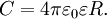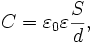Лекция по физике для 10-го физико-математического профильного класса «Электрическая емкость проводника. Единица электроемкости. Конденсатор. Емкость плоского конденсатора. Соединения конденсаторов. Энергия, накопленная в конденсаторе. Применение конденсаторов»
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели и задачи: сформировать представление об электроёмкости вообще и конденсатора в частности, ввести единицу измерения электроёмкости, рассмотреть зависимость ёмкости конденсатора от его геометрической конструкции, соединения конденсаторов, типы конденсаторов и их применение, обратив особое внимание на использование конденсатора в качестве накопителя энергии и выяснив формулы для энергии конденсатора.
УМК: Конденсатор, электрометр, пластина из диэлектрика, набор конденсаторов, проектор, компьютер.
Домашнее задание задано по учебнику Мякишева А.В. для профильных 10-11 классов “Электродинамика” 2011 г., задачи заданы по сборнику Гольдфарба Н.И. с целью ознакомления учащихся с примерами решения задач по данной теме (учащиеся их оформляют в тетради для домашних работ и следующий урок – семинар, посвящён именно решению задач по теме).
Ход урока
рис.1.
На демонстрационном столе собрана установка (см. рис.1).
Если корпус электрометра соединить с землей, то он измеряет напряжение. Зарядим шарик (малый), сообщая ему заряд от разрядника. Видим, что с ростом заряда, растет напряжение между ним и землей. После того как опыт повторили 3-4 раза заряд и напряжение перестают расти.
Следовательно шарик вмещает в себе определенное кол-во зарядов. Если заменить малый шар на большой, то видно, что он вмещает большее количество зарядов.
Электрическая ёмкость С уединённого проводника — это отношение заряда проводника к его потенциалу.
Электроёмкость не зависит от величины заряда и напряжения на проводнике, а характеризует его электрические свойства и определяется размерами и формой проводника.
1Рассмотрим электроёмкость уединённого шара:
Единица электроёмкости : [C] = 1 Ф (фарад) – это электроёмкость такого проводника, потенциал которого изменяется на 1В при сообщении ему заряда в 1 Кл.
Конденсатор – устройство для накопления заряда и энергии. Конденсатор представляет собой два проводника, разделённых тонким слоем диэлектрика. Проводники называют обкладками конденсатора.
На демонстрационном столе установка (см. рис.2)
рис.2
Демонстрируется Приложение 1 (ВИДЕО об устройстве конденсаторов)
Электроемкость конденсатора зависит:
1. От величины заряда C q (одной из обкладок)
2. От напряжения между пластинами
Электроёмкость конденсатора определяется формулой:
Различают конденсаторы также по форме: плоские и сферические. (см. рис.3)
рис.3.
Также конденсаторы различают по диэлектрику:
— Электролитические
— Воздушные
— Слюдяные
— Бумажные. (см. рис.4)
рис.4
Далее учащимся по партам передаются конденсаторы разные по форме, демонстрируются также конденсаторы переменной ёмкости. (см. рис.5).
рис.5
Электрическое поле плоского конденсатора (см.рис.6)
рис.6
Электроемкость плоского конденсатора зависит от геометрических размеров
C S (площадь пластины)
(диэлектрическая проницаемость)
C (расстояние между пластинами)
Рассмотрим энергию заряженного конденсатора.
Т.к. энергия однородного поля равна Wp = Eqd, то для одной пластины Wp = Eqd/2.
Пример 1. Если расстояние между пластинами уменьшили в 2 раза, как изменились емкость, напряжение, напряженность, энергия поля?
Если конденсатор отключен от источника напряжения, то q = const!
| Емкость |
|
Увеличилась |
| Напряжение |
|
уменьшилось |
| Напряженность |
|
Не изменилась |
| Энергия электрического поля |
|
Уменьшилась |
Пример 2. Как изменятся емкость, заряд, напряженность и энергия поля при удалении диэлектрика с ??
Если конденсатор не отключен от источника напряжения, то U = const!
| Емкость |
|
уменьшилась |
| Заряд |
|
уменьшился |
| Напряженность |
|
Не изменилась |
| Энергия электрического поля |
|
уменьшилась |
Соединения конденсаторов:
1) Последовательное (см. рис.7)
q1 = q2
U = U1 + U2
рис.7
2) Параллельное (см. рис.8)
U = U1 = U2
q = q1 + q2
CU = C1U + C2U —> C = C1 + C2
рис.8
Рассмотрим свойства и применение конденсаторов.
Конденсатор – накопитель электроэнергии. Как видно из формулы конденсатор способен хранить электрические заряды тем больше, чем больше его емкость. Если необходимо получить электрический ток большой мощности (N = I2 R), то выгодно иметь большую силу тока, а (I = Q/t), т.е. имея большой заряд, протекающий по проводнику за очень малое время, получаем большую мощность. Конденсатор большой емкости при разрядке дает большую мощность. Пример: фотовспышка
конденсатор – измеритель времени. При зарядке и разрядке конденсатора время этих процессов зависит от емкости конденсатора пропорционально. Это свойство можно использовать для отсчета времени. Например: часы, реле времени ….
Конденсатор в переменном токе. В цепях переменного тока конденсатор периодически перезаряжается, поэтому по подводящим к нему проводникам постоянно проходит ток, а в цепи постоянного тока конденсатор, зарядившись, ток не пропускает. Поэтому конденсатор можно использовать как фильтр для переменного тока. Пример: выпрямители.
Конденсатор и частота переменного тока. В зависимости от частоты переменного тока конденсатор быстро или медленно перезаряжается , при этом оказывая разное сопротивление переменному току. Это используют в частотных фильтрах переменного тока. Например: приемный контур радиоприемника, телевизора, генераторы переменных сигналов….
Демонстрируется Приложение 2 (ВИДЕО о применении конденсаторов).
1. 17. Электрическая емкость уединенного проводника
Уединенным называется проводник, вблизи которого нет других заряженных тел, диэлектриков, которые могли бы повлиять на распределение зарядов данного проводника.
Отношение
величины заряда к потенциалу для
конкретного проводника есть величина
постоянная, называемая электроемкостью (емкостью) С , 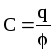 .
.
Таким образом, электроемкость уединенного проводника численно равна заряду, который необходимо сообщить проводнику, чтобы изменить его потенциал на единицу. Опыт показал, что электроемкость уединенного проводника зависит от его геометрических размеров, формы, диэлектрических свойств окружающей среды и не зависит от величины заряда проводника.
Рассмотрим
уединенный шар радиуса R,
находящийся в однородной среде с
диэлектрической проницаемостью .
Ранее было получено, что потенциал шара
равен 
 ,
т.е. зависит только от его радиуса.
,
т.е. зависит только от его радиуса.За единицу емкости принимается 1фарад (Ф). 1Ф — емкость такого уединенного проводника, потенциал которого изменится на 1В при сообщении заряда 1Кл. Фарад — очень большая величина, поэтому на практике используют дольные единицы : миллифарад (мФ, 1мФ=10-3Ф), микрофарад (мкФ, 1мкФ=10-6Ф), нанофарад (нФ, 1нФ=10-9Ф), пикофарад (пФ, 1пФ=10-12Ф).
Уединенные проводники даже очень больших размеров обладают малыми емкостями. Емкостью в 1Ф обладал бы уединенный шар радиуса, в 1500 раз большего радиуса Земли. Электроемкость Земли составляет 0.7 мФ.
1. 18. Взаимная электроемкость. Конденсаторы
Пусть
вблизи заряженного проводника А
находятся незаряженные проводники
или диэлектрики. Под действием поля 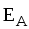 проводника А в телах 1 и 2 возникают
индуцированные (если 1 и 2 проводники)
или связанные (если диэлектрики)
заряды, причем ближе к А будут располагаться
заряды противоположного знака (рис.1.25).
Индуцированные (или связанные) заряды
создают свое поле противоположного
направления, чем ослабляют поле
проводника А, уменьшая его потенциал и
увеличивая его электроемкость.
проводника А в телах 1 и 2 возникают
индуцированные (если 1 и 2 проводники)
или связанные (если диэлектрики)
заряды, причем ближе к А будут располагаться
заряды противоположного знака (рис.1.25).
Индуцированные (или связанные) заряды
создают свое поле противоположного
направления, чем ослабляют поле
проводника А, уменьшая его потенциал и
увеличивая его электроемкость.
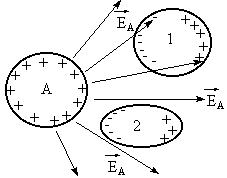 Рис.1.25.
Взаимное влияние проводников.
Рис.1.25.
Взаимное влияние проводников.
Для того, чтобы поле, создаваемое заряженными обкладками, было полностью сосредоточено внутри конденсатора, обкладки должны быть в виде двух близко расположенных пластин, или коаксиальных цилиндров, или концентрических сфер. Соответственно конденсаторы называются плоскими, цилиндрическими или сферическими.
Разность
потенциалов между обкладками
пропорциональна абсолютной величине
заряда обкладки. Поэтому
отношение  есть величина постоянная для конкретного
конденсатора. Она обозначаетсяС и называется взаимной
электроемкостью проводников или
емкостью конденсатора.
Емкость конденсатора численно равна
заряду, который нужно перенести с одной
обкладки конденсатора на другую, чтобы
изменить разность их потенциалов на
единицу.
есть величина постоянная для конкретного
конденсатора. Она обозначаетсяС и называется взаимной
электроемкостью проводников или
емкостью конденсатора.
Емкость конденсатора численно равна
заряду, который нужно перенести с одной
обкладки конденсатора на другую, чтобы
изменить разность их потенциалов на
единицу.
Разность
потенциалов плоского конденсатора
равна 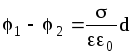 ,
где
,
где поверхностная плотность заряда обкладки.S
— площадь обкладки конденсатора..
Отсюда
емкость плоского конденсатора
поверхностная плотность заряда обкладки.S
— площадь обкладки конденсатора..
Отсюда
емкость плоского конденсатора 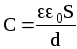 .Из этой
формулы следует, что С плоского конденсатора зависит от
его геометрических размеров, т.е. от S
и d,
и диэлектрической проницаемости
диэлектрика, заполняющего межплоскостное
пространство. Применение в качестве
прослойки сегнетоэлектриков значительно
увеличивает емкость конденсатора,
т.к.
у них достигает очень больших значений.
В очень сильных полях (порядка Епр107 В/м) происходит разрушение диэлектрика
или «пробой», он перестает быть
изолятором и становится проводником.
Это «пробивное напряжение» зависит от
формы обкладок, свойств диэлектрика и
его толщины..
.Из этой
формулы следует, что С плоского конденсатора зависит от
его геометрических размеров, т.е. от S
и d,
и диэлектрической проницаемости
диэлектрика, заполняющего межплоскостное
пространство. Применение в качестве
прослойки сегнетоэлектриков значительно
увеличивает емкость конденсатора,
т.к.
у них достигает очень больших значений.
В очень сильных полях (порядка Епр107 В/м) происходит разрушение диэлектрика
или «пробой», он перестает быть
изолятором и становится проводником.
Это «пробивное напряжение» зависит от
формы обкладок, свойств диэлектрика и
его толщины..
Для получения устройств различной электроемкости конденсаторы соединяют параллельно и последовательно.
Параллельное
соединение конденсаторов (Рис. 1. 26).
В данном случае, так как соединенные
провода-проводники имеют один и тот же
потенциал, то разность потенциалов на
обкладках всех конденсаторов одинакова
и равна  .
Заряды конденсаторов будут
.
Заряды конденсаторов будут
 ,
… ,
,
… , 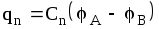 .
.
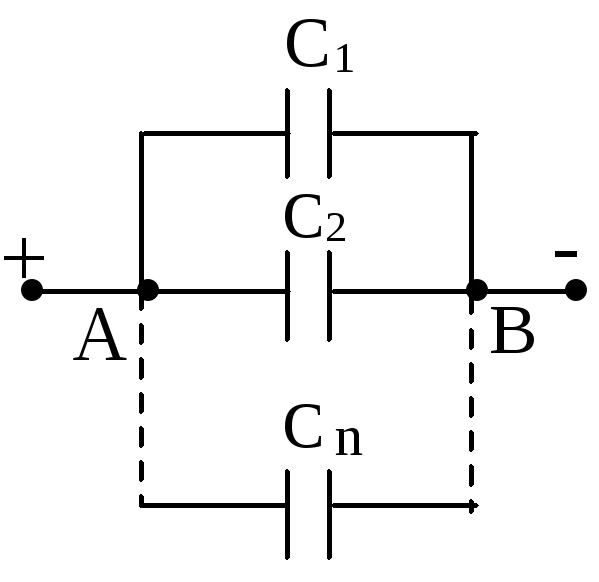
Рис.1.26. Параллельное соединение конденсаторов.
Заряд, запасенный всей батареей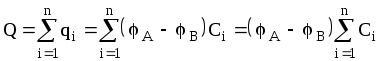 .
.Отсюда
видно, что полная
емкость системы из параллельно соединенных
конденсаторов 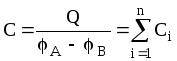 равнасумме
емкостей всех конденсаторов.
равнасумме
емкостей всех конденсаторов.
Последовательное
соединение конденсаторов (Рис. 1. 27).
В данном случае, вследствие электростатической
индукции,
заряды на всех обкладок q
будут равны по модулю, а общая разность
потенциалов складывается из разностей
на отдельных конденсаторах  .
Так как
.
Так как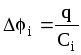 ,
то
,
то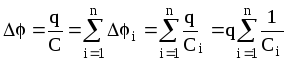 .
Отсюда
.
Отсюда .
.
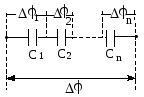
Рис.1.27. Последовательное соединение конденсаторов.
При последовательном соединении конденсаторов обратная величина результирующей емкости равна сумме обратных величин емкостей всех конденсаторов.
Электроёмкость. Конденсаторы
Мы с вами вспоминали о том, что вещества, в которых имеется значительное число свободных носителей зарядов, называются проводниками. Проводники и системы, состоящие из нескольких проводников, обладают одним очень важным свойством: они способны накапливать электрический заряд, а, значит, и электроэнергию, которая может быть использована в дальнейшем (например, при фотосъёмке).

Для характеристики свойства проводника накапливать электрический заряд ввели физическую величину, называемую электрической ёмкостью.
Для объяснения её физического смысла проведём небольшой опыт с уединённым проводником (то есть проводником, который расположен вдали от возможных источников электрического поля как проводящих, так и непроводящих тел).
Итак, присоединим тонким длинным проводником к стержню электрометра с заземлённым корпусом уединённый полый металлический шар.

Теперь, касаясь наэлектризованным проводящим шариком, закреплённым на изолирующей ручке, внутренней поверхности полого металлического шара, будем последовательно сообщать ему одинаковые положительные электрические заряды, увеличивая его суммарный заряд в два, три и так далее раз.
Мы уже с вами знаем, что чем больше сообщённый шару электрический заряд, тем больше его потенциал:

Значит, во сколько раз увеличивается заряд шара, то во столько же раз увеличивается и его потенциал. Но вот отношение электрического заряда к потенциалу не изменяется и остаётся величиной постоянной для данного проводника:

Это отношение принято называть электрической ёмкостью и обозначать большой латинской буквой С. Таким образом, электрическая ёмкость уединённого проводника — это физическая скалярная величина, количественно характеризующая способность проводника накапливать электрический заряд и равная отношению заряда проводника к его потенциалу:

Единицу электрической ёмкости в СИ называют фарад (Ф) в честь Майкла Фарадея — основоположника электродинамики.
1 Ф — электроёмкость такого уединённого проводника, потенциал которого изменяется на 1 В при сообщении ему заряда в 1 Кл:

Фарад (1 Ф) — это очень большая электроёмкость.
Например, в вакууме электроёмкостью один фарад обладал бы шар радиусом R = 9·109 м. Для сравнения, электроёмкость Земли (чей радиус составляет примерно 6400 км) равна 710 мкФ, а человека — примерно 50 пФ.
Для получения нужных значений электроёмкости используют специальный прибор — конденсатор. Он представляет собой систему, состоящую из двух или более проводников и способную накапливать и отдавать электрические заряды.
Простейший конденсатор — это система, состоящая из двух проводников, разделённых слоем диэлектрика, толщина которого мала по сравнению с размерами проводников.

Проводники, образующие конденсатор, называют его обкладками.
Если обкладки конденсатора подсоединить к полюсам источника тока, то на его обкладках конденсатора накопятся противоположные по знаку электрические заряды, модули которых равны.
Процесс накопления зарядов на обкладках называют зарядкой конденсатора.
Процесс нейтрализации зарядов при соединении обкладок конденсатора проводником называют разрядкой конденсатора.
А модуль заряда, находящегося на одной из обкладок конденсатора, называют зарядом конденсатора.
Способность конденсатора накапливать электрические заряды характеризуется скалярной физической величиной, называемой его электрической ёмкостью. Она равна отношению заряда конденсатора к разности потенциалов (или напряжению) между его обкладками:

Если обкладками конденсатора являются две одинаковые параллельные друг другу пластины, то конденсатор называют плоским. Его электростатическое поле в основном сосредоточено между его обкладками и является практически однородным. Несмотря на то, что вблизи краёв пластин однородность поля нарушается, этим часто пренебрегают, если расстояние между пластинами значительно меньше их размеров.
Чтобы установить, от чего зависит электроёмкость плоского конденсатора, проведём несколько опытов с простейшим воздушным конденсатором. Соединим стержень электрометра с одной из пластин, а его корпус с другой. Зарядим конденсатор, подключив его к источнику тока на некоторый промежуток времени. Когда между пластинами конденсатора возникнет разность потенциалов, отключим его от источника тока.

Если каким-либо способом уменьшить площадь взаимного перекрытия пластин при неизменном расстоянии между ними, то, как видим, показания электрометра при этом увеличиваются, хотя сообщённый пластинам при зарядке конденсатора заряд остался неизменным. А так как напряжение между пластинами увеличивается при уменьшении площади перекрытия пластин конденсатора, то его электроёмкость должна уменьшаться (S↓ ⇒ С↓).
Теперь давайте увеличим расстояние между пластинами конденсатора, не меняя площади их перекрытия. Нетрудно заметить, что в этом случае наблюдается возрастание показаний электрометра. А это возможно только при уменьшении электроёмкости конденсатора. Значит, чем больше расстояние между пластинами конденсатора, тем меньше его электроёмкость (d ↑ ⇒ С↓).
Если же между обкладками конденсатора мы поместим какой-нибудь диэлектрик (например, пластину из стекла), то, как видим, показания электрометра уме́ньшатся, что свидетельствует об уменьшении напряжения между обкладками. Следовательно, электроёмкость конденсатора увеличивается (ε ↑ ⇒ С ↑).
В СИ коэффициентом пропорциональности между электроёмкостью конденсатора и определяющими её величинами (S, d, ε) является электрическая постоянная:

Результаты экспериментов позволяют записать формулу для определения электроёмкости плоского конденсатора:

Для получения нужной электроёмкости конденсаторы часто соединяют в батареи, используя при этом параллельное и последовательное соединение.
При параллельном соединении положительно заряженные обкладки конденсаторов соединяют в одну группу, а отрицательно заряженные — в другую.

При таком соединении напряжение на всех конденсаторах одинаковое, но их заряды могут быть разными. При этом полный заряд батареи конденсаторов равен сумме зарядов отдельных конденсаторов:

А её общая электроёмкость равна сумме электроёмкостей каждого из конденсаторов:

Параллельное соединение конденсаторов применяют для получения большой электроёмкости.
При последовательном соединении положительно заряженная обкладка предыдущего конденсатора соединена с отрицательно заряженной обкладкой последующего.

При таком соединении модули зарядов на всех обкладках равны и равны заряду батареи. А суммарный заряд соединённых друг с другом обкладок равен нулю. Напряжение же на полюсах батареи конденсаторов равно сумме напряжений на отдельных конденсаторах:

При этом величина, обратная электроёмкости батареи, равна сумме величин, обратных электроёмкостям отдельных конденсаторов:

Электроемкость плоского конденсатора
Для того, чтобы обеспечить большую емкость обычного проводника, он должен обладать достаточно большими размерами. Однако, на практике требуются устройства, которые при  сравнительно небольших размерах должны иметь способность к накоплению значительных зарядов, то есть обладать значительной электроемкостью. Такие устройства получили широкое распространение и называются конденсаторами.
сравнительно небольших размерах должны иметь способность к накоплению значительных зарядов, то есть обладать значительной электроемкостью. Такие устройства получили широкое распространение и называются конденсаторами.
Устройство конденсатора
Эта система состоит из двух проводников, которые и есть конденсаторы. Они разделены слоем изоляции с толщиной, гораздо меньшей, чем сами проводники, играющие роль обкладок конденсатора.
В состав простейшего плоского конденсатора входят две одинаковые параллельные пластины, расположенные очень близко между собой. Заряды пластин могут быть одинаковыми по модулю и различными по знаку. В этом случае, началом силовых линий электрического поля служит положительно заряженная обкладка конденсатора, а концом является отрицательная обкладка. Поэтому, электрическое поле получается однородным и сосредоточенным внутри конденсатора.
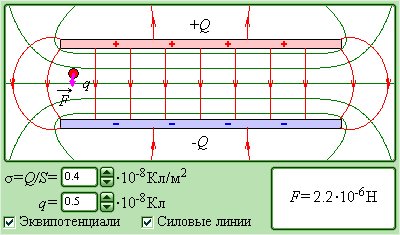
Для того, чтобы зарядить конденсатор, его обкладки должны быть присоединены к источнику напряжения. В отдельных случаях, первая обкладка может соединяться с заземленным полюсом источника питания, при этом, вторая обкладка заземляется.
Значение заряда какой-либо обкладки считается зарядом всего конденсатора, причем окружающие тела совершенно не влияют на разность потенциалов, поскольку электрические поля не могут проникнуть внутрь.
От чего зависит величина электроемкости
От геометрии полностью зависит электроемкость плоского конденсатора, определяемая расстоянием между пластинами, а также их площадью. Таким образом, наибольший заряд можно накопить при максимальной площади пластин. Кроме того, напряжение и расстояние между пластинами находятся между собой в пропорциональной зависимости. Свою роль играют и свойства диэлектрика, расположенного между пластинами. Электроемкость может увеличиться, поскольку диэлектрик способствует ослаблению электрического поля.

Самый простой конденсатор включает в себя металлический корпус, две полоски алюминиевой фольги и бумажная изоляция. Вся конструкция представляет собой небольшой пакет. Для того, чтобы правильно его, необходимо произвести необходимые предварительные расчеты.
Электроемкость — это… Что такое Электроемкость?
- Электроемкость
Электрическая ёмкость — характеристика проводника, характеризующая его способность накапливать электрический заряд. Ёмкость определяется как отношение величины заряда проводника к потенциалу проводника. Ёмкость обозначается как C.
где Q — заряд,
 — потенциал.
— потенциал.В системе СИ ёмкость измеряется в фарадах. В системе СГС в сантиметрах.
Для одиночного проводника ёмкость равна отношению заряда проводника к его потенциалу в предположении, что все другие проводники бесконечно удалены и что потенциал бесконечно удаленной точки принят равным нулю. Она определяется геометрическими размерами и формой проводника и электрическими свойствами окружающей среды (её диэлектрической проницаемостью) и не зависит от материала проводника. К примеру, ёмкость в вакууме проводящего шара радиуса R равна (в системе СИ):
Понятие ёмкости также относится к системе проводников, в частности, к системе двух проводников, разделённых диэлектриком — конденсатору. В этом случае взаимная ёмкость этих проводников (обкладок конденсатора) будет равна отношению заряда, накопленного конденсатором, к разности потенциалов между обкладками. Для плоского конденсатора ёмкость равна:
где S — площадь обкладок, d — расстояние между обкладками, ε — диэлектрическая проницаемость среды между обкладками, ε0 = 8.854*10-12 Ф/м — электрическая постоянная.
Wikimedia Foundation. 2010.
- Электродинамическая постоянная
- Электродрель
Смотреть что такое «Электроемкость» в других словарях:
электроемкость — электроемкость … Орфографический словарь-справочник
электроемкость — сущ., кол во синонимов: 2 • емкость (66) • электроёмкость (1) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Электроемкость* — Это отношение количества электричества, имеющегося на каком либо проводящем теле, к величине потенциала этого тела при условии, что все проводящие тела, находящиеся вблизи этого тела, соединены с землей. Обозначая Э. тела через С, заряд на теле… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Электроемкость — Это отношение количества электричества, имеющегося на каком либо проводящем теле, к величине потенциала этого тела при условии, что все проводящие тела, находящиеся вблизи этого тела, соединены с землей. Обозначая Э. тела через С, заряд на теле… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Электроемкость — электроёмкость ж. 1. Способность тела воспринимать электрический заряд. 2. Величина, характеризующая связь между зарядом, сообщенным проводнику его потенциалом (в физике). Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
электроемкость (затраты электроэнергии на выполнение некоторого экономического показателя) — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN electric intensity … Справочник технического переводчика
электроемкость основных производственных фондов — Отношение всей потребляемой за год предприятием электрической энергии к стоимости основных производственных фондов … Политехнический терминологический толковый словарь
электроемкость продукции — Отношение всей потребляемой за год электрической энергии к годовому объему продукции (в натуральном, условном или стоимостном выражении), выпускаемой предприятием … Политехнический терминологический толковый словарь
Энергоемкость (электроемкость) ВВП — (Energy consumption per GDP unit) — удельный показатель потребления энергоресурсов (электроэнергии) по отношению к ВВП, измеряется обычно в тут (тонны условного топлива) на единицу стоимости ВВП в национальной или иностранной валюте … Экономико-математический словарь
Колебательный разряд — При разряде какого либо наэлектризованного тела, конденсатора, лейденской банки или батареи, состоящей из нескольких таких банок, электрический ток, являющийся в проводнике, при посредстве которого производится разряд, имеет вполне определенное… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Книги
- 10класс. Физика, Сборник. Аудиокурс поможет учащимся в освоении необходимого материала по курсу физики в 10 классе общеобразовательной школы. Важной темой аудиокурса является раздел «Механика», включающая динамику… Подробнее Купить за 124 руб аудиокнига
- Курсы «Подготовка к ЕГЭ по физике», Коллектив авторов. Данный курс посвящен подготовке к итоговой аттестации по школьному курсу по физике, подготовке к сдаче единого государственного экзамена и дальнейшему поступлению школьника в ВУЗ. Главные… Подробнее Купить за 124 руб аудиокнига
2.Конденсаторы. Электроёмкость конденсаторов. Применение конденсаторов.
Электроёмкостьюдвух проводников называют отношение заряда одного из проводников к разности потенциалов между этим проводником и соседним.
Электроёмкость
обозначается буквой 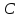 ,
вычисляется по формуле:
,
вычисляется по формуле: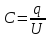 где
где

Единица измерения электроёмкости: Фарад (Ф).
Конденсаторпредставляет собой два проводника, разделённые слоем диэлектрика, толщина которого мала по сравнению с размерами проводников.
Электроёмкость
конденсатора определяется формулой: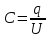 .
.
Конденсаторы бывают разных видов: бумажные, слюдяные, воздушные и т.д. по типу используемого диэлектрика.
Также бывают конденсаторы постоянной и переменной электроёмкости.
Электроёмкость
конденсатора зависит от вида диэлектрика,
расстояния между пластинами и площади
пластин: 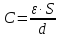 ,
где
,
где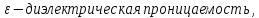


Электрическое
поле сосредоточено внутри конденсатора.
Энергия заряженного конденсатора
вычисляется по формуле: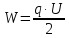 .
.
Основное применение конденсаторов — в радиотехнике. Также они применяются в лампах-вспышках, в газоразрядных лампах.
3.Задача на применение второго закона Ньютона.
Билет № 15
1.Состав ядра атома. Изотопы. Энергия связи ядра атома. Цепная ядерная реакция и условия её протекания. Термоядерные реакции.
Ядроатома любого химического элемента состоит из положительно заряженных протонов (р) и не имеющих заряда нейтронов (n).
Протоны и нейтроны являются двумя зарядовыми состояниями частицы, называемой нуклон.
Количество протонов и нейтронов можно определить по таблице Менделеева.
Порядковый номер – это количество протонов. Чтобы узнать количество нейтронов, нужно из атомной массы вычесть количество протонов.
Например,
в ядре атома кислорода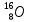 8
протонов и 8 нейтронов.
8
протонов и 8 нейтронов.
У
каждого атома есть изотопы– это
ядра с одним и тем же числом протонов,
но разным количеством нейтронов.
Например, у водорода три изотопа: протий,
дейтерий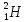 и тритий
и тритий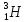 .
.
Энергия,
необходимая для полного разделения
ядра на отдельные нуклоны, называется энергией связи.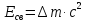
Ядерными реакцияминазывают изменения атомных ядер, вызванные их взаимодействием с элементарными частицами или друг с другом.
В 1938 г. немецкие физики Ган и Штрасман открыли деление урана под действием нейтронов: ядро урана делится на два близких по массе ядра.
У этой реакции есть две важные особенности, которые сделали возможным её практическое применение:
1. При делении каждого ядра урана выделяется значительная энергия.
2. Деление каждого ядра сопровождается вылетом 2-3 нейтронов, которые могут вызвать деление следующих ядер, т.е. сделать реакцию цепной.
Для
осуществления цепной реакции используют
ядра изотопа урана с массовым числом
235, т.е. 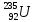 .
Именно они хорошо делятся под действием
как быстрых, так и медленных нейтронов.
.
Именно они хорошо делятся под действием
как быстрых, так и медленных нейтронов.
Ядра
изотопа урана с массовым числом 238 (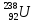 )
используют для получения плутония,
который также используют для цепной
ядерной реакции.
)
используют для получения плутония,
который также используют для цепной
ядерной реакции.
Для осуществления цепной реакции необходимо, чтобы среднее число освобождённых в данной массе нейтронов не уменьшалось с течением времени. Управляемую цепную реакцию проводят в ядерных реакторах, которые конструируют так, чтобы коэффициент размноженияk нейтронов был равен единице. Если число нейтронов будет увеличиваться с течением времени иk>1, то произойдет взрыв.
Термоядерные реакции– это реакции слияния лёгких ядер при очень высокой температуре (примерно 107Кельвинов и выше).
Легче
всего осуществить реакцию синтеза между
тяжелыми изотопами водорода — дейтерием 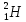 и тритием
и тритием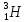 .
При этом в результате получается ядро
гелия
.
При этом в результате получается ядро
гелия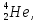 нейтрон
нейтрон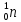 и
выделяется огромная энергия.
и
выделяется огромная энергия.
Работы над созданием управляемой термоядерной реакцией ещё ведутся.
Пока удалось осуществить неуправляемую термоядерную реакцию в водородной бомбе.
Что такое электроемкость конденсатора? :: SYL.ru
Электроемкость конденсатора — это его способность накапливать электрический заряд. Формула электроемкости следующая.
C=q/U
Измеряется эта величина в фарадах. Как правило, емкость элемента очень мала и измеряется в пикофарадах.
В задачах часто спрашивается, как изменится электроемкость конденсатора, если увеличить заряд или напряжение. Это вопрос с подвохом. Проведем другую аналогию.
Представьте, что речь идет про обычную банку, а не конденсатор. Например, у вас она трехлитровая. Аналогичный вопрос: что произойдет со вместимостью банки, если туда налить 4 литра воды? Разумеется, вода просто выльется, но при этом размеры банки никак не изменятся.
То же самое с конденсаторами. Заряд и напряжение никак не влияют на емкость. Этот параметр зависит только от реальных физических размеров.
Формула будет следующей

Только эти параметры влияют на реальную электроемкость конденсатора.
На любом конденсаторе есть маркировка с техническими параметрами.


Разобраться несложно. Достаточно минимальных знаний по электричеству.
Соединение конденсаторов
Конденсаторы, так же как и сопротивления, можно подключать последовательно и параллельно. Кроме этого, в схемах бывают и смешанные соединения.
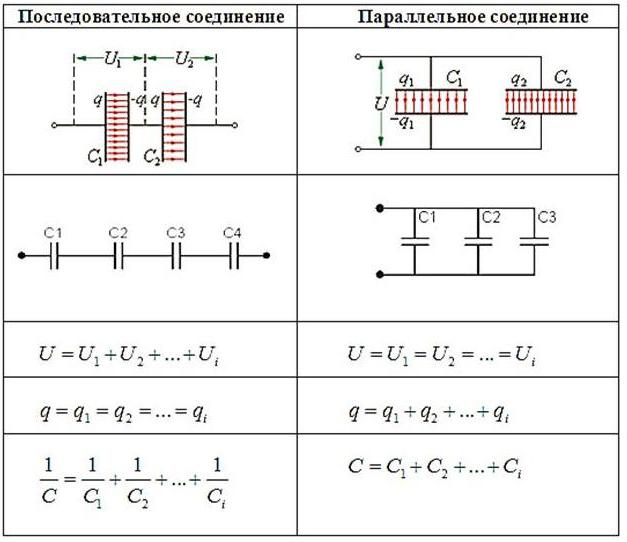
Как видите, электроемкость конденсатора в обоих случаях считается по-разному. Это также относится к напряжению и заряду. По формулам видно, что электроемкость конденсатора, вернее, их совокупности в схеме, будет наибольшей при параллельном соединении. При последовательном общая емкость значительно уменьшается.
При подключении последовательно заряд размещается равномерно. Он будет везде одинаков — как суммарный, так и на каждом конденсаторе. А когда соединение параллельное, суммарный заряд складывается. Это важно помнить при решении задач.
Напряжение считается наоборот. При последовательном соединении складываем, а при параллельном оно равно везде.
Здесь приходится выбирать: если вам нужно больше напряжения, тогда жертвуем емкостью. Если емкость, то огромного напряжения не будет.
Виды конденсаторов
Существует огромное количество конденсаторов. Они отличаются как по размеру, так и по форме.


Разумеется, емкость вычисляется у всех по-разному.
Электроемкость плоского конденсатора
Электроемкость плоского конденсатора определяется проще всего. Эту формулу в основном все и помнят, в отличии от других.
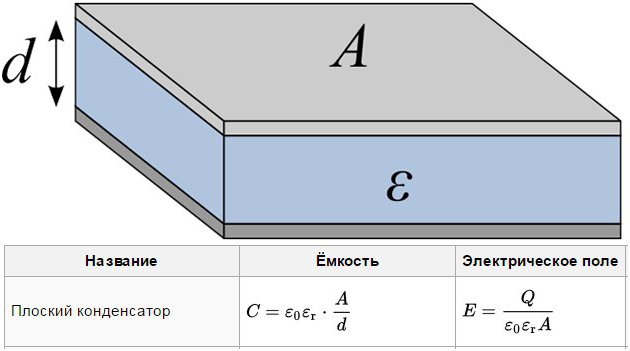
Здесь всё зависит от физических параметров и среды между пластинами.
Сферический конденсатор


Здесь также большое значение имеет, какой диэлектрик или материал помещен внутрь. Так как деталь имеет размер сферы, ее емкость зависит от радиуса.
Цилиндрический конденсатор
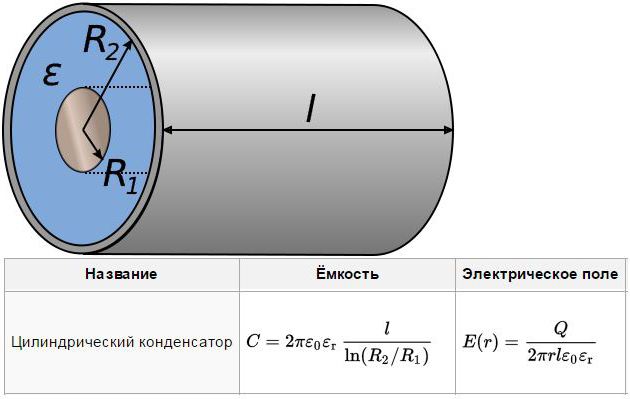
В случае с цилиндрической формой, кроме среды внутри, значение имеют радиусы и длина цилиндра.
Повреждения в конденсаторах
Подумайте, как изменится электроемкость плоского конденсатора, если на нем будут повреждения? Существуют различные сбои, которые могут повлиять на работоспособность конденсаторов.
Например, они рассыхаются или вздуваются. После этого они становятся непригодными для нормальной работы устройства, куда установлены.
Рассмотрим примеры повреждений и выхода из строя конденсаторов. Вздуться могут все сразу.

Иногда из строя выходят только несколько. Такое бывает, когда конденсаторы разных параметров или качества.

Наглядный пример порчи (вздутие, разрыв и выход наружу содержимого).

Если вы увидите вот такие ленты, это крайняя степень повреждения. Хуже и быть не может.

Если вы заметите на устройстве (например на видеокарте в компьютере) такие вздутые конденсаторы, это повод задуматься о замене детали.
Подобные проблемы можно устранить только заменой на аналогичную деталь. У вас должны совпадать все параметры один в один. Иначе работа может быть некорректной или очень кратковременной.
Менять конденсаторы нужно аккуратно, не повредив платы. Выпаивать нужно быстро, не допуская перегрева. Если вы не умеете этого делать, лучше отнесите деталь в ремонт.
Основной причиной разрушения является перегрев, который возникает в случае старения или большого сопротивления в цепи.
Рекомендуется не затягивать с ремонтом. Поскольку у поврежденных конденсаторов изменяется емкость, устройство, где они расположены, будет работать с отклонением от нормы. И со временем это может стать причиной выхода из строя.
Если у вас на видеокарте вздулись конденсаторы, то их своевременная замена может исправить ситуацию. В противном случае может сгореть микросхема или что-то еще. В таком случае ремонт будет стоить очень дорого или вовсе окажется невозможным.
Меры предосторожности
Выше был приведен пример с банкой воды. Там говорилось, что если воды налить больше, то воды выльется. А теперь подумайте, куда могут «вылиться» электроны в конденсаторе? Ведь он запечатан полностью!
Если вы подадите в цепи больше тока, чем тот, на который рассчитан конденсатор, то как только он зарядится, его излишек попытается выйти куда-то. А пространства свободного нет. Результатом будет взрыв. В случае незначительного превышения заряда хлопок будет небольшой. Но если подать колоссальное количество электронов на конденсатор, его просто разорвет, и диэлектрик вытечет.
Будьте аккуратны!




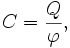
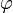 — потенциал.
— потенциал.