Звёздная величина — Википедия
Звёздная величина́ (блеск) — безразмерная числовая характеристика яркости объекта, обозначаемая буквой m (от лат. magnitudo «величина, размер»). Обычно понятие применяется к небесным светилам. Звёздная величина характеризует поток энергии от рассматриваемого светила (энергию всех фотонов в секунду) на единицу площади. Таким образом, видимая звёздная величина зависит и от физических характеристик самого объекта (то есть светимости), и от расстояния до него. Чем меньше значение звёздной величины, тем ярче данный объект. Понятие звёздной величины используется при измерении потока энергии в видимом, инфракрасном и ультрафиолетовом диапазоне. В звёздных величинах измеряется проницающая сила телескопов и астрографов.
Ещё во II веке до н. э. древнегреческий астроном Гиппарх разделил все звёзды на шесть величин. Самые яркие он назвал звёздами первой величины, самые тусклые — звёздами шестой величины, а остальные равномерно распределил по промежуточным величинам.
Как выяснилось позже, связь такой шкалы с реальными физическими величинами логарифмическая, поскольку изменение яркости в одинаковое число раз воспринимается глазом как изменение на одинаковую величину (закон Вебера — Фехнера). Поэтому в 1856 году Норман Погсон предложил следующую формализацию шкалы звёздных величин, ставшую общепринятой[1][2]:
- m1−m2=−2,5lgL1L2{\displaystyle m_{1}-m_{2}=-2{,}5\,\lg {\frac {L_{1}}{L_{2}}}}
где m — звёздные величины объектов, L — освещённости от объектов. Такое определение соответствует падению светового потока в 100 раз при увеличении звёздной величины на 5 единиц.
Данная формула даёт возможность определить только разницу звёздных величин, но не сами величины. Чтобы с её помощью построить абсолютную шкалу, необходимо задать нуль-пункт — блеск, которому соответствует нулевая звёздная величина (0
По современным измерениям, звезда нулевой видимой величины за пределами земной атмосферы создаёт освещённость в 2,54⋅10−6 люкс. Световой поток от такой звезды примерно равен 10
Следующие свойства помогают пользоваться видимыми звёздными величинами на практике:
- Увеличению светового потока в 100 раз соответствует уменьшение видимой звёздной величины ровно на 5 единиц.
- Уменьшение звёздной величины на одну единицу означает увеличение светового потока в 1001/5 ≈ 2,512 раза.
В наши дни понятие звёздной величины используется не только для звёзд, но и для других объектов, например, для Луны и планет. Звёздная величина самых ярких объектов отрицательна. Например, блеск Луны в полной фазе достигает −12,7
Видимая и абсолютная звёздная величина[править | править код]
Широко используется понятие абсолютной звёздной величины (M). Это звёздная величина объекта, которую он имел бы, если бы был на расстоянии 10 парсек от наблюдателя. Абсолютная величина, в отличие от видимой, позволяет сравнивать светимость разных звёзд, поскольку не зависит от расстояния до них.
Наблюдающаяся с Земли звёздная величина называется видимой (m). Это название используется, чтобы отличать её от абсолютной, и применяется даже для величин, измеренных в ультрафиолетовом, инфракрасном или каком-либо другом не воспринимаемом глазом диапазоне излучения (величина, измеренная в видимом диапазоне, называется
Звёздная величина зависит от спектральной чувствительности приёмника излучения (глаза, фотоэлектрического детектора, фотопластинки и т. п.)
- Болометрическая звёздная величина показывает полную мощность излучения звезды (то есть мощность излучения на всех длинах волн). Для её измерения применяется специальное устройство — болометр. Актуальность этой величины связана с тем, что некоторые звёзды (очень горячие и очень холодные) излучают преимущественно не в видимом спектре.
Однако чаще всего звёздные величины измеряют в определённых интервалах длин волн. Для этого разработаны фотометрические системы, в каждой из которых есть набор полос, перекрывающих разные диапазоны волн. В пределах каждой полосы чувствительность максимальна для некоторой длины волны и плавно спадает с удалением от неё.
Самой распространённой фотометрической системой является система UBV, которая состоит из трёх полос, перекрывающих разные интервалы длин волн. В ней для каждого объекта можно измерить 3 звёздные величины:
- Визуальная звёздная величина (V) — звёздная величина в фильтре V, максимум пропускания которого близок к максимуму чувствительности человеческого глаза (555 нм).
- «Синяя» звёздная величина (
- Ультрафиолетовая звёздная величина (U) имеет максимум в ультрафиолетовой области при длине волны около 350 нм.
Разности звёздных величин одного объекта в разных диапазонах (для системы UBV это U − B и B − V) являются показателями цвета объекта: чем они больше, тем более красным является объект. Фотометрическая система UBV определена таким образом, чтобы показатели цвета звёзд спектрального класса А0V равнялись нулю.
Существуют и другие фотометрические системы, в каждой из которых может быть определён свой набор звёздных величин.
- Фотографическая звёздная величина — определяется для спектральной чувствительности несенсибилизированной фотоэмульсии с максимумом чувствительности на длине волны 425 нм; по определению совпадает с визуальной звёздной величиной для звёзд А0V и блеском (6,0 ± 0,5)m. Вместе с фотовизуальной звёздной величиной использовалась в устаревшей фотографической системе звёздных величин.
Звёздные величины некоторых объектов[править | править код]
| Объект | m |
|---|---|
| Солнце | −26,7 (в 400 000 раз ярче полной Луны) |
| Луна в полнолуние | −12,74 |
| −9,5 | |
| Сверхновая 1054 года (максимум) | −6,0 |
| Венера (максимум) | −4,67 |
| Международная космическая станция (максимум) | −4 |
| Земля (при наблюдении с Солнца) | −3,84 |
| Юпитер (максимум) | −2,94 |
| Марс (максимум) | −2,91 |
| Меркурий (максимум) | −2,45 |
| Сатурн (с кольцами; максимум) | −0,24 |
| Звёзды Большого Ковша | +2 |
| Галактика Андромеды | +3,44 |
| Галилеевы спутники Юпитера | +5…6 |
| Уран | +5,5 |
| Самые слабые звёзды, наблюдаемые невооружённым глазом | От +6 до +7,72 |
| Нептун | +7,8 |
| Проксима Центавра | +11,1 |
| Самый яркий квазар | +12,6 |
| Самый слабый объект, заснятый в 8-метровый наземный телескоп | +27 |
| Самый слабый объект, заснятый в космический телескоп «Хаббл» | +31,5 |
| Объект | Созвездие | m |
|---|---|---|
| Сириус | Большой Пёс | −1,47 |
| Канопус | Киль | −0,72 |
| α Центавра | Центавр | −0,27 |
| Арктур | Волопас | −0,04 |
| Вега | Лира | +0,03 |
| Капелла | Возничий | +0,08 |
| Ригель | Орион | +0,12 |
| Процион | Малый Пёс | +0,38 |
| Ахернар | Эридан | +0,46 |
| Бетельгейзе | Орион | +0,50 |
| Альтаир | Орёл | +0,75 |
| Альдебаран | Телец | +0,85 |
| Антарес | Скорпион | +1,09 |
| Поллукс | Близнецы | +1,15 |
| Фомальгаут | Южная Рыба | +1,16 |
| Денеб | Лебедь | +1,25 |
| Регул | Лев | +1,35 |
| Местоположение наблюдателя | m |
|---|---|
| Непосредственно на поверхности Солнца (суммарно со всего диска) | −38,4 |
| Икар (перигелий) | −30,4 |
| Меркурий (перигелий) | −29,3 |
| Венера (перигелий) | −27,4 |
| Земля | −26,7 |
| Марс (афелий) | −25,6 |
| Юпитер (афелий) | −23,0 |
| Сатурн (афелий) | −21,7 |
| Уран (афелий) | −20,2 |
| Нептун (афелий) | −19,3 |
| Плутон (афелий) | −18,2 |
| 631 а. е. | −12,7 (яркость полной Луны) |
| Седна (афелий) | −11,8 |
| 2006 SQ372 (афелий) | −10,0 |
| Комета Хякутакэ (афелий) | −8,3 |
| 0,456 св. года | −4,4 (яркость Венеры) |
| Альфа Центавра | +0,5 |
| Сириус | +2,0 |
| 55 св. лет | +6,0 (порог видимости невооружённым глазом) |
| Ригель | +12,0 |
| Туманность Андромеды | +29,3 |
| 3C 273 (ярчайший квазар) | +44,2 |
| UDFj-39546284 (самый далёкий астрономический объект на 2011 год, с учётом красного смещения) | +49,8 |
- ↑ Сурдин В. Г. Звёзды. — Изд. 2-е, испр. и доп. — М.: Физматлит, 2009. — С. 63. — (Астрономия и астрофизика). — ISBN 978-5-9221-1116-4.
- ↑ 1 2 Сурдин В. Г.. Звёздная величина (рус.). Глоссарий Astronet.ru. Дата обращения 16 сентября 2012. Архивировано 28 ноября 2010 года.
- ↑ Вычислено исходя из того, что звёздная величина на расстоянии 1 а.e. равна −26,7m, что соответствует абсолютной звёздной величине Солнца +4,87m.
Яркость — Википедия
Я́ркость источника света[1] — световой поток, посылаемый в данном направлении, делённый на малый (элементарный) телесный угол вблизи этого направления и на проекцию площади источника[2] на плоскость, перпендикулярную оси наблюдения. Иначе говоря — это отношение силы света, излучаемого поверхностью, к площади её проекции на плоскость, перпендикулярную оси наблюдения.
- B(α)=dI(α)dσcosα{\displaystyle B(\alpha )={\frac {dI(\alpha )}{d\sigma \cos \alpha }}}
В определении, данном выше, подразумевается, если рассматривать его как общее, что источник имеет малый размер, точнее малый угловой размер. В случае, когда речь идёт о существенно протяжённой светящейся поверхности, каждый её элемент рассматривается как отдельный источник. В общем случае, таким образом, яркость разных точек поверхности может быть разной. И тогда, если говорят о яркости источника в целом, подразумевается вообще говоря усреднённая величина. Источник может не иметь определённой излучающей поверхности (светящийся газ, область рассеивающей свет среды, источник сложной структуры — например туманность в астрономии, когда нас интересует его яркость в целом), тогда под поверхностью источника можно иметь в виду условно выбранную ограничивающую его поверхность или просто убрать слово «поверхность» из определения.[источник не указан 2170 дней]
В Международной системе единиц (СИ) измеряется в канделах на м². Ранее эта единица измерения называлась нит (1нт=1кд/1м²), но в настоящее время стандартами на единицы СИ применение этого наименования не предусмотрено.
Существуют также другие единицы измерения яркости — стильб (сб), апостильб (асб), ламберт (Лб):
1 асб = 1/π × 10−4сб = 0,3199 нт = 10−4Лб.[3]
- Вообще говоря, яркость источника зависит от направления наблюдения, хотя во многих случаях излучающие или диффузно рассеивающие свет поверхности более или менее точно подчиняются закону Ламберта, и в этом случае яркость от направления не зависит.
- Последний случай (при отсутствии поглощения или рассеяния средой — см. ниже) позволяет в определении рассматривать и конечные телесные углы и конечные поверхности (вместо бесконечно малых в общем определении), что делает определение более элементарным, однако надо понимать, что в общем случае (к которому при требовании большей точности относятся и большинство практических случаев) определение должно основываться на бесконечно малых или хотя бы физически малых (элементарных) телесных углах и площадках.
- В случае поглощающей или рассеивающей свет среды видимая яркость, конечно, зависит и от расстояния от источника до наблюдателя. Но само введение такой величины, как яркость источника, мотивировано не в последнюю очередь именно тем фактом, что в важном частном случае непоглощающей среды (в том числе вакуума) видимая яркость от расстояния не зависит, в том числе в том важном практическом случае, когда телесный угол определяется размером объектива (или зрачка) и уменьшается с расстоянием (падение с расстоянием от источника силы света точно компенсирует уменьшение этого телесного угла).
- Существует теорема, утверждающая, что яркость изображения никогда не превосходит яркости источника[4].
Яркость L — световая величина, равная отношению светового потока d2Φ{\displaystyle d^{2}\Phi } к геометрическому фактору dΩdAcosα{\displaystyle d\Omega dA\cos \alpha } :
- L=d2ΦdΩdAcosα{\displaystyle L={\frac {d^{2}\Phi }{d\Omega dA\cos \alpha }}}.
Здесь dΩ{\displaystyle d\Omega } — заполненный излучением телесный угол, dA{\displaystyle dA} — площадь участка, испускающего или принимающего излучение, α{\displaystyle \alpha } — угол между перпендикуляром к этому участку и направлением излучения. Из общего определения яркости следуют два практически наиболее интересных частных определения:
Яркость, излучаемая поверхностью dS{\displaystyle dS} под углом α{\displaystyle \alpha } к нормали этой поверхности, равняется отношению силы света I{\displaystyle I}, излучаемого в данном направлении, к площади проекции излучающей поверхности на плоскость, перпендикулярную данному направлению[5]:
- L=dIdScosα{\displaystyle L={\frac {dI}{dS\cos \alpha }}}
Яркость — отношение освещённости E{\displaystyle E} в точке плоскости, перпендикулярной направлению на источник, к элементарному телесному углу, в котором заключён поток, создающий эту освещённость:
- L=dEdΩcosα{\displaystyle L={\frac {dE}{d\Omega \cos \alpha }}}
Яркость измеряется в кд/м2. Из всех световых величин яркость наиболее непосредственно связана со зрительными ощущениями, так как освещённости изображений предметов на сетчатке глаза пропорциональны яркостям этих предметов. В системе энергетических фотометрических величин аналогичная яркости величина называется энергетической яркостью и измеряется в Вт/(ср·м2).
В астрономии яркость — характеристика излучательной или отражательной способности поверхности небесных тел. Яркость слабых небесных источников выражают звёздной величиной площадки размером в 1 квадратную секунду, 1 квадратную минуту или 1 квадратный градус, то есть сравнивают освещённость от этой площадки с освещённостью, даваемой звездой с известной звёздной величиной.
Так, яркость ночного безлунного неба в ясную погоду, равная 2⋅10−4 кд/м², характеризуется звёздной величиной 22,4 с 1 квадратной секунды или звёздной величиной 4,61 с 1 квадратного градуса. Яркость средней туманности равна 19—20 звёздной величины с 1 квадратной секунды. Яркость Венеры — около 3 звёздных величин с 1 квадратной секунды. Яркость площадки в 1 квадратную секунду, по которой распределён свет звезды нулевой звёздной величины, равна 92 500 кд/м². Поверхность, у которой яркость не зависит от угла наклона площадки к лучу зрения, называется ортотропной; испускаемый такой поверхностью поток с единицы площади подчиняется закону Ламберта и называется светлостью; её единицей является ламберт, соответствующий полному потоку в 1 лм (люмен) с 1 м².
Яркость (B) оценивается по максимальному значению яркости светлых участков реестра.[6]
- Солнце в зените — 1,65⋅109 кд/м²[7]
- Солнце у горизонта — 6⋅106 кд/м²[7]
- освещённый солнцем туман — более 12 000 кд/м²[8]
- небо, затянутое светлыми облаками — 10 000 кд/м²[9]
- диск полной Луны — 2500 кд/м²
- дневное ясное небо — 1500—4000 кд/м²[7]
- небо в стратосфере на высоте 19 км — 75 кд/м²[10]
- серебристые облака — иногда до 1—3 кд/м²[11]
- полярные сияния — до 0,2 кд/м²[11]
- ночное небо в полнолуние — 0,0054 кд/м²[12]
- ночное безлунное небо — 0,01[7]—0,0001 кд/м²[9]; 0,000171 кд/м²[13]
- ↑ Под источником света может пониматься как излучающая, так и отражающая или рассеивающая свет поверхность. Также это может быть трёхмерный объект.
- ↑ В случае, когда источник не представляет собой светящуюся поверхность, речь идёт о проекции трёхмерного тела или области пространства, которая считается источником.
- ↑ Апостильб в Большой советской энциклопедии
- ↑ В случае усиливающей среды эта теорема прямо не выполняется или по крайней мере нуждается в аккуратном уточнении понимания её формулировки, формулировка же несколько затруднена тем, что в физическом смысле источником является не только первичный источник, но и среда. Так или иначе, если понимать под яркостью источника лишь яркость первичного источника, она совершенно очевидно может быть превзойдена при распространении света в активной среде.
- ↑ Петровський М. В. Електроосвітлення : конспект лекцій для студентів спеціальності 7.050701 «Електротехнічні системи електроспоживання» всіх форм навчання. — Суми : СумДУ, 2012. — 227 с.
- ↑ Р. М. Степанов. Телевизионные фотоэлектронные приборы. — СПбГЭТУ «ЛЭТИ», 2014. — С. 13. — 191 с.
- ↑ 1 2 3 4 Таблицы физических величин / под ред. акад. И. К. Кикоина. — М.: Атомиздат, 1975. — С. 647.
- ↑ Руководство по определению дальности видимости на ВПП (неопр.) (недоступная ссылка). Дата обращения 24 марта 2017. Архивировано 25 февраля 2017 года.
- ↑ 1 2 Енохович А. С. Справочник по физике.—2-е изд. / под ред. акад. И. К. Кикоина. — М.: Просвещение, 1990. — С. 213. — 384 с.
- ↑ Труды всесоюзной конференции по изучению стратосферы. Л.-М., 1935. — С. 174, 255.
- ↑ 1 2 Ишанин Г. Г., Панков Э. Д., Андреев А. Л. Источники и приемники излучения. — СПб.: Политехника, 1991. — 240 с. — ISBN 5-7325-0164-9.
- ↑ Tousey R., Koomen M.J. The Visibility of Stars and Planets During Twilight // Journal of the Optical Society of America, Vol. 43, N 3, 1953, pp 177—183
- ↑ Andrew Crumey Human Contrast Threshold and Astronomical Visibility
Видимая звёздная величина — Википедия
Материал из Википедии — свободной энциклопедии
 Астероид (65) Кибела и две звезды с указанными для них видимыми звёздными величинами
Астероид (65) Кибела и две звезды с указанными для них видимыми звёздными величинамиВидимая звёздная величина (m) — мера яркости небесного тела (точнее, освещённости, создаваемой этим телом) с точки зрения земного наблюдателя. Обычно используют величину, скорректированную до значения, которое она имела бы при отсутствии атмосферы. Чем ярче объект, тем меньше его звёздная величина.
Уточнение «видимая» указывает только на то, что эта звёздная величина наблюдается с Земли; это уточнение нужно, чтобы отличить её от абсолютной. Оно не указывает на видимый диапазон: видимыми называют и величины, измеренные в инфракрасном или каком-либо другом диапазоне. Величина, измеренная в видимом диапазоне, называется визуальной[1].
В видимой части спектра самая яркая звезда на ночном небе — Сириус, а в инфракрасном J-диапазоне[en] — Бетельгейзе.
| Видны невооружённым глазом[2] | Видимая величина | Яркость относительно Веги | Число звёзд ярче этой видимой величины[3] |
|---|---|---|---|
| Да | −1,0 | 250 % | 1 |
| 0,0 | 100 % | 4 | |
| 1,0 | 40 % | 15 | |
| 2,0 | 16 % | 48 | |
| 3,0 | 6,3 % | 171 | |
| 4,0 | 2,5 % | 513 | |
| 5,0 | 1,0 % | 1 602 | |
| 6,0 | 0,40 % | 4 800 | |
| 6,5 | 0,25 % | 9 096[4] | |
| Нет | 7,0 | 0,16 % | 14 000 |
| 8,0 | 0,063 % | 42 000 | |
| 9,0 | 0,025 % | 121 000 | |
| 10,0 | 0,010 % | 340 000 |
Современная шкала звёздных величин берёт начало в Древней Греции. Её предложил во II веке до н. э. Гиппарх, разделив звезды, видимые невооружённым глазом, по шести величинам. Самые яркие из них он назвал звёздами первой величины (m = 1), а самые слабые — звёздами шестой величины (m = 6). Современная астрономия не ограничивается шестью величинами или только видимым светом. Очень яркие объекты имеют отрицательную величину.
Видимая звёздная величина объектов 1 и 2 определяется как
- m1−m2=−2,5lg(L1L2){\displaystyle m_{1}-m_{2}=-2{,}5\,\mathrm {lg} \left({\frac {L_{1}}{L_{2}}}\right)}
где m — звёздные величины объектов, L — освещённости от этих объектов.
Таким образом, разница в 5 звёздных величин соответствует отношению освещённостей в 100 раз, а разница в одну звёздную величину — в 1001/5 ≈ 2,512 раза.
Общая видимая звёздная величина двух близко расположенных небесных светил получается суммированием видимых величин каждой компоненты. Её значение (mf) вычисляется путём преобразования двух величин (m1) и (m2) к размерности светимости и последующим обратным преобразованием к логарифмическому виду после их сложения:[5]
- mf=−2.5log10(10−m1×0.4+10−m2×0.4){\displaystyle m_{f}=-2.5\log _{10}\left(10^{-m_{1}\times 0.4}+10^{-m_{2}\times 0.4}\right)}
По тому же принципу может быть вычислена общая звёздная величина систем, которые обладают бóльшими уровнями кратности.
Примеры[править | править код]
Видимая звёздная величина полной Луны равна −12,7; яркость Солнца составляет −26,7.
Разница звёздных величин Луны (m1{\displaystyle m_{1}}) и Солнца (m2{\displaystyle m_{2}}):
- m1−m2=(−12,7)−(−26,7)=14,0{\displaystyle m_{1}-m_{2}=(-12,7)-(-26,7)=14,0}
Отношение освещённостей от Солнца и Луны:
- L2/L1=2,512m1−m2=2,51214,0≈400 000{\displaystyle L_{2}/L_{1}=2,512^{m_{1}-m_{2}}=2,512^{14,0}\approx 400~000}
Таким образом, Солнце примерно в 400 000 раз ярче полной Луны.
Светимость — Википедия
Материал из Википедии — свободной энциклопедии
Светимость — название ряда физических величин.
В фотометрии светимость — световая величина, представляющая собой световой поток излучения, испускаемого с малого участка светящейся поверхности единичной площади. Она равна отношению светового потока, исходящего от рассматриваемого малого участка поверхности, к площади этого участка[1]:
- Mv=dΦvdS{\displaystyle M_{v}={\frac {\mathrm {d} \Phi _{v}}{\mathrm {d} S}}},
где dΦv — световой поток, испускаемый участком поверхности площадью dS. Светимость в Международной системе единиц (СИ) измеряется в лм/м². 1 лм/м² — это светимость поверхности площадью 1 м2, излучающей световой поток, равный 1 лм.
Аналогом светимости в системе энергетических фотометрических величин является энергетическая светимость (излучательность). Её определение аналогично определению светимости, но вместо светового потока Φv используется поток излучения Фe. Единица энергетической светимости в СИ — Вт/м².
Светимость в астрономии — полная энергия, излучаемая астрономическим объектом (планетой, звездой, галактикой и т. п.) в единицу времени. Измеряется в абсолютных единицах (СИ — Вт; СГС — эрг/с) либо в единицах светимости Солнца (L⊙ = 3,86⋅1033эрг/с = 3,86⋅1026 Вт)[2].
Светимость астрономического объекта не зависит от расстояния до объекта, от него зависит только видимая звёздная величина. Светимость — одна из важнейших звёздных характеристик, позволяющая сравнивать между собой различные типы звёзд на диаграммах «спектр — светимость», «масса — светимость». Светимость звёзд главной последовательности можно приближённо рассчитать по формуле[3]:
- L=4πR2⋅σT4,{\displaystyle L=4\pi R^{2}\cdot \sigma T^{4},}
где R — радиус звезды, T — температура её фотосферы, σ — постоянная Стефана — Больцмана.
Светимость самых ярких звёзд в миллионы раз превышает светимость Солнца. Светимость квазаров может превышать солнечную в сотни триллионов раз[4].
В экспериментальной физике элементарных частиц светимостью называют параметр ускорителя, характеризующий интенсивность столкновения частиц пучка с частицами фиксированной мишени (интенсивность столкновения частиц двух встречных пучков в случае коллайдеров). Светимость L измеряется в см−2·с−1. При умножении сечения реакции на светимость получается средняя частота протекания этого процесса на данном коллайдере N˙process=L⋅σprocess{\displaystyle {\dot {N}}_{\text{process}}=L\cdot \sigma _{\text{process}}}.
Светимость Большого адронного коллайдера во время первых недель работы пробега была не более 1029 частиц/см²·с, но она продолжает постоянно повышаться. Целью является достижение номинальной светимости в 1,7⋅1034 частиц/см²·с, что по порядку величины соответствует светимостям BaBar (SLAC, США) и Belle (KEK, Япония). Коллайдеру KEKB принадлежит мировой рекорд светимости для ускорителей с встречными пучками — 2,11⋅1034 см−2·с−1[5].
Блеск, яркость и светимость в астрономии. В чем отличие?
Рубрика: Астрономия для чайников Опубликовано 19.08.2019 · Комментарии: 0 · На чтение: 5 мин · Просмотры:Post Views: 2 412
Астрономия — это наука, и как всякая наука, она имеет свою особую терминологию, или, говоря проще, жаргон. Сторонним людям этот жаргон кажется просто бессмысленным набором фраз, а иногда вызывает улыбку. Вот, например, понятия «блеск звезды», «светимость звезды», «яркость звезды». В принципе понятно, что речь идет о том, насколько звезда яркая или тусклая. Но для чего ввели три разных термина? Или это просто синонимы, а фразы означают одно и то же? Давайте разбираться.
Что такое блеск звезды?
Начнем с блеска. Все вы не раз читали фразы вроде «блеск звезды равен…» или «звезда превосходит по блеску планету Сатурн». Звучит немного странно, не правда ли? Блестеть может начищенный пятак, медный таз на солнце, пуговицы на гимнастерке. В конце концов, могут блестеть глаза. Но звезда? Кажется, что во фразе блеск звезды есть что-то нелепое и слегка архаичное.
На самом деле термин блеск звезды — не устаревшее выражение, а самый что ни есть актуальный, современный термин. Под блеском астрономы подразумевают освещенность, которую создает небесный объект (например, звезда) на плоскости, перпендикулярной лучу зрения.
Слишком мудрено? Можно проще: чем выше блеск звезды, тем сильнее освещает она наши глаза, тем лучше мы ее видим! Звезды высокого блеска видны ночью хорошо, мы говорим про них с восхищением: «Какие яркие звезды!» Звезды, чей блеск мал, видны плохо, или вовсе не видны без телескопа. Мы говорим, что эти звезды тусклые.
Как астрономы измеряют блеск звезд?
Раз понятие блеска в астрономии имеет строгое научное определение, значит блеск можно измерить.
Действительно, блеск звезд (да и вообще любых небесных светил) измеряется в звездных величинах. Звездная величина — особая безразмерная физическая величина, которая применяется только в астрономии и астрофизике. Обозначается в виде латинской буквы m над ее числовым значением. Например, блеск Сириуса -1,44<sup>m</sup>. Измеряются звездные величины парадоксальным образом: чем меньше значение m, тем выше блеск небесного объекта. Подробнее читайте в статье «Что такое звездная величина?»
Помимо звездных величин, блеск небесных объектов можно измерять и в традиционных физических величинах, например, в люксах. Связь между звездной величиной и люксом следующая:
m = -14 — 2,5lgJ, где J — значение в люксах.
Таким образом, звезда Вега, имеющая видимый блеск около 0m, создает освещенность 0,00000254 лк. Полная Луна создает освещенность в 0,25 лк.
Яркость звезд
Выше я написал, что про звезды высокого блеска мы говорим, что эти звезды яркие. Значит ли это, что термины блеск и яркость небесного светила имеют один и тот же смысл?
Нет! Яркость — это количество света, приходящее с единицы площади объекта. Поэтому термин яркость применим только к протяженным объектам — Солнцу, Луне, планетам (уже в небольшой телескоп у них видны диски!), кометам, туманностям. А к точечным звездам или не имеющим ширины метеорам термин яркость уже не применим, ведь у них нет площади! Зато применим термин блеск, ведь он характеризует освещенность, которую создают любые небесные тела, хоть туманности, хоть звезды.
Почему же звезды называют яркими? Это просто анахронизм, общеупотребительное выражение, доставшееся нам с прошлых времен, когда блеск астрономы называли интегральной яркостью небесных объектов, а то, что сейчас считается яркостью, — поверхностной яркостью.
Звездное небо и Млечный Путь летом. Фотография усеяна мириадами звезд, которые имеют разный блеск. В случае с Млечным Путем имеет смысл говорить о яркости отдельных его участков. Фото: James Neeley
Светимость звезд
Нам осталось разобраться с последним термином. Что такое светимость?
Светимость — это мощность излучения небесного тела. Другими словами, это полное количество света, которое испускает небесный объект, например, звезда, в единицу времени. Как и светимость обычной лампочки, светимость звезд измеряется в ваттах. Но числа при этом получаются гигантские, поэтому часто астрономы измеряют светимость звезд в светимостях Солнца, то есть сравнивают мощность излучения звезд с мощностью излучения нашей родной звезды.
Давайте для примера взглянем на некоторые яркие звезды, которые видны на небе по вечерам, скажем, в феврале. Возьмем Сириус, самую яркую звезду ночного неба, и звезду Ригель в созвездии Ориона. Ясно, что Сириус — звезда бо́льшего блеска, чем Ригель, ведь она нам кажется ярче, то есть создает бо́льшую освещенность. Ее видимая звездная величина (m) равна -1,47! Ригель светит на нашем небе не так ярко; его блеск равен 0,12m.
Звезда Ригель (бета Ориона) и ее окрестности. Очевидно, что Ригель — самая яркая звезда на этом снимке. Тысячи звезд фона — гораздо более тусклые. Но количественно можно измерить только блеск этих звезд, не яркость! Поэтому астрономы говорят о звездах с большим и меньшим блеском. Фото: Fred Espenak
Но является ли Сириус при этом звездой большей светимости, чем Ригель?
Нет! Сириус светит в 25 раз мощнее Солнца, а Ригель — в 130 тысяч раз мощнее Солнца! Получается, Ригель имеет светимость в 4800 раз большую, чем Сириус! Почему же Сириус имеет на нашем небе бо́льший блеск? Все дело, конечно, в расстоянии до этих звезд. Сириус — одна из ближайших звезд к Земле. Расстояние до нее составляет всего лишь 8 световых лет. Ригель же находится более чем в сто раз дальше, на расстоянии в 860 световых лет от нас. И даже несмотря на это, блеск этих звезд различается не очень сильно! Можно только поражаться, насколько мощно светит Ригель!
Итак, подытожим. Если блеск звезды говорит нам о ее интенсивности на небе, то светимость — о реальной мощности излучения звезды. Блеск нам дан непосредственно, а чтобы вычислить светимость, мы должны знать расстояние до звезды. Термин «яркость» применим только для протяженных объектов, а вот звезд, метеоров, астероидов, коричневых карликов он не касается.
Post Views: 2 412
Абсолютная звёздная величина — Википедия
Материал из Википедии — свободной энциклопедии
Абсолютная звёздная величина — физическая величина, характеризующая светимость астрономического объекта. Для разных типов объектов используются разные определения абсолютной величины.
Абсолютная звёздная величина для звёзд[править | править код]
Абсолютная звёздная величина (M) для звёзд определяется как видимая звёздная величина объекта, если бы он был расположен на расстоянии 10 парсек от наблюдателя. Абсолютная болометрическая (учитывающая полное излучение во всех диапазонах электромагнитных волн) звёздная величина Солнца +4,7[уточнить].
Если известна видимая звёздная величина m{\displaystyle m} и расстояние до объекта d{\displaystyle d}, можно вычислить абсолютную звёздную величину по формуле:
- M=m−5lgdd0{\displaystyle M=m-5\lg {\frac {d}{d_{0}}}}
где d0{\displaystyle d_{0}} = 10 пк ≈ 32,616 световых лет (Также можно воспользоваться формулами: M=m+5−5lgr{\displaystyle M=m+5-5\lg r} и M=m+5+5lgπ′′{\displaystyle M=m+5+5\lg \pi \prime \prime }, где r{\displaystyle r} и π′′{\displaystyle \pi \prime \prime } — расстояние до звезды в парсеках и годичный параллакс в секундах соответственно).
Соответственно, если известны видимая и абсолютная звёздные величины, можно вычислить расстояние по формуле
- d=d010m−M5{\displaystyle d=d_{0}10^{\frac {m-M}{5}}}
Абсолютная звёздная величина связана со светимостью следующим соотношением:
- lgLL⊙=0,4(M⊙−M){\displaystyle \lg {\frac {L}{L_{\odot }}}=0,4(M_{\odot }-M)}
где L⊙{\displaystyle L_{\odot }} и M⊙{\displaystyle M_{\odot }} — светимость и абсолютная звёздная величина Солнца.
Абсолютная звёздная величина для тел Солнечной системы (H)[править | править код]
Для объектов Солнечной системы (планет, астероидов и комет) используется другая версия абсолютной звёздной величины[1][2]. Для них абсолютная величина принимается равной видимой величине, которую они имели бы на расстоянии 1 а. е. от Солнца и от наблюдателя, причём наблюдатель должен видеть полную фазу объекта (то есть теоретически наблюдатель должен находиться в центре Солнца).
Пусть m0 — видимая звёздная величина Солнца, A — геометрическое альбедо планеты, а r — её радиус. Тогда абсолютная звёздная величина g этой планеты может быть выражена следующим образом:
- g=m0−2.5lgAr2{\displaystyle g=m_{0}-2.5\lg {Ar^{2}}},
Поскольку с расстояния в 1 а. е. планета видна под углом ρ, то, выражая угол в секундах дуги, ρ = r / sin 1″. Таким образом можно выразить абсолютную звёздную величину через видимый размер планеты:
- g=m0−2.5lgA−5lgρsin1″=−2.5lgA−5lgρ−0.23{\displaystyle g=m_{0}-2.5\lg {A}-5\lg {\frac {\rho }{\sin {1»}}}=-2.5\lg {A}-5\lg {\rho }-0.23}.
Величина g вычисляется из видимой звёздной величины планеты/астероида. Если из каких-то физических соображений можно сделать оценку геометрического альбедо, то это позволяет нам определить размер астероида, и, наоборот, зная размер астероида, можно определить его геометрическое альбедо.
Есть набор расчётных таблиц для тел с наиболее распространёнными значениями альбедо астероидов (0,25 — 0,05)[3][4][5].
Абсолютная звёздная величина метеоров[править | править код]
Наблюдения метеоров проводятся одновременно в разных точках поверхности Земли. К каждому наблюдателю свет от метеора проходит разное расстояние и испытывает разное поглощение в атмосфере: чем ближе метеор к горизонту, тем большую толщу атмосферы он просвечивает и тем меньше будет его блеск. Типичная высота загорания метеоров — 100 км. Поэтому, в метеорной астрономии принято другое определение абсолютной звёздной величины. А именно, абсолютной называется та звёздная величина метеора M, которую он имел бы, будучи видим в зените на расстоянии 100 км[2].
- M=m−5lgR−K{\displaystyle M=m-5\lg {R}-K},
где K — поправка на поглощение в атмосфере (редукция к зениту), R — расстояние до метеора, m — его видимая звёздная величина.
Блеск и яркость. Видимые и абсолютные звездные величины.
Информацию об астрономических объектах дает приходящий световой поток. Звезды, астероиды и некоторые другие объекты выглядят точечными источниками света. Их излучение характеризует блеск. У протяженных объектов с различными угловыми размерами характеристикой излучения кроме блеска, является яркость.
Яркостью – называется поток излучения, который проходит через перпендикулярную к данному направлению единичную площадку, соприкасающуюся с излучающей поверхностью и заключен внутри единичного телесного угла.
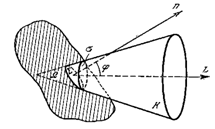
Рисунок 51. Яркость излучающей поверхности.
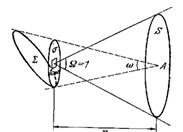
Рисунок 52. Освещенность, создаваемая телом
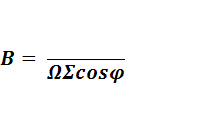 (10)
(10)
Σ – элемент светящейся поверхности.
Ф – световой поток, излучаемый поверхностью Σ внутри конуса с телесным углом Ω.
φ – угол оси конуса с нормалью к светящейся поверхности.
При визуальном наблюдении освещенности сетчатки:
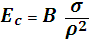 (11)
(11)
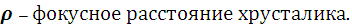
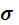 −
диаметр зрачка.
−
диаметр зрачка.
Максимальная освещенность, которую создает объект Е = В ω.
ω – телесный угол, под которым виден объект на небе.
Интенсивность видимого излучения светил определяется по создаваемой ими освещенности Е.
Блеск – это освещенность, создаваемая светилом на приемниках лучистой энергии (глаз, фотопластинка, фотоэлементы и др.). Но освещенность измеряется в люксах, а блеск измеряется в относительных единицах, называемых звездной величиной, обозначается m. Чем больше освещенность светила, тем меньше его звездная величина.
Оценку блеска звездной величины впервые до II в. до н.э. провел греческий астроном Гиппарх. Он разделил объекты на 6 классов звездных величин. Основание – свойство человеческого глаза различать источник по интенсивности излучения, если их яркость отличается приблизительно в 2,5 раза. Это стало известно науке только в XVIII веке.
Освещенности от объектов … — 5m, — 4m, — 3m, -2m, — 1m, 0, 1m, 2m, 3m… образуют убывающую геометрическую прогрессию со знаменателем 2,512.
Звездной величиной называется взятый со знаком минус логарифм по основанию 2,512 от освещенности создаваемой объектом на площадке, перпендикулярной лучам.
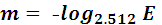 (12)
(12)
Разность звездных величин:
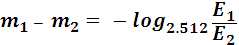 ;
(12,1)
;
(12,1)
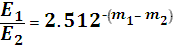 (12,2)
(12,2)
В десятичных логарифмах:
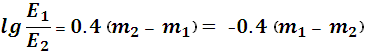 (13)
(13)
Это формула Погсона, которую в 1856 г. при различии блеска ровно в 100 раз считать разность звездных величин равной 5.
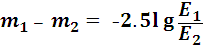 (14)
(14)
Звезда Оm создает на границе земной атмосферы освещенность 2,54 * 10-6 люкс, т.е. как 1 кандела (Кд) с расстояния 600 м. Во всем видимом диапазоне она создает поток 106 квантов на 1 см2 в секунду. В области земных лучей в интервале длин волн 1 Å- это 103 квантов на 1 см2 в секунду. Солнце в зените создает освещенность 137000 лк.
Абсолютная звездная величина
Видимые звездные величины «m» не определяют общей энергии излучения, яркости поверхности. Близкая холодная звезда может иметь видимую звездную величину меньше(казаться ярче), чем далекая горячая.
Чтобы сравнивать звезды, их потоки и освещенность надо отнести к одному расстоянию.
Выбрано стандартное расстояние – 10 пс. Абсолютная звездная величина М – это звездная величина, которую имела бы звезда, если бы находилась на расстоянии 10 пс.
Если r – расстояние до звезды, то связь звездных величин:
0,4 (m — M) = 2 lgr – 2.
M = m + 5 – 5 lgr
lgr = 1 + 0.2 (m — M)
m – M – модуль расстояния.
Таблица 4. Звездные величины некоторых ярких звезд
Звезда | Зв.велич. | Звезда | Зв.велич. |
Альдебаран, α Тельца | 1,06 | Регул, α Льва | 1,34 |
Ригель, β Ориона | 0,34 | Спика, α Девы | 1,21 |
Капелла, α Возничего | 0,21 | Арктур, α Волопаса | 0,24 |
Бетельгейзе, α Ориона | 0,92* | Антарес, α Скорпиона | 1,22* |
Сириус, α Б.Пса | -1,58 | Вега, α Лиры | 0,14 |
Кастор, α Близнецов | 1,99 | Альтаир, α Орла | 0,89 |
Процион, α М.Пса | 0,48 | Денеб, α Лебедя | 1,33 |
Поллукс, β Близнецов | 1,21 | Фомальгаут, α Южной Рыбы | 1,28 |
* — слегка меняет яркость.
Понятие звездной величины можно распространить и на протяженные объекты, так как они тоже создают освещенность.
Т аблица
5. Фотометрические характеристики
некоторых объектов
аблица
5. Фотометрические характеристики
некоторых объектов



