1.1.3 Определить токи во всех ветвях схемы на основании метода наложения
По методу наложения ток в любом участке цепи рассматривается как алгебраическая сумма частных токов, созданных каждой ЭДС в отдельности.
а) Определяем частные токи от ЭДС Е1 при отсутствии ЭДС Е2, т. е. рассчитываем цепь по
Показываем направление частных токов от ЭДС E1 и обозначаем буквой I с одним штрихом (I’). Решаем задачу методом «свертывания»
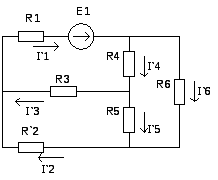

Ток источника

Определяем частные токи от ЭДС Е2 при отсутствии ЭДС Е1


Ток источника

Вычисляем токи ветвей исходной цепи выполняя алгебраическое сложение частных токов, учитывая их направление:

1.1.4 Составить баланс мощностей для заданной схемы
Источники Е1 и Е2 вырабатывают электрическую энергию, т. к. направление ЭДС и тока в ветвях с источниками совпадают. Баланс мощностей для заданной цепи запишется так:

Подставляем числовые значения и вычисляем
 С
учетом погрешности расчетов баланс
мощностей получился.
С
учетом погрешности расчетов баланс
мощностей получился.
1.1.5 Результаты расчетов токов по пунктам 1 и 2 представить в виде таблицы и сравнить
Ток ветви | I1 A | I2 A | I3 A | I4 A | I5 A | I6 A |
Метод расчета | ||||||
Метод контурных токов | 0,429 | 0,081 | 0,510 | 0,291 | 0,219 | 0,138 |
Метод наложения | 0,429 | 0,081 | 0,509 | 0,189 | 0,239 |
1.1.6 Построить потенциальную диаграмму для любого замкнутого контура, включающего обе эдс
Зная ЭДС и внутреннее сопротивление эквивалентного генератора, вычисляем ток в исследуемой ветви:

Возьмем
контур АВCА.
Зададимся обходом контура по часовой
стрелке.
Заземлим одну из точек контура, пусть
это будет точка А. Потенциал
этой точки равен нулю
Зная величину и направление токов ветвей и ЭДС, а также величины сопротивлений, вычислим потенциалы всех точек контура при переходе от элемента к элементу. Начнем обход от точки А.

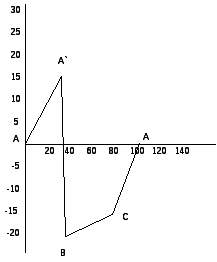
Строим потенциальную диаграмму. По оси абсцисс откладываем сопротивления контура в той последовательности, в которой производим обход контура, прикладывая сопротивления друг к другу, по оси ординат -потенциалы точек с учетом их знака.
1.2 Расчет нелинейных электрических цепей постоянного тока Задание
Построить входную вольтамперную характеристику схемы нелинейной электрической цепи постоянного тока. Определить токи во всех ветвях схемы и напряжения на отдельных элементах, используя полученные вольтамперные характеристики.
R3=45 Ом; U=140В.

ВАХ нэ1-б нэ2-в.
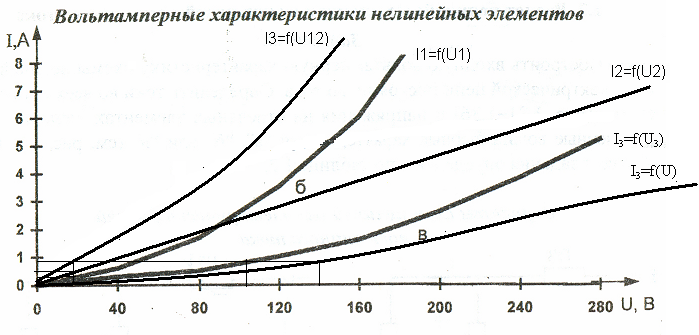
ВАХ линейного
элемента строим по уравнению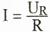 .
Она представляет
собой прямую, проходящую через начало
координат. Для определения координаты
второй точки ВАХ линейного элемента
задаемся произвольным
значением напряжения. Например, UR = 90
В, тогда соответствующее
значение тока
.
Она представляет
собой прямую, проходящую через начало
координат. Для определения координаты
второй точки ВАХ линейного элемента
задаемся произвольным
значением напряжения. Например, UR = 90
В, тогда соответствующее
значение тока

Соединив полученную точку с началом координат, получим ВАХ линейного элемента.
Далее
строится общая ВАХ цепи с учетом схемы
соединения элементов. В нашей цепи
соединение элементов смешанное. Поэтому
графически «сворачиваем» цепь.
Начинаем с разветвленного участка.
Нелинейные
элемент нэ2 и линейный R1
соединены параллельно, их ВАХ I1=f(U1)
и I2=f(U2).
С учетом этого строим общую для них ВАХ.
Для этого задаемся напряжением и
складываем
токи при этом напряжении I3=I1+I2.
Точка пересечения этих значений
тока и напряжения дает одну из точек их
общей ВАХ. В результате
получаем множество точек и по ним строим
ВАХ I
Далее мы имеем характеристики нелинейного элемента I3=f(U3) и нелинейного элемента (нэ12) I3=f(U12), которые соединены между собой последовательно. Строим для них общую ВАХ. В данном случае задаемся током и складываем напряжения. Проделываем это многократно. По полученным точкам строим общую ВАХ цепи I3=f(U).
Дальнейший расчет цепи производим по полученным графикам.
Чтобы найти токи и напряжения на всех элементах цепи, поступаем так: по оси напряжений находим значение напряжения, равное 140 В (точка
Содержание
1.Расчет линейной электрической цепи постоянного тока……………………….. | 4 |
1.1. Для заданной схемы определить все токи в ветвях с помощью уравнений составленных по законам Кирхгофа………………………………………… | 4 |
1.2. Определить ток в ветви с R1методом эквивалентного генератора…….. 1.3. Составить уравнение баланса мощностей……………………………….. 1.4. Определить показания вольтметра……………………………………….. 1.5. Определить ток 1 в ветви c сопротивлением R1 по методу эквивалентного активного двухполюсника и построить график зависимости 1=f(R) при изменении R R1 10R………………………………………………………………………… 1.6. Заменить резистор R1 нелинейным элементом и определить ток в нем.. | 6 9 9 9 10 |
2. Расчет электрической цепи однофазного переменного тока………………… | 11 |
2.1.Определить показания приборов……………………………………….. | 12 |
2.2. Вычислить полную комплексную мощность цепи……………………… | 14 |
2.3. Повысить коэффициент мощности до 0,98 включением необходимого реактивного элемента Х……………………………………………………………. | 15 |
2.4. Построить векторные диаграммы токов и напряжений для режимов до и после компенсации……………………………………………………………… | 16 |
3. Расчет трехфазной цепи…………………………………………………….. | 18 |
3.1. Составить схему включения приемников……………………………… | 19 |
3.2. Составить схему включения ваттметров для измерения активной мощности каждого трехфазного приемника………………………………….. | 20 |
3.3Определить линейные и фазные токи в каждом трехфазном приемнике. Построить векторные диаграммы токов и напряжений……………………. | 20 20 |
Список литературы……………………………………………………………….. | 25 |
1. Расчет линейной электрической цепи постоянного тока
1.1. Для заданной схемы определить токи в ветвях с помощью уравнений составленных по законам Кирхгофа.
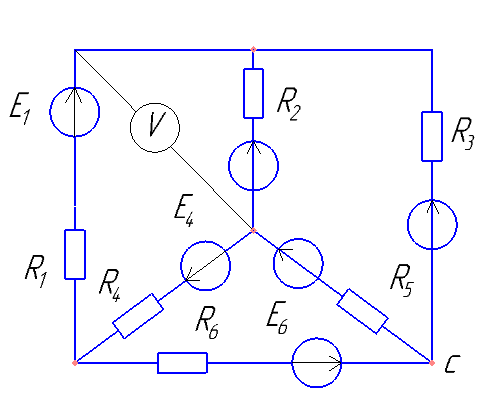 Рис.1
Рис.1

ЭЦ1-810376-07
R1 = 56 Ом
R2 = 91 Ом
R3 = 77 Ом
R4 = 82 Ом
R5 = 82 Ом
R6 = 46 Ом
E2=-99 В
E1=E3= E6=0
E4 =-85 В
E5= -40 В
Рис.2Для данной схемы определим токи в ветвях с помощью уравнений, составленных по законам Кирхгофа.
1). Зададимся произвольно условно положительными направлениями токов;
2). Посчитаем число уравнений по I закону Кирхгофа
nI = ny -1 = 4-1=3, где ny – количество узлов;
nII = nв-( nу -1)=6-(4-1)=3, где nв – количество ветвей.
Составим уравнения по первому закону Кирхгофа для трех узлов и по второму закону Кирхгофа для трех контуров:

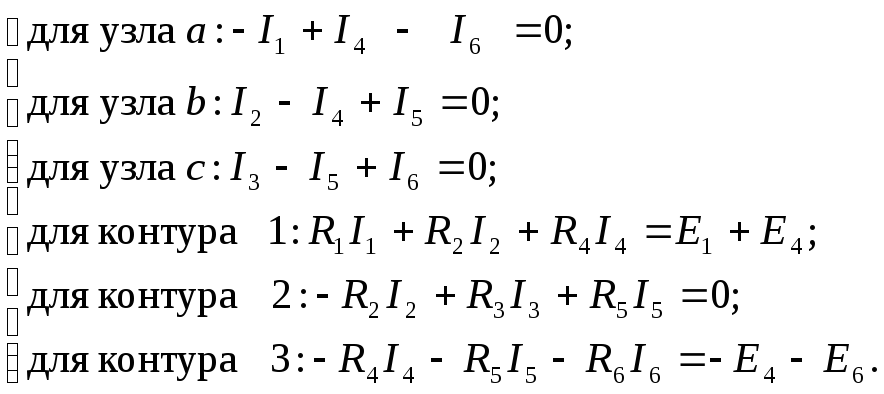
Подставим числовые значения сопротивлений и ЭДС и решим полученную систему уравнений в программе Gauss. Получим :
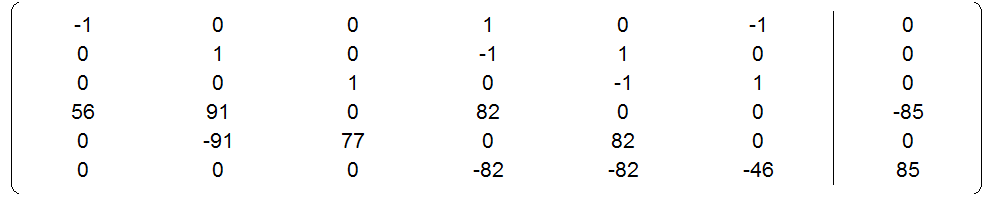
Решим систему, определим токи :
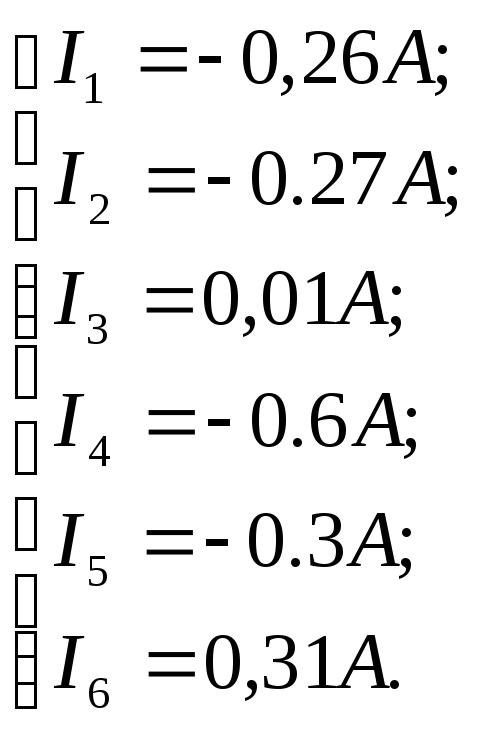
Проверка полученного решения производится составлением баланса мощностей, потребляемых резисторами и получаемых от источников:
Pприем.=R1I12+R2I22+R3I32+R4I42+R5I52+R6I62=56.3.766112+91.6,402052+77.0,00268 2+82.26,189422+82.7,375082+46.4,301902= 48 Вт.
Pист. = E1I1+E4I4+E6I6 =-0,25933+(-85).0,56514+0 .0,30581= 48 Вт.
Pприем = Pист
Баланс мощностей сходится.
1. Расчет линейной электрической цепи постоянного тока
Задание:
Рассчитать схему по законам Кирхгофа.
Определить токи в ветвях методом контурных токов.
Определить ток в ветви с сопротивлением R1 методом эквивалентного генератора.
Составить уравнение баланса мощностей и проверить его подстановкой числовых значений.
Определить показания вольтметра.
Исходная схема:

Определения токов в ветвях по законам Кирхгофа
Зададим направления токов в ветвях и направления обхода контуров:

Определим количество уравнений по законам Кирхгофа:
NI З.К. = 4 – 1 = 3
NIIЗ.К. = 6 – 4 + 1 = 3
Составим уравнения по законам Кирхгофа:
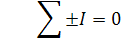
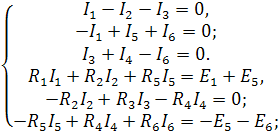
Метод контурных токов
Зададим направления токов в ветвях и направления обхода контуров

Рассчитаем токи в ветвях методом контурных токов:
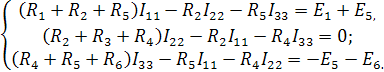


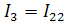

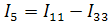

Подставим числовые значения сопротивлений и ЭДС и решим полученную систему уравнений в программе Gauss. Получим:
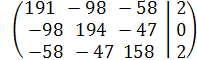

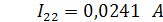
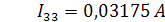
Определим значения токов в ветвях:
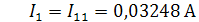
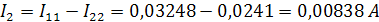
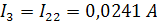
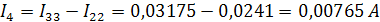


Метод эквивалентного генератора
Преобразуем схему и определим значение напряжения холостого хода Uхх:

Составим систему уравнений, пользуясь методом контурных токов:

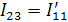
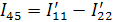

Подставим числовые значения сопротивлений и ЭДС и решим полученную систему уравнений в программе Gauss. Получим:
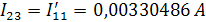


Рассчитаем напряжение холостого хода Uxx:
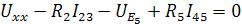

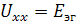
Преобразуем схему и найдем RЭГ:

 =24,75257732
Ом
=24,75257732
Ом
 =23,74226804 Ом
=23,74226804 Ом
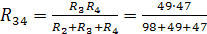 =11,87113402
Ом
=11,87113402
Ом
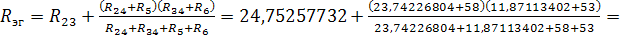
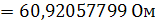

Определим ток в ветви с сопротивлением R1:

Баланс мощностей:


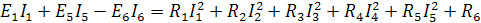
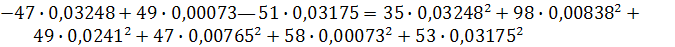
0,12847 Вт =0,12847 Вт
Баланс мощностей сходится.
Определение показаний вольтметра:

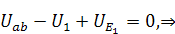

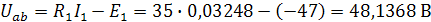
2. Расчёт электрической цепи однофазного переменного тока
Задание:
Определить комплексные действующие значения токов в ветвях схемы.
Определить показания приборов.
Составить баланс активных, реактивных и полных мощностей.
Повысить коэффициент мощности до 0,98 включением необходимого реактивного элемента X.
Построить векторные диаграммы токов и напряжений в одной системе координат.
Исходная схема:

Дано: U = 100 В, F =100 Гц, R1 = 88 Ом, R2 = 10 Ом, L1= 55 мГн, L2 = 0 мГн, C1 = 155 мкФ, C2 = 110 мкФ.
Определение комплексных действующих значений токов в ветвях схемы
Частота
источника, питающего сеть, F
= 100
Гц. Определим частоту 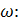

Вычислим  и
найдем z:
и
найдем z:

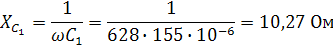
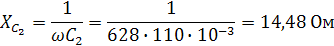
Тогда
Z=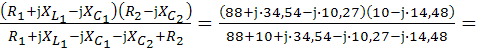
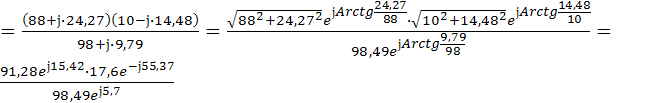 =16,31
=16,31 Ом
Ом
Z1= Ом
Ом
Z2= Ом
Ом
Определим входной ток с помощью закона Ома:
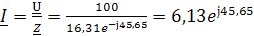 А
А
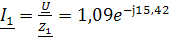 А
А
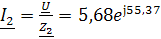 А
А
Определение показаний приборов
1) Показание амперметров
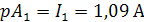

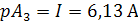
2) Показание вольтметра

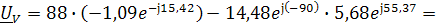
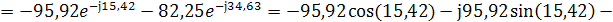
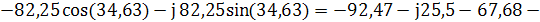
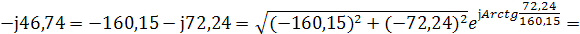

pV=175,69 В
3) Показание фазометра
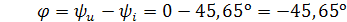
4) Показание ваттметра

Составление баланса активных, реактивных и полных мощностей
Запишем уравнение баланса мощностей:





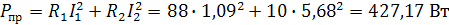


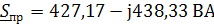

Баланс мощностей соблюдается.
Повышение коэффициента мощности до 0,98 включением необходимого реактивного элемента X.
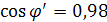

Отсюда:
G=0,042
bC=0,043

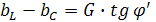
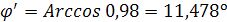

Тогда 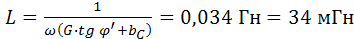
Построение векторных диаграмм токов и напряжений в одной системе координат
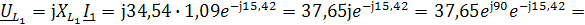
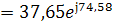 В
В
 В
В

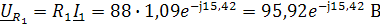

MI: 0,1A:1см MU: 2В:1см

3. Расчёт трёхфазной цепи
Задания:
Составить схему включения приёмников.
Определить комплексы действующих значений фазных и линейных токов.
Составить схему включения ваттметров для измерения активной мощности каждого трёхфазного приёмника.
Рассчитать активную, реактивную и полную мощность каждого приемника.
Построить векторные диаграммы токов и напряжений для каждого приемника.
Исходная схема:

Схема соединения приемников: звезда. Дано: нагрузка: симметричная, U = 220 В, R = 142Ом, L = 8 мГн.
Схема соединения приемников: треугольник. Дано: нагрузка: несимметричная, U = 220 В, Rab = 133 Ом, Rbc = 56 Ом, Rca = 0 Ом, Lab = 0 мГн, Lbc = 0 мГн, Lca = 127 мГн, Cab = 143 мкФ, Cbc = 139 мкФ, Cca = 0 мкФ.
Схема соединения «звезда»
Схема включения приёмников:

2) Определение комплексов действующих значений линейных токов


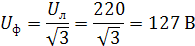
Рассчитаем фазные напряжения:
 В
В
 B
B
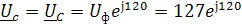 B
B
Представим фазные напряжения в алгебраической форме:
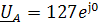 В
В
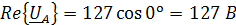


 B
B

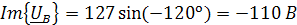

 B
B
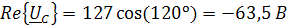
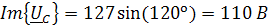


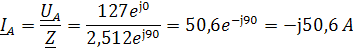

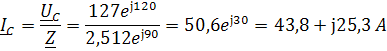
Схема включения ваттметра для измерения активной мощности каждого трёхфазного приёмника:

Показания ваттметра:
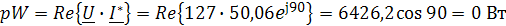
Активная мощность приемников:
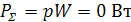
Реактивная мощность приемников:
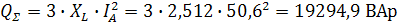
Полная мощность приемников:

Векторные диаграммы токов и напряжений
MI: 1A:1см MU: 6В:1см

Схема соединения «треугольник»
Схема включения приёмников:

Рассчитаем фазные напряжения:
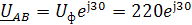 В
В
 B
B
 B
B
Комплексы полных сопротивлений приемников:
 Ом
Ом
 Ом
Ом
 Ом
Ом
Определим комплексы фазных токов по закону Ома:
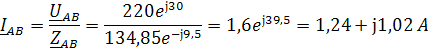
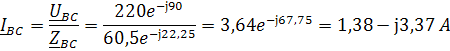
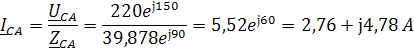
Определим комплексы линейных токов по первому закону Кирхгофа:

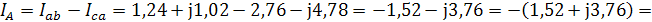

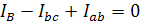



Схема включения ваттметров для измерения активной мощности каждого трёхфазного приёмника:

Показания ваттметров:

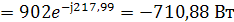
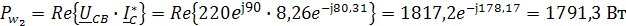
Активная мощность приемников:
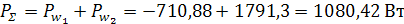
Реактивная мощность приемников:
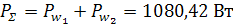
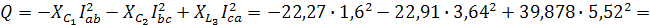

Полная мощность приемников:
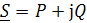
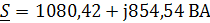
Векторные диаграммы токов и напряжений:
MI: 10A:1см MU: 6В:1см

2.1.Определение комплексных действующих значений токов в ветвях схемы
Для нахождения сопротивлений на индуктивном и емкостном элементах необходимо вычислить круговую частоту:
ω = 2πf=2∙3.14∙100 = 628 c-1
Найдем комплексы полных сопротивлений ветвей схемы:
Z1 = R1 + j( XL1 – XC1 ) = R1 + j( ωL
—  ) = 31 + j(
628·64·10-3 —
) = 31 + j(
628·64·10-3 — 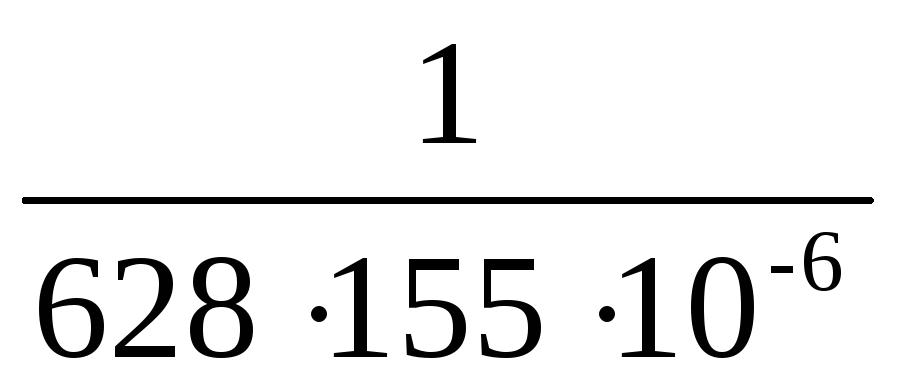 ) =
) =
= 31 + j29,919
= 43,083∙e = 43,083∙e
= 43,083∙e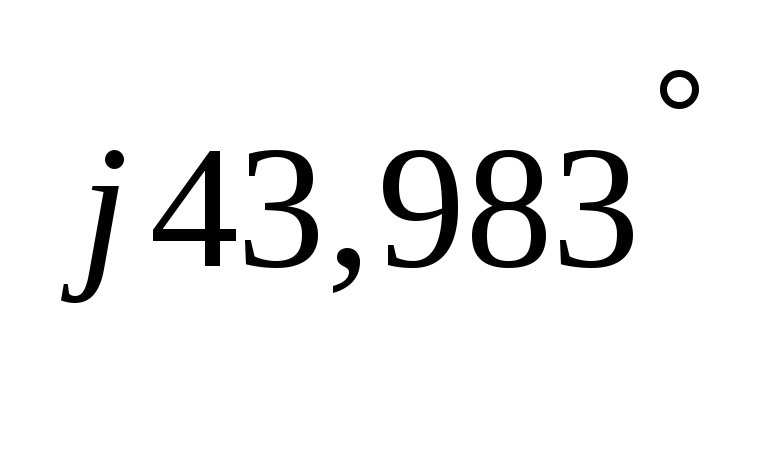 Ом
Ом
Z2 = R2 + jXL2 = R2 + j(ωL2)
= 40 + j(628·64·10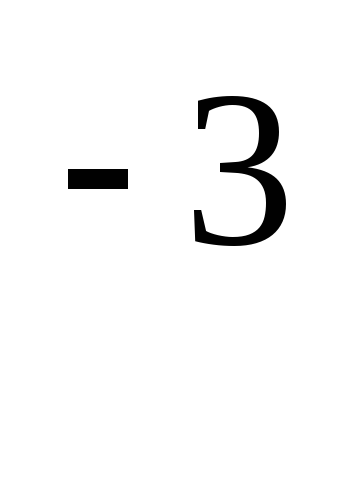 )
= 40 + j40,192 =
)
= 40 + j40,192 =
= 56,704∙e = 56,704∙e
= 56,704∙e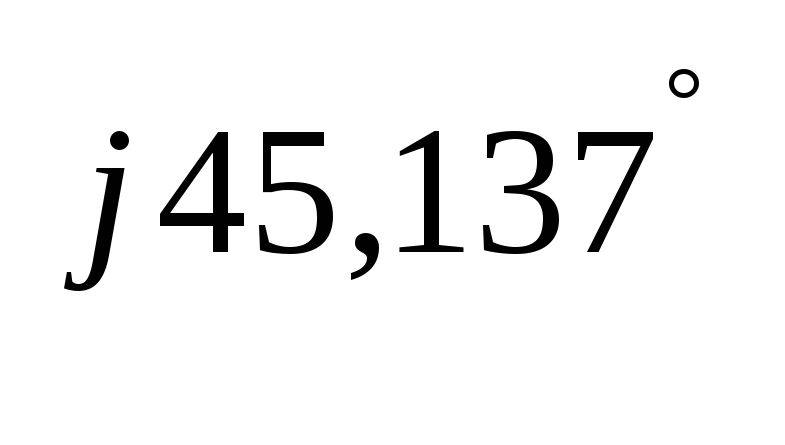 Ом
Ом
 Пусть,
ψu = 0°.
Пусть,
ψu = 0°.
 Тогда, I1 =
Тогда, I1 = 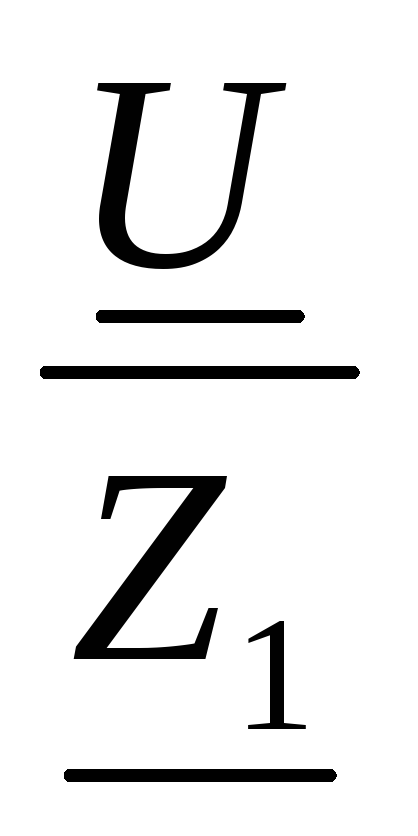 =
=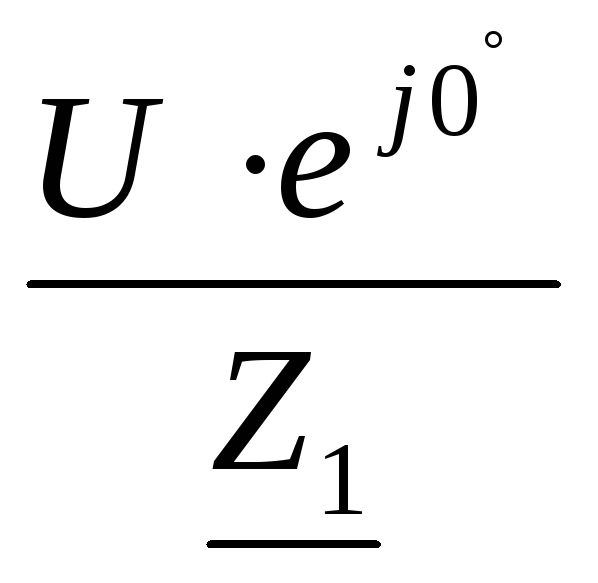 =
=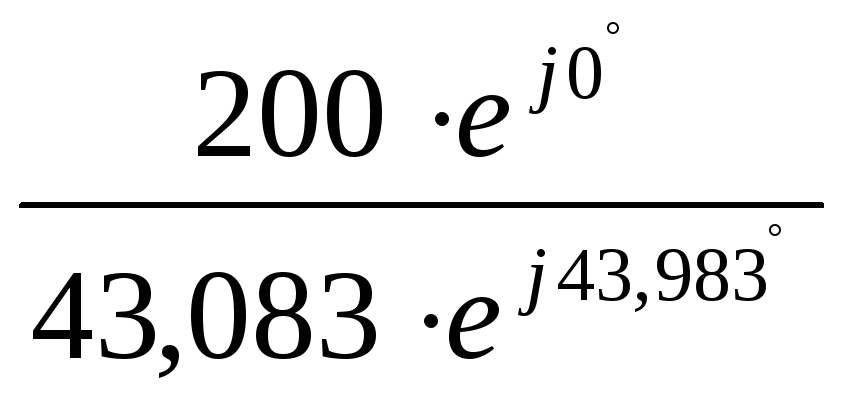 = 4,642·e
= 4,642·e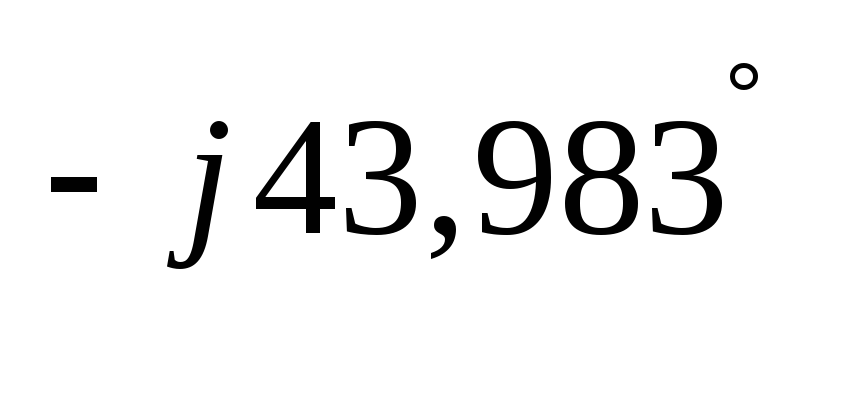 =
4,642·(cos(-43,983°)
+
=
4,642·(cos(-43,983°)
+
+ j∙sin(-43,983°)) = 4,642·(0,72 — j∙0,694) = 3,342 – j∙3,222 А
I2 = 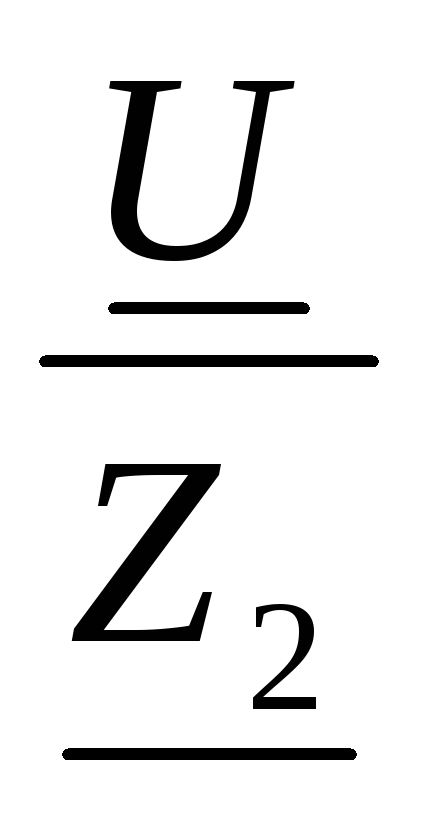 =
= =
= = 3,527∙e
= 3,527∙e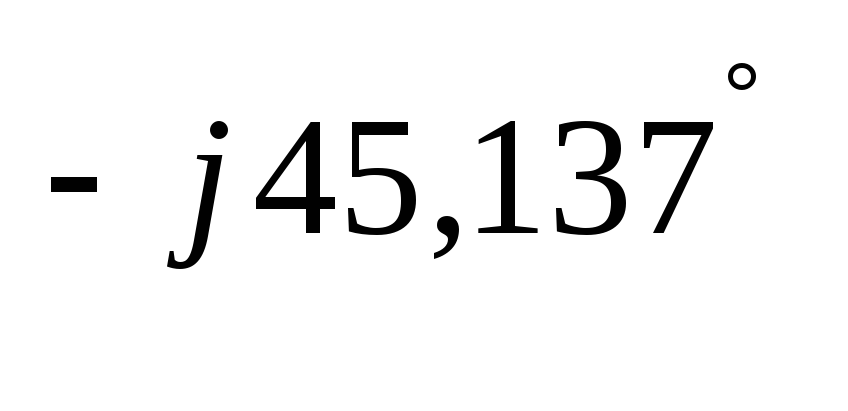 = 3,527∙(cos(-45,137°)
+ j∙sin(-45,137°))
= 3,527∙(0,705 — j∙0,709) = 2,487 — j∙2,501 А
= 3,527∙(cos(-45,137°)
+ j∙sin(-45,137°))
= 3,527∙(0,705 — j∙0,709) = 2,487 — j∙2,501 А
По первому закону Кирхгофа:
I = I1 + I2 = 3,342 – j∙3,222
+ 2,487 — j∙2,501
= 5,829 — j∙5,723
= 8,169∙e = 8,169∙e
= 8,169∙e А
А
2.2. Определение показаний приборов
а) Показания амперметров (показывают только действующее значение тока):
pA1 = I1 = 4,642 А
pA2 = I2 = 3,527 А
pA3 = I = 8,169 А
б) Показание фазометра.
Фазометр показывает разность фаз между током и напряжением:
pφ =φ = ψu – ψi = 0° — (-44,474°) = 44,474°
в) Показание ваттметра.
Так как ваттметр показывает только активную мощность, то для приведенной схемы включения ваттметра:
pW = Re[S] = Re[U∙I*] = 200∙5,829 = 1165,8 Вт.
г) Показание вольтметра:
О пределяем
по второму закону Кирхгофа
пределяем
по второму закону Кирхгофа
(рис.15.):
UV + UR1 – UL2 = 0
UV = I2jωL2 – I1R1 = (2,487 — j∙2,501)∙j∙628∙64∙10-3 —
— (3,342 – j∙3,222)∙31 = j∙99,9575 + 100,52 -103,602 +
+ j∙99,882
=-3,082 + j∙199,8395
= 199,86∙e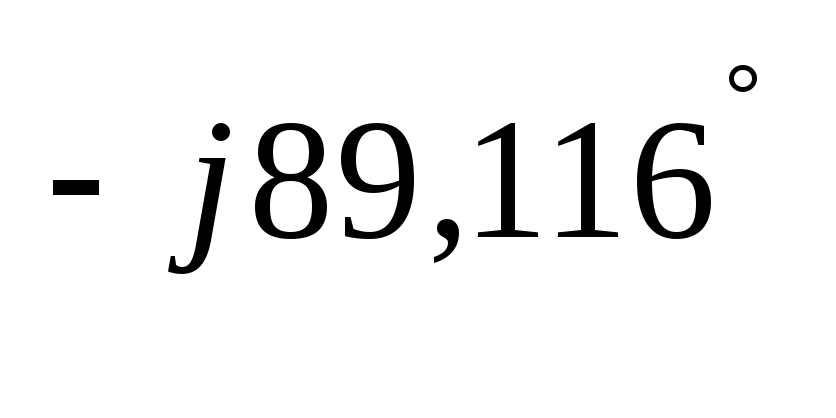 В
В
pV = UV = 199,86 В.
Рис.15.
2.3. Составление баланса активных, реактивных и полных мощностей
Запишем уравнение баланса для полноймощности:

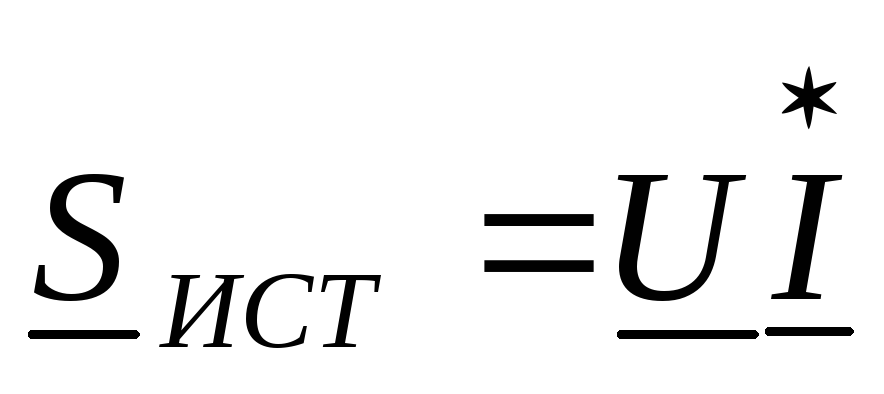 ,
где
,
где — сопряженный комплексный ток.
— сопряженный комплексный ток.
Sист = 200∙(5,829 + j∙5,723) = 1165,8 + j∙1144,6 ВА, где
Pист = Re[Sист] = 1165,8 Вт
Qист = Im[Sист] = 1144,6 ВАр
∑Sпр = ∑Pпр + ∑jQпр
∑Sпр = I12∙Z1 + I22∙Z2 = (4,642)2∙(31 + j29,919) +(3,527)2∙(40 + j40,192) = 667,993 + + j∙644,7 + 497,589 + j∙499,978 = 1165,582 + j∙1144,678 ВА
Pпр = Re[Sпр] = 1165,582 Вт
 Qпр = Im[Sпр]
= 1144,678 ВАр
Qпр = Im[Sпр]
= 1144,678 ВАр
Т
 ак
какPист = Pпр и Qист = Qпр Баланс мощностей соблюдается
ак
какPист = Pпр и Qист = Qпр Баланс мощностей соблюдается
 токи найдены верно.
токи найдены верно.
2.4. Повысить коэффициент мощности до 0,98 включением необходимого реактивного элемента х
Т.к. показание фазометра φ=44,4740>0 ,следовательно,цепь носит активно- индуктивный характер и для того,что бы повысить коэффициент мощности до 0,98 включаемпараллельно емкостной элемент.

Рис.16.
По первому закону Кирхгофа:
I1вх = I2вх + Iс , где I1 вх – токдокомпенсации,I2 вх– токпослекомпенсации.
Iр = Iа∙tgφ
φ1=44,474°
φ2 = arccos(0,98) = 11,478°
I с = I1вх — I2вх = Iа∙(tgφ1 – tgφ2)
=
с = I1вх — I2вх = Iа∙(tgφ1 – tgφ2)
= 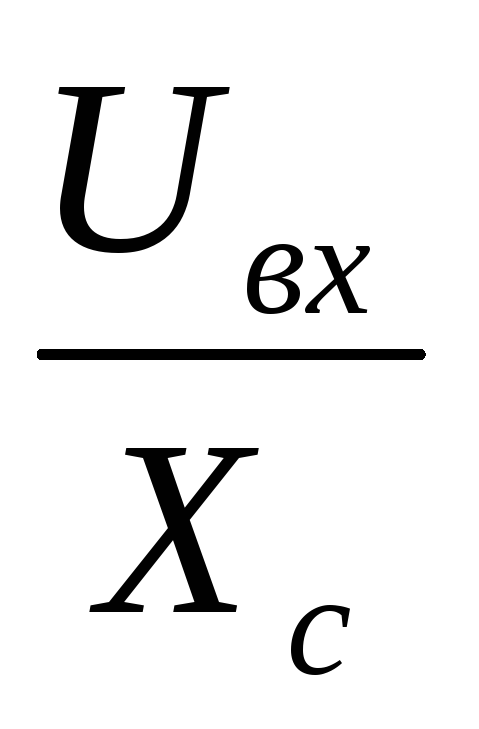 , Iа =
, Iа = 
 C =
C =  =
=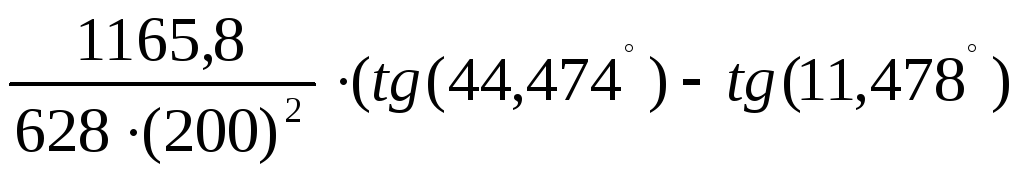 =
36,141мкФ
=
36,141мкФ

Рис.17.
 2.5.
Построение векторных диаграмм
токов и напряжений в одной системе
координат
2.5.
Построение векторных диаграмм
токов и напряжений в одной системе
координат
Определим напряжения на катушках, резисторахи конденсаторе:
UL1 = I1∙j∙XL1 = (3,342 – j∙3,222)∙j∙40,192
=129.499 + j∙134,322
= 186,58∙e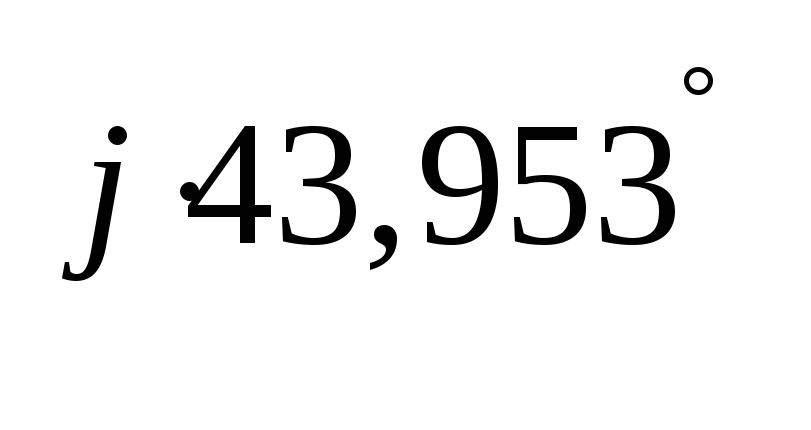 В
В
UL2 = I2∙j∙XL2 = (2,487 — j∙2,501)
∙j∙40,192 =
100,52 + j∙99,958
= 141,76∙e
 В
В
UR1 = I1∙R1 = 4,642·e ∙31
= 143,902·e
∙31
= 143,902·e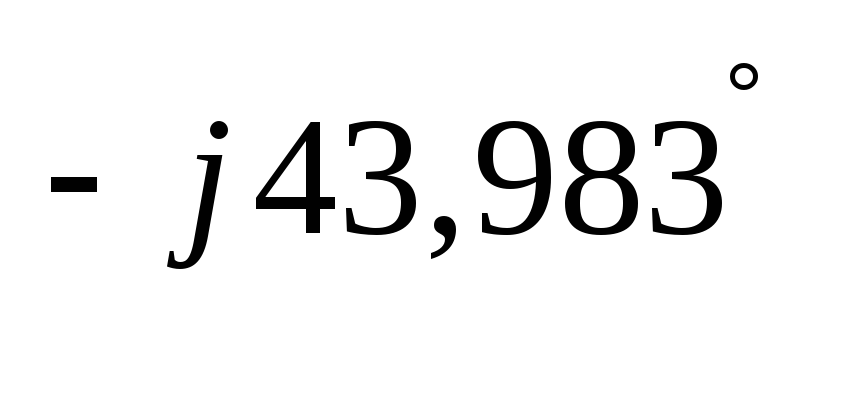 В
В
UR2 = I2∙R2 = 3,527∙e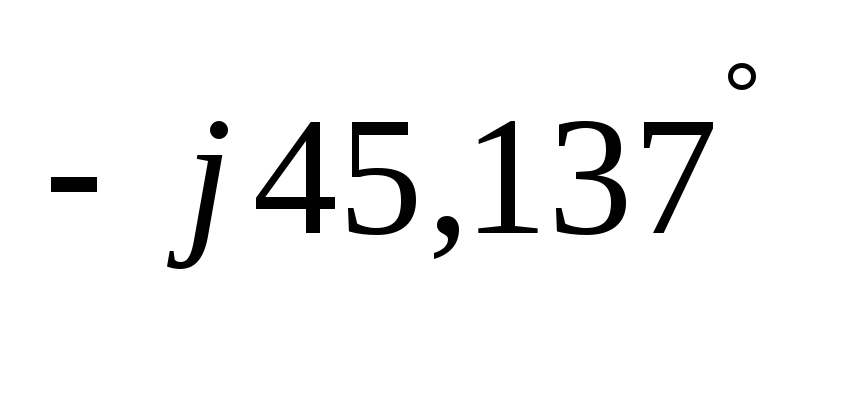 ∙40
= 141,08∙e
∙40
= 141,08∙e В
В
UC1 = — I1∙j∙XC1 = -(3,342 – j∙3,222)∙j∙10,273 = -33,0996 -j∙34,332 =
47,689∙e В.
В.
Масштаб:
MI: 0,05 A : 1мм
MU: 2В : 1мм

 Рис.18.
Рис.18.



ЧАСТЬ 3
РАСЧЕТ ТРЕХФАЗНОЙ ЦЕПИ
Задание:
1.Составить схему включения приемников.
2.Определить комплексы действующих значений фазных и линейных токов.
3.Составить схему включения ваттметров для измерения активной мощности каждого трехфазного приемника.
4.Рассчитать активную, реактивную и полную мощность каждого приемника.
5.Построить векторные диаграммы токов и напряжений для каждого приемника.


Рис.19.
Схема соединения приёмников: звезда с нулевым проводом Дано: Нагрузка: несимметричная U=380 В Ra=101 Ом Rb=65 Ом Rс=73 Ом La=0 Lb=0 Lc=97 мГн Ca=87 мкФ Cb=93 мкФ Cc=0 | Схема соединения приёмников: треугольник Дано: Нагрузка: симметричная U=380 В R=108 Ом L = 76 мГн f=50 Гц |
Решение
Лабораторно-практическое занятие № 2
ИЗУЧЕНИЕ АНАЛИТИЧЕСКИХ МЕТОДОВ РАСЧЕТА ЦЕПЕЙ И ИХ ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА
Типовые задачи
Задача 2.1. Определить показания вольтметра pV (рис.2.1) и указать, в каких режимах работают источники ЭДС (Ri, Ом, Ej, B), используя данные таблицы 2.1.
1. Определение тока.
Поскольку вольтметр имеет бесконечно большое сопротивление, он не оказывает влияние на величину тока рассматриваемой одноконтурной электрической цепи, и поэтому при определении величины тока не играет никакой роли и не учитывается.
Направление тока, как и направление обхода контура, выбирается произвольно (рис.2.2).
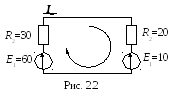 По второму закону
Кирхгофа:
По второму закону
Кирхгофа:
E1— E2 = R1I + R2I = (R1+ R2)I,
I =(E1— E2) /(R1+ R2) =
= (60-10) / (30+20).
2. Определение показания вольтметра.
Показание вольтметра не зависит от того, какая часть схемы рассматривается с целью его определения.
Для определения показания вольтметра составляется уравнение, согласно II закону Кирхгофа (направления обхода контуров показаны на рис. 2.3, а и 2.3,б)

Е1 = R1 I + Uab , Uab = E1 – R1 I = 60 – 30 · 1 = 30, B
или Е2 = R2 I + Uab , Uab = E2 – R2 I = 10 – 20 · 1 = 30, B.
Вольтметр показывает значение, равное Vab, в рассматриваемом случае 30 В.
3.Определение режимов работы источников ЭДС.
Если мощность источника ЭДС P = I E – величина положительная, то источник работает в режиме генератора, в противном случае – в режиме приемника:
P1 = IE1 = 1· 60 = 60, Вт – источник ЭДС E1 в режиме генератора;
P2 = I E2 = 1· 10 = 10, Вт – источник ЭДС E2 в режиме приемника.
Задача
2.2. Рассчитать
цепь методом контурных токов. Составить 
 баланс
мощностей, используя данные таблицы
2.2.
баланс
мощностей, используя данные таблицы
2.2.
Решение
1. Определение токов в ветвях.
Направление токов в ветвях и контурных токов (II IIII) выбираются произвольно, причем целесообразнее чтобы направления контурных токов совпадали с обходами соответствующих контуров (рис. 2.4).
Согласно методу контурных токов составляются уравнения ко II закону Кирхгофа для замкнутых независимых контуров цепи относительно не токов в ветвях, а контурных токов:
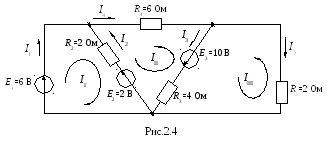
R2 II + R2 III ……………… = —E2 + E1;
+ R2 II +(R2 + R4 + R3) III – R3IIII = (E3 + E2);
……………— R3 III + (R3 + R5) IIII = E3
или 2II + 2 III ………………= — 2 + 6;
2 II + (2 + 6 + 4)III – 4IIII = — 10 – 2;
….………….- 4III+ (4 + 2)IIII= 10,
откуда значения контурных токов:
II = 36/11 А, III= 14/11 А, IIII= 9/11 А
Токи во внешних ветвях:
I1 = II = 36/11 А, I4 = III= 14/11 А, I5 = IIII= 9/11 А,
а токи в смежных ветвях:
I2 = — II– III= — 36 / 11 + 14 / 11 = — 2, А,
I3 = IIII – III= 9 / 11 + 14 / 11 = 23 / 11, А.
2. Составление управления баланса мощности энергии алгебраическая сумма мощностей всех источников цепи равна арифметической сумме мощностей всех ее приемников:
I1E1 + I2 E2 + I3E3 = R2 I2 + R3 I32 + R4 I42 + R5 I52
или в числовом выражении
36/11·6 (-2) 2 + 23/11·10 = 2(-2)2 + 4(23/11)2 + 6(14/11)2 + 2(9/11)2, Вт
402/11 = 402/11, Вт.
Задача 2.3. Определить токи в ветвях электрической цепи методом междуузлового напряжения (Ri, Ом, Ej, В) (рис. 2.5), используя данные таблицы 2.3.
Р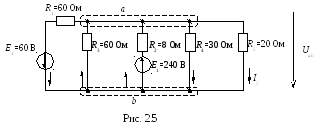 ешение
ешение
1. Определение междуузлового напряжения.
Потенциальные узлы отмечаются буквами с целью соблюдения знаков узловых токов, например, а u b (рис. 2.5), тогда искомое напряжение

где gi = 1/Ri – проводимость i-ой ветви, См, или в числовом выражении
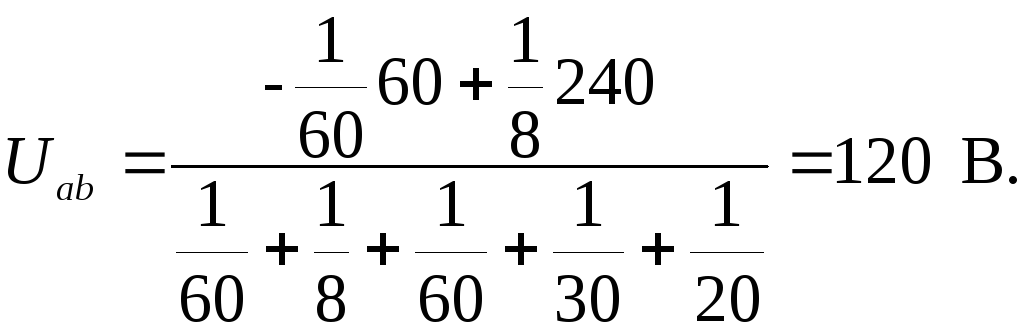
Расчет токов в схеме с одним источником энергии
При расчете токов в электрических цепях с одним источником электрической энергии рассматривают два типа задач: прямуюзадачу иобратную.
Прямая задача. Определить неизвестные токи и напряжение на зажимах источника ЭДС в электрической цепи, схема которой приведена на рис. 1.9, если известен ток четвертой ветвиI4.
Р ешение
этой задачи выполняется с помощью
законов Ома и Кирхгофа.
ешение
этой задачи выполняется с помощью
законов Ома и Кирхгофа.
Четвертая и пятая ветви соединены
параллельно, то есть напряжение  на зажимах этих ветвей одно и то же. По
закону Ома определим это напряжение,
зная ток и сопротивление четвертой
ветви:
на зажимах этих ветвей одно и то же. По
закону Ома определим это напряжение,
зная ток и сопротивление четвертой
ветви: .
.
Тогда ток пятой ветви: 
Ток третьей ветви найдем по первому закону Кирхгофа:
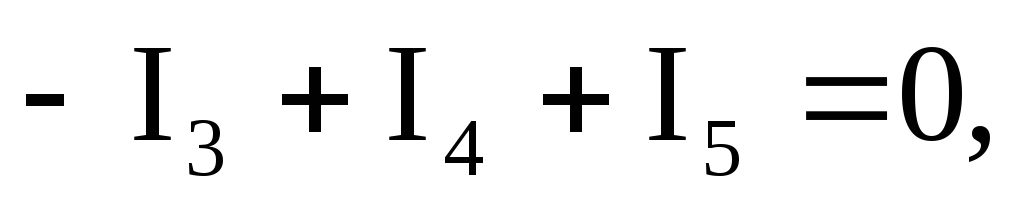 откуда
откуда .
.
Для определения тока второй ветви составим уравнение по второму закону Кирхгофа для контура, образованного второй, третьей и четвертой ветвями:
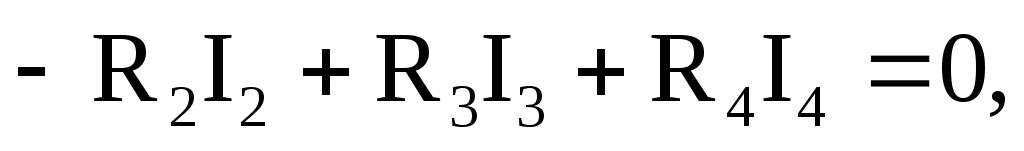
из составленного уравнения найдем ток второй ветви

Ток первой ветви находим, составив уравнение по первому закону Кирхгофа для узла 2:
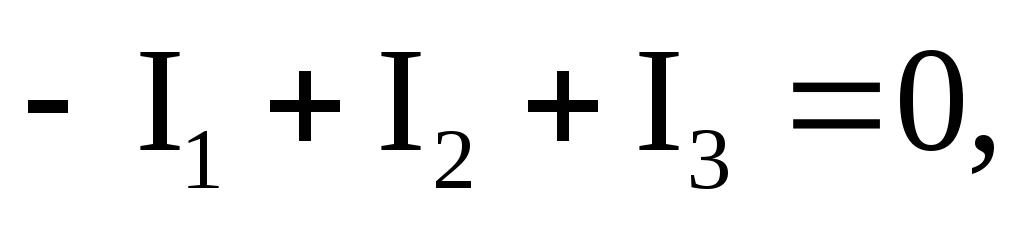 откуда
откуда
ЭДС источника рассчитаем, составив уравнение по второму закону Кирхгофа для контура, образованного первой и второй ветвями:
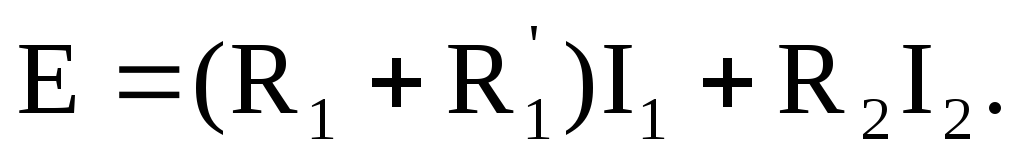
Обратная задача. Определить токи в ветвях электрической цепи, схема которой показана на рис. 1.9, если известны сопротивления приемников и ЭДС источника питания.
Цепь содержит один источник ЭДС. Токи в такой цепи направлены от точки с самым высоким потенциалом (1) через приемники к точке с самым низким потенциалом (5), и можно сразу показать правильные положительные направления токов ветвей.
З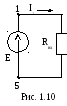 адачу
решаем методом эквивалентных
преобразований.
адачу
решаем методом эквивалентных
преобразований.
Путем последовательных преобразований необходимо определить входное сопротивление цепи относительно зажимов источника, то есть привести схему к виду рис. 1.10.
В такой цепи, содержащей источник и приемник электрической энергии, напряжение на зажимах приемника равно ЭДС и ток, протекающий по цепи, может быть определен с помощью закона Ома:

Рассчитаем входное сопротивление цепи относительно зажимов 1-5.
Найдем сопротивление пятой ветви, содержащей последовательное соединение сопротивлений R5иR6:
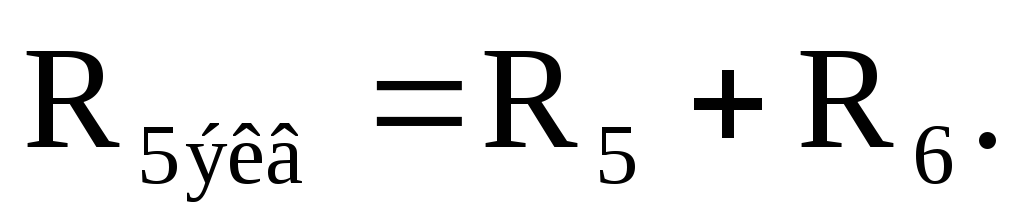
Пятая и четвертая ветви соединены
параллельно, поэтому их эквивалентное
сопротивление, найденное относительно
зажимов 3-4,равно: 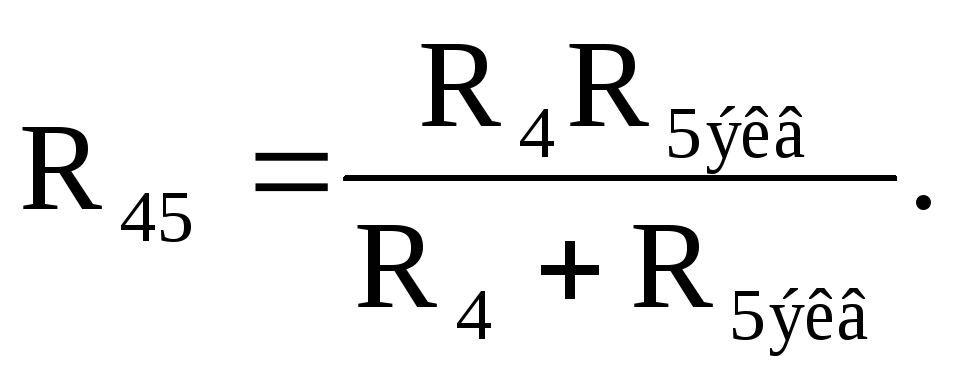
Сопротивление третьей ветви и найденное
сопротивление R45соединены последовательно, их эквивалентное
сопротивление:
Относительно зажимов 2-4 сопротивления второй ветви и сопротивление R345соединены параллельно:
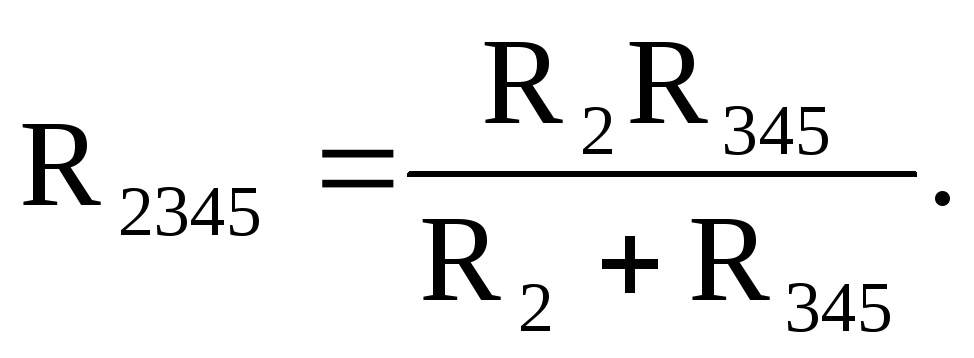
Относительно зажимов источника ЭДС сопротивление R2345и сопротивление первой ветви соединены последовательно, поэтому входное сопротивление можно рассчитать:

Ток ветви, содержащей источник ЭДС, определим по закону Ома:
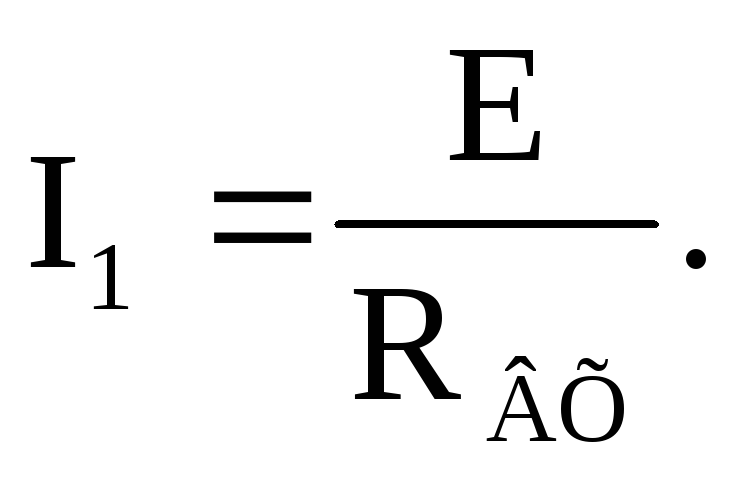
Ток второй ветви определим из уравнения, составленного по второму закону Кирхгофа для контура, образованного первой и второй ветвями:
 ,
откуда
,
откуда
Ток третьей ветви найдем с помощью уравнения, составленного по первому закону Кирхгофа для узла 2:
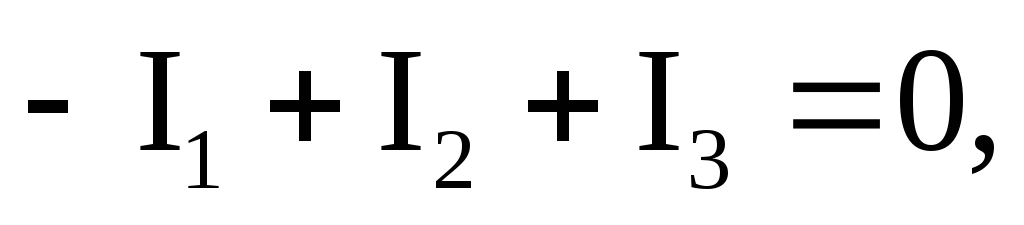 откуда
откуда
Для определения тока четвертой ветви составим уравнение по второму закону Кирхгофа для контура, образованного второй, третьей и четвертой ветвями:
 откуда
откуда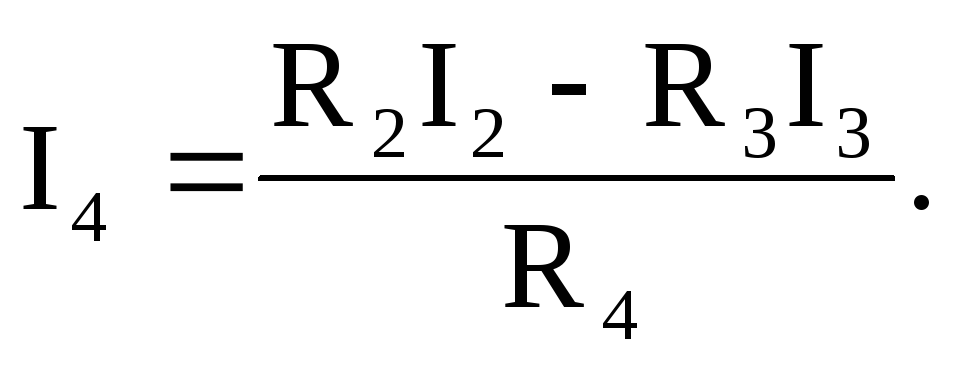
Ток пятой ветви найдем с помощью уравнения, составленного по первому закону Кирхгофа для узла 3:
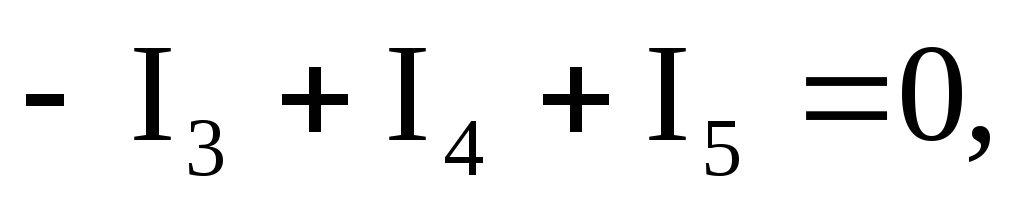 откуда
откуда
9. Метод двух узлов
В электротехнической практике часто встречаются схемы, содержащие только два узла. Для расчета таких схем специально создан метод, получивший название метода двух узлов. Этот метод по существу является частным случаем метода узловых потенциалов.
На рис. 30 приведена обобщенная схема электрической цепи постоянного тока с двумя узлами aиb. Схема состоит изmветвей, часть или все из которых содержат источники ЭДС. В общем случае в некоторых ветвях могут быть и источники тока.
В методе двух узлов за искомое принимают напряжение Uabмежду узламиaиbсхемы. Если при этом один из двух узлов, например, узелbзаземлить и принять его потенциал равным нулю (φb= 0), то потенциал φaвторого узла будет равен напряжениюUab.
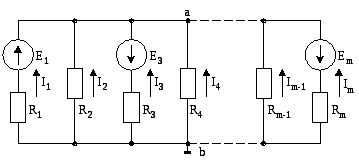
Рис. 30. К методу двух узлов
Воспользуемся методом узловых потенциалов и составим уравнение относительно потенциала φa:
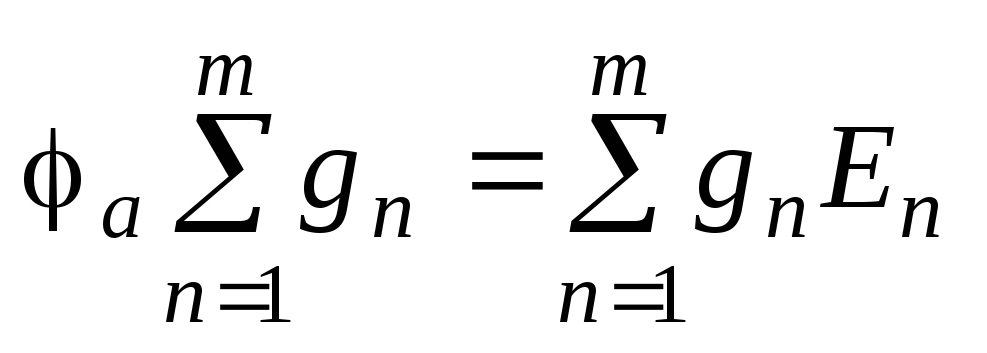 .
.
Решая это уравнение относительно Uab = φa,получаем:
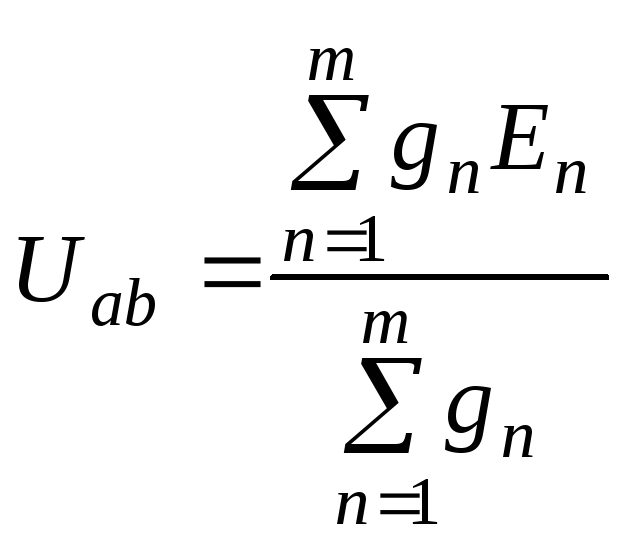 ,
,
где в числителе берется алгебраическая сумма произведений проводимостей gn= 1/Rn и ЭДСEnдля ветвей, содержащих источники ЭДС. (Для ветвей без источников произведениеgnEnобращается в ноль). Члены суммы берутся со знаком плюс, если стрелка источника ЭДС направлена к узлу a, и со знаком минус, если стрелка направлена от узла a. При наличии в части ветвей схемы идеальных источников тока алгебраическая сумма произведенийgnEn будет содержать также токи идеальных источников токаIk. Выбор знака для источника тока такой же, как и для источника ЭДС. Знаменатель формулыUabпредставляет собой арифметическую сумму проводимостей всех ветвей схемы. Причем в этой сумме проводимости ветвей, содержащих идеальные источники тока, равны нулю, т.к. внутреннее сопротивление источника тока равно бесконечности.
После того, как напряжение Uabмежду двумя узлами найдено, можно определить ток в любой ветви схемы по формуле закона Ома для участка цепи с источником ЭДС
 ,
,
где знак ЭДС выбирается исходя из направления ЭДС в n–й ветви.
10. Метод наложения
Метод наложения является следствием общефизического принципа наложения (суперпозиции), согласно которому реакция цепи на сумму отдельных воздействий равна сумме реакций цепи на каждое воздействие в отдельности.
В электротехнической практике в качестве воздействий чаще всего выступают ЭДС, а в качестве реакций – токи.
Для обоснования применения принципа
наложения к анализу электрической цепи
можно использовать формулу (10). В этой
формуле отношение Δpq/Δ
имеет размерность проводимости (См), а
текущий член суммы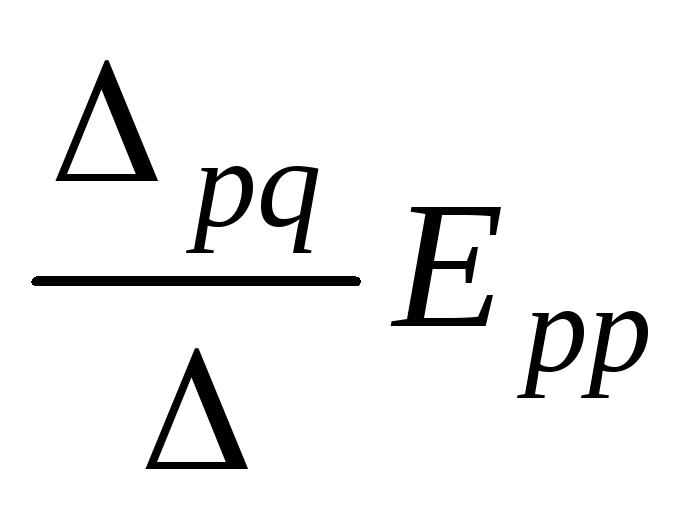 ,
являющийся произведением проводимости
на контурную ЭДС, имеет размерность
тока (А) и представляет собой реакцию
цепи (частичный токq-го
контура) на контурную ЭДСEpp p-го
контура.Поэтому в
соответствии с формулой (10) контурный
ток равен сумме частичных контурных
токов от действия каждой контурной ЭДС
в отдельности. Т.е. формула (10) является
математическим выражением принципа
наложения применительно к контурным
токам.
,
являющийся произведением проводимости
на контурную ЭДС, имеет размерность
тока (А) и представляет собой реакцию
цепи (частичный токq-го
контура) на контурную ЭДСEpp p-го
контура.Поэтому в
соответствии с формулой (10) контурный
ток равен сумме частичных контурных
токов от действия каждой контурной ЭДС
в отдельности. Т.е. формула (10) является
математическим выражением принципа
наложения применительно к контурным
токам.
Согласно методу контурных токов контурные ЭДС представляют собой алгебраические суммы ЭДС источников, действующих в рассматриваемом контуре. Токи ветвей являются алгебраическими суммами контурных токов. Поэтому принцип наложения применим и к токам ветвей. А именно: токи ветвей можно рассматривать как алгебраические суммы частичных токов этих же ветвей от поочередного действия каждого из источников электрической энергии в отдельности:

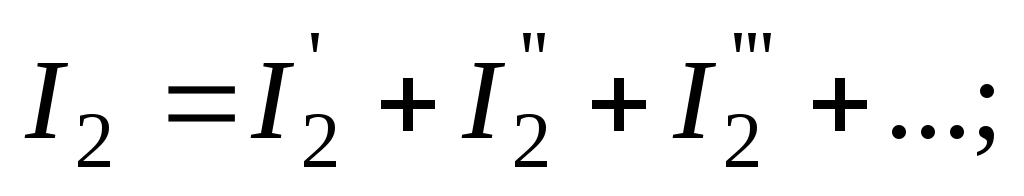
…………………,
где токи с одним, двумя и т.д. штрихами (число штрихов последнего члена каждой суммы равно количеству источников в схеме) – это так называемые частичные токи ветвей.
Методика расчета по методу наложения.
Расчет состоит из f + 1 этапов, где f – количество источников в схеме.
На первом этапе в цепи оставляют только один источник ЭДС или тока. Для остальных источников ЭДС и тока полагают E = 0, Ik = 0 и оставляют только их внутренние сопротивления Ri или проводимости gi. При этом ветви с идеальными источниками тока разрывают, а ветви с идеальными источниками напряжения заменяют короткозамкнутыми перемычками между точками их включения. Далее любым методом (чаще всего с помощью закона Ома) определяют частичные токи I‘ во всех ветвях схемы от действия оставленного источника. Выбранные условные положительные направления частичных токов в ветвях на схеме обозначают стрелками.
На втором этапе оставляют в цепи второй источник и аналогичным образом определяют частичные токи I» во всех ветвях схемы от действия второго источника, также обозначая на схеме направления действия частичных токов I» стрелками.
И т.д., выполняя на каждом новом этапе расчет частичных токов от действия очередного источника ЭДС или тока.
На последнем этапе определяют токи ветвей как алгебраические суммы частичных токов (с учетом направлений частичных токов в ветвях).
Примечание. Расчет мощностей и энергий можно вести только по полным токам ветвей, т.к. мощности и энергии являются квадратичными функциями токов.
Пример 3. Рассчитать токи в ветвях схемы рис. 31 методом наложения. Схема характеризуется следующими параметрами: E4 = 40 В, E6 = 32 В, Ri4 = 1 Ом, Ri6 = 1 Ом, R1 = 6 Ом, R2 = 10 Ом, R3 = 2 Ом, R4 = 7 Ом, R5 = 8 Ом, R6 = 9 Ом.
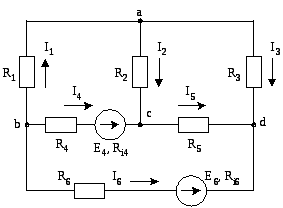
Рис. 31. К методу наложения
Решение
Анализируемая схема является мостовой. В схеме четыре узла и шесть ветвей. В четвертой и шестой ветвях имеются источники с ЭДС E4, E6 и внутренними сопротивлениями источников Ri4, Ri6. Выбранные положительные направления токов ветвей указаны на схеме стрелками.
Расчет токов в рассматриваемой схеме методом наложения необходимо выполнять в три этапа. На первом этапе рассчитаем частичные токи ветвей I‘ от действия источника в шестой ветви. На втором этапе определим частичные токи ветвейI» от действия источника в четвертой ветви. На третьем этапе найдем результирующие токи ветвей.
Первый этап. Удаляем из схемы ЭДС E4, оставив в схеме внутреннее сопротивление Ri4. Схема приобретает вид, изображенный на рис. 32.
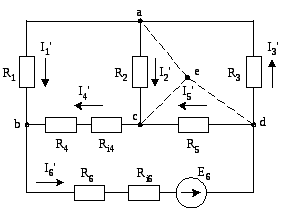
Рис. 32. К первому этапу метода наложения
Заменим контур-треугольник acd эквивалентной звездой (на схеме рис. 32 лучи звезды показаны внутри контура acd пунктиром). Схема приобретает вид, изображенный на рис. 33.

Рис. 33. Схема замещения для первого этапа метода наложения
Для расчета сопротивлений эквивалентной звезды воспользуемся формулами (7):
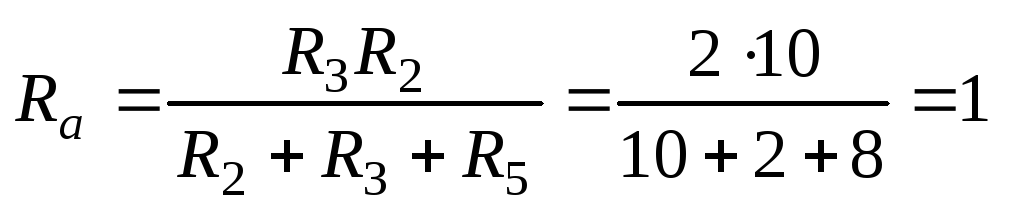 Ом;
Ом;  Ом;
Ом;
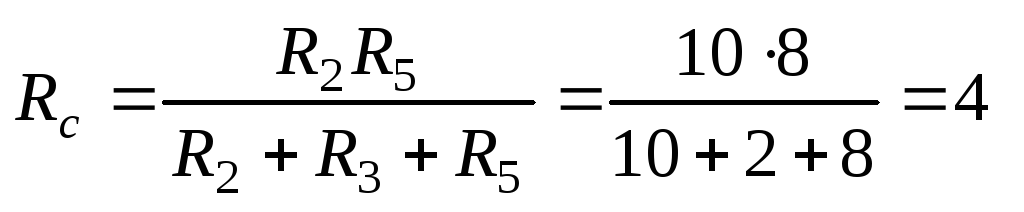 Ом.
Ом.
Схема рис. 33 по структуре соединения ветвей аналогична схеме рис. 16 и представляет собой смешанное соединение в цепи постоянного тока. На схеме рис. 33 первая и четвертая ветви включены параллельно, а шестая ветвь включена последовательно с ними. Определим эквивалентные сопротивления каждой ветви схемы рис. 33.
Первая ветвь
R1a = R1 + Ra = 6 + 1 = 7 Ом.
Четвертая ветвь
R4c = R4 + Ri4 + Rc = 7 + 1 + 4 = 12 Ом.
Шестая ветвь
R6b = R6 + Ri6 + Rb = 9 + 1 + 0,8 = 10,8 Ом.
Применяя формулу (6) для смешанного соединения в цепи постоянного тока, находим входное сопротивление схемы по отношению к ЭДС E6схемы рис. 33:
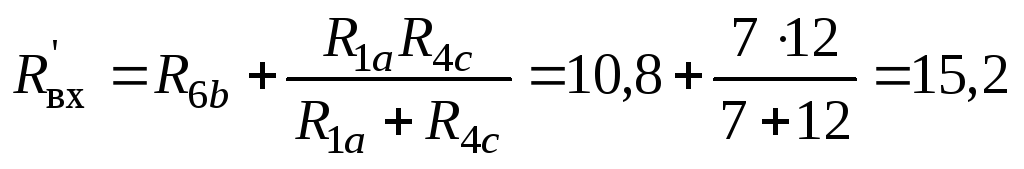 Ом.
Ом.
Далее по закону Ома находим частичный ток шестой ветви
 А.
А.
Для определения частичных токов первой и четвертой ветвей рассчитаем напряжение между узлами eиbсхемы рис. 33:
 В.
В.
Частичные токи первой и четвертой ветвей находим по закону Ома:
 А;
А; 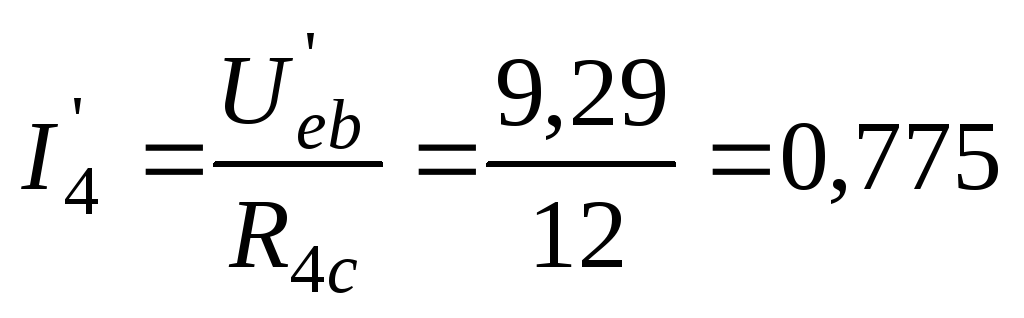 А.
А.
Для нахождения частичных токов второй,
третьей и пятой ветвей схемы рис.
32 необходимо рассчитать напряжения 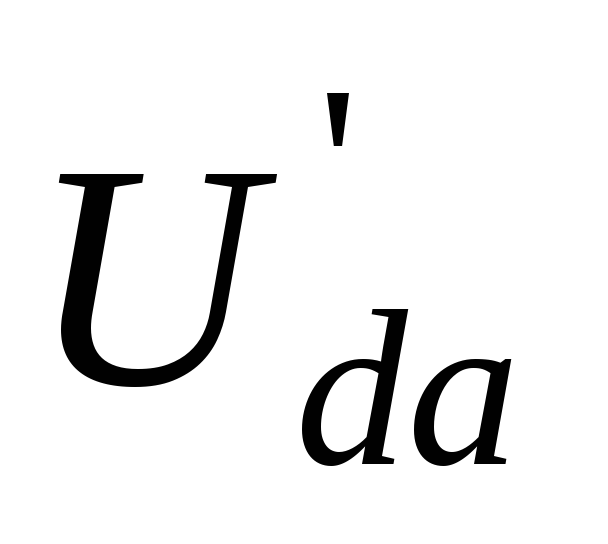 ,
,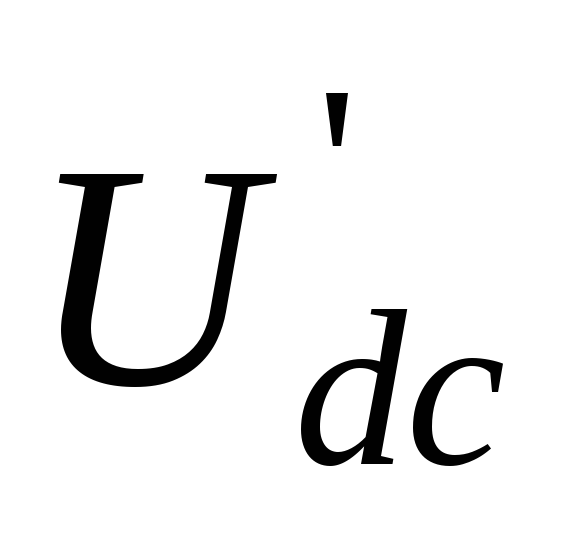 ,
,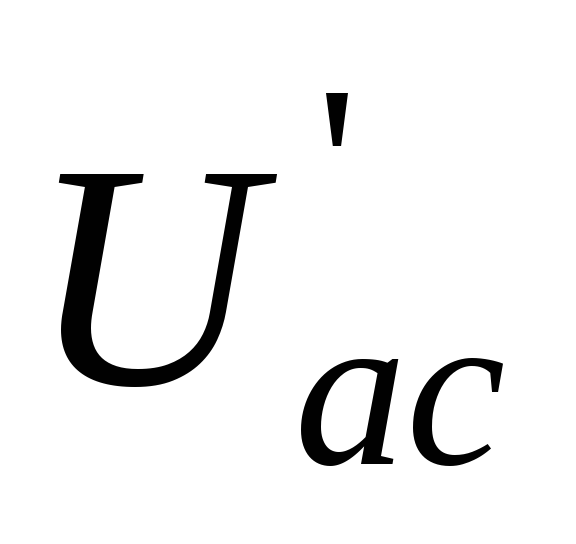 .
Расчет выполняем, используя схему рис.
33:
.
Расчет выполняем, используя схему рис.
33:
 В;
В;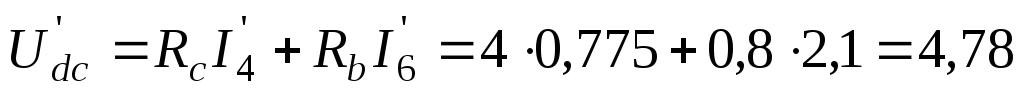 В;
В;
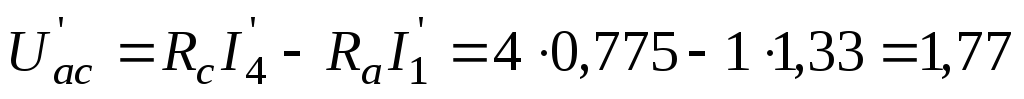 В.
В.
Возвращаемся к схеме рис. 32 и, используя закон Ома для участка цепи, определяем частичные токи второй, третьей и пятой ветвей:
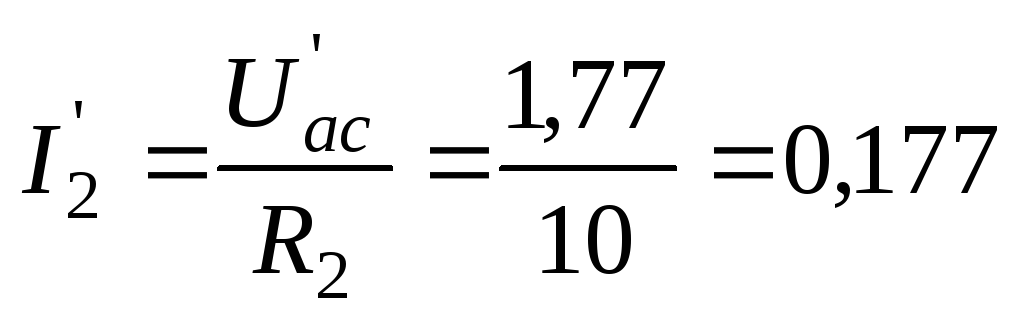 А;
А;  А;
А; 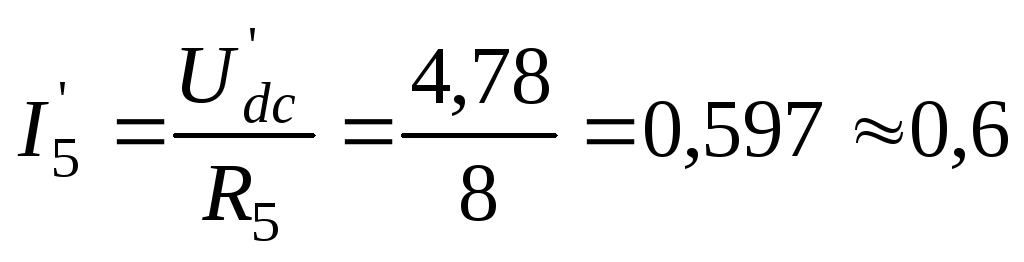 А.
А.
Второй этап.Удалим из исходной схемы (см. рис. 31) ЭДС E6, оставив в схеме внутреннее сопротивление Ri6. Схема приобретает вид, изображенный на рис. 34.

Рис. 34. Ко второму этапу метода наложения
Заменим контур-треугольник acd эквивалентной звездой (на схеме рис. 34 лучи звезды показаны внутри контура acd пунктиром). Схема приобретает вид, изображенный на рис. 35.
Схема рис. 35 – это смешанное соединение в цепи постоянного тока. Численные значения сопротивлений Ra, Rb, Rc эквивалентной звезды схемы рис. 35 те же, что и схемы рис. 33, а именно: Ra = 1 Ом, Rb = 0,8 Ом, Rc = 4 Ом. Поэтому иэквивалентные сопротивления каждой ветви схемы рис. 35 такие же, как и у и схемы рис. 33. Эти сопротивления найдены выше: R1a= = 7 Ом,R4c= 12 Ом, R6b= 10,8 Ом.

Рис. 35. Схема замещения для второго этапа метода наложения
На схеме рис. 35 первая и шестая ветви включены параллельно, а четвертая ветвь включена последовательно с ними. Применяя формулу (6) для смешанного соединения в цепи постоянного тока, находим входное сопротивление по отношению к ЭДС E4схемы рис. 35:
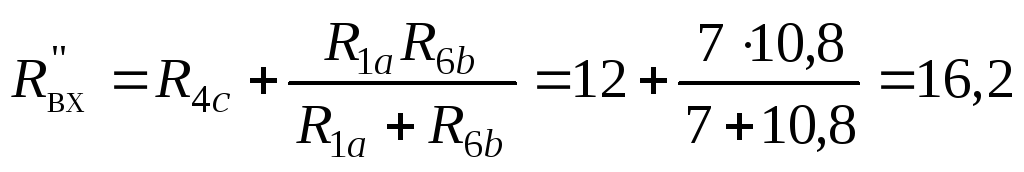 Ом.
Ом.
Далее по закону Ома находим частичный ток четвертой ветви
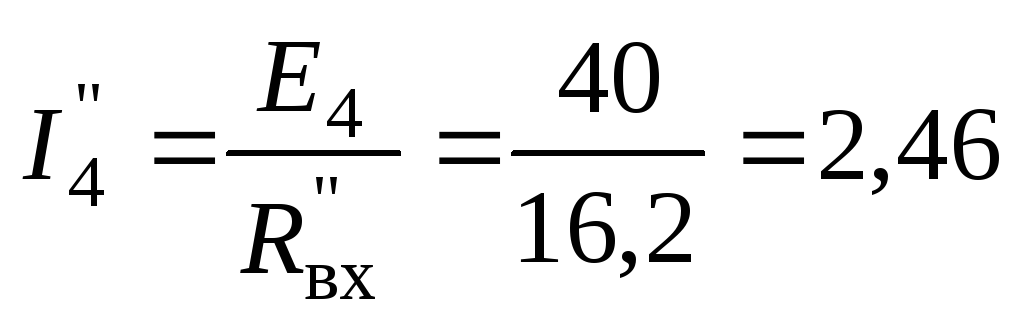 А.
А.
Для определения частичных токов первой и шестой ветвей рассчитаем напряжение между узлами eиbсхемы рис. 35:
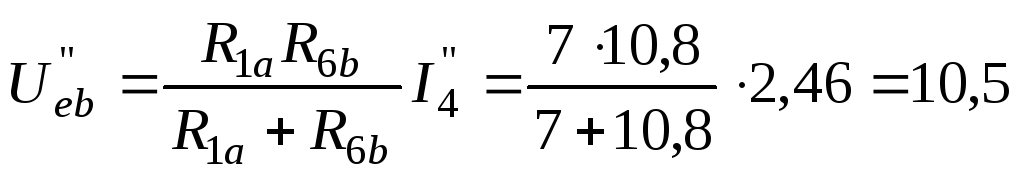 В.
В.
Частичные токи первой и шестой ветвей находим по закону Ома:
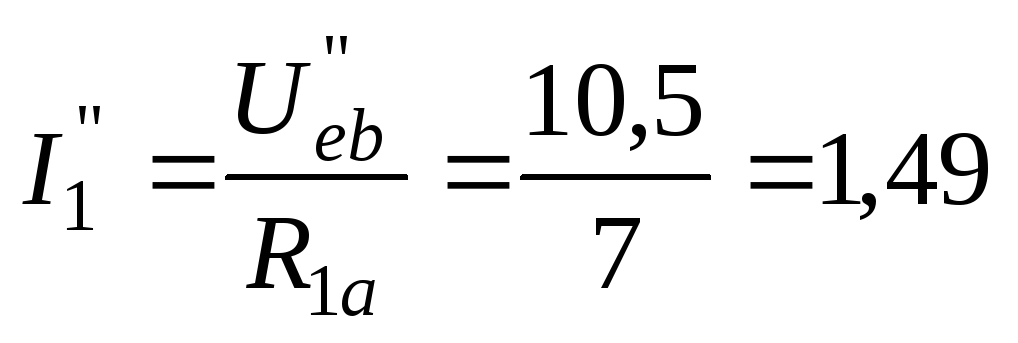 А;
А;  А.
А.
Для нахождения частичных токов второй,
третьей и пятой ветвей схемы рис.
34 необходимо рассчитать напряжения  ,
,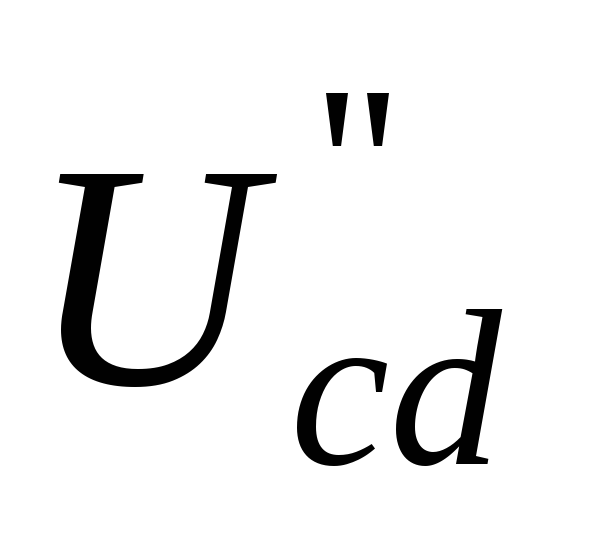 ,
, .
Расчет выполняем, используя схему рис.
35:
.
Расчет выполняем, используя схему рис.
35:
 В;
В; 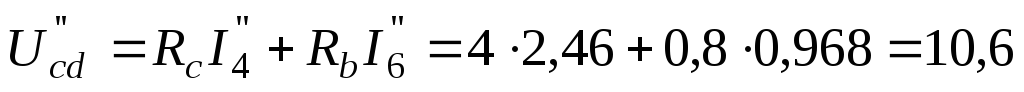 В;
В;
 В.
В.
Возвращаемся к схеме рис. 34 и, используя закон Ома для участка цепи, определяем частичные токи второй, третьей и пятой ветвей:
 А;
А; 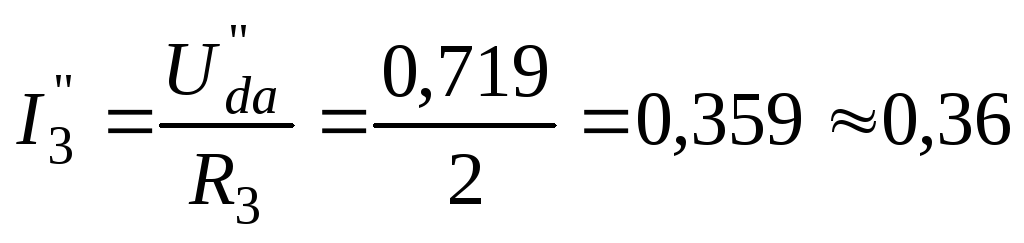 А;
А;  А.
А.
Третий этап.Токи ветвей схемы рис. 31 определяем как алгебраические суммы частичных токов:
 А;
А;  А;
А;
 А;
А;  А;
А;
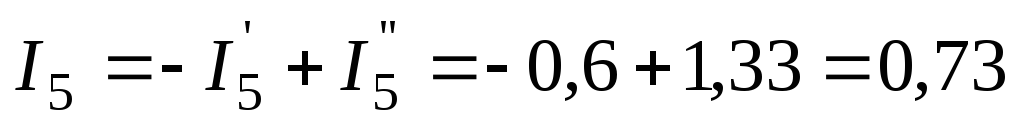 А;
А;  А.
А.



