Понятие силы. Видеоурок. Физика 10 Класс
Сила – это основное понятие динамики, с помощью него мы можем описать взаимодействие тел. На этом уроке мы с вами подробно рассмотрим, что такое сила, какие бывают силы, и к чему приводит то, что некая сила приложена к телу. Кроме того, мы с вами разберем важное понятие равнодействующей всех сил и научимся работать с проекциями сил.
Первые представления о силе связываются у нас с мускульными напряжениями рук, ног – с мускульной силой. Словами «сильный»‚ «слабый» мы в обыденной жизни часто характеризуем действие одного тела на другое, например действие руки на мяч, действие пружины на боек затвора винтовки, давление пара на поршень паровой машины и т. д.
Из прошлого урока мы с вами знаем, что изменение скорости тела происходит из-за взаимодействия его с другими телами. Для того чтобы подробно описать поведение тел при взаимодействии, вводится понятие сила.
Сила – это физическая величина, в результате действия которой тело изменяет свою скорость или деформируется.
Сила характеризуется величиной и направлением (рис. 1).

Рис. 1. Направление действия силы
На тело всегда действует не сила, а другое тело. Сила – это мера взаимодействия тел.
Действуют ли на тело силы?
В физике часто говорят, что на какое-то тело действует сила. Верно ли данное утверждение?
Сила – это мера воздействия. То есть на тело действует не сила, а другое тело. Сила лишь показывает меру того, как эти тела взаимодействуют. Приведем пример. Если вы катаетесь на коньках и сталкиваетесь с другим конькобежцем, то в этом случае некорректно говорить, что вы столкнулись с его массой и скоростью, хотя с помощью массы и скорости можно измерить последствия столкновения. Но все же вы столкнулись именно с конькобежцем.
Однако в языке устоялось выражение «действует сила», поскольку не всегда удобно говорить, что на тело в результате гравитационного взаимодействия действует Земля. Проще сказать, что на тело действует сила тяжести. Важно понимать, что подразумевается под этим выражением.
Обозначается сила следующим образом: 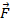 . В системе СИ сила измеряется в ньютонах:
. В системе СИ сила измеряется в ньютонах:
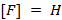
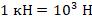
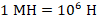

Стрелка сверху указывает на то, что это векторная величина, следовательно, вектор всегда должен соотноситься с СО. Если сила направлена в ту же сторону что и ось 

Рис. 2. Проекции силы на ось 
Сила измеряется с помощью специального прибора. Этот прибор называется динамометром. Динамометр – это прибор для измерения силы или момента силы, он состоит из силового звена (упругого элемента) и отсчетного устройства (рис. 3).

Рис. 3. Динамометр
1 Н – это сила, с которой тело массой приблизительно 100 грамм притягивается к Земле.
Для того чтобы понять, что такое сила в один ньютон, нам нужно вспомнить, что сила, приложенная к телу, изменяет его скорость. Кроме того, вспомним об инертности тел, которая, как мы помним, связана с их массой. Итак:
1 Н– это такая сила, которая меняет скорость тела массой в 1 кг на 1 м/с за каждую секунду.
Примерами сил могут служить:
- Сила тяжести – сила, действующая на тело в результате гравитационного взаимодействия.
- Сила упругости – сила, с которой тело сопротивляется внешней нагрузке. Ее причиной является электромагнитное взаимодействие молекул тела.
- Сила Архимеда – сила, связанная с тем, что тело вытесняет некий объем жидкости или газа.
- Сила реакции опоры – сила, с которой опора действует на тело, находящееся на ней.
- Сила трения – сила сопротивления относительному перемещению контактирующих поверхностей тел.
- Сила поверхностного натяжения – сила, возникающая на границе раздела двух сред.
Итак, из этого урока мы с вами углубили свое понимание понятия силы. Мы вспомнили единицы измерения силы и прибор, с помощью которого измеряется сила.
Список литературы
- Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский. Физика 10. – М.: Просвещение, 2008.
- А.П. Рымкевич. Физика. Задачник 10-11. – М.: Дрофа, 2006.
- О.Я. Савченко. Задачи по физике. – М.: Наука, 1988.
- А.В. Перышкин, В.В. Крауклис. Курс физики. Т. 1. – М.: Гос. уч.-пед. изд. мин. просвещения РСФСР, 1957.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет портал «Youtube» (Источник).
- Интернет портал «Youtube» (Источник).
Домашнее задание
- Решив задачи к данному уроку, вы сможете подготовиться к вопросам 2 ГИА и вопросам А2–А4 ЕГЭ.
- Задачи 131, 135, 137, 138 сб. задач А. П. Рымкевич изд. 10 (Источник).
- Всегда ли при увеличении силы, растягивающей пружину, во столько же раз увеличивается деформация? Как это повлияет на шкалу динамометра?
Рассмотрите следующие вопросы и ответы на них:
Вопрос. Почему сила характеризуется точкой приложения? Ведь в математике мы имеем право параллельно переносить вектор от точки к точке.
Ответ. Вспомните рычаг. Очевидно, что точка, в которой приложена сила к рычагу, сильно влияет на полученный эффект.
Вопрос. Если все тела взаимодействуют, то неужели на мое движение влияет Юпитер или Луна?
Ответ. Действительно, на ваше движение влияет и Юпитер, и Луна, и любая другая планета Солнечной системы. Однако действие этих тел на наше движение очень мало.
Вопрос. Может ли парусное судно двигаться против ветра?
Ответ. Да, может. Техника такого движения подробно описана в книге Я.И. Перельмана «Занимательная физика» (т. 2) (Источник).
Вопрос. Может ли модуль силы быть отрицательным?
Ответ. Нет, модуль силы – величина, большая нуля либо равная нулю. Отрицательной может быть только проекция силы на какую-либо ось.
Сила инерции — Википедия
 Наблюдатель, вращающийся вместе с каруселью, может объяснить отклонение кресел на аттракционе действием центробежной силы инерции
Наблюдатель, вращающийся вместе с каруселью, может объяснить отклонение кресел на аттракционе действием центробежной силы инерцииСи́ла ине́рции (также инерционная сила) — многозначное понятие, применяемое в механике по отношению к трём различным физическим величинам. Одна из них —
Общим для всех трёх величин является их векторный характер и размерность силы. Кроме того, первые две величины объединяет возможность их использования в уравнениях движения, по форме совпадающих с уравнением второго закона Ньютона
Русский термин «сила инерции» произошёл от французского словосочетания фр. force d’inertie. Термин применяется для описания трёх различных векторных физических величин, имеющих размерность силы:
- величин, которые вводят при описании движения тел в неинерциальных система отсчёта — «эйлеровы силы инерции»;
- величины, используемой в принципе Д’Аламбера — «даламберова сила инерции»;
- силы-противодействия из третьего закона Ньютона — «ньютонова сила инерции».
Определения «эйлерова», «даламберова» и «ньютонова» предложены академиком А. Ю. Ишлинским
Эйлерова сила инерции в общем случае складывается из нескольких составляющих различного происхождения, которым также присвоены специальные наименования («переносная», «кориолисова» и др.). Более детально об этом говорится в соответствующем разделе ниже.
В других языках используемые названия сил инерции более явно указывают на их особые свойства: в немецком нем. Scheinkraft[9] («мнимая», «кажущаяся», «видимая», «ложная», «фиктивная» сила), в английском англ. pseudo force[10](«псевдосила») или англ. fictitious force («фиктивная сила»). Реже в английском используются названия «сила д’Аламбера» (англ. d’Alembert force[11]) и «инерционная сила» (англ. inertial force[12]). В литературе, издаваемой на русском языке, по отношению к эйлеровой и даламберовой силам также используют аналогичные характеристики, называя эти силы «фиктивными»[13], «кажущимися»[14], «воображаемыми»[8] или «псевдосилами»[15].
Одновременно с этим в литературе иногда подчёркивают реальность сил инерции[16][17], противопоставляя значение данного термина значению термина фиктивность. При этом, однако, различные авторы вкладывают в эти слова различный смысл, и силы инерции оказываются реальными или фиктивными не в силу отличий в понимании их основных свойств, а в зависимости от избранных определений. Такое употребление терминологии некоторые авторы считают неудачным и рекомендуют просто избегать его в учебном процессе[18][19].
Хотя дискуссия по поводу терминологии ещё не закончена, имеющиеся разногласия не влияют на математическую формулировку уравнений движения с участием сил инерции и не приводят к возникновению каких-либо недоразумений при использовании уравнений на практике.
В классической механике представления о силах и их свойствах основываются на законах Ньютона и неразрывно связаны с понятием «инерциальная система отсчёта». Хотя в наименованиях эйлеровых и даламберовых сил инерции содержится слово сила, эти физические величины силами в смысле, принятом в механике, не являются[20][15].
Действительно, физическая величина, называемая силой, вводится в рассмотрение вторым законом Ньютона, при этом сам закон формулируется только для инерциальных систем отсчёта[21]. Соответственно, понятие силы оказывается определённым только для таких систем отсчёта[22].
Уравнение второго закона Ньютона, связывающее ускорение a→{\displaystyle {\vec {a}}} и массу m{\displaystyle m} материальной точки с действующей на неё силой F→{\displaystyle {\vec {F}}}, записывается в виде
- a→=F→m.{\displaystyle {\vec {a}}={\frac {\vec {F}}{m}}.}
Из уравнения непосредственно следует, что причиной ускорения тел являются только силы, и наоборот: действие на тело не скомпенсированных сил обязательно вызывает его ускорение.
Третий закон Ньютона дополняет и развивает сказанное о силах во втором законе.
Учёт содержания всех законов Ньютона приводит к заключению о том, что силы, о которых идёт речь в классической механике, обладают неотъемлемыми свойствами:
- сила есть мера механического действия на данное материальное тело других тел.[23]
- в соответствии с третьим законом Ньютона силы способны существовать лишь попарно, при этом природа сил в каждой такой паре одинакова[24][25].
- любая сила, действующая на тело, имеет источник происхождения в виде другого тела. Иначе говоря, силы обязательно представляют собой результат взаимодействия тел[26].
Никакие другие силы в классической механике в рассмотрение не вводятся и не используются[22][27]. Возможность существования сил, возникших самостоятельно, без взаимодействующих тел, механикой не допускается[26][28].
Некоторые авторы используют термин «сила инерции» для обозначения силы-противодействия из третьего закона Ньютона. Понятие было введено Ньютоном в его «Математических началах натуральной философии»[29]: «Врождённая сила материи есть присущая ей способность сопротивления, по которой всякое отдельно взятое тело, поскольку оно предоставлено самому себе, удерживает своё состояние покоя или равномерного прямолинейного движения. От инерции материи происходит, что всякое тело лишь с трудом выводится из своего покоя или движения. Поэтому врожденная сила могла бы быть весьма вразумительно названа силою инерции. Эта сила проявляется телом единственно лишь, когда другая сила, к нему приложенная, производит изменение в его состоянии. Проявление этой силы может быть рассматриваемо двояко — и как сопротивление, и как напор.», а собственно термин «сила инерции» был, по словам Эйлера, впервые употреблён в этом значении Кеплером([29], со ссылкой на Е. Л. Николаи).
Для обозначения этой силы-противодействия (действующей на ускоряющее тело со стороны ускоряемого тела[29]) некоторые авторы предлагают использовать термин «ньютонова сила инерции» во избежание путаницы с фиктивными силами, применяемыми при вычислениях в неинерциальных системах отсчёта и при использовании принципа д’Аламбера.
Отголоском мистических и теологических взглядов Ньютона[30] является применённая им терминология при описании силы инерции: «врождённая сила материи», «сопротивление». Такой подход к описанию ньютоновской силы инерции хотя и сохранился в современном обиходе[где?], однако является нежелательным, поскольку вызывает ассоциации с некой способностью тела сопротивляться изменениям, волевым усилием сохранить параметры движения. Максвелл заметил, что с таким же успехом можно было бы сказать, что кофе сопротивляется тому, чтобы стать сладким, так как сладким он становится не сам по себе, а лишь после добавления сахара[29].
Уравнение движения материальной точки в инерциальной системе координат (ИСО), представляющее собой уравнение 2-го закона Ньютона
- ma0=F,{\displaystyle m\mathbf {{a}_{0}} =\mathbf {F} ,}
в неинерциальной системе отсчёта (НСО) приобретает четыре дополнительных члена с размерностью силы — так называемые «силы инерции»[31], иногда называемые «эйлеровыми»:
- ma=F−mdVdt+m[rdΩdt]+2m[vΩ]+m[Ω[rΩ]],{\displaystyle m\mathbf {a} =\mathbf {F} -m{\frac {d\mathbf {V} }{dt}}+m[\mathbf {r} {\frac {d\mathbf {\Omega } }{dt}}]+2m[\mathbf {v} \mathbf {\Omega } ]+m[\mathbf {\Omega } [\mathbf {r} \mathbf {\Omega } ]],}
где:
Классификация[править | править код]
Четыре дополнительных члена в уравнении движения принято рассматривать как отдельные силы инерции, которые получили собственные названия:
- −mdVdt{\displaystyle -m{\frac {d\mathbf {V} }{dt}}} называется поступательной силой инерции. Сила связана с линейным ускорением НСО[32] и противонаправлена ему;
- m[rdΩdt]{\displaystyle m[\mathbf {r} {\frac {d\mathbf {\Omega } }{dt}}]} называется вращательной силой инерции. Сила связана с угловым ускорением НСО[32];
- m[Ω[rΩ]]{\displaystyle m[\mathbf {\Omega } [\mathbf {r} \mathbf {\Omega } ]]} называется центробежной силой. Сила связана с вращением НСО и потому проявляется и в случае равномерного вращения[33];
- 2m[vΩ]{\displaystyle 2m[\mathbf {v} \mathbf {\Omega } ]} называется силой Кориолиса[34].
Первые три силы, не связанные сдвижением точки, объединяются термином «переносные силы инерции»[32].
Примеры использования[править | править код]
В некоторых случаях при расчётах удобно использовать неинерциальную систему отсчёта, например:
- движение подвижных деталей автомобиля удобно описывать в системе координат, связанных с автомобилем. В случае ускорения автомобиля эта система становится неинерциальной;
- движение тела по круговой траектории иногда удобно описывать в системе координат, связанной с этим телом. Такая система координат неинерциальна из-за центростремительного ускорения.
В неинерциальных системах отсчёта стандартные формулировки законов Ньютона неприменимы. Так при ускорении автомобиля, в системе координат, связанной с корпусом автомобиля, незакреплённые предметы внутри получают ускорение в отсутствие какой-либо силы, прикладываемой непосредственно к ним; а при движении тела по орбите, в связанной с телом неинерциальной системе координат тело покоится, хотя на него действует ничем не сбалансированная сила гравитации, выступавшая в качестве центростремительной в той инерциальной системе координат, в которой наблюдалось вращение по орбите.
Для восстановления возможности применения в этих случаях привычных формулировок законов Ньютона и связанных с ними уравнений движения для каждого рассматриваемого тела оказывается удобно ввести фиктивную силу — силу инерции — пропорциональную массе этого тела и величине ускорения системы координат, и противонаправленную вектору этого ускорения.
С использованием этой фиктивной силы появляется возможность краткого описания реально наблюдаемых эффектов в неинерциальной системе отсчёта (в разгоняющемся автомомбиле): «почему при разгоне автомобиля пассажира прижимает к спинке сиденья?» — «на тело пассажира действует сила инерции». В инерциальной системе координат, связанной с дорогой, сила инерции для объяснения происходящего не требуется: тело пассажира в ней ускоряется (вместе с автомобилем), и это ускорение производит сила, с которой сиденье действует на пассажира.
Сила инерции на поверхности Земли[править | править код]
В инерциальной системе отсчёта (наблюдатель вне Земли) тело, находящееся на поверхности Земли, испытывает центростремительное ускорение ac{\displaystyle a_{c}}, по величине совпадающее с ускорением точек поверхности Земли, вызванным её суточным вращением. Это ускорение, в соответствии со вторым законом Ньютона, определяется воздействующей на тело центростремительной силой c{\displaystyle c} (зелёный вектор). Последняя складывается из силы гравитационного притяжения к центру Земли g0{\displaystyle g_{0}} (красный вектор) и силы реакции опоры b{\displaystyle b} (чёрный вектор)[35]. Таким образом, уравнение второго закона Ньютона для рассматриваемого тела в случае инерциальной системы отсчёта имеет вид mac=c{\displaystyle ma_{c}=c} или, что то же самое, mac=g0+b{\displaystyle ma_{c}=g_{0}+b}.
Для наблюдателя, вращающегося вместе с Землёй, тело неподвижно, хотя на него действуют в точности те же силы, что и в предыдущем случае: сила гравитации g0{\displaystyle g_{0}} и реакция опоры b{\displaystyle b}. Противоречия здесь не возникает, поскольку в неинерциальной системе отсчёта, каковой является вращающаяся Земля, применять второй закон Ньютона в обычной форме неправомерно. Вместе с тем в неинерциальной системе отсчёта возможно ввести в рассмотрение силы инерции. В данном случае единственной силой инерции является центробежная сила a{\displaystyle a} (синий вектор), равная произведению массы тела на его ускорение в инерциальной системе отсчёта, взятому со знаком минус, то есть −mac{\displaystyle -ma_{c}}. После введения этой силы уравнение движения тела, приведённое выше, преобразуется в уравнение равновесия тела, имеющее вид g0+a+b=0{\displaystyle g_{0}+a+b=0}.
Сумму сил гравитации g0{\displaystyle g_{0}} и центробежной силы инерции a{\displaystyle a} называют силой тяжести g{\displaystyle g} (жёлтый вектор)[36]. С учётом этого последнее уравнение можно записать в виде g+b=0{\displaystyle g+b=0} и утверждать, что действия силы тяжести и силы реакции опоры компенсируют друг друга. Отметим также, что относительное значение центробежной силы невелико: на экваторе, где такое значение максимально, её вклад в силу тяжести составляет ~0,3 %[37]. Соответственно, невелики и отклонения векторов g{\displaystyle g} и b{\displaystyle b} от радиального направления.
Общий подход к нахождению сил инерции[править | править код]
Сравнивая движение тела в инерциальной и неинерциальной СО, можно прийти к следующему выводу[29]:
Пусть F1→{\displaystyle {\vec {F_{1}}}} есть сумма всех сил, действующих на тело в неподвижной (первой) системе координат, которая вызывает его ускорение a1→{\displaystyle {\vec {a_{1}}}}. Эта сумма находится путём измерения ускорения тела в этой системе, если известна его масса.
Аналогично, F2→{\displaystyle {\vec {F_{2}}}} есть сумма сил, измеренная в неинерциальной системе координат (второй), вызывающая ускорение a2→{\displaystyle {\vec {a_{2}}}}, в общем случае отличающаяся от a1→{\displaystyle {\vec {a_{1}}}} вследствие ускоренного движения второй СО относительно первой.
Тогда сила инерции в неинерциальной системе координат будет определяться разницей:
Fi2→=F2→−F1→{\displaystyle {\vec {F_{i_{2}}}}={\vec {F_{2}}}-{\vec {F_{1}}}} (19)
или:
Fi2→=m(a2→−a1→){\displaystyle {\vec {F_{i_{2}}}}=m({\vec {a_{2}}}-{\vec {a_{1}}})} (20)[29]
В частности, если тело покоится в неинерциальной системе, то есть a2→=0{\displaystyle {\vec {a_{2}}}=0}, то
Fi2→=−F1→{\displaystyle {\vec {F_{i_{2}}}}=-{\vec {F_{1}}}} (21)[29].
Работа сил инерции[править | править код]
В классической физике силы инерции встречаются в двух различных ситуациях в зависимости от системы отсчёта, в которой производится наблюдение[29]. Это — сила, приложенная к связи при наблюдении в инерциальной СО, или сила, приложенная к рассматриваемому телу, при наблюдении в неинерциальной системе отсчёта. Обе эти силы могут совершать работу. Исключением является сила Кориолиса, которая работы не совершает, поскольку всегда направлена перпендикулярно вектору скорости. В то же время сила Кориолиса может изменить траекторию движения тела и, тем самым, способствовать совершению работы другими силами (такими, как сила трения). Примером этому может служить эффект Бэра.
Кроме того, в некоторых случаях бывает целесообразно разделить действующую силу Кориолиса на две составляющие, каждая из которых совершает работу. Суммарная работа, производимая этими составляющими, равна нулю, но такое представление может оказаться полезным при анализе процессов перераспределения энергии в рассматриваемой системе[38].
При теоретическом рассмотрении, когда искусственно сводят динамическую задачу движения к задаче статики, вводят третий вид сил, называемый силами Даламбера, которые работы не совершают ввиду неподвижности тел, на которые эти силы действуют.
Эквивалентность сил инерции и гравитации[править | править код]
Согласно принципу эквивалентности сил гравитации и инерции локально невозможно отличить, какая сила действует на данное тело — гравитационная сила или сила инерции. Различие между силами гравитации и силами инерции классической механики заключается в невозможности устранения сил гравитации в конечной области пространства-времени переходом к какой-либо системе отсчёта[источник?]. В этом смысле глобальные или даже конечные инерциальные системы отсчёта в общей теории относительности в общем случае отсутствуют.
В принципе д’Аламбера в рассмотрение вводятся подлинно отсутствующие в природе силы инерции, которые невозможно измерить никакой физической аппаратурой.
Эти силы вводятся ради использования искусственного математического приёма, основанного на применении принципа Д’Аламбера в формулировке Лагранжа, где задача на движение с помощью введения сил инерции формально сводится к проблеме равновесия[29].
- ↑ 1 2 Тарг С. М. Сила инерции // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. Пойнтинга—Робертсона эффект — Стримеры. — С. 494—495. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
- ↑ Сила инерции — статья из Большой советской энциклопедии.
- ↑ Ишлинский А. Ю. Классическая механика и силы инерции. — М.: «Наука», 1987. — С. 14—15. — 320 с.
- ↑ 1 2 Савельев И. В. Курс общей физики. Том 1. Механика. Молекулярная физика. — М., Наука, 1987. — Тираж 233000 экз. — с. 119—120
- ↑ 1 2 Ландсберг Г. С. Элементарный учебник физики. Том 1. Механика. Теплота. Молекулярная физика. — М., Наука, 1975. — Тираж 350000 экз. — с. 291—292
- ↑ Кошкин Н. И., Ширкевич М. Г. Справочник по элементарной физике.- М., Наука, 1988. — Тираж 300000 экз. — с. 33
- ↑ Ишлинский А. Ю. Классическая механика и силы инерции. — М.: «Наука», 1987. — С. 14—18. — 320 с.
- ↑ 1 2 Ишлинский А. Ю. К вопросу об абсолютных силах и силах инерции в классической механике // Теоретическая механика. Сборник научно-методических статей. — 2000. — № 23. — С. 3—8.
- ↑ Walter Greiner Klassische Mechanik II. Wissenschaftlicher Verlag Harri Deutsch GmbH. Frankfurt am Main. 2008 ISBN 978-3-8171-1828-1
- ↑ ^Richard Phillips Feynman, Leighton R. B. & Sands M. L. (2006). The Feynman Lectures on Physics. San Francisco: Pearson/Addison-Wesley. Vol. I, section 12-5. ISBN 0-8053-9049-9. https://books.google.com/books?id=zUt7AAAACAAJ& <=intitle:Feynman+intitle:Lectures+intitle: on+intitle:Physics&lr=&as_brr=0.
- ↑ ^Cornelius Lanczos (1986). The Variational Principles of Mechanics. New York: Courier Dover Publications. p. 100. ISBN 0-486-65067-7. https://books.google.com/books?id=ZWoYYr8wk2IC&pg=PA103&dq=%22Euler+force%22&lr=&as_brr=0&sig=UV46Q9NIrYWwn5EmYpPv-LPuZd0#PPA100,M1.
- ↑ ^ Max Born & Günther Leibfried (1962). Einstein’s Theory of Relativity. New York: Courier Dover Publications. pp. 76-78. ISBN 0-486-60769-0. https://books.google.com/books?id=Afeff9XNwgoC&pg=PA76&dq=%22inertial+forces%22&lr=&as_brr=0&sig=0kiN27BqUqHaZ9CkPdqLIjr-Nnw#PPA77,M1.
- ↑ Зоммерфельд А. Механика. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 82. — 368 с. — ISBN 5-93972-051-X.
- ↑ Борн М. Эйнштейновская теория относительности. — М.: «Мир», 1972. — С. 81. — 368 с.
- ↑ 1 2 Фейнман Р., Лейтон Р., Сэндс М. Выпуск 1. Современная наука о природе. Законы механики // Фейнмановские лекции по физике. — М.: «Мир», 1965. — С. 225.
- ↑ Седов Л. И. Об основных моделях механики. М.: МГУ, 1992. Стр 17.; Седов Л. И. Очерки, связанные с основами механики и физики. М.: Знание, 1983. Стр 19.
- ↑ Матвеев А. Н. Механика и теория относительности. М.: Высшая школа, 1979. Стр 393. (в 3-е изд. 2003. Стр.393)
- ↑ [1]. Вестник высшей школы. Советская наука, 1987. С. 248.
- ↑ А. Ишлинский при переиздании своей работы удалил эти термины («Классическая механика и силы инерции», 1987, с. 279): … термин «реальная сила» и «фиктивная сила» понимались по-разному. Считаю, что лучше не спорить на эту тему и от упомянутых слов вообще отказаться.
- ↑ «„Силы инерции“ — не силы». Журавлёв В. Ф. Основания механики. Методические аспекты. — М.: ИПМ АН СССР, 1985. — С. 21. — 46 с.
- ↑ Тарг С. М. Краткий курс теоретической механики. — М.: Высшая школа, 1995. — С. 182. — 416 с. — ISBN 5-06-003117-9.
- ↑ 1 2 Журавлёв В. Ф. Основания механики. Методические аспекты. — М.: ИПМ АН СССР, 1985. — С. 19. — 46 с.
- ↑ Тарг С. М. Сила // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. Пойнтинга—Робертсона эффект — Стримеры. — С. 494. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
- ↑ Зоммерфельд А. Механика. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 16. — 368 с. — ISBN 5-93972-051-X.
- ↑ Сивухин Д. В. Общий курс физики. — М.: Физматлит; Изд-во МФТИ, 2005. — Т. I. Механика. — С. 84. — 560 с. — ISBN 5-9221-0225-7.
- ↑ 1 2 Kleppner D., Kolenkow R. J. An Introduction to Mechanics. — McGraw-Hill, 1973. — P. 59—60. — 546 p. — ISBN 0-07-035048-5.
- ↑ Встречается утверждение, что применительно к силе Лоренца сказанное не верно и требует дополнительного уточнения (Матвеев А. Н. Механика и теория относительности. — 3-е изд. — М. Высшая школа 1976. — С. 132). Согласно другой точке зрения, «в электродинамике силы противодействия силам Лоренца приложены к электромагнитному полю (подстрочное примечание: Стоит отметить, что ещё недавно некоторые видные учёные считали, что сила Лоренца вообще не удовлетворяет закону действия и противодействия…) как к физическому объекту, претерпевающему соответствующее влияние» (Седов, Очерки, с. 17).
- ↑ Ишлинский А. Ю. Классическая механика и силы инерции. — М.: «Наука», 1987. — С. 8. — 320 с.
- ↑ 1 2 3 4 5 6 7 8 9 Хайкин, Семён Эммануилович. Силы инерции и невесомость. — 1. — М., «Наука». Главная редакция физико-математической литературы. 1967 г..— С. 129—130, 188—189. — 312 с.
- ↑ Ньютон: Физика в контексте Теологии (рус.). snob.ru. Дата обращения 24 января 2020.
- ↑ Сивухин Д. В. Общий курс физики. — М.: Физматлит, 2005. — Т. I. Механика. — С. 362. — 560 с. — ISBN 5-9221-0225-7.
- ↑ 1 2 3 Егоров Г. В. О силах инерции // Вестник БГУ. 2013. № 1.
- ↑ Ландавшиц, 1988, с. 165—166.
- ↑ Ландавшиц, 1988, с. 165.
- ↑ Китайгородский А. И. Введение в физику. М:Изд.-во «Наука», гл.ред.физико-математической литературы.1973
- ↑ Тарг С. М. Сила тяжести // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. Пойнтинга—Робертсона эффект — Стримеры. — С. 496. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
- ↑ Грушинский Н. П. Основы гравиметрии. — М.: «Наука», 1983. — С. 34. — 351 с.
- ↑ Krigel A. M. The theory of the index cycle in the general circulation of the atmosphere // Geophys. Astrophys. Fluid Dynamics.— 1980.— 16.— p. 1-18.
сила — Толковый словарь Ушакова
С’ИЛА, силы, ·жен.
1. Способность живых существ производить физические действие, энергия, порождаемая способностью управлять движениями мышц. «Какой-то муравей был силы непомерной…» Крылов. «Пригожеством, ростом и силой ты ровни в селе не имел.» Некрасов. «Силы коняге набраться неоткуда.» Салтыков-Щедрин. «Санька… захлопнула дверь изо всей силы.» А.Н.Толстой. Обладать огромной силой. Ударить с силой.
| только ед. Физическое воздействие, насилие. «Смекнул старик, что тут силой не возьмешь.» Салтыков-Щедрин. Действовать убеждением, а не силой. Применять силу.
| только мн. Жизнедеятельность, физическая энергия, бодрость. Выбиться из сил (см. выбиться). Собраться с силами (см. собраться). Лишиться сил. Приняться за работу со свежими силами. В расцвете сил.
2. Напряжение, энергия как причина, выводящая тело, материю из состояния покоя или изменяющая направление, скорость движения (научн.). Центробежная сила. Сила тяжести. Равнодействующая сила. Сила инерции. Сила притяжения земли. Сила натяжения нити.
| только ед. Интенсивность, напряженность чего-нибудь, степень напряжения; в механике — величина, равная произведению массы тела на его ускорение. Сила света. Сила звука. Сила взрыва. Сила ветра. Сила тока. В физике за единицу силы принята дина. Сила, с которой вылетает пробка.
| только мн. Материя, все материальное как источник деятельности, движения, изменений. Производительные силы (см. производительный). «В Советском Союзе идет возрождение многочисленных национальностей, идет подъем хозяйственных сил и национальных культур всех народов.» Молотов. «Наш опыт, опыт строителей коммунистического общества, уже полностью показал, что возможности роста сил ·СССР неограниченно велики.» Молотов. Использование водных сил страны.
3. Способность проявления какой-нибудь деятельности, характерная степенью, устремленностью, напряженностью проявления этой деятельности. Сила воли. Сила ума. Сила привычки. Сила фантазии. Сила таланта. Талант огромной силы. «Плохо верится в добра.» Некрасов. «Человеку прекрасней и шире можно вои развернуть.» Некрасов. Душевные силы.
| только мн. Средство, способ проявления деятельности. «Он всеми силами старался свергнуть с себя бремя этих упреков.» Гончаров. Верю всеми силами души — и посвящу этому делу всю свою жизнь Тургенев.
4. Вообще — источник чего-нибудь, какой-нибудь деятельности, явления. «Ты был всегда ареной деятельной силы, пытливой мысли и труда!» Некрасов. «Непреодолимая сила влекла меня к ней.» А.Тургенев. Советская *****
силы страны. Войти в силу — 1) то же, что взять силу. «Конопляники уже вошли в силу и пускают свой тяжелый, но приятный дух.» А.Тургенев. 2) перен. стать влиятельным, авторитетным. В силах — 1) ·без·доп. и с ·инф. с неослабевшими силами, в состоянии что-нибудь делать (по своему здоровью). Пока я в силах, поработаю. «Я не в силах сносить этой пытки.» Гончаров. 2) с ·инф. иметь возможность, власть (·чаще с отрицанием). «И то, что в жизни взято раз, не в силах рок отнять у нас.» Некрасов. «Только содержащий все общество класс пролетариев в силах произвести социальную революцию.» Ленин. В силе — 1) в таком состоянии, когда есть власть, влияние. «Колхозы и совхозы были слабы, а кулак был еще в силе.» Сталин (о 1924 ·г. ). 2) *****
в силу труд.» Крылов. В силу чего (или, реже, всилу; ·книж.) — вследствие, по причине. В силу создавшихся условий. Лошадиная сила — см. лошадиный. Нечистая сила — см. нечистый. От силы (·прост.) — самое большее, самое вероятное. Ему от силы 20 лет. Здесь от силы два кило. По мере сил — см. мера. По силам или по силе — соответственно возможностям, силам, способностям. По силе возможности (·прост.) — то же, что по мере возможности (см. мера). Под силу — соответствует силам, возможностям, в состоянии справиться с чем-нибудь. «Мне не под силу, брат, я чувствую, что глуп.» Грибоедов. «Современному французскому буржуа ни героизм, ни идеалы уже не под силу.» Салтыков-Щедрин. Рабочая сила — см. рабочий2. Сил нет — 1) отсутствуют силы делать что-нибудь, нет возможности справиться (см. сила в 1 ·знач. ). «Сил нам нет кружиться доле.» Пушкин. «От напора ветра нет сил дышать.» Чехов. 2) перен. употр. при выражении отчаяния, бессилия что-нибудь сделать, чем-нибудь воспрепятствовать чему-нибудь (·разг. ·фам. ). Сил нет, как надоел своей болтовней. Силою в (от, до; воен.) — количеством, численностью. Колонна силою в тысячу штыков. Колонна силою около полка. Силою вещей (·книж.) — по причине сложившихся обстоятельств, условий. Капитализм силою вещей обречен на гибель. Силы небесные (церк., ·устар.) — ·первонач. ангелы как небесное воинство, а позднее вообще — мистические силы неба, божества. С нами крестная сила — см. крестный. Через силу — сверх имеющихся возможностей, сил, способностей. Что есть силы или что было силы (или сил; ·разг.) — изо всех сил. «Комар, что было сил, сонливца укусил.» Крылов. «Что силы есть, хвать друга камнем в лоб.» Крылов.
Источник: Толковый словарь русского языка Ушакова на Gufo.me
Значения в других словарях
- СИЛА — В механике, мера механич. действия на данное материальное тело других тел. Это действие вызывает изменение скоростей точек тела или его деформацию и может иметь место как при непосредств. Физический энциклопедический словарь
- сила — -ы, ж. 1. Способность живых существ напряжением мышц производить физические движения, действия; физическая энергия человека, животного. Малый академический словарь
- сила — сущ., кол-во синонимов… Словарь синонимов русского языка
- сила — • адская ~ • бешеная ~ • богатырская ~ • большая ~ • великая ~ • гигантская ~ • грозная ~ • громадная ~ • дикая ~ • дьявольская ~ • железная ~ • значительная ~ • исключительная ~ • исполинская ~ • колоссальная ~ • крупная ~ • максимальная ~ • мощная ~ •… Словарь русской идиоматики
- сила — орф. сила, -ы Орфографический словарь Лопатина
- Сила — (Деян 15:40; сокращенное слово Силуан 2 Кор 1:19) — один из 70-ти апостолов, называемый в кн. Деяний начальствующим между братьями (15:22) и верным братом (1 Пет 5:16). Библейская энциклопедия архим. Никифора
- Сила — • Sila, Σίλα 1. лес в Бруттии, еще н. Sila. Он тянется от города Консенции (н. Cosenza) до Сицилийского пролива и преимущественно славится смолой, которая из него добывается. Cic. Brut. 22, 85. Strab. 6, 261; 2. город Италии у Адриатического моря. Polib. 34, 11. Словарь классических древностей
- сила — см.: етитский; недетский Толковый словарь русского арго
- сила — СИЛА I. В механике — мера механического воздействия на материальное тело со стороны др. тел или полей; вызывает изменение скоростей точек тела или его деформацию. — движущая сила. Словарь спортивных терминов
- сила — 1. Физическая (мышечная) энергия человека. Богатырская, большая, бычья, великая, воловья, геркулесовская (геркулесова), громадная, дюжая (разг.), железная (разг.), звериная (разг.), крепкая, лошадиная, медвежья, могучая, молодая, молодецкая (разг. Словарь эпитетов русского языка
- сила — Крепость, мощь, держава, власть, вес Поддерживайте дисциплину железной рукой прот. != бессилие, слабость ср. !! власть, значение, достоинство, причина см. >> авторитет, власть, достоинство, значение, причина, суть см. Словарь синонимов Абрамова
- сила — СИЛА -ы; ж. 1. обычно ед. Способность живых существ к физическим действиям, требующим значительного напряжения мышц. Мышечная с. С. рук, ног. С. в руках, ногах у кого-л. Недюжинной силы кто-л. Ударить изо всей силы. Толкнуть кого-л. Толковый словарь Кузнецова
- сила — Сила, силы, силы, сил, силе, силам, силу, силы, силой, силою, силами, силе, силах Грамматический словарь Зализняка
- Сила — Сила (греч. ф-ма арам. имени, соотв. евр. Шаул, в Синод. пер. — Саул («испрошенный»)). С., называемый в посланиях своим лат. именем Силуан (от silva — лес), — один из ближайших сотрудников Павла и, как и апостол, рим. гражданин (Деян 16:37). Библейская энциклопедия Брокгауза
- сила — (интенсивность) звука. Качество звука, зависящее от амплитуды (размаха) колебаний, т. е. от расстояния высшей точки подъема и низшей точки падения звуковой волны: чем сильнее размах, тем сильнее звук. Словарь лингвистических терминов Розенталя
- сила — Общеслав. Родственно лит. siela «убеждение». Ср. убедить. Этимологический словарь Шанского
- сила — : в силу ч е г о и с и л о й ч е г о (вследствие, по причине). Я вышел во двор и бессознательно, в силу стародавней привычки, направился к тому самому цеху, в котором провел не один год (Бахметьев). И скоро силою вещей мы очутились в Париже (Пушкин). Управление в русском языке
- сила — Си́л/а. Морфемно-орфографический словарь
- Сила — орф. Сила, муж. имя (Силич, Силична) Орфографический словарь Лопатина
- сила — • Богатырская (Никитин). • Геркулесовская (Андреев). • Гордая (Кольцов). • Дюжая (Дрожжин). • Крепкая (Коринфский). • Могучая (Фруг). • Молодецкая (Коринфский, Розенгейм). • Мятежная (Фруг). • Непомерная (Крылов, Сологуб). • Сила-моченька (Некрасов). Словарь литературных эпитетов
- сила — Индоевропейское – sei- (связь, соединение). Общеславянское – sila (сила). Слово «сила» известно с древнерусской поры (XI в.) со значениями «естественная способность, свойство», «телесная сила», «духовная сила», «могущество», «власть» и др. Этимологический словарь Семёнова
- сила — СИЛА ж. источник, начало, основная (неведомая) причина всякого действия, движенья, стремленья, понужденья, всякой вещественой перемены в пространстве, или: начало изменяемости мировых явлений, Хомяков. Тяготенье основная сила природы. Толковый словарь Даля
- сила — Превосходство, здорово Словарь воровского жаргона
- сила — I. (иноск.) — множество, пропасть Ср. Лука этакой силы денег (по 100 р. со штуки) дать и сообразить не мог; Лесков. Запечатленный Ангел. 8. II. (иноск.) — сущность дела, причина, основание Ср. «В силу чего-либо поступать». Ср. Фразеологический словарь Михельсона
- Сила — I Си́ла в механике, величина, являющаяся мерой механического действия на данное материальное тело других тел… Большая советская энциклопедия
- сила — сила I ж. 1. Способность живых существ напряжением мышц производить физические движения, действия; физическая энергия. || перен. Физическое воздействие, насилие. Толковый словарь Ефремовой
- сила — си́ла укр. си́ла, блр. сíла, др.-русск., ст.-слав. сила δύναμις, ἰσχύς (Остром., Мар., Зогр., Супр.), болг. си́ла, сербохорв. си̏ла, словен. síla, чеш. sîla, слвц. sila, польск. siɫa, в.-луж., н.-луж. sуɫа. Праслав. silа родственно лит. Этимологический словарь Макса Фасмера
- СИЛА — СИЛА — в механике — мера механического действия на данное материальное тело со стороны других тел… Большой энциклопедический словарь
- сила — СИЛА — СЛАБОСТЬ Физическая сила — физическая слабость. Сила характера — слабость характера. ○ Сила [Л. Толстого] — в критике нашего строя с точки зрения якобы признаваемых этим строем христианских начал. Словарь антонимов русского языка
- Сила — Ы, муж. Стар. редк. Отч.: Силич, Силична. Производные: Силка; Силаша. Происхождение: (Предположительно от лат. Sila — Сила (лес в южной Италии)) Именины: 17 янв., 8 апр., 12 авг. Словарь личных имен
- СИЛА — СИЛА (обозначение F), в широком смысле — причина ударов, толчков или поворотов, испытываемых телом. Сила, действующая на предмет, может 1) уравновешивать равную… Научно-технический словарь
- сила — СИЛА, ы, ж. 1. Величина, являющаяся мерой механического взаимодействия тел, вызывающего их ускорение или деформацию; характеристика интенсивности физических процессов (спец.). Единица силы. Центробежная с. С. тяжести. С. тока. С. света. С. инерции. Толковый словарь Ожегова
- Сила — С’ила (Деян.15:22 ,27,32,34,40; Деян.16:19 ,25,29; Деян.17:4 ,10,14,15; Деян.18:5) — верующий из Иерусалима, начальствующий между братиями и пророк, посланный с ·ап. Павлом в Антиохию. Позже он сопровождал ·ап. Павла в некоторых его путешествиях. Библейский словарь Вихлянцева
- сила — сущ., ж., употр. наиб. часто (нет) чего? силы, чему? силе, (вижу) что? силу, чем? силой, о чём? о силе; мн. что? силы, (нет) чего? сил, чему? силам, (вижу) что? силы, чем? силами, о чём? о силах… Толковый словарь Дмитриева
- сила — Взять силу (простореч.) — усилиться, окрепнуть. ► Огонь силу взял. Даль. Войти в силу 1) то же, что взять силу. ► Конопляники уже вошли в силу и пускают свой тяжелый, но приятный дух. Тургенев. 2) перен. стать влиятельным, авторитетным. Фразеологический словарь Волковой
- сила — Мощь, могущество. Краткий церковнославянский словарь

Консервативные силы — Википедия
Материал из Википедии — свободной энциклопедии
В физике консервати́вные си́лы (потенциальные силы) — это силы, работа которых не зависит от вида траектории, точки приложения этих сил и закона их движения, и определяется только начальным и конечным положением этой точки[1]. Равносильным определением является и следующее: консервативные силы — это такие силы, работа которых по любой замкнутой траектории равна 0.
В теоретической физике выделяют только четыре типа сил, каждая из которых является консервативной (см. Фундаментальные взаимодействия). В школьной программе по физике силы разделяют на консервативные и неконсервативные. Примерами консервативных сил являются: сила тяжести, сила упругости, сила кулоновского (электростатического) взаимодействия. Примером неконсервативной силы является сила трения.
Если в системе действуют только консервативные силы, то механическая энергия системы сохраняется.
Для консервативных сил выполняются следующие равенства:
- ∫C1F→⋅dl→=∫C2F→⋅dl→{\displaystyle \int \limits _{C_{1}}{\vec {F}}\cdot {\vec {dl}}=\int \limits _{C_{2}}{\vec {F}}\cdot {\vec {dl}}} — работа, производимая консервативной силой, определяется только начальным и конечным положением точки её приложения и не зависит от выбора траектории, по которой перемещается тело.
- ∮CF→dl→=0{\displaystyle \oint \limits _{C}{{\vec {F}}d{\vec {l}}}=0} — работа консервативных сил по произвольному замкнутому контуру равна 0;
- ∇×F→=0{\displaystyle \nabla \times {\vec {F}}=0} — ротор консервативных сил равен 0;
- F→=∇U{\displaystyle {\vec {F}}=\nabla U} — консервативная сила является градиентом некой скалярной функции U{\displaystyle U}, называемой силовой. Эта функция равна потенциальной энергии Ep,{\displaystyle E_{p},} взятой с обратным знаком. Соответственно, F→{\displaystyle {\vec {F}}} и Ep{\displaystyle E_{p}} связаны соотношением
- F→=−∇Ep.{\displaystyle {\vec {F}}=-\nabla E_{p}.}
Таким образом, консервативная сила всегда направлена в сторону уменьшения потенциальной энергии.
- ↑ Потенциальная сила // Физический энциклопедический словарь. Гл. ред. Прохоров А. М. — М.: «Советская энциклопедия», 1984. — С. 581. — 944 с.
Классическая теория тяготения Ньютона — Википедия
Класси́ческая тео́рия тяготе́ния Ньютона (Зако́н всемирного тяготе́ния Ньютона) — закон, описывающий гравитационное взаимодействие в рамках классической механики. Этот закон был открыт Ньютоном около 1666 года, опубликован в 1687 году в «Началах» Ньютона.
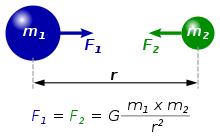
Закон гласит, что сила F{\displaystyle F} гравитационного притяжения между двумя материальными точками с массами m1{\displaystyle m_{1}} и m2{\displaystyle m_{2}}, разделёнными расстоянием r{\displaystyle r}, действует вдоль соединяющей их прямой, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния[1]. То есть:
| F=G⋅m1⋅m2r2{\displaystyle F=G\cdot {m_{1}\cdot m_{2} \over r^{2}}}. | (1) |
Здесь G{\displaystyle G} — гравитационная постоянная, равная[2]6,67408(31)·10−11 м³/(кг·с²).
В ньютоновской теории каждое массивное тело порождает силовое поле притяжения к этому телу, называемое гравитационным полем.
Гравитационное взаимодействие в теории Ньютона распространяется мгновенно, так как сила тяготения зависит только от взаимного расположения притягивающихся тел в данный момент времени. Также для ньютоновских гравитационных сил справедлив принцип суперпозиции: сила тяготения, действующая на частицу со стороны нескольких других частиц, равна векторной сумме сил притяжения со стороны каждой частицы.
Ещё одно важнейшее свойство классической гравитации — принцип эквивалентности[3]. Его следствием является тот факт, что ускорение, сообщаемое заданному телу тяготением, не зависит от массы этого тела, химического состава и других свойств. Это видно из того, что масса входит одинаково в выражение силы в законе тяготения и в выражении силы через ускорение во втором законе Ньютона. Таким образом, в этой теории ускорение точечного или маленького тела под действием гравитационной силы всегда в точности равно напряжённости гравитационного поля[4], определяемой как отношение g→=F→/m.{\displaystyle {\vec {g}}={\vec {F}}/m.}
Сферически симметричное тело создаёт за своими пределами такое же поле, как материальная точка той же массы, расположенная в центре тела. Внутри сферически симметричной оболочки (имеющей сферическую полость или выделенной условно, являясь реально частью какого-то тела) поле, создаваемое ею[5], имеет нулевую напряженность (и, соответственно, постоянный потенциал), то есть, сферически симметричная оболочка не притягивает находящиеся внутри неё тела, и вообще никак на них не действует посредством гравитации.
Сюда следует добавить и то, очевидное из сказанного выше и третьего закона Ньютона, утверждение, что на сферически симметричное тело гравитация сторонних источников также действует в точности как на точечное тело той же массы, расположенное в центре симметрии. А отсюда следует, что и два сферически симметричных тела конечных размеров притягиваются в точности так же, как точечные тела тех же масс, расположенные в их центрах. Это утверждение оказывается достаточно важным для небесной механики, ведь многие небесные тела имеют именно сферически симметричную форму (пусть и не точно), что, в дополнение к тому, что расстояния между небесными телами часто (обычно) во много раз превосходят их размеры, упрощает применение теории к ним, т.к. сила их взаимодействия (в соответствующем приближении, которое оказывается обычно очень хорошим), а соответственно и ускорение, вычисляется так же просто, как для материальных точек — т.е. просто по формуле (1).
Гравитационное поле в теории Ньютона является потенциальным, в связи с этим для его описания можно использовать гравитационный потенциал φ.{\displaystyle \varphi .} В случае, если поле создаётся расположенной в начале координат точечной массой M{\displaystyle M}, гравитационный потенциал определяется формулой:
| φ(r→)=−GMr{\displaystyle \varphi ({\vec {r}})=-G{\frac {M}{r}}}, | (1.1) |
(здесь потенциал на бесконечности, как это делается обычно, принят равным нулю).
В общем случае, когда плотность вещества ρ{\displaystyle \rho } распределена произвольно, φ{\displaystyle \varphi } удовлетворяет уравнению Пуассона:
| Δφ(r→)=−4πGρ(r→){\displaystyle \Delta \varphi ({\vec {r}})=-4\pi G\rho ({\vec {r}})}. | (1.2) |
Решение данного уравнения[6] записывается в виде:
| φ(r→)=−G∫V′ρ(r→′)dV′|r→−r→′|+C{\displaystyle \varphi ({\vec {r}})=-G\int _{V^{\prime }}{\frac {\rho ({\vec {r}}^{\prime })dV^{\prime }}{|{\vec {r}}-{\vec {r}}^{\prime }|}}+C}. | (1.3) |
Здесь r→{\displaystyle {\vec {r}}} — радиус-вектор точки, в которой определяется потенциал, r→′{\displaystyle {\vec {r}}^{\prime }} — радиус-вектор элемента объёма dV′{\displaystyle dV^{\prime }} c плотностью вещества ρ(r→′){\displaystyle \rho ({\vec {r}}^{\prime })}, а интегрирование охватывает все такие элементы; C{\displaystyle C} — произвольная постоянная; чаще всего ее принимают равной нулю, как это сделано в формуле выше для одного точечного источника.
Сила притяжения, действующая в гравитационном поле на материальную точку с массой m{\displaystyle m}, связана с потенциалом формулой:
| F→(r→)=−m∇φ(r→){\displaystyle {\vec {F}}({\vec {r}})=-m\nabla \varphi ({\vec {r}})}. | (1.4) |
Если поле создаётся точечной массой M{\displaystyle M}, расположенной в начале координат, то на точку массой m{\displaystyle m} действует сила
| F→(r→)=−GmMr3⋅r→{\displaystyle {\vec {F}}({\vec {r}})=-G{\frac {mM}{r^{3}}}\cdot {\vec {r}}}. | (1.5) |
Величина этой силы зависит только от расстояния r{\displaystyle r} между массами, но не от направления радиус-вектора r→{\displaystyle {\vec {r}}} (см. формулу в преамбуле).
Траектория материальной точки в гравитационном поле, создаваемом много большей по массе материальной точкой, подчиняется законам Кеплера. В частности, планеты и кометы в Солнечной системе движутся по эллипсам или гиперболам. Влияние других планет, искажающее эту картину, можно учесть с помощью теории возмущений.
С точки зрения физики, гравитационное поле сильно отличается от электростатического — например, массы всегда притягиваются, а заряды могут и отталкиваться, в гравитации нет аналога таким эффектам, как электростатическая индукция и т. д. Однако классические математические модели обеих теорий во многом сходны, а в ряде случаев даже тождественны. В связи с этим для ньютоновской гравитации применимы по сути все те теоретические конструкции и методы решения задач, которые применяются в электростатике. В этом, формальном (но математически вполне содержательном) смысле, можно сказать, что теория одна[7].
Среди теорем и методов, одинаково имеющих силу (и место для применения) в ньютоновской теории гравитации и электростатике, можно назвать теорему Гаусса, теорему Ирншоу, метод изображений, метод конформных отображений, полностью теорию потенциала, не говоря уже о принципе суперпозиции и других разного рода математических принципах и приёмах.
Ньютоновская гравитация гораздо более точно соответствует эксперименту, чем электростатика — она реже даёт существенную ошибку, и величина этой ошибки обычно гораздо меньше. Также можно заметить, что более общие теории для гравитации и электростатики (это соответственно ОТО и электродинамика) совершенно различны.
Точность закона всемирного тяготения Ньютона[править | править код]
Экспериментальная оценка степени точности закона тяготения Ньютона является одним из подтверждений общей теории относительности.[8] Опыты по измерению квадрупольного взаимодействия вращающегося тела и неподвижной антенны показали[9], что приращение δ{\displaystyle \delta } в выражении для зависимости ньютоновского потенциала r−(1+δ){\displaystyle r^{-(1+\delta )}} на расстояниях нескольких метров находится в пределах (2,1±6,2)∗10−3{\displaystyle (2,1\pm 6,2)*10^{-3}}. Другие опыты также подтвердили отсутствие модификаций в законе всемирного тяготения[10].
Закон всемирного тяготения Ньютона в 2007 г. был проверен и на расстояниях, меньших одного сантиметра (от 55 мкм до 9,53 мм). С учетом погрешностей эксперимента в исследованном диапазоне расстояний отклонений от закона Ньютона не обнаружено[11].
Прецизионные лазерные дальнометрические наблюдения за орбитой Луны[12] подтверждают закон всемирного тяготения на расстоянии от Земли до Луны с точностью 3⋅10−11{\displaystyle 3\cdot 10^{-11}}.
Связь с геометрией евклидова пространства[править | править код]
Факт равенства с очень высокой точностью (10−9{\displaystyle 10^{-9}}) показателя степени расстояния в знаменателе выражения для силы тяготения числу 2{\displaystyle 2} отражает евклидову природу трёхмерного физического пространства механики Ньютона. В трёхмерном евклидовом пространстве площадь поверхности сферы точно пропорциональна квадрату её радиуса[13].
- (См. также Ньютон, Исаак#Всемирное тяготение и астрономия).
 Закон всемирного тяготения Ньютона
Закон всемирного тяготения НьютонаСама идея всеобщей силы тяготения неоднократно высказывалась и до Ньютона. Ранее о ней размышляли Эпикур, Гассенди, Кеплер, Борелли, Декарт, Роберваль, Гюйгенс и другие[14]. Кеплер полагал, что тяготение обратно пропорционально расстоянию до Солнца и распространяется только в плоскости эклиптики; Декарт считал его результатом вихрей в эфире[15]. Были, впрочем, догадки с правильной зависимостью от расстояния; Ньютон в письме к Галлею упоминает как своих предшественников Буллиальда, Рена и Гука[16]. Но до Ньютона никто не сумел ясно и математически доказательно связать закон тяготения (силу, обратно пропорциональную квадрату расстояния) и законы движения планет (законы Кеплера).[17].
В своём основном труде «Математические начала натуральной философии» (1687) Исаак Ньютон вывел закон тяготения, основываясь на эмпирических законах Кеплера, известных к тому времени. Он показал, что:
- наблюдаемые движения планет свидетельствуют о наличии центральной силы;
- обратно, центральная сила притяжения приводит к эллиптическим (или гиперболическим) орбитам.
Кроме того, Ньютон достиг существенного продвижения в таких практически значимых темах, связанных с тяготением, как проблема фигуры Земли, теория приливов, предварение равноденствий.
Отметим, что теория тяготения Ньютона уже не была, строго говоря, гелиоцентрической. Уже в задаче двух тел планета вращается не вокруг Солнца, а вокруг общего центра тяжести, так как не только Солнце притягивает планету, но и планета притягивает Солнце. Наконец, выяснилась необходимость учесть влияние планет друг на друга.
Теория Ньютона имела ряд существенных отличий от гипотез предшественников. Ньютон не просто опубликовал предполагаемую формулу закона всемирного тяготения, но фактически предложил целостную математическую модель:
В совокупности эта триада достаточна для полного исследования самых сложных движений небесных тел и тем самым создаёт основы небесной механики. До Эйнштейна никаких принципиальных поправок к указанной модели не понадобилось, хотя математический аппарат оказалось необходимым значительно развить. Последующие исследователи достигли также существенного прогресса в небесной механике, и «астрономическая точность» расчётов вошла в поговорку.
В течение XVIII века закон всемирного тяготения был предметом активной дискуссии (против него выступали сторонники школы Декарта) и тщательных проверок. К концу века стало общепризнанным, что закон всемирного тяготения позволяет с огромной точностью объяснить и предсказать движения небесных тел. Генри Кавендиш в 1798 году осуществил прямую проверку справедливости закона тяготения в земных условиях, используя исключительно чувствительные крутильные весы[18]. Важным этапом стало введение Пуассоном в 1813 году понятия гравитационного потенциала и уравнения Пуассона для этого потенциала; эта модель позволяла исследовать гравитационное поле при произвольном распределении вещества[19]. После этого ньютоновский закон стал рассматриваться как фундаментальный закон природы.
Недостатки классической теории тяготения[править | править код]
В то же время ньютоновская теория содержала ряд трудностей. Главные из них следующие.
- Необъяснимое дальнодействие: сила притяжения передавалась непонятно как через совершенно пустое пространство, причём бесконечно быстро. По существу ньютоновская модель была чисто математической, без какого-либо физического содержания.
- Если Вселенная, как тогда предполагали, евклидова и бесконечна, и при этом средняя плотность вещества в ней ненулевая, то возникает неразрешимый гравитационный парадокс, который поставил под сомнение применимость ньютоновской теории в космологических масштабах.
- В конце XIX века обнаружилась ещё одна проблема: расхождение теоретического и наблюдаемого смещения перигелия Меркурия[20].
В течения XVIII—XIX веков делались неоднократные попытки модифицировать или обобщить классическую теорию тяготения — физики изменяли формулу ньютоновского закона, объясняли механизм тяготения участием мирового эфира. По мере осознания принципов теории относительности начались попытки построить релятивистское обобщение теории гравитации. По-видимому, первую чёткую формулировку проблемы опубликовал Анри Пуанкаре в 1905 году:
Возможно ли найти такой закон, который удовлетворил бы условиям, поставленным Лоренцем [имеются в виду преобразования Лоренца] и одновременно сводился к закону Ньютона во всех случаях, когда скорости небесных тел достаточно малы для того, чтобы можно было пренебречь их квадратами (а также произведениями ускорений на расстояния) по сравнению с квадратом скорости света?
Пуанкаре в статье «О динамике электрона» предложил два варианта релятивистского обобщения закона тяготения. Оба они исключали дальнодействие (скорость гравитации совпадала со скоростью света). Историк науки В. П. Визгин в своей монографии пишет[21]:
Релятивистская теория тяготения, развитая Пуанкаре, не привлекла внимания физиков, хотя в принципиальном отношении она была значительным шагом вперед в развитии гравитационной проблемы. Причины этого невнимания, с нашей точки зрения, таковы:
- теория не объясняла аномальное смещение перигелия Меркурия;
- большинство физиков в 1906—1908 годах не разделяло релятивистской программы;
- формально-алгебраический метод построения теории отодвинул на задний план физические аспекты теории;
- неоднозначность свидетельствовала о незаконченности теории;
- в период преобладания электромагнитно-полевой программы настоящее обобщение ньютоновской теории тяготения требовало использования явного полевого подхода — теория же Пуанкаре не давала уравнений гравитационного поля, из которых можно было получить найденные им лоренц-инвариантные элементарные законы взаимодействия.
Далее наброски релятивистской теории тяготения опубликовали в начале 1910-х годов Макс Абрахам, Гуннар Нордстрём и Альберт Эйнштейн. Все они до создания ОТО не соответствовали данным наблюдений.
Общая теория относительности[править | править код]
На протяжении более двухсот лет после Ньютона физики предлагали различные пути усовершенствования ньютоновской теории тяготения. Эти усилия увенчались успехом в 1915 году — созданием общей теории относительности Эйнштейна, в которой все указанные трудности были преодолены. Теория Ньютона, в полном согласии с принципом соответствия, оказалась приближением более общей теории, применимым при выполнении двух условий:
- Гравитационный потенциал в исследуемой системе не слишком велик: φc2≪1{\displaystyle {\frac {\varphi }{c^{2}}}\ll 1}. В Солнечной системе это условие для большинства движений небесных тел можно считать выполненным — даже на поверхности Солнца отношение |φ|/c2{\displaystyle |\varphi |/c^{2}} составляет всего 2,12⋅10−6{\displaystyle 2{,}12\cdot 10^{-6}}. Заметным релятивистским эффектом является только упомянутое выше смещение перигелия Меркурия[22].
- Скорости движения в этой системе незначительны по сравнению со скоростью света: vc≪1{\displaystyle {\frac {v}{c}}\ll 1}.
В слабых стационарных гравитационных полях уравнения движения переходят в ньютоновы (гравитационный потенциал). Для доказательства покажем, что скалярный гравитационный потенциал в слабых стационарных гравитационных полях удовлетворяет уравнению Пуассона
- ΔΦ=−4πGρ{\displaystyle \Delta \Phi =-4\pi G\rho }.
Известно, что в этом случае гравитационный потенциал имеет вид:
- Φ=−12c2(g44+1){\displaystyle \Phi =-{\frac {1}{2}}c^{2}(g_{44}+1)}.
Найдём компоненту тензора энергии-импульса T44{\displaystyle T_{44}} из уравнений гравитационного поля общей теории относительности:
- Rik=−ϰ(Tik−12gikT){\displaystyle R_{ik}=-\varkappa (T_{ik}-{\frac {1}{2}}g_{ik}T)},
где Rik{\displaystyle R_{ik}} — тензор кривизны. Для Tik{\displaystyle T_{ik}} мы можем ввести кинетический тензор энергии-импульса ρuiuk{\displaystyle \rho u_{i}u_{k}}. Пренебрегая величинами порядка u/c{\displaystyle u/c}, можно положить все компоненты Tik{\displaystyle T_{ik}}, кроме T44{\displaystyle T_{44}}, равными нулю. Компонента T44{\displaystyle T_{44}} равна T44=ρc2{\displaystyle T_{44}=\rho c^{2}} и, следовательно T=gikTik=g44T44=−ρc2{\displaystyle T=g^{ik}T_{ik}=g^{44}T_{44}=-\rho c^{2}}. Таким образом, уравнения гравитационного поля принимают вид R44=−12ϰρc2{\displaystyle R_{44}=-{\frac {1}{2}}\varkappa \rho c^{2}}. Вследствие формулы
- Rik=∂Γiαα∂xk−∂Γikα∂xα+ΓiαβΓkβα−ΓikαΓαββ{\displaystyle R_{ik}={\frac {\partial \Gamma _{i\alpha }^{\alpha }}{\partial x^{k}}}-{\frac {\partial \Gamma _{ik}^{\alpha }}{\partial x^{\alpha }}}+\Gamma _{i\alpha }^{\beta }\Gamma _{k\beta }^{\alpha }-\Gamma _{ik}^{\alpha }\Gamma _{\alpha \beta }^{\beta }}
значение компоненты тензора кривизны R44{\displaystyle R_{44}} можно взять равным R44=−∂Γ44α∂xα{\displaystyle R_{44}=-{\frac {\partial \Gamma _{44}^{\alpha }}{\partial x^{\alpha }}}} и так как Γ44α≈−12∂g44∂xα{\displaystyle \Gamma _{44}^{\alpha }\approx -{\frac {1}{2}}{\frac {\partial g_{44}}{\partial x^{\alpha }}}}, R44=12∑α∂2g44∂xα2=12Δg44=−ΔΦc2{\displaystyle R_{44}={\frac {1}{2}}\sum _{\alpha }{\frac {\partial ^{2}g_{44}}{\partial x_{\alpha }^{2}}}={\frac {1}{2}}\Delta g_{44}=-{\frac {\Delta \Phi }{c^{2}}}}. Таким образом, приходим к уравнению Пуассона:
- ΔΦ=12ϰc4ρ{\displaystyle \Delta \Phi ={\frac {1}{2}}\varkappa c^{4}\rho }, где ϰ=−8πGc4{\displaystyle \varkappa =-{\frac {8\pi G}{c^{4}}}}[23]
Квантовая гравитация[править | править код]
Применение принципа корпускулярно-волнового дуализма к гравитационному полю показывает, что гравитационные волны можно рассматривать как поток квантов поля — гравитонов. В большинстве процессов во Вселенной квантовые эффекты гравитации очень малы. Они становятся существенными лишь вблизи сингулярностей поля тяготения, где радиус кривизны пространства-времени очень мал. Когда он становится близким к планковской длине, квантовые эффекты становятся доминирующими. Эффекты квантовой гравитации приводят к рождению частиц в гравитационном поле чёрных дыр и их постепенному испарению[3]. Построение непротиворечивой квантовой теории гравитации — одна из важнейших нерешённых задач современной физики.
С точки зрения квантовой гравитации, гравитационное взаимодействие осуществляется путём обмена виртуальными гравитонами между взаимодействующими телами. Согласно принципу неопределенности, энергия виртуального гравитона обратно пропорциональна времени его существования от момента излучения одним телом до момента поглощения другим телом. Время существования пропорционально расстоянию между телами. Таким образом, на малых расстояниях взаимодействующие тела могут обмениваться виртуальными гравитонами с короткими и длинными длинами волн, а на больших расстояниях только длинноволновыми гравитонами. Из этих соображений можно получить закон обратной пропорциональности ньютоновского потенциала от расстояния. Аналогия между законом Ньютона и законом Кулона объясняется тем, что масса гравитона, как и масса фотона, равна нулю[24][25]. Разница между законом ньютоновского тяготения и законом Кулона (существует два вида электрических зарядов и один вид «гравитационных зарядов» с притяжением между ними) объясняется тем, что спин фотона равен 1{\displaystyle 1}, а спин гравитона равен 2{\displaystyle 2}[26].
- ↑ Всемирного тяготения закон // Физическая энциклопедия (в 5 томах) / Под редакцией акад. А. М. Прохорова. — М.: Советская Энциклопедия, 1988. — Т. 1. — С. 348. — ISBN 5-85270-034-7.
- ↑ National Institute of Standards and Technology | NIST
- ↑ 1 2 Новиков И. Д. Тяготение //Физический энциклопедический словарь. — под ред. А. М. Прохорова — М., Большая Российская энциклопедия, 2003. — ISBN 5-85270-306-0. — Тираж 10000 экз. — с. 772—775
- ↑ Удобство использования физической величины напряженности связано с тем, что она не зависит от конкретного тела, помещаемого в данную точку, (будет одинаковой, если мы поместим в эту точку разные тела разной массы) и, таким образом, является характеристикой только самого поля, не зависящего непосредственно от тела, на которое оно действует (косвенная зависимость может быть за счёт действия самого этого тела на тела-источники поля, и только при изменении в результате этого воздействия их положения).
- ↑ То есть, речь не идет, конечно, об экранировке гравитационных полей, создаваемых другими источниками, которые могут находиться как внутри оболочки, так и вне её, а только лишь о том поле, которое создаётся самой оболочкой, именно его напряжённость равна нулю (а поля остальных источников тогда по принципу суперпозиции как раз останутся внутри сферической оболочки неизменными, как будто оболочки нет).
- ↑ Это решение естественно получается используя формулу решения с одним точечным источником, приведенную выше, и принцип суперпозиции — то есть просто сложением полей от (бесконечного) множества точечных источников, массой ρdV{\displaystyle \rho dV} каждый, расположенных в соответствующих точках пространства.
- ↑ Это утверждение не столько дело вкуса, сколько указание на то, что можно достаточно свободно пользоваться методами и результатами одной теории применительно к другой, невзирая на то, на электростатическом или гравитационном языке всё описано, соблюдая, конечно, минимально необходимую осторожность, когда дело касается их немногочисленных отличий и особенностей.
- ↑ Д. Д. Иваненко, Г. А. Сарданашвили Гравитация, М.: Едиториал УРСС, 2004, ISBN 5-354-00538-8
- ↑ 10th International conference on General Relativity and Gravitation: Contribut. pap. — Padova, 1983. — Vol. 2, 566 p.
- ↑ Тезисы докладов Всесоюзной конференции «Современные теоретические и экспериментальные проблемы теории относительности и гравитации». — М.: МГПИ, 1984. — 308 с.
- ↑ Ю. Н. Ерошенко Новости физики в сети Internet (по материалам электронных препринтов), УФН, 2007, т. 177, № 2, с. 230
- ↑ Турышев С. Г. «Экспериментальные проверки общей теории относительности: недавние успехи и будущие направления исследований», УФН, 179, с. 3-34, (2009)
- ↑ Бутиков Е.И., Кондратьев А.С. Физика. Книга 1. Механика. — М.: Наука, 1994. — 138 с.
- ↑ Клайн М. Математика. Утрата определённости. — М.: Мир, 1984. — С. 66. Архивная копия от 12 февраля 2007 на Wayback Machine
- ↑ Спасский Б. И. История физики. — Т. 1. — С. 140—141.
- ↑ Ход их рассуждений легко восстановить, см. Тюлина И. А., указ. статья, стр. 185. Как показал Гюйгенс, при круговом движении центростремительная сила F∼{\displaystyle F\sim } (пропорциональна) v2R{\displaystyle v^{2} \over R}, где v{\displaystyle v} — скорость тела, R{\displaystyle R} — радиус орбиты. Но v∼RT{\displaystyle v\sim {\frac {R}{T}}}, где T{\displaystyle T} — период обращения, то есть v
Обсуждение:Сила/Величина силы. Единичная сила — Википедия
Величина силы. Единичная сила (совсем другой вариант текста)[править код]
Принятого общего определения силы в стиле «F = …», где вместо многоточия стояла бы некая математическая формула, не существует.можно убрать —Mikisavex (обс.) 03:13, 5 августа 2017 (UTC) Количественно сила определяется как величина, равная по модулю и противоположная по направлению к той известной силе, которую она способна уравновесить: F→{\displaystyle {\vec {F}}} = -F→{\displaystyle {\vec {F}}}ref. Под уравновешиванием понимается обеспечение ситуации, когда совместное наложение двух воздействий — изучаемого и известного — не приводит к ускорению тела[1].
Единичной (1 ньютон) объявляется сила Funity, сообщающая свободному телу массой 1 кг (например, эталону килограмма) ускорение 1 м/с2.
Располагая каким-либо способом создания единичной силы Funity, можно «воспроизвести» её в любом числе экземпляров. Ориентируя n таких экземпляров сонаправленно и под некоторым углом α к другим n, также сонаправленным, экземплярам, принципиально можно получить известную суммарную силу F→{\displaystyle {\vec {F}}}ref, действующую вдоль биссектрисы угла[1]. Для модуля Fref = 2nFunity•cos(α/2) доступны любые значения. Ради количественной характеризации (измерения) изучаемой силы F, варьированием α и n подбирается уравновешивающая её Fref при совместном приложении к материальной точке.
Данное выше определение силы и соглашение насчёт Funity не базируются на какой-либо математической связи «сила—ускорение»[2], и, соответственно, сила введена независимо от выражения второго закона Ньютона, хотя другие точки зрения на методы дефиниции силы тоже имеют право на существование[2]. —Mikisavex (обс.) 17:46, 4 августа 2017 (UTC)
Величина силы. Единичная сила (новый вариант текста)[править код]
Количественно сила определяется как отношение величин деформации объекта под изучаемым воздействием и под воздействием, которому отвечает единичная сила[3]: F = Δx/Δxunity•Funity. Единичной (1 Н) объявляется сила Funity, сообщающая телу массой 1 кг (эталону килограмма или его копии) ускорение 1 м/с2.
Деформироваться может упругое тело, подвергнутое воздействиям, или, что нагляднее, тестовая пружина с закреплённым на её торце телом. Опыт показал, что изменение во сколько-то раз воздействия на тело влечёт изменение во столько же раз смещения торца пружины Δx. (Подобные наблюдения легли в основу закона Гука.) Это важно для естественности терминологии: сила F, условно говоря, пропорциональна воздействию, то есть реально выступает его мерой. Опытным же путём подтверждена независимость отношения Δxi/Δxj от выбора пружины для любых воздействий i, j, в том числе разнотипных, гарантирующая непротиворечивость определения. Далее, экспериментами с не закреплёнными телами установлено, что сила придаёт им ускорение, причём равные силы вызывают одинаковые ускорения одного и того же тела.
Как видно из формулы для F, сила равна деформации с точностью до калибровочного множителя, «жёсткости», используемой пружины: F = k•Δx, где k = Funity/Δxunity. Воспроизведя единичную силу Funity, можно измерить Δxunity и найти k для любой пружины, а затем использовать её для измерений «в числе».
Данное выше определение силы и соглашение насчёт Funity не базируются на какой-либо математической связи «сила—ускорение»[2], и, соответственно, сила введена независимо от выражения второго закона Ньютона, хотя другие точки зрения на методы дефиниции силы тоже имеют право на существование[2]. —Mikisavex (обс.) 12:30, 3 августа 2017 (UTC)
=== Величина силы. Единичная сила === Сила определяется как величина, пропорциональная продольной деформации объекта (F ~ Δx), вызываемой воздействием на него. Деформироваться может само тело, подвергнутое воздействию, или, что нагляднее, тестовая пружина, на торце которой тело закреплено.
Очевидное кратное увеличение внешнего воздействия (пример: подвешивание двух-трёх одинаковых кирпичей вместо одного) влечёт такое же изменение (удвоение, утроение) смещения торца пружины и, по определению, такое же кратное увеличение силы. Подобные наблюдения лежат в основе закона Гука. Отношение Δxi/Δxj для любых двух сил Fi, Fj не зависит от выбора тестовой пружины, так что осуществимо «сравнительное» измерение сил: F = Fref/Δxref•Δx = k•Δx, где F — исследуемая сила, Δx — создаваемая ею деформация, Δxref — то же для другой силы Fref, взятой для сравнения, k — калибровочный множитель («жёсткость» данной пружины).
На опыте проверяется, что равные силы вызывают одинаковые ускорения любого не закреплённого тела. Единичная сила вводится специальным соглашением: один ньютон — это сила, сообщающая телу массой 1 кг (эталон килограмма задаётся конкретным объектом) ускорение в 1 м/с2. Наличие соглашения логически позволяет воспроизвести силу 1 Н, вычислять жёсткости пружин, а затем измерять силы с их помощью уже «в числе». При этом не используется какой-либо математической связи «сила—ускорение»[2] и, соответственно, сила определена независимо от выражения второго закона Ньютона.вариант утратил актуальность —Mikisavex (обс.) 03:13, 5 августа 2017 (UTC)
- ↑ 1 2 И.Бутиков, А.С.Кондратьев. § 16. Сила — мера взаимодействия // Физика для углубленного изучения 1. Механика. — С. 88—90.
- ↑ 1 2 3 4 5 Матвеев А. Н. Механика и теория относительности. — М.: ОНИКС, 2003. — 432 с. — ISBN 5-329-00742-9 [гл. 5, §§ 19—20].
- ↑ Яворский Б. М., Детлаф А. А. Справочник по физике. — М.: Наука, 1965. — 848 с. [отд. 1, гл. 2]. — в справочнике приведено равенство F1/F2 = Δx1/Δx2 для упругих деформаций; если одну из сил объявить единичной, приходим к сформулированному определению
Живая сила (физика) — Википедия
Материал из Википедии — свободной энциклопедии
У этого термина существуют и другие значения, см. Живая сила.Жива́я си́ла (лат. Vis viva, нем. lebendige Kraft ) — историческое название кинетической энергии. Впервые название введено Лейбницем[1].
Первоначально наименование «живая сила» было дано Лейбницем для произведения массы тела на квадрат его скорости. Впоследствии Гюстав Кориолис внёс в определение термина поправку, определив его, как произведение половины массы тела на квадрат его скорости[2][3], хотя иногда определение живой силы с множителем «½» встречалось и ранее (например, в статьях Д. Бернулли). В результате термин приобрёл то же содержание, что и современный термин «кинетическая энергия».
Фрагмент статьи Д.Бернулли, опубликованной в 1741 году[4], в котором используется определение живой силы с множителем «½».В аналитической механике восемнадцатого века живая сила, принимаемая равной mv2{\displaystyle mv^{2}}, рассматривалась главным образом только как полезный математический артефакт. Ситуация глубоко изменилась под влиянием индустриализации, связанной с широким применением паровых машин. Тогда возник большой практический интерес к механической работе, производимой двигателями. Исходя из той связи, что существует между механической работой и величиной 12mv2{\displaystyle {\frac {1}{2}}mv^{2}}, Кориолис предложил называть живой силой именно эту величину[5]. Комментируя такой подход, Кориолис писал[6]: «Если ранее наименование живая сила давалось произведению массы на квадрат скорости, то это было потому, что не уделялось внимания работе»[7].



