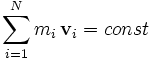Механическая работа и мощность
— 9 —
Если на тело действует сила, то эта сила совершает работу по перемещению этого тела. Прежде чем дать определение работе при криволинейном движении материальной точки, рассмотрим частные случаи:
Сила постоянная
 ,
движение прямолинейное.
,
движение прямолинейное.
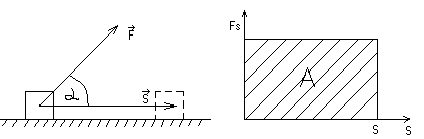
В этом случае механическая работа A равна:
A = F s cos =
=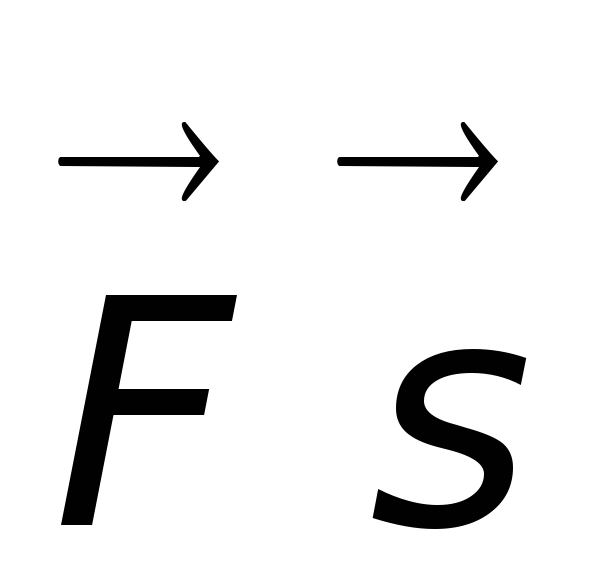 ,
,
или
 × s = FS × s ,
× s = FS × s , где FS – проекция силы 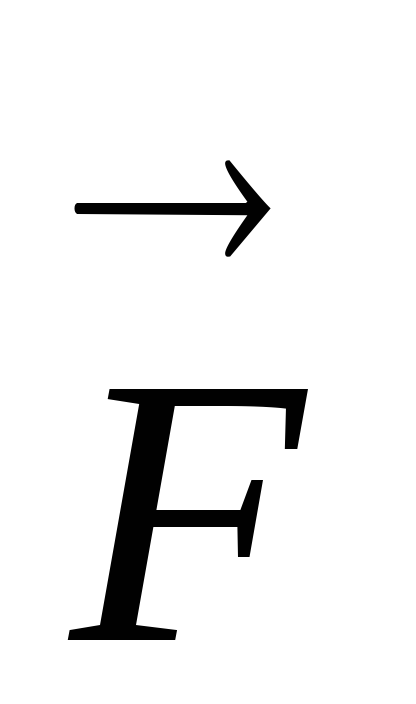 на перемещение. В данном случае Fs=const,
и геометрический смысл работы A – это площадь прямоугольника,
построенного в координатах FS, , s .
на перемещение. В данном случае Fs=const,
и геометрический смысл работы A – это площадь прямоугольника,
построенного в координатах FS, , s .
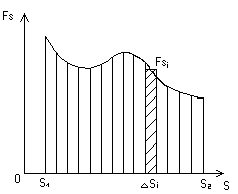
Движение прямолинейное, сила переменная, т.е. F
 const.
const.
Построим график
проекции силы на направление перемещения FS как функции перемещения s.
Полное перемещение представим как сумму
n
малых перемещений  .
Для малого i -ого
перемещения
.
Для малого i -ого
перемещения  работа равна
работа равна 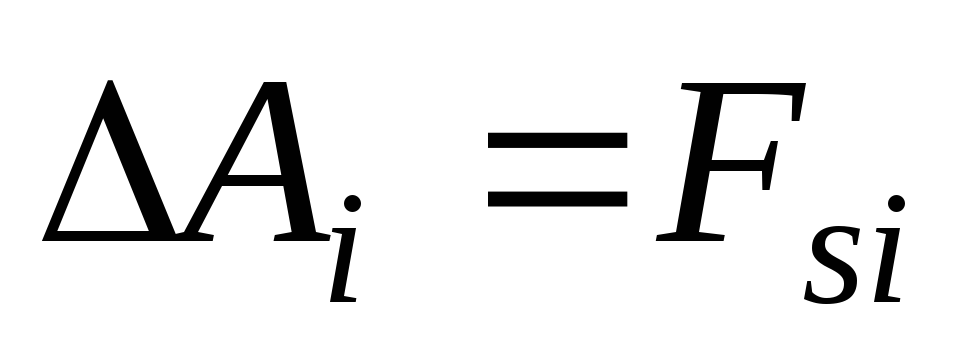

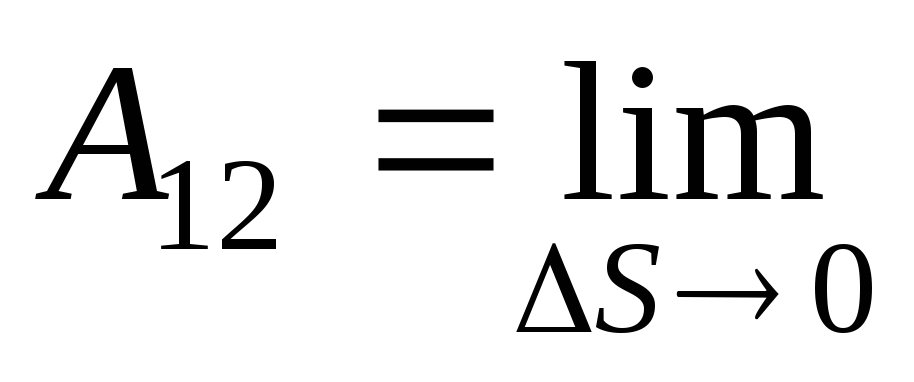
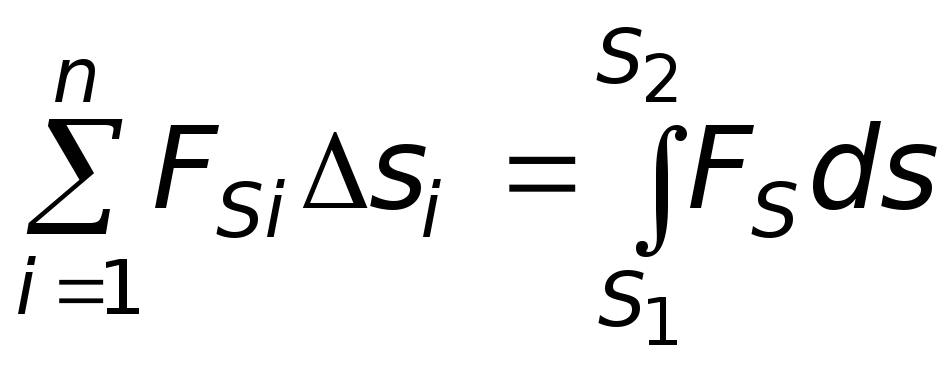 .
.
Величина, стоящая
под интегралом будет представлять
элементарную работу по бесконечно
малому перемещению 
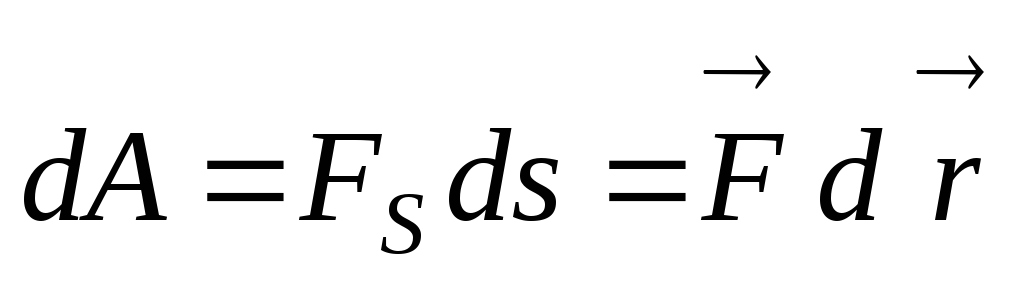 – элементарная
работа.
– элементарная
работа.
Движение криволинейное, сила
 переменная.
переменная.
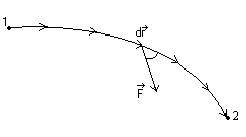
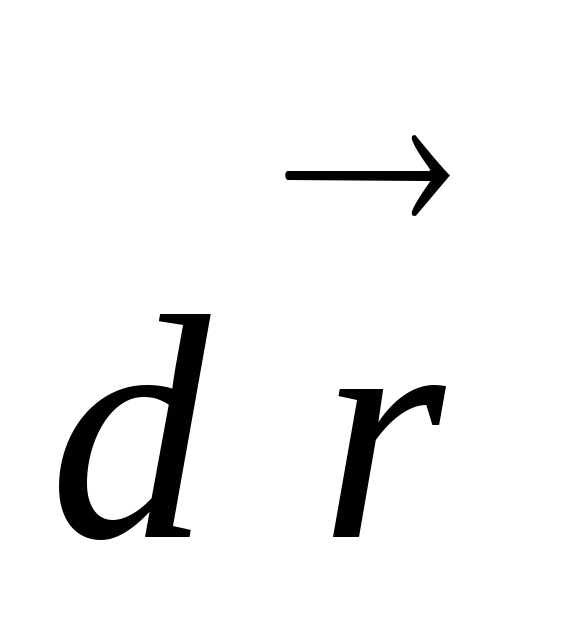 и работу силы
и работу силы 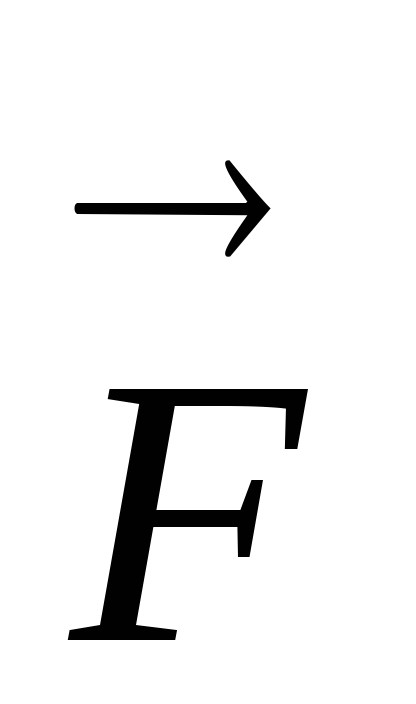
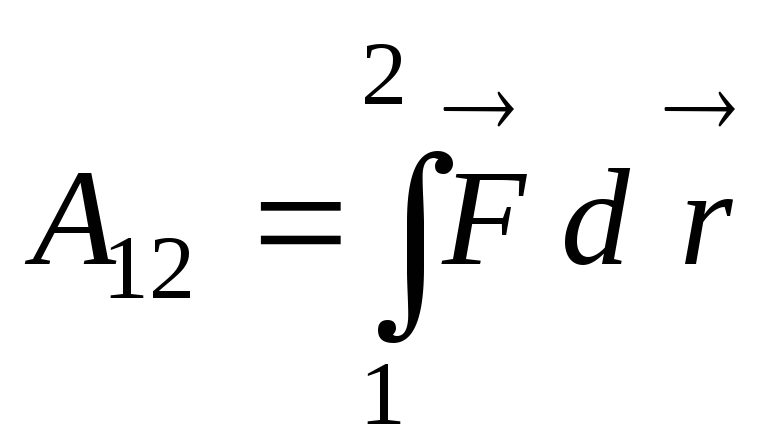 –работа при
криволинейном движении.
–работа при
криволинейном движении.
Пример 1: Работа
силы тяжести 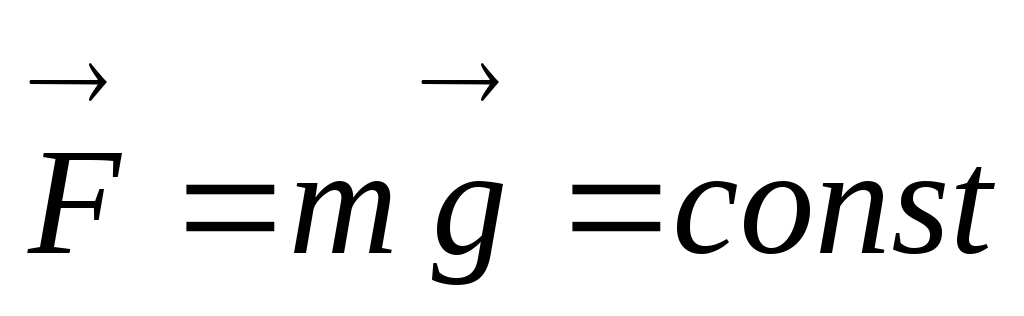 при криволинейном движении материальной
точки.
при криволинейном движении материальной
точки.
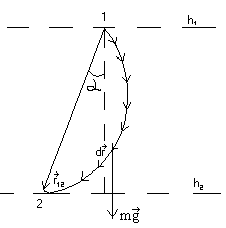
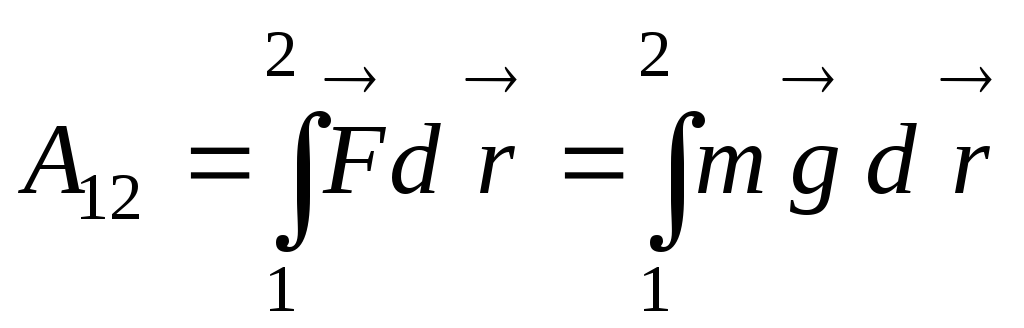 .
. Далее 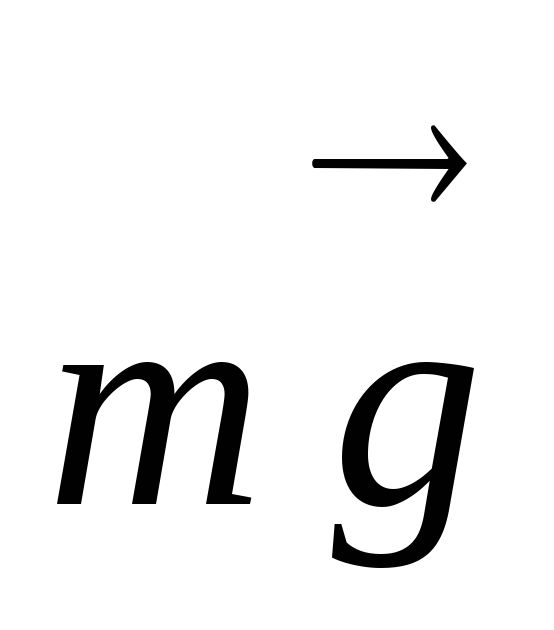 как постоянную величину можно вынести
за знак интеграла, а интеграл
как постоянную величину можно вынести
за знак интеграла, а интеграл 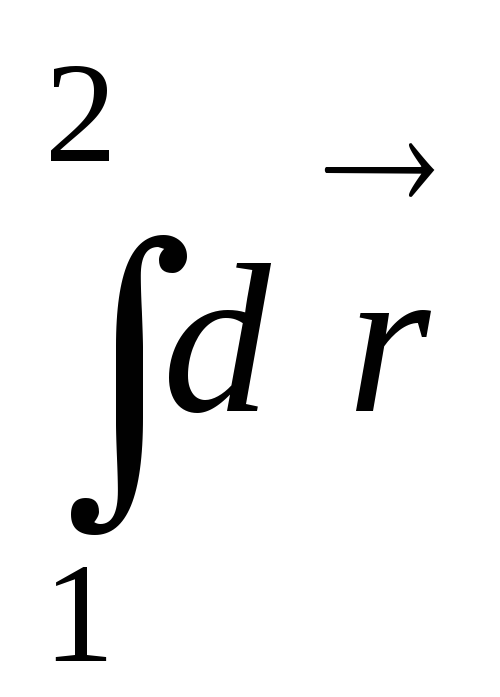 согласно
рисунку будет представлять полное
перемещение
согласно
рисунку будет представлять полное
перемещение 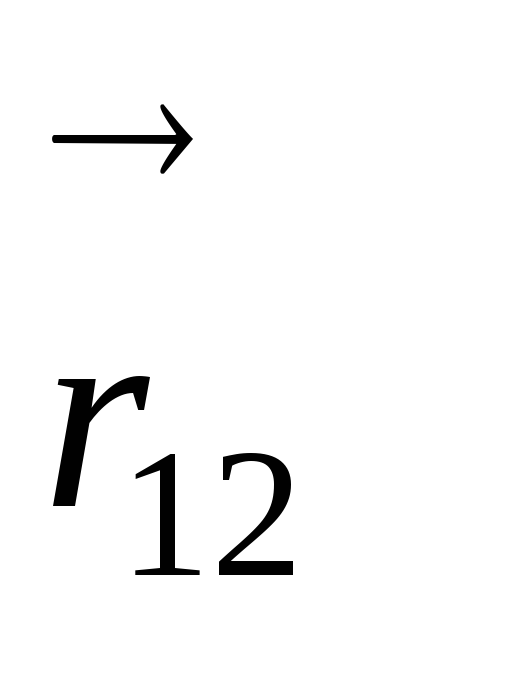 .
. 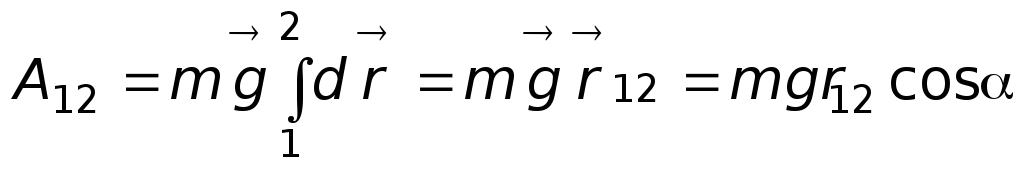 .
.
Если обозначить
высоту точки 1 от поверхности Земли через 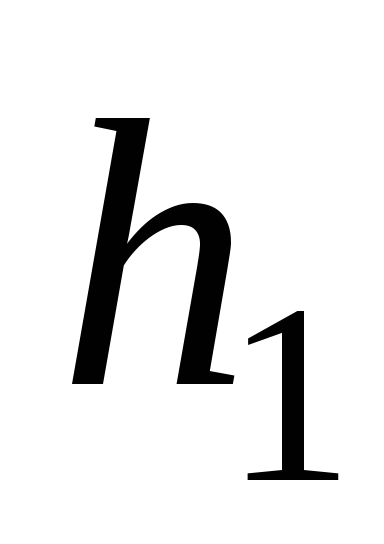 ,
а высоту точки 2 через
,
а высоту точки 2 через 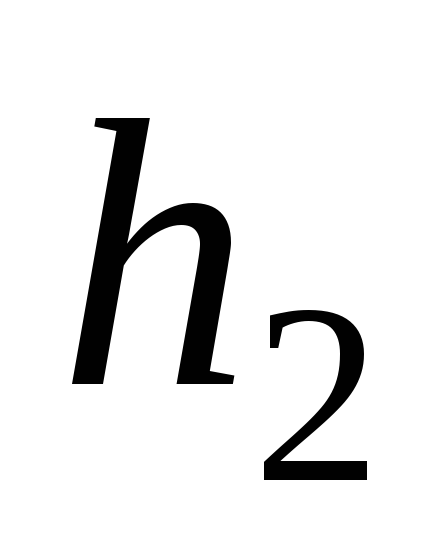
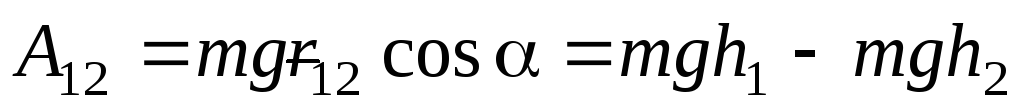 .
.
Мы видим, что в
данном случае работа определяется
положением материальной точки в начальный
и конечный момент времени и не зависит
от формы траектории или пути. Работа
силы тяжести по замкнутому пути равна
нулю: 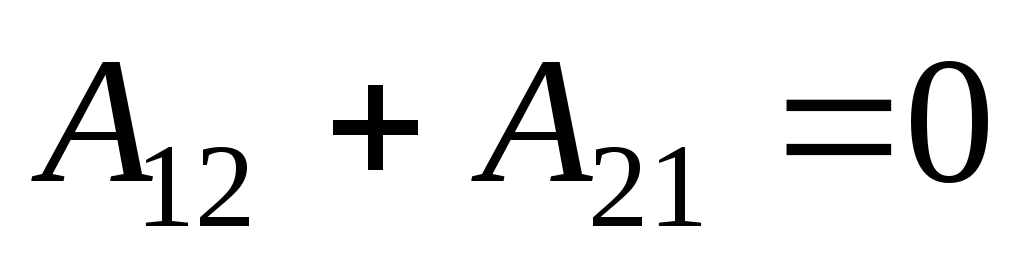 .
.
Силы, работа которых на замкнутом пути равна нулю, называется консервативными.
Пример 2: Работа силы трения.
Это пример неконсервативной силы. Чтобы показать это достаточно рассмотреть элементарную работу силы трения:
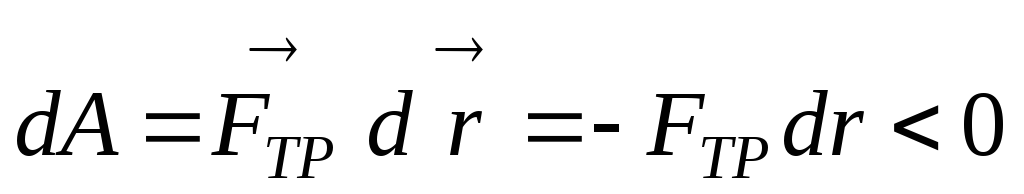 ,
,
т.е. работа силы
трения всегда отрицательная величина
и на замкнутом пути не может быть равной
нулю. Работа, совершаемая в единицу
времени, называется мощностью.
Если за время 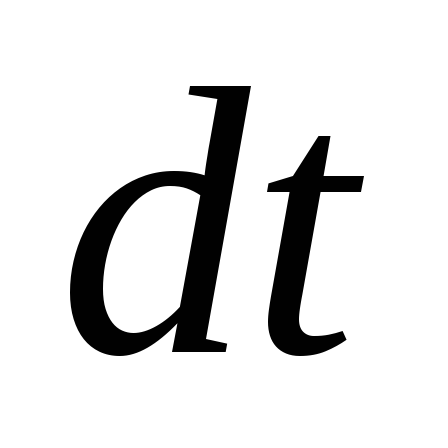 совершается работа
совершается работа  ,
то мощность равна
,
то мощность равна
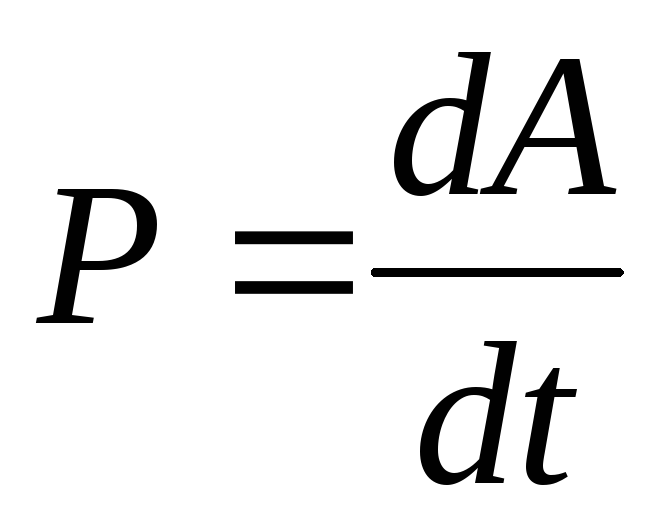
Взяв  в виде
в виде
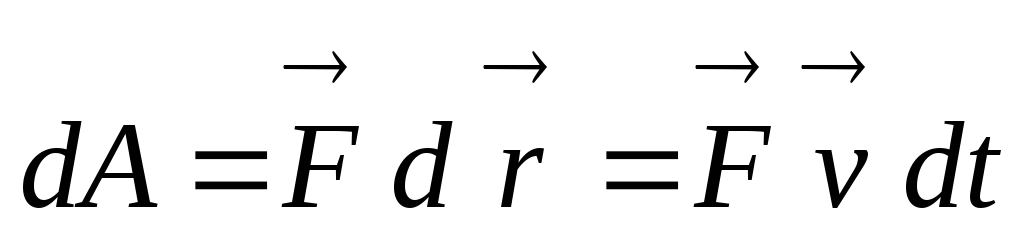 ,
,
получим для мощности выражение:
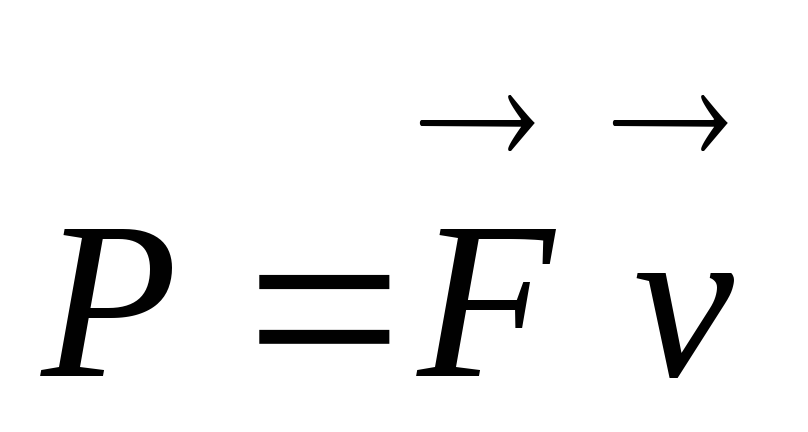 .
.
В СИ единицей
работы является джоуль:  =
1 Дж = 1 Н
=
1 Дж = 1 Н 1
м, а единицей мощности является ватт: 1
Вт = 1 Дж/с.
1
м, а единицей мощности является ватт: 1
Вт = 1 Дж/с.
Механическая энергия.
Энергия является общей количественной мерой движения взаимодействия всех видов материи. Энергия не исчезает и не возникает из нечего: она лишь может переходить из одной формы в другую. Понятие энергии связывает воедино все явления в природе. В соответствии с различными формами движения материи рассматривают разные виды энергии – механическую, внутреннюю, электромагнитную, ядерную и др.
Понятия энергии и работы тесно связаны друг с другом. Известно, что работа совершается за счет запаса энергии и, наоборот, совершая работу, можно увеличить запас энергии в каком-либо устройстве. Другими словами работа – это количественная мера изменения энергии:
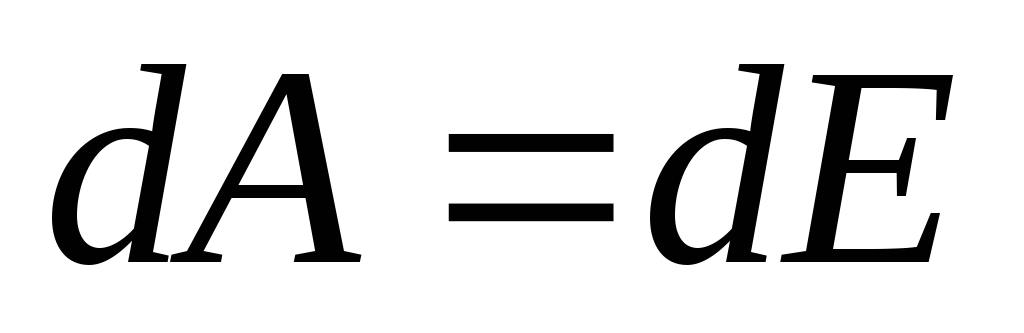
Энергия также как и работа в СИ измеряется в джоулях: [E]=1 Дж.
Механическая энергия бывает двух видов – кинетическая и потенциальная.
Кинетическая
энергия (или энергия
движения) определяется массами и
скоростями рассматриваемых тел.
Рассмотрим материальную точку, движущуюся
под действием силы 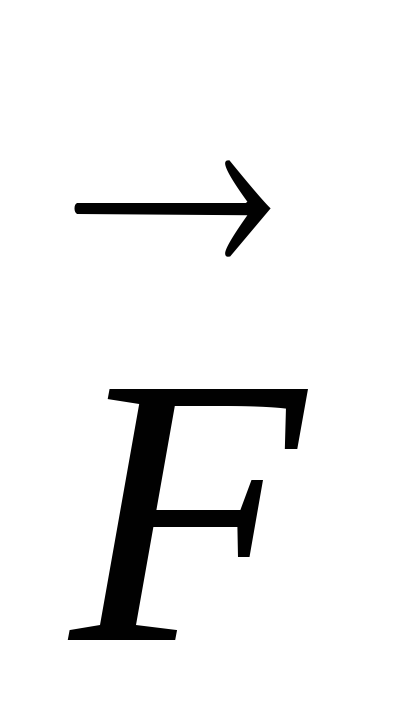 .
Работа этой силы увеличивает кинетическую
энергию материальной точки
.
Работа этой силы увеличивает кинетическую
энергию материальной точки 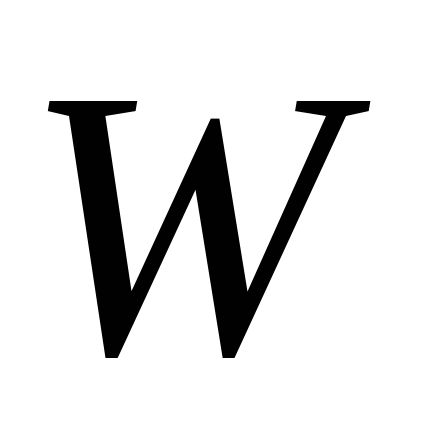 .
Вычислим в этом случае малое приращение
(дифференциал) кинетической энергии:
.
Вычислим в этом случае малое приращение
(дифференциал) кинетической энергии:
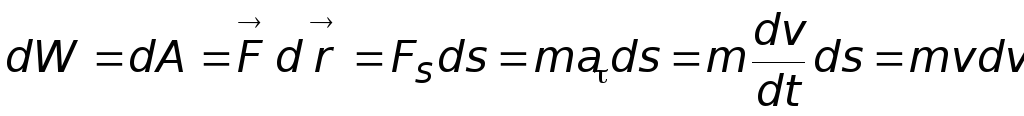 .
.
При вычислении 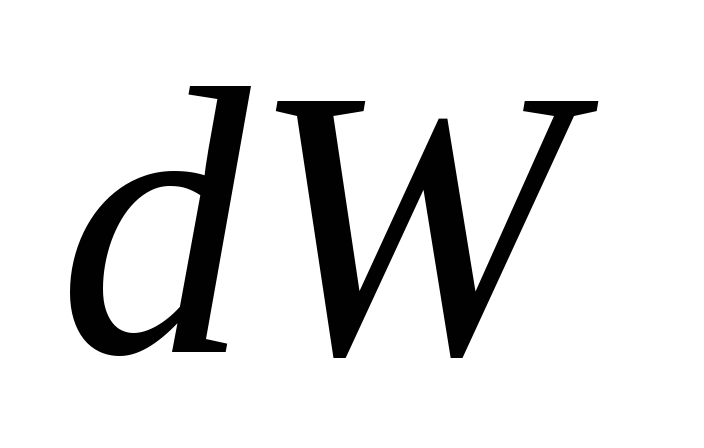 использован
второй закон Ньютона
использован
второй закон Ньютона 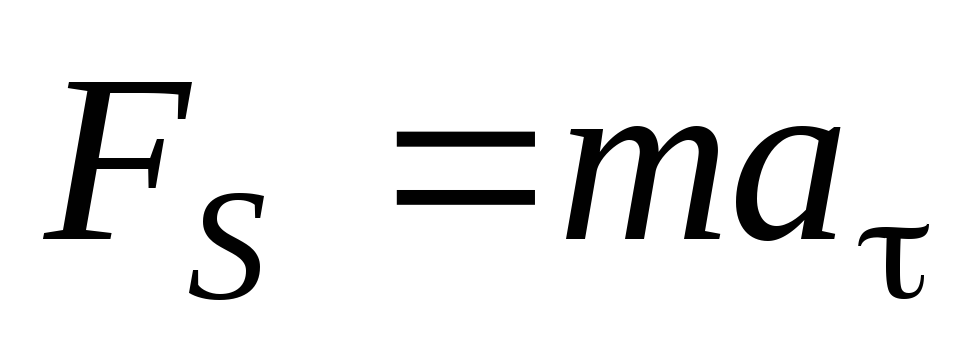 ,
а также
,
а также 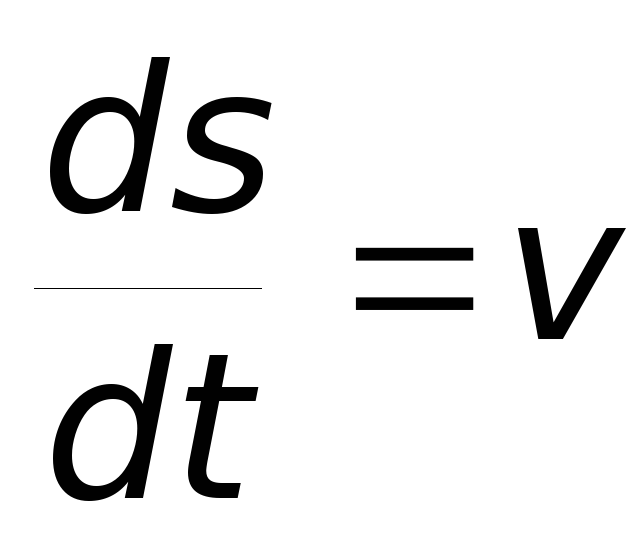 — модуль скорости материальной точки.
Тогда
— модуль скорости материальной точки.
Тогда 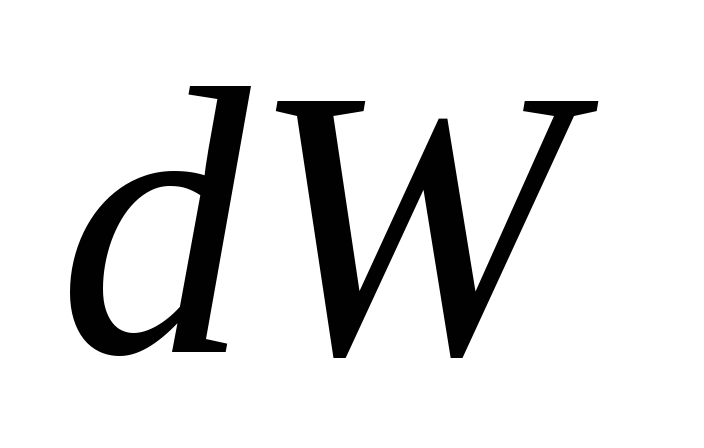 можно представить в виде:
можно представить в виде:
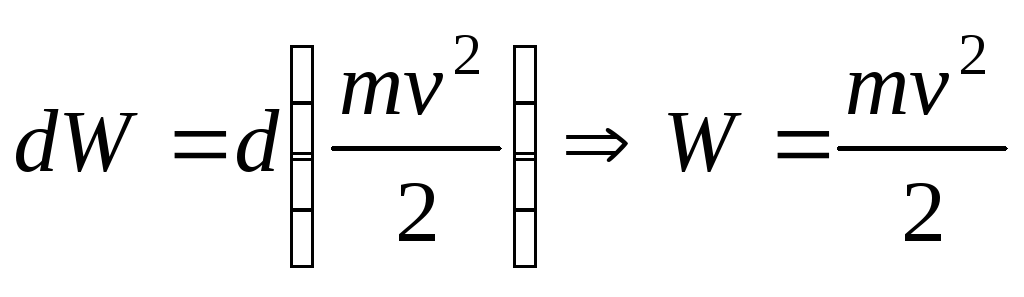
— кинетическая энергия движущейся материальной точки.
Умножив и разделив
это выражение на 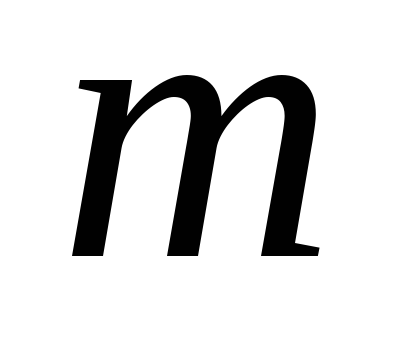 ,
и учитывая, что
,
и учитывая, что 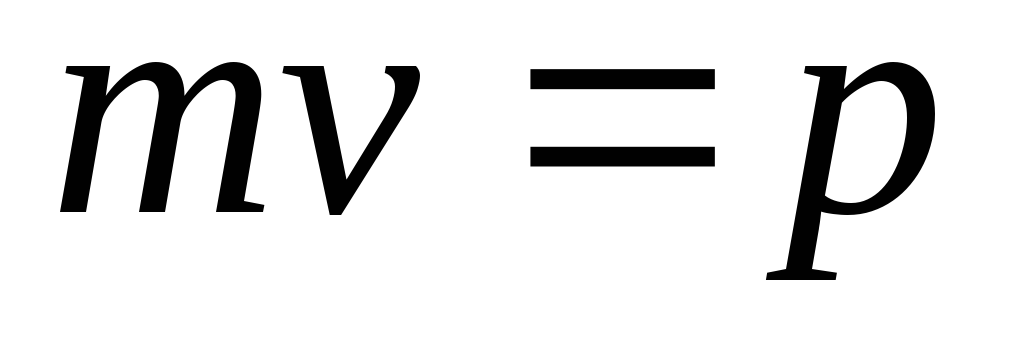 ,
получим
,
получим
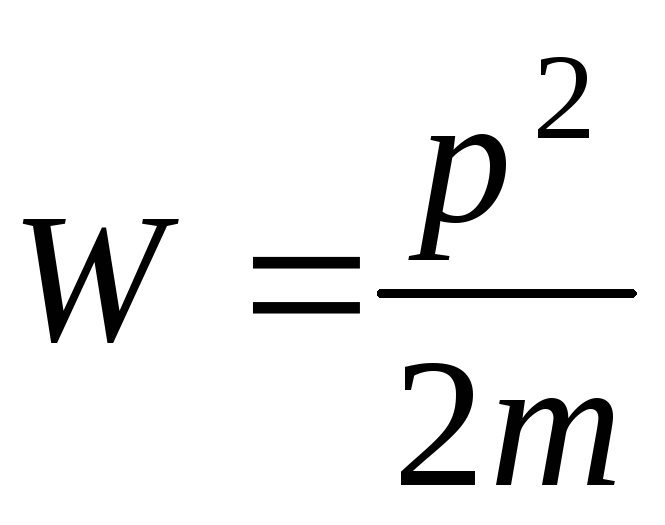 —
—
— связь между импульсом и кинетической энергией движущейся материальной точки.
Потенциальная энергия (или энергия положения тел) определяется действием на тело консервативных сил и зависит только от положения тела.
Мы видели, что
работу силы тяжести 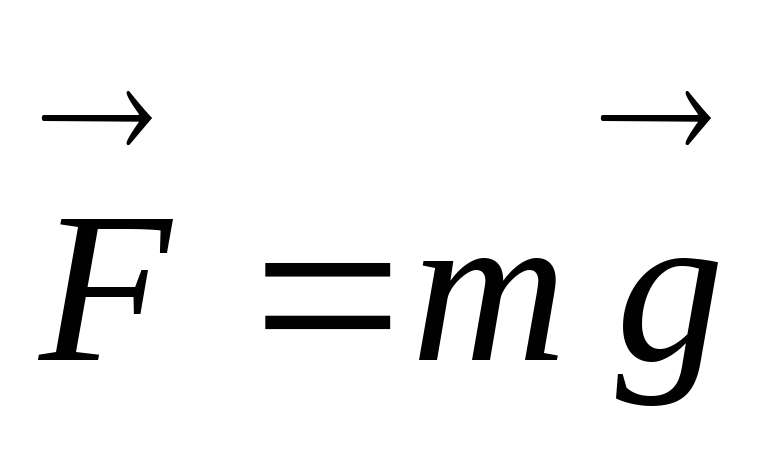 при криволинейном движении материальной
точки
при криволинейном движении материальной
точки 
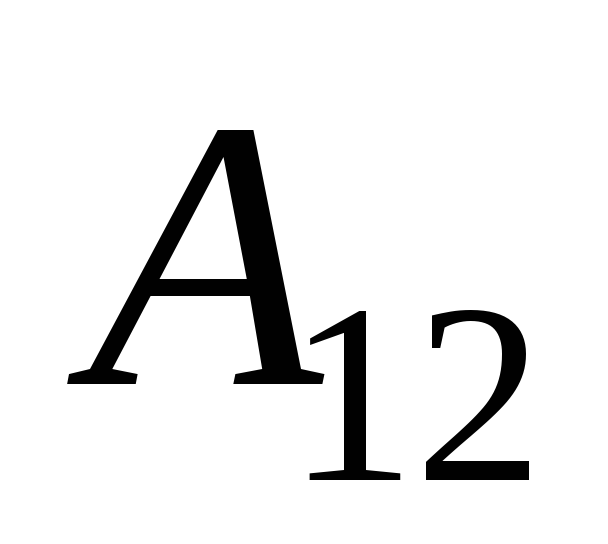 можно представить в виде разности
значений функции
можно представить в виде разности
значений функции 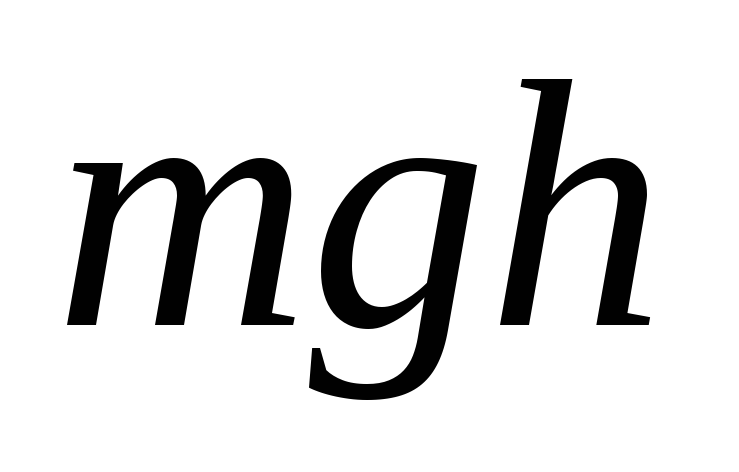 ,
взятых в точке 1 и в точке 2:
,
взятых в точке 1 и в точке 2:
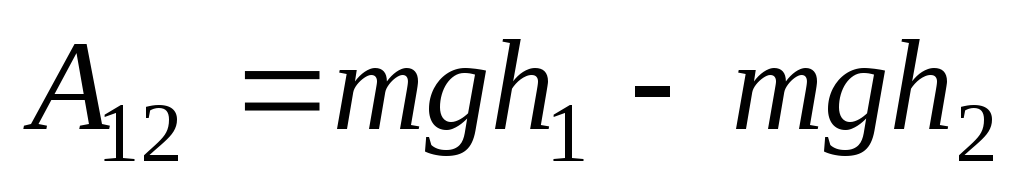 .
.
Оказывается, что
всегда, когда силы консервативны, работу
этих сил на пути 1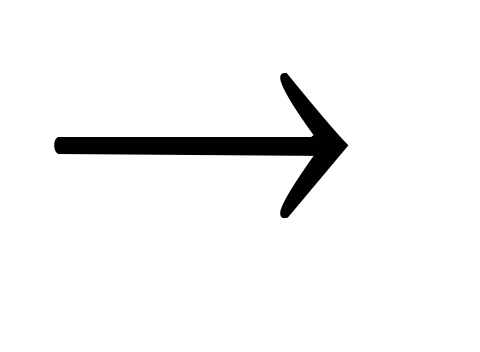 2 можно представить в виде:
2 можно представить в виде:
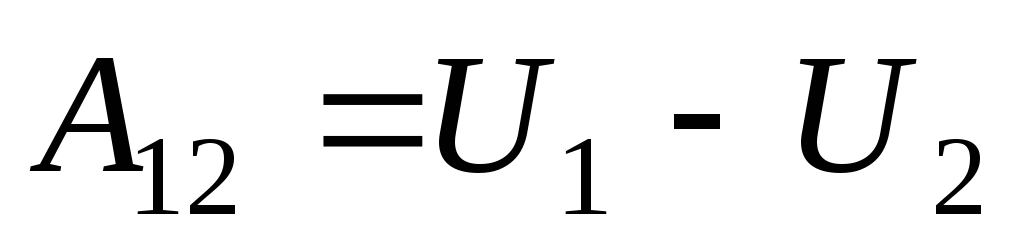 .
.
Функция 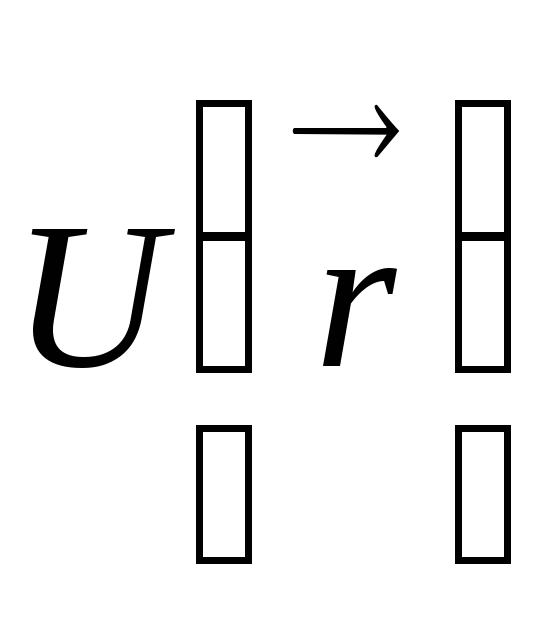 , которая
зависит только от положения тела –
называется потенциальной энергией.
, которая
зависит только от положения тела –
называется потенциальной энергией.
Тогда для элементарной работы получим
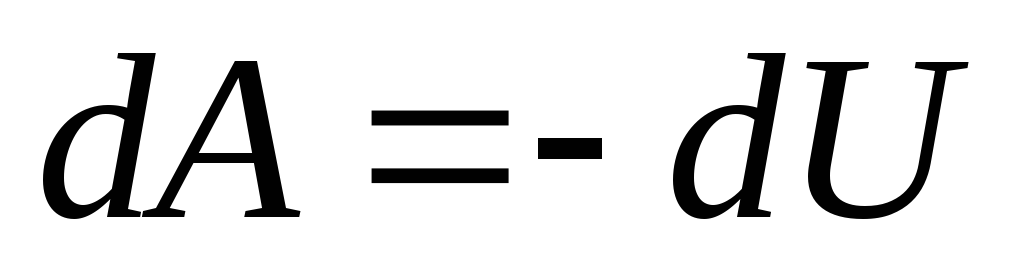 –работа равна
убыли потенциальной энергии.
–работа равна
убыли потенциальной энергии.
Иначе можно сказать, что работа совершается за счёт запаса потенциальной энергии.
Величину  ,
равную сумме кинетической и потенциальной
энергий частицы, называют полной
механической энергией тела:
,
равную сумме кинетической и потенциальной
энергий частицы, называют полной
механической энергией тела:
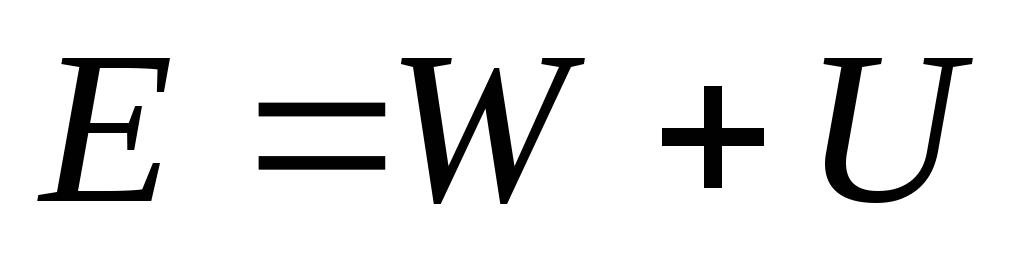 –полная
механическая энергия тела.
–полная
механическая энергия тела.
В заключении
заметим, что используя второй закон
Ньютона 
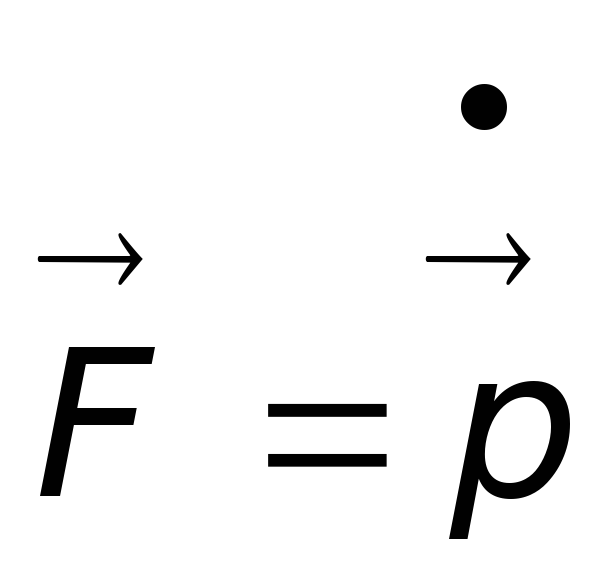 ,
дифференциал кинетической энергии
,
дифференциал кинетической энергии 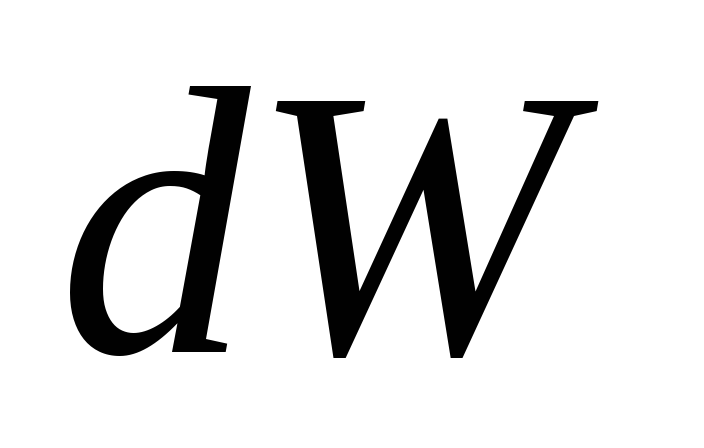 можно представить в виде:
можно представить в виде:
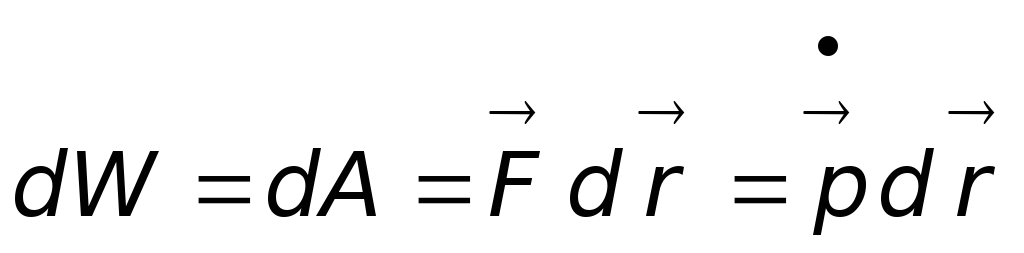 .
.
Дифференциал
потенциальной энергии 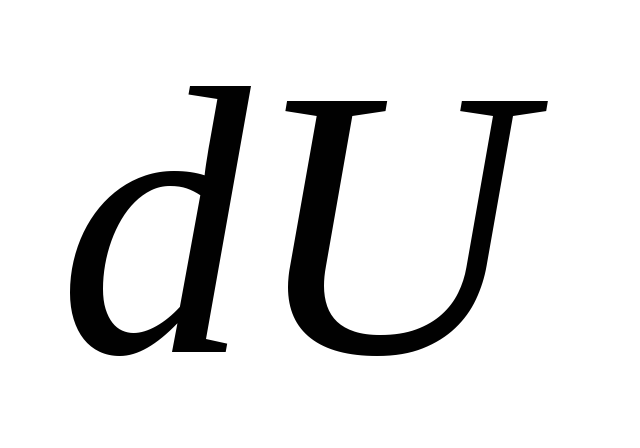 ,
как указывали выше, равен:
,
как указывали выше, равен:
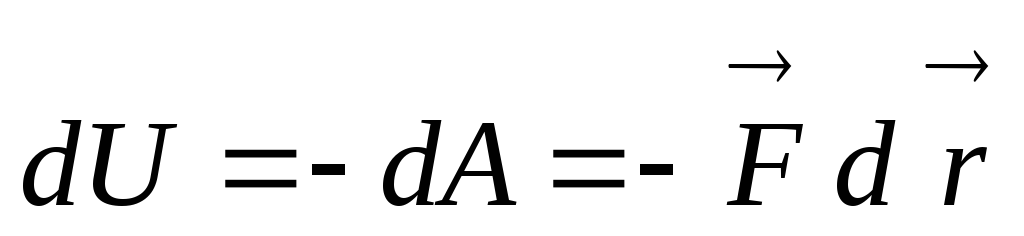 .
.
Таким образом,
если сила 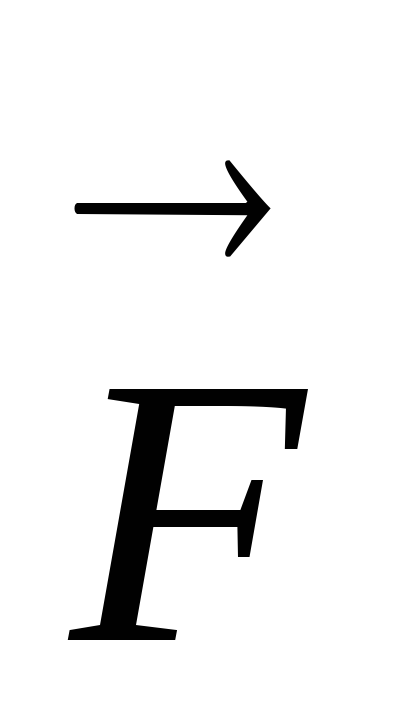 – консервативная сила и отсутствуют
другие внешние силы, то
– консервативная сила и отсутствуют
другие внешние силы, то 
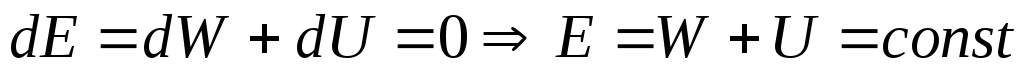 ,
т.е. в этом случае полная механическая
энергия тела сохраняется.
,
т.е. в этом случае полная механическая
энергия тела сохраняется.
1.2.3 Работа сил в механике, энергия. Закон сохранения энергии в механике
Работой постоянной силы F, когда тело движется поступательно и прямолинейно, при прохождении телом пути S, называют величину
А = FScos α = FτS, | (1.90), |
где α— угол между силой F и направлением движения тела. Здесь. Fτ= Fcos α — проекция силы F на направление вектора v скорости тела (рисунок — 1.30).
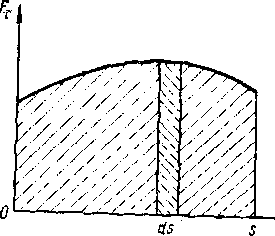
В общем случае тело может двигаться произвольным, достаточно сложным образом, а сила F — изменяться (рисунок — 1.31). Тогда, рассматривая достаточно малое (элементарное) перемещение тела ds, в пределах которой можно считать силу F постоянной, элементарную работу, можно вычислить по формуле:
dА = Fcosαds = Fτds | (1.91). |
Работа, совершаемая силой F на конечном пути s, равна сумме элементарных работ на отдельных бесконечно малых участках пути; эта сумма приводится к интегралу:
A = ∫F cos αds = ∫Fτ ds | (1.92). |
Работа, совершаемая силой F на конечном пути S, графически измеряется площадью заштрихованной на рисунке — 1.31 фигурой, ограниченной, с одной стороны функцией F(t), с другой стороны, ординатами, определяемыми S.
|
|
Рисунок — 1.30 | Рисунок — 1.31 |
Силу F, действующую на материальную точку, называют консервативной, или потенциальной, если работа А, совершаемая этой силой при перемещении точки из одного произвольного положения в другое, не зависит от того, по какой траектории это перемещение произошло. Поэтому при перемещении материальной точки вдоль замкнутой траектории работа консервативной силы тождественно равна нулю. Таким образом, консервативные силы можно определить двумя способами:
1) как силу, работа которой не зависит от пути, по которому частица переходит из одного положения в другое;
2) как силу, работа которой по замкнутому пути равна нулю.
Примерами консервативных сил могут служить силы всемирного тяготения, силы упругости, силы электростатического взаимодействия между заряженными телами.
Все силы, не удовлетворяющие условию консервативности, называются неконсервативными. Характерным примером таких сил являются силы трения скольжения. Сила трения скольжения всегда направлена в сторону, противоположную направлению движения, так чтоcosα = -1. Поэтому работа силы трения скольжения вдоль замкнутой траектории всегда отрицательна и никогда не равна нулю.
Для характеристики скорости совершения работы силой вводится понятие мощности. Мощностью N силы F называется физическая величина, численно равная работе, совершаемой этой силой за единицу времени:
Подставляя в эту формулу выражение для элементарной работы, получим
N = F cosα ds/dt = Fvcosα | (1.94), |
где v — скорость точки приложения силы.
В механике различают два вида энергии, кинетическую и потенциальную. Кинетической энергией тела называют энергию ЕK, являющуюся мерой его механического движения и измеряемую той работой, которую может совершить тело при его торможении до полной остановки. Найдем выражение для кинетической энергии твердого тела В, имеющего массу т и движущегося поступательно со скоростью v.
Пусть тело В тормозится под действием некоторой силой F (в общем случае переменной) и на малом участке пути ds совершает элементарную работу dА = — Fτ ds. По второму закону Ньютона — Fτ= mdv/dt Следовательно, dA = — m (dv/dt) ds = — m (ds/dt) dv = — m v dv. Работа, совершаемая телом В до полной его остановки
A = — ∫ m v dv = mv2/2 | (1.95). |
Итак, кинетическая энергия поступательно движущегося телa, равна половине произведения массы этого тела на квадрат его скорости:
Данная формула справедлива для кинетической энергии материальной точки. Любую механическую систему можно рассматривать как систему материальных точек. Поэтому кинетическая энергия ЕK механической системы равна сумме кинетических энергий всех п материальных точек, образующих эту систему:
Ек= ∑ Еi = ∑mivi2/2 | (1.97), |
где mi, vi — масса и скорость i-й материальной точки. Таким образом, кинетическая энергия системы полностью определяется величинами масс и скоростей движения. входящих в нее материальных точек. Она не зависит от того, каким образом части рассматриваемой системы приобрели данные значения скоростей. Кратко этот важный вывод можно сформулировать следующим образом: кинетическая энергия системы есть функция состояния ее движения.
Если на систему материальных точек или тел действуют консервативные (потенциальные) силы, то можно ввести понятие потенциальной энергии этой системы. В самом деле, работа, совершаемая консервативными силами, не зависит от того, как было осуществлено это перемещение. Работа А1-2 при перемещении системы из одной точки пространства, полностью определяется начальной и конечной местоположениями системы. Это можно выразить в форме
А1-2 = Еп1 – Еп2 | (1.98), |
где Еп — некоторая функция состояния системы, зависящая только от координат всех материальных точек системы. Эту функцию называют потенциальной энергией системы. Отсюда следует, что работа консервативных сил, действующих на механическую систему, равна убыли потенциальной энергии этой системы. Из определения следует, что потенциальная энергия системы в произвольном состоянии равна работе, совершаемой консервативными силами при переводе системы из одного состояния в другое по условию задачи.
Так, например, работа силы тяжести зависит только от разности высот начальной и конечной точек пути. Сила тяжести тела приложена к его центру тяжести. Поэтому работа силы тяжести при любом движении тела равна произведению этой силы на разность высот начального и конечного положений его центра тяжести. Отсюда следует, что работа силы тяжести вдоль замкнутой траектории центра тяжести тела равна нулю, т. е. что сила тяжести, действительно, является консервативной. Потенциальная энергия тела, поднятого на высоту H над поверхностью Земли равна
где Еn0— потенциальная энергия тела, лежащего на поверхности Земли. Обычно принимают Еn0 = 0, так что
Найдем потенциальную энергию упруго деформированного тела. Сила упругости Fynp, как известно из опыта, пропорциональна величине деформации х, т. е. Fynp, =— kх где k — коэффициент упругости, характеризующий упругие свойства тела, а знак минус показывает, что сила упругости направлена в сторону, противоположную направлению деформации: упруго деформированное тело стремится восстановить свои первоначальные форму и размеры.
Элементарная работа, совершаемая силой Fynp при бесконечно малом изменении деформации тела на величину dx равна dА = (Fynpdx) = — kxdx. Работа этой силы при конечном изменении деформации тела, например, при переводе его из недеформированного состояния (х=0) в состояние, соответствующее деформации х, равна
А = — ∫kxdx = — kx2/2 | (1.101). |
Работа А не зависит от хода процесса деформации тела и полностью определяется значениями деформации тела в начальном и конечном состояниях. Следовательно, силы упругости являются консервативными, а потенциальная энергия упруго деформированного тела
Полной механической энергией системы называют величину E, равную сумме кинетической и потенциальной энергий этой системы:
Полная механическая энергия системы — функция ее состояния, так как зависит только от координат, скоростей и масс всех малых частей (материальных точек) системы
Найдем условие, которому должна удовлетворять система тел для того, чтобы ее полная механическая энергия не изменялась с течением времени. Если v — скорость i—й материальной точки с массой ти то ее кинетическая энергия Eкi = mivi2/2. Изменение этой энергии за малый промежуток времени dt, связанное с изменением скорости v, на dvi= aidt (аi— ускорение рассматриваемой материальной точки), равно
dEкi = mi /2[(dvi, vi) + (vi ,dvi,)] = mi(aidt, vi,) = (miаi, vtdt) = (miаi, dri) | (1.104), |
где dri = vidt— приращение радиуса-вектора ri, материальной точки. По второму закону Ньютона miаi = Fi + fi, где Fi и fi — результирующие, соответственно, консервативных и неконсервативных сил, действующих на i—ю материальную точку. Поэтому
dEкi. = (Fi dri) + (fi dri) | (1.105). |
Кинетическая энергия WK всей системы равна сумме кинетических энергий всех п материальных точек, образующих эту систему, а ее изменение за малый промежуток времени dt dЕк = ∑dEкi., т. е.
dЕк =∑(Fi dri) +∑(fi dri) | (1.106). |
Первая сумма в правой части этого уравнения представляет собой суммарную работу dA, совершаемую всеми консервативными силами за промежуток времени dt. Эта работа равна убыли за то же время dt потенциальной энергии системы
Еn = Еnвнутр + Еnвнешн | (1.107), |
∑(Fi dri) = dA = — dЕn | (1.108). |
Вторая сумма в правой части уравнения ∑(fi dri).представляет собой суммарную работу dAнк, совершаемую всеми неконсервативными силами. Таким образом, уравнение можно переписать в форме dЕк + dЕn = dAнк, или
где Е= Е K+ Е n — полная механическая энергия системы.
Если внутренние силы взаимодействия между которыми консервативны, а все внешние силы — стационарны и консервативны, такую систему тел (материальных точек) называют консервативной системой,. Для такой системы dA = dE = 0 и
E = EK+ Eп= const, | (1.110), |
т. е. полная механическая энергия консервативной системы не изменяется с течением времени. Этот закон называют законом сохранения механической энергии. Он справедлив, для замкнутой консервативной системы, т е системы, на которую внешние силы не действуют, а все внутренние силы — консервативны.
Рассмотрим применение закона сохранения механической энергии к расчету абсолютно упругого прямого центрального удара двух тел. Абсолютно упругим называют такой удар, в результате которого не происходит превращения механической энергии системы соударяющихся тел в другие виды энергии. Пусть два абсолютно упругих шара с массами m1 и m2 до удара (рисунок — 1.32, а) движутся поступательно со скоростями v1 и v2, направленными в одну и ту же сторону вдоль линии их центров, причем v1 > v2. Нужно найти скорости шаров u1 и u2 после соударения (рисунок — 1.32, б).
|
|
Рисунок — 1.32 | |
В процессе удара систему соударяющихся тел можно считать замкнутой. Следовательно, для решения этой задачи можно воспользоваться законами сохранения механической энергии и импульса. Перед ударом и после его завершения соударяющиеся тела не деформированы, т. е. потенциальную энергию системы в этих двух состояниях можно считать одинаковой и равной нулю. Тогда из закона сохранения механической энергии имеем
m1v12/2 + m2v22/2 = m1u12/2 + m2u22/2 | (1.111), |
где u1 и u2 скорости этих шаров после соударения. По закону сохранения импульса
m1v1 + m2v2 = m1u1 + m2u2 | (1.112). |
Совместное решение двух последних уравнений дает
u1 = [v1(m1-m2)+ 2m2v2] / (m1+m2), u2 = [v2(m2-m1)+ 2m1v1] / (m1+m2) | (1.113), |
т.е., после упругого соударения тела двигаются каждая со своей скоростью кинетической энергией Е1 и Е2 соответственно.
Систему тел называют диссипативной, если ее механическая энергия постепенно уменьшается за счет преобразования в другие (немеханические) формы энергии. Этот процесс называют процессом диссипации (рассеяния) энергии. В качестве примера рассмотрим диссипацию энергии при абсолютно неупругом прямом центральном ударе двух поступательно движущихся тел.
При абсолютно неупругом ударе происходит диссипация энергии. Изменение ∆E полной механической энергии системы соударяющихся тел равно изменению их кинетической энергии
∆E = ∆Eк =(m1+m2)u2/2 — [m1v12/2 + m2v22/2] | (1.114). |
Общую скорость тел можем найти, применяя закон сохранения импульса для неупругого удара, учитывая, что после соударения они двигаются вместе, имея общую скорость:
u = (m1v1 + m2v2)/ (m1+m2) | (1.115. |
После преобразований, рассеянная энергия равна:
∆E =- m1m2 (v1 –v2)2 /2(m1+m2) | (1.116). |
Механика
Сила.
Силой называется векторная величина , являющаяся мерой воздействия одного тела на другое. Механическое взаимодействие может осуществляться как между непосредственно контактирующими телами (сила трения, сила реакции опоры и т.д.), так и между удаленными телами. Взаимодействия между удаленными телами осуществляется посредством физических полей (гравитационные силы, электромагнитные силы).Особая форма материи, связывающая частицы вещества в единые системы и передающая с конечной скоростью действие одних частиц на другие, называется физическим полем, или просто полем.
Масса.
а) Масса определяет гравитационные свойства тела, т.е. силы, с которыми оно притягивается к другим телам, в частности, к Земле.
б) Масса характеризует инерционные свойства тела (инертность тела), т.е. способность тела сохранить состояние покоя или равномерного прямолинейного движения. Отсюда определение: масса – мера инертности.
Центром
масс системы материальных точек называется
точка, радиус–вектор которой равен 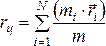 ,
гдеmi ,
,
гдеmi , 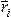 –
соответственно масса и радиус–векторi–ой
точки системы, m = m1+m2+…+mN –
масса всей системы. Радиус–векторы
–
соответственно масса и радиус–векторi–ой
точки системы, m = m1+m2+…+mN –
масса всей системы. Радиус–векторы 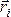 проведены
из центра системы отсчета,i =
1, 2,….N.
проведены
из центра системы отсчета,i =
1, 2,….N.
Импульс.
Импульсом
материальной точки называется векторная
величина, равная произведению ее массы
на ее скорость: 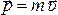 .
Импульс
.
Импульс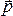 –
вектор, по направлению совпадающий с
направлением скорости
–
вектор, по направлению совпадающий с
направлением скорости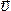 .
.
Импульсом системы материальных точек называется вектор, равный геометрической (векторной) сумме импульсов всех материальных точек системы:
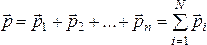 .
.
Используя понятие центра масс, импульс системы равен произведению массы всей системы на скорость ее центра масс
Первый закон Ньютона.
Всякая материальная точка или тело сохраняет состояние покоя или равномерного прямолинейного движения, пока на них не действуют силы или действие сил скомпенсировано.
Системы, в которых выполняется первый закон Ньютона, называются инерциальными. Системы, в которых не выполняется первый закон Ньютона, называются неинерциальными. Инерциальных систем бесконечно много. Любая система, движущаяся относительно данной инерциальной системы равномерно и прямолинейно, является также инерциальной системой.
Второй закон Ньютона.
Скорость
изменения импульса 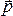 материальной
точки равна действующей на нее силе:
материальной
точки равна действующей на нее силе: 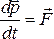 .
.
Если
на материальную точку одновременно
действуют несколько сил, то изменение
её импульса происходит под действием
равнодействующей силы (принцип
суперпозиции или принцип независимости
действия сил на
тело) 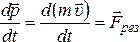 .
.
Ниже даны разные формы записи второго закона Ньютона.
| Второй закон Ньютона в проекциях на координатные оси:
| Второй закон Ньютона в проекциях на касательное и нормальное направления к траектории в данной точке:
где Fτ, Fn –
проекции вектора силы |
Третий закон Ньютона.
Силы,
с которыми два тела действуют друг на
друга, равны по величине, направлены в
противоположные стороны 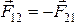 .
.
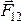 –сила,
действующая со стороны второго тела на
первое, приложена к первому телу,
–сила,
действующая со стороны второго тела на
первое, приложена к первому телу, 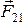 –
сила, действующая на второе тело со
стороны первого, приложена ко второму
телу. По модулю эти силы равны:
–
сила, действующая на второе тело со
стороны первого, приложена ко второму
телу. По модулю эти силы равны: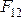 =
=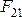 .
.
Закон сохранения импульса.
Полный вектор импульса замкнутой системы есть величина постоянная при любых взаимодействиях внутри данной системы
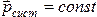 .
.
Если
система незамкнутая, есть внешние силы,
действующие на точки системы, то 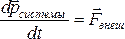 ,
где
,
где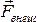 –
вектор внешних сил, равный геометрической
сумме всех внешних сил, действующих на
систему. Следовательно,только
внешние силы изменяют импульс системы.
–
вектор внешних сил, равный геометрической
сумме всех внешних сил, действующих на
систему. Следовательно,только
внешние силы изменяют импульс системы.
Момент
силы, действующий на твердое тело,
относительно точки вращения (полюса) называется
векторная величина, равная векторному
произведению радиус–вектор на направление
силы 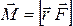 .
Проекция этого вектора на ось, проходящую
через центр вращения , называется
моментом силы относительно оси вращения.
.
Проекция этого вектора на ось, проходящую
через центр вращения , называется
моментом силы относительно оси вращения.
Момент
силы, действующий на твердое тело,
относительно неподвижной оси
вращения Z равен 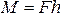 ,
где
,
где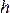 –
плечо силы (перпендикуляр, опущенный
от оси вращения на направление силы,
действующей на тело). Направление момента
сил определяется правилом буравчика.
–
плечо силы (перпендикуляр, опущенный
от оси вращения на направление силы,
действующей на тело). Направление момента
сил определяется правилом буравчика.
Результирующий
момент нескольких сил, действующий на
твердое тело и вызывающий его вращение
вокруг оси, равен геометрической сумме
моментов сил: 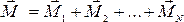 , где N –
число действующих на тело сил.
, где N –
число действующих на тело сил.
Момент
импульса материальной точки (тела)
относительно неподвижной оси
Z называется величина,
равная проекции на эту ось вектора
момента импульса тела относительно
какой–либо точки О, принадлежащей этой
оси: 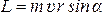 ;
; 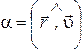 ,
, 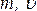 –
соответственно масса тела и его
скорость,
–
соответственно масса тела и его
скорость, –
радиус–вектор от точки О до тела.
–
радиус–вектор от точки О до тела.
Моментом
инерции материальной
точки относительно оси вращения Z называется
физическая величина, численно равная
произведению массы точки на квадрат
расстояния точки до оси вращения 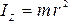 .
.
Моментом
инерции механической системы относительно
неподвижной оси называется физическая
величина, равная сумме произведений
масс всех точек системы на квадраты их
расстояний до оси вращения: 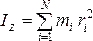 .
.
Второй закон Ньютона для вращательного движения (основное уравнение вращательного движения).
Производная
по времени от момента импульса 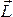 частицы
относительно точки О (полюса) равна моменту
равнодействующей силы относительно
той же точки:
частицы
относительно точки О (полюса) равна моменту
равнодействующей силы относительно
той же точки: 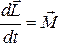 .
.
Если
спроектировать основное уравнение на
выделенную ось вращения Z, то получим
закон Ньютона для вращательного движения
относительно оси вращения 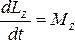
Учитывая,
что 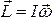 ,
для основного уравнения динамики
вращательного движения получаем:
,
для основного уравнения динамики
вращательного движения получаем: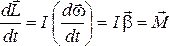 ,
где
,
где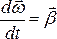 – угловое
ускорение.
– угловое
ускорение.
Закон сохранения момента импульса.
Момент
импульса замкнутой системы относительно
любой неподвижной точки (полюса) не
изменяется с течением времени при любых
взаимодействиях внутри системы: 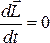 ,
т.е.
,
т.е. 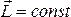
Если результирующий момент сил относительно некоторой оси ОZ, проходящей через точку О, тождественно равен нулю, то и момент импульса относительно этой оси не изменяется с течением времени.
при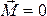
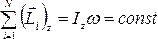 ,
,
где 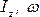 –
соответственно момент инерции и угловая
скорость системы.
–
соответственно момент инерции и угловая
скорость системы.
Работа постоянной силы. Работой постоянной
силы называется
скалярное произведение вектора
силы
Работа – скаляр. Если
на тело действует несколько сил (N –
число сил), и вектор перемещения тела
равен
|
Работа переменной силы. Если
рассматриваемый участок траектории
разбивается на большое число
Рисунок 1.2.1. – Зависимость переменной силы от пути
При
бесконечно большом количестве участков,
на которое разбивается путь ( Силы, работа которых по замкнутому контуру равна нулю, называются потенциальными. В механике к потенциальным силам относятся сила тяжести и сила упругости. |
Энергия. Физическая величина, характеризующая способность тела или системы тел совершить работу, называется энергией. Формы движений в природе различны. Для количественного сравнения разных форм движений и служит понятие энергии.Механическая энергия может быть обусловлена: – или движением тела с некоторой скоростью (кинетическая энергия), – или расположением данного тела в системе других тел определенной конфигурации (потенциальная энергия). Механическая энергия равна сумме потенциальной и кинетической энергий:
| Кинетическая энергия. Кинетической энергией тела называется энергия его механического движения. Изменение кинетической энергии тела под действием силы равно работе этой силы:
Кинетическая
энергия движущегося тела равна Кинетическая энергия механической системы равна сумме механических энергий всех частей системы. Полная
кинетическая энергия вращающегося
тела равна:
| |
Потенциальная энергия. Потенциальная энергия – энергия, определяемая взаимным расположением тел или отдельных частей тела относительно друг друга, т.е. потенциальная энергия зависит от конфигурации системы. Соотношение,
связывающее работу потенциальной
силы с изменением потенциальной
энергии системы, имеет вид: | ||
Потенциальная энергия тяготения. Когда
тело перемещается вблизи Земли, то
говорят, что тело двигается в силовом
поле тяготения Земли
или впотенциальном
поле Земли.
Потенциальная энергия тяготения
равна: | Потенциальная энергия упругости. В
растянутой (или сжатой) пружине на
каждую ее точку действует сила
упругости, в этом случае можно говорить
опотенциальном
поле сил упругости.
Потенциальная энергия упругости
равна ,
гдех –
изменение длины растянутой пружины,
отсчет х ведется
от положения равновесия, в котором
| |
Связь между потенциальной энергией и потенциальной силой. Силы, работа которых по замкнутому пути равна нулю, называются потенциальными (или консервативными). Как указывалось ранее, в механике силы тяготения и упругости – потенциальные силы. Общая связь между потенциальной энергией и потенциальной силой: проекции потенциальной силы на оси координат равны частным производным по этим координатам от потенциальной энергии, взятым с обратным знаком:
В
определении используется понятие
частных производных, т.к. потенциальная
энергия в общем, виде зависит от трех
координат | ||
Связь работа и энергии. Работа – мера изменения энергии(физический смысл работы). Теорема о кинетической энергии: работа всех сил приводит к изменению кинетической энергии теле (или системы тел)
Работа потенциальной силы, приводящая к изменению конфигурации системы, равна приращению потенциальной энергии, взятому со знаком минус:
| ||
Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только посредством сил тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком: А=-(Ек2-Ек1)
По теореме о кинетической
энергии эта работа равна изменению
кинетической энергии тел.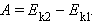
Следовательно 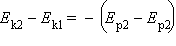
или
|
Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой посредством сил тяготения и сил упругости, остается неизменной.
Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов Ньютона. Сумму E = Ek + Ep называют полной механической энергией. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии.
Механика/Основные определения — это… Что такое Механика/Основные определения?
Предупреждение. Здесь приведены определения некоторых терминов в школьной, элементарной формулировке. При этом некоторыми более сложными эффектами может быть пренебрежено.
Кинематика
Кинематика — изучает геометрические свойства движения тел без учета их масс и действующих на них сил. Рассматривает движение тел без выяснения причин этого движения.
- Материальная точка — тело, размерами и формой которого в данных условиях можно пренебречь.
- Система отсчёта — совокупность тела отсчёта, связанной с ним системы координат и часов.
- Часы — устройство, в котором протекает периодический процесс, положенный в основу отсчета времени.
- Траектория движения материальной точки — линия, описываемая этой точкой в пространстве. В зависимости от формы траектории движение может быть прямолинейным или криволинейным.
- Вектор перемещения — вектор, начальная точка которого совпадает с начальной точкой движения, конец вектора — с конечной.
- Путь — сумма длин всех участков траектории, пройденных точкой за определенное время.
- Средняя скорость — отношение модуля вектора перемещения к промежутку времени, в течение которого это перемещение произошло.
- Мгновенная скорость (скорость) — предел отношения вектора перемещения к промежутку времени, за который это перемещение произошло, при стремлении длительности промежутка времени к нулю.
- Ускорение — характеристика степени неравномерности движения. Определяет быстроту изменения скорости по модулю и направлению.
- Закон сложения скоростей: абсолютная скорость материальной точки равна векторной сумме переносной и относительной скоростей.
- Среднепутевая скорость — отношение пройденного пути к соответствующему промежутку времени.
Вращательное движение тела вокруг неподвижной направленной оси
Вращательное движение тела вокруг неподвижной направленной оси — движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой хх, называемой осью вращения.
- Угловое перемещение — векторная величина, характеризующая изменение угловой координаты в процессе её движения.
- Угловая скорость — векторная величина, характеризующая быстроту вращения материальной точки. Вектор направлен вдоль оси вращения таким образом, чтобы, смотря с его конца, вращение казалось происходящим против часовой стрелки.
- Период вращения (Т) — время, за которое вращающееся тело совершает один полный оборот.
- Частота вращения — число полных оборотов, совершаемых при равномерном движении, в единицу времени.
- Плоское движение — движение плоского тела, при котором все точки тела движутся в некоторой фиксированной плоскости пространства, условно считаемой неподвижной.
Первый закон Ньютона
Первый закон Ньютона:В мире существуют такие системы отсчета, в которых изолированная материальная точка сохраняет состояние покоя или равномерно-прямолинейно движется. Такие системы отсчета называются инерциальными.
Второй закон Ньютона
Второй закон Ньютона: в инерциальных системах отсчета ускорение материальной точки прямо пропорционально векторной сумме сил, действующих на материальную точку, и обратно пропорционально её массе.
Третий закон Ньютона
Третий закон Ньютона: в инерциальных системах отсчета всякое действие одной (первой) материальной точки на другую (вторую), сопровождается воздействием второй материальной точки на первую, т.е имеет характер взаимодействия; силы, с которыми взаимодействуют материальные точки, всегда равны по модулю, противоположно направлены, действуют вдоль прямой, соединяющей эти точки, являются силами одной природы и приложены к разным материальным точкам.
Принцип относительности Галилея
Принцип относительности Галилея: никакими механическими опытами, проводимыми внутри данной инерциальной системы, нельзя установить, покоится эта система или находится в равномерном и прямолинейном движении. Во всех инерциальных системах отсчета законы механики одинаковы.
- Вес тела — сила, с которой тело давит на опору.
Закон Гука
Закон Гука: при достаточно малых деформациях сила упругости пропорциональна величине деформации тела и направлена в сторону, противоположную деформации.
- Импульс тела (материальной точки) — векторная величина, равная произведению массы тела (материальной точки) на её скорость.
- Импульс системы тел (материальных точек) — векторная сумма импульсов всех точек.
- Импульс силы — произведение силы на время её действия (или интеграл по времени, если сила изменяется со временем).
- Закон сохранения импульса: в инерциальной системе отсчета импульс замкнутой системы сохраняется.
- Изменение импульса системы материальных точек — в инерциальной системе отсчета скорость изменения импульса механической системы равна векторной сумме внешних сил, действующих на материальные точки системы.
Центр масс
Центр масс — воображаемая точка С, положение которой характеризует распределение масс этой системы.
- Закон движения центра масс — в инерциальных системах отсчёта центр масс системы движется как материальная точка, в которой находится масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, действующих на систему.
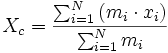 ;
; 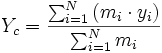 ;
; 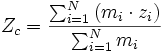
- Система центра масс — система отсчёта, поступательно перемещающаяся в некоторой инерциальной системе, относительно которой центр масс механической системы неподвижен.
Работа, мощность, энергия
- Работа силы равна произведению модуля силы на перемещение и на косинус угла между ними.
- Мощность — отношение работы ко времени, за которое эта работа была совершена.
- Кинетическая энергия — величина, равная половине произведения массы тела на квадрат его скорости.
- Величину, равную произведению масы тела на g на высоту тела над поверхностью Земли, называют потенциальной энергией тела в поле силы тяжести.
- Консервативные силы — силы, работа которых не зависит от пути, пройденного материальной точкой. Зависит только от перемещения.
- Механическая энергия системы — величина, равная сумме кинетической и потенциальной энергий системы.
- В замкнутой системе, в которой действуют только консервативные силы, механическая энергия сохраняется.
- Вторая космическая скорость — скорость, необходимая материальной точке, чтобы покинуть поле тяготения Земли и стать спутником Солнца.
Wikimedia Foundation. 2010.
Определение работы в физике, теория и онлайн калькуляторы
Работа в механике
ОпределениеФизическая величина, называемая работой силы (или просто работой), используется в механике, как численная характеристика обмена энергиями между телами при их взаимодействии.
Допустим, что тело перемещается по прямой линии, и на него действует постоянная сила ($\overline{F}$), образующая угол $\alpha $ с направлением перемещения тела ($\overline{s}$), тогда работа ($A$) этой силы определяется как:
\[A=\overline{F}\overline{s}=Fs{\cos \alpha \ \left(1\right).\ }\]Из формулы (1) следует, что при $\alpha
Если сила не является постоянной величиной то формулу (1) для нахождения механической работы не применяют. Тогда все перемещение тела делят на элементарные отрезки ($d\overline{s}$) на каждом из которых силу можно считать постоянной, а движение точки приложения силы прямолинейным. В этом случае элементарной работой ($dA$) силы $\overline{F}$ на перемещении $d\overline{s}$ называют скалярную величину, которая равна:
\[dA=\overline{F}d\overline{s}=Fds{\cos \alpha \ }\left(2\right),\]где $\alpha $ — угол между векторами $\overline{F\ }и\ d\overline{s}$; $ds$ — модуль элементарного пути. Совокупную работу силы на участке траектории от первой рассматриваемой точки до второй находят как алгебраическую сумму элементарных работ на отдельных бесконечно малых участках. Обычно сумму заменяют интегралом, тогда:
\[A=\int\limits^2_1{dA=\int\limits^2_1{Fds{cos \alpha \ }\left(3\right).}}\]Для того чтобы вычислить интеграл (3) следует знать зависимость силы от пути по траектории на рассматриваемом участке. При графическом задании силы от пути, работу находят как площадь криволинейной трапеции, ограниченной снизу осью абсцисс, сверху графиком F(s), справа и слева ординатами крайних точек.
Термодинамическая работа
В термодинамике работу определяют как:
\[A=\int\limits^{V_2}_{V_1}{pdV(4)},\]где $V_1$ — начальный объем термодинамической системы; $V_2$ — ее конечный объем. Работа считается положительной, если ее выполняет сама термодинамическая система над внешними силами, например, газ расширяется и совершает работу.
Работу можно определить, применив первое начало термодинамики:
\[A=\Delta Q-\Delta U\ \left(5\right),\]где $\Delta Q$ — количество теплоты, получаемое системой; $\Delta U$ — изменение ее внутренней энергии. Для идеального газа, рассматриваемого в качестве термодинамической системы, то формулу (5) записывают как:
\[A=\Delta Q-\frac{i}{2}\nu R\Delta T\ (6),\]где $i$ — число степеней свободы молекулы идеального газа; $\nu =\frac{m}{\mu }$ — количество вещества; $m$ — масса газа; $\mu $ — молярная масса газа; $R$ — универсальная газовая постоянная; $\Delta T$ — изменение температуры газа в расс
Механическая работа
Обычно словом «работа» мы называем действие человека или технического устройства. Например, мы говорим: работает плотник, работает холодильник, работает компьютер. В физике термин «работа» имеет более конкретный (определённый) смысл. Поясним это на нескольких примерах действия сил. Взгляните на рисунок.
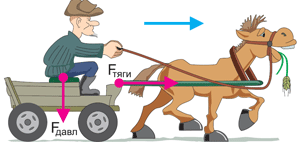 |
Лошадь тянет телегу с некоторой силой, обозначим её Fтяги. Дедушка, сидящий на телеге, давит на неё с некоторой силой. Обозначим её Fдавл. Телега движется вдоль направления силы тяги лошади (вправо), а в направлении силы давления дедушки (вниз) телега не перемещается. Поэтому в физике говорят, что Fтяги совершает работу над телегой, а Fдавл не совершает работу над телегой.
Итак, работа силы над телом или механическая работа – физическая величина, модуль которой равен произведению силы на путь, пройденный телом вдоль направления действия этой силы:
| A = ± ( F||· l ) | A – механическая работа над телом, Дж F|| – сила, параллельная пути тела, Н l – пройденный телом путь, м |
В честь английского учёного Д.Джоуля единица механической работы получила название 1 джоуль (согласно формуле, 1 Дж = 1 Н·м).
Если на рассматриваемое тело действует некоторая сила, значит, на него действует некоторое тело. Поэтому работа силы над телом и работа тела над телом – полные синонимы. Однако, работа первого тела над вторым и работа второго тела над первым – частичные синонимы, поскольку модули этих работ всегда равны, а их знаки всегда противоположны. Именно поэтому в формуле присутствует знак «±». Обсудим знаки работы более подробно.
Числовые значения силы и пути – всегда неотрицательные величины. В отличие от них механическая работа может иметь как положительный, так и отрицательный знаки. Если направление силы совпадает с направлением движения тела, то работу силы считают положительной. Если направление силы противоположно направлению движения тела, работу силы считают отрицательной (берём «–» из «±» формулы). Если направление движения тела перпендикулярно направлению действия силы, то такая сила работу не совершает, то есть A = 0.
Рассмотрите три иллюстрации по трём аспектам механической работы.
 |
Совершение силой работы может выглядеть по-разному с точек зрения различных наблюдателей. Рассмотрим пример: девочка едет в лифте вверх. Совершает ли она механическую работу? Девочка может совершать работу только над теми телами, на которые действует силой. Такое тело лишь одно – кабина лифта, так как девочка давит на её пол своим весом. Теперь надо выяснить, проходит ли кабина некоторый путь. Рассмотрим два варианта: с неподвижным и движущимся наблюдателем.
 |
Пусть сначала мальчик-наблюдатель сидит на земле. По отношению к нему кабина лифта движется вверх и проходит некоторый путь. Вес девочки направлен в противоположную сторону – вниз, следовательно, девочка совершает над кабиной отрицательную механическую работу: Aдев < 0. Вообразим, что мальчик-наблюдатель пересел внутрь кабины движущегося лифта. Как и ранее, вес девочки действует на пол кабины. Но теперь по отношению к такому наблюдателю кабина лифта не движется. Поэтому с точки зрения наблюдателя в кабине лифта девочка не совершает механическую работу: Aдев = 0.
Механика — Википедия
Меха́ника (греч. μηχανική — искусство построения машин) — раздел физики, наука, изучающая движение материальных тел и взаимодействие между ними; при этом движением в механике называют изменение во времени взаимного положения тел или их частей в пространстве[1].
По поводу предмета механики уместно сослаться на слова авторитетного учёного-механика С. М. Тарга из введения к 4-му изданию его широко известного учебника[2] теоретической механики: «Механикой в широком смысле этого слова называется наука, посвящённая решению любых задач, связанных с изучением движения или равновесия тех или иных материальных тел и происходящих при этом взаимодействий между телами. Теоретическая механика представляет собою часть механики, в которой изучаются общие законы движения и взаимодействия материальных тел, то есть те законы, которые, например, справедливы и для движения Земли вокруг Солнца, и для полёта ракеты или артиллерийского снаряда и т. п. Другую часть механики составляют различные общие и специальные технические дисциплины, посвящённые проектированию и расчёту всевозможных конкретных сооружений, двигателей, механизмов и машин или их частей (деталей)»[3].
В приведённом высказывании упущен из виду тот факт, что изучением общих законов движения и взаимодействия материальных тел занимается также и механика сплошных сред (или механика сплошной среды) — обширная часть механики, посвящённая движению газообразных, жидких и твёрдых деформируемых тел. В этой связи академик Л. И. Седов отмечал: «В теоретической механике изучаются движения материальной точки, дискретных систем материальных точек и абсолютно твёрдого тела. В механике сплошной среды … рассматриваются движения таких материальных тел, которые заполняют пространство непрерывно, сплошным образом, и расстояния между точками которых во время движения меняются»[4].
Таким образом, по предмету изучения механика подразделяется на:
Другой важнейший признак, используемый при подразделении механики на отдельные разделы, основан на тех представлениях о свойствах пространства, времени и материи, на которые опирается та или иная конкретная механическая теория. По данному признаку в рамках механики выделяют такие разделы:
Механика занимается изучением так называемых механических систем.
Механическая система обладает определённым числом k{\displaystyle k} степеней свободы, а её состояние описывается с помощью обобщённых координат q1,…qk{\displaystyle q_{1},\dots q_{k}} и соответствующих им обобщённых импульсов p1,…pk{\displaystyle p_{1},\dots p_{k}}. Задача механики состоит в изучении свойств механических систем, и, в частности, в выяснении их эволюции во времени.
Являясь одним из классов физических систем, механические системы по характеру взаимодействия с окружением разделяются на изолированные (замкнутые), закрытые и открытые, по принципу изменения свойств во времени — на статические и динамические.
Наиболее важными механическими системами являются:
Стандартные («школьные») разделы механики: кинематика, статика, динамика, законы сохранения. Кроме них, механика включает следующие (во многом перекрывающиеся по содержанию) механические дисциплины:
Некоторые курсы механики ограничиваются только твёрдыми телами. Изучением деформируемых тел занимаются теория упругости (сопротивление материалов — её первое приближение) и теория пластичности. В случае, когда речь идёт не о жёстких телах, а о жидкостях и газах, необходимо прибегнуть к механике жидкостей и газов, основными разделами которой являются гидростатика и гидрогазодинамика. Общей теорией, изучающей движение и равновесия жидкостей, газов и деформируемых тел, является механика сплошных сред.
Основной математический аппарат классической механики: дифференциальное и интегральное исчисление, разработанное специально для этого Ньютоном и Лейбницем. К современному математическому аппарату классической механики относятся, прежде всего, теория дифференциальных уравнений, дифференциальная геометрия (симплектическая геометрия, контактная геометрия, тензорный анализ, векторные расслоения, теория дифференциальных форм), функциональный анализ и теория операторных алгебр, теория катастроф и бифуркаций. В современной классической механике используются и другие разделы математики. В классической формулировке, механика базируется на трёх законах Ньютона. Решение многих задач механики упрощается, если уравнения движения допускают возможность формулировки законов сохранения (импульса, энергии, момента импульса и других динамических переменных).
Все три закона Ньютона для широкого класса механических систем (консервативных систем, лагранжевых систем, гамильтоновых систем) связаны с различными вариационными принципами. В этой формулировке классическая механика таких систем строится на основе принципа стационарности действия: системы движутся так, чтобы обеспечить стационарность функционала действия. Такая формулировка используется, например, в лагранжевой механике и в гамильтоновой механике. Уравнениями движения в лагранжевой механике являются уравнения Эйлера — Лагранжа, а в гамильтоновой — уравнения Гамильтона.
Независимыми переменными, описывающими состояние системы в гамильтоновой механике, являются обобщённые координаты и импульсы, а в механике Лагранжа — обобщённые координаты и их производные по времени.
Если использовать функционал действия, определённый на реальной траектории системы, соединяющей некую начальную точку с произвольной конечной, то аналогом уравнений движения будут уравнения Гамильтона — Якоби.
Следует отметить, что все формулировки классической механики, основанные на голономных вариационных принципах, являются менее общими, чем формулировка механики, основанная на уравнениях движения. Не все механические системы имеют уравнения движения, представимые в виде уравнения Эйлера — Лагранжа, уравнения Гамильтона или уравнения Гамильтона — Якоби. Тем не менее, все формулировки являются как полезными с практической точки зрения, так и плодотворными с теоретической. Лагранжева формулировка оказалась особенно полезной в теории поля и релятивистской физике, а гамильтонова и Гамильтона — Якоби — в квантовой механике.
Классическая механика основана на законах Ньютона, преобразовании скоростей Галилея и существовании инерциальных систем отсчёта.
Границы применимости классической механики[править | править код]
В настоящее время известно три типа ситуаций, в которых классическая механика перестаёт отражать реальность.
- Свойства микромира не могут быть поняты в рамках классической механики. В частности, в сочетании с термодинамикой она порождает ряд противоречий (см. Классическая механика). Адекватным языком для описания свойств атомов и субатомных частиц является квантовая механика. Подчеркнём, что переход от классической к квантовой механике — это не просто замена уравнений движения, а полная перестройка всей совокупности понятий (что такое физическая величина, наблюдаемое, процесс измерения и т. д.)
- При скоростях, близких к скорости света, классическая механика также перестаёт работать, и необходимо переходить к специальной теории относительности. Опять же, этот переход подразумевает полный пересмотр парадигмы, а не простое видоизменение уравнений движения. Если же, пренебрегая новым взглядом на реальность, попытаться всё же привести уравнение движения к виду F=ma{\displaystyle F=ma}, то придётся вводить тензор масс, компоненты которого растут с ростом скорости. Эта конструкция уже долгое время служит источником многочисленных заблуждений, поэтому пользоваться ей не рекомендуется.
- Классическая механика становится неэффективной при рассмотрении систем с очень большим числом частиц (или же большим числом степеней свободы). В этом случае практически целесообразно переходить к статистической физике.
- ↑ Механика — Статья в Физической энциклопедии
- ↑ На конец 2012 г. выдержал 18 изданий на русском языке и издан в переводах не менее, чем на 14 языках.
- ↑ Тарг С. М. Краткий курс теоретической механики. 4-е изд. — М.: Наука, 1966. — С. 11.
- ↑ Седов, т. 1, 1970, с. 9.
- Билимович Б. Ф. Законы механики в технике. — М.: Просвещение, 1975. — 175 с.
- Голубев Ю. Ф. Основы теоретической механики. 2-е изд. — М.: Изд-во МГУ, 2000. — 720 с. — ISBN 5-211-04244-1.
- Киттель Ч., Найт У., Рудерман М. Механика. Берклеевский курс физики. — М.: Лань, 2005. — 480 с. — ISBN 5-8114-0644-4.
- Ландау Л. Д., Лифшиц Е. М. Теоретическая физика. Т. 1. Механика. 5-е изд. — М.: Физматлит, 2004. — 224 с. — ISBN 5-9221-0055-6.
- Маркеев А. П. Теоретическая механика: Учебник для университетов. 3-е изд. — М.; Ижевск: РХД, 2007. — 592 с. — ISBN 978-5-93972-604-7.
- Матвеев А. Н. Механика и теория относительности. 3-е изд.. — М.: ОНИКС 21 век: Мир и Образование, 2003. — 432 с. — ISBN 5-329-00742-9.
- Седов Л. И. Механика сплошной среды. Том 1.. — М.: Наука, 1970. — 492 с.
- Седов Л. И. Механика сплошной среды. Том 2.. — М.: Наука, 1970. — 568 с.
- Сивухин Д. В. Общий курс физики. Т. 1. Механика. 5-е изд. — М.: Физматлит, 2006. — 560 с. — ISBN 5-9221-0715-1.
- С.П. Стрелков. Механика. — Москва : Наука, 1975. — 560 с. — (Общий курс физики). — 60 000 экз.
- ред. Григорьян А. Т., Погребысский И. Б. История механики с древнейших времен до конца XVIII века. — М.: Наука, 1971. — 296 с. — 3600 экз. (в пер., суперобл.)
- ред. Григорьян А. Т., Погребысский И. Б. История механики с конца XVIII века до середины XX века. — М.: Наука, 1972. — 412 с.
- Хайкин С.Э. Физические основы механики. — 2. — Москва : Наука, 1971. — 752 с. — (Общий курс физики). — 49 000 экз.




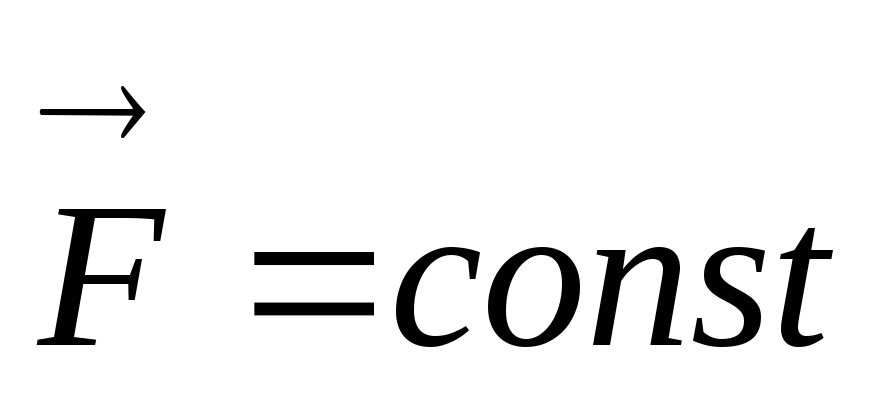 ,
движение прямолинейное.
,
движение прямолинейное.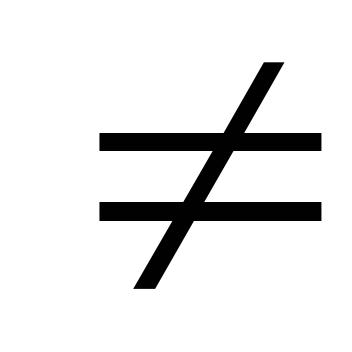 const.
const.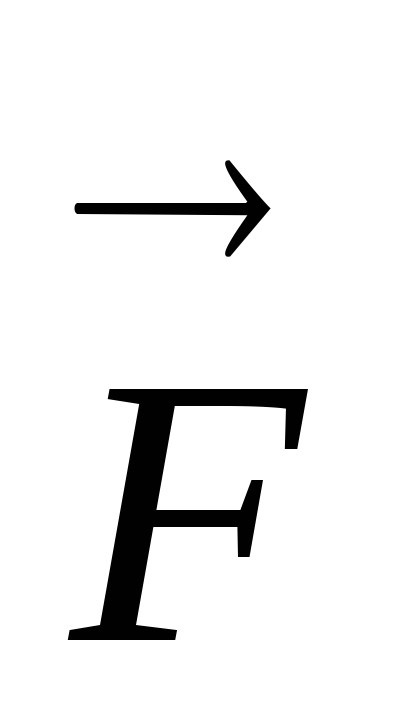 переменная.
переменная.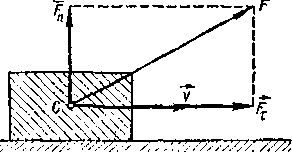
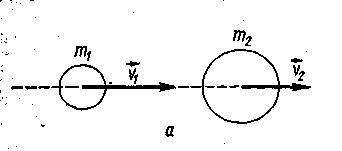
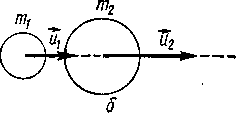
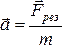
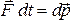 ,
где
,
где 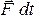 –
импульс силы,
–
импульс силы,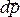 –изменение
импульса тела.
–изменение
импульса тела.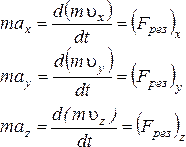
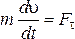 ,
, 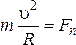 ,
,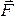 на
нормальное и тангенциальное (касательное)
направления.
на
нормальное и тангенциальное (касательное)
направления.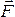 и
вектора перемещения
и
вектора перемещения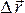 :
: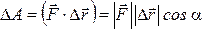 ; где
; где 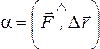 .
.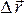 ,
то совершаемая работа равна алгебраической
сумме работ, совершаемых каждой из
действующих на тело сил на этом
перемещении.
,
то совершаемая работа равна алгебраической
сумме работ, совершаемых каждой из
действующих на тело сил на этом
перемещении.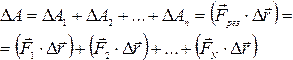 .
.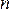 элементарных
участков, то длина пути элементарного
участка будет близка к величине
перемещения на этом участке
элементарных
участков, то длина пути элементарного
участка будет близка к величине
перемещения на этом участке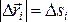 .
Путь ограничен точками С и D (рисунок
1.2.1.).
.
Путь ограничен точками С и D (рисунок
1.2.1.).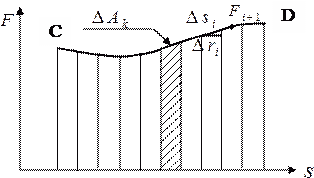
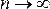 ),
приращения величин перейдут в бесконечно
малые величины
),
приращения величин перейдут в бесконечно
малые величины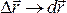 ,
,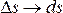 ,
а работа переменной силы на участке
пути
,
а работа переменной силы на участке
пути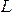 выражается
криволинейным интегралом:
выражается
криволинейным интегралом: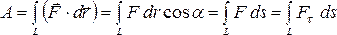 ,
где
,
где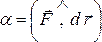 ,
, 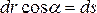 .
Если силу разложить на касательную
и нормальную составляющие, то
работу составляет только
.
Если силу разложить на касательную
и нормальную составляющие, то
работу составляет только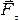 –
касательная составляющая силы,
направленная по касательной в каждой
точке траектории.
–
касательная составляющая силы,
направленная по касательной в каждой
точке траектории.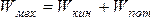
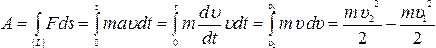 ,
гдеm –
масса тела,
,
гдеm –
масса тела, 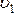 –
начальная скорость,
–
начальная скорость,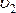 –конечная
скорость.
–конечная
скорость.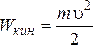 .
Если тело не движется, его кинетическая
энергия равна нулю.
.
Если тело не движется, его кинетическая
энергия равна нулю.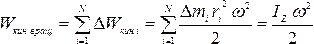 ,
где
,
где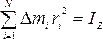 –
момент инерции тела относительно оси
вращения.
–
момент инерции тела относительно оси
вращения.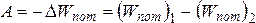 ,где –
приращение потенциальной энергии.
,где –
приращение потенциальной энергии.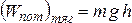 ,гдеh –
расстояние между телом и Землей. Для
потенциальной энергии обязательно
указывается нулевая конфигурация
системы, т.е. точка, где
,гдеh –
расстояние между телом и Землей. Для
потенциальной энергии обязательно
указывается нулевая конфигурация
системы, т.е. точка, где 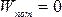 .
.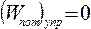 .
.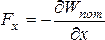 ;
; 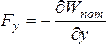 ;
;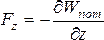 .
.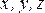 .
.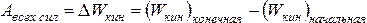 .
.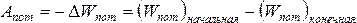 .
.