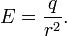Определение напряженность электрического поля: Напряжённость электрического поля — Википедия – Глава 1 электрическое поле — groupnk.ru — Группа НК — комплексные поставки электрооборудования в Москве и регионах

Содержание

Как определить напряженность электрического поля

Прежде чем выяснять, как определить напряженность электрического поля, нужно обязательно понять суть этого явления.

Свойства электрического поля

В создании электрического поля участвуют подвижные и неподвижные заряды. Наличие поля проявляется в его силовом воздействии на них. Кроме того, поле способно создавать индукцию зарядов, находящихся на поверхности проводников. Когда поле создается с помощью неподвижных зарядов, его считают стационарным электрическим полем. Другое название – электростатическое поле. Является одной из разновидностей электромагнитного поля, с помощью которого происходят все силовые взаимодействия, возникающие между заряженными частицами.

В чем измеряется напряженность электрического поля

Напряженность – есть векторная величина, оказывающая силовое воздействие на заряженные частицы. Величина определяется как отношение силы, направленной с его стороны, к величине точечного пробного электрозаряда в конкретной точке этого поля. Пробный электрозаряд вносится в электрополе специально, чтобы можно было рассчитать напряженность.

Кроме теории, существуют практические способы, как определить напряженность электрического поля:

В произвольном электрическом поле, необходимо взять тело, содержащее электрозаряд. Размеры этого тела должны быть меньше, чем размеры тела, с помощью которого генерируется электрическое поле. Для этой цели можно использовать небольшой металлический шарик с электрозарядом. Необходимо измерить заряд шарика с помощью электрометра и поместить в поле. Действующую на шарик силу необходимо уравновесить динамометром. После этого с динамометра снимаются показания, выраженные в ньютонах. Если значение силы разделить на величину заряда, то получится значение напряженности, выраженное в вольт/метр.

Напряженность поля в определенной точке, удаленной от заряда на какую-либо длину, вначале определяется измерением расстояния между ними. Затем, величина делится на полученное расстояние, возведенное в квадрат. К полученному результату применяется коэффициент 9*10^9.
В конденсаторе определение напряженности начинается с измерения напряжения между его пластинами с помощью вольтметра. Далее, необходимо измерить расстояние между пластинами. Значение в вольтах делится на расстояние между пластинами в метрах. Полученный результат и будет значением напряженности электрического поля.

Напряженность электрического поля — это… Что такое Напряженность электрического поля?

Напряжённость электрического по́ля — векторная характеристика электрического поля в данной точке, равная отношению силы 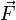$\vec F$ , действующей на пробный заряд, помещенный в данную точку поля, к величине этого заряда q:

$\vec E= \frac{\vec F}{q}$ .

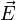По сути, $\vec E$ задает само векторное поле, поскольку его величина и направление меняется в пространстве от точки к точке.

Напряжённость электрического поля точечного заряда

Для системы СИ

Используя потенциал

Вектор 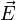$\vec E$ выражается как градиент потенциала, взятый с обратным знаком: 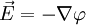$\vec E = - \nabla \varphi$ . К примеру, для точечного заряда, исходя из закона Кулона 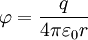$\varphi = \frac{q}{4 \pi \varepsilon_0 r}$ . Так как эквипотенциальные поверхности являются в этом случае сферами, то производная по нормали есть производная по радиусу. Таким образом мы можем прийти к так называемому кулоновскому полю:;

$E = - \frac{\partial \varphi}{\partial n}= -\frac{\partial }{\partial r } \left( \frac{q}{4 \pi \varepsilon_0 r} \right) = \frac{q}{ 4 \pi \varepsilon_0 r^2}$

Используя теорему Остроградского — Гаусса

Из формулы Остроградского-Гаусса вектор 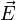$\vec E$ можно определить, зная плотность распределения зарядов. Согласно Формуле О-Г, а также используя уравнение Максвелла 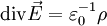$\operatorname{div}{\vec E}=\varepsilon_0^{-1} \rho$ , легко получить:

$\oint\limits_S \vec{E} \cdot \mathrm{d}\vec{S} = \int\limits_V \operatorname{div}{\vec E} \mathrm{d}V = \frac{1}{\varepsilon_0} \int\limits_V \rho \mathrm{d}V = \frac{q_{in}}{\varepsilon_0},$

где q_in — заряд, находящийся внутри замкнутой поверхности S, объемом V. В качестве поверхности интегрирования возьмем сферу (центральная симметрия), тогда

$\oint\limits_S \vec{E} \cdot \mathrm{d}\vec{S} = E \oint\limits_S \mathrm{d}\vec{S} = E \cdot 4 \pi r^2$

И самоочевидно:

$E=\frac{q}{4 \pi \varepsilon_0 r^2}$ .

Как и следовало ожидать, результаты полностью совпали.

Для системы СГС

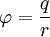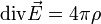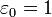Рассуждения аналогичны, вся разница лишь в том, что изменяется вид потенциала $\varphi = \frac{q}{r}$ , уравнение Максвелла $\operatorname{div}{\vec E}=4 \pi \rho$ и $\varepsilon_0 = 1$ . В итоге, получаем в системе СГС:

$E=\frac{q}{r^2}.$

Системы единиц

В системе СГС напряжённость электрического поля измеряется в СГСЭ единицах, в системе СИ — в Ньютонах на Кулон или в Вольтах на метр (В/м или V/m).

См. также

Wikimedia Foundation. 2010.

Напряженность электрического поля

Главное свойство электрического поля – способность действовать на электрические заряды с некоторой силой, поэтому естественно охарактеризовать электрическое поле с помощью силы, действующей на точечный положительный заряд, внесенный в это поле.

Напряженностью электрического поля в данной точке называют физическую величину, численно равную силе, действующей на единичный положительный заряд, помещенный в данную точку и имеющей направление этой силы:

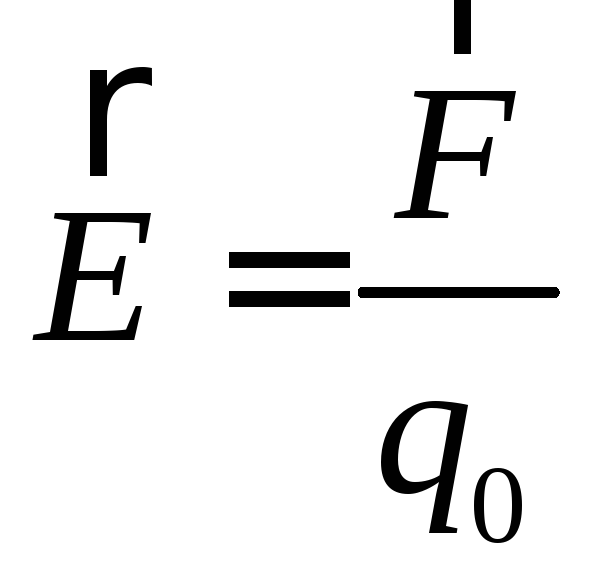. (6.2)

В частности, напряженность в любой точке поля, созданного точечным зарядом (как это следует из закона Кулона), равна

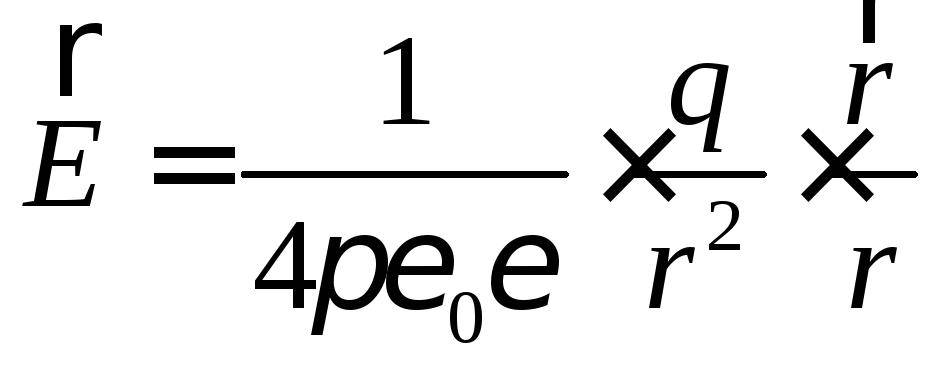. (6.3)

Н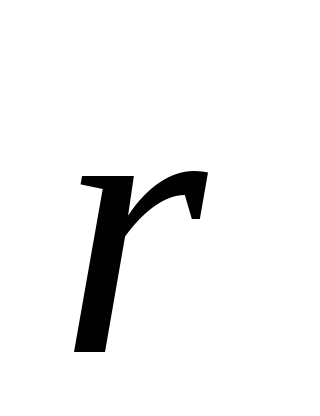апряженность поля не зависит от величины пробного заряда, а определяется величиной и знаком заряда, создающего поле, и положением (координатой) выбранной точки поля. Напряженность поля определяет величину и направление силы, действующей на заряд, помещенный в данную точку поля:

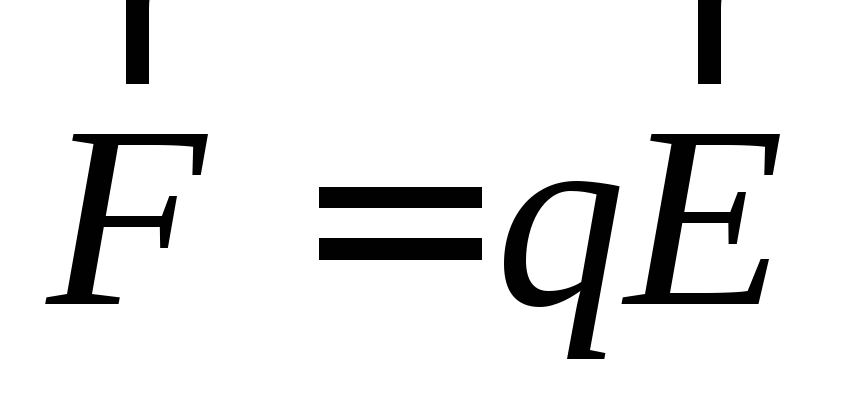(6.4)

Если поле создано двумя или несколькими зарядами, то электрическое поле каждого заряда (как утверждает опыт) не зависит друг от друга, и напряженность электрического поля, поэтому определяется как векторная сумма напряженностей полей, создаваемых отдельными зарядами (рис. 6.1). В этом состоит принцип суперпозиции полей:

. (*)

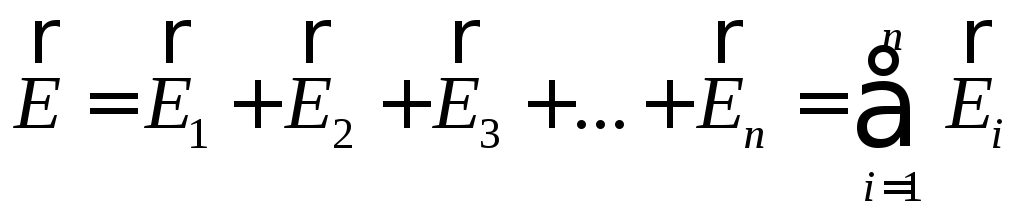Для наглядного (графического) описания электрических полей используется понятие силовой линии поля.

Силовой линией называют линию, проведенную в электрическом поле так (рис. 6.2), чтобы касательная в любой ее точке совпадала с направлением вектора напряженности. Силовой линии приписывают направление, совпадающее с направлением вектора напряженности в каждой ее точке. Так как каждой точке поля соответствует вполне определенный вектор напряженности поля, то силовые линии нигде не пересекаются.

Условились при изображении электрических полей с помощью линий напряженности, число силовых линий, проходящих через единичную поверхность, перпендикулярную к силовым линиям в данной точке поля, выбирать равным напряженности поля Е в данной точке (в этом состоит правило графического изображения полей с помощью силовых линий). При таком условии картина силовых линий электрического поля позволяет наглядно судить как о направлении, так и о величине напряженности поля в каждой точке.

Потенциал электрического поля

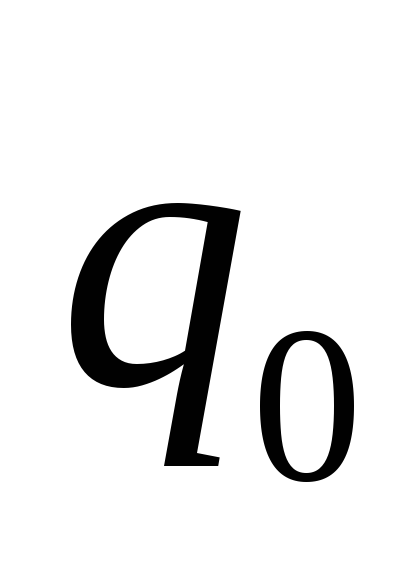
омимо напряженности электрическое поле характеризуется еще одной важной физической величиной – потенциалом.

Рассмотрим перемещение заряда q в поле другого точечного заряда q₀ из точки 1 в точку 2 (рис. 6.3). Работа силы F на элементарном перемещении dl определяется соотношением

, (6.5)

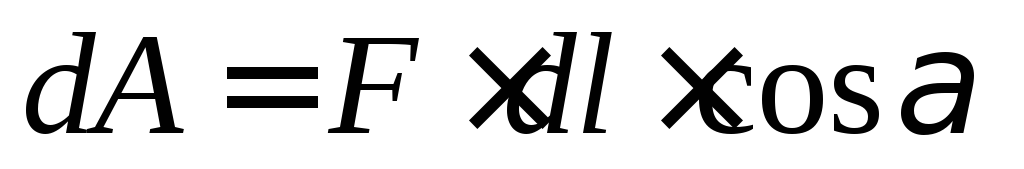
но , значит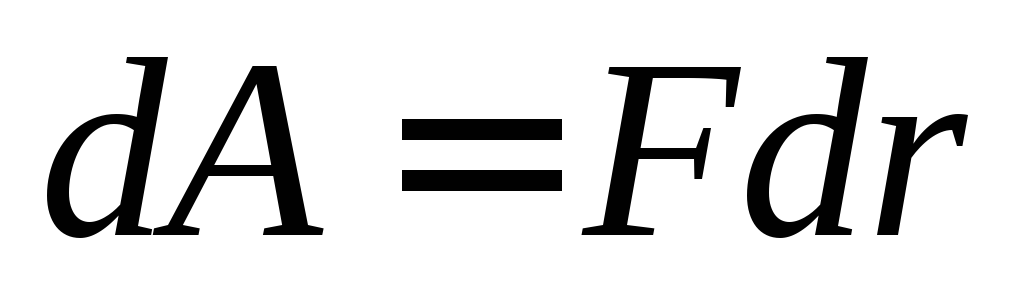. Подставим сюда вместо силы ее значение из закона Кулона, получим:

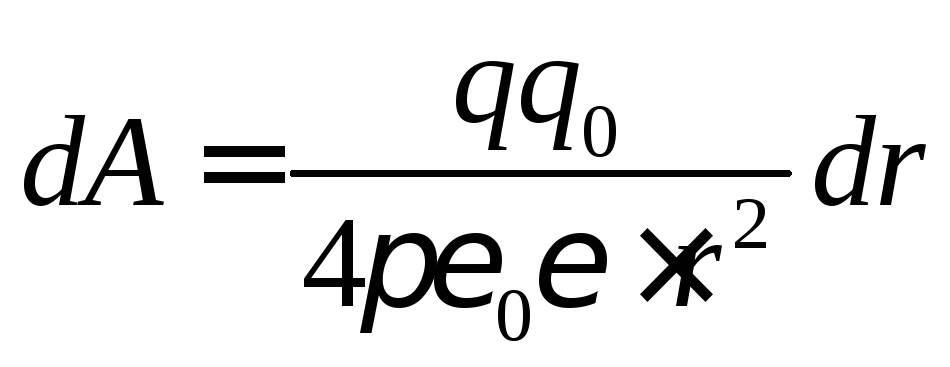. (6.6)

Для вычисления работы перемещения заряда из точки 1 в точку 2 по произвольному пути 1–2 проинтегрируем (6.6) в пределах от r₁до r₂, получим

. (6.7)

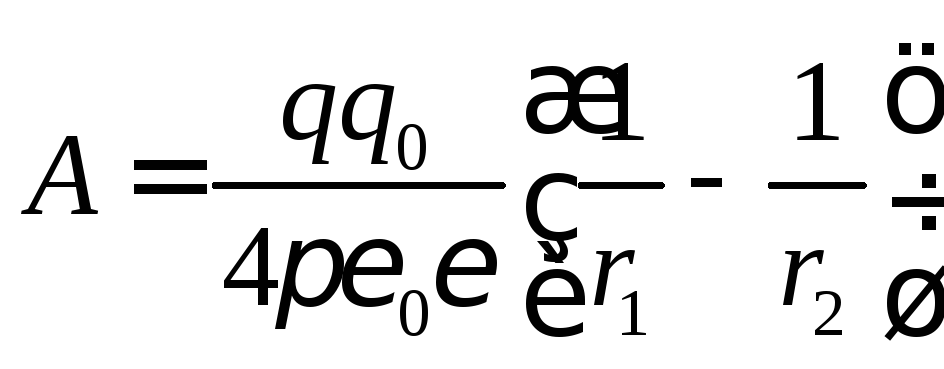
Из выражения (6.7) следует, что работа перемещения электрического заряда не зависит от формы пути, по которому перемещается заряд, а зависит только от начальной и конечной точек. Если заряд q, перемещаясь в электрическом поле, возвращается в исходную точку (r₂= r₁), то работа перемещения заряда по замкнутому пути в электростатическом поле равна нулю. Поля, обладающие указанным свойством, называются потенциальными.

Найдем отношение работы перемещения заряда к величине этого заряда:

. (6.8)

Эта величина не зависит от величины перемещаемого заряда и от пути, по которому он перемещается, и поэтому служит характеристикой поля, созданного зарядом

q₀ , и называется разностью потенциалов или электрическим напряжением.

Разность потенциалов двух точек 1 и 2 электрического поля измеряется работой, совершаемой полем при перемещении единичного положительного заряда между этими точками.

Следует подчеркнуть, что разность потенциалов имеет смысл характеристики поля потому, что работа перемещения заряда не зависит от формы пути. Действительно, если бы работа перемещения заряда зависела от пути, то при перемещении одного и того же заряда между теми же самыми точками поля, это отношение

A / q не являлось бы однозначной характеристикой этих точек поля.

Если выбрать какую-либо точку пространства в качестве начальной точки (точки отсчета), то любой точке можно сопоставить разность потенциалов относительно этой начальной точки.

Для случая поля точечного заряда наиболее простое математическое выражение для потенциала получается, если в качестве начальной выбрать любую точку, удаленную на бесконечность. Тогда работа перемещения положительного заряда q из бесконечности в данную точку поля, созданного другим точечным зарядом q₀ , будет равна

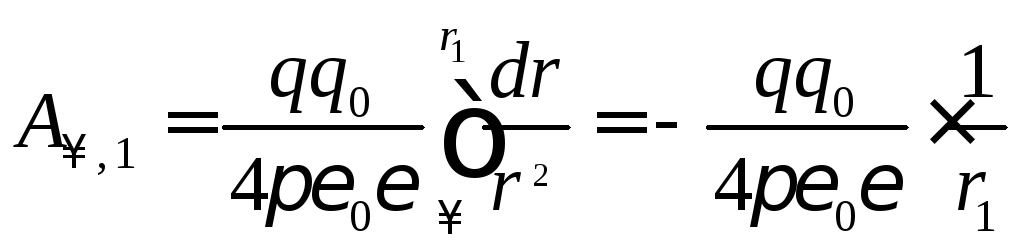. (6.9)

Отношение работы перемещения положительного заряда из бесконечности в данную точку поля к величине этого заряда (работа по перемещению единичного заряда) называется потенциалом данной точки поля:

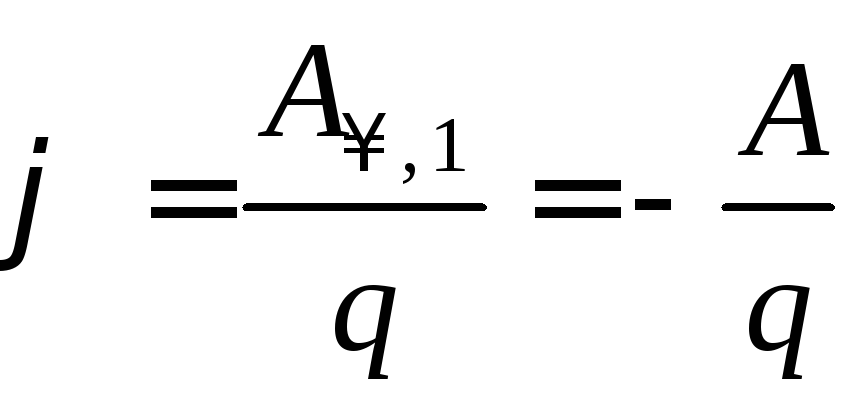. (6.10)

Знак минус в этом выражении означает, что в данном случае работа совершается внешними силами против сил поля.

Очевидно, что напряжение U между произвольными точками 1 и 2 электрического поля и потенциалы этих точек связаны простым соотношением

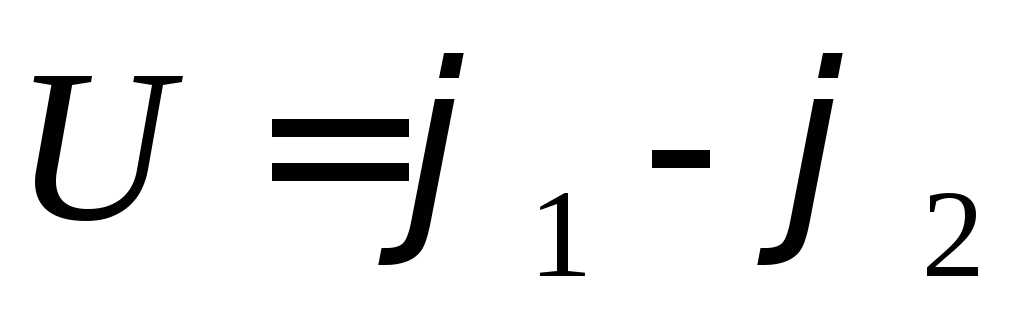. (6.11)

Для поля точечного заряда

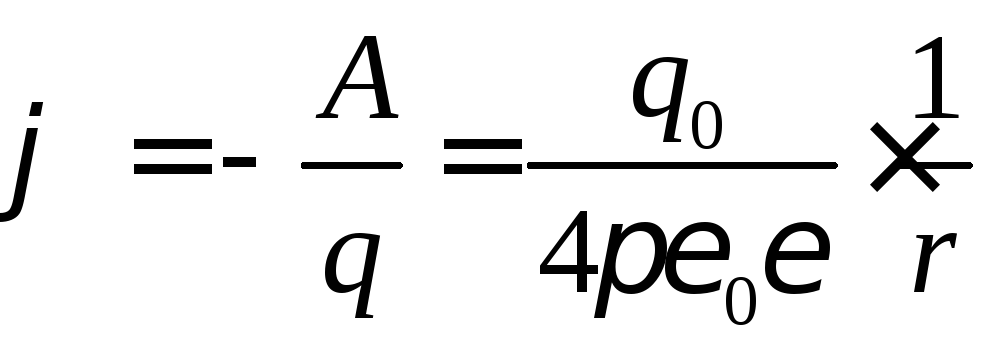. (6.12)

Потенциал любой точки поля, созданного положительным зарядом – положителен и убывает до нуля по мере удаления от заряда. Напротив – потенциал поля, созданного отрицательным зарядом, – отрицательная величина и растет до нуля по мере удаления от заряда.

з выражения для потенциала (6.12) следует, что потенциал любой точки сферической поверхностиS c центром в точке расположения заряда одинаков (рис. 6.4). Такие поверхности называются поверхностями равного потенциала или эквипотенциальными поверхностями.

Работу перемещения заряда можно выразить через разность потенциалов

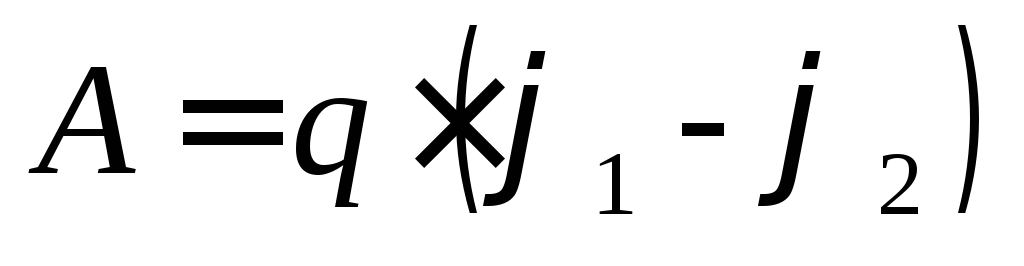. (6.13)

Отсюда следует, что работа перемещения заряда по эквипотенциальной поверхности равна нулю. Это значит, что сила, действующая на заряд, а следовательно, и вектор напряженности поля Е направлены перпендикулярно эквипотенциальной поверхности.

Используя эквипотенциальные поверхности, можно также дать графическое изображение электрического поля.

Результаты, полученные для поля точечного заряда, легко распространить на поля, созданные любым числом точечных зарядов, а так как любое заряженное тело можно представить как совокупность точечных зарядов, то и на поле, созданное любым заряженным телом.

Поля точечных зарядов в соответствии с принципом суперпозиции, накладываясь друг на друга, не влияют друг на друга. Поэтому потенциал поля любого числа зарядов будет равен алгебраической сумме потенциалов полей, созданных отдельными зарядами, т. е.:

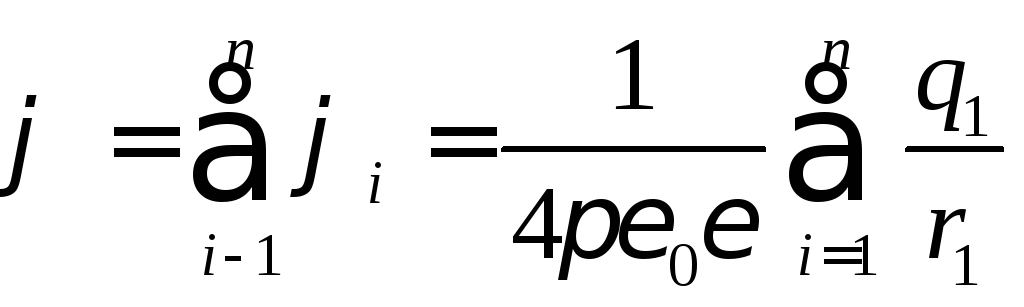. (6.14)

Таким образом, все вышеизложенное в отношении понятия потенциала справедливо и для поля, созданного заряженным телом любой формы, а величину потенциала, в принципе, можно вычислить по формуле (6.14).

Напряжение электрического поля

Электрические заряды не оказывают непосредственное воздействие друг на друга. Каждое заряженное тело может создавать электрическое поле в окружающем пространстве. Такое поле оказывает непосредственное силовое воздействие на остальные заряженные тела.

Электрическое поле и его свойства

Главным свойством электрического поля считается воздействие с определенной силой на электрические заряды. Иными словами, заряженные тела способны взаимодействовать друг с другом исключительно за счет электрических полей, их окружающих.

Исследовать электрическое поле, которое окружает заряженное тело, позволяет так называемый пробный заряд (точечный заряд, небольшой по величине). Такой заряд не может осуществлять заметного перераспределения рассматриваемых зарядов.

Определение 1

Электрическое поле для неподвижных и не изменяющихся со временем зарядов будет называться электростатическим. В большинстве случаев его называют просто электрическим полем.

Если за счет пробного заряда проводится исследование электрического поля, создаваемого несколькими электрически заряженными телами, результирующая сила становится равной геометрической сумме сил, воздействующих на пробный заряд отдельно со стороны каждого из заряженных тел.

Тогда напряженность электрического поля, формируемого системой зарядов в указанной точке пространства, будет зависеть от векторной суммы напряженностей электрополей, создаваемых зарядами в этой же точке по отдельности:

$\vec{E}=\vec{E_1}+vec{E_2}+…$

Такое свойство электрического поля подразумевает его подчинение принципу суперпозиции. Соответственно закону Кулона, напряженность электростатического поля, созданного за счет точечного заряда $Q$ на расстоянии $r$ от него определяет следующая формула:

$E=\frac{Q}{4\pi_0r^2}$

Такое поле названо кулоновским. В этом поле направление вектора $\vec{E}$ будет зависеть от знака заряда $Q$, если $Q$ > $0$, то $\vec{E}$ направляется по радиусу от заряда, если $Q$

С целью наглядного изображения электрополя задействуют силовые линии. Они проводятся таким образом, чтобы направление вектора $\vec{E}$ совпадало в каждой точке с направлением касательной к такой силовой линии. Изображение электрического поля за счет силовых линий требует соблюдения следующего условия: густота таких линий должна оказаться пропорциональной модулю вектора напряженности поля.

Кулоновское поле точечного заряда $Q$ лучше записывать в векторной форме. Для этого проводится радиус-вектор $\vec{r}$. от заряда $Q$ к точке наблюдения. Тогда при условии, что $Q$ > $0$,$\vec{E}$ оказывается параллельным $\vec{r}$. При условии, что $Q$

Пример 1

Примером использования принципа суперпозиции полей выступают силовые линии поля электрического диполя. Такие линии представляют систему из двух равнозначных по модулю зарядов разного знака $q$р, расположенных на определенном расстоянии $L$.

Напряженность однородного электрического поля

Определение 2

Чтобы количественно определить электрическое поле, вводится силовая характеристика в виде напряженности электрического поля. Напряженностью электрополя считается физическая величина, характеризуемая силой воздействия поля на пробный положительный заряд, помещенный в заданную точку пространства.

Определяется такая величина формулой:

$\vec{E}=\frac{\vec{F}}{q}$, где:

$E$ — напряженность электрического поля (Вольт/метр),
$F$ — сила, воздействующая на заряд Q (Ньютон),
$Q$ — заряд (Кулон).

Напряженность электрического поля представляет физическую векторную величину. В неоднородном поле сила, воздействующая на заряд в разных точках поля будет неодинаковой. Напряженность однородного электрополя считается прямо пропорциональной напряжению между пластинами и обратно пропорциональной расстоянию между ними:

$E=\frac{U}{d}$, где:

$E$ — напряженность однородного электрополя (Вольт/метр),
$U$ — напряжение, возникающее между пластинами (Вольт),
$d$ — расстояние между пластинами, которые заряжены (метр).

Напряженность магнитного электрического поля

Замечание 1

Напряженность магнитного электрического поля определяет сила, воздействующая на пробный магнит, помещенный в поле.

Поскольку магнитные полюсы не существуют по отдельности, мы наблюдаем воздействие на южный и северный полюсы пробного магнита противоположно направленных сил. При этом возникает момент пары сил, характеризующий величину напряженности поля в заданном месте.

В магнитном поле у цилиндрической катушки он будет прямо пропорциональным числу витков и силе тока, и при этом и обратно пропорциональным длине катушки.

Направление у вектора напряженности магнитного поля в каждой точке будет совпадающим с направлением силовых линий. Внутри самой катушки (магнита) он направляется от южного полюса к северному, а вне ее — от северного к южному.

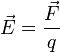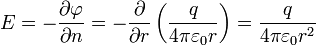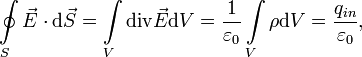
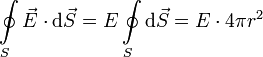
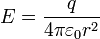Определение напряженность электрического поля: Напряжённость электрического поля — Википедия – Глава 1 электрическое поле