Лекция III.

Цель лекции №3.

Ознакомившись с данной лекцией, студенты должны знать:

1. Цель преобразования электрических цепей.

2. Четко различать участки с последовательным и параллельным соединениями при рассмотрении смешанного соединения проводов.

3. Уметь преобразовывать соединение треугольник в эквивалентную звезду и обратно.

4. Уметь преобразовать источник напряжения в источник тока и обратно.

Преобразование схем электрических цепей.

Целью преобразования электрических цепей является их упрощение, это необходимо для простоты и удобства расчета.

Одним из основных видов преобразования электрических схем является преобразование схем со смешанным соединением элементов. Смешанное соединение элементов

– это совокупность последовательных и параллельных соединений, которые и будут рассмотрены в начале данной лекции.

Последовательное соединение.

На рис. 3-1 изображена ветвь электрической цепи, в которой последовательно включены сопротивления R₁, R₂,…,R_n. Через все эти сопротивления проходит один и тот же ток I. Напряжения на отдельных участках цепи обозначим через U₁, U₂,…, U_n.

Рис. 3-1 Последовательное соединение.

По ЗНК напряжение на ветви

U=U₁+U₂+…+U_n= IR₁+IR₂+…+IR_n=I (R₁+R₂+…R_n)=IRэкв. (1)

Сумма сопротивлений всех участков данной ветви

Называется эквивалентным последовательным сопротивлением.

Поскольку напряжения, которые падают на отдельных сопротивлениях, пропорциональны этим сопротивлениям, можно сказать, что последовательно включенные сопротивления образуют «делитель напряжения». Понятие делителя напряжения широко используется в технике.

Параллельное соединение.

На рис. 3-2 изображена схема электрической цепи с двумя узлами, между которыми включено n параллельных ветвей с проводимостями G₁, G₂,…, G_n. Напряжение между узлами U, оно одинаково для всех ветвей.

Рис.3-2 Параллельное соединение (показать преобразованное).

По ЗТК общий то равен сумме токов отдельных ветвей:

I=I₁+I₂+…+I_n=G₁U+G₂U+…+G_nU=U (G₁+G₂+…+G_n)=UGэкв. (2)

Сумма проводимостей всех ветвей, соединенных параллельно

называется эквивалентной проводимостью.

В случае параллельного сопротивления двух ветвей (n=2) обычно пользуются выражениями, в которые входят сопротивления 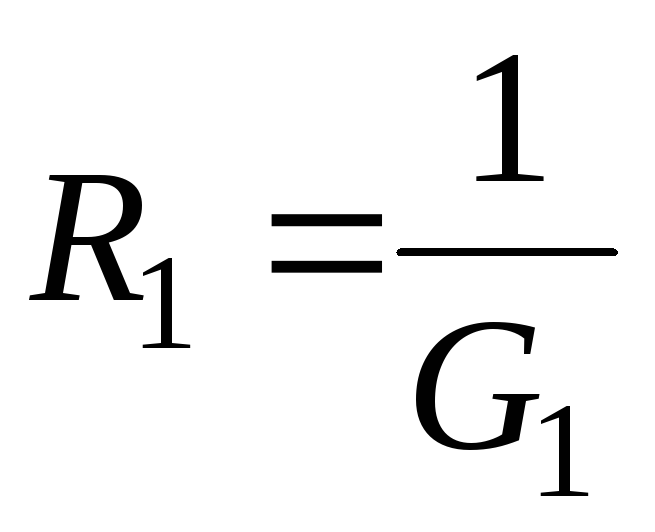и

.

Эквивалентное сопротивление двух параллельно соединенных ветвей равно:

. (3)

Поскольку общий ток делится на отдельные токи ветвей пропорционально проводимостям этих ветвей (или, что тоже самое, обратно пропорционально сопротивлениям этих ветвей), можно сказать, что параллельно включенные сопротивления образуют «делитель токов». Понятие делителя токов используется в технике.

Часто при использовании «ручного» расчета электрических цепей необходимо определить, как ток разделяется по отдельным ветвям параллельно соединенных ветвей.

Из формулы (2) следует, что токи ветвей, соединенных параллельно, пропорциональны проводимостям этих ветвей, т.е. токи делятся по ветвям пропорционально сопротивлениям этих ветвей, или, что тоже самое, обратно пропорционально сопротивлениям этих ветвей.

В случае двух параллельно соединенных сопротивления их общее сопротивление (2) равно:

, тогда суммарный ток I, протекающий по этому эквивалентному сопротивлению, создаст напряжение U, равное:

, чтобы найти ток I₁ в сопротивлении R₁, необходимо разделить выражение на R₁ , а чтобы найти ток I₂ в сопротивлении R₂ найти разделить выражение на R₂:

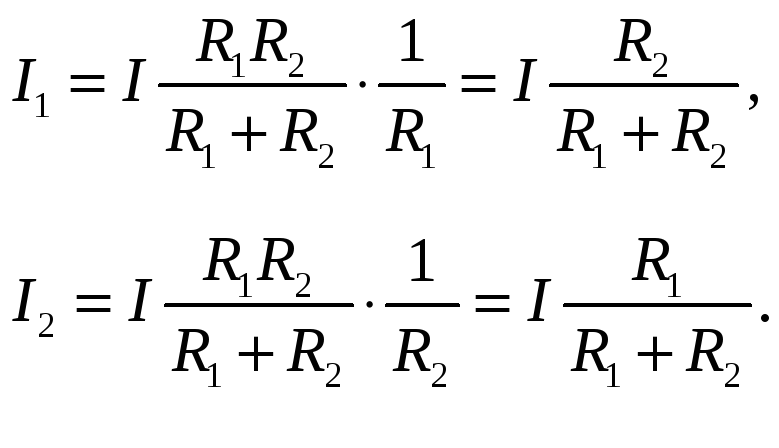
Полученные выражения для токов иногда называют «правилом плеч», которое гласит: ток делится между параллельно включенными сопротивлениями (в делителе токов) обратно пропорционально этим сопротивлениям.

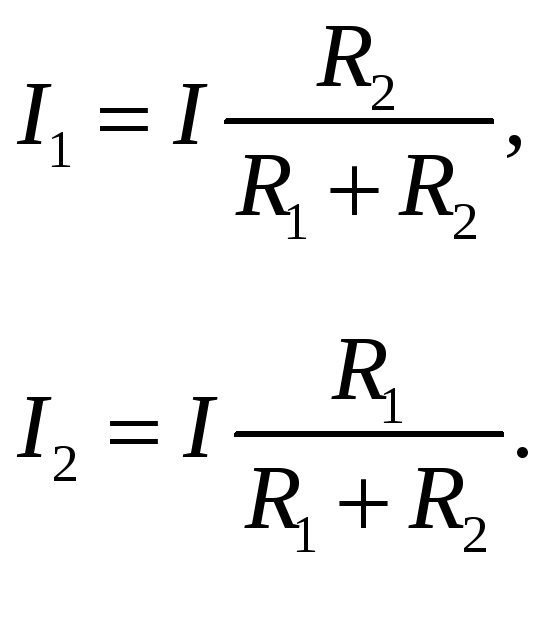(4)

Смешанное соединение.

На рис.3-3 показано смешанное соединение электрической цепи:

Рис.3-3 Смешанное соединение.

Эта схема легко приводится к одноконтурной. Сопротивления R₅ и R₆ включены параллельно, поэтому необходимо вычислить эквивалентное сопротивление данного участка по формуле

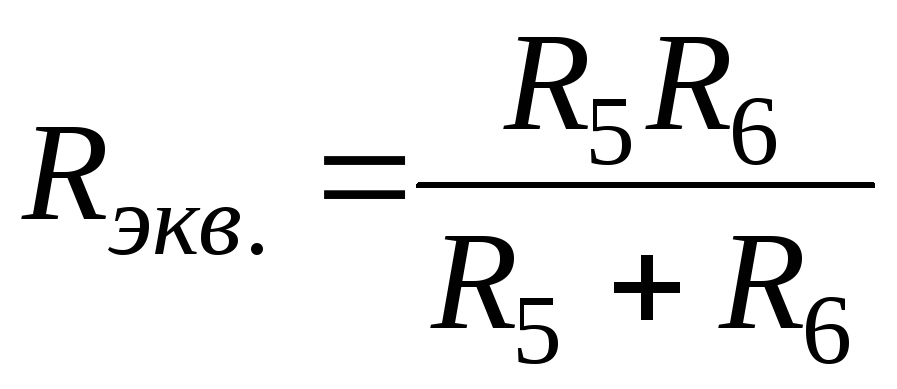
Для понимания полученного результата можно изобразить промежуточную схему (рис. 3-4).

Рис.3-4

Сопротивления R₃, R₄ и R^/_экв. соединены последовательно, и эквивалентное сопротивление участка c-e-f-d равно:

R_экв.=R₃+ R_экв.′ + R₄.

После этого этапа преобразований схема приобретает вид рис. 3-5.

Рис. 3-5

Затем находим эквивалентное сопротивление участка c-d и суммируем его с сопротивлением R₁. Общее эквивалентное сопротивление равно:

.

Полученное сопротивление эквивалентно сопротивлению (рис. 3-6) исходной схемы со смешанным соединением. Понятие “эквивалентно” означает, что напряжение U на входных зажимах и ток I входной ветви остаются неизменными на протяжении всех преобразований.

Рис. 3-6

Преобразование треугольника в эквивалентную звезду.

Преобразованием треугольника в эквивалентную звезду называется такая замена части цепи, соединенной по схеме треугольником, цепью, соединенной по схеме звезды, при которой токи и напряжения в остальной части цепи сохраняются неизменными.

Т.е., под эквивалентностью треугольника и звезды понимается то, что при одинаковых напряжениях между одноименными зажимами токи, входящие в одноименные выводы, одинаковы.

Рис. 3-7. Преобразование треугольника в звезду.

Пусть R₁₂; R₂₃

; R₃₁— сопротивления сторон треугольника;

R₁; R₂; R₃— сопротивления лучей звезды;

I₁₂; I₂₃; I₃₁— токи в ветвях треугольника;

I₁; I₂; I₃— токи, подходящие к зажимам 1, 2, 3.

Выразим токи в ветвях треугольника через подходящие токи I₁, I₂, I₃.

По закону напряжений Кирхгофа сумма падений напряжений в контуре треугольника равна нулю:

I₁₂R₁₂+I₂₃R₂₃+I₃₁R₃₁=0

По закону токов Кирхгофа для узлов 1 и 2

I₃₁=I₁₂+I₁; I₂₃=I₁₂+I₂

При решении этих уравнений относительно I₁₂ получим:

Напряжение между точками 1 и 2 схемы треугольника:

Напряжение между этими же точками схемы звезды равно:

U₁₂=I₁R₁ — I₂R₂.

Т.к. речь идет об эквивалентном преобразовании, то необходимо равенство напряжений между данными точками двух схем, т.е.

Это возможно при условии:

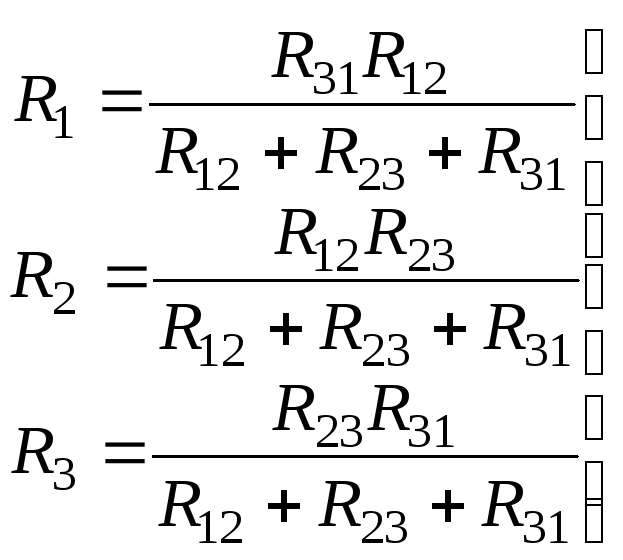
(5)

Третье выражение получено в результате круговой замены индексов.

Исходя из выражения (5) формулируется следующее правило:

Сопротивление луча звезды равно произведению сопротивлений сторон треугольника, прилегающих к этому лучу, деленному на сумму сопротивлений трех сторон треугольника.

Преобразование звезды в эквивалентный треугольник.

При переходе от звезды к треугольнику известными являются сопротивления R₁, R₂, R₃ лучей звезды. Значения сопротивлений треугольника определяются в результате совместного решения уравнений (5):

(6)

Сопротивление стороны треугольника равно сумме сопротивлений прилегающих лучей звезды и произведения их, деленного на сопротивление третьего луча.

Лекция III.

Цель лекции №3.

Ознакомившись с данной лекцией, студенты должны знать:

1. Цель преобразования электрических цепей.

2. Четко различать участки с последовательным и параллельным соединениями при рассмотрении смешанного соединения проводов.

3. Уметь преобразовывать соединение треугольник в эквивалентную звезду и обратно.

4. Уметь преобразовать источник напряжения в источник тока и обратно.

Преобразование схем электрических цепей.

Целью преобразования электрических цепей является их упрощение, это необходимо для простоты и удобства расчета.

Одним из основных видов преобразования электрических схем является преобразование схем со смешанным соединением элементов. Смешанное соединение элементов – это совокупность последовательных и параллельных соединений, которые и будут рассмотрены в начале данной лекции.

Последовательное соединение.

На рис. 3-1 изображена ветвь электрической цепи, в которой последовательно включены сопротивления R₁, R₂,…,R_n. Через все эти сопротивления проходит один и тот же ток I. Напряжения на отдельных участках цепи обозначим через U₁, U₂,…, U_n.

Рис. 3-1 Последовательное соединение.

По ЗНК напряжение на ветви

U=U₁+U₂+…+U_n= IR₁+IR₂+…+IR_n=I (R₁+R₂+…R_n)=IRэкв. (1)

Сумма сопротивлений всех участков данной ветви

Называется эквивалентным последовательным сопротивлением.

Поскольку напряжения, которые падают на отдельных сопротивлениях, пропорциональны этим сопротивлениям, можно сказать, что последовательно включенные сопротивления образуют «делитель напряжения». Понятие делителя напряжения широко используется в технике.

Параллельное соединение.

На рис. 3-2 изображена схема электрической цепи с двумя узлами, между которыми включено n параллельных ветвей с проводимостями G₁, G₂,…, G_n. Напряжение между узлами U, оно одинаково для всех ветвей.

Рис.3-2 Параллельное соединение (показать преобразованное).

По ЗТК общий то равен сумме токов отдельных ветвей:

I=I₁+I₂+…+I_n=G₁U+G₂U+…+G_nU=U (G₁+G₂+…+G_n)=UGэкв. (2)

Сумма проводимостей всех ветвей, соединенных параллельно

называется эквивалентной проводимостью.

В случае параллельного сопротивления двух ветвей (n=2) обычно пользуются выражениями, в которые входят сопротивления и .

Эквивалентное сопротивление двух параллельно соединенных ветвей равно:

. (3)

Поскольку общий ток делится на отдельные токи ветвей пропорционально проводимостям этих ветвей (или, что тоже самое, обратно пропорционально сопротивлениям этих ветвей), можно сказать, что параллельно включенные сопротивления образуют «делитель токов». Понятие делителя токов используется в технике.

Часто при использовании «ручного» расчета электрических цепей необходимо определить, как ток разделяется по отдельным ветвям параллельно соединенных ветвей.

Из формулы (2) следует, что токи ветвей, соединенных параллельно, пропорциональны проводимостям этих ветвей, т.е. токи делятся по ветвям пропорционально сопротивлениям этих ветвей, или, что тоже самое, обратно пропорционально сопротивлениям этих ветвей.

В случае двух параллельно соединенных сопротивления их общее сопротивление (2) равно:

, тогда суммарный ток I, протекающий по этому эквивалентному сопротивлению, создаст напряжение U, равное:

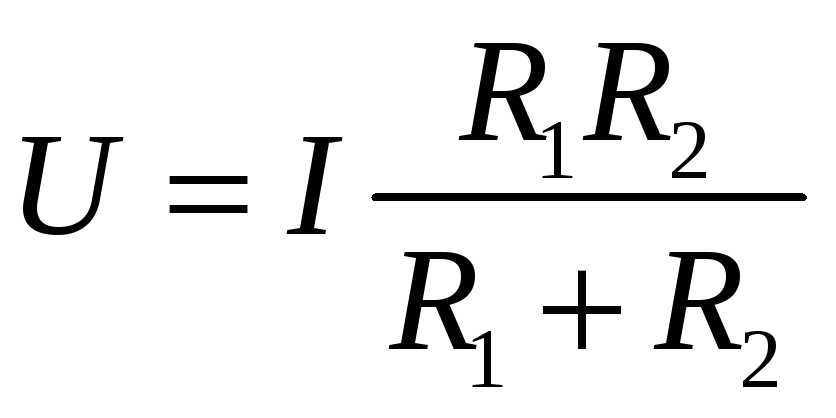, чтобы найти ток I₁ в сопротивлении R₁, необходимо разделить выражение на R₁ , а чтобы найти ток I₂ в сопротивлении R₂ найти разделить выражение на R₂:

Полученные выражения для токов иногда называют «правилом плеч», которое гласит: ток делится между параллельно включенными сопротивлениями (в делителе токов) обратно пропорционально этим сопротивлениям.

(4)

Смешанное соединение.

На рис.3-3 показано смешанное соединение электрической цепи:

Рис.3-3 Смешанное соединение.

Эта схема легко приводится к одноконтурной. Сопротивления R₅ и R₆ включены параллельно, поэтому необходимо вычислить эквивалентное сопротивление данного участка по формуле

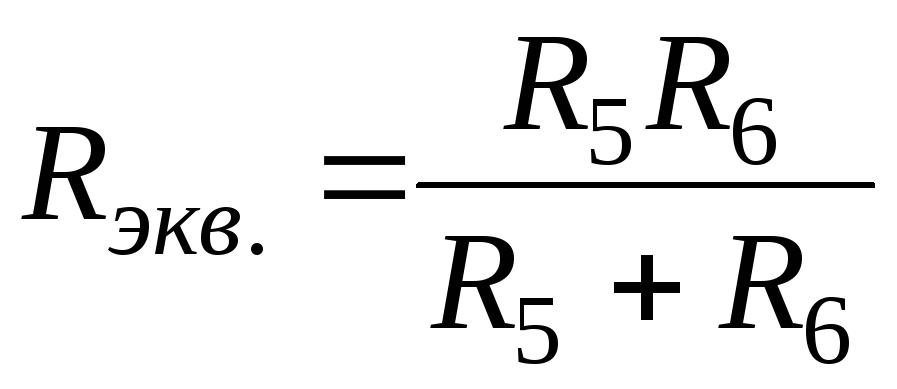
Для понимания полученного результата можно изобразить промежуточную схему (рис. 3-4).

Рис.3-4

Сопротивления R₃, R₄ и R^/_экв. соединены последовательно, и эквивалентное сопротивление участка c-e-f-d равно:

R_экв.=R₃+ R_экв.′ + R₄.

После этого этапа преобразований схема приобретает вид рис. 3-5.

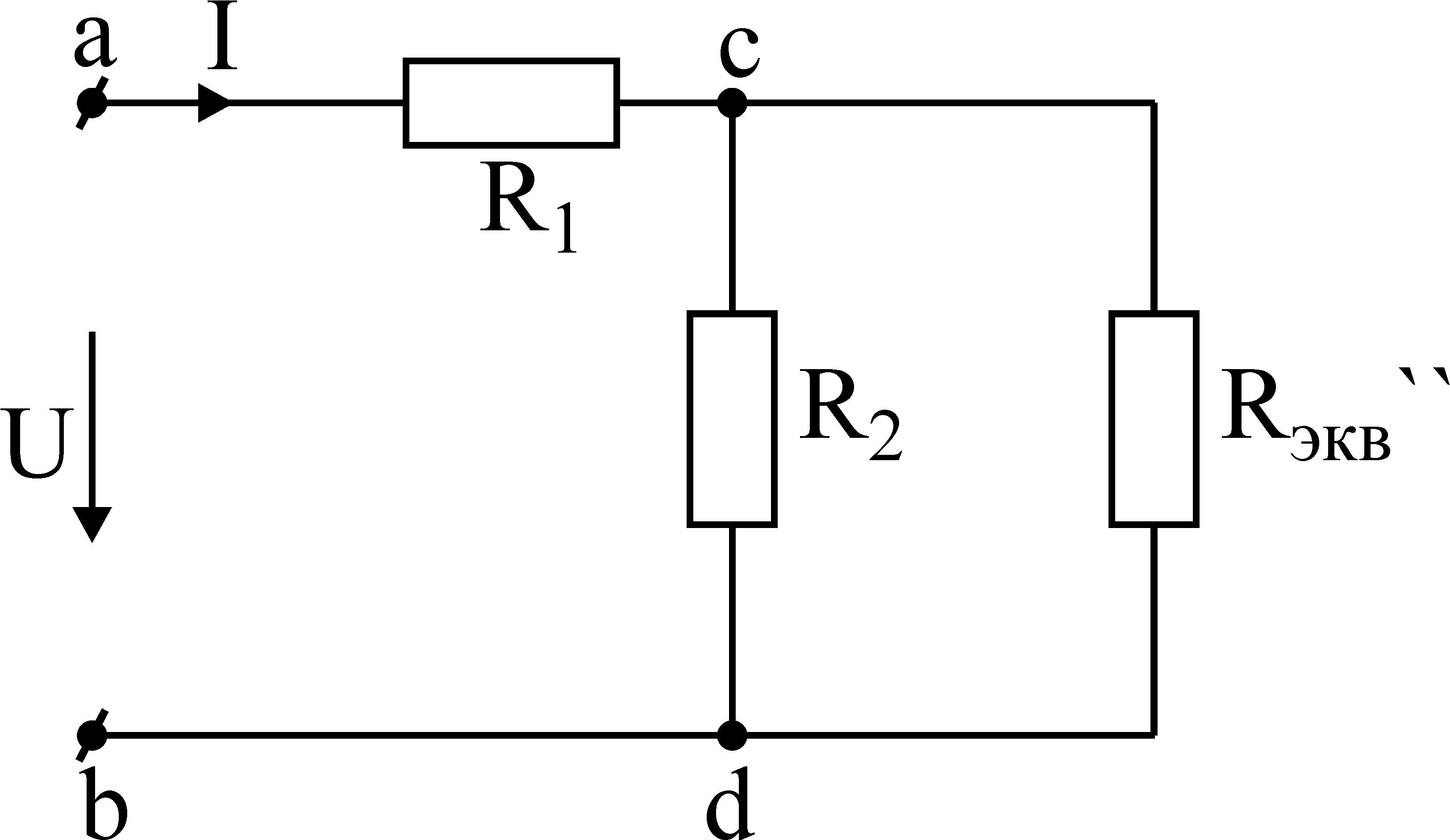
Рис. 3-5

Затем находим эквивалентное сопротивление участка c-d и суммируем его с сопротивлением R₁. Общее эквивалентное сопротивление равно:

.

Полученное сопротивление эквивалентно сопротивлению (рис. 3-6) исходной схемы со смешанным соединением. Понятие “эквивалентно” означает, что напряжение U на входных зажимах и ток I входной ветви остаются неизменными на протяжении всех преобразований.

Рис. 3-6

Преобразование треугольника в эквивалентную звезду.

Преобразованием треугольника в эквивалентную звезду называется такая замена части цепи, соединенной по схеме треугольником, цепью, соединенной по схеме звезды, при которой токи и напряжения в остальной части цепи сохраняются неизменными.

Т.е., под эквивалентностью треугольника и звезды понимается то, что при одинаковых напряжениях между одноименными зажимами токи, входящие в одноименные выводы, одинаковы.

Рис. 3-7. Преобразование треугольника в звезду.

Пусть R₁₂; R₂₃; R₃₁— сопротивления сторон треугольника;

R₁; R₂; R₃— сопротивления лучей звезды;

I₁₂; I₂₃; I₃₁— токи в ветвях треугольника;

I₁; I₂; I₃— токи, подходящие к зажимам 1, 2, 3.

Выразим токи в ветвях треугольника через подходящие токи I₁, I₂, I₃.

По закону напряжений Кирхгофа сумма падений напряжений в контуре треугольника равна нулю:

I₁₂R₁₂+I₂₃R₂₃+I₃₁R₃₁=0

По закону токов Кирхгофа для узлов 1 и 2

I₃₁=I₁₂+I₁; I₂₃=I₁₂+I₂

При решении этих уравнений относительно I₁₂ получим:

Напряжение между точками 1 и 2 схемы треугольника:

Напряжение между этими же точками схемы звезды равно:

U₁₂=I₁R₁ — I₂R₂.

Т.к. речь идет об эквивалентном преобразовании, то необходимо равенство напряжений между данными точками двух схем, т.е.

Это возможно при условии:

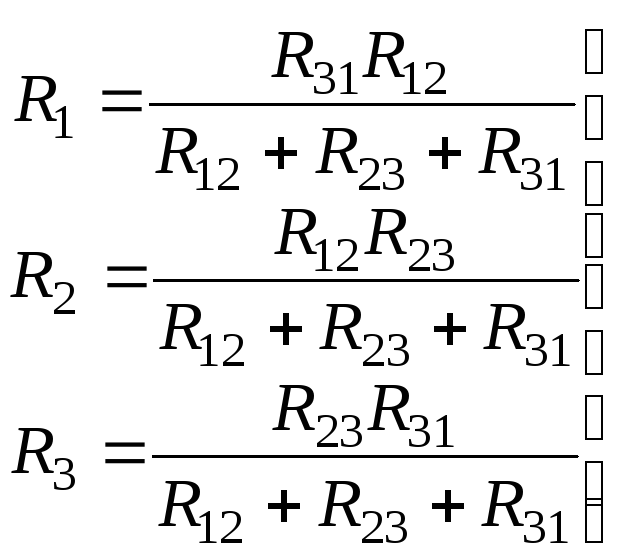
(5)

Третье выражение получено в результате круговой замены индексов.

Исходя из выражения (5) формулируется следующее правило:

Сопротивление луча звезды равно произведению сопротивлений сторон треугольника, прилегающих к этому лучу, деленному на сумму сопротивлений трех сторон треугольника.

Преобразование звезды в эквивалентный треугольник.

При переходе от звезды к треугольнику известными являются сопротивления R₁, R₂, R₃ лучей звезды. Значения сопротивлений треугольника определяются в результате совместного решения уравнений (5):

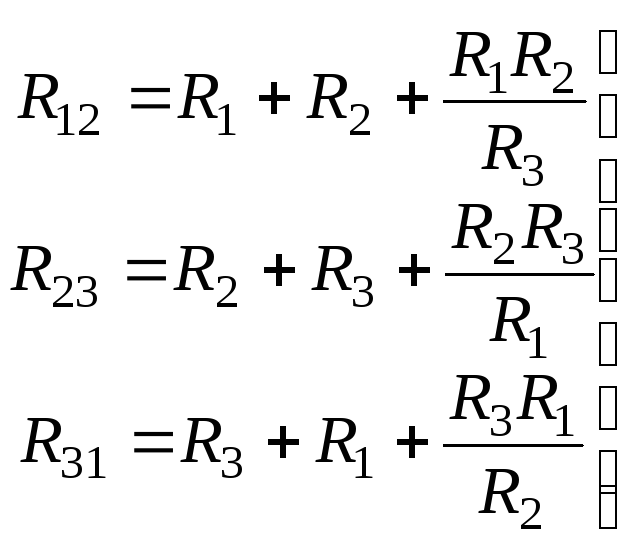(6)

Сопротивление стороны треугольника равно сумме сопротивлений прилегающих лучей звезды и произведения их, деленного на сопротивление третьего луча.

Расчет электрических цепей постоянного тока

Расчет обычных цепей неизменного тока

Целью расчёта электронной цепи неизменного тока является определение неких характеристик на базе начальных данных, из условия задачки. На практике употребляют несколько способов расчёта обычных цепей. Какой-то из них базируется на применении эквивалентных преобразований, позволяющих упростить цепь.

Под эквивалентными преобразованиями в электронной цепи предполагается подмена одних частей другими таким макаром, чтоб электрические процессы в ней не поменялись, а схема упрощалась. Одним из видов таких преобразований является подмена нескольких потребителей, включённых поочередно либо параллельно, одним эквивалентным.

Несколько поочередно соединённых потребителей можно поменять одним, причём его эквивалентное сопротивление равно сумме сопротивлений потребителей, включённых поочередно. Для n потребителей можно записать:

rэ = r1 +r2+…+rn ,

где r1 , r2, …, rn – сопротивления каждого из n потребителей.

При параллельном соединении n потребителей эквивалентная проводимость gэ равна сумме проводимостей отдельных частей, включённых параллельно:

gэ= g1 + g2 +…+ gn .

Беря во внимание, что проводимость является оборотной величиной по отношению к сопротивлению, можно эквивалентное сопротивление найти из выражения:

1/rэ = 1/r1 + 1/r2 +…+ 1/rn,

где r1, r2, …, rn – сопротивления каждого из n потребителей, включённых параллельно.

В личном случае, когда параллельно включены два потребителя r1 и r2, эквивалентное сопротивление цепи:

rэ = (r1 х r2)/(r1 + r2)

Преобразования в сложных цепях, где отсутствует в очевидном виде последовательное и параллельное соединение частей (набросок 1), начинают с подмены частей, включённых в начальной схеме треугольником, на эквивалентные элементы, соединённые звездой.

Набросок 1. Преобразование частей цепи: а — соединённых треугольником, б — в эквивалентную звезду

На рисунке 1, а треугольник частей образуют потребители r1, r2, r3. На рисунке 1, б этот треугольник заменён эквивалентными элементами ra, rb, rc, соединёнными звездой. Чтоб не происходило изменение потенциалов в точках a, b, с схемы, сопротивления эквивалентных потребителей определяются из выражений:

Упрощение начальной цепи можно также выполнить подменой частей, соединённых звездой, схемой, в какой потребители соединены треугольником.

В схеме, изображённой на рисунке 2, а, можно выделить звезду, образованную потребителями r1, r3, r4. Эти элементы включены меж точками c, b, d. На рисунке 2, б меж этими точками находятся эквивалентные потребители rbc, rcd, rbd, соединённые треугольником. Сопротивления эквивалентных потребителей определяются из выражений:

Набросок 2. Преобразование частей цепи: а — соединённых звездой, б — в эквивалентный треугольник

Предстоящее упрощение схем, приведённых на рисунках 1, б и 2, б, можно производить оковём подмены участков с поочередным и параллельным соединением частей их эквивалентными потребителями.

При практической реализации способа расчёта обычный цепи при помощи преобразований выявляются в цепи участки с параллельным и поочередным соединением потребителей, а потом рассчитываются эквивалентные сопротивления этих участков.

Если в начальной цепи в очевидном виде нет таких участков, то, применяя описанные ранее переходы от треугольника частей к звезде либо от звезды к треугольнику, проявляют их.

Данные операции позволяют упростить цепь. Применив их пару раз, приходят к виду с одним источником и одним эквивалентным потребителем энергии. Дальше, применяя законы Ома и Кирхгофа, рассчитывают токи и напряжения на участках цепи.

Расчет сложных цепей неизменного тока

В процессе расчёта сложной цепи нужно найти некие электронные характеристики (сначала токи и напряжения на элементах) на базе начальных величин, данных в условии задачки. На практике употребляются несколько способов расчёта таких цепей.

Для определения токов веток можно использовать: способ, базирующийся на основании конкретного внедрения законов Кирхгофа, способ контурных токов, способ узловых напряжений.

Для проверки корректности вычисления токов нужно составить баланс мощностей. Из закона сохранения энергии следует, что алгебраическая сумма мощностей всех источников питания цепи равна арифметической сумме мощностей всех потребителей.

Мощность источника питания равна произведению его ЭДС на величину тока, протекающего через данный источник. Если направление ЭДС и тока в источнике совпадают, то мощность выходит положительной. В неприятном случае она отрицательна.

Мощность потребителя всегда положительна и равна произведению квадрата тока в потребителе на величину его сопротивления.

Математически баланс мощностей можно записать в последующем виде:

где n – количество источников питания в цепи; m – количество потребителей.

Если баланс мощностей соблюдается, то расчет токов выполнен верно.

В процессе составления баланса мощностей можно узнать, в каком режиме работает источник питания. Если его мощность положительна, то он дает энергию во внешнюю цепь (к примеру, как аккумулятор в режиме разряда). При отрицательном значении мощности источника последний потребляет энергию из цепи (аккумулятор в режиме заряда).

Пацкевич В. А.

Школа для электрика

Расчет электрической цепи: онлайн кальлкулятор

Студенты, которые проходят курс ТОЭ или практикующие инженеры так или иначе должны знать, как рассчитать электрическую цепь. Это несложный, но кропотливый процесс, который требует повышенной внимательности, ведь нужно учесть множество формул, знаков и размерностей. К тому же метод расчета зависит от рода тока, наличия нелинейных элементов или реактивных мощностей. Давайте рассмотрим, что нужно для самостоятельных вычислений, а также как выполнить расчет электрической цепи, используя онлайн калькулятор.

В простейшем случае результатом расчетов является вычисление электрической мощности и её коэффициента (cos Ф). Однако иногда необходимо знать эквивалентное сопротивление элементов нагрузки, эти данные вы можете получить онлайн с помощью нашего калькулятора, когда известно напряжение:

Рассмотрим, как рассчитать электрическую цепь. Для начала нужно вспомнить законы или правила Кирхгофа:

1. Сумма токов в узле цепи равна нулю. Простыми словами — сколько электричества вошло, столько и вышло через точку соединения нескольких ветвей.
2. Сумма ЭДС равна сумме падений напряжения в замкнутом контуре.

Кроме этого нам понадобится Закон Ома, базовые сведения о работе с комплексными числами, понятия активного и реактивного сопротивления и мощности. Комплексные числа в теоретических основах электротехники занимают значимое место во многих задачах, и если нет специализированных калькуляторов, то работа с ними очень затруднительна.

Также полезно знать о том, что работу любой элетросхемы можно представить в виде векторной диаграммы, тогда углы отклонения токов и напряжений зависят от рода нагрузки. При резистивной они направлены в одну сторону, а при индуктивной, емкостной или смешанной — отклонены друг от друга. Угол отклонения используется при вычислении коэффициентов мощности.

Надеемся, предоставленный онлайн калькулятор для расчета электроцепи был для вас полезным! Если возникли вопросы, задавайте их в комментариях под статьей.