Номиналы резисторов. Таблица, онлайн калькулятор

В 1952 году IEC (IEC — международная электротехническая комиссия) утвердила стандартные значения для резисторов, называемый номинальный ряд резисторов.

История создание номинального ряда резисторов началась в первые годы прошлого века, в то время когда большинство резисторов были углеродно-графитовыми с относительно большими производственными допусками (отклонениями).

Паяльная станция 2 в 1 с ЖК-дисплеем

Мощность: 800 Вт, температура: 100…480 градусов, поток возду…

Идея создания номинального ряда довольно простая — установить стандартные значения для резисторов на основе допусков, с которыми они могут быть изготовлены.

Номиналы резисторов

Рассмотрим это на простом примере. Допустим, есть группа резисторов имеющих 10% отклонение от номинала (как в большую, так и в меньшую сторону).

Предположим, что первое предпочтительное значение должно быть равно 100 Ом.

Следовательно, не имеет смысла изготавливать резистор, например на 105 Ом, так как резистор с сопротивлением 105 Ом падает в 10% диапазон допуска резистор на 100 Ом (90…110 Ом).

Поэтому следующее рациональное значение сопротивления должно быть в районе 120 Ом, поскольку резисторы на 100 Ом с допуском 10% имеют значение где-то между 90 Ом и 110 Ом, резистор 120 Ом имеет значение в диапазоне между 108 и 132 Ом, перекрывая тем самым диапазон между 100 и 120 Ом.

Следуя этой логике, стандартные номиналы резисторов с отклонением 10% в диапазоне между 100 и 1000 Ом будут следующие: 100, 120, 150, 180, 220, 270, 330 и так далее (с соответствующим округлением). Это серия резисторов, имеющая маркировку E12, приведена в таблице ниже.

Номиналы резисторов — таблица

Буква «Е» обозначает, что резистор из номинального ряда EIA. Идущее после буквы «Е» число указывает на количество логарифмических шагов в диапазоне от 100 до 1000.

Ниже, в таблице номиналов резисторов, приведены значения сопротивления в диапазоне 100…1000. Сопротивление в любом другом диапазоне (Ом, кОм, мОм) могут быть получены простым делением или умножением данных из таблицы на 10.

Держатель для платы

Материал: АБС + металл, размер зажима печатной платы (max): 20X14 см…

Отличия между сериями:

• Е6 — допуск 20%,
• E12 — допуск 10%
• E24 — допуск 5% (и 2%)
• Е48 — допуск 2%
• E96 — допуск 1%
• E192 — допуск 0,5, 0,25, 0,1% и выше

Номиналы резисторов — онлайн калькулятор

Для удобства приводим калькулятор для быстрого подбора сопротивления из стандартного номинального ряда резисторов.

Примечание: в окошко «Введите необходимое сопротивление» вписывайте значение без префиксов (кОм, МОм). Например, для поиска ближайшего значения для сопротивления 38 Ом – вводим 38. То же самое справедливо и для 38 кОм – вводим 38 (не забывая, что результат относится к кОм)

Калькулятор цветовой маркировки резисторов — Расчёты

33. 1kΩ ± 1%

Маркировка EIA-96

Высокоточные резисторы в сочетании с малыми размерами создали необходимость иметь более компактную маркировку для SMD резисторов. Поэтому была создана система маркировки EIA-96. Основана на серии E96 и предназначена для резисторов с допуском 1%.

В этой системе резистор маркируется тремя знаками: 2 цифры для обозначения значения резистора и 1 буква для множителя. Два первых числа представляют код, который указывает значение сопротивления с тремя значащими цифрами. В таблице ниже приведены значения для каждого кода, которые в основном являются значениями из серии E96. Например, код 04 означает 107 Ом, а 60 означает 412 Ом. Коэффициент умножения дает конечное значение резистора, например:

Использование буквы предотвращает путаницу с другими системами маркировки. Однако обратите внимание, что буква R используется в обеих системах. Для резисторов с допусками, отличными от 1%, существуют разные буквенные таблицы.

Код	Делитель
Z	0.001
Y/R	0.01
X/S	0.1
A	1
B/H	10
C	100
D	1`000
E	10`000
F	100`000

Код	Значение	Код	Значение	Код	Значение	Код	Значение	Код	Значение	Код	Значение
01	100	17	147	33	215	49	316	65	464	81	681
02	102	18	150	34	221	50	324	66	475	82	698
03	105	19	154	35	226	51	332	67	487	83	715
04	107	20	158	36	232	52	340	68	499	84	732
05	110	21	162	37	237	53	348	69	511	85	750
06	113	22	165	38	243	54	357	70	523	86	768
07	115	23	169	39	249	55	365	71	536	87	787
08	118	24	174	40	255	56	374	72	549	88	806
09	121	25	178	41	261	57	383	73	562	89	825
10	124	26	182	42	267	58	392	74	576	90	845
11	127	27	187	43	274	59	402	75	590	91	866
12	130	28	191	44	280	60	412	76	604	92	887
13	133	29	196	45	287	61	422	77	619	93	909
14	137	30	200	46	294	62	432	78	634	94	931
15	140	31	205	47	301	63	442	79	649	95	953
16	143	32	210	48	309	64	453	80	665	96	976

Мощность SMD резистора

Чтобы узнать приблизительную мощность SMD-резистора, измерьте его длину и ширину.

В таблице ниже представлены несколько часто используемых размеров с соответствующими типичными номинальными мощностями. Используйте эту таблицу только в качестве руководства и всегда обращайтесь к спецификации компонента для точного значения.

Типоразмер	Размер в дюймах(ДxШ)	Размер в мм (ДxШ)	Мощность
0201	0.024″ x 0.012″	0.6 мм x 0.3 мм	0,05Вт
0402	0.04″ x 0.02″	1.0 мм x 0.5 мм	0,0625Вт
0603	0.063″ x 0.031″	1.6 мм x 0.8 мм	0,0625Вт
0805	0.08″ x 0.05″	2.0 мм x 1.25 мм	0.1Вт
1206	0.126″ x 0.063″	3.2 мм x 1.6 мм	0.125Вт
1210	0.126″ x 0.10″	3.2 мм x 2. 5 мм	0.25Вт
1812	0.18″ x 0.12″	4.5 мм x 3.2 мм	0.33Вт
2010	0.20″ x 0.10″	5.0 мм x 2.5 мм	0.5Вт
2512	0.25″ x 0.12″	6.35 мм x 3.2 мм	1Вт

.res-eia { margin: 20px 0;} .res-eia .res-eia-bord {margin: 10px auto;width: 360px;border: 1px solid #999;} .res-eia .calc .imp {color: #f00;} .res-eia .calc td {padding: 5px 10px;vertical-align: middle;} .res-eia .math2 {font-weight: bold;} .res-eia .copyr {text-align: right;padding: 0 10px 0;font-size: 10px;background: #F9F9F9;border-top: 1px solid #999;} .table-eia {text-align: center;margin: 20px 0;} .table-eia tr th {background: white;border: 1px solid #ddd;height: auto;padding: 0px 3px;font-size: 14px;line-height: 18px;} .table-eia table {border-collapse: separate;width: auto;margin: 0 auto;}

Онлайн калькулятор цветовой маркировки сопротивления резисторов

Автор Юлия На чтение 5 мин.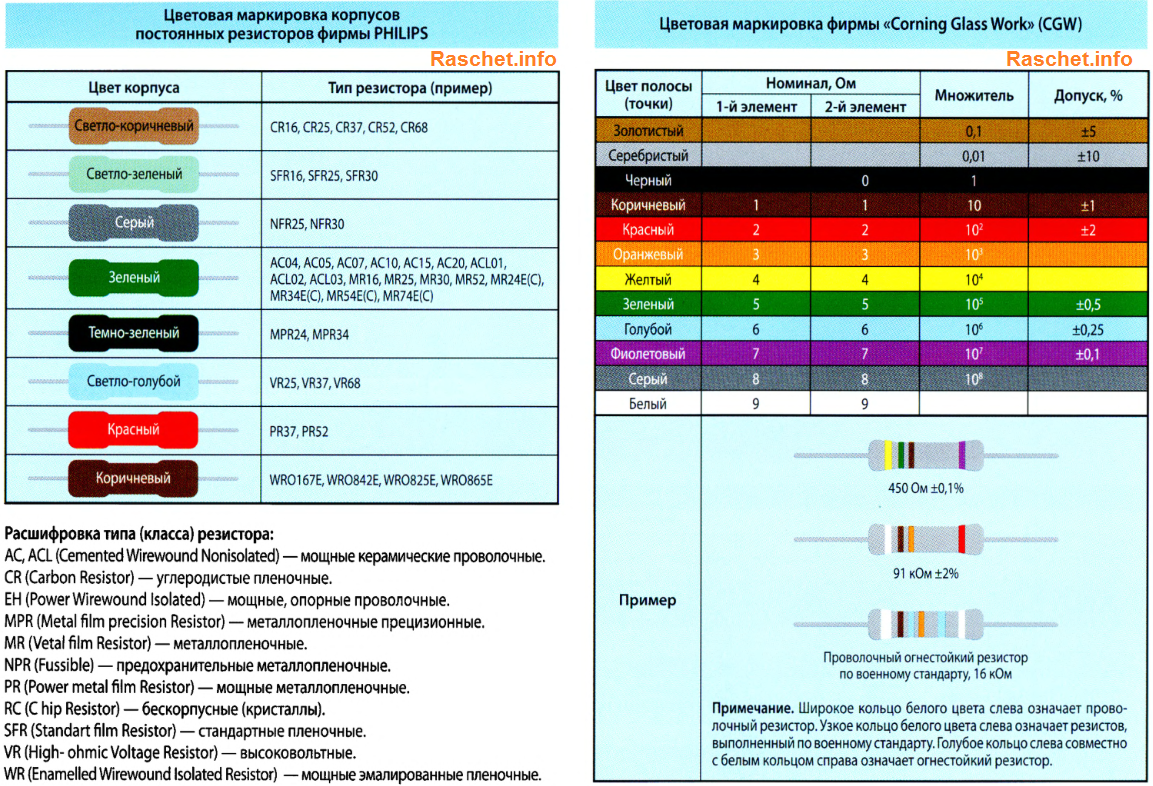 Просмотров 2.5k. Опубликовано 25.12.2019 Обновлено 25.12.2019

Резисторы, в особенности малой мощности — довольно мелкие детали, резистор мощностью 0,125Вт имеет длину несколько миллиметров и диаметр порядка миллиметра. Прочитать на такой детали цифровой номинал сложно, и для них применяют маркировку цветными полосами.

Калькулятор позволяет рассчитывать сопротивление и допуск сопротивления резисторов с цветовой маркировкой в виде 4 или 5 цветных колец. Резистор необходимо расположить так, чтобы кольца были сдвинуты к левому краю или широкая полоса была бы слева.

Основная задача любого резистора – линейное преобразование силы тока (ампер) в напряжение (вольт), ограничение силы тока, ослабление источника питания и поглощение электроэнергии. Резисторы используют во всех сложных схемах и для работы сложных полупроводников. С учетом малого размера элемента нанесение читаемых буквенных или цифровых обозначений невозможно, поэтому применяется цветная маркировка. В статье мы разберем, что означают цветные точки и линии, их цвет, и объясним, как правильно подобрать резистор.

Вводные данные

Для начала обратимся к Википедии, которая дает четкое понимание, что из себя представляет любой резистор. В дословном переводе с английского термин означает сопротивление. И действительно, назначение резисторов с постоянным или переменным значение – линейное преобразование силы тока в напряжение, напряжения в силу и т.д.

Маркировочный цвет, порядок и шифрование цифровых кодов в резисторах определены ГОСТ 175-72 в соответствии с требованиями Публикации 62 Международной электротехнической комиссии. Согласно этим нормативам для идентификации применяются кольца, цвет и количество которых четко регламентированы

Полосы всегда смещены относительно одного вывода, читаются при этом как в арабской письменности — слева направо. Если размер пассивного элемента не позволяет визуально заметно обозначить начало, ширину первой полосы делают толще других приблизительно в 1,5-2 раза.

На резисторах с минимальной величиной допуска (до 10%) наносятся 5 колец, из которых:

• 1, 2, 3 – коэффициент сопротивления, ед.изм. Ом;
• 4 – множитель;
• 5 – максимально допустимое отклонение.

С допустимым отклонением от 10% уже четыре полосы, где:

• 1, 2, 3 – коэффициент сопротивления, ед.изм. Ом;
• 4 – множитель.

Резисторы с допуском 20% имеют только 3 полосы, где также отклонение не указано, но на коэффициент сопротивления отведено только первых 2 кольца.

Мощность резистора можно определить по его габаритам.

Нечасто, но можно встретить и 6-полосное маркирование, где:

• 1, 2, 3 – величина сопротивления, ед.изм. Ом;
• 4 – множитель;
• 5 – нормативный допуск;
• 6 — температурный коэффициент изменения

Последняя (шестая) полоса нужна для понимания того, насколько будет изменяться сопротивление, если корпус пассивного элемента начнет нагреваться.

ВИДЕО: Как работает резистор

Для чего нужны опознавательные признаки?

Самые маленькие резисторы мощностью 0,125 wt длиной всего 3-4 мм, а диаметр – 1 мм. Даже прочитать любую информацию на такой миниатюрке сложно, не говоря уже о том, чтобы нанести ее. Можно, конечно, написать силу тока, например, 4К7, что соответствует 4700 Ом, но этой информации крайне недостаточно.

Цветовая маркировка резисторов гораздо более практична ввиду следующего:

• наносится очень просто;
• легко читаема;
• содержит всю требуемую информацию о номинальных параметрах;
• остается сохранной и видимой в течение всего срока работы.

Также с помощью подсчета количества полос можно определить точность параметров:

• 3 – погрешность 20%;
• 4 – 5-10%;
• 5-6 – 0-0,9%

Для того, чтобы точно узнать, какой именно нужен резистор и с какими полосками, можно самостоятельно установить по таблице или воспользоваться онлайн-калькулятором (в конце статьи).

Универсальная таблица:

С помощью этих табличных значений можно быстро определить номинал пассивного элемента, при этом значение имеет очередность полоски или точки, что позволяет получить числовые данные.

Цвета означают разные данные – цифра отметки, множитель и допустимое отклонение.

Пример:

С помощью универсальной таблицы прочтем, что скрыто на данном элементе. Итак, имеем 4 полосы:

• коричневая,
• черная,
• красная,
• серебристая.

Напоминаем, читать полосы надо слева направо, а единица измерения Ом.

Никогда не маркируется первыми черный, золотой и белый цвета.

Расшифровка:

1. Первое место занимает коричневая полоса, которая обозначает одновременно цифровой символ (1) и множитель (10).
2. Черная (0) – при таком сочетании электрическое сопротивление обозначает 1 кОм – 1К0.
3. Красная – множитель, равен 100.
4. Серебристая – обозначение максимально допустимое отклонение, которое здесь составляет 10%. Эти же данные можно получить путем простого подсчета количества полосок.

Как «прочитать» проволочные резисторы

К этой разновидности пассивных элементов применяется все тот же ГОСТ 175-72 и Публикация 62 МЭК, соответственно, цвета, количество полос и порядок аналогичны «бочонкам», но есть определенные нюансы:

• самая широкая полоса – белая, не читается и обозначает только тип элемента;
• более 4-х десятичных показателей не наносятся;
• последняя в ряду полоса определяет отличительные свойства, зачастую это огнеупорность.

С учетом указанных особенностей лучше сопоставлять данные со сводной таблицей именно проволочных образцов.

Зарубежная продукция

И хотя наши стандарты полностью соответствуют международным, а Публикация 62 и вовсе является императивным стандартом, некоторые компании используют свои правила нанесения полос и выбора цвета, с которыми нужно считаться:

Philips

Имеет свой стандарт символов и цветов, согласно которым наравне с номинальными показателями, резистор передает информацию о технологии производства и характеристике компонентов.

CGW и Panasonic

Используют дополнительные цвета для обозначения дополнительных свойств пассивных элементов цепи.

В целом, все маркировки совпадают с ранее приведенными значениями и таблицами, только эти компании еще больше упростили задачу идентификации номинала. При этом резисторы взаимозаменяемы и никаких требований относительно оригинала ни Philips, ни CGW и Panasonic не выдвигают.

Для того, чтобы точно понимать, какие рабочие характеристики требуются и какие резисторы следует покупать для определенной цели, воспользуйтесь простым сервисом

Путем введения исходных данных можно получить информацию по каждому маркировочному цвету, которому соответствует определенный цифровой код.

ВИДЕО: Расчет сопротивления резистора

Суммарное сопротивление при последовательном соединении. Онлайн калькулятор расчета сопротивления последовательно соединенных резисторов.

Сопротивление параллельной цепи Содержание:

Течение тока в электрической цепи осуществляется по проводникам, в направлении от источника к потребителям. В большинстве подобных схем используются медные провода и электрические приемники в заданном количестве, обладающие различным сопротивлением. В зависимости выполняемых задач, в электрических цепях используется последовательное и параллельное соединение проводников. В некоторых случаях могут быть применены оба типа соединений, тогда этот вариант будет называться смешанным. Каждая схема имеет свои особенности и отличия, поэтому их нужно обязательно заранее учитывать при проектировании цепей, ремонте и обслуживании электрооборудования.

Последовательное соединение проводников

В электротехнике большое значение имеет последовательное и параллельное соединение проводников в электрической цепи. Среди них часто используется схема последовательного соединения проводников предполагающая такое же соединение потребителей. В этом случае включение в цепь выполняется друг за другом в порядке очередности. То есть, начало одного потребителя соединяется с концом другого при помощи проводов, без каких-либо ответвлений.

Свойства такой электрической цепи можно рассмотреть на примере участков цепи с двумя нагрузками. Силу тока, напряжение и сопротивление на каждом из них следует обозначить соответственно, как I1, U1, R1 и I2, U2, R2. В результате, получились соотношения, выражающие зависимость между величинами следующим образом: I = I1 = I2, U = U1 + U2, R = R1 + R2. Полученные данные подтверждаются практическим путем с помощью проведения измерений амперметром и вольтметром соответствующих участков.

Таким образом, последовательное соединение проводников отличается следующими индивидуальными особенностями:

• Сила тока на всех участках цепи будет одинаковой.
• Общее напряжение цепи составляет сумму напряжений на каждом участке.
• Общее сопротивление включает в себя сопротивления каждого отдельного проводника.

Данные соотношения подходят для любого количества проводников, соединенных последовательно. Значение общего сопротивления всегда выше, чем сопротивление любого отдельно взятого проводника. Это связано с увеличением их общей длины при последовательном соединении, что приводит и к росту сопротивления.

Если соединить последовательно одинаковые элементы в количестве n, то получится R = n х R1, где R — общее сопротивление, R1 — сопротивление одного элемента, а n — количество элементов. Напряжение U, наоборот, делится на равные части, каждая из которых в n раз меньше общего значения. Например, если в сеть с напряжением 220 вольт последовательно включаются 10 ламп одинаковой мощности, то напряжение в любой из них составит: U1 = U/10 = 22 вольта.

Проводники, соединенные последовательно, имеют характерную отличительную особенность. Если во время работы отказал хотя-бы один из них, то течение тока прекращается во всей цепи. Наиболее ярким примером является , когда одна перегоревшая лампочка в последовательной цепи, приводит к выходу из строя всей системы.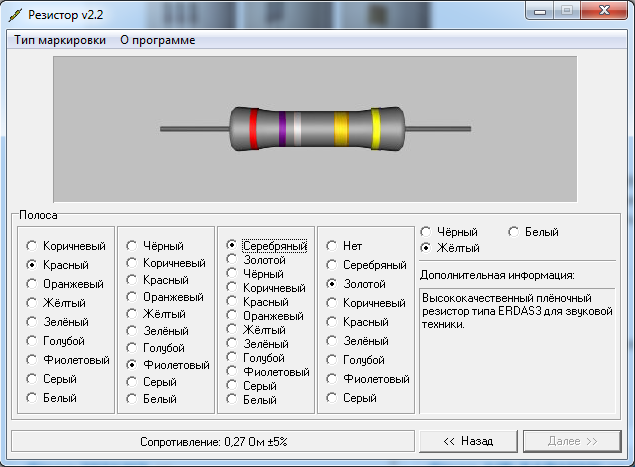 Для установления перегоревшей лампочки понадобится проверка всей гирлянды.

Параллельное соединение проводников

В электрических сетях проводники могут соединяться различными способами: последовательно, параллельно и комбинированно. Среди них параллельное соединение это такой вариант, когда проводники в начальных и конечных точках соединяются между собой. Таким образом, начала и концы нагрузок соединяются вместе, а сами нагрузки располагаются параллельно относительно друг друга. В электрической цепи могут содержаться два, три и более проводников, соединенных параллельно.

Если рассматривать последовательное и параллельное соединение, сила тока в последнем варианте может быть исследована с помощью следующей схемы. Берутся две лампы накаливания, обладающие одинаковым сопротивлением и соединенные параллельно. Для контроля к каждой лампочке подключается собственный . Кроме того, используется еще один амперметр, контролирующий общую силу тока в цепи. Проверочная схема дополняется источником питания и ключом.

После замыкания ключа нужно контролировать показания измерительных приборов. Амперметр на лампе № 1 покажет силу тока I1, а на лампе № 2 — силу тока I2. Общий амперметр показывает значение силы тока, равное сумме токов отдельно взятых, параллельно соединенных цепей: I = I1 + I2. В отличие от последовательного соединения, при перегорании одной из лампочек, другая будет нормально функционировать. Поэтому в домашних электрических сетях используется параллельное подключение приборов.

С помощью такой же схемы можно установить значение эквивалентного сопротивления. С этой целью в электрическую цепь добавляется вольтметр. Это позволяет измерить напряжение при параллельном соединении, сила тока при этом остается такой же. Здесь также имеются точки пересечения проводников, соединяющих обе лампы.

В результате измерений общее напряжение при параллельном соединении составит: U = U1 = U2. После этого можно рассчитать эквивалентное сопротивление, условно заменяющее все элементы, находящиеся в данной цепи. При параллельном соединении, в соответствии с законом Ома I = U/R, получается следующая формула: U/R = U1/R1 + U2/R2, в которой R является эквивалентным сопротивлением, R1 и R2 — сопротивления обеих лампочек, U = U1 = U2 — значение напряжения, показываемое вольтметром.

Следует учитывать и тот фактор, что токи в каждой цепи, в сумме составляют общую силу тока всей цепи. В окончательном виде формула, отражающая эквивалентное сопротивление будет выглядеть следующим образом: 1/R = 1/R1 + 1/R2. При увеличении количества элементов в таких цепях — увеличивается и число слагаемых в формуле. Различие в основных параметрах отличают друг от друга и источников тока, позволяя использовать их в различных электрических схемах.

Параллельное соединение проводников характеризуется достаточно малым значением эквивалентного сопротивления, поэтому сила тока будет сравнительно высокой. Данный фактор следует учитывать, когда в розетки включается большое количество электроприборов. В этом случае сила тока значительно возрастает, приводя к перегреву кабельных линий и последующим возгораниям.

Законы последовательного и параллельного соединения проводников

Данные законы, касающиеся обоих видов соединений проводников, частично уже были рассмотрены ранее.

Для более четкого их понимания и восприятия в практической плоскости, последовательное и параллельное соединение проводников, формулы следует рассматривать в определенной последовательности:

• Последовательное соединение предполагает одинаковую силу тока в каждом проводнике: I = I1 = I2.
• параллельное и последовательное соединение проводников объясняет в каждом случае по-своему. Например, при последовательном соединении, напряжения на всех проводниках будут равны между собой: U1 = IR1, U2 = IR2. Кроме того, при последовательном соединении напряжение составляет сумму напряжений каждого проводника: U = U1 + U2 = I(R1 + R2) = IR.
• Полное сопротивление цепи при последовательном соединении состоит из суммы сопротивлений всех отдельно взятых проводников, независимо от их количества.
• При параллельном соединении напряжение всей цепи равно напряжению на каждом из проводников: U1 = U2 = U.
• Общая сила тока, измеренная во всей цепи, равна сумме токов, протекающих по всем проводникам, соединенных параллельно между собой: I = I1 + I2.

Для того чтобы более эффективно проектировать электрические сети, нужно хорошо знать последовательное и параллельное соединение проводников и его законы, находя им наиболее рациональное практическое применение.

Смешанное соединение проводников

В электрических сетях как правило используется последовательное параллельное и смешанное соединение проводников, предназначенное для конкретных условий эксплуатации. Однако чаще всего предпочтение отдается третьему варианту, представляющему собой совокупность комбинаций, состоящих из различных типов соединений.

В таких смешанных схемах активно применяется последовательное и параллельное соединение проводников, плюсы и минусы которых обязательно учитываются при проектировании электрических сетей. Эти соединения состоят не только из отдельно взятых резисторов, но и довольно сложных участков, включающих в себя множество элементов.

Смешанное соединение рассчитывается в соответствии с известными свойствами последовательного и параллельного соединения. Метод расчета заключается в разбивке схемы на более простые составные части, которые считаются отдельно, а потом суммируются друг с другом.

Проверим справедливость показанных здесь формул на простом эксперименте.

Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.

Замер общего сопротивления при последовательном соединении

Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.

Измерение сопротивления при параллельном соединении

Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:

При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.

Что ещё нужно учитывать при соединении резисторов?

Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт . Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?

Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А ), а сопротивление каждого из них равно 50 Ом , тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт . В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт .

Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.

Подробнее о мощности рассеивания резистора читайте .

Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.

Темы кодификатора ЕГЭ : параллельное и последовательное соединение проводников, смешанное соединение проводников.

Есть два основных способа соединения проводников друг с другом — это последовательное и параллельное соединения. Различные комбинации последовательного и параллельного соединений приводят к смешанному соединению проводников.

Мы будем изучать свойства этих соединений, но сначала нам понадобится некоторая вводная информация.

Проводник, обладающий сопротивлением , мы называем резистором и изображаем следующим образом (рис. 1 ):

Рис. 1. Резистор

Напряжение на резисторе — это разность потенциалов стационарного электрического поля между концами резистора. Между какими именно концами? В общем-то, это неважно, но обычно удобно согласовывать разность потенциалов с направлением тока.

Ток в цепи течёт от «плюса» источника к «минусу». В этом направлении потенциал стационарного поля убывает. Напомним ещё раз, почему это так.

Пусть положительный заряд перемещается по цепи из точки в точку , проходя через резистор (рис. 2 ):

Рис. 2.

Стационарное поле совершает при этом положительную работу .

Так как alt=»q > 0″> и alt=»A > 0″> , то и alt=»\varphi_a — \varphi_b > 0″> , т. е. alt=»\varphi_a > \varphi_b»> .

Поэтому напряжение на резисторе мы вычисляем как разность потенциалов в направлении тока: .

Сопротивление подводящих проводов обычно пренебрежимо мало; на электрических схемах оно считается равным нулю. Из закона Ома следует тогда, что потенциал не меняется вдоль провода: ведь если и , то . (рис. 3 ):

Рис. 3.

Таким образом, при рассмотрении электрических цепей мы пользуемся идеализацией, которая сильно упрощает их изучение. А именно, мы считаем, что потенциал стационарного поля изменяется лишь при переходе через отдельные элементы цепи, а вдоль каждого соединительного провода остаётся неизменным . В реальных цепях потенциал монотонно убывает при движении от положительной клеммы источника к отрицательной.

Последовательное соединение

При последовательном соединении проводников конец каждого проводника соединяется с началом следующего за ним проводника.

Рассмотрим два резистора и , соединённых последовательно и подключённых к источнику постоянного напряжения (рис. 4 ). Напомним, что положительная клемма источника обозначается более длинной чертой, так что ток в данной схеме течёт по часовой стрелке.

Рис. 4. Последовательное соединение

Сформулируем основные свойства последовательного соединения и проиллюстрируем их на этом простом примере.

1. При последовательном соединении проводников сила тока в них одинакова.
В самом деле, через любое поперечное сечение любого проводника за одну секунду будет проходить один и тот же заряд. Ведь заряды нигде не накапливаются, из цепи наружу не уходят и не поступают в цепь извне.

2. Напряжение на участке, состоящем из последовательно соединённых проводников, равно сумме напряжений на каждом проводнике .

Действительно, напряжение на участке — это работа поля по переносу единичного заряда из точки в точку ; напряжение на участке — это работа поля по переносу единичного заряда из точки в точку . Складываясь, эти две работы дадут работу поля по переносу единичного заряда из точки в точку , то есть напряжение на всём участке:

Можно и более формально, без всяких словесных объяснений:

3. Сопротивление участка, состоящего из последовательно соединённых проводников, равно сумме сопротивлений каждого проводника.

Пусть — сопротивление участка . По закону Ома имеем:

что и требовалось.

Можно дать интуитивно понятное объяснение правила сложения сопротивлений на одном частном примере. Пусть последовательно соединены два проводника из одинакового вещества и с одинаковой площадью поперечного сечения , но с разными длинами и .

Сопротивления проводников равны:

Эти два проводника образуют единый проводник длиной и сопротивлением

Но это, повторяем, лишь частный пример. Сопротивления будут складываться и в самом общем случае — если различны также вещества проводников и их поперечные сечения.
Доказательство этого даётся с помощью закона Ома, как показано выше.
Наши доказательства свойств последовательного соединения, приведённые для двух проводников, переносятся без существенных изменений на случай произвольного числа проводников.

Параллельное соединение

При параллельном соединении проводников их начала подсоединяются к одной точке цепи, а концы — к другой точке.

Снова рассматриваем два резистора, на сей раз соединённые параллельно (рис. 5 ).

Рис. 5. Параллельное соединение

Резисторы подсоединены к двум точкам: и . Эти точки называются узлами или точками разветвления цепи. Параллельные участки называются также ветвями ; участок от к (по направлению тока) называется неразветвлённой частью цепи.

Теперь сформулируем свойства параллельного соединения и докажем их для изображённого выше случая двух резисторов.

1. Напряжение на каждой ветви одинаково и равно напряжению на неразветвлённой части цепи.
В самом деле, оба напряжения и на резисторах и равны разности потенциалов между точками подключения:

Этот факт служит наиболее отчётливым проявлением потенциальности стационарного электрического поля движущихся зарядов.

2. Сила тока в неразветвлённой части цепи равна сумме сил токов в каждой ветви.
Пусть, например, в точку за время из неразветвлённого участка поступает заряд . За это же время из точки к резистору уходит заряд , а к резистору — заряд .

Ясно, что . В противном случае в точке накапливался бы заряд, меняя потенциал данной точки, что невозможно (ведь ток постоянный, поле движущихся зарядов стационарно, и потенциал каждой точки цепи не меняется со временем). Тогда имеем:

что и требовалось.

3. Величина, обратная сопротивлению участка параллельного соединения, равна сумме величин, обратных сопротивлениям ветвей.
Пусть — сопротивление разветвлённого участка . Напряжение на участке равно ; ток, текущий через этот участок, равен . Поэтому:

Сокращая на , получим:

(1)

что и требовалось.

Как и в случае последовательного соединения, можно дать объяснение данного правила на частном примере, не обращаясь к закону Ома.
Пусть параллельно соединены проводники из одного вещества с одинаковыми длинами , но разными поперечными сечениями и . Тогда это соединение можно рассматривать как проводник той же длины , но с площадью сечения . Имеем:

Приведённые доказательства свойств параллельного соединения без существенных изменений переносятся на случай любого числа проводников.

Из соотношения (1) можно найти :

(2)

К сожалению, в общем случае параллельно соединённых проводников компактного аналога формулы (2) не получается, и приходится довольствоваться соотношением

(3)

Тем не менее, один полезный вывод из формулы (3) сделать можно. Именно, пусть сопротивления всех резисторов одинаковы и равны . Тогда:

Мы видим, что сопротивление участка из параллельно соединённых одинаковых проводников в раз меньше сопротивления одного проводника.

Смешанное соединение

Смешанное сединение проводников, как следует из названия, может являться совокупностью любых комбинаций последовательного и параллельного соединений, причём в состав этих соединений могут входить как отдельные резисторы, так и более сложные составные участки.

Расчёт смешанного соединения опирается на уже известные свойства последовательного и параллельного соединений. Ничего нового тут уже нет: нужно только аккуратно расчленить данную схему на более простые участки, соединённые последовательно или параллельно.

Рассмотрим пример смешанного соединения проводников (рис. 6 ).

Рис. 6. Смешанное соединение

Пусть В, Ом, Ом, Ом, Ом, Ом. Найдём силу тока в цепи и в каждом из резисторов.

Наша цепь состоит из двух последовательно соединённых участков и . Сопротивление участка :

Ом.

Участок является параллельным соединением: два последовательно включённых резистора и подключены параллельно к резистору . Тогда:

Ом.

Сопротивление цепи:

Ом.

Теперь находим силу тока в цепи:

Для нахождения тока в каждом резисторе вычислим напряжения на обоих участках:

(Заметим попутно, что сумма этих напряжений равна В, т. е. напряжению в цепи, как и должно быть при последовательном соединении.)

Оба резистора и находятся под напряжением , поэтому:

(В сумме имеем А, как и должно быть при параллельном соединении.)

Сила тока в резисторах и одинакова, так как они соединены последовательно:

Стало быть, через резистор течёт ток A.

Последовательным называется такое соединение резисторов, когда конец одного проводника соединяется с началом другого и т.д. (рис. 1). При последовательном соединении сила тока на любом участке электрической цепи одинакова. Это объясняется тем, что заряды не могут накапливаться в узлах цепи. Их накопление привело бы к изменению напряженности электрического поля, а следовательно, и к изменению силы тока. Поэтому

Амперметр А измеряет силу тока в цепи и обладает малым внутренним сопротивлением (R A 0).

Включенные вольтметры V 1 и V 2 измеряют напряжение U 1 и U 2 на сопротивлениях R 1 и R 2 . Вольтметр V измеряет подведенное к клеммам М и N напряжение U. Вольтметры показывают, что при последовательном соединении напряжение U равно сумме напряжений на отдельных участках цепи:

Применяя закон Ома для каждого участка цепи, получим:

где R — общее сопротивление последовательно соединенной цепи. Подставляя U, U 1 , U 2 в формулу (1), имеем

Сопротивление цепи, состоящей из n последовательно соединенных резисторов, равно сумме сопротивлений этих резисторов:

Если сопротивления отдельных резисторов равны между собой, т.е. R 1 = R 2 = … = R n , то общее сопротивление этих резисторов при последовательном соединении в n раз больше сопротивления одного резистора: R = nR 1 .

При последовательном соединении резисторов справедливо соотношение

т.е. напряжения на резисторах прямо пропорциональны сопротивлениям.

Параллельным называется такое соединение резисторов, когда одни концы всех резисторов соединены в один узел, другие концы — в другой узел (рис. 2). Узлом называется точка разветвленной цепи, в которой сходятся более двух проводников. При параллельном соединении резисторов к точкам М и N подключен вольтметр. Он показывает, что напряжения на отдельных участках цепи с сопротивлениями R 1 и R 2 равны. Это объясняется тем, что работа сил стационарного электрического поля не зависит от формы траектории:

Амперметр показывает, что сила тока I в неразветвленной части цепи равна сумме сил токов I 1 и I 2 в параллельно соединенных проводниках R 1 и R 2:

Это вытекает и из закона сохранения электрического заряда. Применим закон Ома для отдельных участков цепи и всей цепи с общим сопротивлением R:

Подставляя I, I 1 и I 2 в формулу (2), получим.

Содержание:

Во всех электрических схемах используются резисторы, представляющие собой элементы, с точно установленным значением сопротивления. Благодаря специфическим качествам этих устройств, становится возможной регулировка напряжения и силы тока на любых участках схемы. Данные свойства лежат в основе работы практически всех электронных приборов и оборудования. Так, напряжение при параллельном и последовательном соединении резисторов будет отличаться. Поэтому каждый вид соединения может применяться только в определенных условиях, чтобы та или иная электрическая схема могла в полном объеме выполнять свои функции.

Напряжение при последовательном соединении

При последовательном соединении два резистора и более соединяются в общую цепь таким образом, что каждый из них имеет контакт с другим устройством только в одной точке. Иначе говоря, конец первого резистора соединяется с началом второго, а конец второго — с началом третьего и т.д.

Особенностью данной схемы является прохождение через все подключенные резисторы одного и того же значения электрического тока. С возрастанием количества элементов на рассматриваемом участке цепи, течение электрического тока становится все более затрудненным. Это происходит из-за увеличения общего сопротивления резисторов при их последовательном соединении. Данное свойство отражается формулой: R общ = R 1 + R 2 .

Распределение напряжения, в соответствии с законом Ома, осуществляется на каждый резистор по формуле: V Rn = I Rn x R n . Таким образом, при увеличении сопротивления резистора, возрастает и падающее на него напряжение.

Напряжение при параллельном соединении

При параллельном соединении, включение резисторов в электрическую цепь выполняется таким образом, что все элементы сопротивлений подключаются друг к другу сразу обоими контактами. Одна точка, представляющая собой электрический узел, может соединять одновременно несколько резисторов.

Такое соединение предполагает течение отдельного тока в каждом резисторе. Сила этого тока находится в обратно пропорциональной . В результате, происходит увеличение общей проводимости данного участка цепи, при общем уменьшении сопротивления. В случае параллельного соединения резисторов с различным сопротивлением, значение общего сопротивления на этом участке всегда будет ниже самого маленького сопротивления отдельно взятого резистора.

На представленной схеме, напряжение между точками А и В представляет собой не только общее напряжение для всего участка, но и напряжение, поступающее к каждому отдельно взятому резистору. Таким образом, в случае параллельного соединения, напряжение, подаваемое ко всем резисторам, будет одинаковым.

В результате, напряжение при параллельном и последовательном соединении будет отличаться в каждом случае. Благодаря этому свойству, имеется реальная возможность отрегулировать данную величину на любом участке цепи.

Калькулятор онлайн для параллельного соединения резисторов: общие сведения, формулы расчета

Параллельное соединение резисторов. Калькулятор для расчета

Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.

Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:

При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.

Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление  R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.

Как рассчитать сложные схемы соединения резисторов

Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.

Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.

Ток, протекающий в цепи параллельно соединенных резисторах

Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.

Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).

Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Таким образом, протекающий общий ток в цепи  можно определить как:

I = I1 + I2

Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:

Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА

Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА

Таким образом, общий ток будет равен:

I = 0,545 мА + 0,255 мА = 0,8 мА

Это также можно проверить, используя закон Ома:

I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)

где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)

И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.

Параллельное соединение резисторов — онлайн калькулятор

Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:

Подведем итог

Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.

Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.

Источник: http://www.joyta.ru/7362-parallelnoe-soedinenie-rezistorov/

Расчет делителя напряжения на резисторах, конденсаторах и индуктивностях — Help for engineer | Cхемы, принцип действия, формулы и расчет

Делитель напряжения используется в электрических цепях, если необходимо понизить напряжение и получить несколько его фиксированных значений.

Состоит он из двух и более элементов (резисторов, реактивных сопротивлений). Элементарный делитель можно представить как два участка цепи, называемые плечами.

Участок между положительным напряжением и нулевой точкой – верхнее плечо, между нулевой и минусом – нижнее плечо.

Делитель напряжения на резисторах может применятmся как для постоянного, так и для переменного напряжений. Применяется для низкого напряжения и не предназначен для питания мощных машин. Простейший делитель состоит из двух последовательно соединенных резисторов:

На резистивный делитель напряжения подается напряжение питающей сети U, на каждом из сопротивлений R1 и R2 происходит падение напряжения. Сумма U1 и U2 и будет равна значению U.

В соответствии с законом Ома (1):

Падение напряжения будет прямо пропорционально значению сопротивления и величине тока. Согласно первому закону Кирхгофа, величина тока, протекающего через сопротивления одинакова. С чего следует, что падение напряжения на каждом резисторе (2,3):

Тогда напряжение на всем участке цепи (4):

Отсюда определим, чему равно значение тока без включения нагрузки (5):

Если подставить данное выражение в (2 и 3), то получим формулы расчета падения напряжения для делителя напряжения на резисторах (6, 7):

Необходимо упомянуть, что значения сопротивлений делителя должны быть на порядок или два (все зависит от требуемой точности питания) меньше, чем сопротивление нагрузки. Если же это условие не выполняется, то при приведенном расчете подаваемое напряжение будет посчитано очень грубо.

Для повышения точности необходимо сопротивление нагрузки принять как параллельно подсоединенный резистор к делителю. А также использовать прецизионные (высокоточные) сопротивления.

Пусть источник питания выдает 24 В постоянного напряжения, примем, что величина сопротивления нагрузки переменная, но минимальное значение равно 15 кОм. Необходимо рассчитать параметры резисторов для делителя, выходное напряжение которого равно 6 В.

Таким образом, напряжения: U=24 B, U2=6 В; сопротивление резисторов не должно превышать 1,5 кОм (в десять раз меньше значения нагрузки). Принимаем R1=1000 Ом, тогда используя формулу (7) получим:

выразим отсюда R2:

Зная величины сопротивления обоих резисторов, найдем падение напряжения на первом плече (6):

Ток, который протекает через делитель, находится по формуле (5):

Схема делителя напряжения на резисторах рассчитана выше и промоделирована:

Использование делителя напряжения очень неэкономичный, затратный способ понижения величины напряжения, так как неиспользуемая энергия рассеивается на сопротивлении (превращается в тепловую энергию). КПД очень низкий, а потери мощности на резисторах вычисляются формулами (8,9):

По заданным условиям, для реализации схемы делителя напряжения необходимы два резистора:

1. R1=1 кОм, P1=0,324 Вт.

2. R2=333,3 Ом, P2=0,108 Вт.

Полная мощность, которая потеряется:

Делитель напряжения на конденсаторах применяется в схемах высокого переменного напряжения, в данном случае имеет место реактивное сопротивление.

Сопротивление конденсатора рассчитывается по формуле (10):

где С – ёмкость конденсатора, Ф;

f – частота сети, Гц.

Исходя из формулы (10), видно, что сопротивление конденсатора зависит от двух параметров: С и f. Чем больше ёмкость конденсатора, тем сопротивление его ниже (обратная пропорциональность). Для ёмкостного делителя расчет имеет такой вид (11, 12):

Еще один делитель напряжения на реактивных элементах – индуктивный, который нашел применение в измерительной технике. Сопротивление индуктивного элемента при переменном напряжении прямо пропорционально величине индуктивности (13):

где L – индуктивность, Гн.

Падение напряжения на индуктивностях (14,15):

Источник: https://h5e.ru/komplektuyushchie/117

Расчет резистора для светодиода, калькулятор расчёта сопротивления

Светодиод имеет очень небольшое внутреннее сопротивление, если его подключить напрямую к блоку питания, то сила тока будет достаточной высокой, чтобы он сгорел.

Медные или золотые нити, которыми кристалл подключается к внешним выводам, могут выдерживать небольшие скачки, но при сильном превышении перегорают и питание прекращает поступать на кристалл.

Онлайн расчёт резистора для светодиода производится на основе его номинальной рабочей силы тока.

Онлайн калькулятор

Онлайн калькулятор покажет вам точное сопротивление  в Омах. Как правило окажется, что резисторы с таким номиналом не выпускаются, и вам будет показан ближайший стандартный номинал. Если не удаётся сделать точный подбор сопротивления, то используйте больший номинал.

Подходящий номинал можно сделать подключая сопротивление параллельно или последовательно. Расчет сопротивления для светодиода можно не делать, если использовать мощный переменный или подстроечный резистор. Наиболее распространены типа 3296 на 0,5W.

При использовании питания на 12В, последовательно можно подключить до 3 LED.

Резисторы бывают разного класса точности, 10%, 5%, 1%. То есть их сопротивление может погрешность в этих пределах в положительную или отрицательную сторону.

Чтобы определить полярность можно подать небольшое напряжение или использовать функцию проверки диодов на мультиметре. Отличается от режима измерения сопротивления, обычно подаётся от 2В до 3В.

Основные параметры

Отличие характеристик кристаллов для дешевых ЛЕД

Так же при расчёте светодиодов следует учитывать разброс параметров, для дешевых они будут максимальны, для дорогих они будут более одинаковыми.  Чтобы проверить этот параметр, необходимо включить их в равных условиях, то есть последовательно.

Уменьшая тока или напряжение снизить яркость до слегка светящихся точек. Визуально вы сможете оценить, некоторые будут светится ярче, другие тускло.  Чем равномернее они горят, тем меньше разброс.

Калькулятор расчёта резистора для светодиода подразумевает, что характеристики светодиодных чипов идеальные, то есть отличие равно нулю.

Напряжение падения для распространенных моделей маломощных до 10W может быть от 2В до 12В. С ростом мощности увеличивается количество кристаллов в COB  диоде, на каждом есть падение. Кристаллы включаются цепочками последовательно, затем они объединяются в параллельные цепи. На мощностях от  10W до 100W снижение растёт с 12В до 36В.

Этот параметр должен быть указан в технических характеристиках LED чипа  и зависит от назначения:

• цвета синий, красный, зелёный, желтый;
• трёхцветный RGB;
• четырёхцветный RGBW;
• двухцветный, теплый и холодный белый.

Особенности дешёвых ЛЕД

Прежде чем подобрать резистор для светодиода на онлайн калькуляторе, следует убедится в параметрах диодов. Китайцы на Aliexpress продают множество led, выдавая их за фирменные. Наиболее популярны модели  SMD3014, SMD 3528, SMD2835, SMD 5050, SMD5630, SMD5730. Всё самое плохое обычно делается под брендом Epistar.

Например, чаще всего китайцы обманывают на SMD5630 и SMD5730. Цифры в маркировке обозначают лишь размер корпуса 5,6мм на 3,0мм.

В фирменных такой большой корпус используется для установки мощных кристаллов на 0,5W , поэтому у покупателей диодов СМД5630 напрямую ассоциируется с мощностью 0,5W.

Хитрый китаец этим пользуется, и в корпус 5630 устанавливает дешевый и слабенький кристалл в среднем на 0,1W , при этом указывая потребление энергии 0,5W.

Китайские светодиодные лампы кукурузы

Наглядным примером будут автомобильные лампы и светодиодные кукурузы, в которых поставлено большое количество слабеньких и некачественных ЛЕД чипов. Обычный покупатель считает, чем больше светодиодов чем лучше светит и выше мощность.

Автомобильные лампы на самых слабых лед 0,1W

Чтобы сэкономить денежку, мои  светодиодные коллеги ищут приличные ЛЕД на Aliexpress. Ищут хорошего продавца, который обещает определённые параметры, заказывают , ждут доставку месяц.

После тестов оказывается, что китайский продавец обманул, продал барахло. Повезёт, если на седьмой раз придут приличные диоды, а не барахло.

 Обычно сделают 5 заказов, и не добившись результата и идут делать заказ в отечественный магазин, который может сделать обмен.

Источник: http://led-obzor.ru/raschet-rezistora-dlya-svetodioda-kalkulyator

Параллельное и последовательное соединение сопротивлений

Как известно, соединение любого элемента схемы, независимо от его назначения, может быть двух видов — параллельное подключение и последовательное. Также возможно и смешанное, то есть последовательно параллельное соединение. Все зависит от назначения компонента и выполняемой им функции. А значит, и резисторы не избежали этих правил.

Последовательное и параллельное сопротивление резисторов это по сути то же самое, что и параллельное и последовательное подключение источников света. В параллельной цепи схема подключения подразумевает вход на все резисторы из одной точки, а выход из другой.

Попробуем разобраться, каким образом выполняется последовательное соединение, а каким — параллельное. И главное, в чем состоит разница между подобными соединениями и в каких случаях необходимо последовательное, а в каких параллельное соединение.

Также интересен и расчет таких параметров, как общее напряжение и общее сопротивление цепи в случаях последовательного либо параллельного соединения. Начать следует с определений и правил.

Способы подключения и их особенности

Внешний вид резисторов и обозначения в схемах

Виды соединения потребителей или элементов играют очень важную роль, ведь именно от этого зависят характеристики всей схемы, параметры отдельных цепей и тому подобное. Для начала попробуем разобраться с последовательным подключением элементов к схеме.

Последовательное соединение

Последовательное подключение — это такое соединение, где резисторы (равно, как и другие потребители или элементы схем) подключаются друг за другом, при этом выход предыдущего подключается на вход следующего.

Подобный вид коммутации элементов дает показатель, равный сумме сопротивлений этих элементов схемы. То есть если r1 = 4 Ом, а r2 = 6 Ом, то при подключении их в последовательную цепь, общее сопротивление составит 10 Ом.

Если мы добавим последовательно еще один резистор на 5 Ом, сложение этих цифр даст 15 Ом — это и будет общее сопротивление последовательной цепи. То есть общие значения равны сумме всех сопротивлений.

При его расчете для элементов, которые подключены последовательно, никаких вопросов не возникает — все просто и ясно. Именно поэтому не стоит даже останавливаться более серьезно на этой.

Совершенно по другим формулам и правилам производится расчет общего сопротивления резисторов при параллельном подключении, вот на нем имеет смысл остановиться поподробнее.

Схема последовательного соединения резисторов

Параллельное соединение

Параллельным называется соединение, при котором все входы резисторов объединены в одной точке, а все выходы — во второй. Здесь главное понять, что общее сопротивление при подобном подключении будет всегда ниже, чем тот же параметр резистора, имеющего наименьшее.

Имеет смысл разобрать подобную особенность на примере, тогда понять это будет намного проще. Существует два резистора по 16 Ом, но при этом для правильного монтажа схемы требуется лишь 8 Ом.

В данном случае при задействовании их обеих, при их параллельном включении в схему, как раз и получатся необходимые 8 Ом. Попробуем понять, по какой формуле возможны вычисления.

Рассчитать этот параметр можно так: 1/Rобщ = 1/R1+1/R2, причем при добавлении элементов сумма может продолжаться до бесконечности.

Попробуем еще один пример. Параллельно соединены 2 резистора, с сопротивлением 4 и 10 Ом. Тогда общее будет равно 1/4 + 1/10, что будет равным 1:(0.25 + 0.1) = 1:0.35 = 2.85 Ом. Как видим, хотя резисторы и имели значительное сопротивление, при подключении их параллельнообщий показатель стал намного ниже.

Так же можно рассчитать общее сопротивление четырех параллельно подключенных резисторов, с номиналом 4, 5, 2 и 10 Ом. Вычисления, согласно формуле, будут такими: 1/Rобщ = 1/4+1/5+1/2+1/10, что будет равным 1:(0.25+0.2+0.5+0.1)=1/1.5 = 0.7 Ом.

Что же касается тока, протекающего через параллельно соединенные резисторы, то здесь необходимо обратиться к закону Кирхгофа, который гласит «сила тока при параллельном соединении, выходящего из цепи, равна току, входящему в цепь». А потому здесь законы физики решают все за нас.

При этом общие показатели тока разделяются на значения, которые являются обратно пропорциональными сопротивлению ветки. Если сказать проще, то чем больше показатель сопротивления, тем меньшие токи будут проходить через этот резистор, но в общем, все же ток входа будет и на выходе.

При параллельном соединении напряжение также остается на выходе таким же, как и на входе. Схема параллельного соединения указана ниже.

Параллельное соединение резисторов

Последовательно-параллельное соединение

Последовательно-параллельное соединение — это когда схема последовательного соединения содержит в себе параллельные сопротивления. В таком случае общее последовательное сопротивление будет равно сумме отдельно взятых общих параллельных. Метод вычислений одинаковый в соответствующих случаях.

Подведем итог

Подводя итог всему вышеизложенному можно сделать следующие выводы:

1. При последовательном соединении резисторов не требуется особых формул для расчета общего сопротивления. Необходимо лишь сложить все показатели резисторов — сумма и будет общим сопротивлением.
2. При параллельном соединении резисторов, общее сопротивление высчитывается по формуле 1/Rобщ = 1/R1+1/R2…+Rn.
3. Эквивалентное сопротивление при параллельном соединении всегда меньше минимального подобного показателя одного из резисторов, входящих в схему.
4. Ток, равно как и напряжение в параллельном соединении остается неизменным, то есть напряжение при последовательном соединении равно как на входе, так и на выходе.
5. Последовательно-параллельное соединение при подсчетах подчиняется тем же законам.

В любом случае, каким бы ни было подключение, необходимо четко рассчитывать все показатели элементов, ведь параметры имеют очень важную роль при монтаже схем. И если ошибиться в них, то либо схема не будет работать, либо ее элементы просто сгорят от перегрузки.

По сути, это правило применимо к любым схемам, даже в электромонтаже. Ведь провод по сечению подбирают также исходя из мощности и напряжения. А если поставить лампочку номиналом в 110 вольт в цепь с напряжением 220, несложно понять, что она моментально сгорит. Так же и с элементами радиоэлектроники.

А потому — внимательность и скрупулезность в расчетах — залог правильной работы схемы.

Источник: https://domelectrik.ru/baza/teoriya/rezistory-na-skheme

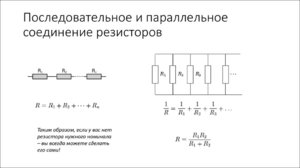
Последовательное и параллельное соединение резисторов

Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.

Общее сопротивление Rобщ

При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.

Напряжение при последовательном соединении

Напряжение при последовательном соединении распределяется на каждый резистор согласно закону Ома:

Т.е чем большее сопротивление резистора, тем большее напряжение на него падает.

Параллельное соединение резисторов

Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.

Общее сопротивление Rобщ

При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.

Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.

Формула общей проводимости при параллельном соединении резисторов:

Формула эквивалентного общего сопротивления при параллельном соединении резисторов:

Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:

Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.

Напряжение при параллельном соединении

Напряжение между точками A и B является как общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности. Поэтому при параллельном соединении на все резисторы упадет одинаковое напряжение.

Электрический ток при параллельном соединении

Через каждый резистор течет ток, сила которого обратно пропорциональна сопротивлению резистора. Для того чтобы узнать какой ток течет через определенный резистор, можно воспользоваться законом Ома:

Смешанное соединение резисторов

Смешанным соединением называют участок цепи, где часть резисторов соединяются между собой последовательно, а часть параллельно. В свою очередь, смешанное соединение бывает последовательного и параллельного типов.

Общее сопротивление Rобщ

Для того чтобы посчитать общее сопротивление смешанного соединения:

• Цепь разбивают на участки с только пареллельным или только последовательным соединением.
• Вычисляют общее сопротивление для каждого отдельного участка.
• Вычисляют общее сопротивление для всей цепи смешанного соединения.

Так это будет выглядеть для схемы 1:

Также существует более быстрый способ расчета общего сопротивления для смешанного соединения. Можно, в соответствии схеме, сразу записывать формулу следующим образом:

• Если резисторы соединяются последоватеьно — складывать.
• Если резисторы соединяются параллельно — использовать условное обозначение «||».
• Подставлять формулу для параллельного соединения где стоит символ «||».

Так это будет выглядеть для схемы 1:

После подстановки формулы параллельного соединения вместо «||»:

Ссылки по теме:

Источник: http://hightolow.ru/resistor3.php

Последовательное и параллельное соединение проводников, резисторов,конденсаторов и катушек индуктивности. Онлайн расчёт

«- Я тебе как электрику объясняю: Надя спит с мужиками последовательно, а Света параллельно. Кто из них шмара вавилонская? — Ну, Света наверное.

— Вот! А мне, как кладовщику, видится немного другое: «поблядушка обыкновенная» — 2 штуки! » «- А теперь скажи мне отрок, как течёт электричество по проводам электрическим, и цепям рукотворным, последовательным да параллельным, от плюса к минусу со скоростью света в вакууме? — С Божьей помощью, батюшка! С Божьей помощью…

» Ну да ладно, достаточно! Шутки — штуками, а пора бы уже дело делать. Так что «Копайте пока здесь! А я тем временем схожу узнаю — где надо…», а заодно набросаю пару-тройку калькуляторов на заданную тему. Итак.

При последовательном соединении проводников сила тока во всех проводниках одинакова, при этом общее напряжение в цепи равно сумме напряжений на концах каждого из проводников.

При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов, а сила тока в цепи равна сумме сил токов в отдельных параллельно соединённых проводниках. Поясним рисунком с распределением напряжений, токов и формулами.Рис.1 Расчёт проведём для 4 резисторов (проводников), соединённых последовательно или параллельно. Если элементов в цепи меньше, то оставляем лишние поля в таблице не заполненными. Заодно, при желании узнать распределение значений токов и напряжений на каждом из элементов при последовательном и параллельном соединениях, есть возможность ввести величину общего напряжения в цепи U. А есть возможность не вводить… Короче, все вводные, помеченные * — к заполнению не обязательны.

РАСЧЁТ СОПРОТИВЛЕНИЙ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
проводников

Теперь, что касается последовательных и параллельных соединений конденсаторов и катушек индуктивности.

Схема, приведённая на Рис.1 для проводников и резисторов, остаётся в полной силе и для катушек с конденсаторами, распределение напряжений и токов тоже никуда не девается, трансформируется лишь осмысление того, что токи эти и напряжения обязаны быть переменными.

Почему переменными? А потому, что для постоянных значений этих величин — сопротивление конденсаторов составляет в первом приближении бесконечность, а катушек — ноль, соответственно и токи будут равны либо нулю, либо бесконечности, а для переменных значений иметь ярко выраженную зависимость от частоты.

Поэтому, для желающих рассчитать величины напряжений и токов в последовательных или параллельных цепях, состоящих из конденсаторов и катушек индуктивности, имеет полный смысл выяснить на странице ссылка на страницу значения реактивных сопротивлений данных элементов при интересующей Вас частоте и подставить эти значения в таблицу для расчёта проводников и резисторов. А в качестве общего напряжения в цепи — подставлять действующее значение амплитуды переменного тока.

Ну а теперь приведём таблицы для расчёта значений ёмкостей и индуктивностей при условии последовательного и параллельного соединений конденсаторов и катушек в количестве от 2 до 4 штук.

Расчёт поведём на основании хрестоматийных формул:

  и       для параллельных цепей и

  и      для последовательных. Как и в предыдущей таблице вводные, помеченные * — к заполнению не обязательны.

РАСЧЁТ ЁМКОСТИ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
конденсаторов

Ну и в завершении ещё одна таблица.

РАСЧЁТ ИНДУКТИВНОСТИ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
катушек

Тут важно заметить, что приведённые в последней таблице расчёты верны только для индуктивно не связанных катушек, то есть для катушек, намотанных на разных каркасах и расположенных на значительных расстояниях друг от друга, во избежание, пересечения взаимных магнитных полей.

Источник: http://vpayaem.ru/information12.html

Параллельное соединение резисторов. Расчеты общего сопротивления, общей мощности. :

Резистор – это элемент электрической схемы, который обладает сопротивлением электрическому току. Классифицируют два типа резисторов: постоянные и переменные (подстроечные). При моделировании той или иной электрической схемы, а также при ремонте электронных изделий, возникает необходимость использовать резистор определенного номинала.

Хотя и существует множество различных номиналов постоянных резисторов, в данный момент под рукой может не оказаться требуемого, либо резистора с таким номиналом не существует. Чтобы выйти из такой ситуации, можно использовать как последовательное так и параллельное соединение резисторов.

О том, как правильно произвести расчет и подбор различных номиналов сопротивлений, будет рассказано в этой статье.

Последовательное соединение резисторов – это самая элементарная схема сборки радиодеталей, оно применяется для увеличения общего сопротивления цепи.

При последовательном соединении, сопротивление используемых резисторов просто складывается, а вот при параллельном соединении необходимо производить расчет по нижеописанным формулам.

Параллельное соединение необходимо для снижения результирующего сопротивления, а также для увеличения мощности, несколько параллельно подключенных резисторов имеют большую мощность, чем у одного.

На фотографии можно увидеть параллельное подключение резисторов.

Ниже представлена принципиальная схема параллельного соединения резисторов.

Общее номинальное сопротивление необходимо рассчитывать по следующей схеме:

R(общ)=1/(1/R1+1/R2+1/R3+1/R n).

Где:

— R(общ) – общее сопротивление;

— R1, R2, R3 и Rn – параллельно подключенные резисторы.

Когда параллельное соединение резисторов состоит всего из двух элементов, в таком случае общее номинальное сопротивление можно высчитать по следующей формуле:

R(общ)=R1*R2/R1+R2.

Где:

— R(общ) – общее сопротивление;

— R1, R2 – параллельно подключенные резисторы.

В радиотехнике существует следующее правило: если параллельное подключение резисторов состоит из элементов одного номинала, то результирующее сопротивление можно высчитать, разделив номинал резистора на количество соединенных резисторов:

R(общ)=R1
.

Где:

— R(общ) – общее сопротивление;

— R – номинал параллельно подключенного резистора;

— n – количество соединенных элементов.

Важно учитывать, что при параллельном соединении результирующее сопротивление всегда будет ниже, чем сопротивление самого малого по номиналу резистора.

Приведем практический пример: возьмем три резистора, со следующими значениями номинального сопротивления: 100 Ом, 150 Ом и 30 Ом. Проведем расчет общего сопротивления, по первой формуле:

R(общ)=1/(1/100+1/150+1/30)=1/(0,01+0,007+0,03)=1/0,047=21,28Ом.

После расчета формулы мы видим, что параллельное соединение резисторов, состоящее из трех элементов, с наименьшим номиналом 30 Ом, в результате дает общее сопротивление в электрической цепи 21,28 Ом, что ниже наименьшего номинального сопротивления в цепи почти на 30 процентов.

Параллельное соединение резисторов чаще всего используют в тех случаях, когда необходимо получить сопротивление с большей мощностью.

В таком случае необходимо взять резисторы одинаковой мощности и с одинаковым сопротивлением.

Результирующая мощность в таком случае рассчитывается путем умножения мощности одного элемента сопротивления на общее количество параллельно подключенных резисторов в цепи.

Например: пять резисторов с номиналом в 100 Ом и с мощностью 1 Вт в каждом, подключенные параллельно, имеют общее сопротивление 20 Ом и мощность 5 Вт.

При последовательном подключении тех же резисторов (мощность так же складывается), получим результирующую мощность 5 Вт, общее сопротивление составит 500 Ом.

Источник: https://www.syl.ru/article/114725/undefined

Параллельное соединение резисторов

В случае последовательного соединения прохождение тока осуществляется только через один проводник. Параллельное соединение резисторов предполагает распределение электрического тока среди нескольких проводников. При добавлении еще одного резистора в электрическую цепь, ток будет частично проходить через разные резисторы.

Схемы последовательного и параллельного соединения

Если рассматривать соединение на примере громкоговорителя, то при последовательном соединении с усилителем мощности подключается только один динамик, поскольку прохождение тока осуществляется только через один проводник. Подключение второго громкоговорителя может быть выполнено разными способами.

При последовательном соединении по обоим устройствам будет протекать одинаковый ток. В этом случае общее сопротивление приборов представляет собой сумму отдельно взятых сопротивлений.

При параллельном соединении протекание тока будет происходить по двум направлениям. Здесь общее значение сопротивления в отличие от последовательного соединения, наоборот, будет уменьшаться. То есть, при параллельном соединении двух сопротивлений, их общее значение будет составлять половину каждого из них.

Если последовательное и параллельное соединение резисторов рассматривается с точки зрения радиоэлектроники, необходимо четко представлять себе, что представляет собой данный элемент и какова его роль в электронных схемах. Эта деталь является неотъемлемой частью многих устройств, благодаря такому свойству, как сопротивление электрическому току.

Резисторы могут быть двух типов – постоянными и переменными, то есть подстроечными. При создании тех или иных электрических схем требуется резистор установленного номинала, которого в данный момент может не оказаться в наличии.

Поэтому приходится использовать элементы с другими номинальными значениями, формула для каждого из которых подтверждает их физические свойства.

Последовательное соединение считается наиболее простым. Оно используется, когда необходимо увеличить общее сопротивление электрической цепи. В этом случае все сопротивления резисторов просто складываются и дают общую сумму. При параллельном соединении, наоборот, можно снизить результирующее сопротивление или увеличить мощность за счет нескольких подключенных резисторов.

Отличие параллельного и последовательного соединения

Последовательное и параллельное соединение резисторов отличаются между собой значениями напряжения. В каждой части параллельных контуров этот показатель будет одинаковым.

Однако, при одном и том же напряжении, сила тока в контурах будет разной.

Кроме того, сопротивление резисторов при параллельном соединении будет существенно отличаться от того же показателя при последовательном соединении.

В процессе использования последовательной схемы наблюдаются обратные явления. Сила тока в каждом сопротивлении будет одна и та же, а напряжение на каждом участке будет отличаться. Это связано с тем, что во время протекания тока, каждый резистор частично забирает приложенное напряжение.

Из-за различного сопротивления резисторов, при последовательном соединении, напряжение в цепи может падать. Для того чтобы подтвердить данное явление, выполняется расчет сопротивления. Все падения напряжения в общей сумме равняются общему напряжению, которое было приложено.

Для проведения вычислений используются формулы, с помощью которых можно получить наиболее точные результаты.

Таким образом, параллельное соединение резисторов, находящихся под одинаковым напряжением, не влияет на режим работы каждого из них. То есть, они совершенно не зависят друг от друга, и ток, проходящий по одному приемнику, не может существенно влиять на другие приемники.

Формула расчета параллельного соединения резисторов

Свои особенности имеет и ток при параллельном соединении резисторов. Попадая в первый узел соединения, он разделяется на столько частей, сколько имеется резисторов, подключенных параллельно. То есть, через сопротивление R1 будет протекать ток I1, а через R2 – ток I2. При попадании во второй узел, они вновь соединяются в один общий ток: I = I1 + I2.

Если какой-либо резистор вышел из строя, то остальные будут нормально функционировать. В этом заключается основное преимущество параллельного соединения. Особенно, это касается двигателей и электрических ламп, работающих от определенного номинального напряжения.

Расчет общего номинального сопротивления осуществляется с помощью формулы: R(общ)=1/(1/R1+1/R2+1/R3+1/R n), где R(общ) – является общим сопротивлением, а R1, R2, R3 и Rn – параллельно подключенными резисторами. Если выполняется параллельное соединение двух резисторов, при котором используется всего лишь два элемента, то в этом случае для расчетов используется следующая схема: R(общ)=R1хR2/R1+R2.

Очень часто в радиоэлектронике приходится пользоваться следующим правилом: если резисторы, подключенные параллельно, имеют один и тот же номинал, то итоговое сопротивление высчитывается путем деления номинала на число подключенных элементов. Такое параллельное соединение резисторов формула представляется следующим образом: R(общ)=R1
, где R(общ) представляет собой сопротивление, R – номинал параллельно подключенного резистора, n – число подключенных элементов.

Для того чтобы рассчитать параллельное соединение резисторов, следует учитывать, что итоговое сопротивление всех подключенных элементов будет всегда ниже, чем сопротивление резистора с самым низким номиналом.

В качестве примера можно рассмотреть схему с тремя резисторами, сопротивления которых составляют 30, 100 и 150 Ом. При использовании основной формулы будет получен следующий результат: R(общ)=1/(1/30+1/100+1/150) =1/(0,03+0,01+0,007)=1/0,047=21,28Ом.

Таким образом, три резистора, соединенные параллельно, с минимальным номиналом 30 Ом, в итоге дадут общее сопротивление электрической цепи 21,28 Ом.

Онлайн калькулятор

В случае больших объемов вычислений, расчет параллельного соединения резисторов выполняется с помощью онлайн-калькулятора. Достаточно всего лишь ввести в нужные окна исходные данные, и после нажатия кнопки получить результат.

Источник: https://electric-220.ru/news/parallelnoe_soedinenie_rezistorov/2014-01-10-487

Онлайн-калькулятор параллельного соединения резисторов

instrument.guru > Электроника > Онлайн-калькулятор параллельного соединения резисторов

Каждый в этой жизни сталкивался с резисторами. Люди с гуманитарными профессиями, как и все, изучали в школе на уроках физики проводники электрического тока и закон Ома.

С резисторами также имеют дело студенты технических университетов и инженеры различных производственных предприятий. Перед всеми этими людьми, так или иначе, вставала задача расчёта электрической цепи при различных видах соединения резисторов. В данной статье речь пойдёт о расчёте физических параметров, характеризующих цепь.

Виды соединений

Резистор — пассивный элемент, присутствующий в каждой электрической цепи. Он предназначен для того, чтобы сопротивляться электрическому току. Существует два вида резисторов:

Зачем же спаивать проводники друг с другом? Например, если для какой-то электрической цепи нужно определённое сопротивление. А среди номинальных показателей нужного нет.

В таком случае необходимо подобрать элементы схемы с определёнными значениями сопротивления и соединить их. В зависимости от вида соединения и сопротивлений пассивных элементов мы получим какое-то определённое сопротивление цепи. Оно называется эквивалентным.

Его значение зависит от вида спайки проводников. Существует три вида соединения проводников:

1. Последовательное.
2. Параллельное.
3. Смешанное.

Значение эквивалентного сопротивления в цепи считается достаточно легко. Однако, если резисторов в схеме очень много, то лучше воспользоваться специальным калькулятором, который считает это значение. При ведении расчёта вручную, чтобы не допускать ошибок, необходимо проверять, ту ли формулу вы взяли.

Последовательное соединение проводников

В последовательной спайке резисторы идут как бы друг за другом. Значение эквивалентного сопротивления цепи равно сумме сопротивлений всех резисторов. Особенность схем с такой спайкой заключается в том, что значение тока постоянно.

Согласно закону Ома, напряжение в цепи равно произведению тока и сопротивления. Так как ток постоянен, то для вычисления напряжения на каждом резисторе, достаточно перемножить значения.

После этого необходимо сложить напряжения всех резисторов, и тогда мы получим значение напряжения во всей цепи.

Расчёт очень простой. Так как с ним имеют дело в основном инженеры-разработчики, то для них не составит труда сосчитать всё вручную. Но если резисторов очень много, то проще воспользоваться специальным калькулятором.

Примером последовательного соединения проводников в быту является ёлочная гирлянда.

Параллельное соединение резисторов

При параллельном соединении проводников эквивалентное сопротивление в цепи считается по-другому. Немного сложнее, чем при последовательном.

Его значение в таких цепях равняется произведению сопротивлений всех резисторов, делённому на их сумму. А также есть и другие варианты этой формулы. Параллельное соединение резисторов всегда снижает эквивалентное сопротивление цепи. То есть, его значение всегда будет меньше, чем наибольшее значение какого-то из проводников.

В таких схемах значение напряжения постоянно. То есть значение напряжения во всей цепи равно значениям напряжений каждого из проводников. Оно задаётся источником напряжения.

Сила тока в цепи равна сумме всех токов, протекающих через все проводники. Значение силы тока, протекающего через проводник. равно отношению напряжения источника к сопротивлению этого проводника.

Примеры параллельного соединения проводников:

1. Освещение.
2. Розетки в квартире.
3. Производственное оборудование.

Для расчёта схем с параллельным соединением проводников лучше пользоваться специальным калькулятором. Если в схеме много резисторов, спаянных параллельно, то гораздо быстрее вы посчитаете эквивалентное сопротивление с помощью этого калькулятора.

Смешанное соединение проводников

Этот вид соединения состоит из каскадов резисторов.

Например, у нас есть каскад из 10 проводников, соединённых последовательно, и после него идёт каскад из 10 проводников, соединённых параллельно.

Эквивалентное сопротивление этой схемы будет равно сумме эквивалентных сопротивлений этих каскадов. То есть, по сути, здесь последовательное соединение двух каскадов проводников.

Многие инженеры занимаются оптимизацией различных схем. Её целью является уменьшение количества элементов в схеме за счёт подбора других, с подходящими значениями сопротивлений. Сложные схемы разбиваются на несколько небольших каскадов, ведь так гораздо проще вести расчёты.

Сейчас, в двадцать первом веке, инженерам стало гораздо проще работать. Ведь несколько десятилетий назад все расчёты производились вручную. А сейчас программисты разработали специальный калькулятор для расчёта эквивалентного сопротивления цепи. В нём запрограммированы формулы, по которым ведутся расчёты.

В этом калькуляторе можно выбрать вид соединения, и потом ввести в специальные поля значения сопротивлений. Через несколько секунд вы уже увидите это значение.

Источник: https://instrument.guru/elektronika/onlajn-kalkulyator-parallelnogo-soedineniya-rezistorov.html

Расчет параллельного соединения резисторов калькулятор онлайн

Параллельное соединение резисторов. Калькулятор для расчета

Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.

Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:

Параллельное соединение резисторов — расчет

Пример №1

При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.

Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов

Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.

Ток, протекающий в цепи параллельно соединенных резисторах

Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.

Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).

Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».

Таким образом, протекающий общий ток в цепи можно определить как:

Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:

Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА

Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА

Таким образом, общий ток будет равен:

I = 0,545 мА + 0,255 мА = 0,8 мА

Это также можно проверить, используя закон Ома:

I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)

где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)

И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.

Параллельное соединение резисторов — онлайн калькулятор

Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:

Подведем итог

Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.

Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.

Калькулятор расчёта параллельного соединения резисторов

Вычислить сопротивление нескольких параллельно соединённых резисторов (до 10)

Впишите любое количество любых номиналов в омах и кликните мышкой в таблице.

Выбрать два имеющихся в наличии номинала E24 и получить результат их параллельного соединения

Если нужен номинал R и имеем резисторы стандарта E24 (+/-5%), тогда вписываем R и кликаем мышкой в таблице. Получим варианты параллельного соединения резисторов R₁ и R₂.

Ещё один калькулятор более точного подбора номинала из резисторов стандарта E48 (+/-2%).

Подбираем (меняем) нужный номинал из того что есть.

Калькуляторы могут быть полезны радиолюбителям-конструкторам, а так же ремонтникам РЭА при затруднении с выбором нужных номиналов резисторов для замены их в цепях электронных устройств.

Замечания и предложения принимаются и приветствуются!

Соединение резисторов, при котором одноименные выводы каждого из элементов собираются в одну точку, называется параллельным. При этом ко всем резисторам подводится один и тот же потенциал, но величина тока через каждый из них будет отличаться. Для составления схем или при замене резисторов в уже существующих цепях важно знать их суммарное сопротивление, как показано на рисунке:

Параллельное соединение резисторов

Данный калькулятор позволяет рассчитать суммарное сопротивление параллельно соединенных резисторов с любым количеством элементов.

Для этого вам необходимо:

• Указать в графе «количество резисторов» их число, в нашем примере их три;
• После того, как вы укажите количество элементов, в поле ниже появится три окошка для ввода значения сопротивления каждого из элементов, к примеру, у вас резисторы сопротивлением 20, 30 и 60 Ом;
• Далее нажмите кнопку «рассчитать» и в окошке «параллельное сопротивление в цепи» вы получите значение сопротивления в 10 Ом.

Чтобы рассчитать другую цепь или при подборе других элементов, нажмите кнопку «сбросить», чтобы обнулить значение параллельно включенных элементов калькулятора.

Для расчета суммарного сопротивления калькулятором используется такое соотношение:

• R_сум — суммарное сопротивление параллельно соединенных элементов
• R₁ — сопротивление первого резистора;
• R₂ — сопротивление второго резистора;
• R₃ — сопротивление третьего резистора;
• R_n — сопротивление n-ого элемента.

Таким образом, в рассматриваемом примере параллельно включены три резистора, поэтому формула для определения суммарного сопротивления будет иметь такой вид:

Чтобы выразить величину суммарного сопротивления необходимо умножить обе половины уравнения на произведение сопротивлений всех трех резисторов. После этого перенести составляющие элементы по правилу пропорции и получить значение сопротивления:

Как видите, расчет параллельного сопротивления резисторов вручную требует немалых усилий, поэтому куда проще его сделать на нашем онлайн калькуляторе.

Обратите внимание, при наличии элементов с сопротивлением в разной размерности Ом, кОм, МОм, их необходимо привести к одной величине, прежде чем производить расчет. К примеру, в Ом и указывать в поле калькулятора для расчета параллельного соединения резисторов значение непосредственно в Омах.

Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.

Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:

Параллельное соединение резисторов — расчет

Пример №1

При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.

Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов

Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.

Ток, протекающий в цепи параллельно соединенных резисторах

Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.

Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).

Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».

Таким образом, протекающий общий ток в цепи можно определить как:

Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:

Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА

Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА

Таким образом, общий ток будет равен:

I = 0,545 мА + 0,255 мА = 0,8 мА

Это также можно проверить, используя закон Ома:

I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)

где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)

И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.

Параллельное соединение резисторов — онлайн калькулятор

Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:

Подведем итог

Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.

Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.

Конвертер величин

Калькулятор параллельных сопротивлений

Калькулятор определяет сопротивление нескольких параллельно соединенных резисторов.

Пример. Рассчитать эквивалентное сопротивление двух резисторов 20 Ом and 30 Ом, соединенных параллельно.

Введите величины сопротивлений в поля R₁, R₂ и т.д., добавляя при необходимости нужное количество полей для ввода, выберите единицы сопротивления в миллиомах (мОм), омах (Ом), килоомах (кОм) или мегаомах (МОм) и нажмите кнопку Рассчитать.

1 мОм = 0,001 Ом. 1 кОм = 1 000 = 10³ Ом. 1 МОм = 1 000 000 = 10⁶ Ом.

Эквивалентное сопротивление R_eq группы параллельно соединенных резисторов является величиной, обратной сумме величин, обратно пропорциональных сопротивлениям этих резисторов.

Иными словами, проводимость G параллельно соединенных резисторов равна сумме проводимостей этих резисторов:

Эта формула для R_eq и используется в данном калькуляторе для расчетов. Например, общее сопротивление трех резисторов 10, 15 и 20 ом, соединенных параллельно, равно 4.62 Ом:

Если параллельно соединены только два резистора, формула упрощается:

Если имеется n соединенных параллельно одинаковых резисторов R, то их эквивалентное сопротивление будет равно

Отметим, что общее сопротивление группы из любого количества соединенных параллельно резисторов всегда будет меньше, чем наименьшее сопротивление резистора в группе и добавление нового резистора всегда приведет к уменьшению эквивалентного сопротивления.

Отметим также, что все резисторы, соединенные параллельно находятся под одним и тем же напряжением. Однако токи, протекающие через отдельные резисторы, отличаются и зависят от их сопротивления. Общий ток через группу резисторов равен сумме токов в отдельных резисторах.

При соединении нескольких резисторов параллельно всегда нужно учитывать их допуски и рассеиваемую мощность.

Примеры применения параллельного соединения резисторов

Одним из примеров параллельного соединения резисторов является шунт в приборе для измерения токов, которые слишком велики для того, чтобы быть напрямую измеренными прибором, предназначенным для измерения небольших токов или напряжений. Для измерения тока параллельно гальванометру или электронному прибору, измеряющему напряжение, подключается резистор с очень маленьким точно известным сопротивлением, изготовленный из материала со стабильными характеристиками. Этот резистор называется шунтом. Измеряемый ток протекает через шунт. В результате на нем падает небольшое напряжение, которое и измеряется вольтметром. Поскольку падение напряжения пропорционально току, протекающему через шунт с известным и точным сопротивлением, вольтметр, подключенный параллельно шунту, можно проградуировать непосредственно в единицах тока (амперах).

Параллельные и последовательные схемы часто используются для получения точного сопротивления или если резистора с требуемым сопротивлением нет или он слишком дорог, если его приобретать в небольших количествах для массового производства. Например, если устройство содержит много резисторов по 20 кОм и необходим только один резистор 10 кОм. Конечно, несложно найти резистор на 10 кОм. Однако для массового производства иногда бывает лучше поставить два резистора на 20 кОм параллельно, чтобы получить необходимые 10 кОм. Это приведет к снижению себестоимости печатной платы, так как будет снижена оптовая цена компонентов, а также стоимость монтажа, так как будет уменьшено количество типоразмеров элементов, которые должен установить на плату автомат установки компонентов.

Последовательное и параллельное соединение проводников, резисторов,

конденсаторов и катушек индуктивности. Онлайн расчёты.

«- Я тебе как электрику объясняю: Надя спит с мужиками последовательно, а Света параллельно. Кто из них шмара вавилонская?
— Ну, Света наверное.
— Вот! А мне, как кладовщику, видится немного другое: «поблядушка обыкновенная» — 2 штуки! »

«- А теперь скажи мне отрок, как течёт электричество по проводам электрическим, и цепям рукотворным, последовательным да параллельным, от плюса к минусу со скоростью света в вакууме?
— С Божьей помощью, батюшка! С Божьей помощью. »

Ну да ладно, достаточно! Шутки — штуками, а пора бы уже дело делать. Так что «Копайте пока здесь! А я тем временем схожу узнаю — где надо. », а заодно набросаю пару-тройку калькуляторов на заданную тему.

Итак.
При последовательном соединении проводников сила тока во всех проводниках одинакова, при этом общее напряжение в цепи равно сумме напряжений на концах каждого из проводников.
При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов, а сила тока в цепи равна сумме сил токов в отдельных параллельно соединённых проводниках.
Поясним рисунком с распределением напряжений, токов и формулами.

Рис.1

Расчёт проведём для 4 резисторов (проводников), соединённых последовательно или параллельно. Если элементов в цепи меньше, то оставляем лишние поля в таблице не заполненными.
Заодно, при желании узнать распределение значений токов и напряжений на каждом из элементов при последовательном и параллельном соединениях, есть возможность ввести величину общего напряжения в цепи U. А есть возможность не вводить.
Короче, все вводные, помеченные * — к заполнению не обязательны.

РАСЧЁТ СОПРОТИВЛЕНИЙ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
проводников

Теперь, что касается последовательных и параллельных соединений конденсаторов и катушек индуктивности.
Схема, приведённая на Рис.1 для проводников и резисторов, остаётся в полной силе и для катушек с конденсаторами, распределение напряжений и токов тоже никуда не девается, трансформируется лишь осмысление того, что токи эти и напряжения обязаны быть переменными.
Почему переменными?
А потому, что для постоянных значений этих величин — сопротивление конденсаторов составляет в первом приближении бесконечность, а катушек — ноль, соответственно и токи будут равны либо нулю, либо бесконечности, а для переменных значений иметь ярко выраженную зависимость от частоты.

Поэтому, для желающих рассчитать величины напряжений и токов в последовательных или параллельных цепях, состоящих из конденсаторов и катушек индуктивности, имеет полный смысл выяснить на странице ссылка на страницу значения реактивных сопротивлений данных элементов при интересующей Вас частоте и подставить эти значения в таблицу для расчёта проводников и резисторов. А в качестве общего напряжения в цепи — подставлять действующее значение амплитуды переменного тока.

Ну а теперь приведём таблицы для расчёта значений ёмкостей и индуктивностей при условии последовательного и параллельного соединений конденсаторов и катушек в количестве от 2 до 4 штук.
Расчёт поведём на основании хрестоматийных формул:

С = С 1 + С 2 +. + С n и 1/L = 1/L 1 + 1/L 2 +. + 1/L n для параллельных цепей и
L = L 1 + L 2 +. + L n и 1/С = 1/С 1 + 1/С 2 +. + 1/С n для последовательных.

Как и в предыдущей таблице вводные, помеченные * — к заполнению не обязательны.

РАСЧЁТ ЁМКОСТИ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
конденсаторов

Ну и в завершении ещё одна таблица.

РАСЧЁТ ИНДУКТИВНОСТИ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
катушек

Тут важно заметить, что приведённые в последней таблице расчёты верны только для индуктивно не связанных катушек, то есть для катушек, намотанных на разных каркасах и расположенных на значительных расстояниях друг от друга, во избежание, пересечения взаимных магнитных полей.

Расчет сопротивления параллельного соединения резисторов

При проектировании электрических схем возникает необходимость использования последовательного и параллельного соединений резисторов. Соединения применяются также и при ремонтах электрооборудования, поскольку в некоторых ситуациях невозможно найти эквивалентный номинал резистора. Выполнить расчет просто, и справиться с этой операцией может каждый.

Типы проводников

Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.

Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.

Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:

1. Проводники (все металлы, ионизированный газ и электролитические растворы).
2. Полупроводники (Si, Ge, GaAs, InP и InSb).
3. Непроводники (диэлектрики или изоляторы).

Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.

Зависимость сопротивления

Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:

1. Температура окружающей среды и материала.
2. Электрические величины.
3. Геометрические свойства вещества.
4. Тип материала, из которого изготовлен проводник (полупроводник).

К электрическим величинам можно отнести разность потенциалов (напряжение), электродвижущую силу (ЭДС) и силу тока. Геометрией проводника является его длина и площадь поперечного сечения.

Электрические величины

Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.

Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн). В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.

Тип и геометрические параметры

Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.

Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:

1. Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.
2. Визуально определить форму материала.
3. Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.

В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S. Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.

Температурные показатели

Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.

В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * [1 + a * (t — 20)]. Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.

Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a Объединение резистивных радиокомпонентов

Для получения необходимого номинала сопротивления применяются два типа соединения резисторов: параллельное и последовательное. Если их соединить параллельно, то нужно два вывода одного резистора подключить к двум выводам другого. Если соединение является последовательным, то один вывод резистора соединяется с одним выводом другого резистора. Соединения используются для получения необходимых номиналов сопротивлений, а также для увеличения рассеивания мощности тока, протекающего по цепи.

Каждое из соединений обладает определенными характеристиками. Кроме того, последовательно или параллельно могут объединяться несколько резисторов. Соединения также могут быть смешанными, т. е. применяться оба типа объединения радиокомпонентов.

Параллельное соединение

При параллельном подключении значение напряжения на всех резисторах одинаковое, а сила тока — обратно пропорциональна их общему сопротивлению. В интернете web-разработчики создали для расчета величины общего сопротивления параллельного соединения резисторов онлайн-калькулятор.

Рассчитывается общее сопротивление при параллельном соединении по формуле: 1 / Rобщ = (1 / R1) + (1 / R2) + …+ (1 / Rn). Если выполнить математические преобразования и привести к общему знаменателю, то получится удобная формула параллельного соединения для расчета Rобщ. Она имеет следующий вид: Rобщ = (R1 * R2 * … * Rn) / (R1 + R2 + … + Rn). Если необходимо рассчитать величину Rобщ только для двух радиокомпонентов, то формула параллельного сопротивления имеет следующий вид: Rобщ = (R1 * R2) / (R1 + R2).

При ремонте или проектировании схемы устройства возникает задача объединения нескольких резистивных элементов для получения конкретной величины сопротивления. Например, значение Rобщ для определенной цепочки элементов равно 8 Ом, которое получено при расчетах. Перед радиолюбителем стоит задача, какие нужно подобрать номиналы для получения нужного значения (в стандартном ряду резисторов отсутствует радиокомпонент с номиналом в 8 Ом, а только 7,5 и 8,2). В этом случае нужно найти сопротивление при параллельном соединении резистивных элементов. Посчитать значение Rобщ для двух элементов можно следующим образом:

1. Номинал резистора в 16 Ом подойдет.
2. Подставить в формулу: R = (16 * 16) / (16 + 16) = 256 / 32 = 8 (Ом).

В некоторых случаях следует потратить больше времени на подбор необходимых номиналов. Можно применять не только два, но и три элемента. Сила тока вычисляется с использованием первого закона Кирхгофа. Формулировка закона следующая: общее значение тока, входящего и протекающего по цепи, равен выходному его значению. Величина силы тока для цепи, состоящей из двух резисторов (параллельное соединение) рассчитывается по такому алгоритму:

1. Ток, протекающий через R1 и R2: I1 = U / R1 и I2 = U / R2 соответственно.
2. Общий ток — сложение токов на резисторах: Iобщ = I1 + I2.

Например, если цепь состоит из 2 резисторов, соединенных параллельно, с номиналами в 16 и 7,5 Ом. Они запитаны от источника питания напряжением в 12 В. Значение силы тока на первом резисторе вычисляется следующим способом: I1 = 12 / 16 = 0,75 (А). На втором резисторе ток будет равен: I2 = 12 / 7,5 = 1,6 (А). Общий ток определяется по закону Кирхгофа: I = I1 + I2 = 1,6 + 0,75 = 2,35 (А).

Последовательное подключение

Последовательное включение резисторов также применяется в радиотехнике. Методы нахождения общего сопротивления, напряжения и тока отличаются от параллельного подключения. Основные правила соединения следующие:

1. Ток не изменяется на участке цепи.
2. Общее напряжение равно сумме падений напряжений на каждом резисторе.
3. Rобщ = R1 + R2 + … + Rn.

Пример задачи следующий: цепочка, состоящая из 2 резисторов (16 и 7,5 Ом), питается от источника напряжением 12 В и током в 0,5 А. Необходимо рассчитать электрические параметры для каждого элемента. Порядок расчета следующий:

1. I = I1 = I2 = 0,5 (А).
2. Rобщ = R1 + R2 = 16 + 7,5 = 23,5 (Ом).
3. Падения напряжения: U1 = I * R1 = 0,5 * 16 = 8 (В) и U2 = I * R2 = 0,5 * 7,5 = 3,75 (В).

Не всегда выполняется равенство напряжений (12 В не равно 8 + 3,75 = 11,75 В), поскольку при этом расчете не учитывается сопротивление соединительных проводов. Если схема является сложной, и в ней встречается два типа соединений, то нужно выполнять расчеты по участкам. В первую очередь, рассчитать для параллельного соединения, а затем для последовательного.

Таким образом, параллельное и последовательное соединения резисторов применяются для получения более точных значений сопротивлений, а также при отсутствии необходимого номинала радиокомпонента при проектировании или ремонте устройств.

Расчет сопротивления резистора для светодиодов: онлайн-калькулятор

Светодиоды пришли на смену традиционным системам освещения – лампам накаливания и энергосберегающим лампам. Чтобы диод работал правильно и не перегорел, его нельзя подключать напрямую в питающую сеть. Дело в том, что он имеет низкое внутреннее сопротивление, потому если подключить его напрямую, то сила тока окажется высокой, и он перегорит. Ограничить силу тока можно резисторами. Но нужно подобрать правильный резистор для светодиода. Для этого проводятся специальные расчеты.

Расчет резистора для светодиода

Чтобы компенсировать сопротивление светодиода, нужно прежде всего подобрать резистор с более высоким сопротивлением. Такой расчет не составит труда для тех, кто знает, что такое закон Ома.

Математический расчет

Исходя из закона Ома, рассчитываем по такой формуле:

где Un – напряжение сети; Uvd – напряжение, на которое рассчитана работа светодиода; Ivd – ток.

Допустим, у нас светодиод с характеристиками:

2,1 -3, 4 вольт – рабочее напряжение (Uvd). Возьмем среднее значение 2, 8 вольт.

20 ампер – рабочий ток (Ivd)

220 вольт – напряжение сети (Un)

В таком случае мы получаем величину сопротивления R = 10, 86. Однако этих расчетов недостаточно. Резистор может перегреваться. Для предотвращения перегрева нужно учитывать при выборе его мощность, которая рассчитывается по следующей формуле:

Для наглядности рекомендуем посмотреть видео:

Графический расчет

Графический способ – менее популярный для расчета резистора на светодиод, но может быть даже более удобный. Зная напряжение и ток диода (их называют еще вольтамперными характеристиками – ВАХ), вы можете узнать сопротивление нужного резистора по графику, представленному ниже:

Тут изображен расчет для диода с номинальным током 20мА и напряжением источника питания 5 вольт. Проводя пунктирную линию от 20 мА до пересечения с «кривой led» (синий цвет), чертим пересекающую линию от прямой Uled до прямой и получаем максимальное значение тока около 50 мА. Далее рассчитываем сопротивление по формуле:

Получаем значение 100 Ом для резистора. Находим для него мощность рассеивания (Силу тока берем из Imax):

Онлайн-калькулятор расчета сопротивления

Задача усложняется, если вы хотите подключить не один, а несколько диодов.

Для облегчения самостоятельных расчетов мы подготовили онлайн-калькулятор расчета сопротивления резисторов. Если подключать несколько светодиодов, то нужно будет выбрать между параллельным и последовательным соединениями между ними. И для этих схем нужны дополнительные расчеты для источника питания. Можно их легко найти в интернете, но мы советуем воспользоваться нашим калькулятором.

Вам понадобится знать:

1. Напряжение источника питания.
2. Характеристику напряжения диода.
3. Характеристику тока диода.
4. Количество диодов.

А также нужно выбрать параллельную или последовательную схему подключения. Рекомендуем ознакомиться с разницей между соединениями в главах, которые мы подготовили ниже.

В каких случаях допускается подключение светодиода через резистор

Никакие диоды, в том числе светодиоды, нельзя включать без ограничения проходящего тока. Резисторы в таком случае просто необходимы. Даже небольшое изменения напряжения вызывают очень сильное изменение тока и, следовательно, перегрев диода.

Параллельное соединение

Для тех, кто уже сталкивался на практике со схемами подключения светодиодного освещения, вопрос о выборе между параллельным и последовательным соединением обычно не стоит. Чаще всего выбирают схему последовательного соединения. У параллельного соединения для светодиодов есть один важный недостаток – это удорожание и усложнение конструкции, потому что для каждого диода нужен отдельный резистор. Но такая схема имеет и большой плюс – если сгорела одна линия, то перестанет светить только один диод, остальные продолжат работу.

Почему нельзя использовать один резистор для нескольких параллельных диодов

Объясняется достаточно просто: если перегорит один светодиод, то на другой (-ие) может попасть больший ток и начнется перегрев. Потому при параллельной схеме подключения каждому диоду нужен отдельный резистор.

Последовательное соединение светодиодов

Именно такое соединение пользуется популярностью. Объясняется такой частый выбор простым примером. Представьте, что в елочной гирлянде для каждого светодиода подобран резистор. А в гирлянде этих лампочек бывает более сотни! Параллельное соединение в данном случае невыгодно и трудоемко.

Можно ли обойтись без резисторов

В бюджетных или просто старых приборах используются резисторы. Также они используются для подключения всего только нескольких светодиодов.

Но есть более современный способ – это понижение тока через светодиодный драйвер. Так, в светильниках в 90% встречаются именно драйверы. Это специальные блоки, которые через схему преобразуют характеристики тока и напряжения питающей сети. Главное их достоинство – они обеспечивают стабильную силу тока при изменении/колебании входного напряжения.

Сегодня можно подобрать драйвер под любое количество светодиодов. Но рекомендуем не брать китайские аналоги! Кроме того, что они быстрей изнашиваются, ещё могут выдавать не те характеристики в работе, которые заявлены на упаковке.

Если светодиодов не так много, подойдут и резисторы вместо достаточно высокого по цене драйвера.

Интересное видео по теме:

В заключение

Пишите комментарии и делитесь статьей в социальных сетях! Если возникли вопросы, можно найти в интернете дополнительные видео для расчета сопротивления резистора и на другие близкие темы.

Калькулятор цветовой маркировки резисторов

Как пользоваться калькулятором?

Перед вами наиболее полный калькулятор цветовой маркировки выводных резисторов.

Работает в двух режимах:

• определение номинала на основе цветовой маркировки;
• определение цветовой маркировки на основе известного номинала.

Калькулятор рассчитан на работу с 4/5/6-полосными резисторами. Минимальное значение — 0.1 Ом, максимальное — 999 ГОм. Значения от 0.1 Ом до 0.99 Ом рассчитываются только на четырехполосном калькуляторе. Значения от 99 ГОм до 999 ГОм — только на пяти- и шестиполосном калькуляторах. Подходящий тип калькулятора будет выбран автоматически в зависимости от введённого значения.

Для определения номинала необходимо указать полосы в том порядке, в котором они нанесены на резистор. В поле «Значение» отобразится номинал резистора согласно указанных цветовых полос.

Для определения цветовой маркировки необходимо ввести в поле «Значение» номинал резистора, выбрать единицу измерения (Ом, кОм, МОм, ГОм), указать точность (не обязательно; по умолчанию это 20%), температурный коэффициент (не обязательно) и нажать кнопку «Рассчитать».

Поле «Результат подсчётов» содержит следующую информацию: 

• точное значение из ряда — если искомый номинал нашелся в соответствующем ряду;
• ближайшее большее  — если есть следующее ближайшее в ряду значение;
• ближайшее меньшее — если есть предыдущее ближайшее в ряду значение.

Что такое ряды или ряды номиналов радиодеталей? Это набор чисельных значений от 1 до 10. Чем выше число в названии ряда тем больше таких значений находится в нём и тем выше точность указанного номинала резистора. Например, ряд E6 содержит следующие номиналы: 1.0, 1.5, 2.2, 3.3, 4.7, 6.8. Соответственно, номиналы радиодеталей согласно этому ряду могут быть 1.5 Ом или 6.8 Ом. Этот ряд имеет точность в 20%. Для получения других номиналов этого ряда используют множитель, например 1000 (от 0.01 до 1000000000). Используя его получаем полный номинал: 1.5 х 1000 = 1500 Ом или 1.5 кОм. Наиболее распространён ряд E24 c допуском 5%.

Таблицы цветовой маркировки резисторов для скачивания: 4 полосы, 5 полос, 6 полос.

Калькулятор цветового кода резистора

• Калькуляторы электрических, радиочастотных и электронных устройств • Онлайн-преобразователи единиц

Определения и расчеты

Резистор и сопротивление

Резистор — это пассивный электрический компонент, который создает электрическое сопротивление в электронных схемах. Резисторы можно встретить практически во всех электрических цепях. Они используются для различных целей, например, для ограничения электрического тока, в качестве делителей напряжения, для обеспечения смещения активных элементов схемы, для завершения линий передачи, в цепях резистор-конденсатор в качестве синхронизирующего компонента… Список бесконечен.

Блок прецизионных декадных резисторов

Электрическое сопротивление резистора или электрического проводника является мерой сопротивления потоку электрического тока. Единицей измерения сопротивления в системе СИ является ом. Любой материал показывает некоторое сопротивление, кроме сверхпроводников, у которых сопротивление нулевое. Дополнительная информация об сопротивлении, удельном сопротивлении и проводимости.

Допуск резистора

Конечно, можно сделать резистор с очень точным сопротивлением, но это будет безумно дорого.Кроме того, относительно редко используются прецизионные резисторы. Для измерений используются очень дорогие резисторы. Здесь мы поговорим о недорогих резисторах, используемых в электрических схемах, не требующих высокой точности. Во многих случаях достаточно точности ± 20%. Для резистора 1 кОм это означает, что приемлем любой резистор со значением в диапазоне от 800 Ом до 1200 Ом. Для некоторых критических компонентов допуск может быть указан как ± 1% или даже ± 0,05%. В то же время 20% резисторы сегодня найти сложно — они были обычным явлением в начале эры транзисторного радио.Резисторы 5% и 1% сегодня очень распространены. Раньше они были относительно дорогими, но сейчас это не так.

Сравнение резисторов SMD 0,1 Вт в корпусах 1608 (1,6 × 0,8 мм) с керамическим резистором 10 Вт 1 Ом

Рассеиваемая мощность

Когда электрический ток проходит через резистор, он нагревается, и электрическая энергия преобразуется в тепловая энергия, которую он рассеивает. Эта энергия должна рассеиваться резистором без чрезмерного повышения его температуры. И не только его температура, но и температура компонентов, окружающих этот резистор.Мощность, потребляемая резистором, рассчитывается как

, где В, в вольтах — это напряжение на резисторе с сопротивлением R в омах, а I — ток в амперах, протекающий через него. Мощность, которую резистор может безопасно рассеивать в течение неопределенного периода времени без ухудшения своих характеристик, называется номинальной мощностью резистора или номинальной мощностью резистора в ваттах . Как правило, чем больше размер резистора, тем больше мощности он может рассеять.Выпускаются резисторы разной мощности, чаще всего от 0,01 Вт до сотен ватт. Угольные резисторы обычно производятся с номинальной мощностью от 0,125 до 2 Вт.

Резисторы с цветовой кодировкой 1/8 Вт, 1/4 Вт, 1/2 Вт и 1 Вт в блоке питания компьютера

Предпочтительные значения

Хотя можно производить резисторы любого номинала, более полезно делать ограниченное количество компонентов, особенно с учетом того, что любой изготовленный резистор подлежит определенному допуску.Стоимость более точных резисторов намного выше, чем их менее точных аналогов. Общая логика требует выбора логарифмической шкалы значений, чтобы все значения были равномерно распределены по логарифмической шкале и соответствовали допуску диапазона. Например, для допуска ± 10% имеет смысл охватить декаду (интервал от 1 до 10, от 10 до 100 и т. Д.) В 12 шагов: 1,0, 1,2, 1,5, 1,8, 2,2, 2,7, 3,3. , 3.9, 4.7, 5.6, 6.8, 8.2, затем 10, 12, 15, 18, 22, 27, 33, 39, 47, 56, 68, 82. Эти значения называются предпочтительными и стандартизированы как E series предпочтительных чисел, которые используются не только для резисторов, но также для конденсаторов, катушек индуктивности и стабилитронов.Каждая серия E (E3, E6, E12, E24, E48, E96 и E192) делит декаду на 3, 6, 12, 24, 48, 96 и 192 шага. Обратите внимание, что серия E3 устарела и почти не используется.

Списки значений серии E

Современный керамический резистор 10 Вт 8,6 Ом (вверху) и резистор VZR 2 Вт 3,3 кОм, произведенный в Советском Союзе в 1969 году

Значения E6 (допуск 20%):

1,0 , 1,5, 2,2, 3,3, 4,7, 6,8.

E12 значения (допуск 10%):

1.0, 1,2, 1,5, 1,8, 2,2, 2,7, 3,3, 3,9, 4,7, 5,6, 6,8, 8,2.

E24 значения (допуск 5%):

1.0, 1.1, 1.2, 1.3, 1.5, 1.6, 1.8, 2.0, 2.2, 2.4, 2.7, 3.0, 3.3, 3.6, 3.9, 4.3, 4.7, 5.1, 5.6, 6.2, 6.8, 7.5, 8.2, 9.1.

E48 значения (допуск 2%):

1,00, 1,05, 1,10, 1,15, 1,21, 1,27, 1,33, 1,40, 1,47, 1,54, 1,62, 1,69, 1,78, 1,87, 1,96, 2,05, 2,15, 2,26, 2.37, 2.49, 2.61, 2.74, 2.87, 3.01, 3.16, 3.32, 3.48, 3.65, 3.83, 4.02, 4.22, 4.42, 4.64, 4.87, 5.11, 5.36, 5.62, 5.90, 6.19, 6.49, 6.81, 7.15, 7.50, 7.87, 8.25, 8.66, 9.09, 9.53.

E96 значения (допуск 1%):

1,00, 1,02, 1,05, 1,07, 1,10, 1,13, 1,15, 1,18, 1,21, 1,24, 1,27, 1,30, 1,33, 1,37, 1,40, 1,43, 1,47, 1,50, 1,54, 1,58, 1,62, 1,65, 1,69, 1,74, 1,78, 1,82, 1,87, 1,91, 1,96, 2,00, 2,05, 2,10, 2,15, 2,21, 2,26, 2,32, 2,37, 2,43, 2,49, 2,55, 2,61, 2,67, 2,74, 2,80, 2,87, 2,94, 3,01, 3,09, 3,16, 3,24, 3,32, 3,40, 3,48, 3,57, 3,65, 3,74, 3,83, 3.92, 4.02, 4.12, 4.22, 4.32, 4.42, 4.53, 4.64, 4.75, 4.87, 4.99, 5.11, 5.23, 5.36, 5.49, 5.62, 5.76, 5.90, 6.04, 6.19, 6.34, 6.49, 6.65, 6.81, 6.98, 7,15, 7,32, 7,50, 7,68, 7,87, 8,06, 8,25, 8,45, 8,66, 8,87, 9,09, 9,31, 9,53, 9,76.

E192 Значения (допуск 0,5% и ниже):

1.00, 1.01, 1.02, 1.04, 1.05, 1.06, 1.07, 1.09, 1.10, 1.11, 1.13, 1.14, 1.15, 1.17, 1.18, 1.20, 1.21, 1,23, 1,24, 1,26, 1,27, 1,29, 1,30, 1,32, 1,33, 1,35, 1,37, 1,38, 1,40, 1,42, 1,43, 1,45, 1.47, 1,49, 1,50, 1,52, 1,54, 1,56, 1,58, 1,60, 1,62, 1,64, 1,65, 1,67, 1,69, 1,72, 1,74, 1,76, 1,78, 1,80, 1,82, 1,84, 1,87, 1,89, 1,91, 1,93, 1,96, 1,98, 2,00, 2,03, 2,05, 2,08, 2,10, 2,13, 2,15, 2,18, 2,21, 2,23, 2,26, 2,29, 2,32, 2,34, 2,37, 2,40, 2,43, 2,46, 2,49, 2,52, 2,55, 2,58, 2,61, 2,64, 2,67, 2,71, 2,74, 2,77, 2,80, 2,84, 2,87, 2,91, 2,94, 2,98, 3,01, 3,05, 3,09, 3,12, 3,16, 3,20, 3,24, 3,28, 3,32, 3,36, 3,40, 3,44, 3,48, 3,52, 3,57, 3.61, 3.65, 3.70, 3.74, 3.79, 3.83, 3.88, 3.92, 3.97, 4.02, 4.07, 4.12, 4.17, 4.22, 4.27, 4.32, 4.37, 4.42, 4.48, 4.53, 4.59, 4.64, 4.70, 4.75, 4.81, 4.87, 4.93, 4.99, 5.05, 5.11, 5.17, 5.23, 5.30, 5.36, 5.42, 5.49, 5.56, 5.62, 5.69, 5.76, 5.83, 5.90, 5.97, 6.04, 6.12, 6.19, 6.26, 6.34, 6.42, 6.49, 6.57, 6.65, 6.73, 6.81, 6.90, 6.98, 7.06, 7.15, 7.23, 7,32, 7,41, 7,50, 7,59, 7,68, 7,77, 7,87, 7,96, 8,06, 8,16, 8,25, 8,35, 8,45, 8,56, 8,66, 8,76, 8,87, 8,98, 9,09, 9,20, 9,31, 9,42, 9,53, 9,65, 9,76, 9,88.

Цветовая кодировка резистора

Маркировка резистора

Большие резисторы, как показано на рисунке, обычно обозначаются цифрами и буквами, и их легко читать.Однако значение не может быть легко напечатано даже с использованием современной технологии печати на небольших резисторах (и других электронных компонентах), особенно если они имеют цилиндрическую форму. Поэтому в течение последних 100 лет для маркировки компонентов использовались цветные полосы. Электронный цветовой код для этой цели был введен в начале 1920 года. Цветовые коды используются не только для резисторов, но и для конденсаторов, диодов, катушек индуктивности и других электронных компонентов.

Цветовой код резистора

Для резисторов используется до шести цветных полос.Наиболее распространенным является четырехполосный цветовой код, в котором первая и вторая полосы представляют первую и вторую значащие цифры значения сопротивления, третья полоса представляет собой десятичный множитель, а четвертая полоса указывает допуск. Между третьей и четвертой полосой есть небольшой, иногда плохо различимый зазор, который помогает различать левую и правую стороны симметричного компонента. Резисторы 20% обычно маркируются всего тремя полосами — у них нет полосы допуска. Их полосы означают цифру, цифру, множитель.

Для резисторов с точностью 2% или более используются пять или более полос, а первые три полосы представляют значение сопротивления. Последняя полоса в 6-полосной маркировке представляет температурный коэффициент в ppm / K (миллионных долях на кельвин). На рисунке выше представлен принцип цветовой маркировки.

Полосы читаются слева направо. Обычно они сгруппированы ближе к левому краю. Если есть видимый зазор между последней цветной полосой и другими полосами, значит, это показывает правую сторону резистора.Кроме того, серебряные или золотые полосы (если есть) всегда на правой стороне. Когда вы определили значение по цветным полосам, сравните его с предпочтительными диаграммами значений. Если его там нет, то попробуйте читать с другого конца. Обратите внимание на , что в данном калькуляторе цветовая маркировка выполнена в соответствии с международным стандартом IEC 60062: 2016 .

Щелкните или коснитесь ссылок, чтобы просмотреть примеры цветовой маркировки:

10 кОм ± 20%, 12 Ом ± 20%, 15 МОм ± 1%, 18 МОм ± 2%, 22 кОм ± 10%, 27 Ом ± 5 %, 33 кОм ± 5%, 39 МОм ± 0.5%, 0,47 Ом ± 0,25%, 0,56 Ом ± 0,1%, 68 Ом ± 0,05%, 0,82 Ом ± 20%

Цифровая маркировка

Числовые значения напечатаны на резисторах для поверхностного монтажа (SMT — технология поверхностного монтажа или SMD — устройство поверхностного монтажа) больших размеров и на более крупных резисторах с осевыми выводами. Поскольку место для маркировки очень мало, иногда бывает непросто прочитать и понять номинал резистора. Маркировка в основном используется для обслуживания, потому что во время производства резисторы подаются в машины для поверхностного монтажа в лентах, которые имеют соответствующую маркировку.Многие, особенно малые резисторы SMD, вообще не имеют маркировки, и после того, как они сброшены с лент, единственный способ определить их сопротивление — это измерить.

39 × 10⁰ = 39 Ом 0,1 Вт SMD резисторы в 1608 (1,6 × 0,8 мм) корпусах

Для маркировки используется несколько систем: трех- или четырехзначное, двухзначное с буквой, трехзначное с буквой, код РКМ , и другие системы. Если вы видите только три цифры, они обозначают значащие цифры, а третья — множитель. Например, 103 на резисторе SMD представляет 10 × 10³ = 10 кОм.

Четырехзначная система используется для резисторов с высокими допусками, например, для резисторов серии E96 или E192. Например, 2743 = 274 × 10³ = 274 кОм.

Для резисторов меньшего размера можно использовать другую систему. Например, для серии E96 используются две цифры плюс одна буква. Эта система может сохранить один символ по сравнению с четырехзначной системой. Это потому, что E96 содержит менее 100 значений, которые могут быть представлены двумя числами, если они пронумерованы последовательно, то есть 01-100, 02-102, 03-105 и т. Д.Буква представляет множитель. Обратите внимание, что производители часто используют собственные системы. Поэтому лучший способ определить сопротивление — всегда измерить его мультиметром.

В Кодексе РКМ, также называемом «нотацией R», вместо десятичного разделителя помещается буква, обозначающая единицу сопротивления, которая не может быть надежно напечатана или просто исчезнет на компонентах или дублированных документах. К тому же этот метод позволяет использовать меньше символов. Например, R22 или E22 означает 0,22 Ом, 2K7 означает 2.7 кОм и 1М5 означает 1,5 МОм.

Измерение резистора 3,3 МОм 0,5 Вт с помощью осциллографа-мультиметра

Измерение сопротивления

Сопротивление можно измерить с помощью аналогового (с помощью иглы) или цифрового омметра или мультиметра с функцией измерения сопротивления. Чтобы измерить сопротивление, подключите щупы к выводам резистора и прочтите значение. Иногда можно измерить сопротивление, не удаляя резистор из цепи. Однако перед подключением мультиметра к измеряемой цепи необходимо отключить питание схемы и разрядить все конденсаторы.

Мультиметр может использоваться не только для измерения сопротивления резисторов, но и контактного сопротивления различных компонентов переключения, таких как реле или переключатели. Например, вы можете определить, нуждается ли кнопка мыши в замене, измерив ее сопротивление, предпочтительно аналоговым мультиметром или цифровым измерителем с аналоговым полосовым дисплеем. Аналоговая гистограмма полезна при диагностике или настройке. Гистограмма действует как стрелка в аналоговом измерителе и может показывать колеблющееся сопротивление, когда цифровой дисплей с мигающими цифрами будет совершенно бесполезен.С помощью этого типа измерителя вы можете легко найти множество периодически возникающих проблем, например, дребезг контактов вибрирующего реле.

В заключение приведу несколько примеров:

Резистор 2,7 кОм ± 5%: красный, фиолетовый, красный, золотой

Резистор 100 кОм ± 5%: коричневый, черный, желтый, золотой.

Резистор 220 кОм ± 5%: красный, красный, желтый, золотой.

Резистор 330 кОм ± 5%: оранжевый, оранжевый, желтый, золотой.

Резистор 390 кОм ± 5%: оранжевый, белый, желтый, золотой.

Резистор 430 кОм ± 5%: желтый, оранжевый, желтый, золотой

Резистор 470 кОм ± 5%: желтый, фиолетовый, желтый, золотой

Резистор 510 кОм ± 5%: зеленый, коричневый, желтый, золотой

Резистор 560 кОм ± 5%: зеленый, синий, желтый, золотой

Резистор 750 кОм ± 5%: фиолетовый, зеленый, желтый, золотой

Резистор 910 кОм ± 5%: белый, коричневый, желтый, золотой

Эта статья написал Анатолий Золотков

Сопротивление провода, онлайн-калькулятор и формула

Онлайн-калькуляторы и формулы для расчета сопротивления проводов

Расчет сопротивления провода онлайн

На этой странице электрическое сопротивление рассчитывается исходя из длины и поперечного сечения провода.Необходимо знать удельное сопротивление или проводимость материала провода.

Обратите внимание, что сопротивление указанной простой длины рассчитывается. Если вы хотите рассчитать общее сопротивление двухполюсного кабеля, например кабель громкоговорителя, вы должны умножить значение на 2. Общее сопротивление = прямая линия + обратная линия.

Удельные значения проводимости наиболее распространенных кабелей:

Материал	Электропроводность
Медь	56.0
Серебро	62,5
Алюминий	35,0

Для просмотра списка других значений удельного сопротивления и проводимости щелкните здесь.

Калькулятор сопротивления проводов

Легенда

\ (\ displaystyle A \) Площадь поперечного сечения (мм ² )

\ (\ displaystyle l \) Длина провода (м)

\ (\ displaystyle R \) Сопротивление провода

\ (\ Displaystyle S \) Проводимость провода

\ (\ displaystyle ρ \) Удельное сопротивление

\ (\ Displaystyle σ \) Удельная проводимость

Формулы сопротивления проводов

Сопротивление провода	\ (\ Displaystyle R = \ гидроразрыва {ρ · l} {A} \) \ (\ displaystyle = \ frac {l} {σ · A} \)
Длина провода	\ (\ Displaystyle л = \ гидроразрыва {R · A} {ρ} \) \ (\ Displaystyle = р · А · σ \)
Площадь поперечного сечения провода	\ (\ Displaystyle А = \ гидроразрыва {l} {R · σ} \) \ (\ Displaystyle = \ гидроразрыва {л · ρ} {R} \)

Эта страница полезна? да Нет Спасибо за ваш отзыв! Извините за это Как мы можем это улучшить? послать

---

Калькулятор цветовой кодировки резистора

| Расчет 3-4-5- и 6-полосных резисторов

3-, 4-, 5- и 6-полосные калькуляторы цветовых кодов резисторов

Цветовые коды резисторов используются для обозначения значения сопротивления, определенного ассоциацией производителей радиооборудования в 1920 году в соответствии с Международным стандартом. Стандарты IEC 60062.

Ниже приведены калькуляторы для различных типов резисторов, таких как 3-полосные, 4-полосные, 5-полосные и 6-полосные резисторы. Пояснения, формулы и диаграммы добавлены под каждым калькулятором цветового кода резистора.

Примечание. Если вы пользуетесь мобильными телефонами, щелкните точки «…» рядом с 3-полосным резистором, чтобы выбрать другие диапазоны, например, 4-полосный, 5-полосный и 6-полосный калькулятор резисторов. Для удобства работы с мобильными телефонами используйте калькулятор в альбомной ориентации.

Калькулятор цветового кода трехполосного резистора

Калькулятор цветового кода трехполосного резистора

В настоящее время он редко используется.Чтобы прочитать полоски трех цветов на резисторе, первая полоска показывает первую значащую цифру. Вторая полоса показывает вторую значащую цифру, а третья полоса показывает множитель. Допуск для трехполосного резистора обычно составляет ± 20% (т.е. без полосы допусков = допуск ± 20%).

Как рассчитать цветовой код трехполосного резистора

Формула для калькулятора трехполосного резистора

1-я цифра. 2-я цифра x множитель

Например, значение сопротивления для показанного трехполосного цветового кода резистора ( коричневый , черный и красный ) в соответствии с таблицей будет:

1.0 x (100) = 1000 Ом с допуском ± 20%.

4-полосный резистор

Калькулятор цветового кода четырехполосного резистора

Это типичные резисторы для использования в электронных схемах. Чтобы прочитать коды четырех цветов полосок на резисторе, первая полоска показывает первую значащую цифру. Вторая полоса показывает вторую значащую цифру. Третья полоска показывает множитель. Четвертая полоса показывает ± допуск в% для четырех полос.

Как рассчитать Цветовой код четырехполосного резистора

Формула для расчета четырехполосного резистора

1 ^st Digit. 2 ^nd цифра x множитель; ± Допуск в%

Например, значение сопротивления для показанного цветового кода 4-полосного резистора ( Коричневый , Черный , Красный и Золотой ) в соответствии с таблицей будет:

1. 0 x (100) = 1000 Ом с допуском ± 5%.

5-полосный резистор

Калькулятор цветового кода пятиполосного резистора

Для высокой точности имеется дополнительная цветная полоса в качестве третьей значащей цифры в цветовом коде 5-полосного резистора. Для считывания пяти цветовых кодов полос на резисторе первый, второй и третий цветовые коды полос показывают соответственно первую значащую, вторую значащую и четвертую значащие цифры. Четвертая полоса показывает множитель. Пятая полоса показывает ± допуск в% для пяти полос.

Как рассчитать цветовой код пятиполосного резистора

Формула для калькулятора 5-полосного резистора

1 ^st Digit. 2 ^nd цифр. 3 ^rd цифра x множитель; ± Допуск в%

Например, значение сопротивления для показанного цветового кода 5-полосного резистора ( Коричневый , Черный , Оранжевый , Красный и Желтый ) в соответствии с таблицей будет:

1.0. 3 x (100) = 10,3 кОм с допуском ± 5%.

Полезно знать:

Существует особый сценарий в случае резистора с цветовым кодом 5-полосного резистора, где четвертая полоса — Gold или Silver . В этом случае первые две полосы показывают первые две значащие цифры, третья — для множителя, четвертая — для допуска, а 5-я — для температурного коэффициента, то же самое в резисторе с цветовым кодом шестиполосного резистора. Единица измерения температурного коэффициента — ppm / K, а более подробную информацию о ppm / K можно найти в цветовом коде 6-полосного резистора.

6-полосный резистор

Калькулятор цветового кода шестиполосного резистора

Для высокой точности и точности предусмотрена дополнительная цветовая полоса в качестве температурного коэффициента в цветовом коде 6-полосного резистора. Чтобы прочитать шесть цветовых кодов полос на резисторе, первый, второй и третий цветовые коды полос показывают первую значащую, вторую значащую и третью значащую цифры соответственно. Четвертая полоса показывает множитель. Пятая полоса показывает ± допуск в%.Шесть диапазонов показывают температурный коэффициент.

Как рассчитать цветовой код пятиполосного резистора

Формула для калькулятора 5-полосного резистора

1 ^st Digit. 2 ^nd цифр. 3 ^rd Разряд x множитель; ± Допуск в%, Температура Коэффициент

Например, значение сопротивления для показанного цветового кода 5-полосного резистора ( Коричневый , Черный , Оранжевый , Красный , Желтый , Коричневый ) согласно таблице будет:

1.0. 3 x (100) = 10,3 кОм с допуском ± 5% 100 ppm / ° C.

Полезно знать

Шестая полоса, используемая для температурного коэффициента в 6-полосном цветовом коде резистора. PPM / K означает «Часть на миллион в Кельвинах ».

Для вышеупомянутого цветового кода для температурного коэффициента, который составляет коричневый , это означает, что сопротивление изменится на 100 частей на миллион на 1 градус Кельвина.

Например,

Указанный выше резистор номиналом 10.3 кОм с допуском ± 5% и 100 ppm / ° C ( Коричневый цвет как 6-я полоса для температурного коэффициента. И мы хотим знать, насколько изменится значение сопротивления, если произойдет изменение температуры на 10 ° C.

(100 x 10ºC / 10 ⁶ ) x 10,3 кОм = отклонение ± 1,03 Ом при 10ºC.

Цветовые коды резисторов

Этот удобный инструмент предназначен для расчета значений 3-полосного, 4-полосного, 5-полосного и 6-полосный резистор в соответствии с их цветовой кодировкой.

Между тем, чтобы узнать, как работает калькулятор цветового кода резистора и как читать напечатанные цветовые коды на конкретном резисторе, чтобы найти их значение, см. Следующие таблицы и диаграмму. Также под каждым калькулятором приведены формулы и таблицы с решенным примером.

В приведенной ниже таблице показаны различные значения для разных цветовых кодов резисторов.

9017 ^st цифра 9018 9018 2 ^nd цифра rd Digit rd Лента

Количество полос	3 полосы	4 полосы	5 полос	6 полос
9017 1
1 st цифра	1 st цифра	1 st цифра
2 nd Диапазон	2 цифра nd	2 nd цифра
3 rd Band	Multiplier	Multiplier	3 rd Digit			НЕТ	Допуск	Множитель	Множитель
5 th Лента	НЕТ	НЕТ	Допуск	Допуск
6 th Band	N / A	N / A	N / A	Температурный коэффициент

Значения цвета для резистора , каждый цвет показывает определенное значение.В случае 3-полосных и 4-полосных резисторов первые две цветные полосы показывают значащие цифры и их значения, в то время как для 5-полосных и 6-полосных резисторов 1

^-й , 2 ^-й и 3 ^-й цветных диапазонов являются показывая значащие цифры и связанные с ними значения.

9018 1

Цвет полосы	Значение
Черный (2 nd и 3 rd Только полосы)
Красный	2
Оранжевый	3
Желтый	Желтый
Синий	6
Фиолетовый	7
Серый	Серый	Серый	Серый

Следующую простую мнемонику можно запомнить, чтобы запомните последовательность цветовых кодов для цветовых кодов резисторов.

• B etter B e R ight O r Y наш Gre при B ig V acation g oes W rong.
• B B ROY из G reat B ritain имел V ery G ood W ife, который носил G old и S Elace.

Второй — для дополнительных цветов в множителе.

Значения цвета для умножителя

Цвет третьей полосы для 3-полосного и 4-полосного резистора или четвертой полосы для 5-полосного и 6-полосного резистора известен как Умножитель . В следующей таблице показаны цвета и соответствующие значения множителя.

ЦВЕТ	МУЛЬТИПЛИКЕР
ЧЕРНЫЙ	1 Ом

1 Ом

ПОМЕЕЦ	1кОм
ЖЕЛТАЯ	10кОм
ЗЕЛЕНЫЙ	100 кОм
СИНИЙ	1 МОм
ФИОЛЕТОВЫЙ	10 МОм
СЕРЫЙ	100 МОм
БЕЛЫЙ
СЕРЕБРЯНЫЙ	0,01 Ом

Значения допуска цвета

В трехполосных цветовых кодах резисторов нет диапазона допуска, поэтому обычно предполагается 20%. Четвертая полоса в цвете 4-полосного резистора используется для значения допуска. В случае 5-полосных и 6-полосных резисторов для допуска используется код полосы 5 ^-й .

ЦВЕТ	Допуск
ЧЕРНЫЙ	НЕТ
BROWN6

0.5% (D) ± 0,05% (A)

± 2% (G)
ОРАНЖЕВЫЙ	± 3%
ЖЕЛТЫЙ		± 4%
СИНИЙ	± 0,25% (C)
ФИОЛЕТОВЫЙ	± 0,10% (B)
БЕЛЫЙ	НЕТ
ЗОЛОТО	± 5% (J)
	9017 % (K)

Буквенные коды допусков для резисторов

• A = 0.05%
• B = 0,1%
• C = 0,25%
• D = 0,5%
• F = 1%
• G = 2%
• J = 5%
• K = 10%
• M = 20 % (Общие)

Значения температурного коэффициента

Шестая полоса шестиполосных резисторов показывает температурный коэффициент в ppm / ºC, который показывает, насколько значение резистора изменяется при изменении температуры. Более подробную информацию о температурном коэффициенте и ppm / ºC и ppm / K можно найти под калькулятором резисторов для 6-диапазона.В шортах PPM / K означает «Часть на миллион в Кельвинах ».

Например,

Указанный выше 6-полосный резистор номиналом 10,3 кОм с допуском ± 5% и 100 ppm / ° C ( Коричневый цвет как 6-я полоса для температурного коэффициента. И мы хотим знать, насколько значение Сопротивление изменится, если произойдет изменение температуры на 10 ° C.

(100 x 10 ° C / 10 ⁶ ) x 10,3 кОм = изменение ± 1,03 Ом более 10 ° C.

ОРАНЖЕВЫЙ

COLOR	Температура Коэффициент (ppm / ºC)
ЧЕРНЫЙ	НЕТ
КОРИЧНЕВЫЙ	100
15
ЖЕЛТЫЙ	25
ЗЕЛЕНЫЙ	НЕТ
СИНИЙ	10
ФИОЛЕТОВЫЙ	5
СЕРЫЙ	N / A

Полезно знать:

• В случае резистора с цветовым кодом 5 полос, где четвертая полоса — Gold или Silver .В этом случае первые две полосы показывают первые две значащие цифры, третья — для множителя, четвертая — для допуска, а 5-я — для температурного коэффициента, то же самое в резисторе с цветовым кодом шестиполосного резистора. Единица измерения температурного коэффициента — ppm / K, а более подробную информацию о ppm / K можно найти в цветовом коде 6-полосного резистора.
• Цвета полос Gold и Silver заменены на цвета Yellow и Grey в случае высоковольтного резистора, чтобы предотвратить попадание частиц, таких как металлы, на покрытие резистора.
• Резистор с нулевым сопротивлением (полоса одного черного цвета) используется в качестве перемычки на печатной плате для соединения дорожек.
• Для высокочувствительных устройств (например, для военных целей) существует диапазон надежности, который показывает частоту отказов в% на 1000 часов работы. Эта полоса недоступна в коммерческих резисторах.

Цветовые коды резисторов SMD

Мы уже обсуждали очень подробный пост о том, как найти значение резисторов SMD с решенными примерами.

Цветовой код резистора Таблицы

Таблица цветового кода резистора

Расчет значения сопротивления 3-полосного, 4-полосного, 5-полосного и 6-полосного цветового кода резистора. Таблица цветов 3, 4, 5 и 6-ти полосного резистора
.

Значимые цифры Цвет Значения для цветовой кодировки резистора.

Значения цвета множителя для цветовой кодировки резистора.

Допустимые значения цвета для цветовых кодов резисторов.

Значения цветов температурного коэффициента для цветовых кодов резисторов.

Похожие сообщения:

Резистор Калькулятор — Инженерной Проекты

[vc_row] [vc_column] [vc_raw_js] JTNDc2NyaXB0JTIwbGFuZ3VhZ2UlM0QlMjJKYXZhU2NyaXB0MS4xJTIyJTNFJTBBJTBBJTJGJTJGJTIwY3JlYXRlJTIwYXJyYXklMjBsaXN0aW5nJTIwYWxsJTIwdGhlJTIwbXVsdGlwbGllciUyMHZhbHVlcyUwQXZhciUyMG11bHRpcGxpZXIlMjAlM0QlMjBuZXclMjBBcnJheSUyOCUyOSUwQW11bHRpcGxpZXIlNUIwJTVEJTIwJTNEJTIwMCUwQW11bHRpcGxpZXIlNUIxJTVEJTIwJTNEJTIwMSUwQW11bHRpcGxpZXIlNUIyJTVEJTIwJTNEJTIwMiUwQW11bHRpcGxpZXIlNUIzJTVEJTIwJTNEJTIwMyUwQW11bHRpcGxpZXIlNUI0JTVEJTIwJTNEJTIwNCUwQW11bHRpcGxpZXIlNUI1JTVEJTIwJTNEJTIwNSUwQW11bHRpcGxpZXIlNUI2JTVEJTIwJTNEJTIwNiUwQW11bHRpcGxpZXIlNUI3JTVEJTIwJTNEJTIwNyUwQW11bHRpcGxpZXIlNUI4JTVEJTIwJTNEJTIwOCUwQW11bHRpcGxpZXIlNUI5JTVEJTIwJTNEJTIwOSUwQW11bHRpcGxpZXIlNUIxMCU1RCUyMCUzRCUyMC0xJTBBbXVsdGlwbGllciU1QjExJTVEJTIwJTNEJTIwLTIlMEElMEElMkYlMkYlMjBjcmVhdGUlMjBhcnJheSUyMGxpc3RpbmclMjBhbGwlMjB0b2xlcmFuY2UlMjB2YWx1ZXMlMEF2YXIlMjB0b2xlcmFuY2UlMjAlM0QlMjBuZXclMjBBcnJheSUyOCUyOSUwQXR vbGVyYW5jZSU1QjAlNUQlMjAlM0QlMjAlMjIlMkIlMkYtNSUyNSUyMiUwQXRvbGVyYW5jZSU1QjElNUQlMjAlM0QlMjAlMjIlMkIlMkYtMTAlMjUlMjIlMEF0b2xlcmFuY2UlNUIyJTVEJTIwJTNEJTIwJTIyJTJCJTJGLTIwJTI1JTIyJTBBJTBBJTJGJTJGJTIwZm9ybWF0JTIwbGFyZ2UlMjB2YWx1ZXMlMjBpbnRvJTIwa2lsbyUyMGFuZCUyMG1lZyUwQWZ1bmN0aW9uJTIwZm9ybWF0JTI4b2htYWdlJTI5JTIwJTdCJTBBJTA5aWYlMjAlMjhvaG1hZ2UlMjAlM0UlM0QlMjAxZTYlMjklMjAlN0IlMEElMDklMDlvaG1hZ2UlMjAlMkYlM0QlMjAxZTYlMEElMDklMDlyZXR1cm4lMjAlMjIlMjIlMjAlMkIlMjBvaG1hZ2UlMjAlMkIlMjAlMjIlMjBNb2htcyUyMiUwQSUwOSU3RCUyMGVsc2UlMjAlN0IlMEElMDklMDlpZiUyMCUyOG9obWFnZSUyMCUzRSUzRCUyMDFlMyUyOSUyMCU3QiUwQSUwOSUwOSUwOW9obWFnZSUyMCUyRiUzRCUyMDFlMyUwQSUwOSUwOSUwOXJldHVybiUyMCUyMiUyMiUyMCUyQiUyMG9obWFnZSUyMCUyQiUyMCUyMiUyMEtvaG1zJTIyJTBBJTA5JTA5JTdEJTIwZWxzZSUyMCU3QiUwQSUwOSUwOSUwOXJldHVybiUyMCUyMiUyMiUyMCUyQiUyMG9obWFnZSUyMCUyQiUyMCUyMiUyMG9obXMlMjIlMEElMDklMDklN0QlMEElMDklN0QlMEElN0QlMEElMEElMkYlMkYlMjBjYWxjdWxhdGUlMjByZXNpc3RhbmNlJTIwYW5kJTIwdG9sZXJhbmNlJTIwdmFsdWVzJTBBZnVuY3Rpb24lMjBjYWxjT2htcyUyOCUyOSUyMCU 3QiUwQSUwOXZhciUyMGZvcm0lMjAlM0QlMjBkb2N1bWVudC5mb3JtcyU1QiUyMmlucHV0JTIyJTVEJTBBJTA5dmFyJTIwZDElMjAlM0QlMjBmb3JtLnRlbnNTZWxlY3Quc2VsZWN0ZWRJbmRleCUwQSUwOXZhciUyMGQyJTIwJTNEJTIwZm9ybS5vbmVzU2VsZWN0LnNlbGVjdGVkSW5kZXglMEElMDl2YXIlMjBtJTIwJTNEJTIwZm9ybS5tdWx0aXBsaWVyU2VsZWN0LnNlbGVjdGVkSW5kZXglMEElMDl2YXIlMjB0JTIwJTNEJTIwZm9ybS50b2xlcmFuY2VTZWxlY3Quc2VsZWN0ZWRJbmRleCUwQSUwOXZhciUyMG9obWFnZSUyMCUzRCUyMCUyOGQxJTIwJTJBJTIwMTAlMjklMjAlMkIlMjBkMiUwQSUwOW9obWFnZSUyMCUzRCUyMGV2YWwlMjglMjIlMjIlMjAlMkIlMjBvaG1hZ2UlMjAlMkIlMjAlMjJlJTIyJTIwJTJCJTIwbXVsdGlwbGllciU1Qm0lNUQlMjklMEElMDlvaG1hZ2UlMjAlM0QlMjBmb3JtYXQlMjhvaG1hZ2UlMjklMEElMDl2YXIlMjB0b2wlMjAlM0QlMjB0b2xlcmFuY2UlNUJ0JTVEJTBBJTA5ZG9jdW1lbnQuZm9ybXMlNUIlMjJvdXRwdXQlMjIlNUQucmVzdWx0LnZhbHVlJTIwJTNEJTIwb2htYWdlJTIwJTJCJTIwJTIyJTJDJTIwJTIyJTIwJTJCJTIwdG9sJTBBJTdEJTBBJTBBJTJGJTJGJTIwcHJlLWxvYWQlMjBhbGwlMjBjb2xvciUyMGltYWdlcyUyMGludG8lMjBpbWFnZSUyMGNhY2hlJTBBdmFyJTIwY29sb3JBcnJheSUyMCUzRCUyMG5ldyUyMEFycmF5JTI4JTIyQmxhY2slMjIlMkMlMjJCbHVlJTIyJTJDJTI yQnJvd24lMjIlMkMlMjJHb2xkJTIyJTJDJTIyR3JheSUyMiUyQyUyMkdyZWVuJTIyJTJDJTIyTm9uZSUyMiUyQyUyMk9yYW5nZSUyMiUyQyUyMlJlZCUyMiUyQyUyMlNpbHZlciUyMiUyQyUyMlZpb2xldCUyMiUyQyUyMldoaXRlJTIyJTJDJTIyWWVsbG93JTIyJTI5JTBBdmFyJTIwaW1hZ2VEQiUyMCUzRCUyMG5ldyUyMEFycmF5JTI4JTI5JTBBZm9yJTIwJTI4aSUyMCUzRCUyMDAlM0IlMjBpJTIwJTNDJTIwY29sb3JBcnJheS5sZW5ndGglM0IlMjBpJTJCJTJCJTI5JTIwJTdCJTBBJTA5aW1hZ2VEQiU1QmNvbG9yQXJyYXklNUJpJTVEJTVEJTIwJTNEJTIwbmV3JTIwSW1hZ2UlMjgyMSUyQzE4MiUyOSUwQSUwOWltYWdlREIlNUJjb2xvckFycmF5JTVCaSU1RCU1RC5zcmMlMjAlM0QlMjAlMjJodHRwJTNBJTJGJTJGd3d3LnRoZWVuZ2luZWVyaW5ncHJvamVjdHMuY29tJTJGd3AtY29udGVudCUyRnVwbG9hZHMlMkYyMDE3JTJGMDElMkYlMjIlMjAlMkIlMjBjb2xvckFycmF5JTVCaSU1RCUyMCUyQiUyMCUyMi5naWYlMjIlMEElN0QlMEElMEFmdW5jdGlvbiUyMHNldFRlbnMlMjhjaG9pY2UlMjklMjAlN0IlMEElMDl2YXIlMjB0ZW5zQ29sb3IlMjAlM0QlMjBjaG9pY2Uub3B0aW9ucyU1QmNob2ljZS5zZWxlY3RlZEluZGV4JTVELnZhbHVlJTBBJTA5ZG9jdW1lbnQudGVucy5zcmMlMjAlM0QlMjBpbWFnZURCJTVCdGVuc0NvbG9yJTVELnNyYyUwQSUwOWNhbGNPaG1zJTI4JTI5JTBBJTdEJTBBZnVuY3Rpb24lMjBzZXRPbmV zJTI4Y2hvaWNlJTI5JTIwJTdCJTBBJTA5dmFyJTIwb25lc0NvbG9yJTIwJTNEJTIwY2hvaWNlLm9wdGlvbnMlNUJjaG9pY2Uuc2VsZWN0ZWRJbmRleCU1RC52YWx1ZSUwQSUwOWRvY3VtZW50Lm9uZXMuc3JjJTIwJTNEJTIwaW1hZ2VEQiU1Qm9uZXNDb2xvciU1RC5zcmMlMEElMDljYWxjT2htcyUyOCUyOSUwQSU3RCUwQWZ1bmN0aW9uJTIwc2V0TXVsdCUyOGNob2ljZSUyOSUyMCU3QiUwQSUwOXZhciUyMG11bHRDb2xvciUyMCUzRCUyMGNob2ljZS5vcHRpb25zJTVCY2hvaWNlLnNlbGVjdGVkSW5kZXglNUQudmFsdWUlMEElMDlkb2N1bWVudC5tdWx0LnNyYyUyMCUzRCUyMGltYWdlREIlNUJtdWx0Q29sb3IlNUQuc3JjJTBBJTA5Y2FsY09obXMlMjglMjklMEElN0QlMEFmdW5jdGlvbiUyMHNldFRvbCUyOGNob2ljZSUyOSUyMCU3QiUwQSUwOXZhciUyMHRvbENvbG9yJTIwJTNEJTIwY2hvaWNlLm9wdGlvbnMlNUJjaG9pY2Uuc2VsZWN0ZWRJbmRleCU1RC52YWx1ZSUwQSUwOWRvY3VtZW50LnRvbC5zcmMlMjAlM0QlMjBpbWFnZURCJTVCdG9sQ29sb3IlNUQuc3JjJTBBJTA5Y2FsY09obXMlMjglMjklMEElN0QlMEFmdW5jdGlvbiUyMHNob3dJbnRybyUyOCUyOSUyMCU3QiUwQSUwOXdpbmRvdy5vcGVuJTI4JTIycmVzaW50cm8uaHRtJTIyJTJDJTIyJTIyJTJDJTIyd2lkdGglM0Q0MDAlMkNoZWlnaHQlM0QzMjAlMkNsZWZ0JTNEMTAwJTJDdG9wJTNEMTAwJTIyJTI5JTBBJTdEJTBBJTBBd2luZG93Lm9ubG9hZCUyMCUzRCU yMGNhbGNPaG1zJTNCJTBBJTNDJTJGc2NyaXB0JTNF [/ vc_raw_js] [/ vc_column] [/ vc_row] [vc_row] [vc_column] [vc_column_text]

Всем привет, прежде всего с Новым годом всех вас.Я надеюсь, что этот год принесет больше счастья в жизнь каждого. 🙂 Сегодня я собираюсь впервые поделиться новым онлайн-инструментом под названием Resistor Calculator . Используя этот онлайн-инструмент, вы можете легко найти значение сопротивления, используя его цветовой код, и я очень рад этому, потому что мы раньше не публиковали ни одного онлайн-инструмента. В ближайшее время мы собираемся поделиться другими такими онлайн-инструментами, и я надеюсь, что эти онлайн-инструменты помогут инженерам в их инженерных проектах.

Я также рассказал, как рассчитать сопротивление вручную, используя его цветовой код и его значение, указанное после этого инструмента для расчета резисторов.Итак, это предложение не только использовать этот калькулятор резисторов, но и научиться делать это вручную, потому что знания всегда полезны, плюс есть шанс, что вы не найдете Интернет, когда захотите использовать наш калькулятор резисторов. 😛 Итак, вот онлайн инструмент для резистора калькулятора : [/ vc_column_text] [vc_raw_html] JTNDc3R5bGUlMjB0eXBlJTNEJTIydGV4dCUyRmNzcyUyMiUzRSUwQSUyM3Jlc2lzdG9yJTIwJTdCdGV4dC1hbGlnbiUzQWNlbnRlciU3RCUwQSUyM3Jlc2lzdG9yJTIwcCUyMCU3QiUwQSUwOXRleHQtYWxpZ24lM0ElMjBsZWZ0JTNCJTBBJTdEJTBBJTIzcmVzaXN0b3IlMjBwcmUlMjAlN0IlMEElMDl0ZXh0LWFsaWduJTNBJTIwbGVmdCUzQiUwQSU3RCUwQXRhYmxlJTIwJTdCJTBBJTA5Ym9yZGVyLWNvbG9yJTNBJTIzMDA4MGZmJTNCJTBBJTA5JTdEJTBBaW5wdXQlMjAlN0IlMEElMDlib3JkZXItY29sb3IlM0ElMjMwMDgwZmYlM0IlMEElN0QlMEEubXlCdXR0b24lMjAlN0IlMEElMDktbW96LWJveC1zaGFkb3clM0FpbnNldCUyMDBweCUyMDFweCUyMDBweCUyMDBweCUyMCUyM2JiZGFmNyUzQiUwQSUwOS13ZWJraXQtYm94LXNoYWRvdyUzQWluc2V0JTIwMHB4JTIwMXB4JTIwMHB4JTIwMHB4JTIwJTIzYmJkYWY3JTNCJTBBJTA5Ym94LXNoYWRvdyUzQWluc2V0JTIwMHB4JTIwMXB4JTIwMHB4JTIwMHB4JTIwJTIzYmJkYWY3JTNCJTBBJTA5YmFja2dyb3VuZCUzQS13ZWJraXQtZ3JhZGllbnQlMjhsaW5lYXIlMkMlMjBsZWZ0JTIwdG9wJTJDJTIwbGVmdCUyMGJvdHRvbSUyQyUyMGNvbG9yLXN0b3AlMjgwLjA1JTJDJTIwJTIzNzliYmZmJTI5JTJDJTIwY29sb3Itc3RvcCUyODElMkMlMjAlMjM zNzhkZTUlMjklMjklM0IlMEElMDliYWNrZ3JvdW5kJTNBLW1vei1saW5lYXItZ3JhZGllbnQlMjh0b3AlMkMlMjAlMjM3OWJiZmYlMjA1JTI1JTJDJTIwJTIzMzc4ZGU1JTIwMTAwJTI1JTI5JTNCJTBBJTA5YmFja2dyb3VuZCUzQS13ZWJraXQtbGluZWFyLWdyYWRpZW50JTI4dG9wJTJDJTIwJTIzNzliYmZmJTIwNSUyNSUyQyUyMCUyMzM3OGRlNSUyMDEwMCUyNSUyOSUzQiUwQSUwOWJhY2tncm91bmQlM0Etby1saW5lYXItZ3JhZGllbnQlMjh0b3AlMkMlMjAlMjM3OWJiZmYlMjA1JTI1JTJDJTIwJTIzMzc4ZGU1JTIwMTAwJTI1JTI5JTNCJTBBJTA5YmFja2dyb3VuZCUzQS1tcy1saW5lYXItZ3JhZGllbnQlMjh0b3AlMkMlMjAlMjM3OWJiZmYlMjA1JTI1JTJDJTIwJTIzMzc4ZGU1JTIwMTAwJTI1JTI5JTNCJTBBJTA5YmFja2dyb3VuZCUzQWxpbmVhci1ncmFkaWVudCUyOHRvJTIwYm90dG9tJTJDJTIwJTIzNzliYmZmJTIwNSUyNSUyQyUyMCUyMzM3OGRlNSUyMDEwMCUyNSUyOSUzQiUwQSUwOWZpbHRlciUzQXByb2dpZCUzQURYSW1hZ2VUcmFuc2Zvcm0uTWljcm9zb2Z0LmdyYWRpZW50JTI4c3RhcnRDb2xvcnN0ciUzRCUyNyUyMzc5YmJmZiUyNyUyQyUyMGVuZENvbG9yc3RyJTNEJTI3JTIzMzc4ZGU1JTI3JTJDR3JhZGllbnRUeXBlJTNEMCUyOSUzQiUwQSUwOWJhY2tncm91bmQtY29sb3IlM0ElMjM3OWJiZmYlM0IlMEElMDktbW96LWJvcmRlci1yYWRpdXMlM0ExNXB4JTNCJTBBJTA5LXdlYmtpdC1ib3JkZXItcmF kaXVzJTNBMTVweCUzQiUwQSUwOWJvcmRlci1yYWRpdXMlM0ExNXB4JTNCJTBBJTA5Ym9yZGVyJTNBMnB4JTIwc29saWQlMjAlMjM4NGJiZjMlM0IlMEElMDlkaXNwbGF5JTNBaW5saW5lLWJsb2NrJTNCJTBBJTA5Y3Vyc29yJTNBcG9pbnRlciUzQiUwQSUwOWNvbG9yJTNBJTIzZmZmZmZmJTNCJTBBJTA5Zm9udC1mYW1pbHklM0FWZXJkYW5hJTNCJTBBJTA5Zm9udC1zaXplJTNBMjhweCUzQiUwQSUwOWZvbnQtd2VpZ2h0JTNBYm9sZCUzQiUwQSUwOXBhZGRpbmclM0ExNXB4JTIwMzVweCUzQiUwQSUwOXRleHQtZGVjb3JhdGlvbiUzQW5vbmUlM0IlMEElMDl0ZXh0LXNoYWRvdyUzQTBweCUyMDFweCUyMDBweCUyMCUyMzUyOGVjYyUzQiUwQSU3RCUwQSUwQS5teUJ1dHRvbjIlMjAlN0IlMEElMDktbW96LWJveC1zaGFkb3clM0FpbnNldCUyMDBweCUyMDFweCUyMDBweCUyMDBweCUyMCUyM2JiZGFmNyUzQiUwQSUwOS13ZWJraXQtYm94LXNoYWRvdyUzQWluc2V0JTIwMHB4JTIwMXB4JTIwMHB4JTIwMHB4JTIwJTIzYmJkYWY3JTNCJTBBJTA5Ym94LXNoYWRvdyUzQWluc2V0JTIwMHB4JTIwMXB4JTIwMHB4JTIwMHB4JTIwJTIzYmJkYWY3JTNCJTBBJTA5YmFja2dyb3VuZCUzQS13ZWJraXQtZ3JhZGllbnQlMjhsaW5lYXIlMkMlMjBsZWZ0JTIwdG9wJTJDJTIwbGVmdCUyMGJvdHRvbSUyQyUyMGNvbG9yLXN0b3AlMjgwLjA1JTJDJTIwJTIzNzliYmZmJTI5JTJDJTIwY29sb3Itc3RvcCUyODElMkMlMjAlMjMzNzhkZTUlMjklMjk lM0IlMEElMDliYWNrZ3JvdW5kJTNBLW1vei1saW5lYXItZ3JhZGllbnQlMjh0b3AlMkMlMjAlMjM3OWJiZmYlMjA1JTI1JTJDJTIwJTIzMzc4ZGU1JTIwMTAwJTI1JTI5JTNCJTBBJTA5YmFja2dyb3VuZCUzQS13ZWJraXQtbGluZWFyLWdyYWRpZW50JTI4dG9wJTJDJTIwJTIzNzliYmZmJTIwNSUyNSUyQyUyMCUyMzM3OGRlNSUyMDEwMCUyNSUyOSUzQiUwQSUwOWJhY2tncm91bmQlM0Etby1saW5lYXItZ3JhZGllbnQlMjh0b3AlMkMlMjAlMjM3OWJiZmYlMjA1JTI1JTJDJTIwJTIzMzc4ZGU1JTIwMTAwJTI1JTI5JTNCJTBBJTA5YmFja2dyb3VuZCUzQS1tcy1saW5lYXItZ3JhZGllbnQlMjh0b3AlMkMlMjAlMjM3OWJiZmYlMjA1JTI1JTJDJTIwJTIzMzc4ZGU1JTIwMTAwJTI1JTI5JTNCJTBBJTA5YmFja2dyb3VuZCUzQWxpbmVhci1ncmFkaWVudCUyOHRvJTIwYm90dG9tJTJDJTIwJTIzNzliYmZmJTIwNSUyNSUyQyUyMCUyMzM3OGRlNSUyMDEwMCUyNSUyOSUzQiUwQSUwOWZpbHRlciUzQXByb2dpZCUzQURYSW1hZ2VUcmFuc2Zvcm0uTWljcm9zb2Z0LmdyYWRpZW50JTI4c3RhcnRDb2xvcnN0ciUzRCUyNyUyMzc5YmJmZiUyNyUyQyUyMGVuZENvbG9yc3RyJTNEJTI3JTIzMzc4ZGU1JTI3JTJDR3JhZGllbnRUeXBlJTNEMCUyOSUzQiUwQSUwOWJhY2tncm91bmQtY29sb3IlM0ElMjM3OWJiZmYlM0IlMEElMDktbW96LWJvcmRlci1yYWRpdXMlM0E3cHglM0IlMEElMDktd2Via2l0LWJvcmRlci1yYWRpdXMlM0E3cHglM0I lMEElMDlib3JkZXItcmFkaXVzJTNBN3B4JTNCJTBBJTA5Ym9yZGVyJTNBMnB4JTIwc29saWQlMjAlMjM4NGJiZjMlM0IlMEElMDlkaXNwbGF5JTNBaW5saW5lLWJsb2NrJTNCJTBBJTA5Y3Vyc29yJTNBcG9pbnRlciUzQiUwQSUwOWNvbG9yJTNBJTIzZmZmZmZmJTNCJTBBJTA5Zm9udC1mYW1pbHklM0FWZXJkYW5hJTNCJTBBJTA5Zm9udC1zaXplJTNBMTRweCUzQiUwQSUwOWZvbnQtd2VpZ2h0JTNBYm9sZCUzQiUwQSUwOXBhZGRpbmclM0E4cHglMjA5cHglM0IlMEElMDl0ZXh0LWRlY29yYXRpb24lM0Fub25lJTNCJTBBJTA5dGV4dC1zaGFkb3clM0EwcHglMjAxcHglMjAwcHglMjAlMjM1MjhlY2MlM0IlMEElN0QlMEElMEEucGFkZGluZzElN0IlMEElMDlwYWRkaW5nLWJvdHRvbSUzQTUwcHglM0IlMEElN0QlMEElM0MlMkZzdHlsZSUzRSUwQSUwQQ == [/ vc_raw_html] [vc_raw_html] JTNDZGl2JTIwc3R5bGUlM0QlMjJwYWRkaW5nJTNBMTBweCUzQmJvcmRlciUzQTEwcHglMjBvdXRzZXQlMjAlMjMwMDgwZmYlM0IlMjAlMjIlM0UlMEElMEElM0NkaXYlMjBpZCUzRCUyMnJlc2lzdG9yJTIyJTNFJTBBJTBBJTNDZGl2JTIwY2xhc3MlM0QlMjJteUJ1dHRvbiUyMiUyMCUzRVJlc2lzdG9yJTIwQ2FsY3VsYXRvciUwQSUzQ2JyJTJGJTNFJTBBJTNDYiUyMHN0eWxlJTNEJTIyZm9udC1zaXplJTNBMTVweCUyMiUzRU9ubGluZSUyMFJlc2lzdG9yJTIwY2FsY3VsYXRvciUyMHVzaW5nJTIwUmVzaXN0b3IlMjBDb2xvciUyMENv ZGUuJTNDJTJGYiUzRSUzQyUyRmRpdiUzRSUwQSUzQ2JyJTJGJTNFJTNDYnIlMkYlM0UlMEElM0NkaXYlMjBzdHlsZSUzRCUyMnBhZGRpbmctbGVmdCUzQTEwcHglM0JwYWRkaW5nLXRvcCUzQTIwcHglM0Jib3JkZXIlM0EycHglMjBzb2xpZCUyMCUyMzAwODBmZiUzQmRpc3BsYXklM0ElMjAtd2Via2l0LWJveCUzQiUyMiUzRSUyMCUwQSUzQ2ltZyUyMHN0eWxlJTNEJTIycGFkZGluZy1yaWdodCUzQTEwcHglM0IlMjIlMjBzcmMlM0QlMjJodHRwJTNBJTJGJTJGd3d3LnRoZWVuZ2luZWVyaW5ncHJvamVjdHMuY29tJTJGd3AtY29udGVudCUyRnVwbG9hZHMlMkYyMDE3JTJGMDElMkZob3d0b3VzZS5wbmclMjIlMkYlM0UlMEElM0N1bCUyMHN0eWxlJTNEJTIydGV4dC1hbGlnbiUzQWxlZnQlM0IlMjIlM0UlMEElM0NsaSUzRVNlbGVjdCUyMHRoZSUyMGNvbG9yJTIwYmFuZHMlMjBvZiUyMHlvdXIlMjByZXNpc3RvciUyMGJ5JTIwdXNpbmclMjB0aGUlMjBmb3VyJTIwY29tYm8lMjBib3hlcyUyMGdpdmVuJTIwYmVsb3cuJTNDJTJGbGklM0UlM0NsaSUzRUFzJTIweW91JTIwY2hhbmdlJTIwdGhlJTIwY29sb3JzJTIwb2YlMjB5b3VyJTIwcmVzaXN0YW5jZSUyMGJhbmRzJTJDJTIwdGhlJTIwdmFsdWUlMjB3aWxsJTIwYmUlMjB1cGRhdGVkJTIwaW4lMjB0aGUlMjBSZXNpc3RvciUyMFZhbHVlJTIwYm94LiUzQyUyRmxpJTNFJTNDJTJGdWwlM0UlMEElM0MlMkZkaXYlM0UlMEElM0NiciUyRiUzRSUwQSUzQ2RpdiUyMHN0eWxlJTNE JTIycGFkZGluZy1sZWZ0JTNBMTBweCUzQnBhZGRpbmctdG9wJTNBMTVweCUzQmJvcmRlciUzQTJweCUyMHNvbGlkJTIwJTIzMDA4MGZmJTNCZGlzcGxheSUzQSUyMC13ZWJraXQtYm94JTNCJTIyJTNFJTIwJTBBJTNDaW1nJTIwc3R5bGUlM0QlMjJwYWRkaW5nLXJpZ2h0JTNBMTBweCUzQiUyMiUyMHNyYyUzRCUyMmh0dHAlM0ElMkYlMkZ3d3cudGhlZW5naW5lZXJpbmdwcm9qZWN0cy5jb20lMkZ3cC1jb250ZW50JTJGdXBsb2FkcyUyRjIwMTclMkYwMSUyRkNvbG9yQ29kZS5wbmclMjIlMkYlM0UlMEElM0Nmb3JtJTIwbmFtZSUzRCUyMmlucHV0JTIyJTIwc3R5bGUlM0QlMjJwYWRkaW5nLWxlZnQlM0E3MHB4JTNCcGFkZGluZy10b3AlM0E3MHB4JTNCJTIyJTNFJTBBJTIwJTIwJTBBJTIwJTIwJTNDc2VsZWN0JTIwbmFtZSUzRCUyMnRlbnNTZWxlY3QlMjIlMjBvbkNoYW5nZSUzRCUyMnNldFRlbnMlMjh0aGlzJTI5JTJDdGhpcy5zdHlsZS5iYWNrZ3JvdW5kQ29sb3IlM0R0aGlzLm9wdGlvbnMlNUJ0aGlzLnNlbGVjdGVkSW5kZXglNUQuc3R5bGUuYmFja2dyb3VuZENvbG9yJTJDJTIwdGhpcy5zdHlsZS5jb2xvciUzRHRoaXMub3B0aW9ucyU1QnRoaXMuc2VsZWN0ZWRJbmRleCU1RC5zdHlsZS5jb2xvciUyMiUyMHN0eWxlJTNEJTIyY29sb3IlM0ElMjNGRkYlM0IlMjBiYWNrZ3JvdW5kLWNvbG9yJTNBJTIzMDAwJTIyJTNFJTBBJTIwJTIwJTBBJTIwJTIwJTBBJTA5JTNDb3B0aW9uJTIwdmFsdWUlM0QlMjJCbGFjayUyMiUy MHNlbGVjdEVEJTIwc3R5bGUlM0QlMjJjb2xvciUzQSUyM0ZGRiUzQiUyMGJhY2tncm91bmQtY29sb3IlM0ElMjMwMDAlMjIlM0UlMjBCbGFjayUwQSUwOSUzQ29wdGlvbiUyMHZhbHVlJTNEJTIyQnJvd24lMjIlMjBzdHlsZSUzRCUyMmNvbG9yJTNBJTIzRkZGJTNCJTIwYmFja2dyb3VuZC1jb2xvciUzQWJyb3duJTIyJTNFJTIwQnJvd24lMEElMDklM0NvcHRpb24lMjB2YWx1ZSUzRCUyMlJlZCUyMiUyMHN0eWxlJTNEJTIyJTIwYmFja2dyb3VuZC1jb2xvciUzQXJlZCUyMiUzRSUyMFJlZCUwQSUwOSUzQ29wdGlvbiUyMHZhbHVlJTNEJTIyT3JhbmdlJTIyJTIwc3R5bGUlM0QlMjIlMjBiYWNrZ3JvdW5kLWNvbG9yJTNBb3JhbmdlJTIyJTNFJTIwT3JhbmdlJTBBJTA5JTNDb3B0aW9uJTIwdmFsdWUlM0QlMjJZZWxsb3clMjIlMjBzdHlsZSUzRCUyMmJhY2tncm91bmQtY29sb3IlM0F5ZWxsb3clMjIlM0UlMjBZZWxsb3clMEElMDklM0NvcHRpb24lMjB2YWx1ZSUzRCUyMkdyZWVuJTIyJTIwc3R5bGUlM0QlMjIlMjBiYWNrZ3JvdW5kLWNvbG9yJTNBZ3JlZW4lMjIlM0UlMjBHcmVlbiUwQSUwOSUzQ29wdGlvbiUyMHZhbHVlJTNEJTIyQmx1ZSUyMiUyMHN0eWxlJTNEJTIyJTIwYmFja2dyb3VuZC1jb2xvciUzQWJsdWUlMjIlM0UlMjBCbHVlJTBBJTA5JTNDb3B0aW9uJTIwdmFsdWUlM0QlMjJWaW9sZXQlMjIlMjBzdHlsZSUzRCUyMiUyMGJhY2tncm91bmQtY29sb3IlM0F2aW9sZXQlMjIlM0UlMjBWaW9sZXQlMEElMDklM0Nv cHRpb24lMjB2YWx1ZSUzRCUyMkdyYXklMjIlMjBzdHlsZSUzRCUyMiUyMGJhY2tncm91bmQtY29sb3IlM0FncmF5JTIyJTNFJTIwR3JheSUwQSUwOSUzQ29wdGlvbiUyMHZhbHVlJTNEJTIyV2hpdGUlMjIlMjBzdHlsZSUzRCUyMmJhY2tncm91bmQtY29sb3IlM0ElMjNGRkYlMjIlM0UlMjBXaGl0ZSUwQSUzQyUyRnNlbGVjdCUzRSUyNm5ic3AlM0IlMjZuYnNwJTNCJTI2bmJzcCUzQiUyNm5ic3AlM0IlMjZuYnNwJTNCJTI2bmJzcCUzQiUyNm5ic3AlM0IlMjZuYnNwJTNCJTI2bmJzcCUzQiUyNm5ic3AlM0IlMjZuYnNwJTNCJTI2bmJzcCUzQiUzQ3NlbGVjdCUyMG5hbWUlM0QlMjJvbmVzU2VsZWN0JTIyJTIwb25DaGFuZ2UlM0QlMjJzZXRPbmVzJTI4dGhpcyUyOSUyQ3RoaXMuc3R5bGUuYmFja2dyb3VuZENvbG9yJTNEdGhpcy5vcHRpb25zJTVCdGhpcy5zZWxlY3RlZEluZGV4JTVELnN0eWxlLmJhY2tncm91bmRDb2xvciUyQyUyMHRoaXMuc3R5bGUuY29sb3IlM0R0aGlzLm9wdGlvbnMlNUJ0aGlzLnNlbGVjdGVkSW5kZXglNUQuc3R5bGUuY29sb3IlMjIlMjBzdHlsZSUzRCUyMmNvbG9yJTNBJTIzRkZGJTNCJTIwYmFja2dyb3VuZC1jb2xvciUzQSUyMzAwMCUyMiUzRSUwQSUwOSUzQ29wdGlvbiUyMHZhbHVlJTNEJTIyQmxhY2slMjIlMjBzZWxlY3RFRCUyMHN0eWxlJTNEJTIyY29sb3IlM0ElMjNGRkYlM0IlMjBiYWNrZ3JvdW5kLWNvbG9yJTNBJTIzMDAwJTIyJTNFJTIwQmxhY2slMEElMDklM0NvcHRpb24lMjB2YWx1 ZSUzRCUyMkJyb3duJTIyJTIwc3R5bGUlM0QlMjJjb2xvciUzQSUyM0ZGRiUzQiUyMGJhY2tncm91bmQtY29sb3IlM0Ficm93biUyMiUzRSUyMEJyb3duJTBBJTA5JTNDb3B0aW9uJTIwdmFsdWUlM0QlMjJSZWQlMjIlMjBzdHlsZSUzRCUyMiUyMGJhY2tncm91bmQtY29sb3IlM0FyZWQlMjIlM0UlMjBSZWQlMEElMDklM0NvcHRpb24lMjB2YWx1ZSUzRCUyMk9yYW5nZSUyMiUyMHN0eWxlJTNEJTIyJTIwYmFja2dyb3VuZC1jb2xvciUzQW9yYW5nZSUyMiUzRSUyME9yYW5nZSUwQSUwOSUzQ29wdGlvbiUyMHZhbHVlJTNEJTIyWWVsbG93JTIyJTIwc3R5bGUlM0QlMjJiYWNrZ3JvdW5kLWNvbG9yJTNBeWVsbG93JTIyJTNFJTIwWWVsbG93JTBBJTA5JTNDb3B0aW9uJTIwdmFsdWUlM0QlMjJHcmVlbiUyMiUyMHN0eWxlJTNEJTIyJTIwYmFja2dyb3VuZC1jb2xvciUzQWdyZWVuJTIyJTNFJTIwR3JlZW4lMEElMDklM0NvcHRpb24lMjB2YWx1ZSUzRCUyMkJsdWUlMjIlMjBzdHlsZSUzRCUyMiUyMGJhY2tncm91bmQtY29sb3IlM0FibHVlJTIyJTNFJTIwQmx1ZSUwQSUwOSUzQ29wdGlvbiUyMHZhbHVlJTNEJTIyVmlvbGV0JTIyJTIwc3R5bGUlM0QlMjIlMjBiYWNrZ3JvdW5kLWNvbG9yJTNBdmlvbGV0JTIyJTNFJTIwVmlvbGV0JTBBJTA5JTNDb3B0aW9uJTIwdmFsdWUlM0QlMjJHcmF5JTIyJTIwc3R5bGUlM0QlMjIlMjBiYWNrZ3JvdW5kLWNvbG9yJTNBZ3JheSUyMiUzRSUyMEdyYXklMEElMDklM0NvcHRpb24lMjB2YWx1ZSUz RCUyMldoaXRlJTIyJTIwc3R5bGUlM0QlMjJiYWNrZ3JvdW5kLWNvbG9yJTNBJTIzRkZGJTIyJTNFJTIwV2hpdGUlMEElM0MlMkZzZWxlY3QlM0UlMjZuYnNwJTNCJTI2bmJzcCUzQiUyNm5ic3AlM0IlMjZuYnNwJTNCJTI2bmJzcCUzQiUyNm5ic3AlM0IlMjZuYnNwJTNCJTI2bmJzcCUzQiUyNm5ic3AlM0IlMjZuYnNwJTNCJTI2bmJzcCUzQiUyNm5ic3AlM0IlM0NzZWxlY3QlMjBuYW1lJTNEJTIybXVsdGlwbGllclNlbGVjdCUyMiUyMG9uQ2hhbmdlJTNEJTIyc2V0TXVsdCUyOHRoaXMlMjklMkN0aGlzLnN0eWxlLmJhY2tncm91bmRDb2xvciUzRHRoaXMub3B0aW9ucyU1QnRoaXMuc2VsZWN0ZWRJbmRleCU1RC5zdHlsZS5iYWNrZ3JvdW5kQ29sb3IlMkMlMjB0aGlzLnN0eWxlLmNvbG9yJTNEdGhpcy5vcHRpb25zJTVCdGhpcy5zZWxlY3RlZEluZGV4JTVELnN0eWxlLmNvbG9yJTIyJTIwc3R5bGUlM0QlMjJjb2xvciUzQSUyM0ZGRiUzQiUyMGJhY2tncm91bmQtY29sb3IlM0ElMjMwMDAlMjIlM0UlMEElMDklM0NvcHRpb24lMjB2YWx1ZSUzRCUyMkJsYWNrJTIyJTIwc2VsZWN0RUQlMjBzdHlsZSUzRCUyMmNvbG9yJTNBJTIzRkZGJTNCJTIwYmFja2dyb3VuZC1jb2xvciUzQSUyMzAwMCUyMiUzRSUyMEJsYWNrJTBBJTA5JTNDb3B0aW9uJTIwdmFsdWUlM0QlMjJCcm93biUyMiUyMHN0eWxlJTNEJTIyY29sb3IlM0ElMjNGRkYlM0IlMjBiYWNrZ3JvdW5kLWNvbG9yJTNBYnJvd24lMjIlM0UlMjBCcm93biUwQSUwOSUzQ29w dGlvbiUyMHZhbHVlJTNEJTIyUmVkJTIyJTIwc3R5bGUlM0QlMjIlMjBiYWNrZ3JvdW5kLWNvbG9yJTNBcmVkJTIyJTNFJTIwUmVkJTBBJTA5JTNDb3B0aW9uJTIwdmFsdWUlM0QlMjJPcmFuZ2UlMjIlMjBzdHlsZSUzRCUyMiUyMGJhY2tncm91bmQtY29sb3IlM0FvcmFuZ2UlMjIlM0UlMjBPcmFuZ2UlMEElMDklM0NvcHRpb24lMjB2YWx1ZSUzRCUyMlllbGxvdyUyMiUyMHN0eWxlJTNEJTIyYmFja2dyb3VuZC1jb2xvciUzQXllbGxvdyUyMiUzRSUyMFllbGxvdyUwQSUwOSUzQ29wdGlvbiUyMHZhbHVlJTNEJTIyR3JlZW4lMjIlMjBzdHlsZSUzRCUyMiUyMGJhY2tncm91bmQtY29sb3IlM0FncmVlbiUyMiUzRSUyMEdyZWVuJTBBJTA5JTNDb3B0aW9uJTIwdmFsdWUlM0QlMjJCbHVlJTIyJTIwc3R5bGUlM0QlMjIlMjBiYWNrZ3JvdW5kLWNvbG9yJTNBYmx1ZSUyMiUzRSUyMEJsdWUlMEElMDklM0NvcHRpb24lMjB2YWx1ZSUzRCUyMlZpb2xldCUyMiUyMHN0eWxlJTNEJTIyJTIwYmFja2dyb3VuZC1jb2xvciUzQXZpb2xldCUyMiUzRSUyMFZpb2xldCUwQSUwOSUzQ29wdGlvbiUyMHZhbHVlJTNEJTIyR3JheSUyMiUyMHN0eWxlJTNEJTIyJTIwYmFja2dyb3VuZC1jb2xvciUzQWdyYXklMjIlM0UlMjBHcmF5JTBBJTA5JTNDb3B0aW9uJTIwdmFsdWUlM0QlMjJXaGl0ZSUyMiUyMHN0eWxlJTNEJTIyYmFja2dyb3VuZC1jb2xvciUzQSUyM0ZGRiUyMiUzRSUyMFdoaXRlJTBBJTA5JTNDb3B0aW9uJTIwdmFsdWUlM0QlMjJHb2xk JTIyJTIwc3R5bGUlM0QlMjJiYWNrZ3JvdW5kLWNvbG9yJTNBZ29sZCUyMiUzRSUyMEdvbGQlMEElMDklM0NvcHRpb24lMjB2YWx1ZSUzRCUyMlNpbHZlciUyMiUyMHN0eWxlJTNEJTIyYmFja2dyb3VuZC1jb2xvciUzQXNpbHZlciUyMiUzRSUyMFNpbHZlciUwQSUzQyUyRnNlbGVjdCUzRSUyNm5ic3AlM0IlMjZuYnNwJTNCJTI2bmJzcCUzQiUyNm5ic3AlM0IlMjZuYnNwJTNCJTI2bmJzcCUzQiUyNm5ic3AlM0IlMjZuYnNwJTNCJTI2bmJzcCUzQiUyNm5ic3AlM0IlMjZuYnNwJTNCJTI2bmJzcCUzQiUyNm5ic3AlM0IlMjZuYnNwJTNCJTI2bmJzcCUzQiUyNm5ic3AlM0IlM0NzZWxlY3QlMjBuYW1lJTNEJTIydG9sZXJhbmNlU2VsZWN0JTIyJTIwb25DaGFuZ2UlM0QlMjJzZXRUb2wlMjh0aGlzJTI5JTJDdGhpcy5zdHlsZS5iYWNrZ3JvdW5kQ29sb3IlM0R0aGlzLm9wdGlvbnMlNUJ0aGlzLnNlbGVjdGVkSW5kZXglNUQuc3R5bGUuYmFja2dyb3VuZENvbG9yJTJDJTIwdGhpcy5zdHlsZS5jb2xvciUzRHRoaXMub3B0aW9ucyU1QnRoaXMuc2VsZWN0ZWRJbmRleCU1RC5zdHlsZS5jb2xvciUyMiUyMHN0eWxlJTNEJTIyYmFja2dyb3VuZC1jb2xvciUzQWdvbGQlMjIlM0UlMEElMDklM0NvcHRpb24lMjB2YWx1ZSUzRCUyMkdvbGQlMjIlMjBzdHlsZSUzRCUyMmJhY2tncm91bmQtY29sb3IlM0Fnb2xkJTIyJTNFJTIwR29sZCUwQSUwOSUzQ29wdGlvbiUyMHZhbHVlJTNEJTIyU2lsdmVyJTIyJTIwc3R5bGUlM0QlMjJiYWNrZ3Jv dW5kLWNvbG9yJTNBc2lsdmVyJTIyJTNFJTIwU2lsdmVyJTBBJTA5JTNDb3B0aW9uJTIwdmFsdWUlM0QlMjJOb25lJTIyJTIwc3R5bGUlM0QlMjJiYWNrZ3JvdW5kLWNvbG9yJTNBd2hpdGUlMjIlM0UlMjBOb25lJTBBJTNDJTJGc2VsZWN0JTNFJTBBJTNDJTJGZm9ybSUzRSUwQSUzQyUyRmRpdiUzRSUwQSUzQ2JyJTJGJTNFJTBBJTNDY2VudGVyJTNFJTBBJTNDc2NyaXB0JTIwYXN5bmMlMjBzcmMlM0QlMjIlMkYlMkZwYWdlYWQyLmdvb2dsZXN5bmRpY2F0aW9uLmNvbSUyRnBhZ2VhZCUyRmpzJTJGYWRzYnlnb29nbGUuanMlMjIlM0UlM0MlMkZzY3JpcHQlM0UlMEElM0MlMjEtLSUyME1pZCUyMDElMjAtLSUzRSUwQSUzQ2lucyUyMGNsYXNzJTNEJTIyYWRzYnlnb29nbGUlMjIlMEElMjAlMjAlMjAlMjAlMjBzdHlsZSUzRCUyMmRpc3BsYXklM0FpbmxpbmUtYmxvY2slM0J3aWR0aCUzQTcyOHB4JTNCaGVpZ2h0JTNBOTBweCUyMiUwQSUyMCUyMCUyMCUyMCUyMGRhdGEtYWQtY2xpZW50JTNEJTIyY2EtcHViLTM0NzI0MTI4OTAyMDU0MjYlMjIlMEElMjAlMjAlMjAlMjAlMjBkYXRhLWFkLXNsb3QlM0QlMjIxMDg5NDM5OTU5JTIyJTNFJTNDJTJGaW5zJTNFJTBBJTNDc2NyaXB0JTNFJTBBJTI4YWRzYnlnb29nbGUlMjAlM0QlMjB3aW5kb3cuYWRzYnlnb29nbGUlMjAlN0MlN0MlMjAlNUIlNUQlMjkucHVzaCUyOCU3QiU3RCUyOSUzQiUwQSUzQyUyRnNjcmlwdCUzRSUwQSUzQyUyRmNlbnRlciUzRSUwQSUzQ2JyJTJGJTNFJTBB JTBBJTNDc2NyaXB0JTIwbGFuZ3VhZ2UlM0QlMjJKYXZhU2NyaXB0MS4xJTIyJTNFJTBBdmFyJTIwZm9ybSUyMCUzRCUyMGRvY3VtZW50LmZvcm1zJTVCJTIyaW5wdXQlMjIlNUQlMEF2YXIlMjB0ZW5zRGlnaXQlMjAlM0QlMjBmb3JtLnRlbnNTZWxlY3Quc2VsZWN0ZWRJbmRleCUwQXZhciUyMHRlbnNDb2xvciUyMCUzRCUyMGZvcm0udGVuc1NlbGVjdC5vcHRpb25zJTVCdGVuc0RpZ2l0JTVELnRleHQlMEF2YXIlMjBvbmVzRGlnaXQlMjAlM0QlMjBmb3JtLm9uZXNTZWxlY3Quc2VsZWN0ZWRJbmRleCUwQXZhciUyMG9uZXNDb2xvciUyMCUzRCUyMGZvcm0ub25lc1NlbGVjdC5vcHRpb25zJTVCb25lc0RpZ2l0JTVELnRleHQlMEF2YXIlMjBtdWx0RGlnaXQlMjAlM0QlMjBmb3JtLm11bHRpcGxpZXJTZWxlY3Quc2VsZWN0ZWRJbmRleCUwQXZhciUyMG11bHRDb2xvciUyMCUzRCUyMGZvcm0ubXVsdGlwbGllclNlbGVjdC5vcHRpb25zJTVCbXVsdERpZ2l0JTVELnRleHQlMEF2YXIlMjB0b2xEaWdpdCUyMCUzRCUyMGZvcm0udG9sZXJhbmNlU2VsZWN0LnNlbGVjdGVkSW5kZXglMEF2YXIlMjB0b2xDb2xvciUyMCUzRCUyMGZvcm0udG9sZXJhbmNlU2VsZWN0Lm9wdGlvbnMlNUJ0b2xEaWdpdCU1RC50ZXh0JTBBdmFyJTIwdGFibGUlMjAlM0QlMjIlM0N0YWJsZSUyMGJvcmRlciUzRDAlMjBhbGlnbiUzRGNlbnRlciUyMCUzRSUzQ2Zvcm0lMjBuYW1lJTNEJTI3b3V0cHV0JTI3JTNFJTIyJTBBdGFibGUlMjAlMkIlM0QlMjAlMjIl M0N0ciUzRSUzQ3RoJTNFJTI2bmJzcCUzQiUyNm5ic3AlM0IlMjZuYnNwJTNCJTI2bmJzcCUzQiUyNm5ic3AlM0IlMjZuYnNwJTNCJTI2bmJzcCUzQiUyNm5ic3AlM0IlMjZuYnNwJTNCJTI2bmJzcCUzQiUyNm5ic3AlM0IlMjZuYnNwJTNCJTI2bmJzcCUzQiUyNm5ic3AlM0IlMjZuYnNwJTNCJTI2bmJzcCUzQiUyNm5ic3AlM0IlMjZuYnNwJTNCJTI2bmJzcCUzQiUyNm5ic3AlM0IlMjZuYnNwJTNCJTI2bmJzcCUzQiUyNm5ic3AlM0IlMjZuYnNwJTNCJTI2bmJzcCUzQiUyNm5ic3AlM0IlMjZuYnNwJTNCJTI2bmJzcCUzQiUyNm5ic3AlM0IlMjZuYnNwJTNCJTI2bmJzcCUzQlJlc2lzdGFuY2UlMjBWYWx1ZSUzQSUzQyUyRnRoJTNFJTIyJTBBdGFibGUlMjAlMkIlM0QlMjIlMjAlM0N0aCUzRSUzQ2lucHV0JTIwdHlwZSUzRCUyN3RleHQlMjclMjBuYW1lJTNEJTI3cmVzdWx0JTI3JTIwc2l6ZSUzRDIwJTIwb25Gb2N1cyUzRCUyN3RoaXMuYmx1ciUyOCUyOSUyNyUzRSUyMiUwQXRhYmxlJTIwJTJCJTNEJTIyJTNDJTJGdGglM0UlM0MlMkZ0ciUzRSUzQ3RyJTNFJTNDdGQlMjBjb2xzcGFuJTNEMiUyMCUzRSUyNm5ic3AlM0IlMjIlMEF0YWJsZSUyMCUyQiUzRCUyMiUzQ2ltZyUyMFNSQyUzRCUyN2h0dHAlM0ElMkYlMkZ3d3cudGhlZW5naW5lZXJpbmdwcm9qZWN0cy5jb20lMkZ3cC1jb250ZW50JTJGdXBsb2FkcyUyRjIwMTclMkYwMSUyRnJlc2xlZnQuZ2lmJTI3JTIwd2lkdGglM0QxMjclMjBoZWlnaHQlM0QxODIlM0UlM0Np bWclMjIlMjAlMkIlMEElMDklMDklMDklMjIlMjBzcmMlM0QlMjdodHRwJTNBJTJGJTJGd3d3LnRoZWVuZ2luZWVyaW5ncHJvamVjdHMuY29tJTJGd3AtY29udGVudCUyRnVwbG9hZHMlMkYyMDE3JTJGMDElMkYlMjIlMjAlMkIlMjB0ZW5zQ29sb3IlMjAlMkIlMjAlMjIuZ2lmJTI3JTIwbmFtZSUzRCUyN3RlbnMlMjclMjB3aWR0aCUzRDIxJTIwaGVpZ2h0JTNEMTgyJTNFJTNDaW1nJTIyJTJCJTBBJTA5JTA5JTA5JTIyJTIwc3JjJTNEJTI3aHR0cCUzQSUyRiUyRnd3dy50aGVlbmdpbmVlcmluZ3Byb2plY3RzLmNvbSUyRndwLWNvbnRlbnQlMkZ1cGxvYWRzJTJGMjAxNyUyRjAxJTJGJTIyJTIwJTJCJTIwb25lc0NvbG9yJTIwJTJCJTIwJTIyLmdpZiUyNyUyMG5hbWUlM0QlMjdvbmVzJTI3JTIwd2lkdGglM0QyMSUyMGhlaWdodCUzRDE4MiUzRSUzQ2ltZyUyMiUyQiUwQSUwOSUwOSUwOSUyMiUyMHNyYyUzRCUyN2h0dHAlM0ElMkYlMkZ3d3cudGhlZW5naW5lZXJpbmdwcm9qZWN0cy5jb20lMkZ3cC1jb250ZW50JTJGdXBsb2FkcyUyRjIwMTclMkYwMSUyRiUyMiUyMCUyQiUyMG11bHRDb2xvciUyMCUyQiUyMCUyMi5naWYlMjclMjBuYW1lJTNEJTI3bXVsdCUyNyUyMHdpZHRoJTNEMjElMjBoZWlnaHQlM0QxODIlM0UlM0NpbWclMjIlMkIlMEElMDklMDklMDklMjIlMjBzcmMlM0QlMjdodHRwJTNBJTJGJTJGd3d3LnRoZWVuZ2luZWVyaW5ncHJvamVjdHMuY29tJTJGd3AtY29udGVudCUyRnVwbG9hZHMlMkYyMDE3JTJGMDEl MkZzcGFjZXIuZ2lmJTI3JTIwd2lkdGglM0QxNyUyMGhlaWdodCUzRDE4MiUzRSUzQ2ltZyUyMiUyQiUwQSUwOSUwOSUwOSUyMiUyMHNyYyUzRCUyN2h0dHAlM0ElMkYlMkZ3d3cudGhlZW5naW5lZXJpbmdwcm9qZWN0cy5jb20lMkZ3cC1jb250ZW50JTJGdXBsb2FkcyUyRjIwMTclMkYwMSUyRiUyMiUyMCUyQiUyMHRvbENvbG9yJTIwJTJCJTIwJTIyLmdpZiUyNyUyMG5hbWUlM0QlMjd0b2wlMjclMjB3aWR0aCUzRDIxJTIwaGVpZ2h0JTNEMTgyJTNFJTNDaW1nJTIyJTJCJTBBJTA5JTA5JTA5JTIyJTIwc3JjJTNEJTI3aHR0cCUzQSUyRiUyRnd3dy50aGVlbmdpbmVlcmluZ3Byb2plY3RzLmNvbSUyRndwLWNvbnRlbnQlMkZ1cGxvYWRzJTJGMjAxNyUyRjAxJTJGcmVzcmlnLmdpZiUyNyUyMCUzRSUyMiUwQXRhYmxlJTIwJTJCJTNEJTIwJTIyJTI2bmJzcCUzQiUzQyUyRnRkJTNFJTNDJTJGdHIlM0UlM0MlMkZmb3JtJTNFJTNDJTJGdGFibGUlM0UlMjIlMEFkb2N1bWVudC53cml0ZSUyOHRhYmxlJTI5JTBBJTNDJTJGc2NyaXB0JTNFJTBBJTNDJTJGZGl2JTNFJTBBJTBBJTNDY2VudGVyJTIwJTNFJTBBJTIwJTIwJTNDcCUzRURldmVsb3BlZCUyMEJ5JTIwJTNDYSUyMGhyZWYlM0QlMjJodHRwJTNBJTJGJTJGd3d3LnRoZWVuZ2luZWVyaW5ncHJvamVjdHMuY29tJTJGJTIyJTNFVEVQJTNDJTJGYSUzRSUyMCU3QyUyMCUzQ2ElMjBocmVmJTNEJTIyaHR0cCUzQSUyRiUyRnd3dy50aGVlbmdpbmVlcmluZ3Byb2plY3RzLmNvbSUy RiUyMiUzRVRoZSUyMEVuZ2luZWVyaW5nJTIwUHJvamVjdHMlM0MlMkZhJTNFJTNDJTJGcCUzRSUwQSUzQyUyRmNlbnRlciUzRSUwQSUzQyUyMS0tJTIwZW5kJTIwZm9vdGVyJTIwLS0lM0UlMEElM0MlMkZkaXYlM0UlMEElM0MlMkZkaXYlM0U = [/ vc_raw_html] [/ vc_column] [/ vc_row] [vc_row] [vc_column] [vc_column_text] Я надеюсь, что вы пользовались этим резистором калькулятором, и это помогло вам в ваших инженерных проектах.Теперь я объясню, как рассчитать сопротивление вручную.

Как рассчитать сопротивление по цветовой шкале ???

• Прежде всего, сопротивление имеет четыре цветных полосы, как показано на рисунке ниже:

• Как вы можете видеть на рисунке выше, на сопротивлении есть четыре цветные полосы, где:
  • Первая полоса — красная.
  • Вторая полоса — зеленая.
  • Третья полоса черная.
  • Четвертая полоса — золото.
• Теперь давайте сначала обсудим эти значения цвета, а затем вернемся к этим полосам.
• Первые три цветных полосы могут иметь девять разных цветовых полос, и эти цвета вместе с их значениями показаны в таблице ниже:

• Теперь вы знаете значения каждой цветовой полосы.
• Итак, теперь позвольте мне рассказать вам, как получить номинал резистора по этим цветовым кодам.
• Значения первой и второй цветовых полос остаются без изменений.
• В приведенных выше примерах первая полоса была красной, а значение красной полосы — 2.
• Вторая полоса была зеленой и ее значение 5.
• Теперь третье значение полосы указывает количество нулей, которые появятся после этих двух значений.
• Итак, поскольку третий цвет черный и его значение равно 0, это означает, что после первых двух значений не будет нуля, поэтому это сопротивление составляет 25 Ом.
• Теперь давайте обсудим четвертую цветовую полосу.
• Обычно это не рассматривается в простом проекте, но вы должны знать, что это значит.
• Четвертая цветная полоса может быть золотой или серебряной, и от нее зависит допуск сопротивления.
• Если четвертая цветная полоса — золото, это означает, что резистор имеет допуск +/- 5%, а если его серебро, то это означает, что он имеет допуск +/- 10%.
• Если четвертая цветная полоса отсутствует, значит, сопротивление имеет только три цветных полосы, значит, у него допуск +/- 20%.
• Итак, теперь давайте обсудим пример другого сопротивления, приведенного ниже:

• Итак, первая полоса — Коричневый , поэтому первое значение — 1.
• Вторая полоса — Черный , поэтому второе значение будет 0.
• Третья полоса — Красный , ее значение — 2, поэтому после первых двух значений будет два нуля.
• Итак, общее значение станет 1000 Ом или, можно сказать, 1 кОм.
• As, последняя полоса серебряная, поэтому допуск +/- 10%.

Итак, это все о калькуляторе резисторов , а также о том, как рассчитать его вручную. Я надеюсь, вам понравилось, и вы собираетесь им пользоваться. Береги себя и получай удовольствие !!! 🙂

[/ vc_column_text] [/ vc_column] [/ vc_row]

Автор: Сайед Зайн Насир

https: // www.theengineeringprojects.com/

Я Сайед Зайн Насир, основатель инженерных проектов (TEP). Я программист с 2009 года, до этого я просто занимаюсь поиском, делаю небольшие проекты, а теперь я делюсь своими знаниями через эту платформу. Я также работаю фрилансером и выполнял множество проектов, связанных с программированием и электрическими схемами. Мой профиль Google +

Калькулятор комбинации резисторов

Эта страница не работает с отключенным JavaScript

Введите необходимое сопротивление резистора в Ом (извините, сейчас нет синтаксического анализа / преобразования единиц измерения), выберите максимальное количество резисторов в комбинации, выберите номиналы резисторов, доступные для создания комбинации (вы даже можете выбрать собственные подмножества E12 или E24), отрегулируйте тип комбинации (только параллельный, только последовательный или оба), нажмите кнопку «Вычислить».
Имейте в виду, близость значения комбинации к требуемой не гарантирует, что вы действительно получите это значение, используя резисторы с допуском ± 10% (E12) или ± 5% (E24).

Каждый дополнительный резистор в комбинации улучшит качество полученных значений примерно на два порядка. Однако запрашиваются комбинации из большего количества резисторов. вызовет более длительный поиск комбинаций (экспоненциальный рост). Калькулятор ограничит максимальное количество резисторов в комбинации в зависимости от количества доступных значений входного резистора.

Желаемое значение
Набор резисторов Пользовательское подмножество E12E24E12 Пользовательское подмножество E24
Макс. # В комбинации 123456
Комбинированный тип Последовательный и параллельный только параллельный Только серия
Compute

• Для наборов входов до 24 значений вы можете запросить комбинации до 6 резисторов.
• Для наборов входов до 36 значений максимальное количество резисторов в комбинации составляет 5
• Для 72 входных значений (включая полный E12) могут быть запрошены комбинации до 4 резисторов
• Для более чем 72 значений будут рассматриваться только комбинации из 3 резисторов

Даже с этими ограничениями полное сканирование всех комбинаций может занять довольно много времени; нажмите кнопку «Отмена» раньше, если вы видите достаточно хороший результат

Комбинация (*: параллельно, +: последовательно)	Значение	Отн.err (% от целевого)	Мин. Значение (% от целевого)	Максимальное значение (% от целевого)

---

Код

доступен на github под CC-BY- NC — это творческое сообщество, совместное использование, указание авторства, некоммерческое использование.
Пока вы используете калькулятор на этой странице, ничего страшного.
Если вы берете код и используете его внутри (не публикуете в Интернете), это тоже нормально.
Если вы берете код с github и используете его на веб-сайте без коммерческих целей, это тоже нормально.
Если вы берете код с github и используете его на веб-сайте, который вы зарабатываете на информации, опубликованной на сайте (даже если за счет рекламы), это нарушение лицензии.

Калькулятор цветовой кодировки резистора

| Circuits4you.com

Электронный цветовой код используется для обозначения значений или номинальных характеристик электронных компонентов, обычно для резисторов , но также для конденсаторов, катушек индуктивности, диодов и других.Отдельный код, 25-парный цветовой код, используется для идентификации проводов в некоторых телекоммуникационных кабелях.

Значения стандартных резисторов и конденсаторов

с кодами IEC и EIA объяснены в предыдущем посте.

Этот инструмент используется для декодирования информации для резисторов с осевыми выводами с цветной полосой. Выберите их цвета, чтобы определить номинал и допуск резистора.

Получить цветовые полосы резистора из номинала резистора

Калькулятор цветового кода четырехполосного резистора

Калькулятор цветового кода пятиполосного резистора

Понимание цветовых кодов

Чтобы отличить левое от правого, есть промежуток между полосами C и D.

полоса
• A — первая значащая цифра значения компонента (левая сторона)
• band B — вторая значащая цифра (некоторые прецизионные резисторы имеют третью значащую цифру, и, следовательно, пять полос).
• band C — десятичный множитель
Полоса
• D , если присутствует, указывает допуск значения в процентах (отсутствие полосы означает 20%)

Например, резистор с полосами желтого, фиолетового, красного и золотого имеет первую цифру 4 (желтый в таблице ниже), вторую цифру 7 (фиолетовый), за которой следуют 2 (красных) нуля: 4700 Ом .Золото означает, что допуск составляет ± 5%, поэтому реальное сопротивление может находиться в пределах от 4465 до 4935 Ом.

Как работает цветовой код резистора?

Значения резистора часто обозначаются цветовым кодом . Практически все резисторы с выводами мощностью до одного ватта отмечены цветными полосами. Кодировка определена в международном стандарте IEC 60062. Этот стандарт описывает коды маркировки резисторов и конденсаторов. Он также включает числовые коды, как, например, часто используемые для резисторов SMD.Цветовой код дается несколькими полосами. Вместе они определяют значение сопротивления, допуск, а иногда и надежность или интенсивность отказов. Количество полос варьируется от трех до шести. Как минимум, две полосы указывают значение сопротивления, а одна полоса служит множителем. Значения сопротивления стандартизированы, эти значения называются предпочтительными значениями.

Таблица цветов резистора

В таблице ниже показано, как определить сопротивление и допуск для резисторов.Таблица также может использоваться для указания цвета полос, если значения известны. Чтобы быстро найти значения резисторов, можно использовать автоматический калькулятор резисторов.

Резисторы с жестким допуском могут иметь три полосы для значащих цифр, а не две, или дополнительную полосу для указания.

Связанные

Калькулятор сопротивления светодиодов размером с бумажник | Лаборатории злых безумных ученых

Это что-то вроде онлайн-калькулятора сопротивления светодиодов, за исключением того, что его можно сложить и положить в кошелек.

Начните с загрузки выкройки здесь (файл PDF 512 КБ). Распечатайте его в режиме высокого качества на лазерном принтере, желательно на «презентационной» бумаге средней плотности. Чтобы получить исходный размер (размер визитной карточки 3,5 x 2 ″), вам может потребоваться отключить автоматическое масштабирование на вашем принтере.

Затем вырежьте узор ножницами или ножом для хобби, следуя контуру обеих частей. Прямая кромка может пригодиться.

Также есть пять коробок на большей части с надписью «[УДАЛИТЬ]», которые, в общем, должны быть удалены.

Есть две линии сгиба на большом элементе (корпусе) и одна на меньшем элементе (слайдер). Используйте прямую кромку, чтобы помочь разложить складки. Плотно согните складку на слайдере, но пока оставьте складки корпуса гибкими.

Как показано на рисунке, в верхней части корпуса имеется откидной клапан. Вставьте ползунок в корпус, загните крышку и плотно согните обе складки корпуса. Лоскут можно удерживать с помощью цельного куска ленты (или клея, если вы амбициозны).

Как пользоваться

Теперь, когда строительство завершено, давайте рассмотрим, как его использовать. Схема нашей модели представлена ​​на схеме на калькуляторе:

Мы предполагаем, что напряжение системы (Vcc) известно. Мы также предполагаем, что вы знаете характеристики светодиода: какой ток вы хотите использовать, и прямое напряжение (Vf) светодиода при работе с этим током. Когда у вас есть эти числа, калькулятор поможет вам выяснить, какое номинал и размер резистора необходимы.

Давайте рассмотрим полный пример. Предположим, что мы хотим запустить красный светодиод от батареи 9 В. Тогда Vcc = 9 В, и наш красный светодиод хочет работать при 20 мА и имеет прямое напряжение Vf = 2 В. Учитывая это, давайте выясним, какой резистор следует выбрать.

Первое, что нам нужно вычислить, — это напряжение «Vr» на резисторе. Для этого выровняйте прямое напряжение (Vf = 2 В) непосредственно под напряжением вашей системы, Vcc = 9 В.
(Если вы уже проделали этот расчет в уме, вы можете сразу перейти к той части, где мы переверните это.)

Напряжение Vr на резисторе появляется в правом нижнем поле, чтобы вы могли прочитать: 7 В.

Затем мы переворачиваем калькулятор.

Наш следующий шаг — найти номинал резистора. Для этого переместим ползунок, чтобы выровнять желаемый ток (в данном случае I = 20 мА) под напряжением резистора (Vr = 7 В):

После того, как это будет выровнено, значение резистора будет указано стрелкой на левой стороне скользящей шкалы, в данном случае около 350 Ом.