Обрыв — линейный провод — Большая Энциклопедия Нефти и Газа, статья, страница 1
Обрыв — линейный провод
Cтраница 1
Обрыв линейного провода в случае соединения потребителя треугольником ведет к образованию однофазной системы. Если, например, обрыв произошел в проводе А ( рис. 6.16 6), то образуются две параллельные ветви ВС и ВАС. Приемники, включенные в фазу ВС, остаются под нормальным напряжением и продолжают работать. Таким образом, в схеме треугольника при обрыве одного линейного провода все приемники продолжают работать, но у большинства приемников напряжение резко снижается, что приводит к нарушению их нормальной работы, например, в случае ламп накаливания — к резкому снижению их накала. [2]
После обрыва линейного провода В нагрузки фаз а и с оказываются соединенными последовательно. [3]
После обрыва линейного провода А общее сопротивление фаз бис станет вдвое большим ( они окажутся соединенными последовательно), а линейное напряжение Ивс, к которому подключены эти фазы, больше фазного в ] / — & раз. [4]
При обрыве линейного провода приемники данной фазы остаются без энергии, а приемники двух других фаз продолжают получать питание от неповрежденных проводов трехфазной системы. При наличии нейтрального провода для приемников, присоединенных к неповрежденным линейным проводам, обрыв чужого линейного провода практически не ощущается. При отсутствии нейтрального провода фазные напряжения на зажимах обоих последовательно соединенных приемников пропорциональны величинам их полных сопротивлений, а при преобладании в одной фазе индуктивной, а в другой емкостной нагрузки может возникнуть резонанс напряжений, сопровождающийся установлением повышенных напряжений на зажимах приемников и резким увеличен нем тока. [5]
При обрыве линейного провода трехфазный потребитель находится под линейным напряжением, так как при этом ни одна из точек нагрузки не будет под потенциалом оборванного линейного провода. [6]
При обрыве линейного провода напряжение на одной из фаз становится равным нулю, а напряжение на двух других фазах равно половине линейного. На рис. 6.13 6 показана векторная диаграмма напряжений потребителя при обрыве одного линейного провода А. Линейные напряжения UAB и UCA также равны половине линейного напряжения U вс и поэтому вершина треугольника линейных напряжений легла на основание его. [8]
При обрыве линейного провода А к двум не поврежденным фазам подводится линейное напряжение UBC 220 В, которое распределится на равные части, так как сопротивления фаз одинаковы: Ui U c t / ec / 2 220 / 2 1 10 В. [9]
Как влияет обрыв линейного провода а работу трехфазного потребителя, соединенного в треугольник. [10]
Рассмотрим случай обрыва линейного провода при трехпроводной симметричной системе для соединения звездой и треугольником. [12]
К чему приводит обрыв линейного провода в трехфазной установке. [13]
В случае соединения приемника треугольником обрыв линейного провода в фазе А ( рис. 5.8, б) изменяет схему так, что две фазы ZAB, ZCA оказываются соединенными последовательно под линейное напряжение U вс. [14]
Страницы: 1 2 3
3.5. Обрыв фаз и обрыв линейного провода при соединении источников и потребителей треугольником
3.5.1. Обрыв фазы ab
Рассмотрим электрическую схему, изображённую на рис.3.20.

Рис.3.20. Электрическая схема трёхфазной системы, соединённой треугольником, с отключенной фазой
При
обрыве фазы ab вектор тока 
 ,
,  ,
,  .
(3.16)
.
(3.16)
На рис.3.21 приведена векторная диаграмма напряжений и токов при обрыве фазы аb нагрузки, соединённой треугольником.

3.5.2. Обрыв фаз ab и bc
Рассмотрим электрическую схему, изображённую на рис.3.22.
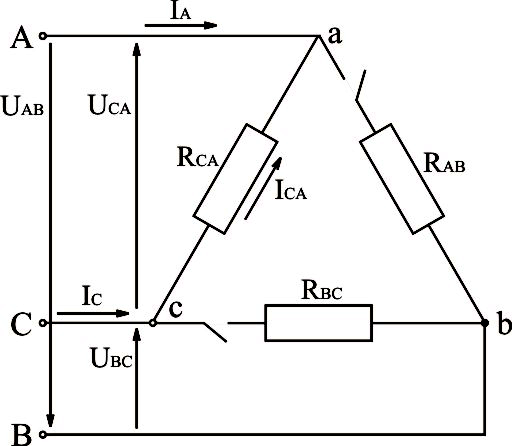
Рис.3.22. Электрическая схема трёхфазной системы, соединённой треугольником, с отключенными двумя фазами
При
обрыве фаз ab и bc векторы токов  и
и 
 ,
, 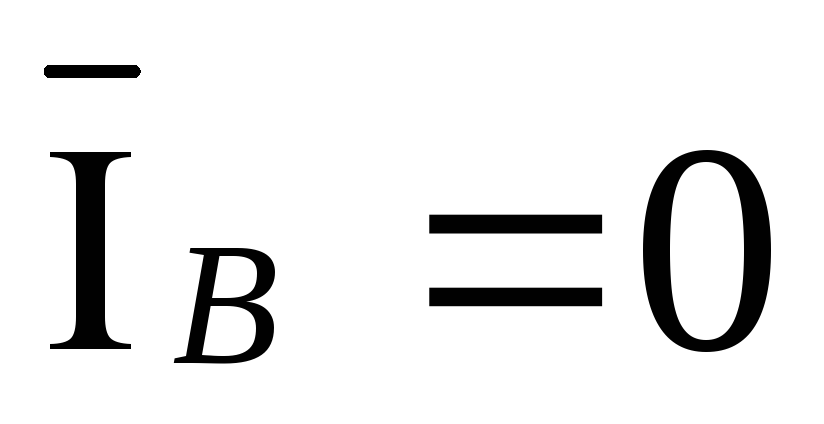 ,
, 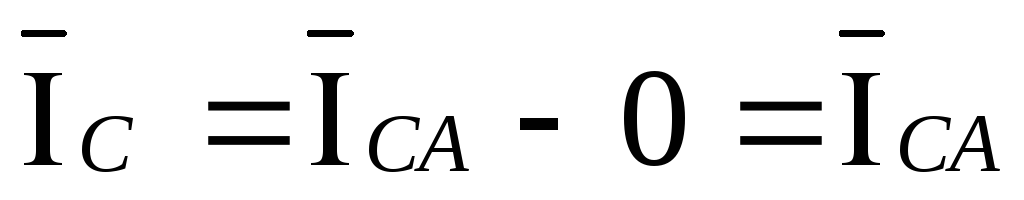 .
(3.17)
.
(3.17)
На рис.3.23 приведена векторная диаграмма напряжений и токов при обрыве фаз аb и bc нагрузки, соединённой треугольником.
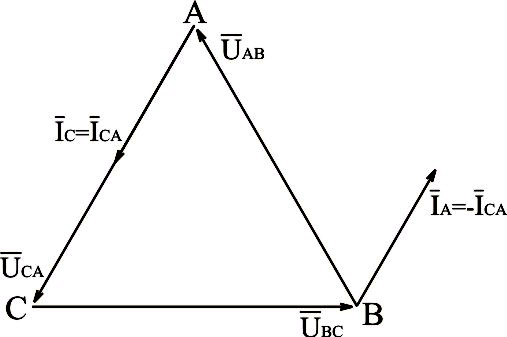
Рис.3.23. Векторная диаграмма напряжений и токов для нагрузки, соединённой треугольником, с отлюченными двумя фазами
3.5.3. Обрыв линейного провода
Рассмотрим
электрическую схему, изображённую на
рис.3.24. Пусть 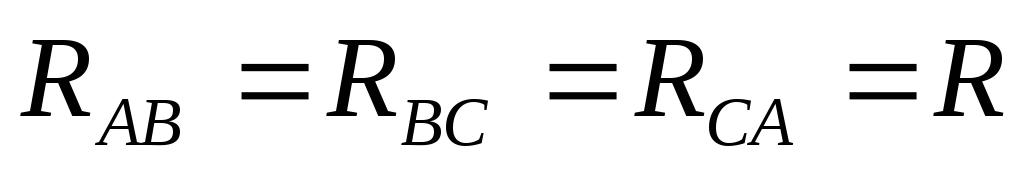 .
.

Рис.3.24. Электрическая схема трёхфазной системы, соединённой треугольником, с отключенным линейным проводом
При
обрыве линейного провода Аa вектор
тока 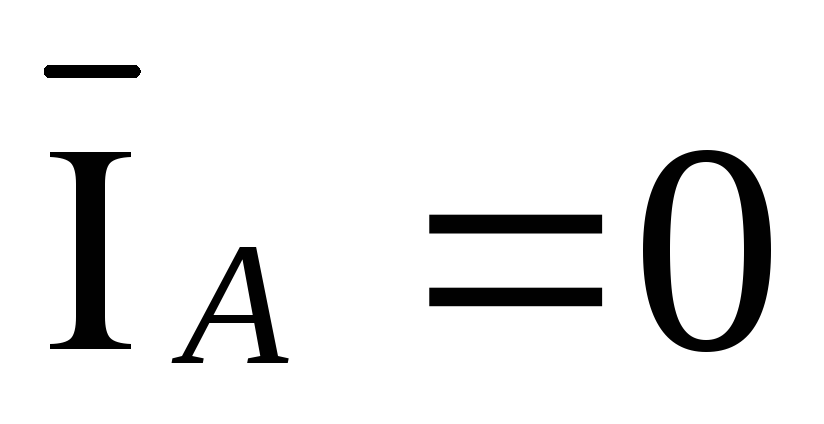 .
Преобразуем схему рис.3.24 в схему рис.3.25.
.
Преобразуем схему рис.3.24 в схему рис.3.25.
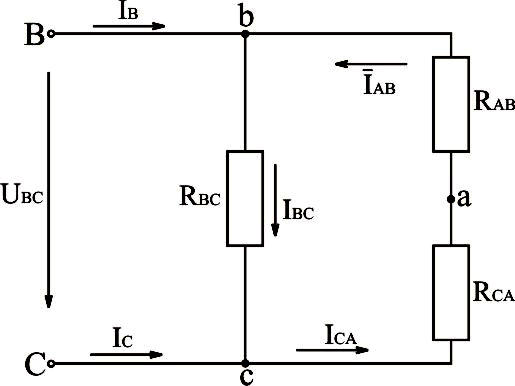
Рис.3.25. Преобразование трёхфазной электрической схемы, соединённой треугольником, с отключенным линейным проводом в однофазную электрическую схему
Из преобразованной схемы следует:

 ,
, .
(3.18)
.
(3.18)По первому закону Кирхгофа:
 ;
; .
(3.19)
.
(3.19)
Используя формулы (3.18) и (3.19), построим векторную диаграмму:
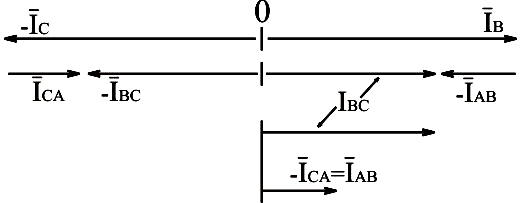
Рис.3.26. Векторная диаграмма токов преобразованной схемы
3.6. Мощность трёхфазной цепи
При
симметричной нагрузке активная мощность
трёхфазной цепи равна сумме активных
мощностей фаз: P
= .
Активную мощность трёхфазной цепи можно
выразить через фазные значения напряжения
и тока:
.
Активную мощность трёхфазной цепи можно
выразить через фазные значения напряжения
и тока:
P
=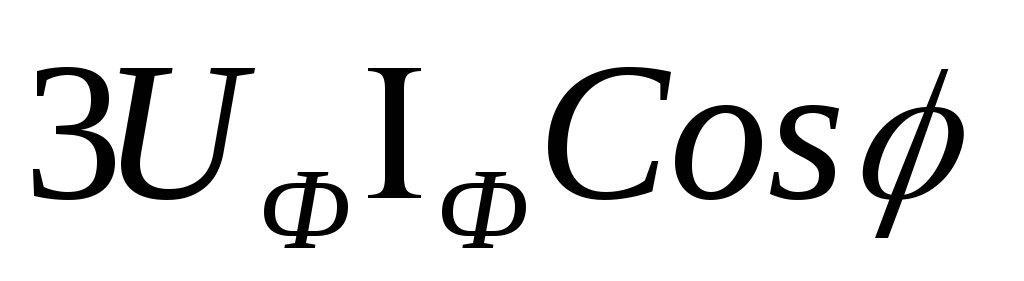
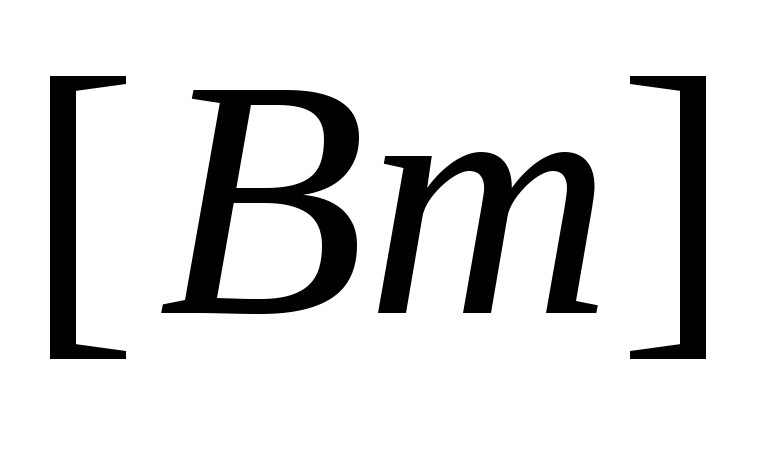
При
соединении звездой соотношения между
фазными и линейными напряжениями и
токами равны:  ,
,  .
При соединении треугольником эти
соотношения равны:
=
.
При соединении треугольником эти
соотношения равны:
=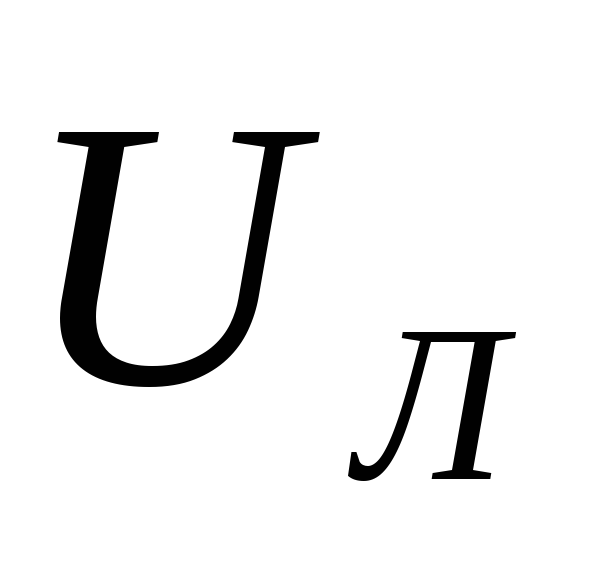 ,
, 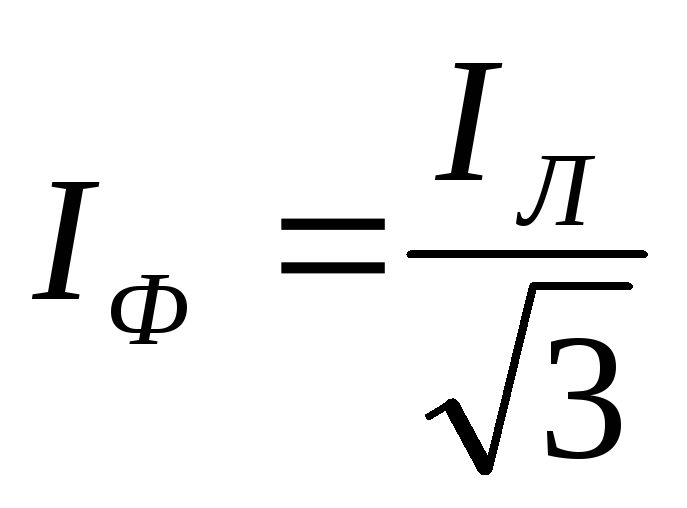 .
В обоих случаях
.
В обоих случаях 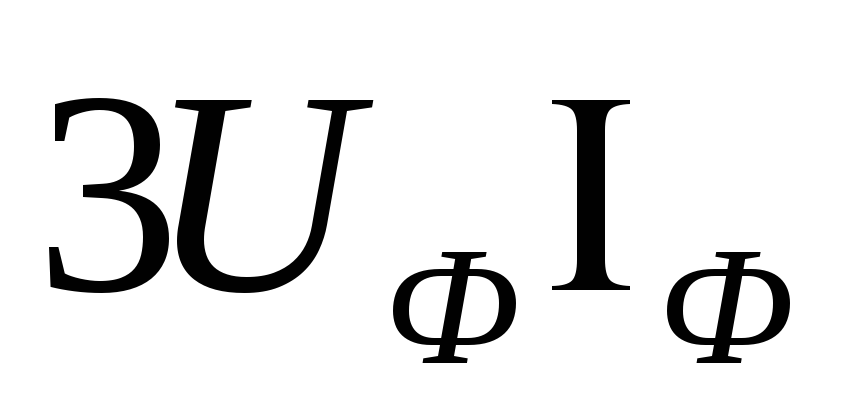
 .
Тогда активную мощность можно выразить
через линейные значения напряжения и
тока:
.
Тогда активную мощность можно выразить
через линейные значения напряжения и
тока:
P
=

 .
(3.21)
.
(3.21)
Реактивная мощность трёхфазной цепи
Q
= =
= .
(3.22)
.
(3.22)
Полная мощность трёхфазной цепи
S
=
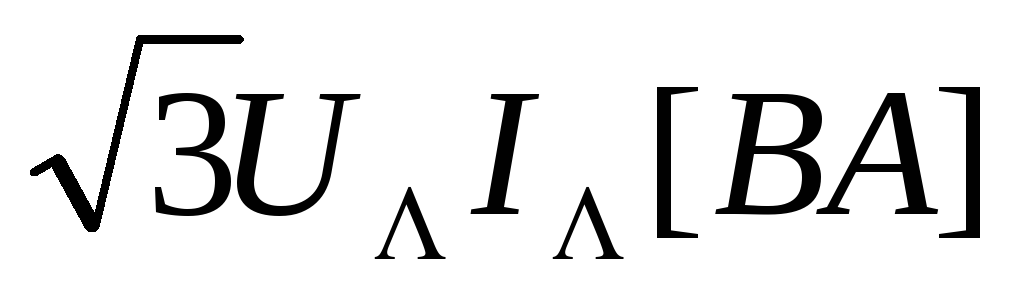 .
(3.23)
.
(3.23)
При расчётах удобно пользоваться следующими формулами:
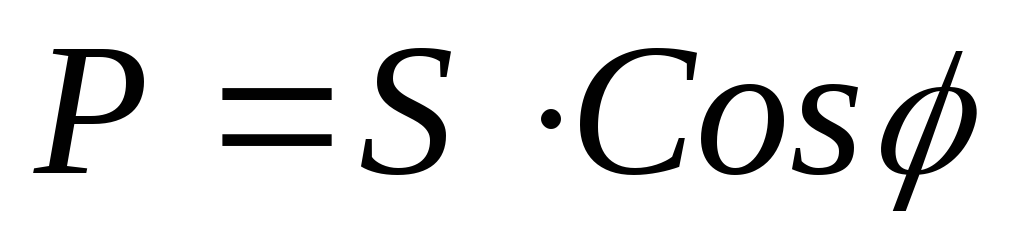 ;
; ;
; =
= ;
; =
= ;
;  =
=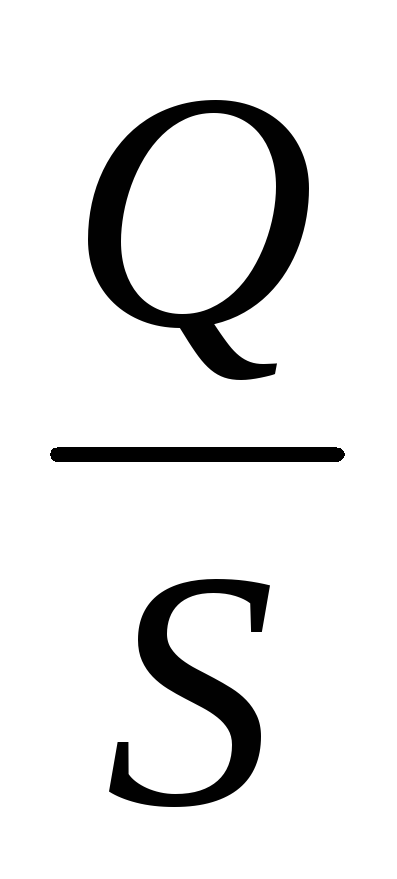 .
.
При несимметричных нагрузках, соединённых звездой или треугольником, активную мощность рассчитывают по формулам:
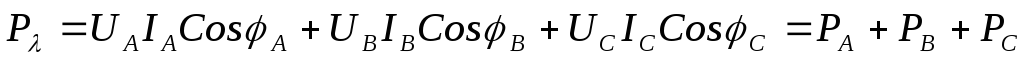 ;
;
 .
.
3.5. Обрыв фаз и обрыв линейного провода при соединении источников и потребителей треугольником
3.5.1. Обрыв фазы ab
Рассмотрим электрическую схему, изображённую на рис.3.20.
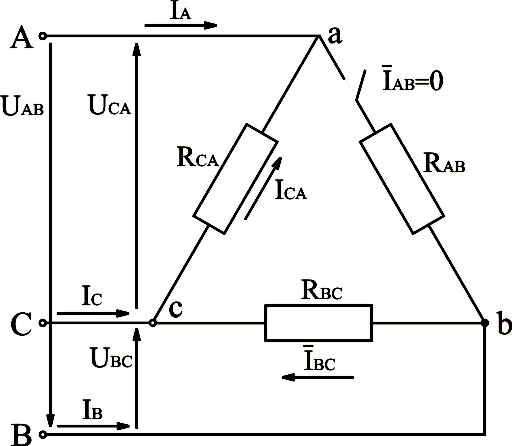
Рис.3.20. Электрическая схема трёхфазной системы, соединённой треугольником, с отключенной фазой
При
обрыве фазы ab вектор тока 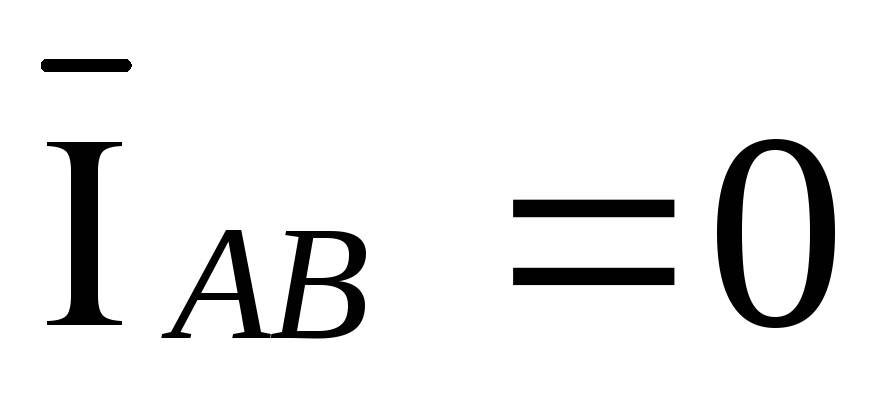 ,
тогда выражения (3.14) преобразуются в
следующий вид:
,
тогда выражения (3.14) преобразуются в
следующий вид:
 ,
,  ,
,  .
(3.16)
.
(3.16)
На рис.3.21 приведена векторная диаграмма напряжений и токов при обрыве фазы аb нагрузки, соединённой треугольником.

Рис.3.21. Векторная диаграмма напряжений и токов для нагрузки, соединённой треугольником, с отлюченной фазой
3.5.2. Обрыв фаз ab и bc
Рассмотрим электрическую схему, изображённую на рис.3.22.

Рис.3.22. Электрическая схема трёхфазной системы, соединённой треугольником, с отключенными двумя фазами
При
обрыве фаз ab и bc векторы токов 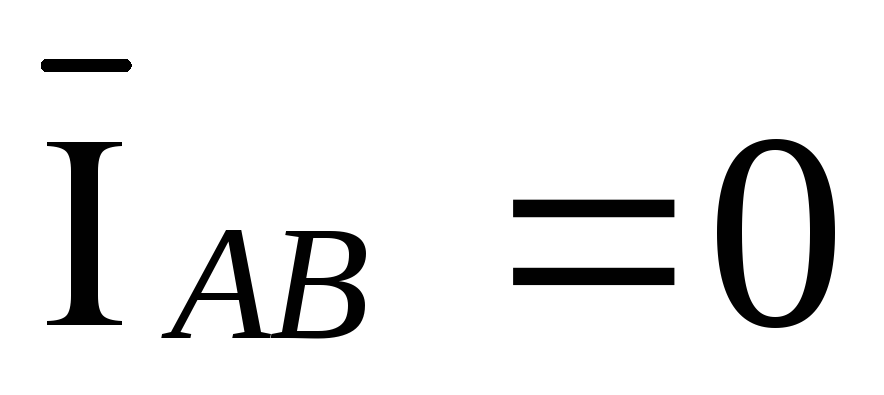 и
и 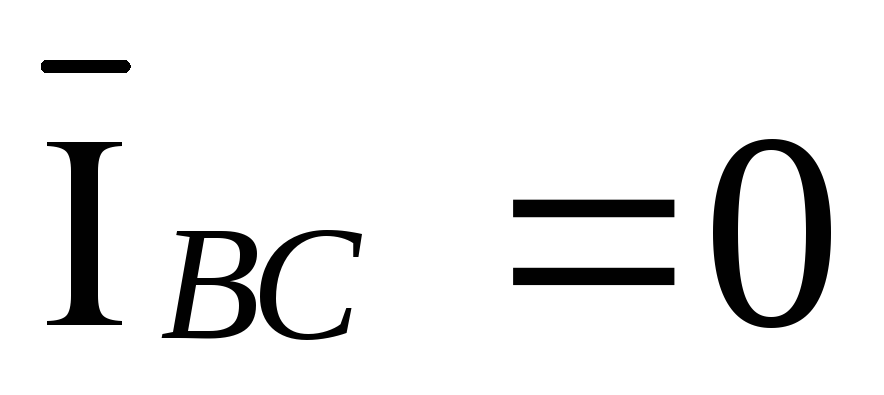 ,
тогда выражения (3.14) преобразуются в
следующий вид:
,
тогда выражения (3.14) преобразуются в
следующий вид:
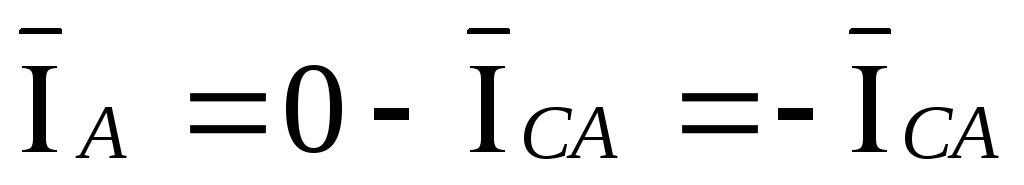 ,
, 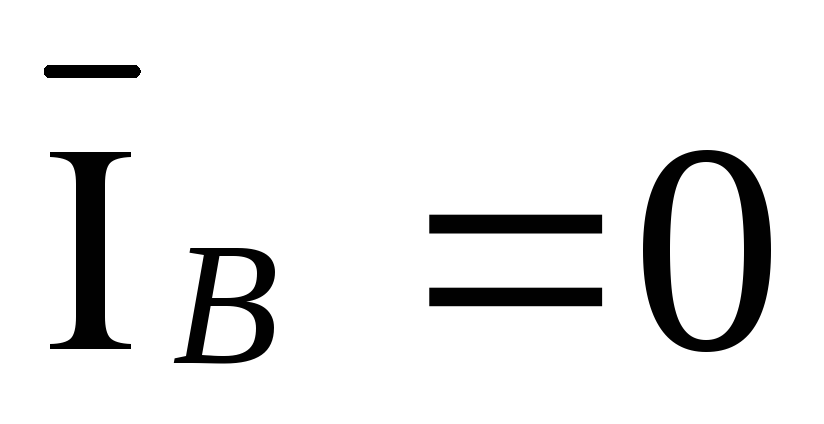 ,
, 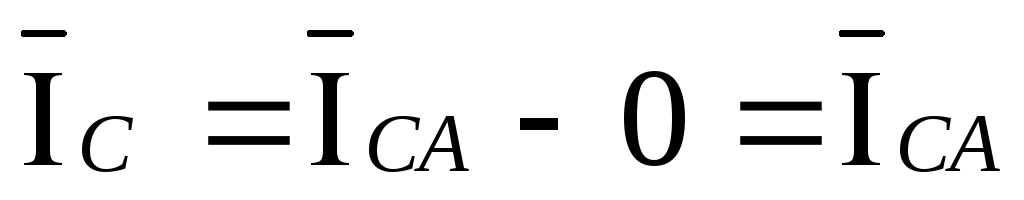 .
(3.17)
.
(3.17)
На рис.3.23 приведена векторная диаграмма напряжений и токов при обрыве фаз аb и bc нагрузки, соединённой треугольником.

Рис.3.23. Векторная диаграмма напряжений и токов для нагрузки, соединённой треугольником, с отлюченными двумя фазами
3.5.3. Обрыв линейного провода
Рассмотрим
электрическую схему, изображённую на
рис.3.24. Пусть  .
.

Рис.3.24. Электрическая схема трёхфазной системы, соединённой треугольником, с отключенным линейным проводом
При
обрыве линейного провода Аa вектор
тока  .
Преобразуем схему рис.3.24 в схему рис.3.25.
.
Преобразуем схему рис.3.24 в схему рис.3.25.
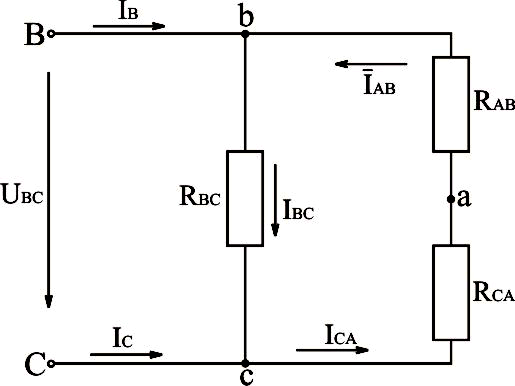
Рис.3.25. Преобразование трёхфазной электрической схемы, соединённой треугольником, с отключенным линейным проводом в однофазную электрическую схему
Из преобразованной схемы следует:
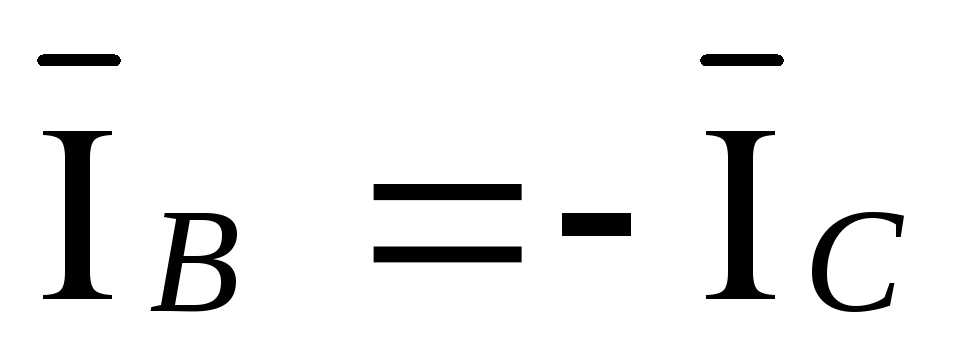 ,
,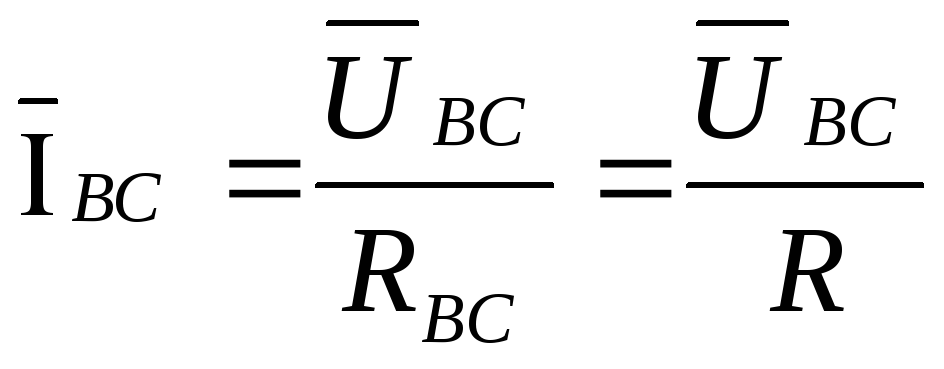 ,
,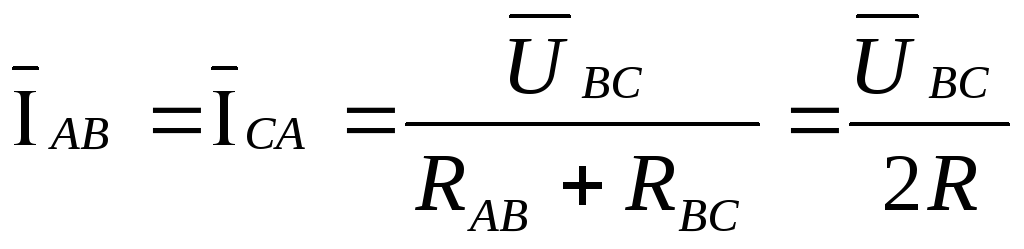 .
(3.18)
.
(3.18)
По первому закону Кирхгофа:
 ;
; .
(3.19)
.
(3.19)
Используя формулы (3.18) и (3.19), построим векторную диаграмму:

Рис.3.26. Векторная диаграмма токов преобразованной схемы
3.6. Мощность трёхфазной цепи
При
симметричной нагрузке активная мощность
трёхфазной цепи равна сумме активных
мощностей фаз: P
=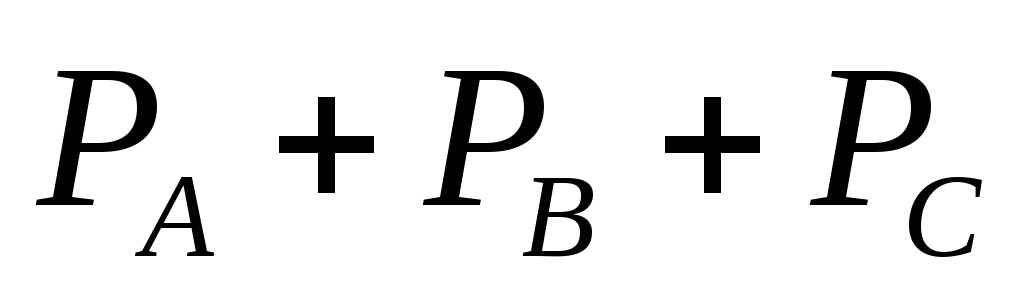 .
Активную мощность трёхфазной цепи можно
выразить через фазные значения напряжения
и тока:
.
Активную мощность трёхфазной цепи можно
выразить через фазные значения напряжения
и тока:
P
=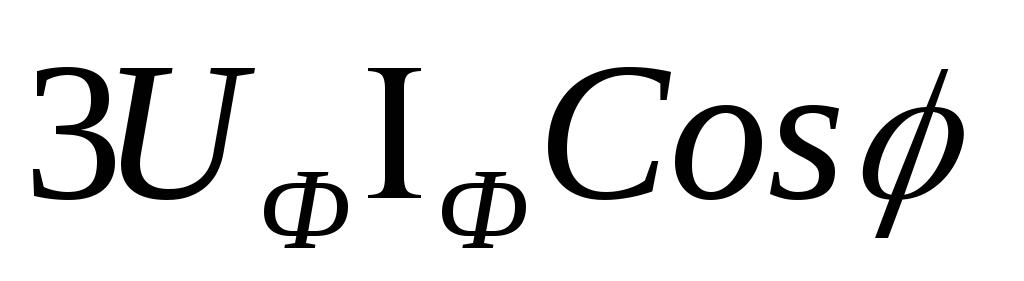
 .
(3.20)
.
(3.20)
При
соединении звездой соотношения между
фазными и линейными напряжениями и
токами равны:  ,
, 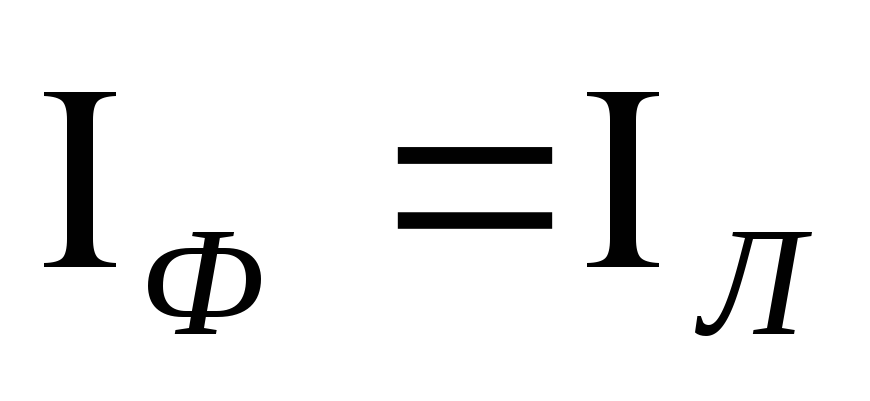 .
При соединении треугольником эти
соотношения равны:
.
При соединении треугольником эти
соотношения равны:  =
=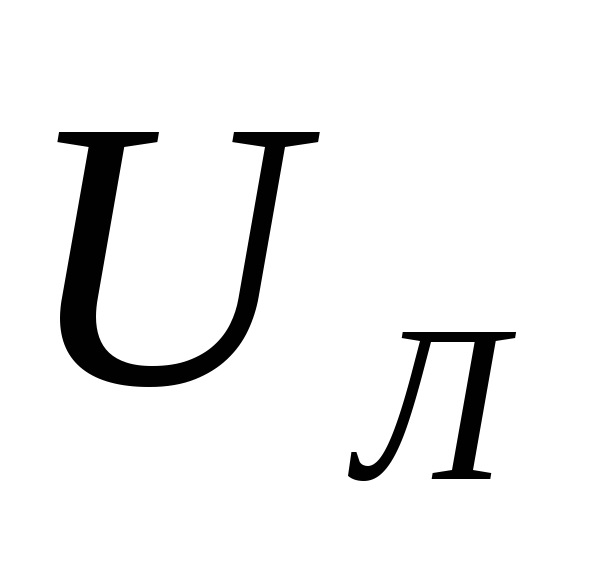 ,
, 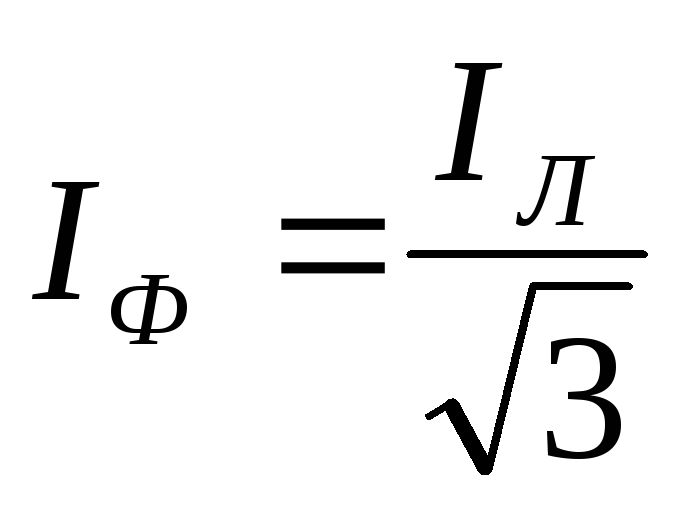 .
В обоих случаях
.
В обоих случаях 
 .
Тогда активную мощность можно выразить
через линейные значения напряжения и
тока:
.
Тогда активную мощность можно выразить
через линейные значения напряжения и
тока:
P
=

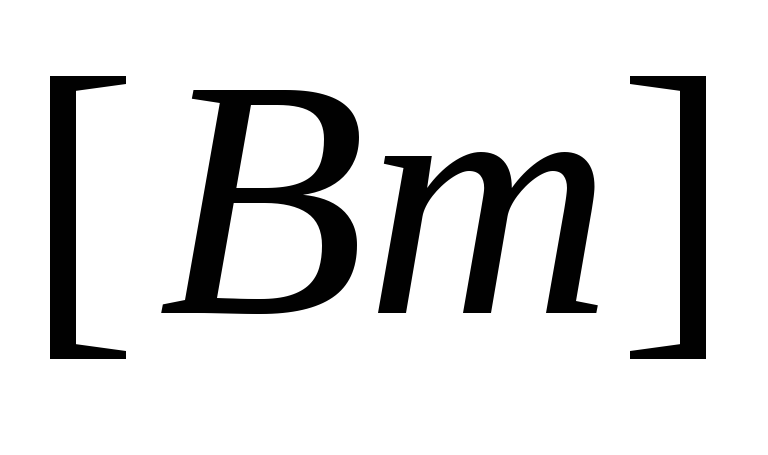 .
(3.21)
.
(3.21)
Реактивная мощность трёхфазной цепи
Q
= =
= .
(3.22)
.
(3.22)
Полная мощность трёхфазной цепи
S
=
 .
(3.23)
.
(3.23)
При расчётах удобно пользоваться следующими формулами:
 ;
;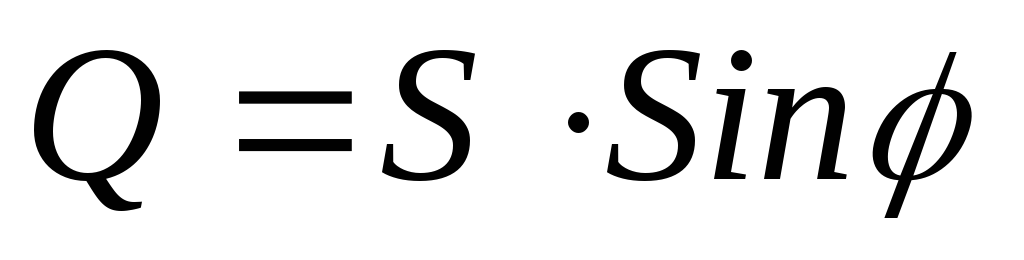 ;
;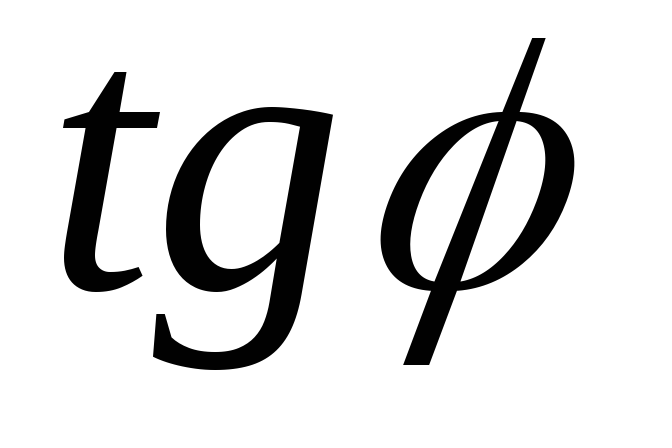 =
=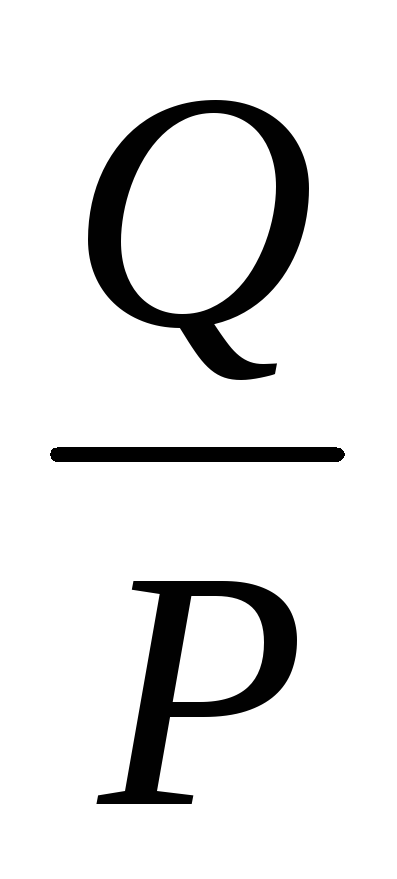 ;
;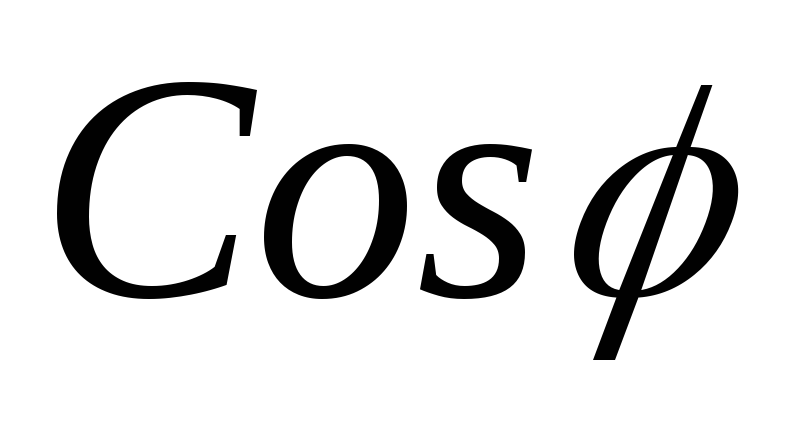 =
= ;
; 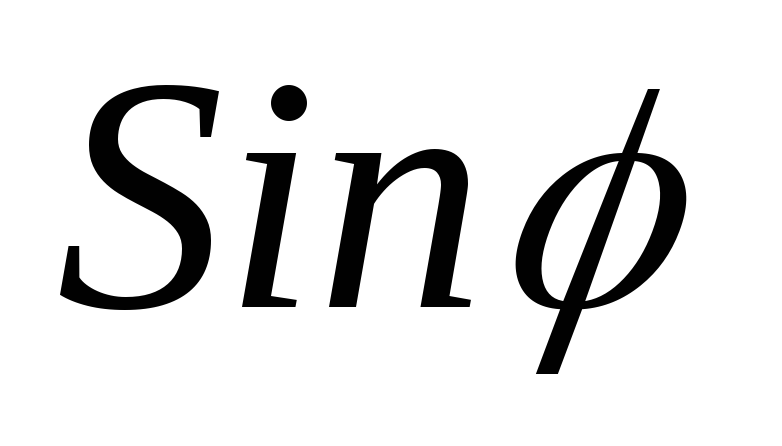 =
= .
.
При несимметричных нагрузках, соединённых звездой или треугольником, активную мощность рассчитывают по формулам:
 ;
;
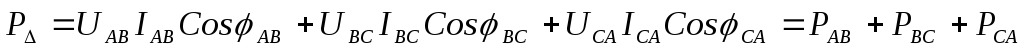 .
.
Аварийные режимы в трехфазных цепях при несимметричной нагрузке Обрыв линейного провода «в» (соединение нагрузки по схеме «треугольник»)
Т ри
приемника энергии с параметрами
ри
приемника энергии с параметрами

 соединены треугольником. Система
линейных напряжений симметрична:
соединены треугольником. Система
линейных напряжений симметрична: Определить токи, построить векторные
диаграммы токов и напряжений (рис.4.24).
Определить токи, построить векторные
диаграммы токов и напряжений (рис.4.24).
Рисунок 4.24 – Схема электрической цепи к задаче
Решение
Изобразим схему замещения электрической цепи (рис.4.24.1):

Рисунок 4.24.1 – Схема замещения электрической цепи
Фазные сопротивления: 

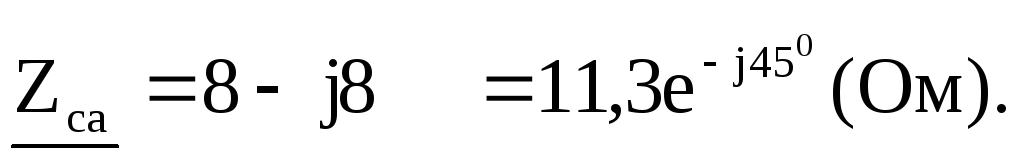
При обрыве линейного провода «В» ветви «ав» и и «вс» будут соединены последовательно, и параллельно ветви «са». Определим фазные токи:
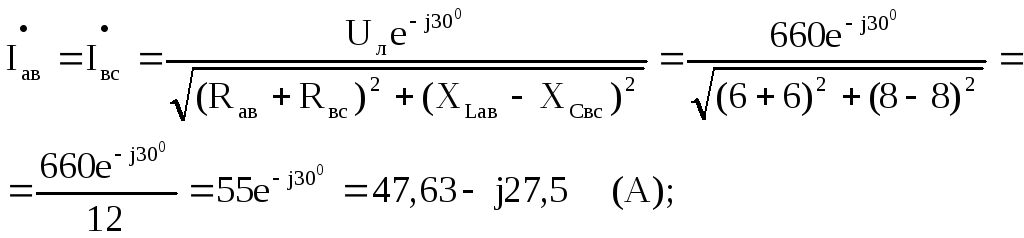

Зная фазные токи, определим фазные напряжения на нагрузке:

Выведем соотношения для линейных и фазных токов, записав уравнения по первому закону Кирхгофа:
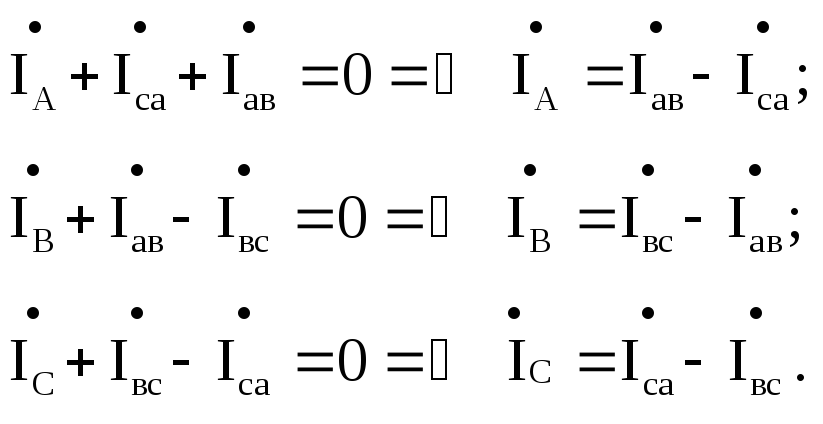
В екторная
диаграмма токов и напряжений приведена
на рисунке 4.24.2
екторная
диаграмма токов и напряжений приведена
на рисунке 4.24.2
Рисунок 4.24.2 – Векторная диаграмма токов и напряжений
Соединение нагрузки по схеме «звезда» Обрыв линейного провода «а» (четырехпроводная «звезда»)
Т ри
приемника энергии с параметрами
ри
приемника энергии с параметрами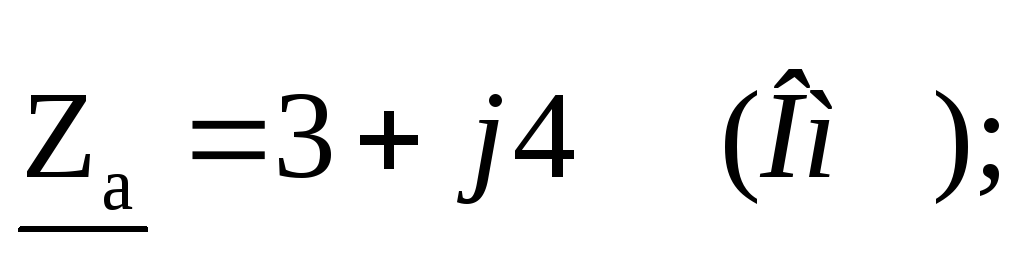

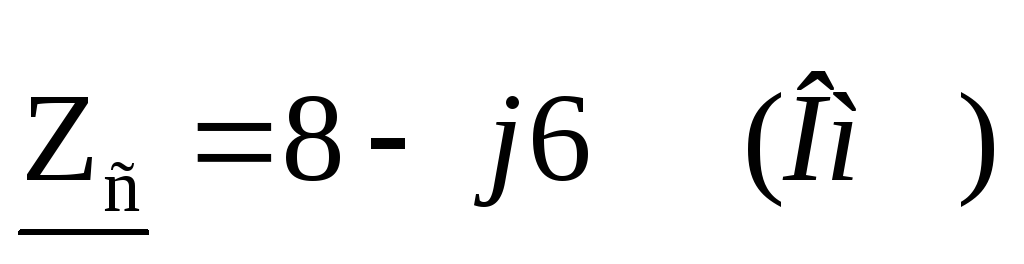 соединены звездой. Система линейных
напряжений симметрична:
соединены звездой. Система линейных
напряжений симметрична: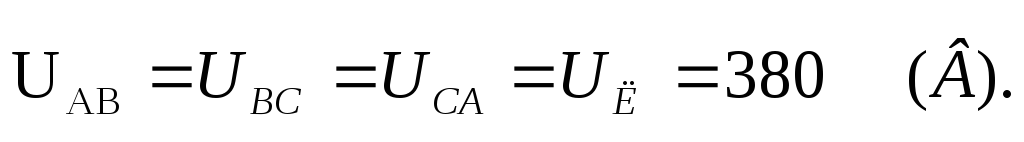 Определить токи, построить векторные
диаграммы токов и напряжений (рис.4.25).
Определить токи, построить векторные
диаграммы токов и напряжений (рис.4.25).
Рисунок 4.25 – Схема электрической цепи
Решение
И зобразим
схему замещения электрической цепи
(рис.4.25.1)
зобразим
схему замещения электрической цепи
(рис.4.25.1)
Рисунок 4.25.1 – Схема замещения электрической цепи
При обрыве линейного провода «А»
напряжение


Сопротивления фаз: 
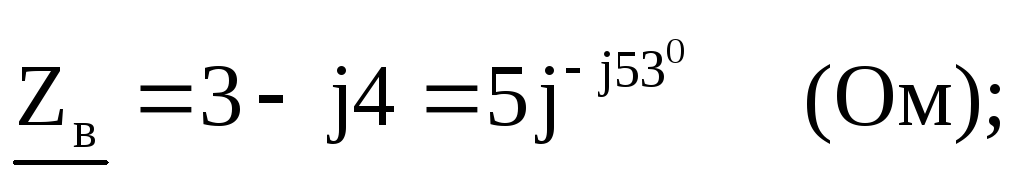

Определим токи: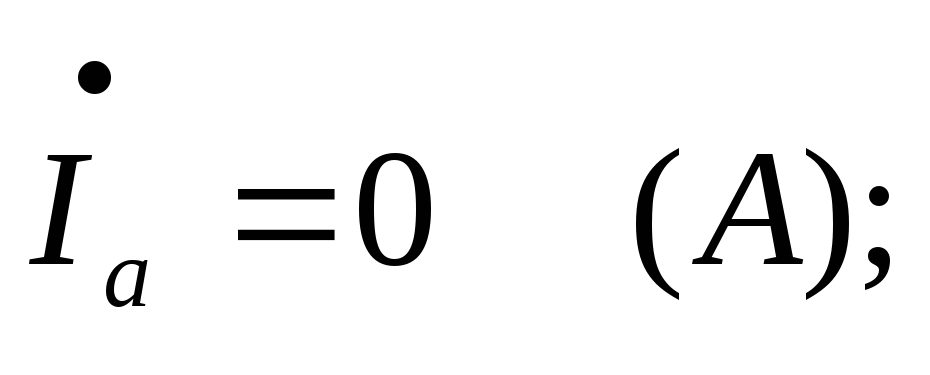

 .
.
Ток в нейтральном проводе определится
как сумма токов  и
и
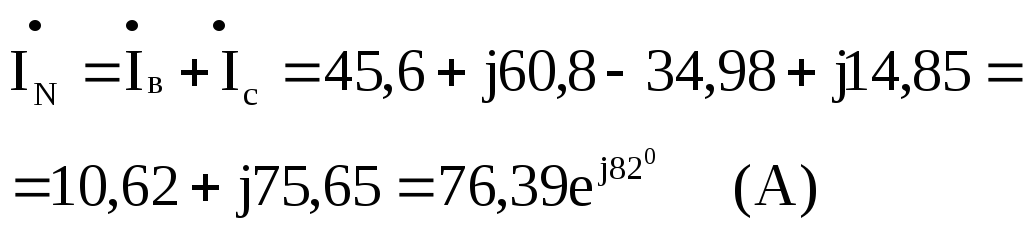
Векторная диаграмма токов и напряжений будет выглядеть следующим образом (рис.4.25.2):

Рисунок 4.25.2 – Векторная диаграмма токов и напряжений при обрыве линейного провода «А» (несимметричная нагрузка)
Трехпроводная «звезда»
Р ассмотрим
данный аварийный режим при обрыве
линейного провода «В»
(рис.4.26).
ассмотрим
данный аварийный режим при обрыве
линейного провода «В»
(рис.4.26).
Рисунок 4.26 – Схема электрической цепи при обрыве линейного провода «В» (несимметричная нагрузка)
Решение
Напряжение  .
Полное сопротивление фаз «А»
и «С»
.
Полное сопротивление фаз «А»
и «С»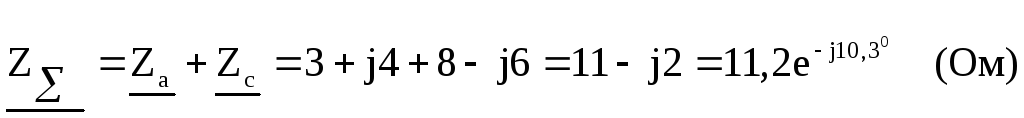 .
.
Токи 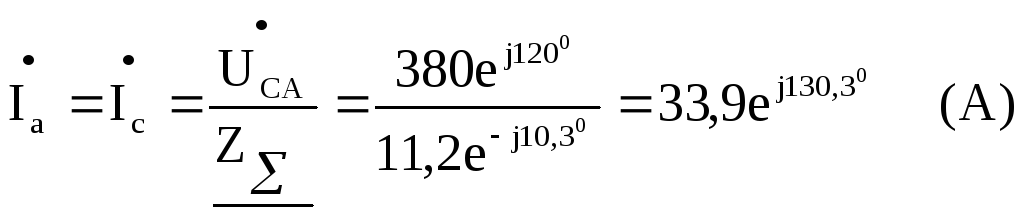 .
.
Для определения фазных напряжений 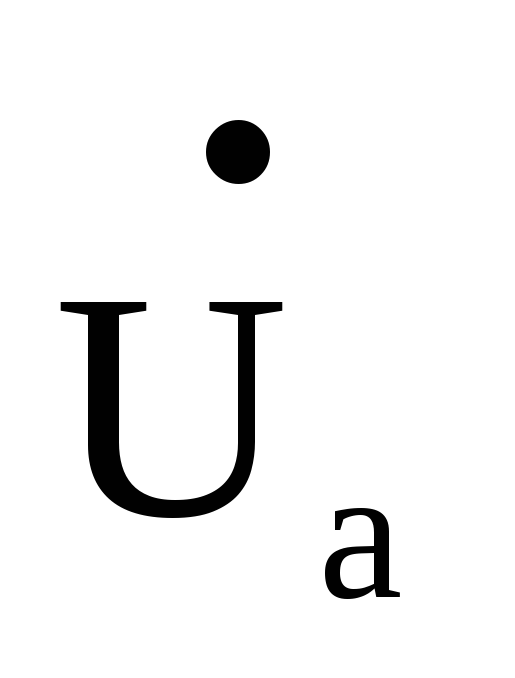 и
и умножим
значения токов
умножим
значения токов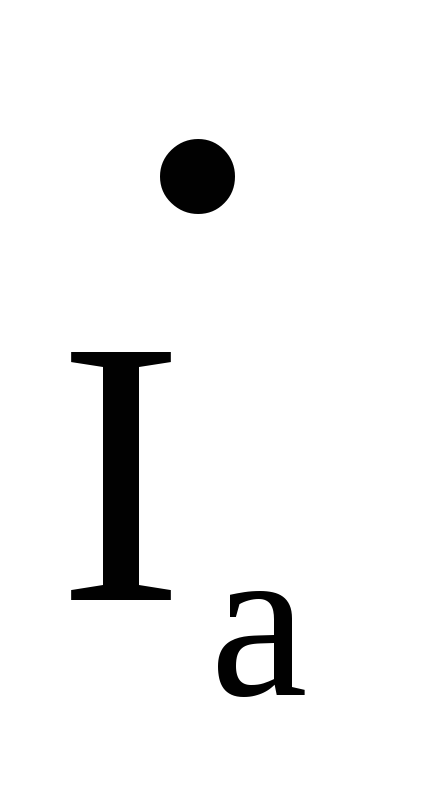 и
и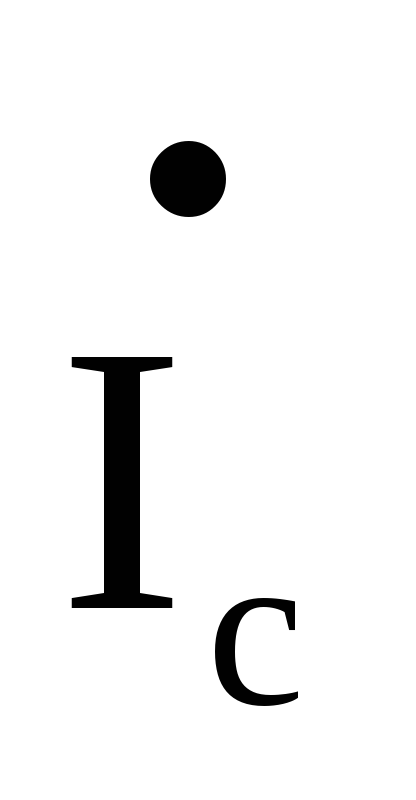 на
соответствующие сопротивления
на
соответствующие сопротивления ;
; .
.
Линейное напряжение  равно сумме напряженийи
равно сумме напряженийи .
.
Векторная диаграмма токов и напряжений примет следующий вид (рис. 4.27)
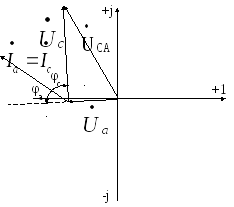
Рисунок 4.27 – Векторная диаграмма токов и напряженийпри обрыве линейного провода «В» (несимметричная нагрузка)
Короткое замыкание в фазе «А»
Три приемника энергии с параметрами 
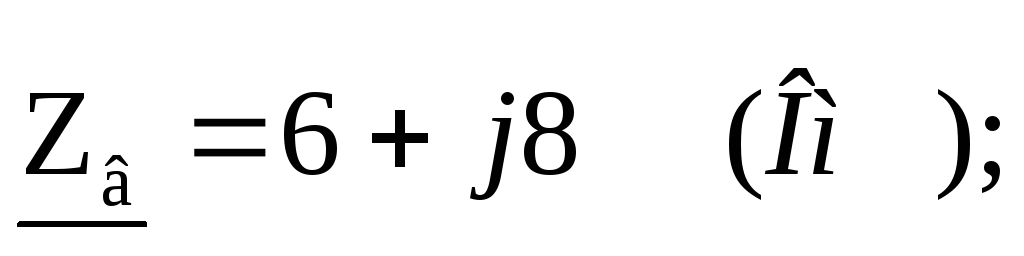
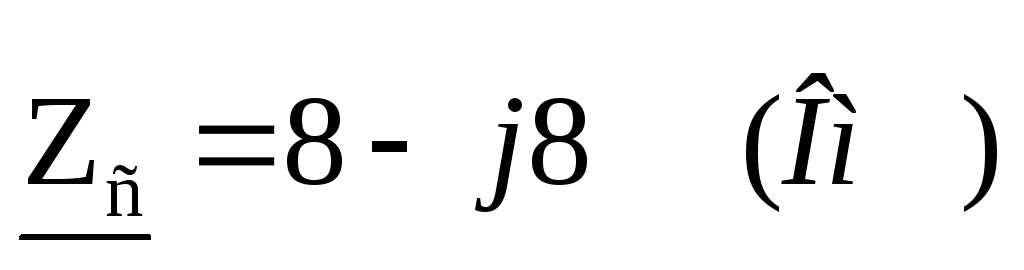 соединены звездой. Система линейных
напряжений симметрична:
соединены звездой. Система линейных
напряжений симметрична: Определить токи, построить векторные
диаграммы токов и напряжений (рис.4.28).
Определить токи, построить векторные
диаграммы токов и напряжений (рис.4.28).

Рисунок 4.28 – Схема электрической цепи при коротком замыкании в фазе «А» (несимметричная нагрузка)
Решение
При коротком замыкании в фазе «А»
фазные напряжение и
и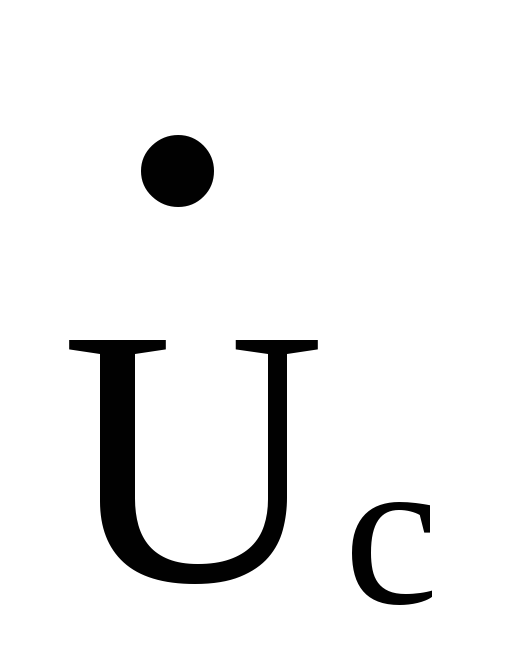 увеличатся до величины линейных:
увеличатся до величины линейных: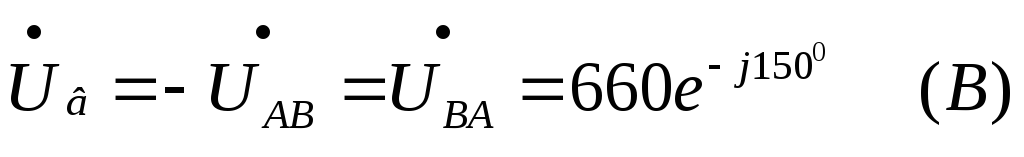 ;
;
Фазные сопротивления: 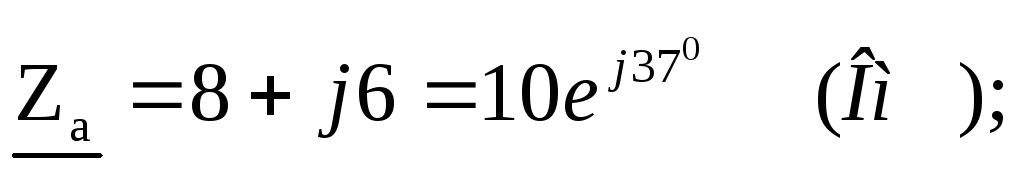

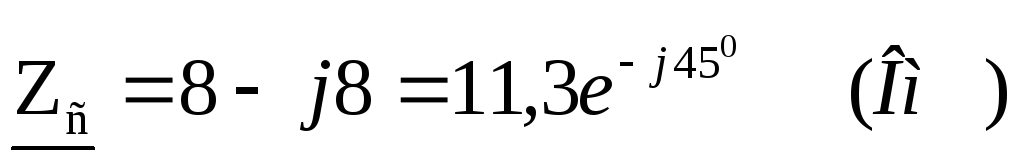 .
.
Определим токи:

 .
.
Используя первый закон Кирхгофа, запишем
систему уравнений: 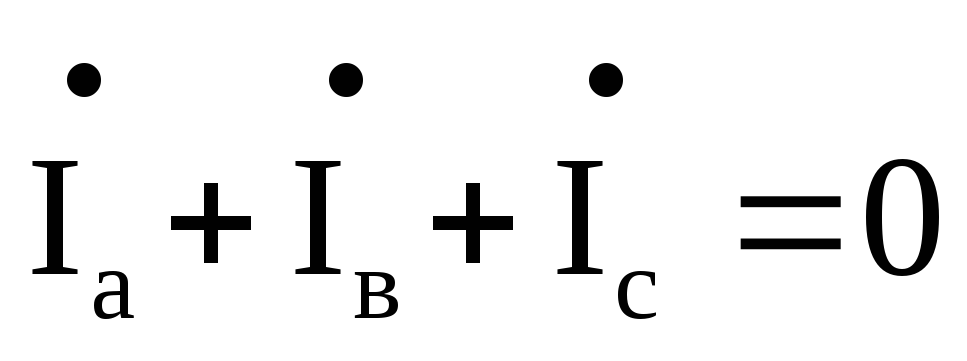 .Отсюда
.Отсюда
В екторная
диаграмма токов и напряжений будет
выглядеть следующим образом (рис.4.29):
екторная
диаграмма токов и напряжений будет
выглядеть следующим образом (рис.4.29):
Рисунок 4.29 – Векторная диаграмма токов и напряженийпри коротком замыкании в фазе «А» (несимметричная нагрузка)
5 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ С НЕСИНУСОИДАЛЬНЫМИ НАПРЯЖЕНИЯМИ И ТОКАМИ
Общие сведения
В предыдущих разделах пособия приводились задачи с расчетом электрических цепей с неизменными параметрами R, L, C, M и при действии источников постоянных или синусоидальных ЭДС или токах. На практике форма ЭДС, напряжения или тока обычно в большей или меньшей степени отличается от постоянной или синусоидальной, причем зависимость от времени может быть периодичной, почти периодической и непериодической. Так на в машинных генераторах переменного тока из- за неравномерности зазора между статором и ротором, который может появится в процессе эксплуатации генератора, форма кривых, наведённых в обмотках ЭДС будет отличатся от синусоидальной, но будет повторятся в каждый период, при этом токи в приемниках, как и ЭДС, так же окажутся периодическими несинусоидальными.
При передачи, радиотелеграфных и телефонных сигналов встречаются кривые тока, которые строго периодичны, но имеют периодически изменяющуюся ошибочную. Такие кривые близки по своим свойствам к периодическим, их называют почти периодическими.
При передаче, например, последовательных импульсов встречаются с напряжениями и токами несинусоидальной непериодической формы.
В этом разделе рассмотрены задачи и методы расчета линейных цепей только с периодическими несинусоидальными напряжениями и токами.
Основные причины возникновения в электрических цепях периодических несинусоидальных напряжений и токов следующие.
Когда источник ЭДС (источник тока) выдает несинусоидальной формы ЭДС (тока), а все элементы цепи (R, L, C, M)– линейные, т.е. не зависящие от тока.
Когда источник ЭДС (источник тока) выдает ЭДС (ток) синусоидальной формы, но один или несколько элементов цепи нелинейные.
Когда источник ЭДС (источник тока) выдает ЭДС (ток) несинусоидальной формы и в составе цепи имеются нелинейные элементы.
Когда источник ЭДС (источник тока) выдает ЭДС (ток) синусоидальной формы, а один или несколько элементов цепи периодически изменяют свою величину во времени.
В последние годы широкое применение управляемых выпрямителей-тиристоров, привело к ухудшению качества (формы) напряжения промышленных сетей, иногда форма кривой искажена так, что становится мало похожей на синусоиду.
Из этого вытекает необходимость в умении анализировать и рассчитывать цепи с несинусоидальными периодическими напряжениями и токами.
Наличие таких напряжений и токов усложняет расчет электрических цепей. Для упрощения расчета его сводят к более простой задаче: расчету определенных составляющих тока и напряжения от постоянной составляющей напряжения и от напряжения нескольких гармонических синусоидальных составляющих с различной частотой. Полные токи напряжения потом определяют в соответствии с принципом наложения.
Такой подход требует предварительно разложения периодических несинусоидальных функций напряжения или тока на составляющие в соответствии с тригонометрическим рядом Фурье.
3.3. Обрыв фазы и короткое замыкание фазы без нулевого провода при соединении источников энергии и потребителей звездой
3.3.1. Обрыв фазы a
Рассмотрим
электрическую схему рис.3.12, в которой  ,
,  ,
, 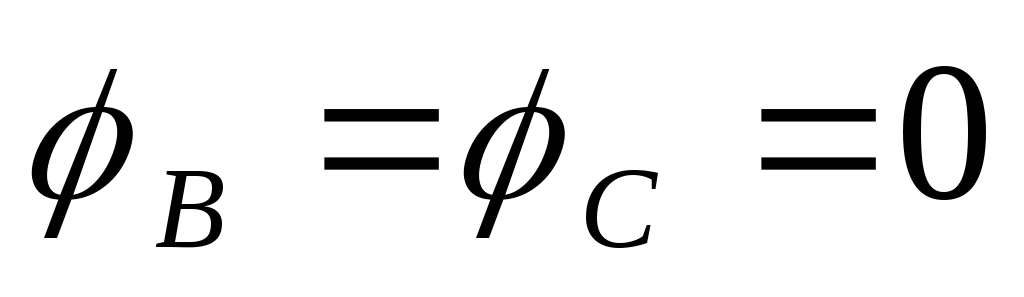 ,
,  .
.
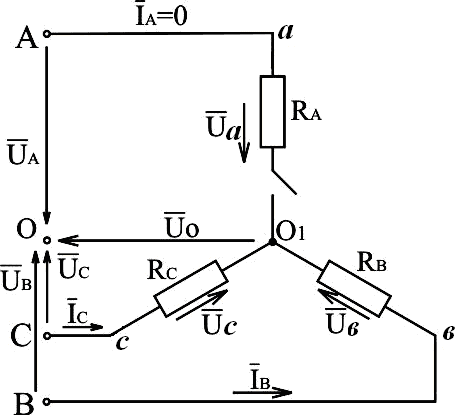
Рис.3.12. Электрическая схема трёхфазной системы, соединённой звездой, без нулевого провода с выключенной фазой
По первому закону Кирхгофа:
 ;
;  . (3.7)
. (3.7)
Преобразуем
рис.3.12 в рис.3.13, откуда следует, что если  ,
тогда
,
тогда
 =
=  =
=  .
(3.8)
.
(3.8)
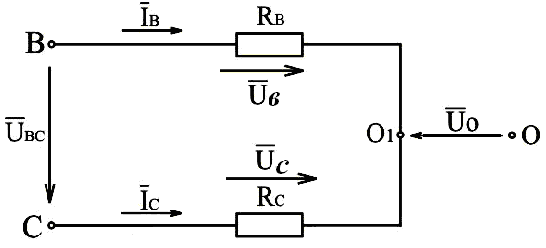
Рис.3.13. Схема, поясняющая построение векторной диаграммы
По второму закону Кирхгофа:
 ;
;
 ;
; .
(3.9)
.
(3.9)
Используя формулы (3.7), (3.8), (3.9) построим векторную диаграмму (рис.3.14).

Рис.3.14. Векторная диаграмма напряжений и токов трёхфазной системы, соединённой звездой, без нулевого провода с выключенной фазой
Рассмотрим пример.
Пусть
фазные генераторные напряжения  равны 220B,
тогда линейные напряжения равны 380B.
Из векторной диаграммы следует, что
равны 220B,
тогда линейные напряжения равны 380B.
Из векторной диаграммы следует, что
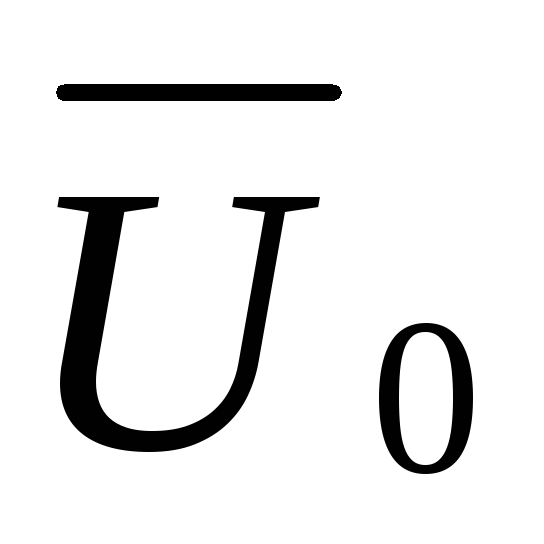 =
=  = 110B и
= 110B и 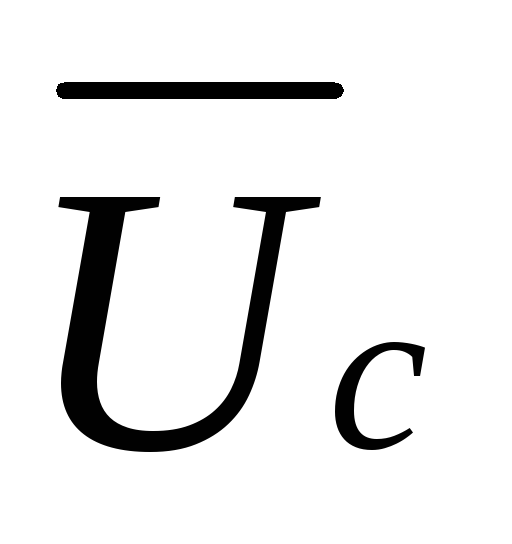 =
= 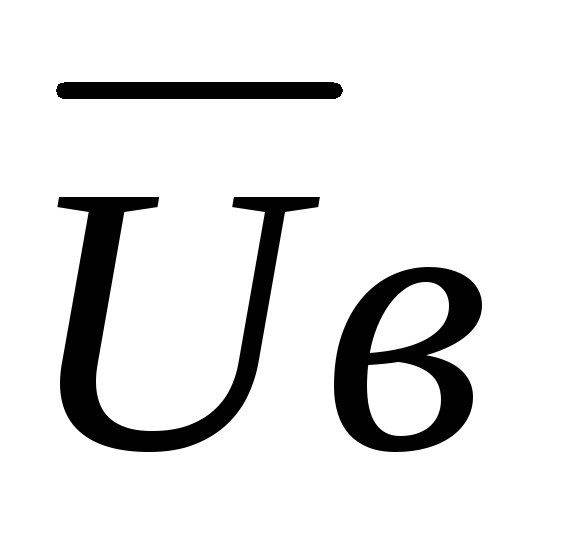 =
= 
 = 220 ∙
= 220 ∙  = 190B,
= 190B,
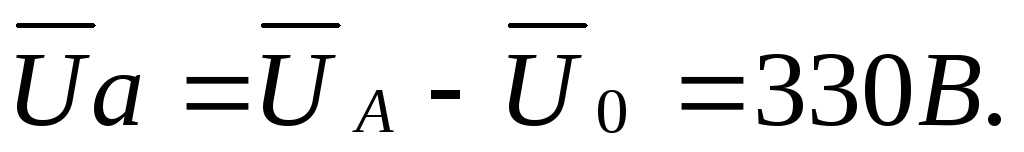
3.3.2. Короткое замыкание фазы a
Рассмотрим
электрическую схему рис.3.15, в которой  ,
,  ,
,
 =
=  ,
, 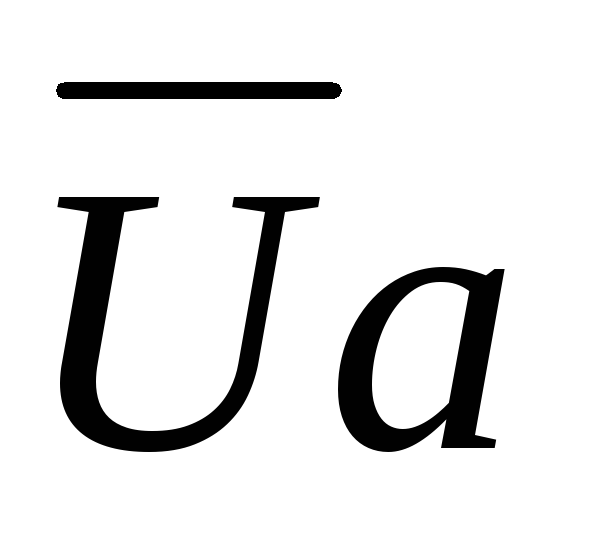 = 0.
= 0.
Воспользуемся преобразованиями:
 ,
так
как
,
так
как 
 ,
,


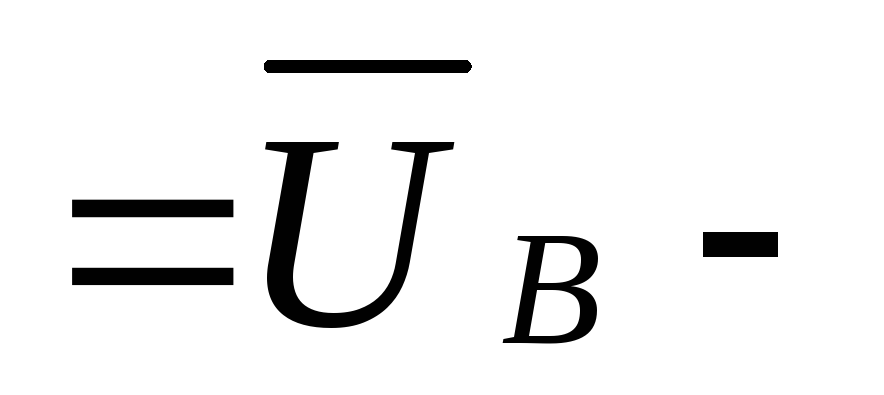


 ,
(3.10)
,
(3.10)
где  —
вектор отрицательного линейного
напряжения;
—
вектор отрицательного линейного
напряжения;
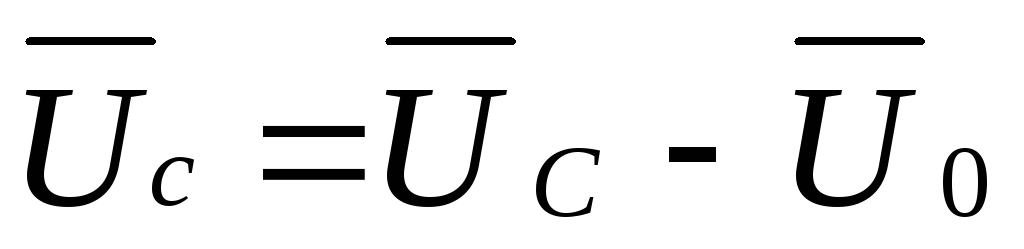



 ,
(3.11)
,
(3.11)
где  —
вектор линейного напряжения.
—
вектор линейного напряжения.

Рис.3.15. Электрическая схема трёхфазной системы, соединённой звездой, без нулевого провода с коротким замыканием фазы
По первому закону Кирхгофа:
 ;
; 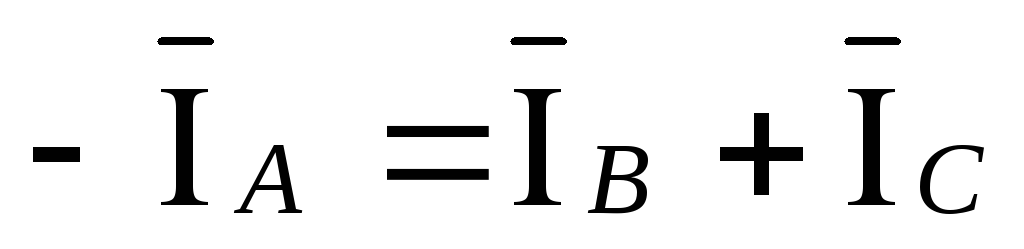 .
(3.12)
.
(3.12)
Используя формулы (3.10), (3.11), (3.12) построим векторную диаграмму, приведённую на рис.3.16.

Рис.3.16. Векторная диаграмма напряжений и токов трёхфазной системы, соединённой звездой, без нулевого провода с коротким замыканием фазы A
Рассмотрим пример.
Пусть 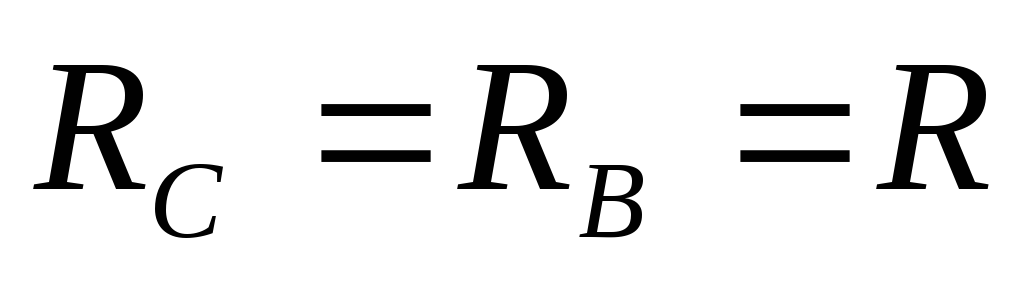
 Ом,
Ом, 

 ,
, 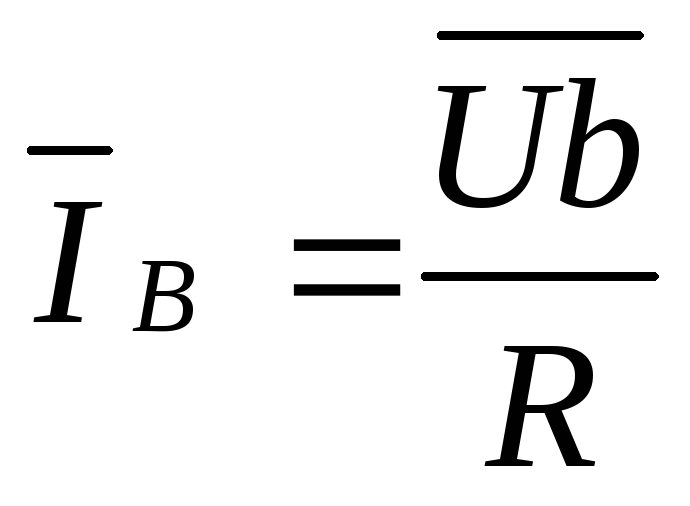
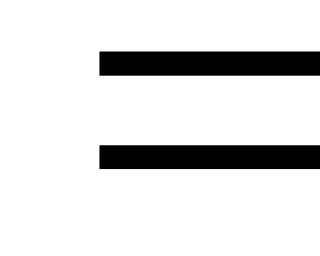 10А,
10А,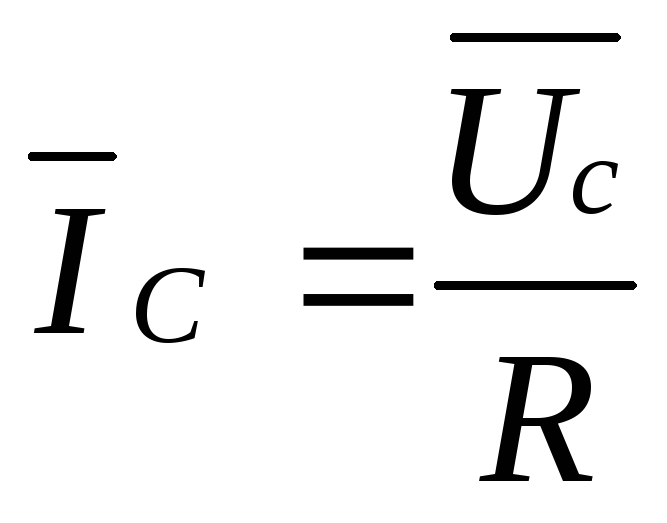
 10А. Из векторной диаграммы следует:
10А. Из векторной диаграммы следует:  ∙
∙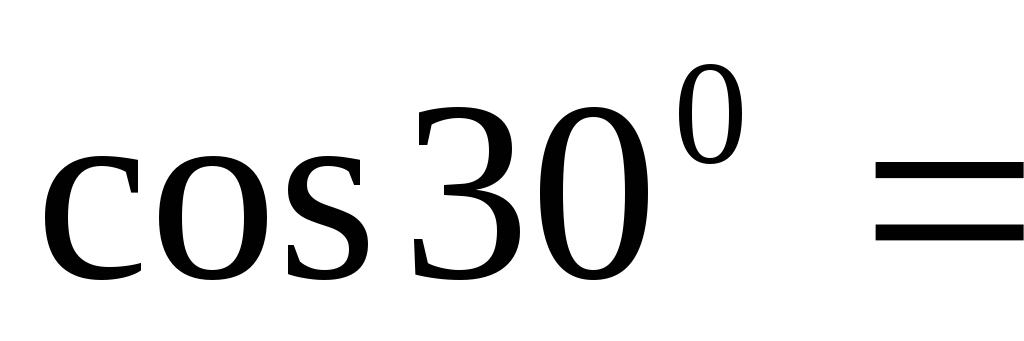 10 ∙
10 ∙  ;
;  = 10 ∙
= 10 ∙ 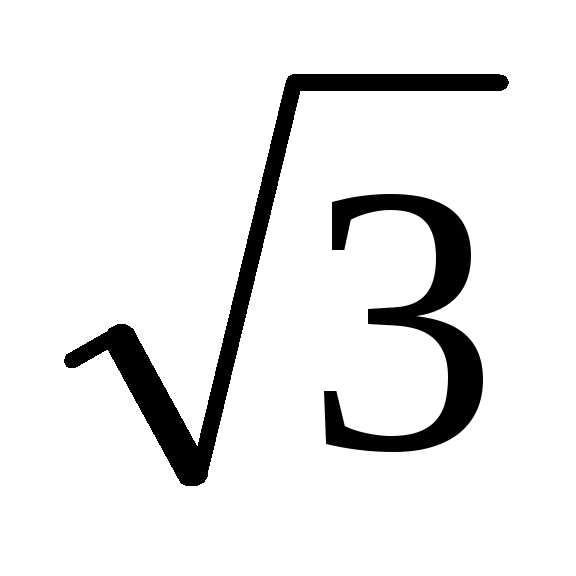 =17,3A.
=17,3A.
3.4. Соединение источников и приёмников электроэнергии треугольником. Соотношения между фазными и линейными напряжениями и токами при симметричной и несимметричной нагрузках
Рассмотрим
схему рис.3.17, в которой трёхфазный
генератор  ,
,  ,
, 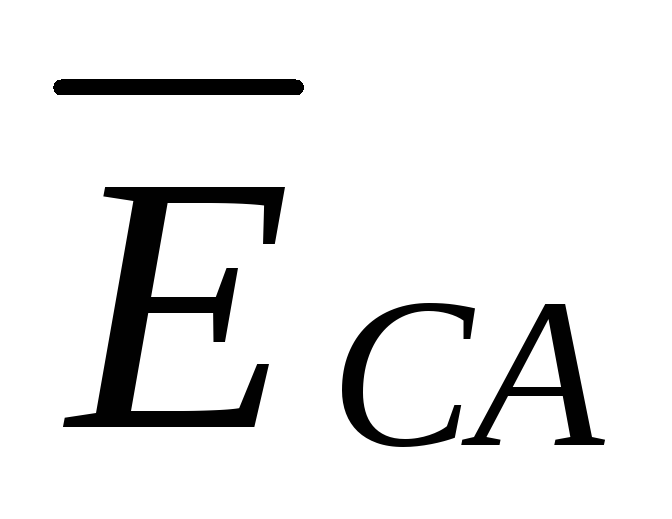 и три активных приемника
и три активных приемника 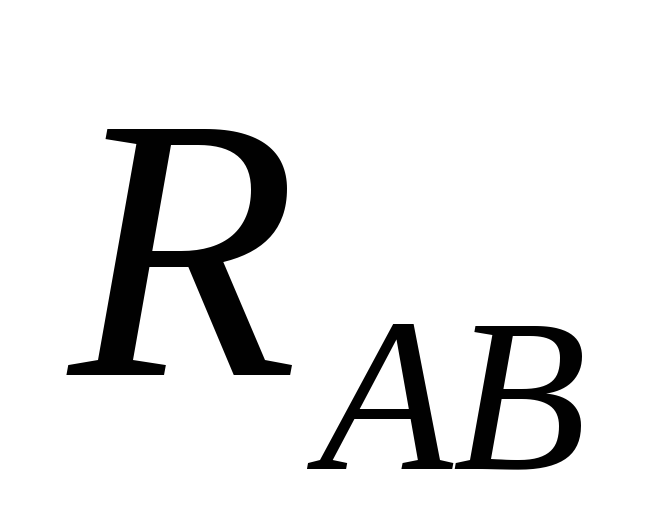 ,
,  ,
,  соединены треугольником.
соединены треугольником.
Из
схемы видно, что линейные напряжения 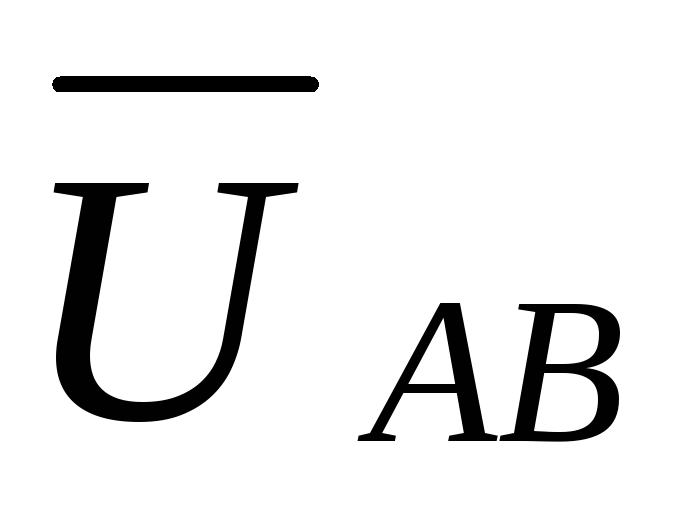 ,
,  ,
,  являются одновременно фазными напряжениями
являются одновременно фазными напряжениями
 ,
(3.13) токи
,
(3.13) токи  ,
,  ,
,  являются линейными и токи
являются линейными и токи 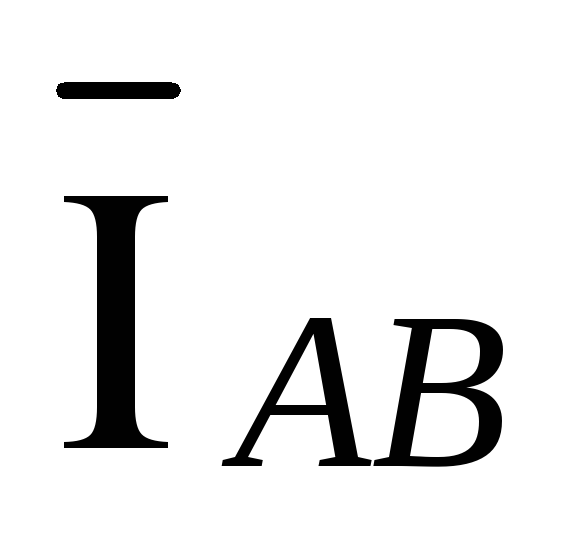 ,
,  ,
,  являются фазными.
являются фазными.
По первому закону Кирхгофа:
 .
(3.14)
.
(3.14)
При
симметричной нагрузке 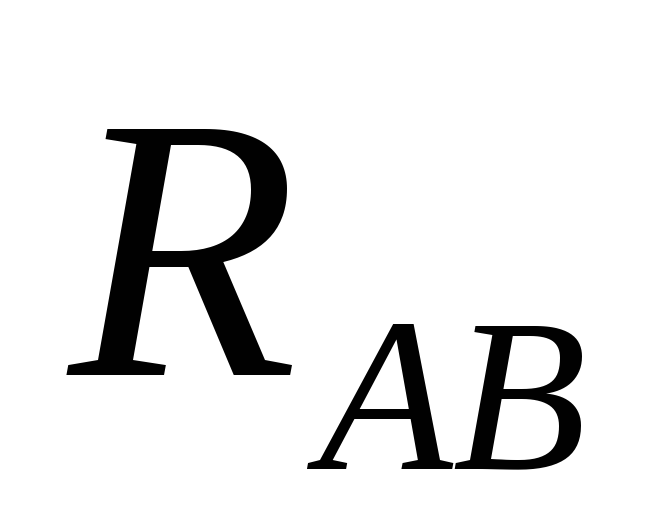


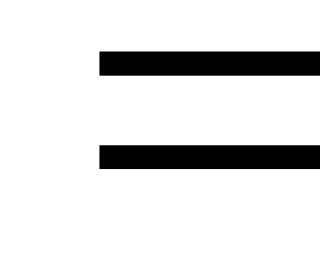
 .
Из выражений (3.14) следует, что геометрическая
сумма линейных токов
.
Из выражений (3.14) следует, что геометрическая
сумма линейных токов  .
.

Рис.3.17. Электрическая схема трёхфазной системы, представленной в виде трёхфазного генератора и активной трёхфазной нагрузки, соединённых треугольником
На рис.3.18 приведена векторная диаграмма напряжений и токов для симметричной нагрузки, соединённой треугольником.
Из
диаграммы видно: 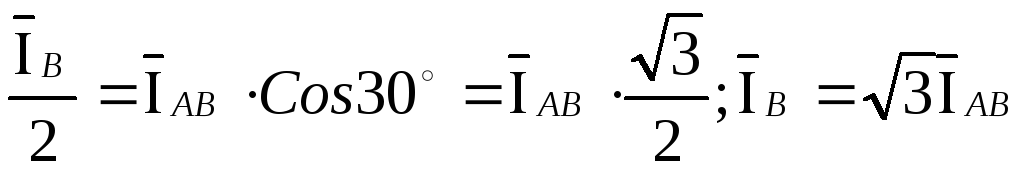 ,
где
,
где  ;
;  .
.
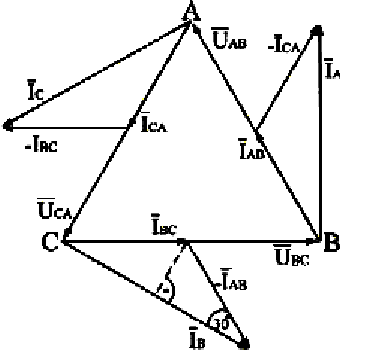
Рис.3.18. Векторная диаграмма напряжений и токов для симметричной нагрузки, соединённой треугольником
Таким образом, при соединении треугольником соотношение между линейными и фазными токами выражается формулой:
 .
(3.15)
.
(3.15)
Если
нагрузка несимметрична, то 
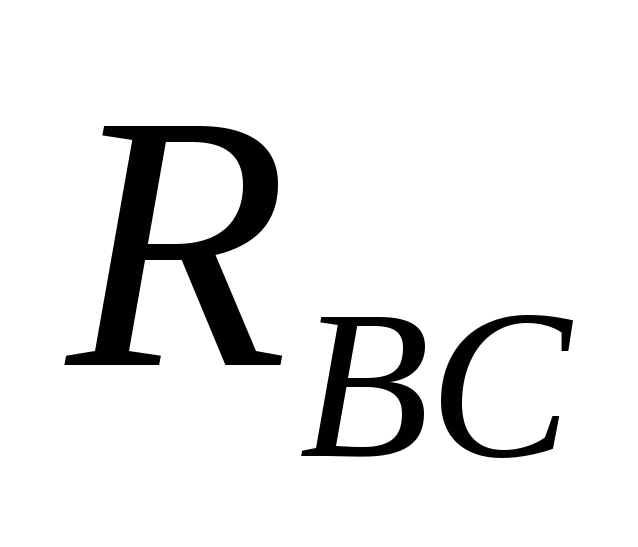

 .
Тогда, используя выражения (3.14), можно
построить векторную диаграмму напряжений
и токов следующего вида:
.
Тогда, используя выражения (3.14), можно
построить векторную диаграмму напряжений
и токов следующего вида:

Рис.3.19. Векторная диаграмма напряжений и токов для несимметричной нагрузки, соединённой треугольником
Трехфазные цепи при соединении треугольником
Особенности включения трехфазных систем треугольником. При соединении трехфазных систем треугольником также используются три гармонических напряжения (4.1), которые были рассмотрены в лекции 15. Однако соединение этих источников выполняется таким образом, что начало одной фазы соединяется с концом другой. На рис. 4.5а показано такое включение трех обмоток генератора и соответствующее ему включение источников напряжения  .
.
Векторная диаграмма для, соединения обмоток генератора по схеме треугольника приведена на рис. 4.5, б. На этой диаграмме полагается, что вектора напряжений генератора имеют значения
 (4.1)
(4.1)
т. е. генератор считается симметричным с прямым чередованием фаз.
При соединении нагрузок треугольником фазные напряжения будут равны линейным, а линейные токи равны геометрической разности двух фазных токов, подходящих к вершине треугольника нагрузок, как показано на рис. 4.6. При этом для положительных направлений токов справедливы следующие соотношения, которые устанавливают связь между линейными и фазными токами
 (4.2)
(4.2)
Фазные токи рассчитываются по известным линейным напряжениям  и проводимостям YAB, YBC, YCA фаз приемников
и проводимостям YAB, YBC, YCA фаз приемников
 (4.3)
(4.3)
Если падения напряжений на проводах линий передачи малы, то можно считать, что напряжения генератора равны соответствующим напряжениям приемника, т. е.  .
.
Из уравнений (26.2) также следует, что при любых значениях фазных токов для линейных токов справедливо выражение
 (4.4)
(4.4)
Следует отметить, что включение нагрузок по схеме треугольника возможно при любом включении обмоток генератора, как по схеме треугольника, так и по схеме звезды. Однако, при включении генератора по схеме звезды фазные напряжения приемника будут равны линейным напряжениям генератора. При этом нулевая точка генератора не используется.
Рассмотрим некоторые частные режимы работы при включении нагрузок по схеме треугольника. К таким режимам относятся:
□ равномерная нагрузка фаз генератора;
□ неравномерная нагрузка фаз генератора;
□ обрыв одной фазы приемника;
□ обрыв двух фаз приемника;
□ обрыв линейного провода.
Короткое замыкание любой фазы приемника приводит к аварийному режиму, так как при этом замыкается накоротко одна из обмоток генератора, и поэтому недопустимо.

Рисунок 4.5

Рисунок 4.6
Равномерная нагрузка фаз генератора.При симметричной системе напряжений генератора, определяемых уравнениями (4.1) и одинаковой нагрузке фаз приемника (YAB = YBC = YCA = Yn) действующие значения токов в фазах равны между собой, поэтому линейные токи связаны с фазными токами соотношением
 (4.5)
(4.5)
Токи в фазах приемника определяются по формулам (4.3) и при равенстве проводимостей имеют значения

Векторная диаграмма для равномерной нагрузки фаз генератора приведена на рис. 4.7а.
Неравномерная нагрузка фаз генератора.Неравномерная нагрузка фаз генератора является наиболее распространенным режимом работы трехфазной системы. Неравномерная нагрузка характеризуется различными значениями проводимостей, включенных в приемнике, т. е. YAB = YBC = YCA. Действующие значения токов в фазах приемника при неравномерной нагрузке и симметричном генераторе пропорциональны проводимостям нагрузки и определяются по формулам (26.3).
Векторная диаграмма для неравномерной нагрузки фаз генератора приведена на рис. 4.7б. Линейные токи при неравномерной нагрузке фаз можно определить по формулам (4.2).
Обрыв одной фазы приемника. При обрыве одной фазы приемника ток в ней будет равен нулю. Токи в других фазах приемника не изменятся, так как не изменятся фазные напряжения.
В линейном проводе, не связанном с оборванной фазой, ток также не изменится. Линейные токи двух других фаз станут равными фазным токам.
Например, при обрыве фазы А-В приемника ток IAВ = 0, а токи других фаз не изменятся. Линейные токи в этом случае будут иметь следующие значения
 . (4.7)
. (4.7)
Векторная диаграмма обрыва фазы А-В приведена на рис. 4.7, в.
Обрыв двух фаз приемника. При обрыве двух фаз приемника ток в них будет равен нулю. Ток в неповрежденной фазе не изменится, так как напряжение на ней сохранится неизменным.
Ток в линейном проводе, подходящем к оборванным фазам, будет равен нулю. Токи в других линейных проводах станут равны фазным токам.
Так, например, при обрыве фаз А-В и В-С фазные токи IАВ = IBC = 0, алинейные токи примут значения
 (4.8)
(4.8)
Векторная диаграмма токов и напряжений при обрыве двух фаз приемник приведена на рис. 4.7, г.
Обрыв линейного провода. При обрыве линейного провода трехфазная система превращается в однофазную. При этом напряжение и ток в фазе, не связанной с оборванным линейным проводом, останутся без изменений.
Две другие фазы, связанные с оборванным линейным проводом, оказываются соединенными последовательно и подключенными параллельно первой фазе.
Так, например, при обрыве линейного провода А фазы А-В и В-С будут включены последовательно и подключены параллельно фазе В-С, напряжение на которой равно UBC.
Токи в фазах определяются уравнениями

Векторная диаграмма токов и напряжений при обрыве линейного провода приведена на рис. 4.7, д.
Трехфазная система звезда — треугольник. Выше было сказано, что способ соединения обмоток генератора не предопределяет способ соединения нагрузок. Поэтому на практике к трехфазному генератору, включенному по схеме звезды, можно подключить нагрузку, соединенную по схеме треугольника. Схема подобного подключения приведена на рис. 4.8.

Рисунок 4.7

Рисунок 4.8
Из этой схемы следует, что каждое плечо треугольника оказывается включенным на линейное напряжение генератора; соединенного по схеме звезды. Поскольку линейное напряжение в 3 раза больше фазного, то токи в фазах симметричного приемника также вырастут в 3 раза. В общем случае их можно определить по формулам
 (4.9)
(4.9)
При расчете от системы звезда-треугольник можно перейти к системе звезда-звезда. При таком преобразовании можно использовать эквивалентность схем звезды и треугольника, при которой сохраняются все напряжения и токи на внешних зажимах этих схем. Такое преобразование приводит в общем случае к эквивалентным сопротивлениям схемы звезды
 (4.10)
(4.10)
Из уравнений (4.10) получим, что для симметричного треугольника с проводимостями YΔ можно найти сопротивления эквивалентной звезды
 (4.11)
(4.11)
откуда следует, что сопротивления эквивалентной звезды для симметричной схемы в три раза меньше сопротивлений треугольника.
Следует отметить, что хотя в результате такого преобразования получается система звезда-звезда, ввести в нее нулевой провод нельзя, так как в реальной схеме этого соединения нет и при введении нулевого провода получается схема, отличная от исходной.
Пример 2. Требуется определить линейные токи в нагрузке, соединенной треугольником, которая подключена к симметричному трехфазному генератору с линейным напряжением Ел = 220 В. Сопротивления фаз приемника имеют значения: ZAB = ZBC = 50 Ом, ZCA = (30 + j40) Ом. Схема соединений генератора t нагрузкой приведена на рис. 4.9, а.
Решение. Приемник с такими нагрузками относится к разряду схем с неравномерной нагрузкой фаз генератора. Для определения линейных токов в такой схеме можно воспользоваться уравнениями (4.2), в которые входят фазные токи, определяемые по уравнениям (4.3). В связи с этим, определим вначале фазные токи, пользуясь уравнениями (4.3)

Далее с помощью формул (4.2) определим линейные токи

Сумма линейных токов в цепи

что подтверждает корректность решения. Векторная диаграмма токов и напряжений в схеме приведена на рис. 4.9б.
Дата добавления: 2018-01-13; просмотров: 2244;
Обрыв фазы при симметричной нагрузке в схеме с нулевым проводом
При обрыве провода, например, в фазе А ток этой фазы становится равным нулю, напряжения и токи в фазах В и С не изменяются, а в нулевом проводе появляется ток
IN = IB + IC. Он равен току, который до обрыва протекал в фазе А (рис. 8.4.2).

Рис.8.4.2
Обрыв фазы при симметричной нагрузке в схеме без нулевого провода
При
обрыве, например, фазы А сопротивления
RAи RBоказываются соединёнными
последовательно и к ним приложено
линейное напряжение UBC. Напряжение
на каждом из сопротивлений составляет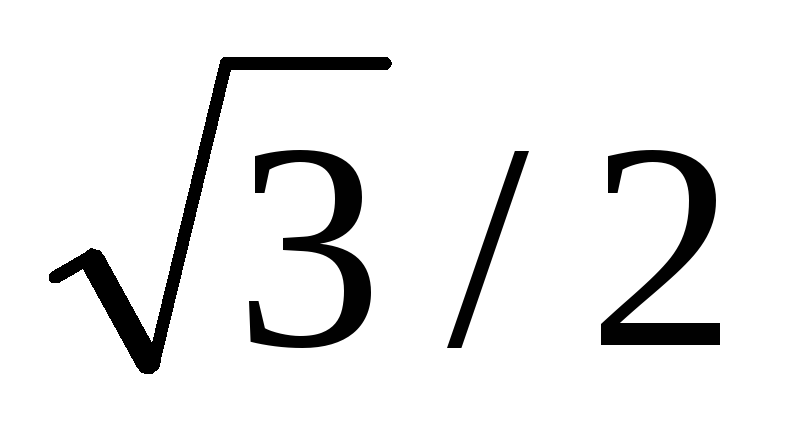 от фазного напряжения в нормальном
режиме. Нулевая точка нагрузки на
векторной диаграмме напряжений смещается
на линию ВС и при RB= RCнаходится точно в середине отрезка ВС
(рис.8.4.3
от фазного напряжения в нормальном
режиме. Нулевая точка нагрузки на
векторной диаграмме напряжений смещается
на линию ВС и при RB= RCнаходится точно в середине отрезка ВС
(рис.8.4.3
)

Рис.8.4.3
Короткие замыкания
При
коротком замыкании фазы нагрузки в
схеме с нулевым проводом ток в этой фазе
становится очень большим (теоретически
бесконечно большим) и это приводит к
аварийному отключению нагрузки защитой.
В схеме без нулевого провода при
замыкании, например, фазы А, нулевая
точка нагрузки смещается в точку «А»
генератора. Тогда к сопротивлениям фаз
В и С прикладываются линейные напряжения.
Токи в этих фазах возрастают в  раз, а ток в фазе А – в 3 раза (рис. 8.4.4).
раз, а ток в фазе А – в 3 раза (рис. 8.4.4).
Короткие замыкания между линейными проводами и в той и в другой схеме приводят к аварийному отключению нагрузки.

Рис.8.4.4
8.4.2. Экспериментальная часть Задание
Экспериментально исследовать аварийные режимы трёхфазной цепи при соединении нагрузки в звезду.
Порядок выполнения работы
Соберите цепь цепь согласно схеме (рис.8.4.5) с сопротивлениями фаз RA=RB=RC=1кОм.Измерения токов можно производить одним – двумя амперметрами, переключая их из одной фазы в другую, либо виртуальными приборами.

Рис.8.4.5
Убедитесь, что обрыв (отключение) нейтрали не приводит к изменению фазных токов.
Убедитесь, что в схеме с нулевым проводом происходит отключение источника защитой при коротких замыканиях как в фазах нагрузки, так и между линейными проводами.
Убедитесь, что в схеме без нулевого провода короткое замыкание в фазе нагрузки не приводит к отключению, а при коротком замыкании между линейными проводами установка отключается.
Проделайте измерения токов и напряжений всех величин, указанных в табл. 8.4.1 в различных режимах и по экспериментальным данным постройте векторные диаграммы для каждого случая в выбранном масштабе.
Ответьте на контрольные вопросы.
Таблица 8.4.1
Режим | UAO, B | UBO, B | UCO, B | UON, B | IA, мА | IB, мА | IC, мА | IN, мА |
RA=1 кОм RB=680 Ом RC=330 Ом Обрыв нейтрали | ||||||||
RA=RB=RC=1 кОм Схема с нейтралью Обрыв фазы А | ||||||||
RA=RB=RC=1 кОм Схема без нейтрали Обрыв фазы А | ||||||||
RA=RB=RC=1 кОм Схема без нейтрали К. З. фазы А |
Векторные диаграммы
RA=1 кОм, RB=680 Ом, RC=330 Ом. Обрыв нейтрали

2. RA= RB= RC =1 кОм, Схема с нейтралью, обрыв фазы А

3. RA= RB= RC =1 кОм, Схема без нейтрали, обрыв фазы А
4. RA= RB= RC =1 кОм, Схема без нейтрали, короткое замыкание фазы А
В опрос:Как изменяется мощность трёхфазной
нагрузки при обрыве фазы в схеме с
нулевым проводом и без него? Как изменяется
мощность при коротком замыкании одной
фазы?
опрос:Как изменяется мощность трёхфазной
нагрузки при обрыве фазы в схеме с
нулевым проводом и без него? Как изменяется
мощность при коротком замыкании одной
фазы?
Ответ: …………



