E (математическая константа) — это… Что такое E (математическая константа)?
e — математическая константа, основание натурального логарифма, иррациональное и трансцендентное число. Иногда число e называют числом Эйлера (не путать с т. н. числами Эйлера I рода) или числом Непера. Обозначается строчной латинской буквой «e».
Играет важную роль в дифференциальном и интегральном исчислении, а также многих других разделах математики.
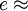 2,718 281 828 459 045 235 360 287 471 352 662 497 757…[1]
2,718 281 828 459 045 235 360 287 471 352 662 497 757…[1]
Способы определения
Число e может быть определено несколькими способами.
Свойства

Данное свойство играет важную роль в решении дифференциальных уравнений. Так, например, единственным решением дифференциального уравнения является функция
является функция  , где c — произвольная константа.
, где c — произвольная константа.- Число e иррационально и даже трансцендентно. Это первое число, которое не было выведено как трансцендентное специально, его трансцендентность была доказана только в 1873 году Шарлем Эрмитом. Предполагается, что e — нормальное число, то есть вероятность появления разных цифр в его записи одинакова.
 , см. формула Эйлера, в частности
, см. формула Эйлера, в частности- Ещё одна формула, связывающая числа е и π, т. н. «интеграл Пуассона» или «интеграл Гаусса»
- Для любого комплексного числа z верны следующие равенства:
- Число e разлагается в бесконечную цепную дробь следующим образом:
![e = [2; \;1, 2, 1, \;1, 4, 1, \;1, 6, 1, \;1, 8, 1, \;1, 10, 1, \ldots] \,](//groupnk.ru/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif) , то есть
, то есть
![e = \lim_{n\to\infty} \frac{n}{\sqrt[n]{n!}}.](//groupnk.ru/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif)
- Представление Каталана:
История
Данное число иногда называют неперовым в честь шотландского учёного Непера, автора работы «Описание удивительной таблицы логарифмов» (1614 год). Однако это название не совсем корректно, так как у него логарифм числа x был равен  .
.
Впервые константа негласно присутствует в приложении к переводу на английский язык вышеупомянутой работы Непера, опубликованному в 1618 году. Негласно, потому что там содержится только таблица натуральных логарифмов, определённых из кинематических соображений, сама же константа не присутствует (см.: Непер).
Предполагается, что автором таблицы был английский математик Отред.
Саму же константу впервые вычислил швейцарский математик Бернулли при анализе следующего предела:
Первое известное использование этой константы, где она обозначалась буквой b, встречается в письмах Лейбница Гюйгенсу, 1690—1691 годы.
Букву e начал использовать Эйлер в 1727 году, а первой публикацией с этой буквой была его работа «Механика, или Наука о движении, изложенная аналитически» 1736 год. Соответственно, e обычно называют числом Эйлера. Хотя впоследствии некоторые учёные использовали букву c, буква e применялась чаще и в наши дни является стандартным обозначением.
Почему была выбрана именно буква e, точно неизвестно. Возможно, это связано с тем, что с неё начинается слово exponential («показательный», «экспоненциальный»). Другое предположение заключается в том, что буквы a, b, c и d уже довольно широко использовались в иных целях, и e была первой «свободной» буквой. Неправдоподобно предположение, что Эйлер выбрал e как первую букву в своей фамилии (нем. Euler).
Способы запоминания
- Для получения приблизительного значения нужно выписать подряд цифры, выражающие число букв в словах следующего стишка, и поставить запятую после первого знака: «Мы порхали и блистали, но застряли в перевале; не признали наши крали авторалли».
- Стишок:
- Два и семь, восемнадцать,
- Двадцать восемь, восемнадцать,
- Двадцать восемь, сорок пять,
- Девяносто, сорок пять.
- Легко запомнить как 2, далее запоминаем 71, потом повторяющиеся 82, 81, 82
- Число e можно запомнить по следующему мнемоническому правилу: два и семь, далее два раза год рождения Льва Толстого (1828), затем углы равнобедренного прямоугольного треугольника (45, 90 и 45 градусов). Стихотворная мнемофраза, иллюстрирующая часть этого правила: «Экспоненту помнить способ есть простой: две и семь десятых, дважды Лев Толстой»
- Цифры 45, 90 и 45 можно запоминать как «год победы над фашистской Германией, затем дважды этот год и снова он»
- В другом варианте правила e связывается с президентом США Эндрю Джексоном: 2 — столько раз избирался, 7 — он был седьмым президентом США, 1828 — год его избрания, повторяется дважды, поскольку Джексон дважды избирался. Затем — опять-таки равнобедренный прямоугольный треугольник.
Доказательство иррациональности
Пускай  рационально. Тогда
рационально. Тогда  , где
, где 
 целые положительные, откуда
целые положительные, откудаУмножая обе части уравнения на 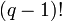 , получаем
, получаем
Переносим 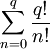 в левую часть:
в левую часть:
Все слагаемые правой части целые, следовательно:
 — целое
— целое
Но с другой стороны
Получаем противоречие.
Интересные факты
- В IPO компании 2004 году было объявлено о намерении компании увеличить свою прибыль на 2 718 281 828 долларов. Заявленная цифра представляет собой первые 10 цифр известной математической константы.
- В языках программирования символу e в экспоненциальных записях числовых литералов соответствует число 10, а не Эйлерово число. Это связано с историей создания и использования языка для математических вычислений FORTRAN[2]:
Я начал программировать в 1960 году на FORTRAN II, используя компьютер IBM 1620. В то время, в 60-е и 70-е годы, FORTRAN использовал только заглавные буквы. Возможно, это произошло потому, что большинство старых устройств ввода были телетайпами, работавшими с 5-битовым кодом Бодо, который не поддерживал строчные буквы. Буква E в экспоненциальной записи тоже была заглавной и не смешивалась с основанием натурального логарифма e, которое всегда записывается маленькой буквой. Символ E просто выражал экспоненциальный характер, то есть обозначал основание системы — обычно таким было 10. В те годы программисты широко использовали восьмеричную систему. И хотя я не замечал такого, но если бы я увидел восьмеричное число в экспоненциальной форме, я бы предположил, что имеется в виду основание 8. Первый раз я встретился с использованием маленькой e в экспоненциальной записи в конце 70-х годов, и это было очень неудобно. Проблемы появились потом, когда строчные буквы по инерции перешли в FORTRAN. У нас существовали все нужные функции для действий с натуральными логарифмами, но все они записывались прописными буквами.
- Таким образом, записи типа
7.38e-43в языках программирования будет соответствовать число , а не
, а не  .
.
Примечания
См. также
Ссылки
Wikimedia Foundation. 2010.
Экспонента и число е: просто и понятно
Перевод большой статьи «An Intuitive Guide To Exponential Functions & e»
Число e всегда волновало меня — не как буква, а как математическая константа. Что число е означает на самом деле?
Разные математические книги и даже моя горячо любимая Википедия описывает эту величественную константу совершенно бестолковым научным жаргоном:
Математическая константа е является основанием натурального логарифма.
Если заинтересуетесь, что такое натуральный логарифм, найдете такое определение:
Натуральный логарифм, ранее известный как гиперболический логарифм, является логарифмом с основанием е, где е – иррациональная константа, приблизительно равная 2.718281828459.
Определения, конечно, правильные. Но понять их крайне сложно. Конечно, Википедия в этом не виновата: обычно математические пояснения сухи и формальны, составляются по всей строгости науки. Из-за этого новичкам сложно осваивать предмет (а когда-то каждый был новичком).
С меня хватит! Сегодня я делюсь своими высокоинтеллектуальными соображениями о том, что такое число е, и чем оно так круто! Отложите свои толстые, наводящие страх математические книжки в сторону!
Число е – это не просто число
Описывать е как «константу, приблизительно равную 2,71828…» — это все равно, что называть число пи «иррациональным числом, приблизительно равным 3,1415…». Несомненно, так и есть, но суть по-прежнему ускользает от нас.
Число пи — это соотношение длины окружности к диаметру, одинаковое для всех окружностей. Это фундаментальная пропорция, свойственная всем окружностям, а следовательно, она участвует в вычислении длины окружности, площади, объема и площади поверхности для кругов, сфер, цилиндров и т.д. Пи показывает, что все окружности связаны, не говоря уже о тригонометрических функциях, выводимых из окружностей (синус, косинус, тангенс).
Число е является базовым соотношением роста для всех непрерывно растущих процессов. Число е позволяет взять простой темп прироста (где разница видна только в конце года) и вычислить составляющие этого показателя, нормальный рост, при котором с каждой наносекундой (или даже быстрее) всё вырастает еще на немного.
Число е участвует как в системах с экспоненциальным, так и постоянным ростом: население, радиоактивный распад, подсчет процентов, и много-много других. Даже ступенчатые системы, которые не растут равномерно, можно аппроксимировать с помощью числа е.
Также, как любое число можно рассматривать в виде «масштабированной» версии 1 (базовой единицы), любую окружность можно рассматривать в виде «масштабированной» версии единичной окружности (с радиусом 1). И любой коэффициент роста может быть рассмотрен в виде «масштабированной» версии е («единичного» коэффициента роста).
Так что число е – это не случайное, взятое наугад число. Число е воплощает в себе идею, что все непрерывно растущие системы являются масштабированными версиями одного и того же показателя.
Понятие экспоненциального роста
Давайте начнем с рассмотрения базовой системы, которая удваивается за определенный период времени. Например:
- Бактерии делятся и «удваиваются» в количестве каждые 24 часа
- Мы получаем вдвое больше лапшинок, если разламываем их пополам
- Ваши деньги каждый год увеличиваются вдвое, если вы получаете 100% прибыли (везунчик!)
И выглядит это примерно так:
Деление на два или удваивание – это очень простая прогрессия. Конечно, мы можем утроить или учетверить, но удваивание более удобно для пояснения.
Математически, если у нас есть х разделений, мы получаем в 2^x раз больше добра, чем было вначале. Если сделано только 1 разбиение, получаем в 2^1 раза больше. Если разбиений 4, у нас получится 2^4=16 частей. Общая формула выглядит так:
рост = 2x
Другими словами, удвоение – это 100% рост. Мы можем переписать эту формулу так:
рост = (1+100%)x
Это то же равенство, мы только разделили «2» на составные части, которыми в сущности и является это число: начальное значение (1) плюс 100%. Умно, да?
Конечно, мы можем подставить и любое другое число (50%, 25%, 200%) вместо 100% и получить формулу роста для этого нового коэффициента. Общая формула для х периодов временного ряда будет иметь вид:
рост = (1+прирост)x
Это просто означает, что мы используем норму возврата, (1 + прирост), «х» раз подряд.
Приглядимся поближе
Наша формула предполагает, что прирост происходит дискретными шагами. Наши бактерии ждут, ждут, а потом бац!, и в последнюю минуту они удваиваются в количестве. Наша прибыль по процентам от депозита магическим образом появляется ровно через 1 год. На основе формулы, написанной выше, прибыль растет ступенчато. Зеленые точки появляются внезапно.
Но мир не всегда таков. Если мы увеличим картинку, мы увидим, что наши друзья-бактерии делятся постоянно:
Зеленый малый не возникает из ничего: он медленно вырастает из синего родителя. После 1 периода времени (24 часа в нашем случае), зеленый друг уже полностью созрел. Повзрослев, он стает полноценным синим членом стада и может создавать новые зеленые клеточки сам.
Эта информация как-то изменит наше уравнение?
Не-а. В случае с бактериями, полусформированные зеленые клетки все же не могут ничего делать, пока не вырастут и совсем не отделятся от своих синих родителей. Так что уравнение справедливо.
В следующий статье мы посмотрим на пример экспоненциального роста ваших денег.
Продолжение
Экспонента — Википедия
Запрос «EXP» перенаправляется сюда; о классе сложности см. Класс EXPTIME.
Экспоне́нта — показательная функция f(x)=exp(x)=ex{\displaystyle f(x)=\exp(x)=e^{x}}, где e{\displaystyle e} — число Эйлера (e≈2,718){\displaystyle (e\approx 2,718)}.
Экспоненциальная функция может быть определена различными эквивалентными способами. Например, через ряд Тейлора:
- ex=1+∑n=1∞xnn!=1+x+x22!+x33!+x44!+⋯{\displaystyle e^{x}=1+\sum _{n=1}^{\infty }{x^{n} \over n!}=1+x+{x^{2} \over 2!}+{x^{3} \over 3!}+{x^{4} \over 4!}+\cdots }
или через предел:
ex=limn→∞(1+xn)n{\displaystyle e^{x}=\lim _{n\rightarrow \infty }\left(1+{\frac {x}{n}}\right)^{n}}
Здесь x{\displaystyle x} — любое комплексное число.
 График экспоненты в комплексной плоскости.
График экспоненты в комплексной плоскости.Легенда
Комплексная экспонента — математическая функция, задаваемая соотношением f(z)=ez{\displaystyle f(z)=e^{z}}, где z{\displaystyle z} есть комплексное число. Комплексная экспонента определяется как аналитическое продолжение экспоненты f(x)=ex{\displaystyle f(x)=e^{x}} вещественного переменного x{\displaystyle x}:
Определим формальное выражение
ez=ex+iy=ex⋅eiy{\displaystyle e^{z}=e^{x+iy}=e^{x}\cdot e^{iy}}.
Определенное таким образом выражение на вещественной оси будет совпадать с классической вещественной экспонентой. Для полной корректности построения необходимо доказать аналитичность функции ez{\displaystyle e^{z}}, то есть показать, что ez{\displaystyle e^{z}} разлагается в некоторый сходящийся к данной функции ряд. Покажем это:
f(z)=ez=ex⋅eiy=eiy∑n=0∞xnn!{\displaystyle f(z)=e^{z}=e^{x}\cdot e^{iy}=e^{iy}\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}}
Сходимость данного ряда легко доказывается:
|eiy∑n=0∞xnn!|≤|∑n=0∞xnn!|≤∑n=0∞|xnn!|=∑n=0∞|x|nn!=e|x|{\displaystyle \left|e^{iy}\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}\right|\leq \left|\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}\right|\leq \sum _{n=0}^{\infty }\left|{\frac {x^{n}}{n!}}\right|=\sum _{n=0}^{\infty }{\dfrac {|x|^{n}}{n!}}=e^{|x|}}.
Ряд всюду сходится абсолютно, то есть вообще всюду сходится, таким образом, сумма этого ряда в каждой конкретной точке будет определять значение аналитической функции f(z)=ez{\displaystyle f(z)=e^{z}}. Согласно теореме единственности, полученное продолжение будет единственно, следовательно, на комплексной плоскости функция ez{\displaystyle e^{z}} всюду определена и аналитична.
Свойства[править | править код]
Аналогично экспонента определяется для элемента произвольной ассоциативной алгебры. В конкретном случае требуется также доказательство того, что указанные пределы существуют.
Матричная экспонента[править | править код]
Экспоненту от квадратной матрицы (или линейного оператора) можно формально определить, подставив матрицу в соответствующий ряд:
- expA=∑k=0∞Akk!.{\displaystyle \exp A=\sum _{k=0}^{\infty }{\frac {A^{k}}{k!}}.}
Определённый таким образом ряд сходится для любого оператора A{\displaystyle A} с ограниченной нормой, поскольку мажорируется рядом для экспоненты нормы A:{\displaystyle A:} exp‖A‖.{\displaystyle \exp \|A\|.} Следовательно, экспонента от матрицы A∈Rn×n{\displaystyle A\in \mathbb {R} ^{n\times n}} всегда определена и сама является матрицей.
С помощью матричной экспоненты легко задать вид решения линейного дифференциального уравнения с постоянными коэффициентами: уравнение x˙=Ax, x∈Rn{\displaystyle {\dot {x}}=Ax,~~~x\in \mathbb {R} ^{n}} с начальным условием x(0)=x0{\displaystyle x(0)=x_{0}} имеет своим решением x(t)=exp(At)x0.{\displaystyle x(t)=\exp(At)x_{0}.}
h-экспонента[править | править код]
Введение h{\displaystyle h}-экспоненты основано на втором замечательном пределе:
eh(x)=(1+h)xh.{\displaystyle e_{h}(x)=(1+h)^{\frac {x}{h}}.}
При h→0{\displaystyle h\to 0} получается обычная экспонента[1].
Обратная функция к экспоненциальной функции — натуральный логарифм. Обозначается lnx{\displaystyle \ln x}:
lnx=logex.{\displaystyle \ln x=\log _{e}x.}
- Лаврентьев М. А., Шабат Б. В. Методы теории функций комплексного переменного. — Издание 5-е, исправленное. — М.: Наука, 1987. — 688 с.
- Хапланов М. Г. Теория функции комплексного переменного (краткий курс). — Издание 2-е, исправленное. — М.: Просвещение, 1965. — 209 с.
ЧИСЛО Е | Энциклопедия Кругосвет
ЧИСЛО e. Число, приближенно равное 2,718, которое часто встречается в математике и естественных науках. Например, при распаде радиоактивного вещества по истечении времени t от исходного количества вещества остается доля, равная e–kt, где k – число, характеризующее скорость распада данного вещества. Обратная величина 1/k называется средним временем жизни атома данного вещества, так как в среднем атом прежде, чем распасться, существует в течение времени 1/k. Величина 0,693/k называется периодом полураспада радиоактивного вещества, т.е. временем, за которое распадается половина исходного количества вещества; число 0,693 приближенно равно loge 2, т.е. логарифму числа 2 по основанию e. Аналогично, если бактерии в питательной среде размножаются со скоростью, пропорциональной их числу в настоящий момент, то по истечении времени t начальное количество бактерий N превращается в Nekt. Затухание электрического тока I в простом контуре с последовательным соединением, сопротивлением R и индуктивностью L происходит по закону I = I0e–kt, где k = R/L, I0 – сила тока в момент времени t = 0. Аналогичные формулы описывают релаксацию напряжений в вязкой жидкости и затухание магнитного поля. Число 1/k часто называют временем релаксации. В статистике величина e–kt встречается как вероятность того, что за время t не произошло событий, наступающих случайно со средней частотой k событий в единицу времени. Если S – сумма денег, вложенных под r процентов с непрерывным начислением вместо начисления через дискретные промежутки времени, то к моменту времени t первоначальная сумма возрастет до Setr/100.
Причина «вездесущности» числа e заключается в том, что формулы математического анализа, содержащие экспоненциальные функции или логарифмы, записываются проще, если логарифмы брать по основанию e, а не 10 или какому-либо другому основанию. Например, производная от log10 x равна (1/x)log10 e, тогда как производная от loge x равна просто 1/x. Аналогично, производная от 2x равна 2xloge 2, тогда как производная от eх равна просто ex. Это означает, что число e можно определить как основание b, при котором график функции y = logb x имеет в точке x = 1 касательную с угловым коэффициентом, равным 1, или при котором кривая y = bx имеет в x = 0 касательную с угловым коэффициентом, равным 1. Логарифмы по основанию e называются «натуральными» и обозначаются ln x. Иногда их также называют «неперовыми», что неверно, так как в действительности Дж.Непер (1550–1617) изобрел логарифмы с другим основанием: неперов логарифм числа x равен 107 log1/e (x/107) (см. также ЛОГАРИФМ).
Различные комбинации степеней e встречаются в математике так часто, что имеют специальные названия. Таковы, например, гиперболические функции
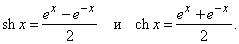
График функции y = ch x называется цепной линией; такую форму имеет подвешенная за концы тяжелая нерастяжимая нить или цепь. Формулы Эйлера
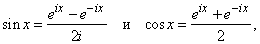
где i2 = –1, связывают число e с тригонометрией. Частный случай x = p приводит к знаменитому соотношению eip + 1 = 0, связывающему 5 наиболее известных в математике чисел.
При вычислении значения e


Значение e с 15 десятичными знаками равно 2,718281828459045. В 1953 было вычислено значение e с 3333 десятичными знаками. Символ e для обозначения этого числа был введен в 1731 Л.Эйлером (1707–1783).
Десятичное разложение числа e непериодично (e – иррациональное число). Кроме того, e, как и p, – трансцендентное число (оно не является корнем никакого алгебраического уравнения с рациональными коэффициентами). Это доказал в 1873 Ш.Эрмит. Впервые было показано, что столь естественным образом возникающее в математике число является трансцендентным.
Проверь себя!
Ответь на вопросы викторины «Математика»
Как звали математика, который в 19 лет решил задачу, не поддававшуюся усилиям лучших геометров со времен Евклида?
I.E. и E.G. — Значение и Перевод Сокращений. » Как Выучить Английский Язык
Добрый день уважаемые читатели блога рассказывающего о том, Как Выучить Английский Язык. Сегодня я решил коснуться таких интересных и достаточно часто встречающихся в английском письменном языке сокращений, как i.e. и e.g. Я расскажу о значении каждого из этих сокращений, а также покажу на примере когда следует употреблять “i.e.”, а когда “e.g.”.
Латинские аббревиатуры «i.e.» и «e.g.» достаточно часто можно встретить в английской литературе, да и вообще в повседневном письменном языке. Скажу даже больше: эти сокращения использовались бы еще чаще, если бы люди были более уверены в понимании того, когда необходимо употребить “i.e.”, а когда “e.g.” Поэтому для начала я предлагаю разобраться, что означают собой эти незамысловатые сокращения.
Сокращение i.e. обычно вставляют в предложение в качестве заменителя “то есть”. Аббревиатура пришла в английский из латинского языка и в не урезанной версии писалась как “id est”. I.e. уместно употреблять в качестве заменителя фразы “другими словами” или “то есть” (как уже упоминалось выше). Это сокращение используют, когда необходимо выделить что-либо более ясно или уточнить.
“E.g.” означает “например”. Как и первая аббревиатура, сокращение e.g. появилось от латинского выражения “exempli gratia” (“ради примера”). “E.g.” уместно использовать в тех случаях, когда вы не намереваетесь перечислять все то, что сейчас обсуждается.
Примеры употребления “i.e.” и “e.g.” :
Пример 1. Места
I.E. (Id Est)
Пример предложения
I am going to the place where I relax best, i.e., the coffee shop.
Объяснение
[Существует только одно место, которое по-моему мнению является наилучшим для отдыха. При помощи “i.e.” я показываю всем, что я особенно люблю расслабляться в этом месте.]
E.G. (Exempli Gratia)
Пример предложения
At the places where I relax well, e.g., Tchibo, I have none of the distractions I have at home.
Объяснение
[Существует большое количество кофеен, которые мне нравятся, к примеру одной из них является сеть кофеен Tchibo]
Аббревиатура “e.g.” может быть использована сразу с несколькими примерами, однако не стоит заканчивать все свои примеры “etc”. Не нужно писать: I like coffee shops, e.g., Tchibo, Starbucks, etc. Вместо этого лучше написать так: There is debate as to whether some of the Ottonian emperors (e.g., Saint Henry II and Otto I the Great) were evil.
Пример 2. Елена Троянская и ее братья и сестры
I.E. (Id Est)
The most beautiful human in Greek mythology, i.e., Leda’s daughter Helen, may have had a unibrow, according to a 2012 book on Helen I’m reading.
[Елена, чья красота стала причиной начала Троянской Войны, считается самой красивой женщиной согласно Греческой мифологии. У нее нет и не может быть соперниц.]
E.G. (Exempli Gratia)
The children of Leda, e.g., Castor and Pollux, were born in pairs.
[Считается, что пара мальчиков, с именами Castor и Pollux, могли быть двойней, однако что касается всех остальных детей Елены Троянской у историков нет такой уверенности. Согласно Греческой мифологии, Елена вылупилась из яйца, но несмотря на такое необычное появление на свет она смогла родить некотрое количество двойнят, и Castor и Pollux — это один из примеров.]
Выделение курсивом I.E. и E.G.
Аббревиатуры i.e. и e.g. — это настолько распространенные латинские сокращения, что абсолютно необязательно выделять их курсивом.
Пищевые добавки (Е***). Описание, обозначение, классификация и расшифровка пищевых добавок — Справочная информация на «Добро ЕСТЬ!»

Рад представить вашему вниманию информацию о пищевых добавках: красителях, консервантах, антиокислителях, усилителях вкуса и т.д. Начну с перечня групп данных веществ, а в дальнейшем буду постепенно выкладывать непосредственно информацию о каждом из них в подробностях. Итак…
Пищевые добавки — вещества, которые в технологических целях добавляются в пищевые продукты в процессе производства, упаковки, транспортировки или хранения продуктов.
Это делается для придания продуктам желаемых свойств, например:
— определённого аромата — ароматизаторы;
— цвета — красители;
— длительности хранения (консерванты) и т.п.
Международные стандарты на пищевые добавки и примеси определяются Объединенным комитетом экспертов Международной сельскохозяйственной организации (JECFA) и Кодексом Алиментариус (Codex Alimentarius), принятом Международной комиссией ФАО/ВОЗ и обязательным к исполнению странами входящими в ВТО. Особенностью Кодекса Алиментариус является то, что он не учитывает токсикологические особенности пищевых добавок.
Классификация пищевых добавок
Для классификации пищевых добавок в странах Евросоюза разработана система нумерации (действует с 1953 года). Каждая добавка имеет уникальный номер, начинающийся с буквы «E». Система нумерации была доработана и принята для международной классификации Кодекс Алиментариус.
Важно отметить, что в настоящее время уже трудно найти какой-либо продукт без упоминания в его составе буквы «Е», а ведь вещество, прячущееся за таким обозначением, может и здоровью навредить.
В любом случае, кто предупрежден, тот вооружен, поэтому давайте перейдем непосредственно к расшифровкам пищевых добавок.
Обозначение пищевых добавок (Е), и их расшифровка
| Группа | Индексы | Технологические функции |
| Е100 — Е199 Красители | 100 — 109 | Желтые |
| 110 — 119 | Оранжевые | |
| 120 — 129 | Красные | |
| 130 — 139 | Синие и фиолетовые | |
| 140 — 149 | Зеленые | |
| 150 — 159 | Коричневые и черные | |
| 160 — 199 | Другие | |
| Е200 — Е299 Консерванты | 200 — 209 | Сорбаты |
| 210 — 219 | Бензоаты | |
| 220 — 229 | Сульфиты | |
| 230 — 239 | Фенолы и формиаты (метаноаты) | |
| 240 — 259 | Нитраты | |
| 260 — 269 | Ацетаты (этаноаты) | |
| 270 — 279 | Лактаты | |
| 280 — 289 | Пропиноаты (пропаноаты) | |
| 290 — 299 | Другие | |
| E300 — E399 Антиокислители | 300 — 305 | Аскорбаты (витамин C) |
| 306 — 309 | Токоферол (витамин E) | |
| 310 — 319 | Галлаты и эриторбаты | |
| 320 — 329 | Лактаты | |
| 330 — 339 | Цитраты | |
| 340 — 349 | Фосфаты | |
| 350 — 359 | Малаты и адипаты (адипинаты) | |
| 360 — 369 | Сукцинаты и фумараты | |
| 370 — 399 | Другие | |
| E400 — E499 Стабилизаторы, загустители, эмульгаторы | 400 — 409 | Альгинта |
| 410 — 419 | Камеди | |
| 420 — 429 | Другие природные вещества | |
| 430 — 439 | Соединения полиоксиэтилена | |
| 440 — 449 | Природные эмульгаторы | |
| 450 — 459 | Фосфаты | |
| 460 — 469 | Соединения целлюлозы | |
| 470 — 489 | Соединения жирных кислот | |
| 490 — 499 | Другие | |
| E500 — E599 Регуляторы pH и вещества против слёживания | 500 — 509 | Неорганические кислоты и основания |
| 510 — 519 | Хлориды и сульфаты | |
| 520 — 529 | Сульфаты и гидроксиды | |
| 530 — 549 | Соединения щелочных металлов | |
| 550 — 569 | Силикаты | |
| 570 — 579 | Стеараты и глюконаты | |
| 580 — 599 | Другие | |
| E600 — E699 Усилители вкуса и аромата | 620 — 629 | Глютаматы |
| 630 — 639 | Инозинаты | |
| 640 — 649 | Другие | |
| E700 — E799 Антибиотики | ||
| E800 — E899 Резерв | ||
| E900 — E999 Прочие | 900 — 909 | Воски |
| 910 — 919 | Глазирователи | |
| 920 — 929 | Вещества, улучшающие мучные изделия | |
| 930 — 949 | Газы для упаковки | |
| 950 — 969 | Подсластители | |
| 990 — 999 | Пенообразователи | |
| E1000 — E1999 Дополнительные вещества |
Вред пищевых добавок
Пищевые добавки используются для улучшения стабильности и сохраняемости продуктов питания, для сохранения пищевой ценности продукта, для различных целей при производстве, обработке, упаковке и хранении.
В СМИ периодически появляются сообщения, что, к примеру: «добавка Е*** — вызывает раковые опухоли», аллергию или расстройство желудка и другие неприятные последствия. Однако нужно понимать, что влияние любого химического вещества на организм человека зависит как от индивидуальных особенностей организма, так и от количества вещества. Для каждой добавки, как правило, определяется допустимая суточная доза потребления (так называемая ДСП), превышение которой влечёт негативные последствия. Для некоторых веществ, применяемых в качестве пищевых добавок, такая доза составляет несколько миллиграмм на килограмм тела (например, E250 — нитрит натрия), для других (например, Е951 — аспартам или E330 — лимонная кислота) — десятые доли грамма на кг тела.
E250 (нитрит натрия) обычно применяют в колбасах, хотя нитрит натрия и является общеядовитым токсичным веществом, в том числе и для млекопитающих (50 процентов крыс погибают при дозе в 180 миллиграмм на килограмм веса), но на практике его не запрещают, так как это «наименьшее зло», обеспечивающее товарный вид продукта и, следовательно, объём продаж (достаточно сравнить красный цвет магазинной колбасы с тёмно-коричневым цветом домашней колбасы). Для копчёных колбас высоких сортов норма содержания нитрита установлена выше, чем для варёных — считается, что их едят в меньших количествах.
Большинство пищевых добавок можно считать вполне безопасными. Со временем, по мере развития аналитических методов и появления новых токсикологических данных, государственные нормативы на содержание примесей в пищевых добавках могут пересматриваться.
Часть добавок, ранее считавшихся безвредными (например, формальдегид E240 в шоколадных батончиках или E121 в газированной воде), позднее были признаны слишком опасными и запрещены; кроме того, добавки, безвредные для одного человека, могут оказать сильное вредное воздействие на другого. Поэтому врачи рекомендуют по возможности оградить от пищевых добавок детей, пожилых и аллергиков.
Некоторые производители в маркетинговых целях не указывают ингредиенты с буквенным кодом E. Они заменяют их на название добавки, например, «глутамат натрия». Ряд производителей использует полную запись — и химическое наименование, и код Е.
Также известность получил Вильжюифский список, в котором вред некоторых пищевых добавок был указан ошибочно.
Таблица опасных для здоровья пищевых добавок

Видео о пищевых добавках
Обсудить эту статью на форуме
//forum.dobro-est.com/pishchevie-dobavki-e- … -rasshifrovka-pishchevih-dobavok-t315.html
Теги: пищевые добавки, пищевые добавки е, вредные пищевые добавки, пищевые добавки таблица, пищевые добавки в продуктах, классификация пищевых добавок, коды пищевых добавок, значение пищевых добавок, группы пищевых добавок, ароматизаторы, красители, консерванты, стабилизаторы, эмульгаторы





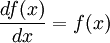 является функция
является функция 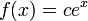 , где c — произвольная константа.
, где c — произвольная константа.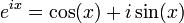 , см. формула Эйлера, в частности
, см. формула Эйлера, в частности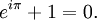
![e = [2; \;1, 2, 1, \;1, 4, 1, \;1, 6, 1, \;1, 8, 1, \;1, 10, 1, \ldots] \,](/800/600/https/dic.academic.ru/pictures/wiki/files/49/1571979fe5689176306c95848b75a781.png) , то есть
, то есть
![e = \lim_{n\to\infty} \frac{n}{\sqrt[n]{n!}}.](/800/600/https/dic.academic.ru/pictures/wiki/files/57/9c678d256067a90ef02d482bac3daa8f.png)
![e=2\cdot\sqrt{\frac{4}{3}}\cdot\sqrt[4]{\frac{6\cdot 8}{5\cdot 7}}\cdot\sqrt[8]{\frac{10\cdot 12\cdot 14\cdot 16}{9\cdot 11\cdot 13\cdot 15}}\cdots](/800/600/https/dic.academic.ru/pictures/wiki/files/48/0801eaa1ae197d9777b780ea6902e619.png)
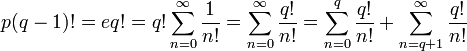
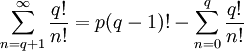
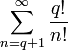 — целое
— целое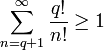
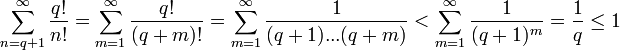
 , а не
, а не 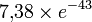 .
.
