26 вопросов и ответов. Теория электрических цепей. Курс лекций

Комплексная спектральная плотность непрерывного сигнала (в дальнейшем для краткости будем говорить: спектр сигнала) вычисляется по формуле прямого преобразования Фурье

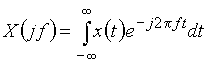. (3)

Сигнал может быть восстановлен по спектру с помощью обратного преобразования Фурье, или интеграла Фурье

. (4)

В соответствии с принципом неопределенности сигнал, имеющий ограниченную протяженность во времени, обладает неограниченным по полосе спектром (рис. 9, а). И наоборот, сигнал с ограниченным спектром имеет бесконечную протяженность во времени (рис. 10,

а). Как следует из этих рисунков, непрерывный сигнал, и ограниченной и бесконечной протяженности во времени, имеет сплошной спектр.

Если сигнал является периодическим, то спектр его – дискретный, т.е. теперь вместо 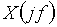используют отсчеты 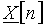. Эта ситуация показана на рис. 9, б. Период сигнала равен длительности сигнала . Интервал дискретизации спектра по частоте F определяется, как известно, периодом сигнала, в данном случае

. Формулы для прямого и обратного преобразований Фурье получаются из (3) и (4) путем замены непрерывной частоты f на дискретные значения nF. При этом следует учесть известную связь между амплитудами гармоник периодического сигнала и отсчетами спектральной плотности непрерывного сигнала: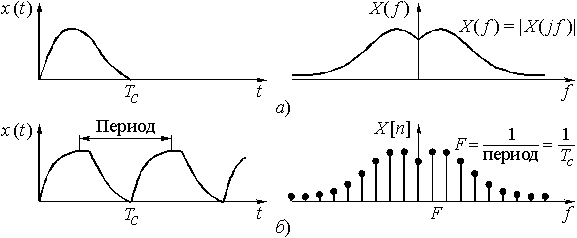

Рис. 9

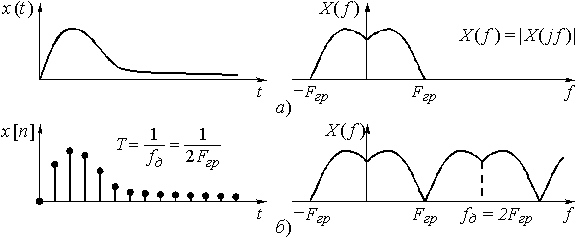
Рис. 10

.

Спектр периодического сигнала вычисляется по формуле

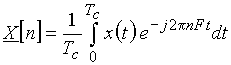. (5)

Сигнал можно восстановить по его дискретному спектру, воспользовавшись формулой

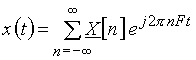. (6)

В соответствии с принципом дуальности можно сказать: если периодическим является спектр, то дискретным будет сигнал (рис. 10, б). Обозначая период повторения спектра 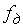, получим интервал дискретизации сигнала .

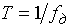Формулы прямого и обратного преобразований Фурье для дискретных сигналов имеют вид

; (7)

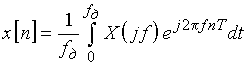. (8)

В формулах (7) и (8) использовано обозначение

.

Пример 4.1. Рассчитаем спектр дискретного сигнала, состоящего из одного отсчета .

Воспользуемся формулой (7), в которую подставим значения заданного сигнала

.

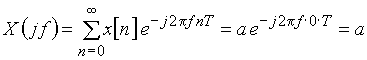Пример 4.2. Рассчитаем спектр экспоненциальной дискретной функции , n³ 0.

График дискретной функции

приведен на рис. 11, а ее отсчеты можно записать в виде последовательности {1; 0,5; 0,25; 0,125; 0,0625; …}.

Рис. 11

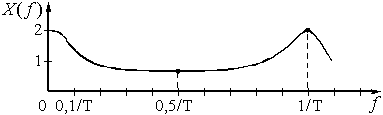
Рис. 12

Спектр дискретной экспоненты рассчитаем по формуле (7)

где для суммирования ряда использована формула

.

Получим выражение для расчета спектра амплитуд 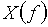, используя формулу Эйлера .

.

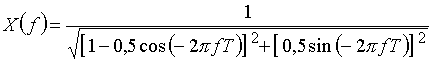Для построения графика будем задавать значения f от 0 до 1/Т с шагом 0,1/T и рассчитывать .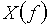

График спектра амплитуд экспоненциальной дискретной функции

приведен на рисунке 12.

Как видно из графика, спектр дискретного сигнала сплошной и периодический с периодом .

Самоконтроль

1. Как рассчитывается спектр непериодического (и периодического) непрерывного сигнала?

2. Как восстановить непрерывный сигнал по его спектру (сплош­ному и дискретному)?

3. Сформулируйте принцип неопределенности.

4. Как рассчитывается спектр дискретного сигнала?

5. Какой спектр у дискретного сигнала: сплошной или дискретный, периодический или непериодический?

6. Как рассчитывается дискретный сигнал, если известен его спектр?

7. Найдите спектр дискретного сигнала, состоящего из одного отсчета .

8. Найдите значения спектра дискретного сигнала, заданного двумя отсчетами 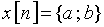, на частотах 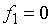и .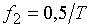

26 вопросов и ответов. Теория электрических цепей. Курс лекций

Получение, передача и обработка непрерывных сигналов (например, речевые сигналы в телефонии и радиовещании, телевизионные сигналы) может осуществляться в аналоговой форме.

На рис. 6 показана RC-цепь, у которой импульсная характеристика, как известно, равна

.

Если задано напряжение на входе цепи и нужно найти напряжение на ее выходе 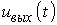, мы можем сделать это, воспользовавшись интегралом свертки:

. (1)

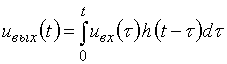
Это известный материал и мы лишь напомним его.

Рис. 6

При передаче аналоговых сигналов необходимо учитывать влияние помех и нестабильность параметров цепи, т.е. их зависимость от времени, температуры, влажности и т.д. Особенно сильно это влияние сказывается на очень низких частотах (меньше 1 Гц) и на частотах выше 20 кГц. В диапазоне сигналов звуковых частот характеристики аналоговых и дискретных цепей и сигналов сопоставимы, и выбор типа сигнала определяется прогрессом в технологии изготовления и применения современных средств микроэлектроники, а они, в свою очередь, ориентированы на цифровые устройства.

Заменим непрерывные сигналы в схеме рис. 6 и формуле (1) их дискретными отсчетами. Чтобы не вносить путаницы, время t заменим дискретными значениями nT, а время t – дискретными значениями mT. Тогда интеграл придется заменить суммой и выражение (1) запишется в виде:

. (2)

Вместо непрерывного сигнала мы будем иметь дело с дискретным сигналом 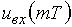и вместо непрерывной импульсной характеристики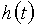

– с дискретной импульсной характеристикой

.

Поскольку любой отсчет сигнала – это число, то формулу (2) можно запрограммировать на ЭВМ. Останется лишь ввести в ЭВМ числа, соответствующие всем дискретным отсчетам и , и она вычислит отсчеты выходного напряжения 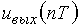. Выражение (2) на языке вычислительной техники называется алгоритмом вычисления выходного сигнала.

Пример 1.3. Рассчитаем отсчеты выходного напряжения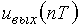 в цепи, приведенной на рис. 6.

Для расчета воспользуемся формулой (2), подставляя в нее соответствующие дискретные отсчеты входного сигнала и дискретные отсчеты импульсной характеристики , графики которых приведены на рис. 6.

;

;

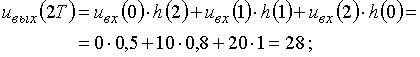
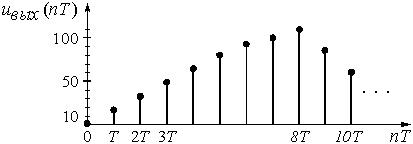
Рис. 7

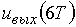Аналогичным образом рассчитываются = 68; = 80,5; = 91; 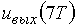= 100,3; = 108,6; = 83,4; 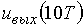= 59 и т.д.

График последовательности 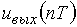приведен на рис. 7.

Таким образом, дискретные сигналы удобны тем, что их можно обрабатывать с помощью ЭВМ. Однако, не следует думать, что дискретные сигналы вносятся в ЭВМ лишь с клавиатуры. Их можно вводить в ЭВМ и выводить из нее непосредственно.

На рис. 8 показано, как это делать. Непрерывный сигнал 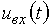подается на ключ, на выходе которого образуются дискретные отсчеты . Но их еще нельзя ввести в машину. Сначала нужно перевести амплитуды отсчетов в двоичный код – ведь только такой код понимает ЭВМ. Выполняет эту операцию кодер. Скажем, если отсчет имеет величину 30 В, то запись числа 30 в двоичном 8-разрядном коде будет такой: 00011110. Закодированные в двоичном коде отсчеты на рисунке обозначены .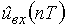

Вычислительные средства (ВС) могут представлять собой универсальную большую ЭВМ, специализированную микро-ЭВМ, микропроцессорное устройство или что-нибудь в этом роде. Главное состоит в том, что в памяти ЭВМ записана программа вычисления, например, выражение (2), и отсчеты импульсной реакции, скажем, RC-цепи. Следовательно, в результате работы программы, ЭВМ будет выдавать закодированные в двоичном коде отсчеты . Декодер преобразует код в амплитуду, и на его выходе появляются дискретные отсчеты выходного напряжения 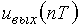. Интерполятор (Инт) восстанавливает функцию между отсчетами. В итоге на выходе системы мы имеем аналоговый сигнал .

Рис. 8

Устройство, состоящее из ключа и кодера и преобразующее непрерывный (аналоговый) сигнал в двоичный код (или, что то же,в цифровой сигнал), называют аналого-цифровым преобразователем (АЦП). Обратное преобразование выполняет цифро-аналоговый преобразователь (ЦАП), содержащий декодер и интерполятор.

Как видим, ЭВМ может сыграть роль реальной цепи. И хотя самой физической цепи может и не быть в наличии, а задана она будет лишь в виде отсчетов импульсной реакции и программы вычислений, мы будем наблюдать на выходе описанной системы такое же выходное напряжение , как и на выходе реальной цепи.

Самоконтроль

1. Почему удобно передавать и обрабатывать дискретные сигналы?

2. Рассчитайте первые два отсчета напряжения на выходе дискретной цепи, имеющей импульсную характеристику

если напряжение на ее входе

3. Поясните по графикам, как работает цепь, изображенная на рис. 8.

3.2. Спектр дискретного сигнала. 3. Дискретные и цифровые сигналы. Радиотехнические цепи и сигналы. Учебное пособие

Перейдем теперь к рассмотрению спектра дискретного сигнала. Очевидно, в соответствии с изложенным выше свойством симметрии преобразования Фурье следует ожидать периодического характера спектральной функции дискретного сигнала.

Итак, дискретный сигнал , как уже подчеркивалось выше, формируется на выходе перемножителя, на один вход которого, подается непрерывный сигнал , а на второй – периодическая последовательность коротких импульсов длительностью

,

с периодом .

Здесь 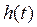– функция, определяющая форму импульсов периодической последовательности. Обычно в качестве периодической последовательности импульсов дискретизации выбирают импульсы прямоугольной формы вида (1.13). Периодическую последовательность импульсов дискретизации можно описать выражением

.

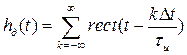Тогда дискретный сигнал запишется в виде

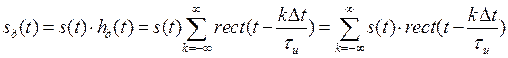. (3.11)

С другой стороны, последовательность прямоугольных импульсов может быть представлена комплексным рядом Фурье

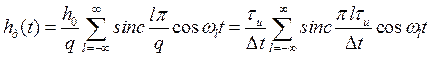. (3.12)

Здесь учтено, что период последовательности равен 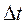, амплитуда единичного импульса 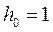, а также .

Теперь можно представить с учетом (3.12) в виде ряда

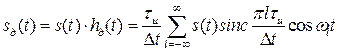. (3.13)

Применим к (3.13) прямое преобразование Фурье

.

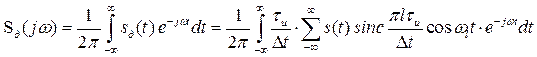Изменив порядок суммирования и интегрирования, запишем

. (3.14)

Так как

,

то

.

В свою очередь

,

.

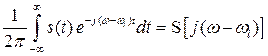Тогда окончательно выражение (3.14) принимает вид

. (3.15)

Спектральный анализ дискретного сигнала существенно упрощается, если предположить, что дискретизация осуществляется последовательностью прямоугольных импульсов единичной площади. В этом случае амплитуда импульса 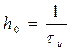и выражение (3.15) запишется следующим образом

.

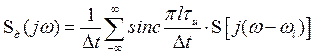Если устремить 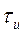к нулю при сохранении единичной площади импульса и перейти к последовательности бесконечно коротких импульсов ( 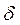-импульсов), т.е.

, (3.16)

то

,

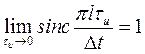а спектральная функция дискретного сигнала примет вид

. (3.17)

На рис. 3.5, а представлен непрерывный сигнал , а на рис. 3.5, б – условное изображения модуля его спектральной функции .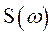

Как известно, спектр непрерывного одиночного сигнала является сплошным.

Спектр же дискретного сигнала, как это следует из (3.16), представляет собой периодическую по частоте последовательность копий спектров исходного сигнала, сдвинутых относительно друг друга на величину (или ), что составляет период последовательности. Очевидно, периодическим по частоте с тем же периодом является и модуль спектра и его аргумент, т.е. фазовый спектр.

Отметим, что (или ) – это частота дискретизации. Таким образом, период спектральной функции дискретного сигнала равен частоте дискретизации. На рис. 3.5. в, г изображены графики дискретного сигнала и модуля его спектра.

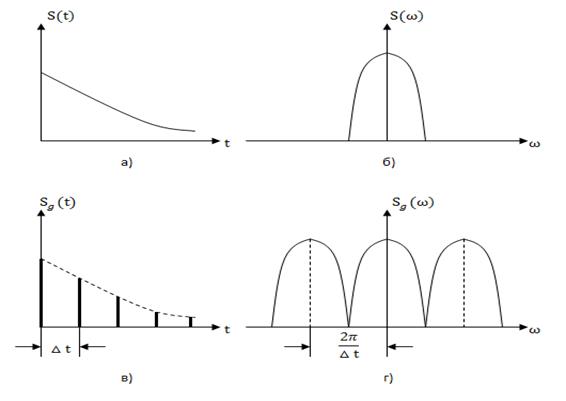
Рис. 3.5

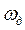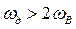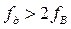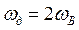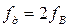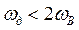Расположение отдельных составляющих периодической функции спектра дискретного сигнала на оси частот зависит от значения частоты дискретизации . На рис. 3.5,г и на рис. 3.6, а, б изображены соответственно функции дискретного сигнала при частотах дискретизации (или ), (или ) и (или 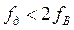). Из этих рисунков следует, что при частоте дискретизации, меньшей чем частота, определяемая пределом Найквиста, копии спектра исходного непрерывного сигнала перекрываются, т.е. имеет место явление наложения спектров. Это приводит к искажению исходного сигнала при его восстановлении. Таким образом, и спектральный анализ дискретного сигнала согласуется с выводами теоремы Котельникова.

Непрерывные и дискретные САУ

Разделяют системы автоматического регулирования САР зависимо от характера сигналов, а также их от их прохождения. Условно их делят на две категории: непрерывные и дискретные, или как их еще называют прерывистые.

Непрерывные

Если в ходе работы данной системы структуры связи не меняются, то такая система имеет название непрерывной. Соответственно сигналы на выходе ее тоже будут непрерывными и представлять собой функцию входящего воздействия и времени. Между выходными и входными элементами такой системы будет существовать связь, которая не будет прерываться во времени. Примером непрерывного устройства может служить:

Здесь ток, протекающий по цепи 4, будет являться непрерывной функцией напряжения на тахогенераторе 5, которое поступает на операционный усилитель 3.

Прерывистые или дискретные системы

Главным отличием их от непрерывных будет то, что в дискретном устройстве сигнал изменяется во времени (работает как реле – контакты замыкаются и размыкаются с определенной периодичность ). Их в свою очередь можно поделить на релейные и импульсные.

Импульсные

В таких системах прерывание сигнала происходит принудительно – специальным прерывающим устройством. Процессы в этих САР протекают также как и в непрерывных САР, но только при появлении импульса. Импульсные системы содержат импульсные элементы и, соответственно, выполняют квантование сигналов по времени.

Релейные

В данном типе устройств размыкание и замыкание производится специальным элементом системы при непрерывном действии сигнала на входе. Замыкание и размыкание производит реле, или же элемент имеющий релейную характеристику. Срабатывание реле происходит при проявлении воздействия на его управляющий орган. Такие системы квантуют сигнал по уровню.

Как правило, для преобразования аналогового сигнала в цифровой применяют устройство, именуемое аналого-цифровыми преобразователями АЦП.

Примером релейного типа САР может послужить:

В такой САР при опускании поплавка ниже определенного уровня – контакт замкнется и двигатель откроет заслонку, выше какого-то уровня –  контакт реле перекинется и двигатель закроет заслонку. Если уровень воды в бассейне находится в норме, то поплавок будет в нейтральном положении, контакт тоже в нейтральном и заслонка окажется в зафиксированном положении. Тип сигнала – релейный контакт.

Также релейные системы тоже делятся на кодово-импульсные и релейно-импульсные, которые могут квантовать сигнал и по времени, и по уровню.

Кодово-импульсные – содержат в управляющем контуре вычислительные цифровые машины (ЦВМ). Их еще называют цифровыми.

В зависимости от конструкции САР их делят на – гидравлические, электрогидравлические,  электронные, электрические, а также электромеханические.

Ниже показаны два сигнала – аналоговый и дискретный:

Красным показан аналоговый сигнал, а синим дискретный.

2. Непрерывные и дискретные сигналы. Дискретизация.

Основной задачей отрасли телекоммуникации является передача сигналов на расстоянии. Первыми передавались простые сигналы, такие как телеграф, посредством азбуки Морзе. Впоследствии, с развитием техники, сначала осуществлялась передача аналоговых (непрерывных) сигналов – звука и видео, а затем цифровых сигналов (к цифровым аудио и видео сигналам добавились данные).

Что же такое непрерывный сигнал? Очевидно, что непрерывный сигнал – это сигнал, изменяющийся во времени непрерывно. Например, звук. Упрощенно, звук – колебания воздуха. Посредством струн – голосовых связок и резонаторов – рта, зубов, языка мы способны создавать определенные колебания воздуха, которые улавливаются ухом и далее распознаются как речь. Эти колебания изменяются непрерывно, несмотря на то, что их интенсивность может изменяться довольно резко (например, когда человек кричит, а затем переходит на шепот). Аналогично создаются колебания различных музыкальных инструментов.

Хорошенько крикнув, мы способны передать звуковые колебания на несколько сот метров (эхо в горах). Однако чтобы передать музыку или речь на 20 километров, хорошенько крикнуть или «бзденькнуть» гитарной струной недостаточно. Здесь нам на помощь приходит микрофон, который преобразует непрерывное колебание воздуха (издаваемое, например, человеком или инструментом), в такой же непрерывный электрический ток, изменяющийся в соответствии с изменениями колебаний воздуха.

В случае аналоговой техники, этот непрерывный сигнал использовался для записи на магнитные ленты, пластинки и т.п. и для передачи на большие расстояния по проводам или радио эфиру. В случае же цифровой техники, этот сигнал, прежде чем использовать оцифровывают с помощью Аналого-цифрового преобразователя.

Рассмотрим процесс этого преобразования подробнее.

Итак, мы имеем некоторый непрерывно меняющийся во времени сигнал x(t):

В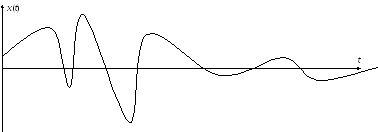цифровой технике только два конечных состояния – 0 и 1. И все данные представляются в виде последовательностей нулей и единиц. Поэтому возникает вопрос о преобразовании аналогового сигнала в такую последовательность. Так как же это осуществить?

Первый шаг – дискретизация. Дискретизация – переход от непрерывного сигнала x(t) к последовательности значений этого сигнала {x[n]}, взятых через определенный интервал времениT_д, называемый периодом дискретизации. Этот процесс отображает следующий рисунок:

Отличие непрерывного сигнала от дискретного состоит в том, непрерывный сигнал существует на всем отрезке времени t, а дискретный сигнал – только в моменты времениi*T_д. Таким образом, дискретный сигнал – по сути ряд (последовательность) значений. Связь элементов этого ряда с исходным сигналом простая:

x[i] =x(i*T_д), i=1,2…N.

Значения x[i] – называют отсчетами.

В цифровой обработке сигналов оперируют выборками сигналов. То есть накапливают определенное количество дискретных отсчетов в буфер. Как только накопится определенное количество, выборка отсчетов передается далее для обработки, и начинает накапливаться новая выборка. Количество отсчетов Nвыборки зависит от задач, типа сигнала и т.д.

Что касается периода дискретизации. Его необходимо выбирать таким, чтобы исходный сигнал можно было восстановить без потерь. Правило выбора минимального шага (периода) при равномерной дискретизации с использованием модели сигнала с ограниченным спектром сформулировано в теореме Котельникова: «Любая непрерывная функция x(t), спектр которой ограничен частотой F_max полностью определяется последовательностью своих значений в моменты времени, отстоящие друг от друга на интервал T_д = 1 \ 2F_max = π \ ω_max».