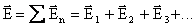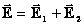Напряжённость электрического поля — это… Что такое Напряжённость электрического поля?
Напряжённость электри́ческого по́ля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы действующей на неподвижный[1]пробный заряд, помещенный в данную точку поля, к величине этого заряда :
- .
Из этого определения видно, почему напряженность электрического поля иногда называется силовой характеристикой электрического поля (действительно, всё отличие от вектора силы, действующей на заряженную частицу, только в постоянном[2] множителе).
В каждой точке пространства в данный момент времени существует свое значение вектора (вообще говоря — разное[3] в разных точках пространства), таким образом, — это векторное поле. Формально это выражается в записи
представляющей напряженность электрического поля как функцию пространственных координат (и времени, т.к. может меняться со временем). Это поле вместе с полем вектора магнитной индукции представляет собой электромагнитное поле
Напряжённость электрического поля в СИ измеряется в вольтах на метр [В/м] или в ньютонах на кулон.
Напряжённость электрического поля в классической электродинамике
Из сказанного выше ясно, что напряженность электрического поля — одна из основных фундаментальных величин классической электродинамики. В этой области физики можно назвать сопоставимыми с ней по значению только вектор магнитной индукции (вместе с вектором напряженности электрического поля образующий тензор электромагнитного поля) и электрический заряд. С некоторой точки зрения столь же важными представляются потенциалы электромагнитного поля (образующие вместе единый электромагнитный потенциал).
Приведем краткий обзор основных контекстов классической электродинамики в отношении напряженности электрического поля.
Сила, с которой действует электромагнитное поле на заряженные частицы
Полная сила, с которой электромагнитное поле (включающее вообще говоря электрическую и магнитную составляющие) действует на заряженную частицу, выражается формулой силы Лоренца:
где q — электрический заряд частицы, — ее скорость, — вектор магнитной индукции (основная характеристика магнитного поля), косым крестом обозначено векторное произведение. Формула приведена в единицах СИ.
Как видим, эта формула полностью согласуется с определением напряженности электрического поля, данном в начале статьи, но является более общей, т.к. включает в себя также действие на заряженную частицу (если та движется) со стороны магнитного поля.
В этой формуле частица предполагается точечной. Однако эта формула позволяет рассчитать и силы, действующие со стороны электромагнитного поля на тела любой формы с любым распределением зарядов и токов — надо только воспользоваться обычным для физики приемом разбиения сложного тела на маленькие (математически — бесконечно маленькие) части, каждая из которых может считаться точечной и таким образом входящей в область применимости формулы.
Остальные формулы, применяемые для расчета электромагнитных сил (такие, как, например, формула силы Ампера) можно считать следствиями
Однако для того, чтобы эта формула была применена (даже в самых простых случаях, таких, как расчет силы взаимодействия двух точечных зарядов), необходимо знать (уметь рассчитывать) и чему посвящены следующие параграфы.
Уравнения Максвелла
Достаточным вместе с формулой силы Лоренца теоретическим фундаментом классической электродинамики являются уравнения электромагнитного поля, называемые уравнениями Максвелла. Их стандартная традиционная форма представляет собой четыре уравнения, в три из которых входит вектор напряженности электрического поля:
Здесь — плотность заряда, — плотность тока, — универсальные константы (уравнения здесь записаны в единицах СИ).
Здесь приведена наиболее фундаментальная и простая форма уравнений Максвелла — так называемые «уравнения для вакуума» (хотя, вопреки названию, они вполне применимы и для описания поведения электромагнитного поля в среде). Подробно о других формах записи уравнений Максвелла — см. основную статью.
Этих четырех уравнений вместе с пятым — уравнением силы Лоренца — в принципе достаточно, чтобы полностью описать классическую (то есть не квантовую) электродинамику, то есть они представляют ее полные законы. Для решения конкретных реальных задач с их помощью необходимы еще уравнения движения «материальных частиц» (в классической механике это законы Ньютона), а также зачастую дополнительная информация о конкретных свойствах физических тел и сред, участвующих в рассмотрении (их упругости, электропроводности, поляризуемости итд итп), а также о других силах, участвующих в задаче (например, о гравитации), однако вся эта информация уже не входит в рамки электродинамики как таковой, хотя и оказывается зачастую необходимой для построения замкнутой системы уравнений, позволяющих решить ту или иную конкретную задачу в целом.
«Материальные уравнения»
Такими дополнительными формулами или уравнениями (обычно не точными, а приближенными, зачастую всего лишь эмпирическими), которые не входят непосредственно в область электродинамики, но поневоле используются в ней ради решения конкретных практических задач, называемыми «материальными уравнениями», являются, в частности:
- Закон Ома,
- Закон поляризации
- в разных случаях многие другие формулы и соотношения.
Связь с потенциалами
Связь напряженности электрического поля с потенциалами в общем случае такова:
где — скалярный и векторный потенциалы. Приведем здесь для полноты картины и соответствующее выражение для вектора магнитной индукции:
В частном случае стационарных (не меняющихся со временем) полей, первое уравнение упрощается до:
Это выражение для связи электростатического поля с электростатическим потенциалом.
Электростатика
Важным с практической и с теоретической точек зрения частным случаем в электродинамике является тот случай, когда заряженные тела неподвижны (например, если исследуется состояние равновесия) или скорость их движения достаточно мала чтобы можно было приближенно воспользоваться теми способами расчета, которые справедливы для неподвижных тел. Этим частным случаем занимается раздел электродинамики, называемый электростатикой.
Как мы уже заметили выше, напряженность электрического поля в этом случае выражается через скалярный потенциал как
или
то есть электростатическое поле оказывается потенциальным полем. ( в этом случае — случае электростатики — принято называть электростатическим потенциалом).
- Также и обратно
Уравнения поля (уравнения Максвелла) при этом также сильно упрощаются (уравнения с магнитным полем можно исключить, а в уравнение с дивергенцией можно подставить ) и сводятся к уравнению Пуассона:
а в областях, свободных от заряженных частиц — к уравнению Лапласа:
Учитывая линейность этих уравнений, а следовательно применимость к ним принципа суперпозиции, достаточно найти поле одного точечного единичного заряда, чтобы потом найти потенциал или напряженность поля, создаваемого любым распределением зарядов (суммируя решения для точечного заряда).
Теорема Гаусса
Очень полезной в электростатике оказывается теорема Гаусса, содержание которой сводится к интегральной форме единственного нетривиального для электростатики уравнения Максвелла:
где интегрирование производится по любой замкнутой поверхности S (вычисляя поток через эту поверхность), Q — полный (суммарный) заряд внутри этой поверхности.
Эта теорема дает крайне простой и удобный способ расчета напряженности электрического поля в случае, когда источники имеют достаточно высокую симметрию, а именно сферическую, цилиндрическую или зеркальную+трансляционную. В частности, таким способом легко находится поле точечного заряда, сферы, цилиндра, плоскости.
Напряжённость электрического поля точечного заряда
В единицах СИ
Для точечного заряда в электростатике верен закона Кулона
или
- .
- .
Исторически закон Кулона был открыт первым, хотя с теоретической точки зрения уравнения Максвелла более фундаментальны. С этой точки зрения он является их следствием. Получить этот результат проще всего исходя из теоремы Гаусса, учитывая сферическую симметрию задачи: выбрать поверхность S в виде сферы с центром в точечном заряде, учесть, что направление будет очевидно радиальным, а модуль этого вектора одинаков везде на выбранной сфере (так что E можно вынести за знак интеграла), и тогда, учитывая формулу для площади сферы радиуса
откуда сразу получаем ответ для E.
Ответ для получается тогда интегрированием E:
Для системы СГС
Формулы и их вывод аналогичны, отличие от СИ лишь в константах.
Напряженность электрического поля произвольного распределения зарядов
По принципу суперпозиции для напряженности поля совокупности дискретных источников имеем:
где каждое
Подставив, получаем:
Для непрерывного распределения аналогично:
где V — область пространства, где расположены заряды (ненулевая плотность заряда), или всё пространство, — радиус-вектор точки, для которой считаем , — радиус-вектор источника, пробегающий все точки области
Системы единиц
В системе СГС напряжённость электрического поля измеряется в СГСЭ единицах, в системе СИ — в ньютонах на кулон или в вольтах на метр (русское В/м, международное V/m).
Литература
Примечания
- ↑ На движущийся заряд действует также магнитное поле, если, конечно, оно имеется (не равно нулю), поэтому в определение напряженности электрического поля вносится условие неподвижности пробного заряда; при условии гарантированного отсутствия магнитного поля неподвижность пробного заряда перестает быть обязательной, однако требование отсутствия магнитного поля в общем случае невозможно (а возможно только в частных классах задач).
- ↑ Для любой частицы ее электрический заряд постоянен. Измениться он может только если от частицы что-то заряженное отделится или если к ней что-то заряженное присоединится.
- ↑ Хотя иногда его значения могут оказываться и одинаковыми в разных точках пространства; если одинаков всюду в пространстве (или какой-то области пространства), говорят об однородном электрическом поле — это всего лишь частный случай электрического поля, хотя и наиболее простой; притом что в реальности электрическое поле может быть однородным лишь приближенно, то есть различия в разных точках пространства есть, но иногда они небольшие и ими можно пренебречь в рамках некоторого приближения.
- ↑ Электромагнитное поле может быть выражено и по-другому, например через электромагнитный потенциал или в несколько иной математической записи (прячущей вектор напряженности электрического поля вместе с вектором магнитной индукции внутрь тензора электромагнитного поля), однако все эти способы записи тесно связаны между собой, таким образом, утверждение о том, что поле — одна из основных составляющих электромагнитного поля не утрачивает смысла.
- ↑ Хотя исторически многие из них были открыты раньше.
См. также
Напряженность электрического поля: формула, единица измерения
Полем с электричеством называют особый вид материи. Он существует вокруг заряда либо вокруг заряженных частиц. Напряжённость – главная силовая характеристика для этого явления. Единица измерения – В/м. Но есть и другие особенности, присущие такому параметру. Формула напряжённости – отдельный вопрос.
Определение
Напряженность относят к величинам физического характера. Как уже говорилось, это силовой параметр. Равен обычно соотношению между силой, действующей на заряженное тело, и значением.

Измерение напряжённости
Важно. Показатель напряжённости относят и к векторным величинам. Определяют, с каким значением действует сила на заряженные предметы. При необходимости упрощает определение направления. Главная единица измерения – ньютон на кулон.
Определение напряжённости упрощает организацию измерения показателя. Если заранее знать значение энергии того или иного тела – проще измерить характеристику, воздействующую на него. Как найти напряжённость – объяснено дальше.
Формула силы электрического поля
В большинстве случаев учёные применяют стандартную формулу:
E = F/q.
Своё значение вектора, который обозначается как E, существует в каждой отдельной временной точке. В форме записи этот показатель тоже имеет свою фиксацию:
E = E (x, y, z, t).
Интересно. Таким образом, это функция пространственных координат. Допустимо изменение характеристики по мере течения времени. За счёт этого происходит образование электромагнитного поля, учитывающего и вектор магнитной индукции. Его регулируют законы термодинамики, то же касается напряжённости электрического поля, формула через заряды тоже давно известна.

Замеры напряжённости
Воздействие поля на заряды
При воздействии полей предполагается, что в полную силу входят магнитные и электрические составляющие. Она выражается в так называемой формуле по силе Лоренца:
F = qE + qv x B
Своим значением наделён каждый элемент в этом определении напряжённости электрического поля, формула без них не будет точной:
- Q – обозначение заряда.
- V – скорость.
- B – вектор относительно магнитной индукции. Это основная характеристика, присущая магнитному пространству. Без неё измерять нельзя.
Косой крест применяют для обозначения векторного произведения. Единицы измерения для формулы – СИ. Заряды тоже становятся частью общей системы.

Специальный прибор
Новые значения – более общие по сравнению с формулой, чьё описание приведено ранее. Причина – в том, что частица под воздействием сил.
Обратите внимание. Предполагается, что частица в этом случае – точечная. Но благодаря этой формуле просто определить воздействие на тела вне зависимости от текущей формы. При этом распределение зарядов и токов внутри не имеет значения. Главное – уметь рассчитывать E и B, чтобы применять формулу правильно. Тогда проще проводить и определение напряжённости поля, формулы с другими цифрами.
Измерение
Напряжённость относят к векторным величинам, оказывающим силовое воздействие на заряженные частицы.
Существуют не только теоретические, но и практические способы для измерения напряжённости.
- Если речь о произвольных – сначала берут тело, содержащее заряд. Это правило распространяется на любые электронные устройства.
Размеры тела должны быть меньше размеров другого тела, генерирующего заряд. Достаточно небольшого металлического шарика, у которого есть свой заряд. Заряд шарика измеряют электрометром, потом приспособление помещают внутрь. Динамометр уравновешивает силу, воздействующую на предмет. После этого можно снять показания с единицей измерения – Ньютонами.

В бытовых условиях
Значение напряжённости получают, разделив значение силы на величину заряда.
- Измерить расстояние – первый шаг, когда определяют напряжённость в конкретной точке, удалённой от тела на какую-либо величину.
Полученную величину разделяют на расстояние, возведённое в квадрат. К полученному результату применяют специальный коэффициент. Его выражение такое: 9*10^9.
- Отдельного изучения заслуживает ситуация с конденсаторами.
В данном случае первый этап – измерение напряжения между пластинами. Предполагается использование вольтметра. Потом определяются с расстоянием между этими пластинами. Единица измерения – метры. Получают результат, который и будет напряжённостью. Направлять её можно по-разному.
Единицы измерения
Ньютоны на кулон, либо вольты на метр – единицы измерения, которые применяют для данного параметра в общепринятых системах.

Соленоиды
Постоянный электрический ток
Электрический ток – направленное движение свободных носителей энергии в веществе или внутри вакуума. Этот показатель появляется при соблюдении главных условий:
- Есть источник энергии.
- Замкнутость пути, который используется для перемещения.
I – буква, которую применяют для обозначения силы тока.

Пример задачи с напряжённостью
Важно. Единица измерения – Амперы. Величина тока зависит от количества электричества или разрядов, которые проходят через поперечное сечение у проводника в единицу времени.
Когда речь о постоянном токе – предполагается, что с течением времени не меняются его направление, основная величина.

Вектор
Амперметр – устройство, применяемое для измерения силы тока. Его подключение к цепи – последовательное. Показатель важен, поскольку от него зависят и сила воздействия и другие подобные параметры. На практике часто встречаются ситуации, когда сила тока заменяется плотностью. В данном случае единица измерения – Ампер на метр квадратный. Площадь сечения проводов выражается в мм2. И плотность тока предполагает опору на эту характеристику.
Электрическое поле можно назвать реально существующим явлением, как и любые предметы. Поле и вещества относят к основным формам существования материи. Способность действовать с силой на заряды – главное свойство. Его используют, чтобы обнаруживать, измерять явления. Ещё одна характеристика – распространение со скоростью света. Это тоже важно для тех, кто занимается изучением подобных факторов.
Электрическое поле. Напряженность электрического поля. | |
Закон Кулона не объясняет механизм передачи электромагнитного взаимодействия: близкодействие (непосредственный контакт) или дальнодействие? Если заряды действуют друг на друга на расстоянии, то скорость передачи взаимодействия должна быть бесконечно большой, взаимодействие должно распространяться мгновенно. На опыте скорость конечна (скорость света с=3.108м/с). |
|
Для объяснения вводится понятие электрического поля (впервые — М. Фарадей) — особый вид материи, существующий вокруг любого электрического заряда и проявляющий себя в действии на другие заряды. |
|
Напряженность — силовая характеристика электрического поля. |
|
Пусть заряд q0 создает поле, в произвольную точку которого мы помещаем положительный заряд q. Во сколько бы раз мы не изменяли заряд q в этой точке, сила взаимодействия изменится во столько же раз (з-н Кулона). |
|
Следовательно: |
|
Напряженность — векторная физическая величина, численно равная отношению силы, действующей на заряд, помещенный в данную точку данного поля, к величине этого заряда. |
|
Напряженность не зависит от величины заряда, помещенного в поле.
|
|
|
|
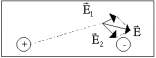
Принцип суперпозиции полей: напряженность поля, созданного системой зарядов равна геометрической сумме напряженностей полей, созданных каждым зарядом. Т.е. напряженности складываются геометрически: (Это опытный факт.) | Пример:
|
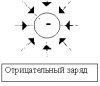
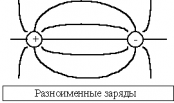
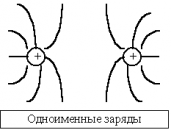
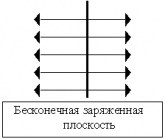
Графическое представление электростатического поля. | |
Силовые линии (линии напряженности) — непрерывные (воображаемые) линии вектор напряженности касателен к каждой точке которых. Способ описания с помощью силовых линий введен Фарадеем. |
|
Свойства: | |
| |
НАПРЯЖЁННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ • Большая российская энциклопедия
-

-

-

В книжной версии
Том 22. Москва, 2013, стр. 36-37
-

Скопировать библиографическую ссылку:
Авторы: Ю. В. Юрьев
НАПРЯЖЁННОСТЬ ЭЛЕКТРИ́ЧЕСКОГО ПО́ЛЯ, векторная физич. величина $E$, силовая характеристика электрич. поля, численно равная отношению силы $F$, действующей со стороны поля на пробный электрич. заряд, помещённый в данную точку поля, к величине этого заряда $q$: $E=F/q$. Пробный заряд $q$ должен быть достаточно мал, чтобы его электрич. поле не изменяло расположения зарядов, создающих исследуемое поле. Направление $E$ совпадает с направлением силы, действующей на положительный пробный заряд. Электрич. поле задаётся распределением векторов $E$ в каждой точке пространства, поэтому вместо термина «Н. э. п.» часто употребляют термин «электрическое поле». Распределение Н. э. п. в пространстве обычно характеризуют с помощью силовых линий электрич. поля – линий, касательные к которым в каждой точке совпадают с направлением вектора $E$. Силовые линии электрич. поля проводят так, чтобы число силовых линий, проходящих через единичную поверхность, перпендикулярную к силовым линиям, было пропорционально модулю $E$ вблизи данной точки. Н. э. п. удовлетворяет принципу суперпозиции, согласно которому Н. э. п. совокупности зарядов в некоторой точке равна геометрич. сумме напряжённостей полей, создаваемых отд. зарядами.
Напряжённость $E$ можно разложить на потенциальную $E_п$ и вихревую (соленоидальную) $E_в$ компоненты (см. Максвелла уравнения). Для потенциальной компоненты: $\text{rot}\:E_п=0,\; E_n=-\text{grad}\:\varphi$, где $\varphi$ – электрич. потенциал. Для вихревой компоненты: $\text{div}\:E_в=0$, $E_в=–𝜕A/𝜕t$, где $A$ – векторный потенциал. $E_п$ создаётся электрич. зарядами, и соответствующие ей силовые линии начинаются на положительных и заканчиваются на отрицательных электрич. зарядах. Так, напр., электростатич. поле (электрич. поле неподвижных электрич. зарядов) имеет только потенциальную компоненту. Компонента $E_в$ возникает при изменении во времени вектора магнитной индукции $B$, и соответствующие ей силовые линии являются замкнутыми. Напр., электрич. поле свободно распространяющейся электромагнитной волны имеет только вихревую компоненту. Под Н. э. п. в среде понимают Н. э. п., усреднённую по физически малому объёму (содержащему большое число атомов среды, но однородному по физич. свойствам).
Единица измерения Н. э. п. в СИ – вольт на метр (В/м).
Теорема Гаусса — Википедия
Теорема Гаусса (закон Гаусса) — один из основных законов электродинамики, входит в систему уравнений Максвелла. Выражает связь (а именно равенство с точностью до постоянного коэффициента) между потоком напряжённости электрического поля сквозь замкнутую поверхность произвольной формы и алгебраической суммой зарядов, расположенных внутри объёма, ограниченного этой поверхностью. Применяется отдельно для вычисления электростатических полей.
Аналогичная теорема, также входящая в число уравнений Максвелла, существует и для магнитного поля (см. ниже).
Также теорема Гаусса верна для любых полей, для которых верен закон Кулона или его аналог (например, для ньютоновской гравитации). При этом она является, как принято считать, более фундаментальной, так как позволяет в частности вывести степень расстояния[1] в законе Кулона «из первых принципов», а не постулировать её (или не находить эмпирически).
В этом можно видеть фундаментальное значение теоремы Гаусса (закона Гаусса) в теоретической физике.
Существуют аналоги (обобщения) теоремы Гаусса и для более сложных полевых теорий, чем электродинамика.
Теорема Гаусса для напряжённости электрического поля в вакууме[править | править код]
Общая формулировка: Поток вектора напряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду.
| СГС | СИ |
|---|---|
|
|
где
Данное выражение представляет собой теорему Гаусса в интегральной форме.
- Замечание: поток вектора напряжённости через поверхность не зависит от распределения заряда (расположения зарядов) внутри поверхности.
В дифференциальной форме теорема Гаусса выражается следующим образом:
| СГС | СИ |
|---|---|
|
|
Здесь ρ{\displaystyle \rho } — объёмная плотность заряда (в случае присутствия среды — суммарная плотность свободных и связанных зарядов), а ∇{\displaystyle \nabla } — оператор набла.
- Теорема Гаусса может быть доказана как теорема в электростатике исходя из закона Кулона (см. ниже). Формула, однако, также верна в электродинамике, хотя в ней она чаще всего не выступает в качестве доказываемой теоремы, а выступает в качестве постулируемого уравнения (в этом смысле и контексте её логичнее называть законом Гаусса[2]).
Теорема Гаусса для электрической индукции (электрического смещения)[править | править код]
Для поля в диэлектрической среде электростатическая теорема Гаусса может быть записана ещё и иначе (альтернативным образом) — через поток вектора электрического смещения (электрической индукции). При этом формулировка теоремы выглядит следующим образом: поток вектора электрического смещения через замкнутую поверхность пропорционален заключённому внутри этой поверхности свободному электрическому заряду:
| СГС | СИ |
|---|---|
|
|
Важный комментарий
Важно заметить, что Q в правой части этого уравнения обозначено не то же самое, что в фундаментальной формулировке ΦE≡∮SEdS=4πQ,{\displaystyle \Phi _{\mathbf {E} }\equiv \oint \limits _{S}\mathbf {E} \,\mathrm {d} \mathbf {S} =4\pi Q,} приведенной выше[3], в начале статьи. Последняя часто называется «формулировкой для вакуума», однако это название чисто условное, она равно применимо и к случаю диэлектрической среды, только под Q здесь необходимо понимать сумму свободного заряда, находящегося внутри поверхности и поляризационного (индуцированного, связанного) заряда диэлектрика, то есть в уравнении для E надо было бы писать в правой части другую букву:
- QΣ=Q+Qb,{\displaystyle Q_{\Sigma }=Q+Q_{b},}
где
- Qb=∮SPdS{\displaystyle Q_{b}=\oint \limits _{S}\mathbf {P} \,\mathrm {d} \mathbf {S} } — связанный заряд внутри поверхности[4],
- P{\displaystyle \mathbf {P} } — вектор поляризации диэлектрика.
Мы же здесь применили одну и ту же букву в правой части просто потому, что такая запись встречается чаще всего, а поскольку та и другая форма уравнения редко используются совместно, так что путаницы не возникает.
Для случая вакуума (отсутствия диэлектрической среды) то и другое уравнения просто совпадают, поскольку тогда Qb=0, в то время как D=E (в системе единиц СИ — пропорциональны.
В дифференциальной форме:
| СГС | СИ |
|---|---|
|
|
Важный комментарий
- Важно понимать, что Q и ρ в этом параграфе обозначены другие величины, чем в предыдущем: величина свободных зарядов и плотность свободных зарядов, то есть зарядов за исключением индуцируемых при поляризации диэлектрической среды (тогда как в предыдущем параграфе имелись в виду полный заряд и полная плотность заряда (подробнее — см. комментрарий в этом параграфе чуть выше). Совпадают эти величины только для случая вакуума (отсутствия диэлектрической среды), когда и сами уравнения этого параграфа переходят по сути в уравнения предыдущего параграфа.
Теорема Гаусса для магнитной индукции[править | править код]
Поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:
- ΦB≡∮SB⋅dS=0,{\displaystyle \Phi _{\mathbf {B} }\equiv \oint \limits _{S}\mathbf {B} \cdot \mathrm {d} \mathbf {S} =0,}
или в дифференциальной форме
- ∇⋅B=0.{\displaystyle \nabla \cdot \mathbf {B} =0.}
Это эквивалентно тому, что в природе не существует «магнитных зарядов» (монополей), которые создавали бы магнитное поле, как электрические заряды создают электрическое поле[5]. Иными словами, теорема Гаусса для магнитной индукции показывает, что магнитное поле является (полностью) вихревым.
Теорема Гаусса для ньютоновской гравитации[править | править код]
Для напряжённости поля ньютоновской гравитации (ускорения свободного падения) теорема Гаусса практически совпадает с таковой в электростатике, за исключением только констант (впрочем, всё равно зависящих от произвольного выбора системы единиц) и, главное, знака[6]:
- Φg≡∮Sg⋅dS=−4πGM,{\displaystyle \Phi _{\mathbf {g} }\equiv \oint \limits _{S}\mathbf {g} \cdot \mathrm {d} \mathbf {S} =-4\pi GM,}
- ∇⋅g=−4πGρ,{\displaystyle \nabla \cdot \mathbf {g} =-4\pi G\rho ,}
где g — напряжённость гравитационного поля, M — гравитационный заряд (то есть масса) внутри поверхности S, ρ — плотность массы, G — ньютоновская константа.
В терминах силовых линий[править | править код]
Теорема Гаусса может быть интерпретирована в терминах силовых линий[7] поля так:
- Поток поля через поверхность есть[8] количество силовых линий, пронизывающих эту поверхность. При этом учитывается направление — силовые линии, пронизывающие поверхность в обратном направлении считаются со знаком минус.
- Силовые линии начинаются или кончаются только на зарядах (начинаются на положительных, кончаются на отрицательных), или могут ещё уходить на бесконечность. Количество силовых линий, исходящих из заряда (начинающихся в нём) равно[9] величине этого заряда (это определение заряда в данной модели). Для отрицательных зарядов всё так же, только заряд равен минус количеству входящих в него (кончающихся на нём) линий.
- Исходя из этих двух положений, теорема Гаусса представляется очевидной в формулировке: количество линий, исходящих из замкнутой поверхности равно суммарному количеству зарядов внутри неё — то есть количеству линий, появившихся внутри неё. Конечно же, подразумевается учёт знаков, в частности, линия, начавшаяся внутри поверхности на положительном заряде может закончиться на отрицательном заряде также внутри неё (если такой там есть), тогда она не даст вклада в поток через эту поверхность, так как или вообще до неё не дойдёт, или выйдет, а потом войдёт обратно (или, вообще говоря, пересечёт поверхность чётное количество раз поровну в прямом и противоположном направлении), что при суммировании с учётом знака даст вклад в поток ноль. То же можно сказать о линиях, начавшихся и закончившихся вне данной поверхности — по той же причине они также дадут нулевой вклад в поток через неё.
В терминах течения несжимаемой жидкости[править | править код]
Теорема Гаусса верна для поля скоростей несжимаемой жидкости. Этот факт позволяет использовать течение несжимаемой жидкости в качестве аналогии (формальной модели), позволяющей прояснить её смысл и наглядно представить её математическое содержание.[10]
Полезно здесь заметить, что даже сама терминология векторного анализа, используемая в электродинамике (и в частности при формулировке теоремы Гаусса) сформировалась почти целиком под влиянием этой аналогии. Достаточно указать на такие термины, как источник поля (применительно к заряду) или поток через поверхность, которые полностью и точно соответствуют в рассматриваемой аналогии понятиям:
- источник жидкости (в смысле места, где жидкость возникает и количественной меры её возникновения — объём, возникающий в единицу времени),
- поток (в смысле количества жидкости, проходящей через поверхность в единицу времени).
В терминах течения несжимаемой жидкости теорема Гаусса формулируется так: Поток жидкости, исходящий из замкнутой поверхности, равен сумме источников, находящихся внутри этой поверхности. Или, более формально: Поток вектора скорости жидкости через замкнутую поверхность равен сумме источников, находящихся внутри этой поверхности. (В сущности, это интегральный вариант уравнения непрерывности для несжимаемой жидкости, выражающего сохранение массы жидкости с учётом постоянства её плотности).
В этой формальной аналогии напряжённость поля заменяется на скорость течения жидкости, а заряд — на источник жидкости (отрицательный заряд — на «отрицательный источник» — «сток»).
Теорема Гаусса как определение заряда[править | править код]
Теорема Гаусса[11] может рассматриваться как определение (величины) заряда.
Так, для точечного заряда очевидно, что поток напряжённости поля через любую поверхность равен потоку через маленькую (бесконечно маленькую) сферу, окружающую этот заряд. Тогда последний (с точностью, быть может, до постоянного коэффициента, в зависимости от нашего произвольного выбора единиц измерения) может быть выбран в качестве определения величины этого заряда.
Вблизи заряда (бесконечно близко к нему) его собственное поле, очевидно, даёт подавляющий вклад в поток через бесконечно маленькую сферу (поскольку поле безгранично растёт с уменьшением расстояния). Значит, остальными полями (порождаемыми другими зарядами) можно пренебречь. Тогда можно увидеть, что данное определение согласуется с обычным (через закон Кулона).
В современной физике обычно принято считать, что определение через закон Гаусса более фундаментально (как и сам закон Гаусса по сравнению с законом Кулона — см. ниже), хотя с определённой точки зрения они просто эквивалентны.
Теорема Гаусса и закон Кулона тесно связаны, как формально, так и по физическому содержанию. В некотором смысле можно утверждать, что теорема Гаусса является интегральной формулировкой закона Кулона или наоборот, что закон Кулона является следствием теоремы (закона) Гаусса.
Что из них считать постулатом, а что следствием — зависит от того, какую аксиоматизацию для электродинамики (или электростатики, если ограничиваться ею) мы выбираем; формально тот или другой выбор практически[12] равноправны, а в случае электростатики это полностью так. Таким образом, выбор того или другого в качестве основания построения теории — вопрос нашего произвольного выбора.
Впрочем, аксиоматизация через закон Гаусса имеет то преимущество, что в законе Гаусса не содержится никаких произвольных параметров (таких, как степень расстояния −2 в законе Кулона), степень расстояния в законе Кулона возникает при этом автоматически из размерности пространства.
Однако, следует сделать оговорку. Если наивно считать, что закон Кулона и теорема Гаусса эквивалентны, то можно рассуждать так: из теоремы Гаусса следует закон Кулона, из закона Кулона следуют уравнения Максвелла для случая электростатики, т.о. второе уравнение Максвелла (о равенстве нулю ротора электрического поля) следует из теоремы Гаусса и является излишним. На самом деле, при выводе закона Кулона из теоремы Гаусса (см. ниже) мы дополнительно используем сферическую симметрию поля точечного заряда, а также нам необходимо ввести принцип суперпозиции, в то время как уравнения Максвелла являются самодостаточными.
Исторически первым был эмпирически открыт закон Кулона. В этом (историческом) смысле теорема Гаусса является его следствием. Именно в связи с этим она называется теоремой, так как первоначально появилась как теорема.
Непосредственно ниже показано, как закон Кулона и закон Гаусса могут быть получены в рамках электростатики[13] друг из друга.
Закон Кулона как следствие закона Гаусса[править | править код]
Исходим из теоремы Гаусса, записав её в единицах системы СИ[14], «Поток ΦE,S{\displaystyle \Phi _{E,S}} вектора напряжённости E{\displaystyle E} через поверхность S{\displaystyle S} пропорционален заряду, заключённому в эту поверхность»:
- ΦE,S=Qε0.{\displaystyle \Phi _{E,S}={\frac {Q}{\varepsilon _{0}}}.}
Для вывода Закона Кулона, будем рассматривать единственный точечный заряд в пределах замкнутой поверхности S, таким образом Q здесь будет величиной этого заряда.
Рассчитаем тот же поток прямым интегрированием по поверхности. Замечаем, что задача имеет сферическую симметрию относительно положения заряда. Из этого делаем вывод, что электрическое поле будет направлено прямо от заряда, а его величина будет одинакова для любых точек, расположенных на одинаковом расстоянии от заряда. Из этого следует, что суммарный поток будет проще всего сосчитать, если в качестве поверхности S выбрать сферу с центром в заряде. Действительно, напряжённость поля E тогда будет всюду ортогональна dS, а абсолютная величина вектора E (будем обозначать её E) будет одинакова везде на этой сфере, и её можно будет вынести за знак интеграла. Итак:
- ΦE,S=∮SE⋅dS=∮SEdS=E∮SdS=ES.{\displaystyle \Phi _{E,S}=\oint \limits _{S}\mathbf {E} \cdot \mathbf {dS} =\oint \limits _{S}EdS=E\oint \limits _{S}dS=ES.}
Имеем:
- {ΦE,S=Qε0ΦE,S=ES{\displaystyle {\begin{cases}\Phi _{E,S}={\frac {Q}{\varepsilon _{0}}}\\\Phi _{E,S}=ES\end{cases}}}
Отсюда:
- ES=Qε0.{\displaystyle ES={\frac {Q}{\varepsilon _{0}}}.}
Осталось подставить сюда для площади сферы S=4πr2{\displaystyle S=4\pi r^{2}} и разрешить уравнение относительно E.
Тогда получаем:
- E=14πε0Qr2,{\displaystyle E={\frac {1}{4\pi \varepsilon _{0}}}{\frac {Q}{r^{2}}},}
то есть — закон Кулона.
Теорема Гаусса как следствие закона Кулона[править | править код]
Элементарное доказательство[править | править код]
Элементарное доказательство строится на двух шагах: доказательстве теоремы для случая одного точечного заряда с использованием геометрических соображений, а затем применении принципа суперпозиции, вследствие которого теорема оказывается доказана для произвольного количества точечных зарядов (а значит и в общем случае).
Исходим из закона Кулона:
- E(r)=qr2er{\displaystyle \mathbf {E} (\mathbf {r} )={\frac {q}{r^{2}}}\mathbf {e} _{r}},
где er{\displaystyle \mathbf {e} _{r}} — единичный вектор в направлении радиус-вектора r{\displaystyle \mathbf {r} }, проведённого из заряда (куда мы поместили начало координат) в точку, где измеряется напряжённость поля E(r){\displaystyle \mathbf {E} (\mathbf {r} )}, r — модуль вектора r, то есть расстояние от заряда до этой точки. (В этом параграфе будем пользоваться только системой СГС, то есть кулоновская константа равна единице. Для перехода в систему СИ достаточно просто добавить множитель. Так же и переход к любой другой системе единиц будет отличаться только кулоновской константой.)
Для одного точечного заряда внутри поверхности[править | править код]
Обозначим поверхность, через которую надо вычислить поток E, буквой S. Полагаем, что наш заряд q находится внутри этой поверхности.
Окружим заряд ещё одной поверхностью — сферой S0 с центром в заряде и радиусом R0 столь малым, что она целиком находится внутри поверхности S. Вычислим поток через S0:
- ΦS0=4πR02E.{\displaystyle \Phi _{S_{0}}=4\pi R_{0}^{2}E.}
Выберем малый (бесконечно малый, малый не только по величине, но и «компактно», то есть так, чтобы он, скажем, мог быть покрыт круговым конусом также малого телесного угла), телесный угол ω{\displaystyle \omega } с вершиной в заряде.
Докажем, что поток ΦS,ω {\displaystyle \Phi _{S,\omega }\ } через площадку поверхности S, вырезаемую этим телесным углом ω{\displaystyle \omega }, равен потоку ΦS0,ω{\displaystyle \Phi _{S_{0},\omega }} через площадку S0,ω{\displaystyle S_{0,\omega }}, вырезаемую им же из сферы S0. Для этого покажем, что
- 1. ΦS,ω =ΦS⊥,ω {\displaystyle \Phi _{S,\omega }\ =\Phi _{S_{\perp ,\omega }}\ } — поток через площадку Sω{\displaystyle S_{\omega }}, вырезаемую телесным углом ω{\displaystyle \omega } из поверхности S, равен потоку через площадку S⊥,ω,{\displaystyle S{\perp ,\omega },} вырезаемую телесным углом ω{\displaystyle \omega } из любой плоскости, перпендикулярной лучам, лежащим внутри ω{\displaystyle \omega }, которые при бесконечно малом телесном угле почти параллельны, отличаясь по направлению бесконечно мало, значит площадка будет одновременно перпендикулярна (говоря строже — почти перпендикулярна) всем им одновременно.
- 2. ΦS⊥,ω=ΦS0,ω.{\displaystyle \Phi _{S\perp ,\omega }=\Phi _{S_{0},\omega }.} — в пределах телесного угла ω{\displaystyle \omega }, поток через площадку, перпендикулярную лучам, равен потоку через площадку сферы S0{\displaystyle S_{0}}.
Первое доказывается замечанием о том, что поток dΦ=E⋅dS{\displaystyle d\Phi =\mathbf {E} \cdot \mathbf {dS} } через малую площадку dS может быть представлен как dΦ=E(dS)⊥{\displaystyle d\Phi =E(dS)_{\perp }}, где (dS)⊥{\displaystyle (dS)_{\perp }} — проекция вектора dS на направление вектора E, то есть площадь проекции данной площадки на плоскость, перпендикулярную E. А применительно к нашему случаю это и означает равенство ΦS⊥,ω{\displaystyle \Phi _{S\perp ,\omega }} и ΦS,ω{\displaystyle \Phi _{S,\omega }}.
Второе видно из соображений подобия и закона Кулона (обозна
Интенсивность (физика) — Википедия
Материал из Википедии — свободной энциклопедии
Интенси́вность — скалярная физическая величина, количественно характеризующая мощность, переносимую волной в направлении распространения. Численно интенсивность равна усреднённой за период колебаний волны мощности излучения, проходящей через единичную площадку, расположенную перпендикулярно направлению распространения энергии. В математической форме это может быть выражено следующим образом:
- I(t)=1T∫tt+TdPdSdt,{\displaystyle I(t)={\frac {1}{T}}\int \limits _{t}^{t+T}{\frac {dP}{dS}}dt,}
где T{\displaystyle T} — период волны, dP{\displaystyle dP} — мощность, переносимая волной через площадку dS{\displaystyle dS}.
Интенсивность волны связана со средней плотностью энергии W{\displaystyle W} в волне и скоростью распространения волны v{\displaystyle v} следующим соотношением:
- I=Wv.{\displaystyle I=Wv.}
Единицей измерения интенсивности в Международной системе единиц (СИ) является Вт/м², в системе СГС — эрг/с·см².
Интенсивность электромагнитного излучения[править | править код]
Электромагнитное излучение (например, свет) представляет собой совокупность волн, колебания в которых совершают напряжённость электрического поля и магнитная индукция. Электромагнитные волны переносят энергию электромагнитного поля, поток которой определяется величиной вектора Пойнтинга. Интенсивность электромагнитного излучения равна усреднённому за период значению модуля вектора Пойнтинга[1]:
- I(t)=1T∫tt+T|S→(t)|dt,{\displaystyle I(t)={\frac {1}{T}}\int \limits _{t}^{t+T}\left|{\vec {S}}(t)\right|dt,}
где вектор Пойнтинга S→(t)=c4π[E→(t)×B→(t)],{\displaystyle {\vec {S}}(t)={\frac {c}{4\pi }}\left[{\vec {E}}(t)\times {\vec {B}}(t)\right],} (в системе СГС), E{\displaystyle E} — напряжённость электрического поля, а B{\displaystyle B} — магнитная индукция.
Для монохроматической линейно поляризованной волны с амплитудой напряжённости электрического поля E0{\displaystyle E_{0}} интенсивность равна:
- I=cE028π.{\displaystyle I={\frac {cE_{0}^{2}}{8\pi }}.}
Для монохроматической циркулярно поляризованной волны это значение в два раза больше:
- I=cE024π.{\displaystyle I={\frac {cE_{0}^{2}}{4\pi }}.}
Звук представляет собой волну механических колебаний среды. Интенсивность звука может быть выражена через амплитудные значения звукового давления p и колебательной скорости среды v:
- I=pv2.{\displaystyle I={\frac {pv}{2}}.}
Электрическая постоянная — Википедия
Материал из Википедии — свободной энциклопедии
Электрическая постоянная (ранее также носила название диэлектрической постоянной) — физическая константа, скалярная величина, входящая в выражения некоторых законов электромагнетизма, в том числе закона Кулона, при записи их в рационализованной форме, соответствующей Международной системе единиц (СИ)[1].
Иногда, используя устаревшую терминологию, называют электрической (или диэлектрической) проницаемостью вакуума[2]. Измеряется в фарадах, делённых на метр.
По определению в СИ электрическая постоянная ε0{\displaystyle \varepsilon _{0}} связана со скоростью света c{\displaystyle c} и магнитной постоянной μ0{\displaystyle \mu _{0}} соотношением[1]
- ε0=1μ0c2.{\displaystyle \varepsilon _{0}={\frac {1}{\mu _{0}c^{2}}}.}
В Международной системе единиц[править | править код]
До изменения СИ 2018—2019 годов[править | править код]
Поскольку в СИ для магнитной постоянной было справедливо точное равенство μ0=4π × 10−7 {\displaystyle \mu _{0}=4\pi \ \times \ 10^{-7}\ }Гн/м, то для электрической постоянной выполнялось соотношение
- ε0=14πc2⋅107{\displaystyle \varepsilon _{0}={\frac {1}{4\pi c^{2}}}\cdot 10^{7}}м/Гн,[3]
также являвшееся точным.
Учитывая, что скорости света в СИ приписано точное значение, по определению равное 299 792 458 м/с, из последнего соотношения следует численное значение ε0{\displaystyle \varepsilon _{0}} в СИ:
- ε0=14π⋅ 2997924582×10−7{\displaystyle \varepsilon _{0}={\frac {1}{4\pi \cdot \ 299792458^{2}\times 10^{-7}}}} Ф/м ≈ 8,85418781762039 · 10−12 Ф·м−1.
Или, выражая то же через основные единицы СИ,
- ε0 ≈ 8,85418781762039 · 10−12 м−3·кг−1·с4·А2.
После изменений СИ 2018—2019 годов[править | править код]
С 2019 года вступили в силу изменения в СИ, включающие, в частности, переопределение ампера на основе фиксации численного значения элементарного заряда. Это привело к тому, что значение электрической постоянной стало экспериментально определяемой величиной, хотя численно её значение осталось прежним с высокой точностью. Значение электрической постоянной, рекомендованное CODATA[4]:
- ε0 = 8,8541878128(13)· 10−12 м−3·кг−1·с4·А2, или Ф·м−1.
В системе СГС[править | править код]
В системе СГС электрическая постоянная как коэффициент, связывающий напряжённость и индукцию электрического поля в вакууме, также может быть введена. При этом в различных вариантах системы СГС электрическая постоянная имеет разную размерность и значение. Конкретно, Гауссова система единиц и система СГСЭ построены так, что электрическая постоянная безразмерна и равна 1, а в системе СГСМ она равна ε0 = 1/c2 ≈ 1,11265005605362 · 10−21 с2·см−2.
Некоторые уравнения электродинамики в СИ[править | править код]
В материальных уравнениях, в вакууме, через электрическую постоянную связаны вектор электрической индукции D{\displaystyle \mathbf {D} } и вектор напряжённости электрического поля E{\displaystyle \mathbf {E} }:
- D=ε0 E.{\displaystyle \mathbf {D} =\varepsilon _{0}\ \mathbf {E} .}
Она также входит в запись закона Кулона (тоже в вакууме):
- F12=14πε0⋅q1q2r122r12r12.{\displaystyle \mathbf {F} _{12}={\frac {1}{4\pi \varepsilon _{0}}}\cdot {\frac {q_{1}q_{2}}{r_{12}^{2}}}{\frac {\mathbf {r} _{12}}{r_{12}}}.}
При использовании СИ произведение электрической постоянной на относительную диэлектрическую проницаемость называют абсолютной диэлектрической проницаемостью.





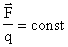 — величина постоянная в данной точке данного поля.
— величина постоянная в данной точке данного поля.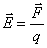
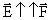 , если q>0.
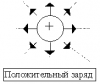
, если q>0. 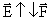 , если q<0. Т.е. вектор напряженности направлен от положительного заряда и к отрицательному.
, если q<0. Т.е. вектор напряженности направлен от положительного заряда и к отрицательному.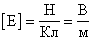 Напряженность в данной точке поля равна 1
Напряженность в данной точке поля равна 1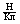 , если на заряд в 1 Кл, помещенный в эту точку, действует сила в 1 Н. (Напряженность равна 1
, если на заряд в 1 Кл, помещенный в эту точку, действует сила в 1 Н. (Напряженность равна 1 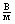 , если между точками электростатического поля, находящимися на расстоянии 1 м друг от друга, существует разность потенциалов 1 В).
, если между точками электростатического поля, находящимися на расстоянии 1 м друг от друга, существует разность потенциалов 1 В).