1.3. Электрическое поле. Напряженность электрического поля. Поле точечного заряда
Электрическое поле — это особый полевой вид материи, основное свойство которого состоит в действии силы на покоящиеся или движущиеся заряды.Электрическое взаимодействие между зарядами в поле передается с очень большой, но конечной скоростью (в вакууме скорость взаимодействия равна скорости светас =3.108м/с).
Электрическое поле может быть создано неподвижными зарядами, в этом случае его называют электростатическим. Оно также может быть порожденопеременным магнитным полем, такое электрическое поленазывают вихревым.
Важным свойством электрического поля является также его способность накапливать и отдавать энергию.
Для обнаружения и исследования электрического поля пользуются “пробным“ зарядом
Р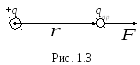 ассмотрим
электрическое поле, созданное точечным
положительным зарядомqв вакууме. Поместим в это поле пробный
зарядqпр.(рис 1.3).
ассмотрим
электрическое поле, созданное точечным
положительным зарядомqв вакууме. Поместим в это поле пробный
зарядqпр.(рис 1.3).
В точке с
радиусом-вектором 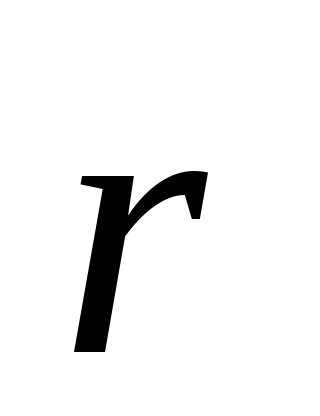 на пробный заряд действует сила
на пробный заряд действует сила

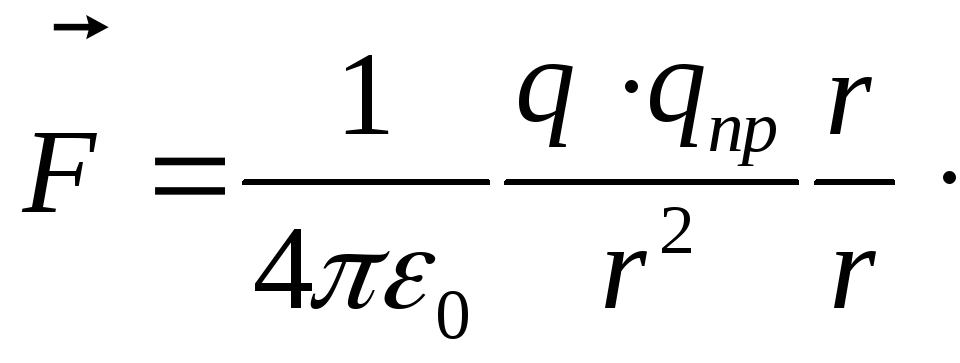
Эта сила зависит
от qпр., qи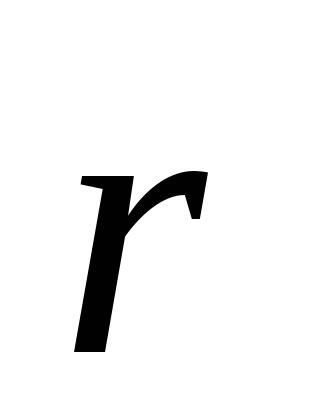 ,
однако отношение
,
однако отношение 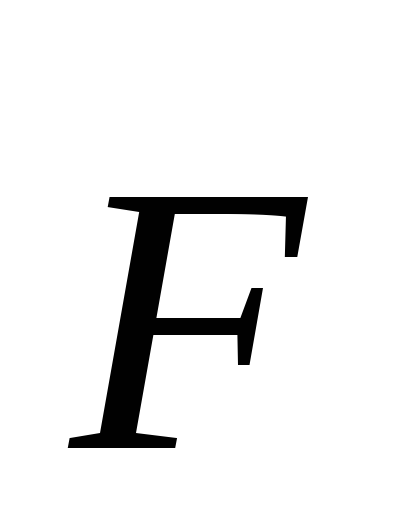 /qпр.будет зависеть лишь от величинq и
/qпр.будет зависеть лишь от величинq и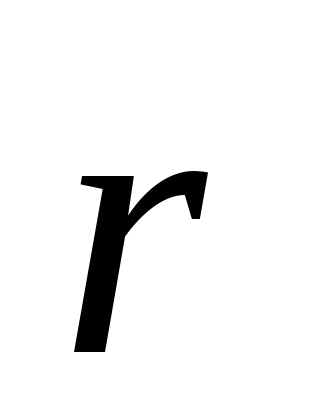 ,
характеризующих поле в данной
точке. Это
отношение обозначают буквой
,
характеризующих поле в данной
точке. Это
отношение обозначают буквой и называютнапряженностью поля:
и называютнапряженностью поля:
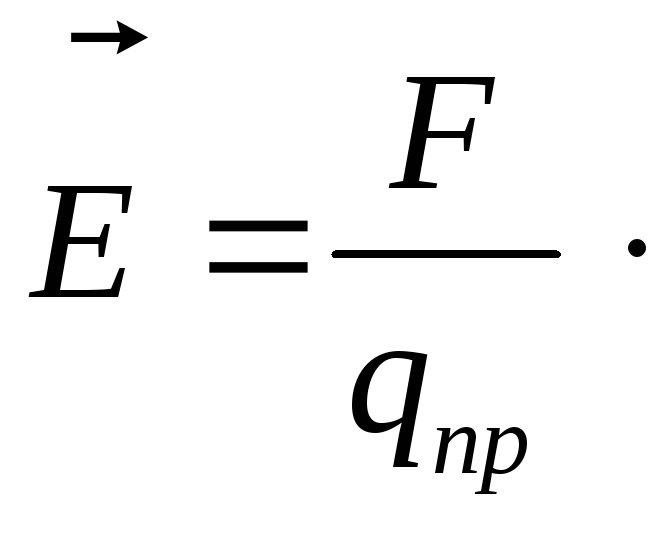
Н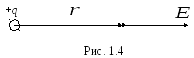 аправлен
вектор
аправлен
вектор вдоль
прямой, проходящей через заряд и данную
точку поля (рис. 1.4).
вдоль
прямой, проходящей через заряд и данную
точку поля (рис. 1.4).
Если заряд, создающий поле, положительный, то напряженность направлена от заряда, если отрицателен — к заряду. В системе СИ единица напряженности электрического поля имеет размерность В/м.
В соответствии с формулой (1.7) напряженность электрического поля — векторная величина, равная силе, действующей на единичный положительный заряд, помещенный в данную точку.
Из формул (1.6) и (1.7) следует, что напряженность электрического поля, созданного точечным зарядом,определяется соотношениями:
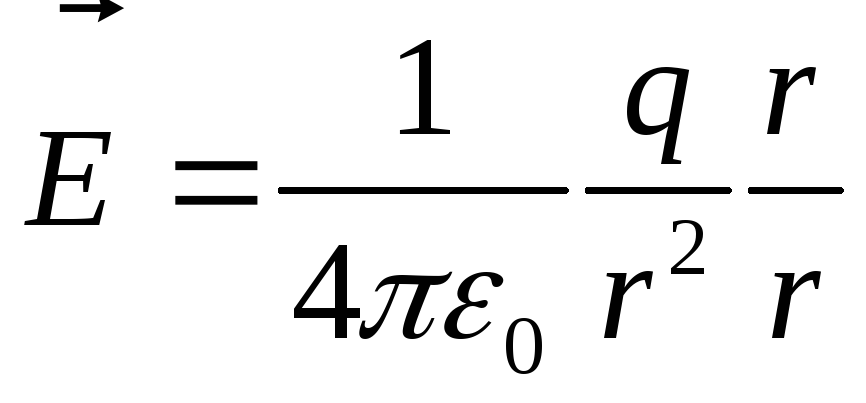 ,
,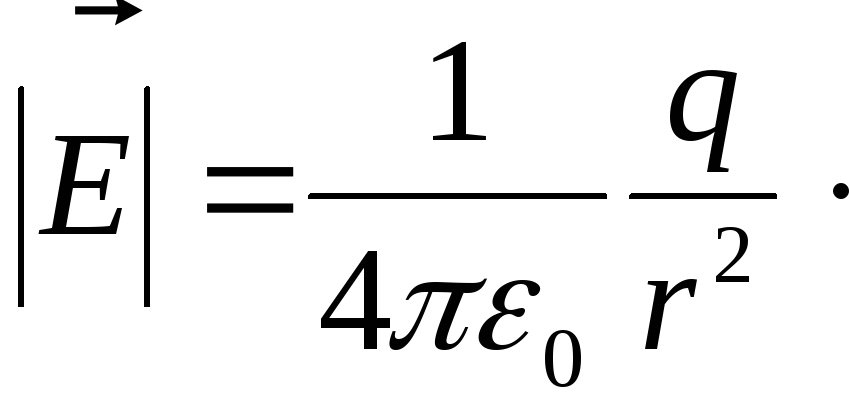 (1.8)
(1.8)
1.4. Принцип суперпозиции электрических полей. Электрический диполь
Напряженность электрического поля — силовая характеристика, поэтому она должна удовлетворять принципу суперпозиции, справедливому для кулоновских сил: напряженность поля системы зарядов равна векторной сумме напряженностей полей, созданных каждым зарядом системы в данной точке. Принцип поясняется

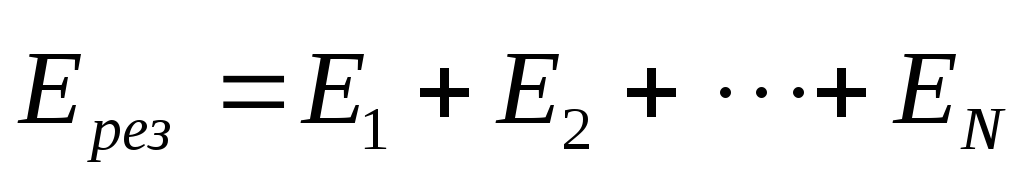 (1.9)
(1.9)
Если поле создано заряженным телом конечных размеров, то разбив его (как показано на рисунке 1.6) на достаточно малые элементы с зарядами dqi, получим систему точечных зарядов, вклад от которых в результирующее поле рассчитывается по формуле (1.8):
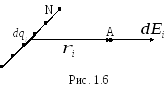
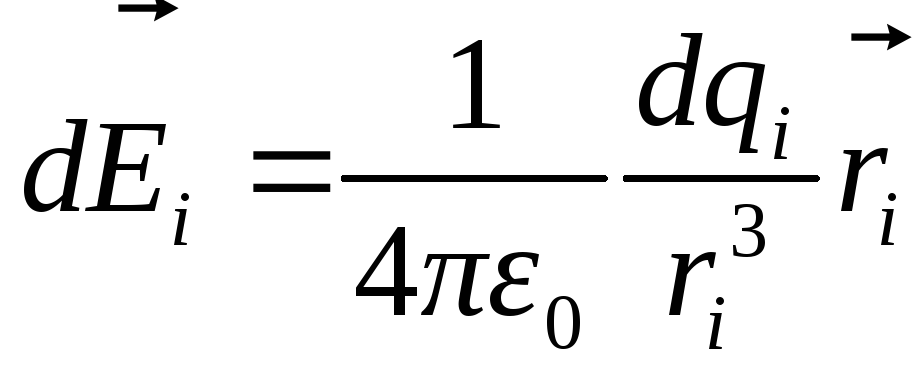 (1.10)
(1.10)
Согласно (1.9) напряженность результирующего поля в точке Аот всехNточечных зарядовdqiможно вычислить, просуммировав элементарные поля:

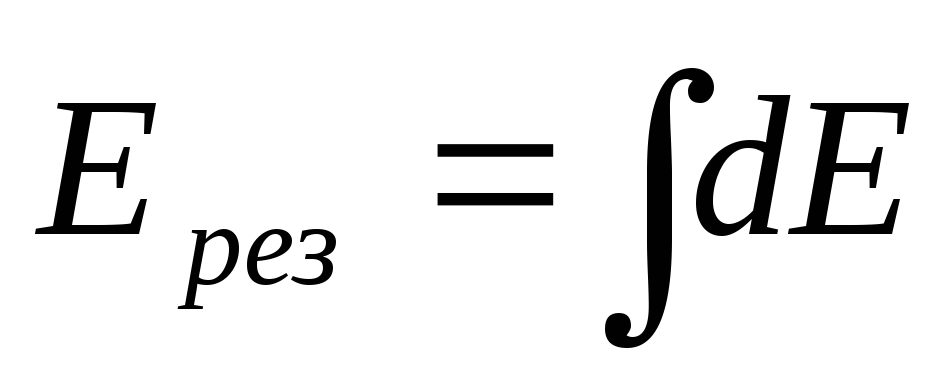 (1.11)
(1.11)
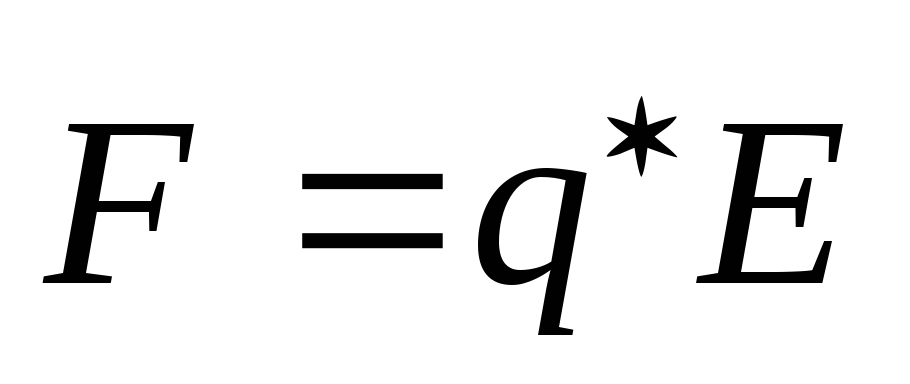 . (1.12)
. (1.12)
Применим принцип
суперпозиции для расчета поля электрического диполя. Так называетсясистема двух одинаковых по величине
разноименных точечных зарядов +q и —q, расстояние между которыми (l)
значительно меньше расстояния (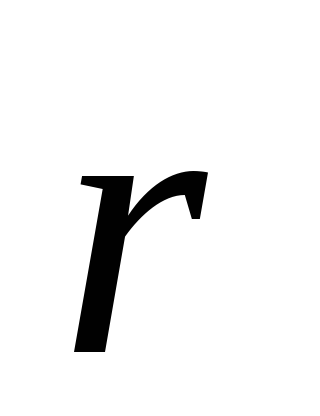 )до тех точек, в которых определяется
электрическое поле (рис. 1.7).
)до тех точек, в которых определяется
электрическое поле (рис. 1.7).
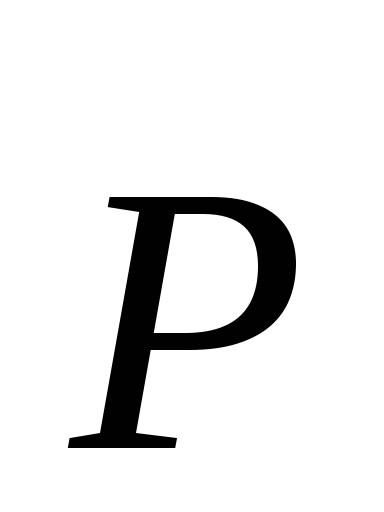 ,
называемойэлектрическим моментом
диполя. Вектор
,
называемойэлектрическим моментом
диполя. Вектор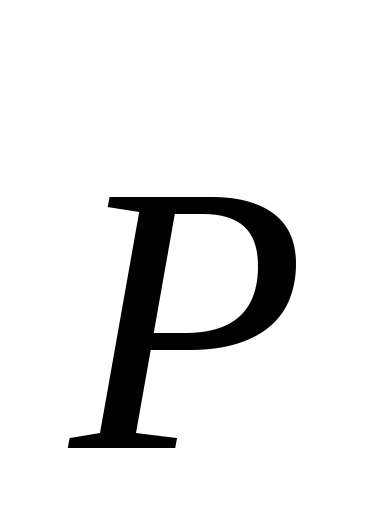 направлен по оси диполя от отрицательного
заряда к положительному и равен:
направлен по оси диполя от отрицательного
заряда к положительному и равен: 
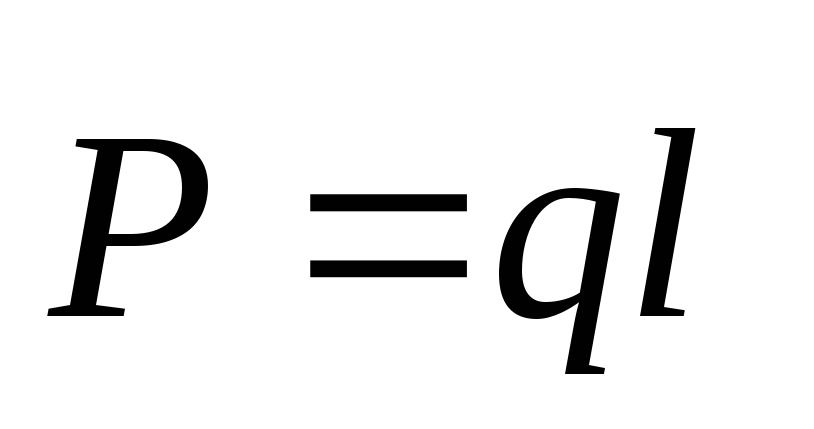
Для расчета электрического поля диполя необходимо в данной точке определить по формуле (1.8) напряженности полей, созданных точечными зарядами +q и -q, и применить принцип суперпозиции.
Расчет показывает,
что напряженность поля, создаваемого
диполем, зависит от 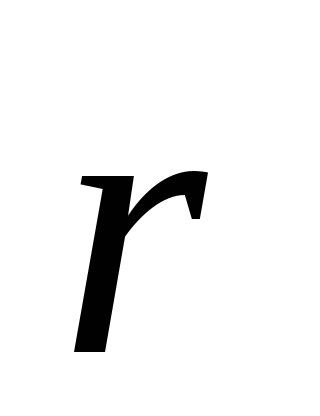 и от угла
и от угла между осью диполя и направлением на
данную точку, т.е.
между осью диполя и направлением на
данную точку, т.е.
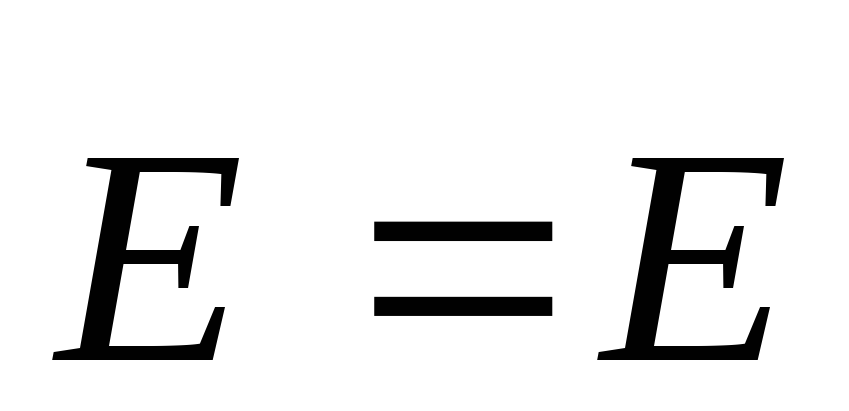 ( r,
( r,
Для модуля вектора  найдено выражение
найдено выражение
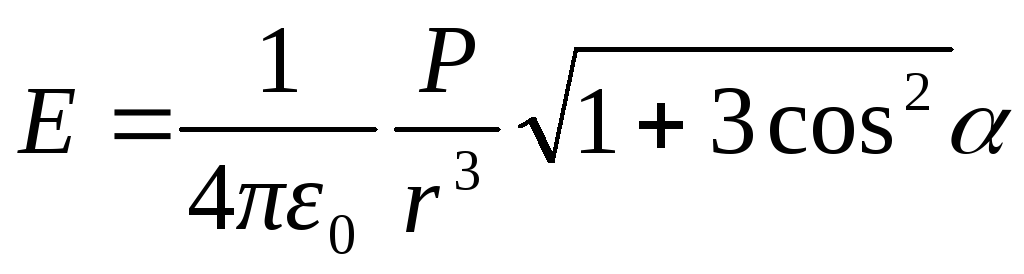 . (1.15)
. (1.15)
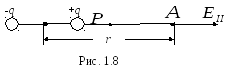
 =0,
получим напряженность на оси диполя
(рис. 1.8):
=0,
получим напряженность на оси диполя
(рис. 1.8): 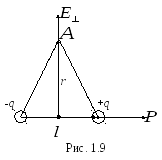
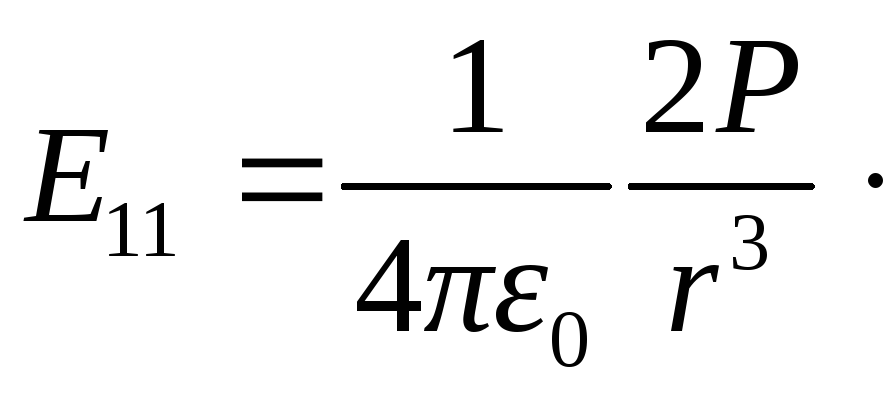 (1.16)
(1.16)
Положив  ,получим напряженность поля на прямой,
проходящей через центр диполя
перпендикулярно его оси (рис. 1.9):
,получим напряженность поля на прямой,
проходящей через центр диполя
перпендикулярно его оси (рис. 1.9):
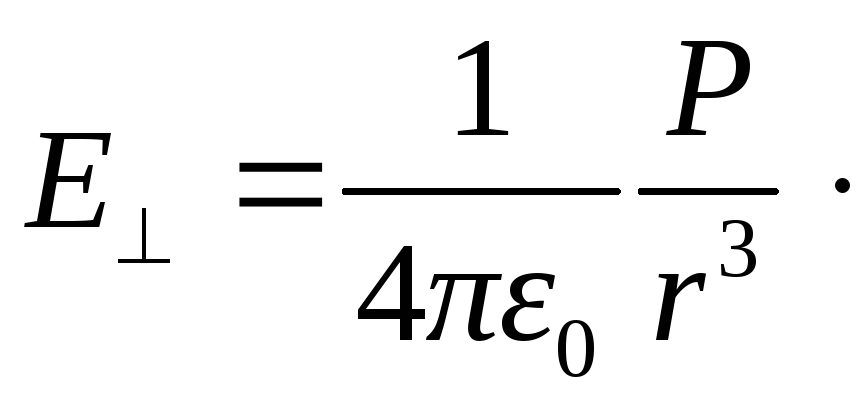 (1.17)
(1.17)
Из сравнения формул (1.16) и (1.17) следует, что напряженность электрического поля в точках, расположенных на оси диполя, в два раза больше, чем на прямой перпендикулярной оси диполя. Отметим, что напряженность поля диполя убывает c ростом
66. Напряженность электрического поля, единицы измерения. Напряженность поля точечного заряда.
Напряженность электрического поля. Количественной характеристикой силового действия электрического поля на заряженные тела служит векторная величина E, называемая напряжённостью электрического поля.
E = F / q пр.
Она определяется отношением силы F, действующей со стороны поля на точечный пробный заряд qпр, помещенный в рассматриваемую точку поля, к величине этого заряда.
Понятие «пробный заряд» предполагает, что этот заряд не участвует в создании электрического поля и так мал, что не искажает его, т. е. не вызывает перераспределения в пространстве зарядов, создающих рассматриваемое поле. В системе СИ единицей напряженности служит 1 В / м, что эквивалентно 1 Н / Кл.
Напряженность поля точечного заряда. Используя закон Кулона (1.1) найдем выражение для напряжённости электрического поля, создаваемого точечным зарядом q в однородной изотропной среде на расстоянии r от заряда:
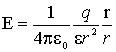 (1.2)
(1.2)
В этой формуле r – радиус-вектор, соединяющий заряды q и qпр. Из (1.2) следует, что напряжённость E поля точечного заряда q во всех точках поля направлена радиально от заряда при q > 0 и к заряду при q < 0.
67. Силовые линии (линии напряженности) электрического поля. Однородное поле
Графическое изображение электрического поля. Метод графического изображения электрического поля был предложен английским физиком Майклом Фарадеем. Суть метода заключается в том, что на чертеже изображаются непрерывные линии, которые называют линиями напряженности, или силовыми линиями.
Правило построения линий напряженности заключается в том, что касательные к ним в каждой точке чертежа совпадают с направлением вектора напряженности поля в изображаемой точке.
Таким образом, силовые линии имеют то же направление, что и напряжённость поля и не пересекаются, так как в каждой точке электрического поля вектор E имеет лишь одно направление.
С помощью силовых линий можно дать количественную характеристику напряжённости электрического поля. Для этого густота, или плотность, силовых линий выбирается пропорционально модулю вектора напряженности. Плотность силовых линий определяется как число линий, пронизывающих единичную поверхность в направлении, перпендикулярном к этой поверхности.
Изображение силовых линий позволяет получать картину поля, которая наглядно показывает, чему равна напряженность в разных частях поля и как она изменяется в пространстве.
Электрическое поле, в котором напряженность одинакова по модулю и направлению в любой точке пространства, называется однородным электрическим полем.
Приблизительно однородным является электрическое поле между двумя разноименно заряженными плоскими металлическими пластинами. Линии напряженности в однородном электрическом поле параллельны друг другу
1.4. Напряженность поля точечного заряда
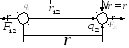
Рис.1.2
Если вспомнить наш первый рис. (по выводу
закону Кулона) и совместить начало
вектора 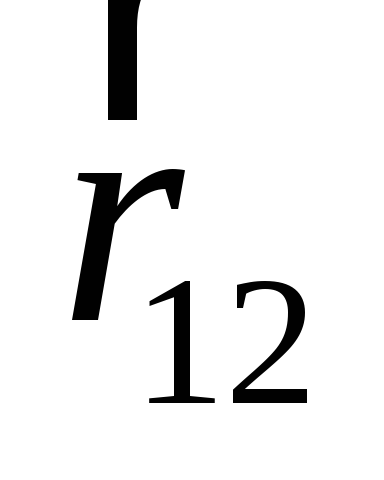 с
положением зарядаq1, который обозначим простоq, то
на основании определения вектора
с
положением зарядаq1, который обозначим простоq, то
на основании определения вектора 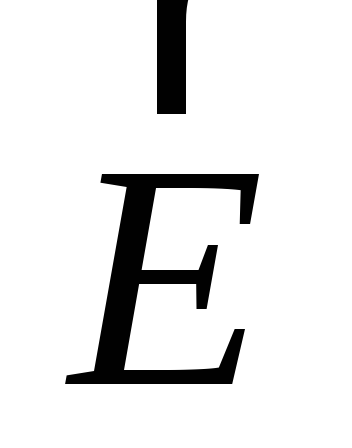 и
закона Кулона, запишем
и
закона Кулона, запишем
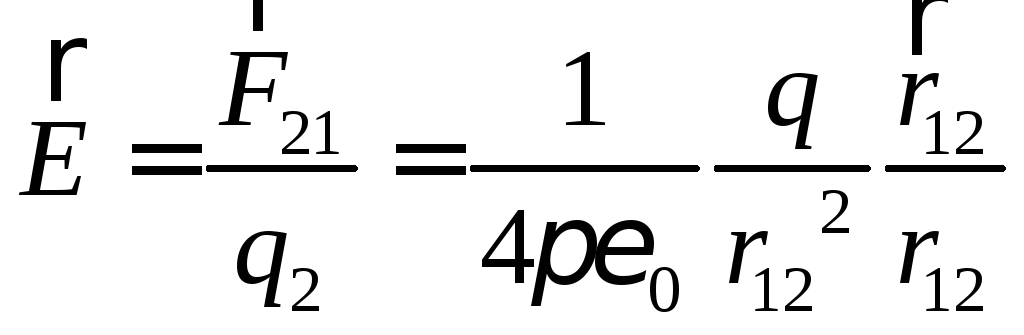 (1.4)
(1.4)
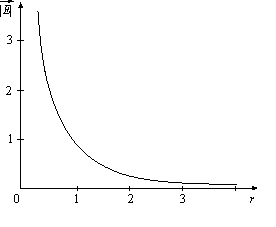
Рис.1.3. Зависимость величины напряженности электрического поля точечного заряда от расстояния до точки наблюдения
На рис.1.3 приведена (в условных единицах) зависимость модуля напряженности электрического поля, созданного точечным зарядом, от расстояния между точечным зарядом и точкой наблюдения, фактически это график функции
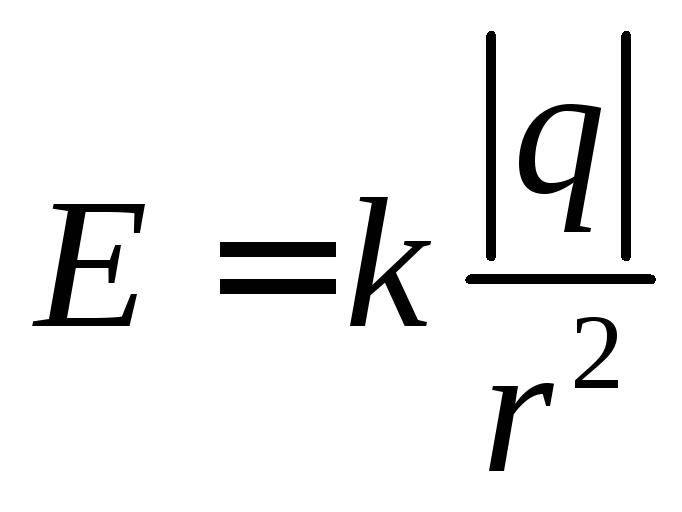 ,
,
которую легко получить из формулы (1.4),
положив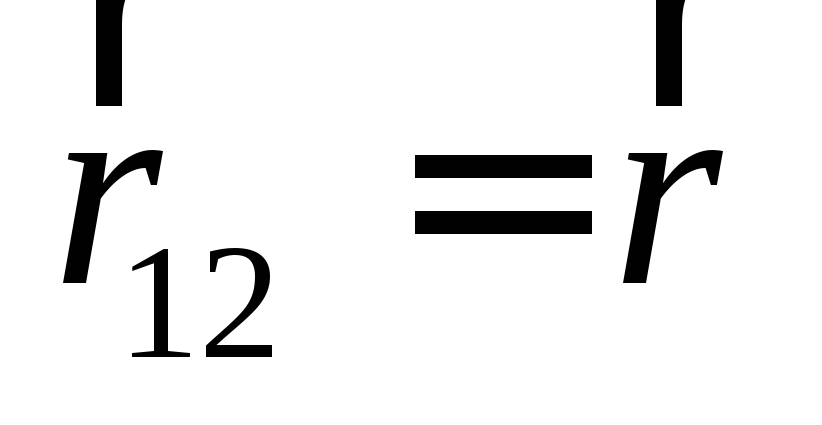 .
.
На рис.1.4 в некотором условном масштабе
изображены поля векторов напряженности 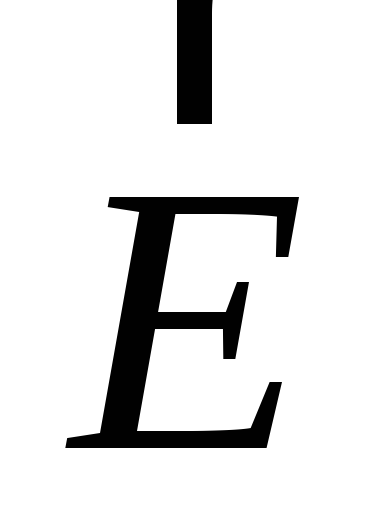 ,
созданные положительным и отрицательным
электрическими точечными зарядами.
Существенным недостатком такого способа
изображения силового векторного поля
,
созданные положительным и отрицательным
электрическими точечными зарядами.
Существенным недостатком такого способа
изображения силового векторного поля 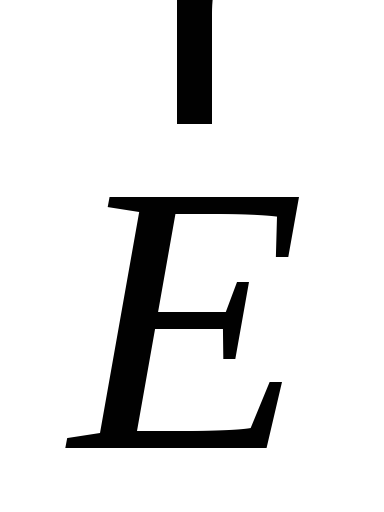 является наложение векторов
напряженности друг на друга, особенно
вблизи источника. На рис.1.4 этого удалось
избежать благодаря специальному выбору
точек наблюдения, в которых изображены
векторы поля.
является наложение векторов
напряженности друг на друга, особенно
вблизи источника. На рис.1.4 этого удалось
избежать благодаря специальному выбору
точек наблюдения, в которых изображены
векторы поля.


а) б)
Рис.1.4. Изображение векторного поля 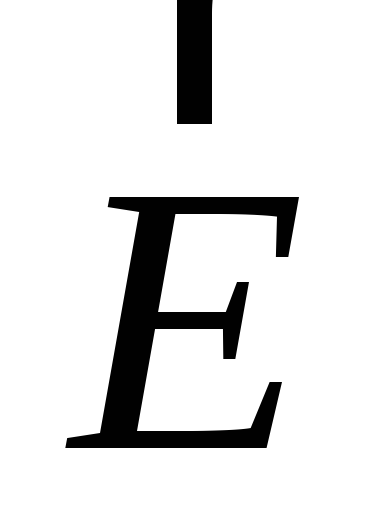 :
а — положительного точечного заряда; б
— отрицательного точечного заряда
:
а — положительного точечного заряда; б
— отрицательного точечного заряда
Иногда для изображения силового поля
удобнее использовать не векторы 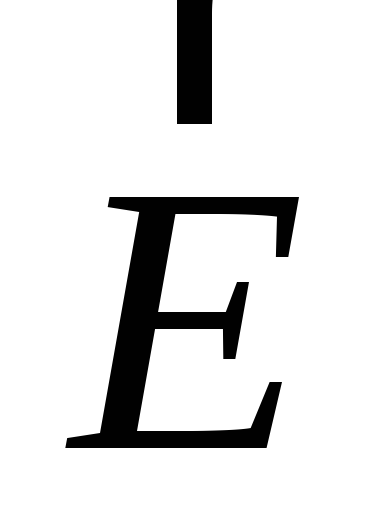 ,
а линии поля (силовые линии).
,
а линии поля (силовые линии).
1.5. Силовые линии электрического поля
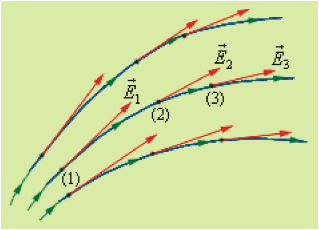
Линия векторного поля (силовая линия) — это математическая линия, касательная к которой в любой ее точке направлена вдоль линии вектора напряженности электрического поля
За положительное направление линий условились считать направления вектора поля, при этом линии поля напряженности идут от положительных зарядов к отрицательным.
Количество линий поля, пронизывающих
единичную площадку, перпендикулярную
вектору 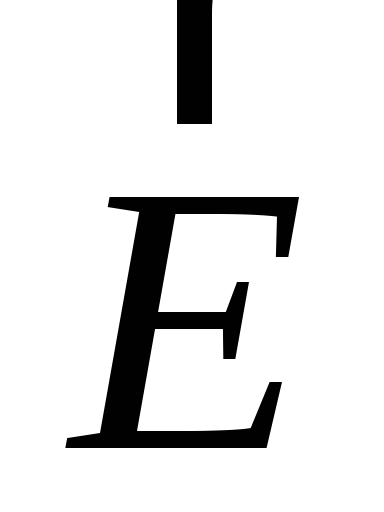 ,
принято полагать пропорциональным
величине этого вектора.
,
принято полагать пропорциональным
величине этого вектора.
Оказывается, электрическое поле устроено так, что можно проводить силовые линии, соблюдая правило густоты и “не обрывая” их в пространстве между зарядами. Это важнейшее свойство силовых линий непосредственно связано с законом Кулона. Рассмотрим, например, поле точечного заряда. При увеличении расстояния от заряда в два раза наблюдаем уменьшение густоты линий поля в четыре раза (число линий в силу их непрерывности не изменится, а площадь поверхности сферы увеличится в четыре раза). Во столько же раз в соответствии с законом Кулона уменьшится напряженность электрического поля. Если бы в формуле, описывающей закон Кулона, содержалось бы 1/r3, а не 1/r2, то напряженность уменьшилась бы в восемь раз, и для соблюдения правила густоты половину силовых линий пришлось бы “оборвать” на пути отrдо 2rв совершенно пустом пространстве.
При изучении следующих тем (например, теоремы Гаусса) к определению силовых линий вернемся еще раз.
а) б)
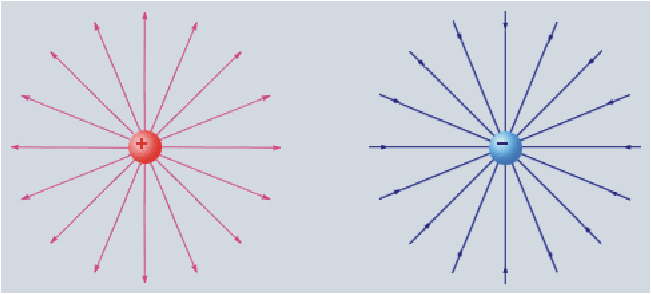
Рис.1.5. Изображение силовых линий поля 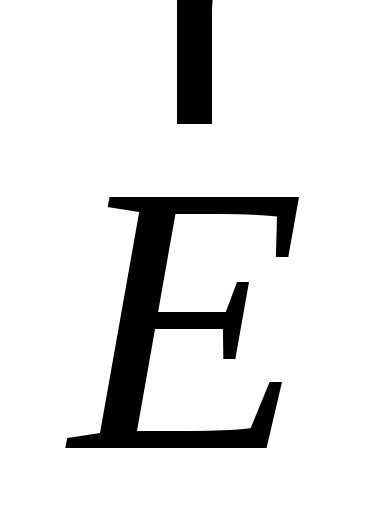 :
а — положительного точечного заряда; б
— отрицательного точечного заряда
:
а — положительного точечного заряда; б
— отрицательного точечного заряда
На рис.1.5 изображены силовые поля,
создаваемые положительными и отрицательными
точечными электрическими зарядами, но
уже с помощью линий поля, а не векторов 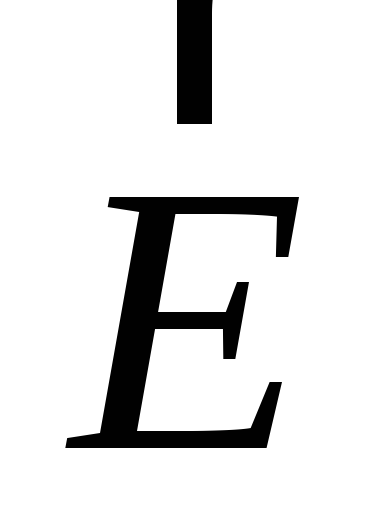 ,
как на рис.1.4. Следует обратить внимание
на серьезный недостаток приведенных
картин — они двумерные, а не трехмерные,
как само электрическое поле, из-за чего
возможны недоразумения. Так, из анализа
рис.1.5 можно заключить, что напряженность
электрического точечного заряда обратно
пропорциональна первой степени расстояния
от заряда до точки наблюдения, а не
второй, что было бы очевидно из
пространственной (а не плоской) картины
силовых линий.
,
как на рис.1.4. Следует обратить внимание
на серьезный недостаток приведенных
картин — они двумерные, а не трехмерные,
как само электрическое поле, из-за чего
возможны недоразумения. Так, из анализа
рис.1.5 можно заключить, что напряженность
электрического точечного заряда обратно
пропорциональна первой степени расстояния
от заряда до точки наблюдения, а не
второй, что было бы очевидно из
пространственной (а не плоской) картины
силовых линий.
Поле точечного заряда и заряженного шара. Принцип суперпозиции полей
Поле точечного заряда и заряженного шара. Принцип суперпозиции полей
«Физика — 10 класс»
Что показывают силовые линии?
Для чего они используются?
Напряжённость поля точечного заряда.
Найдём напряжённость электрического поля, создаваемого точечным зарядом q0. По закону Кулона этот заряд будет действовать на положительный заряд q с силой
Модуль напряжённости поля точечного заряда q0 на расстоянии г от него равен:
Вектор напряжённости в любой точке электрического поля направлен вдоль прямой, соединяющей эту точку и заряд (рис. 14.14), и совпадает с силой, действующей на точечный положительный заряд, помещённый в данную точку.
Силовые линии электрического поля точечного заряда, как следует из соображений симметрии, направлены вдоль радиальных линий (рис. 14.15, а).
Поле заряженного шара.
Рассмотрим теперь вопрос об электрическом поле заряженного проводящего шара радиусом R. Заряд q равномерно распределён по поверхности шара. Силовые линии электрического поля, также из соображений симметрии, направлены вдоль продолжений радиусов шара (рис. 14.15, б).
Распределение в пространстве силовых линий электрического поля шара с зарядом q на расстояниях r ≥ R от центра шара аналогично распределению силовых линий поля точечного заряда q (см. рис. 14.15, а). Следовательно, на расстоянии r ≥ R от центра шара напряжённость поля определяется той же формулой (14.9), что и напряжённость поля точечного заряда, помещённого в центре сферы:
Внутри проводящего шара (r < R) напряженность поля равна нулю.
Принцип суперпозиции полей.
Если на тело действует несколько сил, то согласно законам механики результирующая сила равна геометрической сумме этих сил:
= 1 + 2 + … .
На электрические заряды действуют силы со стороны электрического поля. Если при наложении полей от нескольких зарядов эти поля не оказывают никакого влияния друг на друга, то результирующая сила со стороны всех полей должна быть равна геометрической сумме сил со стороны каждого поля. Опыт показывает, что именно так и происходит на самом деле. Это означает, что напряжённости полей складываются геометрически.
В этом состоит принцип суперпозиции полей.
Если в данной точке пространства различные заряженные частицы создают электрические поля, напряжённости которых 1, 2, 3 и т. д., то результирующая напряжённость поля в этой точке равна сумме напряжённостей этих полей:
= 1 + 2 + 3 + … . (14.11)
Напряжённость поля, создаваемого отдельным зарядом, определяется так, как будто других зарядов, создающих поле, не существует.
Согласно принципу суперпозиции полей для нахождения напряжённости поля системы заряженных частиц в любой точке достаточно знать выражение (14.9) для напряжённости поля точечного заряда.
Для определения направления векторов напряжённостей полей отдельных зарядов мысленно помещаем в выбранную точку положительный заряд.
На рисунке 14.16 показано, как определяется напряжённость поля в точке А, созданного двумя точечными зарядами q1 и q2.
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Электростатика — Физика, учебник для 10 класса — Класс!ная физика
Что такое электродинамика — Электрический заряд и элементарные частицы. Закон сохранения заряд — Закон Кулона. Единица электрического заряда — Примеры решения задач по теме «Закон Кулона» — Близкодействие и действие на расстоянии — Электрическое поле — Напряжённость электрического поля. Силовые линии — Поле точечного заряда и заряженного шара. Принцип суперпозиции полей — Примеры решения задач по теме «Напряжённость электрического поля. Принцип суперпозиции полей» — Проводники в электростатическом поле — Диэлектрики в электростатическом поле — Потенциальная энергия заряженного тела в однородном электростатическом поле — Потенциал электростатического поля и разность потенциалов — Связь между напряжённостью электростатического поля и разностью потенциалов. Эквипотенциальные поверхности — Примеры решения задач по теме «Потенциальная энергия электростатического поля. Разность потенциалов» — Электроёмкость. Единицы электроёмкости. Конденсатор — Энергия заряженного конденсатора. Применение конденсаторов — Примеры решения задач по теме «Электроёмкость. Энергия заряженного конденсатора»
II. Магнитное взаимодействие
F1 = F2 = 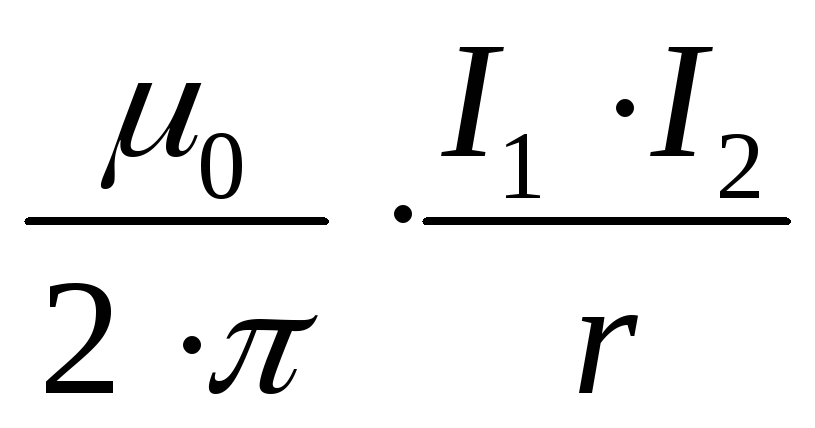 (3)
(3)
— сила взаимодействия между двумя параллельными токами
Ток магнитное полесиловое воздействие
Рис.
3
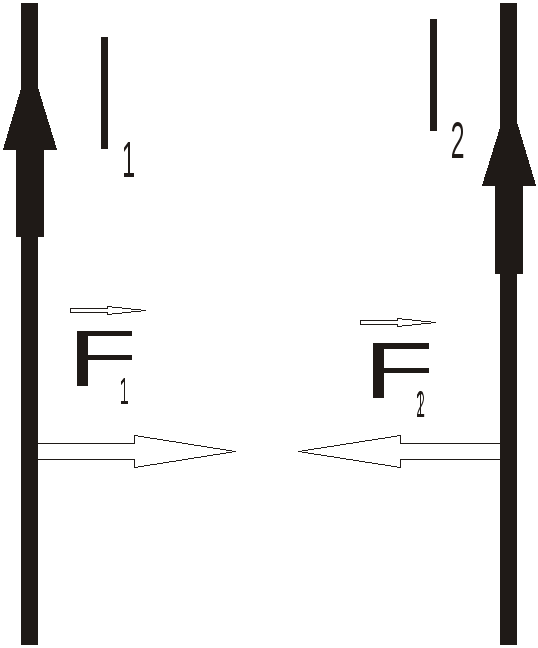
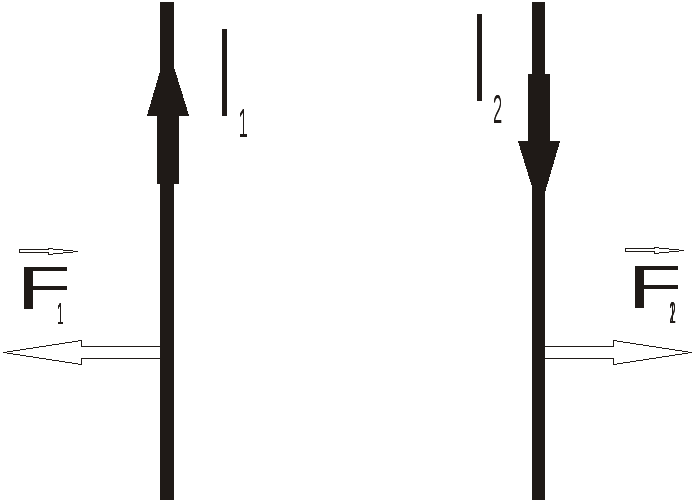 Рис.
3 Взаимодействие постоянных токов
Рис.
3 Взаимодействие постоянных токов
§ 2. Напряженность электростатического поля
Электростатика – раздел физики, который изучает существование и взаимодействие неподвижных зарядов
Электростатическое поле характеризуется двумя взаимосвязанными физическими величинами:
напряженность (силовая характеристика электростатического поля – сила, действующая на единичный неподвижный пробный положительный электрический заряд)
потенциал (энергетич. характеристика поля – работа по перемещению единичного положительного заряда из данной точки в бесконечность. В теории принимают потенциал бесконечно удаленной точки равным нулю
 .
На практикеземли = 0)
.
На практикеземли = 0)
Опыт показывает, что сила F, действующая на неподвижный точечный пробный заряд q, всегда может быть представлена как
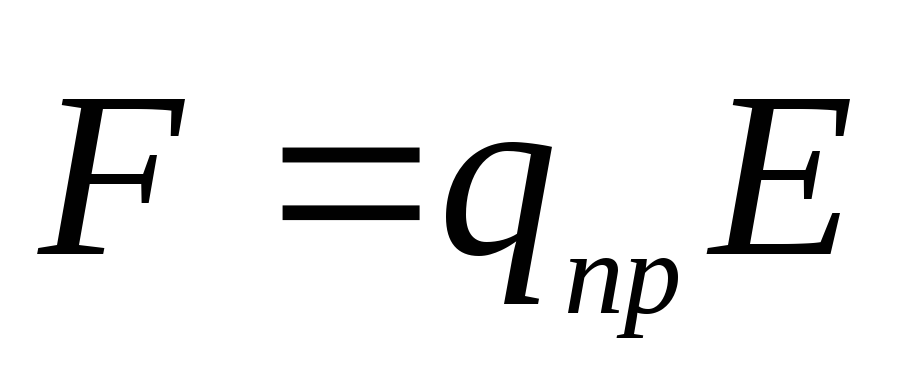 ,
(4)
,
(4)
где
вектор  называют напряженностью электрического поля в данной точке.
Вектор
называют напряженностью электрического поля в данной точке.
Вектор  ,
как видно из
(4), можно
определить как силу, действующую на
единичный положительный неподвижный
заряд. Здесь предполагается, что пробный
заряд qпр должен быть достаточно малым, чтобы его
внесение не вызвало заметного искажения
интересующего нас поля (вследствие
возможного перераспределения создающих
поле зарядов).
,
как видно из
(4), можно
определить как силу, действующую на
единичный положительный неподвижный
заряд. Здесь предполагается, что пробный
заряд qпр должен быть достаточно малым, чтобы его
внесение не вызвало заметного искажения
интересующего нас поля (вследствие
возможного перераспределения создающих
поле зарядов).
Силовая
линия – математическая линия, направление
касательной к которой в каждой точке,
через которую она проходит совпадает
с направлением вектора  ,
а густота пропорциональна модулю вектора
,
а густота пропорциональна модулю вектора .
.
Силовые линии начинаются на “+” заряж. телах и заканчиваются на “-” заряж. телах.
Напряженность поля точечного заряда
Из опыта (закон Кулона) непосредственно следует, что напряженность поля неподвижного точечного заряда q на расстоянии r от него можно представить как
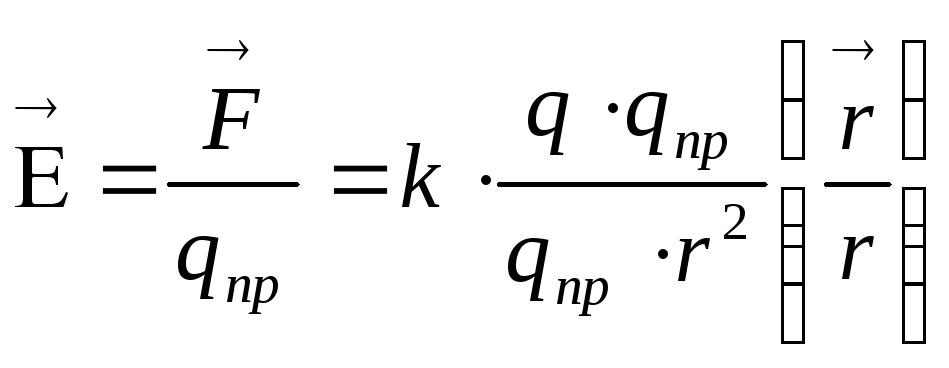
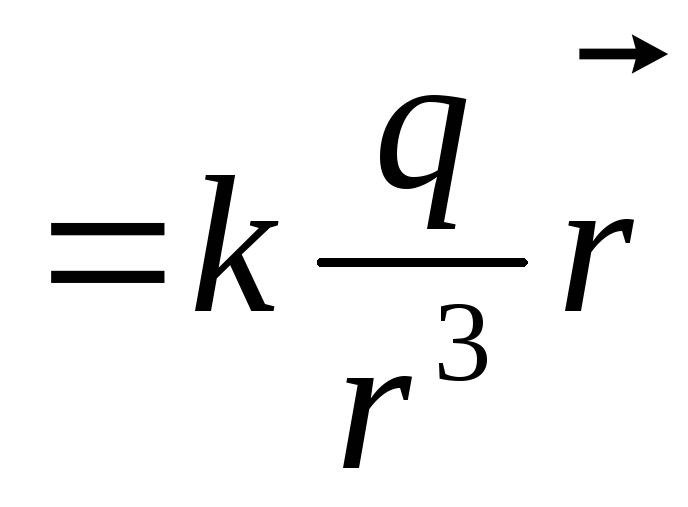 (5)
(5)
где k —
постоянная
вид, которой зависит от выбора системы
отсчета, в системе СИ 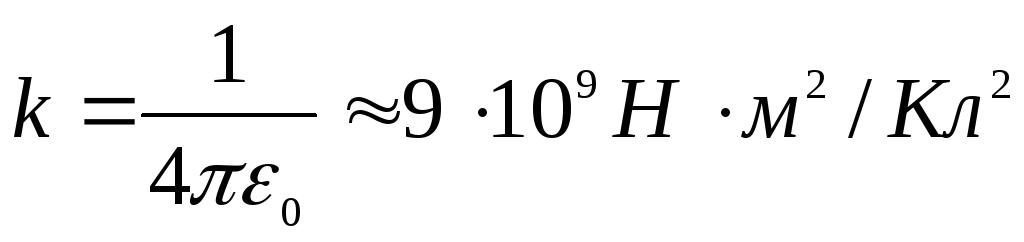 ;
ε0 — электрическая
постоянная;
;
ε0 — электрическая
постоянная; 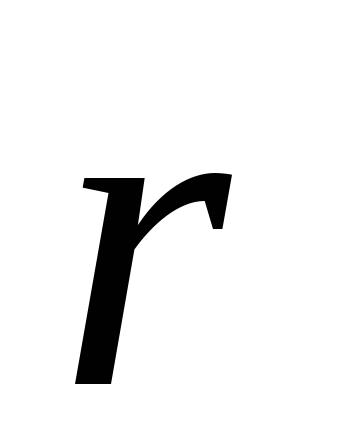 —радиус-вектор, проведенный из центра поля, в котором
расположен заряд q, до интересующей нас точки. Напряженность
поля
—радиус-вектор, проведенный из центра поля, в котором
расположен заряд q, до интересующей нас точки. Напряженность
поля  в системе СИ выражается
в вольтах
на метр (В/м). В зависимости от знака заряда q вектор
в системе СИ выражается
в вольтах
на метр (В/м). В зависимости от знака заряда q вектор  направлен так же, как и
направлен так же, как и 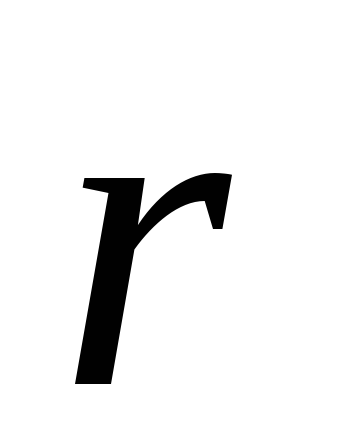 (для
положительного заряда),
или противоположно ему (для отрицательного
заряда).
(для
положительного заряда),
или противоположно ему (для отрицательного
заряда).

Рис. 4
По существу, формула выражает не что иное, как закон Кулона, но в «полевой» форме. Вся совокупность экспериментальных фактов показывает, что этот закон справедлив для расстояний от 10-14 м до нескольких километров, и пока нет никаких оснований ожидать, что этот закон не выполняется и при больших расстояниях.
Принцип суперпозиции
Напряженность поля системы точечных неподвижных зарядов равна векторной сумме напряженностей полей, которые создавали бы каждый из зарядов в отдельности:
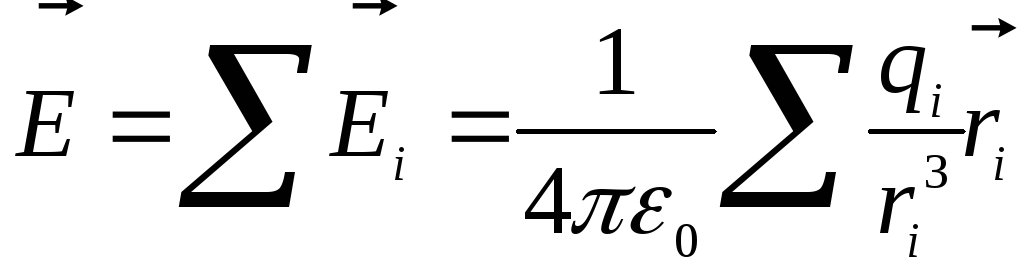 ,
(6)
,
(6)
где ri — расстояние между зарядом qi и интересующей нас точкой поля.
Это утверждение называют принципом суперпозиции (наложения) электрических полей. Поле точечного заряда является фундаментальным, потому что, используя формулу поля точечного заряда и принцип суперпозиции, можно расчитать поле любого (!) заряда.
Распределение зарядов. Для упрощения математических расчетов во многих случаях бывает удобно игнорировать тот факт, что заряды имеют дискретную структуру (электроны, ядра), и считать, что они «размазаны» определенным образом и пространстве. Другими словами, удобно заменить истинное распределение точечных дискретных зарядов фиктивным непрерывным распределением. Это позволяет значительно упрощать расчеты, не внося сколько-нибудь значительной ошибки.
При переходе к непрерывному распределению вводят понятие о плотности зарядов — объемной ρ, поверхностной σ и линейной λ. По определению,
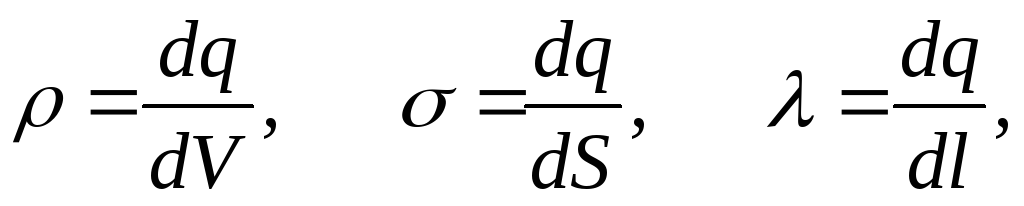 (7)
(7)
где dq — заряд, заключенный соответственно в объеме dV, на поверхности dS и на длине dl.
C учетом этих распределений формула (6) может быть представлена в другой форме. Например, если заряд распределен по объему, то надо заменить qi на dq = ρ dV и ∑ на ∫, тогда
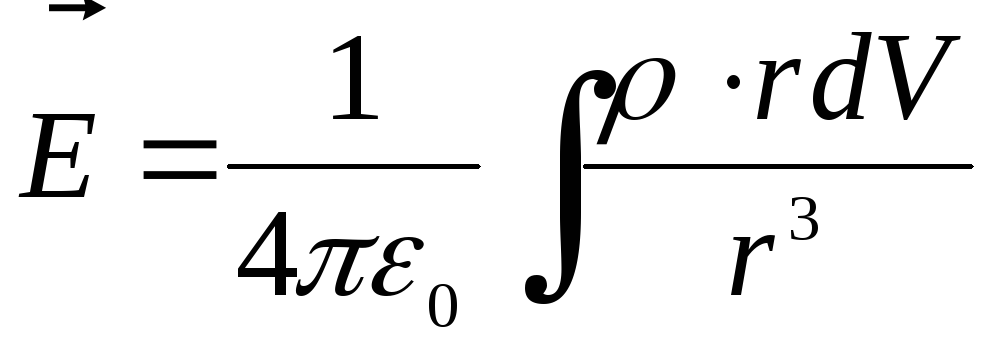 ,
(8)
,
(8)
где интегрирование проводится по всему пространству, в котором ρ отлично от нуля (Рис.5).
 V
V
dV
A
dq 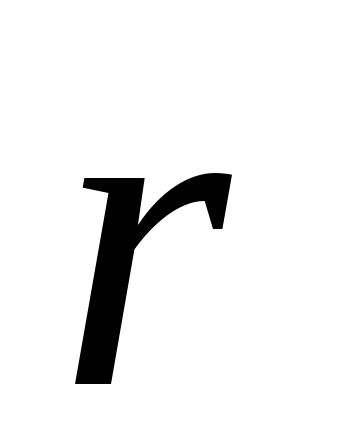
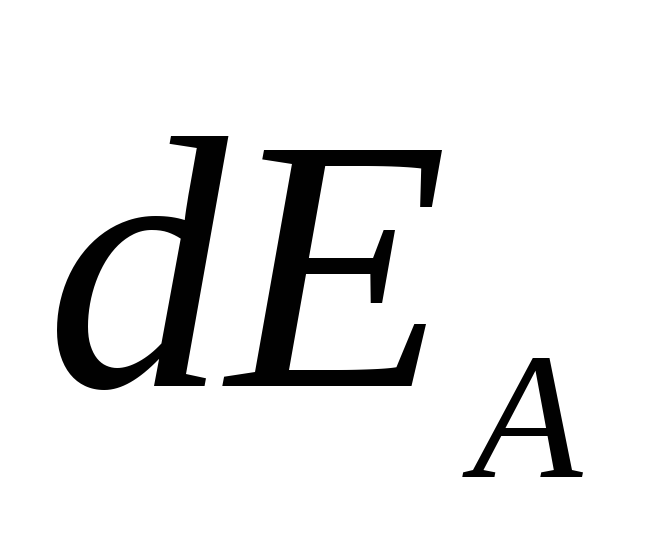
q
Рис. 5
Таким
образом, зная распределение зарядов,
мы можем полностью решить задачу о
нахождении напряженности электрического
поля по формуле
(6), если
распределение дискретно, или по формуле
(8), если
распределение непрерывно. Этот метод
нахождения электрического поля получил
название метод
непосредственного интегрирования.
В общем случае расчет сопряжен со
значительными трудностями (правда, не
принципиального характера). Действительно,
для нахождения вектора  надо вычислить сначала его проекцииЕx , Еy , Еz , а это по
существу, три интеграла типа
(8).
надо вычислить сначала его проекцииЕx , Еy , Еz , а это по
существу, три интеграла типа
(8).
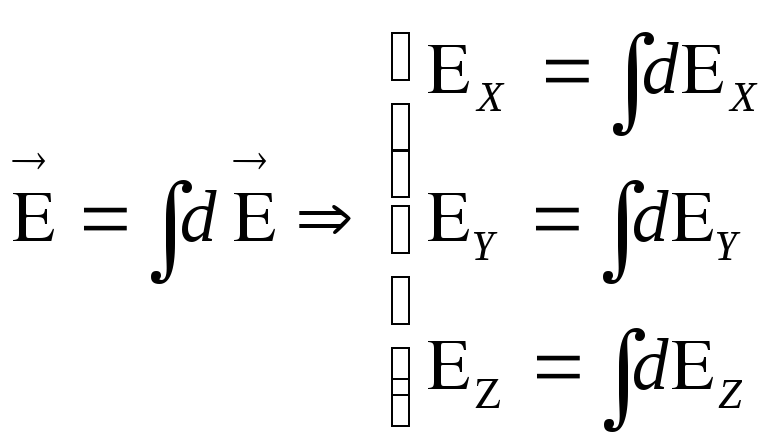 метод
непосредственного интегрирования
метод
непосредственного интегрирования
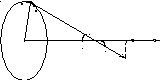
Пример 1 Заряд q > 0 равномерно распределен по тонкому кольцу радиусом R. Найти напряженность Е электрического поля на оси кольца как функцию расстояния z от его центра.
Решение. Легко сообразить, что в данном случае
вектор Е должен быть направлен по оси
кольца (рис.
2). Выделим
на кольце элемент dl. Запишем выражение для составляющей 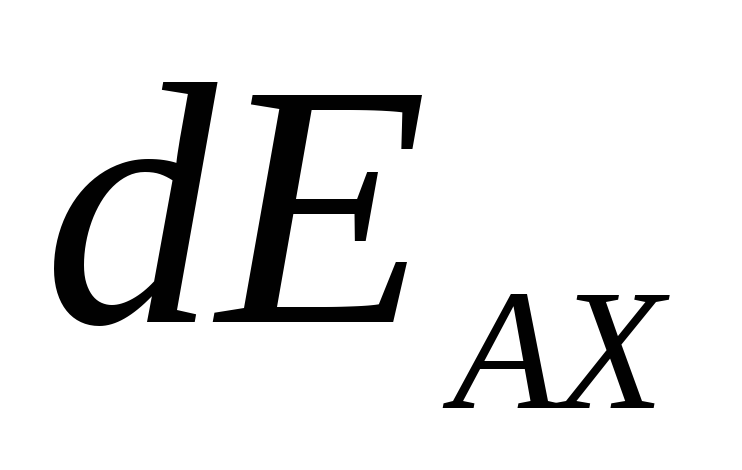 от этого элемента в точке А:
от этого элемента в точке А:
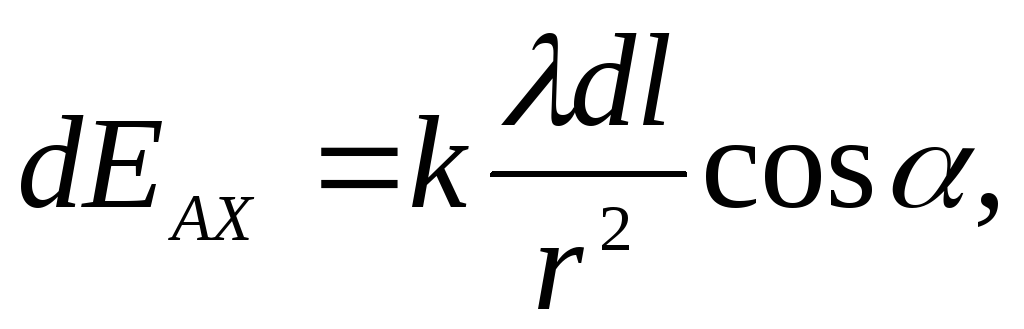
где λ = q/2πR. Для всех элементов кольца r и R будут одними и теми же, поэтому интегрирование этого выражения сводится просто к замене dl на q.
dl
 r
r
R
0 α  x
x
Рис.2
В результате получаем:
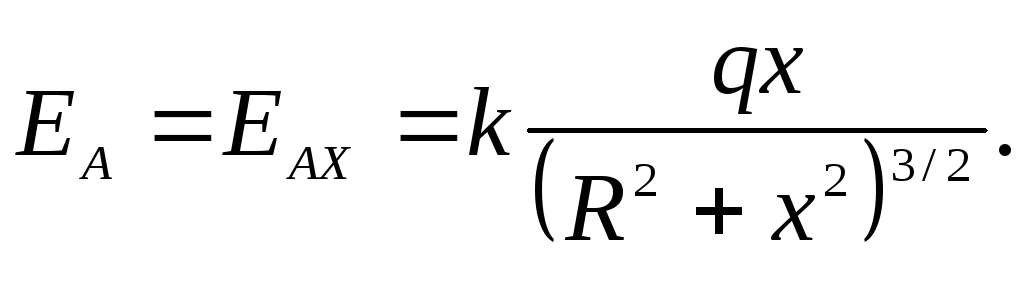
Видно, что при x » а поле Е = q/4πε0x2 , т. е. на больших расстояниях эта система ведет себя как точечный заряд.
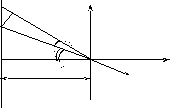 В
Y
В
Y
dl C
A
r dα
α О X
D
r0
Рис. 6
Пример 2:Рассчитать напряженность поля прямой бесконечной нити, равномерно заряженной с линейной плотностьюλ, в точке А, удаленной от нити на расстояние r0 .(рис. 6)Решение.
Разделим нить на столь малые элементы, в пределах которых можно считать заряд точечным. Рассмотрим один такой элемент длиной dlс зарядомdq=λdl(рис. 6).
В точке О элементарная напряженность поля этого заряда
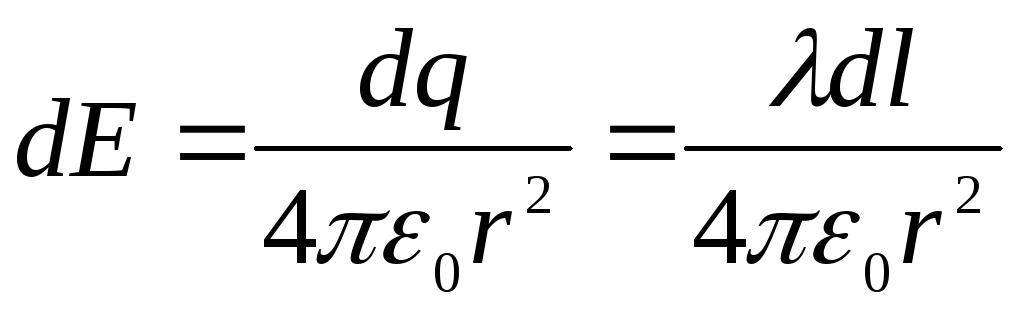 .
.
Из
треугольника ADOнаходим: .
Так как
.
Так как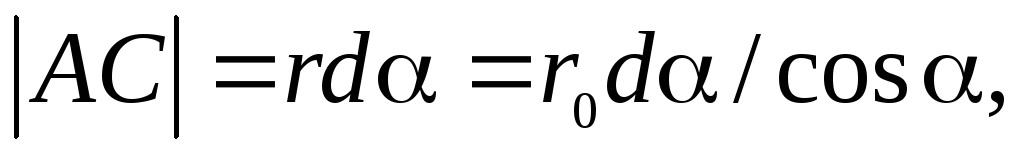 то из треугольникаABCопределяем:
то из треугольникаABCопределяем:
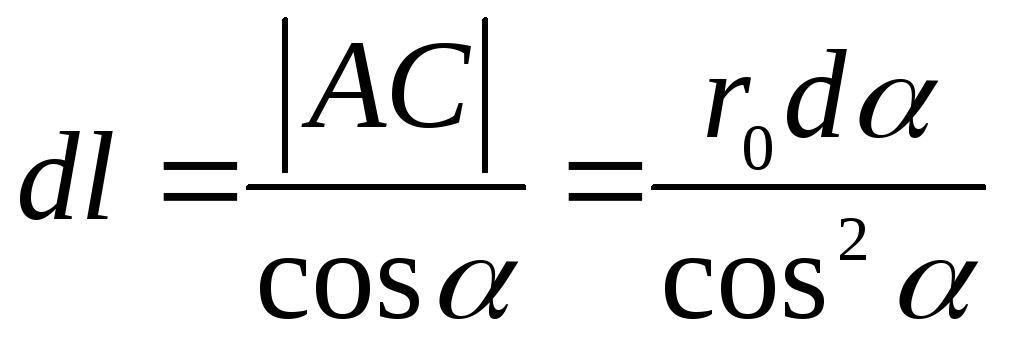 .
.
Подставляя значения r, dα, получаем:
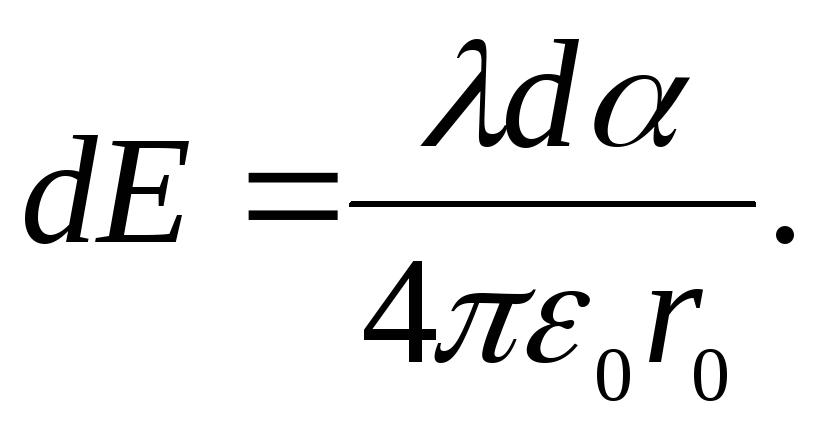
Проекции
вектора  на оси ОXи ОY:
на оси ОXи ОY:
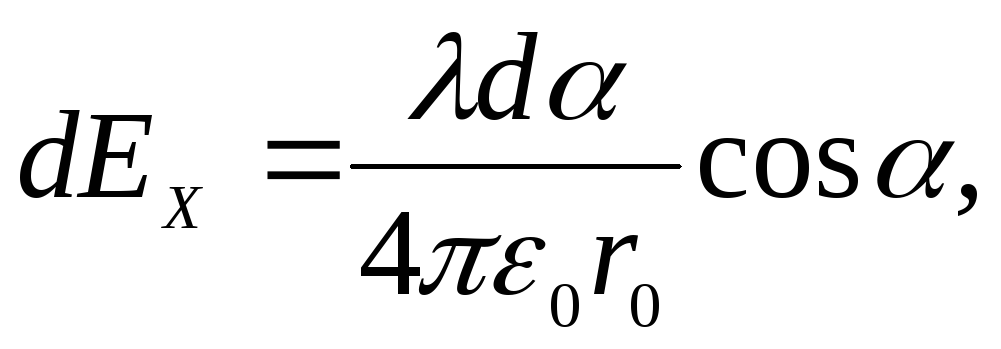
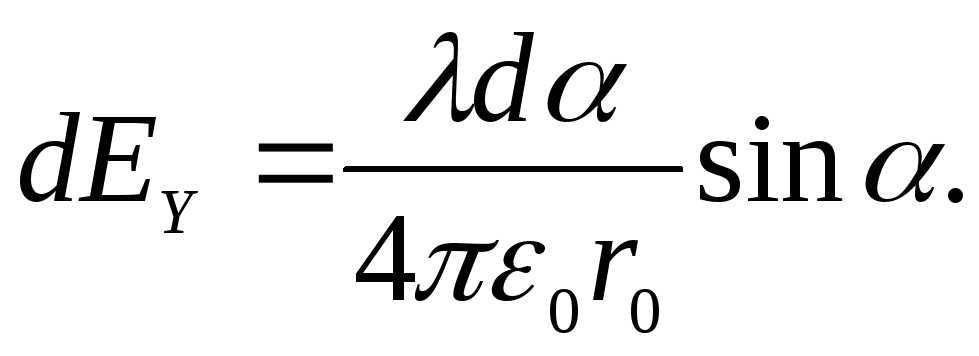
Отсюда после интегрирования получаем:
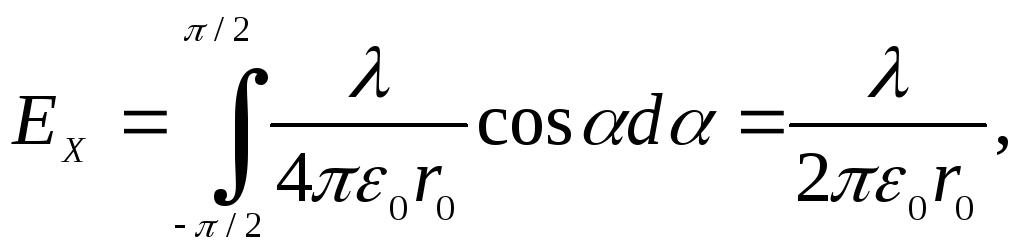

Окончательно получаем:
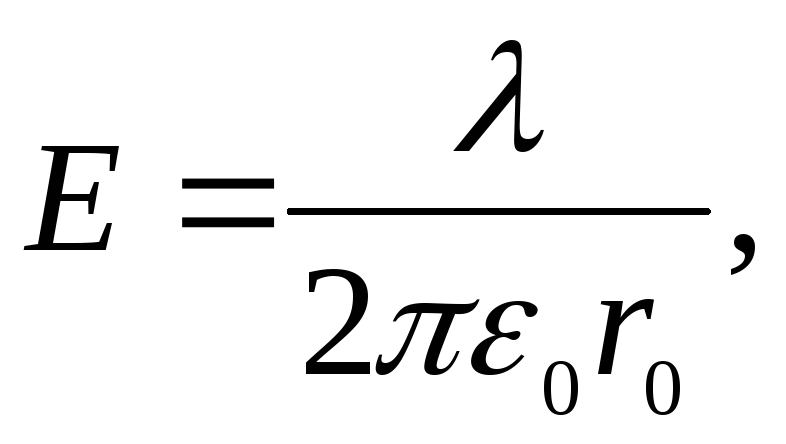
3.1.4 Напряжённость электрического поля. Поле точечного заряда
Видеоурок 1: Напряженность электрического поля
Видеоурок 2: Электрическое поле точечных зарядов
Лекция: Напряжённость электрического поля. Поле точечного заряда
 Электрическое поле
Электрическое полеС помощью закона Кулона мы можем определить силу, с которой взаимодействуют заряды, однако он никоим образом не объясняет природу появления данного взаимодействия. Считается, что для действия одного заряженного тела на другое между телами не обязательно должна быть проводящая среда — взаимодействие происходит даже в вакууме, однако оно изменяется с увеличением расстояния. Данный принцип лежит в основе дальнего действия зарядов.
Иные размышления настаивали на близком действии зарядов. Считается, что действие одного заряда на другой происходит только спустя некоторое время, что характеризуется его скоростью распространения. После этого был сделан вывод, что некая материя является переносчиком действия — это было электромагнитное поле. Однако до тех пор, пока мы рассматриваем неподвижные заряды, речь будет идти исключительно об электрическом поле.
Именно по средствам электрического поля и происходит действие одного заряда на другие. Для того, чтобы определить наличие поля используют пробный заряд. С помощью пробного заряда можно определить не только наличие поля, но и его интенсивность.
 Напряжённость электрического поля
Напряжённость электрического поляИнтенсивность поля характеризуется ФВ, которая определяется отношением силы к величине пробного заряда. Данная величина называется напряженностью.
Вычисляется по формуле:

Е — напряженность электрического поля
F — сила, с которой поле действует на пробный положительный заряд
q — величина этого заряда
Напряженность — это векторная ФВ, что зависит от направления силы и знака пробного заряда.
Измеряется в Н/Кл или В/м.
 Напряжённость поля точечного заряда
Напряжённость поля точечного заряда
Если пробный заряд находится не в вакууме, а в некоторой среде, то в знаменателе дроби появляется диэлектрическая проницаемость среды.
Чем дальше пробный заряд находится от рассматриваемого заряженного тела, тем меньшая сила на него действует. Это говорит о том, что напряженность электрического поля становится меньше по мере отдаления от заряженного тела.
Электрическое поле показывают с помощью специальных линий, которые называются линиями напряженности поля.
21. Электрическое поле. Напряженность поля. Поле точечного заряда. Графическое изображение электростатических полей. Принцип суперпозиции полей. Поле системы зарядов
Взаимодействия зарядов передаются с помощью особого материального посредника, называемого электрическим полем. Взаимодействие двух зарядов q1 и q2 можно объяснить так: в пространстве вокруг заряда q1 существует особая форма материи – электрическое поле, которое и действует непосредственно на заряд q2. Действие электрического поля на помещенный в него заряд является основным его свойством.
Электрическое поле, созданное неподвижными зарядами, называется электростатическим.
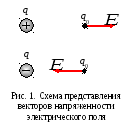
Напряженность электростатического поля
Напряженность
поля  — векторная характеристика
электрического поля. Напряженность
поля в некоторой точке определяется
отношением силы
— векторная характеристика
электрического поля. Напряженность
поля в некоторой точке определяется
отношением силы ,
действующей со стороны поля на
положительный зарядq0,
помещенный в данную точку поля, к величине
этого заряда:
,
действующей со стороны поля на
положительный зарядq0,
помещенный в данную точку поля, к величине
этого заряда:
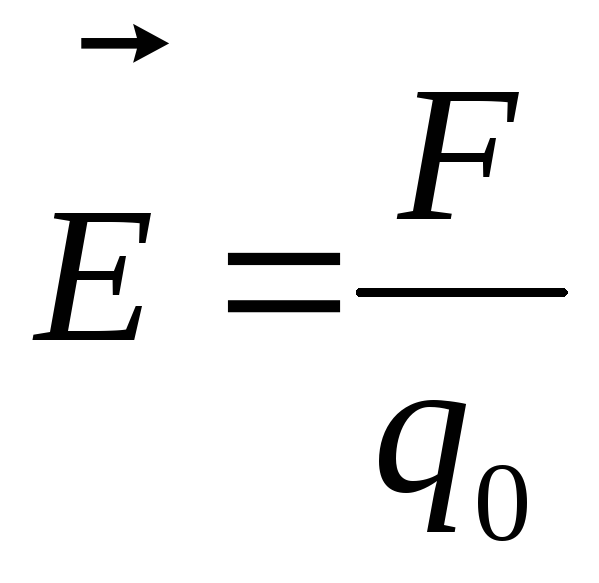 , [
, [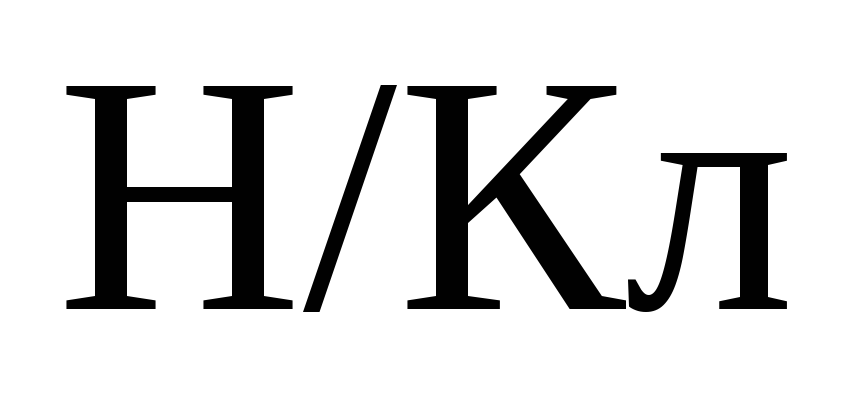 ].
].
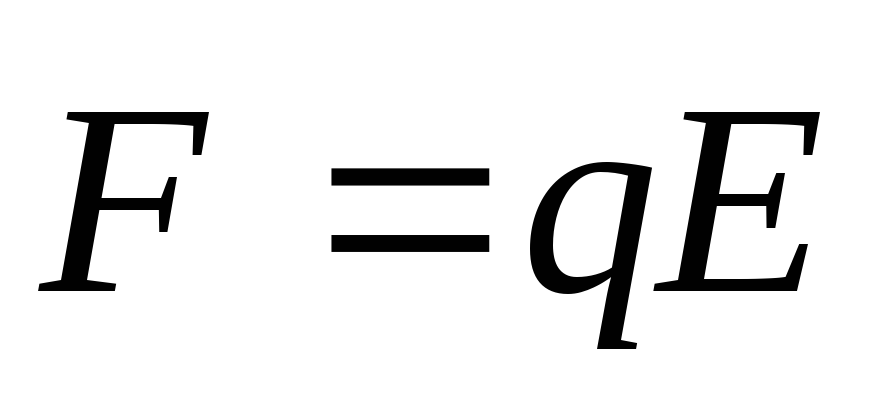 (1)
(1)
Напряженность электрического поля точечного заряда
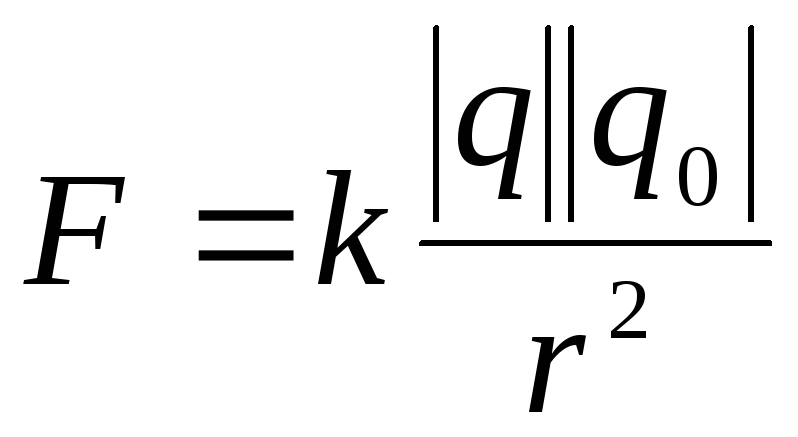

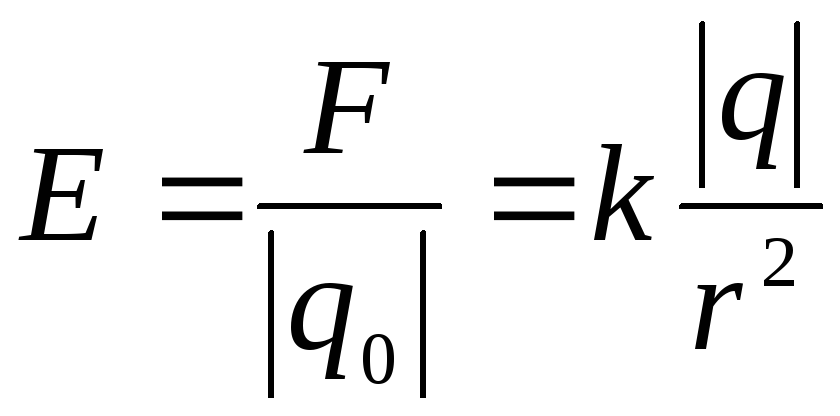

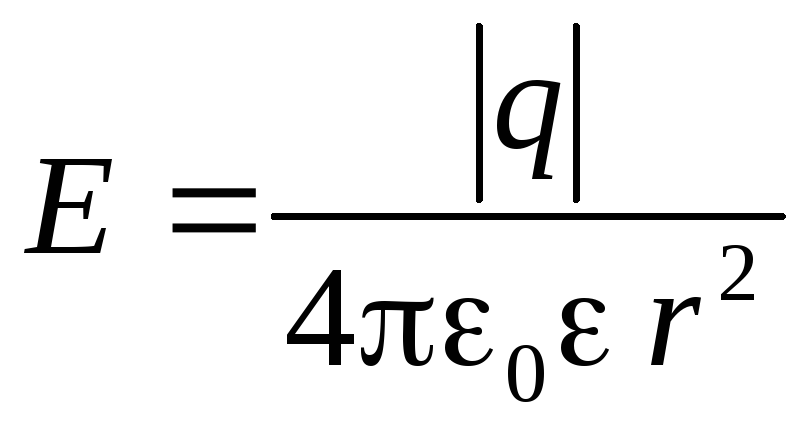 . (2)
. (2)
Принцип суперпозиции полей
Напряженность поля, создаваемая в какой-либо точке пространства системой зарядов, равна векторной сумме напряженностей, создаваемых в этой точке каждым из зарядов:
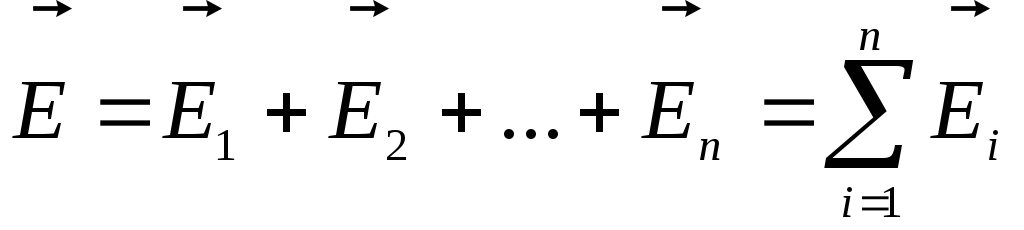 (3)
(3)
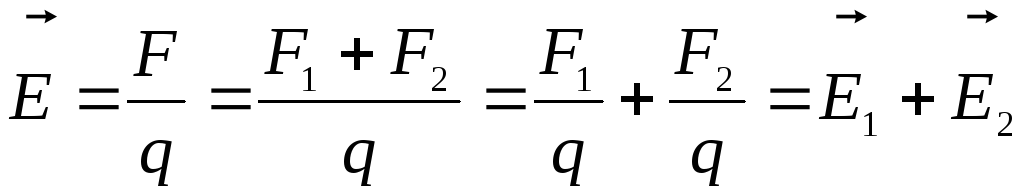
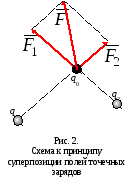
Напряженность
поля непрерывно распределенного заряда: 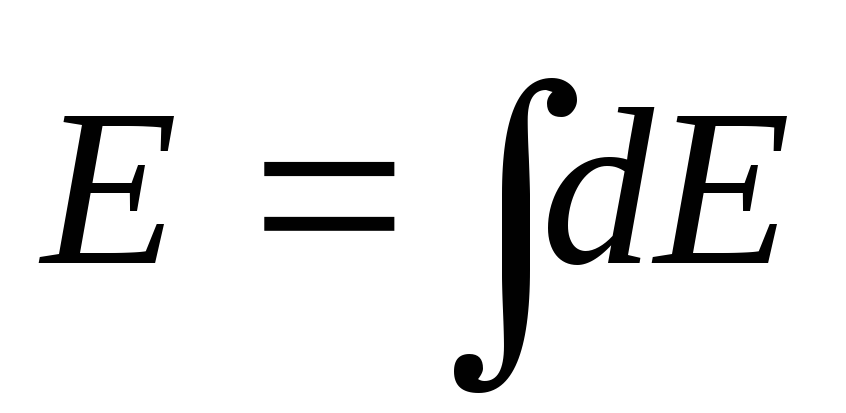 . (4)
. (4)
Характеристики распределенных зарядов
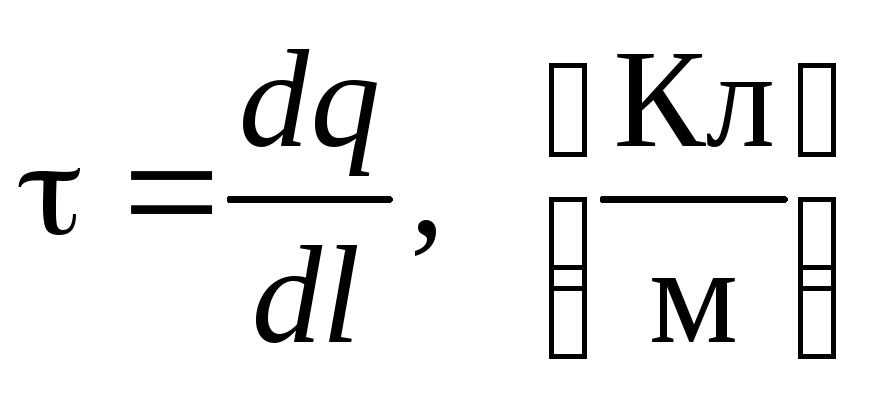 — линейная
плотность зарядов;
— линейная
плотность зарядов;
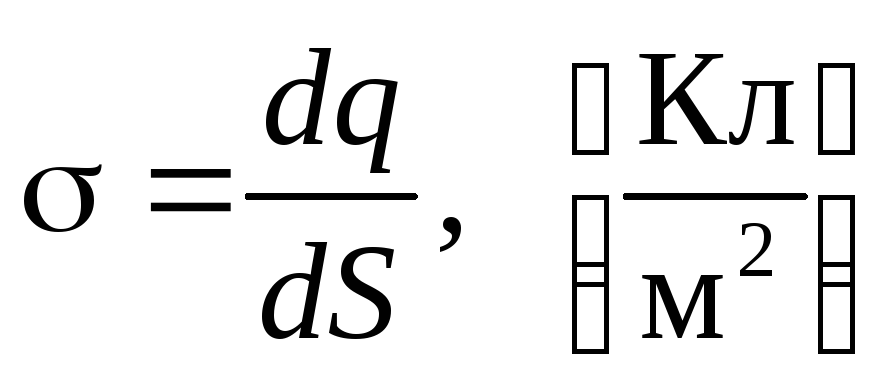 — поверхностная
плотность зарядов;
— поверхностная
плотность зарядов;
 — объемная плотность
зарядов;
— объемная плотность
зарядов;
Графическое изображение электрических полей. Силовые линии

Свойства силовых линий
силовые линии всегда начинаются на положительных зарядах и заканчиваются на отрицательных;
силовые линии начинаются и заканчиваются либо на зарядах, либо уходят в бесконечность;
густота силовых линий (число силовых линий, проходящих через единицу площади) пропорциональна напряженности электрического поля;
силовые линии не пересекаются.
Примеры электрических полей
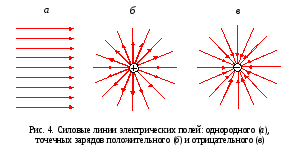


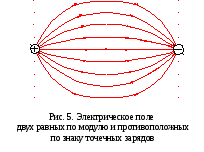
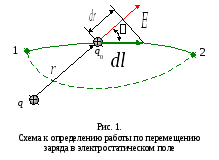
22. Работа сил электростатического поля по перемещению зарядов. Циркуляция вектора напряженности. Потенциальный характер электростатического поля.
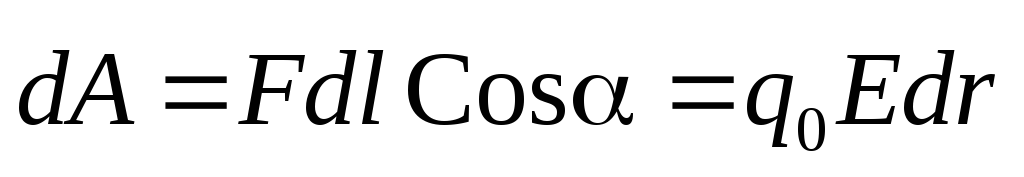 (1)
(1)
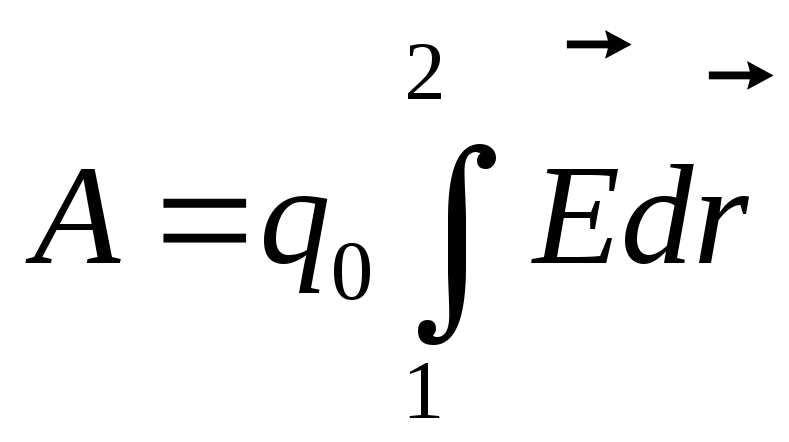 .
(2)
.
(2)
С учетом того, что
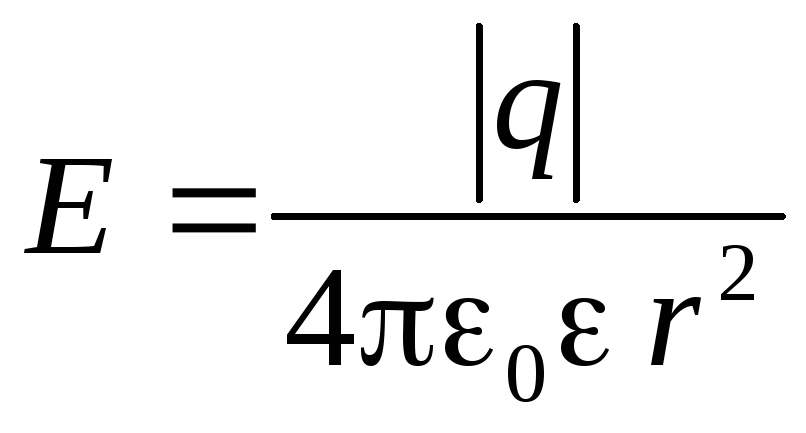
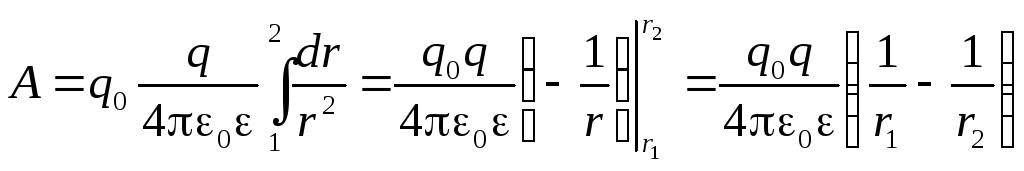 . (3)
. (3)
Работа по перемещению заряда не зависит от формы траектории и пройденного зарядом пути, а зависит только от начального и конечного положения заряда. Такое поле называется потенциальным, а кулоновская сила – консервативной.
При движении заряда по замкнутой траектории (r1 = r2) работа равна нулю
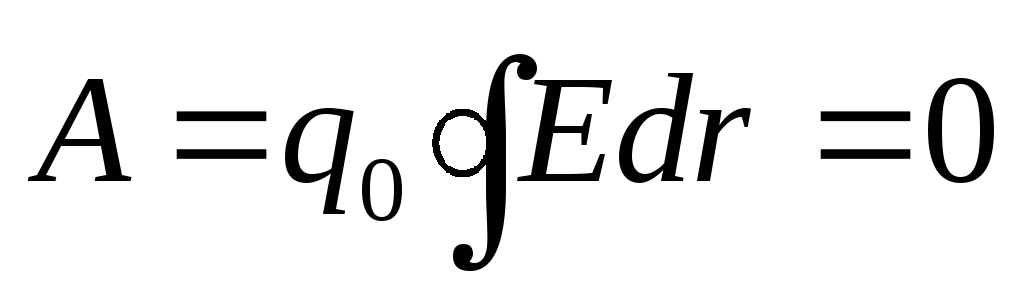 .
(4)
.
(4)
Интеграл  называется циркуляцией
вектора напряженности.
называется циркуляцией
вектора напряженности.
В частном случае
при перемещении заряда q0 из точки 1 с произвольным радиусом r1 = r в бесконечность (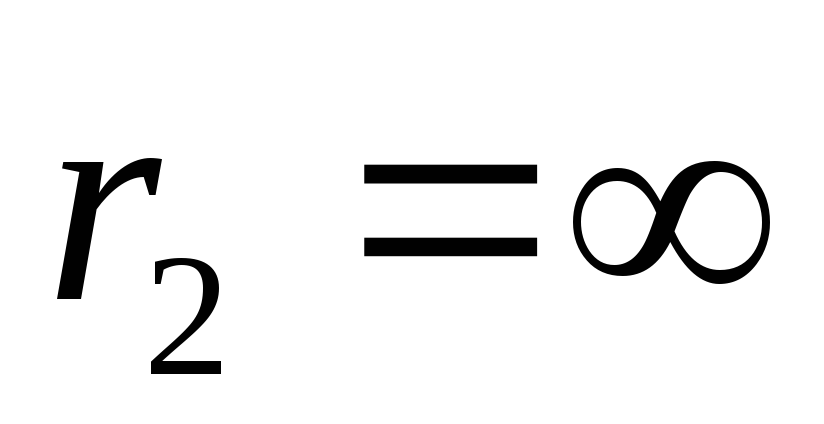 )
)
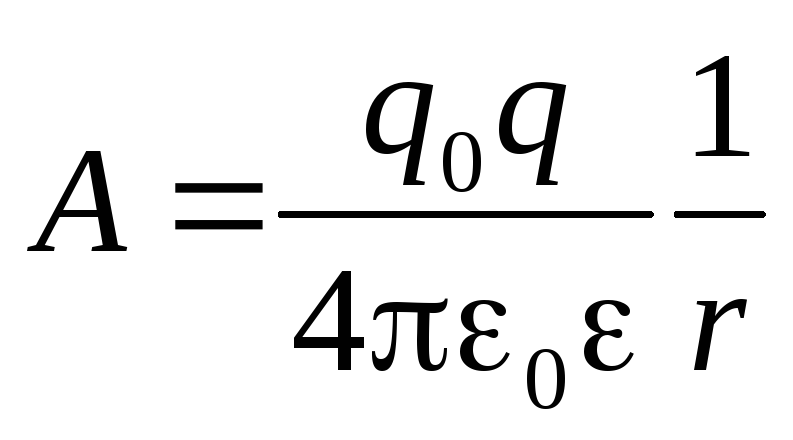 .
(5)
.
(5)




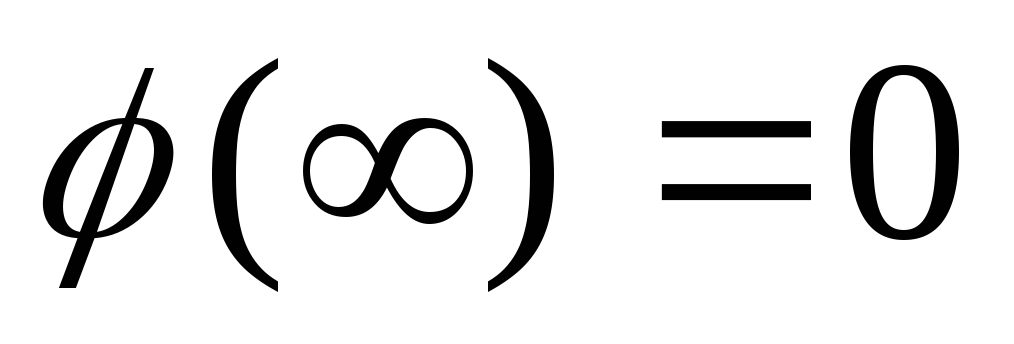 .
На практикеземли = 0)
.
На практикеземли = 0)