Лекция №5 потенциал и разность потенциалов электростатического поля

Наряду с напряжённостью, для характеристики электростатического поля вводят ещё одну физическую величину, называемую потенциалом, которая является энергетической характеристикой этого поля. Она равна

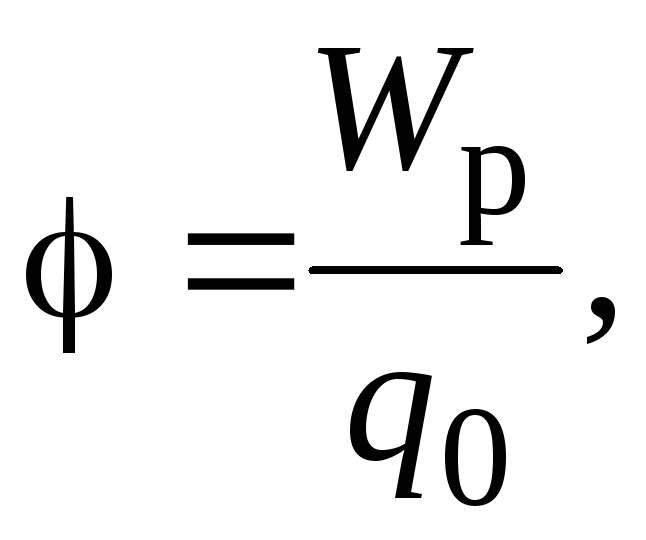(1)

т.е. потенциалом электростатического поля называется отношение потенциальной энергии, которой обладает заряд в некоторой точке поля, к величине этого заряда.

Разность потенциалов находится по формуле:

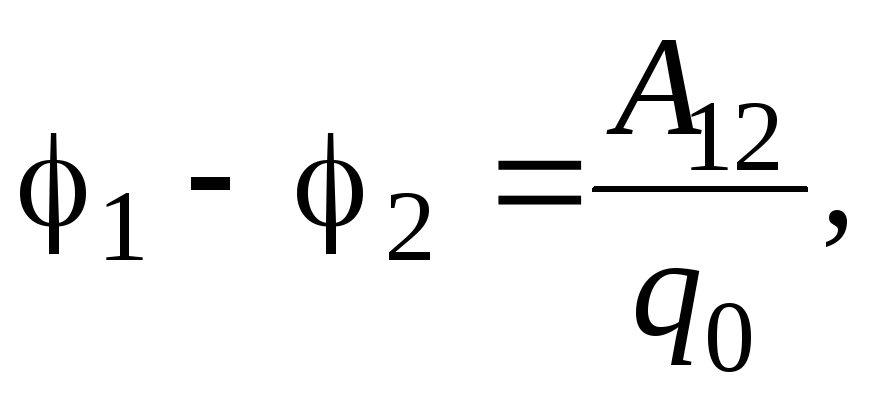(2)

т.е. разностью потенциалов электростатического поля называется отношение работы, совершаемой силами поля при перемещении заряда из одной точки поля в другую, к величине этого заряда.

В системе единиц СИ потенциал и разность потенциалов измеряется в вольтах (B).

Связь между напряжённостью и потенциалом

Электростатическое поле характеризуется двумя физическими величинами  напряжённостью и потенциалом. Они связаны между собой соотношением:

(3)

т.е. проекция напряжённости на какое-либо направление в каждой точке поля равна производной потенциала по данному направлению, взятой с противоположным знаком. Знак минус в выражении (3) указывает на то, что напряжённость в любой точке поля направлена в сторону убывания потенциала.

Из формулы (3) можно найти разность потенциалов ₁ – ₂ между токами, находящимися в однородном электростатическом поле на расстоянии d по линии напряжённости: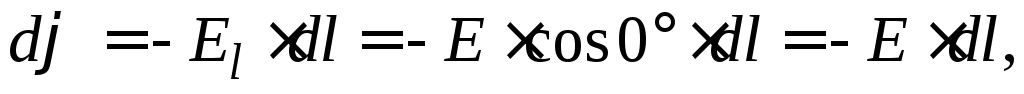

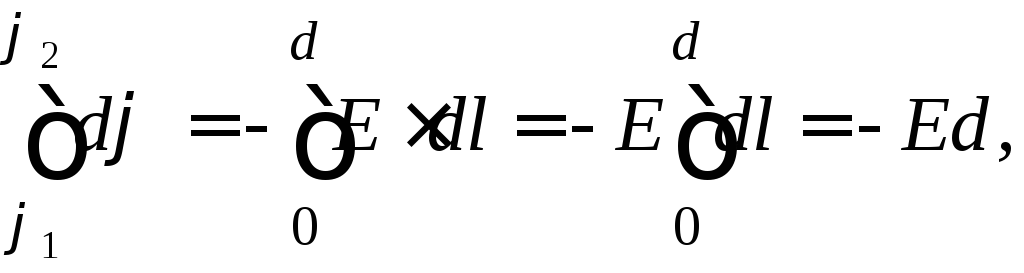
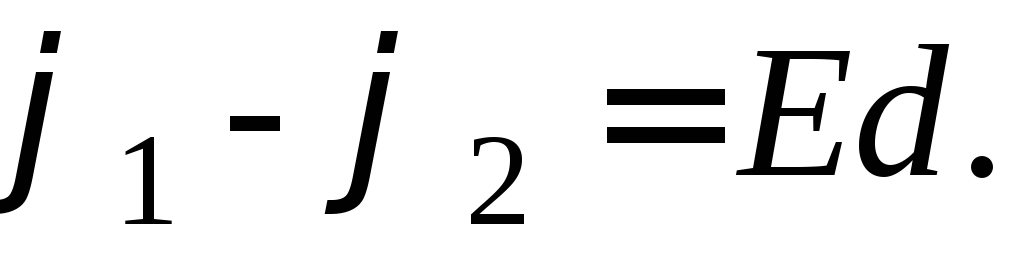(4)

Конденсаторы

Электроёмкостью С конденсатора называется отношение заряда q на конденсаторе к разности потенциалов

₁ – ₂ между его обкладками:

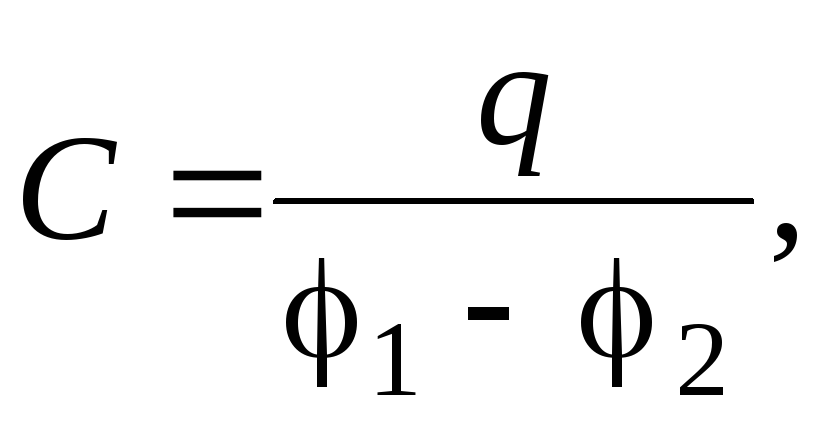(5)

В системе СИ ёмкость измеряется в фарадах.

Энергия заряженного конденсатора

Процесс возникновения разноимённых зарядов на обкладках конденсатора можно представить так, что от одной обкладки отнимается некоторый заряд и передаётся другой. Пусть разность потенциалов между обкладками в какой-то момент времени равна ₁  ₂. Тогда при перемещении элементарного заряда dq изменением этой разности потенциалов можно пренебречь, и элементарная работа dA по переносу данного заряда равна

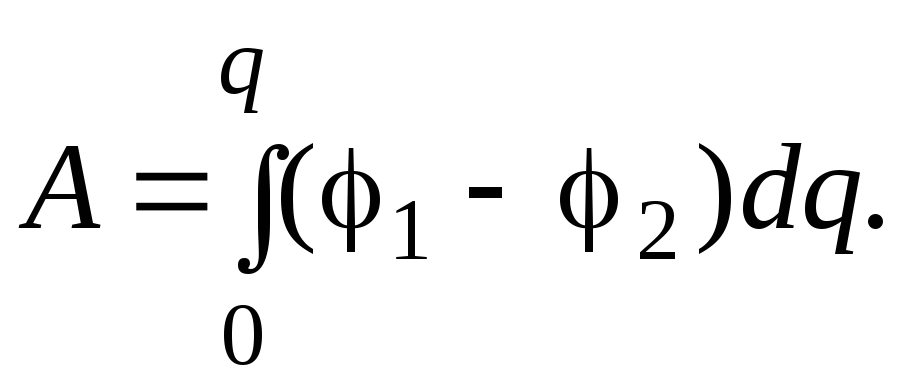dA = (₁  ₂)dq. Полная работа, необходимая для сообщения конденсатору заряда q, находится по формуле Используя формулу ёмкости конденсатора, находим, что₁  ₂ = q/C, где C — ёмкость конденсатора. Тогда 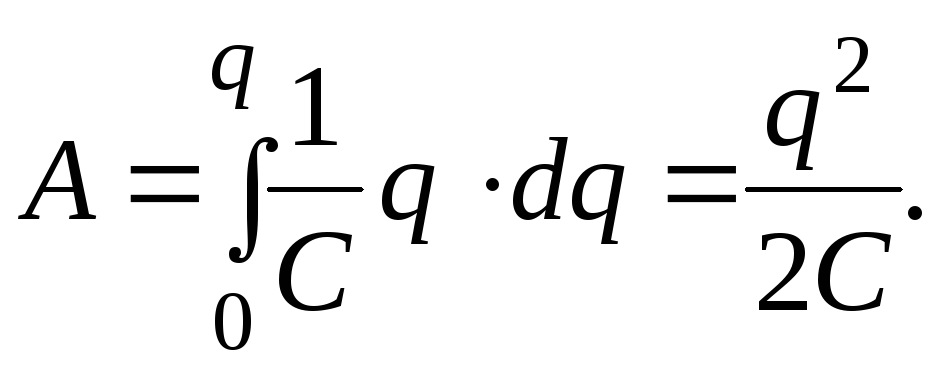Очевидно, что электрическая энергияW_E заряженного конденсатора равна этой работе, т.е.

W_E = q²/(2C). (6)

Учитывая, что q = (₁  ₂)C, выражение (5) запишем в ином виде

W_E = (1/2)C(₁  ₂)². (7)

Энергия электрического поля.

Энергия заряженных проводников запасена в виде электрического поля. Поэтому целесообразно выразить её через напряжённость, характеризующую это поле. Это проще всего проделать для плоского конденсатора. В этом случае ₁  ₂ = Ed, где d — расстояние между обкладками, и C = ₀ S/d. Здесь ₀ — электрическая постоянная,  — диэлектрическая проницаемость диэлектрика, заполняющего конденсатор,

d — расстояние между обкладками конденсатора, S — площадь каждой обкладки. Подставляя эти выражения в (7), получаем

W_E = (1/2)₀E²V. (8)

Здесь V = Sd — объём, занимаемый полем, равный объёму конденсатора.

Введём понятие объёмной плотности энергии. Пусть энергия поля W_E равномерно распределена по объёму V. Тогда объёмная плотность w_E энергии равна:

w_E = W_E /V, (9)

т.е. объёмная плотность энергии —это энергия поля в единице объёма.

В случае конденсатора, заполненного диэлектриком, объёмная плотность энергии, как следует из (7) и (8), находится по формуле

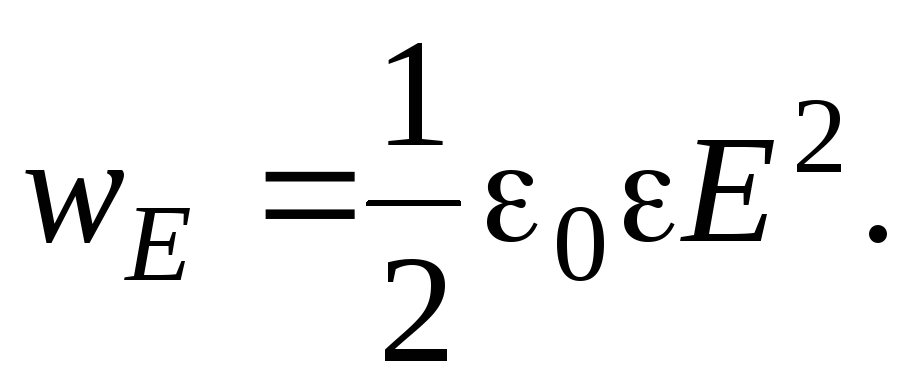(10)

В заключении отметим, что эта формула справедлива не только для конденсатора, но и для других электрических полей, в том числе и для переменных.

Лекция №5 потенциал и разность потенциалов электростатического поля

Наряду с напряжённостью, для характеристики электростатического поля вводят ещё одну физическую величину, называемую потенциалом, которая является энергетической характеристикой этого поля. Она равна

(1)

т.е. потенциалом электростатического поля называется отношение потенциальной энергии, которой обладает заряд в некоторой точке поля, к величине этого заряда.

Разность потенциалов находится по формуле:

(2)

т.е. разностью потенциалов электростатического поля называется отношение работы, совершаемой силами поля при перемещении заряда из одной точки поля в другую, к величине этого заряда.

В системе единиц СИ потенциал и разность потенциалов измеряется в вольтах (B).

Связь между напряжённостью и потенциалом

Электростатическое поле характеризуется двумя физическими величинами  напряжённостью и потенциалом. Они связаны между собой соотношением:

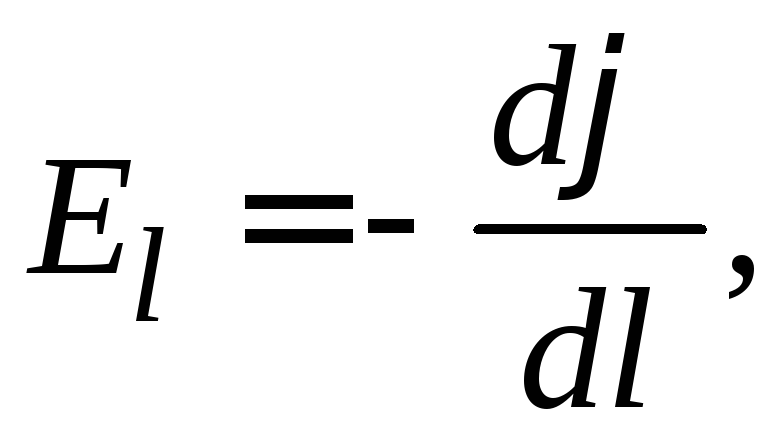(3)

т.е. проекция напряжённости на какое-либо направление в каждой точке поля равна производной потенциала по данному направлению, взятой с противоположным знаком.

Знак минус в выражении (3) указывает на то, что напряжённость в любой точке поля направлена в сторону убывания потенциала.

Из формулы (3) можно найти разность потенциалов ₁ – ₂ между токами, находящимися в однородном электростатическом поле на расстоянии d по линии напряжённости: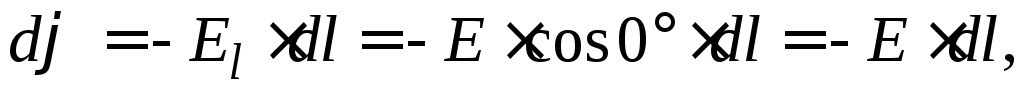

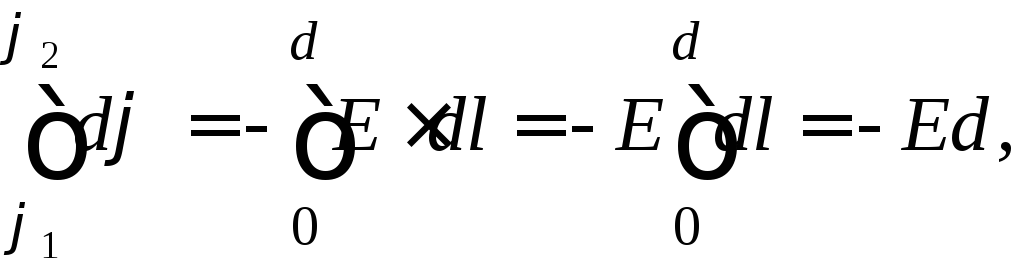
(4)

Конденсаторы

Электроёмкостью С конденсатора называется

отношение заряда q на конденсаторе к разности потенциалов ₁ – ₂ между его обкладками:

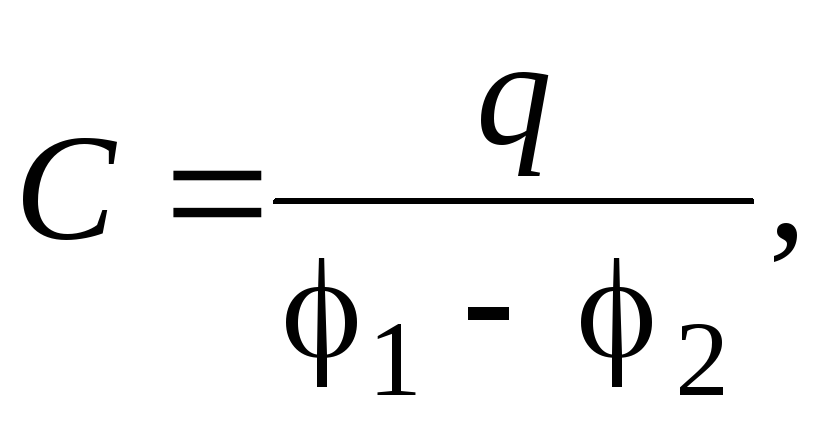(5)

В системе СИ ёмкость измеряется в фарадах.

Энергия заряженного конденсатора

Процесс возникновения разноимённых зарядов на обкладках конденсатора можно представить так, что от одной обкладки отнимается некоторый заряд и передаётся другой. Пусть разность потенциалов между обкладками в какой-то момент времени равна ₁  ₂. Тогда при перемещении элементарного заряда dq изменением этой разности потенциалов можно пренебречь, и элементарная работа

dA по переносу данного заряда равна dA = (₁  ₂)dq. Полная работа, необходимая для сообщения конденсатору заряда q, находится по формуле Используя формулу ёмкости конденсатора, находим, что₁  ₂ = q/C, где C — ёмкость конденсатора. Тогда Очевидно, что электрическая энергияW_E заряженного конденсатора равна этой работе, т.е.

W_E = q²/(2C)

. (6)

Учитывая, что q = (₁  ₂)C, выражение (5) запишем в ином виде

W_E = (1/2)C(₁  ₂)². (7)

Энергия электрического поля.

Энергия заряженных проводников запасена в виде электрического поля. Поэтому целесообразно выразить её через напряжённость, характеризующую это поле. Это проще всего проделать для плоского конденсатора. В этом случае ₁  ₂ = Ed, где d — расстояние между обкладками, и C = ₀ S/d. Здесь ₀ — электрическая постоянная,  — диэлектрическая проницаемость диэлектрика, заполняющего конденсатор, d — расстояние между обкладками конденсатора, S — площадь каждой обкладки. Подставляя эти выражения в (7), получаем

W_E = (1/2)₀E²V. (8)

Здесь V = Sd — объём, занимаемый полем, равный объёму конденсатора.

Введём понятие объёмной плотности энергии. Пусть энергия поля W_E равномерно распределена по объёму V. Тогда объёмная плотность w_E энергии равна:

w_E = W_E /V, (9)

т.е. объёмная плотность энергии —это энергия поля в единице объёма.

В случае конденсатора, заполненного диэлектриком, объёмная плотность энергии, как следует из (7) и (8), находится по формуле

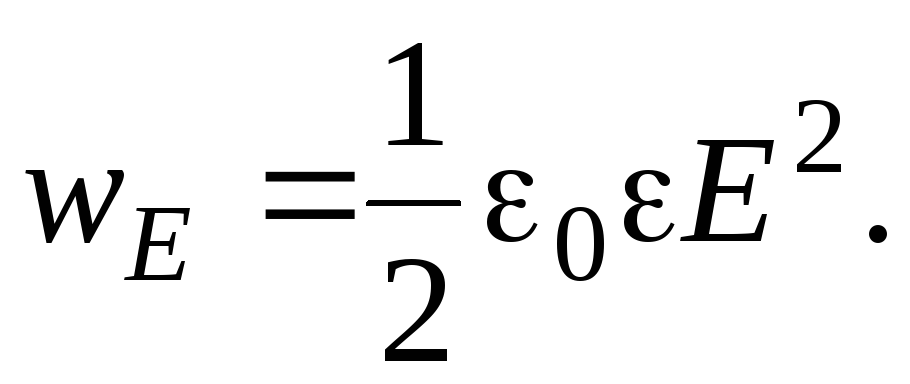(10)

В заключении отметим, что эта формула справедлива не только для конденсатора, но и для других электрических полей, в том числе и для переменных.

1.8. Потенциал и разность потенциалов электрического поля. Связь напряженности электрического поля с его потенциалом

1.8.1. Потенциал и разность потенциалов электрического поля

Так как потенциальная энергия системы электрических зарядов пропорциональна величинам зарядов, то, при помещении в одну и ту же точку поля различных по величине зарядов, будет изменяться потенциальная энергия.

Однако отношение потенциальной энергии системы зарядов к величине помещаемого в данную точку поля электрического заряда остается постоянным, следовательно, оно может служить характеристикой электрического поля.

Потенциальную энергию положительного единичного заряда, помещенного в данную точку поля, называют потенциалом электрического поля . Потенциал электрического поля

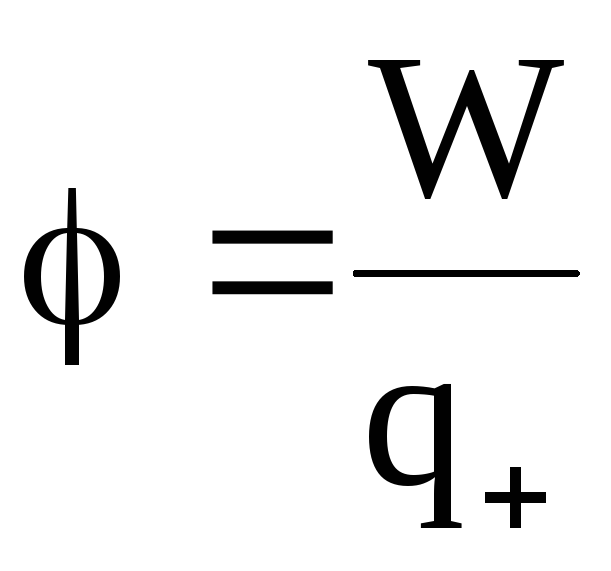. (1.31)

Если поле создано положительным точечным зарядом q, то

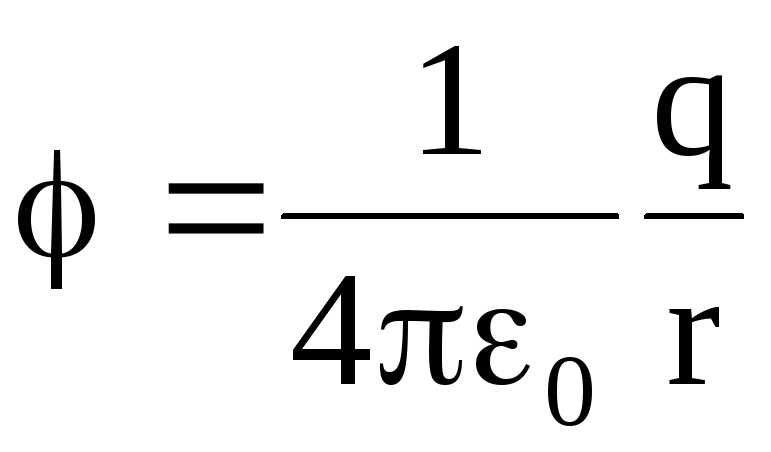, (1.32)

где q – величина заряда, создающего электрическое поле;

r – расстояние от центра заряда до рассматриваемой точки поля.

Потенциал электрического поля системы точечных зарядов равен алгебраической сумме потенциалов полей, создаваемых отдельно взятым зарядом системы:

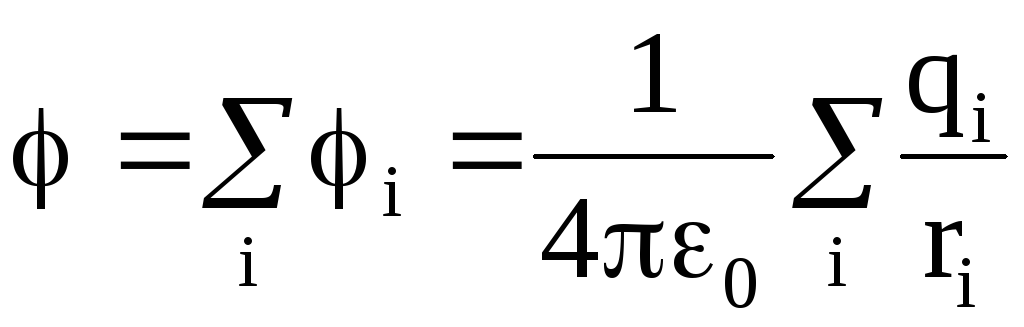, (1.33)

где q_i – величина i-го заряда;

r_i – расстояние от i-го заряда до рассматриваемой точки поля.

Из выражения (1.31)

W = q. (1.34)

Так как работа сил электрического поля равна убыли потенциальной энергии, т.е.

A_1,2 = — W = W₁ — W₂ = q(₁ — ₂), (1.35)

то

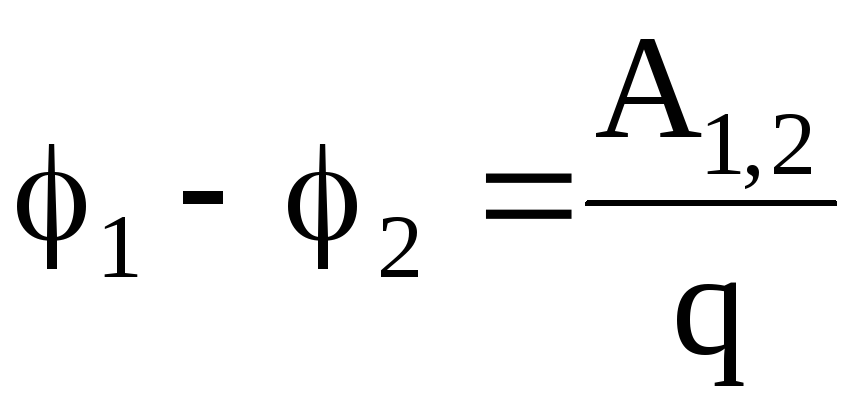. (1.36)

При q = q₊ = 1

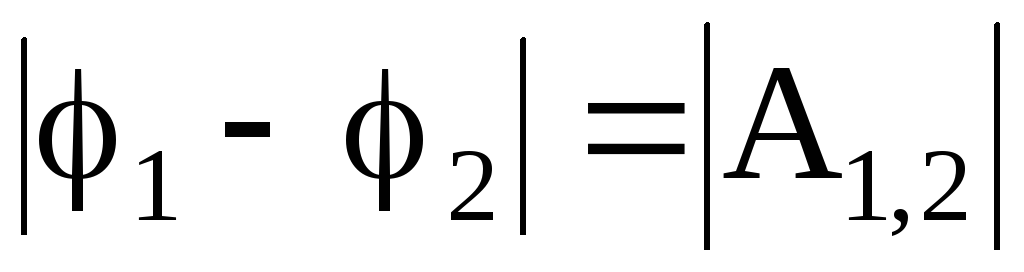. (1.37)

Таким образом, разность потенциалов между двумя точками поля, численно равна работе, которую совершают силы электрического поля по перемещению положительного единичного заряда из одной точки поля в другую.

При перемещении положительного единичного электрического заряда из данной точки поля в бесконечность

A_1, = W₁ — W_ = q_1,

а

. (1.38)

Если q = q₊ = 1, то

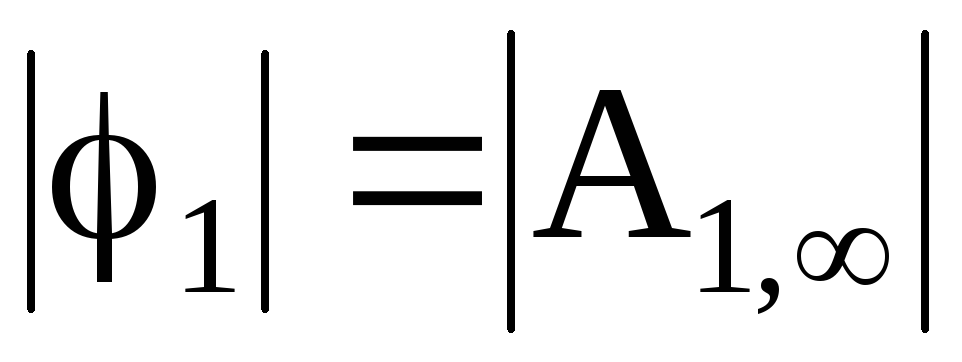. (1.39)

Следовательно, потенциал электрического поля численно равен работе сил электрического поля по перемещению положительного единичного заряда из данной точки поля в бесконечность.

Потенциал и разность потенциалов электрического поля являются его энергетическими характеристиками. В системе СИ потенциал и разность потенциалов измеряются в вольтах.

Один вольт – это потенциал такой точки электрического поля, находясь в которой заряд в 1 Кл обладает потенциальной энергией, равной 1 Дж.

1.8.2. Связь напряженности электрического поля с его потенциалом

Каждая точка электрического поля характеризуется напряженностью и потенциалом (силовой и энергетической характеристиками). Между ними должна существовать связь, которую можно установить исходя из следующих соображений.

Элементарная работа, совершаемая силами электрического поля по перемещению электрического заряда на расстояние dl,

dA = =F∙dl∙cos = F_l∙dl = qE_l∙dl.

Работа совершается за счет убыли (уменьшения) потенциальной энергии:

dA = — dW = — qd.

Следовательно, имеем

qE_ldl = — qd.

Отсюда

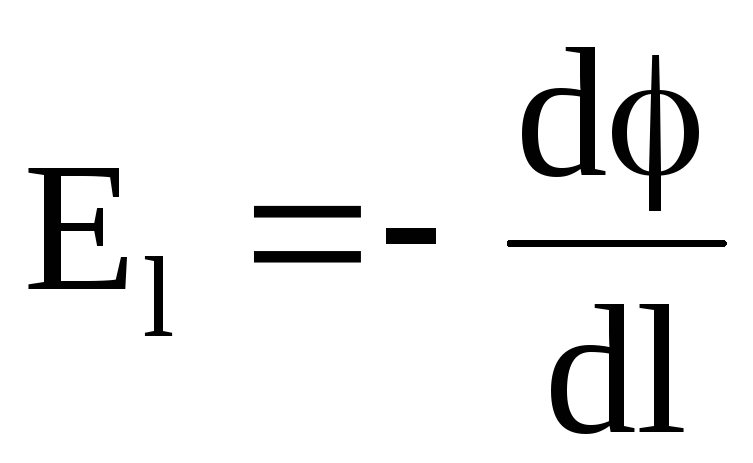, (1.40)

где 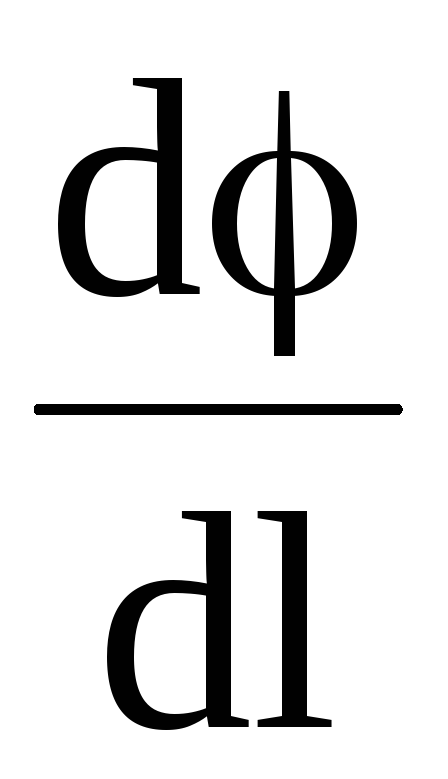характеризует быстроту изменения потенциала в данном направлении l и называется градиентом потенциала;

l – произвольно выбранное направление.

В векторной форме

E = — grad . (1.41)

Знак «минус» означает, что вектор напряженности электрического поля направлен в сторону убывания потенциала.

Проинтегрировав формулу d = — E_ldl, получим

;

.

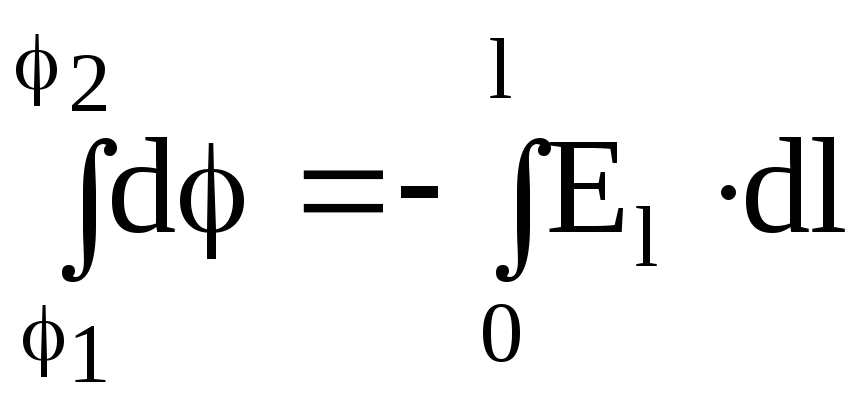Откуда

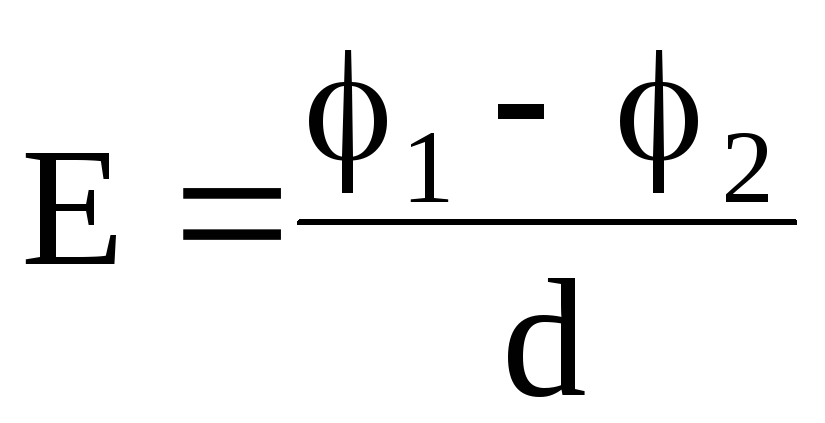, (1.42)

где d = lcos — расстояние между точками 1 и 2 поля.

В векторной форме выражение (1.41), можно представить так:

. (1.43)

Зная теорему Остроградского-Гаусса и связь между напряженностью и потенциалом электрического поля, можно по известной величине определить неизвестную.

Разность потенциалов

Физическая величина, равная работе, которую совершат силы поля, перемещая заряд из одной точки поля в другую, называется напряжением между этими точками поля.

Рассмотрим однородное электростатическое поле (такое поле существует между пластинами плоского заряженного конденсатора вдали от его краев):

Во время перемещения заряда поле совершает работу:

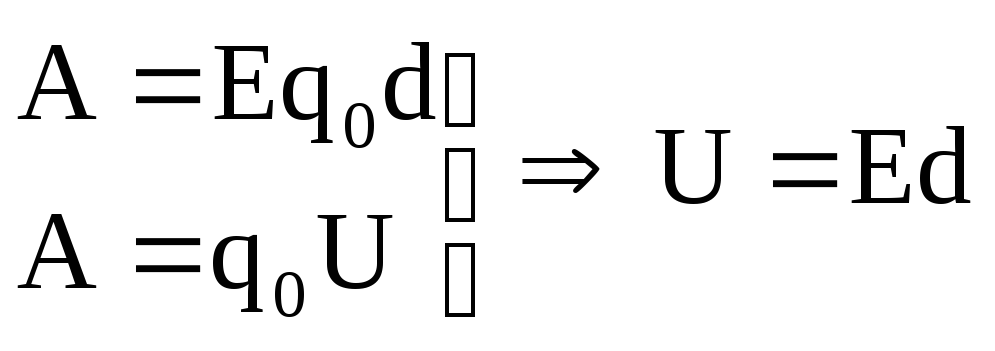
10. Проводник во внешнем электрическом поле (сто происходит, почему индукцируется)

Индукция электростатическая,

наведение в проводниках или диэлектриках электрических зарядов в постоянном электрическом поле.

В проводникахподвижные заряженные частицы — электроны — перемещаются под действиемвнешнегоэлектрическогополя. Перемещение происходит до тех пор, пока заряд не перераспределится так, что созданное им электрическоеполевнутрипроводникаполностью скомпенсируетвнешнееполеи суммарное электрическоеполевнутрипроводникастанет равным нулю. (Если бы этого не произошло, то внутри проводника, помещенного в постоянное электрическое поле, неограниченно долго существовал бы электрический ток, что противоречило бы закону сохранения энергии.) В результате на отдельных участках поверхности проводника (в целом нейтрального) образуются равные по величине наведённые (индуцированные) заряды противоположного знака.

В диэлектриках, помещенных в постоянное электрическое поле, происходит поляризация, которая состоит либо в небольшом смещении положительных и отрицательных зарядов внутри молекул в противоположные стороны, что приводит к образованию электрических диполей(с электрическим моментом, пропорциональным внешнему полю), либо в частичной ориентации молекул, обладающих электрическим моментом, в направлении поля. В том и другом случае электрический дипольный момент единицы объёма диэлектрика становится отличным от нуля. На поверхности диэлектрика появляются связанные заряды. Если поляризация неоднородная, то связанные заряды появляются и внутри диэлектрика. Поляризованный диэлектрик порождает электростатическое поле, добавляющееся к внешнему полю. (См.Диэлектрики.)

11. Электроемкость, конденсатор

Электроемкость – количественная мера способности проводника удерживать заряд.

Простейшие способы разделение разноименных электрических зарядов – электризация и электростатическая индукция – позволяют получить на поверхности тел не большое количество свободных электрических зарядов. Для накопления значительных количеств разноименных электрических зарядов применяются конденсаторы.

Конденсатор – это система из двух проводников (обкладок), разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников. Так, например, две плоские металлические пластины, расположенные параллельно и разделенные слоем диэлектрика, образуют плоский конденсатор.

Если пластинам плоского конденсатора сообщить равные по модулю заряды противоположного знака, то напряженность электрического поля между пластинами будет в два раза больше, чем напряженность поля у одной пластины. Вне пластин напряженность электрического поля равна нулю, т. к. равные заряды разного знака на двух пластинах создают вне пластин электрические поля, напряженности которых равны по модулю, но противоположны по направлению.

Электроемкостью конденсатора называется физическая величина, определяемая отношением заряда одной из пластин к напряжению между обкладками конденсатора:

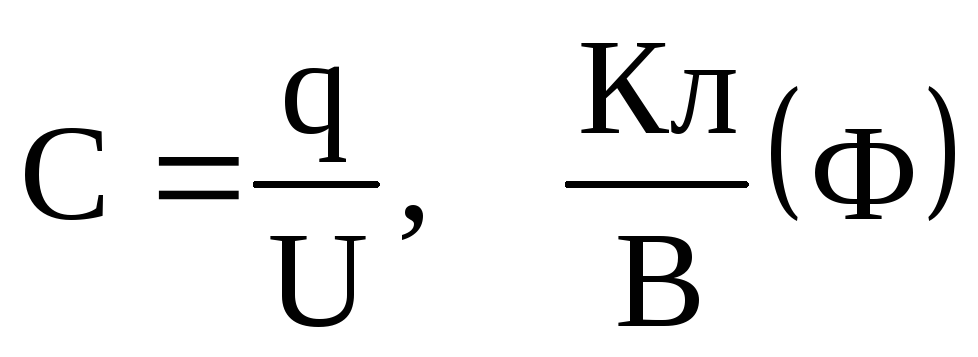
При неизменном положении пластин электроемкость конденсатора является постоянной величиной при любом заряде на пластинах.

За единицу электроемкости в системе СИ принимают Фарад. 1 Ф – электроемкость такого конденсатора, напряжение между обкладками которого равно 1 В при сообщении обкладкам разноименных зарядов по 1 Кл.

Электроемкость плоского конденсатора можно вычислить по формуле:

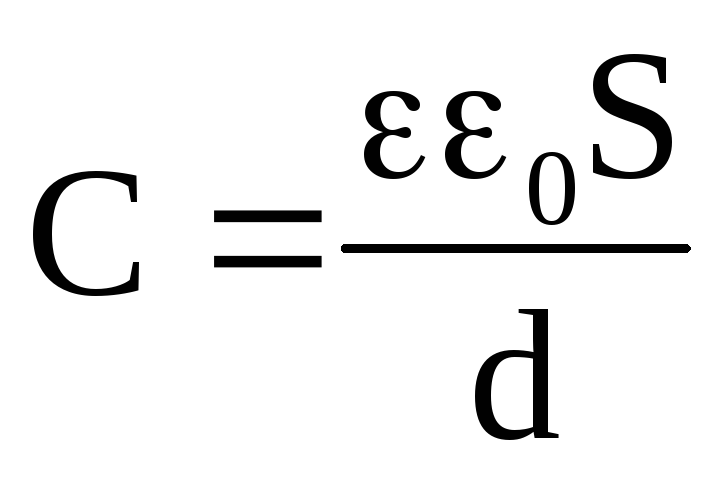, где

S – площадь обкладок конденсатора

d – расстояние между обкладками

–диэлектрическая проницаемость диэлектрика

Электроемкость шара можно вычислить по формуле:

Энергия заряженного конденсатора.

Если внутри конденсатора напряженность поля E, тогда напряженность поля, созданного зарядом одной из пластин E/2. В однородном поле одной пластины находится заряд, распределенный по поверхности другой пластины. Согласно формуле для потенциальной энергии заряда в однородном поле энергия конденсатора равна:

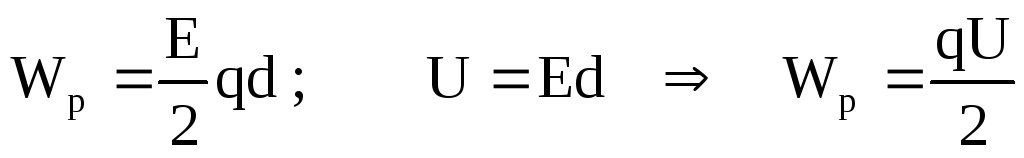
Используя формулу электроемкости конденсатора :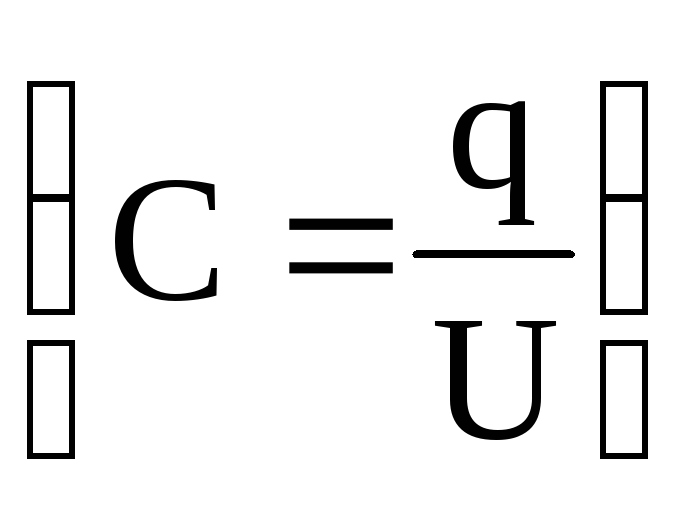

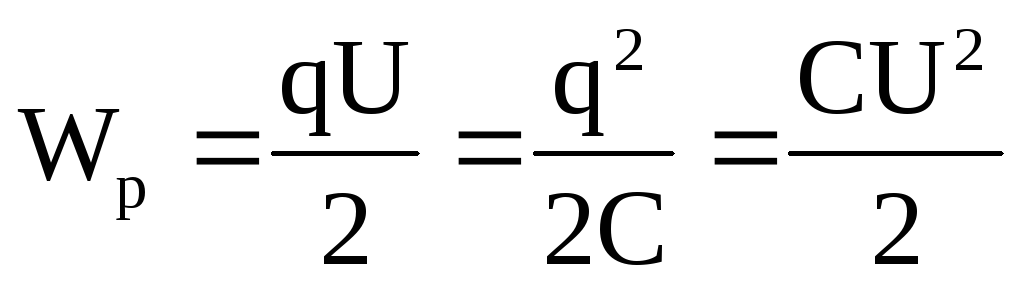
3. Связь между разностью потенциалов и напряженностью

Зная действующую на заряд силу, можно найти и работу, совершаемую при перемещении заряда, поэтому силовая и энергетическая характеристики поля, то есть напряженность и разность потенциалов связаны друг с другом.

Найдем соотношение между разностью потенциалов и напряженностью в однородном поле. Пусть положительный пробный заряд 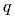перемещается в однородном электростатическом поле с напряженностью 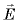в направлении линий напряженности на расстояние 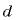(рис. 5.3).

На заряд со стороны поля действует сила 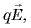направленная вдоль перемещения, поэтому при перемещении на расстояние  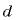поле совершает работу 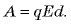Разность потенциалов связана с работой соотношением 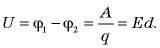Следовательно,

в однородном электростатическом поле с напряженностью 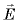разность потенциалов между точками, соединенными вектором 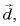направление которого совпадает с направлением напряженности поля, определяется формулой .

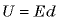Соотношение между напряженностью и разностью потенциалов можно записать также в виде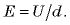

Заметим, что напряженность поля направлена в сторону убывания потенциала. Действительно, если направление перемещения положительного заряда совпадает с направлением напряженности поля, поле совершает положительную работу и, следовательно, потенциальная энергия заряда уменьшается.

Статьи энциклопедии

A. Напряжение — PhysBook

Разность потенциалов. Напряжение

Работа сил электростатического поля по перемещению заряда q₀ из точки 1 в точку 2 поля

\(~A_{12} = W_{p1} — W_{p2} .\)

Выразим потенциальную энергию через потенциалы поля в соответствующих точках:

\(~W_{p1} = q_0 \varphi_1 , W_{p2} = q_0 \varphi_2 .\)

Тогда

\(~A_{12} = q_0 (\varphi_1 — \varphi_2) .\)

Таким образом, работа определяется произведением заряда на разность потенциалов начальной и конечной точек.

Из этой формулы разность потенциалов

\(~\varphi_1 — \varphi_2 = \frac{A_{12}}{q_0} .\)

Разность потенциалов — это скалярная физическая величина, численно равная отношению работы сил поля по перемещению заряда между данными точками поля к этому заряду.

В СИ единицей разности потенциалов является вольт (В).

1 В — разность потенциалов между двумя такими точками электростатического поля, при перемещении между которыми заряда в 1 Кл силами поля совершается работа в 1 Дж.

Разность потенциалов в отличие от потенциала не зависит от выбора нулевой точки. Разность потенциалов φ₁ — φ₂ часто называют электрическим напряжением между данными точками поля:

\(~U = \varphi_1 — \varphi_2 .\)

Напряжение между двумя точками поля определяется работой сил этого поля по перемещению заряда в 1 Кл из одной точки в другую. В электростатическом поле напряжение вдоль замкнутого контура всегда равно нулю.

Работу сил электрического поля иногда выражают не в джоулях, а в электронвольтах. 1 эВ равен работе, совершаемой силами поля при перемещении электрона (е = 1,6·10^-19 Кл) между двумя точками, напряжение между которыми равно 1 В.

1 эВ = 1,6·10^-19 Кл·1 В = 1,6·10^-19 Дж. 1 МэВ = 10⁶ эВ = 1,6·10^-13 Дж.

Электрическое поле графически можно изобразить не только с помощью линий напряженности, но и с помощью эквипотенциальных поверхностей.

Эквипотенциальной называется воображаемая поверхность, в каждой точке которой потенциал одинаков. Разность потенциалов между двумя любыми точками эквипотенциальной поверхности равна нулю.

Следовательно, работа по перемещению заряда вдоль эквипотенциальной поверхности равна 0. Но работа рассчитывается по формуле \(~A = F \Delta r \cos \alpha = q_0E \Delta r \cos \alpha\). Здесь q₀ ≠ 0, Е ≠ 0, Δr ≠ 0. Значит, \(~\cos \alpha = 0 \Rightarrow \alpha = 90^{\circ}\).

Следовательно, линии напряженности перпендикулярны эквипотенциальным поверхностям. Первая эквипотенциальная поверхность металлического проводника — это поверхность самого заряженного проводника, что легко проверить электрометром. Остальные эквипотенциальные поверхности проводятся так, чтобы разность потенциалов между двумя соседними поверхностями была постоянной.

Картины эквипотенциальных поверхностей некоторых заряженных тел приведены на рис. 3.

Рис. 3

Эквипотенциальными поверхностями однородного электростатического поля являются плоскости, перпендикулярные линиям напряженности (рис. 3, а).

Эквипотенциальные поверхности поля точечного заряда представляют собой сферы, в центре которых расположен заряд q (рис. 3, б).

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 231-233.

План-конспект урока по физике на тему «Потенциал и разность потенциалов. Связь между напряжённостью и разностью потенциалов.»

Физика

8″а», 8″б» класс

Тема: Потенциал и разность потенциалов.

Связь между напряжённостью и разностью потенциалов.

Цели урока: обучить навыкам нахождения работы по перемещению заряда в электрическом поле, показать взаимосвязь между напряжённостью и разностью потенциалов, добиться овладения и закрепления качества знаний, дать практику в решении задач.

Дидактическая: обучить навыкам нахождения работы по перемещению заряда в электрическом поле, показать взаимосвязь между напряжённостью и разностью потенциалов, добиться овладения и закрепления качества знаний, дать практику в решении задач.
Воспитательная: сформировать устойчивое осознанное отношение к изучаемому материалу, формировать привычку оказывать помощь товарищам в учении, умения ставить цели и стремления добиваться их.
Развивающая: развивать умения работать в должном темпе, готовность к знанию, организованность, умение владеть собой и преодолевать трудности.

Цели для обучающихся:

Знать: физический смысл потенциала и напряжения.

Уметь: изображать графически поверхности равного потенциала, решать задачи на расчёт потенциала, напряжения, работы электрического поля.

План урока:

1.Проверка домашнего задания.

2.Изучение новой темы.

3.Закрепление нового материала.

4.Домашнее задание.

5.Подведение итогов.

1.Проверка домашнего задания.

1.Записать формулу закона Кулона для

вакуума.

2.Какой буквой обозначается заряд?

3.Чему равен коэффициент пропорциональности?

4.Чему равна напряжённость электрического поля? Записать формулу.

5.В чём измеряется напряжённость.

2. Изучение новой темы.

Работа любого электростатического поля при перемещении в нем заряженного тела из одной точки в другую также не зависит от формы траектории, как и работа однородного поля. На замкнутой траектории работа электростатического поля всегда равна нулю. Поля, обладающие таким свойством, называют потенциальными.

Разность потенциалов (напряжение) между двумя точками равна отношению работы поля при перемещении положительного заряда из начальной точки в конечную к величине этого заряда.

 Каждой точке электрического поля соответствуют определенные значения потенциала и напряженности. Найдем связь напряженности электрического поля с потенциалом.
   Пусть заряд q перемещается в направлении вектора напряженности однородного электрического поля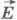из точки 1 в точку 2, находящуюся на расстоянии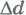от точки 1 (рис.14.28). Электрическое поле совершает работу:

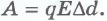
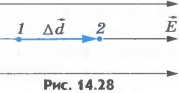
   Эту работу согласно формуле (14.19) можно выразить через разность потенциалов в точках 1 и 2:

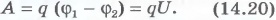
   Приравнивая выражения для работы, найдем модуль вектора напряженности поля:

   В этой формуле U — разность потенциалов между точками 1 и 2, которые связаны вектором перемещения, совпадающим по направлению с вектором напряженности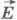(см. рис.14.28).
   Формула (14.21) показывает: чем меньше меняется потенциал на расстоянии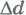, тем меньше напряженность электростатического поля. Если потенциал не меняется совсем, то напряженность поля равна нулю.
   Так как при перемещении положительного заряда в направлении вектора напряженности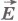 электростатическое поле совершает положительную работу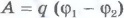, то потенциал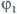больше потенциала.
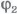   Следовательно, напряженность электрического поля направлена в сторону убывания потенциала.
   Любое электростатическое поле в достаточно малой области пространства можно считать однородным. Поэтому формула (14.21) справедлива для произвольного электростатического поля, если только расстояние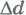настолько мало, что изменением напряженности поля на этом расстоянии можно пренебречь.
   Единица напряженности электрического поля. Единицу напряженности электрического поля в СИ устанавливают, используя формулу (14.21).Напряженность электрического поля численно равна единице, если разность потенциалов между двумя точками на расстоянии 1 мв однородном поле равна 1 В. Наименование этой единицы — вольт на метр (В/м).
   Напряженность можно также выражать в ньютонах на кулон. Действительно,

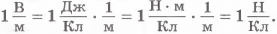
3. Закрепление нового материала.

1. Какие поля называют потенциальными?
   2. Как разность потенциалов между двумя точками поля зависит от работы электрического поля?
   3. Что нужно выбрать прежде, чем говорить о значении потенциала в данной точке поля?

Решение задач:
1.Поле образовано точечным зарядом q = 1,2*10^-7 Кл. Какую работу совершает поле при переносе
одноимённого заряда 1,5*10^-10 Кл из точки В, удалённой от заряда q на расстояние 0,5 м, в точку
А, удалённую от q на расстояние 2 м? Среда – воздух.
2.Пылинка массой 10^-8 г висит между пластинками плоского воздушного конденсатора, к которому
приложено напряжение 5 кВ. Расстояние между пластинками 5 см. Каков заряд пластины?
3.Два заряда по 6 нКл находятся на расстоянии 100 см друг от друга. Какую работу надо совершить,
чтобы сблизить их до расстояния 50 см?
4.Какую скорость приобретает электрон, пролетевший ускоряющую разность потенциалов 10 кВ?
5.Какую работу совершит поле при перемещении заряда 20 нКл из точки с потенциалом 700 В в 
точку с потенциалом 200 В?
6.Напряжение между двумя точками , лежащими на одной линии напряжённости однородного поля,
2 кВ. Найти напряжённость, если расстояние между точками 4 см.

4.Домашнее задание. §33