9.2 Электрическое напряжение — fizikalexcras
Интерактивное изложение материала по теме
Электрическое напряжение. Измерение напряжения Подборка заданий «Электрическое напряжение, сила электрического тока»
Слайд-шоу
«Солнечные батареи»
Слайд-шоу
«Электрическое напряжение в природе»
Рисунок
«Вольтметр»
Подборка
заданий «Электрическое напряжение, сила электрического тока»
Слайд-шоу
«Опасное напряжение»
Слайд-шоу
«Подключение приборов к электрической сети»
Электрический ток – это проходящие через проводник электроны, несущие отрицательный заряд. Объем этого заряда или, иными словами, количество электричества характеризует силу тока. Сила тока одинакова на всех участках цепи. Электроны не могут исчезать или «спрыгивать» с проводов. Поэтому, силу тока мы можем измерить в любом месте электрической цепи. Однако, будет ли одинаковым действие тока на разные участки этой цепи? Проходя по проводам, ток лишь слегка их нагревает, не совершая при этом большой работы.
Определение электрического напряжения
Определение: напряжение электрического тока – это величина, показывающая, какую работу совершило поле при перемещении заряда от одной точки до другой. Напряжение в разных участках цепи будет различным. Напряжение на участке пустого провода будет совсем небольшим, а напряжение на участке с какой-либо нагрузкой будет гораздо большим, и зависеть величина напряжения будет от величины работы, произведенной током.
Напряжение – это физическая величина, характеризующая действие электрического поля на заряженные частицы.
Напряжение показывает, какую работу совершает электрическое поле по перемещению единицы заряда на данном участке цепи. Постоянный ток: Напряжение.
Измеряют напряжение в вольтах (1 В). Для определения напряжения существует формула:
Для определения напряжения существует формула: где U — напряжение,
A – работа, совершенная током по перемещению заряда q на некий участок цепи. Электрическое напряжение
Напряжение на полюсах источника тока
Напряжение на полюсах источника тока означает потенциальную величину энергии, которую может источник придать току. Это как давление воды в трубах. Эта величина энергии,
которая будет израсходована, если к источнику подключить некую нагрузку. Поэтому, чем большее напряжение у источника тока, тем большую работу может совершить ток.Вольтметр
Для измерения напряжения существует прибор, называемый вольтметром. В отличие от амперметра, он подключается параллельно нагрузке. В таком случае вольтметр показывает величину напряжения, приложенного к нагрузке. Для измерения напряжения на полюсах источника тока, вольтметр подключают непосредственно к полюсам прибора.Электрическое напряжение — это… Что такое Электрическое напряжение?
У этого термина существуют и другие значения, см.
Электри́ческое напряже́ние между точками A и B электрической цепи или электрического поля — физическая величина, значение которой равно отношению работы электрического поля, совершаемой при переносе пробного электрического заряда из точки A в точку B, к величине пробного заряда.
При этом считается, что перенос пробного заряда не изменяет распределения зарядов на источниках поля (по определению пробного заряда). В потенциальном электрическом поле эта работа не зависит от пути, по которому перемещается заряд. В этом случае электрическое напряжение между двумя точками совпадает с разностью потенциалов между ними.
Альтернативное определение —
— интеграл от проекции поля эффективной напряжённости поля (включающего сторонние поля) на расстояние между точками A и B вдоль заданной траектории, идущей из точки A в точку B. В электростатическом поле значение этого интеграла не зависит от пути интегрирования и совпадает с разностью потенциалов.
Единицей измерения напряжения в системе СИ является вольт.
Напряжение в цепях постоянного тока
Напряжение в цепи постоянного тока определяется так же, как и в электростатике.
Напряжение в цепях переменного тока
Для описания цепей переменного тока применяются следующие понятия:
Мгновенное напряжение
Мгновенное напряжение есть разность потенциалов между двумя точками, измеренная в данный момент времени. Оно является функцией времени:
Амплитудное значение напряжения
Амплитуда напряжения есть максимальное по модулю значение мгновенного напряжения за весь период колебаний:
Для гармонических (синусоидальных) колебаний напряжения мгновенное значение напряжения выражается как:
Для сети переменного синусоидального напряжения со среднеквадратичным значением 220 В амплитудное равно приблизительно 311,127 В.
Амплитудное напряжение можно измерить с помощью осциллографа.
Среднее значение напряжения
Среднее значение напряжения (постоянная составляющая напряжения) определяется за весь период колебаний, как:
Для чистой синусоиды среднее значение напряжения равно нулю.
Среднеквадратичное значение напряжения
Среднеквадратичное значение (устаревшее наименование: действующее, эффективное) наиболее удобно для практических расчётов, так как на линейной активной нагрузке оно совершает ту же работу (например, лампа накаливания имеет ту же яркость свечения, нагревательный элемент выделяет столько же тепла), что и равное ему постоянное напряжение:
Для синусоидального напряжения справедливо равенство:
В технике и быту при использовании переменного тока под термином «напряжение» имеется в виду именно эта величина, и все вольтметры проградуированы исходя из её определения. Однако конструктивно большинство приборов фактически измеряют не среднеквадратичное, а средневыпрямленное (см. ниже) значение напряжения, поэтому для несинусоидального сигнала их показания могут отличаться от истинного значения.
ниже) значение напряжения, поэтому для несинусоидального сигнала их показания могут отличаться от истинного значения.
Средневыпрямленное значение напряжения
Средневыпрямленное значение есть среднее значение модуля напряжения:
Для синусоидального напряжения справедливо равенство:
На практике используется редко, однако большинство вольтметров переменного тока (те, в которых ток перед измерением выпрямляется) фактически измеряют именно эту величину, хотя их шкала и проградуирована по среднеквадратичным значениям.
Напряжение в цепях трёхфазного тока
В цепях трёхфазного тока различают фазное и линейное напряжения. Под фазным напряжением понимают среднеквадратичное значение напряжения на каждой из фаз нагрузки, а под линейным — напряжение между подводящими фазными проводами. При соединении нагрузки в треугольник фазное напряжение равно линейному, а при соединении в звезду (при симметричной нагрузке или при глухозаземлённой нейтрали) линейное напряжение в раз больше фазного.
На практике напряжение трёхфазной сети обозначают дробью, в знаменателе которой стоит линейное напряжение, а в числителе — фазное при соединении в звезду (или, что то же самое, потенциал каждой из линий относительно земли). Так, в России наиболее распространены сети с напряжением 220/380 В; также иногда используются сети 127/220 В и 380/660 В.
Стандарты
| Объект | Тип напряжения | Значение (на вводе потребителя) | Значение (на выходе источника) |
|---|---|---|---|
| Электрокардиограмма | Импульсное | 1-2 мВ | — |
| Телевизионная антенна | Переменное высокочастотное | 1-100 мВ | — |
| Батарейка AA («пальчиковая») | Постоянное | 1,5 В | — |
| Литиевая батарейка | Постоянное | 3 В — 1,8 В (в исполнении пальчиковой батарейки , на примере Varta Professional Lithium, AA) | — |
| Управляющие сигналы компьютерных компонентов | Импульсное | 3,5 В, 5 В | — |
| Батарейка типа 6F22 («Крона») | Постоянное | 9 В | — |
| Силовое питание компьютерных компонентов | Постоянное | 12 В | — |
| Электрооборудование автомобиля | Постоянное | 12/24 В | — |
| Постоянное | 19 В | — | |
| Сеть «безопасного» пониженного напряжения для работы в опасных условиях | Переменное | 36-42 В | — |
| Напряжение наиболее стабильного горения свечи Яблочкова | Постоянное | 55 В | — |
| Напряжение в телефонной линии (при опущенной трубке) | Постоянное | 60 В | — |
| Напряжение в электросети Японии | Переменное трёхфазное | 100/172 В | — |
| Напряжение в домашних электросетях США | Переменное трёхфазное | 120 В / 240 В (сплит-фаза) | — |
| Напряжение в электросети России | Переменное трёхфазное | 220/380 В | 230/400 В |
| Разряд электрического ската | Постоянное | до 200—250 В | — |
| Контактная сеть трамвая и троллейбуса | Постоянное | 550 В | 600 В |
| Разряд электрического угря | Постоянное | до 650 В | — |
| Контактная сеть метрополитена | Постоянное | 750 В | 825 В |
| Контактная сеть электрифицированной железной дороги (Россия, постоянный ток) | Постоянное | 3 кВ | 3,3 кВ |
| Распределительная воздушная линия электропередачи небольшой мощности | Переменное трёхфазное | 6-20 кВ | 6,6-22 кВ |
| Генераторы электростанций, мощные электродвигатели | Переменное трёхфазное | 10-35 кВ | — |
| Анод кинескопа | Постоянное | 7-30 кВ | — |
| Статическое электричество | Постоянное | 1-100 кВ | — |
| Свеча зажигания автомобиля | Импульсное | 10-25 кВ | — |
| Контактная сеть электрифицированной железной дороги (Россия, переменный ток) | Переменное | 25 кВ | 27,5 кВ |
| Пробой воздуха на расстоянии 1 см | 10-20 кВ | — | |
| Катушка Румкорфа | Импульсное | до 50 кВ | — |
| Пробой трансформаторного масла на расстоянии 1 см | 100-200 кВ | — | |
| Воздушная линия электропередачи большой мощности | Переменное трёхфазное | 35 кВ, 110 кВ, 220 кВ, 330 кВ | 38 кВ, 120 кВ, 240 кВ, 360 кВ |
| Электрофорная машина | Постоянное | 50-500 кВ | — |
| Воздушная линия электропередачи сверхвысокого напряжения (межсистемные) | Переменное трёхфазное | 500 кВ, 750 кВ, 1150 кВ | 545 кВ, 800 кВ, 1250 кВ |
| Трансформатор Тесла | Импульсное высокочастотное | до нескольких МВ | — |
| Генератор Ван де Граафа | Постоянное | до 7 МВ | — |
| Грозовое облако | Постоянное | От 2 до 10 ГВ | — |
См.
 также
такжеСсылки
Физика — 8
ческой энергии, имеющейся у электронов, превращается во внутреннюю энергию проводника, и он нагревается. Для поддержания постоянной скорости упорядоченного движения свободных электронов в электрической цепи и восстановления потерянной ими кинетической энергии необходимо совершение работы. Эту работу во внешней электрической цепи совершает электрическое поле, то есть электрические силы. Работа, совершаемая электрическим полем для перемещения единицы заряда между двумя точками этого поля, является энергетической характеристикой поля и называется электрическим напряжением или напряжением.
| Формула | Единица измерения |
|
U = A 
|
[U] = 1[A] |
| Определение | Определение |
| Электрическое напряжение — это физическая величина, равная отношению работы, совершенной электрическим полем при перемещении заряда между двумя точками, к количеству этого заряда. |
Один вольт (1В) — это такое напряжение между двумя точками электрического поля, когда электрические силы, перемещая заряд в 1 Кл из одной точки в другую, совершают работу в 1 Дж.
|
Как видно из формулы напряжения, работа, совершаемая при перемещении между двумя точками электрического поля, равна произведению количества заряда и электрического напряжения между этими точками:
A = q · U.
Измерение напряжения
Напряжение измеряется вольтметром. В кабинете физики используются два вида вольтметров: лабораторный вольтметр (c) и демонстрационный вольтметр (d).
На шкале вольтметра имеется буква V. На схемах вольтметр обозначается кругом с буквой
V внутри (см.: таблица 6.1.).
Клеммы вольтметра соединяют с теми точками цепи, напряжение между которыми нужно измерить. Например, если нужно измерить напряжение на лампе, то вольтметр соединяется с клеммами этой лампы. Если же нужно определить напряжение на электрическом звонке в цепи,
Зависимость силы тока от напряжения
итак вы написали контрольную работу поэтому домашнего задания сегодня не проверяю мы продолжаем с вами изучение законов постоянного тока собственно законов мы пока еще никаких и не знаем сегодня мы познакомимся самым первым законом что такое электрический ток ариадна можешь сказать это направленное движение заряженных частиц спасибо садись пожалуйста скажите пожалуйста какая физическая величина описывает количественный электрический ток саша ампер это единица измерения эта величина я сама величина как называется сила тока итак сила тока это физическая величина которая описывает электрический ток то есть направленное движение заряженных частиц а благодаря чему эти самые заряженные частицы направлено движутся что их заставляет двигаться пожалуйста напряжение это физическая величина которой описывает то электрического поля и так электрическое поле создаваемые в проводнике заставляет двигаться направлено заряженные частицы то есть причина это электрическое поле следствие это направленное движение заряженных частиц так и запишем после этого запишем тему урока а сейчас за интригую вас причина электрическое поле следствие направленное движение заряженных частиц причина и следствие физика изучает причинно-следственной связи в природе и вот сейчас мы с вами одну из таких причинно-следственных связей установим и так как связана причина и следствие но опять-таки физика наука количественная причина электрическое поле описывается какой физической величиной напряжение между двумя точками электрического поля а следствия ток описывается такой величины как сила тока и вот вопрос как связаны эти самые причины и следствия вот на этот вопрос мы сегодня с вами ответим тема урока зависимость силы тока от напряжения зависимость силы тока от напряжения электрическое сопротивление . закон ома для участка цепи зависимость силы тока от напряжения электрическое сопротивление закон ома для участка цепи мы с вами этот закон будем устанавливать экспериментально потом в 10 или в 11 классе мы выведем его на основании знаний о структуре вещества а сейчас пока что экспериментально для того чтобы изучить этот закон какие нам нужны приборы как он называется вольтметр амперметр нам нужно создать электрический электрическую цепь которую должен еще входить источник тока значит с помощью источника тока мы создадим электрический ток вольтметром мы будем измерять напряжение на каком-то проводнике и амперметром силу тока через этот проводник давайте сейчас сконструируем схему измерительную а потом ее реализуем уже на практике и так нам нужен источник тока что там внутри не важно для нас важно то что этот источник тока должен обеспечивать нам разные напряжения подаваемая в электрическую цепь поэтому напишем так регулируемый источник тока этот источник тока мы подключим к проводнику причем мы будем разные проводники подключать и будем измерять силу тока в этих проводниках силу тока измеряем амперметром который как вы знаете включается в цепь последовательно и вот две клеммы к которым мы будем подключать разные проводники я нарисую этот проводник так вот условно проводники один из них теперь как измерить напряжение на этом проводники куда подключать вольтметр саша к тому к тому участку цепи на который мы хотим измерить напряжение то есть вот между этими двумя выводами надо подключить вольтметр ну давайте я вот сюда его подключил это тоже самое будет вот наша измерительная схема теперь мы эту измерительную схему соберем на практике и заставим ее работать давайте сейчас поделим да скок поделим экран на две части в одной части мы будем видеть схему на доске а в другой части будем видеть эту же самую схему в реальности вот так и так вот это регулируемый источник тока его еще называют выпрямитель теперь проводник в котором мы будем измерять силу тока вот такой смотрите как он работает электрический ток от источника ну тут я уже амперметр подключил по дороге проходит смотрите как через вот этот замкнутый контакт контакт вот с таким штепсель им можно замыкать и размыкать то есть уток идет в обход вот этого проводника но здесь штепселя нет поэтому ток течет по вот этому проводнику а дальше же везде штепсели включены на щиток идет дальше к следующему выводу к следующей клемме и вот чем хороша это систем тем что я вставляю штепсели могу подключать в электрическую цепь различные проводники вот таким образом ну давайте один я вытащу теперь силу тока мы будем с вами измерять амперметром вот этот амперметр ток от источника тока он уже подключен вот идет через один из этих проводников в нашем случае через вот этот кампер метру и вот этот красный провод ведет к другому выводу источника тока амперметр и подключили включаем источник тока смотрите стрелка отклоняется значит ток действительно протекает остается измерить напряжение на этом участке цепи у нас есть вольтметр мы этот вольтметр подключаем как саша сказал параллельно проводнику вот этот вольтметр один вывод подключаем тут минус значит к тому участку который соединён с отрицательным полюсом вот у меня отрицательный полюс значит вот сюда подключаем второй вывод к проводнику ведущему к положительному полюсу так убираем чтобы ничего нам не заслоняла картину есть так протестируем систему стрелка отклоняется и у вольтметра и амперметра можно сделать немножко крупнее и приступить к исследованию сейчас мы с вами возьмем три различных проводника подключим в эту электрическую цепь и будем изучать зависимость тока от напряжения подаваемая подавая различное напряжение на этот проводник и результаты занесем в таблицу сразу заготовим 3 таблицы раз мы решили изучать протекание тока в 3 проводниках так у нас будет три таблицы здесь напишем проводник номер один номер два номер три давайте пусть у вас ширина таблицы будут 6 клеточек здесь будет 3 колонки поскольку мы с вами изучаем зависимость силы тока от напряжения значит в эту таблицу нужно занести напряжение в вольтах далее силу тока в амперах а этот клеточку я пока не буду заполнять оставим ее на потом аналогично будет устроено и вторая таблица и 3 сил напряжения в вольтах сила тока в амперах и еще одна свободная часть таблицы еще один свободный столбец напряжение в вольтах сила тока в амперах подадим 0 вольт 1 вольт 2 вольта 3 вольта можно еще и четыре вольта будет падать и этот опыт проводил уже поэтому я знаю какое напряжение можно подавать во втором случае во втором случае будем подавать напряжение ноль один два три четыре пять вольт и в третьем случае такие же напряжения 0 1 2 3 4 5 готовьте табличку ну что начнем понемножку если подать напряжение 0 вольт как вы думаете какая будет сила тока в проводнике 0 мы не создаем электрического поля поэтому не возникает силы которая толкала бы носители заряда в определенном направлении значит нету движения зарядов силы тока равна нулю это можно понять и без опыта а теперь подадим напряжение 1 вольт скажите пожалуйста как какую меня тут сопротивление включим еще секундочку я так это что-то надо подправить где-то что-то замыкает экспериментальная физика наука капризная требующая к себе уважение к все пошло и так я подал напряжение приблизительно 1 вольт какая сила тока пол ампер давайте запишем 1 вольт это проводник номер один из сила тока 0,5 ампера увеличим напряжение доведем его до 2 вольт какая сила тока приблизительно 1 ампер будем писать 1 ампер все-таки приборы у нас не идеальны точные да и проводник тоже обладают не идеально целым значением величины которую я назову чуть позже итак два вольта создать напряжение два вольта создает ток в 1 ампер теперь подадим напряжение 3 вольта мы увидим что сила тока в проводнике приблизительно полтора ампера запишем и наконец подадимся ток силой подадим напряжение величиной четыре вольта потечет ток силой 2 ампера теперь понятно почему больше четырех вольт я не подаю вы видите что стрелка амперметра дошла до последнего деления шкалы и я даже небольшой такой запашок чувствуешь горячий проводник стал тепловое действие тока проявила себя и так четыре вольта создает ток силой 2 ампера это был проводник номер один теперь этот проводник мы отключаем и включаем проводник номер два вот смотрите я вытаскивал вот этот штырек и повторяем опыт теперь ток будет течь уже не через этот проводник а через вот этот давайте посмотрим что будет подадим напряжение 1 вольт какова сила тока 0 2 ампера нулю соответствует 0 это мы уже знаем когда мы подали напряжение 1 вольт сила тока в цепи в проводнике 0,3 ампера идем дальше подадим напряжение два вольта какова сила тока 0,4 ампера 0,4 ампера подадим 3 вольта как вы думаете ну собственно я уже вам показываю это 0,6 до 3 вольта 0,6 ампера а если я подам четыре вольта будет 08 это ваше предвидение предсказания гипотеза проверим ее на эксперименте пожалуйста все получается 08 ампера и наконец подавая напряжение 5 вольт мы получаем только силой около одного ампера 1 ампер есть второй проводник мы исследовали теперь возьмем третий проводник это третий проводник у нас будет составной я выну все штепсели из этого устройства теперь ток у нас будет идти и через этот и через этот и через этот и через этот проводник последовательно один за другим будет заряд проходить все эти проводники начнем с одного вольта напряжение 1 вольт сила тока сколько 1 10 ампер 0,1 здесь 0 если я подам два вольта как вы думаете какой ток потечет 0 2 ампера подаем действительно 02 подаем напряжение 3 вольта 0 3 ампера 0 3 4 вольта 0 4 ампера 5 вольт 05 ампера вот как давайте выключим эту систему и теперь больше нам уже это это оборудование не понадобится поэтому открываем полностью экран итак мы с вами подавая на три разных проводника они условно называются номер один номер два номер три различное напряжение измеряли силу тока в этих проводниках а вот давайте посмотрим например на вот эту таблицу смотрите 1 вольт создает ток пол ампера два вольта 1 ампер если мы разделим 1 вольт на пол ампера у нас получится сколько 2 чего-то там если мы 2 разделен на 1 получится 2 если мы 3 разделим на полтора получится 2 если 4 разделим на 2 получится 2 скажите пожалуйста вот это частное от деления напряжение от деления напряжения на силу тока она зависит от силы тока частное нет какая бы сила тока не протекала отношения напряжения к силе тока в везде одно и то же следовательно это отношение не является характеристикой электрического поля что же тогда описывает это отношение свойствам чего являются отношения напряжение на концах проводника силе тока в нем измеряемое в вольтах деленных на ампер что характеризует это отношения она характеризует электрическое поле нет она характеризует силу тока нет что же она тогда характеризует свойствам чего являются это отношение ариадна умница это отношение является свойством проводника и мы везде можем записать для данного проводника 2 2 2 2 итак мы с вами выяснили что для этого проводника отношения напряжение на проводнике к силе тока в проводнике равняется двум вольтам на ампер давайте теперь займемся вот этим проводником делить на ноль мы не будем и рассчитаем такое же отношение вольтах на ампер для этого проводника но и сразу приготовим здесь вот так чему равняется здесь это отношения 1 делить на две десятых сколько 5 2 делить на 0 4 5 везде во всех случаях у нас получается пятерка значит если проводник номер один обладает вот таким свойством которые выражаются числом 2 то вот этот проводник обладает этим же свойством но у него другое численное значение у делить на и равняется 5 вольт на ампер ну а здесь чему равняется такое отношение 10 10 10 10 10 10 у деленное на и равняется 10 вольт делить на ампер вот так итак у каждого из этих трех проводников разные свойства у всех у них разные свойства и свойства проводника описывается вот этой величиной скажите пожалуйста а вот если мы возьмем везде одно и то же напряжение например 2 вольта подадим здесь это отношение 2 здесь это отношение 5 а здесь это отношения 10 при одинаковых напряжениях где меньше сила тока в каком из проводников в третьем значит будем говорить так третий проводник оказывает большее сопротивление протекании электрического тока а первый проводник оказывает меньшее сопротивление и вот это отношение давайте и назовем электрическим сопротивлением давайте запишем определение электрическим сопротивлением электрическим сопротивлением называется свойства проводника которая описывается отношениям электрическим сопротивлением называются свойства проводника которая описывается отношениям напряжение на концах проводника которые описываются отношениям напряжение на концах проводника к силе тока в проводнике описывается отношениям напряжение на концах проводника к силе тока в проводнике отписываться отношениям напряжения на концах проводника к силе тока в проводнике как будет по английски сопротивляться to resist по-английски сопротивления resistance поэтому эта величина обозначается большой латинской буквой r большой латинской буквой р р равняется отношению напряжения на концах проводника к силе тока в нем сопротивление проводника в таком случае сопротивление 1 проводника у нас равно двум единицам вольт на ампер 2 5 единица вольт на ампер 3 10 единиц вольт на ампер а если мы сейчас посмотрим на нашу картинку снова то мы увидим что эти величины нас здесь написаны смотрите когда я вытаскивал отсюда штепсель здесь работал проводник номер два когда я отсюда вытаскивал штепсель работал проводник у которого пятерочка здесь написано это и есть значение сопротивления а теперь когда работали все проводники 1 плюс 2 плюс 2 плюс 5 сколько 10 значит сопротивление этих проводников указанной у нас на самом приборе это очень важная характеристика поэтому наверное стоило бы дать особую единицу измерения этой характеристики единица измерения сопротивления получается если мы разделим единицу электрического напряжения на единицу силы тока вольт на ампер но поскольку это очень важная величина то у неё и свое наименование обозначается он и называется кому большая буква о говорит о том что эта единица названа в честь учёного это георг ом георг он брал разные проводники и изучал примерно то же самое что мы с вами только что изучали это сейчас нам легко у нас есть готовый прибор а в те времена эта 19-ый век очень трудно было изготовить проводник допустим который имел бы постоянный диаметр по всей длине вот он такие проводники из разных материалов изготавливают измерял их электрические свойства исследовал и в частности благодаря этому единицы измерения названа в его честь помните я говорил единицы силы тока ампер а потом писал ампер с маленькой буквы если ампир писать с маленькой буквы это значит речь идет о единицы измерения силы тока если словом писать если вы напишете это слово с большой буквы речь идет о бандере мари ампер то здесь должна быть маленькая буква например если в тексте у меня встретиться по цепи ток ток силы 5 ампер я слова ампер должен написать с маленькой буквы точно так же если мы хотим в тексте написать сопротивление проводника равняется 5 o moм 5 он пишется с маленькой буквы но если вы пишите кратко и условие то там используются сокращение единиц поэтому тогда надо писать с большой вот такой интересный интересно такое совпадение и так каждый проводник характеризуется электрическим сопротивлением у этого про не кр-1 равняется 2 ома видите я пишу с большой буквы r 2 равняется 5 м и р 3 равняется 10 комом к сожалению он точнее буква в слове он похоже на нолик чтобы не перепутать смотрите делаем пробел между числом и буквой пишем 5 пробел об или же допустим 50 50 нолик resun худеньким цифра а буковку рисуем широкой чтобы не перепутать что это не 500 метров так всего лишь 50 том речь идет вообще другой физической величине это первая часть нашего разговора а теперь давайте попробуем ту информацию которую мы получили немножко по другим углом рассмотреть мы с вами сейчас делили напряжения на сопротивлении а теперь давайте попробуем изобразить на графике зависимость силы тока от напряжения и тоже есть главная наша задача значит надо построить график по горизонтали которого отложено напряжение поскольку зависимость от напряжения нас интересует а по вертикали сила тока для всех трех проводников и так по горизонтали мы откладываем напряжение в вольтах максимальное напряжение которое здесь у нас фигурирует 5 вольт поэтому пусть это будет у вас 5 сантиметров 10 клеточек 1 2 3 4 5 0 в начале координат обязательно теперь по вертикали максимальное значение силы тока в наших опытах это было 2 ампера пусть 2 ампера будет 10 клеточек то есть один ампер будут 5 клеточек раз два три 4 5 1 ампер раз два три 4 5 2 ампера ну еще одним рисочку сделаем для красоты сила тока в амперах сила тока в амперах рисуем а теперь изобразим на графике те результаты которые сейчас у нас отображены в таблице сначала займемся проводником номер один напряжение 0 сила тока 0 точку ставим в начале координат далее напряжение 1 вольт сила тока пол ампера вот напряжение 1 вольт пол ампера это здесь напряжение два вольта сила тока 1 ампер 1 ампер два вольта 3 вольта создает ток силой полтора ампера четыре вольта ток силой 2 ампера если бы амперметр был на большую силу тока рассчитан мы могли бы подать и напряжение 5 вольт тогда бы ток шел еще больше можно догадаться что ток был бы равен 2 с половиной ампера теперь давайте эти точки отметим если вы аккуратно строили график то можете увидеть что эти точки довольно аккуратно лежат на одной прямой проведем эту прямую вот она и напишем это проводник номер один вы видите что у нас получилось зависимость в виде прямой график зависимости виде прямой второй проводник я уже не буду строить по точкам нетрудно догадаться что если у нас получается график виде прямой то это значит что для его построения достаточно двух точек 1 .
закон ома для участка цепи зависимость силы тока от напряжения электрическое сопротивление закон ома для участка цепи мы с вами этот закон будем устанавливать экспериментально потом в 10 или в 11 классе мы выведем его на основании знаний о структуре вещества а сейчас пока что экспериментально для того чтобы изучить этот закон какие нам нужны приборы как он называется вольтметр амперметр нам нужно создать электрический электрическую цепь которую должен еще входить источник тока значит с помощью источника тока мы создадим электрический ток вольтметром мы будем измерять напряжение на каком-то проводнике и амперметром силу тока через этот проводник давайте сейчас сконструируем схему измерительную а потом ее реализуем уже на практике и так нам нужен источник тока что там внутри не важно для нас важно то что этот источник тока должен обеспечивать нам разные напряжения подаваемая в электрическую цепь поэтому напишем так регулируемый источник тока этот источник тока мы подключим к проводнику причем мы будем разные проводники подключать и будем измерять силу тока в этих проводниках силу тока измеряем амперметром который как вы знаете включается в цепь последовательно и вот две клеммы к которым мы будем подключать разные проводники я нарисую этот проводник так вот условно проводники один из них теперь как измерить напряжение на этом проводники куда подключать вольтметр саша к тому к тому участку цепи на который мы хотим измерить напряжение то есть вот между этими двумя выводами надо подключить вольтметр ну давайте я вот сюда его подключил это тоже самое будет вот наша измерительная схема теперь мы эту измерительную схему соберем на практике и заставим ее работать давайте сейчас поделим да скок поделим экран на две части в одной части мы будем видеть схему на доске а в другой части будем видеть эту же самую схему в реальности вот так и так вот это регулируемый источник тока его еще называют выпрямитель теперь проводник в котором мы будем измерять силу тока вот такой смотрите как он работает электрический ток от источника ну тут я уже амперметр подключил по дороге проходит смотрите как через вот этот замкнутый контакт контакт вот с таким штепсель им можно замыкать и размыкать то есть уток идет в обход вот этого проводника но здесь штепселя нет поэтому ток течет по вот этому проводнику а дальше же везде штепсели включены на щиток идет дальше к следующему выводу к следующей клемме и вот чем хороша это систем тем что я вставляю штепсели могу подключать в электрическую цепь различные проводники вот таким образом ну давайте один я вытащу теперь силу тока мы будем с вами измерять амперметром вот этот амперметр ток от источника тока он уже подключен вот идет через один из этих проводников в нашем случае через вот этот кампер метру и вот этот красный провод ведет к другому выводу источника тока амперметр и подключили включаем источник тока смотрите стрелка отклоняется значит ток действительно протекает остается измерить напряжение на этом участке цепи у нас есть вольтметр мы этот вольтметр подключаем как саша сказал параллельно проводнику вот этот вольтметр один вывод подключаем тут минус значит к тому участку который соединён с отрицательным полюсом вот у меня отрицательный полюс значит вот сюда подключаем второй вывод к проводнику ведущему к положительному полюсу так убираем чтобы ничего нам не заслоняла картину есть так протестируем систему стрелка отклоняется и у вольтметра и амперметра можно сделать немножко крупнее и приступить к исследованию сейчас мы с вами возьмем три различных проводника подключим в эту электрическую цепь и будем изучать зависимость тока от напряжения подаваемая подавая различное напряжение на этот проводник и результаты занесем в таблицу сразу заготовим 3 таблицы раз мы решили изучать протекание тока в 3 проводниках так у нас будет три таблицы здесь напишем проводник номер один номер два номер три давайте пусть у вас ширина таблицы будут 6 клеточек здесь будет 3 колонки поскольку мы с вами изучаем зависимость силы тока от напряжения значит в эту таблицу нужно занести напряжение в вольтах далее силу тока в амперах а этот клеточку я пока не буду заполнять оставим ее на потом аналогично будет устроено и вторая таблица и 3 сил напряжения в вольтах сила тока в амперах и еще одна свободная часть таблицы еще один свободный столбец напряжение в вольтах сила тока в амперах подадим 0 вольт 1 вольт 2 вольта 3 вольта можно еще и четыре вольта будет падать и этот опыт проводил уже поэтому я знаю какое напряжение можно подавать во втором случае во втором случае будем подавать напряжение ноль один два три четыре пять вольт и в третьем случае такие же напряжения 0 1 2 3 4 5 готовьте табличку ну что начнем понемножку если подать напряжение 0 вольт как вы думаете какая будет сила тока в проводнике 0 мы не создаем электрического поля поэтому не возникает силы которая толкала бы носители заряда в определенном направлении значит нету движения зарядов силы тока равна нулю это можно понять и без опыта а теперь подадим напряжение 1 вольт скажите пожалуйста как какую меня тут сопротивление включим еще секундочку я так это что-то надо подправить где-то что-то замыкает экспериментальная физика наука капризная требующая к себе уважение к все пошло и так я подал напряжение приблизительно 1 вольт какая сила тока пол ампер давайте запишем 1 вольт это проводник номер один из сила тока 0,5 ампера увеличим напряжение доведем его до 2 вольт какая сила тока приблизительно 1 ампер будем писать 1 ампер все-таки приборы у нас не идеальны точные да и проводник тоже обладают не идеально целым значением величины которую я назову чуть позже итак два вольта создать напряжение два вольта создает ток в 1 ампер теперь подадим напряжение 3 вольта мы увидим что сила тока в проводнике приблизительно полтора ампера запишем и наконец подадимся ток силой подадим напряжение величиной четыре вольта потечет ток силой 2 ампера теперь понятно почему больше четырех вольт я не подаю вы видите что стрелка амперметра дошла до последнего деления шкалы и я даже небольшой такой запашок чувствуешь горячий проводник стал тепловое действие тока проявила себя и так четыре вольта создает ток силой 2 ампера это был проводник номер один теперь этот проводник мы отключаем и включаем проводник номер два вот смотрите я вытаскивал вот этот штырек и повторяем опыт теперь ток будет течь уже не через этот проводник а через вот этот давайте посмотрим что будет подадим напряжение 1 вольт какова сила тока 0 2 ампера нулю соответствует 0 это мы уже знаем когда мы подали напряжение 1 вольт сила тока в цепи в проводнике 0,3 ампера идем дальше подадим напряжение два вольта какова сила тока 0,4 ампера 0,4 ампера подадим 3 вольта как вы думаете ну собственно я уже вам показываю это 0,6 до 3 вольта 0,6 ампера а если я подам четыре вольта будет 08 это ваше предвидение предсказания гипотеза проверим ее на эксперименте пожалуйста все получается 08 ампера и наконец подавая напряжение 5 вольт мы получаем только силой около одного ампера 1 ампер есть второй проводник мы исследовали теперь возьмем третий проводник это третий проводник у нас будет составной я выну все штепсели из этого устройства теперь ток у нас будет идти и через этот и через этот и через этот и через этот проводник последовательно один за другим будет заряд проходить все эти проводники начнем с одного вольта напряжение 1 вольт сила тока сколько 1 10 ампер 0,1 здесь 0 если я подам два вольта как вы думаете какой ток потечет 0 2 ампера подаем действительно 02 подаем напряжение 3 вольта 0 3 ампера 0 3 4 вольта 0 4 ампера 5 вольт 05 ампера вот как давайте выключим эту систему и теперь больше нам уже это это оборудование не понадобится поэтому открываем полностью экран итак мы с вами подавая на три разных проводника они условно называются номер один номер два номер три различное напряжение измеряли силу тока в этих проводниках а вот давайте посмотрим например на вот эту таблицу смотрите 1 вольт создает ток пол ампера два вольта 1 ампер если мы разделим 1 вольт на пол ампера у нас получится сколько 2 чего-то там если мы 2 разделен на 1 получится 2 если мы 3 разделим на полтора получится 2 если 4 разделим на 2 получится 2 скажите пожалуйста вот это частное от деления напряжение от деления напряжения на силу тока она зависит от силы тока частное нет какая бы сила тока не протекала отношения напряжения к силе тока в везде одно и то же следовательно это отношение не является характеристикой электрического поля что же тогда описывает это отношение свойствам чего являются отношения напряжение на концах проводника силе тока в нем измеряемое в вольтах деленных на ампер что характеризует это отношения она характеризует электрическое поле нет она характеризует силу тока нет что же она тогда характеризует свойствам чего являются это отношение ариадна умница это отношение является свойством проводника и мы везде можем записать для данного проводника 2 2 2 2 итак мы с вами выяснили что для этого проводника отношения напряжение на проводнике к силе тока в проводнике равняется двум вольтам на ампер давайте теперь займемся вот этим проводником делить на ноль мы не будем и рассчитаем такое же отношение вольтах на ампер для этого проводника но и сразу приготовим здесь вот так чему равняется здесь это отношения 1 делить на две десятых сколько 5 2 делить на 0 4 5 везде во всех случаях у нас получается пятерка значит если проводник номер один обладает вот таким свойством которые выражаются числом 2 то вот этот проводник обладает этим же свойством но у него другое численное значение у делить на и равняется 5 вольт на ампер ну а здесь чему равняется такое отношение 10 10 10 10 10 10 у деленное на и равняется 10 вольт делить на ампер вот так итак у каждого из этих трех проводников разные свойства у всех у них разные свойства и свойства проводника описывается вот этой величиной скажите пожалуйста а вот если мы возьмем везде одно и то же напряжение например 2 вольта подадим здесь это отношение 2 здесь это отношение 5 а здесь это отношения 10 при одинаковых напряжениях где меньше сила тока в каком из проводников в третьем значит будем говорить так третий проводник оказывает большее сопротивление протекании электрического тока а первый проводник оказывает меньшее сопротивление и вот это отношение давайте и назовем электрическим сопротивлением давайте запишем определение электрическим сопротивлением электрическим сопротивлением называется свойства проводника которая описывается отношениям электрическим сопротивлением называются свойства проводника которая описывается отношениям напряжение на концах проводника которые описываются отношениям напряжение на концах проводника к силе тока в проводнике описывается отношениям напряжение на концах проводника к силе тока в проводнике отписываться отношениям напряжения на концах проводника к силе тока в проводнике как будет по английски сопротивляться to resist по-английски сопротивления resistance поэтому эта величина обозначается большой латинской буквой r большой латинской буквой р р равняется отношению напряжения на концах проводника к силе тока в нем сопротивление проводника в таком случае сопротивление 1 проводника у нас равно двум единицам вольт на ампер 2 5 единица вольт на ампер 3 10 единиц вольт на ампер а если мы сейчас посмотрим на нашу картинку снова то мы увидим что эти величины нас здесь написаны смотрите когда я вытаскивал отсюда штепсель здесь работал проводник номер два когда я отсюда вытаскивал штепсель работал проводник у которого пятерочка здесь написано это и есть значение сопротивления а теперь когда работали все проводники 1 плюс 2 плюс 2 плюс 5 сколько 10 значит сопротивление этих проводников указанной у нас на самом приборе это очень важная характеристика поэтому наверное стоило бы дать особую единицу измерения этой характеристики единица измерения сопротивления получается если мы разделим единицу электрического напряжения на единицу силы тока вольт на ампер но поскольку это очень важная величина то у неё и свое наименование обозначается он и называется кому большая буква о говорит о том что эта единица названа в честь учёного это георг ом георг он брал разные проводники и изучал примерно то же самое что мы с вами только что изучали это сейчас нам легко у нас есть готовый прибор а в те времена эта 19-ый век очень трудно было изготовить проводник допустим который имел бы постоянный диаметр по всей длине вот он такие проводники из разных материалов изготавливают измерял их электрические свойства исследовал и в частности благодаря этому единицы измерения названа в его честь помните я говорил единицы силы тока ампер а потом писал ампер с маленькой буквы если ампир писать с маленькой буквы это значит речь идет о единицы измерения силы тока если словом писать если вы напишете это слово с большой буквы речь идет о бандере мари ампер то здесь должна быть маленькая буква например если в тексте у меня встретиться по цепи ток ток силы 5 ампер я слова ампер должен написать с маленькой буквы точно так же если мы хотим в тексте написать сопротивление проводника равняется 5 o moм 5 он пишется с маленькой буквы но если вы пишите кратко и условие то там используются сокращение единиц поэтому тогда надо писать с большой вот такой интересный интересно такое совпадение и так каждый проводник характеризуется электрическим сопротивлением у этого про не кр-1 равняется 2 ома видите я пишу с большой буквы r 2 равняется 5 м и р 3 равняется 10 комом к сожалению он точнее буква в слове он похоже на нолик чтобы не перепутать смотрите делаем пробел между числом и буквой пишем 5 пробел об или же допустим 50 50 нолик resun худеньким цифра а буковку рисуем широкой чтобы не перепутать что это не 500 метров так всего лишь 50 том речь идет вообще другой физической величине это первая часть нашего разговора а теперь давайте попробуем ту информацию которую мы получили немножко по другим углом рассмотреть мы с вами сейчас делили напряжения на сопротивлении а теперь давайте попробуем изобразить на графике зависимость силы тока от напряжения и тоже есть главная наша задача значит надо построить график по горизонтали которого отложено напряжение поскольку зависимость от напряжения нас интересует а по вертикали сила тока для всех трех проводников и так по горизонтали мы откладываем напряжение в вольтах максимальное напряжение которое здесь у нас фигурирует 5 вольт поэтому пусть это будет у вас 5 сантиметров 10 клеточек 1 2 3 4 5 0 в начале координат обязательно теперь по вертикали максимальное значение силы тока в наших опытах это было 2 ампера пусть 2 ампера будет 10 клеточек то есть один ампер будут 5 клеточек раз два три 4 5 1 ампер раз два три 4 5 2 ампера ну еще одним рисочку сделаем для красоты сила тока в амперах сила тока в амперах рисуем а теперь изобразим на графике те результаты которые сейчас у нас отображены в таблице сначала займемся проводником номер один напряжение 0 сила тока 0 точку ставим в начале координат далее напряжение 1 вольт сила тока пол ампера вот напряжение 1 вольт пол ампера это здесь напряжение два вольта сила тока 1 ампер 1 ампер два вольта 3 вольта создает ток силой полтора ампера четыре вольта ток силой 2 ампера если бы амперметр был на большую силу тока рассчитан мы могли бы подать и напряжение 5 вольт тогда бы ток шел еще больше можно догадаться что ток был бы равен 2 с половиной ампера теперь давайте эти точки отметим если вы аккуратно строили график то можете увидеть что эти точки довольно аккуратно лежат на одной прямой проведем эту прямую вот она и напишем это проводник номер один вы видите что у нас получилось зависимость в виде прямой график зависимости виде прямой второй проводник я уже не буду строить по точкам нетрудно догадаться что если у нас получается график виде прямой то это значит что для его построения достаточно двух точек 1 . в начале координат 0 0 2 . например при максимальном напряжении 5 вольт 1 ампер вот 5 вольт 1 ампер и теперь мы можем провести прямую сразу это проводник номер два проводник номер три когда мы подаем 5 вольт ток в нем всего лишь пол ампера эту точку мы тоже отмечаем вот она и тоже можно сразу провести прямую проводник номер три рисуем и заодно обращаем внимание вот на такой фактор во сколько раз увеличивается сила тока если увеличить напряжение в два раза в два раза во сколько раз мы увеличиваем напряжение на концах проводника во столько же раз увеличивается сила тока в нем это справедливо для всех этих трех проводников то есть сила тока в проводнике прямо пропорциональна напряжению на этом проводники а теперь это можно записать в виде формулы сила тока в проводнике прямо пропорциональна напряжению на концах этого проводи-ка независимо от того какой проводник номер один номер два или номер 3 а теперь давайте посмотрим как зависит сила тока от от сопротивления проводников возьмем к примеру напряжение четыре вольта и проводник номер один сравним с проводником номер три сопротивление проводника номер 1 2 ома сопротивление проводника номер 3 10 ком напряжение одно и то же четыре вольта ток здесь 2 ампера а здесь ток четыре десятых ампер скажите пожалуйста во сколько раз сила тока уменьшилась в 5 а во сколько раз увеличилось сопротивление было два стола 10 в 10 раз значит с другой стороны сила тока через проводник если увеличить сопротивление в два раза уменьшится в два раза если увеличивать сопротивление в пять раз уменьшится в 5 раз как называется такая зависимость когда обратно пропорциональна значит второй факт который мы установили с вами сила тока обратно пропорциональна сопротивлению проводника а теперь остается объединить эти два факта в 1 оказывается если измерять сопротивление в комах то здесь можно спокойно поставить знак равенства и тогда формула будет выглядеть так и делить на r то что здесь можно поставить знак равенства вы можете посмотреть из таблиц то есть коэффициент пропорциональности равен единице вот это замечательный закон который описывает причину и следствие в связи устанавливать причинно следственную связь между силой тока и напряжением этот закон называется закон ома ну а теперь поскольку вы физически класс я сразу полностью строго объявлю его название закон ома для в учебнике этого нет однородного участка цепи закон ома для однородного участка цепи учебнике написано просто закон ома для участка цепи что такое однородный ребята обратите внимание во всех наших опытах здесь использовался просто кусок провода никаких источников тока по дороге не было вот начало участка цепи до конца как вы знаете вот в источниках тока работают сторонние силы так вот однородным называется участок цепи в котором отсутствуют сторонние силы давайте запишем однородным называется участок цепи в котором отсутствуют сторонние силы однородным называется участок цепи в котором отсутствует сторонние силы что это такое мы с вами помним это силы которые перемещают заряженные частицы против сил электрического поля отсутствует однородной силой сторонние силы ну а теперь собственно закон ома записываем закон ома сила тока в однородном участке цепи сила тока в однородном участке цепи прямо пропорциональна напряжению на концах этого участка сила тока в однородном участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна и обратно пропорциональна сопротивлению участка сила тока в однородном участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна сопротивление участка и обратно пропорциональна сопротивление участка записали это один из центральных законов физики вообще у каждого раздела физике есть какая-то основная задача например основная задача механики определить положение тела в любой момент времени основная задача того раздела который мы с вами занимаемся так скажем теория цепей постоянного тока это найти силу тока в любом участке цепи и вот этот закон позволяет нам это сделать мы теперь понимаем что для того чтобы найти силу тока участке цепи нам нужно знать какое напряжение на этом участке и надо знать сопротивление этого участка а если мы хотим глубже нырнуть то следующий вопрос от чего зависит сопротивления этого участка мы брали разные проводники у них были разные сопротивления выглядели они почти одинаково мы на этот вопрос сегодня отвечать не будем это я просто закинул удочку наперёд впереди интереснейшие уроки где мы выясним от чего зависит это сопротивление а пока что обратите внимание если у вас есть эта формула то из нее вытекают еще 2 если вы знаете напряжение на концах участка цепи и сопротивления вы можете найти силу тока но можно и по другому допустим вы хотите найти сопротивление алгебра отсюда если выразить сопротивление оно равно отношение у напряжения и увеличению сироту силы тока и наоборот если вы хотите найти отсюда напряжения и вам известны силы тока участке цепи и его сопротивления то вы можете это сделать у равняется и умножить на r то есть это очень могущественный закона вот то что я хотел вам рассказать остается только записать домашнее задание домашнее задание по перышки ну параграф 42-44 и там же в перышки не упражнения 29 на страница 126 задание с номерами 1-5 и 7 1-5 и 7 но это мы заканчиваем но мы с вами не расстаёмся пьем чай пока кончен [музыка]
в начале координат 0 0 2 . например при максимальном напряжении 5 вольт 1 ампер вот 5 вольт 1 ампер и теперь мы можем провести прямую сразу это проводник номер два проводник номер три когда мы подаем 5 вольт ток в нем всего лишь пол ампера эту точку мы тоже отмечаем вот она и тоже можно сразу провести прямую проводник номер три рисуем и заодно обращаем внимание вот на такой фактор во сколько раз увеличивается сила тока если увеличить напряжение в два раза в два раза во сколько раз мы увеличиваем напряжение на концах проводника во столько же раз увеличивается сила тока в нем это справедливо для всех этих трех проводников то есть сила тока в проводнике прямо пропорциональна напряжению на этом проводники а теперь это можно записать в виде формулы сила тока в проводнике прямо пропорциональна напряжению на концах этого проводи-ка независимо от того какой проводник номер один номер два или номер 3 а теперь давайте посмотрим как зависит сила тока от от сопротивления проводников возьмем к примеру напряжение четыре вольта и проводник номер один сравним с проводником номер три сопротивление проводника номер 1 2 ома сопротивление проводника номер 3 10 ком напряжение одно и то же четыре вольта ток здесь 2 ампера а здесь ток четыре десятых ампер скажите пожалуйста во сколько раз сила тока уменьшилась в 5 а во сколько раз увеличилось сопротивление было два стола 10 в 10 раз значит с другой стороны сила тока через проводник если увеличить сопротивление в два раза уменьшится в два раза если увеличивать сопротивление в пять раз уменьшится в 5 раз как называется такая зависимость когда обратно пропорциональна значит второй факт который мы установили с вами сила тока обратно пропорциональна сопротивлению проводника а теперь остается объединить эти два факта в 1 оказывается если измерять сопротивление в комах то здесь можно спокойно поставить знак равенства и тогда формула будет выглядеть так и делить на r то что здесь можно поставить знак равенства вы можете посмотреть из таблиц то есть коэффициент пропорциональности равен единице вот это замечательный закон который описывает причину и следствие в связи устанавливать причинно следственную связь между силой тока и напряжением этот закон называется закон ома ну а теперь поскольку вы физически класс я сразу полностью строго объявлю его название закон ома для в учебнике этого нет однородного участка цепи закон ома для однородного участка цепи учебнике написано просто закон ома для участка цепи что такое однородный ребята обратите внимание во всех наших опытах здесь использовался просто кусок провода никаких источников тока по дороге не было вот начало участка цепи до конца как вы знаете вот в источниках тока работают сторонние силы так вот однородным называется участок цепи в котором отсутствуют сторонние силы давайте запишем однородным называется участок цепи в котором отсутствуют сторонние силы однородным называется участок цепи в котором отсутствует сторонние силы что это такое мы с вами помним это силы которые перемещают заряженные частицы против сил электрического поля отсутствует однородной силой сторонние силы ну а теперь собственно закон ома записываем закон ома сила тока в однородном участке цепи сила тока в однородном участке цепи прямо пропорциональна напряжению на концах этого участка сила тока в однородном участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна и обратно пропорциональна сопротивлению участка сила тока в однородном участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна сопротивление участка и обратно пропорциональна сопротивление участка записали это один из центральных законов физики вообще у каждого раздела физике есть какая-то основная задача например основная задача механики определить положение тела в любой момент времени основная задача того раздела который мы с вами занимаемся так скажем теория цепей постоянного тока это найти силу тока в любом участке цепи и вот этот закон позволяет нам это сделать мы теперь понимаем что для того чтобы найти силу тока участке цепи нам нужно знать какое напряжение на этом участке и надо знать сопротивление этого участка а если мы хотим глубже нырнуть то следующий вопрос от чего зависит сопротивления этого участка мы брали разные проводники у них были разные сопротивления выглядели они почти одинаково мы на этот вопрос сегодня отвечать не будем это я просто закинул удочку наперёд впереди интереснейшие уроки где мы выясним от чего зависит это сопротивление а пока что обратите внимание если у вас есть эта формула то из нее вытекают еще 2 если вы знаете напряжение на концах участка цепи и сопротивления вы можете найти силу тока но можно и по другому допустим вы хотите найти сопротивление алгебра отсюда если выразить сопротивление оно равно отношение у напряжения и увеличению сироту силы тока и наоборот если вы хотите найти отсюда напряжения и вам известны силы тока участке цепи и его сопротивления то вы можете это сделать у равняется и умножить на r то есть это очень могущественный закона вот то что я хотел вам рассказать остается только записать домашнее задание домашнее задание по перышки ну параграф 42-44 и там же в перышки не упражнения 29 на страница 126 задание с номерами 1-5 и 7 1-5 и 7 но это мы заканчиваем но мы с вами не расстаёмся пьем чай пока кончен [музыка]
Электрическое напряжение единицы напряжения вольтметр.
 Тема. Электрическое напряжение. Вольтметр. III. Закрепление изученного материала \ Документы \ Для учителя физики
Тема. Электрическое напряжение. Вольтметр. III. Закрепление изученного материала \ Документы \ Для учителя физики При использовании материалов этого сайта — и размещение баннера -ОБЯЗАТЕЛЬНО!!!
Разработку урока предоставила: Толстых Юлия Владимировна, учитель физики и информатики,I квалификационная категория, МОУ СОШ села Кузьминские Отвержки Липецкого района, email:juliy[email protected]
Цель урока:
- Дать понятие напряжения и его объяснение; познакомить с формулой и единицей напряжения; изучить прибор для измерения напряжения и правила включения его в цепь.
- Развивать навыки сборки цепи; мышление; память; речь; интерес к предмету; умение применять полученные знания на практике.
- Воспитание чувства ответственности, коллективизма, добросовестного отношения к выполнению заданий, самодисциплины.
Ход урока по учебнику А.В. Перышкина.
1. Проверка домашнего задания.
Проверка домашнего задания.
Учитель читает вопросы:
- Сила тока обозначается…..
- Сила тока измеряется…..
- Формула для вычисления силы тока…..
- Прибор включается в цепь…..
- Единица электрического заряда…..
- Сколько Ампер в 1 мА?
Ответы: выбрать вариант
- А- I- R
- Вольтметром- часами- амперметром
- F = m a- I = q / t- q = I t
- параллельно- последовательно- первым
- 1 сек- 1 метр- 1 Кулон
- 0,001А- 10А- 100А
Карточки с заданиями раздаются слабым ученикам, а остальные работают у доски и по вопросам
2. Объяснение нового материала.
1. Техника безопасности при работе с электрическим оборудованием.
- Вспомните, ребята, что называют работой тока? Работу электрического поля, создающего ток, называют работой тока.
- Что же это за величина-работа тока? От чего она зависит?
Можно с уверенностью сказать, что она зависит от силы тока, т. е.от электрического заряда, протекающего по цепи в 1с, а так же от новой для вас величины, которая называется электри-ческим напряжением.
е.от электрического заряда, протекающего по цепи в 1с, а так же от новой для вас величины, которая называется электри-ческим напряжением.
Напряжение-это физическая величина, характеризующая электрическое поле и показывающая, какую работу совершает электрическое поле при перемещении единичного положительного заряда из одной точки в другую. Оно обозначается буквой U. Для вычисления напряжения ис-пользуется формула: U = A / q .Единица напряжения названа Вольтом (В) в честь итальянского учёного Алессандро Вольта, создавшего первый гальванический элемент.За единицу напряже-ния принимают такое электрическое напряжение на концах проводника, при котором работа по перемещению электрического заряда в 1Кл по этому проводнику равна 1Дж. 1В = 1Дж / 1КлКроме вольта применяют дольные и кратные ему единицы: милливольт (мВ) и кило-вольт(кВ). 1мВ = 0,001В 1кВ = 1000ВДля измерения напряжения на полюсах источника тока или на каком-нибудь участке цепи применяют прибор, называемый вольтметром. Зажимы вольтметра присоединяют к тем точкам цепи, между которыми надо измерить напряжение. Та-кое включение прибора называют параллельным. Сборка цепи и чертёж схемы, содержащей вольтметр. Объясняется, как обозначается прибор на схеме.
Та-кое включение прибора называют параллельным. Сборка цепи и чертёж схемы, содержащей вольтметр. Объясняется, как обозначается прибор на схеме.
Напряжение
Буква U
Формула U = A / q
Единица 1 Вольт
Дольные единиц ы 1кВ = 1000В
Кратные единицы 1мВ = 0,001В
Прибор вольтметр
Включение в цепь параллельно
Демонстрация вольтметров разного вида с рассказом и объяснением их принципа работы.
3. Закрепление полученных знаний.
На доске записать 2 варианта и вызвать двух учеников для самостоятельной работы.
Переведите данные значения напряжения в Вольт:
1-й вариант:
2-й вариант:
Задания для работы с классом:
Задание 1: Начертите схему электрической цепи, состоящей из аккумулятора, электрического звонка, ключа, вольтметра и амперметра, измеряющих соответственно напряжение на звонке и силу тока в нём.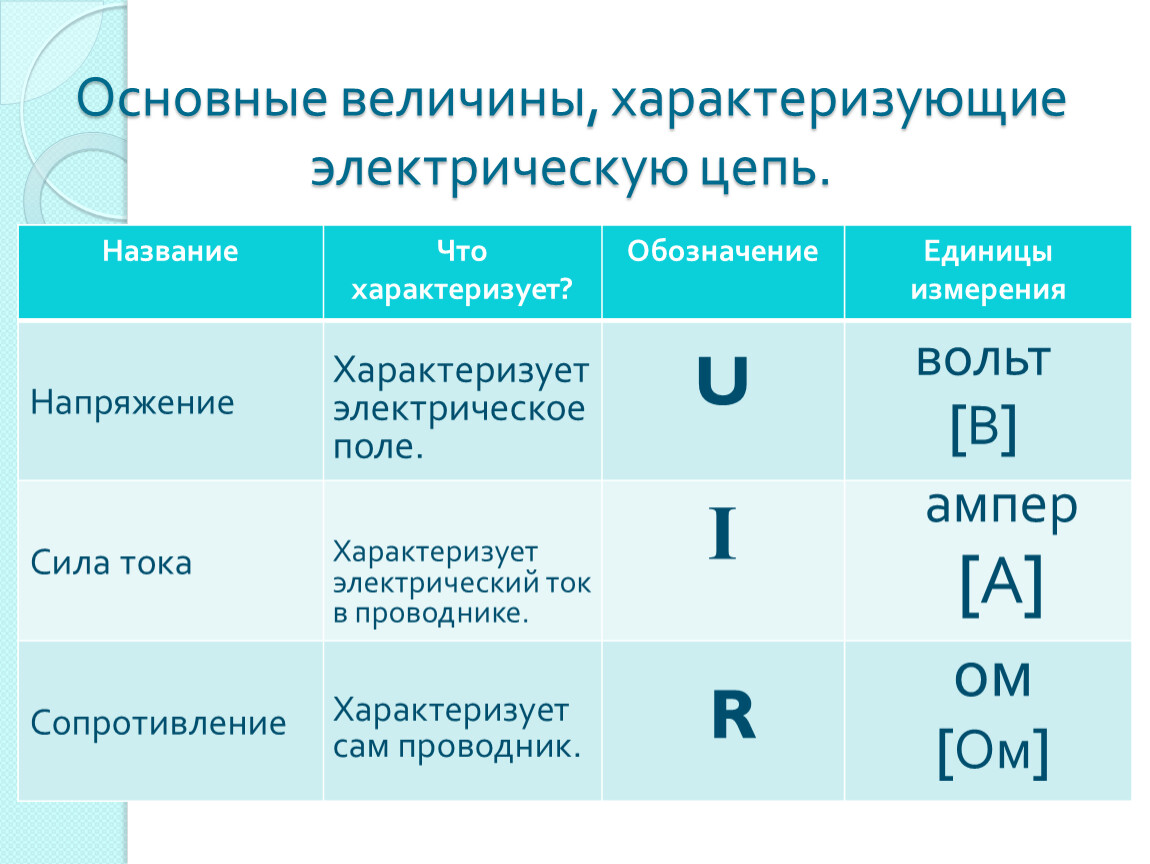 На схеме обозначит знаки зажимов аккумулятора, амперметра и вольтметра, соблюдая правила их соединения. Укажите стрелками направление ток в цепи и направление движения электронов в нём.
На схеме обозначит знаки зажимов аккумулятора, амперметра и вольтметра, соблюдая правила их соединения. Укажите стрелками направление ток в цепи и направление движения электронов в нём.
Задание 2: Какая работа совершается электрическим полем при перемещении заряда в 4,5 Кл через поперечное сечение нити накала лампе, если напряжение на лампе равно 3 В?
(A=Uq=3 B *4,5 Кл= 13,5 Дж)
Задание 3: При прохождении одинакового количества электричества в одном проводнике совершена работа 100 Дж, а в другом – 250 Дж. На каком проводнике напряжение больше? Во сколько раз?
(При прохождении одинакового количества электричества по проводнику, напряжение будет больше в том случае в котором работа тока больше. Во втором случае работа тока больше в 250Дж/100Дж=2,5 раза)
Задание 4: С какими значениями электрического напряжения приходится встречаться человеку в быту? (127В, 220В)
4. Подведение итогов урока.
Опрос по вопросам.
- Что называют работой тока?
- Как объяснить электрическое напряжение на участке цепи?
- Формула для вычисления напряжения.
- Дольные и кратные единицы напряжения.
- Назначение вольтметра и правила включения его в цепь.
Молодцы, ребята! Оценки за урок.
5. Домашнее задание. §39-41 Упр 16 (А.В. Пёрышкин )
Сегодня мы познакомимся ещё с одной физической величиной, но сначала ответьте мне на вопрос: когда тускнеет в лампочках свет, что мы говорим?
(Падает напряжение)
Тема: Электрическое напряжение. Вольтметр. Измерение напряжения.
Повторим и вспомним:
- что такое электрический ток;
- что такое электрическое поле;
- из чего состоит электрическая цепь
Мы узнаем:
ДОМАШНЕЕ ЗАДАНИЕ Да — хлопаем нет – топаемБитва титанов физики
Назовите электрические приборы Найдите условное обозначение
Что же это такое электрический ток?
Вспомним условия существования электрического тока.
Какие частицы переносят электрический заряд в металлах?
Что заставляет эти частицы двигаться?
О силе тока можно судить по показаниям амперметра, либо по действию тока (чем больше накалена нить, тем больше сила тока) Вопрос: от чего зависит сила тока?
Ответ: сила тока зависит от какой-то величины, связанной с источником тока. Источник тока создает электрическое поле, за счет совершения работы по разделению электрических зарядов.
Обычная лампочка и аккумулятор
Лампочка от карманного фонарика и батарейка
Выясним от чего зависит работа тока
Электрическое напряжение характеризует электрическое поле, создаваемое током.. Напряжение (U) показывает какую работу (А) совершает электрическое поле при перемещении единичного положительного заряда (q) из одной точки в другую.Напряжение =
Единица измерения напряжения в системе СИ:
U = 1В «Вольт»
1 Вольт равен электрическому напряжению на участке цепи, где при протекании заряда, равного 1 Кл, совершается работа, равная 1 Дж:
Переведите в систему СИ:
- 200 мВ =
- 6 кВ =
- 0,02 кА =
- 270 мА =
- 20 мин.
 =
= - 2,1 МВ =
2 100 000 В
У игр с напряжением печальный итог
– не любит шутить электрический ток!
СПАСАЙСЯ, КТО МОЖЕТ!
- Напряжение, считающееся безопасным для человека в сухом помещении, составляет до 36 В.
- Для сырого помещения это значение опускается до 12 В.
- Когда человек касается провода, находящегося под напряжением выше 240 В, ток пробивает кожу. Если по проводу течет ток, величина которого еще не смертельна, но достаточна для того, чтобы вызвать непроизвольное сокращение мышц руки (рука как бы “прилипает” к проводу), то сопротивление кожи постепенно уменьшается, и в конце концов ток достигает смертельной для человека величины в 0,1 А. Человеку, попавшему в такую опасную ситуацию, нужно как можно скорее помочь, стараясь “оторвать” его от провода, не подвергая при этом опасности себя.
- Калибровка «0»
- «+» к «+» «-» к «-»
- Включается параллельно
- Условное обозначение
Измеряем напряжение
Определите цену деления прибора:
- 2 В/дел
- 0,5 В/дел
Сборка электрической цепи и измерение напряжения
1. постройте в тетради схему электрической цепи и определите направление тока
постройте в тетради схему электрической цепи и определите направление тока
2. соберите электрическую цепь, ключ должен быть разомкнут
2. Найдите «+» и «-» на аккумуляторе.
3. Рассмотрите вольтметр, определите цену деления
Найдите «0» на вольтметре, вспомните как подключается вольтметр
4. Позовите учителя для проверки электрической цепи
5. Только после разрешения учителя замкните ключ
и определите показания вольтметра
6. Запишите показания вольтметра в тетрадь
Задачи 1. При прохождении по проводнику электрического заряда равного 5 Кл, совершается работа200Дж. Чему равно напряжение на концах этого проводника? А) 1000 В Б) 40 В В) 40 А Г) 0,025 В2. Напряжение на автомобильной лампочке 12 В. Какой заряд прошел через нить накала лампочки, если при этом была совершена работа 1200Дж? А) 0,01Кл Б) 100Кл В) 14400Кл Г)10 В
3.Определите работу, совершенную при прохождении через спираль электроплитки заряда 80 Кл, если она включена в сеть с напряжением 220 В А) 0,36Дж Б) 2,75Дж В) 17600Дж Г) 0,36В
5. Определите цену деления Вольтметра
Определите цену деления Вольтметра
А) 1 В Б) 1,5 В В) 3 В Г) 15 В
4. Необходимо измерить силу тока в лампе и напряжение на ней. Как следует включить по отношению к лампе амперметр и вольтметр?
Итоги урока:
Мы узнали?
А научились?
Домашнее задание
§39-41 Упр. 6 (2,3) Дополнительно(на оценку): 1264,1265 — Лукашик.
Молния
При ударе молнии, например в дерево. Оно нагревается, влага из него испаряется, а давление образовавшегося пара и нагревшихся газов приводят к разрушениям.
Для защиты зданий от грозовых разрядов применяют молниеотводы, которые представляют собой металлический стержень, возвышающийся над защищаемым объектом.
Молния.
В лиственных деревьях ток проходит внутри ствола по сердцевине, где много сока, который под действием тока закипает и пары разрывают дерево.
Причина заключается в том, что между кабелем и севшей на него птицей не возникает разницы напряжений. Ведь сидит она на нем, не соприкасаясь с землей, к тому же сидит только на одном кабеле. Таким образом, напряжения кабеля и птицы абсолютно совпадают. Но если вдруг, взмахнув крыльями, та же птица невзначай коснется соседнего кабеля, но уже с другим напряжением, то адская машина сработает…
Причина заключается в том, что между кабелем и севшей на него птицей не возникает разницы напряжений. Ведь сидит она на нем, не соприкасаясь с землей, к тому же сидит только на одном кабеле. Таким образом, напряжения кабеля и птицы абсолютно совпадают. Но если вдруг, взмахнув крыльями, та же птица невзначай коснется соседнего кабеля, но уже с другим напряжением, то адская машина сработает…
К счастью, кабели обычно располагаются на значительном расстоянии друг от друга, что делает их соприкосновение практически невозможным. Именно поэтому угроза для жизни пернатых ничтожно мала. Но упаси вас Бог проверять это утверждение на практике.
Таким образом, напряжения кабеля и птицы абсолютно совпадают. Но если вдруг, взмахнув крыльями, та же птица невзначай коснется соседнего кабеля, но уже с другим напряжением, то адская машина сработает…
Причина заключается в том, что между кабелем и севшей на него птицей не возникает разницы напряжений. Ведь сидит она на нем, не соприкасаясь с землей, к тому же сидит только на одном кабеле. Таким образом, напряжения кабеля и птицы абсолютно совпадают. Но если вдруг, взмахнув крыльями, та же птица невзначай коснется соседнего кабеля, но уже с другим напряжением, то адская машина сработает…
К счастью, кабели обычно располагаются на значительном расстоянии друг от друга, что делает их соприкосновение практически невозможным. Именно поэтому угроза для жизни пернатых ничтожно мала. Но упаси вас Бог проверять это утверждение на практике.
Почему птицы безнаказанно садятся на провода высоковольтной передачи?
Почему у наэлектризованных людей волосы поднимаются вверх?- Волосы электризуются одноименным зарядом.
 Как известно, одноименные заряды отталкиваются, поэтому волосы, подобно листочкам бумажного султана, расходятся во все стороны.
Если любое проводящее тело, в том числе и человеческое, изолировать от земли, то его можно зарядить до большого потенциала. Так, с помощью электростатической машины тело человека можно зарядить до потенциала в десятки тысяч вольт.
Как известно, одноименные заряды отталкиваются, поэтому волосы, подобно листочкам бумажного султана, расходятся во все стороны.
Если любое проводящее тело, в том числе и человеческое, изолировать от земли, то его можно зарядить до большого потенциала. Так, с помощью электростатической машины тело человека можно зарядить до потенциала в десятки тысяч вольт.
Спасибо за урок! Успехов!
Внимание! Администрация сайта сайт не несет ответственности за содержание методических разработок, а также за соответствие разработки ФГОС.
Данный открытый урок снят на видео 21 января 2016 года на базе МБОУ СОШ №21 г. Нижнекамск Нижнекамского района Республики Татарстан в рамках муниципального конкурса профессионального мастерства «Учитель года — 2016».
В классе в момент съемки присутствовали 20 учащихся 8 класса МБОУ СОШ №21, 16 членов жюри – методисты управления образования г. Нижнекамск, а также учителя и конкурсанты, съемочная группа операторов.
Учащиеся с которым велась работа, были мне не знакомы, следовательно при построении урока мною были учтены и рассмотрены по мере возможности различные ситуации.
Данный видеоролик содержит материал, где я делюсь собственным опытом использования и апробирования моей методической темы «Применение информационно – коммуникационных технологий в педагогической деятельности». Современных детей, которые с рождения приучены гаджетам, увлечь и удивить стоит большого труда. Особенно если кабинет физики с момента открытия школы не обновляется. Интерактивной доски в кабинете не имеется, не смотря на это, с помощью ноутбука и проектора преодолеваю это «препятствие» и нахожу решение как более доступно и интересно преподать урок.
Цели урока: | Предметная: Сформировать понятие «напряжение». Ввести единицы измерения напряжения. Познакомить учащихся с правилами измерения вольтметром. Совершенствовать практические навыки по сборке электрической цепи, чтению и изображению схем, измерения напряжения. |
Задачи урока: | а)формирование представлений о напряжении, организация усвоения основных понятий по данной теме, формирование научного мировоззрения учащихся(предметный результат). б)развитие умения генерировать идеи, выявлять причинно-следственные связи, работать в группе, пользоваться альтернативными источниками информации, формировать умение анализировать факты при наблюдении и объяснении явлений, при работе с текстом учебника(метапредметный результат). в)формирование умений управлять своей учебной деятельностью, формирование интереса к физике при анализе физических явлений, формирование мотивации постановкой познавательных задач, раскрытием связи теории и опыта, развитие внимания, памяти, логического и творческого мышления(личностный результат). |
Методы обучения: | репродуктивный, проблемный, эвристический. |
Формы организации познавательной деятельности обучающихся: | коллективная, индивидуальная, групповая. |
Средства обучения: | учебник, лабораторное оборудование, карточки рефлексии, разноуровневый дидактический материал, ноутбук, проектор, интернет. |
Тип урока | Изучение нового материала |
Работа электрического тока. Напряжение, единица напряжения – 1 Вольт. Вольтметр. Измерение напряжения. | |
Оборудование | Вольтметр, источник тока, лампочка, соединительные провода, ключ, раздаточный материал. Выставка рисунков по теме «Электричество» Физическая газета – дополнение рубрики «Это должен знать каждый», «Исторические сведения», «Факты»… |
Демонстрации | Измерение напряжения на различных участках в цепи |
План урока | Ход урока | Запасной вариант положения |
1) Организационная часть: | Добрый день, ребята! Меня зовут Ахметова Айзаря Занифовна. | |
1 слайд | Девиз урока: «Я слышу – я забываю, я вижу – я запоминаю, я делаю – я понимаю» (Китайская пословица) | |
2) Проверка знаний: 2 слайд | Посмотрите внимательно на экран. Что мы видим на картине? (поле). В жизни это поле мы видим, а с точки зрения электричества поле существует? (да, электрическое) | |
3-4 слайд; 3 анимация «Эл.Ток» | А теперь что наблюдаем? (течение воды в трубе). А в электричестве что может протекать? (эл. ток) | |
Стихотворение (работа в парах, дается 3 ученикам) 1 уч. работает у доски, 2 – работа в парах. | «Как вычисляется сила тока?» – стихотворение Я не зря себя хвалю, | |
Ответ. 8 А 5 слайд Одновременно игра «верю не верю» с остальным классом. | Чему равна сила тока в цепи, если заряд равен 2,4 кКл? Ребята у вас на парте лежат сигнальные карточки зеленого и красного цветов. Я зачитываю предложения, а вы в течении 3 секунд должны поднять красную карточку,если вы не согласны с утверждением, зеленую – если согласны.
| |
Проверка. Самооценка. Проверка у доски задачи. 6 слайд Самооценка. | А сейчас проверим. Кто на все вопросы правильно ответил. Ставит себе 3 балла, если ошиблись 1-2 раза — ставим 2 б, если 3 и более – ставим 1 балл. Отметьте на полях в тетрадях или на листочках у себя. | |
Демонстрация движения груза с динамометром 7 слайд | Из курса 7 класса вы знакомы с термином механическая работа.
| |
Анимация 2 | – Создадим аналогичную ситуацию с электричеством? Т. – И эту работу совершает…. (ЭП) К какому выводу из сказанного мы можем прийти? | |
Определение | Работу сил электрического поля, создающего электрический ток, называют работой тока. В процессе такой работы энергия электрического поля превращается в другой вид энергии – КАКУЮ? (механическую, внутреннюю и др.) ОТ ЧЕГО ЗАВИСИТ РАБОТА ТОКА? (от силы тока, т. е. электрического заряда, протекающего по цепи в 1 с) – в этом вы убедились на предыдущих уроках и при выполнении Л/Р. | |
Исследование Разделившись на 2 группы, ученики замыкают собранные цепи. Сравнить показания амперметра на рис. 63 и 64 Анимация 3 (Демонстрация лампы) | А теперь, ребята, у каждого из вас н парте имеется листочки с надписью «Исследование». Проводники: растворы солей, растворы кислот, серебро, медь, алюминий, золото, вода, графит, медь,) На 2 партах надписи ДИЭЛЕКТРИК и ПРОВОДНИК. На слайде прописано группа диэлектриков и проводников. Каждый находит свой слово в группе и идет к тому столу, где стоит карточка с этим названием. Ребята делятся т.о. на 2 группы и проводят исследование: замыкают собранную цепь.. Ребята, посмотрите на показания амперметра. Озвучьте каждая группа.(Называет каждая группа). Если в цепи с осветительной лампой амперметр показывает меньшую силу тока, а через цепь с лампой от карманного фонаря проходит больший ток, то почему же яркость лампочек различна? (ответы ребят) Идеализированный, частный случай, когда показания амперметров одинаковы. Значит, работа тока зависит не только от силы тока, но и от другой величины…. | |
3) Изучение нового материала: | Так вот, сегодня мы узнаем, что такое напряжение, научимся его измерять, познакомимся с его основными характеристиками. | |
Записать число и тему урока в тетради (На доске) | Тема нашего урока: «Электрическое напряжение. Единицы напряжения» | |
План на доске и 1 один на парту | При знакомстве с новой величиной будем пользоваться уже известным нам планом . Ребята, найдите в учебнике определение, кто нашел — прочтите классу.(стр.91) | |
Определение | Электрическое напряжение – это физическая величина, характеризующая электрическое поле | |
Определение | Вывод: напряжение показывает, какую работу совершает эл. | |
Обозначение Прописываю на доске, одновременно со слайдом | — Обозначается напряжениеU ; — работа А; — заряд буквойq ; | |
Исходя из определения напряжения: зная работу тока на данном участке цепи и весь эл. заряд, прошедший по этому участку, мы можем составить уравнение, т. е. работу тока при перемещении единичного эл. заряда: | Карточка с заданием. | |
Формула для вычисления Анимация 4 | U = A / q → A = Uq ; q = A/U | |
(Мини сообщение) Заранее дать одному ребенку | — Этот портрет вам знаком? (Да, Алессандро Вольта) Как вы думаете единица электрического напряжения как называется? (Вольт). Обратимся к формуле напряжения и попробуем вывести единицу измерения. U = A / q ; 1 В = 1Дж/Кл | |
Единицы измерения | За единицу напряжения принимают, такое эл. напряжение на концах проводника, при котором работа по перемещению эл.заряда в 1 Кл по этому проводнику равна 1 Дж: 1 В = 1Дж/Кл На следующем уроке вы познакомитесь с прибором для измерения напряжения – вольтметр. Подключается он в цепь параллельно, попробуете собрать цепь с использованием вольтметра. | |
Слайд 12 Прибор для измерения Обозначение на схеме Правила подключения | — Как понять смысл напряжения? Электрический ток подобен течению воды в реках и водопадах, т.е. подобен течению воды с более высокого уровня на более низкий. | |
Слайд 13 | Работа, совершаемая падающей водой, зависит от её массы и высоты падения, следовательно, зависит от потенциальной энергии. Чем больше разность уровней воды, тем большую работу совершает вода. Работа силы тока зависит от электрического заряда и напряжения на этом проводнике. Чем больше напряжение на участке цепи, тем больше работа тока при той же величине заряда. В 10 классе мы будем работу электрического поля выражать через разность потенциальной энергии. Если в цепи нет напряжения, то в ней нет и электрического тока (как нет течения в озере или пруде при отсутствии разности уровней в рельефе). | |
4) Домашнее задание: записано на доске заранее | §39-40, пройти тестирование с использованием телефона по теме «Электрическое напряжение». | |
Творческий проект. Слайд 14 | Класс работает над творческим проектом. Попробуем написать свою картину? Ее нужно будет пояснять с точки зрения электричества. | Если не успеваю, тогда Домашняя работа |
Рефлексия (на рисунок лампочки прикрепляют зеленые и красные кружочки при помощи магнитиков). (1 мин) На доске прикреплен ватман, на котором нарисована лампочка. Перед уходом. |
ПЛАН (на доске)
- Определение
- Обозначение
- Единицы измерения
- Формула для вычисления
- Каким прибором измеряется
- Обозначение на схеме
- Правила подключения в цепи
Мини – сообщение
ВОЛЬТА Алессандро — итальянский естествоиспытатель, физик, химик и физиолог. Его важнейшим вкладом в науку явилось изобретение источника постоянного тока, сыгравшее определяющую роль в дальнейших исследованиях электрических и магнитных явлений.
Его важнейшим вкладом в науку явилось изобретение источника постоянного тока, сыгравшее определяющую роль в дальнейших исследованиях электрических и магнитных явлений.
Индивидуальная карточка на сильных учащихся
- Определите напряжение на участке цепи, если при прохождении по нему заряда в 15 Кл током была совершена работа 6 кДж?
- При переносе 60 Кл электричества из одной точки электрической цепи в другую за 12 мин совершена работа 900 Дж. Определите напряжение и силу тока в цепи.
Пробовали ли вы когда-нибудь надувать воздушные шарики на время? Один надувает быстро, а другой за это же время надувает гораздо меньше. Без сомнения, первый совершает большую работу, чем второй.
С источниками напряжения происходит точно так же. Чтобы обеспечить движение частиц в проводнике, надо совершить работу. И эту работу совершает источник. Работу источника характеризует напряжение. Чем оно больше, тем большую работу совершает источник, тем ярче будет гореть лампочка в цепи (при других одинаковых условиях).
Напряжение равно отношению работы электрического поля по перемещению заряда
к величине перемещаемого заряда на участке цепи.
U = A q , где \(U\) — напряжение, \(A\) — работа электрического поля, \(q\) — заряд.
Обрати внимание!
Единица измерения напряжения в системе СИ — [\(U\)] = \(1\) B (вольт).
\(1\) вольт равен электрическому напряжению на участке цепи, где при протекании заряда, равного \(1\) Кл, совершается работа, равная \(1\) Дж: \(1\) В \(= 1\) Дж/1 Кл.
Все видели надпись на домашних бытовых приборах «\(220\) В». Она означает, что на участке цепи совершается работа \(220\) Дж по перемещению заряда \(1\) Кл.
Кроме вольта, применяют дольные и кратные ему единицы — милливольт и киловольт.
\(1\) мВ \(= 0,001\) В, \(1\) кВ \(= 1000\) В или \(1\) В \(= 1000\) мВ, \(1\) В \(= 0,001\) кВ.
Для измерения напряжения используют прибор, который называется вольтметр
.
Обозначаются все вольтметры латинской буквой \(V\), которая наносится на циферблат приборов и используется в схематическом изображении прибора.
В школьных условиях используются вольтметры, изображённые на рисунке:
Основными элементами вольтметра являются корпус, шкала, стрелка и клеммы. Клеммы обычно подписаны плюсом или минусом и для наглядности выделены разными цветами: красный — плюс, черный (синий) — минус. Сделано это с той целью, чтобы заведомо правильно подключать клеммы прибора к соответствующим проводам, подключённым к источнику.
Обрати внимание!
В отличие от амперметра, который включается в разрыв цепи последовательно, вольтметр включается в цепь параллельно.
Включая вольтметр в цепь постоянного тока, необходимо соблюдать полярность.
Сборку электрической цепи лучше начинать со всех элементов, кроме вольтметра, а его уже подключать в самом конце.
Вольтметры делятся на приборы постоянного тока и переменного тока .
Если прибор предназначен для цепей переменного тока, то на циферблате принято изображать волнистую линию. Если прибор предназначен для цепей постоянного тока, то линия будет прямой.
Вольтметр постоянного тока | Вольтметр переменного тока |
Можно обратить внимание на клеммы прибора. Если указана полярность («\(+\)» и «\(-\)»), то это прибор для измерения постоянного напряжения.
Иногда используют буквы \(AC/DC\). В переводе с английского \(AC\) (alternating current) — переменный ток, а \(DC\) (direct current) — постоянный ток.
В цепь переменного тока включается вольтметр для измерения переменного тока. Он полярности не имеет.
Обрати внимание!
Для измерения напряжения можно использовать и мультиметр.
Следует помнить, что высокое напряжение опасно.
Что будет с человеком, который окажется рядом с упавшим оголённым кабелем, находящимся под высоким напряжением?
Так как земля является проводником электрического тока, вокруг упавшего оголённого кабеля, находящегося под напряжением, может возникнуть опасное для человека шаговое напряжение.
Разделы: Физика
Класс: 8
Цель урока: дать понятие напряжение как физической величины характеризующей электрическое поле, создающее электрический ток, вести единицу напряжения.
Оборудование: амперметры двух видов, вольтметры двух видов, портрет Алессандро Вольта.
Ход урока
I. Актуализация знаний.
Проверка домашнего задания. Слайд 2.
- Что такое сила тока? Какой буквой она обозначается?
- По какой формуле находится сила тока?
- Как называется прибор для измерения силы тока? Как он обозначается в схемах?
- Как называется единица силы тока? Как она обозначается?
- Какими правилами следует руководствоваться при включении амперметра в цепь?
- По какой формуле находится электрический заряд, проходящий через поперечное сечение проводника, если известны сила тока и время его прохождения?
- Индивидуальные задания:
1) Через поперечное сечение проводника в 1 с
проходит 6*10 -19 электронов. Какова сила тока
в проводнике? Заряд электрона 1,6*10 -19 Кл.
Какова сила тока
в проводнике? Заряд электрона 1,6*10 -19 Кл.
2) Определите силу тока в электрической лампе,
если через нее за 10 мин проходит электрический
заряд, равный 300 Кл.
3) Какой электрический заряд протекает за 5 мин
через амперметр при силе тока в цепи 0,5 А.
- Проверочная работа (по карточкам):
Вариант I
1.Сколько миллиампер в 0,25 А?
а) 250 мА;
б)25мА;
в) 2,5мА;
г) 0,25мА;
д)0,025мА;
2.Выразите 0,25мА в микроамперах.
а) 250 мкА;
б)25мкА;
в) 2,5мкА;
г) 0,25мкА;
д)0,025мкА;
На рис. 1 изображена схема электрической цепи.
а) у точки М
б) у точки N
а) от точки М к N
б) от точки N к М
Вариант II
1.Выразите 0,025 А в амперметрах.
а) 250 мА;
б)25мА;
в) 2,5мА;
г) 0,25мА;
д)0,025мА;
2. Сколько микроампер в 0,025мА?
Сколько микроампер в 0,025мА?
а) 250 мкА;
б)25мкА;
в) 2,5мкА;
г) 0,25мкА;
д)0,025мкА;
На рис. 2 изображена схема электрической цепи.
3. Где на этой схеме у амперметра знак “+”?
а) у точки М
б) у точки N
4. Какое направление имеет ток в амперметре?
а) от точки М к N
б) от точки N к М
9) Проверка теста. Слайд 3
II. Изучение нового материала.
1. Диск Виртуальная школа Кирилла и Мефодия. Уроки физики Кирилла и Мефодия, 8 класс.
1) Что такое электрический ток?
Ответ учащихся: Электрический ток – это направленное движение заряженных частиц.
2) Каковы условия существования электрического тока?
Ответ учащихся: 1 условие – свободные заряды,
2 условие – должен быть в цепи источник тока.
3) Объяснение учителя:
Направленное движение заряженных частиц
создаётся электрическим полем, которое при этом
совершает работу. Работа, которую совершает
электрический ток при перемещении заряда в 1 Кл
по участку цепи, называется электрическим
напряжением (или просто напряжением).
Работа, которую совершает
электрический ток при перемещении заряда в 1 Кл
по участку цепи, называется электрическим
напряжением (или просто напряжением).
где U – напряжение (В)
А – работа (Дж)
q – заряд (Кл)
Напряжение измеряется в вольтах (В): 1В = 1Дж/Кл.
4) Сообщение ученика: Историческая справка об Алессандро Вольта.
ВОЛЬТА Алессандро (1745-1827), итальянский естествоиспытатель, физик, химик и физиолог. Его важнейшим вкладом в науку явилось изобретение принципиально нового источника постоянного тока, сыгравшее определяющую роль в дальнейших исследованиях электрических и магнитных явлений. В честь него названа единица разности потенциалов электрического поля – вольт.
Вольта был членом-корреспондентом Парижской академии наук, членом-корреспондентом академии наук и литературы в Падуе и членом Лондонского Королевского общества.
В 1800 г. Наполеон открыл университет в Павии, где
Вольта был назначен профессором
экспериментальной физики. По предложению
Бонапарта ему была присуждена золотая медаль и
премия первого консула. В 1802 г. Вольта избирается
в академию Болоньи, через год –
членом-корреспондентом Института Франции и
удостаивается приглашения в Петербургскую
академию наук (избран в 1819). Папа назначает ему
пенсию, во Франции его награждают орденом
Почетного Легиона. В 1809 Вольта становится
сенатором Итальянского королевства, а в
следующем году ему присваивается титул графа. В
1812 г. Наполеон из ставки в Москве назначает его
президентом коллегии выборщиков.
По предложению
Бонапарта ему была присуждена золотая медаль и
премия первого консула. В 1802 г. Вольта избирается
в академию Болоньи, через год –
членом-корреспондентом Института Франции и
удостаивается приглашения в Петербургскую
академию наук (избран в 1819). Папа назначает ему
пенсию, во Франции его награждают орденом
Почетного Легиона. В 1809 Вольта становится
сенатором Итальянского королевства, а в
следующем году ему присваивается титул графа. В
1812 г. Наполеон из ставки в Москве назначает его
президентом коллегии выборщиков.
С 1814 г, Вольта – декан философского факультета в Павии. Австрийские власти даже предоставляют ему право исполнять обязанности декана без посещения службы и подтверждают законность выплаты ему пенсий почётного профессора и экс-сенатора.
5) Дольные и кратные единицы:
1 мВ = 0,001 В;
1 мкВ = 0, 000 001 В;
1 кВ = 1 000 В.
6) Работа с учебником.
Работа с таблицей №7 в учебнике на стр.93.
7) Рабочее напряжение в осветительной сети
жилых домов, социальных объектов – 127 и 220 В.
Опасность тока высокого напряжения.
Правила безопасности при работе с электричеством и электроприборами. Слайд 4.
8) Прибор для измерения напряжения называется вольтметром.
На схемах изображается знаком:
Правила включения вольтметра в цепь найдите в учебнике .
1. Зажимы вольтметра присоединяются к тем точкам цепи, между которыми надо измерить напряжение (параллельно соответствующему участку цепи).
2. Клемму вольтметра со знаком “+” следует соединять с той точкой цепи, которая соединена с положительным полюсом источника тока, а клемму со знаком “ – ” с точкой, которая соединена с отрицательным полюсом источника тока.
Демонстрация двух типов вольтметров.
Отличие вольтметра от амперметра по внешнему виду.
Определение цены деления демонстрационного вольтметра, лабораторного вольтметра.
9) Работа с учебником: (задание по вариантам)
Найдите в учебнике (§ 41) ответы на вопросы:
А) Как с помощью вольтметра измерить напряжение на полюсах источника тока?
Б) Какой должна быть сила тока, проходящего через вольтметр, по сравнению с силой тока в цепи?
III.
 Закрепление изученного материала.
Закрепление изученного материала. - Выразите в вольтах напряжение, равное:
А) U =2 000 мВ =
Б) U = 100 мВ =
В) U = 55 мВ =
Г) U = 3 кВ =
Д) U = 0,5 кВ =
Е) U = 1,3 кВ =
2. Выразите в мВ напряжение, равное:
А) U = 0,5 В =
Б) U = 1,3 В =
В) U = 0,1 В =
Г) U = 1 В =
Д) U = 1 кВ =
Е) U = 0,9 кВ =
3. Решим задачки: Слайд 7. (работа у доски)
А) На участке цепи при прохождении электрическогозаряда25 Кл совершена работа 500 Дж.Чему равно напряжении на этом участке?
Б) Напряжение на концах проводника 220 В. Какая работа будет совершена при прохождении по проводнику электрического заряда, равного 10 Кл?
4. Вопросы на закрепление:
1) Что показывает напряжение в электрической цепи?
2) В каких единицах измеряется напряжение?
3) Кто такой Алессандро Вольта?
4) Как называют прибор для измерения напряжения?
5) Назовите правила включения вольтметра для измерения напряжения на участке цепи?
IV.
 Домашнее задание.
Домашнее задание. § 39 – 41. Упр.16. Подготовиться к лабораторной работе №4 (с.172).
V. Итог урока.
Литература:
- Пёрышкин А.В. Физика. 8кл.: учеб. для общеобразоват. учеб. заведений. – М.:Дрофа, 2007.
- Шевцов В.А. Физика. 8кл.: поурочные планы по учебнику А.В.Пёрышкина.-Волгоград: Учитель, 2007. – 136с.
- Марон А.Е. Физика. 8кл.: учебно-методическое пособие /А.Е.Марон, Е.А.Марон.-6-е изд., стереотип. – М.:Дрофа, 2008.-125с.:ил.-(Дидактические материалы)
- Учебный диск “Кирилла и Мефодия”. Физика.8 класс.
Электрическое напряжение. Вольтметр. Электрические цепи. | Поурочные планы по физике 8 класс
Электрическое напряжение. Вольтметр. Электрические цепи.
27.02.2014 6225 0Цель: ввести понятие
напряжения и познакомить учащихся с единицей измерения напряжения. Побуждать учащихся к преодолению трудностей в
процессе умственной деятельности, воспитать интерес к физике.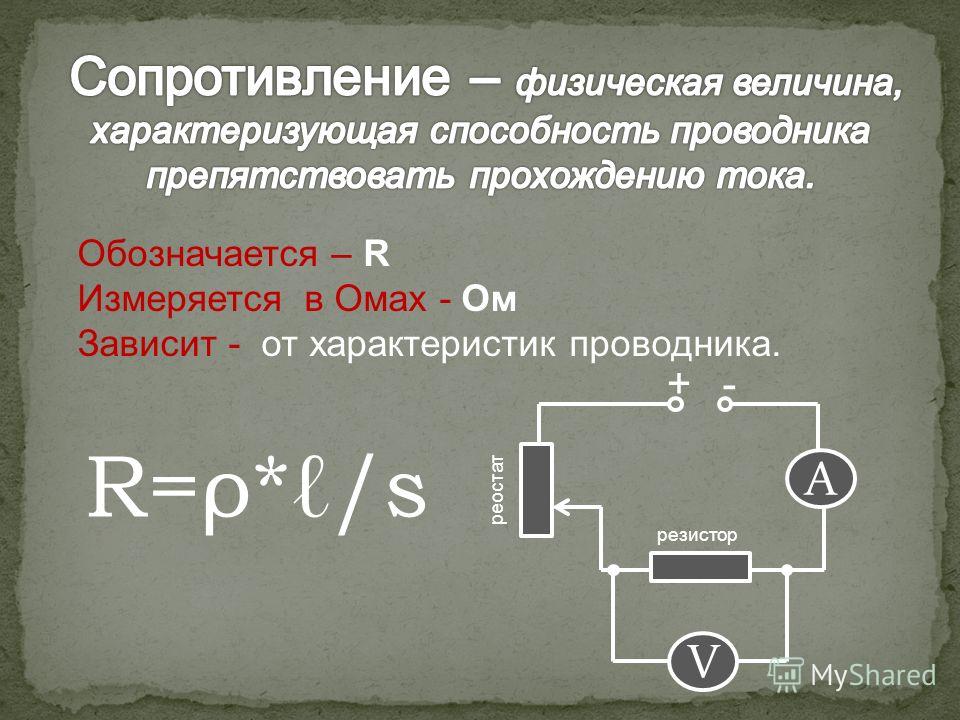
Демонстрации: электрическая схема с лампочками от карманного фонарика и осветительной сети; измерение напряжения вольтметром. Ознакомить с назначением и условным обозначением цепи, научить собирать простейшие электрические цепи
Ход урока
I. Организационный момент
II. Проверка знаний
Чтобы проверить степень усвоения знаний по теме можно в начале урока провести самостоятельную работу по карточкам с разноуровневыми заданиями, например:
Уровень 1
1. Сколько у источника тока полюсов? Какие бывают полюсы?
2. Какие источники тока вы знаете?
Уровень 2
1. Почему тепловое движение электронов в проводнике не может быть названо электрическим током?
2. Могут ли жидкости быть проводниками? Диэлектриками? Приведите примеры.
Уровень 3 .
1. По спирали электролампы проходит 540 Кл электричества за каждые 5 мин. Чему равна сила тока в лампе?
2. При электросварке сила тока достигает 200 А. Какой электрический заряд
проходит через поперечное сечение электрода за 1 мин?
При электросварке сила тока достигает 200 А. Какой электрический заряд
проходит через поперечное сечение электрода за 1 мин?
Уровень 4
1. Скорость направленного движения электронов в металлическом проводнике очень мала, составляет доли миллиметра в секунду. Почему же лампа начинает светиться практически одновременно с замыканием цепи?
2. Гальванометр показывает наличие тока, если к его зажимам присоединить стальную и алюминиевую проволоки, а вторые концы воткнуть в лимон или яблоко. Объясните это явление.
3. Во включенном в цепь приборе сила тока равна 8 мкА. Какое количество электричества проходит через этот прибор в течение 12 мин?
III. Изучение нового материала
План изложения нового материала:
1. Показать, что напряжение характеризует электрическое поле, созданное источником,
2. Напряжение на участке электрической цепи.
3. Единица напряжения — вольт.
4. Сборка электрической цепи (фронтальный
эксперимент).
5. Условные обозначения составляющих электрической цепи.
1. О силе тока можно судить либо по показанию амперметра, либо по
действию тока. Например, чем больше накалена нить лампы, тем больший ток проходит по цепи.
— От каких же факторов зависит сила тока в цепи?
Проведем опыт: замкнем цепь на один аккумулятор и обратим внимание на величину тока в цепи. Если последовательно увеличивать число аккумуляторов, ток в цепи увеличивается.
Вывод: сила тока в цепи зависит от какой-то величины, связанной с источником тока.
Поскольку источник тока создает электрическое поле в цепи, а ток, возникающий
в цепи под действием этого электрического поля, оказывается не одинаковой
величины, то и электрическое поле различных источников будет разным. Электрическое
поле действует с определенной силой на за-, ряженные частицы. Чем больше
величина этой силы, тем больше будет скорость направленного движения заряженных
частиц. Это означает, что через поперечное сечение проводника пройдет в единицу
времени большее число заряженных частиц и будет перенесен больший электрический
заряд, то есть пройдет больший ток.
Действующее в цепи электрическое поле характеризуется особой величиной, называемой напряжением электрического поля или просто напряжением.
Напряжение — это физическая величина, характеризующая действие электрического поля на заряженные частицы.
2. Напряжение на участке электрической цепи. — Как же мы можем судить о напряжении?
Собираем схему, в которую включены последовательно две лампочки. Одна — рассчитанная
на напряжение 220 В, а другая — от фонарика, рассчитанная на 4,5 В. Ток в
обеих лампочках будет примерно одинаков, а следовательно, через лампочки
протекает в единицу времени одно и то же количество электричества. Однако
осветительная лампочка излучает света во много раз больше, чем лампочка для
карманного фонаря. Очевидно, для прохождения некоторого количества
электричества через осветительную лампу требуется большее количество энергии,
чем при протекании заряда через лампочку от карманного фонарика. То есть работа
электрического тока в первой лампочке больше, чем во второй. О величине работы
можно судить по различию в напряжении.
О величине работы
можно судить по различию в напряжении.
Напряжение показывает, какую работу совершает электрическое поле по перемещению единицы заряда на данном участке цепи:
3. Единица напряжения — вольт (В).
Вольт равен такому электрическому напряжению между двумя точками цепи, при котором работа по перемещению электрического заряда в 1 Кл на этом участке равна 1 Дж
4. Изложение нового материала начинается с повторения.
В источнике тока за счет энергии неэлектрического происхождения совершается работа по разделению заряженных частиц. При разделении возникает электрическое поле, которое обладает энергией. Это поле может совершать работу. Чтобы ток существовал, необходимо, кроме поля, наличие замкнутой цепи, в которую включаются потребители энергии электрического тока. Далее знакомство с элементами электрической цепи.
На доске вычерчивается схема простейшей цепи.
В простейших случаях электрическая цепь состоит из: а) источника тока; б)
системы соединительных проводов и управляющих устройств; в) потребителя
электрической энергии.
Даются практические указания по сборке электрической цепи. Учащиеся самостоятельно составляют простейшую цепь по заданной схеме.
Вопросы классу:
Каково назначение источника тока в электрической цепи?
— Какие источники электрического тока вам известны? Каково их назначение? Какую электрическую цепь называют замкнутой? Разомкнутой?
5. Умение чертить схемы электрических цепей и читать готовые схемы вырабатывается у школьников в результате упражнений, которые проводят как на данном уроке, так и на последующих уроках. Полезны задания по составлению схем электропроводки, например:
— Начертите схему цепи, содержащей источник тока и две электрические лампы, каждую из которых включают своим выключателем. Нарисуйте схему соединения батарейки, лампочки, звонка и двух ключей, при которой лампочка загорается при включении звонка, но может быть включена и при неработающем звонке. Нарисуйте схему соединения батарейки, двух лампочек и трех ключей, при которой включение и выключение каждой лампочки производится «своим» ключом, а размыкание третьего ключа позволяет отключить обе лампочки.
IV. Закрепление изученного
Вопросы для закрепления:
— Из какого опыта следует необходимость введения понятия напряжения?
— Какой физической величиной пользуются для измерения напряжения?
Какое напряжение используют в осветительной сети? Напряжение в сети 100 В. Что это означает?
Если в конце урока остается время, его желательно посвятить разбору простых задач по изученной теме:
Задача 1
При прохождении одинакового количества электричества в одном проводнике совершена работа 100 Дж, а в другом — 250 Дж. На каком проводнике напряжение больше? Во сколько раз?
адача 2
Определите напряжение на участке цепи, если при прохождении по нему заряда в 15 Кл током была совершена работа 6 кДж.
Задача 3
При переносе 60 Кл электричества из одной точки электрической цепи в другую за 12 мин совершена работа 900 Дж. Определите напряжение и силу тока в цепи.
Домашнее задание
§ 37 учебника
Физика 8 класс. Напряжение. Единицы напряжения
Физика 8 класс. Конспект. НапряжениеЭлектрическое напряжение. Единицы напряжения. Измерение напряжения.
Электрический ток – это упорядоченное движение заряженных частиц, которое создаётся электрическим полем, а оно при этом совершает работу. Работу сил электрического поля, создающего электрический ток, называют работой тока.
Работа тока зависит от силы тока, то есть от электрического заряда, протекающего по цепи в 1 с. Работа силы тока зависит также от напряжения.
Напряжение – это физическая величина, характеризующая электрическое поле. Напряжение показывает, какую работу совершает электрическое поле при перемещении единичного положительного заряда из одной точки в другую.
Напряжение U равно отношению работы тока A на данном участке к электрическому заряду q, прошедшему по данному участку.
где U – напряжение, А — работа тока, q – электрический заряд.
Единица напряжения называется Вольт, обозначается В.
За единицу напряжения принимают такое электрическое напряжение на концах проводника, при котором работа по перемещению электрического заряда в 1 Кл по этому проводнику равна 1 Дж.
1 В = 1 Дж/Кл
Используют также другие единицы напряжения: милливольт (мВ) и киловольт (кВ)
1 мВ = 0,001 В, 1 кВ = 1000 В
Для измерения напряжения на полюсах источника тока или на каком-нибудь участке цепи применяют прибор, называемый вольтметром.
Зажимы вольтметра присоединяют к тем точкам цепи, между которыми нужно измерить напряжение. Такое включение прибора называется параллельным.
Сила тока в проводнике прямо пропорциональна напряжению на концах проводника: во сколько раз увеличивается напряжение, приложенное к проводнику, во столько же раз увеличивается сила тока в нем.
Конспект составлен на основании теоретического материала учебника «Физика 8 класс» А.В. Перышкин
Скачать конспект:
Похожие записи:
Что такое стресс? Кто хоть раз видел стресс? Стресс — это физическая величина?
Что такое стресс? Кто хоть раз видел стресс? Стресс — это физическая величина?
Профессор И-Хэн Чен, Сианьский университет Цзяотун, 710049, Китайская Республика
электронная почта: [email protected]
Собственно, этот вопрос беспокоит автора уже более 15 лет.
Как хорошо известно, все предыдущие и нынешние исследователи, специализирующиеся в области механики твердого тела в машиностроении или аэрокосмической технике, всегда использовали классическую концепцию напряжения, поскольку они использовали другие физические величины: смещение или деформацию и т. Д.
Однако в мире нет никого, кто когда-либо видел стресс с помощью любого инструмента!
Более того, никто толком не понимал, что такое физический смысл стресса!
Или вместо этого никто не осознавал подробный факт, является ли стресс реальной физической величиной?
Хорошо известно, что для данной геометрической системы координат смещения материальной точки твердого тела, несомненно, являются физическими величинами! Это связано с тем, что смещения материальной точки можно было непосредственно увидеть или измерить с помощью глаз, некоторых современных оптических инструментов или даже электронного микроскопа.
Таким образом, их градации также являются физической величиной в той же точке (или около небольшой области), где существуют непрерывные дифференциалы первого порядка.
Самая большая трудность в том, что такое стресс?
Очевидно, что концепция напряжения сильно отличается от деформации и перемещений, по крайней мере, из-за следующих трех точек зрения:
(1) Во-первых, напряжение невидимо или невозможно измерить с помощью любых существующих инструментов, включая все оптические и электрические инструменты, тогда как смещения или деформации, как известно, можно измерить.Например, некоторые новые оптические инструменты могут быть использованы для уточнения всего 0,01 микрометра смещений и 1 микродеформации, как сообщили GOM или другие корпорации. Более того, некоторые современные электрические микроскопы имеют разрешающую способность 0,18 нанометра!
(2) Во-вторых, классическая концепция напряжения основана на обобщенном законе Гука для упругости, а затем ее расширяют для рассмотрения некоторых структурных проблем пластичности, таких как теория пластической деформации или теория пластической жидкости. В последнее время эта концепция распространилась на микромеханику, механику повреждений и даже наномеханику.Однако, строго говоря, эта концепция возникла не из экспериментальных наблюдений, а из человеческого мозга! Таким образом, это не реальная физическая величина или, другими словами, это псевдофизическая величина, просто воображаемая физическая величина! Этот вопрос легко доказать, потому что в литературе нет никого, кто утверждал бы, что он видел стресс или измерял его!
(3) В-третьих, в нелинейных и неоднородных материалах при некоторых нагрузках имеется много кристаллов (металл) или частиц (керамика) с масштабом в несколько микрон.Вообще говоря, поле напряжений в неоднородном материале не является однородным или даже не уникальным, хотя поле деформации или поле смещения в том же неоднородном материале уникально (поле деформации может быть однозначно выведено из измеренного поля смещения). Из-за зарождения, роста, коалесценции микродефектов (необратимого термодинамического процесса) измеренное поле смещения и вычисленное поле деформации также изменяется. Но каждое поле деформации / смещения может приводить к нескольким различным полям напряжения, в зависимости от различных конститутивных отношений, установленных исследователями (или мозгом исследователей).Другими словами, каждое определяющее отношение дает только особое поле напряжений. Многие определяющие отношения дают множество различных полей напряжений, но исследователи на самом деле не видят и не измеряют свои поля напряжений.
Все становится ясно!
Концепция стресса на самом деле основана на человеческом мозгу, а не на реальных наблюдениях!
Это серьезное препятствие в 21 веке в передовой механике твердого тела для современных материалов, потому что передовая технология способствует тому, что инструменты становятся все меньше и меньше, такие как МЭМС или НЭМС, а затем исследователи, специализирующиеся в механике твердого тела, сталкиваются с некоторой проблемой изучения мелкомасштабной механики, такой как микромеханика или наномеханика.Однако никто не мог сказать нам, применима ли концепция напряжения (как макроскопической и псевдофизической величины) в микомеханике или наномеханике с дефектами?
Если да, он должен сказать нам, почему?
Если нет, он должен сказать нам, какая возможная и альтернативная физическая величина вместо стресса?
Этот вопрос очень ясен, как показано на следующих рисунках (прикрепленных с веб-сайтов).
На рисунке 1 представлена фотография микроскопа.На фото много твердых деталей в неоднородном материале. Вопрос в том, какое напряжение на поверхности каждой детали? Насколько велик стресс? Насколько ценно найти подробное распределение поля напряжений в виде поля смещения или поля деформации? Что еще более важно, с точки зрения микромасштаба, можно ли использовать воображаемое поле напряжений, если оно существует, для введения некоторых феноменологических параметров для оценки разрушения материала?
Рисунок 1.Первый пример фотографии микроскопа прикреплен с сайта.
Рисунок 2. Второй пример фотографии микроскопа, прикрепленной с веб-сайта.
На рисунке 2 также показано подробное поле смещения, а также поле деформации, но никто не смог получить подробное поле напряжений, хотя детальное поле деформации-смещения можно было измерить.
Рисунок 3. Третий пример фотографии микроскопа, прикрепленной с веб-сайта.
На рис. 3 показано еще одно поле смещения с некоторыми трещинами на поверхности.Однако до сих пор неясно, каково поле напряжений, хотя поле деформации-смещения можно измерить.
Более того, некоторые известные эксперты утверждали, что напряжение в их анализах в наномасштабе достигает 100 ГПа! Это напряжение превышает модуль упругости материала? Этот результат свидетельствует о том, что концепция напряжения нереалистична в наномеханике с дефектами.
Конечно, было бы несправедливо отвергать предыдущие взносы на основе так называемого стресс-анализа.Действительно, все классические теории прочности, включая механику разрушения, были созданы на основе анализа напряжений, который принес большой доход и привлек значительное внимание исследователей!
Кроме того, автор не желает просто отбрасывать эту концепцию. Это может перевернуться!
Цель данной статьи — стимулировать дальнейшие дискуссии с другими исследователями, интересующимися этой темой, и представить альтернативную физическую величину для замены концепции напряжения, особенно в неоднородной механике, микромеханике и наномеханике.
С физической точки зрения конфигурационная сила и связанные с ней инвариантные интегралы могут быть полезным выбором вместо работы при анализе напряжений. Это потому, что эти концепции вызваны непосредственно силой Эшелби с дефектами, которая основана на точке зрения энергетического баланса. Фактически, у автора есть несколько начальных попыток в этом направлении исследований [1-17], включая одну книгу [11], в которой суммируются потенциальные применения проектируемых законов сохранения Jk-вектора, M-интеграла и L-интеграла.
Другие достижения в этой области, такие как движущая сила усталостного повреждения (FDDF) для облака микродефектов, будут описаны в следующих статьях автора.
[1] Чен И-Хэн., О вкладе неоднородностей в поле напряжений вблизи вершины вершины в J-интеграл, International Journal of Engineering Science , Vol. 34, 819-829 (1996).
[2] Хан Дж. Дж. И Чен И-Хэн. О вкладе микроотверстия в поле напряжений вблизи вершины в J-интеграл, International Journal of Fracture , Vol.85, 169-183 (1997).
[3] Чжао Л.Г. и Чен И-Хэн. О вкладе субинтерфейсных микротрещин около вершины межфазной трещины в J-интеграл в биматериальных твердых телах, International Journal of Engineering Science , Vol. 35, 387-407 (1997).
[4] Чен И-Хэн. И Цзо Хун, Исследование проблем взаимодействия макротрещины и микротрещины в анизотропных упругих телах. Часть I. Общее решение проблемы и применение J-интеграла, International Journal of Fracture, Vol.91, 61-82 (1998).
[5] Chen Yi-Heng., И Han J. J. Взаимодействие макротрещины и микротрещины в пьезоэлектрических материалах, часть I. Основные формулировки и J-анализ, ASME Journal of Applied Mechanics , Vol. 66, No. 2, 514-521 (1999).
[6] Chen Yi-Heng. И Han J.J. Взаимодействие макротрещины и микротрещины в пьезоэлектрических материалах, Часть II. Численные результаты и обсуждения, Журнал прикладной механики ASME , Vol. 66, No. 2, 522-527 (1999). [7] Тиан У. и Чен И-Хэн., Полубесконечная межфазная трещина, взаимодействующая с подповерхностными матричными трещинами в разнородных анизотропных материалах, Часть I, Основные формулировки и анализ J-интеграла, International Journal of Solids and Structures, Vol. 37, 7717-7730 (2000). [8] Chen Yi-Heng. И Tian W.Y. Полубесконечная межфазная трещина, взаимодействующая с подповерхностными матричными трещинами в разнородных анизотропных материалах, Часть II, Численные результаты и обсуждения, International Journal of Solids and Structures , Vol.37, 7731-7742 (2000). [9] Chen Yi-Heng., M-интегральный анализ для двумерных твердых тел с сильно взаимодействующими трещинами, Часть I. В бесконечно хрупком объекте, International Journal of Solids and Structures ., Vol. 38/18, 3193-3212 (2001).
[10] Чен И-Хэн. М-интегральный анализ для двумерных твердых тел с сильно взаимодействующими трещинами, Часть II. В хрупкой фазе бесконечного биматериала металл / керамика, International Journal of Solids and Structures. , т.38/18, 3213-3232 (2001).
[11] Книги: Достижения в законах сохранения и нормах высвобождения энергии, Kluwer Academic Publishers, Нидерланды (ISBN 1402005008) , 2002 . [12] Чен, Й.Х., и Лу, Т.Дж., (2003) Последние разработки и приложения в инвариантных интегралах, ASME Applied Mechanics Reviews, Vol. 56, 515-552 .
[13] Ли Кью, Чен Й. (2008) Поверхностный эффект и зависимость размера от высвобождения энергии из-за расширения наноразмерных отверстий в плоских упругих материалах, ASME Journal Applied Mechanics, Vol.75, ноябрь.
[14] Hu Y.F., и Chen Yi-Heng, (2009), M-интегральное описание полосы с двумя отверстиями до и после слияния, Acta Mechanica , Vol. 204 (1), 109-.
[15] Ху Ю.Ф. и Чен И-Хэн (2009), M-интегральное описание полосы с двумя трещинами до и после слияния, ASME Journal Applied Mechaics, Vol.76, ноябрь 061017-1-12.
[16] Хуэй Т. и Чен Йи-Хэн (2010), M-интегральный анализ нановключений в плоских упругих материалах при одноосных или двухосных нагрузках, ASME Journal of Applied Mechanics, Vol.77. 021019-1-9.
[17] Хуэй Т., Чен И-Хэн, (2010), M-интеграл двух состояний для нановключения в плоских упругих материалах, ASME Journal of Applied Mechanics, Vol. 77. 024505-1-5.
Напряжение — Типы напряжения, определение и формула
Приведенная ниже формула используется для расчета напряжения:
Напряжение = сила / площадь поперечного сечения
σ = F / A
Где,
σ = Напряжение
F = Сила в Ньютонах (Н)
A = Площадь поперечного сечения в м²
Единицы напряжения = Н / м² или Паскали (Па)
Типы напряжения:
Существуют различные типы стресса в физике, но в основном его можно разделить на три формы:
1.Нормальное напряжение
2. Касательное напряжение или напряжение сдвига
3. Гидравлическое напряжение
Нормальное напряжение:
Напряжение, возникающее при нагрузке на элемент осевой силой, называется нормальной силой. Другими словами, когда прикладываемое напряжение перпендикулярно телу. При изменении длины тела объем объекта напряжения будет нормальным. Он представляет собой символ σ. Единица измерения нормального напряжения в системе СИ — МПа.
Формула ниже используется для расчета нормального напряжения:
Нормальное напряжение = осевое усилие / площадь поперечного сечения
σ = P / A
Нормальное напряжение возникает, когда объект помещены в растяжение или сжатие.
Продольное напряжение:
Когда длина тела изменяет свою длину под действием нормального напряжения, которое применяется, это называется продольным напряжением.
Продольное напряжение = Деформирующая сила / Площадь поперечного сечения
Продольное напряжение = F / A
Продольное напряжение можно разделить на две категории. Растягивающее напряжение можно наблюдать, когда стержень растягивается согласно третьему закону движения Ньютона.Растягиваемая резинка — типичный пример растягивающего напряжения. Противоположным натяжению является сжатие, когда оно воздействует на стержень, который толкается противоположными или равными силами на его концах. Если вы когда-нибудь сжимали в руках резиновый мяч, вы создавали сжимающее напряжение.
Объемное напряжение или объемное напряжение:
Объемное напряжение — это напряжение, при котором объем тела изменяется из-за напряжения. Нормальная нагрузка на тело вызывает изменение длины или объема, а касательное напряжение вызывает изменение формы тела, что называется объемным напряжением.Тело, которое находится под силой давления p, при погружении в жидкость, тело противостоит силе, перпендикулярной поверхности тела.
Объемное напряжение = Сила / Площадь = Давление
Напряжение сдвига:
Напряжение сдвига — это сила, прикладываемая по касательной к площади поверхности плоскости. Когда силы, прикладываемые к поверхности, параллельны ей, и напряжение, действующее на поверхность, также строится по касательной. Этот вид стресса известен как напряжение сдвига.
Распределенное напряжение = Сила / Площадь поверхности = F / A
Напряжение растяжения:
Сила на единицу площади определяется как растягивающее напряжение. Если приложено напряжение, длина тела увеличивается из-за силы. Растягивающее напряжение наблюдается, когда стержень растягивается по третьему закону движения. Резина — распространенный пример растягивающего напряжения. Это количество, связанное с растяжением. Обозначается он σ.
Напряжение сжатия:
Когда мы прикладываем к телу тангенциальную силу, форма и объем тела изменяются.Когда приложено напряжение сжатия, длина тела уменьшается. Напряжение сжатия противоположно напряжению растяжения. Если вы когда-нибудь сжимали в руке пищащую игрушку домашнего животного, вы создаете сжимающую нагрузку на тело.
Касательное напряжение:
Когда мы выражаем силу на единицу площади, это нормальное напряжение и касательное напряжение соответственно. Когда две равные и противоположные деформирующие силы прикладываются параллельно площади поперечного сечения объекта, возникает относительное смещение между противоположными гранями тела, и восстанавливающая сила на единицу площади, развиваемая из-за приложенной тангенциальной силы, называется тангенциальной. стресс.
Гидравлическое напряжение:
Гидравлическое напряжение — это мера внутренней силы на единицу площади, действующей на жидкости. Гидравлическое напряжение — это восстанавливающая сила на единицу площади, когда сила прикладывается жидкостью к телу. Напряжение физически не то же самое, что давление, потому что в давлении учитывается внешняя сила на единицу площади, а в напряжении — это внутренняя сила на единицу площади. В случае жидкостей гидравлическое напряжение определяется таким же образом.
Радиальное напряжение:
Радиальное напряжение рассчитано для толстостенного цилиндра, которое равно манометрическому давлению на внутренней поверхности и равно нулю на внешней поверхности и противоположно ему.Окружное напряжение и продольное напряжение больше, чем радиальное напряжение, поэтому радиальным напряжением можно пренебречь.
Напряжение — это физическая величина, определяющая внутреннюю силу. Напряжение определяется как сила, действующая через «маленькую» границу на единицу площади этой границы. Напряжение — это фундаментальная величина, такая как скорость, крутящий момент (энергия).
В голове возникает один вопрос, на чем можно акцентировать внимание, а на чем — нет. Вы, должно быть, заметили, что есть такие предметы, как резина, которые можно легко растянуть.Другими словами, мы можем объяснить это, когда к любому объекту прилагается растягивающая сила (сила растяжения). Он будет расширяться. Например, резинка легко растягивается. Сила растяжения, приложенная к резиновому объекту. Однако можно ли протянуть железный прут? Ответ — нет, потому что на железный стержень не действует сила натяжения.
Есть некоторые основные положения механики сплошной среды, напряжение — это макроскопическое понятие. Частицы, чтобы мыслить в своем описании и анализе, должны быть достаточно маленькими, чтобы работать как однородные в создании и состоянии, но все же большими, чтобы игнорировать квантовые эффекты и детальные движения молекул.Таким образом, сила между двумя частицами на самом деле является средним значением очень большого числа атомных сил между их молекулами; и в физическом выражении, таком как масса, скорость и силы, он действует через большую часть трехмерных тел, предполагается, что они плавно распределяются по ним.
Давайте обсудим это на примере. Возьмем резиновую трубу и железный стержень, возьмем другой объект квадратной формы, и второй объект висит на резиновой трубе и железном стержне. Подождите некоторое время, затем потяните оба объекта в первом объекте, вы увидите, что первый объект имеет силу растяжения, а другой объект не имеет силы растяжения.
Анализ напряжений — это часть прикладной физики, которая скрывает классификацию внутреннего распределения внутренних сил в твердых телах.
Изучение и проектирование таких конструкций, как плотины, несущие конструкции и туннели, механические части при предписанных или ожидаемых нагрузках, является важной частью инженерного дела. Это также важно во многих других областях; например, в геологии, чтобы изучить теорию тектоники плит, вулканизма и лавин; и в биологии, чтобы понять анатомию живых существ.
12.3 Напряжение, деформация и модуль упругости — University Physics Volume 1
Учебные цели
К концу этого раздела вы сможете:
- Объясните концепции напряжения и деформации при описании упругих деформаций материалов
- Описать виды упругого деформирования предметов и материалов
Модель твердого тела — идеализированный пример объекта, не деформирующегося под действием внешних сил.Это очень полезно при анализе механических систем, а многие физические объекты действительно в значительной степени жесткие. Степень, в которой объект может быть восприниматься как жесткий, зависит от физических свойств материала, из которого он сделан. Например, мяч для пинг-понга, сделанный из пластика, является хрупким, а теннисный мяч, сделанный из резины, эластичен, когда на него воздействуют сжимающие силы. Однако при других обстоятельствах и мяч для пинг-понга, и теннисный мяч могут хорошо отскакивать как твердые тела.Точно так же тот, кто проектирует протезы, может приблизиться к механике человеческих конечностей, моделируя их как твердые тела; однако фактическая комбинация костей и тканей представляет собой эластичную среду.
В оставшейся части этой главы мы переходим от рассмотрения сил, влияющих на движение объекта, к тем, которые влияют на форму объекта. Изменение формы из-за приложения силы называется деформацией. Известно, что даже очень небольшие силы вызывают некоторую деформацию.Деформация испытывается объектами или физическими средами под действием внешних сил — например, это может быть сжатие, сжатие, разрыв, скручивание, срезание или растяжение объектов. На языке физики силы, действующие на деформируемые объекты, описываются двумя терминами: напряжением и деформацией .
Напряжение — это величина, которая описывает величину сил, вызывающих деформацию. Напряжение обычно определяется как сил на единицу площади .Когда силы притягивают объект и вызывают его удлинение, как при растяжении эластичной ленты, мы называем такое напряжение растягивающим напряжением. Когда силы вызывают сжатие объекта, мы называем это напряжением сжатия. Когда объект сжимается со всех сторон, как подводная лодка в глубинах океана, мы называем этот вид напряжения объемным напряжением (или объемным напряжением). В других ситуациях действующие силы могут быть ни растягивающими, ни сжимающими, и все же вызывать заметную деформацию. Например, предположим, что вы держите книгу между ладонями, затем одной рукой вы нажимаете и тянете переднюю обложку от себя, а другой рукой вы нажимаете и тянете заднюю обложку в направлении ты.В таком случае, когда деформирующие силы действуют по касательной к поверхности объекта, мы называем их «поперечными» силами, а вызываемое ими напряжение — поперечным напряжением.
Единицей измерения напряжения в системе СИ является паскаль (Па). Когда сила в один ньютон воздействует на единицу площади квадратного метра, результирующее напряжение составляет один паскаль:
один паскаль = 1.0Па = 1.0N1.0м2. один паскаль = 1.0Па = 1.0N1.0м2.В имперской системе единиц единицей измерения напряжения является «фунт / кв. Дюйм», что означает «фунт на квадратный дюйм» (фунт / дюйм2).(фунт / дюйм2). Еще одна единица измерения объемного напряжения — это атм (атмосфера). Коэффициенты пересчета:
. 1 фунт / кв. Дюйм = 6895 Па и 1 Па = 1,450 × 10–4 фунт / кв. Дюйм · атм = 1,013 × 105 Па = 14,7 фунта / кв. Дюйм. 1 фунт / кв. Дюйм = 6895 Па и 1 Па = 1,450 × 10–4 фунт / кв.Объект или среда под напряжением деформируются. Величина, описывающая эту деформацию, называется деформацией. Деформация задается как частичное изменение длины (при растягивающем напряжении), объема (при объемном напряжении) или геометрии (при напряжении сдвига). Следовательно, деформация — это безразмерное число.Деформация под действием растягивающего напряжения называется деформацией растяжения, деформация под действием объемного напряжения называется объемной деформацией (или объемной деформацией), а деформация, вызванная напряжением сдвига, называется деформацией сдвига.
Чем больше напряжение, тем больше напряжение; однако связь между деформацией и напряжением не обязательно должна быть линейной. Только когда напряжение достаточно низкое, вызываемая им деформация прямо пропорциональна величине напряжения. Константа пропорциональности в этом отношении называется модулем упругости.В линейном пределе низких значений напряжения общее соотношение между напряжением и деформацией составляет
. напряжение = (модуль упругости) × деформация. напряжение = (модуль упругости) × деформация.12,33
Как видно из анализа размеров этого соотношения, модуль упругости имеет ту же физическую единицу, что и напряжение, поскольку деформация безразмерна.
Из уравнения 12.33 также видно, что, когда объект характеризуется большим значением модуля упругости, влияние напряжения невелико.С другой стороны, небольшой модуль упругости означает, что напряжение вызывает большую деформацию и заметную деформацию. Например, напряжение на резиновой ленте вызывает большую деформацию (деформацию), чем такое же напряжение на стальной ленте тех же размеров, потому что модуль упругости резины на два порядка меньше модуля упругости стали.
Модуль упругости при растяжении называется модулем Юнга; то, что для объемного напряжения называется объемным модулем упругости; а напряжение сдвига называется модулем сдвига.Обратите внимание, что соотношение между напряжением и деформацией — это , наблюдаемое соотношение , измеренное в лаборатории. Модули упругости для различных материалов измеряются при различных физических условиях, таких как изменяющаяся температура, и собираются в таблицах технических данных для справки (таблица 12.1). Эти таблицы являются ценными справочными материалами для промышленности и для всех, кто занимается проектированием или строительством. В следующем разделе мы обсудим зависимости деформации от напряжения за пределами линейного предела, представленного уравнением 12.33, в полном диапазоне значений напряжений до точки разрушения. В оставшейся части этого раздела мы изучаем линейный предел, выражаемый уравнением 12.33.
| Материал | Модуль Юнга × 1010 Па × 1010 Па | Объемный модуль × 1010 Па × 1010 Па | Модуль сдвига × 1010 Па × 1010 Па |
|---|---|---|---|
| Алюминий | 7,0 | 7,5 | 2,5 |
| Кость (напряжение) | 1.6 | 0,8 | 8,0 |
| Кость (компрессия) | 0,9 | ||
| Латунь | 9,0 | 6,0 | 3,5 |
| Кирпич | 1,5 | ||
| Бетон | 2,0 | ||
| Медь | 11,0 | 14,0 | 4,4 |
| Коронное стекло | 6.0 | 5,0 | 2,5 |
| Гранит | 4,5 | 4,5 | 2,0 |
| Волосы (человеческие) | 1,0 | ||
| Твердая древесина | 1,5 | 1,0 | |
| Утюг | 21,0 | 16,0 | 7,7 |
| Свинец | 1,6 | 4,1 | 0,6 |
| Мрамор | 6.0 | 7,0 | 2,0 |
| Никель | 21,0 | 17,0 | 7,8 |
| Полистирол | 3,0 | ||
| Шелк | 6,0 | ||
| Паутинка | 3,0 | ||
| Сталь | 20,0 | 16,0 | 7,5 |
| Ацетон | 0.07 | ||
| Этанол | 0,09 | ||
| Глицерин | 0,45 | ||
| Меркурий | 2,5 | ||
| Вода | 0,22 |
Стол 12.1 Приблизительные модули упругости для выбранных материалов
Напряжение при растяжении или сжатии, деформация и модуль Юнга
Напряжение или сжатие возникает, когда две антипараллельные силы равной величины действуют на объект только вдоль одного из его измерений таким образом, что объект не перемещается.Один из способов представить себе такую ситуацию показан на рисунке 12.18. Сегмент стержня либо растягивается, либо сжимается парой сил, действующих по его длине и перпендикулярно его поперечному сечению. Чистый эффект таких сил состоит в том, что стержень изменяет свою длину с исходной длины L0L0, которая была у него до появления сил, на новую длину L , которую он имеет под действием сил. Это изменение длины ΔL = L-L0ΔL = L-L0 может быть либо удлинением (когда L больше исходной длины L0) L0), либо сокращением (когда L меньше исходной длины L0).L0). Напряжение растяжения и деформация возникают, когда силы растягивают объект, вызывая его удлинение, и изменение длины ΔLΔL является положительным. Напряжение сжатия и деформация возникают, когда силы сжимают объект, вызывая его сокращение, а изменение длины ΔLΔL отрицательно.
В любой из этих ситуаций мы определяем напряжение как отношение деформирующей силы F⊥F⊥ к площади A поперечного сечения деформируемого объекта. Символ F⊥F⊥, который мы оставляем для деформирующей силы, означает, что эта сила действует перпендикулярно поперечному сечению объекта.Силы, действующие параллельно поперечному сечению, не изменяют длину объекта. Определение растягивающего напряжения —
. растягивающее напряжение = F⊥A. растягивающее напряжение = F⊥A.12,34
Деформация растяжения — это мера деформации объекта при растягивающем напряжении и определяется как частичное изменение длины объекта, когда объект испытывает растягивающее напряжение.
деформация растяжения = ΔLL0. деформация растяжения = ΔLL0.12,35
Напряжение сжатия и деформация определяются по той же формуле, уравнение 12.34 и уравнение 12.35 соответственно. Единственное отличие от ситуации с растяжением состоит в том, что для сжимающего напряжения и деформации мы берем абсолютные значения правых частей в уравнениях 12.34 и 12.35.
Фигура 12,18 Когда объект находится в состоянии растяжения или сжатия, результирующая сила, действующая на него, равна нулю, но объект деформируется, изменяя свою исходную длину L0.L0. (a) Натяжение: стержень удлинен на ΔL.ΔL. (b) Сжатие: стержень сжимается на ΔL.ΔL. В обоих случаях деформирующая сила действует по длине стержня и перпендикулярно его поперечному сечению.В линейном диапазоне малых напряжений площадь поперечного сечения стержня не изменяется.Модуль Юнга Y — это модуль упругости, когда деформация вызвана либо растягивающим, либо сжимающим напряжением, и определяется уравнением 12.33. Разделив это уравнение на деформацию растяжения, мы получим выражение для модуля Юнга:
Y = растягивающая деформация растяжения = F⊥ / A∆L / L0 = F⊥AL0∆L.Y = растягивающая деформация растяжения = F⊥ / A∆L / L0 = F⊥AL0∆L.12,36
Пример 12,7
Напряжение сжатия в опоре
Скульптура весом 10 000 Н покоится на горизонтальной поверхности на вершине 6.Вертикальный столб высотой 0 м Рис. 12.19. Площадь поперечного сечения столба 0,20 м 20,20 м 2, он выполнен из гранита с удельной массой 2700 кг / м3. 2700 кг / м3. Найдите сжимающее напряжение в поперечном сечении, расположенном на 3,0 м ниже верха столба, и значение сжимающей деформации верхнего 3,0-метрового сегмента столба.Фигура 12,19 Колонна Нельсона на Трафальгарской площади, Лондон, Англия. (кредит: модификация работы Кристиана Бортеса)
Стратегия
Сначала мы находим вес 3.Верхняя часть столба длиной 0 м. Нормальная сила, действующая на поперечное сечение, расположенное на 3,0 м ниже вершины, складывается из веса столба и веса скульптуры. Когда у нас есть нормальная сила, мы используем уравнение 12.34, чтобы найти напряжение. Чтобы найти деформацию сжатия, мы находим значение модуля Юнга для гранита в таблице 12.1 и инвертируем уравнение 12.36.Решение
Объем сегмента колонны высотой h = 3,0мh = 3,0м и площадью поперечного сечения A = 0,20м2A = 0,20м2 составляет V = Ah = (0.20м2) (3,0м) = 0,60м3. V = Ah = (0,20м2) (3,0м) = 0,60м3.При плотности гранита ρ = 2,7 × 103 кг / м3, ρ = 2,7 × 103 кг / м3 масса сегмента столба составляет
m = ρV = (2,7 × 103 кг / м3) (0,60 м3) = 1,60 × 103 кг. m = ρV = (2,7 × 103 кг / м3) (0,60 м3) = 1,60 × 103 кг.Вес сегмента стойки
wp = mg = (1,60 × 103 кг) (9,80 м / с2) = 1,568 × 104 Н. wp = mg = (1,60 × 103 кг) (9,80 м / с2) = 1,568 × 104 Н.Вес скульптуры ws = 1,0 × 104 Н, ws = 1,0 × 104 Н, поэтому нормальная сила на поверхности поперечного сечения, расположенной на 3,0 м ниже скульптуры, составляет
F⊥ = wp + ws = (1.568 + 1.0) × 104N = 2.568 × 104N. F⊥ = wp + ws = (1.568 + 1.0) × 104N = 2.568 × 104N.Следовательно, напряжение
напряжение = F⊥A = 2,568 × 104N0,20м2 = 1,284 × 105Па = 128,4 кПа. напряжение = F⊥A = 2,568 × 104N0,20м2 = 1,284 × 105Па = 128,4 кПа.Модуль Юнга для гранита Y = 4,5 × 1010 Па = 4,5 × 107 кПа. Y = 4,5 × 1010 Па = 4,5 × 107 кПа. Следовательно, деформация сжатия в этом положении равна
. деформация = напряжение Y = 128,4 кПа 4,5 × 107 кПа = 2,85 × 10-6. деформация = напряжение Y = 128,4 кПа 4,5 × 107 кПа = 2,85 × 10-6.Значение
Обратите внимание, что нормальная сила, действующая на площадь поперечного сечения колонны, не постоянна по ее длине, а изменяется от наименьшего значения наверху до наибольшего значения внизу колонны.Таким образом, если опора имеет равномерную площадь поперечного сечения по всей длине, наибольшее напряжение у ее основания.Проверьте свое понимание 12,9
Найдите сжимающее напряжение и деформацию в основании колонны Нельсона.
Пример 12,8
Растяжка стержня
Стальной стержень длиной 2,0 м имеет площадь поперечного сечения 0,30 см2 0,30 см2. Штанга является частью вертикальной опоры, которая удерживает тяжелую платформу массой 550 кг, которая подвешена к нижнему концу штанги.Пренебрегая весом стержня, каково растягивающее напряжение стержня и удлинение стержня под действием напряжения?Стратегия
Сначала мы вычисляем растягивающее напряжение в стержне под весом платформы в соответствии с уравнением 12.34. Затем мы обращаем уравнение 12.36, чтобы найти удлинение стержня, используя L0 = 2,0 м. L0 = 2,0 м. Из таблицы 12.1 модуль Юнга для стали равен Y = 2,0 × 1011 Па. Y = 2,0 × 1011 Па.Решение
Подстановка числовых значений в уравнения дает нам F⊥A = (550 кг) (9.8 м / с2) 3,0 × 10–5 м2 = 1,8 × 108 Па ΔL = F⊥AL0Y = (1,8 × 108 Па) 2,0 × 1011 Па = 1,8 × 10–3 м = 1,8 мм. F⊥A = (550 кг) (9,8 м / s2) 3,0 × 10–5 м2 = 1,8 × 108 Па ΔL = F⊥AL0Y = (1,8 × 108 Па) 2,0 × 1011 Па = 1,8 × 10–3 м = 1,8 мм.Значение
Как и в примере с колонной, растягивающее напряжение в этом примере неоднородно по длине стержня. Однако, в отличие от предыдущего примера, если принять во внимание вес штанги, напряжение в штанге будет наибольшим в верхней части и наименьшим в нижней части штанги, к которой прикреплено оборудование.Проверьте свое понимание 12.10
Проволока длиной 2,0 м растягивается на 1,0 мм под действием нагрузки. Какова деформация растяжения в проволоке?
Объекты часто могут одновременно испытывать напряжение сжатия и растяжения. Рис. 12.20. Один из примеров — длинная полка, загруженная тяжелыми книгами, которая провисает между концевыми опорами под весом книг. Верхняя поверхность полки испытывает напряжение сжатия, а нижняя поверхность полки — растягивающее напряжение.Точно так же длинные и тяжелые балки провисают под собственным весом. В современном строительстве такие деформации изгиба можно практически исключить с помощью двутавровых балок. Рисунок 12.21.
Фигура 12.20 (a) Объект, изгибающийся вниз, испытывает растягивающее напряжение (растяжение) в верхней части и сжимающее напряжение (сжатие) в нижней части. (b) Элитные тяжелоатлеты часто временно сгибают железные прутья во время подъема, как на Олимпийских играх 2012 года. (кредит б: модификация работы Александра Кочерженко)
Фигура 12.21 год Стальные двутавры используются в строительстве для уменьшения деформаций изгиба. (Источник: модификация работы «Инженерный корпус армии США в Европе» / Flickr)
Объемное напряжение, деформация и модуль
Когда вы ныряете в воду, вы чувствуете силу, давящую на каждую часть вашего тела со всех сторон. Тогда вы испытываете объемный стресс или, другими словами, давление. Объемное напряжение всегда имеет тенденцию к уменьшению объема, заключенного на поверхности погружаемого объекта.Силы этого «сжатия» всегда перпендикулярны погружаемой поверхности. Рис. 12.22. Эффект этих сил заключается в уменьшении объема погруженного объекта на величину ΔVΔV по сравнению с объемом V0V0 объекта при отсутствии объемного напряжения. Этот вид деформации называется объемной деформацией и описывается изменением объема по сравнению с исходным объемом:
объемная деформация = ΔVV0. объемная деформация = ΔVV0.12,37
Фигура 12,22 Объект при увеличении объемного напряжения всегда претерпевает уменьшение своего объема.Равные силы, перпендикулярные поверхности, действуют со всех сторон. Эффект этих сил заключается в уменьшении объема на величину ΔVΔV по сравнению с исходным объемом V0.V0.Объемная деформация возникает в результате объемного напряжения, которое представляет собой силу F⊥F⊥, нормальную к поверхности, которая оказывает давление на единицу площади A погруженного объекта. Такая физическая величина, или давление p , определяется как
. давление = p≡F⊥A. давление = p≡F⊥A.12,38
Мы будем изучать давление в жидкостях более подробно в Гидромеханике.Важной характеристикой давления является то, что оно является скалярной величиной и не имеет определенного направления; то есть давление действует одинаково во всех возможных направлениях. Когда вы погружаете руку в воду, вы чувствуете такое же давление, действующее на верхнюю поверхность руки, как на нижнюю, или на боковую, так и на поверхность кожи между пальцами. В этом случае вы ощущаете увеличение давления ΔpΔp по сравнению с тем, что вы привыкли ощущать, когда ваша рука не погружена в воду.Когда ваша рука не погружена в воду, вы чувствуете нормальное давление p0p0 в одну атмосферу, которое служит точкой отсчета. Объемное напряжение — это увеличение давления, или Δp, Δp, по сравнению с нормальным уровнем, p0.p0.
Когда объемное напряжение увеличивается, объемная деформация увеличивается в соответствии с уравнением 12.33. Константа пропорциональности в этом соотношении называется модулем объемной упругости, B или
. B = объемное напряжение, объемная деформация = −ΔpΔV / V0 = −ΔpV0ΔV. B = объемное напряжение, объемная деформация = −ΔpΔV / V0 = −ΔpV0ΔV.12,39
Знак минус, который появляется в уравнении 12.39, предназначен для согласованности, чтобы гарантировать, что B является положительной величиной. Обратите внимание, что знак минус (-) (-) необходим, потому что увеличение ΔpΔp давления (положительная величина) всегда вызывает уменьшение ΔVΔV в объеме, а уменьшение объема является отрицательной величиной. Величина, обратная модулю объемного сжатия, называется сжимаемостью k, k или
. k = 1B = −ΔV / V0Δp.k = 1B = −ΔV / V0Δp.12,40
Термин «сжимаемость» используется в отношении жидкостей (газов и жидкостей).Сжимаемость описывает изменение объема жидкости на единицу увеличения давления. Жидкости, характеризующиеся большой сжимаемостью, относительно легко сжимаются. Например, сжимаемость воды составляет 4,64 × 10–5 / атм. 4,64 × 10–5 / атм, а сжимаемость ацетона составляет 1,45 × 10–4 / атм. 1,45 × 10–4 / атм. Это означает, что при повышении давления на 1,0 атм относительное уменьшение объема для ацетона примерно в три раза больше, чем для воды.
Пример 12.9
Гидравлический пресс
В гидравлическом прессе, рис. 12.23, 250-литровый объем масла подвергается повышению давления на 2300 фунтов на квадратный дюйм. Если сжимаемость масла составляет 2,0 × 10–5 / атм, 2,0 × 10–5 / атм, найдите объемную деформацию и абсолютное уменьшение объема масла при работе пресса.Фигура 12,23 В гидравлическом прессе, когда маленький поршень смещается вниз, давление в масле передается по маслу на большой поршень, заставляя большой поршень двигаться вверх.Небольшая сила, приложенная к маленькому поршню, вызывает большую прижимающую силу, которую большой поршень оказывает на объект, который либо поднимается, либо сжимается. Устройство действует как механический рычаг.
Стратегия
Мы должны обратить уравнение 12.40, чтобы найти объемную деформацию. Во-первых, мы преобразуем увеличение давления из фунтов на квадратный дюйм в атм, Δp = 2300psi = 2300 / 14,7atm≈160atm, Δp = 2300psi = 2300 / 14.7atm≈160atm, и определяем V0 = 250L.V0 = 250L.Решение
Подставляя значения в уравнение, имеем объемная деформация = ΔVV0 = ΔpB = kΔp = (2.0 × 10-5 / атм) (160атм) = 0,0032 ответ: ΔV = 0,0032V0 = 0,0032 (250L) = 0,78L. Объемная деформация = ΔVV0 = ΔpB = kΔp = (2,0 × 10-5 / атм) (160атм) = 0,0032 ответ: ΔV = 0,0032V0 = 0,0032 (250 л) = 0,78 л.Значение
Обратите внимание, что, поскольку сжимаемость воды в 2,32 раза больше, чем у масла, если бы рабочее вещество в гидравлическом прессе этой задачи было заменено на воду, объемная деформация, а также изменение объема были бы в 2,32 раза больше.Проверьте свое понимание 12.11
Если нормальная сила действует на каждую грань кубической 1.Стальной кусок 0-м31,0-м3 заменяют на 1,0 × 107 Н, 1,0 × 107 Н, найдите результирующее изменение объема стального куска.
Напряжение сдвига, деформация и модуль
Понятия напряжения сдвига и деформации относятся только к твердым объектам или материалам. Здания и тектонические плиты являются примерами объектов, которые могут подвергаться сдвиговым напряжениям. В общем, эти концепции не применимы к жидкостям.
Деформация сдвига возникает, когда две антипараллельные силы равной величины прикладываются по касательной к противоположным поверхностям твердого объекта, не вызывая деформации в поперечном направлении к силовой линии, как в типичном примере напряжения сдвига, показанном на рисунке 12.24. Сдвиговая деформация характеризуется постепенным сдвигом ΔxΔx слоев в направлении, касательном к действующим силам. Эта градация ΔxΔx происходит в поперечном направлении на некотором расстоянии L0.L0. Деформация сдвига определяется отношением наибольшего смещения ΔxΔx к поперечному расстоянию L0L0
деформация сдвига = ΔxL0. деформация сдвига = ΔxL0.12,41
Деформация сдвига вызвана напряжением сдвига. Напряжение сдвига возникает из-за сил, действующих на параллелей к поверхности. Для таких сил мы используем символ F∥F∥.Величина F∥F∥ на площадь поверхности A , где применяется сила сдвига, является мерой напряжения сдвига
напряжение сдвига = F∥A. напряжение сдвига = F∥A.12,42
Модуль сдвига является константой пропорциональности в уравнении 12.33 и определяется отношением напряжения к деформации. Модуль сдвига обычно обозначается как S :
. S = напряжение сдвига деформация сдвига = F∥ / AΔx / L0 = F∥AL0Δx.S = напряжение сдвига деформация сдвига = F∥ / AΔx / L0 = F∥AL0Δx.12,43
Фигура 12.24 Объект под напряжением сдвига: две антипараллельные силы равной величины прикладываются по касательной к противоположным параллельным поверхностям объекта. Контур пунктирной линией показывает результирующую деформацию. Направление, перпендикулярное действующим силам, не изменяется, и поперечная длина L0L0 не изменяется. Сдвиговая деформация характеризуется постепенным смещением ΔxΔx слоев в направлении, касательном к силам.Пример 12.10
Старая книжная полка
Уборщик пытается переместить тяжелый старый книжный шкаф по ковровому покрытию, тангенциально толкая поверхность самой верхней полки.Однако единственный заметный эффект от этого усилия аналогичен эффекту, показанному на рисунке 12.24, и он исчезает, когда человек перестает толкать. Книжный шкаф высотой 180 см и шириной 90 см с четырьмя полками глубиной 30 см, частично заполненными книгами. Общий вес книжного шкафа и книг составляет 600,0 Н. Если человек толкает верхнюю полку с силой 50,0 Н, которая перемещает верхнюю полку по горизонтали на 15,0 см относительно неподвижной нижней полки, найдите модуль сдвига книжного шкафа.Стратегия
Единственная важная информация — это физические размеры книжного шкафа, величина тангенциальной силы и смещение, вызываемое этой силой.Мы определяем F∥ = 50.0N, Δx = 15.0cm, F∥ = 50.0N, Δx = 15.0cm, L0 = 180.0cm, L0 = 180.0cm и A = (30.0 cm) (90.0 cm) = 2700.0 cm2, A = (30,0 см) (90,0 см) = 2700,0 см2, и мы используем уравнение 12.43 для вычисления модуля сдвига.Решение
Подставляя числа в уравнения, получаем для модуля сдвига S = F∥AL0Δx = 50.0N2700.0cm2180.0cm.15.0cm. = 29Ncm2 = 29 × 104Nm2 = 209 × 103Pa = 2.222 кПа S = F∥AL0Δx = 50.0N2700.0cm2180.0cm.15.0cm. = 29Ncm2 = 29 × 104Нм2 = 209 × 103Па = 2,222 кПа.Мы также можем найти напряжение сдвига и деформацию соответственно:
F∥A = 50.0N2700,0 см2 = 527 кПа = 185,2 Па ΔxL0 = 15,0 см 180,0 см = 112 = 0,083.F∥A = 50,0N2700,0 см2 = 527 кПа = 185,2 Па ΔxL0 = 15,0 см 180,0 см = 112 = 0,083.Значение
Если человек в этом примере толкнет полку здоровым движением, может случиться так, что индуцированный сдвиг превратит ее в груду мусора. Примерно тот же механизм сдвига ответственен за разрушения засыпанных землей дамб и дамб; и в целом по оползням.Проверьте свое понимание 12,12
Объясните, почему концепции модуля Юнга и модуля сдвига неприменимы к жидкостям.
12,5: Напряжение, деформация и модуль упругости (часть 2)
Объемное напряжение, деформация и модуль
Когда вы ныряете в воду, вы чувствуете силу, давящую на каждую часть вашего тела со всех сторон. Тогда вы испытываете объемный стресс, или, другими словами, давление . Объемное напряжение всегда имеет тенденцию к уменьшению объема, заключенного на поверхности погружаемого объекта. Силы этого «сжатия» всегда перпендикулярны погружаемой поверхности Рис. \ (\ PageIndex {1} \).Эффект этих сил заключается в уменьшении объема погруженного объекта на величину \ (\ Delta \) V по сравнению с объемом V 0 объекта при отсутствии объемного напряжения. Этот вид деформации называется объемной деформацией и описывается изменением объема по сравнению с исходным объемом:
\ [навалом \; деформация = \ frac {\ Delta V} {V_ {0}} \ label {12.37} \]
Рисунок \ (\ PageIndex {1} \): объект при увеличении объемного напряжения всегда претерпевает уменьшение своего объема. Равные силы, перпендикулярные поверхности, действуют со всех сторон.Эффект этих сил заключается в уменьшении объема на величину \ (\ Delta \) V по сравнению с исходным объемом V 0 .Объемная деформация является результатом объемного напряжения, которое представляет собой силу F \ (\ perp \) , перпендикулярную поверхности, которая давит на единицу площади A поверхности погруженного объекта. Такая физическая величина или давление p определяется как
.\ [давление = p \ Equiv \ frac {F _ {\ perp}} {A} \ ldotp \ label {12.38} \]
Мы будем изучать давление в жидкостях более подробно в Гидромеханике.Важной характеристикой давления является то, что оно является скалярной величиной и не имеет определенного направления; то есть давление действует одинаково во всех возможных направлениях. Когда вы погружаете руку в воду, вы чувствуете такое же давление, действующее на верхнюю поверхность руки, как на нижнюю, или на боковую, так и на поверхность кожи между пальцами. В этом случае вы ощущаете увеличение давления \ (\ Delta \) p по сравнению с тем, что вы привыкли ощущать, когда ваша рука не погружена в воду.То, что вы чувствуете, когда ваша рука не погружена в воду, — это нормальное давление p 0 в одну атмосферу, которое служит точкой отсчета. Объемное напряжение — это увеличение давления, или \ (\ Delta \) p, по сравнению с нормальным уровнем, p 0 .
Когда объемное напряжение увеличивается, объемная деформация увеличивается в соответствии с уравнением 12.4.4. Константа пропорциональности в этом соотношении называется объемным модулем упругости B или
.\ [B = \ frac {bulk \; стресс} {объем \; деформация} = \ frac {\ Delta p} {\ frac {\ Delta V} {V_ {0}}} = — \ Delta p \ frac {V_ {0}} {\ Delta V} \ ldotp \ label {12.39} \]
Знак минус, который появляется в уравнении \ ref {12.39}, предназначен для согласованности, чтобы гарантировать, что \ (B \) является положительной величиной. Обратите внимание, что знак минус (-) необходим, потому что увеличение \ (\ Delta \) p давления (положительная величина) всегда вызывает уменьшение \ (\ Delta \) V в объеме, а уменьшение объема является отрицательной величиной. Величина, обратная модулю объемного сжатия, называется сжимаемостью , k, или
.\ [k = \ frac {1} {B} = — \ frac {\ frac {\ Delta V} {V_ {0}}} {\ Delta p} \ ldotp \ label {12.40} \]
Термин «сжимаемость» используется в отношении жидкостей (газов и жидкостей). Сжимаемость описывает изменение объема жидкости на единицу увеличения давления. Жидкости, характеризующиеся большой сжимаемостью, относительно легко сжимаются. Например, сжимаемость воды составляет 4,64 x 10 -5 / атм, а сжимаемость ацетона составляет 1,45 x 10 -4 / атм. Это означает, что при повышении давления на 1,0 атм относительное уменьшение объема для ацетона примерно в три раза больше, чем для воды.
Пример \ (\ PageIndex {1} \): гидравлический пресс
В гидравлическом прессе Рисунок \ (\ PageIndex {2} \) 250-литровый объем масла подвергается повышению давления на 2300 фунтов на кв. Дюйм. Если сжимаемость масла составляет 2,0 x 10 -5 / атм, найдите объемную деформацию и абсолютное уменьшение объема масла при работе пресса.
Рисунок \ (\ PageIndex {2} \): В гидравлическом прессе, когда маленький поршень смещается вниз, давление в масле передается через масло на большой поршень, в результате чего большой поршень перемещается вверх.Небольшая сила, приложенная к маленькому поршню, вызывает большую прижимающую силу, которую большой поршень оказывает на объект, который либо поднимается, либо сжимается. Устройство действует как механический рычаг.Стратегия
Мы должны инвертировать уравнение \ ref {12.40}, чтобы найти объемную деформацию. Сначала мы преобразуем увеличение давления из фунтов на кв. Дюйм в атм, \ (\ Delta \) p = 2300 psi = \ (\ frac {2300} {14.7 \; atm} \) ≈ 160 атм, и определяем V 0 = 250 Л.
Решение
Подставляя значения в уравнение, получаем
\ [навалом \; деформация = \ frac {\ Delta V} {V_ {0}} = \ frac {\ Delta p} {B} = k \ Delta p = (2.{-5} \; / атм) (160 \; атм) = 0,0032 \]
ответ
\ [\ Delta V = 0,0032 V_ {0} = 0,0032 (250 \; L) = 0,78 \; L \ ldotp \]
Значение
Обратите внимание, что, поскольку сжимаемость воды в 2,32 раза больше, чем сжимаемость масла, если бы рабочее вещество в гидравлическом прессе этой задачи было заменено на воду, объемная деформация, а также изменение объема были бы в 2,32 раза больше.
Упражнение \ (\ PageIndex {1} \)
Если нормальная сила действует на каждую грань кубической 1.0-m 3 кусок стали изменить на 1,0 x 10 7 Н, найти результирующее изменение объема куска стали.
Напряжение сдвига, деформация и модуль
Понятия напряжения сдвига и деформации относятся только к твердым объектам или материалам. Здания и тектонические плиты являются примерами объектов, которые могут подвергаться сдвиговым напряжениям. В общем, эти концепции не применимы к жидкостям.
Деформация сдвига возникает, когда две антипараллельные силы равной величины прикладываются по касательной к противоположным поверхностям твердого объекта, не вызывая деформации в поперечном направлении к силовой линии, как в типичном примере напряжения сдвига, показанном на рисунке \ (\ PageIndex {3} \).Деформация сдвига характеризуется постепенным сдвигом слоев \ (\ Delta \) x в направлении, касательном к действующим силам. Эта градация в \ (\ Delta \) x происходит в поперечном направлении на некотором расстоянии L 0 . Деформация сдвига определяется отношением наибольшего смещения \ (\ Delta \) x к поперечному расстоянию L 0
\ [сдвиг \; деформация = \ frac {\ Delta x} {L_ {0}} \ ldotp \ label {12.41} \]
Деформация сдвига вызвана напряжением сдвига. Напряжение сдвига возникает из-за сил, которые действуют параллельно к поверхности.Мы используем символ F \ (\ parallel \) для таких сил. Величина F \ (\ parallel \) на площадь A поверхности, к которой прилагается сила сдвига, является мерой напряжения сдвига
.\ [сдвиг \; стресс = \ frac {F _ {\ parallel}} {A} \ ldotp \ label {12.42} \]
Модуль сдвига является константой пропорциональности в уравнении \ ref {12.33} и определяется отношением напряжения к деформации. Модуль сдвига обычно обозначается \ (S \):
.\ [S = \ frac {сдвиг \; напряжение} {сдвиг \; деформация} = \ frac {\ frac {F _ {\ parallel}} {A}} {\ frac {\ Delta x} {L_ {0}}} = \ frac {F _ {\ parallel}} {A} \ frac { L_ {0}} {\ Delta x} \ ldotp \ label {12.43} \]
Рисунок \ (\ PageIndex {3} \): объект под напряжением сдвига: две антипараллельные силы равной величины прикладываются по касательной к противоположным параллельным поверхностям объекта. Контур пунктирной линией показывает результирующую деформацию. Направление, перпендикулярное действующим силам, не изменяется, и поперечная длина L 0 не изменяется. Деформация сдвига характеризуется постепенным сдвигом слоев \ (\ Delta \) x в направлении, касательном к силам.Пример \ (\ PageIndex {2} \): старая книжная полка
Уборщик пытается переместить тяжелый старый книжный шкаф по ковровому покрытию, тангенциально толкая поверхность самой верхней полки.Однако единственный заметный эффект от этого усилия аналогичен эффекту, показанному на рисунке \ (\ PageIndex {2} \), и он исчезает, когда человек перестает толкать. Книжный шкаф высотой 180 см и шириной 90 см с четырьмя полками глубиной 30 см, частично заполненными книгами. Общий вес книжного шкафа и книг составляет 600,0 Н. Если человек толкает верхнюю полку с силой 50,0 Н, которая перемещает верхнюю полку по горизонтали на 15,0 см относительно неподвижной нижней полки, найдите модуль сдвига книжного шкафа.
Стратегия
Единственная важная информация — это физические размеры книжного шкафа, величина тангенциальной силы и смещение, вызываемое этой силой. Мы идентифицируем F \ (\ parallel \) = 50,0 N, \ (\ Delta \) x = 15,0 см, L 0 = 180,0 см, и A = (30,0 см) (90,0 см) = 2700,0 см 2 , и мы используем уравнение \ ref {12.43} для вычисления модуля сдвига.
Решение
Подставляя числа в уравнения, получаем для модуля сдвига
\ [S = \ frac {F _ {\ parallel}} {A} \ frac {L_ {0}} {\ Delta x} = \ frac {50.{2}} = \ frac {5} {27} \; кПа = 185,2 \; Па \ nonumber \]
\ [\ frac {\ Delta x} {L_ {0}} = \ frac {15.0 \; см} {180.0 \; см} = \ frac {1} {12} = 0,083 \ ldotp \ nonumber \]
Значение
Если человек в этом примере толкнет полку здоровым движением, может случиться так, что индуцированный сдвиг превратит ее в груду мусора. Примерно тот же механизм сдвига ответственен за разрушения засыпанных землей дамб и дамб; и в целом по оползням.
Упражнение \ (\ PageIndex {2} \)
Объясните, почему концепции модуля Юнга и модуля сдвига неприменимы к жидкостям.
Воздействие стресса на организм
В кишечнике есть сотни миллионов нейронов, которые могут функционировать независимо и постоянно взаимодействуют с мозгом, что объясняет способность чувствовать «бабочек» в желудке. Стресс может повлиять на коммуникацию между мозгом и кишечником и может вызвать боль, вздутие живота и другие неприятные ощущения в кишечнике, которые легче почувствовать. В кишечнике также обитают миллионы бактерий, которые могут влиять на его здоровье и здоровье мозга, что может влиять на способность думать и влиять на эмоции.
Стресс связан с изменениями кишечных бактерий, которые, в свою очередь, могут влиять на настроение. Таким образом, кишечные нервы и бактерии сильно влияют на мозг и наоборот.
Стресс в раннем детстве может изменить развитие нервной системы, а также то, как организм реагирует на стресс. Эти изменения могут увеличить риск более поздних заболеваний кишечника или дисфункции.
Пищевод
В состоянии стресса люди могут есть намного больше или намного меньше, чем обычно. Увеличение количества различных продуктов или увеличение употребления алкоголя или табака может привести к изжоге или кислотному рефлюксу.Стресс или истощение также могут усилить регулярно возникающую изжогу. В редких случаях спазмы пищевода могут быть вызваны сильным стрессом и могут быть ошибочно приняты за сердечный приступ.
Стресс также может затруднить глотание пищи или увеличить количество проглатываемого воздуха, что увеличивает отрыжку, газообразование и вздутие живота.
Желудок
Стресс может облегчить боль, вздутие живота, тошноту и другой дискомфорт в желудке.При достаточно сильном стрессе может возникнуть рвота. Кроме того, стресс может вызвать ненужное повышение или снижение аппетита. Нездоровое питание, в свою очередь, может ухудшить настроение.
Вопреки распространенному мнению, стресс не увеличивает выработку кислоты в желудке и не вызывает язвы желудка. Последние на самом деле вызваны бактериальной инфекцией. При стрессе язвы могут причинять больше беспокойства.
Кишечник
Стресс также может облегчить боль, вздутие живота или дискомфорт в кишечнике.Это может повлиять на скорость движения пищи по телу, что может вызвать диарею или запор. Кроме того, стресс может вызвать мышечные спазмы в кишечнике, которые могут быть болезненными.
Стресс может повлиять на пищеварение и на то, какие питательные вещества усваиваются кишечником. Производство газа, связанное с абсорбцией питательных веществ, может увеличиться.
Кишечник имеет плотный барьер для защиты организма от (большинства) пищевых бактерий. Стресс может ослабить кишечный барьер и позволить кишечным бактериям проникнуть в организм.Хотя с большинством этих бактерий легко справляется иммунная система и они не вызывают у нас болезней, постоянная низкая потребность в воспалительном действии может привести к хроническим легким симптомам.
Стресс особенно влияет на людей с хроническими заболеваниями кишечника, такими как воспалительные заболевания кишечника или синдром раздраженного кишечника. Это может быть связано с повышенной чувствительностью кишечных нервов, изменениями микробиоты кишечника, изменениями скорости движения пищи по кишечнику и / или изменениями иммунных реакций кишечника.
Могут ли две физические величины иметь одну и ту же единицу? — MVOrganizing
Могут ли две физические величины иметь одну и ту же единицу?
напряжения и давления.Сила, действующая на единицу площади, называется напряжением. ∴ Единицы измерения напряжения и давления одинаковы.
Какая физическая величина имеет ту же единицу?
Но в основном мы используем только первые три физических величины, то есть массу, длину, время. Размерность представляет собой мощность фундаментальных физических величин, например [MaLbTc], где a, b, c — измерения. Здесь работа и энергия имеют одну и ту же единицу, так что формула размеров также одинакова.
У кого такое же устройство?
Ответ: И импульс, и импульс имеют одну и ту же единицу — кг м / с.
Какой такой же блок СИ?
Ответ. в единицах si системные количества имеют одну и ту же единицу, только если они имеют одинаковые размеры…
Какая единица измерения выполненной работы используется в системе СИ?
Джоуль
Единицы измерения совпадают с размерами?
Измерение — это мера физической переменной (без числовых значений), а единица измерения — это способ присвоить этому измерению число или измерение. Например, длина — это размер, но он измеряется в футах (футах) или метрах (м).английская инженерная система единиц (обычно называемая английскими единицами)
В каком измерении мы живем?
В повседневной жизни мы населяем пространство трех измерений — огромный «шкаф» с высотой, шириной и глубиной, хорошо известный на протяжении веков. Менее очевидно то, что мы можем рассматривать время как дополнительное, четвертое измерение, как показал знаменитый Эйнштейн.
Каковы 7 религиозных измерений?
Используется для понимания всех аспектов религии и ее функций. Эти измерения включают: эмпирический, мифический, доктринальный, этический, ритуальный, социальный и материальный.
Каковы четыре религиозных измерения?
На основе предыдущего теоретического обоснования и исследований автор предлагает модель, которая постулирует четыре основных измерения религии и индивидуальной религиозности, которые частично различны, но взаимосвязаны: вера, связь, поведение и принадлежность.
Что такое духовные измерения?
Духовное измерение включает изучение ключевых принципов, убеждений и ценностей, которые придают смысл и цель вашей жизни.Речь идет о том, чтобы жить в соответствии с вашим «мировоззрением», а также проявлять терпимость по отношению к другим людям, придерживающимся других убеждений и ценностей.
Каковы пять измерений религиозности?
В итоге мы утверждаем, что пять уникальных измерений религиозности, которые важны в жизни подростков, — это религиозные верования, религиозная исключительность, внешняя практика, личная практика и религиозная значимость. Все эти измерения, безусловно, связаны друг с другом.
Напряжение и деформация — Физика в колледже, главы 1-17
Сводка
- Закон штата Гука.
- Объясните закон Гука, используя графическое представление между деформацией и приложенной силой.
- Обсудите три типа деформаций, такие как изменение длины, сдвиг в сторону и изменение объема.
- Опишите на примерах модуль Юнга, модуль сдвига и модуль объемной упругости.
- Определите изменение длины с учетом массы, длины и радиуса.
Теперь мы переходим от рассмотрения сил, влияющих на движение объекта (таких как трение и сопротивление), к тем, которые влияют на форму объекта.Если бульдозер втолкнет машину в стену, машина не сдвинется с места, но заметно изменит форму. Изменение формы из-за приложения силы — это деформация . Известно, что даже очень небольшие силы вызывают некоторую деформацию. При малых деформациях наблюдаются две важные характеристики. Во-первых, объект возвращается к своей исходной форме, когда сила снимается, то есть деформация является упругой для небольших деформаций. Во-вторых, размер деформации пропорционален силе, то есть для малых деформаций соблюдается закон Гука .В форме уравнения закон Гука имеет вид
.[латекс] \ boldsymbol {F = k \ Delta {L},} [/ латекс]
где [латекс] \ boldsymbol {\ Delta {L}} [/ latex] — величина деформации (например, изменение длины), вызванная силой [латекс] \ boldsymbol {F}, [/ latex] и [latex] \ boldsymbol {k} [/ latex] — это константа пропорциональности, которая зависит от формы и состава объекта, а также от направления силы. Обратите внимание, что эта сила является функцией деформации [латекс] \ boldsymbol {\ Delta {L}} [/ latex] — она не постоянна, как кинетическая сила трения.Переставляем это на
[латекс] \ boldsymbol {\ Delta {L} \: =} [/ latex] [латекс] \ boldsymbol {\ frac {F} {k}} [/ латекс]
дает понять, что деформация пропорциональна приложенной силе. На рисунке 1 показано соотношение по закону Гука между удлинением [латекс] \ boldsymbol {\ Delta {L}} [/ latex] пружины или человеческой кости. Для металлов или пружин область прямой линии, к которой относится закон Гука, намного больше. Кости хрупкие, эластичная область небольшая, а перелом резкий.В конце концов, достаточно большое напряжение материала приведет к его разрушению или разрушению. Предел прочности на разрыв — это разрушающее напряжение, которое вызывает остаточную деформацию или разрушение материала.
ЗАКОН КРЮКА
[латекс] \ boldsymbol {F = k \ Delta {L},} [/ латекс]
где [латекс] \ boldsymbol {\ Delta {L}} [/ latex] — величина деформации (например, изменение длины), вызванная силой [латекс] \ boldsymbol {F}, [/ latex] и [latex] \ boldsymbol {k} [/ latex] — это константа пропорциональности, которая зависит от формы и состава объекта, а также от направления силы.
[латекс] \ boldsymbol {\ Delta {L} \: =} [/ latex] [латекс] \ boldsymbol {\ frac {F} {k}} [/ латекс]
Рис. 1. График деформации Δ L в зависимости от приложенной силы F . Прямой отрезок — это линейная область, в которой соблюдается закон Гука. Уклон прямого участка 1 / k . Для больших сил график изогнут, но деформация остается упругой — Δ L вернется к нулю, если сила будет устранена.Еще большие силы деформируют объект до тех пор, пока он окончательно не сломается. Форма кривой возле трещины зависит от нескольких факторов, в том числе от того, как прикладывается сила F . Обратите внимание, что на этом графике наклон увеличивается непосредственно перед трещиной, указывая на то, что небольшое увеличение F дает большое увеличение L рядом с трещиной.Константа пропорциональности [латекс] \ boldsymbol {k} [/ latex] зависит от ряда факторов для материала.Например, гитарная струна из нейлона растягивается при затягивании, а удлинение [латекс] \ boldsymbol {\ Delta {L}} [/ latex] пропорционально приложенной силе (по крайней мере, для небольших деформаций). Более толстые нейлоновые и стальные струны растягиваются меньше при той же приложенной силе, что означает, что они имеют больший [латекс] \ boldsymbol {k} [/ latex] (см. Рисунок 2). Наконец, все три струны возвращаются к своей нормальной длине, когда сила снимается, при условии, что деформация мала. Большинство материалов будут вести себя таким образом, если деформация будет меньше примерно 0.3}. [/ Латекс]
Рис. 2. Одна и та же сила, в данном случае груз ( w ), приложенная к трем разным гитарным струнам одинаковой длины, вызывает три различных деформации, показанные заштрихованными сегментами. Левая нить из тонкого нейлона, посередине — из более толстого нейлона, а правая — из стали.НЕМНОГО РАСТЯНИСЬ
Как бы вы измерили константу пропорциональности [latex] \ boldsymbol {k} [/ latex] резиновой ленты? Если резинка растянулась на 3 см, когда к ней была прикреплена 100-граммовая масса, то насколько она растянулась бы, если бы две одинаковые резинки были прикреплены к одной и той же массе — даже если соединить их параллельно или, наоборот, связать вместе последовательно?
Теперь мы рассмотрим три конкретных типа деформаций: изменения длины (растяжение и сжатие), сдвиг в сторону (напряжение) и изменения объема.Все деформации считаются небольшими, если не указано иное.
Изменение длины [латекс] \ boldsymbol {\ Delta {L}} [/ latex] возникает, когда к проволоке или стержню прилагается сила, параллельная ее длине [латекс] \ boldsymbol {L_0}, [/ latex] либо растягивая (напряжение), либо сжимая. (См. Рисунок 3.)
Рис. 3. (а) Напряжение. Стержень растягивается на длину Δ L , когда сила прилагается параллельно его длине. (б) Сжатие. Тот же стержень сжимается силами той же величины в противоположном направлении.Для очень малых деформаций и однородных материалов Δ L примерно одинаково для одинаковой величины растяжения или сжатия. При больших деформациях площадь поперечного сечения изменяется при сжатии или растяжении стержня.Эксперименты показали, что изменение длины ([latex] \ boldsymbol {\ Delta {L}} [/ latex]) зависит только от нескольких переменных. Как уже отмечалось, [латекс] \ boldsymbol {\ Delta {L}} [/ latex] пропорционален силе [latex] \ boldsymbol {F} [/ latex] и зависит от вещества, из которого сделан объект.Кроме того, изменение длины пропорционально исходной длине [латекс] \ boldsymbol {L_0} [/ latex] и обратно пропорционально площади поперечного сечения проволоки или стержня. Например, длинная гитарная струна растягивается больше, чем короткая, а толстая струна растягивается меньше, чем тонкая. Мы можем объединить все эти факторы в одно уравнение для [latex] \ boldsymbol {\ Delta {L}}: [/ latex]
[латекс] \ boldsymbol {\ Delta {L} \: =} [/ latex] [латекс] \ boldsymbol {\ frac {1} {Y} \ frac {F} {A}} [/ латекс] [латекс] \ boldsymbol {L_0}, [/ латекс]
где [латекс] \ boldsymbol {\ Delta {L}} [/ latex] — это изменение длины, [latex] \ boldsymbol {F} [/ latex] приложенная сила, [латекс] \ boldsymbol {Y} [/ латекс] — это фактор, называемый модулем упругости или модулем Юнга, который зависит от вещества, [латекс] \ boldsymbol {A} [/ latex] — это площадь поперечного сечения, а [латекс] \ boldsymbol {L_0} [/ латекс] — исходная длина.2)} [/ латекс]
Модули Юнга не указаны для жидкостей и газов в таблице 3, потому что они не могут быть растянуты или сжаты только в одном направлении.Обратите внимание, что предполагается, что объект не ускоряется, поэтому на самом деле существуют две приложенные силы величиной [латекс] \ boldsymbol {F} [/ латекс], действующие в противоположных направлениях. Например, струны на Рисунке 3 натягиваются вниз силой величиной [латекс] \ boldsymbol {w} [/ latex] и удерживаются за потолок, что также оказывает силу величиной [латекс] \ boldsymbol {w }. [/ латекс]
Пример 1: Растяжение длинного кабеля
Подвесные тросы используются для перевозки гондол на горнолыжных курортах.2}) (3020 \ textbf {m})} [/ latex]
[латекс] \ boldsymbol {= 18 \ textbf {m}}. [/ Latex]
Обсуждение
Это довольно большое натяжение, но только около 0,6% от длины без опоры. В таких условиях влияние температуры на длину может быть важным.
Кости в целом не ломаются от растяжения или сжатия. Скорее они обычно ломаются из-за бокового удара или изгиба, что приводит к срезанию или разрыву кости. Поведение костей при растяжении и сжатии важно, потому что оно определяет нагрузку, которую кости могут нести.Кости классифицируются как несущие конструкции, такие как колонны в зданиях и деревья. Несущие конструкции обладают особенностями; колонны в здании имеют стальные арматурные стержни, а деревья и кости — волокнистые. Кости в разных частях тела выполняют разные структурные функции и подвержены разным нагрузкам. Таким образом, кость в верхней части бедренной кости расположена в виде тонких листов, разделенных костным мозгом, в то время как в других местах кости могут быть цилиндрическими и заполненными костным мозгом или просто твердыми.Люди с избыточным весом имеют тенденцию к повреждению костей из-за длительного сжатия костных суставов и сухожилий.
Другой биологический пример закона Гука встречается в сухожилиях. Функционально сухожилие (ткань, соединяющая мышцу с костью) должно сначала легко растягиваться при приложении силы, но обеспечивать гораздо большую восстанавливающую силу для большего напряжения. На рисунке 5 показана зависимость напряжения от деформации человеческого сухожилия. Некоторые сухожилия имеют высокое содержание коллагена, поэтому деформация или изменение длины относительно невелико; другие, например, опорные сухожилия (например, в ноге) могут изменять длину до 10%.Обратите внимание, что эта кривая напряжения-деформации является нелинейной, поскольку наклон линии изменяется в разных областях. В первой части растяжения, называемой областью пальца, волокна в сухожилии начинают выравниваться в направлении напряжения — это называется разжатым . В линейной области фибриллы будут растянуты, а в области разрушения отдельные волокна начнут разрываться. Простую модель этой взаимосвязи можно проиллюстрировать параллельными пружинами: разные пружины активируются при разной длине растяжения.Примеры этого приведены в задачах в конце этой главы. Связки (ткань, соединяющая кость с костью) ведут себя аналогичным образом.
Рис. 5. Типичная кривая «напряжение-деформация» для сухожилия млекопитающих. Показаны три области: (1) область пальца ноги (2) линейная область и (3) область разрушения.В отличие от костей и сухожилий, которые должны быть прочными и эластичными, артерии и легкие должны быть легко растяжимыми. Эластические свойства артерий важны для кровотока. Когда кровь выкачивается из сердца, давление в артериях увеличивается, и стенки артерий растягиваются.Когда аортальный клапан закрывается, давление в артериях падает, и артериальные стенки расслабляются, чтобы поддерживать кровоток. Когда вы чувствуете свой пульс, вы чувствуете именно это — эластичное поведение артерий, когда кровь хлынет через каждый насос сердца. Если бы артерии были жесткими, вы бы не чувствовали пульса. Сердце также является органом с особыми эластичными свойствами. Легкие расширяются за счет мышечного усилия, когда мы вдыхаем, но расслабляемся свободно и эластично, когда мы выдыхаем. Наша кожа особенно эластична, особенно для молодых.Молодой человек может подняться от 100 кг до 60 кг без видимого провисания кожи. С возрастом снижается эластичность всех органов. Постепенное физиологическое старение за счет снижения эластичности начинается в начале 20-х годов.
Пример 2: Расчет деформации: насколько укорачивается ваша нога, когда вы стоите на ней?
Вычислите изменение длины кости верхней части ноги (бедренной кости), когда мужчина весом 70,0 кг поддерживает на ней 62,0 кг своей массы, при условии, что кость эквивалентна стержню, равному 40.{-5} \ textbf {m}}. [/ Latex]
Обсуждение
Это небольшое изменение длины кажется разумным, поскольку мы знаем, что кости жесткие. Фактически, даже довольно большие силы, возникающие во время напряженных физических нагрузок, не сжимают и не сгибают кости в значительной степени. Хотя кость более жесткая по сравнению с жиром или мышцами, некоторые из веществ, перечисленных в таблице 3, имеют более высокие значения модуля Юнга [латекс] \ boldsymbol {Y}. [/ Latex] Другими словами, они более жесткие.2} [/ latex]), а отношение изменения длины к длине, [latex] \ boldsymbol {\ frac {\ Delta {L}} {L_0}}, [/ latex], определяется как деформация ( безразмерное количество). Другими словами,
[латекс] \ boldsymbol {\ textbf {stress} = Y \ times \ textbf {stretch}}. [/ Latex]
В этой форме уравнение аналогично закону Гука с напряжением, аналогичным силе, и деформацией, аналогичной деформации. Если снова переписать это уравнение к виду
[латекс] \ boldsymbol {F = YA} [/ latex] [латекс] \ boldsymbol {\ frac {\ Delta {L}} {L_0}}, [/ latex]
мы видим, что он совпадает с законом Гука с константой пропорциональности
[латекс] \ boldsymbol {k \: =} [/ latex] [латекс] \ boldsymbol {\ frac {YA} {L_0}}.[/ латекс]
Эта общая идея о том, что сила и вызываемая ею деформация пропорциональны небольшим деформациям, применима к изменениям длины, боковому изгибу и изменениям объема.
СТРЕСС
Отношение силы к площади, [латекс] \ boldsymbol {\ frac {F} {A}}, [/ latex] определяется как напряжение, измеренное в Н / м 2 .
ШТАМ
Отношение изменения длины к длине, [латекс] \ boldsymbol {\ frac {\ Delta {L}} {L_0}}, [/ latex] определяется как деформация (величина без единицы измерения).Другими словами,
[латекс] \ boldsymbol {\ textbf {stress} = Y \ times \ textbf {stretch}}. [/ Latex]
На рисунке 6 показано, что подразумевается под боковым напряжением или срезающей силой . Здесь деформация называется [латекс] \ boldsymbol {\ Delta {x}} [/ latex], и она перпендикулярна [латексу] \ boldsymbol {L_0}, [/ latex], а не параллельна, как при растяжении и сжатии. Деформация сдвига аналогична растяжению и сжатию и может быть описана аналогичными уравнениями. Выражение для деформации сдвига
[латекс] \ boldsymbol {\ Delta {x} \: =} [/ latex] [латекс] \ boldsymbol {\ frac {1} {S} \ frac {F} {A}} [/ латекс] [латекс] \ boldsymbol {L_0}, [/ латекс]
где [латекс] \ boldsymbol {S} [/ latex] — это модуль сдвига (см. Таблицу 3), а [латекс] \ boldsymbol {F} [/ latex] — сила, приложенная перпендикулярно к [латексу] \ boldsymbol {L_0} [/ latex] и параллельно площади поперечного сечения [latex] \ boldsymbol {A}.[/ latex] Опять же, чтобы препятствовать ускорению объекта, на самом деле есть две равные и противоположные силы [latex] \ boldsymbol {F} [/ latex], приложенные к противоположным граням, как показано на рисунке 6. Уравнение логично — для Например, длинный тонкий карандаш (маленький [латекс] \ boldsymbol {A} [/ latex]) легче согнуть, чем короткий толстый, и оба гнутся легче, чем аналогичные стальные стержни (большие [латекс] \ boldsymbol { S} [/ latex]).
ДЕФОРМАЦИЯ СДВИГА
[латекс] \ boldsymbol {\ Delta {x} \: =} [/ latex] [латекс] \ boldsymbol {\ frac {1} {S} \ frac {F} {A}} [/ латекс] [латекс] \ boldsymbol {L_0}, [/ латекс]
где [латекс] \ boldsymbol {S} [/ latex] — это модуль сдвига, а [latex] \ boldsymbol {F} [/ latex] — это сила, приложенная перпендикулярно к [латексу] \ boldsymbol {L_0} [/ latex] и параллельно площади поперечного сечения [латекс] \ boldsymbol {A}.[/ латекс]
Рис. 6. Сила сдвига прилагается перпендикулярно длине L 0 и параллельно области A , создавая деформацию Δx . Вертикальные силы не показаны, но следует иметь в виду, что в дополнение к двум силам сдвига, F , должны существовать поддерживающие силы, чтобы объект не вращался. Искажающие эффекты этих поддерживающих сил игнорируются при этом лечении.Вес объекта также не показан, поскольку он обычно незначителен по сравнению с силами, достаточно большими, чтобы вызвать значительные деформации.Изучение модулей сдвига в таблице 3 выявляет некоторые характерные закономерности. Например, для большинства материалов модули сдвига меньше модулей Юнга. Кость — замечательное исключение. Его модуль сдвига не только больше, чем модуль Юнга, но и такой же, как у стали. Вот почему кости такие жесткие.
Позвоночный столб (состоящий из 26 позвоночных сегментов, разделенных дисками) обеспечивает основную опору для головы и верхней части тела.Позвоночник имеет нормальную кривизну для стабильности, но это искривление может быть увеличено, что приведет к увеличению силы сдвига на нижних позвонках. Диски лучше выдерживают силы сжатия, чем силы сдвига. Поскольку позвоночник не вертикальный, вес верхней части тела влияет на обе части. Беременным женщинам и людям с избыточным весом (с большим животом) необходимо отвести плечи назад, чтобы поддерживать равновесие, тем самым увеличивая искривление позвоночника и тем самым увеличивая сдвигающий компонент напряжения.Увеличенный угол из-за большей кривизны увеличивает поперечные силы вдоль плоскости. Эти более высокие усилия сдвига увеличивают риск травмы спины из-за разрыва дисков. Пояснично-крестцовый диск (клиновидный диск под последними позвонками) особенно подвержен риску из-за своего расположения.
Модули сдвига для бетона и кирпича очень малы; они слишком изменчивы, чтобы их можно было перечислить. Бетон, используемый в зданиях, может выдерживать сжатие, как в колоннах и арках, но очень плохо противостоит сдвигу, который может возникнуть в сильно нагруженных полах или во время землетрясений.Современные конструкции стали возможны благодаря использованию стали и железобетона. Почти по определению жидкости и газы имеют модули сдвига, близкие к нулю, потому что они текут в ответ на сдвигающие силы.
Пример 3: Расчет силы, необходимой для деформации: гвоздь не сильно изгибается под нагрузкой
Найдите массу картины, висящей на стальном гвозде, как показано на рисунке 7, учитывая, что гвоздь гнет только [латекс] \ boldsymbol {1.80 \: \ mu \ textbf {m}}. [/ Latex] (Предположим, что сдвиг модуль известен с двумя значащими цифрами.)
Рис. 7. Гвоздь, вид сбоку с прикрепленным к нему изображением. Гвоздь очень слабо прогибается (показан намного больше, чем на самом деле) из-за срезающего воздействия поддерживаемого веса. Также показано направленное вверх усилие стенки на гвоздь, демонстрирующее, что равные и противоположные силы прилагаются к противоположным поперечным сечениям гвоздя. См. Пример 3 для расчета массы изображения.Стратегия
Сила [латекс] \ boldsymbol {F} [/ latex] на гвоздь (без учета собственного веса гвоздя) — это вес изображения [латекса] \ boldsymbol {w}.[/ latex] Если мы сможем найти [латекс] \ boldsymbol {w}, [/ latex], тогда масса изображения будет просто [латекс] \ boldsymbol {wg}. [/ latex] Уравнение [латекс] \ boldsymbol { \ Delta {x} = \ frac {1} {S} \ frac {F} {A} L_0} [/ latex] можно решить для [latex] \ boldsymbol {F}. [/ Latex]
Решение
Решение уравнения [латекс] \ boldsymbol {\ Delta {x} = \ frac {1} {S} \ frac {F} {A} L_0} [/ latex] для [латекса] \ boldsymbol {F}, [/ латекс] видим, что все остальные количества можно найти:
[латекс] \ boldsymbol {F \: =} [/ latex] [латекс] \ boldsymbol {\ frac {SA} {L_0}} [/ latex] [латекс] \ boldsymbol {\ Delta {x}}.{-6} \ textbf {m})} [/ latex] [latex] \ boldsymbol {= \: 51 \ textbf {N}}. [/ Latex]
Эта сила 51 Н — это вес [латекс] \ boldsymbol {w} [/ latex] изображения, поэтому масса изображения составляет
[латекс] \ boldsymbol {m \: =} [/ latex] [латекс] \ boldsymbol {\ frac {w} {g}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {F} {g}} [/ latex] [латекс] \ boldsymbol {= \: 5.2 \ textbf {kg}}. [/ latex]
Обсуждение
Это довольно массивное изображение, и впечатляет то, что ноготь прогибается только [латекс] \ boldsymbol {1.80 \: \ mu \ textbf {m}} [/ latex] — количество, не обнаруживаемое невооруженным глазом.
Объект будет сжиматься во всех направлениях, если внутренние силы приложены равномерно ко всем его поверхностям, как показано на рисунке 8. Сжимать газы относительно легко, а жидкости и твердые тела — чрезвычайно сложно. Например, воздух в винной бутылке сжимается, когда она закупорена. Но если вы попытаетесь закупорить бутылку с полными краями, вы не сможете сжать вино — некоторые из них необходимо удалить, если нужно вставить пробку. Причина такой разной сжимаемости заключается в том, что атомы и молекулы разделены большими пустыми пространствами в газах, но плотно упакованы в жидкостях и твердых телах.Чтобы сжать газ, вы должны сблизить его атомы и молекулы. Чтобы сжимать жидкости и твердые тела, вы должны действительно сжать их атомы и молекулы, и очень сильные электромагнитные силы в них препятствуют этому сжатию .
Рис. 8. Внутренняя сила, действующая на все поверхности, сжимает этот куб. Его изменение в объеме пропорционально силе на единицу площади и его первоначальному объему и связано со сжимаемостью вещества.Мы можем описать сжатие или объемную деформацию объекта уравнением.Во-первых, отметим, что сила, «приложенная равномерно», определяется как имеющая одинаковое напряжение или отношение силы к площади [латекс] \ boldsymbol {\ frac {F} {A}} [/ latex] на всех поверхностях. Произведенная деформация представляет собой изменение объема [латекс] \ boldsymbol {\ Delta {V}}, [/ латекс], которое, как было обнаружено, ведет себя очень похоже на сдвиг, растяжение и сжатие, которые обсуждались ранее. (Это неудивительно, поскольку сжатие всего объекта эквивалентно сжатию каждого из его трех измерений.) Связь изменения объема с другими физическими величинами определяется выражением
.[латекс] \ boldsymbol {\ Delta {V} \: =} [/ latex] [латекс] \ boldsymbol {\ frac {1} {B} \ frac {F} {A}} [/ латекс] [латекс] \ boldsymbol {V_0}, [/ латекс]
где [латекс] \ boldsymbol {B} [/ latex] — это модуль объемной упругости (см. Таблицу 3), [latex] \ boldsymbol {V_0} [/ latex] — исходный объем, а [latex] \ boldsymbol {\ frac {F} {A}} [/ latex] — сила на единицу площади, равномерно приложенная внутрь ко всем поверхностям.Обратите внимание, что объемные модули для газов не приводятся.
Какие есть примеры объемного сжатия твердых тел и жидкостей? Одним из практических примеров является производство алмазов промышленного качества путем сжатия углерода с чрезвычайно большой силой на единицу площади. Атомы углерода перестраивают свою кристаллическую структуру в более плотно упакованный узор алмазов. В природе аналогичный процесс происходит глубоко под землей, где чрезвычайно большие силы возникают из-за веса вышележащего материала. Еще один естественный источник больших сжимающих сил — давление, создаваемое весом воды, особенно в глубоких частях океанов.Вода воздействует на все поверхности погружаемого объекта и даже на саму воду. На больших глубинах вода ощутимо сжата, как показано в следующем примере.
Пример 4: Расчет изменения объема с деформацией: насколько вода сжимается на глубинах Великого океана?
Рассчитайте частичное уменьшение объема ([латекс] \ boldsymbol {\ frac {\ Delta {V}} {V_0}} [/ latex]) для морской воды на глубине 5,00 км, где сила на единицу площади [латекс] \ жирный символ {5.2}. [/ Latex]
Стратегия
Уравнение [латекс] \ boldsymbol {\ Delta {V} = \ frac {1} {B} \ frac {F} {A} V_0} [/ latex] является правильным физическим соотношением. Все величины в уравнении, кроме [латекс] \ boldsymbol {\ frac {\ Delta {V}} {V_0}} [/ latex], известны.
Решение
Решение неизвестного [латекса] \ boldsymbol {\ frac {\ Delta {V}} {V_0}} [/ latex] дает
[латекс] \ boldsymbol {\ frac {\ Delta {V}} {V_0}} [/ latex] [latex] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {1} {B} \ frac {F} {A}}.2}} [/ латекс]
[латекс] \ boldsymbol {= 0,023 = 2,3 \%}. [/ Латекс]
Обсуждение
Хотя это и поддается измерению, это незначительное уменьшение объема, учитывая, что сила на единицу площади составляет около 500 атмосфер (1 миллион фунтов на квадратный фут). Жидкости и твердые вещества чрезвычайно трудно сжимать.
И наоборот, очень большие силы создаются жидкостями и твердыми телами, когда они пытаются расшириться, но сдерживаются в этом, что эквивалентно их сжатию до меньшего, чем их нормальный объем.Это часто происходит, когда содержащийся в нем материал нагревается, поскольку большинство материалов расширяются при повышении их температуры. Если материалы сильно стеснены, они деформируют или ломают контейнер. Другой очень распространенный пример — замерзание воды. Вода, в отличие от большинства материалов, при замерзании расширяется, и она может легко сломать валун, разорвать биологическую клетку или сломать блок двигателя, который встанет у нее на пути.
Другие типы деформаций, такие как кручение или скручивание, ведут себя аналогично рассмотренным здесь деформациям растяжения, сдвига и объемных деформаций.
- Закон Гука дан
[латекс] \ boldsymbol {F = k \ Delta {L}}, [/ латекс]
где [latex] \ boldsymbol {\ Delta {L}} [/ latex] — это величина деформации (изменение длины), [latex] \ boldsymbol {F} [/ latex] — это приложенная сила, а [latex ] \ boldsymbol {k} [/ latex] — это константа пропорциональности, которая зависит от формы и состава объекта, а также от направления силы. Соотношение между деформацией и приложенной силой также можно записать как
[латекс] \ boldsymbol {\ Delta {L} \: =} [/ latex] [латекс] \ boldsymbol {\ frac {1} {Y} \ frac {F} {A}} [/ латекс] [латекс] \ boldsymbol {L_0}, [/ латекс]
, где [латекс] \ boldsymbol {Y} [/ latex] — это модуль Юнга , который зависит от вещества, [латекс] \ boldsymbol {A} [/ latex] — это площадь поперечного сечения, а [латекс] \ boldsymbol {L_0} [/ latex] — исходная длина.
- Отношение силы к площади, [латекс] \ boldsymbol {\ frac {F} {A}}, [/ latex] определяется как напряжение , измеренное в Н / м 2 .
- Отношение изменения длины к длине, [латекс] \ boldsymbol {\ frac {\ Delta {L}} {L_0}}, [/ latex], определяется как деформация (безразмерная величина). Другими словами,
[латекс] \ boldsymbol {\ textbf {stress} = Y \ times \ textbf {stretch}}. [/ Latex]
- Выражение деформации сдвига:
[латекс] \ boldsymbol {\ Delta {x} \: =} [/ latex] [латекс] \ boldsymbol {\ frac {1} {S} \ frac {F} {A}} [/ латекс] [латекс] \ boldsymbol {L_0}, [/ латекс]
где [латекс] \ boldsymbol {S} [/ latex] — это модуль сдвига, а [latex] \ boldsymbol {F} [/ latex] — это сила, приложенная перпендикулярно к [латексу] \ boldsymbol {L_0} [/ latex] и параллельно площади поперечного сечения [латекс] \ boldsymbol {A}.[/ латекс]
- Связь изменения объема с другими физическими величинами определяется выражением
[латекс] \ boldsymbol {\ Delta {V} \: =} [/ latex] [латекс] \ boldsymbol {\ frac {1} {B} \ frac {F} {A}} [/ латекс] [латекс] \ boldsymbol {V_0}, [/ латекс]
где [latex] \ boldsymbol {B} [/ latex] — это модуль объемной упругости, [latex] \ boldsymbol {V_0} [/ latex] — это исходный объем, а [latex] \ boldsymbol {\ frac {F} {A }} [/ latex] — это сила на единицу площади, равномерно приложенная внутрь ко всем поверхностям.
Концептуальные вопросы
1: Эластичные свойства артерий важны для кровотока.Объясните важность этого с точки зрения характеристик кровотока (пульсирующий или непрерывный).
2: Что вы чувствуете, когда прощупываете пульс? Измерьте частоту пульса в течение 10 секунд и 1 минуты. Есть ли разница в 6 раз?
3: Изучите различные типы обуви, включая спортивную обувь и стринги. С точки зрения физики, почему нижние поверхности устроены именно так? Какие различия будут иметь для этих поверхностей сухие и влажные условия?
4: Ожидаете ли вы, что ваш рост будет отличаться в зависимости от времени суток? Почему или почему нет?
5: Почему белка может спрыгнуть с ветки дерева на землю и убежать невредимой, а человек может сломать кость при таком падении?
6: Объясните, почему беременные женщины часто страдают растяжением спины на поздних сроках беременности.
7: Уловка старого плотника, чтобы удерживать гвозди от сгибания, когда они забиваются в твердый материал, заключается в том, чтобы крепко удерживать центр гвоздя плоскогубцами. Почему это помогает?
8: Когда стеклянная бутылка, полная уксуса, нагревается, и уксус, и стакан расширяются, но уксус расширяется значительно больше с температурой, чем стекло. Бутылка разобьется, если наполнить ее до плотно закрытой крышки. Объясните, почему, а также объясните, как воздушный карман над уксусом предотвратит разрыв.(Это функция воздуха над жидкостями в стеклянных контейнерах.)
Задачи и упражнения
1: Во время циркового представления один артист качается вверх ногами, свешиваясь с трапеции, держа другого, также перевернутого, за ноги. Если сила, направленная вверх, действующая на более низкую спортсменку, в три раза превышает ее вес, насколько растягиваются кости (бедра) в ее верхних конечностях? Вы можете предположить, что каждый из них эквивалентен одинаковому стержню длиной 35,0 см и радиусом 1,80 см.2}. [/ Latex] Вычислите изменение длины грифеля автоматического карандаша, если постучите им прямо по карандашу с усилием 4,0 Н. Грифель имеет диаметр 0,50 мм и длину 60 мм. б) разумен ли ответ? То есть согласуется ли это с тем, что вы наблюдали при использовании карандашей?
4: Антенны телевещания — самые высокие искусственные сооружения на Земле. В 1987 году физик весом 72,0 кг разместил себя и 400 кг оборудования на вершине одной антенны высотой 610 м для проведения гравитационных экспериментов.Насколько была сжата антенна, если считать ее эквивалентом стального цилиндра радиусом 0,150 м?
5: (a) Насколько альпинист весом 65,0 кг натягивает нейлоновую веревку диаметром 0,800 см, когда она висит на 35,0 м ниже выступа скалы? б) Соответствует ли ответ тому, что вы наблюдали для нейлоновых веревок? Имел бы смысл, если бы веревка была на самом деле тросиком?
6: Полый алюминиевый флагшток высотой 20,0 м по жесткости эквивалентен твердому цилиндру 4.00 см в диаметре. Сильный ветер изгибает полюс так же, как горизонтальная сила в 900 Н. Насколько далеко в сторону прогибается верхняя часть шеста?
7: По мере бурения нефтяной скважины каждая новая секция бурильной трубы выдерживает собственный вес, а также вес трубы и бурового долота под ней. Рассчитайте растяжение новой стальной трубы длиной 6,00 м, которая поддерживает 3,00 км трубы, имеющей массу 20,0 кг / м, и буровое долото 100 кг. Труба по жесткости эквивалентна сплошному цилиндру 5.00 см в диаметре.
8: Рассчитайте усилие, которое настройщик рояля применяет для растяжения стальной рояльной струны на 8,00 мм, если изначально проволока имеет диаметр 0,850 мм и длину 1,35 м.
9: На позвонок действует сила сдвига 500 Н. Найдите деформацию сдвига, принимая позвонок в виде цилиндра высотой 3,00 см и диаметром 4,00 см.
10: Диск между позвонками позвоночника подвергается срезающей силе 600 Н.0} [/ latex] ниже горизонтали с вершиной его шеста и выдерживает напряжение 108 Н. Полый алюминиевый столб высотой 12,0 м эквивалентен по жесткости твердому цилиндру диаметром 4,50 см. а) Насколько он наклонен в сторону? б) Насколько он сжат?
13: Фермер, производящий виноградный сок, наполняет стеклянную бутылку до краев и плотно закрывает ее крышкой. {- 3}} [/ latex]) относительно доступного места.0} [/ latex] с вертикалью. (Ясно, что растяжка должна быть в направлении, противоположном изгибу.)
Рис. 9. Этот телефонный столб находится на изгибе 90 0 линии электропередачи. Оттяжка прикреплена к верху столба под углом 30 0 к вертикали.Сноски
- Приблизительные и средние значения. Модули Юнга [латекс] \ boldsymbol {Y} [/ latex] для растяжения и сжатия иногда различаются, но здесь они усреднены.Кость имеет существенно разные модули Юнга для растяжения и сжатия.
Глоссарий
- деформация
- изменение формы из-за приложения силы
- Закон Гука
- пропорциональное соотношение между силой [латекс] \ boldsymbol {F} [/ latex], действующей на материал, и деформацией [латекс] \ boldsymbol {\ Delta {L}} [/ latex], которую оно вызывает, [латекс] \ boldsymbol {F = k \ Delta {L}} [/ latex]
- предел прочности
- разрушающее напряжение, которое вызовет остаточную деформацию или фракцию материала
- напряжение
- отношение силы к площади
- штамм
- отношение изменения длины к исходной длине
- деформация сдвига
- деформация, перпендикулярная исходной длине объекта
Решения
Задачи и упражнения
1:
[латекс] \ boldsymbol {1.




 =
=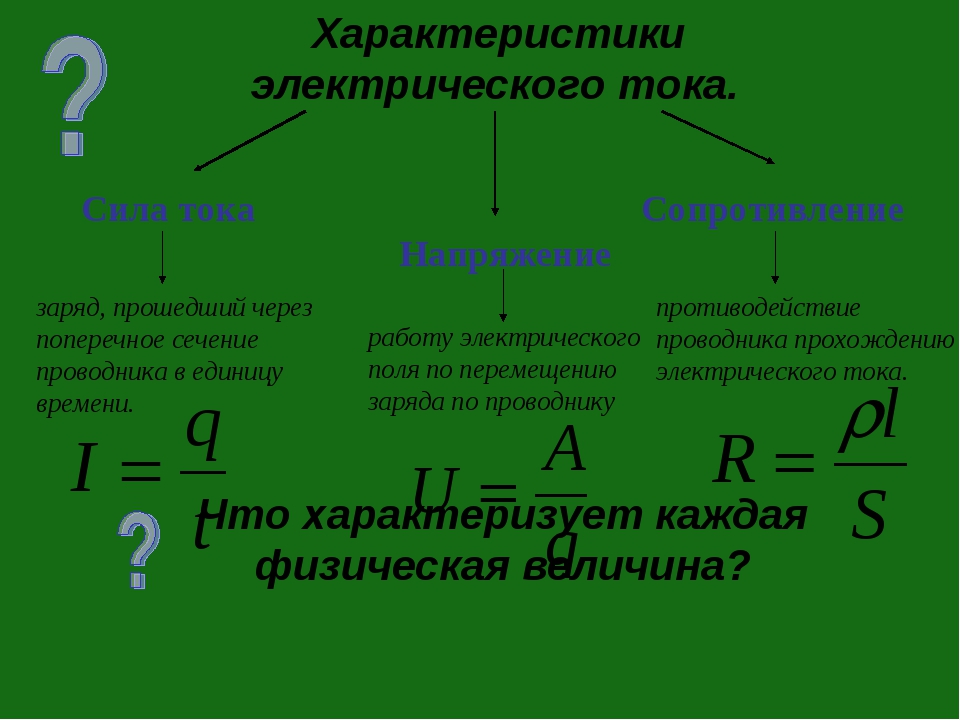 Как известно, одноименные заряды отталкиваются, поэтому волосы, подобно листочкам бумажного султана, расходятся во все стороны.
Если любое проводящее тело, в том числе и человеческое, изолировать от земли, то его можно зарядить до большого потенциала. Так, с помощью электростатической машины тело человека можно зарядить до потенциала в десятки тысяч вольт.
Как известно, одноименные заряды отталкиваются, поэтому волосы, подобно листочкам бумажного султана, расходятся во все стороны.
Если любое проводящее тело, в том числе и человеческое, изолировать от земли, то его можно зарядить до большого потенциала. Так, с помощью электростатической машины тело человека можно зарядить до потенциала в десятки тысяч вольт.
 Всем хорошего настроения и удачной работы. Присаживайтесь.
Всем хорошего настроения и удачной работы. Присаживайтесь. (одновременно)
(одновременно) ток ). кр. карточка
ток ). кр. карточка е. если в механике существует механическая работа, то в электричестве …? (Сущ-ет работа тока)
е. если в механике существует механическая работа, то в электричестве …? (Сущ-ет работа тока) На оборотной стороне написано слово. (На листочках написаны Диэлектрики: дистиллированная вода, стекла, пластмассы, бензол, масла, слюда, фарфор, воздух, резина, смолы различные, дерево;
На оборотной стороне написано слово. (На листочках написаны Диэлектрики: дистиллированная вода, стекла, пластмассы, бензол, масла, слюда, фарфор, воздух, резина, смолы различные, дерево; (которую называют электрическим напряжением или просто напряжением)
(которую называют электрическим напряжением или просто напряжением) поле при перемещении единичного положительного заряда из одной точки в другую.
поле при перемещении единичного положительного заряда из одной точки в другую. Обозначение напряжения В .
Обозначение напряжения В . Заряд q соответствует массе воды, а напряжение – разности уровней, напору воды в реке.
Заряд q соответствует массе воды, а напряжение – разности уровней, напору воды в реке.