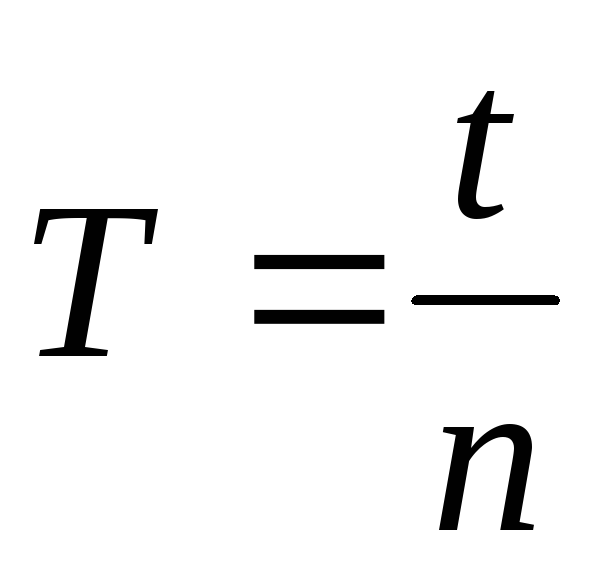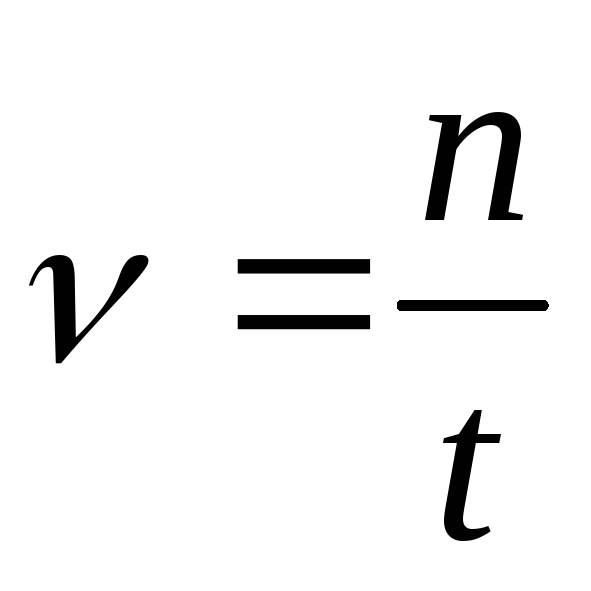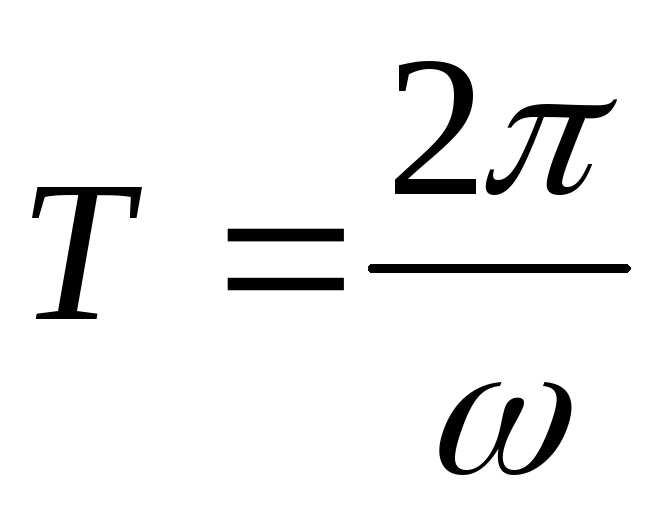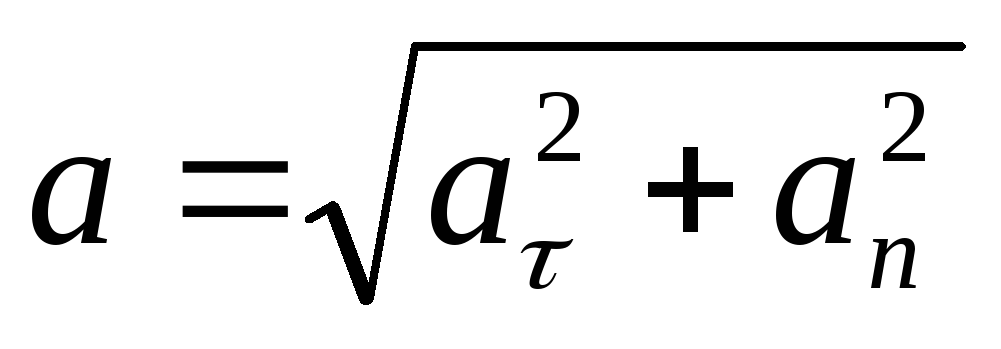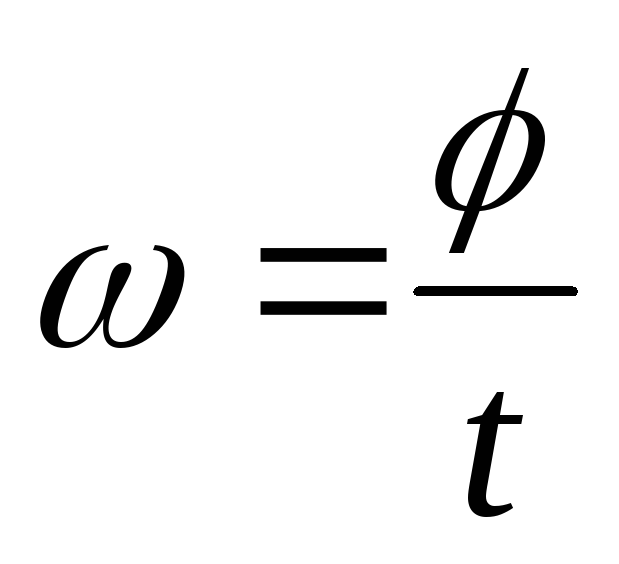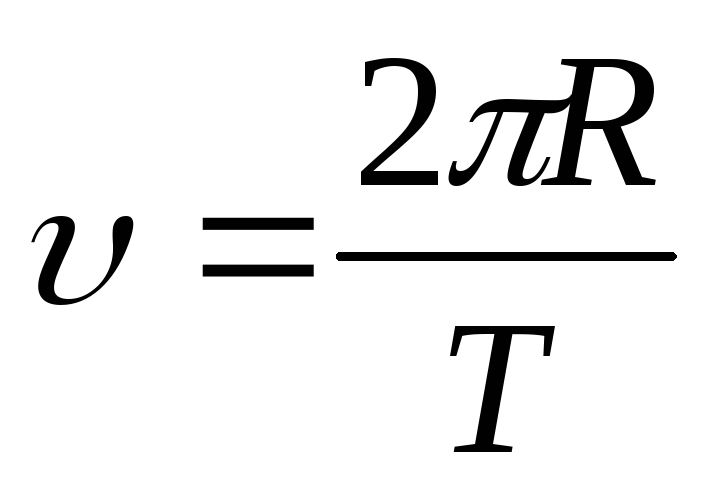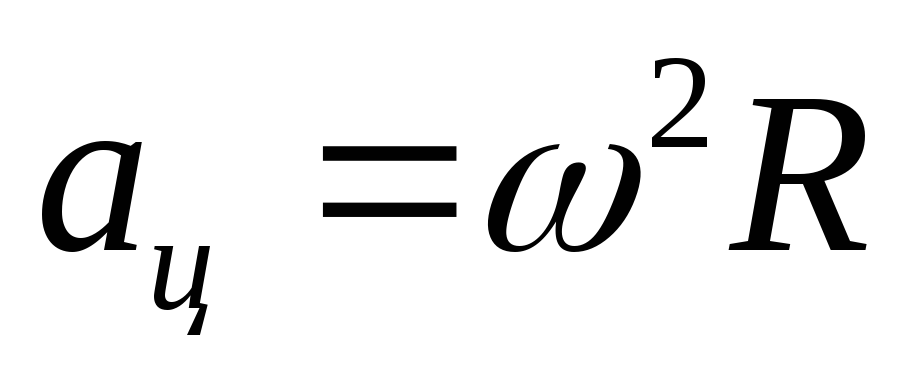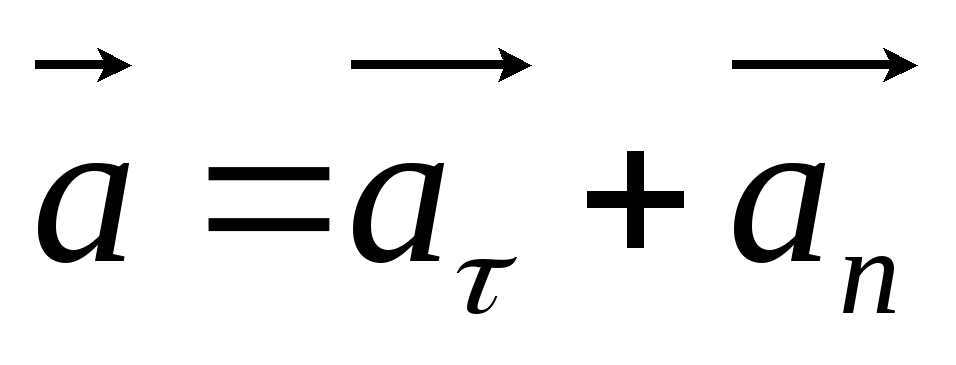42. Как определить направление угловой скорости?
Углова́я ско́рость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:
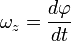 ,
,
а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону. Единица измерения угловой скорости, принятая в системах СИ и СГС) — радианы в секунду. (Примечание: радиан, как и любые единицы измерения угла, — физически безразмерен, поэтому физическая размерность угловой скорости — просто [1/секунда]).Определим угловую скорость как вектор, величина которого численно равна угловой скорости, b направленный вдоль оси вращения, причем, если смотреть с конца этого вектора, то вращение направлено против часовой стрелки
43. Как определить направление углового ускарения?
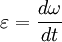 Единица
углового ускорения — радиан в секунду
в квадрате.
Единица
углового ускорения — радиан в секунду
в квадрате.
Углово́е ускоре́ние — псевдовекторная физическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела.
При вращении тела вокруг неподвижной оси, угловое ускорение по модулю равно[1]:
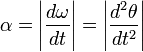
Вектор
углового ускорения α
направлен вдоль оси вращения (в сторону 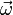 при
ускоренном вращении и противоположно
при
ускоренном вращении и противоположно 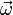 —
при замедленном).
—
при замедленном).
При вращении вокруг неподвижной точки вектор углового ускорения определяется как первая производная от вектора угловой скорости ω по времени[2], то есть
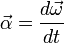 ,
,
и
направлен по касательной к годографу
вектора 
44. При каком условии мы имеем право считать в лабораторной работе №4 «Изучение основного закона динамики вращательного движения» линейное ускорение точек на ободе щкива равным ускорению поступательного движения груза?
Момент
сил создается грузом m, привязанным к
нити Н, которая навита на один из
шкивов. Если момент сил трения Mтр,
приложенный к оси маятника, мал по
сравнению с моментом силы натяжения
нити, то проверка уравнения 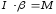
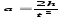 , которое
связано с угловым ускорением
(при отсутствии проскальзывания
нити относительно обода шкива) очевидным
соотношением
, которое
связано с угловым ускорением
(при отсутствии проскальзывания
нити относительно обода шкива) очевидным
соотношением
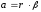 , где
r
— радиус шкива.
, где
r
— радиус шкива.
6. Модуль и направление углового перемещения
Пусть произвольная точка М сначала
находилась в неподвижной плоскости Q(рис. 2). Затем переместилась в подвижной
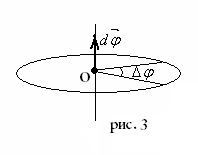
плоскостиPна угол
поворота .
.
Угол поворота (угловое перемещение) будим отсчитывать от неподвижной плоскости Qпо часовой стрелке (см. рис. 3).
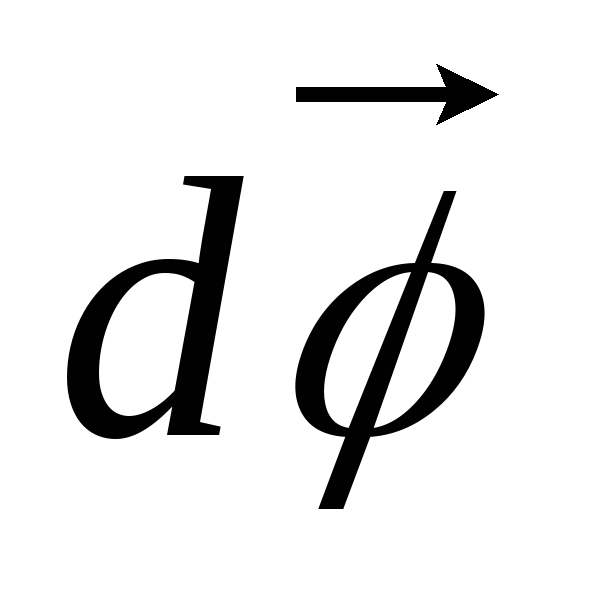

Направление углового
перемещения  совпадает с направлением поступательного
движения острия винта, головка которого
вращается в направлении движения точки
по окружности, т.е. подчиняется правилу
правого винта.
совпадает с направлением поступательного
движения острия винта, головка которого
вращается в направлении движения точки
по окружности, т.е. подчиняется правилу
правого винта.
Модуль углового перемещениязапишется по аналогии с координатой:
7. Модуль и направление угловой скорости
При малом угловом перемещении 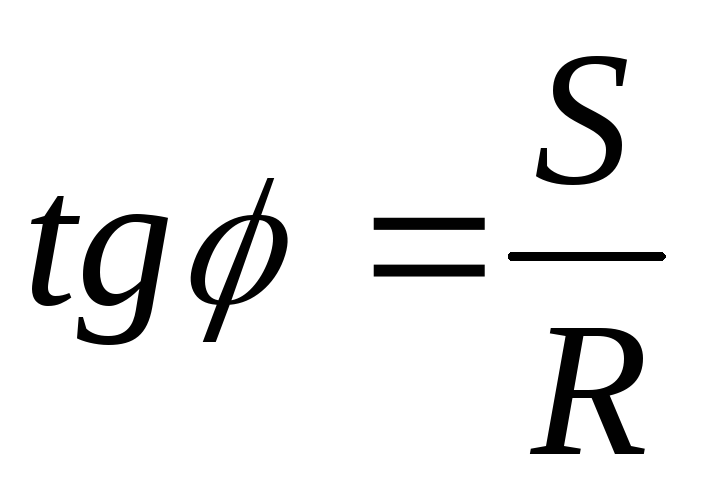
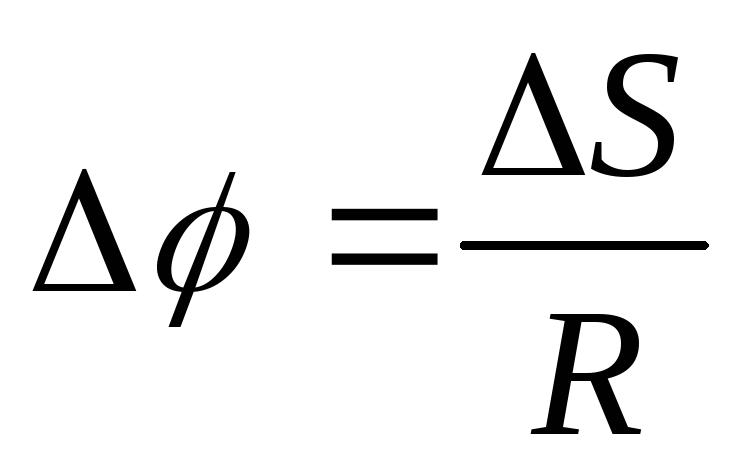 (2)
(2)
Разделим обе части последнего выражения
на  :
:
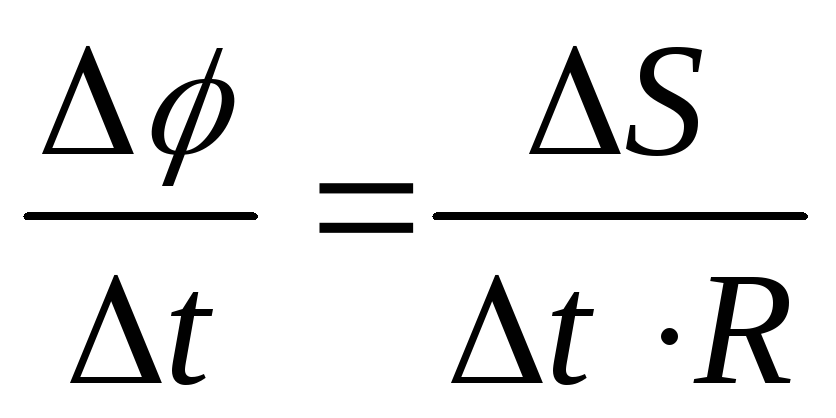 или(3)
или(3)
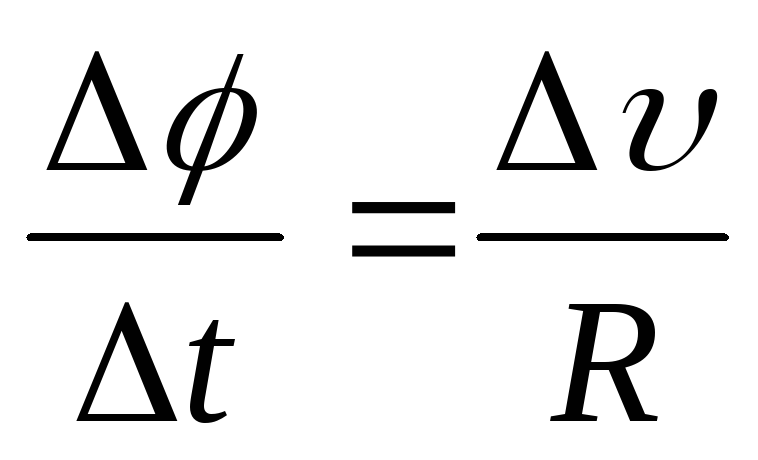
где выражение
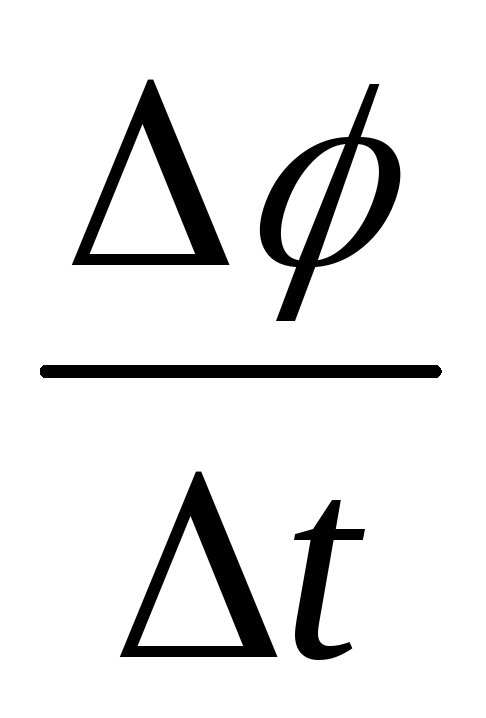 — есть средняя угловая скорость,т.е
— есть средняя угловая скорость,т.е
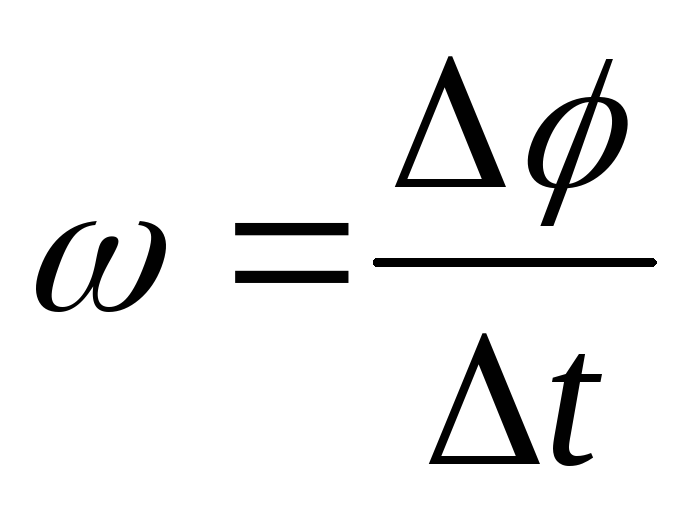 ,(5)
,(5)
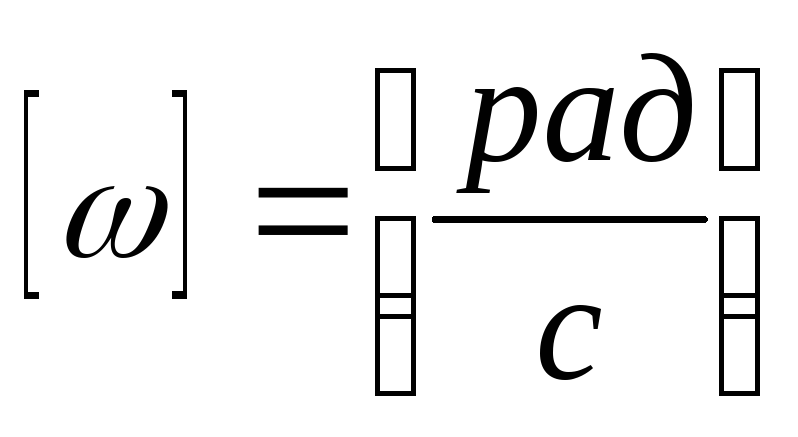

Вектор угловой
скорости направлен вдоль
оси вращения по правилу
правого винта,
т.е. также как и вектор 
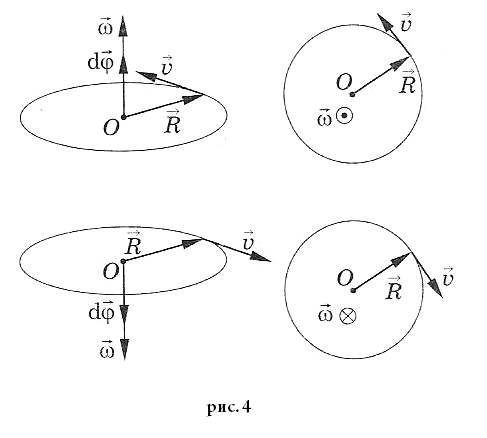
Модуль угловой скорости запишется по аналогии с линейной скоростью:
8. Мгновенная угловая скорость.
Мгновенная угловая скорость равна первой производной углового перемещения по времени:

При равномерном вращении 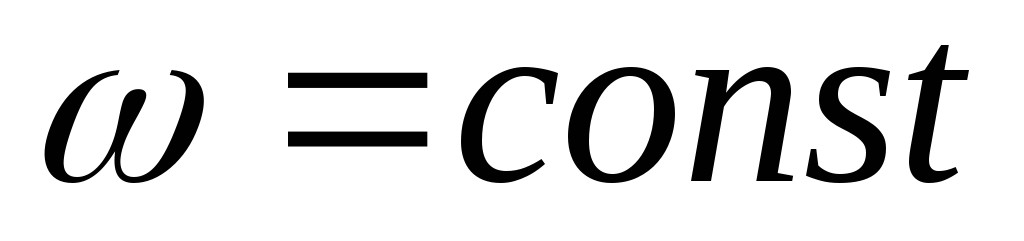 ,
тогда
,
тогда
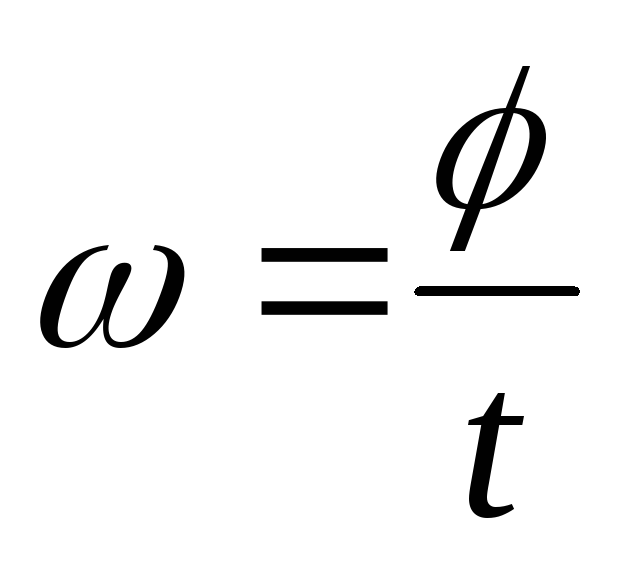 (7)
(7)
9. Связь линейной и угловой скоростей.
Если продолжить (3), то получим:
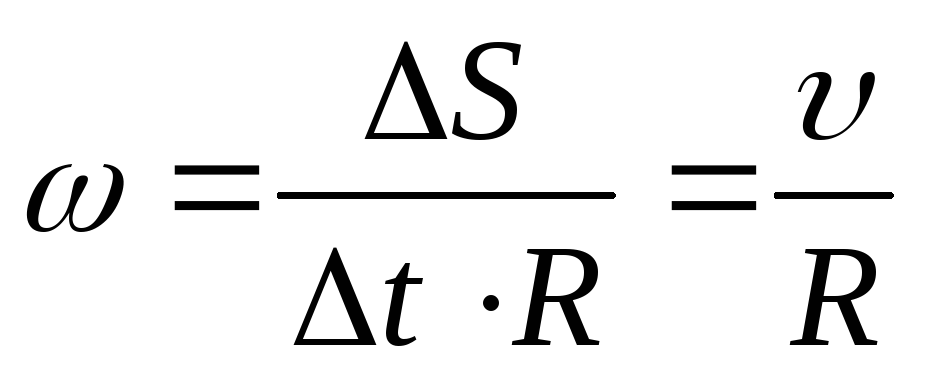 или
или
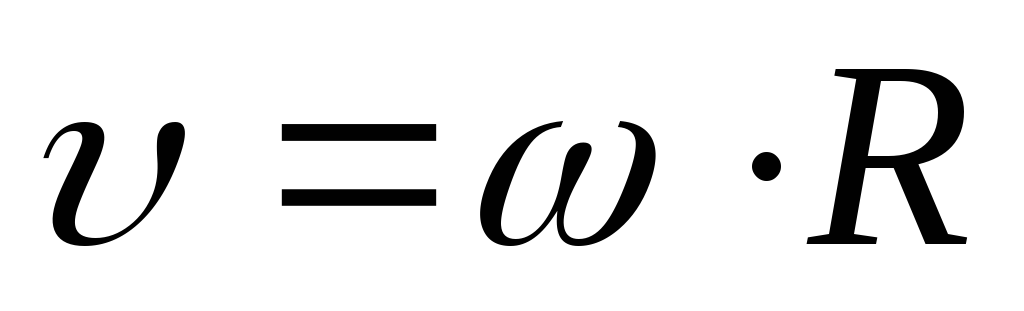 (8)
(8)
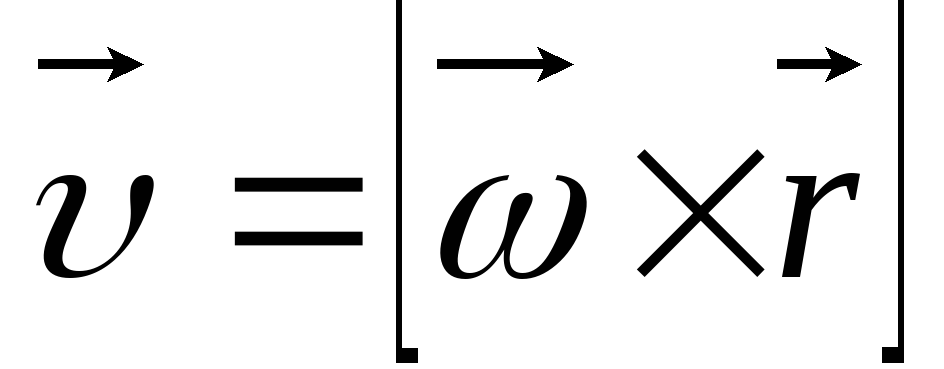

Вектор линейной
скорости совпадает по
направлению
с векторным произведением 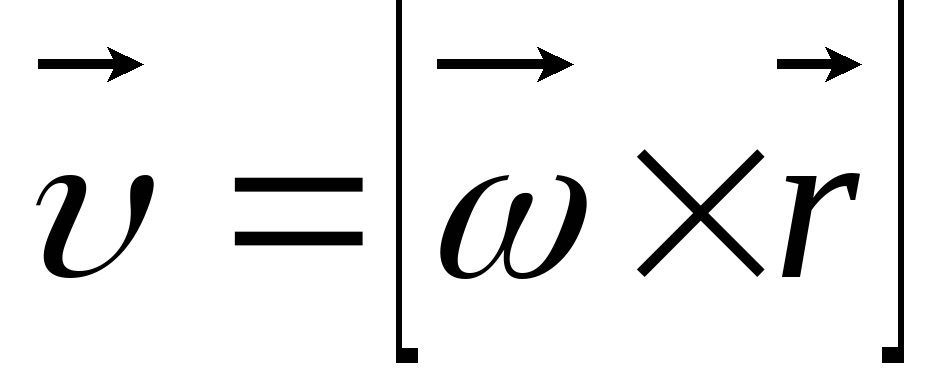 .
Векторное произведение всегда связано
справилом
правого винта:
вращая головку винта по направлению
вектора
.
Векторное произведение всегда связано
справилом
правого винта:
вращая головку винта по направлению
вектора 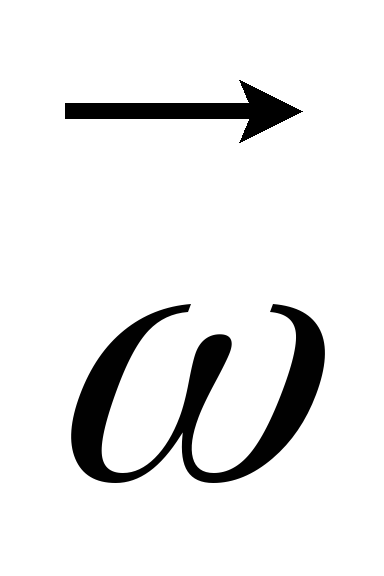 ,
стоящего на первом месте в (9), к вектору
,
стоящего на первом месте в (9), к вектору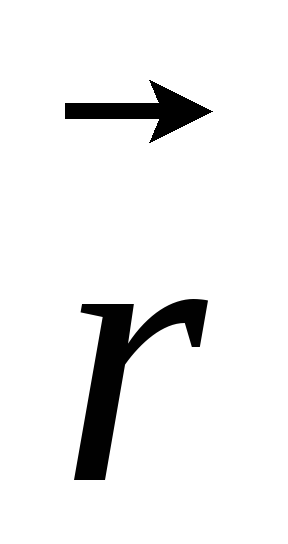
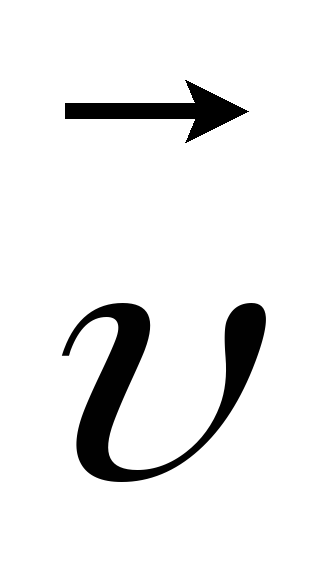 ,
см. рис. 5.
,
см. рис. 5.Модуль векторного произведения:
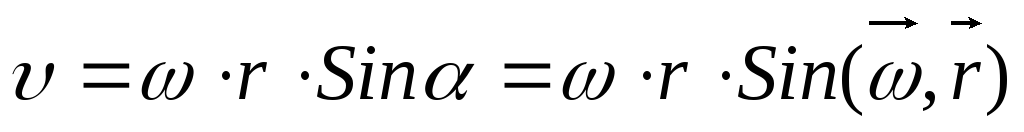 (10)
(10)
10. Модуль и направление углового ускорения.
При
вращении за время  угловая скорость получит приращение
угловая скорость получит приращение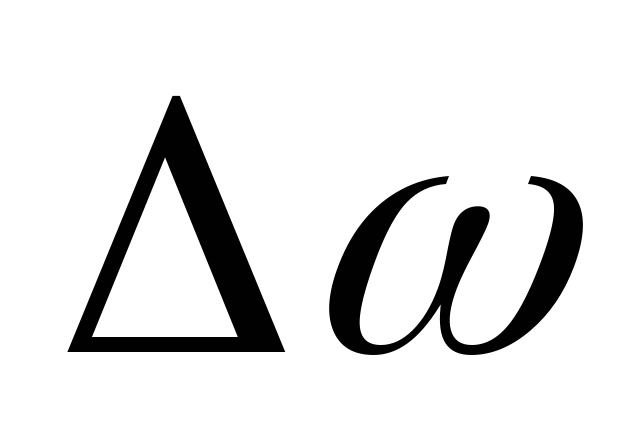 ,
тогда (8) примет вид:
,
тогда (8) примет вид:
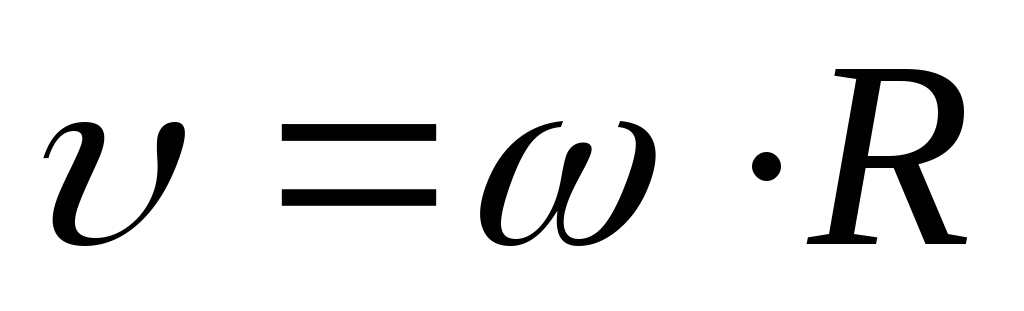

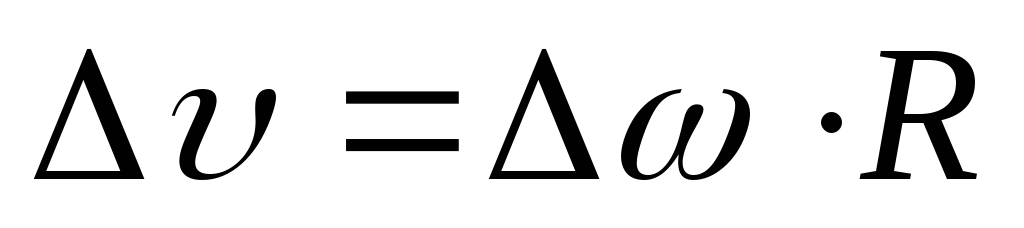 (11)
(11)
Разделим обе части
на  ,
получим:
,
получим:
 ,
(12)
,
(12)
где отношение 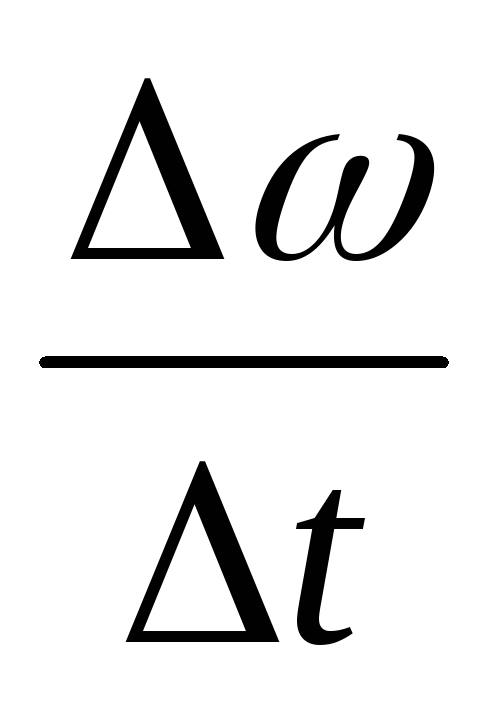 — есть среднее угловое ускорение.
— есть среднее угловое ускорение.
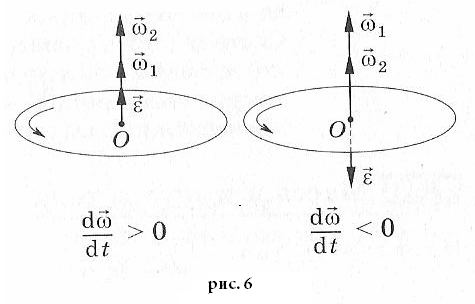 т.е.
т.е.  (13)
(13)
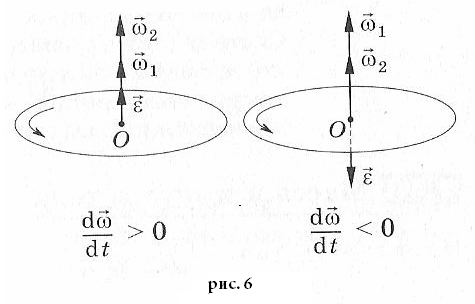
Вектор
углового ускорения  сонаправлен с вектором угловой скости
при
сонаправлен с вектором угловой скости
при и противоположен ему при
и противоположен ему при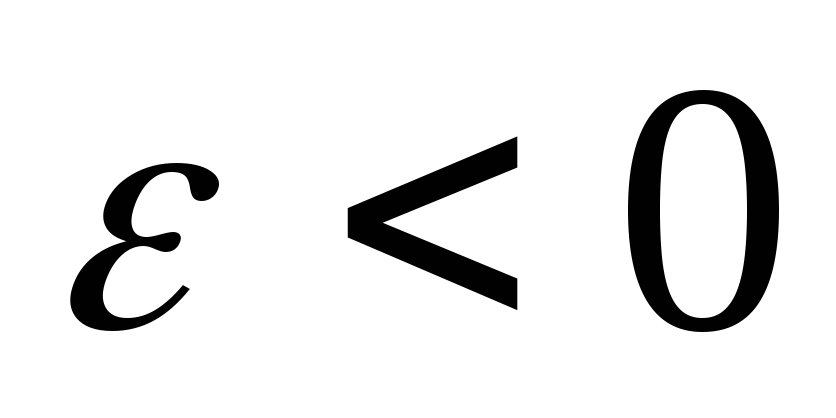 ,
см. рис 6.
,
см. рис 6.
41. Как определить направление момента силы?
Для описания динамики вращательного движения твердого тела необходимо ввести понятие момента силы. Момент силы относительно некоторой точки — это векторное произведение силы на кратчайшее расстояние от этой точки до линии действия силы. Момент силы — аксиальный вектор. Он направлен вдоль оси вращения. Направление вектора момента силы определяется правилом буравчика, а величина его равна M. При этом надо различать понятия момента силы относительно точки и относительно оси. Если сила f приложена к материальной точке А, то моментом силы М относительно произвольной точки О называется векторное произведение радиуса-вектора r, проведенного из точки О к точке А, и вектора силы: М = [ r f ] . Модуль векторного произведения = r f sin a, а направление вектора М определяется правилом правого буравчика: направление первого вектора r по кратчайшему пути вращается к направлению второго вектора f, а движение оси буравчика при этом вращении показывает направление вектора М. Моментом силы относительно произвольной оси z называется векторное произведение радиуса-вектора r и составляющей f силы f , приложенной в точке А: М = [ r f ] где составляющая f представляет собой проекцию силы f на плоскость, перпендикулярную оси z и проходящую через точку А , а r — радиус- вектор точки А, лежащий в этой плоскости. M=Fd, т. е. момент силы равен произведению силы F на длину перпендикуляра d, опущенного из оси на направление силы. Длину перпендикуляра, опущенного из оси на направление силы, называют плечом силы. Значит, момент силы равен произведению величины силы на плечо силы. Ясно, что перенесение точки приложения силы вдоль ее направления не меняет ее момента (рис. 120). Если направление силы проходит через ось вращения, то плечо силы равно нулю; следовательно, равен нулю и момент силы этом случае сила не вызывает вращения тела: сила, момент которой относительно данной оси равен нулю, не вызывает вращения вокруг этой оси. Пользуясь понятием момента силы, мы можем по-новому сформулировать условия равновесия тела, закрепленного на оси и находящегося под действием двух сил. Как мы видели, для равновесия необходимо, чтобы силы стремились вращать тело в противоположных направлениях и чтобы произведения сил на их расстояния до оси были равны. Значит, при равновесии моменты обеих сил должны быть равны по величине и противоположны по знаку. Таким образом, для равновесия тела, закрепленного на оси, алгебраическая сумма моментов действующих на него сил должна быть равна нулю. Так как момент силы определяется произведением величины силы на плечо, то единицу момента мы получим, взяв силу, равную единице, плечо которой также равно единице. Значит, в системе СИ единицей момента силы является момент силы в 1 н, действующей на плече в 1 м, т. е. 1 н*м, в системе СГС —1 дин*см, в системе МКСС— 1 кГ*м. Пользуясь данными § 45, найдем соотношения между этими единицами:1 дин*см = 10-7 н*м; 1 кГ*м = 9,8 н*м.
§ 4. Угловая скорость и угловое ускорение
Рассмотрим твердое тело, которое вращается вокруг неподвижной оси. Тогда отдельные точки этого тела будут описывать окружности разных радиусов, центры которых лежат на оси вращения. Пусть некоторая точка движется по окружности радиуса R (рис.6). Ее положение через промежуток времени t зададим углом . Элементарные (бесконечно малые) углы поворота рассматривают как векторы. Модуль вектора d равен углу поворота, а его направление совпадает с направлением поступательного движения острия винта, головка которого вращается в направлении движения точки по окружности, т. е. подчиняется правилу правого, винта (рис.6). Векторы, направления которых связываются с направлением вращения, называются псевдовекторами или аксиальными векторами. Эти векторы не имеют определенных точек приложения: они могут откладываться из любой точки оси вращения.
Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:
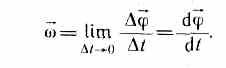

Вектор «в направлен вдоль оси вращения по правилу правого винта, т. е. так же, как и вектор d (рис. 7). Размерность угловой скорости dim=T-1, a . ее единица — радиан в секунду (рад/с).
Линейная скорость точки (см. рис. 6)
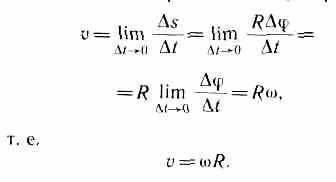
В векторном виде формулу для линейной скорости можно написать как векторное произведение:
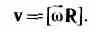
При
этом модуль векторного произведения,
по определению, равен 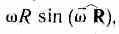
, а направление совпадает с направлением поступательного движения правого винта при его вращении от к R.
Если =const, то вращение равномерное и его можно характеризовать периодом вращения Т — временем, за которое точка совершает один полный оборот, т. е. поворачивается на угол 2. Так как промежутку времени t=T соответствует =2, то = 2/Т, откуда
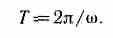
Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени называется частотой вращения:
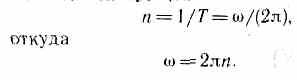
Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:
При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор
13
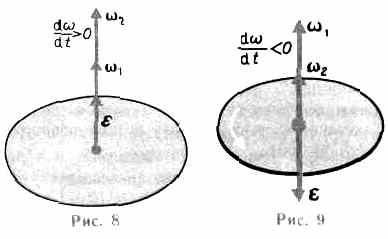
сонаправлен вектору (рис.8), при замедленном.— противонаправлен ему (рис. 9).
Тангенциальная составляющая ускорения
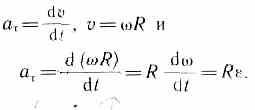
Нормальная составляющая ускорения
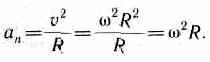
Таким образом, связь между линейными (длина пути s, пройденного точкой по дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение а, нормальное ускорение аn) и угловыми величинами (угол поворота , угловая скорость (о, угловое ускорение ) выражается следующими формулами:
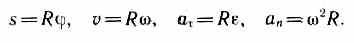
В случае равнопеременного движения точки по окружности (=const)
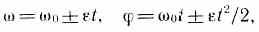
где 0 — начальная угловая скорость.
Контрольные вопросы
• Что называется материальной точкой? Почему в механике вводят такую модель?
• Что такое система отсчета?
• Что такое вектор перемещения? Всегда ли модуль вектора перемещения равен отрезку пути,
пройденному точкой?
• Какое движение называется поступательным? вращательным?
• Дать определения векторов средней скорости и среднего ускорения, мгновенной скорости
и мгновенного ускорения. Каковы их направления?
• Что характеризует тангенциальная составляющая ускорения? нормальная составляющая
ускорения? Каковы их модули?
• Возможны ли движения, при которых отсутствует нормальное ускорение? тангенциальное
ускорение? Приведите примеры.
• Что называется угловой скоростью? угловым ускорением? Как определяются их направления?
• Какова связь между линейными и угловыми величинами?
Задачи
1.1. Зависимость пройденного телом пути от времени задается уравнением s = A+Вt+Сt2+Dt3 (С = 0,1 м/с2, D = 0,03 м/с3). Определить: 1) через какое время после начала движения ускорение а тела будет равно 2 м/с2; 2) среднее ускорение <а> тела за этот промежуток времени. [ 1) 10 с; 2) 1,1 м/с2]
1.2. Пренебрегая сопротивлением воздуха, определить угол, под которым тело брошено к горизонту, если максимальная высота подъема тела равна 1/4 дальности его полета. [45°]
1.3. Колесо радиуса R = 0,1 м вращается так, что зависимость угловой скорости от времени задается уравнением = 2At+5Вt4 (A=2 рад/с2 и B=1 рад/с5). Определить полное ускорение точек обода колеса через t=1 с после начала вращения и число оборотов, сделанных колесом за это время. [а = 8,5 м/с2; N = 0,48]
14
1.4. Нормальное ускорение точки, движущейся по окружности радиуса r=4 м, задается уравнением аn=А+-Bt+Ct2 (A=1 м/с2, В=6 м/с3, С=3 м/с4). Определить: 1) тангенциальное ускорение точки; 2) путь, пройденный точкой за время t1=5 с после начала движения; 3) полное ускорение для момента времени t2=1 с. [ 1) 6 м/с2; 2) 85 м; 3) 6,32 м/с2]
1.5. Частота вращения колеса при равнозамедленном движении за t=1 мин уменьшилась от 300 до 180 мин-1. Определить: 1) угловое ускорение колеса; 2) число полных оборотов, сделанных колесом за это время. [1) 0,21 рад/с2; 2) 360]
1.6. Диск радиусом R=10 см вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением =A+Bt+Ct2+Dt3 (B = l рад/с, С=1 рад/с2, D=l рад/с3). Определить для точек на ободе колеса к концу второй секунды после начала движения: 1) тангенциальное ускорение а; 2) нормальное ускорение аn; 3) полное ускорение а. [ 1) 0,14 м/с2; 2) 28,9 м/с2; 3) 28,9 м/с2]
Векторы угловой скорости и углового ускорения
Вектором угловой скорости твердого тела, вращающегося вокруг неподвижной оси, называется вектор, модуль которого равен абсолютному значению алгебраической угловой скорости и направленный вдоль оси вращения тела в ту сторону, откуда вращение тела видно происходящим против хода часовой стрелки.
Если ввести
единичный вектор  оси вращенияOz, то
оси вращенияOz, то
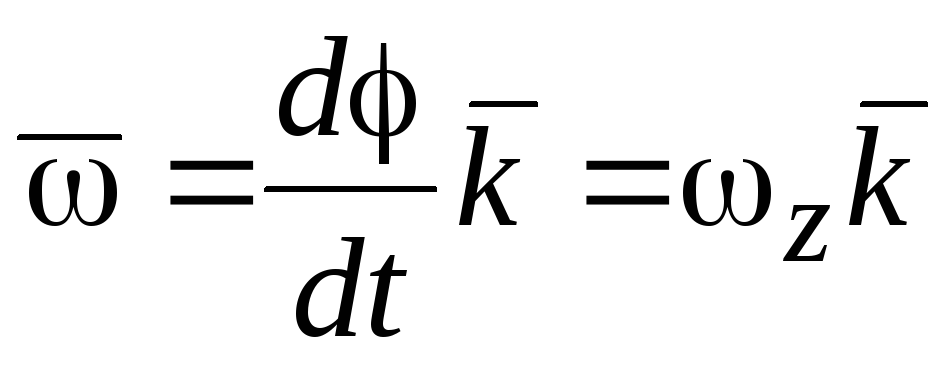 .
(7.11)
.
(7.11)
При 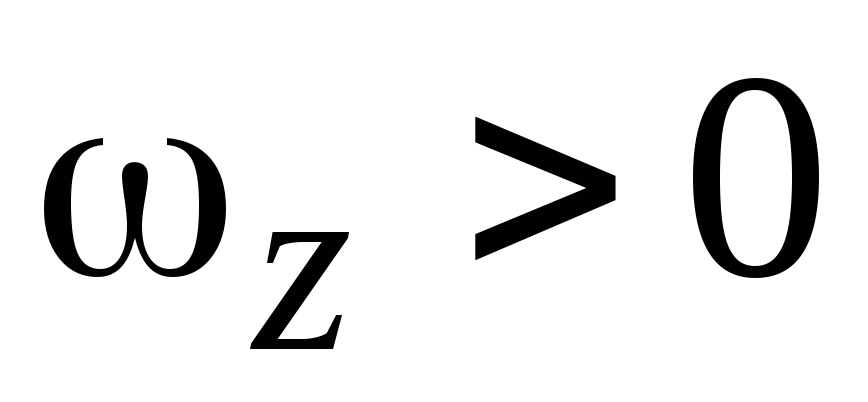 направление вектора
направление вектора совпадает с направлением единичного
вектора
совпадает с направлением единичного
вектора ,
а при
,
а при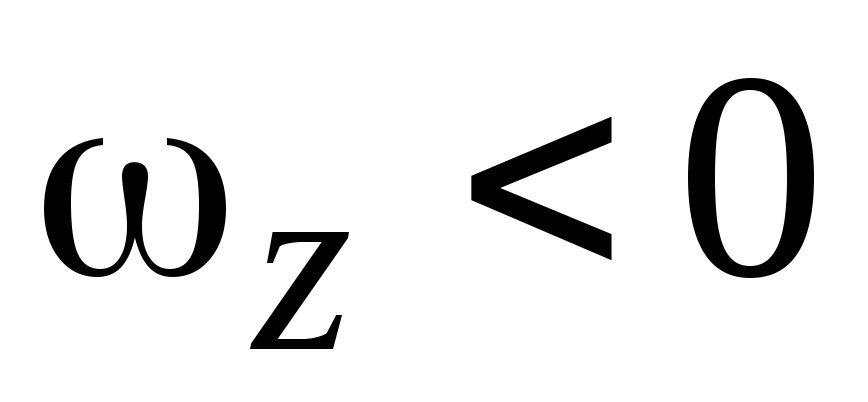 ,
вектор
,
вектор направлен в сторону противоположную
направлению вектора
направлен в сторону противоположную
направлению вектора .
.
Вектором углового ускорения называется вектор, равный производной по времени от вектора угловой скорости.
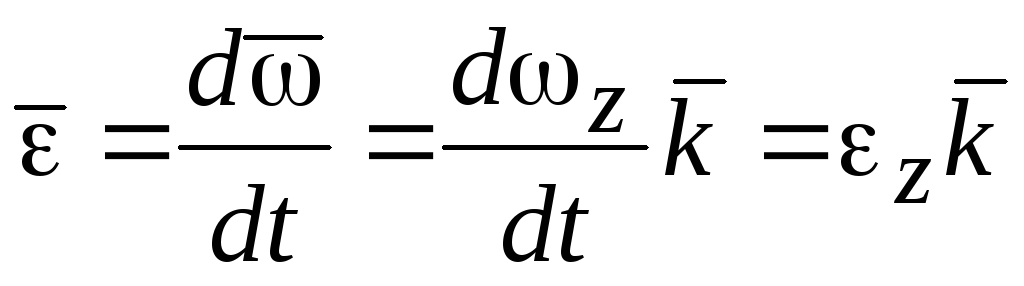 .
(7.12)
.
(7.12)
Из формулы (7.12)
видно, что вектор  направлен, как и вектор
направлен, как и вектор вдоль оси вращения.
вдоль оси вращения.
Таким образом,
величины  и
и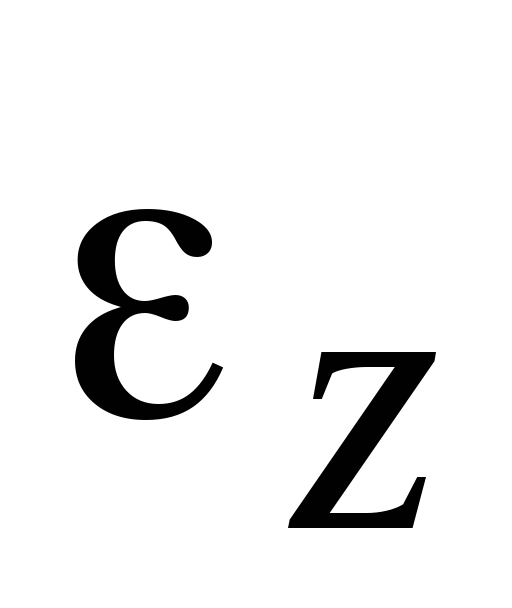 представляют проекции векторов угловой
скорости
представляют проекции векторов угловой
скорости и углового ускорения
и углового ускорения на ось вращенияz.
на ось вращенияz.
Е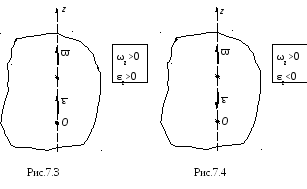 сли
сли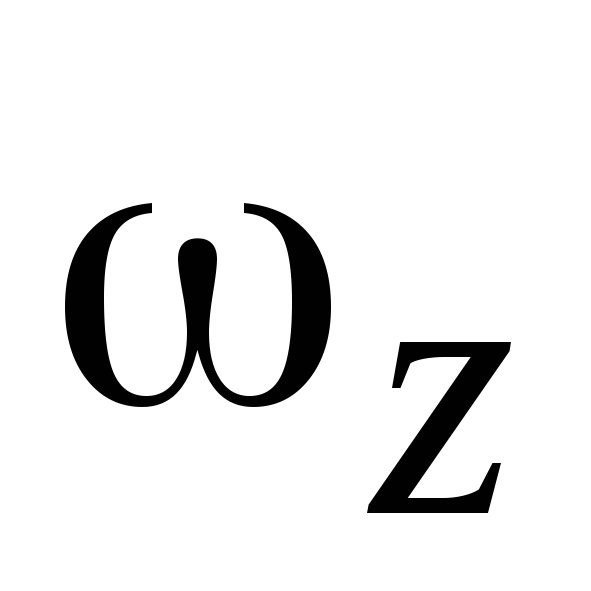 и
и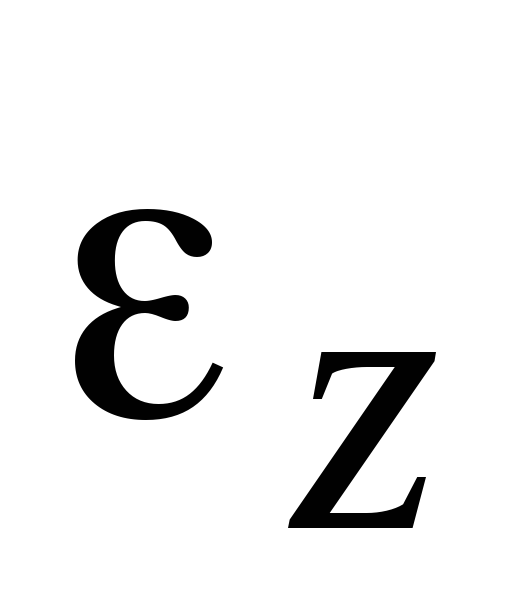 имеют одинаковые знаки, т.е.
имеют одинаковые знаки, т.е.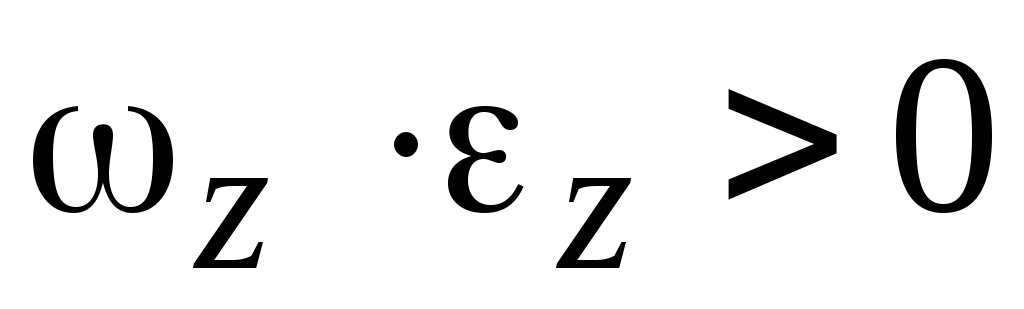 ,
векторы
,
векторы и
и направлены в одну сторону (рис. 7.3) и тело
как мы знаем, вращается ускоренно. Если
направлены в одну сторону (рис. 7.3) и тело
как мы знаем, вращается ускоренно. Если и
и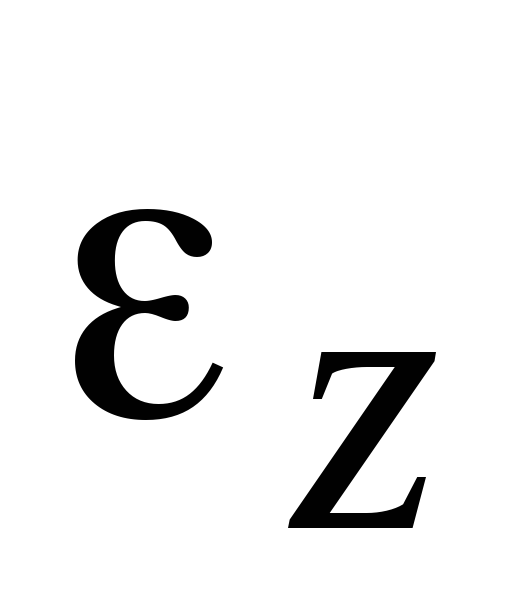 имеют разные знаки, т.е.
имеют разные знаки, т.е.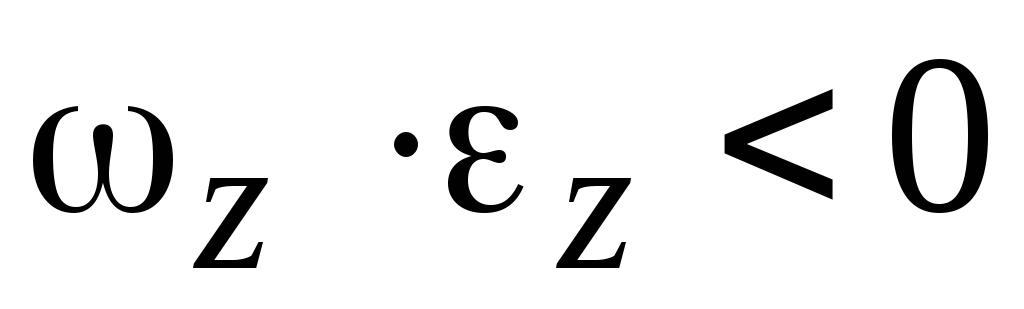 ,
то векторы
,
то векторы и
и направлены в разные стороны (рис. 7.4) и
тело вращается замедленно.
направлены в разные стороны (рис. 7.4) и
тело вращается замедленно.
Векторные формулы для скоростей и ускорений точек тела при вращательном движении
Скорость точки вращающегося твердого тела по модулю и направлению можно представить формулой Эйлера
 ,
(7.13)
,
(7.13)
г де
де — радиус-вектор точки М, проведенный из
произвольной точки оси вращенияOz,
например, из точки О (рис.7.5).
— радиус-вектор точки М, проведенный из
произвольной точки оси вращенияOz,
например, из точки О (рис.7.5).
Убедимся в справедливости этой формулы.
Вектор 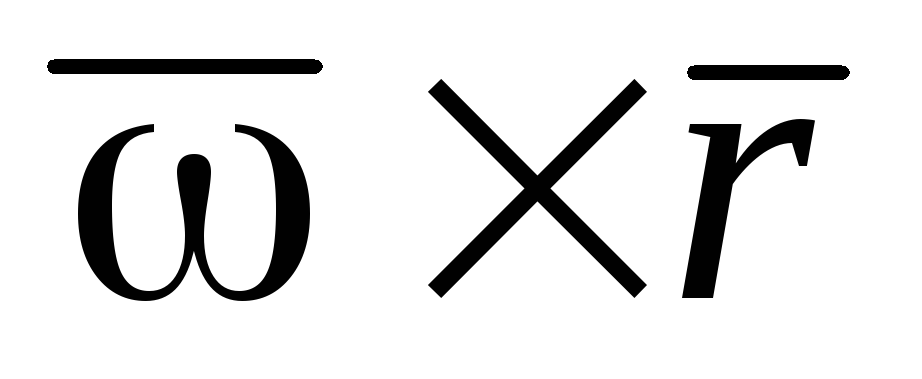 перпендикулярен плоскости, в которой
расположены векторы, входящие в векторное
произведение. По направлению он параллелен
вектору скорости
перпендикулярен плоскости, в которой
расположены векторы, входящие в векторное
произведение. По направлению он параллелен
вектору скорости ,
направленному по касательной к траектории
(окружности) точки. Модуль векторного
произведения равен
,
направленному по касательной к траектории
(окружности) точки. Модуль векторного
произведения равен
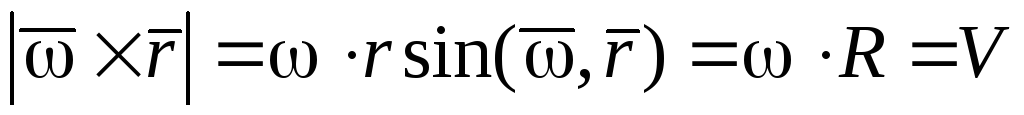 ,
,
т.к. 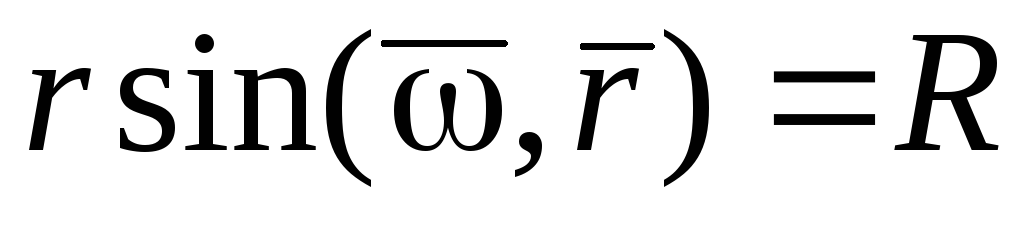 .
.
Таким образом,
векторное произведение 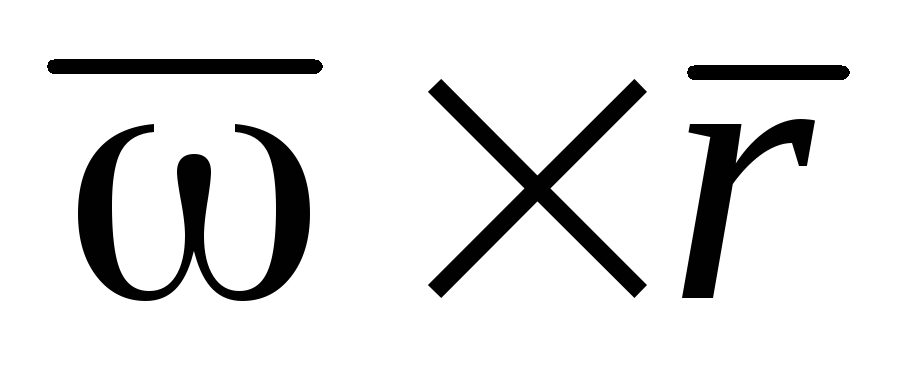 по модулю и направлению определяет
скорость точки при вращательном движении
тела.
по модулю и направлению определяет
скорость точки при вращательном движении
тела.
Ускорение точки по определению равно:
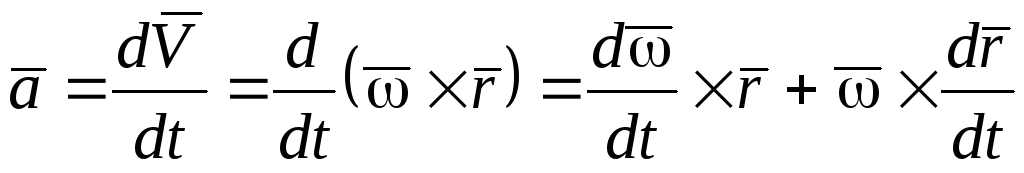 .
.
Так как 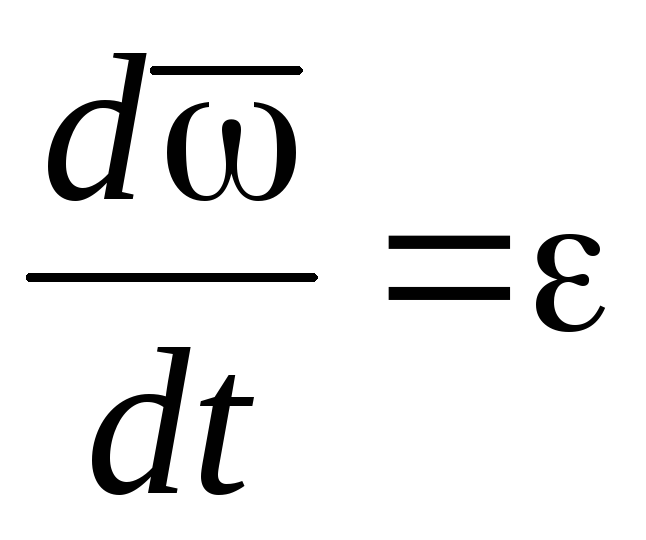 ,
,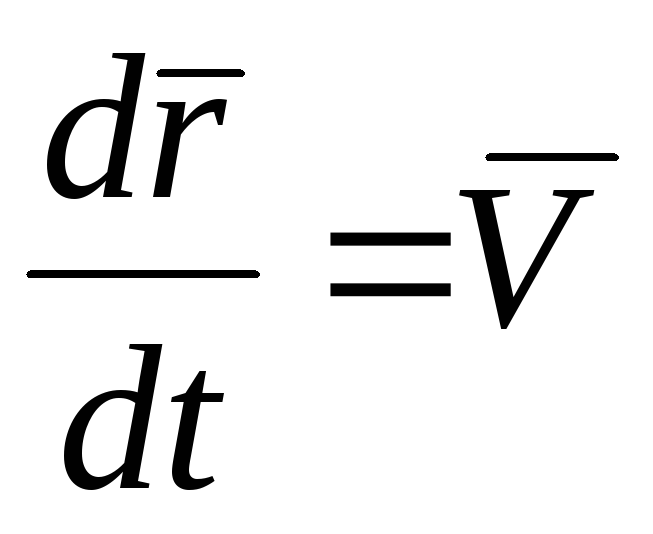 получим
получим
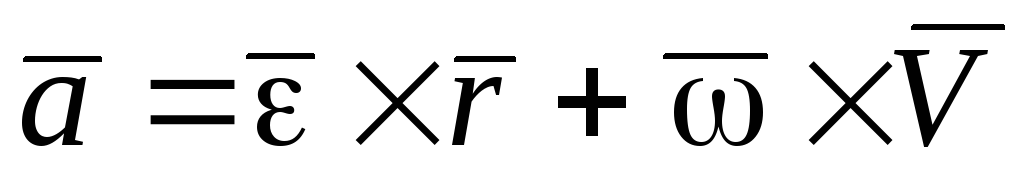 .
(7.14)
.
(7.14)
Вектор  направлен по касательной к траектории
точки. По модулю он равен
направлен по касательной к траектории
точки. По модулю он равен
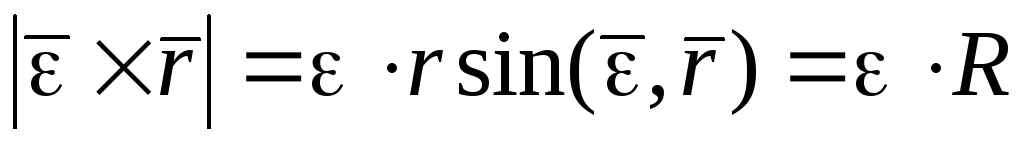
и следовательно эта составляющая ускорения является касательной составляющей ускорения точки М
 .
(7.15)
.
(7.15)
Ее называют также вращательным ускорением.
Вектор
направлен в плоскости окружности радиуса от точкиМ к точке
от точкиМ к точке  .
По модулю он равен
.
По модулю он равен
 ,
,
и, следовательно, эта составляющая ускорения является нормальной составляющей ускорения точки М
 .
(7.16)
.
(7.16)
Ее называют также осестремительным ускорением.
5. Мгновенная угловая скорость.
Мгновенная угловая скорость равна первой производной углового перемещения по времени:
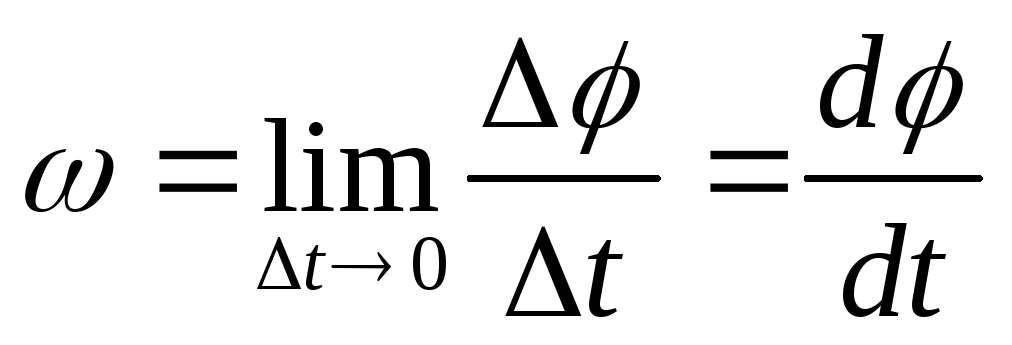 (6)
(6)
При
равномерном вращении 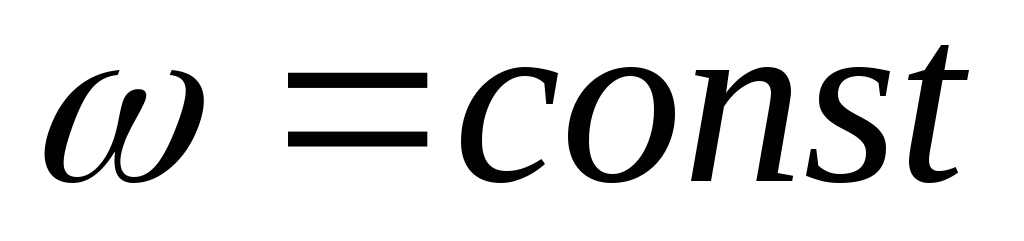 ,
тогда
,
тогда
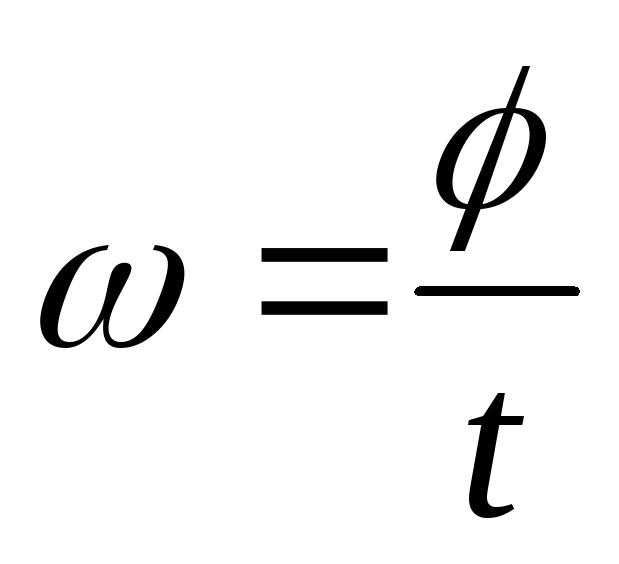 (7)
(7)
6. Связь линейной и угловой скоростей.
Если продолжить (3), то получим:
 или
или
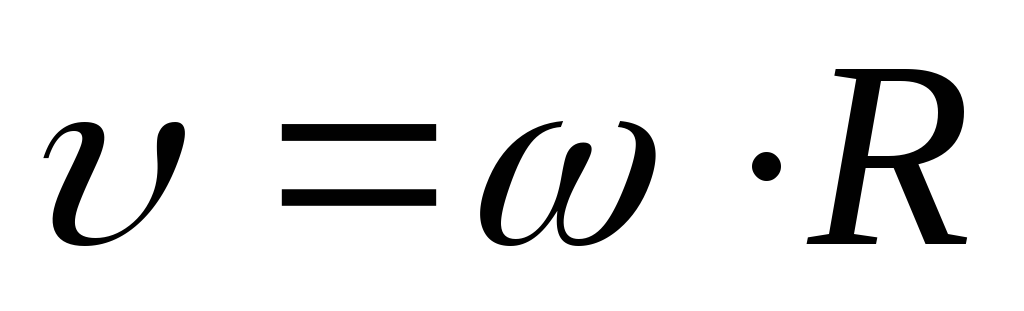 (8)
(8)
 (9)
(9)
Вектор линейной
скоростисовпадает по направлению
с векторным произведением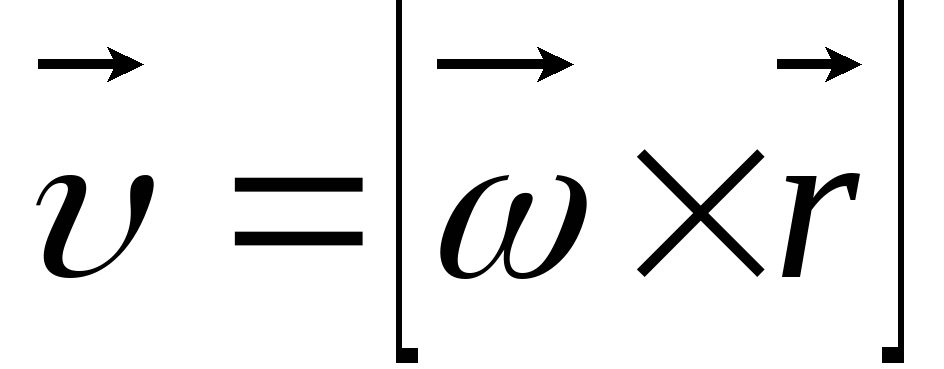 .
Векторное произведение всегда связано
справилом правого
винта: вращая головку винта по
направлению вектора
.
Векторное произведение всегда связано
справилом правого
винта: вращая головку винта по
направлению вектора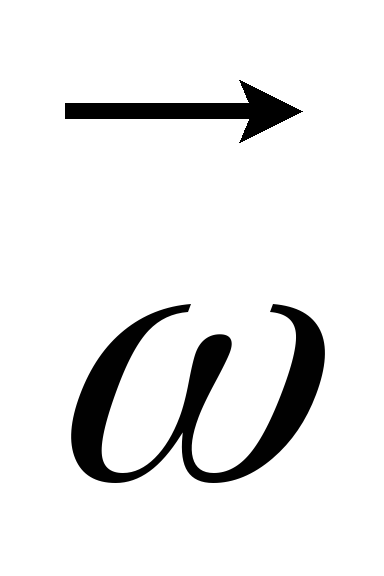 ,
стоящего на первом месте в (9), к вектору
,
стоящего на первом месте в (9), к вектору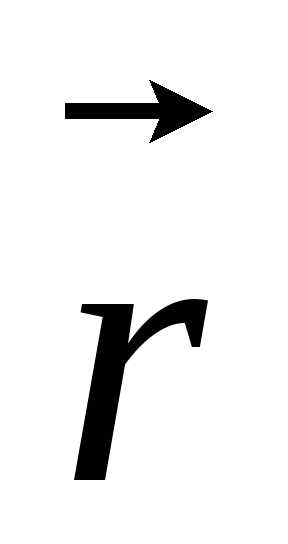 ,
стоящему на втором месте, определяем
по поступательному движению винта
направление третьего вектора
,
стоящему на втором месте, определяем
по поступательному движению винта
направление третьего вектора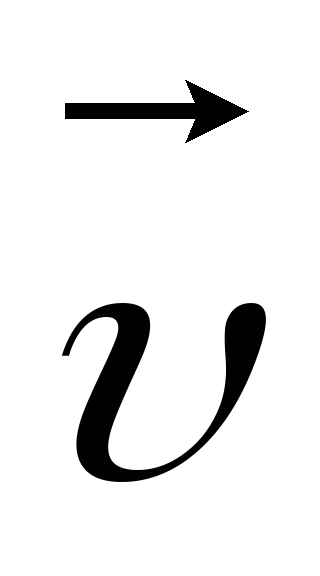 ,
см. рис. 5.
,
см. рис. 5.
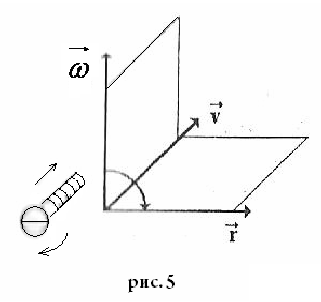
Модуль векторного произведения:
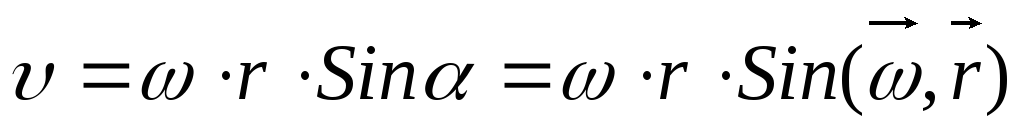 (10)
(10)
7. Модуль и направление углового ускорения.
При
вращении за время  угловая скорость получит приращение
угловая скорость получит приращение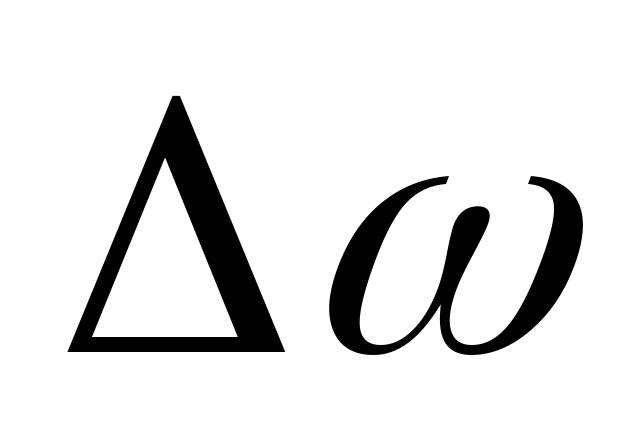 ,
тогда (8) примет вид:
,
тогда (8) примет вид:


 (11)
(11)
Разделим
обе части на  ,
получим:
,
получим:
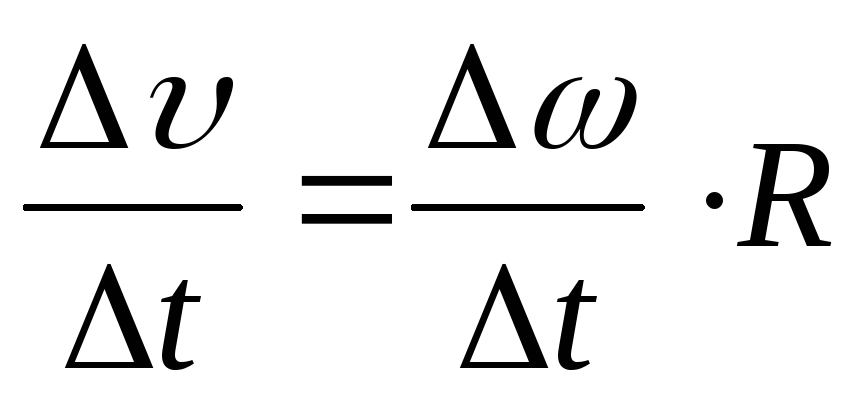 ,
(12)
,
(12)
где
отношение 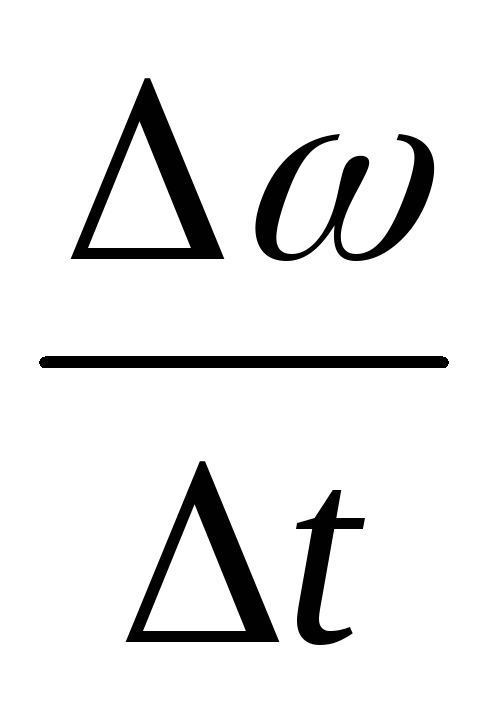 — есть среднее угловое ускорение.
— есть среднее угловое ускорение.
т.е.
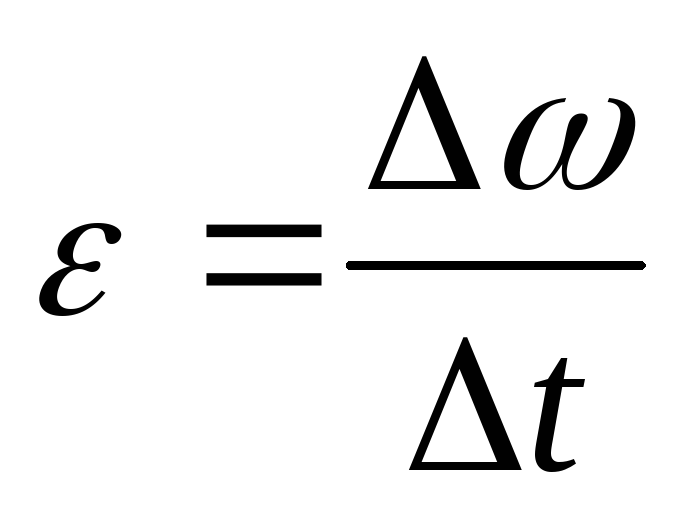 (13)
(13)
Вектор
углового ускорения 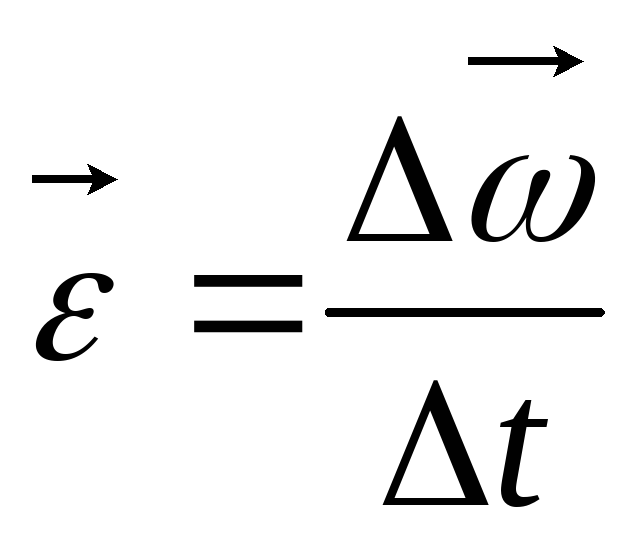 сонаправлен с вектором угловой скости
при
сонаправлен с вектором угловой скости
при и противоположен ему при
и противоположен ему при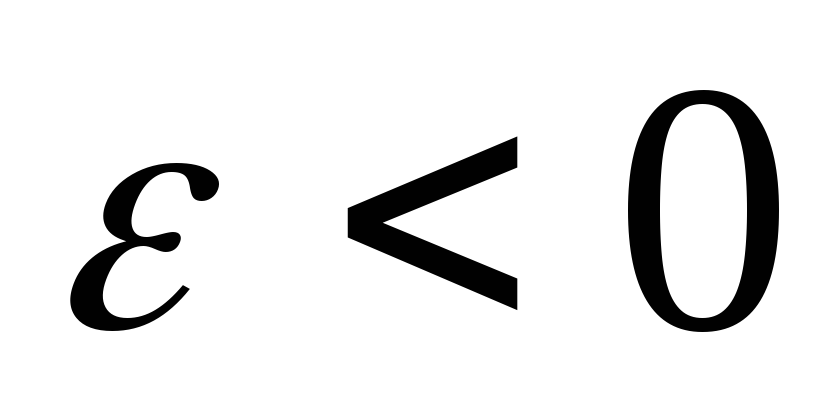 ,
см. рис 6.
,
см. рис 6.
8. Связь тангенциального и углового ускорения.
При
вращении за время  угловая скорость получит приращение
угловая скорость получит приращение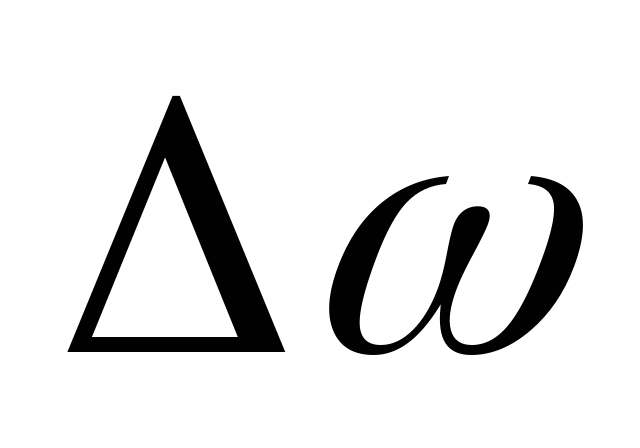 ,
тогда (8) примет вид:
,
тогда (8) примет вид:
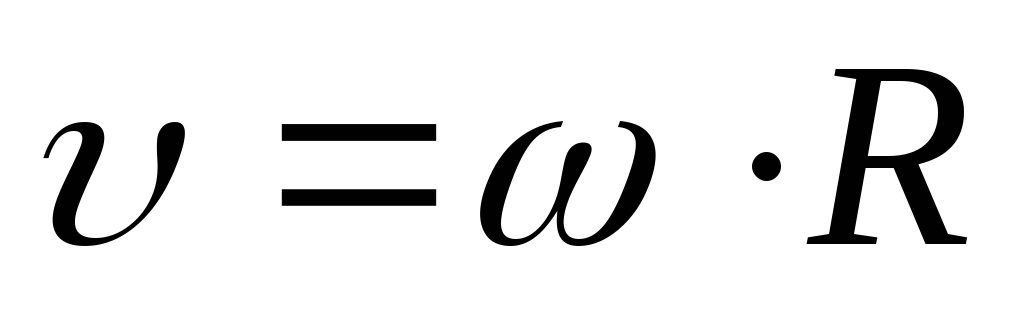

 (14)
(14)
Разделим
обе части на  ,
получим:
,
получим:
 (15)
(15)
или
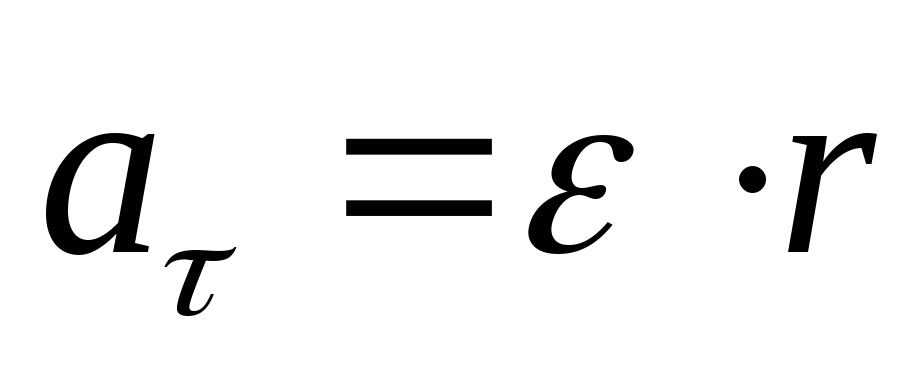 (16)
(16)
Векторное произведение:
 (17)
(17)
Вектор тангенциального
ускорениясовпадает по направлению
с векторным произведением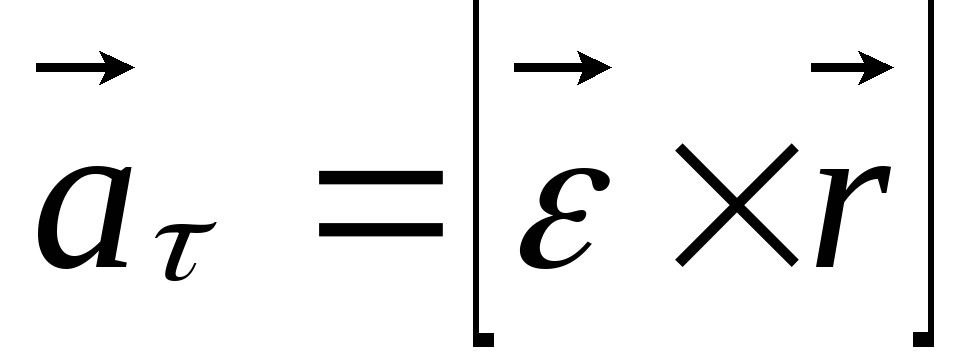 .
Векторное произведение всегда связано
справилом правого
винта: вращая головку винта по
направлению вектора
.
Векторное произведение всегда связано
справилом правого
винта: вращая головку винта по
направлению вектора ,
стоящего на первом месте в (13), к вектору
,
стоящего на первом месте в (13), к вектору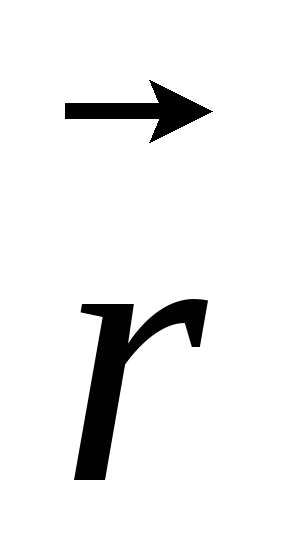 ,
стоящему на втором месте, определяем
по поступательному движению винта
направление третьего вектора
,
стоящему на втором месте, определяем
по поступательному движению винта
направление третьего вектора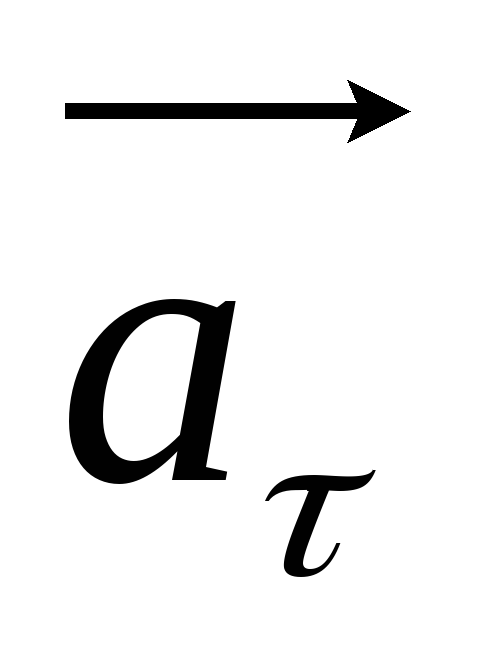 .
.
9. Мгновенное угловое ускорение.
При 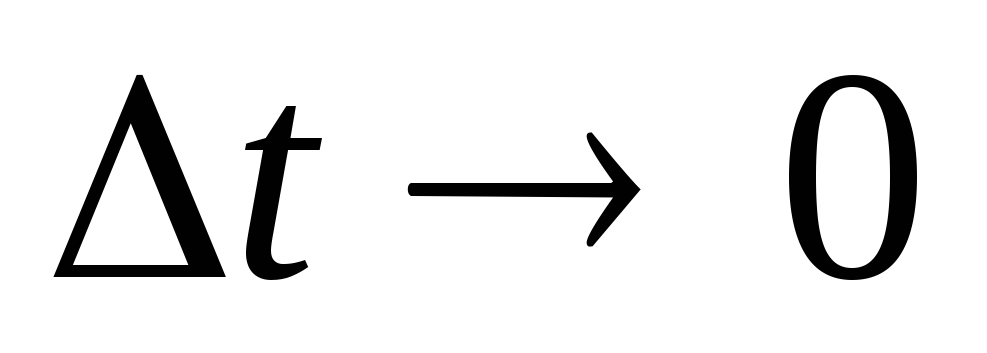 получим мгновенное угловое ускорение:
получим мгновенное угловое ускорение:
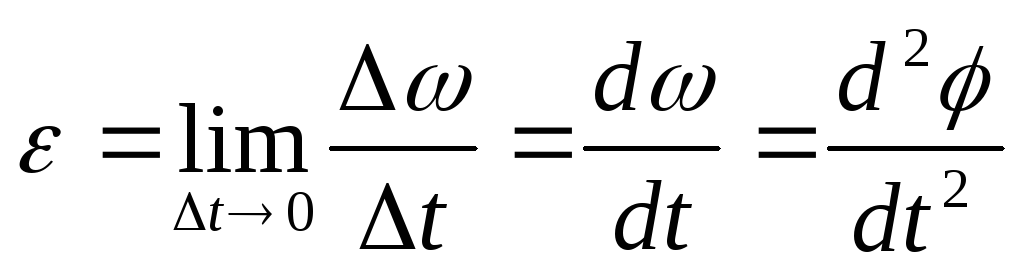 ,
(18)
,
(18)
т.е. мгновенное угловое ускорение численно равно первой производной угловой скорости по времени или – второй производной углового перемещения по времени.
Приложение 1.
тип движения | рисунок, графики | формулы | |
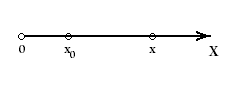
Равномерное движение |
|
| |
Равноускоренное (равнозамедленное) движение |
|
| |
|
| ||
Движение тела, брошенного вертикально вниз |
| При
| |
При
| |||
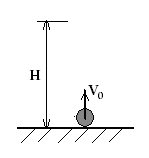
Движение тела, брошенного вертикально вверх |
|
| |
При
| |||
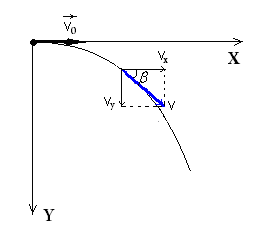
Движение тела, брошенного горизонтально |
|
| |
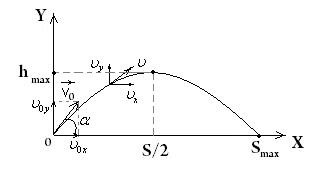
Движение тела, брошенного под углом к горизонту |
|
| |
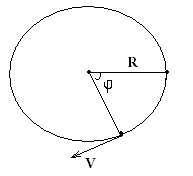
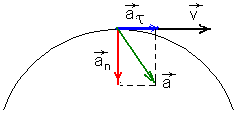
Движение тела по окружности | Т При движении по
криволинейной траектории изменяется
не только модуль скорости, но и ее
направление, поэтому вектор ускорения
представляют в виде двух составляющих:
тангенциального (
Тангенциальное (касательное) ускорение – составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке. (Тангенциальное ускорение характеризует изменение скорости по модулю; Направление
вектора Нормальное
ускорение– составляющая вектора
ускорения, направленная вдоль нормали
к траектории в данной точке. (Нормальное
ускорение характеризует изменение
скорости по направлению. Вектор Модуль полного ускорения при этом определяется соотношением: Направление полного ускоренияопределяют правилом сложения векторов: |
|
|
Движение с постоянным ускорением при действии постоянной силы
Первый этап — определение типа движения.
Второй этап — физическая формулировка задачи: выбор системы отсчета, определение действующих сил и начальных условий.
Третий этап — математическая формулировка задачи: запись уравнений,
Если
md2х/dt2 =F=mа
не равно 0, то движение ускоренное
t = 0, v = v0; x= x0
Четвертый этап — математическое решение задачи.
a = d2х/dt2;
или
a = dv/dt;
Откуда
dv = adt;
Интегрируя обе части
∫ dv =∫ adt;
Взятие интеграла дает
v = at + C
постоянные интегрирования определяюся из начальных условий
Например,
при
t = 0, v = v0;
тогда
v = v0 + at
или используя выражение для скорости
dx/dt = v0 + at;
разделяя переменные
dx =(v0 + at)dt;
перемножая почленно
dx = atdt + v0dt;
Применяя операцию почленного интегрирования(свойство интеграла суммы)
∫dx = ∫ atdt + ∫ v0dt
Получаем интеграл
x = at2/2 + x0 + v0t.
Постоянные интегрирования определяются из начальных условий для координаты частицы и скорости
Следует особо!!!!!! Отметить, что задаются одновременно координата и скорость частицы
Это позволяет делать только классическая механика
Пятый этап — проверка полученного решения.
Прием первый — проверка ответа по размерности.
Прием второй — проверка ответа по заранее очевидным результатам.
Редко используемое и неточное выражение для средней скорости
vср. =(t) t1t2 ∫vdt
Движение материальной точки под действием постоянной силы –размерная задача
Прежде всего, к такому типу движения относится при определенных условиях движение под действием силы тяжести. Сила тяжести, как и любая сила, является векторной величиной. Примем упрощающее предположение,
что ее модуль постоянен. Но так как эта сила направлена к центру Земли, то ее направление в разных точках земной поверхности различно. Однако при исследовании движений тел, перемещающихся на расстояния, которые намного меньше радиуса Земли (R ~ 6000 км), можно
пренебречь кривизной земной поверхности и с хорошей точностью считать, что сила тяжести не меняет своего направления, оставаясь перпендикулярной этой поверхности. В этих условиях сила тяжести может рассматриваться постоянной как по модулю, так и по направлению. Помимо силы тяжести, с постоянными силами приходится часто сталкиваться при рассмотрении работы различных технических устройств, когда их различные детали испытывают действие постоянных сил со стороны других деталей.
Какой вид имеет траектория камня? От чего зависит дальность полета? Аристотель утверждал, например, что на начальном участке траектория брошенного под углом к вертикали тела является прямой линией, и это, вроде бы, подтверждается непосредственными наблюдениями. Потребовалось почти два тысячелетия, чтобы понять, что траектория на самом деле является криволинейной на всех участках полета.
Изучение движения брошенного тела включает в себя несколько этапов, характерных для решения большинства задач механики.
Первый этап — определение типа движения.
Второй этап — физическая формулировка задачи: выбор системы отсчета, определение действующих сил и начальных условий.
любая точка поверхности движется с ускорением, обусловленным вращением Земли вокруг своей оси и вокруг Солнца. Но для многих практических задач этот эффект «неинерциальности» является несущественным, и мы будем полагать, что и в нашей задаче этим эффектом можно пренебречь и считать выбранную систему отсчета инерциальной. В инерциальной системе отсчета справедлив второй закон Ньютона , где теперь под F подразумевается постоянная сила тяжести. Мы изобразили эту силу на рис. 4.2 а для некоторого произвольного момента времени после начала движения, поместив тело известной массы в некоторой произвольной точке над поверхностью. Истинное положение тела в различные моменты времени, то есть траекторию его движения, мы сможем определить только после окончательного решения задачи.
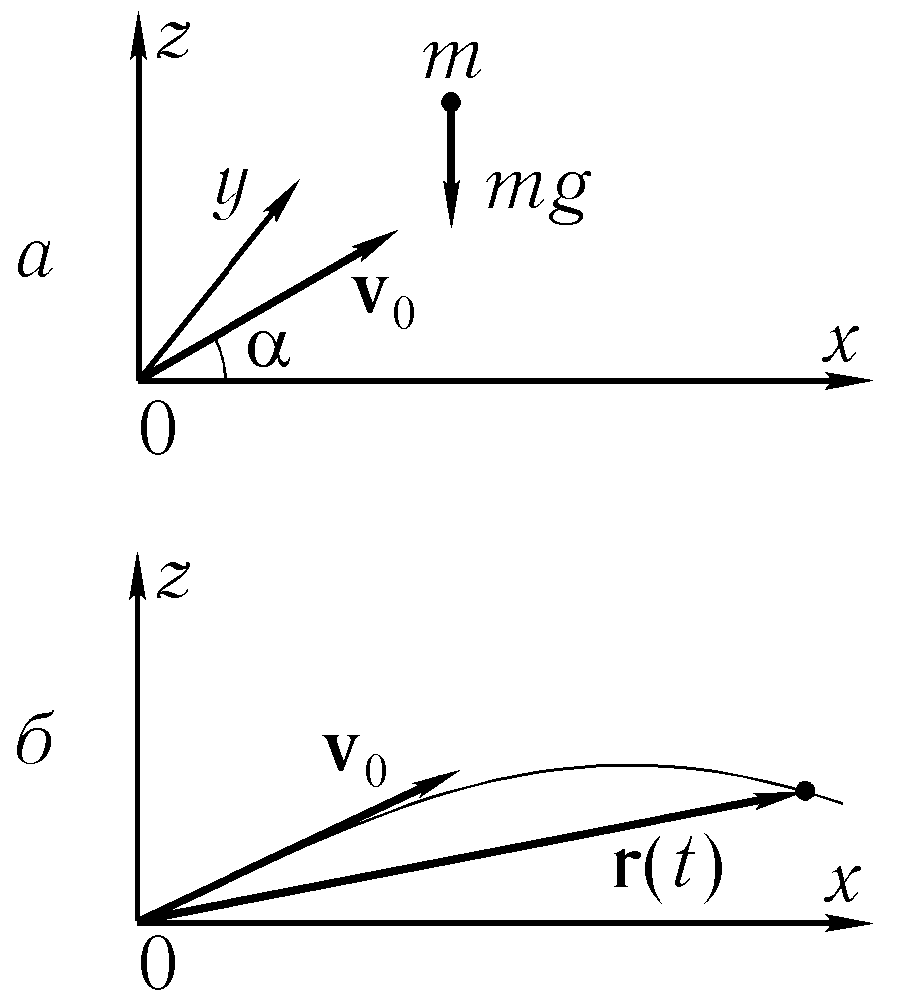
рис 4.2
Третий этап — математическая формулировка задачи: запись уравнений, соответствующих физической формулировке. Уравнение D.3) содержит в качестве неизвестных векторные величиныr(t) и v(t). Поэтому оно фактически представляет собой совокупность трех уравнений для трех проекций вышеупомянутых величин.
Для проекций радиуса-вектора тела введем обозначения: rх= х,rу= у, rz = z. Взяв проекции на оси координат от левой и правой частей уравнения движения, мы получаем три уравнения:

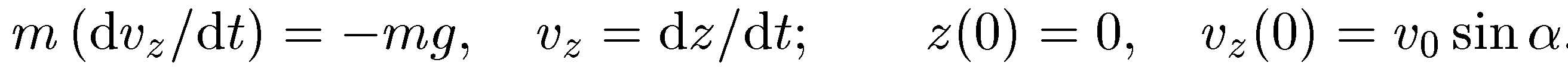
Справа от каждого из уравнений записаны начальные условия, являющиеся
неотъемлемыми элементами физической и математической формулировки задачи. Знак «минус» перед mgв последнем уравнении отражает тот факт, что сила тяжести направлена в отрицательном направлении осиOz.
Четвертый этап — математическое решение задачи.Составляющая скоростиvzимеет вид:
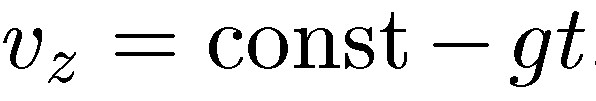
Константу определяем из условия
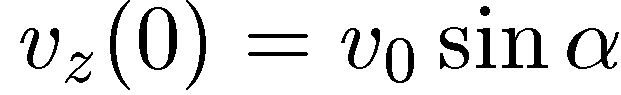
Интегрируем еще раз:
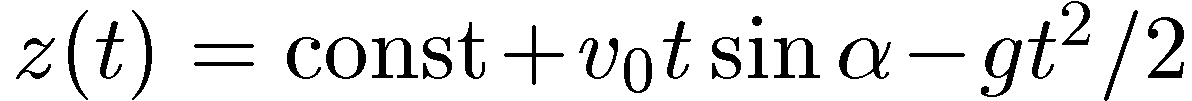
Новую константу определяем из условия z(0) = 0.
окончательно решение:
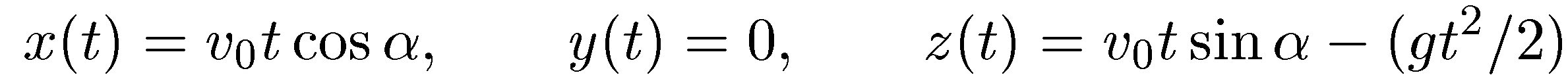
Найденные выражения определяют зависимость от времени всех трех проекций радиуса-вектора тела, движущегося под действием силы тяжести.
Тем самым задача о нахождении траектории движения решена.
достаточно выразить tчерез х в первом из равенств и подставить результат в выражение дляz(t). Это даетуравнение траекториив плоскостиzOx:
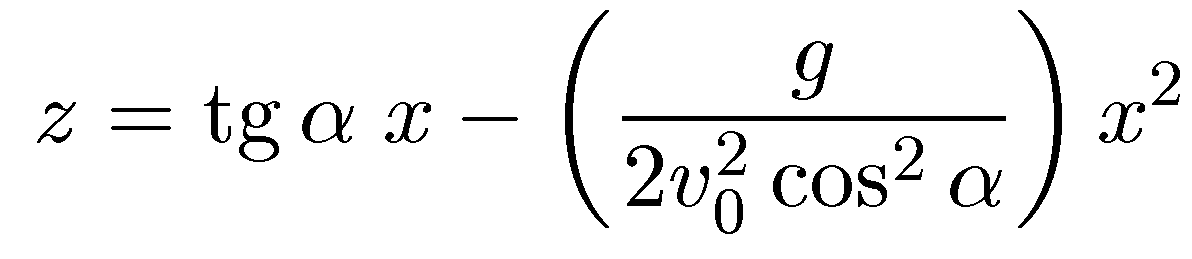
Из геометрии известно, что это соотношение представляет собой уравнение
параболической кривой, и следовательно, ни на одном из участков полета тела его траектория не является прямой линией.
дальность полетатела. При падении на поверхностьz= 0, и из этого условия находим
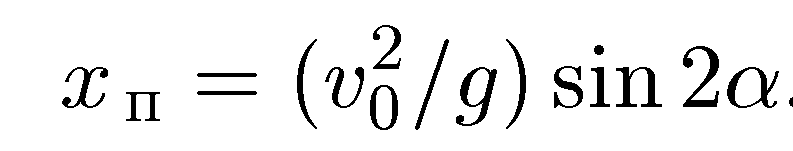
Пятый этап — проверка полученного решения.
Прием первый — проверка ответа по размерности.
Прием второй — проверка ответа по заранее очевидным результатам.
Движение ракеты
Первый этап — определение типа движения.
Второй этап — физическая формулировка задачи: выбор системы отсчета, определение действующих сил и начальных условий.
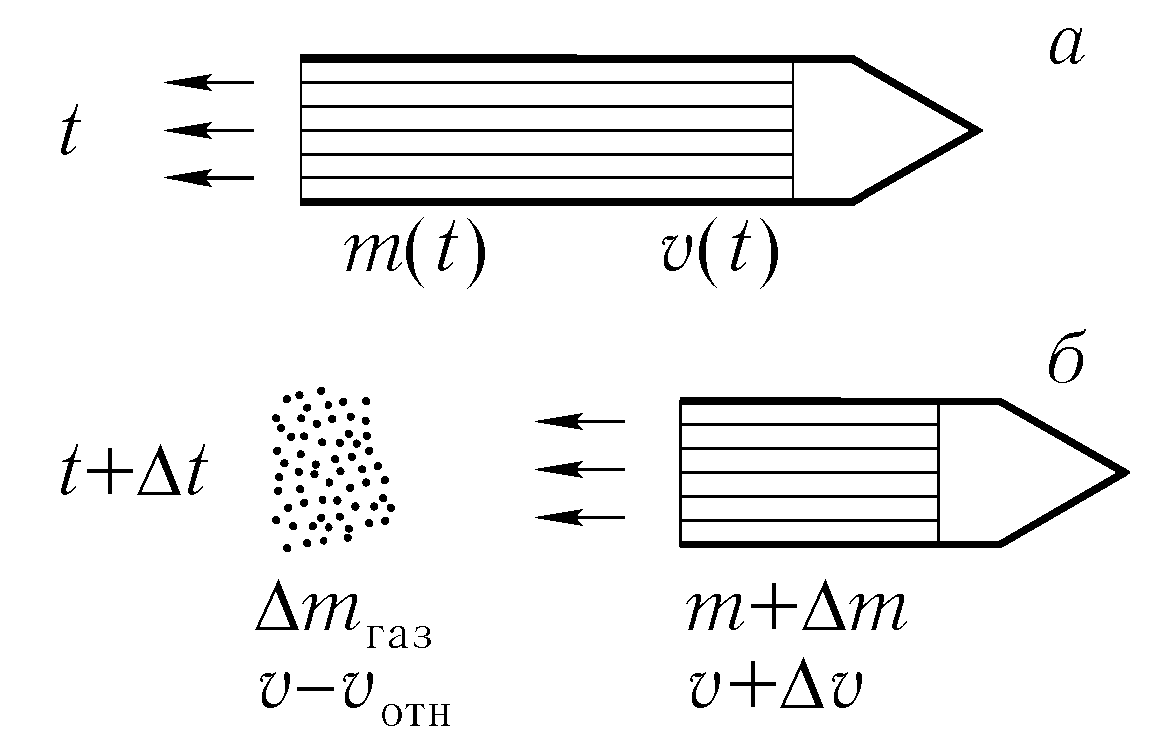
Скорость выброса газов относительно корпуса ракеты-известна(конструкция сопла, тип топлива, параметры горения)-это относительная скорость.
Задача-найти скорость ракеты, массу и т.д.
Третий этап — математическая формулировка задачи: запись уравнений,
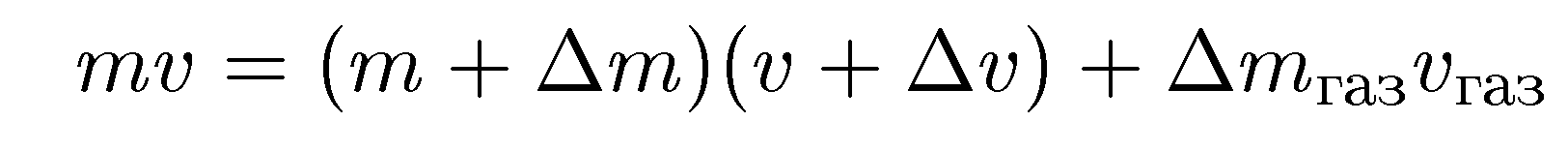
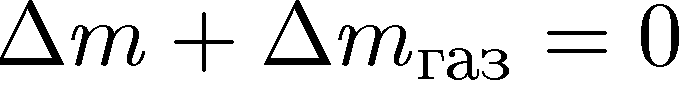
Четвертый этап — математическое решение задачи.
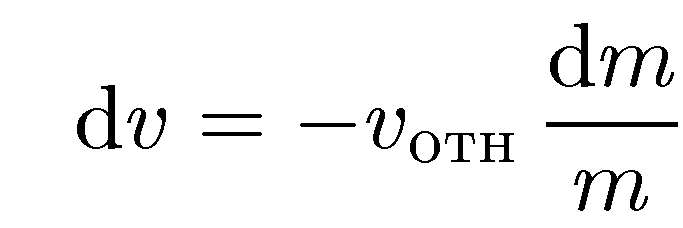
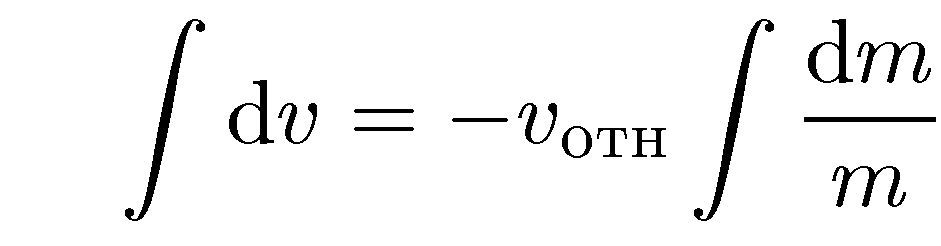

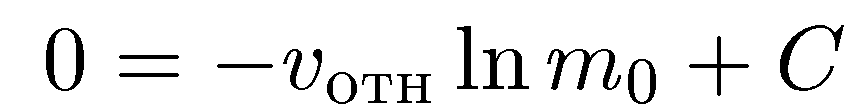

Формула Циолковского
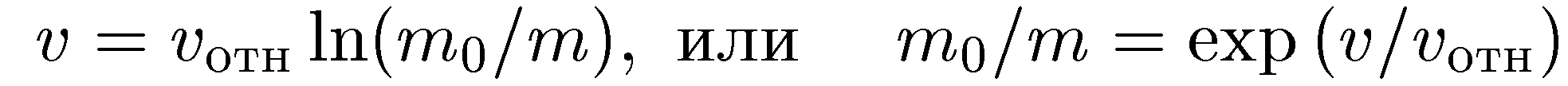
Пятый этап — проверка полученного решения.
Прием первый — проверка ответа по размерности.
Прием второй — проверка ответа по заранее очевидным результатам.
При переменной во времени скорости истечения
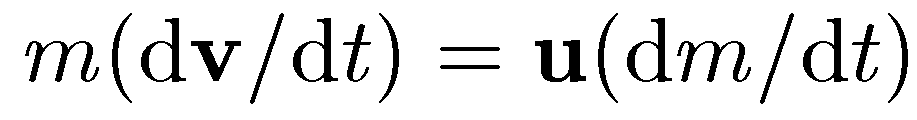
Для описания движения ракеты в поле Земли следует добавить силу
Уравнение Мещерского
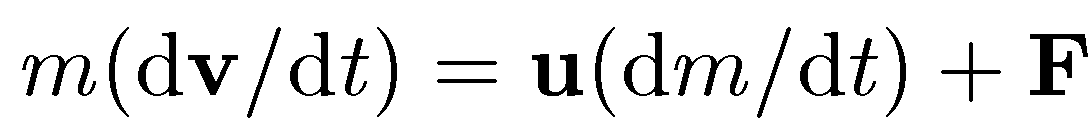
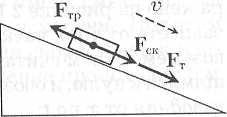
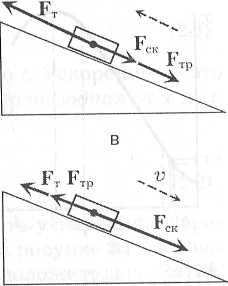
Силы
Сила – степень взаимодействия между объектами
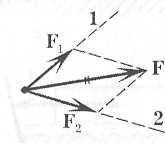
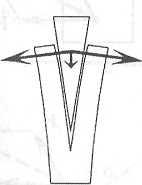
Разложение сил





Определение скоростей и ускорений при вращательном движении
Основные законы и формулы, применяемые при решении задач
Вращательное движение вокруг неподвижной оси
Рассмотри твердое тело, вращающееся вокруг неподвижной оси z. Сделаем рисунок. Ось вращения направим перпендикулярно плоскости рисунка, на нас. Пусть φ – угол поворота тела вокруг оси, отсчитываемый от некоторого начального положения. За положительное направление выберем направление против часовой стрелки. Угловая скорость ω равна производной угла поворота по времени t:
.
При , тело вращается против часовой стрелки; при – по часовой. Вектор угловой скорости направлен перпендикулярно плоскости рисунка. При он направлен на нас; при – от нас.
Угловое ускорение ε равно производной угловой скорости по времени:
.
Вектор углового ускорения также направлен перпендикулярно плоскости рисунка. При он направлен на нас; при – от нас.

Скорость точки при вращательном движении тела вокруг неподвижной оси
Рассмотрим точку A, принадлежащую твердому телу. Опустим из нее перпендикуляр OA на ось вращения. Пусть – расстояние от точки до оси. Траекторией движения точки A является окружность (или дуга) с центром в точке O радиуса .
Абсолютное значение скорости точки A определяется по формуле:
.
Вектор скорости направлен по касательной к траектории (окружности), перпендикулярно отрезку OA. При этом вектор должен производить закручивание в ту же сторону, что и вектор угловой скорости .
Касательное (или тангенциальное) ускорение точки A определяется аналогично скорости:
.
Оно направлено по касательной к окружности, перпендикулярно OA. При этом вектор должен производить закручивание в ту же сторону, что и вектор углового ускорения .

Ускорение точки при вращательном движении тела вокруг неподвижной оси
Нормальное ускорение всегда направлено к центру окружности и имеет абсолютную величину
.
Полное ускорение точки A, или просто ускорение, равно векторной сумме касательного и нормального ускорений:
.
Поскольку векторы и перпендикулярны, то абсолютная величина ускорения точки A определяется по формуле:
.
Поступательное прямолинейное движение
Теперь рассмотрим прямолинейное поступательное движение тела. Направим ось x вдоль его линии движения. Пусть s есть перемещение тела вдоль этой оси относительно некоторого начального положения. Тогда скорость движения всех точек тела равна производной перемещения по времени:
.
При , вектор скорости направлен вдоль оси x. При – противоположно этой оси.
Ускорение точек тела равно производной скорости по времени, или второй производной перемещения по времени:
.
При , вектор ускорения направлен вдоль оси x. При – противоположно.
Соприкосновение тел без проскальзывания
Рассмотрим два тела, находящиеся в зацеплении без проскальзывания. Пусть точка A принадлежит первому телу, а точка B – второму. И пусть, в рассматриваемый момент времени, положения этих точек совпадают. Тогда, если между телами нет проскальзывания, то скорости этих точек равны:
.
Если каждое из тел вращается вокруг неподвижной оси, то равны соответствующие касательные ускорения:
.
Если одно из тел движется поступательно (пусть это второе тело), то ускорение его точек равно касательному ускорению точки соприкосновения первого тела:
.
Пример решения задачи

Условие задачи
Механизм состоит из ступенчатых колес 1, 2, 3, находящихся в зацеплении и связанных ременной передачей, зубчатой рейки 4 и груза 5, привязанного к концу нити, намотанной на одно из колес. Радиусы ступеней колес равны соответственно: у колеса 1 – r1 = 2 см, R1 = 4 см, у колеса 2 – r2 = 6 см, R2 = 8 см, у колеса 3 – r3 = 12 см, R3 = 16 см. На ободьях колес расположены точки A, B и C. Задан закон движения груза: s5 = t3 – 6t (см). Положительное направление для s5 – вниз.
Определить в момент времени t = 2 скорости точек A, C; угловое ускорение колеса 3; ускорение точки B и ускорение рейки 4.
Эта задача – на исследование вращательного движения твердого тела вокруг неподвижной оси. При решении задачи учесть, что проскальзывание в ременной передаче и в точках сцепления колес отсутствует. То есть скорости точек колес, находящихся в зацеплении равны, а скорости точек ремня равны скорости точек, лежащих на ободе колес, связанных ременной передачей.
Дано:
t = 2 с; r1 = 2 см, R1 = 4 см; r2 = 6 см, R2 = 8 см; r3 = 12 см, R3 = 16 см; s5 = t3 – 6t (см).
Решение
Определение скорости и ускорения груза 5
Груз 5 совершает поступательное движение. Поэтому скорости (и ускорения) всех его точек равны. В условии задачи задано смещение s груза относительно некоторого начального положения. Дифференцируя по времени t, находим зависимость скорости точек груза от времени:
.
Дифференцируя скорость груза по времени, находим зависимость ускорения груза от времени:
.
Находим скорость и ускорение груза в заданный момент времени :
см/с;
см/с2.
Определение угловых скоростей и ускорений колес

Решение задачи
Груз 5 связан нитью с внутренним ободом колеса 3. Поэтому скорости точек внутреннего обода колеса 3 равны скорости груза:
.
Отсюда находим угловую скорость колеса 3 для произвольного момента времени:
.
Здесь подразумевается, что и являются функциями от времени t. Дифференцируя по t, находим угловое ускорение колеса 3:
.
Находим значения угловой скорости и углового ускорения в момент времени с. Для этого подставляем найденные значения и при с:
с–1;
с–2.
Рассмотрим колесо 2. Его внутренний обод связан нитью с внешним ободом колеса 3. Поэтому скорости точек на этих ободьях равны:
. Отсюда
.
Дифференцируя по времени, находим угловое ускорение колеса 2 в произвольный момент времени:
.
Подставляем значения для с:
с–1;
с–2.
Рассмотрим колесо 1. Его внутренний обод находится в зацеплении с внешним ободом колеса 2. Поэтому скорости точек на этих ободьях равны:
. Отсюда
.
Дифференцируя по времени, находим угловое ускорение колеса 1 в произвольный момент времени:
.
Подставляем значения для с:
с–1;
с–2.
Итак, мы нашли:
ω1 = 5.3333 с–1, ω2 = 1.3333 с–1, ω3 = 0.5 с–1, ε1 = 10.6667 с–2, ε2 = 2.6667 с–2, ε3 = 1 с–2.
Определение скоростей точек A и C
Точка A лежит на окружности радиуса R1 с центром в точке O1, расположенной на оси вращения. Поэтому скорость этой точки направлена по касательной к окружности и по абсолютной величине равна
см/с.
Точка C лежит на окружности радиуса R3 с центром O3 на оси вращения. Скорость этой точки:
см/с.
Определение ускорения точки B
Точка B лежит на окружности радиуса R2 с центром O2, расположенном на оси вращения. Касательное (или тангенциальное) ускорение этой точки направлено по касательной к окружности в сторону, на которую указывает угловое ускорение (по часовой стрелке). По абсолютной величине оно равно
см/с2.
Нормальное ускорение всегда направлено к центру окружности. По абсолютной величине оно равно
см/с2.
Полное ускорение равно векторной сумме касательного и нормального ускорений:
.
Поскольку касательное ускорение перпендикулярно нормальному, то для абсолютной величины полного ускорения имеем:
см/с2.
Определение ускорения рейки 4
Рейка 4 движется поступательно по направляющим. Она находится в зацеплении с внешним ободом колеса 1. Поэтому ее скорость равна скорости точек внешнего обода колеса 1:
.
Дифференцирую по времени, получаем ускорение рейки в произвольный момент времени:
.
Подставляем численные значения для момента времени t = 2 с:
см/с2.
Ответ
см/с; см/с; с–2; см/с2; см/с2.
Автор: Олег Одинцов. Опубликовано:





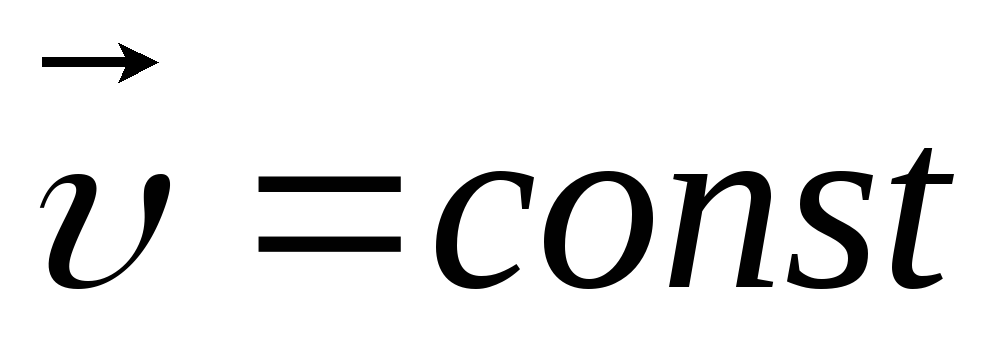
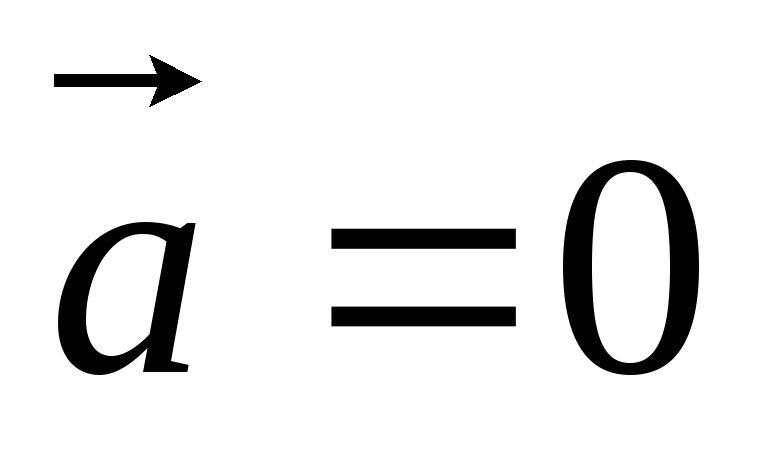
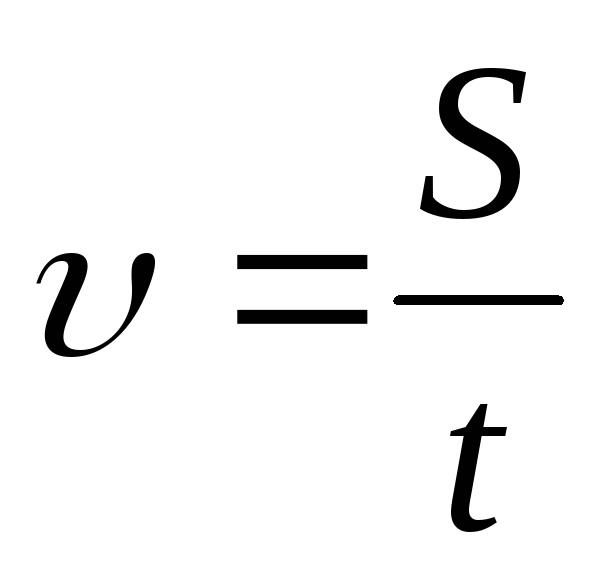

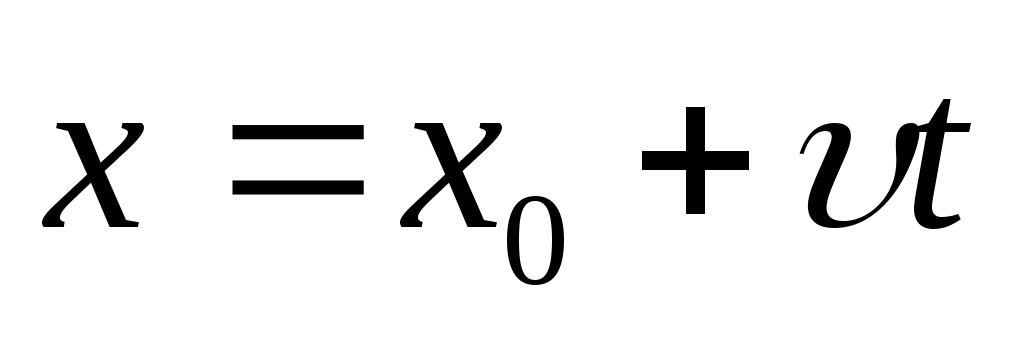

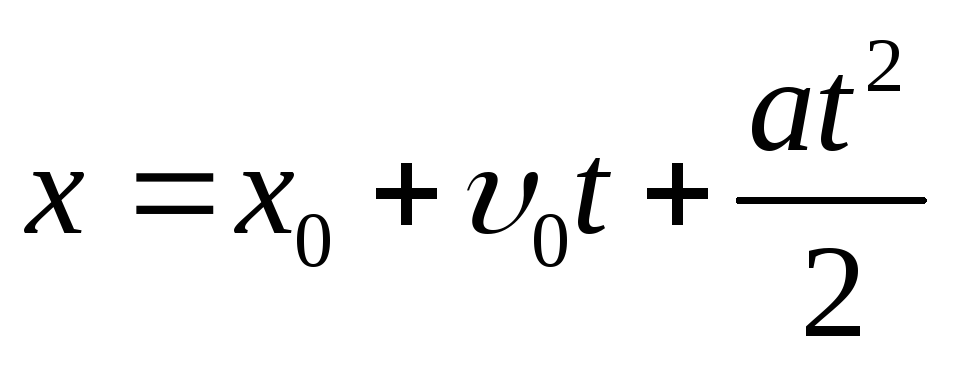
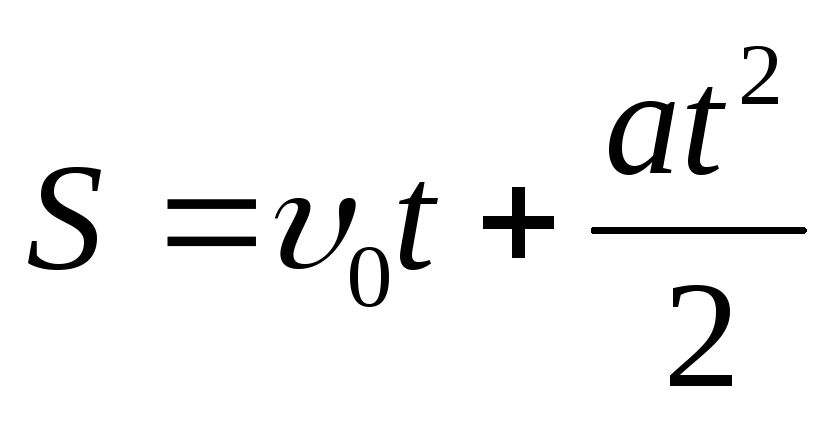
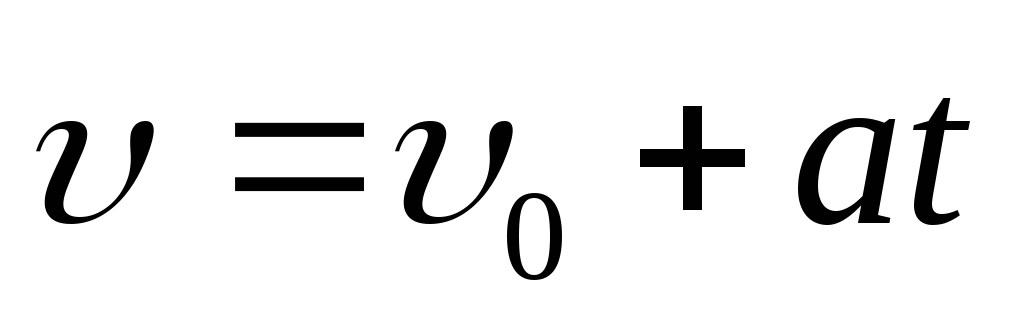
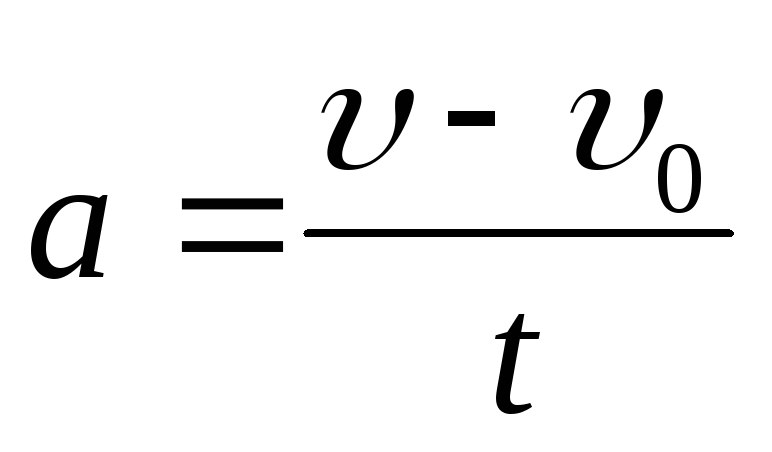

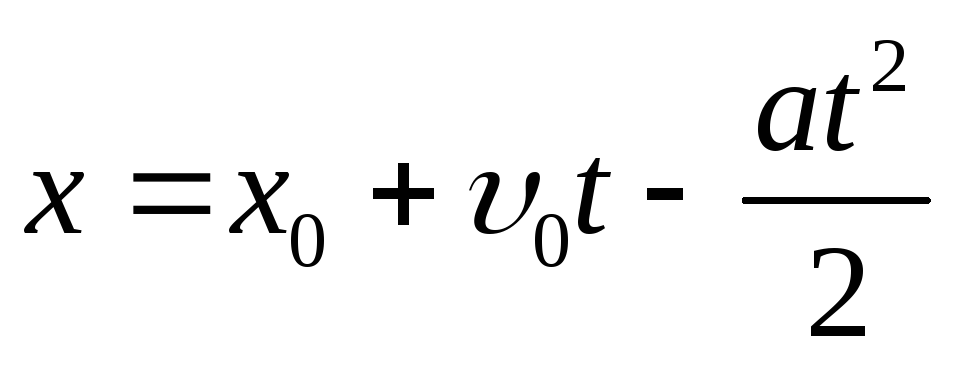
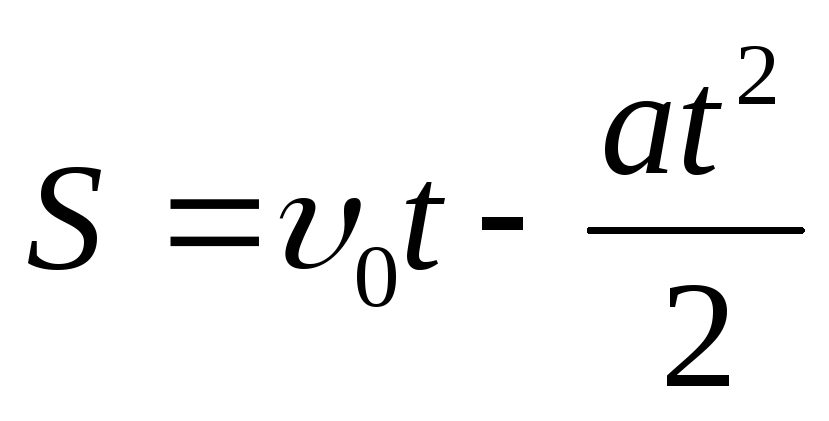


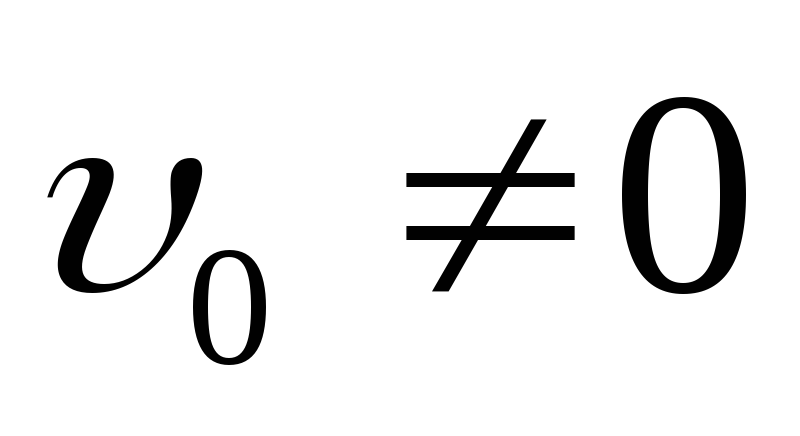

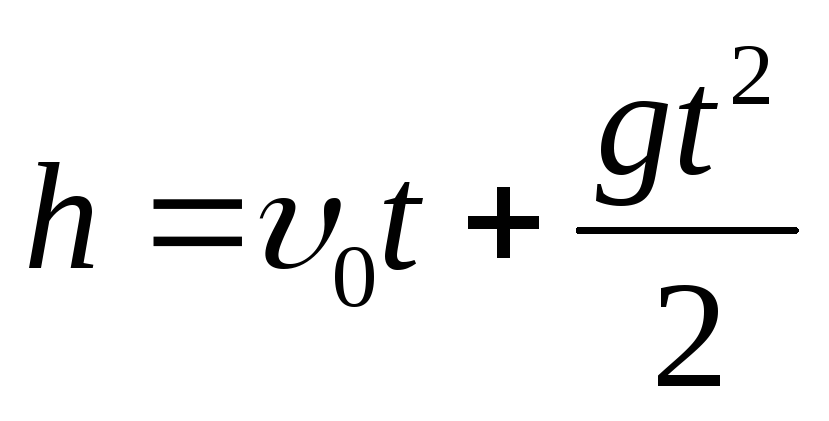
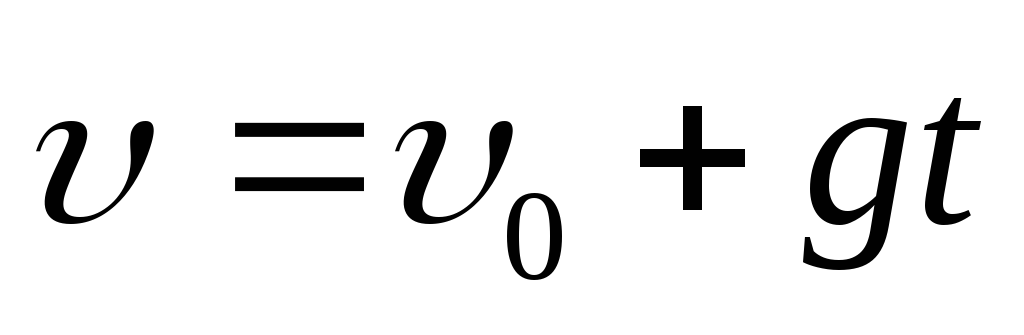
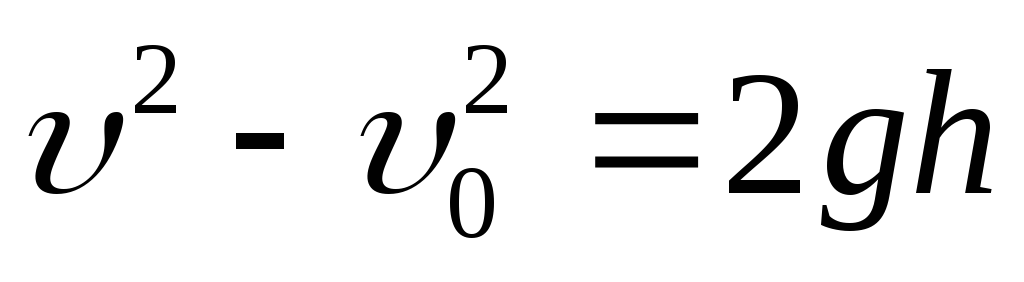
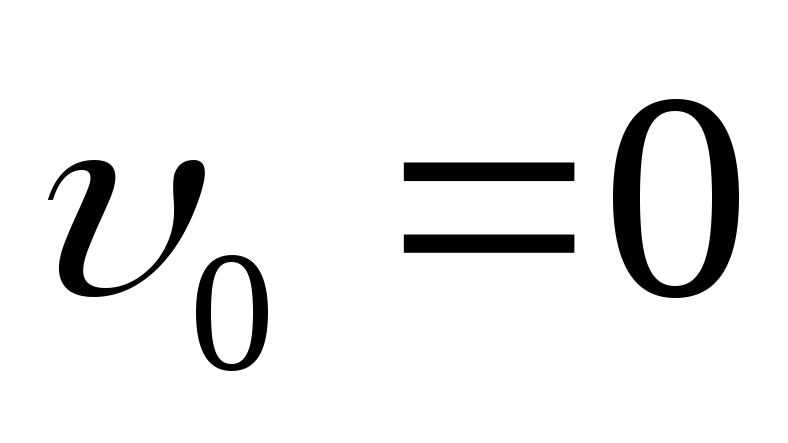
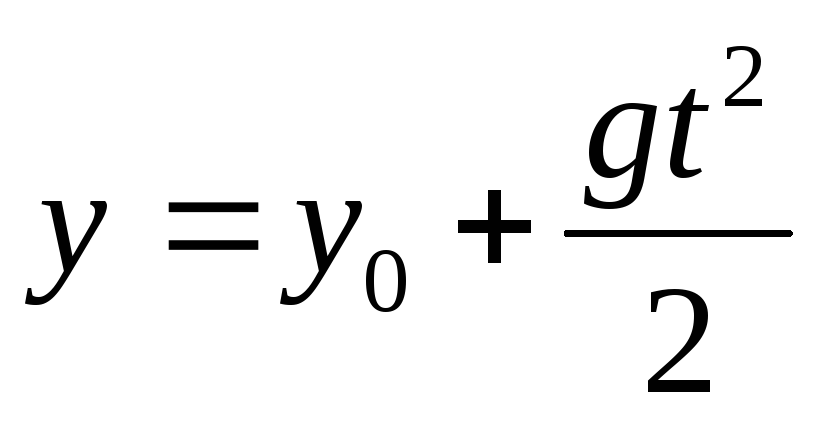
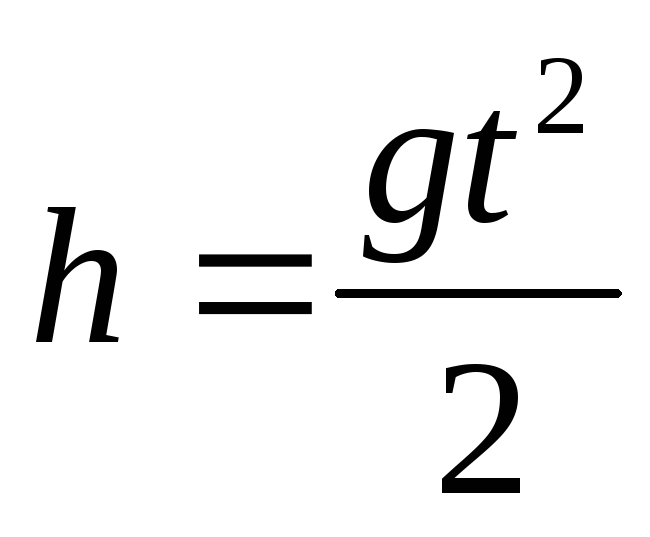
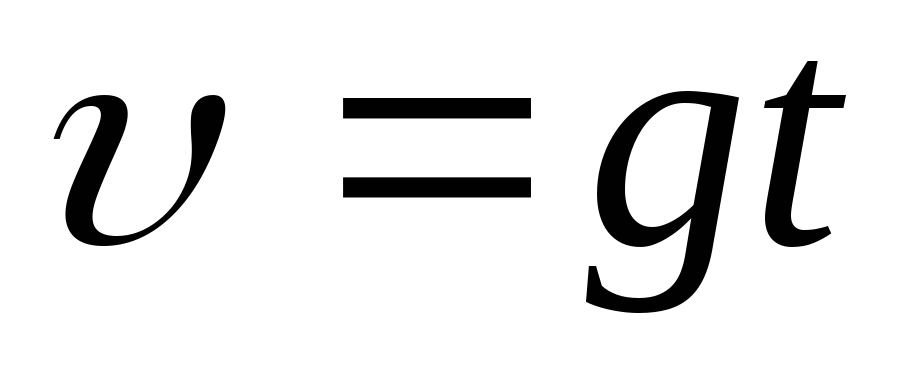
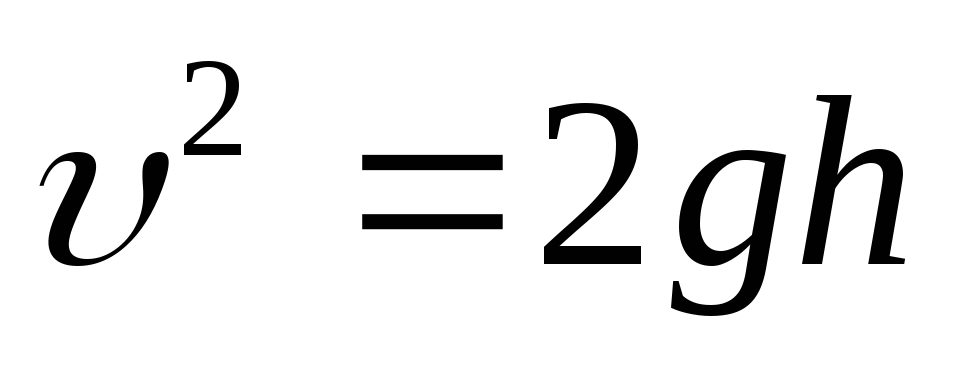

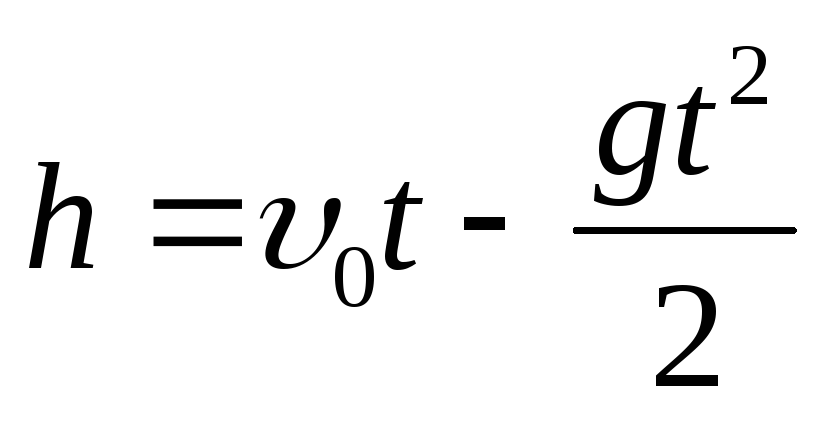
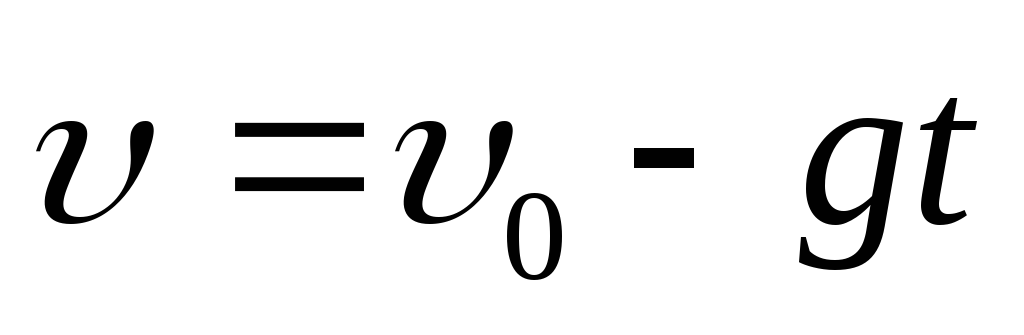

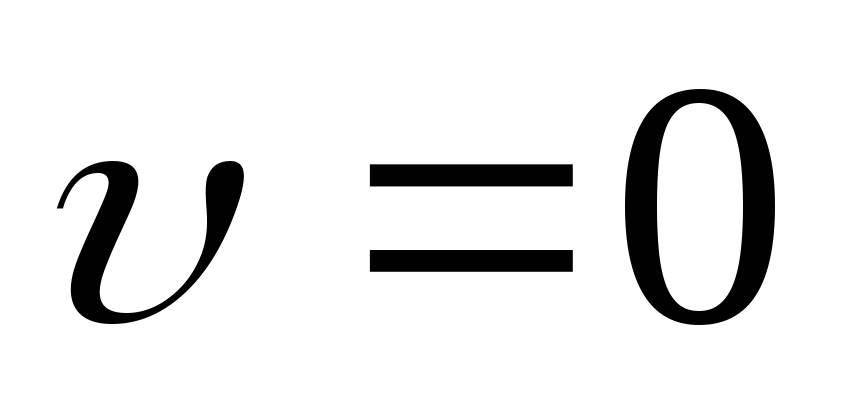
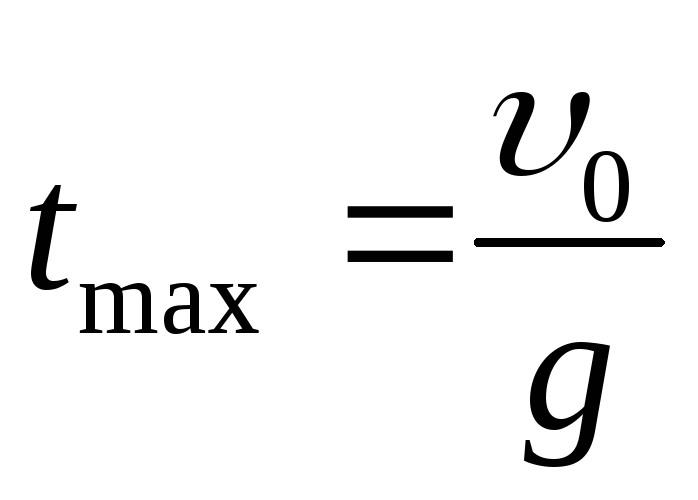

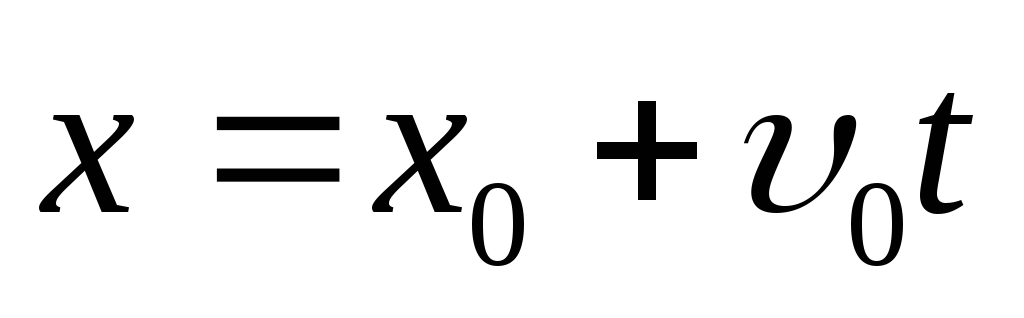 ;
; 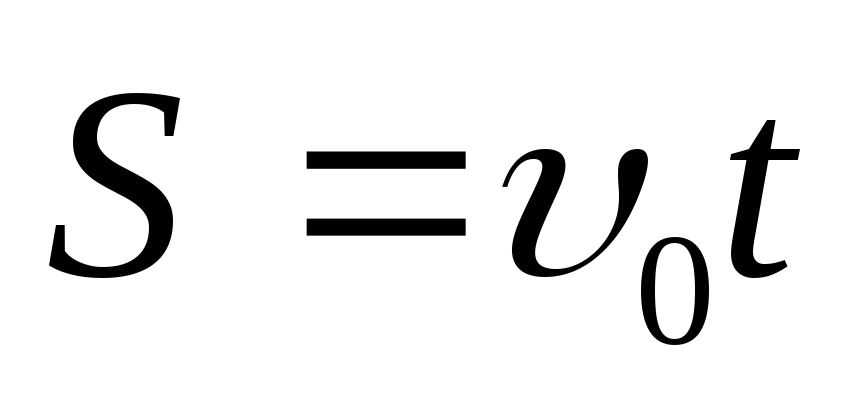
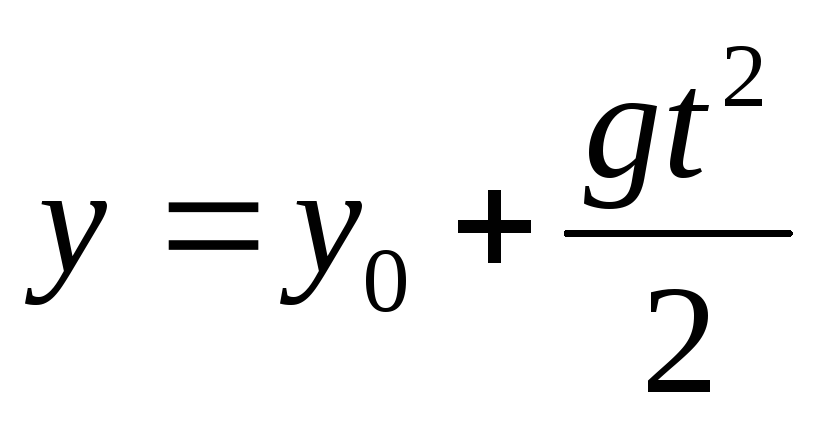 ;
; 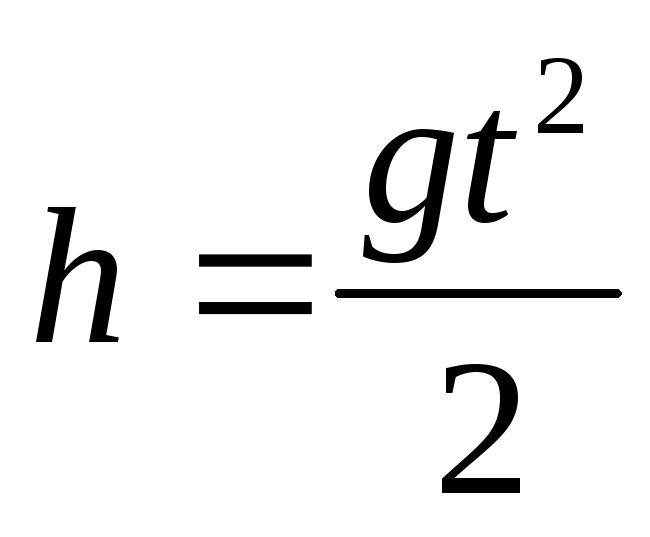

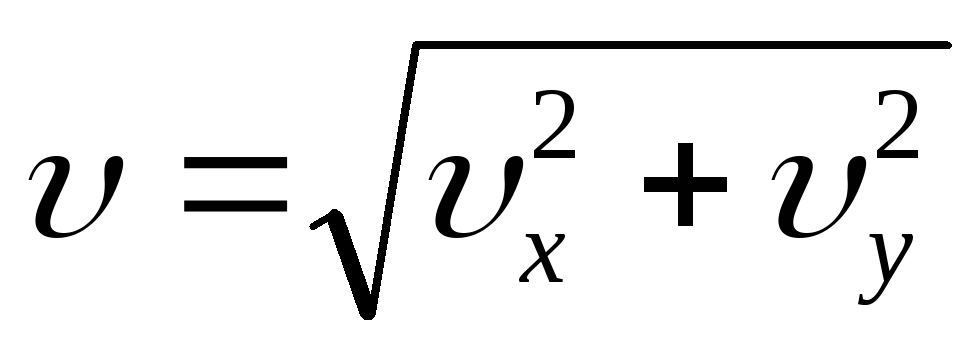
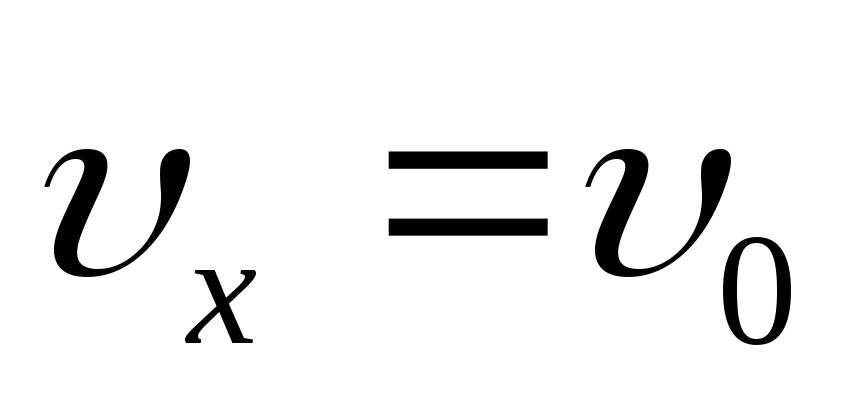 ;
; 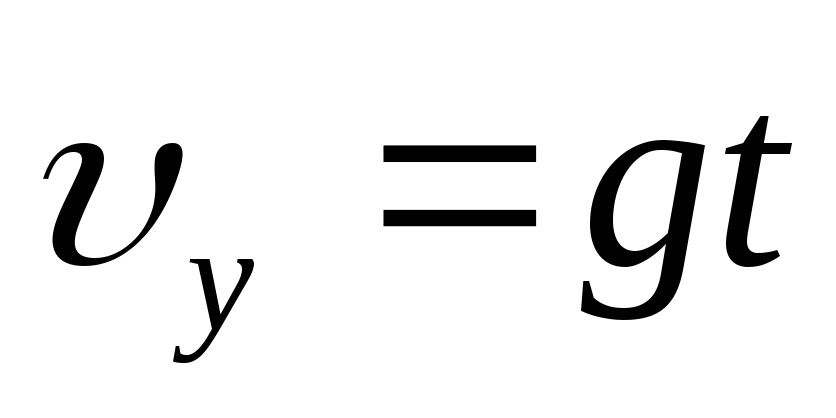
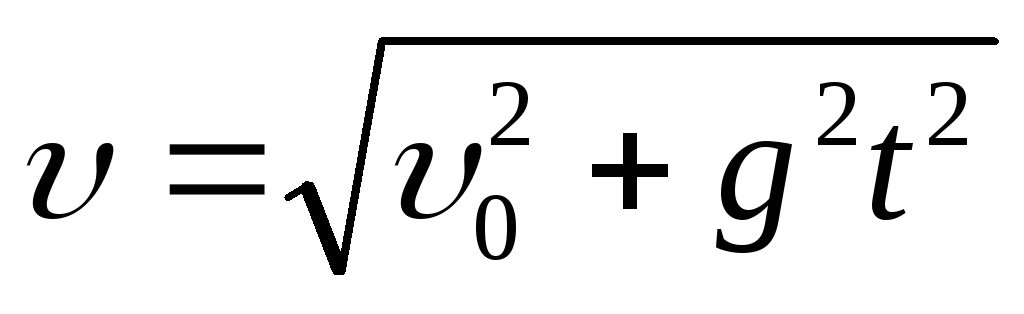
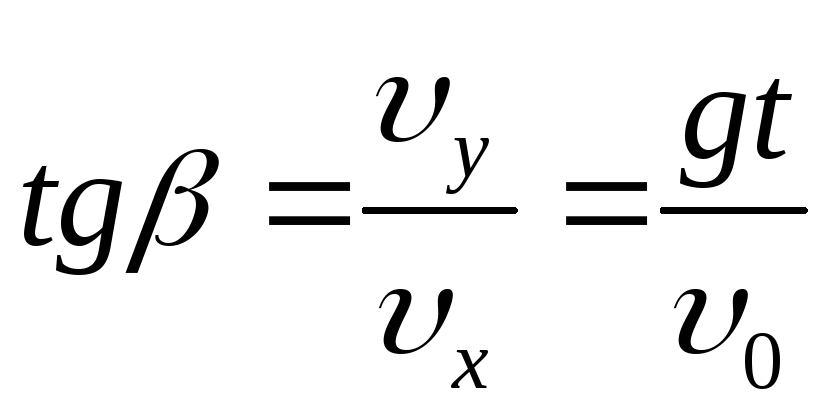
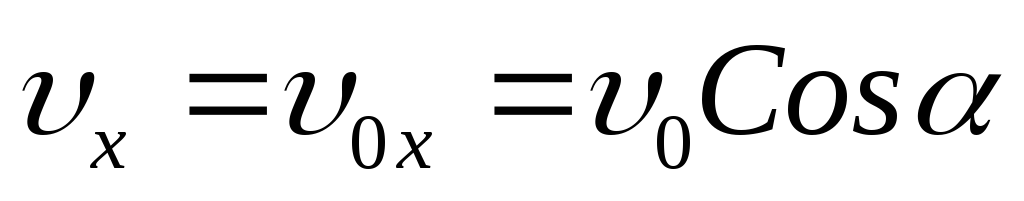

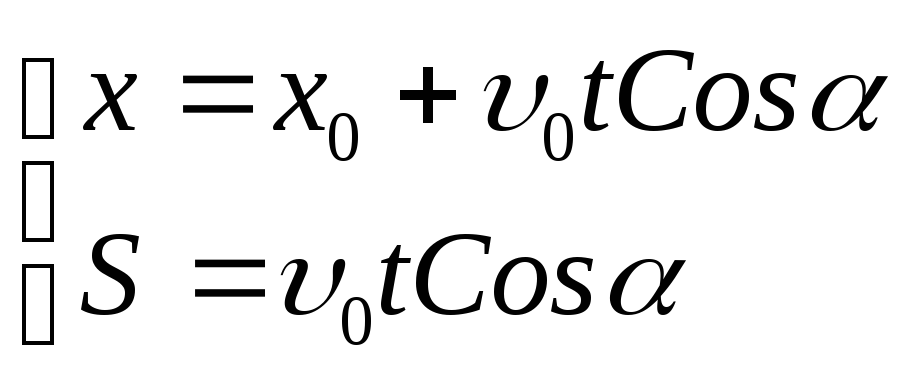

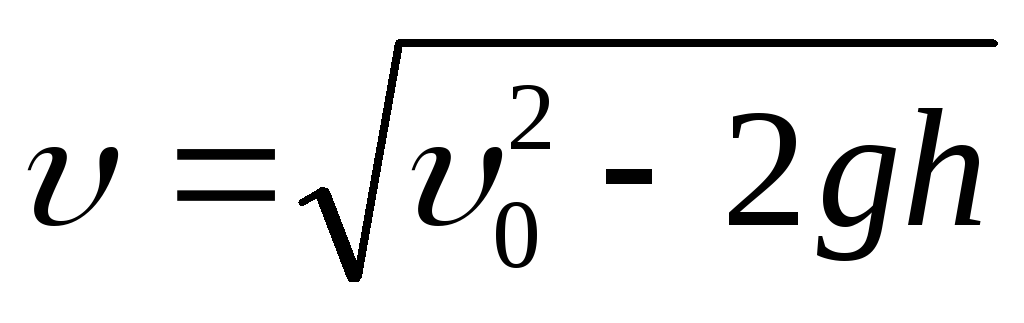

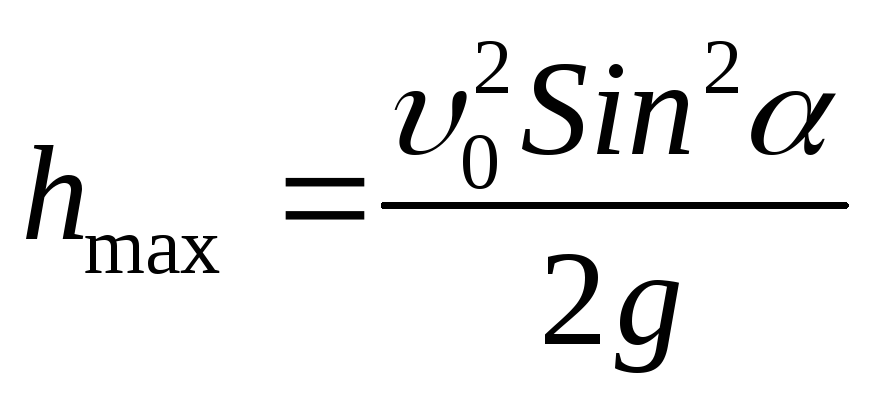
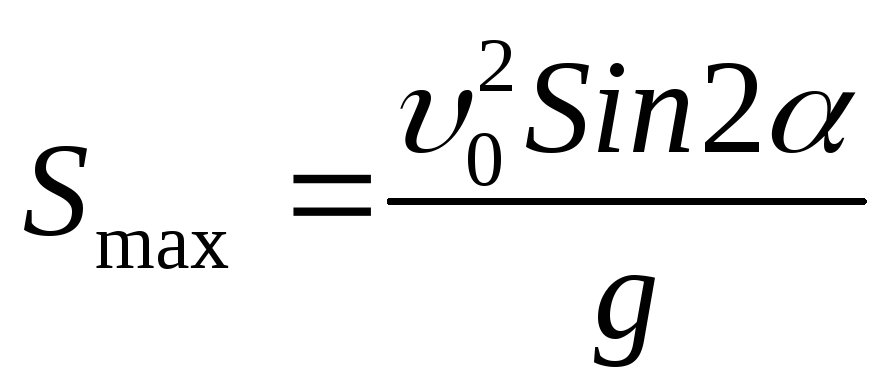
 ангенциальное
и нормальное ускорение.
ангенциальное
и нормальное ускорение.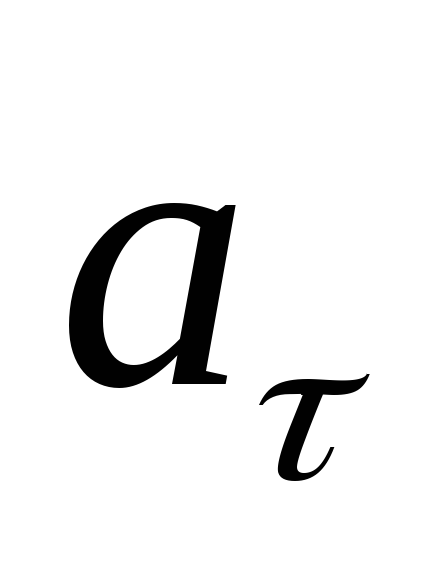 )
и нормального (
)
и нормального (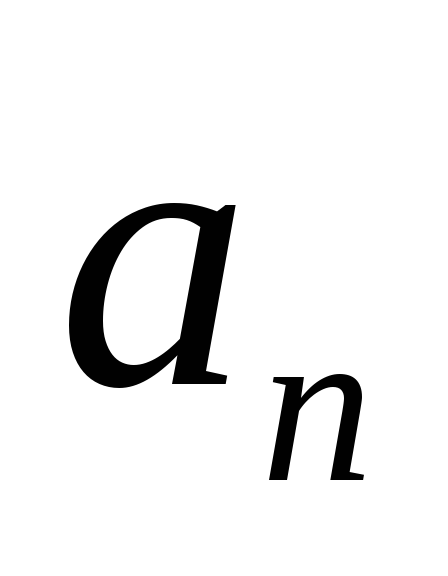 ).
).
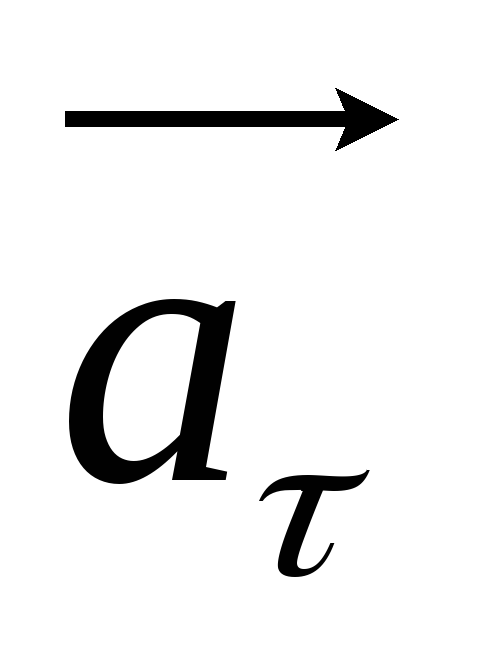 совпадает с направлением линейной
скорости или противоположно ему).
совпадает с направлением линейной
скорости или противоположно ему).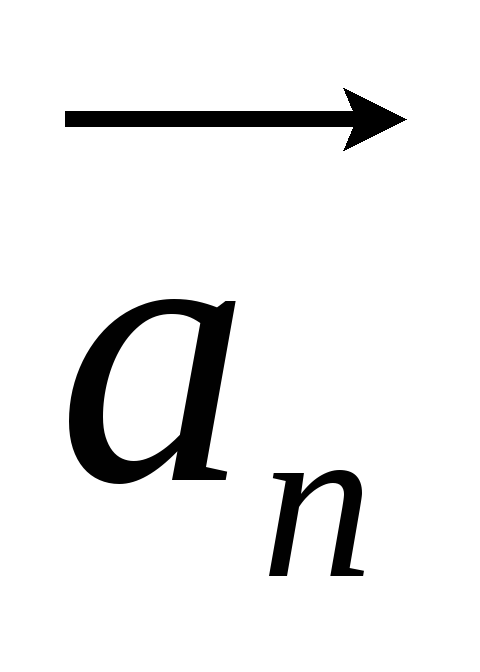 направлен по радиусу кривизны
траектории).
направлен по радиусу кривизны
траектории).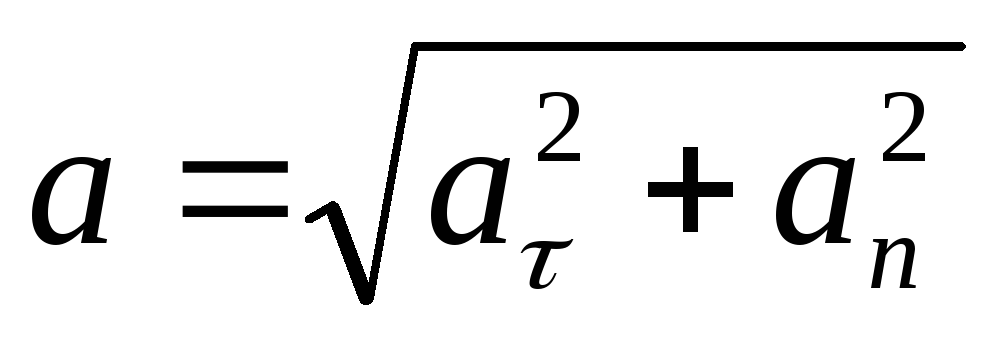 .
. .
.