Формула силы Лоренца в физике

Содержание:

Определение и формула силы Лоренца

Определение

Сила $\bar{F}$ , действующая на движущуюся заряженную частицу в магнитном поле, равная:

$$\bar{F}=q[\bar{v} \times \bar{B}](1)$$

называется силой Лоренца (магнитной силой).

Исходя из определения (1) модуль рассматриваемой силы:

$$F=q v B \sin \alpha(2)$$

где $\bar{v}$ – вектор скорости частицы, q – заряд частицы, $\bar{B}$ – вектор магнитной индукции поля в точке нахождения заряда, $\alpha$ – угол между векторами $\bar{v}$ и $\bar{B}$. Из выражения (2) следует, что если заряд движется параллельно силовым линиям магнитного поля,то сила Лоренца равна нулю. Иногда силу Лоренца стараясь выделить, обозначают, используя индекс: $\bar{F}_L$

Направление силы Лоренца

Сила Лоренца (как и всякая сила) – это вектор. Ее направление перпендикулярно вектору скорости $\bar{v}$ и вектору $\bar{B}$ (то есть перпендикулярно плоскости, в которой находятся векторы скорости и магнитной индукции) и определяется правилом правого буравчика (правого винта) рис.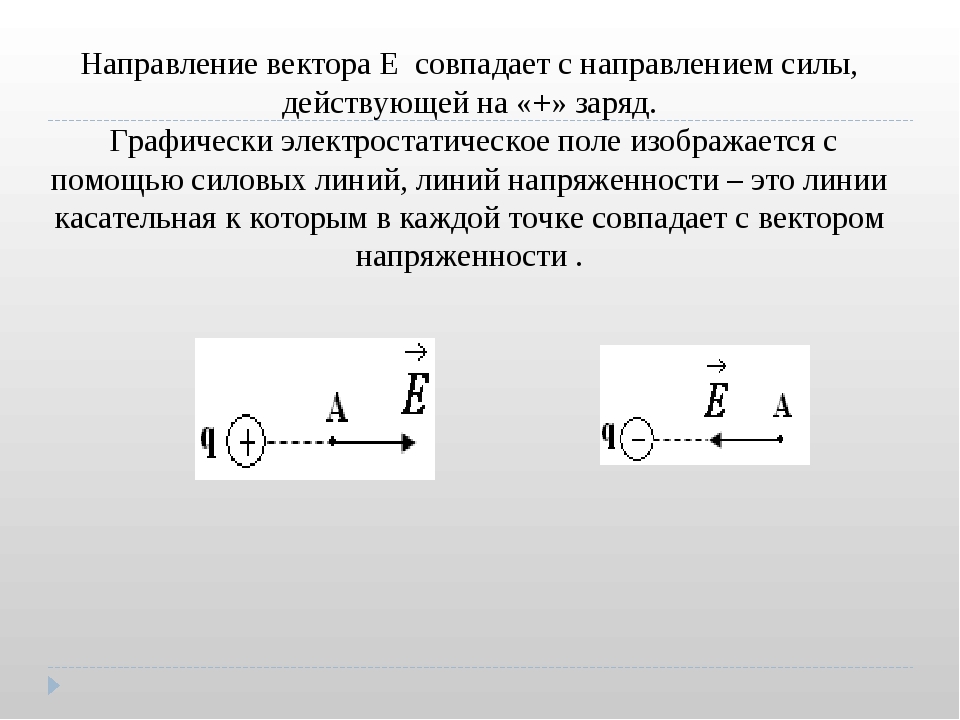

{2}}}}$ – релятивистский множитель Лоренца, c – скорость света в вакууме.

Сила Лоренца — это центростремительная сила. По направлению отклонения элементарной заряженной частицы в магнитном поле делают вывод о ее знаке (рис.2).

Формула силы Лоренца при наличии магнитного и электрического полей

Если заряженная частица перемещается в пространстве, в котором находятся одновременно два поля (магнитное и электрическое), то сила, которая действует на нее, равна:

$$\bar{F}=q \bar{E}+q[\bar{v} \times \bar{B}](4)$$

где $\bar{E}$ – вектор напряженности электрического поля в точке, в которой находится заряд. Выражение (4) было эмпирически получено Лоренцем. Сила $\bar{F}$, которая входит в формулу (4) так же называется силой Лоренца (лоренцевой силой). Деление лоренцевой силы на составляющие: электрическую $(\bar{F} = q \bar{E})$ и магнитную $(\bar{F}=q[\bar{v} \times \bar{B}])$ относительно, так как связано с выбором инерциальной системы отсчета. Так, если система отсчета будет двигаться с такой же скоростью $\bar{v}$, как и заряд, то в такой системе сила Лоренца, действующая на частицу, будет равна нулю.

{2}}{R}(1.4)$$

Из выражения (1.3) получим скорость:

$$v=\frac{q B R}{m}(1.5)$$

Период обращения электрона по окружности можно найти как:

$$T=\frac{2 \pi R}{v}=\frac{2 \pi m}{q B}(1.6)$$

Зная период, можно найти угловую скорость как:

$$\omega=\frac{2 \pi}{T}=\frac{q_{e} B}{m}$$

Ответ. $\omega=\frac{q_{e} B}{m}$

Слишком сложно?

Формула силы Лоренца не по зубам? Тебе ответит эксперт через 10 минут!

Пример

Задание. Заряженная частица (заряд q, масса m) со скоростью vвлетает в область, где имеется электрическое поле напряженностью E и магнитное поле с индукцией B. Векторы $\bar{E}$ и $\bar{B}$ совпадают по направлению. Каково ускорение частицы в моментначалаперемещения в полях, если $\bar{v} \uparrow \bar{B} \uparrow \bar{E}$?

Решение. Сделаем рисунок.

На заряженную частицу действует сила Лоренца:

$$\bar{F}=q \bar{E}+q[\bar{v} \times \bar{B}](2. 1)$$

Магнитная составляющая имеет направление перпендикулярное вектору скорости ($\bar{v}$) и вектору магнитной индукции ($\bar{B}$). Электрическая составляющая сонаправлена с вектором напряжённости ($\bar{E}$) электрического поля. В соответствии со вторым законом Ньютона имеем:

$$\bar{F}=q \bar{E}+q[\bar{v} \times \bar{B}]=m \bar{a}(2.2)$$

Получаем, что ускорение равно:

$$\frac{q \bar{E}+q[\bar{v} \times \bar{B}]}{m}=\bar{a}(2.3)$$

Если скорость заряда параллельна векторам $\bar{E}$ и $\bar{B}$, тогда $[\bar{v} \times \bar{B}]=0$, получим:

$$\bar{a}=\frac{q \bar{E}}{m}$$

Ответ. $\bar{a}=\frac{q \bar{E}}{m}$

Читать дальше: Формула силы натяжения нити.

Действие магнитного поля на движущийся заряд. Сила Лоренца

Действие магнитного поля на движущийся заряд. Сила Лоренца

Подробности

Просмотров: 907

«Физика — 11 класс»

Магнитное поле действует с силой на движущиеся заряженные частицы, в то числе и на проводники с током.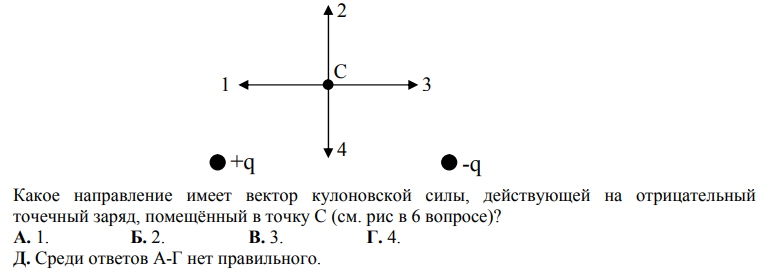

Какова же сила, действующая на одну частицу?

1.
Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца в честь великого голландского физика X. Лоренца, создавшего электронную теорию строения вещества.
Силу Лоренца можно найти с помощью закона Ампера.

Модуль силы Лоренца равен отношению модуля силы F, действующей на участок проводника длиной Δl, к числу N заряженных частиц, упорядоченно движущихся в этом участке проводника:

Так как сила (сила Ампера), действующая на участок проводника со стороны магнитного поля
равна F = | I | BΔl sin α,
а сила тока в проводнике равна

I = qnvS
где
q — заряд частиц
n — концентрация частиц (т.е. число зарядов в единице объема)
v — скорость движения частиц
S — поперечное сечение проводника.

тогда получаем:
На каждый движущийся заряд со стороны магнитного поля действует сила Лоренца, равная:

где α — угол между вектором скорости и вектором магнитной индукции.

Сила Лоренца перпендикулярна векторам и .

2.
Направление силы Лоренца

Направление силы Лоренца определяется с помощью того же

правила левой руки, что и направление силы Ампера:

Если левую руку расположить так, чтобы составляющая магнитной индукции, перпендикулярная скорости заряда, входила в ладонь, а четыре вытянутых пальца были направлены по движению положительного заряда (против движения отрицательного), то отогнутый на 90° большой палец укажет направление действующей на заряд силы Лоренца F_л.

3.
Если в пространстве, где движется заряженная частица, существует одновременно и электрическое поле, и магнитное поле, то суммарная сила, действующая на заряд, равна: = _эл + _л где сила, с которой электрическое поле действует на заряд q, равна F

эл = q.

4.
Cила Лоренца не совершает работы, т.к. она перпендикулярна вектору скорости частицы.
Значит сила Лоренца не меняет кинетическую энергию частицы и, следовательно, модуль ее скорости.
Под действием силы Лоренца меняется лишь направление скорости частицы.

5.
Движение заряженной частицы в однородном магнитном поле

Есть однородное магнитное поле , направленное перпендикулярно к начальной скорости частицы .

Сила Лоренца зависит от модулей векторов скорости частицы и индукции магнитного поля.

Магнитное поле не меняет модуль скорости движущейся частицы, значит остается неизменным и модуль силы Лоренца.
Сила Лоренца перпендикулярна скорости и, следовательно, определяет центростремительное ускорение частицы.
Неизменность по модулю центростремительного ускорения частицы, движущейся с постоянной по модулю скоростью, означает, что

В однородном магнитном поле заряженная частица равномерно движется по окружности радиусом r.

Согласно второму закону Ньютона

Тогда радиус окружности, по которой движется частица, равен:

Время, за которое частица делает полный оборот (период обращения), равно:

6.

Использование действия магнитного поля на движущийся заряд.

Действие магнитного поля на движущийся заряд используют в телевизионных трубках-кинескопах, в которых летящие к экрану электроны отклоняются с помощью магнитного поля, создаваемого особыми катушками.

Сила Лоренца используется в циклотроне — ускорителе заряженных частиц для получения частиц с большими энергиями.

На действии магнитного поля основано также и устройство масс-спектрографов, позволяющих точно определять массы частиц..

Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин

Магнитное поле. Физика, учебник для 11 класса — Класс!ная физика

Магнитное поле и взаимодействие токов — Магнитная индукция. Линии магнитной индукции — Модуль вектора магнитной индукции. Сила Ампера — Электроизмерительные приборы. Громкоговоритель — Действие магнитного поля на движущийся заряд. Сила Лоренца — Магнитные свойства вещества — Примеры решения задач — Краткие итоги главы

Действие магнитного поля на движущийся заряд

| на главную | доп. материалы | физика как наука и предмет | электричество и электромагнетизм |

Организационные, контрольно-распорядительные и инженерно-технические услуги
в сфере жилой, коммерческой и иной недвижимости. Московский регион. Официально.

Опыт показывает, что магнитное поле действует не только на проводники с током, но и на отдельные заряды, движущиеся в магнитном поле. Сила, действующая на электрический заряд Q, движущийся в магнитном поле со скоростью v, называется силой Лоренца и выражается формулой

                                                     (114.1)

где В — индукция магнитного поля, в котором заряд движется.

Направление силы Лоренца определяется с помощью правила левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца направить вдоль вектора v (для Q>0 направления I и v совпадают, для Q<0 — противоположны), то отогнутый большой палец покажет направление силы, действующей на положительный заряд. На рис. 169 показана взаимная ориентация векторов v, В (поле направлено к нам, на рисунке показано точками) и F для положительного заряда. На отрицательный заряд сила действует в противоположном направ­лении. Модуль силы Лоренца (см. (114.1)) равен

где a — угол между v и В.

Отметим еще раз, что магнитное поле не действует на покоящийся электрический заряд. В этом существенное отличие магнитного поля от электрического. Магнитное поле действует только на движущиеся в нем заряды.

Так как по действию силы Лоренца можно найти модуль и направление вектора В, то выражение для силы Лоренца может быть использовано (наравне с другими) для определения вектора магнитной индукции В.

Сила Лоренца всегда перпендикулярна скорости движения заряженной частицы, поэтому она изменяет только направление этой скорости, не изменяя ее модуля. Следовательно, сила Лоренца работы не совершает.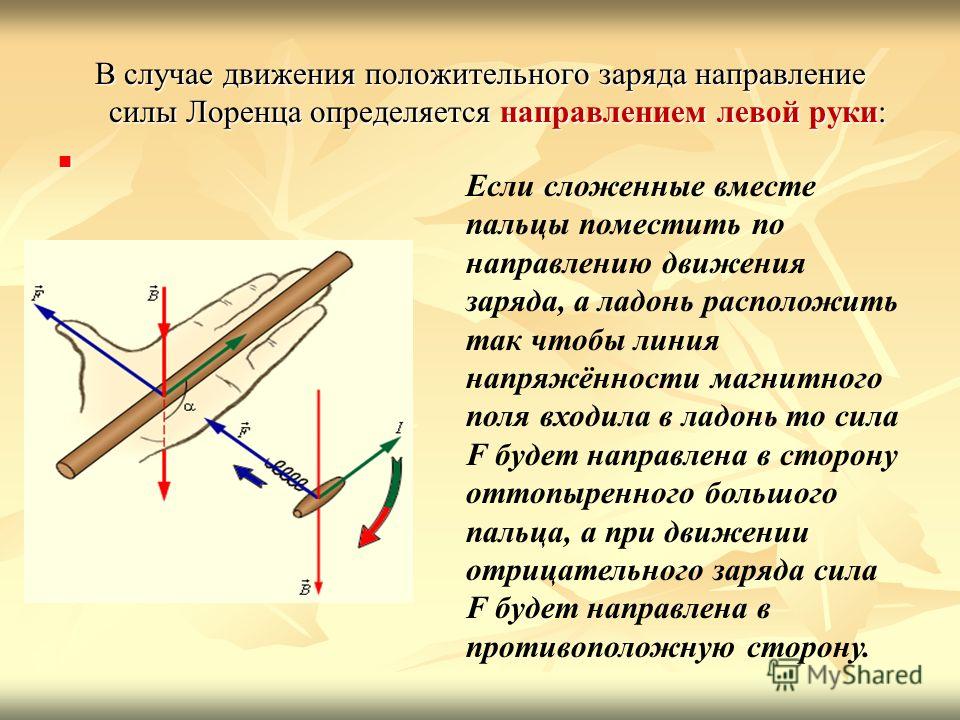 Иными словами, постоянное магнитное поле не совершает работы над движущейся в нем заряженной частицей и кинетическая энергия этой частицы при движении в магнитном поле не изменяется.

Если на движущийся электрический заряд помимо магнитного поля с индукцией В действует и электрическое поле с напряженностью Е, то результирующая сила F, приложенная к заряду, равна векторной сумме сил — силы, действующей со стороны электрического поля, и силы Лоренца:

Это выражение называется формулой Лоренца. Скорость v в этой формуле есть скорость заряда относительно магнитного поля.

---

напряжённость электрического поля — это… Что такое напряжённость электрического поля?

(Е), основная силовая характеристика электрического поля, равная отношению силы, действующей на точечный электрический заряд в данной точке пространства, к величине заряда.

НАПРЯЖЕННОСТЬ ЭЛЕКТРИ́ЧЕСКОГО ПО́ЛЯ (Е), основная силовая характеристика электрического поля (см. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ), определяемая силой (F), действующей на точечный (единичный) положительный электрический заряд (см. ЭЛЕКТРИЧЕСКИЙ ЗАРЯД) (Q_o), помещенный в данную точку поля. Заряд должен быть малым, чтобы не изменять ни величины, ни расположения тех зарядов, которые порождают исследуемое поле (т. е. заряд, не искажающий поля, которое с его помощью изучается, при этом собственным электрическим полем точечного заряда пренебрегают).
Е = F/ Q_o.
В общем случае напряженность поля Е = F/Q. Т.е. напряженность в данной точке пространства есть отношение силы, действующей на заряд, помещенный в эту точку к величине этого заряда.
Единица измерения напряженности электростатического поля — 1Н/Кл =1В/м.
Напряженность 1Н/Кл — это напряженность такого поля, которое на точечный заряд 1 Кл действует силой 1 Н, эту единицу в системе СИ называют В/м.
Напряженность электрического поля — векторная величина. Направление вектора напряженности Е совпадает с направлением кулоновской (см. Кулона закон (см. КУЛОНА ЗАКОН)) силы, действующей на точечный положительный заряд, помещенный в данную точку поля.
Если поле создается положительным зарядом, то вектор напряженности такого поля направлен от заряда вдоль радиуса-вектора, если поле создается отрицательным зарядом, то вектор напряженности поля Е направлен к заряду.
Графической характеристикой поля являются силовые линии (см. СИЛОВЫЕ ЛИНИИ) напряженности электрического поля, касательные к которым в каждой точке совпадают с направлением вектора напряженности.
Для электростатического поля напряженность электрического поля может быть представлена как градиент (см. ГРАДИЕНТ) электрического потенциала (см. ПОТЕНЦИАЛ (в физике)) j;
Е = — gradj.
Вектор напряженности электрического поля направлен в сторону убывания потенциала.
В вакууме напряженность электрического поля удовлетворяет принципу суперпозиции, согласно которому полная напряженность поля в точке равна геометрической сумме напряженностей полей, создаваемых отдельными заряженными частицами.

Высшее образование БГПУ

Сила Ампера. Сила взаимодействия параллельных токов. Контур с то-ком в магнитном поле. Магнитный момент тока. Действие электриче-ского и магнитного полей на движущиеся заряды. Сила Лоренца. Опре-деление удельного заряда электрона. Эффект Холла и его применение. Принцип работы магнитогидродинамических генераторов.

20.1. Сила Ампера. Взаимодействие параллельных токов

При исследовании действия магнитного поля на расположенный в нем прямолинейный проводник с током французский физик А.Ампер пришел к выводу, что модуль этой силы можно рассчитать по формуле

                                                      .                                            (20.1)

Позднее эта сила была названа силой Ампера, а формула – законом Ампера. Направление силы Ампера определяется по правилу левой руки: если левую руку расположить так, чтобы нормальная к проводнику составляющая B_┴ вектора индукции магнитного поля B входила в ладонь, четыре вытянутых пальца были направлены по току, то отогнутый на 90° большой палец покажет направление силы Ампера, которая действует на проводник с током (рис.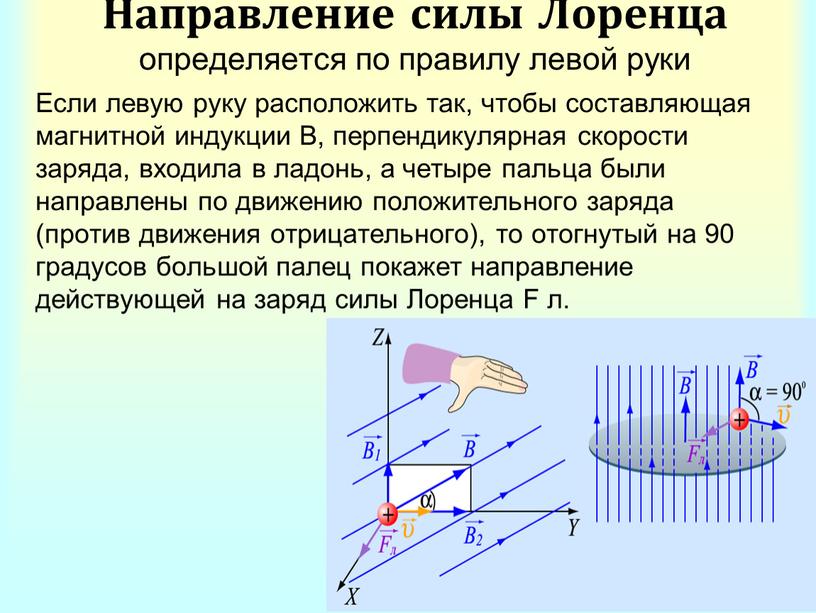 20.1).

 

Рис. 20.1

На основе закона Ампера можно объяснить взаимодействие параллельных проводников с током (рис.20.2).

 

Рис. 20.2

 

Ток I₁ создает в месте расположения проводника с током I₂ магнитное поле B₁, которое действует на ток I₂ с силой F₁₂=B₁I₂l. Ток I₂ в свою очередь также создает магнитное поле, индукция которого в месте расположения проводника с током I₁ равна B₂. Это поле действует на ток I₁ с силой F₂₁=B₂I₁l. Силы F₁₂ и F₂₁ находятся в одной плоскости с проводниками и являются силами притяжения, если токи направлены в одну сторону, и силами отталкивания, если токи направлены в противоположные стороны (рис.20.2).

Если расстояние между проводниками равно d, то индукция магнитного поля, созданного током I₁ в тех точках пространства, где находится второй проводник,

                                                          .                                               (20.2)

Соответственно индукция магнитного поля, созданного током I₂ в тех точках пространства, где расположен первый проводник,

                                                         .                                               (20.3)

Таким образом, для проводников длиной l:

                                                    .                                         (20. 4)

Если проводники находятся в вакууме (μ=1) на расстоянии d=1 м м и токи в них одинаковые и равны единице, то сила взаимодействия между участками проводников длиной по 1 м F₀=μ₀/2π=2·10^–7 Н. Эта формула используется для определения единицы силы тока – ампера – в СИ.

20.2. Контур с током в магнитном поле

Поместим замкнутый контур с током в однородное магнитное поле. Пусть плоскость контура перпендикулярна линиям индукции поля. Если разделить контур на элементы dl, то на каждый из них действует сила dF=IBdl, которая лежит в плоскости контура и направлена к его центру (рис.20.3).

 

Рис. 20.3

Если изменить направление тока на противоположное, то сила dF будет направлена в противоположную сторону (рис.20.4).

 

Рис. 20.4

Значит, силы, которые действуют на замкнутый контур с током в однородном перпендикулярном магнитном поле, могут только деформировать его (растянуть или сжать). Перемещение контура при этом не происходит.

Если расположить контур параллельно направлению линий магнитной индукции (рис.20.5), то на контур будет действовать вращательный момент сил M. Под действием этого момента контур поворачивается так, чтобы его плоскость стала перпендикулярной линиям магнитной индукции.

 

Рис. 20.5

Определим величину вращательного момента. Для этого разделим контур на малые элементы Δl. Выделим два элемента Δl₁ и Δl₂, заключенные между двумя параллельными линиями магнитной индукции, отстоящими друг от друга на расстоянии Δh. На эти элементы со стороны поля действуют силы ΔF₁ и ΔF₂, направленные соответственно перпендикулярно плоскости контура «от нас» и «к нам». Модули этих сил равны: ΔF₁=IBΔl₁sinα₁ и ΔF₂=IBΔl₂sinα₂. Если учесть, что Δl₁sinα₁=Δh, а Δl₂sinα₂=Δh, то очевидно, что эти силы равны по модулю и направлены в противоположные стороны. Они образуют пару сил, момент которой ΔM=ΔF_x=IBΔhx=IBΔS, где x – среднее расстояние между элементами Δl₁ и Δl₂, ΔS=Δhx – площадь, ограниченная линиями магнитной индукции и элементами контура Δl₁ и Δl₂. Очевидно, что весь контур состоит из суммы всех пар элементов. Поэтому суммарный момент действующий на контур, равен

.

Если контур расположен в магнитном поле так, что угол между его нормалью n и вектором магнитной индукции B поля равен β, то под действием проекции вектора B на нормаль к контуру равную B_┴=Bcosβ контур будет растягиваться (сжиматься), а под действием проекции B на плоскость контура Bsinβ – поворачиваться.

Поэтому в общем случае формула расчета вращательного момента имеет вид:

                                                     .                                           (20.5)

Как уже отмечалось, величину p_m=IS называют магнитным моментом контура с током. Это величина векторная, и она совпадает по направлению с еди­ничным вектором нормали n: p_m=ISn. Тогда формулу (20.5) можно записать в векторном виде:

                                                      .                                           (20.6)

Если контур с током поместить в неоднородное магнитное поле, то кроме ориентирующего действия вращательного момента на контур будет действовать сила f в направлении возрастания магнитного поля (рис.20.6).

g

Рис. 20.6

Эта сила является равнодействующей всех сил dF_┴ на каждый элемент тока со стороны составляющей поля B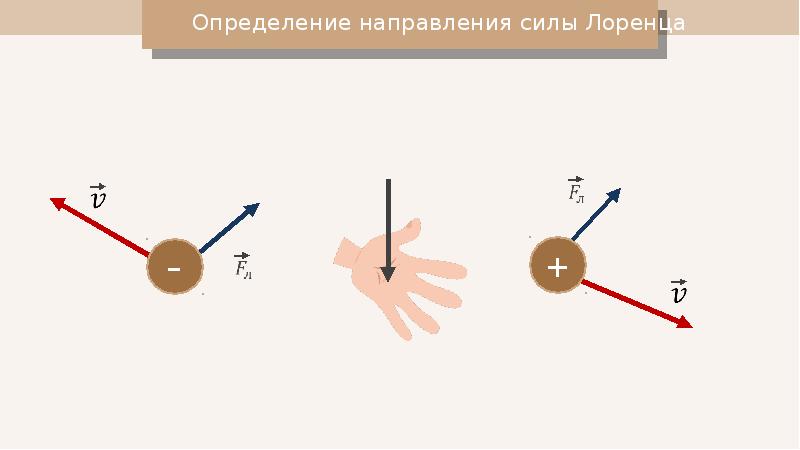_║. Расчет показывает, что модуль силы, которая действует на весь контур, равен:

                                     ,                          (20.7)

где α – угол между векторами p_m и B;  – градиент индукции магнитного поля.

20.3. Сила Лоренца

Как уже отмечалось, на проводник с током, который находится в магнитном поле, действует сила Ампера F_A=IBlsinα. Поскольку ток представляет упорядоченное движение свободных электрических зарядов, то это означает, что магнитное поле действует на каждый из этих зарядов. Сила, действующая на заряд, который движется в магнитном поле, называется силой Лоренца. Х.Лоренц (1853–1928), нидерландский физик, создатель классической электронной теории.

Если учесть, что сила тока в проводнике

,

где q – заряд носителей тока; n – концентрация носителей тока; υ – скорость их упорядоченного движения; S – площадь поперечного сечения проводника, то формула (20. 1) примет вид:

.

Силу Лоренца можно выразить, как

,

где N – общее количество носителей тока в проводнике (N=nV=nSl). С учетом того, что Sl=V (V – объем проводника):

                                                      ,                                           (20.8)

где α – угол между направлением вектора индукции магнитного поля и направлением вектора скорости движения положительного заряда. Направление силы Лоренца, как и силы Ампера, также определяется по правилу левой руки.

20.4. Определение удельного заряда электрона

Под действием силы Лоренца частицы, обладающие электрическим зарядом, движутся в магнитном поле по криволинейным траекториям. Причем если скорость частицы υ _┴ B, то траектория ее движения в магнитном поле представляет окружность (рис.20.7).

 

Рис. 20.7

Определив радиус этой окружности, скорость частицы и величину индукции магнитного поля, можно рассчитать удельный заряд этой частицы. Этот метод используется для определения удельного заряда электрона.

Так, ввиду малости величины силы тяжести, действующей на электрон, движущийся в перпендикулярном магнитном поле, можно записать в соответствии со вторым законом Ньютона:

 или ,

откуда радиус окружности равен

,

а удельный заряд электрона:

                                                          .                                               (20.9)

Для определения скорости необходимо знать ускоряющую разность потенциалов электрического поля. Известно, что на заряженную частицу со стороны электрического поля действует сила

,

где q – заряд частицы, E – напряженность электрического поля. Если скорость частицы υ<<c и электрическое поле является однородным, то она будет двигаться в поле с постоянным ускорением.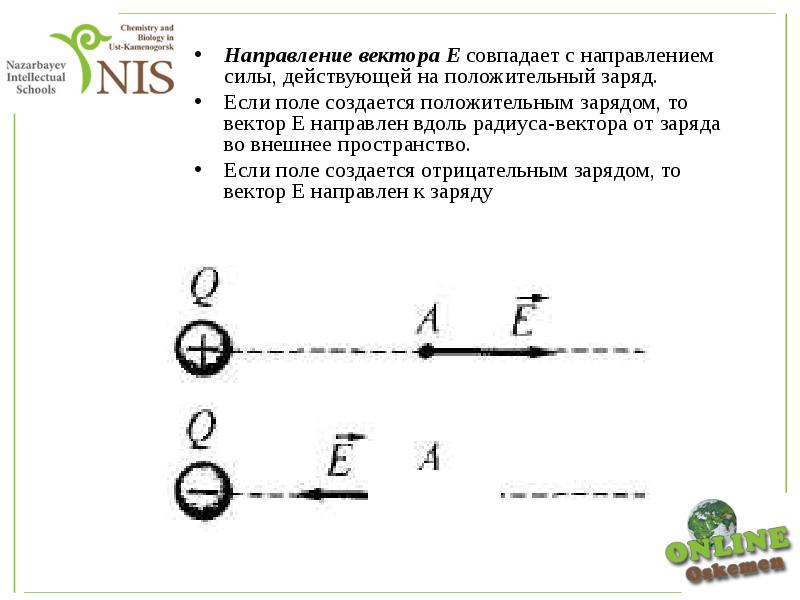

Если скорость частицы в момент включения электрического поля равна нулю, то изменение ее кинетической энергии происходит за счет работы сил поля, т.е.

,

где U – напряжение между точками входа и выхода частицы из электрического поля. Поэтому скорость частицы при выходе из электрического поля

                                                         .                                            (20.10)

С учетом (20.10)выражение (20.9) примет вид:

                                                          .                                             (20.11)

Опыты, проведенные таким образом, позволили рассчитать отношение

Если заряженная частица влетает в магнитное поле так, что направление ее скорости υ образует с вектором индукции магнитного поля B угол α (причем α≠0, α≠π), то траектория движения частицы представляет винтовую линию (рис.20.8).

 

Рис. 20.8

На частицу, которая движется вдоль линий индукции магнитного поля со скоростью υ_y, сила Лоренца не действует.

Перпендикулярная составляющая скорости υ_x обеспечивает движение частицы по окружности радиуса R. Таким образом, под действием двух составляющих скорости υ_y и υ_x частица движется по винтовой линии.

Радиус винтовой траектории согласно формуле (20.9) будет равен:

                                                       ,                                          (20.12)

а шаг винта

                                                      ,                                         (20.13)

где  – период обращения по окружности радиуса R.

Как уже отмечалось ранее, электрическое и магнитное поля являются частями единого электромагнитного поля. Поэтому в произвольной системе отсчета полная сила, с которой электромагнитное поле действует на заряженную частицу, равна векторной сумме электрической F_э и магнитной F_м составляющих, т. е.

.

 

20.5. Эффект Холла

Если пластинку, вдоль которой течет постоянный ток, поместить в перпендикулярное к ней магнитное поле, то между гранями, параллельными направлению тока и поля, возникает разность потенциалов. Это явление впервые исследовал американский физик Е.Холл (1811–1890) в 1879 г., и оно впоследствии было названо эффектом Холла (рис.20.9).

 

Рис. 20.9

Экспериментально определено, что разность потенциалов Холла определяется по формуле:

                              ,                  (20.14)

где b – ширина пластинки, j – плотность тока, B – магнитная индукция поля, R – коэффициент пропорциональности, который называется постоянной Холла.

Эффект Холла можно объяснить согласно электронной теории. Если магнитное поле отсутствует, ток в пластинке обусловлен электрическим полем E₀ (рис.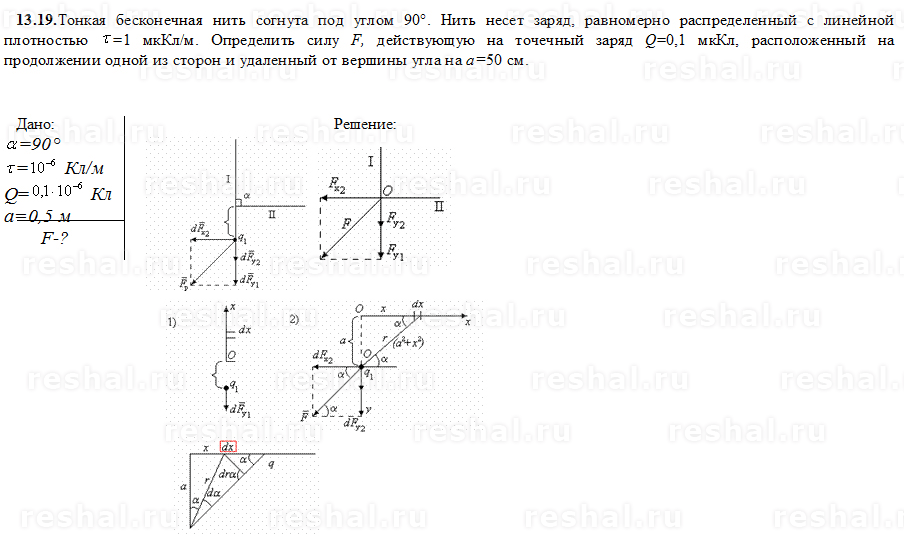 20.10).

 

Рис. 20.10

Потенциал во всех точках поверхности одинаков, в том числе и в точках 1 и 2. Электроны как носители отрицательного заряда двигаются со скоростью υ против вектора плотности тока j. При включении магнитного поля на каждый электрон действует сила Лоренца, направленная вдоль стороны b и численно равная F_л=eυB. Поэтому электроны приобретают составляющую скорости, которая направлена к верхней грани пластинки. Значит, на этой грани накапливается отрицательный заряд, на нижней – положительный. Таким образом, возникает поперечное электрическое поле E_B. Если сила F_B=eE_B уравновесит силу Лоренца F_л=eυB, то установится стационарное равновесие: eE_B=eυB. Откуда E_B=υB. Результирующее поле E равно векторной сумме полей E₀ и E_B. Так как эквипотенциальные линии перпендикулярны вектору напряженности поля E, то точки 1 и 2, которые ранее лежали на одной эквипотенциальной поверхности, уже имеют разный потенциал.

Значит, разность потенциалов между этими точками равна:

                                               .                                  (20.15)

Сравнивая выражения (20.14) и (20.15), определим постоянную Холла:

                                                           .                                              (20.16)

Из формулы (20.14) следует, что величина постоянной Холла, как и разности потенциалов Холла, зависит от концентрации носителей заряда в проводящей пластинке. Так как концентрация носителей тока в полупроводниках значительно меньше, чем в металлах, то и эффект Холла в полупроводниках наблюдать легче.

Эффект Холла используется в датчиках Холла, которые используют для измерения напряженности постоянных и переменных магнитных полей, силы и мощности электрического тока, превращения постоянного ток в переменный, модулирования и детектирования сигналов, анализа спектра частот, «чтения» магнитных записей и во многих элементах автоматики и вычислительной техники.

20.6. Принцип работымагнитогидродинамических генераторов

Магнитогидродинамический (МГД) генератор – энергетическая установка, в которой тепловая энергия рабочего тела (плазмы) превращается в электрическую. Принцип работы МГД-генератора основан на взаимодействии магнитного поля с заряженными частицами, которые движутся в нем (рис.20.11).

 

Рис. 20.11

Если создать поток плазмы в магнитном поле, линии индукции B которого перпендикулярны скорости зарядов υ, то под действием силы Лоренца произойдет их разделение. Это значит, положительные заряды магнитным полем будут отклоняться в одну сторону, а отрицательные – в другую. В результате один электрод заряжается положительно, а второй – отрицательно. Между ними возникает разность потенциалов. Если электроды соединить проводником, то в нем возникнет электрический ток.

Использование МГД-генераторов является перспективным направлением развития тепловой энергетики, так как позволяет получать КПД 60 %, в то время как КПД тепловых станций достигает 40 %. Органическое топливо, которое используется в МГД-генераторах, вместе с нагретым воздухом поступает в камеру сгорания с температурой 3000°C. Там они превращаются в плазму. С целью увеличения электропроводности плазмы в нее могут добавлять специальные присадки – соли калия или цезия, уменьшающие выброс серы в атмосферу, тем самым решая часть экологических проблем.

 

Напряженность электрического поля — как найти? Правила и примеры

Что такое электрическое поле

Однажды Бенджамин Франклин, чей портрет можно увидеть на стодолларовой купюре, запускал воздушного змея во время дождя с грозой. Столь странное занятие он выбрал не просто так, а с целью исследования природы молнии. Заметив, что на промокшем шнуре волоски поднялись вверх (т. е. он наэлектризовался), Франклин хотел прикоснуться к металлическому ключу. Но стоило ему приблизить палец, раздался характерный треск и появились искры. Сработало электрическое поле.

Это случилось в середине XVIII века, но еще целое столетие ученые не могли толком объяснить, как именно заряженные тела взаимодействуют друг с другом, не соприкасаясь. Майкл Фарадей первым выяснил, что между ними есть некое промежуточное звено. Его выводы подтвердил Джеймс Максвелл, который установил, что для воздействия одного такого объекта на другой нужно время, а значит, они взаимодействуют через «посредника».

В современной физике электрическое поле — это некая материя, которая возникает между заряженными телами и обусловливает их взаимодействие. Если речь идет о неподвижных объектах, поле называют электростатическим.

Объекты, несущие одноименные заряды, будут отталкиваться, а тела с разноименными зарядами — притягиваться.

Определение напряженности электрического поля

Для исследования электрического поля используются точечные заряды. Давайте выясним, что это такое.

Точечным зарядом называют такой наэлектризованный объект, размерами которого можно пренебречь, поскольку он слишком мал в сравнении с расстоянием, отделяющим этот объект от других заряженных тел.

Теперь поговорим непосредственно о напряженности, которая является одной из главных характеристик электрического поля. Это векторная физическая величина. В отличие от скалярных она имеет не только значение, но и направление.

Для того, чтобы исследовать электрическую напряженность, нужно в поле заряженного тела q₁ поместить еще один точечный заряд q₂ (допустим, они оба будут положительными). Со стороны q₁ на q₂ будет действовать некая сила. Очевидно, что для расчетов нужно иметь в виду как значение данной силы, так и ее направление, то есть вектор.

Напряженность электрического поля — это показатель, равный отношению силы, действующей на заряд в электрическом поле, к величине этого заряда.

Напряженность является силовой характеристикой поля. Она говорит о том, как сильно влияние поля в данной точке не только на другой заряд, но также на живые и неживые объекты.

Единицы измерения и формулы

Из указанного выше определения понятно, как найти напряженность электрического поля в некой точке:

E = F / q, где F — действующая на заряд сила, а q — величина заряда, расположенного в данной точке.

Если нужно выразить силу через напряженность, мы получим следующую формулу:

F = q × E

Направление напряженности электрического поля всегда совпадает с направлением действующей силы. Если взять отрицательный точечный заряд, формулы будут работать аналогично.

Поскольку сила измеряется в ньютонах, а величина заряда — в кулонах, единицей измерения напряженности электрического поля является Н/Кл (ньютон на кулон).

Принцип суперпозиции

Допустим, у нас есть несколько зарядов, которые перекрестно взаимодействуют и образуют общее поле. Чему равна напряженность электрического поля, создаваемого этими зарядами?

Было установлено, что общая сила воздействия на конкретный заряд, расположенный в поле, является суммой сил, действующих на данный заряд со стороны каждого тела. Из этого следует, что и напряженность поля в любой взятой точке можно вычислить, просуммировав напряжения, создаваемые каждым зарядом в отдельности в той же точке (с учетом вектора). Это и есть принцип суперпозиции.

Е = Е₁+ Е₂+ Е₃… + Е_n.

Это правило корректно для любых полей, за некоторыми исключениями. Принцип суперпозиции не соблюдается в следующих случаях:

• расстояние между зарядами очень мало — порядка 10^-15м;

• речь идет о сверхсильных полях с напряженностью более 10²⁰в/м.

Но задачи с такими данными выходят за пределы школьного курса физики.

Напряженность поля точечного заряда

У электрического поля, создаваемого точечным зарядом, есть одна особенность — ввиду малой величины самого заряда оно очень слабо влияет на другие наэлектризованные тела. Именно поэтому такие «точки» используют для исследований.

Но прежде чем рассказать, от чего зависит напряженность электрического поля точечного заряда, рассмотрим подробнее, как взаимодействуют эти заряды.

Закон Кулона

Предположим, в вакууме есть два точечных заряженных тела, которые статично расположены на некотором расстоянии друг от друга. В зависимости от одноименности или разноименности они могут притягиваться либо отталкиваться. В любом случае на эти объекты воздействуют силы, направленные по соединяющей их прямой.

Закон Кулона Модули сил, действующих на точечные заряды в вакууме, пропорциональны произведению данных зарядов и обратно пропорциональны квадрату расстояния между ними.

Силу электрического поля в конкретной точке можно найти по формуле: где q₁ и q₂ — модули точечных зарядов, r — расстояние между ними.

В формуле участвует коэффициент пропорциональности k, который был определен опытным путем и представляет собой постоянную величину. Он обозначает, с какой силой взаимодействуют два тела с зарядом 1 Кл, расположенные на расстоянии 1 м.

Важно!

Сила взаимодействия двух точечных зарядов остается прежней при появлении сколь угодно большого количества других зарядов в данном поле.

Учитывая все вышесказанное, напряжение электрического поля точечного заряда в некой точке, удаленной от заряда на расстояние r, можно вычислить по формуле:

Итак, мы выяснили, что называется напряженностью электрического поля и от чего зависит эта величина. Теперь посмотрим, как она изображается графическим способом.

Линии напряженности

Электрическое поле нельзя увидеть невооруженным глазом, но можно изобразить с помощью линий напряженности. Графически это будут непрерывные прямые, которые связывают заряженные объекты. Условная точка начала такой прямой — на положительном заряде, а конечная точка — на отрицательном.

Линии напряженности — это прямые, которые совпадают с силовыми линиями в системе из положительного и отрицательного зарядов. Касательные к ним в каждой точке электрического поля имеют то же направление, что и напряженность этого поля.

При графическом изображении силовых линий можно передать не только направление, но и величину напряженности электрического поля (разумеется, условно). В местах, где модуль напряженности выше, принято делать более густой рисунок линий. Есть и случаи, когда густота линий не меняется — это бывает при изображении однородного поля.

Однородное электрическое поле создается разноименными зарядами с одинаковым модулем, расположенными на двух металлических пластинах. Линии напряженности между этими зарядами представляют собой параллельные прямые всюду, за исключением краев пластин и пространства за ними.

Сила Лоренца

Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца в честь великого голландского физика Х. Лоренца (1853 — 1928) — основателя электронной теории строения вещества. Силу Лоренца можно найти с помощью закона Ампера.

Модуль силы Лоренца равен отношению модуля силы F, действующей на участок проводника длиной Δl, к числу N заряженных частиц, упорядоченно движущихся в этом участке проводника:

Рассмотрим отрезок тонкого прямого проводника с током. Пусть длина отрезка Δl и площадь поперечного сечения проводника S настолько малы, что вектор индукции магнитного поля можно считать одинаковым в пределах этого отрезка проводника. Сила тока I в проводнике связана с зарядом частиц q, концентрацией заряженных частиц (числом зарядов в единице объема) и скоростью их упорядоченного движения v следующей формулой:

I = qnvS ( 2 )

Модуль силы, действующей со стороны магнитного поля на выбранный элемент тока, равен:

F = | I |B Δl sin α

Подставляя в эту формулу выражение ( 2 ) для силы тока, получаем:

F = | q | nvS Δl B sin α = v | q | NB sin α, где N = nSΔl — число заряженных частиц в рассматриваемом объеме. Следовательно, на каждый движущийся заряд со стороны магнитного поля действует сила Лоренца, равная: где α — угол между вектором скорости и вектором магнитной индукции. Сила Лоренца перпендикулярна векторам магнитной индукции и скорости упорядоченного движения заряженных частиц. Ее направление определяется с помощью того же правила левой руки, что и направление силы Ампера.

Так как сила Лоренца перпендикулярна скорости частицы, то она не совершает работы. Согласно теореме о кинетической энергии это означает, что сила Лоренца не меняет кинетическую энергию частицы и, следовательно, модуль ее скорости. Под действием силы Лоренца меняется лишь направление скорости частицы.

---

Другие заметки по физике

В каком направлении магнитная сила действует на заряд? — Mvorganizing.org

В каком направлении магнитная сила действует на заряд?

Направление магнитной силы на движущийся заряд перпендикулярно плоскости, образованной v и B, и следует правилу правой руки – 1 (RHR-1), как показано.

Как сравниваются заряды, когда два объекта заряжаются посредством викторины трения?

Как сравниваются заряды, когда два объекта заряжаются за счет трения? Предметы становятся противоположно заряженными и имеют одинаковый заряд. Объекты становятся положительно заряженными и имеют одинаковый заряд. Предметы становятся отрицательно заряженными и имеют разное количество заряда.

Как сравниваются заряды, когда два объекта заряжаются за счет трения, объекты становятся противоположно заряженными и имеют равные количества заряда?

Ответ: Объекты становятся противоположно заряженными и имеют одинаковый заряд. — Трение: два изначально нейтральных объекта трутся друг о друга. Электроны перемещаются от одного объекта к другому: поэтому один объект становится заряженным положительно, а другой — отрицательно.

Какая способность материала препятствовать прохождению заряда?

Тенденция материала противодействовать потоку заряда называется сопротивлением.

Какой материал не позволяет электронам течь?

Материалы, через которые проходит электричество, называются проводниками. Медная проволока — хороший проводник. Материалы, не пропускающие через них электричество, называются изоляторами. Пластик — хороший изолятор.

Какой материал препятствует потоку электронов?

бобби

Вопрос	Ответ
тенденция материала противодействовать потоку электронов называется _____	сопротивление
ток измеряется в _______	ампер
электрическая мощность равна _______ x разность напряжений	текущий
сухая камера используется в льняном свете, чтобы скрыть ____ от света	электрическая энергия

Что препятствует течению тока?

Сопротивление.Противоположностью проводимости является сопротивление — величина, которая описывает, насколько сильно материал препятствует прохождению электрического тока.

В чем причина перетекания заряда?

Отрицательно заряженные электроны удаляются из атомов, атомы остаются в виде положительных ионов. Разность потенциалов между ними заставляет электроны притягиваться обратно, создавая поток электрического заряда: текущее электричество.

Как называется расход потока?

Электрический ток

Какой поток зарядки?

Поток заряда — это процесс подачи или добавления электрического заряда к объекту или потери электрического заряда (в основном электронов) объекта.

Текущий поток заряда?

Ток изначально определялся как поток зарядов от положительного к отрицательному. Позже ученые обнаружили, что ток на самом деле представляет собой поток отрицательно заряженных электронов от отрицательного к положительному.

Как генерируется ток?

Электрический ток можно получить, перемещая металлический провод через магнитное поле. Это также отличается от статического электричества, которое представляет собой накопление зарядов на поверхности. Электрические генераторы вращают катушку проводов через магнитное поле.

Как происходит зарядка?

Электрический заряд создается, когда электроны переносятся на объект или удаляются от него. Поскольку электроны имеют отрицательный заряд, когда они добавляются к объекту, он становится отрицательно заряженным. Когда электроны удаляются из объекта, он становится положительно заряженным.

9,3 Электрическое поле | Электростатика

Рассчитайте напряженность электрического поля \ (\ text {20} \) \ (\ text {m} \) из \ (\ text {7} \) \ (\ text {nC} \) плата.{-1} $} \ end {align *}

Два заряда \ ({Q} _ {1} = — \ text {6} \ text {pC} \) и \ ({Q} _ {2} = — \ text {8} \ text {pC} \ ) разделены расстояние \ (\ text {3} \) \ (\ text {км} \). Какова напряженность электрического поля в точке, \ (\ text {2} \) \ (\ text {km} \) из \ ({Q} _ {1} \) и \ (\ text {1} \) \ (\ text {km} \) из \ ({Q} _ {2} \)? Смысл находится между \ ({Q} _ {1} \) и \ ({Q} _ {2} \).

Нам нужно вычислить электрическое поле на расстоянии от двух данных зарядов.{-1} $} \) в направлении заряда \ (- \ text {8} \) \ (\ text {pC} \).

Формула магнитной силы (заряд-скорость)

Когда заряженная частица движется в магнитном поле, на движущуюся заряженную частицу действует сила. Формула для силы зависит от заряда частицы и векторного произведения скорости частицы и магнитного поля. Направление вектора силы можно найти, вычислив перекрестное произведение, если заданы направления вектора, или с помощью «правила правой руки».Представьте себе вашу правую руку, указательный палец которой направлен в направлении вектора скорости частицы. Затем согните пальцы в направлении вектора магнитного поля. Направление большого пальца — это направление перекрестного произведения векторов. Если заряд положительный, направление силы будет в направлении вашего большого пальца. Если заряд отрицательный, направление силы будет противоположным. Единица силы — ньютоны (Н), единица заряда — кулоны (Кл), единица скорости — метры в секунду (м / с), единица магнитного поля — тесла (Тл).

= вектор магнитной силы (Ньютоны, Н)

q = заряд движущейся частицы (Кулоны, Кл)

= вектор скорости частицы (м / с)

v = величина скорости частицы (м / с)

= вектор магнитного поля (тесла, Тл)

B = величина магнитного поля (тесла, Тл)

= угол между векторами скорости и магнитного поля (радианы)

= вектор направления поперечного произведения (без единиц измерения)

Формула магнитной силы (заряд-скорость) Вопросы:

1) Пучок протонов, каждый из которых имеет заряд, движется через однородное магнитное поле с величиной 0. 60Т. Направление движения протонов — справа от страницы (экрана), а направление магнитного поля — вниз-вправо, под углом от направления протона. Какова величина и направление магнитной силы, действующей на каждый протон?

Ответ: Величину магнитной силы, действующей на протон, можно найти по формуле:

Сила, действующая на каждый протон, имеет величину.

Направление вектора силы можно найти с помощью «правила правой руки». Протоны движутся вправо, поэтому представьте, что ваш указательный палец правой руки направлен в этом направлении. Вектор магнитного поля направлен вниз вправо, поэтому согните пальцы вниз. Ваш большой палец теперь будет указывать на страницу (или экран). Поскольку заряд протонов положительный, это направление вектора силы.

2) Капля масла с зарядом движется со скоростью.К капле прикладывают магнитное поле с величиной и направлением. Какова результирующая магнитная сила, действующая на каплю масла, выраженная в единичном векторе?

Ответ: Магнитную силу, действующую на каплю масла, можно найти, решив кросс-произведение формулы силы:

Перекрестное произведение двух векторов и составляет:

Вектор скорости:

Вектор магнитного поля:

Итак, это:

Магнитная сила, действующая на каплю масла, теперь может быть рассчитана по формуле:

Магнитная сила, действующая на каплю масла, означает, что она имеет величину 2. 88N по направлению.

Solutions HW # 1 — Physics 122

Solutions HW # 1 — Physics 122

---

Solutions Homework Set # 1 — Physics 122

---

Задача 1.

Поскольку две сферы идентичны, общий заряд будет распределен одинаково через них, когда они касаются. Общий начальный заряд равен

Таким образом, окончательный заряд равен

.

---

Задача 2.

Электрическое поле в средней точке, обусловленное зарядом Q, равно

.

Электрическое поле в средней точке, обусловленное зарядом q, равно

.

Знак минус в этих уравнениях означает, что для положительного заряда q, электрическое поле в средней точке будет направлено влево. Общая электрическое поле в средней точке представляет собой векторную сумму электрических полей генерируется двумя зарядами:

Направление электрического поля в средней точке либо к влево или вправо, в зависимости от того, какой из двух зарядов более положительный. Примечание: задача требует величины электрического поля!

---

Задача 3.

Электрическая сила между зарядами в окончательной конфигурации равна равно

---

---

Задача 4.

Рисунок 1. Проблема 4 .

На основании симметрии распределения заряда можно сделать вывод что электрическое поле в точке P будет направлено прямо вверх или прямо вниз для положительного и отрицательного распределения заряда соответственно.Рассмотреть возможность небольшой сегмент пластикового стержня под углом [тета]. Если угловая ширина этого сегмента равна d [theta], то сумма заряда на этом сегмент равен:

Величина полного электрического поля в точке P из-за этого небольшого сегмента. равно:

Из-за аргумента симметрии нам нужно рассматривать только вертикальную компонент этого поля:

Чтобы получить полное электрическое поле в точке P, необходимо просуммировать все сегменты, что эквивалентно изменению [theta] от — [pi] / 2 до + [пи] / 2:

---

---

Задача 5.

Когда шары свешиваются вертикально, действуют только две силы. на них: сила тяжести и напряжение. Они действуют противоположно направлениях, а поскольку система находится в состоянии покоя, результирующая сила, действующая на шары должны быть равны 0 Н. Таким образом:

Примечание: убедитесь, что вы используете правильные единицы измерения. Если вы хотите рассчитать напряжение в Ньютонах, вам нужно использовать кг для массы.

---

Задача 6.

Рис. 2. Задача 6: силы на шаре.

После добавления заряда в систему действуют три силы. каждый шар: гравитационная сила, натяжение и электрическая сила. Эти силы схематически показаны на рисунке 2. Поскольку система находится на в остальном, чистая сила, действующая на каждый мяч, должна быть равна нулю. Рассмотрим вертикаль составляющая чистой силы, действующей на каждый мяч:

Это уравнение сразу говорит нам, каково натяжение каждой нити:

---

Задача 7.

Рассмотрим горизонтальную составляющую чистой силы, действующей на каждый мяч:

Здесь r — расстояние между двумя заряженными шарами. Это уравнение можно переписать, чтобы решить для r:

Используя тригонометрию, мы можем определить следующее соотношение между угол [тета], длина строки l и расстояние r:

Это уравнение можно использовать для решения относительно l:

---

---

Задача 8.

Электрический пробой происходит, когда электрическое поле достигает критического значения. значение Ecrit. Сила на свободный электрон в этом поле равна

Результирующее ускорение равно

Если предположить, что электрон стартует из состояния покоя, его скорость в момент времени t будет равна равно:

Его кинетическая энергия в момент времени t будет равна

.

Задача определяет кинетическую энергию электрона. Предыдущее уравнение можно использовать, чтобы определить, в какое время электрон достигает этого кинетического энергия:

В это время электрон переместится на расстояние d, равное

.

---

---

Задача 9.

Используйте график, показанный в вашем задании, для определения электрического поля. в интересующем месте E (x). Сила, действующая на частицу заряда q, равна равно

Таким образом, соответствующее ускорение, испытываемое этой частицей, равно к

---

---

Задача 10.

Рисунок 3. Проблема 10.

Для расчета электрического поля, создаваемого прямоугольным распределением заряда. сначала рассмотрим электрическое поле, создаваемое одной стороной, например сторона длины L. Возникновение электрического поля очень похоже на к возникновению электрической силы на точечном заряде q из-за бесконечно длинное прямое распределение заряда (см. Пример 2 в Главе 23), за исключением что вместо интегрирования по [theta] между — [pi] / 2 и [pi] / 2, мы необходимо интегрировать в меньшем угловом диапазоне.

Рассмотрим ситуацию, показанную на рисунке 3. Максимальный угол [тета] равен равно

Теперь можно рассчитать электрическое поле в позиции, показанной на рисунке 3. из уравнения (12) в главе 23, изменив пределы интегрирования:

В задаче есть два стержня длиной L, разделенные расстоянием W. Электрическое поле в точке A будет направлено в вертикальном направлении, поскольку горизонтальные компоненты отменяются (см. рисунок 4).Предыдущее уравнение может можно использовать для расчета величины электрического поля из-за этих двух распределение зарядов:

Похожая формула может быть получена для поля в A, созданного двумя стержней длиной W. Полное электрическое поле в точке А равно сумме этих поля:

Рисунок 4. Задача 10.

---

Еще раз о концепции поля — College Physics chapters 1-17

Контактные силы, например, между бейсбольным мячом и битой, в малом масштабе объясняются взаимодействием зарядов в атомах и молекулах в непосредственной близости. Они взаимодействуют посредством сил, которые включают в себя кулоновскую силу . Действие на расстоянии — это сила между объектами, которые находятся недостаточно близко, чтобы их атомы могли «коснуться». То есть они разделены более чем несколькими атомными диаметрами.

Например, заряженный резиновый гребешок притягивает нейтральные кусочки бумаги на расстоянии посредством кулоновской силы. Очень полезно представить объект, окруженный в пространстве силовым полем . Силовое поле переносит силу на другой объект (называемый тестовым объектом) на некотором расстоянии.

Поле — это способ концептуализации и отображения силы, которая окружает любой объект и действует на другой объект на расстоянии без видимой физической связи. Например, гравитационное поле, окружающее Землю (и все другие массы), представляет собой гравитационную силу, которая возникла бы, если бы другая масса была помещена в заданную точку внутри поля.

Таким же образом кулоновское силовое поле, окружающее любой заряд, распространяется по всему пространству. 2} [/ latex], для точечного заряда (частица, имеющая заряд [латекс] \ boldsymbol {Q} [/ latex]), действующего на пробный заряд [латекс] \ boldsymbol {q} [/ latex] на расстоянии [латекс] \ boldsymbol {r} [/ latex] (см. [ссылка]).И величина, и направление кулоновского силового поля зависят от [латекса] \ boldsymbol {Q} [/ latex] и тестового заряда [латекс] \ boldsymbol {q} [/ latex].

Рис. 1. Кулоновское силовое поле из-за положительного заряда Q показано действующим на два разных заряда. Оба заряда находятся на одинаковом расстоянии от Q . (a) Поскольку q ₁ положительное, сила F 1 , действующая на него, является отталкивающей.(b) Заряд q ₂ отрицателен и по величине больше, чем q ₁ , поэтому сила F ₂ , действующая на него, привлекательна и сильнее, чем Ф. ₁ . Таким образом, кулоновское силовое поле не является уникальным в любой точке пространства, потому что оно зависит от тестовых зарядов q ₁ и q ₂ , а также заряда Q .

Для упрощения мы предпочли бы иметь поле, которое зависит только от [latex] \ boldsymbol {Q} [/ latex], а не от тестового заряда [latex] \ boldsymbol {q} [/ latex]. Электрическое поле определяется таким образом, что оно представляет только заряд, создающий его, и уникально в каждой точке пространства. В частности, электрическое поле [латекс] \ boldsymbol {E} [/ latex] определяется как отношение кулоновской силы к испытательному заряду:

[латекс] \ boldsymbol {E =} [/ latex] [латекс] \ boldsymbol {\ frac {F} {q}} [/ latex],

где [латекс] \ boldsymbol {F} [/ latex] — электростатическая сила (или кулоновская сила), действующая на положительный тестовый заряд
[латекс] \ boldsymbol {q} [/ latex]. Подразумевается, что [латекс] \ boldsymbol {E} [/ latex] находится в том же направлении, что и
[латекс] \ boldsymbol {F} [/ latex]. Также предполагается, что [латекс] \ boldsymbol {q} [/ latex] настолько мал, что не меняет распределение заряда, создающее электрическое поле. Единицы электрического поля — ньютоны на кулон (Н / Кл). Если электрическое поле известно, то электростатическая сила, действующая на любой заряд [латекс] \ boldsymbol {q} [/ latex], получается просто умножением заряда на электрическое поле, или [латекс] \ boldsymbol {\ textbf {F} = q \ textbf {E}} [/ latex].2}} [/ латекс]

Таким образом, электрическое поле зависит только от заряда [латекс] \ boldsymbol {Q} [/ latex] и расстояния [латекс] \ boldsymbol {r} [/ latex]; он полностью не зависит от тестового заряда [латекс] \ boldsymbol {q} [/ latex].

Расчет электрического поля точечного заряда

Вычислите силу и направление электрического поля [латекс] \ boldsymbol {E} [/ latex], возникающего из-за точечного заряда 2,00 нКл (нано-кулонов) на расстоянии 5,00 мм от заряда. 5 \; \ textbf {N} / \ textbf {C}.} \ End {array} [/ latex]

Обсуждение

Напряженность электрического поля одинакова в любой точке на расстоянии 5,00 мм от заряда [latex] \ boldsymbol {Q} [/ latex], который создает поле. Он положительный, что означает, что он имеет направление, указывающее от заряда [латекс] \ boldsymbol {Q} [/ latex].

Расчет силы, действующей на точечный заряд электрическим полем

Какую силу оказывает электрическое поле, найденное в предыдущем примере, на точечный заряд [латекс] \ boldsymbol {-0.250 \; \ mu \ textbf {C}} [/ латекс]?

Стратегия

Поскольку мы знаем напряженность электрического поля и заряд в поле, силу, действующую на этот заряд, можно вычислить, используя определение электрического поля [latex] \ boldsymbol {\ textbf {E} = \ textbf {F} / q} [ / latex] преобразован в [latex] \ boldsymbol {\ textbf {F} = q \ textbf {E}} [/ latex].

Раствор

Величина силы, действующей на заряд [латекс] \ boldsymbol {q = -0. 250 \; \ mu \ textbf {C}} [/ latex], оказываемая полем напряженности [латекс] \ boldsymbol {E = 7.5 \; \ textbf {N} / \ textbf {C})} \\ [1em] & \ boldsymbol {0.180 \; \ textbf {N}.} \ End {array} [/ latex]

Поскольку [latex] \ boldsymbol {q} [/ latex] отрицательно, сила направлена ​​противоположно направлению поля.

Обсуждение

Сила привлекательна, как и следовало ожидать от разных зарядов. (Поле было создано положительным зарядом и здесь действует на отрицательный заряд.) Заряды в этом примере типичны для обычного статического электричества, а полученная умеренная сила притяжения аналогична силам, возникающим в статическом цеплении и подобных ситуациях.

Исследования PhET: электрическое поле грез

Играй в мяч! Добавьте заряды в Поле Мечты и посмотрите, как они отреагируют на электрическое поле. Включите фоновое электрическое поле и отрегулируйте направление и величину.

Рис. 2. Электрическое поле снов

Сила, действующая на движущуюся частицу и токопроводящий провод с примерами

Сила, действующая на движущиеся частицы и токопроводящий провод

Как мы узнали ранее, заряженные частицы создают вокруг себя электрическое поле. В электрическом поле на заряженные частицы действует сила F = qE. Движение зарядов в электрическом поле производит ток, в результате чего создается магнитное поле. Это магнитное поле действует на заряженные частицы внутри поля. Эксперименты, проведенные по этому вопросу, показывают, что мы можем найти силу, действующую на провод с током, по следующей формуле:

F = B.i.l.sinß

где B — напряженность магнитного поля, i — сила тока, l — длина провода, а ß — угол между магнитным полем и проводом.

Находим направление силы по правилу правой руки. На приведенном ниже рисунке показано направление тока и силы магнитного поля;

Если угол между током и магнитным полем ß;

1. ß = 0, тогда sinß = 0, F = 0

2. ß = 180, тогда sinß = 0, F = 0

3. ß = 90, тогда sinß = 1, F = B.i.l

Можно сказать, что если направление тока и магнитное поле параллельны друг другу, то на провод не действует сила.

Пример: Какая из магнитных сил, действующих на провода, равна нулю, как показано на рисунке ниже?

Поскольку направления токов i ₁ и i ₂ параллельны направлению магнитного поля, на эти токи не действует сила. F ₁ = F ₂ = 0

i ₃ ток перпендикулярен магнитному полю, таким образом,

F ₃ = B.i ₃ .l

Направление магнитной силы к нам.

Пример: Найдите направления магнитных сил, действующих на токи i1, i ₂ в постоянном магнитном поле.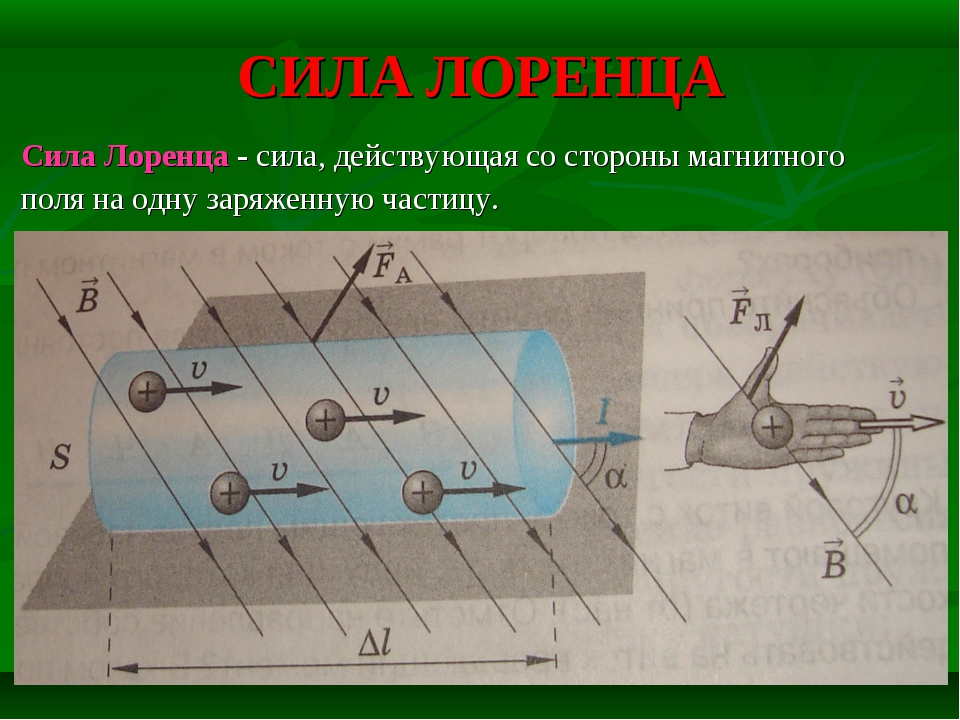

Магнитные силы, действующие на токи i1 и i2, показаны на рисунке ниже.

Сила, действующая на заряженную частицу

Сила, действующая на ток, объяснена выше. Мы узнали, что ток создается движением заряженных частиц. Таким образом, сила, действующая на провод с током, представляет собой сумму сил, действующих на каждую заряженную частицу, через которую проходит этот ток. Если частица имеет заряд q , скорость v и она помещена в магнитное поле с силой B , действующей на эту частицу и ß , расстояние между скоростью и магнитным полем определяется по следующей формуле;

F = q.v.B . sinß

Если;

1. v = 0, тогда F = 0 нет силы, действующей на неподвижную частицу в магнитном поле.

2. ß = 0, тогда sin0 = 0 и F = 0

3. ß = 180, тогда sin180 = 0 и F = 0, силовые линии магнитного поля и скорость частицы параллельны друг другу, тогда на них не действует сила.

4. ß = 90, тогда sin90 = 1, F = q.v.B

Силы токов, переносящих провода друг к другу

Эксперименты, проведенные на этом предмете, показывают, что токи в одном направлении притягиваются друг к другу, поскольку они создают противоположные магнитные поля.Напротив, токи в противоположных направлениях отталкиваются друг от друга, поскольку они создают магнитные поля, имеющие одинаковые направления. Мы находим силу, приложенную к каждому из них, по следующей формуле:

Где; l — длина проводов, d — расстояние между ними.

Экзамены на магнетизм и решения

Магнитное поле вокруг соленоида <Назад		Далее> Трансформеры

Задача по электростатической физике, не можете определить направление результирующей силы?

Привет, Эшли!

Давайте разберемся в проблеме.Как вы знаете, уравнение силы между двумя заряженными частицами:

F = kq ₁ q ₂ / r ²

В направлении x мы смотрим на силу, которую создает заряд 1. при заряде 3. При работе с этим уравнением мы всегда предполагаем, что заряды будут отталкиваться, и результирующий знак в конце определит, верно ли наше предположение или предположение было противоположным:

Q ₁ составляет 4 метра в положительном направлении оси x и имеет заряд -16×10 ^-6 кулонов.

F ₁₃ = kq ₁ q ₃ / r ² = (9×10 ⁹ ) (- 16×10 ^-6 ) (- 4,0×10 ^-6 ) / 16 = 0,036N

Поскольку у нас есть положительный результат, предположение об отталкивании было правильным, и Q ₃ будет испытывать силу 0,036 Н в отрицательном направлении оси x из-за Q ₁ .

Теперь в направлении Y, Q ₂ находится на расстоянии 3 метров и имеет заряд 9,0×10 ^-6 . Опять же, наше предположение будет отталкиванием:

F ₂₃ = kq ₂ q ₃ / r ² = (9×10 ⁹ ) (9.0×10 ^-6 ) (- 4,0×10 ^-6 ) / 16 = -0,036N

Поскольку у нас есть отрицательный результат, предположение об отталкивании было неверным, и Q ₃ будет испытывать силу 0,036N в положительное направление оси Y из-за Q ₂ .

Итак, у нас есть два вектора: 0,036N в положительном направлении Y и 0,036 в отрицательном направлении X. Величина этой силы является просто теоремой Пифагора:

F ² = F _x ² + F _y ² , F ² = (-0.036) ² + (- 0,036) ² = 0,002529, F = 0,0509N

Что касается направления, мы можем сделать это интуитивно — мы знаем, что если величины одинаковы, направление будет кратным 45. градусов (45, 135, 225 или 315). Сила направления Y втянет нас в квадранты 1 и 2, в то время как сила направления X втянет нас в квадранты 2 и 3. Оба этих притяжения имеют общий квадрант 2, поэтому угол составляет 135 градусов.

Математический способ использования функции обратного тангенса для рассчитанных нами компонентов:

tan (theta) = Y / X

Одна вещь, которую следует отметить в отношении функции обратного тангенса, заключается в том, что, когда X отрицателен, мы должны добавить 180 градусов к нему.Это потому, что касательная функция действительна только для положительных значений X.

Итак, на самом деле наш угол:

theta = tan ^-1 (y / x) + 180 = tan ^-1 (0,036 / -0,036) +180 = -45 + 180 = 135 градусов

Таким образом подтверждая наш геометрический подход.

Надеюсь, это поможет!

Кристофер

.