Проверить, является ли векторное поле потенциальным и соленоидальным. Решение задач по высшей математике
Векторное поле называется потенциальным векторным полем если оно является градиентом некоторого скалярного поля . Это скалярное поле называется соответственно потенциалом векторного поля . Векторное поле называется вихревым или соленоидальным векторным полем, если через любую замкнутую поверхность S его поток равен нулю.
Условие задачи
Проверить, является ли векторное поле потенциальным и соленоидальным. В случае потенциальности поля найти его потенциал.
Решение задачи
Задали объемную контрольную? Скоро важный зачет/экзамен? Нет времени на выполнение работы или подготовку к зачету/экзамену, но есть деньги? На сайте 100task.ru можно заказать решение задач, контрольных или онлайн-помощь на зачете/экзамене 〉〉
Если вам сейчас не требуется помощь, но может потребоваться в дальнейшем, то, чтобы не потерять контакт, вступайте в группу ВК.
Проверка на потенциальность
Для потенциальности поля необходимо и достаточно, чтобы
Таким образом, поле является потенциальным.
Проверка на соленоидальность
Для соленоидальности поля:
Таким образом, поле не является соленоидальным.
Вычисление потенциала
Потенциал можно вычислить по формуле:
Выберем в качестве точки точку
К оглавлению решебника по высшей математике 〉
Нахождение потенциала / Теория поля / 3dstroyproekt.ru
В предыдущем разделе мы доказали, что если выполняются условия потенциальности поля $\bar { a } (\mathbf { \textit { M } } )$, то $\varphi (M)=\int\limits_ { \mathop { M_0 M } \limits^\cup } { \bar { a } d\bar { r } } $, где $M_0 \in V$ — фиксированная точка. Обычно, если в точке $\mathbf { \textit { O } } (0,0,0)$ поле не имеет особенностей, то в качестве точки $M_0 (x_0 ,y_0 ,z_0 )$ берётся именно эта точка, если в этой точке поле не определено, берётся другая точка.
Интегрирование ведут по пути, состоящим из отрезков, параллельных координатным осям. В результате получим $\varphi (M)=\int\limits_ { x_0 } ^x { P(x,y_0 ,z_0 )dx } +\int\limits_ { y_0 } ^y { Q(x,y,z_0 )dy } +\int\limits_ { z_0 } ^z { R(x,y,z)dz } $.
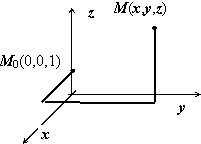
Пример 1
Доказать, что поле $\bar { a } (x,y,z)=\frac { y\cos (xy) } { z } \bar { i } +\frac { x\cos (xy) } { z } \bar { j } -\frac { \sin (xy) } { z^2 } \bar { k } $ потенциально и найти потенциал этого поля.
Решение
Мы будем доказывать, что это поле потенциально в любой односвязной области $\mathbf { \textit { V } } $, не содержащей точку $\mathbf { \textit { O } } (0,0,0)$. Условие безвихревости поля $\bar { a } $:
$rot\bar { a } (M)=\left| { \begin{array} { l } \,\bar { i } \,\,\,\,\bar { j } \,\,\,\bar { k } \\ \frac { \partial } { \partial x } \,\,\frac { \partial } { \partial y } \,\,\frac { \partial } { \partial z } \\ \,P\,\,Q\,\,\,R \\ \end{array} }\right|=\left( { \frac { \partial R } { \partial y } -\frac { \partial Q } { \partial z } }\right)\bar { i } +\left( { \frac { \partial P } { \partial z } -\frac { \partial R } { \partial x } }\right)\bar { j } +\left( { \frac { \partial Q } { \partial x } -\frac { \partial P } { \partial y } }\right)\bar { k } =0$ в координатной форме сводится к равенствам $\frac { \partial R } { \partial y } =\frac { \partial Q } { \partial z } , \frac { \partial P } { \partial z } =\frac { \partial R } { \partial x } , \frac { \partial Q } { \partial x } =\frac { \partial P } { \partial y } $.
В нашем поле $P(x,y,z)=\frac { y\cos (xy) } { z } , Q(x,y,z)=\frac { x\cos (xy) } { z } ,R(x,y,z)=-\frac { \sin (xy) } { z^2 } $. Находим производные:
$\frac { \partial R } { \partial y } =-\frac { x\cos (xy) } { z^2 } $,
$\frac { \partial Q } { \partial z } =-\frac { x\cos (xy) } { z^2 } =\frac { \partial R } { \partial y } $,
$\frac { \partial P } { \partial z } =-\frac { y\cos (xy) } { z^2 } $,
$\frac { \partial R } { \partial x } =-\frac { y\cos (xy) } { z^2 } =\frac { \partial P } { \partial z } $,
$\frac { \partial Q } { \partial x } =\frac { \cos (xy)-xy\sin (xy) } { z } $,
$\frac { \partial P } { \partial y } =\frac { \cos (xy)-xy\sin (xy) } { z } =\frac { \partial Q } { \partial x } $ Потенциальность поля доказана.
Ищем потенциал. Интеграл $\varphi (M)=\int\limits_ { \mathop { M_0 M } \limits^\cup } { \bar { a } d\bar { r } } $ вычисляем по изображённому на рисунке пути, отправляясь от точки $\mathbf { \textit { M } } _ { 0 } $(0,0,1). $\varphi (x,y,z)=\int\limits_0^x { \frac { 0\cdot \cos (x\cdot 0) } { 1 } dx } +\int\limits_0^y { \frac { x\cdot \cos (xy) } { 1 } dy } -\int\limits_1^z { \frac { \sin (xy) } { z^2 } dz } = =\left. { \sin (xy) }\right|_0^y +\left. { \frac { \sin (xy) } { z } }\right|_1^z =\sin (xy)+\left[ { \frac { \sin (xy) } { z } -\sin (xy) }\right]=\frac { \sin (xy) } { z } $.
Если бы мы взяли в качестве точки $\mathbf { \textit { M } } _ { 0 } $ другую точку $\mathbf { \textit { M } } _ { 1 } $, то получили бы выражение, отличающееся на некоторую постоянную { более точно, на $C=\int\limits_ { \mathop { M_0 M_1 } \limits^\cup } { \bar { a } d\bar { r } } )$, поэтому $\varphi (x,y,z)= \frac { \sin (xy) } { z } +C$.
7. Потенциальные векторные поля
A = grad u = 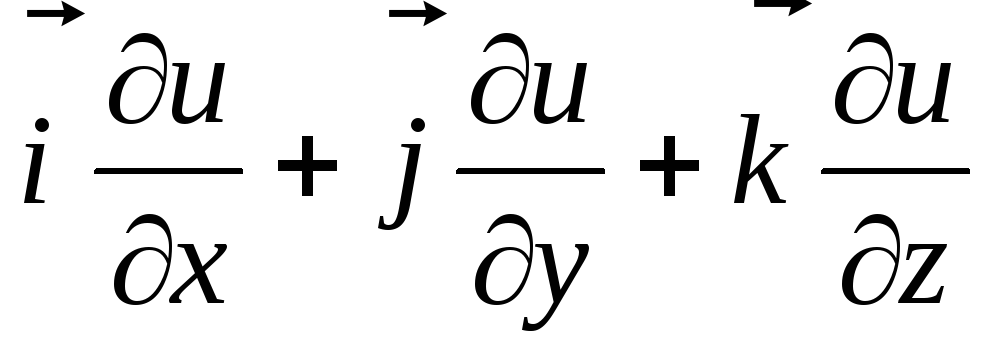 .
(119)
.
(119)
При этом функция и называется потенциалом данного векторного поля.
Примерами потенциальных полей являются поле тяготения точечной массы т, помещенной в начале координат, электрическое поле точечного заряда е, находящегося в начале координат, и другие.
Выясним, при каких условиях векторное поле является потенциальным.
Так как из (119)
следует, что 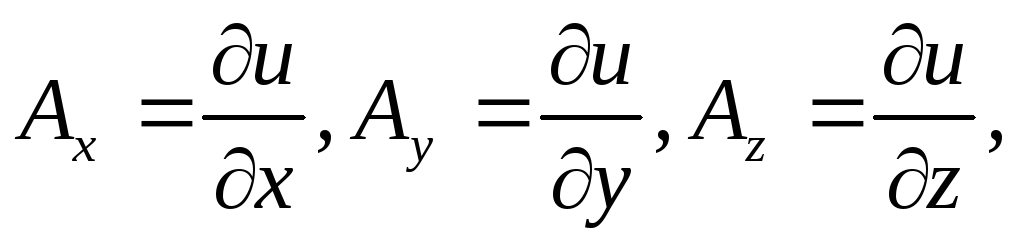 то
то

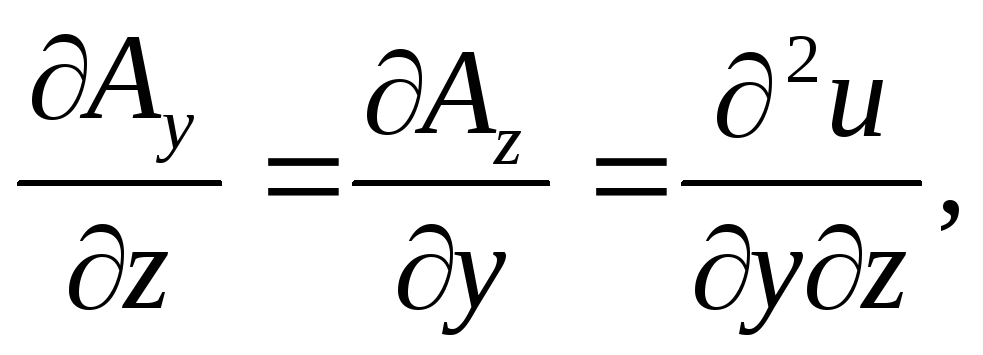
так как смешанная производная второго порядка не зависит от порядка дифференцирования. Из этих равенств легко получаем, что
rot A = 0 – (120)
Определение 28. Векторное поле A = {Ax, Ay, Az}, для которого rot A = 0, называется безвихревым.
Из предыдущих рассуждений следует, что любое потенциальное поле является безвихревым. Можно доказать и обратное, то есть то, что любое безвихревое поле есть поле потенциальное.
Пример 30.
Определить, является
ли векторное поле 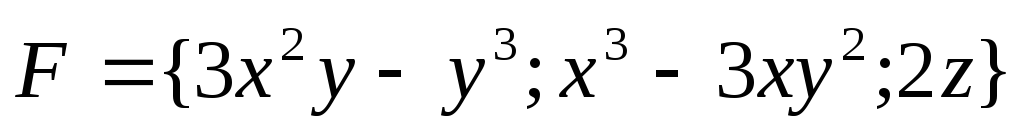 потенциальным. В случае положительного
ответа найти его потенциали в предположении, что в начале координат и = 0.
потенциальным. В случае положительного
ответа найти его потенциали в предположении, что в начале координат и = 0.
Вычислим частные
производные функций 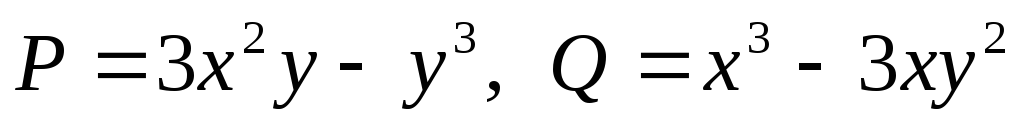 ,
,
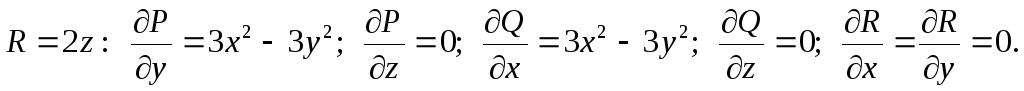
Следовательно, 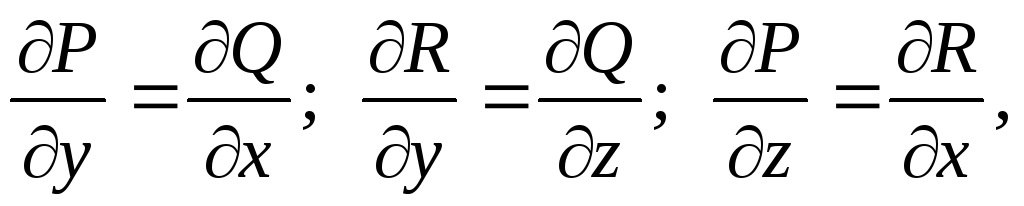
Тогда 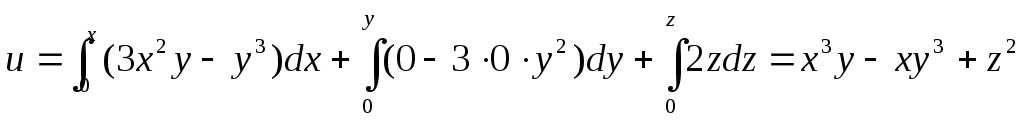 .
.
8. Соленоидальные и гармонические векторные поля
Определение 29. Векторное поле A = {Ax, Ay, Az} называется соленоидальным в области D, если в каждой точке этой области
div A = 0. (121)
Замечание. Так как дивергенция характеризует плотность источников поля
Условием соленоидальности поля является требование, что вектор А является ротором некоторого вектора В: A = rot B. Докажем это.
Действительно,
если 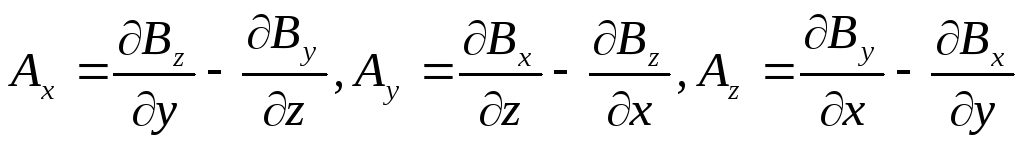 ,
то
,
то
div A =
=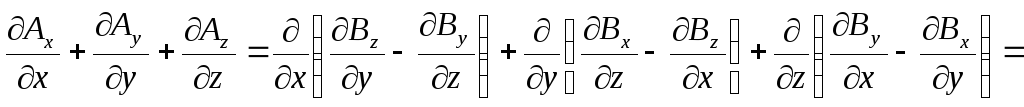
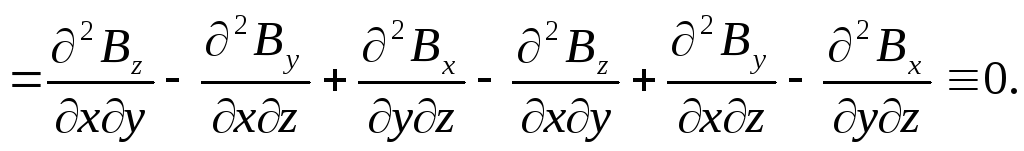
Определение 30. Скалярное поле, задаваемое функцией u = u(x, y, z), называется гармоническим в некоторой области, если функция и в этой области удовлетворяет уравнению Лапласа: Δ и = 0.
Примеры: линейная функция, потенциал электрического поля точечного заряда или поля тяготения точечной массы.
Литература
Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. М.: Наука, 1969.
Кудрявцев Л.Д. Краткий курс математического анализа. М.: Наука, 1989.
Ильин В.А., Позняк Э.Г. Математический анализ. М.: Наука, 1999.
Смирнов В.И. Курс высшей математики.- Т.2. М.: Наука, 1965.
Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. М.: Наука, 1981.
Пискунов Н.С. Дифференциальное и интегральное исчисление. – Т.2. М.: Наука, 1981.
Сборник задач по математике для втузов. Специальные разделы математического анализа (под редекцией А.В.Ефимова и Б.П.Демидовича). – Т.2. М.: Наука, 1981.
Мышкис А.Д. Лекции по высшей математике. М.: Наука, 1973.
69
5. Потенциальное поле Векторное поле


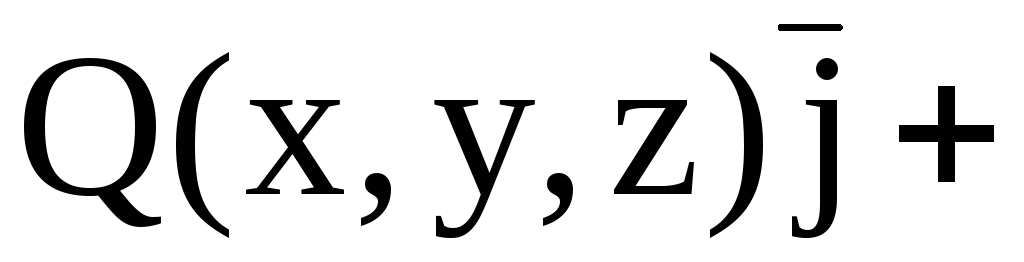
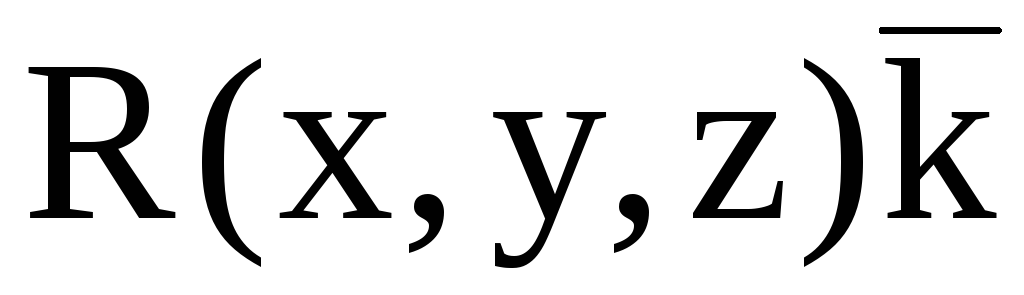
называется
потенциальным, если вектор  является градиентом некоторой скалярной
функции
является градиентом некоторой скалярной
функции 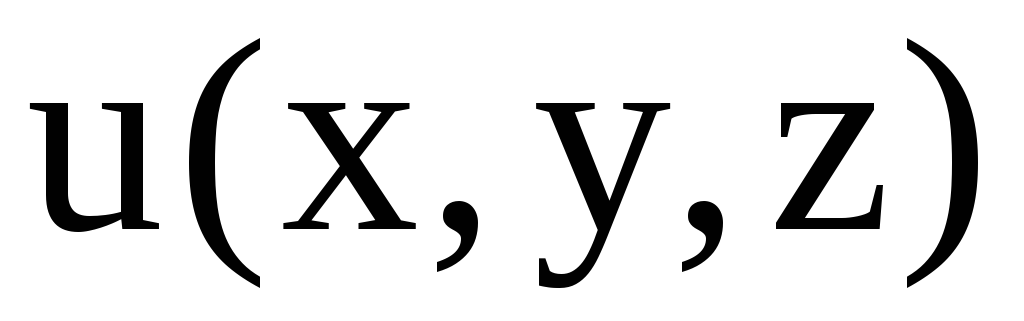
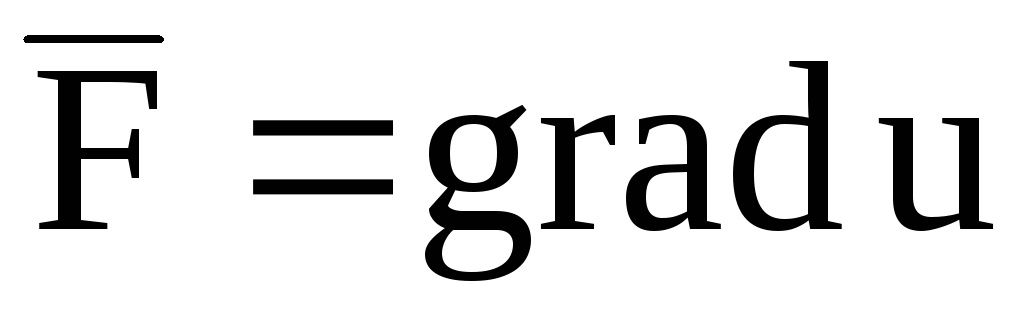 . (1)
. (1)
Функцию
u
в этом случае называют потенциалом
векторного поля  .
.
Напомним,
что работой A
поля  вдоль пути L
называется криволинейный интеграл
вдоль пути L
называется криволинейный интеграл
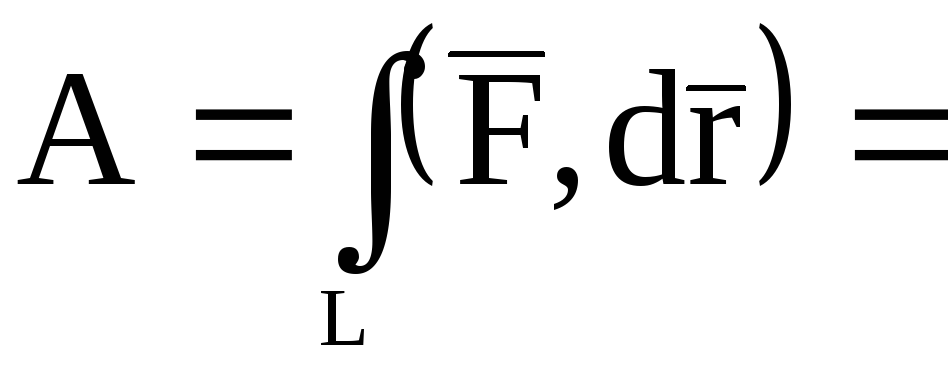
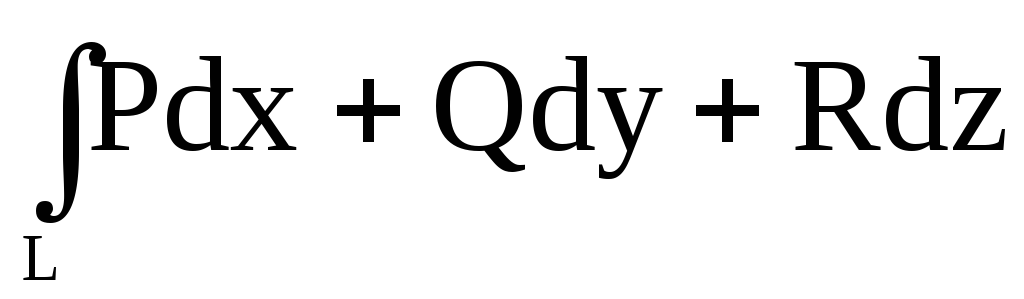
Здесь 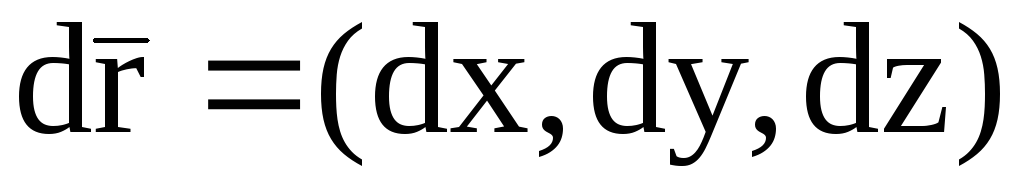 ,
, 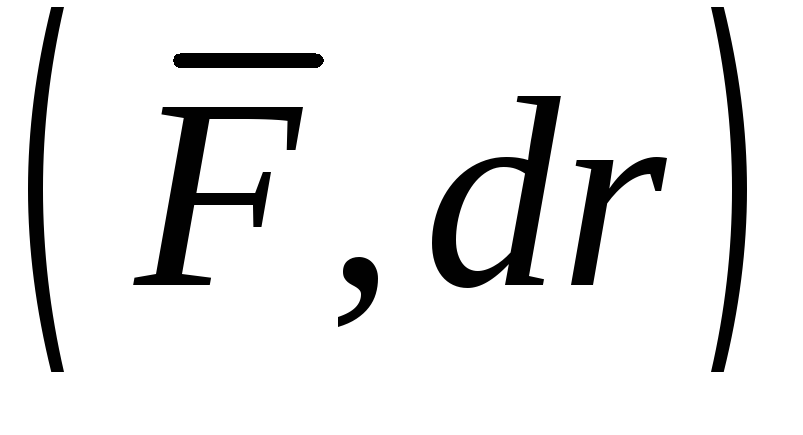 −скалярное
произведение векторов
−скалярное
произведение векторов  и
и 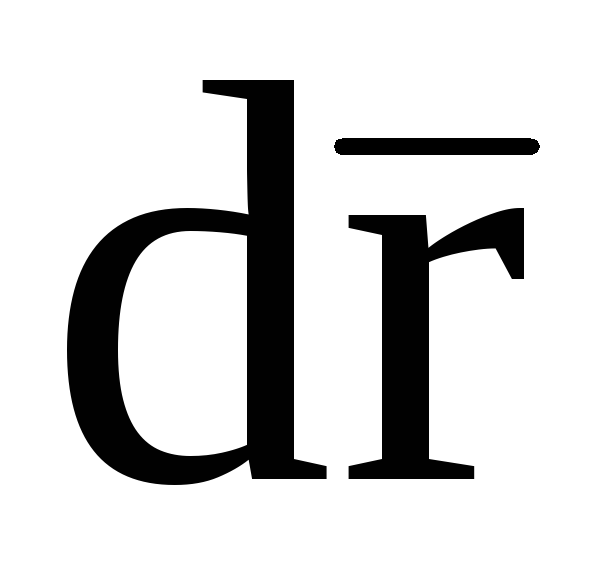 .
.
Работа
векторного поля  не зависит от пути интегрирования, если
для любых точек M1 и M2 и любых двух путей L
не зависит от пути интегрирования, если
для любых точек M1 и M2 и любых двух путей L
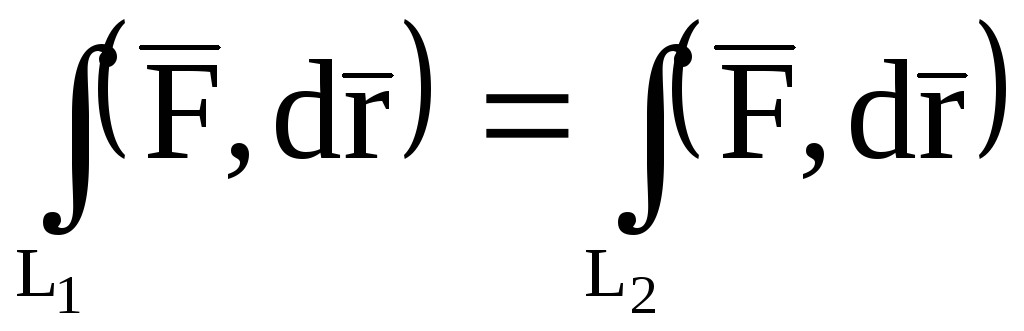 .
.
Область G трехмерного пространства называется односвязной, если на любой замкнутый контур, лежащий в этой области, можно натянуть поверхность, целиком лежащую в области G.
Например, все трехмерное пространство, внутренность сферы являются односвязными областями.
Необходимым
и достаточным условием потенциальности
дважды дифференцируемого векторного
поля  в односвязной области является равенство
нулю ротора этого поля:
в односвязной области является равенство
нулю ротора этого поля:
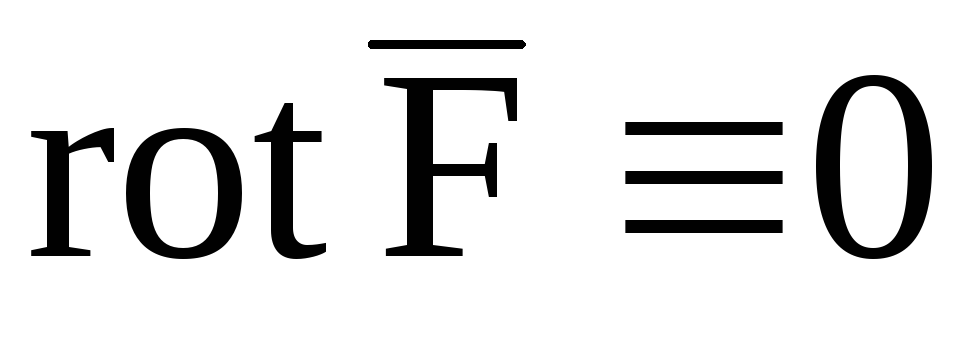 .
(2)
.
(2)
Векторное поле, удовлетворяющее (2), называется безвихревым.
Отметим основные свойства потенциального векторного поля:
1)
Криволинейный интеграл II
рода от потенциального поля  ,
взятый между двумя точками А и В, не
зависит от пути интегрирования и равен
разности значений потенциала поля в
конце и начале пути интегрирования:
,
взятый между двумя точками А и В, не
зависит от пути интегрирования и равен
разности значений потенциала поля в
конце и начале пути интегрирования:
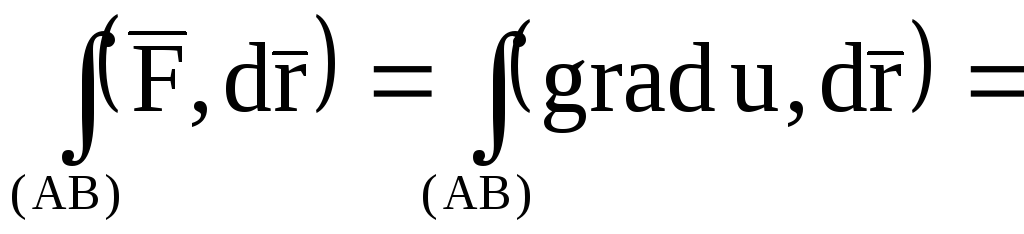

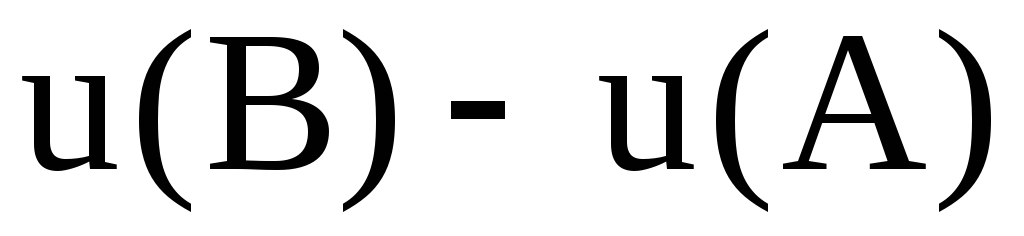 , (3)
, (3)
поскольку

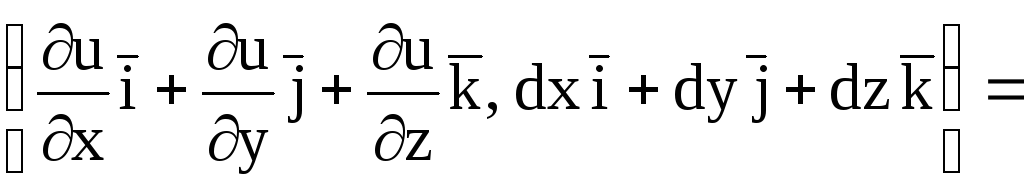
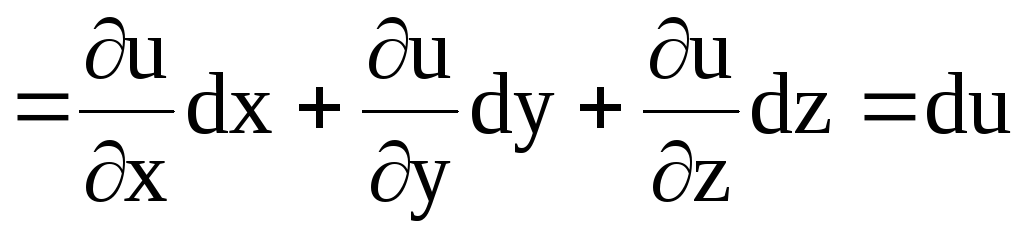 ;
;
2) Циркуляция
потенциального векторного поля  по замкнутому контуру (L),
целиком лежащему в области непрерывности
поля, равна нулю:
по замкнутому контуру (L),
целиком лежащему в области непрерывности
поля, равна нулю:
 ;
;
3) Потенциал 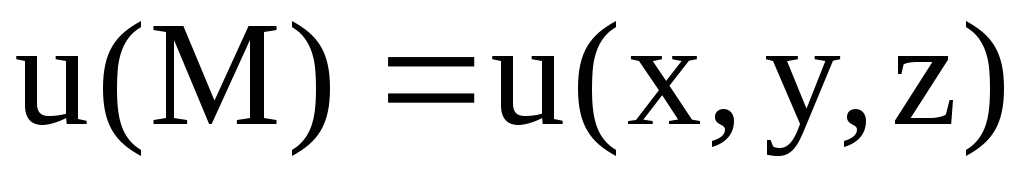 может быть вычислен по формуле:
может быть вычислен по формуле:
 , (4)
, (4)
где 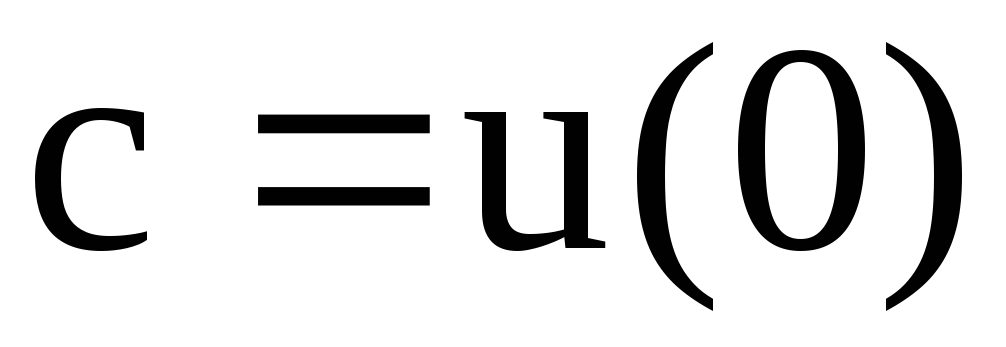 .
.
Для вычисления интеграла (4) выбирается самый простой путь, например, тот, в котором точки 0 и М соединены ломаной со звеньями, параллельными осям координат. В качестве точки 0 выбирают либо начало координат, либо любую другую точку, лежащую в области непрерывности поля.
Пример. Доказать, что поле
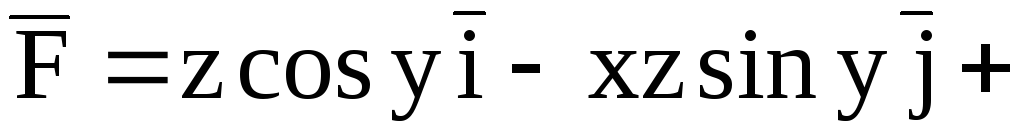

потенциально,
найти его потенциал и вычислить работу
поля  по перемещению материальной точки из
точки M1(1,0,1)
в точку
по перемещению материальной точки из
точки M1(1,0,1)
в точку 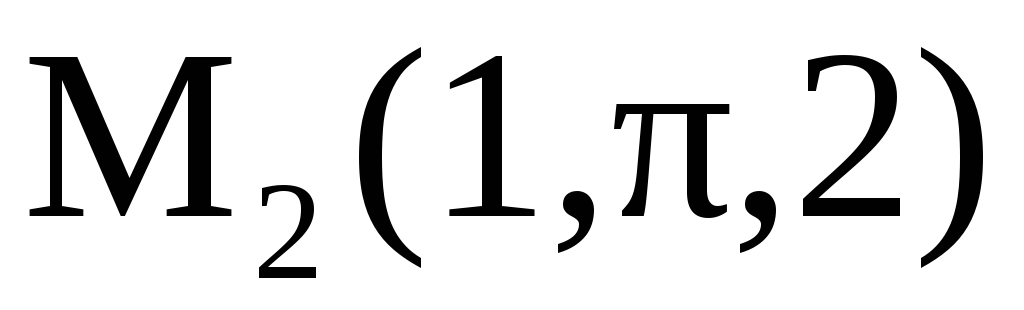 .
.
Решение. Поскольку
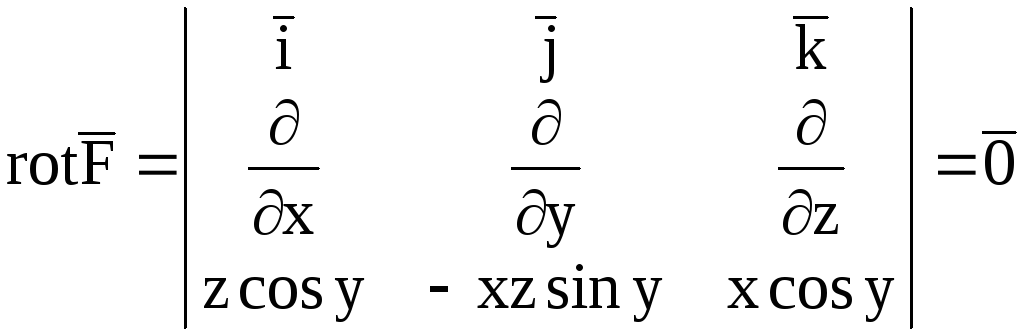 ,
,
то,
согласно условию (2), поле является потенциальным.
является потенциальным.
Найдем его потенциал по формуле (4). За путь интегрирования выбираем ломаную ОАВМ, где О(0,0,0), А(X,0,0), В(X,Y,0), M(X,Y,Z) (рис. 15).
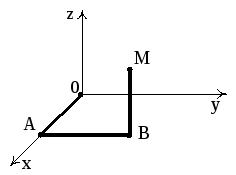
Рис. 15
Тогда получим
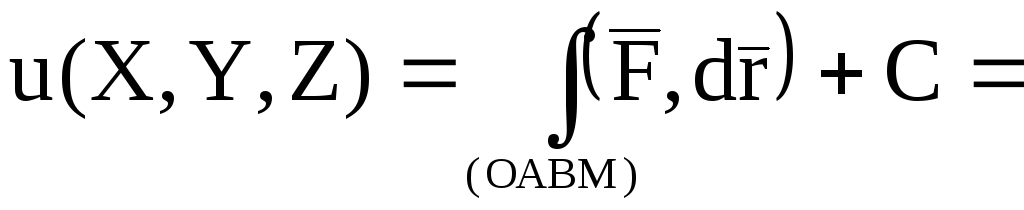

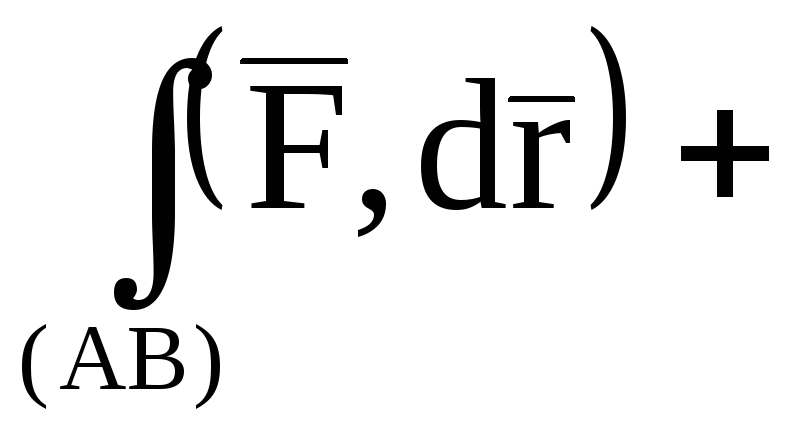
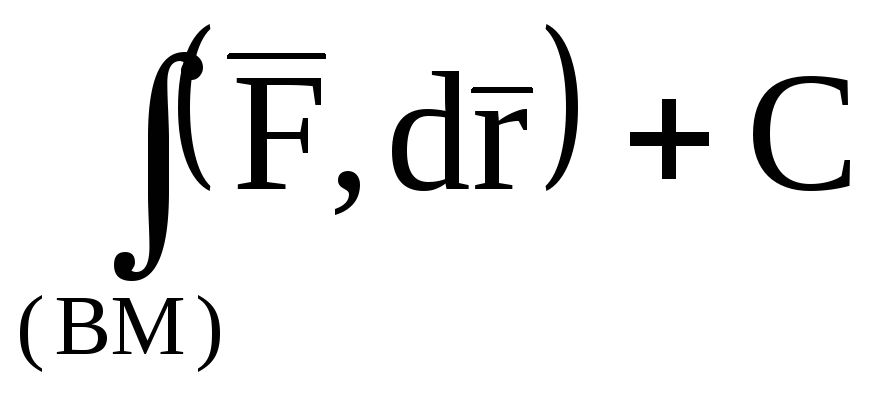 ,
,
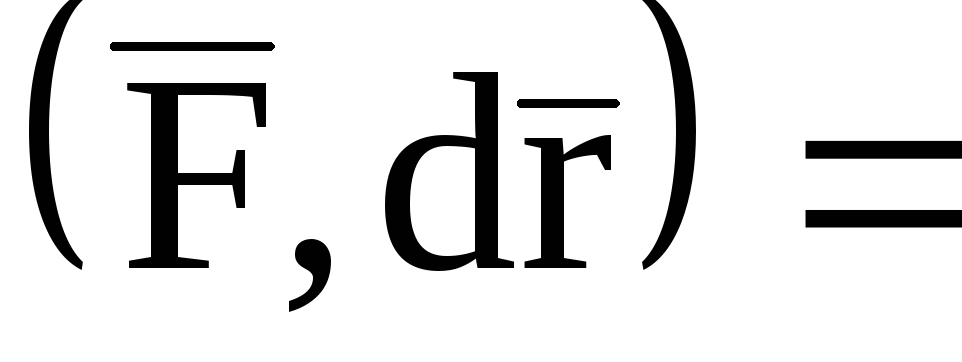
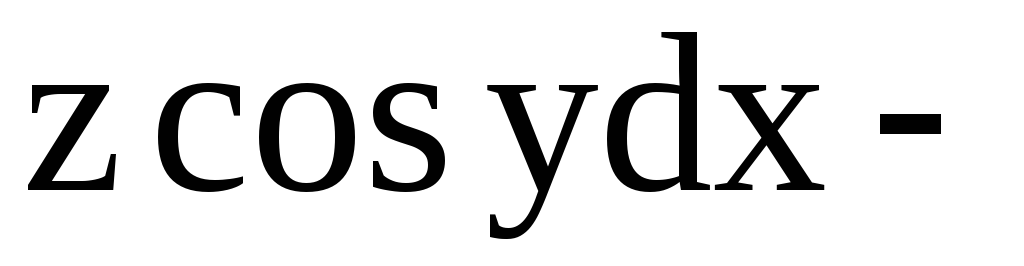

 .
.
Так
как на отрезке ОА: 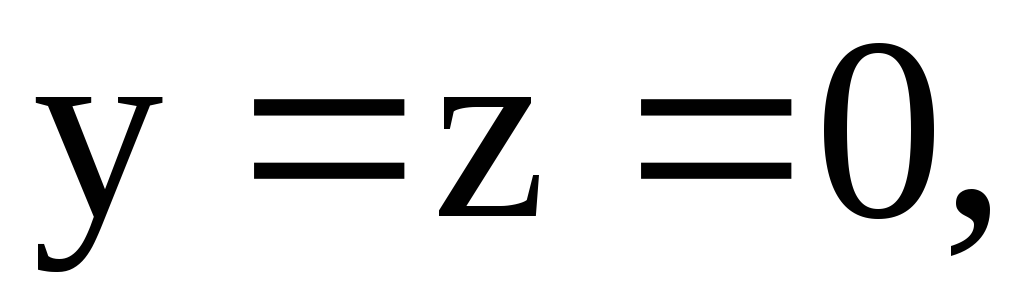
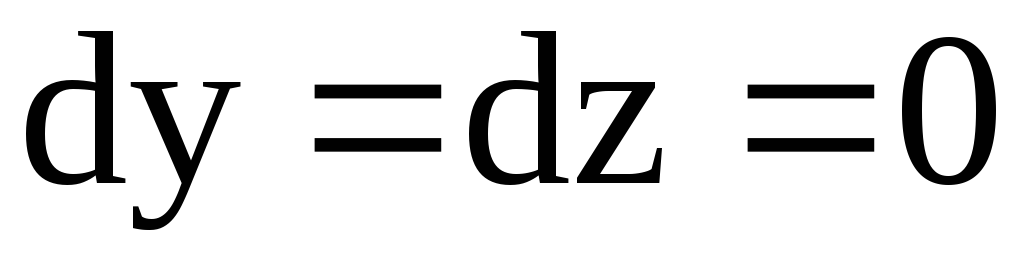 ,
, 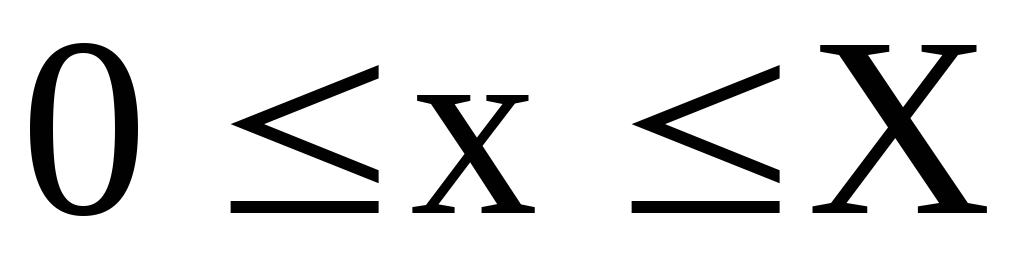 ,
то
,
то
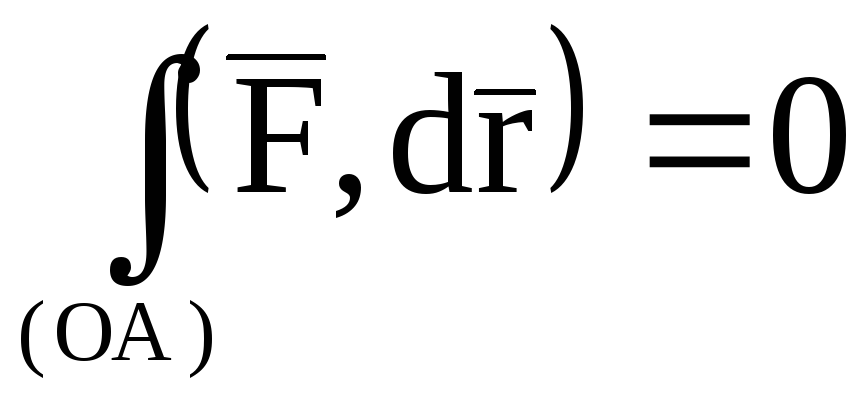 .
.
На
отрезке АВ имеем: 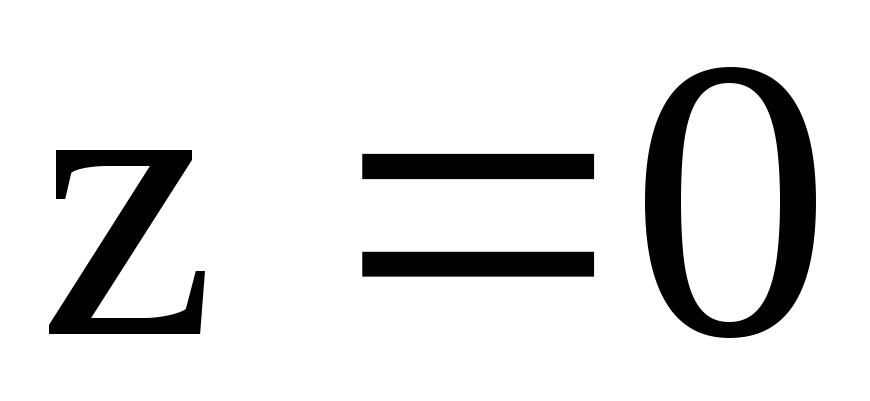 ,
,  ,
, 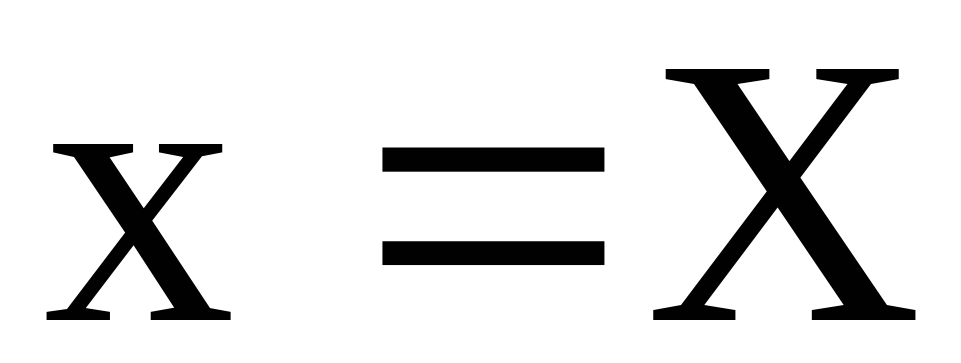 ,
,  и поэтому
и поэтому 
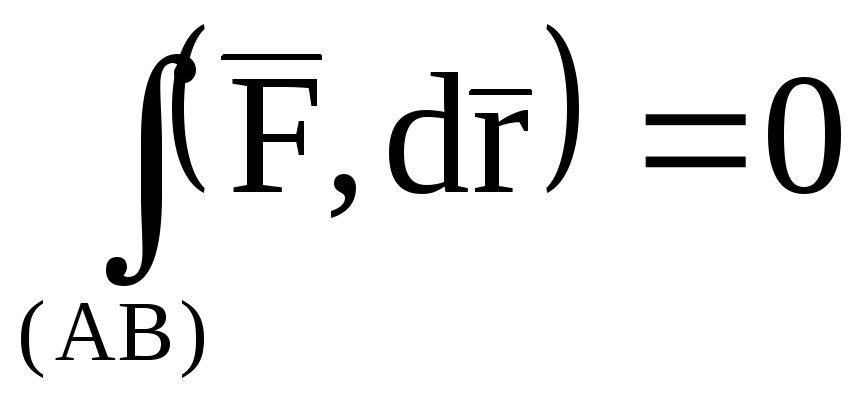 .
.
Наконец,
на отрезке ВМ: 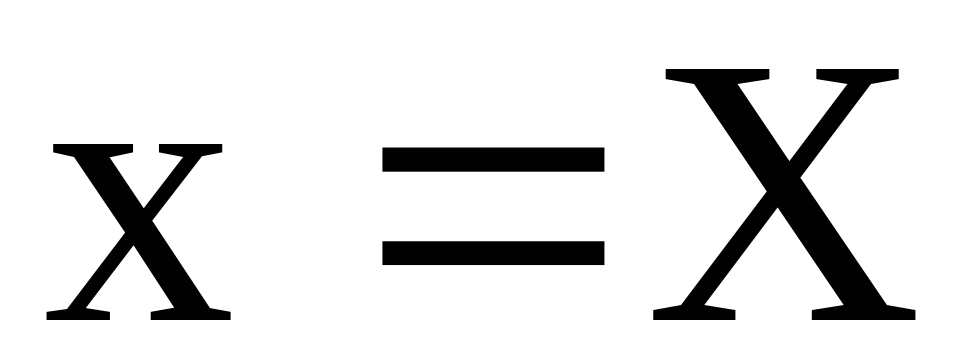 ,
, 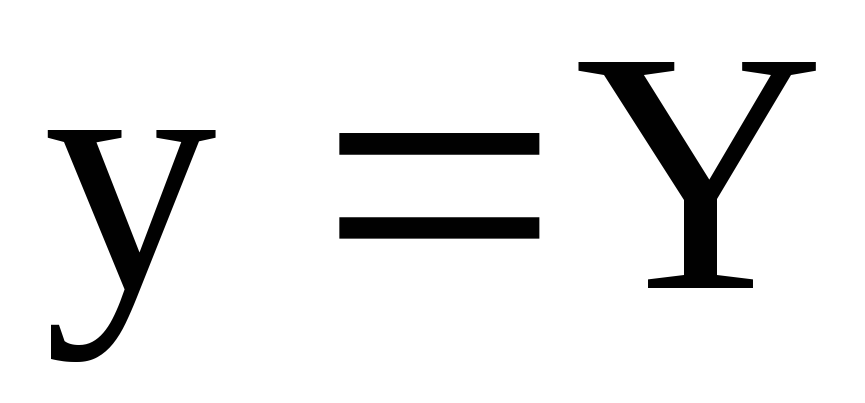 ,
, 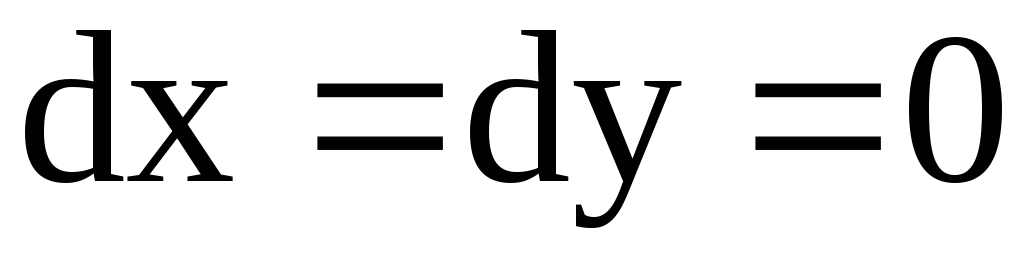 ,
,  и, следовательно,
и, следовательно, 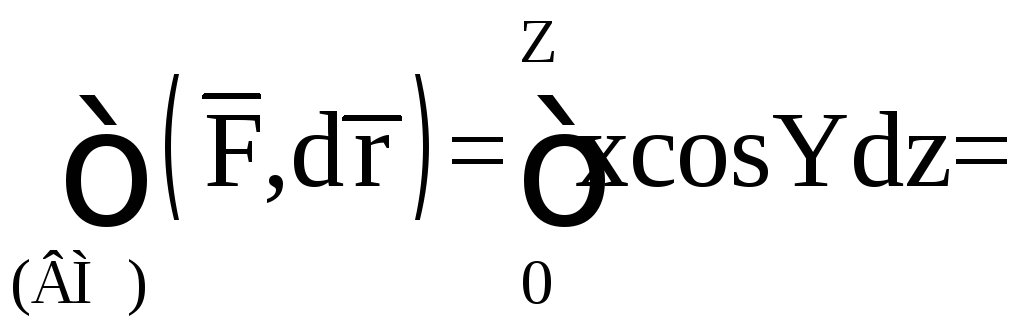
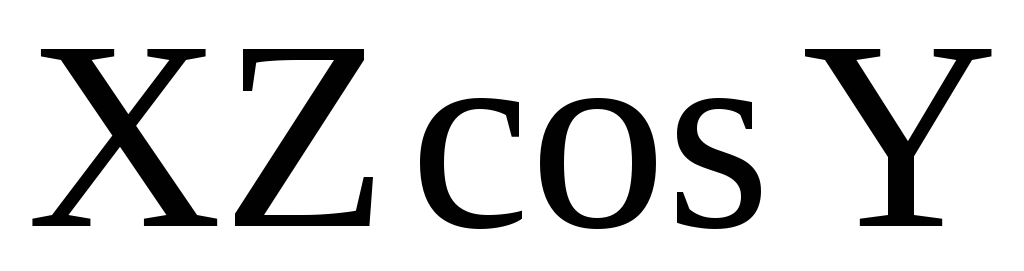 .
.
Таким
образом, 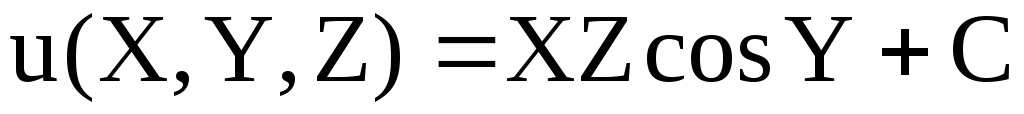 или
или

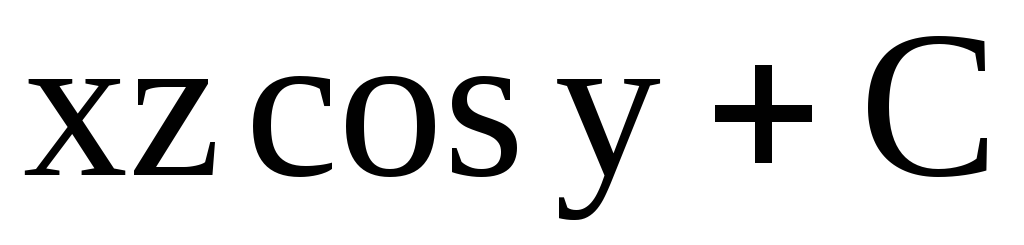 .
.
Сделаем проверку, согласно определению потенциала должно выполняться равенство (1). Имеем
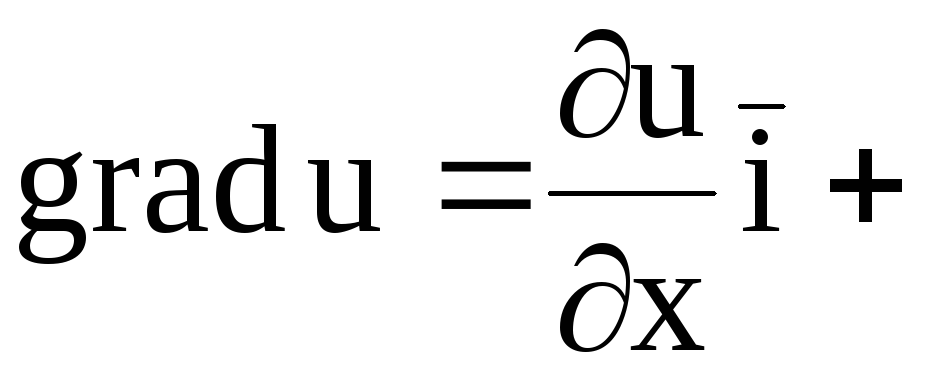

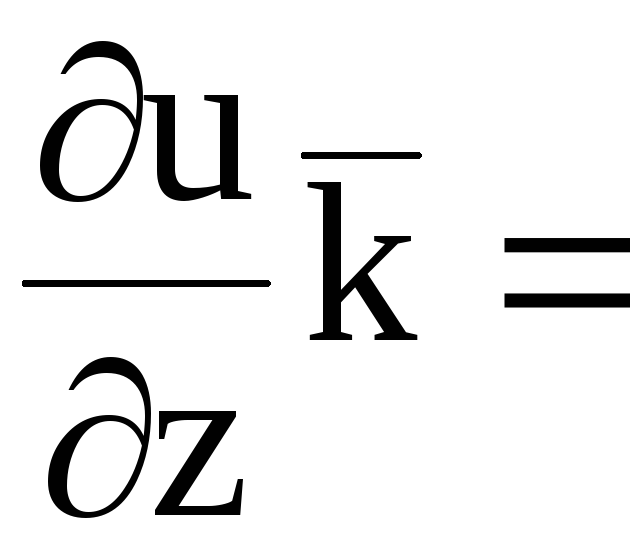
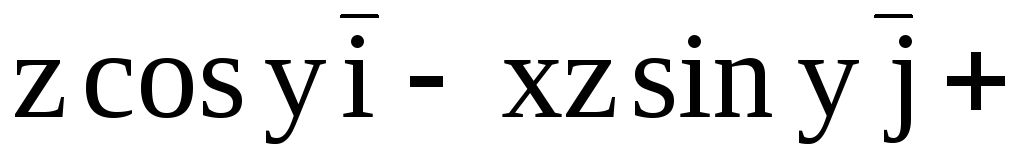
 .
.
Найдем
работу A
по перемещению материальной точки в
поле  из т. M1(1,0,1)
в т. М2(1,
из т. M1(1,0,1)
в т. М2(1, ,2).
Согласно формуле (3)
,2).
Согласно формуле (3)
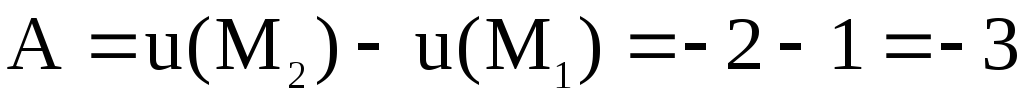 .
.
6. Оператор Гамильтона
6.1. Понятие оператора Гамильтона
Рассмотрим символический оператор «набла», называемый оператором Гамильтона:
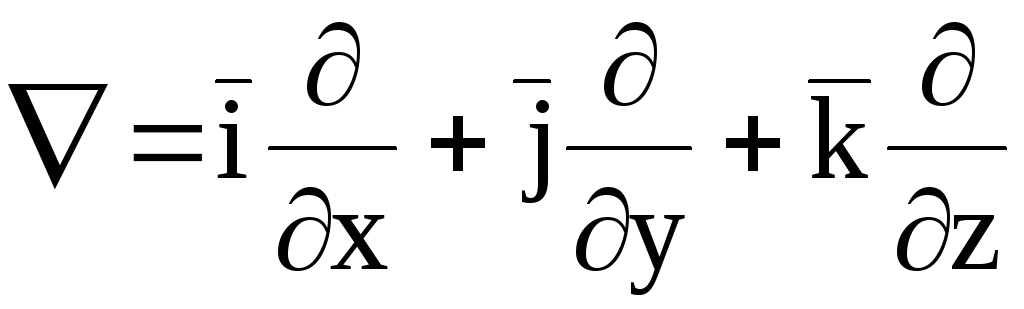 .
.
Многие
операции векторного анализа можно
выразить с помощью оператора Гамильтона,
которому присущи как дифференциальные,
так и векторные свойства, и это позволяет
упростить громоздкие выкладки. Например,
если в области пространства задана
скалярная дифференцируемая функция  ,
то, умножая «вектор»
,
то, умножая «вектор»  на скаляр u,
получим
на скаляр u,
получим
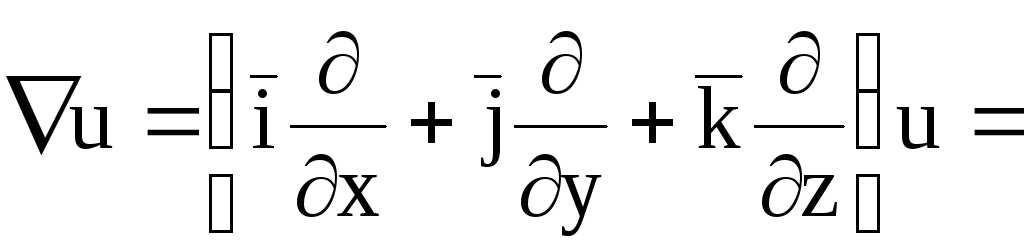
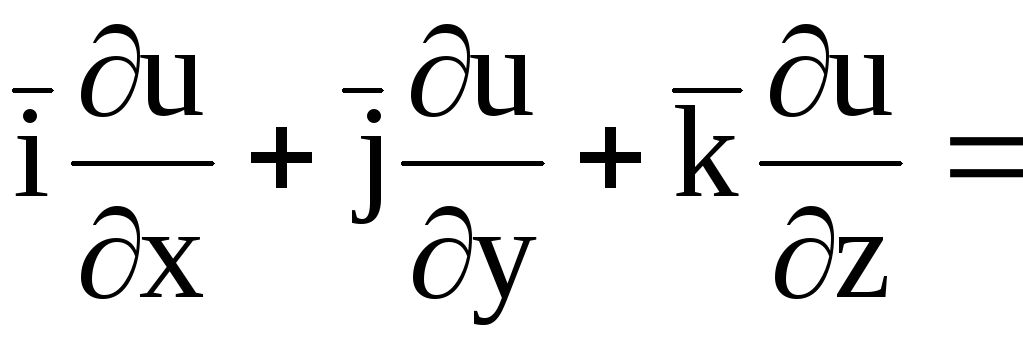
 .
.
Если
в пространстве задана вектор-функция 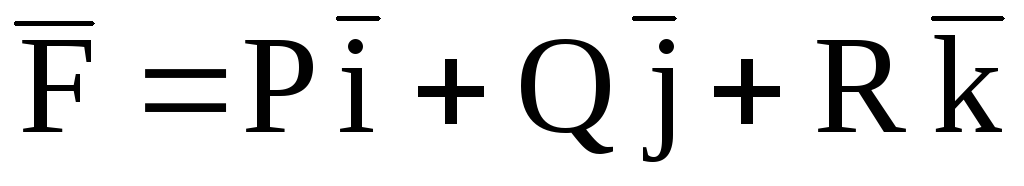 ,
где P,
Q,
R – дифференцируемые функции, то
умножая скалярно
,
где P,
Q,
R – дифференцируемые функции, то
умножая скалярно  на
на  ,
получим
,
получим
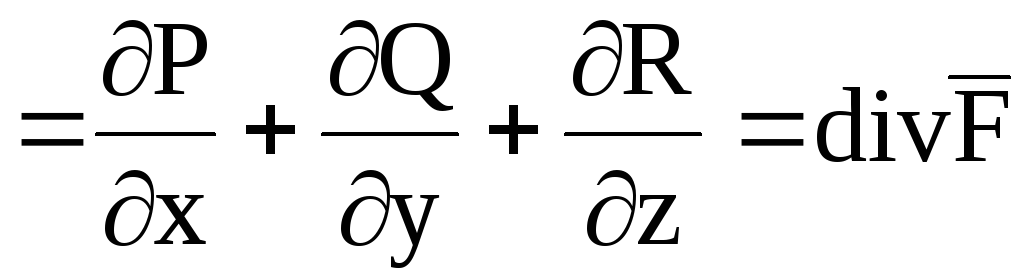 .
.
Для векторного произведения имеем
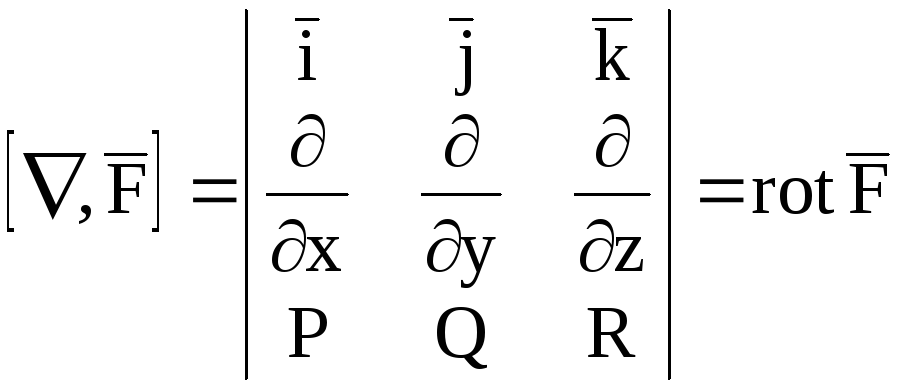 .
.
Методические указания к выполнению семестрового задания (с вариантами заданий), страница 4
Пример.
1) Показать, что поле
вектора 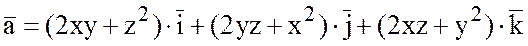 потенциально и найти его потенциал.
потенциально и найти его потенциал.
Решение.
Поле вектора  будет потенциальным, если
будет потенциальным, если  =0.
=0.
Найдем  .
.

Так как  =0, то поле вектора
=0, то поле вектора  потенциально. Найдем потенциал. В
качестве точки
потенциально. Найдем потенциал. В
качестве точки  возьмем (0;0;0).
возьмем (0;0;0).
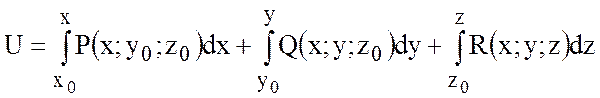 .
.
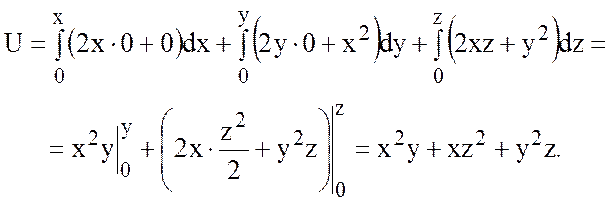
Можно проверить, что
функция U действительно является потенциалом
векторного поля вектора  . Если U потенциал, то
. Если U потенциал, то 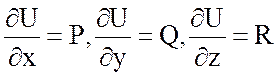 .
.
Найдем 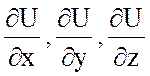 .
.

Ответ: 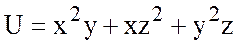 .
.
2) Проверить, будет ли поле вектора
 потенциальным
и найти его потенциал.
потенциальным
и найти его потенциал.
Решение.
Если плоское поле вектора  потенциально, то
потенциально, то 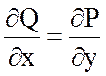 .
.
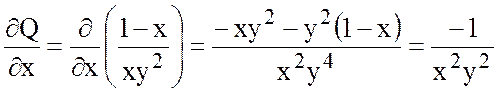 ,
,
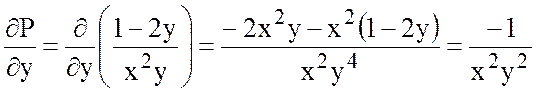 .
.
Так как 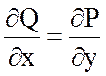 , то поле потенциально. Найдем
потенциал.
, то поле потенциально. Найдем
потенциал.
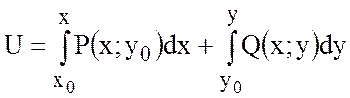 .
.
В качестве точки  возьмем точку (1;1). Точку (0;0)
брать нельзя, так как в этой точке поле вектора
возьмем точку (1;1). Точку (0;0)
брать нельзя, так как в этой точке поле вектора  не
задано, функции Р и Q не существуют в
(0;0).
не
задано, функции Р и Q не существуют в
(0;0).
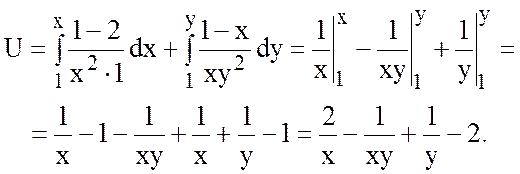
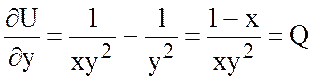
Проверка: 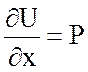 ,
, 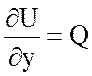 .
.
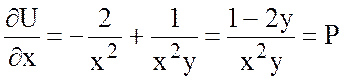 ,
,
 .
.
Ответ: 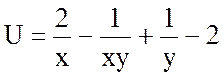 .
.
13 Циркуляция векторного поля
Определение:Циркуляцией вектора  вдоль
замкнутого контура L называется
криволинейный интеграл по этому контуру от скалярного произведения вектора
вдоль
замкнутого контура L называется
криволинейный интеграл по этому контуру от скалярного произведения вектора  на вектор
на вектор 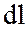 касательной
к контуру:
касательной
к контуру:
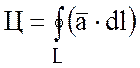 ,
,
если 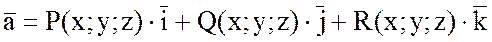 и
и 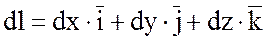 ,
то
,
то
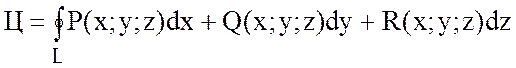 (6)
(6)
Положительным направлением обхода замкнутой кривой L считают направление, при котором область, ограниченная этой кривой, будет оставаться слева.
В силовом поле формула (6) выражает работу при перемещении материальной точки вдоль линии L.
Пример.
1) Найти циркуляцию
векторного поля 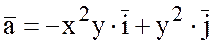 вдоль линии эллипса
вдоль линии эллипса 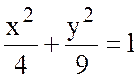
Решение.
По определению циркуляции имеем:
 .
.
Так как 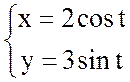 — параметрическое уравнение эллипса,
то
— параметрическое уравнение эллипса,
то
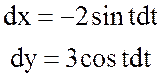 , при этом
, при этом  .
.
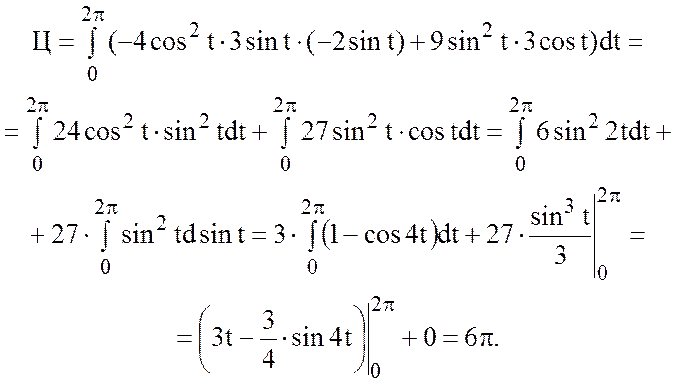
2) Найти циркуляцию векторного поля
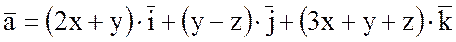 вдоль
линии пересечения плоскости
вдоль
линии пересечения плоскости  с координатными
плоскостями.
с координатными
плоскостями.

Линиями пересечения плоскости  с координатными плоскостями будут
стороны треугольника АВС, т.е.
с координатными плоскостями будут
стороны треугольника АВС, т.е.
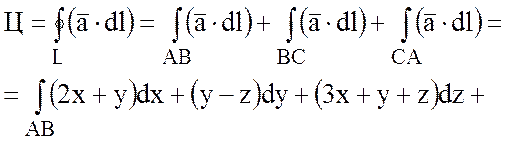

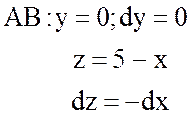 ;
; 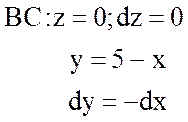 ;
; 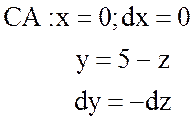 .
.

14 Формула Стокса
Пусть координаты вектора  непрерывны и имеют непрерывные
частные производные, тогда циркуляцию вектора
непрерывны и имеют непрерывные
частные производные, тогда циркуляцию вектора  по
замкнутому контуру L удобно вычислить
по формуле Стокса.
по
замкнутому контуру L удобно вычислить
по формуле Стокса.
Теорема:Циркуляция вектора  по
замкнутому контуру L равна потоку
ротора этого вектора через любую поверхность S, натянутую на контур L.
по
замкнутому контуру L равна потоку
ротора этого вектора через любую поверхность S, натянутую на контур L.
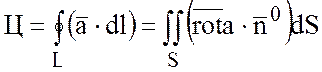 .
.
Предполагается, что
ориентация нормали  к поверхности S согласована с ориентацией контура L так, чтобы из конца нормали обход
контура в выбранном направлении был виден совершающимся против часовой стрелки.
к поверхности S согласована с ориентацией контура L так, чтобы из конца нормали обход
контура в выбранном направлении был виден совершающимся против часовой стрелки.
Так как
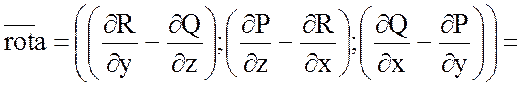
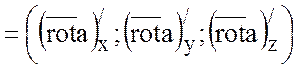 , а
, а 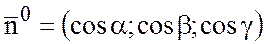 ,
то
,
то

Так как
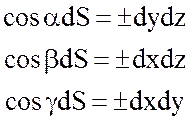 .
.
Из теоремы следует формула Стокса:
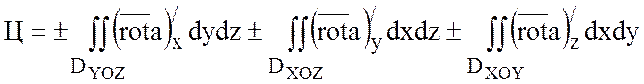 ,
,
где 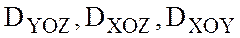 — проекции поверхности S на плоскости YOZ, XOZ, XOY.
— проекции поверхности S на плоскости YOZ, XOZ, XOY.
Из формулы Стокса
следует, что если поле вектора  потенциально, то
тогда
потенциально, то
тогда 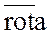 =0 и циркуляция вектора
=0 и циркуляция вектора  потенциального поля равна нулю
потенциального поля равна нулю
Частным случаем формулы
Стокса, когда поле вектора  плоское, будет
формула Грина.
плоское, будет
формула Грина.
Если поле вектора  плоское, то
плоское, то
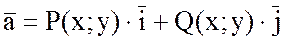 ,
,
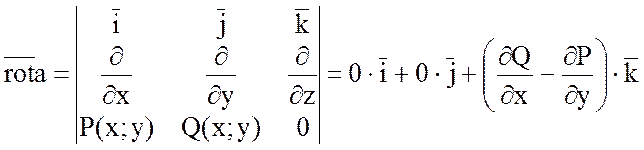 ,
,
так как 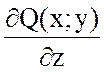 =0 и
=0 и 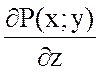 =0.
=0.
Тогда в формуле Стокса 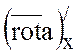 =0 и
=0 и 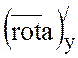 =0
и
=0
и
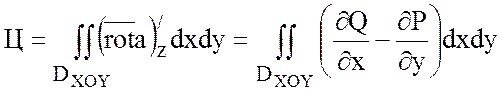 .
.
Примеры.
1) Решим второй пример из рассмотренных ранее вторым способом по формуле Стокса.
Найти циркуляцию векторного поля
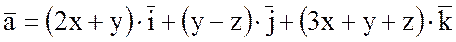 вдоль
линии пересечения плоскости
вдоль
линии пересечения плоскости  с координатными
плоскостями.
с координатными
плоскостями.
Решение.
Найдем 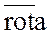 :
:
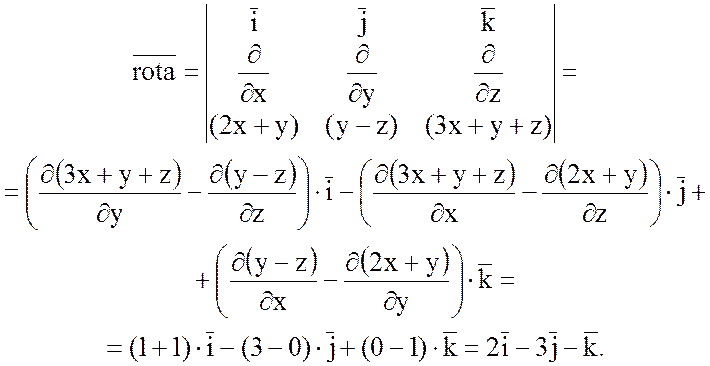
Тогда 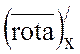 =2,
=2, 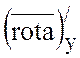 =-3,
=-3, 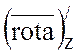 =-1.
=-1.
Найдем циркуляцию по формуле Стокса:
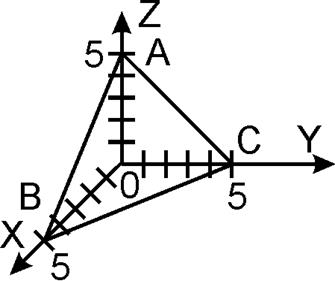
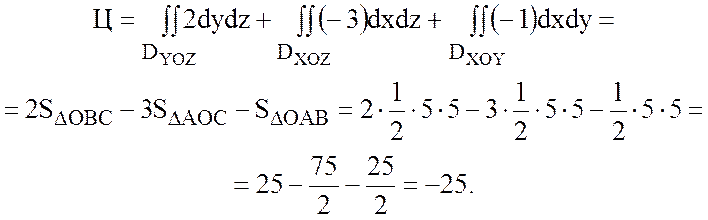
2) Вычислить циркуляцию
вектора 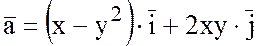 по контуру L, образованному линиями y=x,
по контуру L, образованному линиями y=x,  .
.
Решение.
Так как поле вектора  плоское, то найдем циркуляцию по
формуле Грина:
плоское, то найдем циркуляцию по
формуле Грина:
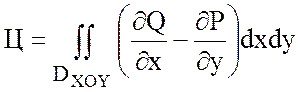 .
.
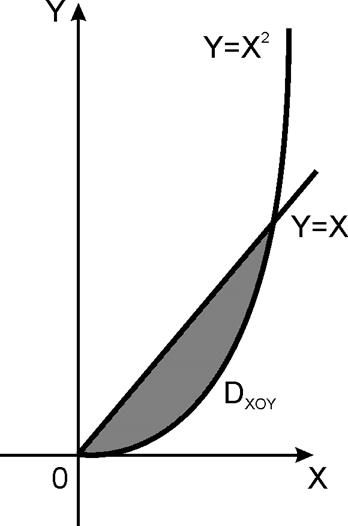

Рисунок 17

15 Оператор Гамильтона. Векторные дифференциальные операции второго порядка
Многие операции векторного анализа могут быть записаны в сокращенной и удобной для расчетов форме с помощью символического оператора Гамильтона «набла».
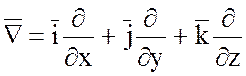 .
.
В этом операторе
соединены дифференциальные и векторные свойства. Формальное умножение  на функцию U(x;y;z) понимают как частное дифференцирование
на функцию U(x;y;z) понимают как частное дифференцирование 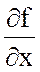 .
.
Правила действия с оператором «набла» таковы:
1) Произведение набла –
вектора 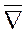 на скалярную функцию U(x;y;z) дает градиент этой функции:
на скалярную функцию U(x;y;z) дает градиент этой функции:
 .
.
2) Скалярное произведение
набла — вектора 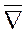 на векторную функцию
на векторную функцию 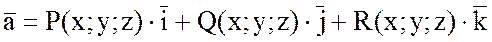 дает дивергенцию этой функции:
дает дивергенцию этой функции:
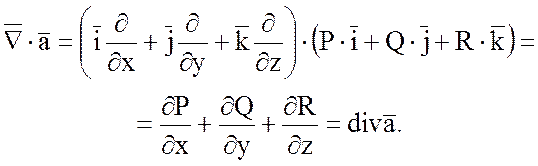
3) Векторное произведение
набла – вектора 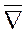 на векторную функцию
на векторную функцию  дает ротор этой функции:
дает ротор этой функции:
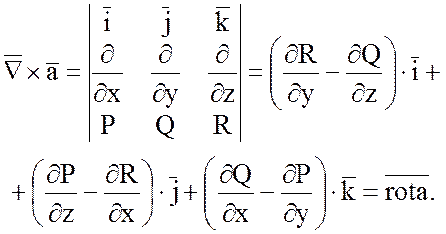
Рассмотрим теперь векторные дифференциальные операции второго порядка.
Пусть задано скалярное
поле U(x;y;z) и нашли градиент этого поля 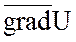 . Поле градиента является векторным
полем и можно найти его дивергенцию и ротор, т.е.
. Поле градиента является векторным
полем и можно найти его дивергенцию и ротор, т.е. 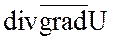 и
и  .
.
а) 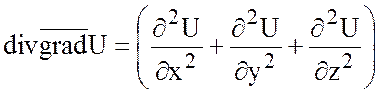 . (*)
. (*)
Действительно, 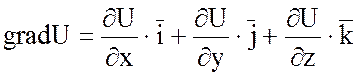 , образуя дивергенцию этого вектора,
мы и получим данную формулу (*). Правая часть формулы (*) называется оператором
Лапласа от функции и обозначается
, образуя дивергенцию этого вектора,
мы и получим данную формулу (*). Правая часть формулы (*) называется оператором
Лапласа от функции и обозначается 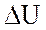 :
:
 .
.
Выражение 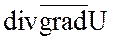 можно с помощью набла – вектора
записать так:
можно с помощью набла – вектора
записать так:
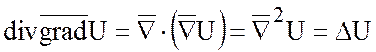 .
.
б) Пусть функция U(x;y;z) имеет непрерывные частные
производные до второго порядка включительно, тогда  =0.
=0.
Это равенство проверяется
просто, так как все координаты  представляют
собой разность вторых смешанных производных функции U, отличающихся лишь порядком дифференцирования, которые
равны, например:
представляют
собой разность вторых смешанных производных функции U, отличающихся лишь порядком дифференцирования, которые
равны, например:
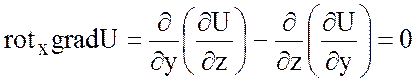 .
.
Это соотношение легко запоминается, если записать его с помощью набла – вектора:
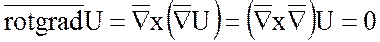 ,
,
так как векторное произведение одинаковых «векторов» равно нулю.
в) 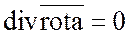 .
.
Образуя дивергенцию от  , получим:
, получим:
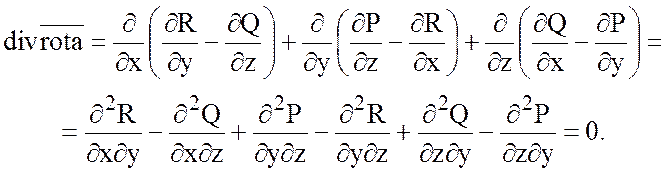
Так как вторые смешанные производные равны, если функции P, Q, R имеют непрерывные частные производные до второго порядка включительно.
С помощью набла – вектора это запишется так:
 .
.
То есть мы имеем смешанное произведение трех «векторов», из которых два вектора одинаковы. Такое произведение равно нулю.
16 Семестровое задание по теме «Теория поля»
Решение задач.
Задача 1.
а) Найти угол между
градиентами функции 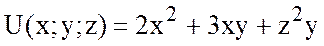 в точках (1;-1;0) и
(2;1;1).
в точках (1;-1;0) и
(2;1;1).
Решение.
 .
.
Найдем градиент функции U в точках (1;-1;0) и (2;1;1):
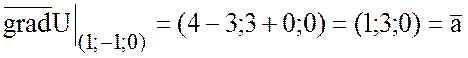 ,
,
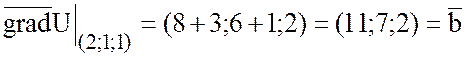 .
.
Тогда косинус угла  между градиентами, т.е. между
векторами
между градиентами, т.е. между
векторами  и
и 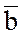 найдем
по формуле:
найдем
по формуле:
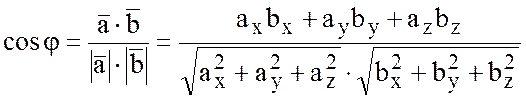 ,
,
Проверить, является ли векторное поле F соленоидальным и потенциальным
Задачи по исследованию векторного поля, что включают нахождение циркуляции, потока рассмотрены на предыдущих уроках. Здесь мы покажем, как быстро проверить, а если и нужно то и доказать, что поле является потенциальным и соленоидальным. Условия за которых это выполняется детально расписанны в объяснениях к вычислениям.
Детальный анализ каждого из примеров позволяет самостоятельно освоить данную тему каждому студенту.
ЗАДАНИЕ 10.4 Проверить, является ли векторное поле F=(5x+4yz) *i+(5y+4xz)*j+(5z+4xy)*k
потенциальным и соленоидным.
Если поле потенциальное, то найти его потенциал.
Решение: Для того, чтобы заданое поле было потенциальным, необходимо и достаточно, чтобы ротор векторного поля был равен нулю rot(F)=0.
За условием выписываем функции, которые необходимы для дальнейших расчетов
P=P(x;y;z)=5x+4yz, Q=Q(x;y;z)=5y+4zx, R=R(x;y;z)=5z+4xy.
Отсюда ротор векторного поля через частичные производные находим по формуле
Из вычислений видим что векторное поле является потенциальным.
Найдем потенциал u=u(x;y;z) заданного векторного поля .
Согласно теории, векторное поле равно градиенту потенциала:
Выпишем компоненты градиента из начального условия F= (5x+4yz) *i+ (5y+4xz) *j+ (5z+4xy) *k
потенциальным и соленоидным. Если полетпотенциальное, то найти его потенциал.
Решение: Для того, чтобы задано поле было потенциальным, необходимо и достаточно, чтобы ротор векторного поля был равен нулю rot (F) =0.
За условием выписываем функции, которые необходимы для дальнейших расчетов
P=P (x;y;z) =5x+4yz, Q=Q (x;y;z) =5y+4zx, R=R (x;y;z) =5z+4xy.
Отсюда ротор векторного поля через частичные производные находим за формулой
Из вычислений видим, что векторное поле является потенциальным.
Найдем потенциал u=u (x;y;z) заданного векторного поля .
Согласно теории векторное поле равно градиенту потенциала :
Выпишем компоненты градиенту из начального условия F=(5x+4yz)*i+(5y+4xz)*j+(5z+4xy)*k
Дальше интегрированием возобновляем потенциал, сначала интегрируем производную по x, потом найденный потенциал дифференцируем по y и приравниваем ко 2 частичной производной, и так далее
Здесь не ставили знак интегрирования, поскольку имеем дело с простыми табличными интегралами, а такая запись экономит время, храня при этом суть операций.
Окончательно записываем потенциал u векторного поля :
u(x;y;z)=2,5(x2+y2+z2)+4xyz+C, где C — произвольная константа.
Чтобы векторное поле было соленоидным, необходимо и достаточно, чтобы его дивергенция была равна нулю
Проверяем это условие:
Она не выполняется, следовательно рассмотреное векторное поле не является соленоидным.
ЗАДАНИЕ 10.5 Проверить будет ли векторное поле F=(x+2yz) *i+(y+2xz)*j+(z+2xy)*k
потенциальным и соленоидным.
Если поле потенциальное, то найти его потенциал.
Решение: Необходимым и достаточным условием, что векторное поле — потенциальное является равенство нулю ротора
Из начального условия записываем P=P(x;y;z)=x+2yz, Q=Q(x;y;z)=y+2xz, R=R(x;y;z)=z+2xy.
По формуле находим ротор векторного поля
Делаем вывод о том, что полет является потенциальным.
Найдем потенциал u(x, y, z).
Градиент равен:
Выписываем частичные производные
а дальше интегрированием возобновляем функцию
Потенциал векторного поля принимает значение
u (x;y;z)=0,5(x2+y2+z2) +2xyz+C,
где C — произвольная константа.
Условие что векторное поле соленоидальное равносильная равенству нулю его дивергенции
Выполняем необходимые расчеты
Из записи видим, что условие не выполняется, следовательно векторное поле не является соленоидным.
ЗАДАНИЕ 10.6 Проверить, является ли векторное поле F=(4x-7yz)*i+(4y-7xz)*j+(4z-7xy)*k
потенциальным и соленоидным.
Если полет потенциальное, то найти его потенциал.
Решение: Полет F является потенциальным, если его ротор равен нулю
За условием выписываем составляющие P=P(x;y;z)=4x-7yz, Q=Q(x;y;z)=4y+7xz, R=R(x;y;z)=4z-7xy
и подставляем в формулу ротора
Получили в результате нуль, можем сделать вывод, что векторное поле является потенциальным.
По
Векторный потенциал — Википедия
У этого термина существуют и другие значения, см. Потенциал.В векторном анализе векторный потенциал — это векторное поле, ротор которого равен заданному векторному полю. Он аналогичен скалярному потенциалу, который определяется как скалярное поле, градиент которого равен заданному векторному полю.
Формально, если v{\displaystyle \mathbf {v} } — векторное поле, векторным потенциалом называется векторное поле A{\displaystyle \mathbf {A} } такое, что
- v=∇×A.{\displaystyle \mathbf {v} =\nabla \times \mathbf {A} .}
Если A{\displaystyle \mathbf {A} } является векторным потенциалом для поля v{\displaystyle \mathbf {v} }, то из тождества
- ∇⋅(∇×A)=0{\displaystyle \nabla \cdot (\nabla \times \mathbf {A} )=0}
(дивергенция ротора равна нулю) следует
- ∇⋅v=∇⋅(∇×A)=0,{\displaystyle \nabla \cdot \mathbf {v} =\nabla \cdot (\nabla \times \mathbf {A} )=0,}
то есть v{\displaystyle \mathbf {v} } должно быть соленоидальным векторным полем.
Для любого соленоидального векторного поля, удовлетворяющего определённым условиям, существует векторный потенциал. В частности, его существование зависит от области, на которой определено поле — в случае многосвязной области потенциал вихревого поля обычно не существует.
Пусть
- v:R3→R3{\displaystyle \mathbf {v} :\mathbb {R} ^{3}\to \mathbb {R} ^{3}}
— дважды непрерывно дифференцируемое соленоидальное векторное поле. Предположим, что v(x){\displaystyle \mathbf {v} \left(\mathbf {x} \right)} убывает достаточно быстро при ‖x‖→∞{\displaystyle \|\mathbf {x} \|\rightarrow \infty }. Определим
- A(x)=14π∇×∫R3v(y)‖x−y‖dy.{\displaystyle \mathbf {A} (\mathbf {x} )={\frac {1}{4\pi }}\nabla \times \int \limits _{\mathbb {R} ^{3}}{\frac {\mathbf {v} (\mathbf {y} )}{\left\|\mathbf {x} -\mathbf {y} \right\|}}\,d\mathbf {y} .}
Тогда A{\displaystyle \mathbf {A} } является векторным потенциалом для v{\displaystyle \mathbf {v} }, то есть
- ∇×A=v.{\displaystyle \nabla \times \mathbf {A} =\mathbf {v} .}
Обобщением этой теоремы является разложение Гельмгольца, согласно которому любое векторное поле может быть представлено как сумма соленоидального векторного поля и безвихревого векторного поля.
Векторный потенциал соленоидального векторного поля определяется неоднозначно. Если A{\displaystyle \mathbf {A} } является векторным потенциалом для v{\displaystyle \mathbf {v} }, также им является
- A+∇m,{\displaystyle \mathbf {A} +\nabla m,}
где m{\displaystyle m} — любая непрерывно дифференцируемая скалярная функция. Это является следствием того факта, что ротор градиента равен нулю.
В электродинамике это даёт неоднозначность при определении потенциалов электромагнитного поля и решается наложением на потенциал дополнительного условия калибровки.
Уравнения Максвелла[править | править код]
Одним из способов записи уравнений Максвелла является формулировка в терминах векторного и скалярного потенциалов. Векторный потенциал A{\displaystyle \mathbf {A} } вводится таким образом, что
- μ0H=B=rotA{\displaystyle \mu _{0}\mathbf {H} =\mathbf {B} =\operatorname {rot} \mathbf {A} } (в системе СИ).
При этом уравнение divB=0{\displaystyle \operatorname {div} \mathbf {B} =0} удовлетворяется автоматически.
Подстановка выражения для A{\displaystyle \mathbf {A} } в
- rotE=−∂B∂t{\displaystyle \operatorname {rot} \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}}
приводит к уравнению
- rot(E+∂A∂t)=0,{\displaystyle \operatorname {rot} \left(\mathbf {E} +{\frac {\partial \mathbf {A} }{\partial t}}\right)=0,}
согласно которому, так же как и в электростатике вводится скалярный потенциал. Однако теперь в E{\displaystyle \mathbf {E} } вносят вклад и скалярный и векторный потенциал:
- E=−gradφ−∂A∂t.{\displaystyle \mathbf {E} =-\operatorname {grad} \;\varphi -{\frac {\partial \mathbf {A} }{\partial t}}.}
Из уравнения rotH=j+∂D∂t{\displaystyle \operatorname {rot} \mathbf {H} =\mathbf {j} +{\frac {\partial \mathbf {D} }{\partial t}}} следует
- rotrotA=μ0j+ε0μ0∂∂t(−gradφ−∂A∂t).{\displaystyle \operatorname {rot} \;\operatorname {rot} \mathbf {A} =\mu _{0}\mathbf {j} +\varepsilon _{0}\mu _{0}{\frac {\partial }{\partial t}}\left(-\operatorname {grad} \;\varphi -{\frac {\partial \mathbf {A} }{\partial t}}\right).}
Используя равенство rotrotA=graddivA−∇2A{\displaystyle \operatorname {rot} \;\operatorname {rot} \mathbf {A} =\operatorname {grad} \;\operatorname {div} \mathbf {A} -\nabla ^{2}\mathbf {A} }, уравнения для векторного и скалярного потенциалов можно записать в виде
- ΔA−grad(divA+1c2∂φ∂t)−1c2∂2A∂t2=−μ0j,{\displaystyle \Delta \mathbf {A} -\operatorname {grad} \left(\operatorname {div} \mathbf {A} +{\frac {1}{c^{2}}}{\frac {\partial \varphi }{\partial t}}\right)-{\frac {1}{c^{2}}}{\frac {\partial ^{2}\mathbf {A} }{\partial t^{2}}}=-\mu _{0}\mathbf {j} ,}
- Δφ+∂∂tdivA=−ρε0.{\displaystyle \Delta \varphi +{\frac {\partial }{\partial t}}\operatorname {div} \mathbf {A} =-{\frac {\rho }{\varepsilon _{0}}}.}
Физический смысл векторного потенциала[править | править код]
В классической электродинамике векторный потенциал достаточно часто трактовался как величина, не имеющая непосредственного физического смысла, формально вводимая лишь для удобства выкладок, хотя уже в структуре действия для классической электродинамики векторный потенциал входит таким прямым образом, что это наводит на мысль о его фундаментальном характере.
В квантовой теории это имеет прозрачный физический смысл прямого влияния векторного потенциала на фазу волновой функции движущейся в магнитном поле частицы. Более того, удалось поставить квантовые эксперименты, показавшие, что векторный потенциал доступен достаточно непосредственному в некотором смысле измерению (по крайней мере, речь идёт о том, что векторный потенциал может влиять наблюдаемым измеримым образом на квантовую частицу даже тогда, когда напряженность магнитного поля в областях, доступных частице, всюду равна нулю, то есть магнитное поле не может оказывать воздействие на частицу через напряженность, а лишь прямо — через векторный потенциал; см. Эффект Ааронова — Бома).
Подобно тому, как скалярный потенциал связан с понятием энергии, векторный потенциал обнаруживает тесную связь с понятием импульса. Так, в случае быстрого отключения магнитного поля частица, находившаяся в нём, получает дополнительный импульс qA.



