Физика_Ответы — Стр 3
| 21 |
Источником электростатического | поля является |
3) неподвижный электрический заряд
ТЗ 208 КТ-3
Стекло при трении о кожу приобретает заряд…
2) положительный
ТЗ 209 КТ-1
Единица измерения потенциала — это…
2) вольт
ТЗ 210 КТ-2
Единица измерения электрического заряда — это.. 2) кулон
ТЗ 211 КТ-3
Величина ѐмкости конденсатора …
3) обратно пропорциональна расстоянию между пластинами
ТЗ 212 КТ-1
Размерность Кл/В определяет величину…
1) электроѐмкости
ТЗ 213 КТ-2
2 заряда по 1 кулону на расстоянии 1 метр взаимодействуют с силой…
5) 9 гиганьютон
ТЗ 214 КТ-3
Вектор напряжѐнности электрического поля направлен…
1) в сторону уменьшения потенциала
ТЗ 215 КТ-1
Электрическое поле это — … 4) векторное поле, определяющее силовое воздействие на
электрические заряды, не зависящее от их скоростей.
ТЗ 216 КТ-2
Два вида зарядов существуют потому, что … 3) обнаружено лишь два взаимодействия заряженных тел – отталкивание и притяжение
ТЗ 217 КТ-3
Взаимодействие электрических зарядов на расстоянии объясняет гипотеза
…
1) электрическое поле первого заряда действует на второй
ТЗ 218 КТ-1
Явление электризации трением объясняет гипотеза
22
2) одно тело теряет электроны, другое приобретает
8.3. Тесты.
ТЗ 219 КТ-2
1) 1А
ТЗ 220 КТ-3
Алюминиевая и медная проволоки имеют одинаковые массы и площадь поперечного сечения. Большее сопротивление имеет …
1) алюминиевая
ТЗ 221 КТ-1
Отметьте правильный ответ Электрическое поле внутри диэлектрика…
1) меньше внешнего
ТЗ 222 КТ-2
Электрическим током через проводящую среду может быть перенесено минимальное количество электричества …
2) равное заряду электрона.
ТЗ 223 КТ-3
Высокий вакуум – состояние газа, при котором длина свободного пробега молекул …
1) больше линейных размеров сосуда
ТЗ 224 КТ-1
Эмиссия – процесс … 1) выхода электронов из металла
ТЗ 225 КТ-2
Ток в вакууме создается … 1) любыми заряженными частицами
ТЗ 226 КТ-3
Ионизация газа – процесс … 1) потери электронов молекулами
ТЗ 227 КТ-1
Несамостоятельный газовый разряд … 1) возникновение тока в газе при действии внешнего ионизатора
ТЗ 228 КТ-2
Самостоятельный газовый разряд …
| 23 |
1) | который продолжается после прекращения действия внешнего |
ионизатора | |
КТ-3 | |
Плазма – сильно ионизированный газ … 1) с равными концентрациями электронов и положительных ионов
ТЗ 230 КТ-1
Сила тока в лампе мощностью 100 Вт в сети с напряжением 220 В равна…
3) 0, 455 А.
ТЗ 231 КТ-2
Выделяемое в проводнике в единицу времени количество теплоты при увеличении силы тока в 4 раза…
4) увеличится в 16 раз.
ТЗ 232 КТ-3
Потребляемая электрической лампой мощность при уменьшении напряжения в 5 раз и неизменном сопротивлении…
4) уменьшится в 25раз.
ТЗ 233 КТ-1
При силе тока в электрической цепи 0,3 А сопротивление лампы равно 10 Ом. Мощность электрического тока, выделяющаяся на нити лампы равна …
3) 3 Вт
ТЗ 234 КТ-2
ЭДС источника тока – разность потенциалов, создаваемая сторонними силами, которая …
1) не зависит от тока
ТЗ 235 КТ-3
Разность потенциалов измеряется в … 1) вольтах (В)
ТЗ 236 КТ-1
Закон Джоуля — Ленца – количество теплоты, выделяемое в проводнике с током пропорционально величине сопротивления и …
1) квадрату тока
ТЗ 237 КТ-2
Узел электрической цепи – точка, в которой сходится … 2) не менее трех проводников
ТЗ 238 КТ-3
1-й закон Кирхгофа – алгебраическая сумма токов узла электрической цепи равна …
24
4) нулю
ТЗ 239 КТ-1
2-й закон Кирхгофа – в замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна …
1) алгебраической сумме напряжений, на всех участках сопротивления цепи
ТЗ 240 КТ-2
Электрическое сопротивление проводника измеряется в … 1) омах
ТЗ 241 КТ-3
Удельное электрическое сопротивление измеряется в … 2) Ом м
ТЗ 242 КТ-1
Электрическая проводимость проводника измеряется в … 2) Сименс
ТЗ 243 КТ-2
При последовательном соединении проводников общее сопротивление цепи равно …
1) сумме сопротивлений отдельных проводников
ТЗ 244 КТ-3
Сопротивление проводника с ростом температуры … 1) увеличивается линейно
ТЗ 245 КТ-1
Электрический ток- … 2) направленное движение электрических зарядов.
ТЗ 246 КТ-2
Сила тока в 1 А есть — … 1) отношение 1 Кл к 1 сек
ТЗ 247 КТ-3
Модуль плотность тока – отношение силы тока к … 1) площади поперечного сечения проводника
ТЗ 248 КТ-1
Закон Ома – сила тока пропорциональна 1) напряжению на данном участке цепи и обратно пропорциональна его сопротивлению
ТЗ 249 КТ-2
Электрическое сопротивление проводника пропорционально …
25
1) удельному сопротивлению и длине проводника и обратно пропорционально его площади поперечного сечения
ТЗ 250 КТ-3
Вольтамперная характеристика … 3) зависимость силы тока от напряжения
ТЗ 251 КТ-1
Процесс изменения силы тока при замыкании или размыкании электрической цепи протекает …
1) по экспоненте
ТЗ 252 КТ-2
Произведение напряжения на силу тока определяет…
3) мощность
ТЗ 253 КТ-3
Наибольшую мощность три электрические лампочки потребляют при их…
1) параллельном соединении
ТЗ 254 КТ-1
Отношение напряжения на участке цепи к силе тока равно…
3) сопротивлению участка цепи.
ТЗ 255 КТ-2
Электрическое сопротивление проводника зависит от… 3) от длины, площади поперечного сечения и материала проводника
ТЗ 256 КТ-3
Напряжение на концах проводника 8В, сопротивление 4 Ом, сила тока равна …
2)2А
9.3.Тесты.
ТЗ 257 КТ-1
Магнитная индукция – это векторная физическая величина, являющаяся … 1) силовой характеристикой магнитного поля
ТЗ 258 КТ-2
Единица магнитной индукции в системе СИ … 1) тесла (Тл)
ТЗ 259 КТ-3
Магнитный поток определяется …
| 26 |
1) скалярным произведением | вектора магнитной индукции на |
элемент поверхности. |
|
ТЗ 260 КТ-1
Единица магнитного потока в системе СИ … 2) вебер (Вб)
ТЗ 261 КТ-2
Закон Ампера описывает силу, действующую на проводник с током в … 1) магнитном поле
ТЗ 262 КТ-3
Напряжѐнность магнитного поля в данной точке определяется законом Био
–Савара – Лапласа и зависит от …
3)расстояния до проводника с током
ТЗ 263 КТ-1
Напряжѐнность магнитного поля измеряется в … 2) теслах (Тл)
ТЗ 264 КТ-2
Взаконе полного тока фигурирует …
1)циркуляция вектора Н
ТЗ 265 КТ-3
По двум параллельным проводникам текут токи в одном направлении и поэтому они …
1) притягиваются
ТЗ 266 КТ-1
Сила Лоренца, действующая на заряд, движущийся с постоянной скоростью v в магнитном поле В пропорциональна …
1) векторному произведению v и В
ТЗ 267 КТ-2
ЭДС Холла, возникающая в проводнике с током, помещѐнном в магнитное поле, пропорциональна …
1) магнитной индукции и расстоянию между электродами проводника
ТЗ 268 КТ-3
Взаимная индукция – это явление возникновения тока в замкнутом контуре при …
1) изменении силы тока в соседнем замкнутом контуре
ТЗ 269 КТ-2
Наибольшую магнитную проницаемость имеют вещества … 3) ферромагнетики
27
ТЗ 270 КТ-3
Единица измерения индуктивности — это…
4) генри
ТЗ 271 КТ-1
Два проводника с однонаправленными токами…
2) притягиваются
ТЗ 272 КТ-2
Энергия магнитного поля катушки индуктивностью 4 Гн и силе тока в ней 3
Аравна…(Дж)
1)18 Дж
ТЗ 273 КТ-3
Трансформатор может работать…
3) на переменном токе
ТЗ 274 КТ-1
Один из основных постулатов теории Максвелла … 1) переменное магнитное поле порождает вихревое электрическое
ТЗ 275 КТ-2
Действующее значение напряжения 220 вольт — его амплитудное значение…
3) 310 вольт
ТЗ 276 КТ-3
Ёмкостное сопротивление конденсатора при увеличении частоты переменного тока в 2 раза…
3)уменьшится в 2 раза
10.3.Тесты.
ТЗ 277 КТ-1
Внешним фотоэффектом называется… 3) выбивание электронов с поверхности металлов под действием света.
ТЗ 278 КТ-2
Внутренним фотоэффектом называется… 1) изменение электрических свойств вещества под действием света без выхода электронов из вещества.
ТЗ 279 КТ-3
Понятие “квант энергии” было введено впервые в физику для объяснения
…
28
1) законов теплового излучения
ТЗ 280 КТ-1
При фотоэффекте кинетическая энергия электронов …
2) линейно зависит от частоты падающего света
ТЗ 281 КТ-2
Гамма-излучение — это поток … 3) квантов электромагнитного излучения, испускаемых атомными ядрами
ТЗ 282 КТ-3
Внешним фотоэффектом называется… 3) Выбивание электронов с поверхности металлов под действием света.
ТЗ 283 КТ-1
Испускание электронов катодом под действием света — это явление…
2) внешнего фотоэффекта
ТЗ 284 КТ-2
Максимальная начальная скорость фотоэлектронов зависит от…
2) частоты света
ТЗ 285 КТ-3
Уравнение Эйнштейна для фотоэффекта представляет собой применение …
1)закона сохранения энергии
11.3.Тесты.
ТЗ 286 КТ-1
Гипотеза Де Бройля о волновых свойствах частиц вещества впоследствии была …
1) подтверждена в экспериментах по дифракции электронов
ТЗ 287 КТ-2
Магнитными и электрическими полями не отклоняется …
4) гамма-излучение
ТЗ 288 КТ-3
Ядро атома состоит из…
1) протонов и нейтронов
ТЗ 289 КТ-1
Планетарная модель атома обоснована…
4) опытами по рассеянию альфа-частиц
29
ТЗ 290 КТ-2
Отметьте правильный ответ Синтез ядра из отдельных протонов и отдельных нейтронов
сопровождается выделением энергии…
4) для любых ядер
ТЗ 291 КТ-3
Частота излучения при переходе атома водорода из второго стационарного состояния в первое…
3) 3R/4
ТЗ 292 КТ-1
Линейчатые спектры дают…
2) одноатомные газы в возбуждѐнном состоянии
ТЗ 293 КТ-2
Частица может иметь заряд, равный … 4) 2 заряда электрона
ТЗ 294 КТ-3
Атомное ядро может иметь заряд … 4) положительный
ТЗ 295 КТ-1
Ядро изотопа радия с массовым числом 226 и зарядовым 88 состоит из…
2) 88 протонов и 138 нейтронов
ТЗ 296 КТ-2
Отметьте правильный ответ Ядро,состоящее из одного протона — это ядро атома…
1) водорода
ТЗ 297 КТ-3
Вкачестве топлива атомных электростанций используется …
1)уран
ТЗ 298 КТ-1
Масса Солнца уменьшается за счет испускания … 4) частиц и электромагнитных волн
ТЗ 299 КТ-2
Модель атома Резерфорда является … 1) неустойчивой системой
| 30 |
Модель атома Бора – электроны | могут двигаться в атоме … |
1) только по определѐнной орбите
.
Электроснабжение с основами электротехники [Архив]
Ответы на модуль 1 (ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ, ТОПОЛОГИЧЕСКИЕ ПАРАМЕТРЫ И МЕТОДЫ РАСЧЕТА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА)1) Напряжение измеряется в следующих единицах: вольт (В).
2) При применении метода параллельного преобразования резистивной схемы эквивалентная проводимость равна: алгебраической сумме проводимостей резистивных элементов.
3) Электрическая мощность связана с величиной напряжения: прямо пропорциональной зависимостью.
4) При методе расчета цепей с помощью законов Кирхгофа действует следующее правило выбора контуров для составления уравнений: каждый после¬дующий контур должен включать в себя хотя бы одну новую ветвь, не охвачен¬ную предыдущими уравнениями.
5) Какое сходство у идеализированных источников напряжения и тока: способны отдавать в электрическую цепь неог¬раниченную мощность.
6) Величина магнитного потока измеряется в следующих единицах: вебер (Вб).
7) При наличии полной симметрии между схемами резистивных цепей звезда – треугольник величина сопротивления элемента схемы треугольник: равна двум величинам сопротивления элемента схемы звезда.
8) Ток измеряется в следующих единицах: ампер (А).
9) Электрическая проводимость обратно пропорциональна: электрическому сопротивлению.
10) Электрическое напряжение – это: энергия, расходуемая на перемещение единицы заряда.
11) По второму закону Кирхгофа в любом замкнутом контуре электрической цепи: алгебраическая сумма па¬дений напряжений на элементах, входящих в контур, равна алгебраической сумме ЭДС.
12) Значение индуктивности прямо пропорционально: потокосцеплению.
13) В индуктивном элементе (реактивное сопротивление) происходит: запасание магнитной энергии.
14) К источнику электрической энергии относится: аккумулятор.
15) По закону Ома для цепи, не содержащей ЭДС: сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.
16) Электрический ток определяется как: произведение электрического заряда и времени.
17) При расчете цепи методом контурных токов применяются: первый и второй законы Кирхгофа.
18) В емкостном элементе (реактивное сопротивление) происходит: запасание электрической энергии.
19) К приемнику электрической энергии относится: электронагреватель.
20) Первый закон Кирхгофа гласит: сумма токов, подходящих к узлу, равна сумме токов, выходящих из узла.
21) Электрическая мощность измеряется в следующих единицах: ватт (Вт).
22) При применении метода последовательного преобразования резистивной схемы эквивалентное сопротивление равно: алгебраической сумме сопротивлений резистивных элементов.
23) В резистивном элементе происходит: не¬обратимое преобразование электромагнитной энергии в тепло или другие виды энергии.
24) Какое из понятий не характеризует геометрию цепи: «элемент».
25) По принципу наложения ток в любой ветви сложной схемы, содержащей несколько источников, равен: алгебраической сумме частичных токов, возникающих в этой ветви от независи¬мого действия каждого источника в от¬дельности.
Ответы на модуль 2 (АНАЛИЗ И РАСЧЕТ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА) по предмету электротехника, электроника и схемотехника.
1) В цепи синусоидального тока с резистивным элементом: ток и напряжение совпадают по фазе.
2) На практике единицей измерения полной мощности в гармонических цепях является: вольт-ампер (ВА).
3) Электрические величины гармонических функций нельзя представить: вещественными числами.
4) При последовательном соединении элементов R, L и C при положительных значениях реактивного сопротивления и угла сдвига фаз электрическая цепь в целом носит следующий характер: активно-индуктивный.
5) Если сдвиг фаз между током и напряжением меньше нуля, то: напряжение опережает ток по фазе.
6) Проекция вращающегося вектора гармонической функции на ось ординат в любой момент времени, равна: мгновенному значению функции времени.
7) В цепи синусоидального тока с катушкой индуктивности: ток опережает напряжение на угол 90º.
8) Коэффициент отношения действующего значения синусоидального напряжения к его амплитудному значению составляет: 0.707.
9) Гармоническим электрическим током называется ток, который: изменяется во времени по своему значению и направлению через равные промежутки времени.
10) Какое из свойств не относится к гармоническому току: после многократной трансформации форма сигнала изменяется.
11) Угловая частота синусоидального тока: обратно пропорциональна периоду колебаний.
12) В цепи синусоидального тока с конденсатором: напряжение опережает ток на угол 90º.
13) По первому закону Кирхгофа в комплексной форме: сумма комплексных значений токов, подходящих к узлу, равна сумме комплексных значений токов, выходящих из узла.
14) Наиболее распространенный переменный ток изменяется в соответствии с функцией: синус.
15) По закону Ома в комплексной форме: комплексное значение тока прямо пропорционально комплексному значению напряжения и обратно пропорционально комплексному значению сопротивления.
16) В цепи синусоидального тока с конденсато¬ром С происходит: обратимый процесс обмена энергией между электрическим полем конденсатора и источником.
17) Амплитудные значения гармонического тока: изменяются по синусоидальному закону.
18) Коэффициент отношения среднего значения синусоидального тока к его максимальному значению составляет: 0.637.
19) По второму закону Кирхгофа в комплексной форме в любом замкнутом контуре электрической цепи: алгебраическая сумма комплексных значений напряжений на сопротивлениях контура равна алгебраической сумме комплексных значений ЭДС.
20) Активная мощность активно-реактивной электрической цепи на переменном токе не зависит от: угловой частоты гармонических колебаний.
21) Активная мощность в цепи синусоидального тока с резистивным элементом всегда больше нуля, что означает: в цепи с резистором протекает необратимый процесс преобразования электроэнергии в другие виды энергии
22) При последовательном соединении элементов R, L и C при отрицательных значениях реактивного сопротивления и угла сдвига фаз электрическая цепь в целом носит следующий характер: емкостный.
23) Деление комплексных чисел может выполняться: только в алгебраической форме.
24) К характеристикам гармонического тока не относится: минимальные значения тока и напряжения.
25) Комплексное число нельзя представить в следующей форме: квадратичной.
Ответы на модуль 3 (КОЛЕБАТЕЛЬНЫЕ КОНТУРЫ. ЯВЛЕНИЯ РЕЗОНАНСА.) по предмету электротехника, электроника и схемотехника.
1) При изменении частоты внешнего источника энергии: изменяются реактивные сопротивления элементов, ток в цепи и на¬пряжения на отдельных участках.
2) Какой из параметров не характеризует свойства параллельного колебательного контура? волновое сопротивление ρ.
3) Полоса пропускания резонансного контура: обратно пропорциональна его добротности.
4) Какое из мероприятий нельзя проводить для повышения коэффициента мощности электрической цепи? для компенсации индуктивной составляющей тока последовательно с приемниками включать конденсаторы.
5) Какое свойство не относится к напряжениям UL и UC на реактивных элементах в цепи, находящейся в режиме резонанса напряжений? напряжения совпадают по фазе и не равны по модулю.
6) Явление резонанса напряжений наблюдается в цепи: с последовательным соединением источника энергии и реактивных элементов L и C.
7) В режиме резонанса напряжений: активное сопротивление равно реактивному сопротивлению.
8) Для параллельного колебательного контура, если сдвиг фаз между напряжением на участке цепи и током меньше нуля, то: общий ток имеет емкостной характер.
9) Активная мощность равна полной мощности в режиме резонанса, если коэффициент мощности: cosφ = 1.
10) Свободные колебания контура не зависят от: частоты вынужденных колебаний источника энергии ω.
11) В режиме резонанса в случае совпадения частоты собственных колебаний wo с частотой вынужденных колебаний источника энергии ω (ωo = ω): амплитуда гармонических колебаний энергии в цепи увеличивается.
12) Условие возникновения резонансного режима можно определить через параметры элементов схемы следующим образом: входное сопротивление (входная проводимость) схемы со стороны выводов источника энергии должно носить реактивный характер.
13) Резонанс напряжений возникает при следующем условии: полное сопротивление цепи имеет минимальное значение и равно активному значению.
14) Для параллельного колебательного контура, если сдвиг фаз между напряжением на участке цепи и током больше нуля, то: общий ток имеет индуктивный характер.
15) Резонанса токов в электрической цепи нельзя достичь следующим способом: изменением параметра активного элемента цепи R.
16) В режиме резонанса токов полная проводимость электрической схемы имеет: максимальное значение и равна значению активной проводимости.
17) Какое из свойств не относится к току источника, протекающему через цепь с элементами R, L и C в режиме резонанса токов? имеет минимальное значение.
18) При наличии в электрической цепи режима резонанса напряжений: ток максимален и совпадает по фазе с напряжением источника.
19) Основное условие возникновения резонанса токов вытекает из следующего условия: реактивная проводимость индуктивного элемента равна реактивной проводимости емкостного элемента.
20) Угол сдвига фаз между напряжением и током в электрической цепи при параллельном соединении элементов R, L и C определяется как арктангенс отношения: общей реактивной проводимости к активной проводимости.
21) Явление резонанса токов наблюдается в электрической цепи: с параллельным соединением источника энергии и реактивных элементов L и C.
22) В электрической цепи возможно появление сво
Закон полного тока
Магнитное поле, создаваемое током, и ток в проводнике неразрывно связаны между собой, следовательно, и величины, характеризующие магнитное поле (магнитный поток, магнитная индукция и т.д.) также связаны с током в проводнике.
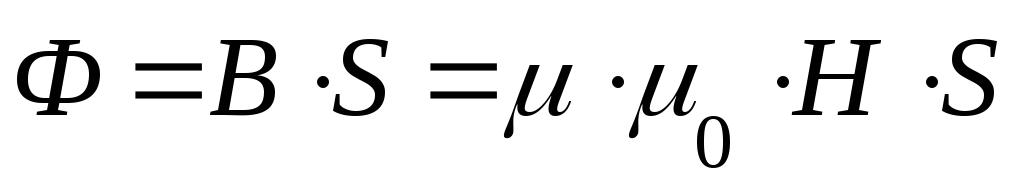
Закон полного тока и устанавливает зависимость между током в проводнике и напряженностью магнитного поля.
Полным токомназывают алгебраическую сумму токов, пронизывающих поверхность, ограниченную контуром ((I)– полный ток).
|
Если ток создает магнитное поле, направление которого совпадает с произвольно выбранным направлением обхода контура, то он берется со знаком «+», а если нет – со знаком «-» |
| Магнитное
поле во всех точках контура будет
различным и по значению
и по направлению, поэтому выделим на
контуре элементарный участок |
с
участком  угол.
Вектор Н можно разложить на две составляющие,
одна из которых совпадает с участком
угол.
Вектор Н можно разложить на две составляющие,
одна из которых совпадает с участком  ,
а вторая – перпендикулярна ему.
,
а вторая – перпендикулярна ему.




Для определения намагничивающей силы для замкнутого контура необходимо просуммировать (проинтегрировать) все магнитные напряжения, вычисленные вдоль этого контура.
Опытным путем установлено, что намагничивающая сила, вычисленная вдоль замкнутого контура, равна полному току (алгебраической сумме токов, пронизывающих поверхность, ограниченную магнитной силовой линией, по которой вычислена намагничивающая сила).

Применение закона полного тока
1. Магнитное поле вокруг прямолинейного проводника с током
| Необходимо определить напряженность поля вокруг проводника в т.А, расположенной от проводника на расстоянии х. Для этого проведем аксонометрическую окружность с радиусом х. Полный ток здесь равен току в проводнике.
|
|
Длина контура равна длине окружности, таким образом, чем дальше точка удалена от проводника, тем напряженность поля в ней будет меньше.
2. Напряженность поля внутри цилиндрического проводника
| Необходимо определить напряженность поля внутри проводника в т.А, расположенной на расстояниихот центра проводника (х<R). Плотность
тока |
проводника
одинакова, поэтому протекающий через
площадь, ограниченную окружностью с
радиусом х,
ток равен 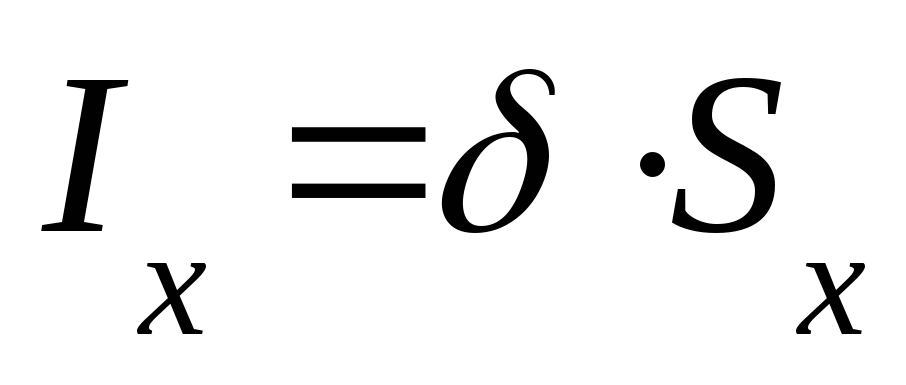 .
С другой стороны плотность тока
.
С другой стороны плотность тока ,
а площадь, ограниченная контуром с
радиусомх:
,
а площадь, ограниченная контуром с
радиусомх:  .
.
 где
где 
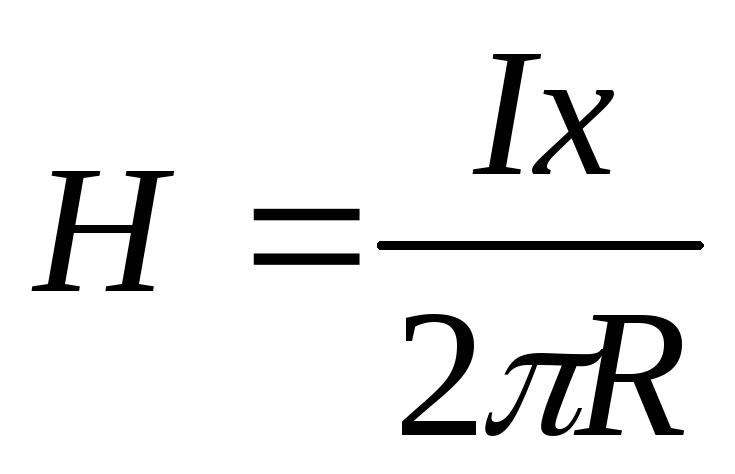
Напряженность поля внутри проводника увеличивается от нуля в центре проводника до максимального значения на его поверхности, а затем по мере удаления от поверхности проводника опять уменьшается.
| Магнитную
индукцию можно определить как |
3. Магнитное поле кольцевой и цилиндрической катушек
| На
кольцевой катушке равномерно намотана
обмотка, имеющая витков. Напряженность поля внутри
сердечника на расстоянии R благодаря симметрии во всех точках
будет одинакова согласно закону
полного тока ( |
Полный
ток  ,
где — число витков.
,
где — число витков.
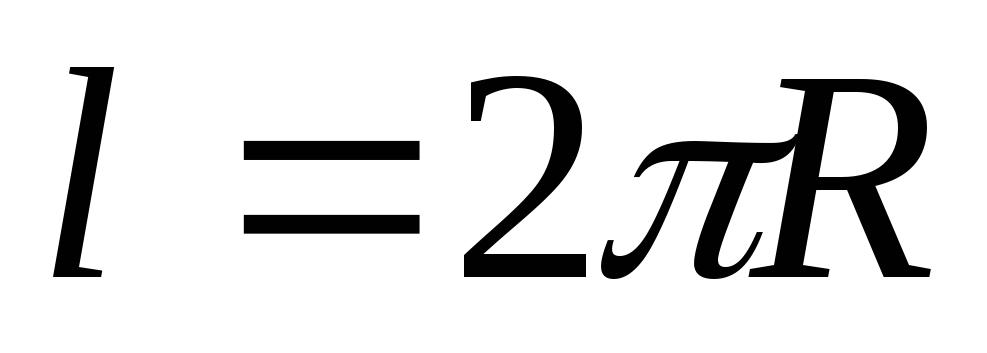 ,
тогда
,
тогда 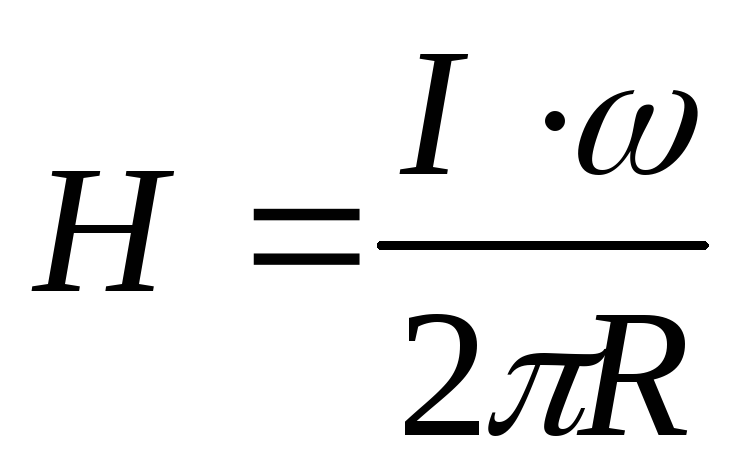

Наибольшая
напряженность и магнитная индукция
будут на внутренней поверхности кольца,
а наименьшие – на внешней поверхности
кольца. Если взять контур с радиусом  или с радиусом
или с радиусом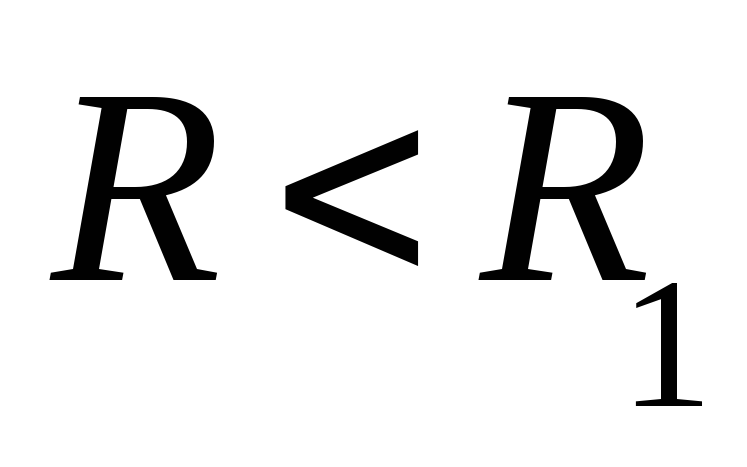 ,
то напряженность и магнитная индукция
в этих точках будут равны нулю, т.к. эти
точки не пронизываются токами.
,
то напряженность и магнитная индукция
в этих точках будут равны нулю, т.к. эти
точки не пронизываются токами.
| Цилиндрические
катушки можно рассматривать
как кольцевую с бесконечно большим
радиусом. Поэтому напряженность поля
цилиндрической катушки определяется
как: |
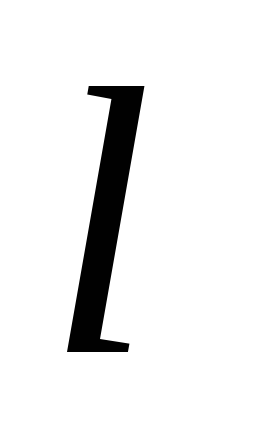 — длина катушки;
— длина катушки;
 — полный ток.
— полный ток.
Сила взаимодействия двух параллельных проводников с токами

Если взять два параллельных проводника с токами, расположенных на расстоянии а друг от друга, то вокруг каждого из них будет возникать собственное магнитное поле, причем проводник с током I1 окажется в магнитном поле проводника с током I2 и наоборот. В результате на проводники будут действовать электромагнитные силы F1 и F2, направление которых определяется по правилу левой руки.
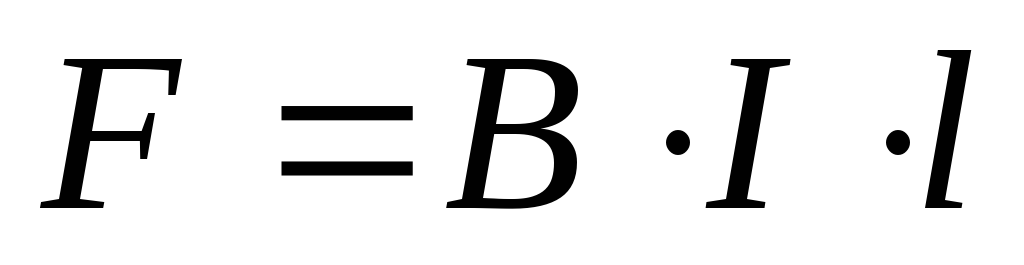

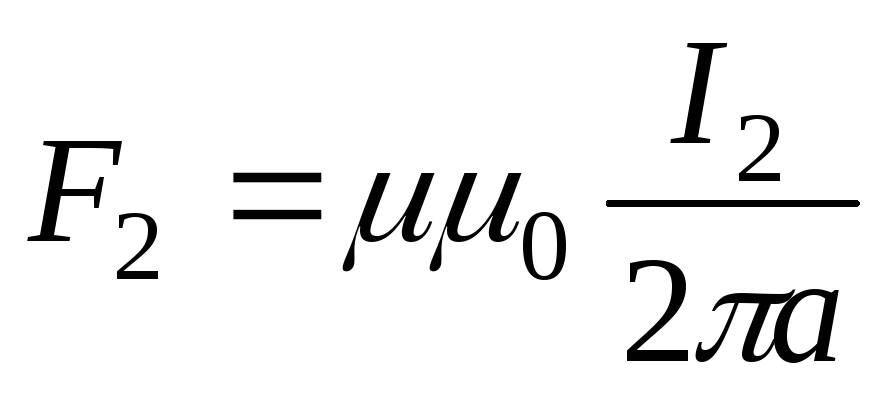






провода с токами
одинакового направления притягиваются
друг к другу с силой F.
провода с токами
одинакового направления притягиваются
друг к другу с силой F.
Закон полного тока | Электрикам


Полным током называют алгебраическую сумму токов, пронизывающих поверхность, ограниченную замкнутым контуром.
Приняв произвольно выбранное направление обхода какого-либо контура в магнитном поле за положительное, будем считать токи, пронизывающие этот контур, положительными, если их направление совпадает с направлением поступательного движения буравчика, рукоятка которого вращается в положительном направлении обхода контура.
Например, на рис. 1 ток I1— положительный, а ток I2 —


отрицательный. Полный ток, пронизывающий контур,


Рис 1. Токи, пронизывающие поверхность, ограниченную контуром
Рис 2. Напряженность магнитного поля провода с током
Магнитная индукция и напряженность поля в отдельных точках, расположенных на контуре, могут иметь или различные или одинаковые значения Допустим, что в точке а вектор индукции и пропорциональный ему вектор напряженности поля образует с элементом длины контура dl угол α. При этом HL = H cosα будет представлять собой касательную к контуру составляющую вектора напряженности магнитного поля. Магнитное напряжение HLdl на элементарном участке контура dl положительно, если направление вектора НL совпадает c выбранным направлением обхода контура, в противном случае оно будет отрицательным.
По закону полного тока МДС F вдоль контура равна полному току, который проходит сквозь поверхность ограниченную этим контуром, т. е.

 или
или 

Если контур совпадает с магнитной линией, то направление вектора напряженности поля совпадает с касательной к контуру и, следовательно, HL=H.
Если, кроме того, индукция B и напряжённость поля H во всех точках контура одинаковы, как вследствие симметрии при обходе вдоль контура рис. 5.17, то в формуле (5 23
напряженность можно вынести за знак суммирования и написать:


где знак 
 обозначает сумму элементарных длин замкнутого контура, т. е. длину этого контура L; следовательно в этом случае
обозначает сумму элементарных длин замкнутого контура, т. е. длину этого контура L; следовательно в этом случае


Выражение 
 иногда называют циркуляцией вектора напряженности магнитного поля по замкнутому контуру. В соответствии с этим изменяют и формулировку закона полного тока.
иногда называют циркуляцией вектора напряженности магнитного поля по замкнутому контуру. В соответствии с этим изменяют и формулировку закона полного тока.
определение и формула для магнитных цепей
В радиотехнических схемах применяют трансформаторы и другие изделия, функциональность которых определена индуктивными характеристиками. В данной публикации представлен закон полного тока, который используют для предварительных расчетов и коррекций устройств с магнитными компонентами.
Для создания работоспособной конструкции нужно правильно вычислить параметры ее компонентов
Определение полного тока
Сутью данного закона является определение взаимной связи между электрическим током и образованным его протеканием магнитным полем. Эта особенность выявлена экспериментальным путем в первой половине XIX века. Позднее была создана формулировка, устанавливающая закон полного тока для магнитного поля. Классическое определение приведено ниже. Однако начинать изучение темы следует с базовых принципов.
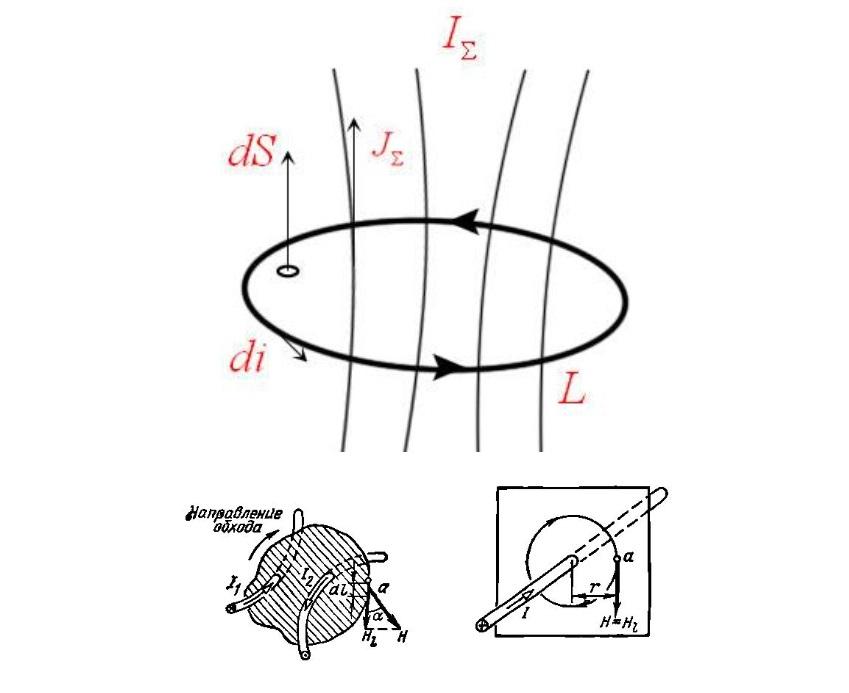
Схематическое изображение физических параметров
На рисунке отмечены следующие компоненты:
- I∑ – суммарный (полный) ток;
- S – пронизываемая (dS – элементарная) площадка;
- dL – элементарный линейный участок.
- J∑ – плотность распределения токов;
- L – кольцевой замкнутый контур;
- H – напряженность магнитного поля в векторном представлении.
Магнитное напряжение вдоль контура
В представленном примере для изучения берут проводники, через которые пропускают электрический ток. В совокупности они образуют сечение с мнимой площадью (S), которая ограничена неким контуром. Пользуясь классическим правилом «буравчика», несложно установить направление вектора (di или Н). Понятно, что в данном случае рассматривается дискретная величина. Вектор магнитной напряженности и полный ток связаны следующей формулой:
I∑ = ∫L*H*dL.
Полный ток
Из приведенного соотношения видно, что сумма токов равна перемещению вектора напряженности магнитного поля по замкнутому контуру. Его циркуляция описывается интегралом приведенных выше компонентов. Из рассмотренных пропорций несложно сделать вывод о том, что полный ток будет зависеть от плотности, контура и элементарной площадки:
I∑ = ∫S*J*ds.
К сведению. В некоторых ситуациях удобнее пользоваться дифференциальной формой представления электромагнитных параметров: ∫S*J*∑ds = ∫S*rotH*ds.
Магнитодвижущая сила
Представленный закон применяют для расчета рабочих характеристик разных устройств:
- одно,- и трехфазных трансформаторов с подключением к сети 220 (380) V, соответственно;
- электродвигателей постоянного тока;
- катушек с тороидальными сердечниками;
- электрических приводов реле и клапанов;
- аналоговых измерительных приборов и датчиков;
- электромагнитов, которые установлены в подъемных механизмах, системах водоочистки.
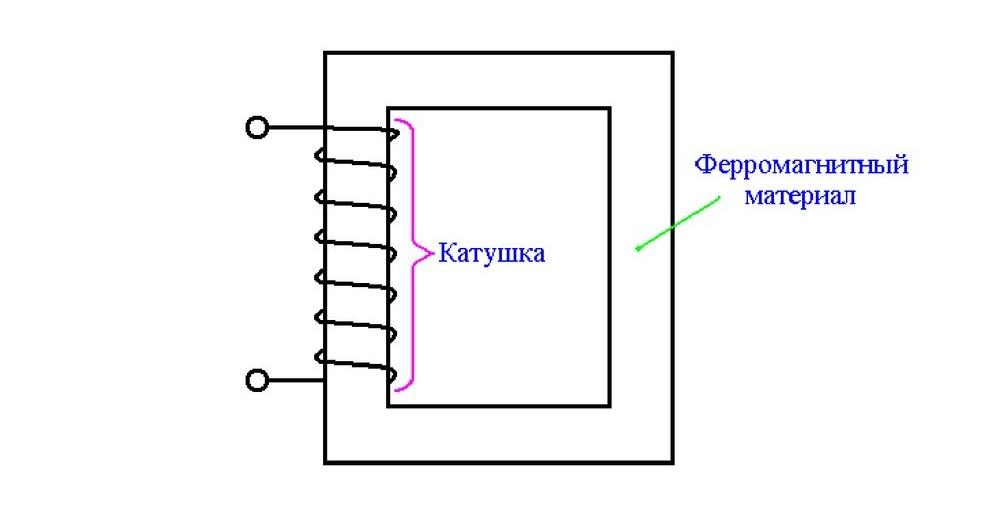
Простая магнитная цепь
Для подробного изучения подойдет несложный пример. В цепи обеспечивается перемещение тока по замкнутому контуру с применением катушки индукции. Созданная магнитодвижущая сила (F) будет зависеть от силы тока (I) в проводнике и количества сделанных витков (W):
F = I * W.
По классическим определениям, ток в цепи появляется при создании разницы потенциалов между точками подключения источника ЭДС. Подобным образом показанная выше сила F провоцирует образование магнитного потока. В данном случае аналогичным образом можно использовать не только правило буравчика, но и технологии расчета цепей. Необходимо только корректно применять отдельные понятия. Так, электрическому сопротивлению соответствует магнитный аналог.
При разделении такого контура на два сегмента справедливым будет следующее выражение:
Н1*L1 + h3*L2 = I *W,
где Н1 и h3 (L1 и L2) напряженность (длина) соответствующих частей.
Последовательным преобразованием можно получить удобную для практического применения формулу закона полного тока:
- h2 = B1/ma1;
- B1 = Ф/S1;
- h3 = B2/ma2;
- B2 = Ф/S2;
- I*W = Ф*L1/ma1*S1 + Ф*L1/ma1*S1 = Ф*Rm1 + Ф*Rm2.
Кроме площади поперечного сечения (S), здесь приведены магнитные параметры разных участков (1 и 2):
- Ф – поток;
- В – индукция;
- ma – проницаемость.
Из этого выражения нетрудно получить значение магнитного сопротивления для каждого участка:
Rm = L/ma*S.
По аналогии с формулой Ома для электрических цепей можно вычислить магнитное напряжение:
U = Ф * Rm.
C учетом частоты питающего сигнала (w) магнитный поток будет зависеть от силы тока и суммарного сопротивления участков цепи:
Ф = (I*w)/(Rm1+Rm2) = (I*w)/∑Rm.
К сведению. По этим же принципам допустимо применение законов Кирхгофа. Так суммарная величина входящих и выходящих магнитных потоков будет равной.
Определение закона полного тока
Важные выводы и пояснения:
- напряженность зависит от источника тока;
- индукция выполняет силовые функции воздействия на движущиеся по цепи заряды;
- параметры поля формируются магнитными свойствами определенной среды.
На практике усиление тока сопровождается пропорциональным изменением поля (магнитной индукции). Базовое правило справедливо при рассмотрении цепей, созданных из серебра, влажного или сухого воздуха, других материалов.
Измененные правила действуют в железе или иной среде с выраженными ферромагнитными свойствами. Именно такие решения применяют при создании трансформаторов и других изделий для улучшения потребительских характеристик.
Для упрощения следует начать изучение физических величин и расчетов на примере нейтральной среды. При отсутствии ферромагнитных параметров можно изобразить магнитное поле несколькими замкнутыми линиями длиной L. В этом случае полный ток (I) будет зависеть от индукции (B) следующим образом:
I = (B*L)/м.
Здесь m – магнитная постоянная, которая в стандартной системе единиц измерения приблизительно равна 1,257*10-7 Генри на метр (Гн/м).
Важно! В действительности подобные идеальные условия встречаются редко, когда индукция сохраняет одинаковые параметры вдоль всей линии контура.
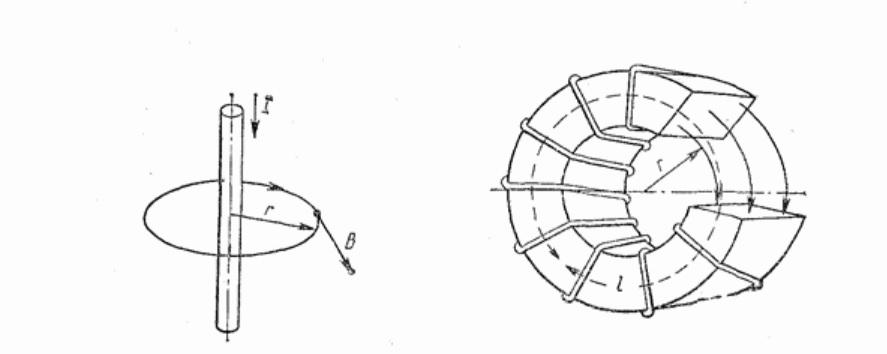
Прямой проводник и тороид
Поле формируется перпендикулярно прямому длинному проводнику. Его линии образуют набор из множества окружностей. Центр каждой из них соответствует продольной оси проводника. Расстояние от нее до кольца – r. Длину (L) вычисляют по стандартной геометрической пропорции:
L = 2π*r.
Если разместить витки симметрично на тороидальном сердечнике из электрически нейтрального фарфора для устранения искажений, линии магнитного поля будут проходить внутри равномерно. Кольца, как показано на рисунке с вырезанным сегментом, образуют замкнутые контуры. В такой конструкции обеспечивается неизменность индукции. Для каждой отдельной линии можно пользоваться формулой:
B*L = B* 2π*r = m*I.
Суммарное значение (полный ток) получают умножением на количество витков (N).
На основе приведенных данных нетрудно вычислить индукцию, которая будет создана внутри нейтрального тороидального кольца при определенной силе тока:
B = m*(I*N/L).
Эта пропорция позволяет сделать определение удельного полного тока:
(IN)o=(I*N)/L.
Зная размеры тора и другие исходные параметры, вычисляют индукцию у внутреннего и наружного края. При необходимости делают коррекции с помощью изменения толщины кольца, количества витков.
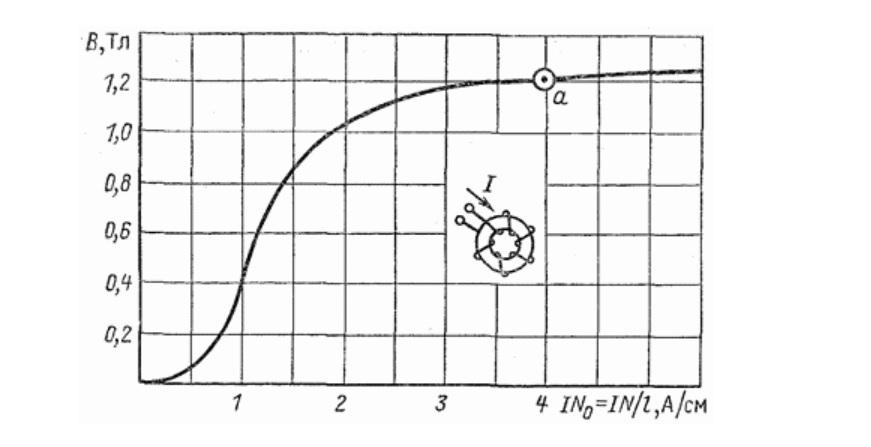
Намагничивание железного кольца
Если на основу из ферромагнитного материала намотать две обмотки (изолированные), будут создан наглядный образец для измерений. Изменяя силу тока в одном проводнике, можно наблюдать за изменением электродвижущей силы по подключенному к другой паре выводов прибору.
На графике приведены результаты эксперимента при использовании кольца, сделанного из железа с минимальным количеством примесей. Если применить закон полного тока для рассмотренного выше примера с нейтральным сердечником в точке «а», должно получиться приблизительно 5*10-4 Тл. Между тем в действительности напряженность составляет для этой силы тока 1,2 Тл при одинаковых размерах тока и количестве сделанных витков.
Корректируют вычисления с учетом поправочного коэффициента – магнитной проницаемости. Следует подчеркнуть, что это параметр не линейный. Максимальный полезный эффект наблюдается при относительно небольших значениях силы тока. Значительный спад после порогового уровня насыщения ограничивает практическое применение рассмотренных свойств.
Формула закона полного тока
В этом разделе приведены формулы для уточненных расчетов и примеры типовых конструкций. Для интегральных вычислений вполне подходит закон Гаусса, который применяют в электростатике.
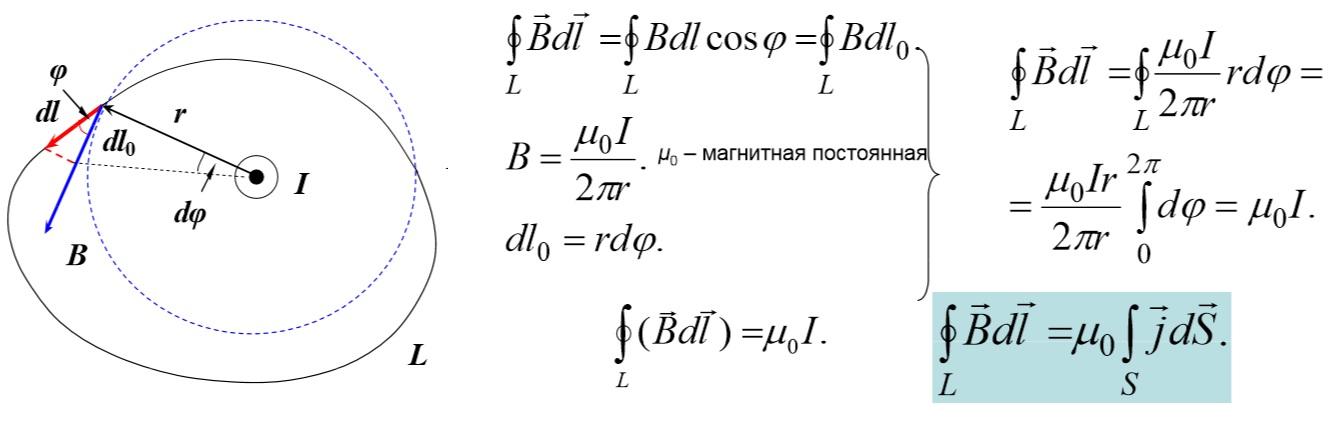
Интегральная формула закона полного тока
Пояснения:
- L – обозначает замкнутый контур, созданный по произвольной траектории;
- векторы В и r направлены перпендикулярно;
- dl (dl0) – элементы произвольной части (силовой линии), соответственно;
- ϕ – угол между элементами.
Из формулы на рисунке понятно, что циркуляция вектора индукции не равняется нулю. Такие поля называют «соленоидальными» или вихревыми. В отличие от электродинамики, в данном случае отсутствуют потенциальные характеристики. Как и в базовом определении, полный ток определяется циркуляцией магнитной индукции (векторное выражение) по контуру произвольной формы, окружающему сумму токов.
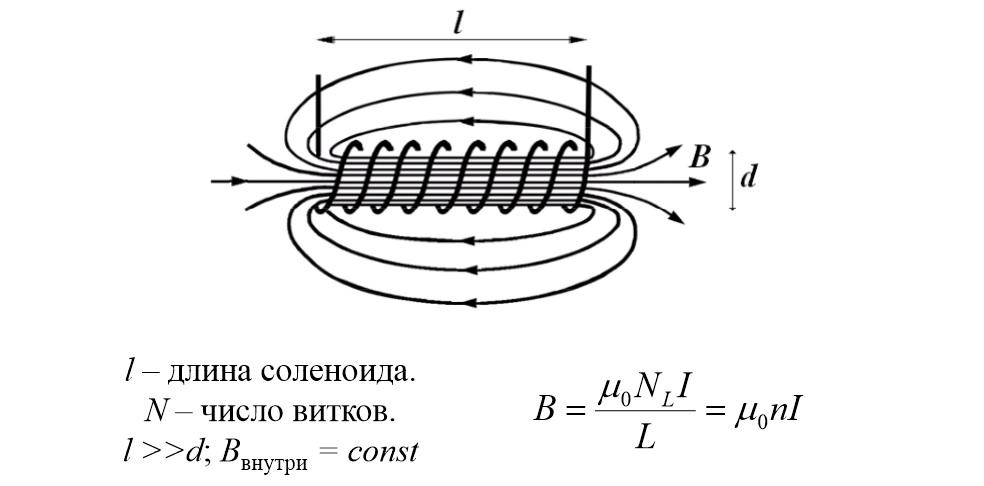
Формула для расчета индуктивности, которую создает длинный соленоид
В этом примере n – число витков обмотки на единицу длины основы.
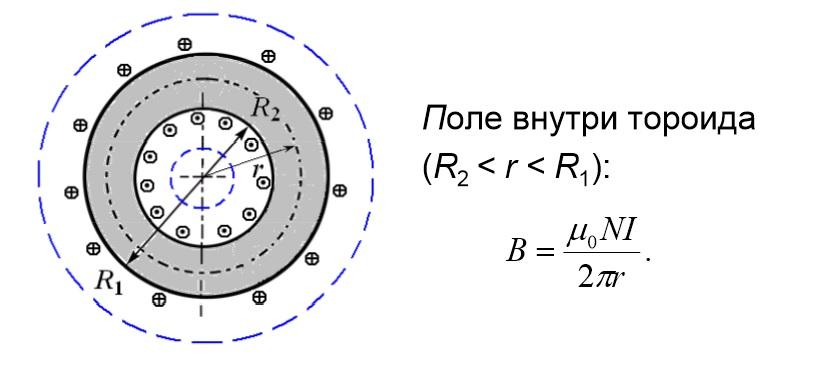
Расчет параметров поля внутри тороида
Параметры:
- количество сделанных витков – N;
- внешний, внутренний и произвольный радиусы – R1, R2 и r.
Следует помнить! Вне тороида магнитное поле равно нулю.
Рассмотренные методики расчетов применяют с учетом реальных условий. Особое значение при выборе компонентов конструкций уделяют ферромагнитным свойствам сердечника. Проводники для обмоток выбирают с запасом, учитывая максимальную силу тока источника.
Видео
Второе уравнение Максвелла. Уравнение непрерывности магнитных линий.
Это уравнение аналогично предыдущему,
но описывает не электрические, а
магнитные явления. Оно связывает
магнитное поле и магнитный заряд. Снова
рассмотрим объем V,
охваченный поверхностью, площадь
которойS. В этом
объеме есть магнитный зарядqм, который создает магнитное поле .
Согласно закону непрерывности магнитных
силовых линий они связаны следующим
соотношением:
.
Согласно закону непрерывности магнитных
силовых линий они связаны следующим
соотношением:
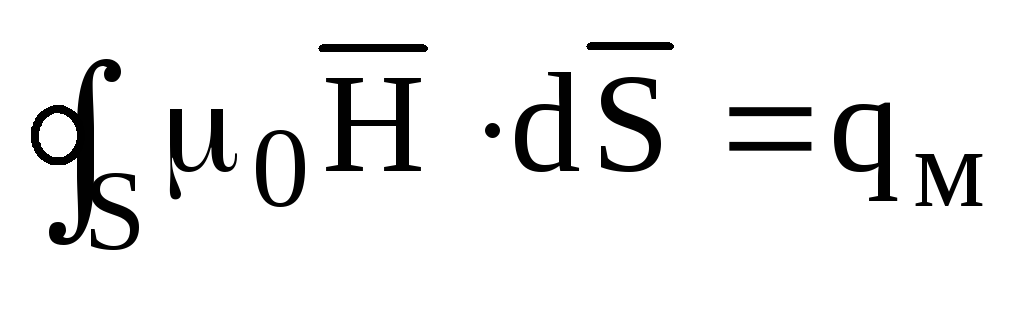 .
(1.20)
.
(1.20)
Известно, что в природе отсутствуют магнитные заряды и в правой части равенства должен стоять ноль. Однако в технических приложениях иногда их приходится искусственно вводить. Например, если в задаче рассматривается поле, создаваемое постоянным магнитом и в интересующий нас объем входит только северный полюс магнита, он и будет играть роль магнитного заряда, создающего магнитное поле.
Если введены магнитные заряды, то можно ввести и их плотность. Тогда последнее равенство можно переписать в дифференциальной форме. Введем плотность магнитных зарядов равенством, аналогичным (1.10).
 (1.21)
(1.21)
Объединяя (1.20), (1.21), пользуясь теоремой Остроградского- Гаусса и рассуждая так же, как в предыдущем разделе, получим:

 ;
;
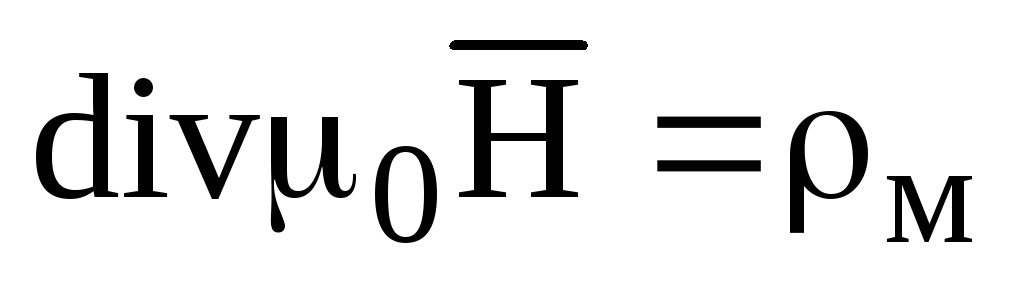 .
(1.22)
.
(1.22)
Источник магнитных силовых линий – магнитные заряды. В природе магнитных зарядов нет и, как правило, магнитные силовые линии непрерывны. Поэтому второе уравнение Максвелла называют уравнением непрерывности магнитных силовых линий.
Допуская существование магнитных зарядов, следует признать и существование магнитных токов, которые можно ввести точно так же, как вводились электрические токи:
 .
(1.23)
.
(1.23)
Для магнитного заряда, как и для электрического, справедлив закон сохранения. С течением времени магнитный заряд может изменяться, но, в соответствии с законом сохранения, это изменение должно происходить только за счет пересечения зарядами поверхности, ограничивающей объем. Процесс движения заряда через поверхность и есть ток через нее. Выразим в (1.23) магнитный ток через его плотность:
 .
(1.24)
.
(1.24)
Получена интегральная форма второго уравнения непрерывности. Чтобы перейти к дифференциальной форме, воспользуемся теоремой Остроградского-Гаусса и заменим интеграл по поверхности от плотности магнитного тока на интеграл по объему отdivjm. Как и ранее, учтем произвольность объемаV. Тогда
 ;
;
 .
(1.25)
.
(1.25)
Получена дифференциальная форма второго уравнения непрерывности, которая утверждает, что изменение магнитного заряда во времени в выбранной точке пространства приводит к возникновению магнитного тока в этой точке.
Третье уравнение Максвелла – закон полного тока
При обсуждении уравнения непрерывности магнитных силовых линий указывалось, что в природе магнитных зарядов не существует, и не они порождают магнитное поле. Обычно магнитное поле возникает вокруг проводника с электрическим током. Это явление количественно описывает закон полного тока. Согласно этому закону циркуляция напряженности магнитного поля по замкнутому контуру равна суммарному току, пронизывающему площадь, охваченную этим контуром.
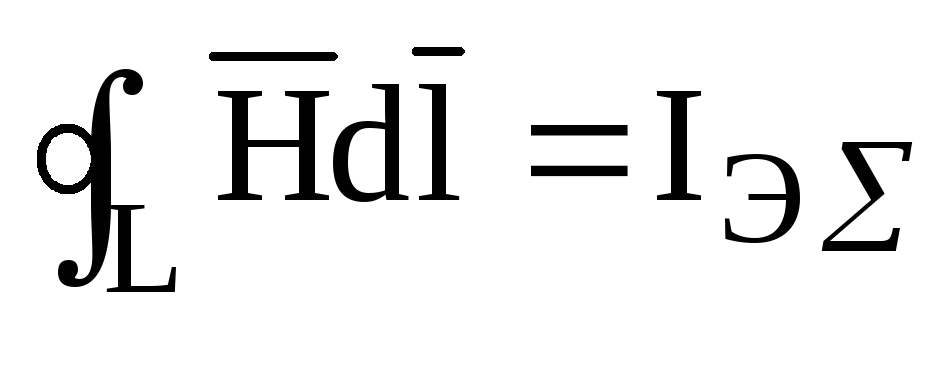 .
(1.26)
.
(1.26)
Выражение в левой части уравнения носит название магнитно-движущей силы.
Закон полного тока следует из определения магнитной индукции. Покажем это. Рассмотрим магнитное поле бесконечно длинного проводника

и
попытаемся получить из него закон
полного тока. Пусть контур L– окружность радиусомr, плоскость
которой перпендикулярна проводнику
с током. Запишем циркуляцию вектора  по этой окружности.
по этой окружности.
 .
.
Закон полного тока записан не для магнитной индукции, а для напряженности магнитного поля. Перейдем в последнем равенстве от магнитной индукции к напряженности магнитного поля.
 =
=
 ;
; ,
,
что полностью совпадает с (1.26).
Получим дифференциальную форму закона. Для этого выразим электрический ток через его плотность
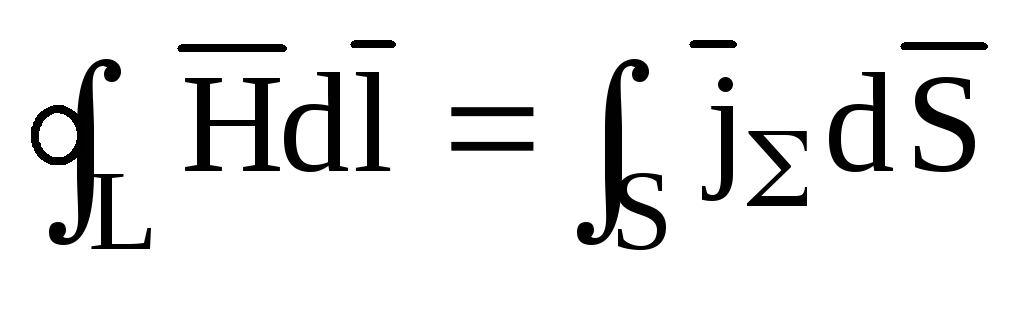 .
.
Используем теорему Стокса для того, чтобы преобразовать циркуляцию напряженности магнитного поля по контуру Lинтегралом от ротора напряженности магнитного поля по площади, ограниченной этим контуром.

Из-за полной произвольности кривой Lэто равенство возможно лишь тогда, когда равны подынтегральные выражения, то есть:
r ot
ot =
=  .
(1.27)
.
(1.27)
Это
и есть дифференциальная форма закона
полного тока. В обе формулировки закона
входит полный ток IЭили его плотность  .
Рассмотрим, из каких составляющих
состоит полный ток. В вакууме нет
носителей заряда, и ток проводимости
отсутствует. Магнитное поле может
возбудить ток, проходящий за пределами
рассматриваемого объема. Такой ток
называютсторонним. Однако существует
еще один вид тока, который называют
током смещения и который существует в
вакууме. С этим током мы сталкиваемся
тогда, когда рассматриваем электрическую
цепь переменного тока, содержащую
конденсатор (рис.1.2). В этой цепи протекает
реактивный ток, который можно рассчитать,
разделив напряжение источника на
сопротивление емкости переменному
току. Выясним природу этого тока. Между
пластинами конденсатора вакуум, и ток
проводимости не может проходить.
Оказывается, что изменение электрического
поля между пластинами, вызванное
изменением заряда на пластинах, можно
интерпретировать как ток. Покажем это.
Выделим замкнутую поверхностьS,охватывающую объемV,
который содержит одну пластину
конденсатора, а другая пластина находится
за пределами объема.qЭ(t)— заряд на этой пластине. Электрические
заряды, перемещаясь по проводнику,
подходят к пластине конденсатора и
накапливаются на ней, изменяя электрическое
поле между пластинами. Этот процесс
описывается первым уравнением Максвелла
– законом Гаусса (см.1.16), который с
учетом знака заряда электрона запишется
так:
.
Рассмотрим, из каких составляющих
состоит полный ток. В вакууме нет
носителей заряда, и ток проводимости
отсутствует. Магнитное поле может
возбудить ток, проходящий за пределами
рассматриваемого объема. Такой ток
называютсторонним. Однако существует
еще один вид тока, который называют
током смещения и который существует в
вакууме. С этим током мы сталкиваемся
тогда, когда рассматриваем электрическую
цепь переменного тока, содержащую
конденсатор (рис.1.2). В этой цепи протекает
реактивный ток, который можно рассчитать,
разделив напряжение источника на
сопротивление емкости переменному
току. Выясним природу этого тока. Между
пластинами конденсатора вакуум, и ток
проводимости не может проходить.
Оказывается, что изменение электрического
поля между пластинами, вызванное
изменением заряда на пластинах, можно
интерпретировать как ток. Покажем это.
Выделим замкнутую поверхностьS,охватывающую объемV,
который содержит одну пластину
конденсатора, а другая пластина находится
за пределами объема.qЭ(t)— заряд на этой пластине. Электрические
заряды, перемещаясь по проводнику,
подходят к пластине конденсатора и
накапливаются на ней, изменяя электрическое
поле между пластинами. Этот процесс
описывается первым уравнением Максвелла
– законом Гаусса (см.1.16), который с
учетом знака заряда электрона запишется
так:

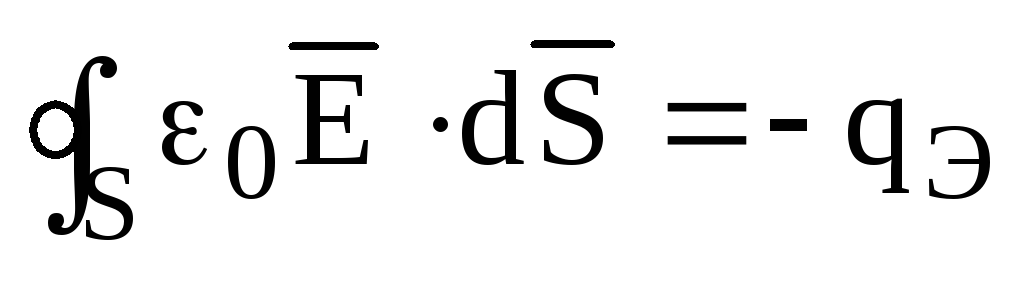 .
.
Если продифференцировать это выражение по времени, то справа окажется производная от заряда, а в соответствии с первым уравнением непрерывности (см.1.15) она вызовет электрический ток. Следовательно, выражение, которое появится в левой части равенства, будет описывать искомый ток. Продифференцируем по времени последнее выражение:
 =
=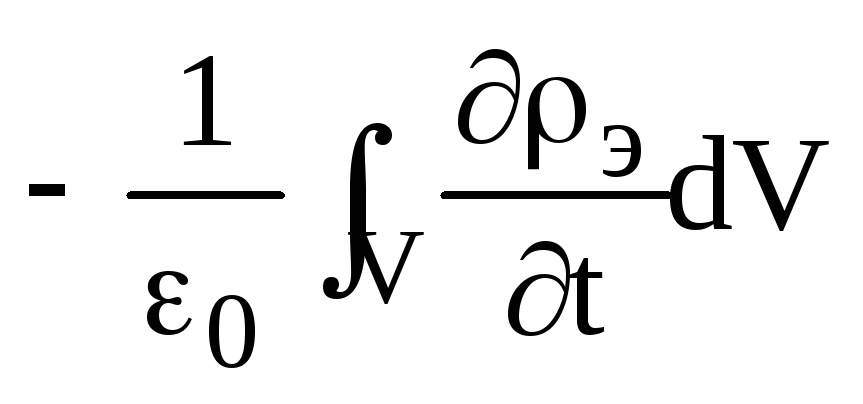 =
=  .
.
Приравнивая подынтегральные выражения для самой левой и самой правой частей равенства, получим:
 . (1.28)
. (1.28)
Итак, кроме стороннего тока, протекающего за пределами рассматриваемого объема, в вакууме существует ток смещения, величина которого зависит от скорости изменения электрического поля во времени. Распишем компоненты полного тока в законе полного тока. Тогда для интегральной формы вместо (1.26) получим
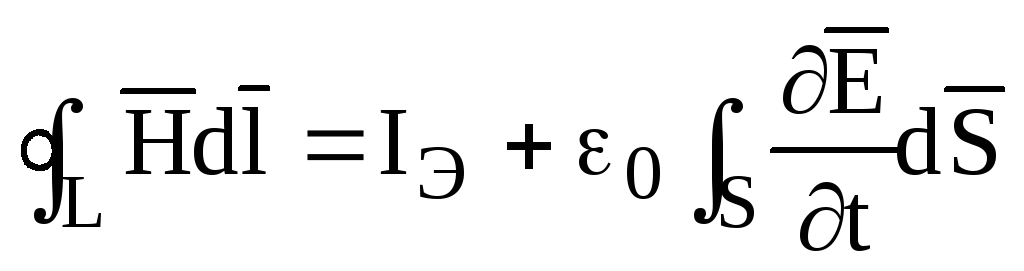 ,
(1.29)
,
(1.29)
а для дифференциальной формы вместо (1.27):
rot =
=  +
+
 . (1.30)
. (1.30)
О законе полного тока: формула для магнитных цепей
В радиоэлектронике применяется ряд законов и постулатов для анализа, как цепей, так и устройств. Сталкиваясь с необходимостью исследования магнитных цепей, применяют закон полного тока для магнитного поля.
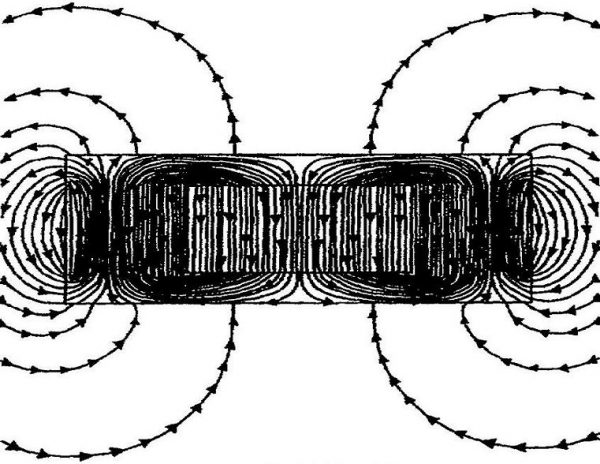
Магнитные потоки трансформатора
Суть закона полного тока
Данный постулат характеризует взаимосвязь между током электрической цепи и магнитным полем, появляющимся в связи с протеканием этого тока.
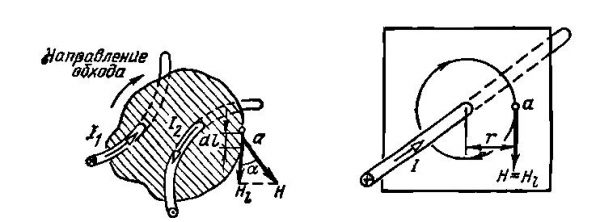
Контур с проводниками под током
Для понимания закона полного тока необходимо представить некоторое число проводников, по которым протекает электрический ток. Множество проводников охватывает некоторый контур, и, соответственно, ограничивает мнимую поверхность S, согласно картинке выше. Направление огибания контура, согласно правилу буравчика, ориентировано по ходу часовой стрелки. Поскольку множество токов является величиной дискретной, то закон полного тока определяется как связь суммарного электрического тока через закольцованный контур L и напряженности магнитного поля, сформированного этим током, и определяется по формуле:
∫LHdl=I∑, где:
- H – вектор напряженности магнитного поля;
- dl – направленный элементарный линейный участок, взятый вдоль контура;
- I∑ – суммарная сила тока.
Сущностью закона полного тока является то, что передвижение вектора напряженности магнитного поля по кольцевому контуру приравнивается сумме всех токов, которые находятся в этом контуре. Это выражение является интегральной формой закона полного тока.
Дополнительная информация. Интеграл произведения вектора напряженности магнитного поля и направленного элементарного линейного участка по кольцевому контуру называется циркуляцией вектора Н.
Если заданный контур пронизывает непрерывный пространственный поток движущихся заряженных частиц с плотностью электрического тока J, то общая величина тока, проходящего сквозь площадку, измеряется по выражению:
I∑=∫sJdS, где dS – элементарная площадка контура S.
Произведение JdS характеризует поток вектора плотности тока J, проходящего через поверхность dS.
Помимо интегральной формы, применяется дифференциальная форма закона полного тока. С целью получения дифференциальной формы выражения полного тока следует заменить интеграл по контуру L на интеграл по площади S. Поскольку теорема Стокса в векторном анализе выражается как:
∫LАdl=∫s rotАdS, то ∫LНdl=∫s rotНdS.
Объединив эти выражения с законом полного тока, в интегральной форме получается:
∫s rotНdS =∫s J∑dS.
Поскольку контур L взят произвольным образом, то интегралы в левой и правой частях выражения равны, если равны подынтегральные выражения. Исходя из этого, выражение преобразовывается в:
rotН=J∑.
Данной формулой выражается закон полного тока в дифференциальной форме.
Практическое применение в расчетах
Закон полного тока является основным законом при расчете магнитных цепей и дает возможность без особых усилий определять напряженность поля.
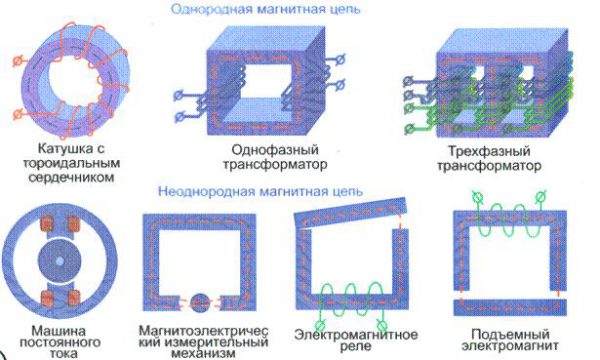
Примеры магнитных цепей
Магнитная цепь являет собой комплекс физических тел, обладающих сильно выраженными магнитными свойствами, магнитодвижущих сил и других условий, по которым смыкается магнитный поток. Магнитодвижущая сила определяется как произведение количества витков катушки на протекающий в ней электрический ток:
F=Iω, где:
- F – магнитодвижущая сила;
- ω – количество витков в катушке;
- I – электрический ток.
Подобно тому, как электродвижущая сила электрической цепи провоцирует возникновение тока, так и магнитодвижущая сила магнитной цепи вызывает магнитный поток. Направление магнитодвижущей силы в схемотехнике определяется на основании правила буравчика.
Параметры, описывающие характеристики магнитной или электрической цепи, являются тождественными. Аналогичными являются и мероприятия по расчету цепей. Постоянные токи в электрических цепях возникают благодаря электродвижущей силе. В магнитных цепях эту функцию выполняет магнитодвижущая сила обмоток. Характеристика сопротивления току в электрической цепи имеет свою аналогию в магнитной цепи в виде магнитного сопротивления.
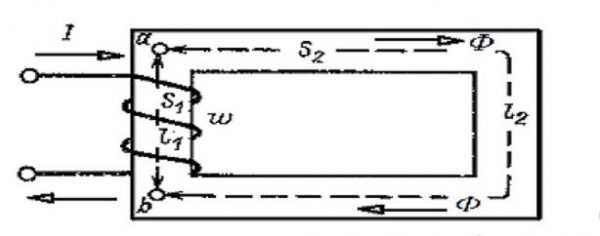
Неразветвленная магнитная цепь
Согласно закону полного тока, выражение, описывающее процессы в магнитной цепи (рис. выше), выглядит так:
Iω=h2L1+h3L2, где:
- h2 – напряженность поля первого участка;
- h3 – напряженность поля второго участка;
- L1 – длина первого однородного участка;
- L2 – длина второго однородного участка.
Поскольку напряженность магнитного поля и магнитная индукции на первом и втором участках равны:
- h2=B1/µа1, где:
- B1 – магнитная индукция;
- µа1 – магнитная проницаемость первого участка.
- B 1=Φ/S1, где:
- Φ – магнитный поток;
- S1 – площадь поперечного сечения первого участка.
- h3=B2/µа2, где:
- B2 – магнитная индукция второго участка;
- µа2 – магнитная проницаемость второго участка.
- B 2=Φ/S2, где:
- Φ – магнитный поток;
- S2 – площадь поперечного сечения второго участка.
выражение, описывающее закон полного тока, преобразовывается в:
Iω=ΦL1/µа1S1+ ΦL2/µа2S2=ΦRм1+ΦRм2, где:
- Rм1=L1/µа1S1 – магнитное сопротивление первого участка;
- Rм2=L2/µа2S2 – магнитное сопротивление второго участка.
Проводя аналогии с электрической цепью, произведение магнитного потока на магнитное сопротивление является магнитным напряжением:
Uм2=ΦRм2=h3L2.
Если выделить из формулы магнитный поток, получается формула, представляющая собой закон Ома для магнитной цепи:
Φ= Iω/Rм1+Rм2= Iω/∑Rм.
Для магнитной цепи, не имеющей магнитодвижущей силы, выражение будет выглядеть как:
Uм=ΦRм=HL.
Аналогично электрическим цепям на магнитные цепи распространяются постулаты Кирхгофа:
- Сумма магнитных потоков, втекающих в узел, равна сумме магнитных потоков, вытекающих из узла. Выражение выглядит как ∑Φк=0;
- Сумма магнитодвижущих сил, находящихся в контуре, равна сумме падений напряжений на всех отрезках цепи, что соответствует выражению ∑Iω=∑Uм=∑HL.
Закон полного тока для магнитных цепей стоит на одном уровне с основными законами, касающимися электрических цепей. Понимание закона полного тока позволит с легкостью проводить расчет и подбор необходимых устройств, в основе работы которых лежат магнитные потоки.







 и допустим, что вектор напряжен-ности
в этой точке образует
и допустим, что вектор напряжен-ности
в этой точке образует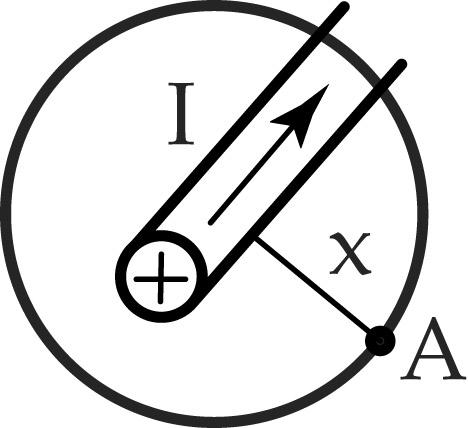






 по всему сечению
по всему сечению
 и для прямолинейного проводника с
током магнитная индукция будет равна
и для прямолинейного проводника с
током магнитная индукция будет равна ,
а внутри проводника с током –
,
а внутри проводника с током –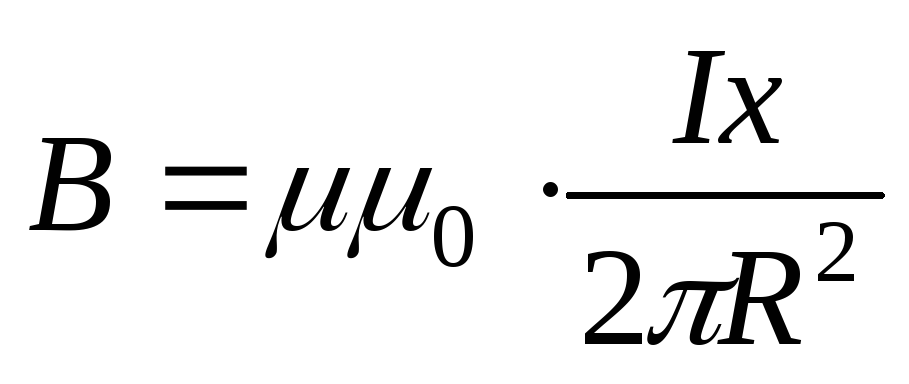

 —
для однородного поля). Определим
напряженность поляН внутри кольцевой катушки.
—
для однородного поля). Определим
напряженность поляН внутри кольцевой катушки.
