Учебная дисциплина ОП.03 Электротехника и электроника

Лекция по теме: «Фазные и линейные напряжения (токи), соотношения между ними. Векторные диаграммы напряжений и токов. Мощность трехфазной цепи переменного тока. Нулевой провод, его значение»

План лекции:

1.Трехфазный переменный ток.

2. Что такое фаза?

3. Фазные и линейные напряжения (токи).

4. Соотношения между фазными и линейными напряжениями (токами).

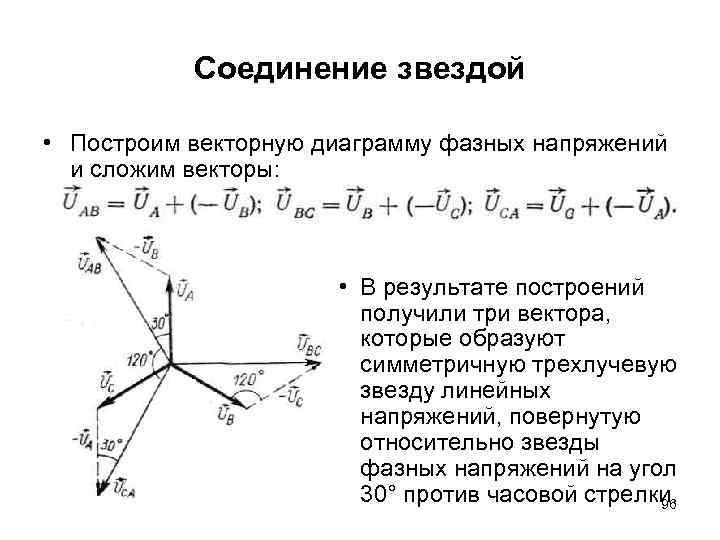
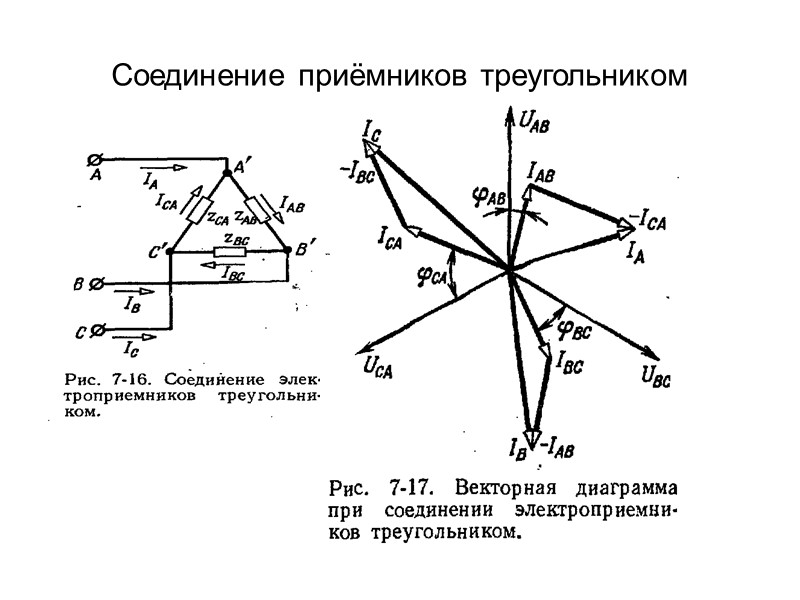
5. Векторные диаграммы напряжений и токов.

6. Мощность трехфазной цепи переменного тока.

7. Нулевой провод, его значение.

Каждая часть многофазной системы, имеющая одинаковую характеристику тока, называется фазой.

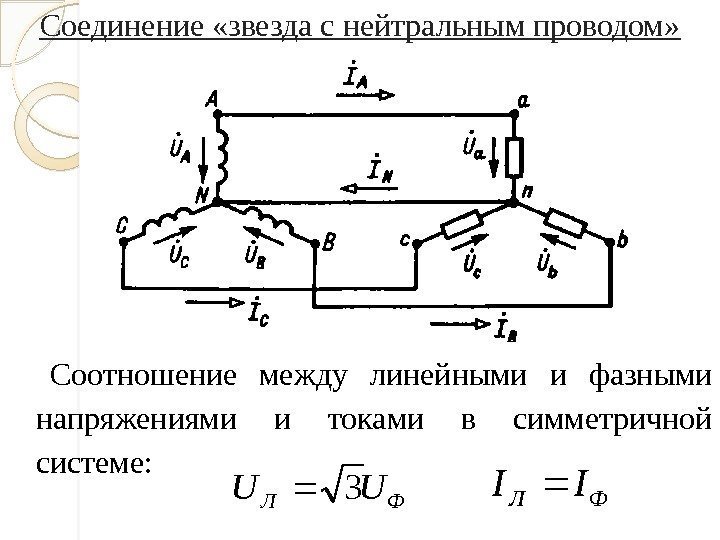
Фазное напряжение – возникает между началом и концом какой-либо фазы. По другому его еще определяют, как напряжение между одним из фазных проводов и нулевым проводом.

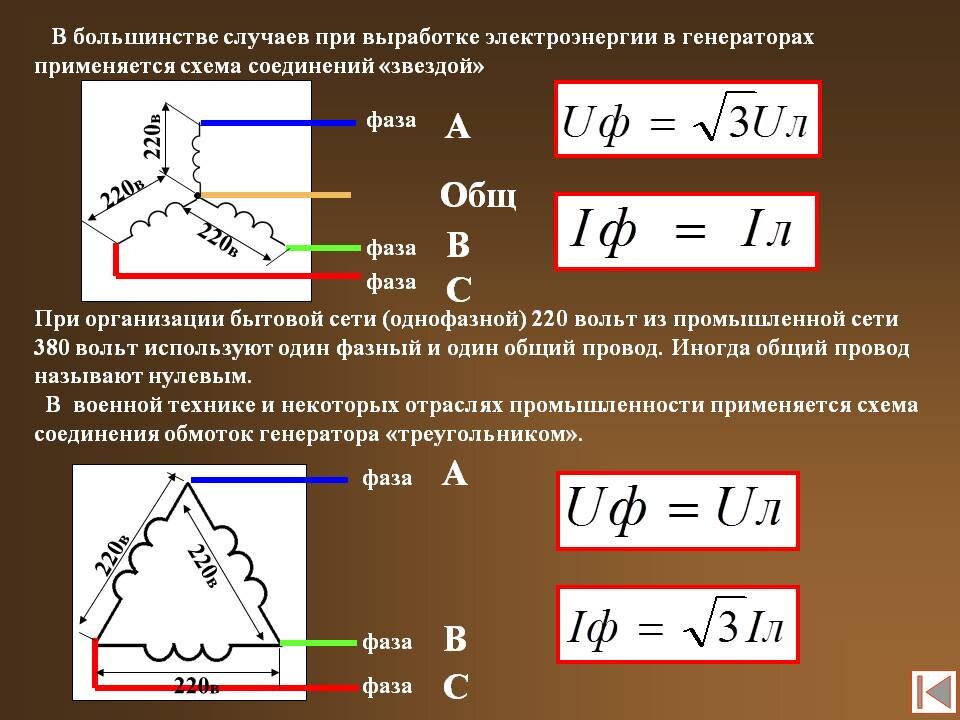
Линейное напряжение — которое определяют еще как межфазное или между фазное – возникающее между двумя проводами или одинаковыми выводами разных фаз. Показатель фазного напряжения составляет примерно 58% от параметров линейного. Таким образом, при нормальных условиях эксплуатации показатели линейных одинаковы и превышают фазные в 1,73 раза. В трехфазной сети напряжение, как правило, оценивают по данным линейного напряжения. Для трехфазных линий, которые отходят от подстанции, устанавливается линейное напряжение номиналом 380 вольт. Это соответствует фазному в 220 В.

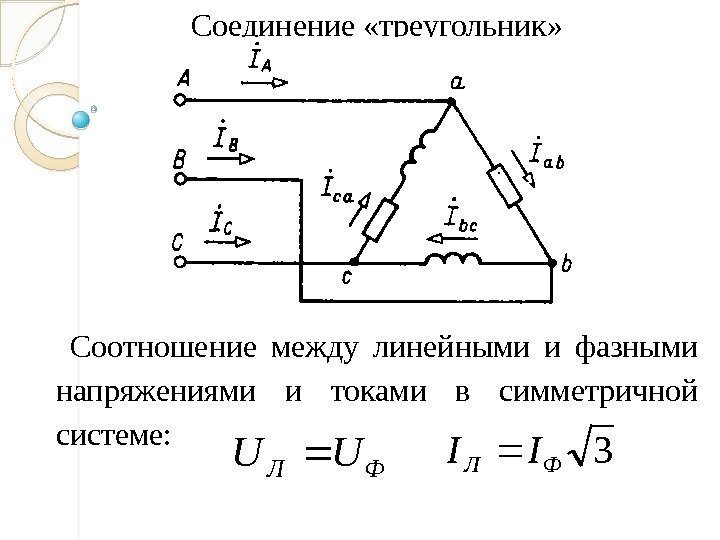
Так, токи, протекающие в каждой фазе, именуют фазными и условно обозначают I_А, I_B, I_C либо условно I_ф. Токи в ветвях нагрузки именуют линейными. Их величина обуславливается величиной фазных напряжений, типом нагрузки. При сугубо активной нагрузке токи идентичны с напряжениями по фазе, а при индуктивной либо емкостной нагрузке, токи могут опережать или отставать от напряжения.

В традиционных электросетях имеет место 2 метода соединения:

— треугольник;

— звезда.

Видео «Построение векторных диаграмм» по ссылке: https://www.youtube.com/ ›watch?v=wcyQvK84lsU

youtube.com›watch?v=XBoF0gFU_FI)

Мощность трехфазной цепи переменного тока

Количество потребленной энергии в сети однофазного тока определяется простейшими расчетами, это не вызывает затруднений. Расчет мощности трехфазной сети сопряжен с некоторыми трудностями: Наличие трех фаз вместо одной; Различные схемы соединения потребителей – «звезда» или «треугольник»; Симметрия или ее отсутствие при распределении нагрузки по фазам.

Для правильного определения и расчета мощности требуется знание нескольких факторов:

— количества фаз питания;

— способа соединения потребителей.

При однофазном подключении используется два провода:

— фазный провод;

— нулевой провод.

Для трехфазной сети характерно наличие трех или четырех проводников (подключение с заземленной нейтралью). При этом используется две различных схемы включения: «Треугольник». Каждая нагрузка подсоединяется с двумя соседними. Напряжение каждой фазы подводится к точкам соединения потребителей. «Звезда». Все три потребителя соединяются в одной точке. Ко вторым концам подключаются фазы питания. Это схема с изолированной нейтралью. В схеме с заземленной нейтралью точка соединения потребителей подключается к нулевому проводнику.

Для измерения мощности применяют специальные измерительные приборы, называемые ваттметрами. При симметричной нагрузке мощность, потребляемая от трехфазной системы, может быть определена одним однофазным ваттметром. В четырехпроводной системе (с нулевым проводом) токовая обмотка ваттметра включается последовательно в один из линейных проводов, а обмотка напряжения — между тем же линейным и нулевым проводами. При  таком включении показание ваттметра определит мощность в одной фазе Рф, а так как при равномерной нагрузке мощности всех фаз  одинаковы, то суммарная мощность трехфазной системы Р = 3 Рф.

В трехпроводной системе обмотка напряжения ваттметра включена на линейное напряжение сети, а по токовой его обмотке протекает линейный

ток. Поэтому мощность трехфазной системы в 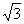 раз больше показания ваттметра P_ω, т. е. Р=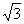

При несимметричной нагрузке одного ваттметра для определений  мощности трехфазной системы недостаточно.

В четырехпроводной системе при несимметричной нагрузке необходимо включение трех ваттметров, обмотки напряжений которых включаются между нулевым и соответствующим линейным проводом. Каждый ваттметр измеряет мощность одной фазы и суммарная мощность трехфазной системы равна сумме показаний трех ваттметров, т. е. Р = Р₁ + Р₂ + Р₃.

В лабораторной практике для этой схемы измерения мощности применяют один ваттметр и специальный переключатель, который без разрыва цепи тока дает возможность включать этот ваттметр как в один, так и в другой линейный провод.

При больших углах сдвига фаз между напряжением и током показания одного из ваттметров могут оказаться отрицательными и для измерения мощности необходимо изменить направление тока в обмотке тока, переключив ее. В этом случае суммарная мощность равна разности показаний ваттметров, т. е. Р = Р₁ — Р₂.

Энергия в трехфазной системе измеряется как однофазными, так и трехфазными счетчиками электрической энергии. Включение однофазных счетчиков в трехфазную сеть подобно включению ваттметров, описанному выше.

Трехфазные счетчики составляются из двух или трех однофазных, размещенных в одном корпусе и имеющих общий счетный механизм, и называются соответственно двухэлементными и трехэлементными. В трехпроводной системе (без нулевого провода) применяют двухэлементные, а в четыре  проводной системе (с нулевым проводом) —трехэлементные счетчики. Схема включения счетчика электрической энергии указывается на съемной крышке, которой закрывается панель зажимов.

Нулевой провод — это провод, использующийся для выравнивания напряжения в фазах. В случае его отсутствия или повреждения могут сгореть подключенные к фазе приборы и даже может начаться пожар. Поэтому необходимо знать принципы работы с ним.

Что такое нулевой провод? Его значение.

При работе с электричеством особого внимания требует нулевой провод. Что это такое, не всегда известно людям, не связанным профессионально с электросетями, и зачастую у них появляется ошибочное заблуждение, что нейтральный кабель – это только заземление. На самом деле, нейтральный проводник соединяет нейтрали установок в трехфазных цепях. Когда на каждую фазу из трех подается разная нагрузка, появляется смещение нейтрали, вызывающее нарушение симметрии напряжений, то есть, нарушение симметрий нагрузки приводит к тому, что у одних потребители будут получать пониженное напряжение, а другие же повышенное.

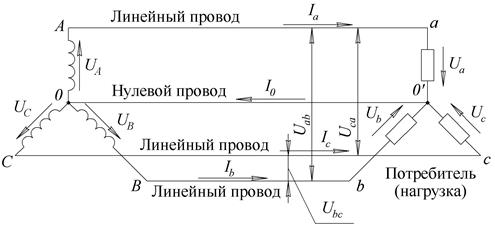
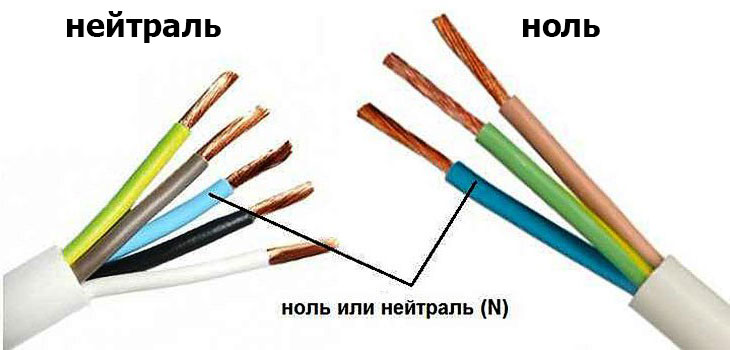
В общей цепи (фаза ноль), той, что приходит на люстру или розетку, есть два провода. Один из них и есть фаза. Именно этот провод находится под напряжением. Фаза в электротехнике сравнима с плюсом в автомобиле — это основное питание для сети.

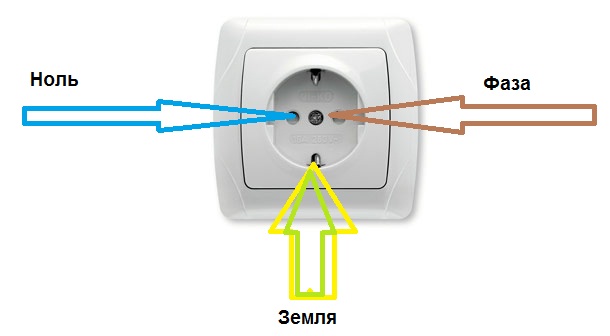
Фаза, ноль, земля в розетке

Нуль — это провод, который не находится под напряжением (это именно то, чем отличается ноль от фазы). Он не перегружен в процессе отбора мощности, но, тем не менее, по нему так же течет электрический ток, только в направлении, обратном фазному. В отсутствии напряжения он является безопасным в плане поражения человека электротоком.

Нуль замыкает электрическую цепь. Без этого провода в цепи не может быть электрического тока, который и дает мощность для питания бытовых приборов. По сути, нулевой провод — это земля.

Начало свое нуль берет от комплектной трансформаторной подстанции 6(10)/0,4 кВ, где трансформатор своей нулевой шиной соединен с контуром заземления. Изначально именно земля является проводником с нулевым потенциалом, и именно поэтому многие путают нуль с землей. ВЛ (воздушная линия электропередачи), выходя из КТП, имеет 4 провода — 3 фазы и нуль, который в начале линии соединен с нулем трансформатора. На протяжении воздушной линии через одну опору производится повторное заземление, которое дополнительно связывает нуль линии с землей, что дает более полноценную связь цепи «фаза — нуль» для того, чтобы у конечного потребителя в розетке было не менее 220В.

Основное назначение нулевого провода — замыкание цепи для создания электрического тока для работы любого электроприбора. Ведь для того, чтобы ток появился, необходима разность потенциалов между двумя проводами. Нуль потому так и называется, что потенциал на нем равен нулю. Отсюда и уровень напряжения 220В — 230В.

В домашних условиях, даже не имея специальных приборов и приспособлений, возможно определить в обычной розетке, какой из двух проводов является фазой, а какой нулем. В этом случае используются электролампа или индикаторная отвертка.

Для поиска нуля и фазы достаточно взять обыкновенный патрон с лампочкой и прикрутить два провода на его штатные места. Затем один из этих проводов подключить к заземляющим ножам в розетке, а второй — к любому из двух силовых разъемов.

Фазным будет являться тот разъем, при подключении к которому лампочка будет загораться. Это происходит потому, что по Правилам устройства электроустановок (ПУЭ), в вводном электрощите нулевые провода всех розеток должны быть соединены с земляными проводами этих же розеток. А отдельно земляная шина должна быть соединена с защитным контуром заземления. Именно это и обеспечивает наличие надежного нуля во всей цепи энергоснабжения дома.

Видео см. по ссылке: https://youtu.be/3Gvp6Q8q3Ks

Вопросы для самоконтроля:

1. Что представляет собой трехфазная цепь? Каковы ее элементы?

2. Что такое фаза трехфазной цепи?

3. В чем преимущества трехфазной цепи перед однофазной?

4. Какая система величин (ЭДС, напряжений, токов) называется трехфазной симметричной?

5. Какое соединение фаз называется соединением в звезду?

6. Какое напряжение называется линейным, фазным? Каковы соотношения между линейными и фазными напряжениями при любой нагрузке и при симметричной нагрузке?

7. Какой ток называется линейным, фазным? Каково соотношение между линейным и фазным токами при соединении фаз приемника в звезду?

8. В чем отличие и преимущества трехпроводных и четырехпроводных цепей?

9. Когда и зачем применяют нейтральный провод?

10. В каком случае отсутствует ток в нейтральном проводе?

11. Как определить мощности трехфазной цепи?

12. Что такое нулевой провод? Каковое его значение?

Домашнее задание:

1.Проработать конспект лекции.

2. Ответить на вопросы для самоконтроля.

3.Выполнить задания в тестовой форме:

Вариант 1

1. Начало первой обмотки при соединении обмоток генератора треугольником соединяется:

1. с началом второй;

2. концом третьей;

3. концом второй;

4. началом третьей;

5. концом третьей.

2. Фазой называют:

1. аргумент синуса;

2. часть многофазной цепи;

3. фазу в начальный момент времени;

4. оба определения ответов 1 и 2 правильны;

5. разность начальных фаз переменных величин.

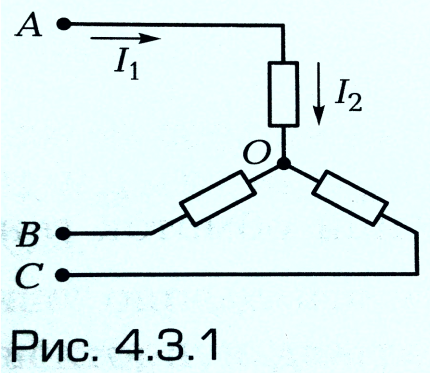
3. Какой из токов в схеме (рис. 4.3.1) линейный, а какой — фазный:

1. оба тока — линейные;

2. оба тока — фазные;

3. ток I₂ — линейный, I₁ — фазный;

4. ток I₂ — фазный, I₁ — линейный;

5. таких токов в данной схеме нет.

4. Симметричная нагрузка соединена звездой. Линейное напряжение 380 В. Фазное напряжение равно:

1. 220 В;

2. 380 В;

3. 250 В;

4. 127В;

5. 660 В.

5. Укажите правильные уравнения, связывающие векторы линейных и фазных токов, если соединение потребителей треугольником (рис. 4.3.2):

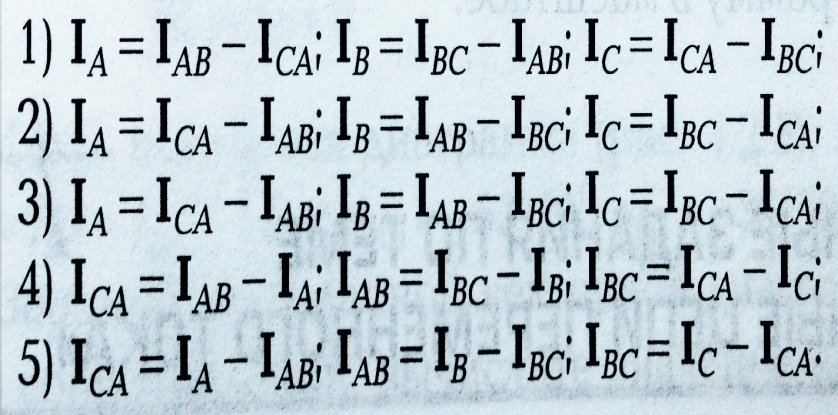
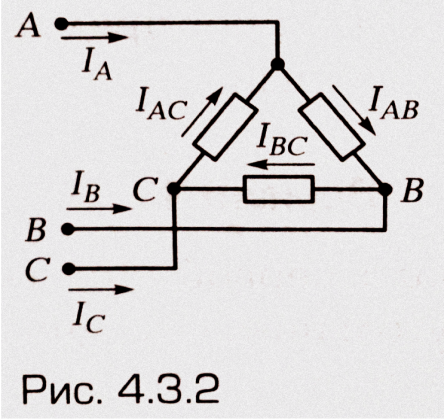
Вариант 2

1. Лампы накаливания с U_H = 127 В включают в трехфазную сеть с линейным напряжением 220 В. Схема включения ламп:

1. звездой;

2. треугольником;

3. звезда с нулевым проводом;

4. лампы нельзя включать в сеть;

5. для ответа недостаточно данных.

2. Действующее значение трехфазной ЭДС при изменении направления вращения катушек:

1. изменится;

2. увеличится в три раза;

3. уменьшится в три раза;

4. изменится на ;

5. не изменится.

3. Ток в нулевом проводе четырехпроводной цепи:

1. не может равняться нулю;

2. может равняться нулю;

3. всегда равен нулю;

4. всегда больше нуля;

5. всегда меньше нуля.

4. Если U_AC = Uс – U_A’, то вектор U_AC при соединении треугольником равен:

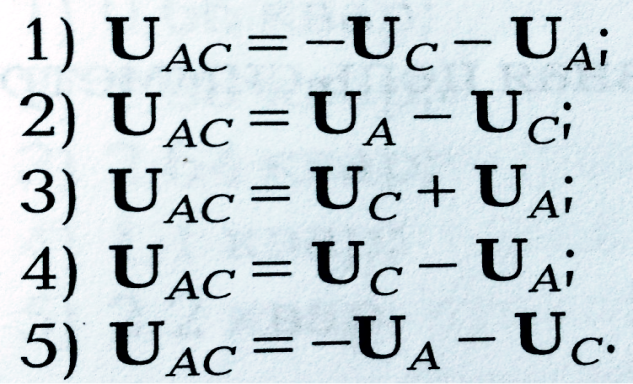
5. В симметричной трехфазной цепи U_ф = 220 В, I_ф = 5 А, cosφ = 0,8. Активная мощность цепи равна:

1. 1,1 кВт;

2. 0,88 кВт;

3. 2,2 кВт;

4. 2,64 кВт;

5. 5,28 кВт.

Вариант 3

1. Если при прочих условиях изменить скорость вращения обмоток, то изменятся:

1. амплитуды и начальные фазы;

2. частота и начальные фазы;

3. ЭДС и начальные фазы;

4. частота и амплитуды;

5. ЭДС и амплитуды.

2. Сумма токов фаз равна нулю при отсутствии нулевого провода:

1. не всегда;

2. всегда;

3. зависит от условий;

4. зависит от числа проводов — 3 или 4;

5. зависит от Z-фазы.

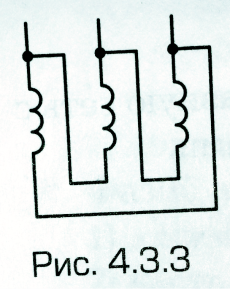
3. Обмотки, показанные на рис. 4.3.3, соединены.

1. звездой;

2. треугольником;

3. последовательно;

4. параллельно;

5. другим способом.

4. При симметричной нагрузке, соединенной треугольником, U_А = 380 В. Фазное напряжение равно:

1. 220 В;

2. 127 В;

3. 660 В;

4. 250 В;

5. 380 В.

5. Дано: U_^ = 220 В; I_^ = 5 A; cosφ = 0,8. Трехфазная цепь симметричная. Активная мощность цепи составляет:

1. 1,1 кВт;

2. 1,14 кВт;

3. 1,52 кВт;

4. 2,2 кВт;

5. 2,06 кВт.

Вариант 4

1. К генератору, обмотки которого соединены в звезду, подходит:

1. 6 соединительных проводов;

2. 3 соединительных провода;

3. 3 или 4 провода;

4. 4 провода;

5. 6 или 3 провода.

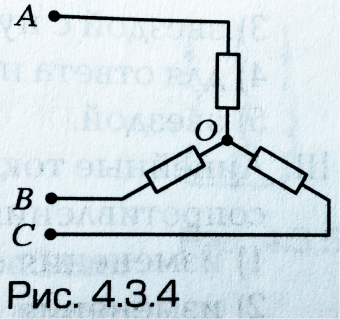
2. Какое напряжение в схеме, показанной на рис. 4.3.4, линейное, а какое — фазное:

1. U_CA — линейное, U_co — фазное;

2. U_AO — линейное, U_BO — фазное;

3. U_AB — линейное, U_BC — фазное;

4. U_BC — линейное, — фазное;

5. U_CO — линейное, — фазное.

3. Будут ли меняться линейные токи при обрыве нулевого провода в случае: а) симметричной нагрузки; б) несимметричной нагрузки:

1. а) будут; б) не будут;

2. а) будут; б) будут;

3. а) не будут; б) не будут;

4. а) не будут; б) будут;

3. Ток I_^ = 2,2 А. Если симметричная нагрузка соединена треугольником, то фазный ток:

1. 3,8 А;

2. 2,2 А;

3. 6,6 А;

4. 1,27 А;

5. 2,54 А.

3. В симметричной трехфазной цепи U_ф = 220 В; I_ф = 5 A; cosφ = 0,8. Реактивная мощность цепи равна:

1. 0,66 квар;

2. 1,98 квар;

3. 2,64 квар;

4. 1,1 квар;

5. 2,2 квар.

Вариант 5

1. В симметричной трехфазной цепи U_A = 220 В, 1_А = 5 A, coscp = 0,8. Реактивная мощность цепи равна:

1. 0,38 квар;

2. 1,1 квар;

3. 1,14 квар;

4. 1,52 квар;

5. 3,04 квар.

2. В трехфазную сеть U_A — 220 В включают двигатель, обмотки которого рассчитаны на 127 В. В этом случае:

1. двигатель нельзя включить в сеть;

2. обмотки двигателя надо соединить треугольником;

3. звездой с нулевым проводом;

4. для ответа недостаточно данных;

5. звездой.

3. Линейные токи при постоянной ЭДС генератора и неизменных сопротивлениях нагрузки могут измениться за счет:

1. изменения фазных напряжений;

2. изменения линейных напряжений;

3. изменения фазных и линейных напряжений.

4. Ток в нулевом проводе при симметричной трехфазной системе токов равен:

1. нулю;

2. значению, меньшему суммы действующих значений фазных токов;

3. значению, большему сумме фазных токов;

4. сумме действующих значений фазных токов;

5. сумме линейных токов.

5. Условия симметричной нагрузки в трехфазной цепи:

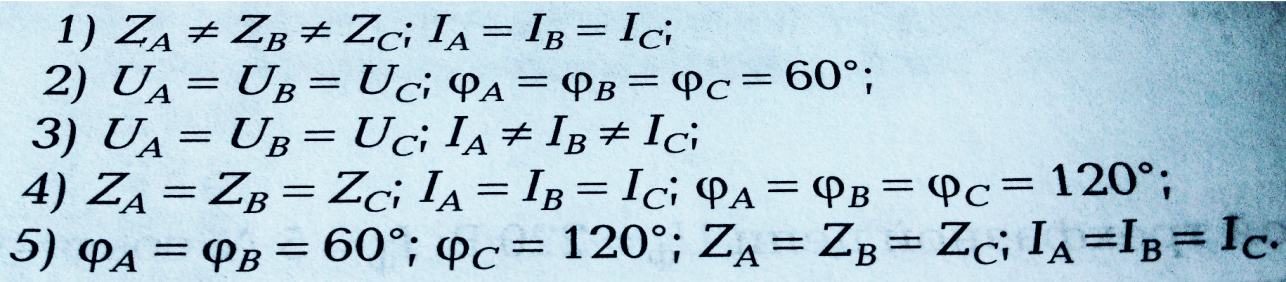
Вариант 6

1. В трехфазной цепи U_^ = 220 В; I_^ = 2 А; Р = 380 Вт. В этом случае соsφ равен:

1. 0,8;

2. 0,5;

3. 0,6;

4. 0,4;

5. 0,7.

2. Трехфазный двигатель, обмотки которого рассчитаны на 127 В, включают в сеть UA = 380 В. Обмотки двигателя надо соеди¬нить:

1. звездой;

2. треугольником;

3. для ответа недостаточно данных;

4. звездой с нулем;

5. двигатель нельзя включать в сеть.

3. Обмотки трехфазного генератора соединены звездой. Конец первой обмотки соединен:

1. с началом второй обмотки;

2. началом третьей обмотки;

3. концом третьей обмотки;

4. концом второй и началом третьей обмоток;

5. концом второй обмотки.

4. Трехфазная симметричная нагрузка потребляет 800 Вт активной мощности. Если при cosφ = 1 потребляется 1000 Вт, то соsφ равен:

1. 0,8;

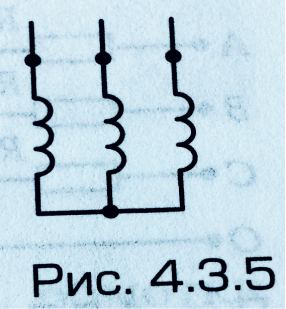
5. Обмотки, показанные на рис. 4.3.5, соединены:

1. звездой с нулевым проводом;

2. треугольником;

3. звездой;

4. другим способом;

5. для ответа недостаточно данных.

4. Вариант 7

1. При соединении обмоток генератора треугольником» начало третьей обмотки соединяется:

1. с концом первой обмотки;

2. началом второй обмотки;

3. концом второй обмотки;

4. началом второй и первой обмоток;

5. концом третьей обмотки.

2. Симметричная нагрузка трехфазной сети соединена звездой, U_^ = 660 В. Фазное напряжение равно:

1. 380 В;

2. 660 В;

3. 220 В;

4. 127 В;

5. 440 B.

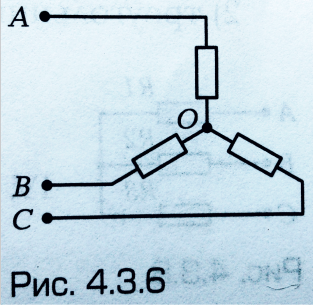
3. Вольтметр для измерения фазного напряжения (рис. 4.3.6) надо включить между точками:

1. А и В;

2. В и С;

3. C и А;

4. А и С;

5. А и О.

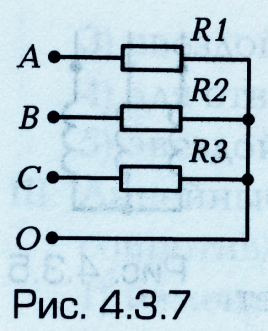
4. Нагрузка в трехфазной цепи (рис. 4.3.7) соединена:

1. звездой;

2. треугольником;

3. параллельно;

4. последовательно;

5. звездой с нулевым проводом.

5. Лампы накаливания с U_H = 220 В включают в трехфазную сеть с U_^ = 220 В. Схема соединения ламп:

1. звездой;

2. треугольником;

3. звездой с нулевым проводом;

4. лампы нельзя включать в сеть;

5. для ответа недостаточно данных.

6. Вариант 8

1. Линейный ток 17,3 А. Фазный ток, если симметричная нагрузка 1 соединена треугольником, равен:

3. 34,6 А

2. Начало второй обмотки при соединении обмоток трехфазного генератора треугольником соединяется:

1. с концом первой обмотки;

2. концом третьей обмотки;

3. началом первой обмотки;

4. началом третьей обмотки;

5. концом второй обмотки.

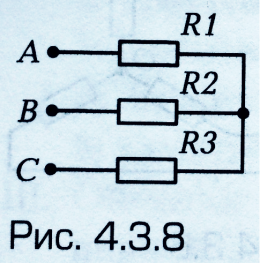
3. Нагрузка в цепи, показанной на рис. 4.3.8, соединена:

1. звездой;

2. треугольником;

3. звездой с нулевым проводом;

4. последовательно;

5. параллельно.

4. К трехфазному генератору, обмотки которого соединены треугольником, подходит соединительных проводов:

1. 4;

2. 3 или 4;

5. В трехфазную сеть с U_^ = 220 В включают двигатель, обмотки которого рассчитаны на 220 В. Соединить обмотки двигателя надо:

1. звездой с нулевым проводом;

2. звездой;

3. треугольником;

4. двигатель нельзя включать в сеть;

5. для ответа недостаточно данных.

Как измерить мощность в цепи трехфазного переменного тока

Мощность в цепи трехфазного тока может быть измерена с помощью одного, двух и трех ваттметров. Метод одного прибора применяют в трехфазной симметричной системе. Активная мощность всей системы равна утроенной мощности потребления по одной из фаз.

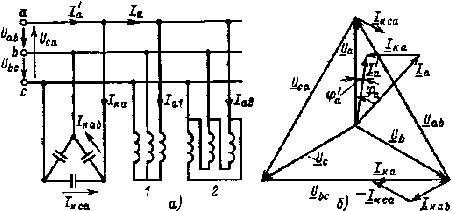
При соединении нагрузки звездой с доступной нулевой точкой или если при соединении нагрузки треугольником имеется возможность включить обмотку ваттметра последовательно с нагрузкой, можно использовать схемы включения, показанные на рис. 1.

 

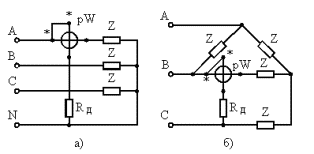
Рис. 1 Схемы измерения мощности трехфазного переменного тока при соединении нагрузок а — по схеме звезды с доступной нулевой точкой; б — по схеме треугольника с помощью одного ваттметра

Если нагрузка соединена звездой с недоступной нулевой точкой или треугольником, то можно применить схему с искусственной нулевой точкой (рис. 2). В этом случае сопротивления должны быть равны Rвт+ Rа = Rb =Rc.

 

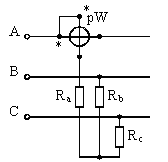
Рис 2. Схема измерения мощности трехфазного переменного тока одним ваттметром с искусственной нулевой точкой

Для измерения реактивной мощности токовые концы ваттметра включают в рассечку любой фазы, а концы обмотки напряжения — на две другие фазы (рис. 3). Полнаяреактивная мощность определяется умножением показания ваттметра на корень из трех. (Даже при незначительной асимметрии фаз применение данного метода дает значительную погрешность).

 

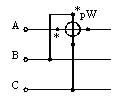
Рис. 3. Схема измерения реактивной мощности трехфазного переменного тока одним ваттметром

Методом двух приборов можно пользоваться при симметричной и несимметричной нагрузке фаз. Три равноценных варианта включения ваттметров для измерения активной мощности показаны на рис. 4. Активная мощность определяется как сумма показаний ваттметров.

При измерении реактивной мощности можно применять схему рис. 5, а с искусственной нулевой точкой. Для создания нулевой точки необходимо выполнить условие равенства сопротивлений обмоток напряжений ваттметров и резистора R. Реактивная мощность вычисляется по формуле

 

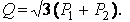
где Р1 и Р2 — показания ваттметров.

По этой же формуле можно вычислить реактивную мощность при равномерной загрузке фаз и соединении ваттметров по схеме рис. 4. Достоинство этого способа в том, что по одной и той же схеме можно определить активную и реактивную мощности. При равномерной загрузке фаз реактивная мощность может быть измерена по схеме рис. 5, б.

Метод трех приборов применяется при любой нагрузке фаз. Активная мощность может быть замерена по схеме рис. 6. Мощность всей цепи определяется суммированием показаний всех ваттметров.

 

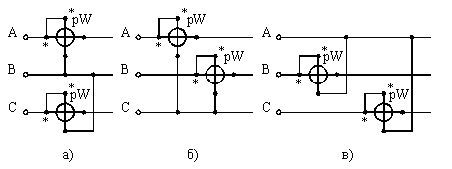
Рис. 4. Схемы измерения активной мощности трехфазного переменного тока двумя ваттметрами а — токовые обмотки включены в фазы А и С; б — в фазы А и В; в — в фазы В и С

Реактивная мощность для трех- и четырехпроводной сети измеряется по схеме рис. 7 и вычисляется по формуле

 

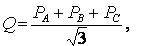
где РA, РB, РC — показания ваттметров, включенных в фазы А, В, С.

 

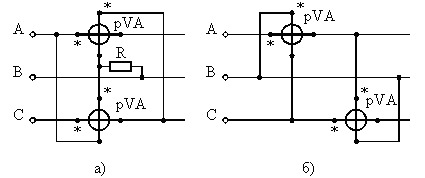
Рис. 5. Схемы измерения реактивной мощности трехфазного переменного тока двумя ваттметрами

 

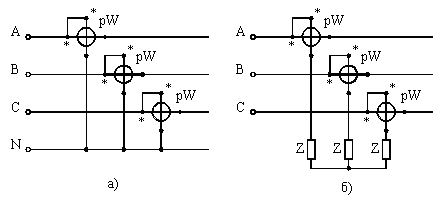
Рис. 6. Схемы измерения активной мощности трехфазного переменного тока тремя ваттметрами а — при наличии нулевого провода; б — с искусственной нулевой точкой

На практике обычно применяют одно-, двух- и трехэлементные трехфазные ваттметры соответственно методу измерения.

Чтобы расширить предел измерения, можно применить все указанные схемы при подключении ваттметров через измерительные трансформаторы тока и напряжения. На рис. 8 в качестве примера показана схема измерения мощности по методу двух приборов при включении их через измерительные трансформаторы тока и напряжения.

 

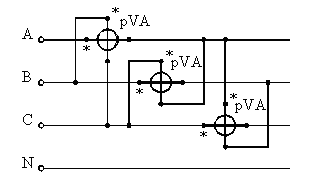
Рис. 7. Схемы измерения реактивной мощности тремя ваттметрами

 

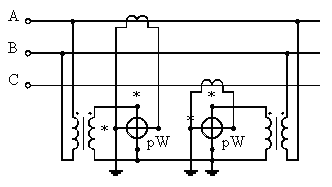
Рис. 8. Схемы включения ваттметров через измерительные трансформаторы.

 

Содержание

Мощность трехфазной цепи — Студопедия

Активная мощность трехфазной цепи равна сумме активных мощностей потребляемых каждой фазой нагрузки:

.

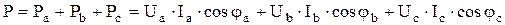При симметричной нагрузке мощности, потребляемые каждой фазой нагрузки равны. В этом случае , а мощность, потребляемая каждой фазой, определяется как: .

где j — угол сдвига между фазным напряжением и током.

Рисунок 4.11 — Векторная диаграмма для несимметричной нагрузки, соединенной треугольником

Реактивная мощность трехфазной цепи равна сумме реактивных мощностей отдельных фаз:

.

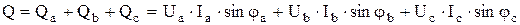При симметричной нагрузке реактивные мощности отдельных фаз равны и реактивная мощность трехфазной цепи 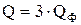, реактивная мощность одной фазы: .

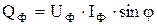Полная мощность трехфазной цепи равна сумме полных мощностей отдельных фаз: .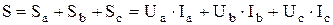

При симметричной нагрузке полная мощность трехфазной цепи 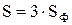, полная мощность одной фазы: .

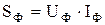При анализе трехфазных цепей удобно пользоваться линейными значениями напряжений и токов.

При соединении нагрузки звездой:

и .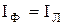

При соединении нагрузки треугольником:

и .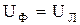

В соответствии с этими выражениями, активная мощность трехфазной цепи, независимо от способа соединения нагрузки определяется по формуле:

.

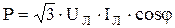Аналогично определяется реактивная и полная мощность:

, .

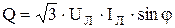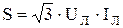При симметричной трехфазной нагрузке активные мощности всех фаз одинаковы, поэтому достаточно измерить активную мощность 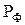одной фазы. Активная мощность трехфазной нагрузки . На рисунке 3.12 показаны схемы включения ваттметра для измерения активной мощности одной фазы при соединении нагрузки звездой с доступной нейтральной точкой (рисунок 3.12 а) и треугольником (рисунок 4.12 б).

Если фазные напряжения и токи симметричной нагрузки недоступны для измерения, то применяют схему с искусственной нейтральной точкой (рисунок 4.13).

В этой схеме цепь напряжения ваттметра с сопротивлением 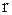и два резистора 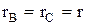образуют симметричную трехфазную нагрузку. Поэтому напряжение на ваттметре 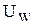равно фазному напряжению нагрузки, соединенной звездой, или в раз меньше фазного напряжения нагрузки, соединенной треугольником.

Ток, протекающий по токовой обмотке ваттметра, равен линейному току и равен фазному току нагрузки, соединенной звездой, или в раз больше фазного тока нагрузки, соединенной треугольником. Следовательно, ваттметр независимо от способа соединения нагрузки измеряет активную мощность одной фазы.

Для измерения активной мощности несимметричной трехфазной нагрузки можно применять схемы описанные выше. Так как при несимметричной нагрузке мощности фаз не равны, то необходимо измерять мощность каждой фазы (то есть включать ваттметры в каждую фазу как показано на рисунке 4.12).

Активная мощность несимметричной трехфазной нагрузки определяется как сумма мощностей отдельных фаз: 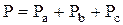. В схеме с искусственной нулевой точкой мощность показываемая ваттметром, включенным в линейные провода фаз А, В, С ( , , ) не равна мощности соответствующих фаз, однако сумма показаний ваттметров равна мощности потребляемой несимметричной трехфазной нагрузкой .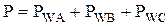

Рисунок 4.12 — Измерение активной мощности в симметричной трехфазной

Чаще всего для измерения мощности в трехфазных трехпроводных цепях с несимметричной нагрузкой используют метод двух ваттметров, включенных в соответствии со схемой на рисунке 4.14. При этом активная мощность несимметричной трехфазной нагрузки равна алгебраической сумме (показания ваттметров могут быть отрицательными) показаний двух ваттметров.

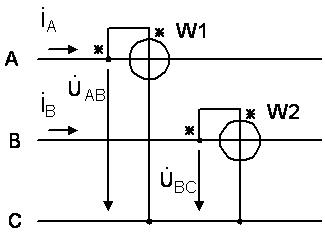
Рисунок 4.14 — Метод двух ваттметров

7. Мощность трехфазной цепи и способы ее измерения

Активная и реактивная мощности трехфазной цепи, как для любой слож­ной цепи, равны суммам соответствующих мощностей отдельных фаз:

,

,

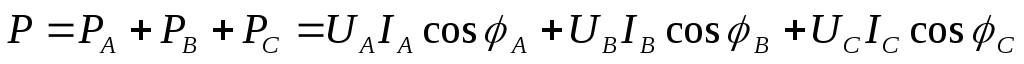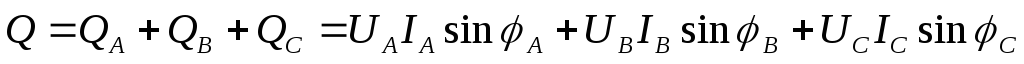где I_A, U_A, I_B, U_B, I_C, U_C – фазные значения токов и напряжений.

В симметричном режиме мощности отдельных фаз равны, а мощность всей цепи мо­жет быть получена путем умножения фазных мощностей на число фаз:

,

,

.

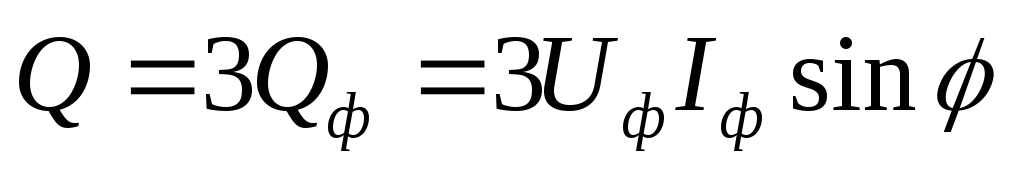В полученных выражениях заменим фазные величины на линейные. Для схемы звезды верны соотношения 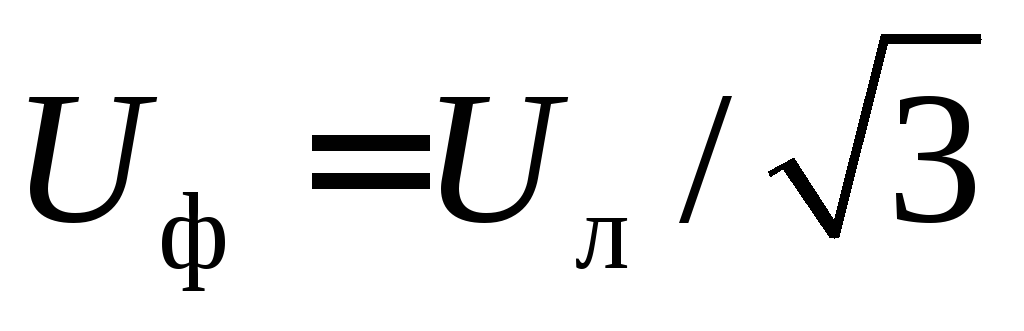;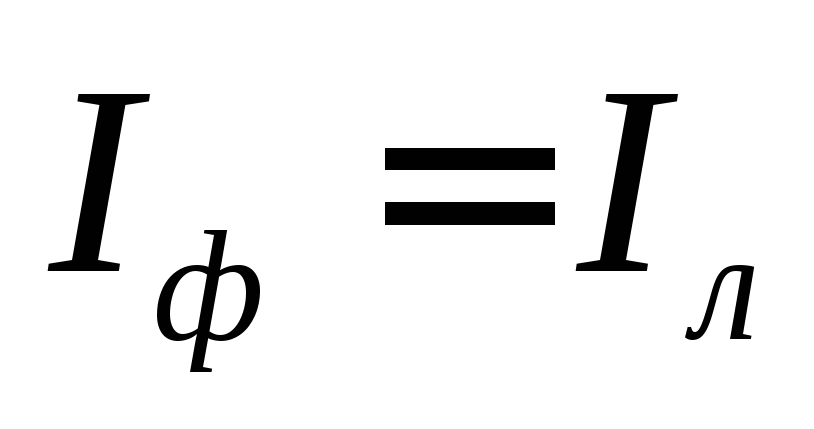, тогда получим:

.

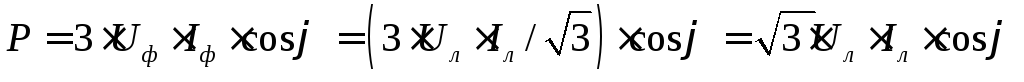Для схемы треугольника верны соотношения: U_ф=U_л ; I_ф=I_л /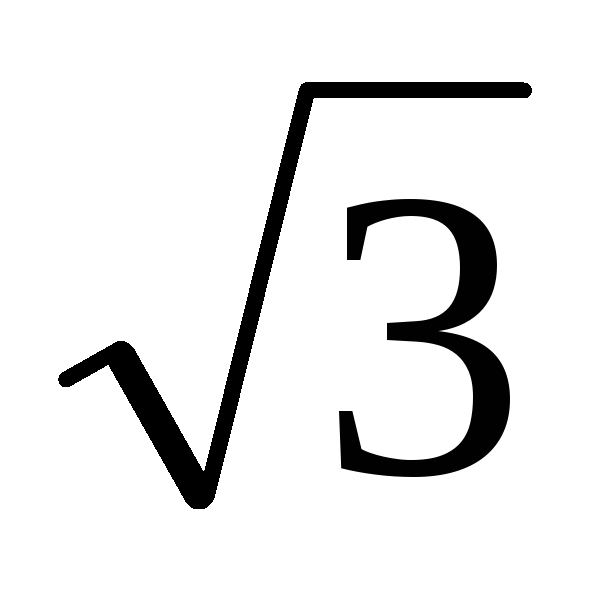, тогда получим:

Следовательно, независимо от схемы соединения (звезда или треуголь­ник) для сим­метричной трехфазной цепи формулы для мощностей имеют оди­наковый вид:

[Вт],

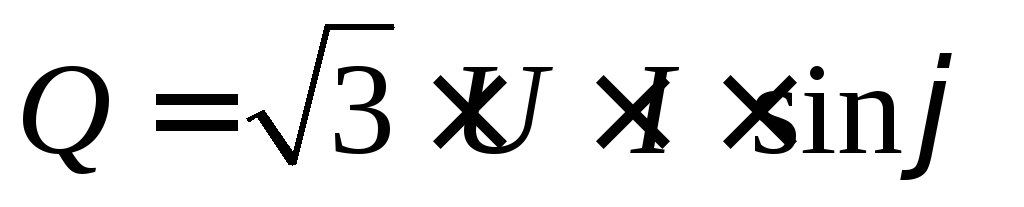[вар],

[ВА].

В приведенных формулах для мощностей трехфазной цепи подразумева­ются линей­ные значения величин U и I, но индексы при их обозначениях не ставятся.

Активная мощность в электрической цепи измеряется прибором, назы­ваемым ватт­метром, показания которого определяется по формуле:

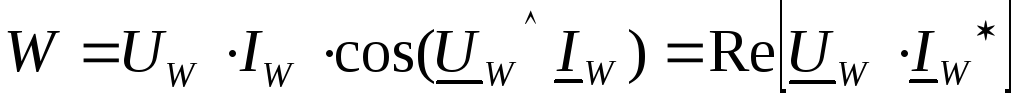, где U_w, I_w  векторы напряжения и тока, подведенные к обмоткам прибора.

Для измерения активной мощности всей трехфазной цепи в зависимости от схемы со­единения фаз нагрузки и ее характера применяются различные схемы включения измери­тельных приборов.

Для измерения активной мощности симметричной трехфазной цепи при­меняется схема с одним ваттметром, который включается в одну из фаз и изме­ряет активную мощ­ность только этой фазы (рис. 99). Активная мощность всей цепи получается путем умножения показания ваттметра на число фаз: 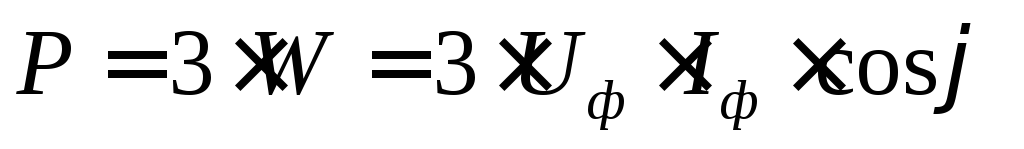. Схема с одним ваттметром мо­жет быть использована только для ориентированной оценки мощности и неприменима для точных и коммерческих измерений.

Для измерения активной мощности в четырехпроводных трехфазных це­пях (при на­личии нулевого провода) применяется схема с тремя приборами (рис. 100), в которой произво­дится измерение активной мощности каждой фазы в отдельности, а мощность всей цепи оп­ределяется как сумма показаний трех ваттметров:

.

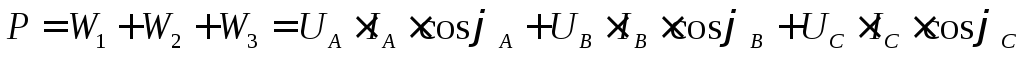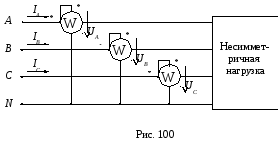
Для измерения активной мощности в трехпроводных трехфазных цепях (при отсутст­вии нулевого провода) применяется схема с двумя приборами (рис. 101).

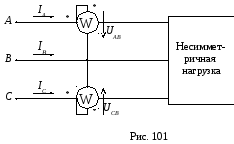
При отсутствии нулевого провода линейные (фазные) ток связаны между собой урав­нением 1-го закона Кирхгофа: 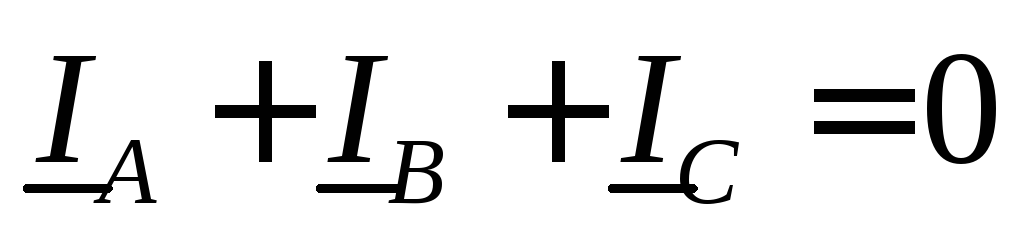. Сумма показаний двух ваттметров равна:

Таким образом, сумма показаний двух ваттметров равна активной трех­фазной мощно­сти, при этом показание каждого прибора в отдельности зависит не только величины на­грузки но и от ее характера.

На рис. 102 показана векторная диаграмма токов и напряжений для сим­метричной на­грузки. Из диаграммы следует, что показания отдельных ваттмет­ров могут быть определены по формулам:

,

.

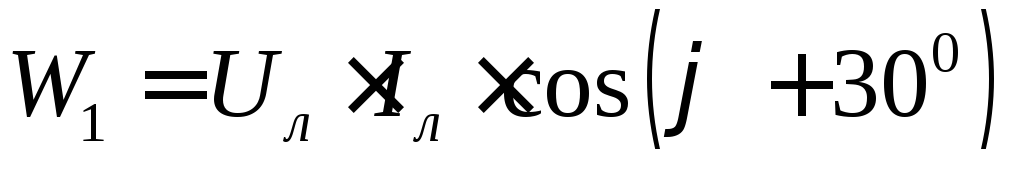Анализ полученных выражений позволяет сделать следующие выводы. При активной нагрузке (φ = 0), показания ваттметров равны (W₁ = W₂).

При активно-индуктивной нагрузке(0 ≤ φ ≤ 90⁰) показание первого ватт­метра меньше, чем второго (W₁ < W₂), а при φ>60⁰ показание первого ваттметра становится отрицательным (W₁<0).

При активно-емкостной нагрузке(0 ≥ φ≥ 90⁰) показание второго ватт­метра меньше, чем первого (W1>W2), а при φ<60⁰ показание второго ватт­метра становится отрицательным.

7.5. Мощность в трехфазных цепях

Трехфазная цепь является обычной цепью синусоидального тока с несколькими источниками.

Активная мощность трехфазной цепи равна сумме активных мощностей фаз

(7.5)

Формула (7.5) используется для расчета активной мощности в трехфазной цепи при несимметричной нагрузке.

При симметричной нагрузке:

При соединении в треугольник симметричной нагрузки

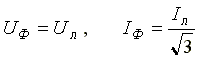
При соединении в звезду

.

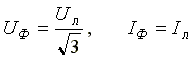В обоих случаях .

3.7. Коэффициент мощности и способы его повышения

Площади поперечного сечения приводов линий электропередачи и электрических сетей, обмоток электрических машин, трансформаторов, электротехнических аппаратов и приборов выбираются, исходя из нагревания, по значению тока в них, который при заданном напряжении переменного тока прямо пропорционален полной мощности S. А энергия, преобразуемая из электрической в другие виды (в механическую, тепловую и т. д.) и используемая в большей части для практических целей, пропорциональна активной энергии и соответствующей ей активной мощности Р.

Как известно, между указанными мощностями и реактивной мощностью существуют соотношения

P = S cos φ; S = √P2 + Q2 .

Входящий в первое выражение cos φ называется коэффициентом мощности и показывает, какую часть полной мощности составляет активная мощность: cos φ = P/S= Р/√P2 + Q2.

Считая, что активная мощность установки, значение кото­рой зависит в основном от мощности приемников, остается постоянной, выясним, к чему приведет увеличение коэффициента мощности установки.

Как следует из приведенных формул, при увеличении cos φ мощность S уменьшается. При Р = const это может происходить лишь за счет уменьшения реактивной мощности Q установки. Снижение мощности S приводит к уменьшению линейного тока Iл . Последнее будет сопровождаться уменьшением потерь напряжения и мощности в сопротивлениях проводов сети, обмотках трансформаторов и генераторов.

Очевидно, при уменьшении тока площади поперечного сечения названных элементов могут быть также уменьшены. В отношении трансформаторов и генераторов это приводит к уменьшению габаритных размеров, расхода дефицитных материалов на изготовление, массы, номинальной мощности и стоимости.

В действующей установке повышение cos φ при существующей площади поперечного сечения проводов позволит увеличить число приемников, которые могут быть подключены к данной сети.

Таким образом, повышение коэффициента мощности дает определенные выгоды во многих отношениях, а поэтому имеет большое народнохозяйственное значение.

Большая часть элементов электрических цепей переменного тока потребляет кроме активной мощности также индуктивную мощность. К ним относятся в первую очередь наиболее распространенные в народном хозяйстве асинхронные электродвигатели. Значительная часть индуктивной мощности потребляется трансформаторами, широко используемыми вразличных установках. Индуктивная мощность потребляется также различными электромагнитными аппаратами, такими, например, как электромагниты, контакторы и магнитные пускатели, реле и т. д.

Для уменьшения индуктивной мощности и увеличения тем самым cos φ необходимо прежде всего:

выбирать правильно двигатели по мощности, так как необоснованное завышение мощности приведет к их работе с недогрузкой, а при этом, как правило, cos φ понижается;

заменять двигатели, работающие с недогрузкой, двигателями меньшей мощности;

сокращать по возможности времена работы двигателей и трансформаторов вхолостую.

Если все же cos φ оказывается недостаточно высоким, прибегают часто к его искусственному повышению. Для этой цели подключают к трехфазной сети компенсирующие устройства, к которым относятся батареи конденсаторов и трехфазные синхронные компенсаторы (см. гл. 11). Последние применяются реже. Батарея конденсаторов соединяется обычно треугольником, как показано на рис. 3.18, а. Батарея конденсаторов потребляет емкостную мощность, которая частично компенсирует индуктивную мощность установки, в результате чего реактивная мощность уменьшается, а коэффициент мощности повышается.   Естественно, что   cos φ  самих  приемников  при  этом остается прежним.

Рис. 3.18. Схема и векторная диаграмма к примеру 3.5

Чтобы уменьшить ток проводов сети, батарею конденсаторов устанавливают по возможности вблизи приемников.

Пример 3.5. К трехфазной сети рис. 3.18, а с линейными напряжениями Uл = 220В подключены два трехфазных приемника. Активная мощность и коэффициент мощности первого приемника P1 = 10 кВт, cos φ1 = 0,7. Фазные сопротивления второго приемника rф = 6 Ом, xLф = 8 Ом, нагрузка симметричная.

Определить токи, мощности и коэффициент мощности cos φ установки из двух приемников. Найти мощность, токи и емкость батареи конденсаторов, если требуется повысить коэффициент мощности до cos φ’ = 0,95. Определить токи и мощности установки из двух приемников и батареи конденсаторов.

Решение. Полная и реактивная мощности первого приемника

S1 = P1/cos φ1 = 14,3 кВ•А,   Q1 = √S12 — P12 ≈ 10,2 квар.

Полное сопротивление и ток фазы второго приемника

z2 = √r22 + x2L2 = 10 Ом;    Iф2 = Uф /z2 = Uл /z2 = 22 А.

Активная и реактивная мощности второго приемника

Р2 = 3I2ф2r2 = 8,7 кВт;   Q2 = 3Iф2xLф ≈ 11,6 квар.

Активная, реактивная и полная мощности установки, состоящей из двух преемников.

Р = P1 + P2 =18,7 кВт;   Q = Q1 + Q2 = 21,8 квар;

S = √P2 + Q2 ≈ 28,7 кВ•А.

Линейный ток и коэффициент мощности установки из двух приемников

Iл = Ia = S√3Uл ≈ 75,5 A;   cos φ = P/S ≈ 0,65.

Мощности установки из приемников и батареи конденсаторов

Р’ = Р = 18,7 кВт;    S’ = P/cos φ’ = 19,68 кВ•А;

Q’ = √S’2 — P’2 = 6,13 квар.

Линейные токи установки из приемников и батареи конденсаторов, мощность и линейные токи батареи конденсаторов

I’л = I’a = S√3Uл = 51,7 A; Qк = Q — Q’ =15,67 квар;

Iк.л = Qк /√3Uл = 41,2 А.

Фазные токи и сопротивление фазы батареи конденсаторов

Iк.л/√3 = 20,8 А; xк.ф = Uф /Iк.ф = Uл /Iк.ф = 10,58 Ом.

Емкость одной фазы и всей батареи конденсаторов

Ск.ф =1/2π/хк.ф = 30 мкФ;    Ск = 3Ск.ф = 90 мкФ.

Векторная диаграмма цепи рис, 3.18, а приведена на рис. 3.18, б. На диаграмме показаны только те токи, которые определяют ток I’a (t. е. Ia и Iкa), а также токи, определяющие ток Iкa (т. е. Iкab и Iкca).

20. Основные понятия и принципы анализа переходных процессов в электрических цепях.

90000 Power Formulas in DC, AC Single Phase & Three Phase Circuits. 90001 90002 90003 Power Formulas in DC, AC Single Phase and AC Three Phase Circuits 90004 90005 90006 Back to basic, below are the simple Power formulas for Single Phase AC Circuit, Three Phase AC Circuits and DC Circuits. You can easily find electric 90003 power in watts 90004 by using the following 90003 power formulas in electric circuits 90004. 90011 90012 90003 Power Formulas in DC Circuits 90004 90015 90016 90017 P = V x I 90018 90017 P = I 90020 2 90021 x R 90018 90017 P = V 90020 2 90021 / R 90018 90027 90006 Where: 90011 90006 90031 90003 P 90004 = 90003 Power 90004 in 90003 Watts 90004 90038 90011 90006 90031 90003 V 90004 = 90003 Voltage 90004 in 90003 Volts 90004 90038 90011 90006 90031 90003 I 90004 = 90003 Current 90004 in 90003 Amperes 90004 90038 90011 90006 90031 R = 90003 Resistance 90004 in 90003 Ohms 90004 ( Ω) 90038 90011 90012 90003 Power Formulas in Single Phase AC Circuits 90004 90015 90016 90017 P = V x I x Cos Ф 90018 90017 P = I 90020 2 90021 x R x Cos Ф 90018 90017 P = V 90020 2 90021 / R (Cos Ф) 90018 90027 90006 Where: 90011 90006 90031 90003 P 90004 = 90003 Power 90004 in 90003 Watts 90004 90038 90011 90006 90031 90003 V 90004 = 90003 Voltage 90004 in 90003 Volts 90004 90038 90011 90006 90031 90003 I 90004 = 90003 Current 90004 in 90003 Amperes 90004 90038 90011 90006 90031 R = 90003 Resistance 90004 in 90003 Ohms 90004 (Ω) 90038 90011 90006 90031 90003 Cos Ф 90004 = 90038 90003 90031 Power Factor 90038 90004 90011 90012 90003 Power Formulas in Three Phase AC Circuits 90004 90015 90016 90017 P = √3 x V 90140 L 90141 x I 90140 L 90141 x Cos Ф 90018 90017 P = 3 x V 90140 Ph 90141 x I 90140 Ph 90141 x Cos Ф 90018 90017 P = 3 x I 90020 2 90021 x R x Cos Ф 90018 90017 P = 3 (V 90020 2 90021 / R) x Cos Ф 90018 90027 90006 Where: 90011 90006 90031 90003 P 90004 = 90003 Power 90004 in 90003 Watts 90004 90038 90011 90006 90031 90003 V 90004 = 90003 Voltage 90004 in 90003 Volts 90004 90038 90011 90006 90031 90003 I 90004 = 90003 Current 90004 in 90003 Amperes 90004 90038 90011 90006 90031 R = 90003 Resistance 90004 in 90003 Ohms 90004 (Ω) 90038 90011 90006 90031 90003 Cos Ф 90004 = 90003 Power Factor 90004 90038 90011 90006 Click imageto enlarge 90011 90006 90211 90211 90011 90006 90011 90006 You may also read: 90011 90016 90017 Basic Electrical Quantities Formulas With Simple Explanation (in DC Circuits.) 90018 90017 Electrical Formulas AC & DC Circuits (Single-φ & 3-φ) 90018 90017 P, V, I, R, Formulas. (Very Simple) 90018 90017 Power, Voltage, Current, Resistance Formulas For DC Circuits (With Easy Explanation) 90018 90017 Basic Electrical Engineering Formulas 90018 90017 Motor HP, input Voltages, Full load Current, Breaker Size, And Copper Wire Size Formulas (Single Phase & 3-Phase Motors) 90018 90027.90000 Single-Phase Power vs Three-Phase Power 90001 90002 Electric Power System 90003 90004 The principal elements of an electric power system are the generating stations, the transmission lines, the substations, and the distribution networks. The generators produce the electricity, the transmission lines move it to regions where it is consumed, and the substations transform it for industrial, commercial, and residential use. 90005 90006 90006 Single-Phase Power vs Three-Phase Power 90004 90009 Finally, the distribution networks carry the electricity to the customers.90010 90005 90004 Both three-phase and single-phase devices can be powered from a three-phase supply. A three-phase circuit is a combination of three single-phase circuits. The current, voltage, and power relations of balanced three-phase AC circuits can be studied by applying the rules that apply to single-phase circuits. 90005 90004 The sine waves of three-phase voltage are separated by 90009 120 electrical degree 90010 because they are generated by three separate sets of armature coils in an 90009 AC generator 90010.These three sets of coils are mounted 120 electrical degrees apart on the generator’s armature. The coil ends could all be brought out of the generator to form three separate single-phase circuits, but they are conventionally interconnected so that only three or four wires are actually brought out of the generator. 90005 90020 90004 Single-phase AC voltage with zero power factor has both voltage and current sine waves in phase, so they cross the zero line together twice in each cycle. 90005 90023 90004 Similarly, a plot of three-phase voltage sine waves, also with zero power factors as shown in 90009 Fig.1 90010, has all three voltage and current waves crossing the zero line twice each cycle together. Each of its three phases, 90009 V1 90010, 90009 V2 90010, and 90009 V3 90010, is separated by 120 electrical degrees. 90005 90004 90009 Power 90010 supplied to each of the three phases of a three-phase circuit also has a sinusoidal waveform, and the total three-phase power supplied to a balanced three-phase circuit remains constant. 90005 90038 90038 Figure 1 — Three-phase voltage waveforms are separated by 120 electrical degrees.90040 90002 Ok, let’s conclude something … 90003 90004 As a result, there are two practical reasons why three-phase power is superior to single-phase power for many applications: 90005 90004 90009 1 90047 st 90048 reason 90010 — Three-phase machines and controls can be smaller, lighter in weight, and more efficient than comparable single-phase equipment. More power is supplied to them in the same period than can be supplied by a single-phase power circuit. 90005 90004 However, the trade-off for this advantage is that three-phase machines and controls are more complex and expensive.90005 90004 90009 2 90047 nd 90048 reason 90010 — Only about 75 percent as much copper wire is required for distributing three-phase power as is required for distributing the same amount of single-phase power. 90005 90004 90009 Resources: 90010 N. Sclater, J. E. Traister — Handbook of electrical design 90005 .90000 3 Phase AC — DC Power Supplies 90001 × 90002 90003 Products 90002 90003 AC-DC Power Supplies 90002 90003 Board Mount 90008 90003 Chassis Mount 90008 90003 External 90008 90003 DIN Rail Mount 90008 90003 Rack Mount 90008 90003 Bench 90008 90003 Configurable 90008 90003 ITE / Industrial 90008 90003 Healthcare 90008 90003 Defense & Avionics 90008 90003 Laboratory 90008 90003 Semifab 90008 90031 90008 90003 DC-DC Converters 90002 90003 Board Mount 90008 90003 Chassis Mount 90008 90003 DIN Rail Mount 90008 90003 ITE / Industrial 90008 90003 Healthcare 90008 90003 Railway 90008 90003 Defense & Avionics 90008 90003 LED Driver 90008 90031 90008 90003 High Voltage AC-DC 90002 90003 Chassis Mount 90008 90003 Rack Mount 90008 90003 Open Stack 90008 90003 Semi-fab 90008 90003 Analytical Instrumentation 90008 90003 ITE / Industrial 90008 90003 Healthcare 90008 90003 Security / Threat Detection 90008 90031 90008 90003 High Voltage DC-DC 90002 90003 Through Hole Mount 90008 90003 Surface Mount 90008 90003 Semi-fab 90008 90003 Analytical Instrumentation 90008 90003 ITE / Industrial 90008 90003 Healthcare 90008 90003 Security / Threat Detection 90008 90031 90008 90003 RF Power Systems 90008 90003 EMI Filters 90008 90031 90008 90003 Applications 90002 90003 Healthcare 90008 90003 Defense & Avionics 90008 90003 Railway 90008 90003 Semiconductor Manufacturing 90008 90003 Custom Power 90008 90003 3 Phase Power Supplies 90008 90031 90008 90003 Resources 90008 90003 Company 90002 90003 About Us 90008 90003 Environment 90008 90003 Certification 90008 90003 Energy Efficiency 90008 90003 Policies 90008 90003 Manufacturing Facilities 90008 90031 90008 90003 Contact 90008 90031 90134 90002 90003 Investors 90008 90003 Careers 90008 90003 90141 en de it fr cn jp ko 90008 90031 90134 90002 90003 90141 90008 90003 90141 90008 90003 90141 90008 90003 90141 90008 90031 90002 90003 Investors 90008 90003 Careers 90008 90003 90141 en de it fr cn jp ko 90008 90031 90141 90141 90002 90003 Products AC-DC Power Supplies DC-DC Converte 90008 90031.90000 Three-Phase Power Equations 90001 90002 Most AC power today is produced and distributed as three-phase power where three sinusoidal voltages are generated out of phase with each other. With single-phase AC power there is only one single sinusoidal voltage. 90003 90004 Real Power 90005 90002 Line to line voltage: 90003 90008 90002 90010 W 90011 applied 90012 = 3 90013 1/2 90014 U 90011 ll 90012 I cos Φ 90017 90003 90002 90010 = 3 90013 1/2 90014 U 90010 90011 ll 90012 90017 I PF (1) 90017 90003 90002 90010 where 90017 90003 90002 90010 W 90011 applied 90012 = real power (W, watts) 90017 90003 90002 90010 U 90010 90011 ll 90012 90017 = line to line voltage (V, volts) 90017 90003 90002 90010 I = current (A, amps) 90017 90003 90002 90010 PF = cos Φ = power factor (0.7 — 0.95) 90017 90003 90055 90002 Line to neutral voltage: 90003 90002 90010 W 90011 applied 90012 = 3 U 90011 ln 90012 I cos Φ (2) 90017 90003 90002 90010 where 90017 90003 90002 90010 U 90011 ln 90012 = line to neutral voltage (V, volts) 90017 90003 90002 For pure resistive load: 90077 PF = cos Φ = 1 90078 90003 90080 90081 90082 resistive loads 90083 converts current into other forms of energy, such as heat 90084 90081 90082 inductive loads 90083 use magnetic fields like motors , solenoids, and relays 90084 90089 90004 Power Factor 90005 90002 Typical power factors: 90003 90094 90095 90096 90097 Device 90098 90097 Power Factor 90098 90101 90102 90103 90096 90105 Lamp, fluorecent uncompensated 90106 90105 0.5 90106 90101 90096 90105 Lamp, fluorecent compensated 90106 90105 0.93 90106 90101 90096 90105 Lamp, incandescent 90106 90105 1 90106 90101 90096 90105 Motor, induction 100% load 90106 90105 0.85 90106 90101 90096 90105 Motor, induction 50% load 90106 90105 0.73 90106 90101 90096 90105 Motor, induction 0% load 90106 90105 0.17 90106 90101 90096 90105 Motor, synchronous 90106 90105 0.9 90106 90101 90096 90105 Oven, resistive heating element 90106 90105 1 90106 90101 90096 90105 Oven, induction compensated 90106 90105 0.85 90106 90101 90096 90105 Pure resistive load 90106 90105 1 90106 90101 90164 90165 90166 Example — Pure Resistive Load 90167 90002 For pure resistive load and 90010 power factor = 1 90017 the real power in a 90010 400/230 voltage (line to line / line to neutral) 20 amps 90017 circuit can be calculated as 90003 90002 90077 W 90078 90011 90077 applied 90078 90012 90077 = 3 90078 90013 90077 1/2 90078 90014 90077 (400 V) (20 A) 1 90078 90003 90002 90077 = 90078 90077 13856 90078 90077 W 90078 90003 90002 90077 = 90078 90077 13.9 90078 90077 kW 90078 90003 90004 Total Power 90005 90008 90002 90010 W = 3 90013 1/2 90014 UI (2) 90017 90003 90055 90004 Brake Horsepower 90005 90008 90002 90010 W 90011 BHP 90012 = 3 90013 1/2 90014 UI PF μ / 746 (3) 90017 90003 90002 90010 where 90017 90003 90002 90010 W 90011 BHP 90012 = brake horse power (hp) 90017 90003 90002 90010 μ = device efficiency 90017 90003 90055.