Коэффициент мощности — Википедия

Синусоидальное напряжение (красная линия) и ток (зелёная линия) синфазны — между ними нет фазового сдвига (φ=0∘{\displaystyle \varphi =0^{\circ }}, cos⁡φ=1{\displaystyle \cos \varphi =1}) — нагрузка полностью активная, нет реактивной составляющей. Мгновенная мощность (синяя линия) и активная мощность (голубая линия) рассчитаны с коэффициентом мощности, равным 1. Как видно, синяя линия (график мгновенной мощности) находится полностью над осью абсцисс (в положительной полуплоскости), вся подводимая энергия преобразуется в работу: переходит в активную мощность, потребляемую нагрузкой. Синусоидальное напряжение (красная линия) и ток (зелёная линия) имеют фазовый сдвиг φ=90∘{\displaystyle \varphi =90^{\circ }} (cos⁡φ=0{\displaystyle \cos \varphi =0}) — нагрузка полностью реактивная, нет активной составляющей. Мгновенная мощность (синяя линия) и активная мощность (голубая линия) рассчитаны с коэффициентом мощности, равным 0. Расположение синей линии (графика мгновенной мощности) на оси абсцисс показывает, что в течение первой четверти цикла вся подводимая мощность временно сохраняется в нагрузке, а во второй четверти цикла возвращается в сеть, и так далее, то есть никакой активной мощности не потребляется, полезной работы в нагрузке не совершается. Синусоидальное напряжение (красная линия) и ток (зелёная линия) имеют фазовый сдвиг φ=45∘{\displaystyle \varphi =45^{\circ }} (cos⁡φ=0,71{\displaystyle \cos \varphi =0{,}71}) — нагрузка имеет и активную, и реактивную составляющие. Мгновенная мощность (синяя линия) и активная мощность (голубая линия) рассчитаны из переменного напряжения и тока с коэффициентом мощности, равным 0,71. Расположение синей линии (графика мгновенной мощности) под осью абсцисс показывает, что некоторая часть подводимой мощности всё же возвращается в сеть в течение части цикла, отмеченного φ.

Коэффицие́нт мо́щности — безразмерная физическая величина, характеризующая потребителя переменного электрического тока с точки зрения наличия в нагрузке реактивной составляющей. Коэффициент мощности показывает, насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.

Численно коэффициент мощности равен косинусу этого фазового сдвига.

Можно показать, что если к источнику синусоидального тока (например, розетка ~230 В, 50 Гц) подключить нагрузку, в которой ток опережает или отстаёт по фазе на некоторый угол от напряжения, то на внутреннем активном сопротивлении источника выделяется повышенная мощность. На практике это означает, что при работе на нагрузку со сдвинутыми напряжением и током от электростанции требуется больше отвода тепла, чем при работе на активную нагрузку; избыток передаваемой энергии выделяется в виде тепла в проводах и может быть довольно значительным.

Коэффициент мощности равен отношению потребляемой электроприёмником активной мощности к полной мощности. Активная мощность расходуется на совершение работы. Полная мощность — геометрическая сумма активной и реактивной мощностей (в случае синусоидальных тока и напряжения). В общем случае полную мощность можно определить как произведение действующих (среднеквадратических) значений тока и напряжения в цепи. Полная мощность равна корню квадратному из суммы квадратов активной и реактивной мощностей. В качестве единицы измерения полной мощности принято использовать вольт-ампер (В∙А) вместо ватта (Вт).

Согласно неравенству Коши—Буняковского, активная мощность, равная среднему значению произведения тока и напряжения, всегда не превышает произведение соответствующих среднеквадратических значений. Поэтому коэффициент мощности принимает значения от нуля до единицы (то есть от 0 до 100 %).

Коэффициент мощности математически можно интерпретировать как косинус угла между векторами тока и напряжения. Поэтому в случае синусоидальных напряжения и тока величина коэффициента мощности совпадает с косинусом угла, на который отстают соответствующие фазы.

В электроэнергетике для коэффициента мощности приняты обозначения cos⁡φ{\displaystyle \operatorname {cos} \varphi } (где φ{\displaystyle \varphi } — сдвиг фаз между силой тока и напряжением) либо λ. Когда для обозначения коэффициента мощности используется λ{\displaystyle \lambda }, его величину обычно выражают в процентах.

При наличии реактивной составляющей в нагрузке кроме значения коэффициента мощности иногда также указывают характер нагрузки: активно-ёмкостный или активно-индуктивный. В этом случае коэффициент мощности соответственно называют опережающим или отстающим.

В случае синусоидального напряжения, но несинусоидального тока, если нагрузка не имеет реактивной составляющей, коэффициент мощности равен доле мощности первой гармоники тока в полной мощности, потребляемой нагрузкой.

Математические расчёты

Треугольник мощностей

Коэффициент мощности необходимо учитывать при проектировании электросетей. Низкий коэффициент мощности ведёт к увеличению доли потерь электроэнергии в электрической сети в общих потерях. Чтобы увеличить коэффициент мощности, используют компенсирующие устройства. Неверно рассчитанный коэффициент мощности может привести к избыточному потреблению электроэнергии и снижению КПД электрооборудования, питающегося от данной сети.

Для расчётов в случае гармонических переменных U{\displaystyle U} (напряжение) и I{\displaystyle I} (сила тока) используются следующие математические формулы:

1. cos⁡φ=PS{\displaystyle \cos \varphi ={\frac {P}{S}}}
2. P=U×I×cos⁡φ{\displaystyle P=U\times I\times \cos \varphi }
3. Q=U×I×sin⁡φ{\displaystyle Q=U\times I\times \sin \varphi }
4. S=U×I=P2+Q2{\displaystyle S=U\times I={\sqrt {P^{2}+Q^{2}}}}

Здесь P{\displaystyle P} — активная мощность, S{\displaystyle S} — полная мощность, Q{\displaystyle Q} — реактивная мощность.

Типовые оценки качества электропотребления

При одной и той же активной мощности нагрузки мощность, бесполезно рассеиваемая на проводах, обратно пропорциональна квадрату коэффициента мощности. Таким образом, чем меньше коэффициент мощности, тем ниже качество потребления электроэнергии. Для повышения качества электропотребления применяются различные способы коррекции коэффициента мощности, то есть его повышения до значения, близкого к единице.

Значение коэффициента мощности	Высокое	Хорошее	Удовлетворительное	Низкое	Неудовлетворительное
cos⁡φ{\displaystyle \operatorname {cos} \varphi }	0,95…1	0,8…0,95	0,65…0,8	0,5…0,65	0…0,5
λ{\displaystyle \lambda }	95…100 %	80…95 %	65…80 %	50…65 %	0…50 %

Например, большинство старых светильников с люминесцентными лампами для зажигания и поддержания горения используют электромагнитные балласты (ЭмПРА), характеризующиеся низким его потреблением, то есть неэффективным электропотреблением. В отличие от них современные светильники, и в том числе компактные люминесцентные («энергосберегающие») лампы имеют ЭПРА, и характеризуются коэффициентом мощности стремящемся к 1, то есть к идеальному значению.

Несинусоидальность

Несинусоидальность — вид нелинейных искажений напряжения в электрической сети, который связан с появлением в составе напряжения гармоник с частотами, многократно превышающими основную частоту сети. Высшие гармоники напряжения оказывают отрицательное влияние на работу системы электроснабжения, вызывая дополнительные активные потери в трансформаторах, электрических машинах и сетях; повышенную аварийность в кабельных сетях; уменьшение коэффициента мощности за счёт мощности искажения, вызванной протеканием токов высших гармоник; а также ограниченное применение батарей конденсаторов для компенсации реактивной мощности.

Источниками высших гармоник тока и напряжения являются электроприёмники с нелинейными нагрузками. Например, мощные выпрямители переменного тока, применяемые в металлургической промышленности и на железнодорожном транспорте, газоразрядные лампы и др.

Коррекция коэффициента мощности

Коррекция коэффициента мощности при помощи конденсаторов

К ухудшению коэффициента мощности (непропорциональному потребляемому току относительно напряжения) приводят реактивная и нелинейная нагрузки. Реактивные нагрузки корректируется внешними реактивностями, именно для них определена величина cos φ.

Коррекция коэффициента мощности ((англ. power factor correction) PFC) — процесс приведения потребления конечного устройства, обладающего низким коэффициентом мощности при питании от силовой сети переменного тока, к состоянию, при котором коэффициент мощности соответствует принятым стандартам.

Технически реализуется в виде той или иной дополнительной схемы на входе устройства.

Данная процедура, необходимая для равномерного использования мощности фазы и исключения перегрузки нейтрального провода трёхфазной сети, обязательна для импульсных источников питания мощностью в 100 и более ватт^{[источник не указан 2743 дня]}. Компенсация обеспечивает отсутствие всплесков тока потребления на вершине синусоиды питающего напряжения и равномерную нагрузку на силовую линию.

Разновидности коррекции коэффициента мощности

• Коррекция реактивной составляющей полной мощности потребления устройства. Выполняется путём включения в цепь реактивного элемента, производящего обратное действие. Например, для компенсации действия электродвигателя переменного тока, обладающего высокой индуктивной реактивной составляющей полной мощности, параллельно цепи питания включается конденсатор.
• Коррекция нелинейности потребления тока в течение периода колебаний питающего напряжения. Если нагрузка потребляет ток непропорционально основной гармонике питающего напряжения, для повышения коэффициента мощности требуется схема пассивного (PPFC) или активного корректора коэффициента мощности (APFC). Простейшим пассивным корректором коэффициента мощности является дроссель с большой индуктивностью, включенный последовательно с питаемой нагрузкой. Дроссель выполняет сглаживание импульсного потребления нагрузки и выделение низшей, то есть основной, гармоники потребления тока, что и требуется.

Ссылки

Что такое коэффициент мощности?

06 июня 2012

Коэффициент мощности — величина, равная отношению активной мощности P, потребляемой нагрузкой, к ее полной мощности S.

Полная мощность — это произведение действующих значений напряжения и тока:

S=U×I, измеряется в вольт-амперах (ВА).

Активная мощность измеряется в ваттах (Вт) и вычисляется по формуле:

P=U×I×λ, где λ — это коэффициент мощности.

Рассмотрим подробнее, что это такое.

Ранее, когда в основном встречались устройства с нагрузкой линейного типа (т.е. при синусоидальном напряжении нагрузка потребляла синусоидальный же ток), более распространено было понятие cosφ («косинус фи»), учитывающее разность фаз между напряжением и током (см. рис. 1).

Рис. 1. Разность фаз между напряжением и током.

Эта величина при условии линейности нагрузки определялась по той же формуле

cosφ=P/S, или из вида осциллограммы.

Однако если форма тока сильно отличается от синусоиды, такого параметра как cosφдля оценки качества потребляемой электроэнергии не достаточно, т.к. необходимо учитывать гармонический состав потребляемого тока (см. рис. 2).

Рис. 2. Кривая тока современного электронного прибора

Поэтому сейчас энергетики оперируют понятием коэффициент мощности.

Обозначается чаще всего λ («лямбда»), PF (Power Factor) или по старинке cosφ:

THD — Total Harmonic Distortion или КНИ (коэффициент нелинейных искажений) — коэффициент, определяемый отношением действующего значения первой гармоники тока к корню из суммы квадратов высших гармоник.

Математический смысл коэффициента мощности — это отношение интеграла произведения мгновенных значений напряжения и тока к произведению корней интегралов квадратов мгновенных значений тока и напряжения:

Физический смысл в том, что активная мощность (т.е. та, которую показывает ваттметр) не совпадает с полной мощностью, т.е. с произведением показаний вольтметра и амперметра, при отличии формы тока от формы напряжения или при несоответствии их фаз.

На рис. 3 хорошо видно, откуда вообще берется этот коэффициент: мгновенная мощность определяется как произведение мгновенного значения тока на мгновенное значение напряжения.

Рис. 3. Откуда берется коэффициент мощности

Т.е. какую-то часть периода (период Т=0,02 секунды при частоте 50 Гц) ток и напряжение совпадают по «знаку» (выделено синим вдоль оси) и их произведение дает положительную величину, а в остальное время (красным) напряжение, к примеру, больше нуля, а ток — меньше, соответственно их произведение меньше нуля. Активная мощность усредняется по периоду (интегрируется), т.е. в первом приближении алгебраически складываются все значения мощности за период и делятся на величину периода, т.е. будут слагаемые со знаком «+» и со знаком «–», поэтому в итоге сумма получится меньше, чем если бы ток и напряжение совпадали по фазе (см. рис. 4).

Рис. 4. Пример, когда ток и напряжение имеют одинаковую форму и совпадают  по фазе — коэффициент мощности равен 1 (или 100%)

В случае с несинусоидальными токами при синусоидальном напряжении все немного сложнее, но смысл тот же — интеграл произведения тока на напряжение за период всегда меньше произведения действующих значений тока и напряжения. Суть в том, что высшие гармоники (т.е. составляющие тока, частота которых кратна основной частоте тока и напряжения) не создают активной мощности (по причине несовпадения частот с напряжением), но нечетные гармоники (3-я — частота 150 Гц, 5-я — частота 250 Гц, 7-я, 9-я и т.д.) создают полную мощность.

Для полноты информации наглядно поясним, что такое высшие гармоники:

1. Так будет выглядеть осциллограмма тока через обычный резистор 2200 Ом при работе в наших сетях (220 В, 50 Гц):

2. Так будет выглядеть ток с частой 150 Гц (т.е. 3×50 Гц — третья гармоника основной частоты) — синяя кривая. Красным цветом — основная частота или первая гармоника:

3. А так будет выглядеть ток, равный сумме 1-й гармоники и 3-й:

4. А если в составе тока будет много высших гармоник:

Примерно такая ситуация наблюдается в компактных люминесцентных и светодиодных лампах ввиду использования в схемах ЭПРА нелинейных элементов (транзисторы, диоды и т.д.). Это означает, что при тех же значениях активной мощности Р и напряжения U, нагрузочный ток энергосберегающих источников освещения больше, чем у ламп накаливания или галогенных.

Если, например, коэффициент мощности светодиодной лампы равен 0,5, то она потребляет в 2 раза больший ток, чем лампа накаливания той же мощности Р.

Потери мощности на нагрев проводов сети пропорциональны квадрату тока:

Таким образом, при соsφ=0,5 потери мощности в сети больше в 4 раза, чем при соs

φ=1. Кроме того, генераторы и трансформаторы будут загружены током в 2 раза больше, и в этом случае требуется примерно в 2 раза большее сечение проводов для обмоток.

Отсюда видно, какое важное значение имеет величина соsφ:

– в электробытовых сетях: квартиры, дачи, частные дома;

– в промышленности: производство с жесткими лимитами электроэнергии;

– в бизнесе: офисы, торговые комплекты, склады;

– а также всюду, где стоит задача минимизировать затраты на электроэнергию.

Почему в нормативных документах требуется повышать коэффициент мощности?

Потому что низкий коэффициент мощности свидетельствует о том, что при низкой потребляемой (и оплачиваемой по времени) активной мощности, ваша нагрузка потребляет бесплатную полную мощность, т.е. фактически вы «гоняете по сетям бесплатный ток», а сетям все равно бесплатный ток или платный — провода греются и даже перегорают, перегружаются трансформаторы и прочее.

Например, известен случай: в одной Подмосковной теплице установили около тысячи КЛЛ на одну сеть — итог: выгорел нулевой провод (по нему при нормальных условиях и линейной нагрузке ток течь не должен вообще).

Поэтому, кстати, стандарты МЭК (стандарт международной электротехнической комиссии) и ГОСТ, соответственно, особенно требовательны к лампам высокой мощности (более 25 Вт).

Коэффициент мощности — WiKi

Синусоидальное напряжение (красная линия) и ток (зелёная линия) синфазны — между ними нет фазового сдвига (φ=0∘{\displaystyle \varphi =0^{\circ }}, cos⁡φ=1{\displaystyle \cos \varphi =1}) — нагрузка полностью активная, нет реактивной составляющей. Мгновенная мощность (синяя линия) и активная мощность (голубая линия) рассчитаны с коэффициентом мощности, равным 1. Как видно, синяя линия (график мгновенной мощности) находится полностью над осью абсцисс (в положительной полуплоскости), вся подводимая энергия преобразуется в работу: переходит в активную мощность, потребляемую нагрузкой. Синусоидальное напряжение (красная линия) и ток (зелёная линия) имеют фазовый сдвиг φ=90∘{\displaystyle \varphi =90^{\circ }} (cos⁡φ=0{\displaystyle \cos \varphi =0}) — нагрузка полностью реактивная, нет активной составляющей. Мгновенная мощность (синяя линия) и активная мощность (голубая линия) рассчитаны с коэффициентом мощности, равным 0. Расположение синей линии (графика мгновенной мощности) на оси абсцисс показывает, что в течение первой четверти цикла вся подводимая мощность временно сохраняется в нагрузке, а во второй четверти цикла возвращается в сеть, и так далее, то есть никакой активной мощности не потребляется, полезной работы в нагрузке не совершается. Синусоидальное напряжение (красная линия) и ток (зелёная линия) имеют фазовый сдвиг φ=45∘{\displaystyle \varphi =45^{\circ }} (cos⁡φ=0,71{\displaystyle \cos \varphi =0{,}71}) — нагрузка имеет и активную, и реактивную составляющие. Мгновенная мощность (синяя линия) и активная мощность (голубая линия) рассчитаны из переменного напряжения и тока с коэффициентом мощности, равным 0,71. Расположение синей линии (графика мгновенной мощности) под осью абсцисс показывает, что некоторая часть подводимой мощности всё же возвращается в сеть в течение части цикла, отмеченного φ.

Коэффицие́нт мо́щности — безразмерная физическая величина, характеризующая потребителя переменного электрического тока с точки зрения наличия в нагрузке реактивной составляющей и мощности искажения (собирательное название — неактивная мощность). Следует отличать понятие «коэффициент мощности» от понятия «косинус фи», который равен косинусу сдвига фазы переменного тока, протекающего через нагрузку, относительно приложенного к ней напряжения. Второе понятие используют в случае синусоидальных тока и напряжения, и только в этом случае оба понятия эквивалентны.

Определение и физический смысл

Коэффициент мощности равен отношению потребляемой электроприёмником активной мощности к полной мощности. Активная мощность расходуется на совершение работы. В случае синусоидальных тока и напряжения полная мощность представляет собой геометрическую сумму активной и реактивной мощностей. Иными словами, она равна корню квадратному из суммы квадратов активной и реактивной мощностей. В общем случае полную мощность можно определить как произведение действующих (среднеквадратических) значений тока и напряжения в цепи. В качестве единицы измерения полной мощности принято использовать вольт-ампер (В∙А) вместо ватта (Вт).

В электроэнергетике для коэффициента мощности приняты обозначения cos⁡φ{\displaystyle \operatorname {cos} \varphi }  (где φ{\displaystyle \varphi }  — сдвиг фаз между силой тока и напряжением) либо λ{\displaystyle \lambda } . Когда для обозначения коэффициента мощности используется λ{\displaystyle \lambda } , его величину обычно выражают в процентах.

Согласно неравенству Коши—Буняковского, активная мощность, равная среднему значению произведения тока и напряжения, всегда не превышает произведение соответствующих среднеквадратических значений. Поэтому коэффициент мощности принимает значения от нуля до единицы (или от 0 до 100 %).

Коэффициент мощности математически можно интерпретировать как косинус угла между векторами тока и напряжения (в общем случае бесконечномерных). Поэтому в случае синусоидальных напряжения и тока величина коэффициента мощности совпадает с косинусом угла, на который отстоят соответствующие фазы.

В случае синусоидального напряжения, но несинусоидального тока, если нагрузка не имеет реактивной составляющей, коэффициент мощности равен доле мощности первой гармоники тока в полной мощности, потребляемой нагрузкой.

При наличии реактивной составляющей в нагрузке кроме значения коэффициента мощности иногда также указывают характер нагрузки: активно-ёмкостный или активно-индуктивный. В этом случае коэффициент мощности соответственно называют опережающим или отстающим.

Прикладной смысл

Можно показать, что если к источнику синусоидального напряжения (например, розетка ~230 В, 50 Гц) подключить нагрузку, в которой ток опережает или отстаёт по фазе на некоторый угол от напряжения, то на внутреннем активном сопротивлении источника выделяется повышенная мощность. На практике это означает, что при работе на нагрузку с реактивной составляющей от электростанции требуется больше отвода тепла, чем при работе на активную нагрузку; избыток передаваемой энергии выделяется в виде тепла в проводах, и в масштабах, например, предприятия потери могут быть довольно значительными.

Не следует путать коэффициент мощности и коэффициент полезного действия (КПД) нагрузки. Коэффициент мощности практически не влияет на энергопотребление самого устройства, включённого в сеть, но влияет на потери энергии в идущих к нему проводах, а также в местах выработки или преобразования энергии (например, на подстанциях). Т.е. счётчик электроэнергии в квартире практически не будет реагировать на коэффициент мощности устройств, поскольку оплате подлежит лишь электроэнергия, совершающая работу (активная составляющая нагрузки). В то же время от КПД непосредственно зависит потребляемая электроприбором активная мощность. Например, компактная люминесцентная («энергосберегающая») лампа потребляет примерно в 1,5 раза больше энергии, чем аналогичная по яркости светодиодная лампа. Это связано с более высоким КПД последней. Однако независимо от этого каждая из этих ламп может иметь как низкий, так и высокий коэффициент мощности, который определяется используемыми схемотехническими решениями.

Математические расчёты

Типовые оценки качества электропотребления

При одной и той же активной мощности нагрузки мощность, бесполезно рассеиваемая на проводах, обратно пропорциональна квадрату коэффициента мощности. Таким образом, чем меньше коэффициент мощности, тем ниже качество потребления электроэнергии. Для повышения качества электропотребления применяются различные способы коррекции коэффициента мощности, то есть его повышения до значения, близкого к единице.

Значение коэффициента мощности	Высокое	Хорошее	Удовлетворительное	Низкое	Неудовлетворительное
cos⁡φ{\displaystyle \operatorname {cos} \varphi }	0,95…1	0,8…0,95	0,65…0,8	0,5…0,65	0…0,5
λ{\displaystyle \lambda }	95…100 %	80…95 %	65…80 %	50…65 %	0…50 %

Например, большинство старых светильников с люминесцентными лампами для зажигания и поддержания горения используют электромагнитные балласты (ЭмПРА), характеризующиеся низким значением коэффициента мощности, то есть неэффективным электропотреблением. Многие компактные люминесцентные («энергосберегающие») лампы, имеющие ЭПРА, тоже характеризуются низким коэффициентом мощности (0,5…0,65). Но аналогичные изделия известных производителей, как и большинство современных светильников, содержат схемы коррекции коэффициента мощности, и для них значение cos⁡φ{\displaystyle \operatorname {cos} \varphi }  близко к 1, то есть к идеальному значению.

Несинусоидальность

Низкое качество потребителей электроэнергии, связанное с наличием в нагрузке мощности искажения, то есть нелинейная нагрузка (особенно при импульсном её характере), приводит к искажению синусоидальной формы питающего напряжения. Несинусоидальность — вид нелинейных искажений напряжения в электрической сети, который связан с появлением в составе напряжения гармоник с частотами, многократно превышающими основную частоту сети. Высшие гармоники напряжения оказывают отрицательное влияние на работу системы электроснабжения, вызывая дополнительные активные потери в трансформаторах, электрических машинах и сетях; повышенную аварийность в кабельных сетях.

Источниками высших гармоник тока и напряжения являются электроприёмники с нелинейными нагрузками. Например, мощные выпрямители переменного тока, применяемые в металлургической промышленности и на железнодорожном транспорте, газоразрядные лампы, импульсные источники питания и др.

Коррекция коэффициента мощности

  Коррекция коэффициента мощности при помощи конденсаторов

Коррекция коэффициента мощности (англ. power factor correction (PFC)) — процесс приведения потребления конечного устройства, обладающего низким коэффициентом мощности при питании от силовой сети переменного тока, к состоянию, при котором коэффициент мощности соответствует принятым стандартам.

К ухудшению коэффициента мощности (изменению потребляемого тока непропорционально приложенному напряжению) приводят нерезистивные нагрузки: реактивная и нелинейная. Реактивные нагрузки корректируются внешними реактивностями, именно для них определена величина cos⁡φ{\displaystyle \cos \varphi } . Коррекция нелинейной нагрузки технически реализуется в виде той или иной дополнительной схемы на входе устройства.

Данная процедура необходима для равномерного использования мощности фазы и исключения перегрузки нейтрального провода трёхфазной сети. Так, она обязательна для импульсных источников питания мощностью в 100 и более ватт^{[источник не указан 3133 дня]}. Компенсация обеспечивает отсутствие всплесков тока потребления на вершине синусоиды питающего напряжения и равномерную нагрузку на силовую линию.

Разновидности коррекции коэффициента мощности

• Коррекция реактивной составляющей полной мощности потребления устройства. Выполняется путём включения в цепь реактивного элемента, производящего обратное действие. Например, для компенсации действия электродвигателя переменного тока, обладающего высокой индуктивной реактивной составляющей полной мощности, параллельно цепи питания включается конденсатор. В масштабах предприятия для компенсации реактивной мощности применяются батареи конденсаторов и других компенсирующих устройств.
• Коррекция нелинейности потребления тока в течение периода колебаний питающего напряжения. Если нагрузка потребляет ток непропорционально приложенному напряжению, для повышения коэффициента мощности требуется схема пассивного (PPFC) или активного корректора коэффициента мощности (APFC). Простейшим пассивным корректором коэффициента мощности является дроссель с большой индуктивностью, включённый последовательно с питаемой нагрузкой. Дроссель выполняет сглаживание импульсного потребления нагрузки и выделение низшей, то есть основной, гармоники потребления тока, что и требуется (правда, это достигается в ущерб форме напряжения, поступающего на вход устройства). Активная коррекция коэффициента мощности ценой некоторого усложнения схемы устройства способна обеспечивать наилучшее качество коррекции, приближая коэффициент мощности к 1.

Ссылки

Коэффициент мощности — Википедия (с комментариями)

Материал из Википедии — свободной энциклопедии

Коэффицие́нт мо́щности — безразмерная физическая величина, характеризующая потребителя переменного электрического тока с точки зрения наличия в нагрузке реактивной составляющей. Коэффициент мощности показывает, насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.

Численно коэффициент мощности равен косинусу этого фазового сдвига.

Можно показать, что если к источнику синусоидального тока (например, розетка ~220 В, 50 Гц) подключить нагрузку, в которой ток опережает или отстаёт по фазе на некоторый угол от напряжения, то на внутреннем активном сопротивлении источника выделяется повышенная мощность. На практике это означает, что при работе на нагрузку со сдвинутыми напряжением и током от электростанции требуется больше энергии; избыток передаваемой энергии выделяется в виде тепла в проводах и может быть довольно значительным.

Коэффициент мощности равен отношению потребляемой электроприёмником активной мощности к полной мощности. Активная мощность расходуется на совершение работы. Полная мощность — геометрическая сумма активной и реактивной мощностей (в случае синусоидальных тока и напряжения). В общем случае полную мощность можно определить как произведение действующих (среднеквадратических) значений тока и напряжения в цепи. Полная мощность равна корню квадратному из суммы квадратов активной и реактивной мощностей. В качестве единицы измерения полной мощности принято использовать вольт-ампер (В∙А) вместо ватта (Вт).

Согласно неравенству Коши—Буняковского, активная мощность, равная среднему значению произведения тока и напряжения, всегда не превышает произведение соответствующих среднеквадратических значений. Поэтому коэффициент мощности принимает значения от нуля до единицы (то есть от 0 до 100 %).

Коэффициент мощности математически можно интерпретировать как косинус угла между векторами тока и напряжения. Поэтому в случае синусоидальных напряжения и тока величина коэффициента мощности совпадает с косинусом угла, на который отстают соответствующие фазы.

В электроэнергетике для коэффициента мощности приняты обозначения cos φ (где φ — сдвиг фаз между силой тока и напряжением) либо λ. Когда для обозначения коэффициента мощности используется λ, его величину обычно выражают в процентах.

При наличии реактивной составляющей в нагрузке кроме значения коэффициента мощности иногда также указывают характер нагрузки: активно-ёмкостный или активно-индуктивный. В этом случае коэффициент мощности соответственно называют опережающим или отстающим.

В случае синусоидального напряжения, но несинусоидального тока, если нагрузка не имеет реактивной составляющей, коэффициент мощности равен доле мощности первой гармоники тока в полной мощности, потребляемой нагрузкой.

Математические расчёты

Коэффициент мощности необходимо учитывать при проектировании электросетей. Низкий коэффициент мощности ведёт к увеличению доли потерь электроэнергии в электрической сети в общих потерях. Чтобы увеличить коэффициент мощности, используют компенсирующие устройства. Неверно рассчитанный коэффициент мощности может привести к избыточному потреблению электроэнергии и снижению КПД электрооборудования, питающегося от данной сети.

Для расчётов в случае гармонических переменных U (напряжение) и I (сила тока) используются следующие математические формулы:

1. <math>\cos \varphi = \frac{P}{S} </math>
2. <math>P = U \times I \times \cos \varphi</math>
3. <math>Q = U \times I \times \sin \varphi</math>
4. <math>S = U \times I = \sqrt{P^2+Q^2} </math>

Здесь <math>P </math> — активная мощность, <math>S </math> — полная мощность, <math>Q </math> — реактивная мощность.

Типовые оценки качества электропотребления

При одной и той же активной мощности нагрузки мощность, бесполезно рассеиваемая на проводах, обратно пропорциональна квадрату коэффициента мощности. Таким образом, чем меньше коэффициент мощности, тем ниже качество потребления электроэнергии. Для повышения качества электропотребления применяются различные способы коррекции коэффициента мощности, то есть его повышения до значения, близкого к единице.

Значение коэффициента мощности	Высокое	Хорошее	Удовлетворительное	Низкое	Неудовлетворительное
cos φ	0,95…1	0,8…0,95	0,65…0,8	0,5…0,65	0…0,5
λ	95…100 %	80…95 %	65…80 %	50…65 %	0…50 %

Например, большинство старых светильников с люминесцентными лампами для зажигания и поддержания горения используют электромагнитные балласты (ЭмПРА), характеризующиеся низким его потреблением, то есть неэффективным электропотреблением. В отличие от них современные светильники, и в том числе компактные люминесцентные («энергосберегающие») лампы имеют ЭПРА, и характеризуются коэффициентом мощности стремящемся к 1, то есть к идеальному значению.

Несинусоидальность

Несинусоидальность — вид нелинейных искажений напряжения в электрической сети, который связан с появлением в составе напряжения гармоник с частотами, многократно превышающими основную частоту сети. Высшие гармоники напряжения оказывают отрицательное влияние на работу системы электроснабжения, вызывая дополнительные активные потери в трансформаторах, электрических машинах и сетях; повышенную аварийность в кабельных сетях; уменьшение коэффициента мощности за счёт мощности искажения, вызванной протеканием токов высших гармоник; а также ограниченное применение батарей конденсаторов для компенсации реактивной мощности.

Источниками высших гармоник тока и напряжения являются электроприёмники с нелинейными нагрузками. Например, мощные выпрямители переменного тока, применяемые в металлургической промышленности и на железнодорожном транспорте, газоразрядные лампы и др.

Коррекция коэффициента мощности

Коррекция коэффициента мощности ((англ. power factor correction) PFC) — процесс приведения потребления конечного устройства, обладающего низким коэффициентом мощности при питании от силовой сети переменного тока, к состоянию, при котором коэффициент мощности соответствует принятым стандартам.

Технически реализуется в виде той или иной дополнительной схемы на входе устройства.

Данная процедура, необходимая для равномерного использования мощности фазы и исключения перегрузки нейтрального провода трёхфазной сети, обязательна для импульсных источников питания мощностью в 100 и более ваттК:Википедия:Статьи без источников (тип: не указан)^{[источник не указан 3190 дней]}. Компенсация обеспечивает отсутствие всплесков тока потребления на вершине синусоиды питающего напряжения и равномерную нагрузку на силовую линию.

Разновидности коррекции коэффициента мощности

• Коррекция реактивной составляющей полной мощности потребления устройства. Выполняется путём включения в цепь реактивного элемента, производящего обратное действие. Например, для компенсации действия электродвигателя переменного тока, обладающего высокой индуктивной реактивной составляющей полной мощности, параллельно цепи питания включается конденсатор.
• Коррекция нелинейности потребления тока в течение периода колебаний питающего напряжения. Если нагрузка потребляет ток непропорционально основной гармонике питающего напряжения, для повышения коэффициента мощности требуется схема пассивного (PPFC) или активного корректора коэффициента мощности (APFC). Простейшим пассивным корректором коэффициента мощности является дроссель с большой индуктивностью, включенный последовательно с питаемой нагрузкой. Дроссель выполняет сглаживание импульсного потребления нагрузки и выделение низшей, то есть основной, гармоники потребления тока, что и требуется.

Напишите отзыв о статье «Коэффициент мощности»

Ссылки

• [electricalschool.info/main/ekspluat/104-kak-povysit-kojefficient-moshhnosti-bez.html Как повысить коэффициент мощности без использования компенсирующих устройств]
• [www.bt.dn.ua/harm/ Суднова В. В., Влияние качества электроэнергии на работу электроприемников]
• [e-audit.ru/quality/no_sinus.shtml Несинусоидальность напряжения]
• [electricalschool.info/main/elsnabg/260-vlijanie-vysshikh-garmonik.html Влияние высших гармоник напряжения и тока на работу электрооборудования]
• [www.gosthelp.ru/gost/gost3761.html ГОСТ 13109-97]
• [ukrm.ru/content/view/68/31/ Оптимизация работы электроприемников — эффективный способ коррекции коэффициента мощности]
• [www.nix.ru/support/faq/show_articles.php?number=616&faq_topics=PFC PFC, Никс, 25.11.2007.]
• [www.compeljournal.ru/enews/2007/9/3 Решения от Texas Instruments для AC/DC- и DC/DC-преобразователей, «Новости электроники», N9, 2007.]
• [www.fcenter.ru/online.shtml?articles/hardware/tower/11259#03 Коррекция фактора мощности // Методика тестирования блоков питания, F-center, 24.12.2004.]
• [energoeducation.ru/wp-content/uploads/2015/07/LAW117393_0_20150905_171103_54007.pdf постановлением Правительства РФ от 20 июля 2011 года № 602 «Об утверждении требований к осветительным устройствам и электрическим лампам, используемым в цепях переменного тока в целях освещения»]
• [www.qgc.ru/upload/medialibrary/b53/b53eeb78ba02d54a9bca43ed4e022f18.pdf ТЕХНИЧЕСКИЙ РЕГЛАМЕНТ Таможенного союза «О требованиях к энергетической эффективности электрических энергопотребляющих устройств» (на стадии принятия)]
• [docs.cntd.ru/document/1200036479 ОСТ 45.183-2001 Установки электропитания аппаратуры электросвязи стационарные. Общие технические требования.]

Отрывок, характеризующий Коэффициент мощности

Вернувшись в Москву из армии, Николай Ростов был принят домашними как лучший сын, герой и ненаглядный Николушка; родными – как милый, приятный и почтительный молодой человек; знакомыми – как красивый гусарский поручик, ловкий танцор и один из лучших женихов Москвы.
Знакомство у Ростовых была вся Москва; денег в нынешний год у старого графа было достаточно, потому что были перезаложены все имения, и потому Николушка, заведя своего собственного рысака и самые модные рейтузы, особенные, каких ни у кого еще в Москве не было, и сапоги, самые модные, с самыми острыми носками и маленькими серебряными шпорами, проводил время очень весело. Ростов, вернувшись домой, испытал приятное чувство после некоторого промежутка времени примеривания себя к старым условиям жизни. Ему казалось, что он очень возмужал и вырос. Отчаяние за невыдержанный из закона Божьего экзамен, занимание денег у Гаврилы на извозчика, тайные поцелуи с Соней, он про всё это вспоминал, как про ребячество, от которого он неизмеримо был далек теперь. Теперь он – гусарский поручик в серебряном ментике, с солдатским Георгием, готовит своего рысака на бег, вместе с известными охотниками, пожилыми, почтенными. У него знакомая дама на бульваре, к которой он ездит вечером. Он дирижировал мазурку на бале у Архаровых, разговаривал о войне с фельдмаршалом Каменским, бывал в английском клубе, и был на ты с одним сорокалетним полковником, с которым познакомил его Денисов.
Страсть его к государю несколько ослабела в Москве, так как он за это время не видал его. Но он часто рассказывал о государе, о своей любви к нему, давая чувствовать, что он еще не всё рассказывает, что что то еще есть в его чувстве к государю, что не может быть всем понятно; и от всей души разделял общее в то время в Москве чувство обожания к императору Александру Павловичу, которому в Москве в то время было дано наименование ангела во плоти.
В это короткое пребывание Ростова в Москве, до отъезда в армию, он не сблизился, а напротив разошелся с Соней. Она была очень хороша, мила, и, очевидно, страстно влюблена в него; но он был в той поре молодости, когда кажется так много дела, что некогда этим заниматься, и молодой человек боится связываться – дорожит своей свободой, которая ему нужна на многое другое. Когда он думал о Соне в это новое пребывание в Москве, он говорил себе: Э! еще много, много таких будет и есть там, где то, мне еще неизвестных. Еще успею, когда захочу, заняться и любовью, а теперь некогда. Кроме того, ему казалось что то унизительное для своего мужества в женском обществе. Он ездил на балы и в женское общество, притворяясь, что делал это против воли. Бега, английский клуб, кутеж с Денисовым, поездка туда – это было другое дело: это было прилично молодцу гусару.
В начале марта, старый граф Илья Андреич Ростов был озабочен устройством обеда в английском клубе для приема князя Багратиона.
Граф в халате ходил по зале, отдавая приказания клубному эконому и знаменитому Феоктисту, старшему повару английского клуба, о спарже, свежих огурцах, землянике, теленке и рыбе для обеда князя Багратиона. Граф, со дня основания клуба, был его членом и старшиною. Ему было поручено от клуба устройство торжества для Багратиона, потому что редко кто умел так на широкую руку, хлебосольно устроить пир, особенно потому, что редко кто умел и хотел приложить свои деньги, если они понадобятся на устройство пира. Повар и эконом клуба с веселыми лицами слушали приказания графа, потому что они знали, что ни при ком, как при нем, нельзя было лучше поживиться на обеде, который стоил несколько тысяч.
– Так смотри же, гребешков, гребешков в тортю положи, знаешь! – Холодных стало быть три?… – спрашивал повар. Граф задумался. – Нельзя меньше, три… майонез раз, – сказал он, загибая палец…
– Так прикажете стерлядей больших взять? – спросил эконом. – Что ж делать, возьми, коли не уступают. Да, батюшка ты мой, я было и забыл. Ведь надо еще другую антре на стол. Ах, отцы мои! – Он схватился за голову. – Да кто же мне цветы привезет?
– Митинька! А Митинька! Скачи ты, Митинька, в подмосковную, – обратился он к вошедшему на его зов управляющему, – скачи ты в подмосковную и вели ты сейчас нарядить барщину Максимке садовнику. Скажи, чтобы все оранжереи сюда волок, укутывал бы войлоками. Да чтобы мне двести горшков тут к пятнице были.
Отдав еще и еще разные приказания, он вышел было отдохнуть к графинюшке, но вспомнил еще нужное, вернулся сам, вернул повара и эконома и опять стал приказывать. В дверях послышалась легкая, мужская походка, бряцанье шпор, и красивый, румяный, с чернеющимися усиками, видимо отдохнувший и выхолившийся на спокойном житье в Москве, вошел молодой граф.
– Ах, братец мой! Голова кругом идет, – сказал старик, как бы стыдясь, улыбаясь перед сыном. – Хоть вот ты бы помог! Надо ведь еще песенников. Музыка у меня есть, да цыган что ли позвать? Ваша братия военные это любят.
– Право, папенька, я думаю, князь Багратион, когда готовился к Шенграбенскому сражению, меньше хлопотал, чем вы теперь, – сказал сын, улыбаясь.
Старый граф притворился рассерженным. – Да, ты толкуй, ты попробуй!
И граф обратился к повару, который с умным и почтенным лицом, наблюдательно и ласково поглядывал на отца и сына.
– Какова молодежь то, а, Феоктист? – сказал он, – смеется над нашим братом стариками.
– Что ж, ваше сиятельство, им бы только покушать хорошо, а как всё собрать да сервировать , это не их дело.
– Так, так, – закричал граф, и весело схватив сына за обе руки, закричал: – Так вот же что, попался ты мне! Возьми ты сейчас сани парные и ступай ты к Безухову, и скажи, что граф, мол, Илья Андреич прислали просить у вас земляники и ананасов свежих. Больше ни у кого не достанешь. Самого то нет, так ты зайди, княжнам скажи, и оттуда, вот что, поезжай ты на Разгуляй – Ипатка кучер знает – найди ты там Ильюшку цыгана, вот что у графа Орлова тогда плясал, помнишь, в белом казакине, и притащи ты его сюда, ко мне.
– И с цыганками его сюда привести? – спросил Николай смеясь. – Ну, ну!…
В это время неслышными шагами, с деловым, озабоченным и вместе христиански кротким видом, никогда не покидавшим ее, вошла в комнату Анна Михайловна. Несмотря на то, что каждый день Анна Михайловна заставала графа в халате, всякий раз он конфузился при ней и просил извинения за свой костюм.
– Ничего, граф, голубчик, – сказала она, кротко закрывая глаза. – А к Безухому я съезжу, – сказала она. – Пьер приехал, и теперь мы всё достанем, граф, из его оранжерей. Мне и нужно было видеть его. Он мне прислал письмо от Бориса. Слава Богу, Боря теперь при штабе.
Граф обрадовался, что Анна Михайловна брала одну часть его поручений, и велел ей заложить маленькую карету.
– Вы Безухову скажите, чтоб он приезжал. Я его запишу. Что он с женой? – спросил он.
Анна Михайловна завела глаза, и на лице ее выразилась глубокая скорбь…
– Ах, мой друг, он очень несчастлив, – сказала она. – Ежели правда, что мы слышали, это ужасно. И думали ли мы, когда так радовались его счастию! И такая высокая, небесная душа, этот молодой Безухов! Да, я от души жалею его и постараюсь дать ему утешение, которое от меня будет зависеть.
– Да что ж такое? – спросили оба Ростова, старший и младший.
Анна Михайловна глубоко вздохнула: – Долохов, Марьи Ивановны сын, – сказала она таинственным шопотом, – говорят, совсем компрометировал ее. Он его вывел, пригласил к себе в дом в Петербурге, и вот… Она сюда приехала, и этот сорви голова за ней, – сказала Анна Михайловна, желая выразить свое сочувствие Пьеру, но в невольных интонациях и полуулыбкою выказывая сочувствие сорви голове, как она назвала Долохова. – Говорят, сам Пьер совсем убит своим горем.
– Ну, всё таки скажите ему, чтоб он приезжал в клуб, – всё рассеется. Пир горой будет.
На другой день, 3 го марта, во 2 м часу по полудни, 250 человек членов Английского клуба и 50 человек гостей ожидали к обеду дорогого гостя и героя Австрийского похода, князя Багратиона. В первое время по получении известия об Аустерлицком сражении Москва пришла в недоумение. В то время русские так привыкли к победам, что, получив известие о поражении, одни просто не верили, другие искали объяснений такому странному событию в каких нибудь необыкновенных причинах. В Английском клубе, где собиралось всё, что было знатного, имеющего верные сведения и вес, в декабре месяце, когда стали приходить известия, ничего не говорили про войну и про последнее сражение, как будто все сговорились молчать о нем. Люди, дававшие направление разговорам, как то: граф Ростопчин, князь Юрий Владимирович Долгорукий, Валуев, гр. Марков, кн. Вяземский, не показывались в клубе, а собирались по домам, в своих интимных кружках, и москвичи, говорившие с чужих голосов (к которым принадлежал и Илья Андреич Ростов), оставались на короткое время без определенного суждения о деле войны и без руководителей. Москвичи чувствовали, что что то нехорошо и что обсуждать эти дурные вести трудно, и потому лучше молчать. Но через несколько времени, как присяжные выходят из совещательной комнаты, появились и тузы, дававшие мнение в клубе, и всё заговорило ясно и определенно. Были найдены причины тому неимоверному, неслыханному и невозможному событию, что русские были побиты, и все стало ясно, и во всех углах Москвы заговорили одно и то же. Причины эти были: измена австрийцев, дурное продовольствие войска, измена поляка Пшебышевского и француза Ланжерона, неспособность Кутузова, и (потихоньку говорили) молодость и неопытность государя, вверившегося дурным и ничтожным людям. Но войска, русские войска, говорили все, были необыкновенны и делали чудеса храбрости. Солдаты, офицеры, генералы – были герои. Но героем из героев был князь Багратион, прославившийся своим Шенграбенским делом и отступлением от Аустерлица, где он один провел свою колонну нерасстроенною и целый день отбивал вдвое сильнейшего неприятеля. Тому, что Багратион выбран был героем в Москве, содействовало и то, что он не имел связей в Москве, и был чужой. В лице его отдавалась должная честь боевому, простому, без связей и интриг, русскому солдату, еще связанному воспоминаниями Итальянского похода с именем Суворова. Кроме того в воздаянии ему таких почестей лучше всего показывалось нерасположение и неодобрение Кутузову.
– Ежели бы не было Багратиона, il faudrait l’inventer, [надо бы изобрести его.] – сказал шутник Шиншин, пародируя слова Вольтера. Про Кутузова никто не говорил, и некоторые шопотом бранили его, называя придворною вертушкой и старым сатиром. По всей Москве повторялись слова князя Долгорукова: «лепя, лепя и облепишься», утешавшегося в нашем поражении воспоминанием прежних побед, и повторялись слова Ростопчина про то, что французских солдат надо возбуждать к сражениям высокопарными фразами, что с Немцами надо логически рассуждать, убеждая их, что опаснее бежать, чем итти вперед; но что русских солдат надо только удерживать и просить: потише! Со всex сторон слышны были новые и новые рассказы об отдельных примерах мужества, оказанных нашими солдатами и офицерами при Аустерлице. Тот спас знамя, тот убил 5 ть французов, тот один заряжал 5 ть пушек. Говорили и про Берга, кто его не знал, что он, раненый в правую руку, взял шпагу в левую и пошел вперед. Про Болконского ничего не говорили, и только близко знавшие его жалели, что он рано умер, оставив беременную жену и чудака отца.

Коэффициент мощности — Википедия. Что такое Коэффициент мощности

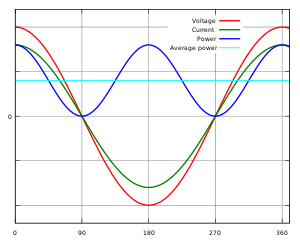Синусоидальное напряжение (красная линия) и ток (зелёная линия) синфазны — между ними нет фазового сдвига (φ=0∘{\displaystyle \varphi =0^{\circ }}, cos⁡φ=1{\displaystyle \cos \varphi =1}) — нагрузка полностью активная, нет реактивной составляющей. Мгновенная мощность (синяя линия) и активная мощность (голубая линия) рассчитаны с коэффициентом мощности, равным 1. Как видно, синяя линия (график мгновенной мощности) находится полностью над осью абсцисс (в положительной полуплоскости), вся подводимая энергия преобразуется в работу: переходит в активную мощность, потребляемую нагрузкой. 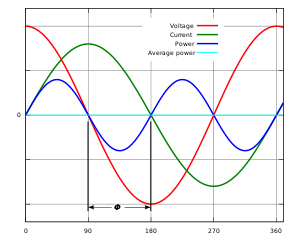Синусоидальное напряжение (красная линия) и ток (зелёная линия) имеют фазовый сдвиг φ=90∘{\displaystyle \varphi =90^{\circ }} (cos⁡φ=0{\displaystyle \cos \varphi =0}) — нагрузка полностью реактивная, нет активной составляющей. Мгновенная мощность (синяя линия) и активная мощность (голубая линия) рассчитаны с коэффициентом мощности, равным 0. Расположение синей линии (графика мгновенной мощности) на оси абсцисс показывает, что в течение первой четверти цикла вся подводимая мощность временно сохраняется в нагрузке, а во второй четверти цикла возвращается в сеть, и так далее, то есть никакой активной мощности не потребляется, полезной работы в нагрузке не совершается. 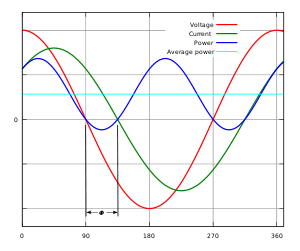Синусоидальное напряжение (красная линия) и ток (зелёная линия) имеют фазовый сдвиг φ=45∘{\displaystyle \varphi =45^{\circ }} (cos⁡φ=0,71{\displaystyle \cos \varphi =0{,}71}) — нагрузка имеет и активную, и реактивную составляющие. Мгновенная мощность (синяя линия) и активная мощность (голубая линия) рассчитаны из переменного напряжения и тока с коэффициентом мощности, равным 0,71. Расположение синей линии (графика мгновенной мощности) под осью абсцисс показывает, что некоторая часть подводимой мощности всё же возвращается в сеть в течение части цикла, отмеченного φ.

Коэффицие́нт мо́щности — безразмерная физическая величина, характеризующая потребителя переменного электрического тока с точки зрения наличия в нагрузке реактивной составляющей. Коэффициент мощности показывает, насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.

Численно коэффициент мощности равен косинусу этого фазового сдвига.

Можно показать, что если к источнику синусоидального тока (например, розетка ~230 В, 50 Гц) подключить нагрузку, в которой ток опережает или отстаёт по фазе на некоторый угол от напряжения, то на внутреннем активном сопротивлении источника выделяется повышенная мощность. На практике это означает, что при работе на нагрузку со сдвинутыми напряжением и током от электростанции требуется больше отвода тепла, чем при работе на активную нагрузку; избыток передаваемой энергии выделяется в виде тепла в проводах и может быть довольно значительным.

Коэффициент мощности равен отношению потребляемой электроприёмником активной мощности к полной мощности. Активная мощность расходуется на совершение работы. Полная мощность — геометрическая сумма активной и реактивной мощностей (в случае синусоидальных тока и напряжения). В общем случае полную мощность можно определить как произведение действующих (среднеквадратических) значений тока и напряжения в цепи. Полная мощность равна корню квадратному из суммы квадратов активной и реактивной мощностей. В качестве единицы измерения полной мощности принято использовать вольт-ампер (В∙А) вместо ватта (Вт).

Согласно неравенству Коши—Буняковского, активная мощность, равная среднему значению произведения тока и напряжения, всегда не превышает произведение соответствующих среднеквадратических значений. Поэтому коэффициент мощности принимает значения от нуля до единицы (то есть от 0 до 100 %).

Коэффициент мощности математически можно интерпретировать как косинус угла между векторами тока и напряжения. Поэтому в случае синусоидальных напряжения и тока величина коэффициента мощности совпадает с косинусом угла, на который отстают соответствующие фазы.

В электроэнергетике для коэффициента мощности приняты обозначения cos⁡φ{\displaystyle \operatorname {cos} \varphi } (где φ{\displaystyle \varphi } — сдвиг фаз между силой тока и напряжением) либо λ. Когда для обозначения коэффициента мощности используется λ{\displaystyle \lambda }, его величину обычно выражают в процентах.

При наличии реактивной составляющей в нагрузке кроме значения коэффициента мощности иногда также указывают характер нагрузки: активно-ёмкостный или активно-индуктивный. В этом случае коэффициент мощности соответственно называют опережающим или отстающим.

В случае синусоидального напряжения, но несинусоидального тока, если нагрузка не имеет реактивной составляющей, коэффициент мощности равен доле мощности первой гармоники тока в полной мощности, потребляемой нагрузкой.

Математические расчёты

Треугольник мощностей

Коэффициент мощности необходимо учитывать при проектировании электросетей. Низкий коэффициент мощности ведёт к увеличению доли потерь электроэнергии в электрической сети в общих потерях. Чтобы увеличить коэффициент мощности, используют компенсирующие устройства. Неверно рассчитанный коэффициент мощности может привести к избыточному потреблению электроэнергии и снижению КПД электрооборудования, питающегося от данной сети.

Для расчётов в случае гармонических переменных U{\displaystyle U} (напряжение) и I{\displaystyle I} (сила тока) используются следующие математические формулы:

1. cos⁡φ=PS{\displaystyle \cos \varphi ={\frac {P}{S}}}
2. P=U×I×cos⁡φ{\displaystyle P=U\times I\times \cos \varphi }
3. Q=U×I×sin⁡φ{\displaystyle Q=U\times I\times \sin \varphi }
4. S=U×I=P2+Q2{\displaystyle S=U\times I={\sqrt {P^{2}+Q^{2}}}}

Здесь P{\displaystyle P} — активная мощность, S{\displaystyle S} — полная мощность, Q{\displaystyle Q} — реактивная мощность.

Типовые оценки качества электропотребления

При одной и той же активной мощности нагрузки мощность, бесполезно рассеиваемая на проводах, обратно пропорциональна квадрату коэффициента мощности. Таким образом, чем меньше коэффициент мощности, тем ниже качество потребления электроэнергии. Для повышения качества электропотребления применяются различные способы коррекции коэффициента мощности, то есть его повышения до значения, близкого к единице.

Значение коэффициента мощности	Высокое	Хорошее	Удовлетворительное	Низкое	Неудовлетворительное
cos⁡φ{\displaystyle \operatorname {cos} \varphi }	0,95…1	0,8…0,95	0,65…0,8	0,5…0,65	0…0,5
λ{\displaystyle \lambda }	95…100 %	80…95 %	65…80 %	50…65 %	0…50 %

Например, большинство старых светильников с люминесцентными лампами для зажигания и поддержания горения используют электромагнитные балласты (ЭмПРА), характеризующиеся низким его потреблением, то есть неэффективным электропотреблением. В отличие от них современные светильники, и в том числе компактные люминесцентные («энергосберегающие») лампы имеют ЭПРА, и характеризуются коэффициентом мощности стремящемся к 1, то есть к идеальному значению.

Несинусоидальность

Несинусоидальность — вид нелинейных искажений напряжения в электрической сети, который связан с появлением в составе напряжения гармоник с частотами, многократно превышающими основную частоту сети. Высшие гармоники напряжения оказывают отрицательное влияние на работу системы электроснабжения, вызывая дополнительные активные потери в трансформаторах, электрических машинах и сетях; повышенную аварийность в кабельных сетях; уменьшение коэффициента мощности за счёт мощности искажения, вызванной протеканием токов высших гармоник; а также ограниченное применение батарей конденсаторов для компенсации реактивной мощности.

Источниками высших гармоник тока и напряжения являются электроприёмники с нелинейными нагрузками. Например, мощные выпрямители переменного тока, применяемые в металлургической промышленности и на железнодорожном транспорте, газоразрядные лампы и др.

Коррекция коэффициента мощности

Коррекция коэффициента мощности при помощи конденсаторов

К ухудшению коэффициента мощности (непропорциональному потребляемому току относительно напряжения) приводят реактивная и нелинейная нагрузки. Реактивные нагрузки корректируется внешними реактивностями, именно для них определена величина cos φ.

Коррекция коэффициента мощности ((англ. power factor correction) PFC) — процесс приведения потребления конечного устройства, обладающего низким коэффициентом мощности при питании от силовой сети переменного тока, к состоянию, при котором коэффициент мощности соответствует принятым стандартам.

Технически реализуется в виде той или иной дополнительной схемы на входе устройства.

Данная процедура, необходимая для равномерного использования мощности фазы и исключения перегрузки нейтрального провода трёхфазной сети, обязательна для импульсных источников питания мощностью в 100 и более ватт^{[источник не указан 2721 день]}. Компенсация обеспечивает отсутствие всплесков тока потребления на вершине синусоиды питающего напряжения и равномерную нагрузку на силовую линию.

Разновидности коррекции коэффициента мощности

• Коррекция реактивной составляющей полной мощности потребления устройства. Выполняется путём включения в цепь реактивного элемента, производящего обратное действие. Например, для компенсации действия электродвигателя переменного тока, обладающего высокой индуктивной реактивной составляющей полной мощности, параллельно цепи питания включается конденсатор.
• Коррекция нелинейности потребления тока в течение периода колебаний питающего напряжения. Если нагрузка потребляет ток непропорционально основной гармонике питающего напряжения, для повышения коэффициента мощности требуется схема пассивного (PPFC) или активного корректора коэффициента мощности (APFC). Простейшим пассивным корректором коэффициента мощности является дроссель с большой индуктивностью, включенный последовательно с питаемой нагрузкой. Дроссель выполняет сглаживание импульсного потребления нагрузки и выделение низшей, то есть основной, гармоники потребления тока, что и требуется.

Ссылки

Коэффициент мощности — это… Что такое Коэффициент мощности?

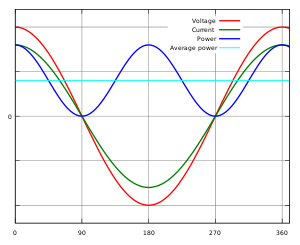Синусоидальное напряжение (красная линия) и ток (зелёная линия) синфазны — между ними нет фазового сдвига (, ) — нагрузка полностью активная, нет реактивной составляющей. Мгновенная мощность (синяя линия) и активная мощность (голубая линия) рассчитаны с коэффициентом мощности, равным 1. Как видно, синяя линия (график мгновенной мощности) находится полностью над осью абсцисс (в положительной полуплоскости), вся подводимая энергия преобразуется в работу: переходит в активную мощность, потребляемую нагрузкой. 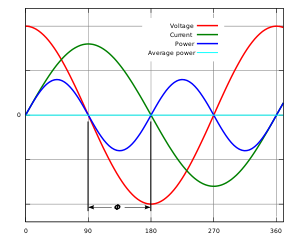Синусоидальное напряжение (красная линия) и ток (зелёная линия) имеют фазовый сдвиг () — нагрузка полностью реактивная, нет активной составляющей. Мгновенная мощность (синяя линия) и активная мощность (голубая линия) рассчитаны с коэффициентом мощности, равным 0. Расположение синей линии (графика мгновенной мощности) на оси абсцисс показывает, что в течение первой четверти цикла вся подводимая мощность временно сохраняется в нагрузке, а во второй четверти цикла возвращается в сеть, и так далее, то есть никакой активной мощности не потребляется, полезной работы в нагрузке не совершается. 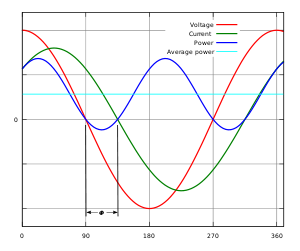Синусоидальное напряжение (красная линия) и ток (зелёная линия) имеют фазовый сдвиг () — нагрузка имеет и активную, и реактивную составляющие. Мгновенная мощность (синяя линия) и активная мощность (голубая линия) рассчитаны из переменного напряжения и тока с коэффициентом мощности, равным 0,71. Расположение синей линии (графика мгновенной мощности) под осью абсцисс показывает, что некоторая часть подводимой мощности всё же возвращается в сеть в течение части цикла, отмеченного φ.

Коэффицие́нт мо́щности — безразмерная физическая величина, характеризующая потребителя переменного электрического тока с точки зрения наличия в нагрузке реактивной составляющей. Коэффициент мощности показывает, насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.

Численно коэффициент мощности равен косинусу этого фазового сдвига.

Можно показать, что если источник синусоидального тока (например, розетка ~220 В, 50 Гц) нагрузить на нагрузку, в которой ток опережает или отстаёт по фазе на некоторый угол от напряжения, то на внутреннем активном сопротивлении источника выделяется повышенная мощность. На практике это означает, что при работе на нагрузку со сдвинутыми напряжением и током от электростанции требуется больше энергии; избыток передаваемой энергии выделяется в виде тепла в проводах и может быть довольно значительным.

Равен отношению потребляемой электроприёмником активной мощности к полной мощности. Активная мощность расходуется на совершение работы. Полная мощность — геометрическая сумма активной и реактивной мощностей (в случае синусоидальных тока и напряжения). В общем случае полную мощность можно определить как произведение действующих (среднеквадратических) значений тока и напряжения в цепи. Полная мощность равна корню квадратному из суммы квадратов активной и неактивной мощностей. В качестве единицы измерения полной мощности принято использовать вольт-ампер (В∙А) вместо ватта (Вт).

Согласно неравенству Коши—Буняковского, активная мощность, равная среднему значению произведения тока и напряжения, всегда не превышает произведение соответствующих среднеквадратических значений. Поэтому коэффициент мощности принимает значения от нуля до единицы (то есть от 0 до 100 %).

Коэффициент мощности математически можно интерпретировать как косинус угла между векторами тока и напряжения. Поэтому в случае синусоидальных напряжения и тока величина коэффициента мощности совпадает с косинусом угла, на который отстают соответствующие фазы.

В электроэнергетике для коэффициента мощности приняты обозначения cos φ (где φ — сдвиг фаз между силой тока и напряжением) либо λ. Когда для обозначения коэффициента мощности используется λ, его величину обычно выражают в процентах.

При наличии реактивной составляющей в нагрузке кроме значения коэффициента мощности иногда также указывают характер нагрузки: активно-ёмкостный или активно-индуктивный. В этом случае коэффициент мощности соответственно называют опережающим или отстающим.

В случае синусоидального напряжения, если нагрузка не имеет реактивной составляющей, коэффициент мощности равен доле мощности первой гармоники тока в полной мощности, потребляемой нагрузкой, и равен коэффициенту искажений тока.

Математические расчёты

Треугольник мощностей

Коэффициент мощности необходимо учитывать при проектировании электросетей. Низкий коэффициент мощности ведёт к увеличению доли потерь электроэнергии в электрической сети в общих потерях. Чтобы увеличить коэффициент мощности, используют компенсирующие устройства. Неверно рассчитанный коэффициент мощности может привести к избыточному потреблению электроэнергии и снижению КПД электрооборудования, питающегося от данной сети.

Для расчётов в случае гармонических переменных U (напряжение) и I (сила тока) используются следующие математические формулы:

Здесь  — активная мощность,  — полная мощность,  — реактивная мощность.

Типовые оценки качества электропотребления

Коэффициент мощности позволяет судить о нелинейных искажениях, вносимых нагрузкой в электросеть. Чем он меньше, тем больше вносится нелинейных искажений. Кроме того, при одной и той же активной мощности нагрузки мощность, бесполезно рассеиваемая на проводах, обратно пропорциональна квадрату коэффициента мощности. Таким образом, чем меньше коэффициент мощности, тем ниже качество потребления электроэнергии. Для повышения качества электропотребления применяются различные способы коррекции коэффициента мощности, то есть его повышения до значения, близкого к единице.

Значение коэффициента мощности	Высокое	Хорошее	Удовлетворительное	Низкое	Неудовлетворительное
cos φ	0,95…1	0,8…0,95	0,65…0,8	0,5…0,65	0…0,5
λ	95…100 %	80…95 %	65…80 %	50…65 %	0…50 %

Например, большинство компактных люминесцентных («энергосберегающих») ламп, имеющих ЭПРА, характеризуются высоким его значением.

Нелинейные искажения тока

Потребители электроэнергии с нелинейной вольт­амперной характеристикой (с коэффициентом мощности, меньшим единицы) создают ток, который меняется непропорционально мгновенному напряжению в сети (как правило, форма тока при этом отличается от синусоидальной). Соответственно искажается форма напряжения на данном участке электросети, что приводит к ухудшению качества электроэнергии. В зависимости от характера нагрузки можно выделить следующие основные виды нелинейных искажений тока: это фазовый сдвиг, вызванный реактивной составляющей в нагрузке, и несинусоидальность формы тока. Несинусоидальные искажения, в частности, имеют место, когда нагрузка несимметрична в разных полуволнах сетевого напряжения.

Несинусоидальность

Несинусоидальность — вид нелинейных искажений напряжения в электрической сети, который связан с появлением в составе напряжения гармоник с частотами, многократно превышающими основную частоту сети. Высшие гармоники напряжения оказывают отрицательное влияние на работу системы электроснабжения, вызывая дополнительные активные потери в трансформаторах, электрических машинах и сетях; повышенную аварийность в кабельных сетях; уменьшение коэффициента мощности за счёт мощности искажения, вызванной протеканием токов высших гармоник; а также ограниченное применение батарей конденсаторов для компенсации реактивной мощности.

Источниками высших гармоник тока и напряжения являются электроприёмники с нелинейными нагрузками. Например, мощные выпрямители переменного тока, применяемые в металлургической промышленности и на железнодорожном транспорте, газоразрядные лампы и др.

Ссылки

Коэффициент использования установленной мощности — Википедия

Материал из Википедии — свободной энциклопедии

Средний КИУМ АЭС в мире, данные EIA.

Коэффицие́нт испо́льзования устано́вленной мо́щности (КИУМ^[1]) — важнейшая характеристика эффективности работы предприятий электроэнергетики. Она равна отношению среднеарифметической мощности к установленной мощности электроустановки за определённый интервал времени^[2]. В ядерной энергетике дают немного другое определение: КИУМ равен отношению фактической энерговыработки реакторной установки за определённый период эксплуатации к теоретической энерговыработке при работе без остановок на номинальной мощности^[3]. Нетрудно заметить, что значение КИУМа при обоих способах подсчёта будет одинаковым, однако последнее определение, во-первых соответствует международному понятию КИУМа (за исключением словосочетания реакторная установка, которое в общем-то можно заменить на электроустановка, определение при этом останется правильным и будет полностью соответствовать международному значению), а во-вторых предполагает более простой подсчёт его значения.

Важность КИУМа заключается в том, что этот параметр характеризует эффективность электростанции в целом, включая не только её технологическое совершенство, но и квалифицированность персонала, организацию работы как руководством самой станции, так и организацию всей отрасли на государственном уровне, а также учитывает многие другие факторы.

В большинстве стран ведётся упорная борьба за высокий КИУМ электростанций, что особенно важно в свете последних мировых тенденций по увеличению энергоэффективности и энергосбережения. Особую роль эта характеристика играет в ядерной энергетике, что связано с некоторыми специфическими особенностями обеспечения высокого КИУМа в этой сфере. По этой причине в СМИ наиболее распространено упоминание этого параметра при освещении показателей работы АЭС.

Предположим, что абстрактная электростанция с электрической мощностью 1000 МВт выработала за 30-дневный месяц 648 000 МВт-часов. В случае, если станция проработала бы этот месяц с полной установленной мощностью, она бы выработала за этот период времени: 1000 МВт × 30 дней × 24 часа = 720 000 МВт-часов. Делим величину выработанной электроэнергии на значение потенциальной выработки с полной загрузкой установленной мощности за этот период и получаем 0,9. Следовательно, КИУМ в этом случае составит 90 %.

Следует отметить, что КИУМ строго зависит от периода времени, за который он подсчитывается, поэтому сообщение о значении КИУМа в какую-то определённую дату не имеет смысла, этот параметр рассчитывается обычно за долгий период, чаще всего за год.

Несмотря на кажущуюся простоту достижения высокого значения КИУМа (достаточно работать на полную мощность и без простоев), этот параметр зависит от множества непростых и сложнопрогнозируемых технических и административных факторов.

Как правило, диспетчерские центры региональных электросетей размещают на электростанциях заявки на ту или иную мощность выработки на каждый час или даже меньшие периоды времени, основываясь на прогнозе потребления. При заметном отклонении фактической выработки и фактического потребления в электросети наблюдается снижение или, что ещё хуже, повышение напряжения и частоты переменного тока, снижение КПД и ресурса энергосистемы в целом. Поэтому за неточное выполнение диспетчерских заявок в любую сторону электростанции штрафуются. Обычно в течение суток потребляемая мощность изменяется в 3-5 раз, с утренним и вечерним пиками, дневным полупиком и ночным спадом, поэтому высокий КИУМ всей энергосистемы невозможен в принципе. По технической способности динамически изменять мощность различным видам электростанций присваивается различная манёвренность. Наименее манёвренными считаются АЭС, из-за потенциальной опасности аварий при смене физических режимов работы реактора, а также теплоэлектростанции на твёрдом топливе, из-за невозможности быстро потушить или разжечь уголь. Тепловые электростанции на жидком топливе и газе более манёвренны, однако КПД их турбин значительно падает при неполной нагрузке. Проще всего маневрировать выработкой ГЭС и ГАЭС, но, за исключением отдельных регионов вроде Сибири, общая выработка гидростанций в энергобалансе не позволяет обойтись только ими.

Для большинства станций возобновляемой энергетики (гидро-, ветро- и солнечной) дополнительным ограничением КИУМ становится неравномерность наличия энергоисточника — необходимых объемов воды, ветра, солнечного освещения.

По данным US Energy Information Administration (EIA), на 2009 год средние КИУМ по США составляли:^[4]

• Атомная энергетика: 90,3 %
• Уголь: 63.8 %
• Тепловые электростанции на природном газе: 42,5 %
• Гидроэлектростанции: 39,8 %
• Другие возобновляемые источники: 33,9 %
• Тепловые электростанции на нефти: 7,8 %

Среди них:

В других странах

• Тепловые солнечные станции с хранением и сжиганием природного газа (в Испании): 63 %^[11]
• Гидроэнергетика, среднее по миру: 44 %,^[12]
• Атомная энергетика: 70 % (среднее за 1971—2009 в США).^[13]
• Атомная энергетика: 88,7 % (среднее за 2006—2012 в США).^[14]