Репетитор-онлайн — подготовка к ЦТ
Пример 15. При замыкании на сопротивление 5,0 Ом батарея элементов дает ток силой 2,0 А. Ток короткого замыкания батареи равен 12 А. Рассчитать наибольшую полезную мощность батареи.
Решение. Проанализируем условие задачи.
1. При подключении батареи к сопротивлению R 1 = 5,0 Ом в цепи течет ток силой I 1 = 2,0 А, как показано на рис. а, определяемый законом Ома для полной цепи:
I1=ℰR1+r,
где ℰ — ЭДС источника тока; r — внутреннее сопротивление источника тока.
2. При замыкании батареи накоротко в цепи течет ток короткого замыкания, как показано на рис. б. Сила тока короткого замыкания определяется формулой
i=ℰr,
где i — сила тока короткого замыкания, i = 12 А.
3. При подключении батареи к сопротивлению R 2 = r в цепи течет ток силой I 2, как показано на рис. в, определяемый законом Ома для полной цепи:
I2=ℰR2+r=ℰ2r;
в этом случае в цепи выделяется максимальная полезная мощность:
Pполезнmax=I22R2=I22r.
Таким образом, для расчета максимальной полезной мощности необходимо определить внутреннее сопротивление источника тока r и силу тока I 2.
Для того чтобы найти силу тока I 2, запишем систему уравнений:
i=ℰr,I2=ℰ2r}
и выполним деление уравнений:
iI2=2.
Отсюда следует:
I2=i2=122=6,0 А.
Для того чтобы найти внутреннее сопротивление источника r, запишем систему уравнений:
I1=ℰR1+r,i=ℰr}
и выполним деление уравнений:
I1i=rR1+r.
Отсюда следует:
r=I1R1i−I1=2,0⋅5,012−2,0=1,0 Ом.
Рассчитаем максимальную полезную мощность:
Pполезнmax=I22r=6,02⋅1,0=36 Вт.
Таким образом, максимальная полезная мощность батареи составляет 36 Вт.
Определение эдс и мощности источника тока
Цель работы: определить ЭДС источника постоянного тока методом компенсации, полезную мощность и КПД в зависимости от сопротивления нагрузки.
Оборудование: исследуемый источник тока, источник стабилизированного напряжения, магазин сопротивления, миллиамперметр, гальванометр.
Теоретическое введение
Источники тока – это устройства, в которых происходит преобразование различных видов энергии (механической, химической, тепловой) в электрическую энергию. В источниках тока происходит разделение электрических зарядов разного знака. Поэтому если источник замкнуть на нагрузку, например на проводник, то по проводнику потечет электрический ток, вызванный движением зарядов под действием электростатического поля. За направление тока принято направление движения положительных зарядов. То есть ток потечет от положительного полюса источника через проводник к отрицательному. Но через источник заряды движутся против сил электростатического поля. Это может происходить только под действием сил не электростатической природы, так называемых сторонних сил. Например, магнитной силы Лоренца в генераторах электростанций, сил диффузии в химических источниках тока.
Характеристикой источника тока является электродвижущая сила – ЭДС. Она равна отношению работы сторонних сил к величине перенесенного заряда:
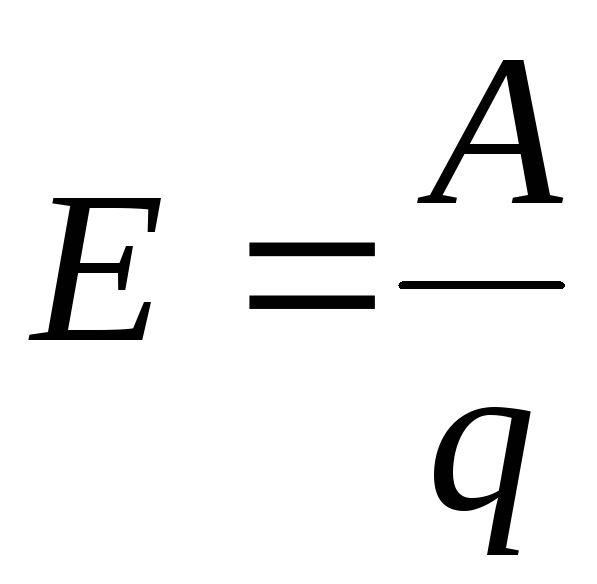 .
(1)
.
(1)
Рассмотрим
электрическую цепь из источника тока
с внутренним сопротивлением r,
замкнутого на нагрузку сопротивлением R.
По закону сохранения энергии работа
сторонних сил 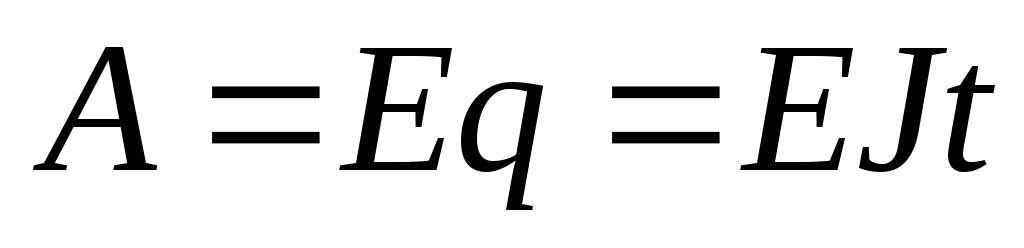
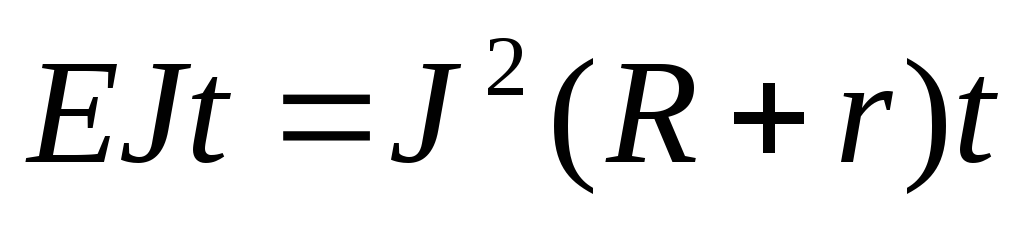 . После
сокращения на Jt получим, что сила тока в цепи равна
отношению ЭДС к полному сопротивлению
электрической цепи:
. После
сокращения на Jt получим, что сила тока в цепи равна
отношению ЭДС к полному сопротивлению
электрической цепи:  .
(2)
.
(2)
Это закон Ома для полной цепи. При отсутствии тока через источник падение напряжения на внутреннем сопротивлении отсутствует и ЭДС равна напряжению между полюсами источника. Единицей измерения ЭДС, как и напряжения, является вольт (В).
ЭДС
можно измерить различными методами.
Если, в простейшем случае, вольтметр c
сопротивлением R подсоединить
к полюсам источника с внутренним
сопротивлением r,
то, по закону Ома, показания вольтметра
будут  .
Это меньше, чем ЭДС, на величину падения
напряжения на внутреннем сопротивлении.
.
Это меньше, чем ЭДС, на величину падения
напряжения на внутреннем сопротивлении.
В компенсационном методе измерения ЭДС
ток через источник не течет (рис. 1). Если
с помощью регулятора блока питания БП
подобрать напряжения на магазине
сопротивлений
компенсационном методе измерения ЭДС
ток через источник не течет (рис. 1). Если
с помощью регулятора блока питания БП
подобрать напряжения на магазине
сопротивлений
Е = J R. (3)
Полезная мощность источника тока при неподвижных проводниках – это тепловая мощность, выделяемая на нагрузке. По закону Джоуля – Ленца Р = J 2R. Подставив силу тока, согласно закону Ома (2), получим формулу зависимости полезной мощности от сопротивления нагрузки:
Работа, энергия, теплота тока. Полезная, полная мощность. Закон Джоуля-Ленца
Мы уже выяснили, что источником движения электронов в проводнике служит электрическое поле, которое совершает работу по переносу заряда:
(1)Проходя через проводник, ток оказывает тепловое воздействие на сам проводник. Данное тепловое воздействие можно описать энергетически:
(2)Формула (2) описывает все энергетические характеристики, связанные с током, для упрощения, мы будем называть данный параметр через
.Используя определения силы тока:
, можем получить: (3)- где
- — время течения тока.
Соотношение (3) называется законом Джоуля-Ленца.
Учитывая закон Ома для участка цепи (
), можно получить следующий ряд уравнений: (4)- где
- — полное сопротивление цепи.
Использование каждого из этих уравнений диктуется условиями задачи.
Мы уже ввели понятие механической мощности
. Тогда соотношения (4) можно адаптировать под мощность: (5)Соотношение (5) определяет полную мощность, потребляемую участком цепи.
Для полной цепи постоянного тока, мощность источника тока/напряжения (т.е. мощность, выдаваемую самим источником), то необходимо использовать закон Ома для полной цепи:
, тогда: (6)- где
- — ЭДС источника,
- — внутреннее сопротивление источника.
Соотношение (6) определяет полную мощность, генерируемую источником тока/напряжения.
Тогда для полной цепи можем определить, так называемую, полезную мощность, т.е. мощность, расходуемую, непосредственно, на потребителя. Пусть в цепи потребляется напряжение
, тогда: (7)Исходя из закона Ома для участка цепи:
(8)Зная связь между ЭДС и напряжением:
Можем получить:
(9)Выражение (7) и (9) — полезная мощность, выдаваемая источником.
Вывод: любая энергетическая характеристика, связанная с током, может быть найдена, исходя из закона Джоуля-Ленца и его форм (4). По поводу мощности дела сложнее: по задаче нужно определить мощность чего нужно определить. Для этого выясняем, с какой цепью работаем:
- для участка цепи: формулы (5)
- для полной цепи:
- в случае вопроса о мощности источника, то формулы (6)
- в случае вопроса о полезной мощности, то формулы (7) и (9)
Поделиться ссылкой:
Понравилось это:
Нравится Загрузка…
1.2. Зависимость полезной мощности источника электрического тока от силы тока и внешнего сопротивления
Рассмотрим электрическую цепь, состоящую из источника постоянного тока и внешнего сопротивления R (рис. 1). При протекании тока через такую цепь источником ЭДС выполняется работа и в цепи выделяется мощность.
П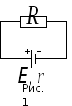 олезной
мощностью называют
мощность, которая выделяется на внешнем
сопротивлении. Из закона Джоуля-Ленца
(10*) полезная
мощность равняется
олезной
мощностью называют
мощность, которая выделяется на внешнем
сопротивлении. Из закона Джоуля-Ленца
(10*) полезная
мощность равняется 
 .
Тогда полезная мощность будет
.
Тогда полезная мощность будет
| (1) |
где  – падение напряжения на внешнем
сопротивлении. При протекании тока по
цепи также выделяется „бесполезная”
мощность – разогревается источник ЭДС.
По закону Джоуля-Ленца эта мощность
равняется
– падение напряжения на внешнем
сопротивлении. При протекании тока по
цепи также выделяется „бесполезная”
мощность – разогревается источник ЭДС.
По закону Джоуля-Ленца эта мощность
равняется
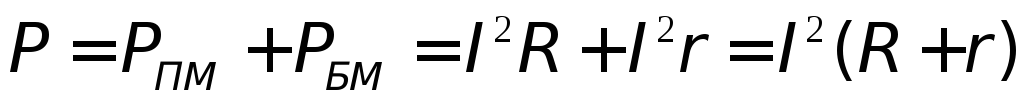 .
Используя закон Ома для полной цепи
.
Используя закон Ома для полной цепи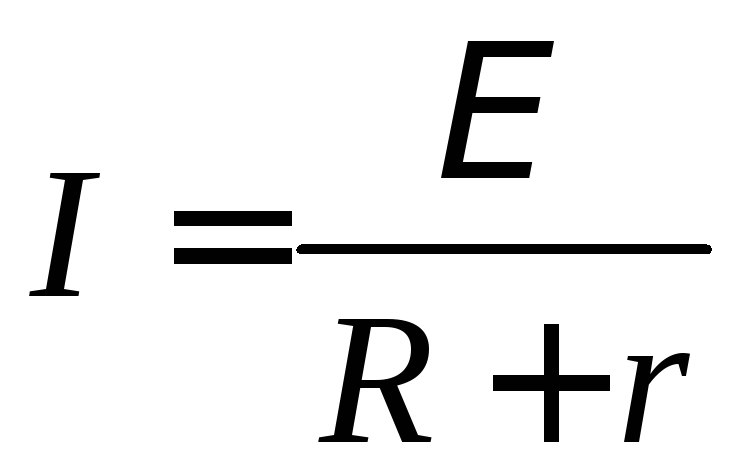 ,
можно найти полную мощность
,
можно найти полную мощность
| (2) |
И
Пусть
в цепи можно менять внешнее сопротивление  .
Проанализируем, как полезная и полная
мощности зависят от силы тока и внешнего
сопротивления.
.
Проанализируем, как полезная и полная
мощности зависят от силы тока и внешнего
сопротивления.
Полезная мощность равняется разности между полной мощностью и „бесполезной”:
| (3) |
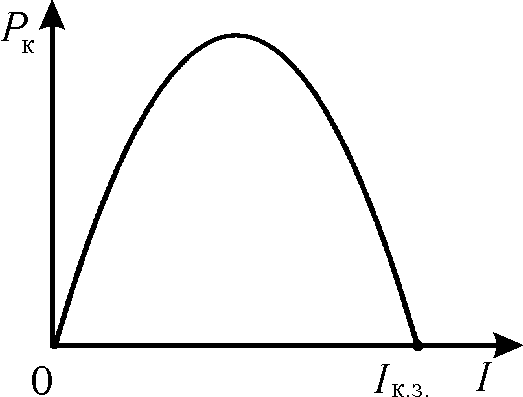


Рис. 2
Из этого выражения видно, что полезная мощность является квадратичной функцией силы тока I. График этой функции будет представлять собой параболу (рис. 2). Из рис. 2
вытекает, что 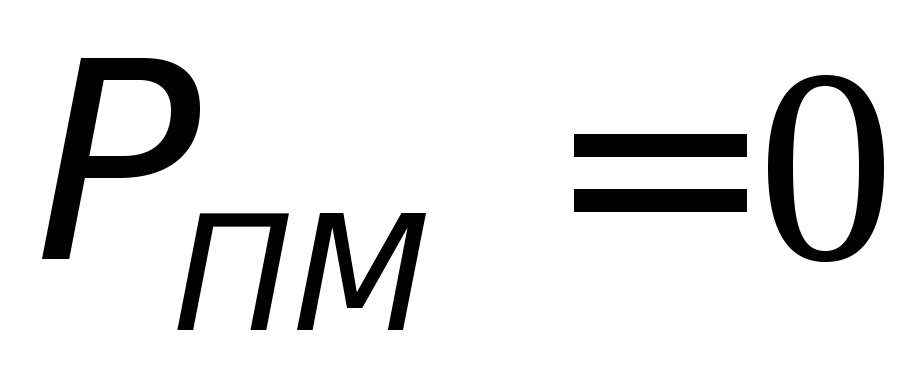 в двух случаях:
в двух случаях:
когда цепь разомкнута (R = ∞), то сила тока в цепи I = 0;
 .
.
Меняя
величину внешнего сопротивления, можно
достичь некоторого значения силы тока
в цепи, при котором полезная мощность
будет максимальной. Найдем этот ток.
Для этого найдем первую производную  и приравняем ее нулю. Из выражения (3)
имеем:
и приравняем ее нулю. Из выражения (3)
имеем:
| (4) |
Отсюда вытекает
| (5) |
а ток  ,
при котором выделяется максимальная
полезная мощность, равняется
,
при котором выделяется максимальная
полезная мощность, равняется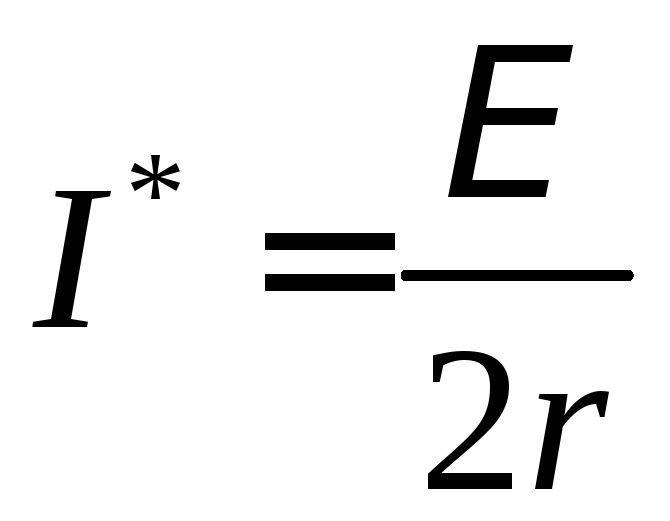 .
С другой стороны, на основании закона
Ома для полной цепи
.
С другой стороны, на основании закона
Ома для полной цепи ,
где
,
где – сопротивление, при котором выделяется
максимальная полезная мощность.
Приравнивая два последних выражения
– сопротивление, при котором выделяется
максимальная полезная мощность.
Приравнивая два последних выражения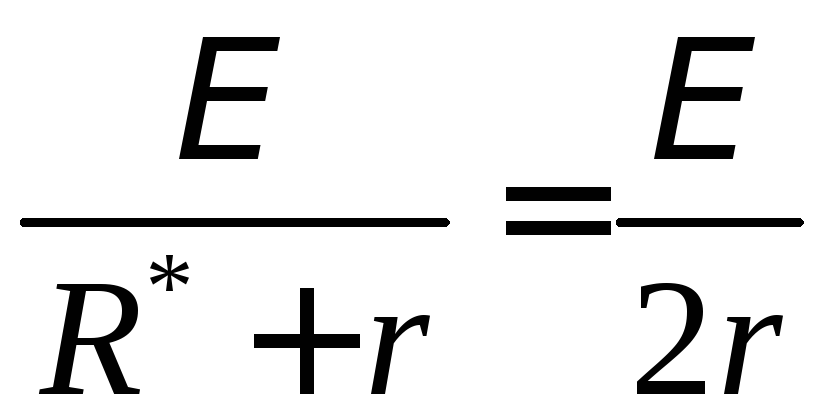 ,
находим, что
,
находим, что
| (6) |
Таким образом, полезная мощность будет максимальной при условии равенства внешнего и внутреннего сопротивлений.
Зависимость
полезной мощности от внешнего сопротивления
можно найти из закона
Джоуля-Ленца 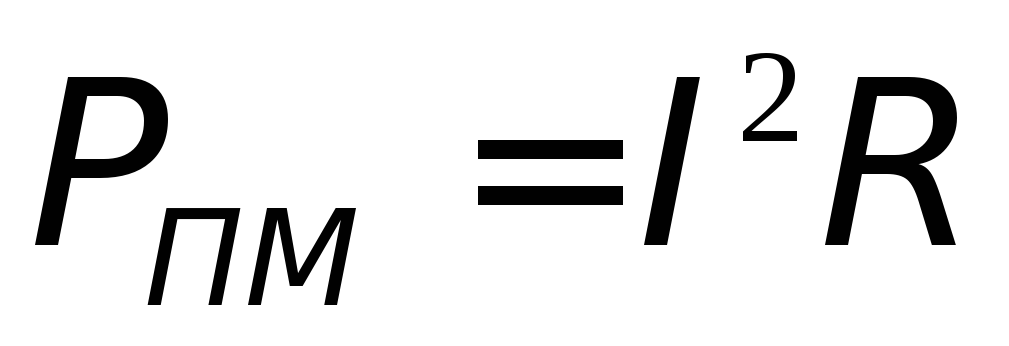 и закона Ома для полной цепи
и закона Ома для полной цепи
| (7) |
График
зависимости 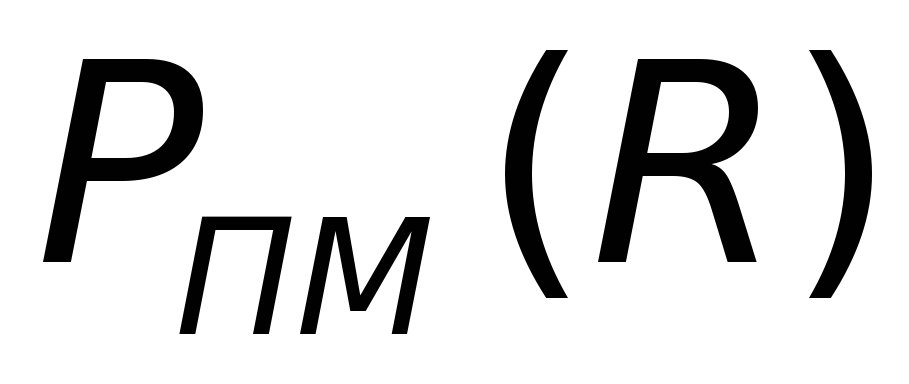 показан на рис. 3 (криваяб).
Максимум функции
показан на рис. 3 (криваяб).
Максимум функции  можно найти, приравнивая
можно найти, приравнивая нулю
нулю
| (8) |
Из
(8) также вытекает ожидаемое равенство 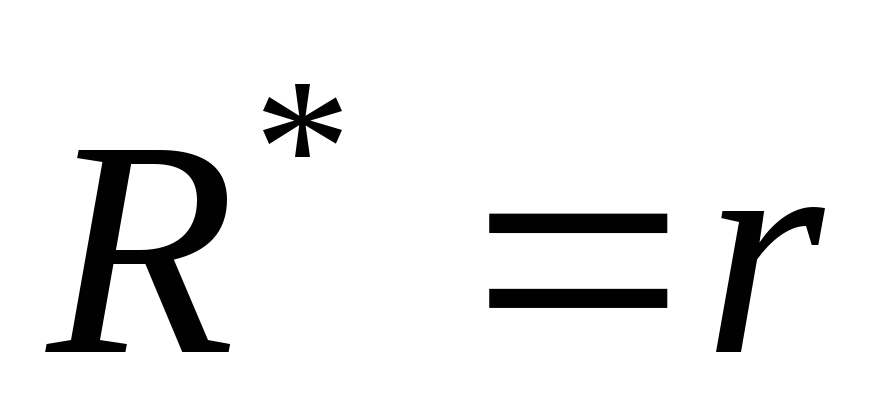 .
.


а – полная мощность
б – корисна потужність
Рис. 3
Рассмотрим теперь, как полная мощность зависит от внешнего сопротивления. Используя выражение (2) и закон Ома для полной цепи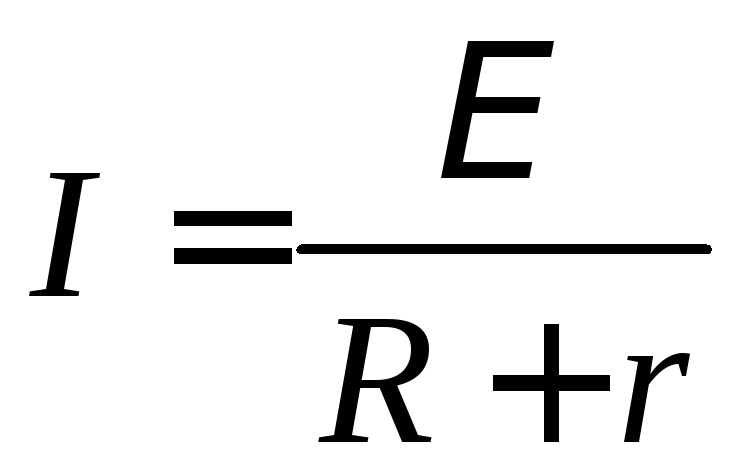 находим зависимость полной мощности
от внешнего сопротивления:
находим зависимость полной мощности
от внешнего сопротивления: 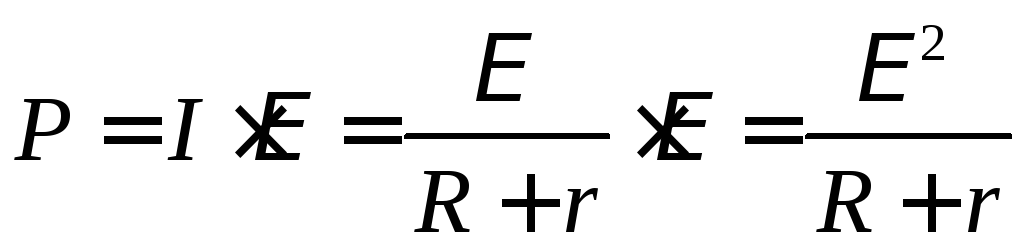 .
(9)
.
(9)
График этой
зависимости показана на рис. 3 (кривая а). При
изменении внешнего сопротивления от
нуля (короткое заключение) до бесконечности
(цепь разомкнута) полная мощность будет
убывать от максимального значения  до нуля.
до нуля.
Зависимость коэффициента полезного действия источника электрического тока от силы тока и внешнего сопротивления цепи
К оэффициент полезного действия (КПД) равняется отношению полезной
мощности (1) к полной мощности (2), которая
выделяется во всей цепи
оэффициент полезного действия (КПД) равняется отношению полезной
мощности (1) к полной мощности (2), которая
выделяется во всей цепи
| (10) |
С начала
найдем зависимость КПД
от силы тока. Если
разделить выражение (3) для полезной
мощности на выражение (1) для полной
мощности, получим
начала
найдем зависимость КПД
от силы тока. Если
разделить выражение (3) для полезной
мощности на выражение (1) для полной
мощности, получим
 (11)
(11)
И так,
КПД представляет собой линейную функцию
от силы тока (рис. 4). Когда I → 0
(цепь разомкнут), то
так,
КПД представляет собой линейную функцию
от силы тока (рис. 4). Когда I → 0
(цепь разомкнут), то  .
При коротком заключении
.
При коротком заключении ,
ток короткого заключения
,
ток короткого заключения
| (12) |
и
КПД будет 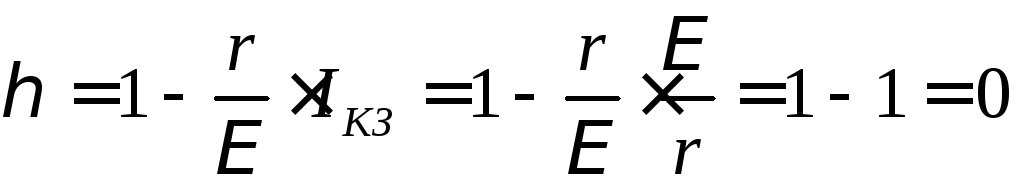 .
.
Чтобы найти зависимость КПД от
внешнего сопротивления,
подставим в (9) выражение для  из закона Ома для участки цепи
из закона Ома для участки цепи ,
а выражение для
,
а выражение для – из закона Ома для полной цепи
– из закона Ома для полной цепи .
Тогда
.
Тогда
| (13) |
Из соотношения (13) вытекает:
Приведенный анализ показывает, что при увеличении внешнего сопротивления КПД асимптотично приближается к единице (рис. 5).
Кпд источника тока.
Перемещая электрические заряды по замкнутой цепи, источник тока совершает работу. Различают полезную и полную работу источника тока. Полезная работа – это та, которую совершает источник по перемещению зарядов во внешней цепи; полная работа – это работа источника по перемещению зарядов во всей цепи:
 —
полезная работа;
—
полезная работа;
 —
полная работа.
—
полная работа.
Соответственно этому, различают полезную и полную мощность источника тока:
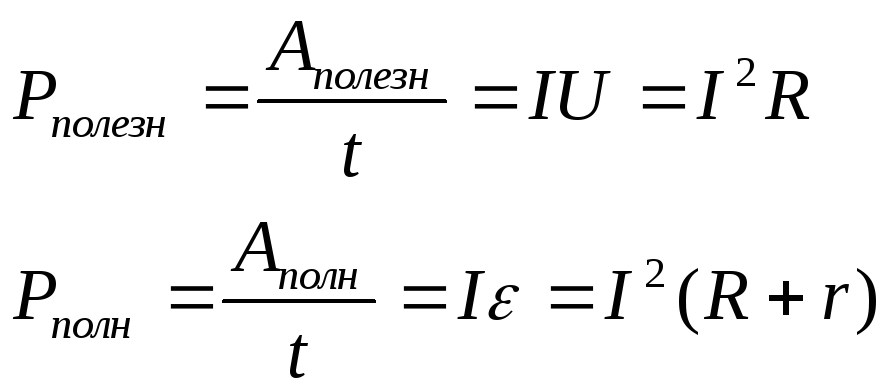
Коэффициентом полезного действия (КПД) источника тока называют отношение:
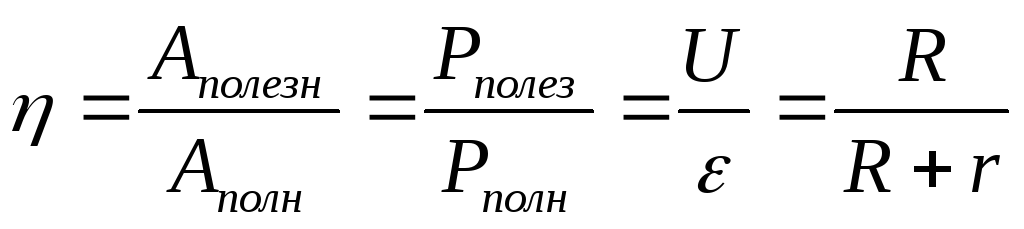
Выясним,
при каком сопротивлении внешней цепи 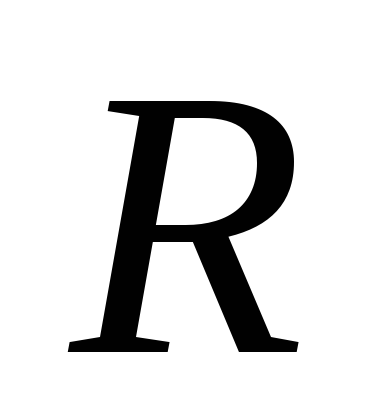 полезная мощностьмаксимальна.
полезная мощностьмаксимальна.
Имеем:  ,
где
,
где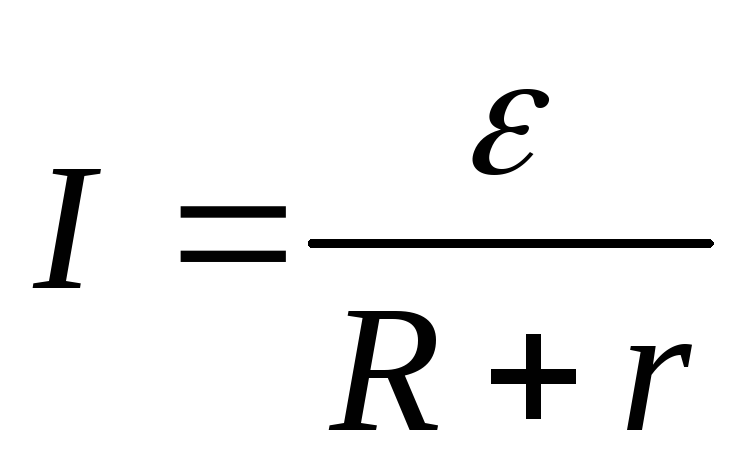 ;
;
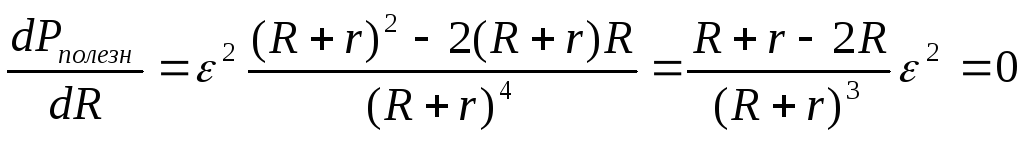
 откуда
откуда  .
.
Условие 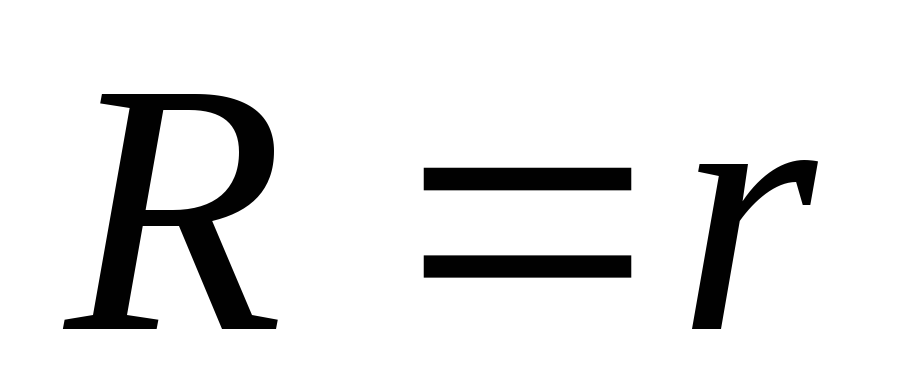 называетсяусловием
согласования источника и нагрузки. В этом случае
мощность, выделяемая источником во
внешней цепи, максимальна.
Отметим, что при выполнении условия
согласования КПД источника тока
называетсяусловием
согласования источника и нагрузки. В этом случае
мощность, выделяемая источником во
внешней цепи, максимальна.
Отметим, что при выполнении условия
согласования КПД источника тока  ,
то есть максимальная полезная мощность и максимальный КПД несовместимы.
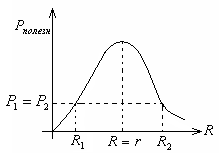
Из приведенного графика видно также,
что одну и ту же полезную мощность можно
получить при двух различных сопротивлениях внешней нагрузки
,
то есть максимальная полезная мощность и максимальный КПД несовместимы.
Из приведенного графика видно также,
что одну и ту же полезную мощность можно
получить при двух различных сопротивлениях внешней нагрузки  .
.
3.2. Сторонние силы. Эдс источника тока. Закон Ома для неоднородного участка цепи и для замкнутой цепи.
Для протекания электрического тока в проводнике необходимо, чтобы на его концах поддерживалась разность потенциалов. Очевидно, для этой цели не может быть использован заряженный конденсатор. Действительно, если включить в цепь проводника заряженный конденсатор и замкнуть цепь, то под действием сил электростатического поля заряды придут в движение, возникнет кратковременный ток, после чего установится равновесное распределение зарядов, при котором потенциалы концов проводника выравниваются и ток прекращается. Другими словами, электростатическое поле конденсатора не может осуществить постоянную циркуляцию зарядов в цепи (то есть электрический ток), что является следствием потенциальности электростатического поля – равенства нулю работы сил электростатического поля по замкнутому контуру. Таким образом, для поддержания постоянного тока в замкнутой цепи необходимо действие сторонних сил неэлектростатического происхождения и не являющихся потенциальными силами.
Э ти
силы могут быть обусловленыхимическими процессами, диффузией носителей заряда через границу двух
разнородных проводников, магнитными полями, другими причинами.
ти
силы могут быть обусловленыхимическими процессами, диффузией носителей заряда через границу двух
разнородных проводников, магнитными полями, другими причинами.
Сторонние силы можно охарактеризовать работой, которую они совершают по перемещению зарядов в замкнутой цепи. Величина, равная работе сторонних сил Аст, отнесенная к единице положительного заряда, называется электродвижущей силой (ЭДС). Единицей измерения ЭДС в СИ (как и напряжения) является В (Вольт).
Работа сторонних сил по замкнутому контуру не равна нулю:

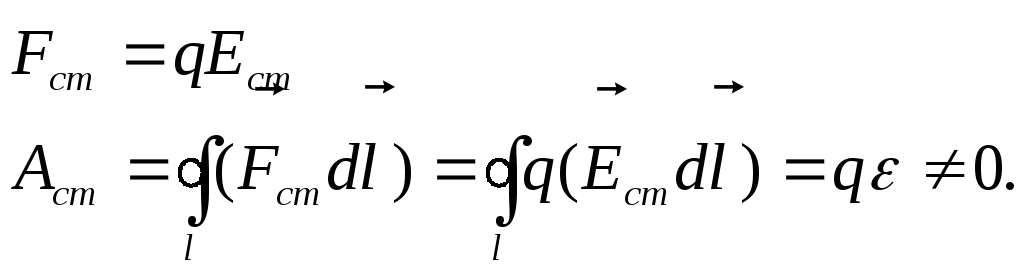
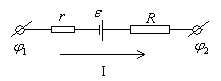
Участок цепи, содержащий источник ЭДС, называется неоднородным. Всякий источник ЭДС характеризуется величиной ЭДС ε и внутренним сопротивлением r.

 —
напряжение на концах участка цепи.
—
напряжение на концах участка цепи.
Закон
Ома для неоднородного
участка цепи имеет вид: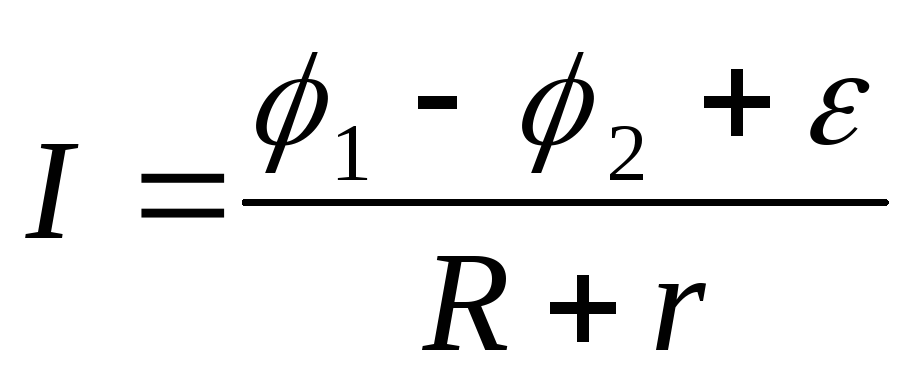
При
соединении концов неоднородного участка
цепи идеальным проводником образуется замкнутая цепь,
в которой потенциалыφ1 и φ2 выравниваются и мы приходим к закону
Ома для замкнутой (или полной) цепи:
потенциалыφ1 и φ2 выравниваются и мы приходим к закону
Ома для замкнутой (или полной) цепи:
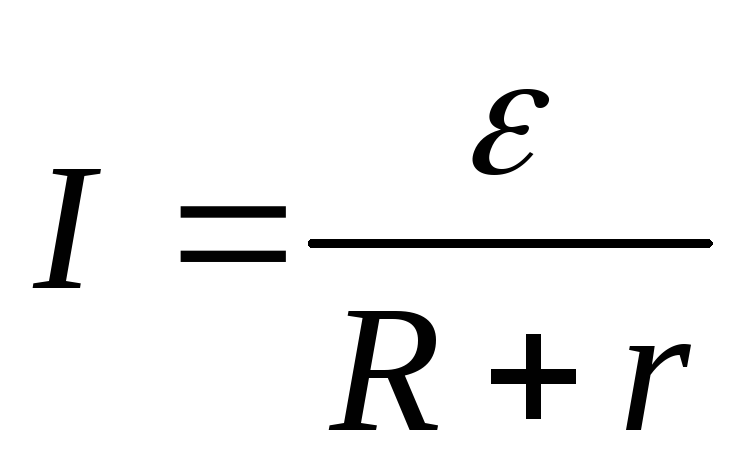
Если
сопротивление внешней цепи  ,
то имеем случайкороткого
замыкания.
В этом случае в цепи течет максимальный ток:
,
то имеем случайкороткого
замыкания.
В этом случае в цепи течет максимальный ток:
При 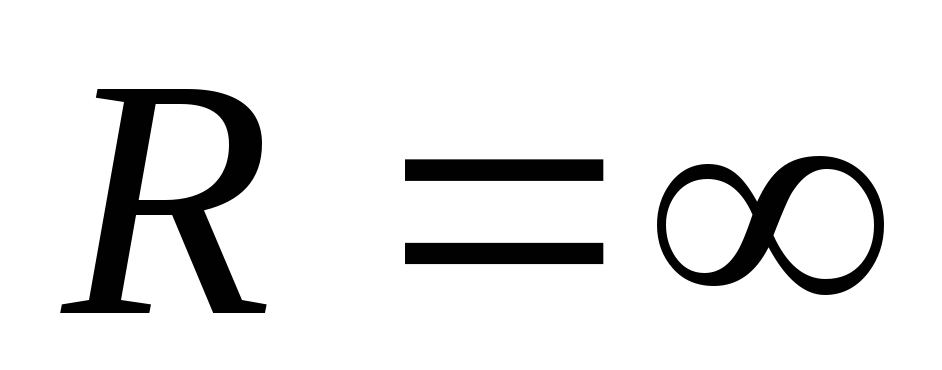 имеем разомкнутую цепь.
В этом случае ток в цепи равен
нулю:
имеем разомкнутую цепь.
В этом случае ток в цепи равен
нулю:
5. Дайте понятие эдс, мощность источника и приёмника электрической энергии. Сформулируйте баланс мощностей. Приведите пример в общем виде.
Источник электрической энергии осуществляет направленное перемещение электрических зарядов по всей замкнутой цепи (рис. 2.3).
Энергия W, которую затрачивает или может затратить источник на перемещение единицы положительного заряда по всей замкнутой цепи, характеризует электродвижущую силу источника Е (ЭДС):
 (1)
(1)

Исходя из формулы (1) следует, что энергия, затраченная источником, равна
Wист= Eq = EIt, (2)
так как q = It, что вытекает
из определения величины тока 
Во всех элементах электрической цепи происходит преобразование энергии
Скорость такого преобразования энергии определяет электрическую мощность элементов электрической цепи
Р= (3)
(3)
Таким образом, мощность источника электрической энергии определяется выражением
 (4)
(4)
Энергия, затраченная на перемещение единицы положительного заряда на каком-либо участке замкнутой цепи, характеризует напряжение или падение напряжения на этом участке (внутреннем или внешнем):
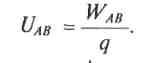
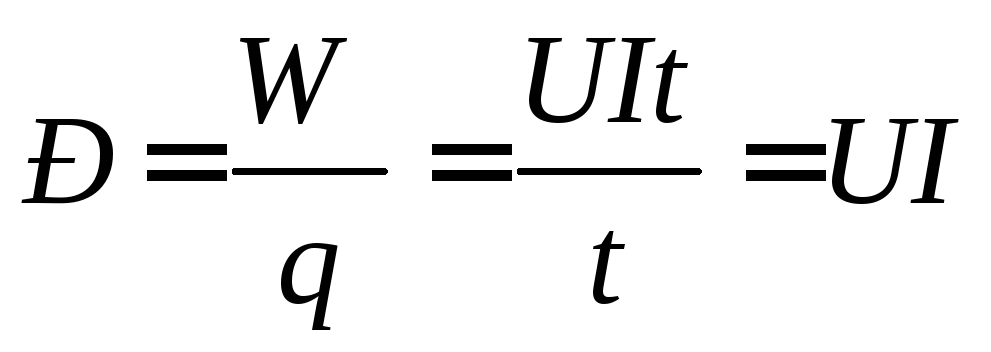 (5)
(5)
Если воспользоваться законом Ома для участка электрической цепи, то полезную мощность можно определить следующим выражением:
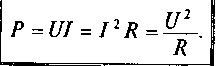 (6)
(6)
Уравнение баланса мощностей:
Сумма мощностей источников электрической энергии равна сумме мощностей приёмников
∑ Е ∙I = ∑ I2∙ R , (7)
где
I – ток в ветви,А;
Е-ЭДС,В;
R-сопротивление, Ом.
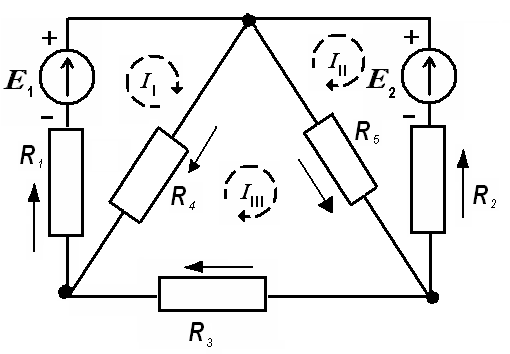
E1I1+E2I2=I12R1+I22R2+I32R3+I42R4+I52R5
6.Объясните принцип построения потенциальной диаграммы электрической цепи. Приведите пример в общем виде.
Потенциал точки – это напряжение между этой точкой и землёй, при этом надо помнить, что потенциал точки из которой ток вытекает больше, чем потенциал точки, в которую он втекает.
Положительный полюс источника имеет потенциал больший, чем отрицательный на величину ЭДС.
Потенциальная диаграмма представляет собой график изменения потенциалов точек цепи от величины сопротивлений участков между этими точками.
Для построения диаграммы необходимо:
Определить все токи в ветвях данного контура.
Одну из точек электрической цепи условно заземлить (потенциал этой точки равен нулю).
Потенциал остальных точек определить по правилу:
Если обходить цепь по направлению тока, то потенциал в каждой точке определяется потенциалом предыдущей точки плюс ЭДС источника, работающего в режиме генератора, минус ЭДС источника, работающего в режиме потребителя, и минус падения напряжения на участке между этими точками цепи. Если контур обходить против тока, то знаки перед ЭДС и падением напряжения изменяются на противоположные.
Изобразить координатные оси, по оси ОХ откладываем величину сопротивлений, по оси ОУ потенциалы соответствующих точек. Выбрать масштаб.
График представляет собой ломаную линию .



7. Раскройте понятия: электрическое сопротивление, удельная электрическая проводимость. (Сформулируйте определения, запишите формулы для расчета и единицы измерения, укажите какими параметрами определяется сопротивление проводника). Сформулируйте закон Ома. Подтвердите примером
Электрическое сопротивление проводника — это способность проводника препятствовать прохождению электрического тока через него.
Обозначается электрическое сопротивление буквой R. Единицей измерения сопротивления является Ом:
[R] = Ом.
Сопротивление R зависит от длины проводникаl, площади поперечного сеченияS и материала проводника 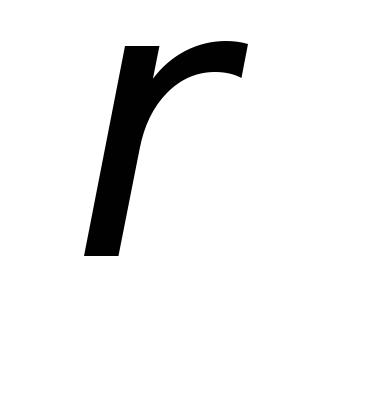 :
:

где  удельное сопротивление проводника,
зависящее от свойства материала
проводника.
удельное сопротивление проводника,
зависящее от свойства материала
проводника.
Единицей измерения удельного сопротивления является
[ ]
= Ом• м,
]
= Ом• м,
поскольку [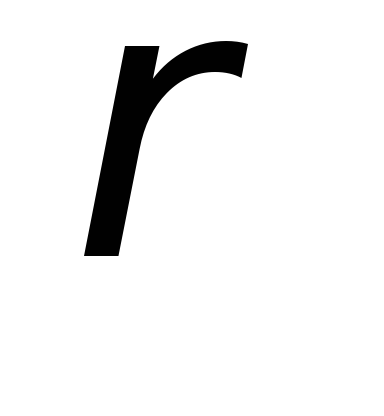 ]
]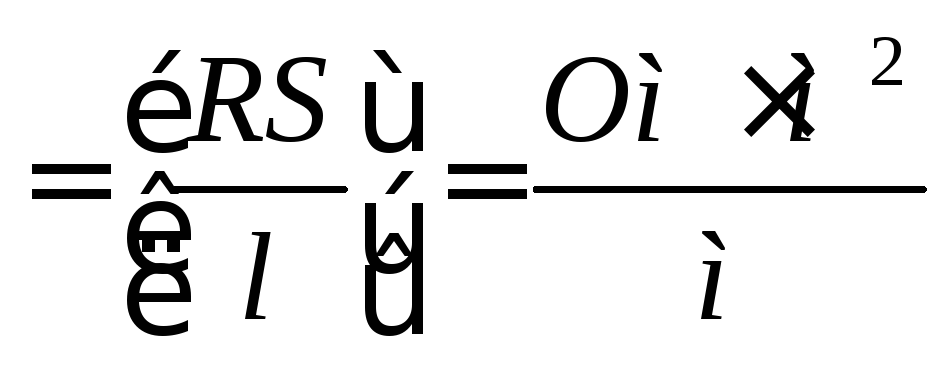
Однако на практике сечение проводников
выражают в мм2. Поэтому [ ]=
]=
Удельное сопротивление проводника
определяет область его применения. Так,
например, для соединения источника с
потребителем применяются металлические
провода с малым удельным сопротивлением
— алюминий, медь. Для обмоток реостатов
нагревательных приборов применяются
сплавы с большим удельным сопротивлением
— нихром, фехраль (при этом уменьшается
длина проводника  ).
).
Величину, обратную сопротивлению, называют проводимостью

Единицей проводимости является сименс
[g] = См (сименс).
Элементы электрической цепи, характеризующиеся сопротивлением R, называют резистивными, а промышленные изделия, предназначенные для выполнения роли сопротивления электрическому току, называются резисторами. Резисторы бывают регулируемые и нерегулируемые, проволочные и непроволочные, пленочные, композиционные и др.
Сопротивление проводников зависит от их температуры.
Сопротивление проводника при любой температуре (с достаточной степенью точности при изменении температуры в пределах 0-100 °С) можно определить выражением
 (2.1)
(2.1)
где R2 — сопротивление
проводника при конечной температуре t°2;
R1— сопротивление
проводника при начальной температуреt1°;  — температурный коэффициент сопротивления.
— температурный коэффициент сопротивления.
Для различных проводников температурный коэффициент сопротивления имеет различные значения.
Закон Ома для замкнутой цепи
Сила тока в электрической цепи с одним источником э.д.с. прямо пропорциональна электродвижущей силе и обратно пропорциональна сумме сопротивлений внешнего и внутреннего участка цепи
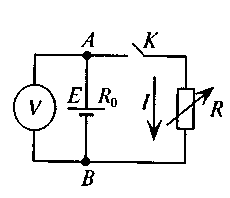

где
R0 — сопротивление источника, Ом;
R — сопротивление потребителя,Ом;
Е-ЭДС,В;
I-ток в цепи,А.
21,Работа, мощность, кпд источника тока. Тепловое действие тока. Закон Джоуля-Ленца.
Если по проводнику течет ток силой I, то за время dt через сечение проводника пройдет заряд:

Заряд, равный dq, в сечении 1 войдет в проводник и точно такой же заряд выйдет из проводника. Можно считать, что за время dt заряд сместился из сечения 1 в сечение 2, при этом над зарядом электростатическими силами совершена работа (см. (3.11)):

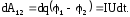
Мощность, развиваемая на участке цепи между точками 1 и 2, по определению равна:

Заменяя, согласно закону Ома (6.5), напряжение U.

получаем формулы для количества тепла dQ и мощности P:
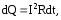 Формулу
называют законом Джоуля-Ленца.
Формулу
называют законом Джоуля-Ленца.

Если измерять тепло в калориях, в формуле (7.3) появляется переводной коэффициент, равный значению 1 Дж в калориях – 0,24 (кал/Дж):
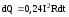 ,
(кал
,
(кал
Точно так же, как выводится закон Ома в дифференциальной форме, выводится закона Джоуля-Ленца в дифференциальной форме. Этот закон определяет количество тепла, выделяющееся в единичном объеме проводника в единицу времени – удельную тепловую мощность тока w:

Рассмотрим однородный цилиндрический проводник. Подставим в формулу (7.4) из (6.6) и (6.2) значения:

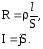
После подстановки получаем:
 (7.6)
(7.6)
где 
Из формулы (7.6) видно, что мощность, выделяемая в единице объема проводника, удельная тепловая мощность тока, равна:
 (7.7)
(7.7)
Для w, пользуясь законом Ома в дифференциальной форме (формула (6.10)), можно записать на основе (7.6) следующие эквивалентные выражения закона Джоуля-Ленца в дифференциальной форме:
 (7.8)
(7.8)
Для количества тепла dQ, выделяющегося в объеме dV за время dt, из (7.8) получаем:
 (7.9)
(7.9)
В случае неоднородного проводника формулы (7.8) и (7.9) позволяют найти количество тепла, выделяемого в каждой точке объема неоднородного проводника.
Если участок цепи неоднородный, то выделяемое количество теплоты по закону сохранения энергии будет равно алгебраической сумме работ кулоновских и сторонних сил.
Действительно, умножив правую и левую части формулы на силу тока I получим
I2R
= (1
2)I
+ 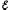 12I.
(5.28)
12I.
(5.28)
Следовательно, из уравнения (5.28) следует, что тепловая мощность
Q = I2R , (5.29)
выделяемая на участке цепи 1-2, равна алгебраической сумме мощностей кулоновских и сторонних сил. Если цепь замкнута, то затраченная мощность
N
=I
 .
(5.30)
.
(5.30)
Если
электрическая цепь замкнута и содержит
источника с ЭДС  ,
то вся затраченная источником тока
работа АЗ = АП + АВНУТ,
,
то вся затраченная источником тока
работа АЗ = АП + АВНУТ,
где
АЗ = I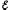 t,
АП = IURt,
АВНУТ =
IUrt.
t,
АП = IURt,
АВНУТ =
IUrt.
Тогда 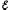 = UR +
Ur =
IR+ Ir, (5.20)
= UR +
Ur =
IR+ Ir, (5.20)
где UR — напряжение на внешнем сопротивлении, Ur — напряжение на внутреннем сопротивлении источника тока.
Мощность
тока можно найти по формуле N
=  .
(5.21)
.
(5.21)
Развиваемая источником тока затраченная мощность
NЗ = NП + NВНУТ, (5.22)
где
NЗ=
I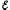 ,
NП = IUR,
NВНУТ=
IUr.
,
NП = IUR,
NВНУТ=
IUr.
КПД источника тока можно найти по формуле
=  .
(5.23)
.
(5.23)
Затраченная источником тока мощность
NЗ =
I =
= /(R+r),
(5.24)
/(R+r),
(5.24)
где
I
= 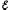 /(R
+ r).
/(R
+ r).
Полезная мощность, выделяемая во внешнем участке цепи
NП = IUR = I2R
=
 .
.
Следовательно,
затраченная и полезная мощности являются
функциями от внешнего сопротивления.
Если R
0, то NП
0; R
,
то NП
0. В этом случае функция NП =
f2 (R)
имеет один максимум. Найдем условие,
при котором полезная мощность максимальна,
т. е. NП =
NП, МАХ.
Для этого производную  приравняем нулю, т. е.
приравняем нулю, т. е.
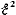 =
0, т. е.
=
0, т. е.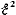 (r2-R2)
= 0. (
(r2-R2)
= 0. (
0, то R
= r
и
= 0,5). Вывод:
Если R
= r
, то полезная мощность максимальна, а
КПД источника тока равно 50%.
0, то R
= r
и
= 0,5). Вывод:
Если R
= r
, то полезная мощность максимальна, а
КПД источника тока равно 50%.




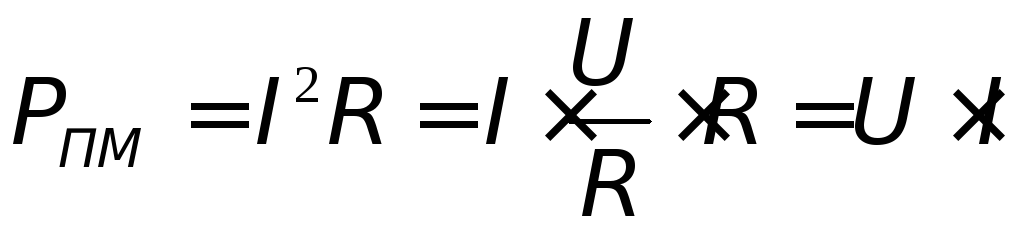 ,
,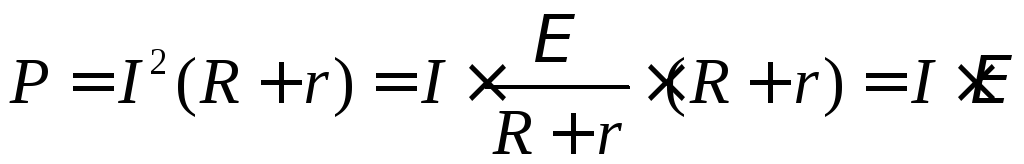 .
. .
.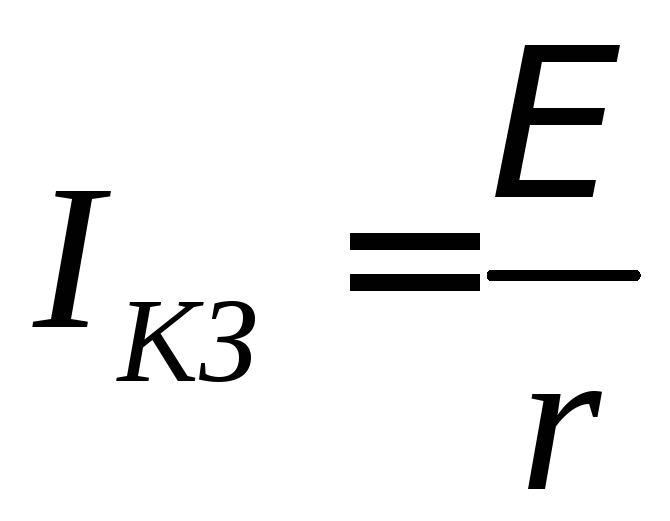 .
. .
. ,
,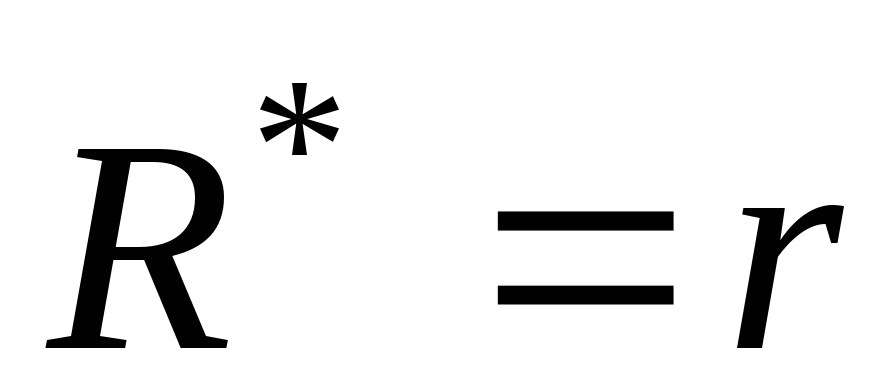 .
. .
.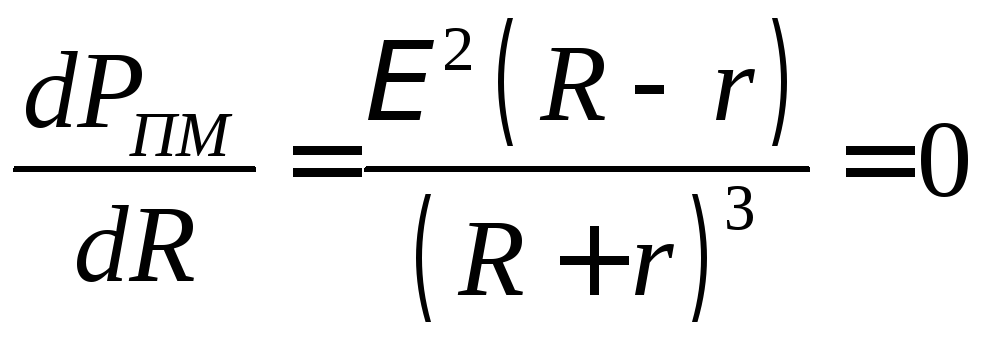 .
.
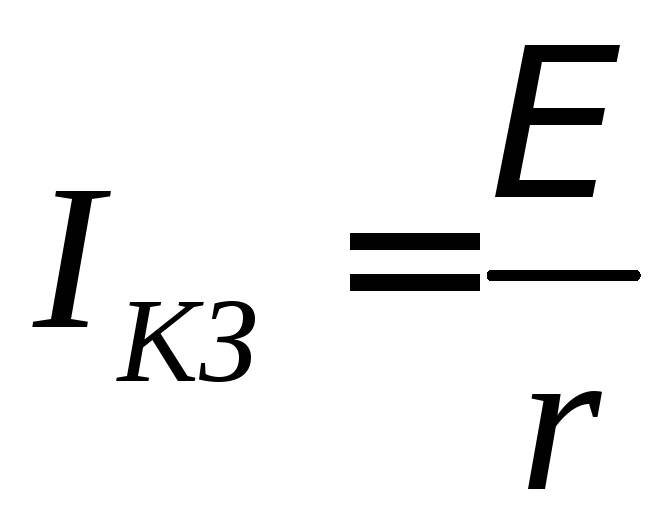
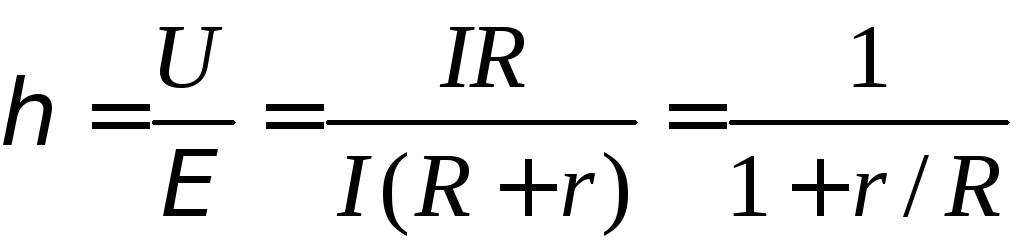 .
.