§ 13. Работа и мощность электрического тока

Электрическая энергия. В природе и технике непрерывно происходят процессы превращения энергии из одного вида в другой (рис. 30). В источниках электрической энергии различные виды энергии превращаются в электрическую энергию. Например, в электрических генераторах 1, приводимых во вращение каким-либо механизмом, происходит превращение в электрическую энергию механической, в термогенераторах 2 — тепловой, в аккумуляторах 9 при их разряде и гальванических элементах 10 — химической, в фотоэлементах 11 — лучистой.
Приемники электрической энергии, наоборот, электрическую энергию превращают в другие виды энергии — тепловую, механическую, химическую, лучистую и пр. Например, в электродвигателях 3 электрическая энергия превращается в механическую, в электронагревательных приборах 5 — в тепловую, в электролитических ваннах 8 и аккумуляторах 7 при их заряде — в химическую, в электрических лампах 6 — в лучистую и тепловую, в антеннах 4 радиопередатчиков — в лучистую.

Рис. 30. Пути превращения энергии из одного вида в другой

Мерой количества энергии является работа. Работа W, совершаемая электрическим током за время t при известном напряжении U силе тока I, равна произведению напряжения на силу тока и на время его действия:

W = UIt (29)

Работа, совершаемая электрическим током силой 1 А при напряжении 1 В в течение 1 с, принята за единицу электрической энергии. Эта единица называется джоулем (Дж). Джоуль, который называют также ватт-секундой (Вт*с), — очень маленькая единица измерения, поэтому на практике для измерения электрической энергии приняты более крупные единицы — ватт-час (1 Вт*ч = 3600 Дж), киловатт-час (1 кВт*ч = 1000 Вт*ч = 3,6*10

6 Дж), мегаватт-час (1 МВт*ч=1000 кВт*ч=3,6*10⁹ Дж).

Электрическая мощность. Энергия, получаемая приемником или отдаваемая источником тока в течение 1 с, называется мощностью. Мощность Р при неизменных значениях U и I равна произведению напряжения U на силу тока I:

P = UI (30)

Используя закон Ома для определения силы тока и напряжения в зависимости от сопротивления R и проводимости G, можно получить и другие выражения для мощности. Если заменить в формуле (30) напряжение U=IR или силу тока I=U/R=UG, то получим

P = I²R (31)

или

P = U²/R = U²G (32)

Следовательно, электрическая мощность равна произведению квадрата силы тока на сопротивление, или электрическая мощность квадрату напряжения, поделенному на сопротивление, либо квадрату напряжения, умноженному на проводимость.

Мощность, которая создается силой тока 1 А при напряжении 1 В, принята за единицу измерения мощности и называется ватт (Вт). В технике мощность измеряют более крупными единицами: киловаттами (1 кВт =1000 Вт) и мегаваттами (1 МВт=1 000 000 Вт).

Потери энергии и коэффициент полезного действия. При превращении электрической энергии в другие виды энергии или наоборот не вся энергия превращается в требуемый вид энергии, часть ее непроизводительно затрачивается (теряется) на преодоление трения в подшипниках машин, нагревание проводов и пр. Эти потери энергии неизбежны в любой машине и любом аппарате.
Отношение мощности, отдаваемой источником или приемником электрической энергии, к получаемой им мощности, называется коэффициентом полезного действия источника или приемника. Коэффициент полезного действия (к. п. д.)

? = P₂/P₁ = P₂/(P₂ + ?P)

(33)

где

Р₂ — отдаваемая (полезная) мощность;
Р₁ — получаемая мощность;
?Р — потери мощности.

К. п. д. всегда меньше единицы, так как в любой машине и любом аппарате имеются потери энергии. Иногда к. п. д. выражают в процентах. Так, тяговые двигатели электровозов и тепловозов имеют к. п. д. 86—92 %, мощные трансформаторы — 96—98 %, тяговые подстанции — 94—96 %, контактная сеть электрифицированных железных дорог — около 90 %, генераторы тепловозов — 92—94 %.
Рассмотрим в качестве примера распределение энергии в электрической цепи (рис. 31). Генератор 1, питающий эту цепь, получает от первичного двигателя 2 (например, дизеля) механическую мощность Р_mx = 28,9 кВт, а отдает электрическую мощность Р

эл = 26 кВт (2,9 кВт составляют потери мощности в генераторе). Поэтому он имеет к. п. д. ?_ген = Р_эл/Р_mx = 26/28,9 = 0,9.

Мощность Р_эл = 26 кВт, отдаваемая генератором, расходуется на питание электрических ламп (6 кВт), на нагрев электрических плиток (7,2 кВт) и на питание электродвигателя (10,8 кВт). Часть мощности ?P_пр = 2 кВт теряется на бесполезный нагрев проводов, соединяющих генератор с потребителями.

Рис. 31. Схема преобразования энергии в электрической цепи

В каждом приемнике электрической энергии также имеют место потери мощности. В электрическом двигателе 3 потери мощности составляют 0,8 кВт (он получает из сети мощность 10,8 кВт, а отдает только 10 кВт), поэтому к. п. д. ?дв = 10/10,8 = 0,925. Из мощности 6 кВт, полученной лампами, лишь незначительная часть идет на Создание лучистой энергии, большая часть ее бесполезно рассеивается в виде тепла. В электрической плитке на нагрев пищи расходуется не вся полученная мощность 7,2 кВт, так как часть созданного ею тепла рассеивается в окружающем пространстве. При рассмотрении электрических цепей наряду с определением токов и напряжений, действующих на отдельных участках, необходимо определять и передаваемую по ним мощность. При этом должен соблюдаться так называемый энергетический баланс мощностей. Это означает, что мощность, получаемая каким-либо устройством (источником тока или потребителем) или участком электрической цепи, должна быть равна сумме отдаваемой ими мощности и потерь мощности, которые возникают в данном устройстве или участке цепи.

Работа и мощность электрического тока. Видеоурок. Физика 10 Класс

На этом уроке мы начнем характеризовать электрический ток с точки зрения его практического применения. Будут выведены различные формулы для вычисления работы тока и мощности тока. Также будет введен закон Джоуля-Ленца (тепловое преобразование электрической энергии).

Электрический ток, конечно же, не стал бы так широко использоваться, если бы не одно обстоятельство. Работу тока или же электроэнергию легко преобразовывать в любую нужную нам энергию или работу: тепловую, механическую, магнитную…

Для практического применения тока прежде всего хочется знать, какую работу можно обратить в свою пользу. Выведем формулу для определения работы тока: 

Формула для работы электрического поля по перемещению заряда нам уже известна:

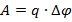
Или же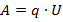 

Узнать, какой заряд переместился полем за промежуток времени t можно из определения силы тока: 

Отсюда: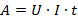 

Так как все величины, входящие в формулу, можно измерить соответствующими приборами (амперметр, вольтметр, часы), формула является универсальной.

Формулу можно также записать в несколько ином виде, используя закон Ома:

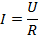
Если в исходную формулу для работы тока подставить силу тока, записанную таким образом, то получим:

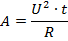
Если же из закона Ома выразить напряжение, то тогда:

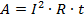
Использование этих формул удобно, когда в цепи присутствует какое-то одно соединение: параллельное для первого случая и последовательное для второго.

Особое внимание следует уделить тепловому действию тока. При прохождении тока через проводник, проводник нагревается. Почему это происходит? Мы уже затрагивали молекулярное строение проводников в теме о сопротивлении и отмечали, что при протекании тока свободные электроны сталкиваются с узлами кристаллической решетки. При этих столкновениях электроны постоянно придают некоторую скорость узлам решетки (рис. 1).

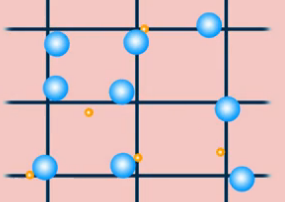
Рис. 1. Взаимодействие электронов с узлами кристаллической решетки

Так как температура – мера теплового движения, в процессе «расталкивания» температура проводника повышается. В какой-то момент наступает равновесие, когда количество энергии, получаемое проводником вследствие прохождения тока, равно количеству энергии, которое он отдает в окружающую среду.

В том случае, когда работа тока не преобразуется в механическую или же ток не имеет химического действия, работа тока эквивалентна количеству теплоты, высвобождающегося в окружающую среду.

Формулу просчета этого количества теплоты впервые независимо друг от друга открыли двое ученых: русский Эмиль Ленц и англичанин Джеймс Джоуль (рис. 2).

Закон Джоуля-Ленца:

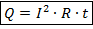
Как видно, правая часть формулы в точности повторяет одну из форм формулы для работы электрического тока.

Всегда следует помнить, что в случае, когда есть какое-либо другое преобразование энергии тока, формула Джоуля-Ленца не выполняется.

 

Рис. 2. Джеймс Джоуль (Источник) и Эмиль Ленц (Источник) соответственно

Наряду с работой тока очень важно отметить мощность тока, так как эта характеристика является ключевой в бытовом использовании электроэнергии (на всех бытовых приборах указано приемлемое напряжение его мощность).

Определение. Мощность – это работа, выполненная за единицу времени (скорость выполнения током работы):

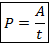
Единица измерения мощности – ватт:

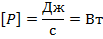
И теперь, используя наши знания о работе тока, мы без труда найдем формулу для мощности тока:

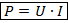
Или же, если использовать другие виды формулы для работы:

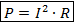
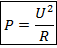
На следующем уроке мы разберем тему «Электродвижущая сила».

 

Список литературы

1. Тихомирова С.А., Яворский Б.М. Физика (базовый уровень) – М.: Мнемозина, 2012.
2. Генденштейн Л.Э., Дик Ю.И. Физика 10 класс. – М.: Илекса, 2005.
3. Мякишев Г.Я., Синяков А.З., Слободсков Б.А. Физика. Электродинамика. – М.: 2010.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Physics.ru (Источник).
2. Constant-current.narod.ru (Источник).
3. Mugo.narod.ru (Источник).

 

Домашнее задание

1. Стр. 105: № 802–805. Физика. Задачник. 10-11 классы. Рымкевич А.П. – М.: Дрофа, 2013. (Источник)
2. Как зависит количество теплоты, которое выделяется в проводнике, в случае параллельного соединения проводников?
3. На фонарике написано «4 В; 1 Вт», а на светильнике – «220 В; 40 Вт». В какой лампе больше сила тока? Сопротивление какой лампы больше и во сколько раз?
4. *Стальной и медный провода одинаковых размеров присоединили к источнику тока сначала параллельно, а потом последовательно. В каком из проводов в каждом случае выделялось большее количество теплоты?

Работа и мощность электрического тока

Работа и мощность электрического тока

Работа электрического тока показывает, какая работа была совершена электрическим полем при перемещении зарядов по проводнику.

Зная две формулы:

I = q/t ….. и ….. U = A/q
можно вывести формулу для расчета работы электрического тока:

Работа электрического тока равна произведению силы тока на напряжение и на время протекания тока в цепи.

Единица измерения работы электрического тока в системе СИ:

[ A ] = 1 Дж = 1A.B.c

НАУЧИСЬ, ПРИГОДИТСЯ

При расчетах работы электрического тока часто применяется
внесистемная кратная единица работы электрического тока: 1 кВт.ч (киловатт-час).

1 кВт.ч = 3 600 000 Дж

В каждой квартире для учета израсходованной электроэнергии устанавливаются специальные приборы-счетчики электроэнергии, которые показывают работу электрического тока, совершенную за какой-то отрезок времени при включении различных бытовых электроприборов.
Эти счетчики показывают работу электрического тока ( расход электроэнергии) в «кВт.ч».

Необходимо научиться рассчитывать стоимость израсходованной электроэнергии!
Внимательно разбираемся в решении задачи на странице 122 учебника (параграф 52)!

МОЩНОСТЬ ЭЛЕКТРИЧЕСКОГО ТОКА

Мощность электрического тока показывает работу тока, совершенную в единицу времени и равна отношению совершенной работы ко времени, в течение которого эта работа была совершена.

(мощность в механике принято обозначать буквой N, в электротехнике — буквой Р так как А = IUt, то мощность электрического тока равна:

Единица мощности электрического тока в системе СИ:

[P] = 1 Вт (ватт) = 1 А.B

КНИЖНАЯ ПОЛКА

Как работает электрочайник?
Как работает электроутюг?
Электрический мотор за 10 секунд!

ИНТЕРЕСНО

В свое время в качестве единицы мощности Дж. Уатт предложил такую единицу, как «лошадиная сила». Эта единица измерения дожила до наших дней. Но в Англии в 1882 г. Британская ассоциация инженеров решила присвоить имя Дж. Уатта единице мощности. Теперь имя Джеймса Уатта можно прочесть на любой электрической лампочке.
Это был первый в истории техники случай присвоения собственного имени единице измерения.
С этого случая и началась традиция присвоения собственных имен единицам измерения

Рассказывают, что …
одну из паровых машин Уатта купил пивовар, чтобы заменить ею лошадь, которая приводила в действие водяной насос. При выборе необходимой мощности паровой машины пивовар определил рабочую силу лошади как восьмичасовую безостановочную работу до полного изнеможения лошади. Расчет показал, что каждую секунду лошадь поднимала 75 кг воды на высоту 1 метр, что и было принято за единицу мощности в 1 лошадиную силу.

ЗНАЕШЬ ЛИ ТЫ

Ток, протекающий в спиралях электроламп, нагревает их до очень высокой температуры.
Поэтому, чтобы спирали служили дольше, их заключают в стеклянные баллоны, заполненные в лампах большой мощности инертным газом.

В баллонах ламп малой мощности (до 40 Вт) — вакуум. Чтобы лампа работала дольше, температура спирали таких ламп ниже, а свет имеет желтый оттенок.

___

Атмосферное электричество опасно проявлением в виде линейных разрядов (молний), которых возникает на нашей планете примерно 100 каждую секунду. Атмосферные электрические заряды могут иметь напряжение до 1 миллиарда вольт, а сила тока молнии достигать 200 тысяч ампер. Время существования молнии оценивается от 0,1 до 1 секунды.
Температура достигает 6-10 тысяч градусов Цельсия.
И если предположить, что электрическая энергия одной молнии может составлять 2500 квт/час, а одна семья из трех человек потребляет в месяц 250 квт/час электричества, то энергии одной молнии хватило бы, чтобы удовлетворить потребность этой семьи на 10 месяцев.

СУМЕЕШЬ ЛИ ТЫ РЕШИТЬ

Две электрические лампы, мощность которых 40 и 100 Вт, рассчитаны на одно и то же напряжение.
Сравните по сопротивлениям нити накала обеих ламп.

Комната освещена с помощью 40 электрических ламп от карманного фонаря, соединенных последовательно и питаемых от городской сети. После того как одна лампа перегорела, оставшиеся 39 снова соединили последовательно и включили в сеть.
Когда в комнате было светлее: при 40 или 39 лампах?

___

Последовательно соединенные медная и железная проволоки одинаковых длины и сечения подключены к аккумулятору. В какой из них выделится большее количество теплоты за одинаковое время?

Два проводника различной длины, но одинакового сечения и материала включены параллельно друг другу в цепь электрического тока. В каком из них будет выделяться большее количество теплоты?

Все бежим к задачкам!

1.4. Работа и мощность постоянного электрического тока

На участке цепи, не содержащей ЭДС, силы электрического поля совершают работу по перемещению электрического заряда

A₁₂=IU₁₂t=Irt=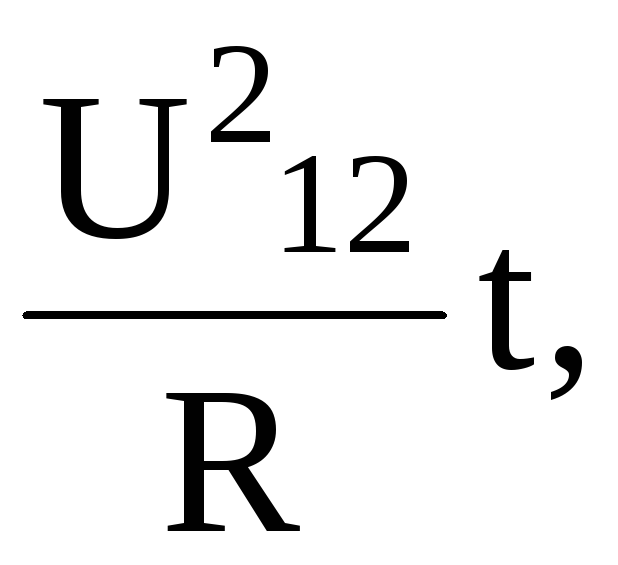

которая выделяется в проводнике в виде тепла.

Если в цепи имеется ЭДС, то работа по перемещению электрического заряда совершается сторонними и электрическими силами, численно равная энергии, выделяющейся в этой цепи.

A=(U₁₂+E)It.

В замкнутой цепи энергия, выделяющаяся в проводнике численно равна работе

A=IU₁₂t+IEt=IEt,

или

A=I²(R+r)t.

Мощность-работа, совершаемая в единицу времени:

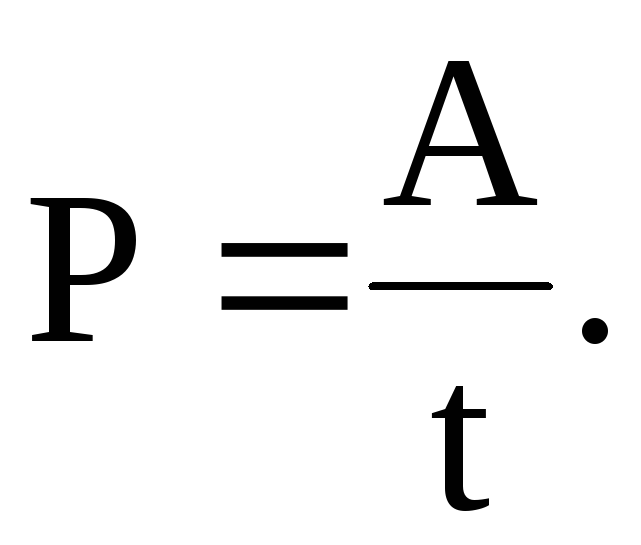
На участке цепи, в котором отсутствует ЭДС, мощность

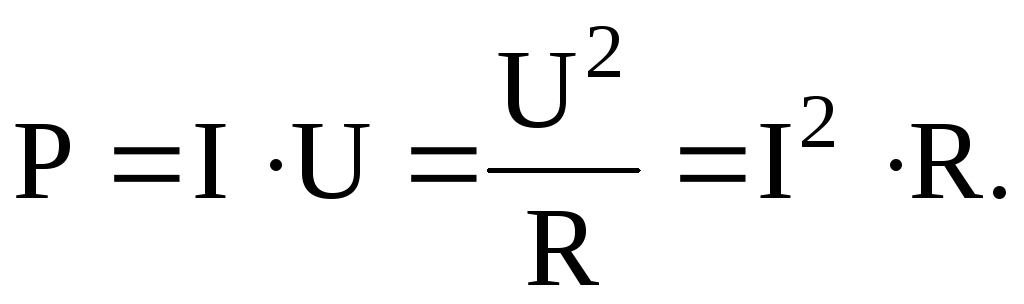
При наличии ЭДС:

P=I×U+I×E.

В замкнутой цепи:

P=I×E=I²(R+r).

Мощность во внешней цепи является полезной мощностью:

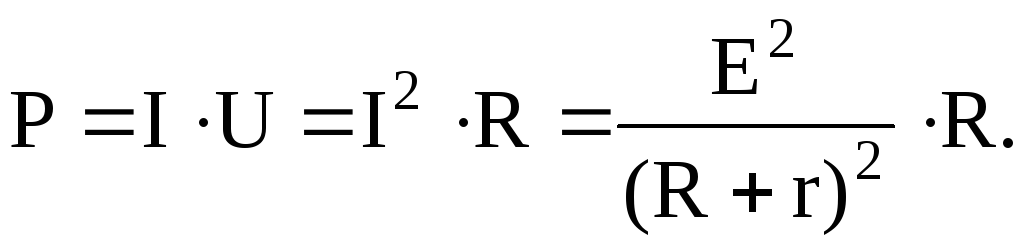
Отношение полезной мощности (мощности во внешней цепи) к мощности развиваемой источником тока (полной мощности) называют коэффициентом полезного действия (КПД):

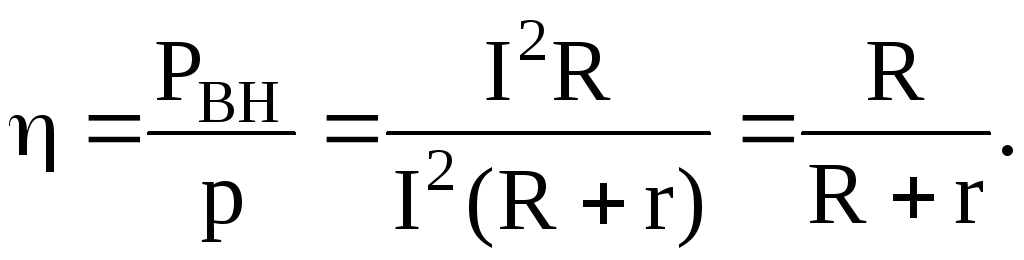
Мощность во внешней цепи максимальна в том случае, когда сопротивление внешнего участка цепи равно внутреннему сопротивлению источника тока (R=r). При этом максимальное значение мощности во внешней цепи оказывается равным:

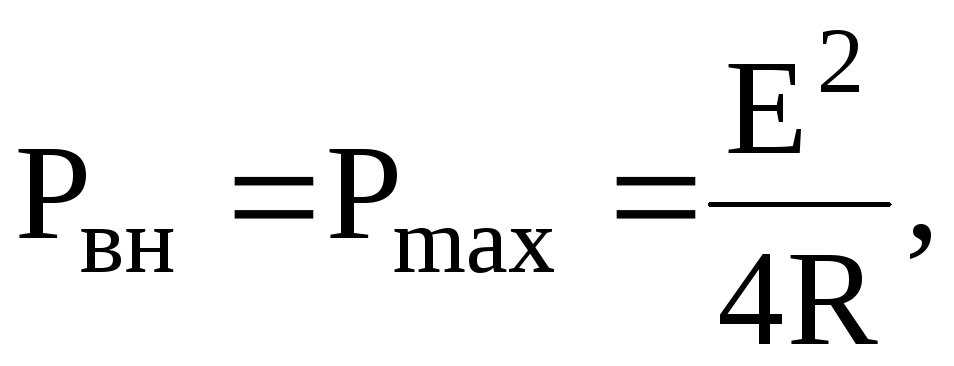
а КПД

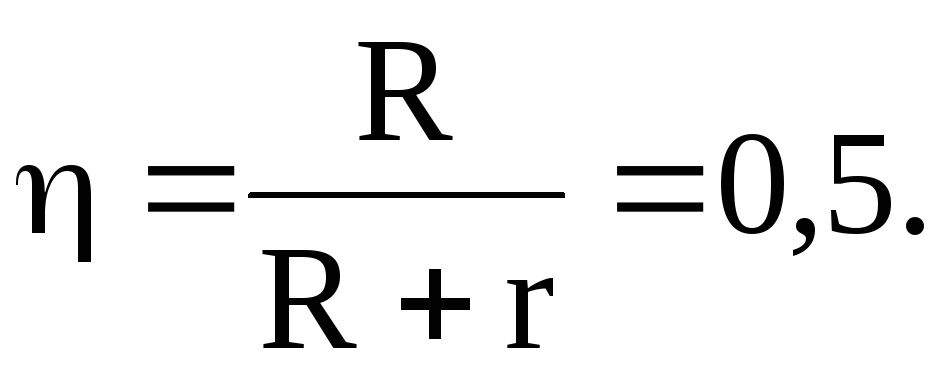
Зависимость КПД источника:

а) от тока во внешней цепи:

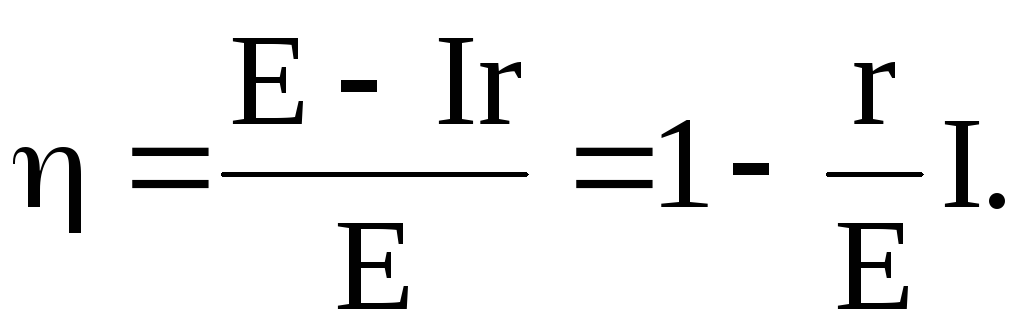
б) от сопротивления внешнего участка цепи:

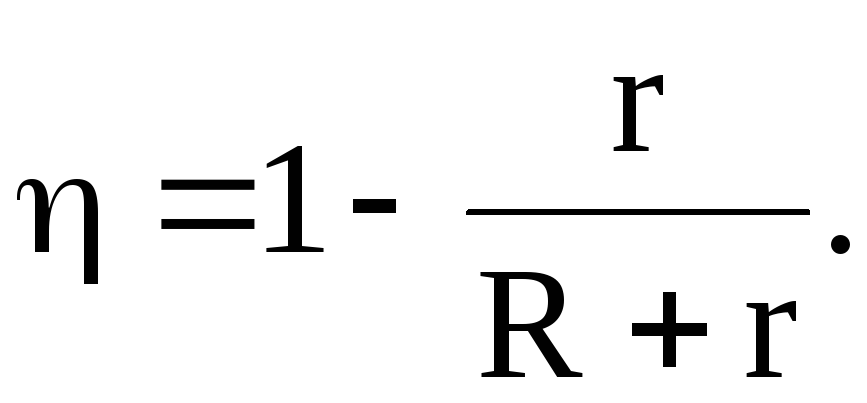
1.4.1. Примеры решения задач

1.4.1.1. Задача. Определить работу электрических сил и количество теплоты, выделяемое ежесекундно, в следующих случаях: 1) в резисторе, по которому идет ток силой I=1 А; разность потенциалов между концами резистора j₁-j₂=2 В; 2) в аккумуляторе, который заряжается током силой I=1 А; разность потенциалов на его зажимах j₁-j₂=2 В, э.д.с. аккумулятора E=1,3 В; 3) в батарее аккумуляторов, которая дает ток силой I=1 А на внешнюю нагрузку; разность потенциалов на зажимах батареи j₁-j₂=2 В, ее э.д.с.E=2,6 В.

Решение. 1. Так как рассматриваемый участок не содержит ЭДС, то по закону Ома для участка однородной цепи, имеем

j₁ -j₂=IR.

Из этого следует, что формулы A=(j₁-j₂)IR и Q=I²Rt в данном случае совпадают. Значит, вся работа электрических сил идет на нагревание резистора:

A=Q=(j₁-j₂)IR=2 (Дж).

2. При зарядке аккумулятора его зажимы присоединяют к источнику, разность потенциалов на полюсах которого постоянна. При этом ток внутри аккумулятора идет от его положительного полюса к отрицательному, т.е. в направлении, обратном току разряда.

Работу электрических сил снова вычислим по формуле

A=(j₁-j₂)IR=2 (Дж).

Чтобы по формуле Q=I²Rt определить количество выделенной теплоты, необходимо найти сопротивление участка цепи, в котором находится аккумулятор. Поскольку этот участок содержит э.д.с., применим закон Ома для участка неоднородной цепи. Учитывая направления тока и э.д.с., запишем в соответствии с правилом знаков

. (1)

Тогда

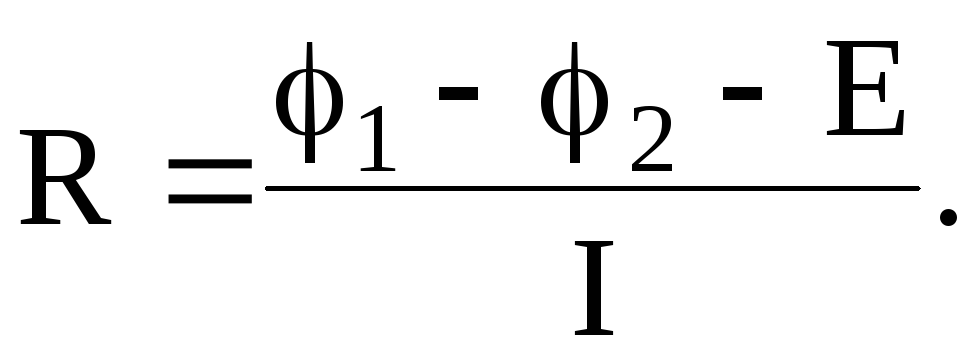(2)

Подставив значение R из (2) в формулу закона Джоуля-Ленца, получим

Q=I²Rt=(j₁ – j₂— E) It=0,7 (Дж).

В данном случае лишь часть работы электрических сил идет на нагревание аккумулятора, остальная же часть (A-Q) превращается в химическую энергию заряжаемого аккумулятора.

3. Работу электрических сил найдем по формуле

A=(j₁-j₂) IR.

При этом обратим внимание на отличие данного случая от предыдущего. Если положительный знак разности потенциалов (j₁ – j₂) сохранился, то направление силы тока на рассматриваемом участке изменилось на противоположное. Следовательно,

A=(j₁-j₂) (-I)t=-2 (Дж). (3)

Отрицательный знак ответа выражает то обстоятельство, что положительные заряды движутся внутри каждого аккумулятора от его низшего потенциала к высшему, т.е. против электрических сил. При этом положительную работу совершают сторонние силы, перемещая заряды внутри аккумуляторов.

Количество теплоты, выделенное в батарее, снова определим по формуле закона Джоуля-Ленца в интегральной форме

Q=I²Rt.

При этом сопротивление r батареи, как и в предыдущем случае, можно вычислить по закону Ома для неоднородного участка цепи

. (4)

Сопротивление батареи можно найти также как разность между сопротивлением всей цепи и сопротивлением внешнего участка цепи

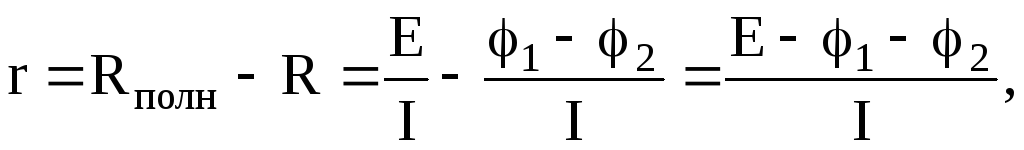
что совпадает с формулой (4). Подставив найденное значение r в формулу закона Джоуля-Ленца, получим

Q=I²Rt=[E-(j₁-j₂)]It=0,6 (Дж). (5)

Этот вариант задачи можно решить еще и по-другому. По данным условиям найдем работу электрических сил на внешнем участке цепи:

A=(j₁-j₂)It=2 (Дж).

Однако работа электрических, т.е. кулоновских (но не сторонних), сил по перемещению зарядов на замкнутом пути всегда равна нулю

A_внутр+A_внеш=0,

откуда

A_внутр=-A_внеш=-2 (Дж),

что совпадает с результатом (3).

Вся энергия, расходуемая батареей, превращается (посредством работы электрических сил) в тепло Q_общ, выделяющееся во всей цепи.

Эту энергию можно вычислить по формуле

A_б=Q_общ=EIt=2,6 (Дж).

Так как на внешнем участке выделяется количество теплоты

Q_внеш=A_внеш=2 (Дж),

то для батареи

Q=Q_общ-Q_внеш=0,6 (Дж),

что совпадает с результатом (5).

1.4.1.2. Задача. Э.д.с. батареи E=12 В. Наибольшая сила тока, которую может дать батарея, I_макс=5 А. Какая наибольшая мощность P_макс может выделиться на подключенном к батарее резисторе с переменным сопротивлением.

Решение. Мощность P тока измеряется работой, совершенной электрическими силами в единицу времени. Поскольку вся работа на внешнем участке цепи идет на нагревание резистора (A=Q), то в данном случае мощность измеряется количеством теплоты, выделяемым в резисторе в единицу времени. Поэтому на основании формулы закона Джоуля-Ленца в интегральной форме для внешнего участка цепи Q==I²Rt, а также закона Ома для замкнутой цепи, получим

P=I²R=E²R/(R+r)², (1)

где R, r-сопротивления внешнего и внутреннего участков цепи соответственно.

Из (1) видно, что при постоянных значениях E, r мощность P во внешней цепи является функцией одной переменной R. Известно, что эту функция имеет максимум при условии r=R (в этом можно убедиться, применив общий метод исследования функций на экстремум с помощью производной). Следовательно,

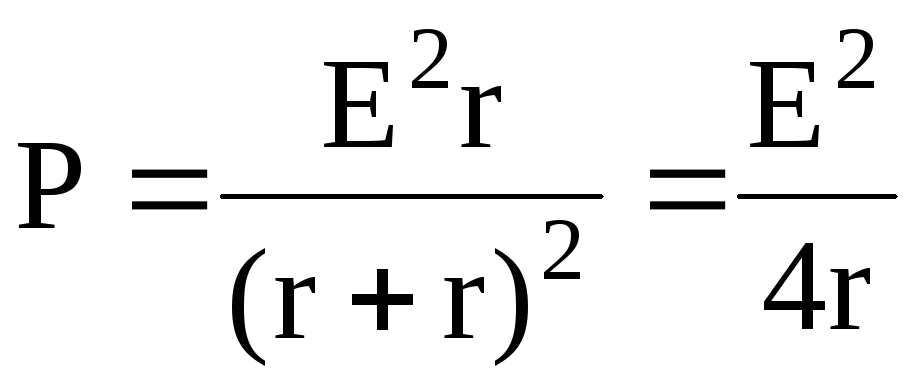. (2)

Таким образом, задача сводится к отысканию сопротивления r внутреннего участка (батареи). Если учесть, что согласно закону Ома для замкнутой цепи наибольшая сила тока I_макс будет при внешнем сопротивлении R=0 (ток короткого замыкания), то

I_макс=E/r,

откуда

r=E I_макс.

Подставив найденное значение внутреннего сопротивления r в формулу (2), получим

P_макс=EI_макс/4=15 (Вт).

1.4.1.3. Задача. Обмотка электрического кипятильника имеет две секции. Если включена одна секция, вода закипает через t₁=10 мин, если другая, то через t₂=20 мин. Через сколько минут закипит вода, если обе секции включить: а) последовательно? б) параллельно? Напряжение на зажимах кипятильника и к.п.д. установки считать во всех случаях одинаковыми.

Решение. При различных включениях секций кипятильника сопротивление цепи различно. Очевидно, искомое время нагревания воды есть некоторая функция сопротивления цепи. Чтобы найти эту функцию, воспользуемся законом Джоуля-Ленца

Q=I²Rt.

Поскольку речь идет об участке цепи, не содержащем э.д.с., к которому применим закон Ома I=(j₁-j₂)/R, запишем в виде

Q=U²t/R. (1)

Отсюда легко определить вид функции t=f(R).

Во всех случаях для нагревания воды требуется одно и то же количество теплоты, определяемое формулой

Q’=cmDt,

где c, m-удельная теплоемкость и масса воды;

Dt-разность температур.

В силу постоянства к.п.д. установки h одним и тем же будет также полное количество теплоты выделенное током, т.е.

Q=Q’/h.

Учитывая также постоянство напряжения на зажимах цепи, из формулы (1), получим

R=U²t/Q=kt, (2)

где k=U²/Q-постоянная величина.

Таким образом, зависимость времени от сопротивления является пропорциональной. Теперь легко найти ответы в обоих случаях.

При последовательном соединении секций общее сопротивление

R_посл=R₁+R₂.

Подставив сюда значения R по формуле (2), получим

kt_посл=kt₁+kt₂,

откуда

t_посл=t₁+t₂=15 (мин).

При параллельном соединении секций сопротивление соединения

R_пар=R₁R₂/(R₁+R₂).

Отсюда, применив соотношение (2), найдем

t_пар=t₁t₂/(t₁+t₂)=7 (мин).

1.4.1.4. Задача. Две медные проволоки одинаковой длины ℓ=1 м и диаметрами d₁=0,1 мм и d₂=0,2 мм, подключенные (поочередно) к зажимам гальванического элемента, нагреваются до одинаковой температуры. Определить внутреннее сопротивление гальванического элемента. Считать отдачу теплоты проволокой в окружающее пространство при постоянной температуре пропорциональной площади ее поверхности.

Решение. При установившемся тепловом режиме, когда температура проволоки перестает повышаться, количество теплоты, выделенное током в 1 с, согласно закону сохранения энергии, должно быть равно количеству теплоты, рассеянному за то же время проволокой в окружающее пространство, т.е. должно выполняться равенство

P_тока=P_расс. (1)

Мощность тока P_тока=I²R выразим через внутреннее сопротивление источника и диаметр проволоки, воспользовавшись законом Ома для замкнутой цепи и формулой сопротивления проводника:

(2)

С другой стороны, согласно условию задачи, имеем

P_расс=kS’=kpdℓ, (3)

где S’-площадь поверхности проволоки, вычисленная как площадь боковой поверхности цилиндра;

k-коэффициент пропорциональности, зависящий от температуры проволоки.

Подставив в уравнение (1) значения P_тока и P_расс по формулам (2), (3) и произведя сокращения, получим

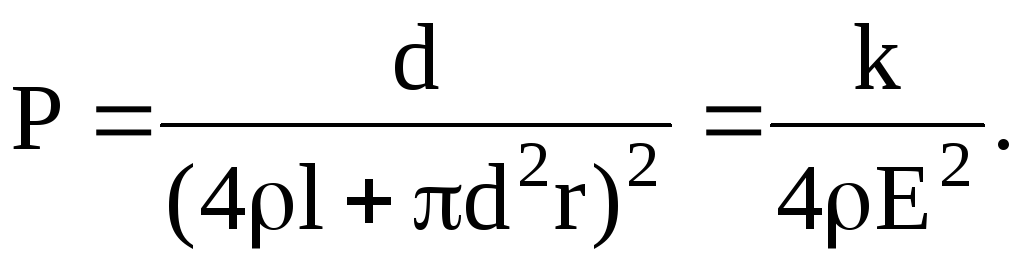(4)

Поскольку при постоянной температуре все величины, стоящие в правой части формулы (4), постоянны, должно выполняться равенство

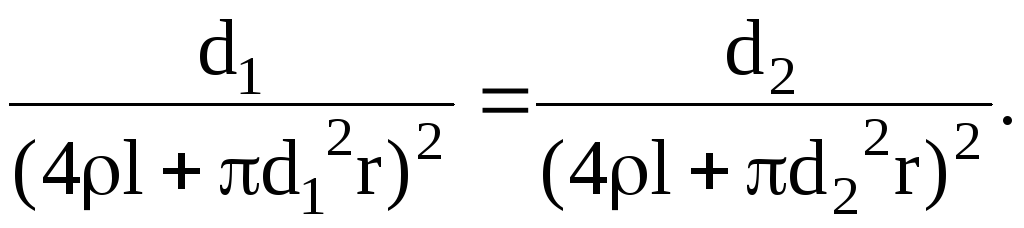(5)

так как диаметрам проволоки d₁, d₂ соответствует по условию одинаковая температура. Чтобы решить уравнение (5) относительно неизвестного r, извлечем из обеих частей уравнения квадратный корень:

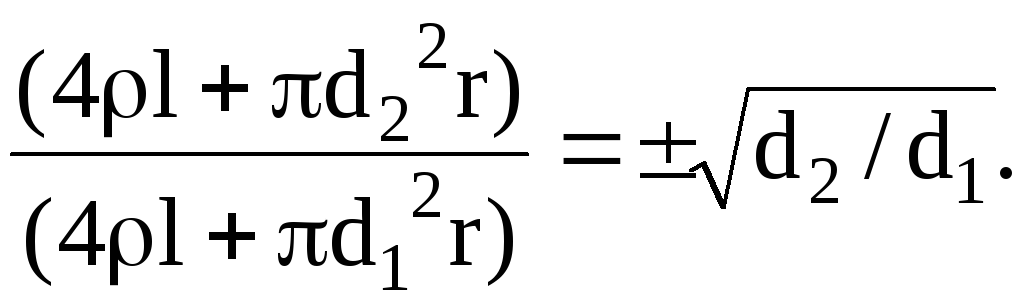
Все слагаемые, стоящие в левой части этого уравнения – заведомо положительные величины, отрицательный знак перед корнем отбрасываем. Решив уравнение относительно r, найдем

Взяв из таблиц значение удельного сопротивления меди, выразив входящие в формулу величины в единицах СИ, выполнив вычисление, получим

r=0,3 (Ом).

13. Работа и мощность электрического тока.

В природе и технике происходят процессы превращения энергии из одного вида в другой. В источниках электрической энергии различные виды энергии превращаются в электрическую энергию. Приемники электрической энергии, наоборот, электрическую энергию превращают в другие виды энергии — тепловую, механическую, химическую.

Мерой количества энергии является работа W, совершаемая электрическим током I за время t при напряжении U и равна:

W=UIt

Работа, совершаемая электрическим током силой 1 А при напряжении 1 В в течение 1 с, принята за единицу электрической энергии. Эта единица называется Джоулем (Дж). Джоуль называют также ватт-секундой (Вт·с).

Энергия, получаемая приемником или отдаваемая источником тока в течение 1 с, называется мощностью. Мощность Р при неизменных значениях U и I равна произведению напряжения U на силу тока I:

Р = U I

Мощность, которая создается силой тока 1 А при напряжении 1 В, принята за единицу измерения мощности и называется Ватт (Вт).

Потери энергии и коэффициент полезного действия. При превращении электрической энергии в другие виды энергии или наоборот в любой машине и любом аппарате неизбежны потери энергии и не вся энергия превращается в требуемый вид.

Отношение мощности, отдаваемой источником или приемником электрической энергии, к получаемой им мощности, характеризуется коэффициентом полезного действия (к. п. д.) источника или приемника.

η = Р₂/Р₁= Р₂ / (Р₂ + ∆Р),

где Р₂ — отдаваемая (полезная) мощность;

Р₁ — получаемая мощность;

∆Р — потери мощности.

К. п. д. всегда меньше единицы, так как в любой машине и любом аппарате имеются потери энергии.

14. Тепловое действие тока

При прохождении электрического тока по проводнику в результате столкновений свободных электронов с его атомами и ионами проводник нагревается. Количество тепла, выделяемого в проводнике при прохождении электрического тока, определяется законом Джоуля — Ленца. Количество выделенного тепла Q равно произведению квадрата силы тока I², сопротивления проводника R и времени t прохождения тока через проводник:

Q =I²Rt.

Допустимая сила и плотность тока. Превращение электрической энергии в тепловую нашло широкое применение в технике.

Однако в электрических машинах и аппаратах, в проводах превращение электроэнергии в тепло не только бесполезно, но и ухудшает работу их работу, а в некоторых случаях может вызвать повреждения и аварии.

Каждый проводник в зависимости от условий, в которых он находится, может пропускать, не перегреваясь, ток силой, не превышающей некоторое допустимое значение. Для определения токовой нагрузки проводов часто пользуются понятием допустимой плотности тока J (сила тока I, приходящаяся на 1 мм² площади s поперечного сечения проводника):

J=I/s

Допустимая плотность тока зависит от материала провода (медь или алюминий), вида применяемой изоляции, условий охлаждения, площади поперечного сечения и пр.

Превышение допустимого значения силы тока в проводнике может вызвать чрезмерное повышение температуры, в результате этого изоляция проводов электродвигателей, генераторов и электрических сетей перегревается, обугливается и даже горит, что может привести к короткому замыканию и пожару. Для того чтобы предотвратить недопустимое увеличение силы тока, во всех электрических установках должны приниматься меры для автоматического отключения от источников электрической энергии тех приемников или участков цепи, в которых имеет место перегрузка или короткое замыкание. Для этой цели в технике широко используют плавкие предохранители и автоматические выключатели.

Нагрев в переходном сопротивлении. Повышенный нагрев проводника, как следует из закона Джоуля — Ленца, может происходить не только вследствие прохождения по нему тока большой силы, но и вследствие повышения сопротивления проводника. Поэтому для надежной работы электрических установок большое значение имеет значение сопротивления в месте соединения отдельных проводников. При неплотном электрическом контакте и плохом соединении проводников (рис. 22) электрическое сопротивление в этих местах (так называемое переходное сопротивление электрического контакта) сильно возрастает, и здесь происходит усиленное выделение тепла. В результате место неплотного соединения проводников будет представлять собой опасность в пожарном отношении, а значительный нагрев может привести к полному выгоранию плохо соединенных проводников. Во избежание этого при соединении проводов на э. п. с. концы их тщательно зачищают, облуживают и впаивают в кабельные наконечники, которые надежно прикрепляют болтами к зажимам электрических машин и аппаратов. Специальные меры принимают и для уменьшения переходного сопротивления между контктами электрических аппаратов, осуществляющих включение и выключение тока.

4. Закон Джоуля-Ленца. Работа и мощность электрического тока.

Закон Джоуля-Ленца: количество тепла Q выделяемое на участке проводника при прохождении тока пропорционально времени прохождения тока, сопротивлению проводника и квадрату силы тока

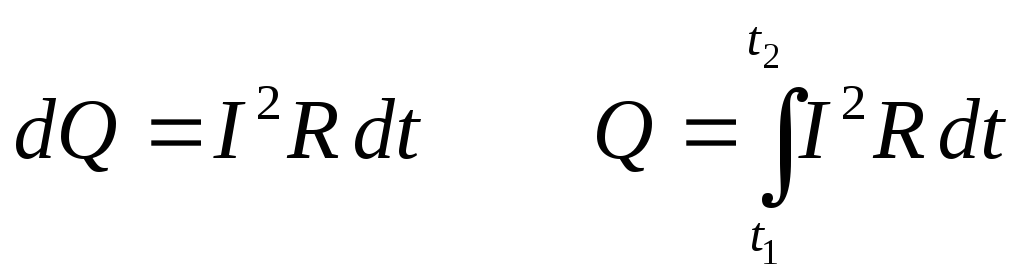
Работа сил электрического поля, создающего электрический ток,

называется работой тока:

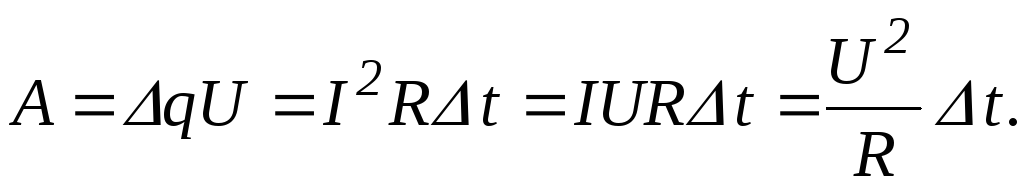
Мощность электрического тока равна отношению работы тока A ко времени t, за которое эта работа совершена:

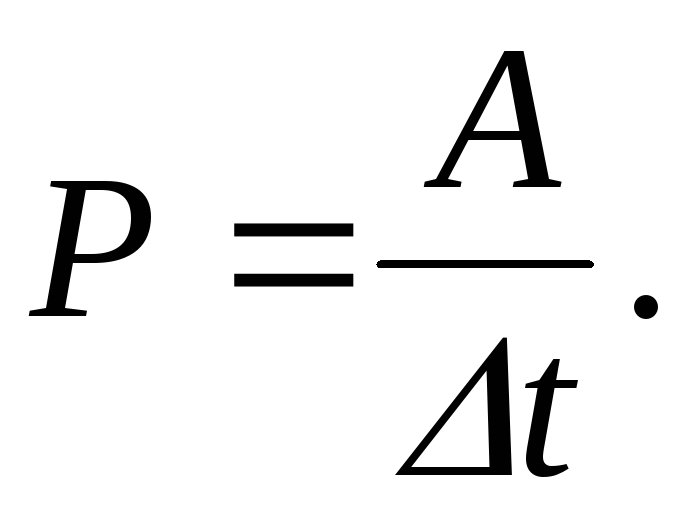
Полезная мощность – мощность, выделяющаяся на внешнем сопротивлении

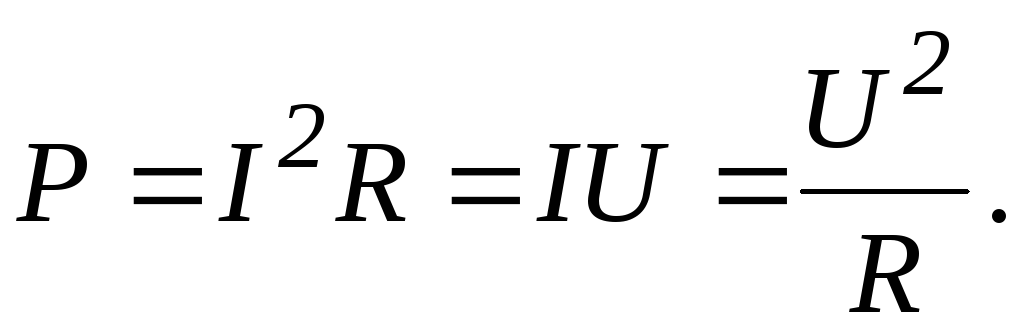
Полная мощность развиваемая источников равна мощности, которая выделяется во всей цепи

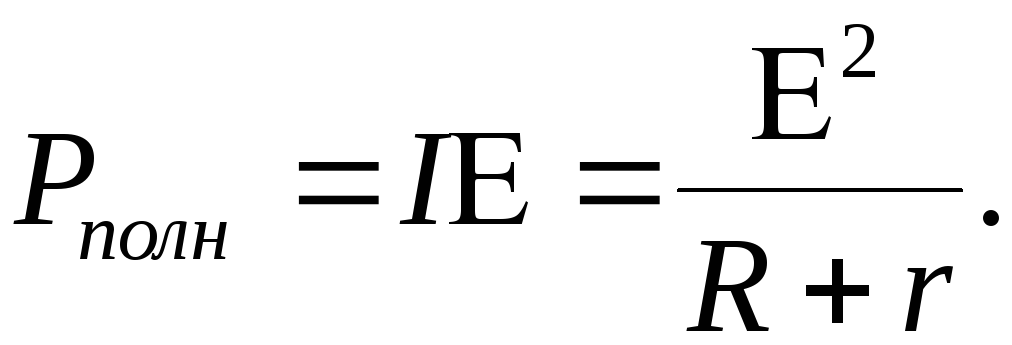
Коэффициент полезного действия (КПД) источника тока равен отношению полезной мощности, выделяемой в цепи, к отношению полной мощности:

3.Разветвленные цепи. Правила Кирхгофа.

Узлами цепи будем называть точки, в которых сходится не менее трех проводников цепи (рис.4).

Первое правило Кирхгофа: алгебраическая сумма токов сходящихся в узле равна нулю:

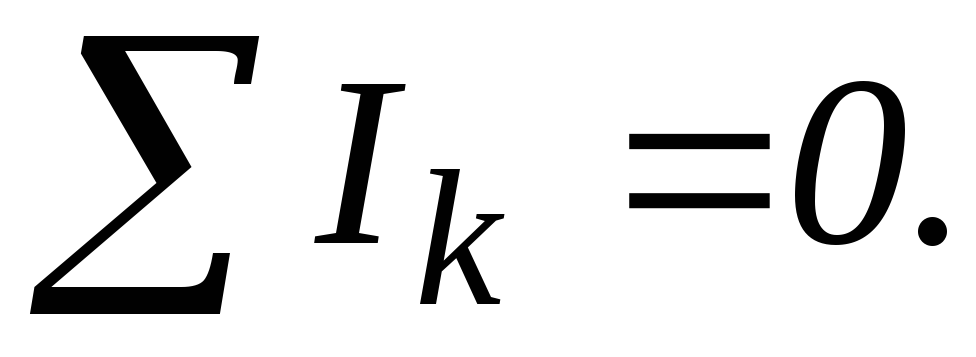
При этом следует соблюдать следующее правило знаков: токи приходящие к узлу считать положительными, уходящие — отрицательными.

Второе правило Кирхгофа: алгебраическая сумма произведений токов на сопротивления в ветвях замкнутого контура равна алгебраической сумме ЭДС, встречающихся в этом контуре:

.

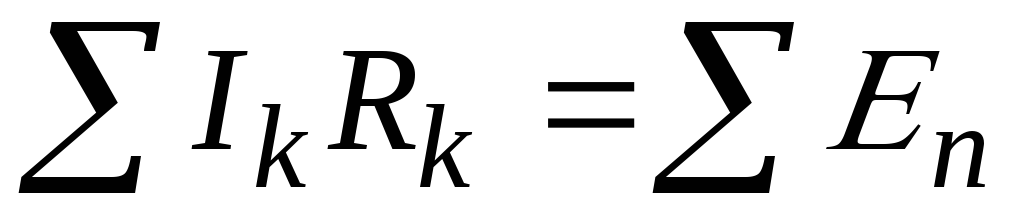При этом следует придерживаться правила знаков: токи, идущие вдоль выбранного нами направления обхода (например по часовой стрелке), считаются положительными, а идущие против направления обхода — отрицательными. Соответственно этому ЭДС которые действуют по выбранному направлению обхода в контуре считаются положительными.

Электромагнетизм

1. Магнитное поле.

Магнитное поле порождается движущимися зарядами. Магнитное поле характеризуется с помощью вектора магнитной индукции . Линии касательные к которым в каждой точке совпадают с направлением вектора магнитной индукции 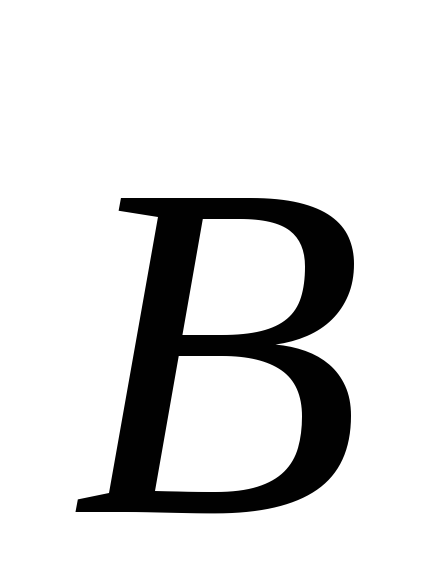в этой точке называются линии магнитной индукции. Магнитная индукция измеряется в теслах: [B] = 1 тл. Направление линий магнитной индукции определяется правилом буравчика.

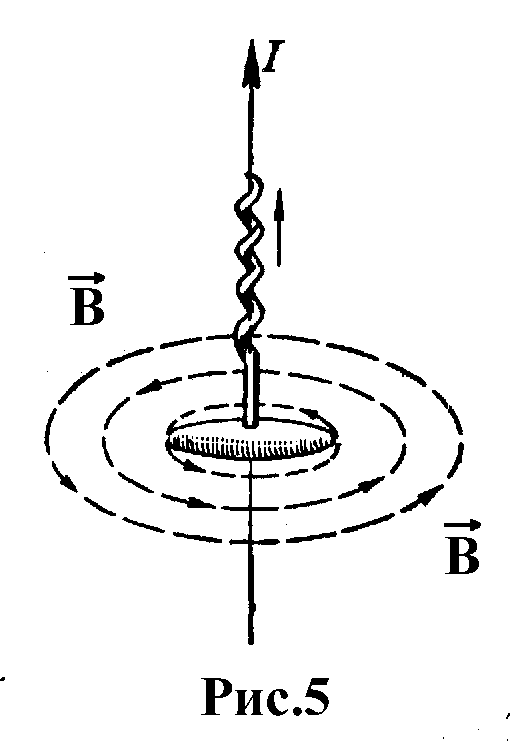
Правило буравчика: если поступательное движение буравчика совпадает с направлением тока, то направление вращения его рукояти даст направление магнитных линий напряженности (рис.5).

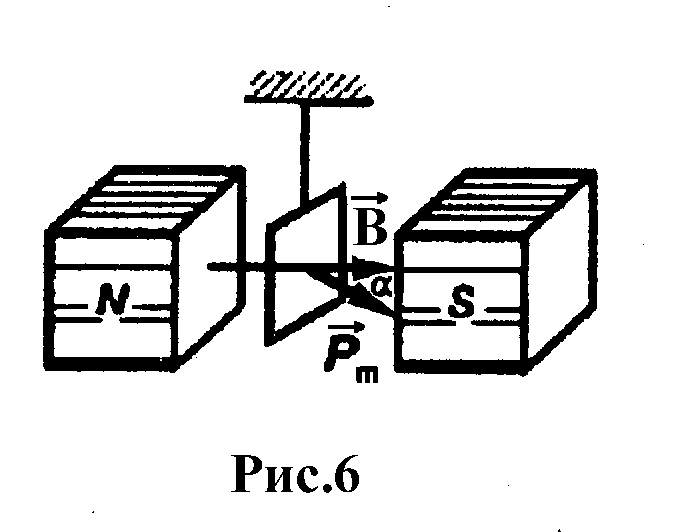
О величине вектора магнитной индукции 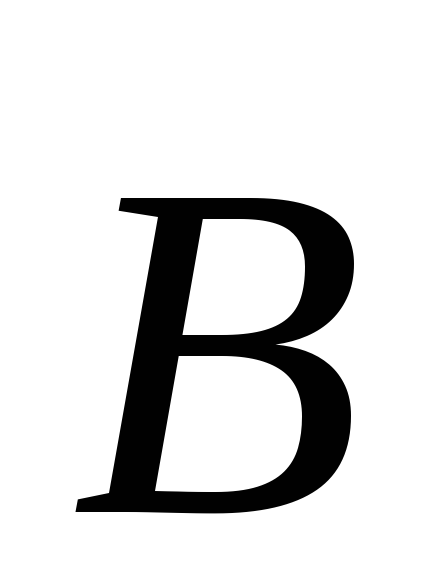судят по величине крутящего момента, испытываемого пробной рамкой при ее повороте в магнитном поле (рис.6) :

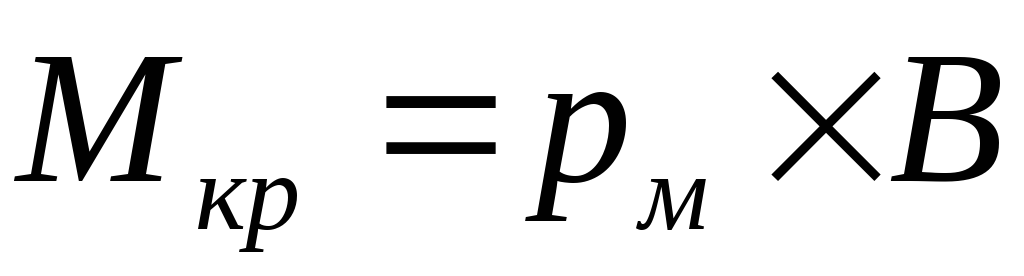или

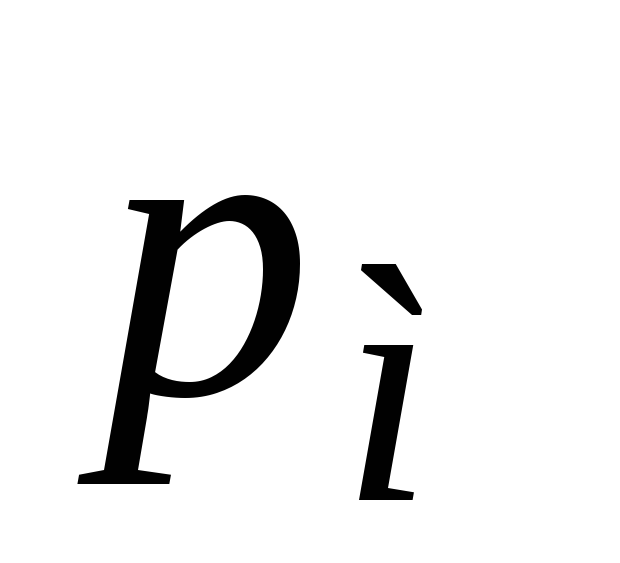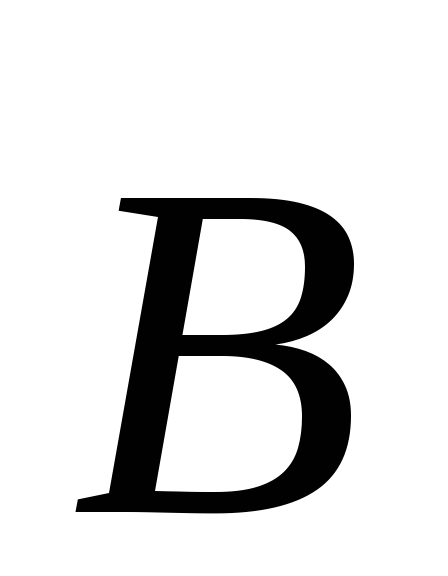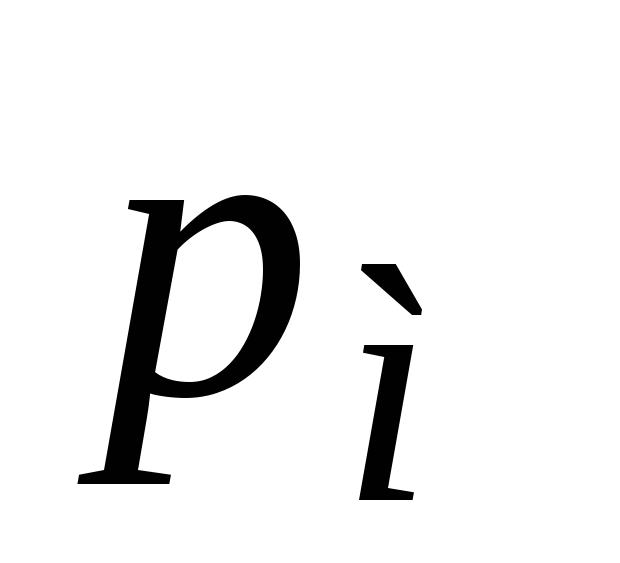 — угол между векторами и ; — магнитный момент контура с током

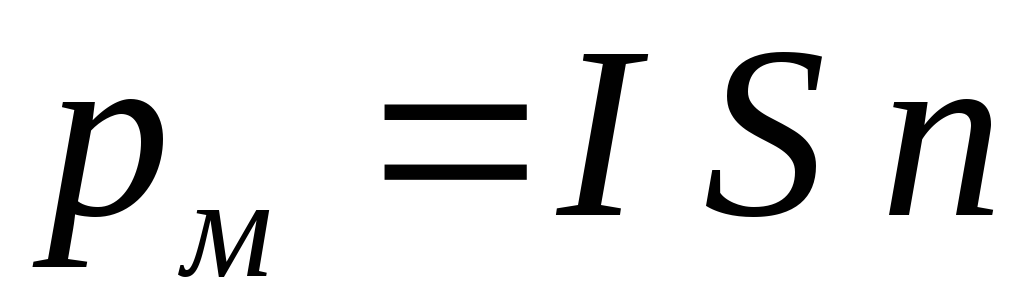или

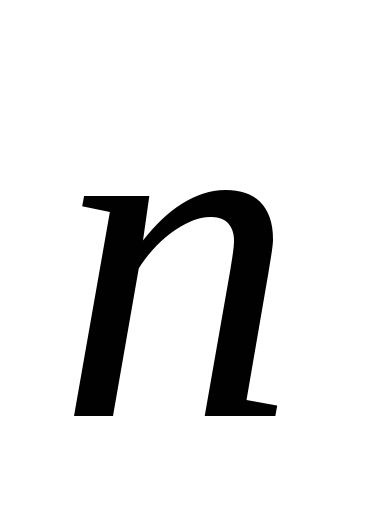
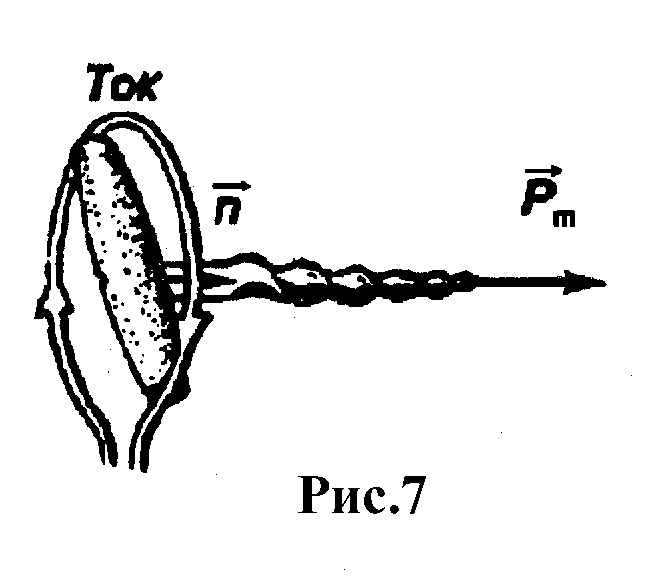— единичный вектор нормали к рамке, направление которого определяется по правилу буравчика (рис.7).

В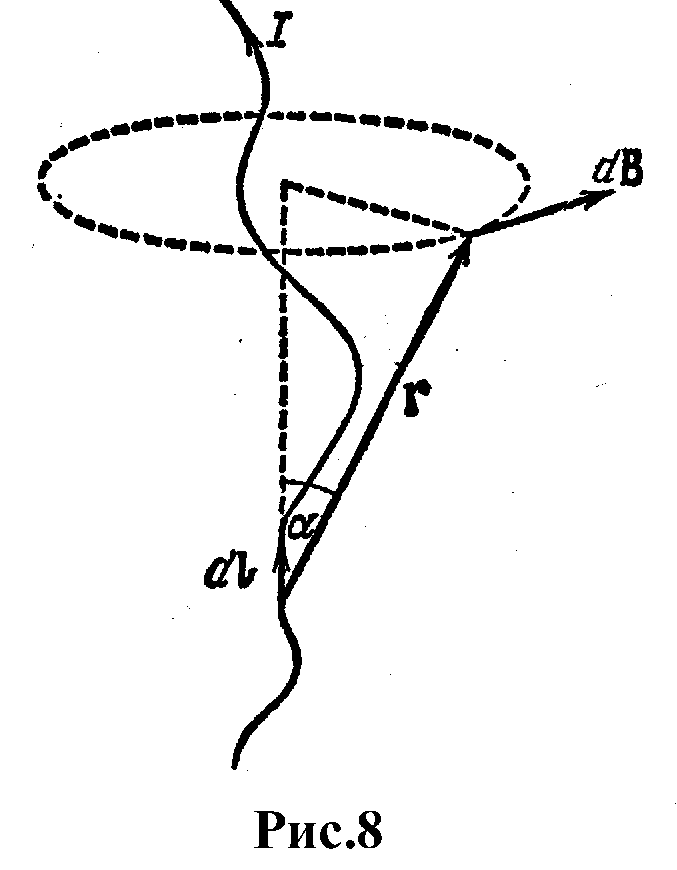еличина магнитной зависит от свойств среды. Характеристика независящая от свойств среды называется вектором напряженностью магнитного поля . Напряженность магнитного поля измеряется в амперах деленных на метр [H] = 1 а/м.

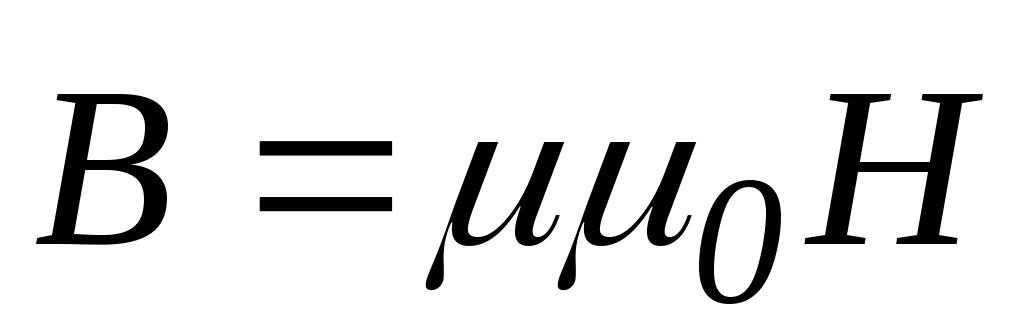
₀ = 4  10^-7 Гн/м — магнитная постоянная;  — магнитная проницаемость среды, для вакуума  = 1.

Чтобы найти суммарную индуктивность или напряженность создаваемую несколькими магнитными полями используют принцип суперпозиции магнитных полей: магнитное поле, создаваемое несколькими источниками, равно векторной сумме напряженностей магнитных полей от каждого источника

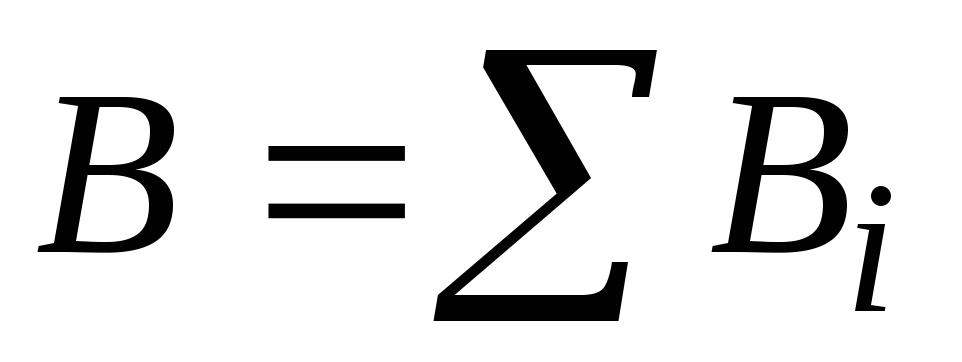
fizika / Работа и мощность электрического тока. Закон Джоуля-Ленца в дифференциальной форме

Работа и мощность электрического тока. Закон Джоуля-Ленца в дифференциальной форме.

Работа электрического тока показывает, какая работа была совершена электрическим полем при перемещении зарядов по проводнику.

Зная две формулы: I = q/t ….. и ….. U = A/q  можно вывести формулу для расчета работы электрического тока: 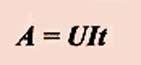  Работа электрического тока равна произведению силы тока на напряжение и на время протекания тока в цепи.

Единица измерения работы электрического тока в системе СИ: [ A ] = 1 Дж = 1A. B . c

НАУЧИСЬ, ПРИГОДИТСЯ !  При расчетах работы электрического тока часто применяется  внесистемная кратная единица работы электрического тока: 1 кВт.ч (киловатт-час).

1 кВт.ч = ………..Вт.с = 3 600 000 Дж

В каждой квартире для учета израсходованной электроэнергии устанавливаются специальные приборы-счетчики электроэнергии, которые показывают работу электрического тока,  совершенную за какой-то отрезок времени при включении различных бытовых электроприборов.  Эти счетчики показывают работу электрического тока ( расход электроэнергии) в «кВт.ч».

Необходимо научиться рассчитывать стоимость израсходованной электроэнергии! Внимательно разбираемся в решении задачи на странице 122 учебника (параграф 52) ! 

МОЩНОСТЬ ЭЛЕКТРИЧЕСКОГО ТОКА

Мощность электрического тока показывает работу тока, совершенную в единицу времени и равна отношению совершенной работы ко времени, в течение которого эта работа была совершена.

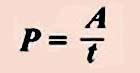
(мощность в механике принято обозначать буквой N, в электротехнике — буквой Р) так как А = IUt, то мощность электрического тока равна:

или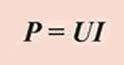 

Единица мощности электрического тока в системе СИ:

[ P ] = 1 Вт (ватт) = 1 А . B

Закон Джо́уля — Ле́нца — физический закон, дающий количественную оценку теплового действия электрического тока. Установлен в 1841 году Джеймсом Джоулем и независимо от него в 1842 году Эмилием Ленцем^[1].

В словесной формулировке звучит следующим образом^[2]

Мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведению плотности электрического тока на величину напряженности электрического поля

Математически может быть выражен в следующей форме:

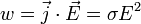
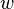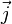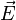где  — мощность выделения тепла в единице объёма,  — плотность электрического тока,  — напряжённость электрического поля, σ — проводимость среды.

Закон также может быть сформулирован в интегральной форме для случая протекания токов в тонких проводах^[3]:

Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивления участка

В математической форме этот закон имеет вид

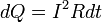
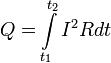
где dQ — количество теплоты, выделяемое за промежуток времени dt, I — сила тока, R — сопротивление, Q — полное количество теплоты, выделенное за промежуток времени от t₁ до t₂. В случае постоянных силы тока и сопротивления: