Работа, энергия и мощность — вспоминаем физику
В текстах, публикуемых на этом сайте, часто встречаются различные термины, которые являются названиями физических величин. Многое мы изучали еще в школьном курсе физике, но знания имеют свойство забываться без постоянного употребления. В серии заметок, объединенных под общим заголовком «Вспоминаем физику» (можно было бы назвать «Снова в школу») мы постараемся напомнить вам, что означают основные термины, какие физические величины за этими терминами скрываются, как они связаны между собой, в каких величинах они измеряются. В общем, дать те основы, которые нужны для понимания публикуемых материалов.
Сайт нас в целом посвящен методам и технологиям получения энергии (конкретно, из возобновляемых источников). Энергия нужна людям для отопления и освещения собственных жилищ, для того, чтобы приводить в движение различные механизмы, которые совершают полезную для людей работу. То есть нам нужно получить в конечном итоге один из трех видов энергии — тепловую, механическую и энергию света. Как будет сказано ниже, в физике различают еще несколько видов энергии, но для нас важны в первую очередь эти три вида. Закончу с предисловиями и приведу те определения энергии, которые приняты в физике.
Работа и энергия
Еще из школьного курса физики (а школу я окончил 50 лет назад) я помню утверждение «Энергия является мерой способности физической системы совершить работу». Википедия дает менее понятное определение, утверждая, что
«Эне́ргия — скалярная физическая величина, являющаяся единой мерой различных форм движения и взаимодействия материи, мерой перехода движения материи из одних форм в другие. Введение понятия энергии удобно тем, что в случае, если физическая система является замкнутой, то её энергия сохраняется в этой системе на протяжении времени, в течение которого система будет являться замкнутой. Это утверждение носит название закона сохранения энергии.»
Энергия является скалярной величиной, для измерения которой применяются несколько разных единиц. Нам наиболее интересны джоуль и киловатт-час.
Джо́уль (русское обозначение: Дж; международное: J) — единица измерения работы, энергии и количества теплоты в Международной системе единиц (СИ). Джоуль равен работе, совершаемой при перемещении точки приложения силы, равной одному ньютону, на расстояние одного метра в направлении действия силы. В электричестве джоуль означает работу, которую совершают силы электрического поля за 1 секунду при напряжении в 1 вольт для поддержания силы тока в 1 ампер.
Впрочем, мы не будем углубляться в основы физики, выясняя, что такое сила и что такое один ньютон, просто примем понятие «энергия» за основу и запомним, что некое количество джоулей характеризует энергию, работу и количество теплоты. Еще одной величиной, с помощью которой измеряют количество энергии, является киловатт-час.
Килова́тт-час (кВт⋅ч) — внесистемная единица измерения количества произведенной или потреблённой энергии, а также выполненной работы. Используется преимущественно для измерения потребления электроэнергии в быту, народном хозяйстве и для измерения выработки электроэнергии в электроэнергетике.
Следует заметить, что правильно писать именно «кВт⋅ч» (мощность, умноженная на время). Написание «кВт/ч» (киловатт в час), часто употребляемое во многих СМИ и даже иногда в официальных документах, неправильно. Такое обозначение соответствует изменению мощности в единицу времени (что обычно никого не интересует), но никак не количеству энергии. Столь же распространённая ошибка — использовать «киловатт» (единицу мощности) вместо «киловатт-час».
В последующих статьях мы будем использовать джоуль и киловатт-час как единицы для оценки количества энергии или работы, имея в виду, что один киловатт-час равен 3,6·10
С точки зрения интересующих нас тем именно свойство энергии совершать работу является основополагающим. Мы не будем выяснять, как физика трактует понятие «работа», будем считать, что это понятие является первоначальным и не определяемым. Только еще раз подчеркнем, что количественно энергия и работа выражаются в одних единицах.
В зависимости от вида энергии или работы величина энергии рассчитывается разными способами:
| В механике: сила, умноженная на длину | E ~ F·l |
| В термодинамике: давление, умноженное на объём | E ~ P·V |
| Импульс, умноженный на скорость | E ~ p·v |
| Масса, умноженная на квадрат скорости | E ~ m·v² |
| В электростатике: заряд, умноженный на напряжение | E ~ q·U |
| Мощность, умноженная на время | E ~ N·t |
Формы и виды энергии
Поскольку энергия, как сказано выше, является только мерой различных форм движения и взаимодействия материи, мерой перехода движения материи из одних форм в другие, различные формы энергии выделяются в соответствии с различными формами движения материи. Таким образом, в зависимости от уровня проявления, можно выделить следующие формы энергии:
- энергия макромира — гравитационная или энергия притяжения тел,
- энергия взаимодействия тел — механическая,
- энергия молекулярных взаимодействий — тепловая,
- энергия атомных взаимодействий — химическая,
- энергия излучения — электромагнитная,
- энергия, заключенную в ядрах атомов, — ядерная.
Гравитационная энергия — энергия системы тел (частиц), обусловленная их взаимным гравитационным тяготением. В земных условиях, это, например, энергия, «запасенная» телом, поднятым на определенную высоту над поверхностью Земли — энергия силы тяжести. Таким образом, энергию, запасенную в водохранилищах гидроэлектростанций, можно отнести к гравитационной энергии.
Механическая энергия — проявляется при взаимодействии, движении отдельных тел или частиц. К ней относят энергию движения или вращения тела, энергию деформации при сгибании, растяжении, закручивании, сжатии упругих тел (пружин). Эта энергия наиболее широко используется в различных машинах — транспортных и технологических.
Тепловая энергия — энергия неупорядоченного (хаотического) движения и взаимодействия молекул веществ. Тепловая энергия, получаемая чаще всего при сжигании различных видов топлива, широко применяется для отопления, проведения многочисленных технологических процессов (нагревания, плавления, сушки, выпаривания, перегонки и т. д.).
Химическая энергия — это энергия, «запасенная» в атомах веществ, которая высвобождается или поглощается при химических реакциях между веществами. Химическая энергия либо выделяется в виде тепловой при проведении экзотермических реакций (например, горении топлива), либо преобразуется в электрическую в гальванических элементах и аккумуляторах. Эти источники энергии характеризуются высоким КПД (до 98 %), но низкой емкостью.
Электромагнитная энергия — это энергия, порождаемая взаимодействием электрического и магнитного полей. Ее подразделяют на электрическую и магнитную энергии. Электрическая энергия — энергия движущихся по электрической цепи электронов (электрического тока).
Электромагнитная энергия проявляется также в виде электромагнитных волн, то есть в виде излучения, включающего видимый свет, инфракрасные, ультрафиолетовые, рентгеновские лучи и радиоволны. Таким образом, один из видов электромагнитной энергии — это энергия излучения. Излучение переносит энергию в форме энергии электромагнитной волны. Когда излучение поглощается, его энергия преобразуется в другие формы, чаще всего в теплоту.
Ядерная энергия — энергия, локализованная в ядрах атомов так называемых радиоактивных веществ. Она высвобождается при делении тяжелых ядер (ядерная реакция) или синтезе легких ядер (термоядерная реакция).
В эту классификацию несколько не укладываются известные нам со школы понятия потенциальной и кинетической энергии. Современная физика считает, что понятия кинетической и потенциальной энергий (а также энергии диссипации) это не формы, а виды энергии:
Кинетическая энергия — энергия, которой обладают тела вследствие своего движения. Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением. Когда тело не движется, кинетическая энергия равна нулю.
Потенциальная энергия
Энергия диссипации (то есть рассеяния) — переход части энергии упорядоченных процессов в энергию неупорядоченных процессов, в конечном счёте — в теплоту.
Дело в том, что каждая из перечисленных выше форм энергии может проявляться в виде потенциальной и кинетической энергии. То есть виды энергии должны трактоваться в обобщенном смысле, ибо они относятся к любой форме движения и, следовательно, к любой форме энергии. Например, имеется кинетическая электрическая энергия, и это не то же самое, что кинетическая механическая энергия. Это кинетическая энергия движения электронов, а не кинетическая энергия механического движения тела. Точно так же потенциальная электрическая энергия это не то же самое, что потенциальная механическая энергия. А химическая энергия складывается из кинетической энергии движения электронов и электрической энергии их взаимодействия друг с другом и с атомными ядрами.
Вообще, насколько я понял при подготовке этого материала, пока не существует общепринятой классификации форм и видов энергии. Впрочем, возможно нам и не нужно до конца разбираться в этих физических понятиях. Важно только помнить, что энергия — это не какая-то реальная материальная субстанция, а только мера, предназначенная для оценки перемещения некоторых форм материи или преобразования одной формы материи в другую.
С понятием энергии и работы неразрывно связано понятие мощности.
Мощность
Мо́щность — физическая величина, равная в общем случае скорости изменения, преобразования, передачи или потребления энергии системы. В более узком смысле мощность равна отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.
В Международной системе единиц (СИ) единицей измерения мощности является ватт, равный одному джоулю, делённому на секунду.
Мощность характеризует способность того или иного устройства совершать работу или производить энергию в течение определенного промежутка времени. Связь между мощностью, энергией и временем выражается следующим соотношением:
Киловатт-час (напомним, что это единица измерения энергии) равен количеству энергии, потребляемой (производимой) устройством мощностью один киловатт (единица мощности) в течение одного часа (единица времени).
Отсюда и уже упомянутое выше равенство 1 кВт⋅ч = 1000 Вт ⋅ 3600 с = 3,6·106 Дж = 3,6 МДж.
Из трех рассмотренных на этой странице единиц именно мощность представляет для нас наибольший интерес, поскольку эта величина будет нам встречаться при рассмотрении и сравнении различных ветро- или гидро-генераторов и солнечных панелей. В этих случаях мощность характеризует способность этих устройств производить энергию. И наоборот, указание мощности на многих бытовых электроприборах характеризует потребление энергии этими приборами. Если мы хотим обеспечить некоторую совокупность бытовых приборов энергией, мы должны сопоставить суммарную потребляемую этими приборами мощность с суммарной мощностью, которую можем получить от производителей энергии.
Но подробнее о мощности мы поговорим в следующих статьях, посвященных конкретным видам энергии. И начнем с электрической энергии, рассмотрим, какими величинами характеризуется электричество и в каких единицах оно измеряется.
9. Энергия, работа, мощность
9.1. Энергия. Работа силы___
Энергия________________________________________________________
Универсальная мера различных форм движения и взаимодействия.
С различными формами движения материи связывают различные виды энергии — механическую, тепловую, электромагнитную, ядерную и др.
Работа силы______________________________________________
Количественная характеристика процесса обмена энергией между взаимодействующими телами.
Работа постоянной силы F, составляющей угол α
с направлением прямолинейного движения тела_
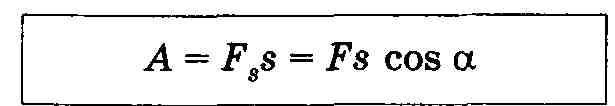
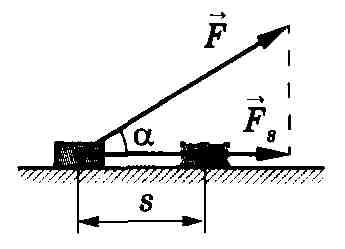Работа
этой силы равна произведению проекции
силы Fs на
направление перемещения (Fs =
F
cos
α),
умноженной на перемещение точки
приложения силы. Элементарная
работа силы 
на
перемещении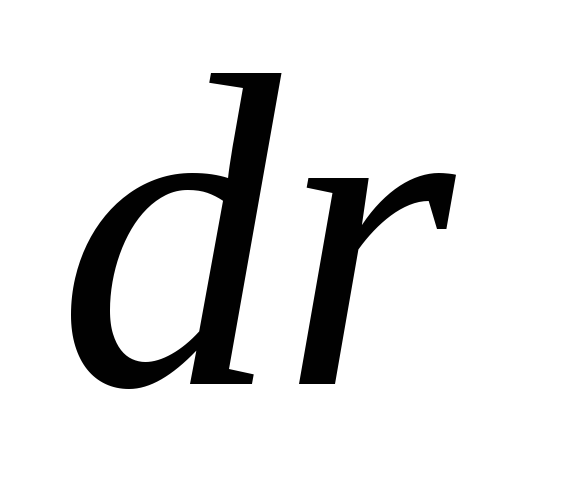 
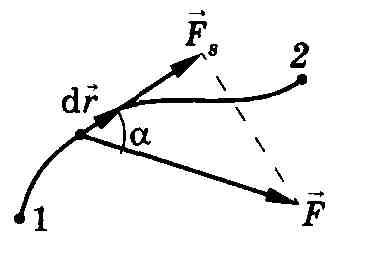
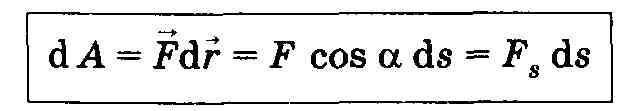[α
— угол между векторами 
и 
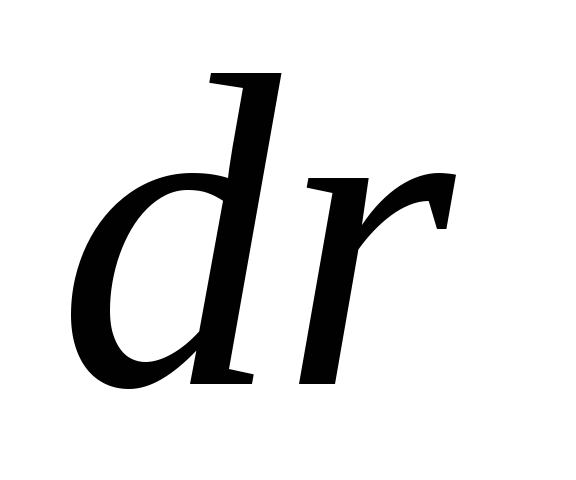;ds
= |
|
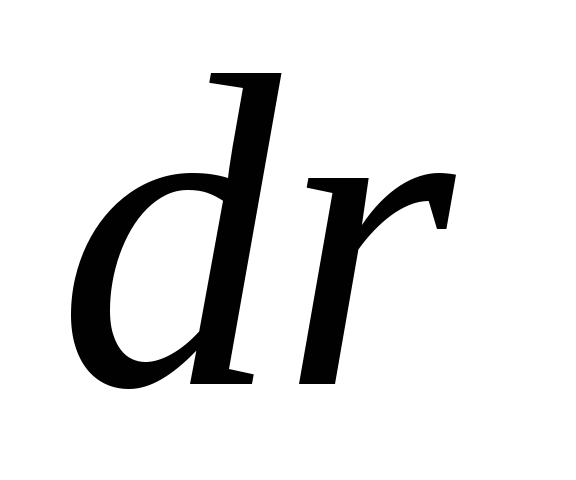— элементарный путь; Fs — проекция
вектора 
на
вектор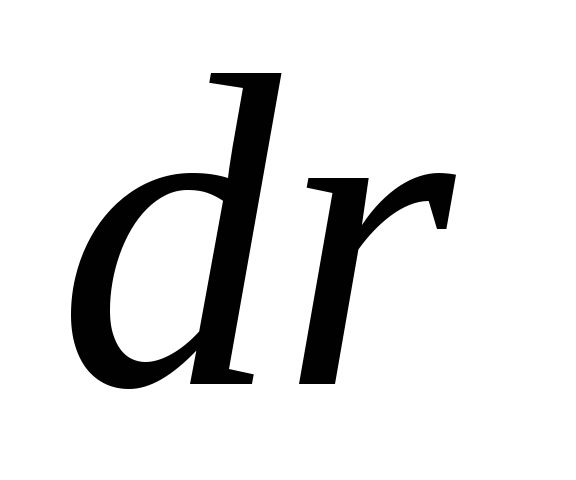 
]
♦ Работа — величина скалярная.
Работа силы на участке траектории 1—2________________________________________________________
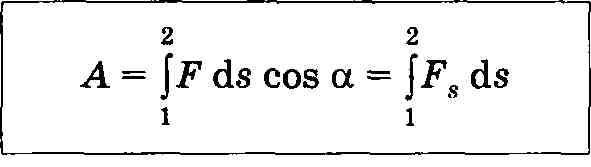
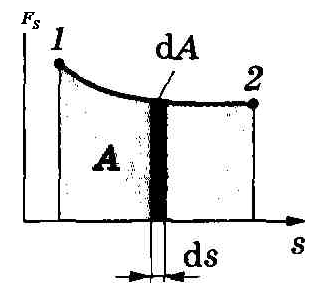Для
вычисления этого интеграла надо
знать зависимость Fs от
s
вдоль траектории 1—2 (пример
на рисунке).
Геометрический смысл выражения для А: искомая работа определяется на графике площадью закрашенной фигуры.
Единица работы
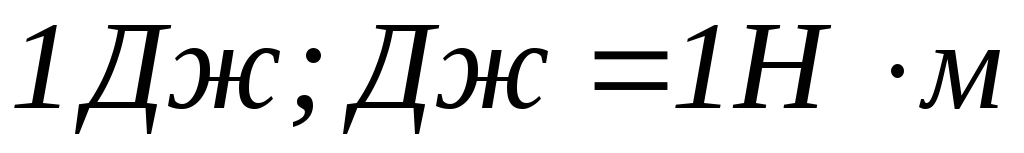1
джоуль — работа, совершаемая силой,
равной 1 Н на пути 1 м.
9.2. Мощность
Ф
изическая
величина, характеризующая скорость
совершения работы.
Мощность, развиваемая силой F
Равна
скалярному произведению вектора силы
на вектор скорости, с которой движется
точка приложения этой силы.
За
время dt сила 
совершает
работу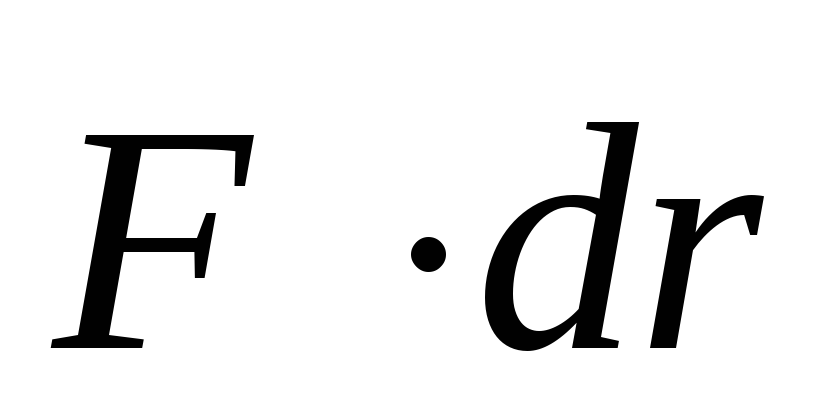 
, и
мощность, развиваемая этой
силой,
в данный момент времени равна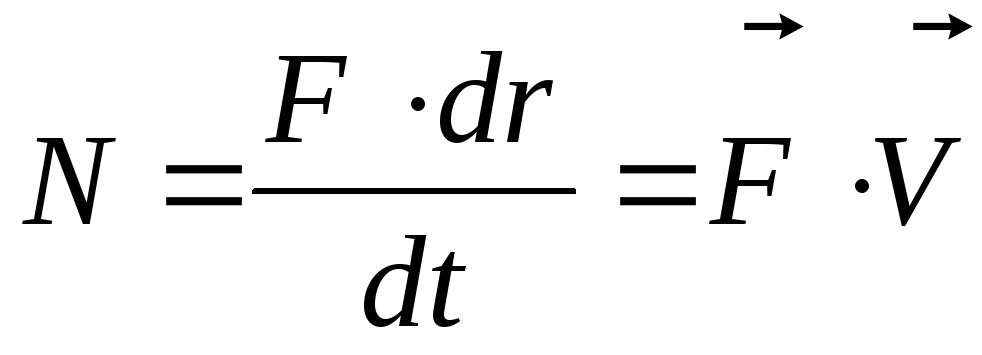 
♦Мощность — величина скалярная.
Единица мощности_
1 ватт — мощность, при которой за время 1 с совершается работа
1
Дж
.
9.3. Кинетическая и потенциальная энергия
Кинетическая энергия_
Кинетическая энергия механической системы
Энергия механического движения этой системы.
Связь работы и кинетической энергии___
dT = dA
Приращение кинетической энергии материальной точки (тела) на элементарном перемещении равно элементарной работе на том же перемещении.
Сила 
, действуя
на покоящееся тело и вызывая его
движение, совершает работу, а энергия
движущегося тела возрастает на величину
затраченной работы. Работа dA
силы 
на
пути, который тело прошло за время
возрастания скорости от 0 до 
, идет
на увеличение кинетической энергии
dT
тела. Можно записать:
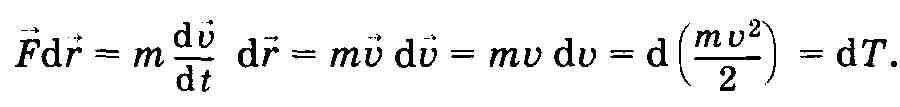
Кинетическая энергия тела массой т, движущегося со скоростью V.
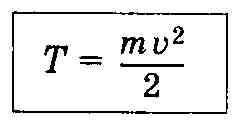Определяется
работой, которую надо совершить, чтобы
сообщить телу данную скорость.
Характерные свойства
Кинетическая энергия Т всегда положительна; неодинакова в разных инерциальных системах отсчета; является функцией состояния системы.
Работа сил при перемещении из точки 1 в точку 2
Теорема о кинетической энергия
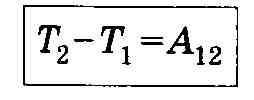Приращение
кинетической энергии материальной
точки на некотором перемещении равно
алгебраической сумме работ всех сил,
действующих на материальную точку на
том же перемещении.
Энергия и мощность электрического тока
В любой замкнутой электрической цепи источник затрачивает электрическую энергию Wистна перемещение единицы положительного заряда по всей цепи: и на внутреннем и на внешнем участках.
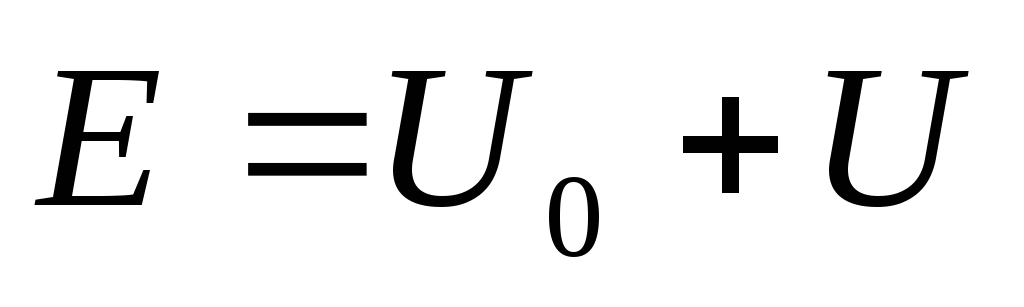и
;
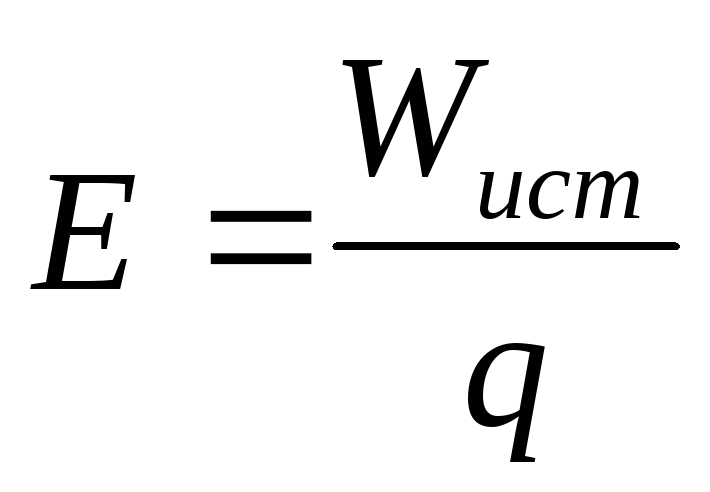Энергия источника определяется выражением: Wист=Eq=EIt= (U0+U)It;
Энергия источника (полезная), которая расходуется на потребителе: W=UIt;
Энергия источника (потери), которая расходуется на внутреннем сопротивлении источника: W=U0It;
Преобразование электрической энергии в другие виды энергий происходит с определенной скоростью. Эта скорость определяет электрическую мощность элементов электрической цепи:
;
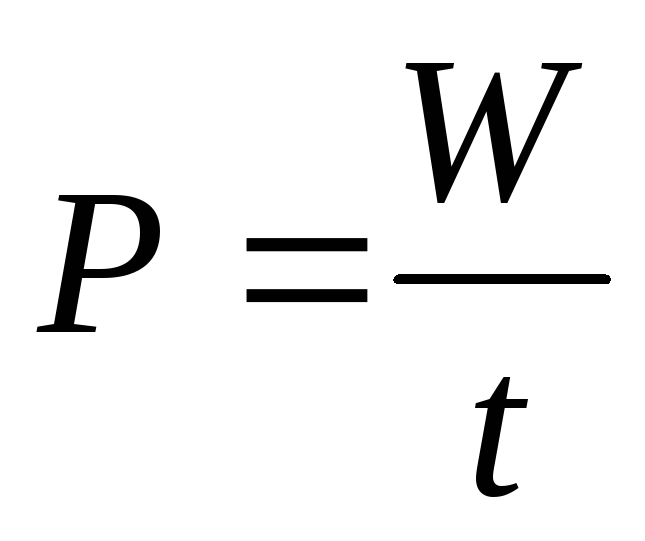Мощность источника определяется соотношением:
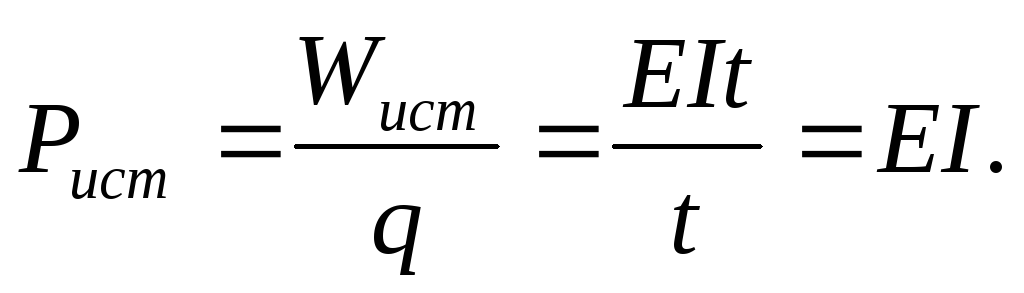
Мощность потребителя определяется соотношением:
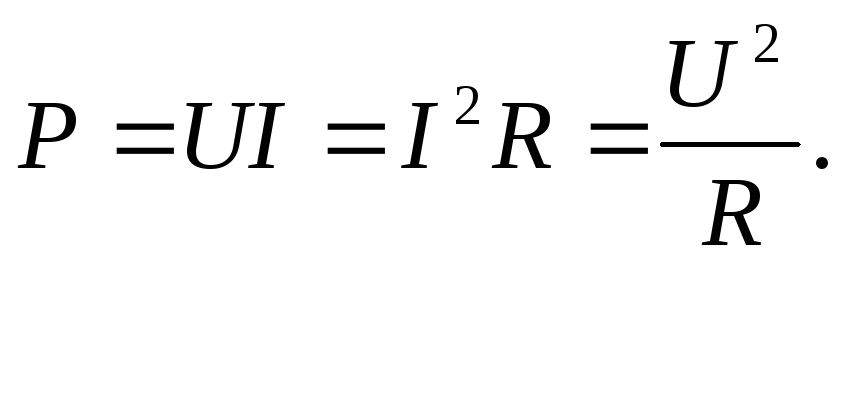
Коэффициент полезного действияэлектрической цепиηопределяется отношением мощности потребителя к мощности источника:
Закон Джоуля — Ленца
Ток, протекая по проводнику, нагревает его (в этом случае электрическая энергия преобразуется в тепловую). Количество выделенного тепла будет определяться количеством электрической энергии, затраченной в этом проводнике.
Дж.
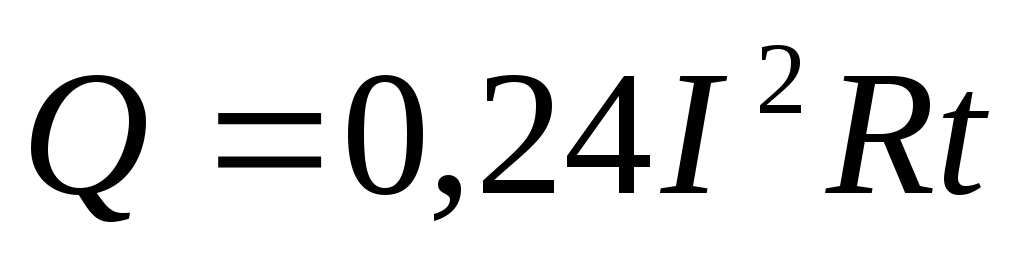(кал).
Коэффициент 0,24 (электротермический эквивалент) устанавливает зависимость между электрической и тепловой энергией.
Часть3: Режимы работы электрических цепей
В электрических цепях все основные элементы делятся на активные и пассивные. Активными считаются элементы, в которых преобразование энергии сопровождается возникновением ЭДС (аккумуляторы, генераторы). Элементы, в которых ЭДС не возникает, называются пассивными.
Параметры электрических цепей:
Ток в замкнутой цепи 
;
Напряжение на клеммах источника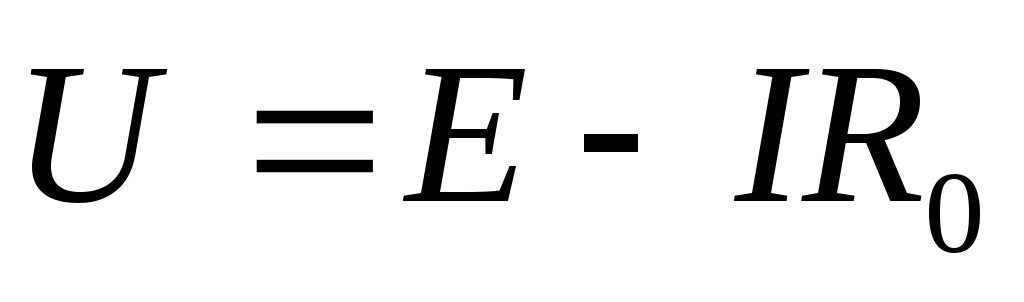 
;
Падение напряжения на сопротивлении
источника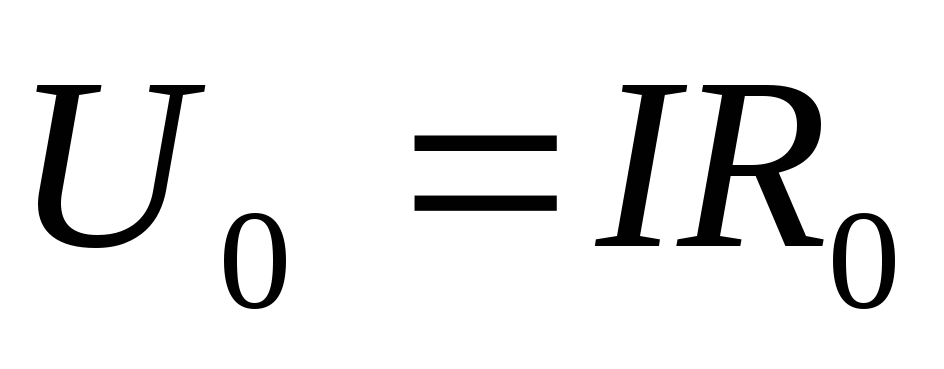 
;
Полезная мощность (мощность потребителя)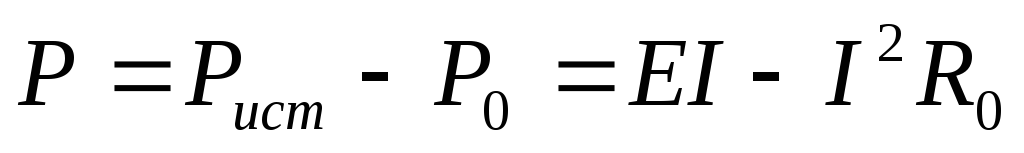 
.
Электрические цепи могут работать в трех режимах:
Условие максимальной отдачи мощности: полезная мощность максимальна, когда сопротивление потребителя R станет равным внутреннему сопротивлению источника R0.
КПД при максимальной отдаче мощности равно 50%, к 100% КПД приближается в режиме, близком к холостому ходу.
Нормальным (рабочим) режимом называют такой режим работы цепи, при котором ток, напряжение и мощность не превышают номинальных значений, заданных заводом-изготовителем.
Источники тока могут работать в режиме генератора и в режиме нагрузки. Источники, ЭДС которых совпадают с направлением тока в цепи, работают в режиме генератора, а источники , ЭДС которых не совпадают с направлением тока, работают в режиме потребителя.
Напряжение источника, работающего в
режиме генератора: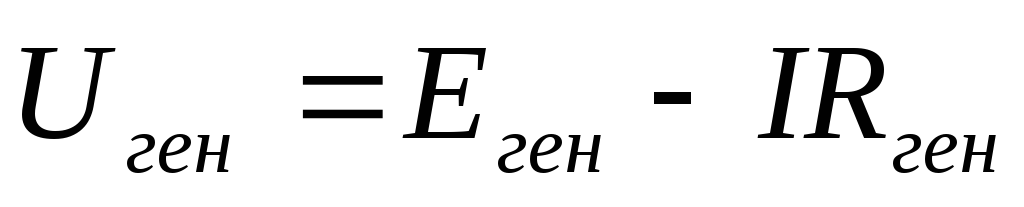 
.
Напряжение источника, работающего в
режиме потребителя: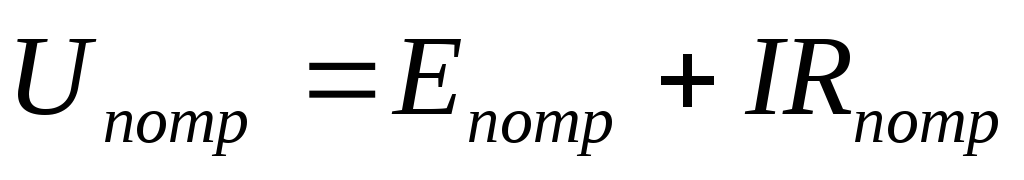 
.
Тема 1.3
Расчет электрических цепей постоянного тока
Основной целью расчета электрической цепи является нахождение ее параметров: ток, напряжение, сопротивление, мощность, КПД. Значения параметров дают возможность оценить условия и эффективность работы электротехнического оборудования и приборов во всех участках электрической цепи.
Для расчета электрических цепей основой служат законы Ома и Кирхгофа, Джоуля-Ленца.
Законы Кирхгофа
К характерным элементам электрической цепи относятся ветвь, узел, контур.
Ветвью электрической цепи называется ее участок, на всем протяжении которого величина тока имеет одинаковое значение. Ветви, которые содержат источники питания называются активными, а которые не содержат их – пассивными.
Узлом электрической цепи называется точка соединения электрических ветвей.
Контуром электрической цепи называют замкнутое соединение, в которое могут входить несколько ветвей.
Первый закон Кирхгофа
Сумма токов входящих в узел равна сумме токов, выходящих из узла. ИЛИ Сумма токов, сходящихся в узле равна нулю.
∑I=0; — математическое выражение первого закона Кирхгофа.
Второй закон Кирхгофа
Алгебраическая сумма ЭДС в замкнутом контуре электрической цепи равна алгебраической сумме падений напряжений на всех участках этой цепи.
;
— математическое выражение второго
закона Кирхгофа.
Последовательное соединение потребителей
Последовательным соединением участков эй цепи называют соединение, при котором через все участки цепи проходит один и тот же ток.
Общее напряжение последовательно
соединенных элементов равно сумме
напряжений на каждом элементе согласно
второму закону Кирхгофа: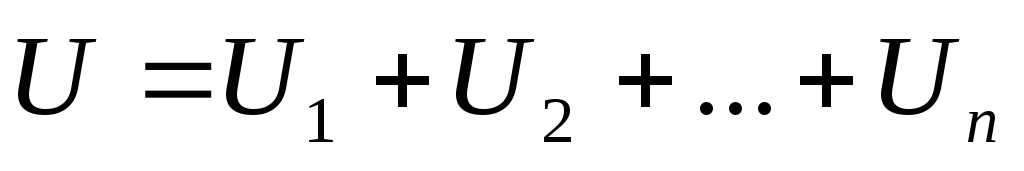 
;
В соответствии с законом Ома: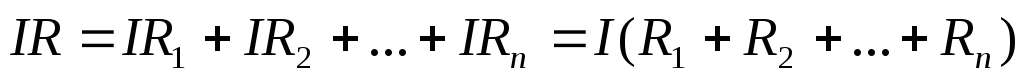 
;
Из этого соотношения следует: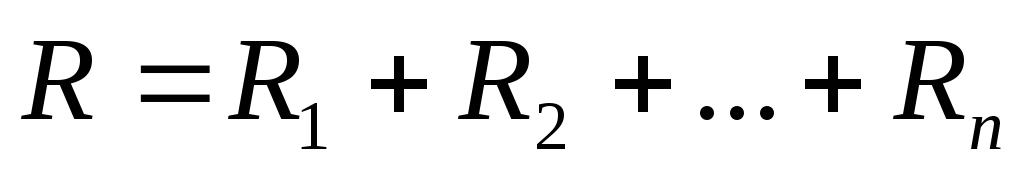
; Таким образом, общее сопротивление
цепи с последовательно соединенными
элементами равно сумме этих сопротивлений.
Параллельное сопротивление потребителей
Параллельным соединением участков электрической цепи называется соединение, при котором все участки цепи присоединяются к одной паре узлов, то есть находятся под действием одного и того же напряжения.
Общий ток такого соединения согласно
первому закона Кирхгофа будет равен
сумме токов в отдельных ветвях: 
;
В соответствии с законом Ома: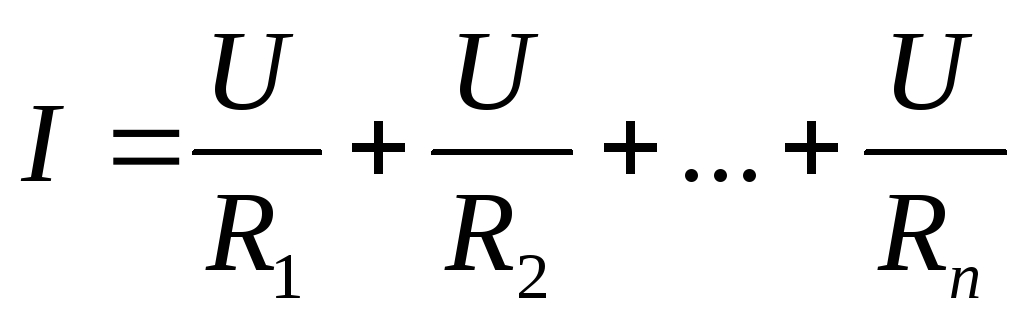
;
Если поделить левую и правую части наU, получим: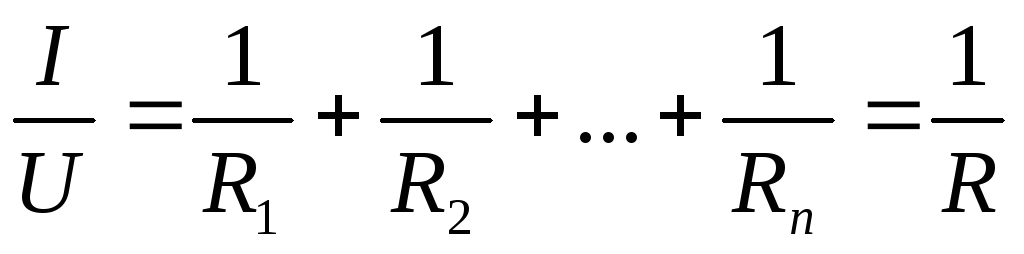
;
Обратная величина общего эквивалентного сопротивления параллельно включенных потребителей равна сумме обратных величин этих потребителей.
Величина, обратная сопротивлению
определяет проводимость потребителя
g. Тогда для параллельно
соединенных потребителей справедливо: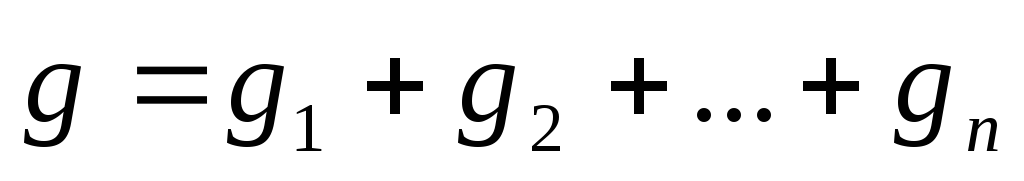
;
Глава 3 Работа и энергия
§11. Энергия, работа, мощность
Энергия — универсальная мера различных форм движения и взаимодействия. С различными формами движения материи связывают различные формы энергии: механическую, тепловую, электромагнитную, ядерную и др. В одних явлениях форма движения материи не изменяется (например, горячее тело нагревает холодное), в других — переходит в иную форму (например, в результате трения механическое движение превращается в тепловое). Однако существенно, что во всех случаях энергия, отданная (в той или иной форме) одним телом другому телу, равна энергии, полученной последним телом.
Изменение механического движения тела вызывается силами, действующими на него со стороны других тел. Чтобы
количественно характеризовать процесс обмена энергией между взаимодействующими телами, в механике вводится понятие работы силы.
Если тело движется прямолинейно и на него действует постоянная сила F, которая составляет некоторый угол а с направлением перемещения, то работа этой силы равна произведению проекции силы Fs на направление перемещения (Fs =Fcos), умноженной на перемещение точки приложения силы:
A = Fss = Fscos. (11.1)
В общем случае сила может изменяться как по модулю, так и по направлению, поэтому формулой (11.1) пользоваться нельзя. Если, однако, рассмотреть элементарное перемещение dr, то силу F можно считать постоянной, а движение точки ее
22
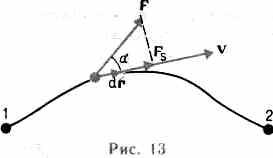
приложения — прямолинейным. Элементарной работой силы F на перемещении dr называется скалярная величина
dА =Fdr = Fcos•ds=Fsds,
где а — угол между векторами F и dr; ds = |dr| — элементарный путь; Fs — проекция вектора F на вектор dr (рис. 13).
Работа силы на участке траектории от точки 1 до точки 2 равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках пути. Эта сумма приводится к интегралу
Для вычисления этого интеграла надо знать зависимость силы Fs от пути s вдоль траектории 1—2. Пусть эта зависимость представлена графически (рис. 14), тогда искомая работа А определяется на графике площадью закрашенной фигуры. Если, например, тело движется прямолинейно, сила F=const и =const, то получим
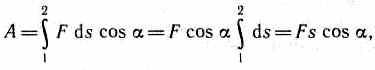
где s — пройденный телом путь (см. также формулу (11.1)).
Из формулы (11.1) следует, что при </2 работа силы положительна, в этом случае составляющая Fs совпадает
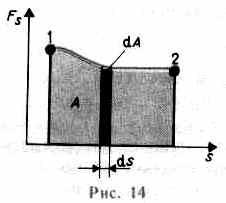
по направлению с вектором скорости движения v (см. рис. 13). Если >/2, то работа силы отрицательна. При =/2 (сила направлена перпендикулярно перемещению) работа силы равна нулю.
Единица работы — джоуль (Дж): 1 Дж — работа, совершаемая силой в 1 Н на пути в 1 м (1 Дж = 1 Н•м).
Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности:
N=da/dt. (11.3)
За время dt сила F совершает работу Fdr, и мощность, развиваемая этой силой, в данный момент времени
N=Fdr/dt=Fv
т. е. равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы; N — величина скалярная.
Единица мощности — ватт (Вт): 1 Вт — мощность, при которой за время 1 с совершается работа в 1 Дж (1 Вт = 1 Дж/с).
11. Работа силы, мощность кин-я и пот-я э. Энергия, работа силы, мощность
Энергия — универсальная мера различных форм движения и взаимодействия. Изменение механического движения тела вызывается силами, действующими на него со стороны других тел. Работы силы — процесс обмена энергией между взаимодействующими телами.
Если
на тело движуещаеся прямолинейно действует постоянная сила F, которая
составляет некоторый угол
с направлением перемещения, то работа
этой силы равна произведению проекции
силы Fs на направление перемещения, умноженной
на перемещение точки приложения силы: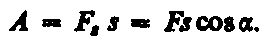
(1)
В
бщем случае сила может изменяться как
по модулю, так и по направлению, поэтому скалярная величина элементарной
работоы силы F на перемещении dr: 
где
— угол между векторами F и dr; ds
= |dr|
— элементарный путь; Fs — проекция вектора F на вектор dr
рис. 1
Работа силы на участке траектории от точки 1 до точки 2 равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках пути: (2)
где s — пройденный телом. При </2 работа силы положительна, если >/2 работа силы отрицательна. При =/2 (сила перпендикулярна перемещению) работа силы равна нулю.
Единица работы — джоуль (Дж): работа, совершаемая силой 1 Н на пути 1 м (1 Дж=1 Н м).
Мощность – величина скорости совершения работы:
(3)
За
время dt сила F
совершает работу Fdr,
и мощность, развиваемая этой силой, в
данный момент ремени:
(4)
т. е. равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы; N — величина скалярная.
Единица мощности — ватт (Вт): мощность, при которой за время 1с совершается работа 1Дж (1Вт = 1Дж/с).
Кинетическая и потенциальная энергии
Кинетическая энергия механической системы — энергия механического движения этой системы.
Сила F, действуя на покоящееся тело и вызывая его движение, совершает работу, а изм-е энергии движущегося тела(dT) возрастает на величину затраченной работы dA. Т . е. dA = dТ
Используя второй закон Ньютона(F=mdV/dt) и ряд др-х преобразований получаем
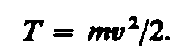(5)
— кинетическая энергия тела массой m,
движущееся со скоростью v.
Кинетическая энергия зависит только от массы и скорости тела.
В разных инерциальных системах отсчета, движущихся друг относительно друга, скорость тела, а следовательно, и его кинетическая энергия будут неодинаковы. Т. о., кинетическая энергия зависит от выбора системы отсчета.
Потенциальная энергия — механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.
В сл-е взаимодействия тел осуществл-х посредством силовых полей(поля упругих, гравитационных сил), работа, совершаемая действующими силами при перемещении тела, не зависит от траектории этого перемещения, а зависит только от начального и конечного положений тела. Такие поля называются потенциальными, а силы, действующие в них, — консервативными. Если же работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такая сила называется диссипативной(сила трения). Тело, находясь в потенциальном поле сил, обладает потенциальной энергией П. Работа консервативных сил при элементарном(бесконечно малом) изменении конфигурации системы равна приращению потенциальной энергии, взятому со знаком минус: dA= — dП (6)
Работа dA — скалярное произведение силы F на перемещение dr и выражение (6) можно записать: Fdr= -dП (7)
При расчётах потенциальную энергию тела в каком-то определенном положении считают равной нулю(выбирают нулевой уровень отсчета), а энергию тела в других положениях отсчитывают относительно нулевого уровня.
Конкретный
вид функции П зависит от характера
силового поля. Например, потенциальная
энергия тела массой т, поднятого на высоту h над поверхностью Земли, равна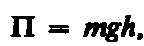
(8)
где высота h отсчитывается от нулевого уровня, для которого П0=0.
Т. к. начало отсчета выбирается произвольно, то потенциальная энергия может иметь отрицательное значение(кинетическая энергия всегда положительна!). Если принять за нуль потенциальную энергию тела, лежащего на поверхности Земли, то потенциальная энергия тела, находящегося на дне шахты(глубина h‘ ), П= —mgh‘.
Потенциальная энергия системы является функцией состояния системы. Она зависит только от конфигурации системы и ее положения по отношению к внешним телам.
Полная механическая энергия системы равна сумме кинетической и потенциальной энергий: E=T+П.
Мощность против энергии: принципиальные различия схожих понятий
23 Марта 2018
Алексей Телегин, ведущий блога по источникам питания Keysight Technologies
Мы продолжаем знакомить читателей с материалами, посвященными базовым понятиям и подходам в использовании источников питания (ИП), современным решениям в данной области и уникальным функциям, помогающим решить самые сложные задачи, возникающие при тестировании. В этом номере менеджер по развитию бизнеса и ведущий раздела по системам электропитания объединенного блога Keysight Technologies в России Алексей Телегин обсуждает такие фундаментальные понятия, как мощность и энергия.
Энергия становится все более ценным товаром, ведь человечество гораздо быстрее находит способы ее потребления, чем способы воспроизводства. Даже если бы мы были способны добывать или преобразовывать энергию в неограниченных количествах, процессы ее производства и потребления все равно оказывали бы огромное влияние на жизнь всей планеты. Для решения проблемы растущих потребностей необходимы более разумные и эффективные способы использования энергии. Нельзя не отметить, что в ряде отраслей происходит постоянное развитие технологий для решения данной задачи, и компания Keysight Technologies является активным участником этого, безусловно, положительного процесса.
Несмотря на то, что мощность и энергия — фундаментальные понятия, и большинство профессионалов прекрасно понимают различие между ними, я иногда встречаю сотрудников, ошибочно использующих одно из этих слов вместо другого. Действительно, эти понятия тесно связаны, но все же являются принципиально разными по смыслу.
Итак, начнем с энергии. Вероятно, лучше всего рассматривать ее с точки зрения классической механики движения заряженных частиц. Уравнение кинетической энергии выглядит следующим образом:
Ek = ½ × m × v2,где Ek — энергия частицы, m — масса, а v — скорость. До тех пор, пока эта движущаяся частица не испытывает воздействия, ее энергия остается неизменной. Но что произойдет с частицей под действием внешней силы? Этот вопрос приводит нас к понятию работы. Механическая работа — это мера силы, зависящая от численной величины, направления силы и от перемещения точки. Если эта сила действует в том же направлении, что и перемещение, работа определяется как положительная. Частица получает энергию. Если сила действует в направлении, противоположном перемещению, тогда работа является отрицательной. Энергия частицы уменьшается. Работа выражается следующим образом:
W = Ek2–Ek1,где Ek1 — энергия частицы до воздействия на нее силы, а Ek2 — энергия частицы после воздействия.
Работа — это количественная мера изменения энергии этой частицы.
Мы подошли к вопросу определения потенциальной энергии. В механике потенциальную энергию можно описать как нечто, что я буду называть возобновляемой силой, приложенной в направлении, противоположном перемещению. В самом типичном случае это будет масса объекта, поднятого на некоторую высоту, на который действует сила тяжести. Это также может быть сила, использованная для растягивания пружины на некоторое расстояние. В случае силы тяжести потенциальную энергию описывает следующая формула:
Ep = m × g × y,где Ep — потенциальная энергия частицы, m — масса, g — сила тяжести, а y — высота частицы над заданной точкой отсчета. Обратите внимание, что вес — это произведение массы на силу тяжести. Работа, складываемая или вычитаемая (соответственно), — это подъем или опускание частицы на вертикальное расстояние под действием силы тяжести.
Для электричества понятия работы и энергии точно такие же, как и в контексте механики. Известно, что энергию нельзя создать или уничтожить, ее можно только преобразовать из одной формы в другую. Энергию света можно преобразовать в электрическую при помощи фотоэлемента. Электрическую энергию можно преобразовать в механическую при помощи электродвигателя и т. д. Эти процессы не являются эффективными на все 100%, потому что значительная доля исходной энергии преобразуется также в тепловую. Общепринятой мерой энергии являются джоули, которые равны одной ватт-секунде. Чаще всего мы сталкиваемся с этим понятием, когда оплачиваем счета за электроэнергию: сумма в них рассчитывается на основании количества киловатт-часов электроэнергии, которая израсходована с момента выставления предыдущего счета.
Как и в механике, энергию в электрических системах можно сохранять — в частности, в реактивных компонентах (катушках индуктивности и конденсаторах). Энергия в катушке вычисляется по формуле:
E = ½× L × I2,где E — энергия в джоулях, L — индуктивность в генри, а I — сила тока в амперах. Катушка индуктивности хранит свою энергию в магнитном поле. Соответственно, энергия конденсатора определяется по формуле:
E = ½× C × V2,где E — энергия в джоулях, C — емкость в фарадах, а V — электрический потенциал в вольтах. Конденсатор хранит свою энергию в электрическом поле.
Надеюсь, что теперь вы имеете более четкое представление о том, что представляет собой энергия (и работа). Далее необходимо связать эти понятия с мощностью.
Мы знаем, как можно увеличить энергию или, наоборот, уменьшить ее в системе под воздействием совершаемой работы, и установили, что совершенная работа приводит к изменению количества энергии. Но необходимо также знать, в течение какого периода выполнялась работа. Ведь она могла совершаться в течение минуты, дня или года. Мощность является мерой скорости, с которой выполняется работа, и энергии, добавляемой в систему или удаляемой из системы.
Средняя мощность = совершаемая работа/интервал времени.Когда мы слышим слово «мощность», чаще всего нам в голову приходит мощность в лошадиных силах, которой обладает какой-нибудь автомобиль (по крайней мере, это утверждение справедливо для большинства автолюбителей). Несмотря на то, что чаще всего это понятие используется в отношении механических систем, лошадиная сила все же остается мерой мощности, точно так же, как и электрическая мощность, которую мы потребляем из розеток у себя дома.
Когда-то, еще во времена тепловых двигателей, Джеймс Ватт придумал термин «лошадиная сила» в качестве средства для сравнения своих паровых двигателей с интенсивностью работы, которую может производить лошадь. Механическая работа — это мера силы (фунты), затраченной на перемещение на расстояние (футы). В результате расчета было принято, что лошадь может переместить 550 футо-фунтов за одну секунду, или производить 550 футо-фунтов мощности в секунду.
Электрическая мощность также является мерой работы, выполняемой за единицу времени. Однако в этом случае она перемещает заряд в 1 Кл (кулон) при потенциале в 1 В (вольт) за 1 с (секунду). Обратите внимание, что 1 А (ампер) равен 1 Кл/с. Одна единица электрической мощности равна одному ватту. Подведем итог:
P (ватты) = Q (кулоны) × V (вольты) / t (секунды) = I (амперы) × V (вольты).Мы говорили о том, что энергия измеряется в ватт-секундах и киловатт-часах. Разделите количество энергии на интервал времени, за который она была использована, и вы получите мощность в ваттах и киловаттах! Какова взаимосвязь между механической и электрической мощностью? Когда появились первые электродвигатели, необходимо было соотнести работу, которую они могли выполнить, с работой тепловых двигателей, которая измерялась в лошадиных силах, где одна лошадиная сила равна 550 футо-фунтов/с. Было определено, что электромотору с КПД, равным 100%, требуется 746 Вт электрической мощности, чтобы произвести одну лошадиную силу механической мощности. Обратите внимание, что оценка работы в лошадиных силах основана на британских единицах измерения физических величин. Мера лошадиной силы на основании метрической системы немного отличается и составляет около 735 Вт.
Итак, теперь вы умеете рассчитывать количество потребляемой мощности электрическими приборами и в лошадиных силах, и в ваттах. В то же время, вы также можете рассчитать мощность двигателя своего автомобиля в ваттах (или киловаттах) вместо лошадиных сил: в наши дни это довольно полезный навык, поскольку мощность в ваттах признается во всем мире, а в лошадиных силах — не везде.
1.Ток, напряжение, энергия и мощность в электрических цепях. Баланс мощностей.
Электри́ческий ток — направленное движение электрически заряженных частиц, например, под воздействием электрического поля. Такими частицами могут являться: в проводниках — электроны, в электролитах — ионы (катионы и анионы), в полупроводниках — электроны и дырки (электронно-дырочная проводимость).
Ток – постоянный(I=const действующее значение переменного тока)
– переменный (i – мгновенное значение переменного тока) i=ImSin(wt)
Напряжение – отношение затраченной энергии для перемещения заряда из одной точки в другую точку цепи. U=dW/dq; W=∫uidt
Электри́ческая мощность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии. S=P+jQ
— полная мощность, ВА (вольт-ампер)
— активная мощность, Вт (ватт)
— реактивная мощность, ВАр (вольт-ампер реактивный)
Название | Напряжение | ток | мощность |
Активное сопрот. | U=Ri | i=U/R | P=I2R=U2g g=1/R |
Индуктивное сопрот. | uL=Ldi/dt | iL=1/L∫uLdt | WL=Li2/2 |
Емкостное сопрот. | uC=1/C∫iCdt | iC=CduC/dt | WC=CU2/2 |
Баланс мощностей:
∑Pист=∑Pпотр
∑IiEi +∑Jk Uk=∑Ij2 Rj
2.Расчет простейших цепей с одним источником энергии (метод эквивалентных преобразований, входная и взаимная проводимости, принцип взаимности и теорема компенсации)
Входные и взаимные проводимости. Входной проводимостью gmm ветви m называется отношение тока Im ветви m к э.д.с. Em источника, помещенного в эту ветвь, при отсутствии э.д.с. в других ветвях:gmm=Im/Em
Взамной (передаточной) проводимостью gkm называется отношение тока Ik ветви k к э.д.с. Em источника ветви m. gkm=Ik/Ek
Принцип взаимности справедлив для линейных электрических цепей с одним источником э.д.с. и может быть сформулирован следующим образом: если источник э.д.с. E действует в любой ветви сколь угодно сложной цепи, не содержащей других источников э.д.с., вызывает в другой ветви ток I, то будучи перенесенным в последнюю, вызовет в первой ветви такой же ток I.
На принципе взаимности основан метод взаимности. Этот метод удобно применять для расчета цепей с одним источником э.д.с., когда его перенос упрощает расчет цепи.
Теорема компенсации. Токи в цепи не изменяются, если любое сопротивление (участок цепи) заменить источником с э.д.с., по величине равной падению напряжения на данном сопротивлении (участке цепи) и направленной навстречу току.
3.Методы расчета сложных электрических цепей. Метод непосредственного применения законов Кирхгофа (последовательность, особенности и пример расчета)
Зако́ны Кирхго́фа (или правила Кирхгофа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи.
Для формулировки законов Кирхгофа, в электрической цепи выделяются узлы — точки соединения трёх и более проводников и контуры — замкнутые пути из проводников. При этом каждый проводник может входить в несколько контуров.
Первый закон (ЗТК, Закон токов Кирхгофа) гласит, что алгебраическая сумма токов в любом узле любой цепи равна нулю (значения вытекающих токов берутся с обратным знаком):
Второй закон (ЗНК, Закон напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений по любому замкнутому контуру цепи равна алгебраической сумме ЭДС, действующих вдоль этого же контура. Если в контуре нет ЭДС, то суммарное падение напряжений равно нулю:
Законы Кирхгофа справедливы для линейных и нелинейных цепей при любом характере изменения во времени токов и напряжений. Токи, втекающие в узел, считаются положительными, а вытекающие — отрицательными.
Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно), перепад напряжения считается положительным, в противном случае — отрицательным.
Законы Кирхгофа, записанные для узлов и контуров цепи, дают полную систему линейных уравнений, которая позволяет найти все токи и напряжения.
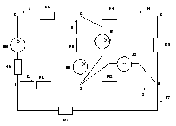
Запишем первый закон Кирхгоффа для 4 – 1 узлов:
узел 2: I5=I4+I8+J8узел 4: J2+I2=I7+I4узел 1: I7+I6=I1
Запишем второй закон Кирхгофа для трех контуров:
контур 15231: I1·R1+I8·R8+I6·(R5+R6)=E8+E6
контур 1341: I1·R1+I2·R2+I7·R7=0
контур 26432: -I4·(R8+R3)-I2·R2+I8·R8=E8