Мощность формулы по физике: Недопустимое название — Викиверситет — groupnk.ru — Группа НК — комплексные поставки электрооборудования в Москве и регионах

Содержание

Мощность | Физика

Одна и та же работа может быть совершена за разное время. Если, например, требуется перенести на какое-то расстояние мешок с песком, то человек это может сделать за несколько минут, а муравью, таскающему по одной песчинке, для этого потребуется несколько лет.

Быстроту совершения работы характеризуют мощностью. Мощность показывает, какая работа совершается за единицу времени (в СИ — за 1 с). Если, например, за 2 с была совершена работа 6 Дж, то за 1 с была совершена работа, в 2 раза меньшая. Разделив 6 Дж на 2 с, мы получим 3 Дж/с. Это и есть мощность.

Итак, чтобы найти мощность, надо работу разделить на время, в течение которого совершалась эта работа:

или

(19.1)

где

N — мощность, А — работа, t — время.

Единицей мощности в СИ является ватт (1 Вт). 1 Вт — это такая мощность, при которой за 1 с совершается работа 1 Дж:

1 Вт = 1 Дж/с.

Эта единица названа в честь английского изобретателя Дж.

Ватта (Уатта), построившего первую паровую машину. Сам Уатт (1736—1819) пользовался другой единицей мощности — лошадиной силой (1 л. с.), которую он ввел с целью возможности сравнения работоспособности паровой машины и лошади:

1 л. с. = 735,5 Вт.

В технике часто применяют более крупные единицы мощности — киловатт и мегаватт:

1 кВт = 1000 Вт, 1 МВт = 1000000 Вт.

Мощность является важной характеристикой любого двигателя. Различные двигатели имеют мощности от сотых и десятых долей киловатта (двигатель электрической бритвы, швейной машины) до миллионов киловатт (двигатели ракет-носителей космических кораблей).

Средняя мощность, развиваемая сердцем, равна 2,2 Вт. А при прыжке с места или рывке при поднятии тяжести человек может развить мощность в тысячу раз больше.
Зная мощность, можно рассчитать работу. Из формулы (19.1) следует, что

A = Nt. (19.2)

Чтобы найти работу, надо мощность умножить на время, в течение которого совершалась работа.

I. Что характеризует мощность? 2. Что показывает мощность? 3. Как находится мощность? 4. Как называется единица мощности в СИ? 5. Как, зная мощность и время, можно рассчитать работу?

Физика. Механика

Представим снова элементарную работу в виде

Удельная величина, равная отношению работы совершенной за время dt к этому времени, называется мощностью:

Другими словами, мощность, развиваемая некоторой силой, равна скорости, с которой эта сила производит работу. Можно сказать и так: средняя за единицу времени мощность численно равна работе совершенной за единицу времени. Если мощность за выбранную единицу времени практически не меняется, то слово «средняя» можно опустить: мощность численно равна работе за единицу времени.

Как видно из определения, мощность равна скалярному произведению силы на скорость перемещения её точки приложения, поэтому работа силы за время от

t₁ до t₂ может быть вычислена следующим образом:

Средняя мощность за этот же промежуток времени равна

За единицу мощности принимается такая мощность, при которой в единицу времени совершается единица работы.

В системе СИ единицей измерения мощности является ватт (Вт):

Внесистемная единица мощности — лошадиная сила (л.с.) — равна 736 Вт. В быту часто используют единицу энергии —

1 кВт•ч = 103 Вт•3600 с=3.6 МДж.

Пример. Вертолет массой m = 3 m висит в воздухе. Определить мощность, развиваемую мотором вертолета, если диаметр ротора равен d = 8 м. При расчете принять, что ротор отбрасывает вниз цилиндрическую струю воздуха диаметром, равным диаметру ротора. Плотность воздуха 1.29 кг/м3.

При решении этой задачи надо применить все известные нам законы динамики. Поскольку это — не одно- и не двухходовая задача, попробуем сначала найти вид окончательного выражения, пользуясь анализом размерности (см. тему 1.3). Искомая мощность зависит от: 1) веса вертолета mg; 2) диаметра винта d, 3) плотности воздуха , то есть искомая формула должна иметь вид

Размерность мощности будет [N] = [ML2T–3].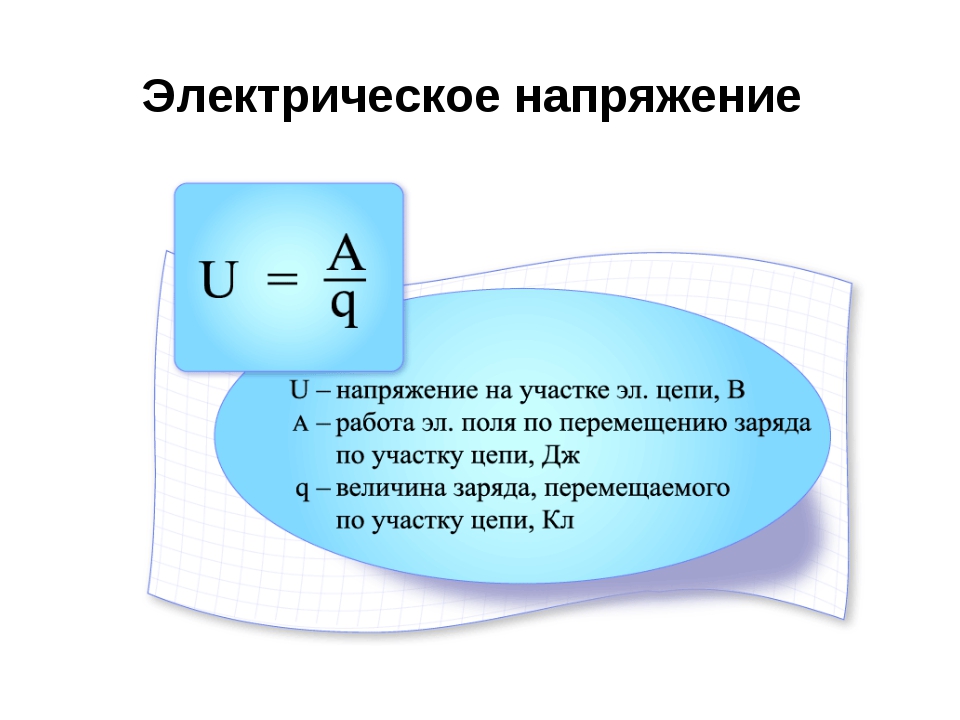 Составляем равенство размерностей в обеих частях искомой формулы:

Решая систему уравнений

находим

то есть искомая мощность двигателя вертолета будет

где C — некий числовой коэффициент.

Решим теперь эту же задачу точно. Пусть — скорость струи воздуха, отбрасываемой винтом. За время частицы воздуха проходят расстояние . Иными словами, за время винт вертолета придает скорость всем частицам воздуха, находящимся в цилиндре с площадью основания и высотой . Масса воздуха в этом объеме равна

а его кинетическая энергия дается выражением

Поскольку мотор передает воздуху кинетическую энергию , то такова и совершаемая им работа. Поэтому развиваемая мотором мощность (без учета потерь мощности во всех трансмиссиях на пути от двигателя до винта) равна

В этом выражении нам надо еще найти скорость струи воздуха, отбрасываемой винтом. Импульс , передаваемый частицам воздуха за время , равен

Из второго закона Ньютона следует, что средняя сила, действующая на отбрасываемый вниз воздух равна . По третьему закону Ньютона такая же сила действует на вертолет со стороны воздуха. Эта сила компенсирует вес вертолета:

Отсюда получаем уравнение

позволяющее найти скорость струи воздуха:

Подставляя найденную скорость в выражение для мощности двигателя вертолета, получаем окончательный результат:

Мы видим, что выражение для мощности действительно оказалось таким, каким ожидалось на основе анализа размерностей. Подставляя числовые данные, находим

Рис.4.5. Мощность в природе и технике

Урок физики «Мощность»

Цели урока:

Познакомиться с мощностью как новой физической величиной;
Развивать умения выводить формулы, пользуясь необходимыми знаниями прошлых уроков; развивать логическое мышление, умение анализировать, делать выводы;
Применять знания по физике в окружающем мире.

Ход урока

«И вечный бой! Покой нам только снится
Сквозь кровь и пыль…
Летит, летит степная кобылица
И мнет ковыль…
И нет конца! Мелькают вёрсты, кручи…
Останови! …Покоя нет! Степная кобылица несется вскачь!»

А.Блок «На поле Куликовом» (июнь 1908 г). ( Слайд 1).

Урок сегодня я хочу начать с вопросов к вам. (Слайд 2).

1. Как вы думаете, имеет ли какое-то отношение лошадь к физике?

2. С какой физической величиной связана лошадь?

Мощность – правильно, это и есть тема нашего урока. Запишем ее в тетрадь.

Действительно, мощность двигателей автомобилей, транспортных средств до сих пор измеряют в лошадиных силах. Сегодня на уроке мы с вами узнаем всё о мощности с точки зрения физики. Давайте подумаем вместе и определим, что мы должны знать о мощности, как о физической величине.

Существует план изучения физических величин: ( Слайд 3).

Определение;
Вектор или скаляр;
Буквенное обозначение;
Формула;
Прибор для измерения;
Единица величины.

Этот план и будут целью нашего урока.

Начнем с примера из жизни. Вам необходимо набрать бочку воды для полива растений. Вода находится в колодце. У вас есть выбор: набрать при помощи ведра или при помощи насоса. Напомню, что в обоих случаях механическая работа, совершенная при этом будет одинаковой. Конечно же, большинство из вас выберут, насос.

Вопрос: В чем разница при выполнении одной и той же работы?

Ответ:

Насос выполнит эту работу быстрее, т.е. затратит меньшее время.

1) Физическая величина, характеризующая быстроту выполнения работы, называют мощностью. ( Слайд 4).

2) Скаляр, т.к. не имеет направления.

3) N.

5) [N] = [ 1 Дж/с] = [1Вт ]

Название этой единицы мощности дано в честь английского изобретателя паровой машины (1784г) Джеймса Уатта. ( Слайд 5).

6) 1 Вт = мощности, при которой за время 1 с совершается работа в 1 Дж. ( Слайд 6).

Самолеты, автомобили, корабли и другие транспортные средства движутся часто с постоянной скоростью. Например, на трассах автомобиль достаточно долго может двигаться со скоростью 100 км/ч. ( Слайд 7).

Вопрос: от чего зависит скорость движения таких тел?

Оказывается, она напрямую зависит от мощности двигателя автомобиля.

Зная, формулу мощности мы выведем еще одну, но для этого давайте вспомним основную формулу для механической работы.

Учащийся выходит к доске для вывода формулы. ( Слайд 8).

Пусть сила совпадает по направлению со скоростью тела. Запишем формулу работы этой силы.

2.При постоянной скорости движения , тело проходит путь определяемой формулой

Подставляем в исходную формулу мощности: , получаем — мощность.

У нас получилась еще одна формула для расчета мощности, которую мы будем использовать при решении задач.

Эта формула показывает ( Слайд 9), что при постоянной мощности двигателя, изменением скорости можно менять силу тяги автомобиля и наоборот, при изменении скорости автомобиля можно менять силу тяги двигателя.

При N = const

v > , F <.

v < , F >.

Вопрос. Когда нужна большая сила тяги?

Ответ:

а)При подъеме в гору. Правильно, тогда водитель снижает скорость.

б) При вспашке земли тракторист движется с малой скоростью, чтобы была большая сила тяги. Для этого водитель, тракторист, машинист, токарь, фрезеровщик часто используют коробку передач, которая позволяет менять скорость. ( Слайд 10).

Мощность всегда указывают в паспорте технического устройства. И в современных технических паспортах автомобилей есть графа:

Мощность двигателя: кВт / л.с.

Следовательно, между этими единицами мощности существует связь.

Вопрос: А откуда взялась эта единица мощности? ( Слайд 11).

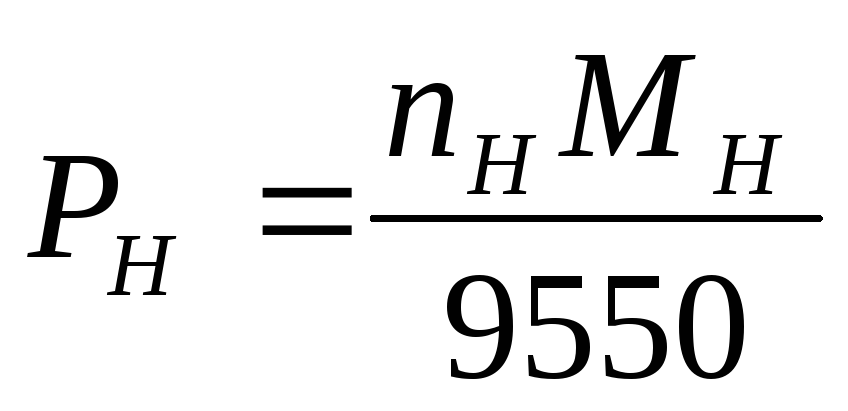
Дж. Уатту принадлежит идея измерять механическую мощность в «лошадиных силах». Предложенная им единица мощности была весьма популярна, но в 1948　г. Генеральной конференцией мер и весов была введена новая единица мощности в международной системе единиц – ватт. ( Слайд 12).

1 л.с. = 735,5 Вт.

1 Вт = ,00013596 л.с.

Эта единица мощности была изъята из обращения с 1 января 1980 г.

Примеры мощностей современных автомобилей. ( Слайд 13,14).

Различные двигатели имеют разные мощности.

Учебник, страница 134, таблица 5. [1]

Вопрос: А какова мощность человека?

Текс учебника, § 54. Мощность человека при нормальных условиях работы в среднем составляет 70-80 Вт. Совершая прыжки, взбегая по лестнице, человек может развивать мощность до 730 Вт, а в отдельных случаях и большую.[1]

Вопрос: А чем «живые двигатели» отличаются от механических? ( Слайд 15).

Ответ: Тем, что «живые двигатели» могут изменять свою мощность в несколько раз.

Закрепление материала.

1.Расскажите все, что вы знаете о мощности. Ответ по плану изучения физической величины.

2. Упр. 29, задача №6. ( Слайд 16).

Дано: СИ Решение:
m = 125кг N = A / t
h = 70 см 0,7 м A = F s s = h
t = 0,3 с F = P = mg
N = mgh / t
N — ? N = 125 кг · 9,8 Н/ кг · 0,7 м / 0,3 с= 2858,3 Вт ≈ 2,9 кВт

Ответ : N ≈ 2,9 кВт.

Домашнее задание: ( Слайд 17).

§ 54.
Записать формулы мощности в таблицу формул.
Упр. 29 (2,5) – 1 уровень.
Упр. 29 (1,3) – 2 уровень.
Упр. 29 (1,4) – 3 уровень.
Задание 18 – на дополнительную оценку ( на листочках).

Литература:

А.В. Перышкин «Учебник физики для 7 класса», Дрофа, Москва, 2006.
А. Блок «На поле Куликовом».
1C: Школа Физика 7 класс

Урок физики по теме «Мощность»

МОУ «Уразовская СОШ №2»

Урок физики

по теме «Мощность»

7 класс

Учитель :Бузунова Н.Н.

Тема урока: Мощность

Цель урока:

Познакомиться с мощностью как новой физической величиной;
Развивать умения выводить формулы, пользуясь необходимыми знаниями прошлых уроков; развивать логическое мышление, умение анализировать, делать выводы;
Создать условия для развития навыков общения и совместной деятельности. Вызвать желание постоянно пополнять свои знания, поддерживать интерес к физике, показывая применение физических явлений на практике

Оборудование: компьютер, проектор.

Тип урока: формирование и совершенствование умений и навыков.

Формы работы: коллективная, индивидуальная, фронтальная,

Средства обучения: объяснительно-иллюстративные, эвристические, исследовательские.

Методы: словесные (фронтальный опрос, проблемная ситуация), наглядные, практические (решение примеров и задач)

Технологии :тестовые, здоровьесберегающие, уровневая дифференциация, ИКТ

Ход урока

Организационный момент.

Цель: проверить готовность к уроку, настроить на рабочий лад, познакомить с планом урока.

II. Актуализация знаний. Проверка выполнения домашнего задания.

Цель: установить правильность, полноту и осознанность выполнения Д/З всеми учащимися; выявить пробелы и определить причины их возникновения.

Сегодня мы продолжим путешествие по «великому» физическому океану истины. Давайте соберемся, улыбнемся друг другу и отправимся в путь.

1.Разгадать кроссворд, определить ключевое слово

-Величина, измеряющаяся в секундах, минутах, часах.

-Физическая величина, измеряемая в джоулях.

— Направленный отрезок прямой, начало которого совпадает с начальным положением точки, а конец – с конечным положением точки

-Способность тела совершать работу.

-Единица измерения энергии.

-Физическая величина, характеризующая действие одного тела на другое, в результате которого другое тело получает ускорение в ИСО.

-Единица пути

-Английский ученый, один из основоположников классической механики.

Мощность – это и есть тема нашего урока. Запишем ее в тетрадь

2.Работа у доски:4 человека по карточкам решают задачи.

Автомобиль проехал расстояние 5 км равномерно. Сила тяги автомобиля — 3 кН. Какую работу совершил автомобиль?(15 МДж)

Вода массой 2 т при падении совершает работу 400 кДж. С какой высоты падает вода?

(20 м)

Трактор тянет плуг с силой 50 кН равномерно по полю, при этом проходит расстояние 30 км. Какую работу совершает трактор? (1500МДж)

Какая масса снега падает с горы при снежной лавине, если лавиной совершается работа 5 МДж, а высота горы 100 м? (5 000 кг)

Остальные

устная работа – заполнить таблицу
Физическая величина
Условное обозначение
Единица измерения
Формула
А
Сила
м
тестовые задания

1. При записи формул механическую работу обозначают буквой…, силу, действующую на тело буквой…, расстояние пройденное телом буквой….

a) A, F, S; б) A, S, F; в) F, A, S; г) S, F, А.

2. В каком из перечисленных случаев механическая работа равна нулю?

а) конькобежец пробегает установленную дистанцию;

б) подъемный кран опускает груз на землю;

в) стрела, выпущенная из лука, поражает цель;

г) человек держит на плечах тяжелый мешок.

3)В Международной системе исчисления механическая работа выражается в

а) кДж; б) МДж; в) мДж; г) Дж.

Физкультминутка

III.Формирование новых умений и навыков.

Цель: ознакомить учащихся с понятием «Мощность»

«И вечный бой! Покой нам только снится
Сквозь кровь и пыль…
Летит, летит степная кобылица
И мнет ковыль…
И нет конца! Мелькают вёрсты, кручи…
Останови! …Покоя нет! Степная кобылица несется вскачь!»

А. Блок «На поле Куликовом» (июнь 1908 г). ( Слайд 1).

(Слайд 2).

1. Как вы думаете, имеет ли какое-то отношение лошадь к физике?

2. С какой физической величиной связана лошадь?

Существует план изучения физических величин: ( Слайд 3).

Определение;
Буквенное обозначение;
Формула;
Единица величины.

Вопрос: В чем разница при выполнении одной и той же работы?

Ответ: Насос выполнит эту работу быстрее, т.е. затратит меньшее время.

1) Физическая величина, характеризующая быстроту выполнения работы, называют мощностью.. ( Слайд 4)

2) Скаляр, т.к. не имеет направления.

3) N

Вывод формулы ( Слайд 5,6).

( Слайд 7)

5) [N] = [ 1 Дж/с] = [1Вт ]

Название этой единицы мощности дано в честь английского изобретателя паровой машины (1784г) Джеймса Уатта. Историческая справка( Слайд 5).

6) 1 Вт = мощности, при которой за время 1 с совершается работа в 1 Дж. ( Слайд 8).

Вопрос: от чего зависит скорость движения таких тел?

Оказывается, она напрямую зависит от мощности двигателя автомобиля.

Учащийся выходит к доске для вывода формулы. ( Слайд 10).

Пусть сила совпадает по направлению со скоростью тела. Запишем формулу работы этой силы.

2.При постоянной скорости движения перемещение точки определяется формулой (в течении этого промежутка времени движение точки практически является равномерным и прямолинейным). Поэтому работа силы, направление которой совпадает или противоположно скорости точки, будет равна

Подставляем в исходную формулу мощности формулу работы , получаем

У нас получилась еще одна формула для расчета мощности, которую мы будем использовать при решении задач.

Эта формула показывает ( Слайд 9), что при постоянной мощности двигателя, изменением скорости можно менять силу тяги автомобиля.

При неизменной мощности двигателя N

Если v , то F ( при увеличении скорости сила, приложенная к движущемуся телу уменьшается)

Если v , то F ( при уменьшении скорости сила, приложенная к движущемуся телу увеличивается)

Вопрос. Когда нужна большая сила тяги?

Ответ: а)При подъеме в гору.

Правильно, тогда водитель снижает скорость.

Мощность двигателя: кВт / л. с.

Следовательно, между этими единицами мощности существует связь.

Вопрос: А появилась эта единица мощности? ( Слайд 11).

1 л.с. = 735,5 Вт.

1 Вт = 0,00013596 л.с.

Эта единица мощности была изъята из обращения с 1 января 1980 г.

Примеры мощностей современных автомобилей. ( Слайд 13,14).

Различные двигатели имеют разные мощности.

таблица 5

Вопрос: А какова мощность человека?

Мощность человека при нормальных условиях работы в среднем составляет 70-80 Вт. Совершая прыжки, взбегая по лестнице, человек может развивать мощность до 730 Вт, а в отдельных случаях и большую.

Вопрос: А чем «живые двигатели» отличаются от механических?

( Слайд 15).

Ответ: Тем, что «живые двигатели» могут изменять свою мощность в несколько раз.

Физкультминутка

IV.Формирование практических умений и навыков.

Цель: закреплять знания и умения в выполнении заданий по данной теме

Задача 1 Спортсмен поднял штангу массой 200 кг за 0,5 с на высоту 2м. Какую мощность он при этом развил?( Слайд 16).

Дано:	СИ	Решение:
m = 200 кг		N = A /∆ t
h = 2м		A = F * h спортсмен совершает работу против силы тяжести
∆t = 0,5 с		A=mgh
		N = mgh / ∆t
N — ?		N = 200 кг · 10 м/с² · 2 м : 0,5 с= 8000 Вт =8 кВт

Ответ : N =8 кВт.

Задача 2 Найдите модуль силы тяги автомобиля, движущегося с постоянной скоростью 20м/с, если двигатель автомобиля развивает мощность 40кВт?

Дано:	СИ	Решение:
V=20 м/с		N=v*F
N = 40кВт	40000Вт	F= N / v
F- ?		F = 40000 Вт: 20 м/с= 2000 Вт =2 кВт

Ответ: F= 2кВт

Задача 3. Двигатель мощностью 5кВт работал 10 мин. Какую работу он при этом совершил?

Дано:	СИ	Решение:
∆t = 10мин	600с	N=А/∆t
N = 5кВт	5000Вт	А= N*∆t
F- ?		А= 5000Вт*600с = 3 000 000 Дж = 3МДж

Ответ: 3 МДж

V. Подведение итогов.

Цель: дать качественную оценку работы класса и отдельных учащихся.

Тестовое задание

При записи формул мощность обозначают буквой …, работу — …,время — …

a) N, A, t; б) A, N, t; в) t, N, А; г) A, t, N.

Для расчета механической мощности используют формулу…

а) б); в) ; г)

Единицей измерения мощности является…

а) Дж; б) Н; в) кг; г) Па; д) Вт.

В Международной системе исчисления мощность выражается в…

а) кВт; б) Вт; в) МВт; г) кВт ч.

Человек развивает наибольшую мощность, когда он…

а) идет по лестнице; в) стоит на лестнице.

б) взбегает по лестнице;

VI.Домашнее задание: параграф 47, выполнить разноуровневые задания задания

Рефлексия.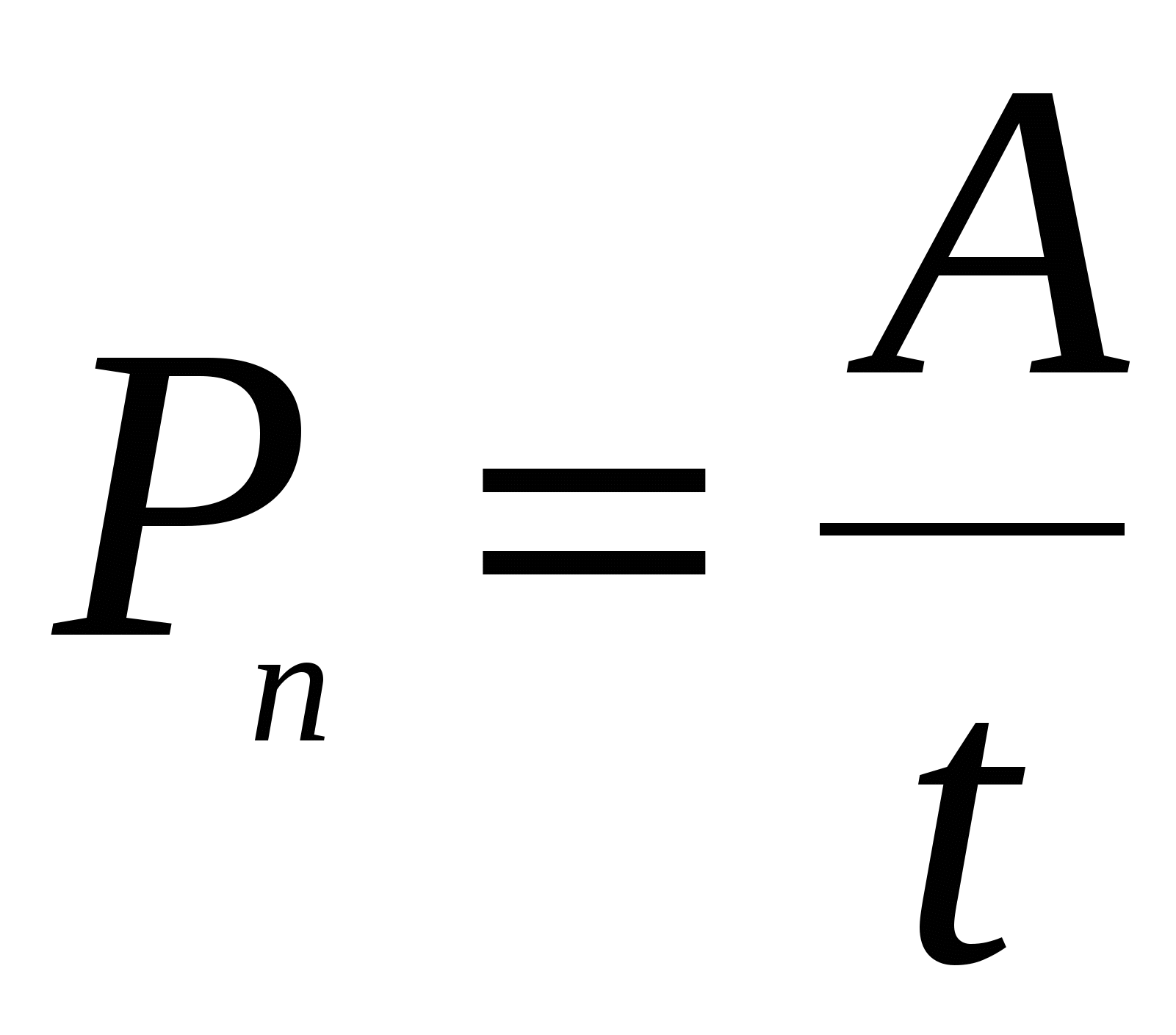 Спасибо всем за работу на уроке. Хочется надеяться, что сегодняшний урок разбудит в вас жажду новых познаний, ведь «великий» океан истины по-прежнему расстилается перед вами, не исследованным до конца! (Слайд)

Полезная мощность: определение в физике

Мощностью в физике называется скорость выполнения работы: сколько затрачивается энергии (или выполняется работы) в единицу времени.

$P = \frac{F \cdot S}{t} \implies P = F \cdot v_{ср}$, где:

$F$ — действующая сила,
$S$ — пройденное расстояние,
$t$ — затраченное время,
$v_{ср}$ — средняя скорость.

Средняя мощность при вращении вычисляется аналогично:

$P = \frac{F \cdot r \cdot \varphi}{t} = \frac{M \cdot \varphi}{t} \implies P = M \cdot \omega_{ср}$, где:

$F$ — сила,
$r$ — радиус до точки приложения силы,
$M$ — вращающий момент,
$\varphi$ — пройденное угловое расстояние,
$\omega_{ср}$ — средняя угловая скорость.

В электротехнике мощность постоянного тока вычисляется как произведение напряжения на его силу:

$P = U \cdot I$

Мощность в системе СИ измеряется в ваттах. Ватт — количество джоулей, затрачиваемых в секунду.

$1 Вт = \frac{Н \cdot м}{с} = \frac{Дж}{с}$

Говоря о полезной мощности, следует делать различие между работой и энергией. С физической точки зрения эти величины взаимозаменяемы, обе измеряются в джоулях. Однако под работой, как правило, подразумевается целенаправленный расход энергии, тогда как просто энергия может означать и явление, происходящее вне человеческих представлений о полезности. Например, при случайном взрыве резервуара с топливом выделяется огромное количество энергии, но называть такое явление работой было бы неправильно.

Соотношение полезной работы к расходу энергии называются коэффициентом полезного действия (КПД). Например, можно поднять груз на высоту 10 м с помощью электролебедки (часть электроэнергии при этом неизбежно преобразуется в ненужное тепло), а можно затащить на ту же высоту по наклонной плоскости (часть энергии будет затрачена на преодоление силы трения). Сопоставляя разные способы подъема груза, мы можем решить, какой из них менее затратен.

Замечание 1

Это рассуждение применимо и к мощности: полезная мощность определяется как та часть затрачиваемой ежесекундно энергии, которая расходуется на выполнение полезной работы, т.е. затрачиваемая в единицу времени энергия за вычетом затрат на преодоление сил трения, паразитных токов, вязкости окружающей среды и т.п.

Готовые работы на аналогичную тему

Расчет средней полезной мощности при поступательном движении производится по формуле

$P = F \cdot v_{ср} \cdot \cos(\alpha)$, где:

$F$ — действующая сила,
$S$ — пройденное расстояние,
$\alpha$ — угол между векторами скорости и силы,
$v_{ср}$ — средняя скорость.

Чем меньше угол между векторами скорости и силы, тем большая часть мощности будет затрачиваться производительно, т.е. на выполнение полезной работы.

Пример 1

Какой мощности требуется лебедка для подъема груза весом 30 кг на высоту 5,5 м за 5,5 с? КПД лебедки принять равным 0,8.

Учитывая, что направления силы и скорости совпадают ($\cos(\alpha) = \cos(0) = 1$), мощность можно найти как

$P = F \cdot v$

Найдем вес груза (действующую на него силу тяжести), умножив массу на ускорение свободного падения:

$F = 9,8 \cdot 20 \approx 300 Н$.

Скорость как отношение перемещения к времени:

$v = \frac{5,5}{5,5} = 1 \frac{м}{с}$

Мощность с учетом КПД:

$P = 0,8 \cdot 300 \cdot 1 \approx 240 Вт $

Ответ: $\approx 240 Вт$.

Работа и мощность тока — материалы для подготовки к ЕГЭ по Физике

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: работа электрического тока, закон Джоуля–Ленца, мощность электрического тока.

Электрический ток снабжает нас энергией. Сейчас мы будем учиться эту энергию вычислять.

Откуда вообще берётся эта энергия? Она возникает за счёт работы электрического поля по передвижению свободных зарядов в проводнике. Поэтому нахождение работы поля — наша первая задача.

Работа тока

Рассмотрим участок цепи, по которому течёт ток . Напряжение на участке обозначим , сопротивление участка равно (рис. 1).

Рис. 1. Участок цепи

За время по нашему участку проходит заряд . Заряд перемещается стационарным электрическим полем, которое совершает при этом работу:

(1)

За счёт работы (1) на рассматриваемом участке может выделяться тепловая энергия или совершаться механическая работа; могут также протекать химические реакции. Короче говоря, данная работа идёт на увеличение энергии нашего участка цепи.

Работа (1) называется работой тока. Термин крайне неудачный — ведь работу совершает не ток, а электрическое поле. Но с укоренившейся терминологией, увы, ничего не поделаешь.

Если участок цепи является однородным, т.е. не содержит источника тока, то для этого участка справедлив закон Ома: . Подставляя это в формулу (1), получим:

(2)

Теперь подставим в (1) вместо тока его выражение из закона Ома :

(3)

Подчеркнём ещё раз: формула (1) получена из самых общих соображений, она является основной и годится для любого участка цепи; формулы (2) и (3) получены из основной формулы с дополнительным привлечением закона Ома и потому годятся только для однородного участка.

Мощность тока

Как вы помните, мощностью называется отношение работы ко времени её совершения. В частности, мощность тока — это отношение работы тока ко времени, за которое эта работа совершена:

Из формул (1)–(3) немедленно получаем соответствующие формулы для мощности тока:

(4)

(5)

(6)

Закон Джоуля–Ленца

Предположим, что на рассматриваемом участке цепи не совершается механическая работа и не протекают химические реакции. Поскольку сила тока постоянна, работа поля не вызывает увеличение кинетической энергии свободных зарядов. Стало быть, работа поля целиком превращается в тепло , которое выделяется на данном участке цепи и рассеивается в окружающее пространство: .

Таким образом, для количества теплоты, выделяющегося на данном участке цепи, мы получаем формулы:

(7)

(8)

(9)

Но часто бывает так, что не вся работа тока превращается в тепло. Например, за счёт работы тока может совершать механическую работу электродвигатель или заряжаться аккумулятор. Тепло, разумеется, будет выделяться и в этих случаях, но только на сей раз получится, что (на величину механической работы, совершённой двигателем, или химической энергии, запасённой аккумулятором).

Оказывается, что в подобных случаях остаётся справедливой формула (8): . Это — экспериментально установленный закон Джоуля-Ленца.

10 формул по физике

Доброго дня уважаемые радиолюбители!
Приветствую вас на сайте “Радиолюбитель“

Формулы составляют скелет науки об электронике. Вместо того, чтобы сваливать на стол целую кучу радиоэлементов, а потом переподключать их между собой, пытаясь выяснить, что же появится на свет в результате, опытные специалисты сразу строят новые схемы на основе известных математических и физических законов. Именно формулы помогают определять конкретные значения номиналов электронных компонентов и рабочих параметров схем.

Точно так же эффективно использовать формулы для модернизации уже готовых схем. К примеру, для того, чтобы выбрать правильный резистор в схеме с лампочкой, можно применить базовый закон Ома для постоянного тока (о нем можно будет прочесть в разделе “Соотношения закона Ома” сразу после нашего лирического вступления). Лампочку можно заставить, таким образом, светить более ярко или, наоборот — притушить.

В этой главе будут приведены многие основные формулы физики, с которыми рано или поздно приходится сталкиваться в процессе работы в электронике. Некоторые из них известны уже столетия, но мы до сих пор продолжаем ими успешно пользоваться, как будут пользоваться и наши внуки.

Соотношения закона Ома

Закон Ома представляет собой взаимное соотношение между напряжением, током, сопротивлением и мощностью. Все выводимые формулы для расчета каждой из указанных величин представлены в таблице:

Искомая величина	Формула
Напряжение, В	U=I*R
Ток, А	I=U/R
Сопротивление, Ом	R=U/I
Мощность, Вт	P=U*I

В этой таблице используются следующие общепринятые обозначения физических величин:

U — напряжение (В),

I — ток (А),

Р — мощность (Вт),

R — сопротивление (Ом),

Потренируемся на следующем примере: пусть нужно найти мощность схемы. Известно, что напряжение на ее выводах составляет 100 В, а ток— 10 А. Тогда мощность согласно закону Ома будет равна 100 х 10 = 1000 Вт. Полученное значение можно использовать для расчета, скажем, номинала предохранителя, который нужно ввести в устройство, или, к примеру, для оценки счета за электричество, который вам лично принесет электрик из ЖЭК в конце месяца.

А вот другой пример: пусть нужно узнать номинал резистора в цепи с лампочкой, если известно, какой ток мы хотим пропускать через эту цепь. По закону Ома ток равен:

I = U / R

Схема, состоящая из лампочки, резистора и источника питания (батареи) показана на рисунке. Используя приведенную формулу, вычислить искомое сопротивление сможет даже школьник.

Что же в этой формуле есть что? Рассмотрим переменные подробнее.

> U пит (иногда также обозначается как V или Е): напряжение питания. Вследствие того, что при прохождении тока через лампочку на ней падает какое-то напряжение, величину этого падения (обычно рабочее напряжение лампочки, в нашем случае 3,5 В) нужно вычесть из напряжения источника питания. К примеру, если Uпит = 12 В, то U = 8,5 В при условии, что на лампочке падает 3,5 В.

> I: ток (измеряется в амперах), который планируется пропустить через лампочку. В нашем случае – 50 мА. Так как в формуле ток указывается в амперах, то 50 миллиампер составляет лишь малую его часть: 0,050 А.

> R: искомое сопротивление токоограничивающего резистора, в омах.

В продолжение, можно проставить в формулу расчета сопротивления реальные цифры вместо U, I и R:

R = U/I = 8,5 В / 0,050 А= 170 Ом

Расчёты сопротивления

Рассчитать сопротивление одного резистора в простой цепи достаточно просто. Однако с добавлением в нее других резисторов, параллельно или последовательно, общее сопротивление цепи также изменяется. Суммарное сопротивление нескольких соединенных последовательно резисторов равно сумме отдельных сопротивлений каждого из них. Для параллельного же соединения все немного сложнее.

Почему нужно обращать внимание на способ соединения компонентов между собой? На то есть сразу несколько причин.

> Сопротивления резисторов составляют только некоторый фиксированный ряд номиналов. В некоторых схемах значение сопротивления должно быть рассчитано точно, но, поскольку резистор именно такого номинала может и не существовать вообще, то приходится соединять несколько элементов последовательно или параллельно.

> Резисторы — не единственные компоненты, которые имеют сопротивление. К примеру, витки обмотки электромотора также обладают некоторым сопротивлением току. Во многих практических задачах приходится рассчитывать суммарное сопротивление всей цепи.

Расчет сопротивления последовательных резисторов

Формула для вычисления суммарного сопротивления резисторов, соединенных между собой последовательно, проста до неприличия. Нужно просто сложить все сопротивления:

Rобщ = Rl + R2 + R3 + … (столько раз, сколько есть элементов)

В данном случае величины Rl, R2, R3 и так далее — сопротивления отдельных резисторов или других компонентов цепи, а Rобщ — результирующая величина.

Так, к примеру, если имеется цепь из двух соединенных последовательно резисторов с номиналами 1,2 и 2,2 кОм, то суммарное сопротивление этого участка схемы будет равно 3,4 кОм.

Расчет сопротивления параллельных резисторов

Все немного усложняется, если требуется вычислить сопротивление цепи, состоящей из параллельных резисторов. Формула приобретает вид:

R общ = R1 * R2 / (R1 + R2)

где R1 и R2 — сопротивления отдельных резисторов или других элементов цепи, а Rобщ -результирующая величина. Так, если взять те же самые резисторы с номиналами 1,2 и 2,2 кОм, но соединенные параллельно, получим

776,47 = 2640000 / 3400

Для расчета результирующего сопротивления электрической цепи из трех и более резисторов используется следующая формула:

Здесь снова величины Rl, R2, R3 и так далее — сопротивления отдельных резисторов, a Rобщ — суммарная величина.

Расчёты ёмкости

Формулы, приведенные выше, справедливы и для расчета емкостей, только с точностью до наоборот. Так же, как и для резисторов, их можно расширить для любого количества компонентов в цепи.

Расчет емкости параллельных конденсаторов

Если нужно вычислить емкость цепи, состоящей из параллельных конденсаторов, необходимо просто сложить их номиналы:

Собщ = CI + С2 + СЗ + …

В этой формуле CI, С2 и СЗ — емкости отдельных конденсаторов, а Собщ суммирующая величина.

Расчет емкости последовательных конденсаторов

Для вычисления общей емкости пары связанных последовательно конденсаторов применяется следующая формула:

Собщ = С1 * С2 /( С1+С2)

где С1 и С2 — значения емкости каждого из конденсаторов, а Собщ — общая емкость цепи

Расчет емкости трех и более последовательно соединенных конденсаторов

В схеме имеются конденсаторы? Много? Ничего страшного: даже если все они связаны последовательно, всегда можно найти результирующую емкость этой цепи:

И здесь опять величины C1, С2, СЗ и так далее — емкости отдельных конденсаторов, а Собщ. — суммарная величина.

Так зачем же вязать последовательно сразу несколько конденсаторов, когда могло хватить одного? Одним из логических объяснений этому факту служит необходимость получения конкретного номинала емкости цепи, аналога которому в стандартном ряду номиналов не существует. Иногда приходится идти и по более тернистому пути, особенно в чувствительных схемах, как, например, радиоприемники.

Расчёт энергетических уравнений

Наиболее широко на практике применяют такую единицу измерения энергии, как киловатт-часы или, если это касается электроники, ватт-часы. Рассчитать затраченную схемой энергию можно, зная длительность времени, на протяжении которого устройство включено. Формула для расчета такова:

ватт-часы = Р х Т

В этой формуле литера Р обозначает мощность потребления, выраженную в ваттах, а Т — время работы в часах. В физике принято выражать количество затраченной энергии в ватт-секундах, или Джоулях. Для расчета энергии в этих единицах ватт-часы делят на 3600.

Расчёт постоянной ёмкости RC-цепочки

В электронных схемах часто используются RC-цепочки для обеспечения временных задержек или удлинения импульсных сигналов. Самые простые цепочки состоят всего лишь из резистора и конденсатора (отсюда и происхождение термина RC-цепочка).

Принцип работы RC-цепочки состоит в том, что заряженный конденсатор разряжается через резистор не мгновенно, а на протяжении некоторого интервала времени. Чем больше сопротивление резистора и/или конденсатора, тем дольше будет разряжаться емкость. Разработчики схем очень часто применяют RC-цепочки для создания простых таймеров и осцилляторов или изменения формы сигналов.

Каким же образом можно рассчитать постоянную времени RC-цепочки? Поскольку эта схема состоит из резистора и конденсатора, в уравнении используются значения сопротивления и емкости. Типичные конденсаторы имеют емкость порядка микрофарад и даже меньше, а системными единицами являются фарады, поэтому формула оперирует дробными числами.

T = RC

В этом уравнении литера Т служит для обозначения времени в секундах, R — сопротивления в омах, и С — емкости в фарадах.

Пусть, к примеру, имеется резистор 2000 Ом, подключенный к конденсатору 0,1 мкФ. Постоянная времени этой цепочки будет равна 0,002 с, или 2 мс.

Для того чтобы на первых порах облегчить вам перевод сверхмалых единиц емкостей в фарады, мы составили таблицу:

Значение емкости конденсатора, мкФ	Емкость конденсатора для расчета
10	0,000 01
1	0,000 001
0,1	0,000 000 1
0,01	0,000 000 01

Расчёты частоты и длины волны

Частота сигнала является величиной, обратно пропорциональной его длине волны, как будет видно из формул чуть ниже. Эти формулы особенно полезны при работе с радиоэлектроникой, к примеру, для оценки длины куска провода, который планируется использовать в качестве антенны. Во всех следующих формулах длина волны выражается в метрах, а частота — в килогерцах.

Расчет частоты сигнала

Предположим, вы хотите изучать электронику для того, чтобы, собрав свой собственный приемопередатчик, поболтать с такими же энтузиастами из другой части света по аматорской радиосети. Частоты радиоволн и их длина стоят в формулах бок о бок. В радиолюбительских сетях часто можно услышать высказывания о том, что оператор работает на такой-то и такой длине волны. Вот как рассчитать частоту радиосигнала, зная длину волны:

Частота = 300000 / длина волны

Длина волны в данной формуле выражается в миллиметрах, а не в футах, аршинах или попугаях. Частота же дана в мегагерцах.

Расчет длины волны сигнала

Ту же самую формулу можно использовать и для вычисления длины волны радиосигнала, если известна его частота:

Длина волны = 300000 / Частота

Результат будет выражен в миллиметрах, а частота сигнала указывается в мегагерцах.

Приведем пример расчета. Пусть радиолюбитель общается со своим другом на частоте 50 МГц (50 миллионов периодов в секунду). Подставив эти цифры в приведенную выше формулу, получим:

6000 миллиметров = 300000 / 50 МГц

Однако чаще пользуются системными единицами длины — метрами, поэтому для завершения расчета нам остается перевести длину волны в более понятную величину. Так как в 1 метре 1000 миллиметров, то в результате получим 6 м. Оказывается, радиолюбитель настроил свою радиостанцию на длину волны 6 метров. Прикольно!

Electric Power — Summary — The Physics Hypertextbook

… electric-сопротивления
electric-power
circuit-r…

Нет постоянных условий .

Механика
1. Кинематика
  1. Движение
  2. Расстояние и перемещение
  3. Скорость и скорость
  4. Разгон
  5. Уравнения движения
  6. Свободное падение
  7. Графики движения
  8. Кинематика и расчет
  9. Кинематика в двух измерениях
  10. Снарядов
  11. Параметрические уравнения
2. Динамика I: Сила
  1. Силы
  2. Сила и масса
  3. Действие-реакция
  4. Масса
  5. Динамика
  6. Статика
  7. Трение
  8. Силы в двух измерениях
  9. Центростремительная сила
  10. Кадры справки
3. Энергия
  1. Работа
  2. Энергия
  3. Кинетическая энергия
  4. Потенциальная энергия
  5. Сохранение энергии
  6. Мощность
  7. Простые машины
4. Dynamics II: Импульс
  1. Импульс и импульс
  2. Сохранение импульса
  3. Импульс и энергия
  4. Импульс в двух измерениях
5. Вращательное движение
  1. Кинематика вращения
  2. Инерция вращения
  3. Вращательная динамика
  4. Статика вращения
  5. Угловой момент
  6. Энергия вращения
  7. Прокатный
  8. Вращение в двух измерениях
  9. Сила Кориолиса
6. Планетарное движение
  1. Геоцентризм
  2. Гелиоцентризм
  3. Вселенская гравитация
  4. Орбитальная механика I
  5. Гравитационная потенциальная энергия
  6. Орбитальная механика II
  7. Плотность вытянутых тел
7. Периодическое движение
  1. Пружины
  2. Простой генератор гармоник
  3. Маятники
  4. Резонанс
  5. Эластичность
8. Жидкости
  1. Плотность
  2. Давление
  3. Плавучесть
  4. Расход жидкости
  5. Вязкость
  6. Аэродинамическое сопротивление
  7. Режимы потока
Теплофизика
1. Тепло и температура
  1. Температура
  2. Тепловое расширение
  3. Атомная природа вещества
  4. Газовые законы
  5. Кинетико-молекулярная теория
  6. Фазы
2. Калориметрия
  1. Явное тепло
  2. Скрытое тепло
  3. Химическая потенциальная энергия
3. Теплопередача
  1. Проводимость
  2. Конвекция
  3. Радиация
4. Термодинамика
  1. Тепло и работа
  2. Диаграммы давление-объем
  3. Двигатели
  4. Холодильники
  5. Энергия и энтропия
  6. Абсолютный ноль
Волны и оптика
1. Волновые явления
  1. Природа волн
  2. Периодические волны
  3. Интерференция и суперпозиция
  4. Интерфейсы и барьеры
2. Звук
  1. Природа звука
  2. Интенсивность
  3. Эффект Доплера (звук)
  4. Ударные волны
  5. Дифракция и интерференция (звук)
  6. Стоячие волны
  7. ударов
  8. Музыка и шум
3. Физическая оптика
  1. Природа света
  2. Поляризация
  3. Эффект Доплера (световой)
  4. Черенковское излучение
  5. Дифракция и интерференция (свет)
  6. Тонкопленочная интерференция
  7. Цвет
4. Геометрическая оптика
  1. Отражение
  2. Преломление
  3. Зеркала сферические
  4. Сферические линзы
  5. Аберрация
Электричество и магнетизм
1. Электростатика
  1. Электрический заряд
  2. Закон Кулона
  3. Электрическое поле
  4. Электрический потенциал
  5. Закон Гаусса
  6. Проводников
2. Электростатические приложения
  1. Конденсаторы
  2. Диэлектрики
  3. Батареи
3. Электрический ток
  1. Электрический ток
  2. Электрическое сопротивление
  3. Электроэнергия
4. цепей постоянного тока
  1. Резисторы в цепях
  2. Батареи в цепях
  3. Конденсаторы в цепях
  4. Правила Кирхгофа
5. Магнитостатика
  1. Магнетизм
  2. Электромагнетизм
  3. Закон Ампера
  4. Электромагнитная сила
6. Магнитодинамика
  1. Электромагнитная индукция
  2. Закон Фарадея
  3. Закон Ленца
  4. Индуктивность
7. Цепи переменного тока
  1. Переменный ток
  2. RC цепи
  3. Цепи РЛ
  4. Цепи LC
8. Электромагнитные волны
  1. Уравнения Максвелла
  2. Электромагнитные волны
  3. Электромагнитный спектр
Современная физика
1. Относительность
  1. Пространство-время
  2. Масса-энергия
  3. Общая теория относительности
2. Quanta
  1. Излучение черного тела
  2. Фотоэффект
  3. Рентгеновские снимки
  4. Антиматерия
3. Волновая механика
  1. Волны материи
  2. Атомарные модели
  3. Полупроводники
  4. Конденсированные вещества
4. Ядерная физика
  1. Изотопы
  2. Радиоактивный распад
  3. Период полураспада
  4. Энергия связи
  5. Деление
  6. Fusion
  7. Нуклеосинтез
  8. Ядерное оружие
  9. Радиобиология
5. Физика элементарных частиц
  1. Квантовая электродинамика
  2. Квантовая хромодинамика
  3. Квантовая динамика вкусов
  4. Стандартная модель
  5. Помимо стандартной модели
Фонды
1. Квартир
  1. Международная система единиц
  2. Гауссова система единиц
  3. Британо-американская система единиц
  4. Разные единицы
  5. Время
  6. Преобразование единиц
2. Измерение
  1. Значащие цифры
  2. По порядку величины
3. Графики
  1. Графическое представление данных
  2. Линейная регрессия
  3. Подгонка кривой
  4. Исчисление
4. Векторы
  1. Тригонометрия
  2. Сложение и вычитание векторов
  3. Векторное разрешение и компоненты
  4. Умножение векторов
5. ссылку
  1. Специальные символы
  2. Часто используемые уравнения
  3. Физические константы
  4. Астрономические данные
  5. Периодическая таблица элементов
  6. Люди в физике
Назад дело
1. Предисловие
  1. Об этой книге
2. Связаться с автором
  1. glennelert.нас
  2. Behance
  3. Instagram
  4. Твиттер
  5. YouTube
3. Аффилированные сайты
  1. hypertextbook.com
  2. midwoodscience.org

Определение силы в физике

Мощность — это скорость выполнения работы или передачи энергии за единицу времени. Мощность увеличивается, если работа выполняется быстрее или энергия передается за меньшее время.

Расчетная мощность

Уравнение для мощности P = W / t

P означает мощность (в ваттах)
Вт — это количество проделанной работы (в Джоулях) или затраченной энергии (в Джоулях)
t — количество времени (в секундах)

С точки зрения математики, мощность — это производная работы по времени.Если работа выполняется быстрее, мощность выше. Если работа выполняется медленнее, мощность меньше.

Поскольку работа — это сила, умноженная на смещение (W = F * d), а скорость — это смещение во времени (v = d / t), мощность равна силе, умноженной на скорость: P = F * v. Большая мощность видна, когда система является одновременно мощной и быстрой по скорости.

Ед. Мощности

Мощность измеряется в энергии (джоулях), деленной на время. Единица измерения мощности в системе СИ — ватт (Вт) или джоуль в секунду (Дж / с). Мощность — это скалярная величина, у нее нет направления.

Лошадиная сила часто используется для описания мощности, выдаваемой машиной. Лошадиная сила — это единица мощности в британской системе измерения. Это мощность, необходимая для подъема 550 фунтов на один фут за одну секунду, и составляет около 746 Вт.

Ватт часто используется по отношению к лампочкам. В этом номинальном значении мощности это скорость, с которой лампа преобразует электрическую энергию в свет и тепло. Лампа с большей мощностью потребляет больше электроэнергии в единицу времени.

Если вы знаете мощность системы, вы можете найти объем работы, который будет произведен, как W = Pt.Если лампочка имеет номинальную мощность 50 Вт, она будет производить 50 джоулей в секунду. За час (3600 секунд) он произведет 180 000 джоулей.

Работа и сила

Когда вы проходите милю, ваша движущая сила перемещает ваше тело, что измеряется по мере выполнения работы. Когда вы пробегаете одну и ту же милю, вы выполняете такой же объем работы, но за меньшее время. Бегун имеет более высокую номинальную мощность, чем ходок, вырабатывая больше ватт. Автомобиль мощностью 80 лошадиных сил может развивать более быстрое ускорение, чем автомобиль мощностью 40 лошадиных сил.В конце концов, обе машины разгоняются до 60 миль в час, но двигатель мощностью 80 л.с. может развивать эту скорость быстрее.

В гонке между черепахой и зайцем заяц обладал большей мощностью и ускорялся быстрее, но черепаха выполняла ту же работу и преодолевала то же расстояние за гораздо большее время. Черепаха показала меньшую мощь.

Средняя мощность

Обсуждая мощность, люди обычно имеют в виду среднюю мощность, P _avg. Это объем работы, выполненной за период времени (ΔW / Δt), или количество энергии, переданной за период времени (ΔE / Δt).

Мгновенная мощность

Какая мощность в конкретное время? Когда единица времени приближается к нулю, для получения ответа требуется расчет, но он приближается к силе, умноженной на скорость.

Мощность

Сила — это энергия! Он измеряется как энергии в единицу времени

Энергия в Джоулях (Дж)
Мощность в Джоулей в секунду (Дж / с), что соответствует специальной единице Вт (Вт)

1 Вт = 1 Джоуль энергии в секунду

1 Вт = 1 Дж / с

Формулы мощности

Нет , не та формула силы!

Мощность — это скорость энергии за раз :

P = Энергия Время

Пример: 3000 Дж энергии используется за 20 секунд, какова мощность?

P = 3000 Дж 20 с = 150 Вт

Мы также можем изменить формулу следующим образом:

		P = Энергия Время
Энергия — это также Сила × Расстояние, поэтому:		P = Сила × Расстояние Время
Расстояние / время — это скорость, поэтому:		P = Сила × Скорость

Пример: эти парни тянут с объединенной силой 4000 Н и управляют скоростью 0.4 м / с, какую мощность они используют?

P = 4000 Н x 0,4 м / с
= 1600 Н м / с
= 1600 Вт

Держись! Действительно ли Н м / с (Ньютон-метр в секунду) то же самое, что Вт (Ватт)?

На самом деле все это одно и то же:

		Мощность:
Начать с:		Н м / с
Ньютон составляет кг м / с ² :		кг м / с ² м / с
Упростить:		кг м ² / с ³
Джоуль составляет кг · м ² / с ² :		Дж / с
Ватт это Дж / с:		Вт

Мощность

1 л.с. (лс) — 745.7 Вт (или 746 Вт для электродвигателей)

Пример: у машины Сэма двигатель мощностью 200 л.с. Что это в ваттах?

200 × 745,7 = 149,140 Вт = 149 кВт (с точностью до кВт)

Что такое киловатт-час?

1 кВтч — это Energy , используемый при мощности 1 кВт в течение 1 часа.

Это маленький радиатор

1 кВт . Сколько энергии он потребляет за час?

1 кВт — это 1000 Вт, что составляет 1000 Дж / с
В часе 3600 секунд

Итак, в час он использует:

1000 Дж / с × 3600 с = 3600000 Дж = 3.6 МДж

Итак, 1 кВт · ч (киловатт-час) — это 3,6 МДж из энергии

Работа, энергия и сила

Определения

Работа можно определить как передачу энергии. В физике мы говорим, что работа выполняется с объектом, когда вы передаете ему энергию. Если один объект передает (отдает) энергию второму объекту, то первый объект работает со вторым объектом.

Работа — это приложение силы на расстоянии. Поднять какой-нибудь груз с земли и положить его на полку — хороший пример работы. Сила равна весу объекта, а расстояние равно высоте полки (W = Fxd).

Принцип работы-энергии — Изменение кинетической энергии объекта равно чистой работе, проделанной с ним.

Энергия может быть определена как способность выполнять работу.2.

Виды энергии

Есть два типа энергии во многих формах:

Кинетическая энергия = Энергия движения

Потенциальная энергия = Накопленная энергия

Формы энергии

Солнечное излучение — инфракрасное тепло, радиоволны, гамма-лучи, микроволны, ультрафиолетовый свет

Атомная / ядерная энергия — энергия, выделяемая в ядерных реакциях.Когда нейтрон расщепляет ядро атома на более мелкие части, это называется делением. Когда два ядра соединяются под воздействием миллионов градусов тепла, это называется синтезом

Электрическая энергия — Производство или использование электроэнергии в течение периода времени, выраженное в киловатт-часах (кВтч), мегаватт-часах (НМ) или гигаватт-часах (ГВтч).

Химическая энергия — Химическая энергия — это форма потенциальной энергии, связанная с разрывом и образованием химических связей. Он накапливается в продуктах питания, топливе и батареях и выделяется в виде других форм энергии во время химических реакций.

Механическая энергия — Энергия движущихся частей машины. Также относится к движениям человека

Тепловая энергия — форма энергии, которая передается разницей температур

Что такое Power

Мощность — это работа, выполненная за единицу времени. Другими словами, мощность — это мера того, насколько быстро можно выполнить работу. Единица мощности — ватт = 1 джоуль / 1 секунда.

Одной из распространенных единиц энергии является киловатт-час (кВтч).Если мы используем один киловатт энергии, одного киловатт-часа энергии хватит на один час.

Расчет работы, энергии и мощности

РАБОТА = W = Fd

Поскольку энергия — это способность выполнять работу, мы измеряем энергию и работу в одних и тех же единицах (Н * м или джоули).

МОЩНОСТЬ (P) — скорость производства (или поглощения) энергии с течением времени: P = E / t

В системе СИ единицы измерения мощности

— ватт, представляющий выработку или поглощение энергии со скоростью 1 Джоуль / сек.Единицей измерения мощности в английской системе является мощность в лошадиных силах, что эквивалентно 735,7 Вт.

См. Также: Работа, энергия и мощность — Как понять и рассчитать счет за энергию.

Попробуйте это упражнение!

1) Сила 20 ньютонов, толкающая объект на 5 метров в направлении силы. Сколько работы сделано?

Пожалуйста, введите свой ответ в отведенное для этого поле:

2) Если вы выполняете 100 джоулей работы за одну секунду (используя 100 джоулей энергии).Сколько энергии используется?

3) 1 лошадиная сила равна сколько ватт?

7.7: Мощность — Физика LibreTexts

Цели обучения

К концу этого раздела вы сможете:

Рассчитайте мощность, рассчитав изменения энергии во времени.
Изучите энергопотребление и расчеты стоимости потребляемой энергии.

Что такое сила?

Сила — это слово вызывает в воображении множество образов: профессиональный футболист, отталкивающий своего противника, драгстер, ревущий от стартовой линии, вулкан, выбрасывающий лаву в атмосферу, или взрывающаяся ракета, как на рисунке.

Рисунок \ (\ PageIndex {1} \): Эта мощная ракета космического корабля «Индевор» работала и потребляла энергию с очень высокой скоростью. (предоставлено NASA)

Эти образы силы имеют общую черту — быстрое выполнение работы, что соответствует научному определению мощности \ (P \) как скорости, с которой выполняется работа.

Мощность

Мощность — это скорость выполнения работы.

\ [P = \ dfrac {W} {t} \]

В системе СИ единица измерения мощности — ватт \ (Вт \), где 1 ватт равен 1 джоуль в секунду \ ((1 \, W = 1 \, J / s) \).

Поскольку работа — это передача энергии, мощность — это также скорость, с которой энергия расходуется. Например, лампочка мощностью 60 Вт потребляет 60 Дж энергии в секунду. Большая мощность означает большой объем работы или энергии, выработанный за короткое время. Например, когда мощный автомобиль быстро разгоняется, он выполняет большой объем работы и потребляет большое количество топлива за короткое время.

Расчет мощности по энергии

Пример \ (\ PageIndex {1} \): расчет мощности для подъема по лестнице

Какая выходная мощность у 60. 2 + mgh, \), где \ (h \) — высота лестницы по вертикали.2) (3,00 \, м)} {3,50 \, s} \]

\ [= \ dfrac {120 \, J + 1764 \, J} {3.50 \, s} \]

\ [= 538 \, W. \]

Обсуждение

Женщина выполняет 1764 Дж работы, чтобы подняться по лестнице, по сравнению со всего лишь 120 Дж, чтобы увеличить свою кинетическую энергию; таким образом, большая часть ее мощности требуется для подъема, а не для ускорения.

Впечатляет, что полезная выходная мощность этой женщины чуть меньше 1 лошадиных сил \ ((1 \, л.с. = 746 \, Вт) \). Люди могут генерировать больше, чем лошадиные силы с помощью мышц ног в течение коротких периодов времени, быстро превращая доступный в крови сахар и кислород в объем работы.(Лошадь может выделять 1 л.с. в течение нескольких часов подряд.) Как только кислород истощается, выходная мощность снижается, и человек начинает быстро дышать, чтобы получить кислород для метаболизма большего количества пищи — это известно как этап аэробных упражнений . Если бы женщина поднималась по лестнице медленно, ее выходная мощность была бы намного меньше, хотя объем выполняемой работы был бы таким же.

Установление связей: расследование на вынос

— Измерьте свою номинальную мощность

Определите собственную номинальную мощность, измерив время, необходимое вам, чтобы подняться по лестнице.2 \) Крошечная часть этого удерживается Землей в течение длительного времени. Наш уровень потребления ископаемого топлива намного превышает скорость его хранения, поэтому они неизбежно будут исчерпаны. Сила означает, что энергия передается, возможно, меняя форму. Невозможно полностью преобразовать одну форму в другую, не потеряв часть ее в виде тепловой энергии. Например, лампа накаливания мощностью 60 Вт преобразует в свет всего 5 Вт электроэнергии, а 55 Вт рассеивается в тепловую энергию.6 \) электроэнергии. Но электростанция потребляет химическую энергию в размере около 2500 МВт, создавая передачу тепла в окружающую среду в размере 1500 МВт. (См. Рисунок.)
Рисунок \ (\ PageIndex {3} \): Огромное количество электроэнергии вырабатывается угольными электростанциями, такими как эта в Китае, но еще большее количество энергии идет на передачу тепла в окружающую среду. Здесь большие градирни необходимы для быстрой передачи тепла по мере его производства. Передача тепла характерна не только для угольных электростанций, но является неизбежным следствием выработки электроэнергии из любого топлива — ядерного, угля, нефти, природного газа и т.п.3 \) Человек в состоянии покоя (вся теплопередача) \ (100 \) Обычная лампа накаливания (общая полезная и теплопередающая) \ (60 \) Сердце, человек в состоянии покоя (общая полезная и теплоотдача) \ (8 \) Часы электрические \ (3 \) Карманный калькулятор \ (10 ^ {- 3} \)
Мощность и энергопотребление
Обычно нам приходится платить за энергию, которую мы используем.Стоимость энергии для электроприбора интересно и легко оценить, если известны его потребляемая мощность и затраченное время. Чем выше уровень энергопотребления и чем дольше прибор используется, тем выше его стоимость. Уровень потребляемой мощности равен \ (P = \ frac {W} {t} = \ frac {E} {t} \), где \ (E \) — энергия, поставляемая электроэнергетической компанией. Таким образом, энергия, потребляемая за время \ (t \), составляет
\ [E = Pt. \]
В счетах за электроэнергию указывается использованная энергия в киловатт-часах \ ((кВт \ cdot ч) \), которая является произведением мощности в киловаттах и времени в часах.Этот блок удобен тем, что потребление электроэнергии на уровне киловатт в течение нескольких часов является типичным.
Пример \ (\ PageIndex {2} \): расчет затрат на энергию
Какова стоимость эксплуатации компьютера мощностью 0,200 кВт, 6,00 ч в день в течение 30,0 дней, если стоимость электроэнергии составляет 0,120 долл. США за \ (кВт \ cdot ч \)?
Стратегия
Стоимость основана на потребленной энергии; таким образом, мы должны найти \ (E \) из \ (E = Pt \), а затем рассчитать стоимость.Поскольку электрическая энергия выражается в \ (кВт \ cdot h \) в начале такой задачи, удобно преобразовать единицы в \ (кВт \) и часы.
Решение
Энергия, потребляемая в \ (кВт \ cdot ч \), составляет
\ [E = Pt = (0.200 \, кВт) (6.00 \, ч / сут) (30.0 \, d) \]
\ [= 36,0 \, кВт \ cdot ч, \]
, а стоимость просто
\ [стоимость = (36,0 \, кВт \ cdot ч) (0,120 $ \, за \, кВт \ cdot ч) = 4,32 доллара \, за \, месяц.\]
Обсуждение
Стоимость использования компьютера в этом примере не является ни чрезмерной, ни незначительной. Понятно, что стоимость — это сочетание силы и времени. Когда и то и другое высокое, например, кондиционер летом, стоимость высока.
Мотивация к экономии энергии стала более убедительной из-за ее постоянно растущей цены. Вооружившись знанием того, что потребляемая энергия является продуктом мощности и времени, вы можете оценить затраты для себя и сделать необходимые оценочные суждения о том, где экономить энергию.Нужно уменьшить либо мощность, либо время. Наиболее экономически выгодно ограничить использование мощных устройств, которые обычно работают в течение длительного времени, например водонагревателей и кондиционеров. Сюда не входят устройства с относительно высокой мощностью, такие как тостеры, потому что они работают всего несколько минут в день. Он также не будет включать электрические часы, несмотря на то, что они используются круглосуточно, потому что они являются устройствами с очень низким энергопотреблением. Иногда можно использовать устройства с большей эффективностью, то есть устройства, потребляющие меньше энергии, для выполнения той же задачи.Одним из примеров является компактная люминесцентная лампа, которая дает в четыре раза больше света на ватт потребляемой мощности, чем ее собрат с лампами накаливания.
Современная цивилизация зависит от энергии, но нынешние уровни потребления и производства энергии не являются устойчивыми. Вероятность связи между глобальным потеплением и использованием ископаемого топлива (с сопутствующим образованием углекислого газа) привела к сокращению использования энергии, а также к переходу на неископаемые виды топлива. Несмотря на то, что энергия в изолированной системе является сохраняемой величиной, конечным результатом большинства преобразований энергии является перенос тепла в окружающую среду, которое больше не используется для выполнения работы.Как мы обсудим более подробно в Термодинамике, способность энергии производить полезную работу «деградировала» при преобразовании энергии.
Сводка
- Мощность — это скорость выполнения работы или в форме уравнения для средней мощности \ (P \) для работы \ (W \), выполненной за время \ (t \), \ (P = W / t \).
- Единицей измерения мощности в системе СИ является ватт (Вт), где \ (1 \, W = 1 \, J / s \).
- Мощность многих устройств, таких как электродвигатели, также часто выражается в лошадиных силах (л.с.), где \ (1 \ space hp = 746 \, W.\)
Глоссарий
мощность
скорость выполнения работ
ватт
(Вт) единица мощности в системе СИ, где \ (1 Вт = 1 Дж / с \)
л.с.
старая единица мощности вне системы СИ, с \ (1 л.с. = 746 Вт \)
киловатт-час
(\ (кВт⋅ч \)) блок, используемый в основном для выработки электроэнергии, поставляемой электроэнергетическими компаниями
Авторы и авторство
Пол Питер Урон (почетный профессор Калифорнийского государственного университета, Сакраменто) и Роджер Хинрикс (Государственный университет Нью-Йорка, колледж в Освего) с авторами: Ким Диркс (Оклендский университет) и Манджула Шарма (Сиднейский университет).Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Power — Мощность и эффективность — Edexcel — GCSE Physics (Single Science) Revision — Edexcel
Когда работа выполняется с объектом, происходит передача энергии. Скорость, с которой эта энергия передается, называется мощностью. Таким образом, чем мощнее устройство, тем больше энергии оно передает каждую секунду.
Расчетная мощность
Уравнение, используемое для расчета мощности, выглядит следующим образом:
\ [power = \ frac {work \ done} {time \ take} \]
\ [P = \ frac {E} {t } \]
Это когда:
- мощность ( P ) измеряется в ваттах (Вт)
- выполненная работа ( E ) измеряется в джоулях (Дж)
- время ( t ) равно измеряется в секундах (с)
Один ватт равен одному джоулю в секунду (Дж / с).Это означает, что на каждый дополнительный джоуль, передаваемый в секунду, мощность увеличивается на один ватт.
Пример
Два электродвигателя используются для подъема груза 2 Н на высоту 10 м по вертикали.
Мотор 1 делает это за 5 секунд.
Второй двигатель делает это за 10 секунд.
Для обоих двигателей переданная энергия — проделанная работа — составляет 20 Дж.
\ [E = F \ times d = 2 \ times 10 = 20 \\ Дж \]
Для первого двигателя:
\ [ P = \ frac {E} {t} = \ frac {20} {5} = 4 \\ W \]
Для второго двигателя:
\ [P = \ frac {E} {t} = \ frac { 20} {10} = 2 \\ W \]
Поскольку один двигатель передает вдвое больше энергии в секунду, можно сказать, что первый двигатель в два раза мощнее, чем второй.
Вопрос
Фен передает 48 000 Дж энергии за одну минуту. Какая мощность у фена?
Показать ответ
\ [P = \ frac {E} {t} \]
\ [P = \ frac {48,000} {60} \]
\ [P = 800 \\ W \]
Мощность — это количество энергии, передаваемое за секунду.
19.4 Электроэнергетика — физика
Цели обучения разделу
К концу этого раздела вы сможете делать следующее:
- Определите электрическую мощность и опишите уравнение электрической мощности
- Расчет электрической мощности в цепях резисторов в последовательном, параллельном и сложном расположении
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим ученикам овладеть следующими стандартами:
- (5) Научные концепции.Студент знает природу сил в физическом мире. Ожидается, что студент:
  - (Ж) проектировать, конструировать и рассчитывать в терминах сквозного тока, разности потенциалов, сопротивления и мощности, используемой элементами электрической цепи, соединенными как в последовательной, так и в параллельной комбинациях.
Кроме того, в Руководстве по физике средней школы рассматривается содержание этого раздела лаборатории под названием «Работа, энергия и мощность в цепях», а также следующие стандарты:
- (6) Научные концепции.Учащийся знает, что в физической системе происходят изменения, и применяет законы сохранения энергии и количества движения. Ожидается, что студент:
  - (С) вычислить механическую энергию, мощность, генерируемую внутри, импульс и импульс физической системы.
Раздел Основные термины
Власть ассоциируется у многих с электричеством. Каждый день мы используем электроэнергию для работы наших современных приборов. Линии электропередачи являются наглядным примером того, как электроэнергия обеспечивает электроэнергию.Мы также используем электроэнергию для запуска автомобилей, работы компьютеров или освещения дома. Мощность — это скорость передачи энергии любого типа; электрическая мощность — это скорость, с которой электрическая энергия передается в цепи. В этом разделе мы узнаем не только, что это означает, но и какие факторы определяют электрическую мощность.
Для начала представим себе лампочки, которые часто характеризуются номинальной мощностью в ваттах. Давайте сравним лампу мощностью 25 Вт с лампой мощностью 60 Вт (см. Рисунок 19.20). Хотя обе работают при одинаковом напряжении, лампа мощностью 60 Вт излучает больше света, чем лампа мощностью 25 Вт. Это говорит нам о том, что выходную мощность электрической цепи определяет нечто иное, чем напряжение.
Лампы накаливания, такие как две, показанные на рисунке 19.20, по сути являются резисторами, которые нагреваются, когда через них протекает ток, и становятся настолько горячими, что излучают видимый и невидимый свет. Таким образом, две лампочки на фото можно рассматривать как два разных резистора.В простой цепи, такой как электрическая лампочка с приложенным к ней напряжением, сопротивление определяет ток по закону Ома, поэтому мы можем видеть, что ток, а также напряжение должны определять мощность.
Рис. 19.20 Слева находится лампочка мощностью 25 Вт, а справа — лампочка мощностью 60 Вт. Почему их выходная мощность различается, несмотря на то, что они работают при одинаковом напряжении?
Формулу мощности можно найти путем анализа размеров. Рассмотрим единицы мощности. В системе СИ мощность указывается в ваттах (Вт), которые представляют собой энергию в единицу времени, или Дж / с
.
Напомним, что напряжение — это потенциальная энергия на единицу заряда, что означает, что напряжение имеет единицы Дж / Кл.
Мы можем переписать это уравнение как J = V × CJ = V × C и подставить его в уравнение для ватт, чтобы получить
W = Js = V × Cs = V × Cs.W = Js = V × Cs = V × Cs.
Но кулон в секунду (Кл / с) — это электрический ток, который мы можем видеть из определения электрического тока, I = ΔQΔtI = ΔQΔt, где ΔΔ Q — заряд в кулонах, а ΔΔ t — время в секундах. Таким образом, приведенное выше уравнение говорит нам, что электрическая мощность равна напряжению, умноженному на ток, или
Это уравнение дает электрическую мощность, потребляемую цепью с падением напряжения В и током I .
Например, рассмотрим схему на Рисунке 19.21. По закону Ома ток, протекающий по цепи, равен
. I = VR = 12 В 100 Ом = 0,12 А. I = VR = 12 В 100 Ом = 0,12 А.
19,49
Таким образом, мощность, потребляемая схемой, составляет
P = VI = (12 В) (0,12 A) = 1,4 Вт. P = VI = (12 В) (0,12 A) = 1,4 Вт.
19,50
Куда уходит эта сила? В этой схеме мощность в основном идет на нагрев резистора в этой цепи.
Рис. 19.21 Простая схема, потребляющая электроэнергию.
При расчете мощности в цепи рисунка 19.21, мы использовали сопротивление и закон Ома, чтобы найти ток. Закон Ома дает ток: I = V / RI = V / R, который мы можем вставить в уравнение для электроэнергии, чтобы получить
P = IV = (VR) V = V2R.P = IV = (VR) V = V2R.
Это дает мощность с точки зрения только напряжения и сопротивления.
Мы также можем использовать закон Ома, чтобы исключить напряжение из уравнения для электрической мощности и получить выражение для мощности только в терминах тока и сопротивления. Если мы запишем закон Ома как V = IRV = IR и используем это, чтобы исключить V в уравнении P = IVP = IV, мы получим
P = IV = I (IR) = I2R.P = IV = I (IR) = I2R.
Это дает мощность с точки зрения только тока и сопротивления.
Таким образом, комбинируя закон Ома с уравнением P = IVP = IV для электроэнергии, мы получаем еще два выражения для мощности: одно через напряжение и сопротивление, а другое через ток и сопротивление. Обратите внимание, что в выражения для электрической мощности входят только сопротивление (не емкость или что-либо еще), ток и напряжение. Это означает, что физической характеристикой схемы, определяющей, сколько мощности она рассеивает, является ее сопротивление.Конденсаторы в цепи не рассеивают электроэнергию — напротив, конденсаторы либо накапливают электрическую энергию, либо отдают ее обратно в цепь.
Чтобы прояснить связь между напряжением, сопротивлением, током и мощностью, взгляните на рисунок 19.22, на котором показано колесо формулы . Количества в центральной четверти круга равны количествам в соответствующей внешней четверти круга. Например, чтобы выразить потенциал V через мощность и ток, мы видим из колеса формул, что V = P / IV = P / I.
Рис. 19.22 Колесо формул показывает, как связаны между собой вольт, сопротивление, ток и мощность. Количества во внутренней четверти окружности равны количеству в соответствующей внешней четверти окружности.
Рабочий пример
Найдите сопротивление лампочки
Типичная старая лампа накаливания имела мощность 60 Вт. Если предположить, что к лампочке приложено 120 В, каков ток через лампочку?
Стратегия
Нам даны напряжение и выходная мощность простой схемы, содержащей лампочку, поэтому мы можем использовать уравнение P = IVP = IV, чтобы найти ток I , протекающий через лампочку.
Решение
Решение P = IVP = IV для тока и вставка данных значений для напряжения и мощности дает
P = IVI = PV = 60 Вт 120 В = 0,50 А. P = IVI = PV = 60 Вт 120 В = 0,50 А.
19,51
Таким образом, половина ампера проходит через лампочку, когда на нее подается 120 В.
Обсуждение
Это значительное течение. Напомним, что в быту используется переменный, а не постоянный ток, поэтому 120 В, подаваемое от бытовых розеток, — это переменная, а не постоянная мощность.Фактически, 120 В — это усредненная по времени мощность, обеспечиваемая такими розетками. Таким образом, средний ток, протекающий через лампочку за период времени, превышающий несколько секунд, составляет 0,50 А.
Рабочий пример
Подогреватели сапог
Чтобы согреть ботинки в холодные дни, вы решили вшить цепь с некоторыми резисторами в стельку ботинок. Вам нужно 10 Вт тепла от резисторов в каждой стельке, и вы хотите, чтобы они работали от двух 9-вольтовых батарей (соединенных последовательно).Какое общее сопротивление вы должны приложить к каждой стельке?
Стратегия
Нам известны требуемая мощность и напряжение (18 В, потому что у нас есть две батареи по 9 В, соединенные последовательно), поэтому мы можем использовать уравнение P = V2 / RP = V2 / R, чтобы найти необходимое сопротивление.
Решение
Решая P = V2 / RP = V2 / R для сопротивления и вставляя заданные напряжение и мощность, получаем
P = V2RR = V2P = (18 В) 210 Вт = 32 Ом. P = V2RR = V2P = (18 В) 210 Вт = 32 Ом.
19,52
Таким образом, общее сопротивление в каждой стельке должно быть 32 Ом.Ω.
Обсуждение
Давайте посмотрим, сколько тока пройдет через эту цепь. У нас есть 18 В, приложенное к сопротивлению 32 Ом, поэтому закон Ома дает
I = VR = 18 В 32 Ом = 0,56 А. I = VR = 18 В 32 Ом = 0,56 А.
19,53
На всех батареях есть этикетки, на которых указано, сколько заряда они могут обеспечить (в единицах тока, умноженного на время). Типичная щелочная батарея на 9 В может обеспечить заряд 565 мА · ч · мА · ч. (таким образом, две батареи 9 В обеспечивают 1130 мА⋅ч мА⋅ч), поэтому эта система обогрева проработает в течение
t = 1130 × 10−3A⋅h0.56A = 2.0h.t = 1130 × 10−3A⋅h0.56A = 2.0h.
19,54
Рабочий пример
Питание через ответвление цепи
Каждый резистор в приведенной ниже схеме имеет сопротивление 30 Ом. Какая мощность рассеивается средней ветвью схемы?
Стратегия
Средняя ветвь схемы содержит последовательно включенные резисторы R3 и R5R3 и R5. Напряжение на этой ветви составляет 12 В. Сначала мы найдем эквивалентное сопротивление в этой ветви, а затем используем P = V2 / RP = V2 / R, чтобы найти мощность, рассеиваемую в ветви.
Решение
Эквивалентное сопротивление: R среднее = R3 + R5 = 30 Ом + 30 Ом = 60 Ом, среднее = R3 + R5 = 30 Ом + 30 Ом = 60 Ом. Мощность, рассеиваемая средней ветвью схемы, составляет
ед. P средний = V2R средний = (12 В) 260 Ом = 2,4 Вт. Средний = V2 R средний = (12 В) 260 Ом = 2,4 Вт.
19,55
Обсуждение
Давайте посмотрим, сохраняется ли энергия в этой цепи, сравнив мощность, рассеиваемую в цепи, с мощностью, обеспечиваемой батареей. Во-первых, эквивалентное сопротивление левой ветви
R влево = 11 / R1 + 1 / R2 + R4 = 11/30 Ом + 1/30 Ом + 30 Ом = 45 Ом.R влево = 11 / R1 + 1 / R2 + R4 = 11/30 Ом + 1/30 Ом + 30 Ом = 45 Ом.
19,56
Мощность по левой ветви
Влево = V2R влево = (12 В) 245 Ом = 3,2 Вт. Влево = V 2 R влево = (12 В) 245 Ом = 3,2 Вт.
19,57
Правая ветвь содержит только R6R6, поэтому эквивалентное сопротивление Rright = R6 = 30ΩRright = R6 = 30Ω. Мощность через правую ветку
Прямо = V2 Правое = (12 В) 230 Ом = 4,8 Вт Правое = V 2 Правое = (12 В) 230 Ом = 4,8 Вт.
19,58
Полная мощность, рассеиваемая схемой, представляет собой сумму мощностей, рассеиваемых в каждой ветви.
P = Pleft + Pmiddle + Pright = 2,4W + 3,2W + 4,8W = 10,4WP = Pleft + Pmiddle + Pright = 2,4W + 3,2W + 4,8W = 10,4W
19,59
Мощность, обеспечиваемая аккумулятором, составляет
, где I — полный ток, протекающий через батарею. Поэтому мы должны сложить токи, проходящие через каждую ветвь, чтобы получить I . Ветви дают токи
Влево = VR влево = 12 В 45 Ом = 0,2667 A В середине = VR в середине = 12 В 60 Ом = 0,20 В вправо = VR В вправо = 12 В 30 Ом = 0,40 А. Влево = VR В влево = 12 В 45 Ом = 0,2667 A В середине = VR в середине = 12 В 60 Ом = 0.20AI right = VR right = 12 В 30 Ом = 0,40 А.
19,61
Суммарный ток
I = левый + Imiddle + Iright = 0,2667A + 0,20A + 0,40A = 0,87A.I = Ileft + Imiddle + Iright = 0,2667A + 0,20A + 0,40A = 0,87A.
19,62
, а мощность, обеспечиваемая аккумулятором, составляет
P = IV = (0,87 A) (12 В) = 10,4 Вт. P = IV = (0,87 A) (12 В) = 10,4 Вт.
19,63
Это та же мощность, которая рассеивается на резисторах цепи, что показывает, что в этой цепи сохраняется энергия.
Практические задачи
16.
Какова формула мощности, рассеиваемой на резисторе?
1. Формула мощности, рассеиваемой в резисторе, P = IV.P = IV.
2. Формула мощности, рассеиваемой в резисторе, P = VI.P = VI.
3. Формула для мощности, рассеиваемой в резисторе: P = IV .
4. Формула мощности, рассеиваемой на резисторе: P = I ² V .
17.
Какова формула мощности, рассеиваемой резистором с учетом его сопротивления и напряжения на нем?
1. Формула мощности, рассеиваемой в резисторе: P = RV2P = RV2
2. Формула мощности, рассеиваемой в резисторе: P = V2RP = V2R
3. Формула мощности, рассеиваемой в резисторе: P = V2RP = V2R
4. Формула мощности, рассеиваемой в резисторе: P = I2RP = I2R
Проверьте свое понимание
18.
Какие элементы схемы рассеивают мощность?
1. конденсаторы
2. индукторы
3. идеальные переключатели
4. резисторы
19.
Объясните словами уравнение мощности, рассеиваемой заданным сопротивлением.
1. Электрическая мощность пропорциональна току через резистор, умноженному на квадрат напряжения на резисторе.
2. Электрическая мощность пропорциональна квадрату тока через резистор, умноженного на напряжение на резисторе.

Мощность формулы по физике: Недопустимое название — Викиверситет

Мощность | Физика

Физика. Механика

Урок физики «Мощность»

Урок физики по теме «Мощность»

Полезная мощность: определение в физике

Готовые работы на аналогичную тему

Работа и мощность тока — материалы для подготовки к ЕГЭ по Физике

Работа тока

Мощность тока

Закон Джоуля–Ленца

10 формул по физике

Electric Power — Summary — The Physics Hypertextbook

Определение силы в физике

Расчетная мощность

Ед. Мощности

Работа и сила

Средняя мощность

Мгновенная мощность

Мощность

Формулы мощности

Пример: 3000 Дж энергии используется за 20 секунд, какова мощность?

Пример: эти парни тянут с объединенной силой 4000 Н и управляют скоростью 0.4 м / с, какую мощность они используют?

Мощность

Пример: у машины Сэма двигатель мощностью 200 л.с. Что это в ваттах?

Что такое киловатт-час?

Это маленький радиатор

Работа, энергия и сила

7.7: Мощность — Физика LibreTexts

Что такое сила?

Расчет мощности по энергии

Мощность и энергопотребление

Сводка

Глоссарий

Авторы и авторство

Power — Мощность и эффективность — Edexcel — GCSE Physics (Single Science) Revision — Edexcel

Расчетная мощность

Пример

19.4 Электроэнергетика — физика

Цели обучения разделу

Поддержка учителей

Поддержка учителей

Раздел Основные термины

Рабочий пример

Найдите сопротивление лампочки

Стратегия

Рабочий пример

Подогреватели сапог

Стратегия

Рабочий пример

Питание через ответвление цепи

Стратегия

Практические задачи

Проверьте свое понимание

Добавить комментарий Отменить ответ