Мощность в цепи постоянного тока
 Здравствуйте! Эту статью можно считать началом знакомства с электричеством. Напряжение, ток, сопротивление – это три главные величины, на которых построены основные законы электротехники и эти величины связаны между собой еще одной – мощностью. А чтобы было проще знакомиться с электротехникой, мы будем рассматривать мощность в цепи постоянного тока. Дело в том, что при расчетах в цепях переменного тока появляется довольно много условий. Впрочем, обо всём по порядку и вы сейчас сами с этим разберётесь.
Здравствуйте! Эту статью можно считать началом знакомства с электричеством. Напряжение, ток, сопротивление – это три главные величины, на которых построены основные законы электротехники и эти величины связаны между собой еще одной – мощностью. А чтобы было проще знакомиться с электротехникой, мы будем рассматривать мощность в цепи постоянного тока. Дело в том, что при расчетах в цепях переменного тока появляется довольно много условий. Впрочем, обо всём по порядку и вы сейчас сами с этим разберётесь.
Для удобства я сразу напишу международные обозначения этих четырёх величин:
U – напряжение (В, вольт)
I – ток (А, ампер)
R – сопротивление (Ом, ом)
P – мощность (Вт, ватт – не надо путать с вольтом, который обозначается только одной буквой В)
Для начала абстрактный пример, чтобы проще было понимать термины, которые я сейчас буду использовать. Допустим, есть магазин товаров (условно это можно представить, как напряжение), есть деньги (условно это будет ток), есть совесть, которая не позволяет вам тратить много или наоборот, шепчет, чтобы вы крупно потратились (это можно считать сопротивлением) и есть купленные товары или продукты, которые вы несёте домой (это мощность). Собственно, на этом примере можно объяснить многие законы, связанные с электрическим током. Все обозначенные величины связаны между собой законом Ома, который гласит, что сила тока в цепи прямо пропорциональна напряжению и обратно пропорциональна сопротивлению цепи, а именно:
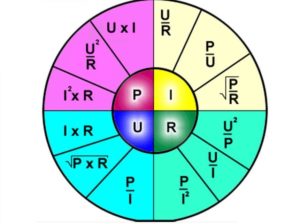
В абстрактном примере – чем больше магазин (напряжение) и чем меньше вам шепчет совесть (сопротивление), тем больше вы тратите денег (сила тока), а когда вы несёте купленный товар домой, вы совершаете работу (мощность). Мощность в цепи постоянного тока это и есть работа, совершаемая электричеством. Мощность это произведение тока на напряжение, а если вместо тока или напряжения подставить соответствующие значения, то можно получить мнемоническую табличку:
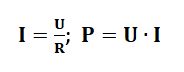
Если теперь в формуле мощности подставить место значения тока формулу тока, то получим следующее: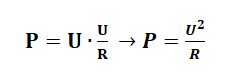
Именно таким образом и получилось 12 формул на основе закона Ома, которые вы видите в мнемонической табличке. Что такое мощность в цепях постоянного тока мы более или менее разобрались, но есть ещё один момент.
Баланс мощностей в цепи постоянного тока.
Собственно, это просто проверка правильности расчетов электрической цепи. Возвращаясь к нашему абстрактному примеру это выглядит так: вы купили товары, забрали их на кассе, отошли от кассы и вам показалось, что ваши пакеты должны быть больше или меньше, чем получились. Тогда вы берёте чек и начинаете сравнивать товар в чеке и товар в наличии. Если товары в чеке и товары в руках совпали, значит всё в порядке. Если мы обратимся к определению, то баланс мощностей – сумма мощностей потребляемых приемниками, равна сумме мощностей отдаваемых источниками.
Как это использовать на практике? Допустим, у нас есть задача, которую нужно решить: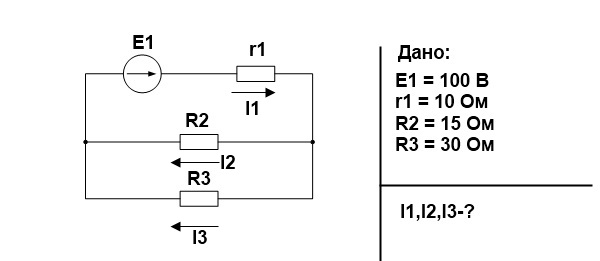
Поскольку решение задачи не является целью этой статьи, я дам уже готовые ответы. 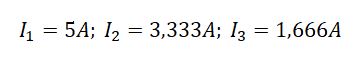
Теперь надо проверить правильно ли были посчитаны токи в задаче. Ток в цепи равен току , следовательно, мощность источника питания (Е1хI1) должна быть равна сумме мощностей сопротивлений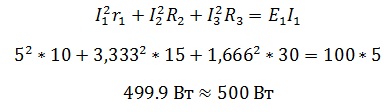
Что мы и получаем с учетом потерь при округлениях.
Таким образом, баланс мощностей в электрической цепи постоянного тока — это ничто иное, как проверка самого себя, своих расчётов.
Как видите, мощность в цепи постоянного тока посчитать довольно легко. Гораздо больше сложностей возникнет, если ток будет переменный. Другими словами, на примере магазина это выглядит так:
Постоянный ток – от входа до выхода прямая линия и вы спокойно идете от начала и до конца без каких-либо приключений.
Переменный ток – магазин представляет из себя зигзаг и вам приходится делать лишние движения.
Поэтому в переменном токе мощность считать немного сложнее, но это уже тема совсем другой статьи.
Поделиться ссылкой:
Похожее
Мощность постоянного тока
Мощность постоянного тока P – это величина, которая показывает какую работу совершил постоянный ток по перемещению электрического заряда за единицу времени. Измеряется электрическая мощность, как и механическая – в ваттах.
Для того чтобы понять что такое электрическая мощность представим себе электрическое поле, в котором находится свободная частица.
Под действием напряженности E электрического поля, частица перемещается из точки a в точку b.

При перемещении частицы из точки a в точку b электрическое поле совершает работу А. Эта работа зависит от напряженности, заряда и расстояния между a и b.

Так как работа зависит еще и от величины заряда, то энергетической характеристикой электрического поля служит напряжение, которое является отношением работы A по перемещению заряда к величине самого заряда Q.

Если заряд равен единичному (Q=1), то получается, что напряжение это есть работа по перемещению единичного заряда из точки a в точку b.

Мощность определяется как отношение работы к промежутку времени , за который была совершена эта работа.

Выходит, что мощность, затрачиваемая на единичный заряд равна

А на некоторое количество зарядов Q

Если присмотреться ко второму множителю, то можно рассмотреть в нем электрический ток, который выражен как скорость изменения заряда. Таким образом, получаем всем известную формулу

Для того чтобы узнать, какое количество энергии выделилось источником постоянного тока, нужно воспользоваться законом Джоуля –Ленца.

Пример
Узнать какое количество энергии получит резистор от источника за 10 секунд, если его сопротивление равно 100 Ом, а ЭДС источника равно 12 В. Сопротивление источника принять равным нулю.

Найдем силу тока по закону Ома

Посчитаем мощность

Такое количество энергии получает резистор за секунду, а за десять секунд он получит в десять раз больше
Рекомендуем прочесть статью о балансе мощностей и о мгновенной мощности.
Преобразование треугольника в звезду
 ra = r1
ra = r1
rb = r2*r3/(r1 + r2 + r3)
rc = r1*r3/(r1 + r2 + r3)
Мощность цепи постоянного тока
Мощность – это работа, производимая в единицу времени. Мощность участка электрической цепи с сопротивлением r равна произведению тока на напряжение на участке: P = I*U.
Отсюда можно получить другие формулы для расчёта мощности, если использовать закон Ома: U = r*I или I = U/r:
P = r*I*I = r*I2 или P = U*U/r = U2/r
[P] = 1 B*1A = 1 B*1 A = 1 Вт
Единицы измерения электрической и механической мощности:
1 Вт = 1 Дж/с = 1 Н*м/с = 0.102 кгс*м/с
1 кгс*м = 9.81 Вт
1 л.с. (лошадиная сила) = 75 кгс*м/с = 736 Вт
1 кВт = 1000 Вт = 102 кгс*м/с = 1.36 л.с.
Сокращением Дж обозначается единица измерения работы или энергии (джоуль). Работу в 1 Дж совершает источник энергии мощностью в 1Вт за 1 с, т. е. 1 Вт*с = 1 Дж = 0.102 кгс*м. 1 кВт*с = 1000 Дж; 1 кВт*ч = 1000*3600 = 3600000 Дж.
Электрическую мощность цепей постоянного тока обычно измеряют вольтметром и амперметром, ваттметром, которым, как правило, измеряется мощность цепей постоянного тока.
Формулы для расчёта работы и энергии в цепях постоянного тока
Величина | Обозначение | Единица величины и её обозначения | Формулы |
Энергия (электрическая работа) | W | :Джоуль (Дж) 1 Дж = 1 Вт*с = 0.102 кгс*м 1 кВт*ч = 1000 Вт*ч = 3.6*106Вт*с = 3.6*106Дж | W = U*I*t W = P*t W = r*I²*t W = (U²/r)*t |
Коэффициент полезного действия электрических установок
Коэффициент полезного действия (к. п. д.) – это отношение полезной мощности к затраченной:
η = полезная мощность/затраченная мощность
η = Рп/Рз = Wп/Wз.
Затраченная мощность Рз всегда больше, чем полезная мощность Рп, на мощность потерь:
ΔР = Рз-Рп.
Электрический нагрев
Основной единицей количества теплоты, в Международной системе СИ, является джоуль (Дж). Это такое количество теплоты, которое выделяется за одну секунду в проводнике, по которому течёт ток 1 А при напряжении 1 В (т. е. при сопротивлении проводника 1 Ом). Отсюда 1 Дж = 1 Вт*с.
Количество выделенной теплоты Q определяется по тем же формулам, что и энергия работа:
Q = W = U*I*t = r*I2*t = (U2/r)*t.
Прежде применялась другая единица количества теплоты – калория (кал).
1 Дж = 1 Вт*с = 0.24 кал
1 кДж = 1000 Дж = 240 кал = 0.24 ккал
1 кВт*ч = 3600 кДж = 860 ккал
Электрическое освещение Основные расчётные соотношения
Величина | Обозначение | Формула | Единица измерения | Обозначение единицы |
Световой поток | F | F = E*S | Люмен | лм |
Сила света | I | I = F/ω | Кандела | кд |
Освещённость | E | E = F/S | Люкс | лк |
Световая отдача | K | K = F/P | Люмен/ватт | лм/Вт |
ω – пространственный угол. Единицей измерения пространственного угла (стерадиан – ср) является пространственный угол, который выделяет на сферической поверхности поверхности радиусом R = 1 м площадь S = 1 м².
Единица силы света кандела ранее называлась свечой (св).
1 лк = 1 лм/1м².
Мощность постоянного и переменного электрического тока.
Мощность постоянного тока
Так как значения силы тока и напряжения постоянны и равны мгновенным значениям в любой момент времени, то мощность можно вычислить по формуле:
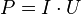 .
.
Для пассивной линейной цепи, в которой соблюдается закон Ома, можно записать:
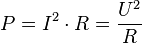 ,
где
,
где 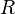 — электрическое
сопротивление.
— электрическое
сопротивление.
Если цепь содержит источник ЭДС, то отдаваемая им или поглощаемая на нём электрическая мощность равна:
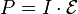 ,
где
,
где 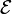 —
ЭДС.
—
ЭДС.
Если
ток внутри ЭДС противонаправлен градиенту
потенциала (течёт внутри ЭДС от плюса
к минусу), то мощность поглощается
источником ЭДС из сети (например, при
работе электродвигателя или
заряде аккумулятора),
если сонаправлен (течёт внутри ЭДС от
минуса к плюсу), то отдаётся источником
в сеть (скажем, при работегальванической
батареи или генератора).
При учёте внутреннего
сопротивления источника
ЭДС выделяемая на нём мощность 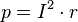 прибавляется
к поглощаемой или вычитается из
отдаваемой.
прибавляется
к поглощаемой или вычитается из
отдаваемой.
Мощность переменного тока[править | править вики-текст]
В цепях переменного тока формула для мощности постоянного тока может быть применена лишь для расчёта мгновенной мощности, которая сильно изменяется во времени и для практических расчётов бесполезна. Прямой расчёт среднего значения мощности требует интегрирования по времени. Для вычисления мощности в цепях, где напряжение и ток изменяются периодически, среднюю мощность можно вычислить, интегрируя мгновенную мощность в течение периода. На практике наибольшее значение имеет расчёт мощности в цепях переменного синусоидального напряжения и тока.
Для
того, чтобы связать понятия полной,
активной, реактивной мощностей
и коэффициента
мощности,
удобно обратиться к теории комплексных
чисел.
Можно считать, что мощность в цепи
переменного тока выражается комплексным
числом таким, что активная мощность
является его действительной частью,
реактивная мощность — мнимой частью,
полная мощность — модулем, а
угол  (сдвиг
фаз) — аргументом. Для такой модели
оказываются справедливыми все выписанные
ниже соотношения.
(сдвиг
фаз) — аргументом. Для такой модели
оказываются справедливыми все выписанные
ниже соотношения.
Активная мощность[править | править вики-текст]
Единица измерения — ватт (W, Вт).
Среднее
за период 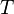 значение
мгновенной мощности называется активной
мощностью:
значение
мгновенной мощности называется активной
мощностью: 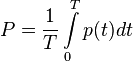 .
В цепях однофазного синусоидального
тока
.
В цепях однофазного синусоидального
тока  ,
где
,
где 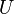 и
и  — среднеквадратичные
значения напряжения и тока,
— среднеквадратичные
значения напряжения и тока, 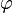 — угол
сдвига фаз между
ними. Для цепей несинусоидального тока
электрическая мощность равна сумме
соответствующих средних мощностей
отдельных гармоник. Активная мощность
характеризует скорость необратимого
превращения электрической энергии в
другие виды энергии (тепловую и
электромагнитную). Активная мощность
может быть также выражена через силу
тока, напряжение и активную составляющую
сопротивления цепи
— угол
сдвига фаз между
ними. Для цепей несинусоидального тока
электрическая мощность равна сумме
соответствующих средних мощностей
отдельных гармоник. Активная мощность
характеризует скорость необратимого
превращения электрической энергии в
другие виды энергии (тепловую и
электромагнитную). Активная мощность
может быть также выражена через силу
тока, напряжение и активную составляющую
сопротивления цепи  или
её проводимость
или
её проводимость 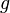 по
формуле
по
формуле 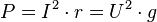 .
В любой электрической цепи как
синусоидального, так и несинусоидального
тока активная мощность всей цепи равна
сумме активных мощностей отдельных
частей цепи, для трёхфазных
цепейэлектрическая
мощность определяется как сумма мощностей
отдельных фаз. С полной мощностью
.
В любой электрической цепи как
синусоидального, так и несинусоидального
тока активная мощность всей цепи равна
сумме активных мощностей отдельных
частей цепи, для трёхфазных
цепейэлектрическая
мощность определяется как сумма мощностей
отдельных фаз. С полной мощностью 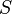 активная
связана соотношением
активная
связана соотношением 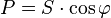 .
.
В теории длинных линий (анализ электромагнитных процессов в линии передачи, длина которой сравнима с длиной электромагнитной волны) полным аналогом активной мощности является проходящая мощность, которая определяется как разность между падающей мощностью и отраженной мощностью.
Реактивная мощность[править | править вики-текст]
Единица измерения — вольт-ампер реактивный (var, вар)
Реактивная
мощность — величина, характеризующая
нагрузки, создаваемые в электротехнических
устройствах колебаниями энергии
электромагнитного поля в цепи
синусоидального переменного тока, равна
произведению среднеквадратичных
значений напряжения 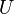 и
тока
и
тока  ,
умноженному на синус угла сдвига
фаз
,
умноженному на синус угла сдвига
фаз 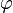 между
ними:
между
ними: 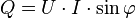 (если
ток отстаёт от напряжения, сдвиг фаз
считается положительным, если опережает —
отрицательным). Реактивная мощность
связана с полной мощностью
(если
ток отстаёт от напряжения, сдвиг фаз
считается положительным, если опережает —
отрицательным). Реактивная мощность
связана с полной мощностью  и
активной мощностью
и
активной мощностью 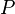 соотношением:
соотношением: 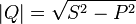 .
.
Физический смысл реактивной мощности — это энергия, перекачиваемая от источника на реактивные элементы приёмника (индуктивности, конденсаторы, обмотки двигателей), а затем возвращаемая этими элементами обратно в источник в течение одного периода колебаний, отнесённая к этому периоду.
Необходимо
отметить, что величина 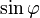 для
значений
для
значений  от
0 до плюс 90° является положительной
величиной. Величина
от
0 до плюс 90° является положительной
величиной. Величина 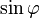 для
значений
для
значений 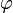 от
0 до −90° является отрицательной величиной.
В соответствии с формулой
от
0 до −90° является отрицательной величиной.
В соответствии с формулой 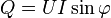 ,
реактивная мощность может быть как
положительной величиной (если нагрузка
имеет активно-индуктивный характер),
так и отрицательной (если нагрузка имеет
активно-ёмкостный характер). Данное
обстоятельство подчёркивает тот факт,
что реактивная мощность не участвует
в работе электрического тока. Когда
устройство имеет положительную реактивную
мощность, то принято говорить, что оно
её потребляет, а когда отрицательную —
то производит, но это чистая условность,
связанная с тем, что большинство
электропотребляющих устройств
(например, асинхронные
двигатели),
а также чисто активная нагрузка,
подключаемая через трансформатор,
являются активно-индуктивными.
,
реактивная мощность может быть как
положительной величиной (если нагрузка
имеет активно-индуктивный характер),
так и отрицательной (если нагрузка имеет
активно-ёмкостный характер). Данное
обстоятельство подчёркивает тот факт,
что реактивная мощность не участвует
в работе электрического тока. Когда
устройство имеет положительную реактивную
мощность, то принято говорить, что оно
её потребляет, а когда отрицательную —
то производит, но это чистая условность,
связанная с тем, что большинство
электропотребляющих устройств
(например, асинхронные
двигатели),
а также чисто активная нагрузка,
подключаемая через трансформатор,
являются активно-индуктивными.
Синхронные генераторы, установленные на электрических станциях, могут как производить, так и потреблять реактивную мощность в зависимости от величины тока возбуждения, протекающего в обмотке ротора генератора. За счёт этой особенности синхронных электрических машин осуществляется регулирование заданного уровня напряжения сети. Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности.
Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии возвращаемой от индуктивной и емкостной нагрузки в источник переменного напряжения.
Полная мощность
Единица полной электрической мощности — вольт-ампер (V·A, В·А)
Полная
мощность — величина, равная произведению
действующих значений периодического
электрического тока  в
цепи и напряжения
в
цепи и напряжения 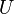 на
её зажимах:
на
её зажимах: 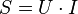 ;
связана с активной и реактивной мощностями
соотношением:
;
связана с активной и реактивной мощностями
соотношением: 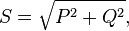 где
где 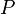 —
активная мощность,
—
активная мощность, 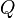 —
реактивная мощность (при индуктивной
нагрузке
—
реактивная мощность (при индуктивной
нагрузке 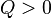 ,
а при ёмкостной
,
а при ёмкостной 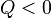 ).
).
Векторная
зависимость между полной, активной и
реактивной мощностью выражается
формулой: 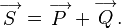
Полная мощность имеет практическое значение, как величина, описывающая нагрузки, фактически налагаемые потребителем на элементы подводящей электросети (провода, кабели, распределительные щиты, трансформаторы, линии электропередачи), так как эти нагрузки зависят от потребляемого тока, а не от фактически использованной потребителем энергии. Именно поэтому полная мощность трансформаторов и распределительных щитов измеряется в вольт-амперах, а не в ваттах.
Комплексная мощность[править | править вики-текст]
Мощность, аналогично импедансу, можно записать в комплексном виде:
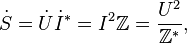 где
где  —
комплексное напряжение,
—
комплексное напряжение, 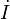 —
комплексный ток,
—
комплексный ток, 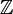 —
импеданс, * — оператор комплексного
сопряжения.
—
импеданс, * — оператор комплексного
сопряжения.
Модуль
комплексной мощности 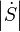 равен
полной мощности
равен
полной мощности 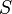 .
Действительная часть
.
Действительная часть 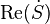 равна
активной мощности
равна
активной мощности 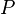 ,
а мнимая
,
а мнимая  —
реактивной мощности
—
реактивной мощности  с
корректным знаком в зависимости от
характера нагрузки.
с
корректным знаком в зависимости от
характера нагрузки.
Электрический ток.Работа, мощность | От урока до экзамена
Кристаллическая решёткаЭлектрический ток. Все металлы являются проводниками электрического тока. Они состоят из пространственной кристаллической решетки, узлы которой совпадают с центрами положительных ионов. Вокруг ионов хаотически движутся свободные электроны.
В металлах электронная проводимость
Электрическим током в металлах называется упорядоченное движение свободных электронов. За направление тока принимают направление движения положительно заряженных частиц.
Электрические заряды могут двигаться упорядоченно под действием электрического поля, поэтому условием для существования эл. тока является наличие электрического поля и свободных носителей эл.заряда.
Сила тока численно равна заряду, протекающему через данное поперечное сечение проводника в единицу времени. Ток называется постоянным, если сила тока и его направление не изменяется с течением времени.
I = 1 Кл/с = 1 А1 ампер (А) равен силе постоянного тока, при котором через любое поперечное сечение проводника за 1 с протекает 1 Кл электричества. I = q0 nvS Силу тока в цепи измеряют амперметром. Условное обозначение в цепи
Работа и мощность тока. Электрический ток снабжает нас энергией. Она возникает за счёт работы электрического поля по передвижению свободных зарядов в проводнике. Рассмотрим участок цепи, по которому течёт ток I. Напряжение на участке обозначим U, сопротивление участка равно R. При протекании тока по однородному участку цепи электрическое поле совершает работу. За время Δt по цепи протекает заряд Δq = I Δt. Электрическое поле на выделенном участке совершает работу. ΔA = U I Δt — эту работу называют работой электрического тока. За счёт работы на рассматриваемом участке может совершаться механическая работа; могут также протекать химические реакции. Если этого нет, то работа эл.поля приводит только к нагреванию проводника. Работа тока равна количеству теплоты, выделяемому проводником с током: — закон Джоуля — Ленца
Мощность электрического тока равна отношению работы тока ΔA к интервалу времени Δt, за которое эта работа была совершена на данном участке: P = IU или . Работа электрического тока в СИ выражается в джоулях (Дж), мощность – в ваттах (Вт).
Закон Ома для замкнутой цепи. Источник тока имеет ЭДС () и сопротивление (r), которое называют внутренним. Электродвижущей силой (ЭДС) называется отношение работы сторонних сил по перемещению заряда q вдоль цепи, к значению этого заряда (1В=1Дж/1Кл). Рассмотрим теперь замкнутую (полную) цепь постоянного тока, состоящую из источника с электродвижущей силой и внутренним сопротивлением r и внешнего однородного участка с сопротивлением R. (R+r) — полное сопротивление цепи. Закон Ома для полной цепи записывается в виде или
Сила тока в электрической цепи прямо пропорциональна ЭДС источника тока и обратно пропорциональна полному сопротивлению цепи.
2.4. Мощность в цепях постоянного тока
Понятие мощности. Мощность – это скорость изменения энергии во времени:
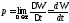 .
.
Умножим и разделим на dq:
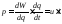
Следовательно, мощность – это произведение напряжения на ток. Единица измерения мощности в общем случае – В⋅А (вольт-ампер).
Используя закон Ома, можно получить другие формулы для мощности в электрических цепях:
− на участке цепи
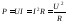 ;
;
− мощность источника постоянного тока:
P = EI;
− мощность приемника:
P =UI = RI⋅I = RI2;
− электрическая энергия:
A = Pt,
где t – время.
Баланс мощностей. Баланс мощностей – это интерпретация закона сохранения энергии в электротехнике.
Определение баланса формулируется следующим образом: мощность генераторов энергии в электрической цепи равна мощности потребителей (нагрузок)
Pг = Рн,
причем
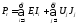
где 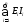 – мощность источников
ЭДС;
– мощность источников
ЭДС;
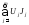 –мощность источников
тока;
–мощность источников
тока;
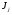 –токи источников
тока;
–токи источников
тока;
 –напряжения на зажимах
источников тока.
–напряжения на зажимах
источников тока.
Эти суммы алгебраические. Источник может как вырабатывать, так и потреблять электрическую энергию (заряд аккумулятора, рис. 2.19).
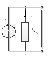

а б
Рис. 2.19. Схема цепи с источником тока в режимах выделения (а) и потребления (б) энергии
Если направления ЭДС и тока через источник ЭДС совпадают, мощность источника записывают в уравнении баланса мощностей с положительным знаком. Он работает в режиме генератора.
При противоположных направлениях ЭДС и тока мощность в уравнении баланса учитывают с отрицательным знаком (режим потребителя).
Ток Iвн и напряжение U направлены в сторону уменьшения потенциала, что и позволяет разметить зажимы источника.
Мощность потребителей (нагрузок)
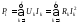
Погрешность расчета баланса мощностей при расчетах электрических цепей не должна превышать (1–3) %.
мощность постоянного тока
Немного о мощности постоянного тока. Не надо долго ходить за примерами и что-то объяснять в том плане, что механическая работа, которую совершает двигатель, выделяемая нагревателем теплота вполне измеримы. От каких же величин зависит совершаемая работа?
Чем дольше потребители тока, будь то лампы или двигатель, включены, тем больше электроэнергии потребляется. И тем больше количество произведенной работы. Но и при простом увеличении количества потребителей сила тока увеличивается, поскольку обычно они включаются параллельно. Следовательно, произведенная электрическая работа возрастает с увеличением силы тока и времени. Но влияет еще и третья величина. Две параллельно включенные лампы потребляют двойную энергию по сравнению с одной. А, значит, и двойной ток. Тот же результат получим, если соединим две лампы последовательно и подадим двойное напряжение (см. рис.1).
Электрическая работа зависит, следовательно, и от напряжения. Поэтому для работы электрического тока в течение отрезка времени получим зависимость:
W=UIt
Здесь U — напряжение, I — сила тока, t — время, W — количество произведенной работы. Теперь о самой мощности. Под мощностью понимают работу, совершаемую за определенное время. Таким образом, P=W/t. Если теперь вместо W подставить выражение для электрической работы, то
P=UIt/t=UI
Таким образом, мощность — это произведение напряжения на силу тока. Единицей мощности служит 1Вт, в честь ее открывателя, шотландского инженера, Джеймса Уайта (1736 — 1819).
Вернувшись назад к формуле
работы тока W=UIt увидим, что это произведение электрической мощности P=UI и времени t, в течение которого эта мощность действует. Если время выразить в часах, то плучим количество потребленной энергии «ватт-час». Такая единица измерения является маленькой, поэтому пользуются «киловатт-часом». 1кВтч=1000Втч
Кстати, кто еще далек от электричества, есть «хитрый» перерасчет электрической мощности в механическую:



