Вектор магн индукции | От урока до экзамена

При прохождении тока по проводнику вокруг него образуется магнитное поле. Векторную характеристику магнитного поля называют вектором магнитной индукции . Это поле оказывает на рамку с током, помещенную в поле, ориентирующее действие. Такое  действием магнитного поля на рамку с током или магнитную стрелку можно использовать для определения направления вектора магнитной индукции. За  принимается направление, который показывает северный полюс N магнитной стрелки. Для определения направления вектора магнитной индукции поля, созданного прямолинейным проводником с током, пользуются правилом буравчика: если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика указывает направление вектора магнитной индукции.

направление вектора магнитного поля прямого проводника с током.

Если между полюсами подковообразного магнита поместить проводник с током, то он будет втягиваться или выталкиваться из поля магнита. Закон, определяющий силу, действующую на отдельный небольшой участок проводника, был установлен в 1820 г. А. Ампером. 

Сила действия однородного маг­нитного поля на проводник с током прямо пропорциональна силе тока, длине проводника, модулю вектора индукции магнитного поля, синусу угла между вектором индукции магнитного поля и проводником:

F=B^.I^.ℓ^. sin α  — закон Ампера.

• Сила Ампера максимальна, если вектор магнитной индукции перпендикулярен проводнику.
• Если вектор магнитной индукции параллелен проводнику, то магнитное поле не оказывает никакого действия на проводник с током, т.е. сила Ампера равна нулю.

Направление силы Ампера (правило левой руки) Если левую руку расположить так, чтобы перпендикулярная составляющая вектора В входила в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90° большой палец покажет направление силы, действующей на проводник с током.

Макроскопическим проявлением силы Лоренца является сила Ампера. Запишем силу, действующую на одну частицу. Если заряженная частица влетает в магнитное поле со скоростью , на нее со стороны магнитного поля действует сила, которую называют силой Лоренца

: ,  a – угол между векторами и . 

• В однородном магнитном поле, направленном перпендикулярно вектору скорости, под действием силы Лоренца заряженная частица будет равномерно двигаться по окружности постоянного радиуса r. Сила Лоренца в этом случае является центростремительной силой:
• Если заряженная частица движется в магнитном поле так, что вектор скорости   составляет с вектором магнитной индукции  угол a , то траекторией движения частицы является винтовая линия с радиусом r.

Если расположить левую руку так, чтобы  составляющая магнитной индукции  , перпендикулярная скорости заряда, входила в ладонь, а четыре вытянутых пальца были направлены по движению положительного заряда, то отогнутый на 90

0 большой палец  укажет направление действующей на заряд силы Лоренца F_л

.

Взаимодействие токов. Модуль вектора магнитной индукции

«Из всех гипотез выбирайте ту,

которая не пресекает дальнейшего

мышления об исследуемых вещах».

Джеймс Максвелл

Данная тема будет посвящена решению задач на взаимодействие токов и определение модуля вектора магнитной индукции.

Задача 1. По контуру протекает ток, равный 5 А. Этот ток создаёт магнитное поле с индукцией 3 мТл. Найдите радиус контура.

ДАНО:	СИ	РЕШЕНИЕ Запишем формулу по которой вычисляется магнитное поле кругового тока Из этой формулы выразим радиус контура

Ответ: 1 см.

Задача 2. Магнитное поле внутри соленоида равно 80 мкТл. Найдите ток, протекающий по виткам соленоида, если на каждый сантиметр соленоида приходится 10 витков.

ДАНО:	СИ	РЕШЕНИЕ Применим формулу, по которой рассчитывается магнитное поле внутри соленоида Из этой формулы выразим силу тока Т.к. все величины входящие в формулу известны, то

Ответ: 157 мА.

Задача 3. К проводнику с сопротивлением 5 Ом приложено напряжение 100 В. Известно, что модуль вектора магнитной индукции поля, создаваемого током в проводнике, равен 2 мТл на расстоянии 2 см от проводника. Найдите магнитную проницаемость среды, в которой находится проводник.

ДАНО:	СИ	РЕШЕНИЕ Запишем формулу для магнитного поля прямого тока Закон Ома для участка цепи Тогда формула для магнитного поля прямого тока с учётом закона Ома будет иметь вид Из этой формулы выразим магнитную проницаемость среды

Ответ: 10.

Задача 4. По двум параллельным тонким проводникам, находящимся на расстоянии 0,1 м друг от друга, протекают токи 3 А и 2 А в противоположных направлениях. Найдите модуль вектора магнитной индукции в точке, находящейся посередине между проводниками.

ДАНО:	РЕШЕНИЕ Запишем принцип суперпозиции полей Магнитное поле прямого тока определяется по формуле Так как векторы B1 и B2 направлены в противоположные стороны, ясно, что модуль результирующего вектора будет равен разности модулей этих векторов

Ответ: 4 мкТл.

Задача 5. По четырём длинным тонким проводникам, проходящим через вершины квадрата со стороной 5 см перпендикулярно его плоскости, текут токи I₁, I₂ по 15 А и I₃, I₄ – по 20 А. По проводникам, проходящим через противолежащие вершины, текут токи в одном направлении, а по проводникам, проходящим через соседние вершины — в противоположных направлениях. Найдите модуль вектора магнитной индукции в центре квадрата.

ДАНО:	СИ	РЕШЕНИЕ Чтобы найти модуль вектора магнитной индукции в центре квадрата, необходимо использовать принцип суперпозиции полей Магнитное поле прямого тока определяется по формуле Длину диагонали квадрата определим из теоремы Пифагора Расстояние от центра квадрата до проводника с током будет равно половине длины диагонали Теперь используем принцип суперпозиции: поскольку векторы B3 и B1 направлены в противоположные стороны, можно просто вычислить разность их модулей, чтобы найти магнитное поле в центре квадрата, создаваемое проводниками 1 и 3 Аналогично для проводников 2 и 4: поскольку векторы B4 и B2 направлены в противоположные стороны, можно просто вычислить разность их модулей, чтобы найти магнитное поле в центре квадрата, создаваемое проводниками 2 и 4 Исходя из условия, разность между токами I1 и I3 равна разности между токами I2 и I4. Поэтому, можем заключить, что модули векторов B1,3 и B2,4 равны Из принципа суперпозиции полей получаем

Ответ: 40 мкТл.

Вектор индукции магнитного поля

Определение

Силовой характеристикой магнитного поля является вектор магнитной индукции $\overrightarrow{B}$. Вектор магнитной индукции является основной характеристикой магнитного поля. Он равен пределу отношения силы, с которой магнитное поле действует на элементарный ток ($Idl$) к произведению тока $(I)$ и величины элемента проводника ($dl$):

Вектор индукции направлен перпендикулярно направлению элементарного тока (или чаще говорят элементу проводника ($\overrightarrow{dl}$)) из (1) и перпендикулярен направлению силы, которая действует со стороны магнитного поля.

Если $\overrightarrow{B}$=const, то магнитное поле называют однородным. Если магнитное поле неизменно во времени, то его называют постоянным.

Иногда модуль вектора индукции однородного магнитного поля определяют как:

где $M_{max}$ — максимальный вращающий момент, действующий на контур с током, который помещен в магнитное поле, $p_m=IS$ — магнитный момент контура ($S$- площадь контура). За направление вектора $\overrightarrow{B}$ принимают направление, в котором устанавливается под действием поля положительная нормаль к контуру с током. Или иначе, говорят, что вектор магнитной индукции направлен в сторону поступательного перемещения правого винта, если его вращать по направлению течения тока в контуре.

Очень часто, определение для вектора магнитной индукции записывают в виде:

где $\overrightarrow{dF}$ — сила, действующая на элемент с током. В том случае, если проводник прямолинейный и магнитная индукция во всех точках постоянна, то формулу (2) можно преобразовать в выражение:

Рис. 1

Модуль вектора индукции можно определить, так же исходя из силы Лоренца ($\overrightarrow{F}$), которая действует на движущуюся, со скоростью $\overrightarrow{v}$ заряженную частицу (заряд q) в магнитном поле:

Основной единицей измерения магнитной индукции в системе СИ является тесла (Тл).

Принцип суперпозиции вектора индукции магнитного поля

Эмпирический доказано, что для магнитного поля выполняется принцип суперпозиции:

Если магнитное поле порождается несколькими токами (движущимися зарядами), то оно равно векторной сумме отдельных полей:

Пример 1

Задание: Проводник имеет форму квадрата, сторона которого равна d, по нему течет ток силы I. Найдите магнитную индукцию поля в точке пересечения диагоналей квадрата.

Решение:

Допустим, что плоскость проводника совпадает с плоскостью рис.2. Зададим направление токов.

Рис. 2

В точке О магнитное поле создают четыре прямолинейные проводника с током. Напряженности всех четырех полей направлены в соответствии с правилом правого винта от нас, перпендикулярно плоскости рисунка. Следовательно, векторную сумму полей в принципе суперпозиции заменим на алгебраическую, запишем:

\[B=B_1+B_2+B_3+B_4\left(1.1\right).\]

Причем из симметрии, очевидно, что модули всех индукций равны, значит, запишем, что:

\[B=4B_1\left(1.2\right).\]

В разделе «Электромагнетизм» мы нашли, формулу для расчета модуля вектора магнитной индукции прямолинейного проводника с током. В применении к нашему случаю модуль $\overrightarrow{B}$ будет иметь вид:

\[B_1=\frac{{\mu }_0I}{4\pi b}\left(cos\alpha -cos\beta \right)\left(1.3\right),\]

углы $\alpha $ и $\beta $ указаны на рис.1. В (1.3) $\beta =\pi -\alpha \to cos\beta ={cos \left(\pi -\alpha \right)\ }=-cos\alpha .$ Перепишем (1.3):

\[B_1=\frac{{\mu }_0I}{2\pi b}cos\alpha \left(1.4\right).\]

Так как мы имеем дело с квадратом, то заметим, что: $b=\frac{d}{2},\alpha =\frac{\pi }{4}\to cos\alpha =\frac{\sqrt{2}}{2}.$ Подставим в (1.4), то что мы получили и (1.4) подставим в (1.2), имеем:

\[B=4\cdot \frac{{\mu }_0I}{\pi d}\cdot \frac{\sqrt{2}}{2}=\frac{2\sqrt{2}}{\pi d}{\mu }_0I.\]

Ответ: $B=\frac{2\sqrt{2}}{\pi d}{\mu }_0I.$

Пример 2

Задание: Бесконечно длинный проводник с током (I) согнут под прямым углом (рис.2). Найдите магнитную индукцию поля в точке А, которая указана на рис. 3.

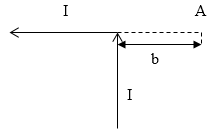
Рис. 3

Решение:

В точке А поле создается двумя частями проводника:

\[\overrightarrow{B}=\overrightarrow{B_{II}}+\overrightarrow{B_{\bot }}\left(2.1\right).\]

Рассмотрим горизонтальный участок, на продолжении которого лежит точка А. Этот участок проводника с током создает поле в точке А индукция $(\overrightarrow{B_{II}})$которого, равна нулю, так как в точке А углы между всеми элементами с током и радиус-векторами будут равны $\pi .\ $Следовательно, векторное произведение ($\left[d\overrightarrow{l}\overrightarrow{r}\right]$), в законе Био — Савара — Лапласа равно нулю:

\[\overrightarrow{B}=\frac{{\mu }_0}{4\pi }\oint{\frac{I\left[d\overrightarrow{l}\overrightarrow{r}\right]}{r^3}}\left(2.2\right),\]

где $\overrightarrow{r}$ — радиус-вектор, проведенный от элемента тока $Id\overrightarrow{l}$ к точке, в которой ищется индукция магнитного поля ($\overrightarrow{B}$).

Индукция магнитного поля бесконечного прямолинейного проводника с током (I) в точке А была бы равна:

\[B’=\frac{{\mu }_0}{2\pi }\frac{I}{b}\left(2.3\right).\]

У нас полу бесконечный проводник, следовательно, из принципа суперпозиции получим, что для нашего проводника индукция равна:

\[{B=B}_{\bot }=\frac{1}{2}B’=\frac{{\mu }_0}{\pi }\frac{I}{b}.\]

Ответ: $B=\frac{{\mu }_0}{\pi }\frac{I}{b}.$

Индукция магнитного поля. Магнитный поток

Многие из вас наверняка замечали, что внешне похожие магниты создают разные по силе магнитные поля.

С другой стороны, вы также знаете, что, например, рамка с током, помещённая между полюсами подковообразного магнита, принимает ориентированное положение, при котором линии магнитного поля перпендикулярны плоскости рамки.

— Так какой же величиной можно охарактеризовать магнитное поле?

Для описания магнитного поля вводится векторная физическая величина, называемая индукцией магнитного поля (или просто магнитной индукцией). Обозначается она большой латинской буквой B.

Давайте поясним смысл этой величины и укажем способ её измерения. Для этого проведём такой опыт. Возьмём проводник, длиной пол метра, подвешенный на динамометре, и поместим его между полюсами подковообразного магнита перпендикулярно его магнитным линиям.

Первоначально проводник уравновешен, а показание динамометра численно равно модулю силы тяжести, действующей на проводник.

Теперь наша задача пропустить по проводнику ток такого направления, чтобы на него подействовала сила Ампера, направленная вертикально вниз. Для этого мы используем правило левой руки: линии магнитного поля должны входить в ладонь перпендикулярно к ней, а отставленный на девяносто градусов большой палец должен быть направлен вертикально вниз. При этом четыре сомкнутых пальца покажут направление тока в проводнике.

Замкнув цепь снимем показания динамометра. Далее определим значение силы Ампера, действующей на проводник, как разность показаний динамометра в конце и начале опыта. Теперь повторим эксперимент при неизменной силе тока, заменив проводник на более длинный и, как и в прошлый раз, найдём значение действующей на проводник силы Ампера.

Видно, что чем длиннее проводник, тем большая сила Ампера на него действует. Следовательно, сила Ампера пропорциональна длине проводника.

Теперь при неизменной длине проводника будем изменять силу тока в нём и, как и в прошлый раз, будем находить значение силы Ампера.

Можно прийти к заключению, что сила Ампера пропорциональна силе тока в проводнике.

Опыты показывают, что сила Ампера зависит и от ориентации проводника в магнитном поле. Она достигает своего максимального значения в случае, когда проводник расположен перпендикулярно линиям поля.

Однако отношение модуля силы Ампера к длине проводника и силе тока не зависит ни от длины проводника, ни от силы тока в нём:

Следовательно, отношение F/l зависит только от свойств магнитного поля и поэтому может служить его количественной характеристикой. Эту характеристику поля называют модулем магнитной индукции.

Таким образом, модуль вектора магнитной индукции — это физическая величина, равная отношению силы, действующей на расположенный перпендикулярно магнитным линиям проводник с током, к произведению силы тока в нём на длину проводника.

Сразу обращаем ваше внимание на то, что по этой формуле можно определить индукцию однородного магнитного поля.

В международной системе единиц за единицу магнитной индукции принята индукция такого магнитного поля, в котором на каждый метр длины проводника при силе тока 1 А действует максимальная сила, равная 1 Н. Эту единицу называют тесла в честь выдающегося югославского физика Николы Тесла.

Отметим, что тесла — это очень крупная единица. Так, например, большой лабораторный электромагнит может создать поле не более 5 Тл. Магнитное поле нашей планеты приблизительно равно 0,5 ∙ 10−4 Тл. И лишь в солнечных пятнах индукция магнитного поля достигает 10 Тл. Поэтому на практике используются более мелкие единицы индукции:

До сегодняшнего дня для графического изображения магнитных полей мы с вами пользовались магнитными линиями — воображаемыми линиями, направление которых совпадает с направлением, на которое указывает северный полюс магнитной стрелки.

За направление же вектора магнитной индукции принимается направление от южного полюса к северному полюсу свободно устанавливающейся стрелки, помещённой в данную точку поля.

Сравните два определения.

Не трудно заметить, что они очень похожи. И это не случайно, дело в том, что более точное название магнитных линий — линии магнитной индукции.

Или, другими словами, линиями магнитной индукции называют линии, касательные к которым в каждой точке поля в направлены так же, как и вектор магнитной индукции.

Например, картина линий магнитной индукции поля, образованного прямолинейным проводником с током, представляет собой систему концентрических окружностей, лежащих в плоскости, перпендикулярной этому проводнику. Проведённые к любой из этих окружностей касательные в любой точке совпадают с направлением вектора магнитной индукции.

Линии магнитной индукции условились проводить так, чтобы по их густоте можно было судить о модуле магнитной индукции: чем гуще линии магнитной индукции, тем больше её модуль.

Теперь, пользуясь понятием «магнитная индукция», дадим более строгое определение однородного и неоднородного магнитного поля. Для начала рассмотрим однородное магнитное поле между полюсами дугообразного магнита.

Магнитные линии здесь расположены параллельно друг другу. А так как во всех точках поля вектор магнитной индукции не только одинаково направлен, но и имеет одно и то же значение, то и густота линий магнитной индукции в любой области поля между полюсами будет одна и та же.

А теперь сравним это поле с неоднородным полем полосового магнита. Не трудно увидеть, что в таком поле вектор магнитной индукции меняется от точки к точке как по направлению, так и по величине.

Таким образом, магнитное поле называют однородным, если во всех его точках магнитная индукция одинакова как по направлению, так и по значению. В противном случае магнитное поле называют неоднородным.

Для объяснения опытов, которые будут проводиться в дальнейшем, нам необходимо ввести ещё одну физическую величину — магнитный поток, которая также является одной из важных характеристик магнитного поля.

Что мы понимаем под потоком в обычной жизни? Кому-то на ум придут потоки воды в реке, кому-то — потоки воздуха. Например, возьмём лист картона с отверстием. Подставив руку с обратной стороны листа, подуем в отверстие — рука явно ощущает поток воздуха. Сильнее дуем — больший поток воздуха. Будем дуть с такой же силой, но уменьшим отверстие — поток уменьшится. И наконец, если плоскость листа бумаги поставим параллельно направлению потока выдуваемого воздуха, ваша рука практически не почувствует влияние воздушного потока.

Аналогично и с магнитным потоком, который можно рассматривать как величину, пропорциональную числу магнитных линий, проходящих через площадь, ограничивающую некоторую поверхность. Поскольку число магнитных линий зависит от их густоты, то, очевидно, что магнитный поток пропорционален модулю вектора индукции магнитного поля: чем больше индукция, тем больший магнитный поток, пронизывает контур.

Вместе с тем магнитный поток зависит и от площади контура: при том же значении магнитной индукции магнитный поток, пронизывающий контур большей площади, будет больше. Следовательно, магнитный поток пропорционален также площади контура.

Очевидно и то, что в случаях, когда линии магнитной индукции перпендикулярны плоскости контура, магнитный поток принимает наибольшее значение. А при изменении ориентации контура в магнитном поле, например, при его вращении вокруг оси, магнитный поток будет уменьшаться, так как будет уменьшаться число линий магнитной индукции, пронизывающей контур. А когда плоскость контура окажется параллельной линиям магнитной индукции, магнитный поток станет равным нулю.

Магнитный поток будет равен нулю и в том случае, если линии магнитной индукции лежат в плоскости контура, не пересекая ограниченную им площадь.

В Международной системе единиц за единицу магнитного потока принят вэбэр, названный в честь немецкого физика Вильгельма Эдуарда Вебера.

1 Вб — это магнитный поток через поверхность площадью 1 м², расположенную в однородном магнитном поле индукцией 1 Тл, перпендикулярной линиям индукции.

Закрепления материала.

Разработка урока «Индукция магнитного поля»

Урок физики в 9 классе по теме «Индукция магнитного поля. Модуль вектора магнитной индукции. Линии магнитной индукции»

Тип урока: постановка учебной задачи

Задачи: обеспечить усвоение знаний об индукции магнитного поля, модуля вектора магнитной индукции, линий магнитной индукции; формировать умение вычислять индукцию маг­нитного поля

Планируемые результаты

Предметные:

научатся записывать формулу взаи­мосвязи модуля вектора магнитной индукции магнитного поля с модулем силы, действующей на проводник, и силой тока в проводнике;

Метапредметные:

познавательные — работать с текстом учебника, выделять главное, си­стематизировать и обобщать полученные сведения об индукции маг­нитного поля; исследовать магнитный поток;

регулятивные — оценивать правильность выполнения учебной задачи, собственные возможности её решения;

коммуникативные — представлять конкретное содержание и представ­лять его в нужной форме

Личностные: развитие настойчивости в дости­жении поставленной цели; разви­тие культуры умственного труда

Образовательные ресурсы: учебник, электронное приложение к учебнику (изд. Дрофа)

Организационная структура урока

Этап урока

Содержание деятельности учителя

Содержание деятельности обучающихся (осуществляемые действия)

Формируемые способы

деятельности

I. Органи­зационный момент

Приветствие. Проверка готовности учащихся к уроку. Со­здание в классе атмосферы психологического комфорта.

Настраиваются на учебную деятельность..

Формировать навыки само­организации

II. Проверка

домашнего

задания

1. Способствую проверке домашнего задания в парах.

2. Фронтальная беседа

— Чем обусловлено существование магнитного поля?
— Что такое магнитные линии?
— Какое магнитное поле называют однородным?

— Как читается правило левой руки для находящегося в магнитном поле проводника с током?

— Какое правило устанавливает связь между направлением тока и направлением его магнитных линий?

— Что еще можно определить по правилу левой руки?

Проверяют домашнее задание у соседа по парте. Фикси­руют найденные ошибки. Оценивают домашнюю работу одноклассника.

Отвечают на вопросы

Умение оценивать

достижения

других людей

III. Актуа­лизация опорных знаний и жизненно­го опыта. Постановка учебной задачи

Предлагаю учащимся найти ассоциации к слову «индук­ция». Полученные слова совместно с учащимися анализи­руются. Делается вывод о понимании этого слова. Вопрос запуска постановки учебной задачи:

• Можно ли сказать, что у меня есть понимание понятий «индукция магнитного поля» и «магнитный поток»? Формулирует учебную задачу:

• Исследовать понятия «индукция магнитного поля» и «магнитный поток»

Ассоциативный ряд: магнит, катушка, физика, поле, магнетизм и т. д.

Осознают важность решения поставленной учебной задачи

Развивать навыки целе полагания

IV. Сообще­ние темы. Постановка цели и задач урока

Сообщаю тему урока. Организую совместное с обучаю­щимися формулирование целей и задач урока:

• Внимательно прочитайте тему урока.

• Как вы сформулировали бы задачи урока исходя из темы урока?

• Что вы изменили бы в предложенных мной задачах урока?

• Чему вы хотели бы научиться?

Записывают в тетрадь тему урока.

Участвуют в формулировании целей и задач урока:

• Усвоить суть понятия «индукция магнитного поля»;

• научиться описывать зависимость магнитного потока от индукции магнитного поля

Формировать

умения

принимать

и сохранять

учебную

задачу

V. Мотиви­рование к учебной деятель­ности

Проблемный опыт. Два разных по силе действия магнита, железные опилки, листы. (Лучше использовать маленький магнит с большей по величине силой, а большой магнит — с меньшей.)

— Какое магнитное поле сильнее?

— Как вы это определили?

Наблюдают за опытом. Делают вывод: Недостаточно знаний, необходима физическая величина, которая характеризовала бы магнитное поле. Она нужна для описания магнитных полей.

Выражать свои мысли. Развивать навыки само­мотивации

VI. Созда­ние ситуа­ции затруд­нения. Изучение нового ма­териала

— Вы знаете, что магнитное поле действует с некоторой силой на проводник с током, помещенный в него. От чего же зависит эта сила?

В учебнике на странице 158 вы сможете найти ответ на этот вопрос.

Но отношение F/Il величина постоянная и может служить количественной характеристикой магнитного поля, она и принимается за модуль вектора магнитной индукции.

• Магнитное поле характеризуется векторной физической величиной, которая обозначается символом В и называет­ся индукцией магнитного поля (или магнитной индукцией). Фрагмент опыта по измерению силы, действующей на помещенный в магнитное поле проводник (эл.приложение к учебнику, изд.Дрофа)

Принимают участие в обсуждении проблемного вопроса. Испытывают определенные трудности при ответах на вопросы.

Делают записи в рабочей тетради.

Выделяют ключевые слова в определении понятия «индукция». Дают определение своими словами.

Делают в ы в о д:

Эта сила зависит от:

— самого поля,

— длины проводника,

— силы тока в нем.

Наблюдают опыт.

Выражать свои мысли в соответст­вии с зада­чей.

Умение об­рабатывать и делать вы­воды.

Помогаю учащимся понять:

• Сила действия магнитного поля на проводник пропор­циональна длине этого проводника и силе тока в нем. Модуль вектора магнитной индукции равен отношению модуля силы, с которой магнитное поле действует на рас­положенный перпендикулярно магнитным линиям провод­ник с током, к силе тока в проводнике и его длине:

В СИ единица магнитной индукции называется тесла (Тл) в честь югославского электротехника Николы Тесла. 1Тл=1Н/(А. м)

Пример. Модуль вектора магнитной индукции Земли равен 0, 00005 Тл.(В_Земли= 0,00005 Тл)

Объясняю учащимся:

• Более точное название магнитных линий — линии маг­нитной индукции (или линии индукции магнитного поля). Линиями магнитной индукции называются линии, каса­тельные к которым в каждой точке поля совпадают

с направлением вектора магнитной индукции.

Организую изучение понятий «однородное и неоднородное магнитное поле». Помогаю понять:

• Магнитное поле называется однородным, если во всех его точках магнитная индукция одинакова. В противном случае поле называется неоднородным.

Записывают в тетрадь формулу.

Анализируют определение: определяют ключевые слова, сопоставляют упомянутые понятия.

Делают записи в рабочей тетради.

Изучают в учебнике пояснения определения с помощью ри­сунка (рис. 113).

Изучают понятия «однородное и неоднородное магнитное поле». Приходят к выводу:

— Чем больше магнитная индукция в данной точке поля, тем с большей силой будет действовать поле в этой точке на магнитную стрелку или движущийся электрический заряд.

Умение с помощью вопросов добывать недостаю­щую инфор­мацию

VII. Закреп­ление изу­ченного ма­териала

Организую беседу по вопросам:

— Как называется векторная величина, которая служит ко­личественной характеристикой магнитного поля?

— Что называется линиями магнитной индукции?

• В каком случае магнитное поле называется однородным, а в каком — неоднородным?

• Как зависит сила, действующая в данной точке магнит­ного поля на магнитную стрелку или движущийся заряд, от магнитной индукции в этой точке?

Отвечают на вопросы.

— Количественной характеристикой магнитного поля служит модуль вектора магнитной индукции.

— Линии магнитной индукции — это линии, касательные

к которым в любой точке совпадают по направлению с вектором магнитной индукции.

• Магнитное поле называется однородным, если во всех его точках значения вектора магнитной индукции совпа­дают. В неоднородных полях вектор магнитной индукции меняется от точки к точке.

• Чем больше магнитная индукция, тем больше сила.

Осуществ­лять актуали­зацию полу­ченных на уроке зна­ний и умений и делать вы­воды.

VIII. Реше­ние заданий

Организую решение задач:

№1. По проводнику длиной 45 см протекает ток силой 20А. Чему равна индукция магнитного поля, в которое помещен проводник, если на проводник действует сила 9 мН?

№2 . Определите модуль силы, действующей на проводник длиной 20 см при силе тока 10А в магнитном поле с индукцией 0,13 Тл.

Организую самостоятельную работу:

№3. В однородном магнитном поле с индукцией 0,82 Тл расположен проводник длиной 1,28 м. Определите силу, действующую на проводник, если сила тока в нем равна 18А.

Доп. Упр.38( 2) в учебнике

Решают в тетрадях, 1 ученик у доски:

№1. Ответ: 1 мТл

№2. Ответ: 0,26 Н

Самостоятельно решают задания.

№3. Ответ: 19 Н

Развитие умений само­стоятельно принимать решения

IX. Подве­дение ито­гов урока. Рефлексия

Организую подведение итогов урока обучающимися. Спо­собствую размышлению обучающихся над вопросами:

• Могу ли я пояснить, что такое индукция магнитного поля?

• С какими трудностями я столкнулся при изучении поня­тия «магнитный поток»?

• Что поменялось в моем мировосприятии после сего­дняшнего урока?

-Достиг ли я поставленных целей и задач?

Подводят итоги своей работы на уроке.

Проводят самооценку, рефлексию

Отслеживать цель учебной деятельности

X. Домаш­нее задание

§ 41 учебника, упр.38 (1),№21 (стр.336)-на повторение

Помогаю учащимся выбрать задания из учебника. Обращаю внимание на возмож­ности и способности учащихся

Выбирают задания, которые будут решать дома. Записывают домашнее задание

Формировать навыки само­организации