Метод векторных диаграмм
Этот метод используется для лучшего понимания и наглядности представления процесса, изменяющегося по гармоническому закону.
Суть
метода: переменные величины 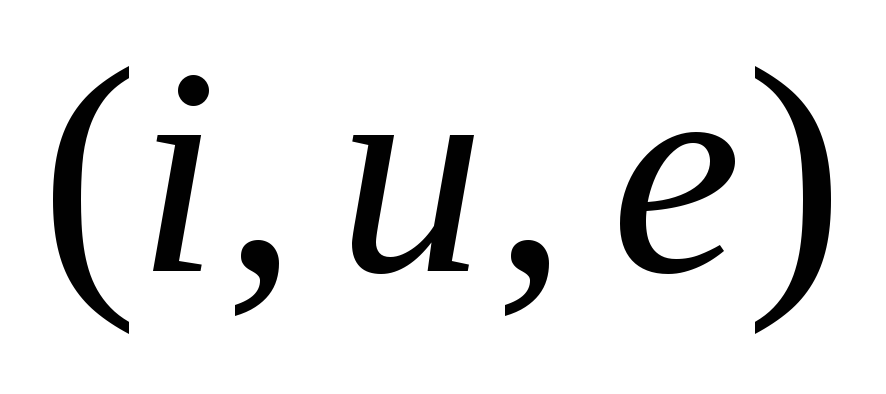 ,
изменяющиеся по гармоническому закону
,
изменяющиеся по гармоническому закону 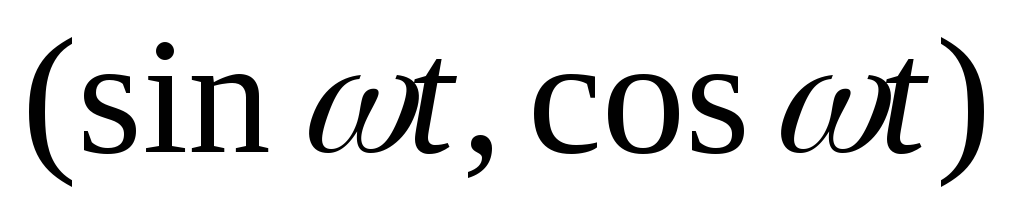 изображаются графически методом
вращающегося вектора амплитуды колебаний.
изображаются графически методом
вращающегося вектора амплитуды колебаний.
Для
этого из произвольной точки О оси ОXоткладывается вектор ,
модуль которого равен амплитуде
рассматриваемого колебания (рис. 6.5).
,
модуль которого равен амплитуде
рассматриваемого колебания (рис. 6.5).
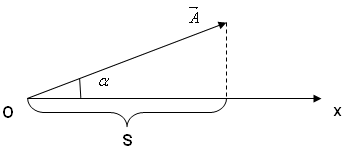
Рис. 6.5. Метод векторных диаграмм
Если
вектор  привести во вращение относительно точки
О против часовой стрелки с циклической
частотой
привести во вращение относительно точки
О против часовой стрелки с циклической
частотой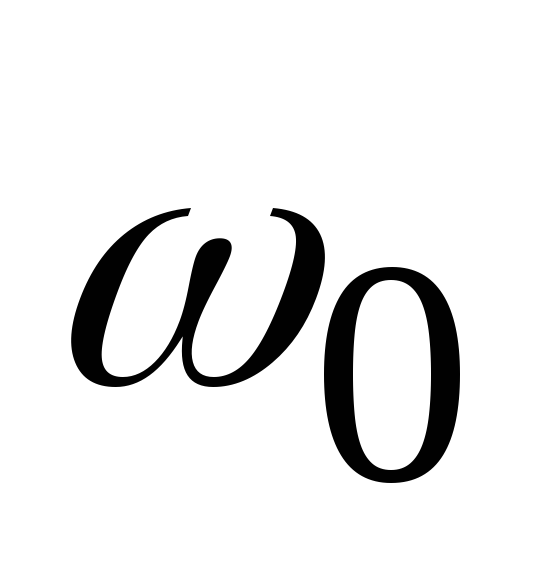 ,
то проекция вектор
,
то проекция вектор на ось ОХ будет изменяться по закону:
на ось ОХ будет изменяться по закону:
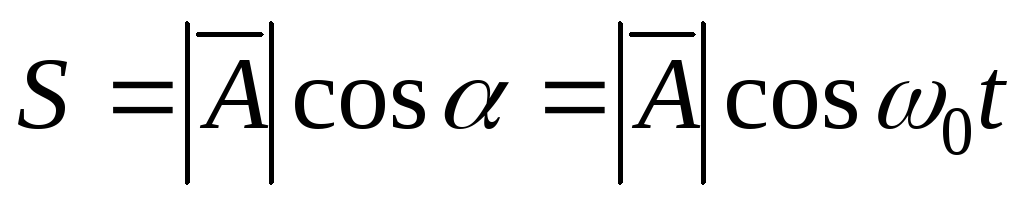 . (6.13)
. (6.13)
Таким образом, достигается эквивалентность вращающегося вектора и гармонического закона (6.5).
В общем случае векторная диаграмма – это совокупность вращающихся против часовой стрелки векторов амплитудных (действующих) значений гармонических величин.
Лекция 7. Действующее значение переменного тока. Связь между током и напряжением в элементах электрической цепи тока
Действующее значение переменного тока равно такому значению постоянного тока, которое за время, равное периоду переменного тока, выделяет в том же сопротивлении такое же количество теплоты, что и данный переменный ток.
Для постоянного тока по закону Джоуля-Ленца
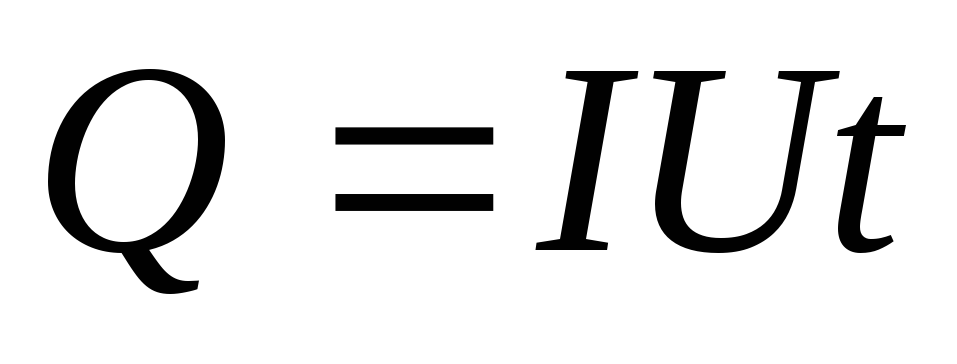 ,
(7.1)
,
(7.1)
где Q– количество теплоты, выделяемое в проводнике.
Если 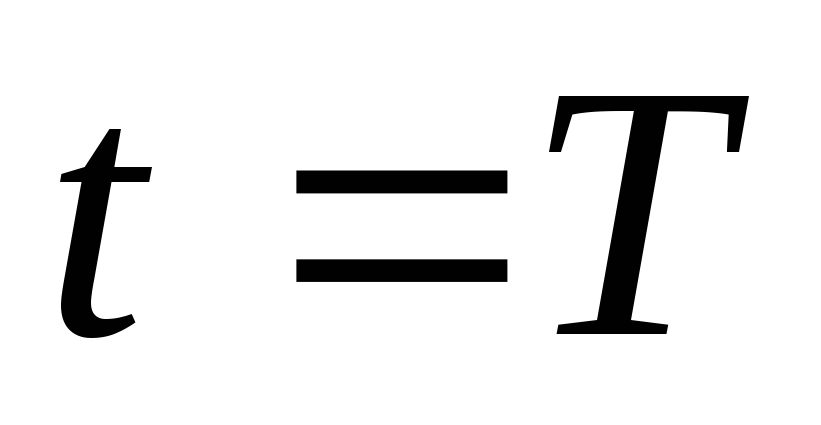 ,
тогда
,
тогда
где Т— период переменного тока.
По закону Ома
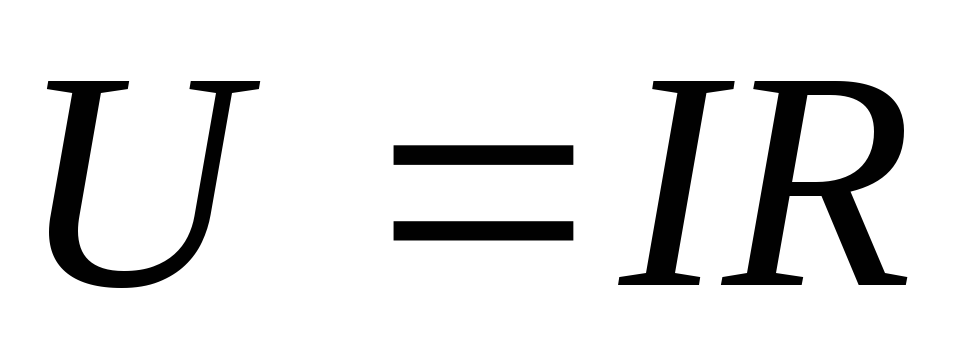 ,
тогда
,
тогда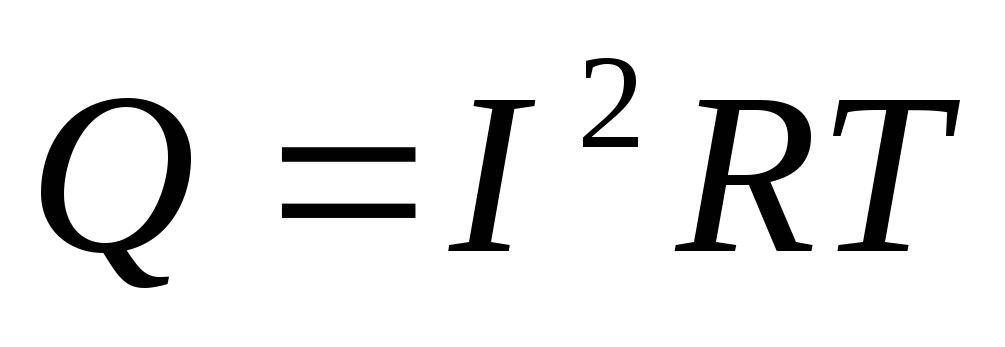 . (7.3)
. (7.3)
Пусть
ток меняется по закону 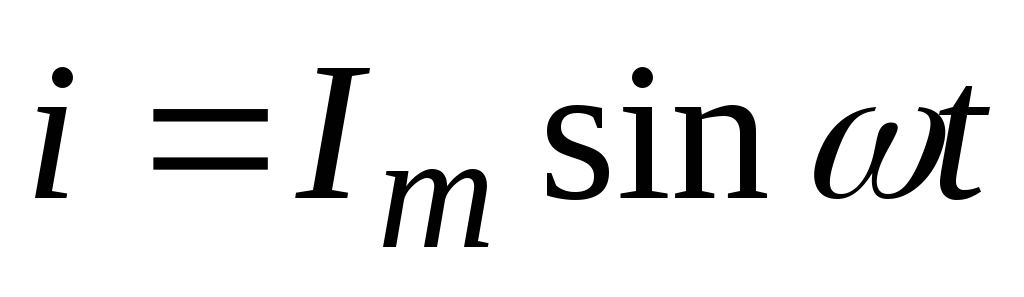 ,
(7.4)
,
(7.4)
где 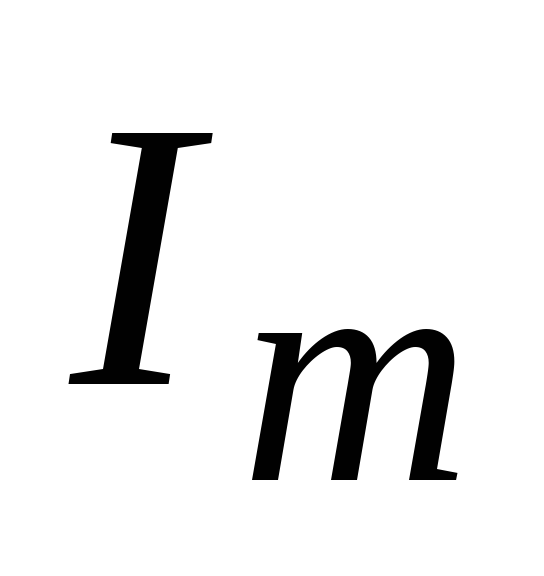 – амплитудное значение переменного
тока.
– амплитудное значение переменного
тока.
Рассмотрим очень малый промежуток времени dt, для которого переменный ток можно считать постоянным (рис. 7.1).
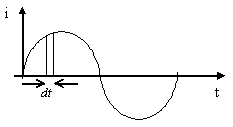
Рис. 7.1. Переменный ток
Тогда по аналогии с выражением (7.3)
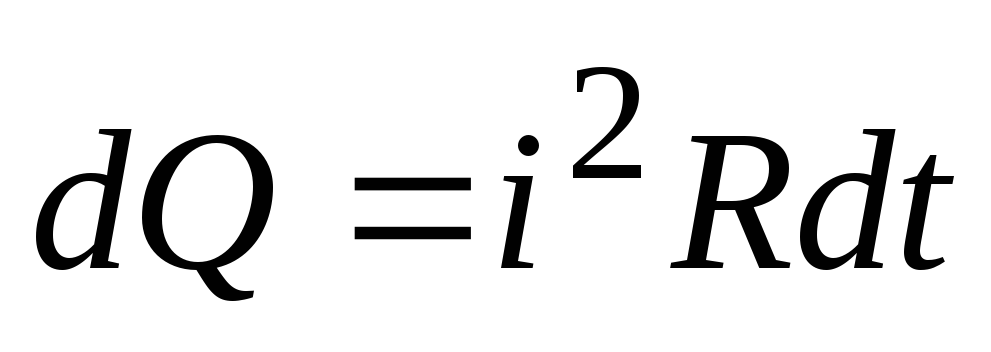 , (7.5)
, (7.5)
где 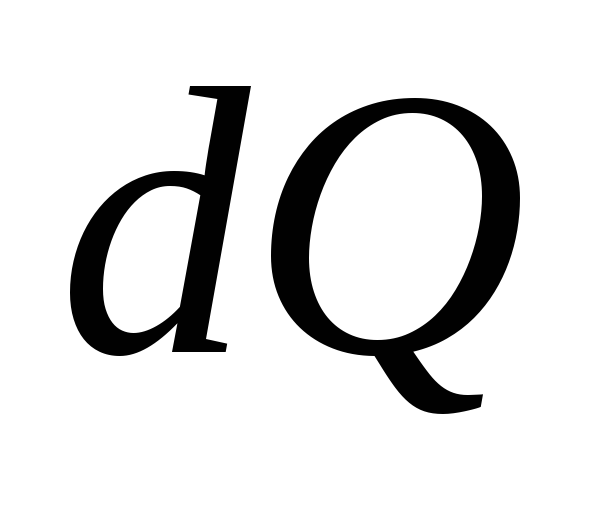 — количество теплоты, которое выделяется
в проводнике за промежуток времени
— количество теплоты, которое выделяется
в проводнике за промежуток времени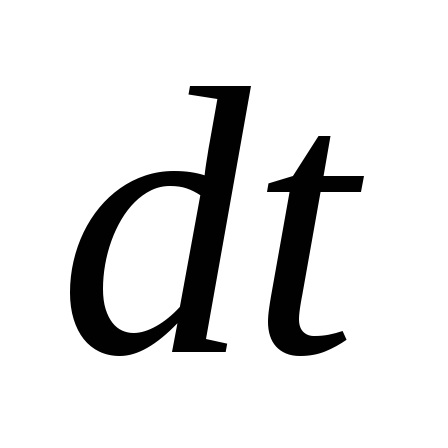 .
.
Для нахождения количества теплоты, выделяющейся в проводнике за период, проинтегрируем выражение (7.5).
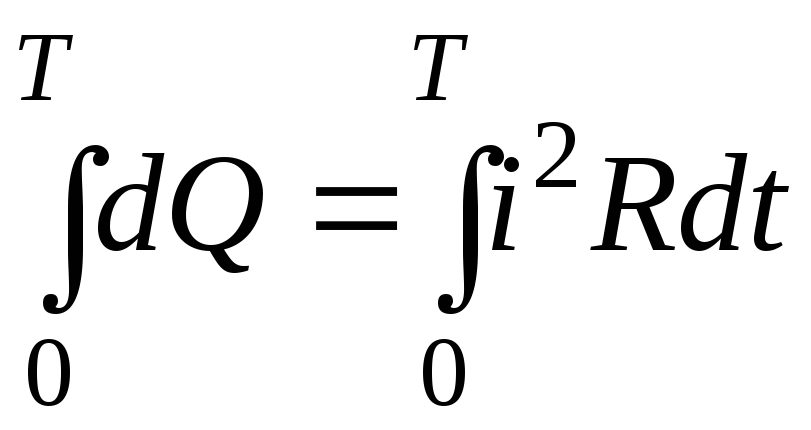 ;
(7.6)
;
(7.6)
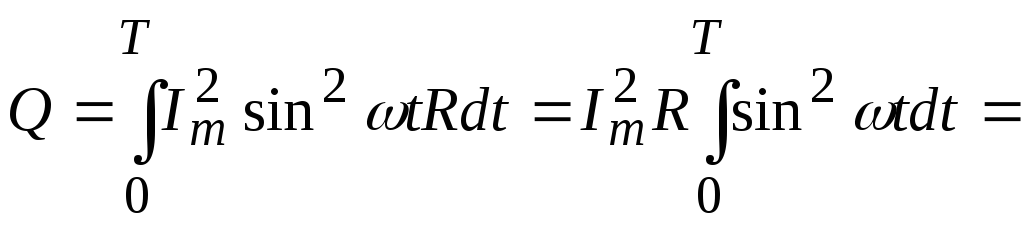
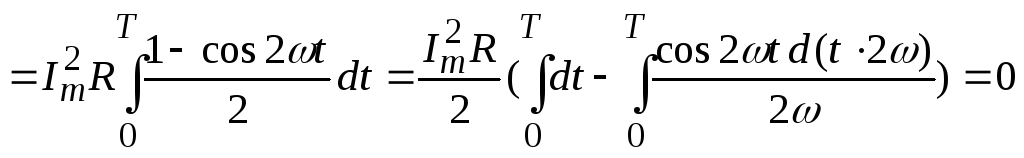

 (7.7)
(7.7)
А в
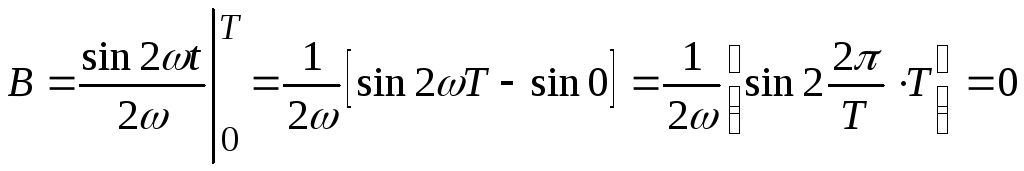 .
(7.8)
.
(7.8)
Вывод. Интеграл от периодической знакопеременной функции за 1 период равен 0.
Геометрически это можно трактовать как площадь под кривой периодической функции (рис 7.2).
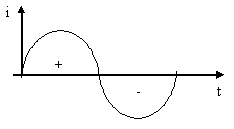
Рис. 7.2. Периодическая функция
Анализируя интеграл А получим:
 ,
т.е.
,
т.е.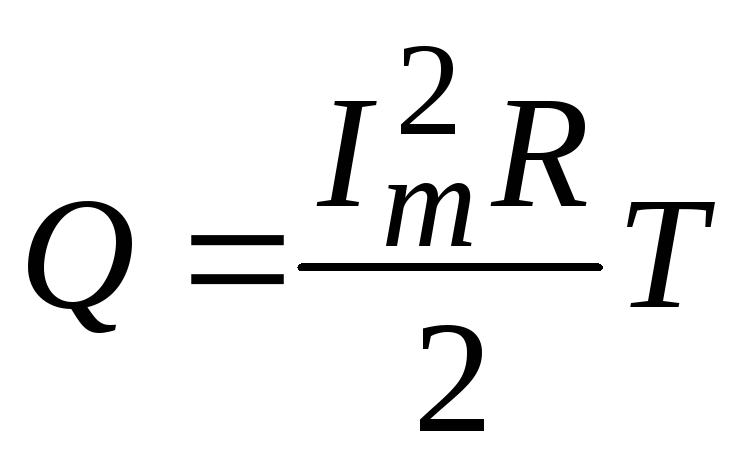 .
(7.9)
.
(7.9)
Сравнивая выражения (7.3) и (7.9) получим:
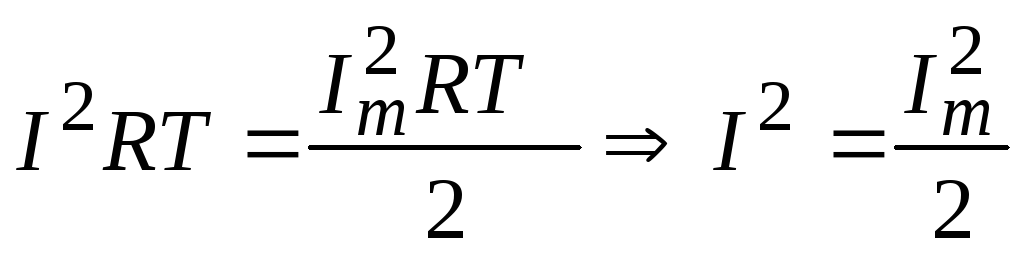 (7.10)
(7.10)
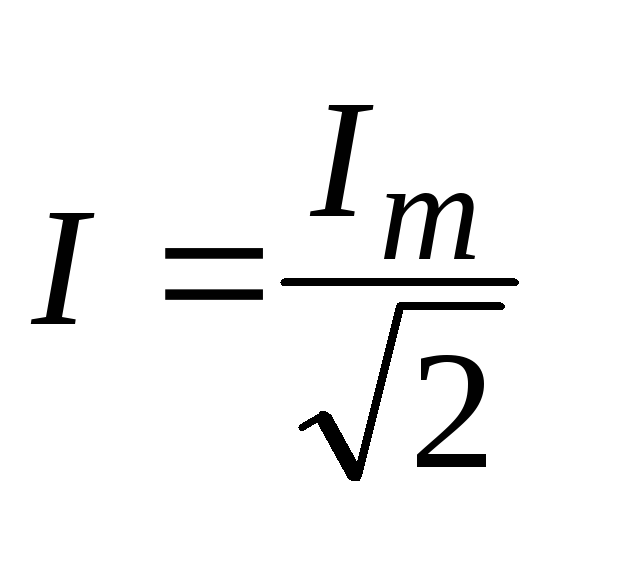 , (7.11)
, (7.11)где I– действующее значение переменного тока.
Связь между током и напряжением в элементах электрической цепи
Активное сопротивление
Пусть имеется цепь переменного тока (рис. 7.3).
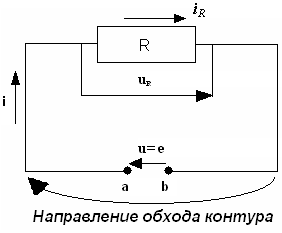
Р ис. 7.3. Электрическая цепьcактивным сопротивлением
Условия:
1) φа > φв;
2) напряжение источника в цепи изменяется по закону
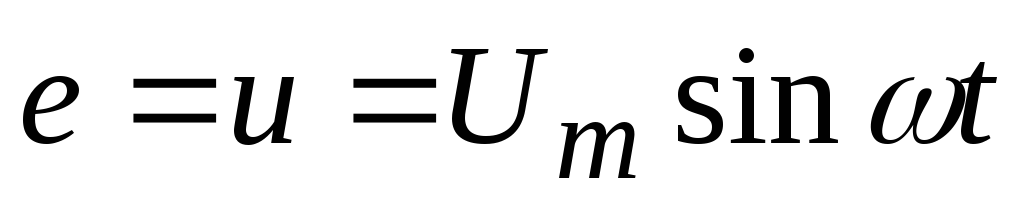 .
(7.12)
.
(7.12)
Запишем второй закон Кирхгофа для электрической цепи (рис. 7.3):
u = uR. (7.13)
По
закону Ома  , (7.14)
, (7.14)
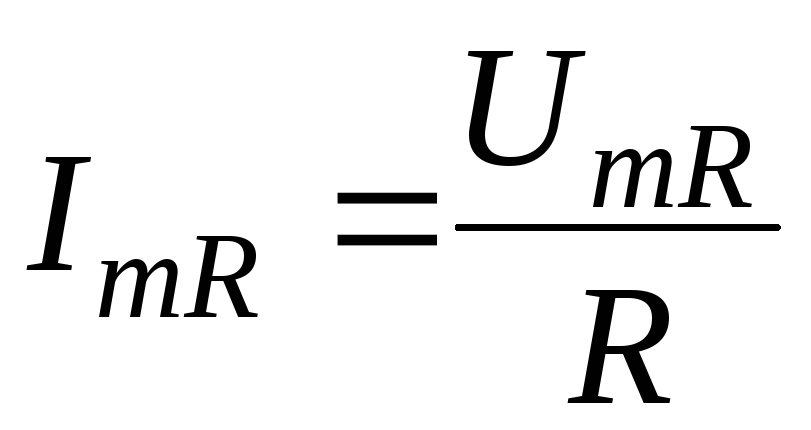 , (7.15)
, (7.15)
где 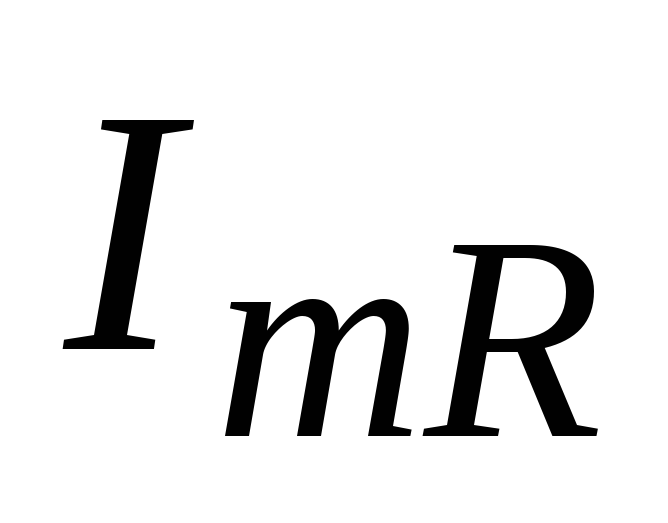 – амплитудное значение тока через
активное сопротивление, т.е.
– амплитудное значение тока через
активное сопротивление, т.е.
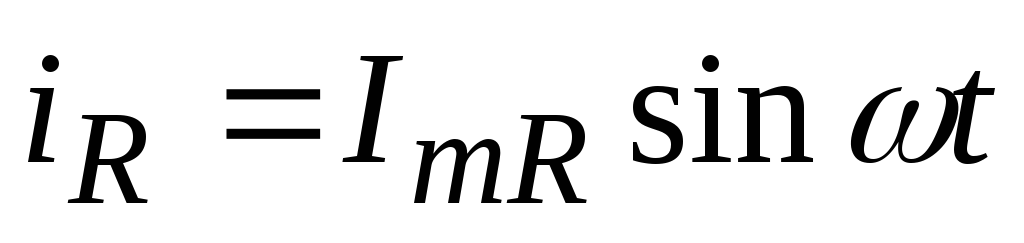 .
(7.16)
.
(7.16)
Сравнивая выражения (7.12) и (7.16) заключаем, что на активном сопротивлении ток и напряжение совпадают по фазе (рис. 7.4).
Поделим
выражение (7.15) на  и получим:
и получим:
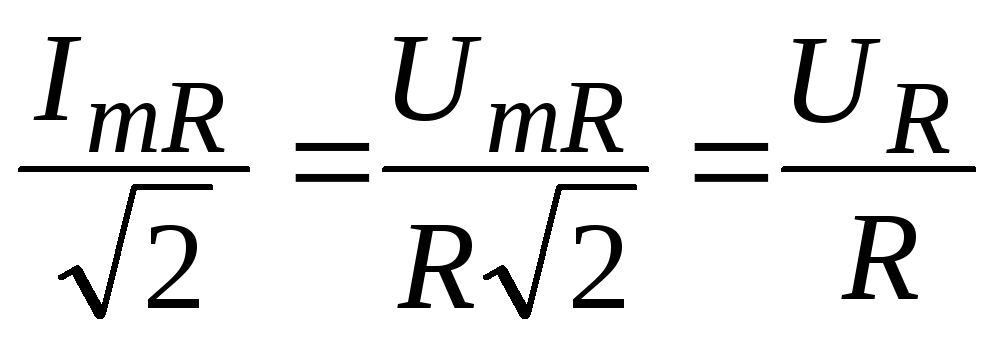 , (7.17)
, (7.17)
где 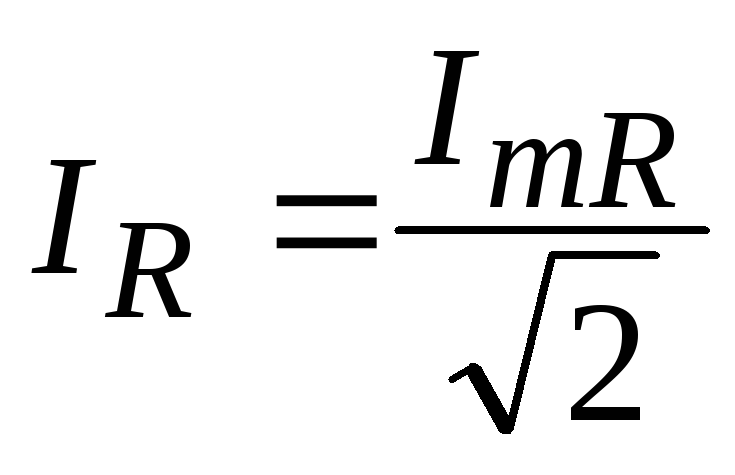 и
и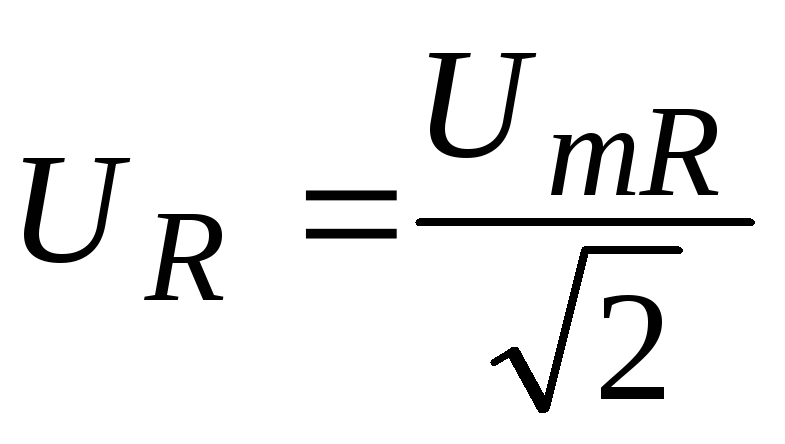
Закон Ома для действующих значений тока и напряжения на активном сопротивлении:
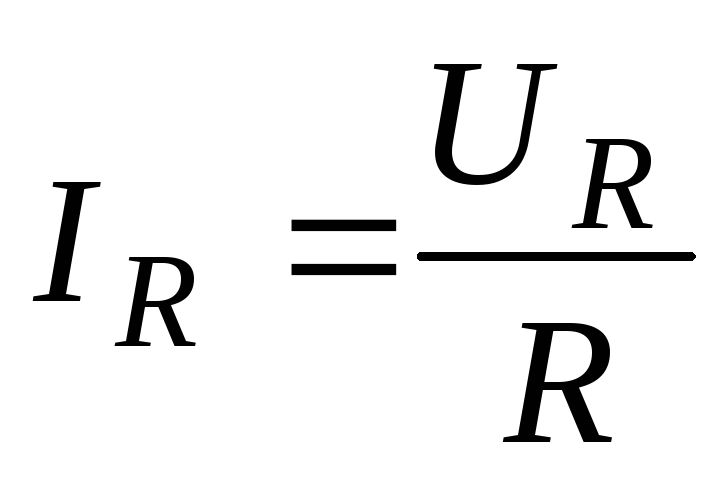 (7.18)
(7.18)
Р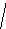 ис.
7.4. Графики тока и напряжения на активном
сопротивлении и векторная диаграмма
ис.
7.4. Графики тока и напряжения на активном
сопротивлении и векторная диаграмма
Векторные диаграммы электрических цепей | FaultAn.ru
При исследовании электрических цепей и моделировании часто пользуются векторными диаграммами токов и напряжений. Под векторной диаграммой понимается совокупность векторов, изображающих синусоидальные функции времени [1].
Воспользуйтесь программой онлайн-расчёта электрических цепей.
Представление синусоидальных функций в виде комплексных чисел
Векторная диаграмма – это удобный инструмент представления синусоидальных функций времени, коими являются, к примеру, напряжения и токи электрической цепи переменного тока.
Рассмотрим, например, произвольный ток, представленный в виде синусоидальной функции
i(t) = 10 sin(ωt + 30°).
Данный синусоидальный сигнал можно представить в виде комплексной величины
I = 10∠30°.
Для формирования комплексного числа используются модуль и фаза синусоидального сигнала.
Закон Ома в комплексной форме
Известно [1], что напряжение U на сопротивлении Z
U = Z ∙ I.
Кроме того, известны соотношения, определяющие активное сопротивление резистора, индуктивное сопротивление катушки и ёмкостное сопротивление конденсатора:
ZR = R, ZL = jXL, ZC = −jXC,
где XL = ωL, XC = 1/(ωC), R – сопротивление резистора, L – индуктивность катушки, C
Векторная диаграмма при последовательном соединении элементов
Для построения векторных диаграмм сперва составляют уравнения по законам Кирхгофа для рассматриваемой электрической цепи.
Рассмотрим электрическую цепь, представленную на рис. 1, и нарисуем для неё векторную диаграмму напряжений. Обозначим падение напряжение на элементах.
 Рис. 1. Последовательное соединение элементов цепи
Рис. 1. Последовательное соединение элементов цепи
Составим уравнение для данной цепи по второму закону Кирхгофа:
UR + UL + UC = E.
По закону Ома падение напряжений на элементах определяется по следующим выражениям:
UR = I ∙ R,
UL = I ∙ jXL,
UC = −I ∙ jXC.
Для построения векторной диаграммы необходимо отобразить приведённые в уравнении слагаемые на комплексной плоскости. Обычно вектора токов и напряжений отображаются в своих масштабах: отдельно для напряжений и отдельно для токов.
Из курса математики известно, что j = 1∠90°, −j = 1∠−90°. Отсюда при построении векторной диаграммы умножение какого-либо вектора на мнимую единицу j приводит к повороту этого вектора на 90 градусов против часовой стрелки, а умножение на −j приводит к повороту этого вектора на 90 градусов по часовой стрелке.
При построении векторной диаграммы напряжений на комплексной плоскости сперва отобразим вектор тока I, после чего относительного него будем отображать вектора падений напряжений (рис. 2) с учётом приведённых выше соотношений для мнимой единицы.
Падение напряжения на резисторе UR совпадает по направлению с током I (т.к. UR = I ∙ R, а R – чисто действительная величина или, простыми словами, нет умножения на мнимую единицу). Падение напряжения на индуктивном сопротивлении опережает вектор тока на 90° (т.к. UL = I ∙ jXL, а умножение на j приводит повороту этого вектора на 90° против часовой стрелки). Падение напряжения на ёмкостном сопротивлении отстаёт от вектора тока на 90° (т.к. UC = −I ∙ jXC, а умножение на −j приводит повороту этого вектора на 90° по часовой стрелке).

Рис. 2. Векторная диаграмма напряжений при последовательном соединении элементов цепи
Следует обратить внимание, что на одной векторной диаграмме изображают только векторы тех величин, у которых частота совпадает!
Векторная диаграмма при параллельном соединении элементов
Рассмотрим электрическую цепь, представленную на рис. 3, и нарисуем для неё векторную диаграмму токов. Обозначим направление токов в ветвях.

Рис. 3. Параллельное соединение элементов цепи
Составим уравнение для данной цепи по первому закону Кирхгофа:
I – IR – IL – IC = 0,
откуда
I = IR + IL + IC.
Определим по закону Ома токи в ветвях по следующим выражениям, учитывая, что 1 / j = −j:
IR = E / R,
IL = E / (jXL) = −j ∙ E / XL,
IC = E / (−jXC) = j ∙ E / XC,
Для построения векторной диаграммы необходимо отобразить приведённые в уравнении слагаемые на комплексной плоскости.
При построении векторной диаграммы токов на комплексной плоскости сперва отобразим вектор ЭДС E, после чего относительного него будем отображать вектора токов токов (рис. 4) с учётом приведённых выше соотношений для мнимой единицы.
Ток в резисторе IR совпадает по направлению с ЭДС E (т.к. IR = E / R, а R – чисто действительная величина или, простыми словами, нет умножения на мнимую единицу). Ток в индуктивном сопротивлении отстаёт от вектора ЭДС на 90° (т.к. IL = −j ∙ E / XL, а умножение на −j приводит повороту этого вектора на 90° по часовой стрелки). Ток в ёмкостном сопротивлении опережает вектор ЭДС на 90° (т.к. IC = j ∙ E / XC, а умножение на j приводит повороту этого вектора на 90° против часовой стрелки). Результирующий вектор тока определяется после геометрического сложения всех векторов по правилу параллелограмма.

Рис. 4. Векторная диаграмма токов при параллельном соединении элементов цепи
Для произвольной цепи алгоритм построения векторных диаграмм аналогичен вышеизложенному с учётом протекаемых в ветвях токов и прикладываемых напряжений.
Обращаем ваше внимание, что на сайте представлен инструмент для построения векторных диаграмм онлайн для трёхфазных цепей.
Список использованной литературы
- Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. Учебник для вузов. Изд. 4-е, переработанное. М., «Энергия», 1975.
Если вам нравится наш контент, помогите в развитии сайта.
Рекомендуемые записи
Методы комплексных амплитуд и векторных диаграмм
Метод комплексных амплитуд
Положение точки на плоскости можно однозначно задать комплексным числом:
Если точка ($А$) вращается, то координаты этой точки изменяются в соответствии с законом:
Используем формулу Эйлера:
запишем $z$ в виде:
где $Re(z)=x$, то есть физическая величина x равна вещественной части комплексного выражения (4). При этом модуль комплексного выражения равен амплитуде колебаний — $a$, его аргумент равен фазе (${\omega }_0t+\delta $). Иногда при взятии реальной части от $z$ знак операции Re опускают и получают символическое выражение:
Выражение (5) не следует принимать буквально. Часто формально упрощают (5):
где $A=ae^{i \delta}$ — комплексная амплитуда колебания. Комплексный характер амплитуды $А$ обозначает, что колебание имеет начальную фазу неравную нулю.
Для того чтобы раскрыть физический смысл выражения типа (6), предположим, что частота колебаний (${\omega }_0$) имеет вещественную и мнимую части, и ее можно представить как:
Тогда выражение (6) можно записать как:
В том случае, если ${\omega }2>0,$ то выражение (8) описывает затухающие гармонические колебания с круговой частотой $\omega1$ и показателем затухания ${\omega }_2$. Если ${\omega }_2
Готовые работы на аналогичную тему
Замечание
Над комплексными величинами можно проводить многие математические операции так, как будто величины являются вещественными. Операции возможны, если они сами линейны и вещественны (такими являются сложение, умножение, дифференцирование по вещественной переменной и другие, но не все). Надо помнить, что комплексные величины сами по себе не соответствуют никаким физическим величинам.
Метод векторных диаграмм
Пусть точка $A$ равномерно вращается по окружности радиуса $r$ (рис.1), скорость ее вращения ${\omega }_0$.

Рисунок 1.
Положение точки $А$ на окружности можно задать с помощью угла $\varphi $. Этот угол равен:
где $\delta =\varphi (t=0)$ величина угла поворота радиус-вектора $\overrightarrow{r}$ в начальный момент времени. Если точка $М$ вращается, то ее проекция на $ось X$ движется по диаметру окружности, совершая гармонические колебания между точками $М$ $N$. Абсциссу точки $А$ можно записать как:
Подобным способом можно представлять колебания любых величин.
Необходимо только принять изображение величины, которая совершает колебания абсциссой точки $А$, которая равномерно вращается по окружности. Можно, конечно использовать и ординату:
Замечание 1
Для того чтобы представлять затухающие колебания, надо брать не окружность, а логарифмическую спираль, которая приближается к фокусу. Если скорость приближения движущейся по спирали точки постоянна и очка движется к фокусу, то проекция этой точки на $ось X$ даст формулы затухающих колебаний.
Замечание 2
Вместо точки можно использовать радиус-вектор, который будет равномерно вращаться вокруг начала координат. Тогда величина, которая совершает гармонические колебания, будет изображаться как проекция этого вектора на $ось X$. При этом математические операции над величиной $x$ заменяют операциями над вектором.
Так операцию суммирования двух величин:
удобнее заменить суммированием двух векторов (используя правило параллелограмма). Векторы выбрать так, что их проекции на избранную $ось X$ являются выражениями $x_1\ и\ x_2$. Тогда результат операции суммирования векторов в проекции на ось абсцисс будет равен $x_1+\ x_2$.
Пример 1
Продемонстрируем применение метода векторных диаграмм.
Итак, представим комплексные числа векторами на комплексной плоскости. Величина, изменяющаяся по гармоническому закону, изображена вектором, который вращается с частотой ${\omega }0$ вокруг своего начала против часовой стрелки. Длина вектора равна амплитуде колебаний.
Графический метод решения, например, уравнения:
\[IZ=U\ \left(1.1\right),\]где $Z=R+i(\omega L-\frac{1}{\omega C})$ — импеданс, представим с помощью рис.2. На этом рисунке изображена векторная диаграмма напряжений в цепи переменного тока.

Рисунок 2.
Учтем, что умножение комплексной величины на комплексную единицу означает ее поворот на угол $90^0$ против часовой стрелки, а умножение на ($-i$) на тот же угол по часовой стрелке. Из рис.2 ледует, что:
\[tg\varphi =\frac{\omega L-\frac{1}{\omega C}}{R}\left(1.2\right),\]где $-\frac{\pi }{2}\le \varphi \le \frac{\pi }{2}.$ Изменение угла $\varphi $ зависит от соотношения между импедансами элементов цепи и частотами. Внешнее напряжение может изменяться по фазе, от совпадающего с напряжением на индуктивности, до совпадающего с напряжением на емкости. Выражается это обычно в виде отношения между фазами напряжений на элементах цепи и фазой внешнего напряжения:
Фаза напряжения на индуктивности ${(U}L=i\omega LI)$ всегда опережает фазу внешнего напряжения на угол от $0$ до $\pi .$
Фаза напряжения на емкости ${(U}C=-\frac{iI}{\omega C}$) всегда отстает от фазы внешнего напряжения на угол между $0$ и —$\ \pi .$
При этом фаза на сопротивлении может как опережать, так и отставать от фазы внешнего напряжения на угол между- $\frac{\pi }{2}$ и $\frac{\pi }{2}$.
Векторная диаграмма (рис.2) позволяет сформулировать следующее:
Фаза напряжения на индуктивности опережает фазу силы тока на $\frac{\pi }{2}$.
Фаза напряжения на емкости отстает на $\frac{\eth }{2}\ $от фазы силы тока.
Фаза напряжения на сопротивлении совпадает с фазой силы тока.
Пример 2
Задание: Продемонстрируйте то, что операцию возведения в квадрат нельзя применять к комплексным величинам как к вещественным числам.
Решение:
Допустим, что надо возвести в квадрат вещественное число $x$. Правильный ответ: $x^2$. Формально применим комплексный метод. Произведем замену:
$x\to x+iy$. Возведем полученное выражение в квадрат, получим:
\[{\left(x+iy\right)}^2=x^2-y^2+2xyi\ \left(2.1\right).\]Вещественная часть выражения (2.1) равна:
\[{Re\left(x+iy\right)}^2=Re\left(x^2-y^2+2xyi\right)=x^2-y^2\ne x^2.\]Причина ошибки в том, что операция возведения в квадрат не является линейной.
Метод векторных диаграмм.
6. Решение многих задач о малых колебаниях значительно упрощается и становится наглядным, если изображать гармонические колебания в виде векторов на плоскости (см. рис.2).
На плоскости проведем ось . Из точки , находящейся на оси , под углом (положительным направлением будем считать направление против часовой стрелки) к построим вектор длиной . При вращении этого вектора с угловой скоростью проекция конца вектора перемещается по оси в интервале значений от до . В соответствии с определением косинуса координата этой проекции изменяется со временем по закону
Таким образом, проекция конца вектора на ось будет совершать гармоническое колебание с амплитудой равной , круговой частотой , равной угловой скорости вращения вектора, и начальной фазой .
Векторное представление колебаний тесно связано также с часто используемым методом представления колебаний с помощью комплексных чисел (см. формулу (3)). Действительно, из формул Эйлера
(9)
следует, что
, (10)
В то же время комплексное число можно также записать в виде
, (11)
где и – полярные координаты (модуль и аргумент комплексного числа).
Соотношения между и приведены на рис.3. Если считать и , то становится очевидным, что гармонические колебания вполне однозначно определяются вектором, вращающимся в комплексной плоскости.
7. Векторное представление колебаний особенно удобно в задачах, где приходится колебания складывать. Возможны случаи, когда тело участвует одновременно в нескольких колебаниях. Если, например, шарик подвесить на пружине к потолку каюты корабля, качающегося на волнах, то движение шарика относительно суши будет складываться из колебаний корабля относительно суши и колебаний шарика относительно корабля.
Если складываемые колебания происходят с одной и той же частотой , то сложив векторы, соответствующие отдельным колебаниям в начальный момент времени , можно утверждать, что с течением времени полученная картинка сложения векторов, вращающихся с угловой скоростью против часовой стрелки, не будет деформироваться. При этом найденная результирующая амплитуда сохраняет свою величину и при времени .
Примеры решения задач
Пример 8.Решим задачу из примера 1 методом векторных диаграмм.
Р е ш е н и е. Приведем первое колебание к стандартному для метода векторных диаграмм виду
и сложим векторно с колебанием .
Из рисунка 4 видно, что результирующая амплитуда колебания равна , а начальная фаза определяется соотношением , что совпадает с решением, полученным в примере 1.
Пример 9.Найти амплитуду колебаний, которые возникают при сложении следующих колебаний одного направления:
, ;
, , .
Решать эту задачу можно по-разному.
Графический способ. На миллиметровой бумаге вычерчиваются графики слагаемых колебаний. Затем по точкам проводят графическое сложение смещений для различных моментов времени. Образуется график гармонической функции (советуем проверить). По клеткам миллиметровой бумаги отсчитывается амплитуда колебания.
Тот, кто силен в тригонометрии, может применить другой способ: сложить функции аналитически, воспользовавшись тригонометрическими соотношениями.
Один из способов основан на применении комплексных чисел. В данном случае предлагаем использовать метод векторных диаграмм.
Р е ш е н и е. а). Отметим сразу же, что оба вектора и (“шляпка” над означает, что это комплексная векторная величина) будут вращаться с одинаковой угловой скоростью . Следовательно, угол между и остается постоянным в любой момент времени . Изобразим вектор . При он образует с осью угол . По формулам приведения . Следовательно, вектор образует с осью отрицательный угол, равный (рис.5).
Сложим векторы и по правилу параллелограмма и получим (длина вектора ). Очевидно, что вектор будет вращаться также с угловой скоростью .
Проекция этого вектора на ось равна сумме проекций слагаемых векторов , следовательно, вектор представляет собой результирующее колебание. Таким образом, результирующее движение будет гармоническим колебанием с частотой и амплитудой 7,0. Амплитуда колебаний, т.е. длина вектора , может быть получена, например, при помощи теоремы ”косинусов’’.
б) Так как , то отстает по фазе от на , а от – на (рис. 6).
В данном случае при сложении трех векторов (см. рис. 7) удобно, построив цепочку слагаемых векторов, воспользоваться правилом, по которому начало результирующего вектора совпадает с началом первого, а конец – с концом последнего из слагаемых векторов.
Из рис. 7 легко определить длину вектора . Составляющая вектора вдоль оси равна , а вдоль оси – . По теореме Пифагора :
Биения
8. Рассмотрим случай, когда два гармонических колебания, происходящие в одном направлении, мало отличаются по частоте. Результирующее движение при этих условиях можно рассматривать как гармонические колебания с пульсирующей амплитудой. Такие колебания называют биениями.
Обозначим частоту одного из колебаний буквой , частоту другого выразим через . Пусть << . Амплитуды обоих колебаний будем полагать одинаковыми и равными .
Пульсации амплитуды результирующего колебания легко объяснимы при рассмотрении векторных диаграмм этих колебаний. Уравнения колебаний будут иметь вид:
, (12)
(13)
На рис.8. изображено взаимное расположение векторов и и вектор результирующего колебания в некоторый момент времени . Вектор ”убежал” от на угол из-за того, что его угловая скорость превышает угловую скорость вектора на . При достижении значения, равного , и будут направлены в противоположные стороны и векторная сумма обратится в нуль.
Через ситуация повторится, амплитуда вновь обратится в ноль. Таким образом, является периодом биений, которые будут происходить с частотой , равной разности частот слагаемых колебаний.
При помощи теоремы ”косинусов” можно рассчитать длину диагонали параллелограмма (рис. 8):
Спроецируем вектор на ось и получим
. (14)
В этом выражении сомножитель изменяется значительно медленнее сомножителя Поэтому можно рассматривать приближенно как гармоническое колебание с медленно меняющейся амплитудой.
Так как амплитуда по определению неотрицательна, то будем называть амплитуду биений величину
. (15)
Пример 10.При сложении двух гармонических колебаний одного направления результирующее колебание точки имеет вид:
,
где дано в секундах. Найти круговые частоты складываемых колебаний и и период результирующего колебания.
Р е ш е н и е. Из формулы (14) следует, что :
1) , рад/с;
2) , то есть рад /с,
а так как рад/с, то рад /с.
Период биений
с.
Вынужденные колебания
9. Применим II закон Ньютона для того, чтобы написать уравнение движения груза массой , подвешенного на пружине с жесткостью в вязкой среде с коэффициентом трения , (например, в воздухе или воде) и колеблющегося под действием гармонической силы :
(16)
Разделив это уравнение на и перенеся члены с и в левую часть, получим неоднородное линейное дифференциальное уравнение второго порядка:
, (17)
где , – коэффициент затухания; – собственная частота колебаний системы. Предположим, что решение (частное, т.е. не содержащее произвольных постоянных) этого уравнения имеет вид:
(18)
Вид решения подсказывает опыт. В самом деле, под действием гармонической силы через определенное время устанавливаются устойчивые колебания с постоянной амплитудой и частотой вынуждающей силы. При этом можно ожидать, что перемещение груза на пружине будет отставать от внешней силы по фазе на .
Дифференцируя (18) по времени, первые два члены уравнения (17) можно записать в следующем виде:
(19)
(20)
Согласно уравнению (17), гармоническое колебание является суммой трех гармонических колебаний то же частоты: (20), (19) и . Если изобразить гармоническое колебание вектором (длиной ), направленным вправо, то вектор (19) длиной будет повернут относительно против часовой стрелки на , а (20) – на угол . Чтобы равенство (17) выполнялось, векторная сумма перечисленных векторов должна совпадать с вектором, изображающим колебание . При получающаяся векторная диаграмм изображена на рис. 9, а при – на рис.10.
В обоих случаях:
или
(21)
Из векторных диаграмм (рис. 9, 10) также получаем, что:
(22)
Окончательное решение уравнения (18) имеет вид:
. (23)
Исследование выражения (21) показывает, что амплитуда вынужденных колебаний в зависимости от частоты вынуждающей силы имеет колоколообразный график, а при достигает максимума . Это явление называется резонансом. При малых коэффициентах затухания ( величина может достигать очень больших значений, что имеет широкое применение в технике.
Читайте также:
Рекомендуемые страницы:
Поиск по сайту
Метод векторных диаграмм
Этот метод используется для лучшего понимания и наглядности представления процесса, изменяющегося по гармоническому закону.
Суть
метода: переменные величины 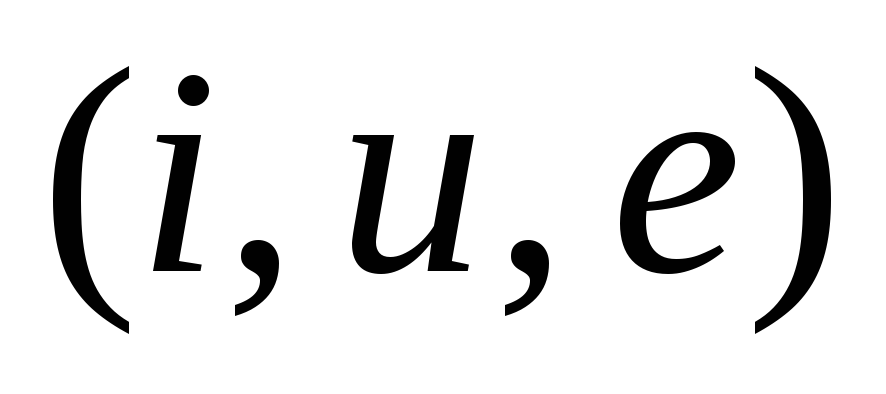 ,
изменяющиеся по гармоническому закону
,
изменяющиеся по гармоническому закону 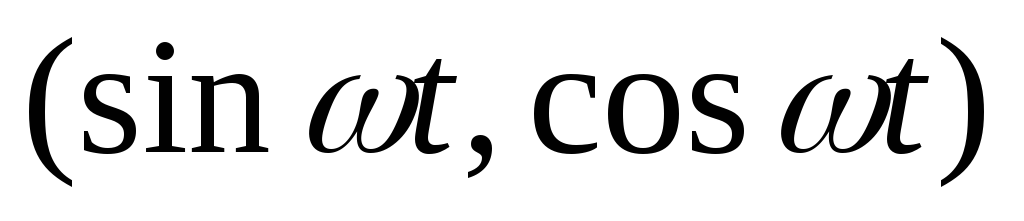 изображаются графически методом
вращающегося вектора амплитуды колебаний.
изображаются графически методом
вращающегося вектора амплитуды колебаний.
Для
этого из произвольной точки О оси ОXоткладывается вектор ,
модуль которого равен амплитуде
рассматриваемого колебания (рис. 6.5).
,
модуль которого равен амплитуде
рассматриваемого колебания (рис. 6.5).

Рис. 6.5. Метод векторных диаграмм
Если
вектор  привести во вращение относительно точки
О против часовой стрелки с циклической
частотой
привести во вращение относительно точки
О против часовой стрелки с циклической
частотой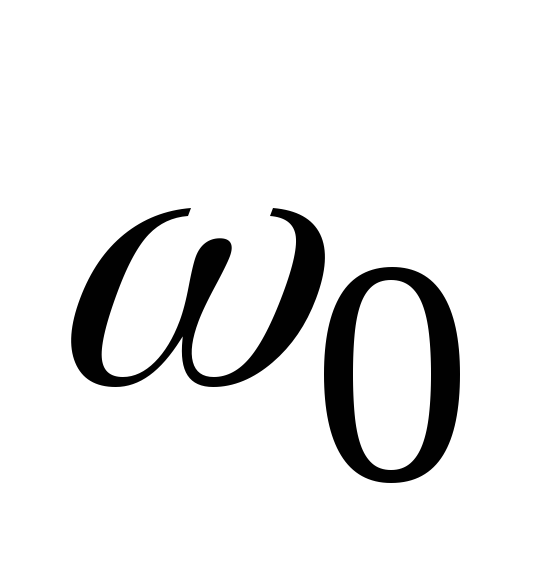 ,
то проекция вектор
,
то проекция вектор на ось ОХ будет изменяться по закону:
на ось ОХ будет изменяться по закону:
 . (6.13)
. (6.13)
Таким образом, достигается эквивалентность вращающегося вектора и гармонического закона (6.5).
В общем случае векторная диаграмма – это совокупность вращающихся против часовой стрелки векторов амплитудных (действующих) значений гармонических величин.
Лекция 7. Действующее значение переменного тока. Связь между током и напряжением в элементах электрической цепи тока
Действующее значение переменного тока равно такому значению постоянного тока, которое за время, равное периоду переменного тока, выделяет в том же сопротивлении такое же количество теплоты, что и данный переменный ток.
Для постоянного тока по закону Джоуля-Ленца
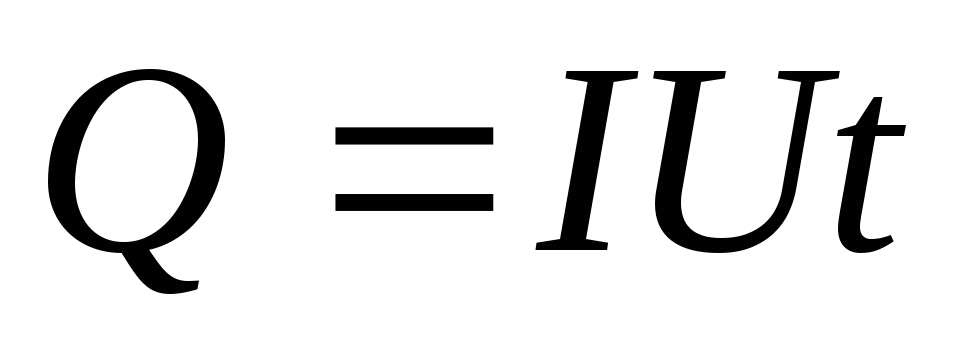 ,
(7.1)
,
(7.1)
где Q– количество теплоты, выделяемое в проводнике.
Если 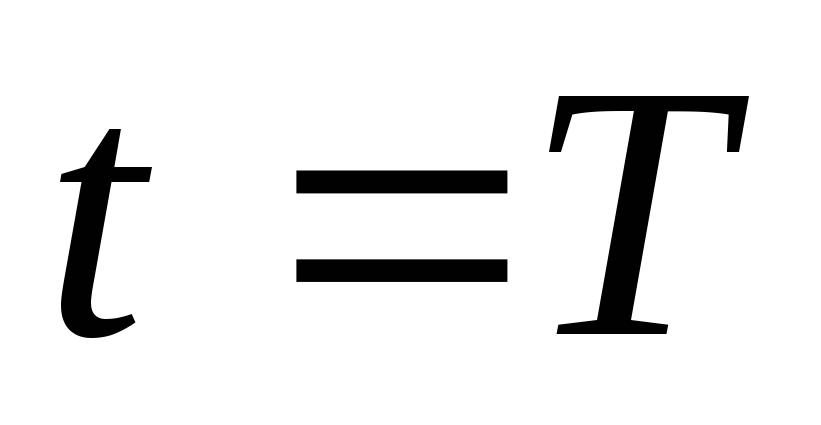 ,
тогда
,
тогда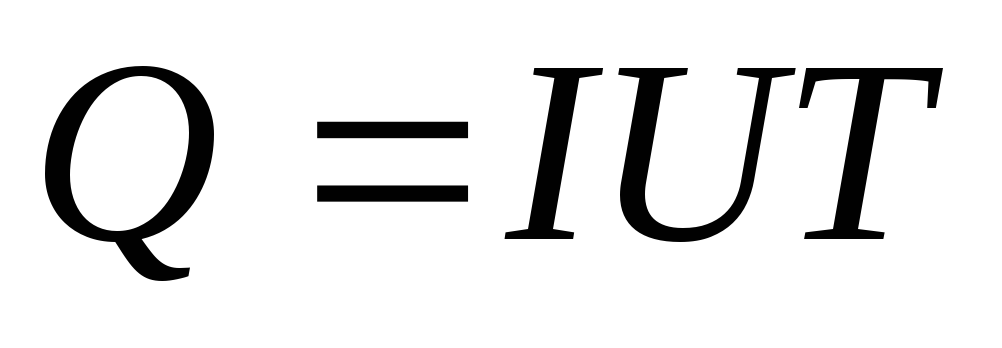 ,
(7.2)
,
(7.2)
где Т— период переменного тока.
По закону Ома
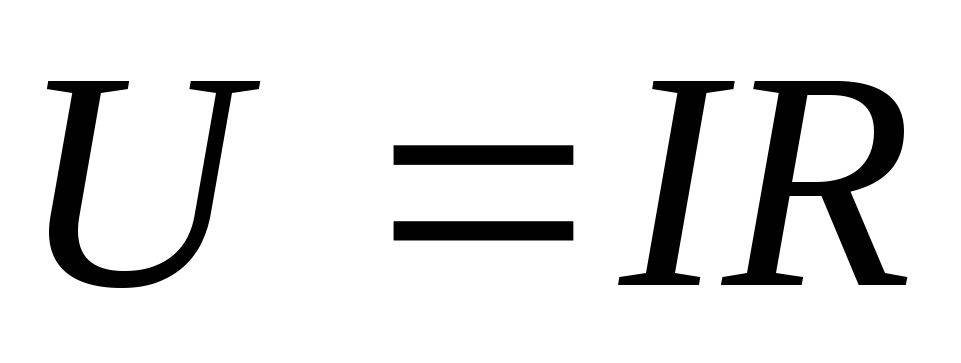 ,
тогда
,
тогда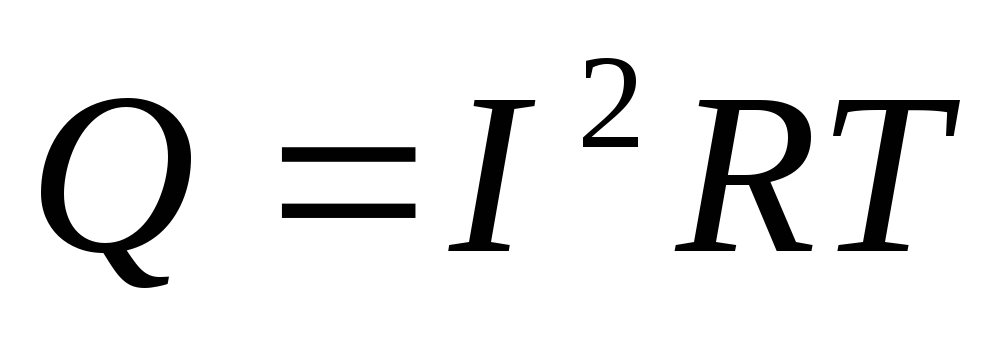 . (7.3)
. (7.3)
Пусть
ток меняется по закону 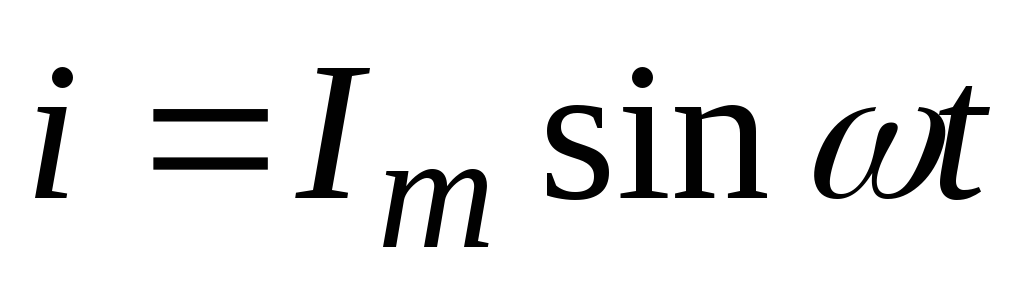 ,
(7.4)
,
(7.4)
где 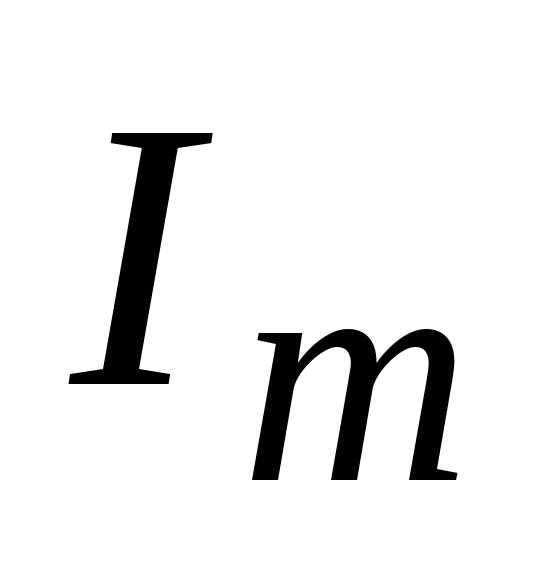 – амплитудное значение переменного
тока.
– амплитудное значение переменного
тока.
Рассмотрим очень малый промежуток времени dt, для которого переменный ток можно считать постоянным (рис. 7.1).
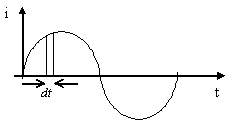
Рис. 7.1. Переменный ток
Тогда по аналогии с выражением (7.3)
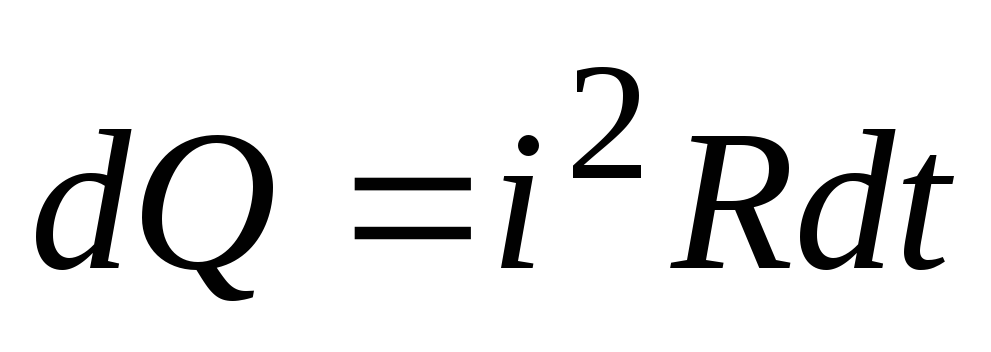 , (7.5)
, (7.5)
где 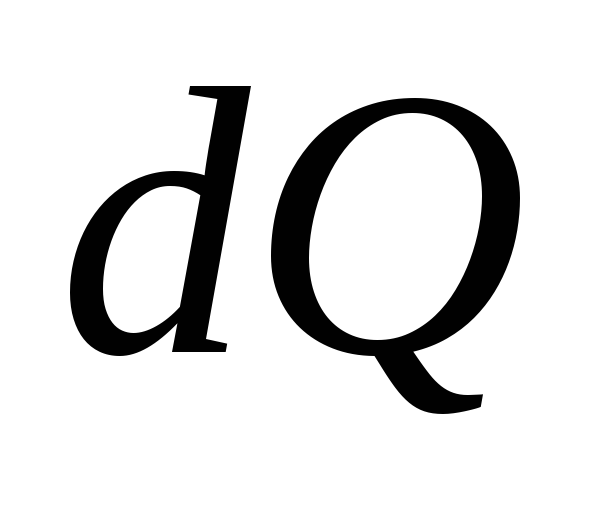 — количество теплоты, которое выделяется
в проводнике за промежуток времени
— количество теплоты, которое выделяется
в проводнике за промежуток времени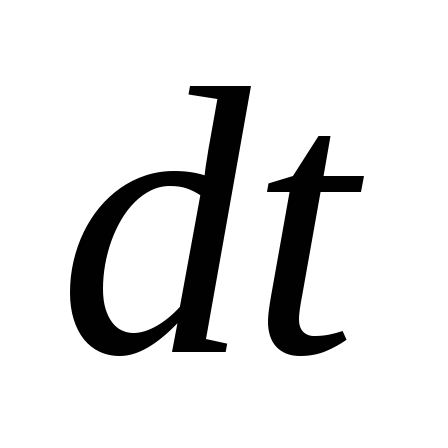 .
.
Для нахождения количества теплоты, выделяющейся в проводнике за период, проинтегрируем выражение (7.5).
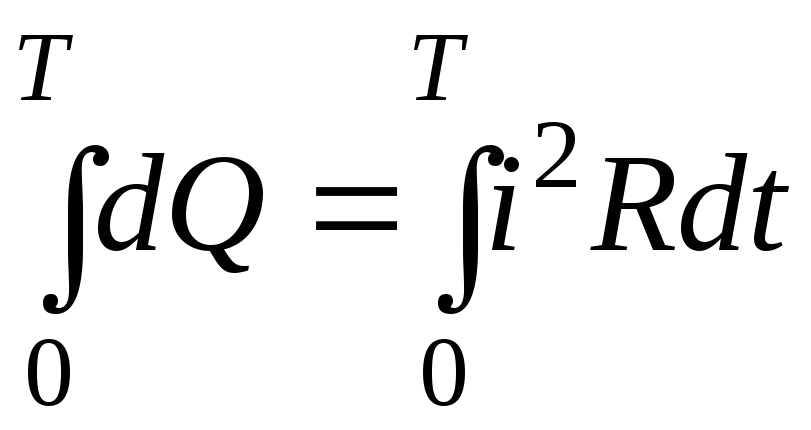 ;
(7.6)
;
(7.6)

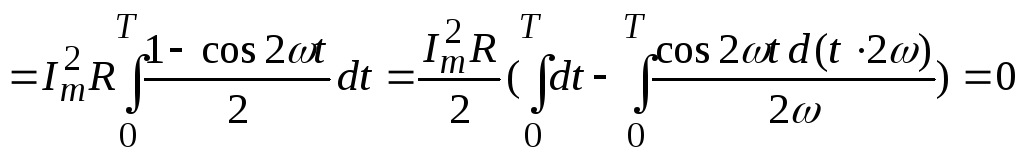

 (7.7)
(7.7)
А в
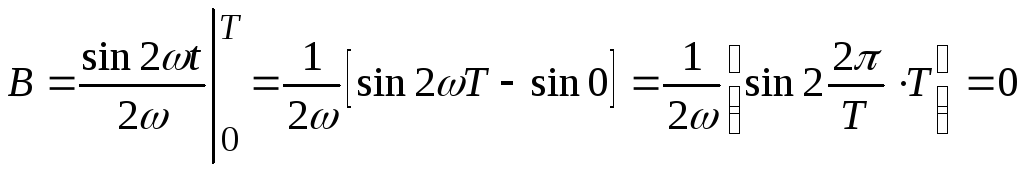 .
(7.8)
.
(7.8)
Вывод. Интеграл от периодической знакопеременной функции за 1 период равен 0.
Геометрически это можно трактовать как площадь под кривой периодической функции (рис 7.2).

Рис. 7.2. Периодическая функция
Анализируя интеграл А получим:
 ,
т.е.
,
т.е.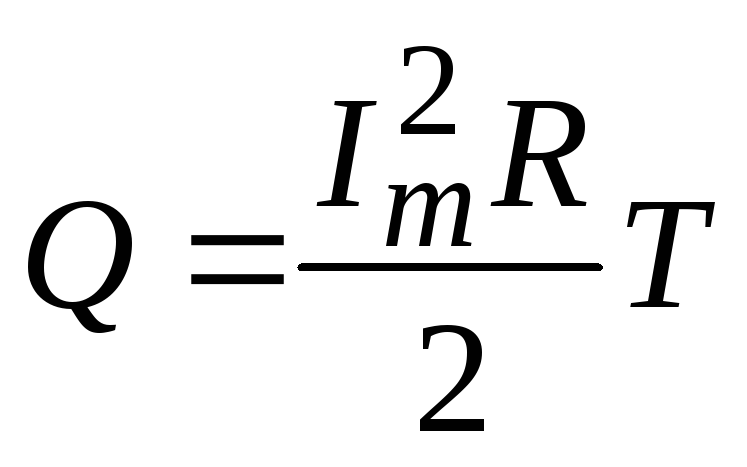 .
(7.9)
.
(7.9)
Сравнивая выражения (7.3) и (7.9) получим:
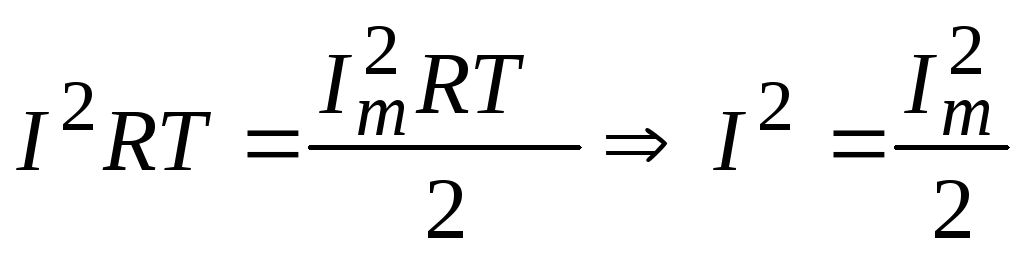 (7.10)
(7.10)
или 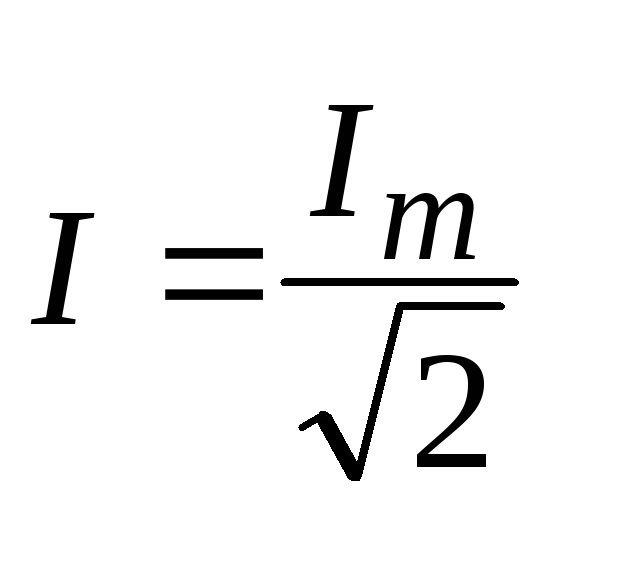 , (7.11)
, (7.11)
где I– действующее значение переменного тока.
Связь между током и напряжением в элементах электрической цепи
Активное сопротивление
Пусть имеется цепь переменного тока (рис. 7.3).

Р ис. 7.3. Электрическая цепьcактивным сопротивлением
Условия:
1) φа > φв;
2) напряжение источника в цепи изменяется по закону
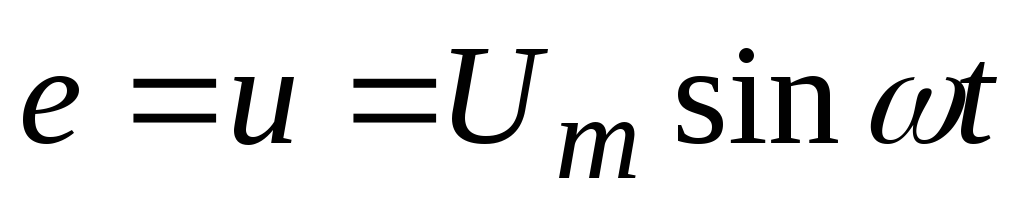 .
(7.12)
.
(7.12)
Запишем второй закон Кирхгофа для электрической цепи (рис. 7.3):
u = uR. (7.13)
По
закону Ома 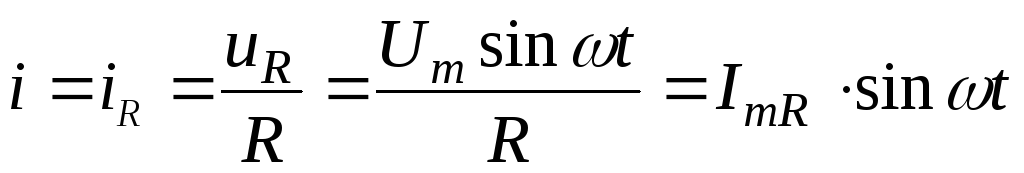 , (7.14)
, (7.14)
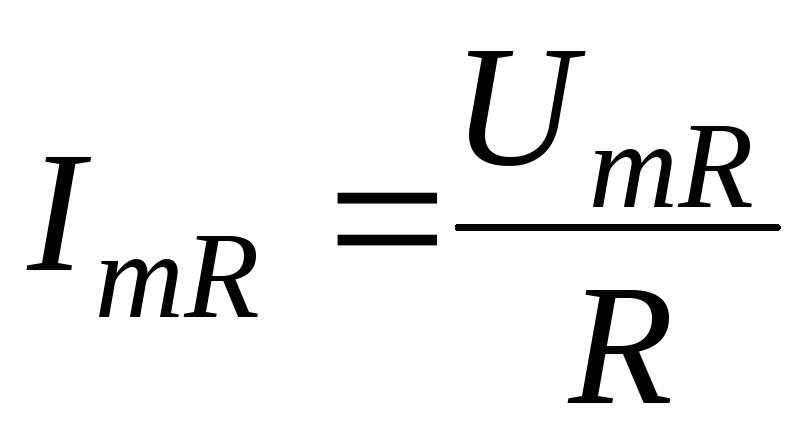 , (7.15)
, (7.15)
где 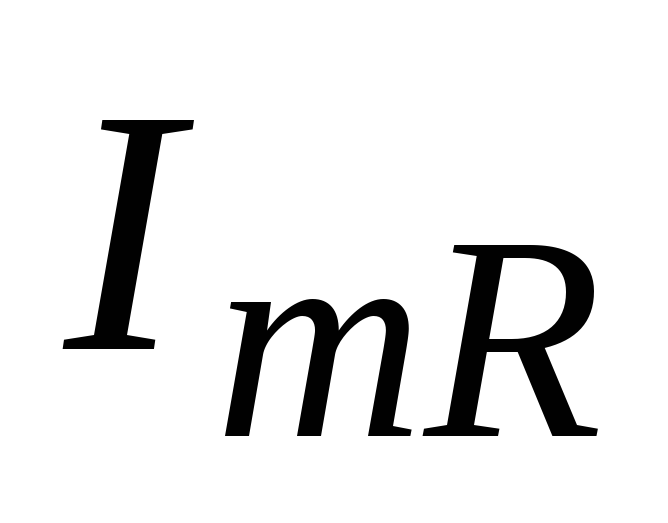 – амплитудное значение тока через
активное сопротивление, т.е.
– амплитудное значение тока через
активное сопротивление, т.е.
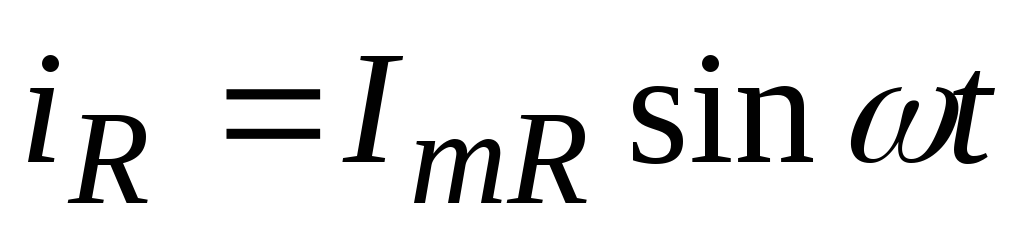 .
(7.16)
.
(7.16)
Сравнивая выражения (7.12) и (7.16) заключаем, что на активном сопротивлении ток и напряжение совпадают по фазе (рис. 7.4).
Поделим
выражение (7.15) на 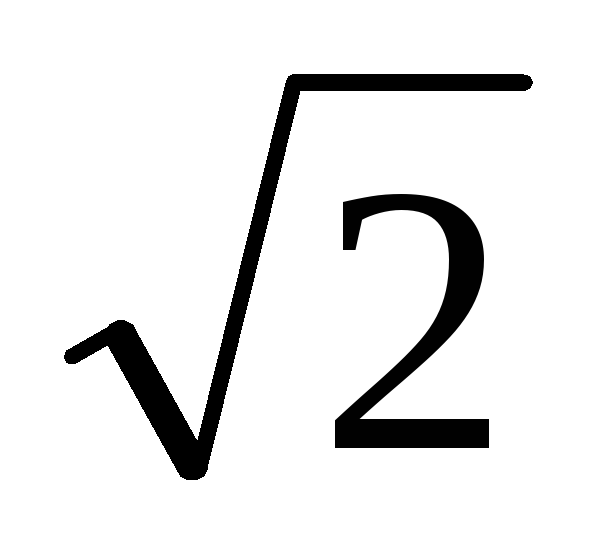 и получим:
и получим:
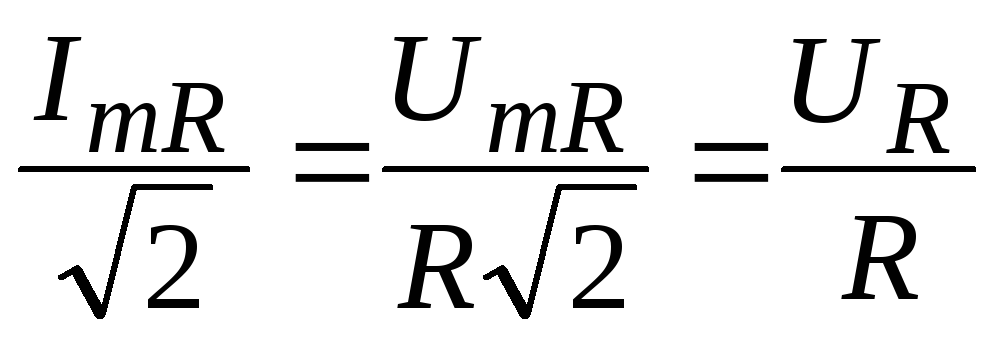 , (7.17)
, (7.17)
где 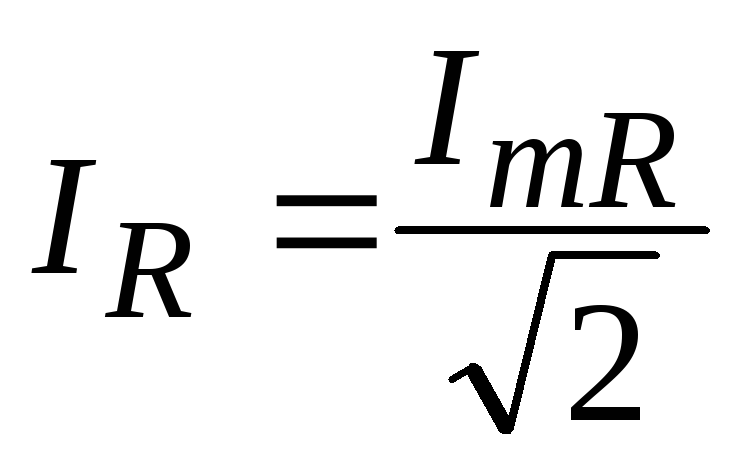 и
и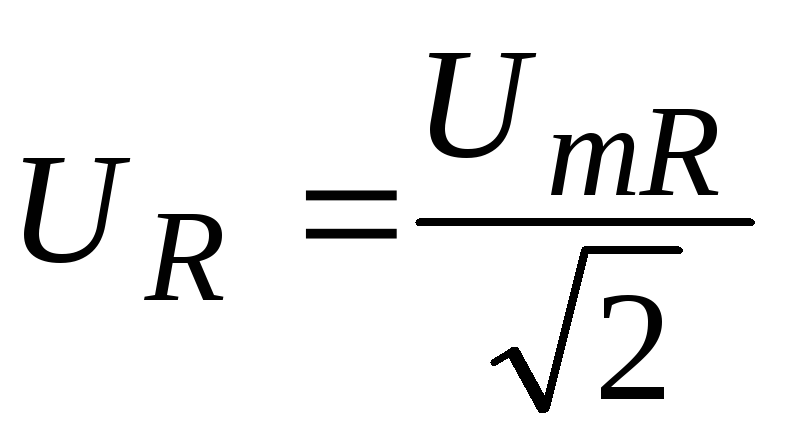 – соответственно действующие значения
тока и напряжения на активном сопротивлении.
– соответственно действующие значения
тока и напряжения на активном сопротивлении.
Закон Ома для действующих значений тока и напряжения на активном сопротивлении:
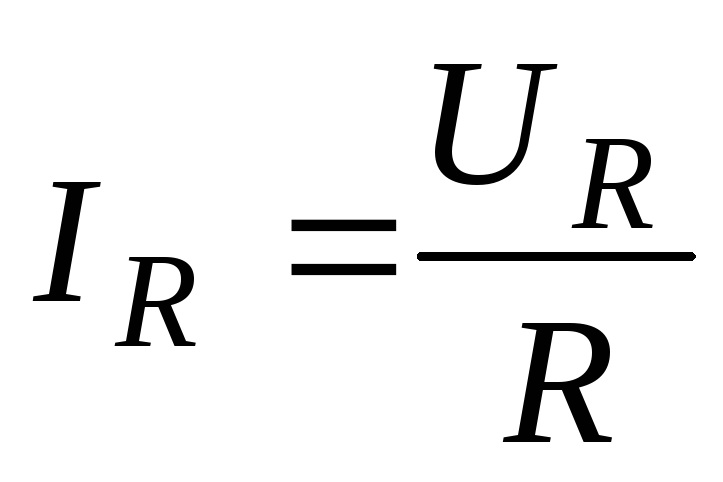 (7.18)
(7.18)
Р ис.
7.4. Графики тока и напряжения на активном
сопротивлении и векторная диаграмма
ис.
7.4. Графики тока и напряжения на активном
сопротивлении и векторная диаграмма
Если в цепь электрического контура, содержащего емкость, индуктивность и сопротивление, включить источник переменной ЭДС (рис.16.5), то в нем, наряду с собственными затухающими колебаниями, возникнут незатухающие вынужденные колебания. Частота этих колебаний совпадает с частотой изменения переменной ЭДС.
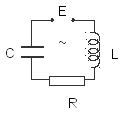
Рис.16.5. Последовательный колебательный RLC-контур.
Ч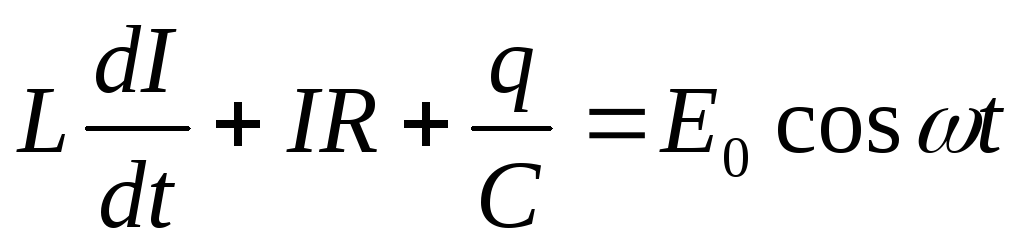 тобы
получить уравнение вынужденных
колебаний, надо, согласно второму
правилу Кирхгофа, приравнять сумму
падений напряжений на элементах контура
приложенной ЭДС:
тобы
получить уравнение вынужденных
колебаний, надо, согласно второму
правилу Кирхгофа, приравнять сумму
падений напряжений на элементах контура
приложенной ЭДС:
и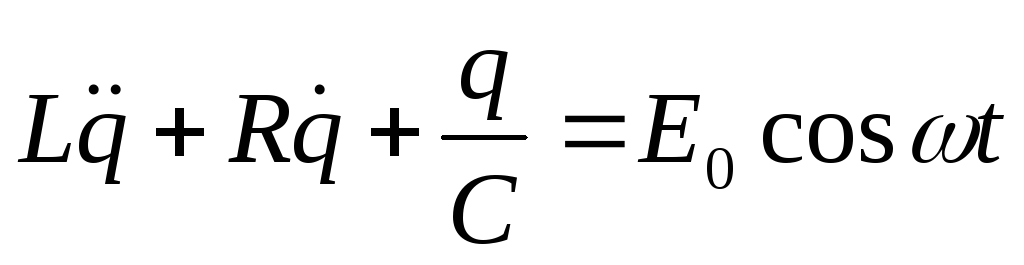 ли
ли
где Е0 — амплитуда переменной ЭДС; ω – ее циклическая частота.
И нтересующее
нас частное решение этого дифференциального
уравнения имеет вид:
нтересующее
нас частное решение этого дифференциального
уравнения имеет вид:
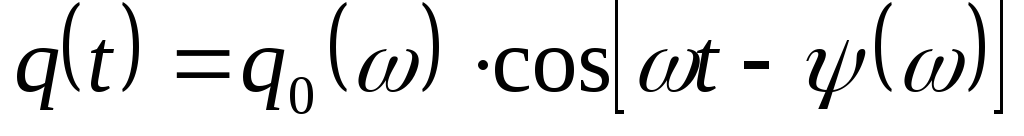
где

Решение соответствующего однородного уравнения, как мы видели в п.5.2, представляет собой свободные затухающие колебания, которые с течением времени становятся исчезающе малыми, и их можно в дальнейшем не учитывать.
Выпишем формулы для силы тока в цепи и падений напряжений на каждом из элементов контура.
Сила тока: 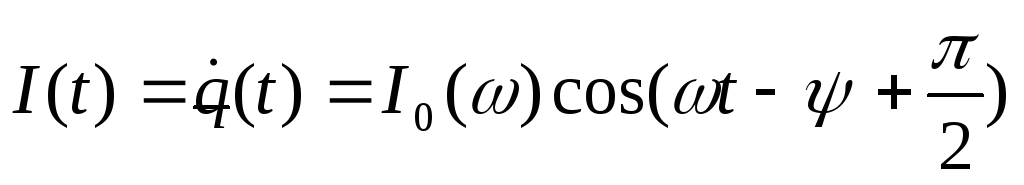 ,
,
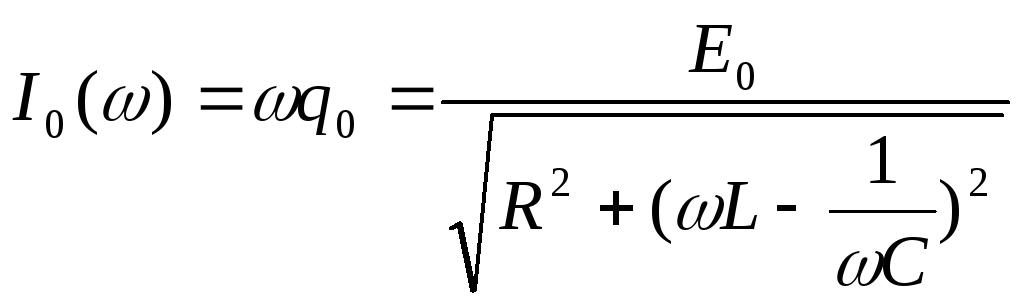 .
.
По аналогии с законом Ома для полной цепи по постоянному току величину
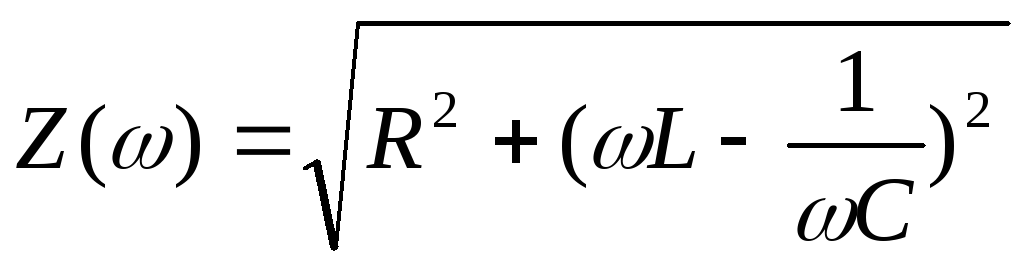
называют полным сопротивлением цепи по переменному току. Эта
величина представляет собой модуль комплексного сопротивления 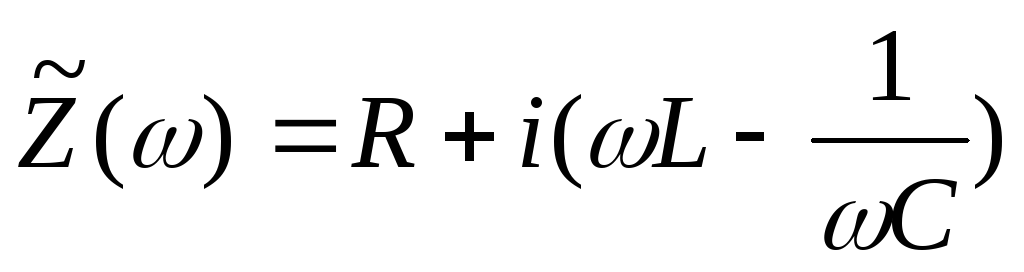 ,
называемого также импедансом цепи.
Сопротивление R называют активным сопротивлением (на нем выделяется тепло). Чисто
мнимые сопротивления ωL и
,
называемого также импедансом цепи.
Сопротивление R называют активным сопротивлением (на нем выделяется тепло). Чисто
мнимые сопротивления ωL и 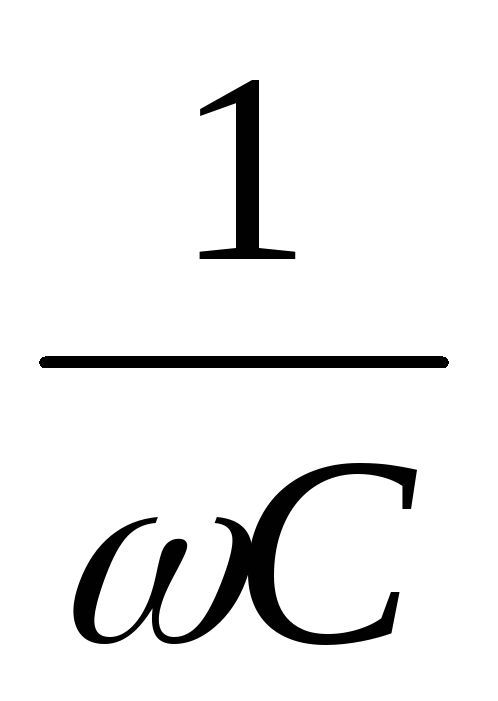 называют соответственно индуктивным и емкостным реактивными сопротивлениями (на них тепло не
выделяется).
называют соответственно индуктивным и емкостным реактивными сопротивлениями (на них тепло не
выделяется).
Напряжение на сопротивлении R:
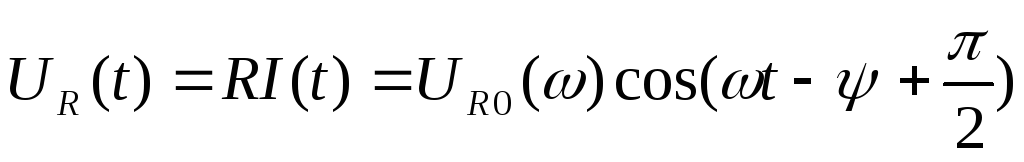 ,
,
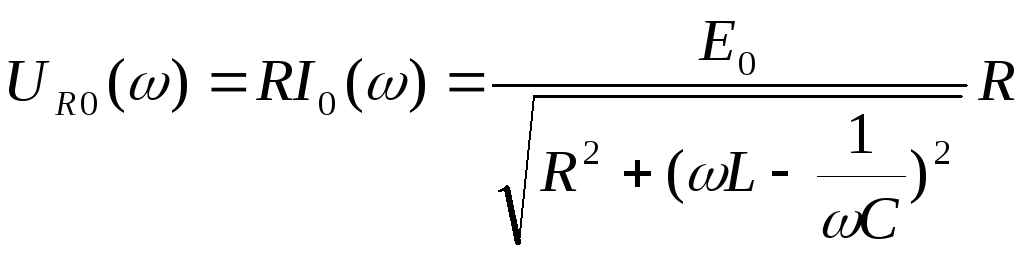 .
.
Напряжение на конденсаторе С:
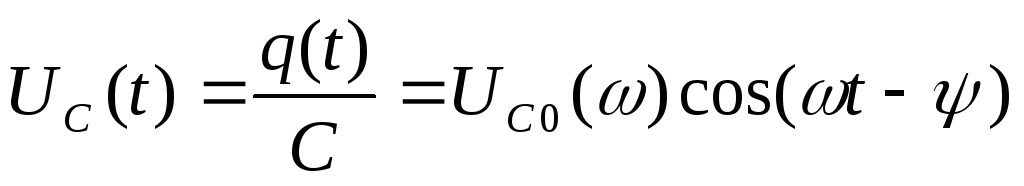 ,
,
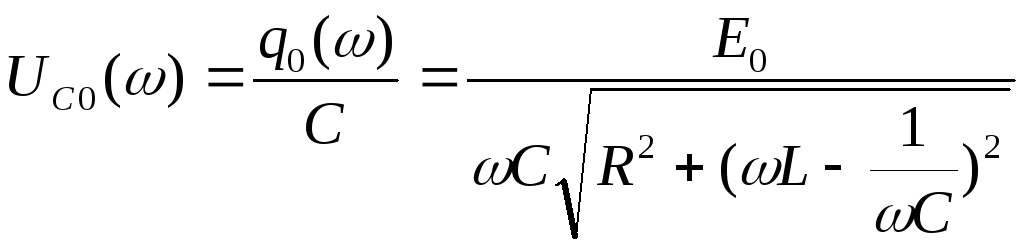 .
.
Напряжение на катушке индуктивности L:
 ,
,
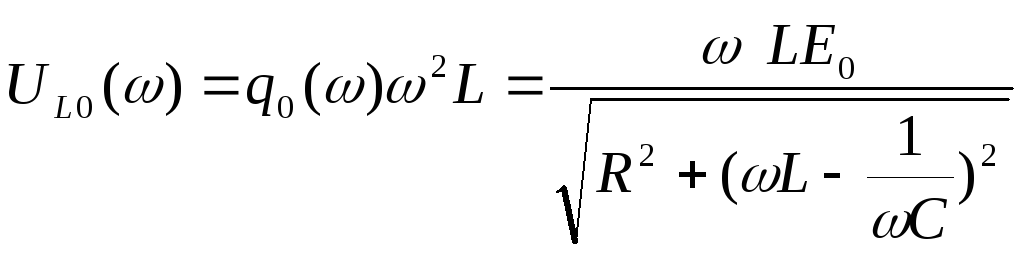 .
.
Сравнивая написанные формулы, видим,
что изменение напряжения на сопротивлении
следует за изменением силы тока в цепи
без отставания или опережения по
фазе, изменение напряжение на конденсаторе отстает по фазе на 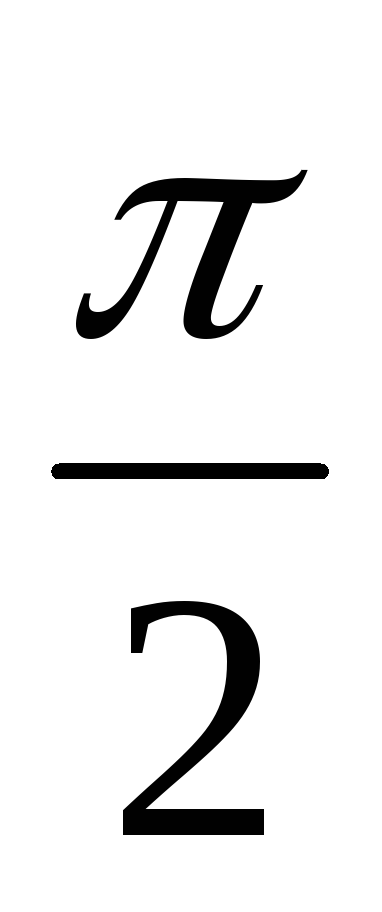 ,
а на индуктивности опережает по
фазе на
,
а на индуктивности опережает по
фазе на 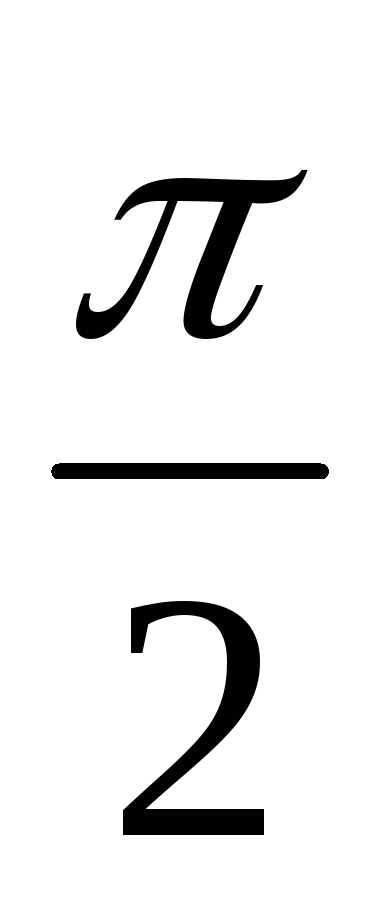 изменение тока. Наглядно это можно
изобразить с помощью векторной
диаграммы (рис.16.6), вещественная
ось которой (ось Х) совпадает с осью
токов. Длина каждого вектора на
этой диаграмме дает амплитуду соответствующего напряжения, а угол,
который составляет данный вектор с осью
токов – сдвиг фазы по отношению к
изменению силы тока в цепи.
изменение тока. Наглядно это можно
изобразить с помощью векторной
диаграммы (рис.16.6), вещественная
ось которой (ось Х) совпадает с осью
токов. Длина каждого вектора на
этой диаграмме дает амплитуду соответствующего напряжения, а угол,
который составляет данный вектор с осью
токов – сдвиг фазы по отношению к
изменению силы тока в цепи.

Рис.16.6. Векторная диаграмма для последовательного RLC-контура.
Амплитуда суммарного напряжения на всех элементах контура, равная амплитуде Е0 действующей
в контуре ЭДС, является результатом
векторного сложения символических
напряжений 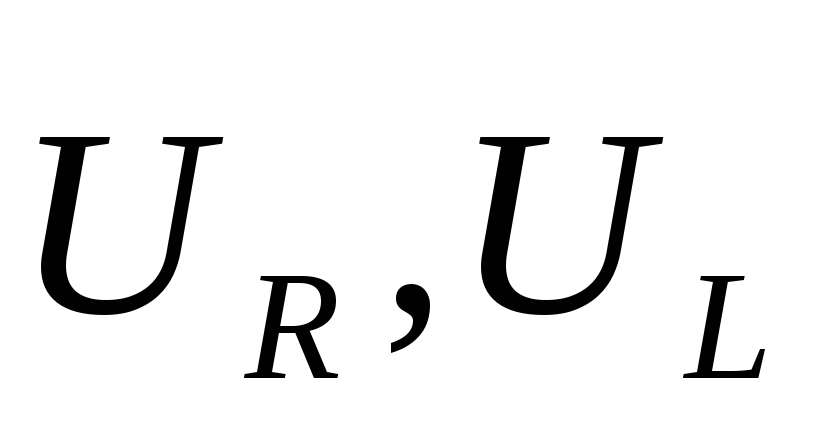 и
и 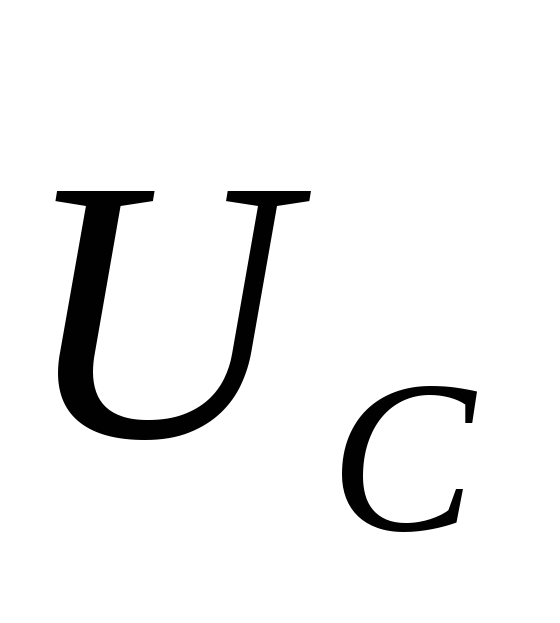 .
Этот вектор образует с осью токов угол
.
Этот вектор образует с осью токов угол 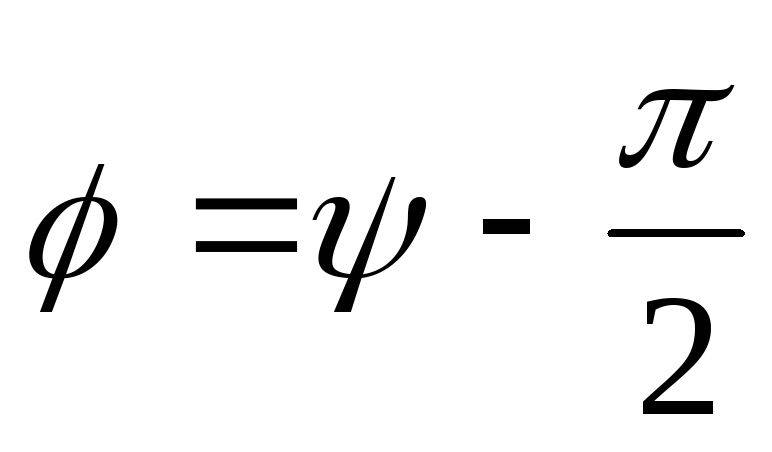 ,
показывающий разность фаз между
током и ЭДС. Тангенс этого угла равен:
,
показывающий разность фаз между
током и ЭДС. Тангенс этого угла равен:
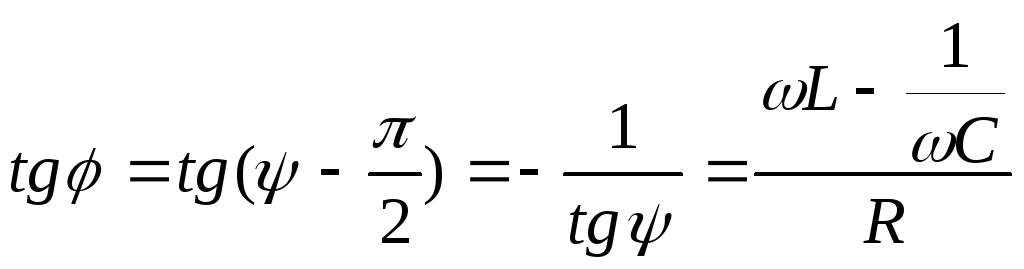 .
.
5.4. Резонансные явления в колебательном контуре. Резонанс напряжений и резонанс токов.
Как следует из приведенных формул, при частоте переменной ЭДС ω, равной
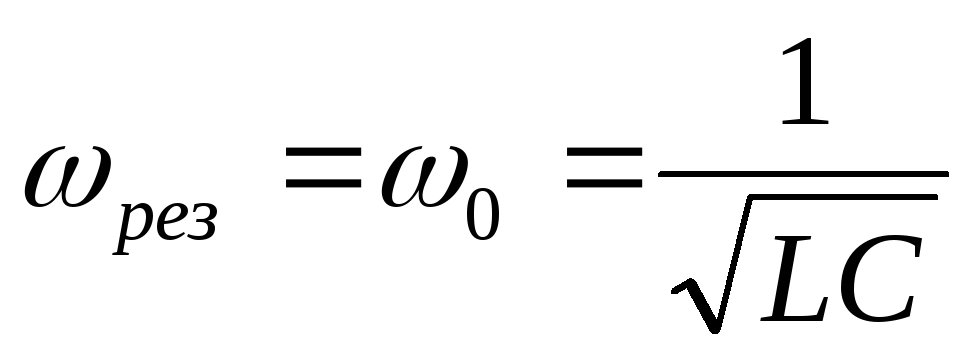 ,
,
амплитудное значение силы тока в
колебательном контуре, принимает максимальное значение 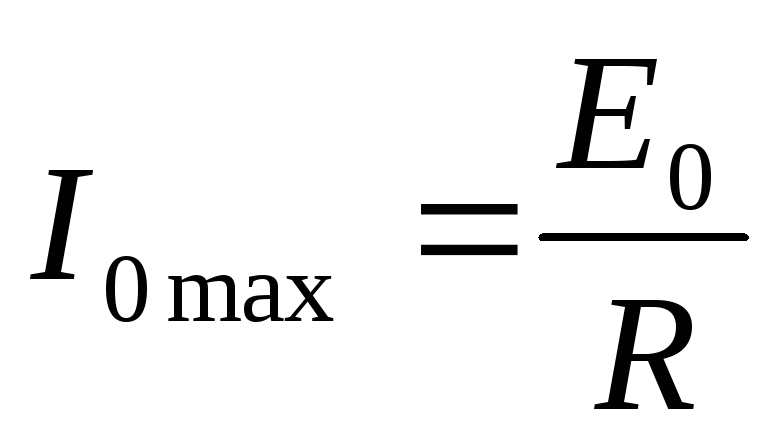 .
При этом амплитуда напряжения на активном сопротивлении R также максимальна и равна UR0 =I0maxR =E0. Падения
напряжения на емкости UC и индуктивности UL одинаковы по амплитуде, но противоположны по фазе, и они взаимно компенсируют друг друга. Это явление,
имеющее место в последовательном колебательном контуре, изображенном на рис.16.5, называется резонансом напряжений. Векторная
диаграмма, соответствующая этому случаю,
показана на рис.16.7.
.
При этом амплитуда напряжения на активном сопротивлении R также максимальна и равна UR0 =I0maxR =E0. Падения
напряжения на емкости UC и индуктивности UL одинаковы по амплитуде, но противоположны по фазе, и они взаимно компенсируют друг друга. Это явление,
имеющее место в последовательном колебательном контуре, изображенном на рис.16.5, называется резонансом напряжений. Векторная
диаграмма, соответствующая этому случаю,
показана на рис.16.7.
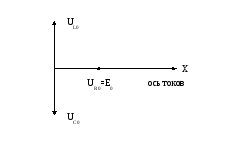
Рис.16.7. Векторная диаграмма при резонансе напряжений.
Максимальное значение амплитуды напряжения на конденсаторе UC0(ω) достигается при частоте

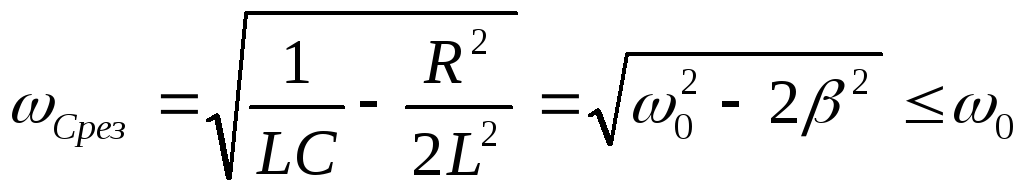 .
.
Резонансные кривые для UC0(ω) представлены на рис.16.8. Максимум получается тем выше и острее, чем меньше коэффициент затухания β, то есть чем меньше активное сопротивление R и больше индуктивность контура L.
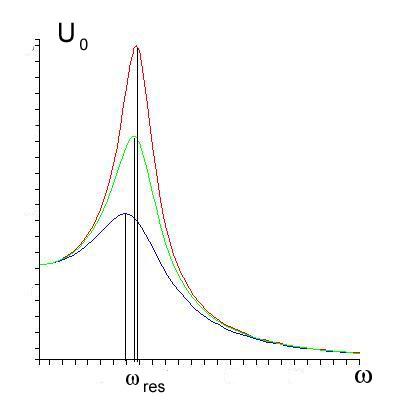
UC0
E0

ωрез ω0
ω
Рис.16.8. Резонансные кривые UC0(ω).
Если источник переменной ЭДС подключить параллельно конденсатору, то получим колебательный контур, который называется параллельным (рис.16.9).

Рис.16.9. Параллельный колебательный RLC-контур.
В таком контуре при 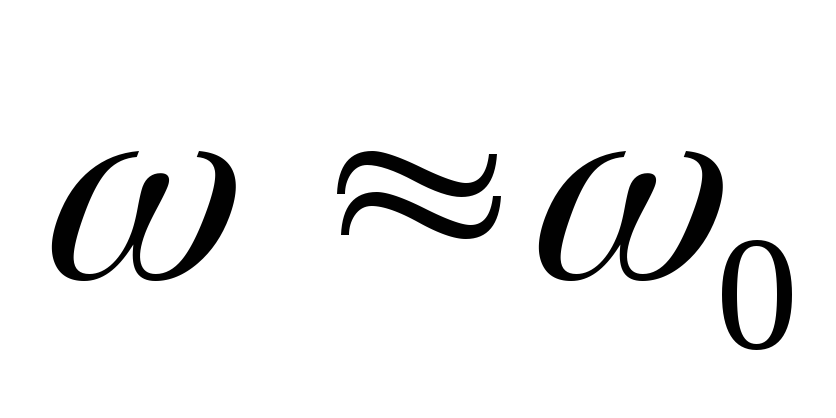 наблюдается другое резонансное явление,
получившее название резонанса токов. При резонансе токов токи, текущие
через емкость и индуктивность одинаковы по амплитуде, но противоположны по
фазе. При этом общий ток в цепи
ЭДС близок к нулю, хотя токи в самом контуре могут быть очень
велики. Векторная диаграмма,
соответствующая этому случаю, приведена
на рис.16.10.
наблюдается другое резонансное явление,
получившее название резонанса токов. При резонансе токов токи, текущие
через емкость и индуктивность одинаковы по амплитуде, но противоположны по
фазе. При этом общий ток в цепи
ЭДС близок к нулю, хотя токи в самом контуре могут быть очень
велики. Векторная диаграмма,
соответствующая этому случаю, приведена
на рис.16.10.
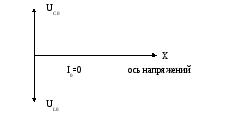
Рис.16.10. Векторная диаграмма при резонансе токов.
Можно показать, что при резонансе токов полное сопротивление Z(ω) параллельного контура максимально и
равно чисто активному сопротивлению R. Резонансная частота,
при которой Z(ω) максимально, определяется из условия
равенства нулю реактивной части
комплексного сопротивления  :
:
ωL(1 – ω2LC) – ωCR2 = 0 ,
откуда
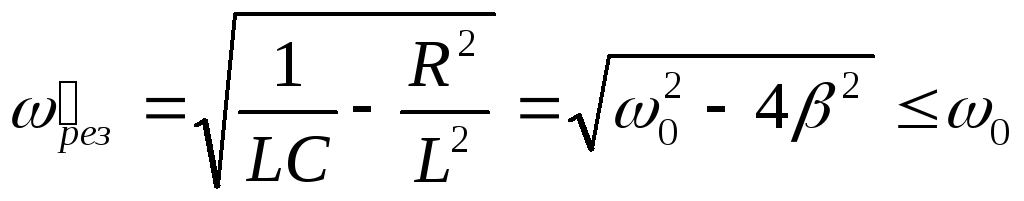 .
.
Р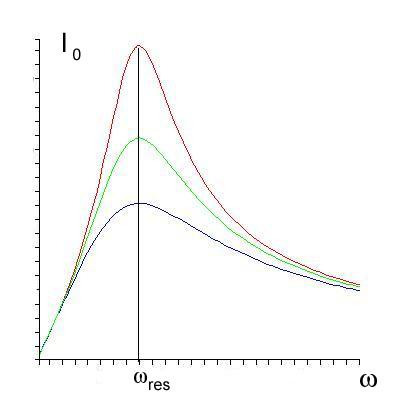 езонансные
кривые для амплитудных значений IC0(ω) тока, текущего через конденсатор,
приведены на рис.16.11.
езонансные
кривые для амплитудных значений IC0(ω) тока, текущего через конденсатор,
приведены на рис.16.11.
IC0
ω

ωрез ω0
Рис.16.11. Резонансные кривые IC0(ω).
Резонансные явления в колебательных контурах широко используются в электро- и радиотехнике (резонансные усилители, частотные фильтры и другие). В частности, явление резонанса используется для выделения из сложного сигнала нужной частотной составляющей. Настроив контур (путем изменения его параметров C и/или L) на одну из выбранных частот, можно получить на конденсаторе напряжение, в Q раз превышающее величину напряжения данной частотной составляющей (см. рис.16.8). Такой процесс осуществляется, например, при настройке радиоприемника на нужную длину волны.
Возможны различные методы и порядок построения векторных диаграмм. Одним из методов построения векторных диаграмм является метод, основанный на использовании промежуточных эквивалентных схем с последовательным соединением элементов. На первом этапе построения векторной диаграммы, используется промежуточная эквивалентная схема, изображенная на рисунке 3.29, с последовательно соединенными элементами, и строится векторная диаграмма для последовательного соединения. А затем выделяется напряжение U23 и строится диаграмма для параллельных ветвей и т.д.
Ниже приведен порядок построения векторной диаграммы разветвленной электрической цепи, приведенной на рисунке 3.34, в котором, на первом этапе строится векторная диаграмма параллельного участка.
 |
Рекомендованный порядок построения векторной диаграммы.
1. Произвольно откладываем вектор напряжения U23.
2. Строим векторную диаграмму токов:
2.1. Вектор тока I2 опережает напряжение U23 на угол j2(активно-емкостной характер), где
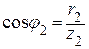 .
.
2.2. Вектор тока I3 отстает от напряжения U23 на угол j3 (активно-индуктивный характер), где
 .
.
2.3. Вектор тока I4 совпадает с направлением напряжения U23 (активный характер).
2.4. Строим вектор I1. Его величина и направление определяется как векторная сумма токов I2, I3, I4.
3. Строим векторную диаграмму напряжений на элементах первой ветви.
3.1. Вектор падения напряжения UL1 на сопротивлении xL1, равный по величине UL1 = I1 xL1 опережает ток I1 на 90° и берет начало с точки 5, конец вектора соответствует точке 2 (рис. 3.35).
3.2. Вектор падения напряжения на сопротивлении r1, равный по величине Ur1 = I1 r1 совпадает с направлением тока I1. Конец вектора совпадает с точкой 5, а начало соответствует точке 1 (рис. 3.35).
3.3. Вектор падения напряжения UC1на сопротивлении xC1, равный по величине UC1 = I1 xC1 отстает от тока I1 на 90° и берет начало с точки 3, конец вектора соответствует точке 4.
3.4. Определим вектор входного напряжения; для этого соединяем точки 1 и 4.
4. Строим векторную диаграмму напряжений параллельной ветви.
4.1. Направление векторов падений напряжений Ur2 и UC2 на сопротивлениях r2и xC2 связано с направлением тока I2. Их величины соответственно равны Ur2 = I2 r2, UC2 = I2 xC2.
4.2. Направление векторов падений напряжений Ur3 и UL3 на сопротивлениях r3и xL3 связано с направлением тока I3. Их величины соответственно равны Ur3 = I3 r3, UL3 = I3 xL3.
4.3. Направление вектора падения напряжения на сопротивлении r4 связано с направлением тока I4. Его величина равна Ur4 = U23.
С помощью векторной диаграммы (рис. 3.35), можно определить напряжения между любыми точками схемы.

Пример 3.4. Рассмотрим порядок построения векторной диаграммы на примере 3.3., расчета электрической цепи, изображенной на рисунке 3.36. Параметры цепи в рассматриваемом примере соответственно равны r1 = 5 (Ом), r2 = 9 (Ом), r3 = 12 (Ом), хС1 = 12 (Ом), хС2 = 12 (Ом), хL3 = 16 (Ом), хL4 = 24 (Ом). Величины токов, определенные в примере 3.3, соответственно равны 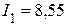 (А),
(А), 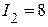 (А),
(А), 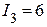 (А).
(А).
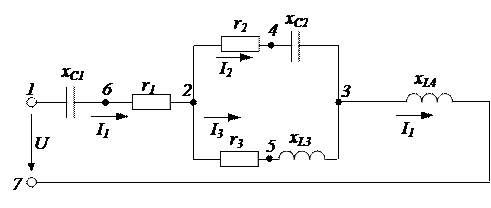
Рисунок 3.36 – Электрическая цепь переменного тока
1. Произвольно откладываем вектор напряжения 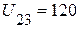 (В).
(В).
2. Строим векторную диаграмму токов.
2.1. Вектор тока I2 = 8 (A) опережает напряжение U23 на угол j2(активно-емкостной режим),
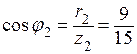

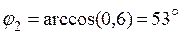 .
.
2.2. Вектор тока I3 = 6 (A) отстает от напряжения U23 на угол j3 (активно-индуктивный характер),
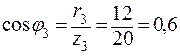

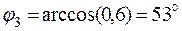 .
.
2.3. Строим вектор I1 = 8,55 (A). Его величина и направление определяется как векторная сумма токов I2 и I3.
3. Строим векторную диаграмму напряжений на элементах первой и четвертой ветвей.
3.1. Вектор падения напряжения Ur1 на сопротивлении r1, равный по величине 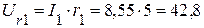 совпадает с направлением тока I1. Конец вектора совпадает с точкой 6, начало соответствует точке 2, (рис. 3.37).
совпадает с направлением тока I1. Конец вектора совпадает с точкой 6, начало соответствует точке 2, (рис. 3.37).
3.2. Вектор падения напряжения UC1на сопротивлении xC1, равный по величине 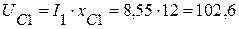 отстает от тока I1 на 90° и берет начало с точки 6, конец вектора соответствует точке 1 (рис. 3.37).
отстает от тока I1 на 90° и берет начало с точки 6, конец вектора соответствует точке 1 (рис. 3.37).
3.3. Вектор падения напряжения UL4 на сопротивлении xL4, равный по величине 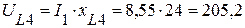 (B) опережает ток I1 на 90° и берет начало с точки 3, конец вектора соответствует точке 7 (рис. 3.37).
(B) опережает ток I1 на 90° и берет начало с точки 3, конец вектора соответствует точке 7 (рис. 3.37).
3.4. Определим вектор входного напряжения 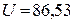 В; для этого соединяем точки 1 и 7.
В; для этого соединяем точки 1 и 7.
4. Строим векторную диаграмму напряжений параллельной ветви.
4.1. Вектор падения напряжения на сопротивлении r2, равный по величине  (B), совпадает с направлением тока I2. Конец вектора совпадает с точкой 3, начало соответствует точке 2, (рис. 3.37).
(B), совпадает с направлением тока I2. Конец вектора совпадает с точкой 3, начало соответствует точке 2, (рис. 3.37).
4.2. Вектор падения напряжения UC2на сопротивлении xC2, равный по величине 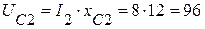 (В), отстает от тока I2 на 90° и берет начало с точки 4, конец вектора соответствует точке 3.
(В), отстает от тока I2 на 90° и берет начало с точки 4, конец вектора соответствует точке 3.
4.3. Вектор падения напряжения на сопротивлении r3, равный по величине 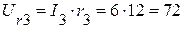 (B), совпадает с направлением тока I3. Конец вектора совпадает с точкой 5, начало соответствует точке 2, (рис. 3.37).
(B), совпадает с направлением тока I3. Конец вектора совпадает с точкой 5, начало соответствует точке 2, (рис. 3.37).
4.4. Вектор падения напряжения UL3 на сопротивлении xL3, равный по величине 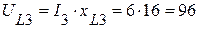 (B), опережает ток I3 на 90° и берет начало с точки 5, конец вектора соответствует точке 3 (рис. 3.37).
(B), опережает ток I3 на 90° и берет начало с точки 5, конец вектора соответствует точке 3 (рис. 3.37).
Векторная диаграмма для рассматриваемого примера, изображена на рисунке 3.37.
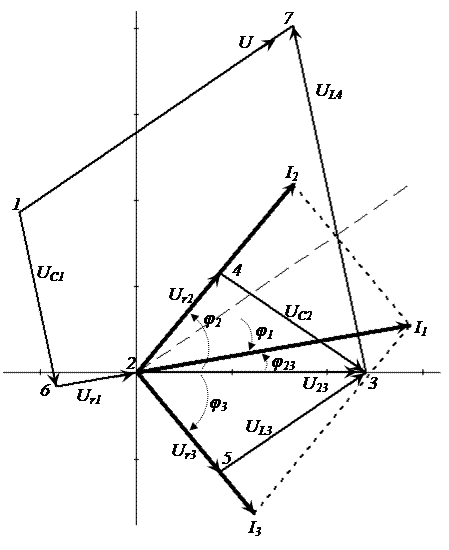
Рисунок 3.37 – Векторная диаграмма
векторная диаграмма — метод параллелограмма
Для Комбинированной Науки (Физики), рисование векторной диаграммы является обязательным.
В общем, даны две известные силы и результирующая сила этих двух сил должна быть найдена с использованием векторной диаграммы .
Существует два метода рисования векторной диаграммы 1) Метод параллелограмма и 2) Метод кончик к хвосту. В этом посте используется метод параллелограмма.
Пример 01
Пример 02
Пример 03
Пример 04
Щелкните здесь, чтобы просмотреть другой пост о методе треугольника с замкнутым контуром (2 силы, 2 неизвестных, 1 известный)
Нажмите здесь, чтобы посмотреть, как метод параллелограмма применяется к разным вопросам
Поделиться:
Нравится:
Нравится Загрузка…
Похожие
Категории: 01 Физические величины, 03 Динамика | Теги: правило параллелограмма, векторная диаграмма | Постоянная ссылка.
,Урок 1 — Добавление вектора: Числовой
Урок 1 — векторное сложение: численноеДобавление вектора: Числовое вычисляет величину и направление результирующего, учитывая величины и направления произвольное количество векторов, которые будут добавлены.
Предпосылки
Студенты должны понимать векторные свойства величины и направления и быть знакомы с графическим добавлением векторов методом Tip-to-Tail.Они также должны иметь знание основ тригонометрии.
Результаты обучения
Студенты научатся рассчитывать величину и направление суммы два вектора (результирующие) с учетом величин и направлений двух векторов быть добавленным. Для этого они научатся использовать закон косинусов и закон синусов. Они также Узнайте, как рассчитать сумму двух векторов, используя компоненты.
Инструкции
Студенты должны понимать функции апплета, которые описаны в Help и ShowMe.Апплет должен быть открытым. Пошаговые инструкции на этой странице быть сделано в апплете. Возможно, вам придется переключаться между инструкциями и апплет, если ваше пространство экрана ограничено.
Содержание
- Описание суммы двух векторов
- Метод 1 — Расчет результирующей с использованием закона косинусов и синусов
- Метод 2 — Расчет результирующего значения с использованием векторных компонентов
Приложение
- Закон косинусов
- Закон Синусов
- Компоненты
Представьте, что вы снова входите в атмосферу космического челнока.Чтобы посадите шаттл безопасно, пилот должен точно подойти к взлетно-посадочной полосе. Для этого пилот должен знать точную скорость шаттла относительно на землю во все времена. При повторном въезде шаттл движется со скоростью 130 м / с при 140 ° относительно воздуха, когда он входит в реактивный поток (большая высота, глобальная циркуляция воздуха), которая движется со скоростью 100 м / с при 60 ° относительно земля. Какова скорость шаттла относительно земли после того, как он входит реактивный поток? Вы можете испытать желание сказать 100 м / с + 130 м / с = 230 м / с.Это, однако, было бы неправильно. Скорость — векторная величина и как таковая две скорости должны быть добавлены как векторы. Апплет будет использоваться для иллюстрации как правильно добавляются два вектора.
Апплет будет использоваться для определения скорости шаттла относительно земля при повторном въезде.
Обведите правильный ответ ниже. Графическое построение результирующего на рисунке 1 показан
- Метод кончика к хвосту сложения векторов
- параллелограмм метод сложения векторов
Результат из упражнения 1 может отображаться в трех режимах.Нажмите на режим
кнопка управления ()
для результирующего, три раза и цикла
в «декартовом» режиме ().
В этом режиме результирующие компоненты x 9009 и y ( r x , r y )
отображаются, как показано на рисунке 2.
Используя кнопку управления режимом, опишите скорость шаттла относительно земля использует все три режима.
- Величина и полярное (положительное) направление результирующего () это (________, ________ град)
- Величина и навигационное направление результирующего () является (________, ________ E из N)
- Декартовы компоненты результирующего () являются (________ , ________)
Как рассчитывается полученный результат? Его можно найти с помощью двух разных методы.
- Метод 1 использует закон косинусов, чтобы найти результирующую величину и Закон синусов для результирующего направления.
- Метод 2 использует векторные компоненты для получения результирующей величины и направление. Каждый метод представлен ниже.
Для расчета величины и направления результирующего как показано на рисунке 1, нам нужна диаграмма, показывающая все соответствующие величины как на рисунке 2 ниже. Рисунок 2 Мы хотим рассчитать величину р из полученного значения и угол α. Угол направления θ результирующего в Полярная (положительная) характеристика тогда равна θ = α + 60 °. Закон косинусов используется для расчета величины ( r ) и закон синусов используется для расчета угла (). Описание этих законов см. В приложении. |
| Согласно рисунку 2, закон косинусов может быть использован для расчета
величина ( р ) результирующего вектора: (Примечание: угол, противоположный вектору равно 60 ° + 40 ° = 100 °.) |
Закон синусов может быть использован для расчета направления (θ) результирующего вектора. Чтобы применить закон синусов, соедините угол (α) с противоположной стороной величины ( v 2 ) и угол 100 ° с противоположной стороной величины ( r ). Следовательно, результирующий вектор имеет величину 177,24 под углом 106,25 ° в полярном (положительном) направлении: |
Используя закон косинусов и синусов, вычислите результат (сумму) следующего два вектора.Добавьте векторы в апплет для просмотра правильного подсказки векторная диаграмма и проверка результата.
1 = 150, 50 ° полярная (положительная)
2 = 200, 150 ° полярная (положительная)
Векторная иллюстрация кончика хвоста: | Результирующая величина (r): | Результирующее направление (θ): (Использование закон синусов и полярная (положительная) спецификация.) |
Используя закон косинусов и синусов, вычислите результат (сумму) следующего два вектора. Добавьте векторы в апплет для просмотра правильного подсказки векторная диаграмма и проверка результата.
1 = 100, 150 ° полярная (положительная)
2 = 75, 250 ° полярная (положительная)
Векторная иллюстрация кончика хвоста: | Результирующая величина (r): | Результирующее направление (θ): (Использование Закон синусов и полярная (положительная) спецификация.) |
| Теперь вычислим сумму тех же двух
векторы 1 и 2 как в предыдущем разделе, но на этот раз с использованием компонентов. Для следующих вычислений вам нужно знать (скалярные) компоненты вектора.Для обзора векторных компонентов, см. приложение. Это особенно легко, если векторы уже даны в терминах их ( x , y ) компонентов, ( v x , v y ) 1 и ( v x , v y ) 2 . Тем не мение, мы будем предполагать, что векторы даны с точки зрения величины и направления [( v 1 , θ 1 ) и ( v 2 , θ 2 )]. Углы измеряются в полярной (положительной) спецификации (или навигации N E). Смотрите рисунок 3. Рисунок 3 Величина и направление 1 и 2 являются: v 1 = 100, θ 1 = 60 ° v 2 = 130, θ 2 = 140 ° | |||||||||||
Добавить два вектора означает добавить соответствующие компоненты.Если компоненты полученного результата обозначены ( р х , р х ), мы получаем:
| |||||||||||
Вы можете указать результат с точки зрения компонентов и остановить расчет на данный момент. Однако, если величина и угол направления Результирующие требуются, они могут быть рассчитаны из компонентов следующим образом.
Опять же, очень полезно сделать диаграмму для иллюстрации углы и другие соответствующие величины участвуют.Смотрите рисунок 4 ниже. Рисунок 4 |
Треугольник, образованный вектором и эти два компонента представляют собой прямоугольный треугольник с вектором в качестве гипотенуза. Поэтому теорема Пифагора может быть использована для вычисления результирующая величина: |
| Из рисунка 4 видно, что направление может быть
рассчитывается с использованием определения тангенса угла. Это подразумевает угол направления значения 180 — 73,75 = 106,24 ° Следовательно, результирующий вектор равен 177,24 при 106,25 ° в полярной (положительное) направление. Вы можете проверить эти значения в апплете, выбрав величина и полярное положительное направление для результирующего: |
В итоге, если два вектора 1 и 2 даны с точки зрения величины и направления, результирующий может быть рассчитан сделав следующее:
- Используйте векторную диаграмму и тригонометрические функции для преобразования векторов в компонент сформироваться.
- Добавьте компоненты (х всего = х 1 + х 2 ) и (у всего = y 1 + y 2 ). Не забудьте включить положительный или отрицательные направления.
- Нарисуй результирующий используя вектор x всего компонент и y всего компонент. Помните включить положительные или отрицательные направления.
- Рассчитайте полученную величину, используя теорему Пифагора (c 2 = 2 + b 2 ).
- Рассчитать направление, используя соответствующую тригонометрическую функцию (тангенс функция).
Это может быть немного больше работы, чем вычислять результат с использованием закона Косинус и закон синусов, как это было сделано в предыдущем разделе. Тем не мение, если два вектора 1 и 2 уже даны в форме компонента, и если нужно получить результат в компоненте Форма, как это часто бывает, расчет проще.
Используя компонентный метод, вычислите результат (сумму) следующего два вектора. Показать все необходимые расчеты и диаграммы ниже и определить направление с использованием полярной (положительной) спецификации. Добавьте векторы на апплет для проверки результирующей величины и направления.
1 = 175, 70 ° полярная (положительная)
2 = 200, полярность 200 ° (положительная)
а.Векторная диаграмма и расчет компонентов на 1 . | б. Векторная схема и расчет компонентов на 2 . |
в. Добавление компонентов и рисование результирующего вектора.
д. Расчет результирующей величины с использованием теоремы Пифагора.
эл. Расчет результирующего направления с использованием функции тангенса.Экспресс направление с точки зрения полярной (положительной) спецификации.
Используя компонентный метод, вычислите результат (сумму) следующего два вектора. Показать все необходимые расчеты и диаграммы, а также определить направление используя полярную (положительную) спецификацию. Добавьте векторы в апплет в порядке проверить результирующую величину и направление.
1 = 185, 45 ° полярная (положительная)
2 = 95, 320 ° полярная (положительная)
| а.Векторная диаграмма и расчет компонентов за 1 . | б. Векторная диаграмма и расчет компонентов за 2 . |
в. Добавление компонентов и рисование результирующего вектора.
д. Расчет результирующей величины с использованием теоремы Пифагора.
эл. Расчет результирующего направления с использованием функции тангенса.Экспресс направление с точки зрения полярной (положительной) спецификации.
Используя компонентный метод, вычислите результат (сумму) следующего два вектора. Показать все необходимые расчеты и диаграммы ниже и определить направление с использованием полярной (положительной) спецификации. Добавьте векторы на апплет для проверки результирующей величины и направления.
1 = (+135, -120) — компоненты2 = (-200, -45) — компоненты
а.Добавление компонентов и рисование результирующего вектора:
б. Расчет полученной величины с использованием теоремы Пифагора:
в. Расчет результирующего направления с использованием функции тангенса: (выразить направление с точки зрения Полярной (положительной) спецификации)
Приложение
| Закон косинусов — это общее уравнение, связывающее три стороны
и один угол в треугольнике.Нет никаких ограничений на треугольник
форма. Три элемента определяют треугольник. Если какие-либо три из четырех элементов
В уравнении закона косинусов приведены уравнения, позволяющие рассчитать
четвертый. На рисунке A1 показан общий треугольник. Три стороны помечены a , b , c , и эти три угла обозначены как α, β, γ. Рисунок А1 |
Существует три уравнения закона косинуса, в зависимости от того, какой угол включен:
c 2 = a 2 + b 2 — 2 ab cos γ (A1)
a 2 = b 2 + c 2 — 2 до н.э. cos α (A2)
b 2 = c 2 + a 2 — 2 ca cos β (A3)
Обратите внимание, что теорема Пифагора является частным случаем этих уравнений, если из углов равен 90 °.Например, если γ = 90 °, то cos γ = 0 и уравнение (A1) сводится к теореме Пифагора:
c 2 = a 2 + b 2 (А4)
Также обратите внимание на знак минус перед косинусом в этих уравнениях. это имеет следующий эффект. Давайте рассмотрим уравнение (1). Если γ <90 ° косинус положительный. Со знаком минус перед косинусом, уравнение (A1) дает значение для c, которое меньше значения, заданного пифагорейцем Теорема (4).Если γ> 90 °, косинус отрицательный. В сочетании с знак минус перед косинусом, термин теперь вносит положительный вклад в правой части уравнения (1), которое дает значение с, которое больше чем тот, который дается теоремой Пифагора.
| Закон синусов — это система уравнений, истинная для любого треугольника.
Это заявляет, что отношение «синус угла, разделенного на длину
противоположная сторона «одинакова для любой пары углов и противоположной стороны. На рисунке A2 показан общий треугольник. Три стороны помечены a , b , c , и эти три угла обозначены как α, β, γ. Рисунок A2 |
Уравнения закона синусов:
(А5)
Треугольник определяется тремя его элементами.Учитывая две стороны и Закон синусов позволяет определить угол, противоположный одной из сторон. другая сторона.
Векторы могут быть описаны в терминах их скалярных компонентов. Вектор в двух измерениях имеет два скалярных компонента, один вдоль оси x и один по оси и . Для вектора эти компоненты обозначены а х и а у , соответственно.На рисунке A3 показаны компоненты для вектора это в первом квадранте. Рисунок A3 скалярных компонентов вектора являются проекциями вектора на оси x и y . На рисунке A3 они показаны зеленым и желтый соответственно. Они называются скалярными компонентами, потому что они являются числами. Скалярные компоненты равны x и y координаты вершины вектора, если хвостовой конец вектора в начале системы координат, как это здесь. |
Вектор на рисунке A3 имеет величину 8 и угол θ с положительный x — ось равна 30 °. Его скалярные компоненты имеют значения:
a x = 6,93, a y = 4,00 (A6)
Для векторов в первом квадранте оба компонента положительны, но для векторов в одном из трех других квадрантов один или оба компонента отрицательны.Для Например, с вектором во втором квадранте, компонент x является отрицательным в то время как y -компонент все еще положителен.
Определение синуса и косинуса подразумевает, что:
a x = a cos θ, a y = a sin θ (A7)
Подстановка a = 8.00 и θ = 30.0 ° в эти уравнения дает значения перечислены в уравнениях (A6) и проиллюстрированы на рисунке A3.
Обратите внимание, что уравнения (A7) являются правильными, даже если вектор находится во втором, третьем или четвертом квадранте. Никаких признаков не нужно менять. любой изменения знака автоматически учитываются знаками косинуса и синусоидальные функции для значений θ в любом из этих других квадрантов.
Физика 20-30 v1.0
© 2004 Alberta Learning (www.learnalberta.ca)
Последнее обновление: 16 июня 2004 г.
,Страница не найдена | MIT
Перейти к содержанию ↓- образование
- Исследовательская работа
- новаторство
- Прием + помощь
- Студенческая жизнь
- Новости
- Alumni
- О MIT
- Больше ↓
- Прием + помощь
- Студенческая жизнь
- Новости
- Alumni
- О MIT
Попробуйте поискать что-нибудь еще! Что вы ищете? Посмотреть больше результатов
Предложения или отзывы?
,1.2 Результат перпендикулярных векторов (ESBK3)
В 10 классе вы узнали о результирующем векторе в одном измерении, мы собираемся расширить его до двух измерений. Напоминаем, что если у вас есть несколько векторов (пока что подумайте о силах), действующих одновременно, вы можете представить результат всех их вместе с одним вектором, известным как результирующий. Результирующий вектор будет иметь тот же эффект , что и все векторы, складывающиеся вместе.
Мы сосредоточимся на примерах, связанных с силами, но очень важно помнить, что это относится ко всем физическим величинам, которые могут быть описаны векторами, силами, смещениями, ускорениями, скоростями и многим другим.
Векторы на декартовой плоскости (ESBK4)
Первое, на что следует обратить внимание, это то, что в 10 классе мы работали с векторами, действующими по одной линии, по одной оси. Теперь мы пойдем дальше и начнем работать с двумя измерениями.Мы можем представить это, используя декартову плоскость, которая состоит из двух перпендикулярных (под прямым углом) осей. Оси являются осью \ (x \) и осью \ (y \). Обычно мы рисуем ось \ (x \) — слева направо (по горизонтали) и ось \ (y \) — вверх и вниз (по вертикали).
Мы можем рисовать векторы на декартовой плоскости. Например, если у нас есть сила \ (\ vec {F} \) величины \ (\ text {2} \) \ (\ text {N} \), действующая в положительном \ (x \) — направлении мы можем нарисовать его как вектор на декартовой плоскости.
Обратите внимание, что длина вектора, измеренная по осям, равна \ (\ text {2} \), указанной величине. Вектор не обязательно должен начинаться с начала координат, но его можно разместить в любом месте на декартовой плоскости. То, где вектор начинается на плоскости, не влияет на физическую величину, пока величина и направление остаются неизменными. Это означает, что все векторы на диаграмме ниже могут представлять одну и ту же силу. Это свойство известно как равенство векторов .
На диаграмме векторы имеют одинаковую величину, потому что стрелки имеют одинаковую длину , и имеют одинаковое направление .Все они параллельны направлению \ (x \) — и параллельны друг другу.
Это в равной степени относится в направлении \ (y \). Например, если у нас есть сила \ (\ vec {F} \) величины \ (\ text {2,5} \) \ (\ text {N} \), действующая в положительном направлении \ (y \) -направление мы можем нарисовать как вектор на декартовой плоскости.
Так же, как и в случае направления \ (x \) -, вектор не обязательно должен начинаться с начала координат, но его можно разместить в любом месте на декартовой плоскости. Все векторы на диаграмме ниже могут представлять одну и ту же силу.
На следующем рисунке показан пример четырех векторов силы, двух векторов, параллельных друг другу и оси \ (y \), а также двух параллельных друг другу и оси \ (x \).
Чтобы подчеркнуть, что векторы перпендикулярны, вы можете видеть на рисунке ниже, что, когда они исходят из одной и той же точки, вектор находится под прямым углом.
Вы можете сделать это! Позвольте нам помочь вам учиться умнее для достижения ваших целей. Практика Siyavula поможет вам в вашем собственном темпе, когда вы будете задавать вопросы онлайн.
Зарегистрируйтесь, чтобы улучшить свои оценки Упражнение 1.1Нарисуйте следующие силы как векторы на декартовой плоскости, возникающие в начале координат:
- \ (\ vec {F} _ {1} = \ text {1,5} \ text {N} \) в положительном \ (x \) — направлении
- \ (\ vec {F} _ {2} = \ text {2} \ text {N} \) в положительном \ (y \) — направлении
Мы выбираем шкалу \ (\ text {1} \) \ (\ text {N} \): \ (\ text {1} \) \ (\ text {cm} \). Теперь мы нарисуем векторы на декартовой плоскости (мы можем разместить векторы в любом месте на декартовой плоскости, мы разместим их, начиная с начала координат):
Нарисуйте следующие силы как векторы на декартовой плоскости:
- \ (\ vec {F} _ {1} = \ text {3} \ text {N} \) в положительном \ (x \) — направлении
- \ (\ vec {F} _ {2} = \ text {1} \ text {N} \) в отрицательном \ (x \) — направлении
- \ (\ vec {F} _ {3} = \ text {3} \ text {N} \) в положительном \ (y \) — направлении
Мы выбираем шкалу \ (\ text {1} \) \ (\ text {N} \): \ (\ text {1} \) \ (\ text {cm} \).Теперь мы нарисуем векторы на декартовой плоскости (мы можем разместить векторы в любом месте на декартовой плоскости):
Нарисуйте следующие силы как векторы на декартовой плоскости:
- \ (\ vec {F} _ {1} = \ text {3} \ text {N} \) в положительном \ (x \) — направлении
- \ (\ vec {F} _ {2} = \ text {1} \ text {N} \) в положительном \ (x \) — направлении
- \ (\ vec {F} _ {3} = \ text {2} \ text {N} \) в отрицательном \ (x \) — направлении
- \ (\ vec {F} _ {4} = \ text {3} \ text {N} \) в положительном \ (y \) — направлении
Мы выбираем шкалу \ (\ text {1} \) \ (\ text {N} \): \ (\ text {1} \) \ (\ text {cm} \).Теперь мы нарисуем векторы на декартовой плоскости (мы можем разместить векторы в любом месте на декартовой плоскости):
Нарисуйте следующие силы как векторы на декартовой плоскости:
- \ (\ vec {F} _ {1} = \ text {2} \ text {N} \) в положительном \ (y \) — направлении
- \ (\ vec {F} _ {2} = \ text {1,5} \ text {N} \) в отрицательном направлении \ (y \) —
- \ (\ vec {F} _ {3} = \ text {2,5} \ text {N} \) в отрицательном \ (x \) — направлении
- \ (\ vec {F} _ {4} = \ text {3} \ text {N} \) в положительном \ (y \) — направлении
Мы выбираем шкалу \ (\ text {1} \) \ (\ text {N} \): \ (\ text {1} \) \ (\ text {cm} \).Теперь мы нарисуем векторы на декартовой плоскости (мы можем разместить векторы в любом месте на декартовой плоскости):
Векторы в двух измерениях не всегда параллельны оси. Мы можем знать, что сила действует под углом к оси, поэтому мы все еще знаем направление силы, и если мы знаем величину, мы можем нарисовать вектор силы. Например, мы можем нарисовать \ (\ vec {F} _ {1} = \ text {2} \ text {N} \), действующий в \ (\ text {45} \) \ (\ text {°} \) в положительное \ (x \) — направление:
Мы всегда указываем угол как против часовой стрелки от положительной оси \ (x \).Поэтому, если бы мы указали отрицательный угол, мы бы измерили его по часовой стрелке от оси \ (x \) -. Например, \ (\ vec {F} _ {1} = \ text {2} \ text {N} \) действует на \ (- \ text {45} \) \ (\ text {°} \) на положительное \ (x \) — направление:
Мы можем использовать множество других способов указания направления вектора. Направление просто должно быть однозначным. До сих пор мы использовали декартову систему координат и угол с осью \ (x \) -, но есть и другие распространенные способы указания направления, которые вам необходимо знать и с которыми удобно работать.
Указания компаса (ESBK5)
Мы можем использовать направления компаса, когда это уместно, чтобы указать направление вектора. Например, если бы мы описывали силы тектонических плит (движущихся участков земной коры), чтобы говорить о силах, связанных с землетрясениями, мы могли бы говорить о силе, которую движущие плиты оказывают друг на друга.
Рисунок 1.1: Карта 15 основных тектонических плит, составляющих земную кору.Четыре основных направления — север, юг, восток и запад при использовании компаса.Они показаны на этом рисунке:
Рисунок 1.2: Эскиз компаса.При указании направления вектора с помощью компаса направления задаются по имени, северу или югу. Если направление находится между двумя направлениями, мы можем объединить имена, например, Северо-Восток находится на полпути между Севером и Востоком. Это может произойти только для направлений под прямым углом друг к другу, вы не можете сказать север-юг, поскольку это неоднозначно.
Подшипники (ESBK6)
Другой способ использования компаса для указания направления числовым способом — использование подшипников.Подшипник — это угол, обычно измеряемый по часовой стрелке с севера. Обратите внимание, , что это отличается от декартовой плоскости, где углы против или против часовой стрелки от положительного направления \ (x \) -.
Результирующий вектор (ESBK7)
В 10 классе вы узнали о сложении векторов в одном измерении. Тот же принцип может быть применен к векторам в двух измерениях. Следующие примеры показывают добавление векторов. Векторы, которые параллельны, могут быть смещены так, чтобы они падали на линию.Векторы, попадающие на одну и ту же линию, называются совместно- векторов. Чтобы добавить коллинеарные векторы, мы используем метод хвоста к голове, который вы изучили в 10 классе. На рисунке ниже мы напоминаем вам о подходе добавления коллинеарных векторов для получения результирующего вектора.
Рисунок 1.3: Добавление коллинеарных векторов для получения результирующего вектора.
На рисунке выше синие векторы находятся в направлении \ (y \) -, а красные — в направлении \ (x \). Два черных вектора графически представляют результирующие значения коллинеарных векторов.
Что мы сделали, так это внедрили метод сложения векторов хвостом к голове для вертикального набора векторов и горизонтального набора векторов.
Рабочий пример 1. Пересмотр: сложение головы к хвосту в одном измерении
Используйте графический метод «голова к хвосту», чтобы определить результирующую силу для игрока в регби, если два игрока в его команде толкают его вперед с силами \ (\ stackrel {\ to} {{F} _ {1}} \ ) = \ (\ text {600} \) \ (\ text {N} \) и \ (\ stackrel {\ to} {{F} _ {2}} \) = \ (\ text {900} \) \ (\ text {N} \) соответственно, и два игрока из противоположной команды отталкивают его назад силами \ (\ stackrel {\ to} {{F} _ {3}} \) = \ (\ text {1 000} \) \ (\ text {N} \) и \ (\ stackrel {\ to} {{F} _ {4}} \) = \ (\ text {650} \) \ (\ text {N} \) соответственно.
Выберите масштаб и направление ссылки
Давайте выберем масштаб \ (\ text {100} \) \ (\ text {N} \): \ (\ text {0,5} \) \ (\ text {cm} \) и для нашей диаграммы мы определим положительное направление как направо.
Выберите один из векторов и нарисуйте его в виде стрелки правильной длины в правильном направлении.
Начнем с рисования вектора \ (\ stackrel {\ to} {{F} _ {1}} \) = \ (\ text {600} \) \ (\ text {N} \), указывающего на положительный направление.Используя наш масштаб \ (\ text {0,5} \) \ (\ text {cm} \): \ (\ text {100} \) \ (\ text {N} \), длина стрелки должна быть \ (\ text {3} \) \ (\ text {cm} \) направо.
Возьмите следующий вектор и начертите его, начиная со стрелки предыдущего вектора.
Следующий вектор — это \ (\ stackrel {\ to} {{F} _ {2}} \) = \ (\ text {900} \) \ (\ text {N} \) в том же направлении, что и \ ( \ stackrel {\ to} {{F} _ {1}} \). Используя шкалу, стрелка должна быть длинной \ (\ text {4,5} \) \ (\ text {cm} \) и направлена вправо.
Возьмите следующий вектор и начертите его, начиная со стрелки предыдущего вектора.
Следующий вектор: \ (\ stackrel {\ to} {{F} _ {3}} \) = \ (\ text {1 000} \) \ (\ text {N} \) в направлении в направлении , Используя шкалу, эта стрелка должна быть \ (\ text {5} \) \ (\ text {cm} \) длинной и указывать на слева .
Примечание: Мы работаем в одном измерении, поэтому эта стрелка будет нарисована сверху первых векторов слева. Это будет сбивать с толку, поэтому мы нарисуем его рядом с реальной линией, чтобы показать вам, как это выглядит.
Возьмите следующий вектор и начертите его, начиная со стрелки предыдущего вектора.
Четвертый вектор — \ (\ stackrel {\ to} {{F} _ {4}} \) = \ (\ text {650} \) \ (\ text {N} \) в обратном направлении. Используя шкалу, эта стрелка должна быть \ (\ text {3,25} \) \ (\ text {cm} \) длинной и указывать налево.
Нарисуйте результат, измерьте его длину и найдите направление
Теперь мы нарисовали все векторы силы, которые применяются к игроку. Результирующий вектор — это стрелка, которая начинается в хвосте первого вектора и заканчивается в начале последнего нарисованного вектора.
Результирующий вектор измеряет \ (\ text {0,75} \) \ (\ text {cm} \), который, используя наш масштаб, эквивалентен \ (\ text {150} \) \ (\ text {N} \ ) и указывает налево ( или — отрицательное направление, или — направление, в котором толкаются члены команды противника).
Вы можете сделать это! Позвольте нам помочь вам учиться умнее для достижения ваших целей. Практика Siyavula поможет вам в вашем собственном темпе, когда вы будете задавать вопросы онлайн.
Зарегистрируйтесь, чтобы улучшить свои оценки Упражнение 1.2Найдите результирующий в направлении \ (x \) -, \ (R_x \) и \ (y \) — направлении \ (R_y \) для следующих сил:
- \ (\ vec {F} _ {1} = \ text {1,5} \ text {N} \) в положительном \ (x \) — направлении
- \ (\ vec {F} _ {2} = \ text {1,5} \ text {N} \) в положительном \ (x \) — направлении
- \ (\ vec {F} _ {3} = \ text {2} \ text {N} \) в отрицательном \ (x \) — направлении
Мы выбираем шкалу \ (\ text {1} \) \ (\ text {N} \): \ (\ text {1} \) \ (\ text {cm} \) и для нашей диаграммы мы определим положительное направление как направо.
Мы начнем с рисования вектора \ (\ stackrel {\ to} {{F} _ {1}} \) = \ (\ text {1,5} \) \ (\ text {N} \), указывающего на положительное направление. Используя наш масштаб \ (\ text {1} \) \ (\ text {N} \): \ (\ text {1} \) \ (\ text {cm} \), длина стрелки должна быть \ (\ text {1,5} \) \ (\ text {cm} \), указывающий направо.
Следующий вектор \ (\ stackrel {\ to} {{F} _ {2}} \) = \ (\ text {1,5} \) \ (\ text {N} \) в том же направлении, что и \ (\ stackrel {\ to} {{F} _ {1}} \). Используя шкалу, стрелка должна быть длинной \ (\ text {1,5} \) \ (\ text {cm} \) и направлена вправо.
Следующий вектор — это \ (\ stackrel {\ to} {{F} _ {3}} \) = \ (\ text {2} \) \ (\ text {N} \) в направлении в направлении . Используя шкалу, эта стрелка должна быть \ (\ text {2} \) \ (\ text {cm} \) длинной и указывать на слева .
Примечание: Мы работаем в одном измерении, поэтому эта стрелка будет нарисована сверху первых векторов слева. Это будет сбивать с толку, поэтому мы нарисуем его рядом с реальной линией, чтобы показать вам, как это выглядит.
Теперь мы нарисовали все заданные векторы силы. Результирующий вектор — это стрелка, которая начинается в хвосте первого вектора и заканчивается в начале последнего нарисованного вектора.
Результирующий вектор измеряет \ (\ text {1} \) \ (\ text {cm} \), который, используя наш масштаб, эквивалентен \ (\ text {1} \) \ (\ text {N} \) и направо ( или в положительном направлении). Это \ (\ vec {R} _ {x} \). Для этого набора векторов у нас нет векторов, указывающих в направлении \ (y \), и поэтому нам не нужно искать \ (\ vec {R} _ {y} \).
Найдите результирующий в направлении \ (x \) -, \ (\ vec {R} _x \) и \ (y \) — направлении, \ (\ vec {R} _y \) для следующих сил:
- \ (\ vec {F} _ {1} = \ text {2,3} \ text {N} \) в положительном \ (x \) — направлении
- \ (\ vec {F} _ {2} = \ text {1} \ text {N} \) в отрицательном \ (x \) — направлении
- \ (\ vec {F} _ {3} = \ text {2} \ text {N} \) в положительном \ (y \) — направлении
- \ (\ vec {F} _ {4} = \ text {3} \ text {N} \) в отрицательном \ (y \) — направлении
Мы выбираем шкалу \ (\ text {1} \) \ (\ text {N} \): \ (\ text {1} \) \ (\ text {cm} \) и для нашей диаграммы мы определим положительное направление как направо.
Прежде чем мы начнем рисовать векторы, отметим длину векторов, используя нашу шкалу:
\ Начать {*} Align \ vec {F} _ {1} & = \ text {2,3} \ text {cm} \\ \ vec {F} _ {2} & = \ text {1} \ text {cm} \\ \ vec {F} _ {3} & = \ text {2} \ text {cm} \\ \ vec {F} _ {4} & = \ text {3} \ text {cm} \ Конец {*} выравниваниеТакже отметим направление, в котором находятся векторы:
\ Начать {*} Align \ vec {F} _ {1} & = \ text {positive} x \ text {-direction} \\ \ vec {F} _ {2} & = \ text {отрицательный} x \ text {-direction} \\ \ vec {F} _ {3} & = \ text {positive} y \ text {-direction} \\ \ vec {F} _ {4} & = \ text {отрицательный} y \ text {-направление} \ Конец {*} выравниваниеТеперь рассмотрим два вектора в направлении \ (x \) -, чтобы найти \ (\ vec {R} _ {x} \):
Теперь мы нарисовали все векторы силы, которые действуют в направлении \ (x \).Чтобы найти \ (\ vec {R} _ {x} \), отметим, что результирующий вектор — это стрелка, которая начинается в хвосте первого вектора и заканчивается в начале последнего нарисованного вектора в этом направлении.
Мы отмечаем, что \ (\ vec {R} _ {x} \) есть \ (\ text {1,3} \) \ (\ text {cm} \) или \ (\ text {1,3} \) \ (\ text {N} \) в положительном \ (x \) — направлении.
Теперь рассмотрим два вектора в направлении \ (y \) -, чтобы найти \ (\ vec {R} _ {y} \):
Теперь мы нарисовали все векторы силы, которые действуют в направлении \ (y \).Чтобы найти \ (\ vec {R} _ {y} \), отметим, что результирующим вектором является стрелка, которая начинается в хвосте первого вектора и заканчивается в начале последнего нарисованного вектора в этом направлении.
Мы отмечаем, что \ (\ vec {R} _ {y} \) — это \ (\ text {1} \) \ (\ text {cm} \) или \ (\ text {1} \) \ (\ text {N} \) в отрицательном направлении \ (y \).
\ (\ vec {R} _ {x} \) = \ (\ text {1,3} \) \ (\ text {N} \) и указывает в положительном \ (x \) — направлении. \ (\ vec {R} _ {y} \) = \ (\ text {1} \) \ (\ text {N} \) и указывает в отрицательном \ (y \) — направлении.
Найдите результирующий в направлении \ (x \) -, \ (\ vec {R} _x \) и \ (y \) — направлении, \ (\ vec {R} _y \) для следующих сил:
- \ (\ vec {F} _ {1} = \ text {3} \ text {N} \) в положительном \ (x \) — направлении
- \ (\ vec {F} _ {2} = \ text {1} \ text {N} \) в положительном \ (x \) — направлении
- \ (\ vec {F} _ {3} = \ text {2} \ text {N} \) в отрицательном \ (x \) — направлении
- \ (\ vec {F} _ {4} = \ text {3} \ text {N} \) в положительном \ (y \) — направлении
Мы выбираем шкалу \ (\ text {1} \) \ (\ text {N} \): \ (\ text {1} \) \ (\ text {cm} \) и для нашей диаграммы мы определим положительное направление как направо.
Прежде чем мы начнем рисовать векторы, отметим длину векторов, используя нашу шкалу:
\ Начать {*} Align \ vec {F} _ {1} & = \ text {3} \ text {cm} \\ \ vec {F} _ {2} & = \ text {1} \ text {cm} \\ \ vec {F} _ {3} & = \ text {2} \ text {cm} \\ \ vec {F} _ {4} & = \ text {3} \ text {cm} \ Конец {*} выравниваниеТакже отметим направление, в котором находятся векторы:
\ Начать {*} Align \ vec {F} _ {1} & = \ text {positive} x \ text {-direction} \\ \ vec {F} _ {2} & = \ text {positive} x \ text {-direction} \\ \ vec {F} _ {3} & = \ text {отрицательный} x \ text {-direction} \\ \ vec {F} _ {4} & = \ text {positive} y \ text {-direction} \ Конец {*} выравниваниеТеперь рассмотрим три вектора в направлении \ (x \) -, чтобы найти \ (\ vec {R} _ {x} \):
Теперь мы нарисовали все векторы силы, которые действуют в направлении \ (x \).Чтобы найти \ (\ vec {R} _ {x} \), отметим, что результирующий вектор — это стрелка, которая начинается в хвосте первого вектора и заканчивается в начале последнего нарисованного вектора в этом направлении.
Мы отмечаем, что \ (\ vec {R} _ {x} \) — это \ (\ text {2} \) \ (\ text {cm} \) или \ (\ text {2} \) \ (\ text {N} \) в положительном \ (x \) — направлении.
Теперь рассмотрим векторы в \ (y \) — направлении, чтобы найти \ (\ vec {R} _ {y} \). Мы замечаем, что у нас есть только один вектор в этом направлении, и поэтому вектор является результирующим.
Мы отмечаем, что \ (\ vec {R} _ {y} \) — это \ (\ text {3} \) \ (\ text {cm} \) или \ (\ text {3} \) \ (\ text {N} \) в положительном \ (y \) — направлении.
\ (\ vec {R} _ {x} \) = \ (\ text {2} \) \ (\ text {N} \) и указывает в положительном \ (x \) — направлении. \ (\ vec {R} _ {y} \) = \ (\ text {3} \) \ (\ text {N} \) и точки в положительном \ (y \) — направлении.
Найдите результирующий в направлении \ (x \) -, \ (\ vec {R} _x \) и \ (y \) — направлении, \ (\ vec {R} _y \) для следующих сил:
- \ (\ vec {F} _ {1} = \ text {2} \ text {N} \) в положительном \ (y \) — направлении
- \ (\ vec {F} _ {2} = \ text {1,5} \ text {N} \) в отрицательном направлении \ (y \) —
- \ (\ vec {F} _ {3} = \ text {2,5} \ text {N} \) в отрицательном \ (x \) — направлении
- \ (\ vec {F} _ {4} = \ text {3} \ text {N} \) в положительном \ (y \) — направлении
Мы выбираем масштаб \ (\ text {1} \) \ (\ text {cm} \): \ (\ text {1} \) \ (\ text {N} \) и для нашей диаграммы мы определим положительное направление как направо.
Прежде чем мы начнем рисовать векторы, отметим длину векторов, используя нашу шкалу:
\ Начать {*} Align \ vec {F} _ {1} & = \ text {2} \ text {cm} \\ \ vec {F} _ {2} & = \ text {1,5} \ text {cm} \\ \ vec {F} _ {3} & = \ text {2,5} \ text {cm} \\ \ vec {F} _ {4} & = \ text {3} \ text {cm} \ Конец {*} выравниваниеТакже отметим направление, в котором находятся векторы:
\ Начать {*} Align \ vec {F} _ {1} & = \ text {positive} y \ text {-direction} \\ \ vec {F} _ {2} & = \ text {отрицательный} y \ text {-direction} \\ \ vec {F} _ {3} & = \ text {отрицательный} x \ text {-direction} \\ \ vec {F} _ {4} & = \ text {positive} y \ text {-direction} \ Конец {*} выравниваниеМы смотрим на векторы в \ (x \) — направлении, чтобы найти \ (\ vec {R} _ {x} \).Мы замечаем, что у нас есть только один вектор в этом направлении, и поэтому вектор является результирующим.
Мы отмечаем, что \ (\ vec {R} _ {x} \) — это \ (\ text {2,5} \) \ (\ text {cm} \) или \ (\ text {2,5} \) \ (\ text {N} \) в отрицательном \ (x \) — направлении.
Теперь рассмотрим три вектора в направлении \ (y \) -, чтобы найти \ (\ vec {R} _ {y} \):
Теперь мы нарисовали все векторы силы, которые действуют в направлении \ (y \). Чтобы найти \ (\ vec {R} _ {y} \), отметим, что результирующим вектором является стрелка, которая начинается в хвосте первого вектора и заканчивается в начале последнего нарисованного вектора в этом направлении.
Мы отмечаем, что \ (\ vec {R} _ {y} \) это \ (\ text {3,5} \) \ (\ text {cm} \) или \ (\ text {3,5} \) \ (\ text {N} \) в положительном \ (y \) — направлении.
\ (\ vec {R} _ {x} \) = \ (\ text {2,5} \) \ (\ text {N} \) и указывает в отрицательном \ (x \) — направлении. \ (\ vec {R} _ {y} \) = \ (\ text {3,5} \) \ (\ text {N} \) и точки в положительном \ (y \) — направлении.
Найдите силу в направлении \ (x \) — \ (F_x \) и \ (y \) — \ (F_y \), которую можно добавить к следующим силам, чтобы сделать результирующим в \ (x \) — направление, \ (R_x \) и \ (y \) — направление, \ (R_y \) ноль:
- \ (\ vec {F} _ {1} = \ text {2,4} \ text {N} \) в положительном \ (y \) — направлении
- \ (\ vec {F} _ {2} = \ text {0,7} \ text {N} \) в отрицательном \ (y \) — направлении
- \ (\ vec {F} _ {3} = \ text {2,8} \ text {N} \) в отрицательном \ (x \) — направлении
- \ (\ vec {F} _ {4} = \ text {3,3} \ text {N} \) в положительном \ (y \) — направлении
Чтобы решить эту проблему, мы нарисуем векторы на декартовой плоскости, а затем посмотрим, что такое результирующий вектор.Затем мы определяем, какой вектор силы добавить, чтобы результирующий вектор был \ (\ text {0} \).
Мы выбираем масштаб \ (\ text {1} \) \ (\ text {cm} \): \ (\ text {1} \) \ (\ text {N} \) и для нашей диаграммы мы определим положительное направление как направо.
Прежде чем мы начнем рисовать векторы, отметим длину векторов, используя нашу шкалу:
\ Начать {*} Align \ vec {F} _ {1} & = \ text {2,4} \ text {cm} \\ \ vec {F} _ {2} & = \ text {0,7} \ text {cm} \\ \ vec {F} _ {3} & = \ text {2,8} \ text {cm} \\ \ vec {F} _ {4} & = \ text {3,3} \ text {cm} \ Конец {*} выравниваниеТакже отметим направление, в котором находятся векторы:
\ Начать {*} Align \ vec {F} _ {1} & = \ text {positive} y \ text {-direction} \\ \ vec {F} _ {2} & = \ text {отрицательный} y \ text {-direction} \\ \ vec {F} _ {3} & = \ text {отрицательный} x \ text {-direction} \\ \ vec {F} _ {4} & = \ text {positive} y \ text {-direction} \ Конец {*} выравниваниеМы смотрим на векторы в \ (x \) — направлении, чтобы найти \ (\ vec {R} _ {x} \).Мы замечаем, что у нас есть только один вектор в этом направлении, и поэтому вектор является результирующим.
Мы отмечаем, что \ (\ vec {R} _ {x} \) есть \ (\ text {2,8} \) \ (\ text {cm} \) или \ (\ text {2,8} \) \ (\ text {N} \) в отрицательном \ (x \) — направлении.
Так что, если мы добавим силу \ (\ text {2,8} \) \ (\ text {N} \) в положительном \ (x \) — направлении, результирующим будет \ (\ text {0} \ ):
Теперь рассмотрим три вектора в направлении \ (y \) -, чтобы найти \ (\ vec {R} _ {y} \):
Теперь мы нарисовали все векторы силы, которые действуют в направлении \ (y \).Чтобы найти \ (\ vec {R} _ {y} \), отметим, что результирующим вектором является стрелка, которая начинается в хвосте первого вектора и заканчивается в начале последнего нарисованного вектора в этом направлении.
Мы отмечаем, что \ (\ vec {R} _ {y} \) — это \ (\ text {5} \) \ (\ text {cm} \) или \ (\ text {5} \) \ (\ text {N} \) в положительном \ (y \) — направлении.
Поэтому, если мы добавим силу \ (\ text {5} \) \ (\ text {N} \) в отрицательном направлении \ (y \) — результирующим будет \ (\ text {0} \):
Мы должны добавить силу \ (\ text {2,8} \) \ (\ text {N} \) в положительном \ (x \) — направлении и силу \ (\ text {5} \) \ (\ text {N} \) в отрицательном \ (y \) — направлении.
Величина результирующих векторов под прямым углом (ESBK8)
Мы применяем тот же принцип к векторам, которые находятся под прямым углом или перпендикулярно друг другу.
Эскизный метод «хвост к голове»
Хвост одного вектора помещается в головку другого, но в двух измерениях векторы могут быть не коллинеарными. Подход состоит в том, чтобы нарисовать все векторы, по одному за раз. Для первого вектора начинаются в начале декартовой плоскости, для второго вектора нарисуйте его из головы первого вектора.Третий вектор должен быть взят из головы второго и так далее. Каждый вектор взят из заголовка предшествующего ему вектора. Порядок не имеет значения, так как результат будет таким же, если порядок другой.
Давайте применим эту процедуру к двум векторам:
- \ (\ vec {F} _ {1} = \ text {2} \ text {N} \) в положительном \ (y \) — направлении
- \ (\ vec {F} _ {2} = \ text {1,5} \ text {N} \) в положительном \ (x \) — направлении
Сначала мы нарисуем декартову плоскость с первым вектором в начале координат:
Следующий шаг — взять второй вектор и нарисовать его из головы первого вектора:
Результирующий, \ (\ vec {R} \), — это вектор, соединяющий хвост первого вектора, нарисованного с головой последнего нарисованного вектора:
Важно помнить, что порядок, в котором мы рисуем векторы, не имеет значения.Если бы мы нарисовали их в обратном порядке, мы получили бы тот же результат, \ (\ vec {R} \). Мы можем повторить процесс, чтобы продемонстрировать это:
Сначала мы нарисуем декартову плоскость со вторым вектором, начинающимся в начале координат:
Следующий шаг — взять другой вектор и нарисовать его из головы вектора, который мы уже нарисовали:
Результирующий, \ (\ vec {R} \), является вектором, соединяющим хвост первого вектора, нарисованного с головой последнего нарисованного вектора (вектор от начальной точки до конечной точки):
Рабочий пример 2: рисование векторов с использованием хвоста к голове
Нарисуйте результат следующих векторов силы методом хвоста к голове:
- \ (\ vec {F} _ {1} = \ text {2} \ text {N} \) в положительном \ (y \) — направлении
- \ (\ vec {F} _ {2} = \ text {1,5} \ text {N} \) в положительном \ (x \) — направлении
- \ (\ vec {F} _ {3} = \ text {1,3} \ text {N} \) в отрицательном направлении \ (y \) —
- \ (\ vec {F} _ {4} = \ text {1} \ text {N} \) в отрицательном \ (x \) — направлении
Рисуем декартову плоскость и первый вектор
Сначала нарисуйте декартову плоскость и силу, \ (\ vec {F} _ {1} \), начиная с начала координат:
Нарисуйте второй вектор
Начиная с заголовка первого вектора, рисуем хвост второго вектора:
Нарисуйте третий вектор
Начиная с заголовка второго вектора, рисуем хвост третьего вектора:
Нарисуйте четвертый вектор
Начиная с заголовка третьего вектора, рисуем хвост четвертого вектора:
Нарисуйте результирующий вектор
Начиная с начала координат, нарисуйте результирующий вектор в заголовке четвертого вектора:
Рабочий пример 3: рисование векторов с использованием хвоста к голове
Нарисуйте результирующее значение следующих векторов силы, используя метод хвоста к голове, сначала определив результирующее значение в
.


