Метод свертывания
Метод свертывания используется для цепей со смешанным соединением потребителей, то есть, когда есть участки с последовательным и параллельным соединением потребителей.
Расчет цепи со смешанным соединением потребителейпроизводится в следующей последовательности:
На схеме отмечаются все токи и узловые точки;
Группы резисторов с явным последовательным или явным параллельным соединением заменяются эквивалентными сопротивлениями;
Замена соединений эквивалентным сопротивлением производится до получения простейшей схемы;
По заданному напряжению и эквивалентному сопротивлению находим общий ток;
Определяем падения напряжения на участках и токи на этих участках;
(привести пример)
Метод преобразования схем
Метод преобразования схем применяют для расчета сложных цепей, в которых невозможно использовать метод свертывания без дополнительных преобразований, так как там присутствуют соединения типа «треугольник» или «звезда». Соединение «треугольник» преобразуют в соединение «звезда» или, наоборот, для того, чтобы потом цепь можно было легко свернуть. Эти преобразования проводятся при условии, что электрические параметры (ее баланс) не нарушаются.
Если есть соединение «треугольник» с узлами А, В, Си сопротивлениямиRАВ ,RВС ,RСА, то его можно преобразовать в соединение «звезда» с общим узлом
АО – RA;
BO – RB;
CO – RC.

Для того, чтобы преобразовать соединение «звезда» с общим узлом Ои сопротивлениями на участках:АО – RA; BO – RB;CO – RC. в соединение «треугольник» с узлами

Метод наложения
Метод наложения используется для расчета сложных электрических цепей, имеющих несколько источников.
Порядок расчета:
В каждой ветви выбираем и показываем на чертеже произвольно направление токов;
Количество расчетных схем в цепи равно количеству источников в исходной схеме;
В каждой расчетной схеме действует только один источник, а остальные заменяются их эквивалентным сопротивлением;
В каждой расчетной схеме методами преобразования и сворачивания находятся частичные токи. Частичным называется ток, протекающий в ветви под действием только одного источника;
Искомые токи в ветвях находятся как алгебраическая сумма частичных токов в этих ветвях.
Метод узлового напряжения
Расчет сложной электрической цепи с несколькими источниками можно произвести с помощью метода узлового напряжения.
Порядок расчета цепи:
Произвольно в ветвях выбираем и показываем на схеме направления токов;
Выбираем базисный узел (φ=0В) и выбираем положительные направления узловых напряжений от независимых узлов к базисному узлу;
Определяем узловые токи, узловые и общие проводимости. При этом токи источников, направленные к узлам, принимают положительными;
Для определения токов в ветвях составляют систему уравнений по первому закону Кирхгофа для узла.
Узловой проводимостью называют сумму проводимостей всех ветвей, присоединенных к данному узлу.
Общей проводимостью называется сумма проводимостей всех ветвей, соединяющих данные два узла.
27. Смешанное соединение пассивных элементов. Метод свертывания.
Смешанным соединением элементов называют все возможные
сочетания последовательного и параллельного соединений. В такой цепи может быть различное число узлов и ветвей. Один из примеров смешанного соединения представлен на схеме (рис. 1.3, а).


а) б)
в)
Рис.1.3 Схема смешанного соединения элементов (а) и ее эквивалентные схемы (б, в)
Для расчета такой схемы необходимо сначала определить эквивалентные сопротивления тех частей схемы, которые представляют собой только последовательное или только параллельное соединение. В предложенной схеме элементы R1иR2соединены между собой последовательно, а элементы R3иR4 – параллельно. Используя приведенные ранее соотношения (1.7) и (1.13), можно заменить R1иR2
R12 =
R1+R2 (1.18)  R34 = (1.19)
R34 = (1.19)
В результате такой эквивалентной замены получится схема, изображенная рис.1.3 (б), в которой элементы R12 и R34 соединены между собой последовательно. Для этой схемы эквивалентное сопротивление
Rэкв=R12 + R34 (1.20) В результате такой эквивалентной замены получим схему, изображенную на рис.1.3 (в). Определим ток, протекающий в этой цепи:
 (1.21)
Это ток источника питания и ток в
элементах R1иR2 реальной
цепи. Найдем напряжения на участке цепи
с сопротивлением R12 и
на участке цепи с сопротивлением R34:
(1.21)
Это ток источника питания и ток в
элементах R1иR2 реальной
цепи. Найдем напряжения на участке цепи
с сопротивлением R12 и
на участке цепи с сопротивлением R34:
U12 = I·R12 ; U34 = I ·R34 (1.22)
Токи
I

 (1.23)
Для проверки правильности расчета схемы
смешанного соединения элементов можно
воспользоваться 1-м и 2-м законами
Кирхгофа, а также законом баланса
мощности. Должны выполняться соотношения:
(1.23)
Для проверки правильности расчета схемы
смешанного соединения элементов можно
воспользоваться 1-м и 2-м законами
Кирхгофа, а также законом баланса
мощности. Должны выполняться соотношения:
I = I3 + I4 ; Uист = U12 + U34 ; Рист=ΣРпр= Р1 + Р2 + Р3 + Р4
Здесь
Р1 = 
 ·R2 ;
Р3 =
·R2 ;
Р3 =  ·R3 ;
Р4 =
·R3 ;
Р4 =  ·R4
.
·R4
.Подобным образом можно рассчитать и другие, более сложные схемы электрических цепей со смешанным соединением элементов.
Существуют и другие схемы эквивалентных преобразований, так как не все схемы сводятся к комбинации последовательно и параллельно соединенных элементов. Такие схемы будут рассмотрены в следующем подразделе.
Метод свертывания используется для цепей со смешанным соединением потребителей, то есть, когда есть участки с последовательным и параллельным соединением потребителей.
28.Соединение конденсаторов.
В электрических цепях применяются различные способы соединения конденсаторов. Соединение конденсаторов может производиться: последовательно, параллельно и последовательно-параллельно (последнее иногда называют смешанное соединение конденсаторов). Существующие виды соединения конденсаторов показаны на рисунке 1.

Параллельное соединение конденсаторов.
Если группа конденсаторов включена в цепь таким образом, что к точкам включения непосредственно присоединены пластины всех конденсаторов, то такое соединение называется параллельным соединением конденсаторов
Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последовательным
Последовательно-параллельным соединением конденсаторов называется цепь имеющая в своем составе участки, как с параллельным, так и с последовательным соединением конденсаторов.
Метод свертывания цепи
Путем упрощения цепи сводят её к последовательному соединению некоторого эквивалентного R с ИИЭЭ.
Вычисляется ток источника или напряжение на полюсах ИТ или ИН.
Н ачинаем
упрощения с какого-либо удаленного от
источника фрагмента, но выбор следует
делать так, чтобы путем логических
заключений происходило приближение к
источнику.
ачинаем
упрощения с какого-либо удаленного от
источника фрагмента, но выбор следует
делать так, чтобы путем логических
заключений происходило приближение к
источнику.
Возможно преобразование «треугольник-звезда».
Выберем R5 для начала рассуждений.
I 5=Ucf/R5
5=Ucf/R5
UR4=Ucd=Ucf
R4 и R5 включены параллельно → R45=R4R5 /(R4+R5)
R3 и R45 включены последовательно → R345=R3+R45
R 2 и R345 включены
параллельно → R2345=R2R345 /(R2+R345)
2 и R345 включены
параллельно → R2345=R2R345 /(R2+R345)
Ubd=I345R345=UR2

Ro=R1+R2345
I1=E/Ro
Теперь, последовательно возвращаясь к предыдущим схемам, можем найти все неизвестные токи и напряжения.
Метод пропорциональных величин
(применим только для линейных цепей)
Выбирается удаленный от источника элемент и задается в нем значение тока 1А(мА) или напряжение 1В.
Выбор элемента делают так, чтобы последовательное применение законов Ома и Кирхгофа позволяло приближаться к полюсам источника.
I5=1А → Ucf=I5R5 → I4=Ucf/R4 → I3=I4+I5 → Ubc=I3R3 → Ubd=Ubc+Ucd → I2=Ubd/R2 → I1=I2+I3 → Uab=I1R1 → Ep=Uab+Ubd – расчетное значение E источника
k=E/Ep – коэффициент пропорциональности, все полученные значения должны увеличиться в k раз
Метод эквивалентного генератора
После замены части цепи, рассматриваемой как ЭГ, на СЗ, можно изобразить новую упрощенную схему цепи.
I н=Eэ/(Rвн.э+Rн)
н=Eэ/(Rвн.э+Rн)
Uн=IнRн=EэRн/(Rвн.э+Rн)
Делитель напряжения
Делитель напряжения – простейшее электротехническое устройство, позволяющее получить меньшее напряжение, если имеется источник с большим ЭДС.
В этом случае ЭДС делится между Rвн,
R1 и Rн.
При увеличении Uвн,1 происходит уменьшение Uн.
этом случае ЭДС делится между Rвн,
R1 и Rн.
При увеличении Uвн,1 происходит уменьшение Uн.
kд=(Rвн+R1+Rн)/Rн >1 – коэффициент деления
Чтобы при подключении нагрузки напряжение делителя падало не более 10% надо, чтобы ток нагрузки был в 5-10 раз меньше, чем ток делителя в ХХ.
Емкость как параметр эц
Емкостью уединенного проводника называют величину q, необходимую для сообщения проводнику φ=1В.
Если проводник не уединен, то φ зависит от формы и от расстояния между проводниками, т.к. на проводниках изменяется распределение q в результате индукции.
A ,
B – проводники, в них есть
свободные носители заряда, возникает
поле с напряженностью E
,
B – проводники, в них есть
свободные носители заряда, возникает
поле с напряженностью E
E=Δφ/d,
где d – расстояние между проводниками
Для реализации емкости используют конденсаторы – систему двух обращенных друг к другу металлических поверхностей.
C =εε0S/d
– емкость плоского конденсатора
=εε0S/d
– емкость плоского конденсатора
В любой точке ЭЦ, даже если в ней нет конденсатора, существует паразитная емкость.
Конденсаторы различаются по номинальному значению и точности, с которой выдерживается на производстве это значение. Чем больше точность, тем более пустой номинальный ряд.
П ри
последовательном включении конденсаторов
общая емкость системы равна:
ри
последовательном включении конденсаторов
общая емкость системы равна:
C=C1C2/(C1+C2)
Для параллельного включения конденсаторов справедлива формула:
C=C1+C2
С течением времени при протекании тока в одном направлении q и Uc увеличиваются независимо от значения тока.

Задача 2.

Рисунок к задаче 2
В приведенной схеме Е=100 В;  Вычислить токи, напряжения и мощности
для всех участков цепи, а также мощность
источника.
Вычислить токи, напряжения и мощности
для всех участков цепи, а также мощность
источника.
Задача 3.
Определить токи в сопротивлениях 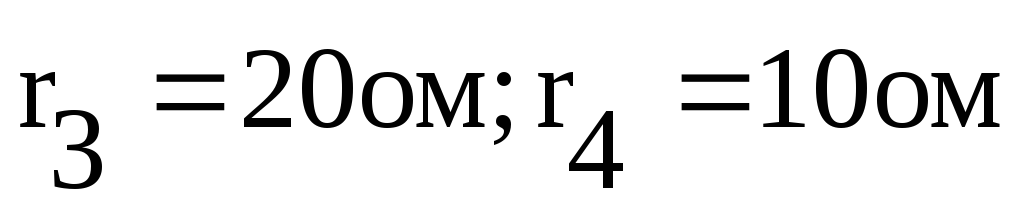 (схема прежняя), если ток источника
составляет 0,6 А.
(схема прежняя), если ток источника
составляет 0,6 А.
Задача 4.
К двум узлам электрической цепи
присоединены три ветви. В средней ветви
последовательно соединены источник
энергии с э.д.с. Е=60 В и внутренним
сопротивлением  Ом
и два сопротивления
Ом
и два сопротивления  Ом
и
Ом
и  Ом.
Одна крайняя ветвь имеет три последовательно
включенных сопротивления:
Ом.
Одна крайняя ветвь имеет три последовательно
включенных сопротивления:  Ом,
Ом, 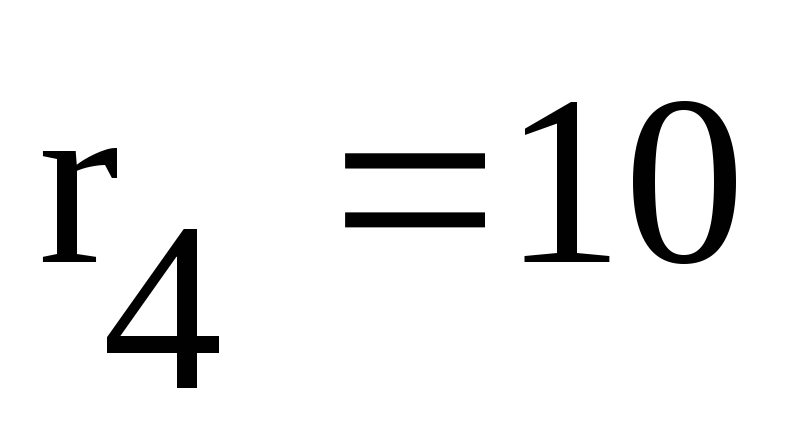 Ом и
Ом и  Ом. Другая крайняя ветвь состоит из
одного сопротивления
Ом. Другая крайняя ветвь состоит из
одного сопротивления  Ом. Составить схему. Определить все
токи, а также напряжения на выходе
источника и между узловыми точками.
Ом. Составить схему. Определить все
токи, а также напряжения на выходе
источника и между узловыми точками.
Задача 5.
Электрическая цепь состоит из трех
ветвей. В средней ветви включены источник
питания с э.д.с. Е=120 В и внутренним
сопротивлением  Ом и последовательно с ним сопротивление
Ом и последовательно с ним сопротивление  Ом. В одной крайней ветви включены
последовательно сопротивления
Ом. В одной крайней ветви включены
последовательно сопротивления  Ом и
Ом и  Ом, в другой крайней ветви – два
параллельно соединенных сопротивления
Ом, в другой крайней ветви – два
параллельно соединенных сопротивления  Ом и
Ом и  Ом и последовательно с ними сопротивление
Ом и последовательно с ними сопротивление  Ом. Составить схему и вычислить все
токи, а также мощности: развиваемую
источником, отдаваемую во внешнюю цепь
и теряемую на внутреннем сопротивлении.
Выполнить проверку расчетов по законам
Кирхгофа.
Ом. Составить схему и вычислить все
токи, а также мощности: развиваемую
источником, отдаваемую во внешнюю цепь
и теряемую на внутреннем сопротивлении.
Выполнить проверку расчетов по законам
Кирхгофа.
Расчет электрических цепей методом эквивалентных сопротивлений (метод свертывания цепи)
Метод эквивалентных сопротивлений применяется для расчета таких электрических цепей, в которых имеются пассивные элементы, включенные между собой последовательно, параллельно или по смешанной схеме. Метод заключается в последовательной замене отдельных групп сопротивлений одним эквивалентным до получения самой простой схемы (см. рис. 13г). Затем определяется каждый ток в цепи.
Рисунок 13. Метод свертывания цепи
Определение эквивалентных сопротивлений
Обратимся к схеме, приведенной на рисунке
13а. Сопротивления  и
и  соединены последовательно. Поэтому
соединены последовательно. Поэтому  .
Эти два сопротивления можно заменить
одним (эквивалентным)
.
Эти два сопротивления можно заменить
одним (эквивалентным)  ,
тогда схема упростится (рисунок 13б).
,
тогда схема упростится (рисунок 13б).
Сопротивления  и
и  включены параллельно и их можно тоже
заменить одним эквивалентным:
включены параллельно и их можно тоже
заменить одним эквивалентным: .
.
Тогда схема еще упростится ( рисунок 13в).
В схеме на рисунке 13в сопротивления  ,
,  и
и  включены последовательно и могут быть
заменены одним эквивалентным
включены последовательно и могут быть
заменены одним эквивалентным  .
Схема еще более упростится (рисунок
13г).
.
Схема еще более упростится (рисунок
13г).
Подобными преобразованиями схему смешанного соединения пассивных элементов с одним источником энергии в большинстве случаев можно привести к простейшей схеме (рисунок 13г). В более сложных схемах методом эквивалентных сопротивлений достигается упрощение, которое значительно облегчает дальнейший расчет.
Определение токов
Определение начинается с простейшей схемы (рисунок 13г).
По закону Ома:  т.к.
т.к.  ;
;  .
.
Зная  легко найти
легко найти 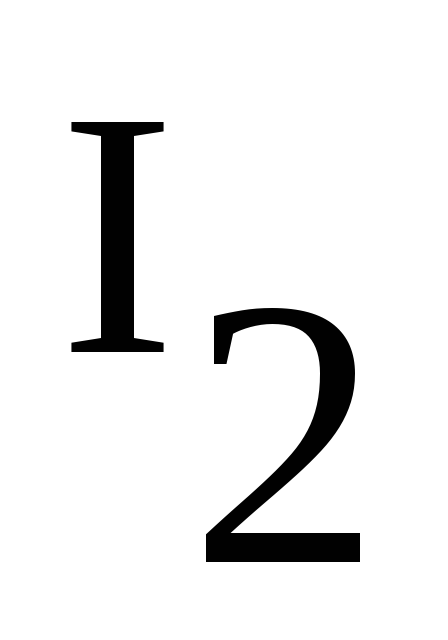 и
и 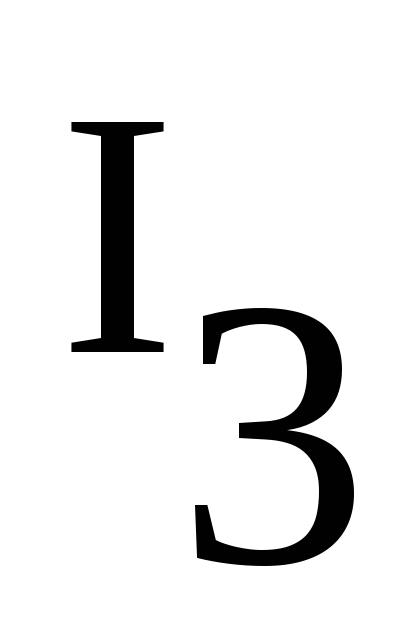 .
. 
 .
.
Задача 1
 = 20 Ом ,
= 20 Ом ,  =30
Ом,
=30
Ом,  = 12 Ом,
= 12 Ом,  = 8 Ом,
= 8 Ом,  = 1,5 Ом,
= 1,5 Ом,  = 160 В,
= 160 В,  =
0,5 Ом. Определить токи во всех элементах
схемы и КПД источника (рисунок 13а).
=
0,5 Ом. Определить токи во всех элементах
схемы и КПД источника (рисунок 13а).
Задача 2
Ток  = 3 А. Величины сопротивления те же.
Определить ЭДС и мощность источника
(рисунок 13а).
= 3 А. Величины сопротивления те же.
Определить ЭДС и мощность источника
(рисунок 13а).
6. Расчет электрических цепей постоянного тока с одним источником методом свертывания
В соответствии с методом свертывания, отдельные участки схемы упрощают и постепенным преобразованием приводят схему к одному эквивалентному (входному) сопротивлению, включенному к зажимам источника. Схема упрощается с помощью замены группы последовательно или параллельно соединенных сопротивлений одним, эквивалентным по сопротивлению. Определяют ток в упрощенной схеме, затем возвращаются к исходной схеме и определяют в ней токи. Рассмотрим схему Пусть известны величины сопротивлений R1, R2, R3, R4, R5, R6, ЭДС Е. Необходимо определить токи в ветвях схемы.
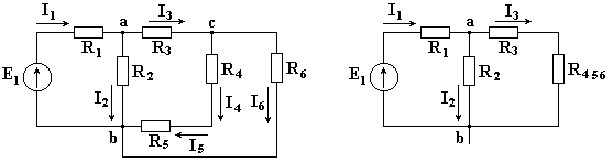 Сопротивления R4 и R5 соединены последовательно, а сопротивление
R6 — параллельно с ними, поэтому их
эквивалентное сопротивление
Сопротивления R4 и R5 соединены последовательно, а сопротивление
R6 — параллельно с ними, поэтому их
эквивалентное сопротивление

После проведенных преобразований схема принимает вид, показанный на рис. 3.2, а эквивалентное сопротивление всей цепи

Ток
I1 в неразветвленной части схемы определяется
по формуле: 
Найдем токи I2 и I3 в схеме на рис. 3.2 по формулам:

I3 = I1 — I2 — формула получается из уравнения, составленного по первому закону Кирхгофа:
I1 — I2 — I3 = 0. Переходим к исходной схеме и определим токи в ней по формулам:

I6 = I3 — I4 (в соответствии с первым законом Кирхгофа I3 — I4 — I6 =0).
7. Расчет электрических цепей постоянного тока с одним источником методом подобия или методом пропорциональных величин
Возьмем
электрическую схему на рис. 3.1, зададимся
произвольным значением тока  в
сопротивлении R6,
наиболее удаленном от источника питания.
По заданному току
в
сопротивлении R6,
наиболее удаленном от источника питания.
По заданному току  и
сопротивлению R6 определим напряжение
и
сопротивлению R6 определим напряжение  .
Далее определим:
.
Далее определим:
 ,
,
 ,
,
 ,
,
 ,
,
 ;
;
 .
.
Находим значение ЭДС
 .
.
Найденное
значение ЭДС  отличается
от заданной величины ЭДС Е.
Вычислим коэффициент подобия
отличается
от заданной величины ЭДС Е.
Вычислим коэффициент подобия .
Умножим на него полученные при расчете
значения токов и напряжений, находим
действительные значения токов цепи.
.
Умножим на него полученные при расчете
значения токов и напряжений, находим
действительные значения токов цепи.
8.
Метод
непосредственного применения
законов
Кирхгофа

На
рис. 4.1 изображена схема разветвленной
электрической цепи. Известны величины
сопротивлений и ЭДС, необходимо
определить токи.
В схеме
имеются четыре узла, можно составить
четыре уравнения по первому закону
Кирхгофа. Укажем произвольно
направления токов. Запишем уравнения:
 Сложим эти уравнения.
Получим тождество 0 = 0. Система уравнений
(4.1) является зависимой.
Если в схеме имеется n узлов, количество
независимых уравнений, которые можно
составить по первому закону Кирхгофа,
равно n — 1.
Для схемы
на рис. 4.1 число независимых уравнений
равно трем.
Сложим эти уравнения.
Получим тождество 0 = 0. Система уравнений
(4.1) является зависимой.
Если в схеме имеется n узлов, количество
независимых уравнений, которые можно
составить по первому закону Кирхгофа,
равно n — 1.
Для схемы
на рис. 4.1 число независимых уравнений
равно трем. Недостающее
количество уравнений составляют
по второму закону Кирхгофа. Уравнения
по второму закону составляют для
независимых контуров. Независимым
является контур, в который входит хотя
бы одна новая ветвь, не вошедшая в другие
контуры.
Выберем три
независимых контура и укажем направления
обхода контуров. Запишем три уравнения
по второму закону Кирхгофа.Решив
совместно системы уравнений (4.2) и (4.3),
определим токи в схеме.
Ток в ветви может иметь отрицательное
значение. Это означает, что действительное
направление тока противоположно
выбранному нами.
Недостающее
количество уравнений составляют
по второму закону Кирхгофа. Уравнения
по второму закону составляют для
независимых контуров. Независимым
является контур, в который входит хотя
бы одна новая ветвь, не вошедшая в другие
контуры.
Выберем три
независимых контура и укажем направления
обхода контуров. Запишем три уравнения
по второму закону Кирхгофа.Решив
совместно системы уравнений (4.2) и (4.3),
определим токи в схеме.
Ток в ветви может иметь отрицательное
значение. Это означает, что действительное
направление тока противоположно
выбранному нами.
Портал ТОЭ — Лекции — Теоретические основы электротехники
2.1 Метод свёртывания. Метод подобия (пропорциональных величин)
Расчёт цепей обычно заключается в определении токов ветвей при известных параметрах источников и приёмников энергии. Методы свёртывания и подобия применимы лишь для самых простых цепей с одним источником.
2.1.1 Метод свёртывания
Метод заключается в определении входного сопротивления относительно зажимов источника, которым называется эквивалентное сопротивление, которое будучи подключённым к зажимам источника вместо пассивной цепи, не изменяет ток источника.
После расчёта эквивалентного сопротивления Zэкв (с использованием правил параграфа 1.8) по закону Ома определяется ток источника (при учёте внутреннего сопротивления источника используется закон Ома для полной цепи):
А затем этот ток распределяется по отдельным ветвям по формуле разброса токов:
2.1.2 Метод подобия
Согласно этому методу в самой удалённой от источника ветви схемы произвольно задаются некоторым значением тока, например, 1 А. Далее, продвигаясь от конца схемы к началу, определяются токи в ветвях и напряжения на различных участках схемы с помощью закона Ома. В конечном итоге определяется значение напряжения источника, которое может отличаться от заданного значения. Например, зад∕расч= K. Тогда в K раз нужно изменить все расчётные токи и напряжения.
МЕТОД ПРЕОБРАЗОВАНИЯ (СВЕРТЫВАНИЯ) ЦЕПЕЙ — Мегаобучалка
Вопросы к экзамену по дисциплине «Электротехника»
Для студентов заочного отделения
Линейная цепь постоянного тока и ее элементы.
Источники энергии постоянного тока, их схемы замещения и характеристики.
Приемники энергии постоянного тока, их схемы включения и преобразования.
Условные передачи максимальной мощности от источника к приемнику.
Законы Ома и Кирхгофа. Баланс мощностей.
Методы расчета простых цепей постоянного тока.
Расчет сложной цепи постоянного тока с применением законов Кирхгофа.
Метод контурных токов.
Метод узлового напряжения.
Метод наложения токов.
Метод эквивалентного генератора.
Потенциальная диаграмма.
Цепь постоянного тока с нелинейными элементами.
Графический расчет нелинейной цепи постоянного тока.
Линейная цепь синусоидального тока.
Изображение синусоидальных токов, э.д.с. и напряжений.
Неразветвленная цепь синусоидального тока с идеальным резистором.
Цепь синусоидального тока с идеальной индуктивной катушкой.
Цепь синусоидального тока с идеальным конденсатором.
Цепь синусоидального тока с последовательным включением R-L-C –элементов.
Цепь синусоидального тока с параллельным включением ветвей, содержащих
R-L-C- элементы.
Повышение коэффициента мощности в однофазной цепи синусоидального тока.
23. Линейные трехфазные цепи. (Общие сведения о приемниках и источниках).
24. Трехфазная цепь по схеме звезда-звезда.
25. Трехфазная цепь по схеме звезда-треугольник.
26. Мощность трехфазной цепи.
27. Измерение активной мощности трехфазной цепи.
28. Магнитная цепь с постоянной МДС (основные сведения).
29. Законы Ома и Кирхгофа для магнитной цепи с постоянной МДС.
30. Расчет магнитной цепи с постоянной МДС.
31. Магнитная цепь с переменной МДС (основные сведения).
32. Уравнение электрического состояния, схема замещения и векторная диаграмма магнитной цепи переменной МДС.
33. Вольт-амперная характеристика магнитной цепи с переменной МДС.
34. Устройство и принципы действия однофазного простейшего трансформатора.
35. Уравнения электрического состояния, схемы замещения и векторные диаграммы однофазного трансформатора при работе на холостом ходу, короткое замыкание и под нагрузкой.
36. Внешняя характеристика и КПД однофазного трансформатора.
37. Устройство и принципы действия трехфазной асинхронной машины.
38. Магнитное поле трехфазной асинхронной машины.
39. Механические свойства трехфазного асинхронного двигателя (АД)
40. Регулирование частоты вращения ротора АД.
41. Пуск в ход АД.
42. Электромагнитное торможение АД.
43. Устройство и принцип действия машины постоянного тока.
44. Способы возбуждения машин постоянного тока.
45. Двигатель постоянного тока с независимым возбуждением (ЭДС обмотки якоря, электромагнитный момент, реакция якоря).
46. Механическая характеристика двигателя постоянного тока с независимым возбуждением (ДТП НВ).
47. Регулирование скорости вращения ДТП НВ.
48. Электромагнитное торможение ДПТ НВ.
49. Устройство и принцип действия синхронной машины.
50. Синхронный двигатель и его механическая характеристика.
Анализ установившихся режимов в линейных электрических цепях постоянного тока
ПРЕОБРАЗОВАНИЕ ЦЕПЕЙ
Резисторы соединены последовательно, если по ним течет один и тот же ток. Эквивалентное сопротивление цепи, состоящей из n последовательно соединенных резисторов, равно сумме их сопротивлений:
. (1.1)
Резисторы соединены параллельно, если они подключены к одной и той же паре узлов. Эквивалентное сопротивление цепи, состоящей из n параллельно соединенных резисторов, определяется из выражения:
(1.2)
В частном случае параллельного соединения двух резисторов эквивалентное сопротивление находится по формуле:
. (1.3)
Если параллельно соединены n одинаковых резисторов, то их эквивалентное сопротивление в n раз меньше одного из них:
.
Преобразование треугольника резисторов в эквивалентную звезду и наоборот проводится по следующей схеме и формулам:
(1.4)
(1.5)
ПРИМЕР 1.1.1
Дано: Ом; Ом; Ом; Ом; Ом; Ом; Ом; Ом.
Определить: .
Решение: Заменим треугольники авс и dfg эквивалентными звездами.
Ом; Ом;
Ом; Ом;
Ом; Ом.
Резисторы R13, R4, R67 и R23, R5, R68 соединены последовательно, поэтому Ом; Ом.
Резисторы R9 и R10 параллельны, следовательно, Ом.
Входное сопротивление цепи Ом.
ПРИМЕР 1.1.2
Дано: Ом.
Определить: .
Решение: Если в ветви, соединяющей два узла, сопротивление отсутствует, то потенциалы этих узлов одинаковы , при , .
Такие узлы целесообразно обозначать одинаковыми буквами или цифрами и схему перечертить так, чтобы каждый узел на ней изображался только один раз.
Решение: Узлы 1 и 3 соединены проводом, сопротивление которого равно нулю. Потенциалы этих узлов одинаковы, поэтому обозначим их буквой а. Аналогично, узлы 2 и 4 обозначим буквой в. Перечертим схему.
Резисторы R1, R2, R3 параллельны, их эквивалентное сопротивление Ом.
МЕТОД ПРЕОБРАЗОВАНИЯ (СВЕРТЫВАНИЯ) ЦЕПЕЙ
При наличии в цепи только одного источника э.д.с. внешнюю по отношению к источнику, часть электрической цепи можно в большинстве случаев рассматривать как смешанное (последовательно-параллельное) соединение резистивных элементов. Расчет таких цепей проводят путем преобразования цепи до эквивалентного сопротивления. Определяют ток в ветви с источником э.д.с., а затем, используя закон Ома, рассчитывают токи в остальных ветвях.



