Т.2. Теоремы и методы расчета сложных резистивных цепей
1. Основные определения
Узлом электрической цепи (схемы) называется точка, в которой сходятся не менее трех ветвей.
Ветвью электрической цепи (схемы) называется участок, состоящий из последовательно включенных элементов, расположенных между двумя смежными узлами.
Сложной называется электрическая цепь (схема), содержащая не менее двух узлов, не менее трех ветвей и не менее двух источников энергии в разных ветвях.
В сложной электрической цепи наблюдаются одновременно в той или иной мере разнородные физические процессы, а именно, процесс генерирования электрической энергии, процесс преобразования электрической энергии в другие виды и процесс обмена энергией между магнитным полем, электрическим полем и источниками энергии. В общем случае для отображения этих физических процессов схема замещения цепи должна содержать кроме источников энергии (
В стационарном
режиме (в режиме постоянного тока)
напряжение на катушке равно нулю
(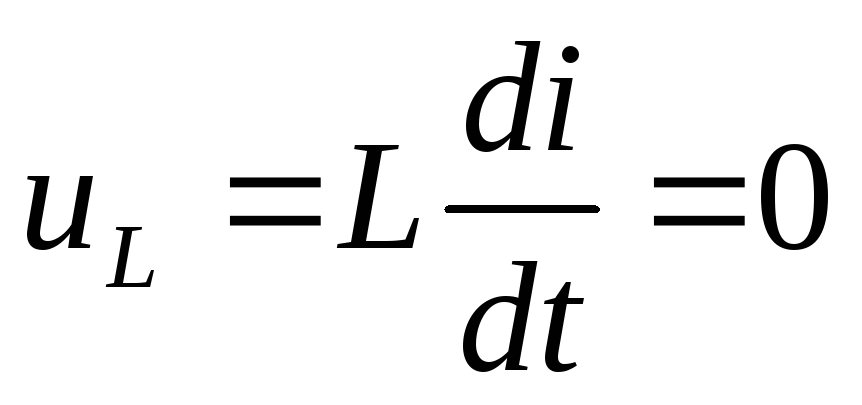 ),
что соответствует короткому замыканию
этого элемента, а при постоянном
напряжении ток в конденсаторе равен
нулю (
),
что соответствует короткому замыканию
этого элемента, а при постоянном
напряжении ток в конденсаторе равен
нулю (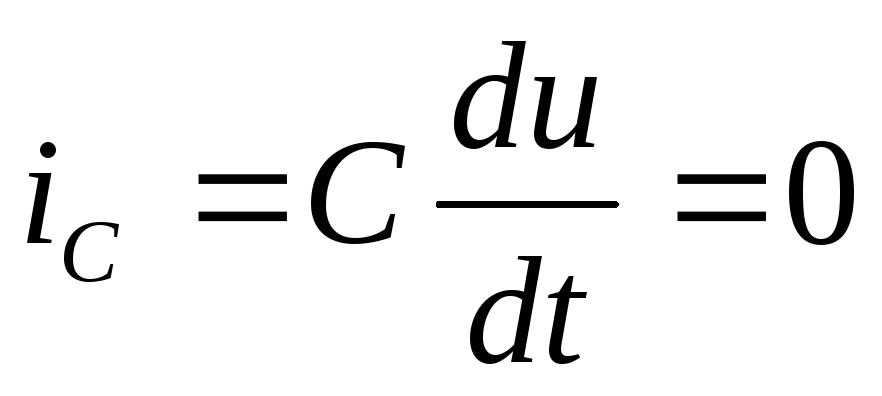 ),
что соответствует разрыву ветви с
этим элементом. Следовательно, на
установившийся режим постоянного тока
схемные элементы
),
что соответствует разрыву ветви с
этим элементом. Следовательно, на
установившийся режим постоянного тока
схемные элементы
В настоящей главе будут рассматриваться только резистивные цепи в режиме постоянного тока. В последующем рассмотренные в данной главе теоремы и методы расчета будут распространены на цепи переменного тока в установившемся синусоидальном режиме.
2. Метод преобразования (свертки) схемы
Если схема электрической цепи содержит только один источник энергии (EилиJ), то пассивная часть схемы может быть преобразована (свернута) к одному эквивалентному элементуRЭ ( рис. 7).
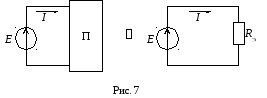
Свертка схемы
начинается с самых удаленных от источника
ветвей, проводится в несколько
этапов до достижения полной свертки.
После полной свертки схемы по закону
Ома определяется ток источника: 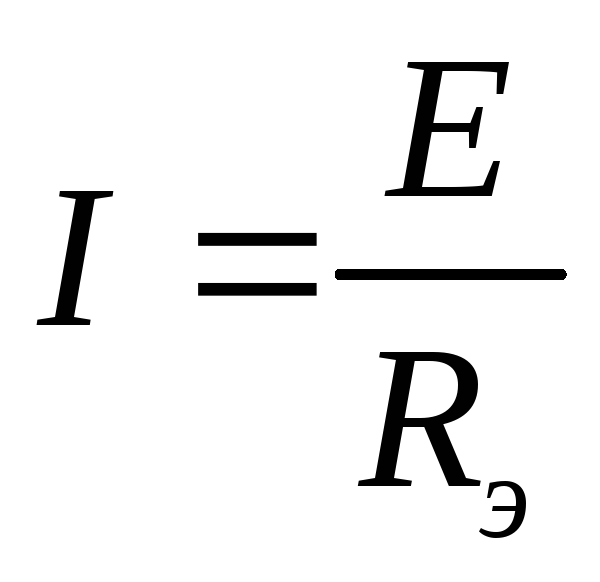
При применении данного метода возможны следующие виды преобразований.
1) Последовательное преобразованиезаключается в замене нескольких элементов, включенных последовательно, одним эквивалентным (рис.8).
Несложно доказать, что справедливы следующие соотношения:
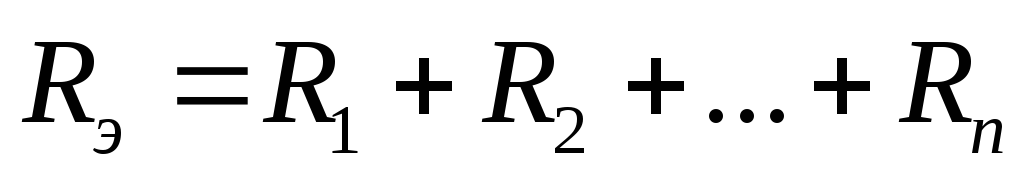 и
и 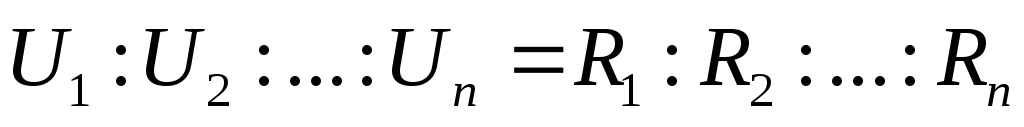
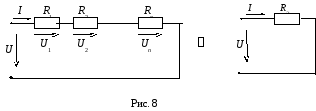
2) Параллельное преобразованиесостоит в замене нескольких элементов, включенных параллельно, одним эквивалентным (рис. 9).
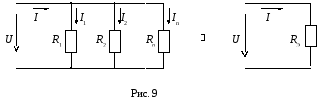
Несложно доказать, что справедливы следующие соотношения:
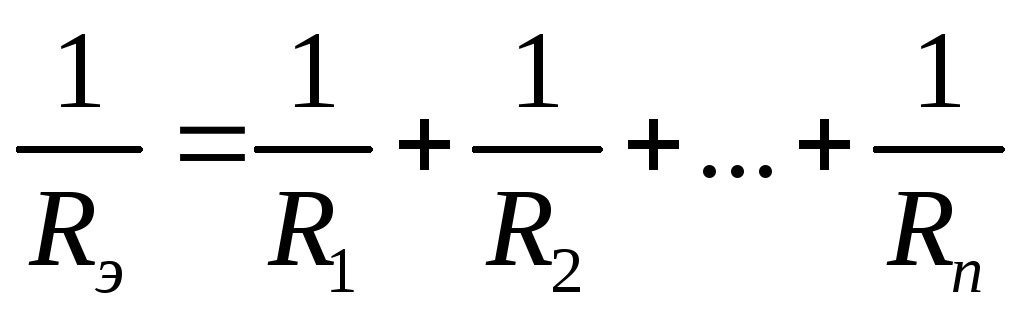
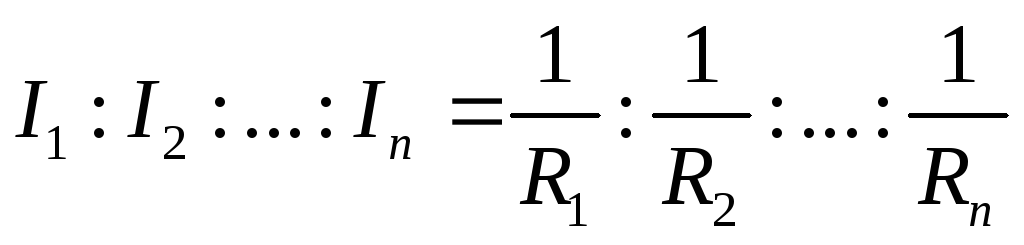
Для двух элементов:  и
и
3) Взаимное преобразование схем звездатреугольник(рис. 4) возникает при свертке сложных схем.
Условием эквивалентности двух схем являются равенства для них токов (I1,I2,I3), напряжений (U12,U23, U
Приравняем входные сопротивления для обеих схем со стороны двух произвольных ветвей при отключенной третей (рис. 10):
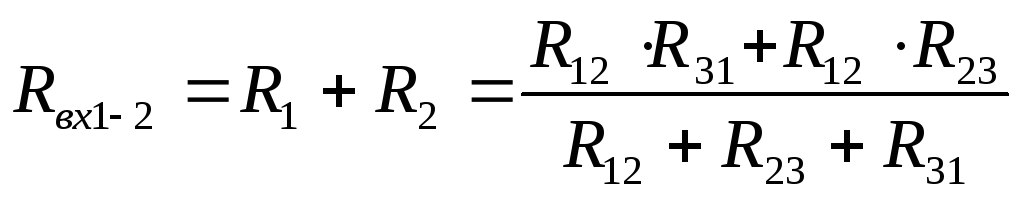 (1)
(1)
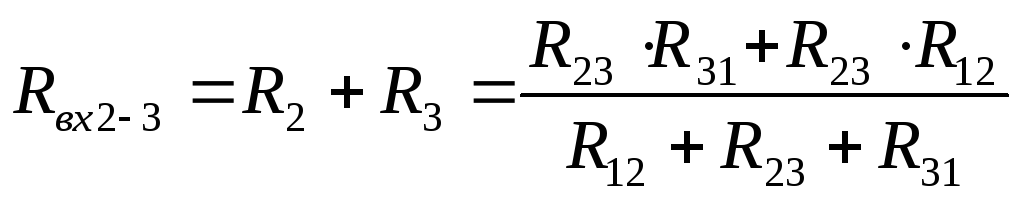 (2)
(2)
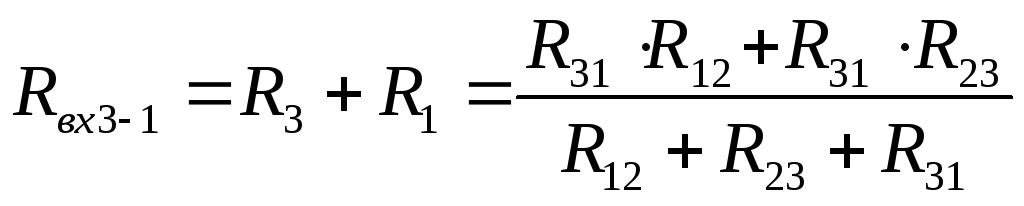 (3)
(3)
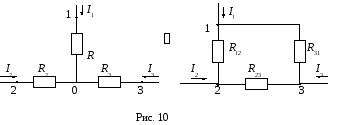
Сложим почленно уравнения (1) и (3) и вычтем из суммы уравнение (2), получим:
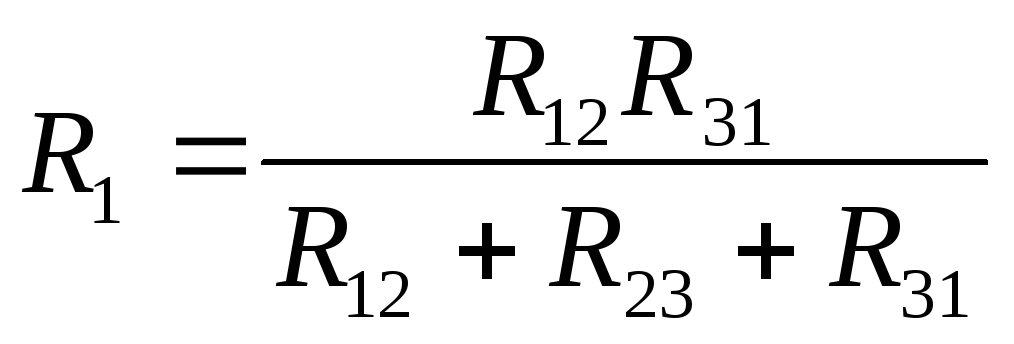 ,
по аналогии:
,
по аналогии: 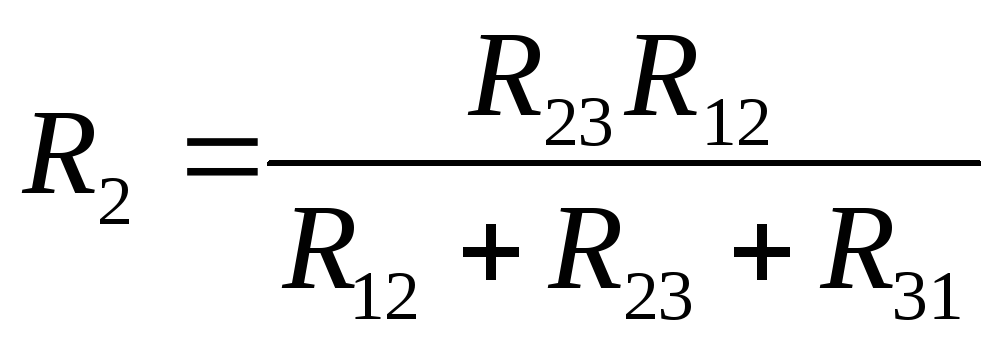 ,
,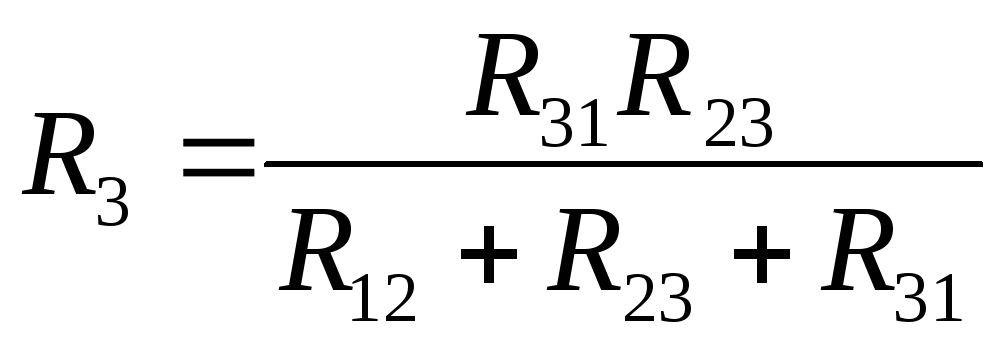 .
.
Приравняем входные проводимости для обеих схем со стороны произвольной вершины и двух других вершин, замкнутых накоротко (рис. 11):
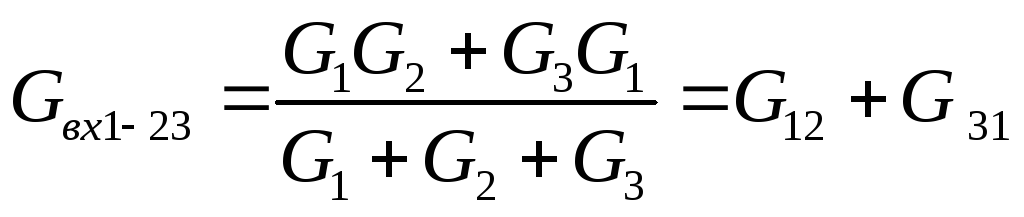 (4)
(4) 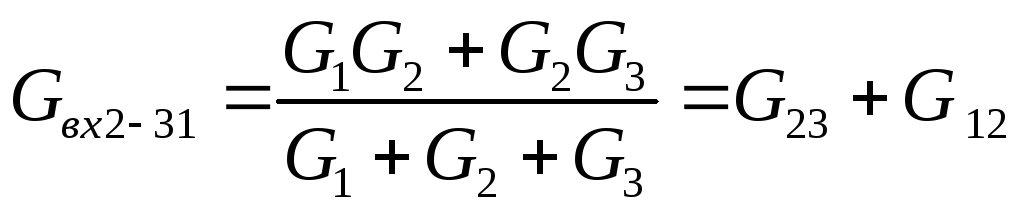 (5)
(5)
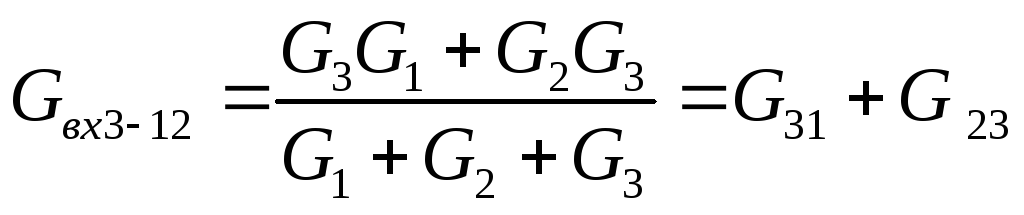
 (6)
(6)
Сложим почленно уравнения (4) и (5) и вычтем уравнение (6), получим:
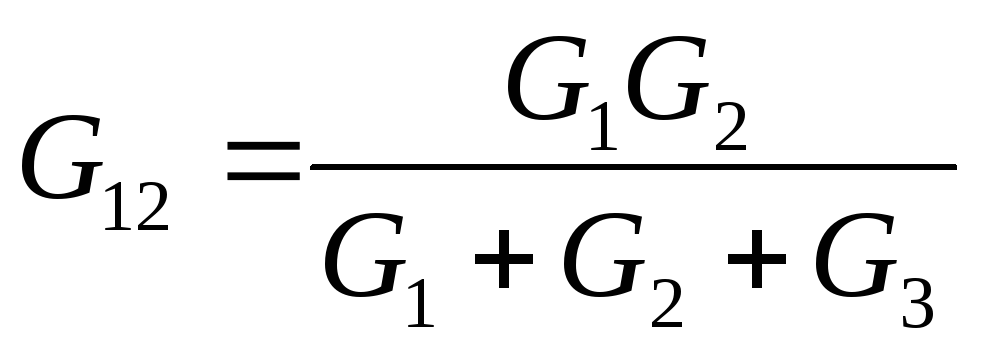 , по аналогии:
, по аналогии: 
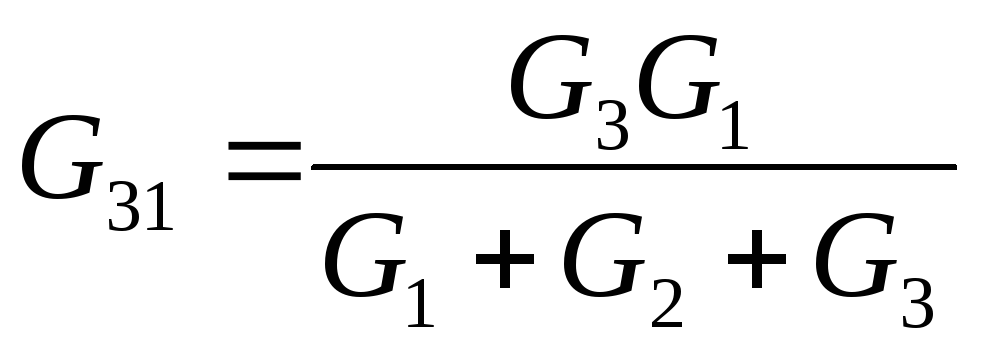 .
. В последних
уравнениях заменим проводимости на
соответствующие им сопротивления 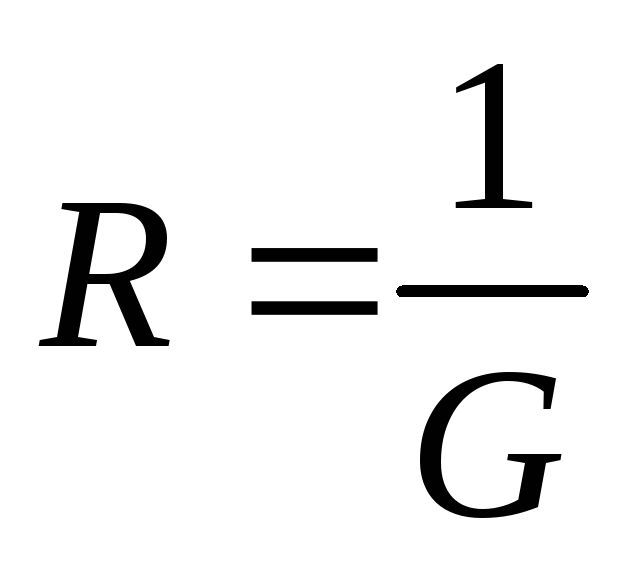 ,
получим:
,
получим:
 ;
; 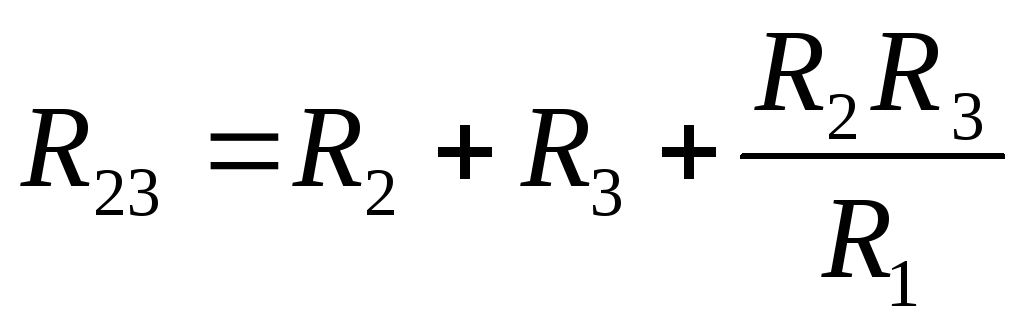 ;
; .
.
При наличии полной
симметрии соотношение между параметрами
эквивалентных схем составляет: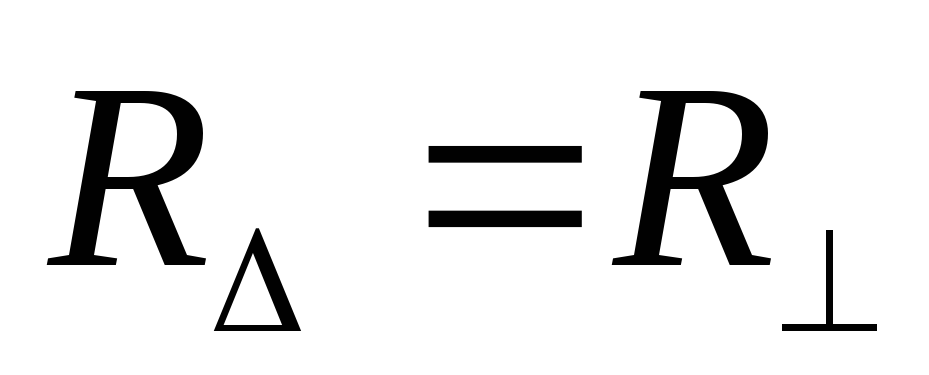
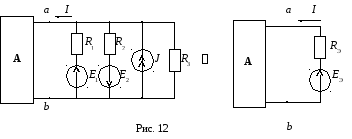
4) Замена параллельных ветвей эквивалентной ветвью (рис. 12) осуществляется согласно теореме об эквивалентном генераторе.
Напряжение холостого хода Uxxaв=EЭ определяется по методу двух узлов:
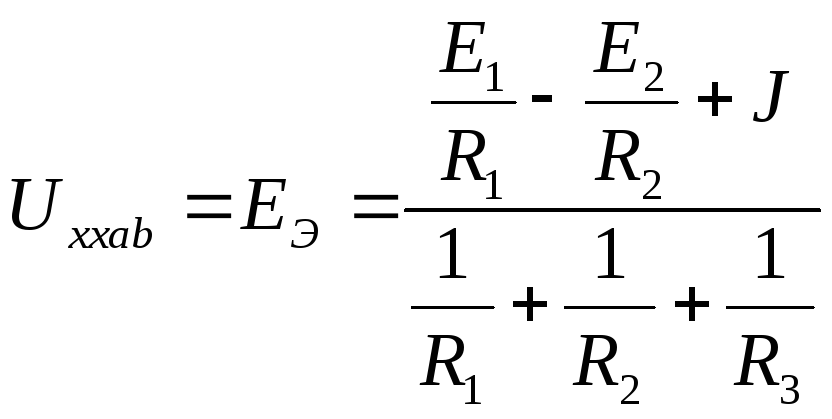 .
.
Эквивалентное входное сопротивление находится методом свертки схемы:

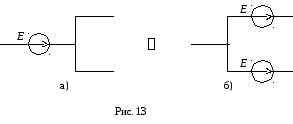
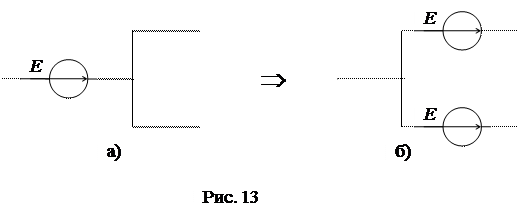
5) Перенос источника ЭДС через узел схемы: источник ЭДС Е можно перенести через узел во все ветви, отходящие от узла (рис. 13а, б.).
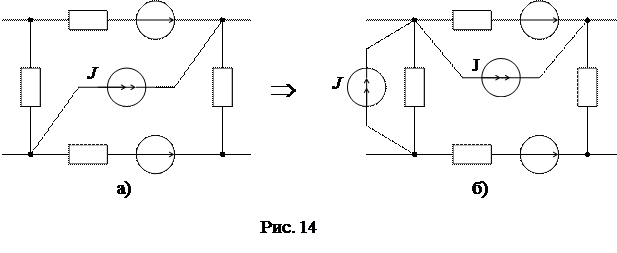
6) Привязка источника тока к произвольному узлу согласно схеме (рис. 14а, б):
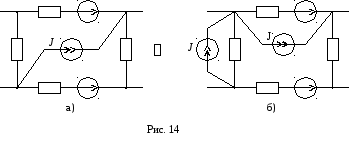
7) Взаимное преобразование схем с источником напряжения и с источником тока согласно схеме
I
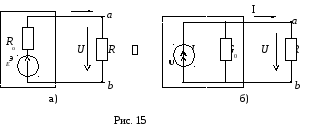
Схемы эквивалентны при равенстве для обеих напряжений U и токов I на нагрузке:
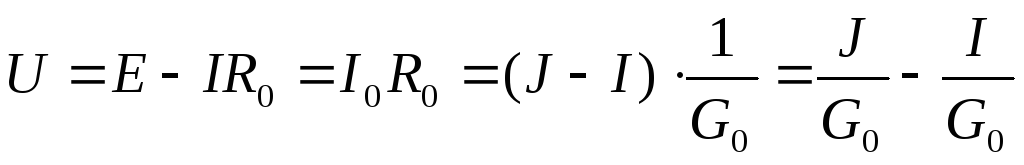 .
.
Сравнивая левые и правые части равенства, получим соотношения между параметрами эквивалентных схем:
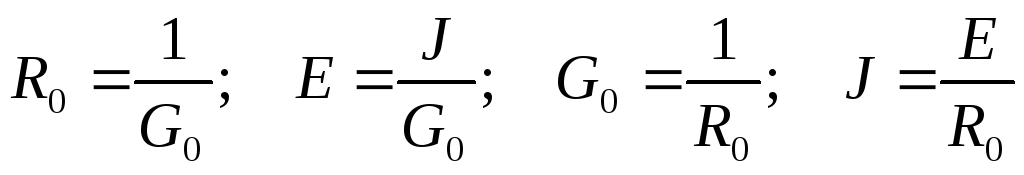 .
.
Лекции / Лекции (1 семестр) / LAB1_2
Лабораторная работа №1
Исследование цепей постоянного тока
Цель работы: Исследование свойств линейных цепей при постоянном воздействии.
Продолжительность работы: 4 часа
Приборы, используемые в работе: Для получения характеристик цепей при гармоническом воздействии в Electronic Workbench можно использовать четыре типа приборов: вольтметр, амперметр, омметр и осциллограф.
Задания к лабораторной работе
1. Метод наложения (суперпозиции)
Суть метода : ток в r-ой ветви равен алгебраической сумме токов, вызываемых каждой из э.д.с. схемы в отдельности. При расчете цепей данным методом поступают следующим образом : поочередно рассчитывают токи, возникающие от действия каждой из э.д.с., мысленно удаляя остальные из схемы (источники э.д.с. закорачиваются, ветви с источниками тока разрываются) , и затем находят токи в ветвях путем алгебраического сложения частичных токов.
.
2. Метод свертки-развертки
Суть метода : при последовательном соединении резисторов их сопротивления складываются R=R1+R2, при параллельном — складываются их проводимости Y=Y1+Y2 (Y1=1/R1,Y2=1/R2). Источники э.д.с. с последовательно соединенными резисторами, заменяются на источники тока с параллельно соединенными резисторами согласно формулам:
Iрез.=E/R , Rрез.=R.
Верны и обратные преобразования,:
Ерез.=I*R , Rрез.=R.
3.Метод взаимности совместно с методом наложения
Суть метода : если необходимо рассчитать ток IS в какой-то ветви схемы содержащей несколько источников э.д.с. (Е1,Е2,…и тд.),необходимо ,включить в эту ветвь схемы источник э.д.с. Е (обычно Е=1В), при этом Е1,Е2,…- закорачиваются а, I1,I2,…-заземляются. Считаются токи от Е (любым способом) в ветвях , где стояли Е1,Е2,..
Получим I(E1),I(E2),…I(En) ,то ток I равен :
IS=E1*I(E1)/E + E2*I(E2)/E+…+En*I(En)/E
(для упрощения формулы можно принять Е=1В).
4.Mетод двух узлов
Часто встречаются схемы, содержащие всего два узла. Наиболее рациональным методом расчета токов в них является метод узловых потенциалов носящий в этом частном случае название метода двух узлов.
Под методом двух узлов понимают метод расчета электрических цепей, в котором за искомое (с его помощью определяют затем токи ветвей) принимают напряжение между двумя узлами схемы.
5. Метод эквивалентного генератора
Суть метода: По отношению к выделенной ветви двухполюсник можно заменить эквивалентным генератором, э.д.с. которого равна напряжению холостого хода на зажимах выделенной ветви, а внутреннее сопротивление равно входному сопротивлению двухполюсника.
Задания к лабораторной работе
Задание 1.
Домашняя подготовка
1. Рассчитать цепи методом наложения для своего варианта.
(определить ток Iнал )
Варианты заданий :
2. Рассчитать цепи методом свертки-развертки для
своего варианта. (определить ток Iсв )
Варианты заданий :
3. Рассчитать цепи методом взаимности совместно с методом
наложения для своего варианта. (определить ток IS )
Варианты заданий :
4. Рассчитать цепи методом двух узлов для своего варианта.
(определить VNODE)
Варианты заданий :
5. Рассчитать цепи методом эквивалентного генератора
для своего варианта.(определить VOPEN,REKV).
Варианты заданий :
Примечание: результаты занести в табл1.
Задание 2.
Лабораторное задание
1.Собрать на рабочем поле WORKBENCH cхемы из домашнего задания и сверить ответы с домашними расчетами.
2.Результаты занести в табл.1
табл.1
Iнал, mA | Iсв, mA | IS, mA | VNODE, V | VOPEN,V | REKV, Om | |
Расчет | ||||||
Экспер. |
Вопросы для самопроверки.
1. Сформулируйте основные методы расчета линейных цепей при постоянном воздействии.
2. В чем состоит упрощение расчетов , при использовании описанных выше методов.
Список литературы:
1.Бессонов Л.Ф. Теоретические основы электротехники:
Высшая школа ,1984. сс. 19 — 40.
13
2.5. Методы преобразования электрических цепей
Некоторые методы преобразования электрических цепей, были рассмотрены ранее. Например, последовательно соединенные n резистивных элементов ветви электрической цепи (рис. 2.79), заменяются одним эквивалентным сопротивлением:
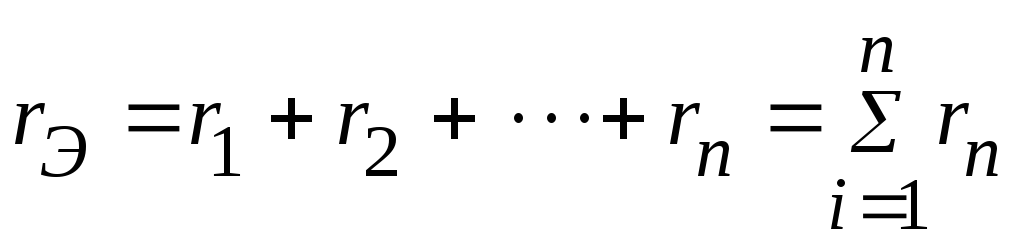 и
и 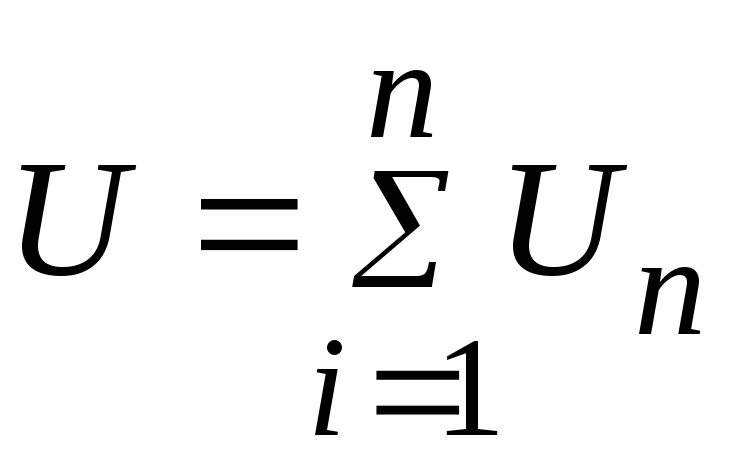 .
.
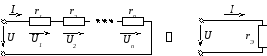
Рисунок 2.79 – Последовательное соединение резистивных элементов
Последовательно соединенные n источников ЭДС ветви электрической цепи (рис. 2.80), заменяются одним эквивалентным ЭДС, равным алгебраической сумме ЭДС источников входящих в соединение:
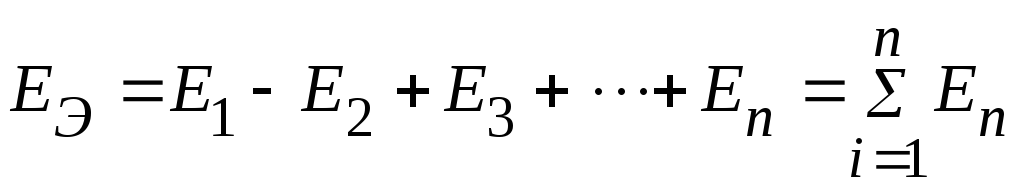 .
.

Рисунок 2.80 – Последовательное соединение ЭДС
Параллельно соединенные n резистивных элементов электрической цепи, представленной на рисунке 2.81, заменяются одним эквивалентным сопротивлением.
Для данного преобразования справедливы следующее соотношение:
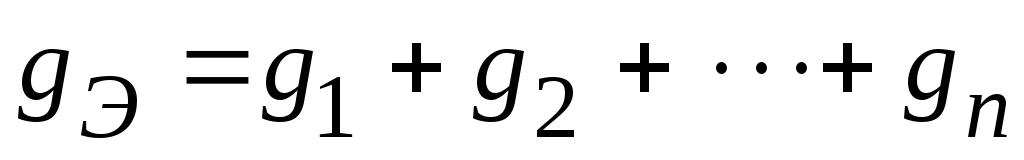 .
.
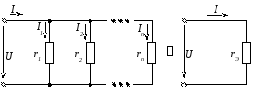
Рисунок 2.81 – Параллельное соединение резистивных элементов
Параллельно соединенные n источников тока электрической цепи (рис. 2.82), заменяются одним эквивалентным источником тока, равным алгебраической сумме токов источников тока, входящих в соединение:
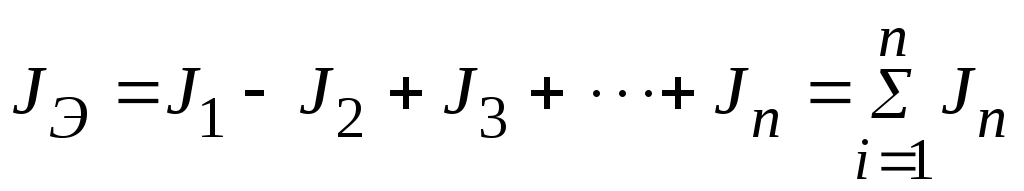 .
.

Рисунок 2.82 – Параллельное соединение источников тока
Вышеуказанные преобразования дают возможность рассчитывать разветвленные электрические цепи цепочного вида с одним источником питания.
2.5.1. Расчет разветвленных цепей цепочного типа
В основе метода расчета подобных цепей используются методы преобразования последовательно и параллельно соединенных элементов, а также закон Ома.
Пример 2.22. Рассмотрим расчет разветвленной цепи цепочного типа на примере электрической цепи, изображенной на рисунке 2.83, с параметрами: E=200 B, r1 = 8 Ом, r2/= 5 Ом, r2//= 15 Ом, r3 =8 Ом, r4 = 10 Ом, r5 = 20 Ом, r6 = 30 Ом. Требуется определить токи во всех ветвях электрической цепи, проверить найденные значения токов, составив баланс мощностей.
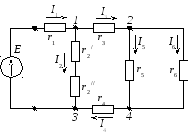
Рисунок 2.83 – Расчетная схема электрической цепи
1. Определяем входное сопротивление всей цепи.
1.1.
На первом этапе последовательно
соединенные сопротивления  и
и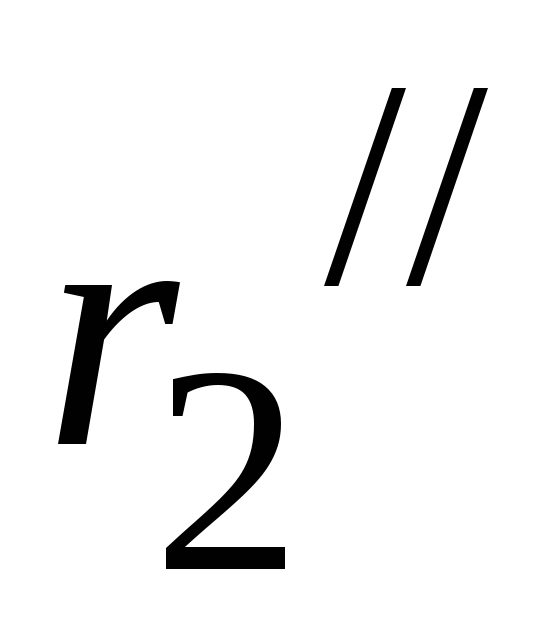 заменяем эквивалентным сопротивлением
заменяем эквивалентным сопротивлением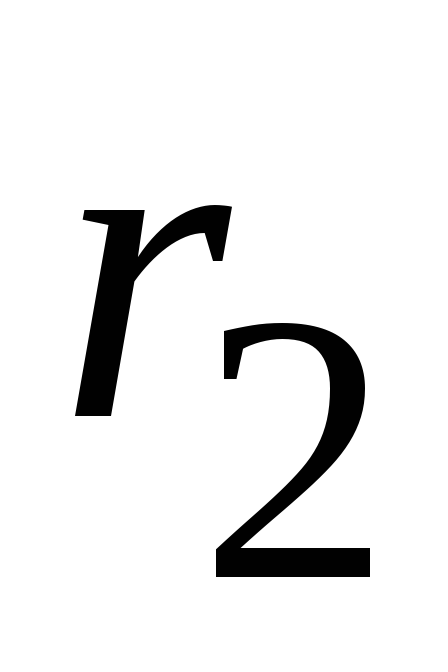 ,
а также параллельно соединенные
,
а также параллельно соединенные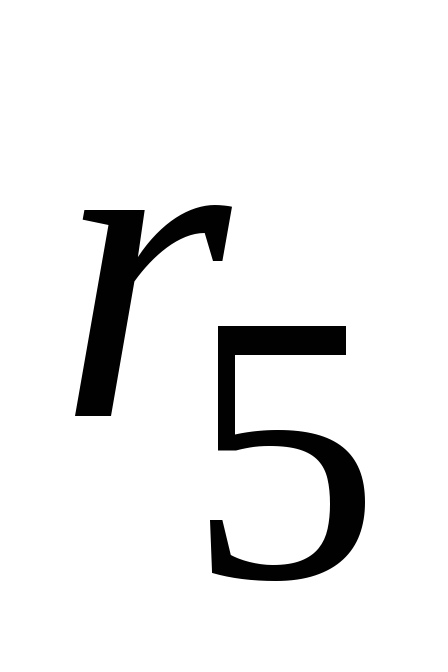 и
и заменяем эквивалентным сопротивлением
заменяем эквивалентным сопротивлением :
:
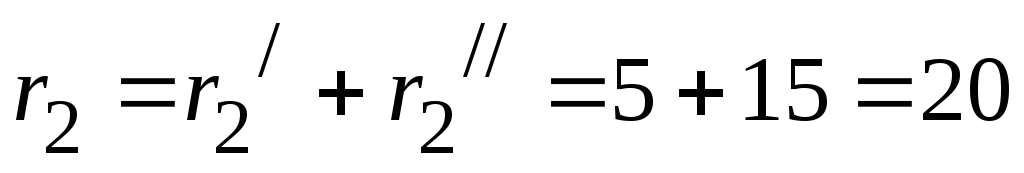 Ом,
Ом,  Ом.
Ом.
В результате схема имеет вид, представленный на рисунке 2.84.
Рисунок 2.84 – Преобразованная электрическая цепь
Последовательно соединенные сопротивления
 ,
,  и
и  заменяем эквивалентным сопротивлением
заменяем эквивалентным сопротивлением  :
:
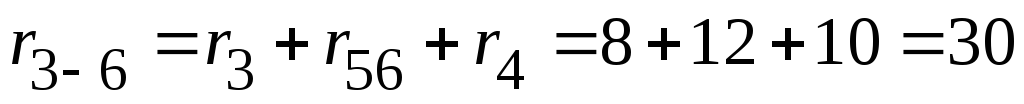 Ом.
Ом.
В результате схема имеет вид, представленный на рисунке 2.85.
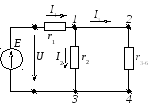
Рисунок 2.85 – Преобразованная электрическая цепь
Параллельно соединенные сопротивления
 и
и  заменяем эквивалентным сопротивлением
заменяем эквивалентным сопротивлением  :
:
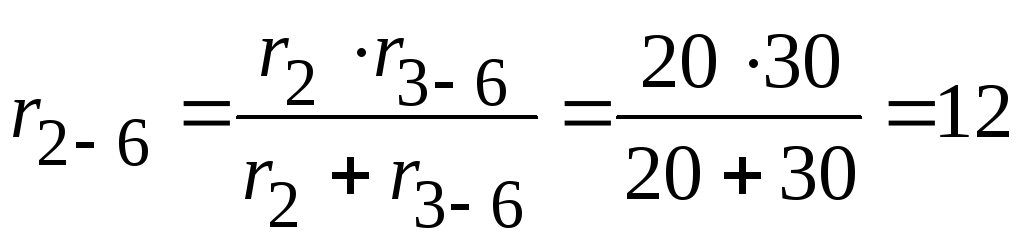 Ом.
Ом.
В результате схема имеет вид, представленный на рисунке 2.86.

Рисунок 2.86 – Преобразованная электрическая цепь
Определяем входное сопротивление всей цепи:
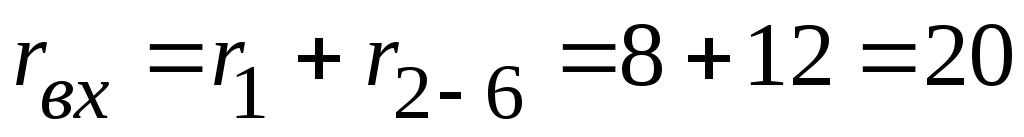 Ом.
Ом.
Определяем токи в ветвях. С этой целью используем закон Ома.
2.1.
Ток 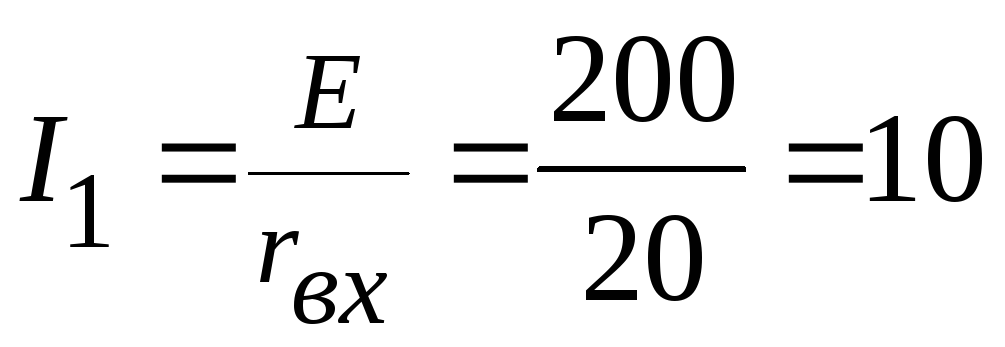 А.
А.
2.2.
Определяем токи 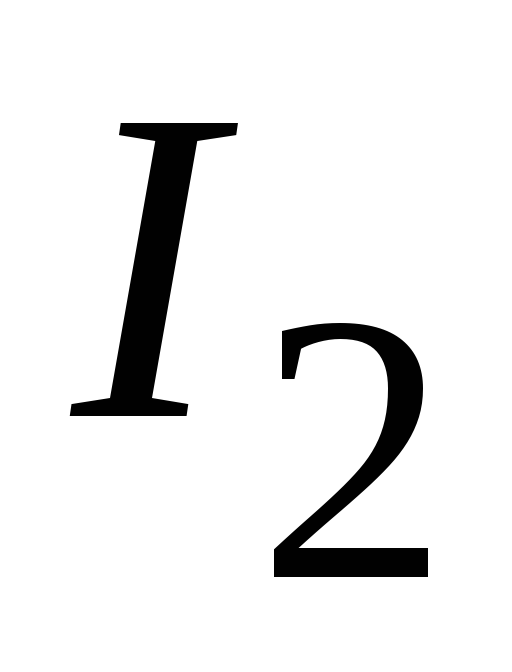 ,
,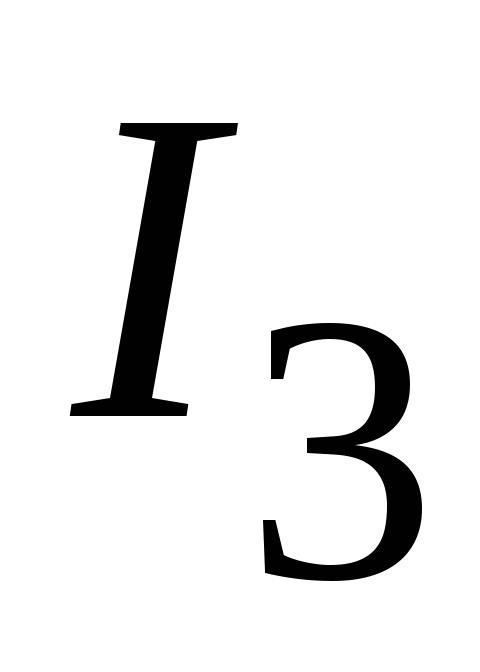 и
и 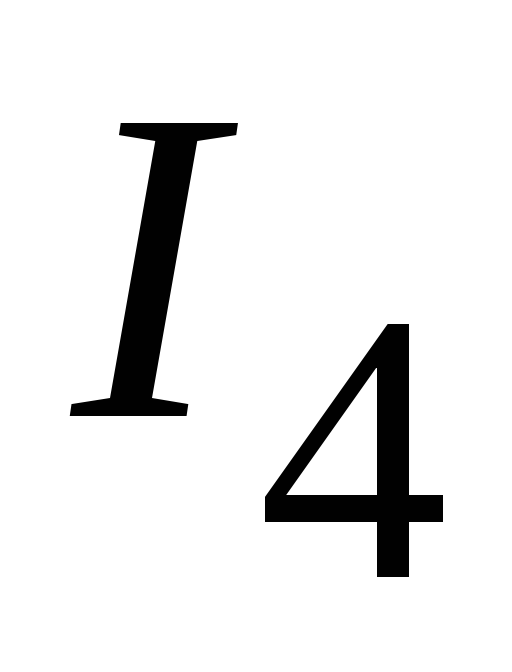 .
Для их определения необходимо
предварительно определить напряжение
.
Для их определения необходимо
предварительно определить напряжение (рис.
2.85).
(рис.
2.85).
2.2.1. Из схемы, приведенной на рисунке 2.86, следует
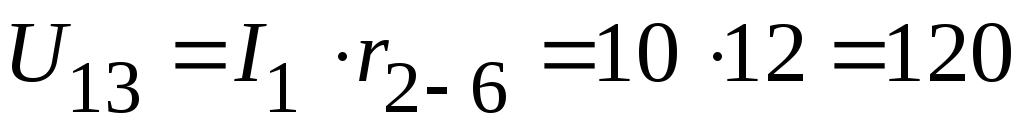 В,
или
В,
или
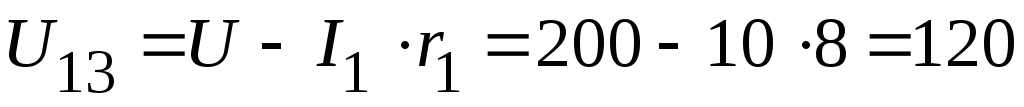 В.
В.
2.2.2. Тогда токи в ветвях:
 А;
А;
 А,
или
А,
или
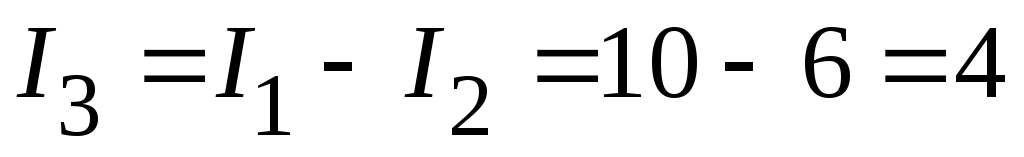 А.
А.
2.3.
Определяем токи 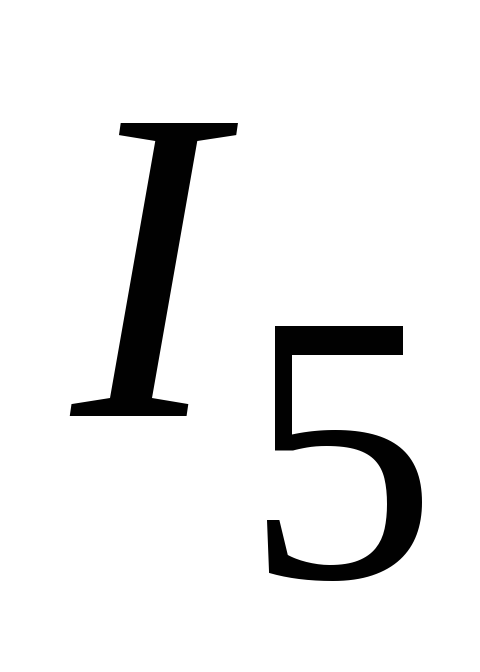 и
и 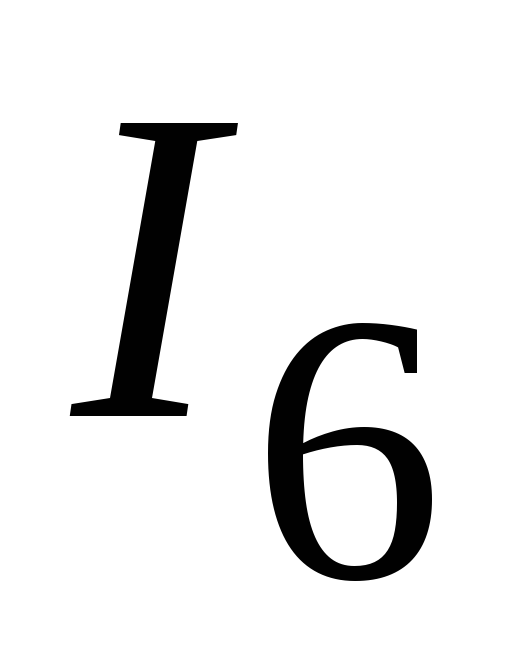 .
Для их определения необходимо
предварительно определить напряжение
.
Для их определения необходимо
предварительно определить напряжение (
рис. 2.83).
(
рис. 2.83).
2.3.1. Из схемы, приведенной на рисунке 2.84, следует
 В,
или
В,
или
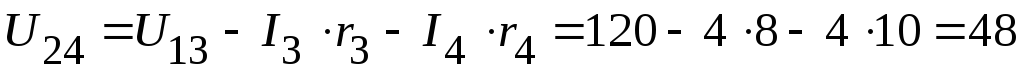 В.
В.
2.3.2. Тогда токи в ветвях:
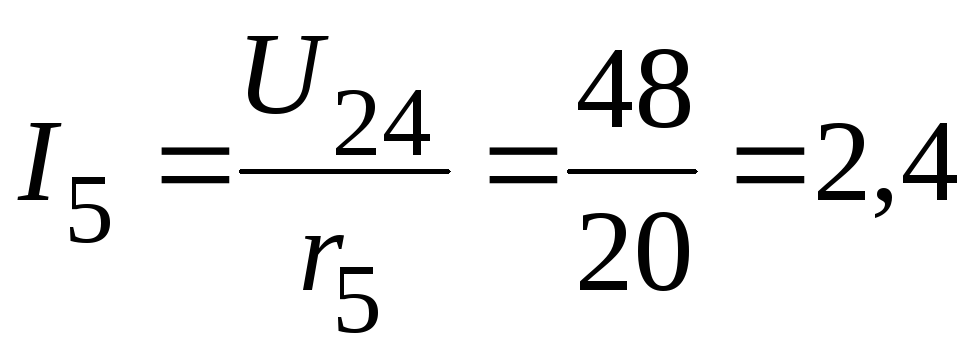 А;
А;
 А,
или
А,
или
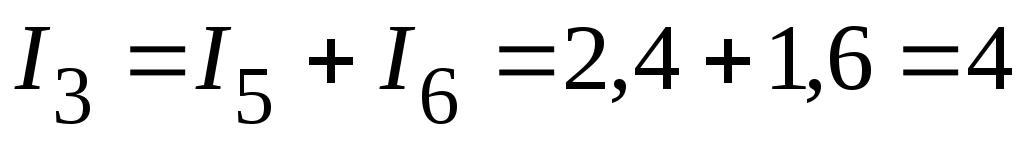 А.
А.
3. Проверяем решение, составив баланс мощностей.
3.1. Мощность, генерируемая источником питания:
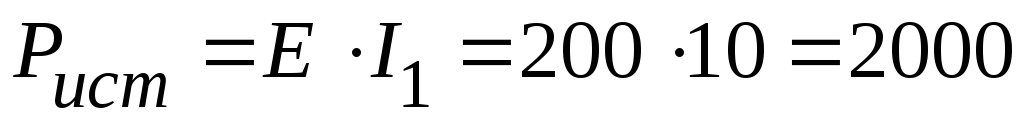 Вт.
Вт.
3.2. Мощность, потребляемая приемниками:
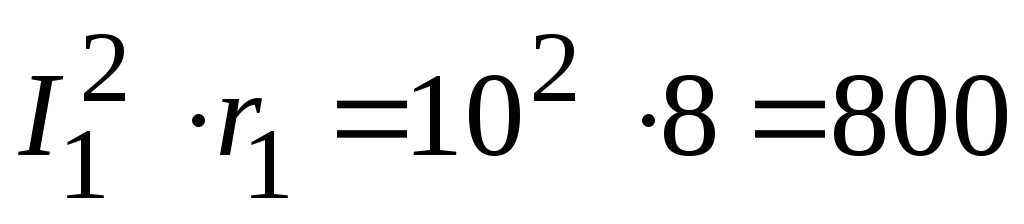 Вт,
Вт,
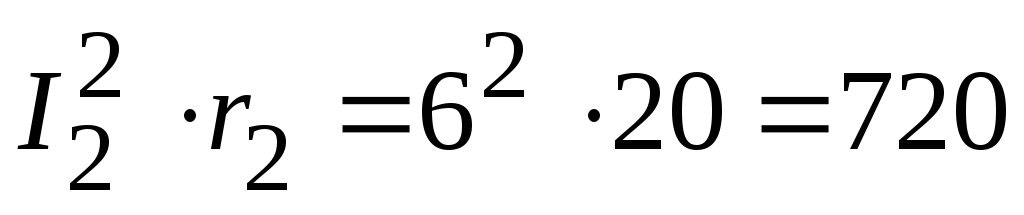 Вт,
Вт,
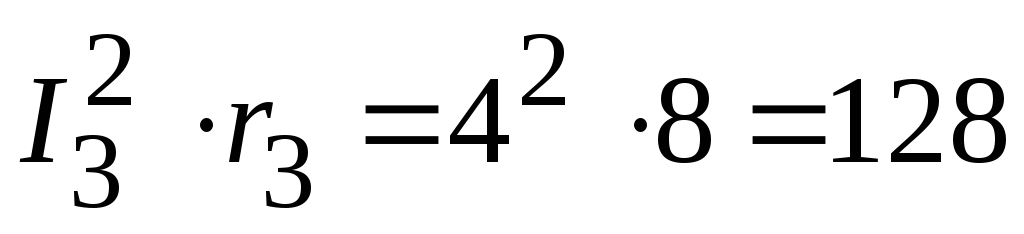 Вт,
Вт,
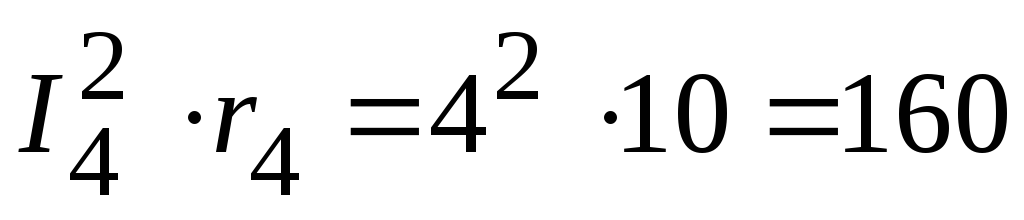 Вт,
Вт,
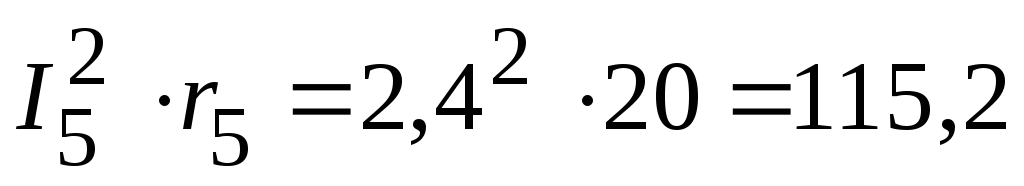 Вт,
Вт,
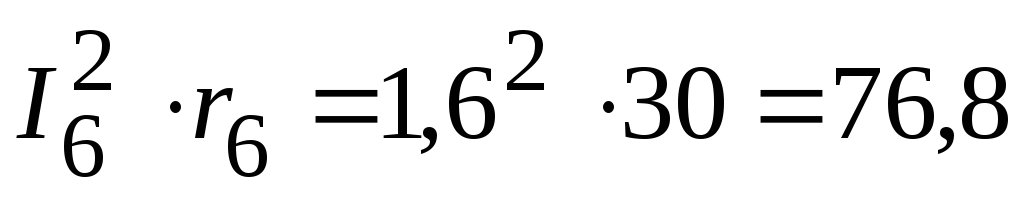 Вт.
Вт.
Суммарная мощность, потребляемая приемниками:
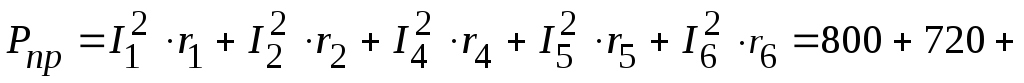
 Вт.
Вт.
3.3.
Из сравнения генерируемой мощности
источниками и потребляемой мощности
приемниками, следует, что погрешность
вычислении  и непревышает
0,5%.
и непревышает
0,5%.
Пример 2.23. Рассмотрим расчет разветвленной цепи цепочного типа на примере электрической цепи, изображенной на рисунке 2.87, с параметрами: E=21 B, r1 =100 Ом, r2=200 Ом, r3 =50 Ом, r4 =150 Ом, r5 =75 Ом, r6 =300 Ом. Требуется определить токи во всех ветвях электрической цепи, проверить найденные значения токов, составив баланс мощностей.
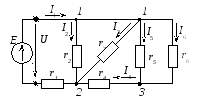
Рисунок 2.87 – Расчетная схема электрической цепи
1. Определяем входное сопротивление всей цепи.
1.1.
На первом этапе параллельно соединенные
сопротивления 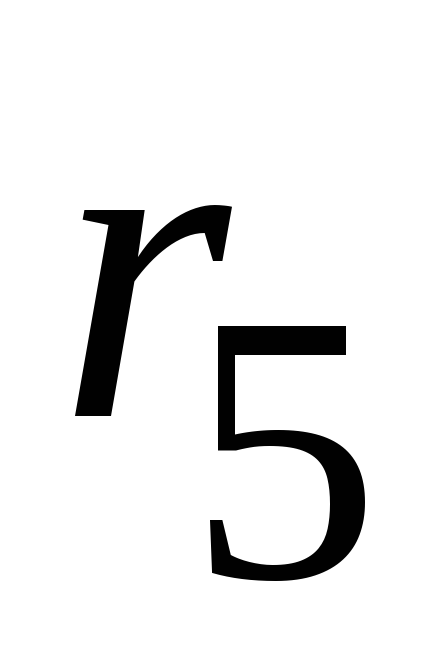 и
и заменяем эквивалентным сопротивлением
заменяем эквивалентным сопротивлением ,
а также параллельно соединенные
,
а также параллельно соединенные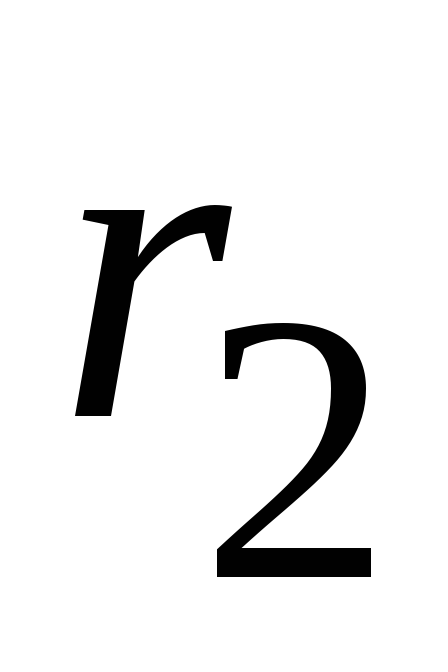 и
и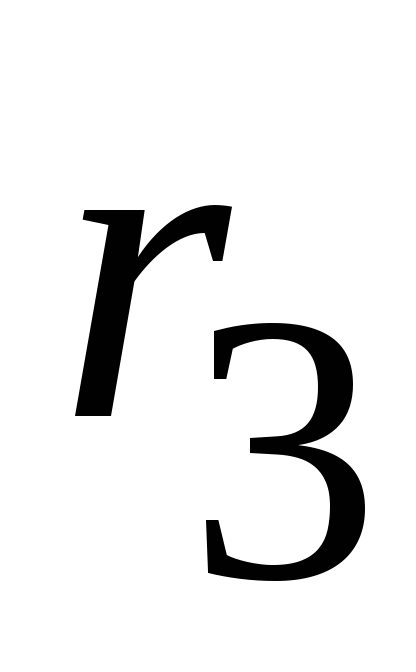 заменяем эквивалентным сопротивлением
заменяем эквивалентным сопротивлением :
:
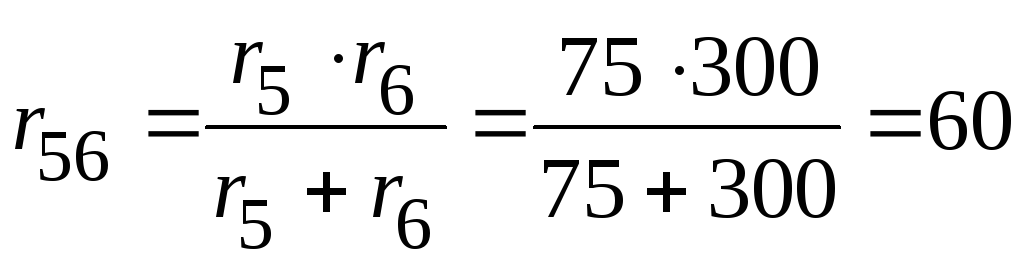 Ом,
Ом,  Ом.
Ом.
В результате схема имеет вид, представленный на рисунке 2.88.
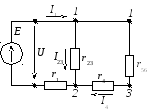
Рисунок 2.88 – Преобразованная электрическая цепь
Последовательно соединенные сопротивления
 и
и  заменяем эквивалентным сопротивлением
заменяем эквивалентным сопротивлением  :
:
 Ом.
Ом.
В результате схема имеет вид, представленный на рисунке 2.89.
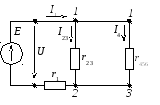
Рисунок 2.89 – Преобразованная электрическая цепь
Параллельно соединенные сопротивления
 и
и  заменяем эквивалентным сопротивлением
заменяем эквивалентным сопротивлением  :
:
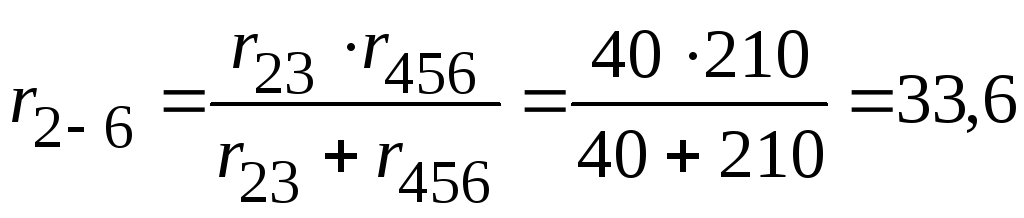 Ом.
Ом.
В результате схема имеет вид, представленный на рисунке 2.90.
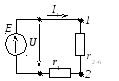
Рисунок 2.90 – Преобразованная электрическая цепь
Определяем входное сопротивление всей цепи:
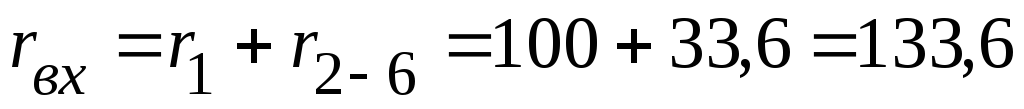 Ом.
Ом.
Определяем токи в ветвях. С этой целью используем закон Ома.
2.1.
Ток 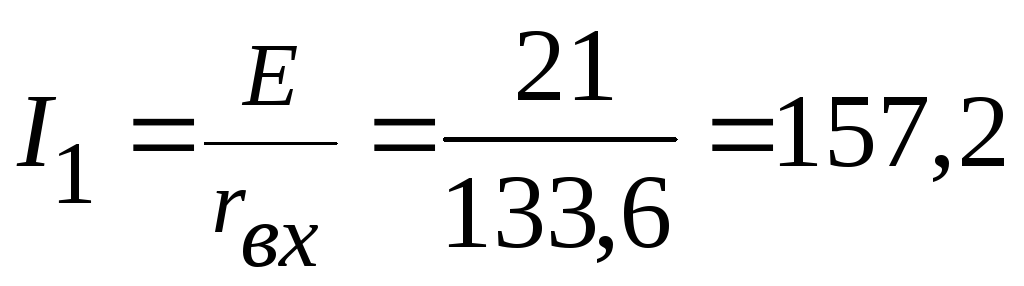 мА.
мА.
2.2.
Определяем токи  ,
, и
и  .
Для их определения необходимо
предварительно определить напряжение
.
Для их определения необходимо
предварительно определить напряжение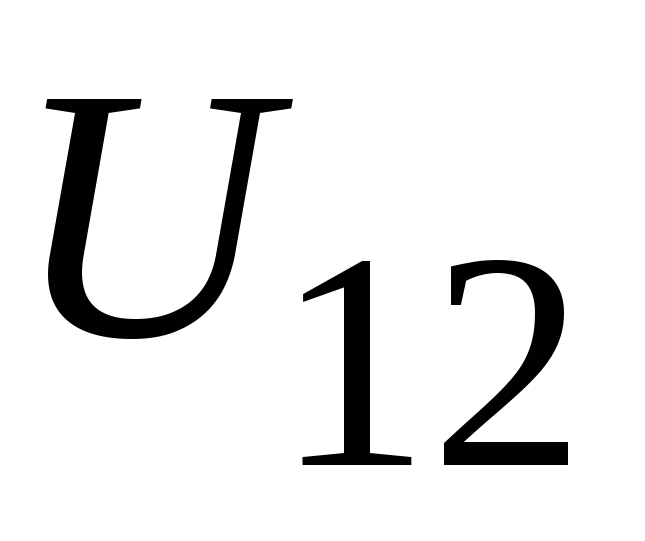 .
.
2.2.1. Из схемы, приведенной на рисунке 2.90, следует
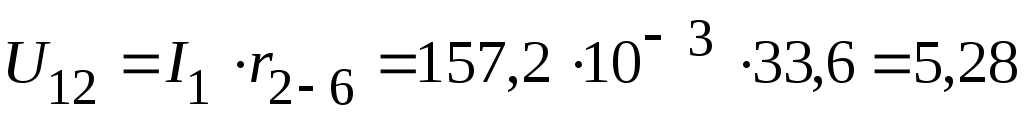 В,
или
В,
или
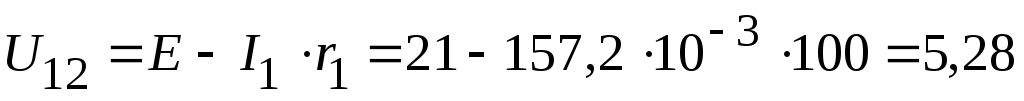 В.
В.
2.2.2. Тогда токи в ветвях:
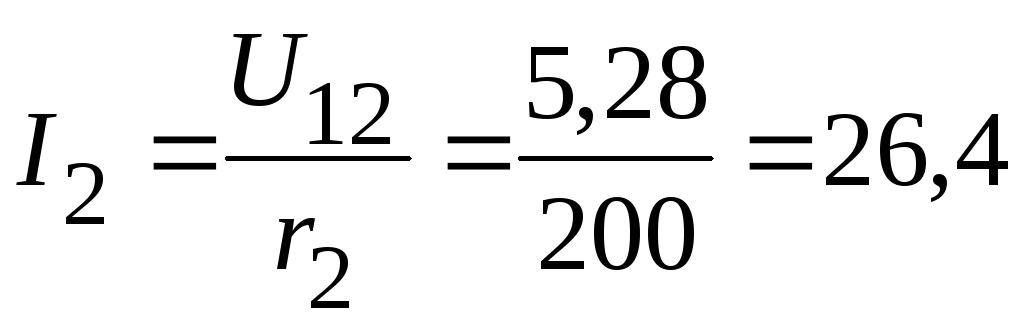 мА;
мА;
 мА,
мА,
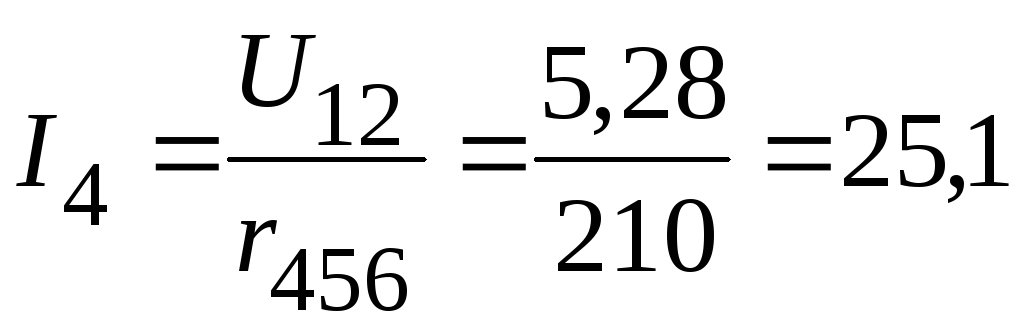 мА,
или
мА,
или
 мА.
мА.
2.3.
Определяем токи 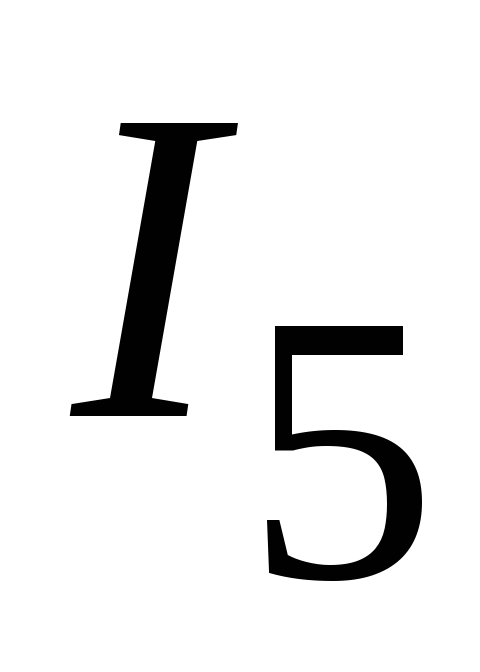 и
и 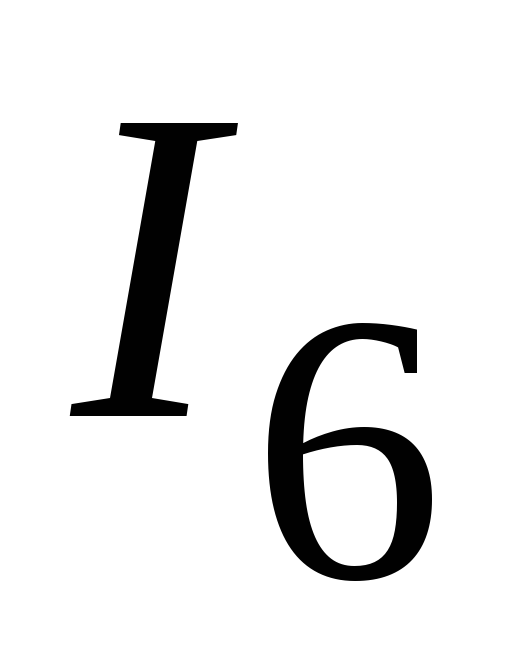 .
Для их определения необходимо
предварительно определить напряжение
.
Для их определения необходимо
предварительно определить напряжение (рис. 2.87).
(рис. 2.87).
2.3.1. Из схемы, приведенной на рисунке 2.88, следует
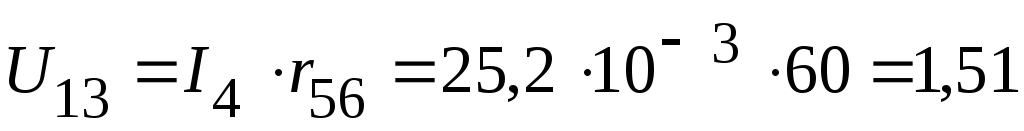 В,
или
В,
или
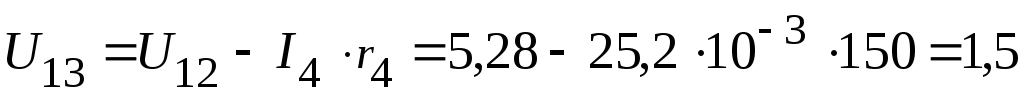 В.
В.
2.3.2. Тогда токи в ветвях:
мА;
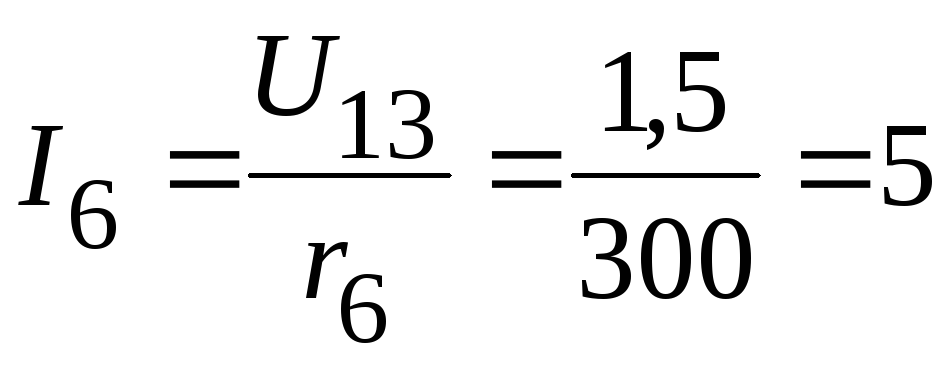 мА,
или
мА,
или
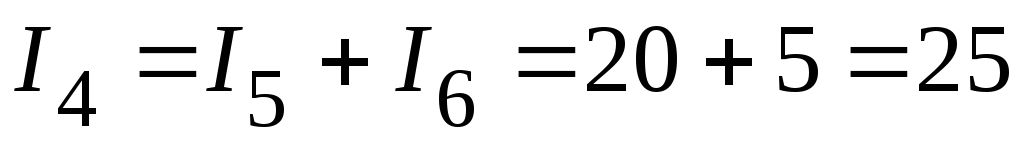 мА.
мА.
3. Проверяем решение, составив баланс мощностей.
3.1. Мощность, генерируемая источником питания:
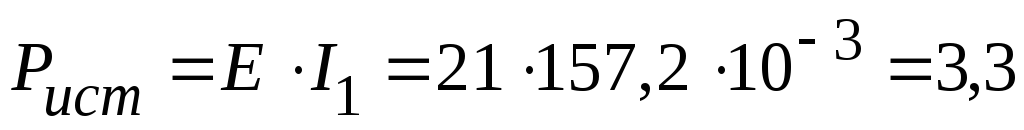 Вт.
Вт.
3.2. Мощность, потребляемая приемниками:
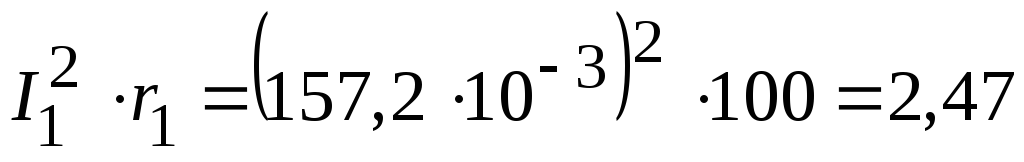 Вт,
Вт,
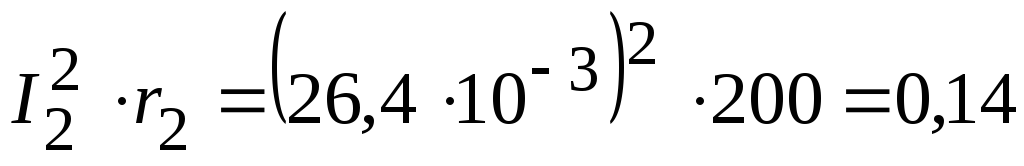 Вт,
Вт,
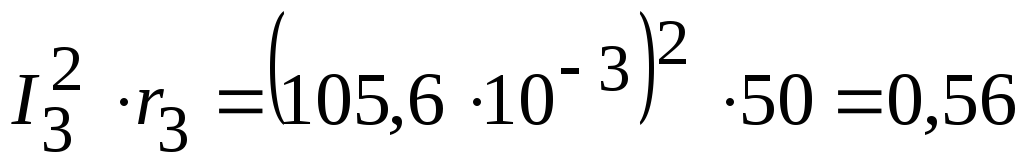 Вт,
Вт,
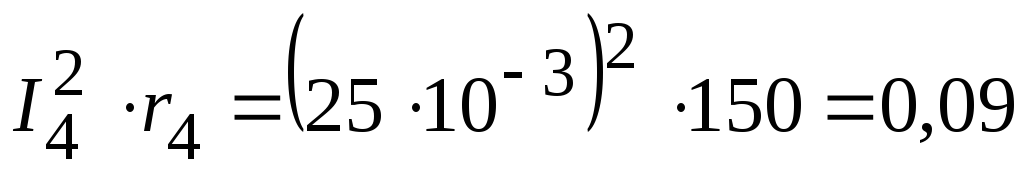 Вт,
Вт,
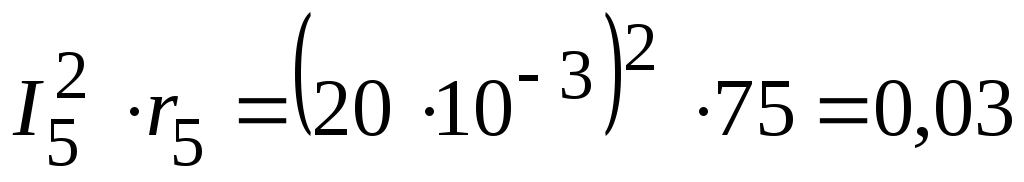 Вт,
Вт,
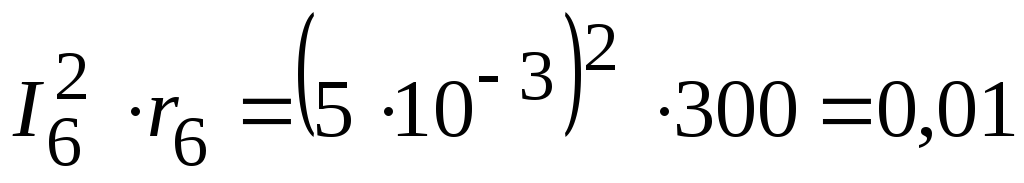 Вт.
Вт.
Суммарная мощность, потребляемая приемниками:
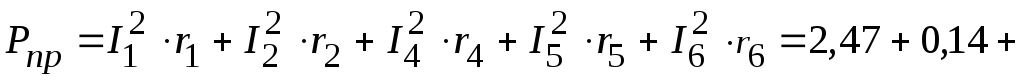
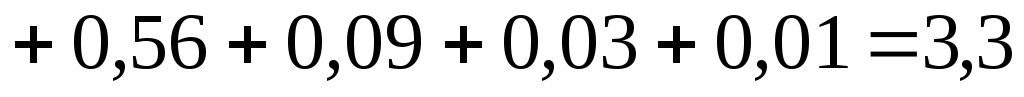 Вт.
Вт.
3.3.
Из сравнения генерируемой мощности
источником и потребляемой мощности
приемниками, следует, что погрешность
вычислении  и непревышает
0,5%.
и непревышает
0,5%.
Метод преобразования (свертки) схемы
Если схема электрической цепи содержит только один источник энергии (E или J), то пассивная часть схемы может быть преобразована (свернута) к одному эквивалентному элементу RЭ( рис. 7).
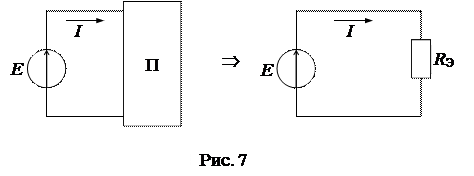 |
Свертка схемы начинается с самых удаленных от источника ветвей, проводится в несколько этапов до достижения полной свертки. После полной свертки схемы по закону Ома определяется ток источника:  . Токи в остальных элементах исходной схемы находятся в процессе обратной развертки схемы. Такой метод расчета токов получил название метода последовательного преобразования (свертки) схемы.
. Токи в остальных элементах исходной схемы находятся в процессе обратной развертки схемы. Такой метод расчета токов получил название метода последовательного преобразования (свертки) схемы.
При применении данного метода возможны следующие виды преобразований.
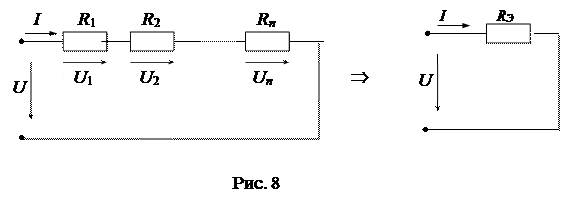
1) Последовательное преобразование заключается в замене нескольких элементов, включенных последовательно, одним эквивалентным (рис. 8).
Несложно доказать, что справедливы следующие соотношения:
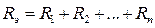 и
и 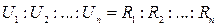
 |
2) Параллельное преобразование состоит в замене нескольких элементов, включенных параллельно, одним эквивалентным (рис. 9).
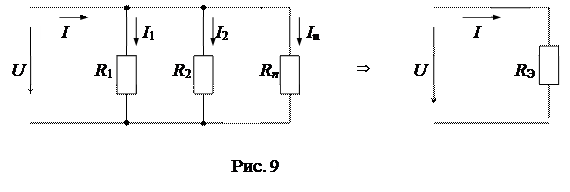 |
Несложно доказать, что справедливы следующие соотношения:
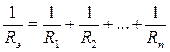 и
и 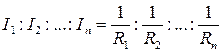
Для двух элементов: 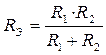 и
и 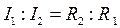
3) Взаимное преобразование схем звезда-треугольник (рис. 4) возникает при свертке сложных схем.
Условием эквивалентности двух схем являются равенства для них токов (I1, I2, I3), напряжений (U12, U23, U31) и входных сопротивлений (R12, R23, R31) и соответственно входных проводимостей ( G12, G23, G31).
Приравняем входные сопротивления для обеих схем со стороны двух произвольных ветвей при отключенной третей (рис. 10):
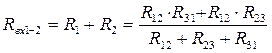 (1)
(1)
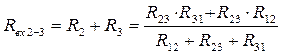 (2)
(2)
 (3)
(3)
 |
Сложим почленно уравнения (1) и (3) и вычтем из суммы уравнение (2), получим:
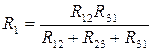 , по аналогии:
, по аналогии: 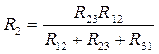 ,
, 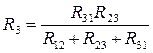 .
.
Приравняем входные проводимости для обеих схем со стороны произвольной вершины и двух других вершин, замкнутых накоротко (рис. 11):
 (4)
(4)
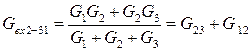 (5)
(5)
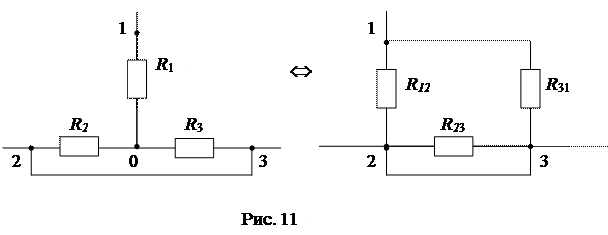
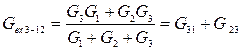 (6)
(6)
Сложим почленно уравнения (4) и (5) и вычтем уравнение (6), получим:
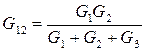 , по аналогии:
, по аналогии: 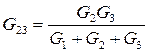 ,
, 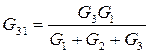 .
.
В последних уравнениях заменим проводимости на соответствующие им сопротивления  , получим:
, получим:
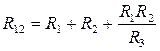 ;
;  ;
;  .
.
При наличии полной симметрии соотношение между параметрами эквивалентных схем составляет: 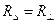 .
.
4) Замена параллельных ветвей эквивалентной ветвью (рис. 12) осуществляется согласно теореме об эквивалентном генераторе.
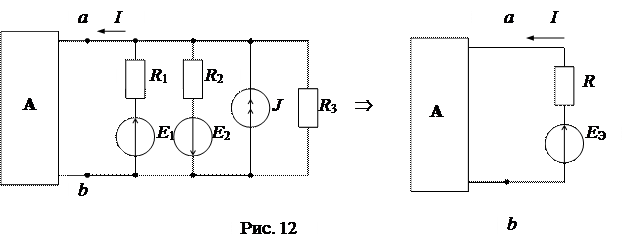 |
Напряжение холостого хода Uxxaв=EЭ определяется по методу двух узлов:
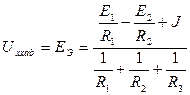 .
.
Эквивалентное входное сопротивление находится методом свертки схемы:
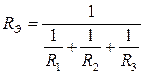 .
.
5) Перенос источника ЭДС через узел схемы: источник ЭДС Е можно перенести через узел во все ветви, отходящие от узла (рис. 13а, б.).
6) Привязка источника токак произвольному узлу согласно схеме(рис. 14а, б):
 |
7) Взаимное преобразование схемс источником напряжения и систочником тока согласно схеме(рис. 15а, б):
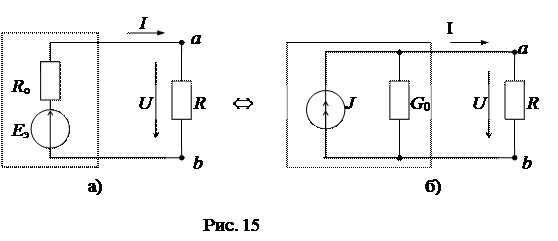 |
Схемы эквивалентны при равенстве для обеих напряжений U и токов I на нагрузке:
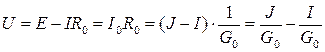 .
.
Сравнивая левые и правые части равенства, получим соотношения между параметрами эквивалентных схем:
 .
.
Дата добавления: 2016-10-18; просмотров: 2051;
Похожие статьи:
принцип эквивалентности, преобразование схем. Методы анализа сложных электрических цепей
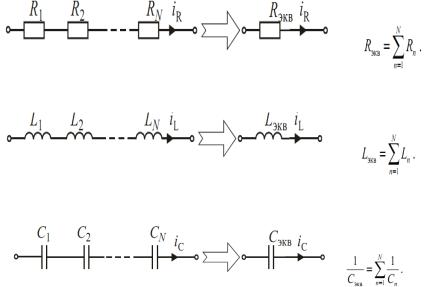
В основе методов преобразования электрических схем лежит принцип эквивалентности, согласно которому токи и напряжения в ветвях схемы не затронутых преобразованием остаются неизменными.
Последовательное соединение элементов:
1. Последовательное соединение резистивных элементов:
2.Последовательное соединение индуктивных элементов:
3.Последовательное | ёмкостных элементов: |

Параллельное соединение элементов:
1.Параллельное соединение резистивных элементов:
2.Параллельное соединение индуктивных элементов:
3.Параллельное соединение ёмкостных элементов:
4.Смешанное соединение резистивных элементов:
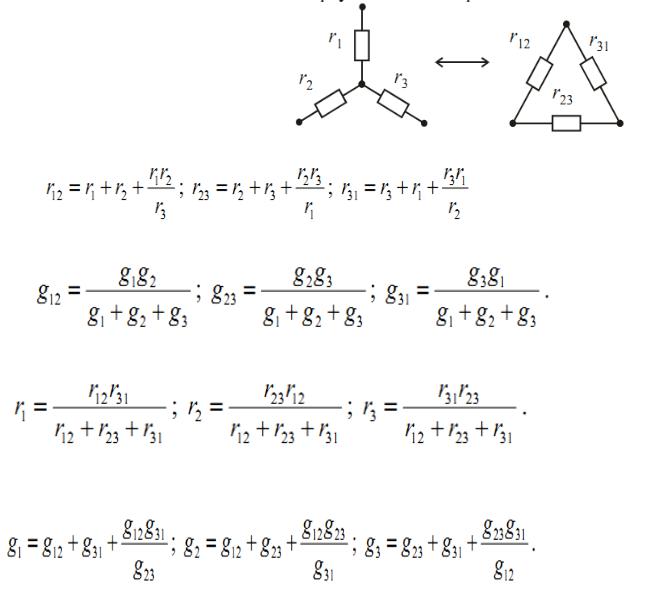
Преобразование из «звезды» в «треугольник» и обратно
Для сопротивлений из «звезды» в
Для проводимостей из «звезды» в «треугольник»
Для сопротивлений из «треугольника» в «звезду»
Для проводимостей из «треугольника» в «звезду»
Методы анализа сложных электрических цепей
постоянного тока: применение законов Кирхгофа, метод контурных токов. Уравнение баланса электрической мощности.
Анализ электрических цепей с одним источником энергии проводится двумя методами: методом эквивалентного преобразования (свертывания схемы) и
методом пропорциональных величин.
При методе свертывания схемы определяется входное или эквивалентное сопротивление путем преобразования сопротивлений: параллельного соединения в последовательное и обратно, треугольника в звезду и обратно и т.д., что упрощает отдельные участки схемы и приводит к одному эквивалентному (входному) сопротивлению относительно зажимов источников питания. В результате схема упрощается и расчет такой схемы можно произвести , используя закон Ома.
К методом анализа сложных цепей относятся:
1.Метод, основанный на применении законов Кирхгофа.
2.Метод контурных токов.
3.Метод узловых потенциалов.
4.Метод наложения.
5.Метод эквивалентного генератора.
Классическим методом расчета электрических цепей с несколькими источниками является непосредственное применение законов Кирхгофа.
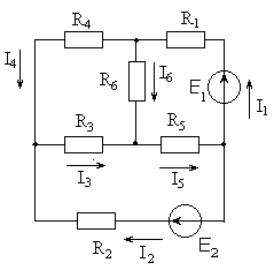
При расчете электрических цепей с применением законов Кирхгофа необходимо:
1.Выбрать положительное направление токов во всех ветвях схемы;
2.Выбрать положительное направление обхода контура;
3.Составить уравнения по законам Кирхгофа;
по первому закону Кирхгофа составить nу-1 уравнение, по второму закону Кирхгофа составить nв –nу +1. Общее число уравнений равно числу ветвей в схеме;
4. Полученную систему уравнений решают относительно
для нахождения токов ветвей для на рисунке:
имеет четыре узла и шесть | ||||||||||
| I1 | I4 | I6 | 0, |
|
|
| |||
уравнений | по законам |
| ||||||||
| I2 |
| I3 | I4 | 0, |
|
|
| ||
вид: |
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
| |
I3 I5 I6 | 0, |
|
|
| ||||||
| I | R I | R I | R 0, |
| |||||
| 3 |
| 3 | 4 |
| 4 | 6 | 6 |
| |
I R I | R I | R E , | ||||||||
| 1 |
| 1 | 5 |
| 5 | 6 | 6 | 1 | |
I2 | R2 I3 R3 I5 R5 E2. | |||||||||
| ||||||||||
Имеем систему из шести уравнений с шестью неизвестными. Выразив токи I1, I2, I5 через I4, I6,I3, получим:
I1 I4 I6,
I2 I3 I4,
I5 I6 I3,
I3 R3 I4 R4 I6 R6 0,
I4 I6 R1 I6 I3 R5 I6 R6 E1,
I3 I4 R2 I3 R3 I6 I3 R5 E2.
Решая данную систему уравнений, можно найти токи ветвей.
Число совместно решаемых уравнений равно числу ветвей схемы (числу неизвестных токов ветвей), поэтому его применение не всегда целесообразно.
В качестве переменных в методе контурных токов принимаются контурные токи.
В схеме выделяют независимые контуры. В каждом контуре произвольно выбирают направление контурных токов. За контурные токи удобно принять токи внешних ветвей схемы, которые входят только в данный контур.
Уравнения составляются на основе второго закона Кирхгофа, выражая токи ветвей через контурные токи.
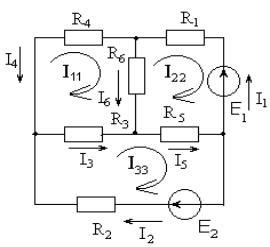
пишем второй закон Кирхгофа:
I4R4 I6R6 I3R3 0,
I6R6 I1R1 I5R5 E1,
I3R3 I5R5 I2R2 E2.
Выразим токи ветвей через контурные:
I11 I4,I22 I1 , I33 I2 ,I6 I11 I22,I3 I33 I11,I5 I33 I22.
После преобразования получим следующую систему уравнений:
I11 R3 R4 R6 I22 R6 I33 R3 0,
I11 R6 I22 R1 R5 R6 I33R5 E1 ,
I11 R3 I22 R5 I33 R3 R2 R5 E2 .
Решив систему уравнений относительно контурных токов, находятся токи ветвей. Правильность решения по методу контурных токов осуществляется на основании второго закона Кирхгофа.
Уравнение баланса электрической мощности.
Баланс мощностей – алгебраическая сумма мощностей, отдаваемых независимыми источниками равняется алгебраической сумме мощностей, потребляемыхn n потребителямиn .
Ek Ik Uk Jk Ik2 Rk
n | k 1 | k 1 | k 1 | |
алгебраическая сумма мощностей, генерируемая | ||||
Где Ek I-k | ||||
источниками э.д.с.; |
|
| ||
k 1 |
|
|
| |
n
k 1 Uk J-k алгебраическая сумма мощностей, генерируемая
источниками тока;
n
I 2 R
k 1 k k- суммарная мощность, потребляемая потребителями в
цепи.
Эти суммы алгебраические. Источник может как вырабатывать, так и потреблять электрическую энергию (заряд аккумулятора).

Если направления ЭДС и тока через источник ЭДС совпадают, мощность источника записывают в уравнении баланса мощностей с положительным знаком. Он работает в режиме генератора. При противоположных направлениях ЭДС и тока мощность в уравнении баланса учитывают с отрицательным знаком (режим потребителя).
Определение знака мощности источника тока поясняет, на котором показана разметка зажимов источника тока, вырабатывающего (а) или потребляющего (б) электрическую энергию. Ток  и напряжение U направлены в сторону уменьшения потенциала, что и позволяет разметить зажимы источника.
и напряжение U направлены в сторону уменьшения потенциала, что и позволяет разметить зажимы источника.
Мощность потребителей (нагрузок) Эта сумма арифметическая.
Погрешность расчета не должна превышать (1–3) %.
Методы расчета электрических цепей постоянного тока
48 | 2. Электрические цепи постоянного тока |
I закон Кирхгофа
Алгебраическая сумма токов в узле электрической цепи равна нулю:
X
I = 0
II закон Кирхгофа
Алгебраическая сумма падений напряжений в контуре электрической цепи равна алгебраической сумме ЭДС в этом же контуре:
XX
I R = E
Методы расчёта электрических цепей постоянного и переменного тока, с точки зрения электротехники, абсолютно аналогичны, однако, математически расчёт цепей переменного тока значительно более сложен, в связи с применением в расчётах комплексных чисел, поэтому рассмотрение методов расчёта мы проведём на примере цепей постоянного тока.
Основная задача расчета электрических цепей –– определить токи и мощности в различных элементах цепи, а также напряжения на отдельных участках.
Исходными данными,обычно, являются значения ЭДС и напряжений, имеющихся в схеме и параметры (сопротивления), либо характеристики (номинальные мощность и напряжение) элементов цепи.
Режим работы источников. По результатам расчета цепи можно определить режим работы источников:
режим источника –– ток в источнике и падение напряжения на нём (или его ЭДС) совпадают по направлению;
режим нагрузки–– ток в источнике и падение напряжения на нём (или его ЭДС) противоположны по направлению.
2.3. Методы расчета электрических цепей постоянного тока | 49 |
Баланс мощностей. Умножив левую и правую часть уравнения по второму закону Кирхгофа на ток получим:
X I 2R = X EI ,
таким образом, в любом замкнутом контуре алгебраическая (т. е. с учётом знака) сумма мощностей источников ЭДС равна сумме мощностей потребляемых всеми сопротивлениями. Это условие называется баланс мощностей и применяется для проверки правильности расчетов электрических цепей.
2.3.1.Метод эквивалентных преобразований (эквивалентного сопротивления)
Идея метода
Идея метода состоит в замене сложной электрической цепи (или её участка) эквивалентной, которая не изменяет режим работы остальной части цепи.
Порядок расчёта
Расчёт, обычно, ведётся для цепей с одним источником питания и начинается с элементов, наиболее удалённых от источника или точек соединения рассматриваемого участка с остальной цепью.
1.Проведём последовательную замену элементов электрической цепи эквивалентными. Преобразования производятся по правилам, рассмотренным в § 1.4 на стр. 34. Целью преобразований является построение цепи, содержащей два эквивалентных элемента –– источник электрической энергии и сопротивление.
2.Находим ток в эквивалентной цепи и, проводя обратное преобразование эквивалентной цепи в исходную, токи в ветвях.
Пример расчёта
Найдём токи в электрической цепи, приведённой на рис. 2.1, сопротивления резисторов и приложенное к цепи напряжение известны.

50 | 2. Электрические цепи постоянного тока | ||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.1. Метод эквивалентных преобразований
Преобразования начнём с наиболее удалённых от источника питания элементов R4 и R5 (рис. 2.2, а). Эти элементы соединены параллельно, следовательно проводимость эквивалентного элемента будет равна сумме проводимостей (см. § 1.4.2 на стр. 35):
G45 = G4 + G5 | 1 |
| 1 | 1 | R45 = | R4R5 | |
| = |
| + |
|
| ||
R45 | R4 | R5 | R4 + R5 | ||||
После замены элементов R4 и R5 на эквивалентный элемент с сопротивлением R45 схема примет вид, привидённый на рис. 2.2, б.
На следующем шаге мы видим, что элементы R3 и R45 соединены последовательно, следовательно эквивалентный им элемент будет иметь сопротивление (см. § 1.4.1 на стр. 34):
R345 = R3 + R45,
после чего мы получим схему, приведённую на рис. 2.2, в. Элементы R2 и R345 соединены параллельно:
R2345 = | R2R345 | , |
| ||
| R2 + R345 | |
полученная эквивалентная схема приведена на рис. 2.2, г.

| 2.3. Методы расчета электрических цепей постоянного тока | 51 | |||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.2. Расчёт методом эквивалентных преобразований
Элементы R1 и R2345 соединены последовательно:
Rэ = R1 + R2345,
итоговая эквивалентная схема на приведена рис. 2.2, д. Рассчитаем токи в ветвях.
Ток, протекающий в цепи (рис. 2.2, д), будет равен:
I = U . Rэ
Так как элементы R1 и R2345 включены последовательно а их сумма равна Rэ, то (рис. 2.2, г):
I = I1 = I2345.
Зная ток I2345, мы можем можем рассчитать напряжение Ucd :
Метод наложения — Википедия
Материал из Википедии — свободной энциклопедии
Метод наложения — метод расчёта электрических цепей, основанный на предположении, что электрический ток в каждой из ветвей электрической цепи при всех включённых генераторах равен сумме токов в этой же ветви, полученных при включении каждого из генераторов по очереди и отключении остальных генераторов (только в линейных цепях).
Метод наложения используется как для расчёта цепей постоянного тока, так и для расчёта цепей переменного тока.
Найти ток I1{\displaystyle I_{1}} методом наложения в цепи, показанной на рисунке. E1=100B{\displaystyle E_{1}=100B}, E2=50B{\displaystyle E_{2}=50B}, R1=R2=R3=10{\displaystyle R_{1}=R_{2}=R_{3}=10} Ом{\displaystyle {\text{Ом}}}.
Пример метода наложенияПри отключённом генераторе 2 ток I1′{\displaystyle I_{1}’} найдём по формуле:
- I1′=E1R1+R2R3R2+R3=10010+10⋅1010+10=6,67A{\displaystyle I_{1}’={\frac {E_{1}}{R_{1}+{\frac {R_{2}R_{3}}{R_{2}+R_{3}}}}}={\frac {100}{10+{\frac {10\cdot 10}{10+10}}}}=6,67A}.
При отключённом источнике 1 ток I2″{\displaystyle I_{2}»} будет
- I2″=E2R2+R1R3R1+R3=5010+10⋅1010+10=3,34A{\displaystyle I_{2}»={\frac {E_{2}}{R_{2}+{\frac {R_{1}R_{3}}{R_{1}+R_{3}}}}}={\frac {50}{10+{\frac {10\cdot 10}{10+10}}}}=3,34A},
а ток I1″{\displaystyle I_{1}»} будет
- I1″=−I2″2=−3,342=−1,67A{\displaystyle I_{1}»=-{\frac {I_{2}»}{2}}=-{\frac {3,34}{2}}=-1,67A}.
Тогда ток I1{\displaystyle I_{1}} при обоих включённых источниках будет равен сумме токов I1′{\displaystyle I_{1}’} и I1″{\displaystyle I_{1}»}:
- I1=I1′+I1″=6,67−1,67=5A{\displaystyle I_{1}=I_{1}’+I_{1}»=6,67-1,67=5A}.
В задаче за положительные направления токов I1′{\displaystyle I_{1}’} и I1″{\displaystyle I_{1}»} приняты направления, совпадающие с направлением, показанным на рисунке для тока I1{\displaystyle I_{1}}. То же самое для тока I2″{\displaystyle I_{2}»}
- Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. — М.: Гардарики, 2002. — 638 с. — ISBN 5-8297-0026-3.




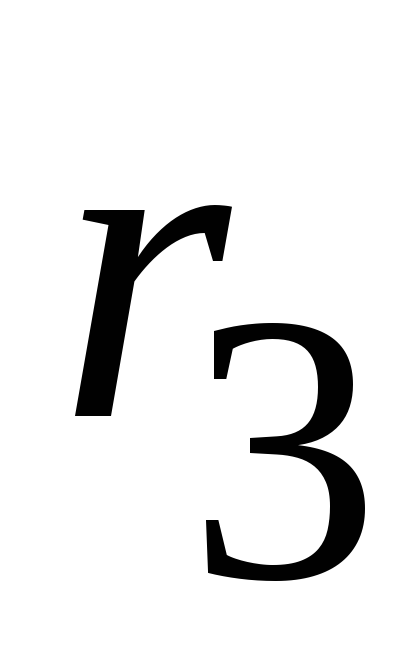 ,
,  и
и 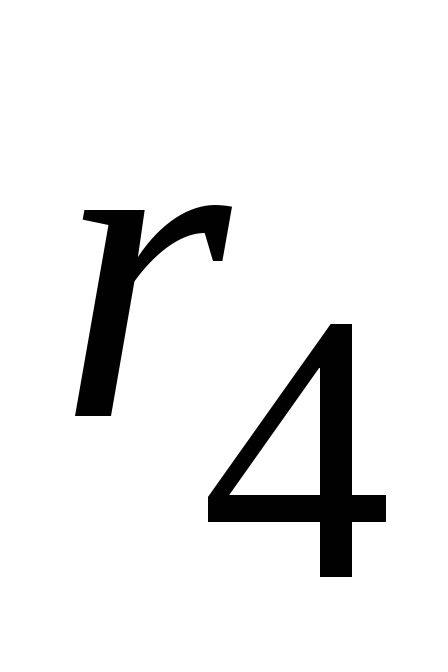 заменяем эквивалентным сопротивлением
заменяем эквивалентным сопротивлением 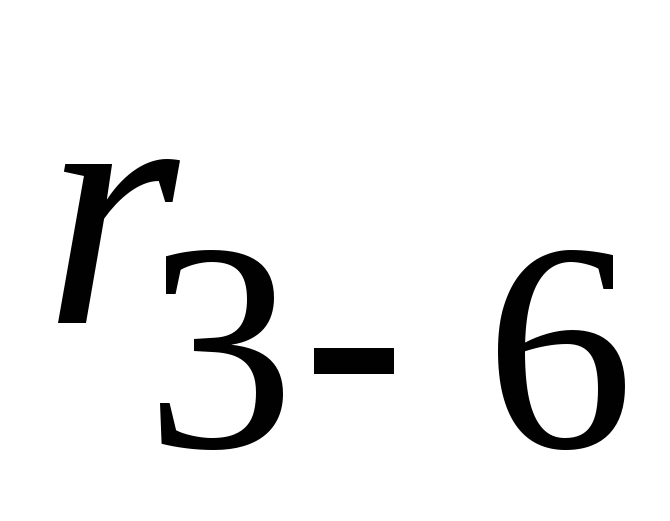 :
: и
и 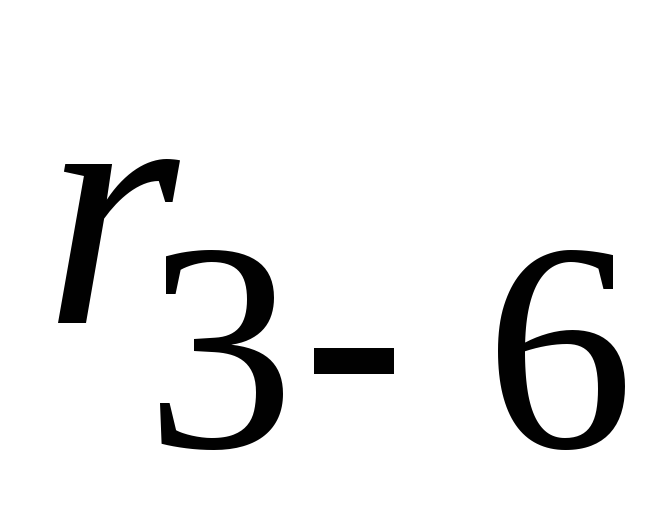 заменяем эквивалентным сопротивлением
заменяем эквивалентным сопротивлением 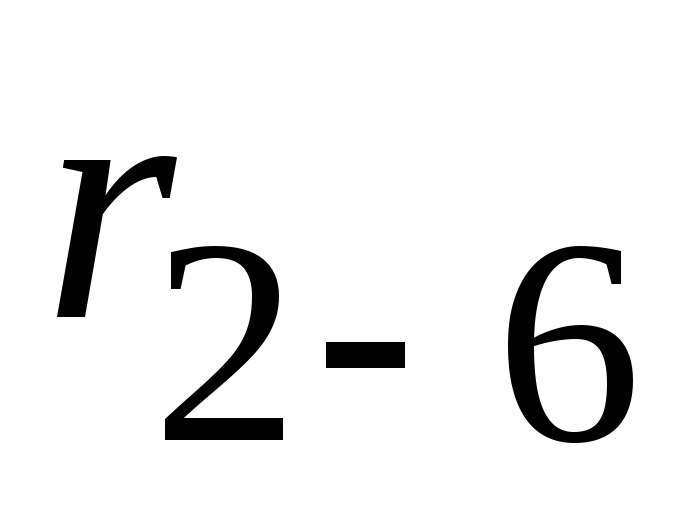 :
: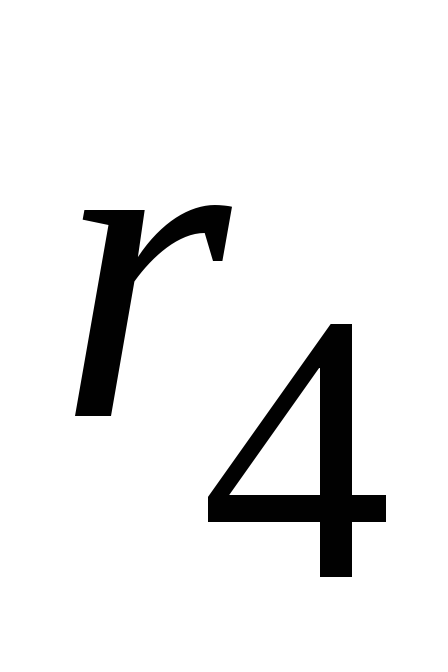 и
и  заменяем эквивалентным сопротивлением
заменяем эквивалентным сопротивлением  :
: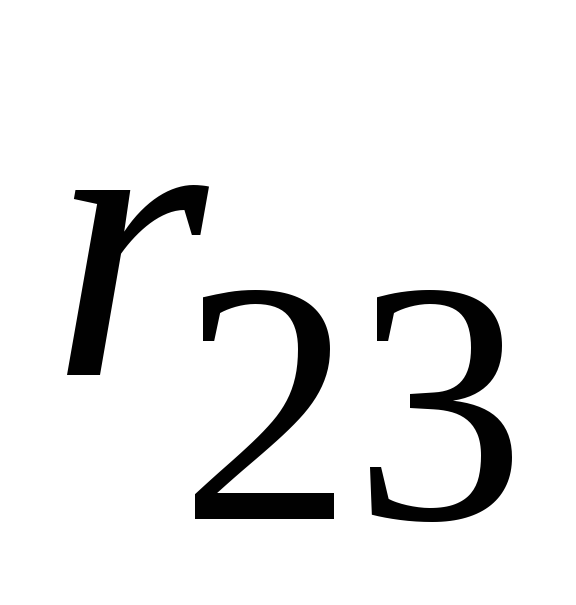 и
и 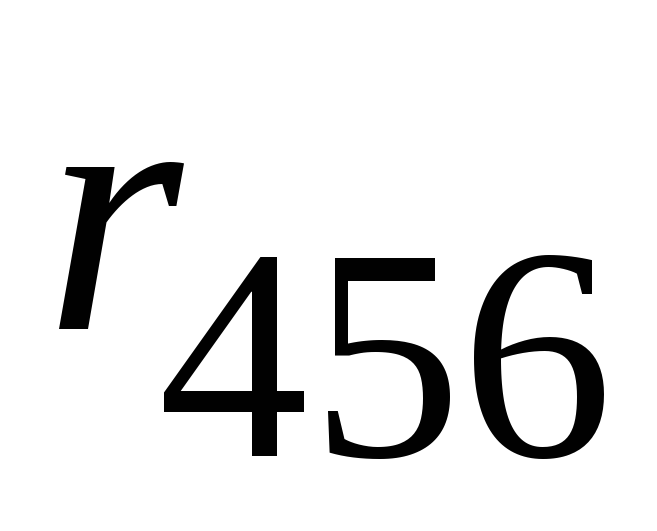 заменяем эквивалентным сопротивлением
заменяем эквивалентным сопротивлением 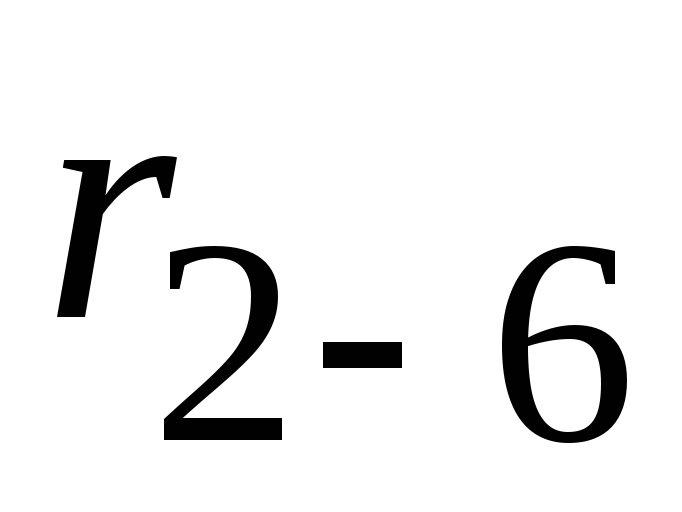 :
: