Матрица Кирхгофа — это… Что такое Матрица Кирхгофа?
Матрица Кирхгофа (Laplacian matrix) — одно из представлений графа с помощью матрицы. Матрица Кирхгофа используется для подсчета остовных деревьев данного графа (матричная теорема о деревьях), а также используется в спектральной теории графов.
Определение
Дан простой граф с вершинами. Тогда матрица Кирхгофа данного графа будет определяться следующим образом:
Также матрицу Кирхгофа можно определить как разность матриц
где — это матрица смежности данного графа, а — матрица, на главной диагонали которой степени вершин графа, а остальные элементы — нули:
Если граф является взвешенным, то определение матрицы Кирхгофа обобщается. В этом случае элементами главной диагонали матрицы Кирхгофа будут суммы проводимостей инцидентных ребер соответствующей вершины. Для смежных (связанных) вершин где — это вес (проводимость) ребра.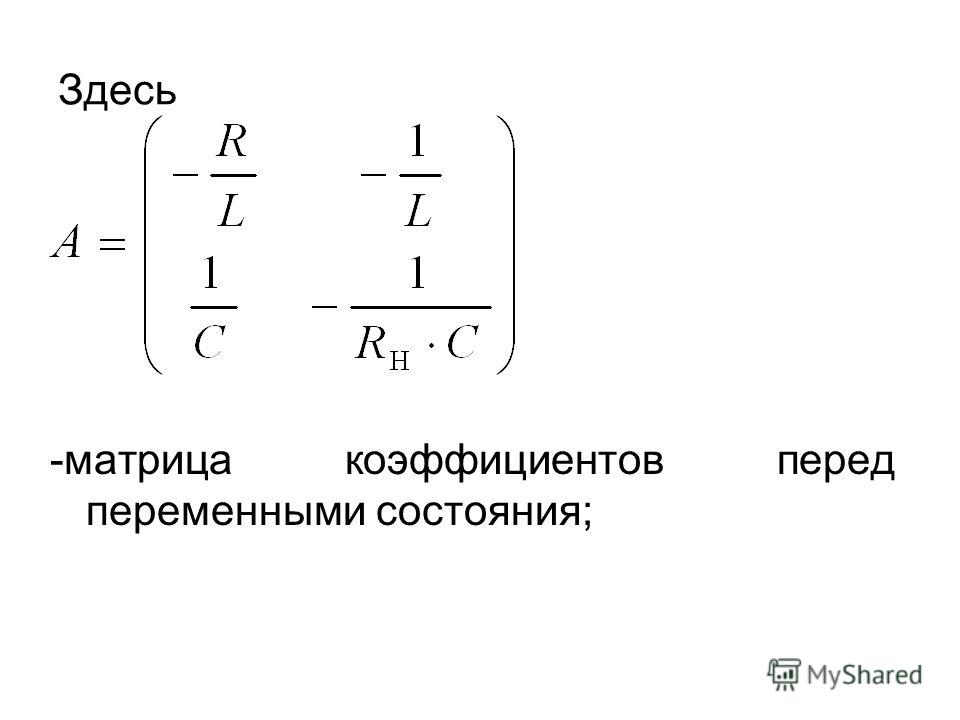
Для взвешенного графа матрица смежности записывается с учетом проводимостей ребер, а на главной диагонали матрицы будут суммы проводимостей ребер инцидентных соответствующим вершинам.
Пример
Пример матрицы Кирхгофа простого графа.
| Помеченный граф | Матрица Кирхгофа |
|---|---|
Свойства
- Сумма элементов каждой строки (столбца) матрицы Кирхгофа равна нулю:
- Определитель матрицы Кирхгофа равен нулю:
- Все алгебраические дополнения симметричной матрицы Кирхгофа равны между собой —
- Если взвешенный граф представляет собой электрическую сеть, то миноры матрицы Кирхгофа позволяют вычислить резистивное расстояние (resistance distance) между точками и данной сети:
,
здесь — постоянная (алгебраическое дополнение) матрицы Кирхгофа, а — алгебраическое дополнение 2-го порядка, то есть определитель матрицы, получающейся из матрицы Кирхгофа вычеркиванием двух строк и двух столбцов .
- 0 является собственным значением матрицы (соответствующих собственный вектор — все единицы), кратность его равна числу связных компонент графа.
- Остальные собственные значения положительны. Второе по малости значение Фидлер назвал индексом связности графа, его с. вектор — вектор Фиддлера.
См. также
Матрица Кирхгофа — Справочник химика 21
Матрица Кирхгофа и конформации молекул [c.144]Матрица Кирхгофа (5.29) в соответствии с формулами (5.34) и [c.70]
Топологические матрицы графов несут в себе полную информацию о глобальной и локальной структурах графа так же, как и его изображение на рисунке. Наиболее часто в теории графов используются матрицы смежности А и инциденции В и несколько реже — матрица Кирхгофа, которая получается из матрицы — А заменой -го элемента главной диагонали на степень -й вершины.
Представляет интерес использование матриц Кирхгофа для анализа и расчета материальных и энергетических балансов технологических схем [58]. Для системы, представленной на рис. 4.13
Уравнение второго закона Кирхгофа для отдельно взятого контура может быть записано как скалярное произведение вектора-строки матрицы [c.52]
Стоящую здесь сумму по всем парам смежных звеньев — / можно записать [75] в матричном виде с помощью матрицы Кирхгофа. Для этого введем матрицу К размера 3 X I, элементы Гаг которой составлены из проекций на декартовы координатные оси (а = 1, 2, 3) радиус-векторов звеньев молекулы. Векторы Г — г, расстояний между смежными звеньями представляются столбцами матрицы КВ.
Таким образом, даже такая минимальная информация о матрице Кирхгофа, как значение ее любого главного минора, позволяет найти свободную энергию полимерной молекулы. Подробность описания конформационной статистики возрастает с увеличением информации о матрице К. Так, зная ее спектр, можно найти средние размеры молекулы и распределение ее радиуса инерции [75]. Эта же информация позволяет вычислить с помощью обобщения теорий Рауза [76] и Зимма [77] динамические свойства гауссовой молекулы в терминах спектра ее времен релаксации [75, 78]. Для этой цели Фореман [78, 79] вместо матрицы К = ВВ , являющейся обобщением на разветвленные молекулы матрицы Зимма [77], использует аналог В В матрицы Рауза [76]. Поскольку отличные от нуля собственные значения матрицы Кирхгофа совпадают со спектром матрицы Рауза, то получающиеся при использовании двух различных подходов выражения идентичны.
Итак, приведем в табл. 9.2 результаты численных расчетов по методу, изложенному в данном пункте и условно названному МКРДГК (метод контурных расходов, на каждом шаге которого проводится разнесение контурных невязок в узлы, ограничивающие одноименные (контурам) хорды, и формируется система уравнений в узловой форме, решаемая методом Гаусса с компактной формой записи, хранения и обработки коэффициентов матрицы Кирхгофа).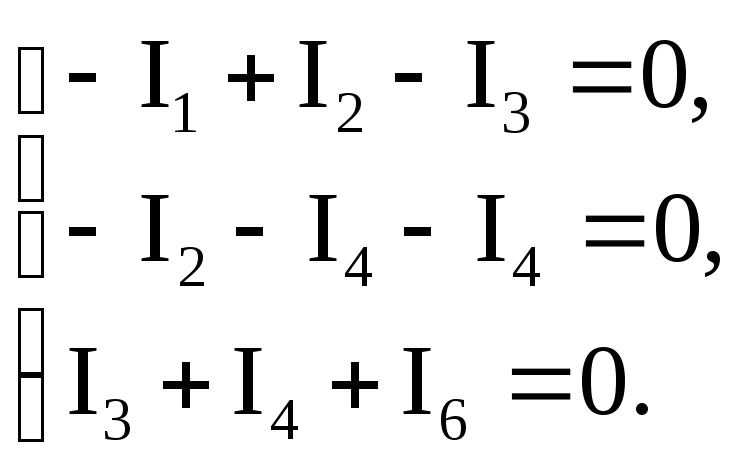
В отличие от электрических цепей при расчете потокораспределения в г д. наиболее распространенным и более эффективным в вычислительном плане является переход к контурным уравнениям. В то же время для учета разреженности матрицы более выгодной оказывается узловая форма записи системы уравнений, поскольку для сложных систем заполненность нулями у матрицы Максвелла меньше, чем у матрицы Кирхгофа. Кроме того, структура матрицы Максвелла совпадает со структурой схемы цепи и не зависит от выбора контуров, что упрощает логику алгоритмов упорядочения исключения переменных. [c.116]
Геометрическая интерпретация подобных шнейных задач наиболее проста их решение определяется пересечением в и-мерном пространстве т — гиперплоскостей (4.9) — по числу независимых узлов. Поскольку определитель квадратной (в таких случаях) матрицы А отличен от нуля, система линейных уравнений первого закона Кирхгофа обязательно имеет ненулевое решение, если она является неоднородной (с ненулевой правой частью).
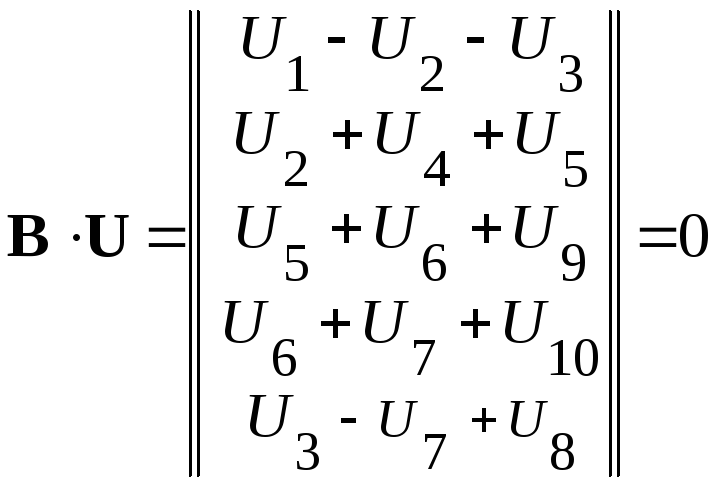 Это означает, в частности, что при одном источнике питания должен существовать по меньшей мере один узел с присоединенной к нему известной нагрузкой, чтобы соответствующая гиперплоскость не проходила через начало координат, а отсекала бы отрезки на осях.
Это означает, в частности, что при одном источнике питания должен существовать по меньшей мере один узел с присоединенной к нему известной нагрузкой, чтобы соответствующая гиперплоскость не проходила через начало координат, а отсекала бы отрезки на осях. Перейдем теперь к виду общего решения системы уравнений первого закона Кирхгофа и соответственно к связи между векторами дГд и Из предыдущего ясно, что ранг матрицы А равен т — 1 и поэтому фундаментальная система решений приведенной системы уравнений Лх = О состоит из л — (/я — 1) = с специально подобранных наборов чисел. В качестве таковых можно взять, как это следует из (4.29) и (4.30), систему из с строк матрицы В, построенной для главной (хордовой) системы контуров. Любая линейная комбинация этих строк с произвольными постоянными коэффициентами х — ( Сь. . ., х ) также будет решением приведенной системы, так что
Элементы этой матрицы являются коэффициентами при х,- (/ = 1,.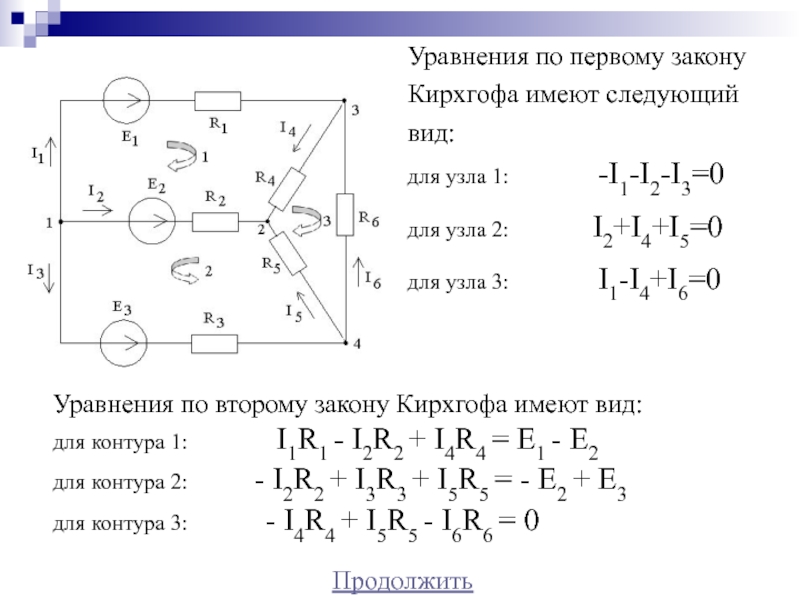 .., 6) в уравнениях второго закона Кирхгофа [c.66]
.., 6) в уравнениях второго закона Кирхгофа [c.66]
Независимо от этого из законов Ома и Кирхгофа и из условия 8.188) находим уравнения (8.184), которые после раскрытия скобок и приведений дают уравнения (8.190) с матрицей коэффициентов (8.191). [c.448]
Из законов Ома и Кирхгофа имеем уравнения (8.200) с матрицей В (8.201) [c.452]
Третий тип уравнений. При умножении уравнения (8.214) и уравнения (8.216) на столбец единиц V справа и при замещении нулями всех элементов, в полученной матрице-столбце VI, кроме начальных и конечных, получаются соответственно закон Кирхгофа для разветвленного тока (ср. уравнение (8.190)) и закон Боденштейна для сложных, в данном случае мономолекулярных обратимых реакций.
Поэтому эпергня (1.32) молекулы просто выражается через матрицу Кирхгофа ее графа [c.177]
Таким образом, в общем случае данные системы линеаризованных (контурных или узловых) уравнений, получаемые на каждом шаге процесса, необходимо решать в полном виде, но с обязательным учетом разреженной (слабозаполненной ненулевыми элементами) структуры матриц коэффициентов этих систем.
Процесс Ньютона в методе контурных расходов (М1СР) реализуется не в общем виде, а с некоторыми особенностями, существенно учитывающими сетевую специфику задачи расчета потокораспределения и связь между матрицами А и В. Во-первых, все приближения д берутся строго удовлетворяющими уравнениям первого закона Кирхгофа. Это будет обеспечено, если данное условие соблюдено для начального приближения т.е. [c.67]
Матрицы /И и N дают возможность записать уравнения состоя т электрической цеон в матричной форме.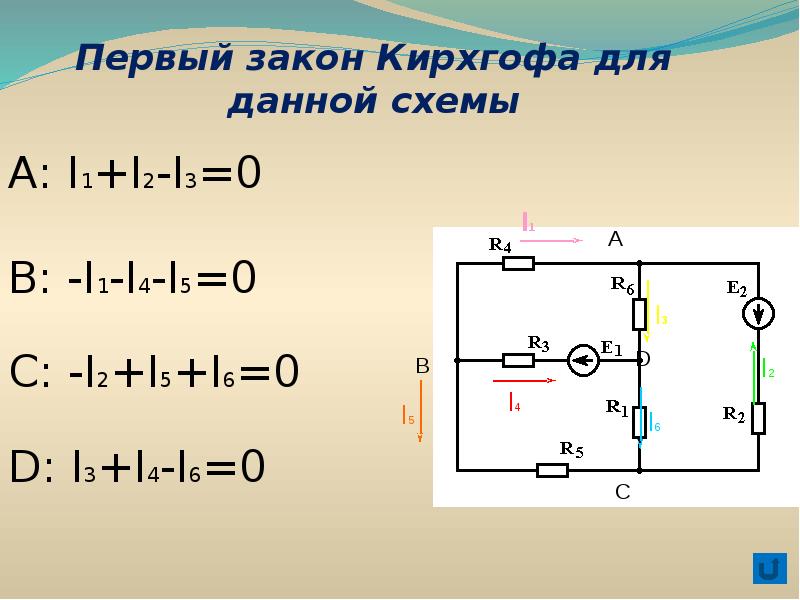 Нелрудно видеть, что СИ. тьма взаимно независимых уравнений первого закона Кирхгофа прсгк тавляется так [c.153]
Нелрудно видеть, что СИ. тьма взаимно независимых уравнений первого закона Кирхгофа прсгк тавляется так [c.153]
Законы Кирхгофа в матричной форме
Для записи законов Кирхгофа в матричной форме необходимо составить топологические матрицы схемы.
Матрица соединений, или узловая А,- это таблица коэффициентов независимых уравнений, составленных по первому закону Кирхгофа для У — 1 узлов. Строки (i) соответствуют узлам (их число равно У- 1), столбцы (j) — ветвям (их число равно В). Элемент матрицы aij = + 1, если ветвь j графа соединена с узлом i и направлена от узла i (положительное направление тока в ветви j выбрано от узла i). Элемент матрицы aij = — 1, если ветвь j графа соединена с узлом i и направлена к узлу i. Элемент матрицы aij = 0, если ветвь j не присоединена к узлу i.
Например, для схемы и графа по рис. 1.14 с У= 4 узлами и В = 6 ветвями для первых трех узлов
что соответствует первым трем уравнениям ( 1. 21а).
21а).
Так как -матрица А определяет, какие ветви присоединены к каждому узлу и как направлены токи в этих ветвях, то произведение матрицы соединений на матрицу-столбец токов ветвей I дает совокупность левых частей уравнений, составленных по первому закону Кирхгофа, и, следовательно, равно нулю:
АI = 0 (1.26а)
— это первый закон Кирхгофа в матричной форме. Для схемы и графа по рис. 1.14
и после выполнения умножения матриц получаем первые три уравнения (1.21а).
Под матрицей соединений иногда понимают матрицу А, записанную для всех узлов схемы.
Матрица сечений Q — это таблица коэффициентов, составленных по первому закону Кирхгофа для сечений. Строки i матрицы соответствуют сечениям (их число равно У — 1), столбцы j — ветвям (их число равно В). Элемент матрицы qij = +1, если ветвь j содержится в сечении i и направлена согласно с направлением сечения. Элемент матрицы qij = -1, если ветвь j содержится в сечении i и направлена противоположно направлению сечения. Элемент матрицы qij = 0, если ветвь j не содержится в сечении i. Для главных сечений составляется матрица главных сечений.
Элемент матрицы qij = 0, если ветвь j не содержится в сечении i. Для главных сечений составляется матрица главных сечений.
Например, для графа рис. 1.14, д при показанных трех главных сечениях
В матричной форме первый закон Кирхгофа можно записать и с матрицей сечений
QI=0 (1.26 б)
После умножения матрицы Q на матрицу-столбец токов I получаются первое и третье (с обратным знаком) уравнения (1.21а) и уравнение (1.216), т. е. независимая система уравнений по первому закону Кирхгофа.
Матрица контуров В — это таблица коэффициентов независимых уравнений, составленных по второму закону Кирхгофа для К = В — (У- 1) независимых контуров. Строки к соответствуют контурам (их число равно К), столбцы j — ветвям (их число равно В).
Элемент матрицы bkj=+1, если ветвь j входит в состав контура k и ее направление совпадает с направлением обхода контура. Элемент матрицы bkj,= -1, если ветвь j входит в состав контура k и ее направление противоположно направлению обхода контура.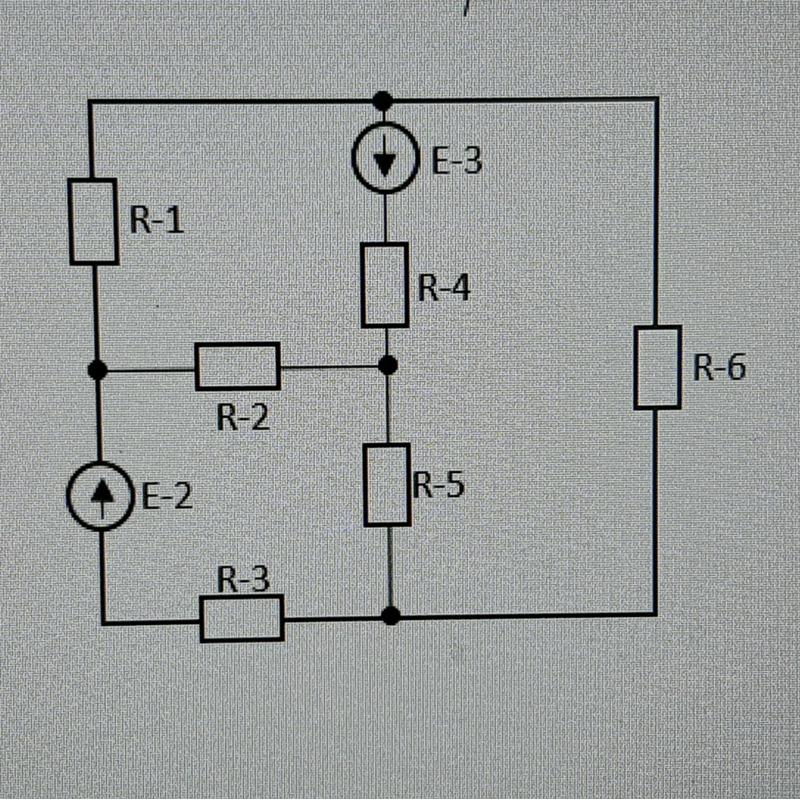 Элемент матрицы bkj = 0, если ветвь j не входит в состав контура k.
Элемент матрицы bkj = 0, если ветвь j не входит в состав контура k.
Матрица В, составленная для главных контуров, приводит непосредственно к независимой системе уравнений по второму закону Кирхгофа. Например, для графа рис. 1.14, д с контурами, состоящими из ветвей 2-4-3 (а), 5-6-4 (б) и 1-6-3 (в) матрица главных контуров при их обходе по направлению движения часовой стрелки
Умножив матрицу В на матрицу-столбец напряжений ветвей, получим матричное уравнение по второму закону Кирхгофа в формулировке (1.20а)
BU = 0, (1.27)
так как каждая строка матрицы В определяет, какие ветви входят в соответствующий контур и с какими знаками должны быть записаны напряжения ветвей.
Для схемы по рис. 1.14, а и ее графа по рис. 1.14, в после умножения на матрицу-столбец напряжений ветвей
получим систему трех независимых уравнений вида (1.20а):
Эта система с учетом равенства и соотношений (1.22а) совпадает с ранее полученной системой (1. 23), (1.246), (1.24а), т. е. с системой вида (1.206).
23), (1.246), (1.24а), т. е. с системой вида (1.206).
Для любой планарной схемы, т. е. схемы, которую можно изобразить на листе без пересекающихся ветвей и проводов, в качестве независимых контуров можно выбирать элементарные контуры-ячейки. Например, для схемы рис. 1.14, а это ячейки I, II, III. Если выбрать направление обхода каждой ячейки по направлению движения стрелки часов, то
После умножения на матрицу-столбец напряжений ветвей U получим другую независимую систему уравнений по второму закону Кирхгофа в форме (1.20 а):
которая после подстановки соотношений (1.22а) приводится к виду (1.206).
Если схема цепи кроме источников ЭДС, как на рис. 1.14, а (и далее рис. 1.20-1.22), содержит и источники тока, то для записи матричных уравнений (1.27) можно рекомендовать преобразование источников тока в источники ЭДС (см. рис. 1.23) или введение понятия обобщенной ветви (см. рис. 1.25).
Основные этапы построения решения
Основные этапы построения решенияОсновные этапы построения решения
Дифференциальные уравнения решаются численно методом Рунге-Кутта.
Чтобы выписать уравнения Кирхгофа для произвольной трубопроводной сети целесообразно привлечь теорию графов.
Топология трубопроводной сети моделируется с помощью ориентированного графа, причем дуги графа соответствуют участкам труб и элементам, имеющим гидравлическое сопротивление, а вершины графа соответствуют концам труб (и точкам их соединения).
Пусть A — матрица инцидентности (точнее базисная подматрица матрицы инцидентности, которая получается из полной матрицы инцидентности в результате отбрасывания какой-нибудь строки — обычно последней). Тогда первый закон Кирхгофа, утверждающий, что сумма расходов, втекающих и вытекающих в любой узел равна нулю, можно записать в виде матричного уравнения
Для записи второго закона Кирхгофа используется матрица базисных циклов В. Эту матрицу можно
получить в результате следующей процедуры. Выберем какое-нибудь остовное дерево
графа (для ускорения процессов сходимости итерационных процессов решения нелинейных
уравнений Кирхгофа рекомендуется выбирать дерево с наименьшим гидравлическим
сопротивлением). Выбор остовного дерева (базисного минора матрицы инцидентности)
разбивает дуги графа на ветви и хорды, при этом соответствующие расходы разбиваются
на базисные и свободные. С учетом этого разбиения уравнение первый закон Кирхгофа
можно переписать в виде:
Эту матрицу можно
получить в результате следующей процедуры. Выберем какое-нибудь остовное дерево
графа (для ускорения процессов сходимости итерационных процессов решения нелинейных
уравнений Кирхгофа рекомендуется выбирать дерево с наименьшим гидравлическим
сопротивлением). Выбор остовного дерева (базисного минора матрицы инцидентности)
разбивает дуги графа на ветви и хорды, при этом соответствующие расходы разбиваются
на базисные и свободные. С учетом этого разбиения уравнение первый закон Кирхгофа
можно переписать в виде:
Здесь At и Ac — квадратная и прямоугольная матрицы, составленные соответственно из базисных столбцов (индекс t от английского слова tree — древо) и остальных (индекс с от английского слова chord — хорда).
Выразим базисные переменные через свободные:
Можно показать, что матрица базисных циклов, соответствующая выбранному остовному дереву имеет вид:
Второй закон Кирхгофа, утверждающий, что сумма падений давления, с учетом действующих напоров, по любому замкнутому контуру равна нулю, можно записать в виде:
Здесь — матрица-столбец, составленная из падений давления на каждом
из участков трубопроводной сети, E матрица-столбец, составленная из действующих
напоров на каждом из участков трубопроводной сети.
Уравнение (1.7) является нелинейным даже в простейшем случае гидравлической сети (в случае гидравлической сети при решении нелинейных уравнений помогает метод Ньютона). В случае паропроводов компоненты векторы определяются из решения системы дифференциальных уравнений, причем решения не являются гладкими функциями. Излом решения образуется в точке появления конденсата. С учетом этих замечаний для решения нелинейных уравнений применим метод минимизации невязок. Введем вектор невязок (residual vector)
и вычислим норму, например евклидову (в конечномерном случае все нормы эквивалентны), этого вектора:
Основы матричных методов расчета электрических цепей. (Лекция N 6)
Рассмотренные методы расчета электрических цепей – непосредственно по законам
Кирхгофа, методы контурных токов и узловых потенциалов – позволяют принципиально
рассчитать любую схему.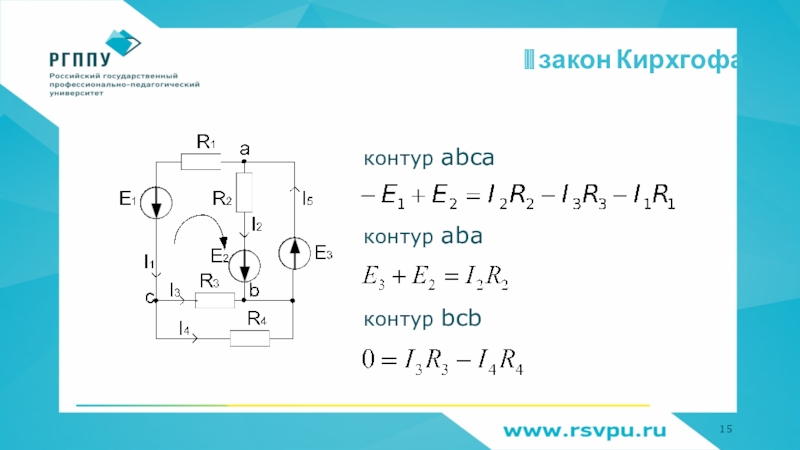 Однако их применение без использования введенных ранее
топологических матриц рационально для относительно простых схем. Использование
матричных методов расчета позволяет формализовать процесс составления уравнений
электромагнитного баланса цепи, а также упорядочить ввод данных в ЭВМ, что особенно
существенно при расчете сложных разветвленных схем.
Однако их применение без использования введенных ранее
топологических матриц рационально для относительно простых схем. Использование
матричных методов расчета позволяет формализовать процесс составления уравнений
электромагнитного баланса цепи, а также упорядочить ввод данных в ЭВМ, что особенно
существенно при расчете сложных разветвленных схем.
Переходя к матричным методам расчета цепей, запишем закон Ома в матричной форме.
Пусть имеем схему по рис. 1, где — источник тока. В соответствии с рассмотренным нами ранее законом Ома для участка цепи с ЭДС для данной схемы можно записать:
| . | (1) |
Однако, для дальнейших выкладок будет удобнее представить ток как сумму токов k-й ветви и источника тока, т.е.:
. |
(2) |
Подставив (2) в (1), получим:
| . | (3) |
Формула (3) представляет собой аналитическое выражение закона Ома для участка цепи с источниками ЭДС и тока (обобщенной ветви).
Соотношение (3) запишем для всех n ветвей схемы в виде матричного равенства
или
| , | (4) |
где Z – диагональная квадратная (размерностью n x n) матрица сопротивлений ветвей, все элементы которой (взаимную индуктивность не учитываем), за исключением элементов главной диагонали, равны нулю.
Соотношение (4) представляет собой матричную запись закона Ома.
Если обе части равенства (4) умножить слева на контурную матрицу В и учесть второй закон Кирхгофа, согласно которому
| , | (5) |
то
| , | (6) |
то есть получили новую запись в матричной форме второго закона Кирхгофа.
Метод контурных токов в матричной форме
В соответствии с введенным ранее понятием матрицы главных контуров В, записываемой для главных контуров, в качестве независимых переменных примем токи ветвей связи, которые и будут равны искомым контурным токам.
Уравнения с контурными токами получаются на основании второго закона Кирхгофа; их число равно числу независимых уравнений, составляемых для контуров, т.е. числу ветвей связи c=n—m+1. Выражение (6) запишем следующим образом:
| . | (7) |
В соответствии с методов контурных токов токи всех ветвей могут быть выражены
как линейные комбинации контурных токов или в рассматриваемом случае токов ветвей
связи. Если элементы j–го столбца матрицы В
умножить соответствующим образом на контурные токи, то сумма таких произведений
и будет выражением тока j–й
ветви через контурные токи (через токи ветвей связи). Сказанное может быть записано
в виде матричного соотношения
Сказанное может быть записано
в виде матричного соотношения
| , | (8) |
где — столбцовая матрица контурных токов; — транспонированная контурная матрица.
С учетом (8) соотношение (7) можно записать, как:
| (9) |
Полученное уравнение представляет собой контурные уравнения в матричной форме. Если обозначить
| , | (10) |
| . | (11) |
то получим матричную форму записи уравнений, составленных по методу контурных токов:
| , | (12) |
где — матрица контурных сопротивлений;
— матрица контурных ЭДС.
В развернутой форме (12) можно записать, как:
| , | (13) |
то есть получили известный из метода контурных токов результат.
Рассмотрим пример составления контурных уравнений.
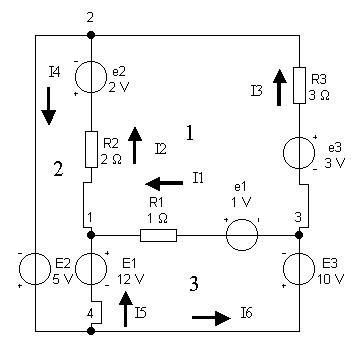
Пусть имеем схему по рис. 2. Данная схема имеет четыре узла (m=4) и шесть обобщенных ветвей (n=6). Число независимых контуров, равное числу ветвей связи,
c=n-m+1=6-4+1=3.
Граф схемы с выбранным деревом (ветви 1, 2, 3) имеет вид по рис. 3.
Запишем матрицу контуров, которая будет являться матрицей главных контуров, поскольку каждая ветвь связи входит только в один контур. Принимая за направление обхода контуров направления ветвей связи, получим:
B
Диагональная матрица сопротивлений ветвей
Z
Матрица контурных сопротивлений
Zk=BZBT
.
Матрицы ЭДС и токов источников
Тогда матрица контурных ЭДС
.
Матрица контурных токов
| . |
Таким образом, окончательно получаем:
,
где ; ; ; ; ; ; ; ; .
Анализ результатов показывает, что полученные три уравнения идентичны тем,
которые можно записать непосредственно из рассмотрения схемы по известным правилам
составления уравнений по методу контурных токов.
Метод узловых потенциалов в матричной форме
На основании полученного выше соотношения (4), представляющего собой, как было указано, матричную запись закона Ома, запишем матричное выражение:
| , | (14) |
где — диагональная матрица проводимостей ветвей, все члены которой, за исключением элементов главной диагонали, равны нулю.
Матрицы Z и Y взаимно обратны.
Умножив обе части равенства (14) на узловую матрицу А и учитывая первый закон Кирхгофа, согласно которому
| , | (15) |
получим:
.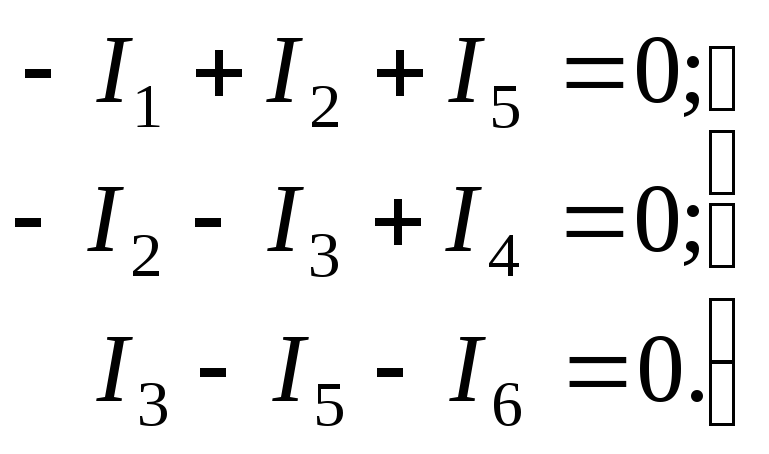 . . |
(16) |
Выражение (16) перепишем, как:
| . | (17) |
Принимая потенциал узла, для которого отсутствует строка в матрице А, равным нулю, определим напряжения на зажимах ветвей:
| . | (18) |
Тогда получаем матричное уравнение вида:
| . | (19) |
Данное уравнение представляет собой узловые уравнения в матричной форме. Если обозначить
| (20) |
| , | (21) |
то получим матричную форму записи уравнений, составленных по методу узловых потенциалов:
| (22) |
где — матрица узловых проводимостей;
— матрица узловых токов.
В развернутом виде соотношение (22) можно записать, как:
| (23) |
то есть получили известный из метода узловых потенциалов результат.
Рассмотрим составление узловых уравнений на примере схемы по рис. 4.
Данная схема имеет 3 узла (m=3) и 5 ветвей (n=5). Граф схемы с выбранной ориентацией ветвей представлен на рис. 5.
Узловая матрица (примем )
АДиагональная матрица проводимостей ветвей:
Y
где .
Матрица узловых проводимостей
.
Матрицы токов и ЭДС источников
Следовательно, матрица узловых токов будет иметь вид:
Таким образом, окончательно получаем:
,
где ; ; ; ; .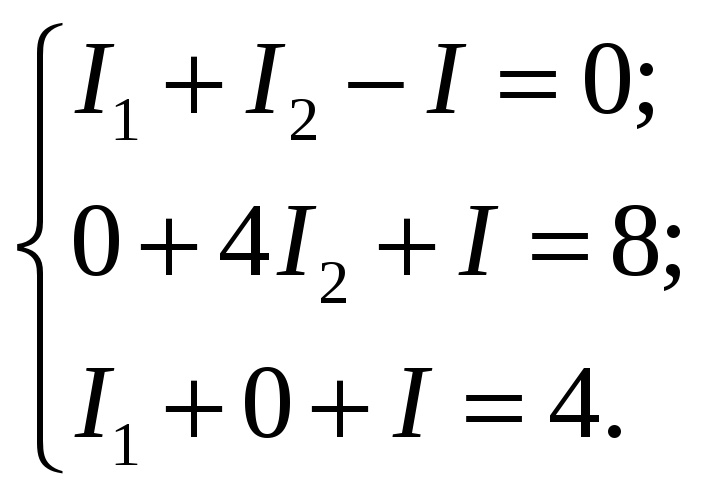
Анализ результатов показывает, что полученные уравнения идентичны тем, которые можно записать непосредственно из рассмотрения схемы по известным правилам составления уравнений по методу узловых потенциалов.
Литература
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
- В чем заключаются преимущества использования матричных методов расчета цепей?
- Запишите выражения матрицы контурных сопротивлений и матрицы контурных ЭДС.

- Запишите выражения матрицы узловых проводимостей и матрицы узловых токов.
- Составить узловые уравнения для цепи на рис. 2.
- Составить контурные уравнения для цепи рис. 4, приняв, что дерево образовано ветвями 3 и 4 (см. рис. 5).
Ответ:
Ответ:
«Мягкая» семантическая сегментация изображений
Редактирование изображений и создание коллажей было бы весьма захватывающим процессом, если бы не приходилось тратить бо́льшую часть времени на кропотливую разметку объектов. Задача еще усложняется, когда границы объектов размыты или присутствует прозрачность. Инструменты “Photoshop”, такие как «магнитное лассо» и «волшебная палочка», не очень интеллектуальны, поскольку ориентируются лишь на низкоуровневые признаки изображения. Они возвращают жёсткие (Hard) границы, которые затем нужно исправлять вручную.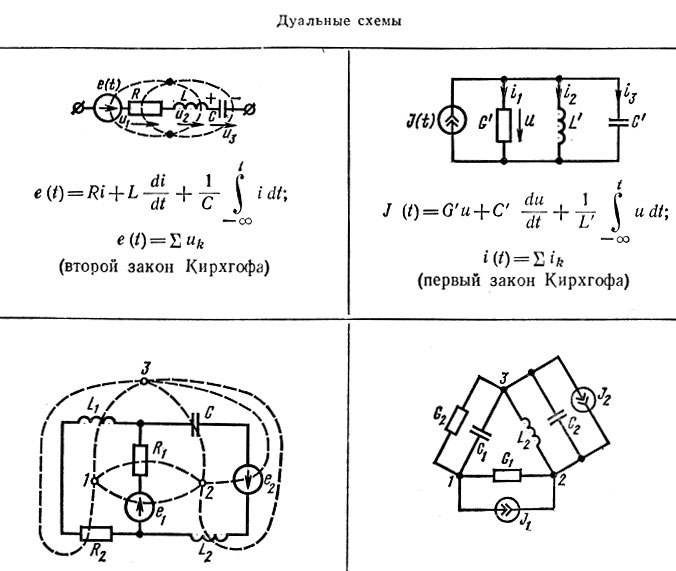 Подход Semantic Soft Segmentation от исследователей Adobe помогают решить эту непростую задачу, разделяя изображение на слои, соответствующие семантически значимым областям, и добавляя плавные переходы на краях.
Подход Semantic Soft Segmentation от исследователей Adobe помогают решить эту непростую задачу, разделяя изображение на слои, соответствующие семантически значимым областям, и добавляя плавные переходы на краях.
«Мягкая» сегментация
Группа исследователей из лаборатории CSAIL в MIT и швейцарского университета ETH Zürich, работающая под руководством Ягыза Аксоя, предложила подойти к этой проблеме, основываясь на спектральной сегментацией, добавив к ней современные достижения глубокого обучения. С помощью текстурной и цветовой информации, а также высокоуровневых семантических признаков, извлечённых нейросетью, по изображению строится граф специального вида. Затем по этому графу строится матрица Кирхгофа (Laplacian matrix). Используя спектральное разложение этой матрицы, алгоритм генерирует мягкие контуры объектов.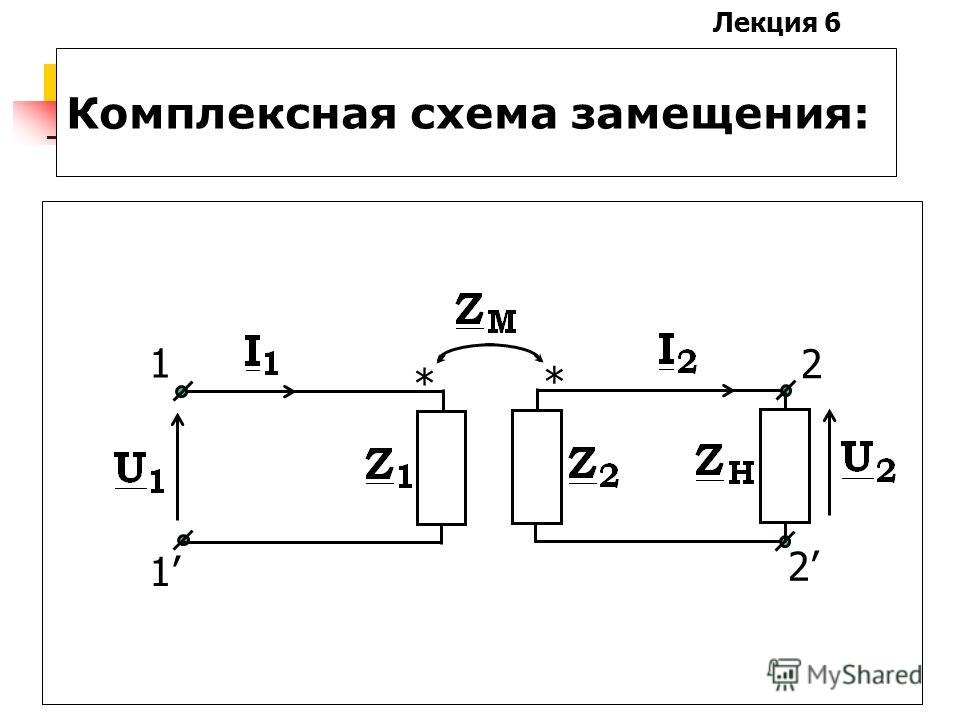 Полученное с помощью собственных векторов разбиение изображения на слои можно затем использовать для редактирования.
Полученное с помощью собственных векторов разбиение изображения на слои можно затем использовать для редактирования.
Обзор предложенного подхода
Описание модели
Рассмотрим метод создания семантически значимых слоёв пошагово:
1. Спектральная маска. Предложенный подход продолжает работу Левина и его коллег, которые впервые использовали матрицу Кирхгофа в задаче автоматического построения маски. Они строили матрицу L, которая задаёт попарное сходство между пикселями в некоторой локальной области. С помощью этой матрицы они минимизируют квадратичный функционал αᵀLα с заданными пользователем ограничениями, где α задаёт вектор значений прозрачности для всех пикселей данного слоя. Каждый мягкий контур является линейной комбинацией K собственных векторов, соответствующих наименьшим собственным значениям L, которая максимизирует так называемую разреженность маски.
2. Цветовая близость. Для вычисления признаков нелокальной цветовой близости исследователи генерируют 2500 суперпикселей и оценивают близость между каждым суперпикселем и всеми суперпикселями в окрестности радиусом 20% размера изображения. Использование нелокальной близости гарантирует, что области с очень похожими цветами останутся связными в сложных сценах, подобных изображённой ниже.
Использование нелокальной близости гарантирует, что области с очень похожими цветами останутся связными в сложных сценах, подобных изображённой ниже.
Нелокальная цветовая близость
3. Семантическая близость. Эта стадия позволяет выделять семантически связные области изображения. Семантическая близость поощряет объединение пикселей, которые принадлежат одному объекту сцены, и штрафует за объединение пикселей разных объектов. Здесь исследователи используют предыдущие достижения в области распознавания образов и вычисляют для каждого пикселя вектор признаков, коррелирующий с объектом, в который входит данный пиксель. Векторы признаков вычисляются с помощью нейросети, о чём мы поговорим далее более подробно. Семантическая близость, как и цветовая, определяется на суперпикселях. Однако, в отличие от цветовой близости, семантическая близость связывает только ближайшие суперпиксели, поощряя создание связных объектов. Сочетание нелокальной цветовой близости и локальной семантической близости позволяет создать слои, которые покрывают разъединённые в пространстве изображения фрагмента одного семантически связанного объекта (например, растительность, небо, другие типы фона).
Семантическая близость
4. Создание слоёв. На этом шаге с помощью вычисленных ранее близостей строится матрица L. Из этой матрицы извлекаются собственные векторы, соответствующие 100 наименьшим собственным значениям, а затем применяется алгоритм разреживания, который извлекает из них 40 векторов, по которым строятся слои. Затем количество слоёв ещё раз уменьшается с помощью алгоритма кластеризации k-means при k = 5. Это работает лучше, чем простое разреживание 100 собственных векторов до пяти, поскольку такое сильное сокращение размерности делает задачу переопределённой. Исследователи выбрали итоговое число контуров равным 5 и утверждают, что это разумное число для большинства изображений. Тем не менее, это число можно изменить вручную в зависимости от обрабатываемого изображения.
Мягкие контуры до и после группировки5. Семантические векторы признаков. Для вычисления семантической близости использовались векторы признаков, посчитанные с помощью нейросети.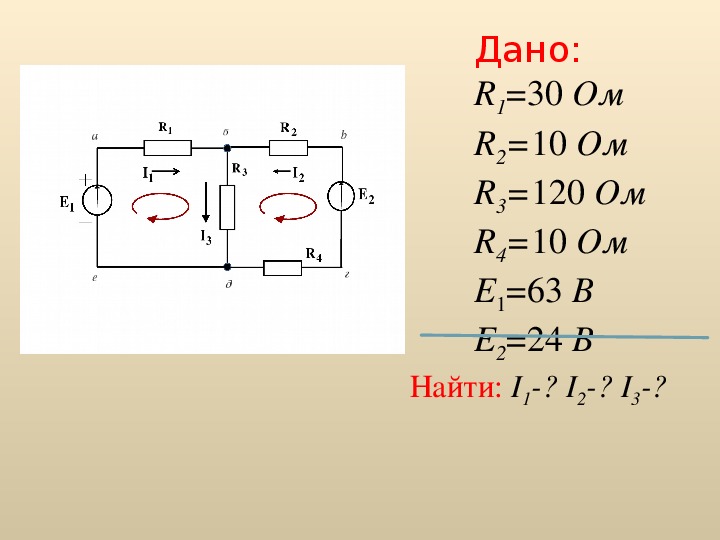 Основой нейросети стала DeepLab-ResNet-101, обученная на задаче предсказания метрики. При обучении поощрялась максимизация L2-расстояния между признаками разных объектов. Таким образом, нейросеть минимизирует расстояние между признаками, соответствующими одному классу, и максимизирует расстояние в другом случае.
Основой нейросети стала DeepLab-ResNet-101, обученная на задаче предсказания метрики. При обучении поощрялась максимизация L2-расстояния между признаками разных объектов. Таким образом, нейросеть минимизирует расстояние между признаками, соответствующими одному классу, и максимизирует расстояние в другом случае.
Качественное сравнение со схожими методами
Изображения, приведённые ниже, показывают результаты работы предложенного подхода (подписанные как «Our result») в сравнении с результатами наиболее близкого подхода мягкой сегментации — спектрального метода построения маски — и двумя state-of-the-art методами семантической сегментации: методом обработки сцен PSPNet и методом сегментации объектов Mask R-CNN.
Качественные сравнения мягкой семантической сегментации с другими подходамиМожно заменить, что PSPNet и Mask R-CNN склонны ошибаться на границах объектов, а мягкие контуры, построенные спектральным методом, часто заходят за границы объектов. При этом описанный метод полностью охватывает объект, не объединяя его с другими, и достигает высокой точности на краях, добавляя мягкие переходы, где это требуется. Однако стоит заметить, что семантические признаки, использованные в данном методе, не различают два разных объекта, принадлежащих к одному классу. В результате множественные объекты представлены на одном слое, что видно на примере изображений жирафов и коров.
Однако стоит заметить, что семантические признаки, использованные в данном методе, не различают два разных объекта, принадлежащих к одному классу. В результате множественные объекты представлены на одном слое, что видно на примере изображений жирафов и коров.
Редактирование изображений с помощью мягких семантических контуров
Ниже приведено несколько примеров применения мягких контуров для редактирования изображений и создания коллажей. Мягкие контуры можно использовать для применения конкретных изменений к разным слоям: добавления размытия, изображающего движение поезда (2), раздельной цветовой коррекции для людей и для фона (5, 6), отдельной стилизации для воздушного шара, неба, ландшафта и человека (8). Конечно, то же самое можно сделать с помощью созданных вручную масок или классических алгоритмов выделения контура, но с автоматическим выделением семантически значимых объектов такое редактирование становится значительно проще.
Использование мягкой семантической сегментации для редактирования изображений
Заключение
Данный метод автоматически создаёт мягкие контуры, соответствующие семантически значимым областям изображения, используя смесь высокоуровневой информации от нейронной сети и низкоуровневых признаков.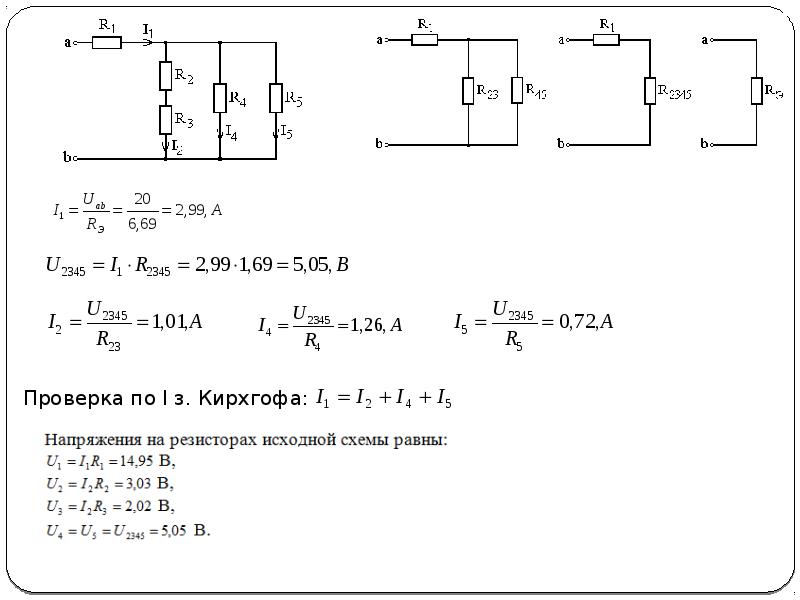 Однако у этого метода есть несколько ограничений. Во-первых, он относительно медленный: время обработки изображения с размерами 640 x 480–3–4 минуты. Во-вторых, этот метод не создаёт отдельные слои для разных объектов одного класса. И в-третьих, как показано ниже, этот метод может ошибиться на начальных этапах обработки в случаях, когда цвета объектов очень похожи (верхний пример), или во время объединения мягких контуров возле больших переходных областей (нижний пример).
Однако у этого метода есть несколько ограничений. Во-первых, он относительно медленный: время обработки изображения с размерами 640 x 480–3–4 минуты. Во-вторых, этот метод не создаёт отдельные слои для разных объектов одного класса. И в-третьих, как показано ниже, этот метод может ошибиться на начальных этапах обработки в случаях, когда цвета объектов очень похожи (верхний пример), или во время объединения мягких контуров возле больших переходных областей (нижний пример).
Случаи ошибок алгоритма
Тем не менее, мягкие контуры, созданные с помощью описанного метода, дают удобное промежуточное представление изображения, позволяющее тратить меньше времени и сил при редактировании изображений.
Топологические матрицы | энергетик
Вернутся в раздел ТОЭ
Топологию цепи в виде матриц называют топологическими матрицами. Выделяют три таких матрицы: узловую матрицу, контурную матрицу и матрицу сечений.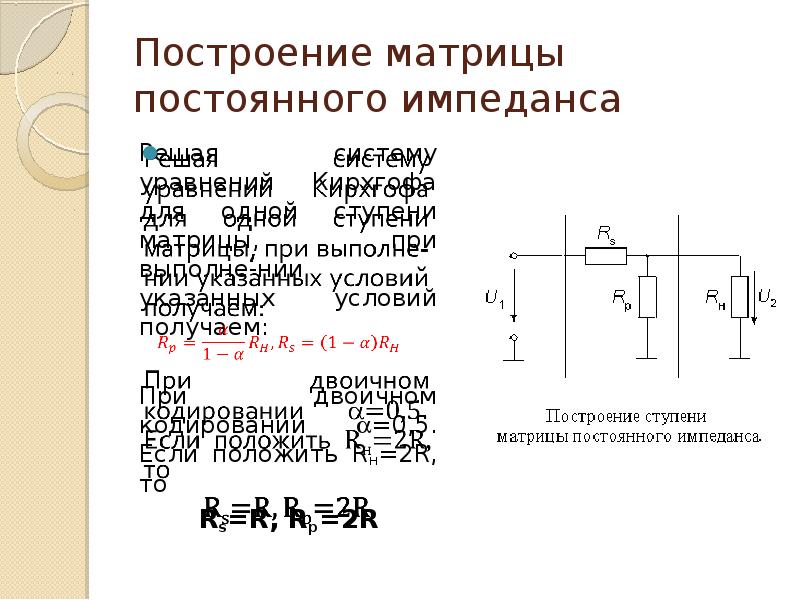
Автор уже коротко опубликовывал в разделе ТОЭ статью на тему Топология электрических сетей, тем не меняя возвращаясь к этой теме давайте вместе вспомним:
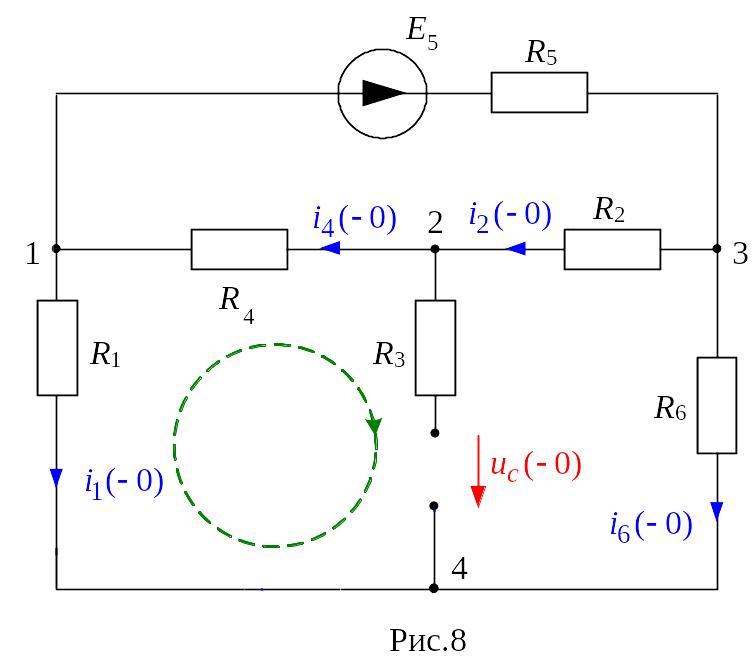
электрическая цепь характеризуется совокупностью элементов, из которых она состоит, и способом их соединения. Соединение элементов электрической цепи наглядно отображается ее схемой. Рассмотрим для примера две электрические схемы (рис. 1, 2), введя понятие ветви и узла.
Рис. 1 и 2
Рис. 3
Ветвью называется участок цепи, обтекаемый одним и тем же током.
Узел – место соединения трех и более ветвей.
Представленные схемы различны и по форме, и по назначению, но каждая из указанных цепей содержит по 6 ветвей и 4 узла, одинаково соединенных. Таким образом, в смысле геометрии (топологии) соединений ветвей данные схемы идентичны.
Топологические (геометрические) свойства электрической цепи не зависят от типа и свойств элементов, из которых состоит ветвь.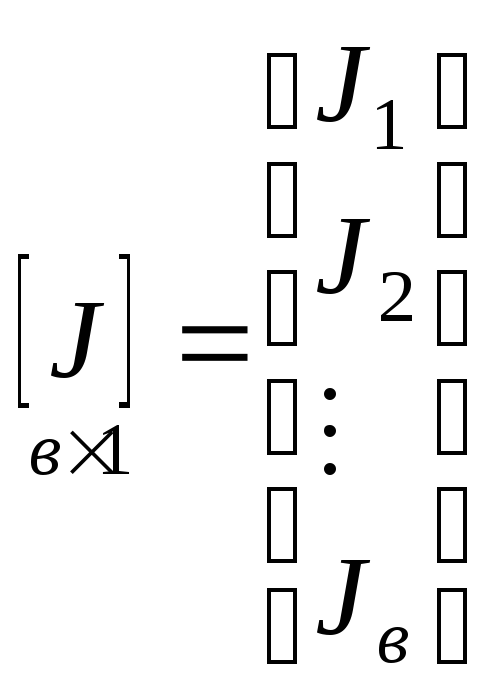 Поэтому целесообразно каждую ветвь схемы электрической цепи изобразить отрезком линии. Если каждую ветвь схем на рис. 1 и 2 заменить отрезком линии, получается геометрическая фигура, показанная на рис. 3.
Поэтому целесообразно каждую ветвь схемы электрической цепи изобразить отрезком линии. Если каждую ветвь схем на рис. 1 и 2 заменить отрезком линии, получается геометрическая фигура, показанная на рис. 3.
Условное изображение схемы, в котором каждая ветвь заменяется отрезком линии, называется графом электрической цепи. При этом следует помнить, что ветви могут состоять из каких-либо элементов, в свою очередь соединенных различным образом.
Отрезок линии, соответствующий ветви схемы, называется ветвью графа. Граничные точки ветви графа называют узлами графа. Ветвям графа может быть дана определенная ориентация, указанная стрелкой. Граф, у которого все ветви ориентированы, называется ориентированным.
Подграфом графа называется часть графа, т.е. это может быть одна ветвь или один изолированный узел графа, а также любое множество ветвей и узлов, содержащихся в графе.
В теории электрических цепей важное значение имеют следующие подграфы:
- Путь – это упорядоченная последовательность ветвей, в которой каждые две соседние ветви имеют общий узел, причем любая ветвь и любой узел встречаются на этом пути только один раз.
 Например, в схеме на рис. 3 ветви 2-6-5; 4-5; 3-6-4; 1 образуют пути между одной и той же парой узлов 1 и 3. Таким образом, путь – это совокупность ветвей, проходимых непрерывно.
Например, в схеме на рис. 3 ветви 2-6-5; 4-5; 3-6-4; 1 образуют пути между одной и той же парой узлов 1 и 3. Таким образом, путь – это совокупность ветвей, проходимых непрерывно. - Контур – замкнутый путь, в котором один из узлов является начальным и конечным узлом пути. Например, для графа по рис. 3 можно определить контуры, образованные ветвями 2-4-6; 3-5-6; 2-3-5-4. Если между любой парой узлов графа существует связь, то граф называют связным.
- Дерево – это связный подграф, содержащий все узлы графа, но ни одного контура. Примерами деревьев для графа на рис. 3 могут служить фигуры на рис. 4.
Рис. 4
- Ветви связи (дополнения дерева) – это ветви графа, дополняющие дерево до исходного графа.
Если граф содержит m узлов и n ветвей, то число ветвей любого дерева , а числа ветвей связи графа .
- Сечение графа – множество ветвей, удаление которых делит граф на два изолированных подграфа, один из которых, в частности, может быть отдельным узлом.

Сечение можно наглядно изобразить в виде следа некоторой замкнутой поверхности, рассекающей соответствующие ветви. Примерами таких поверхностей являются для нашего графа на рис. 3 S1 иS2 . При этом получаем соответственно сечения, образованные ветвями 6-4-5 и 6-2-1-5.
С понятием дерева связаны понятия главных контуров и сечений:
- главный контур – контур, состоящий из ветвей дерева и только одной ветви связи;
- главное сечение – сечение, состоящее из ветвей связи и только одной ветви дерева.
Узловая матрица (матрица соединений) – это таблица коэффициентов уравнений, составленных по первому закону Кирхгофа. Строки этой матрицы соответствуют узлам, а столбцы – ветвям схемы. Для графа на рис. 3 имеем число узлов m=4 и число ветвей n=6. Тогда запишем матрицу Ан, принимая, что элемент матрицы (i –номер строки; j –номер столбца) равен 1, если ветвь j соединена с узлом i и ориентирована от него, -1, если ориентирована к нему, и 0, если ветвь j не соединена с узломi . Сориентировав ветви графа на рис. 3, получим:
Сориентировав ветви графа на рис. 3, получим:
Данная матрица АН записана для всех четырех узлов и называется неопределенной. Следует указать, что сумма элементов столбцов матрицы АН всегда равна нулю, так как каждый столбец содержит один элемент +1 и один элемент -1, остальные нули.
Обычно при расчетах один (любой) заземляют. Тогда приходим к узловой матрице А (редуцированной матрице), которая может быть получена из матрицы АН путем вычеркивания любой ее строки. Например, при вычеркивании строки “4” получим
Число строк матрицы А равно числу независимых уравнений для узлов , т.е. числу уравнений, записываемых для электрической схемы по первому закону Кирхгофа. Итак, введя понятие узловой матрицы А, перейдем к первому закону Кирхгофа.
Первый закон Кирхгофа
Обычно первый закон Кирхгофа записывается для узлов схемы, но, строго говоря, он справедлив не только для узлов, но и для любой замкнутой поверхности, т.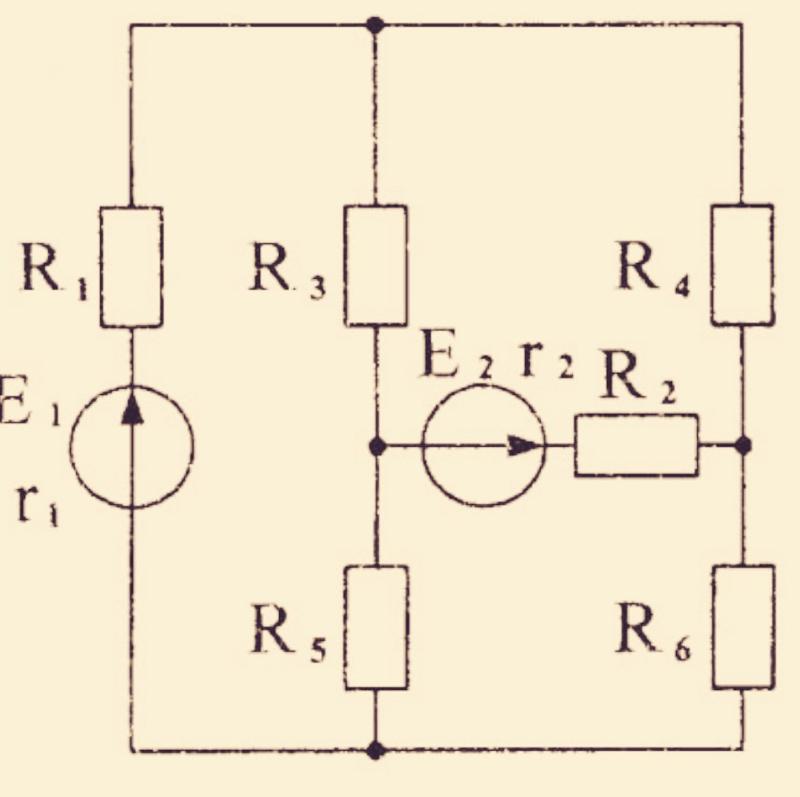 е. справедливо соотношение:
е. справедливо соотношение:
(1)
где — вектор плотности тока; — нормаль к участку dS замкнутой поверхности S.
Первый закон Кирхгофа справедлив и для любого сечения. В частности, для сечения S2 графа на рис. 3, считая, что нумерация и направления токов в ветвях соответствуют нумерации и выбранной ориентации ветвей графа, можно записать:
I1 + I2 — I5 — I6 = 0.
Поскольку в частном случае ветви сечения сходятся в узле, то первый закон Кирхгофа справедлив и для него. Пока будем применять первый закон Кирхгофа для узлов, что математически можно записать, как:
т.е. алгебраическая сумма токов ветвей, соединенных в узел, равна нулю.
При этом при расчетах уравнения по первому закону Кирхгофа записываются для (m-1) узлов, так как при записи уравнений для всех m узлов одно (любое) из них будет линейно зависимым от других, т.е.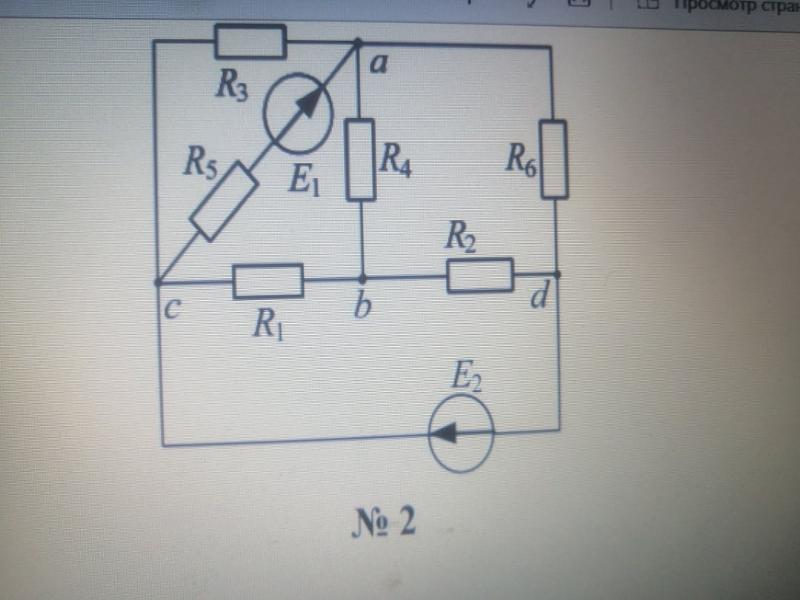 не дает дополнительной информации.
не дает дополнительной информации.
Введем столбцовую матрицу токов ветвей
(2)
Тогда первый закон Кирхгофа в матричной форме записи имеет вид:
– где O — нулевая матрица-столбец. Как видим, в качестве узловой взята матрица А, а не АН, т.к. с учетом вышесказанного уравнения по первому закону Кирхгофа записываются для (m-1) узлов.
В качестве примера запишем для схемы на рис. 3
Отсюда для первого узла получаем
,
что и должно иметь место.
- Контурная матрица (матрица контуров) – это таблица коэффициентов уравнений, составленных по второму закону Кирхгофа. Строки контурной матрицы В соответствуют контурам, а столбцы – ветвям схемы.
Элемент bijматрицы В равен 1, если ветвь j входит в контур i и ее ориентация совпадает с направлением обхода контура, -1, если не совпадает с направлением обхода контура, и 0, если ветвь j не входит в контур i.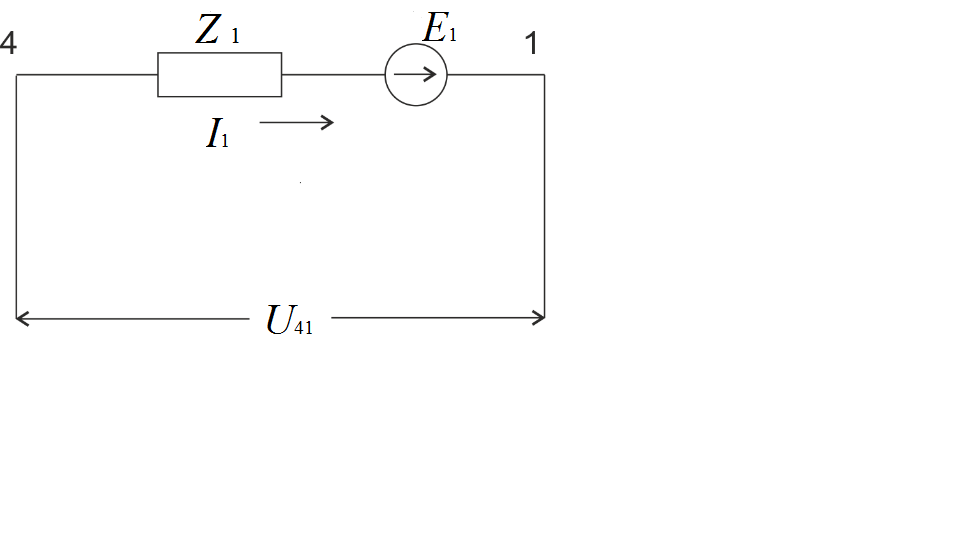
Матрицу В, записанную для главных контуров, называют матрицей главных контуров. При этом за направление обхода контура принимают направление ветви связи этого контура. Выделив в нашем примере (см. рис. 5) дерево, образуемое ветвями 2-1-4, запишем коэффициенты для матрицы В.
Перейдем теперь ко второму закону Кирхгофа
Под напряжением на некотором участке электрической цепи понимается разность потенциалов между крайними точками этого участка, т.е.
(4) |
Просуммируем напряжения на ветвях некоторого контура:
Поскольку при обходе контура потенциал каждой i-ой точки встречается два раза, причем один раз с “+”, а второй – с “-”, то в целом сумма равна нулю.
Таким образом, второй закон Кирхгофа математически записывается, как:
(5) |
— и имеет место следующую формулировку: алгебраическая сумма напряжений на зажимах ветвей (элементов) контура равна нулю. При этом при расчете цепей с использованием законов Кирхгофа записывается независимых уравнений по второму закону Кирхгофа, т.е. уравнений, записываемых для контуров, каждый из которых отличается от других хотя бы одной ветвью. Значение топологического понятия “дерева”: дерево позволяет образовать независимые контуры и сечения и, следовательно, формировать независимые уравнения по законам Кирхгофа. Таким образом, с учетом (m-1) уравнений, составленных по первому закону Кирхгофа, получаем систему из уравнений, что равно числу ветвей схемы и, следовательно, токи в них находятся однозначно.
При этом при расчете цепей с использованием законов Кирхгофа записывается независимых уравнений по второму закону Кирхгофа, т.е. уравнений, записываемых для контуров, каждый из которых отличается от других хотя бы одной ветвью. Значение топологического понятия “дерева”: дерево позволяет образовать независимые контуры и сечения и, следовательно, формировать независимые уравнения по законам Кирхгофа. Таким образом, с учетом (m-1) уравнений, составленных по первому закону Кирхгофа, получаем систему из уравнений, что равно числу ветвей схемы и, следовательно, токи в них находятся однозначно.
Введем столбцовую матрицу напряжений ветвей
Тогда второй закон Кирхгофа в матричной форме записи имеет вид
BU = 0. | (6) |
В качестве примера для схемы рис. 5 имеем
откуда, например, для первого контура получаем
,
что и должно иметь место.
Если ввести столбцовую матрицу узловых потенциалов
причем потенциал последнего узла , то матрица напряжений ветвей и узловых потенциалов связаны соотношением
U=AТ | (7) |
где AТ — транспонированная узловая матрица.
Для определения матрицы В по известной матрице А=АДАС , где АД – подматрица, соответствующая ветвям некоторого дерева, АС — подматрица, соответствующая ветвям связи, может быть использовано соотношение В= (-АТС А-1ТД1).
- Матрица сечений – это таблица коэффициентов уравнений, составленных по первому закону Кирхгофа для сечений.
 Ее строки соответствуют сечениям, а столбцы – ветвям графа.
Ее строки соответствуют сечениям, а столбцы – ветвям графа.
Матрица Q , составленная для главных сечений, называется матрицей главных сечений. Число строк матрицы Q равно числу независимых сечений.
Элемент qij матрицы Q равен 1, если ветвь входит в i-е сечение и ориентирована согласно направлению сечения (за положительное направление сечения принимают направление ветви дерева, входящей в него), -1, если ориентирована противоположно направлению сечения, и 0, если ветвьj не входит в i-е сечение.
В качестве примера составим матрицу Q главных сечений для графа на рис. 5. При указанной на рис. 5 ориентации ветвей имеем
В заключение отметим, что для топологических матриц А, В и Q, составленных для одного и того же графа, выполняются соотношения
АВТ= 0; | (8) |
QВТ= 0, | (9) |
которые, в частности, можно использовать для проверки правильности составления этих матриц.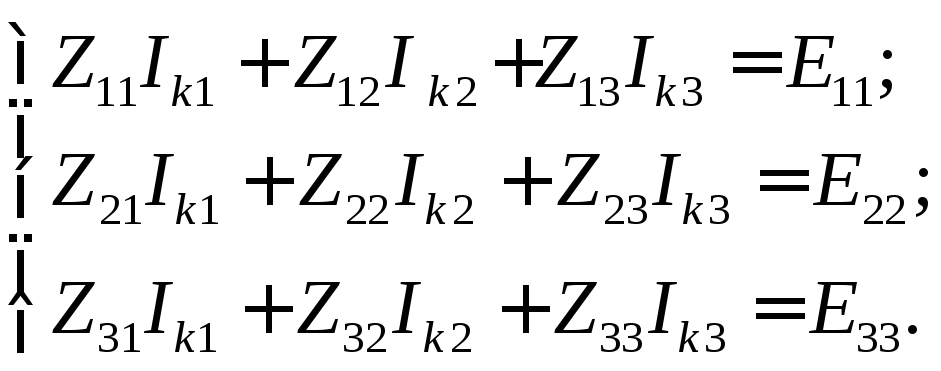 Здесь 0 – нулевая матрица порядка .
Здесь 0 – нулевая матрица порядка .
Приведенные уравнения позволяют сделать важное заключение: зная одну из топологических матриц, по ее структуре можно восстановить остальные.
Вернутся в раздел ТОЭ
Теорема Кирхгофа — алгоритмы конкурентного программирования
Проблема: Вам дан связанный неориентированный граф (с возможным множеством ребер), представленный с помощью матрицы смежности. Найдите количество различных остовных деревьев этого графа.
Следующая формула была доказана Кирхгофом в 1847 году.
Теорема Кирхгофа о матричном дереве
Пусть \ (A \) — матрица смежности графа: \ (A_ {u, v} \) — количество ребер между \ (u \) и \ (v \).3) \) методом Гаусса.
Доказательство этой теоремы довольно сложно и здесь не приводится; план доказательства и варианты теоремы для графов без кратных ребер и для ориентированных графов см. в Википедии. j | }.{(i, j)} \) — это матрица с удаленными двумя строками и двумя столбцами \ (i \) и \ (j \).
j | }.{(i, j)} \) — это матрица с удаленными двумя строками и двумя столбцами \ (i \) и \ (j \).
Теорема Кирхгофа придает этой формуле геометрический смысл.
Практические задачи
Отозванная статья: О матрице Кирхгофа, новом индексе Кирхгофа и энергии Кирхгофа | Journal of Inequalities and Applications
Известно, что существуют довольно широкие приложения, основанные на собственных значениях матрицы смежности в химии [8, 9]. Фактически, один из химически (а также математически) наиболее интересных графов-спектров, основанный на количествах в графике энергии, определяется следующим образом.
Пусть G — (n, m) -граф и пусть A (G) — его матрица смежности, имеющая собственные значения λ1, λ2,…, λn. Отметим, что в [10] эти λ называются собственными значениями графа G и формируют его спектр. Тогда энергия E (G) G определяется как сумма абсолютных значений этих собственных значений как
Мы можем обратиться к [11–13] за более подробной информацией и новыми конструкциями по энергии графа. Ввиду очевидного успеха концепции энергии графа и из-за быстрого уменьшения открытых математических проблем в ее теории, энергии, основанные на собственных значениях других матриц графов, были введены очень широко.Среди них энергия Лапласа LE (G), относящаяся к матрице Лапласа, может рассматриваться как первая [14]. Отметим, что теория инвариантов энергоподобных графов была впервые введена Консонни и Тодескини в [15]. Позже Никифоров [16] распространил определение энергии на произвольные матрицы, что сделало возможным представление энергии падения [17] на основе матрицы падения, и т. Д.
Ввиду очевидного успеха концепции энергии графа и из-за быстрого уменьшения открытых математических проблем в ее теории, энергии, основанные на собственных значениях других матриц графов, были введены очень широко.Среди них энергия Лапласа LE (G), относящаяся к матрице Лапласа, может рассматриваться как первая [14]. Отметим, что теория инвариантов энергоподобных графов была впервые введена Консонни и Тодескини в [15]. Позже Никифоров [16] распространил определение энергии на произвольные матрицы, что сделало возможным представление энергии падения [17] на основе матрицы падения, и т. Д.
Как и в случае других энергий, упомянутых в предыдущем абзаце, мы можем определить новую энергию, рассматривая матрицу Кирхгофа, приведенную в (2), следующим образом.
Если G является (n, m) -графом, то энергия Кирхгофа из G , обозначенная EKf (G), равна
, где каждое δi (с порядком δ1≥δ2≥ ⋯ ≥δn) обозначает собственные значения матрицы Кирхгофа KfA (G). В основном, эти собственные значения называются собственными значениями K — для G .
В основном, эти собственные значения называются собственными значениями K — для G .
3.1. Границы для энергии Кирхгофа
В этом подразделе мы в основном представляем верхние и нижние границы для энергии Кирхгофа, определенной в (6).
Первый результат следующий.
Теорема 1 Пусть G будет графом с n≥2 вершинами . Затем
, где κ — сумма квадратов элементов матрицы Кирхгофа KfA (G).
Доказательство Мы имеем, что
EKf (G) = ∑i = 1n | δi | и i = 1nδi2 = κ = 2∑1≤i По неравенству Коши-Шварца получаем EKf (G) ≤ | δ1 | + | δn | + (n − 2) ∑i = 2n − 1δi2 = | δ1 | + | δn | + (n − 2) (κ − δ12 − δn2). Рассмотрим функцию f (x, y) = x + y + (n − 2) (κ − x2 − y2), где x> 0, y> 0. Теперь наша цель — найти максимальное значение f (x, y). Для этого нам нужно вычислить производные fx = 1 − xn − 2κ − x2 − y2, fy = 1 − yn − 2κ − x2 − y2, fxx = — (κ − y2) n − 2 (κ− x2 − y2) 3/2, fxy = fyx = −xyn − 2 (κ − x2 − y2) 3 / 2andfyy = — (κ − x2) n − 2 (κ − x2 − y2) 3/2. Простым вычислением становится ясно, что из равенства fx = fy = 0 следует x = y = κn, а затем для этого равенства между x и y также верно, что fxx <0andfxxfyy − fxy2 = (N − 2) (κ − x2 − y2) (κ − x2 − y2) 3> 0. Приведенные выше вычисления фактически показывают, что f (x, y) имеет максимальное значение при x = y = κn, а требуемое максимальное значение этой функции равно 2κn + (n − 2) (κ − 2κn) = nκ. Отсюда и результат. □ Следующая лемма необходима для других наших результатов, которые приводятся в этой статье. Лемма 1 Пусть G будет связным графом (n, m) — и пусть δ1, δ2,…, δn будут собственными значениями K — G . Затем и ∑i = 1nδi2 = 2∑1≤i (7) Доказательство Очевидно, что ∑i = 1nδi = Tr [KfA (G)] = ∑i = 1nkii = 0. ∑i = 1nδi2 = Tr [KfA (G)] 2 = ∑i = 1n∑j = 1n (kij) 2 = 2∑1≤i по мере необходимости. □ Теорема 2 Если G является связанным (n, m) — график , , то 2∑1≤i Доказательство В неравенстве Коши-Шварца (∑i = 1naibi) 2≤ (∑i = 1nai2) (∑i = 1nbi2), если мы выберем ai = 1 и bi = | δi |, то получим (∑ я = 1n | δi |) 2≤n∑i = 1nδi2, , из которых EKf (G) 2≤2n∑1≤i Следовательно, это дает верхнюю оценку для EKf (G). Теперь для нижней оценки EKf (G) легко получить неравенство EKf (G) 2 = (∑i = 1n | δi |) 2≥∑i = 1n | δi | 2 = 2∑ 1≤i , что дает непосредственно требуемую нижнюю границу. Следует отметить, что существует второй способ доказательства верхней оценки, который может быть представлен следующим образом. Рассмотрим сумму M = ∑i = 1n∑j = 1n (| δi | — | δj |) 2. Прямым вычислением получаем M = 2n∑i = 1n | δi | 2−2 (∑i = 1n | δi | ∑j = 1n | δj |). Из (7) и определения EKf (G) следует, что M = 4n∑1≤i Здесь, поскольку M≥0, имеем EKf (G) ≤2n∑1≤i Отсюда и результат.□ Далее мы представляем новую нижнюю оценку, которая лучше, чем нижняя оценка, приведенная в теореме 2. Теорема 3 Пусть G будет связным графом (n, m) — и пусть ∇ будет абсолютным значением определителя матрицы Кирхгофа KfA (G). Затем 2∑1≤i Доказательство В свете теоремы 2, если мы покажем справедливость нижней оценки, то это завершит доказательство. По определению энергии Кирхгофа, данному в (6), и равенству в (7) имеем [EKf (G)] 2 = (∑i = 1n | δi |) 2 = ∑i = 1n | δi | 2 + 2∑1≤i (8) Поскольку для неотрицательных значений среднее арифметическое не меньше среднего геометрического, имеем 1n (n − 1) ∑i ≠ j | δi || δj | ≥ (∏i ≠ j | δi || δj | ) 1 / n (n − 1) = (∏i = 1n | δi | 2 (n − 1)) 1 / n (n − 1) = ∏i = 1n | δi | 2 / n = ∇2 / n. (9) После этого, комбинируя уравнения (8) и (9), мы получаем требуемую нижнюю границу. □ Теорема 4 Если G является связанным (n, m) — график , , то EKf (G) ≤2n∑1≤i (10) Доказательство Мы применяем стандартную процедуру (см., Например, [18, 19]), чтобы получить такие оценки сверху. Применяя неравенство Коши-Шварца к двум (n − 1) векторам (1,1,…, 1) и (| δ2 |, | δ2 |,…, | δn |), где каждый δi (2≤ i≤n) является собственным значением K , имеем (∑i = 2n | δi |) 2≤ (n − 1) (∑i = 2n | δi | 2), (EKf (G) −δ1 ) 2≤ (n − 1) (2∑1≤i Теперь рассмотрим функцию f (x) = x + (n − 1) (2∑1≤i Фактически, имея в виду δ1≥1, мы полагаем δ1 = x. Используя ∑i = 1nδi2 = 2∑1≤i получаем, что x2 = δ12≤2∑1≤i Другими словами, x≤2∑1≤i x = 2n∑1≤i Следовательно, f — убывающая функция в интервале 2n∑1≤i и 2n∑1≤i Следовательно, f (δ1) ≤f (2n∑1≤i , поэтому неравенство в (10) выполнено. □ Результаты поиска 115 экспонатов Вычислить тензор Кирхгофа (лапласиан) произвольного гиперграфа Вычислить гиперграф с заданным тензором Кирхгофа (лапласианом) Получить диагонализованную матрицу заданной матрицы Вычислить матричный полином Создает антидиагональную матрицу по заданной антидиагональной Дайте матрицу кофакторов для данной входной матрицы Возвращает псевдослучайную матрицу заданного вида, типа и размера Оцените p-норму Гёльдера числовой матрицы Вычислить знаковую функцию матрицы Сгенерируйте матрицу Безу двух одномерных многочленов Сгенерируйте матрицу Сильвестра двух одномерных многочленов Вычислить матрицу Карлемана функции Сгенерируйте товарищескую матрицу, соответствующую ортогональному полиномиальному ряду Получите расширенную матрицу системы линейных уравнений Сгенерируйте матрицу Гурвица одномерного многочлена Вычислить матрицу Вайнгартена поверхности Сгенерируйте матрицу Якоби, соответствующую ортогональному многочлену Возвращает матрицу коэффициентов системы уравнений. Получите матрицу с 1 в выбранной позиции и нулями в другом месте Вычислить матрицу Якоби векторной функции относительно списка переменных Вычислить матрицу Гессе функции относительно списка переменных Получите неприводимое групповое представление SU (2) для заданного углового момента Сгенерируйте обобщенную сопутствующую матрицу Фидлера одномерного полинома Сгенерируйте трехдиагональную сопутствующую матрицу одномерного полинома Найдите матрицу смежности вершин гиперграфа Оценить матрицы Дирака в любом измерении Преобразование единичного кватерниона в эквивалентную матрицу вращения Преобразуйте матрицу вращения в эквивалентный единичный кватернион Создайте блочно-диагональную матрицу из подматриц Вернуть псевдослучайную унимодулярную матрицу Вычислить матрицу Кэли-Менгера симплекса Создайте двоичную матрицу с повернутой эллиптической областью единиц Вычислить частичный след матрицы Вычислить граничную кривую поля значений матрицы Сгенерируйте сопутствующую матрицу для интерполяционного полинома Ньютона заданного набора точек Вычислить минимальный многочлен квадратной матрицы Найдите нулевые значения и векторы для пучка набора квадратных матриц Проверяет, является ли матрица антидиагональной матрицей Симметричная трехдиагональная матрица для квадратуры Гаусса Изменение матрицы путаницы путем стохастического переворачивания результатов классификации Разложите матрицу на два неотрицательных матричных фактора Восстановить матрицу Якоби из списка пар абсцисс-вес Сгенерируйте ортогональную полиномиальную матрицу Вандермонда, соответствующую заданному вектору Создайте функцию, которая при заданном пороговом значении вероятности создает матрицу неточностей. Вычислить инверсию трехдиагональной матрицы Вычислить свойства пространства строк матрицы Вычислить свойства пространства столбцов матрицы Вычислить пфаффиан антисимметричной (кососимметричной) матрицы Вычислить косо-трехдиагональное разложение антисимметричной матрицы Тридиагонализируйте антисимметричную (кососимметричную) матрицу с помощью алгоритма Парлетта – Рейда. Преобразуйте эрмитово определенный матричный пучок в матрицу с такими же собственными значениями Заменим диагональ произвольной матрицы нулями Дайте сопряженную матрицу квадратной матрицы Вычислить нулевое значение матрицы Добавить столбец справа от матрицы Добавить столбец слева от матрицы Найдите матрицу унимодулярного преобразования, соответствующую решеточной матрице грамиана Численно оценить градиент функции, суммированной по собственным значениям матрицы, относительно параметров матрицы Симметрично переупорядочить строки и столбцы квадратной матрицы Вычислить разложение Смита матрицы одномерных многочленов Получите кофактор матрицы Постройте матрицу точечной диаграммы Вычислить разложение Попова матрицы одномерных многочленов Вычислить оператор формы на поверхности Найдите определитель ковариационной матрицы Разложите матрицу на факторы матрицы независимого анализа компонентов Преобразуйте данные так, чтобы их ковариационная матрица была единичной матрицей. Найдите экземпляр n-мерных векторов, которые создают заданную матрицу расстояний Вычислить полное QR-разложение матрицы Вычислить рациональное разложение Холецкого матрицы Вычислить разложение Аасена симметричной матрицы Вычислить гауссовское разложение Хессенберга матрицы Вычислить разложение Эрмита матрицы одномерных многочленов Определите, является ли набор векторов линейно независимым Возврат равномерно распределенных случайных вращений в кватернионной форме Найдите перестановку, которая минимизирует матричную сумму Дайте антидиагональ матрицы Покажите диски Гершгорина квадратной матрицы Эффективная с точки зрения памяти форма вычисления нулевого пространства матрицы по модулю 2 Вычислить корреляционную матрицу первого порядка из исходной корреляционной матрицы Разложите вектор на линейную комбинацию набора векторов Определите уравнения согласованности, необходимые для того, чтобы система линейных уравнений имела решение Вычислить полярное разложение матрицы Получите полную вариацию матрицы Генерация осевого угла трехмерной матрицы вращения Вычислить определитель Гессе функции по списку переменных Представьте распределение Уишарта Приближаем числовую матрицу как сумму произведений Кронекера Вычислить базис Грёбнера и матрицу преобразования входных полиномов в базис Получить симплексную медиану элементов матрицы Найдите эллипсоидальные точки квартилей матрицы Запишите квадратичное выражение в виде суммы квадратов, исключив смешанные члены, а затем завершив квадраты Вычислить гиперграф с указанным тензором смежности Вычислить тензор смежности произвольного гиперграфа Модель квантового клеточного автомата, которая развивает тензорное произведение набора исходных кубитов с использованием произвольных композиций унитарных операторов за конечное число шагов. Вычислить упругие свойства материала с заданным тензором упругости (матрицей жесткости) Вычислить сокращенный базис для набора векторов вместе с унимодулярной матрицей, которая преобразует векторы в сокращенный базис Возвращает базис для подпространства, охватываемого столбцами матрицы Получить позиции столбцов, которые являются сводными столбцами матрицы Отображение квадратной матрицы в формате судоку-головоломки Выполнение матричных операций над конечным полем Преобразование гиперграфа в граф с той же матрицей расстояний Возвращает базис для подпространства, охватываемого строками матрицы Вычислить контрольные точки кривой Безье, которая интерполирует заданный набор точек. Найдите эффекты строк и столбцов в матрице данных путем многократного вычитания медианы Укажите суммы записей по возрастающим диагоналям квадратной матрицы. Визуализируйте собственные векторы матрицы 2 x 2 или 3 x 3 Вычислить матрицу значений глубины скважины, представляющую диффузор с квадратичным остатком. Эффективная для памяти форма решения линейных систем по модулю 2 Подобно ArrayQ, за исключением того, что он позволяет создавать рваные коллекции вложенных списков. Красиво форматируйте данные в различных структурах в формате сетки Вычислить результат Диксона относительно набора многочленов и переменных Вычислить статистику хи-квадрат, отражающую однородность переходной матрицы цепи Маркова за несколько периодов времени. Решить ортогональную полиномиальную линейную систему Вандермонда Модельные эксперименты по интерференции и дифракции непараксиального оптического поля при произвольной пространственной когерентности Тип Имя Последнее сообщение фиксации Время фиксации Теорема о матричном дереве — это формула для количества остовных деревьев графа в терминах определителя определенной матрицы. Теорема Кирхгофа опирается на понятие матрицы Лапласа графа, которая равна разности между матрицей степеней графа (диагональной матрицей со степенями вершин на диагоналях) и ее матрицей смежности ((0,1) -матрица с 1 в местах, соответствующих элементам, в которых вершины смежны, и 0 в противном случае). Ссылки:
[1] Ричард П. Стэнли, ТЕМЫ АЛГЕБРАИЧЕСКИХ КОМБИНАТОРИЙ. Версия от 1 февраля 2013 г.
[2] Тутте, У. Т. (2001), Теория графов, Cambridge University Press, стр. 138, ISBN 978-0-521-79489-3. В математической области теории графов теорема Кирхгофа или теорема Кирхгофа о матричном дереве, названная в честь Густава Кирхгофа, представляет собой теорему о количестве остовных деревьев в графе, показывающую, что это число может быть вычислено за полиномиальное время как определитель лапласианской матрицы график. Компьютерное моделирование образования трифункциональных и тетрафункциональных полидиметил-силоксановых сетей, которые сшиваются путем конденсации телехелических цепей с многофункциональными сшивающими агентами, было выполнено на системах, содержащих до 1.05 × 10 6 цепей. Спектры собственных значений матриц Кирхгофа для этих сетей были оценены на двух уровнях аппроксимации: (1) включение всех мод средней цепи и (2) подавление мод средней цепи. Используя метод рекурсии Хейдока и Некса, мы смогли эффективно диагонализовать матрицы с 730 498 строками и столбцами без фактического построения матриц такого размера. Маленькие собственные значения были вычислены с использованием алгоритма Ланцоша. Мы демонстрируем следующие результаты: (1) наименьшие собственные значения (с подавленными цепными модами) изменяются как μ — 2 / 3 для достаточно больших μ, где μ — количество переходов в сети; (2) спектры собственных значений матриц Кирхгофа хорошо описываются теорией Маккея для случайных регулярных графов в диапазоне больших собственных значений, но есть значительные отклонения в области малых собственных значений, где вычисленные спектры имеют гораздо больше малых собственных значений, чем случайные регулярные графики; (3) наименьшие собственные значения изменяются как n -1. ПОКАЗЫВАЕТ 1–10 ИЗ 29 ССЫЛКИ СОРТИРОВАТЬ по релевантности Статьи, на которые оказали наибольшее влияние Последнее время Об энергии падения графа (G) и энергия падения IE (G) графика — это недавно предложенные величины, равные, соответственно, сумме квадратных корней из… Развернуть Расстояние сопротивления и нормализованный лапласовский спектр Атомное ветвление в молекулах Определена теоретико-графическая мера расширенного атомного разветвления, которая учитывает влияние всех атомов в молекуле, придавая больший вес ближайшим соседям. Он основан на… Развернуть Энергия графа: старые и новые результаты Пусть G — граф, имеющий n вершин и m ребер. Энергия G, обозначенная E = E (G), является суммой абсолютных значений собственных значений G. Связь между E и полным электроном… Развернуть Энергия графика Аннотация Энергия, E (G) простого графа G определяется как сумма абсолютных значений собственных значений графа G.Если G — k-регулярный граф с n вершинами, то E (G) ⩽k + k (n − 1) (n − k) = B 2 и это… Развернуть Характеристика степени укладки белков Теория графов Новые спектральные индексы для описания молекул Предлагаются два семейства молекулярных дескрипторов, основанные на новых функциях спектра молекул, полученных из любой молекулярной матрицы M (w), рассчитанной по любой схеме взвешивания w. Первый класс… Развернуть Об энергии Лапласа графов
 Более того, для i = 1,2,…, n (i, i) -элемент [KfA (G)] 2 равен ∑j = 1nkijkji = ∑j = 1n (kij) 2. Отсюда получаем
Более того, для i = 1,2,…, n (i, i) -элемент [KfA (G)] 2 равен ∑j = 1nkijkji = ∑j = 1n (kij) 2. Отсюда получаем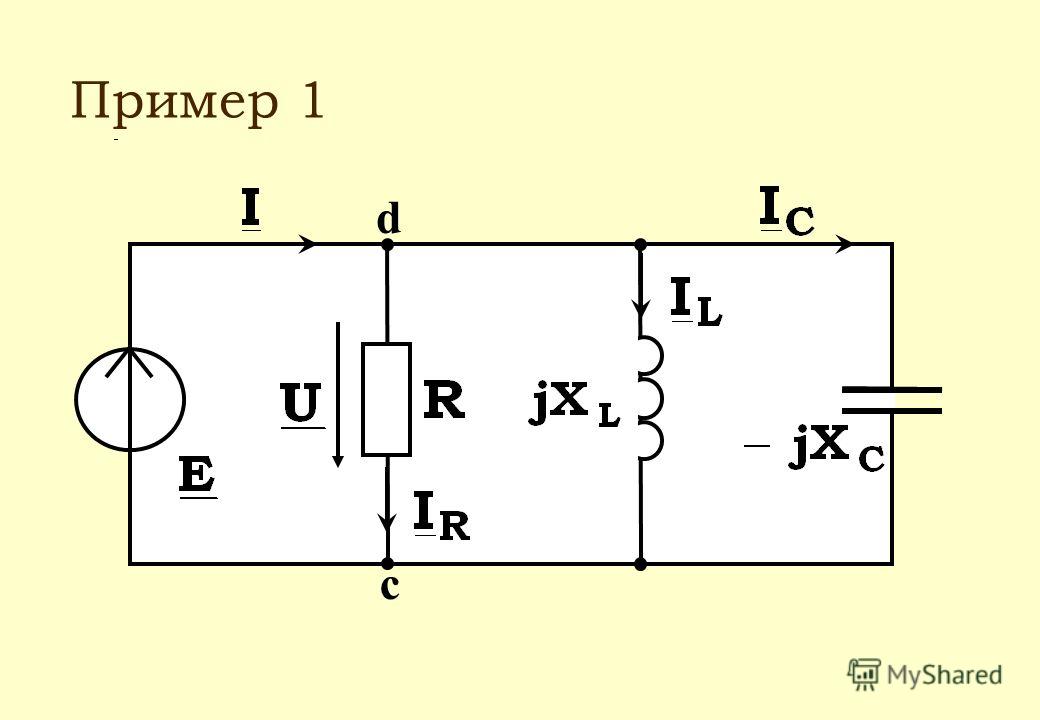
матрица / индекс Кирхгофа | Система ресурсов Wolfram
Ресурс функции: & emsp14;
KirchhoffTensor
Ресурс функции: & emsp14;
Кирхгоф Гиперграф
Ресурс функции: & emsp14;
ДиагонализацияMatrix
Ресурс функции: & emsp14;
Матрица Полином
Ресурс функции: & emsp14;
AntidiagonalMatrix
Ресурс функции: & emsp14;
КофакторMatrix
Ресурс функции: & emsp14;
RandomMatrix
Ресурс функции: & emsp14;
MatrixNorm
Ресурс функции: & emsp14;
MatrixSign
Ресурс функции: & emsp14;
БезоутМатрикс
Ресурс функции: & emsp14;
Сильвестр Матрикс
Ресурс функции: & emsp14;
Карлеман Матрица
Ресурс функции: & emsp14;
Товарищ Матрица
Ресурс функции: & emsp14;
AugmentedMatrix
Ресурс функции: & emsp14;
HurwitzMatrix
Ресурс функции: & emsp14;
WeingartenMatrix
Ресурс функции: & emsp14;
JacobiMatrix
Ресурс функции: & emsp14;
CoefficientMatrix

Ресурс функции: & emsp14;
UnitMatrix
Ресурс функции: & emsp14;
Якобиан Матрица
Ресурс функции: & emsp14;
HessianMatrix
Ресурс функции: & emsp14;
WignerMatrix
Ресурс функции: & emsp14;
ОбобщенныйFiedlerMatrix
Ресурс функции: & emsp14;
Трехдиагональный Спутник Матрица
Ресурс функции: & emsp14;
HypergraphAdjacencyMatrix
Ресурс функции: & emsp14;
DiracMatrix
Ресурс функции: & emsp14;
QuaternionToRotationMatrix
Ресурс функции: & emsp14;
RotationMatrixToQuaternion
Ресурс функции: & emsp14;
БлокDiagonalMatrix
Ресурс функции: & emsp14;
RandomUnimodularMatrix
Ресурс функции: & emsp14;
КэлиМенгер Матрикс
Ресурс функции: & emsp14;
Повернутый эллипс, матрица
Ресурс функции: & emsp14;
MatrixPartialTrace
Ресурс функции: & emsp14;
MatrixFieldOfValues
Ресурс функции: & emsp14;
НьютонСпутникМатрица
Ресурс функции: & emsp14;
МатрицаМинимальноеПолином
Ресурс функции: & emsp14;
MatrixPencilSolve
Ресурс функции: & emsp14;
АнтидиагональныйMatrixQ
Ресурс функции: & emsp14;
Гауссовская квадратурная матрица
Ресурс функции: & emsp14;
ЗамешательствоMatrixFlip
Ресурс функции: & emsp14;
NonNegativeMatrixFactorization
Ресурс функции: & emsp14;
Квадратура Веса ToJacobiMatrix
Ресурс функции: & emsp14;
Ортогональный Полином Вандермонда Матрица
Ресурс функции: & emsp14;
Замешательство, Матрица, Траектория, Функция
Ресурс функции: & emsp14;
Трехдиагональный инверсный
Ресурс функции: & emsp14;
RowSpace
Ресурс функции: & emsp14;
ColumnSpace
Ресурс функции: & emsp14;
Пфаффиан
Ресурс функции: & emsp14;
Наклон Трехдиагональный Декомпозиция
Ресурс функции: & emsp14;
SkewLTLDecomposition
Ресурс функции: & emsp14;
DefinitePencilReduce
Ресурс функции: & emsp14;
Нулевой диагональ
Ресурс функции: & emsp14;
Адъюгат
Ресурс функции: & emsp14;
Аннулирование
Ресурс функции: & emsp14;
AppendColumn
Ресурс функции: & emsp14;
PrependColumn
Ресурс функции: & emsp14;
GramianReduce
Ресурс функции: & emsp14;
NEigenvalueSumGradient
Ресурс функции: & emsp14;
SymmetricSort
Ресурс функции: & emsp14;
PolynomialSmithDecomposition
Ресурс функции: & emsp14;
Кофактор
Ресурс функции: & emsp14;
Парный график разброса
Ресурс функции: & emsp14;
Попов Декомпозиция
Ресурс функции: & emsp14;
Форма Оператор
Ресурс функции: & emsp14;
GeneralizedVariance
Ресурс функции: & emsp14;
Независимый компонентный анализ
Ресурс функции: & emsp14;
ОтбеливаниеТрансформ

Ресурс функции: & emsp14;
FindDistanceInstance
Ресурс функции: & emsp14;
FullQRDecomposition
Ресурс функции: & emsp14;
RationalCholeskyDecomposition
Ресурс функции: & emsp14;
Разложение
Ресурс функции: & emsp14;
Гауссовский Гессенберг Разложение
Ресурс функции: & emsp14;
Многочлен Эрмит Декомпозиция
Ресурс функции: & emsp14;
Линейно-независимый
Ресурс функции: & emsp14;
RandomRotationQuaternion
Ресурс функции: & emsp14;
MinSumPermutation
Ресурс функции: & emsp14;
Противодиагональ
Ресурс функции: & emsp14;
ГершгоринДиски
Ресурс функции: & emsp14;
BitStringNullSpace
Ресурс функции: & emsp14;
FirstOrderCorrelation
Ресурс функции: & emsp14;
Линейная комбинация
Ресурс функции: & emsp14;
Линейные ограничения
Ресурс функции: & emsp14;
Полярное разложение
Ресурс функции: & emsp14;
Всего вариация
Ресурс функции: & emsp14;
AxisAngle
Ресурс функции: & emsp14;
Гессен Детерминант
Ресурс функции: & emsp14;
WishartDistribution
Ресурс функции: & emsp14;
БлижайшийKroneckerПродуктСумма
Ресурс функции: & emsp14;
РасширенныйGroebnerBasis
Ресурс функции: & emsp14;
СимплексМедиан
Ресурс функции: & emsp14;
EllipsoidQuartiles
Ресурс функции: & emsp14;
ДиагонализацияQuadratic
Ресурс функции: & emsp14;
Смежность Гиперграф
Ресурс функции: & emsp14;
AdjacencyTensor
Ресурс функции: & emsp14;
QuantumTensorAutomaton
Ресурс функции: & emsp14;
ElasticData
Ресурс функции: & emsp14;
Расширенная решеткаReduce
Ресурс функции: & emsp14;
КолоннаSpaceBasis
Ресурс функции: & emsp14;
Сводные столбцы
Ресурс функции: & emsp14;
DisplaySudokuГоловоломки
Ресурс функции: & emsp14;
LinearAlgebraMod
Ресурс функции: & emsp14;
HypergraphToGraph
Ресурс функции: & emsp14;
RowSpaceBasis
Ресурс функции: & emsp14;
BezierInterpolatingControlPoints

Ресурс функции: & emsp14;
TukeyMedianПольский
Ресурс функции: & emsp14;
ПротиводиагональВсего
Ресурс функции: & emsp14;
Собственный вектор, участок
Ресурс функции: & emsp14;
КвадратичныйАкустический диффузор

Ресурс функции: & emsp14;
BitStringLinearSolve
Ресурс функции: & emsp14;
Стол Q
Ресурс функции: & emsp14;
NiceGrid
Ресурс функции: & emsp14;
DixonResultant
Ресурс функции: & emsp14;
ChiSquareMarkovChainStatistics
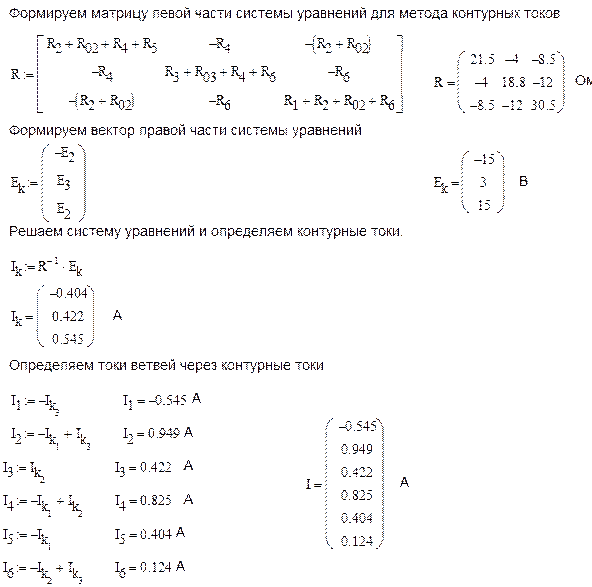
Ресурс функции: & emsp14;
ОртогональныйПолиномVandermondeSolve
Ресурс функции: & emsp14;
OpticalFieldМоделирование
Boussetta / MatrixTreeTheorem: В математической области теории графов теорема Кирхгофа или теорема Кирхгофа о матричном дереве имени Густава Кирхгофа — это теорема о количестве остовных деревьев в графе, показывающая, что это число может быть вычислено за полиномиальное время как определитель.
 матрицы Лапласа графа. GitHub — Boussetta / MatrixTreeTheorem: в математической области теории графов теорема Кирхгофа или теорема Кирхгофа о матричном дереве имени Густава Кирхгофа — это теорема о количестве остовных деревьев в графе, показывающая, что это число может быть вычислено за полиномиальное время как определитель матрицы Лапласа графа.
матрицы Лапласа графа. GitHub — Boussetta / MatrixTreeTheorem: в математической области теории графов теорема Кирхгофа или теорема Кирхгофа о матричном дереве имени Густава Кирхгофа — это теорема о количестве остовных деревьев в графе, показывающая, что это число может быть вычислено за полиномиальное время как определитель матрицы Лапласа графа. Файлы
Постоянная ссылка
Не удалось загрузить последнюю информацию о фиксации.
Около
Ресурсы
Вы не можете выполнить это действие в настоящее время.
Вы вошли в систему с другой вкладкой или окном. Перезагрузите, чтобы обновить сеанс.
Вы вышли из системы на другой вкладке или в другом окне. Перезагрузите, чтобы обновить сеанс.
Моделирование на больших компьютерах упругих сетей: малые собственные значения и спектры собственных значений матрицы Кирхгофа
Аннотация
 78 где n — количество бусинок Роуза в цепочках, составляющих сеть. Расчеты выполняются как для монодисперсного, так и для полидисперсного распределения длин цепей. Как и предсказывает теория, обнаруживаются большие собственные значения, связанные с локализованным движением контактов. Обсуждается связь между малыми собственными значениями и равновесным модулем упругости, а также связь между вязкоупругостью и краем полосы спектра.
78 где n — количество бусинок Роуза в цепочках, составляющих сеть. Расчеты выполняются как для монодисперсного, так и для полидисперсного распределения длин цепей. Как и предсказывает теория, обнаруживаются большие собственные значения, связанные с локализованным движением контактов. Обсуждается связь между малыми собственными значениями и равновесным модулем упругости, а также связь между вязкоупругостью и краем полосы спектра. Отозванная статья: о матрице Кирхгофа, новом индексе Кирхгофа и энергии Кирхгофа
 Развернуть
Развернуть Expand
Expand Generic Graph (общие для направленных / неориентированных) — Sage 9.4 Справочное руководство: Graph Theory
sage: eg1 = Graph ({0: [1, 2], 1: [4], 2: [3, 4], 4: [5], 5: [6]})
мудрец: eg1.all_paths (0, 6)
[[0, 1, 4, 5, 6], [0, 2, 4, 5, 6]]
sage: eg2 = graphs. PetersenGraph ()
sage: sorted (например, 2.all_paths (1, 4))
[[1, 0, 4],
[1, 0, 5, 7, 2, 3, 4],
[1, 0, 5, 7, 2, 3, 8, 6, 9, 4],
[1, 0, 5, 7, 9, 4],
[1, 0, 5, 7, 9, 6, 8, 3, 4],
[1, 0, 5, 8, 3, 2, 7, 9, 4],
[1, 0, 5, 8, 3, 4],
[1, 0, 5, 8, 6, 9, 4],
[1, 0, 5, 8, 6, 9, 7, 2, 3, 4],
[1, 2, 3, 4],
[1, 2, 3, 8, 5, 0, 4],
[1, 2, 3, 8, 5, 7, 9, 4],
[1, 2, 3, 8, 6, 9, 4],
[1, 2, 3, 8, 6, 9, 7, 5, 0, 4],
[1, 2, 7, 5, 0, 4],
[1, 2, 7, 5, 8, 3, 4],
[1, 2, 7, 5, 8, 6, 9, 4],
[1, 2, 7, 9, 4],
[1, 2, 7, 9, 6, 8, 3, 4],
[1, 2, 7, 9, 6, 8, 5, 0, 4],
[1, 6, 8, 3, 2, 7, 5, 0, 4],
[1, 6, 8, 3, 2, 7, 9, 4],
[1, 6, 8, 3, 4],
[1, 6, 8, 5, 0, 4],
[1, 6, 8, 5, 7, 2, 3, 4],
[1, 6, 8, 5, 7, 9, 4],
[1, 6, 9, 4],
[1, 6, 9, 7, 2, 3, 4],
[1, 6, 9, 7, 2, 3, 8, 5, 0, 4],
[1, 6, 9, 7, 5, 0, 4],
[1, 6, 9, 7, 5, 8, 3, 4]]
sage: dg = DiGraph ({0: [1, 3], 1: [3], 2: [0, 3]})
шалфей: отсортировано (dg.all_paths (0, 3))
[[0, 1, 3], [0, 3]]
мудрец: ug = dg.to_undirected ()
sage: sorted (ug.all_paths (0, 3))
[[0, 1, 3], [0, 2, 3], [0, 3]] sage: g = Graph ([(0, 1), (0, 1), (1, 2), (1, 2)], multiedges = True)
sage: g.
PetersenGraph ()
sage: sorted (например, 2.all_paths (1, 4))
[[1, 0, 4],
[1, 0, 5, 7, 2, 3, 4],
[1, 0, 5, 7, 2, 3, 8, 6, 9, 4],
[1, 0, 5, 7, 9, 4],
[1, 0, 5, 7, 9, 6, 8, 3, 4],
[1, 0, 5, 8, 3, 2, 7, 9, 4],
[1, 0, 5, 8, 3, 4],
[1, 0, 5, 8, 6, 9, 4],
[1, 0, 5, 8, 6, 9, 7, 2, 3, 4],
[1, 2, 3, 4],
[1, 2, 3, 8, 5, 0, 4],
[1, 2, 3, 8, 5, 7, 9, 4],
[1, 2, 3, 8, 6, 9, 4],
[1, 2, 3, 8, 6, 9, 7, 5, 0, 4],
[1, 2, 7, 5, 0, 4],
[1, 2, 7, 5, 8, 3, 4],
[1, 2, 7, 5, 8, 6, 9, 4],
[1, 2, 7, 9, 4],
[1, 2, 7, 9, 6, 8, 3, 4],
[1, 2, 7, 9, 6, 8, 5, 0, 4],
[1, 6, 8, 3, 2, 7, 5, 0, 4],
[1, 6, 8, 3, 2, 7, 9, 4],
[1, 6, 8, 3, 4],
[1, 6, 8, 5, 0, 4],
[1, 6, 8, 5, 7, 2, 3, 4],
[1, 6, 8, 5, 7, 9, 4],
[1, 6, 9, 4],
[1, 6, 9, 7, 2, 3, 4],
[1, 6, 9, 7, 2, 3, 8, 5, 0, 4],
[1, 6, 9, 7, 5, 0, 4],
[1, 6, 9, 7, 5, 8, 3, 4]]
sage: dg = DiGraph ({0: [1, 3], 1: [3], 2: [0, 3]})
шалфей: отсортировано (dg.all_paths (0, 3))
[[0, 1, 3], [0, 3]]
мудрец: ug = dg.to_undirected ()
sage: sorted (ug.all_paths (0, 3))
[[0, 1, 3], [0, 2, 3], [0, 3]] sage: g = Graph ([(0, 1), (0, 1), (1, 2), (1, 2)], multiedges = True)
sage: g. all_paths (0, 2, use_multiedges = True)
[[0, 1, 2], [0, 1, 2], [0, 1, 2], [0, 1, 2]] sage: dg = DiGraph ({0: [1, 2, 1], 3: [0, 0]}, multiedges = True)
sage: dg.all_paths (3, 1, use_multiedges = True)
[[3, 0, 1], [3, 0, 1], [3, 0, 1], [3, 0, 1]] sage: g = Graph ([(0, 1, 'a'), (0, 1, 'b'), (1, 2, 'c'), (1, 2, 'd')], multiedges = Правда)
шалфей: г.all_paths (0, 2, use_multiedges = Ложь)
[[0, 1, 2]]
sage: g.all_paths (0, 2, use_multiedges = True)
[[0, 1, 2], [0, 1, 2], [0, 1, 2], [0, 1, 2]]
sage: g.all_paths (0, 2, use_multiedges = True, report_edges = True)
[[(0, 1), (1, 2)], [(0, 1), (1, 2)], [(0, 1), (1, 2)], [(0, 1), (1, 2)]]
sage: g.all_paths (0, 2, use_multiedges = True, report_edges = True, labels = True)
[((0, 1, 'b'), (1, 2, 'd')),
((0, 1, 'b'), (1, 2, 'c')),
((0, 1, 'a'), (1, 2, 'd')),
((0, 1, 'a'), (1, 2, 'c'))]
sage: g.all_paths (0, 2, use_multiedges = False, report_edges = True, labels = True)
[((0, 1, 'b'), (1, 2, 'd'))]
шалфей: г.all_paths (0, 2, use_multiedges = False, report_edges = False, labels = True)
[[0, 1, 2]]
sage: g.
all_paths (0, 2, use_multiedges = True)
[[0, 1, 2], [0, 1, 2], [0, 1, 2], [0, 1, 2]] sage: dg = DiGraph ({0: [1, 2, 1], 3: [0, 0]}, multiedges = True)
sage: dg.all_paths (3, 1, use_multiedges = True)
[[3, 0, 1], [3, 0, 1], [3, 0, 1], [3, 0, 1]] sage: g = Graph ([(0, 1, 'a'), (0, 1, 'b'), (1, 2, 'c'), (1, 2, 'd')], multiedges = Правда)
шалфей: г.all_paths (0, 2, use_multiedges = Ложь)
[[0, 1, 2]]
sage: g.all_paths (0, 2, use_multiedges = True)
[[0, 1, 2], [0, 1, 2], [0, 1, 2], [0, 1, 2]]
sage: g.all_paths (0, 2, use_multiedges = True, report_edges = True)
[[(0, 1), (1, 2)], [(0, 1), (1, 2)], [(0, 1), (1, 2)], [(0, 1), (1, 2)]]
sage: g.all_paths (0, 2, use_multiedges = True, report_edges = True, labels = True)
[((0, 1, 'b'), (1, 2, 'd')),
((0, 1, 'b'), (1, 2, 'c')),
((0, 1, 'a'), (1, 2, 'd')),
((0, 1, 'a'), (1, 2, 'c'))]
sage: g.all_paths (0, 2, use_multiedges = False, report_edges = True, labels = True)
[((0, 1, 'b'), (1, 2, 'd'))]
шалфей: г.all_paths (0, 2, use_multiedges = False, report_edges = False, labels = True)
[[0, 1, 2]]
sage: g.




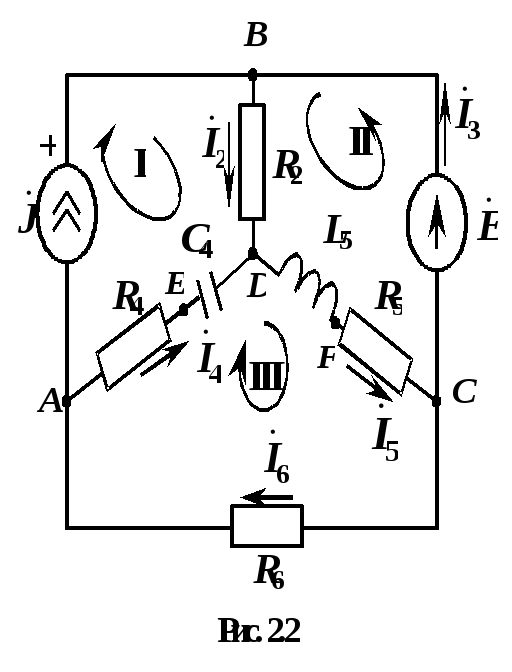
 Например, в схеме на рис. 3 ветви 2-6-5; 4-5; 3-6-4; 1 образуют пути между одной и той же парой узлов 1 и 3. Таким образом, путь – это совокупность ветвей, проходимых непрерывно.
Например, в схеме на рис. 3 ветви 2-6-5; 4-5; 3-6-4; 1 образуют пути между одной и той же парой узлов 1 и 3. Таким образом, путь – это совокупность ветвей, проходимых непрерывно.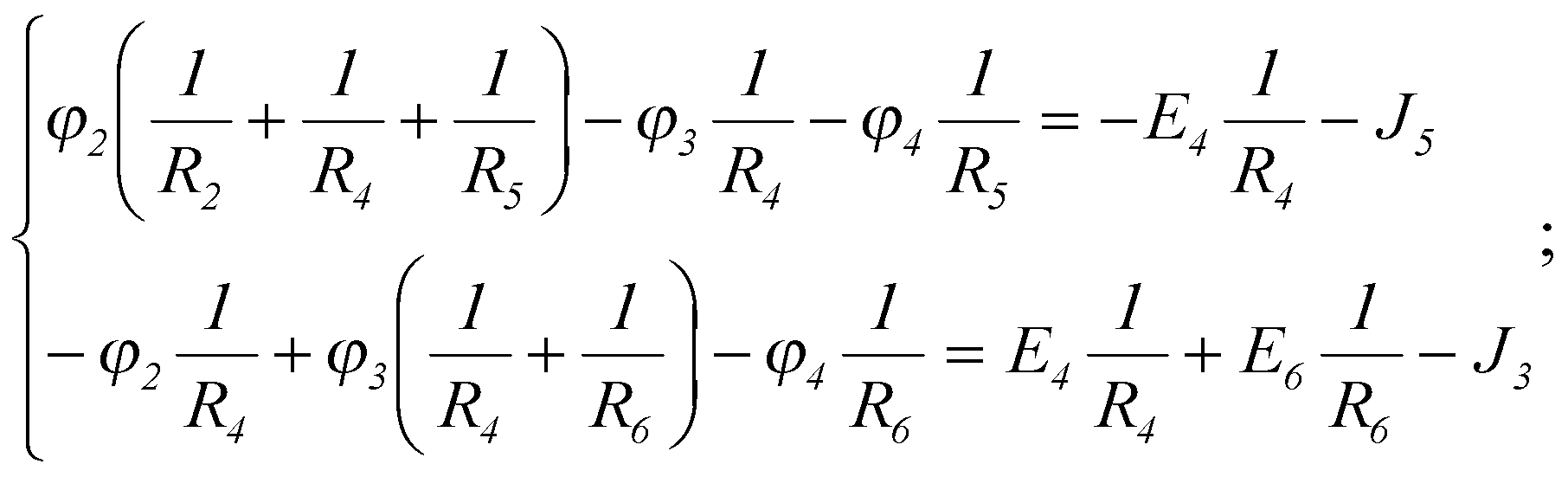
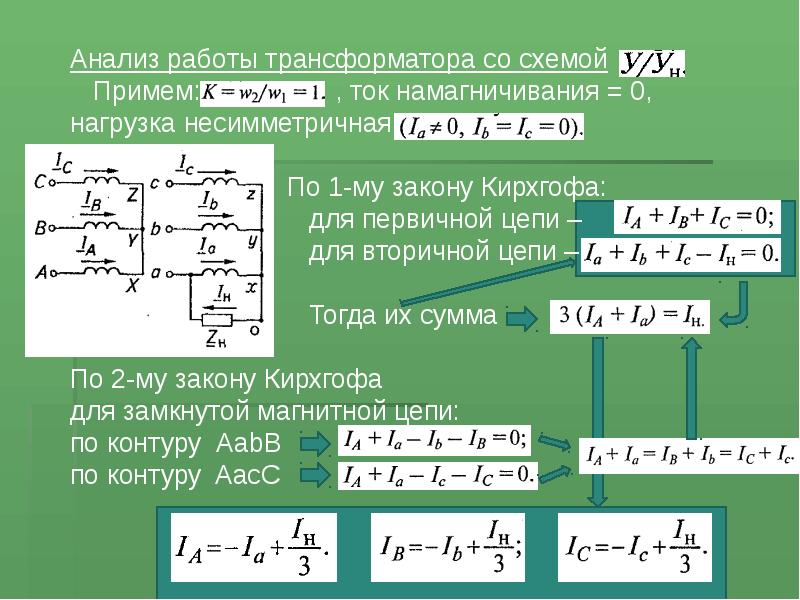 Ее строки соответствуют сечениям, а столбцы – ветвям графа.
Ее строки соответствуют сечениям, а столбцы – ветвям графа.