Матрица Кирхгофа — Википедия

Материал из Википедии — свободной энциклопедии

Матрица Кирхгофа — одно из представлений конечного графа с помощью матрицы. Матрица Кирхгофа представляет дискретный оператор Лапласа для графа. Она используется для подсчета остовных деревьев данного графа (матричная теорема о деревьях), а также в спектральной теории графов.

Дан простой граф  G{\displaystyle \ G} с  |V(G)|=n{\displaystyle \ |V(G)|=n} вершинами. Тогда матрица Кирхгофа  K=(ki,j)n×n{\displaystyle \ K=(k_{i,j})_{n\times n}} данного графа будет определяться следующим образом:

 ki,j:={deg⁡(vi)при i=j,−1при (vi,vj)∈E(G),0в противном случае.{\displaystyle \ k_{i,j}:={\begin{cases}\deg(v_{i})&{\text{при}}\ i=j,\\-1&{\text{при}}\ (v_{i},v_{j})\in E(G),\\0&{\text{в противном случае}}.\end{cases}}}

Также матрицу Кирхгофа можно определить как разность матриц

 K=D−A,{\displaystyle \ K=D-A,}

где  A{\displaystyle \ A} — это матрица смежности данного графа, а  D=(di,j)n×n{\displaystyle \ D=(d_{i,j})_{n\times n}} — матрица, на главной диагонали которой степени вершин графа, а остальные элементы — нули:

 di,j:={deg⁡(vi)if i=j,0otherwise.{\displaystyle \ d_{i,j}:={\begin{cases}\deg(v_{i})&{\mbox{if}}\ i=j,\\0&{\mbox{otherwise}}.\end{cases}}}

Если граф является взвешенным, то определение матрицы Кирхгофа обобщается. В этом случае элементами главной диагонали матрицы Кирхгофа будут суммы весов рёбер, инцидентных соответствующей вершине. Для смежных (связанных) вершин  ki,j=−c(vi,vj){\displaystyle \ k_{i,j}=-c(v_{i},v_{j})}, где  c(vi,vj){\displaystyle \ c(v_{i},v_{j})} — это вес (проводимость) ребра. Для различных не смежных (не связанных) вершин полагается  ki,j=0{\displaystyle \ k_{i,j}=0}.

 ki,j:={∑u∈V(G)(vi,u)∈E(G)c(vi,u)if i=j,−c(vi,vj)if (vi,vj)∈E(G),0otherwise.{\displaystyle \ k_{i,j}:={\begin{cases}\sum _{\begin{smallmatrix}u\in V(G)\\(v_{i},u)\in E(G)\end{smallmatrix}}^{}c(v_{i},u)&{\mbox{if}}\ i=j,\\-c(v_{i},v_{j})&{\mbox{if}}\ (v_{i},v_{j})\in E(G),\\0&{\mbox{otherwise}}.\end{cases}}}

Для взвешенного графа матрица смежности  A{\displaystyle \ A} записывается с учетом проводимостей ребер, а на главной диагонали матрицы  D{\displaystyle \ D} будут суммы проводимостей ребер инцидентных соответствующим вершинам.

 di,j:={∑u∈V(G)(vi,u)∈E(G)c(vi,u)if i=j,0otherwise.{\displaystyle \ d_{i,j}:={\begin{cases}\sum _{\begin{smallmatrix}u\in V(G)\\(v_{i},u)\in E(G)\end{smallmatrix}}^{}c(v_{i},u)&{\mbox{if}}\ i=j,\\0&{\mbox{otherwise}}.\end{cases}}}

Пример матрицы Кирхгофа простого графа.

Помеченный граф	Матрица Кирхгофа
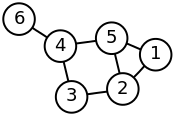	(2−100−10−13−10−100−12−10000−13−1−1−1−10−130000−101){\displaystyle \left({\begin{array}{rrrrrr}2&-1&0&0&-1&0\\-1&3&-1&0&-1&0\\0&-1&2&-1&0&0\\0&0&-1&3&-1&-1\\-1&-1&0&-1&3&0\\0&0&0&-1&0&1\\\end{array}}\right)}

• Сумма элементов каждой строки (столбца) матрицы Кирхгофа равна нулю:

   ∑i=1|V(G)|ki,j=0{\displaystyle \ \sum _{i=1}^{|V(G)|}k_{i,j}=0}.

• Определитель матрицы Кирхгофа равен нулю:

  detK=0{\displaystyle \det K=0}

• Матрица Кирхгофа простого графа симметрична:

   ki,j=kj,ii,j=1,…,|V(G)|{\displaystyle \ k_{i,j}=k_{j,i}\quad i,j=1,\ldots ,|V(G)|}.

• Если взвешенный граф представляет собой электрическую сеть, где вес каждого ребра соответствует его проводимости, то миноры матрицы Кирхгофа позволяют вычислить резистивное расстояние (resistance distance)  Rij{\displaystyle \ R_{ij}} между точками  i{\displaystyle \ i} и  j{\displaystyle \ j} данной сети:

   Rij=K(i,j)K(ij){\displaystyle \ R_{ij}={\frac {K^{(i,j)}}{K_{(ij)}}}},

здесь  K(ij){\displaystyle \ K_{(ij)}} — постоянная (алгебраическое дополнение) матрицы Кирхгофа, а  K(i,j){\displaystyle \ K^{(i,j)}} — алгебраическое дополнение 2-го порядка, то есть определитель матрицы, получающейся из матрицы Кирхгофа вычеркиванием двух строк и двух столбцов  i,j{\displaystyle \ i,j}.

• Существует алгоритм восстановления матрицы Кирхгофа по матрице сопротивлений Rij{\displaystyle R_{ij}}.
  • 0 является собственным значением матрицы (соответствующий собственный вектор — все единицы), кратность его равна числу связных компонент графа.
  • Остальные собственные значения положительны. Второе по малости значение Фидлер назвал индексом связности графа, соответствующий собственный вектор — вектор Фиддлера.

Матрица Кирхгофа — Википедия

Материал из Википедии — свободной энциклопедии

Матрица Кирхгофа — одно из представлений конечного графа с помощью матрицы. Матрица Кирхгофа представляет дискретный оператор Лапласа для графа. Она используется для подсчета остовных деревьев данного графа (матричная теорема о деревьях), а также в спектральной теории графов.

Определение

Дан простой граф  G{\displaystyle \ G} с  |V(G)|=n{\displaystyle \ |V(G)|=n} вершинами. Тогда матрица Кирхгофа  K=(ki,j)n×n{\displaystyle \ K=(k_{i,j})_{n\times n}} данного графа будет определяться следующим образом:

 ki,j:={deg⁡(vi)при i=j,−1при (vi,vj)∈E(G),0в противном случае.{\displaystyle \ k_{i,j}:={\begin{cases}\deg(v_{i})&{\text{при}}\ i=j,\\-1&{\text{при}}\ (v_{i},v_{j})\in E(G),\\0&{\text{в противном случае}}.\end{cases}}}

Также матрицу Кирхгофа можно определить как разность матриц

 K=D−A,{\displaystyle \ K=D-A,}

где  A{\displaystyle \ A} — это матрица смежности данного графа, а  D=(di,j)n×n{\displaystyle \ D=(d_{i,j})_{n\times n}} — матрица, на главной диагонали которой степени вершин графа, а остальные элементы — нули:

 di,j:={deg⁡(vi)if i=j,0otherwise.{\displaystyle \ d_{i,j}:={\begin{cases}\deg(v_{i})&{\mbox{if}}\ i=j,\\0&{\mbox{otherwise}}.\end{cases}}}

Если граф является взвешенным, то определение матрицы Кирхгофа обобщается. В этом случае элементами главной диагонали матрицы Кирхгофа будут суммы весов рёбер, инцидентных соответствующей вершине. Для смежных (связанных) вершин  ki,j=−c(vi,vj){\displaystyle \ k_{i,j}=-c(v_{i},v_{j})}, где  c(vi,vj){\displaystyle \ c(v_{i},v_{j})} — это вес (проводимость) ребра. Для различных не смежных (не связанных) вершин полагается  ki,j=0{\displaystyle \ k_{i,j}=0}.

 ki,j:={∑u∈V(G)(vi,u)∈E(G)c(vi,u)if i=j,−c(vi,vj)if (vi,vj)∈E(G),0otherwise.{\displaystyle \ k_{i,j}:={\begin{cases}\sum _{\begin{smallmatrix}u\in V(G)\\(v_{i},u)\in E(G)\end{smallmatrix}}^{}c(v_{i},u)&{\mbox{if}}\ i=j,\\-c(v_{i},v_{j})&{\mbox{if}}\ (v_{i},v_{j})\in E(G),\\0&{\mbox{otherwise}}.\end{cases}}}

Для взвешенного графа матрица смежности  A{\displaystyle \ A} записывается с учетом проводимостей ребер, а на главной диагонали матрицы  D{\displaystyle \ D} будут суммы проводимостей ребер инцидентных соответствующим вершинам.

 di,j:={∑u∈V(G)(vi,u)∈E(G)c(vi,u)if i=j,0otherwise.{\displaystyle \ d_{i,j}:={\begin{cases}\sum _{\begin{smallmatrix}u\in V(G)\\(v_{i},u)\in E(G)\end{smallmatrix}}^{}c(v_{i},u)&{\mbox{if}}\ i=j,\\0&{\mbox{otherwise}}.\end{cases}}}

Пример

Пример матрицы Кирхгофа простого графа.

Свойства

• Сумма элементов каждой строки (столбца) матрицы Кирхгофа равна нулю:

   ∑i=1|V(G)|ki,j=0{\displaystyle \ \sum _{i=1}^{|V(G)|}k_{i,j}=0}.

• Определитель матрицы Кирхгофа равен нулю:

  detK=0{\displaystyle \det K=0}

• Матрица Кирхгофа простого графа симметрична:

   ki,j=kj,ii,j=1,…,|V(G)|{\displaystyle \ k_{i,j}=k_{j,i}\quad i,j=1,\ldots ,|V(G)|}.

• Если взвешенный граф представляет собой электрическую сеть, где вес каждого ребра соответствует его проводимости, то миноры матрицы Кирхгофа позволяют вычислить резистивное расстояние (resistance distance)  Rij{\displaystyle \ R_{ij}} между точками  i{\displaystyle \ i} и  j{\displaystyle \ j} данной сети:

   Rij=K(i,j)K(ij){\displaystyle \ R_{ij}={\frac {K^{(i,j)}}{K_{(ij)}}}},

здесь  K(ij){\displaystyle \ K_{(ij)}} — постоянная (алгебраическое дополнение) матрицы Кирхгофа, а  K(i,j){\displaystyle \ K^{(i,j)}} — алгебраическое дополнение 2-го порядка, то есть определитель матрицы, получающейся из матрицы Кирхгофа вычеркиванием двух строк и двух столбцов  i,j{\displaystyle \ i,j}.

• Существует алгоритм восстановления матрицы Кирхгофа по матрице сопротивлений Rij{\displaystyle R_{ij}}.
  • 0 является собственным значением матрицы (соответствующий собственный вектор — все единицы), кратность его равна числу связных компонент графа.
  • Остальные собственные значения положительны. Второе по малости значение Фидлер назвал индексом связности графа, соответствующий собственный вектор — вектор Фиддлера.

См. также

Википедия — свободная энциклопедия

Избранная статья

Американская экспедиция на К2 1953 года (англ. 1953 American Karakoram expedition) — американская экспедиция на вершину Чогори под руководством доктора Чарльза Хьюстона, состоявшаяся летом 1953 года и ставившая своей целью первое восхождение на второй по высоте восьмитысячник планеты. Это была пятая по счёту попытка восхождения на К2 и третья со стороны американских альпинистов.

Экспедиция вылетела из Нью-Йорка в Карачи 25 мая 1953 года и после почти месячного перехода к Базовому лагерю у подножия К2 начала свою работу на горе. За чуть менее чем полтора месяца осады ребра Абруццкого (Абруцци) были организованы восемь промежуточных лагерей. В последнем из них (на высоте 7770 м) 2 августа собрались все участники экспедиции, готовясь к финальному рывку. Однако в ночь на 3 августа на гору обрушился шторм, который не утихал последующие две недели. На пятые сутки пережидания непогоды неожиданно тяжело заболел один из сильнейших участников экспедиции Арт Гилки, которому требовалась немедленная эвакуация вниз, но альпинисты смогли её начать лишь 10 августа. Вечером того же дня Арт Гилки погиб в результате схода снежной лавины, но, даже не имея «на руках» больного, все альпинисты смогли спуститься в Базовый лагерь только 15 августа, претерпев все возможные испытания.

Хотя экспедиция не достигла своей главной цели, в альпинистских кругах на десятилетия вперёд она стала эталоном альпинистской взаимовыручки и, по словам Райнхольда Месснера, «самой потрясающей неудачей, которую только можно себе представить».

Хорошая статья

Солове́цкий ка́мень в Санкт-Петербурге — памятник жертвам политических репрессий в СССР и борцам за свободу. Он находится на Петроградской стороне в историческом центре города, на его старейшей площади — Троицкой. Этот сквер расположен рядом с местами, непосредственно связанными с политическими репрессиями в СССР — Домом политкаторжан, тюрьмой и некрополем Петропавловской крепости, Большим домом.

Памятник представляет собой гранитную глыбу, привезённую с территории бывшего Соловецкого лагеря, считающегося символом ГУЛАГа и советского государственного террора в целом. Он был установлен по инициативе и силами бывших политических заключённых и Санкт-Петербургской организации «Мемориал». Авторами памятника выступили художники Юлий Рыбаков и Евгений Ухналёв, которые в советское время сами пережили политическое заключение. Мемориал призван увековечить память не только о жертвах репрессивной системы и о борцах с ней, но в широком смысле он символизирует ценность свободы, прав человека и человеческого достоинства. Соловецкий камень является центральным местом мероприятий, посвящённых памяти жертв государственного террора в СССР, а также других правозащитных акций.

Изображение дня

«Дрозд-отшельник» — один из геоглифов Наски

Матрица Кирхгофа — Википедия

Материал из Википедии — свободной энциклопедии

Матрица Кирхгофа — одно из представлений конечного графа с помощью матрицы. Матрица Кирхгофа представляет дискретный оператор Лапласа для графа. Она используется для подсчета остовных деревьев данного графа (матричная теорема о деревьях), а также в спектральной теории графов.

Определение

Дан простой граф  G{\displaystyle \ G} с  |V(G)|=n{\displaystyle \ |V(G)|=n} вершинами. Тогда матрица Кирхгофа  K=(ki,j)n×n{\displaystyle \ K=(k_{i,j})_{n\times n}} данного графа будет определяться следующим образом:

 ki,j:={deg⁡(vi)при i=j,−1при (vi,vj)∈E(G),0в противном случае.{\displaystyle \ k_{i,j}:={\begin{cases}\deg(v_{i})&{\text{при}}\ i=j,\\-1&{\text{при}}\ (v_{i},v_{j})\in E(G),\\0&{\text{в противном случае}}.\end{cases}}}

Также матрицу Кирхгофа можно определить как разность матриц

 K=D−A,{\displaystyle \ K=D-A,}

где  A{\displaystyle \ A} — это матрица смежности данного графа, а  D=(di,j)n×n{\displaystyle \ D=(d_{i,j})_{n\times n}} — матрица, на главной диагонали которой степени вершин графа, а остальные элементы — нули:

 di,j:={deg⁡(vi)if i=j,0otherwise.{\displaystyle \ d_{i,j}:={\begin{cases}\deg(v_{i})&{\mbox{if}}\ i=j,\\0&{\mbox{otherwise}}.\end{cases}}}

Если граф является взвешенным, то определение матрицы Кирхгофа обобщается. В этом случае элементами главной диагонали матрицы Кирхгофа будут суммы весов рёбер, инцидентных соответствующей вершине. Для смежных (связанных) вершин  ki,j=−c(vi,vj){\displaystyle \ k_{i,j}=-c(v_{i},v_{j})}, где  c(vi,vj){\displaystyle \ c(v_{i},v_{j})} — это вес (проводимость) ребра. Для различных не смежных (не связанных) вершин полагается  ki,j=0{\displaystyle \ k_{i,j}=0}.

 ki,j:={∑u∈V(G)(vi,u)∈E(G)c(vi,u)if i=j,−c(vi,vj)if (vi,vj)∈E(G),0otherwise.{\displaystyle \ k_{i,j}:={\begin{cases}\sum _{\begin{smallmatrix}u\in V(G)\\(v_{i},u)\in E(G)\end{smallmatrix}}^{}c(v_{i},u)&{\mbox{if}}\ i=j,\\-c(v_{i},v_{j})&{\mbox{if}}\ (v_{i},v_{j})\in E(G),\\0&{\mbox{otherwise}}.\end{cases}}}

Для взвешенного графа матрица смежности  A{\displaystyle \ A} записывается с учетом проводимостей ребер, а на главной диагонали матрицы  D{\displaystyle \ D} будут суммы проводимостей ребер инцидентных соответствующим вершинам.

 di,j:={∑u∈V(G)(vi,u)∈E(G)c(vi,u)if i=j,0otherwise.{\displaystyle \ d_{i,j}:={\begin{cases}\sum _{\begin{smallmatrix}u\in V(G)\\(v_{i},u)\in E(G)\end{smallmatrix}}^{}c(v_{i},u)&{\mbox{if}}\ i=j,\\0&{\mbox{otherwise}}.\end{cases}}}

Видео по теме

Пример

Пример матрицы Кирхгофа простого графа.

Помеченный граф	Матрица Кирхгофа
	(2−100−10−13−10−100−12−10000−13−1−1−1−10−130000−101){\displaystyle \left({\begin{array}{rrrrrr}2&-1&0&0&-1&0\\-1&3&-1&0&-1&0\\0&-1&2&-1&0&0\\0&0&-1&3&-1&-1\\-1&-1&0&-1&3&0\\0&0&0&-1&0&1\\\end{array}}\right)}

Свойства

• Сумма элементов каждой строки (столбца) матрицы Кирхгофа равна нулю:

   ∑i=1|V(G)|ki,j=0{\displaystyle \ \sum _{i=1}^{|V(G)|}k_{i,j}=0}.

• Определитель матрицы Кирхгофа равен нулю:

  detK=0{\displaystyle \det K=0}

• Матрица Кирхгофа простого графа симметрична:

   ki,j=kj,ii,j=1,…,|V(G)|{\displaystyle \ k_{i,j}=k_{j,i}\quad i,j=1,\ldots ,|V(G)|}.

• Если взвешенный граф представляет собой электрическую сеть, где вес каждого ребра соответствует его проводимости, то миноры матрицы Кирхгофа позволяют вычислить резистивное расстояние (resistance distance)  Rij{\displaystyle \ R_{ij}} между точками  i{\displaystyle \ i} и  j{\displaystyle \ j} данной сети:

   Rij=K(i,j)K(ij){\displaystyle \ R_{ij}={\frac {K^{(i,j)}}{K_{(ij)}}}},

здесь  K(ij){\displaystyle \ K_{(ij)}} — постоянная (алгебраическое дополнение) матрицы Кирхгофа, а  K(i,j){\displaystyle \ K^{(i,j)}} — алгебраическое дополнение 2-го порядка, то есть определитель матрицы, получающейся из матрицы Кирхгофа вычеркиванием двух строк и двух столбцов  i,j{\displaystyle \ i,j}.

• Существует алгоритм восстановления матрицы Кирхгофа по матрице сопротивлений Rij{\displaystyle R_{ij}}.
  • 0 является собственным значением матрицы (соответствующий собственный вектор — все единицы), кратность его равна числу связных компонент графа.
  • Остальные собственные значения положительны. Второе по малости значение Фидлер назвал индексом связности графа, соответствующий собственный вектор — вектор Фиддлера.

См. также

Матрица Кирхгофа Википедия

Матрица Кирхгофа — одно из представлений конечного графа с помощью матрицы. Матрица Кирхгофа представляет дискретный оператор Лапласа для графа. Она используется для подсчета остовных деревьев данного графа (матричная теорема о деревьях), а также в спектральной теории графов.

Определение[ | ]

Дан простой граф  G{\displaystyle \ G} с  |V(G)|=n{\displaystyle \ |V(G)|=n} вершинами. Тогда матрица Кирхгофа  K=(ki,j)n×n{\displaystyle \ K=(k_{i,j})_{n\times n}} данного графа будет определяться следующим образом:

 ki,j:={deg⁡(vi)при i=j,−1при (vi,vj)∈E(G),0в противном случае.{\displaystyle \ k_{i,j}:={\begin{cases}\deg(v_{i})&{\text{при}}\ i=j,\\-1&{\text{при}}\ (v_{i},v_{j})\in E(G),\\0&{\text{в противном случае}}.\end{cases}}}

Также матрицу Кирхгофа можно определить как разность матриц

 K=D−A,{\displaystyle \ K=D-A,}

где  A{\displaystyle \ A} — это матрица смежности данного графа, а  D=(di,j)n×n{\displaystyle \ D=(d_{i,j})_{n\times n}} — матрица, на главной диагонали которой степени вершин графа, а остальные элементы — нули:

 di,j:={deg⁡(vi)if i=j,0otherwise.{\displaystyle \ d_{i,j}:={\begin{cases}\deg(v_{i})&{\mbox{if}}\ i=j,\\0&{\mbox{otherwise}}.\end{cases}}}

Матрица Кирхгофа — Википедия

Материал из Википедии — свободной энциклопедии

Матрица Кирхгофа — одно из представлений конечного графа с помощью матрицы. Матрица Кирхгофа представляет дискретный оператор Лапласа для графа. Она используется для подсчета остовных деревьев данного графа (матричная теорема о деревьях), а также в спектральной теории графов.

Определение

Дан простой граф  G{\displaystyle \ G} с  |V(G)|=n{\displaystyle \ |V(G)|=n} вершинами. Тогда матрица Кирхгофа  K=(ki,j)n×n{\displaystyle \ K=(k_{i,j})_{n\times n}} данного графа будет определяться следующим образом:

 ki,j:={deg⁡(vi)при i=j,−1при (vi,vj)∈E(G),0в противном случае.{\displaystyle \ k_{i,j}:={\begin{cases}\deg(v_{i})&{\text{при}}\ i=j,\\-1&{\text{при}}\ (v_{i},v_{j})\in E(G),\\0&{\text{в противном случае}}.\end{cases}}}

Также матрицу Кирхгофа можно определить как разность матриц

 K=D−A,{\displaystyle \ K=D-A,}

где  A{\displaystyle \ A} — это матрица смежности данного графа, а  D=(di,j)n×n{\displaystyle \ D=(d_{i,j})_{n\times n}} — матрица, на главной диагонали которой степени вершин графа, а остальные элементы — нули:

 di,j:={deg⁡(vi)if i=j,0otherwise.{\displaystyle \ d_{i,j}:={\begin{cases}\deg(v_{i})&{\mbox{if}}\ i=j,\\0&{\mbox{otherwise}}.\end{cases}}}

Если граф является взвешенным, то определение матрицы Кирхгофа обобщается. В этом случае элементами главной диагонали матрицы Кирхгофа будут суммы весов рёбер, инцидентных соответствующей вершине. Для смежных (связанных) вершин  ki,j=−c(vi,vj){\displaystyle \ k_{i,j}=-c(v_{i},v_{j})}, где  c(vi,vj){\displaystyle \ c(v_{i},v_{j})} — это вес (проводимость) ребра. Для различных не смежных (не связанных) вершин полагается  ki,j=0{\displaystyle \ k_{i,j}=0}.

 ki,j:={∑u∈V(G)(vi,u)∈E(G)c(vi,u)if i=j,−c(vi,vj)if (vi,vj)∈E(G),0otherwise.{\displaystyle \ k_{i,j}:={\begin{cases}\sum _{\begin{smallmatrix}u\in V(G)\\(v_{i},u)\in E(G)\end{smallmatrix}}^{}c(v_{i},u)&{\mbox{if}}\ i=j,\\-c(v_{i},v_{j})&{\mbox{if}}\ (v_{i},v_{j})\in E(G),\\0&{\mbox{otherwise}}.\end{cases}}}

Для взвешенного графа матрица смежности  A{\displaystyle \ A} записывается с учетом проводимостей ребер, а на главной диагонали матрицы  D{\displaystyle \ D} будут суммы проводимостей ребер инцидентных соответствующим вершинам.

 di,j:={∑u∈V(G)(vi,u)∈E(G)c(vi,u)if i=j,0otherwise.{\displaystyle \ d_{i,j}:={\begin{cases}\sum _{\begin{smallmatrix}u\in V(G)\\(v_{i},u)\in E(G)\end{smallmatrix}}^{}c(v_{i},u)&{\mbox{if}}\ i=j,\\0&{\mbox{otherwise}}.\end{cases}}}

Пример

Пример матрицы Кирхгофа простого графа.

Помеченный граф	Матрица Кирхгофа
	(2−100−10−13−10−100−12−10000−13−1−1−1−10−130000−101){\displaystyle \left({\begin{array}{rrrrrr}2&-1&0&0&-1&0\\-1&3&-1&0&-1&0\\0&-1&2&-1&0&0\\0&0&-1&3&-1&-1\\-1&-1&0&-1&3&0\\0&0&0&-1&0&1\\\end{array}}\right)}

Свойства

• Сумма элементов каждой строки (столбца) матрицы Кирхгофа равна нулю:

   ∑i=1|V(G)|ki,j=0{\displaystyle \ \sum _{i=1}^{|V(G)|}k_{i,j}=0}.

• Определитель матрицы Кирхгофа равен нулю:

  detK=0{\displaystyle \det K=0}

• Матрица Кирхгофа простого графа симметрична:

   ki,j=kj,ii,j=1,…,|V(G)|{\displaystyle \ k_{i,j}=k_{j,i}\quad i,j=1,\ldots ,|V(G)|}.

• Если взвешенный граф представляет собой электрическую сеть, где вес каждого ребра соответствует его проводимости, то миноры матрицы Кирхгофа позволяют вычислить резистивное расстояние (resistance distance)  Rij{\displaystyle \ R_{ij}} между точками  i{\displaystyle \ i} и  j{\displaystyle \ j} данной сети:

   Rij=K(i,j)K(ij){\displaystyle \ R_{ij}={\frac {K^{(i,j)}}{K_{(ij)}}}},

здесь  K(ij){\displaystyle \ K_{(ij)}} — постоянная (алгебраическое дополнение) матрицы Кирхгофа, а  K(i,j){\displaystyle \ K^{(i,j)}} — алгебраическое дополнение 2-го порядка, то есть определитель матрицы, получающейся из матрицы Кирхгофа вычеркиванием двух строк и двух столбцов  i,j{\displaystyle \ i,j}.

• Существует алгоритм восстановления матрицы Кирхгофа по матрице сопротивлений Rij{\displaystyle R_{ij}}.
  • 0 является собственным значением матрицы (соответствующий собственный вектор — все единицы), кратность его равна числу связных компонент графа.
  • Остальные собственные значения положительны. Второе по малости значение Фидлер назвал индексом связности графа, соответствующий собственный вектор — вектор Фиддлера.

См. также

Матрица Кирхгофа — это… Что такое Матрица Кирхгофа?

Матрица Кирхгофа (Laplacian matrix) — одно из представлений графа с помощью матрицы. Матрица Кирхгофа используется для подсчета остовных деревьев данного графа (матричная теорема о деревьях), а также используется в спектральной теории графов.

Определение

Дан простой граф с вершинами. Тогда матрица Кирхгофа данного графа будет определяться следующим образом:

Также матрицу Кирхгофа можно определить как разность матриц

где — это матрица смежности данного графа, а — матрица, на главной диагонали которой степени вершин графа, а остальные элементы — нули:

Если граф является взвешенным, то определение матрицы Кирхгофа обобщается. В этом случае элементами главной диагонали матрицы Кирхгофа будут суммы проводимостей инцидентных ребер соответствующей вершины. Для смежных (связанных) вершин где — это вес (проводимость) ребра. Для различных несмежных (несвязанных) вершин полагается .

Для взвешенного графа матрица смежности записывается с учетом проводимостей ребер, а на главной диагонали матрицы будут суммы проводимостей ребер инцидентных соответствующим вершинам.

Пример

Пример матрицы Кирхгофа простого графа.

Помеченный граф	Матрица Кирхгофа

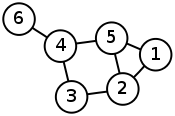Свойства

• Сумма элементов каждой строки (столбца) матрицы Кирхгофа равна нулю:

• Определитель матрицы Кирхгофа равен нулю:

• Все алгебраические дополнения симметричной матрицы Кирхгофа равны между собой — постоянная матрицы Кирхгофа. Для простого графа значение данной постоянной совпадает с числом всех возможных остовов графа (см. Матричная теорема о деревьях).
• Если взвешенный граф представляет собой электрическую сеть, то миноры матрицы Кирхгофа позволяют вычислить резистивное расстояние (resistance distance) между точками и данной сети:

,

здесь  — постоянная (алгебраическое дополнение) матрицы Кирхгофа, а  — алгебраическое дополнение 2-го порядка, то есть определитель матрицы, получающейся из матрицы Кирхгофа вычеркиванием двух строк и двух столбцов .
Существует алгоритм восстановления матрицы Кирхгофа по матрице сопротивлений .

• 0 является собственным значением матрицы (соответствующих собственный вектор — все единицы), кратность его равна числу связных компонент графа.
• Остальные собственные значения положительны. Второе по малости значение Фидлер назвал индексом связности графа, его с. вектор — вектор Фиддлера.

См. также