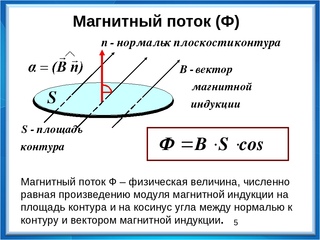
Максимальный магнитный поток: Найти максимальный магнитный поток через прямоугольную рамку, вращающуюся

\prime \left( t \right)\;\;\;\;(1)\]

Магнитный поток через некоторую площадку, помещённую в однородном магнитном поле, можно определить по такой формуле:

\[\Phi = BS\cos \alpha \;\;\;\;(2)\]

В этой формуле $B$ – индукция магнитного поля, $S$ – площадь поверхности, через которую определяется магнитный поток, $\alpha$ – угол между нормалью к площадке и вектором магнитной индукции.

Учитывая, что произведение индукции магнитного поля $B$ на площадь поверхности $S$ дают максимальный магнитный поток $\Phi_{\max}$, то формулу (2) можно записать в следующем виде:

\[\Phi = {\Phi _{\max }}\cos \alpha \;\;\;\;(3)\]

Прямоугольная рамка вращается в магнитном поле, то есть угол $\alpha$ меняется со временем. Чтобы формула (3) стала выглядеть как функция изменения магнитного потока от времени, нужно представить угол $\alpha$ в следующем виде:

\[\alpha = \omega t + {\alpha _0}\]

Здесь $\alpha_0$ – некоторый начальный угол (также называют начальной фазой), а $\omega$ – угловая скорость вращения рамки, которую можно определить через известную частоту $\nu$ по формуле:

\[\omega = 2\pi \nu \]

Учитывая всё написанное, формула (3) примет вид:

\[\Phi = {\Phi _{\max }}\cos \left( {2\pi \nu t + {\alpha _0}} \right)\]

Это выражение подставим в формулу (1):

\[{\rm E_i} = – {\left( {{\Phi _{\max }}\cos \left( {2\pi \nu t + {\alpha _0}} \right)} \right)^\prime }\]

Теперь нужно взять производную, тогда мы получим:

\[{\rm E_i} = {\Phi _{\max }} \cdot 2\pi \nu \cdot \sin \left( {2\pi \nu t + {\alpha _0}} \right)\]

Очевидно, что ЭДС индукции достигнет своего максимального значения, когда синус будет равен единице, поэтому:

\[{{\rm E}_{imax}} = {\Phi _{\max }} \cdot 2\pi \nu \]

Откуда искомый максимальный магнитный поток $\Phi_{\max}$ равен:

\[{\Phi _{\max }} = \frac{{{{\rm E}_{imax} }}}{{2\pi \nu }}\]

Задача решена в общем виде, посчитаем численный ответ (об/с и Гц – это одно и то же):

\[{\Phi _{\max }} = \frac{3}{{2 \cdot 3,14 \cdot 10}} = 0,0478\;Вб = 47,8\;мВб\]

Содержание

Ответ: 47,8 мВб.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

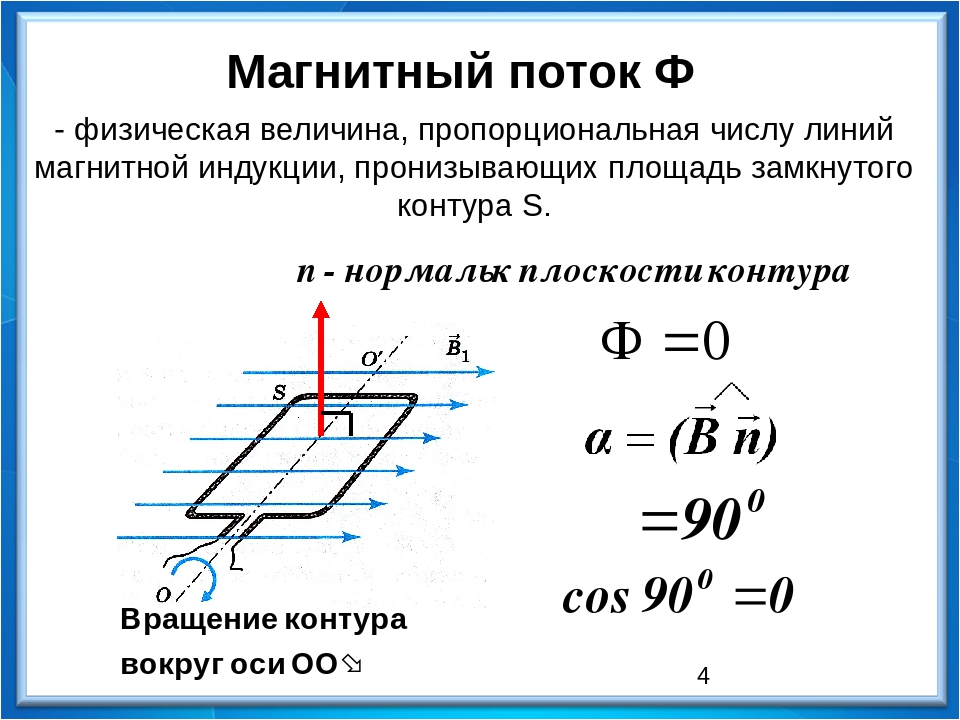
Максимальный магнитный поток. Поток индукции магнитного поля

магнитная индукция — является плотностью магнитного потока в данной точке поля. Единицей магнитной индукции является тесла (1 Тл = 1 Вб/м 2).

Возвращаясь к полученному ранее выражению (1), можно количественно определить магнитный поток через некоторую поверхность как произведение величины заряда, протекающего через проводник совмещенный с границей этой поверхности при полном исчезновении магнитного поля, на сопротивление электрической цепи, по которой протекают эти заряды

В описанных выше опытах с пробным витком (кольцом), он удалялся на такое расстояние, при котором исчезали всякие проявления магнитного поля. Но можно просто перемещать этот виток в пределах поля и при этом в нем также будут перемещаться электрические заряды. Перейдем в выражении (1) к приращениям

Ф + Δ Ф = r (q — Δ q ) => Δ Ф = —rΔ q => Δ q = -Δ Ф/r

где Δ Ф и Δ q — приращения потока и количества зарядов. Разные знаки приращений объясняются тем, что положительный заряд в опытах с удалением витка соответствовал исчезновению поля, т.е. отрицательному приращению магнитного потока.

С помощью пробного витка можно исследовать все пространство вокруг магнита или катушки с током и построить линии, направление касательных к которым в каждой точке будет соответствовать направлению вектора магнитной индукции B (рис. 3)

Эти линии называются линиями вектора магнитной индукции или магнитными линиями .

Пространство магнитного поля можно мысленно разделить трубчатыми поверхностями, образованными магнитными линиями, причем, поверхности можно выбрать таким образом, чтобы магнитный поток внутри каждой такой поверхности (трубки) численно был равен единице и изобразить графически осевые линии этих трубок. Такие трубки называют единичными, а линии их осей —

единичными магнитными линиями . Картина магнитного поля изображенная с помощью единичных линий дает не только о качественное, но и количественное представление о нем, т.

к. при этом величина вектора магнитной индукции оказывается равной количеству линий, проходящих через единицу поверхности, нормальной вектору B , а количество линий, проходящих через любую поверхность равно значению магнитного потока .

Магнитные линии непрерывны и этот принцип можно математически представить в виде

т.е. магнитный поток, проходящий через любую замкнутую поверхность равен нулю .

Выражение (4) справедливо для поверхности s любой формы. Если рассматривать магнитный поток проходящий через поверхность, образованную витками цилиндрической катушки (рис. 4), то ее можно разделить на поверхности, образованные отдельными витками, т.е. s =s 1 +s 2 +…+s 8 . Причем через поверхности разных витков в общем случае будут проходить разные магнитные потоки. Так на рис. 4, через поверхности центральных витков катушки проходят восемь единичных магнитных линий, а через поверхности крайних витков только четыре.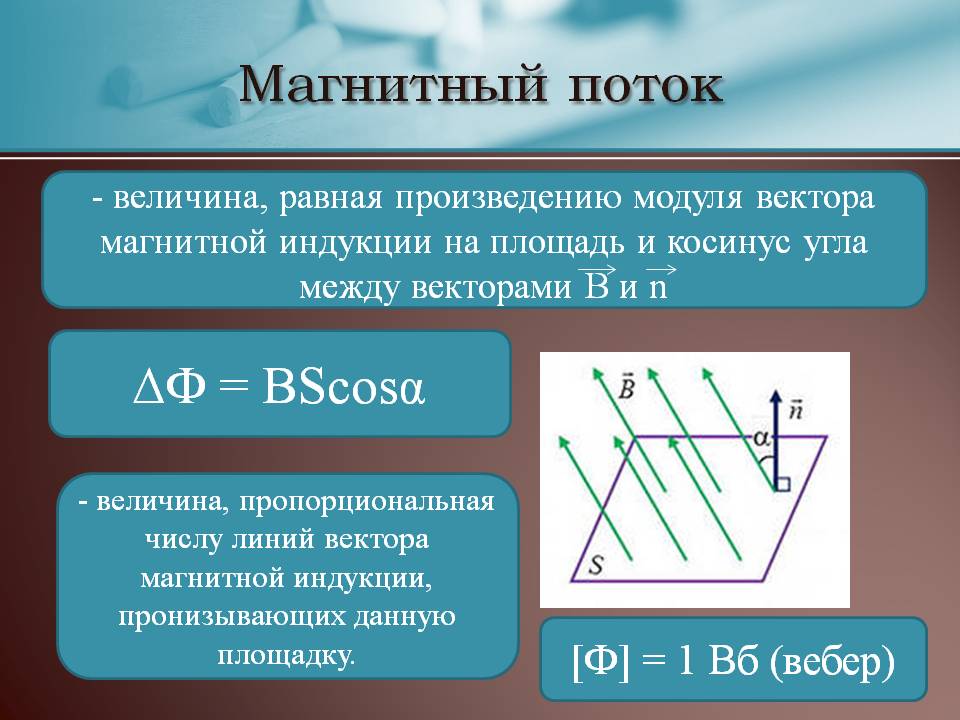

Для того, чтобы определить полный магнитный поток, проходящий через поверхность всех витков, нужно сложить потоки, проходящие через поверхности отдельных витков, или, иначе говоря, сцепляющиеся с отдельными витками. Например, магнитные потоки, сцепляющиеся с четырьмя верхними витками катушки рис. 4, будут равны: Ф 1 =4; Ф 2 =4; Ф 3 =6; Ф 4 =8. Также, зеркально-симметрично с нижними.

Потокосцепление — виртуальный (воображаемый общий) магнитный поток Ψ, сцепляющийся со всеми витками катушки, численно равен сумме потоков, сцепляющихся с отдельными витками: Ψ = w э Ф m , где Ф m — магнитный поток, создаваемый током, проходящим по катушке, а

w э — эквивалентное или эффективное число витков катушки. Физический смысл потокосцепления — сцепление магнитных полей витков катушки, которое можно выразить коэффициентом (кратностью) потокосцепления k = Ψ/Ф = w э.

То есть для приведенного на рисунке случая, двух зеркально-симметричных половинок катушки:

Ψ = 2(Ф 1 + Ф 2 + Ф 3 + Ф 4) = 48

Виртуальность, то есть воображаемость потокосцепления проявляется в том, что оно не представляет собой реального магнитного потока, который никакая индуктивность не может кратно увеличивать, но поведение импеданса катушки таково, что кажется, что магнитный поток увеличивается кратно эффективному количеству витков, хотя реально — это просто взаимодействие витков в том же самом поле.

Если бы катушка увеличивала магнитный поток своим потокосцеплением, то можно было бы создавать умножители магнитного поля на катушке даже без тока, ибо потокосцепление не подразумевает замкнутости цепи катушки, но лишь совместную геометрию близости витков.

Часто реальное распределение потокосцепления по виткам катушки неизвестно, но его можно принять равномерным и одинаковым для всех витков, если реальную катушку заменить эквивалентной с другим числом витков

w э, сохраняя при этом величину потокосцепления Ψ = w э Ф m , где Ф m — поток, сцепляющийся с внутренними витками катушки, а w э — эквивалентное или эффективное число витков катушки. Для рассмотренного на рис. 4 случая w э = Ψ/Ф 4 =48/8=6.

МАГНИТНЫЙ ПОТОК

МАГНИТНЫЙ ПОТОК (символ Ф), мера силы и протяженности МАГНИТНОГО ПОЛЯ. Поток через площадь А под прямым углом к одинаковому магнитному полю есть Ф=mНА, где m — магнитная ПРОНИЦАЕМОСТЬ среды, а Н — интенсивность магнитного поля.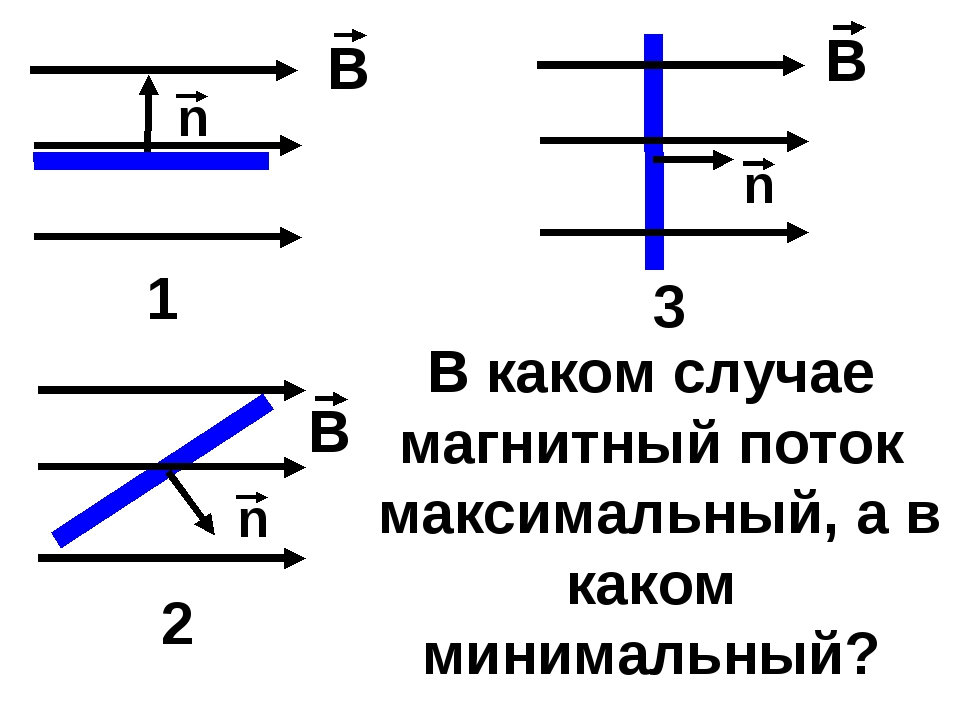 Плотность магнитного потока — это поток на единицу площади (символ В), который равен Н. Изменение магнитного потока через электрический проводник наводит ЭЛЕКТРОДВИЖУЩУЮ СИЛУ.

Научно-технический энциклопедический словарь .

Смотреть что такое «МАГНИТНЫЙ ПОТОК» в других словарях:

Поток вектора магнитной индукции В через какую либо поверхность. Магнитный поток через малую площадку dS, в пределах которой вектор В неизменен, равен dФ = ВndS, где Bn проекция вектора на нормаль к площадке dS. Магнитный поток Ф через конечную… … Большой Энциклопедический словарь

— (поток магнитной индукции), поток Ф вектора магн. индукции В через к. л. поверхность. М. п. dФ через малую площадку dS, в пределах к рой вектор В можно считать неизменным, выражается произведением величины площадки и проекции Bn вектора на… … Физическая энциклопедия

магнитный поток — Скалярная величина, равная потоку магнитной индукции. [ГОСТ Р 52002 2003] магнитный поток Поток магнитной индукции через перпендикулярную магнитному полю поверхность, определяемый как произведение магнитной индукции в данной точке на площадь… … Справочник технического переводчика

МАГНИТНЫЙ ПОТОК — поток Ф вектора магнитной индукции (см.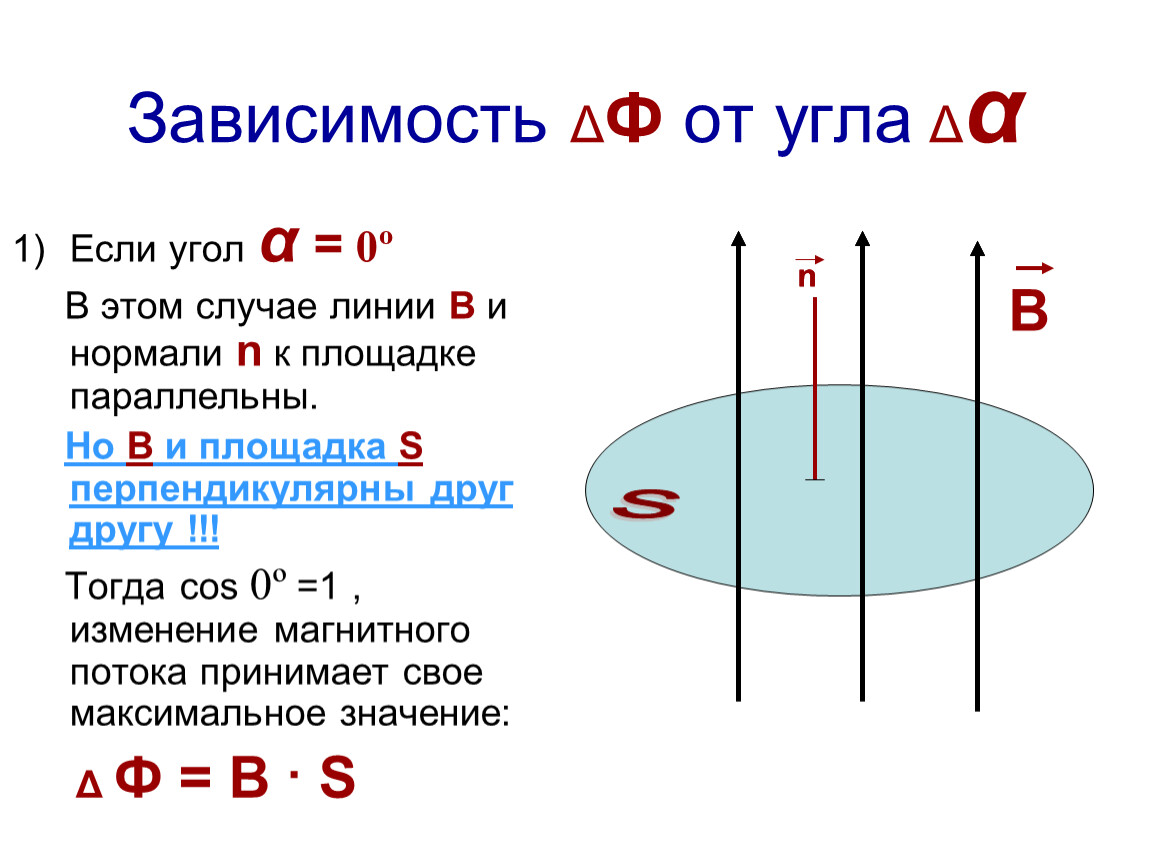 (5)) В через поверхность S, нормальную вектору В в однородном магнитном поле. Единица магнитного потока в СИ (см.) … Большая политехническая энциклопедия

Величина, характеризующая магнитное воздействие на данную поверхность. М. п. измеряется количеством магнитных силовых линий, проходящих через данную поверхность. Технический железнодорожный словарь. М.: Государственное транспортное… … Технический железнодорожный словарь

Магнитный поток — скалярная величина, равная потоку магнитной индукции… Источник: ЭЛЕКТРОТЕХНИКА. ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ ОСНОВНЫХ ПОНЯТИЙ. ГОСТ Р 52002 2003 (утв. Постановлением Госстандарта РФ от 09.01.2003 N 3 ст) … Официальная терминология

Поток вектора магнитной индукции В через какую либо поверхность. Магнитный поток через малую площадку dS, в пределах которой вектор В неизменен, равен dФ = BndS, где Вn проекция вектора на нормаль к площадке dS. Магнитный поток Ф через конечную… … Энциклопедический словарь

Классическая электродинамика … Википедия

магнитный поток — , поток магнитной индукции поток вектора магнитной индукции через какую либо поверхность. Для замкнутой поверхности суммарный магнитный поток равен нулю, что отражает соленоидный характер магнитного поля, т. е. отсутствие в природе … Энциклопедический словарь по металлургии

Магнитный поток — 12. Магнитный поток Поток магнитной индукции Источник: ГОСТ 19880 74: Электротехника. Основные понятия. Термины и определения оригинал документа 12 магнитный по … Словарь-справочник терминов нормативно-технической документации

Книги

, Миткевич В. Ф.. В этой книге содержится многое, на что не всегда обращается должное внимание, когда речь идет о магнитном потоке, и что не было до сих пор достаточно определенно высказано или не было…
Магнитный поток и его преобразование , Миткевич В. Ф.. Эта книга будет изготовлена в соответствии с Вашим заказом по технологии Print-on-Demand. В этой книге содержится многое, на что не всегда обращается должное внимание, когда речь идет о…

Электрический дипольный момент
Электрический заряд
Электрическая индукция
Электрическое поле
Электростатический потенциал

Магнитостатика
Закон Био — Савара — Лапласа Закон Ампера Магнитный момент Магнитное поле Магнитный поток Магнитная индукция

Электродинамика
Векторный потенциал Диполь Потенциалы Лиенара — Вихерта Сила Лоренца Ток смещения Униполярная индукция Уравнения Максвелла Электрический ток Электродвижущая сила Электромагнитная индукция Электромагнитное излучение Электромагнитное поле

Электродинамика

Векторный потенциал
Диполь
Потенциалы Лиенара — Вихерта
Сила Лоренца
Ток смещения
Униполярная индукция
Уравнения Максвелла
Электрический ток
Электродвижущая сила
Электромагнитная индукция
Электромагнитное излучение
Электромагнитное поле

Электрическая цепь
Закон Ома Законы Кирхгофа Индуктивность Радиоволновод Резонатор Электрическая ёмкость Электрическая проводимость Электрическое сопротивление Электрический импеданс

Известные учёные
Генри Кавендиш Майкл Фарадей Никола Тесла Андре-Мари Ампер Густав Роберт Кирхгоф Джеймс Клерк (Кларк) Максвелл Генри Рудольф Герц Альберт Абрахам Майкельсон Роберт Эндрюс Милликен

См.

также: Портал:Физика

Магни́тный пото́к — физическая величина, равная произведению модуля вектора магнитной индукции \vec B на площадь S и косинус угла α между векторами \vec B и нормалью \mathbf{n}. Поток \Phi_B как интеграл вектора магнитной индукции \vec B через конечную поверхность S определяется через интеграл по поверхности:

{{{1}}}

При этом векторный элемент dS площади поверхности S определяется как

{{{1}}}

Квантование магнитного потока

Значения магнитного потока Φ , проходящего через

Напишите отзыв о статье «Магнитный поток»

Ссылки

Отрывок, характеризующий Магнитный поток

– C»est bien, mais ne demenagez pas de chez le prince Ваsile. Il est bon d»avoir un ami comme le prince, – сказала она, улыбаясь князю Василию. – J»en sais quelque chose. N»est ce pas? [Это хорошо, но не переезжайте от князя Василия. Хорошо иметь такого друга. Я кое что об этом знаю. Не правда ли?] А вы еще так молоды.

Вам нужны советы. Вы не сердитесь на меня, что я пользуюсь правами старух. – Она замолчала, как молчат всегда женщины, чего то ожидая после того, как скажут про свои года. – Если вы женитесь, то другое дело. – И она соединила их в один взгляд. Пьер не смотрел на Элен, и она на него. Но она была всё так же страшно близка ему. Он промычал что то и покраснел.
Вернувшись домой, Пьер долго не мог заснуть, думая о том, что с ним случилось. Что же случилось с ним? Ничего. Он только понял, что женщина, которую он знал ребенком, про которую он рассеянно говорил: «да, хороша», когда ему говорили, что Элен красавица, он понял, что эта женщина может принадлежать ему.
«Но она глупа, я сам говорил, что она глупа, – думал он. – Что то гадкое есть в том чувстве, которое она возбудила во мне, что то запрещенное. Мне говорили, что ее брат Анатоль был влюблен в нее, и она влюблена в него, что была целая история, и что от этого услали Анатоля. Брат ее – Ипполит… Отец ее – князь Василий… Это нехорошо», думал он; и в то же время как он рассуждал так (еще рассуждения эти оставались неоконченными), он заставал себя улыбающимся и сознавал, что другой ряд рассуждений всплывал из за первых, что он в одно и то же время думал о ее ничтожестве и мечтал о том, как она будет его женой, как она может полюбить его, как она может быть совсем другою, и как всё то, что он об ней думал и слышал, может быть неправдою.

И он опять видел ее не какою то дочерью князя Василья, а видел всё ее тело, только прикрытое серым платьем. «Но нет, отчего же прежде не приходила мне в голову эта мысль?» И опять он говорил себе, что это невозможно; что что то гадкое, противоестественное, как ему казалось, нечестное было бы в этом браке. Он вспоминал ее прежние слова, взгляды, и слова и взгляды тех, кто их видал вместе. Он вспомнил слова и взгляды Анны Павловны, когда она говорила ему о доме, вспомнил тысячи таких намеков со стороны князя Василья и других, и на него нашел ужас, не связал ли он уж себя чем нибудь в исполнении такого дела, которое, очевидно, нехорошо и которое он не должен делать. Но в то же время, как он сам себе выражал это решение, с другой стороны души всплывал ее образ со всею своею женственной красотою.

В ноябре месяце 1805 года князь Василий должен был ехать на ревизию в четыре губернии. Он устроил для себя это назначение с тем, чтобы побывать заодно в своих расстроенных имениях, и захватив с собой (в месте расположения его полка) сына Анатоля, с ним вместе заехать к князю Николаю Андреевичу Болконскому с тем, чтоб женить сына на дочери этого богатого старика. Но прежде отъезда и этих новых дел, князю Василью нужно было решить дела с Пьером, который, правда, последнее время проводил целые дни дома, т. е. у князя Василья, у которого он жил, был смешон, взволнован и глуп (как должен быть влюбленный) в присутствии Элен, но всё еще не делал предложения.

Магнитными материалами являются те, которые подвержены влиянию особых силовых полей, в свою очередь, немагнитные материалы не подвержены или слабо подвержены силам магнитного поля, которое принято представлять при помощи силовых линий (магнитный поток), обладающих определенными свойствами. Кроме того что они всегда образуют замкнутые петли, они ведут себя так, будто являются эластичными, то есть во время искажения пытаются вернуться в прежнее расстояние и в свою естественную форму.

Невидимая сила

Магниты имеют свойство притягивать к себе некоторые металлы, особенно железо и сталь, а также никель, сплавы никеля, хрома и кобальта. Материалы, создающие силы притяжения, являются магнитами. Существуют различные их типы. Материалы, которые могут легко намагничиваться, называются ферромагнитными. Они могут быть жесткими или мягкими. Мягкие ферромагнитные материалы, такие как железо, быстро теряют свои свойства. Магниты, изготовленные из этих материалов, называются временными. Жесткие материалы, такие как сталь, держат свои свойства гораздо дольше и используются в качестве постоянных.

Магнитный поток: определение и характеристика

Вокруг магнита существует определенное силовое поле, и это создает возможность возникновения энергии. Магнитный поток равен произведению средних силовых полей перпендикулярной поверхности, в которую он проникает. Его изображают при помощи символа «Φ», измеряется он в единицах, называемых Webers (ВБ). Величина потока, проходящего через заданную площадь, будет меняться от одной точки к другой вокруг предмета. Таким образом, магнитный поток — это так называемая мера силы магнитного поля или электрического тока, основанная на общем количестве заряженных силовых линий, проходящих через определенную область.

Раскрывая тайну магнитных потоков

У всех магнитов, независимо от их формы, имеются две области, которые называются полюсами, способными производить определенную цепочку организованной и сбалансированной системы невидимых силовых линий. Эти линии из потока образуют особое поле, форма которого проявляется более интенсивно в некоторых частях по сравнению с другими. Области с наибольшим притяжением называют полюсами. Линии векторного поля не могут быть обнаружены невооруженным глазом. Визуально они всегда отображаются в виде силовых линий с однозначными полюсами на каждом конце материала, где линии более плотные и концентрированные. Магнитный поток — это линии, которые создают вибрации притяжения или отталкивания, показывая их направление и интенсивность.

Линии магнитного потока

Магнитные силовые линии определяются как кривые, перемещающиеся по определенной траектории в магнитном поле. Касательная к этим кривым в любой точке показывает направление магнитного поля в ней же. Характеристики:

Каждая линия потока образует замкнутый контур.

Эти индукционные линии никогда не пересекаются, но имеют тенденцию сокращаться или растягиваться, изменяя в ту или иную сторону свои размеры.

Как правило, силовые линии имеют начало и конец на поверхности.

Имеется также определенное направление с севера на юг.

Силовые линии, которые расположены близко друг к другу, образуя сильное магнитное поле.

Когда соседние полюса одинаковы (север-север или юг-юг), они отталкиваются друг от друга. Когда соседние полюса не совпадают (север-юг или юг-север), они притягиваются друг к другу. Этот эффект напоминает знаменитое выражение о том, что противоположности притягиваются.

Магнитные молекулы и теория Вебера

Теория Вебера опирается на тот факт, что все атомы имеют магнитные свойства благодаря связи между электронами в атомах. Группы атомов соединяются вместе таким образом, что окружающие их поля вращаются в том же направлении.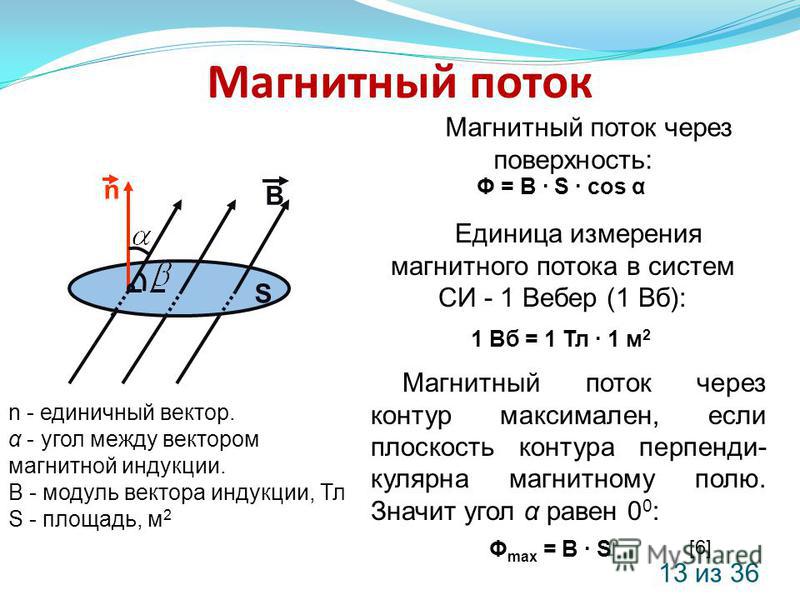 Такого рода материалы состоят из групп крошечных магнитиков (если рассматривать их на молекулярном уровне) вокруг атомов, это означает, что ферромагнитный материал состоит из молекул, которым свойственны силы притяжения. Они известны как диполи и группируются в домены. Когда материал намагничен, все домены становятся единым целым. Материал теряет свою способность притягивать и отталкивать в том случае, если его домены разъединяются. Диполи в совокупности образуют магнит, но по отдельности каждый из них пытается оттолкнуться от однополярного, таким образом притягиваются противоположные полюса.

Поля и полюса

Силу и направление магнитного поля определяют линии магнитного потока. Область притяжения сильнее там, где линии близко расположены друг к другу. Линии находятся ближе всего у полюса стержневого основания, там притяжение наиболее сильное. Сама планета Земля находится в этом мощном силовом поле. Оно действует так, как будто гигантская полосовая намагниченная пластина проходит через середину планеты. Северным полюсом стрелка компаса направлена в сторону точки, называемой Северный магнитный полюс, южным полюсом она указывает на магнитный юг. Однако эти направления отличаются от географических Северного и Южного полюсов.

Природа магнетизма

Магнетизм играет важную роль в электротехнике и электронике, потому что без его компонентов, таких как реле, соленоиды, катушки индуктивности, дроссели, катушки, не будут работать громкоговорители, электродвигатели, генераторы, трансформаторы, счетчики электроэнергии и т. д. Магниты можно найти в естественном природном состоянии в виде магнитных руд. Существуют два основных типа, это магнетит (его также называют оксид железа) и магнитный железняк. Молекулярная структура этого материала в немагнитном состоянии представлена в виде свободной магнитной цепи или отдельных крошечных частиц, которые свободно располагаются в случайном порядке. Когда материал намагничен, это случайное расположение молекул меняется, а крошечные случайные молекулярные частицы выстраиваются таким образом, что они производят целую серию договоренностей. Эта идея молекулярного выравнивания ферромагнитных материалов называется теорией Вебера.

Измерение и практическое применение

Наиболее распространенные генераторы используют магнитный поток для производства электроэнергии. Его сила широко используется в электрических генераторах. Прибор, который служит для измерения этого интересного явления, называется флюксметром, он состоит из катушки и электронного оборудования, которое оценивает изменение напряжения в катушке. В физике потоком называется показатель числа силовых линий, проходящих через определенную область. Магнитный поток — это мера количества магнитных силовых линий.

Иногда даже немагнитный материал может также иметь диамагнитные и парамагнитные свойства. Интересным фактом является то, что силы притяжения могут быть разрушены при нагревании или ударе молоточком из такого же материала, но они не могут быть уничтожены или изолированы, если просто разбить большой экземпляр на две части. Каждой сломанный кусок будет иметь свой собственный северный и южный полюс, и неважно, насколько маленькими по размеру будут эти кусочки.

Если электрический ток, как показали опыты Эрстеда, создает магнитное поле, то не может ли в свою очередь магнитное поле вызывать электрический ток в проводнике? Многие ученые с помощью опытов пытались найти ответ на этот вопрос, но первым решил эту задачу Майкл Фарадей (1791 — 1867).
В 1831 г. Фарадей обнаружил, что в замкнутом проводящем контуре при изменении магнитного поля возникает электрический ток. Этот ток назвали индукционным током.
Индукционный ток в катушке из металлической проволоки возникает при вдвигании магнита внутрь катушки и при выдвигании магнита из катушки (рис. 192),

а также при изменении силы тока во второй катушке, магнитное поле которой пронизывает первую катушку (рис. 193).

Явление возникновения электрического тока в замкнутом проводящем контуре при изменениях магнитного поля, пронизывающего контур, называется электромагнитной индукцией.
Появление электрического тока в замкнутом контуре при изменениях магнитного поля, пронизывающего контур, свидетельствует о действии в контуре сторонних сил неэлектростатической природы или о возникновении ЭДС индукции. Количественное описание явления электромагнитной индукции дается на основе установления связи между ЭДС индукции и физической величиной, называемой магнитным потоком.
Магнитный поток. Для плоского контура, расположенного в однородном магнитном поле (рис. 194), магнитным потоком Ф через поверхность площадью S называют величину, равную произведению модуля вектора магнитной индукции на площадь S и на косинус угла между вектором и нормалью к поверхности:

Правило Ленца. Опыт показывает, что направление индукционного тока в контуре зависит от того, возрастает или убывает магнитный поток, пронизывающий контур, а также от направления вектора индукции магнитного поля относительно контура. Общее правило, позволяющее определить направление индукционного тока в контуре, было установлено в 1833 г. Э. X. Ленцем.
Правило Ленца можно наглядно показать с помощью легкого алюминиевого кольца (рис. 195).

Опыт показывает, что при внесении постоянного магнита кольцо отталкивается от него, а при удалении притягивается к магниту. Результат опытов не зависит от полярности магнита.
Отталкивание и притяжение сплошного кольца объясняется возникновением индукционного тока в кольце при изменениях магнитного потока через кольцо и действием на индукционный ток магнитного поля. Очевидно, что при вдвигании магнита в кольцо индукционный ток в нем имеет такое направление, что созданное этим током магнитное поле противодействует внешнему магнитному полю, а при выдвигании магнита индукционный ток в нем имеет такое направление, что вектор индукции его магнитного поля совпадает по направлению с вектором индукции внешнего поля.
Общая формулировка правила Ленца: возникающий в замкнутом контуре индукционный ток имеет такое направление, что созданный им магнитный поток через площадь, ограниченную контуром, стремится компенсировать то изменение магнитного потока, которым вызывается данный ток.
Закон электромагнитной индукции. Экспериментальное исследование зависимости ЭДС индукции от изменения магнитного потока привело к установлению закона электромагнитной индукции: ЭДС индукции в замкнутом контуре пропорциональна скорости изменения магнитного потока через поверхность, ограниченную контуром.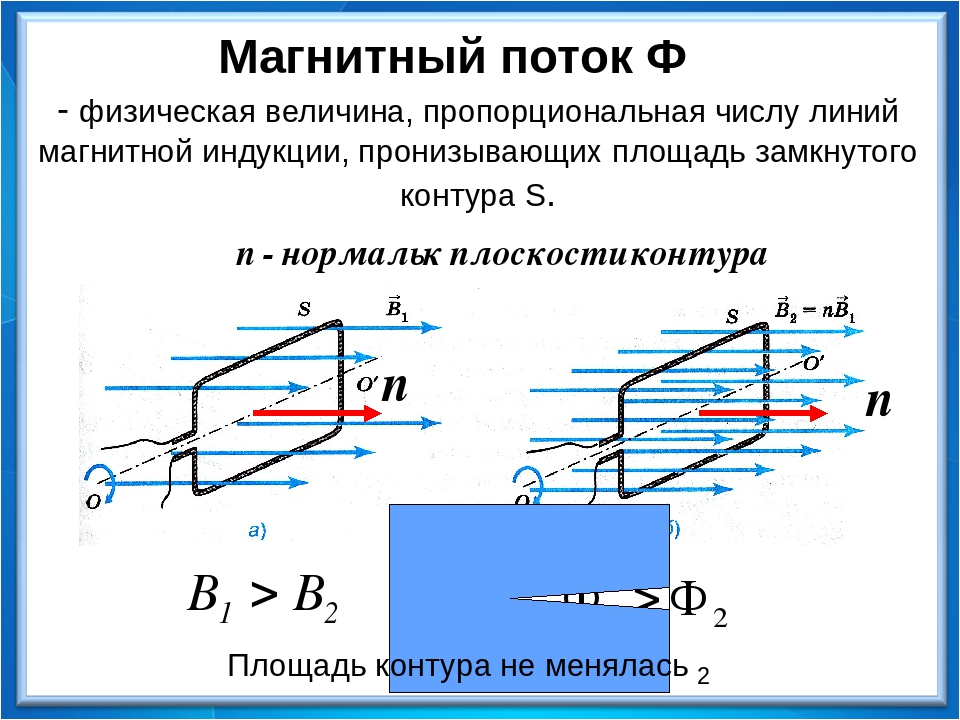
В СИ единица магнитного потока выбрана такой, чтобы коэффициент пропорциональности между ЭДС индукции и изменением магнитного потока был равен единице. При этом закон электромагнитной индукции формулируется следующим образом: ЭДС индукции в замкнутом контуре равна модулю скорости изменения магнитного потока через поверхность, ограниченную контуром:

С учетом правила Ленца закон электромагнитной индукции записывается следующим образом:

ЭДС индукции в катушке. Если в последовательно соединенных контурах происходят одинаковые изменения магнитного потока, то ЭДС индукции в них равна сумме ЭДС индукции в каждом из контуров. Поэтому при изменении магнитного потока в катушке, состоящей из n одинаковых витков провода, общая ЭДС индукции в n раз больше ЭДС индукции в одиночном контуре:

Для однородного магнитного поля на основании уравнения (54.1) следует, что его магнитная индукция равна 1 Тл, если магнитный поток через контур площадью 1 м 2 равен 1 Вб:

Вихревое электрическое поле. Закон электромагнитной индукции (54.3) по известной скорости изменения магнитного потока позволяет найти значение ЭДС индукции в контуре и при известном значении электрического сопротивления контура вычислить силу тока в контуре. Однако при этом остается нераскрытым физический смысл явления электромагнитной индукции. Рассмотрим это явление подробнее.

Возникновение электрического тока в замкнутом контуре свидетельствует о том, что при изменении магнитного потока, пронизывающего контур, на свободные электрические заряды в контуре действуют силы. Провод контура неподвижен, неподвижными можно считать свободные электрические заряды в нем. На неподвижные электрические заряды может действовать только электрическое поле. Следовательно, при любом изменении магнитного поля в окружающем пространстве возникает электрическое поле. Это электрическое поле и приводит в движение свободные электрические заряды в контуре, создавая индукционный электрический ток. Электрическое поле, возникающее при изменениях магнитного поля, называют вихревым электрическим полем.

Работа сил вихревого электрического поля по перемещению электрических зарядов и является работой сторонних сил, источником ЭДС индукции.

Вихревое электрическое поле отличается от электростатического поля тем, что оно не связано с электрическими зарядами, его линии напряженности представляют собой замкнутые линии. Работа сил вихревого электрического поля при движении электри ческого заряда по замкнутой линии может быть отлична от нуля.

ЭДС индукции в движущихся проводниках. Явление электромагнитной индукции наблюдается и в тех случаях, когда магнитное поле не изменяется во времени, но магнитный поток через контур изменяется из-за движения проводников контура в магнитном поле. В этом случае причиной возникновения ЭДС индукции является не вихревое электрическое поле, а сила Лоренца.

Магнитный поток

В этой статье приведены хорошие стартовые задачи по теме “магнитный поток”. Задачи несложные, вполне можно начинать изучать эту тему с их использованием.

Задача 1. За с магнитный поток, пронизывающий проволочную рамку, равномерно уменьшается от некоторого значения до нуля. При этом в рамке генерируется ЭДС, равная 4 В. Чему равен начальный магнитный поток через рамку?
ЭДС равна

Так как поток уменьшился до нуля, то его изменение . Следовательно,

Ответ: 8 Вб

Задача 2. Рамка площадью см с числом витков и сопротивлением Ом находится в однородном магнитном поле, вектор индукции которого перпендикулярен плоскости рамки. Какой заряд пройдет по рамке при ее повороте на 90°? мТл.
Поток через один виток равен , а через витков –

При повороте рамки поток изменится до нуля, следовательно, . Тогда ЭДС

Но ток равен

Тогда

Ответ: 2,5 мКл
Задача 3. За какое время магнитный поток сквозь один виток катушки, содержащей 50 витков, изменился с 5 до 1 мВб, если в результате этого изменения по катушке сопротивлением 100 Ом прошел индукционный ток силой 0,1 А?

По закону Ома

Откуда

Ответ: 0,02 с

Задача 4. Рамка, имеющая 100 витков площадью см каждый, вращается вокруг вертикальной оси, принадлежащей плоскости рамки, в горизонтальном постоянном однородном магнитном поле с индукцией В = 2 мТл. Средняя ЭДС индукции, возникающая на зажимах рамки за четверть периода, равна 8 мВ. Сколько оборотов делает рамка за 10 с?

За четверть периода поток изменяется от максимального до нулевого, так как рамка повернется на 90 градусов за это время. Поэтому

Итак, рамка повернется на 90 градусов за с, следовательно, на 360 градусов она повернется за 0,5 с, ну а за 10 с – успеет повернуться 20 раз.

Ответ: 20 оборотов.
Задача 5. Проволочную рамку поместили в однородное периодически изменяющееся магнитное поле перпендикулярно линиям магнитной индукции. Выберите два верных утверждения.

1) Сила тока будет изменяться обратно пропорционально величине индукции.

2) Сила тока будет периодически изменяться по величине.

3) Сила тока будет равна нулю.

4) Сила тока будет изменяться по направлению.

Так как поле изменяется, то будет меняться поток чрез рамку. Следовательно, в рамке будет наводиться ЭДС, которая тоже будет переменной. И ток вследствие этого будет переменным. Так как поле меняется периодически, то будут периоды, когда индукция нарастает, и будут периоды убывания. Значит, ЭДС будет менять знак, а следовательно, ток тоже будет менять направление.
Ответ: 24
Задача 6. В проволочное кольцо вставили магнит, при этом по кольцу прошел заряд Кл. Определите магнитный поток, пересекающий кольцо, если сопротивление кольца 30 Ом.

Ток равен

Тогда

Ответ: 600 мкВб

Задача 7. Длинную изолированную проволоку А) наматывают на катушку, а концы проволоки присоединяют к гальванометру, Б) складывают вдвое и наматывают на катушку, концы проволоки присоединяют к гальванометру (см. рис.).

К задаче 7

Появится ли индукционный ток в катушке при введении в нее полосового магнита?

1) да, появится ток
2) нет, тока в катушке не будет
3) да, но ток будет появляться только в случае, если сложенный провод намотан по часовой стрелке, а магнит вдвигают северным полюсом
4) да, но ток будет появляться только в случае, если сложенный провод намотан против часовой стрелки, а магнит вдвигают северным полюсом .
В случае А появится, в случае B – нет. В случае A поток изменяется, следовательно, наводится ЭДС, и возникает ток. Катушка, намотанная так, как показано на рисунке, называется бифиллярной. Магнитное поле, созданное одной обмоткой равно и направлено противоположно созданному другой, приводя к взаимонейтрализации магнитных полей. Так что во втором случае в половине провода наводится ЭДС одного знака, а во второй половине провода – ЭДС другого знака, которые компенсируют друг друга.

Ответ: 12
Задача 8. Виток, замкнутый на гальванометр, поместили в пространство между полюсами электромагнита, магнитное поле в котором изменяется по некоторому закону. При этом изменение тока в контуре от времени описывает зависимость на рисунке.

К задаче 8 – рисунок 1

Какой график может соответствовать изменению значения индукции магнитном поле от времени?

К задаче 8 – рисунок 2

Чтобы решить эту задачу, нужно смотреть не на числа, а на фазы изменения тока и индукции в контуре. Ток в первый момент максимален, следовательно, ЭДС максимальна, ведь по фазе они совпадают друг с другом. Поток же всегда опережает ЭДС на 90 градусов, то есть на четверть периода. Остается найти график, сдвинутый на четверть периода от заданного: первый и третий отпадают, из оставшихся подойдет №2. Индукция на этом графике опережает ток как раз на 90 градусов.

Ответ: 2
Задача 9. Координата перемычки, движущейся вдоль оси Х по параллельным металлическим стержням (см. рис.), изменяется по законам:

К задаче 9

А) ;

Б) .

Какой из графиков соответствует зависимости индукционного тока от времени в каждом случае в первые 0,5 с? Вся система находится в поcтоянном однородном магнитном поле, перпендикулярном плоскости, в которой лежат перемычка и стержни.

Графики зависимостей тока от времени

Определим, как меняется скорость. Для этого возьмем производную координаты по времени:

A)
Б)
В момент времени 0,5 с скорость в случае А) будет равна (-1), а в случае Б) – (+2). То есть в первом случае площадь рамки увеличивается, и индукционный ток будет таким, чтобы уменьшить поток, то есть будет направлен против часовой стрелки, а в случае Б) наоборот, по часовой, так как будет стремиться восстановить уменьшающийся поток. Скорость в обоих случаях непостоянна, но меняетсн по линейному закону, значит, ток будет меняться линейно. Графики 1 и 3 – отбрасываем. В первом случае начальная скорость есть, значит, какой-то ток на начало отсчета уже присутствовал, а во втором – нет, поэтому для второго случая выберем график 2, а для первого – 4.

Ответ: 42

Задача 10. В однородном магнитном поле с индукцией В = 5 мТл движется металлический стержень длиной см перпендикулярно вектору магнитной индукции со скоростью 2 м/с (см. рис.). Какова разность потенциалов, возникающая между концами стержня?

К задаче 10

Так как стержень движется перпендикулярно, то угол между линиями индукции и скоростью равен , а синус этого угла – 1, поэтому

Ответ: 5 мВ

ЯВЛЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ.

13.1. Проволочное кольцо радиусом R находится в однородном магнитном поле, с индукцией В. Плоскость кольца перпендикулярна направлению поля. Определить изменение магнитного потока через поверхность, ограниченную кольцом, если его повернуть вокруг одного из диаметров на 180 градусов. Будет ли возникать в этом случае ЭДС индукции? Ответ обосновать.

13.2. Какое явление будет наблюдаться, если поле начнет усиливаться? Записать закон. Показать направление возникающего тока в контуре. Ответ обосновать.

В N

13.3. Показать направление индукционного тока в витке. Описать, как определили направление индукционного тока?

13.4 Что будет происходить со свободно висящим проводящим

кольцом, на которое надвигается северный полюс магнита?

N Записать законы и формулы, которым

подчиняется наблюдаемое явление.

13.5. Контур МNАД, в котором АД движется с некоторой скоростью,

N N А В помещен в магнитное поле, направление линий индукции

которого показан на рисунке. Указать причину возникновения

М Д индукционного тока в контуре и определите его направление.

13.6. Проволочная рамка находится в магнитном поле, созданным бесконечно длинным проводником, лежащим в плоскости рамки. Рамка перемещается

А) параллельно проводнику вправо, оставаясь в своей плоскости;

Б) вращаясь вокруг проводника так, что проводник остается в плоскости рамки на неизменном расстоянии. Индуцируется ли ток в рамке в первом и во втором случаях? Дать объяснение. Назвать и записать закон, описывающий это явление.

13.7. При изменении магнитного потока от его максимального значения до 0 за 0,002с среднее значение ЭДС индукции в контуре было 20В. Найти максимальный магнитный поток.

13.8. Определить среднее значение ЭДС, возникающей в кольце, если кольцо, помещенное перпендикулярно линиям индукции магнитного поля, повернуть на угол 90 градусов за 0,1с. Радиус кольца 5см. Индукция магнитного поля 1Тл.

13.9. Катушка диаметром 10см, имеющая 500 витков, находится в магнитном поле. . Определить среднее значение ЭДС индукции в катушке, если индукция магнитного поля увеличивается от 0 до 2 Тл за 0,1с.

13.10. Скорость самолета с реактивным двигателем 950км/ч. . Определить значение ЭДС индукции, возникающей на концах крыльев самолета, если вертикальная составляющая магнитной индукции земного магнитного поля равна 5·10^-5Тл и размах крыльев самолета 12,5м.

13.11. Ротор, имеющий 100 витков, площадью 4·10^-2м² вращается в однородном магнитном поле, делая 100 оборотов в секунду. Определить максимальное значение ЭДС индукции, если индукция магнитного поля равна 0,8Тл.

13.12. Определить с какой частотой вращается рамка, содержащая 1000 витков площадью15·10^-3м², в магнитном поле индукцией 0,1Тл, если мгновенное значение ЭДС индукции, соответствующее углу поворота 30 градусов, равно 47,1В.

13.13. Прямой проводник длиной 20см помещен в однородное магнитное поле с индукцией 1Тл.Концы проводника замкнуты проводом, находящимся вне поля. Сопротивление всей цепи равно 0,1Ом. Найти силу, с которой нужно действовать на проводник, чтобы перемещать его перпендикулярно линиям индукции со скоростью 2,5 м/с.

13.14. Проволочный виток радиусом R расположен в однородном магнитном поле индукцией В, так его плоскость перпендикулярно направлению магнитного поля. Сравнить заряды, прошедшие по витку при повороте его на 90 градусов и 180 градусов вокруг оси, параллельно плоскости витка. Описать явление, наблюдающееся при таком повороте витка.

13.15. Круговой контур радиусом 2см помещен в однородное магнитное поле с индукцией 0,2Тл. Плоскость контура перпендикулярна направлению магнитного поля. Сопротивление контура равно 1Ом.Какой заряд пройдет через контур при повороте на 180 градусов?.

13.16. Контур со стороной 20см помещен в однородное магнитное поле с индукцией 0,2Тл, направленной от нас. Сопротивление контура равно 1Ом. Какой заряд пройдет через контур при повороте на 90 градусов за 0,01с? Определить направление индукционного тока и найти его величину.

13.17. Катушка, состоящая из 100 витков провода площадью 10см² каждый, помещена в магнитном поле к баллистическому гальванометру. Ось катушки совпадает с направлением поля. При быстром повороте катушки на 180 градусов вокруг ее диаметра через гальванометр проходит электрический заряд 2мкКл. Сопротивление катушки гальванометра 5кОм. Определить индукцию магнитного поля.

13.18. Определить индуктивность контура, если при равномерном изменении тока от 5А до 10А за 0,1с в нем возникает ЭДС самоиндукции 10В.

13.19. Как нужно изменить индуктивность контура, чтобы при неизменном значении тока в нем , энергия магнитного поля увеличилась в 4 раза? Изменится ли при этом магнитный поток сквозь поверхность, ограниченную данным контуром? Ответ обосновать.

13.20. Катушка индуктивностью 0,2Гн подключена к источнику тока. Чему равна ЭДС самоиндукции, если при замыкании ключа ток в катушке возрастает от 0 до 6А за 2с? Какова энергия магнитного поля в катушке при установившемся токе 6А?

магнитный поток пронизывающий

Задача 10312

Плоский контур площадью S = 20 см² находится в однородном магнитном поле (В = 0,03 Тл). Определить магнитный поток Ф, пронизывающий контур, если плоскость его составляет угол φ = 60º с направлением линий индукции.

Задача 10321

Определить магнитный поток Ф, пронизывающий соленоид, если его длина l = 50 см и магнитный момент р_m = 0,4 А·м².

Задача 70259

Какой магнитный поток пронизывал каждый виток катушки, имеющей 100 витков, если при равномерном исчезновении магнитного поля в течение 0,1с в катушке индуцируется э.д.с. 10 В?

Задача 15445

Катушка длиной l = 20 см и диаметром D = 3 см имеет N = 400 витков. По катушке идет ток I = 2 А. Найти индуктивность L катушки и магнитный поток Ф, пронизывающий площадь ее поперечного сечения.

Задача 13676

Колебательный контур содержит катушку с общим числом витков N = 100 индуктивностью L = 10 мкГн и конденсатор емкостью С = 1 кФ. Максимальное напряжение U_m на обкладках конденсатора составляет 100 В. Определите максимальный магнитный поток, пронизывающий катушку.

Задача 11313

Соленоид представляет собой тонкостенный немагнитный цилиндр диаметром D = 20 мм и длиной L = 600 мм на поверхности которого плотно, виток к витку намотана тонкая проволока диаметром d = 0,8 мм и удельным сопротивлением ρ = 12·10^–6 Ом·м. Крайние витки проводника подключаются к источнику, ЭДС которого E = 27 В и внутреннее сопротивление r = 1,5 Ом. На соленоид одето замкнутое кольцо диаметром D_к = 4 см из одного витка той же проволоки, что и обмотка соленоида. Определите: — магнитный поток, пронизывающий кольцо при установившемся токе в цепи соленоида, заряд, протекающий по кольцу при размыкании цепи соленоида, — ЭДС электромагнитной индукции, возникающей в кольце при условии, что время размыкания равно времени релаксации (t_p = Λ/R). Запишите уравнение зависимости силы тока от времени при размыкании цепи соленоида в общем виде и с числовыми коэффициентами.

Задача 12181

Катушка длиной 50 см и диаметром 5 см содержит 200 витков. По катушке течет ток 1 А. Определить индуктивность катушки и магнитный поток, пронизывающий площадь ее поперечного сечения.

Задача 13501

На расстоянии 1 м от длинного прямого провода с током 1 кА находится кольцо радиусом 1 см. Кольцо расположено так, что магнитный поток, пронизывающий его, максимален. Кольцо перемещают вдоль прямой, перпендикулярной проводу, удаляя его от провода. Определите, на какое расстояние переместили кольцо, если за время перемещения по кольцу прошел заряд q = 3,14 нКл. Сопротивление кольца R = 10 Ом.

Задача 15240

Круговой проволочный виток площадью S = 50 cм² находится в однородном магнитном поле. Магнитный поток, пронизывающий виток, Ф = 1 мВб. Определить индукцию магнитного поля, если плоскость витка составляет угол α = 30° с направлением линии индукции.

Задача 15244

По двум длинным параллельным проводам диаметром 2 мм течет ток 10 A. Расстояние между осями проводов 1,2 см. Рассчитать магнитный поток, пронизывающий участок между проводами на протяжении 100 м, если направление тока одном проводе противоположно направлению тока в другом.

Задача 17825

Соленоид представляет собой тонкостенный немагнитный цилиндр диаметром D = 120 мм и длиной L = 900 мм на поверхности которого плотно, виток к витку намотана тонкая проволока диаметром d = 1,0 мм и удельным сопротивлением ρ = 1,6·10^–6 Ом·м. Крайние витки проводника подключаются к источнику, ЭДС которого Е = 27 В и внутренне сопротивление r = 12 Ом. На соленоид одето замкнутое кольцо диаметром D_к = 40 см из одного витка той же проволоки, что и обмотка соленоида.
Определите:
— магнитный поток, пронизывающий кольцо при установившемся токе в цепи соленоида, заряд, протекающий по кольцу при размыкании цепи соленоида,
— ЭДС электромагнитной индукции, возникающей в кольце при условии, что время размыкания равно времени релаксации (t_р = L/R).
Запишите уравнение зависимости силы тока от времени при размыкании цепи соленоида в общем виде и с числовыми коэффициентами.

Задача 17846

Соленоид представляет собой тонкостенный немагнитный цилиндр диаметром D = 50 мм и длиной L = 400 мм на поверхности которого плотно, виток к витку намотана тонкая проволока диаметром d = 0,3 мм и удельным сопротивлением ρ = 2,6·10^–6 Ом·м. Крайние витки проводника подключаются к источнику, ЭДС которого Е = 6 В и внутренне сопротивление r = 0,8 Ом. На соленоид одето замкнутое кольцо диаметром D_к = 10 см из одного витка той же проволоки, что и обмотка соленоида.
Определите:
— магнитный поток, пронизывающий кольцо при установившемся токе в цепи соленоида, заряд, протекающий по кольцу при размыкании цепи соленоида,
— ЭДС электромагнитной индукции, возникающей в кольце при условии, что время размыкания равно времени релаксации (t_р = L/R).
Запишите уравнение зависимости силы тока от времени при размыкании цепи соленоида в общем виде и с числовыми коэффициентами.

Задача 17847

Соленоид представляет собой тонкостенный немагнитный цилиндр диаметром D = 40 мм и длиной L = 800 мм на поверхности которого плотно, виток к витку намотана тонкая проволока диаметром d = 0,6 мм и удельным сопротивлением ρ = 1,7·10^–6 Ом·м. Крайние витки проводника подключаются к источнику, ЭДС которого Е = 12 В и внутренне сопротивление r = 0,5 Ом. На соленоид одето замкнутое кольцо диаметром D_к = 8 см из одного витка той же проволоки, что и обмотка соленоида.
Определите:
— магнитный поток, пронизывающий кольцо при установившемся токе в цепи соленоида, заряд, протекающий по кольцу при размыкании цепи соленоида,
— ЭДС электромагнитной индукции, возникающей в кольце при условии, что время размыкания равно времени релаксации (t_р = L/R).
Запишите уравнение зависимости силы тока от времени при размыкании цепи соленоида в общем виде и с числовыми коэффициентами.

Задача 17848

Соленоид представляет собой тонкостенный немагнитный цилиндр диаметром D = 30 мм и длиной L = 450 мм на поверхности которого плотно, виток к витку намотана тонкая проволока диаметром d = 0,5 мм и удельным сопротивлением ρ = 110·10^–6 Ом·м. Крайние витки проводника подключаются к источнику, ЭДС которого Е = 24 В и внутренне сопротивление r = 0,6 Ом. На соленоид одето замкнутое кольцо диаметром D_к = 10 см из одного витка той же проволоки, что и обмотка соленоида.
Определите:
— магнитный поток, пронизывающий кольцо при установившемся токе в цепи соленоида, заряд, протекающий по кольцу при размыкании цепи соленоида,
— ЭДС электромагнитной индукции, возникающей в кольце при условии, что время размыкания равно времени релаксации (t_р = L/R).
Запишите уравнение зависимости силы тока от времени при размыкании цепи соленоида в общем виде и с числовыми коэффициентами.

Задача 17849

Соленоид представляет собой тонкостенный немагнитный цилиндр диаметром D = 70 мм и длиной L = 840 мм на поверхности которого плотно, виток к витку намотана тонкая проволока диаметром d = 0,4 мм и удельным сопротивлением ρ = 1,6·10^–6 Ом·м. Крайние витки проводника подключаются к источнику, ЭДС которого Е = 110 В и внутренне сопротивление r = 15 Ом. На соленоид одето замкнутое кольцо диаметром D_к = 20 см из одного витка той же проволоки, что и обмотка соленоида.
Определите:
— магнитный поток, пронизывающий кольцо при установившемся токе в цепи соленоида, заряд, протекающий по кольцу при размыкании цепи соленоида,
— ЭДС электромагнитной индукции, возникающей в кольце при условии, что время размыкания равно времени релаксации (t_р = L/R).
Запишите уравнение зависимости силы тока от времени при размыкании цепи соленоида в общем виде и с числовыми коэффициентами.

Задача 17850

Соленоид представляет собой тонкостенный немагнитный цилиндр диаметром D = 80 мм и длиной L = 640 мм на поверхности которого плотно, виток к витку намотана тонкая проволока диаметром d = 0,7 мм и удельным сопротивлением ρ = 2,6·10^–6 Ом·м. Крайние витки проводника подключаются к источнику, ЭДС которого Е = 12 В и внутренне сопротивление r = 3 Ом. На соленоид одето замкнутое кольцо диаметром D_к = 20 см из одного витка той же проволоки, что и обмотка соленоида.
Определите:
— магнитный поток, пронизывающий кольцо при установившемся токе в цепи соленоида, заряд, протекающий по кольцу при размыкании цепи соленоида,
— ЭДС электромагнитной индукции, возникающей в кольце при условии, что время размыкания равно времени релаксации (t_р = L/R).
Запишите уравнение зависимости силы тока от времени при размыкании цепи соленоида в общем виде и с числовыми коэффициентами.

Задача 17851

Соленоид представляет собой тонкостенный немагнитный цилиндр диаметром D = 90 мм и длиной L = 720 мм на поверхности которого плотно, виток к витку намотана тонкая проволока диаметром d = 0,8 мм и удельным сопротивлением ρ = 12·10^–6 Ом·м. Крайние витки проводника подключаются к источнику, ЭДС которого Е = 6 В и внутренне сопротивление r = 2 Ом. На соленоид одето замкнутое кольцо диаметром D_к = 25 см из одного витка той же проволоки, что и обмотка соленоида.
Определите:
— магнитный поток, пронизывающий кольцо при установившемся токе в цепи соленоида, заряд, протекающий по кольцу при размыкании цепи соленоида,
— ЭДС электромагнитной индукции, возникающей в кольце при условии, что время размыкания равно времени релаксации (t_р = L/R).
Запишите уравнение зависимости силы тока от времени при размыкании цепи соленоида в общем виде и с числовыми коэффициентами.

Задача 17852

Соленоид представляет собой тонкостенный немагнитный цилиндр диаметром D = 100 мм и длиной L = 1500 мм на поверхности которого плотно, виток к витку намотана тонкая проволока диаметром d = 0,3 мм и удельным сопротивлением ρ = 1,7·10^–6 Ом·м. Крайние витки проводника подключаются к источнику, ЭДС которого Е = 24 В и внутренне сопротивление r = 10 Ом. На соленоид одето замкнутое кольцо диаметром D_к = 40 см из одного витка той же проволоки, что и обмотка соленоида.
Определите:
— магнитный поток, пронизывающий кольцо при установившемся токе в цепи соленоида, заряд, протекающий по кольцу при размыкании цепи соленоида,
— ЭДС электромагнитной индукции, возникающей в кольце при условии, что время размыкания равно времени релаксации (t_р = L/R).
Запишите уравнение зависимости силы тока от времени при размыкании цепи соленоида в общем виде и с числовыми коэффициентами.

Задача 17853

Соленоид представляет собой тонкостенный немагнитный цилиндр диаметром D = 60 мм и длиной L = 600 мм на поверхности которого плотно, виток к витку намотана тонкая проволока диаметром d = 0,5 мм и удельным сопротивлением ρ = 110·10^–6 Ом·м. Крайние витки проводника подключаются к источнику, ЭДС которого Е = 110 В и внутренне сопротивление r = 20 Ом. На соленоид одето замкнутое кольцо диаметром D_к = 25 см из одного витка той же проволоки, что и обмотка соленоида.
Определите:
— магнитный поток, пронизывающий кольцо при установившемся токе в цепи соленоида, заряд, протекающий по кольцу при размыкании цепи соленоида,
— ЭДС электромагнитной индукции, возникающей в кольце при условии, что время размыкания равно времени релаксации (t_р = L/R).
Запишите уравнение зависимости силы тока от времени при размыкании цепи соленоида в общем виде и с числовыми коэффициентами.

Задача 19642

Имеется два проводящих контура, расположенных в одной плоскости, по одному из которых течет электрический ток, возрастающий по линейному закону.
1) Возникает ли в другом контуре ЭДС индукции?
2) Обращается ли ЭДС индукции во втором контуре в какие-либо моменты времени в нуль?
4) Наводится ли ЭДС самоиндукции в первом контуре (по которому течет ток)?
8) Обращается ли в какие-либо моменты времени в нуль магнитный поток, пронизывающий второй контур? На какие ответы Вы ответили «да»? Укажите сумму их номеров.

Задача 19648

На рисунке изображен график изменения со временем магнитного потока, пронизывающего замкнутый проводящий контур. Укажите номер графика, из приведенных ниже, соответствующего ЭДС индукции, возникающей в этом контуре. Индуктивностью контура пренебречь.

Задача 19651

На рисунке 1 изображен график изменения со временем магнитного потока, пронизывающего замкнутый проводящий контур. Укажите номер графика, из приведенных ниже, соответствующего ЭДС индукции, возникающей в этом контуре. Индуктивностью контура пренебречь.

Задача 20486

Квадратная рамка со стороной 2 см вращается с угловой скоростью 5 рад/с в магнитном поле с индукцией 0,2 Тл вокруг оси, проходящей через середины ее противоположных сторон. Ось вращения перпендикулярна силовым линиям поля. Найти максимальное значение магнитного потока, пронизывающего площадь рамки и зависимость ЭДС индукции, возникающей в рамке, от времени.

Задача 20770

На рисунке представлена зависимость магнитного потока, пронизывающего некоторый контур, от времени. График зависимости ЭДС индукции в контуре от времени представлен на рисунке …

Задача 20774

На рисунке приведена квадратичная зависимость от времени магнитного потока, пронизывающего проводящий контур. При этом зависимости модуля ЭДС индукции, возникающей в контуре, от времени соответствует график …

Учим физику. 11 класс. Урок 11

№ нужного урока

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80,

Домашнее задание 11

№ 921, 922, 923, 924, 925, 926

Магнитный поток, замкнутый контур, изменение, энергия, магнитное поле. ЭДС индукции в движущемся проводнике, в контуре. Тест, курсы по физике

Всего вопросов: 12

Вопрос 1. Единицей измерения магнитного потока в СИ является…

Вопрос 2. Магнитный поток, пронизывающий катушку, изменяется со временем так, как показано на рисунке. В каком промежутке времени модуль ЭДС индукции имеет максимальное значение?

Вопрос 3. Магнитное поле пронизывает рамку так, как показано на рисунке. Не меняя площади рамки, изменяют магнитное поле. На рисунке изображены графики зависимости индукции магнитного поля, пронизывающего контур, от времени. В каком случае в рамке генерируется (наводится) минимальная ЭДС индукции?

Вопрос 4. Магнит перемещают относительно замкнутого проводящего контура, как показано на рисунке. Как будет направлен индукционный ток, возникающий в контуре?

Вопрос 5. В каком направлении относительно замкнутого проводника необходимо двигать магнит, чтобы в проводнике возник электрический ток указанного направления?

Вопрос 6. Магнит вводится в алюминиевое кольцо так, как показано на рисунке. Направление тока в кольце указано стрелкой. Каким полюсом магнит вводится в кольцо?

Вопрос 7. Магнит выводят из кольца так, как показано на рисунке. Какой полюс магнита ближе к кольцу?

Вопрос 8. Как будет направлен ток в контуре 2 при размыкании цепи в контуре 1?

Вопрос 9. Контур В удаляется от контура А. Как будет направлен индукционный ток, возникающий в контуре В?

Вопрос 10. Как будет направлен индукционный ток в контуре В, если контур В удалять от контура А?

Вопрос 11. В вертикальном однородном магнитном поле по П — образному металлическому проводнику, расположенному в горизонтальной плоскости, равномерно со скоростью, модуль которой v, движется перемычка (рис. а). Какой из графиков (1-5) описывает зависимость силы тока от времени (рис. б)?

Вопрос 12. На график (рис. а) показана зависимость магнитного потока, пронизывающего контур, от времени. ЭДС индукции, возникающая в этом контуре, представлена на графике (1-5) (рис. б):

Почему наведенная ЭДС равна нулю при максимальном магнитном потоке?

Когда катушка находится в вертикальном положении, магнитный поток не изменяется (т.е. ЭДС = 0), потому что катушка не «пересекает» силовые линии. Индуцированная ЭДС равна нулю , когда катушки перпендикулярны силовым линиям, и максимум , когда они параллельны. Помните, что наведенная ЭДС — это скорость изменения магнитного потока связи.

Нажмите, чтобы увидеть полный ответ.

Кроме того, почему ЭДС максимальная при нулевом потоке?

По закону Фарадея величина наведенной ЭДС равна скорости изменения магнитного потока , поэтому ее максимальные значения возникают, когда кривая потока имеет наибольший наклон. Индуцированная ЭДС проходит через ноль , когда кривая потока имеет наклон с нулевым . Мы наблюдаем фазовый сдвиг 90 ^o между потоком и индуцированной ЭДС .

Кроме того, как рассчитать максимальную наведенную ЭДС? Закон Фарадея гласит: Индуцированная ЭДС равна скорости изменения магнитного потока. Магнитный поток = Напряженность магнитного поля x Площадь = BA. Следовательно, Индуцированная ЭДС = (изменение плотности магнитного потока x площадь) / изменение во времени. Следовательно, Индуцированная ЭДС = (Bπr ² н) / т.

Кроме того, почему наведенная ЭДС максимальна, когда катушка параллельна магнитному полю?

Магнитный поток составляет максимум , когда плоскость катушки параллельна магнитному полю .Когда якорь поворачивается, то из-за изменения магнитного потока создается наведенная ЭДС . Факторы, от которых зависит э.д.с. : Силу э.м.ф. можно увеличить, увеличив количество витков катушки . Увеличение скорости катушки .

Какая максимальная ЭДС наведена в катушке?

Вы можете обнаружить, что значение e будет максимум при t = 0. Следовательно, максимальная ЭДС равна индуцированной , когда катушка параллельна полю.Но вы сказали, что это максимум , когда движение катушки перпендикулярно полю.

Рассчитайте максимальный магнитный поток, используя уравнение. поток =

Текст расшифрованного изображения: Ширина (м) глубина (м) Величина B (тесла) Угловая скорость, Вт (рад / с) AM 1,25 м 1,25 м 700 мл 12,57 рад / с O: 1.078 Wb щелкните угол или другой параметр, чтобы перезагрузить вашу систему, щелкните время, чтобы возобновить вращение ворот. Время: 1013,5 мс СЕВЕР 0 A, ЮГ B: 700 м при 12,57 рад / с Угол 729.7 ширина: 1,25 м Глубина: 1,25 м Часть 1: Изменение магнитного потока путем изменения угла между магнитным полем B и вектором площади A (Технические данные находятся на страницах 5 и 6) From egn. 2 выше видно, что изменение угла e между вектором магнитного поля B и вектором площади A вызывает максимальное значение магнитного потока, º при углах, 0 = 0 °, или 0 радиан & € = 360 °, или 2n радиан. А 0 имеет отрицательное максимальное значение при 8 = 180 ° или радианах. Это потому, что: cosOºor cos 360º = 1 & cos 180º = -1.Также то же уравнение 2 показывает, что магнитный поток равен нулю для € = 90 ° или радиан & для 8 = 270 ° или радиан. Итак, магнитный поток, как и угн. 2 указывает, изменяется как функция косинуса от e. См. Рис. 3. Если катушка площади A вращается с постоянной угловой скоростью w, то угол поворота задается в любой момент времени t как: 01/2 39/2 2n 8 rad = wt. Для нашего случая, когда w является постоянным, тогда att равно времени одного полного цикла, T (то есть периодического времени), и с тех пор угол, e = 27, поэтому Рисунок 3: Магнитный поток, o как функция угла поворота, 8 .210 Вт = 7 (5) + Из напр. 4 и 5, t = 0 (), и из рисунка мы можем видеть, что $ = 0 fort = & t = * Кроме того, ø является максимальным для t = 0 & t = T и отрицательным максимумом fort = См. Рис. 4. Подставляя egn. 4 в ean. 2, получаем: $ = BAcos (wt) (6) T / 4 5/2 / 13T / 4) T t s Из рисунка 4 мы можем видеть, что при максимальном или отрицательном максимуме изменение D равно нулю. Вы можете проверить это утверждение на рисунке 4: Магнитный поток o, если смотреть на $ в моменты времени в непосредственной близости от t = 0, t & t = функция времени, t.Т. Также из рис. 4 видно, что имеет максимальное отрицательное изменение при t = T / 4 и максимальное положительное изменение при t = (3/4). См. Рис. 5. Какую функцию выполняют точки на рис. 5 E = отрицательное значение закона индукции Фарадея состоит в том, что индуцированная ЭДС, E — это временная скорость отрицательного значения скорости изменения магнитного потока (изменение отрицательного значения фактически происходит в соответствии с законом Ленца). Точное уравнение для скорости изменения $ и индуцированной ЭДС, e из-за изменения угла при вращении показано на рисунке 5: Отрицательная величина скорости изменения € = -временная скорость изменения * = WBA sin ( wt) магнитный поток, как функция времени, предполагают? 0 T4 T / 2 (3T / 4) T tis) Показывает

Предыдущий вопрос Следующий вопрос
РЕШЕНИЕ: Определите максимальный магнитный поток через индуктор, подключенный к стандартной розетке \ left (\ Delta V _ {\ mathrm {r…
Стенограмма видео
в этой задаче, нас просят найти максимум, который говорит, что это помогает Dr.Вы знаете, мы также должны были найти максимум или максимум античного флюса. Так что я был прав в том, что человек тик выглядит нашим максимальным антифлюсом. Благодаря этому в Dr мы можем исходить из определения потока, что основной поток тика задается числом off. Будет ли время нашей площади поперечного сечения таким, чтобы мы находим букву B вместо значения, и мы получаем основной максимальный поток антиквариата через доктора, которым мы ограничились, записывая уравнение для силы X l, которая активна, равна силе покупки f раз l, когда мы знаем, что я беспорядок, равен «Мы беспорядок», разделенный на реакции excel.Итак, если мы заменим значение X l, дамы, что он двое, здесь, и наша смесь I будет, то я, X будет равен квадратному корню из двух умноженных на Ира мс, если вы замените значение на глаз Если вы запишете наши армии в терминах off Max, мы можем получить это, это тоже будет возведено в квадрат. Мы в беспорядке разделены на то, чтобы покупать ф л. Затем мы знаем человека, который чувствовал бы себя внутри в Докторе, то есть Ах, B равно новому количеству членов, умноженному на текущий Бостон в Докторе Максимум, деленном на l l Отсюда длина провода или доктор? Тогда мы можем упростить это до Ын, когда все 10 раз тоже были отключены.Раз мы мс. Мы подставили значение для II руки Mex, которое мы нашли ранее деленное на два, на f l, деленное на l О, мы знаем, что l будет равно вам Знаете что? И квадрат делить на 10 раз делить на плохо. Таким образом, мы заменим значение l на иностранное в Dr, чтобы такое значение студента для l, которое мы легко получаем здесь, отношение для B также будет вызвано, чтобы отклониться, вы знаете, что мы делим m s на два на f раз. Гм, северный край квадрат a разделен на l a, умноженный на l, так что эти l l сократят один n один.Отменяет. У нас осталось выражение, которое представляет собой квадратный корень из двух. Мы — беспорядок, разделенный пополам на F и A. Это романтическое поле, так что хорошо, так что стреляйте в эту пчелу в этом уравнении. Как только мы подставим эту пчелу в это уравнение, мы получим поток Манти как максимальный античный поток через это в Докторе Итак, давайте это понаблюдаем. Итак, мы были. Мы только что нашли квадратный корень из двух. Мы — беспорядок, разделенный на два раза два пи. Извините, если в, где дан поток, настолько хорошо существенен, что это будет здесь, мы придем сюда, тогда замена мертвого нашего выражения становится и отмены n a n a.Эта работа понравилась с этой. У нас тоже остается квадратный корень. Мы — беспорядок, разделенный пополам, это максимум. Как и максимальный магнитный поток, проходящий через него, Ян Доктор
Определение магнитного потока и единица
Магнитный поток определяется как;
«общее количество магнитных силовых линий, проходящих через любую поверхность, расположенную перпендикулярно магнитному полю. Обозначается он φ (греческими буквами фи).
Формула магнитного потока
Магнитный поток также определяется как скалярное произведение магнитного поля B и векторной площади A, как показано на следующем рисунке.
$ \ text {Магнитный} \! \! ~ \! \! \ Text {Flux} = \ text {} \! \! \ Varphi \! \! \ Text {} = BA ~~~ \ text {} \ Cdots \ text {} ~~~~~ \ left (1 \ right) $
Где θ — это угол между B и векторной областью A или внешней нормалью, проведенной к площади поверхности, как показано на рисунке выше. {o}} \ right) $
$ \ varphi = 0 $
Это означает, что поток через область в этой позиции ноль или минимум.{8}} lines \]
Вы также можете прочитать:
Магнитодвижущая сила и Единица
Определение плотности магнитного потока и Единица
Определение интенсивности магнитного потока и Единица
Закон Ленца — University Physics Volume 2
Цели обучения
К концу этого раздела вы сможете:
Используйте закон Ленца для определения направления наведенной ЭДС при изменении магнитного потока
Используйте закон Фарадея с законом Ленца, чтобы определить наведенную ЭДС в катушке и в соленоиде
Направление, в котором индуцированная ЭДС движет ток по проволочной петле, можно определить через отрицательный знак.Однако обычно это направление легче определить с помощью закона Ленца, названного в честь его первооткрывателя Генриха Ленца (1804–1865). (Фарадей также открыл этот закон, независимо от Ленца.) Мы формулируем закон Ленца следующим образом:
Закон Ленца
Направление индуцированной ЭДС движет ток по проволочной петле, чтобы всегда противодействовать изменению магнитного потока, вызывающему ЭДС.
Закон Ленца также можно рассматривать с точки зрения сохранения энергии. Если толкание магнита в катушку вызывает ток, энергия в этом токе должна исходить откуда-то.Если индуцированный ток вызывает магнитное поле, противодействующее увеличению поля магнита, который мы втолкнули, тогда ситуация ясна. Мы приложили магнит к полю и поработали с системой, и это проявилось как ток. Если бы индуцированное поле не противодействовало изменению магнитного потока, магнит был бы втянут, создавая ток без каких-либо действий. Была бы создана электрическая потенциальная энергия, нарушив закон сохранения энергии.
Чтобы определить наведенную ЭДС, вы сначала рассчитываете магнитный поток, а затем получаете Величину, заданную по формуле. Наконец, вы можете применить закон Ленца, чтобы определить значение.Это будет развиваться на примерах, которые иллюстрируют следующую стратегию решения проблем.
Стратегия решения проблем: закон Ленца
Чтобы использовать закон Ленца для определения направлений индуцированных магнитных полей, токов и ЭДС:
Сделайте набросок ситуации для использования при визуализации и записи направлений.
Определите направление приложенного магнитного поля
Определите, увеличивается или уменьшается его магнитный поток.
Теперь определите направление индуцированного магнитного поля. Индуцированное магнитное поле пытается усилить магнитный поток, который уменьшается, или противодействует магнитному потоку, который увеличивается. Следовательно, индуцированное магнитное поле добавляет или вычитает приложенное магнитное поле, в зависимости от изменения магнитного потока.
Используйте правило правой руки 2 (RHR-2; см. Магнитные силы и поля), чтобы определить направление индуцированного тока I , ответственного за индуцированное магнитное поле
Направление (или полярность) наведенной ЭДС теперь может управлять обычным током в этом направлении.
Применим закон Ленца к системе (Рисунок) (а). Мы обозначаем «перед» замкнутой проводящей петли как область, содержащую приближающийся стержневой магнит, а «заднюю часть» петли как другую область. По мере того, как северный полюс магнита движется к петле, поток через петлю из-за поля магнита увеличивается, потому что напряженность силовых линий, направленных от передней части петли к задней, увеличивается. Поэтому в контуре индуцируется ток. По закону Ленца направление индуцированного тока должно быть таким, чтобы его собственное магнитное поле было направлено таким образом, чтобы противодействовало изменяющемуся потоку, вызванному полем приближающегося магнита.Следовательно, индуцированный ток циркулирует так, что силовые линии его магнитного поля через петлю направлены от задней части петли к передней. При использовании RHR-2 поместите большой палец напротив силовых линий магнитного поля, то есть к стержневому магниту. Ваши пальцы сгибаются против часовой стрелки, если смотреть со стороны стержневого магнита. В качестве альтернативы, мы можем определить направление индуцированного тока, рассматривая токовую петлю как электромагнит, который противодействует приближению северного полюса стержневого магнита.Это происходит, когда индуцированный ток течет, как показано, поскольку тогда поверхность петли ближе к приближающемуся магниту также является северным полюсом.
Изменение магнитного потока, вызванное приближением магнита, индуцирует ток в контуре. (а) Приближающийся северный полюс индуцирует ток против часовой стрелки по отношению к стержневому магниту. (b) Приближающийся южный полюс индуцирует ток по часовой стрелке относительно стержневого магнита.
На части (b) рисунка показан южный полюс магнита, движущийся к проводящей петле.В этом случае поток через петлю из-за поля магнита увеличивается, потому что количество силовых линий, направленных от задней части петли к передней, увеличивается. Чтобы противодействовать этому изменению, в петле индуцируется ток, силовые линии которого через петлю направлены спереди назад. Точно так же мы можем сказать, что ток течет в таком направлении, что поверхность петли ближе к приближающемуся магниту является южным полюсом, который затем отталкивает приближающийся южный полюс магнита.При использовании RHR-2 ваш большой палец направлен в сторону от стержневого магнита. Ваши пальцы сгибаются по часовой стрелке, что соответствует направлению индуцированного тока.
Другой пример, иллюстрирующий использование закона Ленца, показан на (Рисунок). Когда переключатель разомкнут, уменьшение тока через соленоид вызывает уменьшение магнитного потока через его катушки, что вызывает ЭДС в соленоиде. Эта ЭДС должна противодействовать вызывающему его изменению (прекращению тока). Следовательно, наведенная ЭДС имеет указанную полярность и движется в направлении исходного тока.Это может вызвать дугу на выводах переключателя при его размыкании.
(а) Соленоид, подключенный к источнику ЭДС. (b) Размыкающий переключатель S прекращает подачу тока, что, в свою очередь, индуцирует ЭДС в соленоиде. (c) Разность потенциалов между концами заостренных стержней создается за счет индукции ЭДС в катушке. Эта разность потенциалов достаточно велика, чтобы образовалась дуга между острыми точками.
Проверьте свое понимание Найдите направление индуцированного тока в проводной петле, показанной ниже, когда магнит входит, проходит и покидает петлю.
Для показанного наблюдателя ток течет по часовой стрелке по мере приближения магнита, уменьшается до нуля, когда магнит центрируется в плоскости катушки, а затем течет против часовой стрелки, когда магнит покидает катушку.
Проверьте свое понимание Проверьте направления наведенных токов на (рисунок).
Сводка
Мы можем использовать закон Ленца для определения направлений индуцированных магнитных полей, токов и ЭДС.
Направление наведенной ЭДС всегда противодействует изменению магнитного потока, которое вызывает ЭДС, результат, известный как закон Ленца.
Концептуальные вопросы
Круглые токопроводящие петли, показанные на прилагаемом рисунке, параллельны, перпендикулярны плоскости страницы и соосны. (a) Когда переключатель S замкнут, в каком направлении индуцируется ток в D ? (b) Когда переключатель разомкнут, каково направление тока, индуцируемого в контуре D ?
а.CW со стороны схемы; б. Против часовой стрелки, если смотреть со стороны схемы
Северный полюс магнита перемещается к медной петле, как показано ниже. Если вы смотрите на петлю сверху магнита, скажете ли вы, что индуцированный ток циркулирует по или против часовой стрелки?
На прилагаемом рисунке показано проводящее кольцо в различных положениях, когда оно движется в магнитном поле. В чем смысл индуцированной ЭДС для каждой из этих позиций?
При входе в петлю наведенная ЭДС создает ток против часовой стрелки, а при выходе из петли индуцированная ЭДС создает непрерывный ток.В то время как петля полностью находится внутри магнитного поля, нет изменения потока и, следовательно, нет индуцированного тока.
Покажите, что и у вас такие же единицы.
Укажите направление индуцированного тока для каждого случая, показанного ниже, наблюдая со стороны магнита.
а. Против часовой стрелки, если смотреть со стороны магнита; б. CW, если смотреть со стороны магнита; c. CW, если смотреть со стороны магнита; d. Против часовой стрелки, если смотреть со стороны магнита; е. CW, если смотреть со стороны магнита; f. нет тока
Проблемы
Одновитковая круглая петля из проволоки радиусом 50 мм лежит в плоскости, перпендикулярной пространственно однородному магнитному полю.За интервал времени 0,10 с величина поля равномерно увеличивается от 200 до 300 мТл. (а) Определите ЭДС, наведенную в петле. (б) Если магнитное поле направлено за пределы страницы, каково направление тока, индуцируемого в петле?
а. ; б. CCW с той же точки зрения, что и магнитное поле
При первом включении магнитного поля поток через 20-витковую петлю изменяется со временем в зависимости от того, где он находится в милливеберах, t — в секундах, а петля находится в плоскости страницы с нормальным направлением единицы. наружу.(а) Какая ЭДС индуцируется в контуре как функция времени? Каково направление индуцированного тока при (b) t = 0, (c) 0,10, (d) 1,0 и (e) 2,0 с?
а. 150 А вниз через резистор; б. 46 А вверх через резистор; c. 0,019 А вниз через резистор
Используйте закон Ленца для определения направления индуцированного тока в каждом случае.
Глоссарий
Закон Ленца
направление наведенной ЭДС противодействует изменению магнитного потока, который ее произвел; это отрицательный знак в законе Фарадея
Что такое максимальное произведение энергии / (BH) max и как оно соответствует марке магнита?
Итак, что такое продукт максимальной энергии ((BH) max), марка магнита и MGO?
Термин «Максимальный энергетический продукт» ((BH) max) является широко используемым, но часто неправильно понимаемым показателем качества магнитов.3.)
Это соглашение кажется разумным, но оно имеет ограничения, поскольку не позволяет прогнозировать магнитные характеристики. Как правило, магнит с более высоким (BH) max будет сильнее, чем магнит с более низким (BH) max, но это по-прежнему не позволяет нам прогнозировать характеристики относительно плотности магнитного поля или генерации потока.
Чтобы предсказать характеристики магнита в конкретном приложении, необходимо знать другие магнитные характеристики материала магнита и физическую геометрию магнита.Прогнозирование производительности не входит в объем данной статьи, но геометрия магнита имеет отношение к обсуждению произведения максимальной энергии.
Формальное определение максимального произведения энергии:
Максимальное произведение энергии или (BH) max магнита — это плотность энергии, которая эквивалентна площади самого большого прямоугольника, который может быть вписан под нормальную кривую, как показано ниже (рисунок 1):
Рис. 1: (BH) max показано в виде вписанного прямоугольника
Это также вершина параболы, состоящей из произведения точек, составляющих нормальную кривую (магнитная индукция и напряженность поля), построенная против напряженности поля, как показано здесь (рисунок 2):
Рисунок 2: (BH) max-Vertex of Parabola
(BH) max Технические пояснения:
(BH) max — это не зависящая от объема магнитная характеристика, что означает, что маленький и большой магнит, сделанный из одного и того же магнитного сплава ND-48 с неодимом, железом и бором, будет иметь одинаковое значение (BH) max, хотя они и создают совершенно разные магнитные поля или потоки.Максимальное произведение энергии, или (BH) max, достигается, когда магнит работает на самом высоком уровне индукции (Гаусс) и при наименьшем объеме для определенного поперечного сечения полюса. Большие объемы магнита будут производить более сильные магнитные поля и больший поток, хотя магнит может не работать при (BH) max.
По отношению к кривой BH или кривой размагничивания, второго квадранта кривой гистерезиса магнита, максимальное произведение энергии — это самый большой прямоугольник, который может быть вписан под нормальную кривую (см. Рисунок 1).Вершина прямоугольника на оси X (напряженность поля) — это рабочая точка Hd при (BH) max, а вершина на оси Y (магнитная индукция) — это рабочая точка Bd при (BH) max.
Кроме того, если известны точки данных (H-B) для нормальной кривой, их произведение может быть рассчитано и затем нанесено на график в зависимости от напряженности поля (ось X). Этот график будет генерировать параболу, и вершина параболы будет находиться в Максимальном произведении энергии для конкретного сорта в единицах MGOe, если B находится в гауссах, а H — в эрстедах (см. Рисунок 2).
Рекламные магнитные характеристики промышленного магнита указаны с допусками. Диапазон остаточной индукции (Br) и коэрцитивной силы (Hc) изменяется там, где рабочие точки Hd и Bd встречаются для (BH) max. Вот почему существует эффективный диапазон для продукта максимальной энергии.
Для того, чтобы магнит работал на максимальной (BH) max, он должен иметь определенную геометрию. Эта геометрия является обычно используемым соотношением в магнитной конструкции и представляет собой отношение длины магнита к диаметру магнита, L / D.(Для некруглых магнитов используется диаметр круга с эквивалентной площадью некруглого полюса.) Поскольку это соотношение, существует бесконечное количество возможностей геометрии магнита для любого конкретного сорта магнита.
Когда конкретный магнит работает на (BH) max, можно сказать, что он имеет наивысший КПД по отношению к плотности энергии. Опять же, когда магнит работает на (BH) max, он может не генерировать достаточно большое магнитное поле для конкретного применения, и поэтому может потребоваться больший объем.Большинство магнитов, используемых в приложениях, не рассчитаны на работу при (BH) макс.
Хотите узнать больше?
У вас есть технические вопросы по разработке и производству магнитов? Присылайте свои вопросы нашим инженерам или свяжитесь с нами по телефону 1-800-492-7939.
Калькулятор максимальной плотности потока (Bmax)
Что такое магнитный поток?
Предположим, что в однородном магнитном поле с интенсивностью магнитной индукции B существует плоскость площадью S, перпендикулярная направлению магнитного поля.Произведение интенсивности магнитной индукции B и площади S называется магнитным потоком, проходящим через эту плоскость, называемым магнитным потоком. Скаляр, символ «Φ».
Обычно магнитный поток определяется интегралом магнитного поля на площади поверхности. Среди них Φ — магнитный поток, B — интенсивность магнитной индукции, S — поверхность, B · dS — скалярное произведение, а dS — бесконечно малый вектор (см. Интегрирование по поверхности). Магнитный поток обычно измеряется измерителем потока.Измеритель потока включает в себя измерительную катушку и схему, которая оценивает изменение напряжения на измерительной катушке для расчета магнитного потока.
Изменение магнитного потока
Величину магнитного потока, проходящего через определенную плоскость, можно наглядно объяснить количеством магнитных линий индукции, проходящих через эту плоскость. В одном и том же магнитном поле, чем больше напряженность магнитной индукции, тем плотнее магнитные линии индукции.Следовательно, чем больше B и больше S, тем больше магнитный поток, а это означает, что количество магнитных линий, проходящих через эту поверхность, больше. Если есть два магнитных потока в противоположных направлениях через плоскость, объединенный магнитный поток в это время является алгебраической суммой магнитных потоков в противоположном направлении (то есть противоположный комбинированный магнитный поток компенсирует оставшийся магнитный поток).
Теорема Гаусса о магнитном поле утверждает, что магнитный поток, проходящий через любую замкнутую поверхность, равен нулю, то есть указывает на то, что магнитное поле является пассивным, и никакой источник или хвост не излучает или не сходится магнитные силовые линии, то есть нет нет изолированного магнитного монополя.B в приведенной выше формуле может быть либо магнитным полем, создаваемым током, магнитным полем, создаваемым изменяющимся электрическим полем, либо суммой двух.
Определение плотности магнитного потока
Плотность магнитного потока отражает количество магнитных силовых линий. Сила магнитного поля обычно выражается интенсивностью магнитной индукции «B».
Единица измерения плотности магнитного потока:
Единица магнитной индукции — Тесла, ее символ — Т, и есть устаревшая единица: Гаусс, ее символ — Гс: 1 Тл = 10000 Гс.
Формула для расчета плотности магнитного потока:
Выражение магнитного потока Φ
1. Φ = BSsinα, где α — угол между направлением магнитного поля и плоскостью.
2. Φ = BScosα, где α — проекционный угол между плоскостью и плоскостью, перпендикулярной направлению магнитного поля.
Если где-то в магнитном поле напряженность магнитной индукции равна B, и имеется поверхность, перпендикулярная магнитному потоку, и ее площадь равна S, то проходящий через нее магнитный поток равен:
Φ = BS
Единицей магнитного потока в формуле является Максвелл (Mx), а единицей силы магнитной индукции B является Гаусс (Гс) в квадратных сантиметрах или Тесла (Тл) в квадратных метрах.
Формулы и уравнения для калькулятора максимальной плотности потока
в трансформаторе,
Bmax = V / (4,44 f N A) …… в Тесла
Bmax = (V x 108) / (4,44 f N A) …… в Гуассе
Где;
Bmax = максимальная плотность потока
В = приложенное действующее напряжение
f = частота
N = количество оборотов обмотки], где V — приложенное напряжение.
A = Площадь поперечного сечения магнитной цепи, заключенной в обмотку (м2)
Формулы и уравнения плотности потока
Bmax = Bmax [AC] + Bmax [DC]
Примечание: в случае отсутствия постоянного тока второй член уравнения опускается.
FAQ
1. Какова максимальная магнитная индукция сердечника трансформатора в настоящее время?
Максимальная магнитная индукция сердечника трансформатора составляет 1,1 Тл. (E = 4,44 кг .kd.kp.flux max .f.N), в основном максимальное количество магнитной индукции зависит от количества витков в обмотке сердечника. Еще одним фактором является воздушный зазор. Если воздушный зазор (кг меньше) будет больше потока.
2. Какая магнитная индукция у силового трансформатора?
Плотность потока — это мера количества магнитных силовых линий на единицу площади поперечного сечения.
3. По какому принципу выбираем магнитную индукцию в сердечнике трансформатора?
Размер трансформатора является основным фактором при выборе плотности потока. По мере увеличения номинальной мощности трансформатора в МВА существует тенденция к использованию более высокой плотности магнитного потока для ограничения размера трансформатора, даже если это означает компромисс с более высоким содержанием гармоник в токе намагничивания. Увеличение магнитной индукции уменьшает габариты трансформатора двумя способами: (1) уменьшение площади поперечного сечения сердечника (2) уменьшение средней длины витка обмотки.

Ответ: 47,8 мВб.

Максимальный магнитный поток. Поток индукции магнитного поля

Смотреть что такое «МАГНИТНЫЙ ПОТОК» в других словарях:

Книги

Квантование магнитного потока

Напишите отзыв о статье «Магнитный поток»

Ссылки

Отрывок, характеризующий Магнитный поток

Невидимая сила

Магнитный поток: определение и характеристика

Раскрывая тайну магнитных потоков

Линии магнитного потока

Магнитные молекулы и теория Вебера

Поля и полюса

Природа магнетизма

Измерение и практическое применение

Рекомендуем также

Магнитный поток

ЯВЛЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ.

магнитный поток пронизывающий

Учим физику. 11 класс. Урок 11

Магнитный поток, замкнутый контур, изменение, энергия, магнитное поле. ЭДС индукции в движущемся проводнике, в контуре. Тест, курсы по физике

Почему наведенная ЭДС равна нулю при максимальном магнитном потоке?

Рассчитайте максимальный магнитный поток, используя уравнение. поток =

РЕШЕНИЕ: Определите максимальный магнитный поток через индуктор, подключенный к стандартной розетке \ left (\ Delta V _ {\ mathrm {r…

Стенограмма видео

Определение магнитного потока и единица

Закон Ленца — University Physics Volume 2

Цели обучения

Сводка

Концептуальные вопросы

Проблемы

Глоссарий

Что такое максимальное произведение энергии / (BH) max и как оно соответствует марке магнита?

Итак, что такое продукт максимальной энергии ((BH) max), марка магнита и MGO?

Калькулятор максимальной плотности потока (Bmax)

Формулы и уравнения для калькулятора максимальной плотности потока

Формулы и уравнения плотности потока

FAQ

Добавить комментарий Отменить ответ