Ответы@Mail.Ru: что такое магнитный поток?

МАГНИТНЫЙ ПОТОК (символ Ф) , мера силы и протяженности МАГНИТНОГО ПОЛЯ. Поток через площадь А под прямым углом к одинаковому магнитному полю есть Ф=mНА, где m — магнитная ПРОНИЦАЕМОСТЬ среды, а Н — интенсивность магнитного поля. Плотность магнитного потока — это поток на единицу площади (символ В) , который равен Н. Изменение магнитного потока через электрический проводник наводит ЭЛЕКТРОДВИЖУЩУЮ СИЛУ.

Магнитным потоком называют поток вектора магнитной индукции В через некую поверхность.

Это магнитный аналог электрического тока, измерятся в Веберах, Вб. Расчет магнитных цепей аналогичен электрическим цепям. Магнитный поток, Вб — электрический ток, А Магнитодвижущая сила, мдс, (количество ампер-витков) — эдс, В Магнитное напряжение, или напряженность измеряется в амперах на метр, А/м — электрическое напряжение, В Магнитное сопротивление аналогично электрическому сопротивлению.

Магни́тный пото́к — физическая величина, равная произведению модуля вектора магнитной индукции на площадь S и косинус угла α между векторамии нормалью {n} . Поток как интеграл вектора магнитной индукции} через конечную поверхность S определяется через интеграл по поверхности

Вращающееся магнитное поле — Википедия

Материал из Википедии — свободной энциклопедии

Векторная сумма (не изображенный вектор, соединяющий начало первого из складываемых векторов и конец третьего) трех магнитных полей, создаваемых тремя катушками статора (синие стрелки) есть вращающееся магнитное поле — вращающийся вектор постоянной длины. Ротор на картинке представляет собой постоянный электромагнит, вращающийся вслед за вращающимся магнитным полем, создаваемым статором (см. Синхронный двигатель).

Вращающееся магнитное поле. Обычно под вращающимся магнитным полем понимается магнитное поле, вектор магнитной индукции которого, не изменяясь по модулю, вращается с постоянной угловой скоростью.

Также вращающимися магнитными полями называют и магнитные поля вращающихся постоянных магнитов.

Существуют вращающиеся магнитные поля ось вращения которых не совпадает с их осью симметрии (например, магнитные поля звезд или планет).

Вращающееся магнитное поле создают, накладывая два или более разнонаправленных переменных, зависящих от времени по синусоидальному закону, магнитных поля одинаковой частоты, но сдвинутых друг относительно друга по фазе.

Вращающееся магнитное поле практически осуществлено независимо в 1888 году итальянским физиком Г. Феррарисом и сербским инженером Н. Тесла^[1].

В электрических машинах[править | править код]

Вращающееся магнитное поле в трёхфазном однополюсном синхронном электродвигателе. Направление поля показано чёрной стрелкой.

Применяется в синхронных и асинхронных машинах.

Разность фаз для двухфазных систем (два перпендикулярных ориентированных электромагнита) в однополюсных машинах должна составлять 90°, а для 3-фазных (три электромагнита, направленных в одной плоскости под углом 120° друг к другу) 120°.

В синхронных генераторах переменного тока ротор является либо постоянным магнитом, либо электромагнитом, питаемым постоянным током — током возбуждения. Вращающееся магнитное поле в таких машинах индуктирует в обмотках статора ЭДС, причём если машина однополюсная, то частота ЭДС равна частоте вращения ротора.

Другие применения[править | править код]

В тахометрах вращающийся постоянный магнит увлекает неферромагнитный металлический диск вал которого снабжён создающей противодействующий вращательный момент.

Счётчики электрической энергии, например, бытовые счётчики, работают по аналогичному принципу — увлечения проводящего неферромагнитного диска вращающимся магнитным полем, создаваемым обмотками тока потребления и напряжения сети.

Также вращающееся магнитное поле применяется в лабораторных мешалках жидкости.

Магнитное поле Земли — Википедия

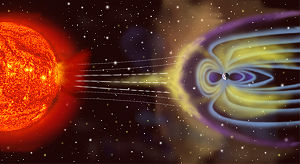Обтекание магнитосферы Земли солнечным ветром

Магни́тное по́ле Земли́ или геомагни́тное по́ле — магнитное поле, генерируемое внутриземными источниками. Предмет изучения геомагнетизма. Появилось 4,2 млрд лет назад

[1].

Строение и характеристики магнитного поля Земли[править | править код]

Собственное магнитное поле Земли (геомагнитное поле) можно разделить на cледующие основные части^[2]:

• главное поле,
• поля мировых аномалий,
• внешнее магнитное поле.

Главное поле[править | править код]

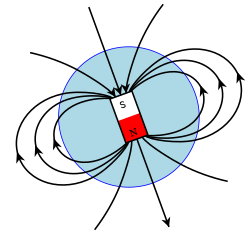Земля как магнитный диполь.

Более чем на 90 % оно состоит из поля, источник которого находится внутри Земли, в жидком внешнем ядре, — эта часть называется главным, основным или нормальным полем

[3]^[4][5]. Оно аппроксимируется в виде ряда по гармоникам — ряда Гаусса, а в первом приближении вблизи поверхности Земли (до трёх её радиусов) близко к полю магнитного диполя, то есть имеет такой вид, как будто земной шар представляет собой полосовой магнит с осью, направленной приблизительно с севера на юг^{[2][6][3][7][8]}. Центр этого диполя смещен относительно центра Земли, а ось наклонена к оси вращения Земли на угол около 10°. На такой же угол отстоят от соответствующих географических полюсов геомагнитные полюса — точки пересечения оси диполя с поверхностью Земли^[4]. Их положение в различные моменты времени вычисляется в рамках той или иной модели магнитного поля, определяющей тем или иным образом первые три коэффициента в ряду Гаусса ^[3]. Эти глобальные модели, такие как Международное геомагнитное аналитическое поле (International Geomagnetic Reference Field, IGRF)^[9] и Всемирная магнитная модель (World Magnetic Model, WMM)^[en][10], создаются различными международными геофизическими организациями, и каждые 5 лет утверждаются и публикуются обновлённые наборы коэффициентов Гаусса, определяющих все данные о состоянии геомагнитного поля и его параметрах^[4]. Так, согласно модели WMM2015, северный геомагнитный полюс (по сути это южный полюс магнита) имеет координаты 80,37° с. ш. и 72,62° з. д., южный геомагнитный полюс — 80,37° ю. ш., 107,38° в. д., наклон оси диполя относительно оси вращения Земли — 9,63° ^[3][11].

Поля мировых аномалий[править | править код]

Реальные силовые линии магнитного поля Земли, хотя в среднем и близки к силовым линиям диполя, отличаются от них местными нерегулярностями, связанными с наличием намагниченных пород в коре, расположенных близко к поверхности. Из-за этого в некоторых местах на земной поверхности параметры поля сильно отличаются от значений в близлежащих районах, образуя так называемые магнитные аномалии^[2][4][7][8]. Они могут накладываться одна на другую, если вызывающие их намагниченные тела залегают на разных глубинах

[5].

Существование магнитных полей протяжённых локальных областей внешних оболочек приводит к тому, что истинные магнитные полюса — точки (вернее, небольшие области), в которых силовые линии магнитного поля абсолютно вертикальны, — не совпадают с геомагнитными, при этом они лежат не на самой поверхности Земли, а под ней^[4][3][6]. Координаты магнитных полюсов на тот или иной момент времени также вычисляются в рамках различных моделей геомагнитного поля путём нахождения итеративным методом всех коэффициентов в ряду Гаусса. Так, согласно актуальной модели WMM, в 2015 г. северный магнитный полюс находился в точке 86° с. ш., 159° з. д., а южный — 64° ю. ш., 137° в.д

[3]. Значения актуальной модели IGRF12 немного отличаются: 86,3° с. ш., 160° з. д., для северного полюса, 64,3° ю. ш., 136,6° в.д для южного^[11].

Соответственно, магнитная ось — прямая, проходящая через магнитные полюса, — не проходит через центр Земли и не является её диаметром^[6][7].

Положения всех полюсов постоянно смещаются — геомагнитный полюс прецессирует относительно географического с периодом около 1200 лет^[2].

Внешнее магнитное поле[править | править код]

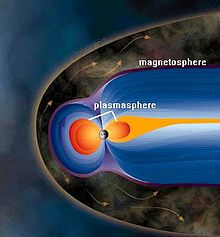
Оно определяется источниками в виде токовых систем, находящимися за пределами земной поверхности, в её атмосфере^[2][4]. В верхней части атмосферы (100 км и выше) — ионосфере — её молекулы ионизируются, формируя плотную холодную плазму, поднимающуюся выше, поэтому часть магнитосферы Земли выше ионосферы, простирающаяся на расстояние до трёх её радиусов, называется плазмосферой. Плазма удерживается магнитным полем Земли, но её состояние определяется его взаимодействием с солнечным ветром — потоком плазмы солнечной короны^[12].

Таким образом, на большем удалении от поверхности Земли магнитное поле несимметрично, так как искажается под действием солнечного ветра: со стороны Солнца оно сжимается, а в направлении от Солнца приобретает «шлейф», который простирается на сотни тысяч километров, выходя за орбиту Луны^[2]. Эта своеобразная «хвостатая» форма возникает, когда плазма солнечного ветра и солнечных корпускулярных потоков как бы обтекают земную магнитосферу — область околоземного космического пространства, ещё контролируемую магнитным полем Земли, а не Солнца и других межпланетных источников^[2][4][7][8]; она отделяется от межпланетного пространства магнитопаузой, где динамическое давление солнечного ветра уравновешивается давлением собственного магнитного поля. Подсолнечная точка магнитосферы в среднем находится на расстоянии 10 земных радиусов R_⊕; при слабом солнечном ветре это расстояние достигает 15—20 R_⊕, а в период магнитных возмущений на Земле магнитопауза может заходить за геостационарную орбиту (6,6 R_⊕)^[2]. Вытянутый хвост на ночной стороне имеет диаметр около 40 R_⊕ и длину более 900 R_⊕; начиная с расстояния примерно 8 R_⊕, он разделен на части плоским нейтральным слоем, в котором индукция поля близка к нулю^[2][4][7][8].

Искажение магнитного поля Земли под действием солнечного ветра

Геомагнитное поле вследствие специфической конфигурации линий индукции создает для заряженных частиц — протонов и электронов — магнитную ловушку. Оно захватывает и удерживает огромное их количество, так что магнитосфера является своеобразным резервуаром заряженных частиц. Общая их масса, по различным оценкам, составляет от 1 кг до 10 кг. Они формируют так называемый радиационный пояс, охватывающий Землю со всех сторон, кроме приполярных областей. Его условно разделяют на два — внутренний и внешний. Нижняя граница внутреннего пояса находится на высоте около 500 км, его толщина — несколько тысяч километров. Внешний пояс находится на высоте 10—15 тыс. км. Частицы радиационного пояса под действием силы Лоренца совершают сложные периодические движения из Северного полушария в Южное и обратно, одновременно медленно перемещаясь вокруг Земли по азимуту. В зависимости от энергии они совершают полный оборот вокруг Земли за время от нескольких минут до суток^[7].

Магнитосфера не подпускает к земле потоки космических частиц^[8]. Однако в её хвосте, на больших расстояниях от Земли напряженность геомагнитного поля, а следовательно, и его защитные свойства, ослабляются, и некоторые частицы солнечной плазмы получают возможность попасть вовнутрь магнитосферы и магнитных ловушек радиационных поясов. Хвост таким образом служит местом формирования потоков высыпающихся частиц, вызывающих полярные сияния и авроральные токи^[2]. В полярных областях часть потока солнечной плазмы вторгается в верхние слои атмосферы из радиационного пояса Земли и, сталкиваясь с молекулами кислорода и азота, возбуждает их или ионизирует, а при обратном переходе в невозбужденное состояние атомы кислорода излучают фотоны с λ = 0,56 мкм и λ = 0,63 мкм, ионизированные же молекулы азота при рекомбинации высвечивают синие и фиолетовые полосы спектра. При этом наблюдаются полярные сияния, особенно динамичные и яркие во время магнитных бурь. Они происходят при возмущениях в магнитосфере, вызванных увеличением плотности и скорости солнечного ветра при усилении солнечной активности^[8][7].

Параметры поля[править | править код]

Наглядное представление о положении линий магнитной индукции поля Земли даёт магнитная стрелка, закреплённая таким образом, что может свободно вращаться и вокруг вертикальной, и вокруг горизонтальной оси (например, в кардановом подвесе), — в каждой точке вблизи поверхности Земли она устанавливается определённым образом вдоль этих линий.

Поскольку магнитные и географические полюса не совпадают, магнитная стрелка указывает направление с севера на юг только приблизительно. Вертикальную плоскость, в которой устанавливается магнитная стрелка, называют плоскостью магнитного меридиана данного места, а линию, по которой эта плоскость пересекается с поверхностью Земли, — магнитным меридианом^[6][8]. Таким образом, магнитные меридианы — это проекции силовых линий магнитного поля Земли на её поверхность, сходящиеся в северном и южном магнитных полюсах^[13]. Угол между направлениями магнитного и географического меридианов называют магнитным склонением. Оно может быть западным (часто обозначается знаком «−») или восточным (знак «+») в зависимости от того, к западу или востоку отклоняется северный полюс магнитной стрелки от вертикальной плоскости географического меридиана^[6][7][8].

Далее, линии магнитного поля Земли, вообще говоря, не параллельны её поверхности. Это означает, что магнитная индукция поля Земли не лежит в плоскости горизонта данного места, а образует с этой плоскостью некий угол — он называется магнитным наклонением^[6][8]. Оно близко к нулю лишь в точках магнитного экватора — окружности большого круга в плоскости, которая перпендикулярна к магнитной оси^[3].

Магнитное склонение и магнитное наклонение определяют направление магнитной индукции поля Земли в каждом конкретном месте. А численное значение этой величины можно найти, зная наклонение и одну из проекций вектора магнитной индукции B{\displaystyle \mathbf {B} } — на вертикальную или горизонтальную ось (последнее оказывается более удобным на практике). Таким образом, три этих параметра — магнитное склонение, наклонение и модуль вектора магнитной индукции B (либо вектора напряжённости магнитного поля H{\displaystyle \mathbf {H} }) — полностью характеризуют геомагнитное поле в данном месте. Их точное знание для максимально большого числа пунктов на Земле имеет чрезвычайно важное значение^[6][8]. Составляются специальные магнитные карты, на которых нанесены изогоны (линии одинакового склонения) и изоклины (линии одинакового наклонения), необходимые для ориентации с помощью компаса^[8].

В среднем интенсивность магнитного поля Земли колеблется от 25 до 65 мкТл (0,25—0,65 Гс) и сильно зависит от географического положения^[3]. Это соответствует средней напряжённости поля около 0,5 Э (40 А/м)^[2]. На магнитном экваторе её величина около 0,34 Э, у магнитных полюсов — около 0,66 Э. В некоторых районах (магнитных аномалий) напряжённость резко возрастает: в районе Курской магнитной аномалии она достигает 2 Э^[7].

Магнитный дипольный момент Земли на 2015 год составлял 7,72⋅10²⁵Гс·см³ (или 7,72⋅10²² А·м²), уменьшаясь в среднем за последние десятилетия на 0,007⋅10²⁵ Гс·см³ в год^[11].

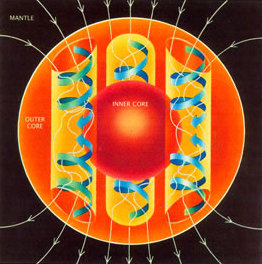Схема динамо-механизма: конвекционные потоки расплавленного металла во внешнем ядре формируют циркулирующие по замкнутому контуру токи, которые генерируют магнитное поле^[14]. Из-за вращения твёрдого ядра согласно теореме Тейлора-Праудмена^[en] скорость потоков постоянна вдоль вертикальной оси образующихся таким образом столбов Тейлора^[en], заключённых внутри цилиндра, ограничивающего внутреннее ядро, и подобных циклонам и антициклонам в атмосфере Земли^[15][16]. Первичные (по/против часовой стрелки) и вторичные (вертикальные сходящиеся/расходящиеся на экваторе) потоки вытягивают и поворачивают линии магнитного поля, превращая азимутальную компоненту в меридиональную и затем обратно^[17].

Впервые объяснить существование магнитных полей Земли и Солнца попытался Дж. Лармор в 1919 году^[18], предложив концепцию динамо, согласно которой поддержание магнитного поля небесного тела происходит под действием гидродинамического движения электропроводящей среды. Однако в 1934 году Т. Каулинг^[en][19] доказал теорему о невозможности поддержания осесимметричного магнитного поля посредством гидродинамического динамо-механизма. А поскольку большинство изучаемых небесных тел (и тем более Земля) считались аксиально-симметричными, на основании этого можно было сделать предположение, что их поле тоже будет аксиально-симметричным, и тогда его генерация по такому принципу будет невозможна согласно этой теореме^[20]. Даже Альберт Эйнштейн скептически относился к осуществимости такого динамо при условии невозможности существования простых (симметричных) решений. Лишь гораздо позже было показано, что не у всех уравнений с аксиальной симметрией, описывающих процесс генерации магнитного поля, решение будет аксиально-симметричным, и в 1950-х гг. несимметричные решения были найдены^[20][15].

С тех пор теория динамо успешно развивается, и на сегодняшний день общепринятым наиболее вероятным объяснением происхождения магнитного поля Земли и других планет является самовозбуждающийся динамо-механизм, основанный на генерации электрического тока в проводнике при его движении в магнитном поле, порождаемом и усиливаемом самими этими токами. Необходимые условия создаются в ядре Земли: в жидком внешнем ядре, состоящем в основном из железа при температуре порядка 4—6 тысяч кельвин, которое отлично проводит ток, создаются конвективные потоки, отводящие от твёрдого внутреннего ядра тепло (генерируемое благодаря распаду радиоактивных элементов либо освобождению скрытой теплоты при затвердевании вещества на границе между внутренним и внешним ядром по мере постепенного остывания планеты). Силы Кориолиса закручивают эти потоки в характерные спирали, образующие так называемые столбы Тейлора^[en]. Благодаря трению слоёв они приобретают электрический заряд, формируя контурные токи. Таким образом, создаётся система токов, циркулирующих по проводящему контуру в движущихся в (изначально присутствующем, пусть и очень слабом) магнитном поле проводниках, как в диске Фарадея. Она создает магнитное поле, которое при благоприятной геометрии течений усиливает начальное поле, а это, в свою очередь, усиливает ток, и процесс усиления продолжается до тех пор, пока растущие с увеличением тока потери на джоулево тепло не уравновесят притоки энергии, поступающей за счет гидродинамических движений^{[14][21][16][22]}. Высказывались предположения, что динамо может возбуждаться за счёт прецессии или приливных сил, то есть что источником энергии является вращение Земли, однако наиболее распространена и разработана гипотеза о том, что это всё же именно термохимическая конвекция^[17].

Математически этот процесс описывается магнитогидродинамическим уравнением индукции^{[en][16][17][23]}

∂B∂t=∇×(u×B)+η∇2B{\displaystyle {\frac {\partial \mathbf {B} }{\partial t}}=\mathbf {\nabla } \times (\mathbf {u} \times \mathbf {B} )+\eta \mathbf {\nabla } ^{2}\mathbf {B} },

где u — скорость потока жидкости, B — магнитная индукция, η = 1/μσ — магнитная вязкость^[en] (коэффициент магнитной диффузии), σ — электропроводность жидкости, а μ — магнитная проницаемость, практически не отличающаяся при такой высокой температуре ядра от μ₀ — проницаемости вакуума. Первое слагаемое в правой части соответствует формированию магнитного поля, а второе — его подавлению. При u=0 (без динамо) решение этого уравнения — поле, полностью угасающее через 6⋅10⁴ лет^[23].

Однако для полного описания необходимо записать систему магнитогидродинамических уравнений. В приближении Буссинеска (в рамках которого пренебрегается т. н. вековым охлаждением и все физические характеристики жидкости полагаются постоянными, кроме силы Архимеда, при расчёте которой учитываются изменения плотности вследствие разности температур и — в общем случае — концентрации лёгких элементов) это^[16][17][23]:

ρ0(∂u∂t+u⋅∇u)=−∇P+ρ0ν∇2u+ρg¯−2ρ0Ω×u+J×B{\displaystyle \rho _{0}\left({\frac {\partial \mathbf {u} }{\partial t}}+\mathbf {u} \cdot \mathbf {\nabla } \mathbf {u} \right)=-\nabla P+\rho _{0}\nu \mathbf {\nabla } ^{2}\mathbf {u} +\rho {\bar {\mathbf {g} }}-2\rho _{0}\mathbf {\Omega } \times \mathbf {u} +\mathbf {J} \times \mathbf {B} }.

Здесь ρ — плотность, ν — кинематическая вязкость, P=p−ρ02|Ω×r|2{\displaystyle P=p-{\frac {\rho _{0}}{2}}|\mathbf {\Omega } \times \mathbf {r} |^{2}} — «эффективное» давление с учётом центробежной силы (хотя в некоторых моделях она полагается пренебрежимо малой), g¯=g0rR0{\displaystyle {\bar {\mathbf {g} }}=g_{0}{\frac {\mathbf {r} }{R_{0}}}} — сила тяготения (R₀ — радиус внешнего ядра), Ω — угловая скорость вращения мантии, полагаемая равной скорости вращения внутреннего ядра, J=1μ∇×B{\displaystyle \mathbf {J} ={\frac {1}{\mu }}\nabla \times \mathbf {B} } — плотность тока согласно закону Ампера, индекс «0» всюду обозначает значения на границе внешнего ядра. Левая часть уравнения — производная от импульса на единицу объёма, то есть производная по времени от величины ρ₀V, увлекаемой движением жидкости; правая часть — сумма сил, вызывающих это изменение импульса: градиент давления^[en], вязкость, гравитация (сила Архимеда), вращение (сила Кориолиса) и магнитное поле (сила Лоренца)^[16].

Вращение Земли — один из важнейших факторов формирования геомагнитного поля, и его механизм схож с процессами в атмосфере Земли, приводящим к завихрению воздушных масс против часовой стрелки в северном полушарии и в обратном направлении в южном — циклонам и антициклонам. Аналогичные завихрения конвекционных потоков в ядре приводят к тому, что отдельные турбулентные конвекционные движения приобретают крупномасштабную (при усреднении по пульсациям скорости) зеркальную асимметрию и в совокупности приводят к генерации динамо в макроскопических масштабах благодаря электродвижущей силе, направленной уже вдоль, а не перпендикулярно среднему (которое определяется усреднением реального поля по его возможным статистическим реализациям) магнитному полю ⟨ε⟩=α⟨B⟩{\displaystyle \langle \mathbf {\varepsilon } \rangle =\alpha \langle \mathbf {B} \rangle }, где ε — ЭДС, а α — коэффициент пропорциональности, из-за которого этот механизм и получил название альфа-эффект^[22][24]. В общем случае α — тензор, однако зеркальная антисимметрия даёт псевдоскаляр, которого и требует по построению эта формула, так как ε — истинный вектор, а B — псевдовектор^[25]. Динамо, основанное исключительно на α-эффекте, называют α²-динамо, поскольку его действие выражается произведением двух членов, содержащих этот коэффициент^[23], — оно характеризуется практически стационарным полем, испытывающим небольшие кратковременные вариации (порядка сотен лет для Земли) и долговременные полные инверсии (порядка миллиона лет для Земли). Возможен также механизм с действием омега-эффекта (более существенного для Солнца, чем для Земли, однако необходимого для объяснения природы наблюдаемого дрейфа геомагнитных неоднородностей) — это измеряемое градиентом скорости дифференциальное вращение, которое из направленного к наблюдателю полоидального (вытянутого вдоль меридианов, B_S) магнитного поля создаёт скрытое в проводящем ядре планеты тороидальное (вытянутое вдоль параллелей, B_T) поле. Альфа-эффект замыкает цикл генерации — превращая тороидальное поле в полоидальное за счёт вихрей, характеризуемых отрицательной спиральностью (эта характеристика выражается соотношением u⋅∇×u{\displaystyle \mathbf {u} \cdot \mathbf {\nabla } \times \mathbf {u} } и непосредственно связана с величиной α) в Северном полушарии и положительной в Южном: восходящие и нисходящие потоки в конвекционных цилиндрах вытягивают и поворачивают B_T-линии в S-направлении^{[26][20][15][17]}. Такая схема обычно называется αω-эффектом, она даёт переменные поля, и при этом B_T>>B_S, тогда как для α²-механизма эти компоненты сравнимы (экспериментально на сегодняшний день удалось получить только грубую оценку |B_S|<|B_T|<100|B_S|). И если источником полоидального поля может быть только альфа-эффект, то тороидального — оба, причём если оба вносят существенный вклад, соответствующий механизм иногда обозначают α²ω. Большинство теоретических моделей магнитного динамо — типа α². В обоих случаях, как альфа, так и омега-эффектов, таким образом снимаются ограничения теоремы Каулинга^[16][23]. Однако существует ряд геометрий течений, для которых динамо также невозможно (например, чисто тороидальное поле скоростей^[23][27]), в то же время при определённых условиях оно возможно и при нулевой суммарной завихрённости ∇×u{\displaystyle \mathbf {\nabla } \times \mathbf {u} } и нулевой спиральности; возможны и другие эффекты, приводящие к возникновению ЭДС, параллельной магнитному полю^[25].

∂T∂t+u⋅∇T=κ∇2T+ϵ{\displaystyle {\frac {\partial T}{\partial t}}+\mathbf {u} \cdot \mathbf {\nabla } T=\kappa \mathbf {\nabla } ^{2}T+\epsilon },

где T — температура, κ = k/(ρc_p) — температуропроводность (коэффициент тепловой диффузии), k — теплопроводность, c_p — удельная теплоёмкость среды при постоянном давлении. Последнее слагаемое, ε, пропорционально выделению тепла, генерируемого теми или иными растворёнными в жидкости источниками (такими как радиоактивный распад), на единицу массы. В моделях, учитывающих перенос не только тепла, но и вещества, записывается соответствующее аналогичное уравнение относительно переменной ξ — массовой доли лёгких элементов (считается, что это сера и кислород) в составе ядра:

∂ξ∂t+u⋅∇ξ=κξ∇2ξ+ϵξ{\displaystyle {\frac {\partial \xi }{\partial t}}+\mathbf {u} \cdot \mathbf {\nabla } \xi =\kappa _{\xi }\mathbf {\nabla } ^{2}\xi +\epsilon _{\xi }},

где κ_ξ — коэффициент (молекулярной) диффузии. В большинстве моделей динамо, однако для простоты разность температур и концентраций лёгких элементов объединяются в одну отвечающую за плавучесть переменную.

∇⋅u=0{\displaystyle \mathbf {\nabla } \cdot \mathbf {u} =0}.

∇⋅B=0{\displaystyle \mathbf {\nabla } \cdot \mathbf {B} =0}.

ρ=ρ0[1−α(T−T0)]{\displaystyle \rho =\rho _{0}\left[1-\alpha (T-T_{0})\right]},

где α — коэффициент линейного теплового расширения (обозначение совпадает с коэффициентом пропорциональности в уравнении для альфа-эффекта). В общем случае, при учёте массопереноса, в квадратных скобках присутствует также слагаемое αξ(ξ−ξ0){\displaystyle \alpha _{\xi }(\xi -\xi _{0})}. Здесь α=−1ρ(∂ρ∂T)P,ξ{\displaystyle \alpha =-{\frac {1}{\rho }}\left({\frac {\partial \rho }{\partial T}}\right)_{P,\xi }}, αξ=−1ρ(∂ρ∂ξ)P,T{\displaystyle \alpha _{\xi }=-{\frac {1}{\rho }}\left({\frac {\partial \rho }{\partial \xi }}\right)_{P,T}}.

Естественно, необходимы также граничные условия для скорости потока, магнитного поля и разности температур, и многое зависит от того, как они ставятся в той или иной модели. Наибольший разброс имеет место в отношении потока тепла и вещества на границах между внутренним и внешним ядром, а также между внешним ядром и мантией, причём существенную роль играет неоднородность мантии и процессов в ней из-за тектоники плит^[16][17][28], которые, что немаловажно, протекают на порядки медленнее, нежели в ядре, что значительно осложняет комплексный анализ задачи.

Удобнее решать эту систему уравнений в безразмерном виде, вводя характерные величины длины, времени, скорости, магнитного поля и т. д.; тогда в них будут входить следующие безразмерные параметры^[16][17][29]:

Параметр	Формула	Определение	Значение в ядре Земли	Примечание
Входные параметры
Число Рэлея	Ra=g0αβ0R03νκ{\displaystyle Ra={\frac {g_{0}\alpha \beta _{0}R_{0}^{3}}{\nu \kappa }}}, где β0 — градиент температур на границе внешнего ядра (при r=R0). В зависимости от модели, встречаются и другие определения: g0αβ0DΩκ{\displaystyle {\frac {g_{0}\alpha \beta _{0}D}{\Omega \kappa }}} (D — толщина внешнего ядра), g0αQ02kκΩ{\displaystyle {\frac {g_{0}\alpha Q_{0}}{2k\kappa \Omega }}} (Q0=4πR02κβ0{\displaystyle Q_{0}=4\pi R_{0}^{2}\kappa \beta _{0}} — полный тепловой поток), g0αβ1R02ηΩ{\displaystyle {\frac {g_{0}\alpha \beta _{1}R_{0}^{2}}{\eta \Omega }}} (β1 — градиент температур на границе внутреннего и внешнего ядра) и т. п.[16]	соотношение интенсивности плавучести и вязкости, определяющее величину энергии, доступной системе для осуществления конвекции: конвекционный механизм теплопереноса будет преобладать над теплопроводностью, при Ra, большем некоторого критического значения	1024-1030, в зависимости от определения[16][23]
Число Экмана	E=ν2ΩR02{\displaystyle E={\frac {\nu }{2\Omega R_{0}^{2}}}}	соотношение вязкости (внутреннего трения) и силы Кориолиса: меньшее значение соответствует более быстрому вращению, и наоборот	10-15
Число Прандтля, а также (при учёте массопереноса) массовое число Прандтля	Pr=νκ{\displaystyle Pr={\frac {\nu }{\kappa }}}, Pc=νκξ{\displaystyle Pc={\frac {\nu }{\kappa _{\xi }}}}	соотношение характерных времён диффузии вязкой и тепловой, то есть кинематической вязкости и температуропроводности	~10-1	предположительно при преобладании турбулентной диффузии все числа Прандтля стремятся к 1, хотя вопрос о турбулентности в ядре изучен ещё недостаточно
Магнитное число Прандтля	Pm=νη{\displaystyle Pm={\frac {\nu }{\eta }}}	соотношение характерных времён диффузии магнитной и вязкой, то есть магнитных сил к силам внутреннего трения	10-6
Число Тейлора	Ta=(2ΩR02ν)2=1E2{\displaystyle Ta=\left({\frac {2\Omega R_{0}^{2}}{\nu }}\right)^{2}={\frac {1}{E^{2}}}}	соотношение между силой Кориолиса и силами вязкого трения
Модифицированное число Рэлея	RaM=αβ0g0R022Ωκ=E⋅Ra{\displaystyle Ra_{M}={\frac {\alpha \beta _{0}g_{0}R_{0}^{2}}{2\Omega \kappa }}=E\cdot Ra}	соотношение между силой Архимеда и силой Кориолиса
Магнитное число Экмана	EM=η2ΩR02=EPm{\displaystyle E_{M}={\frac {\eta }{2\Omega R_{0}^{2}}}={\frac {E}{Pm}}}	соотношение периода вращения и характерного времени магнитного взаимодействия
Соотношение коэффициентов диффузии магнитной и тепловой	q=κη=PmPr{\displaystyle q={\frac {\kappa }{\eta }}={\frac {Pm}{Pr}}}		1,7⋅10-5[23], 2⋅10-7[16]
Вычисляемые величины
Магнитное число Рейнольдса	Rm=u0R0η{\displaystyle Rm={\frac {u_{0}R_{0}}{\eta }}}, где u0 — характерная скорость потока. Локально в каждой точке величина определяется как Rm=|u×B||η

Магнитное дутьё — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 3 января 2015; проверки требуют 7 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 3 января 2015; проверки требуют 7 правок.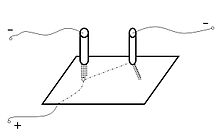 Отклонение дуги при магнитном дутье

Магнитное дутьё — явление отклонения электрической дуги от оси электрода, блуждание конца дуги по изделию при ручной дуговой сварке.

Магнитное дутьё приводит к разбрызгиванию металла при сварке, ухудшению качество шва.

В процессе сварки в сварочной цепи протекает ток в электрической дуге и в сварочной цепи изделия. Эти токи создают магнитное поле.

Взаимодействие магнитного поля цепи тока в изделии с током столба дуги создает силу, направленную к его центру (явление пинч-эффекта). Эта сила, при подключении электрического провода к месту где заканчивается дуга, не вызывает отклонения столба, а возвращает его при отклонении в начальное положение.

Если место подключения провода находится на каком-либо расстоянии от перпендикуляра, то возникающее магнитное поле является поперечным и вызывает отклонение столба. Отклоняющая сила пропорциональна квадрату дугового тока, поэтому магнитное дутье увеличивается при увеличении сварочного тока. Дутье приводит к ограничению сварки постоянным током на больших значениях электрического тока.

Действие магнитного дутья сильно ослабляется при сварке на переменном токе. В этом случае под действием переменного магнитного поля тока в изделии наводится электродвижущая сила. Э. д. с. создает вихревые токи. Создаваемый ими магнитный поток меньше потока, создаваемого постоянным током. В результате при больших переменных токах (1000—2000 А) действие магнитного дутья незначительно.

Из-за магнитного дутья возникают трудности при сварке угловых и стыковых швов.

Магнитное дутьё ослабляется при использовании переменного тока, наклоне электрода, изменении мест подключения сварочного провода к изделию. Так же есть специализированное оборудование, которое полностью убирает эффект магнитного дутья: устройства размагничивания и компенсации магнитного поля.

• Николаев Г. А. Сварка в машиностроении: Справочник в 4-х т. — М.: Машиностроение, 1978 (1-4 т).
• Лесков Г. И. Электрическая сварочная дуга. М.: Машиностроение, 1970. — 335 с.

Эффект Мейснера — Википедия

Материал из Википедии — свободной энциклопедии

Схема Эффекта Мейснера. Показаны линии магнитного поля и их вытеснение из сверхпроводника, находящегося ниже своей критической температуры

Эффект Мейснера, эффект Мейсснера (от нем. Meißner) — полное вытеснение магнитного поля из объёма проводника при его переходе в сверхпроводящее состояние. Впервые явление наблюдалось в 1933 году немецкими физиками В. Мейснером и Р. Оксенфельдом.

При охлаждении сверхпроводника, находящегося во внешнем постоянном магнитном поле, в момент перехода в сверхпроводящее состояние магнитное поле полностью вытесняется из его объёма. Этим сверхпроводник отличается от идеального проводника, у которого при падении сопротивления до нуля индукция магнитного поля в объёме должна сохраняться без изменения.

Отсутствие магнитного поля в объёме проводника позволяет заключить из общих законов магнитного поля, что в нём существует только поверхностный ток. Он физически реален и поэтому занимает некоторый тонкий слой вблизи поверхности. Магнитное поле тока уничтожает внутри сверхпроводника внешнее магнитное поле. В этом отношении сверхпроводник ведёт себя формально как идеальный диамагнетик. Однако он не является диамагнетиком, так как внутри него намагниченность равна нулю.

Эффект Мейснера не может быть объяснён только бесконечной проводимостью. Впервые его природу объяснили братья Фриц и Хайнц Лондоны^[en] c помощью уравнения Лондонов. Они показали, что в сверхпроводнике поле проникает на фиксированную глубину от поверхности — лондоновскую глубину проникновения магнитного поля λ{\displaystyle \lambda }. Для металлов λ∼10−2{\displaystyle \lambda \sim 10^{-2}} мкм.

Чистые вещества, у которых наблюдается явление сверхпроводимости, немногочисленны. Чаще сверхпроводимость бывает у сплавов. У чистых веществ имеет место полный эффект Мейснера, а у сплавов не происходит полного выталкивания магнитного поля из объёма (частичный эффект Мейснера). Вещества, проявляющие полный эффект Мейснера, называются сверхпроводниками первого рода, а частичный — сверхпроводниками второго рода. Однако стоит отметить, что в низких магнитных полях полным эффектом Мейснера обладают все типы сверхпроводников.

У сверхпроводников второго рода в объёме имеются круговые токи, создающие магнитное поле, которое, однако, заполняет не весь объём, а распределено в нём в виде отдельных нитей вихрей Абрикосова. Что же касается сопротивления, оно равно нулю, как и в сверхпроводниках первого рода, хотя движение вихрей под действием текущего тока создаёт эффективное сопротивление в виде диссипативных потерь на передвижение магнитного потока внутри сверхпроводника, чего избегают вводом в структуру сверхпроводника дефектов — центров пиннинга, за которые вихри «цепляются».

«Гроб Магомета» — опыт, демонстрирующий эффект Мейснера в сверхпроводниках^[1].

Происхождение названия[править | править код]

По преданию, гроб с телом пророка Магомета висел в пространстве без всякой поддержки, поэтому этот эксперимент называют «Гроб Магомета».

Постановка опыта[править | править код]

Сверхпроводимость существует только при низких температурах (в ВТСП-керамиках — при температурах ниже 150 К), поэтому предварительно вещество охлаждают, например, при помощи жидкого азота. Далее магнит кладут на поверхность плоского сверхпроводника. Даже в полях, магнитная индукция которых составляет 0,001 Тл, заметно смещение магнита вверх на расстояние порядка сантиметра. При увеличении поля вплоть до критического магнит поднимается всё выше.

Объяснение[править | править код]

Одним из свойств сверхпроводников является выталкивание магнитного поля из области сверхпроводящей фазы. Отталкиваясь от неподвижного сверхпроводника, магнит «всплывает» сам и продолжает «парить» до тех пор, пока внешние условия не выведут сверхпроводник из сверхпроводящей фазы. В результате этого эффекта магнит, приближающийся к сверхпроводнику, «видит» магнит одинаковой полярности и точно такого же размера, — что и вызывает левитацию.

Магнитный монополь — Википедия

Магни́тный монопо́ль — гипотетическая элементарная частица, обладающая ненулевым магнитным зарядом — точечный источник радиального магнитного поля. Магнитный заряд является источником статического магнитного поля совершенно так же, как электрический заряд является источником статического электрического поля.

Магнитный монополь можно представлять как отдельно взятый полюс длинного и тонкого постоянного магнита. Однако у всех известных магнитов всегда два полюса, то есть он является диполем. Если разрезать магнит на две части, то у каждой его части по-прежнему будет два полюса. Все известные элементарные частицы, обладающие электромагнитным полем, являются магнитными диполями.

С созданием физики как науки, основанной на опыте, утвердилось мнение, что электрические и магнитные свойства тел существенно различаются. Это мнение было чётко выражено Уильямом Гильбертом в 1600 году. Установленное Шарлем Кулоном тождество законов притяжения и отталкивания для электрических зарядов и магнитных зарядов — полюсов магнитов, вновь подняло вопрос о сходстве электрических и магнитных сил, однако к концу XVIII века было выяснено, что в лабораторных условиях невозможно создать тело с ненулевым полным магнитным зарядом. Понятие о «магнитно заряженной субстанции» было надолго изгнано из физики после работы Ампера в 1820, в которой было доказано, что контур с электрическим током создаёт такое же магнитное поле, как магнитный диполь.

В 1894 году Пьер Кюри изложил в короткой заметке, что введение магнитных зарядов в уравнения Максвелла производится естественно и только делает их более симметричными.

Сформулированные Максвеллом уравнения классической электродинамики связывают электрическое и магнитное поля с движением заряженных частиц. Эти уравнения почти симметричны относительно электричества и магнетизма. Они могут быть сделаны полностью симметричными, если в дополнение к электрическому заряду qe{\displaystyle q_{\mathrm {e} }} и току ввести некий магнитный заряд qm{\displaystyle q_{\mathrm {m} }} (плотность магнитного заряда ρm{\displaystyle \rho _{\mathrm {m} }}) и магнитный ток (плотность магнитного тока jm{\displaystyle \mathbf {j} _{\mathrm {m} }}):

При этом изменённые уравнения с магнитными монополями переходят в классические уравнения при подстановке ρm=0{\displaystyle \rho _{\mathrm {m} }=0} и jm=0{\displaystyle \mathbf {j} _{\mathrm {m} }=0}, то есть если в рассматриваемой области пространства отсутствуют магнитные заряды. Таким образом можно создать систему уравнений Максвелла с учётом существования магнитных зарядов, при этом классические уравнения просто отражают тот факт, что обычно магнитные заряды не наблюдаются.

Если магнитные заряды существуют, то существование магнитных токов приведёт к существенным поправкам уравнений Максвелла, которые можно наблюдать на макроскопических масштабах.

В новой форме уравнений Максвелла возникают трудности математического описания при помощи вектор-потенциала. При наличии и магнитных и электрических зарядов электромагнитное поле не может быть описано при помощи вектор-потенциала Aμ{\displaystyle \mathbf {A} _{\mu }} (μ=0,1,2,3){\displaystyle (\mu =0,\;1,\;2,\;3)}, непрерывного во всём пространстве. Поэтому при наличии магнитных зарядов уравнения движения заряженных частиц не выводятся из вариационного принципа наименьшего действия. В классической электродинамике это не приводит к принципиальным трудностям (хотя и делает теорию несколько менее красивой), но квантовую динамику невозможно сформулировать вне рамок гамильтонова или лагранжева формализма. ^{[источник не указан 3708 дней]}

Поль Дирак предположил существование частицы с магнитным зарядом и пришёл к нетривиальному заключению, что магнитный заряд предполагаемого монополя не может иметь произвольного значения, но должен быть равен целому кратному определённого количества магнетизма.^[2]

Задача определения векторного потенциала A{\displaystyle A}, дающего магнитное поле H{\displaystyle H}, математически эквивалентна задаче определения системы токов j′{\displaystyle j’}, создающих магнитное поле H′{\displaystyle H’}. Из точки, испускающей постоянный поток магнитного поля, должен вытекать постоянный ток с равномерной плотностью во всех направлениях. Чтобы его поддерживать, надо по проводящей нити подводить ток к этой точке, равный току, исходящему из этой точки по всем направлениям, причем сила этого тока равна магнитному заряду g{\displaystyle g}.^[3] Поскольку расположение такой нити совершенно произвольно, то разность векторных потенциалов равна магнитному полю, создаваемому током, притекающим к точке по одной нити и утекающим по другой нити. Такое магнитное поле можно представить в виде многозначного потенциала, значение которого в каждой точке пространства изменяется при каждом обходе контура, связанного с нитью, на величину силы тока, умноженной на 4π{\displaystyle 4\pi }. Из квантовой механики известно, что волновая функция ψ{\displaystyle \psi }, характеризующая частицу с зарядом e{\displaystyle e} при изменении A→A+grad⁡f{\displaystyle A\rightarrow A+\operatorname {grad} f} как ψ→ψexp⁡(ieℏcf){\displaystyle \psi \rightarrow \psi \exp \left({\frac {ie}{\hbar c}}f\right)}. При обходе контура f=4πg{\displaystyle f=4\pi g}. Но при обходе контура волновая функция не должна измениться, поэтому exp⁡(ieℏc4πg)=1{\displaystyle \exp \left({\frac {ie}{\hbar c}}4\pi g\right)=1}. Комплексное число равно единице, если оно предствлено как exp⁡(2πin){\displaystyle \exp(2\pi in)}, где n{\displaystyle n} — произвольное целое число. Поэтому: ieℏc4πg=2πin{\displaystyle {\frac {ie}{\hbar c}}4\pi g=2\pi in}, где n{\displaystyle n} — целое число. Таким образом, магнитный заряд g{\displaystyle g} частицы должен быть кратен элементарному магнитному заряду g0=ℏc2e{\displaystyle g_{0}={\frac {\hbar c}{2e}}}, где e{\displaystyle e} — элементарный электрический заряд.^[4]

Примечательно обратное утверждение: существование магнитного заряда не противоречит стандартной квантовой механике только в том случае, если электрические заряды всех частиц квантуются. (Таким образом, существование в природе хотя бы одного магнитного монополя с определённым зарядом объяснило бы наблюдаемую на опыте кратность электрических зарядов частиц величине e{\displaystyle e}; магнитный заряд при этом тоже с необходимостью квантовался бы.)

Условие квантования Дирака обобщается на взаимодействие двух частиц, каждая из которых обладает как электрическим, так и магнитным зарядом (такие частицы называется дионами)

e1g2−e2g12πℏc=n.{\displaystyle {\frac {e_{1}g_{2}-e_{2}g_{1}}{2\pi \hbar c}}=n.}

(В используемой системе единиц e{\displaystyle e} и g{\displaystyle g} имеют одинаковую размерность, причём заряд e{\displaystyle e} фиксирован соотношением e2/4πℏc=1/137{\displaystyle e^{2}/4\pi \hbar c=1/137}.)

В нерелятивистском приближении сила, действующая на дион 1 с координатами r{\displaystyle r} и скоростью v{\displaystyle v} со стороны диона 2, закреплённого в начале координат, равна

F=(e1e2+g1g2)r+(e1g2−e2g1)[vr]c4πr3.{\displaystyle F={\frac {(e_{1}e_{2}+g_{1}g_{2})\mathbf {r} +(e_{1}g_{2}-e_{2}g_{1}){\dfrac {[\mathbf {vr} ]}{c}}}{4\pi r^{3}}}.}

Отметим, что входящие в эту формулу комбинации зарядов инвариантны относительно дуального преобразования.

В 1974 А. М. Поляков и Герард ‘т Хоофт (G. ‘t Hooft) независимо обнаружили^[5], что существование магнитного монополя не только возможно, но и обязательно в полевых теориях определённого класса. В моделях великого объединения, рассматривающих симметрию относительно фазовых преобразований волновых функций заряженных частиц как составную часть более широкой неабелевой калибровочной симметрии, электромагнитное поле связано с мультиплетом заряженных калибровочных полей X{\displaystyle X} с большими массами (эти массы возникают при спонтанном нарушении симметрии). Для некоторых калибровочных групп симметрии существуют устойчивые конфигурации полей X{\displaystyle X}, локализованные в области размером l<ℏ/MXc{\displaystyle l<\hbar /M_{X}c} и создающие вне этой области сферически симметричное магнитное поле. Существование таких конфигураций зависит от топологических свойств калибровочной группы, точнее, от того, каким образом в неё вложена подгруппа симметрии, сохранившейся после спонтанного нарушения. Стабильность этих магнитных монополей определяется особым поведением полей на больших расстояниях от центра. Масса магнитного монополя Mm{\displaystyle M_{m}} может быть вычислена, она зависит от конкретной полевой модели, однако во всяком случае должна быть большой, Mm≫MX{\displaystyle M_{m}\gg M_{X}} (по оценке, для широкого класса моделей Mm∼1016GeVc2{\displaystyle M_{m}\sim 10^{16}{\frac {GeV}{c^{2}}}}). Эти магнитные монополи могли бы рождаться в горячей Вселенной вскоре после Большого Взрыва при фазовом переходе, связанном со спонтанным нарушением симметрии и возникновением отличных от нуля однородных скалярных полей в вакууме. Количество рождающихся магнитных монополей определяется процессом развития Вселенной на ранней стадии, поэтому по их отсутствию в настоящее время можно судить об этом процессе. Одно из объяснений того, что реликтовые магнитные монополи не обнаружены, даётся теорией раздувающейся Вселенной (инфляции). Магнитные монополи ‘т Хоофта — Полякова обладают некоторыми необычными свойствами, благодаря которым их было бы легко обнаружить. В частности, взаимодействие с магнитным монополем может стимулировать распад нуклона, предсказываемый некоторыми моделями великого объединения^[6], то есть выступать в качестве катализатора такого распада.

Заряд магнитного монополя[править | править код]

Размерность заряда магнитного монополя совпадает с размерностью электрического заряда в системе СГС:

gD=cℏ2e=e2αE≈137e/2, {\displaystyle g_{D}={\frac {c\hbar }{2e}}={\frac {e}{2\alpha _{E}}}\approx 137e/2,\ }

где c{\displaystyle c} — скорость света в вакууме, ℏ{\displaystyle \hbar } — постоянная Планка и e{\displaystyle e} — элементарный заряд.

В системе СИ размерности магнитного и электрического зарядов различны (конвенция вебера):

gD=he, {\displaystyle g_{D}={\frac {h}{e}},\ }

где h{\displaystyle h} — постоянная Планка.

Конвенция ампер-метра (СИ):

gD=hc2ε0.{\displaystyle g_{D}={\frac {hc^{2}}{\varepsilon _{0}}}.}

Константа связи монополя[править | править код]

Известно, что электрические заряды имеют достаточно малую константу связи (т. н. постоянную тонкой структуры). В системе СГС она имеет следующее значение:

αE=e2cℏ≈1/137. {\displaystyle \alpha _{E}={\frac {e^{2}}{c\hbar }}\approx 1/137.\ }

В СИ мы имеем более громоздкое выражение:

αE=e22hcε0≈1/137, {\displaystyle \alpha _{E}={\frac {e^{2}}{2hc\varepsilon _{0}}}\approx 1/137,\ }

где ε0{\displaystyle \varepsilon _{0}} — электрическая постоянная.

Аналогичным образом можно ввести и магнитную константу связи для системы СГС:

βE=gD2cℏ=14αE=34,25. {\displaystyle \beta _{E}={\frac {g_{D}^{2}}{c\hbar }}={\frac {1}{4\alpha _{E}}}=34{,}25.\ }

Для СИ имеет место выражение:

 — конвенция вебера:

βE=gD22hcμ0=14αE=34,25, {\displaystyle \beta _{E}={\frac {g_{D}^{2}}{2hc\mu _{0}}}={\frac {1}{4\alpha _{E}}}=34{,}25,\ }

 — конвенция ампер-метра:

βE=gD2μ02hc=14αE=34,25, {\displaystyle \beta _{E}={\frac {g_{D}^{2}\mu _{0}}{2hc}}={\frac {1}{4\alpha _{E}}}=34{,}25,\ }

где μ0{\displaystyle \mu _{0}} — магнитная постоянная вакуума. Здесь следует отметить, что магнитная константа значительно больше единицы и поэтому использование пертурбативных методов в квантовой электродинамике для магнитных зарядов не предоставляется возможным.

Масса монополя[править | править код]

Теория Дирака не предсказывает «массу магнитного монополя». Поэтому в настоящее время отсутствует единое мнение по оценке массы монополя (эксперимент только указывает на нижнюю границу). Здесь также можно отметить, что значение массы электрона является чисто экспериментальным фактом и не предсказывается стандартной моделью.

Нижняя оценка массы монополя[править | править код]

Нижнюю оценку для массы монополя можно оценить исходя из классического радиуса электрона (система СИ):

r0=e24πε0m0c2=αEλ02π, {\displaystyle r_{0}={\frac {e^{2}}{4\pi \varepsilon _{0}m_{0}c^{2}}}={\frac {\alpha _{E}\lambda _{0}}{2\pi }},\ }

где λ0{\displaystyle \lambda _{0}} — комптоновская длина волны электрона, m0{\displaystyle m_{0}} — масса электрона.

Аналогичным образом можно ввести значение для классического радиуса магнитного монополя (система СИ (конвенция вебера)):

rD0=gD24πμ0mDc2, {\displaystyle r_{D0}={\frac {g_{D}^{2}}{4\pi \mu _{0}m_{D}c^{2}}},\ }

где mD{\displaystyle m_{D}} — масса монополя. Таким образом, приравнивая классические радиусы, можно получить нижнюю оценку массы монополя:

mD=(gDe)2ε0μ0m0=14αEm0≈4692m0. {\displaystyle m_{D}=\left({\frac {g_{D}}{e}}\right)^{2}{\frac {\varepsilon _{0}}{\mu _{0}}}m_{0}={\frac {1}{4\alpha _{E}}}m_{0}\approx 4692m_{0}.\ }

Неоднократные попытки экспериментального обнаружения магнитного монополя не увенчались успехом. Особенно интенсивно поиски магнитного монополя космического происхождения проводились с начала 80-х годов XX века. Эксперименты можно разделить на несколько групп.

1. Магнитный монополь можно обнаружить непосредственно по связанному с ним магнитному потоку. Прохождение магнитного заряда ng0{\displaystyle ng_{0}} сквозь сверхпроводящий контур изменит поток на 2πΦ0{\displaystyle 2\pi \Phi _{0}}, где Φ0∼2⋅10−3Gm2{\displaystyle \Phi _{0}\sim 2\cdot 10^{-3}Gm^{2}} — квант магнитного потока, и явление электромагнитной индукции приведёт к скачку то

Электромагнит — Википедия

Материал из Википедии — свободной энциклопедии

Прямой провод с током. Ток (I), протекая через провод, создаёт магнитное поле (B) вокруг провода

Электромагнит — устройство, создающее магнитное поле при прохождении электрического тока через него. Обычно электромагнит состоит из обмотки и ферромагнитного сердечника, который приобретает свойства магнита при прохождении по обмотке электрического тока. В электромагнитах, предназначенных, прежде всего, для создания механического усилия также присутствует якорь (подвижная часть магнитопровода), передающий усилие.

Обмотку электромагнитов изготавливают из изолированного алюминиевого или медного провода, хотя есть и сверхпроводящие электромагниты. Магнитопроводы изготавливают из магнитно-мягких материалов — обычно из электротехнической или качественной конструкционной стали, литой стали и чугуна, железо-никелевых и железо-кобальтовых сплавов. Для снижения потерь на вихревые токи (токи Фуко) магнитопроводы выполняют из набора листов.

Извлечение осколков из глаза с помощью электромагнита. 1915

В 1825 году английский инженер Уильям Стёрджен изготовил первый электромагнит, представляющий собой согнутый стержень из мягкого железа с обмоткой из толстой медной проволоки. Для изолирования от обмотки, стержень был покрыт лаком. При пропускании тока железный стержень приобретал свойства сильного магнита, но при прерывании тока он мгновенно их терял. Именно эта особенность электромагнитов и позволила широко применять их в технике^[1][2].

Помимо промышленного использования, магниты стали широко применяться в медицине. Еще в конце XIX — начале XX века на страницах Энциклопедического словаря Брокгауза и Ефрона Мендельсон М. Э. писал, что электромагнит «служит самым лучшим способом для извлечения инородных тел из полости глаза»^[3].

Простейший электромагнит: вокруг ферромагнитного сердечника намотан электропровод в изоляции

Выделяют три типа электромагнитов по способу создания магнитного потока.

Нейтральные электромагниты постоянного тока

Постоянный магнитный поток создается постоянным током в обмотке таким образом, что сила притяжения зависит только от величины и не зависит от направления тока в обмотке.

Поляризованные электромагниты постоянного тока

Присутствуют два независимых магнитных потока — рабочий и поляризующий. Первый создается рабочей (или управляющей) обмоткой. Поляризующий поток чаще всего создается постоянными магнитами, иногда дополнительными электромагнитами, и используется для обеспечения наличия притягивающей силы при выключенной рабочей обмотке. В целом действие такого магнита зависит как от величины, так и от направления электрического тока в рабочей обмотке.

Электромагниты переменного тока

В этих магнитах питание обмотки осуществляется от источника переменного тока, магнитный поток периодически изменяется по величине и направлению, а однонаправленная сила притяжения меняется только по величине, в результате чего сила притяжения пульсирует от нуля до максимального значения с удвоенной частотой по отношению к частоте питающего тока. Широко применяют в электротехнике, начиная от бытовой техники до плит электромагнитных для станков, при магнитопорошковом методе неразрушающего контроля.

Другие классификации[править | править код]

Электромагниты различают также по ряду других признаков: по способу включения обмоток — с параллельными и последовательными обмотками; по характеру работы — работающие в длительном, прерывистом и кратковременном режимах; по скорости действия — быстродействующие и замедленного действия, создающие постоянное или переменное магнитное поле и т. д.

1. ↑ Sturgeon, W. Improved Electro Magnetic Apparatus (неопр.) // Trans. Royal Society of Arts, Manufactures, & Commerce. — London, 1825. — Т. 43. — С. 37—52. cited in Miller, T.J.E. Electronic Control of Switched Reluctance Machines (англ.). — Newnes, 2001. — P. 7. — ISBN 0-7506-5073-7.
2. ↑ Windelspecht, Michael. Groundbreaking Scientific Experiments, Inventions, and Discoveries of the 19th Century, xxii, Greenwood Publishing Group, 2003, ISBN 0-313-31969-3.
3. ↑ Электромагнит в хирургии // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.