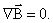fizika / Поток вектора магнитной индукции. Теорема Гаусса для поля вектора магнитной индукции
Поток вектора магнитной индукции. Теорема Гаусса для поля вектора магнитной индукции.
Поток вектора магнитной индукции, пронизывающий площадку S — это величина, равная:
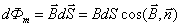
Поток вектора магнитной индукции (магнитный поток) измеряется в веберах (Вб)

Магнитный поток — величина скалярная.
Поток вектора магнитной индукции (магнитный поток) равен числу линий магнитной индукции, проходящих сквозь данную поверхность.
Поток вектора магнитной индукции (магнитный поток) сквозь произвольную замкнутую поверхность равен нулю:
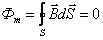
Это теорема Остроградского-Гаусса для магнитного поля.
Она свидетельствует о том, что в природе не существует магнитных зарядов – физических объектов, на которых бы начинались или заканчивались линии магнитной индукции.
Как было показано выше, в
природе нет магнитных зарядов. В 1931 г.
П. Дирак высказал предположение о
существовании обособленных магнитных
зарядов, названных впоследствии монополи
Дирака. Однако до
сих пор они не найдены. Это приводит к
тому, что линии вектора 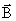 не
имеют ни начала, ни конца. Мы знаем, что
поток любого вектора через поверхность
равен разности числа линий, начинающихся
у поверхности, и числа линий, оканчивающихся
внутри поверхности:
не
имеют ни начала, ни конца. Мы знаем, что
поток любого вектора через поверхность
равен разности числа линий, начинающихся
у поверхности, и числа линий, оканчивающихся
внутри поверхности:
 .
.
В
соответствии с вышеизложенным, можно
сделать заключение, что
поток вектора 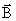 через
замкнутую поверхность должен быть
равен нулю.
через
замкнутую поверхность должен быть
равен нулю.
Таким образом, для любого магнитного поля и произвольной замкнутой поверхности S имеет место условие:
|
| (1.7.1) |
|
Это
теорема Гаусса для 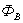 (в
интегральной форме): поток
вектора магнитной индукции через любую
замкнутую поверхность равен нулю.
(в
интегральной форме): поток
вектора магнитной индукции через любую
замкнутую поверхность равен нулю.
Заменив поверхностный интеграл в (1.7.1) объемным, получим:
|
| (1.7.2) |
|
где 
Это условие должно выполняться для любого произвольного объема V, а это, в свою очередь, возможно, если подынтегральная функция в каждой точке поля равна нулю. Таким образом, магнитное поле обладает тем свойством, что его дивергенция всюду равна нулю:
|
| (1.7.3) |
|
В этом его отличие от электростатического поля, которое является потенциальным и может быть выражено скалярным потенциалом φ,магнитное поле – вихревое, или соленоидальное (см. рис. 1.3 и 1.8).
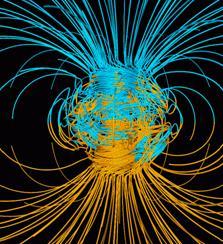
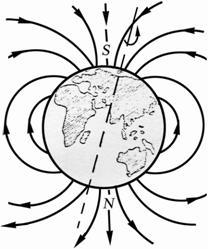
Рис. 1.9
Компьютерная модель магнитного поля Земли, подтверждающая вихревой характер, изображена на рис. 1.9.
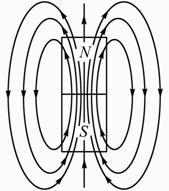
Рис 1.10
На рисунке 1.10 показаны магнитное поле постоянного магнита. Линии магнитной индукции замыкаются в окружающем пространстве.
Репетитор-онлайн — подготовка к ЦТ
Магнитное поле создается постоянными магнитами, движущимися зарядами (токами) и характеризуется вектором магнитной индукции B→.
Магнитное поле — форма материи, посредством которой осуществляется магнитное взаимодействие между движущимися зарядами (токами).
Магнитная индукция — векторная физическая величина, модуль которой равен максимальному вращающему моменту, действующему на рамку с током, деленному на модуль магнитного момента этой рамки:
B=MmaxPm,
где M max — модуль максимального вращающего момента; P m — модуль магнитного момента рамки с током.
Направления векторов B→, M→max и P→m связаны правилом правого винта. В Международной системе единиц магнитная индукция измеряется в теслах (1 Тл).
Силовые линии магнитного поля — линии вектора магнитной индукции B→; с помощью силовых линий производится изображение магнитного поля. Силовые линии магнитного поля являются замкнутыми.
Магнитный момент контура с током — векторная физическая величина, модуль которой равен произведению силы тока в контуре на площадь, ограниченную этим контуром:
P m = IS,
где I — сила тока в контуре; S — площадь, ограниченная этим контуром.
Направление вектора магнитного момента P→m связано с направлением тока правилом правого винта. В Международной системе единиц магнитный момент измеряется в амперах, умноженных на квадратный метр (1 A ⋅ м2).
Механический вращающий момент, действующий на рамку с током, помещенную в магнитное поле, — векторное произведение магнитного момента на индукцию магнитного поля:
M→=[P→m, B→],
где P→m — магнитный момент рамки с током; B→ — вектор индукции магнитного поля.
Магнитное поле оказывает ориентирующее действие на рамку с током. Направление механического вращающего момента M→ определяется правилом правого винта.
Поток вектора магнитной индукции через некоторую площадку — скалярная физическая величина, равная скалярному произведению вектора магнитной индукции B→ на вектор S→:
Ф=B→⋅S→=BScosα,
где S→=S⋅n→; n→ — единичный вектор нормали (перпендикуляра) к площадке; α — угол между векторами B→ и S→.
В Международной системе единиц поток измеряется в веберах (1 Вб).
Магнитный поток, сцепленный с контуром, — скалярная физическая величина, равная произведению индуктивности контура на силу тока в данном контуре:
Фs = LI,
где L — индуктивность контура.
В Международной системе единиц поток, сцепленный с контуром, также измеряется в веберах (1 Вб).
Индуктивность контура — скалярная физическая величина, равная отношению потока, сцепленного с данным контуром, к силе тока в нем:
L=ФsI,
где Фs — поток, сцепленный с контуром.
В Международной системе единиц индуктивность измеряется в генри (1 Гн).
Индуктивность является собственной характеристикой данного контура; она определяется его геометрическими размерами и формой, а также магнитными свойствами среды, в которую помещен этот контур.
Явление электромагнитной индукции заключается в появлении вихревого электрического поля и, как следствие, индукционного тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего площадку, ограниченную данным контуром.
Явление самоиндукции состоит в появлении индукционного тока в замкнутом проводящем контуре при изменении магнитного потока, сцепленного с данным контуром.
Закон Фарадея: ЭДС электромагнитной индукции (самоиндукции) в контуре равна скорости изменения магнитного потока через поверхность, ограниченную этим контуром:
ℰi=−limΔt→0ΔФΔt,
где ΔФ/Δt — скорость изменения магнитного потока; наличие минуса объясняется правилом Ленца.
Правило Ленца: индукционный ток всегда направлен таким образом, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшего этот индукционный ток.
Поток — вектор — магнитная индукция
Поток — вектор — магнитная индукция
Cтраница 1
Поток вектора магнитной индукции В сквозь какую-либо поверхность S называется сокращенно магнитным потоком. [1]
Поток вектора магнитной индукции является скалярной величиной. [2]
Определить поток вектора магнитной индукции, пронизывающий плоскую поверхность площадью 100 сма при индукции 0 2 Тл, если поверхность: а) перпендикуляр-па вектору магнитной индукции; б) параллельна; в) расположена под углом 45 к вектору магнитной индукции; г) расположена под углом 30 к вектору магнитной индукции. [3]
Найти поток вектора магнитной индукции через площадь, охватываемую вертикально расположенной прямоугольной рамкой со сторонами а и b ( сторона b параллельна оси X), если центр рамки лежит на оси X на расстоянии / от начала координат. [4]
Понятие потока вектора магнитной индукции вводится по аналогии с потоком вектора Е электростатического поля. [5]
Понятие потока вектора магнитной индукции широко применяется при расчете магнитных цепей. [6]
Следует ли поток вектора магнитной индукции, линии которого замыкаются полностью внутри проводов обмоток катушки, отнести к потоку рассеяния. [7]
Что называют потоком вектора магнитной индукции. Запишите теорему Гаусса для магнитного поля, объяснив ее физический смысл. [8]
Магнитный поток — поток вектора магнитной индукции ( равно как и магнитные силовые линии) не может обладать инерцией. Инерцией обладает электромагнитное поле как вид материи. [9]
Доказать, что поток вектора магнитной индукции Ф, пронизывающий сверхпроводящий замкнутый виток провода, не меняется при изменении формы ( деформации) витка и при изменении внешнего магнитного поля. [10]
В dS dФ — поток вектора магнитной индукции, пронизывающий эту площадь. [11]
Во сколько раз отличается поток вектора магнитной индукции через торцевую поверхность длинного соленоида от потока через поверхность поперечного сечения соленоида, проходящего через его середину. [12]
В физике пользуются понятием потока вектора магнитной индукции. [13]
Эта формула выражает теорему Гаусса для вектора В: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю. [14]
Вмороженность магнитных линий связана с тем, что при изменении потока вектора магнитной индукции через контур в нем появляются электрические токи, препятствующие изменению этого потока, причем тем большие, чем выше ад; при CR — оо изменение потока индукции становится невозможным. [15]
Страницы: 1 2
Введение
В настоящем пособии кратко изложены некоторые разделы третьей части курса ТОЭ – теория электромагнитного поля.
Все электротехнические устройства при полном и детальном их рассмотрении требуют исследования электромагнитных полей, и соответственно, в той или иной мере, необходимо применение теории электромагнитного поля. Вместе с тем представляет большую ценность возможность сведения задач из области электромагнитных явлений к задачам теории электрических и магнитных цепей, которая оперирует только интегральными величинами – электрическим током, напряжением, магнитным потоком и т. д. Весьма важным является установление критериев, в каких случаях допустимо рассмотрение задач как относящихся к теории цепей и когда необходимо их рассматривать как задачи теории поля.
В тех случаях, когда можно не считаться с конечной скоростью распространения волн в диэлектрике, электрическую цепь называют цепью с сосредоточенными параметрами. При периодических процессах критерием допустимости рассмотрения цепи как цепи с сосредоточенными параметрами является малость линейных размеров цепи и ее элементов по сравнению с длиной электромагнитной волны в диэлектрике. Поэтому при промышленной частоте 50 Гц обычные электромагнитные устройства и электрические цепи, за исключением длинных линий, рассматриваются как обладающие сосредоточенными параметрами. Периодические процессы в них часто называют квазистационарными процессами.
Если протяженность электрической цепи столь велика, что промежуток времени, необходимый для прохождения электромагнитной волны вдоль цепи, становится сравнимым с промежутком времени, в течение которого токи или напряжения в отдельных участках цепи успевают заметно измениться, то такую цепь нужно рассматривать как цепь с распределенными параметрами. В простейшем случае, когда цепь имеет большую протяженность лишь в одном направлении, вводят понятие о параметрах, распределенных по длине цепи. Примером таких цепей являются однородные линии.
Однако и этот метод становится уже невозможным в тех случаях, когда длина электромагнитной волны в диэлектрике сравнима с размерами устройств во всех направлениях. В этом случае используется теория электромагнитного поля.
Существует много важных практических случаев, когда анализ электромагнитных явлений может быть произведен только путем детального изучения электромагнитного поля. В качестве примеров можно указать на задачи в технике высоких напряжений, задачи о поверхностных эффектах или об излучении и распространении электромагнитных волн и т.п.
Исследуя электромагнитное поле, необходимо определять все величины, его характеризующие, в каждой точке пространства. Поэтому мы не можем удовлетвориться интегральной формой уравнений и должны представить их в дифференциальной форме.
1. Общие сведения о теории электромагнитного поля
1.1. Понятие поля. Скалярные и векторные поля
В пространстве задано поле некоторой величины, если в каждой его точке определено значение этой величины.
Физическое
поле – это любая
физическая величина, которая может быть
определена для каждой точки пространства.
Иначе, это область пространства, с каждой
точкой которой связано значение некоторой
физической величины. Физическим полем
является, например, температура. В каждой
точке пространства температура имеет
определенное значение, т.е. в пространстве
существует температурное поле, которое
математически описывается в виде 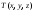 .
Другим примером является электрическое
поле, напряженность
.
Другим примером является электрическое
поле, напряженность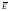 которого также можно определить для
каждой точки пространства.
которого также можно определить для
каждой точки пространства.
Электромагнитное поле – это физическая реальность.Электромагнитное поле представляет собой вид материи, характеризующийся воздействием на заряженные частицы. Как вид материи электромагнитное поле обладает массой, энергией, количеством движения, оно может превращаться в вещество и наоборот.
Электромагнитное поле является совокупностью взаимосвязанных и обуславливающих друг друга электрического и магнитного полей.
Следует помнить, что в природе существует единое электромагнитное поле, а отдельные его стороны электрическое или магнитное поле могут проявляться независимо друг от друга только в частных случаях и при определенных условиях.
Электромагнитное поле может описываться несколькими математическими полями (скалярным полем — полем потенциала, векторным полем — полем вектора напряженности поля).
Векторным полем называют область пространства, каждой точке которой отнесено значение некоторого вектора. Соответственно называют область пространства, каждой точке которой отнесено значение некоторого скаляра.
Векторные и скалярные поля описывают различные свойства физического поля.




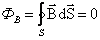 ,
,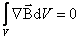 ,
, или
или