Вебер (единица измерения) — Википедия

Материал из Википедии — свободной энциклопедии

У этого термина существуют и другие значения, см. Вебер.

Ве́бер (русское обозначение: Вб, международное: Wb) — единица измерения магнитного потока в Международной системе единиц (СИ).

По определению, изменение магнитного потока через замкнутый контур со скоростью один вебер в секунду наводит в этом контуре ЭДС, равную одному вольту (см. Закон Фарадея). Через основные единицы СИ вебер выражается с помощью соотношения:

Вб =кг·м²·с⁻²·А⁻¹.

Через другие единицы измерения СИ вебер выражается следующим образом:

Вб =В·с =Гн·А.

В соответствии с правилами СИ, касающимися производных единиц, названных по имени учёных, наименование единицы вебер пишется со строчной буквы, а её обозначение «Вб» — с заглавной.

Единица названа в честь немецкого учёного Вильгельма Эдуарда Вебера. Название было установлено Международной электротехнической комиссией (МЭК) в 1930 году

[1]. В 1960 году XI Генеральная конференция по мерам и весам вместе с учреждением СИ приняла это название для единицы магнитного потока в СИ^[2].

Десятичные кратные и дольные единицы образуют с помощью стандартных приставок СИ.

Кратные				Дольные
величина	название	обозначение		величина	название	обозначение
101 Вб	декавебер	даВб	daWb	10−1 Вб	децивебер	дВб	dWb
102 Вб	гектовебер	гВб	hWb	10−2 Вб	сантивебер	сВб	cWb
103 Вб	киловебер	кВб	kWb	10−3 Вб	милливебер	мВб	mWb
106 Вб	мегавебер	МВб	MWb	10−6 Вб	микровебер	мкВб	µWb
109 Вб	гигавебер	ГВб	GWb	10−9 Вб	нановебер	нВб	nWb
1012 Вб	теравебер	ТВб	TWb	10−12 Вб	пиковебер	пВб	pWb
1015 Вб	петавебер	ПВб	PWb	10−15 Вб	фемтовебер	фВб	fWb
1018 Вб	эксавебер	ЭВб	EWb	10−18 Вб	аттовебер	аВб	aWb
1021 Вб	зеттавебер	ЗВб	ZWb	10−21 Вб	зептовебер	зВб	zWb
1024 Вб	иоттавебер	ИВб	YWb	10−24 Вб	иоктовебер	иВб	yWb
применять не рекомендуется

Единица измерения магнитного потока, теория и онлайн калькуляторы

Определение

Элементарный магнитный поток ($dФ$) сквозь малую поверхность $dS$ равен произведению проекции вектора магнитной индукции ($B_n$) на нормаль к элементарной площадке $dS$ на величину этой площадки:

\[dФ=B_ndS\ \left(1\right).\]

Полный поток сквозь всю поверхность $S$ будет равен:

\[Ф=\int\limits_S{B_ndS\ \left(2\right).}\]

Если поверхность $S$ является плоской, находится она в однородном магнитном поле, причем перпендикулярно линиям индукции поля, то магнитный поток можно найти как:

\[Ф=BS\ \left(3\right).\]

Вебер — единица измерения магнитного потока в системе СИ

Единицу измерения магнитного потока можно определить исходя из выражения (3), как:

\[\left[Ф\right]=Тл\cdot м^2=Вб.\]

Единица измерения магнитного потока имеет собственное наименование — вебер (Вб). 1 Вебер — единица измерения магнитного потока в Международной системе единиц (СИ), это магнитный поток, который создает магнитное поле имеющее индукцию 1Тл через поперечное сечение площадью 1 $м^2$.

Иногда 1 вебер определяют иначе. Вебер (единица измерения магнитного потока) — это магнитный поток, при уменьшении которого до нуля, в сцепленной с ним электрической цепи, имеющей сопротивление один ом сквозь поперечное сечение проводника проходит заряд равный одному кулону. Данное определение вебера основывается на формуле:

\[\Delta q=\frac{\Delta Ф}{R}\left(4\right),\]

где $\Delta q$ — заряд, который проходит в замкнутой цепи, при изменении магнитного потока $\Delta Ф$ сквозь поверхность, которую ограничивает цепь; $R$ — сопротивление рассматриваемой цепи. Исходя из формулы (4) вебер можно считать комбинацией следующих единиц:

\[\left[Ф\right]=Вб=Кл\cdot Ом.\]

Производная единица измерения магнитного потока вебер выражается через основные единицы системы СИ как:

\[Вб=Тл\cdot м^2=\frac{кг}{А\cdot с^2}\cdot м^2.\]

Для обозначения кратных и дольных десятичных единиц измерения магнитного потока используют стандартные приставки системы СИ. Например, мВб (мили вебер): $1\ мВб={10}^{-3\ }Вб;;$ ГВб (гига вебер) $1\ ГВб={10}^{6\ }Вб.$

Максвелл — единица измерения магнитного потока в системе СГС

В системе СГС (сантиметр, грамм, секунда) единица измерения магнитного потока, так же как в СИ имеет свое наименование. Она называется максвелл (Мкс). С вебером максвелл соотносится как:

\[1Вб={10}^8Мкс.\]

Максвелл — единица измерения магнитного потока, получил свое название в честь Дж. К. Максвелла в 1900 г.

\[\left[Ф\right]=Мкс=Гс\cdot {см}^2.\]

Через плоский контур, площадью один квадратный сантиметр, находящийся в однородном магнитном поле с индукцией 1 гаусс (Гс) перпендикулярно направлению вектора магнитной индукции, проходит магнитный поток в один максвелл.

Прим

Магнитная индукция и магнитные поток

Напряженность магнитного поля не является основной величиной, характеризующей магнитное поле, хотя определение напряжённости действительно для расчёта катушек без магнитопровода.

Для катушки с магнитопроводом основной величиной характеризующей магнитное поле, является магнитная индукция В. Это векторная величина, т.е. она (как и напряженность) задаётся численным значением и направлением в пространстве. Магнитная индукция определяется по силе, действующей на движущуюся заряженную частицу. При изображении картины магнитного поля при помощи магнитных линий, их рисуют гуще в той части поля, где больше индукция.

Единицей измерения магнитной индукции является тесла (Тл). Ранее применялась другая единица измерения магнитной индукции – гаусс (Гс).

Эти единицы связаны соотношением: 1Тл = 10000Гс.

Произведение магнитной индукции В на площадь S, перпендикулярную вектору магнитной индукции (магнитным линиям), называется магнитным потоком Ф. Таким образом магнитный поток:

Ф = B*S

Единицей измерения магнитного потока является вебер (Вб). При одной и той же напряжённости магнитного поля Н, в разных материалах получаются различные магнитные индукции В. Отношение В/Н называется абсолютной магнитной проницаемостью материала μ_а, т.е.

Абсолютная магнитная проницаемость материала μ_а равна произведению магнитной постоянной (магнитной проницаемости вакуума) μ₀ и относительной магнитной проницаемости μ_r:

раоорропор

Магнитная постоянная

Гн/м (генри на метр, генри единица измерения индуктивности).

Величина μ_rпоказывает, во сколько раз μ_а материала больше, чем магнитная постоянная μ₀.

В материале, магнитная проницаемость которого равна μ_r,

а в вакууме (практически и в воздухе)

где В выражается в теслах, а Н в А/м.

При измерении магнитной индукции в гауссах, а напряжённости магнитного поля в А/см, для магнитной индукции в воздухе получим:

У ферромагнитных материалов относительная магнитная проницаемость μ_r во много раз больше 1, она изменяется с изменением индукции В. Зависимость между В и Н для ферромагнитных материалов чаще изображается графиком в виде кривых намагничивания.

В практических задачах (магнитные цепи электрических машин и аппаратов) для расчёта силы тяги, ЭДС, силы притяжения и т.д. требуется определить магнитный поток Ф или индукцию В. Значение этих величин определяют по кривым намагничивания, если известна напряженность магнитного поля Н, которая, в свою очередь, задаётся магнитным напряжением или МДС.

Величина	Обозначение	Единица величины	Обозначение единицы	Расчётная формула
Напряженность магнитного поля а. в магнитном материале	Н	Ампер на метр	А/м	Н=Iw/l
б. в вакууме (воздухе)
Магнитная сила	F	Ампер		F=wI
Магнитная индукция	В	Тесла (Вебер на 1 м2)	Тл (Вб/м2)
Магнитный поток	Ф	Вебер	Вб	Ф = ВS
Абсолютная магнитная проницаемость		Генри на метр	Гн/м

Задача 1.

Напряжённость магнитного поля катушки

H = 500 А/м. Какова будет магнитная индукция, если в катушку вставить магнитопровод из трансформаторной стали (на рис.), относительная магнитная проницаемость которой μ

r= 2400.

Решение

B = μ_а*Н = μ_о*μ_r*Н = 4*π*10^-7*2400*500 = 1.5 Тл

Задача 2.

Для трансформаторной стали, содержащей 4% Si, магнитная индукция В при напряжённости магнитного поля катушки 500 А/м равна 1.19 Тл (см. кривые намагничивания на рис.). Определить абсолютную магнитную проницаемость трансформаторной стали в рабочей точке μ_а и относительную магнитную проницаемость μ_r. Напомним, что величина μ_r показывает во сколько раз μ_а материала больше, чем магнитная проницаемость

μ_о = 4*π*10^-7.

Решение

Абсолютная магнитная проницаемость

μ_а = В/Н = 1.19/500

μ_а = μ_r*μ_о = 4*π*10^-7*μ_r.

Отсюда

μ_r = μ_а/μ_о = В/Н =1.19/(500*4*π*10^-7) = 1893.9

Задача 3.

По заданным экспериментальным зависимостям В и Н для различных материалов определить коэффициенты полиномов второго порядка, наилучшим способом (по минимуму суммы квадратов ошибок) обеспечивающих аналитическое их описание (математическую модель).

Листовая сталь

Н (А/м)	100	150	200	250	300	350	400	450	500	550
В (Тл)	0.60	0.75	0.86	0.96	1.05	1.12	1.19	1.23	1.30	1.36

Трансформаторная сталь (4% Si)

Н (А/м)	100	200	300	400	500	600
В (Тл)	0.48	0.78	0.96	1.08	1.19	1.27

Литая сталь

Н (А/м)	100	200	300	400	500	600
В (Тл)	0.35	0.60	0.85	1.00	1.10	1.16

Решение

Для оценки коэффициентов полинома

В = a*Н² + b*Н + С

Запишем вектор

Н = [100 150 200 250 300 350 400 450 500 550]’. size A = 10,1

Затем составим матрицу А:

А = [Н^2 Н ones(V(1),1)]

И образуем вектор В:

B = [0.6 0.75 0.86 0.96 1.05 1.12 1.19 1.23 1.3 1.36]’.

Выполним оценку коэффициентов

а х = А\В

С помощью файла sah575.m. В нём выполнены оценки коэффициентов квадратного полинома для листовой стали

а1 = [-0.0206 0.2952 0.3429],

для трансформаторной стали

а2 = [-0.0246 0.3239 0.2000]

и для листовой стали

а3 = [-0.0277 0.2566 0.0150].

Необходимо выполнить расчёты для каждого вида материала в режиме прямых вычислений.

/здесь приводится файл sah 375.m/

Задача 4.

Каков будет магнитный поток Ф в магнитопроводе (см. задачу 1.), если сечение магнитопровода S = 4 см²?

Решение

Магнитный поток, измеряемый в веберах (Вб), равен

Ф = В*S = 1.5*4*10^-4 = 0.0006 Вб

(Тл = Вб/м²)

Задача 5.

Число витков катушки w=500. В магнитопроводе из трансформаторной стали длиной l=25 см необходимо обеспечить магнитную индукцию В=1.19 Тл. Какая м.д.с. и ток необходим для этого?

Решение

По кривой намагничивания трансформаторной стали (см. рис.) находим, что для создания В = 1.19 Тл требуется создать напряжённость магнитного поля Н = 500 А/м. При длине магнитопровода (с катушкой) l = 25 см = 0.25 м необходимая м.д.с. вычисляется по формуле

I*w = H*l = 500 А/м * 0.25 м = 125 А,

Отсюда I = I*w/w = 125/500 = 0.25 А

Задача 6.

Каковы напряжённость, индукция и магнитный поток внутри цилиндрической катушки (рис.) которая имеет длину 20 см, диаметр 3см, число витков 1600 и ток 3 А?

Решение

Напряжённость магнитного поля

Н = I*w/l = 3*1600/0.2 = 24000 А/м

Поскольку катушка без сердечника, то магнитную индукцию следует вычислять по формуле:

В = μ_о*Н = 4*π*10^-7*2.4*10⁴ = 3.02*10^-2 Тл

Сечение катушки

S = π*d²/4 = 3.14*0.03²/4 = 7.06*10^-4 м².

Следовательно, магнитный поток

Ф = В*S = 3.02*10^-2*7.06*10^-4 = 21.3*10^-6 Вб

Дополнение

Задача 1

Какое количество электричества пройдёт через лампу за 3 часа при токе 0,18А?

Решение:

Задача 2

Свинцовый аккумулятор ёмкостью 14А*ч заряжается током I зар = 1.4А. Как долго он должен заряжаться и через сколько времени он разрядится через лампы током Iраз = 0.3А?

Решение:

Зарядка: t = Q/Iзар = 14А*ч/1.4А = 10ч,

т.е. аккумулятор должен заряжаться 10ч

Разрядка: t = Q/Iраз = 14А*ч/0.3А = 47ч,

т.е. лампы горели 47ч. Через лампы прошёл ток 14А*ч, пока аккумулятор не разрядился.

Задача 3

Заряженный аккумулятор имеет ёмкость 28А*ч. 1) Какое количество электричества в кулонах содержит аккумулятор? 2) Какой ток необходим для зарядки аккумулятора за 10ч. Каким током разрядится он за 140ч.?

Решение.

1. 1А*ч = 360 А*с = 3600Кл

28А*ч = 28*3600Кл = 100800 Кл.

2. Iзар = Q/t = 28А*ч/10ч = 2.8А, т.е. аккумулятор зарядится за 10часов током 2.8А

3. Iраз = Q/t = 28А*ч/140ч = 0.2А.

Задача 4

Сколько ампер-часов содержтся в 96480 кулонах (заряд Фарадея)?

1А*ч = 3600А*с = 3600Кл;

96480/3600 = 26.8 А*ч, т.е. 96489 Кл. эквивалентен 26,8 А*ч

Задачи для самостоятельного решения:

1. Какой электрический заряд нужен от гальванического элемента, если он разряжается током 0,05А в течении 12ч.? (0,6 А*ч)

2. Через электродвигатель при токе I проходит количество электричества Q = 7500А*с за время t = 5мин/ Чему равен ток? (30мА)

3. Какой ток протекал по проводнику, если через его поперечное сечение за 30мин прошел заряд 54А*с? (30мА)

4. Через аппарат проходит ток I = 20мА в течение 9мин. Определить количество электричества, которое прошло через аппарат?

5. Аккумулятор ёмкостью 10А*ч заряжается током 4А. Как долго должен заряжаться? (10ч)

Задача 1.

Через медный проводник с площадью поперечного сечения S = 4 мм²

протекает ток I=10А. Какова плотность тока?

Решение:

Плотность тока

J = I/S = 10A/4мм² = 2.5 A/мм²

По площади 1 мм² поперечного сечения протекает ток I = 2.5A;

По всему поперечному сечению S проходит общий ток I = 10А.

По таблице проверить, допустима ли плотность тока 2.5 А/мм²?

Задача 2.

По шине разделительного устройства площадью прямоугольного поперечного сечения (20х80)мм проходит ток I = 1000A. Какова плотность тока в шине?

Решение

Площадь поперечного сечения шины S = 20х80 = 1600 мм². Плотность тока

J = I/S = 1000A/1600 мм² = 0.625A/мм²

Задача 3.

У катушки провод имеет круглое сечение диаметром 0,8мм и допускает плотность тока 2,5А/мм². Какой допустимый ток может проходить по проводу (нагрев не должен превышать допустимый)?

Решение:

Площадь поперечного сечения провода:

Допустимый ток:

Задача 4.

Допустимая плотность тока для обмотки трансформатора J = 2.5 А/мм²

Через обмотку проходит ток I = 4A. Каким должно быть поперечное сечение круглого проводника, чтобы обмотка не перегревалась?

Решение:

Площадь поперечного сечения

S=I/J=

Этому сечению соответствует диаметр провода 1.42мм.

Задача 5.

По изолированному медному проводу сечением 4 мм² проходит максимально допустимый ток 38А (см таблицу). Какая допустимая плотность тока? Чему равны допустимые плотности токов для медных проводов с площадями поперечного сечения 1, 10, 16 мм²?

Решение.

1. Допустимая плотность тока

2. Для сечения 1 мм² допустимая плотность тока (см табл)

3. Для сечения 10 мм² допустимая плотность тока

4. Для сечения 16 мм² допустимая плотность тока

Допустимая плотность тока с увеличением сечения кабеля тоже действительна для проводов с изоляцией класса В.

Задачи для самостоятельного решения.

1. Через обмотку трансформатора должен протекать ток I = 4A. Каким должно быть сечение обмоточного провода при допустимой плотности тока J = 2.5 А/мм² (S = 1.6 мм²)

2. По проводу диаметром 0,3 мм проходит ток 100А. Какова плотность тока (J = 1.415 А/мм²)

3. По обмотке электромагнита из медного изолированного провода диаметром d = 2.26мм (без учёта изоляции) проходит ток 10А. Какова плотность тока? (J= 2.5 А/мм²)

Магнитный поток ℹ️ определение, обозначение и единица измерения, формула, скорость изменения потока, направление вектора магнитной индукции, расчеты

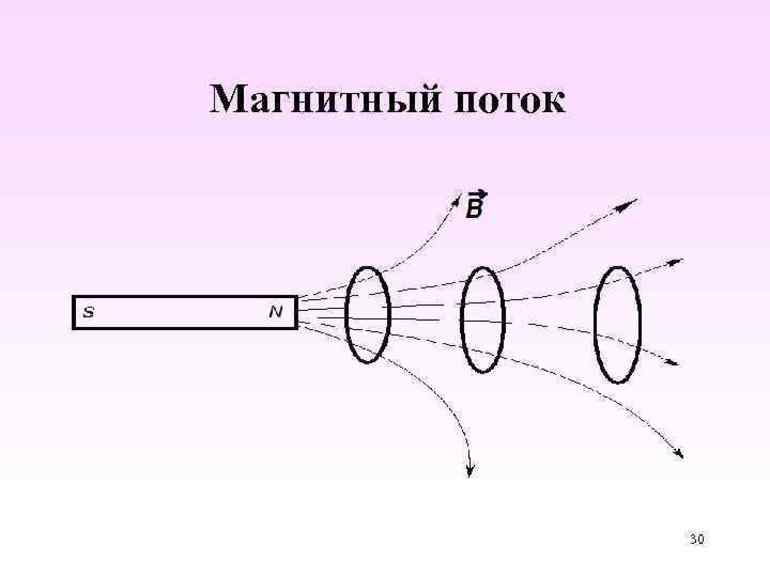
Наблюдение за спектрами

В соответствии с плотностью линий магнитного поля (МП) можно увидеть величину вектора индукции, а согласно направленности силовых рядов — его течение. Наблюдение за спектрами постоянного тока и катушки на самом деле показывает, что при удалении проводника индукция МП уменьшается и довольно быстро.

Магнитный фон называется:

1. С различным выведением в разных точках — гетерогенным. Неоднородный фон — это часть прямолинейного и радиального тока, вне соленоида, неизменённого магнита и т. д.
2. С индукцией во всех точках — однородным полем. Графически такой МФ представлен силовыми линиями, которые считаются равноотстоящими параллельными частями. Этот случай является фоном изнутри длинного соленоида, а также полем между близкими соседними плоскими наконечниками электромагнита.

Произведение индукции поля, проникающего в контур от его области, называется потоком МИ или элементарным МП. Определение было дано и изучено британским физиком Фарадеем. Он отметил, что эта концепция на самом деле позволяет глубже рассмотреть совместный характер магнитных и электрических явлений.

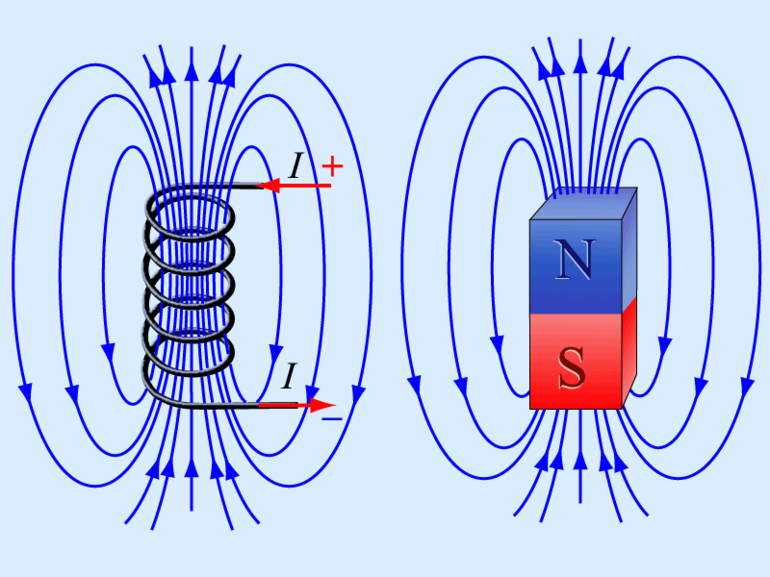
Обозначая поток буквой f, площадью контура S и углом между направлением вектора индукции B и нормальной частью n к области α, можно написать магнитный поток формулой:

F = S cos α.

МП является скалярным размером. Например, поскольку плотность силовых рядов случайного магнитного поля равна его индукции, он уравнивается всему количеству линий, которые проникают в цепь. С изменением поля поток, который пронизывает контур, также меняется.

Единица измерения магнитного потока — вебер. Определение СИ струи считается линия, площадь которой 1 м², оказавшаяся на равномерном фоне с индукцией 1 Вт / м2 и перпендикулярная вектору. Это устройство будет обозначаться:

1 Вт = 1 Вт / м2 — 1 м².

Особенности течения

Скорость изменения магнитного потока генерирует электронный фон, имеющий замкнутые блоки питания (вихревое поле). Этот фон рассматривается в проводнике как циркуляция внешних сил. Это явление называется электрической индукцией, а мощность, которую можно определить, генерируемая в этом случае, является индуцированной ЭДС поверхности

.

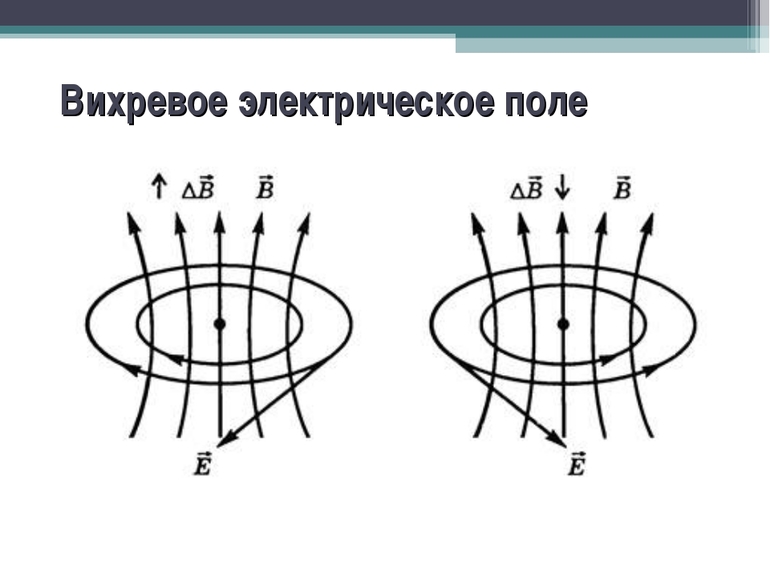
Поток подчёркивает вероятность характеристики всего магнита или видов других источников МП. Если индукция выдвигает на первый план вероятность, характерную её эффекту в любой отдельной точке, поток будет целым. Это вторая по значимости особенность поля. Если МИ функционирует как силовая часть МП, поток считается её энергетической линией.

Возвращаясь к экспериментам, можно сказать, что фактически любая электромагнитная катушка может рассматриваться как 1 закрытая. Это схема, по которой будет течь магнитный поток вектора индукции, тогда ток МИ электронов будет замечен при потокосцеплении.

Таким образом, непосредственно под действием струи в замкнутом проводнике образуется электронный фон. И в течение этого времени он будет генерировать ток.

Магнитная индукция

Согласно прогрессивным научным представлениям об электрических явлениях, МП неразрывно связан с током и не может присутствовать без него. Невозможно предположить электроток без МП. В том числе в случае неизменного магнита связывают этот фон с молекулярными линиями.

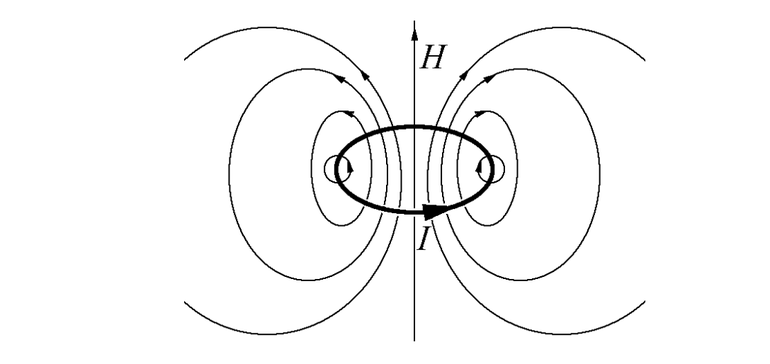
Если в место, где находится МП, поставить иглу, она стремится заимствовать определённое состояние, которое фактически показывает ориентационные качества МП. Скоординированное направление в этой точке места должно учитывать пункт назначения, где установлена ось, — это свободноподвешенная бесконечно небольшая магнитная стрелка, середина которой выровнена с точкой начального места. При этом из 2 возможных направлений вдоль оси стрелки МП символически присваивается назначение от южного конца на север.

Можно получить более яркое представление о направленности поля, если имеется ряд линий, где оси всех стрелок будут относительно касательными. Эти части называются магнитными магистралями.

Набор рядов упоминается как МП. Если бесконечно уменьшать площадь контура, притягивая его к точке, можно прийти к выражению для бесконечно малой стадии d, T активно в контуре маленькой области s, где угол P имеет конкретное значение между нормальностью к плоскости и небольшого контура. В этом случае направлением поля будет точка места, где расположено малое очертание.

Удар на плоскую цепь с током

В таких условиях коэффициент B принимается как характеристика интенсивности МП в этой точке места и называется индукцией МП. Она считается величиной, объединяющей назначение вектора МИ с направлением магнитного поля в этой точке места.

МП, характеризующийся на некоторых участках одинаковым значением вектора МИ, называется равномерным МП. Индукция в международной системе (СИ) измеряется в единицах Тесла (TL). МИ однородного МП составляет 1 т, если она воздействует на плоскую электронную последовательность площадью 5 ‘= 1 м и током 7 = 1 А, расположенную так, что магнитные доли лежат в плоскости цепи p = 0,5 n sin p = 1 с коэффициентом t = 1 Нм.

Область места любой части, что связана с конкретным вектором, называется полем. Понятие строк широко используется для визуального представления ВП. В случае с линейным полем можно увидеть линию, так как сам вектор ориентирован тангенциально в любой точке. Трубчатая линия представляет собой область узла, ограниченную обилием соседних рядов, проделанных сквозь закрытое очертание. Представление векторного поля часто используется при описании различных взаимодействий тела. В частности, в отображении МП упоминается фон вектора магнитной индукции, определяющий в нём части и трубки МИ.

Электрическая зависимость

Британский физик Майкл Фарадей не сомневался в единственной природе явлений магнетизма в своей теореме. Изменяющийся во времени фон создаёт электронный и магнитный вид. В 1831 году Фарадей обнаружил появление индукции, которая легла в основу устройства для генераторов, преобразующих механическую энергию в электронную. А в 1835 г. немецкий математик Карл Гаусс определил аксиому, описывающую обозначение и зависимость напряжённости поля от величины заряда.

Появление электрической индукции замечено в появлении тока в проводящей цепи, которая либо лежит на изменяющемся во времени фоне, либо движется на непременном участке таким образом, что фактически число магнитных витков проникает в контуры трансформаций.

Для своих многочисленных экспериментов Фарадей воспользовался двумя катушками, магнитом, переключателем постоянного тока и гальванометром. Электронный поток мог зависеть и намагничивать кусок железа.

В результате экспериментов Фарадея были заложены основные особенности возникновения электрической индукции, и ток появляется:

• в одной из катушек во время замыкания или размыкания электронной цепи внутри другой части;
• когда энергия протекает в одном из элементов с поддержкой реостата;
• при перемещении катушек относительно друг друга;
• когда неизменный магнит движется относительно.

В замкнутом проводящем контуре ток появляется, когда число линий магнитной индукции изменяется, создавая плоскость, ограниченную цепью. И чем раньше перевести количество рядов МИ, тем больше генерируется индукционный ток в рамке. Это является основной причиной конфигурации численности последовательностей индукции.

Явление позволяет содержать и изменять число линий МИ, делая плоскость площадки, ограниченной неподвижной проводящей цепью, из-за конфигурации тока в катушке, расположенной рядом. Происходит максимальное изменение количества последовательностей МИ из-за смещения схемы на неоднородном фоне, плотность линий которого может изменяться на месте.

Тесла (единица измерения) — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 4 июля 2019; проверки требует 1 правка. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 4 июля 2019; проверки требует 1 правка. У этого термина существуют и другие значения, см. Тесла.

Те́сла (русское обозначение: Тл; международное обозначение: T) — единица индукции магнитного поля в Международной системе единиц (СИ), равная индукции такого однородного магнитного поля, в котором на 1 метр длины прямого проводника, перпендикулярного вектору магнитной индукции, с током силой 1 ампер действует сила 1 ньютон.

Через основные единицы СИ тесла выражается следующим образом:

Через производные единицы СИ тесла выражается соотношениями:

В соответствии с правилами СИ, касающимися производных единиц, названных по имени учёных, наименование единицы тесла пишется со строчной буквы, а её обозначение «Тл» — с заглавной.

Соотношения с другими единицами измерения магнитной индукции:

Единица названа в честь изобретателя Николы Теслы. В Международную систему единиц (СИ) тесла введён решением XI Генеральной конференцией по мерам и весам в 1960 году одновременно с принятием СИ в целом^[1].

• В космическом пространстве магнитная индукция составляет от 0,1 до 10 нанотесла (от 10⁻¹⁰ до 10⁻⁸ Тл).
• Магнитное поле Земли значительно варьируется во времени и пространстве. На широте 50° магнитная индукция в среднем составляет 5⋅10⁻⁵ Тл, а на экваторе (широта 0°) — 3,1⋅10⁻⁵ Тл.
• Сувенирный магнит на холодильнике создает поле около 5 миллитесла.
• Отклоняющие дипольные магниты Большого адронного коллайдера — от 0,54 до 8,3 Тл.
• Стандартное значение магнитной индукции, создаваемой высокопольным магнитно-резонансным томографом, — 1,5 Тл.
• В солнечных пятнах — 0,1 Тл.
• В белых карликах — 100 Тл.
• Рекордное значение постоянного магнитного поля, достигнутое людьми без разрушения установки — 1200 Тл^[2]
• Рекордное значение импульсного магнитного поля, когда-либо наблюдавшегося в лаборатории — 2,8⋅10³ Тл^[3]
• Магнитные поля в атомах — от 1 до 10 килотесла (10³ — 10⁴ Тл).
• На нейтронных звёздах — от 1 до 100 мегатесла (10⁶ — 10⁸ Тл).
• На магнетарах — от 0,1 до 100 гигатесла (10⁸ — 10¹¹ Тл).

Десятичные кратные и дольные единицы образуют с помощью стандартных приставок СИ.

Кратные				Дольные
величина	название	обозначение		величина	название	обозначение
101 Тл	декатесла	даТл	daT	10−1 Тл	децитесла	дТл	dT
102 Тл	гектотесла	гТл	hT	10−2 Тл	сантитесла	сТл	cT
103 Тл	килотесла	кТл	kT	10−3 Тл	миллитесла	мТл	mT
106 Тл	мегатесла	МТл	MT	10−6 Тл	микротесла	мкТл	µT
109 Тл	гигатесла	ГТл	GT	10−9 Тл	нанотесла	нТл	nT
1012 Тл	тератесла	ТТл	TT	10−12 Тл	пикотесла	пТл	pT
1015 Тл	петатесла	ПТл	PT	10−15 Тл	фемтотесла	фТл	fT
1018 Тл	эксатесла	ЭТл	ET	10−18 Тл	аттотесла	аТл	aT
1021 Тл	зеттатесла	ЗТл	ZT	10−21 Тл	зептотесла	зТл	zT
1024 Тл	иоттатесла	ИТл	YT	10−24 Тл	иоктотесла	иТл	yT
применять не рекомендуется

Магнитодвижущая сила — Википедия

Материал из Википедии — свободной энциклопедии

Магнѝтодви́жущая си́ла (МДС) — физическая величина, характеризующая способность электрических токов создавать магнитные потоки. Используется при расчётах магнитных цепей; является аналогом ЭДС в электрических цепях.

Величина измеряется в амперах (СИ) или же в гилбертах (СГС), причём 1 А = 4π10{\displaystyle {\frac {4\pi }{10}}} Гб ≈ 1,257 Гб. На практике для обозначения единицы МДС часто используется термин «ампер-виток», численно равный единице в СИ.

Магнитодвижущая сила F{\displaystyle {\mathcal {F}}} в катушке или электромагните вычисляется по формуле

F=wI,{\displaystyle {\mathcal {F}}=wI,}

где w{\displaystyle w} — количество витков в обмотке, I{\displaystyle I} — ток в проводнике.

Выражение для магнитного потока в магнитной цепи, называемое иногда законом Гопкинсона, имеет следующий вид:

F=ΦRm{\displaystyle {\mathcal {F}}=\Phi R_{m}}

где Φ{\displaystyle \Phi } — величина магнитного потока, Rm{\displaystyle R_{m}} — магнитное сопротивление проводника. Данная запись является аналогом закона Ома в магнитных цепях.

Поток магнитной индукции, теория и примеры

Определение и общие понятия потока магнитной индукции

Исходя из формулы (1), магнитный поток через произвольную поверхность S вычисляется (в общем случае), как:

   

Магнитный поток однородного магнитного поля сквозь плоскую поверхность можно найти как:

   

Для однородного поля, плоской поверхности, расположенной перпендикулярно вектору магнитной индукции магнитный поток равен:

   

Поток вектора магнитной индукции может быть отрицательным и положительным. Это связано с выбором положительного направления . Очень часто поток вектора магнитной индукции связывают с контуром, по которому течет ток. В этом случае положительное направление нормали к контуру связано с направлением течения тока правилом правого буравчика. Тогда, магнитный поток, который создается контуром с током, сквозь поверхность, ограниченную этим контуром является всегда большим нуля.

Единица измерения потока магнитной индукции в международной системе единиц (СИ) – это вебер (Вб). Формулу (4) можно использовать для определения единицы измерения магнитного потока. Одним вебером называют магнитный поток, который проходит сквозь плоскую поверхность площадь, которой 1 квадратный метр, размещенную перпендикулярно к силовым линиям однородного магнитного поля:

   

Теорема Гаусса для магнитного поля

Теорема гаусса для потока магнитного поля отображает факт отсутствия магнитных зарядов, из-за чего линии магнитной индукции всегда замкнуты или уходят в бесконечность, у них нет начала и конца.

Формулируется теорема Гаусса для магнитного потока следующим образом: Магнитный поток сквозь любую замкнутую поверхность (S) равен нулю. В математическом виде данная теорема записывается так:

   

Получается, что теоремы Гаусса для потоков вектора магнитной индукции () и напряженности электростатического поля (), сквозь замкнутую поверхность, отличаются принципиальным образом.

Примеры решения задач