Физика (11 класс)/Магнитное поле. Магнитная индукция — Викиверситет
Магнитное поле[править]
В отличие от заряда покоящегося, который создает вокруг себя электрическое поле, заряд движущийся создает вокруг себя также магнитное поле .
 | Экспериментально установлено, что:
|
Магнитное поле создается постоянными магнитами или проводниками, по которым течет постоянный ток. Вектор магнитной индукции B является важнейшей характеристикой магнитного поля. Линии магнитной индукции — это линии, касательные к которым направлены так же, как и вектор В в данной точке. В отличие от силовых линий электростатического поля, линии магнитной индукции
Для магнитных полей справедлив принцип суперпозиции, дадим его определение.
Определение. Принцип суперпозиции. В любой точке поля вектор магнитной индукции результирующего поля равен сумме векторов полей, создаваемых каждой точкой в отдельности: B=B1+B2+…+Bn{\displaystyle B=B_{1}+B_{2}+…+B_{n}}.Сила, с которой магнитное поле действует на проводник с током, называется силой Ампера.
Fa=BIL sin α.
Где α это угол между вектором магнитной индукции и проводником.
Направление силы Ампера определяется по правилу левой руки.
правило левой руки:
Если расположить левую руку так, чтобы линии магнитной индукции входили в ладонь, а четыре пальца были направлены по току, то отогнутый на 90° большой палец покажет направление силы Ампера. Как видно из формулы, сила Ампера максимальна при α=90° и минимальна при α=0° (т.е. когда линии магнитной индукции параллельны проводнику).
Как было сказано выше, магнитное поле действует не только на проводник с током, но и на движущийся заряд.
Сила Лоренца-это сила с которой магнитное поле действует на движущийся заряд.
Fл=|q|υBsinα
где q- величина заряда, υ-его скорость, B- индукция магнитного поля, α-угол между магнитной индукцией и направлением скорости. Направление СИЛЫ ЛОРЕНЦА можно определить по
ПРАВИЛУ ЛЕВОЙ РУКИ: если расположить ладонь левой руки так, чтобы линии магнитной индукции входили в ладонь, а четыре пальца были направленны по направлению движения положительного заряда (если дан отрицательный заряд, то берем соответственно в противоположную сторону) то отогнутый на 90° большой палец покажет направление действия силы Лоренца.
Магнитный поток[править]
Магнитным потоком(потоком магнитной индукции) Φ через плоскую поверхность площадью S, помещенную в однородное магнитное поле, называется величина:
Φ=BScosα
где B-модуль вектора магнитной индукции, α- угол между вектором B и вектором перпендикулярным к поверхности площадью S. На магнитный поток, как и на магнитное поле распространяется принцип суперпозиции
Φ=Φ1+Φ2+...Φn
Закон электромагнитной индукции[править]
Суть явления электромагнитной индукции состоит в том, что при любом изменении магнитного потока, пронизывающего замкнутый контур, возникает индукционный ток, который существует до тех пор, пока изменяется магнитный поток.
Определить направление индукционного тока можно по правилу Ленца:индукционный ток всегда противодействует причине, вызвавшей его. Закон электромагнитной индукции утверждает, что при изменении магнитного потока в контуре возникает электродвижущая сила индукции , равная скорости изменения магнитного потока через поверхность:
ε=-ΔΦ/Δt
Магнетизм — Физика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Сила Ампера
К оглавлению…
Заряженные тела способны создавать кроме электрического еще один вид поля. Если заряды движутся, то в пространстве вокруг них создается особый вид материи, называемый магнитным полем. Следовательно, электрический ток, представляющий собой упорядоченное движение зарядов, тоже создает магнитное поле. Как и электрическое поле, магнитное поле не ограничено в пространстве, распространяется очень быстро, но все же с конечной скоростью. Его можно обнаружить только по действию на движущиеся заряженные тела (и, как следствие, токи).
Для описания магнитного поля необходимо ввести силовую характеристику поля, аналогичную вектору напряженности E электрического поля. Такой характеристикой является вектор B магнитной индукции. В системе единиц СИ за единицу магнитной индукции принят 1 Тесла (Тл). Если в магнитное поле с индукцией B поместить проводник длиной l с током I, то на него будет действовать сила, называемая

где: В – индукция магнитного поля, I – сила тока в проводнике, l – его длина. Сила Ампера направлена перпендикулярно вектору магнитной индукции и направлению тока, текущего по проводнику.
Для определения направления силы Ампера обычно используют правило «Левой руки»: если расположить левую руку так, чтобы линии индукции входили в ладонь, а вытянутые пальцы были направлены вдоль тока, то отведенный большой палец укажет направление силы Ампера, действующей на проводник (см. рисунок).

Если угол α между направлениями вектора магнитной индукции и тока в проводнике отличен от 90°, то для определения направления силы Ампера надо взять составляющую магнитного поля, которая перпендикулярна направлению тока. Решать задачи этой темы нужно так же как и в динамике или статике, т.е. расписав силы по осям координат или складывая силы по правилам сложения векторов.
Момент сил, действующих на рамку с током
Пусть рамка с током находится в магнитном поле, причём плоскость рамки перпендикулярна полю. Силы Ампера будут сжимать рамку, а их равнодействующая будет равна нулю. Если поменять направление тока, то силы Ампера поменяют своё направление, и рамка будет не сжиматься, а растягиваться. Если линии магнитной индукции лежат в плоскости рамки, то возникает вращательный момент сил Ампера.

где: S — площадь рамки, α — угол между нормалью к рамке и вектором магнитной индукции (нормаль — вектор, перпендикулярный плоскости рамки), N – количество витков, B – индукция магнитного поля, I – сила тока в рамке.
Сила Лоренца
К оглавлению…
Сила Ампера, действующая на отрезок проводника длиной Δl с силой тока I, находящийся в магнитном поле B может быть выражена через силы, действующие на отдельные носители заряда. Эти силы называют силами Лоренца. Сила Лоренца, действующая на частицу с зарядом q в магнитном поле B, двигающуюся со скоростью v, вычисляется по следующей формуле:

Угол α в этом выражении равен углу между скоростью и вектором магнитной индукции. Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или по правилу буравчика (как и сила Ампера). Вектор магнитной индукции нужно мысленно воткнуть в ладонь левой руки, четыре сомкнутых пальца направить по скорости движения заряженной частицы, а отогнутый большой палец покажет направление силы Лоренца. Если частица имеет
Сила Лоренца направлена перпендикулярно векторам скорости и индукции магнитного поля. При движении заряженной частицы в магнитном поле сила Лоренца работы не совершает. Поэтому модуль вектора скорости при движении частицы не изменяется. Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость лежит в плоскости, перпендикулярной вектору индукции магнитного поля, то частица будет двигаться по окружности, радиус которой можно вычислить по следующей формуле:

Сила Лоренца в этом случае играет роль центростремительной силы. Период обращения частицы в однородном магнитном поле равен:

Последнее выражение показывает, что для заряженных частиц заданной массы
Теория о магнитном поле
К оглавлению…
Магнитное взаимодействие токов
Если по двум параллельным проводам идёт ток в одном направлении, то они притягиваются; если в противоположных направлениях, то отталкиваются. Закономерности этого явления были экспериментально установлены Ампером. Взаимодействие токов вызывается их магнитными полями: магнитное поле одного тока действует силой Ампера на другой ток и наоборот. Опыты показали, что модуль силы, действующей на отрезок длиной Δl каждого из проводников, прямо пропорционален силам тока I1 и I2 в проводниках, длине отрезка Δl и обратно пропорционален расстоянию R между ними:

где: μ0 – постоянная величина, которую называют магнитной постоянной. Введение магнитной постоянной в СИ упрощает запись ряда формул. Ее численное значение равно:
μ0 = 4π·10–7 H/A2 ≈ 1,26·10–6 H/A2.
Сравнивая приведенное только что выражение для силы взаимодействия двух проводников с током и выражение для силы Ампера нетрудно получить выражение для индукции магнитного поля создаваемого каждым из прямолинейных проводников с током на расстоянии R от него:

где: μ – магнитная проницаемость вещества (об этом чуть ниже). Если ток протекает по круговому витку, то в центре витка индукция магнитного поля определяется по формуле:

Силовыми линиями магнитного поля называют линии, по касательным к которым располагаются магнитные стрелки. Магнитной стрелкой называют длинный и тонкий магнит, его полюса точечны. Подвешенная на нити магнитная стрелка всегда поворачивается в одну сторону. При этом один её конец направлен в сторону севера, второй — на юг. Отсюда название полюсов: северный (N) и южный (S). Магниты всегда имеют два полюса: северный (обозначается синим цветом или буквой N) и южный (красным цветом или буквой S). Магниты взаимодействуют так же, как и заряды: одноименные полюса отталкиваются, а разноименные – притягиваются. Невозможно получить магнит с одним полюсом. Даже если магнит разломать, то у каждой части будет по два разных полюса.
Вектор магнитной индукции
Вектор магнитной индукции — векторная физическая величина, являющаяся характеристикой магнитного поля, численно равная силе, действующей на элемент тока в 1 А и длиной 1 м, если направление силовой линии перпендикулярно проводнику. Обозначается В, единица измерения — 1 Тесла. 1 Тл — очень большая величина, поэтому в реальных магнитных полях магнитную индукцию измеряют в мТл.
Вектор магнитной индукции направлен по касательной к силовым линиям, т.е. совпадает с направлением северного полюса магнитной стрелки, помещённой в данное магнитное поле. Направление вектора магнитной индукции не совпадает с направлением силы, действующей на проводник, поэтому силовые линии магнитного поля, строго говоря, силовыми не являются.
Силовая линия магнитного поля постоянных магнитов направлена по отношению к самим магнитам так, как показано на рисунке:

В случае магнитного поля электрического тока для определения направления силовых линий используют правило «Правой руки»: если взять проводник в правую руку так, чтобы большой палец был направлен по току, то четыре пальца, обхватывающие проводник, показывают направление силовых линий вокруг проводника:

В случае прямого тока линии магнитной индукции — окружности, плоскости которых перпендикулярны току. Вектора магнитной индукции направлены по касательной к окружности.
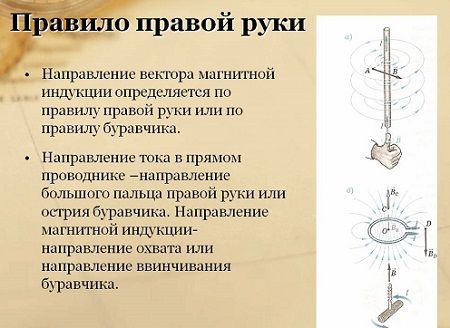
Соленоид — намотанный на цилиндрическую поверхность проводник, по которому течёт электрический ток I. Магнитное поле соленоида подобно полю прямого постоянного магнита. Внутри соленоида длиной l и количеством витков N создается однородное магнитное поле с индукцией (его направление также определяется правилом правой руки):


Линии магнитного поля имеют вид замкнутых линий — это общее свойство всех магнитных линий. Такое поле называют вихревым. В случае постоянных магнитов линии не оканчиваются на поверхности, а проникают внутрь магнита и замыкаются внутри. Это различие электрического и магнитного полей объясняется тем, что, в отличие от электрических, магнитных зарядов не существует.
Магнитные свойства вещества
Все вещества обладают магнитными свойствами. Магнитные свойства вещества характеризуются относительной магнитной проницаемостью μ, для которой верно следующее:

Данная формула выражает соответствие вектора магнитной индукции поля в вакууме и в данной среде. В отличие от электрического, при магнитном взаимодействии в среде можно наблюдать и усиление, и ослабление взаимодействия по сравнению с вакуумом, у которого магнитная проницаемость μ = 1. У диамагнетиков магнитная проницаемость μ немного меньше единицы. Примеры: вода, азот, серебро, медь, золото. Эти вещества несколько ослабляют магнитное поле. Парамагнетики — кислород, платина, магний — несколько усиливают поле, имея μ немного больше единицы. У ферромагнетиков — железо, никель, кобальт — μ >> 1. Например, у железа μ ≈ 25000.
Магнитный поток. Электромагнитная индукция
К оглавлению…
Явление электромагнитной индукции было открыто выдающимся английским физиком М.Фарадеем в 1831 году. Оно заключается в возникновении электрического тока в замкнутом проводящем контуре при изменении во времени магнитного потока, пронизывающего контур. Магнитным потоком Φ через площадь S контура называют величину:

где: B – модуль вектора магнитной индукции, α – угол между вектором магнитной индукции B и нормалью (перпендикуляром) к плоскости контура, S – площадь контура, N – количество витком в контуре. Единица магнитного потока в системе СИ называется Вебером (Вб).
Фарадей экспериментально установил, что при изменении магнитного потока в проводящем контуре возникает ЭДС индукции εинд, равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус:

Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум возможным причинам.
- Магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле. Возникновение ЭДС индукции объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
- Вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре.
При решении задач важно сразу определить за счет чего меняется магнитный поток. Возможно три варианта:
- Меняется магнитное поле.
- Меняется площадь контура.
- Меняется ориентация рамки относительно поля.
При этом при решении задач обычно считают ЭДС по модулю. Обратим внимание также внимание на один частный случай, в котором происходит явление электромагнитной индукции. Итак, максимальное значение ЭДС индукции в контуре состоящем из N витков, площадью S, вращающемся с угловой скоростью ω в магнитном поле с индукцией В:

Движение проводника в магнитном поле
К оглавлению…
При движении проводника длиной l в магнитном поле B со скоростью v на его концах возникает разность потенциалов, вызванная действием силы Лоренца на свободные электроны в проводнике. Эту разность потенциалов (строго говоря, ЭДС) находят по формуле:

где: α — угол, который измеряется между направлением скорости и вектора магнитной индукции. В неподвижных частях контура ЭДС не возникает.
Если стержень длиной L вращается в магнитном поле В вокруг одного из своих концов с угловой скоростью ω, то на его концах возникнет разность потенциалов (ЭДС), которую можно рассчитать по формуле:

Индуктивность. Самоиндукция. Энергия магнитного поля
К оглавлению…
Самоиндукция является важным частным случаем электромагнитной индукции, когда изменяющийся магнитный поток, вызывающий ЭДС индукции, создается током в самом контуре. Если ток в рассматриваемом контуре по каким-то причинам изменяется, то изменяется и магнитное поле этого тока, а, следовательно, и собственный магнитный поток, пронизывающий контур. В контуре возникает ЭДС самоиндукции, которая согласно правилу Ленца препятствует изменению тока в контуре. Собственный магнитный поток Φ, пронизывающий контур или катушку с током, пропорционален силе тока I:

Коэффициент пропорциональности L в этой формуле называется коэффициентом самоиндукции или индуктивностью катушки. Единица индуктивности в СИ называется Генри (Гн).
Запомните: индуктивность контура не зависит ни от магнитного потока, ни от силы тока в нем, а определяется только формой и размерами контура, а также свойствами окружающей среды. Поэтому при изменении силы тока в контуре индуктивность остается неизменной. Индуктивность катушки можно рассчитать по формуле:

где: n — концентрация витков на единицу длины катушки:

ЭДС самоиндукции, возникающая в катушке с постоянным значением индуктивности, согласно формуле Фарадея равна:

Итак ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в ней.
Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии. Энергия Wм магнитного поля катушки с индуктивностью L, создаваемого током I, может быть рассчитана по одной из формул (они следуют друг из друга с учётом формулы Φ = LI):

Соотнеся формулу для энергии магнитного поля катушки с её геометрическими размерами можно получить формулу для объемной плотности энергии магнитного поля (или энергии единицы объёма):

Правило Ленца
К оглавлению…
Инерция – явление, происходящее и в механике (при разгоне автомобиля мы отклоняемся назад, противодействуя увеличению скорости, а при торможении отклоняемся вперёд, противодействуя уменьшению скорости), и в молекулярной физике (при нагревании жидкости увеличивается скорость испарения, самые быстрые молекулы покидают жидкость, уменьшая скорость нагревания) и так далее. В электромагнетизме инерция проявляется в противодействии изменению магнитного потока, пронизывающего контур. Если магнитный поток нарастает, то возникающий в контуре индукционный ток направлен так, чтобы препятствовать нарастанию магнитного потока, а если магнитный поток убывает, то возникающий в контуре индукционный ток направлен так, чтобы препятствовать убыванию магнитного потока.
Правило Ленца для определения направления индукционного тока: возникающий в контуре индукционный ток имеет такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, которое вызывало этот ток.
Все магниты разделяются между собой по силе своего воздействия. Таким образом, существует определенная величина, которая характеризует степень проявления силы того или иного магнита. Если быть более точными, то данная сила создается не самими магнитами, а их магнитными полями. Само магнитное поле зависит от векторной величины, которая известна, как индукция магнитного поля или просто магнитная индукция. ФормулаДля определения величины электромагнитной индукции используется формула B=F/(I*l), где магнитная индукция В, представляющая собой модуль вектора, определяется, как отношение модуля силы F, воздействующей на проводник с током, расположенным перпендикулярно с магнитными линиями, к значению силы тока I, имеющейся в проводнике и длине l самого проводника. Зависимость магнитной индукцииНа электромагнитную индукцию абсолютно не влияют, ни сила тока, ни длина проводника. Она находится в прямой зависимости и связи, только с магнитным полем. Таким образом, при уменьшении силы тока в проводнике, без изменения каких-либо других показателей, происходит уменьшение не индукции, прямо пропорционально связанной с силой тока, а той силы, с которой магнитное поле воздействует на проводник. При этом, значение самой магнитной индукции остается постоянным. Благодаря этим качествам, электромагнитная индукция выступает в роли количественной характеристики магнитного поля.
Измерение магнитной индукции производится в теслах, по формуле: 1 Тл=1 Н/(А*м). Физическую зависимость этой величины от различных факторов, можно определить в ходе проведения несложного эксперимента. Необходимо взять весы, где на одной стороне прикрепляется проводник, а на другой стороне расположены гири. Проводник находится в постоянном электромагнитном поле, при этом, его масса и вес гирь имеют одинаковое значение.
После уравновешивания весов, по проводнику пропускается электрический ток. Вокруг него происходит образование магнитного поля, определяемое в соответствии с правилом правой руки. В результате, наблюдается взаимодействие полей постоянного магнита и самого проводника. При этом, равновесие весов будет нарушено. Из-за протекания тока, сторона весов с проводником начинает опускаться. Для того, чтобы вычислить силу воздействия поля на этот проводник, нужно уравновесить его с помощью гирь. Сила их тяжести рассчитывается по специальной формуле, и будет равняться силе магнитного поля, воздействующей на проводник с током. Соотношение этой силы с длиной проводника и силой тока является постоянной величиной. Данная количественная характеристика находится в зависимости только от поля и представляет собой ни что иное, как модуль вектора магнитной индукции. Линии магнитной индукцииСама индукция магнитного поля характеризуется определенным направлением, представляющим собой линии, отображаемые графически. Эти линии, также получили название магнитных линий, или линий магнитных полей. Так же, как и магнитная индукция, ее линии имеют собственное определение. Они представляют собой линии, к которым проведены касательные во всех точках поля. Эти касательные и вектор магнитной индукции совпадают между собой.
Однородное магнитное поле отличается параллельными линиями магнитной индукции, совпадающими с направлением вектора во всех точках. Если же магнитное поле является неоднородным, произойдет изменение вектора электромагнитной индукции в каждой пространственной точке, расположенной вокруг проводника. Касательные, проведенные к этому вектору, приведут к созданию концентрических окружностей вокруг проводника. Таким образом, в данном случае, линии индукции будут выглядеть в виде расширяющихся окружностей. |
формула, от чего зависит, линии индукции
Все мы знаем, что есть магниты более сильные и менее сильные. Маленький магнитик сможет притянуть пару гвоздей и все, а гораздо более мощный электромагнит домофона удерживает дверь в подъезд так, что несколько взрослых мужчин не смогут открыть ее силой.
Величина, характеризующая величину силы магнита
То есть, мы можем говорить о некой величине, характеризующей величину силы магнитов, а точнее, магнитного поля, создаваемого ими. Магнитное поле характеризуется векторной величиной, которая носит название индукции магнитного поля или магнитной индукции. (см. подробнее электромагнитная индукция)
Обозначается индукция буквой B. Магнитная индукция это не сила, действующая на проводники, это величина, которая находится через данную силу по следующей формуле:
B=F / (I*l)
Или в виде определения:
Модуль вектора магнитной индукции B равен отношению модуля силы F, с которой магнитное поле действует на расположенный перпендикулярно магнитным линиям проводник с током, к силе тока в проводнике I и длине проводника l.
От чего зависит магнитная индукция
Магнитная индукция не зависит ни от силы тока, ни от длины проводника, она зависит только от магнитного поля. То есть, если мы, например, уменьшим силу тока в проводнике, не меняя больше ничего, то уменьшится не индукция, с которой сила тока связана прямо пропорционально, а сила воздействия магнитного поля на проводник. Величина же индукции останется постоянной. В связи с этим индукцию можно считать количественной характеристикой магнитного поля.
Измеряется магнитная индукция в теслах (1 Тл). При этом 1 Тл=1 Н/(А*м) .
Линии индукции магнитного поля
Магнитная индукция имеет направление. Графически ее можно зарисовывать в виде линий. Линии индукции магнитного поля это и есть то, что мы до сих пор в более ранних темах называли магнитными линиями или линиями магнитного поля. Так как мы выше вывели определение магнитной индукции, то мы можем дать определение и линиям магнитной индукции:
Линии магнитной индукции это линии, касательные к которым в каждой точке поля совпадают с направлением вектора магнитной индукции.
В однородном магнитном поле линии магнитной индукции параллельны, и вектор магнитной индукции будет направлен так же во всех точках.
В случае неоднородного магнитного поля, например, поля вокруг проводника с током, вектор магнитной индукции будет меняться в каждой точке пространства вокруг проводника, а касательные к этому вектору создадут концентрические окружности вокруг проводника. Так и будут выглядеть линии индукции магнитного поля расширяющиеся окружности вокруг проводника.
Нужна помощь в учебе?
Предыдущая тема: Обнаружение магнитного поля по его действию на электрический ток
Следующая тема:   Магнитный поток: определение, направление и количество + пример
Все неприличные комментарии будут удаляться.
Напряженность магнитного поля | Формулы и расчеты онлайн
Напряженность магнитного поля можно определить с помощью силы, которая действует на помещенный в поле пробный магнит. Так как магнитные полюсы не существуют по отдельности, на северный и южный полюсы пробного магнита действуют противоположно направленные силы, и возникает момент пары сил. Этот момент характеризует величину напряженности поля в данном месте.
В магнитном поле цилиндрической катушки он прямо пропорционален числу витков и силе тока и обратно пропорционален длине катушки. Направление вектора напряженности магнитного поля в каждой точке совпадает с направлением силовых линий. Внутри катушки (магнита) он направлен от южного полюса к северному, вне катушки — от северного к южному.
Единица СИ напряженности магнитного поля
Единица СИ напряженности магнитного поля:
\[ [H] = \frac{Ампер}{Метр} \]
Эрстед — Единица напряженности магнитного поля
Единица напряженности магнитного поля Эрстед не принадлежит к системе СИ.
\[ 1 Эрстед = \frac{1000}{4π} \frac{Ампер}{метр} \]
\[ 1 \frac{Ампер}{метр} = \frac{4π}{1000} Эрстед \]
Напряженность магнитного поля в цилиндрической катушке
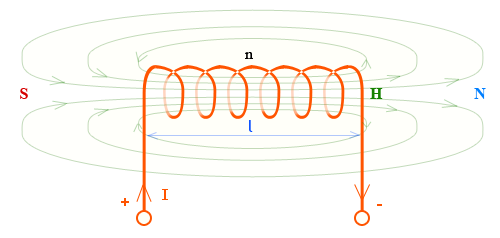
Напряженность магнитного поля в цилиндрической катушке
Если
| H | напряженность магнитного поля внутри цилиндрической катушки, | Ампер/метр |
|---|---|---|
| I | сила тока в катушке, | Ампер |
| n | число витков, | Ампер |
| l | длина катушки (т. е. силовых линий в области однородного поля), | метр |
то напряженность магнитного поля определяется формулой
\[ H = \frac{I·n}{l} \]
Напряженность магнитного поля вокруг прямолинейного проводника
Напряженность Н магнитного поля прямолинейного проводника постоянна вдоль круговой силовой линии.
Если
| H | напряженность магнитного поля прямолинейного проводника, | Ампер/метр |
|---|---|---|
| I | сила тока в проводнике, | Ампер |
| r | расстояние от проводника в плоскости, перпендикулярной проводнику, | метр |
то напряженность магнитного поля определяется формулой
\[ H = \frac{I}{2πr} \]
Напряженность магнитного поля в центре витка с током
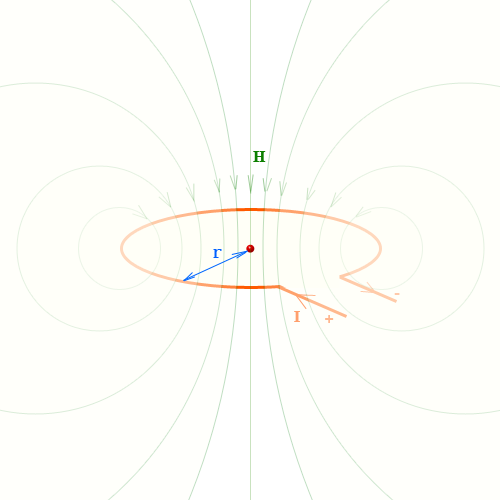
Напряженность магнитного поля в центре витка с током
Если
| H | напряженность магнитного поля в центре витка с током, | Ампер/метр |
|---|---|---|
| I | сила тока в витке, | Ампер |
| r | радиус витка, | метр |
то напряженность магнитного поля определяется формулой
\[ H = \frac{I}{2r} \]
В помощь студенту
Напряженность магнитного поля |
стр. 643 |
|---|
Индукция и напряженность магнитного поля. — КиберПедия
Магнитная индукция—векторная физическая величина, характеризующая магнитное поле.Вектор магнитной индукции всегда направлен по касательной к магнитной линии
Расчетная формула:
Индукция магнитного поля, созданного бесконечно длинным прямым проводником с током
B — магнитная индукция
μ — относительная магнитная проницаемость
μ0 — магнитная постоянная
I — сила тока
r — расстояние до проводника
Магнитная индукция поля в центре кругового тока (витка)
B — магнитная индукция
μ — относительная магнитная проницаемость
μ0 — магнитная постоянная
I — сила тока
R — радиус
Напряженностью магнитного поля называют векторную величину , характеризующую магнитное поле и определяемую следующим образом:,
Напряжённость магнитного поля: бесконечной прямой провод
H — напряжённость магнитного поля
I — сила тока
r — расстояние до проводника
Напряжённость магнитного поля в центре витка
H — напряжённость магнитного поля
I — сила тока
R — радиус
Закон Био-Савара-Лапласа.
Закон БиоСавара Лапласа — Магнитное поле любого тока может быть вычислено как векторная сумма полей, создаваемая отдельными участками токов.
Формулировка
Пусть постоянный ток течёт по контуру γ, находящемуся в вакууме, —точка, в которой ищется поле, тогда индукция магнитного поля в этой точкевыражается интегралом (в системе СИ)
Направление перпендикулярно и , то есть перпендикулярноплоскости, в которой они лежат, и совпадает с касательной к линиимагнитной индукции. Это направление может быть найдено по правилунахождения линий магнитной индукции (правилу правого винта):направление вращения головки винта дает направление , еслипоступательное движение буравчика соответствует направлению тока вэлементе. Модуль вектора определяется выражением (в системе СИ)
Векторный потенциал даётся интегралом (в системе СИ)
2.9.
Поток индукции магнитного поля.
Магнитный поток (поток линий магнитной индукции) через контур численно равен произведению модуля вектора магнитной индукции на площадь, ограниченную контуром, и на косинус угла между направлением вектора магнитной индукции и нормалью к поверхности, ограниченной этим контуром.
Формула работы силы Ампера при движении прямого проводника с постоянным током в однородном магнитном поле.
Таким образом, работа силы Ампера может быть выражена через силу тока в перемещаемом проводнике и изменение магнитного потока через контур, в который включен этот проводник:
Индуктивность контура.
Индуктивность — физ. величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1Ампер за 1 секунду.
Также индуктивность можно рассчитать по формуле:
где Ф — магнитный поток через контур, I — сила тока в контуре.
Единицы измерения индуктивности в системе СИ:
Энергия магнитного поля.
Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии.
2.10.
Электромагнитная индукция.
Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменениимагнитного потока, проходящего через него.
Формула напряжённости магнитного поля
ОПРЕДЕЛЕНИЕНапряжённость магнитного поля равна разности вектора магнитной индукции и вектора намагниченности.
Здесь – напряжённость магнитного поля, – магнитная индукция, – магнитная постоянная, — намагниченность.
Единица измерения напряжённости магнитного поля – А/м (ампер на метр).
Напряжённость – векторная величина, характеризующая интенсивность воздействия магнитного поля на намагниченную заряжённую частицу (пробный магнит) в конкретной точке. В векторной форме уравнение выглядит так:
Примеры решения задач по теме «Напряжённость магнитного поля»
ПРИМЕР 1| Задание | Найти напряжённость магнитного поля в точке, в которой магнитная индукция равна 9 Тл, а намагниченность 7 мА/м. |
| Решение | Переведём кА в А : мА = А. Подставим значения в формулу: |
| Ответ | Напряжённость магнитного поля равна ампер на метр. |
| Задание | Катушка создаёт внутри себя однородное магнитное поле напряжённостью H. Вектор отличается от на угол в плоскости и в плоскости . Вектор отличается от на углы и соответственно. Найти значения Hв проекции на указанные плоскости. В данной системе координат вектор Hсовпадает с осью . |
| Решение | В векторном виде формула напряжённости поля выглядит так:
Если рассмотреть плоскость , то вектор Hбудет катетом прямоугольного треугольника, а вектор – гипотенузой. Угол вежду ними известен: . В плоскости тоже будет катетом, а – гипотенузой. Значит в обоих случаях:
Аналогичные рассуждения верны и для . Значит:
|
| Ответ |
Все формулы по физике
Формула напряжённости электрического поля
Формула удельного веса
Формула количества теплоты
Формула пути
Формула силы натяжения нити