Единицы измерения магнитных величин

      Закон Ампера используется для установления единицы силы тока – ампер.

      Ампер – сила тока неизменного по величине, который, проходя по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого сечения, расположенным на расстоянии один метр, один от другого в вакууме, вызывает между этими проводниками силу в .

,

(2.4.1)

Здесь ; ; ;

      Определим отсюда размерность и величину  в  СИ.

       , следовательно

,  или    .

      Из закона Био–Савара–Лапласа, для прямолинейного проводника с током , тоже можно найти размерность индукции магнитного поля:

      Тесла – единица измерения индукции в  СИ.    .

      Гаусс – единица измерения в Гауссовой системе единиц (СГС).

      1 Тл равен магнитной индукции однородного магнитного поля, в котором на плоский контур с током, имеющим магнитный момент , действует вращающий момент .

Тесла Никола (1856–1943) – сербский ученый в области электротехники и радиотехники. Имел огромное количество изобретений. Изобрел электрический счетчик, частотомер и др. Разработал ряд конструкций многофазных генераторов, электродвигателей и трансформаторов. Сконструировал ряд радиоуправляемых самоходных механизмов. Изучал физиологическое действие токов высокой частоты. Построил в 1899 г. радиостанцию на 200 кВт в Колорадо и радиоантенну высотой 57,6 м в Лонг-Айленде (башня Ворденклиф). Вместе с Эйнштейном и Опенгеймером в 1943 г. участвовал в секретном проекте по достижению невидимости американских кораблей (Филадельфийский эксперимент). Современники говорили о Тесле как о мистике, ясновидце, пророке, способном заглянуть в разумный космос и мир мертвых. Он верил, что с помощью электромагнитного поля можно перемещаться в пространстве и управлять временем.

      Другое определение: 1 Тл равен магнитной индукции, при которой магнитный поток сквозь площадку 1 м², перпендикулярную направлению поля, равен 1 Вб.

      Единица измерения магнитного потока Вб, получила свое название в честь немецкого физика Вильгельма Вебера (1804–1891) – профессора университетов в Галле, Геттингене, Лейпциге.

      Как мы уже говорили, магнитный поток Ф через поверхность S – одна из характеристик магнитного поля (рис. 2.5):

    

Рис. 2.5

      Единица измерения магнитного потока в СИ:

. ,а так как , то .

      Здесь Максвелл (Мкс) – единица измерения магнитного потока в СГС названая в честь знаменитого английского ученого Джеймса Максвелла (1831–1879), создателя теории электромагнитного поля.

      Напряженность магнитного поля Н измеряется в .

,      .

      Сведем в одну таблицу основные характеристики магнитного поля.

Таблица 2.1

Наименование	Обозначение	СИ	СГС	СИ/СГС
Магнитная индукция	В		Гс
Напряженность магнитного поля	Н	А/м	Э
Магнитная постоянная	μ0		1
Поток магнитной индукции	ФB	Вб ( )	Мкс

---

Магнитные поля: опеределение, источники, СанПиН

Магнитное поле Земли

Магнитное поле — это силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения.

Источниками макроскопического магнитного поля являются намагниченные тела, проводники с током и движущиеся электрически заряженные тела. Природа этих источников едина: магнитное поле возникает в результате движения заряженных микрочастиц (электронов, протонов, ионов), а также благодаря наличию у микрочастиц собственного (спинового) магнитного момента.

Переменное магнитное поле возникает также при изменении во времени электрического поля. В свою очередь, при изменении во времени магнитного поля возникает электрическое поле. Полное описание электрического и магнитного полей в их взаимосвязи дают Максвелла уравнения. Для характеристики магнитного поля часто вводят понятие силовых линий поля (линий магнитной индукции).

Для измерения характеристик магнитного поля и магнитных свойств веществ применяют различного типа магнитометры. Единицей индукции магнитного поля в системе единиц СГС является Гаусс (Гс), в Международной системе единиц (СИ) — Тесла (Тл), 1 Тл = 104 Гс. Напряжённость измеряется, соответственно, в эрстедах (Э) и амперах на метр (А/м, 1 А/м = 0,01256 Э; энергия магнитного поля — в Эрг/см

2 или Дж/м², 1 Дж/м² = 10 эрг/см².

Компас реагирует
на магнитное поле Земли

Магнитные поля в природе чрезвычайно разнообразны как по своим масштабам, так и по вызываемым ими эффектам. Магнитное поле Земли, образующее земную магнитосферу, простирается до расстояния в 70—80 тысяч км в направлении к Солнцу и на многие миллионы км в противоположном направлении. У поверхности Земли магнитное поле равно в среднем 50 мкТл, на границе магнитосферы ~ 10^-3 Гс. Геомагнитное поле экранирует поверхность Земли и биосферу от потока заряженных частиц солнечного ветра и частично космических лучей. Влияние самого геомагнитного поля на жизнедеятельность организмов изучает магнитобиология. В околоземном пространстве магнитное поле образует магнитную ловушку для заряженных частиц высоких энергий — радиационный пояс Земли. Содержащиеся в радиационном поясе частицы представляют значительную опасность при полётах в космос. Происхождение магнитного поля Земли связывают с конвективными движениями проводящего жидкого вещества в земном ядре.

Непосредственные измерения при помощи космических аппаратов показали, что ближайшие к Земле космические тела — Луна, планеты Венера и Марс не имеют собственного магнитного поля, подобного земному. Из других планет Солнечной системы лишь Юпитер и, по-видимому, Сатурн обладают собственными магнитными полями, достаточными для создания планетарных магнитных ловушек. На Юпитере обнаружены магнитные поля до 10 Гс и ряд характерных явлений (магнитные бури, синхротронное радиоизлучение и другие), указывающих на значительную роль магнитного поля в планетарных процессах.

© Фото: http://www.tesis.lebedev.ru
Фотография Солнца
в узком спектре

Межпланетное магнитное поле — это главным образом поле солнечного ветра (непрерывно расширяющейся плазмы солнечной короны). Вблизи орбиты Земли межпланетное поле ~ 10

-4—10^-5 Гс. Регулярность межпланетного магнитного поля может нарушаться из-за развития различных видов плазменной неустойчивости, прохождения ударных волн и распространения потоков быстрых частиц, рожденных солнечными вспышками.

Во всех процессах на Солнце — вспышках, появлении пятен и протуберанцев, рождении солнечных космических лучей магнитное поле играет важнейшую роль. Измерения, основанные на эффекте Зеемана, показали, что магнитное поле солнечных пятен достигает нескольких тысяч Гс, протуберанцы удерживаются полями ~ 10—100 Гс (при среднем значении общего магнитного поля Солнца ~ 1 Гс).

Магнитные бури

Магнитные бури — сильные возмущения магнитного поля Земли, резко нарушающие плавный суточный ход элементов земного магнетизма. Магнитные бури длятся от нескольких часов до нескольких суток и наблюдаются одновременно на всей Земле.

Как правило, магнитные бури состоят из предварительной, начальной и главной фаз, а также фазы восстановления. В предварительной фазе наблюдаются незначительные изменения геомагнитного поля (в основном в высоких широтах), а также возбуждение характерных короткопериодических колебаний поля. Начальная фаза характеризуется внезапным изменением отдельных составляющих поля на всей Земле, а главная — большими колебаниями поля и сильным уменьшением горизонтальной составляющей. В фазе восстановления магнитной бури поле возвращается к своему нормальному значению.

Влияние солнечного ветра
на магнитосферу Земли

Магнитные бури вызываются потоками солнечной плазмы из активных областей Солнца, накладывающимися на спокойный солнечный ветер. Поэтому магнитные бури чаще наблюдаются вблизи максимумов 11-летнего цикла солнечной активности. Достигая Земли, потоки солнечной плазмы увеличивают сжатие магнитосферы, вызывая начальную фазу магнитной бури, и частично проникают внутрь магнитосферы Земли. Попадание частиц высоких энергий в верхнюю атмосферу Земли и их воздействие на магнитосферу приводят к генерации и усилению в ней электрических токов, достигающих наибольшей интенсивности в полярных областях ионосферы, с чем связано наличие высокоширотной зоны магнитной активности. Изменения магнитосферно-ионосферных токовых систем проявляются на поверхности Земли в виде иррегулярных магнитных возмущений.

В явлениях микромира роль магнитного поля столь же существенна, как и в космических масштабах. Это объясняется существованием у всех частиц — структурных элементов вещества (электронов, протонов, нейтронов), магнитного момента, а также действием магнитного поля на движущиеся электрические заряды.

Применение магнитных полей в науке и технике. Магнитные поля обычно подразделяют на слабые (до 500 Гс), средние (500 Гс — 40 кГс), сильные (40 кГс — 1 МГс) и сверхсильные (свыше 1 МГс). На использовании слабых и средних магнитных полей основана практически вся электротехника, радиотехника и электроника. Слабые и средние магнитные поля получают при помощи постоянных магнитов, электромагнитов, неохлаждаемых соленоидов, сверхпроводящих магнитов.

Источники магнитного поля

Все источники магнитных полей можно разделить на искусственные и естественные. Основными естественными источниками магнитного поля являются собственное магнитное поле планеты Земля и солнечный ветер. К искусственным источникам можно отнести все электромагнитные поля, которыми так изобилует наш современный мир, и наши дома в частности. Более подробно об электромагнитных полях, их влиянии на человека и способах оценки и экранинирования читайте на нашем сайте.

Транспорт на электроприводе является мощным источником магнитного поля в диапазоне от 0 до 1000 Гц. Железнодорожный транспорт использует переменный ток. Городской транспорт — постоянный. Максимальные значения индукции магнитного поля в пригородном электротранспорте достигают 75 мкТл, средние значения — около 20 мкТл. Средние значения на транспорте с приводом от постоянного тока зафиксированы на уровне 29 мкТл. У трамваев, где обратный провод — рельсы, магнитные поля компенсируют друг друга на гораздо большем расстоянии, чем у проводов троллейбуса, а внутри троллейбуса колебания магнитного поля невелики даже при разгоне. Но самые большие колебания магнитного поля — в метро. При отправлении состава величина магнитного поля на платформе составляет 50-100 мкТл и больше, превышая геомагнитное поле. Даже когда поезд давно исчез в туннеле, магнитное поле не возвращается к прежнему значению. Лишь после того, как состав минует следующую точку подключения к контактному рельсу, магнитное поле вернется к старому значению. Правда, иногда не успевает: к платформе уже приближается следующий поезд и при его торможении магнитное поле снова меняется. В самом вагоне магнитное поле еще сильнее — 150-200 мкТл, то есть в десять раз больше, чем в обычной электричке.

Значения индукции магнитных полей, наиболее часто встречаемых нами в повседневной жизни приведены на диаграмме ниже. Глядя на эту диаграмму становится ясно, что мы подвергаемся воздействию магнитных полей постоянно и повсеместно. По мнению некоторых ученых, вредными считаются магнитные поля с индукцией свыше 0,2 мкТл. Ествественно, что следует предпринимать определенные меры предосторожности, чтобы обезопасить себя от пагубного воздействия окружающих нас полей. Просто выполняя несколько несложных правил Вы можете в значительной мере снизить воздействие магнитных полей на свой организм.

В действующих СанПиН 2.1.2.2801-10 «Изменения и дополнения №1 к СанПиН 2.1.2.2645-10 «Санитарно-эпидемиологические требования к условиям проживания в жилых зданиях и помещениях» сказано следующее: «Предельно допустимый уровень ослабления геомагнитного поля в помещениях жилых зданий устанавливается равным 1,5». Также установлены предельно допустимые значения интенсивности и напряжённости магнитного поля частотой 50 Гц:

• в жилых помещениях — 5 мкТл или 4 А/м;
• в нежилых помещениях жилых зданий, на селитебной территории, в том числе на территории садовых участков — 10 мкТл или 8 А/м.

Исходя из указанных нормативов каждый может рассчитать какое количество электрических приборов может находиться во включённом состоянии и в состоянии ожидания в каждом конкретном помещении или же заказать обследование помещений в нашей фирме, на основании которого будут выданы рекомендации по нормализации жилого пространства.

Видеоматериалы по теме

Небольшой научный фильм о магнитном поле Земли

Использованная литература

1. Большая Советская Энциклопедия.

Эрстед (единица измерения) — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 1 февраля 2018; проверки требует 1 правка. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 1 февраля 2018; проверки требует 1 правка. У этого термина существуют и другие значения, см. Эрстед.

Эрсте́д (русское обозначение Э, международное обозначение Oe) — единица измерения напряжённости магнитного поля в системе СГС. Введена в 1930 году Международной электротехнической комиссией^[1], названа в честь датского физика Ганса Христиана Эрстеда (H. C. Ørsted).

1 эрстед равен напряжённости магнитного поля в вакууме при индукции 1 гаусс.

Согласно формуле, описывающей напряжённость магнитного поля в вакууме, создаваемую прямолинейным тонким бесконечным проводником с током,

H=2Icl,{\displaystyle H=2{\frac {I}{cl}},}

где

на расстоянии 1 см от такого проводника, по которому пропускают ток силой 5 ампер = 5·(с/10) токовых единиц СГСЭ, напряжённость магнитного поля будет равна 1 эрстеду. Также поле в 1 эрстед создаётся в центре бесконечно длинного прямого соленоида в вакууме с плотностью навивки 1000/(4π)≈79,58 витков на метр, по которому пропущен ток в 1 А.

Напряжённость магнитного поля на экваторе планет^[2]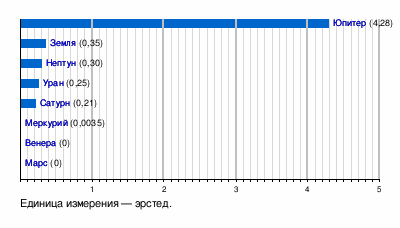

Эрстед в основных единицах СГС выражается как 1 г^1/2·см^−1/2·с⁻¹.

1 эрстед = 1000/(4π) A/м ≈ 79,5774715 А/м.

В геофизике применяется также внесистемная единица измерения напряжённости магнитного поля гамма; 1 гамма = 10⁻⁵ Э.

• Эрстед. // Физическая энциклопедия. В 5 томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.

Магнитная постоянная — Википедия

Материал из Википедии — свободной энциклопедии

Магнитная постоянная (μ0{\displaystyle \mu _{0}}) — физическая константа, скалярная величина, входящая в выражения некоторых законов электромагнетизма в виде коэффициента пропорциональности при записи их в форме, соответствующей Международной системе единиц (СИ)^[1].

Иногда называют магнитной проницаемостью вакуума. Измеряется в генри на метр (или в ньютонах на ампер в квадрате).

В материальных уравнениях, в вакууме, через магнитную проницаемость связаны вектор напряжённости магнитного поля H и вектор магнитной индукции B:

B=μ0 H.{\displaystyle \mathbf {B} =\mu _{0}\ \mathbf {H} .}

Через магнитную постоянную осуществляется связь между относительной и абсолютной магнитной проницаемостью.

В Международной системе единиц[править | править код]

До изменения СИ 2018—2019 годов[править | править код]

Численное значение магнитной постоянной вытекает из определения ампера, единицы силы электрического тока, являющегося одной из основных единиц СИ. Согласно определению, принятому IX Генеральной конференцией по мерам и весам (ГКМВ) в 1948 году и действовавшему до 2019 года, «Ампер есть сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии 1 метр один от другого, вызвал бы на каждом участке проводника длиной 1 метр силу взаимодействия, равную 2⋅10⁻⁷ньютона»^[2][3].

С другой стороны, сила взаимодействия двух расположенных на расстоянии r{\displaystyle r} друг от друга бесконечных параллельных проводников, по которым текут токи I1{\displaystyle I_{1}} и I2{\displaystyle I_{2}}, приходящаяся на единицу длины, выражается соотношением:

F=μ04π2I1I2r.{\displaystyle F={\frac {\mu _{0}}{4\pi }}{\frac {2I_{1}I_{2}}{r}}.}

С учётом определения ампера из этого соотношения следует точное равенство:

μ₀ = 4π · 10⁻⁷ Гн/м.

Соответственно выполняется:

μ₀ ≈ 1,2566370614 · 10⁻⁶ Н/А².

После изменений СИ 2018—2019 годов[править | править код]

С 2019 года вступили в силу изменения в СИ, включающие, в частности, переопределение ампера на основе фиксации численного значения элементарного заряда. Это привело к тому, что значение магнитной постоянной стало экспериментально определяемой величиной, хотя численно её значение осталось прежним с высокой точностью. Значение, рекомендованное CODATA^[4]:

μ₀ = 1,25663706212(19) · 10⁻⁶ Н·А⁻², или Гн·м⁻¹.

В системе СГС[править | править код]

В системе СГС магнитная постоянная как коэффициент, связывающий напряжённость и индукцию магнитного поля в вакууме, также может быть введена. При этом в различных вариантах системы СГС магнитная постоянная имеет разную размерность и значение. В частности, Гауссова система единиц и система СГСМ построены так, что магнитная постоянная равна 1, а в системе СГСЭ она равна 1/c2{\displaystyle 1/c^{2}}.

Магнитная проницаемость — Википедия

Магни́тная проница́емость — физическая величина, коэффициент (зависящий от свойств среды), характеризующий связь между магнитной индукцией B{\displaystyle {B}} и напряжённостью магнитного поля H{\displaystyle {H}} в веществе.

Для разных сред этот коэффициент различен, поэтому говорят о магнитной проницаемости конкретной среды (подразумевая её состав, состояние, температуру и т. д.).

Обычно обозначается греческой буквой μ{\displaystyle \mu }. Может быть как скаляром (у изотропных веществ), так и тензором (у анизотропных).

Впервые этот термин встречается в работе Вернера Сименса «Beiträge zur Theorie des Elektromagnetismus» («Вклад в теорию электромагнетизма») опубликованной в 1881 году^[1].

В общем, соотношение между магнитной индукцией и напряженностью магнитного поля через магнитную проницаемость вводится как:

B→=μH→,{\displaystyle {\vec {B}}=\mu {\vec {H}},}

и μ{\displaystyle \mu } в общем случае здесь следует понимать как тензор, что в компонентной записи имеет вид^[2]:

 Bi=μijHj{\displaystyle \ B_{i}=\mu _{ij}H_{j}}

Для изотропных веществ соотношение:

B→=μH→{\displaystyle {\vec {B}}=\mu {\vec {H}}}

можно понимать в смысле умножение вектора на скаляр (магнитная проницаемость сводится в этом случае к скаляру).

В системе СГС магнитная проницаемость — безразмерная величина, в Международной системе единиц (СИ) вводят как размерную (абсолютную), так и безразмерную (относительную) магнитные проницаемости:

μr=μμ0{\displaystyle \mu _{r}={\frac {\mu }{\mu _{0}}}},

где μr{\displaystyle \mu _{r}} — относительная, а μ{\displaystyle \mu } — абсолютная проницаемость, μ0{\displaystyle \mu _{0}} — магнитная постоянная.

Нередко обозначение μ{\displaystyle \mu } используется не для абсолютной, а именно для относительной магнитной проницаемости (при этом μ{\displaystyle \mu } совпадает с таковым в СГС).

Размерность абсолютной магнитной проницаемости в СИ такая же, как размерность магнитной постоянной, то есть Гн/м или Н/А².

Относительная магнитная проницаемость в СИ связана с магнитной восприимчивостью χ соотношением:

μr=1+χ,{\displaystyle \mu _{r}=1+\chi ,}

а в Гауссовой системе магнитная проницаемость связана с магнитной восприимчивостью χ соотношением:

μ=1+4πχ.{\displaystyle \mu =1+4\pi \chi .}

Вообще говоря, магнитная проницаемость зависит как от свойств вещества, так и от величины и направления магнитного поля для анизотропных веществ (и, кроме того, от температуры, давления и т. д.).

Также она зависит от скорости изменения поля со временем, в частности, для синусоидального изменения поля — зависит от частоты этого колебания (в этом случае для описания намагничивания вводят комплексную магнитную проницаемость, чтобы описать влияние вещества на сдвиг фазы B относительно H). При достаточно низких частотах — небольшой быстроте изменения поля, её можно обычно считать в этом смысле независимой от частоты.

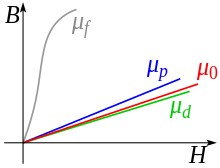Схематический график зависимости ‘B’ от ‘H’ (кривая намагничивания) для ферромагнетиков, парамагнетиков и диамагнетиков, а также для вакуума, иллюстрирующий различие магнитной проницаемости (представляющей собою наклон графика) для: ферромагнетиков (μ_f), парамагнетиков (μ_p), вакуума(μ₀) и диамагнетиков (μ_d)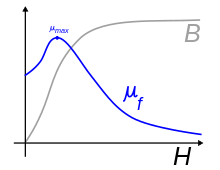

• Магнитная проницаемость сильно зависит от величины поля для нелинейных по магнитной восприимчивости сред (типичный пример — ферромагнетики, для которых характерен магнитный гистерезис). Для таких сред магнитная проницаемость, как независящее от поля число, может указываться приближенно, в линейном приближении.
• Для парамагнетиков и диамагнетиков линейное приближение достаточно хорошо выполняется для широкого диапазона изменения величины поля.

Классификация веществ по значению магнитной проницаемости[править | править код]

Подавляющее большинство веществ относятся либо к классу диамагнетиков (μ⪅1{\displaystyle \mu \lessapprox 1}), либо к классу парамагнетиков (μ⪆1{\displaystyle \mu \gtrapprox 1}). Но существует ряд веществ — (ферромагнетики), например железо, обладают более выраженными магнитными свойствами.

Для ферромагнетиков, вследствие гистерезиса, понятие магнитной проницаемости, строго говоря, неприменимо. Однако, в определённом диапазоне изменения намагничивающего поля (в тех случаях, когда можно было пренебречь остаточной намагниченностью, но до насыщения) можно, в лучшем или худшем приближении, всё же представить эту зависимость как линейную (а для магнитомягких материалов ограничение снизу может быть и не слишком практически существенно), и в этом смысле величина магнитной проницаемости бывает измерена и для них.

Магнитная проницаемость сверхпроводников равна нулю, так как материал выталкивает магнитное поле при переходе в сверхпроводящее состояние, иногда говорят, что сверхпроводники — идеальные диамагнетики.

Абсолютная магнитная проницаемость воздуха приблизительно равна магнитной проницаемости вакуума и в технических расчетах принимается равной^[3] магнитной постоянной = 4π × 10−7{\displaystyle 4\pi \ \times \ 10^{-7}} Гн/м

Магнитные проницаемости некоторых веществ и материалов[править | править код]

Относительная магнитная проницаемость некоторых^[4] веществ[править | править код]

Парамагнетики, μ>1{\displaystyle \mu >1}	(μ−1)⋅10−6{\displaystyle (\mu -1)\cdot 10^{-6}}	Диамагнетики, μ<1{\displaystyle \mu <1}	(1−μ)⋅10−6{\displaystyle (1-\mu )\cdot 10^{-6}}
Азот	0,013	Водород	0,063
Воздух	0,38	Бензол	7,5
Кислород	1,9	Вода	9
Эбонит	14	Медь	10,3
Алюминий	23	Стекло	12,6
Вольфрам	176	Каменная соль	12,6
Платина	360	Кварц	15,1
Жидкий кислород	3400	Висмут	176

Магнитная восприимчивость и магнитная проницаемость некоторых материалов[править | править код]

Medium	Восприимчивость χm (объемная, СИ)	Проницаемость μ, Гн/м	Относительная проницаемость μ/μ0	Магнитное поле	Максимум частоты
Метглас (англ. Metglas)		1,25	1 000 000[5]	при 0,5 Тл	100 кГц
Наноперм (англ. Nanoperm)		10⋅10-2	80 000[6]	при 0,5 Тл	10 кГц
Мю-металл		2,5⋅10-2	20 000[7]	при 0,002 Тл
Мю-металл			50 000[8]
Пермаллой		1,0⋅10-2	8000[7]	при 0,002 Тл
Электротехническая сталь		5,0⋅10-3	4000[7][нет в источнике]	при 0,002 Тл
Никель-цинковый Феррит		2,0⋅10-5 — 8,0⋅10-4	16-640		от 100 кГц до 1 МГц[источник не указан 2907 дней]
Марганец-цинковый Феррит		>8,0⋅10-4	640 (и более)		от 100 кГц до 1 МГц
Сталь		1,26⋅10-4	100[7]	при 0,002 Тл
Никель		1,25⋅10-4	100[7] — 600	при 0,002 Тл
Неодимовый магнит			1,05[9]	до 1,2—1,4 Тл
Платина		1,2569701⋅10-6	1,000265
Алюминий	2,22⋅10-5[10]	1,2566650⋅10-6	1,000022
Дерево			1,00000043[10]
Воздух			1,00000037[11]
Бетон			1[12]
Вакуум	0	1,2566371⋅10-6 (μ0)	1[13]
Водород	-2,2⋅10-9[10]	1,2566371⋅10-6	1,0000000
Фторопласт		1,2567⋅10-6[7]	1,0000
Сапфир	-2,1⋅10-7	1,2566368⋅10-6	0,99999976
Медь	-6,4⋅10-6 или -9,2⋅10-6[10]	1,2566290⋅10-6	0,999994
Вода	-8,0⋅10-6	1,2566270⋅10-6	0,999992
Висмут	-1,66⋅10-4	1	0,999834
Сверхпроводники	−1	0	0

1. ↑ Werner von Siemens, Lebenserinnerungen
2. ↑ Подразумевается суммирование по повторяющемуся индексу (j), то есть запись следует понимать так: μijHj≡∑j=13μijHj.{\displaystyle \mu _{ij}H_{j}\equiv \sum \limits _{j=1}^{3}\mu _{ij}H_{j}.} Эта запись, как легко видеть, означает умножение вектора слева на матрицу по правилам матричного умножения.
3. ↑ Намагничивание стали. Магнитная проницаемость. (неопр.) (недоступная ссылка). Дата обращения 16 июля 2011. Архивировано 19 марта 2011 года.
4. ↑ Магнитная проницаемость. Магнитная проницаемость среды. Относительная магнитная проницаемость. Магнитная проницаемость вещества (неопр.) (недоступная ссылка). Дата обращения 16 июля 2011. Архивировано 12 февраля 2012 года.
5. ↑ «Metglas Magnetic Alloy 2714A», »Metglas» (неопр.) (недоступная ссылка). Metglas.com. Дата обращения 8 ноября 2011. Архивировано 3 июня 2012 года.
6. ↑ «Typical material properties of NANOPERM», »Magnetec» (неопр.) (PDF). Дата обращения 8 ноября 2011.
7. ↑ ^{1 2 3 4 5 6} «Relative Permeability», »Hyperphysics» (неопр.). Hyperphysics.phy-astr.gsu.edu. Дата обращения 8 ноября 2011. Архивировано 3 июня 2012 года.
8. ↑ Nickel Alloys-Stainless Steels, Nickel Copper Alloys, Nickel Chromium Alloys, Low Expansion Alloys (неопр.). Nickel-alloys.net. Дата обращения 8 ноября 2011. Архивировано 3 июня 2012 года.
9. ↑ Juha Pyrhönen, Tapani Jokinen, Valéria Hrabovcová. Design of Rotating Electrical Machines (неопр.). — John Wiley and Sons, 2009. — С. 232. — ISBN 0-470-69516-1.
10. ↑ ^{1 2 3 4} Richard A. Clarke. Clarke, R. »Magnetic properties of materials», surrey.ac.uk (неопр.). Ee.surrey.ac.uk. Дата обращения 8 ноября 2011. Архивировано 3 июня 2012 года.
11. ↑ B. D. Cullity and C. D. Graham (2008), Introduction to Magnetic Materials, 2nd edition, 568 pp., p.16
12. ↑ NDT.net. Determination of dielectric properties of insitu concrete at radar frequencies (неопр.). Ndt.net. Дата обращения 8 ноября 2011. Архивировано 3 июня 2012 года.
13. ↑ точно, по определению.

Магнитодвижущая сила — Википедия

Материал из Википедии — свободной энциклопедии

Магнѝтодви́жущая си́ла (МДС) — физическая величина, характеризующая способность электрических токов создавать магнитные потоки. Используется при расчётах магнитных цепей; является аналогом ЭДС в электрических цепях.

Величина измеряется в амперах (СИ) или же в гилбертах (СГС), причём 1 А = 4π10{\displaystyle {\frac {4\pi }{10}}} Гб ≈ 1,257 Гб. На практике для обозначения единицы МДС часто используется термин «ампер-виток», численно равный единице в СИ.

Магнитодвижущая сила F{\displaystyle {\mathcal {F}}} в катушке или электромагните вычисляется по формуле

F=wI,{\displaystyle {\mathcal {F}}=wI,}

где w{\displaystyle w} — количество витков в обмотке, I{\displaystyle I} — ток в проводнике.

Выражение для магнитного потока в магнитной цепи, называемое иногда законом Гопкинсона, имеет следующий вид:

F=ΦRm{\displaystyle {\mathcal {F}}=\Phi R_{m}}

где Φ{\displaystyle \Phi } — величина магнитного потока, Rm{\displaystyle R_{m}} — магнитное сопротивление проводника. Данная запись является аналогом закона Ома в магнитных цепях.

Энергия электромагнитного поля — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 июня 2016; проверки требуют 3 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 июня 2016; проверки требуют 3 правки.

Эне́ргия электромагни́тного по́ля — энергия, заключенная в электромагнитном поле^{[источник не указан 2652 дня]}. Сюда же относятся частные случаи чистого электрического и чистого магнитного поля.

Работа электрического поля по перемещению заряда[править | править код]

Понятие работы A{\displaystyle A} электрического поля E{\displaystyle E} по перемещению заряда Q{\displaystyle Q} вводится в полном соответствии с определением механической работы:

A=∫F(x)dx=∫Q⋅E(x)dx=Q⋅U,{\displaystyle A=\int F(x)\,dx=\int Q\cdot E(x)\,dx=Q\cdot U,}

где U=∫Edx{\displaystyle U=\int E\,dx} — разность потенциалов (также употребляется термин напряжение).

Во многих задачах рассматривается непрерывный перенос заряда в течение некоторого времени между точками с заданной разностью потенциалов U(t){\displaystyle U(t)}, в таком случае формулу для работы следует переписать следующим образом:

A=∫U(t)dQ=∫U(t)I(t)dt,{\displaystyle A=\int U(t)\,dQ=\int U(t)I(t)\,dt,}

где I(t)=dQdt{\displaystyle I(t)={dQ \over dt}} — сила тока.

Мощность P{\displaystyle P} электрического тока для участка цепи определяется обычным образом, как производная от работы A{\displaystyle A} по времени, то есть выражением:

P(t)=dAdt=U(t)⋅I(t),{\displaystyle P(t)={\frac {dA}{dt}}=U(t)\cdot I(t),}

Это наиболее общее выражение для мощности в электрической цепи.

С учётом закона Ома

U=I⋅R{\displaystyle U=I\cdot R}

электрическую мощность, выделяемую на сопротивлении R{\displaystyle R}, можно выразить как через ток

P=I(t)2⋅R,{\displaystyle P=I(t)^{2}\cdot R,}

так и через напряжение:

P=U(t)2R.{\displaystyle P={{U(t)^{2}} \over R}.}

Соответственно, работа (выделившаяся теплота) является интегралом мощности по времени:

A=∫P(t)dt=∫I(t)2⋅Rdt=∫U(t)2Rdt.{\displaystyle A=\int P(t)\,dt=\int I(t)^{2}\cdot R\,dt=\int {{U(t)^{2}} \over R}\,dt.}

Энергия электрического и магнитного полей[править | править код]

Для электрического и магнитного полей их энергия пропорциональна квадрату напряжённости поля. Строго говоря, термин «энергия электромагнитного поля» является не вполне корректным. Вместо него в физике обычно используют понятие плотности энергии электромагнитного поля (в определённой точке пространства). Общая энергия поля равняется интегралу плотности энергии по всему пространству.

Плотность энергии электромагнитного поля является суммой плотностей энергий электрического и магнитного полей.

В системе СИ:

u=E⋅D2+B⋅h3.{\displaystyle u={\frac {\mathbf {E} \cdot \mathbf {D} }{2}}+{\frac {\mathbf {B} \cdot \mathbf {H} }{2}}.}

В вакууме (а также в веществе при рассмотрении микрополей):

u=ε0E22+B22μ0=ε0E2+c2B22=E2/c2+B22μ0,{\displaystyle u={\varepsilon _{0}E^{2} \over 2}+{B^{2} \over {2\mu _{0}}}=\varepsilon _{0}{\frac {E^{2}+c^{2}B^{2}}{2}}={\frac {E^{2}/c^{2}+B^{2}}{2\mu _{0}}},}

где E — напряжённость электрического поля, B — магнитная индукция, D — электрическая индукция, H — напряжённость магнитного поля, с — скорость света, ε0{\displaystyle \varepsilon _{0}} — электрическая постоянная и μ0{\displaystyle \mu _{0}} — магнитная постоянная. Иногда для констант ε0{\displaystyle \varepsilon _{0}} и μ0{\displaystyle \mu _{0}} — используют термины диэлектрическая проницаемость и магнитная проницаемость вакуума, — которые являются крайне неудачными, и сейчас почти не употребляются.

В системе СГС:^[1]

u=E⋅D+B⋅H8π.{\displaystyle u={\frac {\mathbf {E} \cdot \mathbf {D} +\mathbf {B} \cdot \mathbf {H} }{8\pi }}.}

Энергия электромагнитного поля в колебательном контуре[править | править код]

Энергия электромагнитного поля в колебательном контуре:

W=CU22+LI22,{\displaystyle W={\frac {CU^{2}}{2}}+{\frac {LI^{2}}{2}},}

где:

U — электрическое напряжение в цепи,

C — электроемкость конденсатора,

I — сила тока,

L — индуктивность катушки или витка с током.

Потоки энергии электромагнитного поля[править | править код]

Для электромагнитной волны плотность потока энергии определяется вектором Пойнтинга S (в русской научной традиции — вектор Умова — Пойнтинга).

В системе СИ вектор Пойнтинга равен S=E×H{\displaystyle \mathbf {S} =\mathbf {E} \times \mathbf {H} } (векторному произведению напряжённостей электрического и магнитного полей) и направлен перпендикулярно векторам E и H. Это естественным образом согласуется со свойством поперечности электромагнитных волн.

Вместе с тем, формула для плотности потока энергии может быть обобщена для случая стационарных электрических и магнитных полей и имеет тот же вид: S=E×H{\displaystyle \mathbf {S} =\mathbf {E} \times \mathbf {H} }.

Факт существования потоков энергии в постоянных электрических и магнитных полях может выглядеть странно, но не приводит к каким-либо парадоксам; более того, такие потоки обнаруживаются в эксперименте.