10. Взаимодействие токов. Магнитное поле. Магнитная индукция
Если по двум тонким прямолинейным проводникам текут токи одного направления, то проводники притягиваются, если направления токов противоположны, то проводники отталкиваются.
Сила взаимодействия для прямолинейных проводников, приходящаяся на единицу длины, определяется по формуле:
 ,
,
где а – расстояние между проводниками, 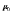 —
магнитная постоянная,
—
магнитная постоянная,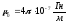 .
.
Взаимодействие токов, осуществляется посредством магнитных полей создаваемых токами.
Подобно
тому, как для исследования электростатического
поля используют пробный точечный заряд,
для исследования магнитного поля
используют пробный ток, циркулирующий
в пробном замкнутом контуре очень малых
размеров. Ориентацию контура в пространстве
характеризуют направлением нормали 
Если внести пробный контур в магнитное поле, то поле оказывает на контур ориентирующее действие, устанавливая его положительной нормалью в определенном направлении. Это направление принимают за направление магнитного поля в данной точке.
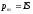 ,
,
где I – сила тока в контуре, S – площадь контура.
Физическую
величину, равную отношению максимального
вращательного момента  ,
действующего на контур, к магнитному
моменту контура называют магнитной
индукцией
,
действующего на контур, к магнитному
моменту контура называют магнитной
индукцией

Магнитная индукция в системе СИ измеряется в теслах (Тл).
Наряду с магнитной индукцией для описания магнитного поля вводится величина, называемая напряженностью магнитного поля. Для вакуума
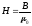 .
.
11. Магнитное поле в веществе. Магнитные свойства вещества
Гипотеза Ампера
Если
проводники, по которым течет ток,
находятся не в вакууме, а в среде, то
магнитное поле может существенно
изменяться. Это обусловлено тем, что
всякое вещество является магнетиком,
т.е. способно намагничиваться. Намагниченное
вещество создает магнитное поле 
 ,
обусловленное токами. Индукция
результирующего поля:
,
обусловленное токами. Индукция
результирующего поля: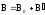 .
.Причина магнитных свойств вещества была объяснена Ампером. Он пришел к выводу, что магнитные свойства любого тела определяются замкнутыми электрическими токами внутри него. Согласно гипотезе Ампера внутри молекул и атомов циркулируют элементарные электрические токи. Если плоскости, в которых циркулируют эти токи, расположены хаотично вследствие теплового движения молекул, то вещество не обнаруживает магнитных свойств. Если вещество намагничено, то токи ориентированы так, что их действия складываются.
Магнитные свойства вещества
Намагничение
магнетика характеризуют магнитным
моментом единицы объема. Эту величину
называют вектором намагничения 

Формула справедлива для неоднородно намагниченного магнетика.
 —
бесконечно малый объем, взятый в
окрестности рассматриваемой точки,
—
бесконечно малый объем, взятый в
окрестности рассматриваемой точки,
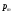 —
магнитный момент отдельной молекулы.
Суммирование производится по всем
молекулам, заключенным в объеме
—
магнитный момент отдельной молекулы.
Суммирование производится по всем
молекулам, заключенным в объеме  .
. Вектор
намагничения связан с напряженностью
магнитного поля в той же точке соотношением  ,
где
,
где —
магнитная восприимчивость вещества
(безразмерная величина).
—
магнитная восприимчивость вещества
(безразмерная величина).
Часто
вместо восприимчивости единицы объема 
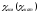 .
.  ,
где
,
где  —
объем киломоля вещества (измеряется в
—
объем киломоля вещества (измеряется в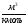 ).
).
В зависимости от знака и величины магнитной восприимчивости все магнетики подразделяются на три группы:
диамагнетики, у которых
 —
отрицательна и мала по абсолютной
величине (
—
отрицательна и мала по абсолютной
величине ( ~
~ ).
).парамагнетики, у которых
 тоже невелика, но положительна (
тоже невелика, но положительна (
 ).
).Ферромагнетики, у которых
 положительна и достигает больших
значений (
положительна и достигает больших
значений ( ~
~ ).
).
Кроме
того, в отличие от диа- и парамагнетиков,
для которых  постоянна, магнитная восприимчивость
ферромагнетиков является функцией
напряженности магнитного поля.
постоянна, магнитная восприимчивость
ферромагнетиков является функцией
напряженности магнитного поля.
Таким
образом, вектор намагничения 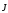 может как совпадать по направлению с
может как совпадать по направлению с (у пара- и ферромагнетиков), так и быть
направленным в противоположную сторону
(у диамагнетиков).
(у пара- и ферромагнетиков), так и быть
направленным в противоположную сторону
(у диамагнетиков).
Магнитное поле. Электромагнитная индукция
285. Магнитное поле — это вид материи, которая порождается движущимися электрическими зарядами и обнаруживается по действию на движущиеся электрические заряды с некоторой силой.
286. Индукция магнитного поля — это физическая величина, равная отношению максимального вращательного момента сил, действующего на рамку с током, помещённую в магнитное поле, к произведению силы тока в рамке на площадь, ограниченную этой рамкой.
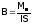
Магнитная индукция измеряется в тесла (Тл)
Второй вариант определения. Индукция магнитного поля — это физическая величина, численно равная отношению максимальной силы, действующей на прямой проводник с током, помещённый в магнитное поле, к произведению силы тока в проводнике на его длину.

287. За направление вектора индукции магнитного поля В принимают направление положительной нормали к рамке с током, помещённой в магнитное поле, при её свободном расположении в этом поле. Направление положительной нормали связано с направлением тока в контуре правилом правого винта.
288. Правило правого винта: винт располагаем так, чтобы при его вворачивании в плоскость рамки вращение головки совпадало с направлением тока в рамке. При этом направление острия винта указывает направление вектора индукции магнитного поля.
289. Во втором определении направление вектора B задаётся правилом левой руки. Левую руку располагаем так, чтобы четыре вытянутых пальца были направлены по направлению тока в проводнике, большой, отогнутый на 900, палец совпадал с направлением максимальной силы, действующей на проводник, тогда вектор индукции магнитного поля будет перпендикулярен ладони.
290. Магнитный момент контура — это величина, равная произведению силы тока в контуре на площадь, ограниченную этим контуром.
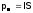
где I — сила тока в контуре, S — площадь ограниченная контуром.
Вектор магнитного момента совпадает по направлению с вектором положительной нормали к контуру, которая связана с направлением тока в контуре правилом правого винта.
291. Закон Ампера: Сила, действующая на проводник с током, помещённый в магнитное поле, равна произведению модуля вектора индукции магнитного поля на силу тока в проводнике, на длину проводника и на синус угла между направлением тока и вектором индукции магнитного поля.

292. Направление силы Ампера можно определить по правилу левой руки: левую руку располагаем так, чтобы вектор индукции магнитного поля был перпендикулярен ладони, четыре пальца были направлены по направлению тока, тогда, отогнутый на 90 градусов большой палец покажет направление силы Ампера.
293. Силовая линия магнитного поля это линия, касательная к которой в любой точке совпадает по направлению с вектором В индукции магнитного поля в этой точке.
294. Сила Лоренца: на электрический заряд, движущийся в магнитном поле со скоростью V, действует сила, модуль которой равен произведению величины этого заряда q, на модуль скорости его движения V, на модуль вектора индукции магнитного поля B и на синус угла между вектором скорости и вектором индукции магнитного поля.

295. Направление силы Лоренца можно определить по правилу левой руки: левую руку располагаем так, чтобы вектор индукции магнитного поля В был перпендикулярен ладони, четыре пальца были направлены по направлению вектора скорости v положительно заряженной частицы, тогда отогнутый на 90 градусов большой палец покажет направление силы Лоренца.
Если частица имеет отрицательный заряд, то вытянутые пальцы левой руки следует направить против направления вектора скорости v.
296. Радиус окружности, по которой со скоростью v, перпендикулярной В, движется в магнитном поле заряженная частица
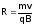
297. Период обращения частицы – это время, затрачиваемое частицей на один полный оборот.
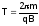
298. Магнитная проницаемость — это число, показывающее, во сколько раз индукция магнитного поля в веществе больше или меньше, чем в вакууме.
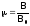
299. Ферромагнетики — это вещества, магнитная проницаемость которых значительно больше 1 и составляет сотни и даже тысячи единиц. Типичными представителями ферромагнетиков являются: железо, никель, кобальт и их сплавы.
300. Домены — это области в ферромагнетике размером порядка 10-5 см, имеющие собственные магнитные поля. В отсутствии внешнего магнитного поля магнитные поля доменов ориентированы произвольно, поэтому кусок ферромагнетика не намагничен. При помещении ферромагнетика во внешнее магнитное поле магнитные поля доменов ориентируются по внешнему полю. Их поля складываются и кусок ферромагнетика намагничивается, приобретая собственное магнитное поле, которое, в свою очередь, складывается с внешним магнитным полем, усиливая его в сотни и даже тысячи раз.
301. Парамагнетики — вещества, в которых вектор магнитной индукции собственного магнитного поля имеет одинаковое направление с вектором индукции намагничивающего поля.
302. Диамагнетики — вещества, в которых вектор индукции собственного магнитного поля направлен противоположно вектору магнитной индукции намагничивающего поля.
303. Электромагнитная индукция — это явление возникновения индукционного тока в замкнутом проводнике при изменении магнитного поля, пересекающего контур, ограниченный этим проводником.
304. Магнитный поток Ф — это скалярная величина, равная произведению модуля вектора индукции магнитного поля B на площадь поверхности S, которую пересекает магнитное поле, и на косинус угла между вектором нормали к контуру и вектором индукции магнитного поля.

Магнитный поток измеряется в веберах (Вб).
305. Поток вектора индукции магнитного поля замкнутого контура через площадь, ограниченную этим контуром прямо пропорционален силе тока в этом контуре
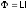
где L — индуктивность контура.
306. Индуктивность контура (катушки) — это величина, численно равная отношению потока вектора индукции магнитного поля через площадь, ограниченную этим контуром, к силе тока, протекающему по контуру и создающему это магнитное поле.
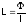
Единица индуктивности — генри (Гн). 1 Гн – это индуктивность такого проводника (катушки индуктивности), в котором ток силой в 1 А создаёт поток магнитной индукции в 1 Вб. 1 Тл — это индукция такого магнитного поля, которое будучи перпендикулярным к площадке в 1 м2 создаёт через неё поток в 1 Вб.
307. Закон Фарадея: ЭДС индукции, возникающая в контуре, прямо пропорциональна скорости изменения магнитного потока, пересекающего площадь, ограниченную этим контуром.

308. Правило Ленца: индукционный ток всегда имеет такое направление, при котором, изменение созданного им магнитного потока противодействует изменению магнитного потока , вызывающего этот ток.
309. ЭДС индукции на концах проводника, движущегося в магнитном поле, равна
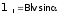
где — угол между вектором В и вектором v движения проводника; В — модуль вектора индукции магнитного поля, l — длина проводника.
310. Самоиндукция — это явление возникновения ЭДС индукции в проводящем контуре при изменении в нем силы тока.
311. Закон самоиндукции: ЭДС самоиндукции, возникающая в электрической цепи при изменении тока в той же цепи, прямо пропорциональна скорости изменения силы тока.
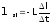
где L — индуктивность электрической цепи (катушки индуктивности).
312. Гипотеза Максвелла: во всех случаях, когда электрическое поле изменяется со временем, оно порождает магнитное поле.
313. Электромагнитное поле — это совокупность переменного электрического поля и неразрывно связанного с ним переменного магнитного поля.
314. Вихревым электрическим полем называют поле, которое порождается изменяющимся магнитным полем. Линии напряжённости вихревого электрического поля замкнутые. Работа по перемещению электрического заряда по замкнутому контуру в таком поле не равна нулю.
315. Энергия магнитного поля может быть вычислена по формуле:

где L — индуктивность, I — сила тока.
316. Колебательный контур — электрическая цепь, состоящая из включенных последовательно конденсатора емкостью С, катушки индуктивностью L и резистора сопротивлением R, в которой могут возникать электромагнитные колебания.
317. Идеальный колебательный контур— это электрическая цепь, состоящая из конденсатора и катушки индуктивности. Конденсатор в колебательном контуре служит для накапливания электрических зарядов, а катушка индуктивности — для создания переменной ЭДС самоиндукции, которая периодически перезаряжает конденсатор. В результате в колебательном контуре возникает периодическое изменение заряда и напряжения на обкладках конденсатора, силы тока и напряжения на катушке индуктивности и т.д., т.е. возникают электромагнитные колебания.
318. Период колебаний в колебательном контуре определяется по формуле

где L — индуктивность, С — электроёмкость. За механизм возникновения электромагнитных колебаний ответственно явление самоиндукции.
319. Полная электромагнитная энергия контура в любой момент времени
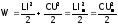
где Im — максимальная сила тока, Um — максимальное напряжение на конденсаторе.
320. Резонансом в электрическом колебательном контуре называется явление резкого возрастания амплитуды вынужденных электрических колебаний (напряжения U, силы тока I, напряжённости электрического поля Е, заряда конденсатора q и т.д.) при совпадении частоты внешнего переменного напряжения с собственной частотой колебательного контура.
321. Условие резонанса в колебательном контуре — индуктивное сопротивление равно емкостному, т.е.

где р — резонансная частота, L — индуктивность, С — ёмкость.
322. Электромагнитная волна — это процесс распространения в пространстве переменного электрического и, неразрывно связанного с ним, переменного магнитного полей. Электромагнитные волны распространяются в вакууме со скоростью 300 000 км/с. В веществе эта скорость меньше.
323. Свойства электромагнитных волн:
1) они отражаются от проводящих поверхностей;
2) на границе диэлектриков частично отражаются, а частично преломляются во второй диэлектрик;
3) им присущи явления интерференции и дифракции;
4) им присуще явление поляризации.
324. Модуляция — это процесс изменения по определённому закону амплитуды, частоты или фазы гармонических колебаний для внесения в колебательный процесс определённой информации.
325. Детектирование — это процесс выделения низкочастотных модулирующих сигналов из модулированных высокочастотных колебаний.
326. Переменным называется электрический ток, сила и направление которого изменяется с течением времени. Наибольшее распространение получил электрический ток, сила и напряжение которого изменяются по гармоническому закону.
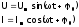
327. Под действующим значением силы (напряжения, ЭДС) переменного тока подразумевают такое значение силы (напряжения, ЭДС) постоянного тока, при пропускании которого через проводник, в последнем выделяется такое же количество теплоты, что и при пропускании переменного тока.
328. Действующее или эффективное значение силы переменного тока, напряжения и ЭДС связаны с их максимальными значениями формулами:

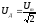
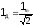
329. ЭДС индукции, возникающая при вращении рамки в однородном магнитном поле
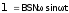
где В — индукция магнитного поля, S — площадь рамки, N — число витков в рамке, — угловая скорость вращения рамки, t — время. Максимальная ЭДС индукции

330. Индуктивное сопротивление

331. Емкостное сопротивление

332. Импеданс (полное сопротивление) электрической цепи при синусоидальных напряжениях и токе)

333. Закон Ома для цепи переменного тока
 или
или 
где Im и Um — амплитудные значения силы тока и напряжения. Iд и Uд — действующие значения силы тока и напряжения.
334. Мощность переменного тока:
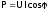
335. Коэффициент мощности:

336. Трансформатором называют электротехническое устройство, служащее для увеличения или уменьшения напряжения переменного тока. В основе работы трансформатора лежит явление электромагнитной индукции.
337. Коэффициентом трансформации называется величина, равная отношению числа витков во вторичной обмотке трансформатора к числу витков в первичной или отношению напряжения на вторичной обмотке к напряжению на первичной обмотке.
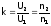
Если k<1, то трансформатор понижающий, а если k>1, то трансформатор повышающий.
Оптика
338. Свет — это электромагнитные волны, длина волны которых лежит в диапазоне от 4,510-7м до 810-7м. Как и все электромагнитные волны, свет распространяется в вакууме со скоростью 300 000 км/с.
339. Геометрическая оптика — раздел оптики, в котором законы распространения света рассматриваются на основе представления о световых лучах.
340. Световой луч — линия, вдоль которой распространяется энергия световых электромагнитных волн.
341. Оптически однородная среда — среда, для которой показатель преломления везде одинаков.
342. Закон прямолинейного распространения света: свет в оптически однородной среде рраспространяется прямолинейно.
343. Скорость света в веществе связана со скоростью света в вакууме соотношением:

где n — абсолютный показатель преломления для этого вещества.
344. Закон отражения света: луч падающий, луч отражённый и перпендикуляр, опущенный в точку падения к границе раздела сред, лежат в одной плоскости. Угол падения равен углу отражения.
345. Закон преломления: луч падающий, луч преломлённый и перпендикуляр, опущенный в точку падения к границе раздела сред, лежат в одной плоскости. Отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных двух сред и называется относительным показателем преломления второй среды относительно первой (n21 )

где — угол падения, — угол преломления. Углы падения и преломления отсчитываются от перпендикуляра к границе раздела сред.
346. Предельным углом полного внутреннего отражения называется такой угол падения из среды с большим показателем преломления на границу его раздела со средой с меньшим показателем преломления, при котором угол преломления равен 900.
347. Полное отражение может наблюдаться только при переходе луча света из среды с большим показателем преломления в среду с меньшим показателем преломления. Закон преломления для этого случая принимает вид:
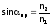
где пр — предельный угол полного отражения; n1 — показатель преломления среды, из которой луч света падает на границу раздела сред; n2 — показатель преломления среды, в которую переходит преломлённый луч.
348. Абсолютный показатель преломления — это число, показывающее во сколько раз скорость света в вакууме больше, чем в данном веществе.
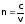
где с — скорость света в вакууме, v — скорость света в веществе.
349. Относительным показателем преломления n21 называется отношение абсолютного показателя второй среды к абсолютному показателю преломления первой среды. Относительный показатель преломления показывает, во сколько раз скорость света во второй среде меньше, чем в первой.
350. Линза — это прозрачное тело, ограниченное с двух сторон сферическими поверхностями или сферической поверхностью и плоскостью.
351. Собирающая линза — это линза, у которой середина толще, чем края.
352. Рассеивающая линза — это линза, у которой края толще , чем середина.
353. Главная оптическая ось линзы — это прямая линия, проведённая через центры сферических поверхностей, ограничивающих линзу.
354. Оптический центр линзы — точка, лежащая на главной оптической оси и обладающая тем свойством, что лучи, проходящие через нее, не преломляются.
355. Фокусом линзы называется точка, в которой пересекаются лучи, пущенные параллельно главной оптической оси.
356. Формула тонкой линзы:

где d — расстояние от предмета до линзы; f — расстояние от линзы до изображения; F — расстояние от линзы до фокуса (фокусное расстояние). Для рассеивающей линзы формула тонкой линзы имеет вид
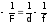
357. Величина обратная фокусному расстоянию называется оптической силой линзы.
Оптическая сила линзы измеряется в диоптриях (дптр.) Оптическая сила рассеивающей линзы отрицательна. 1 дптр — это оптическая сила линзы с фокусным расстоянием 1 м.
358. Оптическая сила тонкой линзы
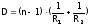
где n — относительный показатель преломления линзы, R1 и R2 – радиусы кривизны поверхностей (R>0 для выпуклой поверхности, R<0 для вогнутой).
359. Увеличением линзы называется отношение линейного размера изображения к линейному размеру предмета

где Н — размер изображения, h — размер предмета.
360. Для построения изображения в линзах используются свойства трёх лучей:
1) Луч, идущий от точки параллельно главной оптической оси, после преломления в линзе проходит через её второй фокус;
2) Луч, проходящий через оптический центр линзы, не преломляется.
3) Луч, прошедший через первый фокус линзы, после преломления в ней, идёт параллельно главной оптической оси.
Если линза рассеивающая, то после преломления в ней, луч параллельный главной оптической оси, будет отклоняться к её краю так, что его продолжение пройдёт через фокус.
27. Магнитное поле, Магнитная индукция. Принцип суперпозиции магнитных полей. Закон Ампера.
Зако́н
Ампе́ра —
закон взаимодействия электрических
токов.
Впервые был установлен Андре
Мари Ампером в 1820 для
постоянного тока. Из закона Ампера
следует, что параллельные проводники с
электрическими токами, текущими в одном
направлении, притягиваются, а в
противоположных — отталкиваются.
Законом Ампера называется также закон,
определяющий силу, с которой магнитное
поле действует
на малый отрезок проводника с током.
Сила  ,
с которой магнитное поле действует на
элемент объёма
,
с которой магнитное поле действует на
элемент объёма 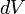 проводника
с током плотности
проводника
с током плотности  ,
находящегося в магнитном поле с
индукцией
,
находящегося в магнитном поле с
индукцией 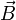 :
:
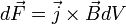 .
.
Модуль силы Ампера можно найти по формуле:
 ,
,
где 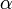 —
угол между векторами магнитной индукции
и тока.
—
угол между векторами магнитной индукции
и тока.
Сила 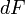 максимальна
когда элемент проводника с током
расположен перпендикулярно линиям
магнитной индукции (
максимальна
когда элемент проводника с током
расположен перпендикулярно линиям
магнитной индукции (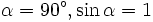 ):
):
 .
.
Магни́тное по́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения[1], магнитная составляющая электромагнитного поля[2]
Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах (и магнитными моментами других частиц, хотя в заметно меньшей степени) (постоянные магниты).
Магни́тная
инду́кция  — векторная величина,
являющаяся силовой характеристикой магнитного
поля (его
действия на заряженные частицы) в данной
точке пространства. Определяет, с
какой силой
— векторная величина,
являющаяся силовой характеристикой магнитного
поля (его
действия на заряженные частицы) в данной
точке пространства. Определяет, с
какой силой  магнитное
поле действует на заряд
магнитное
поле действует на заряд  ,
движущийся со скоростью
,
движущийся со скоростью  .
.
Более
конкретно,  —
это такой вектор, что сила
Лоренца
—
это такой вектор, что сила
Лоренца 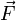 ,
действующая со стороны магнитного
поля[1] на
заряд
,
действующая со стороны магнитного
поля[1] на
заряд 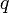 ,
движущийся со скоростью
,
движущийся со скоростью  ,
равна
,
равна
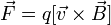
где
косым крестом обозначено векторное
произведение,
α — угол между векторами скорости и
магнитной индукции (направление
вектора 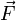 перпендикулярно
им обоим и направлено по правилу
буравчика).
перпендикулярно
им обоим и направлено по правилу
буравчика).
Принцип суперпозиции

Для
магнитного поля, как и для электрического
поля, справедлив принцип суперпозиции:
поле  ,
порождаемое несколькими движущимися
зарядами (токами), равно векторной сумме
полей
,
порождаемое несколькими движущимися
зарядами (токами), равно векторной сумме
полей  ,
порождаемых каждым зарядом (током) в
отдельности:
,
порождаемых каждым зарядом (током) в
отдельности:
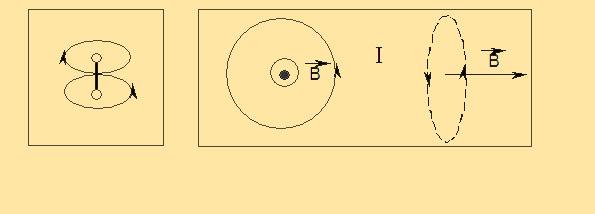
т.е., чтобы найти силу, действующую на точку в пространстве, нужно сложить силы, действующие на неё, как показано на рисунке
Магнитное поле кругового тока представляет собой некую восьмёрку с разделением колец в центре кольца, по которому течёт ток. Его схема показана на рисунке
28. Сила Лоренца. Движение заряженных частиц в магнитом поле.
Сила
Лоренца — сила,
с которой, в рамках классической
физики, электромагнитное
поле действует
на точечную заряженнуючастицу.
Иногда силой Лоренца называют силу,
действующую на движущийся со
скоростью  заряд
заряд  лишь
со сторонымагнитного
поля,
нередко же полную силу — со стороны
электромагнитного поля вообще[1],
иначе говоря, со
стороныэлектрического
лишь
со сторонымагнитного
поля,
нередко же полную силу — со стороны
электромагнитного поля вообще[1],
иначе говоря, со
стороныэлектрического 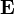 и магнитного
и магнитного  полей.
Выражается в СИ как:
полей.
Выражается в СИ как:

Формула силы Лоренца дает возможность найти ряд закономерностей движения заряженных частиц в магнитном поле. Зная направление силы Лоренца и направление вызываемого ею отклонения заряженной частицы в магнитном поле можно найти знак заряда частиц, которые движутся в магнитных полях.
Для вывода общих закономерностей будем полагать, что магнитное поле однородно и на частицы не действуют электрические поля. Если заряженная частица в магнитном поле движется со скоростью v вдоль линий магнитной индукции, то угол α между векторами v и Вравен 0 или π. Тогда сила Лоренца равна нулю, т. е. магнитное поле на частицу не действует и она движется равномерно и прямолинейно.
В случае, если заряженная частица движется в магнитном поле со скоростью v, которая перпендикулярна вектору В, то сила ЛоренцаF=Q[vB] постоянна по модулю и перпендикулярна к траектории частицы. По второму закону Ньютона, сила Лоренца создает центростремительное ускорение. Значит, что частица будет двигаться по окружности, радиус r которой находится из условия QvB=mv2/r , следовательно
 (1)
(1)
Период вращения частицы, т. е. время Т, за которое она совершает один полный оборот,
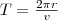
Подствавив (1), получим
 (2)
(2)
т. е. период вращения частицы в однородном магнитном поле задается только величиной, которая обратна удельному заряду (Q/m) частицы, и магнитной индукцией поля, но при этом не зависит от ее скорости (при v<<c). На этом соображении основано действие циклических ускорителей заряженных частиц.
В случае, если скорость v заряженной
частицы направлена под углом α к
вектору В (рис.
170), то ее движение можно задать в виде
суперпозиции: 1) прямолинейного
равномерного движения вдоль поля со
скоростью vparall=vcosα
; 2) равномерного движения со скоростью
vperpend=vsinα
по окружности в плоскости, которая
перпендикулярна полю. Радиус окружности
задается формулой (1) (в этом случае надо
вместо v подставить
vperpend=vsinα).
В результате сложения двух данных
движений возникает движение по спирали,
ось которой параллельна магнитному
полю (рис. 1). Шаг винтовой (спиральной)
линии
случае, если скорость v заряженной
частицы направлена под углом α к
вектору В (рис.
170), то ее движение можно задать в виде
суперпозиции: 1) прямолинейного
равномерного движения вдоль поля со
скоростью vparall=vcosα
; 2) равномерного движения со скоростью
vperpend=vsinα
по окружности в плоскости, которая
перпендикулярна полю. Радиус окружности
задается формулой (1) (в этом случае надо
вместо v подставить
vperpend=vsinα).
В результате сложения двух данных
движений возникает движение по спирали,
ось которой параллельна магнитному
полю (рис. 1). Шаг винтовой (спиральной)
линии 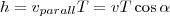
Подставив
в данное выражение (2), найдем 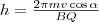
Направление, в котором закручивается спираль, определяется знаком заряда частицы.
Если скорость v заряженной частицы составляет угол α с направлением вектора В неоднородного магнитного поля, у которого индукция возрастает в направлении движения частицы, то r и h уменьшаются с увеличением В. На этом основана фокусировка заряженных частиц в магнитном поле.
Магнитная индукция — это… Что такое Магнитная индукция?
Магни́тная инду́кция — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой магнитное поле действует на заряд , движущийся со скоростью .
Более конкретно, — это такой вектор, что сила Лоренца , действующая со стороны магнитного поля[1] на заряд , движущийся со скоростью , равна
где косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора перпендикулярно им обоим и направлено по правилу буравчика).
Также магнитная индукция может быть определена[2] как отношение максимального механического момента сил, действующих на рамку с током, помещенную в однородное поле, к произведению силы тока в рамке на её площадь.
Является основной фундаментальной характеристикой магнитного поля, аналогичной вектору напряжённости электрического поля.
В системе СГС магнитная индукция поля измеряется в гауссах (Гс), в системе СИ — в теслах (Тл)
- 1 Тл = 104 Гс
Магнитометры, применяемые для измерения магнитной индукции, называют тесламетрами.
Основные уравнения
Поскольку вектор магнитной индукции является одной из основных фундаментальных физических величин в теории электромагнетизма, он входит в огромное множество уравнений, иногда непосредственно, иногда через связанную с ним напряженность магнитного поля. По сути, единственная область в классической теории электромагнетизма, где он отсутствует, это пожалуй разве только чистая электростатика.
- (Здесь формулы приведем в системе единиц СИ, в виде для вакуума[3], где есть варианты для вакуума — для среды; запись в другом виде и подробности — см. по ссылкам).
В магнитостатике
В магнитостатическом пределе[4] наиболее важными являются:
В общем случае
Основные уравнения (классической) электродинамики общего случая (то есть независимо от ограничений магнитостатики), в которых участвует вектор магнитной индукции :
- Формула силы Лоренца
- Следствия из нее, такие как
- Выражение для силы Ампера, действующей со стороны магнитного поля на ток (участок провода с током)
- выражение для вращающего момента, действующего со стороны магнитного поля на магнитный диполь (виток с током, катушку или постоянный магнит):
- выражение для потенциальной энергии магнитного диполя в магнитном поле:
- а также следующих из них выражения для силы, действующей на магнитный диполь в неоднородном магнитном поле и т.д..
- Выражение для силы, действующей со стороны магнитного поля на точечный магнитный заряд:
- (это выражение, точно соответствующее обычному закону Кулона, широко используется для формальных вычислений, для которых ценна его простота, несмотря на то, что реальных магнитных зарядов в природе не обнаружено; также может прямо применяться к вычислению силы, действующей со стороны магнитного поля на полюс длинного тонкого магнита или соленоида).
- Выражение для силы Ампера, действующей со стороны магнитного поля на ток (участок провода с током)
- Следствия из нее, такие как
- Выражение для плотности энергии магнитного поля
- Оно в свою очередь входит (вместе с энергией электрического поля) и в выражение для энергии электромагнитного поля и в лагранжиан электромагнитного поля и в его действие. Последнее же с современной точки зрения является фундаментальной основой электродинамики (как классической, так в принципе и квантовой).
Примечания
- ↑ Если учитывать и действие электрического поля E, то формула (полной) силы Лоренца принимает вид:
- ↑ Это определение с современной точки зрения менее фундаментально, чем приведенное выше (и является просто его следствием), однако с точки зрения близости к одному из практических способов измерения магнитной индукции может быть полезным; также и с исторической точки зрения.
- ↑ То есть в наиболее фундаментальном и простом для ознакомления виде.
- ↑ То есть в частном случае постоянных токов и постоянных электрического и магнитного полей или — приближенно — если изменения настолько медленны, что ими можно пренебречь.
- ↑ Являющаяся частным магнитостатическим случаем закона Ампера — Максвелла (см. в стаье далее).




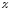 —
отрицательна и мала по абсолютной
величине (
—
отрицательна и мала по абсолютной
величине (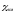 ~
~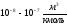 ).
).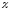 тоже невелика, но положительна (
тоже невелика, но положительна (
 ).
). положительна и достигает больших
значений (
положительна и достигает больших
значений ( ~
~ ).
).