Линейная скорость: формула нахождения
С точки зрения физики абсолютного покоя не существует. Каждое тело и частицы, которые его составляют, находятся в постоянном движении друг относительно друга. Важной кинематической величиной, характеризующей движение, является скорость. В данной статье приведем формулы линейной скорости для различных типов перемещения тел в пространстве.
Что такое линейная скорость?
Речь идет о физической величине, которая показывает, какое расстояние в пространстве проходит тело за единицу времени. Как правило, скорость обозначают буквой v¯, где символ черты говорит о том, что она является векторной величиной. Измеряется скорость в метрах в секунду (м/с), километрах в час (км/ч), милях в час (мил/ч) и других единицах, предполагающих отношение расстояния ко времени.
Вектор скорости v¯ показывает направление реального перемещения тела. Этим он отличается от вектора ускорения, который направлен в сторону действующей силы, но не в сторону движения тела, хотя они могут совпадать.
Мгновенная и средняя скорости

Как найти линейную скорость? Формулу, согласно определению величины, можно записать следующую:
v¯ = dl¯/dt.
Где dl¯ — вектор перемещения тела за время dt. Эта скорость называется мгновенной, поскольку рассчитывается за чрезвычайно короткий промежуток времени dt. Мгновенная скорость в действительности является величиной не стабильной и постоянно меняющейся. Например, представим, что по дороге движется автомобиль. На первый взгляд можно полагать, что в любой момент времени его мгновенная скорость будет постоянной, однако, это не так. Мгновенная скорость испытывает колебания. Если спидометр автомобиля достаточно чувствителен, то он фиксирует эти колебания.
Формула линейной скорости средней ничем не отличается от таковой для мгновенной, однако, измеряется она за более длительный промежуток времени Δt:
v¯ = Δl¯/Δt, где Δt>>dt.
В примере с автомобилем выше, хотя мгновенная скорость испытывает колебания, средняя скорость остается постоянной с определенной точностью на всем участке пути Δl¯.
При решении задач, как правило, используют среднюю скорость. Мгновенная же величина имеет смысл только в случае движения с ускорением.
Равномерное движение по прямой линии
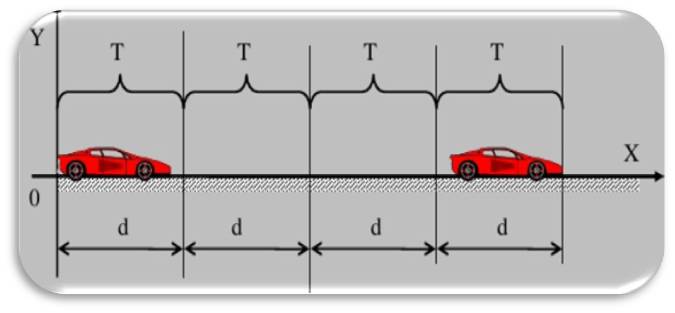
Это идеализированный тип движения, который предполагает, что тело в течение некоторого промежутка времени движется вдоль прямой в пространстве. При этом скорость тела не меняется. Обозначая пройденный путь символом l, получаем формулу:
l = v*t.
Здесь v = const.
Этот тип движения рассматривался еще философами Античной Греции. Они полагали, что для движения тел необходимо прикладывать некоторую силу, поэтому естественным состоянием всех окружающих объектов является покой. Только с приходом эпохи Возрождения благодаря работам Галилея и Ньютона было показано, что если на тело не воздействуют внешние силы, то равномерность и прямолинейность его движения не нарушается.
Скорость при движении по прямой с ускорением
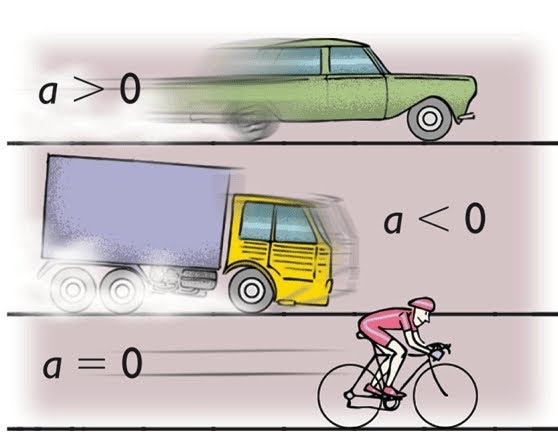
Когда появляется внешняя сила, то ее действие на тело приводит к изменению скорости тела. В динамике эта ситуация описывается вторым законом Ньютона:
F¯ = m*a¯.
Если действие силы F¯ происходит на покоящееся изначально тело массой m, то формула нахождения линейной скорости в любой момент времени t примет вид:
v¯ = a¯*t.
В данном случае обе векторные величины направлены в одну и ту же сторону. Эта формула может применяться для описания разгона какого-либо транспортного средства.
Теперь предположим, что автомобиль двигался с некоторой скоростью v0¯, а затем начал останавливаться. В этой случае соответствующее кинематическое уравнение примет вид:
v¯ = v0¯ + a¯*t.
Поскольку модуль скорости |v¯| авто будет уменьшаться со временем, в скалярной форме это равенство запишется так:
v = v0 — a*t.
В данном случае вектора скорости и ускорения направлены в противоположных направлениях.
Все формулы линейной скорости, приведенные в этом пункте, описывают прямолинейное движение с постоянным ускорением.
Вращение тел

Под вращением понимают тип движения, при котором траектория перемещающегося тела представляет собой окружность. Вращение может происходить вокруг оси или вокруг фиксированной точки. Вращение колеса, планет по своим орбитам, спортсменов во время соревнований по фигурному катанию — все это примеры указанного типа движения.
По аналогии с линейным перемещением, главной формулой динамики вращения является следующая:
M = I*α.
Здесь M и I — моменты силы и инерции, соответственно, α — ускорение угловое.
Для описания вращения удобно пользоваться не линейной, а угловой скоростью. Она определяется так:
ω = θ/t.
Где θ — угол, на который тело повернулось за время t. С записанным ускорением α скорость ω связана следующим равенством:
ω = α*t.
Для измерения всех угловых величин используются радианы.
Формула линейной скорости вращения
Выше отмечалось, что вращение удобно описывать в угловых характеристиках. Тем не менее в некоторых случаях важно знать, чему равна линейная скорость по окружности. Формула для этого случая приведена ниже:
v = ω*r.
Здесь r — радиус окружности, равный расстоянию от любой точки траектории тела до оси вращения. Связывающую линейную и угловую скорость формулу получить несложно самостоятельно. Для этого достаточно рассмотреть, какое расстояние по окружности преодолеет тело за известное время t.
Приведенное выражение можно использовать для вычисления линейных скоростей космических тел, например, нашей Земли, вращающейся вокруг Солнца.
Линейная скорость и центростремительное ускорение
Скорость является величиной векторной. Это означает, что тело получает ускорение не только при изменении модуля величины v, но и при изменении ее направления. Последняя ситуация реализуется во время вращения. Вектор мгновенной скорости тела всегда направлен по касательной к окружности. Если за равные промежутки времени тело описывает равные углы относительно центра вращения, то такое движение является равномерным с точки зрения модуля скорости.
Отклонение от прямолинейного движения во время вращения происходит за счет действия центростремительной силы, вызывающей центростремительное ускорение. Оно направлено всегда перпендикулярно скорости, поэтому изменить ее модуль не может. Ускорение центростремительное ac можно вычислить по формуле:
ac = v2/r.
Абсолютная величина ускорения ac показывает, насколько велики центробежные силы, связанные с инерцией вращающегося тела. Практическим примером является занос автомобиля во время крутого поворота. Заметим, что с уменьшением радиуса ac растет медленнее, чем с увеличением линейной скорости.
Задача на определения линейной скорости нашей планеты

Каждый человек понимает, что если автомобиль движется со скоростью 100 км/ч, то эта цифра является достаточно большой в сравнении со скоростями, с которыми люди сталкиваются в повседневной жизни. Любопытно сравнить указанную цифру со скоростью вращения Земли по своей орбите.
Для оценки этой скорости возьмем следующие данные:
- радиус орбиты — 150 млн км;
- период одного оборота — 365 земных дней.
Для определения требуемой величины воспользуемся формулой линейной и угловой скорости:
v = ω*r.
Значение ω через период T определяется так:
ω = 2*pi/T.
Тогда для v приходим к равенству:
v = 2*pi*r/T.
Подставляя данные из условия задачи, получим линейную скорость 107,5 тысяч км/ч! Эта цифра означает, что наша Земля перемещается в космическом пространстве в 1000 раз быстрее, чем автомобиль движется по дороге. Мы не чувствуем этой гигантскую скорости, поскольку силы гравитации Земли увлекают за собой атмосферу так, что она находится в покое относительно поверхности планеты.
Линейная скорость Википедия
| Скорость | |
|---|---|
| v → = d r → d t {\displaystyle {\vec {v}}={\frac {\mathrm {d} {\vec {r}}}{\mathrm {d} t}}} | |
| Размерность | LT−1 |
| СИ | м/с |
| СГС | см/с |
| вектор | |
Ско́рость (часто обозначается
v
→
{\displaystyle {\vec {v}}}
, от англ. velocity или фр. vitesse, исходно от лат. vēlōcitās) — векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки относительно выбранной системы отсчёта; по определению, равна производной радиус-вектора точки по времени
Термин «скорость» используют в науке и в широком смысле, понимая под ним быстроту изменения какой-либо величины (не обязательно радиус-вектора) в зависимости от другой (чаще подразумеваются изменения во времени, но также в пространстве или любой другой). Так, например, говорят об угловой скорости, скорости изменения температуры, скорости химической реакции, групповой скорости, скорости соединения и т. д. Математически «быстрота изменения» характеризуется производной рассматриваемой величины.
Расширениями понятия скорости являются четырёхмерная скорость, или скорость в релятивистской механике, и обобщённая скорость, или скорость в обобщённых координатах.
Скорость точки в классической механике
Вектор скорости материальной точки в каждый момент времени определяется как производная по времени радиус-вектора
r
→
{\displaystyle {\vec {r}}}
текущего положения этой точки, так что
- v → = d r → d t ≡ v τ τ → , {\displaystyle {\vec {v}}={\mathrm {d} {\vec {r}} \over \mathrm {d} t}\equiv v_{\tau }{\vec {\tau }},}
где τ → ≡ d r → / d s {\displaystyle {\vec {\tau }}\equiv \mathrm {d} {\vec {r}}/\mathrm {d} s} — единичный вектор касательной, проходящей через текущую точку траектории (он направлен в сторону возрастания дуговой координаты s {\displaystyle s} движущейся точки), а v τ ≡ s ˙ {\displaystyle v_{\tau }\equiv {\dot {s}}} — проекция вектора скорости на направление упомянутого единичного вектора, равная производной дуговой координаты по времени и именуемая
- если дуговая координата возрастает, то векторы v → {\displaystyle {\vec {v}}} и τ → {\displaystyle {\vec {\tau }}} сонаправлены, а алгебраическая скорость положительна;
- если дуговая координата убывает, то векторы v → {\displaystyle {\vec {v}}} и τ → {\displaystyle {\vec {\tau }}} противонаправлены, а алгебраическая скорость отрицательна.
Не следует смешивать дуговую координату и пройденный точкой путь. Путь s ~ {\displaystyle {\tilde {s}}} , пройденный точкой за промежуток времени от t 0 {\displaystyle t_{0}} до t {\displaystyle t} , может быть найден так:
- s ~ = ∫ t 0 t | s ˙ | d t ; {\displaystyle {\tilde {s}}=\int _{t_{0}}^{t}|{\dot {s}}|\,\mathrm {d} t\;;}
лишь в случае, когда алгебраическая скорость точки всё время неотрицательна, связь пути и дуговой координаты достаточно проста: путь совпадает с приращением дуговой координаты за время от t 0 {\displaystyle t_{0}} до t {\displaystyle t} (если же при этом начало отсчёта дуговой координаты совпадает с начальным положением движущейся точки, то s ~ {\displaystyle {\tilde {s}}} будет совпадать с s {\displaystyle s} ).
Если алгебраическая скорость точки не меняется с течением времени (или, что то же самое, модуль скорости постоянен), то движение точки называется[5] равномерным (алгебраическое касательное ускорение s ¨ {\displaystyle {\ddot {s}}} при этом тождественно равно нулю).
Предположим, что s ¨ ⩾ 0 {\displaystyle {\ddot {s}}\geqslant {0}} . Тогда при равномерном движении скорость точки (алгебраическая) будет равна отношению пройденного пути s ~ {\displaystyle {\tilde {s}}} к промежутку времени t − t 0 {\displaystyle t-t_{0}} , за который этот путь был пройден:
- s ˙ c p = s ~ t − t 0 . {\displaystyle {\dot {s}}^{\,\mathrm {cp} }={{\tilde {s}} \over t-t_{0}}\;.}
В общем же случае аналогичные отношения
- v → c p = r → − r → 0 t − t 0 ≡ Δ r → Δ t {\displaystyle {\vec {v}}^{\,\,\mathrm {cp} }={{\vec {r}}-{\vec {r}}_{0} \over t-t_{0}}\equiv {\Delta {\vec {r}} \over \Delta {t}}} и s ˙ c p = s − s 0 t − t 0 ≡ Δ s Δ t {\displaystyle {\dot {s}}^{\,\mathrm {cp} }={s-s_{0} \over t-t_{0}}\equiv {\Delta {s} \over \Delta {t}}}
определяют соответственно среднюю скорость точки[6] и её среднюю алгебраическую скорость; если термином «средняя скорость» пользуются, то о величинах v → {\displaystyle {\vec {v}}} и s ˙ {\displaystyle {\dot {s}}} говорят (чтобы избежать путаницы) как о мгновенных скоростях.
Иллюстрация средней и мгновенной скоростиНе следует смешивать два введённых выше понятия средней скорости. Во-первых, v → c p {\displaystyle {\vec {v}}^{\,\,\mathrm {cp} }} — вектор, а s ˙ c p {\displaystyle {\dot {s}}^{\,\mathrm {cp} }} — скаляр. Во-вторых, эти величины могут не совпадать по модулю. Так, пусть точка движется по винтовой линии и за время своего движения проходит один виток; тогда модуль средней скорости этой точки будет равен отношению шага винтовой линии (то есть расстояния между её витками) ко времени движения, а модуль средней алгебраической скорости — отношению длины витка ко времени движения.
Для тела протяжённых размеров понятие «скорости» (тела как такового, а не одной из его точек) не может быть определено; исключение составляет случай мгновенно-поступательного движения. Говорят, что абсолютно твёрдое тело совершает мгновенно-поступательное движение, если в данный момент времени скорости всех составляющих его точек равны[7]; тогда можно, разумеется, положить скорость тела равной скорости любой из его точек. Так, например, равны скорости всех точек кабинки колеса обозрения (если, конечно, пренебречь колебаниями кабинки).
В общем же случае скорости точек, образующих твёрдое тело, не равны между собой. Так, например, для катящегося без проскальзывания колеса модули скоростей точек на ободе относительно дороги принимают значения от нуля (в точке касания с дорогой) до удвоенного значения скорости центра колеса (в точке, диаметрально противоположной точке касания). Распределение скоростей точек абсолютно твёрдого тела описывается кинематической формулой Эйлера.
В декартовых координатах
В прямоугольной декартовой системе координат[8]:
- v = v x i + v y j + v z k . {\displaystyle \mathbf {v} =v_{x}\mathbf {i} +v_{y}\mathbf {j} +v_{z}\mathbf {k} .}
В то же время r = x i + y j + z k , {\displaystyle \mathbf {r} =x\mathbf {i} +y\mathbf {j} +z\mathbf {k} ,} поэтому
Как правило, в любом варианте задания ЕГЭ по физике представлены несколько задач на вращательное движение. Приведем основные определения и законы, необходимые для решения такого рода задач. Угловой скоростью тела, совершающего вращательное движение, называется отношение угла поворота к тому времени , за которое этот поворот произошел
(7.1) |
В этом определении угол должен измеряться в радианах, поэтому размерность угловой скорости рад/с (или 1/с поскольку радиан — безразмерная величина). В принципе, определение (7.1) позволяет найти как среднюю (для больших интервалов времени ), так и мгновенную (при ) угловую скорость. Однако в школьном курсе физики рассматривается только движение с постоянной угловой скоростью, для которого определение (7.1) дает один и тот же результат для любых интервалов времени . Применяя определение (7.1) к полному обороту тела (угол поворота — радиан), получим связь угловой скорости и периода вращения
(7.2) |
Угловую скорость можно ввести не только для точечного тела, но и для протяженного тела. Действительно, при вращении неточечного тела вокруг любой оси все его точки поворачиваются за одинаковое время на одинаковый угол. Поэтому можно говорить об угловой скорости всего тела.
Из формулы (7.2) легко получить связь угловой и обычной скорости вращающегося точечного тела (в этом контексте последнюю всегда называют линейной скоростью). Умножая правую и левую часть формулы (7.2) на радиус окружности и учитывая, что – это длина пути, пройденного за период, получим
(7.3) |
Конечно, для неточечного вращающегося тела нельзя ввести понятие линейной скорости, поскольку у разных точек этого тела линейные скорости будут разными.
Очевидно, при вращательном движении тело всегда имеет ускорение. Действительно, согласно определению (2.1) ускорение тела равно нулю, если не меняется вектор скорости этого тела (т.е. как величина скорости, так и ее направление). При вращательном движении направление скорости обязательно меняется. Можно доказать, что при вращательном движении точечного тела с постоянной по величине линейной скоростью вектор его ускорения в любой момент направлен от тела к центру траектории тела, а его величина равна
(7.4) |
Ускорение (7.3) принято называть центростремительным. Если использовать связь линейной и угловой скорости тела при вращательном движении (7.3), то формулу для центростремительного ускорения можно записать и в таких формах
(7.5) |
Согласно второму закону Ньютона ускорения сообщаются телам силами. Поэтому если тело совершает движение по окружности радиуса с постоянной по величине скоростью (и соответственно угловой скоростью ), на него должна действовать сила, направленная к центру окружности и равная по величине
(7.6) |
Силу (7.6) принято называть центростремительной. Отметим, что термин «центростремительная» связан не с природой этой силы, а с тем, как она действует: в разных ситуациях центростремительной силой может быть и сила тяжести, и сила трения, и сила реакции, и другие силы или их комбинации.
Перечисленных законов и определений достаточно для решения любых задач ЕГЭ на вращательное движение. Рассмотрим их применение к решению задач, приведенных в первой части.
Если период вращения тела задан, то его угловая скорость может быть однозначно определена независимо от размеров тела или радиуса орбиты для точечного тела. В частности, секундная стрелка любых часов поворачивается на угол за одну минуту (конечно, при условии, что они идут «правильно»). Поэтому угловая скорость секундных стрелок любых часов равна рад/мин (задача 7.1.1 – ответ 2).
Для нахождения линейной скорости конца секундной стрелки часов (задача 7.1.2) используем связь угловой и линейной скоростей (7.5). Имеем
(правильный ответ – 2).
Применяя определение угловой скорости к колесу (задача 7.1.3), получаем
(правильный ответ 1).
Из формулы (7.2) имеем
(задача 7.1.4 – правильный ответ 4).
Используя известное расстояние от первой точки до оси вращения и ее центростремительное ускорение (задача 7.1.5), из формулы (7.5) находим квадрат угловой скорости диска
А теперь по формуле (7.5) для второй точки получаем
(ответ 2).
Поскольку скорость автомобиля в задаче 7.1.6 не меняется в процессе движения для сравнения центростремительных ускорений автомобиля в разных точках траектории следует использовать формулу (7.4), из которой находим, что ускорение тем больше, чем меньше радиус траектории (правильный ответ – 3).
Ускорение мальчика из задачи 7.1.7 будет равно нулю, если его скорость относительно земли будет равна нулю. Поэтому при движении мальчика против движения карусели, его скорость относительно карусели равна скорости карусели относительно земли . Если мальчик пойдет в другую сторону с той же скоростью относительно карусели, его скорость относительно земли будет равна . Поэтому центростремительное ускорение мальчика будет равно
(ответ 4).
Тело, находящееся на поверхности вращающегося диска и вращающееся вместе с ним (задача 7.1.8), участвует в следующих взаимодействиях. Во-первых, тело притягивается к земле (сила тяжести), и на него действует поверхность диска (сила нормальной реакции и трения), причем сила трения в каждый момент времени направлена к оси вращения (см. рисунок). Действительно, в отсутствии силы трения тело либо будет оставаться на месте, а диск под ним будет вращаться, либо (если тело имеет скорость) слетит с поверхности диска. Именно сила трения «заставляет» тело вращаться вместе с диском. Поэтому сила трения служит в данной задаче цен-тростремительной силой. Остальные перечисления, данные в условии: «на тело действуют силы тяжести, трения, реакции опоры, центростремительная (или центробежная)» являются неправильными, поскольку в них смешиваются характеристики сил разных типов – первые три касаются природы взаимодействий, вторые – результат действия. Поэтому правильный ответ на вопрос задачи –
Поскольку тело в задаче 7.1.9 вращается с постоянной по величине скоростью по окружности, то его ускорение направлено к центру окружности, и, следовательно, согласно второму закону Ньютона, туда же направлена и результирующая сила, действующая на тело (ответ 2).
Применяя к данному в задаче 7.1.10 телу второй закон Ньютона и учитывая, что его ускорение равно м/с2, получим для равнодействующей =2 Н (ответ 2).
Используя формулу для центростремительного ускорения , находим отношение ускорений материальных точек из
(ответ 1).
Для сравнения центростремительных ускорений материальных точек в задаче 7.2.2 удобно использовать формулу , поскольку в этой задаче одинаковы угловые скорости точек. Получаем
(ответ 3).
Для сравнения центростремительных ускорений тел в задаче 7.2.3 выразим ускорение через радиус окружности и период. Используя формулу (7.2) для периода и (7.5) для центростремительного ускорения, получим
(7.5) |
Поэтому
(ответ 1).
Используя связь угловой и линейной скорости, находим скорости концов часовой и минутной стрелки (задача 7.2.4)
где и – угловые скорости часовой и минутной стрелки соответственно (в рад/час), и – длины часовой и минутной стрелок. Учитывая, что , получаем
(ответ 2).
Телу, вращающемуся вместе с диском на его горизонтальной поверхности (задача 7.2.5), центростремительное ускорение сообщается силой трения
Поэтому при увеличении угловой скорости вращения диска возрастает и сила трения между телом и диском. При некоторой угловой скорости сила трения достигнет максимально возможного для нее значения . Если еще увеличить угловую скорость диска, сила трения уже не сможет удержать тело на диске: тело начнет скользить по поверхности и слетит с поверхности диска. Поэтому значения угловой скорости, при которой тело может вращаться вместе с диском, находится из неравенства
(ответ 4).
В задаче 7.2.6 центростремительной силой является сила натяжения нити. Поэтому из второго закона Ньютона с учетом формулы (7.5) для центростремительного ускорения имеем
(ответ 3).
В задаче 7.2.7 нужно использовать второй закон Ньютона для каждого тела. Силы, действующие на тела, показаны на рисунке. Проекция второго закона Ньютона для дальнего тела на координатную ось, направленную к центру диска, дает
(1) |
На ближнее тело действуют силы натяжения и двух нитей (см. рисунок). Поэтому для него из второго закона Ньютона имеем
Подставляя в эту формулу силу из формулы (1), находим (ответ 2).
В задаче 7.2.8 необходимо использовать то обстоятельство, что угловая скорость всех точек стержня одинакова. Обозначая расстояния от оси вращения до концов стержня как и , имеем
где = 1 м/с и = 2 м/с – линейные скорости концов стержня, м – его длина. Решая эту систему уравнений, найдем расстояния и , а затем и угловую скорость стержня . В результате получим
(ответ 3).
Среднее ускорение тела за некоторый интервал времени (не обязательно малый) определяется по формуле (2.1):
где и – скорости тела в конце и начале интервала времени . За половину периода вектор скорости поворачивается на 180°, поэтому величина разности равна . Поэтому среднее ускорение тела за половину периода равно
(задача 7.2.9 – ответ 1).
Очевидно, при зубчатой передаче совпадают линейные скорости точек на ободе шестерней. Действительно, если бы эти скорости были разными, между поверхностями шестерней было бы проскальзывание, которому препятствуют зубцы шестерней (задача 7.2.10 – ответ 2).
МОУ СОШ №2
Определение линейной и угловой скоростей точки, равномерно движущейся по окружности.
Исследовательская работа
по физике
Выполнил:
Ученик 10 «А» класса
МОУ СОШ №2
Костылев Сергей Анатольевич
Научный руководитель:
Мухина Г.В.
Объект исследования:
Вращающийся диск.
Предмет исследования:
Определение линейной и угловой скорости вращения диска.
Цель работы:
Проверить на практике правильность формулы зависимости линейной скорости от угловой для вращающегося диска V=ω*R
Задача:
Установить зависимость линейной скорости от угловой и радиуса вращения диска: определить линейную и угловую скорости диска.
Гипотеза:
Возможно, что линейная скорость вращения точек зависит от радиуса окружности, по которой двигаются точки диска; линейная и угловая скорости взаимосвязаны ( с увеличением угловой скорости линейная возрастает).
Введение:
При движении по криволинейной траектории, в том числе по окружности, скорость тела может изменяться как по модулю, так и по направлению. Возможно движение, при котором изменяется только направление скорости, а её модуль сохраняется постоянным. Такое движение называется равномерным движением по окружности.
Угловое перемещение измеряют в радианах (рад).
Радиан равен углу между двумя радиусами окружности, длина дуги между которыми равна радиусу.
Движение точки по окружности повторяется через определённые промежутки времени, равные периоду обращения.
Периодом обращения называется время, в течение которого тело совершает один полный оборот. Период обозначается буквой T и измеряют в секундах.
Если за время t тело совершило N оборотов, то период обращения Т равен: Т = t / N
Частотой обращения называют число оборотов тела за одну секунду. ν = N / t
За единицу частоты принят 1 оборот в секунду. Эта единица называется герцем (Гц). 1 герц – это такая частота, при которой тело совершает один оборот за одну секунду. Частота и период обращения связаны следующим образом:
ν = 1 / T ; T = 1 / ν .
Движение тела по окружности характеризуется угловой скоростью. Угловая скорость – физическая величина, равная отношению углового перемещения к промежутку времени, за которое это перемещение произошло. Угловая скорость обозначается буквой ω (омега).
ω = φ / t .
За единицу угловой скорости принимают радиан в секунду
(рад/с).
За время, равное периоду обращения Т, тело совершает полный оборот, т.е. его угловое перемещение равно 2π. Поэтому угловая скорость при равномерном движении тела по окружности: ω = 2π / Т ; или ω = 2πν .
.
Выше рассматривалась такая характеристика криволинейного движения, как мгновенная скорость. Линейная скорость тела, равномерно движущегося по окружности, оставаясь постоянной по модулю, непрерывно изменяется по направлению и в любой точке направлена по касательной к траектории. Линейная скорость обозначается буквой υ.Так как модуль линейной скорости постоянен, то его можно определить по формуле: υ = S / t.
За время, равное периоду обращения, тело проходит путь, равный длине окружности, т.е. S = 2πR, поэтому
υ = 2πR / T.
Записанные равенства позволяют найти соотношение между угловой и линейной скоростями:
υ / ω = (2πR*T) / (T*2π) = R ; таким образом,
υ = ω *R и ω = υ / R.
Практическая часть:
Оборудование:
1)проигрыватель, 2)устройство для записи колебаний маятника, 3)секундомер, 4)транспортир, 5)лист белой бумаги (формат А-4), 6)ножницы, 7)нить, 8)набор иголок.
Ход работы
Определим угловую скорость вращения диска:
ω= φ/ t , где φ — угол поворота
t — время поворота
Угол поворота диска определим с помощью транспортира, время- с помощью записи колебаний маятника.
1)Определим период колебаний маятника по формуле:
T = t / N , где t – время наблюдения
N – число колебаний
Частота колебаний маятника: ν = 1 / Т
2)Включим проигрыватель, расположив над его диском
устройство для записи колебаний маятника,
предварительно прикрепив к диску лист белой бумаги.
На бумаге получим след от неподвижного маятника.
Он будет представлять окружность.
3)Приведём в движение маятник, отклонив его на угол
~ 5 . На листе получим запись колебаний маятника.
Используя её, определим одно полное колебание и
угол, на который повернётся диск за 1 полное
колебание маятника.


 A 4) С помощью транспортира
A 4) С помощью транспортира
определим угол поворота
диска φ= AOB .Время
φ
поворота диска равнопериоду колебания маятника:
 B t = T
B t = T
5) Вычислим угловую скорость
диска по формуле:
ω = φ / t = φ / T
6) Для определения линейной скорости диска
воспользуемся формулой: υ = S / t, где
S – длина дуги АВ ; t – время поворота диска
т.к. t = T, оно уже определено.
Длину дуги найдем с помощью нитки. Воткнём иголки
в бумагу по всей длине дуги и с помощью нитки
найдём путь, пройденный диском от точки А до точки В.
Рассчитаем линейную скорость.
7) Проведём опыт 5 раз для нахождения среднего
значения Ѕ и Т.
Вычисления:
t
T =
=
N
0,99 с
T 1 = =0,099 с
1 = =0,099 с
10 с
1 с
T 2 = = 0,1 с
2 = = 0,1 с
10 с
1,02 с
T 3 = = 0,102 с
3 = = 0,102 с
10 с
0,99 с
T 4 = =0,099 с
4 = =0,099 с
10 с
0,99 с
T 5 = = 0,099 с
5 = = 0,099 с
10 с
T1 +T2 +T3 +T4 +T5 с 0,499
T
 ср. = = =0,099 с
ср. = = =0,099 с
5 5
φ1 рад
ω
 1 = ω1 = 3,5
1 = ω1 = 3,5
T1 с
φ2 рад
ω
 2 = ω2 = 3,5
2 = ω2 = 3,5
T2 с
φ3 рад
ω
 3 = ω3 = 3,4
3 = ω3 = 3,4
T3 с
φ4 рад
ω
 4 = ω4 =3,5
4 = ω4 =3,5
T4 с
φ5 рад
ω
 5 = ω5 = 3,5
5 = ω5 = 3,5
T5 с
ω1 + ω2 + ω3 + ω4 + ω5
ω ср =
ср =
5
рад
ω ср =3,48
ср =3,48
с
S1 + S2 + S3 + S4 +S5 1,13 м
S
 ср = Sср = = 0,226 м
ср = Sср = = 0,226 м
5 5
Sср м
S
 ср = 0,226 м vср = =2,28
ср = 0,226 м vср = =2,28
Tср с
Проверим соотношение: v = ω R
Измерим радиус окружности R.
Определим ω R
И сравним с полученным экспериментально значением линейной скорости.
R =
ωср R =
vср =
Выясним зависимость линейной скорости от радиуса вращения точки. Меняя радиус вращения, определим значение линейной скорости движения точек. Результаты исследования представим в виде графика зависимости линейной скорости от радиуса окружности, по которой движутся точки диска.

Из графика следует, что скорость вращения точек диска пропорциональных радиусу окружности, что соответствует формуле v = ω R
Выводы:
Используя устройство для записи колебаний маятника, можно найти линейную и угловую скорости вращения диска проигрывателя.
vср = 2,28 м/с
ωср = 3,48 рад/с
Линейная и угловая скорости связаны соотношением:
v = ω R
Линейная скорость вращения точек диска зависит от радиуса окружности: чем больше радиус окружности, тем больше линейная скорость.
Используемая литература:
1) Большой справочник Физика. Дрофа, М.: 2008 год.
2) Большая школьная энциклопедия. Том 1. ОЛМА, М.: 2007 Г.
3) «Физика в школе» № 4, 1991 год, стр. 53.
Результаты запишем в таблицу:
опыта
Число
Колебаний
N
Время
Наблюдения
t , с
Период
Т,с
Тср
с
Угол поворота
φ, рад
φср,
рад
Длина дуги,
Ѕ,м
Ѕср,
м
Угловая скорость,
ω,рад\с
ωср
рад\с
υ
м\с
υср
м\с
1
10
0,99
0,099
0,099
3,5
3,5
0,215
0,226
3,5
3,48
2,17
2,28
2
10
1
0,1
3,5
0,23
3,5
2,3
3
10
1,02
0,2
3,5
0,22
3,4
2,15
4
10
0,99
0,099
3,5
0,22
3,5
2,22
5
10
0,99
0,099
3,5
0,245
3,5
2,47


Линейная скорость точки, движущейся равномерно по окружности, равна угловой скорости, умноженной на радиус окружности. линейная скорость равна произведению угловой скорости на радиус тела; период равен удвоенному числу ПИ деленному на угловую скорость; период равен единице деленной на частоту;.Линейное ускорение — изменение скорости тела по модулю. В отличае от углового ускорения — изменения скорости по направлению. Для того чтобы связать линейную скорость v произвольной точки А твердого тела с угловой скоростью ω вращения этого тела вокруг неподвижной оси ОО’, поделим обе части формулы на dt. Учитывая, что dr/dt=v и dφ/dt=ω, получим
v=[ω,r] (1.10)
т.е. линейная скорость вращающейся точки равна векторному произведению угловой скорости на радиус-вектор этой точки. Поступательное и вращательное движение твердого тела Поступательным движением твердого тела называется такое движение, при котором любая прямая, связанная с телом, перемещается в пространстве, оставаясь параллельной самой себе. Другими словами, при поступательном движении отсутствуют какие- либо повороты тела. При вращательном движении все точки тела, лежащие на некоторой прямой, остаются неподвижными во все время движения. Указанная прямая называется осью вращения. Точки тела, не лежащие на оси вращения, движутся в плоскостях, перпендикулярных оси вращения, по окружностям с центром на оси.
Поступательное движение. Понятие материальной точки. Траектория, путь, перемещение, закон движения. Средняя и истинная (мгновенная) скорость. Криволинейное движение. Нормальное и тангенциальное ускорения
| Поступательное движение твердого тела – это движение, при котором любая прямая, связанная с телом, при его движении остается параллельной своему первоначальному положению. |
| Материальная точка – физическая модель объекта Модель – абстрактная система, являющаяся упрощенной копией реальной системы. Материальная точка – тело, размерами которого можно пренебречь в условиях данной задачи. Положение материальной точки характеризуется тремя координатами (x,y,z) или радиус-вектором единичные вектора (орты). Принцип независимости движения Число независимых координат, полностью определяющих положение точки в пространстве, называется число степеней свободы. — радиус вектор. Траектория – кривая, которую описывает радиус вектор материальной точки при её движении. В зависимости от формы траектории движение разделяется на — прямолинейное, — криволинейное. Расстояние, отсчитанное вдоль траектории, (длина участка траектории) называется длиной пути S. — скалярная функция. Направленный отрезок прямой (вектор), соединяющий начальную и конечную точки траектории называется вектором перемещения (перемещением). Скорость движения материальной точки. Понятие о кривизне Материальная точка движется по криволинейной траектории. За время Δt 1 точка проходит путь S 1 и получает приращение Δr 1, За время Δt 2 – Δr 2. Для характеристики движения материальной точки вводится понятие скорости – векторная величина. Вектор средней скорости – отношение перемещения к промежутку времени Вектор средней скорости характеризует изменение положения радиус-вектора. Средняя скорость неравномерного движения – средняя скорость такого равномерного движения, при котором материальная точка за то же время проходит тот же путь. Если стремится к предельному значению. Мгновенная скорость материальной точки – векторная величина, равная первой производной радиус-вектора движущейся точки по времени., следовательно, модуль мгновенной скорости равен первой производной пути по времени: Мгновенная скорость – проекции вектора скорости на оси координат. Криволинейное движение Δφ — угол между касательными в точках, отстоящих друг от друга на расстоянии ΔS. Кривизна траектории характеризует скорость поворота касательной при движении или степень искривленности кривой. Радиус кривизны траектории в данной точке есть величина обратная кривизне Радиус кривизны траектории в данной точке есть радиус окружности, которая сливается на бесконечно малом участке в данном месте с кривой. Нормальное и тангенциальное ускорение нормальное ускорение характеризует изменение скорости по направлению. Вектор направлен в данной точке перпендикулярно скорости к центру кривизны траектории (центростремительное ускорение). тангенциальное ускорение характеризует изменение скорости по величине и направлено вдоль скорости (или в обратную сторону). Любое криволинейное движение можно представить как суперпозицию поступательного и вращательного движений |
- линейная скорость
физ. Скорость движения точки, определяемая по длине пути, пройденного в единицу времени.
Словарь многих выражений. 2014.
- линейка
- линейные меры
Смотреть что такое «линейная скорость» в других словарях:
линейная скорость — Битовая скорость передачи в контрольной точке U x в каком нибудь одном направлении. Это общая скорость данных плюс заголовок решетчатого кодирования (МСЭ Т G.992.3). [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики… … Справочник технического переводчика
линейная скорость — linijinis greitis statusas T sritis automatika atitikmenys: angl. linear velocity vok. lineare Geschwindigkeit, f; Lineargeschwindigkeit, f rus. линейная скорость, f pranc. vitesse linéaire, f … Automatikos terminų žodynas
линейная скорость — linijinis greitis statusas T sritis fizika atitikmenys: angl. linear speed; linear velocity vok. lineare Geschwindigkeit, f; Lineargeschwindigkeit, f rus. линейная скорость, f pranc. vitesse linéaire, f … Fizikos terminų žodynas
Линейная скорость — кровотока – скорость движения частиц крови вдоль сосуда; равна отношению величины объёмной скорости кровотока к площади поперечного сечения сосуда; при увеличении скорости вмешивается турбулентное движение … Словарь терминов по физиологии сельскохозяйственных животных
Линейная скорость выгорания — изменение высоты слоя горючей жидкости в единицу времени в процессе выгорания. Источник: Руководство по тушению нефти и нефтепродуктов в резервуарах и резервуарных парках Линейная скорость выгорания изменение высоты слоя горючей жидкости в… … Словарь-справочник терминов нормативно-технической документации
линейная скорость передачи — скорость передачи символов Количество сигнальных элементов оптического линейного сигнала, передаваемое за единицу времени. Линейная скорость передачи представляет собой результат операций мультиплексирования и кодирования, выполняемых TTE с… … Справочник технического переводчика
Линейная скорость прогрева — изменение толщины гомотермического слоя в единицу времени. Источник: Руководство по тушению нефти и нефтепродуктов в резервуарах и резервуарных парках Линейная скорость прогрева изменение толщины гомотермического слоя в единицу времени … Словарь-справочник терминов нормативно-технической документации
линейная скорость передачи (электросвязь, основные понятия) — линейная скорость передачи скорость передачи символов — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия Синонимы скорость передачи символов EN line digit rate … Справочник технического переводчика
Линейная скорость выгорания — изменение высоты слоя горючей жидкости в единицу времени в процессе выгорания… Источник: РЕКОМЕНДАЦИИ ПО ТУШЕНИЮ ПОЛЯРНЫХ ЖИДКОСТЕЙ В РЕЗЕРВУАРАХ (Согласованы письмом МЧС РФ от 11.04.2007 N 18 6 2 911) … Официальная терминология
Линейная скорость прогрева — изменение толщины гомотермического слоя в единицу времени… Источник: РУКОВОДСТВО ПО ТУШЕНИЮ НЕФТИ И НЕФТЕПРОДУКТОВ В РЕЗЕРВУАРАХ И РЕЗЕРВУАРНЫХ ПАРКАХ (утв. ГУГПС МВД РФ 12.12.1999) … Официальная терминология



