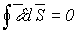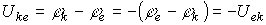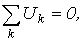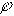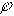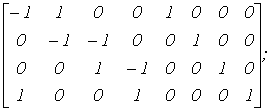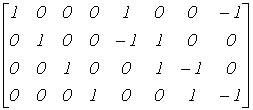Курс лекций. Электротехника и электроника. РАЗДЕЛ 1. Электрические цепи

4

Раздел 1. Электрические цепи Содержание

Стр.
Раздел 1. Электрические цепи ………………………………………………………………	4
Лекция 1.1 Введение. Основные методы анализа линейных
электрических цепей постоянного тока…………………………………………………	7
1.1.1 Общие положения и определения. Элементы цепей и их
характеристики …………………………………………………………………………………	7
1.1.1.1 Источник электрической энергии ………………………………………..	8
1.1.1.2 Приемник электрической энергии ……………………………………..	10
1.1.1.3 Основные определения теории цепей постоянного тока……..	11
1.1.2 Режимы работы электрической цепи ………………………………………..	12
1.1.3 Законы Кирхгофа…………………………………………………………………….	14
1.1.4 Баланс мощности в электрической цепи……………………………………	17
1.1.5 Обзор методов анализа цепей постоянного тока ……………………….	18
Лекция 1.2 Нелинейные цепи постоянного тока…………………………………..	22
1.2.1 Нелинейные цепи общие положения и определения………………….	22
1.2.2 Графоаналитический метод расчета нелинейных цепей…………….	22
1.2.3 Графический метод расчета неразветвленных цепей с
нелинейными элементами ………………………………………………………………..	25
1.2.3.1 Последовательное соединение элементов…………………………..	25
1.2.3.2 Параллельное соединение элементов…………………………………	26
1.2.3.3 Смешанное соединение элементов …………………………………….	28
1.2.3.4 Аналитические расчеты нелинейных цепей ……………………….	30
Лекция 1.3 Цепи однофазного переменного синусоидального тока.
Общие положения и определения ……………………………………………………….	33
1.3.1 Общие положения и определения. Источники
синусоидальных ЭДС и токов……………………………………………………………	33
1.3.2 Причины выбора синусоидальной формы тока и
промышленной частоты……………………………………………………………………	35
1.3.3 Действующее и среднее значения периодических ЭДС,
напряжений и токов………………………………………………………………………….	36
1.3.3.1 Действующее значение периодических ЭДС, напряжений и
токов……………………………………………………………………………………………	36
1.3.3.2 Среднее значение синусоидального переменного тока………	39
1.3.4 Векторные диаграммы ……………………………………………………………..	40
1.3.5 Изображение синусоидальных функций времени
комплексными числами (символический метод) ……………………………….	41
1.3.5.1 Законы Ома и Кирхгофа в комплексной форме ………………….	44
Лекция 1.4 Идеализированные линейные элементы однофазных цепей
синусоидального тока …………………………………………………………………………	46
1.4.1 Идеальный активный элемент…………………………………………………..	46

5
1.4.2 Идеальный индуктивный элемент…………………………………………….	47
1.4.3 Идеальный емкостный элемент ………………………………………………..	49
Лекция 1.5 Полная цепь переменного тока. Мощность в цепи
переменного тока………………………………………………………………………………..	52
1.5.1 Закон Ома для полной цепи переменного тока,
треугольник напряжений………………………………………………………………….	52
1.5.1.1 Закон Ома для Полной цепи переменного тока…………………..	52
1.5.1.2 Треугольники сопротивлений и тока………………………………….	56
1.5.3 Мощность в цепи переменного тока …………………………………………	58
Лекция 1.6 Электрические резонансы…………………………………………………	61
1.6.1 Общая характеристика резонансных цепей……………………………….	61
1.6.2 Резонанс напряжений……………………………………………………………….	62
1.6.3 Резонанс токов…………………………………………………………………………	66
Лекция 1.7 Трехфазные электрические цепи с
симметричными и несимметричными приемниками……………………………	72
1.7.1 Понятие о трехфазных источниках ЭДС и тока. Способы
получения трехфазного тока. Преимущества трехфазной системы
электроснабжения. Способы записи комплексных напряжений
генератора………………………………………………………………………………………..	72
1.7.2 Соединение «звездой». Соотношения между токами и
напряжениями. Симметричный и несимметричный режимы работы.
Роль нулевого провода. Векторные диаграммы…………………………………	75
1.7.3 Соединение «треугольником». Соотношения между токами и
напряжениями. Симметричный и несимметричный режимы работы.
Векторные диаграммы ……………………………………………………………………..	77
1.7.4 Мощность в трехфазной сети. Универсальная формула
мощности…………………………………………………………………………………………	79
1.7.4.1 Измерение активной мощности в трехфазных цепях ………….	80
Лекция 1.8 Магнитные цепи………………………………………………………………..	83
1.8.1 Основные величины, характеризующие магнитное поле и связь
между ними ……………………………………………………………………………………..	83

1.8.2 Закон полного тока. Магнитодвижущая сила. Магнитная цепь и ее

разновидности………………………………………………………………………………….	85
1.8.3 Основные характеристики ферромагнитных материалов. Роль
ферромагнитных материалов в магнитной цепи………………………………..	87
1.8.4 Вебер-амперные характеристики и их построение.
Законы Кирхгофа и Ома для магнитных цепей………………………………….	88
1.8.5 Расчет простых магнитных цепей……………………………………………..	90
Лекция 1.9 Переходные процессы в линейных цепях…………………………..	95
1.9.1 Основные положения и определения………………………………………..	95
1.9.2 Включение катушки на постоянное напряжение. Короткое
замыкание катушки с током. Энергия магнитного поля катушки. ……..	97

6
1.9.3 Заряд и разряд конденсатора. Энергия электрического поля
конденсатора. Законы коммутации …………………………………………………	102
1.9.4 Включение полной цепи RLC на постоянное напряжение ……….	107
1.9.5 Операторный метод расчета переходных процессов. Теорема
Хэвисайда………………………………………………………………………………………	112

7

Лекция 1.1 Введение. Основные методы анализа линейных электрических цепей постоянного тока

План лекции

1)Общие положения и определения. Элементы цепей и их характе- ристики.

2)Режимы работы электрической цепи.

3)Законы Кирхгофа.

4)Баланс мощности в электрической цепи.

5)Обзор методов анализа цепей постоянного тока.

1.1.1Общие положения и определения. Элементы цепей и их характеристики

Электрической цепью называется искусственно созданный путь для электрического тока. Пример электрической цепи дан на рисунке 1.

	a					I			b
E,		+		ΔU			U				R1
R0
						I
	d								c

а

б

Рисунок 1 — Электрическая цепь: а – принципиальная электрическая схема; б – блок схема

Основное назначение электрической цепи — распределение и взаим- ное преобразование электрической и других видов энергии.

Электрическая цепь состоит из трех основных элементов:

-источника электрической энергии;

-приемника электрической энергии;

8

— соединительных проводов.

Рассмотрим каждый из этих элементов цепи подробнее.

1.1.1.1 Источник электрической энергии

Источники электрической энергии разнообразны: гальванические элементы, аккумуляторы, генераторы, термоэлектрические и солнечные батареи и т.д., рисунок 2,а.

Они превращают химическую, механическую, тепловую, световую или энергию других видов в электрическую энергию.

На схемах источники энергии обозначаются так, как показано на ри- сунке 2,б.

Везде RO — внутреннее сопротивление источника энергии.

Гальванический

Электромашинный

Термогенератор Солнечная батарея

элемент

генератор

а

б Рисунок 2 — Условные обозначения источников

В элементах и аккумуляторах, внутреннее сопротивление — это со- противление электролита и граничных слоев между электролитом и элек- тродами, в генераторах — это сопротивление меди обмоток.

Основное назначение источника энергии — создать и постоянно поддерживать в цепи разность потенциалов, разность электрических уровней; создать как бы электрический напор, под воздействием которого и образуется упорядоченное движение электрических зарядов, то есть ток.

Принято зажим высшего потенциала источника обозначать знаком «+», а зажим низшего потенциала знаком «−».

Разность электрических потенциалов количественно определя- ется величиной, которая называется — электродвижущей силой или коротко ЭДС и обозначается на схемах буквой «Е»

9

где ϕ1 — высший потенциал или уровень источника; ϕ 2 — низший потенциал источника.

Направление действия ЭДС обозначается стрелкой, направленной от низшего потенциала к высшему, то есть от «−» к «+».

Работа источника хорошо оценивается с помощью, так называемой внешней характеристики.

Внешней характеристикой называется функциональная зависи- мость напряжения на клеммах источника от величины тока, проте- кающего через источник.

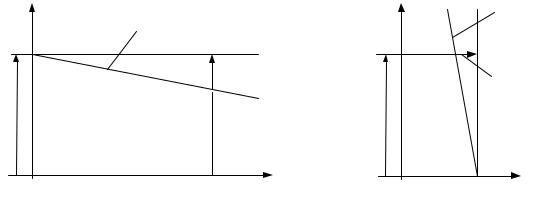
Примерный вид внешних характеристик источников электрической энергии показан на рисунках 3 и 4.

Рисунок 3 — Внешняя характеристика	Рисунок 4 — Внешняя
источника напряжения	характеристика источника тока

Из характеристики видно, что с увеличением тока напряжение на клеммах источника несколько уменьшается за счет потери напряжения на внутреннем сопротивлении RO . В целом, же с ростом тока, напряжение на источнике остается более или менее постоянным.

Подобные характеристики имеют гальванические элементы, аккуму- ляторы, электромашинные генераторы постоянного тока, выпрямители.

На рисунке 4 приведена внешняя характеристика источника элек- трической энергии другого вида.

Здесь, ток вырабатываемый источником остается более или менее постоянным, при значительном изменении напряжения на клеммах источ- ника.

Отличительная особенность таких источников — очень большая вели- чина внутреннего сопротивления, значительно превышающая сопротивле- ние приемника электрической энергии. Данные источники строят по спе- циальным схемам и широко применяют в современной электронике.

10

1.1.1.2 Приемник электрической энергии

Приемники электрической энергии или нагрузки, или потребители — разнообразны. Это могут быть электрические лампы, нагревательные при- боры, электродвигатели и другие устройства.

В нагрузках электрическая энергия преобразуется в тепловую, свето- вую, механическую и другие виды энергии.

На схемах, нагрузка учитывается с помощью соответствующих со- противлений и условно обозначается так, как показано на рисунке 5.

R

Рисунок 5 — Условное изображение нагрузки

В общем случае сопротивление нагрузки R зависит от тока, проте- кающего по нему. Однако, эта зависимость при расчетах цепей использу- ется редко.

На практике, чаще используют зависимость напряжения нагрузки от тока нагрузки, которая называется вольтамперной характеристикой.

Вольтамперной характеристикой называется функциональная зависимость напряжения на зажимах нагрузки от тока, протекающего через нагрузку.

Вольтамперные характеристики могут быть самыми разнообразны- ми, например такими, как показано на рисунке 6.

Рисунок 6 — Вольтамперные характеристики нагрузки

Характеристика «а» называется линейной. Характеристики «b» и «c» называются нелинейными. Поэтому нагрузки бывают линейными и нели- нейными.

Линейным элементом или нагрузкой называют такой, сопротив- ление которого R , при любых значениях тока через него, остается по-

стоянным, а вольтамперная характеристика представляет собой пря- мую линию.

Нелинейным элементом называют такой, сопротивление кото- рого R непостоянно и зависит от величины тока, проходящего через

11

него, а вольтамперная характеристика представляет собой кривую линию.

Только линейные элементы подчиняются закону Ома:

U = RI ; R =	U	;	I =	U	.	(2)
	I			R

Рисунок 7 — Георг Симон Ом. Немецкий физик. Установил основной закон электрической цепи (закон Ома). Член Баварской АН (1845), член- корреспондент Берлинской АН, иностранный почетный член Лондонского Королевского общества (1842).

Соединительные провода

Соединительные провода или линия, обозначены на рисунке 1 — a − b и d − c . Они обеспечивают передачу электрической энергии, транспорти- руют энергию от источника к нагрузке.

Их назначение передать электрическую энергию потребителю с ми- нимальными потерями.

Рассмотрев отдельные элементы, вернемся обратно к электрической цепи, как к сосредоточию всех элементов.

1.1.1.3 Основные определения теории цепей постоянного тока

Цепью постоянного тока называется такая цепь, в которой ЭДС, токи и напряжения остаются постоянными по величине и не зависят от времени.

Цепи делятся на два больших класса:

-линейные;

-нелинейные.

Электрические цепи, содержащие только элементы с линейными вольтамперными характеристиками, называются линейными цепями.

12

Электрические цепи, содержащие элементы с нелинейными ха- рактеристиками называются нелинейными цепями.

Строго говоря, любые цепи нелинейны, однако, если степень нели- нейности мала, то ею пренебрегают и считают такую цепь линейной.

В дальнейшем мы будем рассматривать пока только линейные цепи, так как лишь они подчиняются закону Ома и могут рассчитываться анали- тическими методами.

1.1.2 Режимы работы электрической цепи

Любая электрическая цепь состоит из двух участков:

-внешний участок цепи, с сопротивлением R ;

-внутренний участок цепи, имеющий сопротивление RO .

Внешним участком цепи или внешней цепью называют часть цепи, которая присоединяется извне к зажимам источника.

Внутренним участком цепи или внутренней цепью называют часть цепи, которая проходит внутри источника энергии между его зажимами через электролит или обмотки генератора.

Электрические цепи делятся на замкнутые и разомкнутые.

Замкнутая цепью — такая, в которой имеется непрерывный путь для тока, а общее сопротивление цепи меньше бесконечности,

R + RO < ∞.

Разомкнутой цепью называют такую цепь, в которой путь для тока прерывается, а общее сопротивление равно бесконечности

R + RO = ∞.
По закону Ома для полной цепи имеем I =	E	,
	R + RO
если R + RO < ∞, то I > 0 , если R + RO = ∞, то I = 0 .			(3)
Отсюда следуют выводы:

1)только в замкнутой цепи может протекать ток;

2)в разомкнутой цепи ток не существует, но может существовать напряжение или ЭДС.

Ток протекает по проводнику цепи, поэтому стрелку тока принято

размечать на самом проводнике.

За положительное направление тока во внешней цепи, принято направление от высшего потенциала к низшему, то есть от «+» к «−».

За положительное направление тока во внутренней цепи приня- то направление от низшего потенциала к высшему, то есть от «−» к «+».

13

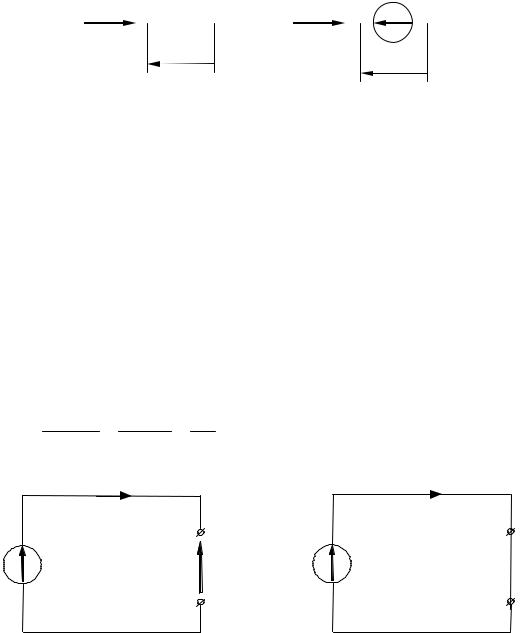
Напряжение на любом участке цепи есть реакция на ток, поэто- му стрелку напряжения принято размечать параллельно элементу и всегда против ранее размеченной стрелки тока. (см. рисунок 8).

		R						E
I					I
				=
+			−		+				−
		U					U = E

Рисунок 8 — Стрелки тока и напряжения

Электрическая цепь может работать в различных режимах, однако все эти режимы, сколько бы их ни было, находятся между двумя крайними режимами — холостым ходом и коротким замыканием.

Режимом холостого хода цепи называют такой режим, при кото- ром сопротивление нагрузки R = ∞ , то есть внешняя цепь разомкнута

(см. рисунок 9). Следовательно,

I XX	=	E	=	E	= 0 .	(4)
		R + RO		∞ + RO

При режиме холостого хода ток холостого хода равен нулю.

Режимом короткого замыкания цепи называется такой режим, при котором сопротивление нагрузки R = 0 , то есть внешняя цепь замкнута накоротко (см. рисунок 10).

Следовательно,

I КЗ	= E =	E =	E = max .	(5)
	R + RO	0 + RO	RO
	IХХ=0
+			+
	E	UХХ =E
—	RО	R=∞
			—
Рисунок 9 — Режим холостого				Рисунок 10 — Режим короткого
	хода			замыкания

Таким образом, при коротком замыкании ток в цепи максимален и ограничивается только величиной внутреннего сопротивления RO источ- ника энергии.

Лекции по общей электротехнике

41 лекция по общей электротехнике:

Лекция № 1. Элементы электрических цепей.

Лекция № 2. Топология электрической цепи.

Лекция № 3. Представление синусоидальных величин с помощью векторов и комплексных чисел.

Лекция № 4. Элементы цепи синусоидального тока. Векторные диаграммы и комплексные соотношения для них.

Лекция № 5. Закон Ома для участка цепи с источником ЭДС.

Лекция № 6. Основы матричных методов расчета электрических цепей.

Лекция № 7. Преобразование энергии в электрической цепи. Мгновенная, активная, реактивная и полная мощности синусоидального тока.

Лекция № 8. Резонансы в цепях синусоидального тока.

Лекция № 9. Векторные и топографические диаграммы.

Лекция № 10. Анализ цепей с индуктивно связанными элементами.

Лекция № 11. Особенности составления матричных уравнений при наличии индуктивных связей и ветвей с идеальными источниками.

Лекция № 12. Методы расчета, основанные на свойствах линейных цепей.

Лекция № 13. Метод эквивалентного генератора.

Лекция № 14. Пассивные четырехполюсники.

Лекция № 15. Электрические фильтры.

Лекция № 16. Трехфазные электрические цепи.

Лекция № 17. Расчет трехфазных цепей.

Лекция № 18. Применение векторных диаграмм для анализа несимметричных режимов.

Лекция № 19. Метод симметричных составляющих.

Лекция № 20. Теорема об активном двухполюснике для симметричных составляющих.

Лекция № 21. Вращающееся магнитное поле.

Лекция № 22. Линейные электрические цепи при несинусоидальных периодических токах.

Лекция № 23. Резонансные явления в цепях несинусоидального тока.

Лекция № 24. Способы составления характеристического уравнения.

Лекция № 25. Операторный метод расчета переходных процессов.

Лекция № 26. Некоторые важные замечания к формуле разложения.

Лекция № 27. Расчет переходных процессов с использованием интеграла Дюамеля.

Лекция № 28. Нелинейные цепи.

Лекция № 29. Расчет нелинейных цепей методом эквивалентного генератора.

Лекция № 30. Нелинейные магнитные цепи при постоянных потоках. Основные понятия и законы магнитных цепей.

Лекция № 31. Общая характеристика задач и методов расчета магнитных цепей.

Лекция № 32. Нелинейные цепи переменного тока в стационарных режимах.

Лекция № 33. Графический метод с использованием характеристик по первым гармоникам.

Лекция № 34. Метод кусочно-линейной аппроксимации.

Лекция № 35. Метод эквивалентных синусоид (метод расчета по действующим значениям).

Лекция № 36. Переходные процессы в нелинейных цепях.

Лекция № 37. Графические методы анализа переходных процессов в нелинейных цепях.

Лекция № 38. Цепи с распределенными параметрами.

Лекция № 39. Линия без искажений.

Лекция № 40. Входное сопротивление длинной линии.

Лекция № 41. Сведение расчета переходных процессов в цепях с распределенными параметрами к нулевым начальным условиям.

Лекции по общей электротехнике

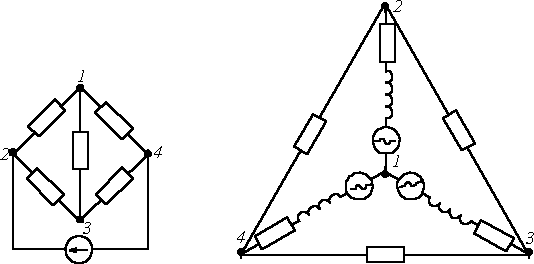
Электрическая цепь характеризуется совокупностью элементов, из которых она состоит, и способом их соединения. Соединение элементов электрической цепи наглядно отображается ее схемой. Рассмотрим для примера две электрические схемы (рис. 1, 2), введя понятие ветви и узла.

Ветвью называется участок цепи, обтекаемый одним и тем же током.

Узел – место соединения трех и более ветвей.

Представленные схемы различны и по форме, и по назначению, но каждая из указанных цепей содержит по 6 ветвей и 4 узла, одинаково соединенных. Таким образом, в смысле геометрии (топологии) соединений ветвей данные схемы идентичны.

Т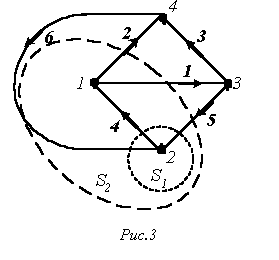опологические (геометрические) свойства электрической цепи не зависят от типа и свойств элементов, из которых состоит ветвь. Поэтому целесообразно каждую ветвь схемы электрической цепи изобразить отрезком линии. Если каждую ветвь схем на рис. 1 и 2 заменить отрезком линии, получается геометрическая фигура, показанная на рис. 3.

Условное изображение схемы, в котором каждая ветвь заменяется отрезком линии, называется графом электрической цепи. При этом следует помнить, что ветви могут состоять из каких-либо элементов, в свою очередь соединенных различным образом.

Отрезок линии, соответствующий ветви схемы, называется ветвью графа. Граничные точки ветви графа называют узлами графа. Ветвям графа может быть дана определенная ориентация, указанная стрелкой. Граф, у которого все ветви ориентированы, называется ориентированным.

Подграфом графа называется часть графа, т.е. это может быть одна ветвь или один изолированный узел графа, а также любое множество ветвей и узлов, содержащихся в графе.

В теории электрических цепей важное значение имеют следующие подграфы:

1. Путь – это упорядоченная последовательность ветвей, в которой каждые две соседние ветви имеют общий узел, причем любая ветвь и любой узел встречаются на этом пути только один раз. Например, в схеме на рис. 3 ветви 2-6-5; 4-5; 3-6-4; 1 образуют пути между одной и той же парой узлов 1 и 3. Таким образом, путь – это совокупность ветвей, проходимых непрерывно.

2. Контур – замкнутый путь, в котором один из узлов является начальным и конечным узлом пути. Например, для графа по рис. 3 можно определить контуры, образованные ветвями 2-4-6; 3-5-6; 2-3-5-4. Если между любой парой узлов графа существует связь, то граф называют связным.

3. Дерево – это связный подграф, содержащий все узлы графа, но ни одного контура. Примерами деревьев для графа на рис. 3 могут служить фигуры на рис. 4.

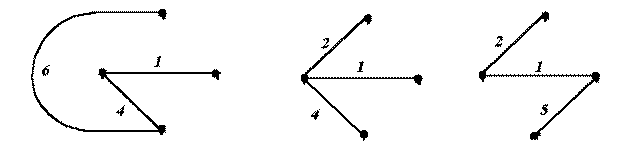
Рис.4

4. Ветви связи (дополнения дерева) – это ветви графа, дополняющие дерево до исходного графа.

Если граф содержит m узлов и n ветвей, то число ветвей любого дерева 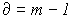, а числа ветвей связи графа .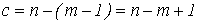

5. Сечение графа – множество ветвей, удаление которых делит граф на два изолированных подграфа, один из которых, в частности, может быть отдельным узлом.

Сечение можно наглядно изобразить в виде следа некоторой замкнутой поверхности, рассекающей соответствующие ветви. Примерами таких поверхностей являются для нашего графа на рис. 3 S₁ иS₂ . При этом получаем соответственно сечения, образованные ветвями 6-4-5 и 6-2-1-5.

С понятием дерева связаны понятия главных контуров и сечений:

• главный контур – контур, состоящий из ветвей дерева и только одной ветви связи;

• главное сечение – сечение, состоящее из ветвей связи и только одной ветви дерева.

Топологические матрицы

Задать вычислительной машине топологию цепи рисунком затруднительно, так как не существует эффективных программ распознавания образа. Поэтому топологию цепи вводят в ЭВМ в виде матриц, которые называют топологическими матрицами. Выделяют три таких матрицы: узловую матрицу, контурную матрицу и матрицу сечений.

1. Узловая матрица (матрица соединений) – это таблица коэффициентов уравнений, составленных по первому закону Кирхгофа. Строки этой матрицы соответствуют узлам, а столбцы – ветвям схемы.

Для графа на рис. 3 имеем число узлов m=4 и число ветвей n=6. Тогда запишем матрицу А_Н , принимая, что элемент матрицы 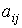(i –номер строки; j –номер столбца) равен 1, если ветвь j соединена с узлом i и ориентирована от него, -1, если ориентирована к нему, и 0, если ветвь j не соединена с узломi . Сориентировав ветви графа на рис. 3, получим

.Данная матрица А_Н записана для всех четырех узлов и называется неопределенной. Следует указать, что сумма элементов столбцов матрицы А_Н всегда равна нулю, так как каждый столбец содержит один элемент +1 и один элемент -1, остальные нули.

Обычно при расчетах один (любой) заземляют. Тогда приходим к узловой матрице А (редуцированной матрице), которая может быть получена из матрицы А_Н путем вычеркивания любой ее строки. Например, при вычеркивании строки “4” получим

.Число строк матрицы А равно числу независимых уравнений для узлов 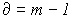, т.е. числу уравнений, записываемых для электрической схемы по первому закону Кирхгофа. Итак, введя понятие узловой матрицы А, перейдем к первому закону Кирхгофа.

Первый закон Кирхгофа

Обычно первый закон Кирхгофа записывается для узлов схемы, но, строго говоря, он справедлив не только для узлов, но и для любой замкнутой поверхности, т.е. справедливо соотношение

(1)

где — вектор плотности тока; 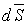— нормаль к участку dS замкнутой поверхности S.

Первый закон Кирхгофа справедлив и для любого сечения. В частности, для сечения S₂ графа на рис. 3, считая, что нумерация и направления токов в ветвях соответствуют нумерации и выбранной ориентации ветвей графа, можно записать

.

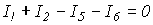Поскольку в частном случае ветви сечения сходятся в узле, то первый закон Кирхгофа справедлив и для него. Пока будем применять первый закон Кирхгофа для узлов, что математически можно записать, как:

(2)

т.е. алгебраическая сумма токов ветвей, соединенных в узел, равна нулю.

При этом при расчетах уравнения по первому закону Кирхгофа записываются для (m-1) узлов, так как при записи уравнений для всех m узлов одно (любое) из них будет линейно зависимым от других, т.е. не дает дополнительной информации.

Введем столбцовую матрицу токов ветвей

I=

Тогда первый закон Кирхгофа в матричной форме записи имеет вид:

– где O — нулевая матрица-столбец. Как видим, в качестве узловой взята матрица А, а не А_Н, т.к. с учетом вышесказанного уравнения по первому закону Кирхгофа записываются для (m-1) узлов.

В качестве примера запишем для схемы на рис. 3

Отсюда для первого узла получаем

,

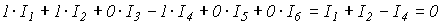что и должно иметь место.

2. Контурная матрица (матрица контуров) – это таблица коэффициентов уравнений, составленных по второму закону Кирхгофа. Строки контурной матрицы Всоответствуют контурам, а столбцы – ветвям схемы.

Элемент b_ij матрицы В равен 1, если ветвь j входит в контур i и ее ориентация совпадает с направлением обхода контура, -1, если не совпадает с направлением обхода контура, и 0, если ветвьj не входит в контурi.

Матрицу В, записанную для главных контуров, называют матрицей главных контуров. При этом за направление обхода контура принимают направление ветви связи этого контура. Выделив в нашем примере (см. рис. 5) дерево, образуемое ветвями 2-1-4, запишем коэффициенты для матрицы В.

 

.

Перейдем теперь ко второму закону Кирхгофа.

Под напряжением на некотором участке электрической цепи понимается разность потенциалов между крайними точками этого участка, т.е.

(4)

Просуммируем напряжения на ветвях некоторого контура:

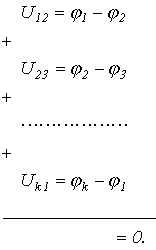
Поскольку при обходе контура потенциал каждой i-ой точки встречается два раза, причем один раз с “+”, а второй – с “-”, то в целом сумма равна нулю.

Таким образом, второй закон Кирхгофа математически записывается, как:

(5)

— и имеет место следующую формулировку: алгебраическая сумма напряжений на зажимах ветвей (элементов) контура равна нулю. При этом при расчете цепей с использованием законов Кирхгофа записывается 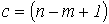независимых уравнений по второму закону Кирхгофа, т.е. уравнений, записываемых для контуров, каждый из которых отличается от других хотя бы одной ветвью. Значение топологического понятия “дерева”: дерево позволяет образовать независимые контуры и сечения и, следовательно, формировать независимые уравнения по законам Кирхгофа. Таким образом, с учетом (m-1) уравнений, составленных по первому закону Кирхгофа, получаем систему из 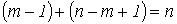уравнений, что равно числу ветвей схемы и, следовательно, токи в них находятся однозначно.

Введем столбцовую матрицу напряжений ветвей

U=

Тогда второй закон Кирхгофа в матричной форме записи имеет вид

В качестве примера для схемы рис. 5 имеем

,

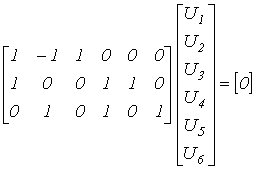откуда, например, для первого контура получаем

,

что и должно иметь место.

Если ввести столбцовую матрицу узловых потенциалов

=

причем потенциал последнего узла 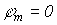, то матрица напряжений ветвей и узловых потенциалов связаны соотношением

U=AТ

(7)

где A^Т — транспонированная узловая матрица.

Для определения матрицы В по известной матрице А=А_ДА_С , где А_Д – подматрица, соответствующая ветвям некоторого дерева, А_С— подматрица, соответствующая ветвям связи, может быть использовано соотношение В= (-А^Т_С А^-1Т_Д1).

3. Матрица сечений – это таблица коэффициентов уравнений, составленных по первому закону Кирхгофа для сечений. Ее строки соответствуют сечениям, а столбцы – ветвям графа.

Матрица Q , составленная для главных сечений, называется матрицей главных сечений. Число строк матрицы Q равно числу независимых сечений.

Элемент q_ij матрицыQ равен 1, если ветвьвходит в i-е сечение и ориентирована согласно направлению сечения (за положительное направление сечения принимают направление ветви дерева, входящей в него), -1, если ориентирована противоположно направлению сечения, и 0, если ветвьj не входит в i-е сечение.

В качестве примера составим матрицу Q главных сечений для графа на рис. 5. При указанной на рис. 5 ориентации ветвей имеем

В заключение отметим, что для топологических матриц А, В и Q, составленных для одного и того же графа, выполняются соотношения

которые, в частности, можно использовать для проверки правильности составления этих матриц. Здесь 0 – нулевая матрица порядка .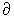

Приведенные уравнения позволяют сделать важное заключение: зная одну из топологических матриц, по ее структуре можно восстановить остальные.

Литература

1. Теоретические основы электротехники. Т.1. Основы теории линейных цепей./Под ред. П.А.Ионкина. Учебник для электротехн. вузов. Изд.2-е , перераб. и доп. –М.: Высш. шк., 1976.-544с.

2. Матханов Х.Н. Основы анализа электрических цепей. Линейные цепи.: Учеб. для электротехн. и радиотехн. спец. 3-е изд. переработ. и доп. –М.: Высш. шк., 1990. –400с.

3. Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.

 

Контрольные вопросы и задачи

1. Сформулируйте основные топологические понятия для электрических цепей.

2. Что такое узловая матрица?

3. Что такое контурная матрица?

4. Что такое матрица сечений?

5. Токи ветвей некоторой планарной цепи удовлетворяют следующей полной системе независимых уравнений:

.

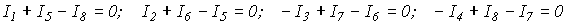Восстановив граф цепи, составить матрицы главных контуров и сечений, приняв, что ветвям дерева присвоены первые номера.

Ответ:

B=

Q=

6. Составить матрицу главных контуров для графа на рис. 3, приняв, что дерево образовано ветвями 2, 1 и 5

Ответ:

B=

7. Решить задачу 5, используя соотношения (8) и (9).

Лекции по электротехнике (1 часть)

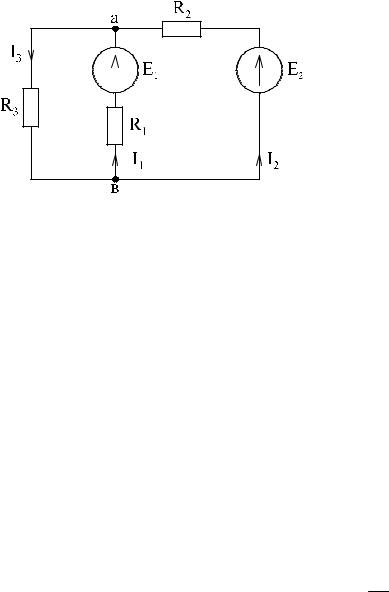
Пример:

ìI1 + I2 — I3 = 0;

ïí- R1I1 — R3I3 = -E1; ;

ïîR1I1 -R2 I2 = E1 — E2

Если при решении системы уравнений значение какого-либо тока получи- лось отрицательным, то это означает, что истинное направление тока проти- воположно выбранному. Данный метод расчета является универсальным, од- нако расчет вручную возможен лишь для несложных схем (4-5 неизвестных тока). Для более сложных схем требуется применение иных методов или вы- числительной техники.

4. Мощность в цепях постоянного тока.

Для оценки энергетических условий важно знать сколь быстро совершается работа.

Отношение работы «А» к соответствующему промежутку времени t опреде- ляет мощность: P = A/ t = UIt / t = UI,[Вт]

Используя закон Ома, можно получить другие формулы для мощности в электрических цепях:

P = UI = I 2 R = U 2 R

5.Баланс мощностей.

Влюбой электрической цепи должен соблюдаться энергетический баланс — баланс мощностей: алгебраическая сумма мощностей всех источников равна арифметической сумме мощностей всех приемников энергии.

k	n			k	n
åUист Iист = åRн Iн		2 ;	åPист = åPn
1	1			1	1
	k		n
	åEi Ii =		åRj I j	2

11

Влевой части равенства слагаемое берется со знаком «+» если Е и I совпа-

дают по направлению и со знаком «-» если не совпадают.

Если направления ЭДС и тока I в источнике противоположны, то физически это означает, что данный источник работает в режиме потребителя.

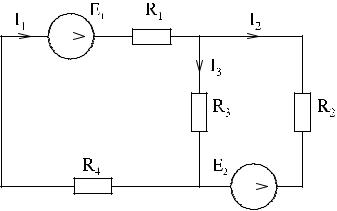
Например:

E1I1 − E2 I2 = I12 R1 + I22 R2 + I32 R3 + I12 R4

Л Е К Ц И Я 3

1.Метод контурных токов.

2.Метод межузлового напряжения.

3.Метод эквивалентного генератора (активного двухполюсника).

1. Метод контурных токов.

Порядок системы уравнений, составленных по законам Кирхгофа, быстро возрастает с ростом сложности схемы, поэтому естественно желание оты- скать менее трудоемкий метод анализа. Таким является метод контурных то- ков. Он позволяет для схемы с «к» узлами и «n» ветвями составлять и решать систему из n-(к-1) уравнений.

По этому методу сначала определяют число независимых контуров в схе- ме: n-(к-1), схему рассматривают как совокупность этих контуров, в каждом из которых задается некоторый контурный ток. Токи смежных ветвей соседних контуров рассматривают как алгебраическую сумму соответствующих контур- ных токов. Токи внешних (независимых) ветвей фактически являются контур- ными токами (по крайней мере, по величине). Далее для каждого контура со- ставляется уравнение по 2-му закону Кирхгофа, где алгебраическая сумма ЭДС в контуре (направление обхода задается контурным током) равна алгеб- раической сумме падений напряжения на сопротивлениях контура от собст- венного контурного тока и от токов в смежных контурах. После решения полу- ченной системы уравнений по известным контурным токам нетрудно опреде- лить направление и величину истинных токов в ветвях схемы.

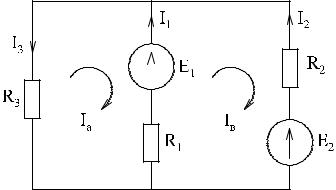
Пример:

Ia , Ib — контурные токи

ì(R1 + R3 )Ia — R1Ib = -E1 íî(R1 + R2 )Ib — R1Ia = E1 — E2

Решаем систему относительно Ia и Ib , а затем находим I1, I2 , I3 :

I1 = Ib — Ia , I2 = -Ib , I3 = -Ia .

2. Метод межузлового напряжения.

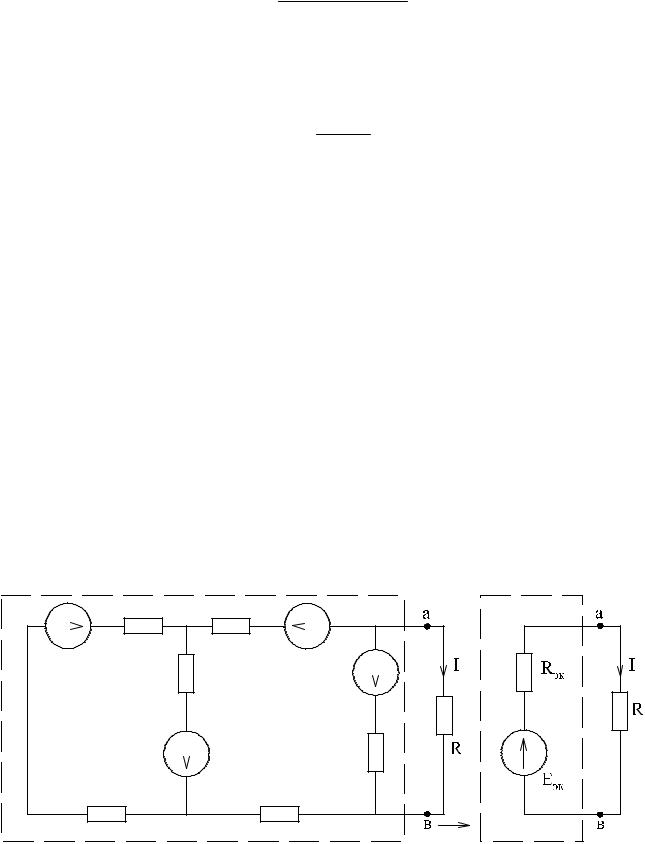
Метод узловых напряжений состоит в определении напряжений между уз- лами сложной электрической цепи путем решения уравнений, составленных по первому закону Кирхгофа, куда в качестве неизвестных входят напряжения между узлами цепи. Рассмотрим применение метода для простейшей цепи с двумя узлами (рис.3), в которой к двум узлам «х» и «y» подключены «n» ветвей.

Пусть величины ЭДС, сопротив- ления резисторов ветвей заданы. Необходимо найти все токи схемы.

По этому методу сначала опреде- ляют напряжение Uхy между узлами «х» и «y» схемы, а затем находят токи всех ветвей.

Предположим, что Uхy известно и направлено от узла «x» к узлу

«y».

Выберем произвольно положительные направления токов ветвей. Причем, в пассивных ветвях токи должны быть направлены от узла с более высоким по- тенциалом (в нашем случае это узел «х») к узлу с низким потенциалом, в актив- ных ветвях направления токов выбираются произвольно.

Применяя к каждой из ветвей закон Ома для активного участка цепи, выра- зим их токи:

I1 = q1(E1 +UXY ), I2 = q2 (E2 +UXY ),

……………………….

In = qn (En +UXY ),

	где — q1 =	1	,	q2 =	1	; ……	qn =	1		— проводимости соответствующей ветви
		R			R			R	n
		1			2

схемы.

По первому закону Кирхгофа для токов ветвей, сходящихся в узле «х», можно записать:

In … − I2 − I1 = 0

Подставляем вместо токов их значения из системы.

qn (En −UXY )…− q2 (E2 +UXY ) − q1(E1 +UXY ) = 0

Из этого равенства определяется напряжение UXY :

UXY = qn En …− q2 E2 − q1E1 qn …+ q2 + q1

или

n

å q1E1

UXY = k =1n

å qk

k =1

Напряжение между узлами параллельной цепи равно алгебраической сум- ме произведений проводимости и ЭДС каждой ветви, деленной на сумму про- водимостей всех ветвей схемы. Произведение GкЕк берут со знаком «+» в том случае, когда направление ЭДС Ек противоположно выбранному условно- положительному направлению Uхy, и со знаком «-«, когда эти направления совпадают.

Зная напряжение Uхy, пользуясь системой уравнений, можно определить токи ветвей схемы.

3. Метод эквивалентного генератора (активного двухполюсника).

Метод эквивалентного генератора используется в тех случаях, когда требу- ется определить ток в какой-либо ветви сложной схемы, а также исследовать, как будет меняться этот ток при изменении сопротивления ветви. Суть метода состоит с том, что действие всей схемы на исследуемую ветвь заменяется дей- ствием некоторого эквивалентного источника ЭДС Еэк с внутренним сопро- тивлением Rэк.

Для полученной схемы ток I определяется из закона Ома:

Следовательно задача распадается на две подзадачи: определение Еэк и опре- деление Rэк.

а) Определение Еэк.

Для того, чтобы найти Еэк достаточно разомкнуть исследуемую ветвь и за- мерить или вычислить напряжение между точками «а» и «в» — Uав, т.к.при ра- зомкнутой ветви Еэк = Uав хх,

б) Определение Rэк.

Rэк это внутреннее сопротивление всей схемы со стороны клемм «а» и «в». Для определения Rэк надо положить равным нулю все ЭДС и вычислить Rэк, используя правила преобразования пассивных цепей.

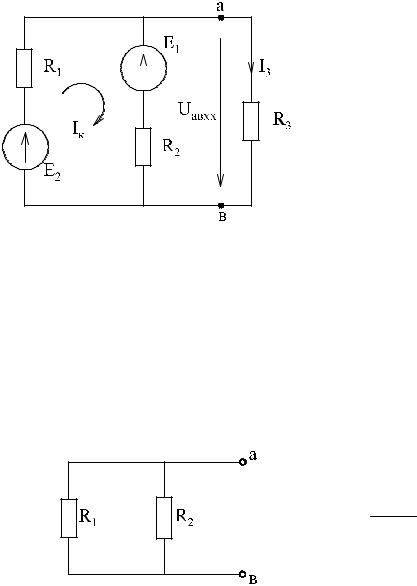
Пример:

Определить ток I3, используя метод эквивалентного генератора.

а) Размыкаем исследуемую ветвь и

вычисляем напряжение на ее концах Uав

Для этого произведем расчет вновь полученной одноконтурной цепи, оп-

	ределив сначала ток IX =	E1	− E2	, а за-
		R1	+ R2

тем напряжение Uав , используя 2-ой закон Кирхгофа (либо закон Ома для активного участка цепи).

UabXX − R2 IX = E2

Откуда

UabXX = E2 + R2 IX

б) Вычисляем Rэк

Rэк = R1+R2

R1 R2

I3 =	UabXX
		.
	Rэк + R3

Л Е К Ц И Я 4

Нелинейные цепи постоянного тока.

1.Нелинейные элементы и цепи.

2.Вольт-амперные характеристики нелинейных элементов.

3.Графоаналитические методы расчета нелинейных цепей.

1. Нелинейные элементы и цепи.

К нелинейным элементам относятся элементы, у которых вольт- амперная характеристика нелинейна. Электрическая цепь, в со- став которой входит хотя бы один нелинейный элемент, называют нелинейной электрической цепью.

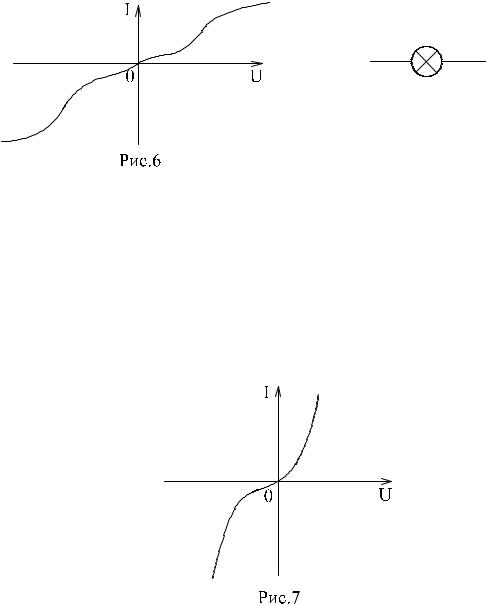
По виду вольт-амперной характеристики различают нелинейные элементы с симметричной и несимметричной характеристиками (по отношению к началу координат). Значение тока в нелинейном эле-

менте с симметричной характеристикой не зависит от полярности приложенного напряжения (рис.4), т.е. сопротивление этого эле- мента не зависит от направления тока в нем. В нелинейном эле-

менте с несимметричной характеристикой значение тока зависит от полярности приложенного напряжения (рис.5), т.е. сопротивление элемента зависит от направления тока в нем.

К нелинейным элементам с симметричной характеристикой от- носятся лампы накаливания, терморезисторы, тиритовые и вилито- вые элементы, бареттеры, электрическая дуга между одинаковыми электродами и другие.

2. Вольт-амперные характеристики нелинейных элементов.

Рассмотрим несколько примеров нелинейных элементов с сим- метричными характеристиками:

а) лампа накаливания

С ростом тока сопротивление нити увеличивается и возрастание тока замедляется (рис.6). Сопротивление не зависит от направления тока.

б) терморезистор С ростом тока сопротивление нити уменьшается (рис.7). Термо-

резистор применяют для компенсации изменений сопротивлений элементов, изготовленных из металлических проводников, сопро- тивление которых увеличивается с увеличением тока в цепи. При

последовательном же включении общее сопротивление цепи не изменяется.

в) тиритовые и вилитовые элементы С увеличением напряжения их проводимость увеличивается. На-

пример:

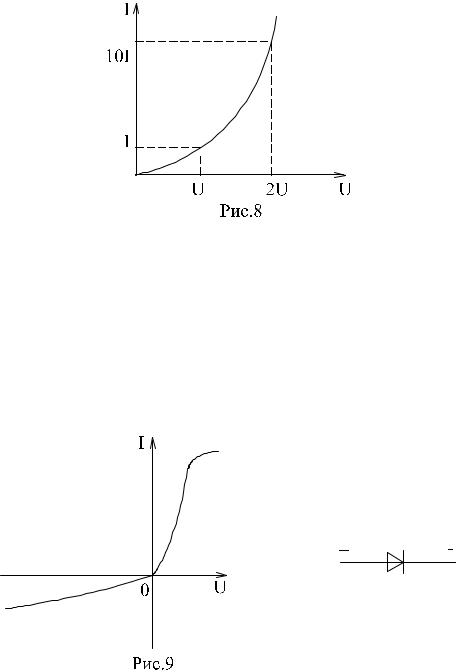
при увеличении напряжения в 2 раза ток I увеличивается в 10 раз (рис.8). Из тиритовых дисков выполняют разрядники, предна- значенные для защиты установок высокого напряжения от перена- пряжений.

К нелинейным элементам с несимметричной вольт-амперной характеристикой относятся электронные лампы, полупроводнико- вые диоды, транзисторы, электрическая дуга при неоднородных электродах и прочие.

Примеры:

а) полупроводниковый диод Проводит электрический ток, если к аноду приложен положи-

тельный потенциал, а к катоду — отрицательный (рис.9).

б) транзистор Ток коллектора различен для разных токов базы (рис.10)

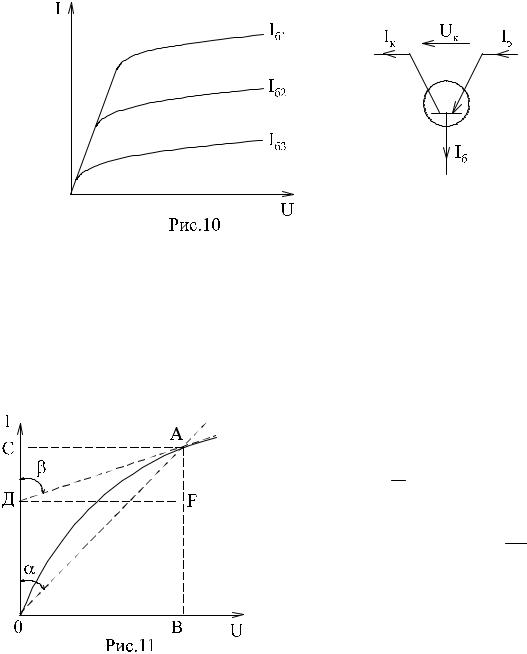
Нелинейные элементы характеризуются двумя параметрами: ста- тическим Rст и дифференциальным Rдиф сопротивлениями. Эти сопротивления изменяются от точки к точке вольт-амперной харак- теристики.

Статическим сопротивлением называется отношение напряжения к току в данной точке (рис.11)

Rст = UI = mRtgα

— масштаб сопротивления mU

mI

Дифференциальное сопротивление определяется производной к ВАХ в точке А, т.е. тангенсом угла наклона касательной в точке А.

R	æ	¶U ö		= m	tgβ
	= ç		÷
диф	è	¶I	øI =Ia	R

3. Графоаналитические методы расчета нелинейных цепей.

Курс лекций. Электротехника и электроника. РАЗДЕЛ 2. Электрические машины

118
Раздел 2. Электрические машины
Содержание
	Стр.
Раздел 2. Электрические машины…………………………………………………….	118
Содержание………………………………………………………………………………………	118

Лекция 2.1	Трансформаторы. Устройство, принцип работы и применение
трансформаторов………………………………………………………………………………		121
2.1.1 Назначение, устройство и принцип действия однофазного
трансформатора ……………………………………………………………………………..		121
2.1.2 Соотношение электрических величин, коэффициент
трансформации ………………………………………………………………………………		122
2.1.3 Эксплуатационные характеристики силовых и специальных
трансформаторов. Режимы работы трансформаторов. Характеристики
трансформаторов. …………………………………………………………………………..		124
2.1.3.1 Внешняя характеристика …………………………………………………		124
2.1.3.2 Мощность и потери энергии в трансформаторе………………..		125
2.1.3.3. Коэффициент полезного действия (КПД) трансформатора 126
Лекция 2.2 Трехфазные и измерительные трансформаторы ……………….		128
2.2.1 Трехфазный трансформатор……………………………………………………		128
2.2.2 Специальный трехфазный трансформатор………………………………		129
2.2.3 Автотрансформатор………………………………………………………………..		130
2.2.4 Измерительные трансформаторы ……………………………………………		131
2.2.4.1 Измерительный трансформатор тока………………………………..		131
2.2.4.2 Измерительный трансформатор напряжения ……………………		132
Лекция 2.3 Асинхронные машины. Устройство и принцип работы…….		135
2.3.1 Круговое вращающееся магнитное поле. Асинхронный и
синхронный принципы вращения……………………………………………………		135
2.3.2 Устройство и принцип действия асинхронного двигателя……….		139
2.3.3 Основные параметры асинхронного двигателя и их связь со
скольжением. Электромагнитный момент и механическая
характеристика двигателя……………………………………………………………….		144
2.3.3.1 Магнитный поток двигателя…………………………………………….		144
2.3.3.2 Ток ротора асинхронного двигателя…………………………………		144
2.3.3.3 Коэффициент мощности ротора……………………………………….		145
2.3.3.4 Вращающий момент асинхронного двигателя ………………….		145
Лекция 2.4	Пуск, реверс и регулирование частоты вращения
асинхронных двигателей …………………………………………………………………..		149
2.4.1 Способы пуска асинхронного двигателя …………………………………		149
2.4.1.1 Прямой пуск асинхронного двигателя………………………………		151

119
2.4.1.2 Переключение статора короткозамкнутого двигателя,
нормально работающего по схеме «Y», на время пуска на
схему « » …………………………………………………………………………………..	152
2.4.1.3 Пуск двигателя с помощью автотрансформатора……………..	154
2.4.1.4 Пуск двигателя с фазным ротором……………………………………	155
2.4.2 Изменение направления вращения (реверс) …………………………….	157
2.4.3 Частота вращения вала асинхронного двигателя и ее
регулирование………………………………………………………………………………..	158
2.4.3.1 Регулирование частоты вращения изменением числа пар
полюсов……………………………………………………………………………………..	158
2.4.3.2 Частотное регулирование скорости вращения асинхронных
двигателей………………………………………………………………………………….	159
2.4.3.2 Регулирование частоты вращения асинхронного двигателя с
фазным ротором…………………………………………………………………………	161
Лекция 2.5 Синхронные машины, устройство и принцип работы и
применение……………………………………………………………………………………….	163
2.5.1 Устройство и принцип действия синхронного генератора и
двигателя ……………………………………………………………………………………….	163
2.5.1.2 Синхронные двигатели…………………………………………………….	167
2.5.2 Потери и КПД синхронной машины ……………………………………….	169
2.5.3 Применение синхронных двигателей………………………………………	170
Лекция 2.6 Машины постоянного тока………………………………………………	173
2.6.1 Принцип работы и устройство, классификация и
применение машин постоянного тока……………………………………………..	173
2.6.1.1 Работа машины в режиме генератора……………………………….	174
2.6.1.2 Работа машины в режиме двигателя…………………………………	176
2.6.1.3 Принцип обратимости……………………………………………………..	177
2.6.1.4 Реакция якоря………………………………………………………………….	177
2.6.1.5 Устройство машины постоянного тока…………………………….	180
2.6.1.6 Потери и коэффициент полезного действия МПТ…………….	182
2.6.1.7 Виды возбуждения машин постоянного тока……………………	182
2.6.2 Механические характеристики машин с разным типом
возбуждения…………………………………………………………………………………..	183
2.6.2.1 Двигатель с независимым возбуждением …………………………	183
2.6.2.2 Двигатель с последовательным возбуждением …………………	184

Лекция 2.7 Пуск, реверс и регулирование частоты вращения двигателей

постоянного тока. ……………………………………………………………………………..	187
2.7.1 Схемы пуска, реверса двигателей постоянного тока………………..	187
2.7.1.1 Пуск ДПТ с независимым возбуждением …………………………	187
2.7.1.2 Реверс двигателя постоянного тока ………………………………….	188
2.7.2 Регулирование скорости вращения двигателей
постоянного тока по якорю и регулирование по обмотке

120
возбуждения…………………………………………………………………………………..	190
2.7.2.1 Реостатное регулирование скорости вращения ДПТ по цепи
якоря………………………………………………………………………………………….	190
2.7.2.2 Регулирование скорости вращения ДПТ изменением
величины магнитного потока. …………………………………………………….	191
2.7.2.3 Регулирование скорости вращения ДПТ изменением
напряжения на его зажимах………………………………………………………..	193

121

Лекция 2.1 Трансформаторы. Устройство, принцип работы и применение трансформаторов

План лекции

1)Назначение, устройство и принцип действия однофазного транс- форматора.

2)Соотношение электрических величин, коэффициент трансформа-

ции.

3)Эксплуатационные характеристики силовых и специальных трансформаторов. Режимы работы трансформаторов. Характеристики трансформаторов.

2.1.1Назначение, устройство и принцип действия однофазного трансформатора

При использовании электрической энергии часто требуется преобра- зовать величины напряжения U и тока I при постоянной мощности P

Например, чтобы при транспортировке электрической энергии поте- ри напряжения и мощности были минимальными, необходимо передавать энергию минимальным током, так как мощность при этом постоянна, а на- пряжение, соответственно, увеличивается:

P = U I = (U → max) (I → min) = const .

(2)

Другой пример, чтобы в электрической печи выделялось много теп- ла, необходимо питать печь током большой величины, а чтобы и здесь со- хранить мощность постоянной, необходимо соответственно снизить на- пряжение.

Таким образом, мощность P в зависимости от конкретных условий может быть получена при различных токах и напряжениях.

Проблема состоит в том, чтобы одновременно менять в одно и то же число раз ток и напряжение.

P = (	U	)( I n ) = (U n		)(	I	) = const ,	(3)
			2
1					n2
	n1

где n1 , n2 – количество раз.

Эта проблема для переменного тока решается специальным электро- магнитным аппаратом — трансформатором.

Трансформатором называется электромагнитный аппарат, ко- торый с помощью магнитного поля преобразует электрическую энер- гию одного напряжения и тока в электрическую энергию другого на- пряжения и тока при сохранении постоянной частоты и мощности.

122

Работа трансформатора основана на законе электромагнитной ин- дукции. Трансформатор не изменяет формы энергии, он лишь преобразует ее компоненты (U и I).

Трансформаторы делятся на два класса: 1) воздушные, у них нет сер- дечника; 2) со стальным сердечником. Первые применяются в высокочас- тотной технике (высокочастотная закалка, сушка). Вторые – в низкочас- тотной сильноточной промышленной технике.

В простейшем случае трансформатор можно представить следую- щим образом.

Рисунок 1 – Схема простейшего трансформатора

Это обмотка, присоединенная к источнику энергии, которая называ- ется первичной или сетевой или входной обмоткой трансформатора со своими параметрами: U1, I1, W1, E1 – первичными напряжением, током, числом витков и ЭДС, соответственно.

Обмотка, присоединенная к нагрузке, называется вторичной обмот- кой трансформатора, а U2,I2,W2,E2 – вторичными напряжением, током, чис- лом витков, ЭДС. Первичная и вторичная обмотки изолированы друг от друга и насажены на общий, набранный из листов электротехнической ста- ли магнитопровод (сердечник).

Энергия, поступающая от источника в первичную обмотку, переда- ется во вторичную обмотку только переменным магнитным потоком. Что- бы полнее передать этот магнитный поток из первичной катушки во вто- ричную и применяют магнитопровод, который направляет почти полно- стью магнитный поток, созданный первичной катушкой, во вторичную.

2.1.2 Соотношение электрических величин, коэффициент трансформации

Величина ЭДС, индуктируемая в каждой обмотке, определяется на основании закона электромагнитной индукции. Мгновенное значение ЭДС, индуктируемой в первичной обмотке трансформатора, запишется

123

	e1 = −	W1dф		, а вторичной обмотки – e2	= −	W2 dф	.	(4)
		dt				dt
	Если напряжение, подводимое к первичной обмотке, синусоидально,
	то и ток и магнитный поток тоже будут синусоидальны
	i = Im sinωt ;							(5)
	Ф = Фm sinωt .							(6)

Учтем (5) и (6) в (4), тогда мгновенные значения ЭДС обмоток мож- но записать как:

e1 =W1Em sin(ωt + 900 ); e2 = W2 Em sin( ωt + 900 ).

Максимальные значения ЭДС равны:

Em1 =W1ωФm =W1 2πfФm ; Em2 =W2ωФm =W2 2πfФm .

Разделив амплитуду ЭДС обмоток на 2 , получим действующие значения ЭДС, индуктируемые в обмотках трансформатора:

E

=

E

m1

=

W1 2πf

Фm

= 4.44W fФ ;

1

2

2

1

m

E

=

Em2

=

W2 2πf

Фm

= 4.44W

fФ .

(9)

2

2

2

2

m

В идеализированном трансформаторе (это трансформатор, в котором отсутствуют электрические и магнитные потери) имеют место следующие соотношения:

− W 1

d ф

e1

=

e1

=

− W 1

=

E 1

d t

,

,

e

2

− W 2

d ф

e

2

− W

2

E

2

d t

E1

=

U1

=

W1

= K12 = const .

(10)

E2

U 2

W2

Выражение (10)

определяет коэффициент трансформации транс-

форматора и имеет место только в идеальном трансформаторе, в реаль- ном трансформаторе эти соотношения несколько нарушаются. Однако при значениях, близких к номинальным, эти отклонения незначительны.

Коэффициентом трансформации трансформатора K12 называется

отношение витков обмотки высокого напряжения к виткам обмотки низ- кого напряжения или напряжений U1 и U2 при холостом ходе трансформа- тора.

124

При K12 >1 трансформатор является понижающим, при K12 <1 транс- форматор будет повышающим.

Трансформатор может работать в любом режиме, который располо- жен между двумя крайними, называемыми режимом холостого хода и ре-

жимом короткого замыкания.

Холостым ходом трансформатора называют такой режим ра- боты, при котором вторичная обмотка разомкнута или замкнута на сопротивлении бесконечно большой величины.

Ток во вторичной обмотке равен нулю. Магнитный поток создается первичной катушкой и называется магнитным потоком холостого хода. Ток первичной катушки при холостом ходе называется током холостого хода трансформатора I0 = I 1XX

IО ≈ (0, 05 0,10)IНОМ .

(11)

Коротким замыканием трансформатора называется такой ре- жим работы, при котором вторичная обмотка замкнута на сопротив- лении, равном 0. При этом напряжение во вторичной цепи равно ну- лю.

Забегая вперед надо сказать, что: коэффициент полезного действия трансформаторов высокий – 0,95 и более, это значит, что потери в нем ма- лы, поэтому, если пренебречь потерями, можно записать:

S1 ≈ S2 ;	(12)
U1 I1 = U 2 I2 = const .	(13)

Таким образом, трансформатор работает аналогично двухплечному рычагу, показанному на рисунке 2.

U1 = I2

U 2 I1

Рисунок 2 – К принципу работы трансформатора

Токи в обмотках трансформатора обратно пропорциональны напря- жениям.

2.1.3 Эксплуатационные характеристики силовых и специальных трансформаторов. Режимы работы трансформаторов. Характеристики трансформаторов.

2.1.3.1 Внешняя характеристика

При увеличении нагрузки напряжение на вторичной обмотке транс- форматора снижается. Данная зависимость характеризуется внешней ха-

рактеристикой трансформатора.

125

Внешней характеристикой трансформатора называется зави- симость вторичного напряжения от вторичного тока трансформатора при постоянном первичном напряжении.

Рисунок 3 – Внешняя характеристика трансформатора

Процентное изменение напряжения трансформатора:

U		=	U2 xx − U2ном	100% .	(14)
	%
			U2 xx
Для современных трансформаторов					U% = (2÷3)% .

Внешняя характеристика зависит от cosϕ2 . Чем меньше cosϕ2 , тем характеристика “ниже” при индуктивном характере нагрузки.

2.1.3.2 Мощность и потери энергии в трансформаторе

Мощность, подводимая к трансформатору (первичная) и снимаемая

на его выходе (вторичная), определяются так
P1 =U1 I1 cosϕ1 – мощность, отданная нагрузке;	(15)
P2 = U2 I2 cosϕ2 – вторичная мощность.	(16)
Баланс мощности трансформатора
P1 = P2 + P ,	(17)

где P – потери в трансформаторе.

В трансформаторе два материала: медь обмотки и железный сердеч- ник, следовательно, два вида потерь энергии.

1. Потери на нагревание меди обмоток (электрические потери):

P	= P + P		= r I 2		+ r I 2 .		(18)
М	1	2	1	1	2	2

2. Потери на нагревание железного сердечника за счет гистерезиса и вихревых токов (железные потери):

PВ=ƒ(В)2, PГ=ƒ(В)2;

P	= Р	В	+ Р	Г	= f ( B )2 .	(19)
Ж

126

Потери в обмотках трансформатора PМ (электрические) зависят от величины токов, протекающих по обмоткам:

PM = f (I12 , I22 )H – называются переменными потерями.

Потери в магнитопроводе (железе) PЖ зависят от частоты тока ƒ1 и магнитной индукции B2:

PM = f (I12 , B22 )H – называются постоянными, так как ƒ и B посто-

янны при неизменном первичном напряжении.

2.1.3.3. Коэффициент полезного действия (КПД) трансформатора

1.1. КПД трансформатора определяется отношением активных мощностей на выходе и входе трансформатора:

η		=	P2	100% =		P2		100% ,	(20)
	%					P2 +
			P1				P
где P = PM + PЖ;						PМ = PМ1 + PМ2;			PЖ = PГ + PВ .

Энергетическая диаграмма трансформатора имеет следующий вид.

Рисунок 4 – Энергетическая диаграмма трансформатора

PЭМ = P1 –

PМ1

– PЖ = E2.I2 = E2

‘I2’ – электромагнитная мощность.

P2 = PЭМ – PМ2 – мощность, отдаваемая нагрузке.

η

=

P1 −

PM −

PЖ

100% = (1−

PM − PЖ

)100% .

(21)

%

P1

P1

Если ввести понятие коэффициента загрузки β, равного

β =

S

=

I2

=

I1

,

(22)

SH

I2H

I2H

где S – текущая мощность трансформатора;

Sн– номинальная мощность трансформатора;

I1 , I2 –текущие значения токов в трансформаторе;

I1H , I2 H – номинальные токи в трансформаторе.

С учетом коэффициента загрузки КПД трансформатора можно запи- сать следующим образом:

				β 2	P +	P
η%	= 1 −				M	Ж		100% .	(23)
		β S		cosφ	+ β 2	P +
			H				P
				2		M	Ж

127

Видим, что КПД трансформатора зависит от cosϕ2 и степени загруз-

ки.

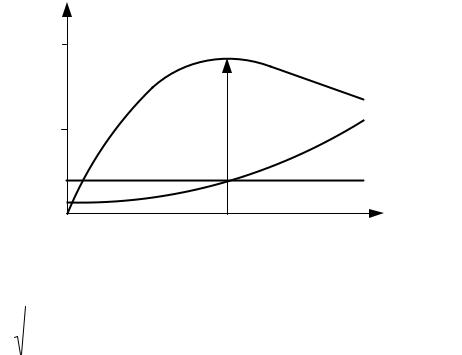
Рисунок 5 – График потерь и КПД трансформатора от нагрузки

Максимальный КПД наступает при условии, что
β Э =		PЖ		, при равенстве PМ = PЖ.	(24)
		PM

Контрольные вопросы

1.Устройство трансформатора (эскизы основных частей, материал и их назначение, охлаждение трансформаторов).

2.Принцип работы однофазного трансформатора.

3.Соотношения между электрическими величинами в трансформа- торе. Коэффициент трансформации. Три режима работы.

4.Потери энергии в трансформаторах.

5.Внешние характеристики трансформаторов.

Лекции по электротехнике (1 часть)

I A = U a Y a ; I B = U b Y b ; I C = U c Y c

I N = U NnY N

(I N = I A + I B + I C )

Как видно, смещение нейтрали вызывает различие фазных напряжений нагрузки.

Случай 3. Обрыв линейного провода А-а в четырехпроводной системе.

Аварийными будем называть случаи обрыва линейных проводов и короткого замыкания фаз нагрузки. В дальнейшем будем рассматривать аварии лишь в фазе «А».

В случае обрыва провода А-а ток I A отсутствует, поэтому

I n = I B + I C

Пренебрегая сопротивлением нейтрального провода, можем записать:

U Nn = 0 ; U b = U B ; U c = U C

Напряжение в месте обрыва U Aa можно определить, записав уравнение второго закона Кирхгофа для внешнего контура: U Aa = U A

Определение токов I B , I C трудностей не представляет, векторная диаграмма строится по аналогии с предыдущими, но с учетом выражений для тока I n и напряженияU Aa .

2. Несимметричная трехпроводная цепь, соединенная звездой. Напряжение смещения нейтрали.

При отсутствии нейтрального провода анализ трехфазной цепи, соединен- ной звездой, можно выполнить, воспользовавшись зависимостями для анализа

четырехпроводной цепи и положив в них проводимость нейтрального провода равной нулю. Тогда получим:

U Nn = U AY a +U B Y b +U C Y c Y a + Y b +Y c

Очевидно, величина смещения нейтрали в этом случае будет максималь- ной, несимметрия фазных напряжений и токов нагрузки здесь усиливается, од- нако, согласно первому закону Кирхгофа, выполняется соотношение:

I n + I B + I C = 0 .

Рассмотрим работу трехпроводной цепи в случае обрыва провода А-а. Электрическое состояние цепи в этом случае полностью определяется соот-

ношением сопротивлений в фазах нагрузки: Z b и Z c . Если Z b = Z c = Z то фазы

симметричны, подставляя в уравнение смещения нейтрали такие проводимо-

сти

Ya = 0 , Y a = Y c = Y

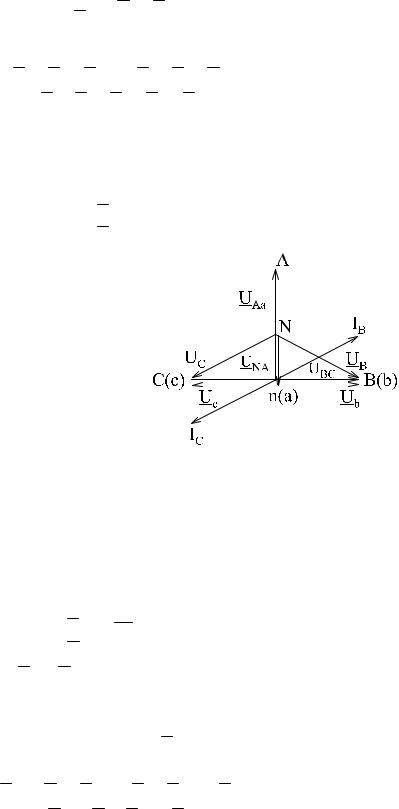
получим

U Nn = U B +U C

2

Далее определяем фазные напряжения нагрузки

U b = U B -U Nn ; U c = U C -U Nn ;

U b -U c = U B -U C = U BC

Согласно первому закону Кирхгофа

I B + I C = 0 ; I B = -I C

т.е. фазные токи уравновешивают друг друга. Вычислим отношение:

U b = -1,

U c

Это означает, что напряжения на- ходятся в противофазе, векторы Ub и Uc противоположны по направ- лению.

Если сопротивления нагрузки однородны , то

		U			b = — Z b < 0
			U
					c	Z c
	Это означает,					что напряжения находятся в противофазе и различны по ве-

личине. Точка n , оставаясь на отрезке ВС, смещается с его середины. Смещение нейтрали также определяется по формуле узлового напряжения,

векторные соотношения для остальных величин сохраняются.

В случае полностью несимметричной нагрузки Z a ¹ Z b ¹ Z c точка n (конец вектора смещения нейтрали) находится вне отрезка ВС. Соотношение

U b = — Zb e j(ϕb −ϕc )
U c	Zc

показывает, что векторы U b и U c различны по величине и не лежат на одной прямой.

При коротком замыкании фазы «а»(Z a = 0) смещение нейтрали становится равным напряжению фазы «А» генератора: U Nn = U A . Напряжения на фазах на- грузки определяем из уравнений второго закона Кирхгофа:

U b = -U A +U B = -(U A -U B ) = -U AB ;

U c = -U c -U A = -U CA .

Ток короткого замыкания фазы определим из уравнения первого закона Кирхгофа для узла «n»:

I A = -I B — I C = -(I b + I c )

Анализ показывает, что при коротком замыкании одной из фаз напряжение на других фазах становится равным линейному. При изменении соотношения

нагрузки фаз Z b и Z c изменяются лишь величины и взаимное расположение векторов токов I A , I B и I C .

Короткое замыкание фазы нагрузки в четырехпроводной цепи недопустимо, поскольку ведет к короткому замыканию соответствующей фазной обмотки ге- нератора.

ЛЕ К Ц И Я 11

1.Трехфазная цепь, соединенная треугольником. Симметричная нагрузка.

2.Трехфазная цепь, соединенная треугольником при несимметричной нагрузке.

3.Мощность трехфазной цепи.

1.Трехфазная цепь, соединенная треугольником. Симметричная

нагрузка.

Соединение обмоток генератора или фаз приемника, при котором начало одной фазы соединяется с концом другой, образуя замкнутый контур, называ- ется соединением треугольником ( ) . Таким образом, нагрузка включается между линейными проводами.

Начало фазы «А» источника питания соединяют с концом фазы «В» и точку соединения обозначают «А». Далее соединяют точки «В» и «Z» (точка «В») и точки «С» и «X» (точка «С»). Направления ЭДС приняты как и при рассмотре- нии схемы соединения звездой.

Подобным образом соединяют треугольником и фазы приемника, сопротив- ления которых обозначены двумя индексами, соответствующими началу и кон- цу фазы.

По фазам приемника протекают фазные токи I ab , I bc , I ca . Условно положи- тельное направление фазных токов приемника принято от точки первого ин- декса к точке второго индекса. Условно положительное направление фазных напряжений U ab ,U bc ,U ca совпадает с положительным направлением фазных то- ков. Условное положительное направление линейных токов I A , I B , I C принято от источника питания к приемнику.

Поскольку каждая фаза нагрузки включена между линейными проводами, то линейное напряжение равно фазному напряжению:

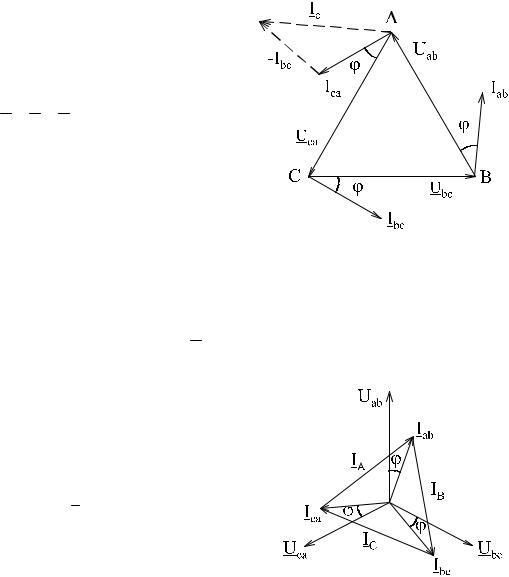
Комплексные токи в фазах нагрузки могут быть определены по закону Ома:

I ab =

U

ab ;

I bc =

U

bc ; I ca

=

U

ca

Z ab

Z bc

Z ca

где

U

ab = UЛ e j30 ;

U

bc = UЛ e− j90 ;

U

ca = UЛ e j150 .

Комплексные токи в линейных проводах связаны с фазными токами пер- вым законом Кирхгофа:

I A = I ab − I ca ; I B = I bc − I ac ; I C = I ca − I bc .

Итак, линейные токи при соединении треугольником равны векторной раз- ности фазных токов тех фаз, которые соединены с данным линейным прово- дом.

Отсюда следует, что векторная сумма линейных токов равна нулю:

I A + I B + I C = 0 .

Система линейных-фазных на- пряжений U ab ,U bc ,U ca при соедине-

нии треугольником образует такой же замкнутый треугольник, как и при соединении звездой.

Если нагрузка симметрична, то

Z ab = Z bc = Z ca = Z ,

и из полученных соотношений следует, что фазные токи нагрузки и линейные токи одинаковы:

I A = I B = I C = IЛ ; I ab = I bc = I ca = IФ = U Ф / Z ,

а их векторы образуют симметричные системы.

Из векторной диаграммы следует, что

при симметричной нагрузке величины линейных и фазных токов связаны соотношением:

I Л = 2IФ cos600

I Л = 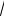3IФ .

2. Трехфазная цепь, соединенная треугольником при несимметричной нагрузке.

В случае несимметичной нагрузки

Z ab ¹ Z bc ¹ Z ca ,

и симметрия векторных систем токов нарушается. Но в любом случае сис-

тема векторов фазных напряжений остается жесткой, а также всегда вы- полняется соотношение между линей- ными токами:

I A + I B + I C = 0 .

В случае обрыва линейного провода А-а при соединении треугольником фазы нагрузки ca и ab оказываются соединенными последовательно, их можно рассматривать как одно общее сопротивление Z = Z ca + Z ab , которое, как и со- противление фазы bc , находится под напряжением U bc .

Согласно второму закону Кирхгофа

U bc + I ca Z ca + I ab Z ab = 0 ,

но поскольку

то

I ca = I ab = I ;

—

U

U

I =

bc

= —

bc

Z ca + Z ab

Напряжения на фазах ca и ab :

Z

U

ca = I Z ca ;

U

ab = I Z ab = —

U

bc —

U

ca .

Рассматривая abc как контур, получим соотношение:

U ab +U bc +U ca = 0

Линейные токи определяются из уравнений первого закона Кирхгофа для узлов «с» и «b», но теперь I c = -I b .

При построении векторной диаграммы может оказаться полезным анализ от- ношения напряжений. Например, при симметричной нагрузке Z ab = Z ca

и			U		ca	= 1
		U
				ab

т.е. векторы U ca и U ab совпадают по фазе и по величине.

Напряжение в месте обрыва определяется таким образом:

	U	Aa =	U	AB −	U	ab ;		3		UAB = UAa
							2

При несимметричной нагрузке отношение U ca является комплексным чис-

U ab

лом, значит, точка «а» находится вне отрезка bc .

В случае обрыва фазы ab нагрузки для анализа электрического состояния цепи можно использовать полученные ранее соотношения между токами и на- пряжениями, учитывая, что

Z ab = ∞ ; I ab = 0

при этом режимы работы остальных фаз не нарушаются, изменяются лишь линейные токи I A и I B .

Соотношения между токами с учетом	I ab = 0 имеют вид:
I A = −Ica ;	I B = I bc

I C = I ca − I bc

Напряжение в месте обрыва равно линейному напряжению Uab .

3. Мощность трехфазной цепи.

Каждую фазу нагрузки в трехфазной цепи можно рассматривать как цепь однофазного переменного тока. Соотношения для мгновенной, активной, ре- активной, полной и комплексной мощностей ранее были получены.

Мгновенные мощности фаз можно определить согласно выражению:

PФ (t) = UФ (t) iФ (t) .

Суммарная мгновенная мощность будет равна

P = Pa + Pb + Pc

Тогда получим

P(t) = 3UФ IФ cosϕ = 3PФ = P

где PФ — активная мощность одной фазы, а P — суммарная активная мощность нагрузки. Получаем вывод: суммарная мгновенная мощность симметричной трехфазной цепи не изменяется во времени и равна суммарной активной мощ- ности всей цепи.

Реактивная и полная мощности определяются так:

Q= 3QФ = 3UФ IФ sinϕ

S = 3SФ = 3UФ IФ

Через линейные токи и напряжения мощности могут быть определены:

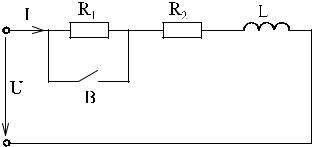
ЛЕ К Ц И Я 12

1.Основные понятия и принципы анализа переходных процессов.

2.Переходные процессы в цепи постоянного тока с последовательным соединением элементов R и L .

3.Переходные процессы в цепи постоянного тока при эксплуатации конденсатора.

1.Основные понятия и принципы анализа переходных процессов.

Процессы в электрических цепях постоянного и переменного тока в уста- новившемся состоянии были рассмотрены в предшествующих лекциях. Эти установившиеся режимы характеризуются тем, что токи в ветвях и напряже-

ния на участках цепи или остаются неизменными или изменяются по одному и тому же закону, например:

	при постоянном напряжении I =	U
		R	U = Um sinωt,
	при синусоидальном напряжении
			i = Im sin(ωt -ϕ).

Эти токи и напряжения называются установившимися токами и напряже- ниями.

Любое изменение состояния электрической цепи (включение, отключение, изменение параметров цепи и т.д.) называется коммутацией. Будем считать, что процесс коммутации осуществляется мгновенно. Энергетическое же со- стояние цепи не может измениться мгновенно.

Пример:

В цепи при разомкнутом вы-

ключателе «В»	протекает уста-
новившийся ток	I1 = U /(R1 + R2 ) ,
определяемый только сопротив-

лением цепи. При замыкании вы- ключателя, т.е. при шунтирова-

нии резистора R1 , установивший-

ся ток в цепи I2 = U / R2 > I1 .

Если предположить, что ток в цепи изменяется мгновенно от I1 до I2 то в

индуктивной катушке в этот момент времени переменным током индуцируется ЭДС самоиндукции

eL = -L Di / 0 ¾® ∞

Но любая самоиндукция препятствует изменению тока в цепи. Поэтому предположение о мгновенном изменении тока в цепи неверно. Только в иде- альном случае, когда L = 0 , можно рассматривать изменение тока как мгновен- ное.

Первый закон коммутации. Ток в цепи с катушкой индуктивности не может измениться скачком.

Второй закон коммутации. Напряжение на зажимах конденсатора или дру- гого емкостного элемента не может измениться скачком.

Индуктивные и емкостные элементы являются инерционными, вследствие

чего для изменения энергетического состояния электрической цепи требуется некоторый промежуток времени, в течение которого происходит процесс, ко-

торый зависит от параметров цепи. Т.е. переход в установившийся режим,			для
которого соответствует строго определенное энергетическое состояние,			на-
пример, для конденсатора	определенное	значение энергии электрического
поля WЭ = CU 2c / 2 и для	индуктивной	катушки энергии магнитного поля

WМ = Li2L / 2 , необходим некоторый промежуток времени t .

В этот промежуток времени (несколько секунд и доли секунды), токи и на- пряжения на отдельных участках цепи могут достигать больших значений ино- гда опасных для электроустановок. Поэтому необходимо уметь рассчиты-

вать токи и напряжения переходных процессов и на основании полученных данных разрабатывать меры защиты электрической цепи.

Переходный процесс можно описать дифференциальным уравнением. Ре- жим линейных электрических цепей с постоянными параметрами R, L и C опи- сывается линейным дифференциальным уравнением с постоянными коэффи- циентами. Так режим цепи синусоидального тока при последовательном со- единении R, L и C и напряжении источника питания U = U m sinωt , описывается

уравнением

di 1

Ri + L dt + C òidt = Um sinωt

Общее (полное) решение дифференциального уравнения запишем в виде

i = i/ + i//

где i — ток в переходном режиме,

i/ — частное решение данного неоднородного уравнения,

i// — общее решение однородного дифференциального уравнения.

Ток i/ называется установившимся током (постоянный ток после окончания переходного процесса).

Ток i// находят при решении уравнения без свободного члена. Физически это означает, что приложенное к цепи напряжение равно нулю, т.е. цепь пред- ставляет замкнутый контур, состоящий из последовательного соединения R, L и C . Ток поддерживается за счет запасов энергии в магнитном и электрическом поле катушки и конденсатора. Так как эти запасы ограничены и при протека- нии тока i// по элементам с сопротивлением происходит рассеяние энергии в виде теплоты, то через некоторое время этот ток становится равным нулю. Ток i// называется свободным, т.к. его определяют в свободном режиме цепи.

Напряжение на элементах цепи U = U / + U // имеет тот же физический смысл, что и ток i в переходном режиме.