Лекция 1.1. Элементы электрических цепей

1.Предмет и задачи дисциплины. Построение курса. Методика работы над учебным материалом.

Электротехника — область науки и техники, использующей электрическое и магнитное явления для практических целей. История развития этой науки занимает два столетия. Она началась после изобретения первого электрохимического источника электрической энергии в 1799 г. Именно тогда началось изучение свойств электрического тока, были установлены основные законы электрических цепей, электрические и магнитные явления стали использоваться для практических целей, были разработаны первые конструкции электрических машин и приборов. Жизнь современного человека без использования электрической энергии немыслима.

Большой вклад в развитие электротехники внесли русские ученые. Так еще в 1802 г. Выдающийся русский ученый В.В. Петров впервые указал на возможность использования электрической дуги для освещения. Было разработано большое число конструкций дуговых ламп освещения. Но наиболее экономичной оказалась электрическая свеча П.Н. Яблочкова (1876г). В предложенной Яблочковым конструкции был впервые применен для практических целей трансформатор. Но главная заслуга изображения в том, что оно повысило спрос на генераторы переменного тока.

Все возрастающая потребность в использовании электрической энергии привело к проблеме ее централизованного производства, передачи на дальние расстояния, распределения и экономичного использования. Решение проблемы привело к разработке и созданию трехфазных электрических цепей. Огромная заслуга в создании элементов таких цепей принадлежит выдающемуся русскому ученому М.О. Доливо-Добровольскому. Он создал трехфазный асинхронный двигатель, трансформатор, разработал четырехпроводную и трехпроводную цепи (1891г.).

Сегодня электрическая энергия используется в технике связи, автоматике, измерительной технике, навигации. Она применяется для выполнения механической работы, нагрева, освещения, используется в технологических процессах (электролиз), в медицине, биологии, астрономии, геологии и др. Столь обширное проникновение электротехники в жизнь человека привело к необходимости включить ее в состав общетехнических дисциплин при подготовке специалистов всех технических специальностей. При этом перед студентами стоят две главные задачи. Первая задача — ознакомиться и усвоить физическую сущность электрических и магнитных явлений. Это позволит понять принципы работы электромагнитных устройств, правильно их эксплуатировать.

Однако, современному специалисту недостаточно знаний одних физических явлений. Поэтому студенты неэлектрических специальностей должны получить навыки в методах расчетов элементарных цепей и устройств, необходимых для успешного изучения последующих прикладных курсов.

Дисциплина «Электротехника и электроника» рассчитана на 80 (88) часов. Из них 40 часов — лекций, 20 часов — практических занятий, 20 (28) часов — лабораторных занятий. Она включает два раздела «Электротехника» и «Электроника», завершается КП, зачетом (экзаменом). Курс построен так, что каждая из 7 тем закрепляется практическими и лабораторными занятиями. Эти виды занятий сопровождаются текущим контролем, который положен в основу формирования рейтинга студента. Поэтому залогом успешного освоения дисциплины является систематическая работа над материалом.

Весь теоретический материал имеет строгое математическое обоснование. Он востребует знания студентов по математике ( разделы векторной алгебры, дифференциального, интегрального, комплексного исчисления, рядов), а также по физике (разделы электричества, магнетизма, молекулярной физики).

Курс лекций. Электротехника и электроника. РАЗДЕЛ 1. Электрические цепи

14

Чтобы ток короткого замыкания не разрушал источника его внут- реннее сопротивление не должно быть слишком малым.

Если записать уравнения электрического состояния цепи, показан-

ной на рисунке 1, по второму закону Кирхгофа, то получим
	E − U − U = 0 , отсюда U = E − U = E − RO I .		(6)
	Из выражения (1.5) следует, что
	U = E при I XX = 0	.	(7)

ЭДС источника численно равна напряжению на его клеммах при холостом ходе.

ЭДС источника отличается от напряжения источника на вели- чину потери напряжения внутри источника.

ЭДС — самое большое напряжение, которое может развивать ис- точник при холостом режиме.

Из выражения (5) следует, что внутреннее сопротивление должно быть минимальным, чтобы внутри источника не было больших потерь на- пряжения.

Из условий (4) и (5) выбирается оптимальное значение величины внутреннего сопротивления RO источника.

1.1.3 Законы Кирхгофа

Рисунок 11 – Великий немецкий физик Густав Роберт Кирхгоф.

Член Берлинской АН ( 1875), член-корреспондент Санкт- Петербургской академии наук (1862)

До сих пор мы рассматривали простые или неразветвленные цепи. Эти цепи решаются с помощью за- кона Ома. Сложные или разветв- ленные цепи рассчитываются при помощи законов Кирхгофа.

Законы Кирхгофа являются основными расчетными законами электротехники. Закон Ома частный случай законов Кирхгофа.

Портрет великого немецкого физика Г.Р. Кирхгофа приведен на рисунке 11.

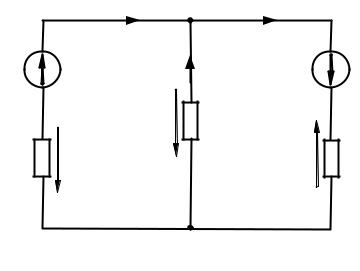
Сложной или разветвленной цепью называют такая, в которой имеется несколько путей для рас- текания токов (см. рисунок 12).

Точки разветвления цепи А и Б — узлы цепи.

Узлами называются точки цепи, в которых соединяются ме-

15

жду собой три или более проводников.

Проводники, соединяющие между собой узлы, называются вет- вями.

Рисунок 12 — Сложная цепь постоянного тока

Ветви бывают двух видов: активные и пассивные.

Активной ветвью называется такая ветвь, которая содержит не только сопротивления, но и источники энергии.

Пассивной ветвью называется такая ветвь, которая содержит только сопротивления, но не содержит источников энергии.

Таким образом, сложная цепь состоит из узлов и ветвей, то есть из 2- х элементов, поэтому и законов Кирхгофа два. Первый закон Кирхгофа управляет узлами, а второй — ветвями (контурами).

Первый закон Кирхгофа гласит:

В любом узле сложной цепи алгебраическая сумма токов равна нулю.

i=n
∑Ii		= 0	,	(8)
i=3	A

где i — количество токов связанных с рассматриваемым узлом; А — обозначение рассматриваемого узла.

Первый закон основан на принципе невозможности накопления электрического заряда в одной точке цепи.

Принято токи, притекающие к узлам цепи, считать положитель- ными и брать со знаком плюс, а токи, оттекающие от узлов, считать отрицательными и брать со знаком минус.

16

Запишем первый закон Кирхгофа для узлов А и Б нашей цепи (рису-

нок 1.10).

i =3

= I1

+ I2

− I3

i =3

= −I1

− I2

+ I3

∑Ii

= 0,

∑Ii

= 0.

(9)

i =1

A

i =1

Б

Сравнивая уравнения между собой, видим, что одно из них является следствием другого. Поэтому в цепи выделяют узлы, которые называют независимыми.

Независимыми узлами называют такие, которые отличаются друг от друга, хотя бы одним током.

Число независимых уравнений, составляемых по первому закону Кирхгофа, равно числу независимых узлов в сложной цепи и равно общему числу узлов в цепи без одного.

Число независимых узлов = n − 1,

(10)

где n — общее число узлов сложной цепи. Ветви сложной цепи, образуют контура. Второй закон Кирхгофа гласит:

В любом контуре сложной цепи алгебраическая сумма ЭДС и напряжений действующих в этом контуре равна нулю.

i=n	k =m
∑Ei	+ ∑Uk = 0	(11)
i=1	k =1

где i – количество источников ЭДС в рассматриваемом контуре; k – количество напряжений входящих в данный контур.

Данная формулировка справедлива, если стрелки напряжений на схеме цепи расставлены против стрелок токов.

Примечание:

В некоторых литературных источниках, стрелки напряжений направляются согласно стрелкам тока. Это допустимо, если использо- вать следующую формулировку второго закона Кирхгофа:

В любом контуре сложной цепи, алгебраическая сумма ЭДС всегда равна алгебраической сумме напряжений действующих в этом контуре.

i =n	k =m
∑Ei	= ∑U k .	(12)
i =1	k =1

Второй закон Кирхгофа записывается только для независимых кон- туров.

Независимыми контурами сложной цепи называются такие, ко- торые отличаются друг от друга хотя бы одним элементом цепи не ис- пользованным в ранее намеченных контурах.

17

Число независимых уравнений, составленных по второму закону

Кирхгофа, равно числу независимых контуров в цепи.
Число уравнений по 2-му закону Кирхгофа = q − n + 1,	(13)
где q — общее число ветвей всей цепи.

При обходе по контуру стрелки ЭДС и напряжений, совпадаю- щие с направлением обхода, берутся со знаком плюс, встречно на- правленные — со знаком минус.

Запишем уравнения электрического состояния контура (см. рисунок 12) по второму закону Кирхгофа:

а) при обходе слева направо E1 + U 2 − U1 = 0;

б) при обходе справа налево − E1 + U1 − U 2 = 0 .

Следовательно, направление обхода контуров можно выбирать про- извольно.

Законы Кирхгофа позволяют рассчитывать самые сложные цепи.

1.1.4 Баланс мощности в электрической цепи

Рассмотрим энергетический баланс в электрической цепи. Пусть за-

дана цепь вида, R I

E1, R01			+	U				+			Е2, R02
			U1		U2
			−
								−
	Рисунок 13 — К балансу мощности

Дано: E1, E2 , RO1, RO2 , R, E1 > E2 .

Найти: Составить баланс.

После расстановки стрелок тока и напряжения по второму закону Кирхгофа электрическое состояние цепи запишется

E1 − U1 − U − U 2 − E2 = 0, отсюда E1 = RO1I + RI + RO2 + E2 .

Умножим обе части равенства на ток I , получим

E I = R

I 2

+ RI 2

+ R

I + E

2

I .

1

O1

O2

Следовательно,

P

= P = E I — мощность, генерируемая в цепи.

Г

1

1

P

= R

I 2

+ RI 2

+ R

I + E

2

I — потребляемая энергия. Таким обра-

H

O1

O2

зом PГ − РН = 0 .

(14)

18

По закону сохранения энергии количество вырабатываемой в цепи энергии всегда равно количеству энергии потребляемой цепью. Следует всегда помнить, при составлении баланса энергии в цепи, что не всякий источник энергии, действующий в цепи, является генератором, а именно:

I			Когда действительный ток через источник совпадает
	+		по направлению с ЭДС источника, то этот источник выра-
	−	Е	батывает энергию, то есть является генератором.
I			Когда действительный ток через источник протекает
			навстречу ЭДС источника, то этот источник потребляет
	+
		Е	энергию, то есть является нагрузкой (пример: зарядка акку-
	−		мулятора).

1.1.5Обзор методов анализа цепей постоянного тока

Внастоящее время разработано много методов для расчета цепей постоянного тока. В зависимости от конфигурации и условий заданной це- пи для расчета цепи применяются различные методы.

Искусство расчетчика состоит в том, что он находит наиболее ра- циональный метод решения к конкретно заданной цепи. Сделаем краткий обзор наиболее употребительных методов расчета цепей.

Метод законов Кирхгофа

Это старейший из расчетных методов. Он основан на составлении уравнений по первому и второму законам Кирхгофа и решении их относи- тельно токов текущих в ветвях. Порядок системы уравнений здесь равен количеству неизвестных токов

Непосредственное применение законов Кирхгофа к расчету сложной цепи приводит к весьма громоздким вычислениям, так как приходится ре- шать систему с большим числом уравнений. Поэтому, этот метод на прак- тике применяется крайне редко в виду его неэкономичности.

Метод контурных токов

Метод контурных токов был предложен известным английским фи- зиком и электротехником Джеймсом К. Максвеллом. По этому методу цепь разбивается на ряд контуров, соприкасающихся друг с другом.

Предполагается, на время расчета, что каждый контур обтекается только присущим ему током, который называется контурным током. Кон- турных токов столько, сколько имеется в цепи независимых контуров. По-

19

скольку, контуров в цепи всегда меньше числа ветвей, то контурных токов в цепи всегда меньше числа реальных токов.

Таким образом, основное преимущество метода контурных токов перед методом законов Кирхгофа состоит в сокращении числа расчетных уравнений.

По известным контурным токам, действительные токи определяются простым алгебраическим сложением.

Метод контурных токов получил широкое распространение в инже- нерной практике, благодаря экономным затратам времени на расчет.

Метод узловых потенциалов

Метод узловых потенциалов основан на первом законе Кирхгофа и на законе Ома. Преимущество метода состоит в том, что он позволяет со- кратить число расчетных уравнений и тем самым уменьшить вычисли- тельную работу.

Согласно методу, один из узлов цепи мысленно заземляется, что не влияет на работу цепи. Потенциалы остальных узлов определяются из ре- шения специальной системы уравнений.

Токи в ветвях находят по разности потенциалов между узлами, с уче- том межузлового сопротивления.

Поскольку узлов в цепи всегда меньше, чем ветвей, метод весьма экономичен.

Метод узлового напряжения

Это частный случай метода узловых потенциалов для цепи с двумя узлами.

Чтобы токи в ветвях были рассчитаны правильно, необходимо с большой точностью находить величину узлового напряжения. В этом один из крупных недостатков метода узлового напряжения.

Указанный метод получил весьма широкое применение в расчетной практике благодаря своей экономичности в вычислительной работе.

Метод наложения (суперпозиции)

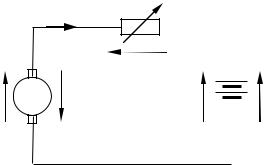
Метод основан на принципе Д’Аламбера — независимости действия сил на линейную систему. Проиллюстрируем принцип Д’Аламбера, рисун- ком 14.

Рисунок 14 — К принципу Д’Аламбера

20

В электрической цепи вместо сил используют ЭДС цепи. Схему ре- шают столько раз, сколько имеется в цепи источников энергии.

Результаты решения алгебраически суммируют.

Метод линейных преобразований

Данный метод основан на использовании закона Ома и формул по- следовательного, параллельного, смешанного соединения сопротивлений, а также перехода от соединения сопротивлений в треугольник к звезде.

Сначала сложная цепь свертывается до предельно простой и решает- ся по закону Ома – прямой путь. Затем, полученное решение развертыва- ется до заданной конфигурации цепи – обратный путь.

Основное условие применимости метода – в цепи должен быть толь- ко один источник питания.

Метод эквивалентного генератора

Метод эквивалентного генератора позволяет определить ток в одной отдельно взятой ветви сложной цепи с сопротивлением Ri , без расчета всех остальных токов.

Суть метода в том, что всю внешнюю по отношению к искомой вет- ви цепь представляют, как некий эквивалентный генератор с напряжением

на зажимах Uixx и некоторым внутренним сопротивлением RКЗ .

Ii

Эквивалентная

схема це-

пи, полученная в результате

RК

Ri

преобразований исходной схе-

U

iXX

мы,

изображена на рисунке 15.

В результате,

искомый

ток определяют по закону Ома

Ii =

Uixx

.

(15)

Рисунок 15 — Эквивалентный

RK + Ri

генератор

Контрольные вопросы

1 Цепи постоянного тока (состав и особенности элементов цепи, где применяются). Режимы работы электрической цепи (холостой ход, нор- мальный, номинальный, короткозамкнутый). Сложная цепь, ветви, узлы. Первый и второй законы Кирхгофа. Закон сохранения энергии.

21

2 Расчет цепи постоянного тока методом законов Кирхгофа (разо- брать на примере).

3 Расчет цепи постоянного тока методом контурных токов (разо- брать на примере).

4 Эквивалентные преобразования в цепях постоянного тока при по- следовательном, параллельном и смешанном соединениях сопротивлений. Эквивалентное преобразование треугольника сопротивлений в звезду.

22

Лекция 1.2 Нелинейные цепи постоянного тока

План лекции

1)Нелинейные цепи (общие понятия).

2)Графоаналитический метод расчета нелинейных цепей.

3)Графический метод расчета нелинейных цепей.

4)Аналитические расчеты нелинейных цепей.

1.2.1Нелинейные цепи общие положения и определения

Электрические цепи, содержащие элементы с нелинейными

вольтамперными характеристиками, называются нелинейными.

Нелинейные элементы делятся на симметричные и несимметричные.

Симметричными нелинейными элементами называются такие, у которых вольтамперные характеристики не зависят от направления тока в них и напряжения на зажимах.

Сюда можно отнести, например, электрические лампы, варисторы, термисторы, катушки со стальными сердечниками.

Несимметричными нелинейными элементами называются та- кие, у которых вольтамперные характеристики различны при разных направлениях тока и напряжения на зажимах.

Сюда можно отнести, например, электрическую дугу с разнородны- ми электродами, полупроводниковые приборы (диоды, транзисторы, тири- сторы).

1.2.2 Графоаналитический метод расчета нелинейных цепей.

Один из методов расчета нелинейных цепей называется графоанали- тическим. Для его использования вводят понятие статического и диффе- ренциального сопротивления нелинейного элемента;

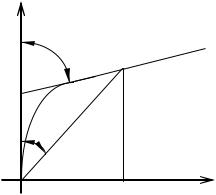
Рассмотрим эти понятия, на примере нелинейного элемента, вольт- амперная характеристика которого, изображена на рисунке 1.

I

Рисунок 1 — К определению статического и дифференциального

сопротивлений

23

На данной кривой, точка А, характеризует рабочий режим элемента. Статическое сопротивление — R , для режима в точке А, определится

следующим образом

	R =	U		=	mU		OC	= mR tgβ		,	(1)
		I			mI		CA
где mU , mI , mR							— масштабы напряжения, тока и сопротивления, соответ-
ственно.
	Статическое сопротивление пропорционально тангенсу угла между
прямой, соединяющей точку А с началом координат и осью токов.
	Дифференциальное сопротивление — R Д , для режима в точке А, оп-
ределится таким образом
	RД =		dU			= mR tgα			.		(2)
				dI

Дифференциальное сопротивление это первая производная от напряжения элемента по току в рабочей точке.

Дифференциальное сопротивление пропорционально тангенсу угла между касательной к вольтамперной характеристике в точке А и осью то- ков.

Для прямолинейных участков вольтамперных характеристик диффе- ренциальное сопротивление можно определить отношением конечного приращения напряжения к конечному приращению тока

R Д =	U	.	(3)
	I

Для элементов с возрастающей характеристикой R Д > 0 , а для эле-

ментов с падающей — RД < 0 .

На линейных участках вольтамперной характеристики величина дифференциального сопротивления остается постоянной, поэтому она и используется в аналитических расчетах.

Если вольтамперная характеристика на некотором участке близко совпадает с прямой линией и работа цепи осуществляется на этом участке, то нелинейный элемент можно заменить источником напряжения и линейным динамическим сопротивлением, то есть ак- тивной линейной ветвью.

Рассмотрим этот прием подробнее. Пусть нам даны вольтамперные характеристики двух элементов 1 и 2, изображенные на рисунке 2.

Работа цепи производится на участках ab и cd соответствующих ха- рактеристик. Найдем параметры и вид эквивалентной линейной цепи, спо- собной на время расчета заменить исходный нелинейный элемент.

Курс лекций. Электротехника и электроника. РАЗДЕЛ 1. Электрические цепи

114

г) Изображение производной функции Для n -ой производной имеем:

d n f (t)

= f

n

(t) ↔ p

n

( p) − f (0) −

f ′(0)

−

f ′′(0)

− … −

f ( n−1) (0)

F

.

(72)

dt

n

p

p

2

p

n−1

Если f (0) = f ′(0) = f ′′(0) = … = f ( n−1) (0) = 0 , то

d n f (t)

= f n (t) ↔ pn F ( p).

(73)

dtn

д) Изображение интеграла функции

t

F ( p)

∫ f (t)dt = φ(t) ↔ φ(0) +

,

(74)

0

p

t

где

φ(0) = ∫ f (t)dt

t=0 —

начальное значение интеграла функции

f (t)

0

при t = 0 .

Если начальное значение интеграла функции при t = 0 равно нулю, то:

	t	F ( p)
	∫ f (t)dt ↔		.	(75)
	0	p

Ход расчетов следующий.

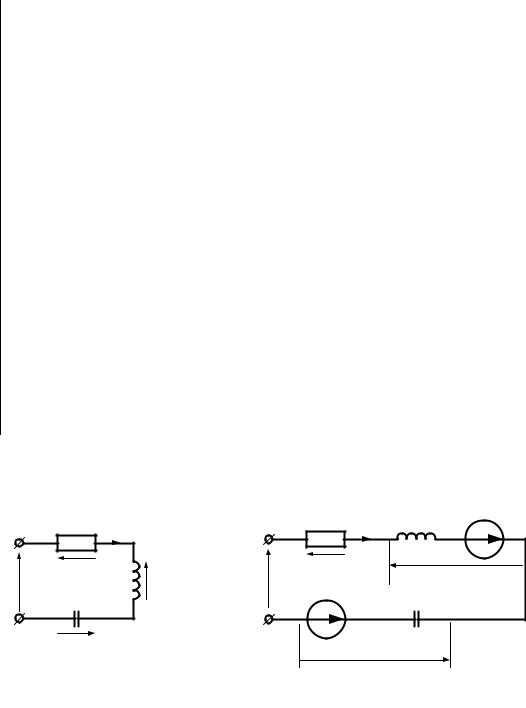
Во-первых, исходная схема преобразуется в операционный вид, ри- сунок 14. При этом:

а б Рисунок 14 – Получение операторной расчетной схемы: а – исходная

схема; б – расчетная схема в операторной форме

-все постоянные величины: ЭДС источника, активные сопротивле- ния в ветвях имеют своими изображениями такие же постоянные величи- ны;

-все индуктивные реактивные сопротивления имеют своими изо- бражениями ω L ↔ p L . Если начальное значение тока в катушке не рав-

но нулю, то последовательно с катушкой включается источник постоянно- го напряжения величиной p L i(0) , который направлен по току;

I ( p) =

				115
— все емкостные реактивные сопротивления имеют своими изобра-
жениями	1	↔ 1	( p C)	. Если начальное значение напряжение на
	(ω C)

конденсаторе отлично от нуля и равно U0 , то последовательно с емкостью включается источник постоянного напряжения величиной U0 . Направле- ние ЭДС источника – против тока.

Затем полученная расчетная схема рассчитывается любым из извест- ных методов расчета цепей. Полученный результат является функцией комплексного переменного p .

Первый закон Кирхгофа в операторной форме:

i=n
∑Ii ( p) = 0 .	(76)

i=1

Второй закон Кирхгофа в операторной форме:

i=n	k =m
∑Ei ( p) − ∑Zk ( p) Ik ( p) = 0;
i=1	k =1
i=n	k =m
∑Ei ( p) + ∑Uk ( p) = 0.
i=1	k =1

Закон Ома в операторной форме:

E( p) .

Z ( p)

Все рассмотренные ранее методы расчета цепей действительны и для расчета переходных режимов операторным методом.

Теорема разложения Хэвисайда

Ранее мы показали, что результат расчета цепи будет иметь форму операторной функции.

Решение в таком виде для практики не пригодно, его необходимо привести обратно в функцию от времени.

Выше мы указывали, что для обратного перехода необходимо в об- щем случае применять интеграл Бромвича. Однако путь этот очень сло- жен. На практике часто пользуются не интегралом Бромвича, а теоремой разложения Хэвисайда.

Теорема разложения представляет собой готовую формулу для опре- деления оригинала функции f (t) по известному изображению этой функ- ции F ( p) . Она является результатом решения интеграла Бромвича для функции F ( p) частного вида.

Функция F ( p) в этом случае должна быть выражена рациональной дробью:

116

H ( p)

a

0

+ a p + a

2

p2 + … + a

m

pm

F ( p) =

=

1

.

(79)

F ( p)

b + b p + b p2 + … + b pn

0

1

2

n

Рациональная дробь (79) кроме того,

должна удовлетворять следующим свойствам:

— наивысшая степень оператора p знаменателя

n должна быть больше наивысшей степени

оператора p числителя m или, в крайнем слу-

чае, равна ей

n ≥ m . Это условие для задач

прикладного характера почти всегда удовле-

творяется.

— корни p1 ,

p2 ,… pk ,… pn знаменателя F ( p) ,

полученные

решением

уравнения F ( p) = 0

должны быть все простые (отсутствуют корни

Рисунок 15 — Оливер

равные друг другу и кратные корни) и не один

из корней не должен ни при каких условиях

Хевисайд (1850 — 1925),

быть корнем числителя

H ( p) (не обращать

английский учёный,

числитель H ( p) в нуль при подстановке в не-

инженер, математик и

физик. Впервые применил

го p1

, p2 ,…

pk ,… pn ). Если есть дополнитель-

преобразования Лапласа

ный n+1 корень, то он может быть равен нулю.

для решения дифференци-

— все вещественные корни должны быть отри-

альных уравнений

цательными, а все комплексные – иметь отри-

цательную вещественную часть.

С учетом вышесказанного получится, что первообразная функция

f (t) операторной функции F ( p)

будет иметь следующий вид:

H ( p)

H (0)

n

H ( pk )

F ( p) =

↔ f (t) =

+ ∑

e pk t .

(80)

F ′( p )

F ( p)

F (0)

k =1

p

k

k

где член H (0)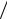 F (0) , который получается от подстановки дополнительного нулевого корня pn+1 = 0 , определяет принужденную составляющую или ус- тановившийся режим для постоянного тока или напряжения;

n	H ( pk )
			e pk t – определяет сумму свободных режимов для тока или на-
∑ p F ′( p )
k =1	k	k

пряжения.

Выражение (80) называется теоремой разложения.

Используя теорему разложения, можно находить начальную функ- цию по ее изображению, не прибегая к интегралу Бромвича, в этом и со- стоит основная ценность теоремы.

117

Контрольные вопросы

1.Понятие о переходном процессе в линейной электрической це- пи. Причины возникновения и сущность переходных процессов.

2.Классический метод расчета. Порядок составления и методы решения уравнений электрической цепи. Свободные и принужденные со- ставляющие.

3.Рассмотреть переходный процесс при включении катушки на постоянное напряжение.

4.Переходный процесс при коротком замыкании катушки с током.

5.Сформулировать первый закон коммутации. Вывести формулу энергии магнитного поля катушки.

6.Рассмотреть переходный процесс при заряде и разряде конден-

сатора.

7.Сформулировать второй закон коммутации. вывести формулу энергии электрического поля конденсатора.

8.Порядок расчета переходных процессов классическим методом. Расчет переходного процесса в последовательной цепи RLC при ее на по- стоянное напряжение.

9.Условия возникновения в цепи колебательных, переходных и апериодических режимов.

10.Операторный метод расчета переходных процессов. Законы Ома

иКирхгофа в операторной форме.

11.Операторные схемы и уравнения цепи.

12.Теорема разложения Хевисайда.

Курс лекций по дисциплине ;Теоретические основы электротехники

Занятие 10. Электрическое сопротивление

а) Электрическое сопротивление и электрическая проводимость.

Свойство материалов препятствовать прохождению через них электрического тока называется электрическим сопротивлением.

С другой стороны можно сказать, что не все материалы препятствуют прохождению через них электрического тока. Говорят, что такие материалы обладают хорошей электропроводностью.

Таким образом, электропроводность и электрическое сопротивление являются взаимообратными величинами.

Сопротивление проводника зависит от его геометрических размеров: его длины и площади поперечного сечения, а также материала, из которого изготовлен проводник..

Для проводников сопротивление прямо пропорционально длине и обратно пропорционально площади их поперечного сечения:

где:l — длина проводника; м.

s — площадь поперечного сечения; м².

— удельное сопротивление, характеризующее электропроводность данного металла,

Ом * м.

Рис. 8.1. Алюминиевый проводник

Величина, обратная электрическому сопротивлению называется электрической проводимостью G.

Где: G – проводимость, См (сименс)

Удельная проводимость, величина, обратная удельному сопротивлению.

 

Удельное сопротивление различных проводников: (·10^-6) [Ом·м]

Серебро 0,016

Медь 0,017

Алюминий 0,03

Вольфрам 0,05

Железо 0,13

Свинец 0,2

Никелин 0,42

Манганин 0,43

Константан 0,5

Ртуть 0,94

Нихром 1,1

Удельное сопротивление проводника зависит от температуры.

где: р_о – удельное сопротивление при 0 градусов,
t – температура,
α – температурный коэффициент сопротивления
( т.е. относительное изменение удельного сопротивления проводника при нагревании его на один градус)

 

 

 

 

 

 

 

 

 

 

Занятие 11. Закон Ома

 

 

а) Закон Ома для участка цепи:

 

Сила тока на участке цепи прямопропорциональна напряжению на этом участке и обратнопропорциональна сопротивлению этого же участка цепи.

Рис.11.1. Схема участка цепи

б) Закон Ома для полной цепи

 

При рассмотрении полной электрической цепи необходимо учитывать, что ток проходит не только по внешней части цепи, но также и по внутренней части цепи, т.е. внутри источника напряжения.

С учетом этого вывода закон Ома для полной цепи формулируется:

Сила тока в цепи прямо пропорциональна электродвижущей силе источника и обратно пропорциональна полному сопротивлению цепи

 

Где: Е – эдс источника, В.

R- сопротивление внешнего участка цепи. Ом.

r₀ – внутреннее сопротивление источника. Ом

Занятие 12 Контрольная работа

 

Контрольные вопросы:

1. Назовите основное свойство электрического поля.

2. Как определяется напряженность электрического поля заряженной сферы?

3. Каковы свойства линий напряженности электрического поля?

4. Что такое потенциал и разность потенциалов?

5. Дайте определение электрической цепи и ее элементов.

6. Какие преобразования энергии происходят в источнике и потребителе?

7. Объясните строение металлического проводника

8. Дайте определение электрического тока и объясните его физическую сущность.

9. От чего зависит сопротивление металлического проводника?

10. Чем отличается напряжение от электродвижущей силы?

11. Что такое электрическая проводимость ?

12. Сформулируйте закон Ома для участка цепи?

13. Сформулируйте закон Ома для полной цепи цепи?

14. Что такое внутреннее сопротивление цепи?

Примечание: Каждому учащемуся необходимо решить задачу, предложенную преподавателем.

Занятие 13. Энергия и мощность электрического тока.

 

а) Энергия электрического тока.

Для создания электрического тока в цепи источник должен обладать необходимой энергией. Величина этой энергии определяется по формуле:

или

Где: W – энергия электрического тока, Вт·ч

U – напряжение на зажимах цепи, В.

I – сила тока, А.

R – сопротивление цепи, Ом.

t – время протекания тока, час.

б) мощность электрического тока

Различные источники электрической энергии могут за один и тот же промежуток времени выдавать различное количество электрической энергии.

Способность источника выдавать в единицу времени определенное количество электрической энергии, а потребитель, соответственно, – потреблять эту энергию характеризуется мощностью источника (потребителя).

Значение мощности электрического тока определяется из выражения :

или

Где: W – энергия электрического тока, Вт·ч

t – время работы источника (потребителя), час.

Р – мощность источника (потребителя), Вт.

U – напряжение, В

I – сила тока, А.

R – сопротивление цепи, Ом.

Мощность, развиваемая источником тока во всей цепи, называется полной мощностью.

Она определяется по формуле

где: Pобщ —полная мощность, развиваемая источником тока во всей цепи, Вт;

Е— э. д. с. источника, В;

I-величина тока в цепи, А.

В общем виде электрическая цепь состоит из внешнего участка (нагрузки) с сопротивлением R и внутреннего участка с сопротивлением R₀ (сопротивлением источника тока).

Заменяя в выражении полной мощности величину э. д. с. через напряжения на участках цепи, получим

Величина UI соответствует мощности, развиваемой на внешнем участке цепи (нагрузке), и называется полезной мощностью  Pпол=UI

Величина U_oI соответствует мощности, бесполезно расходуемой внутри источника, её называют мощностью потерь P_o=U_oI.

Таким образом, полная мощность равна сумме полезной мощности и мощности потерь

P_общ=P_пол+P_о

 

в) Коэффициент полезного действия электрической цепи

Отношение полезной мощности к полной мощности, развиваемой источником, называется коэффициентом полезного действия, сокращенно к. п. д.,и обозначается η

Из определения следует

При любых условиях коэффициент полезного действия η ≤ 1.

Рис.13.1 Энергетическая диаграмма электрической цепи

Рассмотрим элементарную электрическую цепь, содержащую источник ЭДС с внутренним сопротивлением r, и внешним сопротивлением R

Рис.13.2. Схема электрической цепи

КПД определяется как отношение полезной мощности к затраченной:

или

Обычно электрический к. п. д. принято выражать в процентах.

Занятие 14 Тепловое действие тока

 

а) Общие определения

 

В проводнике, по которому течет электрический ток, также как и во всех телах, есть движение молекул. При наличии тока в проводнике движущиеся электрические заряды усиливают движение молекул, что и является причиной повышения температуры проводника. Явление выделения тепла при протекании тока по проводнику может иметь как вредные последствия , так и приносить пользу. Например, с помощью электрического тока можно нагревать спираль электронагревательных приборов. Однако, протекая по изолированному проводу ток нагревает его изоляцию приводя ее к преждевременному износу и разрушению

 

б) Закон Джоуля-Ленца.

Количества теплоты, выделяемой током при прохождении по проводнику зависит от сопротивления проводника, силы тока и времени его прохождения.

Количественные соотношения, имеющие место при нагревании проводника током называются законом Джоуля – Ленца.

Где: Q – количество теплоты [Дж]

в) Элементы тепловой защиты электроаппаратов

Плавкие предохранители применяются для защиты электроустановок от токов короткого замыкания.

Рис.14.1. Плавкие предохранители различных типов

Основным элементом предохранителя является плавкая вставка, которая сгорает (плавится) при значительном повышении тока в сети.

Защитное действие плавкого предохранителя основано на тепловом эффекте электрического тока. Протекая по плавкой вставке ток нагревает ее. Если величина тока значительно возрастает, то количество выделяемой током теплоты становится достаточным для расплавления плавкой вставки.

При расплавлении плавкой вставки электрическая цепь разрывается и потребитель обесточивается.

Этим способом достигается обеспечение сохранности дорогостоящего оборудования.

Рис.14.2. Плавкие вставки предохранителей

 

Контрольный опрос №1
Напишите пары чисел и букв из первого и второго столбцов соответствующие определениям

1. контактный нож
2. фарфоровый корпус
3. крышка
4. болты контактной шайбы
5. болты крышки

 

Занятие 15. Аппараты управления

 

 

а) Кнопки управления

предназначены для замыкания и размыкания цепей дистанционного управления электродвигателями.

Комплект из нескольких кнопок “ПУСК” и “СТОП”, объединенных в одном корпусе

называется кнопочной станцией.

 

 

Рис.15.1. Кнопки управления

 

 

 

 

б)Концевые и путевые выключатели

применяются для переключения цепей управления по мере передвижения элементов механизмов и для автоматического отключения механизма в конце его рабочего пути.

Рис.15.2. Концевые и путевые выключатели

 

в) Магнитный пускатель

– это распространенный электромагнитный аппарат для дистанционного и местного управления электродвигателями и другими установками, а также защиты их от перегрузок и токов короткого замыкания.

Рис.15.3. Магнитный пускатель

г)Тепловое реле

является составной частью магнитного пускателя.

Тепловые реле предназначены для защиты электродвигателей от перегрузок и токов короткого замыкания.

Действие теплового реле основано на изгибании биметаллической пластинки при ее нагревании током перегрузки.

 

 

 

Тепловое реле состоит (см.рисунок)

1-биметаллическая пластинка;

2-нагревательный элемент;

3-кнопка возврата;

4-пружина;

5-тяга;

6-контакт;

7-рычаг;

8 – ось;

Рис.15.4. Внешний вид теплового реле и его схема

 

Работа теплового реле:

При перегрузке электродвигателя в линейных проводах протекают большие токи, значительно больше номинальных значений. Этот ток протекает через нагревательный элемент 2.

Элемент нагревается и нагревает биметаллическую пластинку 1.

Пластинка изгибается вверх, освобождая из зацепления рычаг 7.

Рычаг под действием пружины 4 поворачивается по часовой стрелке на оси 8 и приводит в движение тягу 5, при помощи которой контакты 6 цепи управления размыкаются.

Размыкание контактов в цепи управления магнитного пускателя приводит к разрыву силовой цепи. Электродвигатель отключается, что предотвращает выход его из строя при перегрузке.

При выключении силовой цепи нагревательный элемент 2 остывает, биметаллическая пластинка возвращается в исходное состояние.

Рычаг 7 возвращается в исходное состояние путем нажатия на кнопку возврата.

Занятие 16. Баланс мощностей

 

а) Общие требования к составлению уравнений баланса электрической цепи

 

Из закона сохранения энергии следует, что мощность источников питания в любой момент времени равна сумме мощностей, расходуемой на всех участках цепи.

Это соотношение называют уравнением баланса мощностей.

При составлении уравнения баланса мощностей следует учесть, что если действительные направления ЭДС и тока источника совпадают, то источник ЭДС работает в режиме источника питания, и произведение E I подставляют в со знаком плюс.

Если не совпадают, то источник ЭДС работает в режиме потребителя электрической энергии, и произведение E I подставляют в со знаком минус.

Рассмотрим электрическую цепь, приведенную на рисунке:

Рис.16.1. К расчету баланса электрической цепи

Для цепи, показанной на рисунке уравнение баланса мощностей запишется в виде:

При расчете электрических цепей используются определенные единицы измерения.

Электрический ток измеряется в амперах (А),

– напряжение – в вольтах (В),

– сопротивление – в омах (Ом),

– мощность – в ваттах (Вт),

– электрическая энергия – ватт-час (Вт-час)

– проводимость – в сименсах (См)

Кроме основных единиц используют более мелкие и более крупные единицы измерения:

– миллиампер (1мA = 10^–3А),

– килоампер (1кA = 10³А),

– милливольт (1мВ = 10^–3В),

– киловольт (1кВ = 10³В),

– килоом (1кОм = 10³Ом),

– мегаом (1мОм = 10⁶Ом),

– киловатт (1кВт = 10³Вт),

– киловатт-час (1кВт-час = 10³ ватт-час).

б) Режимы работы электрических цепей

 

Элементами электрической цепи являются различные электротехнические устройства, которые могут работать в различных режимах.

Режимы работы как отдельных элементов, так и всей электрической цепи характеризуются значениями тока и напряжения.

Поскольку ток и напряжение в общем случае могут принимать любые значения, то режимов может быть бесчисленное множество.

Реальная электрическая цепь может быть представлена в виде активного и пассивного двухполюсников

Рис. 16.2. Включение активного и пассивного двухполюсников

Двухполюсником называют цепь, которая соединяется с внешней относительно нее частью цепи через два вывода а и b – полюса.

Режим работы электрической цепи, приведенной на рисунке, определяется изменениями параметров пассивного двухполюсника, в общем случае величиной сопротивления нагрузки Rн.

При анализе электрической цепи рассматривают следующие режимы работы:

– холостого хода,

– номинальный,

– короткого замыкания

– согласованный.

Работа активного двухполюсника под нагрузкой Rн определяется его вольт-амперной (внешней) характеристикой, уравнение которой для данной цепи запишется в виде

Вольт-амперная характеристика строится по двум точкам 1 и 2, соответствующим режимам холостого хода и короткого замыкания

Рис.16.3. Вольт-амперная характеристика

Режим холостого хода

В этом режиме с помощью ключа SA нагрузка Rн отключается от источника питания (см.рисунок).

В этом случае ток в нагрузке становится равным нулю, и как следует из формулы напряжение на зажимах ab становится равным ЭДС Eэ и называется напряжением холостого хода Uхх

 

Режим короткого замыкания

В этом режиме ключ SA в схеме электрической цепи замкнут, а сопротивление Rн=0.

В этом случае напряжение U на зажимах аb становится равным нулю, т.к. U = IRн, а уравнение вольт-амперной характеристики можно записать в виде:

Номинальный режим

Номинальный режим электрической цепи обеспечивает технические параметры как отдельных элементов, так и всей цепи, указанные в технической документации, в справочной литературе или на самом элементе.

Для разных электротехнических устройств указывают свои номинальные параметры. Однако три основных параметра указываются практически всегда:

– номинальное напряжение Uном,

– номинальная мощность Рном

– номинальный ток Iном.

Работа активного двухполюсника под нагрузкой в номинальном режиме определяется следующим уравнением, записанном для номинальных параметров

На вольт-амперной характеристике это уравнение определяется точкой 3 с параметрами Uном и Iном.

При этом на нагрузке выделится активная мощность

Расчеты показывают, что значение сопротивления нагрузки, согласованное с сопротивлением источника, при котором в нагрузку будет предаваться максимальная мощность будет равно:

При этом значение максимальной мощности, которая может выделена в нагрузке Rн будет равна

Полезная мощность, выделяющаяся в нагрузке, определяется уравнением

Полная активная мощность, выделяемая активным двухполюсником, равна

Коэффициент полезного действия

при

Для мощных электротехнических устройств такое низкое значение КПД недопустимо. Но в электронных устройствах и схемах, где величина Р измеряется в милливаттах, с низким КПД можно не считаться, поскольку в этом режиме обеспечивается максимальная передача мощности на нагрузку

 

Занятие 17. Контрольная работа №3 ЭТ У17

Контрольные вопросы

1. Напишите формулу и дайте определение энергии электрического тока
2. Напишите формулу и дайте определение мощности электрического тока
3. Напишите формулу и дайте определение коэффициента полезного действия электрической цепи.
4. Начертите и объясните энергетическую диаграмму электрической цепи.
5. Как проявляется тепловое действие электрического тока и от чего оно зависит?
6. Напишите формулу и объясните закон Джоуля – Ленца.
7. Опишите устройство плавкого предохранителя.
8. Что такое плавкая вставка и как она работает?
9. Перечислите аппараты управления электрическими цепями.
10. Начертите чертеж конструкции теплового реле и перечислите его составные части.
11. Опишите работу теплового реле.
12. Напишите формулу и объясните понятие баланса мощностей электрической цепи.
13. Опишите единицы измерения, используемые при расчете электрических цепей.
14. Опишите режим холостого хода электрической цепи
15. Опишите номинальный режим работы электрической цепи
16. Опишите режим короткого замыкания электрической цепи
17. Что такое вольт-амперная характеристика электрической цепи?
18. Начертите вольт-амперную характеристику цепи и укажите точки холостого хода и короткого замыкания электрической цепи
    

Методическая разработка курс лекций по дисциплине: «Электротехника и электроника»

МИНОБРНАУКИ РОССИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ЮГОРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Сургутский нефтяной техникум (филиал)

Федерального государственного бюджетного образовательного учреждения

высшего профессионального образования

«Югорский государственный университет»

МЕТОДИЧЕСКАЯ РАЗРАБОТКА

КУРС ЛЕКЦИЙ

по дисциплине: «Электротехника и электроника»

раздел: «Цепи постоянного тока»

Преподаватель: О.Н. Кузнецова

2015
Аннотация

В методической разработке представлен конспект лекций раздела» Электрические цепи постоянного тока» дисциплины «Электротехника и электроника».

Данный материал рассчитан на 3 лекционных занятия.

Ценность данной работы заключается в том, что основной теоретический материал, необходимый для получения студентами устойчивых знаний по данной теме, в соответствии с ФГОС третьего поколения, изложен простым и доступным языком.

Методическая разработка содержит примеры карточек контроля, которые позволяют проконтролировать степень усвоения материала по данным темам.

Также к методической разработке приложена презентация по данной теме.
Целью и задачами разработки являются:

• 
  обеспечение процесса обучения наглядными иллюстрациями, простыми для усвоения обучающимися;
  
• 
  совершенствование самостоятельности при получении знаний, умений, навыков;
  
• 
  формирование компетенции различных аспектов учебной деятельности и знаний, необходимых для спланированного продвижения в учении;
  
• 
  развитие у обучающихся логического мышления, интуиции;
  
• 
  развитие интеллектуальных и познавательных способностей.
  

Данной методической разработкой может пользоваться любой преподаватель дисциплины «Электротехника и электроника» или «Физика».

СОДЕРЖАНИЕ:

РАЗДЕЛ № 1 «ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА»

1. 
   Лекция № 1. Тема: «Электрическая цепь, её элементы и параметры»….3
   
2. 
   Лекция № 2.Тема: «Основные законы электротехники»…………………8
   

2.1. Закон Ома………………………………………………………………8

2.2. Первый закон Кирхгофа………………………………………………9

2.3. Второй закон Кирхгофа……………………………………………….9

3. 
   Лекция № 3.Тема: «Способы соединения резисторов»……………..….10
   

3.1. Параллельное соединение резисторов………………………………10

3.2. Последовательное соединение резисторов…………………………11

3.3. Смешанное соединение резисторов…………………………….……12

3.4. Пример расчета смешанного соединения резисторов ……………..13

4. 
   Карточки контроля (Приложения 1, 2, 3)………………………………..15
   

РАЗДЕЛ № 1 «ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА»

Лекция № 1

Тема: «Электрическая цепь, её элементы и параметры»
Электрической цепью называют совокупность устройств, предназначенных для получения, передачи, преобразования и использования электрической энергии.

Условное обозначение элементов электрической цепи:

Е, — источник ЭДС

, — потребитель

Источники ЭДС:

а) аккумуляторы

б) генераторы

в) конденсаторы
Потребители (нагрузка):

1. 
   электрические бытовые приборы,
   

б) осветительные приборы,

в) электрические двигатели,

г) трансформаторы и т.д.
Основными элементами, без которых невозможно создать электрическую цепь являются:

1. источник энергии

2. провода

3. потребитель

Рис. 1 простейшая электрическая цепь

Так же в электрическую цепь включаются: аппараты коммутации, электроизмерительные приборы, различные устройства защиты, преобразовательные и распределительные устройства.

Любая электрическая цепь характеризуется:

1. электрическим током,

2. электродвижущей силой (ЭДС),

3. электрическим напряжением,

4. электрической мощностью,

5. электрическим сопротивлением.
Электрическим токомназывают направленное движение заряженных частиц (электронов).

Значение тока определяется совокупным электрическим зарядом Q всех частиц проходящих за единицу времени через поперечное сечение проводника за единицу времени.

Единица измерения электрического тока – Ампер (А).

В практических расчетах используют понятие плотности тока:

Электрический ток, не изменяющийся по направлению в течение времени называется постоянным током.

Постоянный ток может быть:

Пульсирующим Сглаженным

Электрический ток, изменяющий свое значение и направлении в течении времени периодически называется переменным током.

Электрический ток измеряется амперметром, который включается в цепь последовательно.

Электродвижущей силой(Е) – называется величина равная энергии получаемой внутри источника единичным электрическим зарядом.

E – [B] (Вольт)

ЭДС получается в результате работы не электрических сил (химическая реакция, механическая энергия…)

Э.Д.С. измеряется вольтметром, при отключенной нагрузке, т.е. при разомкнутой цепи.

Напряжение(U) – величина, которая показывает, какая энергия преобразуется (расходуется) в потребителе, каждым единичным зарядом.

U – [B] (Вольт).

Напряжение измеряется вольтметром при замкнутой цепи.

Вольтметр включается в цепь параллельно.

При движении электронов в проводнике, они сталкиваются с атомами и молекулами материала, испытывая при этом противодействия своему движению, которое называется электрическим сопротивлением(R).

R – [Ом]

Электрическое сопротивление измеряется омметром.

Электрическое сопротивление проводника зависит от физико-химических параметров проводника и находится по формуле:

Сопротивление проводника зависит от температуры. Эта зависимость выражается формулой:

R₂ = R₁ [ 1+

R₁ и R₂ сопротивление проводника при начальной и конечной температурах.

— температурный коэффициент сопротивления

Любой элемент электрической цепи имеет большее или меньшее сопротивление.

Элемент с большим сопротивлением называется резистором.

Наряду с сопротивлением любой проводник обладает электрической проводимостью.

Удельная электрическая проводимость (G) характеризует свойство вещества проводить электрический ток

Учитывая эти определения, получим расчетные формулы для электрических цепей постоянного тока

Электрическая мощность (P) – это величина характеризующая скоростью выполняемой работы.

Единица измерения:[Вт]- ватт, [кВт] – киловатт.

Мощность, отдаваемая источником.

Мощность,потребляемая нагрузкой (мощность потребителя).

При прохождении тока по проводнику, электроны сталкиваются с молекулами вещества, в результате чего часть энергии электронов теряется, что приводит к нагреву проводника.

Количество теплоты, выделенной в проводнике, находится по закону Джоуля – Ленца.

Количество теплоты, выделяемой при прохождении тока в проводнике, пропорционально , сопротивлению и времени прохождения тока.
Лекция № 2

Тема: «Основные законы электротехники»

1. Закон Ома

Ток, протекающий по цепи прямо пропорционален напряжению, приложенному к цепи (участку цепи) и обратно пропорционален сопротивлению цепи (участку цепи).

С учетом внутреннего сопротивления источника ЭДС можно записать:

E = U_вн+ U_внеш= I · R_вн + I · R_внеш = I ( R_вн+ R_внеш)

Тогда получим:

Напряжение на зажимах цепи:

U = E – U_внут= E – I · R_внут

Любая электрическая цепь содержит узлы, контуры и ветви.

Контуром называют любой замкнутый участок цепи, проходящий по нескольким ветвям (участкам).

Ветвью называют участок цепи, расположенный между 2-мя узлами по которому протекает один и тот же ток.

Узлом называют место соединения трех и большего числа ветви(проводов).

При расчете любой электрической цепи применяют законы Кирхгофа.

2. Первый закон Кирхгофа

Алгебраическая сумма токов входящих в узел, равна алгебраической сумме токов выходящих из узла или сумма всех токов в узле равна нулю.

Этот закон применяют для составления токового уравнения для любого узла электрической цепи.

При составлении уравнения нужно помнить что токи, направленные к узлу берут со знаком (+), а токи, направленные от узла со знаком (-).

Токовое уравнение для узла А записанное по первому закону Кирхгофа.

3.Второй закон Кирхгофа

Алгебраическая сумма Э.Д.С., действующих в любом замкнутом контуре, равна алгебраической сумме напряжений на каждом сопротивлении этого контура:

;

или

Напряжение, действующее в любом замкнутом контуре равно сумме напряжений на каждом сопротивлении этого контура.

Пример:

Лекция № 3

Тема: «Способы соединения резисторов»

1. 
   Параллельное соединение сопротивлений.
   

Параллельным называется соединение, при котором все участки цепи присоединяются к одной паре узлов и находятся под одним напряжением.

Признак параллельного соединения: наличие двух общих узлов.

Рассмотрим свойства:

1. 
   Напряжение на всех ветвях одинаково и равно напряжениюна зажимах цепи.
   

2. Ток в неразветвленной части цепи I равен сумме токов ветвей

3. Эквивалентное сопротивление цепи находится

а) через проводимости, если цепь содержит 3 или большее количество ветвей:

Где:

б) Если цепь содержит 2 ветви, то находится по формуле

В) Если цепь содержит n ветвей с одинаковыми сопротивлениями то:

2. Последовательное соединение резисторов.

Последовательным называют соединение, при котором резисторы соединены друг за другом без разветвлений.

Признак последовательного соединения:отсутствие узлов между резисторами.

Рассмотрим свойства соединения.

1. 
   Ток, протекающий через все сопротивления одинаковый.
   

2. 
   Напряжение на зажимах цепи равно сумме напряжений на всех сопротивлениях.
   

3. 
   Эквивалентное сопротивление цепи равно сумме всех R.
   

По закону Ома напряжения на зажимах цепи и на сопротивлениях рассчитывают

; ;

Видим, что при последовательном соединении резисторов напряжения на них прямо пропорциональны сопротивлению, т.е. напряжение U прямопропорционально сопротивлению R

Поэтому если изменить значения сопротивлений, то произойдет перераспределение напряжения на участках цепи.

3. Смешанное соединение

Смешанным называют соединение, которое содержит участки с последовательным и параллельным соединением.

При расчете цепи со смешанным соединением необходимо знать свойства последовательного и параллельного соединений и пользоваться ими, а также знать и применять законы Ома и Кирхгофа.

Сначала необходимо выделить участки цепи, на которых видно, какое — либо соединение (последовательное или параллельное).

Пользуясь свойствами начать сворачивать первоначальную цепь до одного эквивалентного сопротивления с составлением схем замещения.

Пользуясь схемами замещения произвести расчет всех параметров на участках цепи.

Пример расчета параметров электрической цепи со смешанным соединением резисторов:

Решение:

1. 
   Находим эквивалентное сопротивление:
   

б)

2. 
   Находим напряжение :
   

3. 
   Находим ток :
   

4. 
   Находим ток :
   

5. 
   Находим напряжение на зажимах цепи :
   

6. 
   Мощность, потребляемая цепью:
   

7. 
   Электроэнергия, потребляемая цепью за 8 часов работы:
   

8. 
   При замыкании накоротко резистора , цепь будет иметь вид:
   

ОБРАЗЦЫ КАРТОЧЕК КОНТРОЛЯ И ПРОВЕРКИ ЗНАНИЙ

ПО РАЗДЕЛУ: «ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА»
Приложение 1

Карточки контроля к теме: «Электрическая цепь, её элементы и параметры»

Вариант 1	Вариант 2	Вариант 3

Вариант 1	Вариант 2	Вариант 3

Приложение 2

Карточки контроля к теме: «Основные законы электротехники»

Приложение 3

Карточки контроля к теме: «Способы соединения резисторов»

Перечень рекомендуемых учебных изданий, Интернет – ресурсов, дополнительной литературы

Основная литература:

1. 
   Б.В. Покрепин. «Оператор по добыче нефти и газа».Волгоград: Ин — Фолио, 2011.
   
2. 
   А.И. Снарев. «Расчеты машин и оборудования для добычи нефти и газа». – М.: Инфра-инженерия, 2010.
   
3. 
   С.П. Никитенко. «Нефтегазопромысловое оборудование». — Волгоград: Ин — Фолио, 2008.
   
4. 
   Б.Г. Меньшов, И.И. Суд. «Электрооборудование нефтяной промышленности». – М.: Недра, 2008.
   

Дополнительная литература:

1. 
   Кацман М. И. «Электрические машины» — М.: Высшая школа, 2010.
   
2. 
   «Справочник мастера по ремонту нефтегазового технологического оборудования». Том 1, 2. – М.: Инфра-инженерия, 2008.
   
3. 
   А.Г. Молчанов, В.Л. Чичеров. «Нефтепромысловые машины и механизмы». – М.: Недра, 2003.
   
4. 
   А.А. Раабен, П.Е. Шевалдин, Н.Х. Максутов. «Ремонт и монтаж нефтепромыслового оборудования». – М.: Недра, 2003.
   
5. 
   В.И. Блохин, Б.И. Моюхейн, Б.М. Парфенов и др. «Электропривод новых буровых установок с применением тиристорных преобразователей». – М.: ВНИИОНГ.
   

Интернет-ресурсы:

1.http://e—scientist.ru/

2. http://www.vsya—elektrotehnika.ru/

3. http://electricalschool.info/main/elsnabg/

4. http://www.mephi.ru/sdudents/labs/chair8/