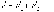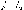Кулоновское поле это – кулоновское поле — это… Что такое кулоновское поле? — groupnk.ru — Группа НК — комплексные поставки электрооборудования в Москве и регионах

Содержание

Поле кулоновское — Справочник химика 21

Адсорбция полярных молекул на поверхностях, имеющих электрические заряды. Прн адсорбции полярных молекул на адсорбенте, имеющем на поверхности ионы или диполи, возникает взаимодействие диполя адсорбата с электростатическим полем адсорбента. Если молекулы адсорбата невелики и обладают периферически расположенными диполями (например, молекулы воды и аммиака), они ориентируются в электростатическом поле адсорбента. Возникает так называемое ориентационное кулоновское взаимодейст- [c.495]
Кулоновское поле — поле точечного заряда. Ядро и электрон можно считать точечными, так как их размеры в 10 раз меньше размеров атома. [c.24]

Электростатические силы тем больше, чем выше заряд ионов и чем меньше ионные радиусы. Поле кулоновских сил имеет сферическую симметрию, что приводит к ненаправленно-сти ионной связи. Можно выделить три особенности строения ионных соединений.

[c.347]

Если применить эти результаты при изучении поведения электрического диполя в поле кулоновских сил, то из уравнений (229) и (236) можно получить [c.83]

ВНЕШНЕЕ ПОЛЕ (КУЛОНОВСКАЯ ЗАДАЧА) [c.20]

Эффект поля (кулоновский эффект) передача через пространство в соответствии с законами электростатики . [c.56]

При вращении электрона вокруг ядра атома в поле кулоновских сил он может иметь только дискретные орбиты, а не бесконечное число, предсказываемое классической механикой. [c.26]

Третий важный вклад в расчет спектра бензола принадлежит Паризеру [1956 (а)]. Он включил в рассмотрение взаимодействие всех конфигураций, возникающих из основного состояния при одноэлектронных возбуждениях. Гамильтониан был построен таким же способом, как это рассмотрено в гл. 5 для теории самосогласованного поля кулоновские интегралы вычислены по методу Паризера — Парра (гл. 5). Результаты расчетов Паризера приведены в табл. 36.

[c.182]

Электрическое напряжение (символ U, единица — вольт, В) — физическая величина, численно равная работе, совершаемой полем кулоновских сил при перемещении одиночного положительного заряда на участке электрической цепи, на концах которой измеряют электрическое напряжение. Вольт В — 1 ZbK Кл. [c.512]

При больших энергиях фотонов в кулоновском поле ядер образуются электронно-позитронные пары. Возникающей паре передается энергия фотона за вычетом энергии покоя пары, равной 2 = =1,022 МэВ. Указанное значение энергии является порогом для этого процесса. Сечение процесса образования пар медленно растет в области энергий от 1,02 до 4 МэВ, а затем возрастает в логарифмической зависимости от энергии. Нестабильность позитрона в среде приводит к его аннигиляции с испусканием в большинстве случаев двух фотонов с энергией 0,511 МэВ. Сечение образования пар пропорционально 2 + 2, где первый член отвечает ядерным процессам, а второй — процессам в поле электронов.

[c.45]

Поле, создаваемое атомным остовом, хотя и не кулоновское, имеет центральную симметрию, как и поле ядра в водородоподобном атоме, благодаря чему и здесь квантовые числа пи/ сохраняют свое значение. Однако в отличие от водородоподобного атома энергия электрона зависит не только от п, но и от /, вырождение относительно I снимается электрон движется в поле не одного ядра, но остова, и энергия электрона зависит от того, как он поляризует остов (нарушает его центральную симметрию) и как он проникает внутрь остова. Поляризация же и проникновение зависят от типа орбитали, т. е. от квантового числа /. Электроны в атоме можно разделить на квантовые слои. Квантовый слой, или уровень, — совокупность электронов с данным главным квантовым числом п. Внутри уровня электроны разделяются по энергии на подуровни 5, / и т. д. в соответствии с квантовым числом / (рис. 10). Наиболее проникающими [c.35]

Механизм взаимодействия капель в постоянном поле такой же, как и в переменном поле. Однако диполь-дипольное контактирование в электростатическом поле усиливается кулоновским взаимодействием частиц, сопровождаемым интенсивным встречным движением капель. В результате улучшается обработка и очистка светлых нефтепродуктов. [c.375]

Однако содержание ионов в растворителях с малой диэлектрической проницаемостью очень мало по сравнению с содержанием полярных молекул из-за незначительной степени диссоциации растворов электролитов (10 —10 моль/л). Средние межионные расстояния при этом очень велики, и растворы в отношении ионов жидкости являются весьма разбавленными. Даже относительно сильное кулоновское поле, связанное с малым значением е среды, не вызывает существенных межионных взаимодействий.

[c.27]

Основной силой, действующей на частицу в электрофильтре, является кулоновская сила действия электрического поля на заряд частицы. Эта сила вне области короны направлена к осадительному электроду. Скорость в м/с перемещения частиц под действием этой силы (или скорость дрейфа частиц) в направлении, перпендикулярном осадительному электроду, рассчитывают по формулам [c.21]

Известно, что силовые лииии изолированного электрического заряда распространяются равномерно во все стороны пространства, образуя сферические эквипотенциальные поверхности напряженностей поля. Эти силовые линии одного и того же заряда не могут пересекаться. При кулоновском взаимодействии двух неподвижных противоположно заряженных частиц боковое давление силовых трубок, окружающих центральную силовую трубку (уравнения 10 и 11), обеспечивает параллельность распространения силовых линий и прямолинейность их траектории между протоном и электроном. Поэтому для определения напряженности поля такой центральной силовой трубки можно использовать уравнение напряженности поля между пластинами плоского конденсатора при сравнительно малом расстоянии между пластинами [12]

[c.22]

Капли, попадая в электрическое поле, поляризуются, и их форма приближается к эллипсоидальной (рис. 1.1). Соударение и слияние капель происходит за счет кулоновского взаимодействия противоположных по знаку поляризационных зарядов частиц, оказавшихся вблизи друг от друга. Из электростатики известно, что заряд поляризации qn = Еа . Следовательно, сила взаимодействия, определяющая сближение и слияние капель [c.8]

При адсорбции иона на поверхности диэлектрика, также состоящего из ионов, между ионами адсорбента и адсорбированным ионом должны возникать

Центральные силы и их поля — Википедия

Центральная сила — сила, линия действия которой при любом положении тела, к которому она приложена, проходит через точку, называемую центром силы (точка K{\displaystyle K} на рис.1)^[1].

Примерами центральных сил являются силы тяготения и Кулона, направленные вдоль линии, соединяющей точечные массы или точечные заряды.

[3] не могут быть представлены конечным количеством материальных точек. В случае распределённых систем общим подходом является разбиение их на очень большое (в пределе бесконечное) количество элементов малого (в пределе стремящегося к нулю) размера каждый (которые и рассматриваются как материальные точки), между которыми действуют центральные силы в соответствии с определением, данным выше. Таким образом, в этом случае центральной, собственно, является каждая элементарная сила, а реальная сила является суммой (суперпозицией) таких элементарных сил.

Классическая физика вводит также понятие поля центральной силы для области трёхмерного пространства, в котором действуют центральные силы. ^[4]

Рис.1 К определению центральной силы: α{\displaystyle \alpha } частица в поле атомного ядра.(опыт Резерфорда)

Для любой центральной силы F→{\displaystyle {\vec {F}}} выполняется соотношение
M→=r→×F→=0,{\displaystyle {\vec {M}}={\vec {r}}\times {\vec {F}}=0,}

(где M — момент сил, r→{\displaystyle {\vec {r}}} — радиус-вектор с началом в центре силы), свидетельствующее о равенстве нулю момента силы относительно центра силы:

Этим полям соответствуют кулоновские силы (силы электростатического взаимодействия) и силы гравитационные (силы Всемирного тяготения). Сходство между ними заключается в том, что они могут быть обнаружены во время взаимодействия материальных объектов, причем в случае гравитации свойством, обуславливающим это взаимодействие, является масса, а в случае кулоновского взаимодействия — заряд, этой массой переносимый. Заряды, не связанные с массой, классической физике неизвестны.

Величина, характеризующая интенсивность центрального силового поля, представляет собой вектор, направленный по линии, соединяющей точечный источник и заданную точку поля.

Потенциальные центральные поля[править | править код]

Работа центральной силы[править | править код]

Элементарная работа dA{\displaystyle dA} силы, в том числе и центральной силы, есть скалярная величина, исчисляемая изменением энергии при перемещении точки приложения силы F→{\displaystyle {\vec {F}}} (в общем случае изменяющей свою величину и направление), при перемещении на столь малый отрезок своей траектории, что на нём вектор силы может считаться неизменным, то есть на расстояние d→r{\displaystyle {\vec {d}}r} :

dA=F→d→r=Fcos⁡αdr{\displaystyle dA={\vec {F}}{\vec {d}}r=F\cos \alpha dr} (5)

где α{\displaystyle \alpha } есть угол между этими векторами. Поскольку cos⁡α=cos⁡(−α){\displaystyle \cos \alpha =\cos(-\alpha )}, то направление отсчёта угла значения не имеет.

При перемещении на расстояние от r1{\displaystyle r_{1}} до r2{\displaystyle r_{2}}, весь пройденный путь можно разбить на i{\displaystyle i} элементарных участков. И тогда полная работа A{\displaystyle A} будет суммой этих элементарных работ с тем большей точностью, чем на большее количество участков n{\displaystyle n} будет разбита траектории, что выражается знаком интеграла, как предела этой суммы :

A=lim∑i=1nFicosi⁡αi dri=∫r1r2F→rdr→(6){\displaystyle A=\lim \sum _{i=1}^{n}{F_{i}}\cos _{i}\alpha _{i}\ dr_{i}=\int \limits _{r_{1}}^{r_{2}}{\vec {F}}_{r}d{\vec {r}}(6)}

Рассматривая движение в декартовой системе координат, центральную силу можно представить в виде геометрической суммы её проекций на координатные оси:

F→=F→x+F→y+F→z=Fxi→+Fyj→+Fzk→(7){\displaystyle {\vec {F}}={\vec {F}}_{x}+{\vec {F}}_{y}+{\vec {F}}_{z}=F_{x}{\vec {i}}+F_{y}{\vec {j}}+F_{z}{\vec {k}}(7)}

где i→{\displaystyle {\vec {i}}} ,j→{\displaystyle {\vec {j}}} ,k→{\displaystyle {\vec {k}}} суть единичные векторы (орты) для своих осей.

Потенциал поля[править | править код]

Не для всякого поля силы совершаемая ею работа зависит лишь от положения начальной и конечной точек движения. Иными словами, не зависит от формы пути.

Упомянутый интеграл не будет зависеть от формы пути лишь в том случае, если будет существовать некая первообразная функция U{\displaystyle U}, в выражении полного дифференциала которой:

dU=∂U∂xdx+∂U∂ydy+∂U∂zdz(8){\displaystyle dU={\frac {\partial U}{\partial x}}dx+{\frac {\partial U}{\partial y}}dy+{\frac {\partial U}{\partial z}}dz(8)}

её частные производные будут соответствовать проекциями силы (по существующему обычному соглашению — с точностью до знака):

dU=−Fxdx−Fydy−Fzdz(9){\displaystyle dU=-F_{x}dx-F_{y}dy-F_{z}dz(9)}

В этом случае функция U{\displaystyle U} будет называться потенциальной функцией, а поле силы — потенциальным полем.^[5]

Но это станет возможным лишь при одновременном выполнении равенств:

∂Fy∂z=∂Fz∂y;∂Fz∂x=∂Fx∂z;∂Fx∂y=∂Fy∂x(10){\displaystyle {\frac {\partial F_{y}}{\partial z}}={\frac {\partial F_{z}}{\partial y}};{\frac {\partial F_{z}}{\partial x}}={\frac {\partial F_{x}}{\partial z}};{\frac {\partial F_{x}}{\partial y}}={\frac {\partial F_{y}}{\partial x}}(10)}

Для центральных сил это условие выполняется. Поле, в котором выполнены эти условия, называется безвихревым полем. Поэтому потенциальные поля суть поля безвихревые.^[5]

Знак минус в формуле, связывающей потенциальную функцию и силу, определяется желанием отождествить потенциальную функцию с потенциальной энергией^[6] (в противном случае можно было бы обойтись без знака минус, что иногда и делается при введении потенциальной функции чисто формально, особенно для векторного поля, не имеющего характера силы).

Связь с потенциальной энергией естественно осуществляется через работу.

Представляется естественным считать, что вектор напряжённости поля направлен ОТ источника поля, (что привычно принимается при описании электростатического поля при взаимодействии одноимённых зарядов^[7]) Тогда, зафиксировав точку, находящуюся на расстоянии r1{\displaystyle r_{1}} от центрального заряда и предоставив ему свободу, получим, что он под действием силы будет удаляться в бесконечность. При этом совершённая полем работа будет равна:

Ar1=∫r11F→rdr→(11){\displaystyle A_{r_{1}}=\int \limits _{r_{1}}^{\mathcal {1}}{\vec {F}}_{r}d{\vec {r}}(11)}.

То же можно сказать и в случае, если поле продвинуло тело дальше r2>r1{\displaystyle r_{2}>r_{1}} и, следовательно, проделало больше работы и потому разница работ на пути между точками больше нуля.

И эти работы может быть названа с точностью до постоянной потенциалом точки: Ul1{\displaystyle U_{l1}} и Ul2{\displaystyle U_{l2}}, подразумевая под потенциалом возможность совершить работу, которая для более близкой точки выше, чем у более далёкой.

Тогда совершённая полем работа будет равна разности потенциалов, взятой со знаком «минус»

A=∫r1r2F→rdr→=Ul1−Ul2=−ΔU(12){\displaystyle A=\int \limits _{r_{1}}^{r_{2}}{\vec {F}}_{r}d{\vec {r}}=U_{l1}-U_{l2}=-\Delta U(12)}

Таким образом работа силы на пути из начальной точки в конечную равна изменению потенциальной функции, являющейся скалярной функцией расстояния. В таком случае для каждой точки пути можно с точностью до постоянной величины приписать свой потенциал:U{\displaystyle U}

Поле как градиент потенциала[править | править код]

В поле центральной силы её составляющая по данной оси представляет собой скорость изменения потенциальной функции по этой же оси или же градиент функции по заданному направлению.

Для описания изменения потенциальной функции по произвольному направлению в теории поля введён векторный дифференциальный оператор, имеющий вид:

∇≡∂∂xi→+∂∂yj→+∂∂zk→(13){\displaystyle \nabla \equiv {\frac {\partial }{\partial x}}{\vec {i}}+{\frac {\partial }{\partial y}}{\vec {j}}+{\frac {\partial }{\partial z}}{\vec {k}}(13)}

Применяя этот оператор к потенциальной функции получаем, что в данной точке поля сила является (с точностью до знака) градиентом потенциала:

F→=Fxi→+Fyj→+Fzk→=F→x+F→y+F→z=−∇U≡−gradU(14).{\displaystyle {\vec {F}}=F_{x}{\vec {i}}+F_{y}{\vec {j}}+F_{z}{\vec {k}}={\vec {F}}_{x}+{\vec {F}}_{y}+{\vec {F}}_{z}=-\nabla U\equiv -\mathbf {grad} U(14).}

Знак минус, по обычному соглашению присутствующий в этой формуле, связан с тем, чтобы функция U могла быть отождествлена с потенциальной энергией (хотя чисто формально потенциальная функция могла бы быть выбрана и с другим знаком, если такого отождествления не предполагается).

Кулоновское поле[править | править код]

Напряженность кулоновского поля определяется вектором E→{\displaystyle {\vec {E}}}, равным:

E→=CQQr→r3(15){\displaystyle {\vec {E}}=C_{Q}{\frac {Q{\vec {r}}}{r^{3}}}(15)}

или, переходя, к скалярной форме записи:

E=CQQr2(16){\displaystyle E=C_{Q}{\frac {Q}{r^{2}}}(16)}

Здесь E=‖E→‖{\displaystyle E=\lVert {\vec {E}}\rVert }; Q{\displaystyle Q} — заряд тела -источника силы; r=‖r→‖{\displaystyle r=\lVert {\vec {r}}\rVert },есть расстояние до точки, где определяется интенсивность, а константа CQ{\displaystyle C_{Q}} зависит от диэлектрической постоянной среды ε{\displaystyle \varepsilon }, (для пустого пространства равная 1), в которой существует поле:

CQ=14πεε0{\displaystyle C_{Q}={\frac {1}{4\pi \varepsilon \varepsilon _{0}}}}, где:

ε0{\displaystyle \varepsilon _{0}} есть диэлектрическая постоянная вакуума. В таком случае для вакуума

CQ=14πε0{\displaystyle C_{Q}={\frac {1}{4\pi \varepsilon _{0}}}} = 1010{\displaystyle 10^{10}} Vm/As в Международной системе единиц^[8],

Кулоновские силы[править | править код]

Объектом действия кулоновского поля является материальное тело, несущее заряд q{\displaystyle q}

В таком случае на него действует механическая (ньютонова) сила электрического происхождения, равная произведению величины заряда на напряжённость поля:

или, с учётом ():

F→q=CQqQr→r3(17){\displaystyle {\vec {F}}_{q}=C_{Q}{\frac {qQ{\vec {r}}}{r^{3}}}(17)} или, в скалярном представлении:

Fq=CQqQr2(18){\displaystyle F_{q}=C_{Q}{\frac {qQ}{r^{2}}}(18)}

Специфической особенностью кулоновского поля является то, что вектор его напряжённости направлен либо ОТ источника поля в случае совпадение знака заряда источника и объекта взаимодействия, либо направлен К источнику в случае разноимённости зарядов. Это значит, что заряженные материальные тела в первом случае будут испытывать отталкивающую силу, а в противоположном — силу сближающую их.

Ещё одним свойством кулоновского поля является техническая возможность выделить область пространства, в котором оно будет в требуемой степени отсутствовать (клетка Фарадея)

Поле гравитации[править | править код]

В русскоязычной литературе интенсивность поля тяготения называют «ускорением свободного падения» g→{\displaystyle {\vec {g}}}, за рубежом иногда её называют напряжённостью гравитационного поля.

g→=GMr→r3(19){\displaystyle {\vec {g}}=G{\frac {M{\vec {r}}}{r^{3}}}(19)}

Или, переходя к скалярной форме записи: g=GMr2(20){\displaystyle g=G{\frac {M}{r^{2}}}(20)}

Здесь g=‖g→‖{\displaystyle g=\lVert {\vec {g}}\rVert }; M{\displaystyle M} — масса тела -источника гравитации; r=‖r→‖{\displaystyle r=\lVert {\vec {r}}\rVert } есть расстояние до точки, где определяется интенсивность, а константа G{\displaystyle G} есть гравитационная постоянная, равная по современным данным G=6,6742∗10−11m3kg∗s2{\displaystyle G=6,6742*10^{-11}{\frac {m^{3}}{kg*s^{2}}}}, ^[9]

Силы гравитации[править | править код]

Объектом действия поля гравитации является материальное тело, имеющее массу m{\displaystyle m}

В таком случае на него действует механическая сила, равная произведению массы m{\displaystyle m} тела на напряжённость поля. Существенно, что между массой, входящей во второй закон Ньютона и массой того же тела, подверженного действию гравитации, нет никакой разницы в величине. Тогда, с учётом ():

F→g=mg→(21){\displaystyle {\vec {F}}_{g}=m{\vec {g}}(21)}

или, в скалярном представлении:

Fg=mg (22){\displaystyle F_{g}=mg\ (22)}

Специфической особенностью сил гравитации является то, что они всегда являются силами притяжения. Кроме того, силы гравитации всепроникающи, и от них невозможно защититься никаким экраном. Это свойство объединяет силы гравитации с фиктивными силами инерции, существующими в любой неинерциальной системе отсчёта. Подобная аналогия имеет своей основой фундаментальные свойства пространства, изучения которых выходит за рамки классической физики.^[10]

Потенциал поля гравитации[править | править код]

Подставляя в (6) значение силы Всемирного тяготения из (20), получаем с учётом того, что работа была совершена против поля:

A=−GmM∫r1r2r→r3dr→=−GmM(1r2−1r1)=U2−U1{\displaystyle A=-GmM\int \limits _{r_{1}}^{r_{2}}{\frac {\vec {r}}{r^{3}}}d{\vec {r}}=-GmM\left({\frac {1}{r_{2}}}-{\frac {1}{r_{1}}}\right)=U_{2}-U_{1}} (23)

Таким образом каждой точке гравитационного поля можно с точностью до постоянной присвоить свой потенциал, как:

Ur=−GmM(1r){\displaystyle U_{r}=-GmM\left({\frac {1}{r}}\right)}^[11](24)

Движение под действием центральной силы[править | править код]

В общем случае любую траекторию тела, рассматриваемого как материальная точка, можно представить в виде пространственной кривой, состоящей из сопряжённых поворотов в различных плоскостях вокруг мгновенных центров поворота с различными значениями радиуса поворота rc{\displaystyle r_{c}} на том же Рис 1.Применение представления о траектории реального трёхмерного тела смысла не имеет.

Но кривизна траектории отнюдь не значит, что на тело действует некая сила, для каждого момента являющейся силой центростремительной.

Замечание

Последняя оговорка весьма существенна. Так, например, для земного наблюдателя бомба, сброшенная с летящего равномерно и прямолинейно летательного аппарата движется по параболе. Но для пилота она падает вертикально под действием единственной в данном случае силы тяжести (если не принимать во внимание снос из-за сопротивления воздуха). Никаких сил, вызывающих искривление траектории, здесь нет. Центростремительные силы возникают не потому, что траектория крива, но потому, что они являются выражением реально имеющего место силового взаимодействия движущегося объекта со своим окружением.

Считается, что в центре силы находится источник силы, которым может быть тяготеющая масса, либо электрический заряд в случае, если рассматриваемая сила есть характеристика соответствующего силового поля. Центр силы в общем случае не совпадает с мгновенным центром поворота — точка C{\displaystyle C} на Рис. Это совпадение имеет место лишь при повороте тела по дуге окружности. ^[4]

Как видно на Рис.1 единственная действующая между телами α{\displaystyle \alpha } и K{\displaystyle K} сила F→{\displaystyle {\vec {F}}} может быть разложена на две составляющие: F→=F→t+F→n{\displaystyle {\vec {F}}={\vec {F}}_{t}+{\vec {F}}_{n}} (2)

При этом F→t{\displaystyle {\vec {F}}_{t}} есть тангенциальная сила, в зависимости от направления движения тела по своей траектории на рисунке либо тормозящая его движение, либо ускоряющая его.

F→n{\displaystyle {\vec {F}}_{n}} есть сила, направленная по нормали к касательной к траектории в сторону мгновенного центра и потому являющаяся центростремительной силой.^[12]

Непосредственно из определения понятий о моментах силы и момента количества движения (момента импульса) следует экспериментально подтверждаемый факт, что скорость изменения момента импульса вращающегося тела L→{\displaystyle {\vec {L}}} прямо пропорциональна величине приложенного к телу момента силы M→{\displaystyle {\vec {M}}}:

dL→dt=M→(3){\displaystyle {\frac {d{\vec {L}}}{dt}}={\vec {M}}(3)}

Однако в поле центральной силы её момент всегда равен нулю (Формула (1)). Из этого непосредственно следует, что при любом движении тела в поле центральной силы момент количества движения движущегося под её действием тела остаётся постоянным:

L→=const(4){\displaystyle {\vec {L}}=const(4)}. Но, поскольку постоянство вектора есть одновременно и сохранение его направления в пространстве, то заметаемая при движении тела площадка всегда лежит в одной и той же плоскости. Из этого следует, что любая траектория движения тела под действием центральной силы есть плоская кривая.

Наиболее часто движение тел в гравитационном поле изучают в области небесной механики, где преобладают гравитационные воздействия, и потому изучаемая система взаимодействующих сил может рассматриваться как консервативная система, то есть такая, в которой сохраняется полная энергия тела в виде суммы потенциальной и кинетической энергии.^[4]

E=Wk+Wp{\displaystyle E=W_{k}+W_{p}} (25), где:

Wk=m2(vn2+vt2)(26){\displaystyle W_{k}={\frac {m}{2}}(v_{n}^{2}+v_{t}^{2})(26)} причём vn{\displaystyle v_{n}} и vt{\displaystyle v_{t}} соответствуют скоростям, создаваемым нормальной и тангенциальной составляющей действующей на тело силы на Рис.1

$v_{t}$ Рис.2 К вопросу о зависимости параметров орбиты от полной энергии планеты

Воспользовавшись определением кинетического момента:L=mrvt{\displaystyle L=mrv_{t}} получаем для кинетической энергии тангенциального движения соотношение:

Wk(t)=L22mr2(27){\displaystyle W_{k}(t)={\frac {L^{2}}{2mr^{2}}}(27)} .

А для движения по нормали к траектории: Wk(n)=mvn22(28){\displaystyle W_{k}(n)={\frac {mv_{n}^{2}}{2}}(28)}

Wp=GmMr(29){\displaystyle W_{p}={\frac {GmM}{r}}(29)}

Тогда выражение для полной энергии тела будет иметь вид:

E=mvn22+L22mr2−GmMr(30){\displaystyle E={\frac {mv_{n}^{2}}{2}}+{\frac {L^{2}}{2mr^{2}}}-{\frac {GmM}{r}}(30)}

Введя в рассмотрение эффективный потенциал U∗{\displaystyle U^{*}} :

U∗=L22mr2−GmMr(31){\displaystyle U^{*}={\frac {L^{2}}{2mr^{2}}}-{\frac {GmM}{r}}(31)}

Получаем возможность связать диапазон изменения длины радиус-вектора траектории тела с запасённой им энергией, что представлено на рис.2^[13]

Так при минимальной энергии движущегося тела E3{\displaystyle E_{3}} тело движется по круговой орбите с радиусом

1.Закон Кулона.

Точечный заряд — это заряженное тело, размеры которого много меньше других разме-

ров, характерных для данной задачи. В частности, размеры точечных зарядов пренебрежимо

малы по сравнению с расстояниями между ними .Закон Кулона. Сила взаимодействия двух неподвижных точечных зарядов в вакууме пря-

мо пропорциональна произведению абсолютных величин зарядов и обратно пропорциональна

квадрату расстояния между ними.

F=k*((q1q2)/r²). F-сила, r–расстояние, Коэффициент пропорциональности- k.

Закон Кулона с электрической постоянной выглядит так: F =

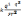
в диэлектрике: : F =Диэлектрическая проницаемость вакуума, как видим, равна единице. Во всех остальных случаях диэлектрическая проницаемость больше единицы.

2. Электрическое поле. Материальное электрическое поле.

Электрическое поле — один из двух компонентов электромагнитного поля, представляющий собой векторное поле^[1], существующее вокруг телили частиц, обладающих электрическим зарядом, а также возникающий при изменении магнитного поля Электрическое поле неподвижных и не меняющихся со временем зарядов называется электростатическим. Во многих случаях для краткости это поле обозначают общим термином – электрическое поле

Если с помощью пробного заряда исследуется электрическое поле, создаваемое несколькими заряженными телами, то результирующая сила оказывается равной геометрической сумме сил, действующих на пробный заряд со стороны каждого заряженного тела в отдельности. Следовательно, напряженность электрического поля, создаваемого системой зарядов в данной точке пространства, равна векторной сумме напряженностей электрических полей, создаваемых в той же точке зарядами в отдельности:

Это свойство электрического поля означает, что поле подчиняется принципу суперпозиции.

В соответствии с законом Кулона напряженность электростатического поля, создаваемого точечным зарядом Q на расстоянии r от него, равна по модулю

Это поле называется кулоновским. В кулоновском поле направление вектора зависит от знака заряда Q: если Q > 0, то вектор направлен по радиусу от заряда, если Q < 0, то вектор 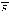направлен к заряду.

Напряженность электрического поля – векторная физическая величина. Направление вектора

в каждой точке пространства совпадает с направлением силы, действующей на положительный пробный заряд. Кулоновское поле точечного заряда Q удобно записать в векторной форме. Для этого нужно провести радиус-вектор

от зарядаQ к точке наблюдения. Тогда при Q > 0 вектор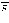

параллелен

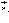а приQ

антипараллелен

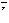Следовательно, можно записать:

где r – модуль радиус-вектора

. Важной характеристикой электрического диполя является так называемый дипольный момент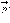

где – вектор, направленный от отрицательного заряда к положительному, модуль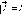Диполь может служить электрической моделью многих молекул.

3.Напряженность и индукция электрического поля.

Напряженность электростатического поля — это силовая характеристикаэлектростатического поля, численно равная силе, действующей на единичный положительный заряд.Напряженность электростатического поля — векторная величина.

Напряженность электрического поля:E = F/Qпробный

Напряженность электростатического поля (точечного заряда):

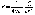
где r — расстояние от заряда Q, создающего поле, до точки поля, в которой определяется напряженность.

Единица напряженности — вольт на метр (В/м)

Электростатическое поле представляется графически силовыми линиямиили линиями напряженности . (D), векторная величина, характеризующая электрич. поле и равная сумме двух векторов разл. природы: напряжённости электрического поля Е — гл. хар-ки поля и поляризации среды Р, к-рая определяет электрич. состояние в-ва в этом поле. В Гаусса системе единицD=E+4pP, (1)в СИD=e0E+P, (1′)где e0 — размерная константа, наз. электрической постоянной или диэлектрич. проницаемостью вакуума.В изотропном в-ве, не обладающем сегнетоэлектрич. св-вами, при слабых полях вектор поляризации прямо пропорц. напряжённости поля. В системе ГауссаР=cеЕ, (2)где cе — пост. безразмерная величина, наз. диэлектрической восприимчивостью. Для сегнетоэлектриков cе зависит от Е, и связь между Р и Е становится нелинейной.Подставив выражение (2) в (1), получим:D =(1+4pce)E=eE. (3)Величинаe=1+4pcе (4)наз. диэлектрической проницаемостью в-ва.

В системе СИ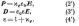

1. Электрический заряд. Закон кулона.

Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия.

Электрический заряд обычно обозначается буквами q или Q.

Совокупность всех известных экспериментальных фактов позволяет сделать следующие выводы:

Существует два рода электрических зарядов, условно названных положительными и отрицательными.
Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.
Одноименные заряды отталкиваются, разноименные – притягиваются. В этом также проявляется принципиальное отличие электромагнитных сил от гравитационных. Гравитационные силы всегда являются силами притяжения.

Величина заряда не зависит от того, движется этот заряд или покоится.

Электрические заряды могут исчезать и возникать вновь. Однако всегда возникают или исчезают два элементарных заряда противоположных знаков.

Закон сохранения электрических зарядов: суммарный заряд электрически изолированной системы не может измениться. Система называется электрически изолированной, если через ограничивающую её поверхность не могут проникать заряженные частицы.

Точечным зарядом называют заряженное тело, размерами которого в условиях данной задачи можно пренебречь.

Закон Кулона: сила взаимодействия двух неподвижных точечных зарядов пропорциональна величина каждого из зарядов и обратнопропорциональна квадрату расстояния между ними.

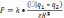
Ε- относительная диэлектрическая проницаемость среды- показывает во сколько раз сила взаимодействия между зарядами в вакууме > силы взаимодействия между теми же зарядами на том же расстоянии в данной среде, величина постоянная для данной среды. Если среда не оговаривается, то ей является вакуум ε=1, для воздуха ε=1.

2.Напряжённость электростатического поля. Принцип суперпозиции. Силовые линии электростатического поля.

Электростатическое поле – электрическое поле неподвижных и не меняющихся со временем зарядов.

напряженность электрического поля, создаваемого системой зарядов в данной точке пространства, равна векторной сумме напряженностей электрических полей, создаваемых в той же точке зарядами в отдельности:

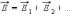
В соответствии с законом Кулона напряженность электростатического поля, создаваемого точечным зарядом Q на расстоянии r от него, равна по модулю:

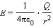
Это поле называется кулоновским. В кулоновском поле направление вектора зависит от знака заряда Q: если Q > 0, то вектор направлен по радиусу от заряда, если Q < 0, то вектор направлен к заряду.

Силовые линии показывают направление напряжённость поля

Принцип суперпозиции — электростатический потенциал, создаваемый в данной точке системой зарядов, есть сумма потенциалов отдельных зарядов.

результат воздействия на частицу нескольких внешних сил есть просто сумма результатов воздействия каждой из сил.
Взаимодействие между двумя частицами не изменяется при внесении третьей частицы, также взаимодействующей с первыми двумя.

Кулоновский барьер — Википедия

Материал из Википедии — свободной энциклопедии

Куло́новский барье́р — потенциальный барьер, который необходимо преодолеть атомным ядрам (которые заряжены положительно) для того, чтобы сблизиться друг с другом для возникновения притяжения, вызванного короткодействующим сильным взаимодействием нуклонов (ядерными силами). Кулоновский барьер есть следствие того, что, согласно закону Кулона, одноимённо заряженные тела отталкиваются. На малых расстояниях (порядка 1 фм) ядерные силы между двумя протонами сильнее кулоновских сил, расталкивающих одноимённо заряженные частицы; однако ядерные силы убывают с ростом расстояния значительно быстрее кулоновских сил. В результате зависимость суммарного потенциала взаимодействия ядер от расстояния имеет максимум (вершину кулоновского барьера) на некотором расстоянии.

Сила взаимодействия двух протонов или двух легких ядер как функция расстояния между ними.

Кулоновский барьер препятствует ходу термоядерной реакции в плазме. Дело в том, что даже при температурах в несколько тысяч кельвинов (когда вещество уже переходит в состояние плазмы), кинетической энергии ядер всё ещё недостаточно для их сближения на расстояние, при котором ядерные силы притяжения станут больше сил кулоновского отталкивания. Только при температурах порядка миллионов кельвинов вероятность преодолеть кулоновский барьер за счёт туннелирования становится заметной, и начинает идти самоподдерживающаяся термоядерная реакция. Именно такие условия реализуются в центре звёзд, в частности, внутри Солнца.

Кулоновским барьером называют также потенциальный барьер, который должна преодолеть альфа-частица для вылета из ядра при альфа-распаде. Логически этот термин не совсем правилен, поскольку кулоновское взаимодействие отталкивает альфа-частицу от ядра (тем самым способствуя её вылету), тогда как притяжение альфа-частицы к ядру обусловлено ядерными силами; потенциальный барьер, препятствующий альфа-распаду, создаётся именно ядерными силами. Кулоновский барьер (вместе с менее значимым центробежным барьером) при альфа-распаде преодолевается благодаря туннелированию. Вероятность туннелирования сильно (экспоненциально) зависит от высоты и ширины преодолеваемого барьера, поэтому период полураспада альфа-активных ядер быстро растёт с уменьшением энергии распада: ядра с энергией распада около 8 МэВ распадаются за микросекунды (например, ²¹⁴Po), тогда как альфа-распад с энергией около 2 МэВ происходит в среднем за время, значительно превышающее возраст Вселенной (например, ¹⁸⁰W).

Величина кулоновского барьера определяется формулой

Bk=Zze2R{\displaystyle B_{k}={\frac {Zze^{2}}{R}}}

где Z{\displaystyle \ Z}, z{\displaystyle \ z} — атомные номера налетающей (вылетающей) частицы и ядра соответственно, R{\displaystyle \ R} — эффективный радиус ядра (расстояние, на котором сильное взаимодействие начинает преобладать над кулоновским), e{\displaystyle \ e} — заряд электрона.

Кулоновское увлечение — Википедия

Материал из Википедии — свободной энциклопедии

Кулоновское увлечение (англ. Coulomb drag) — процесс взаимодействия пространственно разделённых зарядов посредством кулоновского взаимодействия. Проявляется в двухслойных структурах с металлическими слоями, разделёнными туннельно непрозрачным изолятором, когда ток, протекающий в одном из слоёв, создаёт ток в другом слое при замкнутой электрической цепи в этом слое или напряжение при разомкнутой цепи^[1]. Эффект был теоретически предсказан в работе советского учёного М. Б. Погребинского^[2].

Рассмотрим два проводника, разделённых непроводящим материалом. (В случае гетероструктуры, состоящей из GaAs — квантовых ям, разделённых барьером в виде AlAs). Туннельный ток между квантовыми ямами при низких температурах отсутствует в такой структуре благодаря достаточно толстому слою изолятора (AlAs). Тем не менее, электрическое поле носителей заряда в одном слое может влиять на носители тока во втором слое. Оказывается, что при протекании тока в одном слое, называемом активным слоем, носители заряда из второго слоя — соответственно, пассивного, — испытывают увлечение. В этом случае импульс и энергия носителей активного слоя может переноситься в пассивный слой и создавать ток при замкнутой цепи или напряжение, препятствующее протеканию тока, при разомкнутой цепи. Это, в частности, приводит к дополнительному электрическому сопротивлению в активном слое из-за трения^[1]. Тогда кулоновское увлечение может дать информацию о деталях электрон-электронного взаимодействия в разных слоях полупроводника.

Чтобы описать взаимодействие между слоями, вводят следующую характеристику (сопротивление увлечения, англ. drag resistance)

RD=−V2I1{\displaystyle R_{D}=-{\frac {V_{2}}{I_{1}}}},

где V₂ — напряжение, измеренное в пассивном слое, I₁ — ток активного слоя.

Феноменологическая модель[править | править код]

Погребинский рассмотрел взаимодействие двух проводящих слоёв в модели Друде^[3].

dv1dt=em1E1+em1[v1×B]−v1τ1−v1−v2τD{\displaystyle {\frac {d{\textbf {v}}_{1}}{dt}}={\frac {e}{m_{1}}}{\textbf {E}}_{1}+{\frac {e}{m_{1}}}[{\textbf {v}}_{1}\times {\textbf {B}}]-{\frac {{\textbf {v}}_{1}}{\tau _{1}}}-{\frac {{\textbf {v}}_{1}-{\textbf {v}}_{2}}{\tau _{D}}}},

dv2dt=em2E2+em2[v2×B]−v2τ2−v2−v1τD{\displaystyle {\frac {d{\textbf {v}}_{2}}{dt}}={\frac {e}{m_{2}}}{\textbf {E}}_{2}+{\frac {e}{m_{2}}}[{\textbf {v}}_{2}\times {\textbf {B}}]-{\frac {{\textbf {v}}_{2}}{\tau _{2}}}-{\frac {{\textbf {v}}_{2}-{\textbf {v}}_{1}}{\tau _{D}}}},

где e — заряд электрона, v_i, m_i, E_i, τ_i — дрейфовая скорость, эффективна масса, электрическое поле, время релаксации по импульсам для частиц в слое i, соответственно. Первое слагаемое описывает кулоновскую силу, второе — силу Лоренца, третье — затухание, и последнее отвечает за взаимодействие между слоями с соответствующим временем увлечения τ_D. При малом взаимодействии между слоями, когда τ_D>>τ_i, транспорт полностью независим в двух слоях и теория Друде даёт обычные выражения для тензора сопротивления (см. магнитосопротивление). В другом предельном случае сильного взаимодействия или идеальных проводников, когда τ_D<<τ_i, тензор сопротивления определяется взаимодействием между слоями и создаётся ситуация идеального увлечения. В промежуточном случае нужно ввести обычный тензор ραβ(ij){\displaystyle \rho _{\alpha \beta }^{(ij)}}, где индексы i, j относятся к разным проводящим слоям, а греческие индексы α, β определяют пространственные компоненты. Тогда для компонент тензора сопротивлений^[3]

ρxx(12)=−m2e2n1τD{\displaystyle \rho _{xx}^{(12)}=-{\frac {m_{2}}{e^{2}n_{1}\tau _{D}}}},

ρxx(11)=m1e2n1(1τ1+1τD){\displaystyle \rho _{xx}^{(11)}={\frac {m_{1}}{e^{2}n_{1}}}\left({\frac {1}{\tau _{1}}}+{\frac {1}{\tau _{D}}}\right)},

ρyx(11)=Ben1{\displaystyle \rho _{yx}^{(11)}={\frac {B}{en_{1}}}}.

Заметим, что отсутствует холловское увлечение и вклад в кулоновское увлечение вносит только продольная компонента тензора сопротивлений и она в этой модели не зависит от магнитного поля.

↑ ¹ ² Narozhny, 2016, с. 2.
↑ Pogrebinskii, M. B. Mutual drag of carriers in a semiconductor-insulator-semiconductor system (англ.) // Sov. Phys. Semicond.. — 1977. — Vol. 11. — P. 372.
↑ ¹ ² Narozhny, 2016, с. 4.

Центральные силы и их поля

Центральная сила — сила, линия действия которой при любом положении тела, к которому она приложена, проходит через точку, называемую центром силы (точка на Рис.1). Тело при этом, как правило, рассматривается как материальная точка, а центр также считается точечным, обычно^[1] совпадая с физическим источником силы; в простейшем случае он фиксирован в пространстве.

Проще всего центральные силы вводятся для физических систем, состоящих из конечного числа объектов, размерами которых можно пренебречь (материальных точек), или, иногда, некоторых эквивалентных им, состоящих из протяжённых объектов с фиксированной внутренней структурой^[2]. Распределенные системы, в которых действуют центральные силы, в общем случае^[3] не могут быть представлены конечным количеством материальных точек. В случае распоеделенных систем общим подходом является разбиение их на очень большое (впределе бесконечное) количество элементов малого (в пределе стремящегося к нулю) размера каждый, которые и рассматриваются как материальные точки — между которыми действуют центральные силы в соответствии с определением, данным выше. Таким образом, в этом случае центральной, собственно, является каждая элементарная сила, а реальная сила является суммой (суперпозицией)) таких элементарных сил.

Kлассическая физика вводит также понятие поля центральной силы для области трёхмерного пространства, в котором действуют центральные силы. ^[4]

Рис.1 К определению центральной силы: частица в поле атомного ядра.(опыт Резерфорда)

Для любой центральной силы выполняется соотношение

(где — радиус-вектор с началом в центре силы), свидетельствующее о равенстве нулю момента силы относительно центра силы:

Силовые поля

Этим полям соответствуют кулоновские силы (силы электростатического взаимодействия) и силы гравитационные (силы Всемирного тяготения. Сходство между ними заключается в том, что они могут быть обнаружены во время взаимодействия материальных объектов, причем в случае гравитации свойством, обуславливающим это взаимодействие, является масса, а в случае кулоновского взаимодействия — заряд, этой массой переносимый. Заряды, не связанные с массой, классической физике неизвестны.

При сохранении подобия в геометрических размерах тел и их взаимного расстояния, силы взаимного тяготения, равно как и силы электростатические (кулоновские) растут пропорционально 4-й степени абсолютных размеров рассматриваемой модели. В то же самое время в случае электрического взаимодействия, где между величиной заряда и размерами тел, несущих эти заряды, нет определённой связи, силы взаимодействия ослабляются пропорционально 2-й степени абсолютных размеров . Поэтому при сравнении этих сил в микромире доминируют Кулоновские силы, а в масштабах Вселенной — силы Всемирного тяготения.

Интенсивность силового поля

В ряде случаев в рассматриваемом силовом поле оказывается возможным определить пространственно локализованный его источник (нем. Quelle).

Одним из основных свойств рассматриваемых здесь полей является их экспериментально подтверждаемая аддитивность, иначе называемая принципом суперпозиции, заключающегося в том, что действие поля, создаваемого несколькими источниками на объект своего воздействия независимы друг от друга при любом значении их интенсивности. Это позволяет ввести в рассмотрение понятие о «точечном источнике» с чётко определённым его пространственным расположении и сформулировать понятие об суммарной интенсивности поля нескольких источников как сумму этих воздействий с учётом геометрии конкретной задачи.

Интенсивность определяется в заданной точке пространства силой, которая могла бы подействовать на единичный «пробный объект» с заданным свойством, который мог бы находиться в этой точке или же в действительности находящийся в ней. Выбор «пробного объекта» есть предмет договорённости. При необходимости источник поля и объект его воздействия могут поменяться местами.

Величина, характеризующая интенсивность центрального силового поля представляет собой вектор направленный по линии соединяющей точечный источник и заданную точку поля.

Потенциальные центральные поля

Работа центральной силы

Элементарная работа силы, в том числе и центральной силы, есть скалярная величина, исчисляемая изменением энергии при перемещении точки приложения силы (в общем случае изменяющей свою величину и направление), при перемещении на столь малый отрезок своей траектории, что на нём вектор силы может считаться неизменным, то есть на расстояние :

(5)

где есть угол между этими векторами. Поскольку , то направление отсчёта угла значения не имеет.

При перемещении на расстояние от до , весь пройденный путь можно разбить на элементарных участков. И тогда полная работа будет суммой этих элементарных работ с тем большей точностью, чем на большее количество участков будет разбита траектории, что выражается знаком интеграла, как предела этой суммы :

Рассматривая движение в Декартовой системе координат центральную силу можно представить в виде геометрической суммы её проекций на координатные оси:

где , , суть единичные векторы (орты) для своих осей.

Потенциал поля

Не для всякого поля силы совершаемая ею работа зависит лишь от положения начальной и конечной точек движения . Иными словами, не зависит от формы пути.

Упомянутый интеграл не будет зависеть от формы пути лишь в том случае, если будет существовать некая первообразная функция , в выражении полного дифференциала которой:

В этом случае функция будет называться потенциальной функцией, а поле силы -потенциальным полем. ^[5]

Но это станет возможным лишь при одновременном выполнении равенств:

Связь с потенциальной энергией естественно осуществляется через работу.

Представляется естественным считать, что вектор напряжённости поля направлен ОТ источника поля, (что привычно принимается при описании электростатического поля при взаимодействии одноимённых зарядов ^[7] )Тогда, зафиксировав точку, находящуюся на расстоянии от центрального заряда и предоставив ему свободу, получим, что он под действием силы будет удаляться в бесконечность. При этом совершённая полем работа будет равна:

То же можно сказать и в случае, если поле продвинуло тело дальше и, следовательно, проделало больше работы и потому разница работ на пути между точками больше нуля.

И эти работы может быть названа с точностью до постоянной потенциалом точки : и , подразумевая под потенциалом возможность совершить работу, которая для более близкой точки выше, чем у более далёкой.

Тогда совершённая полем работа будет равна разности потенциалов , взятой со знаком «минус»

Поле как градиент потенциала

Знак минус, по обычному соглащению присутстсвующий в этой формуле, связан с тем, чтобы функция U могла быть отождествлена с потенциальной энергией (хотя чиcто формально потенциальная функция могла бы быть выбрана и с другим знаком, если такого отождествления не предполагается).

Кулоновское поле

Напряженность кулоновского поля определяется вектором , равным:

или, переходя, к скалярной форме записи:

Здесь ; — заряд тела -источника силы; ,есть расстояние до точки, где определяется интенсивность, а константа зависит от диэлектрической постоянной среды , (для пустого пространства равная 1), в которой существует поле:

, где:

есть диэлектрическая постоянная вакуума. В таком случае для вакуума

= Vm/As в Международной системе единиц ^[8],

Кулоновские силы

Объектом действия кулоновского поля является материальное тело, несущее заряд

или, с учётом ():

или, в скалярном представлении:

Специфической особенностью кулоновского поля является то, что вектор его напряжённости направлен либо ОТ источника поля в случае совпадение знака заряда источника и объекта взаимодействия, либо направлен К источнику в случае разноимённости зарядов. Это значит, что заряжённые материальные тела в первом случае будут испытывать отталкивающую силу, а в противоположном — силу сближающую их.

Поле гравитации

В русскоязычной литературе интенсивность поля тяготения называют «ускорением свободного падения» за рубежом иногда её называют напряжённостью гравитационного поля.

Или, переходя, к скалярной форме записи:

Здесь ; — масса тела -источника гравитации; есть расстояние до точки, где определяется интенсивность, а константа есть гравитационная постоянная, равная по современным данным , ^[9]

Силы гравитации

Объектом действия поля гравитации является материальное тело,имеющее массу

В таком случае на него действует механическая сила, равная произведению массы тела на напряжённость поля. Существенно, что между массой, входящей во Второй закон Ньютона и массой того же тела, подверженного действию гравитации нет никакой разницы в величине. Тогда, с учётом ():

или, в скалярном представлении:

Специфической особенностью сил гравитации является то, что они всегда являются силами притяжения. Кроме того, силы гравитации всепроникающи и от них невозможно защититься никаким экраном. Это свойство объединяет силы гравитации с фиктивными силами инерции, существующими в любой неинерциальной системе отсчёта. Подобная аналогия имеет своей основой фундаментальные свойства пространства, изучения которых выходит за рамки классической физики.^[10]

Потенциал поля гравитации

( 23)

^[11](24)

Движение под действием центральной силы

В общем случае любую траекторию тела, рассматриваемого как материальная точка, можно представить в виде пространственной кривой, состоящей из сопряжённых поворотов в различных плоскостях вокруг мгновенных центров поворота C с различными значениями радиуса поворота на том же Рис 1.Применение представления о траектории реального трёхмерного тела смысла не имеет.

Замечание

Последняя оговорка весьма существенна. Так, например, для земного наблюдателя бомба, сброшенная с летящего равномерно и прямолинейно летательного аппарата движется по параболе. Но для пилота она падает вертикально под действием единственной в данном случае силы тяжести (Если не принимать во внимание снос из-за сопротивления воздуха).Никаких сил, вызывающих искривление траектории здесь нет. Центростремительные силы возникают не потому, что траектория крива,но потому, что они являются выражением реально имеющего место силового взаимодействия движущегося объекта со своим окружением.

Считается, что в центре силы находится источник силы которым может быть тяготеющая масса, либо электрический заряд в случае, если рассматриваемая сила есть характеристика соответствующего силового поля. Центр силы в общем случае не совпадает с мгновенным центром поворота — точка на Рис. Это совпадение имеет место лишь при повороте тела по дуге окружности. ^[4]

Как видно на Рис.1 единственная действующая между телами и сила может быть разложена на две составляющие: (2)

При этом есть тангенциальная сила, в зависимости от направления движения тела по своей траектории на рисунке либо тормозящая его движение, либо ускоряющая его.

есть сила, направленная по нормали к касательной к траектории в сторону мгновенного центра и потому являющаяся центростремительной силой.^[12]

Непосредственно из определения понятий о моментах силы и момента количества движения (момента импульса)следует экспериментально подтверждаемый факт, что скорость изменения момента импульса вращающегося тела прямо пропорциональна величине приложенного к телу момента силы :

Однако в поле центральной силы её момент всегда равен нулю (Формула (1)).Из этого непосредственно следует, что при любом движении тела в поле центральной силы момент количества движения движущегося под её действием тела остаётся постоянным:

. Но, поскольку постоянство вектора есть одновременно и сохранение его направления в пространстве, то заметаемая при движении тела площадка всегда лежит в одной и той же плоскости. Из этого следует, что любая траектория, движения тела под действием центральной силы есть плоская кривая.

Наиболее часто движение тел в гравитационном поле изучают в области небесной механики, где гравитационное воздействия преоблаают и потому изучаемая система взаимодействующих сил может рассматриваться, как консервативная система , т.е. такая, в которой сохраняется полная энергия тела в виде суммы потенциальной и кинетической энергии.^[4]

(25),где:

причём и соответствуют скоростям, создаваемым нормальной и тангенциальной составляющей действующей на тело силы на Рис.1

Рис.2 К вопросу о зависимости параметров орбиты от полной энергии планеты

Воспользовавшись определением кинетического момента: получаем для кинетической энергии тангенциального движения соотношение:

А для движения по нормали к траектории:

Тогда выражение для полной энергии тела будет иметь вид:

Введя в рассмотрение эффективный потенциал :

Получаем возможость связать диапазон изменения длины радиуса -вектора траектории тела с запасённой им энергией, что представлено на рис.2 ^[13]

Так при минимальной энергии движущегося тела тело движется по круговой орбите с радиусом

Если энергия движения тела больше, скажем ,траектория тела будет представлять эллипс с малой полуосью и большой .

Наконец, при энергии тела разойдутся, сблизившись на минимальное расстояние

Примечания

↑ Иногда бывает удобно — и удаётся — рассматривать как центр силы не её физический источник, а некоторую фиктивную точку. Так например при изучении движения двух точечных тел, между которыми действуют центральные силы, удобно рассматривать в качестве такого центра центр масс системы — потому что он неподвижен.
↑ Имеются в виду сферически симметричные объекты (или объекты, досаточно мало отличающиеся от сферически симметричных, так чтобы можно было считать их сферически симметричными в рамках рабочего приближения).
↑ По сути — почти в любом случае кроме описанных выше; даже в таком простом случае, как кулоновское взаимодействие абсолютно твердых тел несферической формы с фиксированными на них распределенными зарядами, обычно невозможно свести вычисление сил к силам между небольшим количеством материальных точек.
↑ ¹ ² ³ Физический энциклопедический словарь/ Гл. ред. А.М.Прохоров. Ред.кол. Д.М.Алексеев, А.М. Бонч-Бруевич,А.С.Боровик-Романов и др. -М.: Сов.энциклопедия, 1983.-323 с.,ил, 2 л.цв.ил.
↑ ¹ ² Бронштейн И. Н. Семендяев К. А. Справочник по математике. М.: Издательство «Наука» Редакция справочной физико-математической литературы.1964.
↑ Поскольку сохраняться должна сумма потенциальной и кинетической энергий, в направлении действия силы (которая может разгонять в этом направлении частицу, увеличивая тем самым ее кинетическую энергию) потенциальная энергия убывает.
↑ Тамм,И.Е. Основы теории электричества
↑ ГОСТ 8.417-2002. Единицы величин
↑ Ulrich Leute. Physik und ihre Anwendungen in Technik und Umwelt: Carl Hanser Verlag; München, Wien- 2004 ISBN 3-446-22884-5
↑ Хайкин, Семён Эммануилович|С. Э. Хайкин. Силы инерции и невесомость. М.,1967 г. Издательство «Наука».Главная редакция физико-математической литературы.
↑ Ulrich Leute. Physik und ihre Anwendungen in Technik und Umwelt: Carl Hanser Verlag; München, Wien- 2004 ISBN 3-446-22884-5
↑ Klaus Dransfeld, Paul Kleine, Georg Michael Kalvius. Physik I. Oldenbourg Wissenschaftsverlag GmbH 2001 ISBN 3-486-25416-2
↑ ‘

Кулоновское поле это – кулоновское поле — это… Что такое кулоновское поле?

Поле кулоновское — Справочник химика 21

Центральные силы и их поля — Википедия

Потенциальные центральные поля[править | править код]

Работа центральной силы[править | править код]

Потенциал поля[править | править код]

Поле как градиент потенциала[править | править код]

Кулоновское поле[править | править код]

Кулоновские силы[править | править код]

Поле гравитации[править | править код]

Силы гравитации[править | править код]

Потенциал поля гравитации[править | править код]

Движение под действием центральной силы[править | править код]

1.Закон Кулона.

3.Напряженность и индукция электрического поля.

1. Электрический заряд. Закон кулона.

2.Напряжённость электростатического поля. Принцип суперпозиции. Силовые линии электростатического поля.

Кулоновский барьер — Википедия

Кулоновское увлечение — Википедия

Феноменологическая модель[править | править код]

Центральные силы и их поля

Силовые поля

Интенсивность силового поля

Потенциальные центральные поля

Работа центральной силы

Потенциал поля

Поле как градиент потенциала

Кулоновское поле

Кулоновские силы

Поле гравитации

Силы гравитации

Потенциал поля гравитации

Движение под действием центральной силы

Примечания

Добавить комментарий Отменить ответ