Круговая частота Википедия

Углова́я частота́ (синонимы: радиальная частота, циклическая частота, круговая частота, частота вращения) — скалярная физическая величина, мера частоты вращательного или колебательного движения. В случае вращательного движения угловая частота равна модулю вектора угловой скорости. В Международной системе единиц (СИ) и системе СГС угловая частота выражается в радианах в секунду, её размерность обратна размерности времени (радианы безразмерны).

Угловая частота является производной по времени от фазы колебания:

ω=∂φ/∂t.{\displaystyle \omega =\partial \varphi /\partial t.}

Другое распространённое обозначение ω=φ˙.{\displaystyle \omega ={\dot {\varphi }}.}

Угловая частота связана с частотой ν соотношением^[1]

ω=2πν.{\displaystyle \omega ={2\pi \nu }.}

В случае использования в качестве единицы угловой частоты градусов в секунду связь с обычной частотой будет следующей:

ω=360∘ν.{\displaystyle \omega ={360^{\circ }\nu }.}

В случае вращательного движения угловая частота численно равна углу, на который повернется вращающееся тело за единицу времени (то есть равна модулю вектора угловой скорости), в случае колебательного движения — приращению полной фазы колебания за единицу времени. Численно угловая (циклическая) частота равна числу циклов (колебаний, оборотов) за 2π единиц времени.

Введение циклической частоты (в её основной размерности — радианах в секунду) позволяет упростить многие формулы в теоретической физике и электронике. Так, резонансная циклическая частота колебательного LC-контура равна ωLC=1/LC,{\displaystyle \omega _{LC}=1/{\sqrt {LC}},} тогда как обычная резонансная частота νLC=1/(2πLC).{\displaystyle \nu _{LC}=1/(2\pi {\sqrt {LC}}).}

В то же время ряд других формул усложняется. Решающим соображением в пользу циклической частоты стало то, что переводные множители 2π и 1/(2π), появляющиеся во многих формулах при использовании радианов для измерения углов и фаз, исчезают при введении циклической частоты.

См. также[ | ]

Примечания

Частота среза — Википедия

Материал из Википедии — свободной энциклопедии

Частота́ сре́за (частота отсе́чки) fc{\displaystyle f_{c}} — частота, выше или ниже которой мощность выходного сигнала некоторого линейного частотно-зависимого объекта, например, электронной схемы уменьшается в два раза^[2] от мощности в полосе пропускания при воздействии на вход неизменного по амплитуде сигнала.

Амплитудно-частотная характеристика на частоте среза имеет спад до уровня −log10⁡2{\displaystyle -\log _{10}2} (приблизительно −3 дБ) относительно уровня в полосе пропускания.

Пример вычисления частоты среза и коэффициента передачи на частоте среза фильтра нижних частот 1-го порядка[править | править код]

Фильтр нижних частот (ФНЧ) 1-го порядка имеет комплексную передаточную функцию H(s){\displaystyle H(s)} вида:

H(s)=11+αs,{\displaystyle H(s)={\frac {1}{1+\alpha s}},}

где s{\displaystyle s} — комплексная переменная преобразования Лапласа;

α{\displaystyle \alpha } — параметр фильтра, константа.

В случае подачи на вход фильтра гармонического сигнала с частотой ω{\displaystyle \omega } в установившемся режиме комплексная передаточная функция имеет вид:

H(jω)=11+αjω,{\displaystyle H(j\omega )={\frac {1}{1+\alpha j\omega }},}

где буквой j{\displaystyle j} обозначена мнимая единица;

ω{\displaystyle \omega } — угловая частота.

Эта функция имеет единственный полюс (частота, при которой знаменатель дроби обращается в 0) на частоте ωc=2πfc=1/α,{\displaystyle \omega _{c}=2\pi f_{c}=1/{\alpha },} fc{\displaystyle f_{c}} — частота среза.

Модуль коэффициента передачи этого ФНЧ в зависимости от частоты (эту функцию принято называть амплитудно-частотной характеристикой) имеет вид:

|H(jω)|=|11+αjω|=11+α2ω2.{\displaystyle \left|H(j\omega )\right|=\left|{\frac {1}{1+\alpha j\omega }}\right|={\sqrt {\frac {1}{1+\alpha ^{2}\omega ^{2}}}}.}

Модуль коэффициента передачи на частоте полюса:

|H(jωc)|=11+α2ωc2=12.{\displaystyle \left|H(j\omega _{\mathrm {c} })\right|={\sqrt {\frac {1}{1+\alpha ^{2}\omega _{\mathrm {c} }^{2}}}}={\frac {1}{\sqrt {2}}}.}

То есть, на частоте полюса коэффициент передачи уменьшается в 2.{\displaystyle {\sqrt {2}}.} В рассмотренном примере частота среза равна частоте полюса.

1. ↑ Порядок фильтра равен порядку (степени алгебраического уравнения) знаменателя передаточной функции (ЛАФЧХ) фильтра. Как правило^{[уточнить]}, порядок фильтра равен количеству входящих в него сосредоточенных реактивных элементов.
2. ↑ При этом амплитуда сигнала на частоте среза равна 12≈0,707{\displaystyle {\frac {1}{\sqrt {2}}}\approx 0,707} от амплитуды сигнала в полосе пропускания.

Волновое число — Википедия

Волново́е число́ (также^[1] называемое пространственной частотой ^[2]) — это отношение 2π радиан к длине волны:

k≡2πλ,{\displaystyle k\equiv {\frac {2\pi }{\lambda }},}

пространственный аналог угловой частоты^[3].

Обычное обозначение^[4]: k{\displaystyle k}.

Определение: волновым числом k называется быстрота роста фазы волны φ по пространственной координате^[5]:

k≡dφdx.{\displaystyle k\equiv {\frac {d\varphi }{dx}}.}

В одномерном случае волновому числу обычно приписывают знак минус, если волна распространяется в отрицательном направлении (против оси). В многомерном — это обычно синоним абсолютной величины волнового вектора или его компонент (несколько волновых чисел по количеству осей координат), также может быть проекцией волнового вектора на некоторое определенное выбранное направление.

Поскольку в большинстве случаев волновое число имеет смысл только применительно к монохроматической волне (строго монохроматической или по крайней мере почти монохроматической), производную в определении можно (для этих самых распространенных случаев) заменить на выражение с конечными разностями:

k≡ΔφΔx.{\displaystyle k\equiv {\frac {\Delta \varphi }{\Delta x}}.}

Исходя из этого, можно получить разные более-менее удобные формулировки^[6]:

• Волновое число есть разность фазы волны (в радианах) в один и тот же момент времени в пространственных точках на расстоянии единицы длины (одного метра).
• Волновое число есть количество пространственных периодов (горбов) волны, приходящееся на 2π метров.
• Волновое число равно числу радиан волны на отрезке в 1 метр.

В спектроскопии волновым числом часто называют просто величину, обратную длине волны (1/λ), измеряемую обычно в обратных сантиметрах (см⁻¹). Такое определение отличается от обычного отсутствием множителя 2π.

Единица измерения — рад·м⁻¹, физическая размерность м⁻¹ (в системе СГС: см⁻¹).

Используется в физике, математике^[7] (преобразование Фурье) и таких приложениях, как обработка изображений.

k≡2πλ=2πνvφ=ωvφ,{\displaystyle k\equiv {\frac {2\pi }{\lambda }}={\frac {2\pi \nu }{v_{\varphi }}}={\frac {\omega }{v_{\varphi }}},}

где:

λ —  длина волны,

ν{\displaystyle \nu } (греческая буква «ню») — частота,

v{\displaystyle v}_φ — фазовая скорость волны,

ω — угловая частота.

Для монохроматической бегущей волны можно записать:

φ=kx−ωt{\displaystyle \varphi =kx-\omega t} — для фазы;

u(x,t)=const⋅cos(kx−ωt+φ0){\displaystyle u(x,t)=const\cdot \mathrm {cos} (kx-\omega t+\varphi _{0})} — для самой волны;

или

u(x,t)=const⋅ei(kx−ωt){\displaystyle u(x,t)=const\cdot e^{i(kx-\omega t)}}

 — для комплексной волны; здесь φ0{\displaystyle \varphi _{0}} может быть спрятано в const{\displaystyle const},

для монохроматической стоячей волны:

u(x,t)=const⋅cos(k⋅(x−x0))cos(ω⋅(t−t0)).{\displaystyle u(x,t)=const\cdot \mathrm {cos} (k\cdot (x-x_{0}))\mathrm {cos} (\omega \cdot (t-t_{0})).}

Волновое число точно определено для монохроматической волны. К волнам другого вида волновое число относится через понятие спектра (то есть через преобразования Фурье), то есть немонохроматическая волна вообще говоря содержит в разных пропорциях монохроматические компоненты с разными волновыми числами; впрочем, почти монохроматические волны могут приближенно быть описаны как волны с определенным волновым числом (их спектр в основном сосредоточен вблизи одного значения волнового числа).

Иногда, например, в квазигеометрическом (квазиклассическом) приближении, можно рассматривать волновое число (волновой вектор) как медленно меняющийся в пространстве, то есть волну не как монохроматическую, а как квазимонохроматическую. В этом случае, естественно, лучше использовать определение волнового числа (волнового вектора) с производной, а не с конечными разностями.

В сущности, единственный физически осмысленный случай, когда волновое число (волновой вектор) может меняться с x, даже относительно быстро, это случай формализма интеграла по траекториям. В этом случае в теории для описания волны присутствуют волны весьма специального вида:

u(x,t)=ei∫(kdx−ωdt),{\displaystyle u(x,t)=e^{i\int (kdx-\omega dt)},}

для которых упомянутое вполне корректно и осмысленно.

В квантовой физике связывается с компонентой импульса по данному направлению:

px=ℏkx,{\displaystyle p_{x}=\hbar k_{x},}

где

p_x —  компонента импульса по направлению x (для одномерной системы — полный импульс),

k_x —  волновое число (компонента волнового вектора) по направлению x (для одномерной системы — просто волновое число),

ħ — редуцированная постоянная Планка (постоянная Дирака).

Поскольку константа Планка — универсальная константа, можно выбором системы единиц просто сделать ħ = 1. Тогда

px=kx,{\displaystyle p_{x}=k_{x},}

то есть в квантовой физике понятия компоненты импульса и волнового числа по сути совпадают. Это можно считать одним из фундаментальных принципов квантовой механики.

То же можно сказать для полного импульса и волнового числа без указания направления абсолютной величины волнового вектора):

p=ℏk,{\displaystyle p=\hbar k,}

а в единицах ħ = 1:

p=k{\displaystyle p=k}

В частном случае, для света в вакууме (и, в принципе, любых других безмассовых полей; приближенно — для ультрарелятивистских частиц) можно также написать:

k=Eℏc,{\displaystyle k={\frac {E}{\hbar c}},}

где

E — энергия,

ħ — редуцированная постоянная Планка (постоянная Дирака),

c — скорость света в вакууме.

1. ↑ Это практически полные синонимы, различающиеся несколько лишь традиционными предпочтениями употребления в разных областях, так, термин волновое число в основном употребляется в физике (впрочем, наряду с термином пространственная частота), в математике же и различных приложениях (таких, как обработка изображений) обычно употребляется для сходного понятия термин пространственная частота и даже просто частота. Дополнительно заметим, что для термина пространственная частота (частота) нередко допускается многомерное понимание, то есть он употребляется и в качестве практического синонима термина волновой вектор, тогда как для термина волновое число такое употребление по понятным причинам практически исключено. Впрочем, компоненты волнового вектора могут называться волновыми числами по осям координат.
2. ↑ Физическая энциклопедия. В 5 томах/ Гл. ред. А. М. Прохоров. Ред. кол. Д. М. Алексеев, А. М. Балдин.- М.: Советская энциклопедия + Большая российская энциклопедия. — 1998.
3. ↑ Круговая частота измеряется в радианах в секунду, волновое число — в радианах на метр
4. ↑ Зачастую используются и другие, как правило, оговоренные явно.
5. ↑ В одномерном случае выбор пространственной координаты однозначен (с точностью до зеркального отражения), в многомерном же случае по умолчанию координата x выбирается так, чтобы совпадать с направлением максимальной скорости роста фазы, то есть перпендикулярно фазовому фронту; в этом случае волновое число есть абсолютная величина волнового вектора. Наконец иногда направление x задается явно и может не совпадать с упомянутым только что; тогда обычно говорят о волновом числе по направлению x и явно указывают это в обозначении: kx{\displaystyle k_{x}}.
6. ↑ Включая и формулировку в начале статьи
7. ↑ В математике (и многих приложениях) — в основном в терминологической форме пространственная частота или даже просто частота.

Длина волны — Википедия

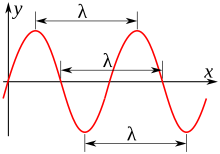График волны функции (например, физической величины) y, распространяющейся вдоль оси Оx, построенный в фиксированный момент времени (t = const). Длина волны λ может быть измерена как расстояние между парой соседних максимумов y (x) либо минимумов, либо как удвоенное расстояние между соседними точками, в которых y = 0

Длина́ волны́ — расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе^[1][2].

Длина́ волны́ (в линии передачи) — расстояние в линии передачи, на котором фаза электромагнитной волны вдоль направления распространения меняется на 2π^[3].

Длину волны можно также определить:

• как расстояние, измеренное в направлении распространения волны, между двумя точками в пространстве, в которых фаза колебательного процесса отличается на 2π{\displaystyle 2\pi };
• как путь, который проходит фронт волны за интервал времени, равный периоду колебательного процесса;
• как пространственный период волнового процесса.

Представим себе волны, возникающие в воде от равномерно колеблющегося поплавка, и мысленно остановим время. Тогда длина волны — это расстояние между двумя соседними гребнями волны, измеренное в радиальном направлении. Длина волны — одна из основных характеристик волны наряду с частотой, амплитудой, начальной фазой, направлением распространения и поляризацией. Для обозначения длины волны принято использовать греческую букву λ{\displaystyle \lambda }, размерность длины волны — метр.

Как правило, длина волны используется применительно к гармоническому или квазигармоническому (например, затухающему или узкополосному модулированному) волновому процессу в однородной, квазиоднородной или локально однородной среде. Однако формально длину волны можно определить по аналогии и для волнового процесса с негармонической, но периодической пространственно-временной зависимостью, содержащей в спектре набор гармоник. Тогда длина волны будет совпадать с длиной волны основной (наиболее низкочастотной, фундаментальной) гармоники спектра.

Длина волны — пространственный период волнового процесса[править | править код]

Волна — колебательный процесс, развивающийся (распространяющийся) в пространстве и во времени, в связи с этим изменяющаяся в волновом процессе физическая величина является функцией пространственных координат и времени (то есть особого вида пространственно-временной функцией). Волновой процесс в частности может быть периодическим (например, гармоническим). По аналогии с «временны́м» периодом T{\displaystyle T} [с] (интервалом времени, за который периодический колебательный процесс повторяется) длину волны λ{\displaystyle \lambda } [м] можно рассматривать как

пространственный период волнового процесса. Следует заметить, что «временно́й» круговой частоте ω=2πf=2π/T{\displaystyle \omega =2\pi f=2\pi /T} [радиан/с], показывающей, на сколько радиан изменится фаза колебания за 1 с, соответствует «пространственная круговая частота» k=2π/λ{\displaystyle k=2\pi /\lambda } [радиан/м], называемая волновым числом и показывающая, на сколько радиан отличаются фазы колебательного процесса в двух точках в пространстве, расположенных вдоль направления распространения волны на расстоянии 1 м друг от друга. При этом очевидно, что фазы колебательного процесса в двух таких точках, расположенных друг от друга на расстоянии в λ{\displaystyle \lambda }, отличаются ровно на 2π{\displaystyle 2\pi }.

Получить соотношение, связывающее длину волны с фазовой скоростью v{\displaystyle v} и частотой f{\displaystyle f} можно из определения. Длина волны соответствует пространственному периоду волны, то есть расстоянию, которое точка с постоянной фазой «проходит» за интервал времени, равный периоду T{\displaystyle T} колебаний, поэтому

λ=vT=vf=2πvω.{\displaystyle \lambda =vT={\frac {v}{f}}={\frac {2\pi v}{\omega }}.}

Для электромагнитных волн в вакууме скорость v{\displaystyle v} в этой формуле равна скорости света (299 792 458 м/с), и длина волны λ=299792458 m/sf{\displaystyle \lambda ={\frac {299\,792\,458~{\text{m/s}}}{f}}}. Если значение f{\displaystyle f} подставить в герцах, то λ{\displaystyle \lambda } будет выражена в метрах.

Радиоволны делят на диапазоны по значениям длин волн, например, 10…100 м — декаметровые (короткие) волны, 1…10 м — метровые, 0.1…1,0 м — дециметровые и т. п. Механизмы и условия распространения радиоволн, степень проявления эффекта дифракции, отражающие свойства объектов, предельная дальность радиосвязи и радиолокации сильно зависят от длины волны. Как правило, габаритные размеры антенн сравнимы либо (справедливо всегда для антенн направленного действия) превышают рабочую длину волны радиоэлектронного средства.

В оптически более плотной среде (слой выделен тёмным цветом) длина электромагнитной волны сокращается. Синяя линия — распределение мгновенного ( t = const) значения напряжённости поля волны вдоль направления распространения. Изменение амплитуды напряжённости поля, обусловленное отражением от границ раздела и интерференцией падающей и отражённых волн, на рисунке условно не показано.

Длина электромагнитной волны в среде короче, чем в вакууме:

λ=cnν,{\displaystyle \lambda ={\frac {c}{n\nu }},}

где n=εμ>1{\displaystyle n={\sqrt {\varepsilon \mu }}>1} — показатель преломления среды;

ε{\displaystyle \varepsilon } — относительная диэлектрическая проницаемость среды;

μ{\displaystyle \mu } — относительная магнитная проницаемость среды.

Величины n{\displaystyle n}, μ{\displaystyle \mu } и ε{\displaystyle \varepsilon } могут существенно зависеть от частоты ν{\displaystyle \nu } (явление дисперсии). Поскольку для большинства сред в радиочастотном диапазоне μ≈1{\displaystyle \mu \approx 1} (для диэлектриков μ=1{\displaystyle \mu =1}, для ферромагнетиков с ростом частоты μ→1{\displaystyle \mu \rightarrow 1}), то в инженерной практике используют величину 1/ε<1{\displaystyle 1/{\sqrt {\varepsilon }}<1}, которую называют коэффициентом укорочения. Она равна отношению длины волны в среде к длине волны в вакууме. Например, для полиэтилена (используется в радиочастотном диапазоне как изоляционный материал с малыми потерями) ε{\displaystyle \varepsilon } = 2,56, и коэффициент укорочения 1/ε{\displaystyle 1/{\sqrt {\varepsilon }}} = 1/1,6 = 0,625.

Напротив, длина электромагнитной волны (поперечномагнитной, поперечноэлектрической) в волноводах может быть не только больше, чем в среде с тем же значением ε{\displaystyle \varepsilon }, но и больше, чем вакууме, поскольку фазовая скорость электромагнитной волны в волноводе превышает скорость электромагнитной волны в среде с тем же ε{\displaystyle \varepsilon }.

Волнам де Бройля также соответствует определённая длина волны. Частице с энергией E{\displaystyle E} и импульсом p{\displaystyle p}, соответствуют:

• частота: ν=Eh,{\displaystyle \nu ={\frac {E}{h}},}
• длина волны: λ=hp,{\displaystyle \lambda ={\frac {h}{p}},}

где h{\displaystyle h} — постоянная Планка.

Видеоурок: длина волны

Приближённо, с погрешностью около 0,07 % рассчитать длину радиоволны в свободном пространстве можно так: 300 делим на частоту в мегагерцах, получаем длину волны в метрах. Другой способ — запомнить какую-нибудь удобную пару f{\displaystyle f} ↔ λ{\displaystyle \lambda }, например, частоте 100 МГц соответствует длина волны 3 м; тогда оценив, во сколько раз требуемая частота выше или ниже 100 МГц, можно определить длину волны. Например, 1 МГц ниже 100 МГц в 100 раз, значит 1 МГц ↔ 3 м × 100 = 300 м

Примеры характерных частот и длин волн: частоте 50 Гц (частота тока в электросети) соответствует длина радиоволны 6000 км; частоте 100 МГц (радиовещательный FM-диапазон) — 3 м; 900 (1800) МГц (мобильные телефоны) — 33,3 (16,7) см; 2,4 ГГц (Wi-Fi) — 12,5 см; 10 ГГц (бортовые радиолокационные станции системы управления вооружением современных самолётов-истребителей) — 3 см. Видимый свет представляет собой электромагнитное излучение c длинами волн от 380 до 780 нм^[4].

1. ↑ Колебания и волны // Физика : Учебник для 11 класса общеобразовательных учреждений / Г. Я. Мякишев, Б. Б. Буховцев. — 12-е изд. — М. : Просвещение, 2004. — С. 121. — 336 с. — 50 000 экз. — ISBN 5-09-013165-1.
2. ↑ Определение не вполне корректно, поскольку (1) в одинаковой фазе колебания происходят и на фронте волны, и расстояние между точками на фронте может быть произвольным, в том числе и нулевым; (2) чтобы расстояние между двумя точками равнялось длине волны, колебание должно происходить не в одинаковой фазе, а со сдвигом фаз в 2π{\displaystyle 2\pi }, и расположены точки должны быть вдоль линии распространения
3. ↑ ГОСТ 18238-72. Линии передачи сверхвысоких частот. Термины и определения.
4. ↑ ГОСТ 7601-78. Физическая оптика. Термины, буквенные обозначения и определения основных величин Архивная копия от 23 марта 2013 на Wayback Machine

Период, частота, амплитуда и фаза переменного тока

Период и частота переменного тока

Время, в течение которого совершается одно полное изме­нение ЭДС, то есть один цикл колебания или один полный оборот радиуса-вектора, называется периодом колебания пере­менного тока (рисунок 1).

Рисунок 1. Период и амплитуда синусоидального колебания. Период — время одного колебания; Аплитуда — его наибольшее мгновенное значение.

Период выражают в секундах и обозначают буквой Т.

Так же используются более мелкие единицы измерения периода это миллисекунда (мс)- одна тысячная секунды и микросекунда (мкс)- одна миллионная секунды.

1 мс =0,001сек =10^-3сек.

1 мкс=0,001 мс = 0,000001сек =10^-6сек.

1000 мкс = 1 мс.

Число полных изменений ЭДС или число оборотов ради­уса-вектора, то есть иначе говоря, число полных циклов колеба­ний, совершаемых переменным током в течение одной секунды, называется частотой колебаний переменного тока.

Частота обо­значается буквой f и выражается в периодах в секунду или в герцах.

Одна тысяча герц называется килогерцом (кГц), а миллион герц — мегагерцом (МГц). Существует так же единица гигагерц (ГГц) равная одной тысячи мегагерц.

1000 Гц = 10³ Гц = 1 кГц;

1000 000 Гц = 10⁶ Гц = 1000 кГц = 1 МГц;

1000 000 000 Гц = 10⁹ Гц = 1000 000 кГц = 1000 МГц = 1 ГГц;

Чем быстрее происходит изменение ЭДС, то есть чем бы­стрее вращается радиус-вектор, тем меньше период колебания Чем быстрее вращается радиус-вектор, тем выше частота. Таким образом, частота и период переменного тока являются величинами, обратно пропорциональными друг другу. Чем больше одна из них, тем меньше другая.

Математическая связь между периодом и частотой переменного тока и напряжения выра­жается формулами

Например, если частота тока равна 50 Гц, то период будет равен:

Т = 1/f = 1/50 = 0,02 сек.

И наоборот, если известно, что период тока равен 0,02 сек, (T=0,02 сек.), то частота будет равна:

f = 1/T=1/0,02 = 100/2 = 50 Гц

Частота переменного тока, используемого для освещения и промышленных целей, как раз и равна 50 Гц.

Частоты от 20 до 20 000 Гц называются звуковыми часто­тами. Токи в антеннах радиостанций колеблются с частотами до 1 500 000 000 Гц или, иначе говоря, до 1 500 МГц или 1,5 ГГц. Такие вы­сокие частоты называются радиочастотами или колебаниями высокой частоты.

Наконец, токи в антеннах радиолокационных станций, станций спутниковой связи, других спецсистем (например ГЛАНАСС, GPS) колеблются с частотами до 40 000 МГц (40 ГГц) и выше.

Амплитуда переменного тока

Наибольшее значение, которого достигает ЭДС или сила тока за один период, называется амплитудой ЭДС или силы переменного тока. Легко заметить, что амплитуда в масштабе равна длине радиуса-вектора. Амплитуды тока, ЭДС и напряжения обозначаются соответственно бук­вами Im, Em и Um (рисунок 1).

Угловая (циклическая) частота переменного тока.

Скорость вращения радиуса-вектора, т. е. изменение ве­личины угла поворота в течение одной секунды, называется угловой (циклической) частотой переменного тока и обозначается греческой буквой ? (оме­га). Угол поворота радиуса-вектора в любой данный момент относительно его начального положения измеряется обычно не в градусах, а в особых единицах — радианах.

Радианом называется угловая величина дуги окружности, длина которой равна радиусу этой окружности (рисунок 2). Вся окружность, составляющая 360°, равна 6,28 радиан, то есть 2.

Рисунок 2. Радиан.

Тогда,

1рад = 360°/2

Следовательно, конец радиуса-вектора в течение одного периода пробегают путь, равный 6,28 радиан (2). Так как в тече­ние одной секунды радиус-вектор совершает число оборотов, равное частоте переменного тока f, то за одну секунду его ко­нец пробегает путь, равный 6,28 * f радиан. Это выражение, характеризующее скорость вращения радиуса-вектора, и будет угловой частотой переменного тока — ?.

Итак,

?= 6,28*f = 2f

Фаза переменного тока.

Угол поворота радиуса-вектора в любое данное мгновение относительно его начального положения называется фазой переменного тока. Фаза характеризует величину ЭДС (или тока) в данное мгновение или, как говорят, мгновенное значение ЭДС, ее направление в цепи и направление ее изменения; фаза пока­зывает, убывает ли ЭДС или возрастает.

Рисунок 3. Фаза переменного тока.

Полный оборот радиуса-вектора равен 360°. С началом но­вого оборота радиуса-вектора изменение ЭДС происходит в том же порядке, что и в течение первого оборота. Следова­тельно, все фазы ЭДС будут повторяться в прежнем поряд­ке. Например, фаза ЭДС при повороте радиуса-вектора на угол в 370° будет такой же, как и при повороте на 10°. В обо­их этих случаях радиус-вектор занимает одинаковое положе­ние, и, следовательно, мгновенные значения ЭДС будут в обоих этих случаях одинаковыми по фазе.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Похожие материалы:

Добавить комментарий

круговая частота — с английского на русский

См. также в других словарях:

• круговая частота — угловая частота циклическая частота Величина ω=2πf=2π/Т, где f частота, Т период колебания. [Система неразрушающего контроля. Виды (методы) и технология неразрушающего контроля. Термины и определения (справочное пособие). Москва 2003… …   Справочник технического переводчика

• КРУГОВАЯ ЧАСТОТА — то же, что угловая частота …   Большой Энциклопедический словарь

• Круговая частота — Угловая частота (синонимы: радиальная частота, циклическая частота, круговая частота)  скалярная величина, мера частоты вращательного или колебательного движения. В случае вращательного движения, угловая частота равна модулю вектора угловой… …   Википедия

• круговая частота — то же, что угловая частота. * * * КРУГОВАЯ ЧАСТОТА КРУГОВАЯ ЧАСТОТА, то же, что угловая частота (см. УГЛОВАЯ ЧАСТОТА) …   Энциклопедический словарь

• круговая частота — угловая частота периодических колебаний; угловая частота; отрасл. круговая частота Число периодов колебаний в 2π единиц времени …   Политехнический терминологический толковый словарь

• круговая частота — kampinis dažnis statusas T sritis fizika atitikmenys: angl. angular frequency; cyclic frequency; radian frequency vok. Kreisfrequenz, f; Winkelfrequenz, f rus. круговая частота, f; угловая частота, f; циклическая частота, f pranc. fréquence… …   Fizikos terminų žodynas

• круговая частота — kampinis dažnis statusas T sritis automatika atitikmenys: angl. angular frequency; circular frequency vok. Kreisfrequenz, f; Winkelfrequenz, f rus. круговая частота, f; угловая частота, f pranc. fréquence angulaire, f; fréquence circulaire, f …   Automatikos terminų žodynas

• круговая частота — kampinis dažnis statusas T sritis Standartizacija ir metrologija apibrėžtis Virpesio fazės kitimo sparta, išreiškiama formule: ω = 2πf; čia f – dažnis. Kampinio dažnio ω matavimo vienetas yra rad/s (radianas per sekundę), o dažnio f – Hz (hercas) …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

• КРУГОВАЯ ЧАСТОТА — то же, что угловая частота …   Большой энциклопедический политехнический словарь

• КРУГОВАЯ ЧАСТОТА — то же, что угловая частота …   Естествознание. Энциклопедический словарь

• круговая частота — угловая скорость …   Словарь русских синонимов по технологиям автоматического контроля

угловая+(круговая)+частота — с русского на английский

 

угловая частота
Скорость изменения фазы синусоидального электрического тока, равная частоте синусоидального электрического тока, умноженной на 2π.
Примечание — Аналогично определяют угловые частоты синусоидальных электрического напряжения, электродвижущей силы, магнитного потока и т. д.
[ ГОСТ Р 52002-2003]

EN

angular frequency
pulsatance
ω
product of the frequency of a sinusoidal quantity and the factor 2π
NOTE – For the quantity Am cos (ω t + θ0), the angular frequency is ω.
[IEV number 101-14-36 ]

FR

pulsation
produit de la fréquence d’une grandeur sinusoïdale par le facteur 2π
NOTE – Pour la grandeur Am cos (ω t + θ0), la pulsation est ω.
[IEV number 101-14-36 ]

Практика остановила свой выбор на синусоидальных колебаниях переменных электрических величин. В дальнейшем, говоря о токе, э. д. с., напряжении и магнитном потоке, мы будем считать их изменяющимися по закону синуса.

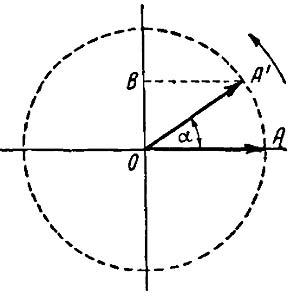
Фиг. 130. Вращение вектора вокруг оси

Пусть мы имеем вектор ОА (фиr. 130), выражающий в масштабе какую-либо переменную синусоидальную величину, например ток. Будем вращать с постоянной скоростью вектор вокруг точки О против часовой стрелки. Конец вектора будет описывать окружность, а угол, на который поворачивается вектор, будет меняться с течением времени.
Угловая скорость или угловая частота ω (омега) вращения равна углу поворота вектора в единицу времени: ω=α/t, откуда α=ωt.
Часто вместо градуса пользуются другой единицей измерения угла – радианом. Радианом называется угол, дуга которого равна радиусу. Если длина окружности С=2πR, то она содержит 2πR/R=2π радиан.
За один оборот радиус-вектор ОА будет иметь один период вращения продолжительностью Т секунд.
Угловая частота в этом случае выразится: ω=α/t=2π/T рад/сек.
Так как 1/Т=f, то ω=2πf рад/сек.
[Кузнецов М. И. Основы электротехники. М, «Высшая Школа», 1964]

Тематики

• электротехника, основные понятия

Синонимы

EN

DE

FR