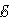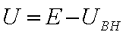14)Мощность и кпд источника постоянного тока!!!
Полная
мощность источника, то есть работа,
совершаемая сторонними силами за
единицу времени, равна |
Во
внешней цепи выделяется мощность |
Отношение |
 называется коэффициентом
полезного действия источника.
называется коэффициентом
полезного действия источника.
На рис. 1.11.1 графически представлены зависимости мощности источника Pист, полезной мощности
 ,
и внутренним сопротивлениемr.
Ток в цепи может изменяться в пределах
от I = 0
(при
,
и внутренним сопротивлениемr.
Ток в цепи может изменяться в пределах
от I = 0
(при 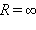 )
до
)
до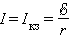 (приR = 0).
(приR = 0).
|
Рисунок 1.11.1.Зависимость ощности источника Pист,мощности во внешней цепи P и КПД источника η от силы тока |
Из приведенных графиков видно, что максимальная мощность во внешней цепи Pmax, равная
|
достигается при R = r. При этом ток в цепи
|
а КПД источника равен 50 %. Максимальное значение КПД источника достигается при I → 0, т. е. при R → ∞. В случае короткого замыкания полезная мощность P = 0 и вся мощность выделяется внутри источника, что может привести к его перегреву и разрушению. КПД источника при этом обращается в нуль.
15)Разветвленные цепи!! Правила Кирхгофа и их применение!!!
В разветвленных цепях можно выделить узловые точки (узлы), в которых сходятся не менее трех проводников (рис. 1.10.1). Токи, втекающие в узел, принято считать положительными; вытекающие из узла – отрицательными.
В узлах цепи постоянного тока не может происходить накопление зарядов. Отсюда следует первое правило Кирхгофа
Алгебраическая сумма сил токов для каждого узла в разветвленной цепи равна нулю:
|
Первое правило Кирхгофа является следствием закона сохранения электрического заряда.
В разветвленной цепи всегда можно выделить некоторое количество замкнутых путей, состоящих из однородных и неоднородных участков. Такие замкнутые пути называютсяконтурами
|
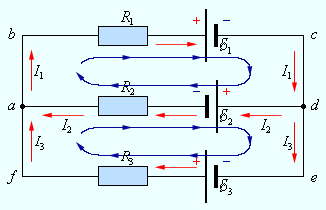
Рисунок 1.10.2. |
В цепи можно выделить три контура abcd, adef и abcdef. Из них только два являются независимыми (например, abcd и adef), так как третий не содержит никаких новых участков.
Второе правило Кирхгофа является следствием обобщенного закона Ома.
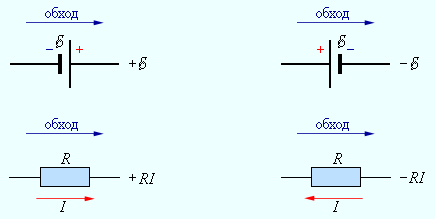
Запишем обобщенный закон Ома для участков, составляющих один из контуров цепи, изображенной на рис. 1.10.2, например, abcd. Для этого на каждом участке нужно задатьположительное направление тока и положительное направление обхода контура. При записи обобщенного закона Ома для каждого из участков необходимо соблюдать определенные «правила знаков», которые поясняются на рис. 1.10.3.
|
Рисунок 1.10.3. |
Для участков контура abcd обобщенный закон Ома записывается в виде:
Для
участка bc: I1R1 = Δφbc – 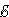 1.
1.
Для
участка da: I2R2 = Δφda – 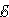 2.
2.
Складывая левые и правые части этих равенств и принимая во внимание, что Δφbc = – Δφda , получим:
Второе правило Кирхгофа можно сформулировать так: алгебраическая сумма произведений сопротивления каждого из участков любого замкнутого контура разветвленной цепи постоянного тока на силу тока на этом участке равна алгебраической сумме ЭДС вдоль этого контура.
Первое
и второе правила Кирхгофа, записанные
для всех независимых
узлов и контуров разветвленной цепи,
дают в совокупности необходимое и
достаточное число алгебраических
уравнений для расчета значений напряжений
и сил токов в электрической цепи. Для
цепи, изображенной на рис. 1.10.2, система
уравнений для определения трех неизвестных
токов I1,I2 и I
I1R1 + I2R2 = – |
– I2R2 + I3R3 = |
– I1 + I2 + I3 = 0. |
Таким образом, правила Кирхгофа сводят расчет разветвленной электрической цепи к решению системы линейных алгебраических уравнений. Это решение не вызывает принципиальных затруднений, однако, бывает весьма громоздким даже в случае достаточно простых цепей. Если в результате решения сила тока на каком-то участке оказывается отрицательной, то это означает, что ток на этом участке идет в направлении, противоположном выбранному положительному направлению.
Электротехника часть 3 электрические цепи
Всем доброго времени суток. В прошлой статье я рассказал о таких понятиях, как электрический ток, напряжение, сопротивление и основополагающем законе постоянного тока – законе Ома. Но этого, несомненно, мало для полного понимания процессов и возникающих закономерностей при функционировании электронных схем. В дальнейших статьях я постепенно буду формировать целостную картину такой интересной области техники как электроника.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Составные части электрических цепей
Как известно, для того, чтобы электрический ток в проводниках существовал длительное время необходимо, во-первых, существование разности потенциалов или напряжения, а во-вторых, восполнение необходимого количества разноимённых зарядов для возникновения этой разности потенциалов. Данным условиям соответствует некоторая совокупность элементов называемая электрической цепью.
Таким образом, электрической цепью называется совокупность устройств и объектов, которые образуют путь для электрического тока и электромагнитные процессы, в которых могут быть описаны с помощью понятий ЭДС, напряжения и электрического тока. Кроме того, для протекания электрического тока необходима замкнутая электрическая цепь. В общем случае электрическая цепь состоит из источника электрической энергии, приемника электрической энергии, соединительных проводов, а также вспомогательных элементов, выполняющих разнообразные функции.
Источником электрической энергии является устройство, которое выполняет преобразование неэлектрической энергии в электрическую. Например, аккумуляторы осуществляют преобразование энергии химических реакций в электрическую энергию, а генераторы – преобразование механической энергии. Таким образом, как известно из предыдущей статьи источники энергии называют также источниками ЭДС.
Приёмником электрической энергии, также называемые нагрузками является устройство, в котором выполняется действие противоположное источнику энергии, то есть электрическая энергия преобразуется в неэлектрическую. Например, в лампочке электрическая энергия преобразуется в световую и тепловую энергию, а в электродвигателе – в механическую энергию.
К вспомогательным устройствам относятся различные коммутирующие, распределительные и измерительные приборы и объекты.
Электрические цепи изображают на чертежах в виде принципиальных электрических схем, где каждому элементу электрической цепи соответствует свой графический элемент. Принципиальные схемы показывают назначение каждого элемента цепи, а также его взаимодействие с остальными элементами, однако при расчётах они не очень удобны. Поэтому при расчётах пользуются так называемыми схемами замещения, которые также как и принципиальные схемы изображаются с помощью графических элементов, однако элементы схем замещения выбираются так, чтобы с необходимым приближением описать работу электрической цепи. Пример изображения принципиальных электрических схем и схем замещения показано ниже
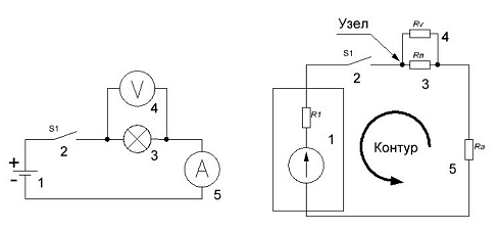

Принципиальная схема (слева) и схема её замещения (справа).
Схемы замещения состоят из следующих элементов: контур, ветвь и узел. Ветвь – это один элемент либо последовательное соединение нескольких элементов. Узел – место соединения трёх и более ветвей. Контур – замкнутый путь, проходящий по ветвям так, чтобы ни один узел и ни одна ветвь не встречались больше одного раза.
Таким образом, зная параметры всех элементов схемы замещения, возможно при помощи законов электротехники определить электрическое состояние всей электрической цепи, то есть рассчитать режим её работы.
Источник ЭДС и источник тока
При анализе электрических цепей, часто используют понятие идеального элемента, то есть такого элемента, в котором сосредоточен только один параметр, в отличие от реального элемента, в котором кроме одного основного параметра имеют место быть паразитные параметры. Например, резистор можно представить в виде идеального сопротивления, однако в реальном резисторе присутствует как емкость (например, между выводами), так и индуктивность (в проволочном резисторе, где используется намотанная на керамический каркас проволока). То есть идеальные элементы используются для упрощения анализа электрической цепи.
Источники энергии в электрических цепях при анализе схем также упрощают, кроме того их делят на два типа: источники ЭДС и источники тока. Рассмотрим каждый из них в отдельности.
Идеальный источник ЭДС характеризуется тем, что напряжение на его выводах не зависит от протекающего через него тока, то есть внутри такого источника ЭДС отсутствуют пассивные элементы (сопротивление R, индуктивность L, емкость С), и поэтому падение напряжения на пассивных элементах отсутствует.
Таким образом, напряжение на его выводах равно ЭДС, а ток теоретически не имеет ограничения, то есть если замкнуть его выходные зажимы, то электрический ток должен быть бесконечно большим. Поэтому идеальный источник ЭДС можно рассматривать, как источник бесконечной мощности. Однако в реальности ток имеет конечное значение, так как падение напряжения на внутреннем сопротивлении при коротком замыкании выводов уравновешивает ЭДС источника. Таким образом, реальный источник ЭДС можно изобразить в виде идеального источника ЭДС с последовательно подключённым пассивным элементом, который ограничивает мощность, отдаваемую во внешнюю цепь.
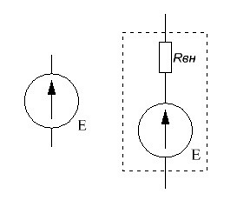

Источники ЭДС: идеальный (слева) и реальный (справа).
Идеальный источник тока характеризуется тем, что ток протекающий через него не зависит от напряжения, которое присутствует на его выводах, то есть сопротивление внутри источника тока бесконечно велико и поэтому параметры внешних элементов электрической цепи не влияют на ток протекающий через источник.
Таким образом, при бесконечном увеличении сопротивления также увеличивается напряжение на выводах идеального источника тока, поэтому и мощность растёт до бесконечности, то есть получается источник бесконечной мощности. Так как в реальности мощность всё же конечна, то реальный источник тока изображается, как идеальный источник тока с параллельно подключенным пассивным компонентом, характеризующим внутренние параметры источника тока, и ограничивает мощность, отдаваемую во внешнюю цепь.
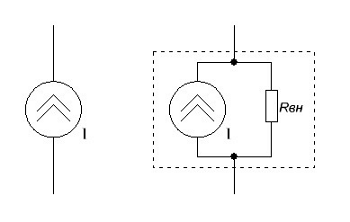

Источники тока: идеальный (слева) и реальный (справа).
Закон Ома для полной цепи
В предыдущей статье я рассказал о законе Ома, который устанавливает зависимость между напряжением и током, протекающим через участок цепи. Однако при попытке его применить ко всей цепи, содержащей кроме сопротивления ещё и источник напряжения, приводит к неверным результатам, так как реальный источник напряжения, как мы знаем, имеет некоторое внутреннее сопротивление.


Закон Ома для полной цепи.
Поэтому полное сопротивление цепи является суммой внутреннего сопротивления источника энергии RВН (обычно небольшого) и внешнего сопротивления нагрузки RН (практически всегда значительно большего, чем RВН), поэтому для полной цепи закон Ома будет иметь следующий вид
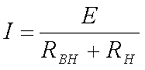
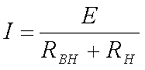
Проанализировав данное выражение можно прийти к следующим практически выводам:
При подключении к источнику питания нагрузки, напряжение источника питания меньше его ЭДС, так как на внутреннем сопротивлении RВН источника питания происходит падение некоторого напряжения UВН


Следовательно, при отключенной нагрузке напряжение источника питания будет равно ЭДС. Данное приложение используется для измерения ЭДС источников питания.
- Напряжение источника питания при подключении различных нагрузок изменяется, причем, чем меньше величина сопротивления нагрузки, тем меньше величина напряжения источника питания, так как разная величина сопротивления нагрузки вызывает разный ток в цепи, а следовательно изменяется падение напряжение на внутреннем сопротивлении источника
- В некоторых случаях возникает необходимость в измерении внутреннего сопротивления источника энергии. Это возможно сделать с помощью следующей схемы
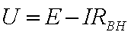
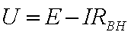


Схема для измерения источника энергии.
В начале проводят замер ЭДС источника питания Е, путём размыкая ключа S1, затем замыкая ключ S1 замеряют протекающий по цепи ток I и напряжение источника питания под нагрузкой UH. Таким образом, вычисляют падение напряжения на внутреннем сопротивлении источника питания UВН. Тогда, величина внутреннего сопротивления RВН будет вычислена, как отношение внутреннего падения напряжения к протекающему в цепи току
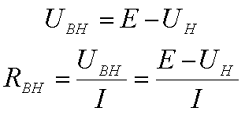
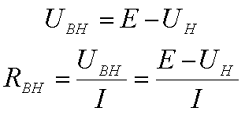
Например, при разомкнутом ключе S1 напряжение на выходе источника питания составило U = E = 1,5 В. При замыкании ключа S1 ток составил I = 0,18 А, а напряжение составило UH = 1,42 В. Тогда внутренне сопротивление RВН источника питания составит
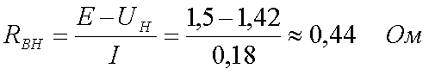
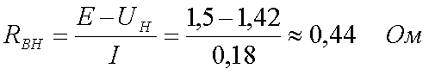
КПД источника энергии
Кроме внутреннего сопротивления RВН и ЭДС Е источник энергии характеризуется также коэффициентом полезного действия КПД при работе на конкретную нагрузку RН.
Коэффициентом полезного действия КПД источника энергии называется отношение мощности приёмника энергии (мощности нагрузки) или полезной мощности РН к мощности источника энергии Р. Как известно мощность выражается произведением напряжения на ток протекающий через источник энергии, то есть по отношению к источнику энергии это будет
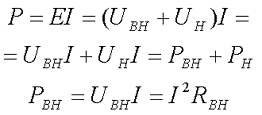
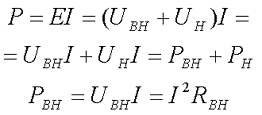
где PBH – мощность потерь внутри источника энергии.
Таким образом, КПД будет равен
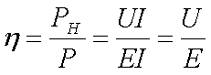
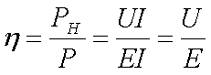
Из вышесказанного возникает резонный вопрос, при каком КПД в нагрузку отдается наибольшая мощность? Можно было бы предположить, что максимальная мощность в нагрузку поступает при КПД η = 1 или 100 %, однако в этом случае напряжение U на источнике питания равняется ЭДС Е, то есть ток в цепи равен нулю I = 0, а значит и мощность на нагрузке также равна нулю Р = 0


Данный режим называется режимом холостого хода.
Другой случай, когда КПД η = 0, в этом случае ток имеет максимальное значение и фактически ограничен лишь внутренним сопротивлением источника питания I = E/RBH. Следовательно, напряжение нагрузки равно нулю UH = 0 и мощность в нагрузке также нулевая Р = 0


Данный режим называется режимом короткого замыкания.
Не вдаваясь в длинные расчёты сказу сразу, что максимальная мощность на нагрузке выделяется при КПД η = 0,5 или 50 %, в этом случае напряжение на нагрузке равно падению напряжения на внутреннем сопротивлении источника питания UH = UBH, то есть сопротивление нагрузки равно внутреннему сопротивлению источника питания.
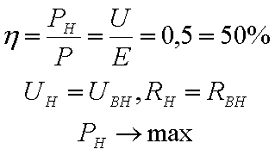
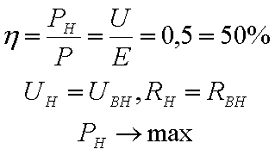
Данный режим называется режимом согласованной нагрузки.
В данном режиме работает большинство слаботочных устройств автоматики, телемеханики и электросвязи, где низкий КПД не влечёт значительных потерь энергии. Однако в мощных устройствах стараются проектировать устройства так чтобы КПД η = 0,95…0,98.
Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.
1.5. Электрическая энергия и электрическая мощность
1.5.1. Электрическая энергия
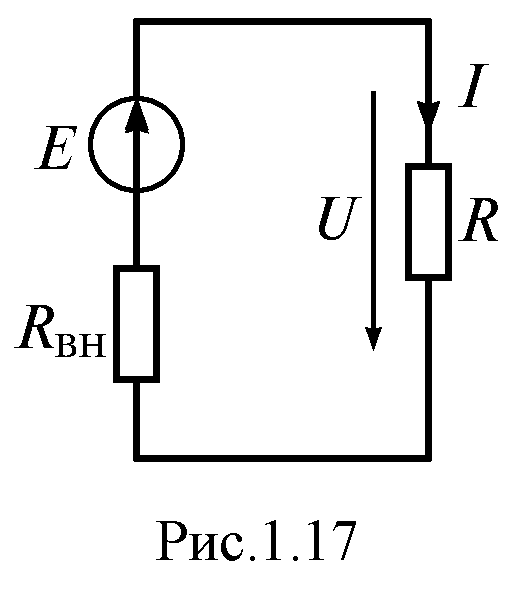
Рис. 1.13
Изобразим схему простейшей электрической цепи, состоящей из источника ЭДС с внутренним сопротивлением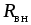 и приемника с сопротивлением
и приемника с сопротивлением (рис. 1.13).
(рис. 1.13).Из закона Ома (1.9)
 .
.
Учитывая, что 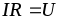
 .
(1.13)
.
(1.13)
Умножим левую и правую части уравнения
на 
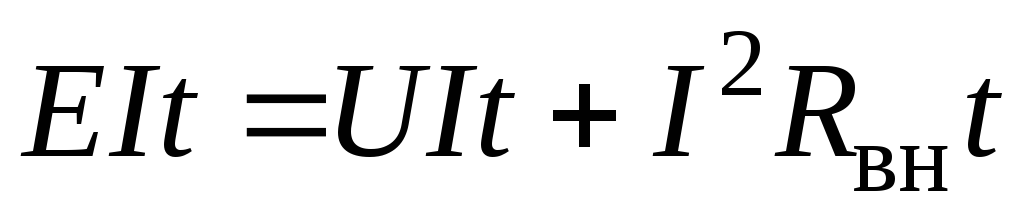 ,
(1.14)
,
(1.14)
где  – работа (энергия) источника.
– работа (энергия) источника.
Так как 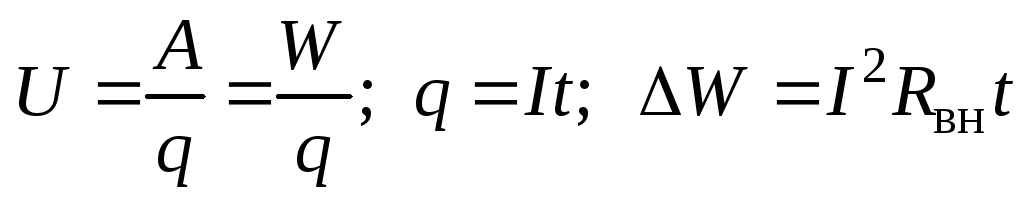
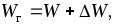 (1.15)
(1.15) где 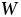 – энергия, передаваемая потребителю;
– энергия, передаваемая потребителю;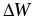 – энергия, расходуемая на потери во
внутреннем сопротивлении источника.
– энергия, расходуемая на потери во
внутреннем сопротивлении источника.
Следует отметить, что работа и энергия – понятия равноценные. Энергия – способность источника совершать работу. Чтобы измерить энергию источника, надо измерить работу, которую он совершает, расходуя эту энергию.
Размерность энергии 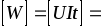 В·А·с=Дж.
В·А·с=Дж.
На практике за единицу энергии принимают 1 кВт·ч= 3600000Дж.
1.5.2. Электрическая мощность
Электрическая мощность 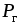 –
это физическая величина, характеризующая
скорость передачи или преобразования
электрической энергии
–
это физическая величина, характеризующая
скорость передачи или преобразования
электрической энергии

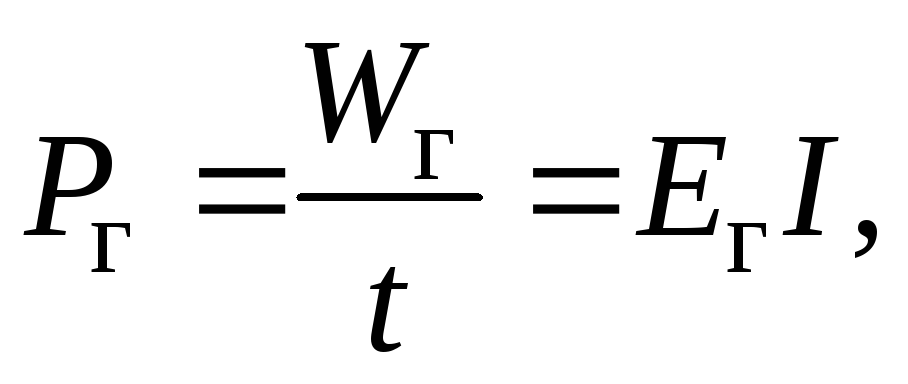 (1.16)
(1.16)
Размерность мощности – ватт (вт). 1вт– мощность, при которой за одну секунду совершается работа в один джоуль.
Мощность, отдаваемая (полезная) источником энергии потребителю (приемнику)
 (1.17)
(1.17)
Потери мощности во внутреннем сопротивлении
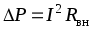 .
(1.18)
.
(1.18)
При работе источника на нагрузку в виде сопротивления преобразование электрической энергии в электрическую мощность выражают с помощью закона Джоуля-Ленца. Мощность, выделяемая (или потребляемая) в сопротивлении R:
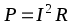 .
.
1.5.3. Кпд источника энергии
Отношение мощности приемника (полезной
мощности) 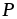 к мощности источника энергии
к мощности источника энергии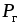 называется его коэффициентом полезного
действия (КПД):
называется его коэффициентом полезного
действия (КПД):
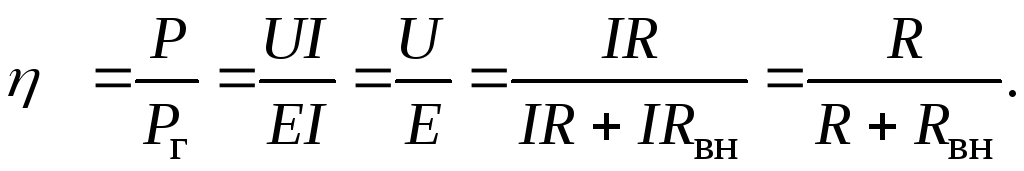 (1.19)
(1.19)
Из последней формулы видно, что чем
меньше внутреннее сопротивление  ,
тем выше КПД источника. Определим, при
каком условии источник энергии
развивает полезную максимальную
мощность. Преобразуем формулу (1.17),
учитывая (1.9)
,
тем выше КПД источника. Определим, при
каком условии источник энергии
развивает полезную максимальную
мощность. Преобразуем формулу (1.17),
учитывая (1.9)
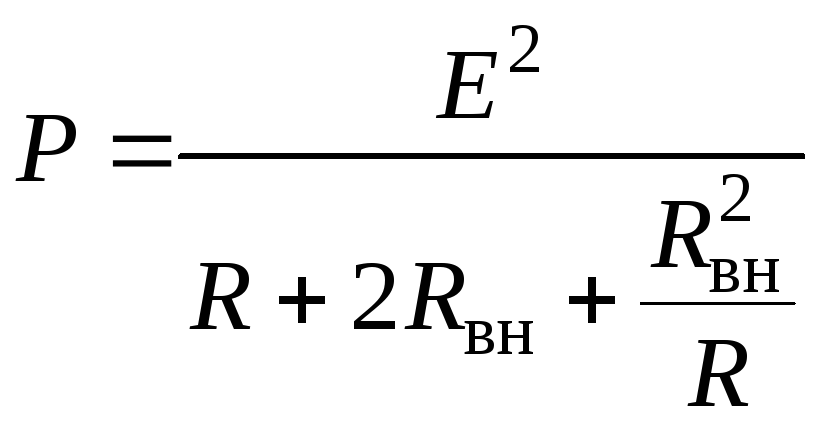 .
(1.20)
.
(1.20)
Исследуем уравнение (1.20) на максимум
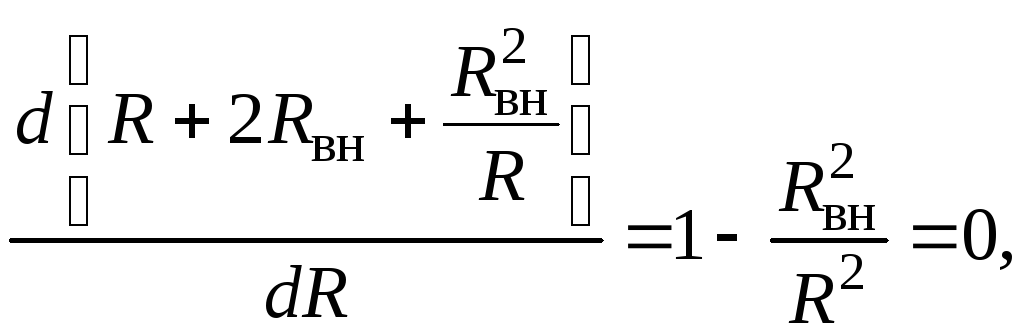 (1.21)
(1.21)
отсюда 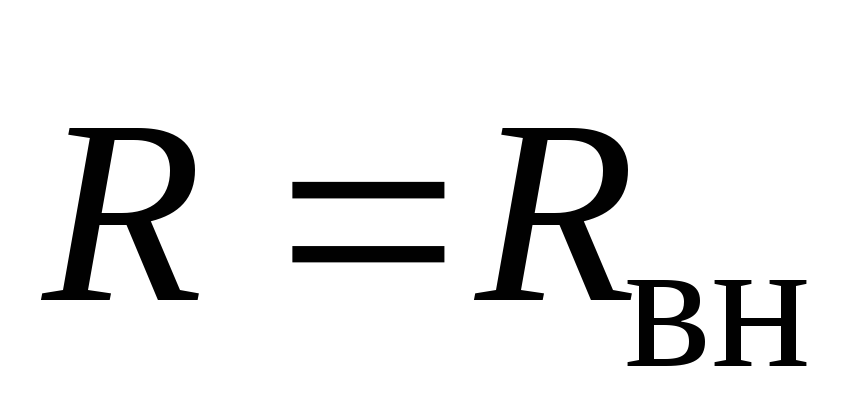 .
.
Тогда формула (1.20) приобретает вид
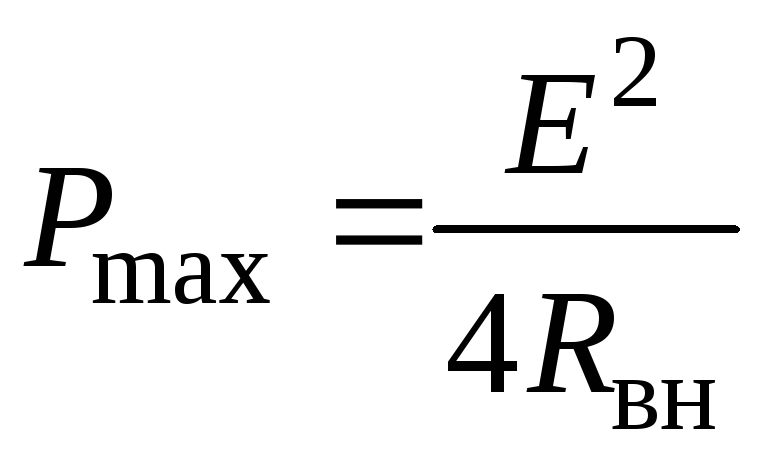 .
(1.22)
.
(1.22)
Таким образом,
источник ЭДС развивает максимальную
полезную мощность, когда внешнее
сопротивление 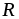 равно
внутреннему сопротивлению источника.
равно
внутреннему сопротивлению источника.
Однако такой режим является невыгодным, так как в этом случае 50 % энергии теряется во внутреннем сопротивлении источника
 (1.23)
(1.23)
Режим цепи, при котором внешнее
сопротивление цепи равно внутреннему
сопротивлению источника энергии,
называется режимом согласованной
нагрузки. Такой режим используется
в телемеханике, электросвязи и автоматике,
где передаются малые мощности. Мощные
источники, как правило, работают на
приемник сопротивлением = (10…20)
= (10…20)  ,
обеспечивая максимальный КПД (более 95
%).
,
обеспечивая максимальный КПД (более 95
%).
1.6. Закон Ома для участка цепи, содержащего эдс
Рассмотрим участок цепи, содержащий сопротивление и ЭДС (рис. 1.14).

Рис. 1.14
Разность потенциалов между точками  и
и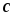 равна напряжению
равна напряжению
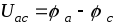 .
.
Выразим потенциал точки  через потенциал точки
через потенциал точки .
С этой целью сначала выражаем потенциал
точки
.
С этой целью сначала выражаем потенциал
точки через потенциал точки
через потенциал точки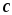 ,
затем потенциал точки
,
затем потенциал точки – через потенциал точки
– через потенциал точки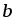 (учитывая при этом, что ток протекает
от более высокого потенциала к более
низкому и направление действия ЭДС
указывает на возрастание потенциала).
(учитывая при этом, что ток протекает
от более высокого потенциала к более
низкому и направление действия ЭДС
указывает на возрастание потенциала).
Для схемы на рис. 1.14 а
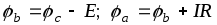
или
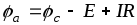 .
.
Тогда
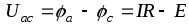 .
(1.24)
.
(1.24)
Для схемы на рис. 1.14 б:

или
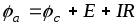 .
.
Тогда
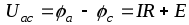 .
(1.25)
.
(1.25)
Из уравнения (1.24) для схемы (рис. 1.14 а)
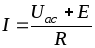 .
(1.26)
.
(1.26)
Из уравнения (1.25) для схемы (рис. 1.14 б)
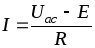 .
(1.27)
.
(1.27)
В общем случае
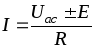 .
(1.28)
.
(1.28)
Последнее уравнение выражает в математической форме закон Ома для участка цепи, содержащего ЭДС.
| Речь в данной статье пойдёт о всем знакомого, но многим не понятного термина коэффициент полезного действия (КПД). Что же это такое? Давайте разберёмся. Коэффициент полезного действия, далее по тексту (КПД) — характеристика эффективности системы какого-либо устройства, в отношении преобразования или передачи энергии. Определяется отношением полезной использованной энергии к суммарному количеству энергии, полученному системой. Обозначается обычно ? (« эта»). ? = Wпол/Wcyм. КПД является безразмерной величиной и часто измеряется в процентах. Математически определение КПД может быть записано в виде: n=(A:Q ) х100 %, где А — полезная работа, а Q — затраченная работа. В силу закона сохранения энергии КПД всегда меньше единицы или равен ей, то есть невозможно получить полезной работы больше, чем затрачено энергии! Просматривая разные сайты, часто удивляюсь, как радиолюбители сообщают, вернее, хвалят свои конструкции, за высокий КПД, не имея понятия, что это такое! Для наглядности на примере рассмотрим упрощенную схему преобразователя, и узнаем, как найти КПД устройства. Упрощенная схема изображена на рис.1
Форум по теории Обсудить статью РАСЧЁТ КПД ПРЕОБРАЗОВАТЕЛЯ |
КПД (коэффициент полезного действия) источника электрического тока. Формулы
Нами было введено понятие КПД (коэффициент полезного действия):
(1)Воспользуемся введёнными нами понятиями мощности электрического тока:
(2) (3)Исходя из (1) — (3), можем ввести КПД разными способами:
(4)Соотношение (4) используется в случае возможности достаточно простого нахождения параметров напряжения и ЭДС.
(5)Соотношение (5) используется, когда имеется полная информация о самой цепи (возможность рассчитать её полное сопротивление).
Поделиться ссылкой:
Понравилось это:
Нравится Загрузка…





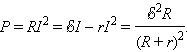
 равное
равное
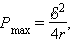
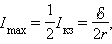
 1 –
1 – 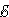 2,
2, 2 +
2 +