Конспект лекций электротехника — Стр 2
ЛЕКЦИЯ № 2
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПЕРЕМЕННОГО ОДНОФАЗНОГО ТОКА
Переменный ток широко применяется в различных областях электротехники. Электрическая энергия почти во всех случаях производится, распределяется и потребляется в виде энергии переменного тока. Широкое применение переменного тока в различных областях техники объясняется легкостью его получения и преобразования, а также простотой устройства генераторов и двигателей переменного тока, надежностью их работы и удобством эксплуатации.
Генерирование переменного электрического тока практически легче осуществляется в машинах с вращающимися проводниками.
Переменный ток, меняет свое значение и направление определенное число раз в секунду. При переменном токе электроны движутся вдоль провода сначала в одном направлении, затем на мгновение останавливаются, далее движутся в обратную сторону, опять останавливаются и снова повторяют движение вперед и назад. То есть электроны совершают в проводе колебания. Вследствие своей малой скорости движения (Vэл = 10-4 м/с = 0,1 мм/с ) электроны при таких колебаниях успевают сделать лишь небольшие перемещения вдоль провода.
Наиболее часто встречается, так называемый синусоидальный переменный ток. Изменение электрических величин (силы тока, напряжения, э.д.с.) со временем показывает плавная кривая линия, называемая синусоидой.
Электрические цепи, в которых значения и направления э.д.с., напряжения и тока периодически изменяются со временем по синусоидальному закону, называются цепями синусоидального тока. Иногда их называют просто цепями переменного тока.
Для переменного тока была выбрана синусоидальная форма, так как она обеспечивает более экономичные производство, передачу, распределение и использование электрической энергии.
Кроме того именно синусоидальная форма электрических величин остается неизменной во всех участках сколь угодно сложной электрической цепи, то есть индуктивные и емкостные элементы входящие в состав электрических цепей не изменяют синусоидальной формы.
В большинстве стран выбрана частота переменного тока 50 Гц (США и Канада — 60 Гц). Эта частота является наиболее оптимальной, поскольку переменные токи низкой частоты 25 — 40 Гц вызывают заметное для глаза мигание электрических ламп накаливания, а повышение частоты приводит к росту э.д.с. самоиндукции и дополнительным потерям при передаче электроэнергии.
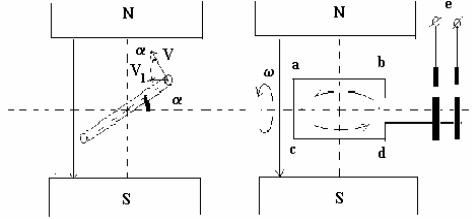
Рассмотрим процесс возникновения синусоидальной э.д.с. Простейшим генератором синусоидальной э.д.с. может служить прямоугольная рамка, равномерно вращающаяся в однородном магнитном поле с угловой скоростью . Пронизывающий катушку (рамку) магнитный поток во время вращения рамки abcd индуцирует в ней на основании закона электромагнитной индукции э.д.с. е.
Нагрузку подключают к генератору с помощью щеток, прижимающихся к двум контактным кольцам, которые соединены с катушкой (рамкой).
Значение наведенной в рамке э.д.с. в каждый момент времени пропорционально магнитной индукции В, размеру активной части рамки l = ab + cd , скорости пересечения магнитных линий VH :
e = BlVH.
Причем скорость VH зависит от ориентации рамки :
VH = V sin ,
где V — линейная скорость движения рамки, — угол описывающий положение рамки (ориентацию относительно вектора магнитной индукции).
В случае равномерного вращения рамки угол поворота зависит от времени следующим образом :
= t.
Следовательно, э.д.с. индуцируемая в равномерно вращающейся рамке определяется : e = BlVsin t.
Сомножители, стоящие перед sin t представляют собой максимальное значение наведенной э.д.с. :
em = BlV.
Тогда
e = emsin t.
Если в начальный момент времени рамка распологалась не по нормали к силовым линиям, а под углом
e то = t + e и
e = emsin ( t+ e ).
Электрические цепи переменного тока по сравнению с цепями постоянного тока имеют ряд особенностей. Эти особенности определяются во-первых, тем, что в состав цепей переменного тока входят новые элементы: трансформаторы, конденсаторы, катушки индуктивности, во-вторых тем, что переменные токи и напряжения в этих элементах порождают переменные электрические и магнитные поля, которые в свою очередь приводят к возникновению явления самоиндукции, взаимной индукции и токов смещения.
Все это оказывает существенное влияние на протекающие электрической цепи процессы. Анализ процессов в цепях усложняется.
Врезисторах в цепях постоянного тока электрическая энергия преобразуется в тепловую. В цепях переменного тока помимо преобразования электрической энергии в тепловую происходит накапливание энергии в магнитном и электрическом полях, то есть кроме параметра сопротивления R, цепь характеризуется еще и параметрами индуктивности и емкости L, C.
Для цепи переменного синусоидального тока большое значение имеет частота f. От частоты зависит влияние емкостей и индуктивностей на процессы в цепи.
Особенности цепей синусоидального тока обуславливают ряд новых, специфических для этих цепей явлений : сдвиг фаз, явление резонанса, появление реактивных мощностей.
При расчете режимов цепи синусоидального тока максимально используются понятия, формулы и методы расчета цепей постоянного тока.
Вцепях переменного тока направление э.д.с., токов и напряжений изменяются два раза за период. Однако при расчете цепи синусоидального тока необходимо составлять уравнения по законам Кирхгофа, а они требуют задания определенных направлений э.д.с., токов и напряжений. Поєтому положительные направления токов, как и для цепи постоянного тока, выбирают произвольно.
Законы Кирхгофа, расмотренные ранее для цепей постоянного тока, справедливы и для мгновенных значений синусоидальных токов, напряжений и э.д.с.
Первый закон Кирхгофа :
Алгебраическая сумма мгновенных значений токов в узле равна нулю :
N
ik 0,
k 1
где N — число ветвей, соединенных в узле.
Второй закон Кирхгофа :
Алгебраическая сумма напряжений на резистивных, индуктивных и емкостных элементах контура в данный момент времени равна алгебраической сумме э.д.с. в том же контуре в тот же момент времени.
При составлении уравнений контур обходят в одном произвольно выбранном направлении, алгебраически суммируя напряжения и э.д.с. Если положительное направление напряжения и э.д.с. совпадает с направлением обхода, то это напряжение или э.д.с. записываются со знаком “ + ” плюс, если не совпадает, то со знаком “ — ”.
Закон Ома для мгновенных значений напряжения и тока справедлив только для резистивных элементов ( I = U/R ).
ПАРАМЕТРЫ ПЕРЕМЕННОГО ТОКА.
Для количественной характеристики переменного тока служат служат следующие параметры. Мгновенные значения тока, напряжений и э.д.с. — это их значения в любой момент времени:
i = imsin ( t+ i ), u = umsin ( t+ u ),
e = emsin ( t+ e ).
Амплитудные значения тока, напряжения и э.д.с. im ,um ,em — максимальные значения мгновенных значений.
Период Т — промежуток времени, в течение которого ток совершает полное колебание и принимает прежнее по величине мгновенное значение. Период измеряется в секундах.
Угловая частота — характеризует скорость вращения катушки генератора в магнитном поле. Измеряется в рад/с. Связана с периодом следующей формулой :
= 2 /Т.
Циклическая частота (частота) f — величина, обратная периоду и характеризующая число полных колебаний тока за 1с. Частота измеряется [Гц] = 1/с и определяется :
f = 1/Т.
Частота и угловая частота связаны между собой следующим образом :
= 2 f.
Фаза. Аргументы периодических функций называют фазой. Фазы характеризуют значения соответствующих величин в заданный момент времени. Значение фазы в начальный момент времени называется начальной фазой. Начальная фаза определяет значение соответствующей величины в начальный момент времени.
Действующие значения I, U, E. Пользоваться амплитудными значениями тока и напряжения не всегда удобно. Например, очевидно, что переменный ток с амплитудой 10 А имеет меньшую мощность, чем постоянный ток 10 А. Значение постоянного тока все время равно 10 А, а переменный ток достигает 10 А только в моменты, соответствующие амплитудному значению. В другие моменты ток меньше 10 А и даже доходит до нуля.
За основу для измерения постоянного тока положено сопоставление его среднего теплового действия с тепловым действием постоянного тока. Определенное посредством такого сравнения значение силы тока называется действующим значением.
Действующим значением переменного тока называется такой постоянный ток, при котором выделяется в резистивном элементе с активным сопротивлением R за период то же количество энергии, что и при действии переменного тока.
Энергия, которая выделяется в резистивном элементе при переменном токе :
T | T |
|
W i 2Rdt im2 | sin2 tRdt. | |
0 | 0 |
|
При постоянном токе выделяется энергия :
W I 2RT .
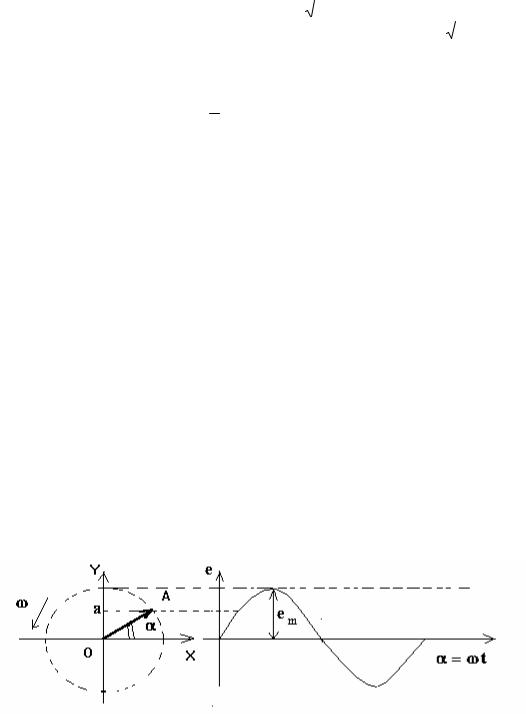
Приравнивая правые части получим действующее значение тока :
|
| T | i |
|
|
|
|
|
I ( | 1 | im2 sin2 tdt)1/ 2 | m |
| 0707,im. |
|
| |
T |
|
|
|
|
| |||
2 |
|
| ||||||
0 |
|
|
|
| ||||
Таким образом, действующее значение тока меньше | амплитудного в | 2 | раз. Аналогично | |||||
определяются действующие значения э.д.с. и напряжения. |
|
|
|
|
|
| ||
Когда говорят о значении напряжения, э.д.с. и тока в цепях переменного тока, то имеют в виду их действующие значения. Шкалы измерительных приборов переменного тока проградуированы в действующих значениях. Например, если прибор показывает 10 А, то это значит, что амплитуда тока : im = 
 2I = 1,41 10 = 14,1 A,
2I = 1,41 10 = 14,1 A,
Напряжение в сети 220 В означает, что действующее напряжение в осветительной сети составляет 220 В. Амплитудное значение напряжения в осветительной сети равно 311 В. Амплитудное значение напряжения нужно принимать во внимание, например при выборе изоляции.
МЕТОД ВЕКТОРНЫХ ДИАГРАММ.
Электрическое состояние цепей переменного тока, так же как и цепей постоянного тока, описывается уравнениями Кирхгофа. Однако при анализе цепей переменного синусоидального тока математический аппарат становится очень громоздким, так как все уравнения содержат электрические величины, изменяющиеся по гармоническому закону.
Для упрощения анализа и расчета цепей переменного тока в электротехнике используют метод
векторных диаграмм.
В электротехнике векторами изображаются изменяющиеся гармонически э.д.с., напряжения и токи, но в отличие от векторов, которыми изображались силы и скорости в механике, эти вектора вращаются с постоянной угловой скоростью и не означают направления действия.
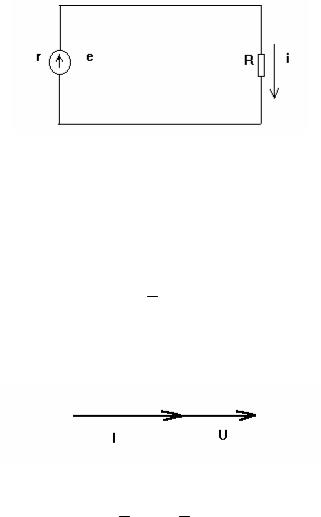
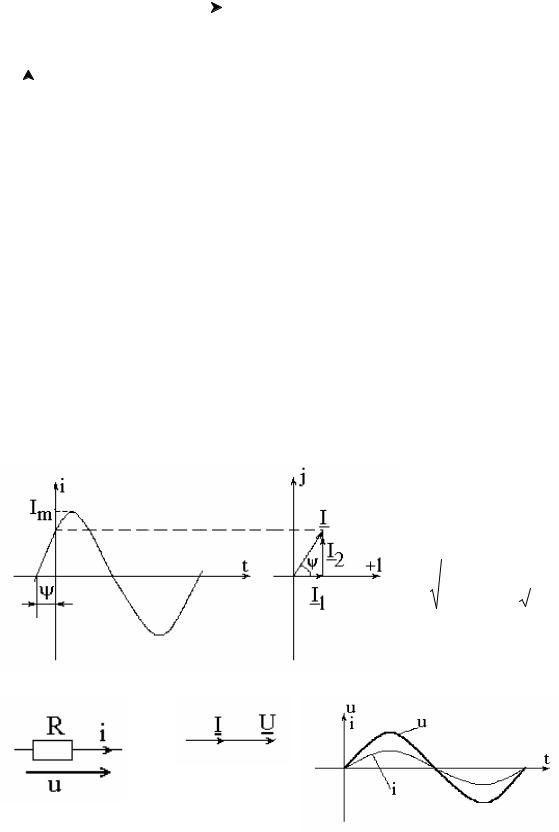
Допустим, что радиус-вектор ОА, представляющий собой в определенном масштабе амплитудное значение э.д.с. em вращается с постоянной угловой частотой = 2 f против часовой стрелки. Проекция ОА на OY будет равна
Oa = OA sin .
Выразив ОА через амплитудное значение э.д.с. em и угол через t , получим выражение мгновенного значения э.д.с. изменяющейся синусоидально :
e = em sin t.
График мгновенных значений э.д.с. изображен в правой части рисунка.
За начало отчета выбран момент времени, когда радиус-вектор совпадает с горизонтальной осью ( ось Х ). Если в начальный момент времени t = 0, ОА совпадает с линией, расположенной под углом к оси Х, то проекция ОА, а следовательно, и э.д.с. будут соответственно равны :
Oa = OA sin ( t + ), e = em sin ( t + е).
Аналогично можно представить в виде векторов, вращающихся против часовой стрелки с постоянной угловой частотой , напряжение и ток.
Совокупность нескольких вращающихся векторов, в начальный момент времени, соответствующих уравнениям электрической цепи, называется векторной диаграммой.
Обычно векторные диаграммы строят не для амплитудных значений, а для действующих значений. При построении векторных диаграмм обычно один из векторов распологают на плоскости
произвольно, остальные же вектора — под соответствующими углами к исходному. При этом в подавляющем большинстве случаев можно обойтись без нанесения осей координат.
Векторные диаграммы позволяют, не прибегая к вычислениям, исследовать характер изменений той или иной величины, определяющей режим работы электрической цепи.
АНАЛИЗ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПЕРЕМЕННОГО СИНУСОИДАЛЬНОГО ТОКА.
В общем случае электрическая цепь переменного тока может содержать резистивные, индуктивные и емкостные элементы, параметрами которых являются сопротивление, индуктивность и емкость. Анализ и расчет таких цепей значительно сложней, чем цепей постоянного тока. Прежде чем разбирать общий случай цепи содержащей все выше перечисленные элементы рассмотрим частные случаи.
1.Электрическая цепь с активным сопротивлением.
Рассмотрим электрическую цепь, содержащую только резистивный элемент с активным сопротивлением. Под активным сопротивлением понимают сопротивление проводников переменному току. Активные сопротивления непрерывно потребляют энергию.
Сопротивление резистора в цепи переменного тока может отличаться от сопротивления того же резистора в цепи постоянного тока. Это различие обусловлено поверхностным эффектом, при котором ток вытесняется к поверхности проводника, и зависит от частоты. С увеличением частоты сопротивление растет. Однако при относительно небольших частотах, например 50 Гц, его увеличением можно пренебречь.
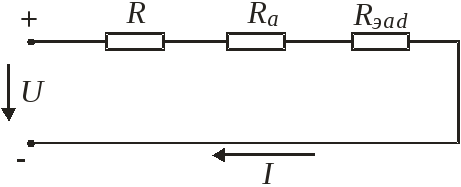
Рассмотрим цепь состоящую из источника э.д.с.
e = em sin t.
и резистора сопротивлением R :
Если r << R, то ток в цепи зависит главным образом от э.д.с. и сопротивления нагрузки — источник в этом случае называют источником э.д.с. или напряжения, так как на его выводах
e= u.
Поэтому в цепи переменного тока действует напряжение :
u = um sin t.
Мгновенное значение силы тока в цепи с активным сопротивлением определяется законом Ома:
i = u / R = um sin t /R = im sin t.
Отсюда следует закон Ома для амплитудных значений : im = um / R,
а разделив левую и правую части равенства на 
 2, получим закон Ома для действующих значений :
2, получим закон Ома для действующих значений :
I = U / R.
Сопоставляя выражения для мгновенных и действующих значений тока и напряжения, можно прийти к выводу, что токи и напряжения в цепи с активным сопротивлением совпадают по фазе.
Векторная диаграмма для цепи с активным сопротивлением имеет вид :
Мгновенная мощность цепи равна произведению мгновенных значений тока и напряжения. Мощность определяет скорость расхода энергии, и следовательно, для цепей переменного тока является величиной переменной. Мгновенная мощность по определению равна :
P =ui= um im sin2 t = (um /
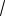 2) ( im /
2) ( im /
 2)(1 — cos 2 t) = UI — UIcos2 t.
2)(1 — cos 2 t) = UI — UIcos2 t.
Мгновенная мощность, оставаясь все время положительной колеблется около уровня UI.
В цепи с активным сопротивлением энергия все время поступает от источника к приемнику и необратимо преобразуется в нем в теплоту и рассеивается в окружающей среде.
Для определения расхода энергии за длительное время целесообразно пользоваться средним значением мощности. Для вывода выражения средней мощности найдем сначала расход энергии в цепи за полупериод :
| T / 2 |
| T / 2 |
|
| T / 2 | T / 2 |
| T |
| |
W |
| Pdt | (UI | UI | cos2 t)dt | UIdt | UI | cos2 tdt | UI | ||
| |||||||||||
| 0 |
| 0 |
|
| 0 | 0 | 2 |
| ||
Разделив полученное выражние на Т / 2, получим среднюю скорость расхода
энергии:
P UI .
Электрическая энергия, которая преобразуется на активном сопротивлении в тепловую называется
активной мощностью.
Активная мощность измеряется ваттметром.
2.Электрическая цепь с индуктивным элементом.
Огромное влияние на процессы протекающие в цепях имеет явление электромагнитной индукции. Явление электромагнитной индукции заключается в том, что изменение магнитного поля вокруг проводника, связанное с пересечением проводника магнитными силовыми линиями, вызывает появление э.д.с. в этом проводнике.
При этом безразлично, будет ли изменяться магнитное поле относительно проводника или проводник будет перемещаться в магнитном поле.
При изменении тока в проводнике изменяется магнитный поток, создаваемый этим током. Изменение магнитного потока индуцирует в проводнике э.д.с., действие которой по правилу Ленца направлено на поддержание предшествующего состояния поля (Правило Ленца: Индуцируемая э.д.с. стремится противодействовать причине, ее вызывающей). Такое явление называется самоиндукцией. Явление самоиндукции в проводниках характеризуется индуктивностью L. Индуктивность это размерный коэффициент пропорциональности между скоростью изменения тока во времени и индуцируемой при этом э.д.с.
e = — L (di / dt)
Знак минус в формуле отражает правило Ленца. Индуктивность измеряется в Генри.
Значение индуктивности L зависит от конструкции элементов цепи. Так для катушки с числом витков
N, магнитопроводом длины l, площади S и магнитной проницаемостью :
L = 0 N2 S / l
Индуктивностью обладают также одиночный прямой провод, двухпроводная линия, коаксиальный кабель.
Обмотки электрических машин, трансформаторов, реле, катушки индуктивности обладают значительной индуктивностью.
Переменный ток встречает в проводниках не только омическое сопротивление. Непрерывное противодействие э.д.с., препятствующее изменению переменного тока, создает в цепи дополнительное сопротивление. Это дополнительное сопротивление называют индуктивным сопротивлением. Таким образом, катушки и разные обмотки, поскольку в них есть индуктивность, оказывают большее сопротивление переменному току, чем постоянному.
Параметрами катушек индуктивности являются активное сопротивление и индуктивность. Рассмотрим вначале катушку, активное сопротивление которой настолько мало, что им можно пренебречь. Применим к рассматриваемому замкнутому контуру второй закон Кирхгофа.

Вслучае цепей переменного тока второй закон Кирхгофа формулируется для мгновенных значений следующим образом:
Алгебраическая сумма напряжений на всех элементах контура в данный момент времени равна алгебраической сумме э.д.с. в том же контуре, в тот же момент времени.
При составлении уравнений контур обходят в одном произвольно выбранном направлении, алгебраически суммируя напряжения и э.д.с.
Если положительное направление напряжения и э.д.с. совпадает с направлением обхода контура, то это напряжение или э.д.с. записываются со знаком “ + “, если не совпадают, то со знаком » — «.
Под действием синусоидального напряжения в цепи с катушкой протекает синусоидальный ток :
i= im sin t.
Врезультате вокруг этой катушки возникает переменное магнитное поле и в катушке наводится э.д.с.
самоиндукции.
e + eL = 0.
При исследовании цепей с э.д.с. самоиндукции условились положительное направление э.д.с. самоиндукции брать совпадающим, с положительным направлением тока, который наводит эту э.д.с. Но э.д.с. источника равна его внешнему напряжению (у источника э.д.с. внутреннее сопротивление r 0 и э.д.с. не зависит от тока нагрузки проходящего через источник e = u = const):
e = u,
а э.д.с. самоиндукции и ток связаны уравнением :
eL = — L di/dt.
Если ток со временем увеличивается, то di/dt > 0 и eL < 0, то есть ток самоиндукции направлен навстречу току, обусловленному внешним источником, и тормозит его возростание. Если ток со временем падает, то di/dt < 0 и eL > 0, то есть индукционный ток имеет тоже направление как и убывающий ток в контуре, и замедляет его убывание. Таким образом, контур, обладая индуктивностью, приобретает электрическую инертность, заключающуюся в том, что любое изменение тока тормозится тем сильнее, чем больше индуктивность.
Второй закон Кирхгофа для рассматриваемой электрической цепи : u = -eL.
Напряжение источника целиком идет на уравновешивание eL.
u = L di/dt = im L cos t = um sin ( t + /2 ),
где
um = im L.
Сопоставляя мгновенные значения тока и напряжения приходим к выводу, что ток в цепи с индуктивным элементом отстает по фазе от напряжения на /2.
Векторная диаграмма цепи с индуктивным элементом имеет вид :
Выведем закон Ома для этой цепи. Из um = im L следует, что | im=um/ L. Введем обозначение: |
ХL = L.

Эта величина называется реактивным индуктивным сопротивлением, или просто индуктивным сопротивлением.
Закон Ома для мгновенных значений:
im=um / ХL
Закон Ома для действующих значений :
I= U / ХL.
Сувеличением частоты тока индуктивное сопротивление увеличивается. Физически это объясняется тем, что возрастает скорость изменения тока, а следовательно, и э.д.с. самоиндукции.
Иногда необходимо увеличить сопротивление в цепи переменного тока, в этом случае в цепь включают катушку со стальным сердечником, называемую дросселем. Большая самоиндукция мешает увеличению тока и поддерживает его в моменты спада. Дроссели применяются: в электросварке, в различных выпрямителях, в радиотехнических устройствах. Для защиты электрических сетей от токов короткого замыкания устанавливают реакторы — большие катушки из толстого медного провода. Для обычного перменного тока они представляют очень небольшое сопротивление. При мгновенном увеличении тока короткого замыкания в реакторе индуктируется большая э.д.с. самоиндукции. Она противодействует этому увеличению и ограничивает ток короткого замыкания до безопасной величины, чем защищает ценное оборудование — генераторы, трансформаторы, электродвигатели — от разрушения.
Обычно катушки и обмотки имеют значительное индуктивное сопротивление. Когда нужно, чтобы катушка в цепи переменного тока не имела индуктивного сопротивления, а только активное, то провод на катушку накладывают так: весь провод складывают вдвое и тогда наматывают на катушку. Обмотка выполненная таким образом, называется бифилярной, или двухвитковой.
Осутствие индуктивности в таких катушках обьясняется тем, что магнитные поля, создающиеся противоположно направленными токами в двух половинах обмотки, взаимно компенсируются. Поэтому катушка в целом не создает магнитного потока и в ее витках не индуктируется э.д.с.
Как и для цепи с активным элементом, мгновенное значение мощности определяется произведением мгновенных значений напряжений и тока :
p =ui = um im sin t sin ( t + /2 ) = (um /
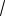 2)( im /
2)( im /
 2) sin t cos t) = UI sin 2 t.
2) sin t cos t) = UI sin 2 t.
Среднее значение мощности:
|
| 1 | T | |
uidt 0. | ||||
P | ||||
T | ||||
| 0 | |||
Физически это объясняется преобразованием энергии источника в энергию магнитного поля катушки и возвращением накопленной энергии источнику. В среденем катушка не потребляет энергии, и следовательно, активная мощность P = 0.
Для количественной характеристики интенсивности обмена энергией между источником и индуктивными элементами служит величина называемая реактивной мощностью:
Q = UI.
Измеряется реактивная мощность в единицах, которые называются вольт-ампер реактивный или сокращенно вар.
Реактивными называются сопротивления, которые в среднем не потребляют энергию.
3.Электрическая цепь с емкостным элементом.
Если в цепь постоянного тока подключить конденсатор, то тока в цепи не будет, так как она разрывается диэлектриком, находящимся между пластинами конденсатора.
При включении конденсатора в цепь переменного тока обнаружим, что ток проходит по цепи, несмотря на ее разрыв диэлектриком в конденсаторе.
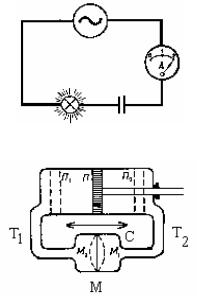
Чтобы понять, почему переменный ток проходит по цепи, рассмотрим работу установки; изображенную на рисунке:
Поршень П двигается в цилиндре вправо и влево. В сосуде С имеется упругая перепонка М, которая делит цепь на две части. При перемещении поршня влево вода, опускаясь по трубе Т1, начнет давить на перепонку М, которая, выгнувшись, займет положение М1; в трубе Т2 вода в этот момент будет подниматься вверх.
Непрерывное перемещение поршня создает непрерывное движение жидкости в цепи. Перепонка периодически выгибается то вправо, то влево, создавая давление на воду.
Источник переменного тока выполняет работу, подобную поршню, а конденсатор в цепи переменного тока можно сравнить с упругой перепонкой. Напряжение электрической цепи похоже на давление поршня на воду, а перемещение воды имеет сходство с током в электрической цепи. Напряжение источника периодически меняет свой знак. Поэтому за первый полупериод одна обкладка конденсатора заряжается положительно, а другая — отрицательно.
В начале следующего полупериода меняется знак напряжения источника, и конденсатор перезаряжается.
При каждой перезарядке конденсатора по цепи то в одном, то в другом направлении будет проходить ток. Этот ток не проходит сквозь диэлектрик конденсатора, так же, как вода не проходит сквозь перепонку М. Когда ток перезарядки конденсатора проходит через лампу, то он накаляет ее нить.
Такой ток называют емкостным током. Таким образом, переменный ток по цепи с конденсатором проходит.
Проанализируем процессы в цепи емкостным элементом. Зададимся напряжением на зажимах источника
u = um sin t,
тогда ток в цепи также будет изменяться по синусоидальному закону. Ток определяется по формуле : i = dq/dt.
Электрический заряд на обкладках конденсатора связан с напряжением на конденсаторе и его емкостью формулой :
q = Cu.
Следовательно :
i = dq/dt = Cdu/dt = um С cos t = um С sin ( t + /2 ).
Таким образом, ток в цепи с емкостью опережает по фазе напряжение на угол /2.
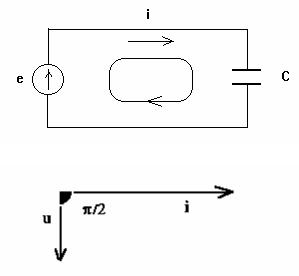
Векторная диаграмма напряжения и тока для цепи с емкостным элементом имеет вид :
Физически это объясняется тем, что напряжение на конденсаторе возникает за счет разделения зарядов на его обкладках в результате протекания тока. Следовательно, напряжение появляется только после возникновения тока.
Получим закон Ома для цепи с емкостным элементом. В формуле :
i = um С sin ( t + /2 )
введем обозначение
Хc = 1 / С,
где Хc — емкостное сопротивление.
Закон Ома для амплитудных и действующих значений имеет вид :
im = um / Хc, | I = U / Xc. |
Емкостное сопротивление уменьшается с ростом частоты. Это объясняется. тем что при большой частоте через поперечное сечение диэлектрика в единицу времени протекает больший заряд при том же напряжении, что эквивалентно уменьшению сопротивления в цепи.
Рассмотрим энергетические характеристики в цепи с емкостью. Пусть начальная фаза тока в цепи равна нулю, тогда
i = im sin t .
Поскольку напряжение на емкости отстает от тока на угол /2 , то
u = um sin ( t — /2 ) = — um сos t.
Мгновенная мощность вычисляется по формуле :
p = ui = — um im sin t сos t = — UI sin 2 t.
Графики напряжения, тока и мгновенной мощности показаны ниже на рисунке. В цепи с емкостью, так же как в цепи с индуктивностью, происходит переход энергии от источника к нагрузке, и наоборот. В данном случае энергия источника преобразуется в энергию электрического поля конденсатора и наоборот. Средняя активная мощность в цепи с емкостью также равна нулю.
Для количественной характеристики интенсивности обмена энергией между источником и конденсатором служит реактивная мощность:
Q = UI.
1.2. Конспект лекций по дисциплине Электротехника, электроника и схемотехника . Электротехника.
Модуль 1
Лекция 1.
План а
Основные понятия и законы электрических цепей.
Элементы цепи и её топологические параметры
Схемы замещения источников питания и их взаимное преобразование. Закон Ома. Законы Кирхгофа
Мощность источника энергии и баланс мощностей.
КПД источника энергии
Основные понятия
Электротехника — обширная область практического применения электромагнитных явлений, происходящих в электротехническом устройстве.
Электротехническое устройство — система заряженных тел и проводников с током.
Для практического применения электромагнитных явлений в электротехническом устройстве необходимо по крайней мере установить связь между переменными системы (потенциалами, зарядами, токами, магнитными потоками) и параметром системы.
Переменные системы делятся на две категории: известные, независимые (сигналы) и определяемые, зависимые (реакция).
Обозначив сигналы вектором
 ;
реакцию вектором
;
реакцию вектором ;
параметры системы вектором
;
параметры системы вектором можно сформулировать две основные
задачи электротехники:
можно сформулировать две основные
задачи электротехники:1. Анализ: Дано
 и
и ;
определить
;
определить ;
т.е. при заданной системе (
;
т.е. при заданной системе ( )
и возмущениях (
)
и возмущениях ( )
в результате анализа получается реакция
системы (
)
в результате анализа получается реакция
системы ( ).
).2. Синтез: Дано
 и
и ;
определить
;
определить ;
т.е. требуется определить такую систему
(
;
т.е. требуется определить такую систему
( ),
чтобы при заданных возмущениях (
),
чтобы при заданных возмущениях ( )
обеспечивала требуемую реакцию (
)
обеспечивала требуемую реакцию ( ).
).Для решения задач электротехники (как и задач во многих других областях знаний) исходя из физических процессов в системе переходят к модельному представлению системы, т.е. к такому упрощению системы, которое с одной стороны сохраняла бы все существенные ее свойства, с другой поддавалась бы решению доступными математическими средствами.
План: б
Классификация и математические модели двухполюсников резистивного, емкостного, индуктивного типа и взаимная индуктивность.
Источники электрической энергии и их режимы работы.
Эквивалентные преобразования.
Зависимые управляемые и неуправляемые источники энергии и их примеры.
Сигналы возмущения в схемах.
Электрические измерительные приборы и их погрешности.
Электрической
цепью называется система заряженных частиц
и проводников с током, которые могут
быть описаны такими интегральными
понятиями, как ток (I),
напряжение (U),
ЭДС 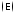 ,
мощность
,
мощность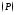 и энергия
и энергия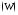 ,
или для их мгновенных значений
,
или для их мгновенных значений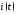 ,
,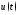 ,
,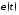 ,
,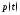 и
и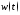 соответственно.
соответственно.
Элементы цепи призваны отображать свойства тех частей, из чего состоит цепь:
генерировать энергию или преобразовывать другие виды энергии в электрическую;
рассеивать энергию;
накапливать энергию в магнитном поле;
накапливать энергию в электрическом поле.
Реальные элементы обычно обладают несколькими свойствами. Например, катушка индуктивности состоит из провода (имеет сопротивление) и индуктивности (электромагнитного свойства), а так как может работать на высоких частотах, тогда возникает еще и межвитковая емкость. Таким образом, индуктивность обладает несколькими свойствами, а также и другие элементы. Поэтому в электротехнике используют математические модели элементов.
Конспект лекций электротехника — Стр 5
Ia = Ua/Za; Ib = Ub/Zb; Ic = Uc/Zc;
cos a = Ra/Za; cos b = Rb/Zb; cos c = Rc/Zc.
При симметричной нагрузке достаточно выполнить расчет для одной фазы.
Найдем для такой цепи напряжение между нейтральными точками. Так как для симметричной нагрузки Ya = Yb = Yc, то смещение нейтрали определяется:
UN = Yа(UA + UB + UC)/( YN + 3Ya ),
но при симметричной системе напряжений
UA + UB + UC = 0.
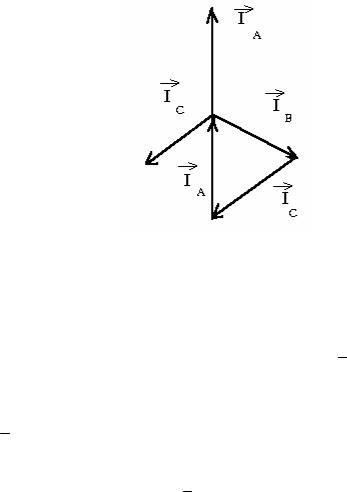
Поэтому при симметричной нагрузке нейтральные точки генератора и приемника совпадают и напряжение между ними равно нулю. Отсюда следует, что при симметричной нагрузке ток в нулевом проводе будет равен нулю. К такому же выводу можно прийти рассмотрев векторную диаграмму токов из которой так же следует равенство нулю тока в нулевом проводе
IN = Ia + Ib + Iс = 0
Таким образом, если нагрузка равномерная, то необходимость в нейтральном проводе отпадает. Трехфазная цепь без нейтрального провода является трехпроводной.
Соединения звездой при несимметричной нагрузке.
При несимметричной нагрузке сопротивления приемников не одинаковы. Для несимметричных нагрузок применяют только четырехпроводные цепи, так как между нейтральными точками появляется напряжение и напряжения на фазах нагрузки становятся различными. При этом нарушается
соотношение между фазными и линейными напряжениями UЛ = 
 3 UФ, причем на одних фазах нагрузки напряжение становиться большим, а на других — меньшим.
3 UФ, причем на одних фазах нагрузки напряжение становиться большим, а на других — меньшим.
Наличие нейтрального провода в цепи с несимметричной нагрузкой позволяет выравнивать напряжение на фазах приемника и поддерживать их неизменными, равными фазным напряжениям
источника UЛ/
 3, то есть нейтральный провод обеспечивает симметрию фазных напряжений приемника. Иначе говоря, при наличии нейтрального провода, когда ZN=0, даже при несимметричной нагрузке фазные напряжения приемника равны друг другу и соблюдается соотношение между
3, то есть нейтральный провод обеспечивает симметрию фазных напряжений приемника. Иначе говоря, при наличии нейтрального провода, когда ZN=0, даже при несимметричной нагрузке фазные напряжения приемника равны друг другу и соблюдается соотношение между
фазными и линейными напряжениями UЛ = 
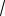 3 UФ.
3 UФ.
Если нагрузка несимметричная и нейтральный провод имеет конечное сопротивление ZN 0, то токи в фазах приемника и нулевом проводе будут определяться выражениями:

IA = Ua/Za = (UA — UN)Ya
IB = Ub/Zb = (UB — UN)Yb
IC = Uc/Zc = (UC — UN)Yc
IN = UN/ZN = UNYN = IA + IB + IC.
Рассмотрим аврийные ситуации в трехпроводной системе.
1.Обрыв одной из фаз нагрузки. В исходном состоянии нагрузка симметричная (для простоты считаем ее активной), система фазных токов симметрична, нейтрали совпадают и система фазных напряжений приемника также симметрична. Рассмотрим случай обрыва линейного провода А.
В этом случае Ya = 0, Yb = Yc = Y0 , смещение нейтрали определяется:
UN = Y0( UB + UC)/2Y0 = — UA/2
поскольку UA + UB + UC = 0.
Этому случаю соответствует такая векторная диаграмма:
При этом фазное напряжение UA увеличивается в 1,5 раза, а UB и UC уменьшаются в 2/
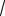 3, так как они становятся равными половине линейного напряжения.
3, так как они становятся равными половине линейного напряжения.
Ток в фазе А равен нулю, а токи в фазах В и С уменьшаются в 2/ 
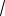 3 раза из-за уменьшения напряжений UB и UC. Так как нагрузка активная, то токи будут совпадать по фазе с фазными напряжениями.
3 раза из-за уменьшения напряжений UB и UC. Так как нагрузка активная, то токи будут совпадать по фазе с фазными напряжениями.
2. Короткое замыкание одной из фаз приемника. Например Za = 0 => Ya = .
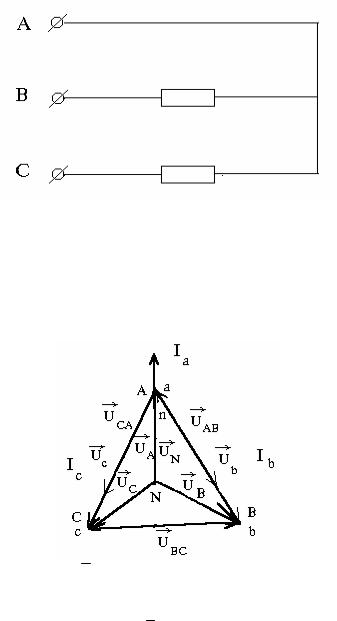
Напряжение смещения нейтрали:
UN = (UA + UBYb/Ya + UCYc/Ya)/( 1 + Yb/Ya + Yc/Ya) = UA.
Следовательно, нейтральная точка приемника переместится в точку а — напряжение в фазе а будет равно нулю, а фазы нагрузки b и с будут находиться под линейными напряжениями. Этому случаю соответствует такая векторная диаграмма:
Фазные токи Iс и Ib возростают в 
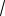 3, совпадая по фазе со своими напряжениями. Ток в проводе а находится из уравнения:
3, совпадая по фазе со своими напряжениями. Ток в проводе а находится из уравнения:
Ia = — ( Ib + Iс).
Как видно из векторной диаграммы ток ia в 
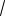 3 раз больше токов Ib и Ic и в 3 раза больше тока в исходном режиме.
3 раз больше токов Ib и Ic и в 3 раза больше тока в исходном режиме.
Трехфазные цепи при соединении приемников треугольником.
При соединении приемников электрической энергии треугольником отдельные фазы приемника присоединяются к линейным проводам, идущим от генератора:
При этом каждая фаза приемника непосредственно включается на линейное напряжение, которое в то же время будет и фазным:
Ua = Uab; Ub = Ubc; Uc = Uca;
Для определения связи между линейными и фазными токами воспользуемся I законом Кирхгофа. Применим его к узлам: a, b, c.
За положительное направление фазных токов выбирается направление от начала фазы к ее концу. С учетом того что фазы нагрузки у нас соединены последовательно положительными направлениями будут: a b, b c, c a.
За положительные направления линейных токов принимают направление от генератора к приемнику. Тогда получим
для узла а |
| Ia + Ica = Iab | Ia = Iab — Ica |
для узла b |
| Ib + Iab = Ibc | Ib = Ibc — Iab |
для узла с |
| Ic + Ibc = Ica | Ic = Ica — Ibc |
Этим уравнениям соответствует векторная диаграмма:
Если нагрузка фаз симметричная ( Za = Zb = Zc; a = b = c ), то действующие значения фазных токов равны между собой и токи сдвинуты по фазам на одинаковые углы от соответствующих напряжений. Рассмотрим треугольник, образованный векторами Ia, Iab, -Ica:
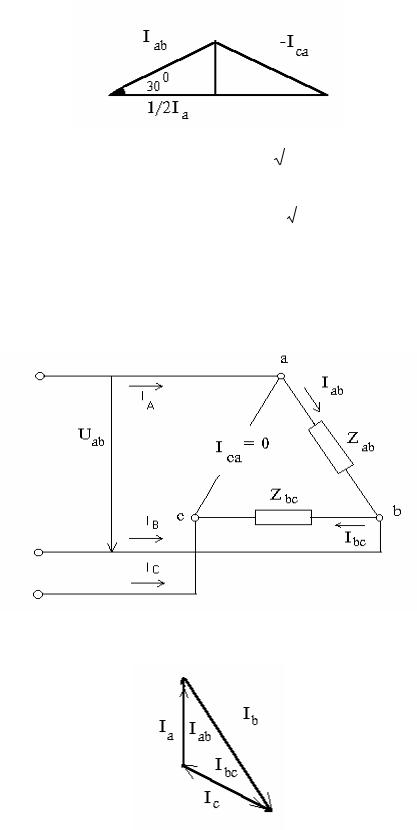
Из этого треугольника следует, что |
|
|
|
|
1/2 Ia = Iab cos 300 Ia = | 3 | Iab. | ||
При симметричной нагрузке: |
|
|
|
|
Ia = Ib = Ic = IЛ, Iab = Ibc = Iac = IФ | ||||
Действующие значения линейных токов больше, чем фазные в |
| 3 | . | |
Из векторной диаграммы видно, линейные токи отстают от фазных на 300. Рассмотрим аврийные ситуации при соединении приемников треугольником.
1.Обрыв одной из фаз нагрузки.
При обрыве фазы са фазный ток Ica = 0. Другие фазные токи не изменяются. Линейный провод оказывается включенным последовательно с фазой ab , поэтому линейный ток Ia = Iab. По этой же причине Ic = -Ibc . Таким образом, Ia и Ic по значению становятся равными фазным токам.
Линейный ток Ib определяется так же как и в исходном режиме Ib = Ibc — Iab , и поэтому остается неизменным. Этому случаю соответствует векторная диаграмма:
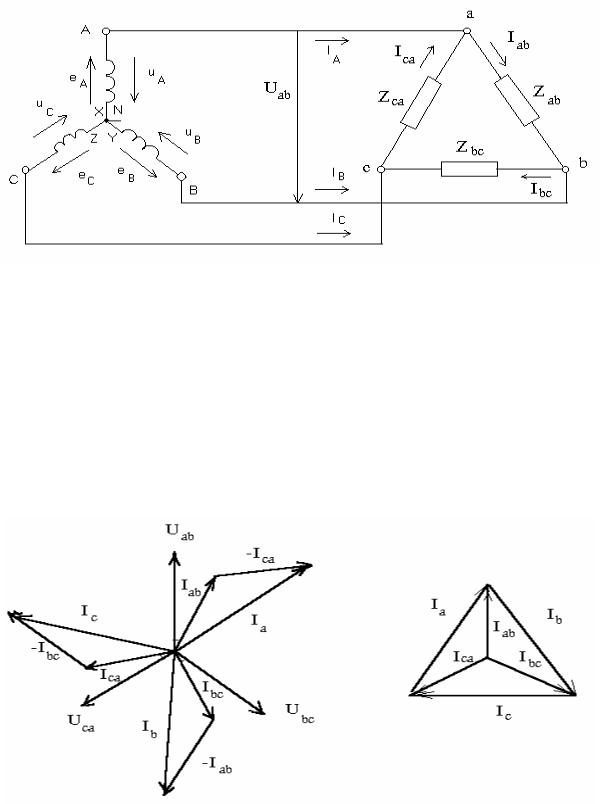
2.Обрыв линейного провода.
При обрыве провода а (перегорание предохранителя) трехфазная цепь преобразуется в однофазную цепь:

Фазы приемника образуют две параллельные ветви, к которым подводится напряжение Ubc. Ток в ветви Zbc остается неизменным, так как по-прежнему определяется тем же напряжением Ubc. Ток в ветвях Zab и Zca , включенных последовательно, совпадает по фазе с током Ibc , так как тоже определяется напряжением Ubc. По значению он в два раза меньше тока Ibc , так как Zab = Zca = Zbc.
Линейный ток Ib = Ibc + Iab совпадает по фазе с током Ibc , а по значению в 1,5 раза больше тока Ibc. Ток Ic равен по значению Ib , а по фазе ему противоположен. Векторная диаграмма токов такой однофазной цепи изображена на рисунке:
МОЩНОСТЬ ТРЕХФАЗНЫХ ЦЕПЕЙ.
Активная мощность трехфазного тока равна сумме мощностей всех трех фаз, а именно
P = Pa + Pb + Pc = UaIa cos a + UbIb cos b + UcIc cos c
При симметричной нагрузке
P = 3Pф = 3UфIф cos .
Реактивная мощность трехфазной цепи
Q = Qa + Qb + Qc = UaIa sin a + UbIb sin b + UcIc sin c
При симметричной нагрузке
Q = 3Qф = 3UфIф sin .
Полная мощность
S = ( P2 + Q2)1/2.
Полная мощность при симметричной нагрузке
S = 3UфIф.
Обычно в качестве паспортных данных для трехфазных приемников приняты линейные напряжения и токи. Поэтому мощности трехфазных приемников целесообразно выражать через линейные напряжения и токи. При таких обозначениях индекс “л” у линейного напряжения и тока не указывают.
Так как при соединении симметричной нагрузки треугольником Uф=Uл=U и Iф=Iл/ | 3=I/ | 3, а при | |||||
соединении симметричной нагрузки звездой Uф=Uл/ | 3 | =U/ | 3 | и Iф=Iл=I, то независимо от схемы | |||
соединения фаз приемника произведение UфIф=UI/ | 3 | оказывается одинаковым. | Таким | образом, | |||
независимо от схемы соединения симметричной нагрузки имеет место следующие выражения для мощностей
P = 
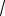 3UI cos , Q =
3UI cos , Q = 
 3UI sin , S =
3UI sin , S = 
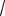 3UI.
3UI.
Если известны активная мощность, линейные напряжения и ток при симметричной нагрузке, то коэффициент мощности определяется по формуле:
cos = P/(
 3UI)
3UI)
ЛЕКЦИЯ № 6
ТРАНСФОРМАТОРЫ
Электрическая энергия вырабатывается на электростанциях синхронными генераторами с напряжением до 35 кВ. Для непосредственного безопасного использования потребителями это напряжение очень велико (220В, 380В, 660В) а для экономичной передачи на большие расстояния, поскольку обычно приемники электрической энергии расположены на некотором расстоянии от электростанций, очень низкое (1150 кВ). При заданной передаваемой мощности линией электропередачи, чем выше напряжение, тем меньше будет значение тока и тем меньше получается требуемое сечение проводов линии электропередачи. Поэтому в месте производства электрической энергии — на электрических станциях — выгодно повышать напряжение до сотен тысяч Вольт и выше, а затем передавать энергию по проводам потребителям.
Изменение напряжения до необходимых значений осуществляется с помощью трансформаторов.
Трансформатором называется статическое электротехническое устройство, служащее для преобразования переменного тока одного напряжения в переменный ток другого напряжения той же частоты.
Электрическая энергия при передаче от электростанции до потребителей преобразуется с помощью тансформаторов около 5 — 7 раз.
В цепях переменного тока использование трансформаторов позволяет изменять напряжения, ток и число фаз.
Трансформаторы относятся к высоконадежным электротехническим устройствам, поскольку они не имеют движущихся частей и скользящих контактных соединений.
По назначению трансформаторы делятся на силовые и специального назначения. Силовые трансформаторы служат для передачи и распределения электрической энергии, а также для питания различных электротехнических устройств. К трансформаторам специального назначения относятся измерительные, сварочные трансформаторы, для прогрева бетона, для перносных светильников, питания электроинструментов и другие.
По числу фаз трансформаторы делятся на однофазные и трехфазные.
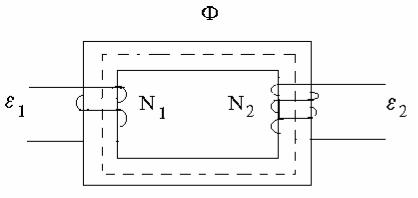
УСТРОЙСТВО ТРАНСФОРМАТОРОВ.
Трансформатор состоит из стального магнитопровода, на который намотаны обмотки :
Обмотка, подключаемая к источнику электрической энергии, называется первичной обмоткой, а обмотка к которой подключается нагрузка называется вторичной.
Если через трансформатор необходимо осуществить питание двух и более нагрузок с разным напряжением, то выполняется соответствующее число вторичных обмоток. Такие трансформаторы называются многообмоточными.
Существуют тансформаторы состоящие из одной обмотки. Такие трансформаторы называются автотрансформаторами. В случае повышающего авторансформатора э.д.с. подводится к части обмотки, а вторичная э.д.с. снимается с части обмотки. В понижающем автотрансформаторе
напряжение сети подается на всю обмотку, а вторичная э.д.с. снимается с части обмотки. Автотрансформаторы позволяют регулировать напряжение в широких пределах.
Магнитопровод трансформаторов изготавливают из стальных листов толщиной 0,35 — 0,5 мм. Стальные пластины сердечника трансформатора изолируют друг от друга бумажной, лаковой изоляцией или окалиной, что позволяет уменьшить потери мощности в магнитопроводе за счет того, что вихревые токи замыкаются в плоскости поперечного сечения отдельной пластины. Чем меньше толщина листа, тем меньше сечение проводника, по которому протекает вихревой ток, и тем болше его сопротивление. В результате вихревой ток и потери мощности на нагрев магнитпровода уменьшаются. Обмотки трансформаторов обычно выполняют из медного провода круглого или прямоугольного сечения. Для лучшей магнитной связи между обмотками их стремятся расположить как можно ближе друг к другу. Обычно их распологают на одном стержне. Обмотки изолируют как от стержня магнитопровода, так и друг от друга. В качестве изоляции применяют электротехнический картон, специальную бумагу или ткань, пропитанную лаком.
По расположению обмоток относительно друг от друга различают концентрические, изготовленные в виде цилиндров, и чередующиеся, когда обмотки расположены друг за другом. В случае концентрической намотки обмоток первой
наматывается обмотка низшего напряжения, а поверх нее размещается обмотка высшего напряжения. По способу охлаждения трансформаторы делятся на сухие и маслянные. Сухие трансформаторы имеют естественное воздушное охлаждение, которое может быть ипользовано только для трансформаторов малой мощности. При увеличении мощности увеличивается нагрев обмоток. Чтобы обеспечить допустимую для изоляции температуру нагрева, применяют более интенсивные способы отвода тепла. Для этого магнитопровод с обмотками помещают в специальный бак, заполненный трансформаторным маслом. Масло является одновременно и охлаждающей и изолирующей средой. Интенсивность охлаждения обеспечивается как за счет большей по сравнению с воздухом теплопроводности масла, так и за счет того, что поверхность бака по сравнению с поверхностью тансформатора значительно больше. Этот способ охлаждения называется естественным маслянным охлаждением. В трансформаторах большой мощности применяют систему принудительного масляного охлаждения при котором масло специальными насосами прокачивается через специальные теплообменники, которые в свою очередь охлаждаются водой или воздухом.
ПРИНЦИП ДЕЙСТВИЯ ТРАНСФОРМАТОРОВ.
Принцип действия трансформаторов основан на явлении взаимной индукции.
При подсоединении первичной обмотки трансформатора к источнику переменного напряжения с э.д.с.1 в ней возникает переменный ток, создающий в магнитном сердечнике переменный магнитный поток, который практически полностью локализован в железном сердечнике и, следовательно почти целиком пронизывает витки вторичной обмотки. Применение магнитопровода с большой магнитной проводимостью способствует увеличению магнитного потока и усилению электромагнитной связи между обмотками. Замыкаясь магнитный поток оказывается сцепленным как с первичной, так и вторичной обмотками.
Изменение этого магнитного потока вызывает во вторичной обмотке появление э.д.с. взаимной индукции, а в первичной э.д.с. самоиндукции.
Ток в первичной обмотке определяется по второму закону Кирхгофа :
е1 + еi1 = i1R1 ==> е1 — d(N1 Ф) / dt = i1R1,
где R1 — активное сопротивление первичной обмотки. Из-за малости R1 падение напряжения I1R1 мало по сравнению с каждой из двух э.д.с. Поэтому
e1 N1 dФ/dt.
Во вторичной обмотке возникает э.д.с. взаимной индукции :
e2 = -N2 dФ/dt.
Сравнивая две последние формулы мы можем найти э.д.с., возникающую во вторичной обмотке :
e2 = -N2 e1/ N1,
где знак «минус», что э.д.с. в первичной и вторичной обмотках отличаются по фазе на 1800. Отношение вторичной э.д.с. к первичной называется коэффициентом трансформации трансформатора
:
k = e2/e1 = N2/N1
При незначительном активном сопротивлении источника. э.д.с. примерно равна напряжению в цепи. Э.д.с. вторичной обмотки при разомкнутой вторичной обмотке (то есть при отсутствии в ней тока и падения напряжения) равна напряжению на концах обмотки. Тогда
k = e2/e1 =u2 /u1 = N2/N1
Коэффициент трансформации может быть определен на основании измерений напряжения на входе и выходе ненагруженного трансформатора.
Коэффициент трансформации может быть как больше, так и меньше единицы.
Если необходимо повысить напряжение источника питания, то число витков вторичной обмотки делают больше числа витков первичной обмотки. Такой трансформатор называется повышающим. Если напряжение надо понизить, то необходимо, чтобы число витков в первичной обмотке было больше, чем во вторичной обмотке. В этом случае трансформатор будет понижающим.
Учитывая высокий к.п.д. трансформаторов, можно считать, что мощность потребляемая из сети примерно равна мощности отдаваемой нагрузке :
S1 S2 ===> i1 u1 i2 u2 .
Отсюда следует:
i1/i2 = u2 /u1.
Мы видим, что во сколько раз увеличивается напряжение во столько же раз уменьшается ток.
По обмотке высшего напряжения проходит меньший ток, поэтому ее делают из провода соответственно меньшего сечения, но она имеет меньшее большее число витков. Обмотка низшего напряжения — с большим током — имеет большее сечение провода, но меньшее число витков. По сечению провода легко отличить обмотку высшего напряжения от обмотки низшего напряжения трансформатора.
Если ко вторичной обмотке трансформатора подключены потребители, через которые замыкается цепь этой обмотки, то по ней проходит ток i2 , направленный (по закону Ленца) противоположно току в первичной обмотке i1 .
Эти токи создают в сердечнике трансформатора два противоположно направленных магнитных потока Ф1 и Ф2, которые вместе образуют общий магнитный поток
Ф = Ф1 — Ф2
Этот общий поток и индуктирует э.д.с. в обмотках трансформатора. Поскольку Е1 = U1, а напряжение U1, которое подводится от источника, обычно не изменяется, то и Е1 почти всегда неизменна. Э.д.с. Е1 индуктируется магнитным потоком Ф, который также вследствие этого должен быть постоянной величиной.
Таким образом, величина общего потока в сердечнике трансформатора всегда постоянна.
При холостом ходе трансформатора, когда i2 = 0, магнитный поток Ф2 также равен нулю. Общий поток Ф трансформатора равен потоку Ф1.
Если же цепь вторичной обмотки замкнуть на потребитель, то возникший ток i2 вторичной обмотки создаст, поток Ф2, противоположный потоку Ф1. Поток Ф2 будет размагничивать сердечник трансформатора.
Так как общий поток Ф = Ф1 — Ф2 не изменяется, то размагничивающее действие потока Ф1 должно быть уравновешено увеличенным намагничивающим потоком Ф1. Таким образом, всякое увеличение тока i2 и его потока Ф2 способствует увеличению потока Ф1, до такой величины, чтобы разность этих потоков Ф1 — Ф2 была равна общему неизменному потоку трансформатора Ф.
Поскольку увеличение потока Ф1 возможно только вследствие увеличения тока i1, который создает этот поток, то всякое увеличение или уменьшение нагрузки (тока i2) во вторичной обмотке трансформатора вызывает соответствующее увеличение или уменьшение тока i1, в первичной обмотке трансформатора. Иногда это явление называют «саморегулированием» трансформатора. Оно основано на законе сохранения и преобразования энергии.
РЕЖИМЫ РАБОТЫ ТРАНСФОРМАТОРОВ
1.Номинальный режим, режим при номинальных значениях тока и напряжения первичной обмотки трансформатора.
2.Рабочий режим (основной режим), при котором напряжение первичной обмотки близко к номинальному значению или равно ему, а ток определяется нагрузкой трансформатора.
3.Режим холостого хода — это режим ненагруженного трансформатора при котором цепь вторичной обмотки разомкнута или подключена к приемнику с очень большим сопротивлением, например, к вольтметру.
4.Режим короткого замыкания трансформатора, режим при котором его вторичная обмотка закорочена или подключена к приемнику с очень маленьким сопротивлением нагрузки, например к амперметру. Короткое замыкание трансформатора в условиях эксплуатации создает аварийный режим,
так как токи в первичной и вторичной обмотках возростают в несколько десятков раз по сравнению с номинальным. Поэтому в цепях с трансформаторами предусматривается защита, которая при коротком замыкании автоматически отключает трансформатор.
Режимы короткого замыкания и холостого хода возникают при аварийных ситуациях или специально создаются при испытании трансформаторов.
КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ
При работе трансформаторов возникают потери в ферромагнитном сердечнике при перемагничивании (потери в стали Рст) и электрические потери в обмотках (потери в меди Рэл). Поэтому активная мощность потребляемая трансформатором из сети отличается от активной мощности отдаваемой трансформатором нагрузке.
Отношение активной мощности отдаваемой трансформатором приемнику к активной мощности подведенной к трансформатору из сети называется его коэффициентом полезного действия.
= Р2 / Р1 = Р2 / (Р2 + Рст + Рэл).
К.П.Д. трансформаторов зависит так же от загруженности трансформатора и от характера нагрузки, то есть коэфициента мощности приемника.
Загрузка трансформатора в рабочем режиме оценивается коэффициентом
= Р2 /Sн cos = I2 / I2н
где Р2 — полезная мощность трансформатора; Sн — номинальная полная мощность; cos — коэффициент мощности нагрузки; I2 — ток во вторичной обмотке; I2н — номинальный ток вторичной обмотки.
Активная мощность отдаваемая трансформатором приемнику при любом характере нагрузки и произвольной загруженности определяется выражением:
P2 = I2U2cos 2 = I2U2cos 2 = Sн cos 2
Потери в стали не зависят от нагрузки и загруженности трансформатора и равны потерям холостого хода. Потери в меди пропорциональны квадрату тока и определяются мощностью потребляемой трансформатором при опыте короткого замыкания. ( Рк ). При произвольной нагрузке трансформатора потери в меди расчитываются с учетом загруженности трансформатора:
Pэл = 2 Рк .
Поэтому в общем случае для произвольной нагрузки К.П.Д. трансформатора определяется:
= Sн cos 2 / ( Sн cos 2 + Рст + 2 Рк).
Потери в стали не зависят от нагрузки. Потери в меди увеличиваются одновременно с увеличением тока нагрузки. При небольших нагрузках преобладают индуктивные потери в стали, cos трансформатора небольшой и работа его неэкономична. Следовательно, нужно стремиться к наиболее полной нагрузке трансформатора, так как при этом потери в меди хотя и увеличиваются, но по отношению ко всей мощности они будут составлять меньшую их часть. Поэтому при увеличении нагрузки к.п.д. трансформатора увеличивается.
К.П.Д. у мощных трансформаторов достигает 95 — 99 %, а у трансформаторов малой и средней мощности 70 — 90 %.
Краткий конспект лекций к первой части курса «Теоретические основы электротехники»
85
Павлов В. ЭС-104
Оглавлени
Краткий конспект лекций 1
1
2
Павлов В. ЭС-104 2
Введение 5
Общие определения цепей и их параметров 5
Активные элементы 7
Эквивалентные преобразования источников электрической энергии 8
Свойства линейных электрических цепей 9
Основные уравнения электрических цепей. Законы Кирхгофа. 10
ЛИНЕЙНЫЕ ЦЕПИ ПОСТОЯННОГО ТОКА 12
Эквивалентные преобразования пассивных цепей 12
Расчет цепей по законам Кирхгофа 14
Метод контурных токов 15
Метод узловых напряжений 17
Метод наложения 18
Свойство взаимности 20
Теорема о компенсации 22
Метод эквивалентного источника напряжения 23
(теорема Гельмгольца-Тевенена) 23
Метод эквивалентного источника тока 26
(теорема Нортона) 26
Потенциальная диаграмма. 28
Баланс мощностей 29
Топология электрической цепи 30
Топологические матрицы графов 32
ЛИНЕЙНЫЕ ЦЕПИ С ИСТОЧНИКАМИ ГАРМОНИЧЕСКИХ ЭДС И ТОКОВ 36
Периодические напряжения и токи 36
Генератор синусоидального напряжения 37
37
Временная диаграмма 38
Векторная диаграмма 38
Действующие и средние значения периодических ЭДС и токов 39
Разность фаз напряжения и тока. Параметры цепей переменного тока. 41
Активное сопротивление в цепи переменного тока. 41
Индуктивное сопротивление в цепи переменного тока. 41
Емкостное сопротивление в цепи переменного тока. 42
Установившийся режим в цепи с последовательным соединением активного сопротивления, индуктивности и емкости 43
Установившийся режим в цепи с параллельным соединением активного сопротивления, индуктивности и емкости 45
Энергетические соотношения в цепях синусоидального тока 47
Комплексный метод расчета электрических цепей 50
Комплексные сопротивления и проводимости 53
Перевод комплексных величин в показательную форму: 55
Перевод показательных величин в комплексную форму: 55
Основные законы электрических цепей в комплексной форме 55
Мощность в комплексной форме. Баланс мощностей 57
Резонансные явления в электрических цепях. 58
Частотные характеристики. 58
Резонанс напряжений 59
Частотные характеристики последовательного R-L-C контура. 61
Резонансные характеристики 61
Параллельный колебательный контур. Резонанс токов. 63
Частотные характеристики цепи с параллельным соединением элементов. 64
Резонансные кривые при параллельном соединении элементов 64
Цепи с взаимной индукцией 65
Последовательное и параллельное соединения 65
индуктивно связанных катушек 65
Векторные диаграммы: 66
При параллельном соединении катушек их напряжение одинаково. 67
Трансформатор без стального сердечника 68
Трехфазные системы токов и напряжений 71
Энергия и мощность в трехфазных цепях 74
ОСНОВЫ ТЕОРИИ ЧЕТЫРЕХПОЛЮСНИКОВ 75
Уравнения четырехполюсников 75
Холостой ход и короткое замыкание четырехполюсника 77
Определение параметров четырехполюсника 78
ПЕРИОДИЧЕСКИЕ НЕСИНУСОИДАЛЬНЫЕ НАПРЯЖЕНИЯ И ТОКИ 81
В ЛИНЕЙНЫХ ЦЕПЯХ 81
Разложение периодических функций в ряд Фурье 81
Действующее значение и мощность при несинусоидальных 83
напряжениях и токах 83
Расчет линейных цепей при несинусоидальных напряжениях и токах 84
Введение 4
Общие определения цепей и их параметров 4
Активные элементы 6
Эквивалентные преобразования источников электрической энергии 7
Свойства линейных электрических цепей 7
Основные уравнения электрических цепей. Законы Кирхгофа. 9
ЛИНЕЙНЫЕ ЦЕПИ ПОСТОЯННОГО ТОКА 10
Эквивалентные преобразования пассивных цепей 10
Расчет цепей по законам Кирхгофа 12
Метод контурных токов 13
Метод узловых напряжений 15
Метод наложения 16
Свойство взаимности 18
Теорема о компенсации 19
Метод эквивалентного источника напряжения 20
(теорема Гельмгольца-Тевенена) 20
Метод эквивалентного источника тока 23
(теорема Нортона) 23
Потенциальная диаграмма. 25
Баланс мощностей 26
Топология электрической цепи 27
Топологические матрицы графов 29
ЛИНЕЙНЫЕ ЦЕПИ С ИСТОЧНИКАМИ ГАРМОНИЧЕСКИХ ЭДС И ТОКОВ 33
Периодические напряжения и токи 33
Генератор синусоидального напряжения 34
Временная диаграмма 34
Векторная диаграмма 35
Действующие и средние значения периодических ЭДС и токов 36
Разность фаз напряжения и тока. Параметры цепей переменного тока. 37
Активное сопротивление в цепи переменного тока. 37
Индуктивное сопротивление в цепи переменного тока. 37
Емкостное сопротивление в цепи переменного тока. 38
Установившийся режим в цепи с последовательным соединением активного сопротивления, индуктивности и емкости 38
Установившийся режим в цепи с параллельным соединением активного сопротивления, индуктивности и емкости 40
Энергетические соотношения в цепях синусоидального тока 42
Комплексный метод расчета электрических цепей 45
Комплексные сопротивления и проводимости 48
Перевод комплексных величин в показательную форму: 49
Перевод показательных величин в комплексную форму: 49
Основные законы электрических цепей в комплексной форме 49
Мощность в комплексной форме. Баланс мощностей 50
Резонансные явления в электрических цепях. 51
Частотные характеристики. 51
Резонанс напряжений 52
Частотные характеристики последовательного R—L—C контура. 54
Резонансные характеристики 54
Параллельный колебательный контур. Резонанс токов. 55
Частотные характеристики цепи с параллельным соединением элементов. 57
Резонансные кривые при параллельном соединении элементов 57
Цепи с взаимной индукцией 58
Последовательное и параллельное соединения 58
индуктивно связанных катушек 58
Векторные диаграммы: 59
При параллельном соединении катушек их напряжение одинаково. 60
Трансформатор без стального сердечника 61
Трехфазные системы токов и напряжений 63
Энергия и мощность в трехфазных цепях 66
ОСНОВЫ ТЕОРИИ ЧЕТЫРЕХПОЛЮСНИКОВ 67
Уравнения четырехполюсников 67
Холостой ход и короткое замыкание четырехполюсника 69
Определение параметров четырехполюсника 70
ПЕРИОДИЧЕСКИЕ НЕСИНУСОИДАЛЬНЫЕ НАПРЯЖЕНИЯ И ТОКИ 72
В ЛИНЕЙНЫХ ЦЕПЯХ 72
Разложение периодических функций в ряд Фурье 72
Действующее значение и мощность при несинусоидальных 74
напряжениях и токах 74
Расчет линейных цепей при несинусоидальных напряжениях и токах 75
Конспект по электротехнике на тему » Электрические цепи постоянного тока»
ЛЕКЦИЯ № 2
Электрические цепи постоянного тока.
ПЛАН
Понятие об электрических цепях, электрический ток, электродвижущая сила, закон Ома, электрическое сопротивление и проводимость.
Электрическая цепь – это совокупность устройств и объектов, образующих путь для электрического тока, электромагнитные процессы в которых могут быть описаны с помощью понятий об электродвижущей силе, электрическом токе и электрическом напряжении.
Любая электрическая цепь состоит из следующих трех групп элементов, выполняющих определенную функцию:
— источники электрической энергии;
— приемники электрической энергии;
— вспомогательные элементы.
Источники электрической энергии (активные элементы) – это элементы электрической цепи, в которых происходит преобразование химической, тепловой, механической и других видов энергии в электрическую. Источниками электрической энергии являются, например, гальванические элементы, аккумуляторы, солнечные батареи, генераторы электрических станций и др.
Приемники электрической энергии (пассивные элементы) – это элементы электрической цепи, в которых происходит преобразование электрической энергии в другие виды энергии, а также ее запасание. Приемниками электрической энергии являются электрические двигатели, лампы накаливания, нагревательные элементы, громкоговорители, резисторы, конденсаторы, индуктивные катушки и др.
Вспомогательные элементы – это элементы электрической цепи, предназначенные для защиты, измерения, соединения источников и приемников электроэнергии и других вспомогательных функций. Вспомогательными элементами являются выключатели, предохранители, измерительные приборы, соединительные провода, разъемы и др. Для подключения к остальной части цепи каждый элемент цепи имеет внешние выводы, называемые также зажимами или полюсами. В зависимости от числа внешних выводов различают двухполюсные (резистор, конденсатор, катушка индуктивности) и многополюсные (транзистор, трансформатор, электронная лампа и др.) элементы.
В теории цепей предполагается, что каждый элемент цепи полностью характеризуется зависимостью между током и напряжениями на его зажимах, при этом процессы, имеющие место внутри элементов, не рассматриваются. В основе теории электрических цепей лежит принцип моделирования. В соответствии с этим принципом реальные элементы цепи заменяются их упрощенными моделями, построенными из идеализированных элементов. Используют пять основных типов идеализированных двухполюсных элементов: — идеальный резистор; — идеальный конденсатор; — идеальная индуктивная катушка; — идеальный источник напряжения; — идеальный источник тока.
В простейшем случае модель реального элемента может состоять из одного идеализированного элемента, в более сложных случаях она представляет собой соединение нескольких идеализированных элементов. Например, моделью реальной индуктивной катушки может быть последовательное соединение идеальной индуктивности и идеального резистора, учитывающего сопротивление проводов катушки. Кроме двухполюсных использую также многополюсные идеализированные элементы – управляемые источники тока и напряжения, идеальные трансформаторы и др.
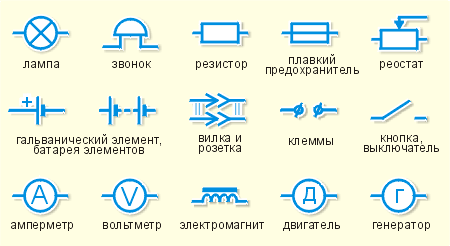
Графические обозначения в электрических схемах

Направленное движение заряженных частиц называется электрическим током.
За направление электрического тока принято направление движения положительных свободных зарядов. Для существования электрического тока в проводнике необходимо создать в нем электрическое поле.
Количественной мерой электрического тока служит сила тока I – скалярная физическая величина, равная отношению заряда Δq, переносимого через поперечное сечение проводника (рис. 1) за интервал времени Δt, к этому интервалу времени: I=ΔqΔt
Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным.
Рисунок 1.Упорядоченное движение электронов в металлическом проводнике и ток I. S – площадь поперечного сечения проводника, E−→ – электрическое поле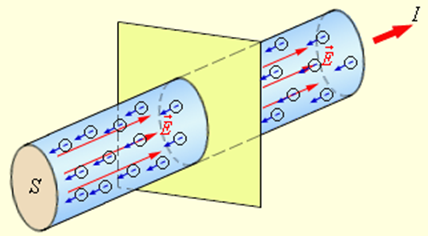
В Международной системе единиц СИ сила тока измеряется в Амперах (А). Единица измерения тока 1 А устанавливается по магнитному взаимодействию двух параллельных проводников с током.
Немецкий физик Г. Ом в 1826 году экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника:
I=1RU;U=IR
где R = const.
Величину R принято называть электрическим сопротивлением. Проводник, обладающий электрическим сопротивлением, называется резистором. Данное соотношение выражает закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.
В СИ единицей электрического сопротивления проводников служит Ом (Ом). Сопротивлением в 1 Ом обладает такой участок цепи, в котором при напряжении 1 В возникает ток силой 1 А.
Проводники, подчиняющиеся закону Ома, называются линейными. Графическая зависимость силы тока I от напряжения U (такие графики называются вольт-амперными характеристиками, сокращенно ВАХ) изображается прямой линией, проходящей через начало координат. Следует отметить, что существует много материалов и устройств, не подчиняющихся закону Ома, например, полупроводниковый диод или газоразрядная лампа. Даже у металлических проводников при токах достаточно большой силы наблюдается отклонение от линейного закона Ома, так как электрическое сопротивление металлических проводников растет с ростом температуры.
Для участка цепи, содержащего ЭДС, закон Ома записывается в следующей форме: IR=U12=ϕ1−ϕ2+E=Δϕ12+E; I=UR
Это соотношение принято называть обобщенным законом Ома или законом Ома для неоднородного участка цепи.
На рис. 1.8.2 изображена замкнутая цепь постоянного тока. Участок цепи (cd) является однородным.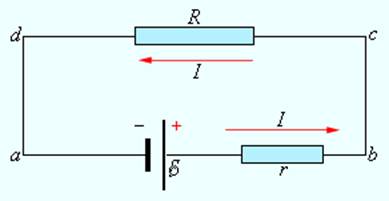
Рисунок 1.8.2.
Цепь постоянного тока По закону Ома
IR=Δϕcd
Участок (ab) содержит источник тока с ЭДС, равной E.
По закону Ома для неоднородного участка, Ir=Δϕab+E
Сложив оба равенства, получим: I(R+r)=Δϕcd+Δϕab+E
Но Δϕcd=Δϕba=−Δϕab.
Поэтому : I=ER+r
Эта формула выражает закон Ома для полной цепи: сила тока в полной цепи равна электродвижущей силе источника, деленной на сумму сопротивлений однородного и неоднородного участков цепи (внутреннего сопротивления источника).
Сопротивление r неоднородного участка на рис. 1.8.2 можно рассматривать как внутреннее сопротивление источника тока. В этом случае участок (ab) на рис. 1.8.2 является внутренним участком источника. Если точки a и b замкнуть проводником, сопротивление которого мало по сравнению с внутренним сопротивлением источника (R ≪r), тогда в цепи потечет ток короткого замыкания
Iкз=Er
Сила тока короткого замыкания – максимальная сила тока, которую можно получить от данного источника с электродвижущей силой E и внутренним сопротивлением r. У источников с малым внутренним сопротивлением ток короткого замыкания может быть очень велик и вызывать разрушение электрической цепи или источника. Например, у свинцовых аккумуляторов, используемых в автомобилях, сила тока короткого замыкания может составлять несколько сотен ампер. Особенно опасны короткие замыкания в осветительных сетях, питаемых от подстанций (тысячи ампер). Чтобы избежать разрушительного действия таких больших токов, в цепь включаются предохранители или специальные автоматы защиты сетей.
Опорный конспект по ТОЭ
МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Уфимский государственный авиационный технический университет
ОПОРНЫЙ КОНСПЕКТ ПО ТЕОРИИ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
1
МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Уфимский государственный авиационный технический университет
Кафедра теоретических основ электротехники
ОПОРНЫЙ КОНСПЕКТ ПО ТЕОРИИ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
2
Составители : Л.Е.Виноградова, В.С.Лукманов, Л.С.Медведева,И.Е.Чечулина
УДК 621.3(076.5)
Опорный конспект по теории электрических цепей : методические указания / УГАТУ- Сост. Л.Е.Виноградова, В.С.Лукманов,Л.С.Медведева, И.Е.Чечулина- Уфа, 1997, -35 с.
Методические указания предназначены для студентов, изучающих курсы “ Теоретические основы электротехники ” , “ Теоретическая электротехника ”, “ Основы теории цепей”. Материал разбит на основные темы в соответствии со
стандартной программой и содержит краткие теоретические сведения в виде формул, таблиц, векторных диаграмм и электрических схем.
Ил. 58 . Табл.30 . Библиограф.: 3 назв.
Рецензент: профессор каф.АП, д-р техн.наук Шаймарданов Ф.А.
5
1.2 Методы контурных токов и узловых потенциалов
R 1 R 3
|
| R 2 |
|
| ìI | I | (R | 1 | + R | 2 | + R | 5 | ) — I | II | R | 2 | — | ||
|
|
|
| ï |
|
|
|
|
|
|
|
| |||||||
E 1 | I I | I I I | E | ï | -IIIIR 5 | = E1 + E2 |
|
|
|
| |||||||||
|
|
|
| 3 | ï-II R 2 + III (R 2 + R 3 + R 4 ) — | ||||||||||||||
|
| E |
|
| í |
|
|
|
|
| == -E2 | — E3 |
|
|
| . | |||
| R | 2 | R 4 |
| ï- IIIIR 4 |
|
|
|
| ||||||||||
| 5 |
| ï | -II R 5 | — III R 4 + |
|
|
|
| ||||||||||
|
|
|
|
|
|
|
|
| |||||||||||
|
|
|
|
| ï | + IIII (R 4 + R 5 + R 6) = E6 | |||||||||||||
|
| IIII |
|
| î | ||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
| E 6 | R 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
R 1 | R 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
| R 2 | I II |
|
|
|
|
|
|
|
| IIII = -J6, |
|
|
|
|
| ||
E 1 | I I | E | II (R1+R2+R5) — IIIR2 — IIIIR5 = E1 + E2, |
| |||||||||||||||
|
| E |
| 3 |
| ||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
| R | 2 | R 4 |
| -IIR2 + III (R2+R3+R4) — IIIIR4 =-E2 — E3. |
| |||||||||||||
| 5 |
|
| ||||||||||||||||
IIII
9
Теорема о взаимных приращениях
|
|
|
|
| I m | Im = Imo |
| −Gmm R m | ||||
|
|
|
|
|
| |||||||
I n |
|
|
|
|
|
|
| R m | 1+ G mm R m |
| ||
|
|
|
|
|
|
| ||||||
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
| −G mn R m | ||
| A |
|
|
|
|
| In = Imo | |||||
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
| R m | 1 + Gmm R m | |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Коэффициенты передачи
KU = U2 / U1
KI = I2 / I1
KR = U2 / I1
KG = I2 / U1
KP = P2 / P1
2 Линейные цепи при гармонических воздействиях
2.1 Пассивный двухполюсник при синусоидальном токе
i(t) = Imsin(wt+y ) = Im[I mejωt]
I = Iejψ = I1+ jI2
|
| 1 T 2 |
| Im |
| ||
I = |
| 0ò i dt = |
|
|
| ||
T |
|
|
| ||||
2 |
| ||||||
w = 2pf
uR=Ri | UR=RI | ZR=R | YR=G=1/R |
Кафедра Энергетики Краткий конспект лекций по электротехнике для специальностей ртп, ртб, ртмо
Лектор : профессор Меньков Б.В.
Москва 2007 г.
Компьютерная графика выполнена студентами:
Кислицын И.Э, Борисов Д.Г, Набока Р.Р., Семенова К.М (все РТМО-05), Пустовая Л.Г., Потапов К.С.(оба РТБ-05-1), Минькеева И. (РТП-05), Абранин А. (РТБ-05-2).
Текст лекций сохранен, в основном, по студенческим конспектам.
Электротехника – эта отрасль науки и техники, которая занимается производством передач и переходов тока при управлении электрической энергии.
Расчеты сводятся по заданным значениям ЕДС напряжения, определяя токи и мощи потребителя. Токи определяем, для того чтобы по известной плотности тока и сопротивлению определять их сечения и габарит, т.е. нагрузка в электротехнике – это величины тока и мощности, но не напряжения. Напряжение не является нагрузкой.
В природе существуют три главных типа нагрузки:
1. Сопротивление 2. Индуктивность 3. Ёмкость


Элементы электрической цепи.

ЭДС источника может быть замерена вольтметром в режиме холостого хода, когда ток равен нулю. (R0 = 0)
Уравнение баланса мощностей

Этим уравнением должен заканчиваться каждый электротехнический расчёт.
Соединения различных элементов называются электрической цепью, а графическое изображение цепи – электрической схемой. Электрические схемы могут быть принципиальными, расчетными ( замещения) и монтажными.
Электрическая схема показывает, как осуществляется соединение элементов рассматриваемой цепи. В электрической схеме соединения элементов образуют ветви, узлы, контуры.
Участок электрической цепи, по которому проходит ток одного и того же значения и направления, называется ветвью.
Замкнутая электрическая цепь, образованная одной или несколькими ветвями, называется контуром, а место соединения трёх или более ветвей – узлом. На схеме узел изображается точкой.
Вся электротехника базируется на двух законах Кирхгофа. Оба закона были установлены на основании многочисленных опытов и потому получили название
Опытные Законы Кирхгофа.
Опытные Законы Кирхгофа.
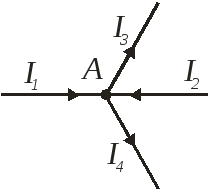
Согласно I-му закону Кирхгофа алгебраическая сумма токов в любом узле электрической цепи равна нулю:
∑ Iκ = 0
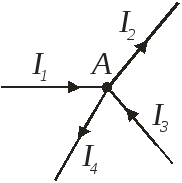
І1+І3-І2-І4=0
Согласно II-му закону Кирхгофа алгебраическая сумма ЭДС источников питания в любом контуре равна алгебраической сумме падений напряжения на элементах этого контура.
ΣЕ=ΣU
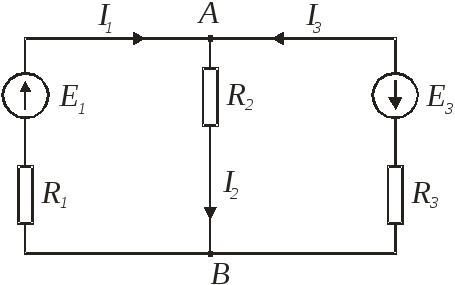
При расчете по первому закону Кирхгофа составляется число уравнений на единицу меньше числа узлов. Перед расчетом назначаются условно положительные направления.
І1+І3— І2=0 (1)
Число уравнений должно быть равно числу ветвей.
Для любого замкнутого контура нужно выбрать направление обхода. Направление обхода по часовой стрелке.
Е1=І1 · R1+ І2 · R2 (2)
Е1+ Е3= І1 · R1— І3 · R3 (3)
Решая эти уравнения мы определяем токи І1, І2, І3; если получилось со знаком «+», то действительное (расчетное) направление тока совпадает с назначено ранее условноположительным направлением ветвей, если со знаком «-», то условноположительное направление ветвей необходимо поменять на обратное.
По известному значению плотности тока, мы определяем S=І / q.
Расчет заканчиваем уравнением баланса мощностей.
Правило:
При составлении уравнений по второму закону Кирхгофа в каждое последующее уравнение необходимо вводить дополнительный контур или одну из ветвей, чтобы не было уравнений тождественных.
Для уменьшения вычислительной работы по первому закону Кирхгофа, предложено ряд методов, основанных на применение законов Кирхгофа.
Метод контурных токов.
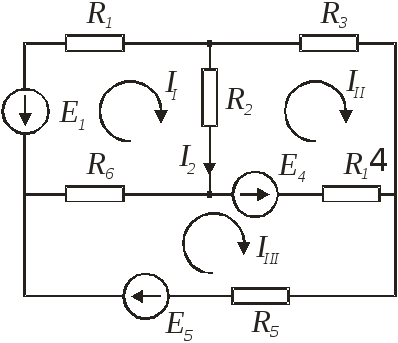
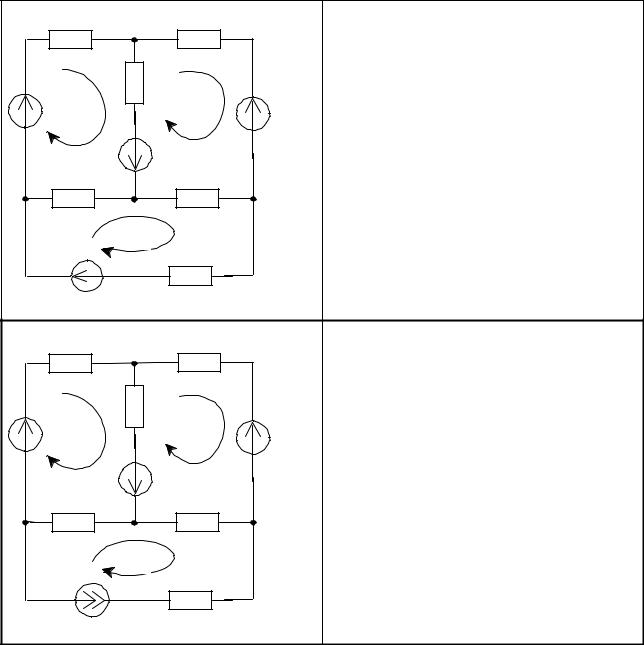
Три расчетных контура по которым протекает свой контурный ток. По первому закону Кирхгофа составляем три уравнения, и по второму закону Кирхгофа – три уравнения. Общее число ветвей 6.
Е1= І1·( R1+ R2 + R6) – ІІІ· R2 – ІІІІ·R6;
— E4=ІІІ· (R2+R3+R4) – ІІ·R2 – ІІІІ·R4 ;
E4+E5=ІІІІ· (R4+R5+R6) – ІІ·R6 – ІІІ·R4 ;
Решая эти уравнения определяем контурные токи.
Правило знаков:
Для определения действительных токов в ветвях, ток в не разветвленной ветви равен контурному, если контурный ток получился со знаком «+», если контурный ток со знаком «-», то равен контурному, но направлен в противоположную сторону.
В смежных ветвях действительный ток равен алгебраической сумме смежных контурных токов.
Знак алгебраической суммы определяется направлением первого тока в правой части.
Расчет заканчиваем уравнением баланса мощностей для действительных токов.
Метод двух узлов или узлового напряжения.
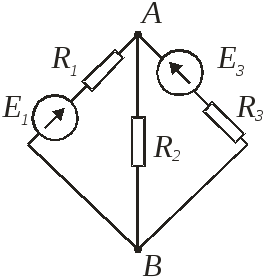
Если ЭДС направлена в сторону положительного узла со знаком (+), и наоборот со знаком (-). Расчет заканчивается уравнением баланса мощностей.
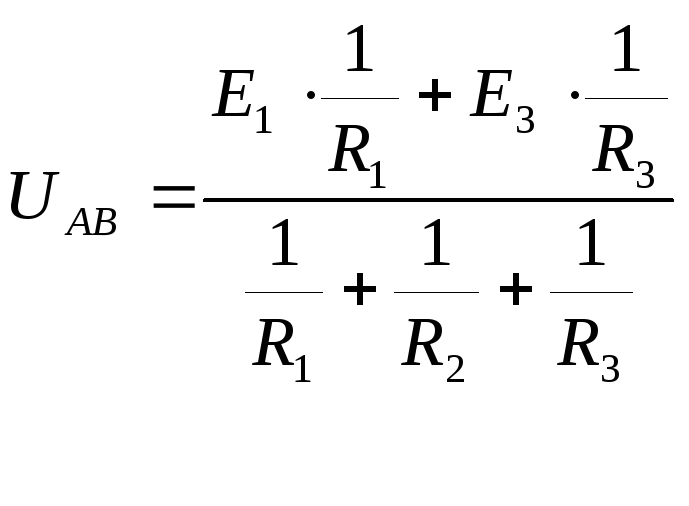
Токи в ветвях определяются по закону Ома.
Электрические цепи бывают: простые и сложные. Простые, когда один источник электрической энергии и схему можно свернуть (упростить) до минимального параметра L,R,C. Сложные – когда с двумя или более источниками электрической энергии.
При свертке можно преобразовать схему между узлами, если оставить потенциалы между точками преобразования.
Преобразование соединения в звезду и треугольник.
Найти токи в ветвях звезды и треугольника. Звезда – когда в узле сходятся три луча.

Если бы рассчитывали непосредственно по первому и второму закону Кирхгофа, то пришлось бы по первому закону Кирхгофа составить три уравнения и по второму закону Кирхгофа три уравнения.
Можно преобразовать схему, если оставим потенциалы: φa, φb, φc.
Получилась звезда с сопротивлениями Ra, Rb, Rc.
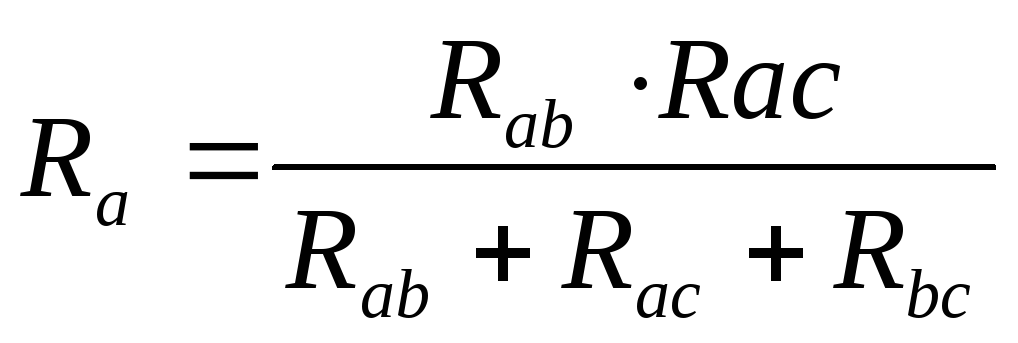
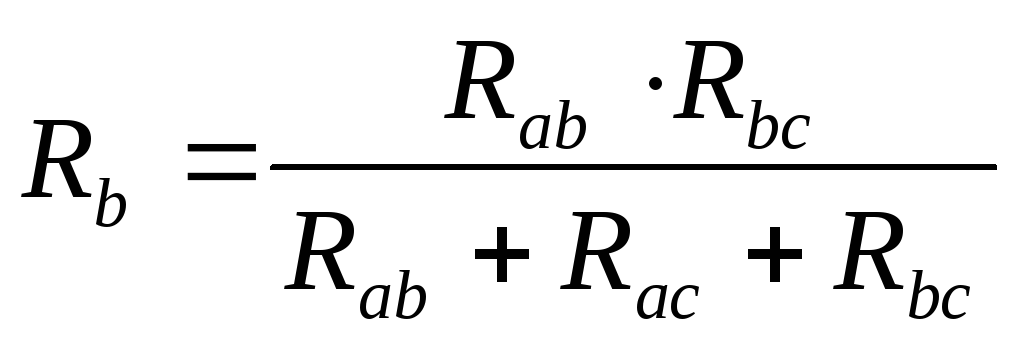

Таким же образом можно сопротивление звезды преобразовать в треугольники.
Линейные электрические цепи синусоидального переменного тока.
Синусоидальная — единственная форма тока, потому что косинус является производной от синуса. Это возможность использования уравнения Эйлера для расчета их применять комплексные числа.
Число полных изменений синусоиды за 1 секунду называется частотой переменного тока.
Время в течении которого синусоида полностью изменяется, называется периодом.
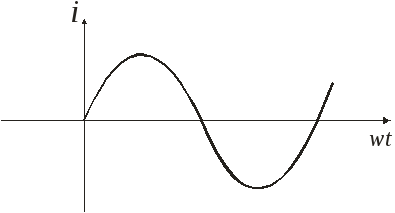

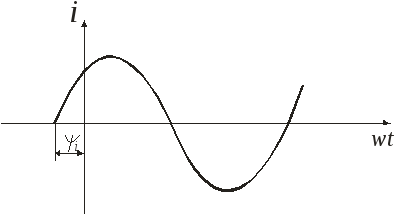

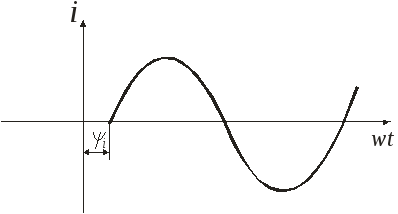
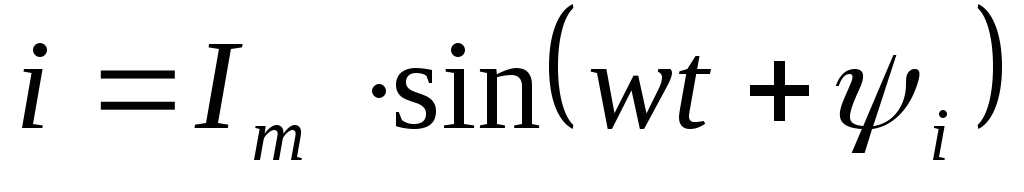
где Im — максимальное, или амплитудное, значение тока,
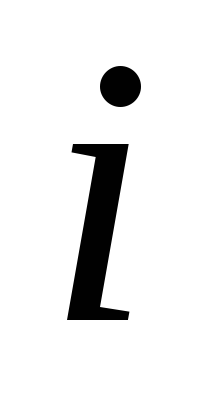 —
мгновенное значение тока i(t),
—
мгновенное значение тока i(t),
 — угловая частота или скорость
изменения аргумента функции,
— угловая частота или скорость
изменения аргумента функции,
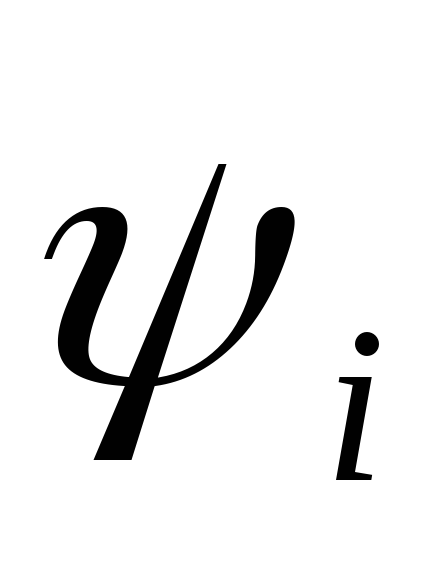 — начальная фаза (аргумент функции
в момент времени (момент включения),
принятый за начало отсчета, т.е. при t = 0),
— начальная фаза (аргумент функции
в момент времени (момент включения),
принятый за начало отсчета, т.е. при t = 0),
аргумент синусоидальной функции  ,
называется фазой , и определяет
значение функции i(t)
в любой момент времени.
,
называется фазой , и определяет
значение функции i(t)
в любой момент времени.
Условились, что какая-то величина
переменного тока I, U, E будет равна какой-то величине постоянного
тока, если у них будет одинаковая
температура нагрева  .
.
Значение периодического тока, равное
такому значению постоянного тока,
который за время одного периода произведет
тот же самый тепловой или электродинамический
эффект, что и периодический ток, называют действующим значением периодического
тока (среднеквадратичным значением
тока за период или эффективным): 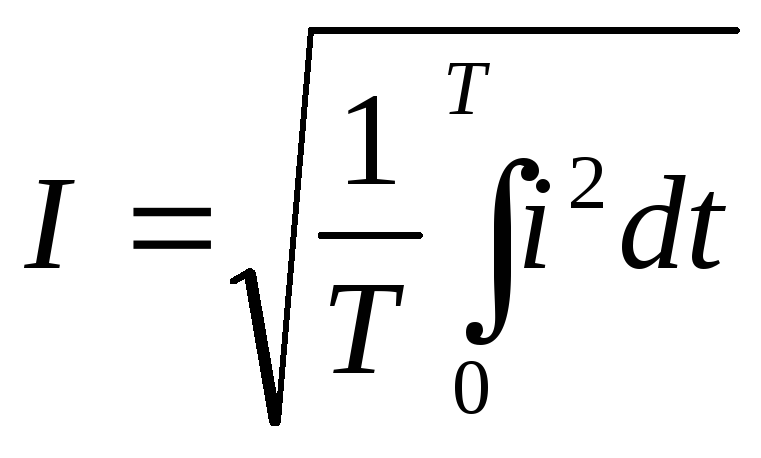

Аналогично определяются действующие значения ЭДС и напряжения.
Обозначим через I некоторый постоянный ток, при протекании
которого по тому же участку цепи за
время T выделится такое же количество тепла.
Тогда с учетом того, что 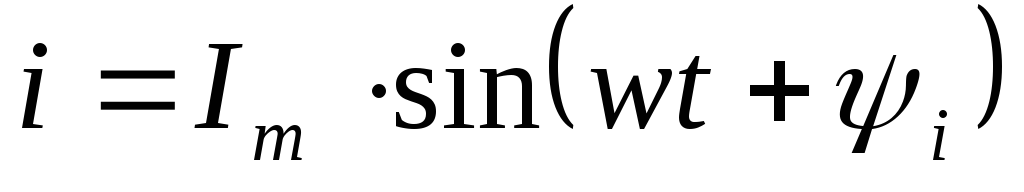 получим:
получим:
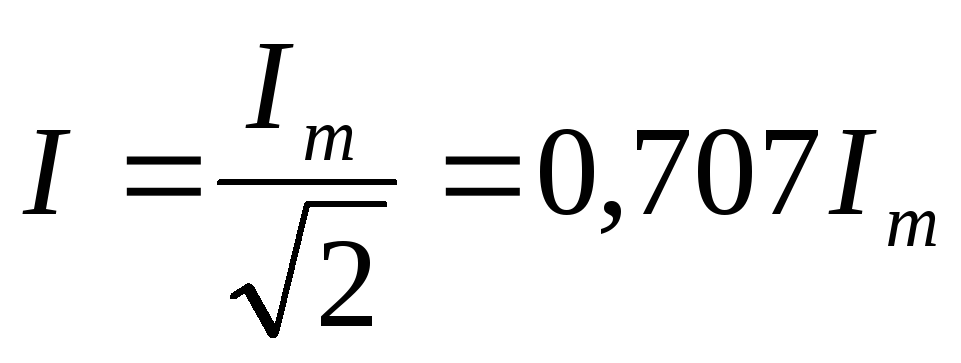 ,
аналогично
,
аналогично 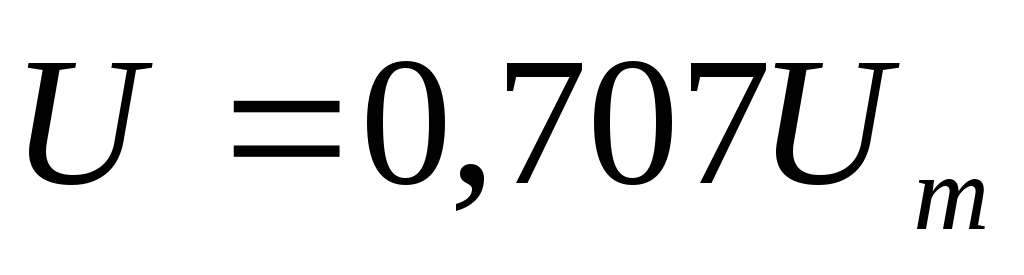 ,
,  .
.
Подавляющее большинство приборов для измерения в цепях синусоидального переменного тока показывают именно эти действующие значения (тока I, напряжения U, ЭДС E).
Расчеты цепей переменного тока при включении активного, индуктивного и емкостного сопротивления (R, L, C).
В цепи переменного тока
наблюдается эффект вытеснения тока в
периферии сечения, у периферии  больше, чем у центра. Но так как частоты
низкие (50 Гц), то пренебрегаем этим
явлением и считаем, что активное и
омическое сопротивления одинаковы.
больше, чем у центра. Но так как частоты
низкие (50 Гц), то пренебрегаем этим
явлением и считаем, что активное и
омическое сопротивления одинаковы.
Активное сопротивление R в цепи синусоидального переменного тока.
Считается, что напряжение прикладывается сразу и достигает своего значения сразу.
Забегая вперед, напишем, что на участке с активным сопротивлением, ток повторяет функцию напряжения, совпадая с ним по фазе, на индуктивном сопротивлении всегда на этом участке ток начинается с нуля и отстает от напряжения на определенный угол, а на участке с емкостью напряжение на емкости начинается с нуля, а ток опережает это напряжение на определенный угол.
В цепях переменного тока доказывается положение о том, что уравнения и методы цепей постоянного тока могут быть записаны как для мгновенных значений, так для векторных и комплексных величин.
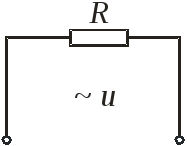

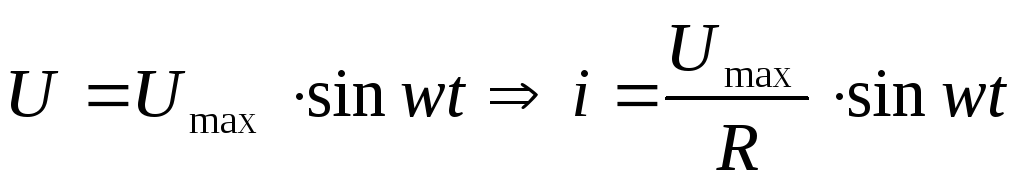
Сравниваем фазы напряжения и тока, видим их совпадения. На участке с активным сопротивлением ток и напряжение совпадают по фазе.
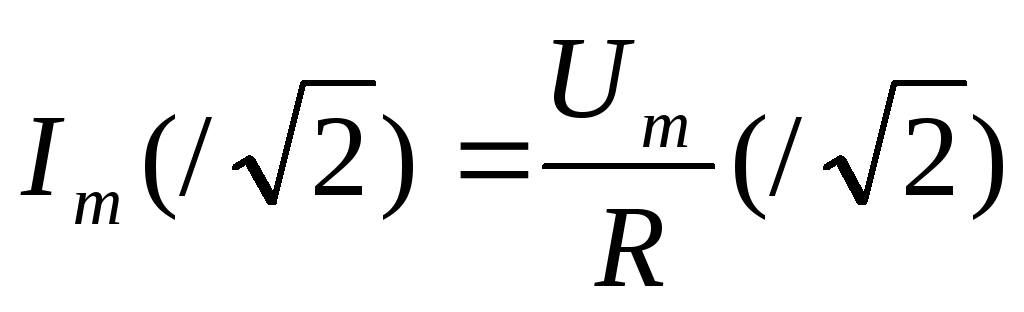
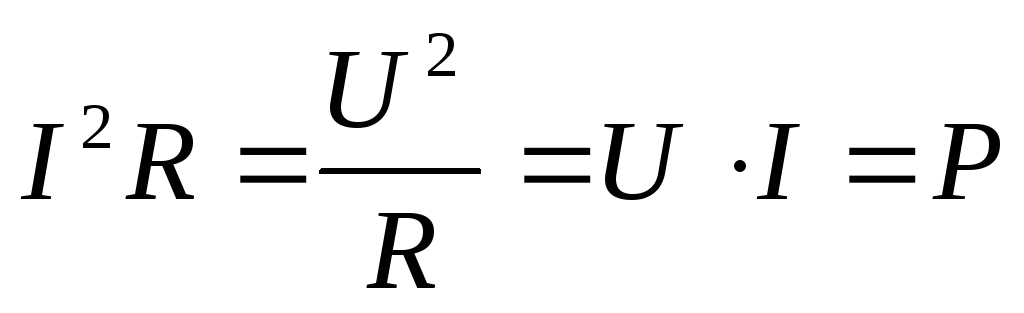 (Вт, кВт) – активная мощность в цепи
с активным сопротивлением.
(Вт, кВт) – активная мощность в цепи
с активным сопротивлением.
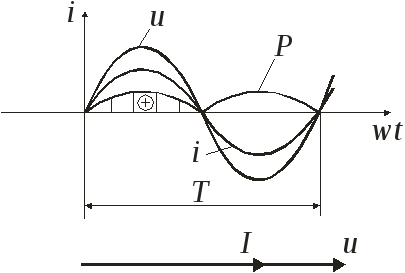
Индуктивность в цепи синусоидального переменного тока.
Положительное направление ЭДС совпадает
с током. Т.к. магнитное поле собственное  ЭДС самоиндукции.
ЭДС самоиндукции.
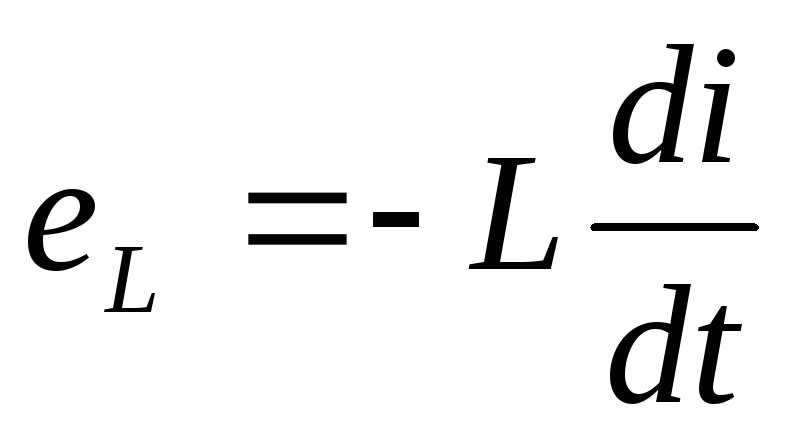

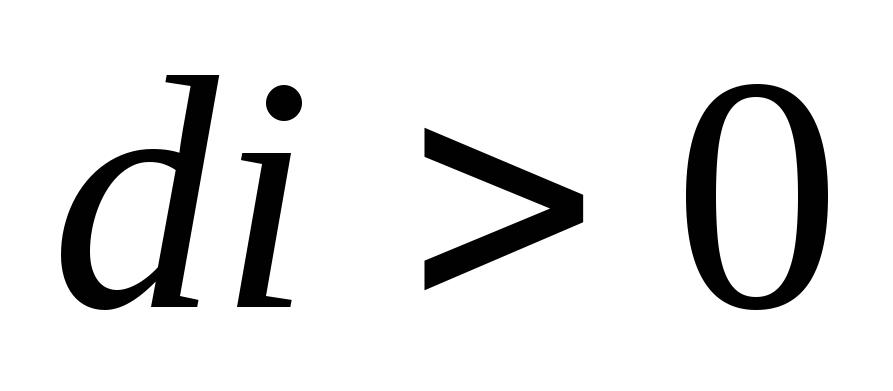
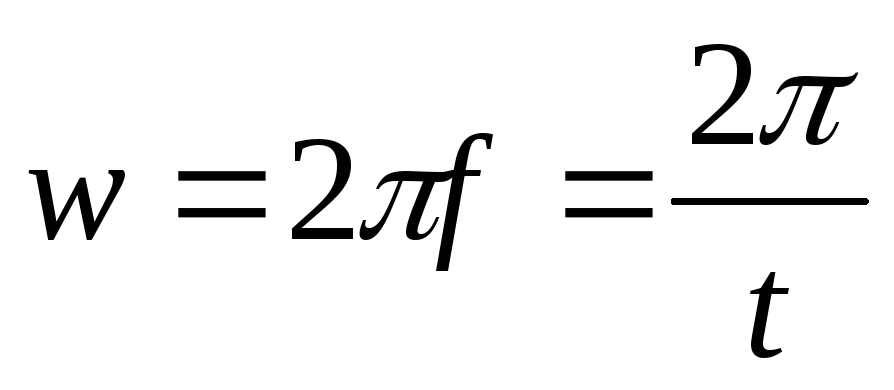
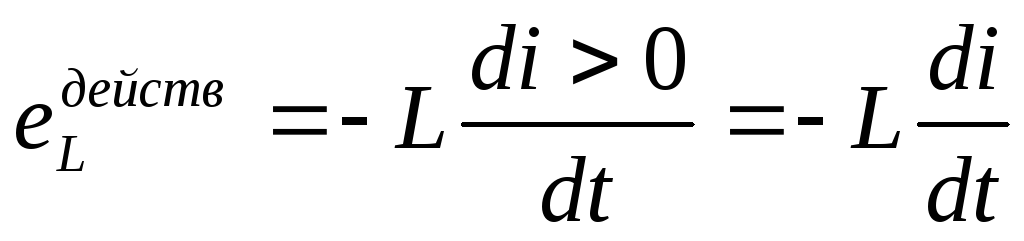
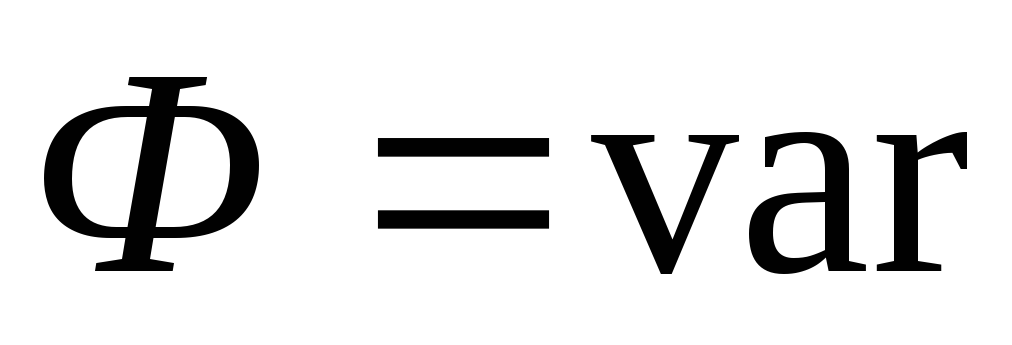
При возрастании тока ЭДС самоиндукции направлена против тока, не дает ему увеличиваться, стабилизирует процесс.
Если 

Действительное направление ЭДС совпадает с током, не давая ему исчезнуть.
Закон Ленца об ЭДС самоиндукции. Из схемы:
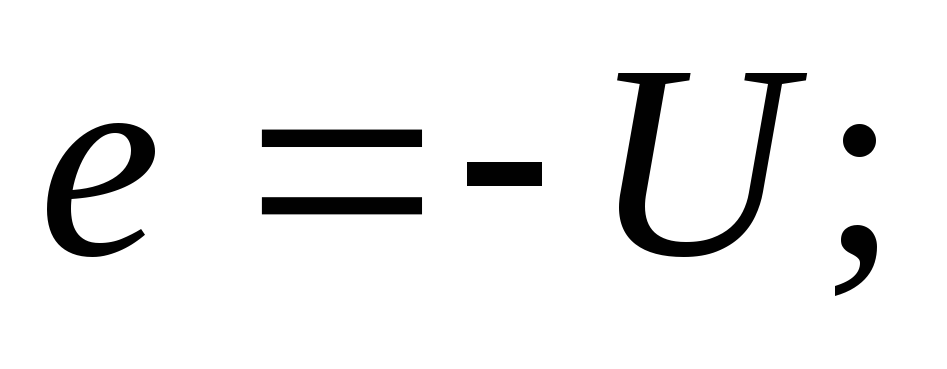
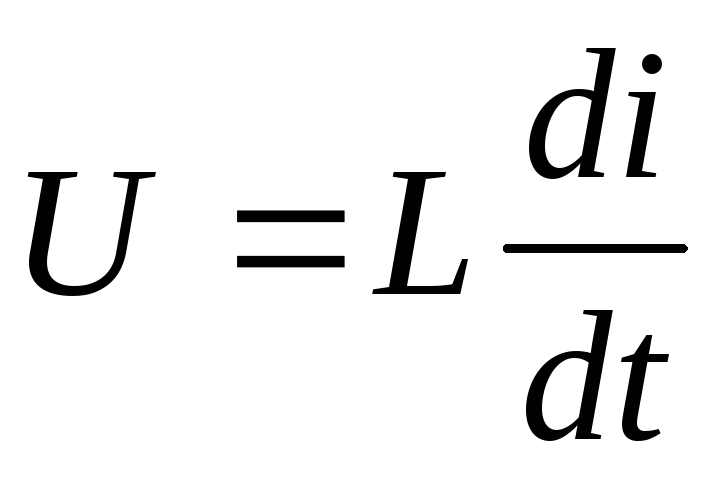

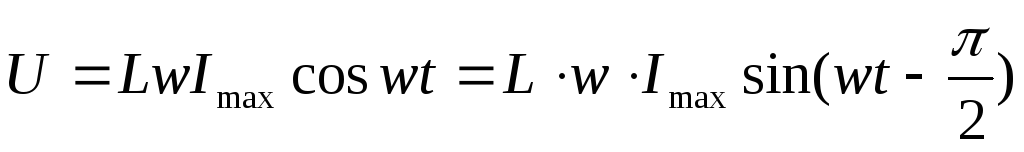
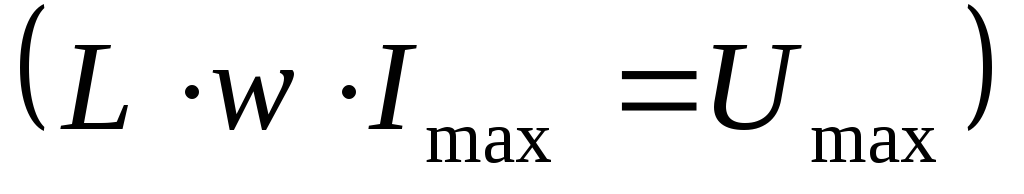
На участке с индуктивностью ток отстает по фазе от напряжения на угол 90° (π/2).
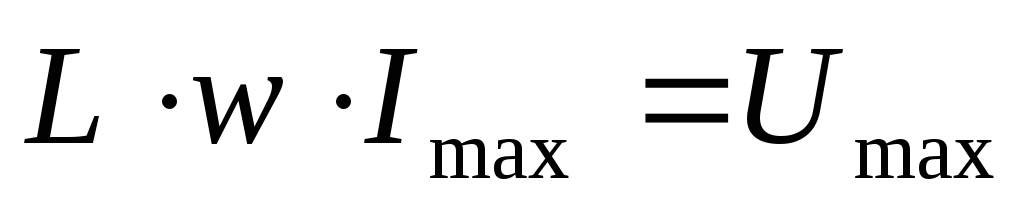
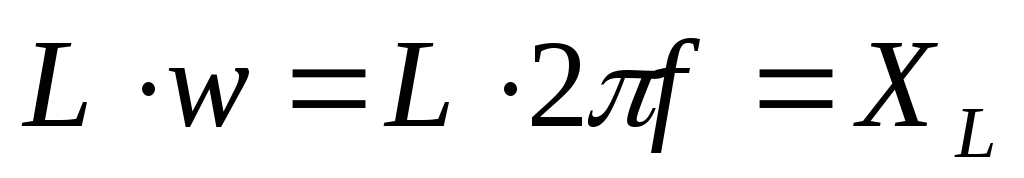
В правом уравнении ЭДС самоиндукции XL – искусственно введенное реактивное сопротивление, которое заменяет собой действие ЭДС самоиндукции.
 — закон Ома для участка с индуктивностью.
— закон Ома для участка с индуктивностью.
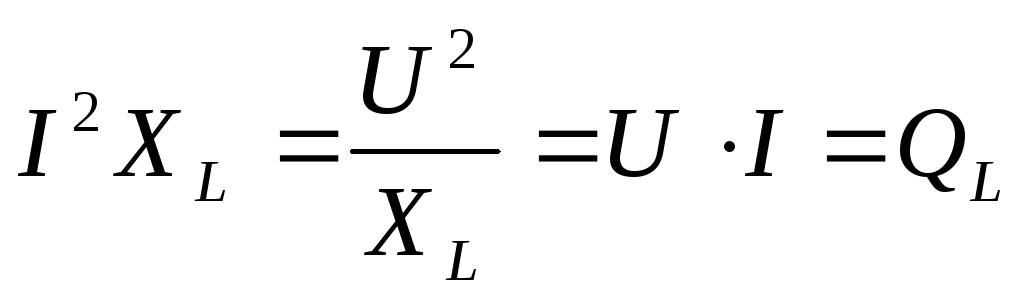 — реактивная мощность, вредная (Вар,
кВар).
— реактивная мощность, вредная (Вар,
кВар).
π / 2

Емкость в цепи синусоидального переменного тока.
Емкость – два проводника, а между ними диэлектрик.

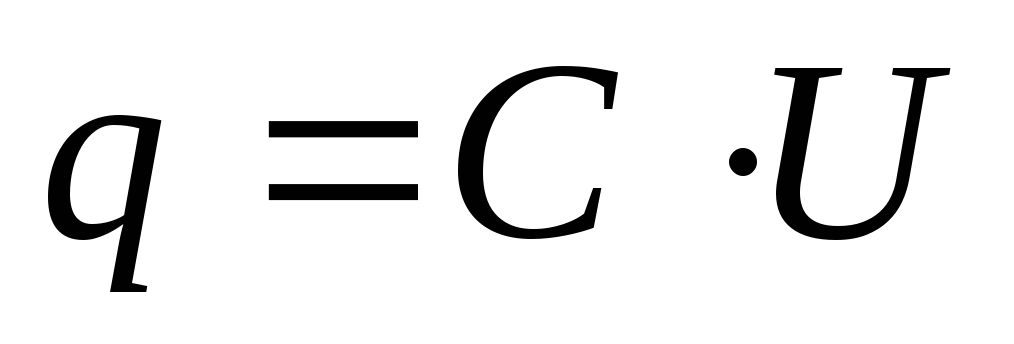
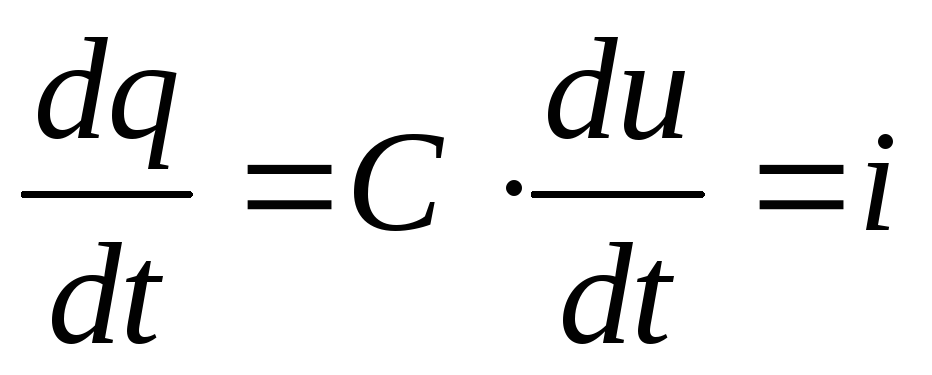
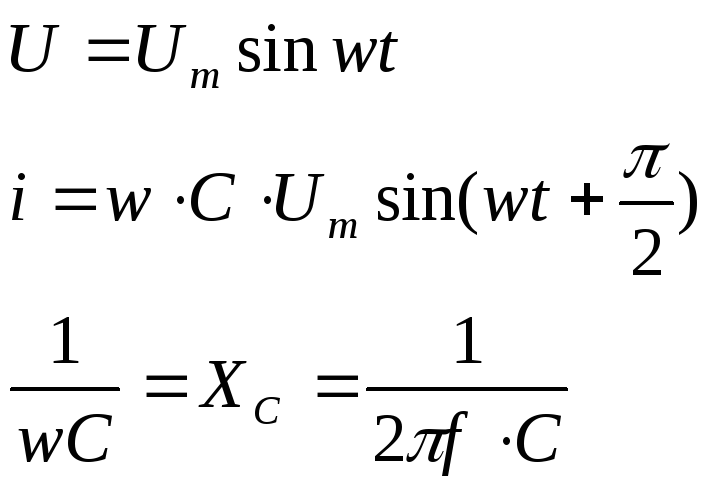
На участке с емкостью ток опережает приложенное к емкости напряжение на угол 90° (π/2). XC – емкостное сопротивление.
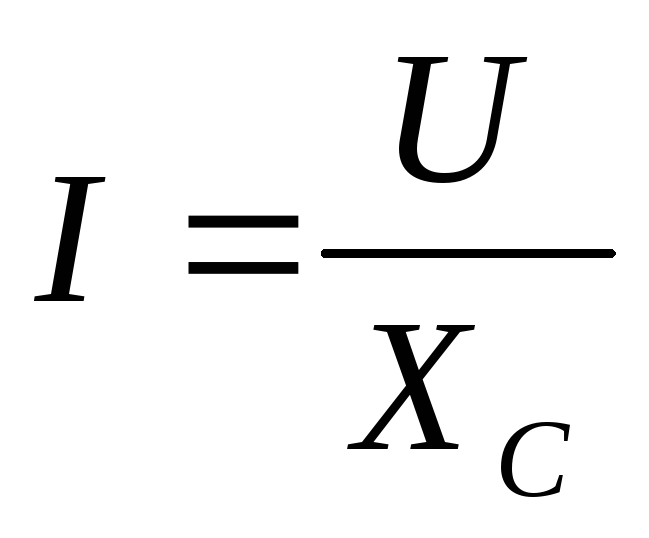 — закон Ома для участка с емкостью.
— закон Ома для участка с емкостью.
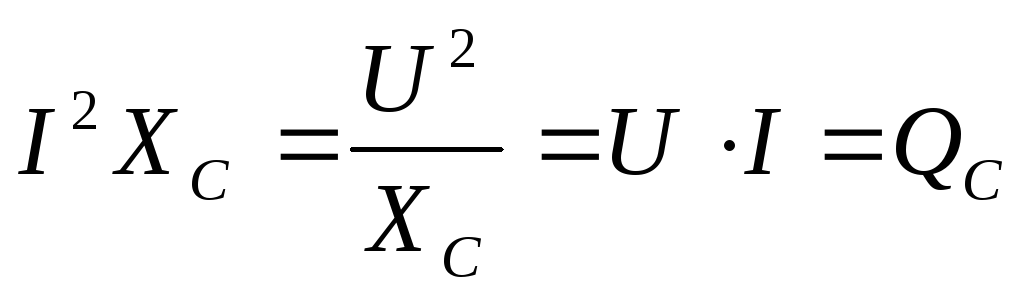 — реактивная емкостная мощность (Вар,
кВар).
— реактивная емкостная мощность (Вар,
кВар).
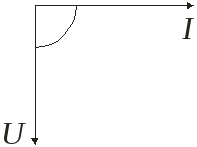
π / 2
Из того, что ток на индуктивности отстает от напряжения, а на емкости опережает реактивная мощность индуктивности в любой момент времени находится в противофазе с емкостной, они стремятся друг друга уничтожить.
Последовательное соединение R, L, C.
для мгновенных значений — 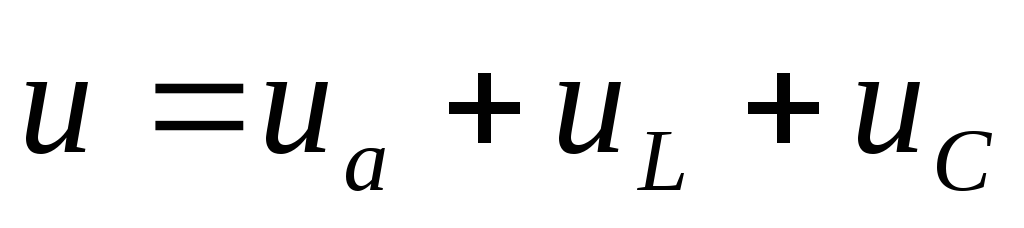
для векторных значений — 
для комплексных значений — 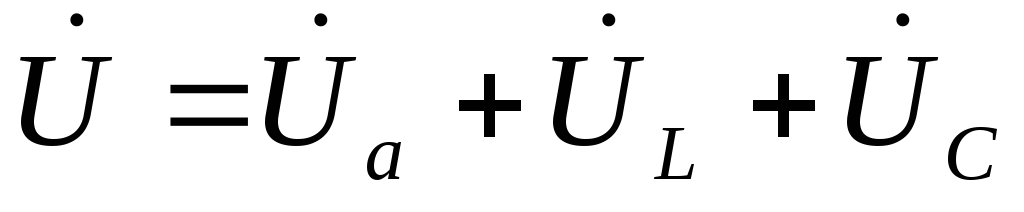

Целесообразно векторную диаграмму строить для общей для данного вида соединений величины. Для последовательного соединения целесообразно строить относительно тока, для параллельного – относительно напряжения.
Пусть характер цепи активно-индуктивный,
т.е. 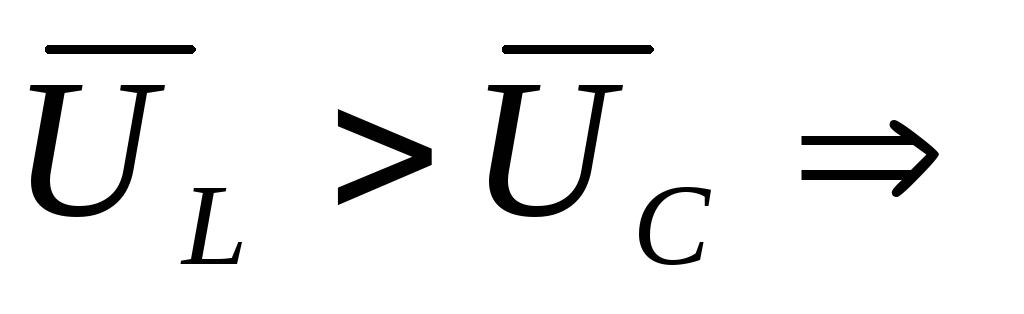 ток отстает от напряжения на некоторый
угол φ.
ток отстает от напряжения на некоторый
угол φ.

φ
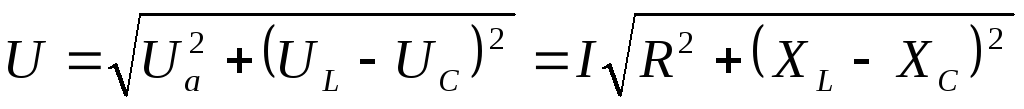
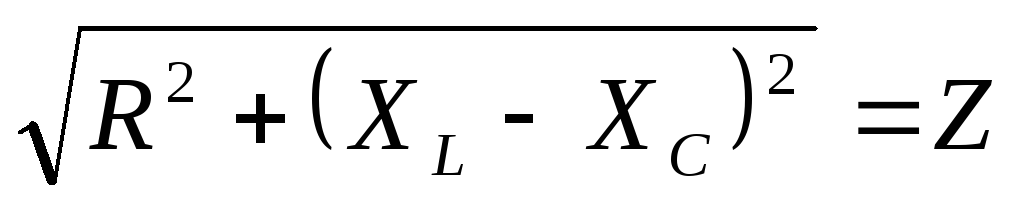 — модуль полного сопротивления цепи
переменного тока.
— модуль полного сопротивления цепи
переменного тока.
 — закон Ома для цепи переменного тока.
— закон Ома для цепи переменного тока.
Модуль полного сопротивления в цепи переменного тока.

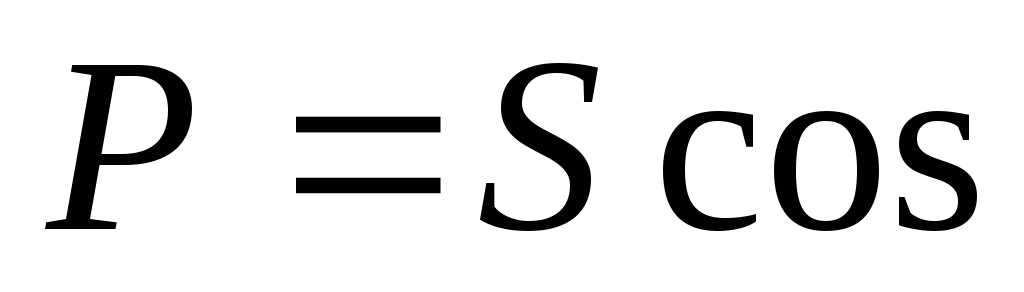 φ (Вт, кВт)
φ (Вт, кВт)
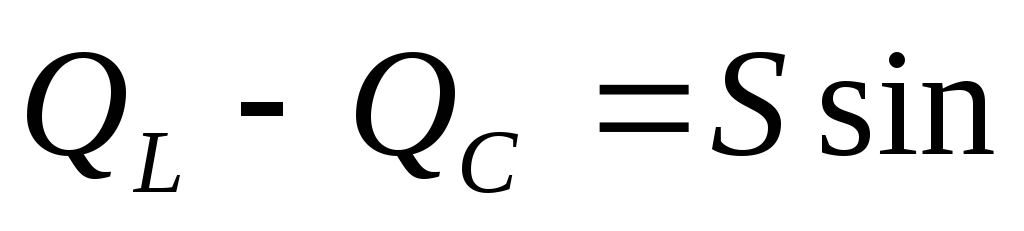 φ (Вар, кВар)
φ (Вар, кВар)
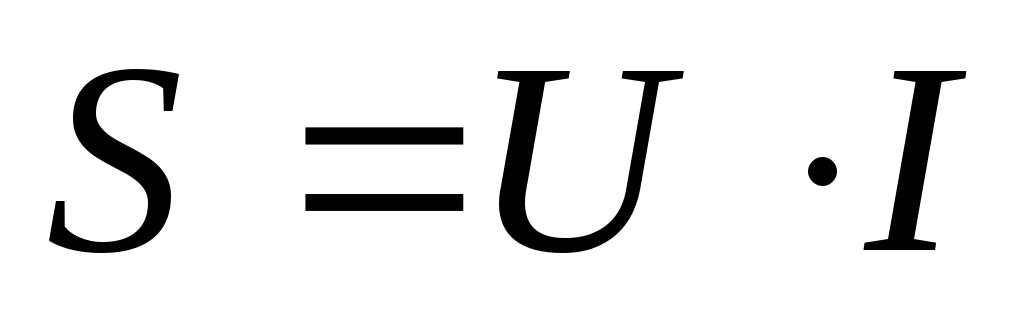 (ВА, кВА)
(ВА, кВА)
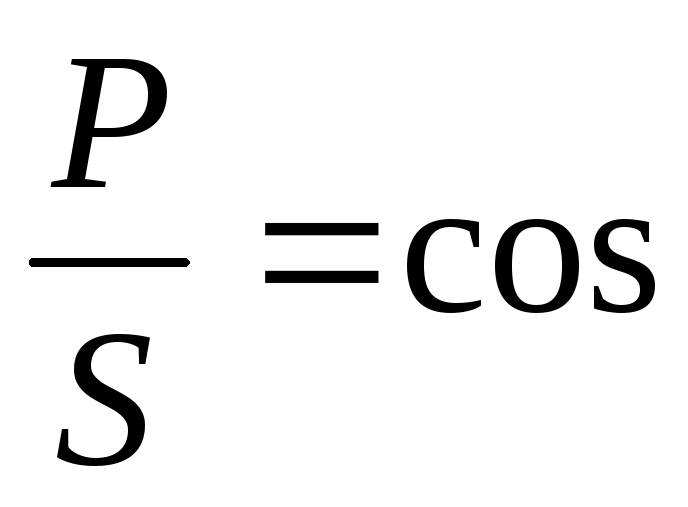 φ – какая часть производимой мощности
идет на совершение полезной работы.
φ – какая часть производимой мощности
идет на совершение полезной работы.
Символический метод или расчет цепей
с применением комплексных чисел.
Диаграмму напряжений поместим на
комплексную плоскость ( ),
умножение на j есть
поворот комплексного числа на 90° против
часовой стрелки.
),
умножение на j есть
поворот комплексного числа на 90° против
часовой стрелки.
|ejφ|
= 1 =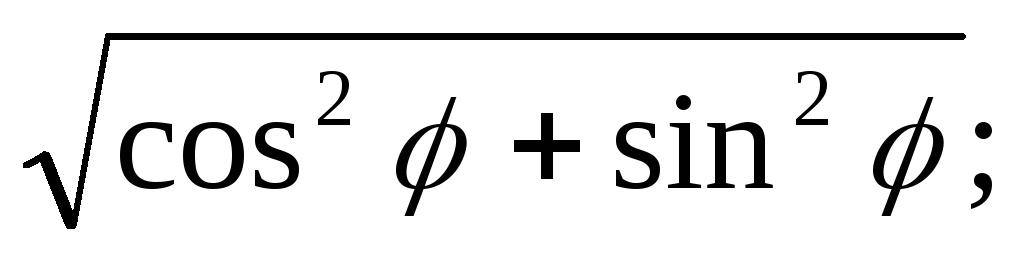



Z – полное комплексное сопротивление цепи переменного тока.
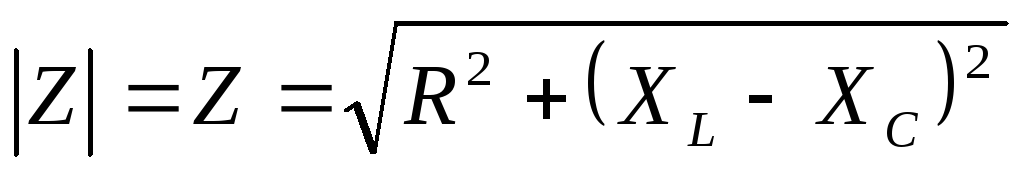 — модуль комплексного сопротивления
— модуль комплексного сопротивления
До сих пор мы имели дело с модулем полного
комплексного сопротивления  .
.
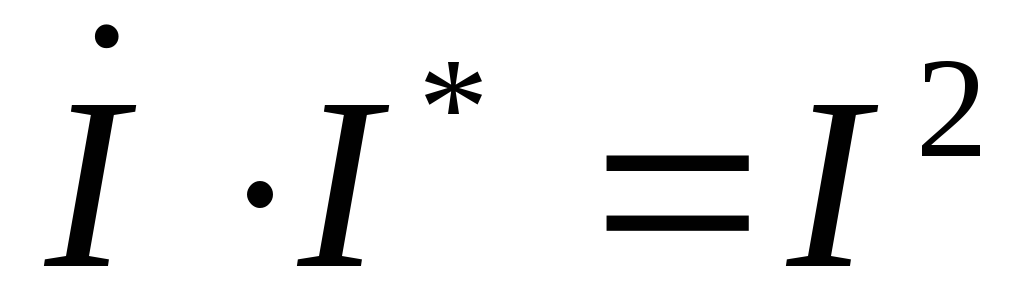
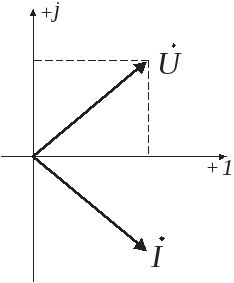
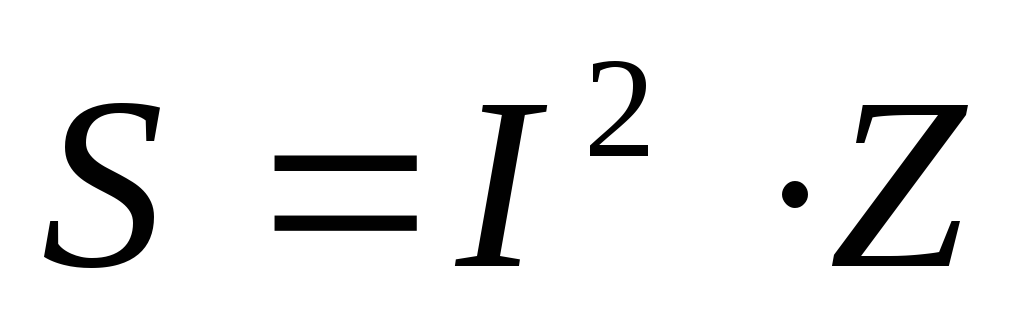
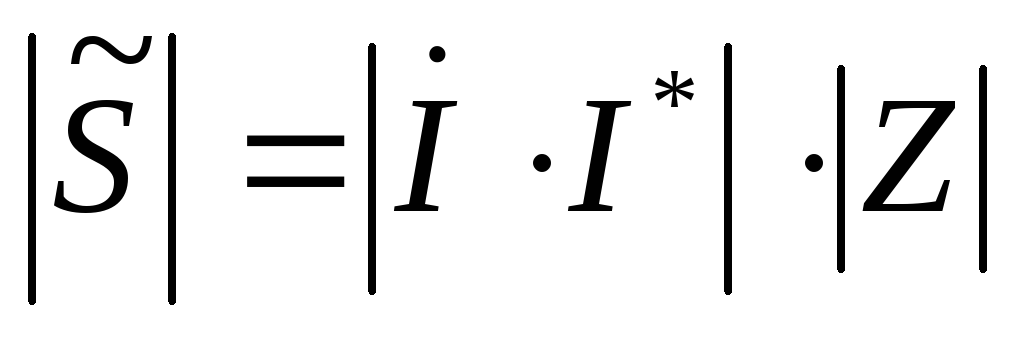
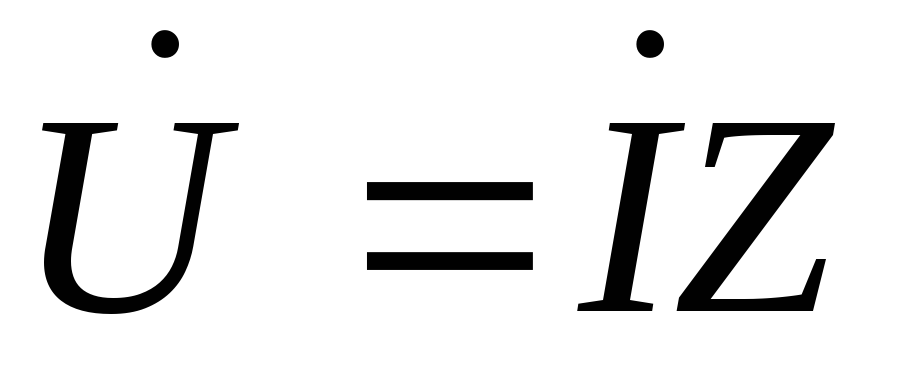
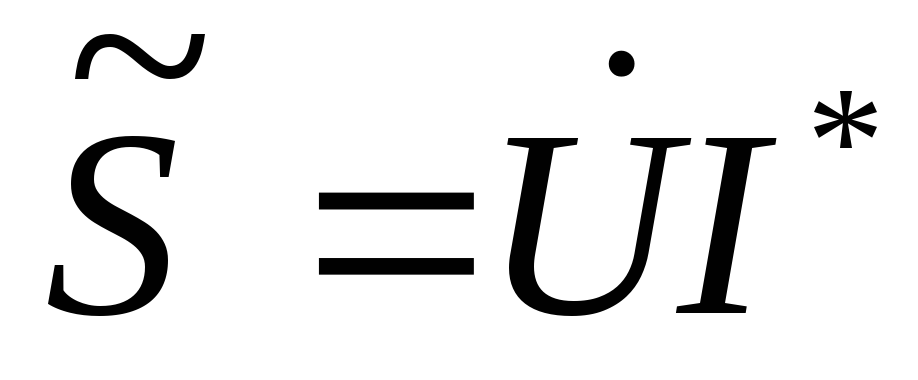 — полная комплексная мощность –
произведение комплекса напряжения на
сопряженный комплекс тока.
— полная комплексная мощность –
произведение комплекса напряжения на
сопряженный комплекс тока.
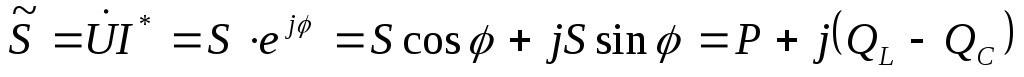
Все электротехнические расчеты выполняются с помощью комплексных чисел. Применение комплексных чисел при расчете цепей синусоидального переменного тока позволяет перейти от геометрических операций над векторами к алгебраическим действиям над комплексными числами (алгебраически складываются действительные части с коэффициентами мнимой части комплексного числа). Поэтому все методы, законы, уравнения постоянного тока могут быть использованы в цепях переменного тока, но записанные с помощью комплексных чисел. Можно применять метод двух узлов, контурных токов и т.д.
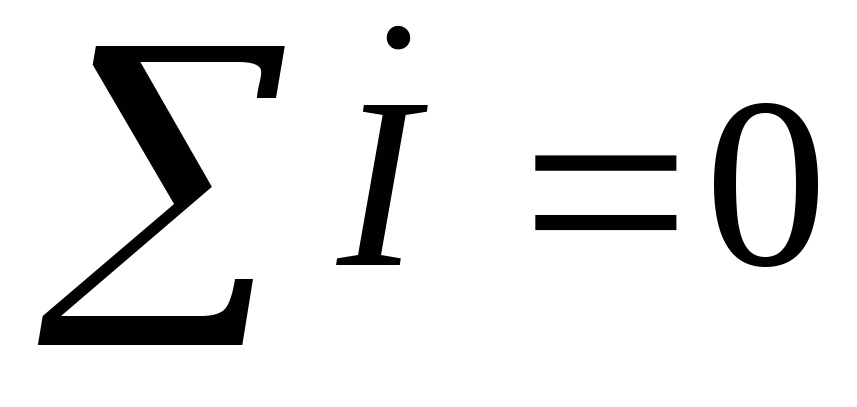
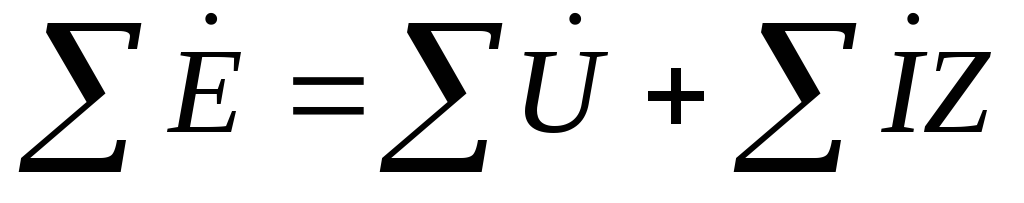
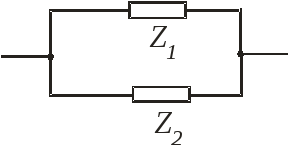

Перед расчетом какой-либо цепи ее предварительно необходимо преобразовать в комплексной форме для применения символического метода.


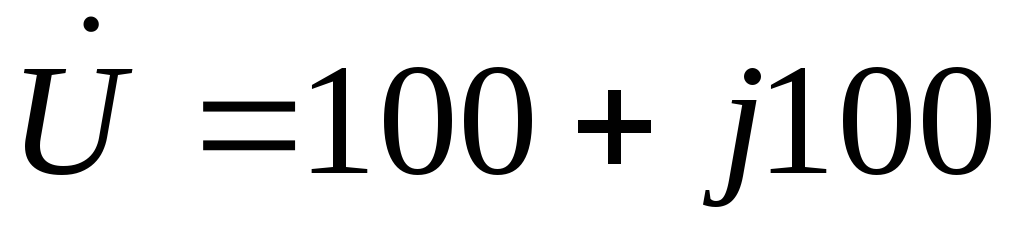 В
В 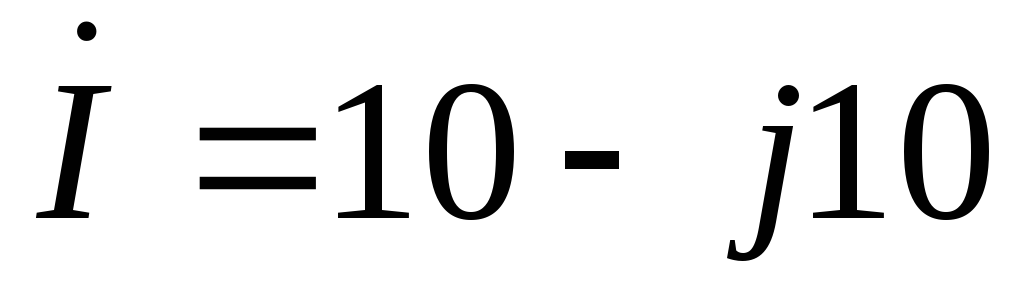 А
А
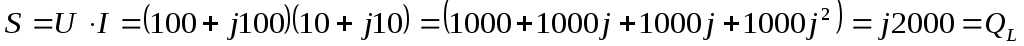 Вар
Вар
Пример 1: нагрузка чисто индуктивная.
Расчеты символическим методом производятся над действующими значениями токов и напряжений. Если имеется начальная фаза, то действующее значение равно 0,707 амплитудного, wt = 0, t = 0 и остается синус начальной фазы.
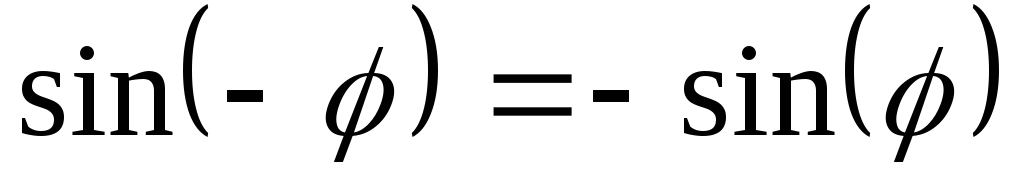
Перед расчетом необходимо реальную схему преобразовать в прямоугольники.
1) 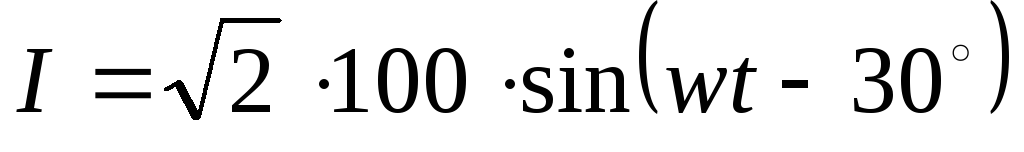

Резонансы в электрических цепях в.
При последовательном ХL и ХC (рис1) возможен последовательный резонанс напряжений. Если же ХL и ХC соединены параллельно (рис2), то может возникнуть параллельный резонанс, или резонанс токов.
Под резонансом электрических цепей понимают такое состояние, когда частоты свободных и вынужденных колебаний совпадают, ток и напряжения совпадают по фазе. Когда нагрузка становится чисто активной, потребляется чисто активная мощность, реактивная мощность равна 0, а полная мощность S = P.
Резонанс напряжений.
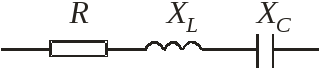
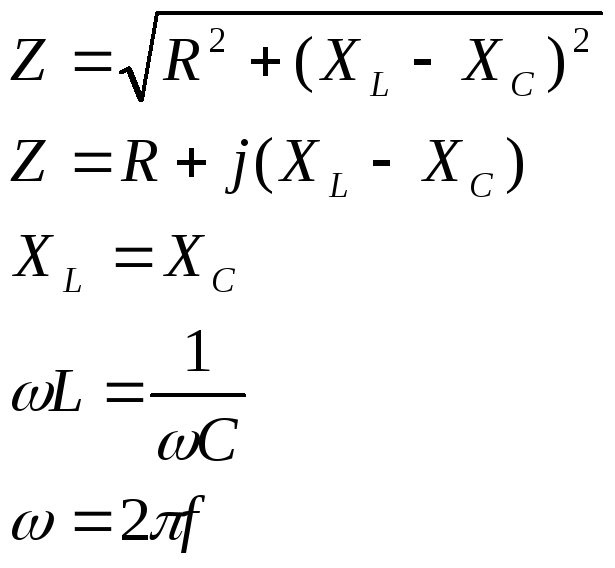
Резонанс напряжений, может быть, достигнут тремя путями:
Изменить частоту
Изменить индуктивность
Изменить емкость


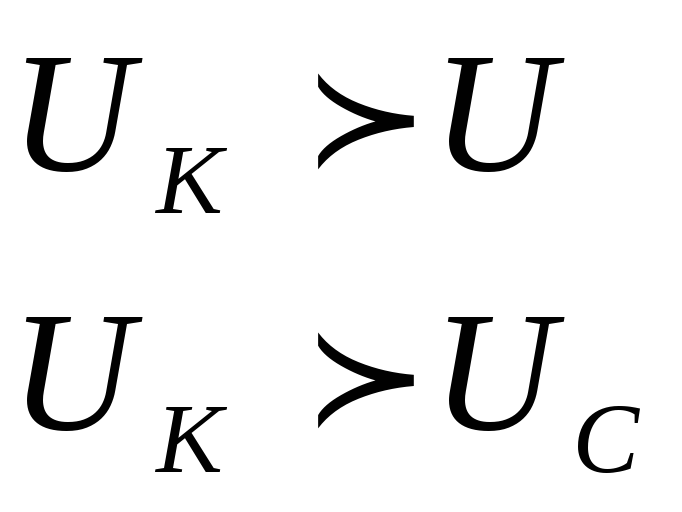
При резонансе напряжения, напряжения ХL и ХC находятся в противофазах, их разность равна 0. Но сами могут достигать значительных значений.
Q – добротность контура, показывающая во сколько раз напряжение на индуктивности и ли на емкости превышает напряжение в сети.
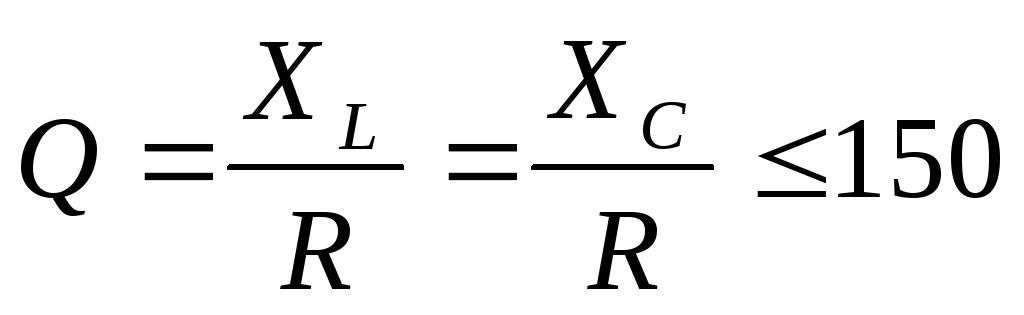
Резонанс напряжений вещь вредная, и его надо предусматривать.
При резонансе ток не только совпадает по фазе, но и достигает max-го значения.
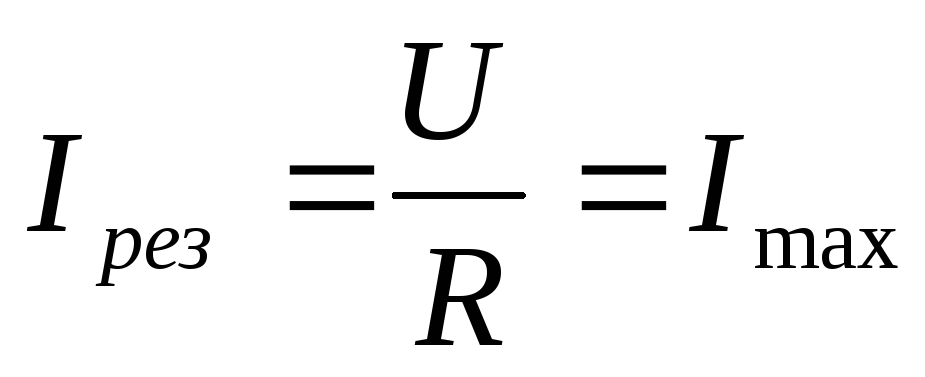
Резонанс напряжения – это когда частоты вынужденных колебаний (сети) совпадают с колебаниями собственной частоты.
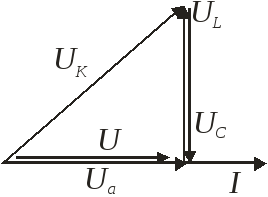
Резонанс токов. (или параллельный резонанс)
В этом случае может возникнуть в колебательном контуре резонанс токов, который характеризуется совпадением по фазе I и U в неразветвленной части коэффициент мощности равен 1. Когда отсутствует во внешней цепи реактивная мощность, а проводимость становится чисто активной и равная сумме активных проводимостей параллельных ветвей.
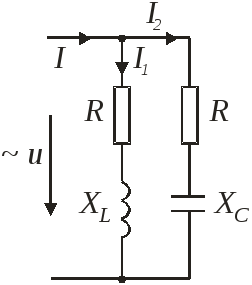
Общая проводимость

В цепи параллельного тока активная проводимость зависит так же от реактивного сопротивления:
1 XL
2 XC
Резонанс тока наступает, когда 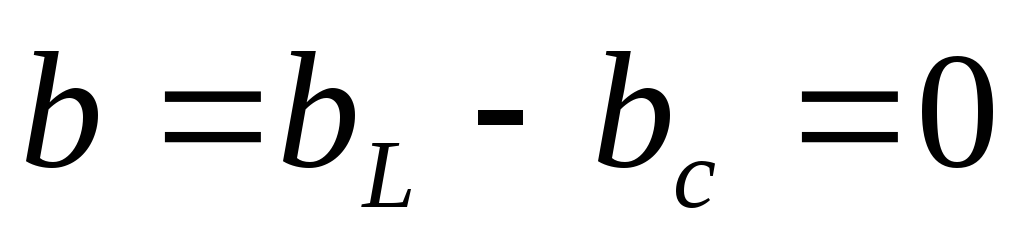
Кроме того, резонансного тока можно добиться изменением частоты ХL и ХC, а так же активных сопротивлений этих ветвей.
При этом ток будет
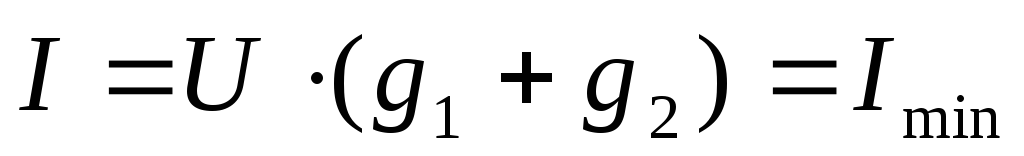
Ток в неразветвленной части контура будет совпадать по фазе с общим напряжением.
По первому закону Кирхгофа

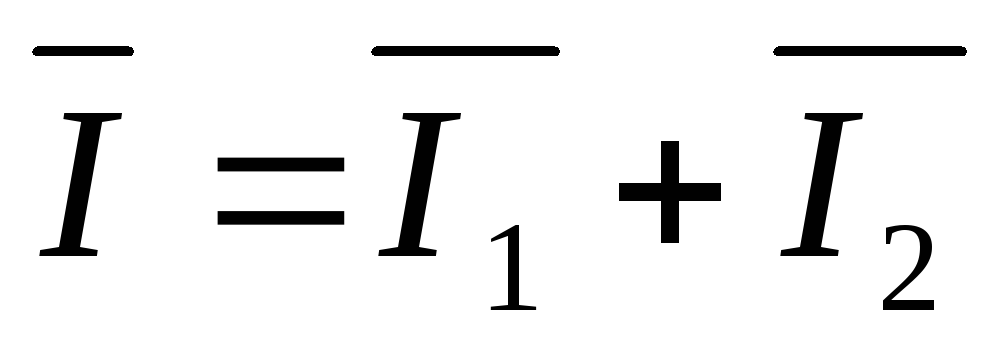
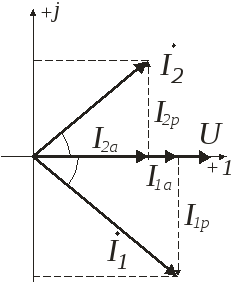
φ2
φ1
Из векторной диаграммы видно, что при резонансе тока реактивная составляющая индуктивного = реактивной составляющей емкостного и находятся с ней в противофазах.
Общий ток в неразветвленной фазе равен сумме активных составляющих токов 1 и 2 и совпадает по фазе с приложенными напряжениями.
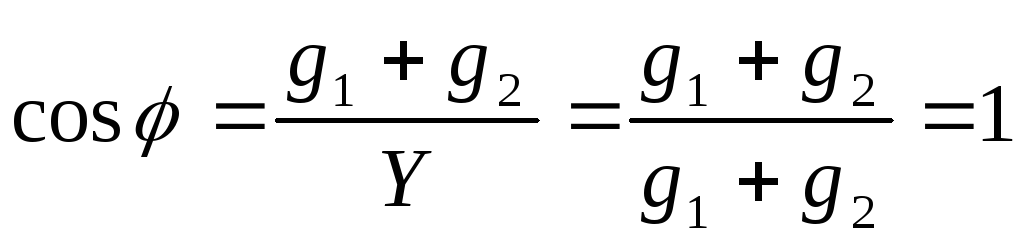
Явление резонанса тока явление полезное
и служит для искусственного увеличения  ,
а следовательно к уменьшению
реактивно-индуктивной мощности, а при
их равенстве
,
а следовательно к уменьшению
реактивно-индуктивной мощности, а при
их равенстве 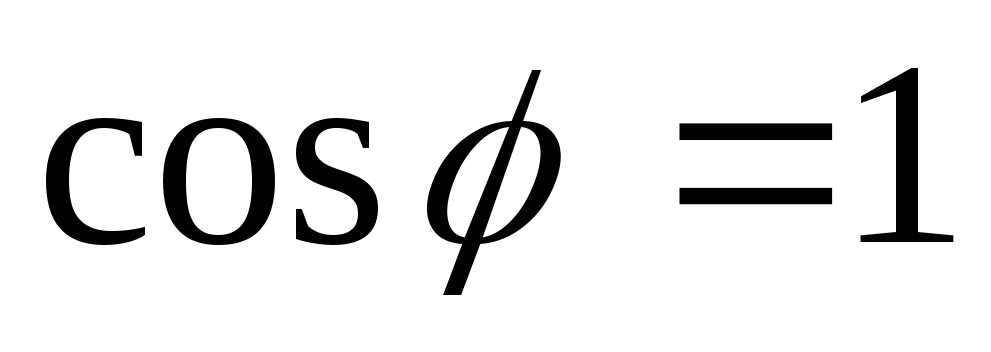
Пример:
Пусть потребитель имеет активно-индуктивный характер.
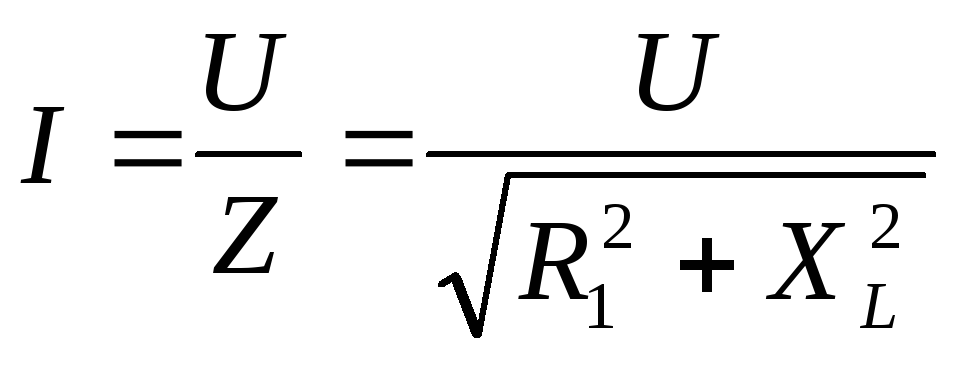
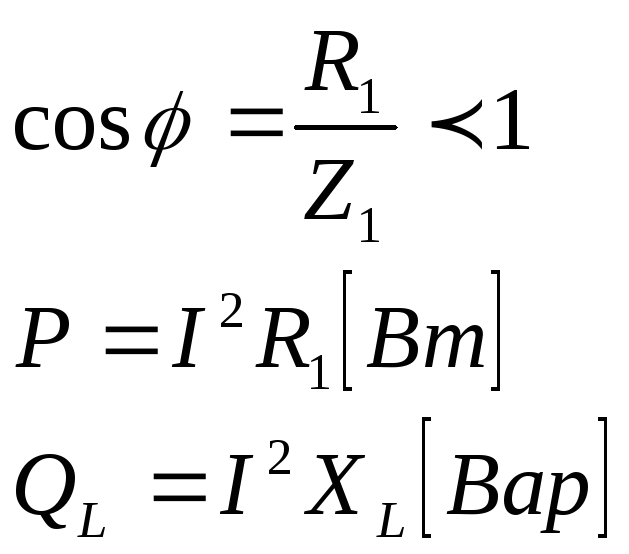
Нужна мощность, чтобы подключить еще один потребитель, тогда у нас будет

При этом из сети будет забираться чисто активная мощность меньше прежней S, то есть создается запас по мощности для подключения дополнительного потребителя.
Этот способ увеличения  до 1 называется способом улучшения
до 1 называется способом улучшения  ,
способом получения чисто активной
мощности.
,
способом получения чисто активной
мощности.
Пример:
Дано (Комплексное) мгновенное выражение для тока.
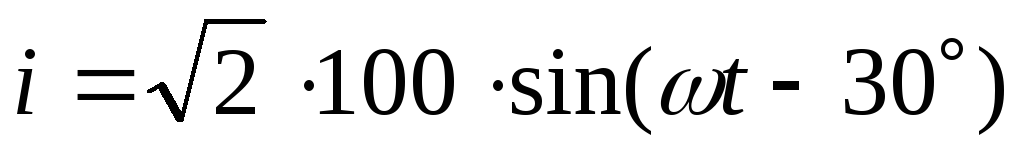
i=50
Комплекс тока i=50А, начальная
фаза 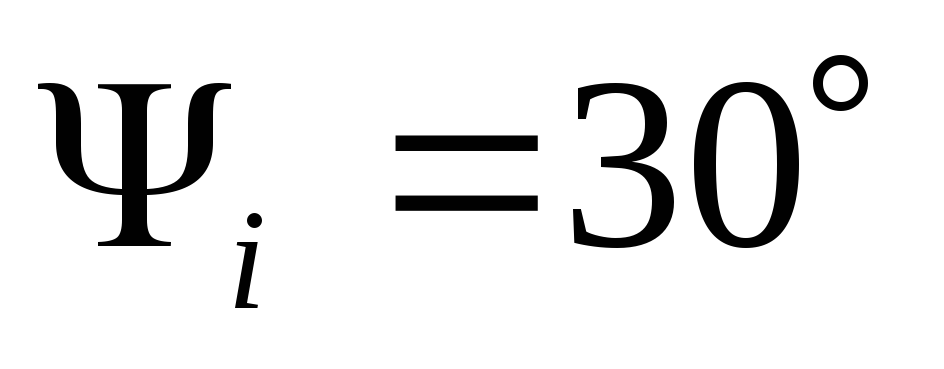 запишем выражение мгновенного значения
тока:
запишем выражение мгновенного значения
тока:
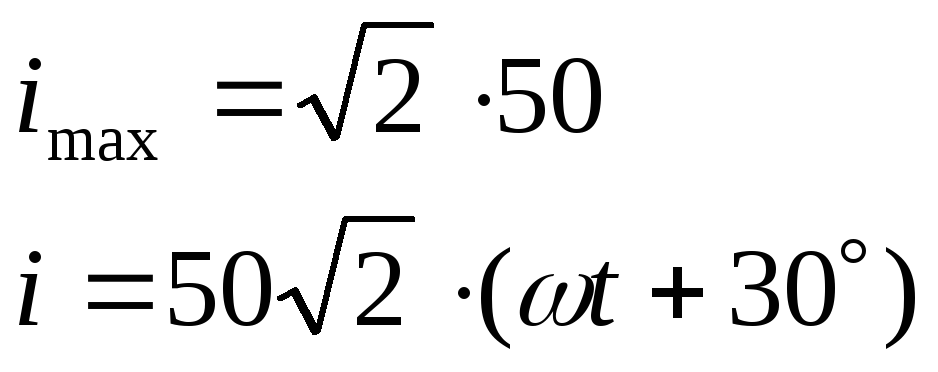
Трехфазные системы синусоидального тока.
Преимущество:
1) Возможность получения кругового вращающегося магнитного поля.
2) И поток, и магнитное поле постоянны в любой точке.
3) Минимальные потери при канализации этой системы.
4) Простота расчета.
Пример трехфазного асинхронного двигателя:

Схема трехфазного асинхронного двигателя:

Обмотки статора сдвинуты на 120 градусов. В каждой обмотке при вращении индуктора отдельно наводится синусоидальная однофазная ЭДС, которая конструктивно сдвинута одна относительно другой на 120 градусов. А, Б, С – фазы.
e
eA
eB
eC

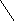
 А, eВ, eс.
А, eВ, eс. 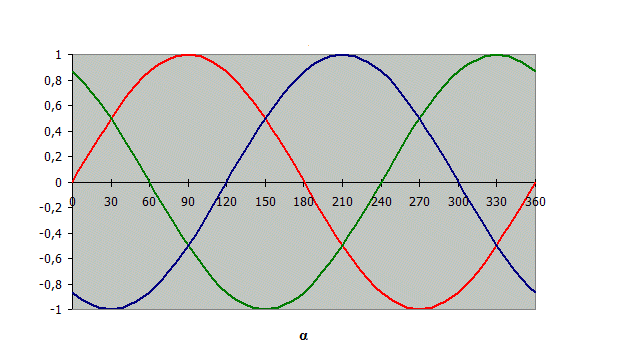 eА + eB + eC.
= 0
eА + eB + eC.
= 0 ! Алгебраическая сумма ЭДС равна нулю в любой момент времени.
Это дает основание записать, как это было доказано в 1-фазном токе с помощью комплексных чисел для действующих значений комплексов:
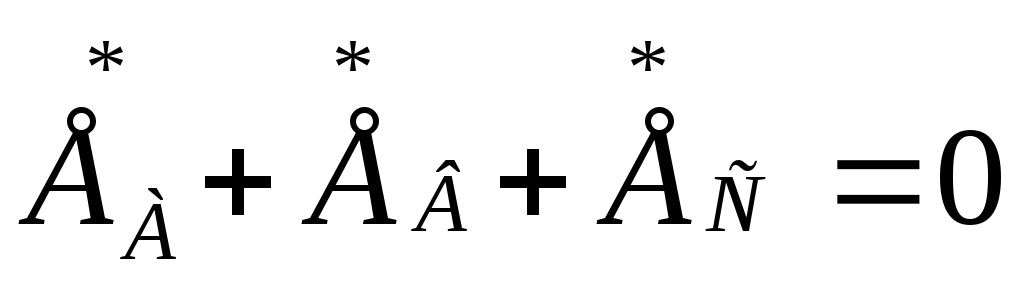

Следовательно, под трехфазной системой ЭДС понимают три отдельных однофазных ЭДС одинаковой частоты, амплитуды, но сдвинутых на 120 градусов по отношению к друг другу. И если концы этих обмоток соединить в одну точку, то получим звезду фазных ЭДС.
Если последовательность достижения максимумов ЭДС АВСАВСАВС и т.д., то это прямая последовательность. Если последовательность АСВАСВАСВ и т.д. то это обратная последовательность.
При прямой последовательности получается круговое вращательное магнитное поле по часовой стрелке, при обратной — против часовой. Если изобразить 3-х фазную систему на комплексной поверхности, причем по оси действительных отложить направление А.
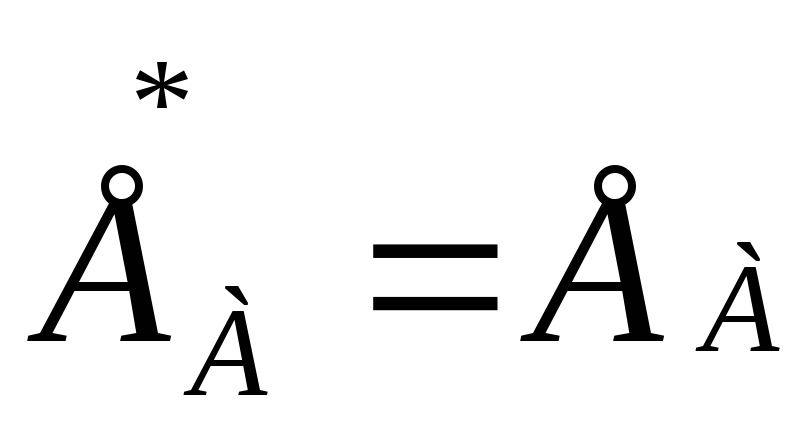




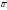 ;
реакцию вектором
;
реакцию вектором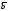 ;
параметры системы вектором
;
параметры системы вектором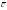 можно сформулировать две основные
задачи электротехники:
можно сформулировать две основные
задачи электротехники: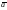 и
и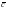 ;
определить
;
определить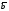 ;
т.е. при заданной системе (
;
т.е. при заданной системе (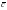 )
и возмущениях (
)
и возмущениях (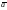 )
в результате анализа получается реакция
системы (
)
в результате анализа получается реакция
системы (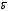 ).
).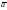 и
и ;
определить
;
определить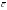 ;
т.е. требуется определить такую систему
(
;
т.е. требуется определить такую систему
( ),
чтобы при заданных возмущениях (
),
чтобы при заданных возмущениях ( )
обеспечивала требуемую реакцию (
)
обеспечивала требуемую реакцию ( ).
).