Электрический импеданс — Википедия
Электри́ческий импеда́нс (ко́мплексное электри́ческое сопротивле́ние[1]) (англ. impedance от лат. impedio «препятствовать») — комплексное сопротивление между двумя узлами цепи или двухполюсника для гармонического сигнала.
Это понятие и термин ввёл физик и математик О. Хевисайд в 1886 году[2][3].
Резистор — пассивный элемент, обладающий чисто активным сопротивлением. Реактивная составляющая комплексного сопротивления резистора равна нулю, так как соотношение между напряжением на резисторе и током через него не зависит от частоты тока/напряжения и является пассивным элементом, поскольку не содержит внутренних источников энергии. Если к его концам приложить некоторое напряжение U (подсоединить источник напряжения), то через резистор пойдёт электрический ток I. Если через резистор пропустить электрический ток I (подсоединить источник тока), то между концами резистора возникнет падение напряжения
- R=UI.{\displaystyle R={\frac {U}{I}}.}
Применение понятия «электрическое сопротивление» к реактивным элементам (катушка индуктивности и конденсатор) при постоянном токе приводит к тому, что:
- сопротивление идеальной катушки индуктивности стремится к нулю:
- если пропустить через идеальную катушку индуктивности некоторый постоянный ток I, то при любом значении I, падение напряжения на катушке будет нулевым:
- U=0;{\displaystyle U=0;}
- R=UI=0I=0;{\displaystyle R={\frac {U}{I}}={\frac {0}{I}}=0;}
- если приложить к конденсатору некоторое постоянное напряжение U, то при любом значении U, ток через конденсатор будет нулевым:
- I=0;{\displaystyle I=0;}
- R=UI=U0=∞.{\displaystyle R={\frac {U}{I}}={\frac {U}{0}}=\infty .}
Это справедливо лишь для постоянного тока и напряжения. В случае же приложения к реактивному элементу переменного тока и напряжения, свойства реактивных элементов существенно иные:
- напряжение между выводами катушки индуктивности не равно нулю;
- ток, протекающий через конденсатор, не будет равен нулю.
Такое поведение не может быть описано в терминах активного сопротивления для постоянного тока, поскольку активное сопротивление предполагает постоянное, не зависящее от времени соотношение тока и напряжения, то есть отсутствие фазовых сдвигов между током и напряжением.
Было бы удобно иметь некоторый параметр аналогичный активному сопротивлению и для реактивных элементов, который бы связывал ток и напряжение на них подобно активному сопротивлению в формуле закона Ома для постоянного тока.
Такую характеристику можно ввести, если рассмотреть свойства реактивных элементов при воздействиях на них гармонических сигналов. В этом случае ток и напряжение оказываются связаны некой константой (подобной в некотором смысле активному сопротивлению), которая и получила название «
Импедансом z^(jω){\displaystyle {\hat {z}}(j\omega )\;} называется отношение комплексной амплитуды напряжения гармонического сигнала, прикладываемого к двухполюснику, к комплексной амплитуде тока, протекающего через двухполюсник в установившемся режиме, то есть после завершения переходных процессов. Для линейных пассивных цепей с постоянными параметрами в установившемся режиме импеданс не зависит от времени. Если время t в математическом выражении для импеданса не сокращается, значит, для данного двухполюсника понятие импеданса неприменимо.
| z^(jω)=u^(jω,t)i^(jω,t)=U(ω)ej(ωt+ϕu(ω))I(ω)ej(ωt+ϕi(ω))=U(ω)ejϕu(ω)I(ω)ejϕi(ω)=U^(jω)I^(jω){\displaystyle {\hat {z}}(j\omega )\;={\frac {{\hat {u}}(j\omega ,t)\;}{{\hat {i}}(j\omega ,t)\;}}={\frac {U(\omega )e^{j(\omega t+\phi _{u}(\omega ))}}{I(\omega )e^{j(\omega t+\phi _{i}(\omega ))}}}={\frac {U(\omega )e^{j\phi _{u}(\omega )}}{I(\omega )e^{j\phi _{i}(\omega )}}}={\frac {{\hat {U}}(j\omega )\;}{{\hat {I}}(j\omega )\;}}} | (1) |
- Здесь:
Исторически сложилось, что в электротехнике обозначение импеданса, комплексных амплитуд и других комплексных функций частоты записывают как f(jω){\displaystyle f(j\omega )}, а не f(ω){\displaystyle f(\omega )}. Такое обозначение подчёркивает, что используются комплексные представления гармонических функций вида ejωt{\displaystyle e^{j\omega t}}. Кроме того, над символом, обозначающим комплексный сигнал или комплексный импеданс, обычно ставят «домик» или точку: U˙(jω){\displaystyle {\dot {U}}(j\omega )\;} чтобы отличать от соответствующих действительных величин.
Алгебраическая форма[править | править код]
Если рассматривать комплексный импеданс как комплексное число в алгебраической форме, то действительная часть соответствует активному сопротивлению, а мнимая — реактивному. То есть двухполюсник с импедансом z^(jω){\displaystyle {\hat {z}}(j\omega )\;} можно рассматривать как последовательно соединенные резистор с сопротивлением ℜ(z^(jω)){\displaystyle \Re ({\hat {z}}(j\omega ))} и чисто реактивный элемент с импедансом ℑ(z^(jω)){\displaystyle \Im ({\hat {z}}(j\omega ))}
Рассмотрение действительной части полезно при расчёте мощности, выделяемой в двухполюснике, поскольку мощность выделяется только на активном сопротивлении.
Тригонометрическая форма[править | править код]
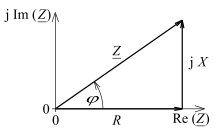
Если рассматривать импеданс как комплексное число в тригонометрической форме, то модуль соответствует отношению амплитуд напряжения и тока (сдвиг фаз не учитывается), а аргумент — сдвигу фазы между током и напряжением, то есть на сколько фаза тока отстаёт от фазы напряжения или опережает.
Понятие импеданса в классической форме применимо, если при приложении к двухполюснику гармонического напряжения, ток, вызванный этим напряжением, также гармонический той же частоты. Для этого необходимо и достаточно, чтобы двухполюсник был линейным и его параметры не менялись со временем и закончились переходные процессы. Если это условие не выполнено, то импеданс не может быть найден по следующей причине: невозможно получить выражение для импеданса, не зависящее от времени t, поскольку при вычислении импеданса множитель ejωt{\displaystyle e^{j\omega t}} в (1) не сокращается.
- Однако и для линейных двухполюсников (для которых зависимость от времени сокращается) импеданс всё же зависит от частоты (за исключением случая когда двухполюсник сводится к схеме из одних резисторов и импеданс оказывается действительной величиной).
Практически это означает, что импеданс может быть вычислен для любого двухполюсника, состоящего из резисторов, катушек индуктивности и конденсаторов, то есть из линейных пассивных элементов. Также импеданс хорошо применим для активных цепей, линейных в широком диапазоне входных сигналов (например, цепи на основе операционных усилителей). Для цепей, импеданс которых не может быть найден в силу указанного выше ограничения, бывает полезным найти импеданс в малосигнальном приближении — для бесконечно малой амплитуды сигнала для конкретной рабочей точки. Для этого необходимо перейти к эквивалентной схеме и искать импеданс для неё.
Обобщенный импеданс в s-плоскости и преобразование Лапласа[править | править код]
Импедансы, определённые через комплексную частоту jω{\displaystyle j\omega }, позволяют вычислять частотный отклик некоторой линейной цепи, возбуждаемой гармоническим сигналом, причём только в установившемся режиме. Для расчёта отклика цепи на сигнал, произвольно изменяющийся во времени применяется обобщенный импеданс — функции комплексной переменной s=σ+jω{\displaystyle s=\sigma +j\omega } и отклик цепи во временно́й области вычисляется через обратное преобразование Лапласа, причем в таких вычислениях возбуждающий сигнал fin(t){\displaystyle f_{in}(t)} из временного представления должен быть предварительно преобразован в комплексное представление Ft(s){\displaystyle F_{t}(s)} через прямое преобразование Лапласа:
- Ft(s)=∫0∞fin(t)e−stdt.{\displaystyle F_{t}(s)=\int _{0}^{\infty }f_{in}(t)e^{-st}\,dt.}
Комплексный отклик системы выражается обычным способом через преобразованное комплексное представление возбуждающего сигнала и комплексную передаточную функцию системы H(s){\displaystyle H(s)}:
- Ft,H(s)=H(s) Ft(s).{\displaystyle F_{t,H}(s)=H(s)\ F_{t}(s).}
| Двухполюсник | Обобщённый импеданс |
|---|---|
| Резистор | R{\displaystyle R\,} |
| Катушка индуктивности | sL{\displaystyle sL\,} |
| Конденсатор | 1sC{\displaystyle {\frac {1}{sC}}\,} |
Комплексная передаточная функция вычисляется обычным методом расчёта электрических цепей, например, по правилам Кирхгофа, в формулы в качестве сопротивлений подставляются обобщённые импедансы. Обобщённые импедансы пассивных двухполюсников приведены в таблице. Например, обобщённый импеданс цепи, состоящей из последовательно включённых резистора и катушки индуктивности будет R+sL{\displaystyle R+sL}.
Отклик цепи во временно́й области вычисляется обратным преобразованием Лапласа:
- fF,H(t)=L−1[H(s) Ft(s)]=12πi∫σ1−j⋅∞σ1+j⋅∞estH(s) Ft(s)ds,{\displaystyle f_{F,H}(t)={\mathcal {L}}^{-1}[H(s)\ F_{t}(s)]={\frac {1}{2\pi i}}\int \limits _{\sigma _{1}-j\cdot \infty }^{\sigma _{1}+j\cdot \infty }e^{st}H(s)\ F_{t}(s)\,ds,}
- где σ1 {\displaystyle \sigma _{1}\ } — некоторое вещественное число, выбираемое из условий сходимости интеграла.
- Пример вычисления временно́го отклика RC-фильтра нижних частот на ступенчатое возмущение
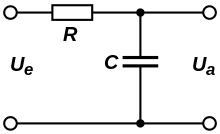 Пассивный RС-фильтр нижних частот 1-го порядка
Пассивный RС-фильтр нижних частот 1-го порядкаПростейший фильтр нижних частот 1-го порядка изображён на рисунке и состоит из последовательно соединённых резистора и конденсатора, образующего делитель напряжения для входного сигнала где выходной сигнал снимается с конденсатора, обобщённый комплексный коэффициент передачи HRC(s){\displaystyle H_{RC}(s)} такого делителя:
- HRC(s)=1/sCR+1/sC=1sRC+1=1sT+1,{\displaystyle H_{RC}(s)={\frac {1/sC}{R+1/sC}}={\frac {1}{sRC+1}}={\frac {1}{sT+1}},}
- где обозначено T=RC{\displaystyle T=RC} — постоянная времени RС-цепи.
Ступенчатый входной сигнал можно выразить через функцию Хевисайда h(t){\displaystyle h(t)}:
- Uin(t)=U0 h(t),{\displaystyle U_{in}(t)=U_{0}\ h(t),}
- где U0{\displaystyle U_{0}} — амплитуда ступеньки.
Преобразование Лапласа входного сигнала:
Fin(s)=L[U0 h(t)]=∫0∞e−stU0h(t)dt=U0/s.{\displaystyle F_{in}(s)={\mathcal {L}}[U_{0}\ h(t)]=\int \limits _{0}^{\infty }e^{-st}\,U_{0}\,h(t)\,dt=U_{0}/s.}
- Uout(t)=L−1[HRC(s) Fin(s)]=12πi∫σ1−j⋅∞σ1+j⋅∞est1sT+1⋅U0sds=U0(1−e−t/T).{\displaystyle U_{out}(t)={\mathcal {L}}^{-1}[H_{RC}(s)\ F_{in}(s)]={\frac {1}{2\pi i}}\int \limits _{\sigma _{1}-j\cdot \infty }^{\sigma _{1}+j\cdot \infty }e^{st}{\frac {1}{sT+1}}\cdot {\frac {U_{0}}{s}}\,ds=U_{0}(1-e^{-t/T}).}
Таким образом, получен отклик цепи при нулевом начальном условии (UC=0{\displaystyle U_{C}=0} при t=0{\displaystyle t=0}), такой же, как и при применении другого метода расчёта, например, из решения обыкновенного дифференциального уравнения.
Для практического применения расчета цепей (и других расчётов) составлены подробные таблицы прямого и обратного преобразования Лапласа многих часто встречающихся при расчётах функций.
Комбинируя преобразование Лапласа с использованием его свойств и интеграл Дюамеля обычно относительно легко найти отклики во временной области самых различных линейных электрических цепей.
Идеальные элементы[править | править код]
Резистор[править | править код]
Для резистора импеданс всегда равен его сопротивлению R и не зависит от частоты:
| zR=R{\displaystyle z_{R}=R} | (2) |
Конденсатор[править | править код]
Ток и напряжение для конденсатора связаны соотношением:
| i(t)=CdUdt.{\displaystyle i(t)=C{\frac {dU}{dt}}.} | (3) |
Отсюда следует, что при напряжении
| u^(jω,t)=U(ω)ej(ωt+ϕu(ω)){\displaystyle {\hat {u}}(j\omega ,t)=U(\omega )e^{j(\omega t+\phi _{u}(\omega ))}} | (4) |
ток, текущий через конденсатор, будет равен:
| i^(jω,t)=Cddt(U(ω)ej(ωt+ϕu(ω)))=jωCU(ω)ej(ωt+ϕu(ω)).{\displaystyle {\hat {i}}(j\omega ,t)=C{\frac {d}{dt}}\left(U(\omega )e^{j(\omega t+\phi _{u}(\omega ))}\right)=j\omega CU(\omega )e^{j(\omega t+\phi _{u}(\omega ))}.} | (5) |
После подстановки (4) и (5) в (1) получаем:
| z^C(jω)=1jωC=−jωC.{\displaystyle {\hat {z}}_{C}(j\omega )={\frac {1}{j\omega C}}=-{\frac {j}{\omega C}}.} | (6) |
Катушка индуктивности[править | править код]
Аналогичное рассмотрение для катушки индуктивности приводит к результату:
| z^L(jω)=jωL.{\displaystyle {\hat {z}}_{L}(j\omega )\;=j\omega L.} | (7) |
Общий случай[править | править код]
Для произвольного двухполюсника, состоящего из элементов с известным импедансом, нет необходимости производить приведенные выше вычисления с целью нахождения импеданса. Импеданс находится по обычным правилам расчёта сопротивления сложной цепи, то есть используются формулы для сопротивления при параллельном и последовательном соединении резисторов. При этом все математические операции производятся по правилам действий над комплексными числами. Например, импеданс идеальных последовательно соединенных резистора, конденсатора и катушки индуктивности будет равен:
| Z^(jω) =R+1jωC+jωL=R−jωC+jωL=R+j(−1ωC+ωL).{\displaystyle {\hat {Z}}(j\omega )\ =R+{\frac {1}{j\omega C}}+j\omega L=R-{\frac {j}{\omega C}}+j\omega L=R+j\left(-{\frac {1}{\omega C}}+\omega L\right).} | (8) |
Экспериментальное измерение импеданса[править | править код]
Прямое измерение импеданса требует измерения амплитуд синусоидальных напряжения и тока изучаемого двухполюсника, и одновременного измерения сдвига фазы между ними.
Импеданс также часто измеряют компенсационными методами с помощью мостов переменного тока, подобными мосту Уитстона для постоянного тока, при таких измерениях мост балансируют изменением эталонных реактивного и активного элементов, по величине реактивного и активного сопротивления эталонных элементов, требуемого для балансировки моста, определяется измеряемый импеданс.
В силовых устройствах измерение импеданса может потребовать одновременного измерения и подачи питания на работающее устройство.
Измерение импеданса устройств и линий передач является практической задачей в радиотехнике и других областях.
Измерения импеданса обычно проводятся на одной частоте, но если требуется определить зависимость импеданса от частоты, то измерения проводят на нескольких частотах в нужном диапазоне частот.
Активная и реактивная составляющие импеданса обычно выражают в омах, но могут использоваться связанные с импедансом величины, например, в радиотехнике, линиях передачи, коэффициент стоячей волны или коэффициент отражения имеют бо́льшее удобство.
Сопротивление устройства можно рассчитать путем деления комплексных напряжения и тока. Полное сопротивление устройства рассчитывается путем подачи синусоидального напряжения на устройство последовательно с эталонным резистором и измерения напряжений на резисторе и на самом устройстве. Выполнение этого измерения на нескольких частотах тестирующего сигнала обеспечивает определение фазового сдвига и величины импеданса[5].
Измерение отклика исследуемой цепи на импульсный тестирующий сигнал можно использовать в сочетании с быстрым преобразованием Фурье для измерения импеданса различных электрических устройств[5].
LCR-измеритель (индуктивность L, емкость C и сопротивление R) или измеритель иммитанса — это устройство, обычно используемое для измерения индуктивности, сопротивления и ёмкости компонента. Из этих значений можно рассчитать полное сопротивление на любой частоте.
Введение импеданса позволяет описывать поведение двухполюсника с реактивными свойствами при воздействии на него гармонического сигнала. Кроме того, в случае негармонического сигнала импеданс применяется столь же успешно. Для этого сигнал раскладывается на спектральные компоненты при помощи ряда Фурье или преобразования Фурье и рассматривается воздействие каждой спектральной компоненты. Вследствие линейности двухполюсника сумма откликов на спектральные компоненты равна отклику на исходный негармонический сигнал или применять преобразование Лапласа.
Комплексные сопротивления и проводимости
Отношение
комплексного напряжения к комплексному
току называют комплексным
сопротивлением цепи и обозначают  .
.
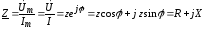 ,
,
где R, X и z – активное, реактивное и полное сопротивления цепи.
С другой стороны:
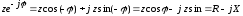 .
.
Тогда полное сопротивление z получим из соотношений:
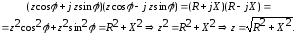
В случае последовательного соединения элементов R,L,C комплексное сопротивление запишется в виде:
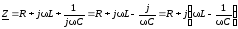 .
.
Отношение
комплексного тока к комплексному
напряжению называют комплексной
проводимостью цепи и обозначают 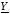 :
:
 ,
,
где 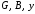 –активная,
реактивная и полная проводимости цепи.
–активная,
реактивная и полная проводимости цепи.
Поскольку комплексная проводимость есть величина обратная комплексному сопротивлению, то:
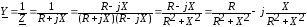 .
.
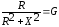 ;
;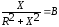 .
. Тогда:  .
.
С
другой стороны: 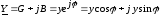 .
.
Тогда полную проводимость у получим из соотношений:
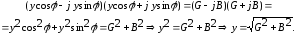
В случае параллельного соединения элементов
 .
.
Очевидно,
что 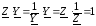 .
.
Перевод комплексных величин в показательную форму:
3 + j2
1.
Находим модуль: 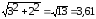 .
.
2.
Находим аргумент: 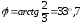 .
.
Окончательно: 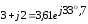
3 − j2
1.
Находим модуль: 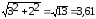 .
.
2.
Находим аргумент: 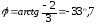 .
.
Окончательно: 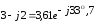 .
.
Перевод показательных величин в комплексную форму:
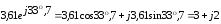 ;
;
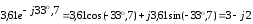
Основные законы электрических цепей в комплексной форме
Законы
электрических цепей переменного тока
в комплексной форме имеют такой же вид,
как и для цепей постоянного тока, с
заменой соответствующих постоянных
величин комплексными: 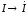 ,
,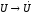 ,
,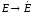 ,
,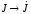 ,
,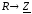
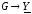 .
. Закон
Ома в
комплексной форме имеют вид:  .
.
Достоинство этих выражений заключается в том, что в них учитывается как связь между действующими значениями тока и напряжения, так и сдвиг фаз между ними.
Первый
закон Кирхгофа в применении
к узлу: 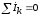 .
.
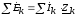 .
.Возможность использовать соотношения для цепей постоянного тока справедлива и для эквивалентных преобразований.
При
последовательном соединении
комплексное сопротивление всей цепи
равно алгебраической сумме комплексных
сопротивлений отдельных ее участков: 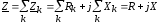 .
.
При параллельном соединении комплексная проводимость всей цепи равна алгебраической сумме комплексных проводимостей отдельных ее участков:
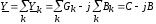 .
.При смешанном соединении:
Расчет сложных цепей переменного тока комплексным методом осуществляется с помощью тех же методов, что и цепей постоянного тока при замене соответствующих величин их комплексными аналогами.
Мощность в комплексной форме. Баланс мощностей
В качестве комплексной мощности понимают произведение комплексного напряжения на сопряженную комплексную величину тока. В результате чего, получаем комплексную мощность:
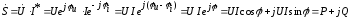 .
.
Вещественная часть комплексной мощности равна активной мощности
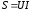 .
.Баланс мощности:
1. Сумма комплексных мощностей для всех ветвей электрической цепи равна 0.
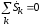 ,
откуда
,
откуда 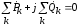 .
.
Такое
равенство возможно только в том случае,
если 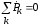
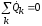 .
.2. Поскольку в каждой цепи есть источники и приемники, то
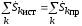
Источники ЭДС и токов можно разделить:
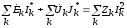 .
.
Действительно, мощность, потребляемую приемником, мы можем представить как:
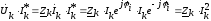 .
.
С другой стороны,
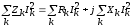
и для мощности источников
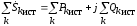 .
.
Следовательно, 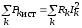 и
и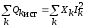 .
.
Резонансные явления в электрических цепях. Частотные характеристики.
Ранее было доказано, что действующее значение силы тока в R, L,C цепочке определяет соотношение:
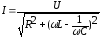 .
.
Так
как индуктивное и емкостное сопротивления
зависят от частоты (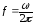 ),
то сила тока вR, L,C также будет зависеть от частоты источника
питания. Из приведенного выражения
следует, что ток будет максимален при:
),
то сила тока вR, L,C также будет зависеть от частоты источника
питания. Из приведенного выражения
следует, что ток будет максимален при:

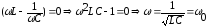 ,
,
где  −резонансная
частота контура.
−резонансная
частота контура.
В
том случае, когда 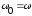 в цепи наблюдаетсяявление резонанса.
в цепи наблюдаетсяявление резонанса.
На
этой резонансной частоте 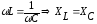 ,
а, следовательно, в цепи действует чисто
активное сопротивлениеR,
поэтому напряжение и ток при резонансе
совпадают по фазе.
,
а, следовательно, в цепи действует чисто
активное сопротивлениеR,
поэтому напряжение и ток при резонансе
совпадают по фазе.
Частоты, при которых наблюдается явление резонанса, называются резонансными частотами.
Покажем зависимость I (ω) для фиксированных значениях напряжения U, индуктивности L и емкости С при двух различных значения R:

Резонансными называют электрические цепи, в которых могут возникать явления резонанса напряжения или тока.
Комплексное сопротивление — это… Что такое Комплексное сопротивление?
- Комплексное сопротивление
Реактивное сопротивление — электрическое сопротивление, обусловленное передачей энергии электрическому или магнитному полю (и обратно).
Реактивное сопротивление определяет мнимую часть импеданса:
- Z = R + iX, где Z — импеданс, R — величина активного сопротивления, X — величина реактивного сопротивления, i — мнимая единица.
В зависимости от величины X какого-либо элемента электрической цепи, говорят о трёх случаях:
Величина реактивного сопротивления может быть выражена через величины индуктивного и ёмкостного сопротивлений:
Индуктивное сопротивление (XL) обусловлено возникновением ЭДС самоиндукции. Электрический ток создает магнитное поле. Изменение тока, и как следствие изменение магнитного поля, вызывает ЭДС самоиндукции, которая препятствует изменению тока. Величина индуктивного сопротивления зависит от индуктивности элемента и частоты протекающего тока:
Ёмкостное сопротивление (XC). Величина ёмкостного сопротивления зависит от ёмкости элемента С и также частоты протекающего тока:См. также
Активное сопротивлние
Wikimedia Foundation. 2010.
- Комплексное соединение
- Комплексные вещества
Смотреть что такое «Комплексное сопротивление» в других словарях:
комплексное сопротивление — Комплексная величина, равная отношению комплексного действующего значения синусоидального электрического напряжения на выводах пассивной электрической цепи или ее элемента к комплексному действующему значению синусоидального электрического тока в … Справочник технического переводчика
КОМПЛЕКСНОЕ СОПРОТИВЛЕНИЕ — то же, что импеданс. Физическая энциклопедия. В 5 ти томах. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988 … Физическая энциклопедия
комплексное сопротивление — kompleksinė varža statusas T sritis fizika atitikmenys: angl. complex resistance vok. komplexer Widerstand, m rus. комплексное сопротивление, n pranc. résistance complexe, f … Fizikos terminų žodynas
комплексное сопротивление обмотки — Импеданс измерительной обмотки, сочлененной с проводящим контролируемым изделием. [Система неразрушающего контроля. Виды (методы) и технология неразрушающего контроля. Термины и определения (справочное пособие). Москва 2003 г.] Тематики виды… … Справочник технического переводчика
комплексное сопротивление электрической цепи — Комплексная величина, равная отношению комплексного напряжения на зажимах данной цепи к комплексному току в этой цепи … Политехнический терминологический толковый словарь
Сопротивление — Сопротивление: В Викисловаре есть статья «сопротивление» Электрическое сопротивление физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока. Сопротивление разговорное название резистора … Википедия
комплексное полное сопротивление — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN vector impedance … Справочник технического переводчика
сопротивление — 3.93 сопротивление (resistance): Способность конструкции или части конструкции противостоять действию нагрузок. Источник: ГОСТ Р 54382 2011: Нефтяная и газовая промышленность. Подводные трубопроводные системы. Общие технические требования … Словарь-справочник терминов нормативно-технической документации
комплексное (электрическое) сопротивление — 154 комплексное (электрическое) сопротивление Комплексная величина, равная отношению комплексного действующего значения синусоидального электрического напряжения на выводах пассивной электрической цепи или ее элемента к комплексному действующему… … Словарь-справочник терминов нормативно-технической документации
сопротивление короткого замыкания четырехполюсника — 199 сопротивление короткого замыкания четырехполюсника Комплексное или операторное сопротивление пассивного четырехполюсника со стороны одной пары выводов, когда другая пара замкнута накоротко Источник: ГОСТ Р 52002 2003: Электротехника. Термины… … Словарь-справочник терминов нормативно-технической документации
Комплексные сопротивления.
При анализе и расчете цепей синусоидального тока особенный интерес представляет сопоставление по амплитуде и начальной фазе тока и напряжения одного и того же пассивного участка электрической цепи. В самом удобном и компактном виде это сопоставление осуществляется с помощью комплексных чисел.
Введем понятие комплексного сопротивления,которое определяется отношением комплексной амплитуды напряжения к комплексной амплитуде тока:
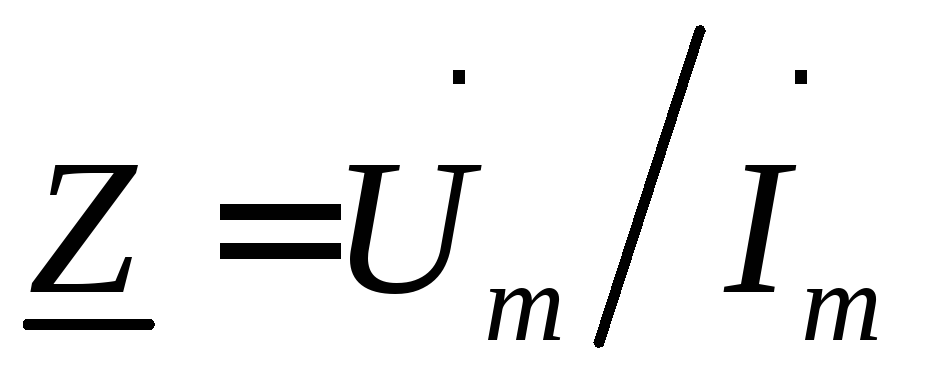 . (26)
. (26)
Комплексное число 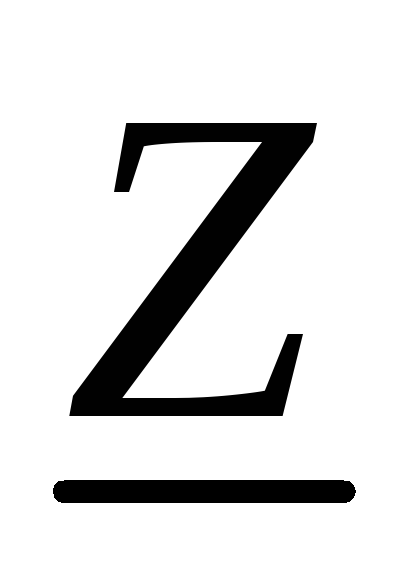 дает информацию как о соотношении
амплитуд
дает информацию как о соотношении
амплитуд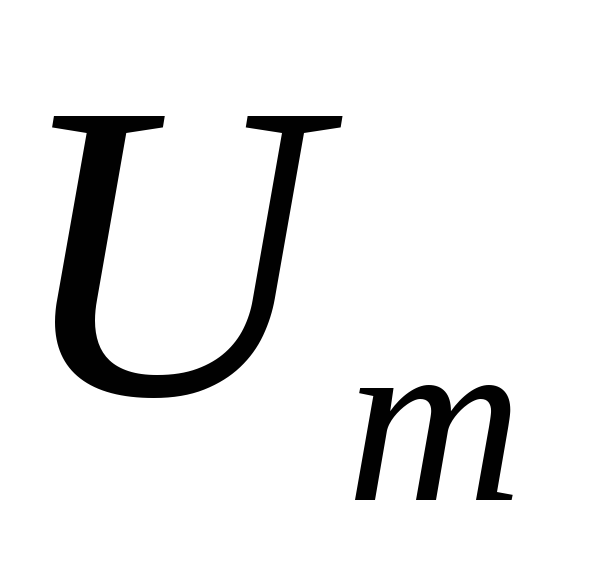 и
и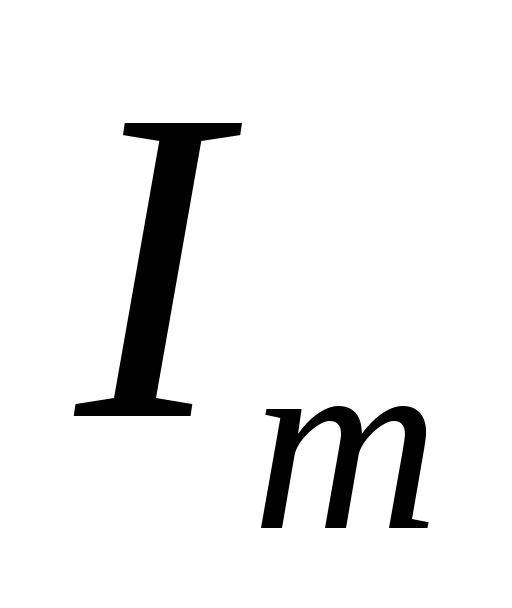 ,
так и о сдвиге фаз между напряжением и
током. Действительно,
,
так и о сдвиге фаз между напряжением и
током. Действительно,
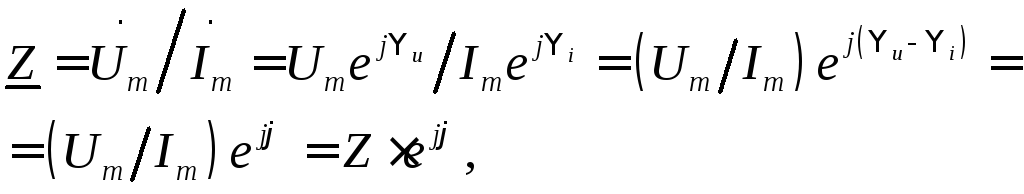
где Z – модуль, a 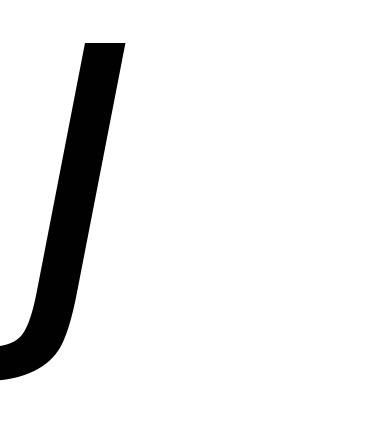 – аргумент комплексного сопротивления.
– аргумент комплексного сопротивления.
Модуль комплексного сопротивления Z, называемый полным сопротивлением, равен отношению амплитуды напряжения к амплитуде тока:
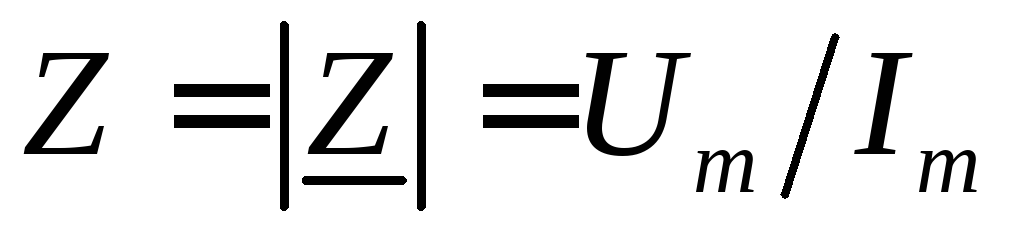 . (27)
. (27)
Аргумент комплексного сопротивления 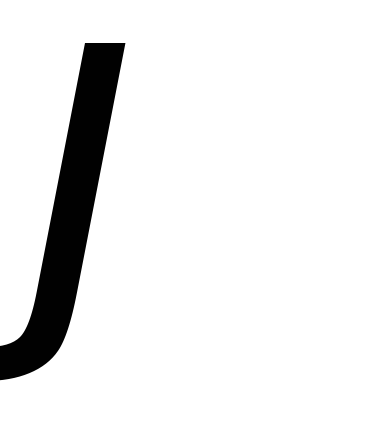 равен разности начальных фаз напряжения
и тока:
равен разности начальных фаз напряжения
и тока:
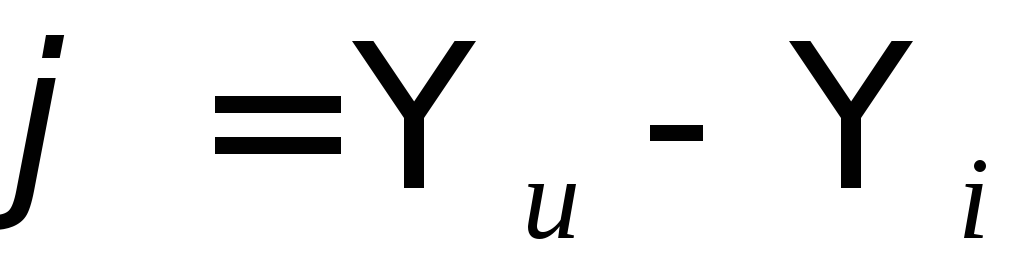 . (28)
. (28)
Комплексное сопротивление можно выразить также через комплексные действующие значения напряжения и тока:
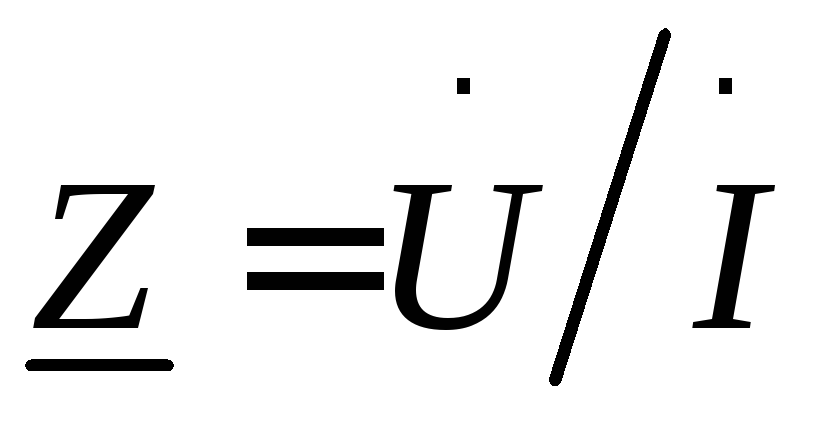 . (29)
. (29)
Отметим, что обозначение комплексного
сопротивления отличается от обозначения
комплексных токов и напряжений – вместо
точки над буквой символ комплексного
сопротивления имеет черту снизу. Это
различие объясняется тем, что сам
комплекс 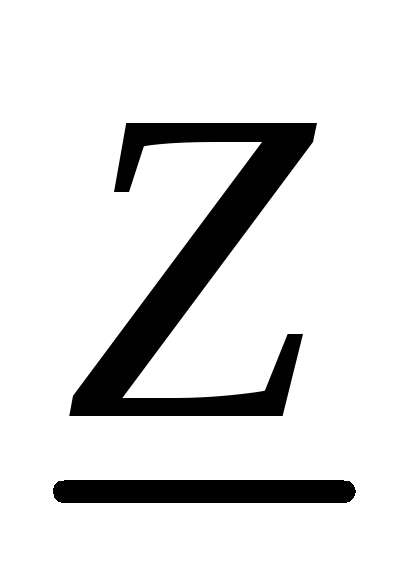 не служит изображением синусоидальной
функции, а является комплексным числом,
с помощью которого сопоставляются
комплексные изображения напряжения и
тока.
не служит изображением синусоидальной
функции, а является комплексным числом,
с помощью которого сопоставляются
комплексные изображения напряжения и
тока.
Соотношения
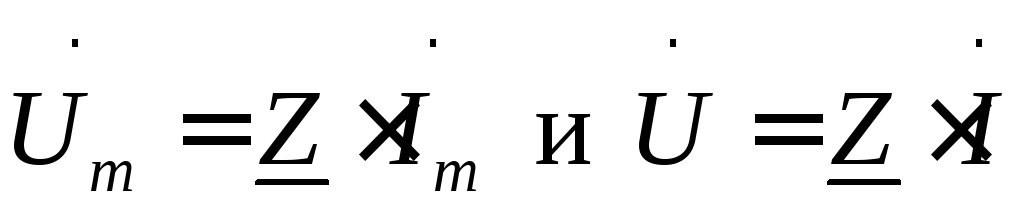 , (30)
, (30)
аналогичные по форме записи закону Ома для цепи постоянного тока, называют законом Ома в комплексной форме соответственно для амплитудных и действующих значений.
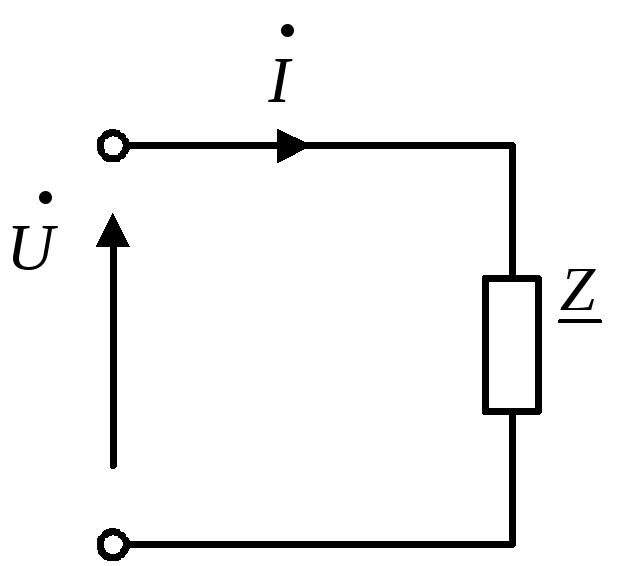
Рисунок 9 Комплексные обозначения на схеме замещения.
Обозначение комплексного сопротивления на схемах замещения приведено на рисунке 9.
Электрическая цепь сR- элементом.
Определим ток R- элемента,
схема замещения которого показана на
рисунке 10а, если он подключен к источнику
синусоидального напряжения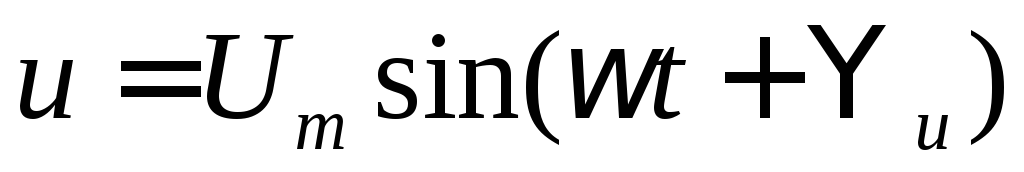 .
.
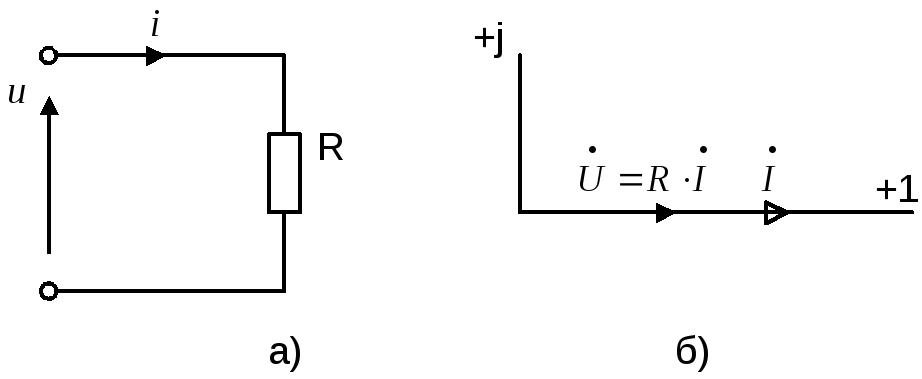
Рисунок 10
Для записи уравнения электрического
состояния цепи синусоидального тока
предварительно необходимо, так же как
и в цепях постоянного тока, выбрать
положительные направления тока и
напряжения. Тот факт, что ток и напряжение
в цепях синусоидального тока в течение
периода изменяют свое направление на
противоположное, не лишает смысла
наличие стрелок положительных направлений:
истинное направление тока (напряжения)
совпадает со стрелкой в моменты времени,
когда 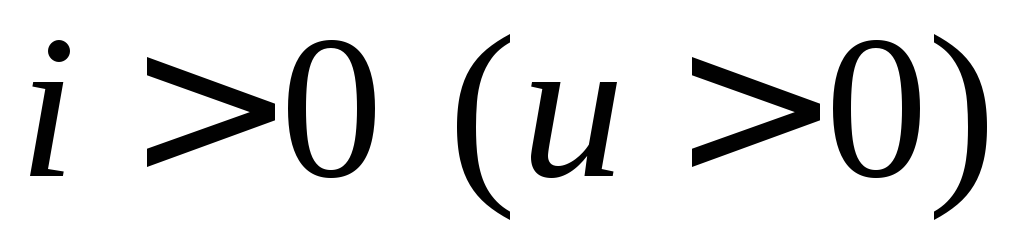 ,
и противоположно стрелке, если
,
и противоположно стрелке, если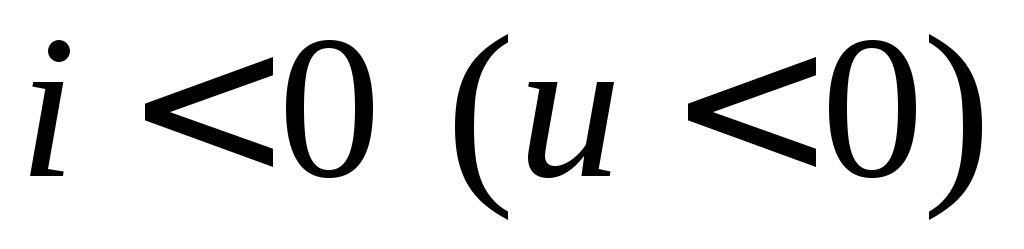 .
На участках электрической цепи, содержащих
пассивные элементы, положительные
направления тока и напряжения, так же
как и в цепях постоянного тока, выбирают
совпадающими.
.
На участках электрической цепи, содержащих
пассивные элементы, положительные
направления тока и напряжения, так же
как и в цепях постоянного тока, выбирают
совпадающими.
Мгновенные значения тока и напряжения
R- элемента, стрелки
положительных направлений которых
показаны на рисунке 10а, связаны законом
Ома: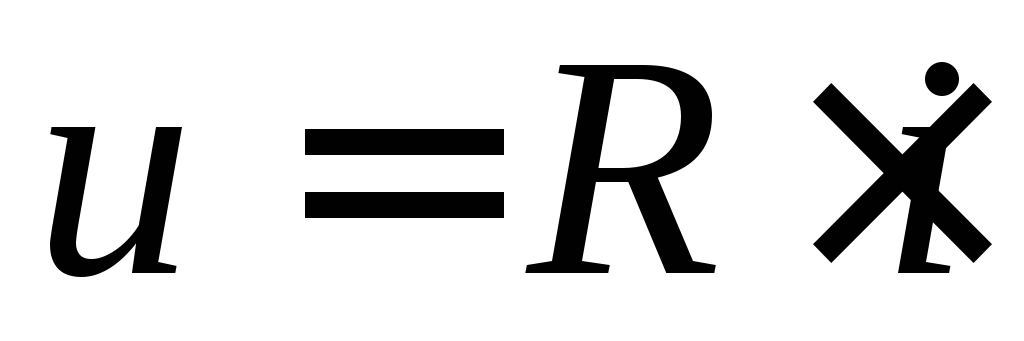 .
Следовательно, при заданном синусоидальном
напряжении источника ток в резистивном
элементе будет также синусоидальным:
.
Следовательно, при заданном синусоидальном
напряжении источника ток в резистивном
элементе будет также синусоидальным:
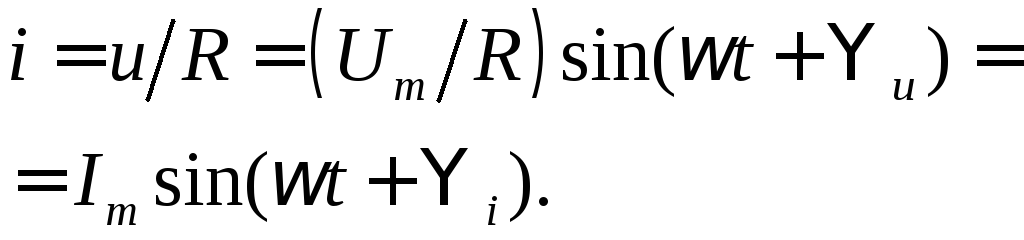 (31)
(31)
Из (31) следует, что ток и напряжение в рассматриваемом случае имеют одинаковую частоту и совпадают по фазе, а соотношение между амплитудными значениями определяется законом Ома:
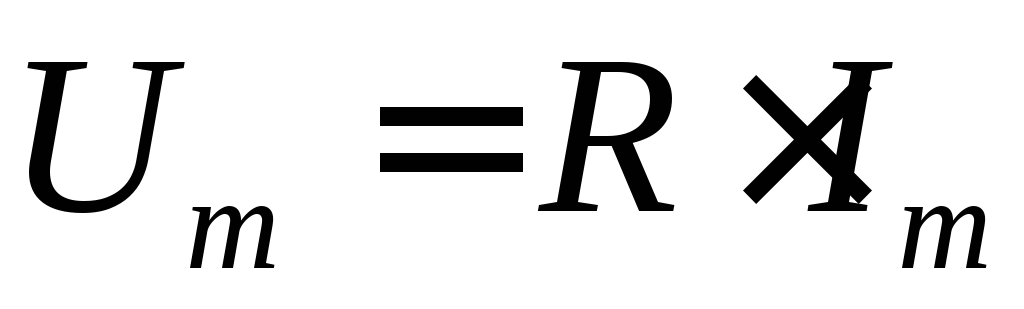 ; (32)
; (32)
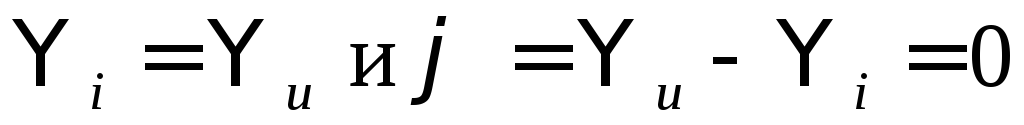 . (33)
. (33)
Поделив правую и левую части (32) на 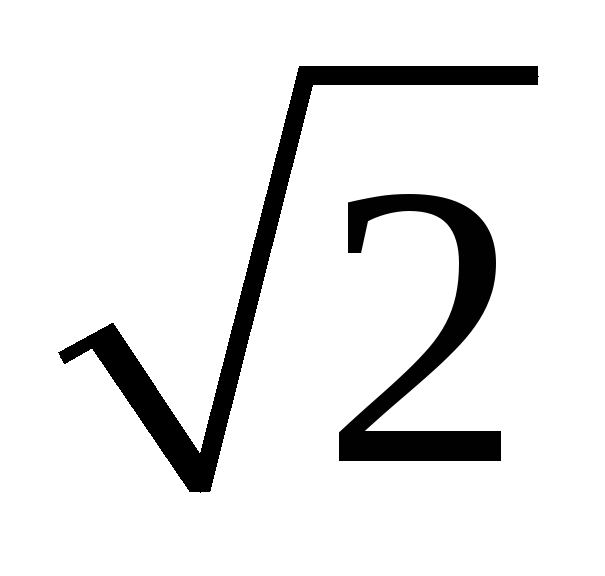 ,
можно записать закон Ома для действующих
значений напряжения и тока:
,
можно записать закон Ома для действующих
значений напряжения и тока:
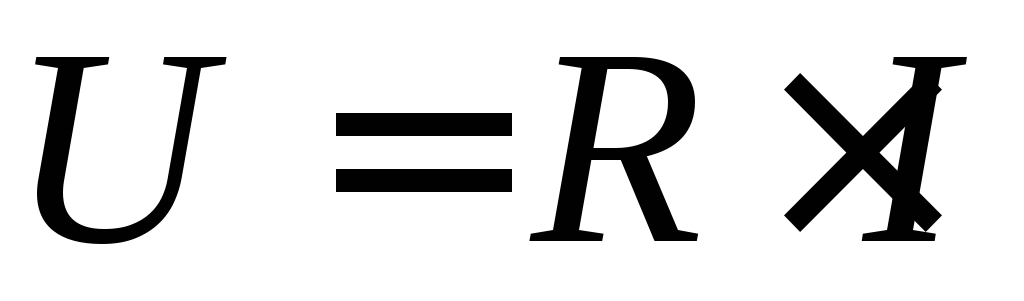 . (34)
. (34)
Соотношение между напряжением и током
R- элемента можно записать
и в комплексной форме. Если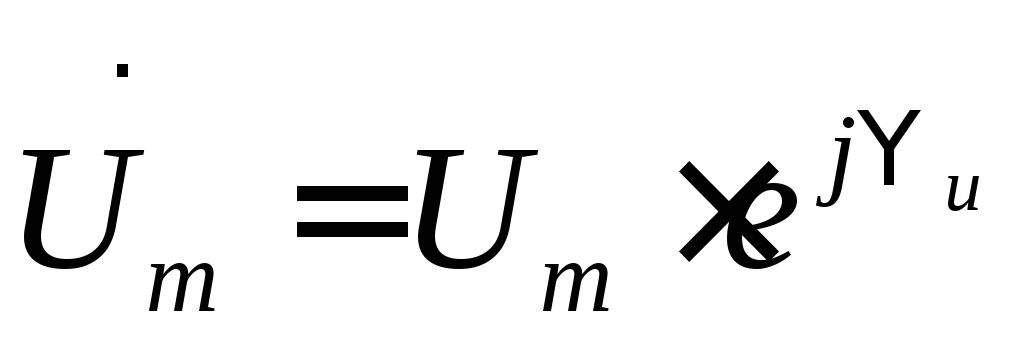 и
и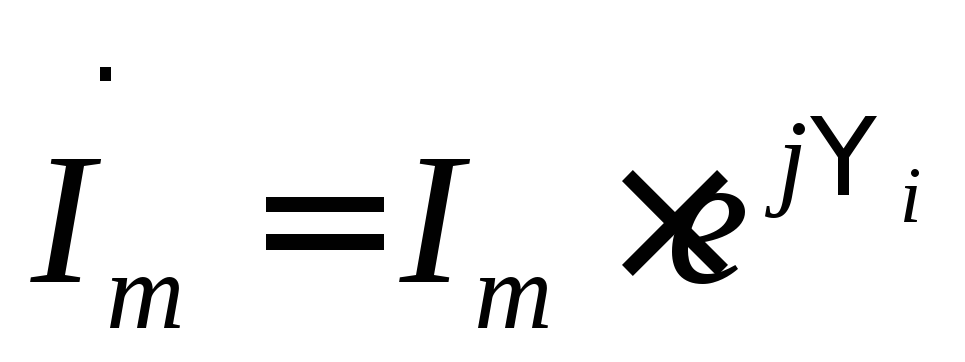 ,
то комплексное сопротивление
,
то комплексное сопротивление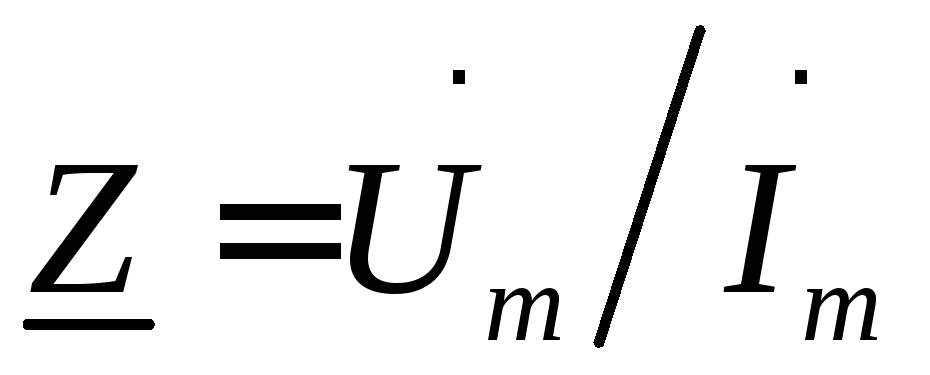 или
или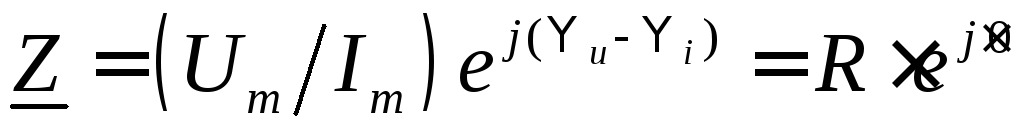 ,
т.е.
,
т.е.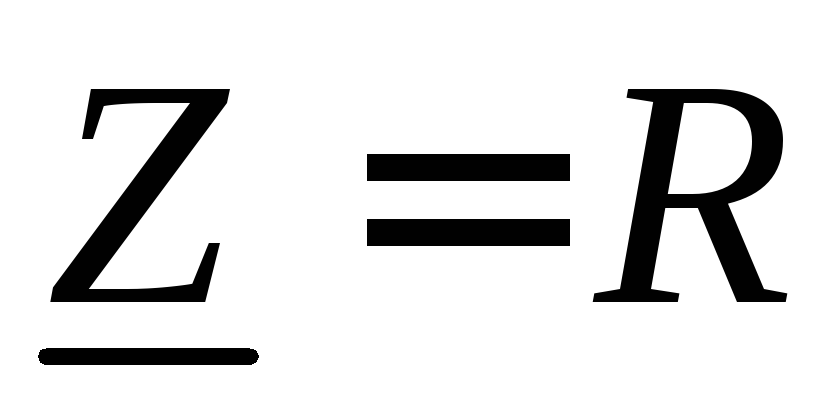 ,
следовательно,
,
следовательно,
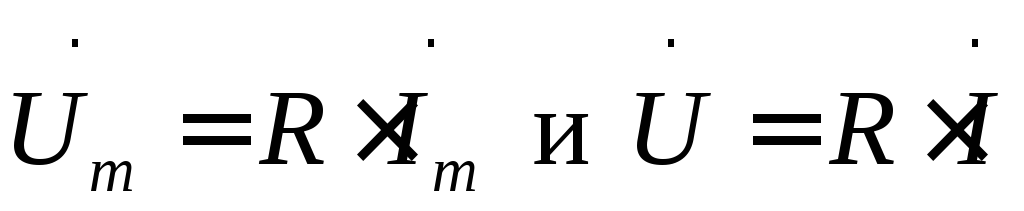 . (35)
. (35)
Комплексное сопротивление резистивного элемента является положительным действительным числом, равным значению активного сопротивления R. Соотношения (35) называют законом Ома соответственно для комплексных амплитуд и комплексных действующих значений напряжения и тока.
На рисунке 10б построена векторная диаграмма цепи рисунка 10а – вектор тока в R- элементе совпадает по фазе с вектором напряжения.
Рассмотрим энергетические процессы в
цепи с R- элементом. Работу,
совершаемую в электрической цепи, будем
характеризовать скоростью поступления
энергии, т.е. мгновенной мощностью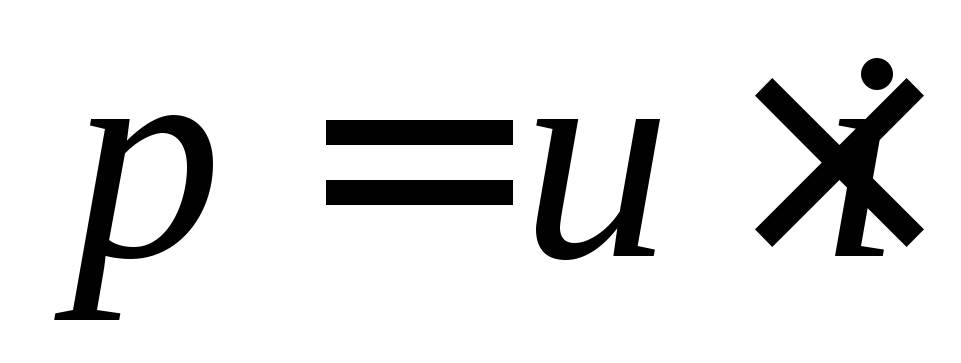 .
В любой момент времени истинные
направления тока и напряжения совпадают
и, следовательно, мгновенная мощность
всегда положительна, т. е. R- элемент
потребляет электрическую энергию от
источника и необратимо преобразует ее
в другие виды энергии. Скорость поступления
энергии в течение периода не остается
постоянной:
.
В любой момент времени истинные
направления тока и напряжения совпадают
и, следовательно, мгновенная мощность
всегда положительна, т. е. R- элемент
потребляет электрическую энергию от
источника и необратимо преобразует ее
в другие виды энергии. Скорость поступления
энергии в течение периода не остается
постоянной:
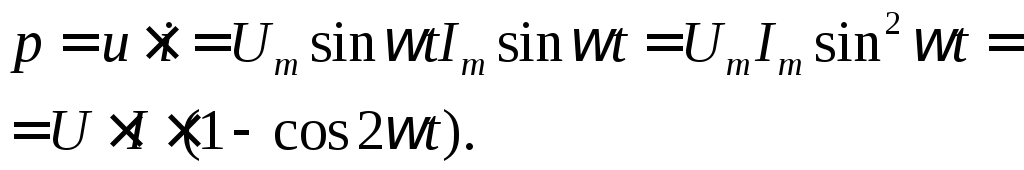 (36)
(36)
Мощность колеблется с угловой частотой 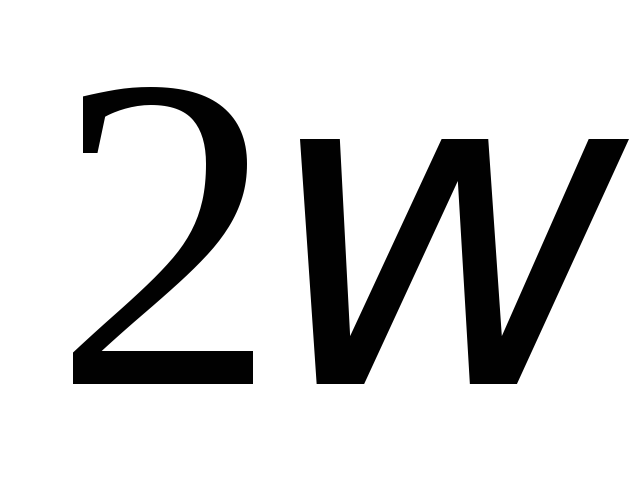 в пределах от
в пределах от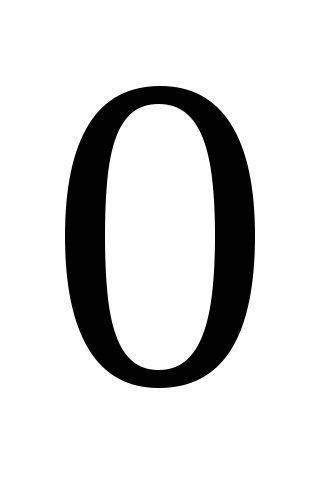 до
до .
.
Энергетический процесс принято характеризовать средним значением мощности за период, которое называют активной мощностью и обозначают буквой Р:
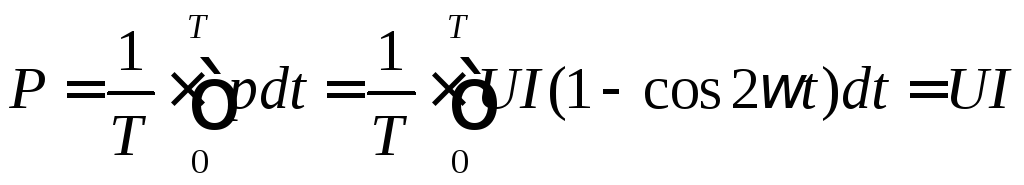 . (37)
. (37)
С учётом (34) полученное выражение преобразуется к виду
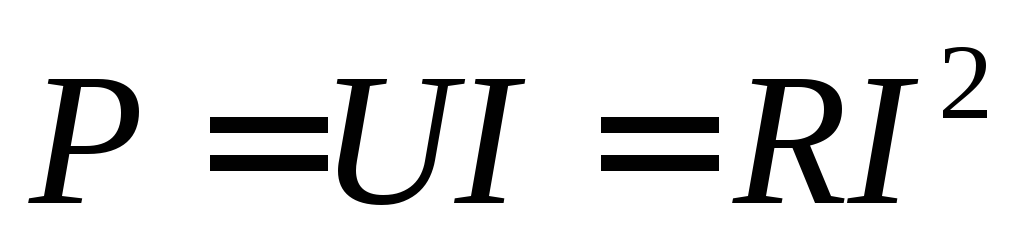 . (38)
. (38)
Активная мощность характеризует работу, совершаемую в электрической цепи за период, т. е. определяет электрическую энергию W, необратимо преобразовавшуюся в другие виды энергии:
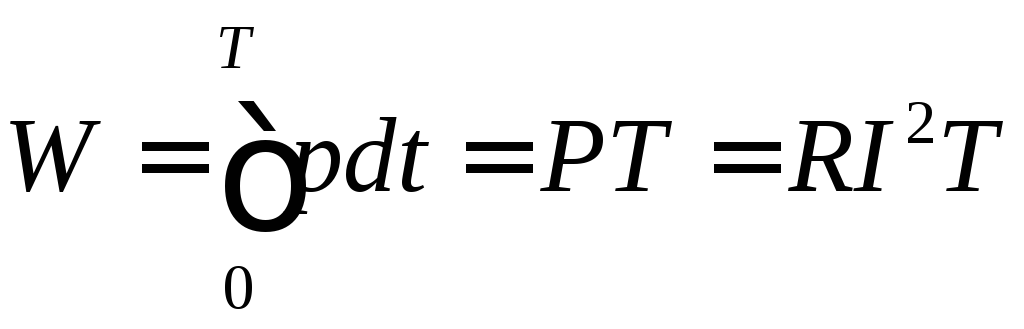 . (39)
. (39)
Таким образом, ток с действующим значением  по совершаемой им работе эквивалентен
постоянному току, имеющему то же значение
по совершаемой им работе эквивалентен
постоянному току, имеющему то же значение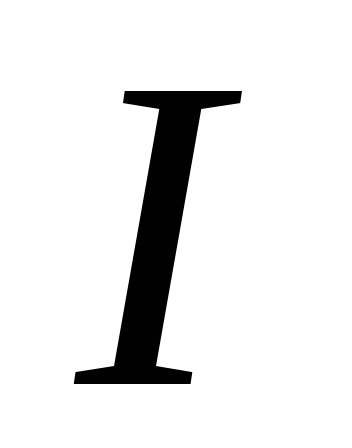 .
.
Комплексное сопротивление элемента (участка цепи)
Под комплексным сопротивлением понимают отношения комплексной амплитуды входного напряжения к комплексной амплитуде входного тока:
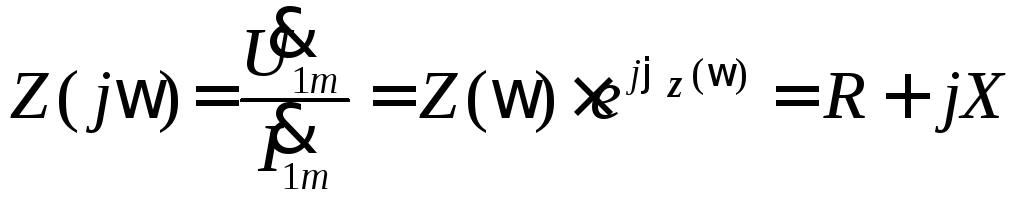 . (1.6)
. (1.6)
где Z –модуль комплексного сопротивления, φ=ψu — ψi – начальная фаза или аргумент комплексного сопротивления; R — активного сопротивления, X– реактивному сопротивлению, причем Z=(R2+X2)1/2, а φz(ω)=ψu—ψi =arctg(X/R).
По виду записи комплексного сопротивления можно судить о характере участка цепи: Z=R – активное (резистивное) сопротивление; Z=R+jX — активно-индуктивное сопротивление; Z=R – j X — активно-емкостное
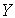 —
комплексная проводимость, величина,
обратная комплексному сопротивлению:
—
комплексная проводимость, величина,
обратная комплексному сопротивлению:
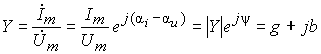 ПОСТРОЕНИЕ
ВЕКТОРНЫХ ДИАГРАММ НА ВРАЩАЮЩЕЙСЯ
КОМПЛЕКСНОЙ ПЛОСКОСТИ.
ПОСТРОЕНИЕ
ВЕКТОРНЫХ ДИАГРАММ НА ВРАЩАЮЩЕЙСЯ
КОМПЛЕКСНОЙ ПЛОСКОСТИ.
Для облегчения построения векторных диаграмм на вращающейся плоскости необходимо запомнить следующие основные положения:
а) В цепи с активным сопротивлениемток и напряжение совпадают по фазе.
б) В идеализированной цепи только с индуктивным сопротивлением без потерь напряжение по фазе опережает ток на угол, равный 90 градусов
в) В цепи с чисто емкостным сопротивлением без потерь ток опережает по фазе напряжение на угол +90 градусов.
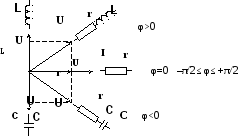
Рис.2.1.Мнемоническая схема, поясняющая возможные повороты радиусов-векторов при различном включении r-L-Cэлементов.
При построении векторных диаграмм надо начинать построение с вектора напряжения или тока общего для всей анализируемой цепи. В частности при последовательном включение элементов цепи надо начинать с построения вектора тока, протекающего через все элементы цепи. При параллельном включении элементов цепи построение векторной диаграммы надо начинать с вектора общего приложенного напряжения, а затем строить вектора токов, протекающих через каждую из ветвей электрической цепи. Возможные сдвиги фаз векторов напряжения в электрических цепях, состоящих из различных комбинаций r-L-C элементов, приведены на мнемонической схеме (см. рис.2.1.).
Радиус–вектора на схеме и ниже выделяются жирным шрифтом или точками (черточками) над ними.
Расчет цепей методом комплексных амплитуд
Метод комплексных амплитуд состоит в следующем:
1) исходная схема электрической цепи заменяется комплексной схемой замещения, в которой:
а) все пассивные элементы заменяются их комплексными сопротивлениями, как показано на рис. 4.27.
б )
все токи и напряжения в схеме заменяются
их комплексными амплитудами, т.е.х(t) =Xm cos(0t – x) Xm=Xm e–jx.
)
все токи и напряжения в схеме заменяются
их комплексными амплитудами, т.е.х(t) =Xm cos(0t – x) Xm=Xm e–jx.

R
ZR=R
C
ZC=1/(jC)
L
ZL=jL
Рис. 4.27 2 )
Расчет электрической цепи сводится к
составлению уравнений состояния цепи
на основе законов Ома и Кирхгофа в
комплексной форме и нахождениюкомплексных
амплитуд токов или напряжений на
интересующих нас участках цепи, т.е.Ym = Ym e–jy.
)
Расчет электрической цепи сводится к
составлению уравнений состояния цепи
на основе законов Ома и Кирхгофа в
комплексной форме и нахождениюкомплексных
амплитуд токов или напряжений на
интересующих нас участках цепи, т.е.Ym = Ym e–jy.
3) Запись окончательного решения состоит в замене рассчитанных комплексных амплитуд на гармонические функции времени, т.е.
Y m=Ym e –jy y(t) =Ym cos(0t – y).
m=Ym e –jy y(t) =Ym cos(0t – y).
Пример 1. Алгоритм метода рассмотрим на примере анализа цепи, схема которой приведена на рис. 4.29.
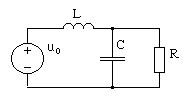
Рис. 4.29. RLC-цепь второго порядка
На вход цепи
подается синусоидальное воздействие 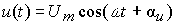 .
Параметры воздействия и элементов цепи
известны:Um=1
В, ω =1 с-1 , φ u=900 , R=1
Ом, L=1
Гн, C=1
Ф. Требуется определить токи и напряжения
ветвей, построить векторную диаграмму.
.
Параметры воздействия и элементов цепи
известны:Um=1
В, ω =1 с-1 , φ u=900 , R=1
Ом, L=1
Гн, C=1
Ф. Требуется определить токи и напряжения
ветвей, построить векторную диаграмму.
Решение.
Представим воздействие в комплексной форме:
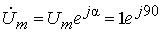 .
.
Построим схему замещения цепи в частотной области, заменив элементы цепи комплексными двухполюсниками, как это показано на рис. 4.30.
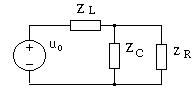
Рис. 4.30. Схема замещения цепи в частотной области
3. Произведем расчет реакций (токов и напряжений) в комплексной области. При этом можно воспользоваться законами Кирхгофа и Ома в комплексной форме, а также известными методами расчета резистивных цепей:
 ,
,  ,
,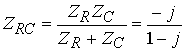 ,
,
 ,
,
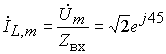 ,
, 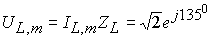 ,
,
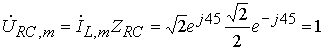 ,
,
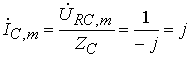 ,
, 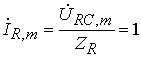 .
.
Построим векторную диаграмму для токов и напряжений в цепи. Для этого на комплексной плоскости откладываются в соответствующем масштабе найденные токи и напряжения, как показано на рис. 4.31.

Рис. 4.31. Векторная диаграмма
Построение
векторной диаграммы, как правило,
является конечным результатом решения
подобных задач. Векторная диаграмма
показывает амплитуду и начальную фазу
любого тока или напряжения. При
необходимости записать временную
функцию тока или напряжения, это всегда
можно сделать, имея векторную диаграмму.
Например, напряжение на L-элементе
имеет амплитуду 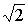 ,
а начальную фазу 1350,
значит, во временной области это
напряжение можно записать так:
,
а начальную фазу 1350,
значит, во временной области это
напряжение можно записать так:
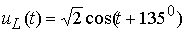 .
.
Пример 2. Задана эквивалентная схема цепи синусоидального тока (рис. 10) и ее параметры.
Выполнить следующие действия:
Рассчитать токи в ветвях и напряжения на элементах схемы;
Составить и проверить баланс полных, активных и реактивных мощностей;
Построить векторную диаграмму токов для узла а.
Расчет проводим символическим методом в следующем порядке:
1. Рассчитываем
сопротивление всех элементов схемы
(учитываем, что 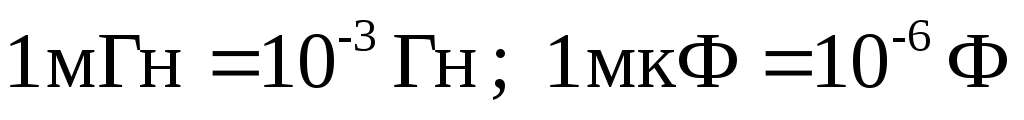 )
)

2. Представляем ЭДС источника в виде комплекса действующего значения. Определяем комплексные сопротивления и проводимости ветвей
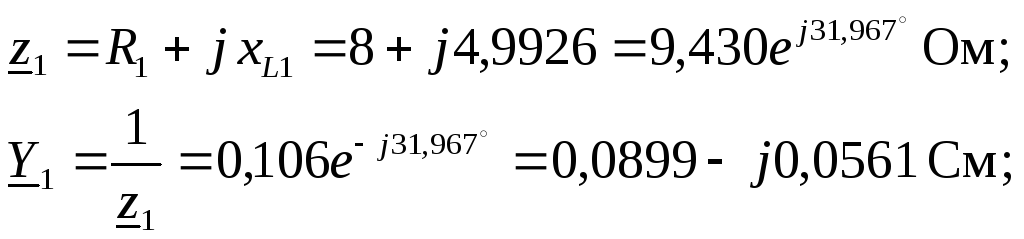

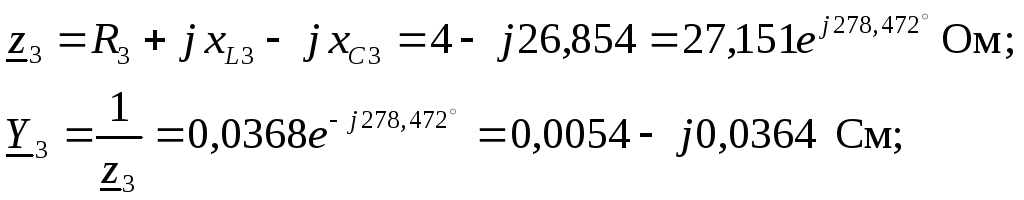
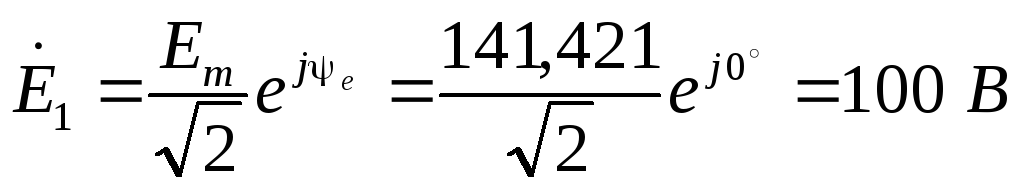 .
.
3. Рассчитываем токи в ветвях методом двух узлов. Задаем произвольно положительное направление токов в ветвях и положительное направление узлового напряжения. Используя основную формулу метода, рассчитываем узловое напряжение
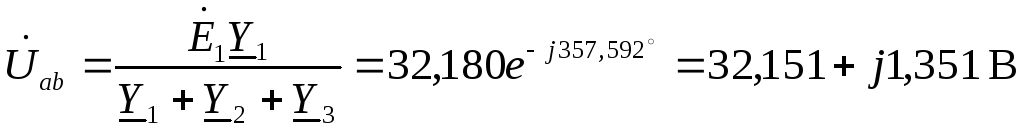 .
.
Определяем токи в ветвях, используя обобщенный закон Ома
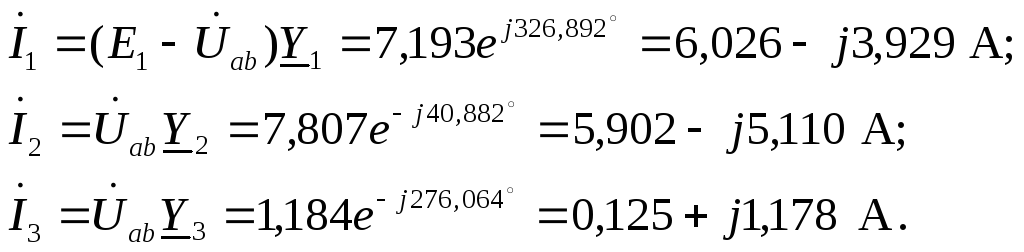
Проверяем корректность промежуточных расчетов, составив уравнение по первому закону Кирхгофа для узла а
 .
.
Комплексная абсолютная погрешность расчета составляет
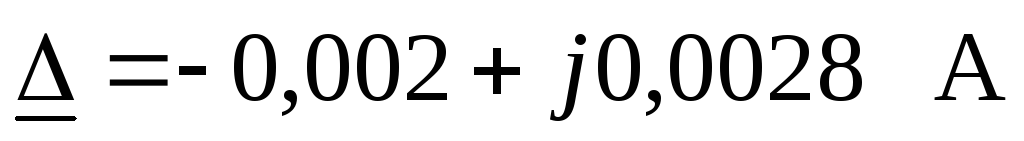 .
.
Определяем ее модуль
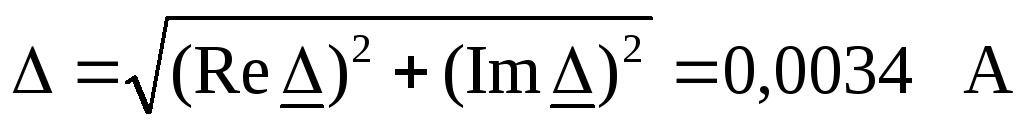 .
.
Рассчитываем относительную погрешность определения токов
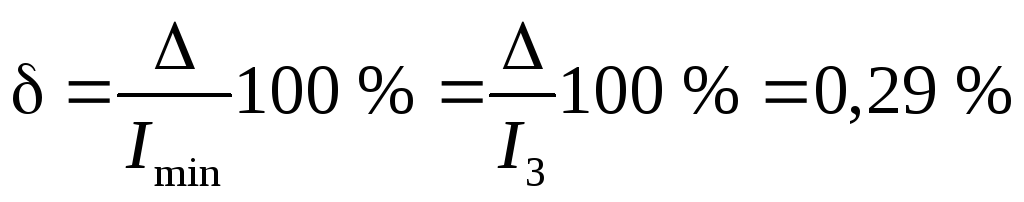 .
.
Поскольку  ,
расчет токов корректен. Первый пункт
задания выполнен.
,
расчет токов корректен. Первый пункт
задания выполнен.
4. Составляем и проверяем баланс мощностей
Рассчитываем полную комплексную мощность, развиваемую источником, а также его активную и реактивную мощность. При этом используем закон Джоуля – Ленца в комплексной форме записи
 ,
,

 .
.
Определяем суммарную активную и реактивную мощность на приемниках. При этом также используем закон Джоуля – Ленца
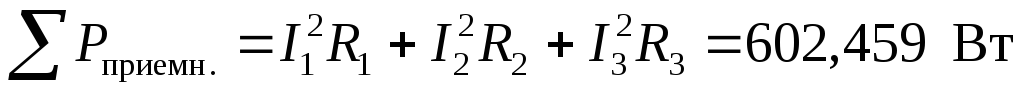 ;
;
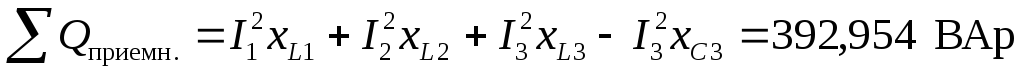 .
.
Рассчитываем суммарную полную комплексную мощность на приемниках
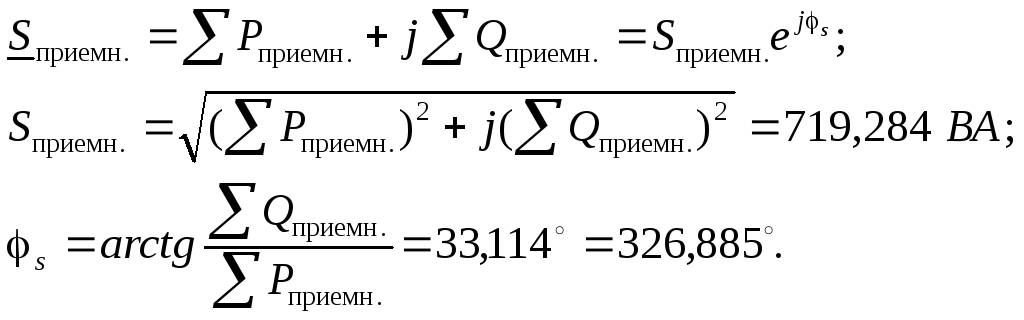
Проверяем корректность расчета, рассчитав модуль относительной погрешности определения полных мощностей
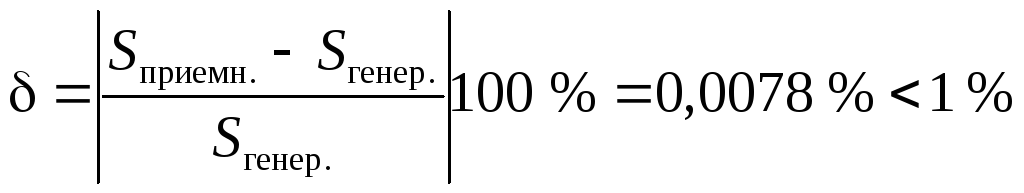 .
.
Расчет проведен корректно. Второй пункт задания выполнен.
5. Строим векторную
диаграмму токов на комплексной плоскости,
используя их действительные (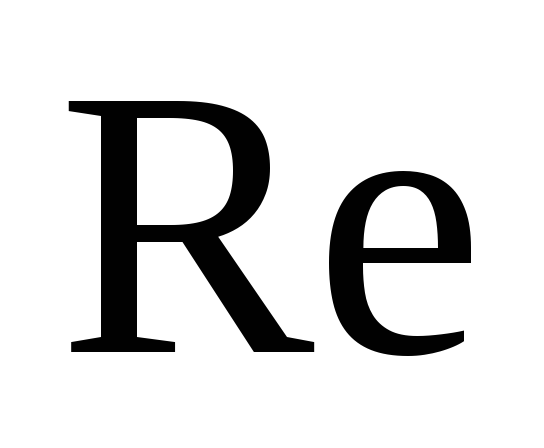 )
и мнимые (
)
и мнимые (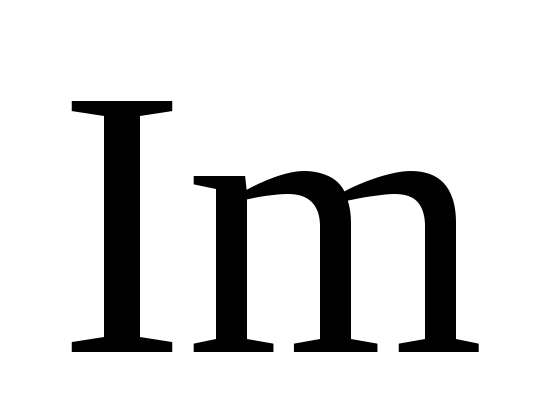 )
составляющие. Задаемся масштабом по
току
)
составляющие. Задаемся масштабом по
току ,
делим указанные составляющие токов на
масштаб и откладываем получающиеся
отрезки в сантиметрах вдоль осей
комплексной плоскости (с учетом знаков
составляющих).
,
делим указанные составляющие токов на
масштаб и откладываем получающиеся
отрезки в сантиметрах вдоль осей
комплексной плоскости (с учетом знаков
составляющих).
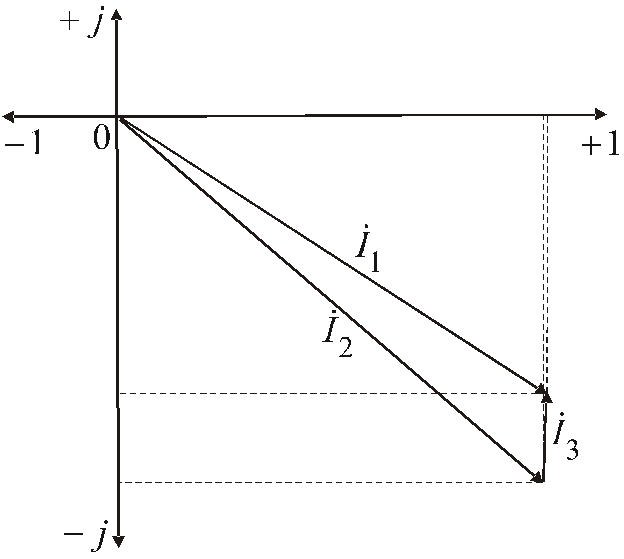
Рис. 11.
Результаты построения (рис. 11) наглядно иллюстрируют корректность проведенных расчетов. Итак, третий пункт и все задание выполнены.
При выполнении задания №2 можно также воспользоваться рекомендуемой литературой [2, 3, 4].
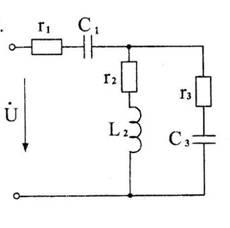
Пример 6. Для цепи, изображенной на рис. 1 требуется:
Определить комплексным методом действующие значения напряжений и токов на всех участках цепи.
Определить активные, реактивные и полные мощности каждого участка цепи и всей цепи.
Составить баланс активных и реактивных мощностей и оценить погрешность расчета.
П
 остроить
векторную диаграмму токов и напряжений.
остроить
векторную диаграмму токов и напряжений.
Рис. 1
Исходные данные: U = 127 В , r1 = 15 Ом , C1 = 60 мкФ, r2 = 10 Ом , L2 = 80 мГн, r3 = 15 Ом , C3 = 90 мкФ. Частота питающего напряжения 50 Гц.
Лекция 1.3. Комплексные сопротивления и проводимости элементов электрических цепей
1.Комплексное сопротивление
Введение комплексного представления токов и напряжений требует определить и сопротивление элементов электрических цепей в комплексной форме — Z.
Хороши известно, что сопротивление резистора определяется как отношение напряжения на резисторе к току, протекающему через него. Если напряжение и ток представлены в комплексной форме, то

Но на предыдущей лекции было установлено,
что 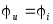 .
Поэтому
.
Поэтому
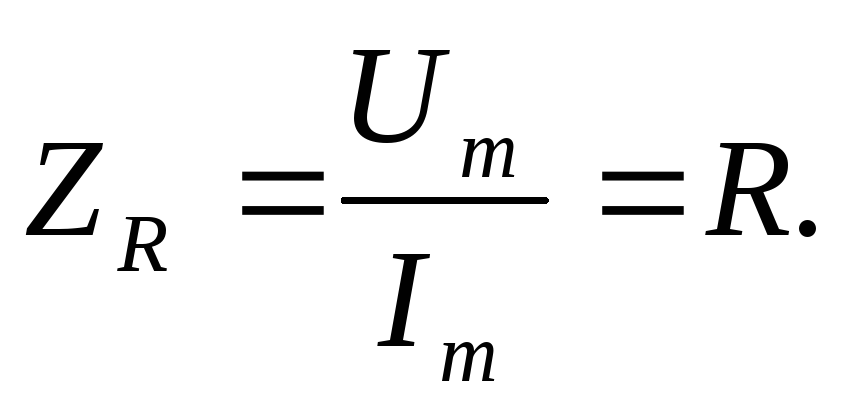 (3.1)
(3.1)
Таким образом видим, что комплексное сопротивление резистора выражается только действительным числом. Оно не вносит фазовых искажений между токами и напряжением. Чтобы подчеркнуть этот факт такое сопротивление часто называют активным.
Комплексное сопротивление емкости определяется отношением
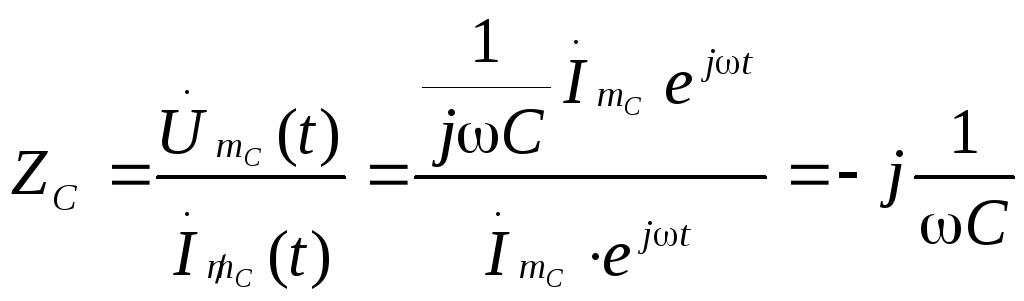 .
(3.2)
.
(3.2)
Видим, что комплексное сопротивление емкости переменному току выражается мнимым числом. Мнимая единица -jфизически определяет сдвиг фаз между током и напряжением на 90о. Это хорошо согласуется с ее максимальным значением
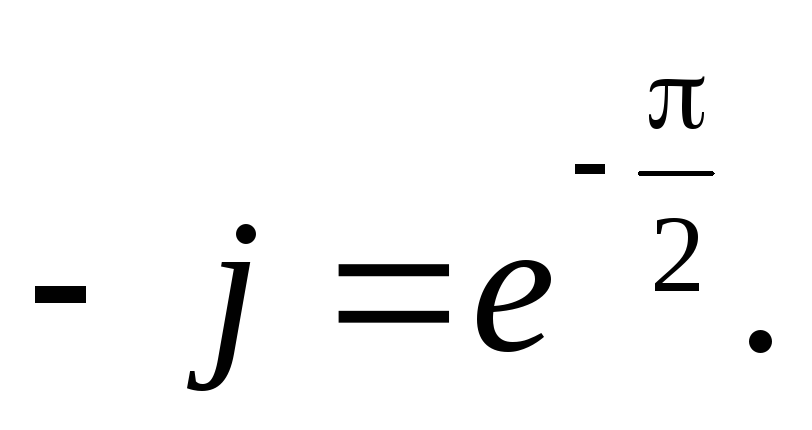
Поэтому на емкости напряжение отстает от тока на 90о. Это означает, что сначала растет ток, протекающий через конденсатор, затем, с некоторым отставанием увеличивается заряд и напряжение.
Коэффициент 1/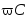 определяет величину сопротивления в
Омах. Он обратно пропорционален частоте,
называется емкостным сопротивлением
и обозначается ХС, т.е.
определяет величину сопротивления в
Омах. Он обратно пропорционален частоте,
называется емкостным сопротивлением
и обозначается ХС, т.е.
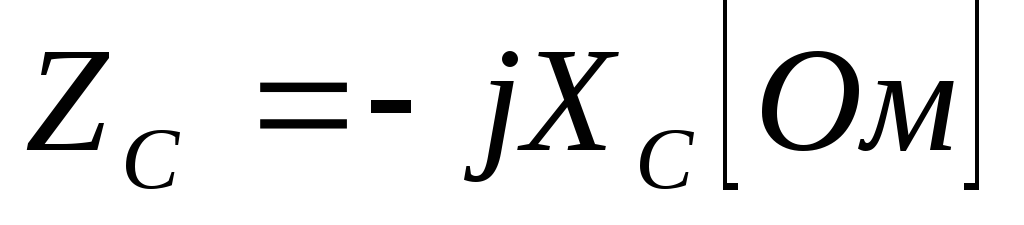 .
(3.3)
.
(3.3)
Комплексное сопротивление индуктивности определяется отношением
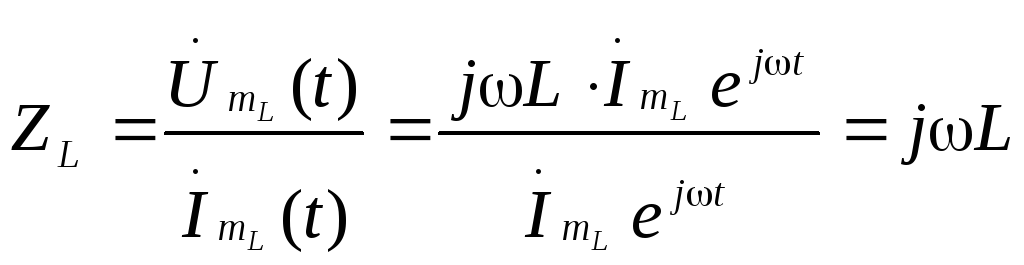 .
(3.4)
.
(3.4)
И в этом случае сопротивление выражается мнимым числом. Но так как это число положительное, то это означает, что на индуктивности напряжение опережает ток на 90о.
Коэффициент Lопределяет величину сопротивления в Омах. Он пропорционален частоте, называется индуктивным сопротивлением и обозначается ХL, т.е.
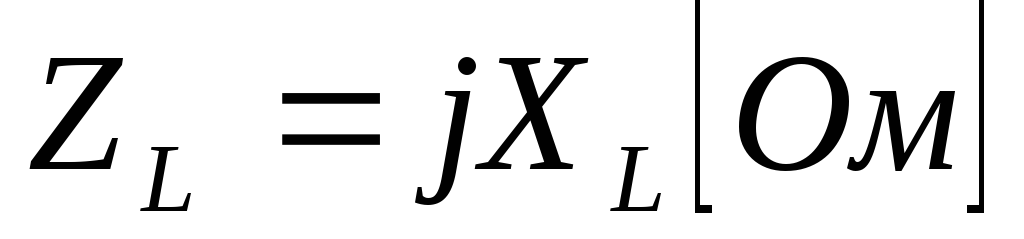 .
(3.5)
.
(3.5)
Чтобы подчеркнуть тот факт, что сопротивления емкости и индуктивности выражаются мнимыми числами, их называют реактивными сопротивлениями, а конденсатор и индуктивность — реактивными элементами цепи.
Определим теперь комплексное
сопротивление электрической цепи,
содержащей активные и реактивне элементы,
например последовательно включенные
R,Lи С
элементы (рис.3.1). Такая цепь представляет
замкнутый к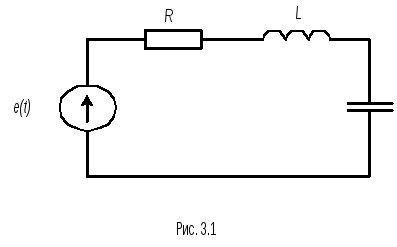 онтур,
поэтому для нее справедлив второй закон
Кирхгофа
онтур,
поэтому для нее справедлив второй закон
Кирхгофа
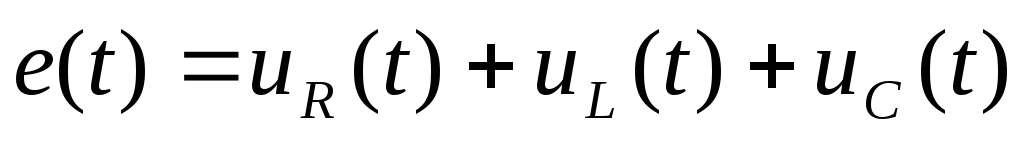 .
(3.6)
.
(3.6)
В последнем выражении проведем замену символов мгновенных напряжений и ЭДС на их комплексные изображения по правилам, определенным в лекции 1.2. Такой прием получил название символического метода. Так как ток протекающий через все элементы последовательной цепи одинаков, то (3.6) приходит к виду
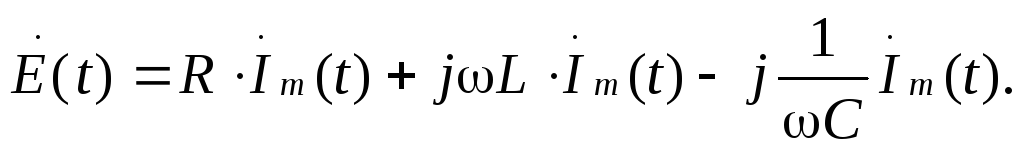
Преобразуем это выражение к виду
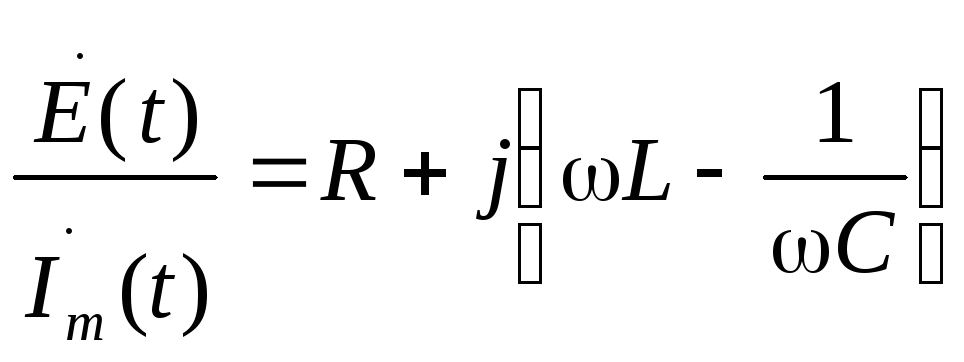 .
.
По определению выражение в правой части последнего равенства есть ни что иное, как комплексное сопротивление цепи рис.3.1, т.е.
 (3.7)
(3.7)
где R- действительная часть или активное сопротивление цепи.
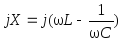 —
мнимая часть или реактивное сопротивление
цепи.
—
мнимая часть или реактивное сопротивление
цепи.
Выражение (3.7) представляет комплексное сопротивление в алгебраической форме. Соотношения между составляющими комплексного сопротивления находятся в полном соответствии с соотношениями для комплексного представления тока. Но для большей наглядности вводится понятие треугольника сопротивления (рис.3.2).
В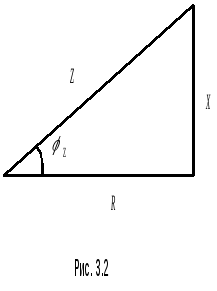 треугольнике — гипотенуза определяется
модулем комплексного сопротивленияZ,
причем
треугольнике — гипотенуза определяется
модулем комплексного сопротивленияZ,
причем
 (3.8)
(3.8)
Противолежащий катет — реактивным сопротивлением X, причем
 (3.9)
(3.9)
Угол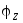 определяет сдвиг фаз между током и
напряжением, который вносится комплексным
сопротивлением цепи, причем
определяет сдвиг фаз между током и
напряжением, который вносится комплексным
сопротивлением цепи, причем
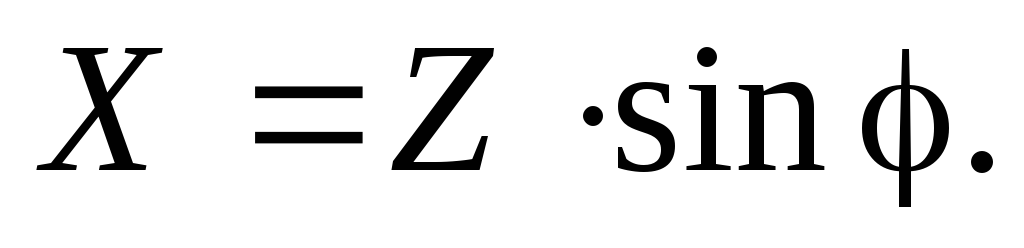 (3.10)
(3.10)
Учитывая выражения (3.8) (3.11) легко перейти от алгебраической к тригонометрической форме комплексного сопротивления
Z 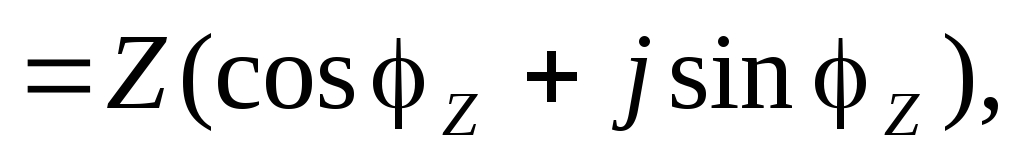 (3.12)
(3.12)
aприменив формулу Эйлера получить показательную форму
Z 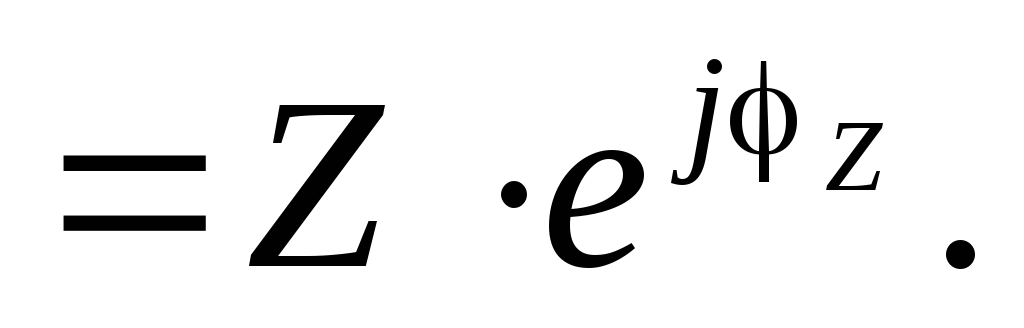 (3.13)
(3.13)
Теперь можно записать закон Ома для участка цепи без источника ЭДС в комплексном изображении
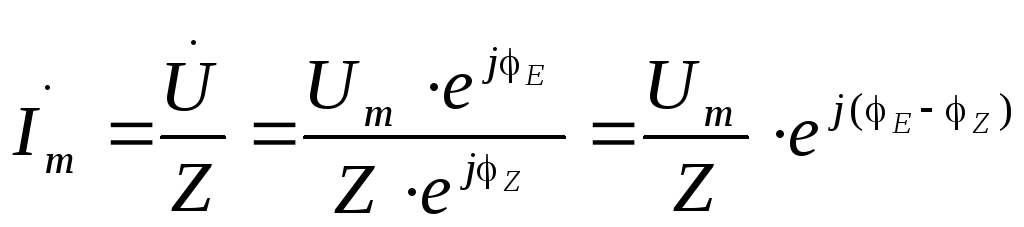 (3.14)
(3.14)
Выражение (3.14) показывает, что в цепях переменного тока модуль тока определяется отношением модуля напряжения (его амплитудного значения) к модулю комплексного сопротивления, а фаза тока определяется разностью фаз напряжения и комплексного сопротивления. Отсюда вытекает еще одно полезное для практики выражение
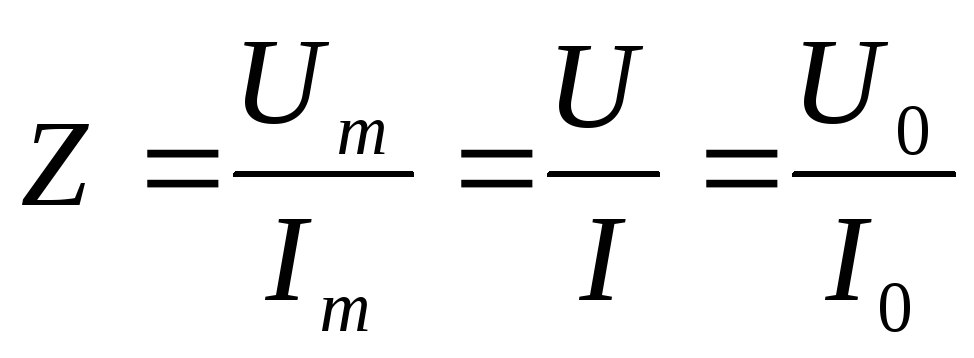 .
(3.15)
.
(3.15)
3. Рассчитываем комплексные сопротивления фаз приемника
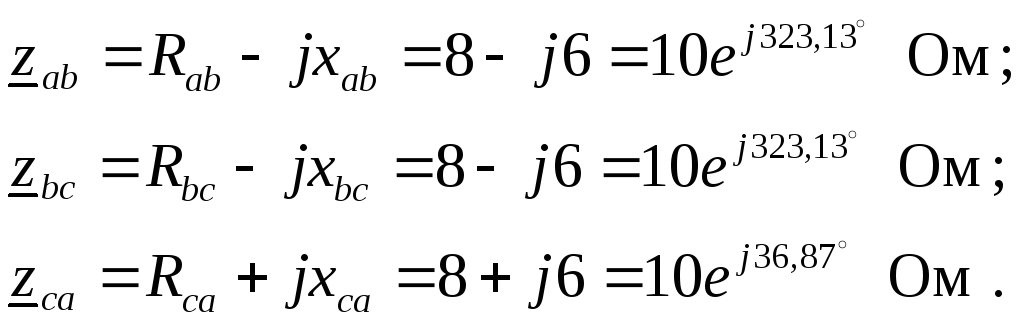
По закону Ома определяем фазные токи
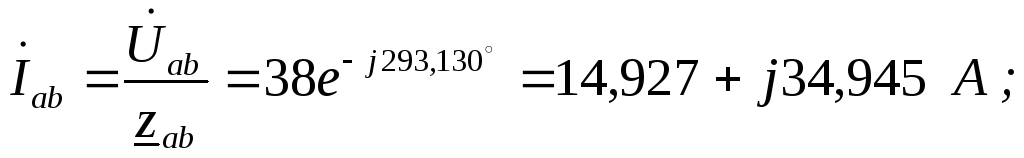
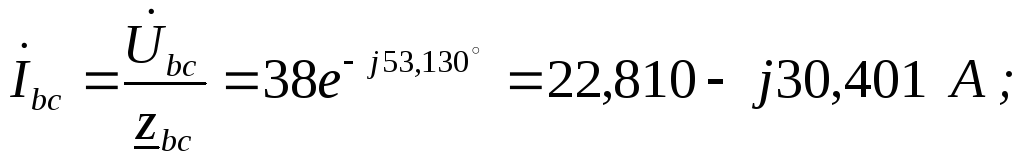
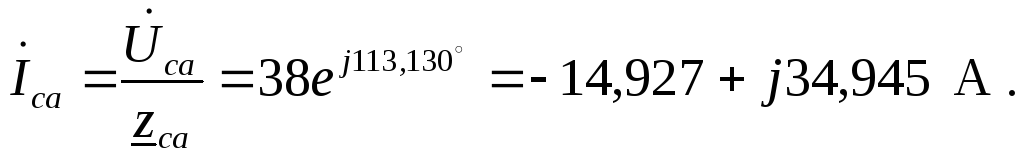
5. Рассчитываем линейные токи, используя первый закон Кирхгофа

6. Определяем полные комплексные, полные активные и реактивные мощности каждой фазы и эти же мощности на всем трехфазном приемнике

При этом
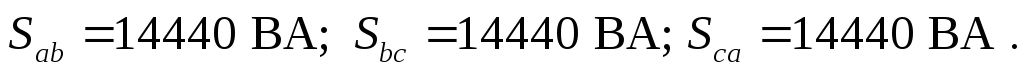
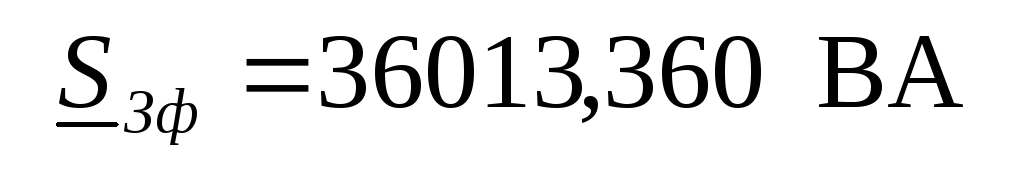
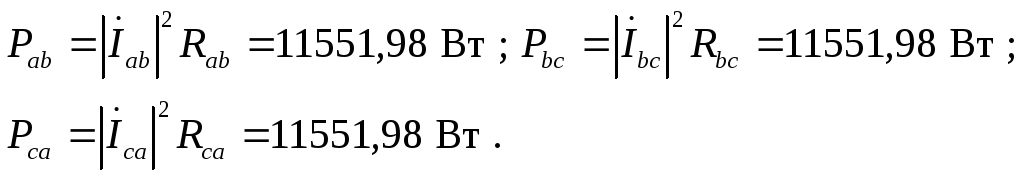
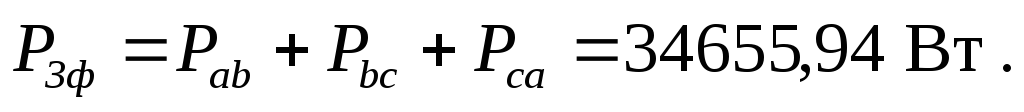
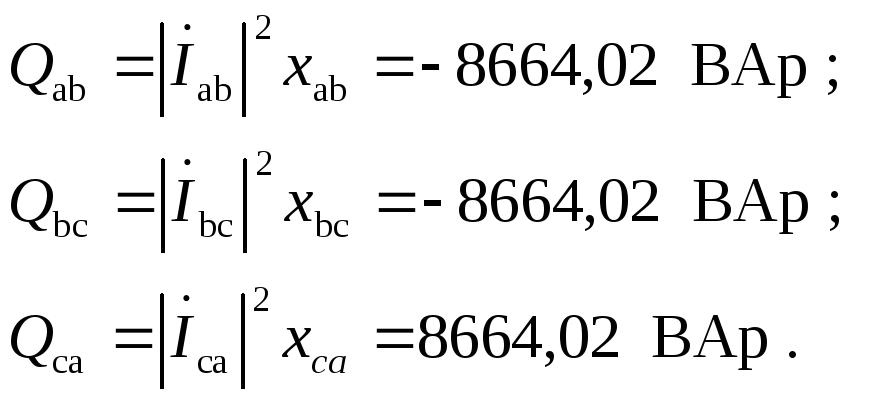
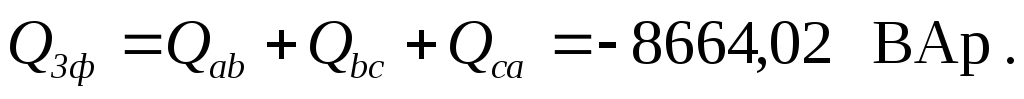
Без специальной проверки видно, что баланс мощностей подтверждается. Следовательно расчеты проведены корректно.
7. Строим векторную
диаграмму токов, напряжений и ЭДС.
Задаемся масштабами по току и по
напряжению: 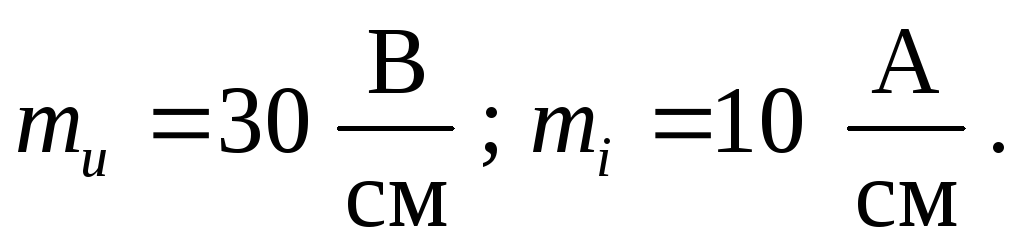
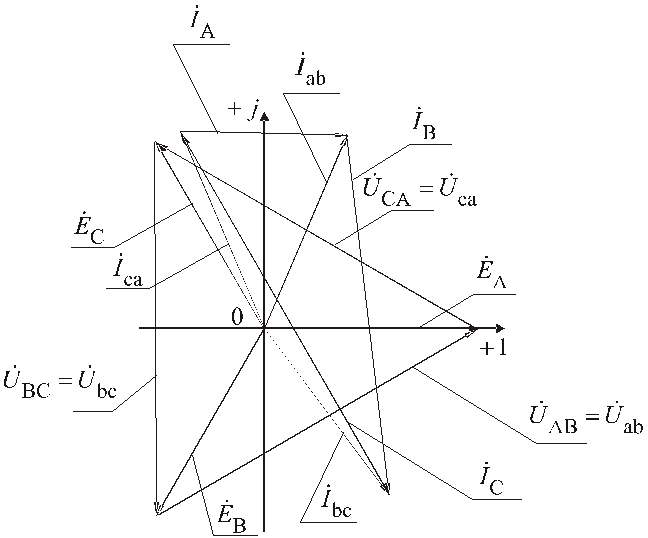
Рис. 13.
Третий пункт и все задание выполнены.
При выполнении задания №3 можно воспользоваться рекомендуемой литературой [2, 3, 6,7].
Пример 2 . Расчет трехфазной цепи с несимметричной нагрузкой (звезда)
К трехфазному источнику подключена цепь (рис. 1). Значения линейного напряжения, активных, индуктивных и емкостных сопротивлений приемников приведены ниже. Требуется:
Определить фазные и линейные токи для заданной схемы соединения, а также ток в нейтральном проводе для схемы «звезда».
Определить активную и реактивную мощности, потребляемые цепью.
Построить векторную диаграмму напряжений и токов.
Исходные данные:
UЛ
= 220 В, XC1 = 10 Ом, R2 = 9 Ом, XL2 = 13 Ом, XL3 = 8
Ом 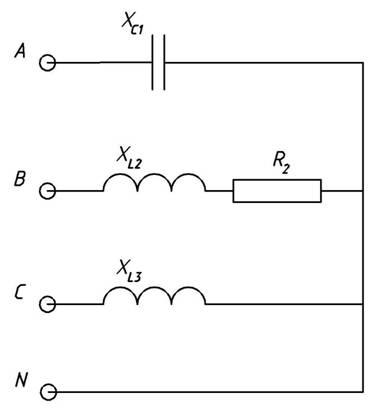 Рис.
1Решение
Рис.
1Решение
1. Определим фазные напряжения для данной схемы типа «звезда»:
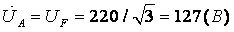
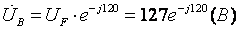
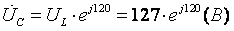
2. Определим комплексные эквивалентные сопротивления каждой фазы:
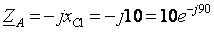 (Ом)
(Ом) 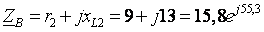 (Ом)
(Ом)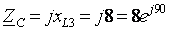 (Ом)
(Ом)
3. Определим фазные токи (для соединения типа «звезда» фазные токи равны линейным):
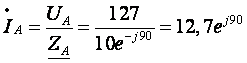 (А)
(А)  (А)
(А)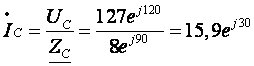 (А)
(А)
4. Определим комплекс действующего значения тока в нейтральном проводе:
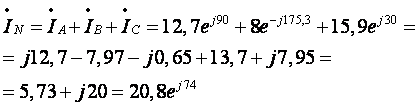
5. Определим активную мощность
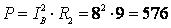 (Вт)
(Вт)
6. Определим реактивную мощность.
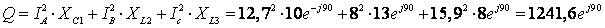 (вар)
(вар)
7. Построим векторную диаграмму
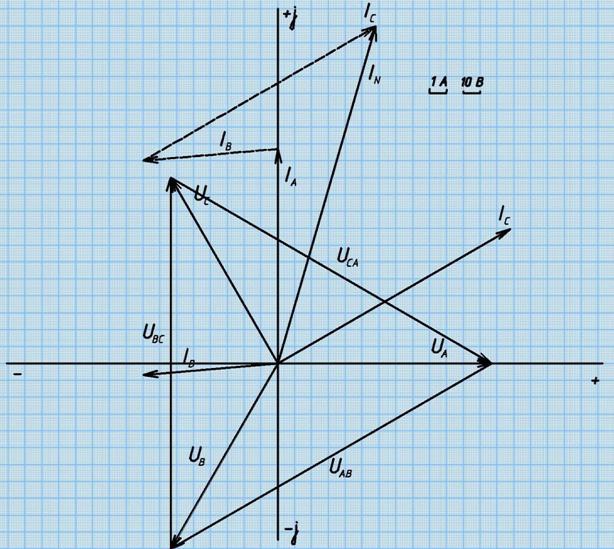
Пример 3. Расчет трехфазной цепи с несимметричной нагрузкой (треугольник) К трехфазному источнику подключен несимметричный трехфазный приемник (рис. 1). Значения линейного напряжения, активных, индуктивных и емкостных сопротивлений приемников приведены ниже. Требуется:
Определить фазные и линейные токи для заданной схемы соединения, а также ток в нейтральном проводе для схемы «звезда».
Определить активную, реактивную и полную мощности, потребляемые цепью.
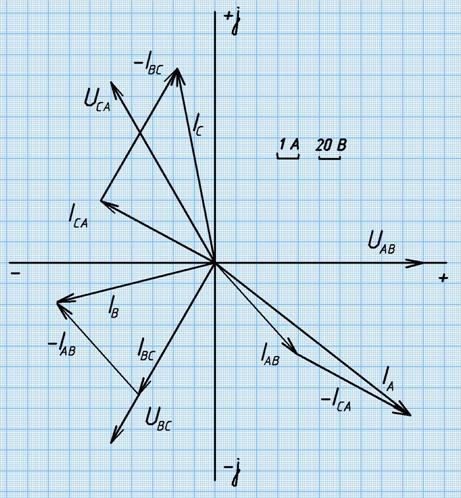
Построить векторную диаграмму напряжений и токов.
Исходные данные:
UЛ
= 220 В, R1 = 25 Ом, XC = 18 Ом, XL = 28 Ом, R2 = 30 Ом, R3
= 30 Ом. 
Рис. 1 Решение.
1. Определим фазные напряжения для данной схемы типа «треугольник»:
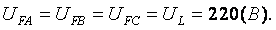
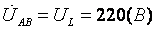
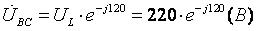
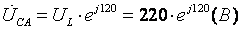
2. Определим комплексные эквивалентные сопротивления каждой фазы:
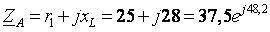 (Ом)
(Ом)  (Ом)
(Ом)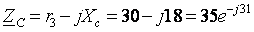 (Ом)
(Ом)
3. Определим фазные токи:

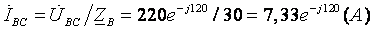
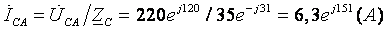
4. Определим комплексы действующих значений линейных токов:
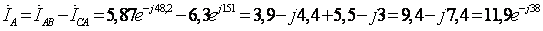 (A)
(A)
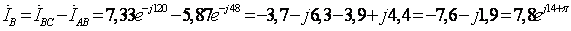 (A)
(A)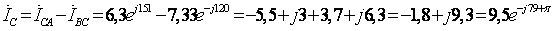 (A)
(A)
5. Определим активную мощность цепи:
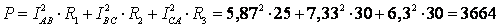 (Вт)
(Вт)
6. Определим реактивную мощность цепи:
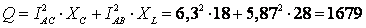 (вар)
(вар)
7. Построим векторную диаграмму.
Контрольные вопросы к экзамену (зачету) по разделу Электротехника
Контрольные вопросы к зачету (экзамену ) по разделу «Основы электротехники».
Электрическая цепь постоянного тока, электрический ток и напряжение.
Линейные и нелинейные элементы электрической цепи их свойства.
Пассивные элементы электрической цепи: сопротивление, индуктивность, емкость.
Активные элементы электрической цепи: источники ЭДС и источники тока.
Закон Ома для замкнутой электрической цепи.
Закон Ома для участка цепи без источника ЭДС.
Первый закон Кирхгофа.
Второй закон Кирхгофа.
Баланс мощностей в цепях постоянного тока.
Тепловое действие тока. Закон Джоуля-Ленца.
Переменный ток. Параметры переменного синусоидального тока.
Представление синусоидального тока проекциями вращающегося вектора. Векторная диаграмма.
Представление синусоидального тока комплексными величинами.
Метод комплексных амплитуд. Закон Ома для участка цепи без источников ЭДС в комплексной форме.
Метод комплексных амплитуд. Законы Кирхгофа в комплексной форме.
Катушка индуктивности в цепи синусоидального тока.
Конденсатор емкостью С в цепи синусоидального тока.
Цепь с последовательным соединением R, L и C. Резонанс напряжений и условия его возникновения.
Цепь с параллельным соединением R, L и C. Резонанс токов и условия его возникновения.
Последовательное соединение элементов R, L и C. Треугольники напряжений и сопротивлений.
Параллельное соединение элементов R, L и C. Треугольники токов и проводимостей.
Мощность в цепи синусоидального тока. Мгновенная мощность.
Мощность в цепи синусоидального тока. Активная, реактивная, полная и комплексная мощность.
Мощность в цепи синусоидального тока. Баланс мощностей в цепи синусоидального тока.
Мощность в цепи синусоидального тока. Коэффициент мощности и способы его улучшения.
.Трехфазные электрические цепи. Основные определения. Линейные и фазные токи и напряжения. Маркировка фазы. Способы соединения генераторов и приемников типа звезда и треугольник. Трехпроводные и четырехпроводные цепи. Нейтральный провод.
Нелинейные электрические цепи. Аппроксимация нелинейных характеристик.
Электрические фильтры. Низкочастотные сглаживающие фильтры.
Электрические фильтры. Резонансные полосовые и заградительные фильтры.
Понятие о многофазных цепях и системах.
Линейные и фазные величины в трехфазных электрических цепях.
Трехфазные цепи типа «звезда-звезда» с нулевым проводом.
Трехфазные цепи типа «звезда-треугольник».
Переходные процессы. Первый закон коммутации.
Переходные процессы. Второй закон коммутации.
Переходные процессы. Включение RL-цепи в источник постоянного тока.
Переходные процессы. Включение RC-цепи в источник постоянного тока.
. Расчет цепей постоянного тока с одним или несколькими нелинейными элементами.
Основные магнитные величины. Магнитные цепи постоянного тока.
Магнитные цепи переменного тока. Ферромагнитные материалы.
Расчет катушки с магнитопроводом и воздушным зазором.
. Энергия и основные потери в магнитопроводе.
Трансформаторы. Конструкция и параметры. Схема замещения. Основные режимы работы.
Асинхронные электродвигатели. Конструкция и параметры. Схемы замещения.
Синхронные электрические машины переменного тока.
Электрические машины постоянного тока.
Электробезопасность. Характеристики поражения человека электрическим током.
Второй спсок
Темы рефератов.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Самостоятельная работа студентов состоит в изучении ряда теоретических вопросов по темам дисциплины, перечень которых приведен в таблице 5 и составления рефератов..
Таблица 5
№ п/п | Тема дисциплины |
1 | 2 |
1 | Тема 1. Электрические цепи. Основные определения, топологические параметры |
2 | Тема 2. Методы расчета линейных электрических цепей |
3 | Тема З. Однофазный переменный ток |
4 | Тема 4. Электрические цепи трехфазного тока. |
5 | Тема 5. Магнитные цепи и электромагнитные устройства. |
6 | Тема 6. Трансформаторы |
7 | Тема 7. Асинхронные машины |
8 | Тема 8. Машины постоянного тока (МПТ) |
9 | Тема 9. Синхронные машины |
10 | Тема 10. Электрические измерения и приборы |
11 | Тема 11. Основы электроники и элементной базы современных электронных устройств |
12 | Тема 12. Источники вторичного электропитания |
13 | Тема 13. Усилители электрических сигналов |
14 | Тема 14. Импульсные и автогенераторные устройства |
15 | Тема 15. Основы цифровой электроники |
16 | Тема 16. Микропроцессорные средства |




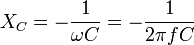
 остроить
векторную диаграмму токов и напряжений.
остроить
векторную диаграмму токов и напряжений.