Принцип работы термопары и компенсация напряжения на холодном спае

    Термопары — маленькие, прочные и сравнительно недорогие устройства. Вдобавок из всех температурных датчиков они работают в самом широком диапазоне температур. Термопары незаменимы при измерении высоких температур (вплоть до 2300 °С) в агрессивных средах. Они вырабатывают на выходе термоЭДС в диапазоне от микровольт до милливольт, однако требуют стабильного усиления для последующей обработки. К тому же необходимо применять компенсацию напряжения на холодном спае, которая вкратце будет обсуждена ниже. Они гораздо более линейны, чем многие другие датчики, а их нелинейность на сегодняшний день хорошо изучена и описана в специальной литературе.

    В табл. 2 приведены наиболее распространенные термопары. При их изготовлении обычно применяют такие металлы, как железо, платина, родий, рений, вольфрам, медь, алюмель (сплав никеля с алюминием), хромель (сплав никеля с хромом) и константан (сплав меди и никеля).

Таблица 2

Хромель-алюмель	-184…1260	39	К
Платина (13%)/родий-платина	0…1593	11,7	R
Платина (10%)/родий-платина	0…1538	10,4	S
Медь-константан	-184…400	45	Т

    На рис. 1 представлены зависимости ЭДС от температуры трех наиболее распространенных типов термопар, у которых температура опорного спая поддерживается равной 0 °С. Термопары типа J наиболее чувствительны и развивают наибольшее выходное напряжение при одном и том же изменении температуры. С другой стороны, термопары типа S являются наименее чувствительными. Как видно из приведенных характеристик, сигналы, развиваемые термопарами, очень малы и требуют малошумящих усилителей с большим коэффициентом усиления и малым дрейфом. Это необходимо учитывать при проектировании схем обработки сигналов с термопарных датчиков.

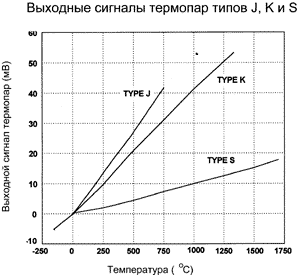
Рис. 1

    Чтобы понять поведение термопар, рассмотрим, как изменяется их выходной сигнал при изменении температуры чувствительной части термопары (горячего спая). Рисунок 1 показывает связь между температурой горячего спая и выходным сигналом, развиваемым разными типами термопар (во всех случаях температура холодного спая поддерживается равной 0 °С). Очевидно, что отдача термопар нелинейна, но природа этой нелинейности до сих пор не вполне ясна.

    Рисунок 2 показывает, как зависит от температуры горячего спая коэффициент линейности (Seebeck coefficient), то есть прирост выходного напряжения, соответствующий росту температуры горячего спая на 1 °С, иными словами, первая производная зависимости выходного сигнала от температуры. Отметим, что мы по-прежнему рассматриваем тот случай, когда температура холодного спая поддерживается равной 0 °С.

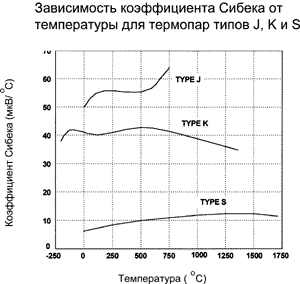
Рис. 2

    При выборе термопары для производства замеров температур в достаточно широком диапазоне следует выбирать ту термопару, коэффициент линейности которой изменяется менее других в рамках этого диапазона.

    Например, для термопары типа J в диапазоне от 200 до 500 °С коэффициент линейности изменяется менее чем на 1 мкВ/°С, что делает ее идеальной для использования в этом диапазоне.

    Приведенные на рис. 1 и 2 данные полезны вдвойне: во-первых, рис. 1 показывает диапазон и чувствительность трех типов термопар, так что разработчик может с одного взгляда определить, что термопара типа S имеет самый широкий диапазон измерений, но типа J — более чувствительная; во-вторых, знание коэффициента Сибека (рис. 2) позволяет быстро определить, какова линейность выбранной термопары. Используя рис. 2, разработчик для работы в диапазоне 400…800 °С выберет термопару типа К, коэффициент линейности которой в этой области минимальный, а для диапазона 900…1700 °С — типа S. Поведение коэффициента линейности термопары оказывается определяющим в тех случаях, когда некоторое отклонение от заданной температуры критичнее, чем само значение заданной температуры. Эти данные также показывают, какими характеристиками должны обладать устройства, работающие в схеме управления совместно с той или иной термопарой.

    Чтобы успешно использовать термопары, необходимо понимать основные принципы их работы. Рассмотрим схемы, изображенные на рис. 3.

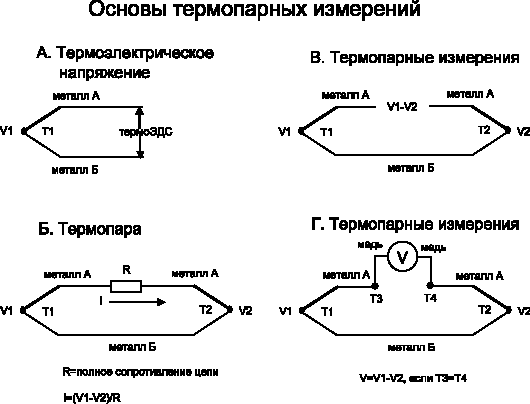
Рис. 3

    Если мы соединим два разнородных металла при какой-либо температуре, превышающей абсолютный нуль (-273,16 °С), то между ними будет разность потенциалов (так называемая, термоЭДС — Thermoelectric EMF, или «контактная разность потенциалов»), которая является функцией температуры соединения (рис. 3, а). Если мы соединим два провода в двух местах, сформируются два спая (рис. 3, б) Если эти спаи имеют разную температуру, то в цепи образуется термоЭДС, по проводникам потечет ток, величина которого определяется значением термоЭДС и сопротивлением проводников.

    Разорвав один из проводников, мы увидим, что напряжение в точках разрыва будет равным термоЭДС, и если замерить это напряжение, то полученное значение можно использовать, чтобы определить разность температур между двумя спаями (рис. 3, в).

    Необходимо помнить, что термопара изменяет разницу температур между двумя спаями, а не абсолютную температуру в одном из них. Определить температуру в измеряемом спае мы можем лишь в том случае, если знаем температуру второго спая (часто называемого «опорным» или «холодным»).

    Но не так легко измерить напряжение, образуемое термопарой. Предположим, что мы подключили вольтметр в контур схемы (рис. 3, г). Провода, подключенные к вольтметру, также образуют термопары в месте их присоединения. Если обе эти дополнительные термопары находятся под одинаковой температурой (не имеет значения, какой), то они не окажут воздействия на общую термоЭДС системы. Если же их температуры различаются, то могут возникнуть ошибки. Поскольку каждая пара находящихся в контакте разнородных металлов вырабатывает термоЭДС (включая медь/припой, ковар/медь (ковар — сплав, используемый для формирования подложки микросхемы), алюминий/ковар [в соединении внутри микросхемы)), очевидно, что в реальных рабочих контурах возникают гораздо более серьезные проблемы, чем описано выше. Поэтому необходимо постараться обеспечить, чтобы все контакты разнородных металлов в контуре вокруг термопары (естественно, помимо спаев самой термопары) находились при одинаковой температуре.

    Термопары создают напряжение, хотя и очень маленькое, но не требующее токового возбуждения. Показанная на рис. 3, г термопара имеет два спая (T1 — температура измерительного спая, Т2 — опорного). Если Т2 = Т1, тогда V2 = V1 и выходное напряжение V = 0. Выходное напряжение термопары обычно определено как значение, полученное при поддержании температуры холодного спая, равной 0 °С. Отсюда и происхождение термина «холодный спай» или «спай при температуре тающего льда». Таким образом, если измерительный спай будет помещен в среду с нулевой температурой, на выходе термопары будет нулевое напряжение.

    Чтобы проводить высокоточные измерения, необходимо тщательно поддерживать температуру холодного спая, которая должна быть строго определена (хотя не обязательно равна 0°С). Простая реализация этого требования представлена на рис. 4. Ванна с тающим льдом может быть легко реализована в любых условиях, хотя на практике это не всегда удобно.

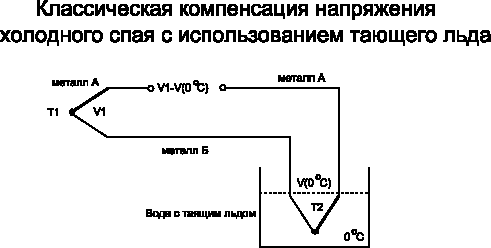
Рис. 4

    Сегодня «спай при температуре тающего льда» с требуемой для его реализации ванной со льдом и водой успешно вытесняется электроникой. Температурный датчик другого типа (чаще полупроводниковый, а иногда и термистор) измеряет температуру холодного спая, а полученный результат используется для формирования дополнительного напряжения в цепи термопары, компенсирующего разницу между фактической температурой холодного соединения и его идеальным значением (обычно 0 °С), как показано на рис. 5. В идеале напряжение компенсации должно подбираться строго в зависимости от разности напряжений. Корректирующее напряжение является функцией от температуры опорного спая Т2, причем более сложной, нежели простая линейная зависимость, описываемая произведением КхТ2, где К — простая константа. На практике, поскольку холодные спаи обычно находятся при температуре лишь на несколько десятков градусов выше 0 °С и ее значение колеблется в пределах ±10 °С, линейная аппроксимация компенсирующего напряжения оказывается допустимой. Другими словами, хотя реальное значение корректирующего напряжения и определяется многочленом в соответствии с формулой V=K

1хT+K₂хT²+K₃хT³+…, но значения коэффициентов К₂, К₃и т. д. очень малы для всех известных типов термопар. Значения этих коэффициентов для всех термопар можно найти в справочной литературе.

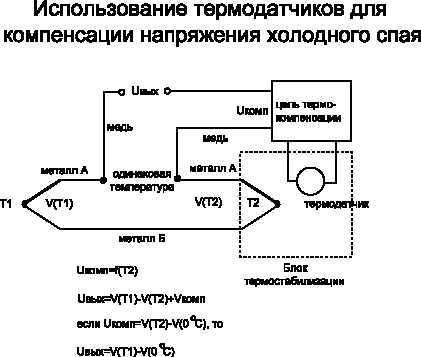
Рис. 5

    Когда используется электронная компенсация напряжения на холодном спае, на практике соединение проводов с концами термопары заключают в изотермический блок, как показано на рис. 6. Когда соединения металл А — медь и металл В — медь находятся при одной температуре, это эквивалентно спаю металл А — металл В, как показано на рис. 5.

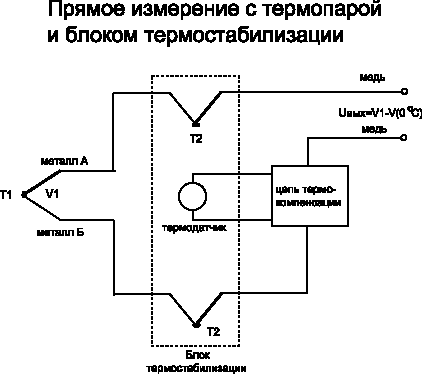
Рис. 6

    Схема, приведенная на рис. 7, обеспечивает измерение температуры от 0 °С до 250 °С при помощи термопары типа К с компенсацией напряжения холодного спая. Питание схемы осуществляется однополярным напряжением от 3,3 до 12 В. Причем схема была спроектирована таким образом, чтобы коэффициент преобразования составлял 10 мВ/°С.

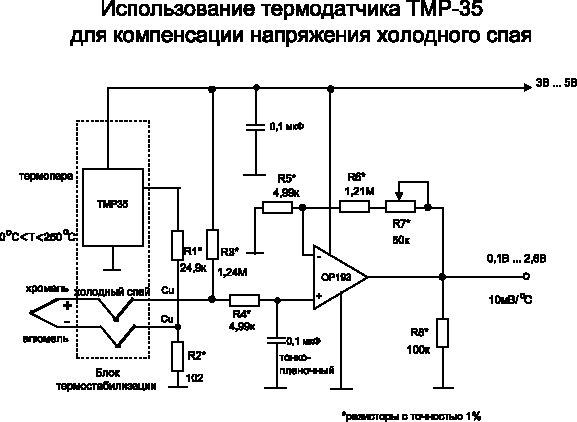
Рис. 7

    Коэффициент передачи термопары типа К приблизительно равен 41 мкВ/°С. Следовательно, примененный для компенсации датчик напряжения с температурным коэффициентом 10 мВ/°С ТМР35 используется с делителем на R1 и R2, обеспечивающим требуемое значение 41 мкВ/°С. Ликвидация неизотермичности между дорожками печатной платы и проводами термопары предотвращает появление ошибок в процессе измерения при изменении температур. Такая компенсация подходит для схем, работающих при температуре окружающей среды от 20 до 50 °С.

    Если температура рабочего спая термопары достигла 250 °С, ее выходное напряжение будет составлять 10,151 мВ. Поскольку при этом выходной сигнал схемы должен быть равен 2,5 В, то усилитель должен иметь коэффициент усиления, равный 246,3. Выбор R4, равного 4,99 кОм, предопределяет для R5 значение 1,22 МОм. Наиболее близкое однопроцентное значение для R5 составляет 1,21 МОм, в связи с чем для точной настройки размаха выходного сигнала совместно с R5 используется потенциометр сопротивлением 50 кОм.

    Хотя ОР193 допускает питание от одного источника, его выходные каскады не предназначены для работы в режиме rail-to-rail и минимальное значение сигнала на его выходе не должно быть ниже +0,1 В. С этой целью резистор R3 добавляет ко входу ОУ небольшое напряжение, увеличивающее выходной сигнал на 0,1 В для питающего напряжения 5 В. Это смещение (соответствующее 10 °С) должно быть вычтено после обработки или считывания сигнала с выхода ОР193. R3 также обеспечивает определение обрыва термопары: если термопара отсутствует, выходной сигнал становится больше чем 3 В. Резистор R7 балансирует входное сопротивление ОР193 по постоянному току, а пленочный конденсатор емкостью 0,1 мкФ снижает помехи от термопары на его неинвертирующем входе.

    AD594/AD595 — инструментальный усилитель и компенсатор напряжения холодного спая, выполненный в одном чипе (рис. 9). Эта микросхема осуществляет привязку к «точке таяния льда» и содержит предварительно откалиброванный усилитель, который обеспечивает получение выходного напряжения высокого уровня (10 мВ/°С) непосредственно с выхода термопары. AD594/AD595 может быть использована как линейный усилитель-компенсатор либо в качестве переключаемого контроллера, используемого для постоянного или мобильного управления и регулирования. Схема может быть также использована для прямого усиления компенсируемого напряжения, выполняя при этом функции преобразователя температуры в напряжение с коэффициентом преобразования 10 мВ/°С. В ряде случаев очень важно, чтобы чип находился при той же температуре, что и холодный спай термопары. Обычно это достигается путем размещения обоих в непосредственной близости друг от друга и изоляции их от источников тепла.

    AD594/AD595 включает датчик повреждения термопары, который показывает, что либо один, либо оба конца термопары отсоединены от микросхемы. Аварийный выход достаточно гибкий и в состоянии формировать ТТL-сигнал. Прибор запитывается от одного положительного источника (напряжение на нем может быть всего 5 В), но подача отрицательного напряжения позволяет измерить температуру ниже 0 °С. Для уменьшения самонагрева собственное потребление AD594/AD595 (без нагрузки) снижено до 160 мкА, при этом микросхемы в состоянии отдать в нагрузку ток до ±5мА.

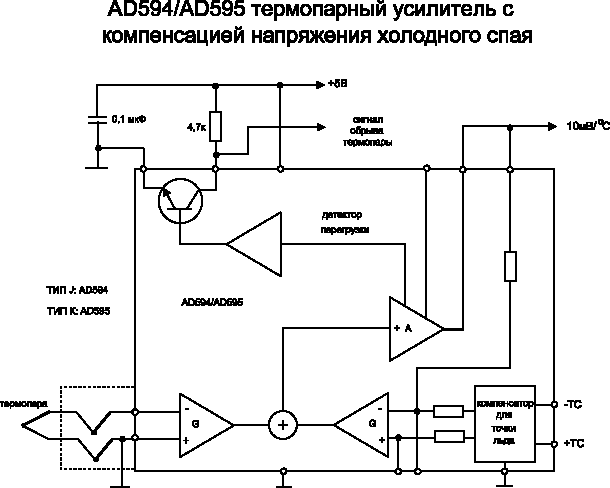
Рис. 8

    Благодаря лазерной подгонке сопротивлений внутри AD594 схема настроена на работу с термопарами типа J (железо/константан), а AD595 — с термопарами типа К (хромель/алюмель). Напряжения смещения и коэффициенты усиления микросхем могут изменяться при помощи внешних элементов, так что каждая из них может быть перекалибрована под термопару любого другого типа. Допустимо также с помощью внешних элементов осуществить более точную калибровку термопары для специальных применений.

    AD594/AD595 выпускаются в двух модификациях: «С» и «А», — калибрующихся с точностью ±1 °С и ±3 °С соответственно. Оба исполнения допускают поддержание температуры холодного спая в пределах от 0°С до 50 °С. Схема, представленная на рис.9, непосредственно работает с термопарой типа J (AD594) или типа K AD595) и позволяет измерять температуру от 0 °С до 300 °С.

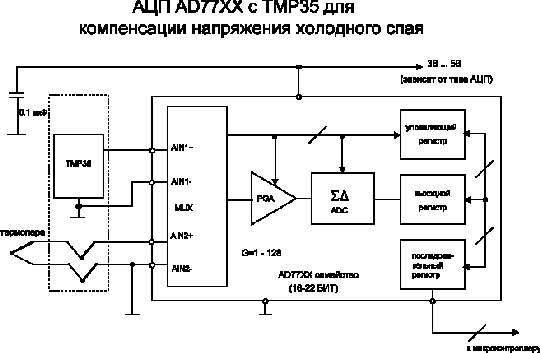
Рис. 9

    AD596/AD597 — монолитные контроллеры, оптимизированные для использования в условиях любых температур в различных случаях. В них осуществляется компенсация напряжения холодного спая и усиление сигналов с J- или K-термопары таким образом, чтобы получить сигнал, пропорциональный температуре. Схемы могут быть подстроены так, чтобы обеспечить выходное напряжение 10 мВ/°С непосредственно от термопар типа J или K. Каждый из чипов размещен в металлическом корпусе с десятью выводами и настроен на работу при температуре окружающей среды от 25 °С до 100 °С.

    AD596 усиливает сигналы термопары, работающей в температурном диапазоне от -200 °С до +760 °С, рекомендованном для термопар типа J, в то время как AD597 работает в диапазоне от -200 °С до +1250 °С (диапазон термопар типа K). Усилители откалиброваны с точностью ±4 °С при температуре окружающей среды 60 °С и характеризуются температурной стабильностью 0,05°С/°С при изменении температуры окружающей среды в пределах от 25 °С до 100 °С.

    Все вышеописанные усилители не в состоянии компенсировать нелинейность термопары: они способны лишь корректировать и усиливать сигнал с термопарного выхода. АЦП с высокой разрешающей способностью, входящие в семейство AD77хx, могут использоваться для прямой оцифровки сигнала с выхода термопары, без предварительного усиления. Преобразование и линеаризацию осуществляет микроконтроллер, сопряженный с таким АЦП, как показано на рис.10. Два мультиплексируемых входа АЦП используются для прямой оцифровки сигнала с термопары и с теплового датчика, находящегося в контакте с ее холодным спаем. Вход PGA (программируемого усилителя) программируется на усиление от 1 до 128, и разрешающая способность АЦП лежит в пределах от 16 до 22 бит в зависимости от того, какая из микросхем выбрана пользователем. Микроконтроллер осуществляет как компенсацию напряжения холодного спая, так и линеаризацию характеристики

Программная компенсация температуры «холодного спая» при работе с термопарой

Эта статья родилась, как часть статьи про датчик для работы с термопарой ads1118.
Дело в том, что для повышения точности, компенсировать «холодный спай» необходимо. Первоначально, я имея ряд отсчетов, подобрал некую магическую формулу, которая давала неплохие результаты. Но обоснования ей не было. НО потом, возникла идея, как сделать правильно. А в процессе реализации, стало ясно, что это может быть достаточно простым и универсальным решением для любой ситуации.

Под катом много математики и нет картинок и одна картинка ).

И чтобы далеко не ходить, обещанная картинка с температурой в доме:

Для тех, кому надо результат:
Берем приложенный файл. Делаем 3 замера:
Нагреваем плату с «холодным спаем» и измеряем температуру 100 градусов (кипящую воду).
Остужаем плату (например в холодильнике), и снова измеряем темепературу 100 градусов и 0 градусов.
Заносим данные в верхний левый угол таблицы.
Подбираем коэффициент КТ (первая срока), так, чтобы ошибка была минимальной.
Полученные 4 числа: КТ, С, К1 и К2 используем для перевода «попугаев» в температуру.
Если хочется оптимизаций, то она описана в конце статьи.
Все. Дальше, только математика 🙂

Постановка задачи:
Мы измеряем температуру с помощью термопары, и неким образом знаем температуру «холодного спая» (например припаяв рядом специальную микросхему и читая ее данные).
Задача: нужно минимизировать ошибку измерения имея на входе некое волшебное число А — величина с термопары («горячий спай») и некое волшебное число B — величина температуры «холодного спая», а так-же найти коэффициент самой термопары.

Предварительные мысли:
Как правильно обратил внимание уважаемый DeepSOIC в комментарии к первоначальной статье:

Напряжение на термопаре пропорционально разности температур между её спаем и её разъёмом. Разъём называют «холодный спай» — cold junction — который кстати вовсе не обязательно холодный, просто так называется. Т.е. термопара измеряет не температуру, а разность температур. Чтобы получить полную температуру, нужно измеренную разность температур приплюсовать к температуре холодного спая.

Как бы это все понятно, но для себя в мозгу фразу:

термопара измеряет не температуру, а разность температур

я уяснил только прочитав этот комментарий. Спасибо огромное!!!

Т.е. нам по сути, необходимо просто прибавить температуру к той, что дает термопара. Проблема в том, что, разница не постоянна, и зависит и от температуры обоих спаев. Приходиться долго экспериментировать, изучать закон изменения разницы. + еще нужно найти коэффициент самой термопары (КТ)… И тут,

Эврика:
А зачем нам все это делать? Если мы допустим, что закон линеен (не линейный закон, мы все равно не вычислим, да и точность нам нужна не до тысячных), то получается элементарная задача:
Дано: 2 числа А и В. Необходимо:
1) Найти КТ
2) Вычислить некое число, линейно зависящее от А, В и КТ.
Из математики, мы получаем единственный вариант:
ЧИСЛО (Ч) = ВОЛШЕБНАЯ КОНСТАНТА (С) + ВОЛШЕБНЫЙ КОЭФФИЦИЕНТ 1 (К1) * А + ВОЛШЕБНЫЙ КОЭФФИЦИЕНТ 2 (К2) * В
Все что нам необходимо, это найти 3 волшебных числа. Т.е. решить систему линейных уравнений с 3-мы неизвестными. Для этого нужно иметь 3 уравнения. Не вопрос: проводим 3 замера (и еще 3 для контроля), подставляем, решаем. Важное дополнение по итогам обсуждения:
необходимо 3-е измерение брать при значительном изменении температуры «холодного спая». Это даст более точное решение.
Например так:
Нагреваем плату с «холодным спаем» и измеряем температуру 100 градусов (кипящую воду).
Остужаем плату (например в холодильнике), и снова измеряем темепературу 100 градусов и 0 градусов.
Остается найти КТ, как число, которое дает минимальную ошибку для тестовых замеров. ВСЕ!!! Самое интересное, что система не явно, дает самый точный результат, при правильно КТ. Т.е. мы можем просто менять в условиях задачи КТ и смотреть, где ошибка меньше, там точнее КТ.
Математика за нас, учла и смещение 0, и взаимное влияние коэффициентов друг на друга и КТ. Для каждой схемы, решение будет разное. Но решение не зависит от внешних факторов. Оно зависит только от реализации схемы, и учитывает все погрешности и не точности (например разброс номиналов резисторов) — они получаются учтены в результатах тестовых измерений, и в решении они тоже учитываются. Кроме того, системе не важно в каких «попугаях» заданы числа А и В. Единственное требование: (достаточно точная для задачи) линейность этих «попугаев».

Пример из моей задачи:

КТ = 5
Температура Горячий спай Холодный спай
    0          -116	    3334
    0          -122	    3488
    0          -124	    3500
   100          389	    3432
   100          382	    3564
Система уравнений:
28,7414	= C + К1 * -116 + К2 * 3334
28,5902	= C + К1 * -122 + К2 * 3488
30,9189	= C + К1 *  389 + К2 * 3432

Решение:
K1 = 0,0044687231
K2 = -0,000878236
C = 32,1877900423

Итог для последнего измерения:
Ч = 32,1877900423 + 0,0044687231 * 382 - 0,000878236 * 3564 = 30,7648
Смещение = 3564 / 30,7648 = 115,8466
Результат = 382 + 115,8466 = 497,8466
Температура = 497,8466 / 5 = 99,5693
Все результаты:
Смещение	Результат	Температура	Ошибка
116,0000	  0,0000	   0,0000	 0,00
122,0463	  0,0463	   0,0093	 0,01
122,5497	 -1,4503	  -0,2901	 0,29
111,0248	500,0248	 100,0050	 0,00
115,8466	497,8466	  99,5693	 0,43

Должен заметить, что коэффициент КТ, подобран по минимальной ошибке.
Например, при КТ = 6 получается так:

Смещение	Результат	Температура	Ошибка
116,0000	  0,0000	   0,0000	 0,00
119,4133	 -2,5867	  -0,4311	 0,43
119,5223	 -4,4777	  -0,7463	 0,75
206,0085	595,0085	  99,1681	 0,83
208,3491	590,3491	  98,3915	 1,61

Для упрощения расчетов, я приложил файлик с готовыми формулами. Надо только подставить данные и подобрать КТ.
ВНИМАНИЕ: никаких макросов я не использовал. Если они есть, значит это вирус!!! Будьте внимательны!!!

Оптимизация:
Если посмотреть на алгоритм, то расчеты это куча умножений и делений дробных чисел. Это и на ПК не быстро, а уж в МК и подавно… Поэтому я использую хитрость: работу с фиксированной запятой. В итоге, работа только с целыми числами!!!
Суть: все 3 коэффициента: С, К1 и К2 я умножаю на 65536 (думаю понятно почему 65536 :)):

K1 = 0,0044687231 * 65536 = 293
K2 = -0,000878236 * 65536 = -58
C = 32,1877900423 * 65536 = 2109459

В результате, число Ч автоматически увеличивается в 65536 раз. Только все операции целочисленные. При вычислении смещения, мы предварительно умножаем значение холодного спая на 65536 и при ЦЕЛОЧИСЛЕННОМ делении 65536 исчезает… 🙂 Конечно, точность немного страдает… Но скорость вырастает на порядки…
Но и тут еще можно поднять точность, используя целые числа, т.к. смещение число не большое, и 1-ка очень важна (1% точности). Мы умножаем значение холодного спая не на 65536, а на 131072. И после деления, прибавляем единичку и делим на 2, чтобы компенсировать ошибку. В итоге получаем округление до 0.5 )
В приложенном файле, есть оба варианта (дробное и целое).
Целое дает ТОЧНЫЙ(!!!) результат на тестовых данных. Ошибка 0.

ОБНОВЛЕНИЕ:

Пояснения по решению, или ответы на вопросы:

По сути мы хотим получить две прямые (но нас интересует их сумма).

Первая прямая — горячий спай,
t1 = k1 * A + c1
Вторая — холодный
t2 = k2 * B + c2

Нас интересует их сумма
t = k1 * A + k2 * B + c (где с = с1 + с2)

0          -122         3488
0          -124         3500
100          389         3432

      1   -116   3334
      1   -122   3488
      1    389   3432

К сожалению, мы НЕ ищем прямое преобразование А-В в температуру и НЕ решаем описанные уравнения. Это было бы идеально. И для расчетов (2 умножения, 2 сложения) очень просто и не напряжно для МК. Проблема в том, что это НЕ работает 🙁

По факту, как правильно заметили:

Вообще самое правильное это сначала измеренную температуру холодного спая преобразовать в эквивалентное термо ЭДС (Как если бы холодный спай был при нуле, а рабочий при измеренной температуре), затем сложить это напряжение с измеренным с термопары, а потом уже обратно преобразовать эту сумму в температуру. Таким образом полностью компенсируются нелинейности.

Т.е. системой уравнений, мы как раз и ищем КОЭФФИЦИЕНТЫ для расчета КОЭФФИЦИЕНТА КОМПЕНСАЦИИ «холодного спая» для заданных условий.

Не понятно откуда взялись числа 28,7414 28,5902 30,9189

Это как раз и есть КОЭФФИЦИЕНТы КОМПЕНСАЦИИ «холодного спая» для заданных условий. Они разные для разных данных.
При дальнейших расчетах, мы делим на этот коэффициент, тем самым внося нелинейность в формулу перевода «попугаев» в температуру.

Пояснение 2, математическое:
Пусть:
t – измеряемая температура
vx – измеренное значение «холодного спая»
vg — измеренное значение «горячего спая»
vg0 — измеренное значение «горячего спая» если бы измерение проводилось при vx = 0
КТ – коэффициент перевода vg0 в t:

(1)	t = vg0/КТ

Но как правило, vx не равно 0, поэтому нам надо привести vx к нулю, изменив vg на некую величину, зависящую от vx:
Пусть kx – коэффициент компенсации:

(2)	vg0 = vg + vx/kx,     vx = 0

Предположим, что kx линейно зависит от vx и vg:

(3)	kx = c + k1 * vx + k2 * vg

Для нахождения c, k1 и k2, необходимо решить систему линейных уравнений с 3-мя неизвестными для известных kx, vx, vg. vx и vg мы измеряем непосредственно.
kx мы находим по формуле (1) и (2), зная температуру в точках измерения:

(4)	kx = vx/(vg0 - vg) и vg0 = t * KT 	=>	 kx = vx/(t * KT - vg)

Итого из (3) и (4):

(5)	vx/(t * KT - vg) = c + k1 * vx + k2 * vg

Но (5) это уже не линейное уравнение, поэтому проще всего подобрать КТ по минимальной ошибке решая систему линейных уравнений для каждого КТ.

Компенсация холодного спая в практике применения термоэлектрических преобразователей

Компенсация холодного спая в практике применения термоэлектрических преобразователей

На сегодняшний день термопары получили наибольшее распространение среди датчиков измерения температуры. Использование термопар в большом диапазоне температур более эффективно по сравнению с такими решениями, как термопреобразователь сопротивления (ТПС), термистор, или интегральный датчик температуры (ИДТ). Термопары используются, например, в автомобилях или бытовой технике. Вдобавок, их надежность, стабильность и малое время отклика делают термопары наилучшим выбором для многих видов оборудования.

Однако и в применении термопар есть некоторые сложности, в первую очередь – значительная нелинейность характеристик. К тому же, ТПС и ИДТ обычно обладают лучшими характеристиками по чувствительности и точности, что важно для прецизионных решений. Выходной сигнал термопары имеет очень малый уровень и требует усиления или применения цифровых преобразователей высокой разрядности для обработки сигнала.

Но, несмотря на все перечисленные недостатки, низкая стоимость, легкость применения и широкий температурный диапазон до сих пор являются причинами популярности термоэлектрических преобразователей.

Основные сведения о термопарах

Термопары относятся к дифференциальным измерителям температуры. Конструктивно они представляют из себя два термоэлектрода из разных металлов, один из которых принимается за положительный, другой – за отрицательный. В таблице 1 представлены наиболее распостраненные типы термопар, используемые металлы или сплавы и температурный диапазон для каждого варианта. Каждый тип термопар обладает уникальными термоэлектрическими свойствами в определенном для них температурном диапазоне.

Таблица 1. Основные характеристики термопар       

Тип	Положительный Металл/Сплав	Отрицательный Металл/Сплав	Температурный диапазон, °С
T	Медь	Константан	-200…350
J	Железо	Константан	0…750
K	Хромоникелевый сплав	Алюмель	-200…1250
E	Хромоникелевый сплав	Константан	-200…900

При соединении двух металлов (пайкой или сваркой) получают два перехода (спая), как показано на рис. 1а, разность потенциалов образуется в цепи вследствие разности температур спаев. Это явление называется эффектом Зеебека, он состоит в преобразовании тепловой энергии в электрическую. Эффект Зеебека обратен эффекту Пельтье, заключающемуся в преобразовании электрической энергии в тепловую, что применяется в частности в термоэлектрических охладителях. На рис. 1 показано, что выходное напряжение Vвых – это разница между потенциалами холодного и горячего спаев. Т.к. Vгор и Vхол образуются за счет разности температур спаев, Vвых является функцией этой разности. Коэффициент, равный отношению разности потенциалов к разности температур, известен как коэффициент Зеебека.

Рис. 1а. Напряжение в цепи в результате эффекта Зеебека

Рис. 1б. Наиболее распространенная схема реализации термопары

На рисунке 1б показана наиболее часто употребляемая схема использования термопары. Здесь использован третий металл (т.н. металл-посредник), что дает дополнительный спай. В этом примере каждый термоэлектрод соединен с медным проводом. Пока между ними нет разности температур, металл-посредник не оказывает никакого влияния на выходное напряжение. Эта схема позволяет использовать термопару без отдельного опорного спая. Напряжение Vвых так и остается функцией от разности температур холодного и горячего спаев, определяемой коэффициентом Зеебека. Однако до тех пор, пока измеряется именно разница температур, для определения актуальной температуры горячего спая необходимо знать температуру холодного.

Самый простой метод – поддержание температуры холодного спая на уровне 0°C. В этом случае Vвых = Vгор, и измерение напряжения дает непосредственную информацию о температуре горячего спая.

Раньше этот вариант считался стандартом при использовании термопар, однако сейчас обеспечение такого охлаждения холодного спая зачастую непрактично. Для получения результатов измерения в абсолютных величинах необходимо знать температуру холодного спая. Выходное напряжение термопары должно быть компенсировано с учетом влияния потенциала холодного спая при ненулевой температуре. Это и называется – компенсация холодного спая.

Выбор устройства для измерения температуры холодного спая

Данные о температуре холодного спая можно получить с помощью различных датчиков и устройств. Среди самых распространенных – резистивный температурный преобразователь (РТП), термистор и интегральный датчик температуры (ИДТ). Каждое из этих устройств имеет свои достоинства и недостатки, поэтому применение того или иного датчика определяется условиями конкретной задачи.

Для устройств с высокими требованиями по точности лучшим выбором будет калиброванный платиновый РТП с его широким температурным диапазоном. Однако это решение – дорогостоящее.

Термисторы и ИДТ – недорогая альтернатива РТП в случаях, когда требования к точности не столь строгие. У термисторов рабочий температурный диапазон шире, однако ИДТ используются чаще из-за линейности характеристик. Корректировка нелинейности термисторов может требовать слишком много ресурсов от микроконтроллера устройства. ИДТ обладают превосходной линейностью характеристик, но узким диапазоном измерений.

Итак, измеритель температуры холодного спая выбирается, исходя из требований к системе. На выбор оказывают влияние точность, диапазон измерения температур, линейность характеристик и стоимость.

Решение числовых задач

Когда вы определились с методом компенсации холодного спая, скомпенсированное выходное напряжение должно быть преобразовано в данные о температуре. Самый простой метод – воспользоваться таблицами, предоставленными Национальным Бюро Стандартов США (NBS) (значения расчетных коэффициентов можно найти в справочной литературе, базирующейся на ГОСТ Р 8.585-2001 ГСИ. «Термопары. Номинальные статические характеристики преобразования»). Поиск данных в этих таблицах программным путем требует определенного объема памяти для их хранения, но это быстрое и точное решение в случаях, когда измерения повторяются с большой частотой. Два других метода для преобразования напряжения в данные требуют больших ресурсов, чем поиск данных в таблицах: 1) линейная аппроксимация с помощью полиномов; 2) аналоговая линеаризация выходного сигнала термопары.

Линейная аппроксимация программным путем популярна, т.к. необходима память только для хранения заранее известных коэффициентов полинома. Недостаток этого метода в том, что время измерения зависит от скорости расчета полиномов высокой степени. Время на расчет растет с возрастанием степени полинома, что обычно происходит при увеличении диапазона измерений прибора. Для температур, при измерении которых требуется использование полиномов высоких степеней, применение таблиц может оказаться более эффективным и точным.

До того, как появилось программное обеспечение современного уровня, аналоговая линеаризация достаточно часто применялась для преобразования напряжения в температурные данные (в дополнение к ручному поиску данных в таблицах). Этот аппаратный метод основывался на использовании аналоговых схем для корректировки нелинейности сигнала термопары. Точность зависела от реализации аналоговой корректировки. Такой подход до сих пор используется в мультиметрах, принимающих сигнал с термопар.

РАЗДЕЛ 7: Датчики температуры

РАЗДЕЛ 7: ДАТЧИКИ ТЕМПЕРАТУРЫ

Уолт Кестер, Джеймс Брайнт, Уолт Юнг

!Работа термопар и компенсация температуры холодного спая

!Резистивные датчики температуры

!Термисторы

!Полупроводниковые датчики температуры

!Мониторинг температуры микропроцессоров

Введение

В современных электронных устройствах измерение температуры чрезвычайно важно, особенно если речь идет о дорогих малогабаритных компьютерах или других портативных устройствах с плотно упакованными электронными компонентами, которые рассеивают заметную мощность в виде тепловой энергии. Знание температуры системы можно также использовать для управления зарядом аккумуляторных батарей и для предотвращения повреждения дорогостоящих микропроцессоров.

Портативное высоко потребляющее оборудование часто имеет охлаждающий вентилятор для поддержания внутренней температуры на нужном уровне. Для того чтобы продлить жизненный цикл аккумуляторных батарей, вентилятор должен работать только тогда, когда это необходимо. Точное управление работой вентилятора требует знания критических температур, которые измеряются с помощью соответствующих датчиков температуры.

♦Для мониторирования (наблюдения)

♦Портативного оборудования

♦Температуры центрального процессора

♦Температуры аккумуляторной батареи

♦Температуры окружающей среды

♦Для компенсации

♦Для компенсации дрейфа генератора в сотовых телефонах

♦Для компенсации температуры холодного спая термопар

♦Для управления

♦Зарядом аккумуляторной батареи

♦Управление процессом удержания температуры

Рис.7.1. Применение датчиков температуры.

Точные измерения температуры требуется и для других приложений, таких как управление технологическими процессами и специальный инструментарий. В большинстве случаев, вследствие малых выходных сигналов и их нелинейности, выходные сигналы с датчиков должны быть отнормированы соответствующим образов и усилены перед тем как выполнять их последующую обработку.

©АВТЭКС Санкт-Петербург (812) 567-7202, http://www.autexspb.da.ru, E-mail: [email protected] Автор перевода: Горшков Б.Л.

Термопары и компенсация холодного спая

Лекция 7. Датчики температуры

7.1. Общие сведения

7.2. Термопары и компенсация холодного спая

7.3. Резистивные датчики температуры

7.4. Термисторы

7.5. Полупроводниковые датчики температуры

7.6. Датчики температуры с цифровым выходом

7.7. Термореле и регуляторы с установкой температуры

Общие сведения

Различают следующие датчики и направления при построении температурных контрольно-измерительных устройств:

для мониторирования (наблюдения)

• портативного оборудования,

• температуры центрального процессора,

• температуры аккумуляторной батареи,

• температуры окружающей среды; для компенсации

• дрейфа генератора в сотовых телефонах,

• температуры холодного спая термопар; для управления

• зарядом аккумуляторной батареи,

• процессом удержания температуры.

Практически все температурные датчики достаточно нелинейны, исключение составляют интегральные датчики. Резистивные датчики достаточно точны, но требуют внешнего тока возбуждения и, следовательно, оптимальной схемой включения такого датчика будет мостовая схема. Термисторы наиболее чувствительны, но и наиболее нелинейны. Полупроводниковые датчики температуры являются самыми точными, но имеют узкий диапазон применения (от –55 °С до +150 °С).

Таблица 2.5 Типы датчиков температуры

Термопары	РДТ	Термисторы	Полупроводниковые датчики температуры
Самый широкий диапазон температур (от –184 °С до +2300 °С)	Диапазон от –200 °С до +850 °С	Диапазон от 0 °С до +100 °С	Диапазон от –55 °С до +150 °С
Высокая точность и повторяемость	Высокая линейность	Низкая линейность	Линейность 1 °С Точность 1 °С
Необходимость компенсации холодного спая	Требует внешнего возбуждения	Требует внешнего возбуждения	Требует внешнего возбуждения
Низкое выходное напряжение	Низкая стои- мость	Высокая чувствительность	Типовой выходной сигнал 10 мВ/К, 20 мВ/К или 1 мА/К

В табл. 2.5 приведены наиболее популярные типы температурных датчиков.

Термопары и компенсация холодного спая

Термопары являются относительно недорогими датчиками, причем они функционируют в широком диапазоне температур, а при измерении высоких температур (до + 2300 °С) и в агрессивных средах термопары практически незаменимы. Тем не менее они дают на выходе милливольтные сигналы и требуют точного усиления для проведения дальнейшей их обработки. Еще одним недостатком при применении термопар является компенсация температуры холодного спая (см. ниже). Как правило, термопары достаточно линейны. Наиболее известные термопары приведены в табл. 2.6, а на рис. 2.17 показаны кривые зависимости напряжения от температуры для трех широко используемых термопар.

Термопары изготавливают из следующих металлов: железо, платина, родий, рений, вольфрам, медь, алюмель (сплав никеля и алюминия), хромел (сплав никеля и хрома) и константан (сплав меди и никеля).

Рассмотрим основы функционирования термопар. Известно, что при соединении двух разнородных металлов при температуре выше абсолютного нуля между ними появляется разность потенциалов (термоЭДС), которая является функцией температуры спая (соединения) (рис. 2.17, а). Другими словами, каждая пара разнородных металлов, находящихся в контакте друг с другом, генерирует термоэлектрическую ЭДС.

Таблица 2.6 Термопары

Материал контакта	Типовой температурный диапазон, °С	Номинальная чувствительность, мкВ/°С	Обозначение по ANSI
Платина (6 %) Родий-платина (30 %) Родий	От 38 до 1800	7.7	B
Вольфрам (5 %) Рений-вольфрам (26 %) Рений	От 0 до 2300		C
Хромел-константан	От 0 до 982		E
Железо-константан	От 0 до 760		J
Хромел-алюмель	От –184 до 1260		K
Платина (13 %) Родий-платина	От 0 до 1593	11,7	R
Платина (10 %) Родий-платина	От 0 до 1538	10,4	S
Медь-константан	От 184 до 400		T

Металл А Металл А

V1 V1 V2 а в

R

Металл А Металл А

V1 V2 V1 V2

R = полное сопротивление цепи V = (V1 — V2), если Т3 = Т4

I = (V1 — V2) / R г _б

Рис. 2.17. Основы работы термопары: а – термоэлектрическое напряжение; б – термопара; в – измерение с помощью термопары; г – измерение с помощью термопары

Для того чтобы сформировать два спая (рис. 2.17, б), соединим между собой два термопарных провода с обоих концов. Если оба спая находятся при различных температурах, то в цепи появится результирующая ЭДС и потечет ток, определяемый величиной ЭДС и полным сопротивлением цепи. Если разорвать один из проводов, то напряжение в точках разрыва будет равно величине результирующей термоЭДС в цепи, и если измерить это напряжение, то можно использовать его для расчета разности температур двух спаев

(рис. 2.17, в) [8].

Примечание. Термопара измеряет разницу температур двух спаев, а не абсолютную температуру одного из спаев.

Замер температуры на измерительном спае можно проводить только в том случае, если известна температура другого спая (называемого часто опорным или холодным спаем).

Подключим вольтметр к цепи термопар (рис. 2.17, г). В местах подключения образуются дополнительные термопары из проводов вольтметра и проводов цепи. Если эти подключения находятся при разных температурах, то они будут вносить ошибки.

Следовательно, необходимо, чтобы все пары контактов в цепи, содержащей термопару, находились при одной и той же температуре, кроме, разумеется, измерительных контактов термопар.

Термопары не требуют внешнего возбуждения. Как правило, для измерения используются два спая (рис. 2.18): Т1 – измерительный спай и Т2 – опорный (холодный) спай. Если Т1 = T2,то V1= V2и выходное напряжение V = 0. Выходные напряжения термопар определяются по отношению к температуре опорного спая при 0 °С (см. рис. 2.18).

Именно отсюда произошел термин холодный спай или спай точки таяния льда. Из вышеизложенного следует, что термопара дает выходное напряжение 0 В при температуре измерительного спая 0 °С. Однако необязательно иметь температуру холодного спая, равную 0 °С. Достаточно знать его текущую температуру (рис. 2.19). На рисунке показано, что вместо ванны таящего льда используется другой температурный датчик, который измеряет температуру холодного спая, и его сигнал используется для введения напряжения в измерительную цепь термопары. Этот сигнал компенсирует разницу между действительной температурой холодного спая и ее идеальной величиной (0

°С).

На практике используют компесационные коэффициенты термопар для определения величины выходного напряжения (V = K·Т2). Таким образом, расчет напряжения термопары с температурой ее измерительного спая Т °С и опорного спая при температуре 0 °С производится при помощи полинома V = K1·Т + K2·–Т² + K3·Т³+ … . Следует учесть, что величины коэффициентов K2, K3и т. д. весьма малы для большинства известных типов термопар.

Как правило, для компенсации холодного спая свободные концы термопары устанавливаются в специальном изотермическом блоке (рис. 2.20).

Рис. 2.18. Классическая компенсация температуры холодного спая при использовании опорного спая, находящегося при температуре таяния льда (0 °С)

Vcomp = f(T2)

Vout= V(T1) — V(T2) + Vcomp

еслиVcomp = V(T2) — V(0°C), тоVout= V(T1) — V(0°C)

Рис. 2.19. Использование датчика температуры для компенсации холодного спая

Рассмотрим схему сопряжения микропроцессорной системы с термопарой типа К (рис. 2.21). Здесь обеспечивается компенсация холодного спая для температур от 0 °С до 250 °С [9]. Схема работает от одного источника питания от +3,3 В до +12 В и формирует передаточную характеристику выходного напряжения 10 мВ/°С. Термопара типа К имеет коэффициент Зеебека приблизительно 41 мкВ/°С (см. ниже), поэтому на холодном спае устанавливается датчик температуры с температурным коэффициентом 10 мВ/°С – микросхема ТМР35. Он используется совместно с делителем R1и R2 для того, чтобы ввести компенсирующий температурный коэффициент холодного спая противоположного знака величиной –41мкВ/°С.

Рис. 2.20. Установка термопарных проводников непосредственно в изотермическом блоке

Указанное включение препятствует появлению ошибки измерения температуры, обусловленной непосредственным соединением между проводниками термопары и трассами печатных проводников платы. Данная компенсация работает исключительно хорошо в диапазоне температур окружающей среды от 20 °С до 50 °С.

По диапазону измерения 250 °С термопара дает изменение выходного напряжения в 10.151 мВ. Поскольку требуемое изменение выходного сигнала по верхнему пределу составляет 2.5 В, усиление в цепи будет 246.3. Выбор R4 = 4.99 кОм даст величину К5 = 1.22 MОм. Поскольку ближайшая величина 1 % резистора R5составляет 1.21 MОм, используется дополнительный потенциометр 50 кОм для точной настройки выходного напряжения по верхнему пределу. Интегральная схема ОР193 является операционным усилителем с однополярным питанием, его выходной каскад не работает в режиме от питания до питания, и его выходной сигнал доходит только до потенциала +0.1 В относительно земли. По этой причине для смещения выходного напряжения приблизительно на 0.1 В устанавливается дополнительный резистор R3на источник питания 5 В. Это напряжение смещения (10 °С) вычитается при расчетах результатов измерений. Резистор R3также обеспечивает определение обрыва цепи термопары, устанавливая величину выходного напряжения больше 3 В, если термопара оборвана. Резистор R7балансирует входной импеданс операционного усилителя ОР193, а пленочный конденсатор 0.1 мкФ уменьшает величину шума на неинвертирующем входе.

Зарубежной промышленностью выпускаются интегральные схемы инструментальных усилителей с компенсацией холодного спая. Например, ИС AD594/AD595 от AnalogDevices (рис. 2.22) [9]. Он включает в себя компенсатор холодного спая на температуру таяния льда и калиброванный усилитель с непосредственным подключением к выходу термопары и выходным сигналом высокого уровня (10 мВ/°С). Переключение перемычек на выводах установки режима позволяет использовать ИС в качестве линейного усилителя-компенсатора или релейного регулятора температуры, использующего фиксированное значение или дистанционное управление точкой установки температуры. ИС можно использовать для прямого усиления напряжения компенсации, получая тем самым отдельный преобразователь температуры в градусах Цельсия с выходным сигналом 10 мВ/°С. Важно помнить, что ЧИП ИС был при той же самой температуре, что и холодный спай термопары, что обычно достигается установкой их обоих в непосредственной близости друг от друга и изолированием от источников тепла.

Рис. 2.21. Использование датчика температуры (ТМР35) для компенсации холодного спая термопары

Более совершенные ИС AD596/AD597 являются релейными регуляторами с установкой температуры, которые используются при высоких температурах, например в устройствах, связанных с управлением печами. Для получения внутреннего сигнала, пропорционального температуре, устройство выполняет компенсацию холодного спая и усиливает сигналы термопар типа

J/K [10].

Рис. 2.22. Монолитные усилители термопар AD594/AD595 с компенсацией холодного спая

Рис. 2.23. АЦП семейства AD77XX, используемый совместно с температурным датчиком ТМР35 для компенсации температуры холодного спая

Рис. 2.24. Выходные напряжения для термопар типов J, К, S

Рис. 2.25. Зависимость коэффициента Зеебека для термопары от температуры

Однако вышеперечисленные устройства не производят компенсацию нелинейности термопар (рис. 2.24). Для компенсации нелинейности термопары рекомендуется использовать высокоточный АЦП и последующую программную обработку сигнала. На рис. 2.23 представлена микропроцессорная система, предназначенная для квантования напряжения с термопары. Для анализа выхода температурного датчика холодного спая используются два мультиплексных входа АЦП. Входной усилитель программируется на усиление от 1 до 128, а разрешение АЦП составляет от 16 до 22 разрядов (в зависимости от выбранного конкретного АЦП). Микроконтроллер выполняет арифметические действия по компенсации температуры холодного спая и линеаризации характеристики термопары [11].

Известно, что коэффициент Зеебека (изменение выходного напряжения при изменении температуры чувствительного спая) меняется с температурой измерительного спая, поэтому при выборе термопары для выполнения измерений в заданном диапазоне температур необходимо выбирать термопару, коэффициент Зеебека которой в меньшей степени меняется в заданном рабочем диапазоне (рис. 2.25) [8].

Например, для измерения температуры в диапазоне от 200 °С до 500 °С необходимо применять термопару J-типа, так как она имеет коэффициент Зеебека, меняющийся менее чем на 1 мкВ/°С в данном промежутке.

Компенсация холодного спая термопары | Уголок радиолюбителя

В предыдущей статье мы рассмотрели принцип работы термопары, и в частности метод измерения температуры с использованием «холодного спая» эталонного показателя. Устранение из системы измерения «холодного спая» и соответствующих ему контактов очень желательно в большинстве случаев применения, в частности для промышленных систем.

Это не только упрощает использование термопары, но также исключает необходимость обращения с потенциально большим количеством дополнительных входных каналов сбора данных и считывания датчиков отсчета.

Компенсация холодного спая термопары

Первое предположение, которое можно сделать, это то, что измерительный прибор термопары или плата сбора данных должны быть разработаны и построены таким образом, чтоб их внутренние цепи имели соответствующую термоэлектрическую компенсацию электромагнитных полей.

Затем можно сосредоточиться на том, что происходит между входом измерителя и термопарой. Основной причиной погружения датчика в ледяную ванну — получение на стыке известную температуру (0°C). Однако любая температура была бы хорошая, если только она была бы известна.

Из рисунка 1 (в предыдущей статье) следует, что подключение термопары к входам вольтметра, приводит к образованию дополнительных контактов в цепи в точках соединений, и каждое из них может также генерировать и термоэлектрическое электромагнитное поле. В случае идеальной насадки эти (J2 и J3) будут иметь одинаковую температуру.

Этого можно достичь путем размещения их в изотермическом корпусе (рис. 2а).

В свою очередь, мы можем переместить эталонный датчик вне ледяной ванны, в изотермический блок (рисунок 2b). Благодаря этому концы прибора и эталонного датчика (J2, J3 и J4) имеют одинаковую температуру. Эта температура может быть измерена через бесконтактный датчик, такой как термистор или полупроводниковый датчик температуры, находящийся в контакте с изотермическим блоком.

Последний шаг упрощения измерительной цепи термопары является удаление отрезка провода линии 2 от контакта (J4) к входу прибора (J3). Закон о промежуточных металлах гласит, что размещение третьего металла между двумя различными металлическими контакта термопары не влияет на выходное напряжение, пока два контакта, образованные дополнительным металлом имеют одинаковую температуру.

Так как эти контакты находиться в изотермическом блоке, то их температура одинакова. В этом случае датчик термопары можно представить себе, соединение медь и линия 1, с линией 2 в качестве промежуточного металла

Кинев В.К вопросу о компенсации температуры холодного спая при измерении температуры с помощью термопар

Квопросу о компенсации температуры холодного спая при измерении температуры с помощью термопар

Василий Кинёв, Сергей Рогожников

В статье рассматривается методика компенсации температуры холодного спая при преобразовании измеренной модулем аналогового ввода программируемого контролера термо-ЭДС термопары в значение измеряемой температуры нагретого тела. Также рассмотрен пример построения библиотечного FBD-блока для измерения температуры c помощью термопары с НСХ XK(L) в программном пакете UltraLogik для модуля аналогового ввода ADAM-5018

Введение

Несколько лет назад у одного из авторов статьи состоялась беседа со специалистом по метрологии, во время которой он рассказал, что на их предприятии внедряется система автоматизации и КИП одного из технологических процессов производства меди на основе программируемых контроллеров. При метрологической проверке каналов измерения температуры с помощью термопар с НСХ XK(L) обнаружена ошибка в измерении, которая в диапазоне до 6000С достигала 80С. Позднее, при разработке FBD-библиотеки для разработки систем автоматизации и КИП с использованием программируемых в программном пакете UltraLogik контроллеров ADAM-5510, мы обнаружили одну методическую неточность в прилагаемой с пакетом FBD-библиотеке «ADAM», касающуюся компенсации температуры холодного спая. Это и явилось причиной написания данной статьи.

Коротко о явлении Зеебека

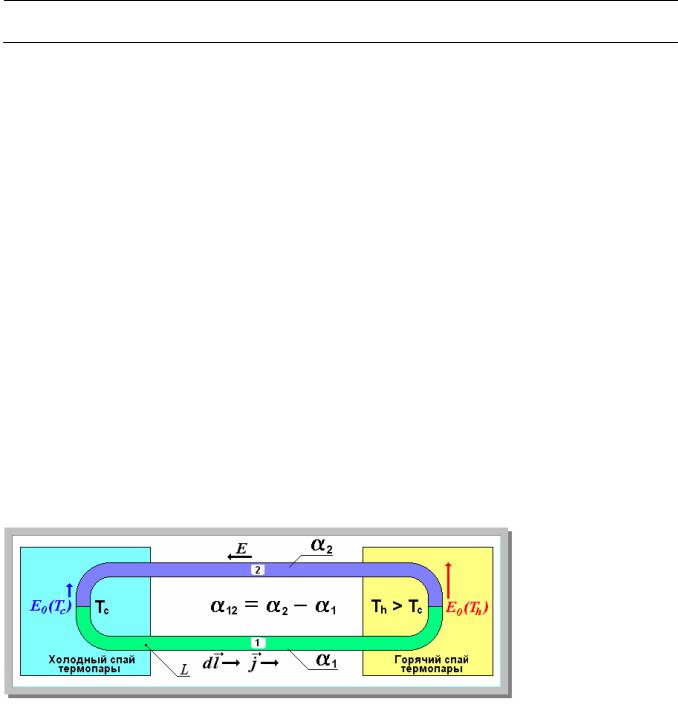
Измерение температуры нагретых тел с помощью термопар основано на физическом явлении, открытом в 1821 году Зеебеком (T.Seebeck). Явлением Зеебека называют возникновение электродвижущей силы Е в замкнутой электрической цепи, составленной из последовательно соединенных разнородных проводников, если места их контакта (спаи) поддерживают при разных температурах. Величину Е называют термо-ЭДС [1]. На рисунке №1 изображена электрическая цепь, составленная из проводников различных материалов 1 и 2. Спаи находятся при температурах

Tc и Th>Tc. Такая цепь называется термоэлементом или термопарой.

Рисунок №1. Иллюстрация к явлению Зеебека (направления E0 указаны в предположении Th>Tc>00C).

Из теории термоэлектрических явлений известно, что выражение для вектора плотности электрического тока j в отсутствие магнитного поля имеет вид [1]:

j = -(α grad T + grad(ϕ – µ/e))/ρ (1)

Здесь: T — температура,

e — модуль электрического заряда электрона, ρ — удельное сопротивление, α — удельная термоэлектродвижущая сила,

µ — химический потенциал электронов,

ϕ — электрический потенциал,

(µ — eϕ) — электрохимический потенциал.

Закон Ома для контура L: E = IR; отсюда дифференциал dE = IdR = jS(ρ/S)dl = ρ(jdl) (S – площадь сечения проводника, dl – дифференциал длины контура). Следовательно, для нахождения E нужно взять криволинейный интеграл от ρj по dl, обойдя замкнутый контур L против часовой стрелки.

			r	= ∫ρ rj dlr = −∫α gradT dlr+				∫grad (µ −eϕ)dlr =
	E = ∫IdR = ∫(S rj )ρdl						1
	L	L	S	L	L		e	L
	= −∫α			T	T	T			T
		∂T dl +0 = −∫α dT = −∫h			α1 dT − ∫c α2 dT =∫h (α2 −α1 )dT =∫h α12 dT =
	L	∂l	L	T	T	T			T
				c	h	c			c
	T	T				E0 (T ) = T∫α12 dT ,					dE0
	= ∫h α12 dT − ∫c α12 dT =E0 (Th ) −E0 (Tc ), где:								α12	=
											dT
	0	0						0

В выражении (1) криволинейный интеграл от второго слагаемого будет равен нолю, так как электрохимический потенциал – функция непрерывная, а интеграл по замкнутому контуру от градиента непрерывной функции равен нолю. В интеграле от первого слагаемого составляющие градиента в плоскости сечения проводников равны нолю и (grad T).dl = (дT/дl)dl = dT. В результате интегрирования по замкнутому контуру L получаем формулу для вычисления E:

E = E0(Th) – E0(Tc), (2)

где: E0 = f(T) – функция, являющаяся интегралом от α12 = α2 – α1 по dT с переменным верхним пределом, равным T, при нижнем пределе интегрирования, равном 00С.

В свою очередь α12 = dE/dT является функцией температуры и зависит от сочетания материалов 1 и 2. Приближенные значения α12 для некоторых материалов для температур, близких к 00С, приведены в таблице №1, когда вторым электродом термопары является свинец [2]. Знак «плюс» указывает, что у спая с большей температурой ток направлен в сторону от свинцового проводника к проводнику из таблицы, при знаке «минус» — в обратном направлении.

Таблица№1. Приближенные значения удельных термоэлектродвижущих сил некоторых проводников относительно свинца при 0…1000С [2].

	Проводник	α12, мкВ/0С
	Свинец	0
	Медь	+3,2
	Серебро	+2,7
	Никель	-20,8
	Железо	+15,0
	Платина	-4,4
	Аллюмель	-17,3
	Копель	-38,0
	Хромель	+24,0
	Платинородий	+2,0

Значения функций E0 = f(T), называемых номинальными статическими характеристиками преобразования (НСХ), для различных типов термопар, применяемых в практике измерения температуры, затабулированы в ГОСТ 3044-84 [3]. Там же приводятся коэффициенты an полиномиальной аппроксимации данных функций E0 = f(T) = Σ an Tn. На рисунке №2 приведены графики для E0(T) и α12(T) для хромель-копелевой термопары XK(L).

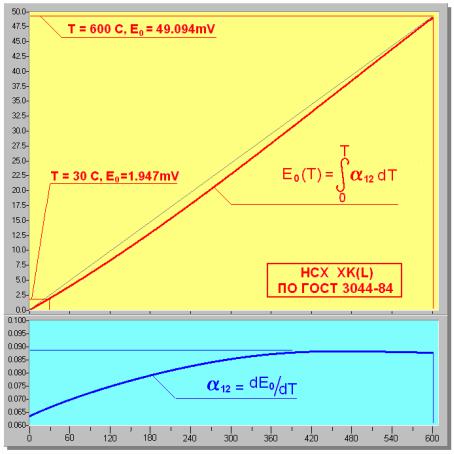
Рисунок №2. Графики зависимости E0(T) и α12(T) для хромель-копелевой термопары XK(L).

Рассмотрим пример хромель-копелевой термопары XK(L). Какова будет термо-ЭДС E, если спаи термопары находятся при температурах: Th = 6000C, Tc = 300C?

Согласно ГОСТ 3044-84: E0(600) = 49,094мВ, E0(30) = 1,947мВ, следовательно, термо-ЭДС при данных температурах спаев E = 49,094 – 1,947 = 47,147мВ.

Измерение температуры с помощью термопар

Важным для нас является следующее свойство явления Зеебека [1]: если в разрыв одной из ветвей термоэлемента (термопары) включить последовательно любое количество проводников другого состава, все спаи которых находятся при одной и той же температуре, то термо-ЭДС в такой цепи будет равна термо-ЭДС исходного термоэлемента (термопары). Это свойство позволяет нам включить в цепь термопары, со стороны холодного спая, какой-либо измерительный прибор для измерения термо-ЭДС E: милливольтметр, АЦП модуля аналогового ввода контроллера и так далее.

Поставим задачу: известен тип термопары (известна функция E0 = f(T)), известно (измерено) значение термо-ЭДС Е, известна (измерена) температура холодного спая Tc; как вычислить температуру горячего спая Th?

Вернемся к соотношению (2) E = E0(Th) – E0(Tc), которое разрешим относительно E0(Th): E0(Th) = E + E0(Tc). Нам известна по ГОСТ 3044-84 функция E0 = f(T) = Σ an Tn, следовательно, E0(Tc) мы можем вычислить и правая часть E + E0(Tc) будет известна. Располагая табличными значениями функции E0 = f(T), можно, например, методом наименьших квадратов построить полиномиальную аппроксимацию обратной к ней функции T = f -1(E0) = Σ bk E0k. Такие полиномы для применяющихся в практике термопар построены, в частности, в библиотеке «Нормализаторы» программного пакета UltraLogik. Таким образом, мы можем вычислить Th по формуле:

Th = f -1(E0(Th)) = f -1(E + E0(Tc)) = Σ bk (E + Σ an Tcn)k

(3)

Данная формула лежит в основе вычисления температуры горячего спая термопары с помощью измерения термо-ЭДС термопары и температуры холодного спая термопары.

Вернемся к рассмотренному ранее примеру хромель-копелевой термопары XK(L): предположим, что мы измерили термо-ЭДС E = 47,147мВ, измерили температуру холодного спая Tc = 300C. Какова температура Th горячего спая?

Находим E + Σ an Tcn = 47,147 + 1,947 = 49,094мВ. Отсюда: Th = f -1(49,094) = 6000C.

Пусть функция E0 = f(T), график которой проходит через начало координат, пренебрежительно мало отличается от линейной функции. Тогда и график функции T = f -1(E0) также проходит через начало координат, и пренебрежительно мало отличается от прямой линии. В этом случае можно приближенно предположить:

Th = f -1(E0(Th)) = f -1(E + f (Tc)) = f -1(E) + f -1( f (Tc)) = f -1(E) + Tc = Σ bk Ek + Tc

(4)

Если это свойство распространить на функции, график которых значительно отличается от прямой линии, то использование формулы (4) приведет к неоправданной погрешности вычислений.

Еще раз вернемся к рассмотренному выше примеру с XK(L): E = 47,147мВ, Tc = 300C. Если применить формулу (4), то получим: Th = f -1(47,147) + 30 = 577,82 + 30 = 607,820С.

Ошибка составляет: ∆Th = 7,820C (δTh = 1,3%). Полагаем, что это как раз те восемь градусов, о которых упоминалось в начале данной статьи.

FBD-блок для термопары XK(L) для ADAM-5018

Рассмотрим пример построения в программном пакете UltraLogik библиотечного FBDблока для хромель-копелевой термопары с НСХ XK(L) по ГОСТ 3044-84. Блок построен на основании формулы (3). Коэффициенты bk взяты из библиотеки «Нормализаторы». Для нахождения E0(Tc) построен полином второй степени, так как в интервале -20…+500С он дает результаты с хорошей точностью и нет необходимости использовать из ГОСТ 3044-84 полином восьмой степени, построенный для температур –200…+8000С.

Таблица №2. Сравнение полинома E0(Tc) = Tc (0,06325 + 0,000055 Tc) с данными из [3].

	Tc	E0	E0	∆E0
		[3]	Вычисл.
	0С	мВ	мВ	мВ
	-20	-1,240	-1,2430	-0,0030
	-10	-0,626	-0,6270	-0,0010
	0	0,000	0,0000	0,0000
	5	0,318	0,3176	-0,0004
	10	0,638	0,6380	0,0000
	15	0,961	0,9611	0,0001
	20	1,287	1,2870	0,0000
	25	1,616	1,6156	-0,0004
	30	1,947	1,9470	0,0000
	35	2,282	2,2811	-0,0009
	40	2,618	2,6180	0,0000
	45	2,957	2,9576	0,0006
	50	3,299	3,3000	0,0010

Реализация и внешний вид FBD-блока SENSOR_ТС_L показан на рисунке №3.

Блок предназначен для измерения температуры в интервале 0…6000C термопарой ХK(L) с помощью модуля ADAM-5018, сконфигурированного под биполярный сигнал с разрешением 16bit. Входы и выходы блока:

Inp (INTEGER)	— вход кода с модуля ADAM-5018,
Gnf (INTEGER)	— коэффициент усиления конфигурации модуля ADAM-5018,

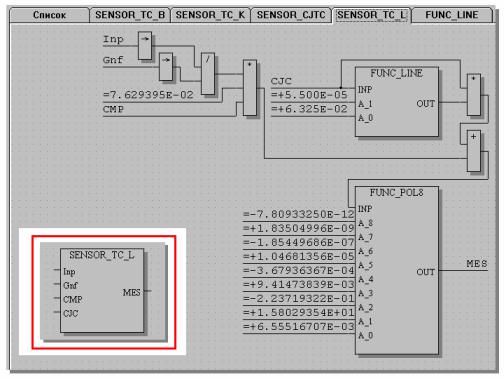
CMP (FLOAT)	— коэффициент коррекции преобразования напряжения в код,
CJC (FLOAT)	— температура холодного спая в 0С,
MES (FLOAT)	— температура горячего спая в 0С.

Использованные здесь библиотечные блоки FUNC_LINE и FUNC_POL8 вычисляют значение линейной функции y = a0+a1x и значение полинома 8 степени y = a0+a1x +…+a8x8 соответственно и в пояснениях не нуждаются.

Gnf не рекомендуется выбирать больше 16, так как при этом напряжение с датчика температуры холодного спая модуля ADAM-5018 может выйти за пределы шкалы преобразования. CMP – это аналог настроечного резистора в приборах. При правильно откалиброванном модуле СМР = 1. Если же есть некоторое отклонение при преобразовании напряжения в код, то его можно компенсировать, вводя значение близкое к единице (но у нас не возникала необходимость в этом). Блок для измерения температуры холодного спая мы не обсуждаем, так как реализация такого блока для модуля ADAM-5018 приведена в библиотеке «ADAM» пакета UltraLogik.

Рисунок №3. Реализация и внешний вид блока SENSOR_TC_L.

Заключение

Мы ограничились примером FBD-блока для хромель-копелевой термопары. Для термопары ХА(К) при измерении температур до 10000С ошибка при применении формулы (4) незначительна.

В случае платино-родиевой термопары с НСХ ПР(В) компенсацию выполнять не целесообразно, поскольку в интервале температур 0…530С E0(T) принимает значения разного знака и не выходит за пределы интервала -0,003…+0,003мВ. Тем более, если ее выполнить по формуле Th = Σ bk Ek + Tc, то это может привести к погрешности до 4%.

Действительно, пусть термо-ЭДС E = 4,833мВ, Tc = 400С. Так как E0(40) = 0,000мВ [3], то по формуле (3) Th = Σ bk (E + 0)k = Σ bk Ek = 10000С; если же мы воспользуемся приближенной формулой (4) Th = Σ bk Ek + Tc = 1000 + 40 = 10400С, то ошибка преобразования составит неприемлемое значение δ = 100.(1040-1000)/1000 = 4%.

Отсюда следует, что при разработке программ контроллеров в части измерения температуры с помощью термопар, к каждому типу термопар следует подходить индивидуально, исследуя его номинальную статическую характеристику, в нашем обозначении функцию E0 = f(T), в том диапазоне температур, в котором нужно будет вести измерения.

Литература

1.Яворский Б.М., Детлаф А.А. Справочник по физике для инженеров и студентов. Издание шестое: Издательство «Наука», М., 1974.

2.Физический энциклопедический словарь. Том пятый: Издательство «Советская энциклопедия», М., 1966

3.ГОСТ 3044-84. Преобразователи термоэлектрические. Номинальные статические характеристики преобразования: Издательство стандартов, М., 1987