Законы Кирхгофа для расчёта электрических цепей
При расчёте электрических цепей, в том числе для целей моделирования, широко применяются законы Кирхгофа, позволяющие полностью определить режим её работы.
Прежде чем перейти к самим законам Кирхгофа, дадим определение ветвей и узлов электрической цепи.
Ветвью электрической цепи называется такой её участок, который состоит только из последовательно включённых источников ЭДС и сопротивлений, вдоль которого протекает один и тот же ток. Узлом электрической цепи называется место (точка) соединения трёх и более ветвей. При обходе по соединённым в узлах ветвям можно получить замкнутый контур электрической цепи. Каждый контур представляет собой замкнутый путь, проходящий по нескольким ветвям, при этом каждый узел в рассматриваемом контуре встречается не более одного раза [1].
Первый закон Кирхгофа применяется к узлам и формулируется следующим образом: алгебраическая сумма токов в узле равна нулю:
∑i = 0,
или в комплексной форме
∑I = 0.
Второй закон Кирхгофа применяется к контурам электрической цепи и формулируется следующим образом: в любом замкнутом контуре алгебраическая сумма напряжений на сопротивлениях, входящих в этот контур, равна алгебраической сумме ЭДС:
∑Z ∙ I = ∑E.
Количество уравнений, составляемых для электрической цепи по первому закону Кирхгофа, равно Nу – 1, где Nу – число узлов. Количество уравнений, составляемой для электрической цепи по второму закону Кирхгофа, равно Nв – Nу + 1, где
Опишем методику составления уравнений по законам Кирхгофа. Рассмотрим её на примере электрической цепи, представленной на рис. 1.
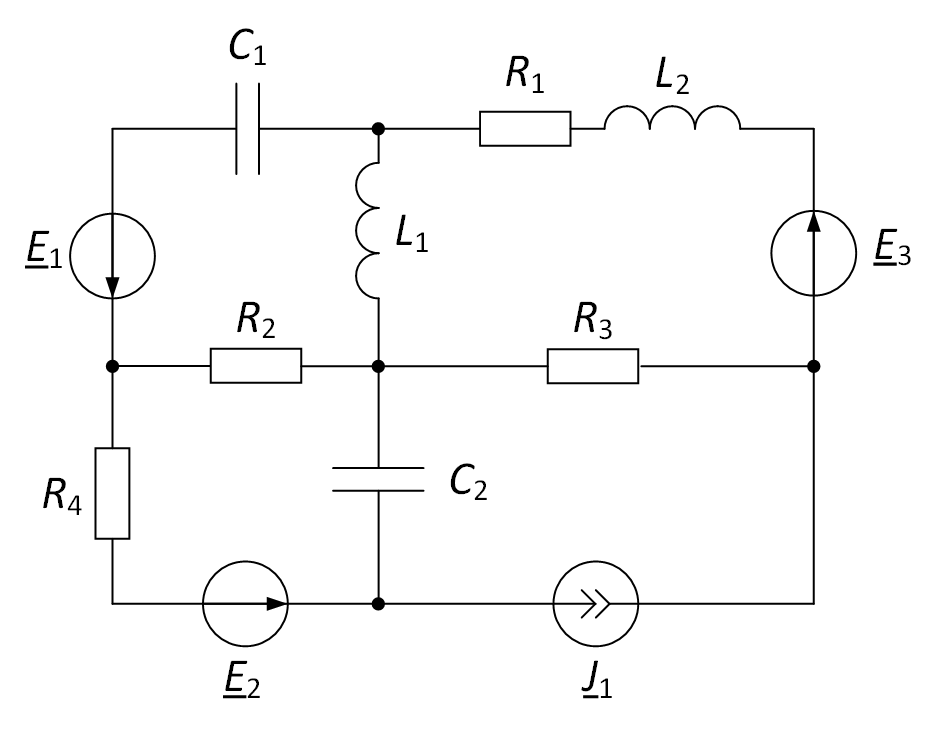
Рис. 1. Рассматриваемая электрическая цепь
Для начала необходимо задать произвольно
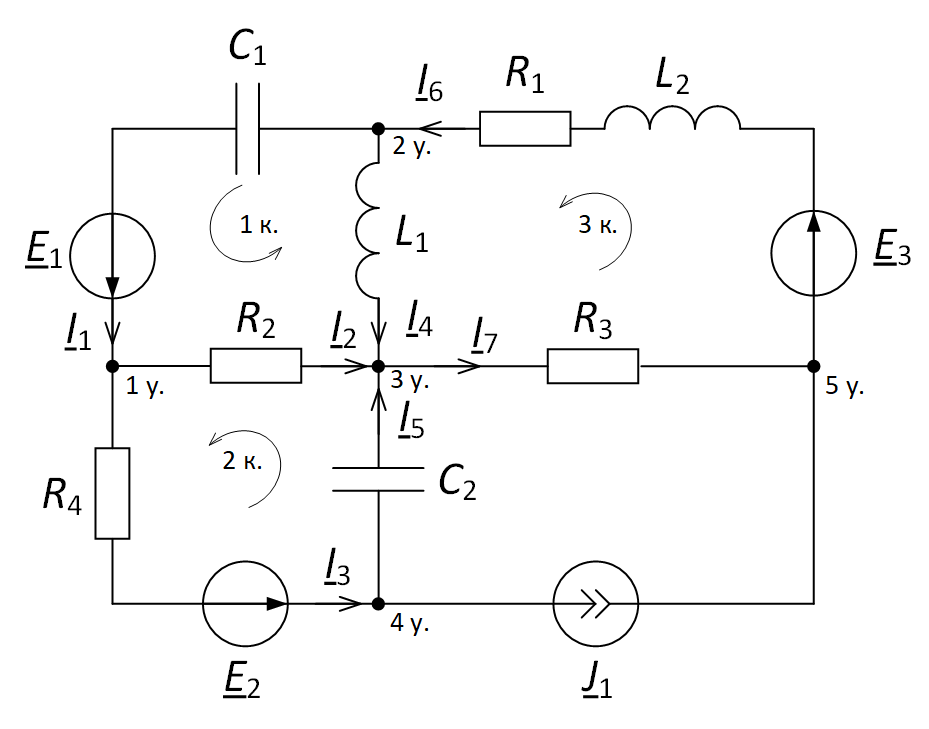
Рис. 2. Задание направления токов и направления обхода контуров для электрической цепи
Количество уравнений, составляемых по первому закону Кирхгофа, в данном случае равно 5 – 1 = 4. Количество уравнений, составляемых по второму закону Кирхгофа, равно 3, хотя «окошек» в данном случае 4. Но напомним, что «окошко», содержащее источник тока J1, не рассматривается.
Составим уравнения по первому закону Кирхгофа. Для этого «втекающие» в узел токи будем брать со знаком «+», а «вытекающие» — со знаком «-». Отсюда для узла «1 у.» уравнение по первому закону Кирхгофа будет выглядеть следующим образом:
I1 – I2 – I3 = 0;
для узла «2 у.» уравнение по первому закону Кирхгофа будет выглядеть следующим образом:
—I1 – I4 + I6 = 0;
для узла «3 у.»:
I2 + I4 + I5 – I
для узла «4 у.»:
I3 – I5 – J1 = 0
Уравнение для узла «5 у.» можно не составлять.
Составим уравнения по второму закону Кирхгофа. В этих уравнениях положительные значения для токов и ЭДС выбираются в том случае, если они совпадают с направлением обхода контура. Для контура «1 к.» уравнение по второму закону Кирхгофа будет выглядеть следующим образом:
ZC1 ∙ I1 + R2 ∙ I2 – ZL1 ∙ I4 = E1;
для контура «2 к.» уравнение по второму закону Кирхгофа будет выглядеть следующим образом:
-R2 ∙ I2 + R4 ∙ I3 + ZC2 ∙ I5 = E2;
для контура «3 к.»:
ZL1 ∙ I4 + (ZL2 + R1) ∙ I6 + R3 ∙ I7 = E3,
где ZC = — 1/(ωC), ZL = ω
Таким образом, для того, чтобы найти искомые токи, необходимо решить следующую систему уравнений:
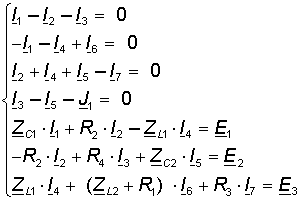
В данном случае это система из 7 уравнений с 7 неизвестными. Для решения данной системы уравнений удобно пользоваться Matlab. Для этого представим эту систему уравнений в матричной форме:
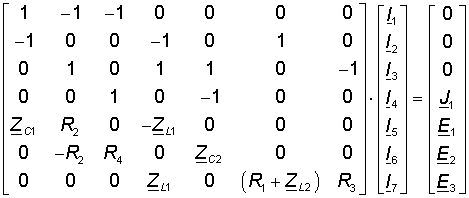
Для решения данной системы уравнений воспользуемся следующим скриптом Matlab:
>> syms R1 R2 R3 R4 Zc1 Zc2 Zl1 Zl2 J1 E1 E2 E3;
>> A = [1 -1 -1 0 0 0 0;
-1 0 0 -1 0 1 0;
0 1 0 1 1 0 -1;
0 0 1 0 -1 0 0;
Zc1 R2 0 -Zl1 0 0 0;
0 -R2 R4 0 Zc2 0 0;
0 0 0 Zl1 0 (R1+Zl2) R3];
>> b = [0;
0;
0;
J1;
E1;
E2;
E3];
>> I = A\bВ результате получим вектор-столбец I
Список использованной литературы
- Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. Учебник для вузов. Изд. 4-е, переработанное. М., «Энергия», 1975.
Рекомендуемые записи
Вопрос 19. Первый закон Кирхгофа, узловые уравнения. Второй закон Кирхгофа, контурные уравнения.
Узел— точка, в которой сходятся не менее 3-х токов.
Ветвь— участок цепи, по которому течёт один и тот же ток.
Контур— любой замкнутый путь в схеме.
Первый закон Кирхгофа
Для любого узла сумма токов, приходящих к узлу, равна сумме токов, отходящих от узла.

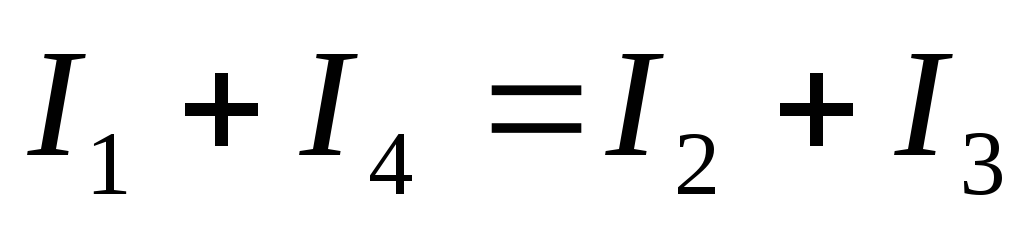
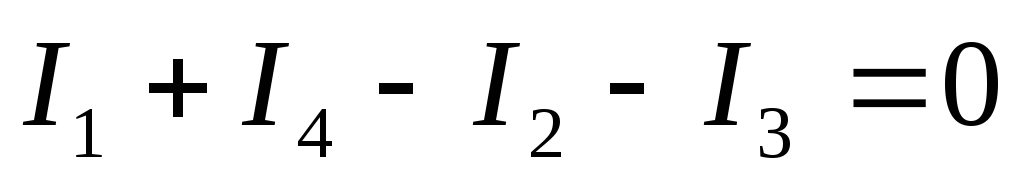
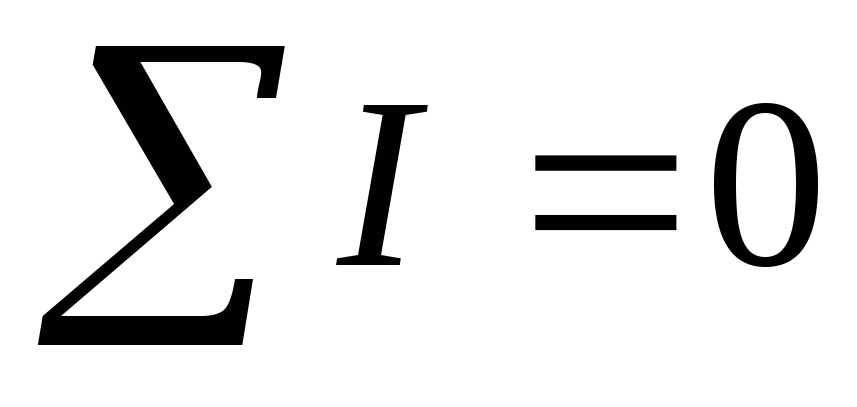
Для любого узла электрической цепи алгебраическая сумма токов равна нулю.
Второй закон Кирхгофа
Для любого замкнутого контура алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на участках этого контура.
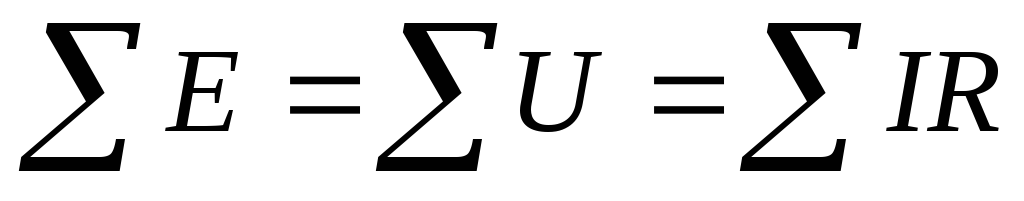
Порядок составления контурных уравнений:
Выбираем произвольное направление тока ветвей.
Если в схеме n узлов, то составляем n – 1 уравнение по первому закону Кирхгофа.
Выбираем произвольное направление обхода контура.
Если направление обхода и ЭДС совпадают, то она входит в уравнение со знаком “+”, если нет — со знаком “–”.
Если ток ветви и направление обхода совпадают, то падение напряжения входит в уравнение со знаком “+”, если нет — со знаком “–”.
Если при расчёте получился отрицательный ток, значит его направление противоположно выбранному.
Задача
С оставить
контурные уравнения для решения сложной
электрической цепи.
оставить
контурные уравнения для решения сложной
электрической цепи.
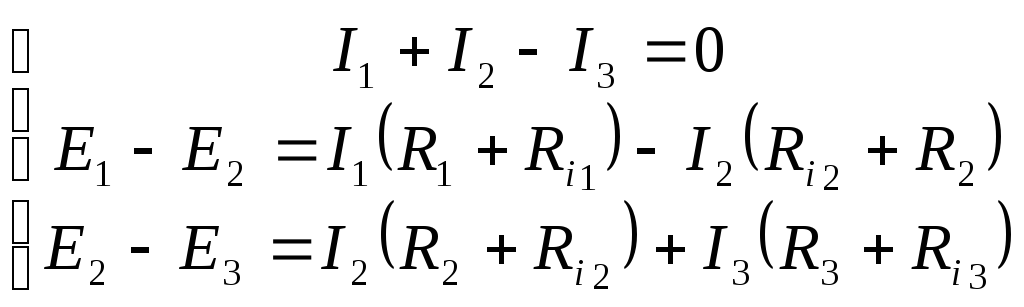
Вопрос 20. Расчёт сложных электрических цепей методом контурных токов.
Метод контурных токовпозволяет решать меньшее количество уравнений, чем при расчёте сложных электрических цепей методом уравнений Кирхгофа.
Порядок расчёта:
Выбираем произвольное направление контурного (расчётного) тока.
Составляем уравнение по второму закону Кирхгофа для контурных токов. При записи учитываем падение напряжения от контурного (собственного) тока и контурных токов соседних контуров.
Решаем полученную систему уравнений и рассчитываем контурные токи.
Рассчитываем действительные токи ветвей по правилу:
Если в ветви течёт один контурный ток, то действительный ток равен контурному току. Если два и более — то действительный равен их алгебраической сумме и направлен в сторону большего.
Задача
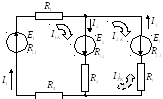
Найти и направить все токи в электрической цепи методом контурных токов.
Используя алгоритм, составляется система уравнений:
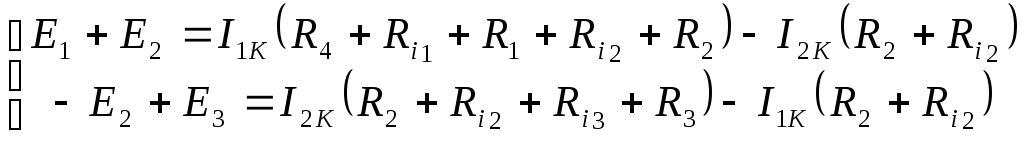
Пусть при решении получили контурные токи:
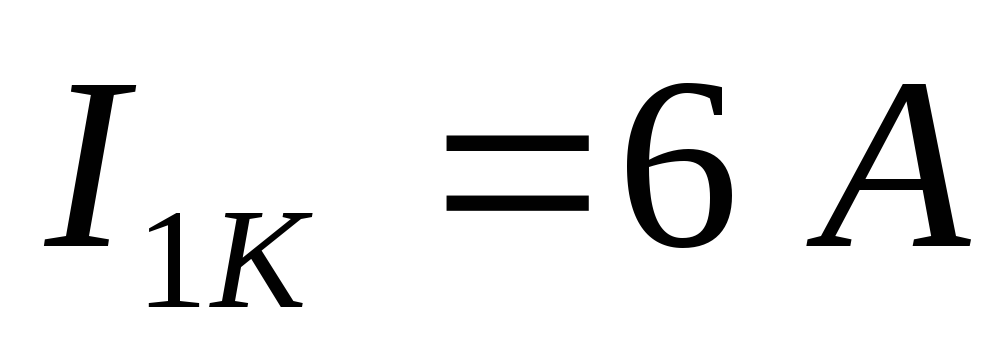
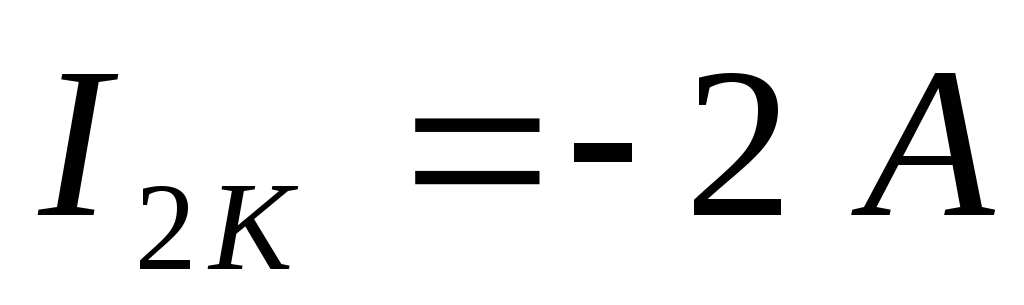

Тогда можно рассчитать действительные токи:

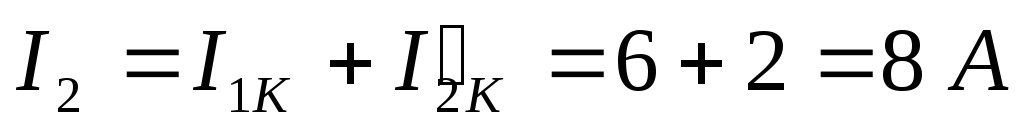
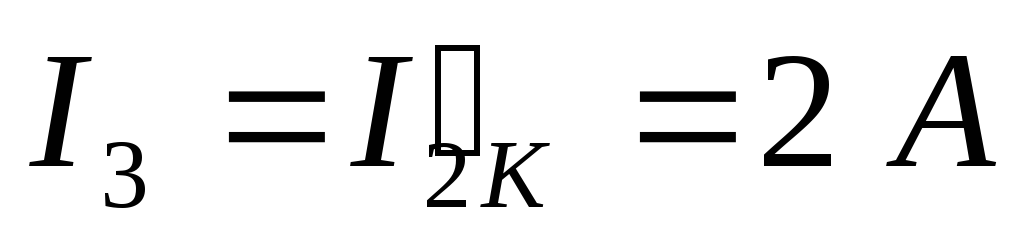
Вопрос 21. Расчёт сложных электрических цепей методом двух узлов.
Рассмотрим метод узловых напряжений(двух узлов) на примере.
Задача
Определить токи ветвей и направить их.
Порядок расчёта:
обозначаем узлы А и Б: под узлом А обозначаем узел, к которому направлена большая ЭДС;
все токи направляем к узлу А;
рассчитываем проводимость каждой ветви по формуле
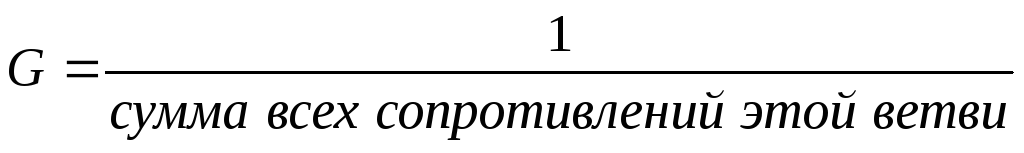 :
:

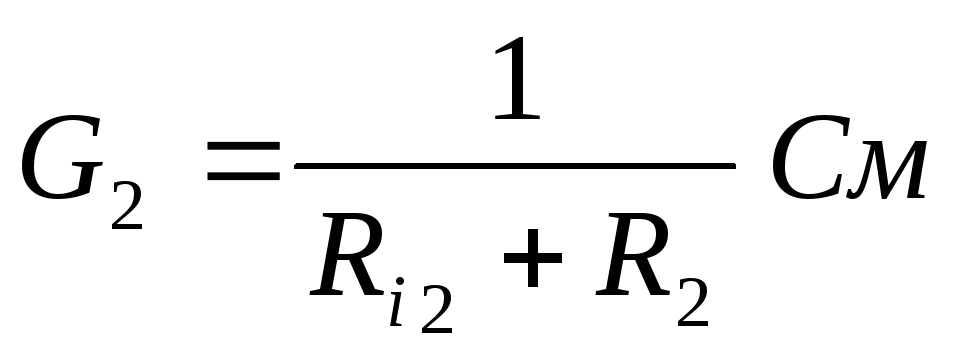
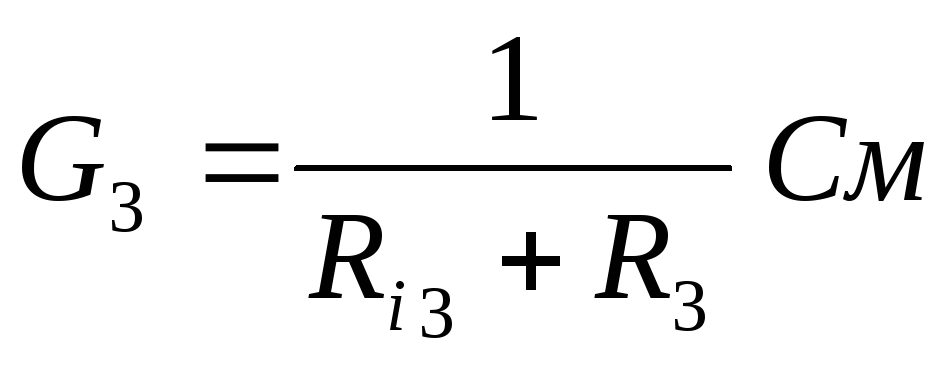

Рассчитываем напряжение
 между двумя узлами по формуле:
между двумя узлами по формуле:

В формулу Eвходит со знаком “+”, если она направлена к узлу А; если от узла — то со знаком “–”.

Находим токи ветвей:
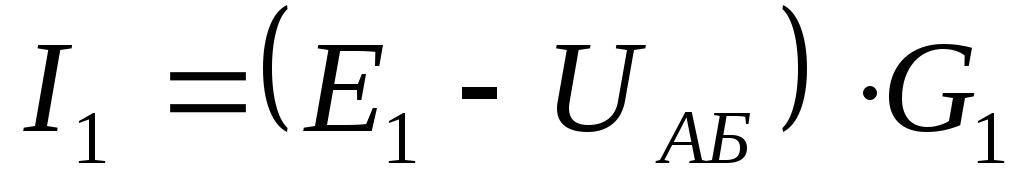
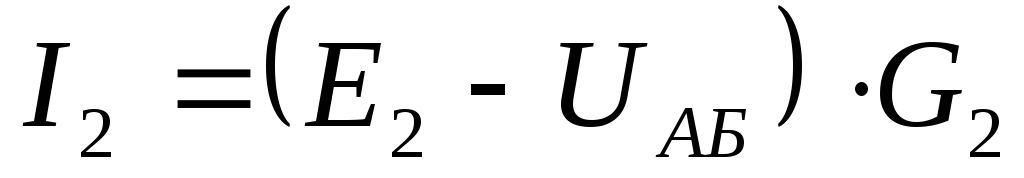
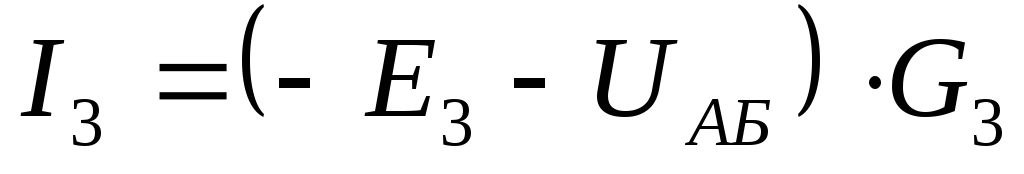
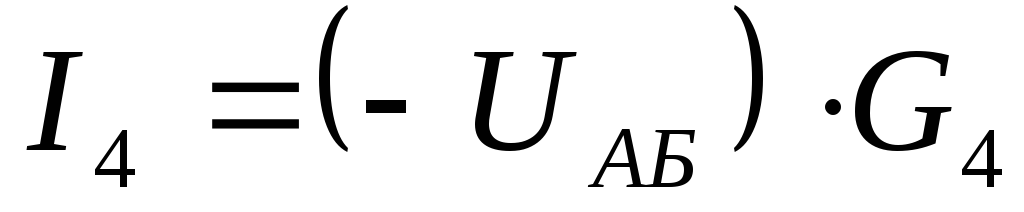
Изменяем направление отрицательных токов.
Вопрос 22. Расчёт сложных электрических цепей методом эквивалентного генератора.
Методом эквивалентного генераторанаходят ток в одной ветви. Особенно удобно, если сопротивление этой ветви изменяется.
Согласно теореме об эквивалентном
генераторе, любой активный двухполюсник
можно заменить эквивалентной ЭДС (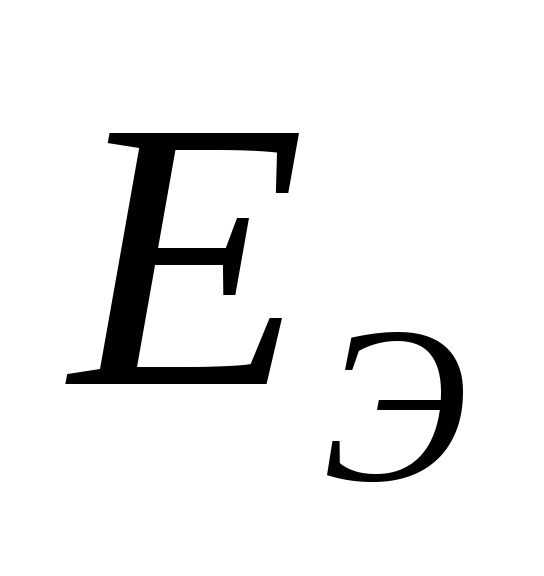 )
и эквивалентным внутренним сопротивлением
(
)
и эквивалентным внутренним сопротивлением
(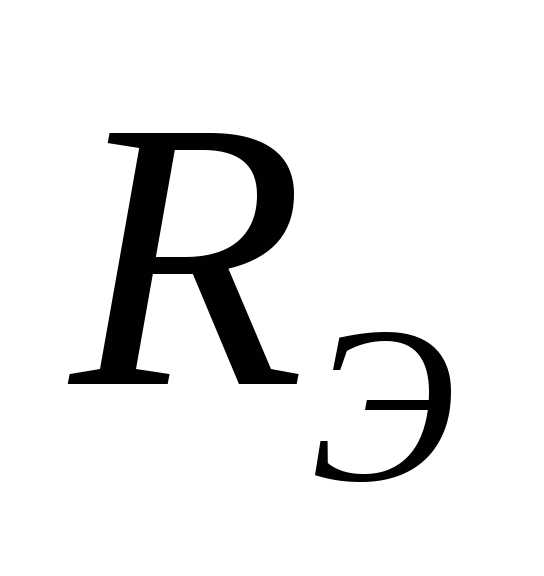 ).
То, что обведено пунктиром на схеме 1,
— активный двухполюсник:
).
То, что обведено пунктиром на схеме 1,
— активный двухполюсник:
Схема 1А | Схема 1Б |
Чтобы найти 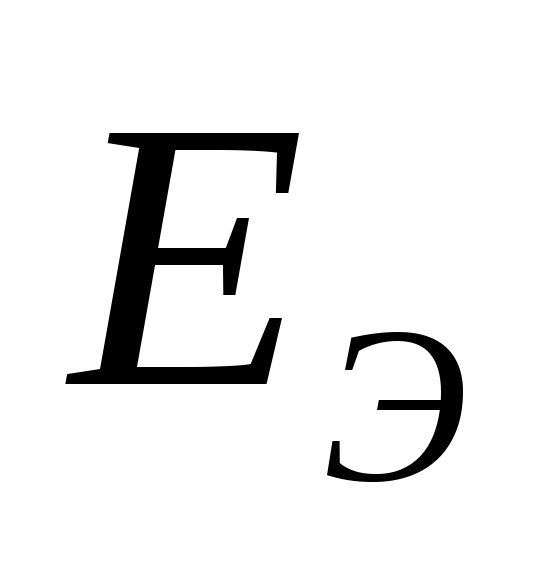 ,
надо разомкнуть ветвь АБ и найти
напряжение на зажимах разомкнутой
ветви. Оно будет равно
,
надо разомкнуть ветвь АБ и найти
напряжение на зажимах разомкнутой
ветви. Оно будет равно :
:
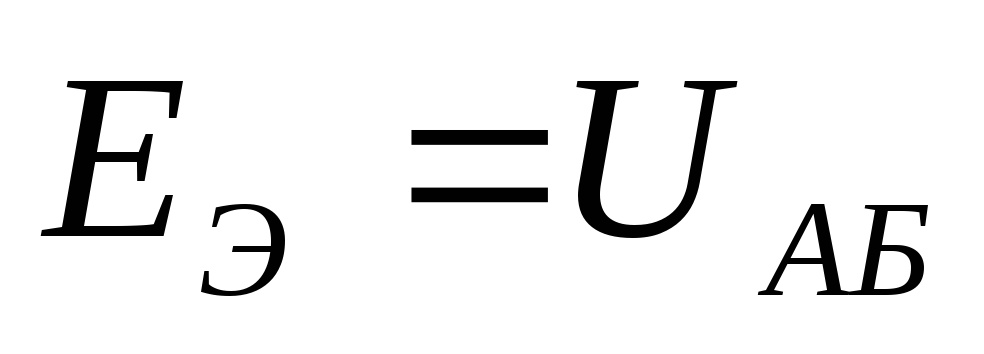
Чтобы найти 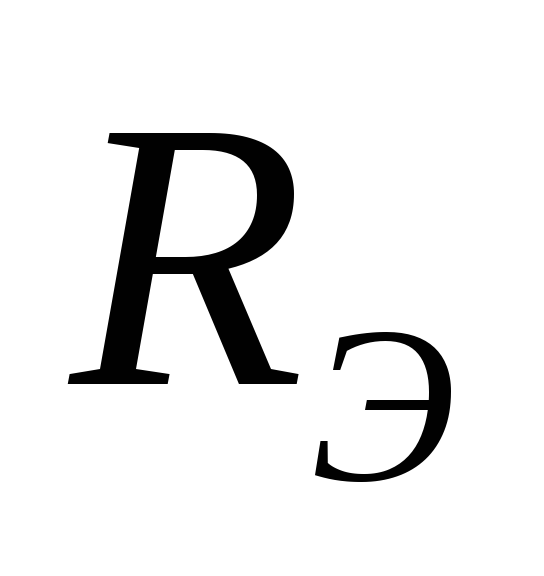 ,
надо разомкнуть ветвь АБ, убрать все
источники, оставив их внутренние
сопротивления. Далее необходимо
рассчитать сопротивление цепи по
отношению к зажимам АБ. Это и будет
,
надо разомкнуть ветвь АБ, убрать все
источники, оставив их внутренние
сопротивления. Далее необходимо
рассчитать сопротивление цепи по
отношению к зажимам АБ. Это и будет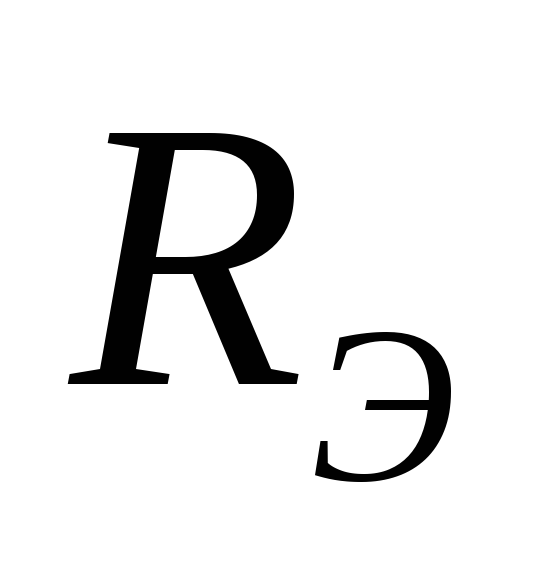 .
.
Если известны  и
и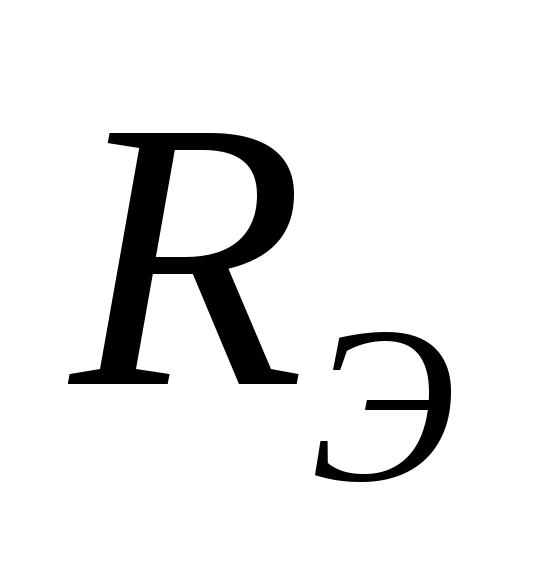 ,
то:
,
то:
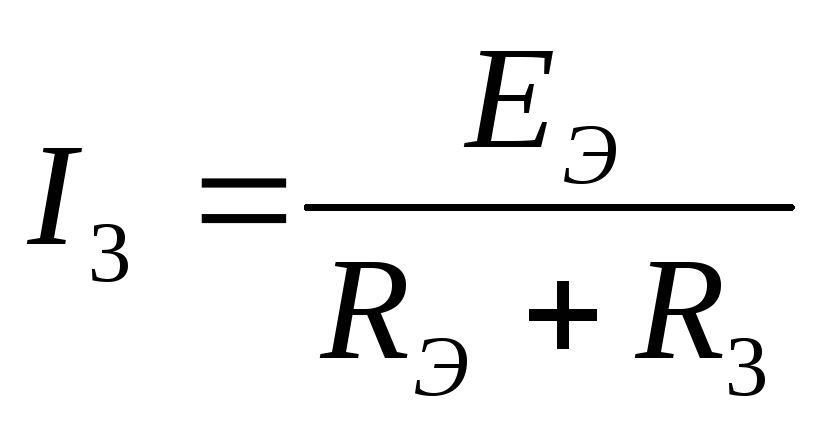
Задача
Дано (для схемы 1А):
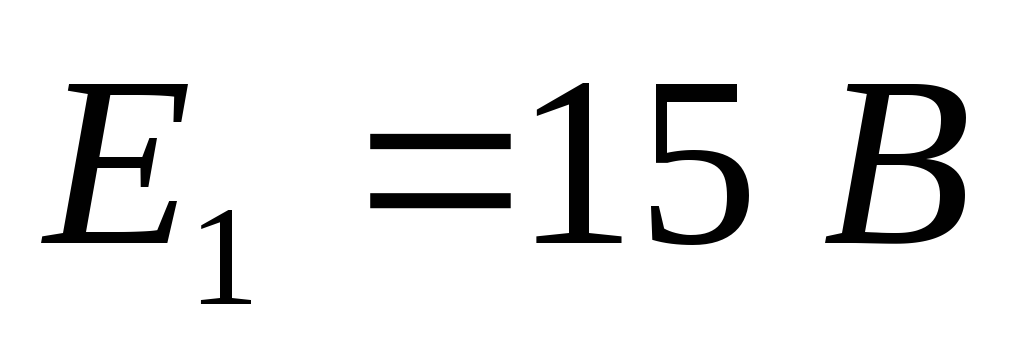
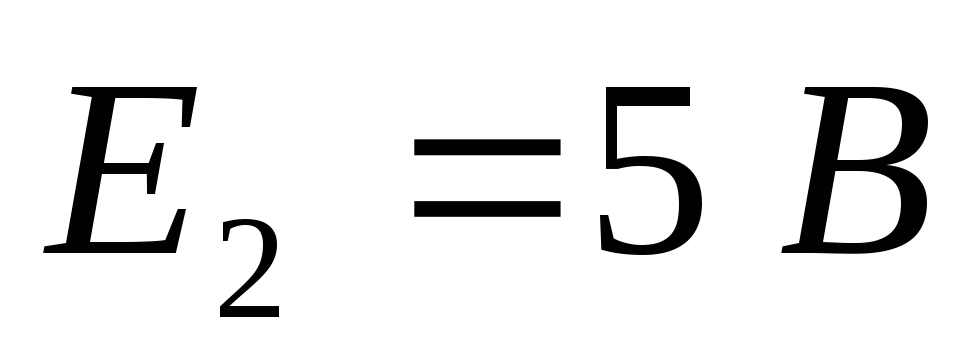
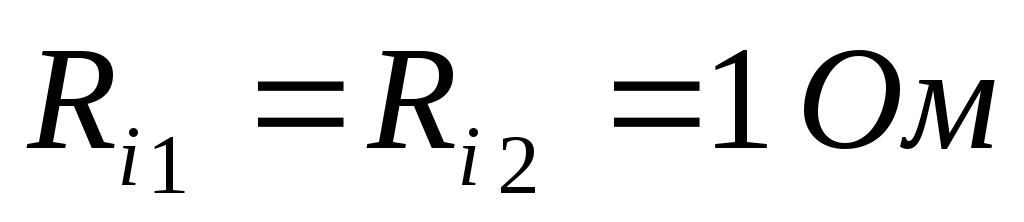
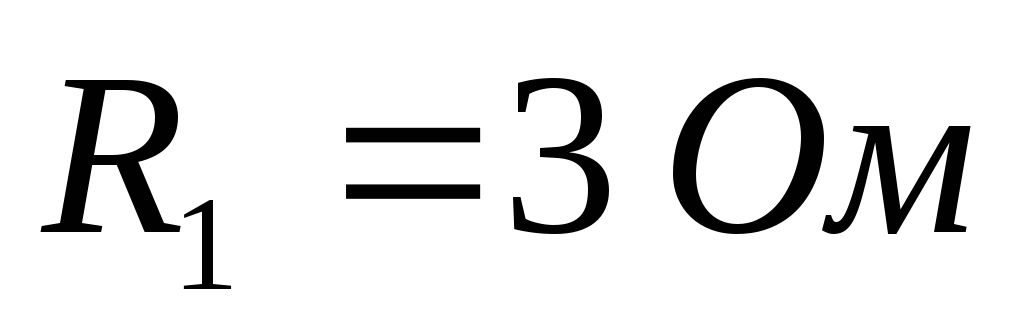

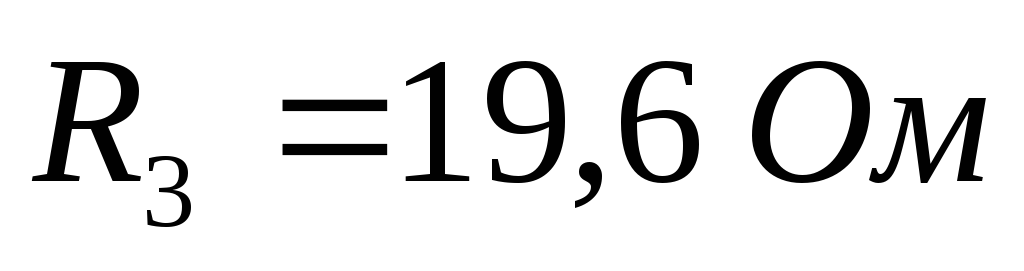
Найти ток 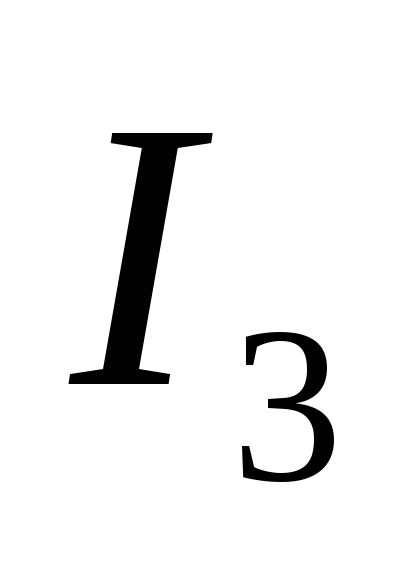 в цепи (методом эквивалентного
генератора).
в цепи (методом эквивалентного
генератора).
Разомкнутая цепь приведена на схеме:
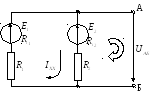
Находим ток холостого хода:
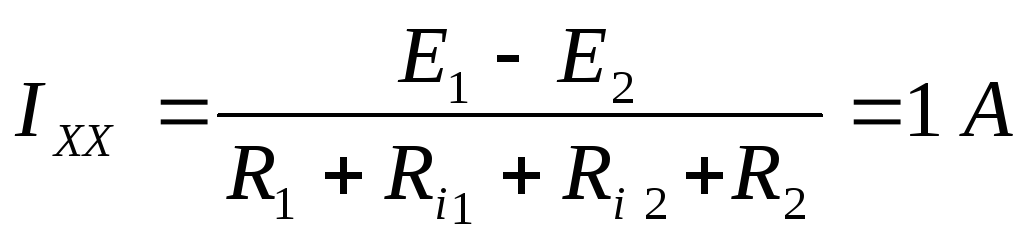
Найдём  :
:
Обходим контур по второму закону
Кирхгофа так, чтобы он замкнулся через
напряжение 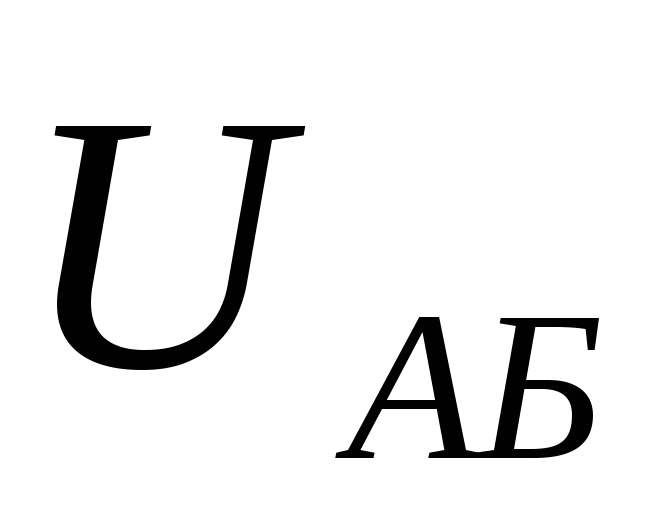 (лучше взять такой контур, где меньше
элементов):
(лучше взять такой контур, где меньше
элементов):
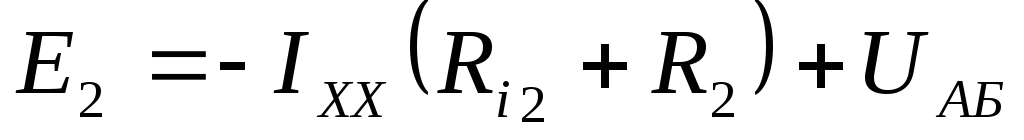
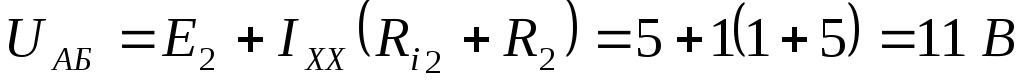
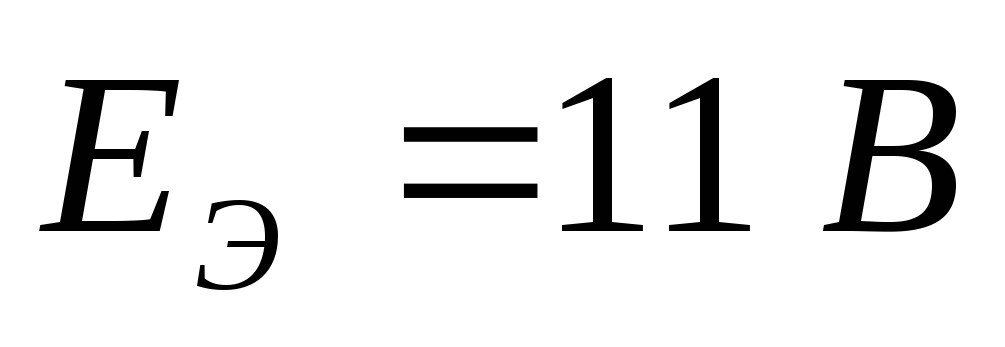
Находим  :
:


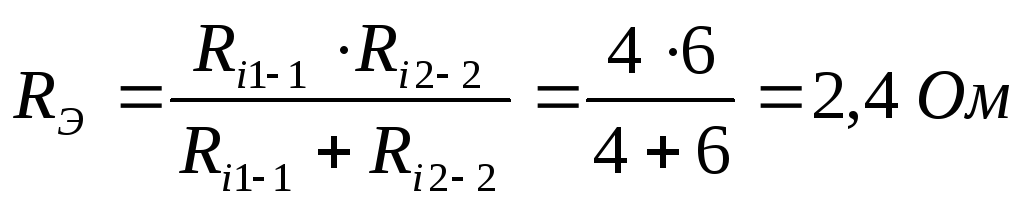
Далее можно выразить искомый ток:
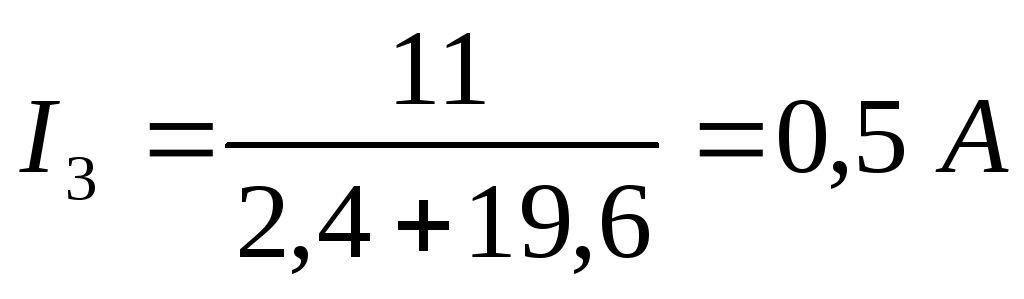
1) Составить уравнения по законам Кирхгофа.
Некоммерческое акционерное общество
«АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ»
Кафедра теоретических основ электротехники

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №1
По дисциплине «Основы теории цепей»
На тему «Расчет линейных электрических цепей постоянного тока с зависимыми источниками»
Специальность «Информационные системы»
Выполнил Ануарбеков Шыңғыс Группа ИС-16-2
Принял доцент каф. ТОЭ Айтжанов Н.М.
_________ «____»____________2017г.
Алматы 2017
Содержание
Введение……………………………………………………………………………………………………3
Задание………………………………………………………………………………………………………4
Расчетная часть………………………………………………………………………………………….6
Уравнения по законам Кирхгофа………………………………………………………..6
Метод контурных токов……………………………………………………………………..7
Метод узловых потенциалов………………………………………………………………9
Сравнение результатов МКТ и МУП…………………………………………………10
Метод эквивалентного генератора……………………………………………………..11
Напряжение на зажимах источника тока……………………………………………13
Баланс мощностей…………………………………………………………………………….13
Заключение………………………………………………………………………………………………14
Список литературы…………………………………………………………………………………..15
Введение
Цель работы: умение составлять систему уравнений по законам Кир-хгофа; применение закона Ома; получение навыков расчётов электрических цепей постоянного тока с зависимыми источниками методами контурных токов, методом узловых потенциалов, эквивалентного генератора.
В цепи действуют независимые источники напряжения с ЭДС Е1, Е2, Е3, источник тока J и зависимый источник напряжения Еи , управляемый током. Номер схемы определяется по таблице 1.1, числовые значения параметров цепи приведены в таблицах 1.2 и 1.3.
Таблица 1.1
Год поступления | Первая буква фамилии | |||||||||
Четный | А БЯ | ГЭЕ | ЖЗЩ | КЛ | МН | ОПР | СТУ | ФЧЦ | ХШИ | ДЮВ |
№ схемы | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.6 | 1.7 | 1.8 | 1.9 | 1.10 |
МЭГ | I1 | I3 | I4 | I2 | I1 | I4 | I3 | I3 | I1 | I2 |
Таблица 1.2
Год поступления | Последняя цифра номера студенческого билета | |||||||||
Четный | 0 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
E1, В | 25 | 20 | 30 | 40 | 20 | 25 | 15 | 35 | 40 | 15 |
E2, В | 10 | 15 | 25 | 20 | 30 | 20 | 15 | 10 | 20 | 25 |
E3, В | 25 | 30 | 35 | 20 | 30 | 20 | 25 | 15 | 30 | 10 |
J, А | 3 | 5 | 2 | 6 | 4 | 10 | 8 | 5 | 3 | 5 |
r, Ом | 10 | 20 | 15 | 16 | 25 | 30 | 35 | 40 | 15 | 20 |
Таблица 1.3
Год поступления | Предпоследняя цифра номера студенческого билета | |||||||||
Четный | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
R1, Ом | 25 | 20 | 15 | 20 | 10 | 30 | 20 | 10 | 30 | 15 |
R2, Ом | 15 | 30 | 20 | 12 | 20 | 10 | 20 | 25 | 40 | 20 |
R3, Ом | 20 | 16 | 25 | 35 | 30 | 20 | 30 | 16 | 10 | 30 |
R4, Ом | 30 | 20 | 30 | 40 | 15 | 40 | 15 | 25 | 20 | 30 |
R, Ом | 6 | 10 | 8 | 10 | 10 | 15 | 20 | 15 | 5 | 8 |
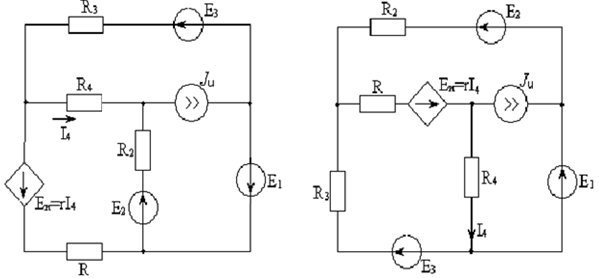
Рисунок 1.1
Задание:
1) Составить уравнения по законам Кирхгофа.
2) Рассчитать токи во всех ветвях методом контурных токов.
3) Рассчитать токи во всех ветвях методом узловых потенциалов. 4) Сравнить результаты, полученные в пунктах 2, 3 и свести их в
одну таблицу.
5) Рассчитать ток в одной ветви методом эквивалентного генератора (см. таблицу 1.1).
6) Определить напряжение на зажимах источника тока.
7) Проверить выполнение баланса мощности.
Расчетная часть
Первый
закон Кирхгофа: алгебраическая сумма
токов в узле электрической цепи равна
нулю: 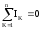 .
Со знаком «+» записываются токи,
направленные к узлу, со знаком «-»
записываются токи, направленные от узла
(или наоборот). Число уравнений,
составляемых по первому закону Кирхгофа,
равно
.
Со знаком «+» записываются токи,
направленные к узлу, со знаком «-»
записываются токи, направленные от узла
(или наоборот). Число уравнений,
составляемых по первому закону Кирхгофа,
равно 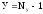 ,
где
,
где  —
число узлов в цепи. В цепи (рис 1.1) имеются
4 узла, исходя из этого У = 4-1 = 3 (количество
уравнений по I
закону Кирхгофа). Следовательно,
достаточно записать уравнения для узлов
1, 2 и 3.
—
число узлов в цепи. В цепи (рис 1.1) имеются
4 узла, исходя из этого У = 4-1 = 3 (количество
уравнений по I
закону Кирхгофа). Следовательно,
достаточно записать уравнения для узлов
1, 2 и 3.
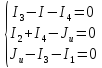
Второй
закон Кирхгофа: в любом замкнутом контуре
электрической цепи алгебраическая
сумма напряжений на сопротивлениях,
входящих в этот контур равна алгебраической
сумме ЭДС: 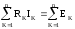 .
Напряжения записываются со знаком «+», если
положительное направление тока
.
Напряжения записываются со знаком «+», если
положительное направление тока 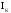 совпадает с направлением обхода контура,
со знаком «-», если направление тока
совпадает с направлением обхода контура,
со знаком «-», если направление тока 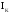 противоположно
направлению обхода контура; ЭДС
противоположно
направлению обхода контура; ЭДС 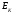 ,
направления, которых совпадают с
направлением обхода контура, записываются
со знаком «+», а ЭДС
,
направления, которых совпадают с
направлением обхода контура, записываются
со знаком «+», а ЭДС  ,
направленные против обхода контура –
со знаком «-». Число уравнений, составляемых
по второму закону Кирхгофа, равно:
,
направленные против обхода контура –
со знаком «-». Число уравнений, составляемых
по второму закону Кирхгофа, равно: 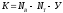 ,
где
,
где 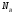 — число ветвей,
— число ветвей,  — число источников тока. Исходя из этого,
в цепи (рис 1.1) 6 ветвей, 1 источник тока
и как было выше сказано – 4 узла.
Следовательно, для второго закона
Кирхгофа понадобится К = 6-1-3=2 уравнения.
Выбираем два независимых контура, не
имеющих источника тока, затем произвольно
выбираем обход контура (рис 1.1). И для
каждого контура (внешний контур и контур
1241) запишем уравнение по II
закону Кирхгофа:
— число источников тока. Исходя из этого,
в цепи (рис 1.1) 6 ветвей, 1 источник тока
и как было выше сказано – 4 узла.
Следовательно, для второго закона
Кирхгофа понадобится К = 6-1-3=2 уравнения.
Выбираем два независимых контура, не
имеющих источника тока, затем произвольно
выбираем обход контура (рис 1.1). И для
каждого контура (внешний контур и контур
1241) запишем уравнение по II
закону Кирхгофа:
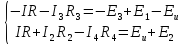
Общая система уравнений по законам Кирхгофа будет выглядеть следующим образом

2) Рассчитать токи во всех ветвях методом контурных токов.
Составим систему уравнений по методу контурных токов для цепи постоянного тока (рис 1.2):

Рисунок 1.2.

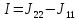

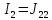
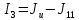
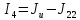 ,
где
,
где 
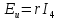 =
=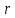 (
(
Решение: 

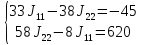 =
=
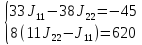 =
=
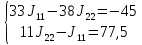 =
=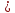
 =
=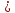
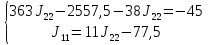 =
=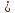
 =
=
 =
=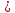
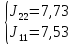 =
=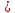
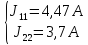 ,
тогда
,
тогда
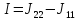 =7,73
– 7,53 = 0,2А
=7,73
– 7,53 = 0,2А
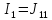 =
7,53А
=
7,53А
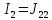 =
7,73А
=
7,73А
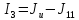 =
10 – 7,53 = 2,47А
=
10 – 7,53 = 2,47А
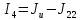 =
010– 7,73 = 2,27А
=
010– 7,73 = 2,27А
3) Рассчитать токи во всех ветвях методом узловых потенциалов.
Метод
узловых потенциалов позволяет уменьшить
число уравнений системы до числа 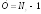 .
Суть метода
узловых потенциалов заключается в
определении потенциалов узлов
электрической цепи, токи рассчитываются
по закону Ома. При составлении уравнений
по методу узловых потенциалов, потенциал
одного из узлов принимают равным нулю,
для определения потенциалов оставшихся
узлов составляются уравнения.
.
Суть метода
узловых потенциалов заключается в
определении потенциалов узлов
электрической цепи, токи рассчитываются
по закону Ома. При составлении уравнений
по методу узловых потенциалов, потенциал
одного из узлов принимают равным нулю,
для определения потенциалов оставшихся
узлов составляются уравнения.
Возьмем
узел 3 за базовый и будем считать, что
он равен нулю. Автоматически значение
потенциала в узле 4 становится равным 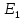 .
.
(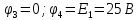 ).
).
Составим систему уравнений по методу узловых потенциалов для цепи постоянного тока (рис 1.3), так как значения потенциалов в узлах 3 и 4 известны, то нам необходимо составить систему из 2 уравнений для узлов 1 и 2:
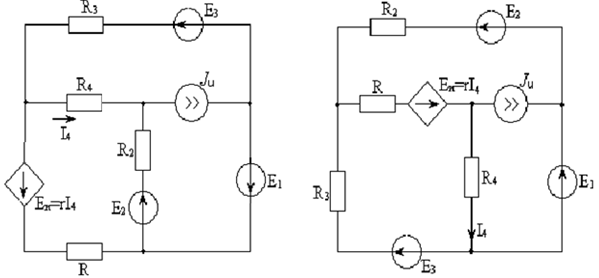
Рисунок 1.3
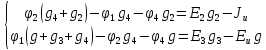
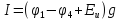
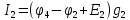
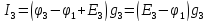
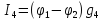
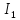 найдем,
применив I
закон Кирхгофа
найдем,
применив I
закон Кирхгофа 
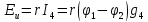

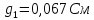
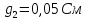
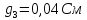

Решение: 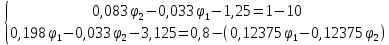
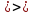
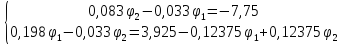
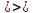

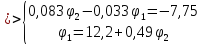

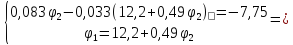
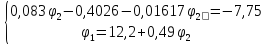

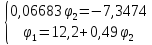
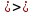
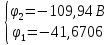 ,
тогда
,
тогда
 =0,99*68,2694
= 67,586706В
=0,99*68,2694
= 67,586706В
 =
0,115 А
=
0,115 А
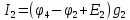 =
7,47А
=
7,47А
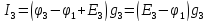 =
2,46А
=
2,46А
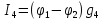 =
2,25А
=
2,25А
 7,35А
7,35А
Формула второго закона Кирхгофа
Какой бы сложной не была электрическая цепь, она имеет элементы двух видов: узлы и замкнутые контуры. Узлом цепи называют точку разветвления цепи, в которой сходятся три или более проводника с током. Расчеты в любой самой сложной цепи можно провести, используя закон Ома и закон сохранения заряда. Для упрощения расчетов цепей постоянного тока используют правила (законы) Кирхгофа, которые позволяю составить линейные уравнения вычисления сил токов, текущих в элементах цепи.
Падение напряжения это произведение силы тока на сопротивление (). Если в цепи источников ЭДС будет несколько, то следует ЭДС суммировать, учитывая знаки. ЭДС принято считать положительной, если при обходе контура первым встречается отрицательный полюс источника. Направление обхода контура выбирают произвольно, (по часовой стрелке или против нее). Один раз выбрав направление обхода контура при решении задачи не следует его изменять.
Теперь к самой формуле, отображающей второй закон Кирхгофа:
Формула второго закона Кирхгофа говорит о том, что сумма произведений силы токов (I) (с учетом знака) на внешние и внутренние сопротивления всех участков замкнутого контура равны сумме величин ЭДС () источников, которые включены в данный контур (суммирование ЭДС происходит с учетом знаков). При составлении и уравнений с использованием формулы второго закона Кирхгофа необходимо внимательно следить за расстановкой знаков токов и ЭДС.
Система уравнений, которая получается при использовании первого и второго правил Кирхгофа является полной и дает возможность отыскать все токи. При составлении уравнений, используя правила Кирхгофа, надо следить за тем, чтобы новое уравнение имело хотя бы одну величину, которая еще не вошла в предыдущие уравнения. Кроме того, необходимо, чтобы система уравнений имела число уравнений равное количеству неизвестных.
Второе правило Кирхгофа следует из того, что электрическое напряжение по замкнутому контуру равно нулю, то есть это правило является следствием основного свойства электростатического поля, которое заключается в том, что работа поля при движении заряда по замкнутой траектории равна нулю.
Примеры решения задач по теме «Второй закон Кирхгофа»
Электротехника: Второй закон Кирхгофа.
Второй закон (правило) Кирхгофа — алгебраическая сумма напряжений на элементах контура электрической цепи равна нулю.Контур электрической цепи — замкнутый проводящий ток путь образованный элементами электрической цепи.
Рассмотрим схему на рисунке 1:
Рисунок 1 — Схема с одним контуром
В этой схеме присутствуют: источник ЭДС и резисторы R1, R2 и R3; эти элементы образуют замкнутый путь проводящий ток т.е. контур. Напряжение на источнике ЭДС равно E и направлено так как показано на рисунке 1 стрелочкой справа от источника. Стрелка на условном обозначении источника направлена в сторону противоположную направлению напряжения на источнике ЭДС (иногда это запутывает при расчёте схем но так принято обозначать источник ЭДС). Направления падений напряжений на резисторах указаны стрелками (рис. 1). Для составления уравнения, по второму закону Кирхгофа, необходимо выбрать направление обхода контура (по часовой стрелке или против). В схеме на рисунке показано направление по часовой стрелке. Запишем уравнение по второму закону Кирхгофа:
Напряжения резисторов вошли в левую часть уравнения со знаком плюс т.к. направление обхода контура совпадает с направлениями напряжений на резисторах. Напряжение источника ЭДС E вошло в правую часть со знаком плюс т.к. направление обхода контура не совпадает с направлением напряжения источника. Можно также записать напряжение источника в левой части уравнения со знаком минус (что, в принципе, тоже самое):
Уравнение (2) больше подходит для определения второго закона Кирхгофа приведенного выше.
Напряжения совпадающие по направлению с обходом контура записаны со знаком плюс а напряжение источника не совпадающее с обходом контура — со знаком минус и вся эта алгебраическая сумма равна нулю. Теперь, из выражения (2), зная три каких либо напряжения можно найти четвёртое. Обычно расчёт цепи сводится к нахождению токов во всех ветвях или потенциалов всех узлов т.к. зная эти величины (токи ветвей или потенциалы узлов), сопротивления всех элементов и напряжения источников ЭДС (и токи всех источников тока) можно найти напряжение на любом элементе и ток любого элемента. В схеме на рисунке 1 для определения напряжений U1, U2 и U3 достаточно знать ток I т.к. он одинаков для всех элементов цепи (R1, R2, R3, E). Умножением тока I на сопротивление R1 находится напряжение U1, умножением тока I на сопротивление R2 находится напряжение U2, умножением тока I на сопротивление R3 находится напряжение U3. Учитывая это можно привести уравнение (1) к виду:
Из уравнения (3) можно найти ток I. Т.к. контур один то и ток в уравнении один но если схема содержит больше одно контура то и токов будет больше. Вынеся ток I за скобки и поделив обе части уравнения на сумму сопротивлений R1, R2 и R3 получаем уравнение для нахождения тока I, но этот ток можно найти и другим способом например заменой последовательного соединения резисторов R1, R2 и R3 одним резистором R123 и делением напряжения E на сопротивление резистора R123.
Сопротивление резистора R123 равно сумме сопротивлений резисторов R1, R2 и R3. Ток находится из уравнения:
Если в контуре содержится больше одного источника ЭДС то уравнение, по второму закону (правилу) Кирхгофа, составляется аналогично.
Рисунок 2 — Схема с двумя источниками ЭДС
Запишем уравнение, по второму закону Кирхгофа, для контура в схеме на рисунке 2:
Напряжение E2 источника E2 записано в правой части уравнения со знаком минус т.к. оно совпадает по направлению с обходом контура. Заменяя напряжения на резисторах произведениями тока I на сопротивления резисторов получим уравнение:
Из уравнения (6) может быть найден ток I.
Если схема имеет больше одного контура то Закон (правило) Кирхгофа все равно выполняется для всех контуров. Уравнения по второму закону Кирхгофа, в таком случае, составляются аналогично тому как в примерах выше. Отличие будет только в том что необязательно для всех элементов будет один и тот же ток. В случае если схема имеет больше одного контура можно считать что через каждый элемент течет свой ток. Напряжение на элементе, в таком случае, находится умножением сопротивления этого элемента (если этот элемент например резистор) на ток данного элемента.
Рисунок 3 — Часть схемы имеющей больше одного контура
Рисунок 4 — Часть схемы имеющей больше одного контура и ветвь из двух элементов
Рисунок 4 — Часть схемы имеющей больше одного контура, ветвь из двух элементов и элементы напряжения на на которых имеют направления не совпадающие с выбранным направлением обхода контура
При составлении уравнений по второму закону Кирхгофа не стоит слишком много времени уделять выбору направлений обходов контуров и направлений токов (они (направления обходов и токов) выбираются произвольно) так как реальные направления токов определяются при решении этих уравнений.
Пример:
Направление напряжения на элементе R1 такое же как и направление тока этого элемента по тому что принято считать что ток течёт от большего потенциала к меньшему а напряжение направлено также (от большего потенциала к меньшему).
Пример составления уравнений по законам Кирхгофа для разветвленной цепи
Рассмотрим пример составления уравнений по законам Кирхгофа для разветвленной электрической цепи постоянного тока. Для данной электрической цепи необходимо рассчитать токи в каждой ветви. Для расчета токов будет пользоваться законами Кирхгофа.
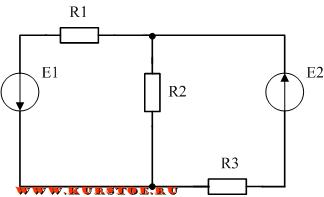
Составляем уравнения по первому закону кирхгофа. Согласно алгоритма задаемся направлением токов в ветвях электрической схемы.
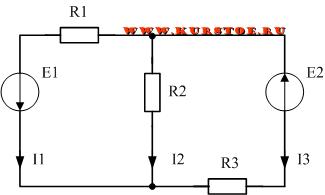
Количество уравнений равно количеству узлов минус один. У нас в схеме два узла. Значит будет одно уравнение. Т.к. все токи втекают в узел, то берем их с одним знаком, например плюс. В результате уравнение по первому закону будет таким.
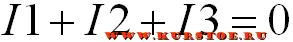
Составим уравнения по второму правилу Кирхгофа. По алгоритму необходимо задаться обходом независимых контуров.
В электрической цепи три контура. Контура обозначены стрелочками.
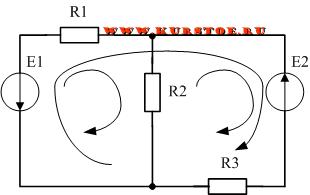
Из них только любые два являются независимыми контурами.
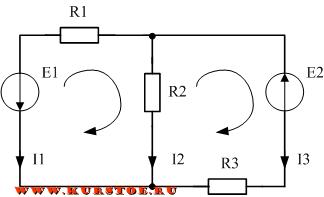
Для каждого независимого контура составляем уравнение по второму закону Кирхгофа.
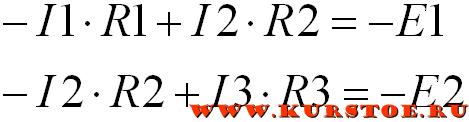
В первом уравнении перед током I1 поставлен минус, т.к. направление обхода первого (слева) контура не совпадает с направление протекающего тока I1.
Перед током I2 в первом уравнении поставлен плюс, т.к. направление обхода первого контура совпадает с направление протекающего тока I2.
Перед ЭДС 1 поставлен минус, т.к. направление действия ЭДС 1 не совпадает с направление обхода первого контура.
Во втором уравнении перед током I2 поставлен минус, т.к. направление обхода второго контура не совпадает с направление протекающего тока I2.
Перед током I3 во втором уравнении поставлен плюс, т.к. направление обхода второго контура совпадает с направление протекающего тока I3.
Перед ЭДС 2 поставлен минус, т.к. направление действия ЭДС 2 не совпадает с направление обхода второго контура.
Выполняем объединение уравнений в систему. Решаем систему уравнений с тремя неизвестными I1, I2, I3 любым известным способом.
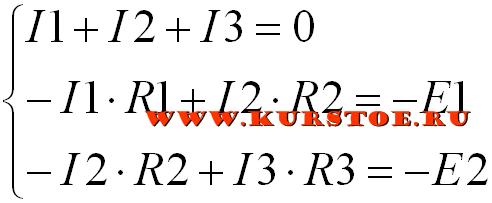




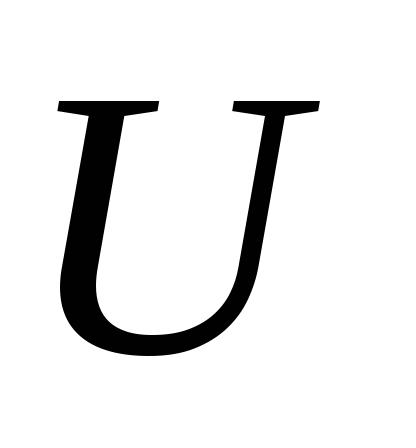 между двумя узлами по формуле:
между двумя узлами по формуле:
