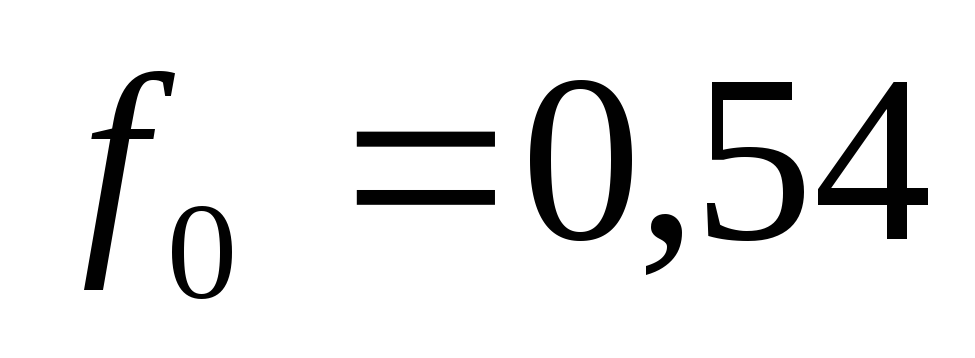коэффициент заполнения — это… Что такое коэффициент заполнения?
3.15 коэффициент заполнения (fill ratio), φ: Отношение объема источника шума под кожухом к внутреннему объему кожуха.
Примечание — Если форма источника шума затрудняет расчет его объема, то можно в качестве объема источника принять объем огибающего параллелепипеда по ГОСТ 31275.
Коэффициент заполнения — максимально возможный объем СПГ по отношению к общему объему резервуара (определяет разработчик резервуара).
3.13 коэффициент заполнения (fill ratio) φ: Отношение объема источника шума под кожухом к внутреннему объему кожуха.
Примечание — Если форма источника шума затрудняет расчет его объема, то можно в качестве объема источника принять объем огибающего параллелепипеда по ГОСТ 31275.
2.15 коэффициент заполнения: Отношение площади пикселя, отведенной для отображения информации, к полной площади пикселя.
3.11 коэффициент заполнения: Отношение теоретического объема, заполненного металлом, определяемого исходя из массы и плотности, к действительному объему, полученному после сдавливания при определенной нагрузке набора (пакета) листов.
3.10 коэффициент заполнения: Отношение теоретического объема, заполненного металлом, определяемого исходя из массы и плотности, к действительному объему, полученному после сдавливания при определенной нагрузке набора (пакета) листов.
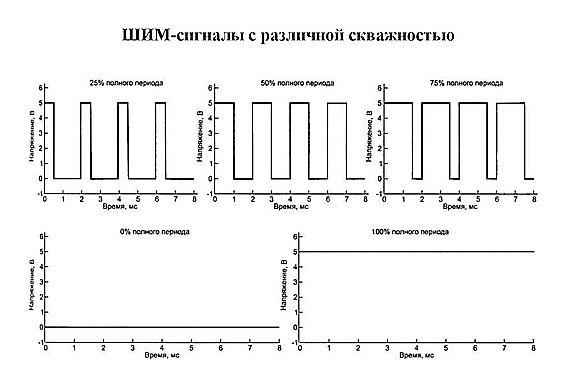
3.10 коэффициент заполнения (duty factor): Отношение длительности импульса к периоду следования импульсов в периодической импульсной последовательности.
11. Коэффициент заполнения
Отношение длительности импульса к длительности периода
Смотри также родственные термины:
47. Коэффициент заполнения вихретокового проходного преобразователя
Fill factor of encircling eddy current probe
Отношение площади поперечного сечения объекта контроля к меньшей из площадей поперечного сечения, эквивалентного витка измерительной или возбуждающей обмотки проходного вихретокового преобразователя
где — площадь поперечного сечения эквивалентного витка измерительной обмотки;
— площадь поперечного сечения эквивалентного витка обмотки возбуждения
57.
Коэффициент заполнения
D. Belastungsfaktor
Отношение среднеарифметического значения нагрузки энергоустановки потребителя к максимальному за установленный интервал времени
3.1.63 коэффициент заполнения графика нагрузки энергоустановки потребителя (коэффициент заполнения): Отношение среднеарифметического значения нагрузки энергоустановки потребителя к максимальному за установленный интервал времени.
[ГОСТ 19431-84, пункт 57]
207. Коэффициент заполнения жилы
Коэффициент заполнения
Отношение площади поперечного сечения многопроволочной токопроводящей жилы к площади, ограниченной описанным около нее контуром
13.5.2. Коэффициент заполнения кабельных каналов
Необходимо, чтобы коэффициент заполнения основывался на показателях длины и прямолинейности канала и гибкости проводов. Рекомендуется, чтобы расположение каналов и их размеры позволяли легко укладывать на место провода и кабели.
7.1.9. Коэффициент заполнения круга
Отношение площади поперечного сечения стержня к площади круга с диаметром, равным диаметру стержня трансформатора
Примечание. При наличии в сечении стержня каналов площадь поперечного сечения каналов не включается в площадь поперечного сечения стержня
34. Коэффициент заполнения лесосплавного хода
Е. Coefficient of floating route filling
Отношение площади, занятой плывущими бревнами или сплоточными единицами в пределах рассматриваемого участка лесосплавного хода, к общей площади этого участка
19. Коэффициент заполнения несущего винта
Коэффициент заполнения
σ
Величина, определяемая соотношением
7.1.15. Коэффициент заполнения окна магнитной системы
Отношение суммарной площади поперечного сечения металла всех витков всех обмоток в окне магнитной системы к площади окна
68. Коэффициент заполнения питателя роторного снегоочистителя
Коэффициент заполнения питателя
Отношение фактической объемной производительности снегоочистителя к пропускной способности питателя
67. Коэффициент заполнения ротора снегоочистителя
Коэффициент заполнения ротора снегоочистителя
Коэффициент заполнения ротора
Отношение фактической объемной производительности снегоочистителя к пропускной способности ротора
7.1.10. Коэффициент заполнения сечения стержня (ярма)
Отношение активного сечения стержня (ярма) к площади его поперечного сечения
7.1.11. Коэффициент заполнения сталью
Отношение активного сечения стержня к площади круга с диаметром, равным диаметру стержня трансформатора.
Примечание. Коэффициент заполнения сталью равен произведению коэффициента заполнения круга и коэффициента заполнения сечения стержня
Словарь-справочник терминов нормативно-технической документации. academic.ru. 2015.
Коэффициент заполнения — Энциклопедия по машиностроению XXL
В случае утолщения входной кромки трубопровода от 0 до б = = б/П,( — 0,05 интенсивность отрыва потока от стенок заметно уменьшается и коэффициент заполнения сечения увеличивается ( с = 0,6).
Принимая для струйки, выходящей из отверстия решетки, коэффициент заполнения сечения (контракции) ас 0,65 и коэффициент скорости фск = 0,95, получим согласно формулам (1.23) и (1.24) для наиболее узкого сечения общей струи (х/ ЛГк 0,7 х= = = 140 мм) при ( — 0,38 следующие значения относительных скоростей шах/и р = [c.217]
Уточнить формулы (1.13) можно введением коэффициента заполнения 1-го блока ai=Viм Vi (где Vi—полный объем блока Уш — примерный объем деталей блока), тогда
Вторую ветвь базы данных составляют массивы условно-постоянной информации. Прежде всего сюда относятся справочные данные, характеризующие марки сталей и других магнитных материалов, таблицы стандартных размеров голого и изолированного проводов различных марок. Сюда включаются также различные эмпирические коэффициенты заполнения, обработки, запаса и пр. ), а также массив ограничений, накладываемых на геометрические размеры и диктуемых требованиями их технологической выполнимости.
[c.85]
), а также массив ограничений, накладываемых на геометрические размеры и диктуемых требованиями их технологической выполнимости.
[c.85]
Большой наглядностью обладает способ сравнения циклов на Т — s-диаграммах. Если сравнивать произвольный цикл, вписанный в цикл Карно, то площадь вписанного цикла меньше, чем площадь цикла Карно. Отношение из этих площадей называют коэффициентом заполнения цикла. Чем больше коэффициент заполнения, тем ближе приближаются к наиболее эффективному преобразованию теплоты в работу.
Активное и внутреннее реактивное сопротивления условного одно-виткового индуктирующего провода при коэффициенте заполнения g = 0,9 и глубине проникновения тока в медь [c.258]
При конструировании приборов, их механизмов и деталей необходимо обеспечить 1) надежность и точность выполнения заданных функций 2) удобство, простоту и безопасность эксплуатации. При этом компоновка прибора, конструкция корпуса, расположение, форма, размеры, окраска и освещение шкал, указателей и других средств отображения информации, а также рукояток управления и переключателей должны удовлетворять требованиям эргономики 3) внешний вид, форму и размеры элементов конструкции, их окраску и отделку, соответствующую требованиям технической эстетики 4) компактность конструкции — малые размеры и вес при высоком коэффициенте заполнения объема 5) прочность, жесткость и износостойкость деталей 6) удобство конструкции для профилактических осмотров, ремонта и транспортировки
 398]
398]
Назовем коэффициентом заполнения диаграммы скоростей
Коэффициент заполнения т] = = (R/R ) = 0,5. По диаграмме на [c.103]
Если индуктор имеет w витков, расположенных в один ряд, то следует / j, Х2 , Xj, / ( умножить на w rj следует также разделить на коэффициент заполнения g = 0.8 -н 0,9 делится на w. [c.116]
Наиболее распространенный вид индуктора для закалки внутренней поверхности — кольцевой индуктор для закалки цилиндрической поверхности (см. рис. 8-12, 8-15). Особенностью этого индуктора является то, что коэффициент заполнения магнитопро-вода сталью на внутренней его кромке больше, чем на внешней. Это затрудняет изготовление таких индукторов при диаметрах, меньших 50 мм. В последнем случае вместо стали лучше применять феррит, особенно если частота выше 2500 гц. В остальном работа такого индуктора протекает так же как и плоского.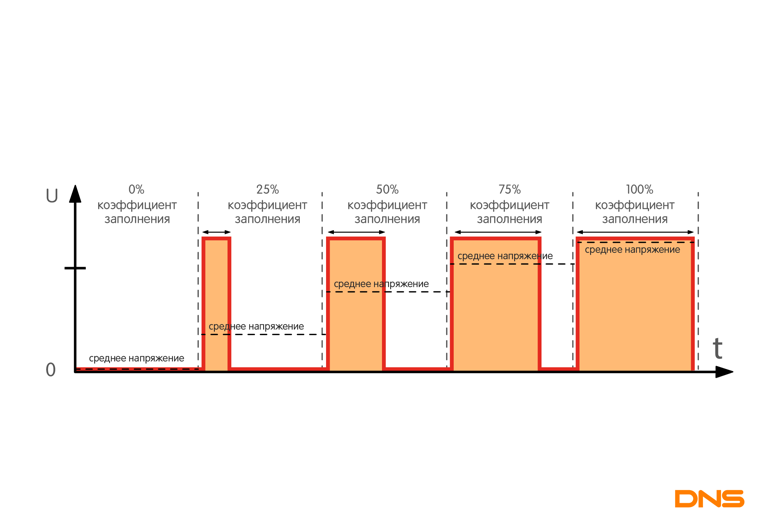
Приближенно полную работу деформации образца можно вычислить, умножив площадь прямоугольника с основанием А1 — ОО4 и высотой Рд на коэффициент заполнения диаграммы И, тогда А = Рд -А1 г . В частности, для стали 11 = 0,8—0,9. [c.73]
В индукционной печи с плазмотроном последний особо полезен для расплавления кусковой шихты с малым коэффициентом заполнения тигля, а также для перегрева расплава перед разливкой или в процессе его обработки [68, 80]. [c.98]
TO выходная здс проходного преобразователя с коэффициентом заполнения т) = 1 [c.6]
Комплексную индуктивность измерительной катушки можно выразить через компоненты комплексной магнитной проницаемости ii и Ц2, собственную индуктивность катушки Lo и коэффициент заполнения т] [c.102]
Для оценки эффективности реализации приведенных схем целесообразно ввести следующие показатели коэффициент заполнения профиля и коэффициент использования импульсов. [c.61]
[c.61]
Коэффициент заполнения профиля Кз отражает степень заполнения профиля, подлежащего контурно-лучевой обработке зонами лазерного воздействия [c.61]
Расчет момента центробежной муфты со стальными щариками производят аналогично. При определении массы шариков, расположенных в одной полости муфтты, объем полости умножают на коэффициент заполнения К, учитывающий пустоты между шариками. Обычно принимают К= 0,5…0,7. [c.333]
При радиальном растекании узкой струи по фронту такой решетки наибольшими скоростями будут обладать центральные струйки, протекающие нормально или под небольшими углами наклона к поверхности решетки наименьшие скорости будут у промежуточных струек, которые почти полностью стелятся по фронтальной поверхности решетки. Кроме этого, центральные струйки будут иметь и большую массу, так как коэффициент заполнения сечения ( сжатия ) центральных отверстий при протекании через них струек нормально к поверхности решеаки получается наибольшим. Коэффициент заполнения сеченнй остальных отверстий уменьшается с увеличением угла наклона к фронтальной поверхности решетки т. е. с удалением от оси струи. Исключение составляют отверстия, расположенные вблизи стенки корпуса аппарата, у которой струйки изменяют свое направление нормально к решетке. В результате, струйки, выходящие из центральных каналов спрямляющей решетки, с большой кинетической энергией и массой будут подсасывать более слабые периферийные струйки, за исключением пристенных (рис. 3.5, г). Как видно из сравнения рис. 3.5, в и г, характер профиля скорости в последнем случае будет близок к характеру профиля скорости за перфорированной решеткой с меиьшпм значением ( р при отсутствии за ней спрямляюищй решетки. Так оно и должно быть, так как спрямляющая решетка устраняет влияние увеличенной радиальности растекания потока по фронту решетки и нет большого отличия в поведении струек, протекающих через отверстия решетки при больших и малых значениях р.
[c.83]
Коэффициент заполнения сеченнй остальных отверстий уменьшается с увеличением угла наклона к фронтальной поверхности решетки т. е. с удалением от оси струи. Исключение составляют отверстия, расположенные вблизи стенки корпуса аппарата, у которой струйки изменяют свое направление нормально к решетке. В результате, струйки, выходящие из центральных каналов спрямляющей решетки, с большой кинетической энергией и массой будут подсасывать более слабые периферийные струйки, за исключением пристенных (рис. 3.5, г). Как видно из сравнения рис. 3.5, в и г, характер профиля скорости в последнем случае будет близок к характеру профиля скорости за перфорированной решеткой с меиьшпм значением ( р при отсутствии за ней спрямляюищй решетки. Так оно и должно быть, так как спрямляющая решетка устраняет влияние увеличенной радиальности растекания потока по фронту решетки и нет большого отличия в поведении струек, протекающих через отверстия решетки при больших и малых значениях р.
[c.83]
Гранецентрированная кубическая и гексагональная илотно-упакованная (da = 1,633) рен 1еткн — наиболее компактные в них коэффициент заполнения объема атомами равен 74 «о. [c.16]
[c.16]
При уменьшении координационного числа в решетке Г12 до 6 коэффициент заполнения составляет около 50 о, а при коордппа ционном числе 4 — B ei o около 25 %. [c.16]
Под коэффициентом заполнения цикла подразумевается отношение площади даппого цикла в Гя-днаграмме к площади цикла Карно, осущест-пленного U том же нптервллс температур, [c.322]
Этот процесс совершенствования циклов тепловых машин называют карнотизацией цикла. Повышение средней температуры подвода теплоты и понижение средней температуры отвода теплоты эквивалентно увеличению коэффициента заполнения цикла. [c.89]
Площадь сечения стержня с учетом изоляции 6 = SJk , где /г, 0,9 — коэффициент заполнения, учитывающий межлисто- [c.282]
Вычерчивается пространственная схема, в процессе выполнения кС Торой определяется взаимное расположение элементов Конструкции в пространстве. Сначала наносятся на бумагу оси валиков, делительные окружности колес и пунктиром габаритные контуры двигателя, редуктора, сельсина и т. д. (см. рис. 28.8, б, г). Затем нг носятся контуры корпуса механизма. При этом стремятся получить наименьшие габаритные размеры корпуса механизма, высокий коэффициент заполнения объема Кз и обеспечить неооходимые условия для эксплуатации, сборки, осмотра и ремонта механизма. (К = где Кд — объем, занимаемый деталями и элементами механизма — объем параллелепипеда, ограничивающего габариты механизма.)
[c.405]
д. (см. рис. 28.8, б, г). Затем нг носятся контуры корпуса механизма. При этом стремятся получить наименьшие габаритные размеры корпуса механизма, высокий коэффициент заполнения объема Кз и обеспечить неооходимые условия для эксплуатации, сборки, осмотра и ремонта механизма. (К = где Кд — объем, занимаемый деталями и элементами механизма — объем параллелепипеда, ограничивающего габариты механизма.)
[c.405]
Провода с высокопрочной эмалевой изоляцией получают с использованием лаков на основе синтетических полимеров, пленка которых не нуждается в поверхностной защите, что позволяет уменьшить толщину изоляции это существенно влияет на размеры многовитковых многослойных аппаратных катушек и увеличивает коэффициент заполнения пазов электрических машин. Например, при номинальном диаметре медного провода 1 мм толщина изоляции провода марки ПЭЛБД с масляной эмалевой, изоляцией и двойной обмоткой хлопчатобумажной пряжей составляет 0,165 мм, а провода марки ПЭВ-1 с изоляцией на основе поливинилацеталевого лака (с однослойной изоляцией) — 0,04 мм, провода ПЭВ-2 (с двухслойной изоляцией) — 0,05 мм. Двухслойная изоляция более надежна в механическом и электрическом отношении, чем однослойная с точки зрения наличия случайно ослабленных мест, имеет значительно большее пробивное напряжение.
[c.260]
Двухслойная изоляция более надежна в механическом и электрическом отношении, чем однослойная с точки зрения наличия случайно ослабленных мест, имеет значительно большее пробивное напряжение.
[c.260]
Принятые величины. Переохлаждение конденсата А к = = 0,7 °С теплоемкость конденсата с =4,175 кДж/(кг-°С). Разность температур 8i = 4,7 °С температура забортной охлаждающей воды fi = 23 °С, ее теплоемкость Сц, = 3,925 кДж/(кг-°С), плотность р = 1020 кг/м скорость охлаждающей воды в трубах w = 2,0 м/с. Наружный диаметр труб d = = 0,019 м, внутренний dg = 0,016 5 м, шаг труб s = 28 мм. Коэффициент загрязнения рз = 0,9, коэффициент = 0,83, коэффициент заполнения трубной доски Т1тр = 0,58. Число ходов охлаждающей воды 2=2. Толщина трубной доски 8 = 0,03 м. [c.182]
В дефектоскопах, как правило, используются дифференциальные ВТП самосравнения с малой базой, с однородным и неоднородным полем в зоне контроля. Применение ВТП с неоднородным полем обусловлено стремлением уменьшить длину возбуждающей катушки с целью сокращения общей длины ВТП при контроле объектов большого диаметра.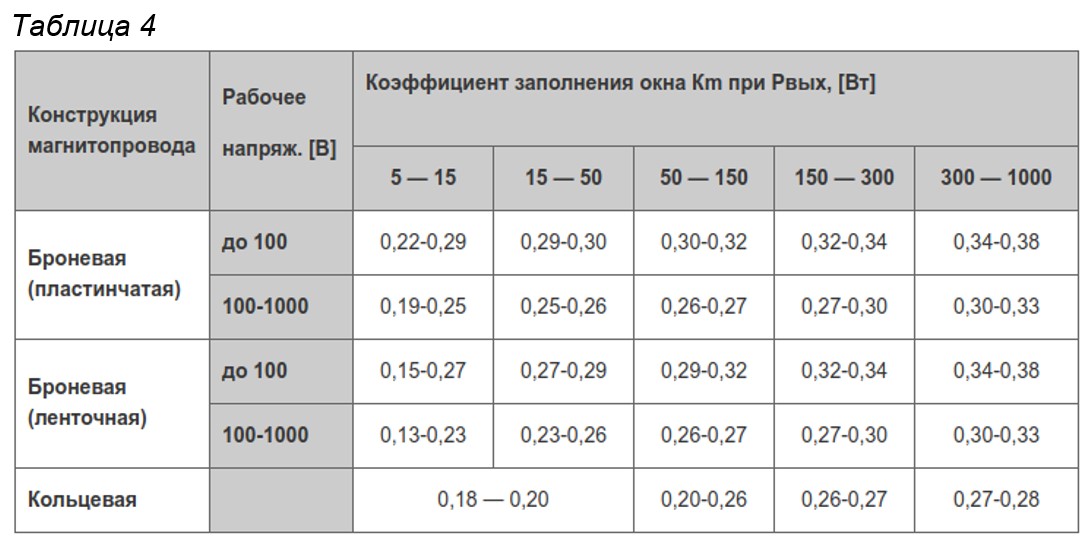 Однако при этом приходится принимать меры для стабилизации положения объекта. Для уменьшения возможных радиальных перемещений объекта в ВТП, а также для поддержания коэффициента заполнения t] на определенном уровне, определяющем чувствительность, дефектоскопы снабжают набором ВТП различного диаметра. При использовании ВТП с однородным полем можно значительно уменьшить число их типоразмеров, компенсируя изменение чувствительности при изменении г) регулированием возбуждающего тока.
[c.139]
Однако при этом приходится принимать меры для стабилизации положения объекта. Для уменьшения возможных радиальных перемещений объекта в ВТП, а также для поддержания коэффициента заполнения t] на определенном уровне, определяющем чувствительность, дефектоскопы снабжают набором ВТП различного диаметра. При использовании ВТП с однородным полем можно значительно уменьшить число их типоразмеров, компенсируя изменение чувствительности при изменении г) регулированием возбуждающего тока.
[c.139]
Развитие статистических методов позволяет наиболее полно оценить шероховатость поверхности, так как, помимо высотных характеристик, эти методы определяют закон распределения неровностей по высоте, коэффициент заполнения профиля, регулярную и случайную составляющие профиля, радиусы закругления неровностей, шаг неровностей, углы наклона боковых сторон профиля к средней линии и другие параметры. По Пекленику, профиль поверхности может быть характеризован автокорреляционной функцией [130].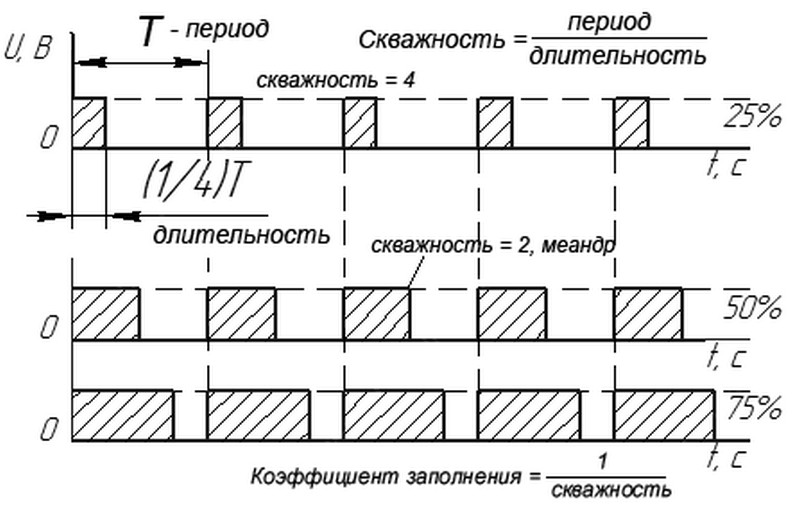 По данным работы [125], автокорреляционная функция, полностью характеризующая профиль исследуемой поверхности при условии, что функция профиля х) стационарна и одновременно подчиняется распределению Гаусса, выражается двумя следующими зависимостями
[c.24]
По данным работы [125], автокорреляционная функция, полностью характеризующая профиль исследуемой поверхности при условии, что функция профиля х) стационарна и одновременно подчиняется распределению Гаусса, выражается двумя следующими зависимостями
[c.24]
В соответствии с первой схемой осуществления процесса контурно-лучевой обработки предполагается, что 8 = 5 = 0 (рис. 38, а). Эта схема может быть использована в том случае, если по эксплуатационным требованиям, предъявляемым к изготовляемой детали, допускается наличие необлученных участков между зонами лазерного воздействия. Схема, показанная на рис. 38, а, характеризуется малым коэффициентом заполнения профиля (Кз = 0,8) и сравнительно высоким коэффициентом использования импульсов (Ки = = 0,68), что обусловливает довольно высокую производительность и скорость обработки. Отличительной чертой этой схемы является также отсутствие взаимноперекрытых участков зон лазерного воздействия, так как коэффициент перекрытия в этом случае равен единице. [c.61]
[c.61]
Коэффициент заполнения графика — Энциклопедия по машиностроению XXL
Так, по ЕЭС СССР и по отдельным наиболее характерным ОЭС коэффициент заполнения графика нагрузки 102 [c.102]Отношение средней нагрузки к максимальной называется коэффициентом заполнения графика ( а) [c.16]
Коэффициенту заполнения графика ij. отвечает коэффициент использования установ- [c.17]
Для сокраш,ения затрат машинного времени в вычислительный комплекс в некоторых случаях вводятся вместо относительно сложных зависимостей и алгоритмов упрощенные соотношения, выявленные после выполнения определенного объема расчетов (накопления опыта). В частности, такой прием применяется для организации сокращенного расчета режимов использования ТЭС путем обхода некоторых внутригодовых интервалов, с эквивалентным определением затрат на топливо за эти интервалы по упрощенным зависимостям. Аналогичным образом опыт, накапливаемый при полных расчетах по каждому году, позволяет затем производить полные расчеты не для каждого года, а показатели пропущенных лет получать интерполяцией. Подобный прием применяется при определении величины ремонтного резерва, коэффициента заполнения графика ремонтов и при дифференциации коэффициента готовности по внутригодовым интервалам специальная модель графика ремонтов используется лишь для отдельных характерных вариантов, в алгоритм же вычислительного комплекса введены обобщенные уравнения.
[c.204]
Аналогичным образом опыт, накапливаемый при полных расчетах по каждому году, позволяет затем производить полные расчеты не для каждого года, а показатели пропущенных лет получать интерполяцией. Подобный прием применяется при определении величины ремонтного резерва, коэффициента заполнения графика ремонтов и при дифференциации коэффициента готовности по внутригодовым интервалам специальная модель графика ремонтов используется лишь для отдельных характерных вариантов, в алгоритм же вычислительного комплекса введены обобщенные уравнения.
[c.204]
Плановое потребление электроэнергии в рабочий день составляет 108 тыс. кВт-ч. Число часов работы равно 24. Среднечасовая нагрузка 108 24 = 4,5 МВт. Коэффициент заполнения графика (за рабочий день декабря предыдущего года при максимальной нагрузке в часы максимума нагрузки энергосистемы) равен 0,75. [c.72]
Максимальная нагрузка равна 6,2 МВт (зафиксированная в часы максимума нагрузки энергосистемы в рабочий день декабря предыдущего года). Коэффициент заполнения графика равен 0,82. Прирост предельной потребляемой мощности собственными потребителями, установленной энергосистеме на месяц (отчетного года), равен 4,5 %.
[c.73]
Коэффициент заполнения графика равен 0,82. Прирост предельной потребляемой мощности собственными потребителями, установленной энергосистеме на месяц (отчетного года), равен 4,5 %.
[c.73]
Наряду С ЭТИМ, если суточный график нагрузки имеет коэффициент нагрузки (коэффициент заполнения графика) меньше 1, то на каждую 0,1 снижения коэффициента нагрузки этого трансформатора допускается перегрузка в 3% сверх номинальной мощности трансформатора на все часы максимума, если температура охлаждающей среды не превышает + 35° С. [c.224]
Коэффициент заполнения графика Гм (зима/лето).. Отношение суточного минимума нагрузки к максимуму т (зима/лето). . . 0,88/0,92 0,75/0,82 0,84/0,87 0,65/0,69 0,88/0,92 0,78/0,82 0,90/0,87 0,77/0,77 0,91/0,94 0,84/0,89 [c.16]
Будем понимать под коэффициентом заполнения отношение площади фигуры, ограниченной графиком 0″ (т) и осью абсцисс, к площади описанного прямоугольника, т. е. Хзп =
[c.21]
е. Хзп =
[c.21]На фиг. 5 представлен ряд механических характеристик с различными коэффициентами заполнения а на фиг. 6 приведена кривая зависимости коэффициента а от yi. При построении графика т и Пг приняты численно равными друг другу к взят равным 0,1. Из графика видно, что коэффициент а тем больше, чем меньше коэффициент заполнения механической характеристики. С другой стороны, из приведенного на фиг. 7 графика / =/(0 следует, что увеличение передаточного числа [c.108]
Характерным для суточного графика является также коэффициент использования максимальной нагрузки (коэффициент заполнения суточного графика) [c.10]
Значения коэффициента неравномерности графиков нагрузки энергосистем СССР для среднего рабочего дня декабря составляют от 0,6 в европейской части СССР до 0,85 в Сибири, коэффициента заполнения — соответственно от 0,8 до 0,9. [c.10]
Соответственно коэффициент использования годовой максимальной нагрузки (коэффициент заполнения годового графика продолжительности нагрузок) равен
[c. 11]
11]
Поляры несущего винта, т, е. графики зависимости Ср/а от t/q, построены для винта с коэффициентом заполнения [c.81]
О расчете характеристик вертолета полная мощность неизвестна, так что требуются еще последовательные приближения, но их выполняют графически, а не численно. Наибольщая трудность при таком графическом рещении состоит в необходимости интерполирования между графиками при расчете полной мощности. Графики характеристик строят для конкретного набора параметров несущего винта, но влияние массовой характеристики лопасти оказалось малым. При указанном выборе переменных влияние коэффициента заполнения винта также невелико. Из оставшихся параметров наиболее важен градиент крутки, так что для каждого значения этого параметра нужно [c.290]
НИТЬ расчет индуктивных скоростей при небольшом увеличении времени счета. Результаты расчетов аэродинамических нагрузок при переменном поле индуктивных скоростей представлены на рис. 13.8—13.14. Рассматривался трехлопастный шарнирный винт с коэффициентом заполнения о = 0,1. Градиент крутки 0кр составлял —8°, а массовая характеристика лопасти у была равна 8. В разд. 5.6 рассмотрены нагрузки этого же винта, определенные при постоянной индуктивной скорости. Все графики
[c.659]
13.8—13.14. Рассматривался трехлопастный шарнирный винт с коэффициентом заполнения о = 0,1. Градиент крутки 0кр составлял —8°, а массовая характеристика лопасти у была равна 8. В разд. 5.6 рассмотрены нагрузки этого же винта, определенные при постоянной индуктивной скорости. Все графики
[c.659]
На фиг. 15 приведены графики экспериментальных исследований зависимости коэффициента заполнения от скорости движения диска для двух способов ориентации. Как видно из графика, коэффициент заполнения для диска с расположением карманов по хорде (диск № 1, фиг. 7) в определенном диапазоне не зависит от скорости. Для отношения [c.137]
| Фиг. 17. График влияния угла наклона диска на коэффициент заполнения. |
Для определения коэффициента прохождения звука в этом случае можно воспользоваться графиками статьи [56], если заменить на оси ординат коэффициент отражения коэффициентом прохождения, а на оси абсцисс — коэффициент заполнения 1—коэффи- [c.
 115]
115]При действии ветра под углом к плоскости симметрии пространственной конструкции из двух параллельных ферм нагрузка на нее сначала увеличивается с ростом угла скольжения р (рис. 3.39), потому что при малых углах стержни задней фермы выходят иэ тени передних. При углах р = 20+-30° нагрузка на конструкцию достигает наибольшего значения. С увеличением расстояния между фермами нагрузка на обе растет все меньше. При бесконечно большом расстоянии между фермами характер изменения нагрузки в зависимости от угла скольжения приближается к графику сопротивления изолированной (одинарной) фермы. При отношении 6/с 1,5 рост нагрузки становится уже малым и зависимость ее с увеличением угла р все более приближается к случаю, когда Ь/ = оо. Влияние коэффициента заполнения фермы в пределах 0,25—0,4 проявляется в повышении нагрузки характер ее зависимости от угла р остается примерно одинаковым. При угле р=70° нагрузка на две фермы составляет приблизительно 0,25 наибольшей величины нагрузки с дальнейшим ростом угла р она изменяется мало. [c.77]
[c.77]
Коэффициент заполнения графика нагрузки среднего раЗочего дня декабря [c.100]
Специфические условия работы забойных электроприемников заметно влияют на формирование суммарной электрической нагрузки добычного участка. Это хорошо видно на графике изменения во времени тока и напряжения в электрической сети, от которой питается угледобывающий комплекс (рис. 1.2). Обычно коэффициент заполнения графиков электрических нагрузок ЭП комплексно-механизированных лав за сутки близок к 0,5, а за смену достигает 0,7 (см. рис. 1.1, а). При этом в течение почти 50 % времени работы комбайна текущее значение нагрузки ЭП превышает 30-минутный максимум, поскольку непрерывное время работы комбайна, как правило, значительно меньше времени осреднения нагрузки.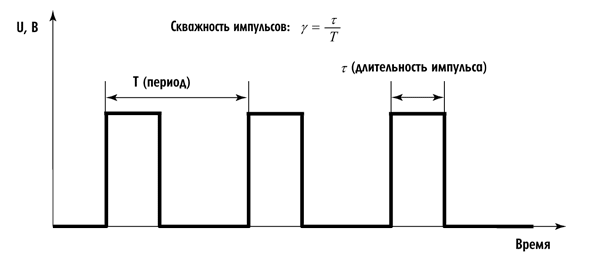 [c.26]
[c.26]
Режим и структура электропотребления находят свое отражение в нагрузке энергосистем и наиболее характерно определяются суточными графиками нагрузки. По сравнению с основными развитыми капиталистическими странами графики наг1рузки энергетических систем в СССР являются более плотными, характеризуются высоким коэффициентом заполнения, что объясняется сравнительно большим удельным весом промышленности в общем потреблении электроэнергии. За 1975— 1980 гг. годовое число часов использования максимума нагрузки увеличилось на 210 ч, что было вызвано, в частности, проведением мероприятий по выравниванию графика нагрузок потребителями, а также напряженными режимными условиями в ЕЭС СССР. Необходимо отметить, что доля коммунально-бытовых и сельскохозяйственных потребителей непрерывно повышалась. [c.99]
Входящие в (4-79) относительная площадь фактического конта.относительное сближение е находим по формулам (4-75). Получаем т ., = 0,000288 и 8 = 0,0309. По графику рис. 4-29 для Лср = = 46-10 м, коэффициент заполнения адгезивом впадин мпкронеров-ностей = 0,6.
[c.268]
По графику рис. 4-29 для Лср = = 46-10 м, коэффициент заполнения адгезивом впадин мпкронеров-ностей = 0,6.
[c.268]
В работе [К-42] приведены графики аэродинамических характеристик вертолета при полете вперед, основанные на численном определении нагрузок винта и махового движения. При выполнении расчетов не использовано предположение о малости углов, учтено влияние срыва, сжимаемости воздуха и зоны обратного обтекания, а в качестве характеристик сечений лопасти взяты экспериментальные аэродинамические коэффициенты профиля (NA A 0012) в стационарном потоке. Распределение индуктивных скоростей предполагалось равномерным, эффекты радиального течения и динамического срыва не учитывались. Расчеты были выполнены для винта с прямоугольными в плане линейно-закрученными лопастями при следующих значениях параметров коэффициент заполнения а — 0,062 (рассмотрено введение поправки на заполнение), массовая характеристика лопасти V = 7,6, неоперенная часть до го = 0,2, коэффициент концевых потерь В = 0,97, относ горизонтальных шарниров
[c. 293]
293]
Проходные преобразователи чаще всего используют для дефектоскопии протяженных объектов, особенно объектов цилиндрической формы. Для прутков, проволоки, труб и других объектов круглого сечения, получаемых прокаткой плп волоченпем, наиболее характерны узкие продольные дефекты (тре щины, закаты, волосовины, риски и т. д.). Они оказывают такое же влияние на преобразователь, как бесконечно узкий и бесконечно длинный разрез глубиной к, направленный в глубь цилиндра по радиусу (рис. 23, дефект типа А). На рпс. 24, а представлена диаграмма зависимости относительной комплексной величины приращения напряжения измерительной обмотки проходного трансформаторного преобразователя от глубины поверхностного дефекта й (/г выражена в долях диаметра цилиндра) для различных значений обобщенного параметра 3 . Диаграмма справедлива для неферромагнитного бесконечно длинного цилиндра при коэффициенте заполнения = 1. На рис 24, б приведен соответствую щип график для модуля АС/.
[c. 117]
117]
Рассмотрение типовых графиков усилий (см. рис. 7.1, 7.2, 21.9) позволяет сделать выводы о применимости того или иного привода. Например, для процессов группы III прессы небольших усилий целесообразно не оснащать насосным аккумуляторным приводом. Его гидравлический коэффициент будет незначителен вследствие малой степени заполнения графика усилий. Нецелесообразен здесь и насосный безакку.муляторный привод в простейшем исполнении (насос постоянной подачи и одноцилиндровый пресс). 1Мощность привода не будет использована в достаточной мере. Целесообразно прн.менение привода от насосов различных характеристик. [c.274]
Цилиндрический, конический редукторы — т = фрК10 , где ф — коэффициент заполнения определить по графикам в зависимости от межосевого расстояния для цилиндрического редуктора (см. рис. 12.1) в зависимости от внешнего конусного расстояния — для конического (см.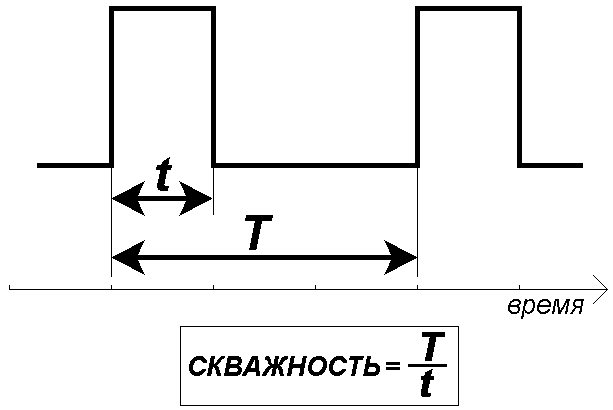 рис. 12.2)
[c.262]
рис. 12.2)
[c.262]
На рис. 2-4 показан примерный суточный график технологической нагрузки теплоемкого предприятия. Степень неравномерности теплопотреблення характеризует коэффициент заполнения суточного графика А ц.с (усредненный за характерные сутки), определяется как отношение среднечасовой иагрузки Ст.ср к максимальной часовой за сутки Ст.макс- [c.20]
Планирование зоны хранения
Издание «Современный склад», №6, 2007 г. // Июнь, 2007
Планирование зоны хранения — один из этапов логистического проектирования склада, направленный на решение следующих трех основных задач: определение конструкции мест хранения (типоразмеров), вычисление потребности в ячейках каждого из выбранных типоразмеров и распределение ячеек по стеллажам в зоне хранения.
Конструкция мест хранения непосредственно влияет на выбор вида и количества стеллажного и погрузочного оборудования. От того, какие типы мест хранения будут выбраны и как они будут размещены на складе, зависят затраты на оснащение, стоимость единицы хранения товара, эффективность использования складского пространства, трудовых и технических ресурсов.
Представленная в настоящей публикации методика, использующаяся в проектах AXELOT, обладает достаточной гибкостью и универсальностью и позволяет получить точный результат при условии наличия данных о весогабаритных характеристиках товара и статистики товародвижения за 1–2 года.
Согласно методике, процесс проектирования мест хранения включает в себя следующие подэтапы:
- Выбор оптимальных типоразмеров ячеек с учетом габаритных характеристик товаров
- Расчет потребности в ячейках каждого из выбранных типоразмеров для зон хранения и отбора товаров.
- Составление схемы размещения стеллажей
Выбор типоразмеров ячеек
Имея перечень товаров, подлежащих размещению на складе, а также данные о габаритах и весе упаковок, можно определить оптимальные типоразмеры ячеек, которые впоследствии будут использоваться на складе.
Для этого на основании оценки параметров имеющихся помещений и стеллажных конструкций необходимо выбрать несколько типоразмеров ячеек, которые в принципе возможно использовать. Затем следует рассчитать максимальное количество упаковок с товаром, которые могут разместиться в каждой из выбранных ячеек, и определить коэффициент заполнения по весу и объему.
Затем следует рассчитать максимальное количество упаковок с товаром, которые могут разместиться в каждой из выбранных ячеек, и определить коэффициент заполнения по весу и объему.
Из всего многообразия ячеек в дальнейших расчетах следует использовать те из них, которые имеют максимальный коэффициент заполнения по объему, а коэффициент заполнения по весу при этом не превышает допустимые значения. Пример расчета коэффициента заполнения приведен в таблицах 1–3.
Таблица 1. Данные о товарах
|
код |
Наименование |
Учетная Единица |
Длина, мм |
Ширина, мм |
Высота, мм |
Вес, кг |
объем, м3 |
|
0001 |
Сухой корм для кошек в картонных коробках по 400 гр |
шт. |
50 |
150 |
250 |
0,5 |
0,0019 |
|
0002 |
Сухой корм для собак, в мешках по 15 кг |
шт. |
730 |
400 |
220 |
15,5 |
0,0642 |
|
0003 |
Консервированный корм для собак в жестяных банках по 400 гр |
шт. |
75 |
75 |
110 |
0,5 |
0,0006 |
Таблица 2. Выбранные типоразмеры ячеек
|
|
ячейка 1 |
ячейка 2 |
ячейка 3 |
|
длина, мм |
1200 |
1200 |
1000 |
|
ширина, мм |
800 |
800 |
400 |
|
высота, мм |
1400 |
500 |
650 |
|
объем, м3 |
1,344 |
0,48 |
0,26 |
|
Максимальный вес товара на поддоне, кг |
750 |
750 |
750 |
Таблица 3.
 Расчет коэффициента заполнения ячеек
Расчет коэффициента заполнения ячеек|
Код товара |
Максимальное количество упаковок с товаром, которое может разместиться в ячейке |
Проверка ограничения по весу (Произведение количества товара в ячейке и веса одной единицы) |
Расчет коэффициента заполнения объема ячейки (отношение объема товара к объему яейки) |
||||||
|
ячейка 1 |
ячейка 2 |
ячейка 3 |
ячейка 1 |
ячейка 2 |
ячейка 3 |
ячейка 1 |
ячейка 2 |
ячейка 3 |
|
|
0001 |
600 |
240 |
80 |
300 |
120 |
40 |
0,84 |
0,94 |
0,58 |
|
0002 |
12 |
4 |
2 |
186 |
62 |
31 |
0,57 |
0,54 |
0,49 |
|
0003 |
1920 |
640 |
325 |
960 |
320 |
162,5 |
|
0,83 |
0,77 |
Первый шаг вычислений — определение количества упаковок, которое может разместиться в каждой из выбранных ячеек (таблица 3).
 В данном случае количество вычисляется по формуле:
В данном случае количество вычисляется по формуле:, где
К — количество товара в ячейке
Д — длина, мм
Ш — ширина, мм
В — высота, мм
На практике используются более сложные расчеты, которые учитывают возможность вращения упаковок и различные способы их укладки на поддон.
Следующий шаг — вычисление веса товара и определение ячеек, которые не могут быть использованы из-за превышения нагрузки на полку. В нашем примере третья позиция номенклатуры при укладке на поддон высотой 1,4 м превышает допустимый вес, поэтому для данного товара ячейка №1 использоваться не может.
Далее рассчитываем коэффициент заполнения ячейки по формуле:
В случае если в габариты ячеек включен сам поддон, а также пространство между товаром и элементами стеллажа, необходимое для удобной и безопасной работы, оптимальным считается значение коэффициента от 0,56 до 0,75.
Если указывается «чистый объем», то оптимальный коэффициент заполнения должен быть не менее 0,7.
В ситуации, когда в результате расчетов ни одна из выбранных ячеек не удовлетворяет указанным критериям, необходимо выбрать дополнительные типоразмеры ячеек или изменить параметры используемых.
В идеале окончательный перечень ячеек должен состоять из таких типоразмеров, коэффициент заполнения которых любым товаром из перечня номенклатуры был бы не менее 0,7. Поскольку на складе могут храниться товары с существенно различающимися габаритными характеристиками, номенклатуру следует разделить на товарные группы и перечень типоразмеров ячеек определять для каждой группы отдельно.
Расчет необходимого количества ячеек
Для определения количества ячеек зоны хранения используются нормативные значения уровня запаса для каждого товара. К сожалению, в большинстве случаев консультанты AXELOT сталкиваются с отсутствием такой информации у заказчика, поэтому расчеты производятся для диапазона объема товара. Нижняя граница диапазона — средний уровень запаса товара (за последнее полугодие). В качестве верхней границы, как правило, используется значение суммарного объема поставок за месяц, если на складе коэффициент оборачиваемости товаров за год близок к 12.
В качестве верхней границы, как правило, используется значение суммарного объема поставок за месяц, если на складе коэффициент оборачиваемости товаров за год близок к 12.
Ольга Каверина, консультант по складской логистике компании AXELOT
Менеджеры AXELOT будут рады ответить на все вопросы по тел. +7(495)961-26-09. Также вы можете написать нам через форму
Обратная связь
Вольт-амперная характеристика, как работают солнечные элементы
Для генерации электричества от солнца вам нужен солнечный модуль, который состоит из одного или многих солнечных фотоэлектрических элементов. Когда на солнечный элемент падает солнечных свет, материал солнечного элемента поглощает часть солнечного света (фотоны). Каждый фотон имеет малое количество энергии. Когда фотон поглощается, он инициирует процесс освобождения электрона в солнечном элементе. Вследствие того, что обе стороны фотоэлектрического элемента имеют токоотводы, в цепи возникает ток когда фотон поглощается. Солнечный элемент генерирует электричество, которое может быть использовано сразу или сохранено в аккумуляторной батарее.
Солнечный элемент генерирует электричество, которое может быть использовано сразу или сохранено в аккумуляторной батарее.
Принцип действия фотоэлектрического элемента
- 1.свет (фотоны)
- 4.слой p-n перехода
- 2.фронтальный контакт
- 5.позитивный слой
- 3.негативный слой
- 6.задний контакт
Пока солнечный элемент освещается, процесс образования свободных электронов продолжается и генерируется электричество, то есть наблюдается фотоэлектрический эффект. Материалы, из которых делается элемент – это полупроводники с особыми свойствами.
Простейшая конструкция солнечного элемента (СЭ) – прибора для преобразования энергии солнечного излучения – на основе монокристаллического кремния показана на рис.1. На малой глубине от поверхности кремниевой пластины p-типа сформирован p-n-переход с тонким металлическим контактом. На тыльную сторону пластины нанесён сплошной металлический контакт.
Рис.2. Зонная модель разомкнутого p-n-перехода: а) – в начальный момент освещения; б) – изменение зонной модели под действием постоянного освещения и возникновение фотоЭДС
Когда СЭ освещается, поглощённые фотоны генерируют неравновесные электрон-дырочные пары. Электроны, генерируемые в p-слое вблизи p-n-перехода, подходят к p-n-переходу и существующим в нем электрическим полем выносятся в n-область. Аналогично и избыточные дырки, созданные в n-слое, частично переносятся в p-слой (рис. 2а). В результате n-слой приобретает дополнительный отрицательный заряд, а p-слой – положительный. Снижается первоначальная контактная разность потенциалов между p- и n-слоями полупроводника, и во внешней цепи появляется напряжение (рис. 2б). Отрицательному полюсу источника тока соответствует n-слой, а p-слой – положительному.
Электроны, генерируемые в p-слое вблизи p-n-перехода, подходят к p-n-переходу и существующим в нем электрическим полем выносятся в n-область. Аналогично и избыточные дырки, созданные в n-слое, частично переносятся в p-слой (рис. 2а). В результате n-слой приобретает дополнительный отрицательный заряд, а p-слой – положительный. Снижается первоначальная контактная разность потенциалов между p- и n-слоями полупроводника, и во внешней цепи появляется напряжение (рис. 2б). Отрицательному полюсу источника тока соответствует n-слой, а p-слой – положительному.
Величина установившейся фотоЭДС при освещении перехода излучением постоянной интенсивности описывается уравнением вольт-амперной характеристики (ВАХ) (рис. 3):
U = (kT/q)ln((Iph-I)Is/+1)
где Is– ток насыщения, а Iph – фототок.
Рис.3. Вольт-амперная характеристика солнечного элемента
ВАХ поясняет эквивалентная схема фотоэлемента (рис. 4), включающая источник тока Iph=SqN0Q, где S – площадь фотоэлемента, а коэффициент собирания Q – безразмерный множитель (<1), показывающий, какая доля всех созданных светом электронно-дырочных пар (SN0) собирается p-n-переходом. Параллельно источнику тока включен p-n-переход, ток через который равен Is[eqU/kT-1]. p-n-Переход шунтирует нагрузку, и при увеличении напряжения ток через него быстро возрастает. В нагрузку (сопротивление R) отбирается ток I.
4), включающая источник тока Iph=SqN0Q, где S – площадь фотоэлемента, а коэффициент собирания Q – безразмерный множитель (<1), показывающий, какая доля всех созданных светом электронно-дырочных пар (SN0) собирается p-n-переходом. Параллельно источнику тока включен p-n-переход, ток через который равен Is[eqU/kT-1]. p-n-Переход шунтирует нагрузку, и при увеличении напряжения ток через него быстро возрастает. В нагрузку (сопротивление R) отбирается ток I.
Уравнение ВАХ справедливо и при освещении фотоэлемента светом произвольного спектрального состава, изменяется лишь значение фототока Iph. Максимальная мощность отбирается в том случае, когда фотоэлемент находится в режиме, отмеченном точкой а (см. рис. 3).
Рис.4. Эквивалентная схема солнечного элемента
Максимальная мощность, снимаемая с единицы площади, равна
P = Iph*U = x*Iкз*Uхх,
где x – коэффициент формы или коэффициент заполнения вольт-амперной характеристики, Iкз – ток короткого замыкания, Uхх – напряжение холостого хода.
Солнечные модули могут генерировать электричество в течение 20 и более лет. Износ происходит в основном от воздействия окружающей среды. Хорошо смонтированная солнечная батарея будет надежным, тихим и чистым источником энергии в течение многих лет.
Дополнительная информация: М. Мейтин. “Пусть всегда будет солнце!”
Солнечные элементы. Коэффициент заполнения вольт-амперной характеристики
Коэффициент заполнения ВАХ солнечного элемента (fill factor – FF) – это отношение реальной мощности (Vpmax x Ipmax) к гипотетической мощности Voc x Isc. Этот коэффициент является одным из основых параметров, по которому можно судить о качестве фотоэлектрического преобразователя. Типичные качественные серийно выпускаемые солнечные элементы имеют коэффициент заполнения ВАХ > 0.70. Бракованные элементы, которые обычно продаются на eBay или китайских аукционах или интернет-магазинах (grade B), имеют коэффициент заполнения ВАХ в диапазоне от 0. 4 до 0.65. У аморфных элементов и других тонкопленочных фотоэлектрических преобразователей коэффициент заполнения ВАХ находится в диапазоне 0.4 – 0.7.
4 до 0.65. У аморфных элементов и других тонкопленочных фотоэлектрических преобразователей коэффициент заполнения ВАХ находится в диапазоне 0.4 – 0.7.
На рисунке справа теоретическая мощность – это площадь квадрата, а реальная мощность соответствует границе голубой фигуры. FF – это отношение площади голубой фигуры к площади суммы голубой и красной фигур. Можно сказать, что чем больше FF, тем меньше потери в элементе из-за внутреннего сопротивления.
Коэффициент заполнения ВАХ может также использоваться для определения сопротивления солнечного элемента.
Коэффициент заполнения ВАХ (FF) = (Vmpp x Impp) / (Voc x Isc)
где:
Vmpp = напряжение в точке максимальной мощности (ТММ)
Impp = ток в ТММ
Voc = напряжение холостого хода
Isc = ток короткого замыкания
График ниже иллюстрирует ВАХ элементов c различным коэффициентом заполнения.
Как видно, обе кривые имеют одинаковые Voc и Isc, однако элемент c меньшим FF (нижний график) вырабатывает меньше мощности в ТММ. Обычный человек может быть легко обманут замерами только тока КЗ и напряжения ХХ. На eBay и youtube.com есть много предложений, где продавцы измеряют эти 2 параметра у модулей c поломанными элементами и уверяют, что модуль работает “как целый”.
При производстве каждый солнечный элемент тестируется и при этом измеряется его ВАХ и FF. Если fill factor меньше 0,7, то элемент классифицируется как Grade B и используется для продажи “самоделкиным” или производителям супер-дешевых модулей (которые должны уведомлять покупателей, что модули сделаны из низкокачественных элементов – однако на практике недобросовестные продавцы и производители этого не делают).
Эта статья прочитана 14171 раз(а)!
Продолжить чтение
59
Технология солнечных элементов PERC: Почему она будет доминировать в ближайшем будущем? Последние несколько лет технология изготовления солнечных элементов PERC является одним из фаворитов научно-исследовательских работ в фотоэлектрической индустрии, и уже стала стандартом при серийном производстве фотоэлектрических модулей. PERC означает Passivated…
PERC означает Passivated…51
Как работают MPPT контроллеры? Что такое MPPT контроллеры, для чего они нужны и в чем их отличие от контроллеров с ШИМ описано по ссылке. На этой странице дана более подробная техническая информация Методы поиска точки максимальной мощности (ТММ) солнечной батареи…
Волоконная оптика. Термины и определения – РТС-тендер
ГОСТ 25462-82
Группа Т35
Дата введения 1984-01-01
ВВЕДЕН В ДЕЙСТВИЕ Постановлением Государственного комитета СССР по стандартам от 29 сентября 1982 года N 3825
Настоящий стандарт устанавливает применяемые в науке, технике и производстве термины и определения основных понятий в области волоконной оптики.
Термины, установленные настоящим стандартом, обязательны для применения в документации всех видов, научно-технической, учебной и справочной литературе.
Для каждого понятия установлен один стандартизованный термин. Применение терминов-синонимов стандартизованного термина запрещается.
Применение терминов-синонимов стандартизованного термина запрещается.
Для отдельных стандартизованных терминов в стандарте приведены в качестве справочных краткие формы, которые разрешается применять в случаях, исключающих возможность их различного толкования. Установленные определения можно, при необходимости, изменять по форме изложения, не допуская нарушения границ понятий.
В стандарте приведен алфавитный указатель содержащихся в нем терминов.
Стандартизованные термины набраны полужирным шрифтом, краткая форма — светлым.
Термин | Определение |
1. Волоконная оптика | Раздел оптики, в котором рассматривают направленную передачу излучения и связанную с ним информацию по волоконным световодам |
2. Световод | Направляющий канал для передачи оптического излучения, состоящий из сердцевины, окруженной отражающей оболочкой (оболочками) |
3. Многожильный волоконный световод Многожильный световод | Совокупность волоконных световодов, объединенных по всей длине материалом оболочки |
4. Сердцевина волоконного световода Сердцевина | Светопроводящая часть волоконного световода со средним значением показателя преломления, превышающим показатель преломления отражающей оболочки |
5. Отражающая оболочка волоконного световода Оболочка | Покрытие сердцевины волоконного световода, обеспечивающее ее оптическую изоляцию и механическую защиту |
6. | Волоконный световод с плавным изменением показателя преломления по сечению от оси световода к его периферии |
7. Волоконнооптический жгут | Изделие из волоконных световодов, жестко скрепленных у торцов |
8. Волоконнооптическая пластина | Изделие из параллельно расположенных и жестко скрепленных по всей длине волоконных световодов с длиной, меньшей поперечного сечения |
9. Волоконнооптический преобразователь | Изделие из волоконных световодов с заданной схемой расположения их концов |
10. Фокон | Изделие из волоконных световодов с увеличивающимся или уменьшающимся по длине сечением |
11. Коэффициент заполнения | Отношение суммы площадей торцов сердцевин к площади торца изделия из волоконных световодов |
12. Угол скоса торца волоконного световода Угол скоса | Угол между оптической осью волоконного световода и нормалью к поверхности торца волоконного световода |
13. Угол входа луча в волоконный световод Угол входа | Угол между лучом в пространстве предметов и оптической осью волоконного световода |
14. Угол распространения луча в волоконном световоде Угол распространения | Угол между лучом в волоконном световоде и его оптической осью |
15. Угол выхода луча из волоконного световода Угол выхода | Угол между лучом в пространстве изображений и оптической осью волоконного световода |
16. Расчетный апертурный угол | Наибольший угол между оптической осью волоконного световода и лучом в пространстве предметов, проходящим по волоконному световоду без виньетирования |
17. Расчетная числовая апертура волоконного световода Расчетная числовая апертура | Произведение показателя преломления среды на входе волоконного световода и абсолютного значения синуса его расчетного апертурного угла |
Апертура волоконного световода числовая расчетная | 17 |
Апертура числовая расчетная | 17 |
Жгут волоконнооптический | 7 |
Коэффициент заполнения | 11 |
Коэффициент заполнения изделия из волоконных световодов | 11 |
Оболочка | 5 |
Оболочка волоконного световода отражающая | 5 |
Оптика волоконная | 1 |
Пластина волоконнооптическая | 8 |
Преобразователь волоконнооптический | 9 |
Световод | 2 |
Световод волоконный | 2 |
Световод волоконный градиентный | 6 |
Световод волоконный многожильный | 3 |
Световод многожильный | 3 |
Сердцевина | 4 |
Сердцевина волоконного световода | 4 |
Угол апертурный расчетный | 16 |
Угол волоконного световода апертурный расчетный | 16 |
Угол входа | 13 |
Угол входа луча в волоконный световод | 13 |
Угол выхода | 15 |
Угол выхода луча из волоконного световода | 15 |
Угол распространения | 14 |
Угол распространения луча в волоконном световоде | 14 |
Угол скоса | 12 |
Угол скоса торца волоконного световода | 12 |
Фокон | 10 |
Текст документа сверен по:
официальное издание
М. : Издательство стандартов, 1982
: Издательство стандартов, 1982
| PVEducation
Ток короткого замыкания и напряжение холостого хода — это максимальные ток и напряжение, соответственно, от солнечного элемента. Однако в обеих этих рабочих точках мощность солнечного элемента равна нулю. «Коэффициент заполнения», более известный под аббревиатурой «FF», представляет собой параметр, который в сочетании с V oc и I sc определяет максимальную мощность солнечного элемента. FF определяется как отношение максимальной мощности от солнечного элемента к произведению V oc и I sc , так что:
$$ FF = \ frac {P_ {MP}} {V_ {OC} \ times I_ {SC}} $$
Графически FF — это мера «прямоугольности» солнечного элемента, а также площадь самого большого прямоугольника, который будет соответствовать кривой IV.FF проиллюстрирован ниже.
График выходного тока ячейки (красная линия) и мощности (синяя линия) как функции напряжения. Также показаны точки тока короткого замыкания элемента (I sc ) и напряжения холостого хода (V OC ), а также точка максимальной мощности (V mp , I mp ). Щелкните график, чтобы увидеть, как изменяется кривая для ячейки с низким FF.
Также показаны точки тока короткого замыкания элемента (I sc ) и напряжения холостого хода (V OC ), а также точка максимальной мощности (V mp , I mp ). Щелкните график, чтобы увидеть, как изменяется кривая для ячейки с низким FF.
Поскольку FF является мерой «прямоугольности» ВАХ, солнечный элемент с более высоким напряжением имеет более высокий возможный FF, поскольку «закругленная» часть ВАХ занимает меньшую площадь.Максимальный теоретический FF солнечного элемента может быть определен путем дифференцирования мощности солнечного элемента по напряжению и определения, где оно равно нулю. Следовательно:
$$ \ frac {d (I V)} {d V} = 0 $$
подача:
$$ V_ {MP} = V_ {OC} — \ frac {nkT} {q} ln (\ frac {q V_ {MP}} {nkT} +1) $$
Это неявное уравнение, но оно быстро сходится при повторении. Начиная с V MP = 0,9 × V OC в качестве начального условия, после одной итерации возникает ошибка <1% и незначительная (<0. 01%) после трех итераций. Альтернативой является использование функций Ламберта (см. Ниже). Подстановка значения V MP обратно в уравнение диода дает I MP , а затем FF. Более часто используемое эмпирическое выражение для FF:
01%) после трех итераций. Альтернативой является использование функций Ламберта (см. Ниже). Подстановка значения V MP обратно в уравнение диода дает I MP , а затем FF. Более часто используемое эмпирическое выражение для FF:
, где v oc определяется как «нормализованный V oc «:
Приведенные выше уравнения показывают, что чем выше напряжение, тем выше возможная FF. Однако большие колебания напряжения холостого хода в данной материальной системе относительно редки.Например, на одном солнце разница между максимальным напряжением холостого хода, измеренным для кремниевого лабораторного устройства и типичного коммерческого солнечного элемента, составляет около 120 мВ, что дает максимальные значения FF соответственно 0,85 и 0,83. Однако изменение максимального FF может быть значительным для солнечных элементов, изготовленных из разных материалов. Например, у солнечного элемента на основе GaAs FF может приближаться к 0,89.
Приведенное выше уравнение также демонстрирует важность фактора идеальности, также известного как «n-фактор» солнечного элемента.Фактор идеальности является мерой качества перехода и типа рекомбинации в солнечном элементе. Для простых механизмов рекомбинации, обсуждаемых в разделе Типы рекомбинации, n-фактор имеет значение 1. Однако некоторые механизмы рекомбинации, особенно если они большие, могут вводить механизмы рекомбинации 2. Высокое значение n не только ухудшает FF. , но поскольку он также обычно сигнализирует о высокой рекомбинации, он дает низкие напряжения холостого хода.
Ключевым ограничением в уравнениях, описанных выше, является то, что они представляют максимально возможную FF, хотя на практике FF будет ниже из-за наличия паразитных резистивных потерь, которые обсуждаются в разделе «Эффекты паразитных сопротивлений».Следовательно, FF чаще всего определяется путем измерения ВАХ и определяется как максимальная мощность, деленная на произведение I sc * V oc , т. Е .:
Е .:
Точное определение V
MPУравнение солнечного элемента:
$$ I = I_L-I_0 \ left [\ exp \ left (\ frac {V} {nV_t} \ right) -1 \ right] $$
\ (мощность = V \ умножить на I \) и, кроме того, член -1 не влияет на V MP
$$ P = V I_L- V I_0 \ exp \ left (\ frac {V} {nV_t} \ right) $$
V MP — это когда производная мощности по V равна нулю:
$$ 0 = I_L- I_0 \ exp \ left (\ frac {V_ {MP}} {nV_t} \ right) \ left (1+ \ frac {V_ {MP}} {nV_t} \ right) $$
V>> V t и перестановка дает:
$$ \ frac {I_L} {I_0} = \ exp \ left (\ frac {V_ {MP}} {nV_t} \ right) \ left (\ frac {V_ {MP}} {nV_t} \ right) $$
W-функция Ламберта является решением класса экспоненциальных функций.x \ Leftrightarrow X = W (Y) $$
так получаем:
$$ \ frac {V_ {MP}} {nV_t} = W \ left (\ frac {I_L} {I_0} \ right) $$
$$ V_ {MP} = nV_t W \ left (\ frac {I_L} {I_0} \ right) $$
, используя выражение для V OC , мы также можем записать:
$$ V_ {MP} = nV_t W \ left (\ exp \ left (\ frac {V_ {OC}} {nV_t} \ right) \ right) $$
Поскольку выражение внутри W () всегда действительное и положительное, нам всегда нужна только основная ветвь функции Ламберта W, W 0 . Функция Ламберта W является трансцендентной функцией, очень похожей на функцию логарифмирования. Хотя он недоступен на большинстве калькуляторов, он доступен в расширенных математических пакетах, таких как Matlab или Python. При дальнейшем анализе W-функцию Ламберта можно также использовать для других элементов солнечных элементов и при наличии паразитных сопротивлений.
Функция Ламберта W является трансцендентной функцией, очень похожей на функцию логарифмирования. Хотя он недоступен на большинстве калькуляторов, он доступен в расширенных математических пакетах, таких как Matlab или Python. При дальнейшем анализе W-функцию Ламберта можно также использовать для других элементов солнечных элементов и при наличии паразитных сопротивлений.
Что такое формула коэффициента заполнения? — Mvorganizing.org
Что такое формула коэффициента заполнения?
«Коэффициент заполнения», более известный под аббревиатурой «FF», представляет собой параметр, который вместе с Voc и Isc определяет максимальную мощность солнечного элемента.FF определяется как отношение максимальной мощности солнечного элемента к произведению Voc и Isc, так что: F F = P M P V O C × I S C.
Может ли коэффициент заполнения быть больше 1?
Как вы можете прочитать выше, в соответствии с правилами аналитической геометрии невозможно, чтобы значение коэффициента заполнения любого солнечного элемента могло быть больше 1. Поскольку математическое соотношение тока и напряжения можно объяснить только с помощью «уравнения Шокли».
Поскольку математическое соотношение тока и напряжения можно объяснить только с помощью «уравнения Шокли».
Что такое «SQ Limit»?
a) Предел эффективности детального баланса Shockley-Queisser (предел S-Q) и текущие записи эффективности различных солнечных элементов.
Как увеличить коэффициент заполнения?
Коэффициент заполнения — это мера прямоугольности ВАХ. По мере увеличения прямоугольности увеличивается коэффициент заполнения. Прямоугольность увеличивается за счет: — уменьшения обратного тока насыщения Is.
Как коэффициент заполнения влияет на точку максимальной мощности?
Коэффициент заполнения определяется как отношение максимальной мощности солнечного элемента к произведению напряжения холостого хода Voc и тока короткого замыкания Isc. В табличных данных это часто используется для оценки максимальной мощности, которую может обеспечить ячейка с оптимальной нагрузкой при заданных условиях, P = FF * Voc * Isc.
Как определить точку максимальной мощности?
MPP также можно найти как точку, в которой произведение тока и напряжения равно наибольшему значению. Расчет мощности показывает, что MPP имеет напряжение VMPP = 4,934, ток IMPP = 0,100 A, мощность P = 0,491 Вт. Эти данные могут быть более четко визуализированы на графике.
Расчет мощности показывает, что MPP имеет напряжение VMPP = 4,934, ток IMPP = 0,100 A, мощность P = 0,491 Вт. Эти данные могут быть более четко визуализированы на графике.
Что лучше MPPT или PWM?
ШИМ-контроллер работает с относительно постоянной эффективностью сбора урожая независимо от размера массива.Контроллер PWM дешевле, чем MPPT, поэтому является более экономичным выбором для небольшой системы. Контроллер MPPT намного менее эффективен в приложениях с низким энергопотреблением.
Как определить максимальную мощность солнечной панели?
Есть много разных способов попытаться использовать солнечную панель на максимальной мощности. Один из самых простых — подключить батарею к солнечной панели через диод. Этот метод описан здесь в статье «Сбор энергии с помощью солнечных панелей малой мощности».
Какую мощность вырабатывает солнечная панель мощностью 300 Вт?
Что можно запустить с солнечной панелью на 300 ватт? Панель на 300 Вт, которая получает 8 часов солнечного света в день, будет производить почти 2,5 киловатт-часа в день. Если мы умножим это на 365 дней в году, мы получим около 900 киловатт-часов в год. Короче говоря, каждая панель будет обеспечивать 900 киловатт-часов каждый год.
Если мы умножим это на 365 дней в году, мы получим около 900 киловатт-часов в год. Короче говоря, каждая панель будет обеспечивать 900 киловатт-часов каждый год.
Как рассчитать текущую мощность солнечной панели?
Как рассчитать мощность солнечной панели
- Мощность солнечной панели x среднее количество часов солнечного света x 75% = суточная мощность ватт-часов.В качестве примера предположим, что у вас есть солнечные панели на 250 ватт и вы живете в месте, где вы получаете 5 часов солнечного света в день.
- 250 Вт x 5 часов x 0,75 = 937,5 ватт-часов в сутки.
- 937,5 / 1000 = 0,937.
Как можно повысить эффективность солнечной панели?
Узнайте, как повысить эффективность солнечных панелей и увеличить потребление энергии с помощью этих четырех советов.
- Оттенок. Проблема: тень является основным ингибитором солнечных батарей, так как это форма блокировки солнечного света.
- Погода. Проблема: погодные условия являются основным фактором в работе солнечных панелей.

- Ориентация.
- Содержание.
Какой тип солнечной панели наиболее эффективен?
монокристаллический
Могут ли зеркала увеличить мощность солнечных батарей?
Значительное увеличение выработки энергии на уровне системы за счет использования зеркал может сильно изменить способ установки солнечных панелей на солнечных фермах в это время искусственно завышенных цен на панели, поступающие из-за пределов США.С.
Какие факторы влияют на эффективность солнечной панели?
Какие факторы влияют на эффективность солнечных панелей?
- Температура. Температура влияет на эффективность фотоэлектрического элемента из-за внутренних характеристик полупроводникового материала.
- Эффективность преобразования энергии.
- Солнечные тени.
- Ориентация, наклон, широта места и климатические условия.
- Эксплуатация и мониторинг.
- archelios ™ Suite.
Как температура влияет на эффективность фотоэлемента?
Температурный коэффициент показывает, в процентах на градус Цельсия, сколько энергии потеряет солнечная панель при повышении температуры на 1 градус выше 25 ° C (77 ° F). И наоборот, на каждый градус Цельсия ниже 25 ° C максимальная эффективность этой солнечной панели увеличивается на 0,38%.
И наоборот, на каждый градус Цельсия ниже 25 ° C максимальная эффективность этой солнечной панели увеличивается на 0,38%.
Какова максимальная мощность солнечной панели?
Солнечные панели обычно имеют выходную мощность от 250 до 400 Вт, но некоторые панели превышают отметку в 400 Вт.Солнечная панель с максимальной мощностью — это SunPower E-Series, коммерческая линейка солнечных панелей.
Можете ли вы сфокусировать свет на солнечной панели?
Да, фокусировка света на солнечных батареях увеличит электрическую мощность. Обычно солнечные элементы необходимо охлаждать, если вы концентрируете на них много света, что увеличивает стоимость. Кроме того, вам нужно повернуть солнечный элемент плюс линзу, чтобы линза фокусировалась на солнечном элементе, что значительно увеличивает стоимость.
Улучшается ли технология солнечных панелей?
Современные коммерческие солнечные панели в среднем преобразуют 17-19% падающей на них световой энергии в электричество. Всего 10 лет назад это было 12%. Более эффективные солнечные элементы означают, что мы могли бы получать намного больше, чем сегодняшние 2,4% мирового производства электроэнергии от солнца. Солнечная энергия уже является самой быстрорастущей энергетической технологией в мире.
Всего 10 лет назад это было 12%. Более эффективные солнечные элементы означают, что мы могли бы получать намного больше, чем сегодняшние 2,4% мирового производства электроэнергии от солнца. Солнечная энергия уже является самой быстрорастущей энергетической технологией в мире.
Какие новейшие технологии в солнечных батареях?
В наиболее эффективных солнечных панелях, доступных в 2021 году, используются IBC-элементы высокой чистоты N-типа производства SunPower и LG. Компания REC недавно выпустила серию Alpha, в которой используются высокопроизводительные клетки HJT N-типа, эффективность которых близка к уровню клеток IBC.
Что такое новейшие солнечные технологии?
Тонкопленочные солнечные элементы второго поколения кажутся одной из самых многообещающих фотоэлектрических технологий благодаря своей узкой конструкции (в 350 раз меньше светопоглощающих слоев по сравнению со стандартными Si-панелями), легкому весу, гибкости и простоте установки.
Что такое новейшая технология солнечных панелей?
Oxford PV, компания, занимающаяся солнечными технологиями, разработала солнечные элементы, которые преобразуют более 28% получаемого солнечного света в электричество.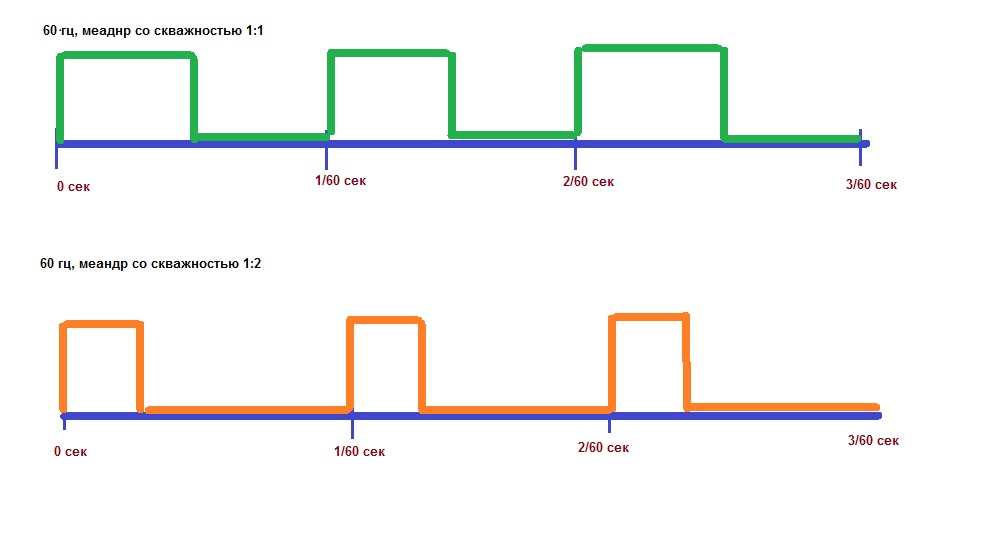 Они обнаружили, что покрытие традиционных солнечных элементов тонким слоем кристаллического материала, называемого перовскитом, может увеличить выработку электроэнергии.
Они обнаружили, что покрытие традиционных солнечных элементов тонким слоем кристаллического материала, называемого перовскитом, может увеличить выработку электроэнергии.
Какие 10 лучших солнечных панелей?
Из всех компаний, которые в настоящее время производят солнечные панели, главными именами, которые чаще всего ассоциируются с лучшими солнечными панелями на рынке, являются:
- SunPower.
- LG.
- Panasonic.
- Silfab.
- ЯЧЕЙКИ Q.
- Canadian Solar.
- JinkoSolar.
- Trina Solar.
Работают ли солнечные батареи ночью?
Солнечные панели не производят энергию ночью или когда солнце закрыто. Вместо этого они продолжают обеспечивать электроэнергией через сетевые измерения, при которых избыточная энергия передается в энергосистему общего пользования, часто работающую на ископаемом топливе, для компенсации затрат.
Работают ли солнечные панели при снегопаде?
Солнечные батареи работают на снегу? Когда солнечная панель покрыта снегом, она не может производить электричество. Однако солнечные батареи, как правило, неплохо сбрасывают снег — сами панели поглощают солнечное тепло, а также его свет, они устанавливаются лицом к солнцу и часто находятся на склоне.
Однако солнечные батареи, как правило, неплохо сбрасывают снег — сами панели поглощают солнечное тепло, а также его свет, они устанавливаются лицом к солнцу и часто находятся на склоне.
Работают ли солнечные батареи во время дождя?
Солнечные панели по-прежнему будут работать, даже если свет отражается или частично блокируется облаками. Дождь действительно помогает поддерживать эффективную работу ваших панелей, смывая пыль и грязь.
Почему важно понимать коэффициент заполнения солнечной батареи? Как это влияет на эффективность фотоэлементов?
Фактор заполнения и эффективность солнечной батареиТрудно понять коэффициент заполнения солнечных элементов ? А обязательно ли знать коэффициент заполнения и эффективность солнечного элемента?
Ответ: Нет !! Это несложно, но необходимо понять, если вы хотите знать, как повысить эффективность солнечной батареи?
Понимание фактора заполнения и оптимизации эффективности солнечных элементов не является достаточно гибким, если у вас есть достаточно времени, чтобы прочитать эту статью. В этой статье рассказывается о коэффициенте заполнения и эффективности солнечного элемента.
В этой статье рассказывается о коэффициенте заполнения и эффективности солнечного элемента.
С продолжающимся ростом глобального потепления и сокращением структуры ископаемого топлива цель альтернативных источников энергии становится все более и более насущной.
В этой статье я подчеркивал коэффициент заполнения солнечных элементов, их поведение, влияние и факторы, влияющие на эффективность солнечных элементов.
Солнечный фотоэлектрический (PV) элемент может преобразовывать световую энергию в электрическую в некоторых полупроводниковых материалах, таких как кремний, галлий и т. Д.
Реализация более значительного потенциала от только части солнечного излучения требует исследования рабочих параметров солнечного фотоэлектрического модуля. Коэффициент заполнения (FF), напряжение холостого хода (VOC) и ток короткого замыкания (ISC) являются тремя важными жизненно важными параметрами.
Максимальное увеличение всех трех параметров необходимо для эффективной работы.
- Коэффициент заполнения (FF).
- Напряжение холостого хода (VOC).
- Ток короткого замыкания (ISC).
Хорошее понимание технических особенностей факторов важно для рентабельной работы.
Давайте начнем с коэффициента заполнения и эффективности солнечных элементов, их определения и формулы, а также оценим ограничивающий характер в различных обстоятельствах.
Давайте углубимся !!
Что означает коэффициент заполнения и эффективность солнечного элемента? Значение коэффициента заполнения по формуле :Коэффициент заполнения (FF) обычно является мерой эффективности солнечного фотоэлектрического модуля.
FF — это отношение максимальной мощности (P max ) к произведению V OC и I SC , т. Е . :
:
Это коэффициент фактической наивысшей достижимой мощности.
Здесь,
- Напряжение холостого хода (В OC ): Наибольшее напряжение, которое может генерировать солнечная фотоэлектрическая панель (при стандартных условиях тестирования). Поскольку к выходной цепи не подключена нагрузка, ток не генерируется.
- Ток короткого замыкания (I SC ): Наибольший ток, который может генерировать солнечная фотоэлектрическая панель (при стандартных условиях тестирования).Поскольку провода панели подключены напрямую, т. Е. Закорочены, напряжение отсутствует.
Максимальная мощность (P макс ) возникает, когда комбинации тока и напряжения приводят к наиболее значительной мощности.
Это не происходит ни в условиях разомкнутой цепи (V OC ) , ни в условиях короткого замыкания (I SC ) .
Как и на I SC , напряжение в идеале равно нулю, а при В OC ток в ячейке тоже считается идеально нулевым.
Следовательно, P max не возникает при максимальном токе; скорее, это происходит при определенном токе (I MPP ) , который меньше, чем I SC .
Аналогично, P max не возникает при максимальном напряжении; скорее, это происходит при определенном напряжении (V MPP ), которое меньше, чем V OC .
Таким образом,
P макс. = V MPP x I MPPЗдесь V MPP & I MPP — это напряжение и ток соответственно в точке максимальной мощности на зависимости тока (I) от тока.кривая напряжения (В) (т. е. кривая ВАХ).
Фактор заполнения солнечных элементов:- Коэффициент заполнения (FF) солнечного фотоэлектрического модуля обычно составляет около 80% для кремниевых элементов.

- А солнечные элементы, изготовленные из GaAs, могут дать максимальный коэффициент заполнения 89%.
Эффективность солнечного элемента — это определение производственной мощности солнечной панели.
Это отношение максимальной мощности к входной мощности.
Здесь P max — это максимальная мощность, которую солнечная фотоэлектрическая панель может генерировать при стандартных условиях тестирования.
Коэффициент заполнения и эффективность солнечного элементаИ, P в — это солнечное излучение, то есть лучистая энергия, испускаемая солнцем.
Как правило, существует три разновидности солнечных панелей, а именно
- Монокристаллический,
- поликристаллический и
- Тонкопленочный.

Эффективность преобразования трех типов солнечных батарей варьируется в зависимости от материала конструкции и технологии.
Тип солнечной энергии | Строительство | КПД (%) |
и. Монокристаллический | Чистый кремний | 20 |
ii.Поликристаллический | Слитые вместе фрагменты кристалла кремния | 15–17 |
iii. Тонкопленочный | Теллурид кадмия (CdTe), аморфный кремний (a-Si) и селенид меди, индия, галлия (CIGS) или с любой такой смесью из различных материалов | 11 (приблизительно) |
- Монокристаллические солнечные панели: Их производственным материалом является чистый кремний.
 Они самые дорогие и самые эффективные. Монокристаллические солнечные панели могут достигать эффективности более 20%.
Они самые дорогие и самые эффективные. Монокристаллические солнечные панели могут достигать эффективности более 20%.
- Поликристаллические солнечные панели: Их технология изготовления немного отличается от других, даже несмотря на то, что производственным материалом является кремний. Фрагменты кристалла кремния сплавились вместе, чтобы произвести поликристаллические солнечные панели.
Целью разработки поликристаллической солнечной панели было снижение стоимости, но она также стала менее эффективной.
Обычно он может достигать КПД 15-17%.
Этот разрыв в эффективности между двумя вышеупомянутыми панелями может скоро сократиться с постоянно совершенствующейся технологией.
- Тонкопленочные солнечные панели: Уникальная особенность тонкопленочных панелей заключается в том, что в процессе их производства часто используются другие материалы (кроме кремния).
Тонкопленочная солнечная панель может быть изготовлена из теллурида кадмия (CdTe), аморфного кремния (a-Si) и селенида меди, индия, галлия (CIGS) или любой такой смеси из различных материалов.
Эффективность тонкопленочной солнечной панели является минимальной (примерно 11%) среди трех типов солнечных панелей.
Разница между КПД и коэффициентом заполнения в солнечном элементе: Фактор заполнения и эффективность солнечной батареиКПД
| Коэффициент заполнения |
и.Это отношение максимальной мощности, которую солнечная фотоэлектрическая панель может генерировать в стандартных условиях тестирования, к входной мощности | и. Это отношение максимальной мощности к теоретической. |
ii. | ii. |
iii.Вы можете максимизировать эффективность фотоэлектрической панели за счет увеличения коэффициента заполнения (FF), V OC и I SC . | iii. Максимально достижимая мощность (теоретическая) зависит от нескольких факторов, таких как тип кремния, используемый для создания солнечных фотоэлектрических модулей. Любое отклонение от ожидаемого значения коэффициента заполнения может свидетельствовать о неисправности модуля. |
Глубокая зависимость от ископаемых видов топлива (уголь, нефть, природный газ и т. Д.)) для производства электроэнергии привело нас в довольно неопределенное будущее.
Мы можем удовлетворить постоянно растущие потребности в электроэнергии с помощью альтернативных источников энергии с такими характеристиками, как находчивость, долговечность и т. Д.
Всесторонняя проверка факторов, которые могут способствовать недостаточной эффективности фотоэлемента в настоящее время становится все более актуальной.
Давайте углубимся в влияние этих факторов —
1. Фактор заполнения: Между двумя солнечными фотоэлектрическими панелями одна с меньшим значением коэффициента заполнения будет иметь меньшую эффективность, чем другая.
2. Солнечный спектр и температура: Солнечный спектр и температура влияют на эффективность фотоэлектрической панели.
Солнечная фотоэлектрическая панель вырабатывает электричество, используя лучи солнечного света. Однако он снижает эффективность с увеличением освещенности.
Предположим, что температура фотоэлектрической панели выходит за пределы оптимального или рабочего значения температуры.
В этом случае перегретая фотоэлектрическая панель вызывает падение V OC и I SC , за которым следует снижение КПД.
3. Интенсивность света: Интенсивность света существенно влияет на коэффициент заполнения (FF). Следовательно, на эффективность влияет изменение интенсивности освещения.
Следовательно, на эффективность влияет изменение интенсивности освещения.
- FF увеличивается при облучении менее 500 Вт / м 2 (низкое облучение)
- FF уменьшается при облучении более 500 Вт / м 2 (сильное облучение).
Аналогично
- Эффективность увеличивается логарифмически при облучении менее 400 Вт / м 2 (низкое облучение)
- Тем не менее, КПД не уменьшается и не увеличивается при облучении более 400 Вт / м 2 (сильное облучение).
4. Накопление пыли: Плотность накопления пыли на поверхности фотоэлектрической панели снижает качество и коэффициент заполнения солнечного элемента.
- Мощность солнечного фотоэлектрического модуля может быть уменьшена на 20% после одиночной пыльной бури и на 50% в течение шести месяцев.

Согласно другому исследованию, мощность солнечного фотоэлектрического модуля может быть уменьшена на 35% за месяц в тропическом климате.
Как повысить эффективность солнечного элемента:Давайте посмотрим правде в глаза, технология преобразования фото солнечной фотоэлектрической панели должна быть улучшена, чтобы добиться значительного прогресса и продемонстрировать необычайный рост в качестве альтернативного источника энергии.
Не могли бы мы проверить некоторые хаки, чтобы взломать эффективность?
- Чтобы смягчить влияние факторов окружающей среды (влажность или накопление пыли), вы должны изучить соответствующее географическое положение перед установкой солнечной фотоэлектрической системы.
- Для получения более высокой производительности необходимо расширить возможности оптимизации в соответствии с универсальным климатом.
- Вместо того, чтобы использовать обобщенную технику установки солнечной фотоэлектрической системы, необходимо учитывать такие факторы, как доминирующее направление ветра или угол установки.

- Поскольку эффективность солнечного элемента снижается с повышением температуры элемента (из-за термической деградации солнечного элемента), вы должны поддерживать оптимальную температуру поверхности солнечной панели.
- Вы можете уменьшить явление перегрева фотоэлектрической панели с помощью воздушного или водяного охлаждения.
- Вы можете использовать характеристики антибликового материала для улучшения характеристик фотоэлектрической панели.
- Солнечные элементы не могут достичь 100% эффективности, поскольку солнечный спектр испускает фотоны с широким диапазоном энергий.Только для определенных спектральных диапазонов полупроводниковых материалов световая энергия может быть преобразована в электрическую. Теоретический максимальный КПД 33,7
- Процесс преобразования энергии не может завершиться на 100% из-за внутренних резистивных или оптических потерь.
 Когда световая энергия отражается и рассеивается или преобразуется в энергию удара, это предотвращает полное использование огромного источника энергии.
Когда световая энергия отражается и рассеивается или преобразуется в энергию удара, это предотвращает полное использование огромного источника энергии.
Глубокое понимание системы имеет решающее значение.Мы можем выбрать подходящий модуль и приложить все усилия, чтобы обеспечить максимальную выработку энергии от фотоэлектрической панели. Один из способов повысить эффективность — сконцентрироваться на установке фотоэлемента в подходящее положение с учетом условий окружающей среды.
Накопление пыли приводит к снижению коэффициента заполнения солнечного элемента. Это мера того, насколько солнечный элемент действует как идеальный источник (при стандартных условиях тестирования). Ограничение скопления пыли и концентрации росы на фотоэлектрической панели повысит эффективность фотоэлектрического модуля.
Источники запасов энергии ограничены по своей природе, и соответствующие технологии для добычи угля и добычи нефти или природного газа еще не реализованы. Необходима щедрая маржа для повышения производительности солнечных элементов, чтобы создать устойчивый и безопасный сценарий, зависящий от возобновляемых источников энергии .
Необходима щедрая маржа для повышения производительности солнечных элементов, чтобы создать устойчивый и безопасный сценарий, зависящий от возобновляемых источников энергии .
Коэффициент заполнения фотоэлемента в фотоэлектрической панели должен быть максимальным. Сосредоточьтесь на факторах, влияющих на эффективность солнечных панелей. На месте установки не должно быть какой-либо инфраструктуры затенения.Солнечные фотоэлектрические панели должны находиться в такой среде, где невозможно плотное скопление пыли или грязи.
Каталожные номера:
- «Влияние интенсивности освещения на параметры солнечных элементов» М. Чегаар, А. Хамзауи, А. Намода, П. Пети, М. Эллери и А. Хергут
- «Влияние накопления пыли на выходную мощность солнечных фотоэлектрических модулей» Мухаммед Дж. Адинойи, Сайед А.М. Сказал
- «Влияние естественной пыли на характеристики фотоэлектрических панелей в Бангладеш», автор — Md.
 Мизанур Рахман, доктор Аминул Ислам, A.H.M. Задидул Карим и Асрафул Хак Рони
Мизанур Рахман, доктор Аминул Ислам, A.H.M. Задидул Карим и Асрафул Хак Рони
Коэффициент заполнения индекса SQL Server с эталоном производительности
В этой статье мы подробно рассмотрим, как работает коэффициент заполнения индекса SQL Server.
Индекс Коэффициент заполнения
Коэффициент заполнения индекса SQL Server — это процентное значение для заполнения страницы данных данными в SQL Server. Этот параметр доступен в свойствах индекса для управления хранением данных на страницах данных.Он играет жизненно важную роль в настройке производительности запросов. Значение по умолчанию — 0 в свойстве индекса SQL Server для каждого индекса таблиц, это предотвращает заполнение 100% хранилища на каждой странице данных. Мы можем изменить это значение, сравнив производительность по характеру данных и размеру данных.
Например. Значение коэффициента заполнения, установленное на «100», обеспечит 100% -ное заполнение хранилища данных на странице данных, а «90» позволит сохранить 90% -ное заполнение страницы данных, а остальная часть пространства будет свободна, что может быть использовано для модификации данных на страницу, а не для вставки новых записей.
Вот небольшой тест на примере. Я добавил одну таблицу [tbl_user] в базу данных [auth] .
ИСПОЛЬЗОВАТЬ [auth] GO СОЗДАТЬ ТАБЛИЦУ [dbo]. [Tbl_user] ( user_id bigint IDENTITY (1,1) PRIMARY KEY, fname varchar (128) NULL, lname varchar ( 128) NULL, email varchar (128) NULL ) |
Мы проведем тест с двумя статистическими данными и проанализируем набор результатов.
- Без Фактор заполнения
- с коэффициентом заполнения
без коэффициента заполнения
Значение коэффициента заполнения индекса SQL Server по умолчанию равно 0 (100%). При 100% использовании страницы могут возникнуть проблемы с описанием при выполнении крупноразмерной таблицы или обновления данных в таблице, так как не останется места для модификации данных / с.
Как в этой ситуации будут реструктурированы строки? будет он на той же странице или перемещен на новую? Будет подробно рассмотрено с примером и образцами данных.
Первичный ключ определен в столбце user_id таблицы; проверьте значения по умолчанию по индексу. Свойство Фактор заполнения установлен на «0 (ноль)», который также может быть добавлен в индекс с помощью команды SQL при добавлении индекса.
Запрос на получение номера страницы, выделенной для таблицы:
Пример: в таблицу вставлено 256 строк, а текущее значение коэффициента заполнения индекса равно 0 (100%). Запрос, как показано ниже:
ВЫБРАТЬ a.database_id,
a.object_id,
a.extent_page_id,
a.allocated_page_page_id,
a.next_page_file_id,
a.previous_page_page_id
FROM sys.dm_db_ID ), NULL, NULL, ‘DETAILED’) a
INNER JOIN sys.indexes i ON i.object_id = a.object_id AND i.index_id = a.index_id
WHERE page_type = 1 —page_type_desc = ‘DATA_PAGE’
90В запросе указан page_type = 1, который возвращает только страницы данных.

Количество страниц данных для таблицы также можно узнать с помощью команды DBCC . Запрос, как показано ниже:
DBCC IND (аутентификация, tbl_user, -1)
Две страницы 352 и 384 (результат на снимке экрана выше) выделены для хранения 256 строк. Теперь, когда используется команда DBCC PAGE, она возвращает те же строки, а также возвращает заголовок и шестнадцатеричный дамп страницы данных на основе заданных параметров.Имейте в виду, что перед выполнением трассировки флаг «3604» должен быть включен в сеансе для получения вывода запроса в клиенте
.DBCC TRACEON (3604)
DBCC PAGE (db_name / db_id, file id, page_id, 0/1/2/3)
Четвертый параметр определяет подробный вывод этой команды:
0 — только заголовок страницы
1 — Заголовок страницы и шестнадцатеричный дамп всех строк со слотами
2 — Заголовок страницы и шестнадцатеричный дамп всех строк
3 — Заголовок страницы и объяснение строки
DBCC PAGE (‘auth’, 1, 352, 1)
или
Вывод запроса 1.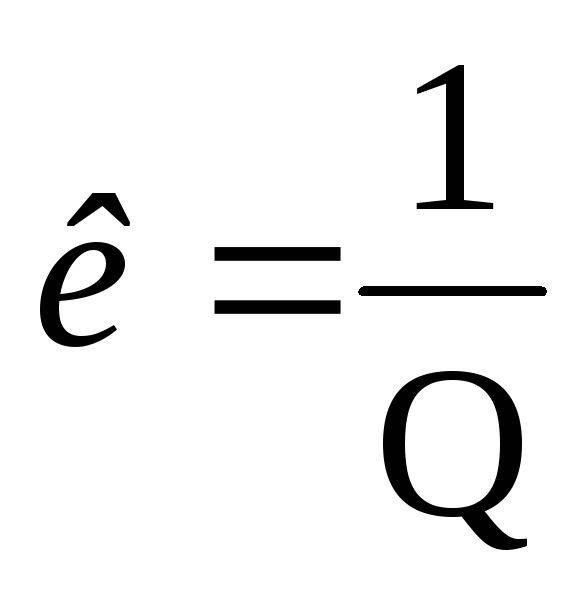 01:
01:
| СТРАНИЦА: (1: 352) | ||||||||
| ЗАГОЛОВОК СТРАНИЦЫ: | ||||||||
| Страница @ 0x00000260EDF48000 | ||||||||
| m_pageId = (1: 352) | m_pageId = (1: 352) | m_header_type_header_type_ | 5 905 = 0x0 | m_level = 0 | m_flagBits = 0x200 | |||
| m_objId (AllocUnitId.idObj) = 180 | m_indexId (AllocUnitId.idInd) = 256 | |||||||
| Метаданные: AllocUnitId = 72057594049724416 | ||||||||
| Метаданные: PartitionId = 72057594043301888 | Метаданные: IndexId = 1 | |||||||
| 5 = (1: 354) | ||||||||
| pminlen = 12 | m_slotCnt = 147 | m_freeCnt = 15 | ||||||
| m_freeData = 7883 | m_reservedCnt = 0 | m_reservedCnt = 0 | m_reservedCnt = 0 | m_reservedCnt = 0 | m_reservedCnt = 0 | m_xactReserved = 0 | m_xdesId = (0: 0) | m_ghostRecCnt = 0 |
| m_tornBits = 1792311503 | DB Frag ID = 1 | |||||||
Смотрите здесь, все поля содержат довольно значимые данные в разделе PAGE HEADER ..jpg.c99d317725161904ea2c952a4ad5a310.jpg) m_slotCnt = 147 представляет количество строк / записей на странице, а остальные 109 записей помещаются на вторую страницу.
m_slotCnt = 147 представляет количество строк / записей на странице, а остальные 109 записей помещаются на вторую страницу.
Что произойдет, если мы обновим строки на первой странице?
Теперь давайте попробуем обновить данные в существующей таблице, объединив user_id с email в столбце email в таблице. Это потребует больше места для обновления строк на странице, однако для коэффициента заполнения установлено значение «100%», и мы заполнили страницу 100% данными, поэтому на странице не осталось свободного места.Обновим таблицу и проверим источник страниц.
ОБНОВЛЕНИЕ tbl_user SET email = CAST (user_id AS VARCHAR (10)) + email |
После обновления таблицы список страниц, которые мы получаем для таблицы с помощью запроса, возвращает 3 строки вместо 2 (см. Предыдущий набор результатов). Теперь данные распределены по 3 страницам, а строки реструктурированы. Даже команда DBCC PAGE помогает отслеживать количество строк на отдельной странице.
Теперь данные распределены по 3 страницам, а строки реструктурированы. Даже команда DBCC PAGE помогает отслеживать количество строк на отдельной странице.
DBCC TRACEON (3604) DBCC PAGE (9, 1, 352, 1) |
Перед запуском оператора обновления в таблице было 147 строк (см. Вывод запроса 1.01), поскольку строки были реструктурированы на 3 страницы, а первая страница теперь заполнена 73 строками. Этот процесс разделения строк займет больше времени для выполнения этой операции и может потреблять больше ресурсов ЦП и памяти, а также для тяжелой таблицы на основе транзакций обновление таблицы без фактора заполнения индекса SQL Server также может генерировать блокировки.
Вывод запроса 1.02:
| m_pageId = (1: 368) | m_headerVersion = 1 | m_type = 1 | ||||
| m_typeFlagBits = 0x0 | m_level = 0 | m_2008js_elevel = 0 | m_2008js_gbits = 0 | m_indexId (AllocUnitId. idInd) = 256 idInd) = 256 | ||
| Метаданные: AllocUnitId = 72057594050052096 | ||||||
| Метаданные: PartitionId = 72057594043629568 | 1 | 1 | 0)m_nextPage = (1: 449) | |||
| pminlen = 12 | m_slotCnt = 73 | m_freeCnt = 3935 | ||||
| m_freeData = 7247 | m eservedCnt = 0 | m_lsn = (37: 104: 93) | ||||
| m_xactReserved = 0 | m_xdesId = (0: 0) | m_ghostRecCnt = 0 | ||||
| m_tornBits1 | ||||||
здесь также важно обращать внимание на фрагментацию индекса при работе над фактором заполнения индекса SQL Server.Для этой таблицы у нас есть 66,66% счетчика фрагментации после выполнения обновления таблицы. Фрагментация индекса влияет на производительность индекса в SQL Server. Следовательно, при более высоком значении фрагментации фактора заполнения стоимость будет высокой, поэтому ее следует использовать, применяя правильную величину для этого параметра. Мы можем проверить фрагментацию по запросу ниже.
Мы можем проверить фрагментацию по запросу ниже.
ВЫБЕРИТЕ dbschemas. [Имя] как «Схема», dbtables. [Имя] как «Таблица», dbindexes.[имя] как «Индекс», indexstats.avg_fragmentation_in_percent, indexstats.page_count FROM sys.dm_db_index_physical_stats (DB_ID (), NULL, NULL, NULL, NULL) AS indexstats JNTBINS INNULL sys.dm_db_index_stats . [object_id] = indexstats. [object_id]INNER JOIN sys.schemas dbschemas on dbtables. [schema_id] = dbschemas. [schema_id] INNER JOIN sys.indexes AS dbindexes ON dbindexes. [object_id_id] ] И indexstats.index_id = dbindexes.index_id ГДЕ indexstats.database_id = 9 ЗАКАЗАТЬ indexstats.avg_fragmentation_in_percent desc |
с коэффициентом заполнения:
Значение коэффициента заполнения регулирует процент данных, которые должны быть заполнены на каждой странице данных. В этом примере значение коэффициента заполнения индекса SQL Server, заданное параметром 80 в первичном индексе, означает, что на каждой странице таблицы будет 20% свободного пространства, а 80% пространства будет выделено для хранения данных.Чтобы применить изменения в коэффициенте заполнения, индекс всегда будет перестраиваться.
В этом примере значение коэффициента заполнения индекса SQL Server, заданное параметром 80 в первичном индексе, означает, что на каждой странице таблицы будет 20% свободного пространства, а 80% пространства будет выделено для хранения данных.Чтобы применить изменения в коэффициенте заполнения, индекс всегда будет перестраиваться.
Теперь мы снова вставили те же 256 строк в ту же таблицу, чтобы проверить выделенное количество страниц в таблице. На этот раз данные разделены на 3 страницы, тогда как они были разделены на две страницы без коэффициента заполнения.
Глядя на количество строк на первой странице, мы видим, что 118 строк сохранены (Query Output 2.01) по сравнению с данными предыдущего результата (коэффициент заполнения 100%), разделенными на 2 страницы при вставке данных и 147 строк на первой странице ( Вывод запроса 1.01).
Здесь остается 20% свободного места на каждой странице для вставки новой строки в таблицу в соответствии с величиной коэффициента заполнения.
DBCC TRACEON (3604) DBCC PAGE (auth, 1, 368, 1) |
Вывод запроса 2.01:
| ЗАГОЛОВОК СТРАНИЦЫ: | |||
| Страница @ 0x00000260F6CB2000 | |||
| m_pageId = (1: 368) | m_headerVersion = 1 | m_type_letype = 1 05 | m_type_le = 1 |
| m_objId (AllocUnitId.idObj) = 183 | m_indexId (AllocUnitId.idInd) = 256 | ||
| Метаданные: AllocUnitId = 72057594049921024 | |||
| Метаданные: PartitionId = 720549690 | 7 m_prevPage = (0: 0) | m_nextPage = (1: 376) | |
| pminlen = 12 | m_slotCnt = 118 | m_freeCnt = 1607 | |
| m_freeCnt = 1607 | |||
| m_freeData = | m_freeData = 6 36: 3352: 61) | ||
| m_xactReserved = 0 | m_xdesId = (0: 0) | m_ghostRecCnt = 0 | |
| m_tornBits = 1731328174 | 9049 ID фрагмента | ||
Давайте снова обновим таблицу, как в предыдущем примере, и проверим размещение строк в структуре страницы.Здесь мы обнаруживаем, что на первой странице изменений не обнаружено, и даже мы видим, что больше свободного места занято существующими строками. Принято считать, что никакие страницы не реорганизовываются и избегают блокировок целевых строк и строк, зависимых от страницы.
ОБНОВЛЕНИЕ tbl_user SET email = CAST (user_id AS VARCHAR (10)) + email DBCC PAGE (auth, 1, 368, 1) |
Вывод запроса 2.02:
| m_pageId = (1: 368) | m_headerVersion = 1 | m_type = 1 | ||
| m_typeFlagBits = 0x0 | m_level = 0 | m_flagBitsidObj) = 194 | m_indexId (AllocUnitId.idInd) = 256 | |
| Метаданные: AllocUnitId = 72057594050641920 | ||||
| Метаданные: PartitionId = | ||||
| Метаданные: PartitionId = 720549: | m_prevPage = (0: 0)m_nextPage = (1: 376) | |||
| pminlen = 12 | m_slotCnt = 118 | m_freeCnt = 1361 | ||
| m_184_reserved 37: 3856: 131) | ||||
| m_xactReserved = 0 | m_xdesId = (0: 0) | m_ghostRecCnt = 0 | ||
| m_tornBits = 0 | DB Frag ID = 1 | |||




 PERC означает Passivated…
PERC означает Passivated… Волоконный световод
Волоконный световод Градиентный волоконный световод
Градиентный волоконный световод Коэффициент заполнения изделия из волоконных световодов
Коэффициент заполнения изделия из волоконных световодов Расчетный апертурный угол волоконного световода
Расчетный апертурный угол волоконного световода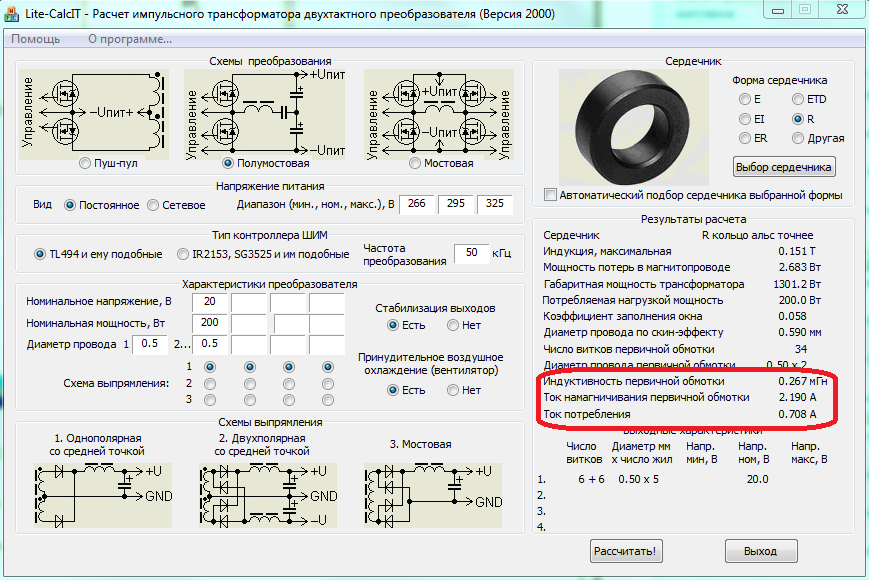
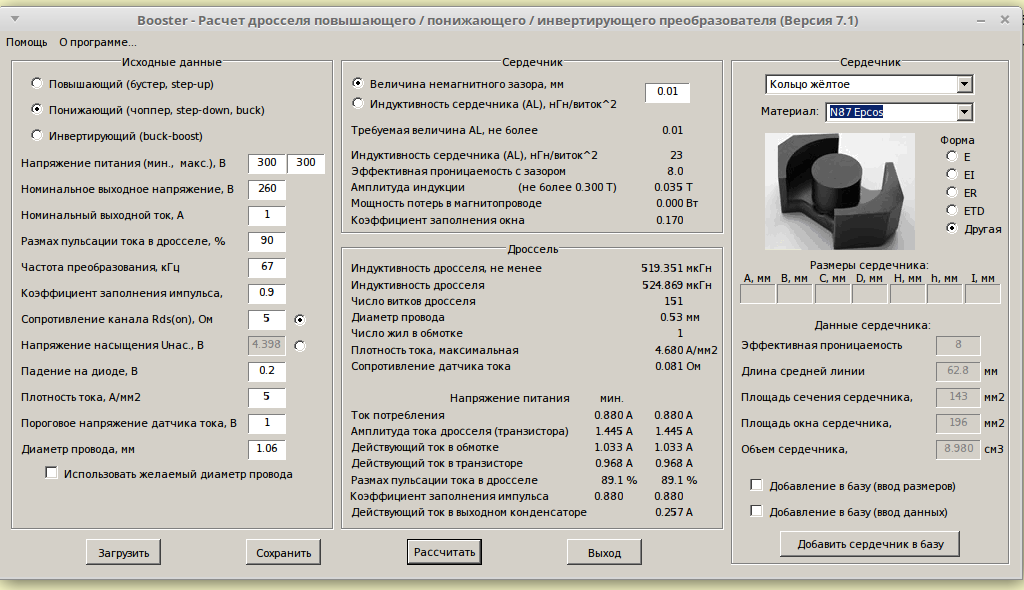

 Они самые дорогие и самые эффективные. Монокристаллические солнечные панели могут достигать эффективности более 20%.
Они самые дорогие и самые эффективные. Монокристаллические солнечные панели могут достигать эффективности более 20%.

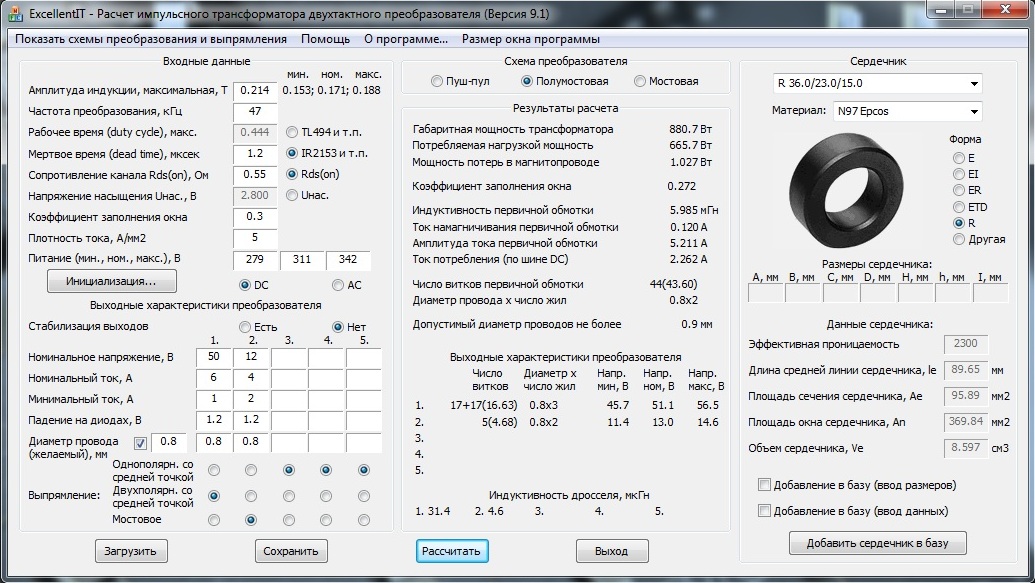
 Когда световая энергия отражается и рассеивается или преобразуется в энергию удара, это предотвращает полное использование огромного источника энергии.
Когда световая энергия отражается и рассеивается или преобразуется в энергию удара, это предотвращает полное использование огромного источника энергии.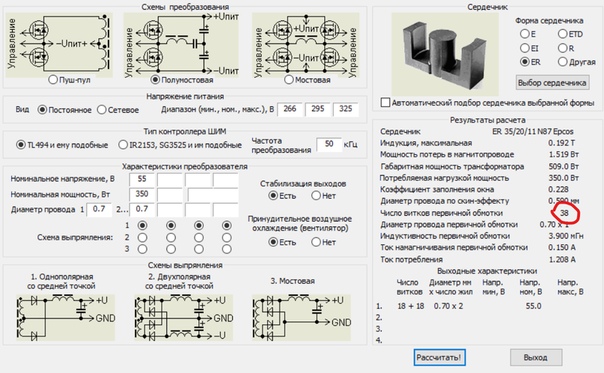 Мизанур Рахман, доктор Аминул Ислам, A.H.M. Задидул Карим и Асрафул Хак Рони
Мизанур Рахман, доктор Аминул Ислам, A.H.M. Задидул Карим и Асрафул Хак Рони